高二数学导数及其应用综合检测综合测试题

合集下载

2014-2015学年人教a版数学选修2-2第1章《导数及其应用》综合检测(含答案)

第一章综合检测时间120分钟，满分150分。

一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的)1．(2013·天津红桥区高二段测)二次函数y ＝f (x )的图象过原点且它的导函数y ＝f ′(x )的图象是如图所示的一条直线，y ＝f (x )的图象的顶点在( )A ．第Ⅰ象限B ．第Ⅱ象限C ．第Ⅲ象限D ．第Ⅳ象限[答案] A[解析] 设f (x )＝ax 2＋bx ＋c ，∵二次函数y ＝f (x )的图象过原点，∴c ＝0，∴f ′(x )＝2ax ＋b ，由y ＝f ′(x )的图象可知，2a <0，b >0，∴a <0，b >0，∴－b 2a >0，4ac －b 24a ＝－b 24a>0，故选A.2．(2013·华池一中高二期中)曲线y ＝－1x 在点(12，－2)处的切线方程为( )A ．y ＝4xB ．y ＝4x －4C ．y ＝4(x ＋1)D ．y ＝2x －4[答案] B[解析] ∵y ′＝1x 2，∴y ′|x ＝12＝4，∴k ＝4，∴切线方程为y ＋2＝4(x －12)，即y ＝4x －4.3．(2014·淄博市临淄区学分认定考试)下列函数中，x ＝0是其极值点的函数是( ) A ．f (x )＝－x 3B ．f (x )＝－cos xC ．f (x )＝sin x －xD ．f (x )＝1x[答案] B[解析] 对于A，f′(x)＝－3x2≤0恒成立，在R上单调递减，没有极值点；对于B，f′(x)＝sin x，当x∈(－π，0)时，f′(x)<0，当x∈(0，π)时，f′(x)>0，故f(x)＝－cos x在x＝0的左侧区间(－π，0)内单调递减，在其右侧区间(0，π)内单调递增，所以x＝0是f(x)的一个极小值点；对于C，f′(x)＝cos x－1≤0恒成立，在R上单调递减，没有极值点；对于D，f(x)＝1x在x＝0没有定义，所以x＝0不可能成为极值点，综上可知，答案选B.4．(2013·北师大附中高二期中)已知函数f(x)＝－x3＋ax2－x－1在(－∞，＋∞)上是单调函数，则实数a的取值范围是( )A．(－∞，－3)，∪(3，＋∞) B．(－3，3)C．(－∞，－3]∪[3，＋∞) D．[－3，3][答案] D[解析] f′(x)＝－3x2＋2ax－1，∵f(x)在(－∞，＋∞)上是单调函数，且f′(x)的图象是开口向下的抛物线，∴f′(x)≤0恒成立，∴Δ＝4a2－12≤0，∴－3≤a≤3，故选D.5．(2013·武汉实验中学高二期末)设函数f(x)在定义域内可导，y＝f(x)的图象如下图所示，则导函数y＝f′(x)的图象可能是( )[答案] A[解析] f(x)在(－∞，0)上为增函数，在(0，＋∞)上变化规律是减→增→减，因此f′(x)的图象在(－∞，0)上，f′(x)>0，在(0，＋∞)上f′(x)的符号变化规律是负→正→负，故选A.6．(2012·陕西文，9)设函数f (x )＝2x＋ln x ，则( )A ．x ＝12为f (x )的极大值点B ．x ＝12为f (x )的极小值点C ．x ＝2为f (x )的极大值点D ．x ＝2为f (x )的极小值点[答案] D[解析] 由f ′(x )＝－2x 2＋1x ＝1x (1－2x)＝0可得x ＝2.当0<x <2时，f ′(x )<0，f (x )单调递减，当x >2时f ′(x )>0，f (x )单调递增．所以x ＝2为极小值点．7．(2014·天门市调研)已知函数f (x )＝a sin x －b cos x 在x ＝π4时取得极值，则函数y＝f (3π4－x )是( )A ．偶函数且图象关于点(π，0)对称B ．偶函数且图象关于点(3π2，0)对称C ．奇函数且图象关于点(3π2，0)对称D ．奇函数且图象关于点(π，0)对称 [答案] D[解析] ∵f (x )的图象关于x ＝π4对称，∴f (0)＝f (π2)，∴－b ＝a ，∴f (x )＝a sin x －b cos x ＝a sin x ＋a cos x ＝2a sin(x ＋π4)，∴f (3π4－x )＝2a sin(3π4－x ＋π4)＝2a sin(π－x )＝2a sin x .显然f (3π4－x )是奇函数且关于点(π，0)对称，故选D.8．(2013·武汉实验中学高二期末)定义域为R 的函数f (x )满足f (1)＝1，且f (x )的导函数f ′(x )>12，则满足2f (x )<x ＋1的x 的集合为( )A ．{x |－1<x <1}B ．{x |x <1}C ．{x |x <－1或x >1}D ．{x |x >1}[答案] B[解析] 令g (x )＝2f (x )－x －1，∵f ′(x )>12，∴g ′(x )＝2f ′(x )－1>0，∴g (x )为单调增函数，∵f(1)＝1，∴g(1)＝2f(1)－1－1＝0，∴当x <1时，g (x )<0，即2f (x )<x ＋1，故选B.9．(2013·华池一中高二期中)若关于x 的方程x 3－3x ＋m ＝0在[0,2]上有根，则实数m 的取值范围是( )A ．[－2,2]B ．[0,2]C ．[－2,0]D ．(－∞，－2)∪(2，＋∞)[答案] A[解析] 令f (x )＝x 3－3x ＋m ，则f ′(x )＝3x 2－3＝3(x ＋1)(x －1)，显然当x <－1或x >1时，f ′(x )>0，f (x )单调递增，当－1<x <1时，f ′(x )<0，f (x )单调递减，∴在x ＝－1时，f (x )取极大值f (－1)＝m ＋2，在x ＝1时，f (x )取极小值f (1)＝m －2.∵f (x )＝0在[0,2]上有解，∴⎩⎪⎨⎪⎧f1<0，f 2>0，∴⎩⎪⎨⎪⎧m －2≤0，2＋m ≥0，∴－2≤m ≤2.10．(2013·河南安阳中学高二期末)f (x )是定义在(0，＋∞)上的非负可导函数，且满足xf ′(x )＋f (x )≤0，对任意正数a 、b ，若a 0)，则F ′(x )＝xf ′(x )＋f (x )≤0，∴F (x )在(0，＋∞)上为减函数，∵0<a f (b )，即af (a )>bf (b )，与选项不符；由于xf ′(x )＋f (x )≤0且x >0，f (x )≥0，∴f ′(x )≤－f xx≤0，∴f (x )在(0，＋∞)上为减函数，∵0<a f (b )， ∴bf (a )>af (b )，结合选项知选A.11．(2014·天门市调研)已知函数f (x )的导函数f ′(x )＝a (x －b )2＋c 的图象如图所示，则函数f (x )的图象可能是( )[答案] D[解析] 由导函数图象可知，当x <0时，函数f (x )递减，排除A ，B ；当0<x <x 1时，f ′(x )>0，函数f (x )递增．因此，当x ＝0时，f (x )取得极小值，故选D.12．(2013·泰安一中高二段测)已知函数f (x )的导函数的图象如图所示，若△ABC 为锐角三角形，则一定成立的是( )A ．f (sin A )>f (cosB ) B ．f (sin A )<f (cos B )C ．f (sin A )>f (sin B )D ．f (cos A )<f (cos B )[答案] A[解析] 由导函数图象可知，x >0时，f ′(x )>0，即f (x )单调递增，又△ABC 为锐角三角形，则A ＋B >π2，即π2>A >π2－B >0，故sin A >sin(π2－B )>0，即sin A >cos B >0，故f (sin A )>f (cos B )，选A.二、填空题(本大题共4个小题，每小题4分，共16分，把正确答案填在题中横线上) 13．(2013·华池一中高二期中)已知f (x )＝x 3＋3x 2＋a (a 为常数)，在[－3,3]上有最小值3，那么在[－3,3]上f (x )的最大值是________．[答案] 57[解析] f ′(x )＝3x 2＋6x ＝3x (x ＋2)，当x ∈[－3，－2)和x ∈(0,3]时，f ′(x )>0，f (x )单调递增，当x ∈(－2,0)时，f ′(x )<0，f (x )单调递减，∴极大值为f (－2)＝a ＋4，极小值为f (0)＝a ，又f (－3)＝a ，f (3)＝54＋a ，由条件知a ＝3，∴最大值为f (3)＝54＋3＝57.14．(2014·湖北重点中学高二期中联考)已知函数f (x )＝13ax 3＋12ax 2－2ax ＋2a ＋1的图象经过四个象限，则实数a 的取值范围是________．[答案] (－65，－316)[解析] f ′(x )＝ax 2＋ax －2a ＝a (x －1)(x ＋2)，由f (x )的图象经过四个象限知，若a >0，则⎩⎪⎨⎪⎧f－2>0，f 1<0，此时无解；若a <0，则⎩⎪⎨⎪⎧f－2<0，f 1>0，6 5<a<－316，综上知，－65<a<－316.∴－15．(2014·泉州实验中学期中)已知函数f (x )＝x 3－3x ，若过点A (1，m )(m ≠－2)可作曲线y ＝f (x )的三条切线，则实数m 的取值范围为________．[答案] (－3，－2)[解析] f ′(x )＝3x 2－3，设切点为P (x 0，y 0)，则切线方程为y －(x 30－3x 0)＝(3x 20－3)(x －x 0)，∵切线经过点A (1，m )，∴m －(x 30－3x 0)＝(3x 20－3)(1－x 0)，∴m ＝－2x 30＋3x 20－3，m ′＝－6x 20＋6x 0，∴当0<x 0<1时，此函数单调递增，当x 0<0或x 0>1时，此函数单调递减，当x 0＝0时，m ＝－3，当x 0＝1时，m ＝－2，∴当－3<m <－2时，直线y ＝m 与函数y ＝－2x 30＋3x 20－3的图象有三个不同交点，从而x 0有三个不同实数根，故过点A (1，m )可作三条不同切线，∴m 的取值范围是(－3，－2)．16．如图阴影部分是由曲线y ＝1x、y 2＝x 与直线x ＝2、y ＝0围成，则其面积为______．[答案] 23＋ln2[解析] 由⎩⎪⎨⎪⎧y 2＝x ，y ＝1x ，得交点A (1,1)由⎩⎪⎨⎪⎧x ＝2y ＝1x得交点B ⎝ ⎛⎭⎪⎫2，12.故所求面积S ＝⎠⎛01x d x ＋⎠⎛121xd x＝23x 32| 10＋ln x | 21＝23＋ln2. 三、解答题(本大题共6个大题，共74分，解答应写出文字说明，证明过程或演算步骤) 17．(本题满分12分)设函数f (x )＝ln x ＋ln(2－x )＋ax (a >0)． (1)当a ＝1时，求f (x )的单调区间；(2)若f (x )在(0,1]上的最大值为12，求a 的值．[解析] 函数f(x)的定义域为(0,2)，f ′(x )＝1x －12－x＋a ，(1)当a ＝1时，f ′(x )＝－x 2＋2x 2－x ，∴当x ∈(0，2)时，f ′(x )>0，当x ∈(2，2)时，f ′(x )<0，所以f (x )的单调递增区间为(0，2)，单调递减区间为(2，2)；(2)当x ∈(0,1]时，f ′(x )＝2－2xx 2－x＋a >0，即f (x )在(0,1]上单调递增，故f (x )在(0,1]上的最大值为f (1)＝a ，因此a ＝12.18．(本题满分12分)(2014·韶关市曲江一中月考)已知函数f (x )＝ax 3＋cx ＋d (a ≠0)是R 上的奇函数，当x ＝1时，f (x )取得极值－2.(1)求函数f (x )的解析式；(2)求函数f (x )的单调区间和极大值；(3)证明：对任意x 1、x 2∈(－1,1)，不等式|f (x 1)－f (x 2)|<4恒成立． [解析] (1)∵f (x )是R 上的奇函数， ∴f (－x )＝－f (x )，即－ax 3－cx ＋d ＝－ax 3－cx －d ，∴d ＝－d ， ∴d ＝0(或由f (0)＝0得d ＝0)． ∴f (x )＝ax 3＋cx ，f ′(x )＝3ax 2＋c ，又当x ＝1时，f (x )取得极值－2，∴⎩⎪⎨⎪⎧f 1＝－2，f ′1＝0，即⎩⎪⎨⎪⎧a ＋c ＝－2，3a ＋c ＝0，解得⎩⎪⎨⎪⎧a ＝1，c ＝－3.∴f (x )＝x 3－3x .(2)f ′(x )＝3x 2－3＝3(x ＋1)(x －1)，令f ′(x )＝0，得x ＝±1，当－1<x <1时，f ′(x )<0，函数f (x )单调递减；当x <－1或x >1时，f ′(x )>0，函数f (x )单调递增；∴函数f (x )的递增区间是(－∞，－1)和(1，＋∞)；递减区间为(－1,1)．因此，f (x )在x ＝－1处取得极大值，且极大值为f (－1)＝2.(3)由(2)知，函数f (x )在区间[－1,1]上单调递减，且f (x )在区间[－1,1]上的最大值为M ＝f (－1)＝2.最小值为m ＝f (1)＝－2.∴对任意x 1、x 2∈(－1,1)，|f (x 1)－f (x 2)|<M －m ＝4成立．即对任意x 1、x 2∈(－1,1)，不等式|f (x 1)－f (x 2)|<4恒成立．19．(本题满分12分)(2014·北京海淀期中)已知函数f (x )＝x 2－2(a ＋1)x ＋2a ln x (a >0)．(1)当a ＝1时，求曲线y ＝f (x )在点(1，f (1))处的切线方程；(2)求f(x)的单调区间；(3)若f(x)≤0在区间[1，e]上恒成立，求实数a的取值范围．[解析] (1)∵a ＝1，∴f (x )＝x 2－4x ＋2ln x ， ∴f ′(x )＝2x 2－4x ＋2x(x >0)，f (1)＝－3，f ′(1)＝0，所以切线方程为y ＝－3.(2)f ′(x )＝2x 2－2a ＋1x ＋2a x＝2x －1x －ax(x >0)，令f ′(x )＝0得x 1＝a ，x 2＝1，当0<a <1时，在x ∈(0，a )或x ∈(1，＋∞)时，f ′(x )>0，在x ∈(a,1)时，f ′(x )<0，∴f (x )的单调递增区间为(0，a )和(1，＋∞)，单调递减区间为(a,1)；当a ＝1时，f ′(x )＝2x －12x≥0，∴f (x )的单调增区间为(0，＋∞)；当a >1时，在x ∈(0,1)或x ∈(a ，＋∞)时，f ′(x )>0，在x ∈(1，a )时，f ′(x )<0，∴f (x )的单调增区间为(0,1)和(a ，＋∞)，单调递减区间为(1，a )．(3)由(2)可知，f (x )在区间[1，e]上只可能有极小值点，∴f (x )在区间[1，e]上的最大值必在区间端点取到，∴f (1)＝1－2(a ＋1)≤0且f (e)＝e 2－2(a ＋1)e ＋2a ≤0，解得a ≥e 2－2e2e －2.20．设函数f (x )＝x 3－92x 2＋6x －a .(1)对于任意实数x, f ′(x )≥m 恒成立，求m 的最大值； (2)若方程f (x )＝0有且仅有一个实根，求a 的取值范围． [解析] (1)f ′(x )＝3x 2－9x ＋6＝3(x －1)(x －2)．因为x ∈(－∞，＋∞)．f ′(x )≥m ，即3x 2－9x ＋(6－m )≥0恒成立．所以Δ＝81－12(6－m )≤0，得m ≤－34，即m 的最大值为－34.(2)因为当x <1时，f ′(x )>0；当1<x <2时，f ′(x )<0；当x >2时f ′(x )>0. 所以当x ＝1时，f (x )取极大值f (1)＝52－a ，当x ＝2时，f (x )取极小值f (2)＝2－a .故当f (2)>0或f (1)<0时，方程f (x )＝0仅有一个实根，解得a <2或a >52.21．(本题满分12分)(2014·荆州中学、龙泉中学、宜昌一中、襄阳四中期中联考)已知函数f (x )＝ln x ＋ax ＋1，a 为常数．(1)若a ＝92，求函数f (x )在[1，e ]上的值域；(e 为自然对数的底数，e ≈2.72)(2)若函数g(x)＝f(x)＋x在[1,2]上为单调减函数，求实数a的取值范围．[解析] (1)由题意f ′(x )＝1x－a x ＋12，当a ＝92时，f ′(x )＝1x －92x ＋12＝x －22x －12x x ＋12. ∵x ∈[1，e ]，∴f (x )在[1,2)上为减函数，[2，e ]上为增函数，又f (2)＝ln2＋32，f (1)＝94，f (e )＝1＋92e ＋2，比较可得f (1)>f (e )，∴f (x )的值域为[ln2＋32，94]．(2)由题意得g ′(x )＝1x－a x ＋12＋1≤0在x ∈[1,2]上恒成立，∴a ≥x ＋12x＋(x ＋1)2＝x 2＋3x ＋1x＋3恒成立，设h (x )＝x 2＋3x ＋1x＋3(1≤x ≤2)，∴当1≤x ≤2时，h ′(x )＝2x ＋3－1x2>0恒成立，∴h (x )max ＝h (2)＝272，∴a ≥272，即实数a 的取值范围是[272，＋∞)．22．(本题满分14分)(2014·北京海淀期中)如图，已知点A (11,0)，直线x ＝t (－1<t <11)与函数y ＝x ＋1的图象交于点P ，与x 轴交于点H ，记△APH 的面积为f (t )．(1)求函数f (t )的解析式； (2)求函数f (t )的最大值．[解析] (1)由已知AH ＝11－t ，PH ＝t ＋1，所以△APH 的面积为f (t )＝12(11－t )t ＋1，(－1<t <11)．(2)解法1：f ′(t )＝33－t 4t ＋1，由f ′(t )＝0得t ＝3，函数f (t )与f ′(t )在定义域上的情况如下表：t (－1,3) 3 (3,11)所以当t ＝3时，函数f (t )取得最大值8. 解法2.由f (t )＝12(11－t )t ＋1＝1211－t2t ＋1，－1<t <11，设g (t )＝(11－t )2(t ＋1)，－1<t <11，则g ′(t )＝－2(11－t )(t ＋1)＋(11－t )2＝(t －11)(t －11＋2t ＋2)＝3(t －3)(t －11)．g (t )与g ′(t )在定义域上的情况见下表：t (－1,3) 3 (3,11) g ′(t ) ＋ 0 － g (t )单调递增极大值单调递减所以当t ＝3所以当t ＝3时，函数f (t )取得最大值12g3＝8.一、选择题1．若曲线y ＝x 2＋ax ＋b 在点(0，b )处的切线方程是x －y ＋1＝0，则( ) A ．a ＝1，b ＝1 B ．a ＝－1，b ＝1 C ．a ＝1，b ＝－1 D ．a ＝－1，b ＝－1[答案] A[解析] y ′＝2x ＋a ，∴y ′|x ＝0＝(2x ＋a )|x ＝0＝a ＝1，将(0，b )代入切线方程得b ＝1.2．(2014·浙江杜桥中学期中)已知函数f (x )＝x 3＋ax 2＋3x －9在x ＝－3时取得极值，则a ＝( )A ．2B ．3C ．4D ．5[答案] D[解析] f ′(x )＝3x 2＋2ax ＋3，由条件知，x ＝－3是方程f ′(x )＝0的实数根，∴a ＝5.3．函数y ＝2x 3－3x 2－12x ＋5在[0,3]上的最大值，最小值分别是( ) A ．5，－15 B ．5，－4 C ．－4，－15D ．5，－16[答案] A[解析] ∵y ′＝6x 2－6x －12＝0，得x ＝－1(舍去)或x ＝2，故函数y ＝f (x )＝2x 3－3x2－12x ＋5在[0,3]上的最值可能是x 取0,2,3时的函数值，而f (0)＝5，f (2)＝－15，f (3)＝－4，故最大值为5，最小值为－15，故选A.4.⎠⎛241xd x 等于( )A ．－2ln2B ．2ln2C ．－ln2D ．ln2[答案] D[解析] 因为(ln x )′＝1x，所以 ⎠⎛241xd x ＝ln x |42＝ln4－ln2＝ln2.5．(2013·吉林白山一中高二期末)已知定义在R 上的函数f (x )的导函数f ′(x )的大致图象如图所示，则下列结论一定正确的是( )A ．f (b )>f (c )>f (d )B ．f (b )>f (a )>f (e)C ．f (c )>f (b )>f (a )D ．f (c )>f (e)>f (d )[答案] C[解析] 由图可知f ′(x )在(－∞，c )和(e ，＋∞)上取正值，在(c ，e)上取负值，故f (x )在(－∞，c )和(e ，＋∞)上单调递增，在(c ，e)上单调递减，∵a <b <c ，∴f (a )<f (b )<f (c )，故选C.6．已知函数f (x )＝4x ＋3sin x ，x ∈(－1，1)，如果f (1－a )＋f (1－a 2)<0成立，则实数a 的取值范围为( )A ．(0,1)B ．(1，2)C ．(－2，－2)D ．(－∞，－2)∪(1，＋∞)[答案] B[解析] ∵f (x )＝4x ＋3sin x ，x ∈(－1,1)，∴f ′(x )＝4＋3cos x >0在x ∈(－1,1)上恒成立，∴f (x )在(－1,1)上是增函数，又f (x )＝4x ＋3sin x ，x ∈(－1,1)是奇函数，∴不等式f (1－a )＋f (1－a 2)<0可化为f (1－a )<f (a 2－1)，从而可知，a 须满足⎩⎪⎨⎪⎧－1<1－a <1，－1<a 2－1<1，1－a <a 2－1.解得1<a < 2.7．设f ′(x )是函数f (x )的导函数，将y ＝f (x )和y ＝f ′(x )的图象画在同一个直角坐标系中，不可能正确的是( )[答案] D[解析] A 中，当f (x )为二次函数时，f ′(x )为一次函数，由单调性和导数值的符号关系知A 可以是正确的，同理B 、C 都可以是正确的，但D 中f (x )的单调性为增、减、增，故f ′(x )的值应为正负正，因此D 一定是错误的．8．函数y ＝f (x )的图象如图所示，则y ＝f ′(x )的图象可能是( )[答案] D[解析] 由f (x )的图象知，f (x )在(－∞，0)上单调递增，在(0，＋∞)上单调递减，∴在(0，＋∞)上f ′(x )≤0，在(－∞，0)上f ′(x )≥0，故选D.9．如果1N 能拉长弹簧1cm ，为了将弹簧拉长6cm ，所耗费的功为( ) A ．0.18J B ．0.26J C ．0.12JD ．0.28J[解析] 设F(x)＝kx，当F(x)＝1时，x＝0.01m，则k＝100，∴W＝∫0.060100x d x＝5010．(2014·甘肃省金昌市二中、临夏中学期中)已知函数f (x )＝ln x ，则函数g (x )＝f (x )－f ′(x )的零点所在的区间是( )A ．(0,1)B ．(1,2)C ．(2,3)D ．(3,4)[答案] B[解析] 由题可知g (x )＝ln x －1x ，∵g (1)＝－1<0，g (2)＝ln2－12＝ln2－ln e>0，∴选B.11．已知三次函数f (x )＝13x 3－(4m －1)x 2＋(15m 2－2m －7)x ＋2在R 上是增函数，则m的取值范围是( )A ．m <2或m >4B ．－4<m <－2C ．2<m <4D ．以上皆不正确[答案] D[解析] f ′(x )＝x 2－2(4m －1)x ＋15m 2－2m －7，由题意得x 2－2(4m －1)x ＋15m 2－2m －7≥0恒成立，∴Δ＝4(4m －1)2－4(15m 2－2m －7) ＝64m 2－32m ＋4－60m 2＋8m ＋28 ＝4(m 2－6m ＋8)≤0， ∴2≤m ≤4，故选D.12．(2014·浙江省五校联考)已知函数f (x )＝13x 3＋12mx 2＋m ＋n2x 的两个极值点分别为x 1、x 2，且0<x 1<1<x 2，点P (m ，n )表示的平面区域内存在点(x 0，y 0)满足y 0＝log a (x 0＋4)，则实数a 的取值范围是( )A ．(0，12)∪(1,3)B ．(0,1)∪(1,3)C ．(12，1)∪(1,3]D ．(0,1)∪[3，＋∞)[答案] B[解析] f ′(x )＝x 2＋mx ＋m ＋n2，由条件知，方程f ′(x )＝0的两实根为x 1、x 2且0<x 1<1<x 2，∴⎩⎪⎨⎪⎧f ′0>0，f ′1<0，∴⎩⎪⎨⎪⎧m ＋n2>0，1＋m ＋m ＋n2<0，∴⎩⎪⎨⎪⎧m ＋n >0，3m ＋n <－2，由⎩⎪⎨⎪⎧m ＋n ＝0，3m ＋n ＝－2，得⎩⎪⎨⎪⎧m ＝－1，n ＝1，∴⎩⎪⎨⎪⎧x 0<－1，y 0>1.由y 0＝log a (x 0＋4)知，当a >1时，1<y 0<log a 3，∴1<a <3；当0<a <1时，y 0＝log a (x 0＋4)>loga3，由于y 0>1，log a 3<0，∴对∀a ∈(0,1)，此式都成立，从而0<a <1，综上知0<a <1或1<a <3，故选B.二、填空题13．(2014·杭州七校联考)若函数f (x )＝x 3－3bx ＋b 在区间(0,1)内有极值，则实数b 的取值范围是________．[答案] (0,1)[解析] f ′(x )＝3x 2－3b ，∵f (x )在(0,1)内有极值， ∴f ′(x )＝0在(0,1)内有解，∴0<b <1.14．(2013·泰州二中高二期中)函数f (x )＝x 3＋ax 2＋3x －9，已知f (x )在x ＝－3时取得极值，则a ＝________.[答案] 5[解析] f ′(x )＝3x 2＋2ax ＋3，由条件知，x ＝－3是f ′(x )＝0的根，即f ′(－3)＝0，∴27－6a ＋3＝0，∴a ＝5.15．对正整数n ，设曲线y ＝x n(1－x )在x ＝2处的切线与y 轴交点的纵坐标为a n ，则数列⎩⎨⎧⎭⎬⎫a n n ＋1的前n 项和是__________________． [答案] 2n ＋1－2[解析] ∵y ＝x n(1－x )，∴y ′＝(x n)′(1－x )＋(1－x )′·x n＝n ·x n －1(1－x )－x n.f ′(2)＝－n ·2n －1－2n ＝(－n －2)·2n －1.在点x ＝2处点的纵坐标为y ＝－2n. ∴切线方程为y ＋2n＝(－n －2)·2n －1(x －2)．令x ＝0得，y ＝(n ＋1)·2n， ∴a n ＝(n ＋1)·2n，∴数列⎩⎨⎧⎭⎬⎫a n n ＋1的前n 项和为22n－12－1＝2n ＋1－2.16．(2014·哈六中期中)已知函数f (x ＋2)是偶函数，x >2时f ′(x )>0恒成立(其中f ′(x )是函数f (x )的导函数)，且f (4)＝0，则不等式(x ＋2)f (x ＋3)<0的解集为________．[答案] (－∞，－3)∪(－2,1)[解析] ∵函数y ＝f (x ＋2)是偶函数，∴其图象关于y 轴对称，∵y ＝f (x ＋2)的图象向右平移两个单位得到y ＝f (x )的图象，∴函数y ＝f (x )的图象关于直线x ＝2对称，∵x >2时，f ′(x )>0，∴f (x )在(2，＋∞)上单调递增，在(－∞，2)上单调递减，又f (4)＝0，∴f (0)＝0，∴0<x <4时，f (x )<0，x <0或x >4时，f (x )>0，由(x ＋2)f (x ＋3)<0得⎩⎪⎨⎪⎧x ＋2<0，fx ＋3>0，(1)或⎩⎪⎨⎪⎧x ＋2>0，f x ＋3<0.(2)由(1)得⎩⎪⎨⎪⎧x <－2，x ＋3<0或x ＋3>4，∴x <－3；由(2)得⎩⎪⎨⎪⎧x >－2，0<x ＋3<4.∴－2<x <1，综上知，不等式的解集为(－∞，－3)∪(－2,1) 三、解答题17．(2013·四川达州诊断)已知函数f (x )＝x 3＋ax 2－3bx ＋c (b >0)，且g (x )＝f (x )－2是奇函数．(1)求a 、c 的值；(2)若函数f (x )有三个零点，求b 的取值范围． [解析] (1)∵g (x )＝f (x )－2是奇函数， ∴g (－x )＝－g (x )对x ∈R 成立， ∴f (－x )－2＝－f (x )＋2对x ∈R 成立， ∴ax 2＋c －2＝0对x ∈R 成立， ∴a ＝0且c ＝2.(2)由(1)知f (x )＝x 3－3bx ＋2(b >0)， ∴f ′(x )＝3x 2－3b ＝3(x －b )(x ＋b )，令f ′(x )＝0得x ＝±b ，x (－∞，－b )－b (－b ，b )b(b ，＋∞)f ′(x ) ＋ 0 － 0 ＋ f (x )增极大值减极小值增依题意有⎩⎨⎧f －b >0，fb <0，∴b >1，故正数b 的取值范围是(1，＋∞)．18．在曲线y ＝x 3(x ≥0)上某一点A 处作一切线使之与曲线以及x 轴围成图形的面积为112，试求过切点A 的切线方程． [解析] 设切点A (x 0，x 30)，切线斜率k ＝y ′|x ＝x 0＝3x 20.∴切线的方程为y －x 30＝3x 20(x －x 0)．令y ＝0，得x ＝2x 03.依题意S ＝∫x 00x 3d x －12×(x 0－2x 03)·x 3＝14x 40－16x 40＝112x 40＝112， ∵x 0≥0，∴x 0＝1.∴切线方程为y －1＝3(x －1)，即3x －y －2＝0.19．(2014·福建安溪一中、养正中学联考)已知函数f (x )＝x 3＋ax 2＋bx ＋5，若曲线f (x )在点(1，f (1))处的切线斜率为3，且x ＝23时，y ＝f (x )有极值．(1)求函数f (x )的解析式；(2)求函数f (x )在[－4,1]上的最大值和最小值． [解析] f ′(x )＝3x 2＋2ax ＋b ，(1)由题意得，⎩⎪⎨⎪⎧f ′23＝3×232＋2a ×23＋b ＝0，f ′1＝3×12＋2a ×1＋b ＝3.解得⎩⎪⎨⎪⎧a ＝2，b ＝－4.经检验得x ＝23时，y ＝f (x )有极小值，所以f (x )＝x 3＋2x 2－4x ＋5.(2)由(1)知，f ′(x )＝3x 2＋4x －4＝(x ＋2)(3x －2)．令f ′(x )＝0，得x 1＝－2，x 2＝23，f ′(x )，f (x )的值随x 的变化情况如下表： x －4 (－4，－2)－2 (－2，23)23 (23，1) 1 f ′(x ) ＋ 0 － 0 ＋ f (x )单调递增极大值单调递减极小值单调递增函数值－111395274∵f (3)＝27，f (－2)＝13，f (－4)＝－11，f (1)＝4，∴f (x )在[－4,1]上的最大值为13，最小值为－11.20．(2013·海淀区高二期中)已知函数f (x )＝a 23x 3－2ax 2＋bx ，其中a 、b ∈R ，且曲线y＝f (x )在点(0，f (0))处的切线斜率为3.(1)求b的值；(2)若函数f(x)在x＝1处取得极大值，求a的值．[解析] (1)f′(x)＝a2x2－4ax＋b，由题意f′(0)＝b＝3.(2)∵函数f (x )在x ＝1处取得极大值， ∴f ′(1)＝a 2－4a ＋3＝0，解得a ＝1或a ＝3. ①当a ＝1时，f ′(x )＝x 2－4x ＋3＝(x －1)(x －3)，x 、f ′(x )、f (x )的变化情况如下表：x (－∞，1)1 (1,3) 3 (3，＋∞)f ′(x ) ＋0 －0 ＋ f (x )极大值极小值②当a ＝3时，f ′(x )＝9x 2－12x ＋3＝3(3x －1)(x －1)，x 、f ′(x )、f (x )的变化情况如下表：x (－∞，13)13 (13，1) 1 (1，＋∞)f ′(x ) ＋0 －0 ＋ f (x )极大值极小值综上所述，若函数f (x )在x ＝1处取得极大值，a 的值为1.21．(2013·武汉实验中学高二期末)已知曲线f (x )＝ax 2＋2在x ＝1处的切线与直线2x －y ＋1＝0平行．(1)求f (x )的解析式；(2)求由曲线y ＝f (x )与y ＝3x 、x ＝0、x ＝1、x ＝2所围成的平面图形的面积． [解析] (1)由已知得：f ′(1)＝2，求得a ＝1， ∴f (x )＝x 2＋2.(2)由题意知阴影部分的面积是：S ＝⎠⎛01(x 2＋2－3x )d x ＋⎠⎛12(3x －x 2－2)d x＝(13x 3＋2x －32x 2)|10＋(32x 2－13x 3－2x )|21＝1. 22．(2013·福州文博中学高二期末)设f (x )＝ln x ，g (x )＝f (x )＋f ′(x )． (1)求g (x )的单调区间和最小值； (2)讨论g (x )与g (1x)的大小关系；(3)求a 的取值范围，使得g (a )－g (x )<1a对任意x >0成立．[解析] (1)由题设知g (x )＝ln x ＋1x，∴g ′(x )＝x －1x 2，令g ′(x )＝0，得x ＝1. 当x ∈(0,1)时，g ′(x )<0，故(0,1)是g (x )的单调递减区间．当x ∈(1，＋∞)时，g ′(x )>0，故(1，＋∞)是g (x )的单调递增区间，因此，x ＝1是g (x )的唯一极值点，且为极小值点，从而是最小值点，所以最小值为g (1)＝1.(2)g (1x)＝－ln x ＋x ，设h (x )＝g (x )－g (1x )＝2ln x －x ＋1x，则h ′(x )＝－x －12x 2.当x ＝1时，h (1)＝0，即g (x )＝g (1x)．当x ∈(0,1)∪(1，＋∞)时，h ′(x )<0，h ′(1)＝0，因此，h (x )在(0，＋∞)内单调递减．文档可能无法思考全面，请浏览后下载!19 / 31 当0<x <1时，h (x )>h (1)＝0，即g (x )>g (1x)，当x >1时，h (x )<h (1)＝0，即g (x )<g (1x)． (3)由(1)知g (x )的最小值为1，所以g (a )－g (x )<1a 对任意x >0成立⇔g (a )－1<1a，即ln a <1，从而得0<a <e ，即a 的取值范围为(0，e)．。

高二数学选修2-2导数及其应用测试题(含答案)

高二数学选修2-2导数及其应用测试题一、选择题(本大题共12小题，每小题5分，共60分)1．设xx y sin 12-=，则='y （）． A ．x x x x x 22sin cos )1(sin 2--- B ．xx x x x 22sin cos )1(sin 2-+- C ．x x x x sin )1(sin 22-+- D ．xx x x sin )1(sin 22--- 2．设1ln)(2+=x x f ，则=)2('f （）． A ．54 B ．52 C ．51 D ．53 3．已知2)3(',2)3(-==f f ，则3)(32lim3--→x x f x x 的值为（）． A ．4- B ．0 C ．8 D ．不存在4．曲线3x y =在点)8,2(处的切线方程为（）．A ．126-=x yB ．1612-=x yC ．108+=x yD ．322-=x y 5．已知函数d cx bx ax x f +++=23)(的图象与x 轴有三个不同交点)0,(),0,0(1x ，)0,(2x ，且)(x f 在1=x ，2=x 时取得极值，则21x x ⋅的值为（）A ．4B ．5C ．6D ．不确定6．在R 上的可导函数c bx ax x x f +++=22131)(23，当)1,0(∈x 取得极大值，当)2,1(∈x 取得极小值，则12--a b 的取值范围是（）． A ．)1,41( B ．)1,21( C ．)41,21(- D ．)21,21(-7．函数)cos (sin 21)(x x e x f x +=在区间]2,0[π的值域为（）． A ．]21,21[2πe B ．)21,21(2πe C ．],1[2πe D ．),1(2πe 8.076223=+-x x 在区间)2,0(内根的个数为（）A ．0B ．1C ．2D ．39．1. 已知函数)(x f y =在0x x =处可导，则hh x f h x f h )()(lim 000--+→等于（）A ．)(0/x fB ．２)(0/x fC ．－２)(0/x fD ．０10．如图是导函数/()y f x =的图象，那么函数()y f x =在下面哪个区间是减函数( )A. 13(,)x xB. 24(,)x xC.46(,)x xD.56(,)x x第Ⅱ卷（非选择题，共90分）二、填空题（每小题4分，共16分。

(完整版)高二数学导数及其应用测试题

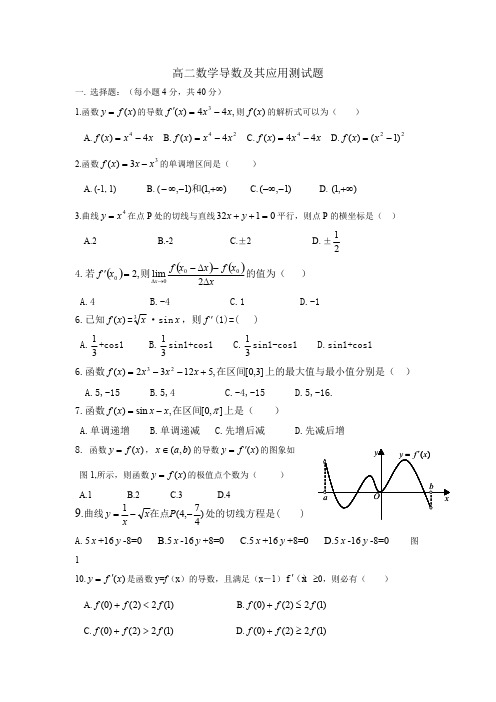
2.函数 f (x) 3x x3 的单调增区间是（）
A. (-1, 1)
B. ( ,1)和(1,) C. (,1)
D. (1,)
3.曲线 y x 4 在点 P 处的切线与直线 32x y 1 0 平行，则点 P 的横坐标是（）
A.2
B.-2
C.±2
4.若
f
x0
2,则 lim x0
f
x0
x
2x
f
x0 的值为（
1
D. ±
2 ）
A.4
B.-4
C.1
D.-1
6.已知 f (x) = 3 x ·sin x ，则 f (1)=( )
A. 1 +cos1 3
B. 1 sin1+cos1 3
C. 1 sin1-cos1 3
D.sin1+cos1
6.函数 f (x) 2x3 3x2 12x 5,在区间[0,3] 上的最大值与最小值分别是（）
；
三.解答题（5 个小题，共 44 分） 15.(8 分)已知函数 f (x) 1 x3 x2 , x [1,3] ，求函数 f (x) 的最大值和最小值.
3
16.(8 分)已知函数 f (x) ax3 bx2 3x在x ±1 处都取得极值.
(1)讨论 f (1)和f (1) 是函数 f (x) 的极大值还是极小值；
The shortest way to do many things is
高二数学导数及其应用测试题
答题卡
班级
；姓名
；得分
；
一.选择题（本大题共 10 个小题,每小题 4 分，共 40 分）题 1 2 3 4 5 6 7 8 9 10 号答案

高二数学导数与其应用综合检测综合测试题

第一章导数及其应用综合检测时间120分钟，满分150分一、选择题（本大题共12个小题，每小题 5 分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）2+ ax^ b在点（Q>1. （2010全国H文，7若曲线y= xb处的切线方程是x- y+ 1= 0,则（）A. a= 1, b= 1B. a=- 1, b= 1C. a= 1 , b=- 1D. a=- 1, b=- 1［答案］A ［解析］y' = 2+ a,二y' |x= 0= （2+ a）= 0= a= 1, 将（0, b代入切线方程得b= 1.2. —物体的运动方程为s= 2tsi+t,贝陀的速度方程为（）A. v= 2sin+t 2tco+st 1B. v= 2sin+t 2tcostC. v= 2sintD. v= 2sin+t 2cos+t 1［答案］ A［解析］因为变速运动在t0 的瞬时速度就是路程函数y= s（在t o 的导数，S = 2sin+ 2tco+t 1，故选 A.2+ 3x在点A（2,1处的切线的斜率是A. 4B. 5C. 6D. 73. 曲线y= x( )［答案］D ［解析］由导数的几何意义知，曲线y =x2+ 3>在点A（2,1处的切线的斜率就是函数y= x2+ 3x在x= 2时的导数，y' F2= 7,故选4•函数y= x|x（关3）卅1（）A. 极大值为2= 5,极小值（0= 1B. 极大值（2= 5,极小值为3= 1C. 极大值（2= 5,极小值（0=f（3=1D. 极大值（2= 5,极小值为3=1, f（- 1 = —3［答案］B［解析］尸x|x—3）卅1'3—3哭+ 1 （X0或x>3）=x—x 3+ 3^+ 1 （0C 点3）3+ 3）?+ 1 （g x< 3）2—6x （xv或x>3）二Y = 3x—3x 2+ 6x (g无极极大极小值二f(x极大=f(2” 5, f(x极小=f(3)= 1 故应选 B.5. (2009安徽理'9已知函数f(x在R上满足f(x)=2+ 8x- 8则曲线y= f(x在点(1 f(1)处的切2f(2- x—x线方程是()A. y= 2x- 1B. y= xC. y= 3x- 2D. y=-2灶3［答案］A ［解析］本题考查函数解析式的求法、导数的几何意义及直线方程的点斜式.•・• f(x片2(2- x—x2+ 8x- 8・•・ f(2- x)= 2fQ— x2- 4灶4・•・f(x片x2, ••• f' (x片2x•••曲线y= f(x在点(1, f(1)处的切线斜率为2,切线方程为y—1= 2(—1, •••尸2" 1.3+ ax+ 3x- 9 已知f(x)在x= — 3 时6•函数f(()= x取得极值，则a等于()A. 2B. 3C. 4D. 52＋2ax＋3，［答案］D ［解析］f (x片3xT f(x在x=- 3时取得极值，x=- 3是方程3x+ 2axF 3= 0的根,.•・a= 5,故选D.7•设f(x) g(x 分别是定义在R 上的奇函数和偶函则不等式f(Xg(x )v 的解集是( )［答案］D［解析］令F(x #fx)g (x)易知F(x 为奇函数，又当 x<0时，F (x)5+ f(x)g (x)>0 即 F (x)>0 知 F(x) 在—x, 0内单调递增，又 F(x 为奇函数，所以 Fx 在(0 + )内也单调递增，且由奇函数知f (0片0,・•・R0) =0.又由 g — 3)= Q 知 g(3#0 二 F — 3> 0,进而 F(3#0于是Rx)= f(x)g(x 的大致图象如图所示・•・ F[x > f(x) g *)<0的解集为(―* ,— 3U (0,3)故应选D.8 •下面四图都是同一坐标系中某三次函数及其导函数的图象，其中一定不正确的序号是数•当 XV0寸，f‘ (xgx )+ f(Xg(x)>0 且 g(- 3> 0,A. (- 3,0卩(3 + )B. (- 3,0^ (0,3)C.(—「一 3)U (3 2)D. (—「一3U (0,3)A.①②B.③④ C ・①③ D ①④［答案］B ［解析］③不正确；导函数过原点，但三次函数在 x = 0不存在极值； ④不正确；三次函数先增后减再增，而导函数先负后正再负•故应选所以41xd = lnx2= ln4— ln2= ln2.A . m<或 m>4B — 4<<— 2 C. 2<m<4 D .以9. （201醐南理，5） 41xdX 等于(A . — 2ln2 B. 2l n2 C. — ln2 D. ln2［答案］D［解析］10已知三次函数1 3— (4m- f(x = 3x1)i + (15m — 2m—7)炸 2在 x € (—g, g ）是增函数，则m 的取值濶上皆不正确2— 2(4m 1)灶 15rf［答案］D ［解析］f (x ^x—2m — 7 由题意得 )2— 2(4— 1)炸 15r 2— 2m — 7> 0恒成立，・•・△ =4(4r — 12— 4(15i^— 2m — 7)=64m — 32m+ 4- 60rf ^ 8rnP 28 =4(rfi — 6mb 8)c 0,・•・2< 4,故选3+ bX + c 灶d 在区间—1,2上是减11 已知 f(x = x 函数，那么 b + c( )15 15 C.有最小值 2 D.有最小值— 2 ［答案］B析］由题意f' (x = 3x f ' (x)c 0恒成立.F (— 1戶 0 所以F (2 戸 0 2b — c — 3> 015A 有最大值 2 B.有最大值- 15 22+ 2b 冷 c 在［—1,2上,［解 /\ /勺—o即4b^ c+ 12C 0令b+ c= z b= —c+ z 如图过一6, 32得z 最大，12设、g(x 是定义:为R 的恒大于0的可导函［答案］Cf(x)［解析］令F(x)=g(x) f (xgx)—斶(x)则 F ' (»=2(x) <0gfx 、g(x 是定义域为R 恒大于零的实数・•・FFx 在R 上为递减函数，f(x) f(b)gx)>g(b)・•・ fx )g(b)>fgx)•故选.IF二、填空题(本大题共4个小题，每小题 4分，分•将正确答案填在题中横线上)最大值b + E — 6—15 2故选数，且 f ' (xg(x —f(x)g (x)<0则当a<x<时有)A. f(X)g(x)>bgb)B. f(x)g(afa)g(x)C ・ f(X)g(b)(bgx) D. f(x)g(x)fx)当 x € (a, b 时，共16dx 广-113 - 3^ ----------- .［(1 甘5x) '2［答案】72 ［解析］取F(x护—从而F'（沪1 3 则1 dx 3= F（- 1）-（11＋5x）－（11＋5x）-272.10 36010$ 10 X2— 1ax14若函数f(x =则数a 的取值范0是［答案］a > 0［答案］—2［解析］本小题主要考查导数的几何意义和数函数的有关性质.k = y~ X 产 n + 1 二切线-y — 1= (n+ 1)X — 1,1F(— 2=— ------ 21 11 72= — =的单调土区间，+ ［解析］f (x > ax-1=a+2,x由题意得， a + *恒成立，1a > — 2, x € (0,xx )恒成立，・•・a> 0.n」(n € N *)在点(1,1)15 (200陕西理，16设曲=x处的切线与轴的交点的横坐^为令s n = Igx,则ai__ 22+ ?a)9的值为令y= 0, x= ,・•・a=lg212 99二原式=lg lg _ ? _ lg2 3 1001 2 99 1 =lg X >? X 2 3 100 lg —21001,y^= x与直线x= 2,［答案］3+ ln22=兀y _［解析］由 1 ,得交点A(1,1). 戶xx= 2由1得交点B22 3 y=x故所求面积1 xck+2 .I _21xdx16如图阴影部分是由曲线y=1=3xln|ln2.三、解答题（本大题共6个小题，共74分．解答应写2出文字说明、证明过程或演算步)=lrx + ln(2- x 片 axa>0)(1 当 a = 1时，求f(x 的单调区间 1(2若f(x 在 (0,1上的最大值为求a 的值.2 ［解析］函数f(x 的定义域2) 厂(x A厂—x 十2，所以f(x 的单调递x(2- x) 增区为 2)单调递驱间2 2；2— 2x十a>0x(2- x)即f(x)在 (0,1上单调递增，故x 在(0,1上的最大值17 (本题分12分)(201江西理， 19设函数f(x)(1当 a = 1 时，f ' (x)= (2当 x € (0,1 时，厂(x A 为A a 因此a=1 2.2— 4x)d 冶求a b 的值;(2求函数f(x 的单调区间与极值点. ［分析］考查利用导数研究函数的单调性，极值点的性质，以及分类讨论思想.L2—3a.［解析］(1)f (x = 3x因为x23—3x所以S=b(护 0).x2)d —2— 4x)dx. 2(2xoo13/ = 2x- x ,3x=2^— 4x133x23—2x=4.3— 3axP19 (本题满分12分)设函数f(x)= x(1若曲线y = f(x 在点(2 f(2)处与直线y = 8相切，(2x2—4x)d冶因为曲线y= f(x在点(2 f(2处与直线y= 8相切，f (2= 0, 3(4- a= 0,所以即f(2= 8. 8- 6升b= 8.解得a= 4, b= 24.2—a)a^ 0)・(2)' (x片3(x当a<0寸，F (x)>0函数f(x)在(—x,+x上单调递增，此时函数fx没有极值点.当a>0寸，由(x片0得x= ±a.V当x€ (—^，― a时，F (x)>0函数f(x单调递增；当x€ (―- a a时，f' (x)<0函数f(x单调递减当x€ ( a,+ *)时，f (x)>0函数f(x)单调递增.此时x=—a是fx的极大值点，x= a是f(x)的极小值点.12+ lnx.20 (本题分12分)已知函数f(x^2x(1求函数fx的单调5间1 2(2求证：当X>1时，2十l nx< 3_ 2x 3x［解析］(1依题意知函数的定义域为x>Q}1•・• F ())= x+，故f (x)>0x二f(x的单调增0间为土x).2 3—12—lnx(2设炸3x 2x1 ・•・ g (x)= 2x— x—x2 x＋1)•'当x〉1时，g （x片（X— i）>0，（2xx1 ・•・g(y 在 (1, + g )上为增函数，・•・g(x)>g 件)6>012 ・•・当x>1时，2x 3x2+ lnx< 3.3- 92+ 6x- a.21 (本题分12分)设函数f(x)= x 2x(1对于任意实数 x, f' (x p m 恒成立，求 m 的最大值； (2若方程fx )= 0有且仅有一个实根求a 的取值范围.求参数的范围问题.2- 9灶 6= 3(— 1)(- 2)［解析］(1)f (x = 3x(2因为当 x<1 时，f (x)>0 当 1<xv 时,F (x)<0 当 x>2时 f［分析］本题主要考查导数的应用及转化思以及因为 x € (-g ,g ). F (x p m ,即 3x2- 9灶(6m p 0恒成立.所以 4=8— 12(— m 齐 0,得 me3，即m 的最 4大值为-34.(x)>0.所以当x= 1时，f(x取极大值f(1)=2当x= 2 时，f(x取极小值f(2#2— a.故当f(2)>或f(1)v时，方程f(x# 0仅有一个实根5解得a<2或a>2.3+ aX+22 (本题分14分)已知函数f(x片—xia€ R)._ 2 -上递增，在区间3(1若函数y= f(x在区间2,+ 上递减，求a的值；3(2当x€ ［0,1时，设函数尸f(x图象上任意一点处勺切线的倾斜角为，若给定常数a€［十g ,求B的取2值范围(3在(1 的条件下，是否存在实数m使得函数g(x)=x—5x+ (2— mx2+ 1(n€ R)的图象与函数y= f(x的图象恰有三个交点•若存在，请求出实数m的值；若不存在，试说明理由.2［解析］(1依题意f3= 0,2 22+ 2ax= —由f'(X片—3x+ 2ax得—33 2+ 2a•= 0,即- 一a=I 丿=0,即a=3(2当x€ [0,1 时，tan0= f (x片一3x23.3 x －2＋ a丄、由a€ --k oo得 3 ，+ o-.2 € 2—f a 1 2①当3 €,1，即a€ <2」 a2 ,3 时，f' (x ma— 3f(x)!in—f (0—0. _2此时（K tan9<a3.a②当€ (1 Z),卩a€ (3 Z)时，f (x ma^F ⑴3=2a- 3 f‘(x}i尸f (0)= 0,此时，C K tan0< 2a- 3.23 a又v 0 € [0, n, ) 当2<K 3时，6€ 0, arctan3 当a>3时，0 € [Q arctan-舀)]4— 5X+ (2- mX2+ 1(m€ R) （3函数戶f（x与g（x^ x的图象恰有3个交点，等价于方程一x3+ x2+ 1= x—5）3+ （2- m）x2+ 1恰有3个不等实根，・•・x4— 4x+ （1— mx2= 0,显然=0是其中一个根（二重根）,方程x2—4炸（1— m= 0有两个非零不等实根，则电丄O A E丄)寸石L H <H S (X &H A W (X )4H A報®生M 00&训宦LI E M o A E ...象恰有3个交点．2, y A 2x—4x18 (本题分.12分)求曲线A 2—x所围成图形的面灭「2得XA,XA2.［解析］由y= 2x- x2—4xy=2x由图可知，所求图形的面积S A2(2—x)d十|。

高二数学《导数及其应用》单元检测题

高二数学《导数及其应用》单元检测题.选择题(每小题5分，共60 分)f(x) ax bx c f (1) 2 f ( 1)A . 4 B. 2 C.2 D.42. 函数f(x) lg x 11的零点所在的区间是xA.0,1 B. 1,2 C. 2,3 D. 3,10 3.已知函数f(x)在R上满足f(x) 2f (2 x) x2 8x 8，则曲线y= f (x)在点(1, f (1))处的切线方程是A. y 2x 1B. y xC. y 3x- 2D. y 2x 34.曲线y x3 3x2在点(1, 2)处的切线方程为A. y 3x 1B. y 3x+3C. y 3x 5D. y 2x5.设y 2,则y =A.2B. 2C.0D.以上都不是6.已知f(x) x(2014 ln x)，若 f (x°) 2013 ,则X。

A . 1B . l n 2 C. 1 D . ee7.曲线y x2 11在点P (1, 12)处的切线与y轴交点的纵坐标是A.-9B.-3C.9D.158.函数f(x) c 32x ax ,若f⑵1，则aA.4B.-C.-4D. 14 49.函数f(x) 3 亠=ax + bx 在x= 1处有极值—2,，则a, b的值分别为A.1, —3B.1,3C. —1,3D.--1, —310.函数f(x) 3=x —3x(|x| v 1)A.有最大值,但无最小值B. 有最大值，也有最小值C.无最大值,也无最小值D. 无最大值，但有最小值2・ '11. y x sinx，贝y yA. 2xsinx B . x2 cosx2 2C. 2xcosx x cosx D . 2xsinx x cosxn12. 函数f (x) = x + 2cosx在［0 ,空］上取得最大值时x为n n nA.0B."6C. —D. —二.简答题(每小题5分，共20分)X13. 过原点作曲线y e的切线，则切线的方程为 __________________ .114. 设函数f(x) = x(ex + 1) + qx2，则函数f(x)的单调递增区间为_____________15. 若曲线y X 1(a€ R)在点(1,2)处的切线经过坐标原点，则a =。

高二数学第三章导数及其应用9份同步测试题(有答案)

高二数学第三章导数及其应用9份同步测试题（有答案）第三章导数及其应用3．1变化率与导数3．1．1变化率问题双基达标（限时20分钟）1．函数y＝f(x)在x0到x0＋Δx之间的平均变化率f（x0＋Δx）－f（x0）Δx中，Δx不可能是()．A．大于0B．小于0C．等于0D．大于0或小于0答案C2．如果质点M按规律s＝3＋t2运动，则在一小段时间2，2.1]中相应的平均速度是()．A．4B．4.1C．0.41D．3解析＝（3＋2.12）－（3＋22）0.1＝4.1.答案B3．函数y＝x2＋x在x＝1到x＝1＋Δx之间的平均变化率为()．A．Δx＋2B．2Δx＋(Δx)2C．Δx＋3D．3Δx＋(Δx)2解析ΔyΔx＝f（1＋Δx）－f（1）Δx＝（1＋Δx）2＋（1＋Δx）－（12＋1）Δx＝Δx＋3.答案C4．已知函数y＝2＋1x，当x由1变到2时，函数的增量Δy＝________．解析Δy＝2＋12－(2＋1)＝－12.答案－125．一个作直线运动的物体，其位移s与时间t的关系是s＝3t－t2，则物体在t＝0到t＝2之间的平均速度为________．解析物体在t＝0到t＝2之间的平均速度为（3×2－22）－02－0＝1. 答案16．已知函数f(x)＝2x＋1，g(x)＝－2x，分别计算在下列区间上f(x)及g(x)的平均变化率；(1)－3，－1]；(2)0，5]．解(1)函数f(x)在区间－3，－1]上的平均变化率为f（－1）－f（－3）（－1）－（－3）＝2×（－1）＋1]－2×（－3）＋1]2＝2，g(x)在区间－3，－1]上的平均变化率为g（－1）－g（－3）（－1）－（－3）＝－2×（－1）]－－2×（－3）]2＝－2.(2)函数f(x)在区间0，5]上的平均变化率为f（5）－f（0）5－0＝（2×5＋1）－（2×0＋1）5＝2，g(x)在区间0，5]上的平均变化率为g（5）－g（0）5－0＝－2×5－（－2×0）5＝－2.综合提高（限时25分钟）7．已知函数f(x)＝2x2－4的图象上一点(1，－2)及邻近一点(1＋Δx，－2＋Δy)，则ΔyΔx等于()．A．4B．4xC．4＋2ΔxD．4＋2(Δx)2解析ΔyΔx＝f（1＋Δx）－f（1）Δx＝2（1＋Δx）2－2Δx＝4＋2Δx.答案C8．一质点的运动方程是s＝4－2t2，则在时间段1，1＋Δt]内相应的平均速度为()．A．2Δt＋4B．－2Δt－4C．4D．－2Δt2－4Δt解析＝4－2（1＋Δt）2－（4－2×12）Δt＝－4Δt－2（Δt）2Δt＝－2Δt －4.答案B9．已知圆的面积S与其半径r之间的函数关系为S＝πr2，其中r∈(0，＋∞)，则当半径r∈1，1＋Δr]时，圆面积S的平均变化率为________．解析当r∈1，1＋Δr]时，圆面积S的平均变化率为ΔSΔr＝π（1＋Δr）2－πΔr＝π＋2π•Δr＋（Δr）2π－πΔr＝2π＋πΔr.答案2π＋πΔr10．国家环保局在规定的排污达标的日期前，对甲、乙两家企业进行检查，其连续检测结果如图所示．治污效果更好的企业是(其中W表示排污量)________．解析ΔWΔt＝W（t1）－W（t2）Δt，在相同的时间内，由图可知甲企业的排污量减少的多，∴甲企业的治污效果更好．答案甲企业11．假设在生产8到30台机器的情况下，生产x台机器的成本是c(x)＝x3－6x2＋15x(元)，而售出x台的收入是r(x)＝x3－3x2＋12x(元)，则生产并售出10台至20台的过程中平均利润是多少元？解由题意，生产并售出x台机器所获得的利润是：L(x)＝r(x)－c(x)＝(x3－3x2＋12x)－(x3－6x2＋15x)＝3x2－3x，故所求的平均利润为：L＝L（20）－L（10）20－10＝87010＝87(元)．12．(创新拓展)婴儿从出生到第24个月的体重变化如图，试分别计算第一年与第二年婴儿体重的平均变化率．解第一年婴儿体重平均变化率为11.25－3.7512－0＝0.625(千克/月)；第二年婴儿体重平均变化率为14.25－11.2524－12＝0.25(千克/月)．。

(完整版)高中数学选修22导数及其应用单元测试卷

章末检测一、选择题1.设 f(x)为可导函数，且知足 lim f 1－f 1－2x＝－ 1，则过曲线 y＝ f(x)上点 (1，f(1)) 处的切线x→02x斜率为 ()B.－1D. －2答案B分析lim f 1 － f 1－ 2x＝ lim f 1－2x－f 1＝－ 1，即 y′ |x＝1＝－ 1，则 y＝f(x)在点 (1，f(1))x→ 02x x→0－ 2x处的切线斜率为－ 1.2.函数 y＝ x4－ 2x2＋ 5 的单一减区间为 ()A.( －∞，－ 1)和 (0,1)B.( － 1,0)和 (1，＋∞ )C.(－ 1,1)D.( －∞，－ 1)和 (1，＋∞ )答案A分析y′＝ 4x3－ 4x＝4x(x2－ 1)，令 y′ <0 得 x 的范围为 (－∞，－ 1)∪ (0,1)，应选 A.3.一物体在变力F(x)＝5－ x2(力单位： N ，位移单位： m)作用下，沿与F(x)成 30°方向做直线运动，则由 x＝1 运动到 x＝ 2时 F(x)做的功为 ()23A. 3 JB. 3J43C.3J 3 J答案C分析因为 F(x)与位移方向成30°角 .如图： F 在位移方向上的分力F ′＝F ·cos 30，°W＝2(51 3312－ x2) · cos 30x＝°d2(5－ x2)dx＝5x－ x322311＝3×8＝43(J). 2334.若 f(x)＝ x2＋ 21f(x)dx，则1f(x)dx 等于 ()001A.－1B.－3第1页共6页1C.3答案B分析∵ f(x)＝ x2＋ 21f(x)dx，11∴1f(x)dx) 1f(x)dx＝ ( x3＋ 2x0300＝1＋21f(x)dx，31∴1f(x)dx＝－3.5.已知函数 f(x)＝－ x3＋ ax2－ x－ 1 在(－∞，＋∞ )上是单一函数，则实数 a 的取值范围是 ( )A.( －∞，－ 3)B.[ － 3， 3]C.( 3，＋∞ )D.( －3，3)答案B分析 f ′(x)＝－ 3x2＋2ax－ 1≤0 在 (－∞，＋∞ )恒建立，＝4a2－12≤0?－3≤ a≤ 3. 6.设 f(x)＝ xln x，若 f′ (x0)＝2，则 x0等于 ()2 B.ln 2 C.ln 22答案D分析∵ f′ (x)＝x(ln x)′＋ (x)′ ·lnx＝ 1＋ ln x，∴f′ (x0)＝1＋ ln x0＝ 2，∴ln x0＝ 1，∴x0＝e.17.设函数 f(x)＝3x－ ln x(x＞0)，则 y＝ f(x)()1，1， (1， e)内均有零点A. 在区间e1B. 在区间e， 1， (1， e)内均无零点1， 1内无零点，在区间(1， e)内有零点C.在区间e1D.在区间e，1内有零点，在区间(1， e)内无零点答案Cx－ 3分析由题意得 f ′ (x)＝3x，令 f′ (x)＞0得 x＞ 3；令 f′ (x)＜ 0 得 0＜ x＜3；令 f′ (x)＝0得 x＝3，故知函数 f(x)在区间 (0,3)上为减函数，在区间(3，＋∞)为增函数，在点x＝ 3 处有极小值 1－ ln 3 ＜ 0；又 f(1)＝1＞0， f(e)＝e－1＜ 0， f1＝1＋1＞0. 33e3e第2页共6页8.已知一物体在力F(x)＝ 4x－ 1(单位： N) 的作用下，沿着与力 F 同样的方向，从x＝ 1 m 处运动到 x＝ 3 m 处，则力 F(x)所做的功为 ()A.10 JB.12 JC.14 JD.16 J答案C3分析力 F(x)所做的功 W＝3F(x)dx＝3(4x－ 1)dx＝ (2x2－ x)＝ 14(J).1119.由 x 轴和抛物线y＝ 2x2－ x 所围成的图形的面积为()A. 5(2x2－ x)dxB.5(x－ 2x2)dxC.1(x－ 2x2)dx 2D.1(x＋ 2x2)dx 2答案C11分析先计算出抛物线与x 轴的交点的横坐标，分别为 x1＝ 0，x2＝2，且在 0＜x＜2内，函数1图象在 x 轴下方，则由定积分的几何意义可知，所求图形面积的积分表达式为2 (x－ 2x2)dx.10.函数 f(x)＝ xe x－ e x＋1的单一递加区间是 ()A.( －∞， e)B.(1 ， e)C.(e，＋∞ )D.(e － 1，＋∞ )答案D分析x x x＋1xf ′(x)＝ e ＋ xe － e＝(x－e＋ 1)e ，由 f′ (x)＞ 0，得 x＞ e－ 1.应选 D.二、填空题11.若曲线 y＝ kx＋ ln x 在点 (1 ，k)处的切线平行于 x 轴，则 k＝.答案－ 11分析求导得 y′＝ k＋x，依题意 k＋1＝ 0，因此 k＝－ 1.12.已知函数 f(x)＝－ x3＋ ax 在区间 (－ 1,1)上是增函数，则实数 a 的取值范围是.答案a≥ 3分析由题意应有f′ (x)＝－ 3x2＋ a≥0 在区间 (－ 1,1)上恒建立，则a≥ 3x2在 x∈ (－ 1,1)时恒建立，故a≥ 3.13.已知函数y＝xf′ (x)的图象如下图( 此中 f′ (x)是函数 f(x)的导函数 )，给出以下说法：第3页共6页①函数 f(x)在区 (1，＋∞ )上是增函数；②函数 f(x)在区 (－1,1)上无性；1③函数 f(x)在 x＝－获得极大；④函数 f(x)在 x＝1 获得极小.此中正确的法有.答案①④分析从象上能够，当x∈ (1，＋∞ )，xf′ ( x)＞0，于是f′ ( x)＞0，故f(x)在区(1，＋∞ )上是增函数，故① 正确；当 x∈ (－1,1)， f′ (x)＜ 0，因此函数f(x) 在区 (－ 1,1)上是减函数，②，③也；当 0＜x＜ 1 ， f(x)在区 (0,1) 上是减函数，而在区(1，＋∞ )上是增函数，因此函数f(x)在x＝ 1 获得极小，故④正确 .n ＋1*)在 (1,1)的切与 x 的交点的横坐 x n， log2 015x1＋ log2 015x214.曲 y＝ x(n∈N＋⋯＋ log 2 015x2 014的.答案－1分析∵ y′ |x＝1＝ n＋1，∴切方程y－ 1＝ (n＋ 1)(x－ 1)，令 y＝0，得 x＝1－1＝n，即 x n＝n. n＋ 1 n＋ 1n＋ 1∴log 2 015x1＋ log 2 015x2＋⋯＋ log2 015x2 014＝log 2 015(x1·x2·⋯·x2 014)1 2 2 014＝ log2 0151＝－ 1.＝ log 2 015··⋯ ·2 3 2 015 2 015三、解答15.函数 f( x)＝2x3－ 3(a＋ 1)x2＋ 6ax＋ 8，此中 a∈R .已知 f(x)在 x＝ 3 获得极 .(1)求 f( x)的分析式；(2)求 f( x)在点 A(1,16)的切方程.解 (1)f′ (x)＝ 6x2－ 6(a＋ 1)x＋ 6a.∵ f(x) 在 x＝ 3 获得极，∴f′ (3)＝ 6× 9－ 6(a＋ 1)× 3＋ 6a＝ 0，解得 a＝ 3.∴f(x) ＝2x3－ 12x2＋ 18x＋ 8.第4页共6页(2)A 点在 f(x)上，由 (1) 可知 f ′ (x)＝ 6x 2－ 24x ＋ 18，f ′ (1) ＝ 6－ 24＋18＝ 0，∴ 切线方程为 y ＝ 16.2 3 616.设 3<a<1 ，函数 f(x)＝ x 3－ 2ax 2＋ b (－ 1≤x ≤ 1)的最大值为1，最小值为－2 ，求常数 a ，b.解令 f ′( x)＝ 3x 2－ 3ax ＝ 0，得 x 1＝ 0，x 2＝a.a 3f(0) ＝b ， f( a)＝－ 2 ＋ b,3f(－ 1)＝－ 1－ 2a ＋ b ，3f(1) ＝1－ 2a ＋ b.23因为 3<a<1，因此 1－ 2a<0，故最大值为 f(0) ＝ b ＝ 1，因此 f(x)的最小值为f(－1) ＝－3 a ＋ b ＝－ 3 1－ a ，2 2因此－ 3 a ＝－ 662 ，因此 a ＝3 .2故 a ＝ 36，b ＝ 1.17.已知函数 f(x)＝ ( x ＋1)ln x －x ＋ 1.(1)若 xf ′ (x)≤ x 2＋ax ＋ 1，求 a 的取值范围；(2)求证 (x － 1)f(x)≥ 0.(1)解 f ′ (x)＝x ＋ 1＋ ln x － 1＝ln x ＋1， xf ′ (x)＝xln x ＋ 1，而 xf ′ (x)≤ x 2＋ax ＋ 1 等价于 ln xx x－ x ≤ a.令 g(x)＝ ln x － x ，则 g ′ (x)＝1x － 1，当 0＜ x ＜ 1 时， g ′ (x)＞ 0；当 x ＞ 1 时， g ′ (x)＜＝ 1 是 g(x)的极大值点，也是最大值点， ∴ g(x)≤ g(1) ＝－ 1.综上可知， a 的取值范围是 [－ 1，＋ ∞ ).(2)证明由(1) 知， g(x)≤ g(1) ＝－ 1，即 ln x －x ＋ 1≤ 0.当 0＜ x ＜ 1 时， f( x)＝ (x ＋ 1)ln x － x ＋ 11－ 1＝ xln x ＋ (ln x － x ＋ 1)≤ 0；当 x ≥ 1 时， f(x)＝ ln x ＋ (xln x － x ＋1)＝ ln x ＋ x ln x ＋ x ＝ ln x －11x ln －＋ 1 ≥ 0.∴(x － 1)f(x) ≥0.第 5页共6页18.已知函数 f(x)＝－ 1 3 2 23x ＋ 2ax － 3a x ＋b(a ＞0).7(1) 当 f( x)的极小值为－ 3，极大值为－ 1 时，求函数 f(x)的分析式；(2) 若 f( x)在区间 [1,2] 上为增函数，在区间 [6，＋∞ )上为减函数，务实数a 的取值范围 .解 (1)f ′ (x)＝－ x 2＋ 4ax － 3a 2＝－ (x － a)(x － 3a)，令 f ′ (x)≥ 0，得 a ≤ x ≤ 3a ，令 f ′ (x)≤0，得 x ≥ 3a 或 x ≤ a ，∴ f(x)在 (－ ∞， a]上是减函数，在[a,3a]上是增函数，在 [3a ，＋ ∞ )上是减7函数， ∴ f( x) 在 x ＝ a 处取极小值，在x ＝ 3a 处取极大值 . 由已知有f a ＝－ 3，即f 3a ＝－ 1，13337－ 3a ＋ 2a － 3a＋ b ＝－ 3， a ＝ 1， 1 解得b ＝－ 1，－ 3× 27a 3＋18a 3－ 9a 3＋ b ＝－ 1，∴ f(x) ＝－ 1x 3＋ 2x 2－ 3x －1. 3(2)由 (1)知 f(x)在 (－ ∞， a]上是减函数，在[a,3a] 上是增函数，在 [3a ，＋ ∞)上是减函数， ∴要a ≤ 1，2≤ a ≤1.使 f(x)在区间 [1,2] 上为增函数，在区间 [6，＋∞)上是减函数，则一定有 3a ≥ 2，解得3a ≤ 6，3第 6页共6页。

期末专题02 导数及其应用大题综合(精选30题)(解析版)-备战期末高二数学

期末专题02导数及其应用大题综合（精选30题）1．（22-23高二下·江西·期末）已知函数()()2ln 21f x x x f x '=+.(1)求()1f '的值；(2)求()f x 在点()()22e ,ef 处的切线方程.【答案】(1)2-(2)222e 0x y --=【分析】（1）求出函数的导函数，再代入1x =计算可得；（2）由（1）可得()2ln 4f x x x x =-，求出()2e f ，()2e f '，再由点斜式求出切线方程.【详解】（1）因为()()2ln 21f x x x f x '=+，所以()2ln 22(1)f x x f ''=++，代入1x =得：()()()12ln1221221f f f '''=++=+，所以()12f '=-.（2）由（1）可得()2ln 4f x x x x =-，则()2ln 2f x x '=-所以()22222e ln e 4e 0e f =-=，()222ln e 22f =-=，所以切线方程为202(e )y x -=-，即222e 0x y --=.2．（22-23高二下·安徽亳州·期末）设函数()3e ax bf x x x +=-，曲线()y f x =在点()()1,1f 处的切线方程为1y x =-+．(1)求a b ，的值；(2)设函数()()g x f x '=，求()g x 的极值点；【答案】(1)1,1a b =-=(2)()g x 的极大值点为0和33【分析】（1）求出函数()f x 的导数，再利用导数的几何意义列式求解作答.（2）利用（1）的结论求出()g x ，再利用导数求出极值点作答.【详解】（1）函数3R ()e ,ax b f x x x x +=-∈，求导得()()2313e ax bf x a x x ++'=-，因为()f x 在(1,(1))f 处的切线方程为1y x =-+，于是(1)110f =-+=，(1)1f '=-，则()311e 013e 1a ba ba ++⎧-⨯=⎪⎨-+=-⎪⎩，解得11a b =-⎧⎨=⎩，所以1,1a b =-=.（2）由（1）得()()()23113e x f x x g x x -+='-=-，求导得()()1266e x x g x x x -+'+-=-，令2660x x -+=，解得3x =±1e 0x -+>成立，由()0g x '<，得03x <<3x >+，函数()g x 递减；由()0g x '>，得0x <或33x <<，函数()g x 递增，所以()g x 的极大值点为0和33.3．（22-23高二下·安徽合肥·期末）函数()e ln x f x x =-，()f x '是()f x 的导函数：(1)求()f x '的单调区间；(2)证明：()2f x >．【答案】(1)()f x '单调递增区间为()0,∞+，无递减区间(2)证明见解析【分析】（1）对()()g x f x '=求导后，由导数的正负可求出函数的单调区间；（2）由（1）知()f x '单调递增区间为()0,∞+，然后根据零点存在性定理可得存在01,12x ⎛⎫∈ ⎪⎝⎭，使得()0001e 0xf x x '=-=，从而可求得()f x 的单调区间和最小值，进而可证得结论.【详解】（1）由()e ln x f x x =-，得()()1e 0xf x x x '=->，令()()()1e 0xg x f x x x '==->，则()210x g x x'=+>e 恒成立，所以()f x '单调递增区间为()0,∞+，无递减区间；（2）由（1）知()()1e 0xf x x x'=->，()f x '单调递增区间为()0,∞+，因为121e 202f ⎛⎫'=-< ⎪⎝⎭，()1e 10f '=->，所以存在01,12x ⎛⎫∈ ⎪⎝⎭，使得()0001e 0xf x x '=-=，所以当00x x <<时，()0f x '<，当0x x >时，()0f x ¢>，所以()f x 在区间()00,x 上单调递减，在()0,x +∞上单调递增，所以()()0000min 01e 2ln x f x f x x x x ==-=+≥，当且仅当001x x =，即01x =时取等号，因为01,12x ⎛⎫∈ ⎪⎝⎭，所以等号取不到，所以()2f x >，得证．【点睛】关键点点睛：此题考查导数的应用，考查利用导数求函数的单调区间和最值，第（2）问解题的关键是根据函数的单调性结合零点存在性定理可求得函数的最值，考查数学转化思想，属于中档题.4．（22-23高二下·河北石家庄·期末）已知函数32()f x x x ax b =-++，若曲线()y f x =在(0,(0))f 处的切线方程为1y x =-+．(1)求a ，b 的值；(2)讨论函数()y f x =在区间()2,2-上的单调性．【答案】(1)1a =-；1b =(2)在12,3⎛⎫-- ⎪⎝⎭和()1,2上单调递增，在1,13⎛⎫- ⎪⎝⎭上单调递减【分析】（1）根据函数的切线方程即可求得参数值；（2）先求函数的导函数，判断函数单调性.【详解】（1）令0x =，由1y x =-+，则()10y f ==，由()32f x x x ax b =-++，可得(0)1==f b ．又2()32f x x x a '=-+，所以(0)1f a '==-.（2）由（1）可知32()1f x x x x =--+，()()2()321311f x x x x x '=--=+-，令()0f x '>，解得13x <-或1x >；令()0f x '<，解得113-<<x ，所以()f x 在1(2,)3--和(1，2)上单调递增，在1,13⎛⎫- ⎪⎝⎭上单调递减．5．（22-23高二下·安徽合肥·期末）已知函数()sin 2()f x x ax a =--∈R ．(1)当12a =时，讨论()f x 在区间π0,2⎡⎤⎢⎥⎣⎦上的单调性；(2)若当0x ≥时，()e cos 0xf x x ++≥，求a 的取值范围．【答案】(1)()f x 在π0,3⎡⎤⎢⎥⎣⎦上单调递增，在ππ,32⎛⎤⎥⎝⎦上单调递减(2)(,2]-∞【分析】（1）求导，由导数正负即可求解（2）利用导数求证e 1x x ≥+和sin x x ≥，即可结合零点存在性定理求解.【详解】（1）当12a =时，1()sin 22f x x x =--，1()cos 2f x x '=-，当ππ32x <≤时，()0f x '<；当π03x ≤≤时，()0f x '≥．所以()f x 在π0,3⎡⎤⎢⎥⎣⎦上单调递增，在ππ,32⎛⎤ ⎥⎝⎦上单调递减.（2）设()e sin cos 2x h x x x ax =++--，由题意知当0x ≥时，()0h x ≥．求导得()e cos sin x h x x x a '=+--．设()e cos sin x x x x a ϕ=+--，则()e sin cos x x x ϕ=--，令e 1x y x =--，则e 1x y '=-，当0,0,x y '>>当0,0,x y '<<故函数e 1x y x =--在()0,∞+单调递增，在(),0∞-单调递减，所以e 1x x ≥+；令()sin m x x x =-，可得()1cos 0m x x '=-≥，故()m x 在0x ≥单调递增时，sin x x ≥．所以当0x ≥时，()e sin cos 1cos 1cos 0x x x x x x x x ϕ'=--≥+--=-≥．故()ϕx 在[0,)+∞上单调递增，当0x ≥时，min ()(0)2x a ϕϕ==-，且当x →+∞时，()x ϕ→+∞．若2a ≤，则()()0h x x ϕ'=≥，函数()h x 在[0,)+∞上单调递增，因此[0,)x ∀∈+∞，()(0)0h x h ≥=，符合条件．若2a >，则存在0[0,)x ∈+∞，使得()00x ϕ=，即()00h x '=，当00x x <<时，()0h x '<，则()h x 在()00,x 上单调递减，此时()(0)0h x h <=，不符合条件．综上，实数a 的取值范围是(,2]-∞．【点睛】方法点睛：对于利用导数研究函数的综合问题的求解策略：1、通常要构造新函数，利用导数研究函数的单调性，求出最值，从而求出参数的取值范围；2、利用可分离变量，构造新函数，直接把问题转化为函数的最值问题．3、根据恒成立或有解求解参数的取值时，一般涉及分离参数法，但压轴试题中很少碰到分离参数后构造的新函数能直接求出最值点的情况，进行求解，若参变分离不易求解问题，就要考虑利用分类讨论法和放缩法，注意恒成立与存在性问题的区别．6．（22-23高二下·吉林白城·期末）已知函数()e xf x ax =+在()()0,0f 处的切线与直线l ：240x y -+=垂直．(1)求()f x 的单调区间；(2)若对任意实数x ，()232f x x b ≥--+恒成立，求整数b 的最大值．【答案】(1)单调递减区间为(),ln 3-∞，单调递增区间为()ln 3,+∞．(2)1【分析】（1）利用导数的几何意义得出3a =-，再利用导数判断单调区间即可；（2）分离参数将问题转化为2e 332x x b ++≥恒成立，利用导数求最值结合隐零点计算即可.【详解】（1）由()e xf x a '=+，得()01k f a '==+，又切线与直线l ：240x y -+=垂直，所以2k =-，即3a =-．所以()e 3xf x '=-，令()0f x '=，得ln3x =，当ln3x <时，()0f x '<，()f x 单调递减；当ln3x >时，()0f x ¢>，()f x 单调递增．所以()f x 的单调递减区间为(),ln 3-∞，单调递增区间为()ln 3,+∞．（2）对任意实数x ，()232f x x b ≥--+恒成立，即对任意实数2,e 332x x x x b +-+≥恒成立．设()2e 33x g x x x =+-+，即()min 12b g x ≤．()e 23x g x x =+-'，令()()e 23x h x g x x '==+-，所以()e 20'=+>xh x 恒成立，所以()e 23x g x x =+-'在R 上单调递增．又1202g ⎛⎫'=< ⎪⎝⎭，()1e 10g '=->，所以存在01,12x ⎛⎫∈ ⎪⎝⎭，使得()00g x '=，即00e 230xx +-=，所以00e 32xx =-．当()0,x x ∈-∞时，()00g x '<，()g x 单调递减；当()0,x x ∈+∞时，()00g x '>，()g x 单调递增．所以()()02000min e 33x g x g x x x ==+-+2220000005132335624x x x x x x ⎛⎫=-+-+=-+=-- ⎪⎝⎭，当01,12x ⎛⎫∈ ⎪⎝⎭时，200152564x x <-+<，所以()01151,28g x ⎛⎫∈ ⎪⎝⎭，由题意知()012b g x ≤且b ∈Z所以1b ≤，即整数b 的最大值为1．7．（22-23高二下·福建福州·期末）已知函数2()2ln f x a x x a =-+，R a ∈．(1)讨论函数()f x 的单调性；(2)证明:()*11112ln 1(2341)n n n +>++++∈+N ．【答案】(1)答案见解析(2)证明见解析【分析】（1）求得()222x af x x-+='，分0a ≤和0a >，两种情况讨论，结合导数的符号，进而求得函数()f x 的单调区间；（2）由（1），根据题意，得到()()max10f x f ==，即22ln 1x x ≤-，当n ∈*N 时，结合22ln 111n n n n ⎛⎫⎛⎫<- ⎪ ⎪++⎝⎭⎝⎭，2112ln 1n n n n --⎛⎫⎛⎫<- ⎪ ⎪⎝⎭⎝⎭，L ，2112ln 122⎛⎫⎛⎫<- ⎪ ⎪⎝⎭⎝⎭，将不等式累加后，即可求解.【详解】（1）解：由函数2()2ln f x a x x a =-+，可得()f x 的定义域为(0,)+∞，且()22222a x a f x x x x-='+=-若0a ≤，可得()0f x '<，()f x 在(0,)+∞上单调递减；若0a >，令()0f x '=，因为0x >，可得x =当(x ∈时，()0f x ¢>，()f x 单调递增；当)x ∈+∞时，()0f x '<，()f x 单调递减，综上可得：当0a ≤时，()f x 在(0,)+∞上单调递减；当0a >时，()f x的递增区间为(，递减区间为)+∞.（2）证明：由（1）知，当1a =时，()f x 的递增区间为()01,，递减区间为()1,+∞，所以()()max 10f x f ==，所以()0f x ≤，即22ln 1x x ≤-，当n ∈*N 时，可得：2222ln 111112ln 1112ln 122n n n n n n n n ⎧⎛⎫⎛⎫<-⎪ ⎪ ⎪++⎝⎭⎝⎭⎪⎪--⎛⎫⎛⎫⎪<-⎪ ⎪ ⎨⎝⎭⎝⎭⎪⎪⎪⎛⎫⎛⎫⎪<- ⎪ ⎪⎪⎝⎭⎝⎭⎩，将不等式累加后，可得222111112ln 11212n n n n n n n n n n n --⎛⎫⎛⎫⎛⎫⎛⎫<+++-<+++- ⎪ ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭⎝⎭ 1111111111212n n n n⎫=-+-++--=-++⎪+⎝⎭ ，即()11112ln 12341n n +>+++++ .8．（22-23高二下·吉林长春·期末）已知函数()ln x f x a x a=-，()e xg x ax a =-．（e 2.71828=⋅⋅⋅为自然对数的底数）(1)当1a =时，求函数()y f x =的极大值；(2)已知1x ，()20,x ∈+∞，且满足()()12f x g x >，求证：21e 2xx a a +>．【答案】(1)1-(2)证明见解析【分析】（1）运用导数研究()f x 的单调性，进而求得其最大值.（2）同构函数()ln h x x x =-，转化为()21e x x h h a ⎛⎫> ⎪⎝⎭，结合换元法2112,e xx t t a ==，分别讨论11t ≥与101t <<，当11t ≥时运用不等式性质即可证得结果，当101t <<时运用极值点偏移即可证得结果.【详解】（1）当1a =时，()ln f x x x =-，定义域为()0,∞+，则()111xf x x x-'=-=，()001f x x '>⇒<<，()01f x x '<⇒>，所以()f x 在()0,1上单调递增，在()1,+∞上单调递减，故()f x 的极大值为()11f =-；（2）由题意知，0a >，由()()12f x g x >可得2112ln e x x a x ax a a->-，所以2211lnln e e x x x x a a->-，令()ln h x x x =-，由（1）可知，()h x 在()0,1上单调递增，在()1,+∞上单调递减，则()21e xx h h a ⎛⎫> ⎪⎝⎭，令11x t a=，22e xt =，又1>0x ，20x >，所以10t >，21t >，则()()12h t h t >，①若11t ≥，则122t t +>，即21e 2x x a+>，所以21e 2x x a a +>；②若101t <<，设()31,t ∈+∞，且满足()()31h t h t =，如图所示，则()()()312h t h t h t =>，所以321t t <<，下证：312t t +>．令()()()()2ln ln 222F x h x h x x x x =--=---+，()0,1x ∈，则()()()221112022x F x x x x x -'=+-=>--，所以()()()2F x h x h x x =--在()0,1x ∈上单调递增，所以()()10F x f <=，所以()()()11120F t h t h t =--<，即()()112h t h t <-，又因为()()31h t h t =，所以()()312h t h t <-，3t ，()121,t -∈+∞，所以312t t >-，即312t t +>，又因为321t t <<，所以122t t +>，即21e 2xx a a +>．由①②可知，21e 2xx a a +>得证.【点睛】方法点睛：极值点偏移问题的一般题设形式：1.若函数()f x 存在两个零点12,x x 且12x x ≠，求证：1202x x x +>（0x 为函数()f x 的极值点）；2.若函数()f x 中存在12,x x 且12x x ≠满足2()()1f x f x =，求证：1202x x x +>（0x 为函数()f x 的极值点）；3.若函数()f x 存在两个零点12,x x 且12x x ≠，令1202x x x +=，求证：()00f x '>；4.若函数()f x 中存在12,x x 且12x x ≠满足2()()1f x f x =，令1202x x x +=，求证：()00f x '>.9．（22-23高二下·广西南宁·期末）已知函数()ln 1f x a x ax =-+（a ∈R ，且0a ≠）.(1)讨论a 的值，求函数()f x 的单调区间；(2)求证：当2n ≥时，1111ln 2ln 3ln n n n-+++> .【答案】(1)见解析(2)证明见解析【分析】（1）求出函数导数，分0,0a a ><分类讨论即可得解；（2）当1a =时利用函数单调性可得ln 1≤-x x ，放缩可得()110ln 1x x x >>-，根据裂项相消法求和即可得证.【详解】（1）由()ln 1f x a x ax =-+知函数定义域为(0,)+∞，()()1a x af x a x x-'=-=，①当0a >时，若01x <<，则()0f x '>，若1x >，()0f x '<，所以()f x 的单调递增区间为(0,1)，单调递减区间为(1,)+∞；②当a<0时，若01x <<，则()0f x '<，若1x >，()0f x '>，所以()f x 的单调递减区间为(0,1)，单调递增区间为(1,)+∞.（2）令1a =，则()ln 1f x x x =-+，所以(1)0f =，由（1）可知()f x 在[1,)+∞上单调递减，故()(1)0f x f ≤=，（当1x =时取等号)，所以()ln 10f x x x =-+≤，即ln 1≤-x x ，当2x ≥时，0ln 1(1)x x x x <<-<-，即0ln 1)(x x x <<-，即()110ln 1x x x >>-令x n =，则()1111ln 11n n n n n>=---，所以11111111111ln 2ln 3ln 1223341n n n +++>-+-+-++-- 111n n n-=-=，故当2n ≥时，1111ln 2ln 3ln n n n-+++> .【点睛】关键点点睛：1a =时，利用函数单调性得出ln 1≤-x x ，当2x ≥时，放缩得出0ln 1)(x x x <<-，变形得出()110ln 1x x x >>-是解题的关键，再由裂项相消法及不等式的性质即可得解.10．（22-23高二下·山东德州·期末）已知函数()1ln 2f x a x x x=--，a ∈R .(1)当1a =时，判断()f x 的零点个数；(2)若()1e 2e xf x x x+++≥恒成立，求实数a 的值.【答案】(1)()f x 的零点个数为0(2)a e=-【分析】（1）求导得函数的单调性，即可由单调性求解最值，进而可判断，（2）将问题转化为e ln e x a x +≥，构造函数()e ln x F x a x =+和()e xg x x a =+，()0,x ∈+∞，利用导数求解函数的单调性，分类讨论并结合零点存在性定理即可求解.【详解】（1）当1a =时，()()1ln 20f x x x x x=-->，则()()()2222222111121212x x x x x x f x x x x x x +--++--=+-==-=-'，当()0,1x ∈，()0f x ¢>，函数()f x 在()0,1上单调递增，当()1,x ∈+∞，()0f x '<，函数()f x 在()1,+∞上单调递减，所以()()max 11230f x f ==--=-<，所以()f x 的零点个数为0.（2）不等式()1e 2e xf x x x+++≥，即为e ln e x a x +≥，设()e ln xF x a x =+，()0,x ∈+∞，则()e e x x a x aF x x x+=+='，设()e xg x x a =+，()0,x ∈+∞，当0a ≥时，()0g x >，可得()0F x '>，则()F x 单调递增，此时当()1,1e,x F ==而当01x <<时，()e F x <，故不满足题意；当0a <时，由()()1e 0xg x x '=+>，()g x 单调递增，当x 无限趋近0时，()g x 无限趋近于负数a ，当x 无限趋近正无穷大时，()g x 无限趋近于正无穷大，故()0g x =有唯一的零点0x ，即00e 0xx a +=，则00e x ax =-，()00ln ln x x a +=-，当()00,x x ∈时，()0g x <，可得()0F x '<，()F x 单调递减；当()0,x x ∈+∞时，()0g x >，可得()0F x '>，()F x 单调递增，所以()()()0000min 0e ln ln x aF x F x a x a a x x ⎡⎤==+=-+--⎣⎦()()00001ln ln a a a ax a a a x x x ⎛⎫=---=--+ ⎪⎝⎭，因为00x >，可得0012x x +≥，当且仅当01x =时，等号成立，所以()()001ln ln 2a a a x a a ax ⎛⎫--+≥-- ⎪⎝⎭因为()e F x ≥恒成立，即()ln 2e a a a --≥恒成立，令()()ln 2h a a a a =--，(),0a ∈-∞，可得()()()ln 12ln 1h a a a =-='-+--，当(),e a ∈-∞-时，()0h a '>，()h a 单调递增；当()e,0a ∈-时，()0h a '<，()h a 单调递减，所以()()e e h a h ≤-=，即()e h a ≤又由()e h a ≥恒成立，则()()ln 2e h a a a a =--=，所以a e =-.【点睛】对于利用导数研究函数的综合问题的求解策略：1、通常要构造新函数，利用导数研究函数的单调性，求出最值，从而求出参数的取值范围；2、利用可分离变量，构造新函数，直接把问题转化为函数的最值问题．3、根据恒成立或有解求解参数的取值时，一般涉及分离参数法，但压轴试题中很少碰到分离参数后构造的新函数能直接求出最值点的情况，进行求解，若参变分离不易求解问题，就要考虑利用分类讨论法和放缩法，注意恒成立与存在性问题的区别．11．（22-23高二下·河北张家口·期末）已知函数()ln f x x x =.(1)求函数()f x 的单调区间和极值；(2)若方程()21f x x =-的两个解为1x 、2x ，求证：122e x x +>.【答案】(1)减区间为10,e ⎛⎫ ⎪⎝⎭，增区间为1,e ⎛⎫+∞ ⎪⎝⎭，极小值为11e e f ⎛⎫=- ⎪⎝⎭，无极大值；(2)证明见解析【分析】（1）求出函数()f x 的定义域与导数，利用函数的单调性、极值与导数的关系可得出结果；（2）设()()21h x f x x =-+，利用导数分析函数()h x 的单调性与极值，分析可知120e x x <<<，要证122e x x +>，即证()()112e h x h x >-，构造函数()()()2e p x h x h x =--，其中0e x <<，利用导数分析函数()p x 在()0,e 上的单调性，证明出()0p x >对任意的()0,e x ∈恒成立，即可证得结论成立.【详解】（1）解：函数()ln f x x x =的定义域为()0,∞+，且()ln 1f x x '=+，令()0f x '=可得1ex =，列表如下：x10,e ⎛⎫ ⎪⎝⎭1e1,e ⎛⎫+∞ ⎪⎝⎭()f x '-+()f x 减极小值增所以，函数()f x 的减区间为10,e ⎛⎫ ⎪⎝⎭，增区间为1,e ⎛⎫+∞ ⎪⎝⎭，极小值为11e e f ⎛⎫=- ⎪⎝⎭，无极大值.（2）解：设()()21ln 21h x f x x x x x =-+=-+，其中0x >，则()ln 1h x x '=-，令()0h x '<，可得0e x <<，此时，函数()h x 在()0,e 上单调递减，令()0h x '>，可得e x >，此时，函数()h x 在()e,+∞上单调递增，所以，e x =是函数()h x 的极小值点，因为函数()h x 有两个零点1x 、2x ，设12x x <，则120e x x <<<，即()()120h x h x ==且120e x x <<<，要证122e x x +>，即证21e 2e x x >->，因为函数()h x 在()e,+∞上单调递增，所以，只需证明：()()212e h x h x >-，即证()()112e h x h x >-，令()()()()()2e ln 2e ln 2e 44e p x h x h x x x x x x =--=----+，其中0e x <<，则()()()2ln ln 2e 2ln 2e 2p x x x x x '=+--=--，因为0e x <<，则()()22222e e e 0,e x x x -=--+∈，所以，()()22ln 2e 2ln e 20p x x x '=--<-=，故函数()p x 在()0,e 上为减函数，又因为()e 0p =，所以，()0p x >对任意的()0,e x ∈恒成立，则()()()1112e 0p x h x h x =-->，即()()112e h x h x >-，故122e x x <+成立.【点睛】方法点睛：证明极值点偏移的相关问题，一般有以下几种方法：（1）证明122x x a +<（或122x x a +>）：①首先构造函数()()()2g x f x f a x =--，求导，确定函数()y f x =和函数()y g x =的单调性；②确定两个零点12x a x <<，且()()2f x f x =，由函数值()1g x 与()g a 的大小关系，得()()()()()1112122g x f x f a x f x f a x =--=--与零进行大小比较；③再由函数()y f x =在区间(),a +∞上的单调性得到2x 与12a x -的大小，从而证明相应问题；（2）证明212x x a <（或212x x a >）（1x 、2x 都为正数）：①首先构造函数()()2a g x f x f x ⎛⎫=- ⎪⎝⎭，求导，确定函数()y f x =和函数()y g x =的单调性；②确定两个零点12x a x <<，且()()12f x f x =，由函数值()1g x 与()g a 的大小关系，得()()()2211211a a g x f x f f x f x x ⎛⎫⎛⎫=-=-⎪ ⎪⎝⎭⎝⎭与零进行大小比较；③再由函数()y f x =在区间(),a +∞上的单调性得到2x 与21a x 的大小，从而证明相应问题；（3121212ln ln 2x x x xx x -+<<-证明极值点偏移：①由题中等式中产生对数；②将所得含对数的等式进行变形得到1212ln ln x x x x --；③利用对数平均不等式来证明相应的问题.12．（22-23高二下·湖南·期末）已知函数()()2e 3xf x a x a =-+∈R .(1)若方程()0f x =有3个零点，求实数a 的取值范围；(2)若()()224x x x f x ϕ=-++-有两个零点()1212,x x x x <，求证：0ea <<2121e e x x x x --<+.【答案】(1)36(0,e(2)证明见解析【分析】（1）将问题转化为y a =与()23e xx g x -=有三个不同的交点，利用导数研究函数()g x 的性质，从而结合图象即可求得实数a 的范围；（2）利用导数求得函数()x ϕ的单调性，再利用零点存在定理证得0a <2121221e 1ex x x x x x ++-<+，构造函数()e 2e 1t h t t =--，利用导数证得()()00H t H >=即可得证.【详解】（1）解：令()0f x =，即得2e 30xa x -+=，即23ex x a -=方程有三个零点，即直线y a =与曲线()23ex x g x -=有三个不同的交点，可得()()()22132323e e e x x xx x x x x x g x +--+--==-=-'，所以当(),1x ∈-∞-或()3,x ∈+∞时，()0g x '<，()g x 单调递减；当()1,3x ∈-时，()0g x '>，()g x 单调递增，所以当=1x -时，()g x 有极小值为()2e g x =-，当3x =时，()g x 有极大值为()36e g x =，当x →+∞时，()0g x →，且当x ≥()0g x >，所以作出函数()23e xx g x -=的图象如图所示，所以数形结合可知360e a <<，即实数a 的取值范围为36(0,)e.（2）解：因为()()22421e xx x x f x x a ϕ=-++-=+-，当0a ≤时，()x ϕ单调递增，不可能有两个零点，所以0a >，此时()2e xx a ϕ=-'，令()0x ϕ'=，得2lnx a =，所以当2,ln x a ⎛⎫∈-∞ ⎪⎝⎭时，()0x ϕ'>；当2ln ,x a ∞⎛⎫∈+ ⎪⎝⎭时，()0x ϕ'<，故()x ϕ在区间2,ln a ∞⎛⎫- ⎪⎝⎭上单调递增，在区间2ln ,a ∞⎛⎫+ ⎪⎝⎭上单调递减，所以222ln 2ln 122ln 1a a a ϕ⎛⎫=+-=- ⎪⎝⎭，若()x ϕ有两个零点，则2ln 0a ϕ⎛⎫> ⎪⎝⎭21ln 2a >，所以0ea <<，当0a <<时，2ln 0a ϕ⎛⎫> ⎪⎝⎭，121e 02a ϕ-⎛⎫-=-< ⎪⎝⎭，211ln 22a >>-，故存在112,ln 2x a ⎛⎫∈- ⎪⎝⎭，使得()10f x =，又当x 趋向于+∞时，()x ϕ趋向于-∞，故存在22ln ,x a ⎛⎫∈+∞ ⎪⎝⎭，使得()20f x =，故0a <<，则满足121221e 21ex x x a x a ⎧+=⎨+=⎩，可得212121e 21x x x x -+=+212e x x -=，2121e e x x x x --<+，只需证2121221e e e x x x x x x ---<+，两边同乘以1e x ，可得2121221e 1ex x x x x x ++-<+，因为112x >-，221ln 2x a >>，所以120x x +>，令1202x x t +=>，即证2e 1e 2t tt-<，即证2e 2e 10t t t -->，令()2e 2e 1(0)t t h t t t =-->，可得()()()22e 21e 2e e 1t t t th t t t =-+=--'，令()()e 10t H t t t =-->，()e 10tH t =->'，故()H t 在区间()0,∞+上单调递增，故()()00H t H >=，因此()0h t '>，所以()h t 在区间()0,∞+上单调递增，故()()00h t h >=，因此原不等式成立.【点睛】方法技巧：对于利用导数研究不等式的恒成立与有解问题的求解策略：1、通常要构造新函数，利用导数研究函数的单调性，求出最值，从而求出参数的取值范围；2、利用可分离变量，构造新函数，直接把问题转化为函数的最值问题．3、根据恒成立或有解求解参数的取值时，一般涉及分离参数法，但压轴试题中很少碰到分离参数后构造的新函数能直接求出最值点的情况，进行求解，若参变分离不易求解问题，就要考虑利用分类讨论法和放缩法，注意恒成立与存在性问题的区别．13．（22-23高二下·湖南长沙·期末）已知函数2()ln f x x x x =-+．(1)证明()0f x ≤；(2)关于x 的不等式222ln 0ee x axx xx ax x -+-+≤恒成立，求实数a 的取值范围．【答案】(1)证明见解析(2)[1,)+∞【分析】（1）根据题意，求得并化简得到(21)(1)()x x f x x+-'=-，得出函数()f x 的单调区间，结合()()1≤f x f ，即可可证；（2）根据题意把不等式转化为22ln 2ln e 2ln e ln x ax x x x ax x x --+≤-+-，根据()e x g x x =+为增函数，转化为2ln x x a x +≥恒成立，令2ln ()x x h x x +=，求得312ln ()x xh x x --'=，得出函数()h x 的单调区间和最大值(1)1h =，即可求解.【详解】（1）由函数2()ln f x x x x =-+，可得1(21)(1)()21x x f x x x x'+-=-+=-，令()0f x '>，可得01x <<；令()0f x '<，可得1x >，所以()f x 在区间()0,1上单调递增，在区间(1,)+∞上单调递减，所以()()10f x f ≤=，即()0f x ≤．（2）由不等式222ln 0e ex axx x x ax x -+-+≤，可得22ln 2ln e 2ln e ln x ax x x x ax x x --+≤-+-，因为()e x g x x =+为增函数，则22ln ln x ax x x ≤--，即2ln x xa x +≥在(0,)+∞恒成立，令2ln ()x x h x x +=，可得312ln ()x xh x x --'=，再令()12ln m x x x =--，可得()210m x x'=--<，所以()m x 单调递减，又因为()10m =，所以当()0,1x ∈时，()0m x >，()0h x '>，函数()h x 在()0,1上单调递增；当()1,x ∈+∞时，()0m x <，()0h x '<，函数()h x 在()1,+∞上单调递减，即()h x 在区间()0,1上单调递增，在区间(1,)+∞上单调递减，所以()h x 最大值为(1)1h =，所以实数a 的取值范围为[1,)+∞．【点睛】方法点睛：对于利用导数研究不等式的恒成立与有解问题的求解策略：1、通常要构造新函数，利用导数研究函数的单调性，求出最值，从而求出参数的取值范围；2、利用可分离变量，构造新函数，直接把问题转化为函数的最值问题；3、根据恒成立或有解求解参数的取值时，一般涉及分离参数法，但压轴试题中很少碰到分离参数后构造的新函数能直接求出最值点的情况，进行求解，若参变分离不易求解问题，就要考虑利用分类讨论法和放缩法，注意恒成立与存在性问题的区别．14．（22-23高二下·福建莆田·期末）已知函数()2ln f x ax x =--，其中a ∈R .(1)讨论()f x 的单调性；(2)若()f x 有两个零点1x ，2x ，且213x x ≥，求12x x 的最小值.【答案】(1)答案见解析(2)49e 【分析】（1）求出函数的导函数，再分0a ≤、0a >两种情况讨论，分别求出函数的单调性；（2）依题意可得11222ln 02ln 0ax x ax x --=⎧⎨--=⎩，即可得到12121212ln ln ln ln 4x x x x a x x x x -++==-+，从而得到()121121221ln 4ln 1x x x x x x x x ++=-，令12x t x =，10,3t ⎛⎤∈ ⎥⎝⎦，令()1ln 1t g t t t +=-，10,3t ⎛⎤∈ ⎥⎝⎦，利用导数求出()g t 的最小值，即可求出12x x 的最小值.【详解】（1）()2ln f x ax x =--定义域为()0,∞+，且()11ax f x a x x-'=-=，当0a ≤时，()0f x '<恒成立，所以()f x 在()0,∞+上单调递减；当0a >时，令()0f x '=得1x a=，当10,x a ⎛⎫∈ ⎪⎝⎭时，()0f x '<；当1,x a ⎛⎫∈+∞ ⎪⎝⎭时，()0f x ¢>，所以()f x 在10,a ⎛⎫ ⎪⎝⎭上单调递减，在1,a ⎛⎫+∞ ⎪⎝⎭上单调递增.综上可得：当0a ≤时()f x 在()0,∞+上单调递减；当0a >时()f x 在10,a ⎛⎫ ⎪⎝⎭上单调递减，在1,a ⎛⎫+∞ ⎪⎝⎭上单调递增.（2）因为()()120f x f x ==，所以11222ln 02ln 0ax x ax x --=⎧⎨--=⎩，所以()1212ln ln a x x x x -=-，()1212ln ln 4a x x x +=++，所以12121212ln ln ln ln 4x x x x a x x x x -++==-+，所以()112121121122221ln 4ln ln 1x x x x x xx x x x x x x x +++==--，令12xt x =，因为213x x ≥，所以1213x x ≤，即103t <≤，所以()121ln 4ln 1t x x t t ++=-，10,3t ⎛⎤∈ ⎥⎝⎦，令()1ln 1t g t t t +=-，10,3t ⎛⎤∈ ⎝⎦，则()()()()()2211ln 11ln 2ln 11t t t t t t tt t g t t t +⎛⎫+--+-- ⎪⎝⎭'==--，令()12ln h t t t t=--，()0,1t ∈，则()()22211210t h t t t t-=+-=>'，所以()h t 在()0,1上单调递增，又()10h =，所以()0h t <，即()0g t '<，所以()g t 在10,3⎛⎤⎥⎝⎦上单调递减，所以()12ln 33g t g ⎛⎫≥= ⎪⎝⎭，所以()12ln 42ln 3x x +≥，即2ln 3412e x x -≥，即1249e x x ≥，当且仅当2112439e x x x x =⎧⎪⎨=⎪⎩，即1223e x x ==时等号成立，所以12x x 的最小值为49e .【点睛】方法点睛：导函数中常用的两种常用的转化方法：一是利用导数研究含参函数的单调性，常化为不等式恒成立问题．注意分类讨论与数形结合思想的应用；二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理．15．（22-23高二下·贵州黔东南·期末）已知函数()ln ,R f x ax x a =-∈.(1)讨论函数()f x 的单调性；(2)当1a =时，设()()()21x g x f x -=，求证：函数()g x 存在极大值点0x ，且()0222e 3g x <<.【答案】(1)答案见解析(2)证明见解析【分析】（1）求出函数的导数，分类讨论，判断导数正负，即可判断函数单调性；（2）求出函数()()()21x g x f x -=的导数，由此构造函数，利用导数判断其单调性，确定函数()g x 的极值点0x ，并判断其范围，进而化简()0g x 的表达式，即可证明结论.【详解】（1）由函数()ln ,R f x ax x a =-∈的定义域为(0,)+∞，则()11ax f x a x x-'=-=，当0a ≤时，()0f x '<，()f x 在(0,)+∞上单调递减；当0a >时，当10x a<<时，()0f x '<，则()f x 在1(0,a 上单调递减；当1x a>时，()0f x ¢>，则()f x 在1(,)a +∞上单调递增；故当0a ≤时，()f x 在(0,)+∞上单调递减；当0a >时，()f x 在1(0,a上单调递减，在1(,)a +∞上单调递增；（2）当1a =时，由（1）可知()ln f x x x =-，()f x 在(0,1)上单调递减，在(1,)+∞上单调递增，故()(1)1f x f ≥=；故当1a =时，()()()()2211ln x x g x f x x x--==-，则()()()()2221121(ln )1(1)1(2ln 2)(ln )(ln )x x x x x x x x x g x x x x x -------+-'==--，令1()2ln 2,(0)h x x x x x =-+->，则222222121(1)()10x x x h x x x x x -+-'=-+==≥，仅当1x =时等号成立，故1()2ln 2h x x x x=-+-在(0,)+∞上单调递增，且2211()2ln 310,(e )6e 033h h -=+->=-<，即存在唯一201(e ,3x -∈，使得0()0h x =，当00x x <<时，()0h x <；当01x x <<时，()0h x >；则当00x x <<时，()0g x '>；当01x x <<时，()0g x '<，当1x >时，()0g x '>，即()g x 在0(0,)x 单调递增，在0(),1x 单调递减，在(1,)+∞单调递增，故函数()g x 存在极大值点，即为0x ；由0()0h x =，即00012ln 20x x x -+-=，故()()()()()()222200000020000000111211111ln 1(2)1222x x x x x g x x x x x x x x x ----====---+--+，由于201(e ,)3x -∈，故()002g x x =，且2022(2e ,3x -∈，即()0222e 3g x <<.【点睛】难点点睛：本题考查了导数的综合应用问题，涉及到判断函数的单调性以及函数极值问题，解答的难点在于第二问证明不等式()0222e 3g x <<，解答时要注意零点问题的解决，并判断零点201(e ,)3x -∈.16．（22-23高二下·江苏镇江·期末）已知函数()3f x x ax =-.(1)当1a =-时，求函数在点()()1,1f 处的切线方程；(2)若函数()f x 存在不同的极值点12,x x ，且以()()()()1122,,,A x f x C x f x 为对角线的正方形ABCD 的四顶点A B C D ､､､都在函数()y f x =的图像上，求2a 的值.【答案】(1)420x y --=(2)2278a +=【分析】（1）把1a =-代入函数解析式，可求切点坐标，利用导数求切线斜率，可求函数在点()()1,1f 处的切线方程；（2）利用导数求出极值点，得,A C 两点坐标，由AC 的中点为原点O ，ABCD 为正方形，可求D 点坐标，代入在函数()f x 中，可求出2a 的值.【详解】（1）当1a =-时，()3f x x x +，()12f =，故切点坐标为()1,2，()231f x x ='+，故切点处切线的斜率为()14f '=，切线方程为()241y x -=-，即420x y --=.（2）函数()3f x x ax =-，定义域为R ，()23f x x a '=-，()f x 存在不同的极值点12,x x ，则有0a >，()0f x ¢>，解得x <x >；()0f x '<，解得x <则()f x 在,⎛-∞ ⎝⎭和⎫+∞⎪⎪⎝⎭上单调递增，在⎛ ⎝⎭上单调递减，得x =x则有2,23,,939A a C ⎛⎛- ⎪ ⎪ - ⎪⎝⎭⎝⎭，AC 的中点为原点O ，正方形ABCD ，过C 作CC '垂直于x 轴，过D 作DD '垂直于y 轴，垂足分别为,C D ''，则有OCC ODD ''≅ ，所以D ⎫⎪⎪⎝⎭，D 点在函数()y f x =的图像上，则有f ⎝⎭即322993a ⎛⎛-= ⎝⎭⎝⎭，化简得42854810a a --=，解得2278a +=.【点睛】方法点睛：导数是研究函数的单调性、极值()最有效的工具，而函数是高中数学中重要的知识点，所以在历届高考中，对导数的应用的考查都非常突出，从高考来看，对导数的应用的考查主要从以下几个角度进行：(1)考查导数的几何意义，往往与解析几何、微积分相联系．(2)利用导数求函数的单调区间，判断单调性；已知单调性，求参数．(3)利用导数求函数的最值(极值)，解决生活中的优化问题．(4)考查数形结合思想的应用．17．（22-23高二下·辽宁大连·期末）已知函数()()2cos ln 11f x x x =++-．(1)判断函数()f x 在区间π0,2⎛⎫⎪⎝⎭上零点和极值点的个数，并给出证明；(2)若0x ≥时，不等式()1f x ax <+恒成立，求实数a 的取值范围．【答案】(1)函数()f x 在区间π0,2⎛⎫⎪⎝⎭上只有一个极值点和一个零点，证明见解析(2)实数a 的取值范围是[)1,+∞【分析】（1）首先求函数的导数，并利用二阶导数判断导数的单调性，并结合零点存在性定理证明极值点个数，并结合函数单调性，以及端点值判断函数零点个数；（2）首先由不等式构造函数()()2cos ln 12g x x x ax =++--，()0x >，并求函数的导数，根据()00g =，以及()01g a '=-，分1a ≥，01a ≤<，a<0三种情况讨论不等式恒成立的条件.【详解】（1）函数()f x 在区间π0,2⎛⎫⎪⎝⎭上只有一个极值点和一个零点，证明如下，()12sin 1f x x x '=-++，设()()12sin 1t x f x x x '==-++，()()212cos 1t x x x '=--+，当π0,2x ⎛⎫∈ ⎪⎝⎭时，()0t x '<，所以()f x '单调递减，又()010f '=>，π12220π2π212f ⎛⎫'=-+=-+< ⎪+⎝⎭+，所以存在唯一的π0,2α⎛⎫∈ ⎪⎝⎭，使得()0f α'=，所以当()0,x α∈时，()0f x ¢>，当π,2x α⎛⎫∈ ⎪⎝⎭时，()0f x '<，所以()f x 在()0,α单调递增，在π,2α⎛⎫⎪⎝⎭单调递减，所以α是()f x 的一个极大值点，因为()02110f =-=>，()()0f f α>>，ππln 11022f ⎛⎫⎛⎫=+-< ⎪ ⎪⎝⎭⎝⎭，所以()f x 在()0,α无零点，在π,2α⎛⎫⎪⎝⎭上有唯一零点，所以函数()f x 在区间π0,2⎛⎫⎪⎝⎭上只有一个极值点和一个零点；（2）由()1f x ax ≤+，得()2cos ln 120x x ax ++--≤，令()()2cos ln 12g x x x ax =++--，()0x >，则()00g =，()12sin 1g x x a x'=-+-+，()01g a '=-，①若1a ≥，则1a -≤-，当0x ≥时，ax x -≤-，令()()ln 1h x x x =+-，则()1111x h x x x -'=-=++，当0x ≥时，()0h x '≤，所以()h x 在[)0,∞+上单调递减，又()00h =，所以()()0h x h ≤，所以()ln 10x x +-≤，即()ln 1xx ≤+又cos 1≤x ，所以()220g x x x ≤+--=，即当0x ≥时，()1f x ax ≤+恒成立，②若01a ≤<，因为当π0,2x ⎛⎫∈ ⎪⎝⎭时，()g x '单调递减，且()010a g =->'，π120π212g a ⎛⎫'=-+-< ⎪⎝⎭+，所以存在唯一的π0,2β⎛⎫∈ ⎪⎝⎭，使得()0g β'=，当()0,x ∈β时，()0g x '>，()g x 在()0,β上单调递增，不满足()0g x ≤恒成立，③若a<0，因为()()()()()()444444e 12cos e 1ln e e 1222cos e 1e 10g a a -=-+---=---->不满足()0g x ≤恒成立，综上所述，实数a 的取值范围是[)1,+∞.【点睛】关键点点睛：本题考查利用导数解决函数零点，不等式恒成立问题，本题第一问需要求函数的二阶导数，利用二阶导数分析一阶导数的单调性，结合零点存在性定理判断零点问题，第二问的关键是()00g =这个条件，再根据()01g a '=-，讨论a 的取值.18．（22-23高二下·福建龙岩·期末）已知函数()ln f x ax x =-．(1)讨论()f x 的单调性；(2)已知()()g x xf x b =+，且12,x x 是()g x 的两个零点，12x x <，证明：()()211211x ax b x ax -<<-．【答案】(1)答案见解析(2)证明见解析【分析】（1）求导后分0a ≤与0a >两种情况讨论即可；（2）根据12,x x 是()g x 的两个零点可得()12211221ln ln x x x x b ax x x x -=--，再将所证不等式转化为1222111ln 1x x x x x x -<<-，进而令211xt x =>，再构造函数求导分析单调性证明即可.【详解】（1）()11(0)ax f x a x x x-='-=>，①若0a ≤，则()0f x '<，即()f x 在()0,∞+单调递减，②若0a >，令()0f x ¢>，有1x a >，令()0f x '<，有10x a <<，即()f x 在10,a ⎛⎫ ⎪⎝⎭单调递减，在1,a ⎛⎫+∞ ⎪⎝⎭单调递增，综上：0a ≤，()f x 在()0,∞+单调递减，若0a >，()f x 在10,a ⎛⎫ ⎪⎝⎭单调递减，在1,a ⎛⎫+∞ ⎪⎝⎭单调递增．（2）()()2ln ln g x x ax x b ax x x b =-+=-+，令()0g x =得：2ln 0ax x x b -+=，因为0x >，ln 0bax x x -+=，因为12,x x 是()g x 的两个零点，所以，112212ln 0,ln 0b bax x ax x x x -+=-+=，所以()12211211ln ln 0a x x x x b x x ⎛⎫-+-+-= ⎪⎝⎭，()12211221ln ln x x x x b ax x x x -=--，要证明()()211211x ax b x ax -<<-，只需证122121ax x x b ax x x -<<-，即证明21212121ln ln x x x x x x x x --<-<--变形为1222111ln 1x x x x x x -<<-，令211xt x =>，则证明11ln 1t t t-<<-，设()()1ln 11h t t t t ⎛⎫=--> ⎪⎝⎭，()210t h t t -'=>，()h t 在()1,+∞单调递增，所以()()10h t h >=，即1ln 1t t>-，设()()ln 1u t t t =--，()10tu t t-'=<，()u t 在()1,+∞单调递减，所以，()()10u t u <=，即，ln 1t t <-，综上：()()211211x ax b x ax -<<-．19．（22-23高二下·安徽阜阳·期末）已知函数()21ln e 2f x x x x x =+-.(1)讨论()f x 的单调性；(2)令()()()212e 12eg x f x x a x =++++，若不等式()0g x ≥恒成立，求a 的最小值.【答案】(1)答案见解析(2)2-【分析】（1）求得()ln e f x x x =+'，令()()h x f x ='，得到()0h x '>，结合10e f '⎛⎫= ⎪⎝⎭，进而求得函数()f x 的单调区间；（2）求得()ln 12e g x x x a =+++'，令()()x g x ϕ'=，求得()0x ϕ'>，得到()g x '在()0,x ∈+∞上单调递增，结合()()2e0a g -+'<，()e 0a g -'>，得出存在()()20e ,e aa x -+-∈，使得()000ln 12e 0g x x x a '=+++=，进而得出函数的单调性，结合不等式()0g x ≥恒成立等价于()min 0()0g x g x =≥，得到010ex <≤，得到00ln 2e 12a x x -=++≤，即可求解.【详解】（1）解：函数()21ln e 2f x x x x x =+-的定义域为()0,∞+，可得()ln e f x x x =+'，令()()h x f x ='，则()1e 0h x x=+>'，所以()h x 单调递增，即()f x '单调递增.又因为1110e f ⎛⎫=-+= ⎪⎝⎭'，所以当10,e ⎛⎫∈ ⎪⎝⎭x 时，()0f x '<，当1,e x ⎛⎫∈+∞ ⎪⎝⎭时，()0f x ¢>，所以函数()f x 的单调递减区间为10,e ⎛⎫⎪⎝⎭，单调递增区间1,e ∞⎡⎫+⎪⎢⎣⎭.（2）解：由题意知()22ln e eg x x x x ax =+++，可得()ln 12e g x x x a =+++'，令()()x g x ϕ'=，可得()12e 0x xϕ+'=>，所以()x ϕ在()0,x ∈+∞上单调递增，即()g x '在()0,x ∈+∞上单调递增，又由()()()()2222e e212e e 10ea aa g a a -+-++=-+++⋅+≤-+<'，()e 12e e 0a a g a a --=-++⋅+>'，。

高二数学-选修2-2-导数及其应用测试卷-(含答案)

高二数学-选修2-2-导数及其应用测试卷-(含答案)高二数学导数及其应用测试题 (含答案)一、选择题(本大题共12小题，每小题5分，共60分每小题5分，共60分).1.若对任意x ，有f ′(x )＝4x 3，f (1)＝－1，则此函数为( B )A ．f (x )＝x 4B ．f (x )＝x 4－2C ．f (x )＝x 4＋1D ．f (x )＝x 4＋2 2.设函数()xf x xe =,则（ D ）A ．1x =为()f x 的极大值点B ．1x =为()f x 的极小值点C ．1x =-为()f x 的极大值点D ．1x =-为()f x 的极小值点解析:()(1)xf x x e '=+,令()0,f x '=得1x =-,1x <-时,()0f x '<,()xf x xe =为减函数;1x >-时,()0f x '>,()xf x xe =为增函数,所以1x =-为()f x 的极小值点,选D. 3．函数y ＝(3－x 2)e x 的单调递增区是（ D ）A.(－∞,0)B. (0,＋∞)C. (－∞,－3)和(1,＋∞)D. (－3,1) 解析：2222(3)(23)023031x x x y xe x e e x x x x x '=-+-=--+>⇒+-<⇒-<<∴函数y ＝(3－x 2)e x 的单调递增区是(－3,1)4.设a >0,b >0. （ A ）A ．若2223ab a b +=+,则a >bB ．若2223a b a b+=+,则a <bC ．若2223aba b -=-,则a >bD．若2223a b a b-=-,则a <b【解析】若2223aba b +=+,必有2222aba b +>+.构造函数:()22x f x x=+,则()2ln 220x f x '=⋅+>恒成立,故有函数()22x f x x=+在x >0上单调递增,即a >b 成立.5.已知函数aa bx ax xx f 7)(223--++=在1=x 处取得极大值10，则ba 的值为（ A ） A.32- B.2- C.2-或32- D. 不存在【解析】由题2'()32f x x ax b=++，则23201710a b a b a a ++=⎧⎨++--=⎩，解得21a b =-⎧⎨=⎩，或69a b =-⎧⎨=⎩，经检验69a b =-⎧⎨=⎩满足题意，故23a b =-，选A 。

高二数学导数的综合运用试题答案及解析

高二数学导数的综合运用试题答案及解析1.已知函数f（x）=alnx﹣ax﹣3（a＜0）．（1）求函数f（x）的单调区间；（2）若函数y=f（x）的图象在点（2，f（2））处的切线的倾斜角为45°，对于任意的t∈[0，1]，函数g（x）=x3+x2[f′（x）+m]在区间（t，2）上总不是单调函数，其中f′（x）为f（x）的导函数，求实数m的取值范围．【答案】（1）的单调递增区间为（1，＋∞），单调递减区间为（0,1]；（2）．【解析】解题思路：（1）求导，利用导数的正负确定函数的单调区间；（2）求导，利用零点存在定理判定在总存在零点.规律总结：利用导数研究函数的单调性、极值、最值及与函数有关的综合题，都体现了导数的重要性；此类问题往往从求导入手，思路清晰；但综合性较强，需学生有较高的逻辑思维和运算能力.试题解析：（1）根据题意知，，当时，的单调递增区间为（1，＋∞），单调递减区间为（0,1]．（2）∵，∴，∴.∴，∴.∵在区间上总不是单调函数，且，∴由题意知：对于任意的，恒成立，∴∴.【考点】1.函数的单调性；2.函数的单调性的逆用.2.已知函数．（Ⅰ）当时，求在区间上的最值；（Ⅱ）讨论函数的单调性.【答案】(1)(2)当时，在单调递增当时，在单调递增，在上单调递减．当时，在单调递减；【解析】(1)利用函数的单调性与导数的关系；(2)解决类似的问题时，注意区分函数的最值和极值.求函数的最值时，要先求函数在区间内使的点，再计算函数在区间内所有使的点和区间端点处的函数值，最后比较即得;(4)若可导函数在指定的区间上单调递增（减），求参数问题，可转化为恒成立，从而构建不等式，要注意“=”是否可以取到.试题解析：解：（Ⅰ）当时，，∴．∵的定义域为，∴由得．∴在区间上的最值只可能在取到，而，∴．（Ⅱ）．①当，即时，在单调递减；②当时，在单调递增；③当时，由得或（舍去）∴在单调递增，在上单调递减；综上，当时，在单调递增；当时，在单调递增，在上单调递减．当时，在单调递减；【考点】(1)利用导数求函数的最值；（2）利用导数求函数的单调区间.3.设f(x)＝2x3＋ax2＋bx＋1的导数为f′(x)，若函数y＝f′(x)的图象关于直线x＝－对称，且f′(1)＝0.（1）求实数a，b的值；（2）求函数f(x)的极值．【答案】（1）a＝3. b＝－12.（2）函数f(x)在x1＝－2处取得极大值f(－2)＝21，在x2＝1处取得极小值f(1)＝－6.【解析】（1）先求出的导函数f′(x)=，由函数y＝f′(x)的图象关于直线x＝－对称及二次函数的性质求出，再由f′(1)＝0求出；（2）将（1）中的值代入导函数中，利用导函数研究函数的单调性，根据单调性及极值的有关知识求出的极值.试题解析：（1）由题知f′(x)= ，由函数y＝f′(x)的图象关于直线x＝－对称得，，解得a＝3，由f′(1)＝0即解得b＝－12. 所以a＝3. b＝－12. 6分（2）由（1）知a＝3， b＝－12，所以f′(x)= =，当＜-2或＞1时，＞0，当-2＜＜1时，＜0，所以单调增区间为（-，-2），（1，+），单调减区间为（-2,1），所以函数f(x)在x1＝－2处取得极大值f(－2)＝21，在x2＝1处取得极小值f(1)＝－6. 12分考点:常见函数的导数，导数的运算法则，二次函数的对称性，函数的极值4.已知函数（，为常数），当时，函数有极值，若函数有且只有三个零点，则实数的取值范围是．【解析】∵=，由当时函数有极值知，，解得，所以=，所以当或时，＞0，当时，＜0，则在（-，0）和（1，+）上是增函数，在（0,1）上是减函数，所以当=0时，取极大值=，当=1时，取极小值=，要使有三个零点，则，解得0＜＜，所以的取值范围为（0，）.【考点】常见函数的导数，导数的综合运用，函数零点，数形结合思想5.已知函数（为常数）的图像与轴交于点，曲线在点处的切线斜率为-1.（1）求的值及函数的极值；（2）证明：当时，；（3）证明：对任意给定的正数，总存在，使得当，恒有.【答案】（1），极小值为无极大值；（2）证明见解析；（3）证明见解析．【解析】解题思路：（1）利用导数的几何意义求，再进一步求极值；（2）构造函数，即证；（3）结合（2）的结论，对进行分类讨论.规律总结：这是一道典型的导函数问题，综合性较强，要求我们要有牢固的基础知识（包括函数的性质、常见解题方法、数形结合等）.试题解析：解法一：（1）由，得.又,得.所以.令,得.当时, 单调递减;当时, 单调递增.所以当时, 取得极小值,且极小值为无极大值.（2）令,则.由（1）得,故在R上单调递增,又,因此,当时, ,即.（3）①若,则.又由（2）知，当时, .所以当时, .取,当时，恒有.②若,令,要使不等式成立，只要成立.而要使成立，则只要,只要成立.令,则.所以当时,在内单调递增.取,所以在内单调递增.又.易知.所以.即存在,当时，恒有.综上，对任意给定的正数c，总存在,当时,恒有.解法二：（1）同解法一（2）同解法一（3）对任意给定的正数c，取由（2）知，当x>0时，，所以当时，因此，对任意给定的正数c，总存在,当时,恒有.【考点】1.导数的几何意义；2.导数在研究函数中的应用.6.设函数在定义域内可导,的图象如下右图所示,则导函数可能为( )【答案】D【解析】本题考查函数图象与导函数的关系：函数图象上升，则的图象在轴上方，反之亦然；函数图象下降，则的图象在轴下方.经验证D符合条件.【考点】函数图象与导函数图象的关系.7.已知函数的图象为曲线E．(1)若a = 3，b = -9，求函数f(x)的极值；(2)若曲线E上存在点P，使曲线E在P点处的切线与x轴平行，求a，b的关系．【答案】（1），；（2）.【解析】（1）欲求函数极值应先求函数导数，并求出的根，再判断在根左右导数是否异号，若成立则此根为极值点，代入函数解析式可求极值.（2）对于存在性问题，一般假设存在然后依条件求出，若有则有，若无则假设不成立.试题解析：(1)当时，.令，可得.+0-0+当时，，当时， 5分，设切点为，则曲线在点P的切线的斜率由题意知有解∴即． 10分【考点】（1）函数导数与极值；（2）函数导数与切线.8.定义在上的函数，是它的导函数，且恒有成立，则（）A．B．C．D．【答案】D【解析】由于，又因为，从而有：；构造函数则，从而有在上是增函数，所以有即：，故选Ｄ．【考点】函数的导数．9.已知函数：f(x)＝x3＋ax2＋bx＋c，过曲线y＝f(x)上的点P(1，f(1))的切线方程为y＝3x＋1(1)y＝f(x)在x＝－2时有极值，求f(x)的表达式；(2)函数y＝f(x)在区间[－2,1]上单调递增，求b的取值范围．【答案】(1) f(x)＝x3＋2x2－4x＋5; (2) b≥0【解析】(1)先由函数导数的几何意义用含a,b,c的代数式表达出函数在点P处的切线方程，再与已知的切线相比较可得关于a,b,c的两个方程；另又因为y＝f(x)在x＝－2时有极值，所以f′(－2)＝0再得到一个关于a,b,c的方程，三个字母三个方程，通过解方程组就可求得字母a,b,c的值，从而求得f(x)的表达式； (2) 由函数y＝f(x)在区间[－2,1]上单调递增，知其导函数f′(x)在[－2,1]上恒有f′(x)≥0，注意到(1)中的①式:2a+b=0,所以有，从而有3x2－bx＋b≥0在[－2,1]上恒成立，分离参数转化为函数的最值问题，可求得b的取值范围.试题解析：(1)由f(x)＝x3＋ax2＋bx＋c,求导数得f′(x)＝3x2＋2ax＋b，过y＝f(x)上点P(1，f(1))的切线方程为：y－f(1)＝f′(1)(x－1)，即y－(a＋b＋c＋1)＝(3＋2a＋b)(x－1)而过y＝f(x)上P(1，f(1))的切线方程为：y＝3x＋1即又∵y＝f(x)在x＝－2时有极值，故f′(－2)＝0 ∴－4a＋b＝－12③由①②③相联立解得a＝2，b＝－4，c＝5,所以f(x)＝x3＋2x2－4x＋5(2)y＝f(x)在区间[－2,1]上单调递增又f′(x)＝3x2＋2ax＋b，由(1)知2a＋b＝0∴f′(x)＝3x2－bx＋b依题意f′(x)在[－2,1]上恒有f′(x)≥0，即3x2－bx＋b≥0在[－2,1]上恒成立注意到，所以3x2－bx＋b≥0在[－2,1]上恒成立等价于：，令知当时，当时，所以在[-2，1）上有最大值为，故知，且当x=1时f′(x)≥0也成立,所以【考点】1.导数的几何意义;2.函数的极值与最值.10.对于三次函数，定义是的导函数的导函数，若方程有实数解，则称点为函数的“拐点”，可以证明，任何三次函数都有“拐点”，任何三次函数都有对称中心，且“拐点”就是对称中心，请你根据这一结论判断下列命题：①任意三次函数都关于点对称：②存在三次函数,若有实数解，则点为函数的对称中心；③存在三次函数有两个及两个以上的对称中心；④若函数，则:其中所有正确结论的序号是( )．A．①②④B．①②③C．①③④D．②③④【答案】A【解析】①的二阶导数为，令得，根据题意得对称中心为，故①正确；②存在，例如三次函数，得，而就是的对称中心；③任何三次函数经过一次求导以后得到的是一个二次函数，二次函数再求一次导以后得到的是一个一次函数，而一次函数只有一个解，所以只有一个拐点，也就是说只有一个对称中心，所以说任何三次函数都只有一个对称中心；④,,得，所以的对称中心是即，所以有，所以，④正确。

高二数学导数及其应用综合检测综合测试题

导数及其应用综合检测一、选择题(本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．若曲线y＝x2＋ax＋b在点(0，b)处的切线方程是x－y＋1＝0，则()A．a＝1，b＝1B．a＝－1，b＝1C．a＝1，b＝－1D．a＝－1，b＝－12．一物体的运动方程为s＝2t sin t＋t，则它的速度方程为() A．v＝2sin t＋2t cos t＋1B．v＝2sin t＋2t cos tC．v＝2sin tD．v＝2sin t＋2cos t＋13.函数f(x)=(x-3)e x的递增区间是( )(A)(-∞，2) (B)(0，3)(C)(1，4) (D)(2，+∞)4．函数y＝x|x(x－3)|＋1()A．极大值为f(2)＝5，极小值为f(0)＝1B．极大值为f(2)＝5，极小值为f(3)＝1C．极大值为f(2)＝5，极小值为f(0)＝f(3)＝1D．极大值为f(2)＝5，极小值为f(3)＝1，f(－1)＝－35．函数f(x)＝x3＋ax2＋3x－9，已知f(x)在x＝－3时取得极值，则a等于()A．2 B．3 C．4 D．56．设f(x)，g(x)分别是定义在R上的奇函数和偶函数．当x<0时，f′(x)g(x)＋f(x)g′(x)>0，且g(－3)＝0，则不等式f(x)g(x)<0的解集是()A．(－3,0)∪(3，＋∞)B．(－3,0)∪(0,3)C．(－∞，－3)∪(3，＋∞)D．(－∞，－3)∪(0,3)7．函数f(x)=(x2-2x)e x的图像大致是( )8．已知三次函数f (x )＝13x 3－(4m －1)x 2＋(15m 2－2m －7)x ＋2在x ∈(－∞，＋∞)是增函数，则m 的取值范围是( )A ．m <2或m >4B ．－4<m <－2C ．2<m <4D ．以上皆不正确9．设f (x )、g (x )是定义域为R 的恒大于0的可导函数，且f ′(x )g (x )－f (x )g ′(x )<0，则当a <x f (b )g (b )B ．f (x )g (a )>f (a )g (x )C ．f (x )g (b )>f (b )g (x )D ．f (x )g (x )>f (a )g (x )10．下面四图都是同一坐标系中某三次函数及其导函数的图象，其中一定不正确的序号是()A ．①②B ．③④C ．①③D ．①④二、填空题(本大题共5个小题，每小题5分，共25分．将正确答案填在题中横线上)11.函数xe y lnx的导数y ′=___________.12．若函数f (x )＝ax 2－1x 的单调增区间为(0，＋∞)，则实数a 的取值范围是________．13.若函数f(x)=x 3-3x-a 在区间［0，3］上的最大值、最小值分别为m,n,则m-n=________.14. f(x)=x 3+x 2f ′(1)+3xf ′(-1),则f ′(1)+f ′(-1)= ________． 15．设曲线y ＝x n ＋1(n ∈N *)在点(1,1)处的切线与x 轴的交点的横坐标为x n ，令a n ＝lg x n ，则a 1＋a 2＋…＋a 99的值为________．三、解答题(本大题共6个小题，共74分．解答应写出文字说明、证明过程或演算步骤)16．设函数f (x )＝ln x ＋ln(2－x )＋ax (a >0)． (1)当a ＝1时，求f (x )的单调区间；(2)若f (x )在(0,1]上的最大值为12，求a 的值． 17．(本题满分12分)设函数f (x )＝x 3－3ax ＋b (a ≠0)．(1)若曲线y ＝f (x )在点(2，f (2))处与直线y ＝8相切，求a ，b 的值； (2)求函数f (x )的单调区间与极值点． 18．(本题满分12分)已知函数f (x )＝12x 2＋ln x .(1)求函数f (x )的单调区间； (2)求证：当x >1时，12x 2＋ln x <23x 3. 19．设函数f (x )＝x 3－92x 2＋6x －a .(1)对于任意实数x, f ′(x )≥m 恒成立，求m 的最大值； (2)若方程f (x )＝0有且仅有一个实根，求a 的取值范围． 20.某分公司经销某种品牌产品，每件产品的成本为3元，并且每件产品需向总公司交a 元(3≤a ≤5)的管理费，预计当每件产品的售价为x 元(9≤x ≤11)时，一年的销售量为(12-x)2万件.(1)求分公司一年的利润L(万元)与每件产品的售价x 的函数关系式； (2)当每件产品的售价为多少元时，分公司一年的利润L 最大，并求出L 的最大值Q(a).21．(本题满分14分)已知函数f (x )＝－x 3＋ax 2＋1(a ∈R )． (1)若函数y ＝f (x )在区间⎝ ⎛⎭⎪⎫0，23上递增，在区间⎣⎢⎡⎭⎪⎫23，＋∞上递减，求a 的值；(2)当x ∈[0,1]时，设函数y ＝f (x )图象上任意一点处的切线的倾斜角为θ，若给定常数a ∈⎝ ⎛⎭⎪⎫32，＋∞，求θ的取值范围；(3)在(1)的条件下，是否存在实数m，使得函数g(x)＝x4－5x3＋(2－m)x2＋1(m∈R)的图象与函数y＝f(x)的图象恰有三个交点．若存在，请求出实数m的值；若不存在，试说明理由．。

新课标高二数学选修2-2第一章导数及其应用测试题（含答案）

新课标⾼⼆数学选修2-2第⼀章导数及其应⽤测试题（含答案）新课改⾼⼆数学选修2-2第⼀章导数及其应⽤测试题第Ⅰ卷（选择题，共40分）⼀、选择题(本⼤题共10⼩题，每⼩题4分，共40分)1．设xx y sin 12-=，则='y （）．A ．x x x x x 22sin cos )1(sin 2---B ．xx x x x 22sin cos )1(sin 2-+- C ．x x x x sin )1(sin 22-+- D ．xx x x sin )1(sin 22---2．设1ln )(2+=x x f ，则=)2('f （）．A ．54 B ．52 C ．51 D ．53 3．已知2)3(',2)3(-==f f ，则3)(32lim3--→x x f x x 的值为（）．A ．4-B ．0C ．8D ．不存在 4．曲线3x y =在点)8,2(处的切线⽅程为（）．A ．126-=x yB ．1612-=x yC ．108+=x yD ．322-=x y 5.满⾜()()f x f x '=的函数是A . f (x )＝1－x B. f (x )＝x C . f (x )＝0D . f (x )＝16.曲线34y x x =-在点（－1，－3）处的切线⽅程是A . 74y x =+ B. 72y x =+ C. 4y x =- D. 2y x =-7.若关于x 的函数2m n y mx -=的导数为4y x '=,则m n +的值为 A. -4 B. 1- C. D . 48.设ln y x x =-，则此函数在区间(0,1)内为A ．单调递增， B.有增有减 C.单调递减， D.不确定 9．函数3()31f x x x =-+在闭区间[-3，0]上的最⼤值、最⼩值分别是A . 1，－1 B. 3，-17 C. 1，－17 D. 9，－1910.函数)(x f 的定义域为开区间),(b a ，导函数)(x f '在),(b a 内的图象如图所⽰，则函数)(x f 在开区间),(b a 内有极⼩值点 A 1个B 2个C 3个D 4个第Ⅱ卷（⾮选择题，共60分）⼆、填空题（每⼩题5分，共15分。

高二数学《导数及其应用》单元检测题

2.函数 f ( x ) = lg x - 的零点所在的区间是A .1B . ln 2C .D . e高二数学《导数及其应用》单元检测题一．选择题（每小题５分，共 60 分）12 3 4 5 6 7 8 9 10 11 121.若 f ( x ) = ax 4 + bx 2 + c 满足 f '(1) = 2 ，则 f '(-1) =A. -4B. -2C.2D.41xA. (0,1)B. (1,2 )C. (2,3 )D. (3,10)3.已知函数 f ( x ) 在 R 上满足 f ( x ) = 2 f (2 - x) - x 2 + 8x - 8 ，则曲线 y= f ( x ) 在点(1, f (1)) 处的切线方程是A. y = 2 x - 1B. y = xC. y = 3x-2D. y = -2 x + 34.曲线 y = - x 3 + 3x 2 在点（1，2）处的切线方程为A. y = 3x - 1B. y = -3x +3C. y = 3x + 5D. y = 2 x5.设 y = π 2 ，则 y ˊ=A.2 πB. π 2C.0D.以上都不是6.已知 f ( x ) = x(2014 - ln x) ，若 f '( x ) = 2013 ，则 x =0 01 e7.曲线 y = x 2 + 11 在点 P （1，12）处的切线与 y 轴交点的纵坐标是A.-9B.-3C.9D.15C.-4D.-11.y=x sin x，则y=12.函数f(x)＝x＋2cosx在[0，]上取得最大值时x为A.0B.π63213.过原点作曲线y=e的切线，则切线的方程为_____________.215.若曲线y=x+1（α∈R）在点（1，2）处的切线经过坐标原点，则α=________。

8.函数f(x)=-2x+ax3，若f'(2)=1，则a=A.4B.11 449.函数f(x)＝ax3＋bx在x＝1处有极值－2，则a，b的值分别为A.1,－3B.1,3C.－1,3D.－1,－310.函数f(x)＝x3－3x(|x|＜1)A.有最大值，但无最小值B.有最大值，也有最小值C.无最大值，也无最小值D.无最大值，但有最小值2'A．2x sin x B．x2cos xC．2x cos x+x2cos x D．2x sin x+x2cos xπ2ππC. D.二.简答题（每小题5分，共20分）x114.设函数f(x)＝x(ex＋1)＋x2，则函数f(x)的单调递增区间为_________α16.若曲线y=kx+ln x在点(1,k)处的切线平行于x轴,则k=______.17.已知函数 f ( x) = x - 3x + ax + 2 ，曲线 y = f ( x) 在点 (0, 2) 处的切线与 x 轴ln x ，若函数 f ( x) 在 [ 2，+ ∞)上为减函数，求实数 a 的最小三.解答题（共 70 分）32交点的横坐标为 -2 .(1)求 a ；(2)证明：当 k < 1 时，曲线 y = f ( x) 与直线 y = kx - 2 只有一个交点.18.设函数值；f ( x ) = x- ax19.已知函数f(x)2xalnx2(a0).若曲线y f(x)在点P(1,f(1))处的切线与直线y x2垂直，求函数y f(x)的单调区间；20.已知数列 a n 的首项 a 1 = 5 ，且 a n +1 = 2a n + 1（1）求数列 a n 的通项公式；{ }{ }（2）设 f ( x) = a 1x + a 2 x 2 … +a n x n (n ∈ N + ) ,求 a 1 + 2a 2 + 3a 3 … +na n .21.已知函数 f ( x) = ax 3 + bx 2 - 3x(a, b ∈ R ) 在点 (1, f (1)) 处的切线方程为 y + 2 = 0 . （1）求函数 f ( x) 的解析式；（2）若经过点 M (2, m ) 可以作出曲线 y = f ( x) 的三条切线，求实数 m 的取值范围.(Ⅰ)若xf'(x)≤x+ax+1，求a的取值范围；22.已知函数f(x)=(x+1)ln x-x+1.2(Ⅱ)证明：(x-1)f(x)≥0.第()单元检测题参考答案（仅供参考）1 B 2C3A4A5C6A7C8B9A10C11D12B二.简答题答案:21.解析：y′=e x，设切点的坐标为(x，e x0)，切线的斜率为k，则k=e x0，故切线方程为y﹣e x0=e x0(x﹣x0)，又切线过原点，∴﹣e x0=e x0(﹣x)，∴x0=1，y0=e，k=e.则切线方程为y=ex，故答案为y=ex.26.[-1,+∞)27.2[解析]：y'=αxα-1，则k=α，故切线方程y=αx过点（1，2）解得α=2 30.-1求导得y'=k+1x,依题意k+1=0,所以k=-1.三.解答题答案:33.（I）f'(x)=3x2-6x+a，f'(0)=a.曲线y=f(x)在点（0,2）处的切线方程为y=ax+2。

高二数学选修2-2导数及其应用测试题(含答案)(可编辑修改word版)

x 2 + 1 1 高二数学选修 2-2 导数及其应用测试题一、选择题(本大题共 12 小题，每小题 5 分，共 60 分，在每小题给出的四个选项中，只有一项是符合题目要求的，请将所选答案写在答题卡上)1 - x2 1. 设 y = sin x，则 y ' = （）．- 2x sin x - (1 - x 2 ) cos xA ．sin 2x - 2x sin x + (1 - x 2 )-2x sin x + (1 - x 2 ) cos xB ．sin 2 x - 2x sin x - (1 - x 2 )C.D ．sin xsin x2．设 f (x ) = ln ，则 f '(2) = （）．4 2 13 A.B ．C ．D ．55552x - 3 f (x ) 3．已知 f (3) = 2, f '(3) = -2 ，则limx →3x - 3的值为（）．A. - 4B. 0C ． 8D ．不存在4. 曲线 y = x 3 在点(2,8) 处的切线方程为（）．A ． y = 6x - 12 C ． y = 8x + 10B ． y = 12x - 16 D ． y = 2x - 325. 已知函数 f (x ) = ax 3 + bx 2+ cx + d 的图象与 x 轴有三个不同交点(0,0),(x ,0)， (x ,0) ，且 f (x ) 在 x = 1， x = 2 时取得极值，则 x 1 ⋅ x 2 的值为（）A ．4B ．5C ．6D ．不确定6. 在 R 上的可导函数 f (x ) =1 x 3 + 1 ax 2+ 2bx + c ，当 x ∈ (0,1) 取得极大值，当 x ∈ (1,2) 3 2b - 2取得极小值，则的取值范围是（）．a - 1A. ( 1 4,1)B. ( 1 2,1)C. (- 1 , 1 )2 4D. (- 1 , 1 )2 27.函数 f (x ) = 1 e x(sin x + cos x ) 在区间 2 [0, ]的值域为（）．2A ．[ 1, 2 1e 2 ]2B ． ( 1 , 1 2 2e 2 )C ．[1, e 2 ]D ． (1, e 2)23 4V a42 n8.积分⎰-a a 2-x2dx=（）．A.1a24x 2 y 2B.1a22C.a2D.2a29.由双曲线-a 2b 2积为（）= 1，直线y =b, y =-b 围成的图形绕y 轴旋转一周所得旋转体的体A.8ab23B.8a2b3C.4a2b3D.4ab2310.由抛物线y 2= 2x 与直线y =x - 4 所围成的图形的面积是（）．38 16A．18 B．C．D ．163 311.设底面为等边三角形的直棱柱的体积为V ，则其表面积最小时，底面边长为（）．Ａ．3V Ｂ．32V Ｃ．D．23V12.某人要剪一个如图所示的实心纸花瓣，纸花瓣的边界由六段全等的正弦曲线弧y = sin x(0 ≤x ≤) 组成，其中曲线的六个交点正好是一个正六边形的六个顶点，则这个纸花瓣的面积为（）．A．6 + 3 32B．12 +3 3 22C．6+2D．6 +3 3 22第Ⅱ卷（非选择题，共90 分）二、填空题（每小题4 分，共16 分。

高二数学导数及其应用试题答案及解析

高二数学导数及其应用试题答案及解析1.函数的导数是（）A．B．C．D．【答案】D【解析】===【考点】基本函数的求导公式、积的求导法则点评：本题比较简单，直接代入求导公式运算。

要求学生熟记公式。

2.已知直线是的切线，则的值为（）A．B．C．D．【答案】C【解析】，则∴切点为，曲线过∴，。

【考点】切线方程、对数运算。

点评：根据导数的几何意义，先把切点利用k表示，再利用切点是切线和曲线的公共点代入已知方程求值。

3.在曲线y=2x2－1的图象上取一点（1， 1）及邻近一点（1+Δx,1+Δy）,则等于A．4Δx+2Δx2B．4+2Δx C．4Δx+Δx2D．4+Δx【答案】B【解析】∵△y=2（1+△x）2-1-1=2△x2+4△x，∴=4+2△x，故选B．【考点】本题主要考查导数的概念。

点评：遵循“算增量，求比值”，细心计算。

4.（2006年福建卷）统计表明，某种型号的汽车在匀速行驶中每小时的耗油量（升）关于行驶速度（千米/小时）的函数解析式可以表示为：已知甲、乙两地相距100千米。

（I）当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？（II）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？【答案】（I）当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地耗油17.5升。

（II）当汽车以80千米/小时的速度匀速行驶时，从甲地到乙地耗油最少，最少为11.25升.【解析】分析：结合物理知识进行求解.解：（I）当时，汽车从甲地到乙地行驶了小时，要耗没（升）。

答：当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地耗油17.5升。

（II）当速度为千米/小时时，汽车从甲地到乙地行驶了小时，设耗油量为升，依题意得令得当时，是减函数；当时，是增函数。

当时，取到极小值因为在上只有一个极值，所以它是最小值。

答：当汽车以80千米/小时的速度匀速行驶时，从甲地到乙地耗油最少，最少为11.25升.【考点】本小题主要考查函数、导数及其应用。

【高二】导数及其应用综合检测综合测试题(有答案)

【高二】导数及其应用综合检测综合测试题（有答案）第一章导数及其应用综合检测时间120分钟，满分150分。

一、(本大题共12个小题，每小题5分后，共60分后．在每小题得出的四个选项中，只有一项就是合乎题目建议的)1．(2021?全国ⅱ文，7)若曲线y＝x2＋ax＋b在点(0，b)处的切线方程是x－y＋1＝0，则( )a．a＝1，b＝1b．a＝－1，b＝1c．a＝1，b＝－1d．a＝－1，b＝－1[答案] a[解析] y′＝2x＋a，∴y′x＝0＝(2x＋a)x＝0＝a＝1，将(0，b)代入切线方程得b＝1.2．一物体的运动方程为s＝2tsint＋t，则它的速度方程为( )a．v＝2sint＋2tcost＋1b．v＝2sint＋2tcostc．v＝2sintd．v＝2sint＋2cost＋1[答案] a[解析] 因为变速运动在t0的瞬时速度就是路程函数y＝s(t)在t0的导数，s′＝2sint＋2tcost＋1，故选a.3．曲线y＝x2＋3x在点a(2,10)处的切线的斜率就是( )a．4b．5c．6d．7[答案] d[解析] 由导数的几何意义言，曲线y＝x2＋3x在点a(2,10)处的切线的斜率就是函数y＝x2＋3x在x＝2时的导数，y′x＝2＝7，故挑选d.4．函数y＝xx(x－3)＋1( )a．极大值为f(2)＝5，极小值为f(0)＝1b．极大值为f(2)＝5，极小值为f(3)＝1c．极大值为f(2)＝5，极小值为f(0)＝f(3)＝1d．极大值为f(2)＝5，极小值为f(3)＝1，f(－1)＝－3[答案] b[解析] y＝xx(x－3)＋1＝x3－3x2＋1 (x<0或x>3)－x3＋3x2＋1 (0≤x≤3)∴y′＝3x2－6x (x<0或x>3)－3x2＋6x (0≤x≤3)x变化时，f′(x)，f(x)变化情况如下表中：x(－∞，0)0(0,2)2(2,3)3(3，＋∞)f′(x)＋0＋0－0＋f(x)?无极值?极大值5?极小值1?∴f(x)很大＝f(2)＝5，f(x)极小＝f(3)＝1故应选b.5．(2021?安徽理，9)未知函数f(x)在r上满足用户f(x)＝2f(2－x)－x2＋8x－8，则曲线y＝f(x)在点(1，f(1))处的切线方程就是( )a．y＝2x－1b．y＝xc．y＝3x－2d．y＝－2x＋3[答案] a[解析] 本题考查函数解析式的带发修行、Auron数的几何意义及直线方程的点斜式．∵f(x)＝2f(2－x)－x2＋8x－8，∴f(2－x)＝2f(x)－x2－4x＋4，∴f(x)＝x2，∴f′(x)＝2x，∴曲线y＝f(x)在点(1，f(1))处的切线斜率为2，切线方程为y－1＝2(x－1)，∴y＝2x－1.6．函数f(x)＝x3＋ax2＋3x－9，已知f(x)在x＝－3时取得极值，则a等于( )a．2b．3c．4d．5[答案] d[解析] f′(x)＝3x2＋2ax＋3，∵f(x)在x＝－3时获得极值，∴x＝－3是方程3x2＋2ax＋3＝0的根，∴a＝5，故挑选d.7．设f(x)，g(x)分别是定义在r上的奇函数和偶函数．当x<0时，f′(x)g(x)＋f(x)g′(x)>0，且g(－3)＝0，则不等式f(x)g(x)<0的解集是( )a．(－3,0)∪(3，＋∞)b．(－3,0)∪(0,3)c．(－∞，－3)∪(3，＋∞)d．(－∞，－3)∪(0,3)[答案] d[解析] 令f(x)＝f(x)?g(x)，易知f(x)为奇函数，又当x<0时，f′(x)g(x)＋f(x)g′(x)>0，即f′(x)>0，知f(x)在(－∞，0)内单调递增，又f(x)为奇函数，所以f(x)在(0，＋∞)内也单调递增，且由奇函数知f(0)＝0，∴f(0)＝0.又由g(－3)＝0，言g(3)＝0∴f(－3)＝0，进而f(3)＝0于是f(x)＝f(x)g(x)的大致图象如图所示∴f(x)＝f(x)?g(x)<0的解集为(－∞，－3)∪(0,3)，故应选d.8．下面四图都就是同一坐标系中某三次函数及其Auron函数的图象，其中一定不恰当的序号就是( )a．①②b．③④c．①③d．①④[答案] b[解析] ③不恰当；Auron函数过原点，但三次函数在x＝0不存有极值；④不恰当；三次函数先减后减至再减，而导函数先负后正再正数．故高文瑞b.9．(2021?湖南理，5)241xdx等于( )a．－2ln2b．2ln2c．－ln2d．ln2[答案] d[解析] 因为(lnx)′＝1x，所以241xdx＝lnx42＝ln4－ln2＝ln2.10．已知三次函数f(x)＝13x3－(4－1)x2＋(152－2－7)x＋2在x∈(－∞，＋∞)是增函数，则的取值范围是( )a．<2或>4b．－4<c．2<<4d．以上皆不恰当[答案] d[解析] f′(x)＝x2－2(4－1)x＋152－2－7，由题意得x2－2(4－1)x＋152－2－7≥0恒成立，∴δ＝4(4－1)2－4(152－2－7)＝642－32＋4－602＋8＋28＝4(2－6＋8)≤0，∴2≤≤4，故挑选d.11．已知f(x)＝x3＋bx2＋cx＋d在区间[－1,2]上是减函数，那么b＋c( )a．存有最大值152b．有最大值－152c．存有最小值152d．有最小值－152[答案] b[解析] 由题意f′(x)＝3x2＋2bx＋c在[－1,2]上，f′(x)≤0恒成立．所以f′(－1)≤0f′(2)≤0即2b－c－3≥04b＋c＋12≤0令b＋c＝z，b＝－c＋z，例如图过a－6，－32得z最大，最大值为b＋c＝－6－32＝－152.故高文瑞b.12．设f(x)、g(x)是定义域为r的恒大于0的可导函数，且f′(x)g(x)－f(x)g′(x)<0，则当aa．f(x)g(x)>f(b)g(b)b．f(x)g(a)>f(a)g(x)c．f(x)g(b)>f(b)g(x)d．f(x)g(x)>f(a)g(x)[答案] c[解析] 令f(x)＝f(x)g(x)则f′(x)＝f′(x)g(x)－f(x)g′(x)g2(x)<0f(x)、g(x)是定义域为r恒大于零的实数∴f(x)在r上以递增函数，当x∈(a，b)时，f(x)g(x)>f(b)g(b)∴f(x)g(b)>f(b)g(x)．故高文瑞c.二、题(本大题共4个小题，每小题4分，共16分．将正确答案填在题中横线上)13.－2－1dx(11＋5x)3＝________.[答案] 772[解析] 挑f(x)＝－110(5x＋11)2，从而f′(x)＝1(11＋5x)3则－2－1dx(11＋5x)3＝f(－1)－f(－2)＝－110×62＋110×12＝110－1360＝772.14．若函数f(x)＝ax2－1x的单调减区间为(0，＋∞)，则实数a的值域范围就是________．[答案] a≥0[解析] f′(x)＝ax－1x′＝a＋1x2，由题意得，a＋1x2≥0，对x∈(0，＋∞)恒成立，∴a≥－1x2，x∈(0，＋∞)恒设立，∴a≥0.15．(2021?陕西理，16)设曲线y＝xn＋1(n∈n*)在点(1,1)处的切线与x轴的交点的横坐标为xn，令an＝lgxn，则a1＋a2＋…＋a99的值为________．[答案] －2[解析] 本小题主要考查导数的几何意义和对数函数的有关性质．k＝y′x＝1＝n＋1，∴切线l：y－1＝(n＋1)(x－1)，令y＝0，x＝nn＋1，∴an＝lgnn＋1，∴原式＝lg12＋lg23＋…＋lg99100＝lg12×23×…×99100＝lg1100＝－2.16．如图阴影部分是由曲线y＝1x，y2＝x与直线x＝2，y＝0围成，则其面积为________．[答案] 23＋ln2[解析] 由y2＝x，y＝1x，得交点a(1,1)由x＝2y＝1x得交点b2，12.故所求面积s＝01xdx＋121xdx＝23x3210＋lnx21＝23＋ln2.三、解答题(本大题共6个小题，共74分．解答应写出文字说明、证明过程或演算步骤)17．(本题满分12分后)(2021?江西理，19)设立函数f(x)＝lnx＋ln(2－x)＋ax(a>0)．(1)当a＝1时，求f(x)的单调区间；(2)若f(x)在(0,1]上的最大值为12，谋a的值．[解析] 函数f(x)的定义域为(0,2)，f′(x)＝1x－12－x＋a，(1)当a＝1时，f′(x)＝－x2＋2x(2－x)，所以f(x)的单调递增区间为(0，2)，单调递减区间为(2，2)；(2)当x∈(0,1]时，f′(x)＝2－2xx(2－x)＋a>0，即f(x)在(0,1]上单调递增，故f(x)在(0,1]上的最大值为f(1)＝a，因此a＝12.18．(本题满分12分后)谋曲线y＝2x－x2，y＝2x2－4x所围起图形的面积．[解析] 由y＝2x－x2，y＝2x2－4x得x1＝0，x2＝2.由图所述，所求图形的面积为s＝02(2x－x2)dx＋02(2x2－4x)dx＝02(2x－x2)dx－02(2x2－4x)dx.因为x2－13x3′＝2x－x2，23x3－2x2′＝2x2－4x，所以s＝x2－13x320－23x3－2x220＝4.19．(本题满分12分后)设立函数f(x)＝x3－3ax＋b(a≠0)．(1)若曲线y＝f(x)在点(2，f(2))处与直线y＝8相切，求a，b的值；(2)求函数f(x)的单调区间与极值点．[分析] 考查利用导数研究函数的单调性，极值点的性质，以及分类讨论思想．[解析] (1)f′(x)＝3x2－3a.因为曲线y＝f(x)在点(2，f(2))处与直线y＝8相切，所以f′(2)＝0，f(2)＝8.即3(4－a)＝0，8－6a＋b＝8.解得a＝4，b＝24.(2)f′(x)＝3(x2－a)(a≠0)．当a<0时，f′(x)>0，函数f(x)在(－∞，＋∞)上单调递增，此时函数f(x)没有极值点．当a>0时，由f′(x)＝0得x＝±a.当x∈(－∞，－a)时，f′(x)>0，函数f(x)单调递增；当x∈(－a，a)时，f′(x)<0，函数f(x)单调递增；当x∈(a，＋∞)时，f′(x)>0，函数f(x)单调递增．此时x＝－a就是f(x)的极大值点，x＝a就是f(x)的极小值点．20．(本题满分12分)已知函数f(x)＝12x2＋lnx.(1)求函数f(x)的单调区间；(2)求证：当x>1时，12x2＋lnx<23x3.[解析] (1)依题意言函数的定义域为{xx>0}，∵f′(x)＝x＋1x，故f′(x)>0，∴f(x)的单调减区间为(0，＋∞)．(2)设g(x)＝23x3－12x2－lnx，∴g′(x)＝2x2－x－1x，∵当x>1时，g′(x)＝(x－1)(2x2＋x＋1)x>0，∴g(x)在(1，＋∞)上以增函数，∴g(x)>g(1)＝16>0，∴当x>1时，12x2＋lnx<23x3.21．(本题满分12分)设函数f(x)＝x3－92x2＋6x－a.(1)对于任一实数x,f′(x)≥恒设立，谋的最大值；(2)若方程f(x)＝0有且仅有一个实根，求a的取值范围．[分析] 本题主要考查导数的应用领域及转变思想，以及谋参数的范围问题．[解析] (1)f′(x)＝3x2－9x＋6＝3(x－1)(x－2)．因为x∈(－∞，＋∞)．f′(x)≥，即3x2－9x＋(6－)≥0恒设立．所以δ＝81－12(6－)≤0，得≤－34，即的最大值为－34.(2)因为当x<1时，f′(x)>0；当12时f′(x)>0.所以当x＝1时，f(x)挑极大值f(1)＝52－a，当x＝2时，f(x)取极小值f(2)＝2－a.故当f(2)>0或f(1)<0时，方程f(x)＝0仅有一个实根，Champsaura<2或a>52.22．(本题满分14分)已知函数f(x)＝－x3＋ax2＋1(a∈r)．(1)若函数y＝f(x)在区间0，23上递减，在区间23，＋∞上递增，谋a的值；(2)当x∈[0,1]时，设函数y＝f(x)图象上任意一点处的切线的倾斜角为θ，若给定常数a∈32，＋∞，求θ的取值范围；(3)在(1)的条件下，与否存有实数，使函数g(x)＝x4－5x3＋(2－)x2＋1(∈r)的图象与函数y＝f(x)的图象恰存有三个交点．若存有，命令出来实数的值；若不存有，先行表明理由．[解析] (1)依题意f′23＝0，由f′(x)＝－3x2＋2ax，得－3232＋2a?23＝0，即a＝1.(2)当x∈[0,1]时，tanθ＝f′(x)＝－3x2＋2ax＝－3x－a32＋a23.由a∈32，＋∞，得a3∈12，＋∞.①当a3∈12，1，即a∈32，3时，f′(x)ax＝a23，f(x)in＝f′(0)＝0.此时0≤tanθ≤a23.②当a3∈(1，＋∞)，即a∈(3，＋∞)时，f′(x)ax＝f′(1)＝2a－3，f′(x)in＝f′(0)＝0，此时，0≤tanθ≤2a－3.又∵θ∈[0，π)，∴当32当a>3时，θ∈[0，arctan(2a－3)]．(3)函数y＝f(x)与g(x)＝x4－5x3＋(2－)x2＋1(∈r)的图象恰存有3个交点，等价于方程－x3＋x2＋1＝x4－5x3＋(2－)x2＋1恰存有3个左右实根，∴x4－4x3＋(1－)x2＝0，似乎x＝0就是其中一个根(二重根)，方程x2－4x＋(1－)＝0有两个非零不等实根，则δ＝16－4(1－)>01－≠0∴>－3且≠1故当>－3且≠1时，函数y＝f(x)与y＝g(x)的图象恰存有3个交点．。

(完整版)高二数学周测卷--导数及其应用(含答案)

2019 —2020 学年第二学期高二数学周测试卷一、选择题 (本大题共 12 小题，每题 5 分，共 60 分．在每小题给出的四个选项中，只有一项为哪一项切合题目要求的) 1．设函数 y＝f(x)在(a，b)上可导，则 f(x)在(a，b)上为增函数是f′(x)>0 的()A ．必需不充分条件B．充分不用要条件C．充分必需条件D．既不充分也不用要条件分析y＝f(x)在(a，b)上 f′(x)>0? y＝f(x)在 (a，b)上是增函数，反之， y＝f(x)在(a，b)上是增函数 ? f′(x)≥0?/ f′(x)>0.答案 A2．若曲线y＝f(x)在点 (x0，f(x0))处的切线方程是2x＋y－1＝0，则( )A ．f′(x0)>0 C．f′(x0)＝ 0 B．f′(x0)<0 D．f′(x0)不存在分析曲线 y＝f(x)在点 (x0，f(x0))处的切线的斜率为f′(x0)＝－ 2<0. 答案 B3．曲线 y＝31x3－2 在点 (－1，－53)处切线的倾斜角为 ()A ．30° B．45° C．135° D．150°分析 y′＝x2，k＝tanα＝y′|x＝－1＝(－1)2＝1，∴α＝45 °.答案 B4．曲线f(x)＝x3＋x－2 的一条切线平行于直线y＝4x－1，则切点 P0的坐标为( )A ．(0，－ 1)或(1,0)B ．(1,0)或(－1，－ 4)C ．(－1，－ 4)或(0，－ 2)D ．(1,0)或(2,8)分析设P 0 0， 0 ，则 ′ 0 ＝ 2 ＝，0＋(x y ) f (x ) 3x 1 4∴x 02＝1，∴x 0＝1，或 x 0＝－ 1.∴P 0 的坐标为 (1,0)或(－1，－ 4)．答案 B5．以下函数中，在 (0，＋∞ )上为增函数的是 ( )A ．＝ 2B ．＝ 3－x y sin x y x C ．y ＝xe xD ．y ＝－ x ＋ln(1＋x)分析关于 C ，有 y ′＝ (xe x)′＝e x＋xe x＝e x(x ＋1)>0. 答案 C 6 ．已知函数＝ 3 －3x 2－9x ，x ∈(－2,2)，则 f(x)有( ) f(x) x A ．极大值 5，极小值为－ 27 B ．极大值 5，极小值为－ 11 C ．极大值 5，无极小值 D ．极小值－ 27，无极大值分析 f ′(x)＝3x 2－－9 6x＝ 3(x ＋1)(x －3)．当 x<－1 时， f ′(x)>0，当－ 1<x<3 时， f ′(x)<0.∴x ＝－ 1 是 f(x)的极大值点．且极大值为 f(－1)＝5，在 (－2,2)内无极小值．答案 C7．函数 y ＝2x 3＋x 2 的单一递加区间是 ()1 1A ．(－∞，－3)∪(0 ，＋∞ ) B．(－6，＋∞ )1 1 C．(－∞，－3)和(0，＋∞ ) D．(－∞，－6)分析 y′＝6x2＋2x＝ 2x(3x＋1)，1令 y′>0，得 x<－3，或 x>0.∴函数 y＝2x3＋ x2的单一增区间为1(－∞，－3)和(0，＋∞)．答案 C8．如图是函数 y＝f(x)的导函数的图象，给出下边四个判断：①f(x)在区间 [－2，－ 1] 上是增函数；② x＝－ 1 是 f(x)的极小值点；③ f(x)在区间 [－1,2]上是增函数，在区间 [2,4] 上是减函数；④ x＝2 是 f(x)的极小值点．此中，全部正确判断的序号是 ( )A ．①②B．②③C．③④D．①②③④分析由函数 y＝f(x)的导函数的图象可知：(1)f(x)在区间 [－2，－1]上是减函数，在[ －1,2]上是增函数，在[2,4] 上是减函数；(2)f(x)在 x＝－ 1 处获得极小值，在 x＝2 处获得极大值．故②③正确．答案 B9．已知 f(x)＝x2＋2xf′(1)，则 f′(0)等于 ( )A ．0 B．－ 4 C．－ 2 D．2分析 f′(x)＝2x＋2f′(1)，∴f′(1)＝2＋2f′(1)，即 f′(1)＝－ 2，∴f′(x)＝2x－4，∴ f′(0)＝－ 4.答案 B10．函数 f(x)＝－ x3＋x2＋x－2 的零点个数及散布状况为()1A ．一个零点，在－∞，－3内1B．二个零点，分别在－∞，－3，(0，＋∞ )内1 1C．三个零点，分别在－∞，－3，－3，0，(1，＋∞ )内1D．三个零点，分别在－∞，－3，(0,1)，(1，＋∞ )内1分析利用导数法易得函数f(x)在(－∞，－3)内单一递减，在1 1 59－3，1 内单一递加，在 (1，＋∞ )内单一递减，而 f －3 ＝－27<0，f(1)＝－ 1<0，故函数 f(x)的图象与 x 轴仅有一个交点，且交点横坐标1在－∞，－3内答案 A11．关于R 上可导的随意函数f(x)，若知足(x－1)f′(x)≥0，则必有 ( )A ．f(0)＋f(2)<2f(1) B．f(0)＋f(2)≤2f(1)C．f(0)＋f(2)≥2f(1) D．f(0)＋f(2)>2f(1)分析当 1≤x≤2 时，f′(x)≥0，则 f(2)≥f(1)；而当 0≤x≤1 时， f′(x)≤0，则 f(1)≤f(0)，进而 f(0)＋f(2)≥2f(1)．答案 C12．设 f(x)是定义在 R 上的可导函数，且知足f′(x)>f(x)，对随意的正数 a，下边不等式恒建立的是 ( )A．f(a)<e a f(0) B．f(a)>e a f(0)f 0 f 0 C．f(a)< e a D．f(a)> e a分析结构函数 g(x)＝f xx，则 g′(x)＝f′ x －f x>0，故函数 g(x)＝xe ef xx在 R 上单一递加，因此 g(a)>g(0)，即f aa >f 00，即 f(a)>e a f(0)．e e e答案 B二、填空题 (本大题共 4 小题，每题 5 分，共 20 分．把答案填在题中的横线上 )1 3 2＝________. 13．若函数 f(x)＝3x －f′(1) ·x＋2x＋5，则 f′(2)分析∵f′(x)＝x2－′＋，2f (1)x 2∴f′(1)＝1－2f′(1)＋2.∴f′(1)＝1.∴f′(x)＝ x2－2x＋2.∴f′(2)＝22－2×2＋2＝2.答案 2114．过点 (2,0)且与曲线 y＝x相切的直线的方程为 ________．分析：设所求切线与曲线的切点为P(x0，y0)，∵ y′＝－12，∴ y′|x＝x0＝－12，所求切线的方程为x x01y－y0＝－(x－x0)．∵点 (2,0)在切线上，∴0－y0＝－12(2－x0)，∴ x20y0＝2－x0.① x0又∵ x0y0＝1，②x0＝1，由①②解得∴所求直线方程为x＋y－2＝0.y0＝1，答案 x＋y－2＝0.1 15．设函数 f(x)＝x m＋ax 的导数为 f′(x)＝2x＋1，则数列f n (n ∈N＋)的前 n 项和是 ________．m －1＋a＝2x＋1，得m＝2，分析： f′(x)＝mx a＝1.1 1 1 1则 f(x)＝x2＋x，f n ＝n n＋1＝n－n＋1，其和为1－1＋1－1＋1－1＋＋1－ 1 ＝1－ 1 ＝ n .1 2 2 3 3 4 n ＋n＋1 n＋1n 1答案nn＋116．已知函数 f(x)＝1mx2＋ lnx－2x 在定义域内是增函数，则实数 m 的2取值范围为 ________．1分析：依据题意，知 f′(x)＝mx＋x－2≥0 对全部 x>0 恒建立，∴m≥－1x2＋2x，令 g(x)＝－1x2＋2x＝－1x－1 2＋1，则当1x＝1 时，函数 g(x)获得最大值 1，故 m≥1.答案 [1，＋∞ )三、解答题 (本大题共 6 个小题，共 70 分．解答应写出文字说明、证明过程或演算步骤 )17．(10 分)已知函数 f(x) ＝13x3－4x＋m 在区间 (－∞，＋∞ )上有极大28值3 .(1)务实数 m 的值；(2)求函数 f(x) 在区间 (－∞，＋∞ )的极小值．解 f′(x) ＝x2－4＝(x＋2)(x－2)．令 f ′(x)＝0，得 x＝－ 2，或 x＝2.故 f(x) 的增区间 (－∞，－ 2)和(2，＋∞),减区间为 (－2,2)．(1)当 x＝－ 2，f(x) 获得极大值，8 28故 f( －2)＝－3＋8＋m＝3，∴ m＝4.(2)由(1)得 f(x) ＝13x3－4x＋4，4又当 x＝2 时， f(x) 有极小值 f(2)＝－3.18．(12 分) 已知函数f (x)x3bx 2 ax d 的图象过点P（0,2 ）, 且在点 M ( 1, f ( 1)) 处的切线方程为 6x y 7 0.(1) 求函数 y f (x) 的分析式；(2) 求函数 y f (x) 的单一区间 .解（Ⅰ）由 f ( x) 的图象经过 P （ 0， 2），知 d=2，因此 f ( x) x 3 bx 2cx 2, f ( x) 3x 2 2bx c. 由在 M ( 1, f ( 1)) 处的切线方程是 6x y7 0 知6f ( 1) 7 0,即 f ( 1) 1, f ( 1)6.3 2b c 6,即2b c 3, 解得 b c3.故所求的分析式是1 b c2 b c 0,1.f ( x) x 3 3x 23x 2.（ 2） f ( x) 3x 26x 3. 令 3x 2 6x 3 0,即 x 2 2x 10. 解得x 1 1 2, x 2 1 2. 当 x12,或 x 1 2时 , f ( x)0; 当12x 12时 , f ( x) 0. 故 f ( x) x 3 3x 23x 2在 (,12) 内是增函数，在 (12 ,12) 内是减函数，在 (12, ) 内是增函数 .19.(12 分) 已知函数 f (x)ax33(a 2) x 2 6x 32（1）当 a 2 时，求函数 f (x) 极小值；（2）试议论曲线 y f ( x) 与 x 轴公共点的个数解（1） a 2 时f '(x) 3ax23(a 2) x6 3a(x2)( x 1),2a由 f ( x) 0 得x 1或xa2 由 f ( x) 0 得x 1aaf ( x) 极小值为 f (1)2（）①若 a 0 ，则 f ( x)3(x2， f ( x) 的图像与 x 轴只有一个交点；2 1)②若 a 0 ，f ( x) 极大值为 f (1)a 0 ， Q f (x) 的极小值为 f ( 2)0，2af (x) 的图像与 x 轴有三个交点；③若 0 a 2 ，f (x)的图像与x 轴只有一个交点；④若 a 2 ，则 f ' ( x) 6( x 1)2 0 ， f ( x) 的图像与x轴只有一个交点；⑤若 a 2 ，由（ 1）知f ( x)的极大值为 f ( 2 ) 4( 1 3 ) 2 3 0 ， f ( x) 的图像a a 4 4与 x 轴只有一个交点；综上知，若 a 0, f ( x) 的图像与x轴只有一个交点；若 a 0 ，f ( x)的图像与 x 轴有三个交点。

高二数学导数及其应用综合检测综合测试题

第一章导数及其应用综合检测时间120分钟，满分150分。

一、选择题(本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．(2010·全国Ⅱ文，7)若曲线y＝x2＋ax＋b在点(0，b)处的切线方程是x－y＋1＝0，则( ) A．a＝1，b＝1 B．a＝－1，b＝1C．a＝1，b＝－1 D．a＝－1，b＝－1[答案] A [解析] y′＝2x＋a，∴y′|x＝0＝(2x ＋a)|x＝0＝a＝1，将(0，b)代入切线方程得b＝1.2．一物体的运动方程为s＝2t sin t＋t，则它的速度方程为( )A．v＝2sin t＋2t cos t＋1 B．v＝2sin t＋2t cos tC．v＝2sin t D．v＝2sin t＋2cos t＋1 [答案] A[解析] 因为变速运动在t0的瞬时速度就是路程函数y＝s(t)在t0的导数，S′＝2sin t＋2t cos t＋1，故选A.3．曲线y＝x2＋3x在点A(2,10)处的切线的斜率是( )A ．4B ．5C ．6D ．7[答案] D [解析] 由导数的几何意义知，曲线y ＝x 2＋3x 在点A (2,10)处的切线的斜率就是函数y ＝x 2＋3x 在x ＝2时的导数，y ′|x ＝2＝7，故选D.4．函数y ＝x |x (x －3)|＋1( )A ．极大值为f (2)＝5，极小值为f (0)＝1B ．极大值为f (2)＝5，极小值为f (3)＝1C ．极大值为f (2)＝5，极小值为f (0)＝f (3)＝1D ．极大值为f (2)＝5，极小值为f (3)＝1，f (－1)＝－3[答案] B[解析] y ＝x |x (x －3)|＋1＝⎩⎪⎨⎪⎧ x 3－3x 2＋1 (x <0或x >3)－x 3＋3x 2＋1 (0≤x ≤3) ∴y ′＝⎩⎪⎨⎪⎧ 3x 2－6x (x <0或x >3)－3x 2＋6x (0≤x ≤3)x 变化时，f ′(x )，f (x )变化情况如下表：f (x ) 无极值极大值5 极小值1 极大极小B.5．(2009·安徽理，9)已知函数f (x )在R 上满足f (x )＝2f (2－x )－x 2＋8x －8，则曲线y ＝f (x )在点(1，f (1))处的切线方程是( )A ．y ＝2x －1B ．y ＝xC ．y ＝3x －2D ．y ＝－2x ＋3[答案] A [解析] 本题考查函数解析式的求法、导数的几何意义及直线方程的点斜式．∵f (x )＝2f (2－x )－x 2＋8x －8，∴f (2－x )＝2f (x )－x 2－4x ＋4，∴f (x )＝x 2，∴f ′(x )＝2x ，∴曲线y ＝f (x )在点(1，f (1))处的切线斜率为2，切线方程为y －1＝2(x －1)，∴y ＝2x －1.6．函数f (x )＝x 3＋ax 2＋3x －9，已知f (x )在x ＝－3时取得极值，则a 等于( )A ．2B ．3C ．4D ．5[答案] D [解析] f ′(x )＝3x 2＋2ax ＋3，∵f (x )在x ＝－3时取得极值，∴x＝－3是方程3x2＋2ax＋3＝0的根，∴a＝5，故选D.7．设f(x)，g(x)分别是定义在R上的奇函数和偶函数．当x<0时，f′(x)g(x)＋f(x)g′(x)>0，且g(－3)＝0，则不等式f(x)g(x)<0的解集是( )A．(－3,0)∪(3，＋∞) B．(－3,0)∪(0,3) C．(－∞，－3)∪(3，＋∞) D．(－∞，－3)∪(0,3)[答案] D[解析] 令F(x)＝f(x)·g(x)，易知F(x)为奇函数，又当x<0时，f′(x)g(x)＋f(x)g′(x)>0，即F′(x)>0，知F(x)在(－∞，0)内单调递增，又F(x)为奇函数，所以F(x)在(0，＋∞)内也单调递增，且由奇函数知f(0)＝0，∴F(0)＝0.又由g(－3)＝0，知g(3)＝0 ∴F(－3)＝0，进而F(3)＝0于是F(x)＝f(x)g(x)的大致图象如图所示∴F(x)＝f(x)·g(x)<0的解集为(－∞，－3)∪(0,3)，故应选D.8．下面四图都是同一坐标系中某三次函数及其导函数的图象，其中一定不正确的序号是( )A．①② B．③④ C．①③ D．①④[答案] B [解析] ③不正确；导函数过原点，但三次函数在x＝0不存在极值；④不正确；三次函数先增后减再增，而导函数先负后正再负．故应选B.9．(2010·湖南理，5)⎠⎜⎛241xd x等于( )A．－2ln2 B．2ln2 C．－ln2 D．ln2[答案] D [解析] 因为(ln x)′＝1x，所以⎠⎜⎛241xdx＝ln x|42＝ln4－ln2＝ln2.10．已知三次函数f(x)＝13x3－(4m－1)x2＋(15m2－2m －7)x ＋2在x ∈(－∞，＋∞)是增函数，则m 的取值范围是( )A ．m <2或m >4B ．－4<m <－2C ．2<m <4D ．以上皆不正确[答案] D [解析] f ′(x )＝x 2－2(4m －1)x ＋15m 2－2m －7，由题意得x 2－2(4m －1)x ＋15m 2－2m －7≥0恒成立，∴Δ＝4(4m －1)2－4(15m 2－2m －7)＝64m 2－32m ＋4－60m 2＋8m ＋28＝4(m 2－6m ＋8)≤0，∴2≤m ≤4，故选D.11．已知f (x )＝x 3＋bx 2＋cx ＋d 在区间[－1,2]上是减函数，那么b ＋c ( )A ．有最大值152B ．有最大值－152C ．有最小值152D ．有最小值－152[答案] B[解析] 由题意f ′(x )＝3x 2＋2bx ＋c 在[－1,2]上，f ′(x )≤0恒成立．所以⎩⎪⎨⎪⎧ f ′(－1)≤0f ′(2)≤0即⎩⎪⎨⎪⎧ 2b －c －3≥04b ＋c ＋12≤0令b ＋c ＝z ，b ＝－c ＋z ，如图过A ⎝ ⎛⎭⎪⎫－6，－32得z 最大，最大值为b ＋c ＝－6－32＝－152.故应选B. 12．设f (x )、g (x )是定义域为R 的恒大于0的可导函数，且f ′(x )g (x )－f (x )g ′(x )<0，则当a <x f (b )g (b )B ．f (x )g (a )>f (a )g (x )C ．f (x )g (b )>f (b )g (x )D ．f (x )g (x )>f (a )g (x )[答案] C[解析] 令F (x )＝f (x )g (x )则F ′(x )＝f ′(x )g (x )－f (x )g ′(x )g 2(x )<0 f (x )、g (x )是定义域为R 恒大于零的实数∴F (x )在R 上为递减函数，当x ∈(a ，b )时，f (x )g (x )>f (b )g (b )∴f (x )g (b )>f (b )g (x )．故应选C.二、填空题(本大题共4个小题，每小题4分，共16分．将正确答案填在题中横线上)13.⎠⎜⎛－2－1d x(11＋5x )3＝________. [答案] 772 [解析] 取F (x )＝－110(5x ＋11)2，从而F ′(x )＝1(11＋5x )3 则⎠⎜⎛－2－1d x (11＋5x )3＝F (－1)－F (－2)＝－110×62＋110×12＝110－1360＝772. 14．若函数f (x )＝ax 2－1x的单调增区间为(0，＋∞)，则实数a 的取值范围是________．[答案] a ≥0[解析] f ′(x )＝⎝⎛⎭⎪⎫ax －1x ′＝a ＋1x 2，由题意得，a ＋1x 2≥0，对x ∈(0，＋∞)恒成立， ∴a ≥－1x 2，x ∈(0，＋∞)恒成立，∴a ≥0. 15．(2009·陕西理，16)设曲线y ＝x n ＋1(n ∈N *)在点(1,1)处的切线与x 轴的交点的横坐标为x n ，令a n ＝lg x n ，则a 1＋a 2＋…＋a 99的值为________．[答案] －2[解析] 本小题主要考查导数的几何意义和对数函数的有关性质． k ＝y ′|x ＝1＝n ＋1，∴切线l ：y －1＝(n ＋1)(x －1)，令y ＝0，x ＝nn ＋1，∴a n ＝lg nn ＋1，∴原式＝lg 12＋lg 23＋…＋lg 99100＝lg 12×23×…×99100＝lg 1100＝－2. 16．如图阴影部分是由曲线y ＝1x，y 2＝x 与直线x ＝2，y ＝0围成，则其面积为________．[答案] 23＋ln2[解析] 由⎩⎪⎨⎪⎧ y 2＝x ，y ＝1x ，得交点A (1,1)由⎩⎪⎨⎪⎧ x ＝2y ＝1x 得交点B ⎝⎛⎭⎪⎫2，12. 故所求面积S ＝⎠⎜⎛01x d x ＋⎠⎜⎛121x d x ＝23x 32| 10＋ln x | 21＝23＋ln2.三、解答题(本大题共6个小题，共74分．解答应写出文字说明、证明过程或演算步骤)17．(本题满分12分)(2010·江西理，19)设函数f (x )＝ln x ＋ln(2－x )＋ax (a >0)．(1)当a ＝1时，求f (x )的单调区间；(2)若f (x )在(0,1]上的最大值为12，求a 的值． [解析] 函数f (x )的定义域为(0,2)，f ′(x )＝1x －12－x＋a ， (1)当a ＝1时，f ′(x )＝－x 2＋2x (2－x )，所以f (x )的单调递增区间为(0，2)，单调递减区间为(2，2)；(2)当x ∈(0,1]时，f ′(x )＝2－2xx (2－x )＋a >0，即f (x )在(0,1]上单调递增，故f (x )在(0,1]上的最大值为f (1)＝a ，因此a ＝12.18．(本题满分12分)求曲线y ＝2x －x 2，y ＝2x 2－4x 所围成图形的面积．[解析] 由⎩⎪⎨⎪⎧y ＝2x －x 2，y ＝2x 2－4x 得x 1＝0，x 2＝2.由图可知，所求图形的面积为S ＝⎠⎜⎛02(2x －x 2)d x ＋|⎠⎜⎛02(2x 2－4x )d x |＝⎠⎜⎛02(2x －x 2)d x －⎠⎜⎛02(2x 2－4x )d x . 因为⎝⎛⎭⎪⎫x 2－13x 3′＝2x －x 2，⎝ ⎛⎭⎪⎫23x 3－2x 2′＝2x 2－4x ，所以S ＝⎝ ⎛⎭⎪⎫x 2－13x 3⎪⎪⎪⎪2－⎝ ⎛⎭⎪⎫23x 3－2x 2⎪⎪⎪⎪2＝4.19．(本题满分12分)设函数f (x )＝x 3－3ax ＋b (a ≠0)．(1)若曲线y ＝f (x )在点(2，f (2))处与直线y ＝8相切，求a ，b 的值；(2)求函数f (x )的单调区间与极值点．[分析] 考查利用导数研究函数的单调性，极值点的性质，以及分类讨论思想．[解析] (1)f ′(x )＝3x 2－3a .因为曲线y ＝f (x )在点(2，f (2))处与直线y ＝8相切，所以⎩⎪⎨⎪⎧f ′(2)＝0，f (2)＝8.即⎩⎪⎨⎪⎧3(4－a )＝0，8－6a ＋b ＝8.解得a ＝4，b ＝24.(2)f ′(x )＝3(x 2－a )(a ≠0)．当a <0时，f ′(x )>0，函数f (x )在(－∞，＋∞)上单调递增，此时函数f (x )没有极值点．当a >0时，由f ′(x )＝0得x ＝±a .当x ∈(－∞，－a )时，f ′(x )>0，函数f (x )单调递增；当x ∈(－a ，a )时，f ′(x )<0，函数f (x )单调递减；当x ∈(a ，＋∞)时，f ′(x )>0，函数f (x )单调递增．此时x ＝－a 是f (x )的极大值点，x ＝a 是f (x )的极小值点．20．(本题满分12分)已知函数f (x )＝12x 2＋ln x .(1)求函数f (x )的单调区间； (2)求证：当x >1时，12x 2＋ln x <23x 3.[解析] (1)依题意知函数的定义域为{x |x >0}， ∵f ′(x )＝x ＋1x，故f ′(x )>0，∴f (x )的单调增区间为(0，＋∞)． (2)设g (x )＝23x 3－12x 2－ln x ，∴g ′(x )＝2x 2－x －1x，∵当x >1时，g ′(x )＝(x －1)(2x 2＋x ＋1)x>0，∴g (x )在(1，＋∞)上为增函数，∴g (x )>g (1)＝16>0，∴当x >1时，12x 2＋ln x <23x 3.21．(本题满分12分)设函数f (x )＝x 3－92x 2＋6x －a .(1)对于任意实数x, f ′(x )≥m 恒成立，求m 的最大值；(2)若方程f (x )＝0有且仅有一个实根，求a 的取值范围．[分析] 本题主要考查导数的应用及转化思想，以及求参数的范围问题．[解析] (1)f ′(x )＝3x 2－9x ＋6＝3(x －1)(x －2)．因为x ∈(－∞，＋∞)．f ′(x )≥m ，即3x 2－9x ＋(6－m )≥0恒成立．所以Δ＝81－12(6－m )≤0，得m ≤－34，即m 的最大值为－34.(2)因为当x <1时，f ′(x )>0；当1<x <2时，f ′(x )<0；当x >2时f ′(x )>0.所以当x ＝1时，f (x )取极大值f (1)＝52－a ，当x ＝2时，f (x )取极小值f (2)＝2－a .故当f (2)>0或f (1)<0时，方程f (x )＝0仅有一个实根，解得a <2或a >52.22．(本题满分14分)已知函数f (x )＝－x 3＋ax 2＋1(a ∈R )．(1)若函数y ＝f (x )在区间⎝ ⎛⎭⎪⎫0，23上递增，在区间⎣⎢⎡⎭⎪⎫23，＋∞上递减，求a 的值； (2)当x ∈[0,1]时，设函数y ＝f (x )图象上任意一点处的切线的倾斜角为θ，若给定常数a ∈⎝ ⎛⎭⎪⎫32，＋∞，求θ的取值范围；(3)在(1)的条件下，是否存在实数m ，使得函数g (x )＝x 4－5x 3＋(2－m )x 2＋1(m ∈R )的图象与函数y ＝f (x )的图象恰有三个交点．若存在，请求出实数m 的值；若不存在，试说明理由．[解析] (1)依题意f ′⎝ ⎛⎭⎪⎫23＝0，由f ′(x )＝－3x 2＋2ax ，得－3⎝ ⎛⎭⎪⎫232＋2a ·23＝0，即a＝1.(2)当x ∈[0,1]时，tan θ＝f ′(x )＝－3x 2＋2ax ＝－3⎝⎛⎭⎪⎫x －a 32＋a 23.由a ∈⎝ ⎛⎭⎪⎫32，＋∞，得a 3∈⎝ ⎛⎭⎪⎫12，＋∞.①当a 3∈⎝ ⎛⎦⎥⎤12，1，即a ∈⎝ ⎛⎦⎥⎤32，3时，f ′(x )max ＝a 23，f (x )min ＝f ′(0)＝0.此时0≤tan θ≤a 23.②当a3∈(1，＋∞)，即a ∈(3，＋∞)时，f ′(x )max＝f ′(1)＝2a －3，f ′(x )min ＝f ′(0)＝0，此时，0≤tan θ≤2a －3.又∵θ∈[0，π)，∴当32<a ≤3时，θ∈⎣⎢⎡⎦⎥⎤0，arctan a 23，当a >3时，θ∈[0，arctan(2a －3)]．(3)函数y ＝f (x )与g (x )＝x 4－5x 3＋(2－m )x 2＋1(m ∈R )的图象恰有3个交点，等价于方程－x 3＋x 2＋1＝x 4－5x 3＋(2－m )x 2＋1恰有3个不等实根，∴x 4－4x 3＋(1－m )x 2＝0，显然x ＝0是其中一个根(二重根)，方程x 2－4x ＋(1－m )＝0有两个非零不等实根，则⎩⎪⎨⎪⎧Δ＝16－4(1－m )>01－m ≠0∴m >－3且m ≠1故当m>－3且m≠1时，函数y＝f(x)与y＝g(x)的图象恰有3个交点．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

导数及其应用综合检测
时间120分钟，满分150分。

一、选择题(本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)
1．(2010·全国Ⅱ文，7)若曲线y＝x2＋ax＋b在点(0，b)处的切线方程是x－y＋1＝0，则()
A．a＝1，b＝1B．a＝－1，b＝1
C．a＝1，b＝－1 D．a＝－1，b＝－1
2．一物体的运动方程为s＝2t sin t＋t，则它的速度方程为()
A．v＝2sin t＋2t cos t＋1 B．v＝2sin t＋2t cos t
C．v＝2sin t D．v＝2sin t＋2cos t＋1
3．曲线y＝x2＋3x在点A(2,10)处的切线的斜率是()
A．4 B．5 C．6 D．7
4．函数y＝x|x(x－3)|＋1()
A．极大值为f(2)＝5，极小值为f(0)＝1
B．极大值为f(2)＝5，极小值为f(3)＝1
C．极大值为f(2)＝5，极小值为f(0)＝f(3)＝1
D．极大值为f(2)＝5，极小值为f(3)＝1，f(－1)＝－3
5．(2009·安徽理，9)已知函数f(x)在R上满足f(x)＝2f(2－x)－x2＋8x－8，则曲线y＝f(x)在点(1，f(1))处的切线方程是()
A．y＝2x－1 B．y＝x C．y＝3x－2 D．y＝－2x＋3
6．函数f(x)＝x3＋ax2＋3x－9，已知f(x)在x＝－3时取得极值，则a等于() A．2 B．3 C．4 D．5
7．设f(x)，g(x)分别是定义在R上的奇函数和偶函数．当x<0时，f′(x)g(x)
＋f (x )g ′(x )>0，且g (－3)＝0，则不等式f (x )g (x )<0的解集是( )
A ．(－3,0)∪(3，＋∞)
B ．(－3,0)∪(0,3)
C ．(－∞，－3)∪(3，＋∞)
D ．(－∞，－3)∪(0,3)
8．下面四图都是同一坐标系中某三次函数及其导函数的图象，其中一定不正确的序号是( )
A ．①②
B ．③④
C ．①③
D ．①④
9．(2010·湖南理，5)⎠⎛2
4
1x d x 等于( ) A ．－2ln2 B ．2ln2 C ．－ln2 D ．ln2
10．已知三次函数f (x )＝13x 3－(4m －1)x 2＋(15m 2－2m －7)x ＋2在x ∈(－∞，
＋∞)是增函数，则m 的取值范围是( )
A ．m <2或m >4
B ．－4<m <－2
C ．2<m <4
D ．以上皆不正确
11．已知f (x )＝x 3＋bx 2＋cx ＋d 在区间[－1,2]上是减函数，那么b ＋c ( )
A ．有最大值152
B ．有最大值－152
C ．有最小值152
D ．有最小值－152
12．设f (x )、g (x )是定义域为R 的恒大于0的可导函数，
且f ′(x )g (x )－f (x )g ′(x )<0，则当a <x f (b )g (b )
B ．f (x )g (a )>f (a )g (x )
C ．f (x )g (b )>f (b )g (x )
D ．f (x )g (x )>f (a )g (x )
二、填空题(
本大题共4个小题，每小题4分，共16分．将正确答案填在题中横线上)
13.⎠⎜⎛－2
－1d x (11＋5x )3＝________.
14．若函数f (x )＝ax 2－1x 的单调增区间为(0，＋∞)，则实数a 的取值范
围是________．
15．(2009·陕西理，16)设曲线y ＝x n ＋1(n ∈N *)在点(1,1)处的切线与x 轴的
交点的横坐标为x n ，令a n ＝lg x n ，则a 1＋a 2＋…＋a 99的值为________．
16．如图阴影部分是由曲线y ＝1x ，y 2＝x 与直线x ＝2，y ＝0围成，则其
面积为________．
三、解答题(本大题共6个小题，共74分．解答应写出文字说明、证明过程或演算步骤)
17．(本题满分12分)(2010·江西理，19)设函数f (x )＝ln x ＋ln(2－x )＋ax (a >0)．
(1)当a ＝1时，求f (x )的单调区间；
(2)若f (x )在(0,1]上的最大值为12，求a 的值．
18．(本题满分12分)求曲线y ＝2x －x 2，y ＝2x 2－4x 所围成图形的面积．
19．(本题满分12分)设函数f (x )＝x 3－3ax ＋b (a ≠0)．
(1)若曲线y ＝f (x )在点(2，f (2))处与直线y ＝8相切，求a ，b 的值；
(2)求函数f (x )的单调区间与极值点．
20．(本题满分12分)已知函数f (x )＝12x 2＋ln x .
(1)求函数f (x )的单调区间；
(2)求证：当x >1时，12x 2＋ln x <23x 3.
21．(本题满分12分)设函数f (x )＝x 3－92x 2＋6x －a .
(1)对于任意实数x, f ′(x )≥m 恒成立，求m 的最大值；
(2)若方程f (x )＝0有且仅有一个实根，求a 的取值范围．
22．(本题满分14分)已知函数f (x )＝－x 3＋ax 2＋1(a ∈R )．
(1)若函数y ＝f (x )在区间⎝ ⎛⎭⎪⎫0，23上递增，在区间⎣⎢⎡⎭
⎪⎫23，＋∞上递减，求a 的值； (2)当x ∈[0,1]时，设函数y ＝f (x )图象上任意一点处的切线的倾斜角为θ，若
给定常数a ∈⎝ ⎛⎭
⎪⎫32，＋∞，求θ的取值范围； (3)在(1)的条件下，是否存在实数m ，使得函数g (x )＝x 4－5x 3＋(2－m )x 2＋1(m ∈R )的图象与函数y ＝f (x )的图象恰有三个交点．若存在，请求出实数m 的值；若不存在，试说明理由．。