全等三角形证明题培优提高经典例题练习题

合集下载

全等三角形培优(含答案)

全等三角形培优(含答案)1.已知三角形ABC中，AB=4，AC=2，D为BC中点，AD为整数，求AD。

2.已知四边形BCDE中，BC=DE，∠B=∠E，∠C=∠D，F为CD中点，证明∠1=∠2.3.已知三角形ABC中，∠1=∠2，CD=DE，EF//AB，证明EF=AC。

4.已知三角形ABC中，AD平分∠BAC，AC=AB+BD，证明∠B=2∠C。

6.如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上。

证明BC=AB+DC。

7.已知AB=CD，∠A=∠D，证明∠B=∠C。

8.P为∠BAC平分线上一点，AC>AB，证明PC-PB<AC-AB。

9.已知在三角形ABC中，E为AB中点，AF=BD，BD=5，AC=7，求DC。

10.如图，已知AD∥BC，∠PAB的平分线与∠CBA的平分线相交于E，CE的连线交AP于D，证明AD+BC=AB。

11.如图，△ABC中，AD为∠CAB的平分线，且AB=AC+CD，证明∠C=2∠B。

12.如图，AE、BC交于点M，F点在AM上，BE∥CF，BE=CF，证明AM是△ABC的中线。

13.已知三角形ABC中，AB=AC，BD⊥AC，CE⊥AB，垂足分别为D、E，BD、CE相交于点F，证明BE=CD。

14.在直角三角形ABC中，AC=BC，直线MN经过点C，且AD⊥XXX于D，BE⊥XXX于E。

当直线MN绕点C旋转到图1的位置时，证明：①△ADC≌△CEB；②DE=AD+BE。

当直线MN绕点C旋转到图2的位置时，①中的结论不成立。

15.如图所示，已知AE⊥AB，AF⊥AC，AE=AB，AF=AC。

证明：（1）EC=BF；（2）EC⊥BF。

16.如图，已知AC∥BD，EA、EB分别平分∠CAB和∠DBA，CD过点E，不能证明AB与AC+BD相等。

17.如图，△ABC是等腰直角三角形，∠ACB=90°，AD是BC边上的中线，过C作CE垂直于AB交于E，证明AE=BE。

人教版八年级数学上册三角形全等的证明培优综合训练(含答案)

人教版八年级数学上册三角形全等的证明培优综合训练（含答案）考点1 利用SSS求证三角形全等1．如图，点B，F，C，E在同一条直线上，点A，D在直线BC的异侧，AB＝DE，AC＝DF，BF＝EC．（1）求证：△ABC≌△DEF；（2）若∠BFD＝150°，求∠ACB的度数．2．如图，C是AB的中点，AD=CE，CD=BE．求证：(1)△DCA≌△EBC；(2)AD//CE．3．已知：如图，已知线段AB、CD相交于点O、AD、CB的延长线交于点E、OA=OC、EA=EC，求证：∠A=∠C、考点2 利用SAS求证三角形全等4．如图，在△ABC和△DEF中，点B、F、C、E在同一直线上，AB=DE，BF=CE，AB‖DE，求证：△ABC≅△DEF．5．在△ABC中,AD为边BC上的中线,延长AD到点E,使DE=AD,连接BE.△ABC的面积与△ABE的面积相等吗?说明理由6．两组邻边分别相等的四边形我们称它为筝形，如图，在筝形ABCD中，AB＝AD，BC ＝DC，AC，BD相交于点O．(1)求证：①△ABC≌△ADC；②OB＝OD，AC⊥BD；(2)如果AC＝6，BD＝4，求筝形ABCD的面积．考点3 利用AAS 或ASA 求证三角形全等7．已知：在ABC 中，90BAC ∠=︒，AB AC =，直线m 经过点A ，BD ⊥直线m ，CE ⊥直线m ，垂足分别为点D 、E ．（1）证明：BDA AEC ≌；（2）3BD =，4CE =，求DE 的长．8．如图，已知AD 为ABC ∆的中线，延长AD ，分别过点B ，C 作BE AD ⊥，CF AD ⊥．求证：BED CFD ∆≅∆．9．如右图，已知,90AB AC BAC BE CE =∠=︒,⊥于点E ，延长BE CA 、相交于点F ，求证：ADC AFB ≌10．如图，已知E 、F 在AC 上，AD //CB ，且∠D=∠B ，AE=CF ．求证：DF=BE ．考点4 利用HL 求证三角形全等11．在ABC 中，AB CB =，90ABC ∠=︒，F 为AB 延长线上一点，点E 在BC 上，且AE CF =．（1）求证：ABE CBF ≌；（2）若30CAE ∠=︒，求ACF ∠度数．12．如图，已知AE =DE ，AB ⊥BC ，DC ⊥BC ，且AB =EC ．求证：BC =AB ＋DC ．13．如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD．（1）证明：Rt△BCE≌Rt△DCF；（2）若AB=21，AD=9，求AE的长．14．如图：AD是ABC的高，E为AC上一点，BE交AD于F，且有BF＝AC，FD＝CD、求 .证：BE AC考点5 全等三角形综合15．已知点P为∠EAF平分线上一点，PB⊥AE于B，PC⊥AF于C，点M、N分别是射线AE、AF上的点，(1)如图1，当点M在线段AB上，点N在线段AC的延长线上，且PM=PN，求证：BM=CN；(2)在(1)的条件下，直接写出线段AM、CN与AC之间的数量关系_______．(3)如图2，当点M在线段AB的延长线上，点N在线段AC上时，∠MAN+MPN=180°，若AC：PC=2：1，PC=4，求四边形ANPM的面积．16．如图，在平面直角坐标系中，A、B坐标为（6，0）、（0，6），P为线段AB上的一点．（1）如图1，若P为AB的中点，点M、N分别是OA、OB边上的动点，且保持AM＝ON，则在点M、N运动的过程中，探究线段PM、PN之间的位置关系与数量关系，并说明理由．（2）如图2，若P为线段AB上异于A、B的任意一点，过B点作BD⊥OP，交OP、OA分别于F、D两点，E为OA上一点，且∠PEA＝∠BDO，试判断线段OD与AE的数量关系，并说明理由．答案1．解：（1）证明：BF EC =∵，BF FC EC FC ∴+=+，BC EF ∴=，在ABC ∆和DEF ∆中，AB DE AC DF BC EF =⎧⎪=⎨⎪=⎩，()ABC DEF SSS ≅∆∆∴；（2）150BFD ∠=︒，180BFD DFE ∠+∠=︒， 30DFE ∴∠=︒，由（1）知，ABC DEF ∆≅∆，ACB DFE ∴∠=∠，30ACB ∴∠=︒．2.（1）证明：点C 是AB 的中点，AC BC ∴=；在DCA ∆与EBC ∆中，AD CE CD BE AC BC =⎧⎪=⎨⎪=⎩，()DCA EBC SSS ∴∆≅∆，（2）证明：DCA EBC ∆≅∆，A BCE ∴∠=∠，//AD CE ∴．3.如图，连结OE在、OEA 和、OEC 中OA OC EA EC OE OE =⎧⎪=⎨⎪=⎩、、OEA、、OEC （SSS ）、、A ＝、C （全等三角形的对应角相等）4.∵BF=CE ，∴BF+FC=CE+FC ，即BC=EF ．∵AB ∥DE ，∴∠B=∠E ．在△ABC 和△DEF 中AB DE B E BC EF =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△DEF （SAS ）5.△ABC 与△ABE 的面积相等．理由：∵AD 为边BC 上的中线，∴BD=CD ，在△BDE 和△CAD 中，BD DC BDE CDA DE AD =⎧⎪∠=∠⎨⎪=⎩，∴△BDE ≌△CAD、SAS、，BDE ABD CAD ABD S S S S +=+，即△ABC 与△ABE 的面积相等．6.(1)证明：①在△ABC 和△ADC 中，AB=AD ，BC=DC ，AC=AC ，∴△ABC ≌△ADC （SSS ）.②∵△ABC ≌△ADC ，∴∠BAO=∠DAO.∵AB=AD ，∠BAO=∠DAO ，OA=OA ，∴△ABO ≌△ADO （SAS ）.∴OB=OD ，AC ⊥BD.(2)筝形ABCD 的面积=△ABC 的面积+△ACD 的面积=12×AC×BO+12×AC×DO=12×AC×(BO+DO)=12×AC×BD=12×6×4=12. 7.（1）证明：∵BD m ⊥，CE m ⊥，∴90ADB CEA ∠=∠=︒，∴90ABD BAD ∠+∠=︒，∵AB AC ⊥，∴90BAD CAE ∠+∠=︒，∴ABD CAE ∠=∠，在BDA 和AEC 中，90ADB CEA ABD CAEAB AC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩， ∴()BDA AEC AAS ≅；（2）∵BDA AEC ≅△△，∴BD AE =，AD CE =，∴7DE DA AE BD CE =+=+=．8.证明：∵AD 是△ABC 的中线，∴ BD ＝CD ，∵ BE ⊥AD ，CF ⊥AD ，∴∠E ＝∠CFD ＝90°在Rt △BDE 和Rt △CDF 中，90BDE CDF E CFD BD CD ∠=∠⎧⎪∠=∠=⎨⎪=⎩，∴ Rt △BDE ≌Rt △CDF （AA S ）9.、、BAC=90°，、、BAF=180°-、BAC=90°，、、BAF=、CAD ，、F+、ABF=90°，∵CE ⊥BE ，、、CEF=90°，、、F+、ACD=90°，、、ABF=、ACD ，在、ADC 和、AFB 中，BAF CAD AC ABACD ABF ∠=∠⎧⎪=⎨⎪∠=∠⎩，、、ADC ≌、AFB （ASA ）．10.解：证明：∵AE=CF ，∴AE -EF=CF -EF即AF=CE ，∵AD ∥CB ，∴∠A=∠C ，在△ADF 和△CBE 中，A C AF CE DB ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ADF ≌△CBE （ASA ），∴DF=BE ．11.（1）证明：∵∠ABC=90°，∴∠CBF=∠ABE=90°，在Rt △ABE 和Rt △CBF 中，AE CF AB BC=⎧⎨=⎩， ∴Rt △ABE ≌Rt △CBF （HL ）；（2）解：∵AB=BC ，∠ABC=90°，∴∠CAB=∠ACB=45°，又∵∠BAE=∠CAB -∠CAE=45°-30°=15°，由（1）知：Rt △ABE ≌Rt △CBF ，∴∠BCF=∠BAE=15°，∴∠ACF=∠BCF+∠ACB=15°+45°=60°．12.∵AB ⊥BC ，DC ⊥BC ，∴∠B=∠C=90°，在Rt △AEB 和Rt △EDC 中，AB EC AE DE =⎧⎨=⎩， ∴Rt △AEB ≌Rt △EDC （HL ），∴DC=BE ，∵BC=BE+CE ，∴AB+DC=BC ．13.（1）∵AC 平分∠BAD ，CE ⊥AB 于E ，CF ⊥AD 于F ， ∴CF=CE ，∠DFC=∠BEC=90°，在Rt △BCE 和Rt △DCF 中，CE CF BC CD =⎧⎨=⎩， ∴Rt △BCE ≌Rt △DCF （HL ）；（2）∵AC 平分∠BAD ，CE ⊥AB 于E ，CF ⊥AD 于F ， ∴CF=CE ，∠CFA=∠CEA=90°，在Rt △AFC 和Rt △AEC 中，CF CE AC AC =⎧⎨=⎩，∴Rt △AFC ≌Rt △AEC （HL ），∴AF=AE ，由（1）知Rt △BCE ≌Rt △DCF ，则BE=DF ，∵AB=21，AD=9，∴AB=AE+EB=AF+EB=AD+DF+ DF =AD+2DF=9+2DF=21，解得，DF=6，∴AE=AF=AD+DF=9+6=15，即AE 的长是15．14.证明： ∵AD ⊥BC ，∴∠BDF ＝∠ADC ＝90°．又∵BF ＝AC ，FD ＝CD ，∴△RtADC ≌Rt △BDF （HL ）．∴∠EBC ＝∠DAC ．又∵∠DAC ＋∠ACD ＝90°，∴∠EBC ＋∠ACD ＝90°．∴BE ⊥AC ．15.（1）证明：点P 为EAF ∠平分线上一点，PB AE ⊥于B ，PC AF ⊥于C ， PB PC ∴=，在Rt PBM ∆和Rt PCN ∆中，PB PC PM PN =⎧⎨=⎩， Rt PBM Rt PCN ∴∆≅∆，BM CN ∴=；（2）AM CN AC +=，理由如下：在Rt PBA ∆和Rt PCA ∆中，PB PC AP AP =⎧⎨=⎩， Rt PBA Rt PCA ∴∆≅∆，AB AC ∴=，AM CN AM BM AB AC ∴+=+==，故答案为：AM CN AC +=；（3）:2:1AC PC =，4PC =，8AC ∴=，PB AE ⊥，PC AF ⊥，90ABP ACP ∴∠=∠=︒，180MAN BPC ∴∠+∠=︒，又180MAN MPN ∠+∠=︒， MPB NPC ∴∠=∠，在PBM ∆和PCN ∆中，BPM CPN PB PCPBM PCN ∠=∠⎧⎪=⎨⎪∠=∠⎩， PBM PCN ∴∆≅∆，∴四边形ANPM 的面积=四边形ABPC 的面积1842322=⨯⨯⨯=． 16.解：（1）结论：PM ＝PN ，PM ⊥PN ．理由如下：如图1中，连接OP ．∵A 、B 坐标为（6，0）、（0，6），∴OB ＝OA ＝6，∠AOB ＝90°，∵P为AB的中点，∴OP＝12AB＝PB＝P A，OP⊥AB，∠PON＝∠P AM＝45°，∴∠OP A＝90°，在△PON和△P AM中，ON AMPON PAMOP AP=⎧⎪∠=∠⎨⎪=⎩，∴△PON≌△P AM（SAS），∴PN＝PM，∠OPN＝∠APM，∴∠NPM＝∠OP A＝90°，∴PM⊥PN，PM＝PN．（2）结论：OD＝AE．理由如下：如图2中，作AG⊥x轴交OP的延长线于G．∵BD⊥OP，∴∠OAG＝∠BOD＝∠OFD＝90°，∴∠ODF+∠AOG＝90°，∠ODF+∠OBD＝90°，∴∠AOG＝∠DBO，∵OB＝OA，∴△DBO≌△GOA，∴OD＝AG，∠BDO＝∠G，∵∠BDO＝∠PEA，∴∠G＝∠AEP，在△P AE和△P AG中，AEP GPAE PAGAP AP∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△P AE≌△P AG（AAS），∴AE＝AG，∴OD＝AE．。

成都市第三十七中学八年级数学上册第十二章《全等三角形》经典测试(提高培优)

一、选择题1．如图，△ABC ≌△ADE ，AB ＝AD ，AC ＝AE ，∠B ＝28︒，∠E ＝95︒，∠EAB ＝20︒，则∠BAD 等于（）A ．75︒B ．57︒C ．55︒D ．77︒2．如图，△ACB ≌△A′C B′，∠ACB ＝70°，∠ACB′＝100°，则∠BCA′度数是（）A ．40°B ．35C ．30°D ．45°3．如图，在ABC 中，AB AC =，点D ，E 在BC 上，连接AD ，AE ，若只添加一个条件使DAB EAC ∠=∠，则添加的条件不能为（）A ．BD CE =B ．AD AE =C ．BE CD = D ．DA DE = 4．如图，在ABC 和AEF 中，EAC BAF ∠=∠，EA BA =，添加下面的条件：①EAF BAC ∠=∠；②E B ∠=∠；③AF AC =；④EF BC =，其中可以得到ABC AEF ≌△△的有（）个．A ．1B ．2C ．3D ．45．下列说法正确的（）个．①0.09的算术平方根是0.03；②1的立方根是±1；③3.1＜10＜3.2；④两边及一角分别相等的两个三角形全等．A ．0B ．1C ．2D ．36．如图所示，已知AB ∥CD ，BAC ∠与ACD ∠的平分线交于点O ，OE AC ⊥于点E ，且3OE cm =，则点O 到AB ，CD 的距离之和是（）A ．3cmB ．6cmC ．9cmD ．12cm7．如图，AB AC =，AD AE =，55A ︒∠=，35C ︒∠=，则DOE ∠的度数是（）A ．105︒B ．115︒C ．125︒D ．130︒8．下列说法正确的是（）①近似数232.610⨯精确到十分位；②在2，()2--，38-，2--中，最小的是38-；③如图所示，在数轴上点P 所表示的数为15-+；④用反证法证明命题“一个三角形最多有一个钝角”时，首先应假设“这个三角形中有两个钝角”；⑤如图，在ABC 内一点P 到这三条边的距离相等，则点P 是三个角平分线的交点．A ．1B ．2C ．3D ．49．下列说法不正确的是（）A ．三边分别相等的两个三角形全等B ．有两边及一角对应相等的两个三角形全等C ．有两角及一边对应相等的两个三角形全等D ．斜边和一条直角边分别相等的两个直角三角形全等10．下列各命题中，假命题是（）A ．有两边及其中一边上的中线对应相等的两个三角形全等B ．有两边及第三边上高对应相等的两个三角形全等C ．有两角及其中一角的平分线对应相等的两三角形全等D ．有两边及第三边上的中线对应相等的两三角形全等11．如图，已知△ABC 的周长是20，OB ，OC 分别平分∠ABC 和∠ACB ，OD ⊥BC 于，且OD=2，△ABC 的面积是（）A ．20B ．24C ．32D ．4012．如图，点D 在线段BC 上，若1802ACE ABC x ∠=︒-∠-︒，且BC DE =，AC DC =，AB EC =，则下列角中，大小为x ︒的角是( )A ．EFC ∠B ．ABC ∠ C ．FDC ∠D ．DFC ∠ 13．如图，在△ABC 中，点E 和F 分别是AC ，BC 上一点，EF ∥AB ，∠BCA 的平分线交AB 于点D ，∠MAC 是△ABC 的外角，若∠MAC ＝α，∠EFC ＝β，∠ADC ＝γ，则α、β、γ三者间的数量关系是（）A ．β＝α+γB ．β＝2γ﹣αC ．β＝α+2γD ．β＝2α﹣2γ 14．如图，AB ＝4cm ，AC ＝BD ＝3cm ，∠CAB ＝∠DBA ，点P 在线段AB 上以1cm/s 的速度由点A 向点B 运动，同时，点Q 在线段BD 上由点B 向点D 运动．设运动时间为t （s ），当△ACP 与△BPQ 全等时，则点Q 的运动速度为（）cm/s ．A ．0.5B ．1C ．0.5或1.5D ．1或1.5 15．如图，在下列条件中，不能判断△ABD ≌△BAC 的条件是（）A ．∠D=∠C ， ∠BAD=∠ABCB ．BD=AC ， ∠BAD=∠ABC C ．∠BAD=∠ABC ， ∠BAD=∠ABCD ．AD=BC ，BD=AC二、填空题16．如图，AC=BC ，请你添加一个条件，使AE=BD ．你添加的条件是：________．17．如图，在Rt ABC △中，90C ∠=︒，AD 平分BAC ∠交BC 于点D ．若3BC =，且:5:4BD DC =，5AB =，则ABD △的面积是______．18．如图，ABC 中，D 是AB 上的一点，DF 交AC 于点E ，AE CE =，//CF AB ，若四边形DBCF 的面积是26cm ，则ABC 的面积为______2cm ．19．如图，△ABC ≌△DEF ，由图中提供的信息，可得∠D ＝__________°．20．如图，AC AE =，AD AB =，90ACB DAB ∠=∠=︒，33BAE ∠=︒，//CB AE ，AC 与DE 相交于点F ．（1）DAC ∠=______．（2）当1AF =时，BC 的长为______．21．如图，在△ABC 中，∠ABC 的平分线与外角∠ACE 的平分线交于点D ，若∠D ＝20°，则∠A ＝_____．22．如图，ABC ADE ≅，延长BC ，分别交AD ，ED 于点F ，G ，若120EAB ∠=︒，30B ∠=︒，10CAD ∠=︒，则CFD ∠=________︒．23．如图，ABC 中，∠C ＝90°，AD 平分∠BAC ， AB ＝5，CD ＝2，则ABD △的面积是______24．如图，在四边形ABCD 中，90A ∠=︒，3AD =，连接BD ，BD CD ⊥，BD 平分ABC ∠．若P 是BC 边上一动点，则DP 长的最小值为______．25．如图，AB ＝8cm ，AC ＝5cm ，∠A ＝∠B ，点P 在线段AB 上以2cm/s 的速度由点A 向B 运动，同时，点Q 以x cm/s 的速度从点B 出发在射线BD 上运动，则△ACP 与△BPQ 全等时，x 的值为_____________26．如图，在ABC 中，AD 平分BAC ∠，P 为线段AD 上的一个动点，PE AD ⊥交直线BC 于点E ．若35B ∠=︒，85ACB ∠=︒，则E ∠的度数为______．三、解答题27．如图，CB 为ACE ∠的角平分线，F 是线段CB 上一点，,CA CF B E =∠=∠，延长EF 与线段AC 相交于点D ．（1）求证：AB FE =；（2）若,//ED AC AB CE ⊥，求A ∠的度数．28．如图，AB CB ⊥，DC CB ⊥，点E 、F 在BC 上，BE CF =，再添加一个什么条件后可推出AF DE =，写出添加的条件并完成证明．29．作图：已知ABC 和线段r ，请在ABC 内部作点P ，使得点P 到AC 和BC 的距离相等，并且点A 到点P 的距离等于定长r ．（不写作法，保留痕迹）30．如图1，在平面内取一个定点O ，自O 引一条射线O x ，设M 是平面内一点，点O 与点M 的距离为m （m ＞0）, 以射线O x 为始边，射线OM 为终边的∠x OM 的度数为x °（x≥0）．那么我们规定用有序数对（m ，x °）表示点M 在平面内的位置，并记为M （m ，x °）．例如，在如图2中，如果OG=4，∠x OG=120°，那么点G 在平面内的位置记为G （4，120°）．（1）如图3，如果点N 在平面内的位置记为N （6，35°），那么ON= ；xON ∠= °；（2）如图4，点A ，点B 在射线O x 上，点A ，B 在平面内的位置分别记为（a ，0°）,（2a，0°）点A，E，C在同一条直线上. 且OE=BC．用等式表示∠OEA与∠ACB之间的数量关系，并证明．。

全等三角形的证明及计算大题专项训练(30道)(含答案)

全等三角形的证明及计算大题专项训练（30道）考卷信息：本套训练卷共30题，培优篇15题，拔尖篇15题，题型针对性较高，覆盖面广，选题有深度，可深化学生对全等三角形工具的应用及构造全等三角形！1．（2021春•道里区期末）如图，点A ，C 在EF 上，AD ∥BC ，DE ∥BF ，AE ＝CF ．（1）求证：△ADE ≌△CBF ；（2）直接写出图中所有相等的线段（AE ＝CF 除外）．【解题思路】（1）利用ASA 证明△ADE ≌△CBF 即可；（2）根据△ADE ≌△CBF 即可得图中所有相等的线段．【解答过程】（1）证明：∵AD ∥BC∴∠DAC ＝∠BCA ，又∵∠DAC +∠EAD ＝180°，∠BCA +∠FCB ＝180°，∴∠EAD ＝∠FCB ，∵DE ∥BF ，∴∠E ＝∠F ，在△ADE 和△CBF 中，{∠EAD =∠FCB AE =CF ∠E =∠F，∴△ADE ≌△CBF （ASA ），（2）∵△ADE ≌△CBF ，∴ED ＝FB ，DA ＝BC ，EC ＝F A ．∵AD ∥BC ，∴∠DAC ＝∠BCA ，在△ADC 和△CBA 中，{AD =CB ∠DAC =∠CBA AC =CA，∴△ADC ≌△CBA （SAS ），∴AB ＝CD ；∴图中所有相等的线段有：ED ＝FB ，DA ＝BC ，AB ＝CD ，EC ＝F A ．2．（2021春•宁德期末）如图，AB ，CD 交于点O ，AC ＝DB ，∠ACD ＝∠DBA ．（1）说明△AOC ≌△DOB 的理由；（2）若∠ACD ＝94°，∠CAO ＝28°，求∠OCB 的度数．【解题思路】（1）直接利用AAS 即可证明△AOC ≌△DOB ；（2）利用三角形外角的性质得到∠COB ，再根据△AOC ≌△DOB 得到OC ＝OB ，即可求得∠OCB ．【解答过程】解：（1）在△AOC 和△DOB 中，{∠AOC =∠DOB ∠ACO =∠DBO AC =DB，∴△AOC ≌△DOB （AAS ）；（2）∵∠ACD ＝94°，∠CAO ＝28°，∴∠COB ＝∠ACD +∠CAO ＝122°，∵△AOC ≌△DOB ，∴OC ＝OB ，∴∠OCB ＝（180°﹣122°）÷2＝29°．3．（2021春•沙坪坝区校级期末）如图，在△ABC 中，AC ＝BC ，点D 在AB 边上，点E 在BC 边上，连接CD ，DE ．已知∠ACD ＝∠BDE ，CD ＝DE ．（1）猜想AC 与BD 的数量关系，并证明你的猜想；（2）若AD ＝3，BD ＝5，求CE 的长．【解题思路】（1）利用AAS 证明△ADC ≌△BED ，即可得结论；（2）结合△ADC ≌△BED ，可得AC ＝BD ＝5，BE ＝AD ＝3，进而可得CE 的长．【解答过程】解：（1）AC ＝BD ，理由如下：∵AC ＝BC ，∴∠A ＝∠B ，在△ADC 和△BED 中，{∠A =∠B ∠ACD =∠BED CD =DE，∴△ADC ≌△BED （AAS ），∴AC ＝BD ；（2）由（1）知：△ADC ≌△BED ，∴AC ＝BD ＝5，BE ＝AD ＝3，∴BC ＝AC ＝5，∴CE ＝BC ﹣BE ＝2．4．（2021春•渝中区校级期末）如图，点E 在△ABC 的边AC 上，且∠ABE ＝∠C ，AF 平分∠BAE 交BE 于F ，FD ∥BC 交AC 于点D ．（1）求证：△ABF ≌△ADF ；（2）若BE ＝7，AB ＝8，AE ＝5，求△EFD 的周长．【解题思路】（1）根据平行线的性质得到∠ADF ＝∠C ，等量代换得到∠ABF ＝∠ADF ，由角平分线的定义得到∠BAF ＝∠CAF ，根据全等三角形的判定定理即可得到结论；（2）根据全等三角形的性质得到AD ＝AB ＝8，BF ＝DF ，由线段的和差得到DE ＝AD ＝AE ＝8﹣5＝3，根据三角形的周长公式即可得到结论．【解答过程】解：（1）∵FD ∥BC ，∴∠ADF ＝∠C ，∵∠ABF ＝∠C ，∴∠ABF ＝∠ADF ，∵AF 平分∠BAE ，∴∠BAF ＝∠CAF ，在△ABF 和△ADF 中，{∠BAF =∠DAF ∠ABF =∠ADF AF =AF，∴△ABF ≌△ADF （AAS ）；（2）∵△ABF ≌△ADF ，∴AD ＝AB ＝8，BF ＝DF ，∵AE ＝5，∴DE ＝AD ﹣AE ＝8﹣5＝3，∴△EFD 的周长＝EF +DF +DE ＝EF +BF +DE ＝BE +DE ＝7+3＝10．5．（2021春•北碚区校级期末）如图，已知D 是AC 上一点，AB ＝DA ，AB +DC ＝ED ，AE ＝BC ．（1）求证：△ABC ≌△DAE ，（2）若∠BAE ＝125°，求∠DCB 的度数．【解题思路】（1）根据SSS 证明三角形全等即可．（2）利用全等三角形的性质以及三角形内角和定理求解即可．【解答过程】（1）证明：∵DE ＝AB +DC ，AB ＝AD ，∴DE ＝AD +DC ＝AC ，在△ABC 和△DAE 中，{AB =AD AC =DE BA =AE，∴△ABC ≌△DAE （SSS ）．（2）解：∵△ABC ≌△DAE ，∴∠EAD ＝∠B ，∴∠B +∠BAC ＝∠EAD +∠BAC ＝∠EAB ＝125°，∴∠DCB ＝180°﹣（∠B +∠BAC ）＝180°﹣125°＝55°．6．（2021春•莱芜区期末）如图，已知AD 、BC 相交于点O ，AB ＝CD ，AM ⊥BC 于点M ，DN ⊥BC 于点N ，BN ＝CM ．（1）求证：△ABM ≌△DCN ；（2）试猜想OA 与OD 的大小关系，并说明理由．【解题思路】（1）根据HL 可证明：△ABM ≌△DCN ；（2）根据AAS 证明△AMO ≌△DNO 可得结论．【解答过程】（1）证明：∵BN ＝CM ，∴BN +MN ＝MN +CM ，即CN ＝BM ，∵AM ⊥BC 于点M ，DN ⊥BC 于点N ，∴∠AMB ＝∠DNC ＝90°，在Rt △ABM 和Rt △DCN 中，{AB =CD BM =CN， ∴Rt △ABM ≌Rt △DCN （HL ）；（2）解：OA ＝OD ，理由如下：∵Rt △ABM ≌Rt △DCN ，∴AM ＝DN ，在△AMO 和△DNO 中，{∠AOM =∠DNO ∠AMO =∠DNO AM =DN，∴△AMO ≌△DNO （AAS ），∴OA ＝OD ．7．（2021春•静安区期末）如图，已知四边形ABCD 中，AB ∥CD ，AD ∥BC ．E 为BD 上一点，且BE ＝AD ，∠DEF ＝∠ADC ，EF 交BC 的延长线于点F ．（1）AD 和BC 相等吗？为什么？（2）BF 和BD 相等吗？为什么？【解题思路】（1）根据平行线的性质和全等三角形的判定和性质得出△ABD 与△CDB 全等，进而利用全等三角形的性质解答即可；（2）根据平行线的性质和全等三角形的判定和性质得出△EFB 与△CDB 全等，进而解答即可．【解答过程】解：（1）AD ＝CB ，理由如下：∵AD ∥BC ，∴∠ABD ＝∠CDB ，同理可得，∠ADB ＝∠CBD ，在△ABD 与△CDB 中，{∠ABD =∠CDB BD =DB ∠ADB =∠CBD，∴△ABD ≌△CDB （ASA ），∴AD ＝CB ；（2）BF ＝BD ，理由如下：∵AD ＝CB ，BE ＝AD ，∴BC ＝BE ，∵∠DEF ＝∠ADC ，∴∠DEF ﹣∠DBF ＝∠ADC ﹣∠ADB ，即∠EFB ＝∠CDB ，在△EFB 与△CDB 中，{∠EFB =∠CDB BC =BE ∠FBE =∠DBC，∴△EFB ≌△CDB （ASA ），∴FB ＝DB ．8．（2021春•沙坪坝区校级月考）如图，△ABC 中，CD ⊥AB ，垂足为D ．BE ⊥AC ，垂足为G ，AB ＝CF ，BE ＝AC ．（1）求证：AE ＝AF ；（2）求∠EAF 的度数．【解题思路】（1）利用SAS 证明△AEB ≌△F AC 可证明结论；（2）由全等三角形的性质可得∠E ＝∠CAF ，由余角的定义可求得∠EAF 的度数．【解答过程】（1）证明：∵CD ⊥AB ，BE ⊥AC ，∴∠CAD +∠ACD ＝∠CAD +∠EBA ＝90°，∴∠ACD ＝∠EBA ，在△AEB 和△F AC 中，{AB =FC ∠EBA =∠ACF BE =CA，∴△AEB ≌△F AC （SAS ），∴AE ＝F A ；（2）解：∵△AEB ≌△F AC ，∴∠E ＝∠CAF ，∵∠E +∠EAG ＝90°，∴∠CAF +∠EAG ＝90°，即∠EAF ＝90°．9．（2021春•铁岭月考）已知：如图，AB ＝AC ，∠1＝∠2．（1）找出图中的所有全等三角形（直接写出）；（2）求证：AD ＝AE ．【解题思路】（1）直接根据全等三角形的判定可得答案；（2）先根据SAS 证得△ABF ≌△ACF ，再根据ASA 证得△BDF ≌△CEF ，然后根据全等三角形的性质可得结论．【解答过程】解：（1）△ABF ≌△ACF ，△BDF ≌△CEF ，△ADF ≌△AEF ，△ADC ≌△AEB ；（2）证明：在△ABF 和△ACF 中，{AB =AC ∠1=∠2AF =AF，∴△ABF ≌△ACF （SAS ），∴∠B ＝∠C ，BF ＝CF ．在△BDF 和△CEF 中，{∠B =∠C BF =CF ∠BFD =∠CFE，∴△BDF ≌△CEF （ASA ），∴BD ＝CE ，∴AB ﹣BD ＝AC ﹣CE ，∴AD ＝AE ．10．（2021•南岗区模拟）已知：在△ABC 和△DBE 中，AB ＝DB ，BC ＝BE ，其中∠ABD ＝∠CBE ．（1）如图1，求证：AC ＝DE ；（2）如图2，AB ＝BC ，AC 分别交DE ，BD 于点F ，G ，BC 交DE 于点H ，在不添加任何辅助线的情况下，请直接写出图2中的四对全等三角形．【解题思路】（1）根据SAS 证明△ABC 与△DBE 全等，利用全等三角形的性质解答即可．（2）根据全等三角形的判定解答即可．【解答过程】证明：（1）∵∠ABD ＝∠CBE ，∴∠ABD +∠DBC ＝∠CBE +∠DBC ，即∠ABC ＝∠DBE ，在△ABC 与△DBE 中，{AB =DB ∠ABC =∠DBE BC =BE，∴△ABC ≌△DBE （SAS ），∴AC ＝DE ；（2）由（1）得△ABC ≌△DBE ，∴∠A ＝∠D ，∠C ＝∠E ，AB ＝DB ，BC ＝BE ，∴AB ＝BE ，∵AB ＝BC ，∴∠A ＝∠C ，∴∠A ＝∠E ，在△ABG 与△EBH 中，{∠A =∠E AB =BE ∠ABD =∠EBC，∴△ABG ≌△EBH （ASA ），∴BG ＝BH ，在△DBH 与△CBG 中，{BG =BH ∠DBH =∠CBG DB =CB，∴△DBH ≌△CBG （SAS ），∴∠D ＝∠C ，∵DB ＝CB ，BG ＝BH ，∴DG ＝CH ，在△DFG 与△CFH 中，{∠DFG =∠CFH ∠D =∠C DG =CH，∴△DFG ≌△CFH （AAS ）．11．（2021•三水区一模）如图，AB ＝AC ，直线l 过点A ，BM ⊥直线l ，CN ⊥直线l ，垂足分别为M 、N ，且BM ＝AN ．（1）求证△AMB ≌△CNA ；（2）求证∠BAC ＝90°．【解题思路】（1）由HL证明△AMB≌△CNA即可；（2）先由全等三角形的性质得∠BAM＝∠ACN，再由∠CAN+∠ACN＝90°，得∠CAN+∠BAM＝90°，即可得出结论．【解答过程】证明：（1）∵BM⊥直线l，CN⊥直线l，∴∠AMB＝∠CNA＝90°，在Rt△AMB和Rt△CNA中，{AB=CABM=AN，∴Rt△AMB≌Rt△CNA（HL）；（2）由（1）得：Rt△AMB≌Rt△CNA，∴∠BAM＝∠ACN，∵∠CAN+∠ACN＝90°，∴∠CAN+∠BAM＝90°，∴∠BAC＝180°﹣90°＝90°．12．（2021•广州模拟）如图，在△ABC中，∠ACB＝90°，AC＝BC，点E是∠ACB内部一点，连接CE，作AD⊥CE，BE⊥CE，垂足分别为点D，E．（1）求证：△BCE≌△CAD；（2）若BE＝5，DE＝7，则△ACD的周长是30．【解题思路】（1）根据条件可以得出∠E＝∠ADC＝90°，进而得出△CEB≌△ADC；（2）利用（1）中结论，根据全等三角形的性质即可解决问题；【解答过程】（1）证明：∵BE ⊥CE ，AD ⊥CE ，∴∠E ＝∠ADC ＝90°，∴∠EBC +∠BCE ＝90°．∵∠BCE +∠ACD ＝90°，∴∠EBC ＝∠DCA ．在△BCE 和△CAD 中，{∠E =∠ADC ∠EBC =∠DCA BC =AC，∴△BCE ≌△CAD （AAS ）；（2）解：∵：△BCE ≌△CAD ，BE ＝5，DE ＝7，∴BE ＝DC ＝5，CE ＝AD ＝CD +DE ＝5+7＝12．∴由勾股定理得：AC ＝13，∴△ACD 的周长为：5+12+13＝30，故答案为：30．13．（2020春•越秀区校级期中）已知：△ABN 和△ACM 的位置如图所示，∠1＝∠2，AB ＝AC ，AM ＝AN ．求证：（1）∠BAN ＝∠CAM ；（2）∠ODA ＝∠OEA ．【解题思路】（1）由∠1＝∠2，则∠1+∠MAN ＝∠2+∠MAN ，即∠BAN ＝∠CAM ；（2）先证△ACM ≌△ABN （SAS ），得∠M ＝∠N ，再证△ADN ≌△AEM （ASA ），即可得出结论．【解答过程】证明：（1）∵∠1＝∠2，∴∠1+∠MAN ＝∠2+∠MAN ，即∠BAN ＝∠CAM ；（2）在△ACM 和△ABN 中，{AM =AN ∠CAM =∠BAN AC =AB，∴△ACM ≌△ABN （SAS ），∴∠M ＝∠N ，在△ADN 和△AEM 中，{∠DAN =∠EAM AN =AM ∠N =∠M，∴△ADN ≌△AEM （ASA ），∴∠NDA ＝∠MEA ，即∠ODA ＝∠OEA ．14．（2020•江北区模拟）如图，在△ABC 中，AD 是BC 边上的中线，E 是AB 边上一点，过点C 作CF ∥AB ，交ED 的延长线于点F ．（1）求证：△BDE ≌△CDF ；（2）当AD ⊥BC ，AE ＝2，CF ＝1时，求AC 的长．【解题思路】（1）根据平行线的性质得到∠B ＝∠FCD ，∠BED ＝∠F ，由AD 是BC 边上的中线，得到BD ＝CD ，于是得到结论；（2）根据全等三角形的性质得到BE ＝CF ＝1，求得AB ＝AE +BE ＝3，于是得到结论．【解答过程】证明：∵CF ∥AB ，∴∠B ＝∠FCD ，∠BED ＝∠F ，∵AD 是BC 边上的中线，∴BD ＝CD ，在△BDE 和△CDF 中，{∠B =∠FCD ∠BED =∠F BD =CD，∴△BDE ≌△CDF （AAS ）；（2）∵△BDE ≌△CDF ，∴BE ＝CF ＝1，∴AB ＝AE +BE ＝2+1＝3，∵AD ⊥BC ，BD ＝CD ，∴AC ＝AB ＝3．15．（2020秋•萧山区月考）如图，已知在△ABC 中，BD ⊥AC 于D ，CE ⊥AB 于E ，F 是BD 上一点，BF ＝AC ，G 是CE 延长线上一点，CG ＝AB ，连接AG ，AF ．（1）试说明∠ABD ＝∠ACE ；（2）探求线段AF ，AG 有什么关系？并请说明理由．【解题思路】（1）根据的等角的余角相等，即可证明∠ACG ＝∠ABF ；（2）根据SAS 推出△ABF ≌△GCA 即可解决问题；【解答过程】（1）证明：∵BD 、CE 是△ABC 的高，∴∠ADB ＝∠AEC ＝90°，∴∠ABF +∠BAD ＝90°，∠GCA +∠BAD ＝90°，∴∠ABF ＝∠GCA ，（2）结论：AF ＝AG ，AF ⊥AG ．理由如下：在△ABF 和△GCA 中，{AB =CG ∠ABF =∠GCA BF =AC，∴△ABF ≌△GCA （SAS ），∴AF ＝AG ，∠GAC ＝∠AFB ，∵∠AFB＝∠ADB+∠F AD，∠GAC＝∠GAF+∠F AD，∴∠GAF＝∠ADF，∵∠ADF＝90°，∴∠GAF＝90°，∴AG⊥AF，AG＝AF．16．（2021•张家界模拟）如图，四边形ABCD中，AB＝BC＝2CD，AB∥CD，∠C＝90°，E是BC的中点，AE与BD相交于点F，连接DE（1）求证：△ABE≌△BCD；（2）判断线段AE与BD的数量关系及位置关系，并说明理由；（3）若CD＝1，试求△AED的面积．【解题思路】（1）由平行线的性质得出∠ABE+∠C＝180°，得出∠ABE＝90°＝∠C，再证出BE＝CD，由SAS证明△ABE≌△BCD即可；（2）由全等三角形的性质得出AE＝BD，证出∠ABF+∠BAE＝90°，得出∠AFB＝90°，即可得出结论；（3）由全等三角形的性质得出BE＝CD＝1，求出CE＝BC﹣BE＝1，得出CE＝CD，△AED的面积＝梯形ABCD的面积﹣△ABE的面积﹣△CDE的面积，即可得出答案．【解答过程】（1）证明：∵AB∥CD，∴∠ABE+∠C＝180°，∵∠C＝90°，∴∠ABE＝90°＝∠C，∵E是BC的中点，∴BC＝2BE，∵BC＝2CD，∴BE＝CD，在△ABE和△BCD中，{AB=BC∠ABE=∠CBE=CD，∴△ABE≌△BCD（SAS）；（2）解：AE＝BD，AE⊥BD，理由如下：由（1）得：△ABE≌△BCD，∴AE＝BD，∵∠BAE＝∠CBD，∠ABF+∠CBD＝90°，∴∠ABF+∠BAE＝90°，∴∠AFB＝90°，∴AE⊥BD；（3）解：∵△ABE≌△BCD，∴BE＝CD＝1，∵AB＝BC＝2CD＝2，∴CE＝BC﹣BE＝1，∴CE＝CD，∴△AED的面积＝梯形ABCD的面积﹣△ABE的面积﹣△CDE的面积=12（1+2）×2−12×2×1−12×1×1=3 2．17．（2020秋•台江区校级期中）如图，A，B，C三点共线，D，C，E三点共线，∠A＝∠DBC，EF⊥AC 于点F，AE＝BD．（1）求证：C是DE的中点；（2）求证：AB＝2CF．【解题思路】（1）过D 作DH ⊥AC 的延长线与H ，根据全等三角形的判定证得△AEF ≌△BDH ，得到EF ＝DH ，再证得△EFC ≌△DHC 得到CE ＝CD ，即可证得即可证得结论；（2）由（1）得，△AEF ≌△BDH ，△EFC ≌△DHC ，根据全等三角形的性质得到AF ＝BH ，CF ＝CH ，再根据线段的和差即可证得结论．【解答过程】证明：（1）过D 作DH ⊥AC 的延长线与H ，∴∠EFC ＝∠DHC ＝90°，在△AEF 和△BDH 中，{∠A =∠DBC ∠AFE =∠BHD =90°AE =BD，∴△AEF ≌△BDH （AAS ），∴EF ＝DH ，在△EFC 和△DHC 中，{∠FCE =∠HCD ∠EFC =∠DHC =90°EF =DH，∴△EFC ≌△DHC （AAS ），∴CE ＝CD ，∴C 是DE 的中点；（2）由（1）得，△AEF ≌△BDH ，△EFC ≌△DHC ，∴AF ＝BH ，CF ＝CH ，∴AB +BF ＝BF +FH ，FH ＝2FC ，∴AB ＝FH ，∴AB ＝2CF ．18．（2021春•铁岭月考）如图，△AOC 和△BOD 中，OA ＝OC ，OB ＝OD ，∠AOC ＝∠BOD ＝α（0＜α＜90°），AD 与BC 交于点P ．（1）求证：△AOD ≌△COB ；（2）求∠APC （用含α的式子表示）；（3）过点O 分别作OM ⊥AD ，ON ⊥BC ，垂足分别为点M 、N ，请直接写出OM 和ON 的数量关系．【解题思路】（1）由∠AOC ＝∠BOD ，可得∠AOD ＝∠COB ，然后根据SAS 可得结论；（2）根据全等三角形的性质得∠OAD ＝∠OCB ，再根据三角形外角性质可得答案；（3）根据全等三角形的性质得∠MAO ＝∠NCO ，由垂直定义得∠AMO ＝∠CNO ，再根据全等三角形的判定与性质可得结论．【解答过程】解：（1）∵∠AOC ＝∠BOD ，∴∠AOC +∠COD ＝∠BOD +∠COD ，∴∠AOD ＝∠COB ，在△AOD 和△COB 中，{OA =OC ∠AOD =∠COB OD =OB，∴△AOD ≌△COB （SAS ）；（2）由（1）可知△AOD ≌△COB ，∴∠OAD ＝∠OCB ，令AD 与OC 交于点E ，则∠AEC ＝∠OAD +∠AOC ＝∠OCB +∠APC ，∴∠AOC ＝∠APC ，∵∠AOC ＝α，∴∠APC ＝α；（3）∵△AOD ≌△COB ，∴∠P AP ＝∠BCO ，即∠MAO ＝∠NCO ，∵OM ⊥AD ，ON ⊥BC ，∴∠AMO ＝∠CNO ＝90°，在△AOM 和△CON 中，{∠MAO =∠NCO ∠AMO =∠CNO OA =OC，∴△AOM ≌△CON （AAS ），∴OM ＝ON ．19．（2020秋•花都区月考）如图所示，BD 、CE 是△ABC 的高，点P 在BD 的延长线上，CA ＝BP ，点Q 在CE 上，QC ＝AB ．（1）探究P A 与AQ 之间的关系；（2）若把（1）中的△ABC 改为钝角三角形，AC ＞AB ，∠A 是钝角，其他条件不变，上述结论是否成立？画出图形并证明你的结论．【解题思路】（1）由条件可得出∠1＝∠2，可证得△APB ≌△QAC ，可得结论；（2）根据题意画出图形，结合（1）可证得△APB ≌△QAC ，可得结论．【解答过程】（1）结论：AP ＝AQ ，AP ⊥AQ 证明：∵BD 、CE 是△ABC 的高， ∴BD ⊥AC ，CE ⊥AB ，∴∠1+∠CAB ＝90°，∠2+∠CAB ＝90°， ∴∠1＝∠2，在△QAC 和△APB 中，{QC =AB ∠1=∠2CA =BP，∴△QAC ≌△APB （SAS ），∴AQ ＝AP ，∠QAC ＝∠P ，而∠DAP +∠P ＝90°，∴∠DAP +∠QAC ＝90°，即∠QAP ＝90°，∴AQ ⊥AP ；即AP ＝AQ ，AP ⊥AQ ；（2）上述结论成立，理由如下：如图所示：∵BD 、CE 是△ABC 的高，∴BD ⊥AC ，CE ⊥AB ，∴∠1+∠CAE ＝90°，∠2+∠DAB ＝90°， ∵∠CAE ＝∠DAB ，∴∠1＝∠2，在△QAC 和△APB 中，{QC =AB ∠1=∠2CA =BP，∴△QAC ≌△APB （SAS ），∴AQ ＝AP ，∠QAC ＝∠P ，∵∠PDA ＝90°，∴∠P +∠P AD ＝90°，∴∠QAC +∠P AD ＝90°，∴∠QAP ＝90°，∴AQ ⊥AP ，即AP ＝AQ ，AP ⊥AQ ．20．（2020春•萍乡期末）在△ABC 中，AB ＝AC ，D 是直线BC 上一点，以AD 为一边在AD 的右侧作△ADE ，使AE ＝AD ，∠DAE ＝∠BAC ，连接CE ，设∠BAC ＝∠1，∠DCE ＝∠2．（1）如图①，当点D 在线段BC 上移动时，试说明：∠1+∠2＝180°；（2）如图②，当点D 在线段BC 的延长线上移动时，请猜测∠1与∠2有怎样的数量关系？并说明理由．【解题思路】（1）由“SAS ”可证△BAD ≌△CAE ，可得∠ACE ＝∠ABD ，由三角形的内角和定理可得结论；（2）由“SAS ”可证△BAD ≌△CAE ，可得∠ACE ＝∠ABD ，由三角形的内角和定理和平角的定义可得结论．【解答过程】证明：（1）∵∠DAE ＝∠BAC ，∴∠BAD ＝∠CAE ，在△ABD 和△ACE 中，{AB =AC ∠BAD =∠CAE AD =AE，∴△BAD ≌△CAE （SAS ），∴∠ACE ＝∠ABD ，∵∠BAC +∠ABD +∠ACB ＝180°，∴∠BAC +∠ACB +∠ACE ＝∠BAC +∠BCE ＝180°，∴∠1+∠2＝180°；（2）∠1＝∠2，理由如下：∵∠DAE ＝∠BAC ，∴∠BAD ＝∠CAE ，在△ABD 和△ACE 中，{AB =AC ∠BAD =∠CAE AD =AE，∴△BAD ≌△CAE （SAS ），∴∠ACE ＝∠ABD ，∵∠BAC +∠ABD +∠ACB ＝180°，∠ACE +∠ACB +∠DCE ＝180°，∴∠1＝∠2．21．（2020春•揭阳期末）已知△ABC ，点D 、F 分别为线段AC 、AB 上两点，连接BD 、CF 交于点E ．（1）若BD ⊥AC ，CF ⊥AB ，如图1所示，试说明∠BAC +∠BEC ＝180°；（2）若BD 平分∠ABC ，CF 平分∠ACB ，如图2所示，试说明此时∠BAC 与∠BEC 的数量关系；（3）在（2）的条件下，若∠BAC ＝60°，试说明：EF ＝ED ．【解题思路】（1）根据余角的性质得到∠DEC ＝∠BAC ，由于∠DEC +∠BEC ＝180°，即可得到结论；（2）根据角平分线的性质得到∠EBC =12∠ABC ，∠ECB =12∠ACB ，于是得到结论；（3）作∠BEC 的平分线EM 交BC 于M ，由∠BAC ＝60°，得到∠BEC ＝90°+12∠BAC ＝120°，求得∠FEB ＝∠DEC ＝60°，根据角平分线的性质得到∠BEM ＝60°，推出△FBE ≌△EBM ，根据全等三角形的性质得到EF ＝EM ，同理DE ＝EM ，即可得到结论．【解答过程】解：（1）∵BD ⊥AC ，CF ⊥AB ，∴∠DCE +∠DEC ＝∠DCE +∠F AC ＝90°，∴∠DEC ＝∠BAC ，∠DEC +∠BEC ＝180°，∴∠BAC +∠BEC ＝180°；（2）∵BD 平分∠ABC ，CF 平分∠ACB ，∴∠EBC =12∠ABC ，∠ECB =12∠ACB ，∠BEC ＝180°﹣（∠EBC +∠ECB ）＝180°−12（∠ABC +∠ACB ）＝180°−12（180°﹣∠BAC ）＝90°+12∠BAC ；（3）作∠BEC 的平分线EM 交BC 于M ，∵∠BAC ＝60°，∴∠BEC ＝90°+12∠BAC ＝120°，∴∠FEB ＝∠DEC ＝60°，∵EM 平分∠BEC ，∴∠BEM ＝60°，在△FBE 与△EBM 中，{∠FBE =∠EBM BE =BE ∠FEB =∠MEB，∴△FBE ≌△EBM （ASA ），∴EF ＝EM ，同理DE ＝EM ，∴EF ＝DE ．22．（2020秋•淇滨区校级期中）（1）如图1所示，△ACB 和△ECD 都是等腰三角形，A 、C 、D 三点在同一直线上，连接BD 、AE ，并延长AE 交BD 于点F ，试判断AE 与BD 的数量关系及位置关系，并证明你的结论．（2）若△ECD 绕顶点C 顺时针转任意角度后得到图2，图1中的结论是否仍然成立？请说明理由．【解题思路】（1）根据SAS 推出△ACE ≌△BCD ，根据全等三角形的性质得出∠CAE ＝∠DBC ，根据∠ACB ＝90°求出∠CAE +∠AEC ＝90°，求出∠DBC +∠BEF ＝90°，根据三角形内角和定理求出∠BFE ＝90°即可；（2）根据SAS 推出△ACE ≌△BCD ，根据全等三角形的性质得出∠CAE ＝∠DBC ，根据∠ACB ＝90°求出∠CAE +∠AOC ＝90°，求出∠DBC +∠BOE ＝90°，根据三角形内角和定理求出∠BFO ＝90°即可．【解答过程】（1）AE ⊥BD ．证明：在△ACE 和△BCD 中{AC =BC ∠ACE =∠BCD CE =CD∴△ACE ≌△BCD （SAS ），∴∠CAE ＝∠DBC ，∵∠ACB ＝90°，∴∠CAE +∠AEC ＝90°，∵∠CAE ＝∠DBC ，∠AEC ＝∠BEF ，∴∠DBC +∠BEF ＝90°，∴∠BFE ＝180°﹣90°＝90°，∴AE ⊥BD ；（2）解：结论还成立，理由是：∵∠ACB ＝∠ECD ，∴∠ACB +∠BCE ＝∠ECD +∠BCE ，即∠ACE ＝∠BCD ，在△ACE 和△BCD 中{AC =BC ∠ACE =∠BCD CE =CD∴△ACE≌△BCD（SAS），∴∠CAE＝∠DBC，∵∠ACB＝90°，∴∠CAE+∠AOC＝90°，∵∠CAE＝∠DBC，∠AOC＝∠BOE，∴∠DBC+∠BOE＝90°，∴∠BFO＝180°﹣90°＝90°，∴AE⊥BD．23．（2020秋•蒙阴县期中）在△ABC中，∠ACB＝90°，AC＝BC，直线MN经过点C，且AD⊥MN于点D，BE⊥MN于点E．（1）当直线MN绕着点C旋转到如图1所示的位置时，求证：①△ADC≌△CEB；②DE＝AD+BE；（2）当直线MN绕着点C旋转到如图2所示的位置时，①找出图中一对全等三角形；②DE、AD、BE之间有怎样的数量关系，并加以证明．【解题思路】（1）根据余角和补角的性质易证得∠DAC＝∠ECB，已知∠ADC＝∠CEB＝90°，AC＝CB，根据全等三角形的判定AAS即可证明△ADC≌△CEB，根据各边的相等关系即可得DE＝AD+BE．（2）同理可证得△ADC≌△CEB，再根据各边的相等关系可得DE＝AD﹣BE．【解答过程】（1）证明：∵AD⊥MN，BE⊥MN，∴∠ADC＝∠CEB＝90°，∴∠DAC+∠ACD＝90°，∵∠ACB＝90°，∴∠ACD+∠BCE＝180°﹣90°＝90°，∴∠DAC＝∠ECB；在△ADC和△CEB中，∠ADC＝∠CEB，∠DAC＝∠ECB，AC＝CB，∴△ADC≌△CEB（AAS）①，（7分）∴DC＝EB，AD＝CE，∴DE＝AD+BE．（9分）（2）解：同理可得△ADC≌△CEB①；（11分）∴AD＝CE，CD＝BE，∴DE＝AD﹣BE②．（14分）24．（2018秋•环翠区期末）（1）如图1，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，E、F分别是边BC、CD上的点，若∠EAF=12∠BAD，可求得EF、BE、FD之间的数量关系为BE+DF＝EF．（只思考解题思路，完成填空即可，不必书写证明过程）（2）如图2，在四边形ABCD中，AB＝AD，∠B+∠ADC＝180°，E、F分别是边BC、CD延长线上的点，若∠EAF=12∠BAD，判断EF、BE、FD之间的数量关系还成立吗，若成立，请完成证明，若不成立，请说明理由．【可借鉴第（1）问的解题经验】【解题思路】（1）线段EF、BE、FD之间的数量关系是BE+DF＝EF．如图1中，延长CB至M，使BM ＝DF，连接AM，利用全等三角形的性质解决问题即可．（2）结论：EF+DF＝BE．如图2中，在BE上截取BM＝DF，连接AM，证明△ABM≌△ADF（SAS），推出AM＝AF，∠BAM＝∠DAF，再证明△AEM≌△AEF（SAS），可得结论．【解答过程】解：（1）线段EF、BE、FD之间的数量关系是BE+DF＝EF．如图1，延长CB至M，使BM＝DF，连接AM，∵∠ABC +∠D ＝180°，∠ABC +∠1＝180°，∴∠1＝∠D ，在△ABM 和△ADF 中，{AB =AD ∠1=∠D BM =DF，∴△ABM ≌△ADF （SAS ），∴AM ＝AF ，∠3＝∠2，∵∠EAF =12∠BAD ，∴∠4+∠4＝∠EAF ，∴∠GAM ＝∠3+∠4＝∠2+∠4＝∠EAF ，在△MAE 和△F AE 中，{AM =AF ∠MAE =∠FAE AE =AE，∴△MAE ≌△F AE （SAS ），∴EF ＝EM ，∵EM ＝BM +BE ＝BE +DF ，∴EF ＝BE +FD ；故答案为：BE +DF ＝EF ．（2）结论：EF +DF ＝BE ．理由：在BE 上截取BM ＝DF ，连接AM ，∵∠B +∠ADC ＝180°，∠ADC +∠ADE ＝180°，∴∠B ＝∠ADF ，在△ABM 与△ADF 中，{BM =DF ∠ABM =∠ADF AB =AD，∴△ABM ≌△ADF （SAS ），∴AM ＝AF ，∠BAM ＝∠DAF ，∵∠EAF =12∠BAD ，∴∠EAF ＝∠EAM ，在△AEM 与△AEF 中，{AM =AF ∠EAF =∠EAM AE =AE，∴△AEM ≌△AEF （SAS ），∴EM ＝EF ，即BE ﹣BM ＝EF ，即BE ﹣DF ＝EF ，∴EF +DF ＝BE ．25．（2021春•和平区期末）如图，在△ABC 中，AC ＝BC ，点D 在边AB 上，AB ＝4BD ，连接CD ，点E ，F 在线段CD 上，连接BF ，AE ，∠BFC ＝∠AEC ＝180°﹣∠ACB ．（1）①∠FBC 与∠ECA 相等吗？说明你的理由；②△FBC 与△ECA 全等吗？说明你的理由；（2）若AE ＝11，EF ＝8，则请直接写出BF 的长为 3 ；（3）若△ACE 与△BDF 的面积之和为12，则△ABC 的面积为 48 ．【解题思路】（1）①连接BC ，由已知及∠AEC ＝180°﹣∠AED ，可得到∠ACB ＝∠AED ．再证明∠CAE ＝∠BCF ，由三角形内角和定理可得∠FBC ＝∠ECA ；②利用“ASA ”证明△FBC ≌△ECA ；（2）由（1）中全等三角形的结论及已知可得到BF 的长；（3）由（1）中结论可得S △FBC ＝S △ECA ，所以S △ECA +S △BDF ＝12＝S △FBC +S △BDF ＝S △DBC ，根据AB ＝4BD ，可得到S △DBC =14S △ABC ＝12，从而可得△ABC 的面积．【解答过程】解：（1）①∠FBC ＝∠ECA ，理由如下：连接BC ，如右图．∵∠BFC ＝∠AEC ＝180°﹣∠ACB ，且∠AEC ＝180°﹣∠AED ，∴∠ACB ＝∠AED ．由外角定理可得∠AED ＝∠ACD +∠CAE ，又∠ACB ＝∠ACD +∠BCF ，∴∠CAE ＝∠BCF ，由三角形内角和定理可得∠FBC ＝∠ECA ．②△FBC 与△ECA 全等，理由如下：在△FBC 和△ECA 中，{∠FBC =∠ECA BC =CA ∠BCF =∠CAE，∴△FBC ≌△ECA （ASA ）．（2）由（1）中②可知，FC ＝AE ＝11，BF ＝CE ，又EF ＝8，∴CE ＝FC ﹣EF ＝11﹣8＝3，∴BF ＝3，故答案为：3．（3）由（1）中结论可知S△FBC＝S△ECA，∴S△ECA+S△BDF＝12＝S△FBC+S△BDF＝S△DBC，又AB＝4BD，∴S△DBC=14S△ABC＝12，∴S△ABC＝48．故答案为：48．26．（2020•岱岳区一模）已知∠ABC＝90°，点D是直线AB边上的点，AD＝BC．（1）如图1，点D在线段AB上，过点A作AF⊥AB，且AF＝BD，连接DC、DF、CF，试判断△CDF 的形状并说明理由；（2）如图2，点D在线段AB的延长线上，点F在点A的左侧，其他条件不变，以上结论是否仍然成立？请说明理由．【解题思路】（1）利用SAS证明△F AD≌△DBC，再利用全等三角形的性质得出FD＝DC，即可判断三角形的形状；（2）利用SAS证明△F AD和△DBC全等，再利用全等三角形的性质得出FD＝DC，∠FDC＝90°，即可得出结论．【解答过程】（1）△CDF是等腰直角三角形，理由如下：∵AF⊥AB，∴∠A＝90°，在△F AD和△DBC中，∵{AF=BD∠A=∠B=90°AD=BC，∴△F AD≌△DBC（SAS），∴∠ADF＝∠BCD，DF＝DC，∵∠BDC+∠BCD＝90°，∴∠ADF+∠CDB＝90°，∴∠FDC＝180°﹣90°＝90°，又∵DF＝DC，∴△CDF是等腰直角三角形；（2）仍然成立，理由如下：∵AF⊥AB，∴∠A＝90°，在△F AD和△DBC中，∵{AF=BD∠A=∠DBC=90°AD=BC，∴△F AD≌△DBC（SAS），∴∠ADF＝∠BCD，DF＝DC，∵∠BDC+∠BCD＝90°，∴∠ADF+∠BDC＝90°，即∠FDC＝90°，又∵DF＝DC，∴△CDF是等腰直角三角形．27．如图（1），线段AD∥BC，连接AB、CD，取CD中点E，连接AE，AE平分∠BAD．（1）线段AB与AD、BC之间存在怎样的等量关系？请说明理由．（2）如果点C在AB的左侧，其他条件不变，如图（2）所示，那么（1）中的结论还成立吗？如果成立，请说明理由；如果不成立，请写出新的结论，并说明理由．【解题思路】（1）延长AE ，BF 交于点F ，即可求证△ADE ≌△FCE ，即可求得CF ＝AD ，AB ＝BF ，即可求得AB ＝AD +BC ；（2）不成立，新的结论为：AB +BC ＝AD ．延长AE ，BF 交于点F ，可证△ADE ≌△FCE 和AB ＝BF ，即可解题．【解答过程】解：（1）延长AE ，BF 交于点F ，∵AE 平分∠BAD ，∴∠BAF ＝∠DAF ，∵AD ∥BC ，∴∠AFB ＝∠DAF ，∴AB ＝BF ，在△ADE 和△FCE 中，{∠DAE =∠EFC ∠AED =∠FEC DE =CE，∴△ADE ≌△FCE （AAS ），∴CF ＝AD ，∵BF ＝BC +CF ，∴AB ＝BC +AD ；（2）不成立，新结论为：AB ＝AD ﹣BC ．延长AE ，BF 交于点F ，证明：∵AE 平分∠BAD ，∴∠BAF ＝∠DAF ，∵AD ∥BC ，∴∠AFB ＝∠DAF ，∴AB ＝BF ，在△ADE 和△FCE 中，{∠DAE =∠EFC ∠AED =∠FEC DE =CE，∴△ADE ≌△FCE （AAS ），∴CF ＝AD ，∵BF +BC ＝CF ，∴AB +BC ＝AD ．28．（2021春•章丘区期末）如图，CD 是经过∠BCA 顶点C 的一条直线，CA ＝CB ，E 、F 分别是直线CD 上两点，且∠BEC ＝∠CF A ＝α．（1）若直线CD 经过∠BCA 的内部，且E 、F 在射线CD 上．①如图1，若∠BCA ＝90°，α＝90°，则BE ＝ CF ；②如图2，若0°＜∠BCA ＜180°，请添加一个关于α与∠BCA 关系的条件 α+∠BCA ＝180° ，使①中的结论们然成立，并说明明理由；（2）如图3，若线CD 经过∠BCA 的外部，a ＝∠BCA ，请提出关于EF ，BE ，AF 三条线段数量关系的合理猜想，并简述理由．【解题思路】（1）由∠BCA ＝90°，∠BEC ＝∠CF A ＝α＝90°，可得∠CBE ＝∠ACF ，从而可证△BCE ≌△CAF ，故BE ＝CF ．（2）若BE ＝CF ，则可使得△BCE ≌△CAF ．根据题目已知条件添加条件，再使得一对角相等，△BCE ≌△CAF 便可得证．（3）题干已知条件可证△BCE ≌△CAF ，故BE ＝CF ，EC ＝F A ，从而可证明EF ＝BE +AF ．【解答过程】解：（1）∵∠BEC ＝∠CF A ＝α＝90°，∴∠BCE +∠CBE ＝180°﹣∠BEC ＝90°．又∵∠BCA ＝∠BCE +∠ACF ＝90°，∴∠CBE ＝∠ACF ．在△BCE 和△CAF 中，{∠BEC =∠CFA ，∠CBE =∠ACF ，BC =AC ．∴△BCE ≌△CAF （AAS ）．∴BE ＝CF ．（2）α+∠BCA ＝180°，理由如下：∵∠BEC ＝∠CF A ＝α，∴∠BEF ＝180°﹣∠BEC ＝180°﹣α．又∵∠BEF ＝∠EBC +∠BCE ，∴∠EBC +∠BCE ＝180°﹣α．又∵α+∠BCA ＝180°，∴∠BCA ＝180°﹣α．∴∠BCA ＝∠BCE +∠ACF ＝180°﹣α．∴∠EBC ＝∠FCA ．在△BCE 和△CAF 中，{∠CBE =∠ACF ，∠BEC =∠CFA ，BC =CA ．∴△BCE ≌△CAF （AAS ）．∴BE ＝CF ．（3）EF ＝BE +AF ，理由如下：∵∠BCA ＝α，∴∠BCE +∠ACF ＝180°﹣∠BCA ＝180°﹣α．又∵∠BEC ＝α，∴∠EBC +∠BCE ＝180°﹣∠BEC ＝180°﹣α．∴∠EBC ＝∠FCA ．在△BEC 和△CF A 中，{∠EBC =∠FCA ，∠BEC =∠FCA ，BC =CA ．∴△BEC ≌△CF A （AAS ）．∴BE ＝CF ，EC ＝F A ．∴EF ＝EC +CF ＝F A +BE ，即EF ＝BE +AF ．29．（2020春•南岸区期末）在∠MAN 内有一点D ，过点D 分别作DB ⊥AM ，DC ⊥AN ，垂足分别为B ，C ．且BD ＝CD ，点E ，F 分别在边AM 和AN 上．（1）如图1，若∠BED ＝∠CFD ，请说明DE ＝DF ；（2）如图2，若∠BDC ＝120°，∠EDF ＝60°，猜想EF ，BE ，CF 具有的数量关系，并说明你的结论成立的理由．【解题思路】（1）根据题目中的条件和∠BED ＝∠CFD ，可以证明△BDE ≌△CDF ，从而可以得到DE ＝DF ；（2）作辅助线，过点D 作∠CDG ＝∠BDE ，交AN 于点G ，从而可以得到△BDE ≌△CDG ，然后即可得到DE ＝DG ，BE ＝CG ，再根据题目中的条件可以得到△EDF ≌△GDF ，即可得到EF ＝GF ，然后即可得到EF ，BE ，CF 具有的数量关系．【解答过程】解：（1）∵DB ⊥AM ，DC ⊥AN ，∴∠DBE ＝∠DCF ＝90°，在△BDE 和△CDF 中，∵{∠BED =∠CFD ，∠DBE =∠DCF ，BD =CD ，∴△BDE ≌△CDF （AAS ）．∴DE ＝DF ；（2）EF ＝FC +BE ，理由：过点D 作∠CDG ＝∠BDE ，交AN 于点G ，在△BDE 和△CDG 中，{∠EBD =∠GCD BD =CD ∠BDE =∠CDG，∴△BDE ≌△CDG （ASA ），∴DE ＝DG ，BE ＝CG ．∵∠BDC ＝120°，∠EDF ＝60°，∴∠BDE +∠CDF ＝60°．∴∠FDG ＝∠CDG +∠CDF ＝60°，∴∠EDF ＝∠GDF ．在△EDF 和△GDF 中，{DE =DG ∠EDF =∠GDF DF =DF，∴△EDF ≌△GDF （SAS ）．∴EF ＝GF ，∴EF＝FC+CG＝FC+BE．30．（2021春•揭东区期末）已知点C为线段AB上一点，分别以AC、BC为边在线段AB同侧作△ACD和△BCE，且CA＝CD，CB＝CE，∠ACD＝∠BCE，直线AE与BD交于点F．（1）如图1，求证：△ACE≌△DCB．（2）如图1，若∠ACD＝60°，则∠AFB＝120°；如图2，若∠ACD＝90°，则∠AFB＝90°；（3）如图3，若∠ACD＝β，则∠AFB＝180°﹣β（用含β的式子表示）并说明理由．【解题思路】（1）求出∠ACE＝∠DCB，根据SAS证出两三角形全等即可；（2）根据全等三角形性质得出∠AEC＝∠DBC，∠CDB＝∠CAE，求出∠EAB+∠DBA＝∠ACD，∠AFB ＝180°﹣（∠EAB+∠DBC），代入求出即可；（3）根据全等三角形性质得出∠AEC＝∠DBC，∠CDB＝∠CAE，求出∠EAB+∠DBA＝∠ACD，∠AFB ＝180°﹣（∠EAB+∠DBC），代入求出即可．【解答过程】（1）证明：∵∠ACD＝∠BCE，∴∠ACD+∠DCE＝∠BCE+∠DCE，∴∠ACE＝∠DCB，在△ACE和△DCB中∵{AC=CD∠ACE=∠DCB CE=CB，∴△ACE≌△DCB；（2）解：∵∠ACD＝60°，∴∠CDB+∠DBC＝∠ACD＝60°，∵△ACE≌△DCB，∴∠AEC＝∠DBC，∠CDB＝∠CAE，∴∠CAE+∠DBC＝60°，∴∠AFB＝180°﹣60°＝120°；当∠ACD＝90°时，∵∠ACD＝90°，∴∠CDB+∠DBC＝∠ACD＝90°，∵△ACE≌△DCB，∴∠AEC＝∠DBC，∠CDB＝∠CAE，∴∠CAE+∠DBC＝90°，∴∠AFB＝180°﹣90°＝90°；故答案为：120°，90°；（3）解：当∠ACD＝β时，∠AFB＝180°﹣β，理由是：∵∠ACD＝β，∴∠CDB+∠DBC＝∠ACD＝β，∵△ACE≌△DCB，∴∠AEC＝∠DBC，∠CDB＝∠CAE，∴∠CAE+∠DBC＝β，∴∠AFB＝180°﹣（∠CAE+∠DBC）＝180°﹣β；故答案为：180°﹣β．。

(完整)全等三角形提高练习精选27题及答案

全等三角形提高练习精选27题及答案1•如图所示，△ ABC ^A ADE , BC 的延长线过点 E,/ ACB= / AED=105 / CAD=10 ° ,Z B=50。

，求/DEF 的度数。

2•如图，△ AOB 中，/ B=30。

，将A AOB 绕点O 顺时针旋转52。

，得到厶A'OB ', 边A 'B '与边OB 交于点C （A '不在OB 上）,则/ A 'CO 的度数为多少？3•如图所示，在△ ABC 中，/ A=90 ° ,D 、E 分别是 AC 、若厶ADB ◎△ EDB ^A EDC ，则/ C 的度数是多少？4•如图所示，把△ ABC 绕点C 顺时针旋转35°，得到△ A'B'C , A '' 交 AC 于点 D ，若/ A 'DC=90 °,^U/A= ____________6•如图，Rt A ABC 中，/ BAC=90 ° ,AB=AC ，分别过点 B C 作过点A 的垂线BC 、CE,垂足分另【J 为 D 、E , 若 BD=3 , CE=2，贝U DE= ____________7•如图，AD 是厶ABC 的角平分线，DE 丄AB , DF 丄AC ,垂足分别是 E 、F ,连接EF, 交AD 于G , AD 与EF 垂直吗？证明你的结论。

AE G5•已知，如图所示, 则AD 是多AB=AC , AD 丄 BC 于 D ，且 AB+AC+BC=50cm,ABA'B'AO14. 如图所示，已知△ ABC 和厶BDE 都是等边三角形，下列结论：① AE=CD ;②BF=BG ; ③BH 平分/ AHD ; ④/ AHC=60 ° ;⑤厶BFG 是等边三角形； ⑥FG// AD , E其中正确的有()A . 3 个 B. 4 个 C. 5 个 D. 6 个C H8•如图所示，在△ ABC 中，AD 为/ BAC 的角平分线,2积是 28cm ,AB=20cm , AC=8cm ，求 DE 的长。

中考数学全等三角形证明经典50题(含答案)+经典因式分解练习题100道

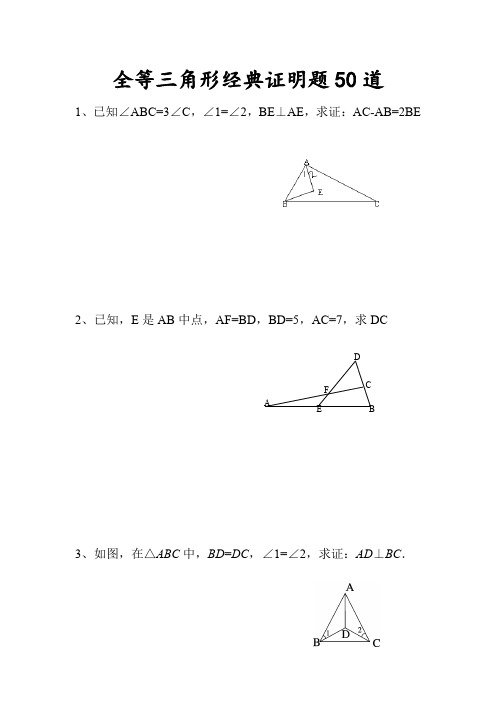
全等三角形经典证明题50道1、已知∠ABC=3∠C ，∠1=∠2，BE ⊥AE ，求证：AC-AB=2BE2、已知，E 是AB 中点，AF=BD ，BD=5，AC=7，求DC3、如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ．FAEDC B4．如图，OM平分∠POQ，MA⊥OP,MB⊥OQ，A、B为垂足，AB交OM于点N．求证：∠OAB=∠OBA5．（5分）如图，已知AD∥BC，∠P AB的平分线与∠CBA的平分线相交于E，CE的连线交AP于D．求证：AD+BC=AB．PCEDBA6．（6分）如图①，E、F分别为线段AC上的两个动点，且DE ⊥AC于E，BF⊥AC于F，若AB=CD，AF=CE，BD交AC于点M．（1）求证：MB=MD，ME=MF（2）当E、F两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．7．已知：如图，DC ∥AB ，且DC =AE ，E 为AB 的中点，（1）求证：△AED ≌△EBC ．（2）观看图前，在不添辅助线的情况下，除△EBC 外，请再写出两个与△AED 的面积相等的三角形．（直接写出结果，不要求证明）：8．（7分）如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ．求证：BD =2CE ．OEDCB AFE D CB A25、如图：DF=CE ，AD=BC ，∠D=∠C 。

求证：△AED ≌△BFC 。

证明：∵DF=CE ， ∵DF-EF=CE-EF ，即DE=CF ，在∵AED 和∵BFC 中，∵ AD=BC ， ∵D=∵C ，DE=CF ∵∵AED ∵∵BFC （SAS ）26、（10分）如图：AE 、BC 交于点M ，F 点在AM 上，BE ∥CF ，BE=CF 。

求证：AM 是△ABC 的中线。

全等三角形证明题培优(38题)(方法)

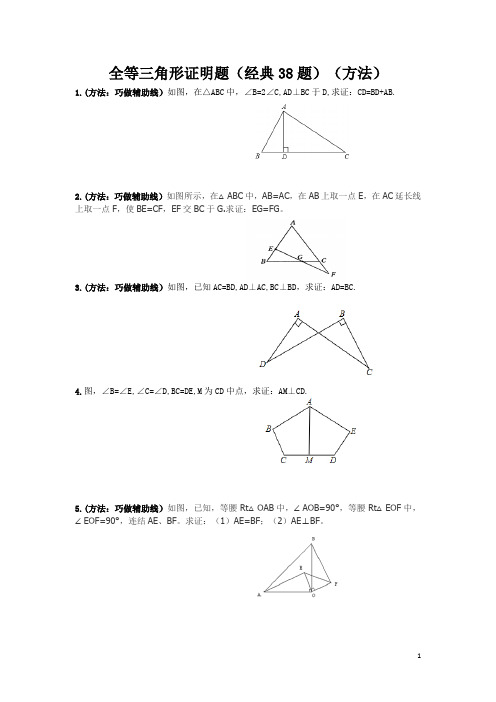
全等三角形证明题（经典38题）（方法）1.(方法：巧做辅助线）如图，在△ABC中，∠B=2∠C,AD⊥BC于D,求证：CD=BD+AB.2.(方法：巧做辅助线）如图所示，在△ABC中，AB=AC，在AB上取一点E，在AC延长线上取一点F，使BE=CF，EF交BC于G.求证：EG=FG。

3.(方法：巧做辅助线）如图，已知AC=BD,AD⊥AC,BC⊥BD，求证：AD=BC.4.图，∠B=∠E,∠C=∠D,BC=DE,M为CD中点，求证：AM⊥CD.5.(方法：巧做辅助线）如图，已知，等腰Rt△OAB中，∠AOB=90°，等腰Rt△EOF中，∠EOF=90°，连结AE、BF。

求证：（1）AE=BF；（2）AE⊥BF。

6.(方法：巧做辅助线）如图，在△ABC中，AB=AC，E在线段AC上，D在AB的延长线，连D E交BC于F，过点E作EG⊥BC于G．（1）若∠A=50°，∠D=30°，求∠GEF的度数；（2）若BD=CE，求证：FG=BF+CG．7.(方法：火眼金睛找条件）如图所示，∠BAC=∠DAE=90°，M是BE的中点，AB=AC，AD=AE，求证：（1）CD=2AM,（2）AM⊥CD．8.(方法：火眼金睛找条件）已知：如图，点C为线段AB上一点，△ACM, △CBN都是等边三角形，AN交MC于点E，BM交CN于点F.(1)求证：AN=BM;(2)求证：△CEF为等边三角形9.(方法：火眼金睛找条件）如图，在△ABC中，AD平分∠BAC，E为BC的中点，过点E 作EF∥AD交AB于点G，交CA的延长线于点F．求证：BG=CF．FDE CBA(2)10.(方法：巧做辅助线）如图，AB=AE,∠ABC=∠AED,BC=ED,点F 是CD 的中点，求证：AF ⊥CD.11.(方法：巧做辅助线）如图，在正方形ABCD 中，M 、N 分别是BC 、CD 上的点，∠MAN=45°．求证：MB+ND=MN ．12.(方法：巧做辅助线）已知：如图，ABCD 是正方形，∠FAD=∠FAE ．求证：BE+DF=AE ．13.(方法：火眼金睛找条件）如图E 为正方形ABCD 边BC 的中点，F 为DC 的中点，BF 与AE 有何关系？请解释你的结论。

全等三角形培优专题训练(供参考)

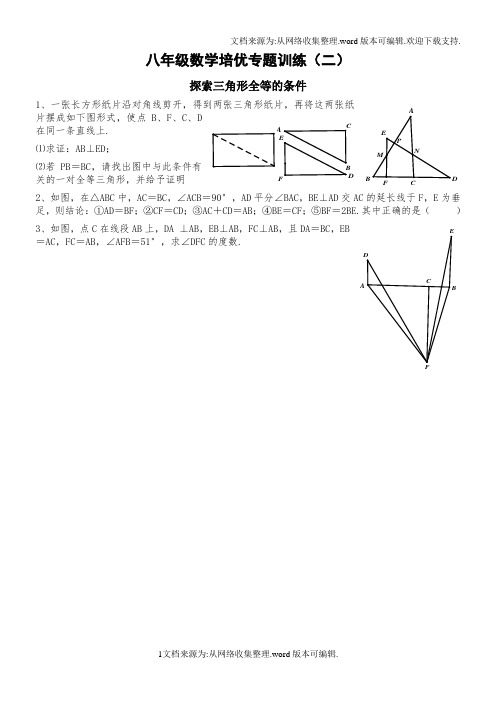
八年级数学培优专题训练（二）探索三角形全等的条件1、一张长方形纸片沿对角线剪开，得到两张三角形纸片，再将这两张纸片摆成如下图形式，使点B 、F 、C 、D在同一条直线上.⑴求证：AB ⊥ED ；⑵若PB ＝BC ，请找出图中与此条件有关的一对全等三角形，并给予证明2、如图，在△ABC 中，AC ＝BC ，∠ACB ＝90°，AD 平分∠BAC ，BE ⊥AD 交AC 的延长线于F ，E 为垂足，则结论：①AD ＝BF ；②CF ＝CD ；③AC ＋CD ＝AB ；④BE ＝CF ；⑤BF ＝2BE.其中正确的是（）3、如图，点C 在线段AB 上，DA ⊥AB ，EB ⊥AB ，FC ⊥AB ，且DA ＝BC ，EB ＝AC ，FC ＝AB ，∠AFB ＝51°，求∠DFC 的度数.A4、如图，四边形ABCD中，AB∥CD，AD∥BC，O为对角线AC的中点，过点O作一条直线分别与AB、CD交于点M、N，点E、F在直线M、N上，且OE＝OF.⑴图中共有几对全等三角形，请把它们都写下来；⑵求证：∠MAE＝∠NCF5、在△ABC中，高所在直线AD和BE交于H点，且BH＝AC，则∠ABC＝_____________.6、下列三个判断：⑴有两边及其中一边上的高对应相等的两个三角形全等；⑵有两边及第三边上的高对应相等的两个三角形全等；⑶一边及其它两边上的高对应相等的两个三角形全等.上述判断是否正确？若正确，说明理由；若不正确，请举出反例.E八年级数学培优专题训练（三）全等三角形的应用全等三角形常用来转移线段和角，用它来证明：①线段和角的等量关系②线段和角的和差倍分关系③直线与直线的平行或垂直等位置关系1、如图，已知BD、CE分别是△ABC的边AC和AB上的高，点P在并证明.2、如图，AD是△ABC的高，E为AC上一点，BE交AD于点F，且BF＝AC，FD＝CD，求证：BE⊥AC3、（2012·阜新中考）如图,在△ABC中,AB＝AC,AD＝AE,∠BAC＝∠DAC＝90°.⑴当点D在AC上时,如图①,线段BD,CE有怎样的数量和位置关系?证明你猜想的结论.⑵将图①中的△ADE绕点A顺时针旋转α角(0°＜α＜90°)，如图②，线段BD、CE有怎样的数量关系和位置关系？问明理由.B②4、在△ABC中，AB＝AC，点D是直线 BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD＝AE，∠DAE＝∠BAC，连接CE.⑴如图①，当点D在线段BC上时，若∠BAC＝90°，则∠BCE＝_______度.⑵设∠BAC＝α，∠BCE＝βa、如图②，当点D在线段BC上移动时，α，β之间有怎样的数量关系？请说明理由.b、当点D在直线BC上移动时，α，β之间有怎样的数量关系？请直接写出你的结论.①②辅助线作法之连接法在几何证明中，常通过添加辅助线来构造全等三角形.常见的添加辅助线方法有：连接法、截长补短法、倍长中线法、翻折法、旋转法以及利用特殊条件构造全等三角形等等.1、如图，△ABC的两条高BD，CE相交于点P，且PD＝PE.证明∶AC＝AB2、已知AB＝DE，BC＝EF，∠B＝∠E，AF＝CD求证：AC∥DF3、如图，AB交CD于点O，AD、CB的延长线相交于点E，且OA＝OC，EA＝EC.∠A＝∠C吗？点O在∠AEC的平分线上吗？A辅助线作法之倍长中线法在题目条件中含有中线的问题，我们常用的辅助线就是将中线延长一倍，其目的是为了得一对全等三角形，将分散的条件集中到一个三角形中去.1、△ABC中，AB＝5，AC＝3，求中线AD的取值范围.2、如图，在△ABC中，AD是∠BAC的平分线，又是BC上的中线求证：AB＝AC3、（2014·襄阳初三模拟）在△ABC中，D是边BC上的一点，且CD＝AB，∠BAD＝∠BDA，AE是△ABD的中线.求证∶AC＝2AEB文档来源为:从网络收集整理.word版本可编辑.欢迎下载支持.4、（竞赛014）△ABC中，D为BC的中点，DE⊥DF交AB，AC于点E，F.求证：BE＋CF＞EF6、（竞赛015）例：已知AD是△ABC的中线，BE交AC于点E，交AD于点F，且AE＝EF.求证:AC＝BFB辅助线作法之截长补短法截长法：在第三条线段上截下一段使其等于两条线段中的一条，再证明剩余部分与另一条相等. 补短法：把两条线段中的一条补到另一条线段上去，证明所得新线段与第三条线段相等. 1、已知AC ∥BD ，EA ，EB 分别平分∠CAB 和∠DBA ，点E 在CD 上.求证：AB ＝AC ＋BD2、在四边形ABCD 中，AC 平分∠BAD ，CE ⊥AB 于点E ，且AE ＝½（AB ＋AD ）.求证∶∠B ＋∠D ＝180°3、如图，已知△ABC 中，∠A ＝90°，AB ＝AC ，D 为AC 的中点，AE ⊥BD 于E ，延长AE 交BC 于F.求证：∠ADB ＝∠CDF4、如图，∠C ＝90°，AC ＝BC ，AD 是∠BAC 的角平分线. 求证∶AC ＋CD ＝AB12、如图，已知AB ＝CD ＝AE ＝BC ＋DE ＝2，∠ABC ＝∠AED ＝90°，求五边形ABCDE 的面积.AB辅助线作法之利用特殊条件构造全等三角形2、（2012·“华罗庚杯”）如图，在△ABC 中，AC ＝½AB ，AD 平分∠BAC ，且AD ＝BD求证：CD ⊥AC八年级数学培优专题训练（八）全等三角形在动态几何中的运用1、(竞赛·014·3)如图，△ABC 的边BC 在直线l 上，AC ⊥BC ，且AC ＝BC.△EFP 的边FP 也在直线l 上，边EF 与边AC 重合，且EF ＝FP.⑴在图①中,请你通过观察、测量、猜想并写出AB 与AP 所满足的数量关系和位置关系; ⑵将△EFP 沿直线l 向左平移到图②的位置时,EP 交AC 于点Q,连接AP,BQ.猜想并写出BQ 与AP 所满足的数量关系和位置关系,并证明你的猜想;⑶将△EFP 沿直线l 向左平移到图③的位置时,EP 的延长线交AC 的延长线于点Q,连接AP,BQ.你认为⑵中所猜想的BQ 与AP 的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.B探究角平分线一、知识清单角平分线的定义：从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的角平分线.三角形的角平分线定义：三角形的一个角的平分线与这个角的对边相交，连结这个角的顶点和与对边交点的线段叫做三角形的角平分线（也叫三角形的内角平分线）. 由定义可知，三角形的角平分线是一条线段.角平分线性质:1、角平分线上的点，到这个角的两边的距离相等.2、角平分线分得的两个角相等，都等于该角的一半.3、三角形的三条角平分线交于一点，且到各边的距离相等，这个点称为内心.二、方法点拨证明角平分线有两种方法:一是运用定义证明两个角相等;二是运用角平分线的判定方法.三、规律清单①遇到角平分线,可从角平分线上的某一点向角的两边作垂线段(图1).②遇到角平分线,常可利用翻折法或截长补短法解题(图2).③有两条角平分线(内角或外角)交于一点,则连接该点与三角形第三个顶点的线段会平分一个内角或外角(图3).④有垂直于角平分线的线段,则延长这条线段以利用三线合一解题(图4).⑤遇到角内的一点到角的两边有垂线段时,就连接这点与角的顶点,看能否平分已知角(图5).⑥遇到有多条角平分线时,可尝试用整体的思想解题(图6).⑦有翻折条件时,除注意全等的结论,还应关注折线就是角平分线、是对称轴（如图7）.⑧角平分线、平行线、等腰三角形三个条件中出现任意两个,常可直接得到另一个(如图8）.四、真题训练1、(2011·鄂州·竞赛·018 ·重庆中考）如图，△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP相交于点P，若∠BPC＝40°，则∠CAP＝_____________.2、(竞赛·019)如图，∠B＝∠C＝90°，M是BC的中点，DM平分∠ADC.求证:AM平分∠DABB3、(竞赛·019)如图,在△ABC 中,∠BAC ＝90°,AB ＝AC,BE 平分∠ABC,CE ⊥BE.求证:CE ＝12BD4、如图，在△ABC 中，AD 平分∠BAC ，BD ＝CD 求证：∠B ＝∠C5、如图，在Rt △ABC 中，∠C ＝90°，AC ＝BC ，AD 是∠BAC 的平分线，交BC 于D ，DE ⊥AB 于E ，若AB ＝10cm ，则△DBE 的周长是多少？6、（2011，恩施中考）AD 是△ABC 的角平分线，DF ⊥AB ，垂足为F ，DE ＝DG ，△ADG 和△AED 的面积分别为50和39，则△EDF 的面积为多少？B7、如图，△ABC 中，AD 平分∠BAC ，DG ⊥BC 且平分BC ，DE ⊥AB 于E ，DF ⊥AC 于F.求证：BE ＝CF8、在△ABC 中，AD 是∠BAC 的平分线，E 、F 分别为AB 、AC 上的点，且∠EDF ＋∠BAF ＝180°⑴求证：DE ＝DF⑵如果把最后一个条件改为AE ＞AF ，且∠AED ＋∠AFD ＝180°，那么结论还成立吗？ 9、如图，已知AB ＝AC ，BE ⊥AC 于E ，CF ⊥AB 于F ，BE 与CF 交于点D 求证：点D 在∠BAC 的平分线上.10、如图，在四边形ABCD 中，对角线AC 平分∠BAD ，AB ＞AD ，下列结论正确的是( )A.AB －AD ＞CB －CDB.AB －AD ＝CB －CDC.AB －AD ＜CB －CDD.AB －CD 与CB －CD 的大小关系不确定11、（竞赛014）如图，已知△ABC 中，∠B ＝60°，∠BAC ，∠BCA 的平分线AD ，CE 相交于点O.求证：DC ＋AE ＝AC12、(竞赛·019)如图，已知△ABC ，P 为内角平分线AD 、BE 、CF 的交点，过点P 作PG ⊥BC 于G 点。

全等三角形经典培优题型(含标准答案)

三角形培优练习题1已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD2已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠23已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC4已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C5已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE6如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

求证：BC=AB+DC 。

已知：AB=CD ，∠A=∠D ，求证：∠B=∠C78.P 是∠BAC 平分线AD 上一点，AC>AB ，求证：PC-PB<AC-ABCDBA BC DEF 2 1ADBCA B CD ABACDF2 1 E9已知，E 是AB 中点，AF=BD ，BD=5，AC=7，求DC10．如图，已知AD ∥BC ，∠P AB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ．11如图，△ABC 中，AD 是∠CAB 的平分线，且AB =AC +CD ，求证：∠C =2∠B12如图：AE 、BC 交于点M ，F点在AM 上，BE∥CF ，BE=CF 。

求证：AM 是△ABC 的中线。

13已知：如图，AB =AC ，BD ⊥AC ，CE ⊥AB ，垂足分别为D 、E ，BD 、CE 相交于点F 。

求证：BE =CD ．14在△ABC 中，︒=∠90ACB ，BC AC =，直线MN 经过点C ，且MN AD ⊥于D ，MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时，求证： ①ADC ∆≌CEB ∆；②BE AD DE +=；(2)当直线MN 绕点C 旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，说明理由.15如图所示，已知AE ⊥AB ，AF ⊥AC ，AE=AB ，AF=AC 。

全等三角形培优(含答案)

三角形培优练习题1 已知：AB=4 ，AC=2 ，D 是BC 中点，AD 是整数，求ADAB CD2 已知：BC=DE ，∠B=∠E，∠C=∠D，F 是CD 中点，求证：∠1=∠2A21B EC F D3 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=ACA21FCDEB4 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠CACB D15 已知：AC 平分∠BAD ，CE⊥AB ，∠B+∠D=180°，求证：AE=AD+BE6 如图，四边形ABCD 中，AB ∥DC，BE、CE 分别平分∠ABC 、∠BCD，且点 E 在AD 上。

求证：BC=AB+DC 。

7 已知：AB=CD ，∠A= ∠D，求证：∠B=∠CA DB C8.P 是∠BAC 平分线AD 上一点，AC>AB ，求证：PC-PB<AC-ABCAP DB9 已知，E 是AB 中点，AF=BD ，BD=5 ，AC=7 ，求DCDCFAE B10．如图，已知AD∥BC，∠PAB 的平分线与∠CBA 的平分线相交于E，CE 的连线交AP 于D．求证：AD +BC=AB．PCEDA B11 如图，△ABC 中，AD 是∠CAB 的平分线，且AB=AC+CD，求证：∠C=2∠BACD B12 如图：AE、BC交于点M，F 点在AM上，BE∥CF，BE=CF。

求证：AM是△ABC的中线。

AFBC ME313 已知：如图，AB=AC，BD AC，CE AB，垂足分别为D、E，BD、CE 相交于点F。

求证：BE =CD．CDFEB A14 在△ABC 中，ACB 90 ，AC BC ，直线M N 经过点C ，且AD MN 于D ，BE MN 于E .(1) 当直线M N 绕点C 旋转到图 1 的位置时，求证：①ADC ≌CEB；②DE AD BE ；(2) 当直线M N 绕点C 旋转到图 2 的位置时，（1）中的结论还成立吗？若成立，由.请给出证明；若不成立，说明理15 如图所示，已知AE⊥AB，AF⊥AC，AE=AB，AF=AC。

全等三角形证明题培优提高经典例题练习题

全等三角形证明题培优提高经典例题练习题1.已知直角三角形ABC中，AB=AC，AD⊥AE，AD=AE，求证BE=CD。

证明：连接BD、CE，由于AB=AC，所以∠___∠ACB，又AD⊥AE，所以∠BAD=∠CAE，因此△ABD≌△___，从而BD=CE。

又因为___⊥AC，所以BD⊥CE，因此△BDE≌△___，从而BE=CD。

2.已知直角三角形ABC中，AB⊥BC，AD⊥DC，AB=AD，求证EB=ED。

证明：连接AE，由于AB⊥BC，所以∠ABC=90°，又AB=AD，所以△ABD为等腰直角三角形，因此∠BAD=45°。

又因为AD⊥DC，所以∠ADC=90°，因此∠BAC=45°。

又因为AB=AE，所以△ABE为等腰直角三角形，因此∠BAE=45°。

因此△ABE和△ABD为全等三角形，从而EB=ED。

3.已知AB、CD交于O点，CE//DF，CE=DF，AE=BF，求证∠___=∠BDF。

证明：连接OF，因为CE//DF，所以∠___∠___，又因为CE=DF，所以△CEO≌△DFO，从而∠CEO=∠DFO。

又因为AE=BF，所以△AEO≌△BFO，从而∠AEO=∠___。

因此∠___=∠CEO+∠AEO=∠DFO+∠BFO=∠BDF。

4.在等边三角形ABC中，AB=AC，过A作GE∥BC，角平分线BD、CF交于点H，它们的延长线分别交GE于E、G，证明△HBE≌△___。

证明：因为AB=AC，且GE∥BC，所以△ABE和△ACG为全等三角形，从而BE=CG。

又因为BD和CF为角平分线，所以∠ABD=∠___，∠ACD=∠CBD，从而∠ABD+∠___∠FBC+∠CBD=180°，因此四边形ABCF为内接四边形。

因为H是角平分线的交点，所以HB=HC。

又因为BE=CG，所以△HBE和△HCG为全等三角形，从而HE=GC。

5.在三角形ABC中，点D在AB上，点E在BC上，BD=BE，且△BEA≌△BDC，证明△ABC为等腰三角形。

全等三角形提高32题含答案

全等三角形提高32题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD2. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠23. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC4. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠ CA BC DEF 21 ADBCBACDF2 1 E5. 已知：AC 平分∠BAD ，CE ⊥AB ， ∠B+∠D=180°，求证：AE=AD+BE6. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

求证：BC=AB+DC 。

CDBA7. 已知：AB//ED ，∠EAB=∠BDE ，AF=CD ，EF=BC ，求证：∠F=∠C8．如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ．9．如图，OM 平分∠POQ ，MA ⊥OP ,MB ⊥OQ ，A 、B 为垂足，AB 交OM 于点N ．求证：∠OAB =∠OBADCBA FE10．如图，已知AD ∥BC ，∠P AB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ．11．如图，△ABC 中，AD 是∠CAB 的平分线，且AB =AC +CD ，求证：∠C =2∠BPEDCBA D CBA12．如图①，E 、F 分别为线段AC 上的两个动点，且DE ⊥AC 于E ，BF ⊥AC 于F ，若AB =CD ，AF =CE ，BD 交AC 于点M ．（1）求证：MB =MD ，ME =MF（2）当E 、F 两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．13．已知：如图，DC ∥AB ，且DC =AE ，E 为AB 的中点，（1）求证：△AED ≌△EBC ．（2）观看图前，在不添辅助线的情况下，除△EBC 外，请再写出两个与△AED 的面积相等的三角形．（直接写出结果，不要求证明）：OEDCBA14．如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ．求证：BD =2CE ．15、如图：AE 、BC 交于点M ，F 点在AM 上，BE ∥CF ，BE=CF 。

全等三角形证明题专练(培优)

1.（★★★）已知：BD CE 、是ABC ∆的高，点P 在BD 的延长线上，BP AC =，点Q 在CE 上，CQ AB =，求证：⑴AP AQ =；⑵AP AQ ⊥．PDQCBEA2.（★★★）如图，已知在ABC ∆中，AD 是BC 边上的中线，E 是AD 上一点，延长BE 交AC 于F ，AF EF =，求证：AC BE =．FEDC BA3.（★★★★）已知AD 为ABC ∆的中线，ADB ∠，ADC ∠的平分线分别交AB 于E 、交AC 于F ．求证：BE CF EF +>．FE AB D C4.（★★）如图，已知AB =DC ，AD =BC ，O 是BD 中点，过O 点的直线分别交DA 、BC 的延长线于E ，F ．求证：∠E =∠F5.（★★）如图，ABC ∆中，AB AC =，90BAC ∠=︒，D 是BC 中点，ED FD ⊥，ED 与AB 交于E ，FD 与AC 交于F ．求证：BE AF =，AE CF =．ABCDE F6.（★★★）如图所示，已知ABC ∆中，AD 平分BAC ∠，E 、F 分别在BD 、AD 上．DE CD =，EF AC =．求证：EF ∥ABFA CD E B7.（★★★）如图所示，在ABC ∆中，AD 平分BAC ∠，AD AB =，CM AD ⊥于M ，求证2AB AC AM +=．MD CBA8.（★★★）如图，已知在ABC ∆中，3ABC C ∠=∠，12∠=∠，BE AE ⊥．求证：2AC AB BE -=．21ECBA9.（★★★）已知：如图，点C为线段AB上一点，ACM∆、CBN∆是等边三角形．（1）求证：AN BM=．（2）求证：CD=CE (3) 求证：CF平分∠MCN （4）求证：DE∥AB10.（★★★）等边ABD∆和等边CBD∆的边长均为1，E是BE AD⊥上异于A D、的任意一点，F是CD上一点，满足1AE CF+=，当E F、移动时，试判断BEF∆的形状．DFECBA11．（★★★★）如图，在ABC∆中，BE是∠ABC的平分线，AD BE⊥，垂足为D。

三角形全等培优证明题100题(有答案)

全等三角形证明题专项练习(100题)1．已知如图，△ABC≌△ADE，∠B=30°，∠E=20°，∠BAE=105°，求∠BAC的度数．∠BAC=_________．2．已知：如图，四边形ABCD中，AB∥CD，AD∥BC．求证：△ABD≌△CDB．3．如图，点E在△ABC外部，点D在边BC上，DE交AC于F．若∠1=∠2=∠3，AC=AE，请说明△ABC≌△ADE 的道理．4．如图，△ABC的两条高AD，BE相交于H，且AD=BD．试说明下列结论成立的理由．（1）∠DBH=∠DAC；（2）△BDH≌△ADC．5．如图，在△ABC中，D是BC边的中点，DE⊥AB，DF⊥AC，垂足分别为E、F，且DE=DF，则AB=AC，并说明理由．6．如图，AE是∠BAC的平分线，AB=AC，D是AE反向延长线的一点，则△ABD与△ACD全等吗？为什么？7．如图所示，A、D、F、B在同一直线上，AF=BD，AE=BC，且AE∥BC．求证：△AEF≌△BCD．8．如图，已知AB=AC，AD=AE，BE与CD相交于O，△ABE与△ACD全等吗？说明你的理由．9．如图，在△ABC中，AB=AC，D是BC的中点，点E在AD上，找出图中全等的三角形，并说明它们为什么是全等的．10．如图所示，CD=CA，∠1=∠2，EC=BC，求证：△ABC≌△DEC．11．已知AC=FE，BC=DE，点A、D、B、F在一条直线上，要使△ABC≌△FDE，应增加什么条件？并根据你所增加的条件证明：△ABC≌△FDE．12．如图，已知AB=AC，BD=CE，请说明△ABE≌△ACD．13．如图，△ABC中，∠ACB=90°，AC=BC，将△ABC绕点C逆时针旋转角α（0°＜α＜90°）得到△A1B1C，连接BB1．设CB1交AB于D，A1B1分别交AB，AC于E，F，在图中不再添加其他任何线段的情况下，请你找出一对全等的三角形，并加以证明．（△ABC与△A1B1C1全等除外）14．如图，AB∥DE，AC∥DF，BE=CF．求证：△ABC≌△DEF．15．如图，AB=AC，AD=AE，AB，DC相交于点M，AC，BE相交于点N，∠DAB=∠EAC．求证：△ADM≌△AEN．16．将两个大小不同的含45°角的直角三角板如图1所示放置在同一平面内．从图1中抽象出一个几何图形（如图2），B、C、E三点在同一条直线上，连接DC．求证：△ABE≌△ACD．17．如图，已知△ABC是等边三角形，D、E分别在边BC、AC上，且CD=CE，连接DE并延长至点F，使EF=AE，连接AF、BE和CF．请在图中找出所有全等的三角形，用符号“≌”表示，并选择一对加以证明．18．如图，已知∠1=∠2，∠3=∠4，EC=AD．（1）求证：△ABD≌△EBC．（2）你可以从中得出哪些结论？请写出两个．19．等边△ABC边长为8，D为AB边上一动点，过点D作DE⊥BC于点E，过点E作EF⊥AC于点F．（1）若AD=2，求AF的长；（2）求当AD取何值时，DE=EF．20．巳知：如图，AB=AC，D、E分别是AB、AC上的点，AD=AE，BE与CD相交于G．（Ⅰ）问图中有多少对全等三角形？并将它们写出来．（Ⅱ）请你选出一对三角形，说明它们全等的理由（根椐所选三角形说理难易不同给分，即难的说对给分高，易的说对给分低）21．已知：如图，AB=DC，AC=BD，AC、BD相交于点E，过E点作EF∥BC，交CD于F，（1）根据给出的条件，可以直接证明哪两个三角形全等？并加以证明．（2）EF平分∠DEC吗？为什么？22．如图，己知∠1=∠2，∠ABC=∠DCB，那么△ABC与△DCB全等吗？为什么？23．如图，B，F，E，D在一条直线上，AB=CD，∠B=∠D，BF=DE．试证明：（1）△DFC≌△BEA；（2）△AFE≌△CEF．24．如图，AC=AE，∠BAF=∠BGD=∠EAC，图中是否存在与△ABE全等的三角形？并证明．25．如图，D是△ABC的边BC的中点，CE∥AB，E在AD的延长线上．试证明：△ABD≌△ECD．26．如图，已知AB=CD，∠B=∠C，AC和BD相交于点O，E是AD的中点，连接OE．（1）求证：△AOB≌△DOC；（2）求∠AEO的度数．27．如图，已知AB∥DE，AB=DE，AF=DC．（1）求证：△ABF≌△DEC；（2）请你找出图中还有的其他几对全等三角形．（只要直接写出结果，不要证明）28．如图：在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连接AD、AG．（1）求证：△ABD≌△GCA；（2）请你确定△ADG的形状，并证明你的结论．29．如图，点D、F、E分别在△ABC的三边上，∠1=∠2=∠3，DE=DF，请你说明△ADE≌△CFD的理由．30．如图，在△ABC中，∠ABC=90°，BE⊥AC于点E，点F在线段BE上，∠1=∠2，点D在线段EC上，给出两个条件：①DF∥BC；②BF=DF．请你从中选择一个作为条件，证明：△AFD≌△AFB．31．如图，在△ABC中，点D在AB上，点E在BC上，AB=BC，BD=BE，EA=DC，求证：△BEA≌△BDC．32．阅读并填空：如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D．请说明△ADC≌△CEB的理由．解：∵BE⊥CE于点E（已知），∴∠E=90°_________，同理∠ADC=90°，∴∠E=∠ADC（等量代换）．在△ADC中，∵∠1+∠2+∠ADC=180°_________，∴∠1+∠2=90°_________．∵∠ACB=90°（已知），∴∠3+∠2=90°，∴_________．在△ADC和△CEB中，.∴△ADC≌△CEB （A．A．S）33．已知：如图所示，AB∥DE，AB=DE，AF=DC．（1）写出图中你认为全等的三角形（不再添加辅助线）；（2）选择你在（1）中写出的全等三角形中的任意一对进行证明．34．如图，点E在△ABC外部，点D在BC边上，DE交AC于点F，若∠1=∠2=∠3，AC=AE．试说明下列结论正确的理由：（1）∠C=∠E；（2）△ABC≌△ADE．35．如图，在Rt△ABC中，∠ACB=90°，AC=BC，D是斜边AB上的一点，AE⊥CD于E，BF⊥CD交CD的延长线于F．求证：△ACE≌△CBF．36．如图，在△ABC中，D是BC的中点，DE∥CA交AB于E，点P是线段AC上的一动点，连接PE．探究：当动点P运动到AC边上什么位置时，△APE≌△EDB？请你画出图形并证明△APE≌△EDB．37．已知：如图，AD∥BC，AD=BC，E为BC上一点，且AE=AB．求证：（1）∠DAE=∠B；（2）△ABC≌△EAD．38．如图，D为AB边上一点，△ABC和△ECD都是等腰直角三角形，∠ACB=∠DCE=90°，CA=CB，CD=CE，图中有全等三角形吗？指出来并说明理由．39．如图，AB=AC，AD=AE，∠BAC=∠DAE．求证：△ABD≌△ACE．40．如图，已知D是△ABC的边BC的中点，过D作两条互相垂直的射线，分别交AB于E，交AC于F，求证：BE+CF＞EF．41．如图所示，在△MNP中，H是高MQ与NE的交点，且QN=QM，猜想PM与HN有什么关系？试说明理由．42．如图，在△ABC中，D是BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于G点，DE⊥GF，交AB于点E，连接EG．（1）求证：BG=CF；（2）请你判断BE+CF与EF的大小关系，并证明你的结论．43．如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于E，AD⊥CE于D，AD=2.5cm，DE=1.7cm，求BE的长．44．如图，小明在完成数学作业时，遇到了这样一个问题，AB=CD，BC=AD，请说明：∠A=∠C的道理，小明动手测量了一下，发现∠A确实与∠C相等，但他不能说明其中的道理，你能帮助他说明这个道理吗？试试看．45．如图，AD是△ABC的中线，CE⊥AD于E，BF⊥AD，交AD的延长线于F．求证：CE=BF．46．如图，已知AB∥CD，AD∥BC，F在DC的延长线上，AM=CF，FM交DA的延长线上于E．交BC于N，试说明：AE=CN．47．已知：如图，△ABC中，∠C=90°，CM⊥AB于M，AT平分∠BAC交CM于D，交BC于T，过D作DE∥AB 交BC于E，求证：CT=BE．48．如图，已知AB=AD，AC=AE，∠BAE=∠DAC．∠B与∠D相等吗？请你说明理由．49．D是AB上一点，DF交AC于点E，DE=EF，AE=CE，求证：AB∥CF．50．如图，M是△ABC的边BC上一点，BE∥CF，且BE=CF，求证：AM是△ABC的中线．51．四边形ABCD中，AD=BC，BE=DF，AE⊥BD，CF⊥BD，垂足分别为E、F．（1）求证：△ADE≌△CBF；（2）若AC与BD相交于点O，求证：AO=CO．52．如图，已知点B，E，C，F在一条直线上，AB=DF，AC=DE，∠A=∠D．（1）求证：AC∥DE；（2）若BF=13，EC=5，求BC的长．53．如图，BD⊥AC于点D，CE⊥AB于点E，AD=AE．求证：BE=CD．54．如图，点O是线段AB和线段CD的中点．（1）求证：△AOD≌△BOC；（2）求证：AD∥BC．55．如图：点C是AE的中点，∠A=∠ECD，AB=CD，求证：∠B=∠D．56．如图，已知△ABC和△DAE，D是AC上一点，AD=AB，DE∥AB，DE=AC．求证：AE=BC．57．如图，AB∥CD，E是CD上一点，BE交AD于点F，EF=BF．求证：AF=DF．58．如图，点B、E、C、F在同一条直线上，AB=DE，AC=DF，BE=CF，求证：AB∥DE．59．如图，点D是AB上一点，DF交AC于点E，DE=FE，FC∥AB求证：AE=CE．60．如图，点A、C、D、B四点共线，且AC=BD，∠A=∠B，∠ADE=∠BCF，求证：DE=CF．61．如图，点A，B，C，D在同一条直线上，CE∥DF，EC=BD，AC=FD．求证：AE=FB．62．已知△ABN和△ACM位置如图所示，AB=AC，AD=AE，∠1=∠2．（1）求证：BD=CE；（2）求证：∠M=∠N．63．如图，BE⊥AC，CD⊥AB，垂足分别为E，D，BE=CD．求证：AB=AC．64．如图，在△ABC和△CED中，AB∥CD，AB=CE，AC=CD．求证：∠B=∠E．65．如图，在△ABC中，AD平分∠BAC，且BD=CD，DE⊥AB于点E，DF⊥AC于点F．（1）求证：AB=AC；（2）若AD=2，∠DAC=30°，求AC的长．66．如图，Rt△ABC≌Rt△DBF，∠ACB=∠DFB=90°，∠D=28°，求∠GBF的度数．67．如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．求证：△ABC≌△BAD．68．已知：如图，点B、F、C、E在一条直线上，BF=CE，AC=DF，且AC∥DF．求证：△ABC≌△DEF．69．已知：点A、C、B、D在同一条直线，∠M=∠N，AM=CN．请你添加一个条件，使△ABM≌△CDN，并给出证明．（1）你添加的条件是：；（2）证明：．70．如图，AB=AC，AD=AE．求证：∠B=∠C．71．如图，在△ABC中，AD是△ABC的中线，分别过点B、C作AD及其延长线的垂线BE、CF，垂足分别为点E、F．求证：BE=CF．72．一个平分角的仪器如图所示，其中AB=AD，BC=DC．求证：∠BAC=∠DAC．73．在数学课上，林老师在黑板上画出如图所示的图形（其中点B、F、C、E在同一直线上），并写出四个条件：①AB=DE，②BF=EC，③∠B=∠E，④∠1=∠2．请你从这四个条件中选出三个作为题设，另一个作为结论，组成一个真命题，并给予证明．题设：；结论：．（均填写序号）证明：74．如图，在△ABC和△DEF中，AB=DE，BE=CF，∠B=∠1．求证：AC=DF．（要求：写出证明过程中的重要依据）75．如图，已知AB=DC，AC=DB．求证：∠1=∠2．76．如图，D、E分别为△ABC的边AB、AC上的点，BE与CD相交于O点．现有四个条件：①AB=AC；②OB=OC；③∠ABE=∠ACD；④BE=CD．（1）请你选出两个条件作为题设，余下的两个作为结论，写出一个正确的命题：命题的条件是和，命题的结论是和（均填序号）；（2）证明你写出的命题．77．如图，已知AB∥DE，AB=DE，AF=DC，请问图中有哪几对全等三角形并任选其中一对给予证明．78．如图所示，在梯形ABCD中，AD∥BC，∠B=∠C，点E是BC边上的中点．求证：AE=DE．79．如图，给出下列论断：①DE=CE，②∠1=∠2，③∠3=∠4．请你将其中的两个作为条件，另一个作为结论，构成一个真命题，并加以证明．80．已知：如图，∠ACB=90°，AC=BC，CD是经过点C的一条直线，过点A、B分别作AE⊥CD、BF⊥CD，垂足为E、F，求证：CE=BF．81．如图，在△ABC中，AC⊥BC，AC=BC，D为AB上一点，AF⊥CD交于CD的延长线于点F，BE⊥CD于点E，求证：EF=CF﹣AF．82．如图，在△ABC中，∠BAC=90°，AB=AC，若MN是经过点A的直线，BD⊥MN于D，EC⊥MN于E．（1）求证：BD=AE；（2）若将MN绕点A旋转，使MN与BC相交于点O，其他条件都不变，BD与AE边相等吗？为什么？（3）BD、CE与DE有何关系？83．已知：如图，△ABC中，AB=AC，BD和CE为△ABC的高，BD和CE相交于点O．求证：OB=OC．84．在△ABC中，∠ACB=90°，D是AB边的中点，点F在AC边上，DE与CF平行且相等．试说明AE=DF的理由．85．如图，在△ABC中，D是边BC上一点，AD平分∠BAC，在AB上截取AE=AC，连接DE，已知DE=2cm，BD=3cm，求线段BC的长．86．如图：已知∠B=∠C，AD=AE，则AB=AC，请说明理由．87．如图△ABC中，点D在AC上，E在AB上，且AB=AC，BC=CD，AD=DE=BE．（1）求证△BCE≌△DCE；（2）求∠EDC的度数．88．已知：∠A=90°，AB=AC，BD平分∠ABC，CE⊥BD，垂足为E．求证：BD=2CE．89．如图，已知：AB=CD，AD=BC，过BD上一点O的直线分别交DA、BC的延长线于E、F．（1）求证：∠E=∠F；（2）OE与OF相等吗？若相等请证明，若不相等，需添加什么条件就能证得它们相等？请写出并证明你的想法．90．如下图，AD是∠BAC的平分线，DE垂直AB于点E，DF垂直AC于点F，且BD=DC．求证：BE=CF．91．如图，在矩形ABCD中，AB=8，BC=12，点E是BC的中点，连接AE，将△ABE沿AE折叠，点B 落在点F处，连接FC，（1）求CF的长。

全等三角形经典题型50题(含答案)

全等三角形证明经典50题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。

因为 BC=ED,CF=DF,∠BCF=∠EDF 。

所以三角形BCF 全等于三角形EDF(边角边)。

所以 BF=EF,∠CBF=∠DEF 。

连接BE 。

在三角形BEF 中,BF=EF 。

所以 ∠EBF=∠BEF 。

又因为 ∠ABC=∠AED 。

所以 ∠ABE=∠AEB 。

所以 AB=AE 。

在三角形ABF 和三角形AEF 中，AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。

所以三角形ABF 和三角形AEF 全等。

所以 ∠BAF=∠EAF (∠1=∠2)。

ADBC4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC 证明：过E 点，作EG//AC ，交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE （AAS ）∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ，AD=AD ∴⊿AED ≌⊿ABD （SAS ）∴∠AED=∠B ，DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F ，使EF ＝EB ，连接CF 因为CE ⊥AB 所以∠CEB ＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ，所以△CEB ≌△CEF 所以∠B ＝∠CFE 因为∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC 所以△ADC ≌△AFC （SAS ）所以AD ＝AF 所以AE ＝AF ＋FE ＝AD ＋BE12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。