运筹学建模例题和判断题
运筹学建模例题和判断题

【例1-2】某商场决定:营业员每周连续工作5天后连续休息2天,轮流休息。
根据统计,商场每天需要的营业员如表1-2所示。
表1-2 营业员需要量统计表星期需要人数星期需要人数一300 五480二300 六600三350 日550四400(2)在例1.2中,如果设x j(j=1,2,…,7)为工作了5天后星期一到星期日开始休息的营业员,该模型如何变化.【例1-3】合理用料问题。
某汽车需要用甲、乙、丙三种规格的轴各一根,这些轴的规格分别是1.5,1,0.7(m),这些轴需要用同一种圆钢来做,圆钢长度为4 m。
现在要制造1000辆汽车,最少要用多少圆钢来生产这些轴?如果要求余料最少,数学模型如何变化;【例1-4】配料问题。
某钢铁公司生产一种合金,要求的成分规格是:锡不少于28%,锌不多于15%,铅恰好10%,镍要界于35%~55%之间,不允许有其他成分。
钢铁公司拟从五种不同级别的矿石中进行冶炼,每种矿物的成分含量和价格如表1-4所示。
矿石杂质在治炼过程中废弃,现要求每吨合金成本最低在例1.4中,若允许含有少量杂质,但杂质含量不超过1%,模型如何变化.【例1-5】投资问题。
某投资公司拟将5000万元的资金用于国债、地方国债及基金三种类型证券投资,每类各有两种。
每种证券的评级、到期年限及每年税后收益率见表1-5所示。
序号证券类型评级到期年限每年税后收益率(%)1 国债1 1 8 3.22 国债2 1 10 3.83 地方债券1 24 4.34 地方债券2 3 6 4.75 基金1 4 3 4.26 基金2 5 4 4.6决策者希望:国债投资额不少于1000万,平均到期年限不超过5年,平均评级不超过2。
问每种证券各投资多少使总收益最大。
【例1-6】均衡配套生产问题。
某产品由2件甲、3件乙零件组装而成。
两种零件必须经过设备A、B上加工,每件甲零件在A、B上的加工时间分别为5分钟和9分钟,每件乙零件在A、B上的加工时间分别为4分钟和10分钟。
运筹学试题与答题

一、判断题(正确的打“√”,错误的打“×”):1.图解法只能解决包含两个决策变量的线性规划问题.( 是 )2.线性规划具有无界解,则可行域无界.( 是 )3.若线性规划问题的可行域存在,则可行域是一个凸集.( 是 )4.单纯形法求解线性规划问题时每换基迭代一次必使目标函数值下降一次.( 错 )每迭代一次,目标函数的值都会增加,即增量大于05.用单纯形法求解线性规划问题时,如果表中所有的检验数0≤j σ,则表中的基可行解为最优解.( 是 )0≤j σ,则非基变量都<=06.对偶问题的对偶就是原问题.( 恩 )8.互为对偶问题,原问题有最优解,对偶问题也有最优解.( 恩 )且目标函数的值也一样9.任意一个运输问题一定存在最优解.( 是的)运输问题一定存在最优解10.线性规划问题的最优解只能在极点上达到.(错 )11.对偶单纯形法是直接解对偶问题的一种方法.( 错 )有区别的。
通过判断b 列的正负来进行迭代的。
12.原问题具有无界解,对偶问题无可行解.( 恩 )13.可行解是基解.( 错)14.标准型中的变量要求非正.( 恩 )大于015.线性规划的基本最优解是最优解.( 恩 )16.对产销平衡运输问题,各产地产量之和等于各销地销量之和.( 恩 )18.用单纯形法求解线性规划问题时,一定要将问题化为标准型.( 恩 )19.匈亚利解法是求解运输问题的一种方法.(错 )匈牙利(康尼格)法是求解及小型(优化方向为极小)指派问题的一种方法20.运输问题必存在有限最优解.( 错 )当非基变量为0时有无穷多最优解(关于其退化问题)二、填空题:1.规划问题的数学模型由 目标函数 、 约束条件 、 决策变量 三个要素组成。
2.满足变量非负约束条件的 基解 称为基可行解。
3.线性规划的约束条件个数与其对偶问题的 决策变量个数 相等;4.如原问题有可行解且目标函数值无界,则其对偶问题 无可行解 ;反之,对偶问题有可行解且目标函数值无界,则其原问题 无可行解 。
《运筹学》模拟试题及参考答案

《运筹学》模拟试题及参考答案一、判断题(在下列各题中,你认为题中描述的内容为正确者,在题尾括号内写“√”,错误者写“×”。
)1. 图解法提供了求解线性规划问题的通用方法。
( )2. 用单纯形法求解一般线性规划时,当目标函数求最小值时,若所有的检验数C j-Z j ≥0,则问题达到最优。
( )3. 在单纯形表中,基变量对应的系数矩阵往往为单位矩阵。
( )4. 满足线性规划问题所有约束条件的解称为基本可行解。
( )5. 在线性规划问题的求解过程中,基变量和非基变量的个数是固定的。
( )6. 对偶问题的目标函数总是与原问题目标函数相等。
( )7. 原问题与对偶问题是一一对应的。
( )8. 运输问题的可行解中基变量的个数一定遵循m+n-1的规则。
( )9. 指派问题的解中基变量的个数为m+n。
( )10. 网络最短路径是指从网络起点至终点的一条权和最小的路线。
( )11. 网络最大流量是网络起点至终点的一条增流链上的最大流量。
( )12. 工程计划网络中的关键路线上事项的最早时间和最迟时间往往不相等。
( )13. 在确定性存贮模型中不许缺货的条件下,当费用项目相同时,生产模型的间隔时间比订购模型的间隔时间长。
( )14. 单目标决策时,用不同方法确定的最佳方案往往是一致的。
( )15. 动态规划中运用图解法的顺推方法和网络最短路径的标号法上是一致的。
( )二、简述题1. 用图解法说明线性规划问题单纯形法的解题思想。
2. 运输问题是特殊的线性规划问题,但为什么不用单纯形法求解。
3. 建立动态规划模型时,应定义状态变量,请说明状态变量的特点。
三、填空题1. 图的组成要素;。
2. 求最小树的方法有、。
3. 线性规划解的情形有 、 、 、 。
4. 求解指派问题的方法是 。
5. 按决策环境分类,将决策问题分为 、 、 。
6. 树连通,但不存在 。
四、下列表是线性规划单纯形表(求Z max ),请根据单纯形法原理和算法。
运筹学习题判断题及答案(通用篇)

运筹学习题判断题及答案(通用篇)一、判断题1. 线性规划问题中,目标函数必须是线性函数。
()答案:错误。
线性规划问题的目标函数可以是线性函数,也可以是非线性函数。
但是,当目标函数为非线性函数时,该问题就不再是线性规划问题。
2. 在目标规划中,若决策变量有上界和下界,则称为有界决策变量。
()答案:正确。
在目标规划中,有界决策变量是指决策变量具有上界和下界限制。
3. 对偶问题与原问题具有相同的可行域。
()答案:错误。
对偶问题与原问题具有相同的解,但可行域一般不同。
4. 在整数规划中,若决策变量取值为整数,则该问题一定为整数规划问题。
()答案:错误。
整数规划问题要求决策变量取整数值,但并非所有决策变量取整数值的问题都是整数规划问题。
例如,线性规划问题的决策变量也可以取整数值。
5. 在动态规划中,最优子结构的性质是指一个问题的最优解包含了其子问题的最优解。
()答案:正确。
动态规划的最优子结构性质是指问题的最优解可以通过求解子问题的最优解来构造。
6. 网络流问题是图论中的一个特殊问题,它涉及到图中各顶点之间的流量分配。
()答案:正确。
网络流问题确实是图论中的一个特殊问题,主要研究如何在图中各顶点之间进行流量分配,使得整个网络的流量达到最大。
7. 在排队论中,顾客到达率和服务率是描述排队系统性能的关键指标。
()答案:正确。
顾客到达率和服务率是排队论中描述排队系统性能的两个重要指标,它们分别表示单位时间内到达系统的顾客数和单位时间内服务完毕的顾客数。
8. 在库存管理中,经济订货批量(EOQ)模型适用于确定最优订货量和订货周期。
()答案:正确。
经济订货批量(EOQ)模型是库存管理中的一种重要模型,用于确定最优订货量和订货周期,以降低库存成本。
9. 在非线性规划中,库恩-塔克(KKT)条件是判断约束非线性规划问题最优解的必要条件。
()答案:正确。
库恩-塔克(KKT)条件是约束非线性规划问题最优解的必要条件,它提供了一种求解约束非线性规划问题的方法。
运筹学建模例题和判断题

运筹学建模例题和判断题集团标准化工作小组 #Q8QGGQT-GX8G08Q8-GNQGJ8-MHHGN#【例1-2】某商场决定:营业员每周连续工作5天后连续休息2天,轮流休息。
根据统计,商场每天需要的营业员如表1-2所示。
表1-2 营业员需要量统计表j业员,该模型如何变化.【例1-3】合理用料问题。
某汽车需要用甲、乙、丙三种规格的轴各一根,这些轴的规格分别是,1,(m),这些轴需要用同一种圆钢来做,圆钢长度为4 m。
现在要制造1000辆汽车,最少要用多少圆钢来生产这些轴如果要求余料最少,数学模型如何变化;【例1-4】配料问题。
某钢铁公司生产一种合金,要求的成分规格是:锡不少于28%,锌不多于15%,铅恰好10%,镍要界于35%~55%之间,不允许有其他成分。
钢铁公司拟从五种不同级别的矿石中进行冶炼,每种矿物的成分含量和价格如表1-4所示。
矿石杂质在治炼过程中废弃,现要求每吨合金成本最低在例中,若允许含有少量杂质,但杂质含量不超过1%,模型如何变化.【例1-5】投资问题。
某投资公司拟将5000万元的资金用于国债、地方国债及基金三种类型证券投资,每类各有两种。
每种证券的评级、到期年限及每年税后收益率见表1-5所示。
决策者希望:国债投资额不少于1000万,平均到期年限不超过5年,平均评级不超过2。
问每种证券各投资多少使总收益最大。
【例1-6】均衡配套生产问题。
某产品由2件甲、3件乙零件组装而成。
两种零件必须经过设备A、B上加工,每件甲零件在A、B上的加工时间分别为5分钟和9分钟,每件乙零件在A、B上的加工时间分别为4分钟和10分钟。
现有2台设备A和3台设备B,每天可供加工时间为8小时。
为了保持两种设备均衡负荷生产,要求一种设备每天的加工总时间不超过另一种设备总时间1小时。
怎样安排设备的加工时间使每天产品的产量最大在例中,假定同种设备的加工时间均匀分配到各台设备上,要求一种设备每台每天的加工时间不超过另一种设备任一台加工时间1小时,模型如何变化.【例1-13】将下例线性规划化为标准型【例3-2 】在例3-1中,假设此人还有一只旅行箱,最大载重量为12公斤,其体积是。
运筹学考试重点
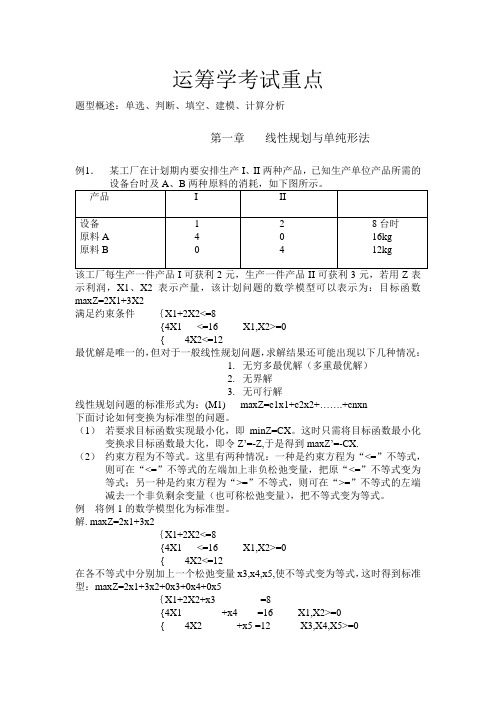
运筹学考试重点题型概述:单选、判断、填空、建模、计算分析第一章线性规划与单纯形法例1.某工厂在计划期内要安排生产I、II两种产品,已知生产单位产品所需的示利润,X1、X2表示产量,该计划问题的数学模型可以表示为:目标函数maxZ=2X1+3X2满足约束条件{X1+2X2<=8{4X1 <=16 X1,X2>=0{ 4X2<=12最优解是唯一的,但对于一般线性规划问题,求解结果还可能出现以下几种情况:1.无穷多最优解(多重最优解)2.无界解3.无可行解线性规划问题的标准形式为:(M1) maxZ=c1x1+c2x2+…….+cnxn下面讨论如何变换为标准型的问题。
(1)若要求目标函数实现最小化,即minZ=CX。
这时只需将目标函数最小化变换求目标函数最大化,即令Z’=-Z,于是得到maxZ’=-CX.(2)约束方程为不等式。
这里有两种情况:一种是约束方程为“<=”不等式,则可在“<=”不等式的左端加上非负松弛变量,把原“<=”不等式变为等式;另一种是约束方程为“>=”不等式,则可在“>=”不等式的左端减去一个非负剩余变量(也可称松弛变量),把不等式变为等式。
例将例1的数学模型化为标准型。
解. maxZ=2x1+3x2{X1+2X2<=8{4X1 <=16 X1,X2>=0{ 4X2<=12在各不等式中分别加上一个松弛变量x3,x4,x5,使不等式变为等式,这时得到标准型:maxZ=2x1+3x2+0x3+0x4+0x5{X1+2X2+x3 =8{4X1 +x4 =16 X1,X2>=0{ 4X2 +x5 =12 X3,X4,X5>=0其中松弛变量x3,x4,x5表示没有被利用的资源,当然也没有利润。
(3)若存在取值无约束的变量Xk,可令Xk=X’k-X’’k,其中X’k,X’’k>=0。
线性规划问题解的概念1.可行解2.基3.基可行解4.可行基线性规划问题的几个定理:定理1 若线性规划问题存在可行域,则其可行域D是凸集。
运筹学练习及解答

运筹学练习:一、判断(√)1、线性规划问题中,必须有一个要实现的目标。
(×)2、在基可行解中基变量一定为非零。
(√)3、如果一个线性规划问题有两个不同的最优解,则它有无穷多个最优解。
(√)4、在用单纯形法解线性规划问题时,任何一个人工变量都不应该在最优解的基变量组合中。
(×)5、如果一个线性规划问题有可行解,则它必有最优解。
(√)6、运输问题中,用闭回路法和用位势法算出的检验数是一样的。
(√)7、运输问题模型是一种特殊的线性规划模型,因而运输问题也可用单纯形法求解。
(×)8、运输问题的运价表的某一行的所有ij c 同乘以一个非零常数,其最优调运方案不变。
(√)9、运输表中给出初始基可行解后,从每一空格出发的闭回路是唯一的。
(×)10、不平衡运输问题不一定有最优解。
二、填空1、线性规划是试图合理地分配各种 资源 以最优地实现某个 目标 的规划方法。
2、标准线性规划问题的特点是:(1)要求目标函数 极大化 ,(2)约 束条件取 等式 ,(3)变量 为非负 。
3、在线性规划问题的图解法中,如果存在最优解,则这个最优解将处于 可行域的 顶点处 。
4、解总运费最小的运输问题时,确定最优解的条件是:所有非基变量的 检验数均不为 负 数。
5、解运输问题一般采用 表上作业 法,确定检验数的方法有 闭回路法和 用位势法 三、简答题1、试用图解法求解下述线性规划问题⎪⎩⎪⎨⎧≥≤+≤++=0,152315322110max 21212121x x x x x x x x z解:先在直角坐标系中作出可行域,再作目标函数的等值线,可以看出,当目标函数的等值线平移到两直线1523,15322121=+=+x x x x 的交点时,目标函数值最大。
即,最优解为:3,321==x x ,2、某商场对售货员的需求情况如下表所示,为保证售货人员充分休息,每周工作五天,休息两天,并要求休息的两天是连续的。
《运筹学》课程考试试卷试题(含答案)

《运筹学》课程考试试卷试题(含答案)一、选择题(每题5分,共25分)1. 运筹学的核心思想是()A. 最优化B. 系统分析C. 预测D. 决策答案:A2. 在线性规划中,约束条件可以用()表示。
A. 等式B. 不等式C. 方程组D. 矩阵答案:B3. 以下哪个不是运筹学的基本模型?()A. 线性规划B. 整数规划C. 非线性规划D. 随机规划答案:D4. 在目标规划中,以下哪个术语描述的是决策变量的偏离程度?()A. 目标函数B. 约束条件C. 偏差变量D. 权重系数答案:C5. 在动态规划中,以下哪个概念描述的是在决策过程中,某一阶段的最优决策对后续阶段的影响?()A. 最优子结构B. 无后效性C. 最优性原理D. 阶段性答案:B二、填空题(每题5分,共25分)1. 运筹学是一门研究在复杂系统中的______、______和______的科学。
答案:决策、优化、实施2. 在线性规划中,若目标函数为最大化,则其标准形式为______。
答案:max z = c^T x3. 在非线性规划中,若目标函数和约束条件均为凸函数,则该规划问题为______。
答案:凸规划4. 在目标规划中,若决策变量x_i的权重系数为w_i,则目标函数可以表示为______。
答案:min Σ(w_i d_i^+ + w_i d_i^-)5. 在动态规划中,若状态变量为s_n,决策变量为u_n,则状态转移方程可以表示为______。
答案:s_{n+1} = f(s_n, u_n)三、判断题(每题5分,共25分)1. 线性规划问题的最优解一定在可行域的顶点处取得。
()答案:正确2. 在整数规划中,若决策变量为整数,则目标函数和约束条件也必须为整数。
()答案:错误3. 目标规划中的偏差变量可以是负数。
()答案:正确4. 在动态规划中,最优策略具有最优子结构。
()答案:正确5. 在非线性规划中,若目标函数为凸函数,则约束条件也必须为凸函数。
运筹学建模例题和判断题

【例1-2】某商场决定:营业员每周连续工作5天后连续休息2天,轮流休息。
根据统计,商场每天需要的营业员如表1-2所示。
表1-2 营业员需要量统计表123456714567125671236712347123452345634567min 3003003504004806005500,1,2,,7jZ x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x j =++++++⎧++++≥⎪++++≥⎪⎪++++≥⎪++++≥⎪⎨++++≥⎪⎪++++≥⎪++++≥⎪⎪≥=⎩(2)在例中,如果设x j (j=1,2,…,7)为工作了5天后星期一到星期日开始休息的营业员,该模型如何变化.123456723456345671456712567123671234712345min 3003003504004806005500,1,2,,7jZ x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x j =++++++⎧++++≥⎪++++≥⎪⎪++++≥⎪++++≥⎪⎨++++≥⎪⎪++++≥⎪++++≥⎪⎪≥=⎩【例1-3】合理用料问题。
某汽车需要用甲、乙、丙三种规格的轴各一根,这些轴的规格分别是,1,(m ),这些轴需要用同一种圆钢来做,圆钢长度为4 m 。
现在要制造1000辆汽车,最少要用多少圆钢来生产这些轴10112345134678924578910min 221000243210002324510000,1,210j jj Z x x x x x x x x x x x x x x x x x x x x x j ==⎧++++≥⎪++++++≥⎪⎨+++++≥⎪⎪≥=⋯⎩∑, 如果要求余料最少,数学模型如何变化;23457891012345134678924578910min 0.30.50.10.40.30.60.20.5221000243210002324510000,1,210j Z x x x x x x x x x x x x x x x x x x x x x x x x x x x x j =+++++++⎧++++≥⎪++++++≥⎪⎨+++++≥⎪⎪≥=⋯⎩,【例1-4】配料问题。
运筹学建模练习题

运筹学建模练习题如买进的杂粮当⽉到货,但需到下⽉才能卖出,且规定“货到付款”。
公司希望本季末库存2000担,问应采取什么样的买进卖出的策略使3个⽉总的获利最⼤?2、超级市场上班的员⼯数量如果能随商城客流量⼤⼩⽽调整,则可在满⾜⼀定服务质量的前提下,减少⼈⼒资源的投⼊,从⽽可以降低运作成本。
某超市根据统计,在超市员⼯可以选择上全时班(连续⼯作8⼩时)或上半时班(连续⼯作4⼩时),但上半时班的员⼯⼈数不能超过每⼀时段使⽤员⼯总数的50%。
超市按⼯作⼩时付给员⼯⼯资,上全时班和上半时班的⼩时⼯资率相同,请为该超市构造⼀个数学模型,使每天使⽤的员⼯费⽤最⼩。
3、某种牌号的鸡尾酒酒系由三种等级的酒兑制⽽成。
已知各种等级酒的每天供应量和单位成本如下:等级i:供应量1500单位/天,成本6元/单位;等级ii:供应量2000单位/天,成本4.5元/单位;/天,成本3元/单位;等级iii:供应量1000单位pl 兑制要求配⽐必须严格满⾜;p2企业获取尽可能多的利润;p3 红⾊商标酒每天量不低于2000单位------------------- 时磊5说------ - --- --------4、某快餐店坐落在⼀个旅游景点中,这个旅游景点远离市区,平时游客不多,⽽在每个星期六游客猛增,快餐店主要为旅客提供低价位的快餐服务,该快餐店雇佣了两名正式员⼯,正式员⼯每天⼯作8个⼩时,其余⼯作由临时⼯来担任,临时⼯每天⼯作4个⼩时,在星期六,该快餐店从上午营业到下午10点关门,根据游客就餐情况,在星期六每个营业⼩时所需职⼯数(包括正式⼯和临时⼯)如表所⽰:已知⼀名正式职⼯11点开始上班,⼯作4⼩时后,休息1⼩时,⽽后再⼯作4⼩时;另⼀名正式职⼯13点开始上班,⼯作4⼩时后,休息1个⼩时,⽽后再⼯作4个⼩时,⼜知零时⼯每⼩时的⼯资为4元。
在满⾜对职⼯需求的条件下,如何安排临时⼯的班次,使得临时⼯的成本最⼩?5、某化⼯⼚⽣产两种⽤于轮船上的粘合剂A和B。
管理运筹学(物流)总复习题建模题

管理运筹学总复习题(物流管理专业)四、建模题(只建模,不求解)1. 某农场打算添购一批拖拉机以完成每年三季度的生产任务:春种330公顷,夏管130公顷,秋收470公顷。
可供选择的拖拉机型号、单台市场价格以及拖拉机的使用能力参数如下:单台拖拉机的使用能力(公顷) 拖拉机 型号 购买价格 (元) 春种 夏管 秋收 A 型 B 型 C 型 D 型50000 45000 44000 5300030 29 32 3117 16 18 1445 40 42 44问每种拖拉机各购买几台,才能顺利地完成全年的各项生产任务,并且还能保证总的花费最少。
试就这一问题建立数学模型。
2. 某工厂生产A 、B 两种产品,已知生产A 每公斤要用煤6吨、电4度、劳动力3个;生产B 每公斤要用煤4吨、电5度、劳动力10个。
又知,每公斤A 、B 的利润分别为7万元和12万元。
现在该工厂只有煤360吨、电200度、劳动力300个。
问在这种情况下,各生产A 、B 多少公斤,才能获最大利润?3. 某企业生产甲、乙、丙三种产品,已知有关数据如下表所示:问在这种情况下,各生产甲、乙、丙三种产品各生产多少件,才能获最大利润,建立数学模型。
4. 某公司有一级质检人员8名,二级质检人员10名。
此公司每天(按8小时计算)至少有1800个工件需要质量检验,一级检验人员每小时可检验工件25个,检验的准确率为98%,每小时的工资为7元;二级检验人员每小时可检验工件15个,检验的准确率为95%,每小时的工资为5元;检验人员每出现一次错检,将给公司造成2元的经济损失。
问公司应该选拔多少位一级和二级检验人员从事质检工作,才能使质量方面的花费最小,请你建立该问题的数学模型。
5. 现要截取2.9米、2.1米和1.5米的元钢各100根,已知原材料的长度是7.4米,问应如何下料,才能使所消耗的原材料最省。
试构造此问题的数学模型。
6. 某炼油厂生产三种牌号的汽油,70#,80#和85#汽油。
运筹学_判断题及模拟试卷

注意:1、运筹学考1、2、5、6章,题目都是书上的例题,这是判断题。
2、题型:填空,选择,判断,建模,计算。
3、发现选择题中一个错误,第6章第2题,答案应该C。
4、大部分建立模型和计算是第一章内容,加选择判断题目已经发给你们了,主要考对概念,性质,原理,算法的理解。
判断题一、线性规划1.若线性规划存在最优解则一定存在基本最优解2.若线性规划无界解则其可行域无界3.可行解一定是基本解4.基本解可能是可行解5.线性规划的可行域无界则具有无界解6.最优解不一定是基本最优解7.x j的检验数表示变量x j增加一个单位时目标函数值的改变量8.可行解集有界非空时,则在极点上至少有一点达到最优值9.若线性规划有三个最优解X(1)、X(2)、X(3),则X=αX(1)+(1-α)X(3)及X=α1X(1)+α2X(2)+α3X(3)均为最优解,其中10.任何线性规划总可用大M单纯形法求解11.凡能用大M法求解也一定可用两阶段法求解12.两阶段法中第一阶段问题必有最优解13.两阶段法中第一阶段问题最优解中基变量全部非人工变量,则原问题有最优解14.任何变量一旦出基就不会再进基15.人工变量一旦出基就不会再进基16.普通单纯形法比值规则失效说明问题无界15.将检验数表示为λ=C B B-1A-C的形式,则求极大值问题时基可行解是最优解的充要条件是λ≥018.当最优解中存在为零的基变量时,则线性规划具有多重最优解19.当最优解中存在为零的非基变量时,则线性规划具唯一最优解20.可行解集不一定是凸集21.将检验数表示为的形式,则求极小值问题时,基可行解为最优解当且仅当λj≥0,j=1,2,…,n22.若线性规划存在基本解则也一定存在基本解可行解23.线性规划的基本可行解只有有限多个24.在基本可行解中基变量一定不为零25.123 123123123 max34 |25|5010100,0,0Z x x xx x xx x xx x x=+-++≤⎧⎪-+≥⎨⎪≥≥≥⎩是一个线性规划数学模型二对偶规划1.任何线性规划都存在一个对应的对偶线性规划2.原问题(极大值)第i个约束是“≥”约束,则对偶变量y i≥03.互为对偶问题,或者同时都有最优解,或者同时都无最优解4.对偶问题有可行解,则原问题也有可行解5.原问题有多重解,对偶问题也有多重解在以下6~10中,设X*、Y*分别是的可行解6.则有CX*≤Y*b7.CX*是w的下界8.当X*、Y*为最优解时,CX*=Y*b;9.当CX*=Y*b时,有Y*X s+Y s X*=0成立10.X*为最优解且B是最优基时,则Y*=C B B-1是最优解11.对偶问题有可行解,原问题无可行解,则对偶问题具有无界解12.原问题无最优解,则对偶问题无可行解13.对偶问题不可行,原问题无界解14.原问题与对偶问题都可行,则都有最优解15.原问题具有无界解,则对偶问题不可行16.若某种资源影子价格为零,则该资源一定有剩余17.原问题可行对偶问题不可行时,可用对偶单纯形法计算18.对偶单纯法换基时是先确定出基变量,再确定进基变量19.对偶单纯法是直接解对偶问题问题的一种方法20.对偶单纯形法比值失效说明原问题具有无界解21.在最优解不变的前提下,基变量目标系数c i的变化范围可由式确定22.在最优基不变的前提下,常数b r的变化范围可由式确定,其中为最优基B的逆矩阵第r列23.减少一约束,目标值不会比原来变差24.增加一个变量,目标值不会比原来变好25.当b i在允许的最大范围内变化时,最优解不变三、整数规划1.整数规划的最优解是先求相应的线性规划的最优解然后取整得到2.部分变量要求是整数的规划问题称为纯整数规划3.求最大值问题的目标函数值是各分枝函数值的上界4.求最小值问题的目标函数值是各分枝函数值的下界5.变量取0或1的规划是整数规划6.整数规划的可行解集合是离散型集合7. 0-1规划的变量有n个,则有2n个可行解8.6x1+5x2≥10、15或20中的一个值,表达为一般线性约束条件是6x1+5x2≥10y1+15y2+20y3,y1+y2+y3=1,y1、y2、y3=0或19. 高莫雷(R.E.Gomory)约束是将可行域中一部分非整数解切割掉10.隐枚举法是将所有变量取0、1的组合逐个代入约束条件试算的方法寻找可行解四、目标规划1.正偏差变量大于等于零,负偏差变量小于等于零2.系统约束中没有正负偏差变量3.目标约束含有正负偏差变量4.一对正负偏差变量至少一个大于零5.一对正负偏差变量至少一个等于零6.要求至少到达目标值的目标函数是max Z=d+7.要求不超过目标值的目标函数是 min Z=d-8.目标规划没有系统约束时,不一定存在满意解9.超出目标值的差值称为正偏差10.未到达目标的差值称为负偏差五、运输与指派问题1.运输问题中用位势法求得的检验数不唯一2.平衡运输问题一定有最优解3.不平衡运输问题不一定有最优解4.产地数为3,销地数为4的平衡运输问题有7个基变量5.m+n-1个变量组构成一组基变量的充要条件是它们不包含闭回路6.运输问题的检验数就是其对偶变量7.运输问题的检验数就是对偶问题的松驰变量8.运输问题的位势就是其对偶变量9.不包含任何闭回路的变量组必有孤立点10.含有孤立点的变量组一定不含闭回路11.用一个常数k加到运价矩阵C的某列的所有元素上,则最优解不变12.令虚设的产地或销地对应的运价为一任意大于零的常数c(c>0),则最优解不变13.若运输问题的供给量与需求量为整数,则一定可以得到整数最优解14.按最小元素法求得运输问题的初始方案, 从任一非基格出发都存在唯一一个闭回路15.运输问题中运价表的每一个元素都分别乘于一个常数,则最优解不变16.运输问题中运价表的每一个元素都分别加上一个常数,则最优解不变17.5个产地6个销地的平衡运输问题有11个变量18.5个产地6个销地的平衡运输问题有30个变量19.5个产地6个销地的销大于产的运输问题有11个基变量20.产地数为3销地数为4的平衡运输中,变量组{x11,x13,x22,x33,x34}可作为一组基变量六、网络模型1.容量不超过流量2.最大流问题是找一条从起点到终点的路,使得通过这条路的流量最大3.容量C ij是弧(i,j)的最大通过能力4.流量f ij是弧(i,j)的实际通过量5.可行流是最大流的充要条件是不存在发点到收点的增广链6.截量等于截集中弧的流量之和7.任意可行流量不超过任意截量8.任意可行流量不小于任意截量9.存在增广链说明还没有得到最大流量10.存在增广链说明已得到最大流11.找增广链的目的是:是否存在一条从发点到收点的路,使得可以增加这条路的流量12.狄克斯屈拉算法是求最大流的一种标号算法13.破圈法是:任取一圈,去掉圈中最长边,直到无圈14.避圈法(加边法)是:去掉图中所有边,从最短边开始添加,加边的过程中不能形成圈,直到连通(n-1条边)15.连通图一定有支撑树16.P是一条增广链,则后向弧上满足流量f ≥017.P是一条增广链,则前向弧上满足流量f ij≤C ij18.可行流的流量等于每条弧上的流量之和19.最大流量等于最大流20.最小截集等于最大流量七、网络计划1.网络计划中的总工期是网络图中的最短路的长度2.紧前工序是前道工序3.后续工序是紧后工序4.虚工序不需要资源,是用来表达工序之间的衔接关系的虚设活动5.A完工后B才能开始,称A是B的紧后工序6. 单时差为零的工序称为关键工序7.关键路线是由关键工序组成的一条从网络图的起点到终点的有向路8.关键路线一定存在9.关键路线存在且唯一10.计划网络图允许有多个始点和终点11.事件i的最迟时间T L(i)是指以事件i为完工事件的工序最早可能结束时间12.事件i的最早时间T E(i)是以事件i为开工事件的工序最早可能开工时间13.工序(i,j)的事件i与j的大小关系是i < j14.间接成本与工程的完工期成正比15.直接成本与工程的完工期成正比16.17.18.19.20.1 线性规划1= "对"2= "对"3 = "错"4= "对"5= "错"6 = "对"7= "对"8= "对"9 = "对" 10= "对" 11= "对" 12 = "对" 13= "错" 14= "错" 15= "对" 16= "对" 17= "对" 18 = "错" 19= "错" 20 = "错" 21= "对" 22 = "错" 23= "对"24 = "错"25 = "错" 2对偶问题1="对"2= "错"3 = "对"4= "错"5 = "错"6= "错"7 = "错"8= "对"9= "对"10 = "对"11 = "对"12= "错"13 = "错"14 = "对"15 = "对"16 = "错"17 = "错"18= "对"19 = "错"20= "错"21= "对"22 = "错"23= "对"24= "错"25= "错"3 整数规划1= "错"2 = "错"3 = "对"4 = "对"5 = "对"6= "对"7 = "错"8= "对"9 = "对"10= "错4 目标规划1="错"2 = "对"3 = "对"4 = "错"5= "对"6 = "错"7= "错"8 = "错"9 = "对"10= "对"5 运输问题1 = "错"2 = "对"3 = "错"4 = "错" 5= "对"6 = "错"7 = "对"8 = "对" 9= "对" 10= "错"11 = "对"12 = "对"13 = "对"14 = "对"15 = "对"16 = "对"17 = "错"18 = "对"19 = "对" 6 网络模型1 = "错"2 = "错"3 = "对"4 = "对"5 = "对"6 = "错"7 = "对"8 = "错"9 = "对"10 = "错"11 = "对"12 = "错"13 = "对"14 = "对"15 = "对"16 = "错"17 = "错"18 = "错"19 = "错"7 网络计划1 = "错 "2 = "对"3 = "错"4 = "对"5= "错"6 = "错"7 = "对"8 = "对"9= "错"10 = "错"11 = "错"12= "对"12= "对"14 = "对"15 = "错"16 = "错"17 = "对"18 = "对"19 = "错"20 = "错" 20 = "错" 20 = "对"《运筹学》模拟试题及参考答案一、判断题(在下列各题中,你认为题中描述的内容为正确者,在题尾括号内写“√”,错误者写“×”。
运筹学例题解析

运筹学例题解析(共6页) -本页仅作为预览文档封面,使用时请删除本页-(一)线性规划建模与求解B.样题:活力公司准备在5小时内生产甲、乙两种产品。
甲、乙两种产品每生产1单位分别消耗2小时、1小时。
又根据市场需求信息,乙产品的产量应该至少是甲产品产量的3倍。
已知甲、乙两种产品每销售1单位的利润分别为3百元和1百元。
请问:在5小时内,甲、乙两种产品各生产多少单位,才能够使得总销售利润最大要求:1、建立该问题的线性规划模型。
2、用图解法求出最优解和最大销售利润值,并写出解的判断依据。
如果不存在最优解,也请说明理由。
解:1、(1)设定决策变量: 设甲、乙两种产品分别生产x 1、x2单位 。
(2)目标函数: max z=2 x 1+x 2(3)约束条件如下:12211225..3,0+≤⎧⎪≥⎨⎪≥⎩x x s t x x x x2、该问题中约束条件、目标函数、可行域和顶点见图1所示,其中可行域用阴影部分标记,不等式约束条件及变量约束要标出成立的方向,目标函数只结论:本题解的情形是: 无穷多最优解 ,理由: 目标函数等值线z=2 x 1+x 2与约束条件2 x 1+x 2≤5的边界平行 。
甲、乙两种产品的最优产量分别为 (5,0)或(1,3)单位;最大销售利润值等于 5 百元。
(二)图论问题的建模与求解样题A.正考样题(最短路问题的建模与求解,清华运筹学教材编写组第三版267-268页例13)某企业使用一台设备,每年年初,企业都要做出决定,如果继续使用旧的,要付维修费;若购买一台新设备,要付购买费。
但是变卖旧设备可以获得残值收入,连续使用1年、2年、3年、4年以上卖掉的设备残值分别为8万元、6万元、3万元和0万元。
试制定一个5年的更新计划,使总支出最少。
已知设备在各年的购买费与维修费如表2所示。
要求:(1)建立某种图论模型;(2)求出最少总支出金额。
解:(1)建立图论——最短路问题模型。
①设点Vi 表示第i年年初,虚设一个点V6,表示第五年年底;②弧(Vi , Vj)表示第i年初购进一台设备一直使用到第j年初(即第i-1年年底)再卖掉并获得残值收入;③弧(Vi , Vj)上的权数表示第i年初购进一台设备,一直使用到第j年初所需支付的购买、维修及抵扣残值收入以后的全部费用(单位:万元)。
运筹学复习题及参考答案

中南大学网络教育课程考试复习题及参考答案运筹学一、判断题:1.图解法与单纯形法虽然求解的形式不同,但从几何上理解,两者是一致的。
[ ]2.线性规划问题的每一个基本解对应可行解域的一个顶点。
[ ]3.任何线性规划问题存在并具有惟一的对偶问题。
[ ]4.已知y i*为线性规划的对偶问题的最优解,若y i*>0,说明在最优生产计划中第i种资源已完全耗尽。
[ ]5.单纯形迭代中添加人工变量的目的是为了得到问题的一个基本可行解。
[ ]6.订购费为每订一次货所发生的费用,它同每次订货的数量无关。
[ ]7.如果线性规划问题存在最优解,则最优解一定可以在可行解域的顶点上获得。
[ ]8.用单纯形法求解Max型的线性规划问题时,检验数Rj>0对应的变量都可以被选作入基变量。
[ ]9.对于原问题是求Min,若第i个约束是“=”,则第i个对偶变量yi≤0。
[ ]10.用大M法或两阶段法单纯形迭代中若人工变量不能出基(人工变量的值不为0),则问题无可行解。
[ ]11.如图中某点vi有若干个相邻点,与其距离最远的相邻点为vj,则边[vi,vj]必不包含在最小支撑树内。
[ ] 12.在允许缺货发生短缺的存贮模型中,订货批量的确定应使由于存贮量的减少带来的节约能抵消缺货时造成的损失。
[ ] 13.根据对偶问题的性质,当原问题为无界解时,其对偶问题无可行解,反之,当对偶问题无可行解时,其原问题具有无界解。
[ ] 14.在线性规划的最优解中,若某一变量xj为非基变量,则在原来问题中,改变其价值系数cj,反映到最终单纯形表中,除xj的检验数有变化外,对其它各数字无影响。
[ ] 15.运输问题是一种特殊的线性规划问题,因而其求解结果也可能出现下列四种情况之一:有惟一最优解,有无穷多最优解,无界解,无可行解。
[ ]16.动态规划的最优性原理保证了从某一状态开始的未来决策独立于先前已做出的决策。
[ ]17.一个动态规划问题若能用网络表达时,节点代表各阶段的状态值,各条弧代表了可行方案的选择。
运筹学 考题与答案

一、填空题:1. 表1中给出某线性规划问题计算过程中的一个单纯形表,目标函数为654228max x x x z ++=,约束条件为≤,表中321,,x x x 为松弛变量,表中解的目标函数值为14=z 。
(1)a =______,b =______,c =______,d =______,e =______,f =______,g =______; (2)表中给出的解为___________(提示:最优解,满意解,可行解……)。
2.在单纯形法的计算中,按照最小比值θ来确定换出基的变量时,有时出现存在两个以上相同的最小比值,从而出现_______现象。
3.使用动态规划方法解决多阶段决策问题,首先要将实际问题写成动态规划模型,此时要用到5个概念:_______、_______、_______、状态转移方程和指标函数。
二、判断题1.图解法同单纯形法虽然求解的形式不同,但从几何上理解,两者是一致的。
( )2.根据对偶问题的性质,当原问题为无界解时,其对偶问题无可行解;反之,当对偶问题无可行解时,其原问题具有无界解。
( )3.运输问题时一种特殊的线性规划模型,因而求解结果也可能出现下列四种情况之一:唯一最优解、无穷多最优解、无界解、无可行解。
( )4.动态规划中,定义状态时应保证在各个阶段中所作决策的相互独立性。
( )5.求图的最小支撑树以及求图中一点至另一点的最短路问题,都可以归结为求解整数规划问题。
( )三、简答题1.简述影子价格的经济意义。
2.简述不确定型决策方法中的悲观准则。
四、计算题1.用图解法求解下列线性规划问题,并指出问题是具有唯一最优解、无穷多最优解、无界解或无可行解。
(8分)⎪⎩⎪⎨⎧≥≥+≥++=0,5.14312.46min 21212121x x x x x x st x x z 2.已知表2为求解某线性规划问题的最终单纯形表,表中4x ,5x 为松弛变量,问题的约束为≤形式。
运筹学建模例题和判断题

【例1-2】某商场决定:营业员每周连续工作5天后连续休息2天,轮流休息。
根据统计,商场每天需要的营业员如表1-2所示。
123456714567125671236712347123452345634567min 3003003504004806005500,1,2,,7jZ x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x j =++++++⎧++++≥⎪++++≥⎪⎪++++≥⎪++++≥⎪⎨++++≥⎪⎪++++≥⎪++++≥⎪⎪≥=⎩(2)在例1.2中,如果设x j (j=1,2,…,7)为工作了5天后星期一到星期日开始休息的营业员,该模型如何变化.123456723456345671456712567123671234712345min 3003003504004806005500,1,2,,7jZ x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x j =++++++⎧++++≥⎪++++≥⎪⎪++++≥⎪++++≥⎪⎨++++≥⎪⎪++++≥⎪++++≥⎪⎪≥=⎩【例1-3】合理用料问题。
某汽车需要用甲、乙、丙三种规格的轴各一根,这些轴的规格分别是1.5,1,0.7(m ),这些轴需要用同一种圆钢来做,圆钢长度为4 m 。
现在要制造1000辆汽车,最少要用多少圆钢来生产这些轴?10112345134678924578910min 221000243210002324510000,1,210j jj Z x x x x x x x x x x x x x x x x x x x x x j ==⎧++++≥⎪++++++≥⎪⎨+++++≥⎪⎪≥=⋯⎩∑, 如果要求余料最少,数学模型如何变化;23457891012345134678924578910min 0.30.50.10.40.30.60.20.5221000243210002324510000,1,210j Z x x x x x x x x x x x x x x x x x x x x x x x x x x x x j =+++++++⎧++++≥⎪++++++≥⎪⎨+++++≥⎪⎪≥=⋯⎩,【例1-4】配料问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【例1-2】某商场决定:营业员每周连续工作5天后连续休息2天,轮流休息。
根据统计,商场每天需要的营业员如表1-2所示。
表1-2 营业员需要量统计表123456714567125671236712347123452345634567min 3003003504004806005500,1,2,,7jZ x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x j =++++++⎧++++≥⎪++++≥⎪⎪++++≥⎪++++≥⎪⎨++++≥⎪⎪++++≥⎪++++≥⎪⎪≥=⎩(2)在例1.2中,如果设x j (j=1,2,…,7)为工作了5天后星期一到星期日开始休息的营业员,该模型如何变化.123456723456345671456712567123671234712345min 3003003504004806005500,1,2,,7jZ x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x j =++++++⎧++++≥⎪++++≥⎪⎪++++≥⎪++++≥⎪⎨++++≥⎪⎪++++≥⎪++++≥⎪⎪≥=⎩【例1-3】合理用料问题。
某汽车需要用甲、乙、丙三种规格的轴各一根,这些轴的规格分别是1.5,1,0.7(m ),这些轴需要用同一种圆钢来做,圆钢长度为4 m 。
现在要制造1000辆汽车,最少要用多少圆钢来生产这些轴?10112345134678924578910min 221000243210002324510000,1,210j jj Z x x x x x x x x x x x x x x x x x x x x x j ==⎧++++≥⎪++++++≥⎪⎨+++++≥⎪⎪≥=⋯⎩∑, 如果要求余料最少,数学模型如何变化;23457891012345134678924578910min 0.30.50.10.40.30.60.20.5221000243210002324510000,1,210j Z x x x x x x x x x x x x x x x x x x x x x x x x x x x x j =+++++++⎧++++≥⎪++++++≥⎪⎨+++++≥⎪⎪≥=⋯⎩,【例1-4】配料问题。
某钢铁公司生产一种合金,要求的成分规格是:锡不少于28%,锌不多于15%,铅恰好10%,镍要界于35%~55%之间,不允许有其他成分。
钢铁公司拟从五种不同级别的矿石中进行冶炼,每种矿物的成分含量和价格如表1-4所示。
矿石杂质在治炼过程中废弃,现要求每吨合金成本最低1234512451345135123451234512min 3402601802301900.250.40.20.080.280.10.150.20.050.150.10.050.150.10.250.30.20.40.170.550.250.30.20.40.170.350.70.7Z x x x x x x x x x x x x x x x x x x x x x x x x x x x x =+++++++≥+++≤++=++++≤++++≥+3450.40.80.4510,1,2,,5jx x x x j ⎧⎪⎪⎪⎪⎨⎪⎪+++=⎪⎪≥=⎩ 在例1.4中,若允许含有少量杂质,但杂质含量不超过1%,模型如何变化.1234512451345135123451234512min 3402601802301900.250.40.20.080.280.10.150.20.050.150.10.050.150.10.250.30.20.40.170.550.250.30.20.40.170.350.70.7Z x x x x x x x x x x x x x x x x x x x x x x x x x x x x =+++++++≥+++≤++=++++≤++++≥+3450.40.80.450,1,2,,0.95jx x x x j ⎧⎪⎪⎪⎪⎨⎪⎪+++≥⎪⎪≥=⎩【例1-5】投资问题。
某投资公司拟将5000万元的资金用于国债、地方国债及基金三种类型证券投资,每类各有两种。
每种证券的评级、到期年限及每年税后收益率见表1-5所示。
决策者希望:国债投资额不少于1000万,平均到期年限不超过5年,平均评级不超过2。
问每种证券各投资多少使总收益最大。
1234561234561212456123456max 0.2560.380.1720.2820.1260.1845000100023035200,1,2,,6j Z x x x x x x x x x x x x x x x x x x x x x x x x x x j =+++++⎧+++++≤⎪+≥⎪⎪--+++≤⎨⎪+-+--≤⎪⎪≥=⎩【例1-6】均衡配套生产问题。
某产品由2件甲、3件乙零件组装而成。
两种零件必须经过设备A 、B 上加工,每件甲零件在A 、B 上的加工时间分别为5分钟和9分钟,每件乙零件在A 、B 上的加工时间分别为4分钟和10分钟。
现有2台设备A 和3台设备B ,每天可供加工时间为8小时。
为了保持两种设备均衡负荷生产,要求一种设备每天的加工总时间不超过另一种设备总时间1小时。
怎样安排设备的加工时间使每天产品的产量最大121212121212max 1..21354960910144046604660Z ys t y x y x x x x x x x x x x x y =≤≤+≤+≤≤+≤≥--,,在例1.6中,假定同种设备的加工时间均匀分配到各台设备上,要求一种设备每台每天的加工时间不超过另一种设备任一台加工时间1小时,模型如何变化.1212121212121212max 1..213549609101440549106023549106023Z ys t y x y x x x x x x x x x x x x x x x y =≤≤+≤+≤++≤++-+≤≥-+,,【例1-13】将下例线性规划化为标准型1212112max ||||54Z x x x x x x x unr=--⎧+≥⎪≤⎨⎪⎩、112211223114max ()()540Z x x x x x x x x x x x x x x x x x x ''''''=-+-+''''''⎧-+--=⎪'''-+=⎨⎪''''''≥、、、、、【例3-2 】在例3-1中,假设此人还有一只旅行箱,最大载重量为12公斤,其体积是0.02m 3。
背包和旅行箱只能选择其一,建立下列几种情形的数学模型,使所装物品价值最大。
(1)所装物品不变;(2)如果选择旅行箱,则只能装载丙和丁两种物品,价值分别是4和3,载重量和体积的约束为1111111122222222000000000000x x x x x x x x x x x x x x x x ⎧⎧≥≥⎪⎪'''==⎨⎨<<⎪⎪⎩⎩⎧⎧≥≥⎪⎪'''==⎨⎨<-<⎪⎪⎩⎩,,,,-,,,,,111111222222||,||,x x x x x x x x x x x x ''''''=+=-''''''=+=-1211221231236(1)4610(1)2420(1)1011,2,3j x x y Mx x y M x x y M y y y y j ⎧+≤+-⎪+≥--⎪⎪+≤+-⎨⎪++=⎪⎪==⎩或,+≤+≤1212121.80.61.5220x x x x(1)1211121122221.20.8102 2.52in max 4310,,011,210t 522i i Z x x y x y a x x nd y x x y eger y y i y +++=+≤≤+=≥==+或(2)12212121211211221.20.8102max 43()1.80.612(2.5)()1.5220()10,,011,t 25n 2i i i x x My x x M Z x x a x x My b c x x My d y y x y i d eger y an +≤+≤=++≤++≤++≥+===或+【例3-3】试引入0-1变量将下列各题分别表达为一般线性约束条件 (1)x 1+x 2≤6或4x 1+6x 2≥10或2x 1+4x 2≤20 (2)若x 1≤5,则x 2≥0,否则x 2≤8 (3)x 2取值0,1,3,5,7121122123123646102420(31)011,22,3j x x y M x x y M x x y M y y y y j ⎧+≤+⎪+≥⎪⎪+≤+⎨⎪++-=-⎪⎪==⎩或,(2)21125(1)8(1)015x y M x y M y M M x x y y ≥-≤⎧⎪>--⎪⎪⎨⎪≤+-⎪+⎪=⎩或 (3)2123412343571011,2,3,4j x y y y y y y y y y j ⎧=+++⎪+++⎨⎪==⎩≤或,【例3-4】企业计划生产4000件某种产品,该产品可自己加工、外协加工任意一种形式生产.已知每种生产的固定费用、生产该产品的单件成本以及每种生产形式的最大加工数量(件)限制如表3-2所示,怎样安排产品的加工使总成本最小.1122331231201,2,3min (5008)(8005)(6007)40001500,20000,101,2,3j j j jZ y x y x y x x x My x x x x x y j j =+++++⎧⎪++≥-≤=⎪⎨≤≤⎪⎪≥==⎩或,用分枝-隐枚举法求解下列BIP 问题123451234512345min 362462712(311)45310(311)011,2,3,4jZ x x x x x x x x x x a x x x x x b x j =-++-⎧+-++≤-⎪++-+≥-⎨⎪==⎩或,解 (1)令x 2=1-x '2及x 5=1-x '5,代入模型后整理得123451234512345min 362476279(311)4533(311)011,2,3,4jZ x x x x x x x x x x a x x x x x b x j ''=++++-⎧''--+-≤-⎪''-+--≥-⎨⎪==⎩或,142531425314253min 234676729(311)4353(311)011,2,3,4jZ x x x x x x x x x x a x x x x x b x j ''=++++-⎧''+--≤-⎪''-+≥-⎨⎪==⎩---或,【例4-1】某企业在计划期内计划生产甲、乙、丙三种产品。
