2017高一数学竞赛试题
数学竞赛试题高一及答案

数学竞赛试题高一及答案一、选择题(每题5分,共20分)1. 若函数f(x) = 2x^2 + 3x + 1的图像关于直线x = -1/2对称,则下列哪个函数的图像也关于直线x = -1/2对称?A. g(x) = x^2 + 2x + 3B. h(x) = -x^2 + 2x - 3C. i(x) = x^2 - 2x + 3D. j(x) = -x^2 - 2x - 3答案:B2. 已知集合A = {1, 2, 3},集合B = {2, 3, 4},则A∪B等于:A. {1, 2, 3, 4}B. {1, 2, 3}C. {2, 3}D. {1, 3, 4}答案:A3. 若方程x^2 - 5x + 6 = 0的两个根为α和β,则α + β的值为:A. 1B. 2C. 3D. 5答案:C4. 函数y = |x - 2| + 3的图像与x轴交点的个数是:A. 0B. 1C. 2D. 3答案:B二、填空题(每题5分,共20分)1. 已知等差数列的前三项依次为2, 5, 8,则该数列的第五项为________。
答案:112. 圆的方程为x^2 + y^2 - 6x - 8y + 25 = 0,则圆心坐标为________。
答案:(3, 4)3. 函数y = sin(x)在区间[0, π]上的最大值为________。
答案:14. 已知三角形的三边长分别为3, 4, 5,则该三角形的面积为________。
答案:6三、解答题(每题15分,共30分)1. 证明:若一个三角形的两边长分别为a和b,且满足a^2 + b^2 =c^2(c为第三边长),则该三角形为直角三角形。
证明:根据勾股定理,若三角形的两边长为a和b,且满足a^2 + b^2 = c^2,则第三边c所对的角θ为直角,即θ = 90°。
因此,该三角形为直角三角形。
2. 解方程:2x^2 - 3x - 2 = 0。
解:首先,我们计算判别式Δ = b^2 - 4ac = (-3)^2 - 4*2*(-2) = 9 + 16 = 25。
2017年高中数学联赛一二试及详解版

2017年全国高中数学联赛A 卷一试一、填空题1.设)(x f 是定义在R 上的函数,对任意实数x 有1)4()3(-=-⋅+x f x f .又当70<≤x 时,)9(l o g )(2x x f -=,则)100(-f 的值为__________.2.若实数y x ,满足1cos 22=+y x ,则y x cos -的取值范围是__________.3.在平面直角坐标系xOy 中,椭圆C 的方程为1109:22=+y x ,F 为C 的上焦点,A 为C 的右顶点,P 是C 上位于第一象限内的动点,则四边形OAPF 的面积的最大值为__________.4.若一个三位数中任意两个相邻数码的差不超过1,则称其为“平稳数”.平稳数的个数是5.正三棱锥ABC P -中,1=AB ,2=AP ,过AB 的平面α将其体积平分,则棱PC 与平面α所成角的余弦值为__________.6.在平面直角坐标系xOy 中,点集}{1,0,1,),(-==y x y x K .在K 中随机取出三个点,则这三点中存在两点之间距离为5的概率为__________.7.在ABC ∆中,M 是边BC 的中点,N 是线段BM 的中点.若3π=∠A ,ABC ∆的面积为3,则⋅的最小值为__________.8.设两个严格递增的正整数数列{}{}n n b a ,满足:20171010<=b a ,对任意正整数n ,有n n n a a a +=++12,n n b b 21=+,则11b a +的所有可能值为__________.二、解答题9.设m k ,为实数,不等式12≤--m kx x 对所有[]b a x ,∈成立.证明:22≤-a b .10.设321,,x x x 是非负实数,满足1321=++x x x ,求)53)(53(321321x x x x x x ++++的最小值和最大值.11.设复数21,z z 满足0)Re(1>z ,0)Re(2>z ,且2)Re()Re(2221==z z (其中)Re(z 表示复数z 的实部). (1)求)Re(21z z 的最小值;(2)求212122z z z z --+++的最小值.2017年全国高中数学联赛A 卷二试一.如图,在ABC ∆中,AC AB =,I 为ABC ∆的内心,以A 为圆心,AB 为半径作圆1Γ,以I 为圆心,IB 为半径作圆2Γ,过点I B ,的圆3Γ与1Γ,2Γ分别交于点Q P ,(不同于点B ).设IP 与BQ 交于点R .证明:CR BR ⊥二.设数列{}n a 定义为11=a , ,2,1,,,,1=⎩⎨⎧>-≤+=+n n a n a n a n a a n n n n n .求满足20173≤<r a r 的正整数r 的个数.三.将3333⨯方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻连个小方格的颜色不同,则称它们的公共边为“分隔边”.试求分隔边条数的最小值.四.设n m ,均是大于1的整数,n m ≥,n a a a ,,,21 是n 个不超过m 的互不相同的正整数,且n a a a ,,,21 互素.证明:对任意实数x ,均存在一个)1(n i i ≤≤,使得x m m x a i )1(2+≥,这里y 表示实数y 到与它最近的整数的距离.2017年全国高中数学联赛A卷一试答案1.2.3.4.6.7.9.10.2017年全国高中数学联赛A卷二试答案一.二、。
2017年全国高中数学联赛陕西赛区试题(一试)解析pdf版

abc ( a ≥1 且 a Z ) abc
f '(a )
bc(a b c) abc b 2 c bc 2 ≥0 (a b c) 2 (a b c) 2
所以 f ( a ) 在 [1, ) 上单调递增 所以 f ( a ) min f (1) 令 g (b)
A、
1 2
B、
1 3
C、
2 2
D、
3 3
【解析】由 AOB 60 , OA OB b ,得 A
3 1 2 a, 2 a , B (0, a ) ,所以直线 AB 为
y
3 xa 3
3 y xa 3 由 2 2 x y 1 a 2 b2
A
Q
D P Q1 B
C
1 1 1 AC , PP AC , QQ1 AC , 1 2 2 2
P1 C1 B1
因 为 AC PR, AC PQ, AC QR , 所 以 RR1 平 面
R D1 A1 R1
PQR , PP 1 平面 PQR , QQ1 平面 PQR ,所以三棱柱
4
)4∴Βιβλιοθήκη 4≤
4
≤
5 4
∴
2 ≤ sin( ) ≤ 1 2 4
∴ 4 5 ≤ 10 sin(
4
) 4 ≤ 4 10
∴ B y 4 5 ≤ y ≤ 4 10
∵A 中的元素是 3 的倍数的正整数,而 B 中的元素是 3 的倍数的有 3 和 6 ∴集合 A B 中元素的个数有 2 个 所以选 B 8、设 x ≥ y 0,若存在实数 a, b 满足 0≤ a ≤ x ,0≤ b ≤ y ,且
2017年广西高一数学竞赛“创新杯”决赛试卷(含参考答案)

2017年广西高一“创新杯”决赛试卷参考答案一、选择题(每小题6分,共36分)1.如果1=++cc bb aa ,则abcabc 的值为 ( _★_ )A.1-B. 1C. 1±D. 与c b a ,,的值有关【答案】A解:c c b b a a ,,的取值是1或-1,因为1=++c c b b a a ,所以c c b b a a ,,中有2个1,1个-1.c b a ,,中有两正一负,所以0<abc ,.1-=abcabc2.已知非零实数a b 、满足:2210a ab b a b ++-+=+,则a b +的值等于 ( _★_ )A .1-B .0C .1D .2 【答案】B解:由题设得22211102a b a b ⎡⎤++++-=⎣⎦()()(),则0a b =+,10a =+,10b -=,故0a b =+.3.方程 3)2(22=-+x x x 的所有实数根之和为 ( ★ ) A .1 B.3 C.5 D .7 【答案】C 解:方程22()32x x x +=-化为2222(2)3(2)x x x x -+=-。
即3251060x x x -+-=,2(1)(46)0x x x --+=。
解得1x =。
经检验1x =是原方程的根。
∴ 原方程所有实数根之和为5。
4.如图,四边形ABHK 是边长为6的正方形,点C 、D 在边AB 上,且AC =DB =1,点P 是线段CD 上的动点,分别以AP 、PB 为边在线段AB 的同侧作正方形AMNP 和正方形BRQP ,E 、F 分别为MN 、QR 的中点,连接EF ,设EF 的中点为G ,则当点P 从点C 运动到点D 时,点G 移动的路径长为 ( _★_ ) A.1 B. 2 C. 3 D. 6【答案】B解:设KH 中点为S ,连接PE 、ES 、SF 、PF 、PS ,可证明四边形PESF 为平行四边形,∴G 为PS 的中点,即在点P 运动过程中,G 始终为PS 的中点,所以G 的运行轨迹为△CSD 的中位线,∵CD =AB -AC -BD =6-1-1=4,∴点G 移动的路径长为421⨯=2.5.已知,,x y z 为三个非负实数,且满足325231x y z x y z ++=⎧⎨+-=⎩,设37s x y z =+-,则s 的最大值是 ( _★_ ) A .57-B. 75-C. 111D. 111- 【答案】D 解:由方程组解出73711x z y z=-⎧⎨=-⎩,由,x y 非负实数,可解得37711z ≤≤,∵373(73)711732s x y z z z z z =+-=-+--=-,取711z =代入即可求得,111max -=s6.()f x 是定义在R 上的函数,若0)1(=f ,且对任意x R ∈,满足)()2(x f x f -+≤2,)()6(x f x f -+≥6,则=)2017(f ( _★_ )A. 2015B. 2016C. 2017D. 2018 【答案】B解:∵ 对任意x R ∈,满足)()2(x f x f -+≤2,∴[][][](6)()(6)(4)(4)(2)(2)()6f x f x f x f x f x f x f x f x +-=+-+++-+++-≤,又)()6(x f x f -+≥6因此,(6)()6f x f x +-=,(6)()6f x f x +=+. ∴ (6)()6f x k f x k +=+,*k N ∈.∴ .20163366)1()33661()2017(=⨯+=⨯+=f f f二、填空题(每小题9分,共54分)7.已知实数x ,y 满足x 2+3x +y -4=0,则x +y 的最大值为 . 【答案】5解:由x 2+3x +y -4=0得y =-x 2-3x +4,把y 代入x +y 得:x +y =x -x 2-3x +4=-x 2-2x +4=-(x +1)2+5≤5,∴x +y 的最大值为5.8.设a =,且ab = 1,则a 2 + b 2的值为 .【答案】98解:因25a ===+,及ab = 1知,625)23(23232-=-=+-=b ,故a 2 + b 2 = (a + b )2– 2ab = 100 – 2 = 98.9.若f ex dx cx bx ax x +++++=+23455)12(,则e d c b a +-+-的值是 .【答案】2解:f ex dx cx bx ax x +++++=+23455)12( ,当x =0时,1=f ,当1-=x 时,1-=+-+-+-f e d c b a ,2-=-+-+-e d c b a2=+-+∴e d c b a -.10.如图所示,BC 是半圆⊙O 的直径,EF ⊥BC 于点F ,5BFFC=. 已知AB = 8,AE = 2.则AD 的长为 .【答案】231+ 解:联结BE .由BC 为直径知∠BEC = 90°.故BE == 又由Rt △BFE ∽Rt △EFC ,知225BE BF EF BE BF EC EC EF FC EC FC==⇒==⇒=由割线定理得()AE AE EC AD AB +===11.我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l :34+=kx y 与x轴、y 轴分别交于A 、B ,∠OAB =30°,点P 在x 轴上,⊙P 与l 相切,当P 在线段OA 上运动时,使得⊙P 成为整圆的点P 个数是 .【答案】6解:∵直线l :y =kx +与x 轴、y 轴分别交于A 、B ,∴B (0,4),∴OB =在Rt △AOB 中,∠OAB =30°,∴OA OB =×4=12,∵⊙P 与l 相切,设切点为M ,连接PM ,则PM ⊥AB ,∴PM =12P A ,设P (x ,0),∴P A =12﹣x ,∴⊙P 的半径PM =12PA =6-12x ,∵x 为整数,PM 为整数,∴x 可以取0,2,4,6,8,10,6个数,∴使得⊙P 成为整圆的点P 个数是6.12.黑板上写有1001,,31,21,1⋅⋅⋅共100个数字.每次操作先从黑板上的数中选取2个数b a ,,然后删去b a ,,并在黑板上写上数ab b a ++,则经过99次操作后,黑板上剩下的数是 . 【答案】100解:1)1)(1(-++=++b a ab b a ,∵计算结果与顺序无关,∴顺次计算得:21)121)(11(=-++,31)131)(12(=-++,41)141)(13(=-++,…… 1001)11001)(199(=-++.13.(本小题满分20分)已知实数a ,b ,c 满足a +b +c =13,a 2+b 2+c 2=77,abc =48,求cb a 111++的值. 解:因为a +b +c =13,所以(a +b +c )2=a 2+b 2+c 2+2(ab +bc +ca )=169. ……………… 5分 因为a 2+b 2+c 2=77,所以ab +bc +ca =46. ……………… 10分 又因为abc =48,所以2423111=++=++abc ca bc ab c b a . ……………… 20分14.(本小题满分20分)如图,⊙O 的直径AB =2,AM 和BN 是它的两条切线,DE 切⊙O 于E ,交AM 于D ,交BN 于C .设AD =x ,BC =y . (1)求y 关于x 的关系式;(2)求四边形ABCD 的面积S ,并证明:S ≥2.解:(1)过点D 作BC DF ⊥于F ,则DF AB // ∵AB 是直径,AM 、BN 是切线∴AB BN AB AM ⊥⊥, ∴BN AM //∴四边形ABFD 为平行四边形又∵∠ABC =90°,∴四边形ABFD 为矩形.∴2==AB FD ,x AD BF ==∵DE 、DA ,CE 、CB 都是切线 ∴根据切线长定理,得x AD DE ==,y CB CE ==在DFC Rt ∆中,x y BF BC CF y x CE DE DC DF -=-=+=+==,,2∴222)(2)(x y y x -+=+化简,得)0(1>=x xy ……………………………… 10分 (2))0(,1)(21>+=+=x xx BC AD AB S ABCD,即)0(,1>+=x xx S ……………………………… 15分 ∵2)1(21xx x x -=-+≥0当且仅当1=x 时,等号成立 ∴xx 1+≥2,即S ≥2.……………………………… 20分15.(本小题满分20分)已知,a b 为正整数,求22324M a ab b =---能取到的最小正整数值.解:因,a b 为正整数,要使得22324M a ab b =---的值为正整数,则有2a ≥. 当2a =时,b 只能为1,此时 4.M =故M 能取到的最小正整数值不超过4. 当3a =时,b 只能为1或2.若1,18b M ==;若2b =,则7M =.当4a =时,b 只能为1或2或3.若1,38b M ==;若2,24b M ==;若3,b =则2M =.……… 10分(下面考虑:22324M a ab b =---的值能否为1?)(反证法)假设1M =,则223241a ab b ---=,即22325a ab b -=+,2(3)25a a b b -=+ ①因b 为正整数,故25b +为奇数,从而a 为奇数,b 为偶数, 不妨设21,2a m b n =+=,其中,m n 均为正整数,则22222(3)(21)3(21)(2)4(332)3a a b m m n m m mn n ⎡⎤-=++-=+--+⎣⎦即2(3)a a b -被4除所得余数为3,而252(2)141b n n +=+=+被4除所得余数为1, 故①式不可能成立,故1M ≠.因此,M 能取到的最小正整数值为2.……………… 20分。
2017年全国高中数学联赛一试(B卷)答案

成立,求实 成立.由于
解:设 t 2 x ,则 t [2, 4] ,于是
对所有
t a 5 t (t a ) 2 (5 t ) 2 (2t a 5)(5 a ) 0 . ………………8 分 对给定实数 a ,设 f (t ) (2t a 5)(5 a ) ,则 f (t ) 是关于 t 的一次函数或常 值函数.注意 t [2, 4] ,因此 f (t ) < 0 等价于 f (2) (1 a )(5 a ) 0, ………………12 分 f (4) (3 a )(5 a ) 0, 解得 3 a 5 . 所以实数 a 的取值范围是 3 a 5 . ………………16 分 10. ( 本 题 满 分 20 分 ) 设 数 列 {an } 是 等 差 数 列 , 数 列 {bn } 满 足 2 , n 1, 2, . bn an1an2 an (1)证明:数列 {bn } 也是等差数列; (2) 设数列 {an } 、 并且存在正整数 s, t , 使得 as bt {bn } 的公差均是 d 0 , 是整数,求 a1 的最小值. 解: (1)设等差数列 {an } 的公差是 d ,则 2 2 bn1 bn ( an2an3 an 1 ) ( an1an2 an ) an2 ( an3 an1 ) ( an1 an )( an1 an ) an2 2d ( an1 an ) d
2017 年全国高中数学联合竞赛一试(B 卷) 参考答案及评分标准
说明: 1. 评阅试卷时,请依据本评分标准. 填空题只设 8 分和 0 分两档;其他各题的 评阅,请严格按照本评分标准的评分档次给分,不得增加其他中间档次. 2. 如果考生的解答方法和本解答不同,只要思路合理、步骤正确,在评卷时可 参考本评分标准适当划分档次评分, 解答题中第 9 小题 4 分为一个档次, 第 10、 11 小题 5 分为一个档次,不得增加其他中间档次. 一、填空题:本大题共 8 小题,每小题 8 分,共 64 分. 1. 在等比数列 {an } 中, a2 2, a3 3 ,则
2017年全国高中数学联赛新疆赛区预赛高一试题及详解

12017年全国高中数学联赛新疆赛区预赛高一试题详解一.填空题(本大题共8小题,每小题8分,共64分,把答案填在横线上)1.已知函数()f x 是R 上的减函数,且是奇函数.若,m n 满足不等式组()(2)0,(1)0,f m f n f m n +-≤⎧⎨--≤⎩则5m n -的取值范围是 .2.已知1231,2,3x x x ===是满足432()f x x ax bx cx d =++++的三个零点,则(0)(4)f f += .3.已知1a >,则4log 162log a a +的最小值为 .4.在Rt ABC ∆中,60C ∠=.以C 为圆心,BC 为半径的圆交AC 于D 点.连接BD .弧BD 与弦BD 将ABC ∆分为三部分(如图).则三部分面积之比123::S S S = .5.已知A 从甲地到乙地用了整数个小时,且A 每小时走的公里数与他从甲地到乙地所用时间相同. B 从甲地到乙地每小时走2公里,且每走4公里休息1小时,公用了11小时,则甲乙两地距离为 公里.6.已知在ABC ∆中,tan ,(1tan ,tan A B C +成等差数列,则B ∠的最小值为 .7.已知直线2017ax by +=与圆22100x y +=有公共点,且公共点的横、纵坐标均为整数,则这样的直线E 为AB 上一点,1AE =.现将BCE ∆沿CE 折起,使得点B 在平面ABCD 上共有 条.8.已知数列{n a }首项为2,且满足16341n n n S a +=+-,则n S 的最大值为 . 二.解答题(本大题共3小题,其中第1题16分,第2,3小题各20分,共56分)1.(1)对于任意的,0a b >,求证: 1111()4a b a b≤++; (2)设123,,0x x x >,且1231111x x x ++=.求证:12312312313321231213232x x x x x x x x x x x x x x x x x x x x x ++++++++≤+++.2.已知已,,x y z 是正数,且满足2222223,4,7.x y xy y z yz z x zx ⎧++=⎪++=⎨⎪++=⎩求x y z ++.(1)求椭圆的方程;3.如图,边长为2的等边三角形ABC ∆中,D 是BC 的中点. ,E F 分别是边,AB AC 上的动点.(1)若120EDF ∠=,求证:AE AF +为定值;(2)若60EDF ∠=,此时AE AF +是否为定值?若是,请给出证明;否则,求出AE AF +的取值范围.。
2017年全国高中数学联合竞赛一试(A卷)(含参考答案及评分标准)

答案: 13, 20 . 解:由条件可知: a1 , a2 , b1 均为正整数,且 由于 ,故 . .反复运用 {an } 的递推关系知 , 因此 而 21a1 a10 b10 512b1 2b1 (mod 34) , ,故有 . 另一方面,注意到 ,有 . 当 当 时,①,②分别化为 时,①,②分别化为 ,此时 当 . ,得到唯一的正整数 ,无解. ,得到唯一的正整数 ,故 ②
( x1 + 3x2 + 5 x3 )( x1 +
x2 x3 1 5x + ) = ( x1 + 3x2 + 5 x3 )(5 x1 + 2 + x3 ) 3 5 5 3 2 1 1 5x ≤ ⋅ ( x1 + 3x2 + 5 x3 ) + (5 x1 + 2 + x3 ) 5 4 3
1 PP PF 1 1 P 2F 1 2 4 2 PF 1 2 P 2 F2 PP 1 2 4 2 , ………………15 分 (例如, 当 z1 z2 2 2 i 时,F2 恰是 PP 等号成立当且仅当 F2 位于线段 PP 1 2 上 1 2 的中点) . 综上可知, z1 2 z2 2 z1 z2 的最小值为 4 2 . …………20 分
① ② ③
a b a b ab f k m 1 . 2 2 2
由① ② 2 ③知, a b ( a b) 2 4, =f ( a ) f ( b ) 2 f 2 2 故ba 2 2 .
2
1 14 ………………10 分 = 6 x1 + x2 + 6 x3 20 3 1 9 2 ≤ ( 6 x1 + 6 x2 + 6 x3 ) = , 20 5 1 1 9 = x1 = , x2 0, = x3 当 时不等式等号成立,故欲求的最大值为 . ………20 分 2 2 5 11. ( 本 题 满 分 20 分 ) 设 复 数 z1 , z2 满 足 Re( z1 ) 0, Re( z2 ) 0 , 且
2017年第10届全国中学数理化竞赛高一数学试题答案(初赛)

二、填空题(每题 8 分,共 48 分) 9 9.-2 解析 函数f(x)的定义域是不等式ax2+abx+b≥0 的解集.不等式ax2+abx+b≥0 的解集为 a<0, 1+2=-b, {x|1≤x≤2},所以 b 1×2=a, 3 a=-2, 3 9 所以a+b=-2-3=-2. 解得 b=-3,
y f 0 x 2 的图像,作该图像在 x 轴下方的部分关于 x 轴的对称图形得到图 3,其中 x 轴
上方的部分即是 f 2 x f1 x 2 的图像.易得所求面积为 7.
y
y
y (1,2) 1
(-1,2)
1
o
x
-1
o
1
x
-3
o
-1
3
x
图1
图2
图3
三、解答题(共 70 分) 13.(23 分)
特级教师 王新敞
126. com wxckt @
1 1 1 1 对于①,f(x)=x-x , f ( ) =x-x=-f(x),满足“倒负”变换;对于②, f ( ) = x x
1 1 1 x ,0 x 1, x , x 1, 1 1 1 1 不满足 “倒负” 变换; 对于③, f ( ) = 0, 1, 即 f ( ) = 0, x 1, x +x=f(x), x x x x,0 x 1 1 x , x 1 1 故 f ( ) =-f(x),满足“倒负”变换.综上可知,满足“倒负”变换的函数是①③. x
2017年全国高中数学联赛湖北省预赛试题参考答案及评分标准(高一年级)

6 6 2 3 2 2说明:1. 评阅试卷时,请依据本评分标准. 填空题只设9分和0分两档;其他各题的评阅, 请严格按照本评分标准的评分档次给分,不要增加其他中间档次.2. 如果考生的解答方法和本解答不同,只要思路合理、步骤正确,在评卷时可参考本评分标准适当划分档次评分,解答题中5分为一个档次,不要增加其他中间档次.一、填空题(本大题共10小题,每小题9分,共90分.)1.已知非空集合 A = {x | m +1 ≤ x ≤ 2m -1}, B = {x | x 2 - 2x -15 ≤ 0} ,且 A ⊆ B ,则实数 m 的取值范围是 [2,3] .2. 已知正项等比数列{a n }满足a 6 + a 5 + a 4 - a 3 - a 2 - a 1 = 49 ,则a 9 + a 8 + a 7 的最小值为 196 .3. 设函数 f (x ) = x 3 + ax 2 + bx + c ( x ∈R ),其中a ,b , c 为互不相同的非零整数,且 f (a ) = a 3 , f (b ) = b 3 ,则a + b + c = 18 .4 . 设△ ABC 的内角 A , B ,C 的对边分别是 a ,b , c , 若 cos A = 3cos B = 4 cos C ,则a b ct a n A = . 3 5.设函数 f (x ) = (1) x + ( 2) x + (5) x , x ∈[0,+∞) ,则该函数图象上整点的个数为 3 .2 3 66 . 已知 O 为△ ABC 的外心, D 为 BC 的中点, 若 AO ⋅ AD = 4 , BC = 2 ,则 AD = .7. 已知正实数a ,b 满足ab (a + b ) = 4 ,则2a + b 的最小值为 2 .8. 设 x , y ∈R ,则 P = (x +1- cos y )2 + (x -1+ sin y )2 的最小值为 3 - 2 .9. 若关于 x 的方程 | x | x +1= k x 2 恰有两个不同的实数根,则实数k 的取值范围为(-∞, 0) (0, 4). 10. 将与 70 互素的所有正整数从小到大排成数列,这个数列的第 2017 项为 5881 .二、解答题(本题满分 60 分,每小题 20 分。
2017年全国高中数学联合竞赛试题及解答.(A卷)

2 2 1 AM AN 3 AB AC 4 AB AC , 8
由 3 S ABC
1 3 AB AC sin A AB AC 得 AB AC 4 2 4
2
所以 AB AC 2 ,所以 3 AB
AC 8 3 ,当且仅当 AB
x x1 3x 2 5 x3 x1 2 3
★解析:由柯西不等式
x3 的最小值和最大值。 5 x2 5 x3 3 x3 5 1
2
x x x1 3x 2 5 x3 x1 x1 3 x 2 x1 2 3 3 5
当 x1 1 , x 2 0 , x 3 0 时取等号,故所求的最小值为 1 ; 又 x1 3 x 2 5 x 3 x1
x 2 x3 1 5x x1 3 x 2 5 x 3 5 x1 2 x 3 3 5 5 3
2
512 b1 ② 55
★证明:记 f ( x ) x kx m , x a, b ,则 f ( x ) 1,1 。于是
2
f (a ) a 2 ka m 1 ①; f (b) b 2 kb m 1 ② ab ab 2 ab )( ) k( ) m 1 ③ 2 2 2 ①+②- 2 ③知 f(
2017 年全国高中数学联合竞赛一试(A 卷)
一、填空题:本大题共 8 个小题,每小题 8 分,共 64 分。 2017A1、设 f ( x ) 是定义在 R 上函数,对任意的实数 x 有 f ( x 3) f ( x 4) 1 ,又当 0 x 7 时, f ( x ) log 2 (9 x ) ,则 f ( 100) 的值为 ◆答案:
2017年全国高中数学联赛一试(B卷)答案

2017 年全国高中数学联合竞赛一试(B卷)参考答案及评分标准说明:1. 评阅试卷时,请依据本评分标准. 填空题只设 8 分和 0 分两档;其他各题的评阅,请严格按照本评分标准的评分档次给分,不得增加其他中间档次.2. 如果考生的解答方法和本解答不同,只要思路合理、步骤正确,在评卷时可参考本评分标准适当划分档次评分,解答题中第 9 小题 4 分为一个档次,第 10、11 小题 5 分为一个档次,不得增加其他中间档次.一、填空题:本大题共 8 小题,每小题 8 分,共 64 分.1. 在等比数列{a } 中,a2, a 3,则a 1a2011的值为.3n23a 7a2017答案:8.9a 3 a a a a 1 8 解:数列{a } 的公比为q 3,故.a 2 q 6 ( a 1 a 2011 ) q 6n 2 a 7a 201792. 设复数 z 满足z 9 1022 i ,则 z z 的值为.答案:.5 a , b R .由条件得解:设z a b i,( a 9) b i 10 a ( 10b 22) i . 比较两边实虚部可得 a + 9 = 10 a ,b = −10b + 22,解得a 1, b 2 ,故z 1 2 i ,进而 z 5 .3. 设 f ( x ) 是定义在R 上的函数,若 f ( x ) x 2 是奇函数, f ( x ) 2x 是偶函数, 则 f (1) 的值为 .答案: 7.4f ( 1) 1 , 解:由条件知, f (1) 1f ( 1) ( 1) 2 f ( 1) 1, f (1) 221 ,即 f (1) 7两式相加消去 f ( 1) ,可知2 f (1) 3 .244. 在 ABC 中,若sin A 2sin C ,且三条边a , b , c 成等比数列,则cos A 的值为 .答案:42.解:由正弦定理知,ac sinsin C A 2 ,又b 2ac ,于是a : b : c 2 : 2 : 1,从而由余弦定理得,cos A b2c2a 2(2) 2122 22. 4 2 bc 2 2 15. 在正四面体 ABCD 中,E , F 分别在棱 AB , AC 上,满足BE = 3, EF = 4 ,且EF 与面BCD 平行,则∆DEF 的面积为.1答案:233 .解:由条件知,EF 平行于BC .因为正四面体 ABCD 的各个面是全等的正三角形,故AE AF EF 4, AD AB AE BE 7 .由余弦定理得,DE AD 2 AE 2 2 AD AE cos 6049 16 28 37 ,同理有DF 37 .作等腰 DEF 底边EF 上的高DH ,则EH12 EF 2 ,故DH DE 2 EH 2 33 ,于是S DEF12 EF DH 233 .6. 在平面直角坐标系 xOy 中,点集K ( x , y ) | x , y 1, 0, 1 .在K 中随机取出三个点,则这三个点两两之间距离均不超过 2 的概率为 .答案:145.解:注意K 中共有 9 个点,故在K 中随机取出三个点的方式数为种.当取出的三点两两之间距离不超过 2 时,有如下三种情况:(1)三点在一横线或一纵线上,有 6 种情况.(2)三点是边长为1, 1, 2 的等腰直角三角形的顶点,有4 4 16 种情况.(3)三点是边长为2, 2, 2 的等腰直角三角形的顶点,其中,直角顶点位于(0, 0) 的有 4 个,直角顶点位于( 1, 0), (0, 1) 的各有一个,共有8 种情况.综上可知,选出三点两两之间距离不超过 2 的情况数为 ,进而所求概率为30 5 . 14 847. 设a 为非零实数,在平面直角坐标系 xOy 中,二次曲线 x 2 ay 2 a 2 0 的 焦距为 4,则a 的值为 .答案:1 217.解:二次曲线方程可写成 x 2 y2 1.显然必须 a 0 ,故二次曲线为双曲 a 2ay 2x 2222 21 .则c ( a )( a )a a ,注意到焦距( a )2 ( a )2c 4 ,可知a 2 a 4 ,又a 0,所以a 117.28. 若正整数a , b , c 满足2017 10 a 100b 1000c ,则数组( a , b , c ) 的个数为.答案:574 .解:由条件知c20172 .1000当c1时,有10b20.对于每个这样的正整数b,由10b a201知,2相应的a的个数为202 10b.从而这样的正整数组的个数为20b 10 2当c2时,由20 b 2017 .进而200 2017 201 ,,知b20 a100 10故a200, 201.此时共有2组(a,b,c).综上所述,满足条件的正整数组的个数为.二、解答题:本大题共3小题,满分56分.解答应写出文字说明、证明过程或演算步骤.9.(本题满分16分)设不等式2x a5 2x对所有成立,求实数a的取值范围.解:设t2x,则t[2, 4],于是对所有成立.由于t a 5 t ( t a ) 2 (5 t)2(2 t a 5)(5 a) 0 .………………8 分对给定实数a,设f(t) (2t a5)(5a),则f(t)是关于t的一次函数或常值函数.注意t[2, 4],因此f(t) 0等价于………………12 分f (4) (3 a )(5 a) 0,解得3a5.所以实数a的取值范围是3a5.………………16 分10.(本题满分20分)设数列{a n}是等差数列,数列{b n}满足b a a a 2, n 1, 2,.n n 1 n 2 n(1)证明:数列{b n}也是等差数列;(2)设数列{a n}、{b n}的公差均是d0,并且存在正整数s,t,使得a s b t是整数,求a1的最小值.解:(1)设等差数列{a n}的公差是d,则b n1b n( a n2a n3 a n21)( a n1a n2a n2)a n2( a n3 a n1) ( a n1 a n)( a n1 a n)a n22 d ( a n1 a n) d(2a n2a n1a n ) d .所以数列{b n}也是等差数列.………………5 分(2)由已知条件及(1)的结果知.因为,故.这样b a an 2 a 2 ( a d )( a 2 d ) a2n n 1 n n n n3da n 2d2a n 2 .………………10分9若正整数s,t满足,则3a b a a 2a ( s 1) d a ( ts ts t 9 1 12a s t 22 Z . 13 9 s t 2 2记l 2a ,则l Z ,且18a 3(3l1 3 91 整数,故,从而.又当时,有ab1 17 1 Z .13 18 18综上所述, a 1 的最小值为181.1)d92s t 1) 1是一个非零的………………15 分………………20 分11. (本题满分 20 分)在平面直角坐标系 xOy 中,曲线C 1 : y 2 4x ,曲线 C2 : ( x 4) 2 y 28 .经过C 1 上一点P 作一条倾斜角为45 的直线l ,与C 2 交于两个不同的点Q , R ,求 PQ PR 的取值范围.解:设P (t 2 , 2t ) ,则直线l 的方程为 y x 2t t 2 ,代入曲线C 2 的方程得, ( x 4) 2 ( x 2t t 2 ) 2 8 ,化简可得 2 x 2 2(t 2 2t 4) x (t 2 2t ) 2 8 0 .①由于l 与C 2 交于两个不同的点,故关于x 的方程①的判别式 为正.计算得,(t 2 2t 4) 2 2((t 2 2t ) 2 8) (t 2 2t ) 2 8(t 2 2t ) 16 2(t 2 2t ) 2 164(t 2 2t ) 2 8(t 2 2t )(t 2 2t ) (t 2 2t 8)t (t 2)(t 2)(t 4) ,因此有 t ( 2, 0) (2,4) . ②………………10 分设Q , R 的横坐标分别为x 1 , x 2 ,由①知,x x t 22t 4, x x 1((t 2 2t ) 2 8) ,121 2 2因此,结合l 的倾斜角为45 可知,PQ PR 2( x 1t 2 ) 2( x 2 t 2 ) 2 x 1 x 2 2 t 2 ( x 1 x 2 ) 2t 4(t 2 2t ) 2 8 2t 2 (t 2 2t 4) 2t 4t 4 4t 3 4t 2 8 2t 4 4t 3 8t 2 2t 4t 4 4t 2 8 (t 2 2) 2 4 .③………………15 分由②可知,t 2 2 ( 2, 2) (2, 14) ,故( t 2 2) 2 [0,4) (4, 196) ,从而由③得,PQ PR (t 2 2) 2 4 [4, 8) (8, 200) .………………20 分注 1:利用C 24 2 t t2的圆心到l 的距离小于C 2 的半径,列出不等式2,2 2同样可以求得②中t 的范围.注 2:更简便的计算 PQ PR 的方式是利用圆幂定理.事实上,C 2 的圆心为 M (4, 0) ,半径为r 2 2 ,故PQ PRPM 2 r 2 (t 2 4) 2 (2t ) 2 (22) 2 t 4 4t 2 8 .4。
2017年福建省高一数学竞赛试题(原卷排版+解析)

6
3
6
∴ 1 c 1 ,且 1 c 1 。
66
2
6
∴ c1。 6
6
此时, f (0) 1 ,可见 f (x) 在区间 1,1 上的最小值为 f (0) 。
6
∴ f (x) 的对称轴为 x 0 ,即 1 a 0 , a 1 。
3
3
∴ f (x) 1 x2 1 。 36
2xy yz 1 ,当且仅当 x 2y ,且 y z ,即 x 2 , y z 1 时,等
2
10
10
号成立。
所以, 2xy yz 的最大值为 1 。 2
三、解答题(第 13、14、15、16 题每题 16 分,第 17 题 14 分,满分 78 分)
13.已知 f (x) ax2 (1 a)x c ,且当 1 x 1时, f (x) 1 恒成立。
2017 年福建省高一数学竞赛试题
(考试时间:5 月 14 日上午 8:30-11:00)
一、选择题(每小题 6 分,共 36 分)
1.已知集合A来自 xx2 x3
0,x Z
,则集合
A 中所有元素的和为(
)
A. 1
B.0
C.2
D.3
【答案】 B
【解答】由 x 2 0 ,得 2 x 3。又 x Z 。因此 A 2,1,0,1,2 。
也是 1,0 ,则 a m 的值为
。
【答案】 5 2
【解答】当 a 1时, f (x) 在 1,0 上为增函数,依题意有
3
f (1) loga (1 m) 1,方程组无解。 f (0) loga (0 m) 0
2017年浙江省高中数学竞赛试卷

2017年浙江省高中数学竞赛试卷一、填空题:本大题共10个小题,每小题8分,共80分. 1.在多项式310(1)(2)x x -+的展开式中6x 的系数为 . 2.已知3)a -=,则实数a = .3.设2()f x x ax b =++在[]0,1中有两个实数根,则22a b -的取值范围为 .4.设x ,y R ∈,且222222sin cos cos cos sin sin 1sin()x x x y x yx y -+-=+,则x y -= .5.已知两个命题,命题p :函数()log a f x x =(0x >)单调递增;命题q :函数2()1g x x ax =++ (x R ∈).若p q ∨为真命题,p q ∧为假命题,则实数a 的取值范围为 .6.设S 是5(0,)8中所有有理数的集合,对简分数q S p ∈,(,)1p q =,定义函数1()q q f p p +=,则2()3f x =在S 中根的个数为 . 7.已知动点P ,M ,N 分别在x 轴上,圆22(1)(2)1x y -+-=和圆22(3)(4)3x y -+-=上,则||||PM PN +的最小值为 .8.已知棱长为1的正四面体P ABC -,PC 的中点为D ,动点E 在线段AD 上,则直线BE 与平面ABC 所成的角的取值范围为 .9.已知平面向量a r ,b r ,c r ,满足||1a =r ,||2b =r ,||3c =r ,01λ<<,若0b c ⋅=r r,则|(1)|a b c λλ---r r r所有取不到的值的集合为 .10. 已知22,0,()1,0,x x f x x x -<⎧⎪=⎨-≥⎪⎩方程()|()240f x f x ax +---=有三个根123x x x <<.若32212()x x x x -=-,则实数a = .二、解答题:本大题共5个小题,满分120分,将答案填在答题纸上)11. (本题满分20分)设1()f x =1()n f x +,1,2,n =L .对每个n , 求()n f x 3x =的实数解.12. (本题满分20分)已知椭圆22162x y +=的右焦点为F ,过F 的直线(2)y k x =-交椭圆于P ,Q 两点(0)k ≠.若PQ 的中点为原点,直线ON 交直线3x =于M . (I)求MFQ ∠的大小; (Ⅱ)求PQMF的最大值.13. (本题满分20分)设数列{}n a 满足:1|2|2n n a a +-=,||2n a ≤,1,2,3,n =L . 证明:如果1a 为有理数,则从某项后{}n a 为周期数列.14. (本题满分30分)设1a ,2a ,3a ;1b ,2b ,3b Z +∈,证明:存在不全为零的数1λ,2λ, {}30,1,2λ∈,使得112233a a a λλλ++和112233b b b λλλ++同时被3整除.15. (本题满分30分)设{}12,,n a a a σ=…,为{}1,2,,n …的一个排列,记11()ni i i F a a σ+==∑,11n a a +=,求min ()F σ.。
江西省萍乡市2017年高一数学竞赛试题(含解析)

2017年江西省萍乡市高一年级数学竞赛试卷第Ⅰ卷(共60分)一、填空题(每题10分,共80分.)1. 若是单位向量,且,则__________.【答案】0【解析】2. 函数的值域为__________.【答案】【解析】时,x-1时,1-x<0, <-1综上值域为故答案为点睛:分段函数求值域,先分段求,再求并集,注意的是指数函数都是大于0的3. 4个函数,,,图象的交点数共有__________.【答案】5故答案为54. 若,则__________.【答案】0.........5. 已知,,,则__________.【答案】【解析】∵cosα+cosβ+cosγ=sinα+sinβ+sinγ=0,∴cosγ=−cosα−cosβ,sinγ=−sinα−sinβ,∵=1,∴=1,整理得:2+2(cosαcosβ+sinαsinβ)=1,即cosαcosβ+sinαsinβ=−,∴cos(β−α)= −,∵0⩽α<β<2π,∴0<β−α<2π∴β−α=或.①∴同理可得:cos(γ−β)=−−,解得:γ−β=或②。
cos(γ−α)= −;解得:γ−α=或③。
∵0⩽α<β<γ<2π,∴β−α=,γ−β=,γ−α=.故β−α的值为.点睛:本题主要考查了同角平方关系的应用,解题的关键是要发现sin2γ+cos2γ=1,从而可得α,β的基本关系,但要注意出现多解时一定要三思而后行.6. 甲乙两人玩猜数学游戏,先由甲心中想一个数字,记为,再由乙猜甲刚才所想的数字,把乙猜的数字记为,其中,若,称甲乙“心相近”,现任意两人玩这游戏,则他们心相近的概率为__________.【答案】【解析】7. 在中,角所对边分别为,若,则__________.【答案】【解析】又A为锐角,所以A=8. 将10个数1,2,3,…,9,10按任意顺序排列在一个圆圈上,设其中连续相邻的3数之和为,则的最大值不小于__________.【答案】18【解析】设10个在圆圈上的排列的数依次为其中于是=故中必有一个不小于18故答案为18二、解答题(共70分)9. 已知函数()是偶函数,若对一切实数都成立,求实数的取值范围.【答案】【解析】试题分析:函数()是偶函数得出,证明出当时,为增函数,,根据单调性去掉f,得出,即得解试题解析:()是偶函数,当时,,得对一切都成立,所以,.于是设,,所以,当时,为增函数.,,于是,即,所以即对一切实数都成立.点睛:型如的题目肯定会用到函数的奇偶性,单调性,所以做题时从这两方面着手即可.10. 记表示不超过实数的最大整数,在数列中,,(),证明:.【答案】见解析【解析】试题分析:由()知,数列为正项递增数列.把化为,两边同除得,裂项相消求和即得解.试题解析:由()知,数列为正项递增数列.又,所以,.化为,两边同除得.因此,故11. 如图,定直线与定相离,为上任意一点,为的两条切线,为两切点,其垂足为点,交于点,证明:为定长.【答案】见解析【解析】试题分析:因为,,由射影定理,得,因为,所以,四点共圆,由圆幂定理得结合两个等式即得解.试题解析:连,设为,的交点,因为,,由射影定理,得因为,所以,四点共圆.由圆幂定理,得所以,即(定值),所以,为定长.12. 有()个整数:,,…,,满足,,证明能被4整除.【答案】见解析【解析】试题分析:反证法来解决问题,若为奇数,由,得均为奇数推出矛盾,所以,中必有偶数,如果中仅有一个偶数,推出矛盾,所以中必至少有2个偶数,即得证试题解析:首先,为偶数,事实上,若为奇数,由,得均为奇数,而奇数个奇数和应为奇数,且不为0,这与矛盾,所以,为偶数所以,中必有偶数.如果中仅有一个偶数,则中还有奇数个奇数,从而,也为奇数,矛盾,所以,中必至少有2个偶数.由知,能被4整除.。
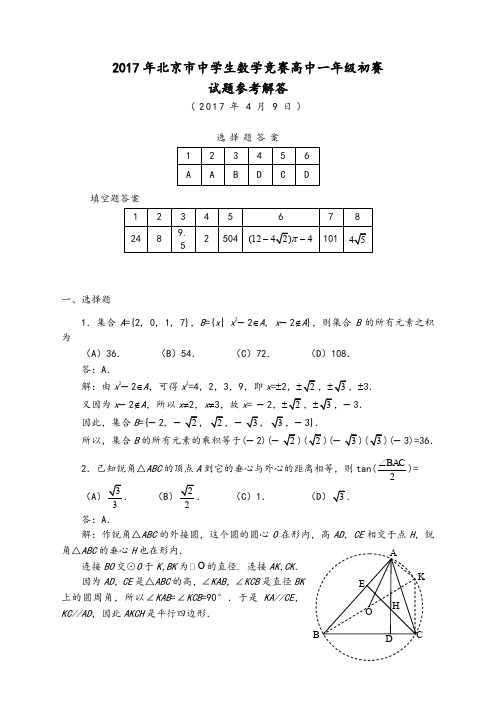
2017北京市高一数学初赛试题及解答
2017年北京市中学生数学竞赛高中一年级初赛试题参考解答(2017年4月9日)选择题答案填空题答案一、选择题1.集合A ={2, 0, 1, 7},B ={x | x 2−2∈A , x −2∉A },则集合B 的所有元素之积为(A )36. (B )54.(C )72. (D )108. 答:A .解:由x 2−2∈A ,可得x 2=4,2,3,9,即x =±2,,±3. 又因为x −2∉A ,所以x ≠2,x ≠3,故x = −2,,,−3. 因此,集合B ={−2, −−−3}.所以,集合B 的所有元素的乘积等于(−2)(−−−3)=36.2.已知锐角△ABC 的顶点A 到它的垂心与外心的距离相等,则tan(2BAC∠)= (A. (B . (C )1. (D 答:A .解:作锐角△ABC 的外接圆,这个圆的圆心O 在形内,高AD ,CE 相交于点H ,锐角△ABC 的垂心H 也在形内.连接BO 交⊙O 于K ,BK 为O 的直径. 连接AK ,CK . 因为AD ,CE 是△ABC 的高,∠KAB ,∠KCB 是直径BK 上的圆周角,所以∠KAB =∠KCB =90°.于是KA//CE ,KC//AD ,因此AKCH 是平行四边形.所以KC =AH =AO =12BK . 在直角△KCB 中,由KC =12BK ,得∠BKC =60°,所以∠BAC =∠BKC =60°. 故tan(2BAC∠)= tan30°.3.将正奇数的集合{1, 3, 5, 7, …}从小到大按第n 组2n −1个数进行分组:{1},{3, 5, 7},{9, 11, 13, 15, 17},…,数2017位于第k 组中,则k 为 (A )31. (B )32. (C )33. (D )34. 答:B.解:数2017是数列a n = 2n −1的第1009项.设2017位于第k 组,则1+3+5+…+(2k −1)≥1009,且1+3+5+…+(2k −3)<1009.即k 是不等式组221009(1)1009k k ⎧≥⎨-<⎩的正整数解,解得k =32,所以2017在第32组中. 4.如图,平面直角坐标系x -O -y 中,A , B 是函数y =1x在第I 象限的图象上两点,满足∠OAB =90°且AO = AB ,则等腰直角△OAB 的面积等于(A )12. (B )2. (C)2. (D)2.答:D .解:依题意,∠OAB =90°且AO = AB ,∠AOB =∠ABO =45°.过点A 做y 轴垂线交y 轴于点C ,过点B 做y 轴平行线,交直线CA 于点D .易见△COA ≌△DAB .设点A (a , 1a ),则点B (a +1a , 1a − a ).因为点B 在函数y =1x 的图象上,所以(a +1a )(1a− a )=1即21a− a 2=1. 因此S △ABC =12OA 2=12(21a + a 2) =122=. 5.已知f (x ) = x 5 + a 1x 4 + a 2x 3 + a 3x 2 + a 4x + a 5,且当m =1, 2, 3, 4时,f (m )=2017m ,则f (10)−f (−5)=(A )71655. (B )75156. (C )75615. (D )76515. 答:C .解:因为 当m =1, 2, 3, 4时,f (m )=2017m ,所以1, 2, 3, 4是方程f (x )−2017x =0的四个实根,由于5次多项式f (x )−2017x 有5个根,设第5个根为p ,则f (x )−2017x = (x −1)(x −2)(x −3)(x −4)(x −p )即 f (x ) = (x −1)(x −2)(x −3)(x −4)(x −p )+2017x .所以f (10)=9×8×7×6(10−p )+2017×10,f (−5)=−6×7×8×9(5+p )−2017×5,因此f (10)− f (−5)=15(9×8×7×6+2017)=75615.6.已知函数2||,,()42,.x x a f x x ax a x a ≤⎧=⎨-+>⎩若存在实数m ,使得关于x 的方程f (x )=m有四个不同的实根,则a 的取值范围是(A )17a >. (B )16a >. (C )15a >. (D )14a >.答:D .解:要使方程f (x )=m 有四个不同的实根,必须使得y =m 的图像与y =f (x )的图像有4个不同的交点.而直线与y =|x |的图像及二次函数的图像交点都是最多为两个,所以y =m 与函数y =|x |, x ≤a 的图像和y =x 2−4ax +2a , x >a 的图像的交点分别都是2个.而存在实数m ,使y =m 与y =|x |, x ≤a 的图像有两个交点,需要a >0,此时0<m ≤a ;又因为y =x 2−4ax +2a , x >a 顶点的纵坐标为242(4)4a a ⨯-,所以,要y =m 与y =x 2−4ax +2a ,x >a 的图像有两个交点,需要m >242(4)4a a ⨯-.因此y =m 的图像与y =f (x )的图像有4个不同的交点需要满足:0<m ≤a 且m >242(4)4a a ⨯-,解得14a >.二、填空题1. 用[x ]表示不超过x 的最大整数,设[99]S =++++,求的值.答:24.解:因为12≤1, 2, 3<22,所以12,因此1===,共3个1;同理,22≤4, 5, 6, 7, 8<32,因此,2=====,共5个2;又32≤9, 10, 11, 12, 13, 14, 15<42,因此=[15]3===,共7个3;依次类推,[23]4=====,共9个4;[34]5=====,共11个5;[47]6=====,共13个6;[62]7=====,共15个7;[79]8=====,共17个8;[98]9=====,共19个9.S= (++)+(++++)+…+([99]++)= 1×3+2×5+3×7+4×9+5×11+6×13+7×15+8×17+9×19=615. 因为242=576<615=S <625=252,即2425,所以,.2.确定(201721log 2017×201741log 2017×201781log 2017×2017161log 2017×2017321log 2017)15的值.答:8. 解:原式=(20172017log 2×20172017log 4×20172017log 8×20172017log 16×20172017log 32)15=(2×4×8×16×32)15= (21×22×23×24×25)15=(21+2+3+4+5)15=(215)15=23=8.3.已知△ABC 的边AB厘米,BCCA 厘米,求△ABC 的面积. 答:9.5平方厘米.解:注意到13=32+22,29=52+22,34=52+32,作边长为5厘米的正方形AMNP ,分成25个1平方厘米的正方形网格,如图.根据勾股定理,可知,AB厘米,BCCA 因此△ABC 的面积可求.△ABC 的面积=5×5−12×3×5−12×2×5−12×2×3=9.5(平方厘米).4. 设函数()f x =的最大值为M ,最小值为N ,试确定M +N的值.答:2.解:由已知得22)()11x x f x x ++=++因为)())(())]x x x x ++-=-- =22ln(()1())ln10x x -+--==,所以()))x x +-=-,NA MBP因此,)x是奇函数.进而可判定,函数()g x=为奇函数.则g(x)的最大值M1和最小值N1满足M1+N1= 0.因为M =M1+1,N = N1+1,所以M + N = 2.5.设A是数集{1, 2, …, 2017}的n元子集,且A中的任意两个数既不互质,又不存在整除关系,确定n的最大值.答:504.解:在数集{1, 2, …, 2017}中选取子集,使得子集中任意两个数不互质,最大的子集是偶数集{2, 4, …, 2016}共1008个元素,但其中,有的元素满足整除关系,由于1010的2倍是2020,所以集合A={1010, 1012, 1014, …, 2016}中,任意两个数既不互质,又不存在整除关系,A中恰有504个元素.事实上504是n的最大值.因为若从{1009, 1011, …, 2017}中任取一个奇数,会与A中的与它相邻的偶数互质;若从{1, 2, 3, …, 1008}中任取一数,则它的2倍在A中,存在整除关系.6.如图,以长为4厘米的线段AB的中点O为圆心、2厘米为半径画圆,交AB的中垂线于点E和F. 再分别以A、B为圆心,4厘米为半径画圆弧交射线AE于点C,交射线BE于点D. 再以E为圆心DE为半径画圆弧DC,求这4条实曲线弧连接成的“卵形”AFBCDA的面积.(圆周率用π表示,不取近似值)答:(12−)π−4平方厘米.解:半圆(O, 2)的面积=12π×22=2π.因为AO=OB=2,所以AB=AC=BD=4,AE=BE,ED=EC=4−.又∠AEB=∠CED=90°,∠EAB =∠EBA=45°,因此,扇形BAD的面积=扇形ACB的面积=18π×42=2π,△AEB的面积=12×4×2=4,直角扇形EDC的面积=14π(4−)2= 6π−π,卵形AFBCDA的面积 = 半圆(O, 2)的面积+扇形BAD的面积+扇形ACB的面积−△AEB的面积+直角扇形EDC的面积= 2π+2×2π−4+6π−π= (12−)π−4(平方厘米).BFADCEO7. 已知22()1005000x f x x x =-+,求f (1)+f (2)+…+f (100)的值.答:101.解:设g (x ) = x 2−100x +5000,则g (100−x ) = (100−x )2−100(100−x )+5000=1002−200x +x 2−1002+100x +5000= x 2−100x +5000= g (x ),即 g (k ) = g (100−k ).所以 f (k ) + f (100−k ) =22(100)()(100)k k g k g k -+- =22(100)()k k g k +-=2, 又 f (50) =2250=150100505000-⨯+, f (100)22100==2.1001001005000-⨯+ 所以, f (1)+ f (2)+…+ f (100)= (f (1)+ f (99))+ (f (2)+ f (98))+…+ (f (49)+ f (51))+ f (50)+ f (100) = 2×49+1+2=101.8.如图,在锐角△ABC 中,AC = BC = 10,D 是边AB 上一点,△ACD 的内切圆和△BCD 的与BD 边相切的旁切圆的半径都等于2,求AB 的长.答:解:线段AB 被两圆与AB 的切点及点D 分成四段,由于两圆半径相等,再根据切线长定理,可知中间两段相等,于是可将这四段线段长度分别记为a , b , b , c ,由于圆O 2的切线长CE = CG ,所以BC +a = CD +b = (AC −c +b )+b ,而AC = BC ,所以a +c = 2b .由等角关系可得△AO 1F ∽△O 2BE ,得12OF B E A F OE =,即22ac =,由此推出ac = 4. 分别计算△BCD 和△ACD 的面积: 12(),2BCD S BC CD BD ∆=⨯+-12()2ACD S AC CD AD ∆=⨯++ 所以24ACD BCD S S AD BD AB a c b b ∆∆-=+==++=. ①又设由C 引向AB 的高为h ,可得1()2ACD BCD S S c a h ∆∆-=-=②由①、②两式可得4b =将a +c = 2b ,ac = 4代入,化简得42251000b b -+=DA CBD A CB E G FO 1 O 2 · a b b c·解得b2=5或b2=20,即b b ,(负根舍).于是,AB = a+c+2b = 4b AB .若AB ,△ABC为钝角三角形,不合题设△ABC是锐角三角形的要求.所以AB的长为.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017高一数学竞赛试题
导读:我根据大家的需要整理了一份关于《2017高一数学竞赛试题》的内容,具体内容:在我们的学习生活中,考试试卷的练习是我们的重要学习方式,我们应该认真地对待每一份试卷!下面是有我为你整理的2017高一数学竞赛试题,希望能够帮助到你!一、选择题:(本大...
在我们的学习生活中,考试试卷的练习是我们的重要学习方式,我们应该认真地对待每一份试卷!下面是有我为你整理的2017高一数学竞赛试题,希望能够帮助到你!
一、选择题:(本大题共12小题,每题5分,共60分,在每小题给出的四个选项中,只有一个是符合题目要求的)
1.已知 , 为集合I的非空真子集,且 , 不相等,若,则
( )
A. B. C. D.
2.与直线的斜率相等,且过点(-4,3)的直线方程为 ()
A. = 32
B. =32
C. =32
D. =-32
3. 已知过点和的直线的斜率为1,则实数的值为 ( )
A.1
B.2
C.1或4
D.1或2
4. 已知圆锥的表面积为6 ,且它的侧面展开图是一个半圆,则这个圆锥的底面半径为 ( )
A. B.2 C. D.
5. 在空间中,给出下面四个命题,则其中正确命题的个数为 ()
①过平面外的两点,有且只有一个平面与平面垂直;
②若平面内有不共线三点到平面的距离都相等,则∥;
③若直线l与平面内的无数条直线垂直,则l;
④两条异面直线在同一平面内的射影一定是两平行线;
A.3
B.2
C.1
D.0
6. 已知函数定义域是,则函数的定义域是 ( )
A. B. C. D.
7. 直线在同一坐标系中的图形大致是图中的 ( )
8. 设甲,乙两个圆柱的底面面积分别为,体积为,若它们的侧面积相等且,则的值是 ( )
A. B. C. D.
9.设函数,如果,则的取值范围是 ( )
A. 或
B.
C.
D. 或
10.已知函数没有零点,则实数的取值范围是 ()
A. B. C. D.
11.定义在R上的偶函数满足:对任意的,有 .则 ( )
A. B.
C. D.
12. 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各个面中,直角三角形的个数是 ( )
A.1
B.2
C.3
D.
第Ⅱ卷(非选择题,共90分)
二、填空题:(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)..
13.已知增函数,且,则的零点的个数为
14. 已知在定义域上是增函数,则的取值范围是
15. 直线恒过定点
16. 高为的四棱锥S-ABCD的底面是边长为1的正方形,点S、A、B、C、D均在半径为1的同一球面上,则底面ABCD的中心与顶点S之间的距离为
三、解答题(17题10,其余每题12分)
17.已知一个空间组合体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,请说出该组合体由哪些几何体组成,并且求出该组合体的表面积和体积
18.已知偶函数的定义域为 ,且在上是增函数,试比较与的大小。
19. 已知方程 + +6- =0( ).
(1)求该方程表示一条直线的条件;
(2)当为何实数时,方程表示的直线斜率不存在?求出这时的直线方程;
(3)已知方程表示的直线在轴上的截距为 -3,求实数的值;
20. 已知函数,判断函数的奇偶性,单调性,并且求出值域
21. 如图,长方体﹣中,,, ,点分别在上, .过点的平面与此长方体的面相交,交线围成一个正方形.
(1)在图中画出这个正方形(说明画法和理由)
(2)求平面把该长方体分成的两部分体积的比值.
22. 如图,三棱锥P-A BC中,平面PAC 平面ABC, ABC= ,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//面PBC.
(1)证明:EF// BC.
(2)证明:AB 平面PFE.
(3)若四棱锥P-DFBC的体积为7,求线段BC的长.
答案
一、ACACD,BCBDA,DB
13、1个 14、 15、(-2,3) 16、1
17、解:解:由一个半球和一个圆柱组成的...2分
表面积是: ...6分
体积是: ... 10分
18、解: ...5分
因为函数为偶函数,且在上是增函数,所以在是减函数...8分
所以 ...12分
19、解:解:(1)当x,y的系数不同时为零时,方程表示一条直线,令m2―2m―3=0,解得m=-1或m=3;
令2m2+m-1=0,解得m=-1或m= .
所以方程表示一条直线的条件是mR,且m-1....4分
(2)由(1)易知,当m= 时,方程表示的直线的斜率不存在,此时的方程为x= ,它表示一条垂直于轴的直线 (8)
(3)依题意,有 =-3,所以3m2-4m-15=0.所以m=3,或m=- ,由(1)知所求m=- ....12分
20、解:函数的定义域是,...2分
因为,所以函数是奇函数。
...4分,设,则
当时,,所以,所以在上是减函数;...8分
当时,,所以,所以在上也是减函数。
由,,所以或 ...12分
21、解:
(Ⅰ)交线围成的正方形EHGF如图:在面ABCD中做HG平行于BC,连接EH,FG且HB=GC=6,则E F平行且等于HG,所以四边形EFGH是平行四边形,EF平行于 ,所以EF垂直面 ,所以EF垂直于EH,且经过计算可知EH=FG=10,所以EFGH是正方形...6分
(Ⅱ)作EMAB,垂足为M,则AM= A1E=4,EB1=12,EM=AA1=8.
因为EHGF为正方形,所以EH=EF=BC=10.于是MH= .
因为长方体被平面分为两个高为10的直棱柱,
所以其体积的比值为 ( 也正确)...12分
22、(1)证明: EF//面PBC.EF 面ABC, 面PBC 面ABC=BC,
所以根据线面平行的性质可知EF// BC. ...4分
(2)由DE=EC,PD=PC可知:E为等腰 PDC中D C边的中点,
故PE AC,又平面PAC 平面ABC,
平面PAC 面ABC=AC,PE 平面PAC, PE AC,
所以PE 平面ABC,
所以PE AB,因为 ABC= ,EF// BC.所以AB EF
所以AB 面PEF...8分
(3)设BC= ,在直角三角形ABC中,AB= ,,EF// BC知 AFE相似于 ABC,所以
由AD= AE, ,
从而四边形DFBC的面积为,
由(2)可知PE是四棱锥P-DFBC的高,PE= ,
所以V=所以,所以或者,
所以BC=3或BC= ...12分。
