九年级数学正方形练习题(含答案)
中考数学复习----《正方形的性质》知识点总结与专项练习题(含答案解析)

中考数学复习----《正方形的性质》知识点总结与专项练习题(含答案解析)知识点总结1.正方形的定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形2.正方形的性质:①具有平行四边形的一切性质。
②具有矩形与菱形的一切性质。
所以正方形的四条边都相等,四个角都是直角。
对角线相互平分且相等,且垂直,且平分每一组对角,把正方形分成了四个全等的等腰直角三角形。
正方形既是中心对称图形,也是轴对称图形。
对角线交点是对称中心,对角线所在直线是对称轴,过每一组对边中点的直线也是对称轴。
练习题1.(2022•黄石)如图,正方形OABC的边长为,将正方形OABC绕原点O顺时针旋转45°,则点B的对应点B1的坐标为()A.(﹣2,0)B.(2,0)C.(0,2)D.(0,2)【分析】连接OB,由正方形的性质和勾股定理得OB=2,再由旋转的性质得B1在y轴正半轴上,且OB1=OB=2,即可得出结论.【解答】解:如图,连接OB,∵正方形OABC的边长为,∴OC=BC=,∠BCO=90°,∠BOC=45°,∴OB===2,∵将正方形OABC绕原点O顺时针旋转45°后点B旋转到B1的位置,∴B 1在y 轴正半轴上,且OB 1=OB =2,∴点B 1的坐标为(0,2),故选:D .2.(2022•广州)如图,正方形ABCD 的面积为3,点E 在边CD 上,且CE =1,∠ABE 的平分线交AD 于点F ,点M ,N 分别是BE ,BF 的中点,则MN 的长为( )A .26B .23C .2﹣3D .226− 【分析】连接EF ,由正方形ABCD 的面积为3,CE =1,可得DE =﹣1,tan ∠EBC ===,即得∠EBC =30°,又AF 平分∠ABE ,可得∠ABF =∠ABE =30°,故AF ==1,DF =AD ﹣AF =﹣1,可知EF =DE =×(﹣1)=﹣,而M ,N 分别是BE ,BF 的中点,即得MN =EF =. 【解答】解:连接EF ,如图:∵正方形ABCD 的面积为3,∴AB =BC =CD =AD =,∵CE =1,∴DE=﹣1,tan∠EBC===,∴∠EBC=30°,∴∠ABE=∠ABC﹣∠EBC=60°,∵AF平分∠ABE,∴∠ABF=∠ABE=30°,在Rt△ABF中,AF==1,∴DF=AD﹣AF=﹣1,∴DE=DF,△DEF是等腰直角三角形,∴EF=DE=×(﹣1)=﹣,∵M,N分别是BE,BF的中点,∴MN是△BEF的中位线,∴MN=EF=.故选:D.3.(2022•贵阳)如图,“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形.若图中的直角三角形的两条直角边的长分别为1和3,则中间小正方形的周长是()A.4B.8C.12D.16【分析】根据题意和题目中的数据,可以计算出小正方形的边长,然后即可得到小正方形的周长.【解答】解:由题意可得,小正方形的边长为3﹣1=2,∴小正方形的周长为2×4=8,故选:B.4.(2022•青岛)如图,O为正方形ABCD对角线AC的中点,△ACE为等边三角形.若AB=2,则OE 的长度为( )A .26B .6C .22D .23【分析】首先利用正方形的性质可以求出AC ,然后利用等边三角形的性质可求出OE .【解答】解:∵四边形ABCD 为正方形,AB =2,∴AC =2,∵O 为正方形ABCD 对角线AC 的中点,△ACE 为等边三角形,∴∠AOE =90°,∴AC =AE =2,AO =,∴OE =×=. 故选:B .5.(2022•泰州)如图,正方形ABCD 的边长为2,E 为与点D 不重合的动点,以DE 为一边作正方形DEFG .设DE =d 1,点F 、G 与点C 的距离分别为d 2、d 3,则d 1+d 2+d 3的最小值为( )A .2B .2C .22D .4【分析】连接AE ,那么,AE =CG ,所以这三个d 的和就是AE +EF +FC ,所以大于等于AC ,故当AEFC 四点共线有最小值,最后求解,即可求出答案.【解答】解:如图,连接AE ,∵四边形DEFG 是正方形,∴∠EDG =90°,EF =DE =DG ,∵四边形ABCD 是正方形,∴AD =CD ,∠ADC =90°,∴∠ADE =∠CDG ,∴△ADE ≌△CDG (SAS ),∴AE =CG ,∴d 1+d 2+d 3=EF +CF +AE ,∴点A ,E ,F ,C 在同一条线上时,EF +CF +AE 最小,即d 1+d 2+d 3最小,连接AC ,∴d 1+d 2+d 3最小值为AC ,在Rt △ABC 中,AC =AB =2,∴d 1+d 2+d 3最小=AC =2, 故选:C .6.(2022•黔东南州)如图,在边长为2的等边三角形ABC 的外侧作正方形ABED ,过点D 作DF ⊥BC ,垂足为F ,则DF 的长为( )A .23+2B .5﹣33C .3﹣3D .3+1【分析】方法一:如图,延长DA 、BC 交于点G ,利用正方形性质和等边三角形性质可得:∠BAG =90°,AB =2,∠ABC =60°,运用解直角三角形可得AG =2,DG =2+2,再求得∠G =30°,根据直角三角形性质得出答案.方法二:过点E 作EG ⊥DF 于点G ,作EH ⊥BC 于点H ,利用解直角三角形可得EH =1,BH =,再证明△BEH ≌△DEG ,可得DG =BH =,即可求得答案.【解答】解:方法一:如图,延长DA、BC交于点G,∵四边形ABED是正方形,∴∠BAD=90°,AD=AB,∴∠BAG=180°﹣90°=90°,∵△ABC是边长为2的等边三角形,∴AB=2,∠ABC=60°,∴AG=AB•tan∠ABC=2×tan60°=2,∴DG=AD+AG=2+2,∵∠G=90°﹣60°=30°,DF⊥BC,∴DF=DG=×(2+2)=1+,故选D.方法二:如图,过点E作EG⊥DF于点G,作EH⊥BC于点H,则∠BHE=∠DGE=90°,∵△ABC是边长为2的等边三角形,∴AB=2,∠ABC=60°,∵四边形ABED是正方形,∴BE=DE=2,∠ABE=∠BED=90°,∴∠EBH=180°﹣∠ABC﹣∠ABE=180°﹣60°﹣90°=30°,∴EH=BE•sin∠EBH=2•sin30°=2×=1,BH=BE•cos∠EBH=2cos30°=,∵EG⊥DF,EH⊥BC,DF⊥BC,∴∠EGF=∠EHB=∠DFH=90°,∴四边形EGFH是矩形,∴FG=EH=1,∠BEH+∠BEG=∠GEH=90°,∵∠DEG+∠BEG=90°,∴∠BEH=∠DEG,在△BEH和△DEG中,,∴△BEH≌△DEG(AAS),∴DG=BH=,∴DF=DG+FG=+1,故选:D.7.(2022•随州)七巧板是一种古老的中国传统智力玩具,如图,在正方形纸板ABCD中,BD为对角线,E,F分别为BC,CD的中点,AP⊥EF分别交BD,EF于O,P两点,M,N分别为BO,DO的中点,连接MP,NF,沿图中实线剪开即可得到一副七巧板.则在剪开之前,关于该图形,下列说法正确的有()①图中的三角形都是等腰直角三角形;②四边形MPEB是菱形;③四边形PFDM的面积占正方形ABCD面积的.A.只有①B.①②C.①③D.②③【分析】①利用正方形的性质和中位线的性质可以解决问题;②利用①的结论可以证明OM≠MP解决问题;③如图,过M作MG⊥BC于G,设AB=BC=x,利用正方形的性质与中位线的性质分别求出BE和MG即可判定是否正确.【解答】解:①如图,∵E,F分别为BC,CD的中点,∴EF为△CBD的中位线,∴EF∥BD,∵AP⊥EF,∴AP⊥BD,∵四边形ABCD为正方形,∴A、O、P、C在同一条直线上,∴△ABC、△ACD、△ABD、△BCD、△OAB、△OAD、△OBC、△OCD、△EFC都是等腰直角三角形,∵M,N分别为BO,DO的中点,∴MP∥BC,NF∥OC,∴△DNF、△OMP也是等腰直角三角形.故①正确;②根据①得OM=BM=PM,∴BM≠PM∴四边形MPEB不可能是菱形.故②错误;③∵E,F分别为BC,CD的中点,∴EF∥BD,EF=BD,∵四边形ABCD是正方形,且设AB=BC=x,∴BD=x,∵AP⊥EF,∴AP⊥BD,∴BO=OD,∴点P在AC上,∴PE=EF,∴PE=BM,∴四边形BMPE是平行四边形,∴BO=BD,∵M为BO的中点,∴BM=BD=x,∵E为BC的中点,∴BE=BC=x,过M作MG⊥BC于G,∴MG=BM=x,∴四边形BMPE的面积=BE•MG=x2,∴四边形BMPE的面积占正方形ABCD面积的.∵E、F是BC,CD的中点,∴S△CEF=S△CBD=S四边形ABCD,∴四边形PFDM的面积占正方形ABCD面积的(1﹣﹣﹣)=.故③正确.故选:C.8.(2022•宁波)将两张全等的矩形纸片和另两张全等的正方形纸片按如图方式不重叠地放置在矩形ABCD内,其中矩形纸片和正方形纸片的周长相等.若知道图中阴影部分的面积,则一定能求出()A.正方形纸片的面积B.四边形EFGH的面积C.△BEF的面积D.△AEH的面积【分析】根据题意设PD=x,GH=y,则PH=x﹣y,根据矩形纸片和正方形纸片的周长相等,可得AP=x+y,先用面积差表示图中阴影部分的面积,并化简,再用字母分别表示出图形四个选项的面积,可得出正确的选项.【解答】解:设PD=x,GH=y,则PH=x﹣y,∵矩形纸片和正方形纸片的周长相等,∴2AP+2(x﹣y)=4x,∴AP=x+y,∵图中阴影部分的面积=S矩形ABCD﹣2△ADH﹣2S△AEB=(2x+y)(2x﹣y)﹣2ו(x﹣y)(2x+y)﹣2ו(2x﹣y)•x=4x2﹣y2﹣(2x2+xy﹣2xy﹣y2)﹣(2x2﹣xy)=4x2﹣y2﹣2x2+xy+y2﹣2x2+xy=2xy,A、正方形纸片的面积=x2,故A不符合题意;B、四边形EFGH的面积=y2,故B不符合题意;C、△BEF的面积=•EF•BQ=xy,故C符合题意;D、△AEH的面积=•EH•AM=y(x﹣y)=xy﹣y2,故D不符合题意;故选:C.9.(2022•重庆)如图,在正方形ABCD中,AE平分∠BAC交BC于点E,点F是边AB上一点,连接DF,若BE=AF,则∠CDF的度数为()A.45°B.60°C.67.5°D.77.5°【分析】根据正方形的性质和全等三角形的判定和性质,可以得到∠ADF的度数,从而可以求得∠CDF的度数.【解答】解:∵四边形ABCD是正方形,∴AD=BA,∠DAF=∠ABE=90°,在△DAF和△ABE中,,△DAF≌△ABE(SAS),∠ADF=∠BAE,∵AE平分∠BAC,四边形ABCD是正方形,∴∠BAE=∠BAC=22.5°,∠ADC=90°,∴∠ADF=22.5°,∴∠CDF=∠ADC﹣∠ADF=90°﹣22.5°=67.5°,故选:C.10.(2022•重庆)如图,在正方形ABCD中,对角线AC、BD相交于点O.E、F分别为AC、BD上一点,且OE=OF,连接AF,BE,EF.若∠AFE=25°,则∠CBE的度数为()A.50°B.55°C.65°D.70°【分析】利用正方形的对角线互相垂直平分且相等,等腰直角三角形的性质,三角形的内角和定理和全等三角形的判定与性质解答即可.【解答】解:∵四边形ABCD是正方形,∴∠AOB=∠AOD=90°,OA=OB=OD=OC.∵OE=OF,∴△OEF为等腰直角三角形,∴∠OEF=∠OFE=45°,∵∠AFE=25°,∴∠AFO=∠AFE+∠OFE=70°,∴∠F AO=20°.在△AOF和△BOE中,,∴△AOF ≌△BOE (SAS ).∴∠F AO =∠EBO =20°,∵OB =OC ,∴△OBC 是等腰直角三角形,∴∠OBC =∠OCB =45°,∴∠CBE =∠EBO +∠OBC =65°.故选:C .11.(2022•益阳)如图,将边长为3的正方形ABCD 沿其对角线AC 平移,使A 的对应点A ′满足AA ′=31AC ,则所得正方形与原正方形重叠部分的面积是 .【分析】由正方形边长为3,可求AC =3,则AA ′=AC =,由平移可得重叠部分是正方形,根据正方形的面积公式可求重叠部分面积.【解答】解:∵正方形ABCD 的边长为3,∴AC =3,∴AA ′=AC =, ∴A ′C =2,由题意可得重叠部分是正方形,且边长为2,∴S 重叠部分=4.故答案为:4.12.(2022•海南)如图,正方形ABCD 中,点E 、F 分别在边BC 、CD 上,AE =AF ,∠EAF =30°,则∠AEB = °;若△AEF 的面积等于1,则AB 的值是 .【分析】利用“HL”先说明△ABE与△ADF全等,得结论∠BAE=∠DAF,再利用角的和差关系及三角形的内角和定理求出∠AEB;先利用三角形的面积求出AE,再利用直角三角形的边角间关系求出AB.【解答】解:∵四边形ABCD是正方形,∴AB=AD,∠BAD=∠B=∠D=90°.在Rt△ABE和Rt△ADF中,,∴Rt△ABE≌Rt△ADF(HL).∴∠BAE=∠DAF.∴∠BAE=(∠BAD﹣∠EAF)=(90°﹣30°)=30°.∴∠AEB=60°.故答案为:60.过点F作FG⊥AE,垂足为G.∵sin∠EAF=,∴FG=sin∠EAF×AF.∵S△AEF=×AE×FG=×AE×AF×sin∠EAF=1,∴×AE2×sin30°=1.即×AE2×=1.∴AE=2.在Rt△ABE中,∵cos∠BAE=,∴AB=cos30°×AE=×2=.故答案为:.13.(2022•广西)如图,在正方形ABCD中,AB=42,对角线AC,BD相交于点O.点E是对角线AC上一点,连接BE,过点E作EF⊥BE,分别交CD,BD于点F,G,连接BF,交AC于点H,将△EFH沿EF翻折,点H的对应点H′恰好落在BD上,得到△EFH′.若点F为CD的中点,则△EGH′的周长是.【分析】作辅助线,构建全等三角形,先根据翻折的性质得△EGH'≌△EGH,所以△EGH′的周长=△EGH的周长,接下来计算△EGH的三边即可;证明△BME≌△FNE(ASA)和△BEO≌△EFP(AAS),得OE=PF=2,OB=EP=4,利用三角函数和勾股定理分别计算EG,GH和EH的长,相加可得结论.【解答】解:如图,过点E作EM⊥BC于M,作EN⊥CD于N,过点F作FP⊥AC于P,连接GH,∵将△EFH沿EF翻折得到△EFH′,∴△EGH'≌△EGH,∵四边形ABCD是正方形,∴AB=CD=BC=4,∠BCD=90°,∠ACD=∠ACB=45°,∴BD=BC=8,△CPF是等腰直角三角形,∵F是CD的中点,∴CF=CD=2,∴CP=PF=2,OB=BD=4,∵∠ACD=∠ACB,EM⊥BC,EN⊥CD,∴EM=EN,∠EMC=∠ENC=∠BCD=90°,∴∠MEN=90°,∵EF⊥BE,∴∠BEF=90°,∴∠BEM=∠FEN,∵∠BME=∠FNE,∴△BME≌△FNE(ASA),∴EB=EF,∵∠BEO+∠PEF=∠PEF+∠EFP=90°,∴∠BEO=∠EFP,∵∠BOE=∠EPF=90°,∴△BEO≌△EFP(AAS),∴OE=PF=2,OB=EP=4,∵tan∠OEG==,即=,∴OG=1,∴EG==,∵OB∥FP,∴∠OBH=∠PFH,∴tan∠OBH=tan∠PFH,∴=,∴==2,∴OH=2PH,∵OP=OC﹣PC=4﹣2=2,∴OH=×2=,在Rt△OGH中,由勾股定理得:GH==,∴△EGH′的周长=△EGH的周长=EH+EG+GH=2+++=5+.故答案为:5+.14.(2022•无锡)如图,正方形ABCD的边长为8,点E是CD的中点,HG垂直平分AE 且分别交AE、BC于点H、G,则BG=.【分析】设CG=x,则BG=8﹣x,根据勾股定理可得AB2+BG2=CE2+CG2,可求得x 的值,进而求出BG的长.【解答】解:连接AG,EG,∵E是CD的中点,∴DE=CE=4,设CG=x,则BG=8﹣x,在Rt△ABG和Rt△GCE中,根据勾股定理,得AB2+BG2=CE2+CG2,即82+(8﹣x)2=42+x2,解得x=7,∴BG=BC﹣CG=8﹣7=1.故答案是:1.15.(2022•江西)沐沐用七巧板拼了一个对角线长为2的正方形,再用这副七巧板拼成一个长方形(如图所示),则长方形的对角线长为.【分析】根据图形可得长方形的长是正方形的对角线为2,长方形的宽是正方形对角线的一半为1,然后利用勾股定理即可解决问题.【解答】解:根据图形可知:长方形的长是正方形的对角线为2,长方形的宽是正方形对角线的一半为1,则长方形的对角线长==.故答案为:.。
北师大版九年级数学上册《1.3 正方形的性质与判定》 同步练习试题

1.3 正方形的性质与判定一.选择题1.下列说法错误的是()A.对角线互相垂直的平行四边形是矩形B.矩形的对角线相等C.对角线相等的菱形是正方形D.两组对边分别相等的四边形是平行四边形2.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E,若∠CBF=25°,则∠AED=()A.60°B.65°C.70°D.75°3.如图,两把完全一样的直尺叠放在﹣起,重合的部分构成一个四边形,给出以下四个论断:①这个四边形可能是正方形②这个四边形一定是菱形③这个四边形不可能是矩形④这个四边形一定是轴对称图形,其中正确的论断是()A.①②B.③④C.①②④D.①②③④4.如图,以△ABC的各边为边,在边BC的同侧分别作三个正方形ABDI,BCFE,ACHG,对于四边形ADEG的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是()A.若△ABC为任意三角形,则四边形ADEG是平行四边形B.若∠BAC=90°,则四边形ADEG是矩形C.若AC=AB,则四边形ADEG是菱形D.若∠BAC=135°且AC=AB,则四边形ADEG是正方形5.如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE与BF相交于O;下列结论:(1)AE=BF;(2)AE⊥BF;(3)AD=OE;(4)S△AOB=S四边形DEOF.其中正确的有()A.4个B.3个C.2个D.1个二.填空题6.如图,平面内直线l1∥l2∥l3∥l4,且相邻两条平行线间隔均为1,正方形ABCD四个顶点分别在四条平行线上,则正方形的面积为.7.如图,正方形ABCD的边长为5,AG=CH=4,BG=DH=3,连接GH,则线段GH的长为.8.如图,在边长为2的正方形ABCD中,点E、F分别是边AB,BC的中点,连接EC,FD,点G、H分别是EC,FD的中点,连接GH,则GH的长度为.9.如图,已知正方形ABCD的边长为7,点E,F分别在AD、DC上,AE=DF=3,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为.10.如图,四边形ABCD为正方形,AB为边向正方形外作等边三角形ABE、CE与DB相交于点F,则∠AFD=度.11.如图,在正方形ABCD的外侧,作等边三角形ABE,则∠DEB的度数为度.12.如图,若四边形ABCD是正方形,△CDE是等边三角形,则∠EAB的度数为.13.如图,四边形ABCD是一个正方形,E是BC延长线上的一点,且AC=EC,则∠DAE =.14.如图,已知正方形ABCD的边长为1,连接AC、BD,CE平分∠ACD交BD于点E,则DE=.15.已知:正方形ABCD中,对角线AC、BD相交于点O,∠DBC的平分线BF交CD于点E,交AC于点F,OF=1,则AB=.三.解答题16.如图,在△ABC中,AC=BC=6,∠ACB>90°,∠ABC的平分线交AC于点D,E是AB上点,且BE=BC,CF∥ED交BD于点F,连接EF,ED.(1)求证:四边形CDEF是菱形;(2)当∠ACB=度时,四边形CDEF是正方形,请给予证明;并求此时正方形的边长.17.已知:如图,菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.(1)求证:四边形ABCD是正方形.(2)E是OB上一点,DH⊥CE,垂足为H,DH与OC相交于点F,求证:OE=OF.18.如图,正方形ABCD中,AB=4,点E是对角线AC上的一点,连接DE.过点E作EF ⊥ED,交AB于点F,以DE、EF为邻边作矩形DEFG,连接AG.(1)求证:矩形DEFG是正方形;(2)求AG+AE的值;(3)若F恰为AB中点,连接DF交AC于点M,请直接写出ME的长.19.如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)求证:矩形DEFG是正方形;(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.20.如图,已知平行四边形ABCD中,对角线AC、BD交于点O,E是DB延长线上一点,且△ACE是等边三角形.(1)求证:四边形ABCD是菱形;(2)若∠AEB=2∠EAB,求证:四边形ABCD是正方形.21.以△ABC的各边,在边BC的同侧分别作三个正方形.他们分别是正方形ABDI,BCFE,ACHG,试探究:(1)如图中四边形ADEG是什么四边形?并说明理由.(2)当△ABC满足什么条件时,四边形ADEG是矩形?(3)当△ABC满足什么条件时,四边形ADEG是正方形?参考答案一.选择题1.解:对角线互相垂直的平行四边形是菱形,故选项A错误;矩形的对角线相等,故选项B正确;对角线相等的菱形是正方形,故选项C正确;两组对边分别相等的四边形是平行四边形,故选项D正确;故选:A.2.解:∵四边形ABCD是正方形,∴∠ABC=90°,BA=DA,∠BAE=∠DAE=45°.又AE=AE,∴△ABE≌△ADE(SAS).∴∠ADE=∠ABE=90°﹣25°=65°.∴∠AED=180°﹣45°﹣65°=70°.故选:C.3.解:过点D作DE⊥AB于E,DF⊥BC于F.∵两张长方形直尺的宽度相等,∴DE=DF,又∵平行四边形ABCD的面积=AB•DE=BC•DF,∴AB=BC,∴平行四边形ABCD为菱形.当∠DAB=90°时,这个四边形是正方形,∴这个四边形一定是轴对称图形,故选:C.4.解:A、∵四边形ABDI、四边形BCFE、四边形ACHG都是正方形,∴AC=AG,AB=BD,BC=BE,∠GAC=∠EBC=∠DBA=90°.∴∠ABC=∠EBD(同为∠EBA的余角).在△BDE和△BAC中,,∴△BDE≌△BAC(SAS),∴DE=AC=AG,∠BAC=∠BDE.∵AD是正方形ABDI的对角线,∴∠BDA=∠BAD=45°.∵∠EDA=∠BDE﹣∠BDA=∠BDE﹣45°,∠DAG=360°﹣∠GAC﹣∠BAC﹣∠BAD=360°﹣90°﹣∠BAC﹣45°=225°﹣∠BAC,∴∠EDA+∠DAG=∠BDE﹣45°+225°﹣∠BAC=180°,∴DE∥AG,∴四边形ADEG是平行四边形(一组对边平行且相等),正确,故本选项不符合题意;B、∵四边形ABDI和四边形ACHG是正方形,∴∠DAI=45°,∠GAC=90°,∵∠BAC=90°,∴∠DAG=360°﹣45°﹣90°﹣90°=135°,∵四边形ADEG是平行四边形,∴四边形ADEG不是矩形,错误,故本选项符合题意;C、∵四边形ADEG是平行四边形,∴若要四边形ADEG是菱形,则需AD=AG,即AD=AC.∵AD=AB,∴当AB=AD,即AB=AC时,四边形ADEG是菱形,正确,故本选项不符合题意;D、∵当∠BAC=135°时,∠DAG=360°﹣45°﹣90°﹣135°=90°,即平行四边形ADEG是平行四边形,∵当AB=AD,即AB=AC时,四边形ADEG是菱形,∴四边形ADEG是正方形,即当∠BAC=135°且AC=AB时,四边形ADEG是正方形,正确,故本选项不符合题意;故选:B.5.解:∵四边形ABCD是正方形,∴AB=AD,∠BAF=∠ADE=90°.∵CE=DF,∴AF=DE.在△ABF和△DAE中,,∴△ABF≌△DAE.∴AE=BF,故(1)正确.∵△ABF≌△DAE,∴∠AFB=∠AED.∵∠AED+∠DAE=90°,∴∠AFB+∠DAE=90°,∴∠AOF=90°,即AE⊥BF,故(2)正确.∵△ABF≌△DAE,∴S△ABF=S△ADE.∴S△AOB=S△ABF﹣S△AOF,S四边形DEOF=S△ADE﹣S△AOF,即∴S△AOB=S四边形DEOF.如图所示:过点E作EG⊥AB,则EG=AD.∵HE>OE,GE>HE,∴GE>OE.∴AD>OE,故(3)错误.故选:B.二.填空题6.解:过C点作EF⊥l2,交l1于E点,交l4于F点.∵l1∥l2∥l3∥l4,EF⊥l2,∴EF⊥l1,EF⊥l4,即∠CED=∠BFC=90°.∵ABCD为正方形,∴∠BCD=90°.∴∠DCE+∠BCF=90°.又∵∠DCE+∠CDE=90°,∴∠CDE=∠BCF.在△CDE和△BCF中,∴△CDE≌△BCF(AAS),∴BF=CE=2.∵CF=1,∴BC2=12+22=5,即正方形ABCD的面积为5.故答案为:5.7.解:如图,延长BG交CH于点E,在△ABG和△CDH中,,∴△ABG≌△CDH(SSS),∴∠1=∠5,∠2=∠6,∵AG=CH=4,BG=DH=3,AB=5,∴AG2+BG2=AB2,∴∠AGB=∠CHD=90°,∴∠1+∠2=90°,∠5+∠6=90°,又∵∠2+∠3=90°,∠4+∠5=90°,∴∠1=∠3=∠5,∠2=∠4=∠6,在△ABG和△BCE中,,∴△ABG≌△BCE(ASA),∴BE=AG=4,CE=BG=3,∠BEC=∠AGB=90°,∴GE=BE﹣BG=4﹣3=1,同理可得HE=1,在Rt△GHE中,GH===,故答案为:.8.解:连接CH并延长交AD于P,连接PE,∵四边形ABCD是正方形,∴∠A=90°,AD∥BC,AB=AD=BC=2,∵E,F分别是边AB,BC的中点,∴AE=CF=×2=1,∵AD∥BC,∴∠DPH=∠FCH,∵∠DHP=∠FHC,∴△PDH≌△CFH(AAS),∴PD=CF=1,∴AP=AD﹣PD=1,∴PE==,∵点G,H分别是EC,FD的中点,∴GH=EP=.9.解:∵四边形ABCD是正方形,∴AB=DA,∠BAE=∠ADF=90°,在△BAE和△ADF中,,∴△BAE≌△ADF(SAS),∴∠ABE=∠DAF,∵∠ABE+∠BEA=90°,∴∠DAF+∠BEA=90°,∴∠AGE=90°,∴∠BGF=90°,∵点H为BF的中点,∴GH=BF,又∵BC=CD=7,DF=3,∠C=90°,∴CF=4,∴BF===,∴GH=,故答案为:.10.解:∵∠CBA=90°,∠ABE=60°,∴∠CBE=150°,∵四边形ABCD为正方形,三角形ABE为等边三角形∴∠BEC=15°,∵∠FBE=∠DBA+∠ABE=105°,∴∠BFE=60°,在△CBF和△ABF中,,∴△CBF≌△ABF(SAS),∴∠BAF=∠BCE=15°,又∠ABF=45°,且∠AFD为△AFB的外角,∴∠AFD=∠ABF+∠F AB=15°+45°=60°.故答案为60.11.解:∵四边形ABCD是正方形∴AB=AD,∠BAD=90°∵△ABE是等边三角形∴AE=AB,∠BAE=∠BEA=60°∴AD=AE,∠DAE=150°∴∠AED=∠ADE=(180°﹣∠DAE)=15°∴∠DEB=∠BEA﹣∠AED=60°﹣15°=45°故答案为:45.12.解:∵∠ADE=∠BCE=90°+60°=150°,AD=BC,DE=CE,∴△ADE≌△BCE,∴AE=BE,∴∠EAB=∠EBA.∵正方形中AD=DC,等边三角形中DC=DE,∴AD=DE,∵∠ADE=90°+60°=150°,∴∠DEA==15°,同理∠CEB=15°,∴∠AEB=60°﹣15°﹣15°=30°,∴∠EAB==75°.故答案为75°.13.解:∵四边形ABCD是正方形,∴∠ACB=45°,AD∥BC,∵AC=EC,∴∠E=∠CAE,∵∠ACB=∠E+∠CAE=2∠E,∴∠E=∠ACB=22.5°,∵AD∥BC,∴∠DAE=∠E=22.5°.故答案为:22.5°.14.解:过E作EF⊥DC于F,∵四边形ABCD是正方形,∴AC⊥BD,∵CE平分∠ACD交BD于点E,∴EO=EF,在Rt△COE和Rt△CFE中,∴Rt△COE≌Rt△CFE(HL),∴CO=FC,∵正方形ABCD的边长为1,∴AC=,∴CO=AC=,∴CF=CO=,∴EF=DF=DC﹣CF=1﹣,∴DE==﹣1,另法:因为四边形ABCD是正方形,∴∠ACB=45°=∠DBC=∠DAC,∵CE平分∠ACD交BD于点E,∴∠ACE=∠DCE=22.5°,∴∠BCE=45°+22.5°=67.5°,∵∠CBE=45°,∴∠BEC=67.5°,∴BE=BC,∵正方形ABCD的边长为1,∴BC=1,∴BE=1,∵正方形ABCD的边长为1,∴AC=,∴DE=﹣1,故答案为:﹣1.15.解:如图作FH∥BC交BD于点H.∵四边形ABCD是正方形,∴∠OBC=∠OCB=45°,OB=OC,∠BOC=90°∵FH∥BC,∴∠OHF=∠OBC,∠OFH=∠OCB,∴∠OHF=∠OFH,∴OH=OF=1,FH==,∵BF平分∠OBC,∴∠HBF=∠FBC=∠BFH,∴BH=FH=,∴OB=OC=1+,∴BC=OB=2+.故答案为2+.三.解答题16.证明:(1)如图,连接EC,交BD于点O∵BE=BC,BD平分∠ABC∴EO=CO,BD⊥CE∴EF=FC,DE=CD,∵CF∥DE∴∠DFC=∠FDE,且EO=CO,∠FOC=∠DOE ∴△DOE≌△FOC(AAS)∴DE=CF∴EF=FC=CD=DE∴四边形EFCD是菱形(2)当∠ACB=120度时,四边形CDEF是正方形,理由如下:∵∠ACB=120°,BC=AC∴∠ABC=∠BAC=30°∵BD平分∠ABC∴∠DBC=15°,且BD⊥EC∴∠BCO=75°∴∠ACE=45°,∵四边形EFCD是菱形∴∠FCD=2∠ACE=90°∴四边形CDEF是正方形,∴∠ADE=90°如图,过点C作CP⊥AB于点P,∵BC=AC=6,∠ABC=30°,CP⊥AB∴CP=3,BP=CP=3,AB=2BP=6,∴AE=AB﹣BE=6﹣6∵∠A=30°,∠ADE=90°∴DE=AE=3﹣317.(1)证明:∵四边形ABCD是菱形,∴AD∥BC,∠BAD=2∠DAC,∠ABC=2∠DBC,∴∠BAD+∠ABC=180°,∵∠CAD=∠DBC,∴∠BAD=∠ABC,∴2∠BAD=180°,∴∠BAD=90°,∴四边形ABCD是正方形;(2)证明:∵四边形ABCD是正方形,∴AC⊥BD,AC=BD,CO=AC,DO=BD,∴∠COB=∠DOC=90°,CO=DO,∵DH⊥CE,垂足为H,∴∠DHE=90°,∠EDH+∠DEH=90°,∵∠ECO+∠DEH=90°,∴∠ECO=∠EDH,在△ECO和△FDO中,,∴△ECO≌△FDO(ASA),∴OE=OF.18.解:(1)如图,作EM⊥AD于M,EN⊥AB于N.∵四边形ABCD是正方形,∴∠EAD=∠EAB,∵EM⊥AD于M,EN⊥AB于N,∴EM=EN,∵∠EMA=∠ENA=∠DAB=90°,∴四边形ANEM是矩形,∵EF⊥DE,∴∠MEN=∠DEF=90°,∴∠DEM=∠FEN,∵∠EMD=∠ENF=90°,∴△EMD≌△ENF,∴ED=EF,∵四边形DEFG是矩形,∴四边形DEFG是正方形.(2)∵四边形DEFG是正方形,四边形ABCD是正方形,∴DG=DE,DC=DA=AB=4,∠GDE=∠ADC=90°,∴∠ADG=∠CDE,∴△ADG≌△CDE(SAS),∴AG=CE,∴AE+AG=AE+EC=AC=AD=4.(3)如图,作EH⊥DF于H.∵四边形ABCD是正方形,∴AB=AD=4,AB∥CD,∵F是AB中点,∴AF=FB∴DF==2,∵△DEF是等腰直角三角形,EH⊥AD,∴DH=HF,∴EH=DF=,∵AF∥CD,∴AF:CD=FM:MD=1:2,∴FM=,∴HM=HF﹣FM=,在Rt△EHM中,EM==.19.解:(1)如图,作EM⊥BC于M,EN⊥CD于N,∴∠MEN=90°,∵点E是正方形ABCD对角线上的点,∴EM=EN,∵∠DEF=90°,∴∠DEN=∠MEF,∵∠DNE=∠FME=90°,在△DEN和△FEM中,,∴△DEN≌△FEM(ASA),∴EF=DE,∵四边形DEFG是矩形,∴矩形DEFG是正方形;(2)CE+CG的值是定值,定值为6,理由如下:∵正方形DEFG和正方形ABCD,∴DE=DG,AD=DC,∵∠CDG+∠CDE=∠ADE+∠CDE=90°,∴∠CDG=∠ADE,在∴△ADE和△CDG中,,∴△ADE≌△CDG(SAS),∴AE=CG,∴CE+CG=CE+AE=AC=AB=×3=6是定值.20.证明:(1)∵四边形ABCD是平行四边形,∴AO=CO.∵△ACE是等边三角形,∴AE=CE.∴BE⊥AC.∴四边形ABCD是菱形.(2)从上易得:△AOE是直角三角形,∴∠AEB+∠EAO=90°∵△ACE是等边三角形,∴∠EAO=60°,∴∠AEB=30°∵∠AEB=2∠EAB,∴∠EAB=15°,∴∠BAO=∠EAO﹣∠EAB=60°﹣15°=45°.又∵四边形ABCD是菱形.∴∠BAD=2∠BAO=90°∴四边形ABCD是正方形.21.解:(1)图中四边形ADEG是平行四边形.理由如下:∵四边形ABDI、四边形BCFE、四边形ACHG都是正方形,∴AC=AG,AB=BD,BC=BE,∠GAC=∠EBC=∠DBA=90°.∴∠ABC=∠EBD(同为∠EBA的余角).在△BDE和△BAC中,,∴△BDE≌△BAC(SAS),∴DE=AC=AG,∠BAC=∠BDE.∵AD是正方形ABDI的对角线,∴∠BDA=∠BAD=45°.∵∠EDA=∠BDE﹣∠BDA=∠BDE﹣45°,∠DAG=360°﹣∠GAC﹣∠BAC﹣∠BAD=360°﹣90°﹣∠BAC﹣45°=225°﹣∠BAC∴∠EDA+∠DAG=∠BDE﹣45°+225°﹣∠BAC=180°∴DE∥AG,∴四边形ADEG是平行四边形(一组对边平行且相等).(2)当四边形ADEG是矩形时,∠DAG=90°.则∠BAC=360°﹣∠BAD﹣∠DAG﹣∠GAC=360°﹣45°﹣90°﹣90°=135°,即当∠BAC=135°时,平行四边形ADEG是矩形;(3)当四边形ADEG是正方形时,∠DAG=90°,且AG=AD.由(2)知,当∠DAG=90°时,∠BAC=135°.∵四边形ABDI是正方形,∴AD=AB.又∵四边形ACHG是正方形,∴AC=AG,∴AC=AB.∴当∠BAC=135°且AC=AB时,四边形ADEG是正方形.。
2021年九年级数学中考一轮复习正方形的判定与性质中考真题演练2(附答案)

2021年九年级数学中考一轮复习正方形的判定与性质中考真题演练2(附答案)1.已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.(1)当∠MAN绕点A旋转到BM=DN时(如图1),请你直接写出BM、DN和MN的数量关系:__________.(2)当∠MAN绕点A旋转到BM≠DN时(如图2),(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)当∠MAN绕点A旋转到如图3的位置时,线段BM、DN和MN之间又有怎样的数量关系?请写出直接写出结论.2.如图,正方形ABCD,G是BC边上任意一点(不与B、C重合),DE⊥AG于点E,BF ∥DE,且交AG于点F.(1)求证:AF﹣BF=EF;(2)四边形BFDE是否可能是平行四边形,如果可能,请指出此时点G的位置,如不可能,请说明理由.3.已知:如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F分别是边BC,CD上的点,且∠EOF=90°.求证:CE=DF.4.如图,已知正方形ABCD的边长为1,正方形CEFG的面积为S1,点E在DC边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为S2,且S1=S2.(1)求线段CE的长;(2)若点H为BC边的中点,连接HD,求证:HD=HG.5.如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.(1)求证:平行四边形ABCD是矩形;(2)请添加一个条件使矩形ABCD为正方形.6.如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F.(1)求证:四边形CDOF是矩形;(2)当∠AOC多少度时,四边形CDOF是正方形?并说明理由.7.如图,在△ABC中,点D是边BC的中点,DE⊥AC、DF⊥AB,垂足分别是E、F,且BF=CE.(1)求证:DE=DF;(2)当∠A=90°时,试判断四边形AFDE是怎样的四边形,并证明你的结论.8.如图,已知四边形ABCD为正方形,AB=22,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.①求证:矩形DEFG是正方形;②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.9.如图(1),已知四边形ABCD的四条边相等,四个内角都等于90°,点E是CD边上一点,F是BC边上一点,且∠EAF=45°.(1)求证:BF+DE=EF;(2)若AB=6,设BF=x,DE=y,求y关于x的函数解析式,并写出x的取值范围;(3)过点A作AH⊥FE于点H,如图(2),当FH=2,EH=1时,求△AFE的面积.10.取一张正方形的纸片进行折叠,具体操作过程如下:第一步:如图1,先把正方形ABCD对折,折痕为MN.第二步:点G在线段 MD上,将△GCD沿GC翻折,点D恰好落在MN上,记为点P,连接BP.(1)判断△PBC的形状,并说明理由;(2)作点C关于直线AP的对称点C′,连接PC′、DC′.①在图2中补全图形,并求出∠APC′的度数;②猜想∠PC′D的度数,并加以证明;(温馨提示:当你遇到困难时,不妨连接AC′、CC′,研究图形中特殊的三角形)11.问题提出(1)如图1,将直角三角板的直角顶点P放在正方形ABCD的对角线AC上,一条直角边经过点B,另一条直角边交边DC于点E,线段PB和线段PE相等吗?请证明;问题探究(2)如图2,移动三角板,使三角板的直角顶点P在对角线AC上,一条直角边经过点B,另一条直角边交DC的延长线于点E,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由;问题解决(3)继续移动三角板,使三角板的直角顶点P在对角线AC上,一条直角边经过点B,另一条直角边交DC的延长线于点E,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.12.综合与实践问题情境:在数学活动课上,老师出示了这样一个问题:如图1,在矩形ABCD 中,AD=2AB ,E 是AB 延长线上一点,且BE=AB ,连接DE ,交BC 于点M ,以DE 为一边在DE 的左下方作正方形DEFG ,连接AM .试判断线段AM 与DE 的位置关系.探究展示:勤奋小组发现,AM 垂直平分DE ,并展示了如下的证明方法:证明:∵BE=AB ,∴AE=2AB .∵AD=2AB ,∴AD=AE .∵四边形ABCD 是矩形,∴AD ∥BC . ∴EM EB DM AB=.(依据1) ∵BE=AB ,∴1EM DM =.∴EM=DM . 即AM 是△ADE 的DE 边上的中线,又∵AD=AE ,∴AM ⊥DE .(依据2)∴AM 垂直平分DE .反思交流:(1)①上述证明过程中的“依据1”“依据2”分别是指什么?②试判断图1中的点A 是否在线段GF 的垂直平分线上,请直接回答,不必证明; (2)创新小组受到勤奋小组的启发,继续进行探究,如图2,连接CE ,以CE 为一边在CE 的左下方作正方形CEFG ,发现点G 在线段BC 的垂直平分线上,请你给出证明;探索发现:(3)如图3,连接CE ,以CE 为一边在CE 的右上方作正方形CEFG ,可以发现点C ,点B 都在线段AE 的垂直平分线上,除此之外,请观察矩形ABCD 和正方形CEFG 的顶点与边,你还能发现哪个顶点在哪条边的垂直平分线上,请写出一个你发现的结论,并加以证明.参考答案1.解:(1)BM+DN=MN.理由如下:如图4,把△AND绕点A顺时针旋转90°得到△ABF,则由题意可得:点C、B、F三点共线,∴由旋转的性质可得:BF=DN,AF=AN,∠BAF=∠DAN,∵∠BAD=90°,∠MAN=45°,∴∠BAM+∠DAN=45°,∴∠BAF+∠BAM=45°=∠MAF=∠MAN,又∵AM=AM,∴△AMF≌△AMN,∴MF=MN,又∵MF=BM+BF,BF=DN,∴MN=BM+DN;(2)成立,理由如下:如图5,把△ADN绕点A顺时针旋转90°,得到△ABE,则可得E、B、M三点共线.∴∠EAM=90°﹣∠NAM=90°﹣45°=45°,AE=AN,BE=DN,又∵∠NAM=45°,∴∠EAM=∠NAM,∴在△AEM与△ANM中,,∴ME=MN,∵ME=BE+BM=DN+BM,∴DN+BM=MN;(3)DN-BM=MN.理由如下:如图6,在DC上截取DE=BM,连接AE,∵∠ADE=∠ABM=90°,AD=AB,∴△ADE≌△ABM,∴AE=AM,∠DAE=∠BAM,∵∠BAM+∠BAN=∠MAN=45°,∴∠DAE+∠BAN=45°,∴∠EAN=90°-∠DAE-∠BAN=45°=∠MAN,又∵AN=AN,∴△EAN≌△MAN,∴EN=MN,又∵DN-DE=EN,∴DN-BM=MN.2.解:(1)证明:∵四边形ABCD是正方形,∴AB=AD,∠BAF+∠DAE=90°,∵DE⊥AG,∴∠DAE+∠ADE=90°,∴∠ADE=∠BAF,又∵BF∥DE,∴∠BFA=90°=∠AED,∴AE=BF,∴AF﹣BF=AF﹣AE=EF;(2)不可能,理由是:如图,若要四边形BFDE是平行四边形,已知DE∥BF,则当DE=BF时,四边形BFDE为平行四边形,∵DE=AF,∴BF=AF,即此时∠BAF=45°,而点G不与B和C重合,∴∠BAF≠45°,矛盾,∴四边形BFDE不可能是平行四边形.3.证明:∵四边形ABCD为正方形,∴OD=OC,∠ODF=∠OCE=45°,∠COD=90°,∴∠DOF+∠COF=90°,∵∠EOF=90°,即∠COE+∠COF=90°,∴∠COE=∠DOF,∴△COE≌△DOF(ASA),∴CE=DF.4.解:(1)设正方形CEFG的边长为a,∵正方形ABCD的边长为1,∴DE=1﹣a,∵S1=S2,∴a2=1×(1﹣a),解得,(舍去),,即线段CE的长是;(2)证明:∵点H为BC边的中点,BC=1,∴CH=0.5,∴DH==,∵CH=0.5,CG=,∴HG=,∴HD=HG.5.(1)证明:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵∠OBC=∠OCB,∴OB=OC,∴AC=BD,∴平行四边形ABCD是矩形;(2)解:AB=AD(或AC⊥BD答案不唯一).理由:∵四边形ABCD是矩形,又∵AB=AD,∴四边形ABCD是正方形.或:∵四边形ABCD是矩形,又∵AC⊥BD,∴四边形ABCD是正方形.6.(1)证明:∵OD平分∠AOC,OF平分∠COB(已知),∴∠AOC=2∠COD,∠COB=2∠COF,∵∠AOC+∠BOC=180°,∴2∠COD+2∠COF=180°,∴∠COD+∠COF=90°,∴∠DOF=90°;∵OA=OC,OD平分∠AOC(已知),∴OD⊥AC,AD=DC(等腰三角形的“三合一”的性质),∴∠CDO=90°,∵CF⊥OF,∴∠CFO=90°∴四边形CDOF是矩形;(2)当∠AOC=90°时,四边形CDOF是正方形;理由如下:∵∠AOC=90°,AD=DC,∴OD=DC;又由(1)知四边形CDOF是矩形,则四边形CDOF是正方形;因此,当∠AOC=90°时,四边形CDOF是正方形.7.(1)证明:∵DE⊥AC,DF⊥AB,∴∠BFD=∠CED=90°,在Rt△BDF和Rt△CDE中,∵,∴Rt△BDF≌Rt△CDE(HL),∴DE=DF;(2)答:四边形AFDE是正方形.证明:∵∠A=90°,DE⊥AC,DF⊥AB,∴四边形AFDE是矩形,又∵Rt△BDF≌Rt△CDE,∴DF=DE,∴四边形AFDE是正方形.22.解:①过E作EM⊥BC于M点,过E作EN⊥CD于N点,如图所示:∵正方形ABCD,∴∠BCD=90°,∠ECN=45°,∴∠EMC=∠ENC=∠BCD=90°,且NE=NC,∴四边形EMCN为正方形.∵四边形DEFG是矩形,∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°,∴∠DEN=∠MEF,又∠DNE=∠FME=90°.在△DEN和△FEM中,∵∠DNE=∠FME,EN=EM,∠DEN=∠FEM,∴△DEN≌△FEM(ASA),∴ED=EF,∴矩形DEFG为正方形,②CE+CG的值为定值,理由如下:∵矩形DEFG为正方形,∴DE=DG,∠EDC+∠CDG=90°.∵四边形ABCD是正方形,∵AD=DC,∠ADE+∠EDC=90°,∴∠ADE=∠CDG.在△ADE和△CDG中,∵AD=CD,∠ADE=∠CDG,DE=DG,∴△ADE≌△CDG(SAS),∴AE=CG,∴AC=AE+CE=2AB=2×22=4,∴CE+CG=4 是定值.解:(1)如图1中,将△ADE绕点A顺时针旋转90°得到△ABH,∵四边形ABCD是正方形,∴AB=AD=CD=BC,∠BAD=90°,∵∠EAF=45°,∴∠BAF+∠BAH=∠BAF+∠DAE=45°,∴∠FAH=∠FAE=45°,∵AF=AF,AH=AE,∴△AFH≌△AFE(SAS),∴EF=FH,∵FH=BH+BF=DE+BF,∴EF=BF+DE;(2)∵AB=BC=CD=6,BF=x,DE=y,∴EF=x+y,FC=6=﹣x,EC=6﹣y,在Rt△ECF中,∵EF2=CF2+EC2,∴(x+y)2=(6﹣x)2+(6﹣y)2,∴y=3662+6xx(0≤x≤6);(3)如图2中,将△ADE绕点A顺时针旋转90°得到△ABM.由(1)可知△AFM≌△AFH,∵AB⊥FM,AH⊥EF,∴AB=AH,设AB=BC=CD=AD=x,∵∠ABF=∠AHF=90°,∵AF=AF.AB=AH,∴Rt△AFB≌Rt△AFH(HL),∴BF=FH=2,同理可证:DE=EH=1,∴CF=x﹣2,EC=x﹣1,在Rt△ECF中,∵EF2=CF2+EC2,∴32=(x﹣2)2+(x﹣1)2,∴x=317 +或317-(舍弃),∴S△AEF=12•EF•AH=12317+9317+8.解:(1)△PBC是等边三角形,理由如下:∵四边形ABCD是正方形,∴AB=BC=CD,∠ABC=90°,由折叠的性质得:BN=NC=12BC=12PC,MN⊥BC,∴PB=PC,∠PNC=90°,在Rt△PNC中,sin∠NPC=12NCPC=,∴∠NPC=30°,∴∠PCB=60°,∴△PBC是等边三角形;(2)①补全图形如图2所示:由①得:∠PCB=∠PBC=∠BPC=60°,PB=PC=BC,∵∠ABC=90°,∴∠ABP=90°﹣60°=30°,∵AB=BC,∴AB=PB,∴∠BAP=∠BPA=12(180°-∠PBC)=75°,∴∠APC=∠BPA+∠BPC=75°+60°=135°,∵C关于直线AP的对称点为C′,∴∠APC'=∠APC=135°;②连接AC',CC',如图3所示:由对称的性质得:AC=AC',∠CAP=∠C'AP=30°,∴∠CAC'=60°,∴△CAC'是等边三角形,∴AC'=CC',∠AC'C=60°,在△AC'D 和△CC'D 中,{AC CC AD CDC D C D=='=''', ∴△AC'D ≌△CC'D (SSS ),∴∠AC'D=∠CC'D=12∠AC'C=30°, ∵∠AC'P=∠ACP=15°,∴∠PC'D=15°.9.解:(1)如图1,过点P 作PM ⊥BC ,PN ⊥CD ,垂足分别为M ,N ,∵四边形ABCD 为正方形,∴∠BCD =90°,AC 平分∠BCD ,∵PM ⊥BC ,PN ⊥CD ,∴四边形PMCN 为正方形,PM =PN ,∵∠BPE =90°,∠BCD =90°,∴∠PBC +∠CEP =180°,而∠CEP +∠PEN =180°,∴∠PBM =∠PEN ,在△PBM 和△PEN 中, { PBM PEN PMB PNE PM PN∠=∠∠=∠= ∴△PBM ≌△PEN(AAS),∴PB =PE(2)如图2,PB =PE 还成立.理由如下:过点P 作PM ⊥BC ,PN ⊥CD ,垂足分别为M ,N ,∵四边形ABCD 为正方形,∴∠BCD =90°,AC 平分∠BCD ,∵PM ⊥BC ,PN ⊥CD ,∴四边形PMCN 为正方形,PM =PN ,∴∠MPN =90°,∵∠BPE =90°,∠BCD =90°,∴∠BPM +∠MPE =90°,而∠MPE +∠EPN =90°,∴∠BPM =∠EPN ,在△PBM 和△PEN 中, { PMB PNE PM PN BPM EPN∠=∠=∠=∠∴△PBM≌△PEN(ASA),∴PB=PE (3)如图3,PB=PE还成立.理由如下:过点P作PM⊥BC交BC 的延长线于点M,PN⊥CD的延长线于点N,∵四边形ABCD为正方形,∴∠BCD=90°,AC 平分∠BCD,∵PM⊥BC,PN⊥CD,∴四边形PMCN为正方形,PM=PN,∴∠MPN=90°,∵∠BPE=90°,∠BCD=90°,∴∠BPM+∠BPN=90°,而∠BPN+∠EPN=90°,∴∠BPM=∠EPN,在△PBM和△PEN中,{PMB PNEPM PNBPM EPN∠=∠=∠=∠∴△PBM≌△PEN(ASA),∴PB=PE12.解:由问题情景知,AM⊥DE,∵四边形DEFG是正方形,∴DE∥FG,∴点A在线段GF的垂直平分线上.(2)证明:过点G作GH⊥BC于点H,∵四边形ABCD是矩形,点E在AB的延长线上,∴∠CBE=∠ABC=∠GHC=90°,∴∠BCE+∠BEC=90°.∵四边形CEFG为正方形,∴CG=CE,∠GCE=90°,∴∠BCE+∠BCG=90°.∴∠2BEC=∠BCG.∴△GHC≌△CBE.∴HC=BE,∵四边形ABCD是矩形,∴AD=BC.∵AD=2AB,BE=AB,∴BC=2BE=2HC,∴HC=BH.∴GH垂直平分BC.∴点G在BC的垂直平分线上.(3)答:点F在BC边的垂直平分线上(或点F在AD边的垂直平分线上).过点F作FM⊥BC于点M,过点E作EN⊥FM于点N.∴∠BMN=∠ENM=∠ENF=90°.∵四边形ABCD是矩形,点E在AB的延长线上,∴∠CBE=∠ABC=90°,∴四边形BENM为矩形.∴BM=EN,∠BEN=90°.∴∠1+∠2=90°.∵四边形CEFG为正方形,∴EF=EC,∠CEF=90°.∴∠2+∠3=90°.∴∠1=∠3.∵∠CBE=∠ENF=90°,∴△ENF≌△EBC.∴NE=BE.∴BM=BE.∵四边形ABCD是矩形,∴AD=BC.∵AD=2AB,AB=BE.∴BC=2BM.∴BM=MC.∴FM垂直平分BC.∴点F在BC边的垂直平分线上。
2019届中考数学复习《矩形、菱形、正方形》专项训练题含答案

2019届初三数学中考复习矩形、菱形、正方形专项复习练习1.已知平行四边形ABCD,AC,BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为矩形的是( )A.∠BAC=∠DCA B.∠BAC=∠DACC.∠BAC=∠ABD D.∠BAC=∠ADB2. 如图,矩形ABCD的对角线AC与BD相交于点O,∠ADB=30°,AB=4,则OC=( )A.5 B.4 C.3.5 D.33. 如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为( )A.2 B.3 C. 3 D.2 34. 如图,在▱ABCD中,对角线AC与BD交于点O,若增加一个条件,使▱ABCD成为菱形,下列给出的条件不正确的是( )A.AB=AD B.AC⊥BD C.AC=BD D.∠BAC=∠DAC5. 下列说法:①四边相等的四边形一定是菱形;②顺次连接矩形各边中点形成的四边形一定是正方形;③对角线相等的四边形一定是矩形;④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分.其中正确的有( )A.4个 B.3个 C.2个 D.1个6. 如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=2,BD=2,则菱形ABCD的面积为( )A.2 2 B. 2 C.6 2 D.8 27. 如图,矩形ABCD的对角线AC与BD相交于点O,C E∥BD,DE∥AC,AD=23,DE=2,则四边形OCED 的面积( )A.2 3 B.4 C.4 3 D.88. 如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC =23,∠AEO=120°,则FC的长度为( )A.1 B.2 C. 2 D. 39. 如图,矩形纸片ABCD中,AD=4 cm,把纸片沿直线AC折叠,点B落在点E处,AE交DC于点O,若AO=5 cm,则AB的长为( )A.6 cm B.7 cm C.8 cm D.9 cm10. 如图,在△ABC中,点D是边BC上的点,(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )A.若AD⊥BC,则四边形AEDF是矩形B.若AD垂直平分BC,则四边形AEDF是矩形C.若BD=CD,则四边形AEDF是菱形D.若AD平分∠BAC,则四边形AEDF是菱形11. 如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE,将△ADE沿AE对折至△AFE,延长EF 交边BC于G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC =3.6.其中正确结论的个数是( )A.2个B.3个C.4个D.5个12. 在菱形ABCD中,∠A=30°,在同一平面内,以对角线BD为底边作顶角为120°的等腰三角形BDE,则∠EBC的度数为_______________________.13. 在平行四边形ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是___________.14. 如图,在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为_______.15. 如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则cos∠AEF的值是____.16. 如图,在△ABC中,∠ACB=90°,点D,E分别是BC,AB上的中点,连接DE并延长至点F,使EF=2DE,连接CE,AF.(1)证明:AF=CE;(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.参考答案:1---11 CBDCC AAACD D12. 45°或105°13. ①③④14. 3015.2 216. 解:(1)在△ABC中,点D,E分别是边BC,AB上的中点,∴DE是△ABC的中位线,∴DE∥AC,DE=12 AC,∵EF=2DE,∴EF∥AC,EF=AC,∴四边形ACEF是平行四边形,∴AF=CE(2)当∠B=30°时,四边形ACEF为菱形.理由:在△ABC中,∠B=30°,∠ACB=90°,∴∠BAC=60°,AC=12AB=AE,∴△AEC为等边三角形,∴AC=CE,又∵四边形ACEF为平行四边形.∴四边形ACEF为菱形2019-2020学年数学中考模拟试卷一、选择题1.如图,已知////AB CD EF,那么下列结论正确的是()A.AD BCDF CE=B.BC DFCE AD=C.CD BCEF BE=D.CD ADEF AF=2.已知二次函数y=(x+m)2–n的图象如图所示,则一次函数y=mx+n与反比例函数y=mnx的图象可能是()A. B. C. D.3.如图,点E在△DBC的边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论:①BD=CE;②∠ABD+∠ECB=45°;③BD⊥CE;④BE2=2(AD2+AB2)﹣CD2.其中正确的是()A.①③④B.②④C.①②③D.①②③④4.下列所述图形中,是中心对称图形,但不是轴对称图形的是A.正三角形B.平行四边形C.正五边形D.圆5.在的环湖越野赛中,甲乙两选手的行程(单位:)随时间(单位:)变化的图象如图所示,根据图中提供的信息,下列说法中,错误的是:( )A.出发后1小时,两人行程均为;B.出发后1.5小时,甲的行程比乙多;C.两人相遇前,甲的速度小于乙的速度;D.甲比乙先到达终点.6.下列运算正确的是()A. B. C. D.7.在数列3、12、30、60……中,请你观察数列的排列规律,则第5个数是( )A.75 B.90 C.105 D.1208.估计的值应在()A.8和9之间B.9和10之间C.10和11之间D.11和12之间9.下列形状的地砖中,不能把地面作既无缝隙又不重叠覆盖的地砖是()A.正三角形B.正方形C.正五边形D.长方形10.下列说法正确的个数是()①一组数据的众数只有一个②样本的方差越小,波动性越小,说明样本稳定性越好③一组数据的中位数一定是这组数据中的某一数据④数据:1,1,3,1,1,2的众数为4 ⑤一组数据的方差一定是正数.A.0个B.1个C.2个D.4个11.八年级6班的一个互助学习小组组长收集并整理了组员们讨论如下问题时所需的条件:如图所示,在四边形ABCD中,点E、F分别在边BC、AD上,____,求证:四边形AECF是平行四边形. 你能在横线上填上最少且简捷的条件使结论成立吗?条件分别是:①BE=DF;②∠B=∠D;③BAE=∠DCF;④四边形ABCD是平行四边形.其中A、B、C、D四位同学所填条件符合题目要求的是()A.①②③④B.①②③C.①④D.④12.如图1,一个扇形纸片的圆心角为90°,半径为4.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为()A .43π-B .83π-C .83π-D .843π- 二、填空题13.在实数范围内分解因式:24x -=______________________.14.将一个含有45°角的直角三角板摆放在矩形上,如图所示,若∠1=40°,则∠2=________.15.将一个直角三角板和一把直尺如图放置,如果∠α=43°,则∠β的度数是__________.16.如果在五张完全相同的纸片背后分别写上平行四边形、矩形、菱形、正方形、等腰梯形,打乱后随机抽取其中一张,那么抽取的图形既是轴对称图形又是中心对称图形的概率等于_____. 17.如图,已知第一象限内的点A 在反比例函数上,第二象限的点B 在反比例函数上,且OA ⊥OB ,,则k 的值为________________ .18.从0,1,2,3这四个数字中任取3个数,取得的3个数中不含2的概率是________ 三、解答题19.某贮水塔在工作期间,每小时的进水量和出水量都是固定不变的.从凌晨4点到早8点只进水不出水,8点到12点既进水又出水,14点到次日凌晨只出水不进水.下图是某日水塔中贮水量y (立方米)与x (时)的函数图象.(1)求每小时的进水量;(2)当8≤x≤12时,求y与x之间的函数关系式;(3)从该日凌晨4点到次日凌晨,当水塔中的贮水量不小于28立方米时,直接写出x的取值范围.20.某小区应政府号召,开展节约用水活动,效果显著.为了了解该小区节水情况,随机对小区的100户居民节水情况进行抽样调查,其中3月份较2月份的节水情况如图所示.(1)补全统计图;(2)计算这100户居民3月份较2月份的平均节水量;(3)已知该小区共有5000户居民,根据上面的计算结果,估计该小区居民3月份较2月份共节水多少吨?21.如图,在Rt△ABC中,∠C=90°,D是AC边上一点,tan∠DBC=43,且BC=6,AD=4.求cosA的值.22.已知关于x的一元二次方程x2﹣(m+2)x+2m=0.(1)求证:不论m为何值,该方程总有两个实数根;(2)若直角△ABC的两直角边AB、AC的长是该方程的两个实数根,斜边BC的长为3,求m的值.23.定义:若一个三角形一条边上的高长为这条边长的一半,则称该三角形为这条边上的“半高”三角形,这条高称为这条边上的“半高”,如图,△ABC是BC边上的“半高”三角形.点P在边AB上,PQ∥BC交AC于点Q,PM⊥BC于点M,QN⊥BC于点N,连接MQ.(1)请证明△APQ为PQ边上的“半高”三角形.(2)请探究BM,PM,CN之间的等量关系,并说明理由;(3)若△ABC的面积等于16,求MQ的最小值24.“全民阅读”活动,是中央宣传部、中央文明办和新闻出版总署贯彻落实关于建设学习型社会要求的一项重要举措.读书必须要讲究方法,只有按照一定的方法去阅读,才能取得事半功倍的效果.常用的阅读方法有:A.圈点批注法;B.摘记法;C.反思法:D.撰写读后感法;E.其他方法.某县某中学张老师为了解本校学生使用不同阅读方法读书的情况,随机抽取部分本校中学生进行了调查,通过数据的收集、整理绘制成以下不完整的统计图表,请根据图表中的信息解答下列问题:中学生阅读方法情况统计表(1)请你补全图表中的a,b,c数据:a=,b=,c=;(2)若该校共有中学生960名,估计该校使用“反思法”读书的学生有人;(3)小明从以上抽样调查所得结果估计全县6000名中学生中有1200人采用“撰写读后感法”读书,你同意小明的观点吗?请说明你的理由.(4)该校决定从本次抽取的“其他方法”4名学生(记为甲,乙,丙,丁)中,随机选择2名成为学校阅读宣讲志愿者,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.25.(某中学九年级学生共600人,其中男生320人,女生280人.该校对九年级所有学生进行了一次体育模拟测试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成如下的统计表:(1)a=; b=;(2)若将该表绘制成扇形统计图,那么Ⅲ类所对应的圆心角是°;(3)若随机抽取的学生中有64名男生和56名女生,请解释“随机抽取64名男生和56名女生”的合理性;(4)估计该校九年级学生体育测试成绩是40分的人数.【参考答案】*** 一、选择题二、填空题 13.()()22x x +- 14.85° 15.47° 16.3517. 18.14三、解答题19.(1)每小时的进水量为5立方米;(2)当8≤x≤12时,y =3x+1;(3)3792x 剟. 【解析】 【分析】(1)由4点到8点只进水时,水量从5立方米上升到25立方米即能求每小时进水量;(2)由图象可得,8≤x≤12时,对应的函数图象是线段,两端点坐标为(8,25)和(12,37),用待定系数法即可求函数关系式;(3)由(2)的函数关系式即能求在8到12点时,哪个时间开始贮水量不小于28立方米,且能求出每小时的出水量;14点后贮水量为37立方米开始每小时减2立方米,即能求等于28立方米的时刻 【详解】解:(1)∵凌晨4点到早8点只进水,水量从5立方米上升到25立方米 ∴(25﹣5)÷(8﹣4)=5(立方米/时) ∴每小时的进水量为5立方米.(2)设函数y =kx+b 经过点(8,25),(12,37)8251237k b k b +=⎧⎨+=⎩解得:31k b =⎧⎨=⎩∴当8≤x≤12时,y =3x+1 (3)∵8点到12点既进水又出水时,每小时水量上升3立方米 ∴每小时出水量为:5﹣3=2(立方米) 当8≤x≤12时,3x+1≥28,解得:x≥9 当x >14时,37﹣2(x ﹣14)≥28,解得:x≤372∴当水塔中的贮水量不小于28立方米时,x 的取值范围是9≤x≤372【点睛】本题考查了一次函数的应用,解题关键是理解图象中横纵坐标代表的意义并结合题意分析图象的每个分段函数.20.(1)见解析;(2)这100户居民3月份较2月份的平均节水量为1.48 t ;(3)估计该小区5000户居民3月份较2月份共节水7400 t.【解析】【分析】(1)从图中可获得节水量在0.4-0.8t 的有5户,0.8-1.2t 的有20户,1.6-2.0t 的有30户,2.0-2.4t 的有10户,样本共100户,可求得节水1.2-1.6t 的有35户,补全图形即可;(2)运用加权平均数公式把组中值当作每组数据,户数看成权,可求得平均节水量;(3)利用样本估计总体可得结果.【详解】解:(1)100-5-20-30-10=35(户).∴节水1.2~1.6吨的有35户.补全统计图如下.(2)由统计图得每小组中的组中值分别为0.40.82+=0.6,0.8 1.22+=1.0,1.2 1.62+=1.4,1.6 2.02+=1.8,2.0 2.42+=2.2, 所以这100户居民3月份较2月份的平均节水量 =0.65 1.020 1.435 1.830 2.210100⨯+⨯+⨯+⨯+⨯=1.48(t). 答:这100户居民3月份较2月份的平均节水量为1.48 t;(3)由题意可得1.48×5000=7400(t).答:估计该小区5000户居民3月份较2月份共节水7400 t.【点睛】本题考查从统计图表中获取信息的能力,加权平均数的应用和统计中用样本估计总体的思想.21 【解析】【分析】先在Rt △BDC 中,利用锐角三角函数的定义求出CD 的长,由AC=AD+DC 求出AC 的长,然后在Rt △ABC 中,根据勾股定理求出AB 的长,从而求出 cosA 的值.【详解】解:在Rt △BDC 中, tan ∠DBC=43, 且BC=6 , ∴ tan ∠DBC=DC BC =6DC =43, ∴CD=8,∴AC=AD+DC=12,在Rt △ABC 中,,∴ cosA =ACAB =5. 【点睛】本题主要考查解直角三角形.熟练掌握三角函数的定义是解题的关键.22.(1)见解析;(2【解析】【分析】(1)根据一元二次方程根的判别式和非负数的性质即可得到结论;(2)根据勾股定理和一元二次方程根的判别式解方程即可得到结论.【详解】(1)∵△=[﹣(m+2)]2﹣4×2m=(m ﹣2)2≥0,∴不论m 为何值,该方程总有两个实数根;(2)∵AB 、AC 的长是该方程的两个实数根,∴AB+AC =m+2,AB•AC=2m ,∵△ABC 是直角三角形,∴AB 2+AC 2=BC 2,∴(AB+AC )2﹣2AB•AC=BC 2,即(m+2)2﹣2×2m=32,解得:m ,∴m又∵AB•AC=2m ,m 为正数,∴m【点睛】本题考查了一元二次方程根的判别式,勾股定理,熟练掌握勾股定理是解题的关键.23.(1)见解析;(2)2PM =BM+CN ,理由见解析;(3)5. 【解析】【分析】(1)根据平行相似,证明△APQ ∽△ABC ,利用相似三角形对应边的比等于对应高的比:PQ AK BC AR =,由“半高”三角形的定义可结论;(2)证明四边形PMNQ 是矩形,得PQ =MN ,PM =KR ,代入AR =12BC ,可得结论;(3)先根据△ABC 的面积等于16,计算BC 和AR 的长,设MN =x ,则BM+CN =8﹣x ,PM =QN =12(8﹣x ),根据勾股定理表示MQ ,配方可得最小值.【详解】(1)证明:如图,过A 作AR ⊥BC 于R ,交PQ 于K ,∵△ABC 是BC 边上的“半高”三角形,∴AR =12BC , ∵PQ ∥BC ,∴△APQ ∽△ABC , ∴PQ AK BC AR=, ∴AK AR 1PQ BC 2==, ∴AK =12PQ , ∴△APQ 为PQ 边上的“半高”三角形.(2)解:2PM =BM+CN ,理由是:∵PM ⊥BC ,QN ⊥BC ,∴∠PMN =∠MNQ =∠MPQ =90°,∴四边形PMNQ 是矩形,∴PQ =MN ,PM =KR ,∵AK =12PQ ,AR =12BC , ∴AK+RK =12(BM+MN+CN ), 12PQ+PM =12BM+12MN+12CN , ∴2PM =BM+CN ;(3)解:∵△ABC 的面积等于16, ∴12BC AR ⋅=16, ∵AR =12BC , 1122BC BC ⋅⋅=16, BC =8,AR =4,设MN =x ,则BM+CN =8﹣x ,PM =QN =12(8﹣x ),∵MQ ==∴当x =85时,MQ 有最小值是5.【点睛】本题是三角形的综合题,考查的是新定义:“半高”三角形,涉及到相似三角形的性质和判定、三角形面积、勾股定理及新定义的理解和运用等知识,解决问题的关键是作辅助线解决问题.24.(1)32,8,10%;(2)96;(3)1200人;(4)16. 【解析】【分析】(1)先根据“摘记法”的频数及其频率求得总人数,再根据频数、频率与总数间的关系可得a 、b 、c 的值;(2)总人数乘以样本中“反思法”学生所占比例可得;(3)利用总人数乘以撰写读后感法的百分比即可解答(4)用树状图表示出四人中随机抽取两人有12种可能,即可解答【详解】解:(1)本次调查的学生有:20÷25%=80,a =80×40%=32,b =80×(100﹣40﹣25﹣20﹣5)%=80×10%=8,c =(100﹣40﹣25﹣20﹣5)%=10%,故答案为:32,8,10%;(2)若该校共有中学生960名,估计该校使用“反思法”读书的学生有:960×10%=96人,故答案为:96;(3)同意小明的观点;理由如下:全县6000名中学生中采用“撰写读后感法”读书的有:6000×20%=1200人;(4)树状图如图所示,∵从四人中随机抽取两人有12种可能,恰好是甲和乙的有2种可能, ∴抽取两人恰好是甲和乙的概率是21=126.【点睛】此题考查树状图法,扇形统计图,解题关键在于看懂图中数据25.(1)a =54;b =0.45; (2)72°;(3)“随机抽取64名男生和56名女生”比较合理;(4)该校九年级学生体育测试成绩是40分的人数约为180人.【解析】【分析】(1)先利用一类的频数除以频率计算出总频数c,再用总频数减去其余三类,即可得到a,再用a的频数除以总频数即可得到b(2)圆周角为360°,第三类占总数的0.2,所以第三类的圆心角=360°×0.2(3)根据九年级学生共600人,其中男生320人,女生280人进行反推即可解答(4)利用总人数乘频率即可解答【详解】(1)总频数=36÷0.3=120,a的频数=总频数-36-24-6=54,b频率=54÷120=0.45,a=54;b=0.45;(2)0.2×360°=72°;(3)∵6432056280== 120600120600,,∴“随机抽取64名男生和56名女生”比较合理;(4)0.3×600=180(人)答:该校九年级学生体育测试成绩是40分的人数约为180人.【点睛】此题考查了频数分布表,圆周角,用样本估计总体,熟练掌握运算法则是解题关键2019-2020学年数学中考模拟试卷一、选择题1.一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是()A.此抛物线的解析式是y=﹣15x2+3.5B.篮圈中心的坐标是(4,3.05)C.此抛物线的顶点坐标是(3.5,0)D.篮球出手时离地面的高度是2m2.下列等式一定成立的是()A.2a﹣a=1 B.a2•a3=a5C.(2ab2)3=2a3b6D.x2﹣2x+4=(x﹣2)23.某店在开学初用880元购进若干个学生专用科学计算器,按每个50元出售,很快就销售一空,据了解学生还急需3倍数量这种计算器,由于量大,每个进价比上次优惠1元,该店又用2580元购进所需计算器,该店第一次购进计算器的单价为()A.20元B.42元C.44元D.46元4.二次函数y=x2+bx的对称轴为直线x=2,若关于x的一元二次方程x2+bx﹣t=0(t为实数)在﹣1<x<4的范围内有解,则t的取值范围是()A.0<t<5 B.﹣4≤t<5 C.﹣4≤t<0 D.t≥﹣45.如图,在▱ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=4,则△CEF的周长为()A.8B.9.5C.10D.11.56.关于的一元二次方程有两个相等的实数根,那么的值是()A. B. C. D.7.如图,AB∥CD,直线MN与AB、CD分别交于点E、F,FG平分∠EFD,EG⊥FG于点G,若∠CFN=110°,则∠BEG=( )A.20°B.25°C.35°D.40°8.如图1,等边△ABD与等边△CBD的边长均为2,将△ABD沿AC方向向右平移k个单位到△A′B′D′的位置,得到图2,则下列说法:①阴影部分的周长为4;②当k=当k;正确的是( )A.①B.①②C.①③D.①②③9.若x是不等于1的实数,我们把11x-称为x的差倒数,如2的差倒数是11x-=﹣1,﹣1的差倒数为11(1) --=12,现已知x1=13,x2是x1的差倒数,x3是x2的差倒数,x4是x3的差倒数,…,依此类推,则x2019的值为()A.﹣13B.﹣2 C.3 D.410.如图,已知直线y=34x﹣6与x轴、y轴分别交于B、C两点,A是以D(0,2)为圆心,2为半径的圆上一动点,连结AC、AB,则△ABC面积的最小值是()A.26 B.24 C.22 D.2011.华为手机Mate X在5G网络下能达的理论下载速度为603 000 000B/s,3秒钟内就能下载好1GB的电影,将603 000 000用科学计数法表示为()A.603×610B.6.03×810C.60.3×710D.0.603×91012.如图,在△ABC中,AC=BC,∠C=90°,折叠△ABC使得点C落在AB边上的E处,连接DE、CE,下列结论:①△DEB是等腰直角三角形;②AB=AC+CD;③BE BDAC AB;④S△CDE=S△BDE.其中正确的个数是()A.1 B.2 C.3 D.4二、填空题13.定义:若抛物线的顶点与x轴的两个交点构成的三角形是直角三角形,则这种抛物线被称为:“直角抛物线”.如图,直线l:y=15x+b经过点M(0,14),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…B n(n,y n) (n为正整数),依次是直线l上的点,第一个抛物线与x轴正半轴的交点A1(x1,0)和A2(x2,0),第二个抛物线与x轴交点A2(x2,0)和A3(x3,0),以此类推,若x1=d(0<d<1),当d为_____时,这组抛物线中存在直角抛物线.14.如图,点为等边内一点,若,,,则的度数是__________.15.如图,正三角形ABC的边长为2,点A,B的圆上,点C在圆内,将正三角形ABC绕点A 逆时针旋转,当边AC第一次与圆相切时,旋转角为_____.16.抛物线 221y x =-的顶点坐标是________.17.命题“若a =b ,则a 3=b 3.”是真命题.它的逆命题“若a 3=b 3,则a =b”是_____(填真或假)命题.18.如图,直线y 1=mx 经过P(2,1)和Q(-4,-2)两点,且与直线y 2=kx +b 交于点P ,则不等式kx +b >mx >-2的解集为_________________.三、解答题19.关于x 的一次函数y =ax+b 与反比例函数y =k x(x >0)的图象交于点A (m ,4)和点B (4,1). (1)求m 的值和反比例函数的解析式;(2)求一次函数的解析式.20.如图1,在平面直角坐标系xOy 中,A (0,4),B (8,0),C (8,4).(1)试说明四边形AOBC 是矩形.(2)在x 轴上取一点D ,将△DCB 绕点C 顺时针旋转90°得到△D'CB'(点D'与点D 对应).①若OD =3,求点D'的坐标.②连接AD'、OD',则AD'+OD'是否存在最小值,若存在,请直接写出最小值及此时点D'的坐标;若不存在,请说明理由.21.抛物线L :y =a (x ﹣x 1)(x ﹣x 2)(常数a≠0)与x 轴交于点A (x 1,0),B (x 2,0),与y 轴交于点C ,且x 1•x 2<0,AB =4,当直线l :y =﹣3x+t+2(常数t >0)同时经过点A ,C 时,t =1.(1)点C 的坐标是 ;(2)求点A ,B 的坐标及L 的顶点坐标;(3)在如图2 所示的平面直角坐标系中,画出L 的大致图象;(4)将L 向右平移t 个单位长度,平移后y 随x 的增大而增大部分的图象记为G ,若直线l 与G 有公共点,直接写出t 的取值范围.22.从沈阳到大连的火车原来的平均速度是180千米/时,经过两次提速后平均速度为217.8干米/时,这两次提速的百分率相同.(1)求该火车每次提速的百分率;(2)填空:若沈阳到大连的铁路长396千米,则第一次提速后从甲地到乙地所用的时间比提速前少用了小时.23.立定跳远是嘉兴市体育中考的抽考项目之一,某校九年级(1),(2)班准备集体购买某品牌的立定跳远训练鞋.现了解到某网店正好有这种品牌训练鞋的促销活动,其购买的单价y(元/双)与一次性购买的数量x(双)之间满足的函数关系如图所示.(1)当10≤x<60时,求y关于x的函数表达式;(2)九(1),(2)班共购买此品牌鞋子100双,由于某种原因需分两次购买,且一次购买数量多于25双且少于60双;①若两次购买鞋子共花费9200元,求第一次的购买数量;②如何规划两次购买的方案,使所花费用最少,最少多少元?24.如图,在Rt△ABC中,∠ACB=90°.(1)请用直尺和圆规作∠ABC的平分线,交AC于点D(保留作图痕迹,不要求写作法和证明);(2)在(1)作出的图形中,若∠A=30°,BC,则点D到AB的距离等于.25.设a ,b 是任意两个不等实数,我们规定满足不等式a≤x≤b 的实数x 的所有取值的全体叫做闭区间,表示为[a ,b].对于一个函数,如果它的自变量x 与函数值y 满足:当m≤x≤n 时,有m≤y≤n,我们就称此函数闭区间[m ,n]上的“闭函数”.如函数y =﹣x+4.当x =1时,y =3;当x =3时,y =1,即当1≤x≤3时,有1≤y≤3,所以说函数y =﹣x+4是闭区间[1,3]上的“闭函数”(1)反比例函数2019y x是闭区间[1,2019]上的“闭函数”吗?请判断并说明理由. (2)若二次函数y =x 2﹣2x ﹣k 是闭区间[1,2]上的“闭函数”,求k 的值;(3)若一次函数y =kx+b (k≠0)是闭区间[m ,n]上的“闭函数”,求此函数的解析式(用含m ,n 的代数式表示).【参考答案】***一、选择题二、填空题13.1120、1320、32014.150°15.75°16.(0,-1)17.真18.-4<x <2三、解答题19.(1)m =1,y =4x ;(2)y =﹣x+5; 【解析】【分析】(1)把B 点坐标代入反比例函数解析式,即可求出m 的值,从而求出反比例函数的解析式和m 的值;(2)求得A 点坐标,进而把A 、B 点的坐标代入一次函数y =kx+b 的解析式,就可求出a 、b 的值,从而求得一次函数的解析式.【详解】(1)∵点B (4,1)在反比例函数y =k x (x >0)的图象上, ∴1=4k , ∴k =4. ∴反比例函数的解析式为y =4x∵点A(m,4)在反比例函数y=4x的图象上,∴4=4m,∴m=1.(2)点A(1,4)和点B(4,1)在一次函数y=ax+b的图象上,∴4 41 a ba b+=⎧⎨+=⎩解得15 ab=-⎧⎨=⎩∴一次函数的解析式为y=﹣x+5.【点睛】本题考查了反比例函数和一次函数的交点问题,能够熟练运用待定系数法求得函数的解析式是解题的关键.20.(1)见解析;(2)①D'的坐标为(4,9),②AD'+OD',点D'的坐标是(4,2).【解析】【分析】(1)根据矩形的判定证明即可;(2)①当点D在原点右侧时,根据旋转的性质和矩形的性质解答即可;②当点D在原点左侧时,根据旋转的性质和矩形的性质解答即可.【详解】(1)∵A(0,4),B(8,0),C(8,4).∴OA=4,BC=4,OB=8,AC=8,∴OA=BC,AC=OB,∴四边形AOBC是平行四边形,∵∠AOB=90°,∴▱AOBC是矩形;(2)∵▱AOBC是矩形,∴∠ACB=90°,∠OBC=90°,∵△D'CB'将△DCB绕点C顺时针旋转90°得到(点D'与点D对应),∴∠D'B'C=∠DBC=90°,B'C=BC=4,D'B'=DB,∠BCB'=90°,即点B'在AC边上,∴D'B'⊥AC,①如图1,当点D在原点右侧时:D'B'=DB=8﹣3=5,∴点D'的坐标为(4,9);②如图2,当点D在原点左侧时:D'B'=DB=8+3=11,∴点D'的坐标为(4,15),综上所述:点D'的坐标为(4,9)或(4,15).AD'+OD',点D'的坐标是(4,2).【点睛】此题考查四边形的综合题,关键是根据旋转的性质和矩形的性质解答.21.(1) 点C的坐标是(0,3); (2)A(1,0),B(﹣3,0),L的顶点坐标为(﹣1,4);(3)见解析;(4)t≥1 2【解析】【分析】(1)把t=1代入y=﹣3x+t+2,令x=0,求得相应的y值,即可得到点C的坐标;(2)根据待定系数法,可得函数解析式;(3)根据描点法,可得函数图象;(3)根据平移规律,可得G的解析式,根据函数与不等式的关系,可得答案.【详解】(1)直线的解析式为y=﹣3x+3,当x=0时,y=3,即C点坐标为(0,3),故答案为:(0,3);(2)当y=0时,﹣3x+3=0,解得x1=1,即A(1,0),由点A(x1,0),B(x2,0),且x1•x2<0,AB=4,得1﹣x2=4,解得x2=﹣3,即B(﹣3,0);L:y=a(x﹣1)(x+3),将C(0,3)坐标代入L,得a=﹣1,∴L的解析式为y=﹣(x﹣1)(x+3),即y=﹣(x+1)2+4,∴L的顶点坐标为(﹣1,4);(3)函数图象如图所示:;(4)L向右平移t个单位的解析式为y=﹣(x+1﹣t)2+4,a=﹣1<0,当x≤t﹣1时,y随x的增大而增大.若直线l与G有公共点时,则有当x=﹣1+t时,G在直线l的上方,即﹣(t﹣1+1﹣t)2+4≥﹣3(t﹣1)+t+2,解得t≥12.【点睛】本题考查了二次函数综合题,解(1)的关键是利用自变量与函数值的对应关系;解(2)的关键是待定系数法;解(3)的关键是描点法,解(4)的关键是利用函数值的大小得出不等式,还利用了函数图象平移的规律.22.(1)该火车每次提速的百分率为10%.(2)0.2.【解析】【分析】(1)设该火车每次提速的百分率为x,根据提速前的速度及经两次提速后的速度,即可得出关于x的一元二次方程,解之取其正值即可得出结论;(2)利用第一次提速后的速度=提速前的速度×(1+提速的百分率)可求出第一次提速后的速度,再利用少用的时间=两地间铁路长÷提速前的速度﹣两地间铁路长÷第一次提速后的速度,即可求出结论.【详解】(1)设该火车每次提速的百分率为x,依题意,得:180(1+x)2=217.8,解得:x1=0.1=10%,x2=﹣2.1(舍去),答:该火车每次提速的百分率为10%;(2)第一次提速后的速度为180×(1+10%)=198(千米/时),第一次提速后从甲地到乙地所用的时间比提速前少用的时间为396396180198-=0.2(小时),故答案为:0.2.【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.23.(1)y=150﹣x;(2)①第一批购买数量为30双或40双.②第一次买26双,第二次买74双最省钱,最少9144元.【解析】【分析】(1)若购买x双(10<x<60),每件的单价=140﹣(购买数量﹣10),依此可得y关于x的函数关系式;(2)①设第一批购买x双,则第二批购买(100﹣x)双,根据购买两批鞋子一共花了9200元列出方程求解即可.分两种情况考虑:当25<x≤40时,则60≤100﹣x<75;当40<x<60时,则40<100﹣x<60.②把两次的花费与第一次购买的双数用函数表示出来.【详解】解:(1)购买x双(10<x<60)时,y=140﹣(x﹣10)=150﹣x.故y关于x的函数关系式是y=150﹣x;(2)①设第一批购买x双,则第二批购买(100﹣x)双.当25<x≤40时,则60≤100﹣x<75,则x(150﹣x)+80(100﹣x)=9200,解得x1=30,x2=40;当40<x<60时,则40<100﹣x<60,则x(150﹣x)+(100﹣x)[150﹣(100﹣x)]=9200,解得x=30或x=70,但40<x<60,所以无解;答:第一批购买数量为30双或40双.②设第一次购买x双,则第二次购买(100﹣x)双,设两次花费w元.当25<x≤40时w=x(150﹣x)+80(100﹣x)=﹣(x﹣35)2+9225,∴x=26时,w有最小值,最小值为9144元;当40<x<60时,w=x(150﹣x)+(100﹣x)[150﹣(100﹣x)]=﹣2(x﹣50)2+10000,∴x=41或59时,w有最小值,最小值为9838元,综上所述:第一次买26双,第二次买74双最省钱,最少9144元.【点睛】考查了一元二次方程的应用,根据实际问题列一次函数关系式,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.24.(1)作图见解析;(2)1.【解析】【分析】(1)根据角平分线的尺规作图可得;(2)作DE⊥AB于E,设DE=DC=x,由∠A=30°,BC AD=2DE=2x,AB=2BC=由BC2+AC2=AB2得到关于x的方程,解之可得.【详解】(1)如图所示,BD即为所求;。
九年级数学中考复习课题矩形、菱形、正方形AB组习题专题课后训练分层练习B组提高题含答案解析

九年级数学中考复习课题矩形、菱形、正方形AB组习题专题课后训练分层练习B组提高题含答案解析A组1.下列性质中,菱形具有而平行四边形不具有的性质是()A.对边平行且相等B.对角线互相平分C.对角线互相垂直D.对角互补解:A、平行四边形的对边平行且相等,所以A选项错误;B、平行四边形的对角线互相平分,所以B选项错误;C、菱形的对角线互相垂直,平行四边形的对角线互相平分,所以C选项正确;D、平行四边形的对角相等,所以D选项错误.故选C.2.矩形具有而菱形不一定具有的性质是()A.对边分别相等B.对角分别相等C.对角线互相平分D.对角线相等解:矩形的性质有:①矩形的对边相等且平行,①矩形的对角相等,且都是直角,①矩形的对角线互相平分、相等;菱形的性质有:①菱形的四条边都相等,且对边平行,①菱形的对角相等,①菱形的对角线互相平分、垂直,且每一条对角线平分一组对角;①矩形具有而菱形不一定具有的性质是对角线相等,故选D.3.顺次连接四边形ABCD各边中点所成的四边形为菱形,那么四边形ABCD的对角线AC 和BD只需满足的条件是()A.相等B.互相垂直C.相等且互相垂直D.相等且互相平分解:因为原四边形的对角线与连接各边中点得到的四边形的关系:①原四边形对角线相等,所得的四边形是菱形;①原四边形对角线互相垂直,所得的四边形是矩形;①原四边形对角线既相等又垂直,所得的四边形是正方形;①原四边形对角线既不相等又不垂直,所得的四边形是平行四边形.因为顺次连接四边形ABCD各边中点所成的四边形为菱形,所以四边形ABCD的对角线AC和BD相等.故选A.4.已知菱形的两条对角线长分别是6cm和8cm,则菱形的边长是()A.12cm B.10cm C.7cm D.5cm解:如图:①菱形ABCD中BD=8cm,AC=6cm,①OD=BD=4cm,OA=AC=3cm,在直角三角形AOD中AD===5cm.故选D.5.如图,菱形纸片ABCD,①A=60°,P为AB中点,折叠菱形纸片ABCD,使点C落在DP所在的直线上,得到经过点D的折痕DE,则①DEC等于75度.解:连接BD,①四边形ABCD为菱形,①A=60°,①①ABD为等边三角形,①ADC=120°,①C=60°,①P为AB的中点,①DP为①ADB的平分线,即①ADP=①BDP=30°,①①PDC=90°,①由折叠的性质得到①CDE=①PDE=45°,在①DEC中,①DEC=180°﹣(①CDE+①C)=75°.故答案为:75.6.如图:在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则DE的长是3.解:如图,连接CE,,设DE=x,则AE=8﹣x,①OE①AC,且点O是AC的中点,①OE是AC的垂直平分线,①CE=AE=8﹣x,在Rt①CDE中,x2+42=(8﹣x)2解得x=3,①DE的长是3.故答案为:3.7.如图,矩形ABCD中,对角线AC、BD交于点O,点E是BC上一点,且AB=BE,①1=15°,则①2=30°.解:①四边形ABCD是矩形,①①ABC=①BAD=90°,OB=OD,OA=OC,AC=BD,①OB=OC,OB=OA,①①OCB=①OBC,①AB=BE,①ABE=90°,①①BAE=①AEB=45°,①①1=15°,①①OCB=①AEB﹣①EAC=45°﹣15°=30°,①①OBC=①OCB=30°,①①AOB=30°+30°=60°,①OA=OB,①①AOB是等边三角形,①AB=OB,①①BAE=①AEB=45°,①AB=BE,①OB=BE,①①OEB=①EOB,①①OBE=30°,①OBE+①OEB+①BEO=180°,①①OEB=75°,①①AEB=45°,①①2=①OEB﹣①AEB=30°,故答案为:30°.8.如图,在Rt①ABC中,①ACB=90°,D为AB的中点,AE①CD,CE①AB,连接DE交AC于点O.(1)证明:四边形ADCE为菱形.(2)BC=6,AB=10,求菱形ADCE的面积.证明:(1)①在Rt①ABC中,①ACB=90°,D为AB中点,①CD=AB=AD,又①AE①CD,CE①AB①四边形ADCE是平行四边形,①平行四边形ADCE是菱形;(2)在Rt①ABC中,AC===8.①平行四边形ADCE是菱形,①CO=OA,又①BD=DA,①DO是①ABC的中位线,①BC=2DO.又①DE=2DO,①BC=DE=6,①S菱形ADCE===24.B组9.如图:点P是Rt①ABC斜边AB上的一点,PE①AC于E,PF①BC于F,BC=15,AC=20,则线段EF的最小值为()A.12B.6C.12.5D.25解:如图,连接CP.①①C=90°,AC=3,BC=4,①AB===25,①PE①AC,PF①BC,①C=90°,①四边形CFPE是矩形,①EF=CP,由垂线段最短可得CP①AB时,线段EF的值最小,此时,S①ABC=BC•AC=AB•CP,即×20×15=×25•CP,解得CP=12.故选A.10.如图,在菱形ABCD中,①BAD=80°,AB的垂直平分线交对角线AC于点F,点E为垂足,连接DF,则①CDF为()A.80°B.70°C.65°D.60°解:如图,连接BF,在①BCF和①DCF中,①CD=CB,①DCF=①BCF,CF=CF①①BCF①①DCF①①CBF=①CDF①FE垂直平分AB,①BAF=×80°=40°①①ABF=①BAF=40°①①ABC=180°﹣80°=100°,①CBF=100°﹣40°=60°①①CDF=60°.故选D.11.如图,在菱形ABCD中,①A=110°,E,F分别是边AB和BC的中点,EP①CD于点P,则①FPC的度数为()A.55°B.50°C.45°D.35°解:延长PF交AB的延长线于点G.如图所示:在①BGF与①CPF中,,①①BGF①①CPF(ASA),①GF=PF,①F为PG中点.又①由题可知,①BEP=90°,①EF=PG,①PF=PG,①EF=PF,①①FEP=①EPF,①①BEP=①EPC=90°,①①BEP﹣①FEP=①EPC﹣①EPF,即①BEF=①FPC,①四边形ABCD为菱形,①AB=BC,①ABC=180°﹣①A=70°,①E,F分别为AB,BC的中点,①BE=BF,①BEF=①BFE=(180°﹣70°)=55°,①①FPC=55°;故选:A.12.如图,矩形ABCD中,对角线AC、BD交于点O,点E是BC上一点,且AB=BE,①1=15°,则①2=30°.解:①四边形ABCD是矩形,①①ABC=①BAD=90°,OB=OD,OA=OC,AC=BD,①OB=OC,OB=OA,①①OCB=①OBC,①AB=BE,①ABE=90°,①①BAE=①AEB=45°,①①1=15°,①①OCB=①AEB﹣①EAC=45°﹣15°=30°,①①OBC=①OCB=30°,①①AOB=30°+30°=60°,①OA=OB,①①AOB是等边三角形,①AB=OB,①①BAE=①AEB=45°,①AB=BE,①OB=BE,①①OEB=①EOB,①①OBE=30°,①OBE+①OEB+①BEO=180°,①①OEB=75°,①①AEB=45°,①①2=①OEB﹣①AEB=30°,故答案为:30°.13.(2019•绍兴)如图,在直线AP上方有一个正方形ABCD,①P AD=30°,以点B为圆心,AB长为半径作弧,与AP交于点A,M,分别以点A,M为圆心,AM长为半径作弧,两弧交于点E,连结ED,则①ADE的度数为15°或45°.【分析】分点E与正方形ABCD的直线AP的同侧、点E与正方形ABCD的直线AP的两侧两种情况,根据正方形的性质、等腰三角形的性质解答.解:①四边形ABCD是正方形,①AD=AE,①DAE=90°,①①BAM=180°﹣90°﹣30°=60°,AD=AB,当点E与正方形ABCD的直线AP的同侧时,由题意得,点E与点B重合,①①ADE=45°,当点E与正方形ABCD的直线AP的两侧时,由题意得,E′A=E′M,①①AE′M为等边三角形,①①E′AM=60°,①①DAE′=360°﹣120°﹣90°=150°,①AD=AE′,①①ADE′=15°,故答案为:15°或45°.14.如图:在①ABC中,CE、CF分别平分①ACB与它的邻补角①ACD,AE①CE于E,AF①CF 于F,直线EF分别交AB、AC于M、N.(1)求证:四边形AECF为矩形;(2)试猜想MN与BC的关系,并证明你的猜想;(3)如果四边形AECF是菱形,试判断①ABC的形状,直接写出结果,不用说明理由.(1)证明:①AE①CE于E,AF①CF于F,①①AEC=①AFC=90°,又①CE、CF分别平分①ACB与它的邻补角①ACD,①①BCE=①ACE,①ACF=①DCF,①①ACE+①ACF=(①BCE+①ACE+①ACF+①DCF)=×180°=90°,①三个角为直角的四边形AECF为矩形.(2)结论:MN①BC且MN=BC.证明:①四边形AECF为矩形,①对角线相等且互相平分,①NE=NC,①①NEC=①ACE=①BCE,①MN①BC,又①AN=CN(矩形的对角线相等且互相平分),①N是AC的中点,若M不是AB的中点,则可在AB取中点M1,连接M1N,则M1N是①ABC的中位线,MN①BC,而MN①BC,M1即为点M,所以MN是①ABC的中位线(也可以用平行线等分线段定理,证明AM=BM)①MN=BC;法二:延长MN至K,使NK=MN,因为对角线互相平分,所以AMCK是平行四边形,KC①MA,KC=AM因为MN①BC,所以MBCK是平行四边形,MK=BC,所以MN=BC(3)解:①ABC是直角三角形(①ACB=90°).理由:①四边形AECF是菱形,①AC①EF,①EF①AC,①AC①CB,①①ACB=90°.即①ABC是直角三角形.15.如图,在①ABC中,①ABC=90°,BD为AC的中线,过点C作CE①BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.(1)求证:BD=DF;(2)求证:四边形BDFG为菱形;(3)若AG=13,CF=6,求四边形BDFG的周长.(1)证明:①①ABC=90°,BD为AC的中线,①BD=AC,①AG①BD,BD=FG,①四边形BGFD是平行四边形,①CF①BD,①CF①AG,又①点D是AC中点,①DF=AC,①BD=DF;(2)证明:①BD=DF,①四边形BGFD是菱形,(3)解:设GF=x,则AF=13﹣x,AC=2x,①在Rt①ACF中,①CFA=90°,①AF2+CF2=AC2,即(13﹣x)2+62=(2x)2,解得:x=5,①四边形BDFG的周长=4GF=20.。
九年级数学正方形的判定(基础)(含答案)

正方形的判定(基础)一、单选题(共10道,每道10分)1.下列说法,错误的是( )A.所有的平行四边形都是中心对称图形B.矩形是轴对称图形C.菱形不是轴对称图形D.正方形既是轴对称图形也是中心对称图形答案:C解题思路:所有平行四边形均为中心对称图形,对称中心为对角线的交点;矩形是轴对称图形,对称轴为过中心且与边垂直的直线;菱形是轴对称图形,对称轴为对角线所在直线;综上,A,B,D正确,C错误.试题难度:三颗星知识点:略2.平行四边形、矩形、菱形、正方形都具有的是( )A.对角线互相平分B.对角线互相垂直C.对角线相等D.每一条对角线平分一组对角答案:A解题思路:所有平行四边形均满足对角线互相平分;矩形对角线相等但不垂直,不平分一组对角;菱形对角线相互垂直但不相等,平分一组对角;正方形对角线相等,互相垂直,且平分一组对角.综上,A正确.试题难度:三颗星知识点:略3.正方形的一条对角线长为4,则这个正方形的面积是( )A.8B.C. D.16答案:A解题思路:正方形的一条对角线长为4,则边长为,面积为8试题难度:三颗星知识点:略4.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,连接CE,则∠BCE的度数是( )A.22.5°B.25°C.30°D.无法确定答案:A解题思路:如图,∵四边形ABCD是正方形,AE=AC∴∠CAB=∠ACB=45°,∠ACE=(180°-45°)=67.5°∴∠BCE=∠ACE-∠ACB=22.5°试题难度:三颗星知识点:略5.如图,在正方形ABCD的外侧,作等边△ABE,则∠BED的的度数为( )A.15°B.35°C.45°D.55°答案:C解题思路:∵四边形ABCD为正方形,△ABE为等边三角形∴AD=AB,∠DAB=90°,AE=AB,∠EAB=∠AEB=60°∴△ADE为等腰三角形,且∠EAD=150°∴∠AED=15°∴∠BED=∠AEB-∠AED=60°-15°=45°试题难度:三颗星知识点:略6.如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为( )A.5B.C.7D.答案:D解题思路:由旋转性质,则△ADE≌△ABF∴S四AECF=S△ABF+S四ABCE=S△ADE+S四ABCE=S正ABCD=25∴AD=5∴Rt△ADE中,∠D=90°,AD=5,DE=2,由勾股定理得AE=试题难度:三颗星知识点:略7.如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是( )A. B.5C. D.20答案:C解题思路:如图,连接BD交AC于点O.∵四边形ABCD为正方形,AE=CF∴AO=OC,BO=OD,BD⊥AC∴AO-AE=CO-OF,即EO=OF∴四边形BEDF为菱形∵AC=8,CF=2∴OC=OD=4,OF=OC-FC=2Rt△DOF中,∠DOF=90°,OF=2,OD=4,由勾股定理得DF=故菱形BEDF的周长为4DF=试题难度:三颗星知识点:略8.如图,在正方形ABCD中,点E是BC上的一点,点F是CD延长线上的一点,且BE=DF,连接AE,AF,EF.若AE=5,则EF的长为( )A. B.C.10D.无法确定答案:A解题思路:∵四边形ABCD为正方形,BE=DF∴AB=AD,∠B=∠ADC=∠ADF=90°∴△ABE≌△ADF∴AE=AF,∠BAE=∠DAF∴∠EAF=∠DAF+∠DAE=∠BAE+∠DAE=∠BAD=90°∴△EAF为等腰直角三角形且AE=5∴EF=AE=试题难度:三颗星知识点:略9.如图,正方形ABCD中,AB=6,G是BC的中点,将△ABG沿AG对折至△AFG,延长GF 交DC于点E,则DE的长是( )A.1B.C.2D.答案:C解题思路:如图,连接AE.∵四边形ABCD为正方形,△ABG沿AG对折至△AFG∴AF=AB=AD,∠AFG=∠B=∠D=90°∴∠AFE=∠D=90°∵AE=AE∴Rt△AFE≌Rt△ADE(HL)∵G是BC的中点,BC=6,若设DE=x则CG=3,FG=BG=3,EF=DE=x,CE=6-xRt△CGE中,由勾股定理CG2+CE2=EG2即32+(6-x)2=(3+x)2,解得x=2∴DE的长是2试题难度:三颗星知识点:略10.如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BH⊥AE,垂足为点H,延长BH交CD于点F,连接AF.若正方形边长是5,BE=2,则AF的长为( )A.4B.C. D.答案:B解题思路:∵四边形ABCD为正方形∴AB=BC,∠ABC=∠C=90°∵BH⊥AE∴∠BAE+∠BEA=90°,∠EBH+∠BEA=90°∴∠BAE=∠EBH∴△ABE≌△BCF(ASA)∴CF=BE∵BC=5,BE=2∴AD=5,DF=3则Rt△ADF中,利用勾股定理可得AF=试题难度:三颗星知识点:略。
1.3.1正方形的性 同步练习(含答案)2021——2022学年北师大版九年级数学上册

1.3.1正方形的性质同步练习一.选择题(共12小题)1.如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设∠CBE=α,则∠AFP为()A.2αB.90°﹣αC.45°+αD.90°﹣α2.如图,正方形ABCD的边长为4,点E在AB上,BE=3,过点E作EF∥BC,分别交BD,CD于点G,F.若点M,N分别为DG,EC的中点,则线段MN的长为()A.B.C.2.5D.1.53.如图,在边长为6的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为()A.2B.C.3D.第1题第2题第3题4.如图,在正方形ABCD的外侧,作等边三角形CDE,连接AE.则∠DAE的度数是()A.15°B.20°C.12.5°D.10°5.如图,已知F、E分别是正方形ABCD的边AB与BC的中点,AE与DF交于P.则下列结论成立的是()A.BE=AE B.PC=PDC.∠EAF+∠AFD=90°D.PE=EC6.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD 于点N.若四边形MOND的面积是1,则AB的长为()A.1B.C.2D.2第4题第5题第6题7.如图,把含30°的直角三角板PMN放置在正方形ABCD中,∠PMN=30°,直角顶点P在正方形ABCD的对角线BD上,点M,N分别在AB和CD边上,MN与BD交于点O,且点O为MN的中点,则∠AMP的度数为()A.60°B.65°C.75°D.80°8.如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M,N 分别是DC,DF的中点,连接MN.若AB=7,BE=5,则MN=()A.B.C.6D.9.如图,已知正方形ABCD的边长为4,P是对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.给出下列结论:①PD=EC;②四边形PECF的周长为8;③AP=EF;④EF的最小值为2.其中正确结论有几个()A.1B.2C.3D.4第7题第8题第9题10.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,H是AF的中点,CH=3,那么CE的长是()A.3B.4C.D.11.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=6,F为DE的中点.若OF 的长为1,则△CEF的周长为()A.14B.16C.18D.1212.如图,在正方形ABCD中,点M,N为CD,BC上的点,且DM=CN,AM与DN交于点P,连接AN,点Q为AN中点,连接PQ,若AB=10,DM=4,则PQ的长为()A.4B.8C.D.第10题第11题第12题二.填空题(共3小题)13.如图,在正方形ABCD内有一点P,若AP=4,BP=7,DP=9,则∠APB的度数为.14.如图,E是边长为2的正方形ABCD的对角线AC上一点,且AE=AB,F为BE上任意一点,FG⊥AC于点G,FH⊥AB于点H,则FG+FH的值是.15.如图,正方形ABCD,延长BC至点E,使CE=CD.直线EF分别交AB、CD于点F、G,在FG上取点H,使∠BHF=45°,若FH=6,△DEF的面积为130,则DG的长为.第13题第14题第15题三.解答题(共7小题)16.如图,点P在正方形ABCD的对角线AC上,点E在边BC上,且PE=PB.(1)求证:PE=PD;(2)试探究BC2,EC2,PE2三者之间满足的等量关系,并证明你的结论.17.如图,四边形ABCD为正方形,点E、F分别是AB、CD的中点,DG⊥CF于点G.(1)求证:AE∥CF;(2)求证:∠AGE=90°;(3)若正方形的边长为2,则线段CG的长度为.18.如图,已知四边形ABCD为正方形,△CDE为等边三角形.(1)求证:AE=BE;(2)若AB=10,求△BCE的面积.19.如图,在正方形ABCD中,AB=,E为正方形ABCD内一点,DE=AB,∠EDC=α(0°<α<90°),连结CE,AE,过点D作DF⊥AE,垂足为点F,交CE的延长线于点G,连结AG.(1)当α=20°时,求∠DAE的度数;(2)判断△AEG的形状,并说明理由;(3)当GF=1时,求CE的长.20.如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.(1)证明:△ADG≌△DCE;(2)连接BF,求证:AB=FB.21.如图,在正方形ABCD和正方形CEFG中,点D在CG上,H是AF的中点.(1)求证:CH=AF;(2)若BC=1,CE=3,求CH的长.22.正方形ABCD中,点P是边CD上的任意一点,连接BP,O为BP的中点,作PE⊥BD.连接EO,AE,EC.于E,连接ED,AE,EC.(1)当∠DAE=25°时,求∠AEC的度数;(2)当∠PBC=15°时,DP=4,求正方形的边长;(3)当AE=时,求BP的长.1.3.1正方形的性质同步练习参考答案与试题解析一.选择题(共12小题)1.如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设∠CBE=α,则∠AFP为()A.2αB.90°﹣αC.45°+αD.90°﹣α【解答】解:∵四边形PBEF为正方形,∴∠PBE=90°,∵∠CBE=α,∴∠PBC=90°﹣α,∵四边形APCD、PBEF是正方形,∴AP=CP,∠APF=∠CPB=90°,PE=PB,在△APF和△CPB中,,∴△APF≌△CPB(SAS),∴∠AFP=∠PBC=90°﹣α.故选:B.2.如图,正方形ABCD的边长为4,点E在AB上,BE=3,过点E作EF∥BC,分别交BD,CD于点G,F.若点M,N分别为DG,EC的中点,则线段MN的长为()A.B.C.2.5D.1.5【解答】解:连接ME、MF、MC,∵ABCD为正方形,BD为对角线,EF∥BC,AB=4,∴∠BDC=45°,AB=BC=CD=EF=4,∠EFD=90°,∵M为GD中点,∴FM=,∴DM=MF,∠MFG=45°,在△EMF和△CMD中,,∴△EMF≌△CMD(SAS),∴∠FME=∠DMC,∴∠EMC=∠DMF=90°,∵N为EC中点,∴,在Rt△EBC中,BE=3,BC=4,∴EC=5,∴MN=2.5.故选:C.3.如图,在边长为6的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为()A.2B.C.3D.【解答】证明:∵四边形ABCD是正方形,∴AB=AD,∴把△ABF绕点A逆时针旋转90°至△ADG,可使AB与AD重合,如图:∴∠BAF=∠DAG,∵∠BAD=90°,∠EAF=45°,∴∠BAF+∠DAE=45°,∴∠EAF=∠EAG,∵∠ADG=∠ADC=∠B=90°,∴∠EDG=180°,点E、D、G共线,在△AFE和△AGE中,,∴△AFE≌△AGE(SAS),∴EF=EG,即:EF=EG=ED+DG,∵E为CD的中点,边长为6的正方形ABCD,∴CD=BC=6,DE=CE=3,∠C=90°,∴设BF=x,则CF=6﹣x,EF=3+x,在Rt△CFE中,由勾股定理得:EF2=CE2+CF2,∴(3+x)2=32+(6﹣x)2,解得:x=2,即BF=2,故选:A.4.如图,在正方形ABCD的外侧,作等边三角形CDE,连接AE.则∠DAE的度数是()A.15°B.20°C.12.5°D.10°【解答】解:∵四边形ABCD是正方形,∴∠ADC=90°,AD=DC,∵△CDE是等边三角形,∴DE=DC,∠EDC=60°,∴∠ADE=90°+60°=150°,AD=ED,∴∠DAE=∠DEA=(180°﹣∠ADE)=15°,故选:A.5.如图,已知F、E分别是正方形ABCD的边AB与BC的中点,AE与DF交于P.则下列结论成立的是()A.BE=AE B.PC=PDC.∠EAF+∠AFD=90°D.PE=EC【解答】解:∵F、E分别是正方形ABCD的边AB与BC的中点,∴AF=BE,在△AFD和△BEA中,,∴△AFD≌△BEA(SAS),∴∠FDA=∠EAB,又∵∠FDA+∠AFD=90°,∴∠EAB+∠AFD=90°,即∠EAF+∠AFD=90°,故C正确,A、B、D无法证明其成立,故选:C.6.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD 于点N.若四边形MOND的面积是1,则AB的长为()A.1B.C.2D.2【解答】解:∵四边形ABCD是正方形,∴∠MDO=∠NCO=45°,OD=OC,∠DOC=90°,∴∠DON+∠CON=90°,∵ON⊥OM,∴∠MON=90°,∴∠DON+∠DOM=90°,∴∠DOM=∠CON,在△DOM和△CON中,,∴△DOM≌△CON(ASA),∵四边形MOND的面积是1,四边形MOND的面积=△DOM的面积+△DON的面积,∴四边形MOND的面积=△CON的面积+△DON的面积=△DOC的面积,∴△DOC的面积是1,∴正方形ABCD的面积是4,∵AB2=4,∴AB=2,故选:C.7.如图,把含30°的直角三角板PMN放置在正方形ABCD中,∠PMN=30°,直角顶点P在正方形ABCD的对角线BD上,点M,N分别在AB和CD边上,MN与BD交于点O,且点O为MN的中点,则∠AMP的度数为()A.60°B.65°C.75°D.80°【解答】解:在Rt△PMN中,∠MPN=90°,∵O为MN的中点,∴OP=,∵∠PMN=30°,∴∠MPO=30°,∴∠DPM=150°,在四边形ADPM中,∵∠A=90°,∠ADB=45°,∠DPM=150°,∴∠AMP=360°﹣∠A﹣∠ADB﹣∠DPM=360°﹣90°﹣45°﹣150°=75°.故选:C.8.如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M,N 分别是DC,DF的中点,连接MN.若AB=7,BE=5,则MN=()A.B.C.6D.【解答】解:连接CF,∵正方形ABCD和正方形BEFG中,AB=7,BE=5,∴GF=GB=5,BC=7,∴GC=GB+BC=5+7=12,∴CF===13,∵M,N分别是DC,DF的中点,∴MN=CF=,9.如图,已知正方形ABCD的边长为4,P是对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.给出下列结论:①PD=EC;②四边形PECF的周长为8;③AP=EF;④EF的最小值为2.其中正确结论有几个()A.1B.2C.3D.4【解答】解:连接PC,①∵BD是正方形的对角线,则∠PDF=45°,而PF⊥CD,则△PDF为等腰直角三角形,∴PD=PF,∵PE⊥BC,∴∠PEC=∠PFC=90°,∵四边形ABCD为正方形,∴∠BCD=90°,∴四边形PECF是矩形,∴CE=PF,∴PD=CE;故①正确;②∵四边形PECF为矩形,∴四边形PECF的周长=2CE+2PE=2CE+2BE=2BC=8;故②正确;③∵四边形PECF为矩形,∵四边形ABCD为正方形,∴AD=CD,∠ADC=∠CDP,在△ADP和△CDP中,,∴△ADP≌△CDP(SAS),∴AP=PC,∴AP=EF;故③正确;④由EF=PC=AP,∴当AP最小时,EF最小,则当AP⊥BD时,即AP=BD=2时,EF的最小值等于2;故④正确;综上,①②③④正确.故选:D.10.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,H是AF的中点,CH=3,那么CE的长是()A.3B.4C.D.【解答】解:连接AC,CF,如图,∵四边形ABCD和四边形CEFG为正方形,∴∠ACF=45°×2=90°.∵H是AF的中点,CH=3,∴AF=2CH=6.在Rt△ABC中,AC=BC=.在Rt△ACF中,CF==.在Rt△ECF中,∵CE2+EF2=CF2,CE=EF,∴CE=CF==.故选:D.11.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=6,F为DE的中点.若OF 的长为1,则△CEF的周长为()A.14B.16C.18D.12【解答】解:在正方形ABCD中,BO=DO,BC=CD,∠BCD=90°,∵F为DE的中点,∴OF为△DBE的中位线,ED=2CF=2EF,∴△CEF的周长为EF+EC+FC=ED+EC,∵OF=1,∴BE=2OF=2,∵CE=6,∴BC=BE+CE=2+6=8,∴CD=BC=8,在Rt△CED中,∠ECD=90°,CD=8,CE=6,∴ED=,∴△CEF的周长为EF+EC+FC=ED+EC=10+6=16,故选:B.AN中点,连接PQ,若AB=10,DM=4,则PQ的长为()A.4B.8C.D.【解答】解:在正方形ABCD中,AD=CD,∠ADC=∠DCN=90°,在△ADM与△DCN中,∵AD=CD,DM=CN,∠ADC=∠DCN,∴△ADM≌△DCN(SAS),∴∠DAM=∠CDN,∴∠DMA=∠CND,在△DPM中∠PDM+∠PMD=90°,∴∠DPM=90°'∵∠DPM=∠APN,∴△ANP为直角三角形,AN为直角三角形的斜边,由直角三角形的性质得PQ=AN,在△ANB中AN==2,故选:C.二.填空题(共3小题)13.如图,在正方形ABCD内有一点P,若AP=4,BP=7,DP=9,则∠APB的度数为135.【解答】解:∵四边形ABCD为正方形,∴∠ABC=90°,BA=BC,∴△BAP绕点A逆时针旋转90°可得△ADE,由旋转的性质得,ED=BP=7,AE=AP=4,∠PBE=90°,∠AED=∠APB,∴△APE为等腰直角三角形,∴PE=AP=4,∠AEP=45°,在△PED中,∵PD=9,ED=7,PE=4,∴DE2+PE2=DP2,∴△PED为直角三角形,∠PED=90°,∴∠AED=90°+45°=135°,∴∠APB=135°,故答案为:135°.14.如图,E是边长为2的正方形ABCD的对角线AC上一点,且AE=AB,F为BE上任意一点,FG⊥AC于点G,FH⊥AB于点H,则FG+FH的值是.【解答】解:如图,过点E作EM⊥AB于M,连接AF,∵四边形ABCD是正方形,∴∠CAB=45°,∴∠AEM=90°﹣∠CAM=45°,∴AM=EM,∴△AEM是等腰直角三角形,∵AB=AE=2,∴EM=AE•sin45°=2×=,∵S△ABE=S△AEF+S△ABF,∴S△ABE=AB•EM=AE•FG+AB•FH,∴EM=FG+FH=,故答案为.15.如图,正方形ABCD,延长BC至点E,使CE=CD.直线EF分别交AB、CD于点F、G,在FG上取点H,使∠BHF=45°,若FH=6,△DEF的面积为130,则DG的长为 6.5.【解答】解:连接DH,∵四边形ABCD是正方形,∴∠A=∠ABC=90°,∴∠BFE=90°﹣∠BEF,∵∠DFE=180°﹣∠FDE﹣∠DEF,∠AFD=180°﹣∠DFE﹣∠BFE,∠BFE=180°﹣∠FHB﹣∠FBH且∠BHF =45°,∴∠DFH=45°=∠FHB,∴DF∥BH,∴∠BAF+∠FHD+∠FDH=180°,∴∠BHF=∠FBH=45°,∴∠DHF=90°,∴△FHD为等腰直角三角形,∴DH=6,∴FG•DH÷2=DG•AD÷2=65,∴DG=6.5.故答案为:6.5.三.解答题(共7小题)16.如图,点P在正方形ABCD的对角线AC上,点E在边BC上,且PE=PB.(1)求证:PE=PD;(2)试探究BC2,EC2,PE2三者之间满足的等量关系,并证明你的结论.【解答】(1)证明:∵四边形ABCD是正方形,∴BC=DC,∠ACB=∠ACD,在△PBC和△PDC中,,∴△PBC≌△PDC(SAS),∴PB=PD,∵PE=PB,∴PE=PD;(2)解:BC2+EC2=2PE2,证明如下:连接DE,如图所示:∵四边形ABCD是正方形,∴∠BCD=90°,BC=CD,由(1)得:△PBC≌△PDC,∴∠PBC=∠PDC,∵PE=PB,∴∠PBC=∠PEB,∴∠PDC=∠PEB,∵∠PEB+∠PEC=180°,∴∠PDC+∠PEC=180°,∴△PDE是等腰直角三角形,∴DE2=PE2+PD2=2PE2,在Rt△CDE中,由勾股定理得:CD2+EC2=DE2,∴BC2+EC2=2PE2.17.如图,四边形ABCD为正方形,点E、F分别是AB、CD的中点,DG⊥CF于点G.(1)求证:AE∥CF;(2)求证:∠AGE=90°;(3)若正方形的边长为2,则线段CG的长度为.【解答】解:(1)∵AF=CE,AF=CE,∴四边形AFCE是平行四边形,∴AE∥CF;(2)如图,取AE和DG交于H,∵CF∥AE,DG⊥CF,∴DG⊥AE于H,∴△DGE是等腰三角形,∴H是DG的中点,∴AG=AD,在△ADE和△AGE中,,∴△ADE≌△AGE(SSS),∴∠AGE=∠ADE=90°;(3)∵AG=AD=2,DE=1,∴AE=,又∵GH⊥AE,∴,解得HG=,∴DG=,∴,故答案为.18.如图,已知四边形ABCD为正方形,△CDE为等边三角形.(1)求证:AE=BE;(2)若AB=10,求△BCE的面积.【解答】(1)证明:∵四边形ABCD为正方形,∴AD=BC,∠ADC=∠BCD=90°,∵△CDE为等边三角形,∴ED=EC,∠EDC=∠ECD=60°,∴∠ADE=∠BCE,∴△ADE≌△BCE(SAS),∴AE=BE;(2)解:过E点作EF⊥AB,垂足为F,∵AE=BE,∴AF=BF,∵AB=10,∴BF=5,∵BC=AB=10,∴S△BCE=BC•BF=×10×5=25.19.如图,在正方形ABCD中,AB=,E为正方形ABCD内一点,DE=AB,∠EDC=α(0°<α<90°),连结CE,AE,过点D作DF⊥AE,垂足为点F,交CE的延长线于点G,连结AG.(1)当α=20°时,求∠DAE的度数;(2)判断△AEG的形状,并说明理由;(3)当GF=1时,求CE的长.【解答】解:(1)∵四边形ABCD是正方形,∴∠ADC=90°,AB=AD,∵∠CDE=20°,∴∠ADE=70°,∵DE=AB,∴DA=DE,∴∠DAE=∠DEA=×(180°﹣70°)=55°.(2)结论:△AEG是等腰直角三角形.理由:∵AD=DE,DF⊥AE,∴DG是AE的垂直平分线,∴AG=GE,∴∠GAE=∠GEA,∵DE=DC=AD,∴∠DAE=∠DEA,∠DEC=∠DCE,∵∠DAE+∠DEA+∠DEC+∠DCE+∠ADC=360°,∴∠DEA+∠DEC=135°,∴∠GEA=45°,∴∠GAE=∠GEA=45°,∴∠AGE=90°,∴△AEG为等腰直角三角形.(3)如图,连接AC,∵四边形ABCD是正方形,∴AC=AB=,∵△AEG为等腰直角三角形,GF⊥AE,∴GF=AF=EF=1,∴AG=GE=,∵AC2=AG2+GC2,∴10=2+(EC+)2,∴EC=(负根已经舍弃).20.如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.(1)证明:△ADG≌△DCE;(2)连接BF,求证:AB=FB.【解答】证明:(1)∵四边形ABCD是正方形,∴∠ADG=∠C=90°,AD=DC,又∵AG⊥DE,∴∠DAG+∠ADF=90°=∠CDE+∠ADF,∴∠DAG=∠CDE,∴△ADG≌△DCE(ASA);(2)如图所示,延长DE交AB的延长线于H,∵E是BC的中点,∴BE=CE,又∵∠C=∠HBE=90°,∠DEC=∠HEB,∴△DCE≌△HBE(ASA),∴BH=DC=AB,即B是AH的中点,又∵∠AFH=90°,∴Rt△AFH中,BF=AH=AB.21.如图,在正方形ABCD和正方形CEFG中,点D在CG上,H是AF的中点.(1)求证:CH=AF;(2)若BC=1,CE=3,求CH的长.【解答】(1)证明:如图,延长AD交EF于M,连接AC,CF,∵四边形ABCD和四边形GCEF是正方形,∴∠ACD=∠GCF=45°,∴∠ACF=90°,∵H为AF的中点,∴;(2)解:方法一:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,∴AB=BC=1,CE=EF=3,∠E=90°,则AM=BC+CE=1+3=4,FM=EF﹣AB=3﹣1=2,∠AMF=90°,在Rt△AMF中,由勾股定理得:=,∴.方法二:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,∴AB=BC=1,CE=EF=3,∠E=90°,∴AC=,CF=3,∴AF==,∴.22.正方形ABCD中,点P是边CD上的任意一点,连接BP,O为BP的中点,作PE⊥BD.连接EO,AE,EC.于E,连接ED,AE,EC.(1)当∠DAE=25°时,求∠AEC的度数;(2)当∠PBC=15°时,DP=4,求正方形的边长;(3)当AE=时,求BP的长.【解答】解:(1)∵四边形ABCD是正方形,∴∠ADE=∠CDE=45°,又∵∠DAE=25°,∴∠AEB=∠ADE+∠DAE=45°+25°=70°,在△DAE和△DCE中,,∴△DAE≌△DCE(SAS),∴∠DEA=∠DEC,∴∠AEB=∠CEB,∴∠AEC=2∠AEB=2×70°=140°;(2)∵∠PBC=15°,∴∠PBD=30°,∠BPC=75°,∵PE⊥BD,∴∠BPE=60°,∴∠DPE=180°﹣75°﹣60°=45°,∵DP=4,∠DPE=∠EDP=45°,∴DE=EP=DP=2,在Rt△EBP中,∠EBP=30°,∴BE=EP=2,∴DB=2+2,∴DC=DB=2+;(3)连接OC,在△BAE和△BCE中,,∴△BAE≌△BCE(SAS),∴EC=AE=,在Rt△EBP中,O为BP中点,∴EO=BO=OP,同理:OC=OB=OP,∴OE=OC,∵∠EBP=45°﹣∠PBC,OE=OB,∴∠EOP=2(45°﹣∠PBC)=90°﹣2∠PBC,又∵∠POC=2∠PBC,∴∠EOC=90°﹣2∠PBC+2∠PBC=90°,∴EO⊥OC,在△OCE中,OC=OE,OE⊥OC,∴OE=OC=EC=×=,∴BP=2OE=2。
2020北师大版九年级数学上《正方形的判定》常考题(含详细的答案解析)

【文库独家】正方形的判定常考题一、选择题(共21小题)1、下列五个命题:(1)若直角三角形的两条边长为5和12,则第三边长是13;(2)如果a≥0,那么=a(3)若点P(a,b)在第三象限,则点P(﹣a,﹣b+1)在第一象限;(4)对角线互相垂直且相等的四边形是正方形;(5)两边及第三边上的中线对应相等的两个三角形全等.其中不正确命题的个数是()A、2个B、3个C、4个D、5个2、下列命题中,正确命题是()A、两条对角线相等的四边形是平行四边形B、两条对角线相等的四边形是矩形C、两条对角线互相垂直平分的四边边是菱形D、两条对角线平分且相等的四边形是正方形3、下列命题中,真命题是()A、两条对角线垂直的四边形是菱形B、对角线垂直且相等的四边形是正方形C、两条对角线相等的四边形是矩形D、两条对角线相等的平行四边形是矩形4、下列说法中错误的是()A、两条对角线互相平分的四边形是平行四边形B、两条对角线相等的四边形是矩形C、两条对角线互相垂直的矩形是正方形D、两条对角线相等的菱形是正方形5、下列说法中,不正确的是()A、有三个角是直角的四边形是矩形B、对角线相等的四边形是矩形C、对角线互相垂直的矩形是正方形D、对角线互相垂直的平行四边形是菱形6、如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE.连接DE,DF,EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②四边形CDFE不可能为正方形,③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是()A、①②③B、①④⑤C、①③④D、③④⑤7、如图,已知四边形ABCD是平行四边形,下列结论中不正确的是()A、当AB=BC时,它是菱形B、当AC⊥BD时,它是菱形C、当∠ABC=90°时,它是矩形D、当AC=BD时,它是正方形8.下列命题中正确的是()A、两条对角线互相平分的四边形是平行四边形B、两条对角线相等的四边形是矩形C、两条对角线互相垂直的四边形是菱形D、两条对角线互相垂直且平分的四边形是正方形9、已知四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是()A、∠D=90°B、AB=CDC、AD=BCD、BC=CD10、如图,将一张长方形纸片对折两次,然后剪下一个角,打开.如果要剪出一个正方形,那么剪口线与折痕成()A、22.5°角B、30°角C、45°角D、60°角11、在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是()A、AC=BD,AB∥CD,AB=CDB、AD∥BC,∠A=∠CC、AO=BO=CO=DO,AC⊥BDD、AO=CO,BO=DO,AB=BC12、用两个全等的直角三角形拼下列图形:(1)平行四边形(不包含菱形、矩形、正方形);(2)矩形;(3)菱形;(4)正方形;(5)等腰三角形,一定可以拼成的图形是()A、(1)(2)(5)B、(2)(3)(5)C、(1)(4)(5)D、(1)(2)(3)13、下列说法中,错误的是()A、一组对边平行且相等的四边形是平行四边形B、两条对角线互相垂直且平分的四边形是菱形C、四个角都相等的四边形是矩形D、邻边相等的菱形是正方形14、下列说法中错误的是()A、一组对边平行且一组对角相等的四边形是平行四边形B、每组邻边都相等的四边形是菱形C、四个角都相等的四边形是矩形D、对角线互相垂直平分的四边形是正方形15、四边形ABCD的对角线AC和BD相交于点O,设有下列条件:①AB=AD;②∠DAB=90°;③AO=CO,BO=DO;④矩形ABCD;⑤菱形ABCD,⑥正方形ABCD,则下列推理不成立的是()A、①④⇒⑥B、①③⇒⑤C、①②⇒⑥D、②③⇒④16、在下列命题中,是真命题的是()A、两条对角线相等的四边形是矩形B、两条对角线互相垂直的四边形是菱形C、两条对角线互相平分的四边形是平行四边形D、两条对角线互相垂直且相等的四边形是正方形17、下列说法中错误的是()A、四个角相等的四边形是矩形B、对角线互相垂直的矩形是正方形C、对角线相等的菱形是正方形D、四条边相等的四边形是正方形18、下列说法正确的是()A、对角线相等的四边形是矩形B、有一组邻边相等的矩形是正方形C、菱形的四条边、四个角都相等D、三角形一边上的中线等于这边的一半19、下列说法错误的是()A、平行四边形的内角和与外角和相等B、一组邻边相等的平行四边形是菱形C、对角线互相平分且相等的四边形是矩形D、四条边都相等的四边形是正方形20、矩形的四个内角平分线围成的四边形()A、一定是正方形B、是矩形C、菱形D、只能是平行四边形21、下列命题正确的是()A、一组对边平行,另一组对边相等的四边形是平行四边形B、对角线互相垂直的四边形是菱形C、对角线相等的四边形是矩形D、一组邻边相等的矩形是正方形二、填空题(共3小题)22、如图,在四边形ABCD中,AB=BC=CD=DA,对角线AC与BD相交于点O,若不增加任何字母与辅助线,要使四边形ABCD是正方形,则还需增加一个条件是_________.23、要使一个菱形ABCD成为正方形,则需增加的条件是_________.(填一个正确的条件即可)24、把“直角三角形,等腰三角形,等腰直角三角形”填入下列相应的空格上.(1)正方形可以由两个能够完全重合的_________拼合而成;(2)菱形可以由两个能够完全重合的_________拼合而成;(3)矩形可以由两个能够完全重合的_________拼合而成.三、解答题(共6小题)25、如图,点D是线段AB的中点,点C是线段AB的垂直平分线上的任意一点,DE⊥AC于点E,DF⊥BC于点F.(1)求证:CE=CF;(2)点C运动到什么位置时,四边形CEDF成为正方形?请说明理由.26、已知:如图,D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别是E、F,且BF=CE.(1)求证:△ABC是等腰三角形;(2)当∠A=90°时,试判断四边形AFDE是怎样的四边形,证明你的结论.27、如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.(1)求证:四边形ABCD是菱形;(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.28、已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥A N,垂足为点E,(1)求证:四边形ADCE为矩形;(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.29、如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.(1)求证:△BED≌△CFD;(2)若∠A=90°,求证:四边形DFAE是正方形.30、如图,在Rt△ABC与Rt△ABD中,∠ABC=∠BAD=90°,AD=BC,AC,BD相交于点G,过点A作AE∥DB交CB 的延长线于点E,过点B作BF∥CA交DA的延长线于点F,AE,BF相交于点H.(1)图中有若干对三角形是全等的,请你任选一对进行证明;(不添加任何辅助线)(2)证明:四边形AHBG是菱形;(3)若使四边形AHBG是正方形,还需在Rt△ABC的边长之间再添加一个什么条件?请你写出这个条件.(不必证明)答案与评分标准一、选择题(共21小题)1、下列五个命题:(1)若直角三角形的两条边长为5和12,则第三边长是13;(2)如果a≥0,那么=a(3)若点P(a,b)在第三象限,则点P(﹣a,﹣b+1)在第一象限;(4)对角线互相垂直且相等的四边形是正方形;(5)两边及第三边上的中线对应相等的两个三角形全等.其中不正确命题的个数是()A、2个B、3个C、4个D、5个考点:勾股定理;二次根式的性质与化简;点的坐标;全等三角形的判定;正方形的判定。
人教版数学中考复习《正方形的计算和证明问题》专项练习(含答案)
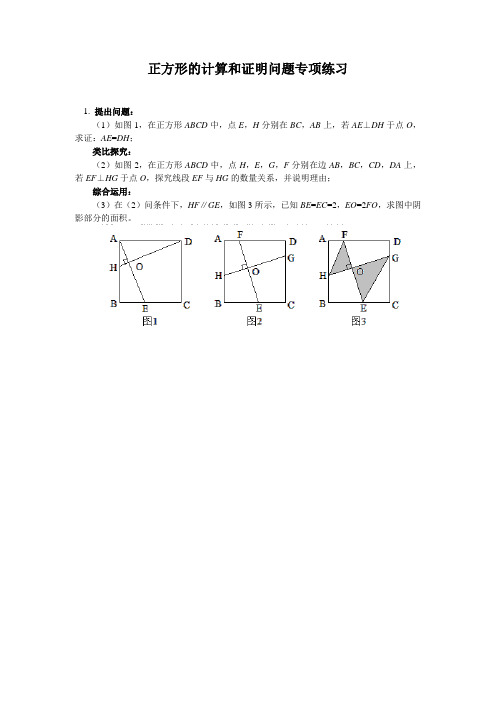
正方形的计算和证明问题专项练习1. 提出问题:(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;类比探究:(2)如图2,在正方形ABCD中,点H,E,G,F分别在边AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由;综合运用:(3)在(2)问条件下,HF∥GE,如图3所示,已知BE=EC=2,EO=2FO,求图中阴影部分的面积。
2. 如图1,点O 为正方形ABCD 的中心。
(1)将线段OE 绕点O 逆时针方向旋转︒90,点E 的对应点为点F ,连接EF ,AE ,BF ,请依题意补全图1;(2)根据图1中补全的图形,猜想并证明AE 与BF 的关系;(3)如图2,点G 是OA 中点,△EGF 是等腰直角三角形,H 是EF 的中点,︒=∠90EGF ,AB =2=GE ,△EGF 绕G 点逆时针方向旋转α角度,请直接写出旋转过程中BH 的最大值。
3. 如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(﹣4,4)。
点P从点A 出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动。
连接BP,过P点作BP 的垂线,与过点Q平行于y轴的直线l相交于点D。
BD与y轴交于点E,连接PE。
设点P 运动的时间为t(s)。
(1)∠PBD的度数为,点D的坐标为(用t表示);(2)当t为何值时,△PBE为等腰三角形?(3)探索△POE的周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值。
正方形的计算和证明问题专项练习参考答案1.(1)证明:∵四边形ABCD是正方形,∴AB=DA,∠ABE=90°=∠DAH。
∴∠HAO+∠OAD=90°。
∵AE⊥DH,∴∠ADO+∠OAD=90°。
∴∠HAO=∠ADO。
初中数学 正方形 练习题(含答案)

第五章四边形第29课时正方形1.阅读下面材料:已知:如图,在正方形ABCD中,边AB=a1.第1题图按照以下操作步骤,可以从该正方形开始,构造一系列的正方形,它们之间的边满足一定的关系,并且一个比一个小.请解决以下问题:(1)完成表格中的填空:①;②;③;④.(2)根据以上第三步、第四步的作法画出第三个正方形CHIJ(不要求尺规作图).数学文化专练2. (2019绵阳)公元三世纪,我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是125,小正方形面积是25,则(sinθ-cosθ)2=()第2题图A. 15 B.55 C.355 D.95七巧板3. (2019苏州)“七巧板”是我们祖先的一项卓越创造,可以拼出许多有趣的图形,被誉为“东方魔板”.图①是由边长为10 cm的正方形薄板分为7块制作成的“七巧板”,图②是用该“七巧板”拼成的一个“家”的图形,该“七巧板”中7块图形之一的正方形边长为cm(结果保留根号).第3题图参考答案中考试题中的核心素养核心素养提升1. 解:(1)①斜边和一条直角边分别相等的两个直角三角形全等;②(2-1)a1;③(2-1)2a1;④(2-1)n-1a1.(2)所画正方形CHIJ见解图.第1题解图数学文化专练2. A【解析】∵大正方形的面积是125,小正方形面积是25,∴大正方形的边长为55,小正方形的边长为5,∴55cos θ-55sin θ=5,∴cos θ-sin θ=55,∴(sin θ-cos θ)2=[-(cos θ-sin θ)]2=15.3. 522【解析】如解图,由题意可知正方形ABCD的边长AB=10 cm,∵△AOB是等腰直角三角形,∴AO=BO=52.∵△BEF是等腰直角三角形,∴BE=EF.∵四边形OEFG是正方形,∴OE=EF=BE,∴OE=52 2.第3题解图。
2024年数学九年级上册几何基础练习题(含答案)

2024年数学九年级上册几何基础练习题(含答案)试题部分一、选择题(每题2分,共20分)1. 在直角三角形ABC中,∠C是直角,AC=3cm,BC=4cm,求AB的长度。
A. 5cmB. 6cmC. 7cmD. 8cm2. 在等腰三角形ABC中,AB=AC,∠BAC=60°,求∠ABC的度数。
A. 60°B. 120°C. 30°D. 45°3. 在平行四边形ABCD中,AB=CD,AD=BC,∠A=90°,求∠C的度数。
A. 90°B. 45°C. 135°D. 180°4. 在梯形ABCD中,AB//CD,AD=BC,∠ABC=60°,求∠ADC的度数。
A. 60°B. 120°C. 90°D. 45°5. 在正方形ABCD中,对角线AC和BD相交于点O,求∠AOD的度数。
A. 45°B. 90°C. 135°D. 180°6. 在圆O中,半径OA=5cm,弦AB=8cm,求∠AOB的度数。
A. 30°B. 60°C. 90°D. 120°7. 在三角形ABC中,∠BAC=90°,BC=10cm,AC=6cm,求AB的长度。
A. 8cmB. 12cmC. 16cmD. 20cm8. 在等边三角形ABC中,AB=AC=BC,求∠ABC的度数。
A. 60°B. 120°C. 30°D. 45°9. 在矩形ABCD中,AB=CD,AD=BC,∠ABC=90°,求∠ADC的度数。
A. 90°B. 45°C. 135°D. 180°10. 在菱形ABCD中,AB=BC=CD=DA,∠ABC=60°,求∠ADC的度数。
2021年九年级中考数学复习强化练习——正方形及四边形综合问题

正方形及四边形综合问题一、选择题1. 下列条件不能判断▱ABCD是正方形的是()A.∠ABC=90°且AB=ADB.AB=BC且AC⊥BDC.AC⊥BD且AC=BDD.AC=BD且AB=BC2. 下列说法,正确的个数有 ()①正方形既是菱形又是矩形;②有两个角是直角的四边形是矩形;③菱形的对角线相等;④对角线互相垂直平分且相等的四边形是正方形.A.1个B.2个C.3个D.4个3. 如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边的正方形EFGH的周长为()A. 2B. 2 2C. 2+1D. 22+14. 如图正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于点O,则∠DOC的度数为()A.60°B.67.5°C.75°D.54°5. (2020·威海)如图,在▱ABCD中,对角线BD⊥AD,AB=10,AD=6,O为BD的中点,E为边AB上一点,直线EO交CD于点F,连结DE,BF.下列结论不成立的是()A.四边形DEBF为平行四边形B.若AE=3.6,则四边形DEBF为矩形C.若AE=5,则四边形DEBF为菱形D.若AE=4.8,则四边形DEBF为正方形6. 如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为()A. 2B. 3C. 2D. 17. 已知在平面直角坐标系中放置了5个如图X3-1-10所示的正方形(用阴影表示),点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3在x轴上.若正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是()A.3+318 B.3+118C.3+36 D.3+168. (2020·东营)如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC 、BD 相交于点O ,过点P 分别作AC 、BD 的垂线,分别交AC 、BD 于点E 、F ,交AD 、BC 于点M 、N ,下列结论:①△APE ≌△AME ;②PM+PN=AC ;③222PE PF PO ;④△POF ∽△BNF ;⑤点O 在M 、N 两点的连线上.其中正确的是( )A. ①②③④B. ①②③⑤C. ①②③④⑤D. ③④⑤A BCDEFMNOP二、填空题9. 如图,在正方形ABCD 中,AC 为对角线,点E 在AB 边上,EF ⊥AC 于点F ,连接EC ,AF=3,若△EFC 的周长为12,则EC 的长为 .10. 如图,E ,F是正方形ABCD 的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF 的周长是 .11. ▱ABCD的对角线AC 与BD 相交于点O ,且AC ⊥BD ,请添加一个条件:________,使得▱ABCD 为正方形.12. 如图,正方形ABCO 的顶点C ,A 分别在x 轴,y 轴上,BC 是菱形BDCE 的对角线,若∠D =60°,BC =2,则点D 的坐标是________.13. 如图,在正方形ABCD 中,点E ,N ,P ,G 分别在边AB ,BC ,CD ,DA 上,点M ,F ,Q 都在对角线BD 上,且四边形MNPQ 和AEFG 均为正方形,则S 正方形MNPQS 正方形AEFG的值等于________.14. 如图,正方形ABCD的边长为22,对角线AC,BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为________.15. 如图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是________.16. 如图,正方形ABCD的面积为3 cm2,E为BC边上一点,∠BAE=30°,F 为AE的中点,过点F作直线分别与AB,DC相交于点M,N.若MN=AE,则AM的长等于________cm.三、解答题17. 如图,在正方形ABCD中,E是DC边上一点(与D,C不重合),连接AE,将△ADE沿AE所在的直线折叠得到△AFE,延长EF交BC于点G,连接AG,作GH⊥AG,与AE的延长线交于点H,连接CH.显然AE是∠DAF的平分线,EA是∠DEF的平分线.仔细观察,请逐一找出图中其他的角平分线(仅限于小于180°的角的平分线),并说明理由.18. 如图①,在四边形ABCD中,点P是AB上一点,点E在射线DP上,且∠BED=∠BAD,连接AE.(1)若AB=AD,在DP上截取点F,使得DF=BE,连接AF,求证:△ABE≌△ADF;(2)如图②,若四边形ABCD是正方形,点P在AB的延长线上,BE=1,AE=32,求DE的长;(3)如图③,若四边形ABCD是矩形,AD=2AB,点P在AB的延长线上,AE=5 BE,若AE=nDE,求n的值.图①图②图③19. 已知正方形ABCD中,点E在BC上,连接AE,过点B作BF⊥AE于点G,交CD于点F.(1)如图①,连接AF,若AB=4,BE=1,求证:△BCF≌△ABE;(2)如图②,连接BD,交AE于点N,连接AC,分别交BD、BF于点O、M,连接GO,求证:GO平分∠AGF;(3)如图③,在第(2)问的条件下,连接CG,若CG⊥GO,AG=nCG,求n的值.20. (2020·河南)将正方形ABCD的边AB绕点A逆时针旋转至AB′,记旋转角为.连接BB′,过点D作DE垂直于直线BB′,垂足为点E,连接DB′,CE.(1)如图1,当=60°时,△DEB′的形状为,连接BD,可求出BBCE′的值为;(2)当0°<<360°且≠90°时,①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;②当以点B′、E、C、D为顶点的四边形是平行四边形时,请直接写出BEB E′的值.正方形及四边形综合问题-答案一、选择题1. 【答案】B[解析]A.▱ABCD中,若∠ABC=90°,则▱ABCD是矩形,再由AB=AD 可得是正方形,故此选项错误;B.▱ABCD中,若AB=BC,则▱ABCD是菱形,再由AC⊥BD仍可得是菱形,不能判定为正方形,故此选项正确;C.▱ABCD中,若AC⊥BD,则▱ABCD是菱形,再由AC=BD可得是正方形,故此选项错误;D.▱ABCD中,若AC=BD,则▱ABCD是矩形,再由AB=BC可得是正方形,故此选项错误.故选B.2. 【答案】B3. 【答案】B【解析】∵正方形ABCD的面积为1,∴BC=CD=1,∵E、F是边的中点,∴CE=CF=12,∴EF=(12)2+(12)2=22,则正方形EFGH的周长为4×22=2 2.4. 【答案】A[解析]连接BF,∵E为AB中点,FE⊥AB,∴EF垂直平分AB,∴AF=BF.∵AF=2AE,∴AF=AB,∴AF=BF=AB,∴△ABF为等边三角形,∴∠FBA=60°,BF=BC,∴∠FCB=∠BFC=15°,∵四边形ABCD为正方形,∴∠DBC=45°,根据三角形的外角等于与它不相邻的两个内角的和得∠DOC=15°+45°=60°.5. 【答案】:∵O为BD的中点,∴OB=OD,∵四边形ABCD为平行四边形,∴DC∥AB,∴∠CDO=∠EBO,∠DFO=∠OEB,∴△FDO≌△EBO(AAS),∴OE=OF,∴四边形DEBF为平行四边形,故A选顶结论正确,若AE=3.6,AD=6,∴,又∵,∴,∵∠DAE=∠BAD,∴△DAE∽△BAD,∴AED=∠ADB=90°.故B选项结论正确,∵AB=10,AE=5,∴BE=5,又∵∠ADB=90°,∴DE AB =5,∴DE =BE ,∴四边形DEBF 为菱形. 故C 选项结论正确,∵AE =3.6时,四边形DEBF 为矩形,AE =5时,四边形DEBF 为菱形, ∴AE =4.8时,四边形DEBF 不可能是正方形. 故D 不正确. 故选:D .6. 【答案】B【解析】∵AB =2,∴BF =2,又∵BM =12BC =1,由勾股定理得FM =FB 2-BM 2= 3.7. 【答案】⎝⎛⎭⎪⎫72,0D 解析:过小正方形的一个顶点D 3作FQ ⊥x 轴于点Q ,过点A 3作A 3F ⊥FQ 于点F .∵正方形A 1B 1C 1D 1的边长为1,∠B 1C 1O =60°,B 1C 1∥B 2C 2∥B 3C 3, ∴∠B 3C 3E 4=60°,∠D 1C 1E 1=30°,∠E 2B 2C 2=30°, ∴D 1E 1=12D 1C 1=12,∴D 1E 1=B 2E 2=12, ∴cos30°=B 2E 2B 2C 2=12B 2C 2,解得:B 2C 2=33.∴B 3E 4=36,cos30°=B 3E 4B 3C 3.解得:B 3C 3=13. 则D 3C 3=13. 根据题意得出:∠D 3C 3Q =30°,∠C 3D 3Q =60°,∠A 3D 3F =30°, ∴D 3Q =12×13=16,FD 3=D 3A 3·cos30°=13×32=36.则点A3到x轴的距离FQ=D3Q+FD3=16+36=3+16.8. 【答案】B【解析】本题考查了垂线、平行线和正方形的性质,全等三角形的判定与性质、等腰直角三角形的判断和性质、相似三角形的判定和性质,是常见问题的综合,灵活的运用所学知识是解答本题的关键.综合应用垂线、平行线和正方形的性质,全等三角形的判定与性质、等腰直角三角形的判断和性质、相似三角形的判定和性质等知识,逐个判断5个结论的正确性,得出结论.①∵正方形ABCD,∴∠APE=∠AME=45°,∵PM⊥AE,∴∠AEP=∠AEM=90°,∵AE=AE,∴△APE≌△AME(ASA);②过点N作NQ⊥AC于点Q,则四边形PNQE是矩形,∴PN=EQ,∵正方形ABCD,∴∠P AE=∠MAE=45°,∵PM⊥AE,∴∠PEA=45°,∴∠P AE=∠APE,PE=NQ,∴△APE等腰直角三角形,∴AE=PE,同理得:△NQC等腰直角三角形,∴NQ=CQ,∵△APE≌△AME,∴PE=ME,∴PE=ME= NQ=CQ,∴PM=AE+CQ,∴PM+PN=AE+CQ+EQ=AC,即PM+PN=AC成立;③∵正方形ABCD,∴AC⊥BD,∴∠EOF是直角,∵过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,∴∠PEO和∠PFO是直角,∴四边形PFOE 是矩形,∴PF=OE,在R t△PEO中,有PE2+OE2=PO2,∴PE2+PF2=PO2,即PE2+PF2=PO2成立;④△BNF是等腰直角三角形,点P不在AB的中点时,△POF不是等腰直角三角形,所以△POF与△BNF不一定相似,即△POF∽△BNF不一定成立;⑤∵△AMP是等腰直角三角形,△PMN∽△AMP,∴△PMN是等腰直角三角形,∵∠MPN=90°,∴PM=PN,∵AP=22PM,BP=22PN,∴AP=BP,∴点P是AB的中点,又∵O为正方形的对称中点,∴点O在M、N两点的连线上.综上,①②③⑤成立,即正确的结论有4个,答案选B.二、填空题9. 【答案】5[解析]∵四边形ABCD是正方形,AC为对角线,∴∠F AE=45°,又∵EF⊥AC,∴∠AFE=90°,∴∠AEF=45°,∴EF=AF=3,∵△EFC的周长为12,∴FC=12-3-EC=9-EC,在Rt△EFC中,EC2=EF2+FC2,∴EC2=9+(9-EC)2,解得EC=5.10. 【答案】8 [解析]如图,连接BD 交AC 于点O ,∵四边形ABCD 为正方形,∴BD ⊥AC ,OD=OB=OA=OC , ∵AE=CF=2,∴OA -AE=OC -CF ,即OE=OF ,∴四边形BEDF 为平行四边形,且BD ⊥EF , ∴四边形BEDF 为菱形, ∴DE=DF=BE=BF , ∵AC=BD=8,OE=OF==2,∴由勾股定理得:DE===2,∴四边形BEDF 的周长=4DE=4×2=8,故答案为:8.11. 【答案】∠BAD =90°(答案不唯一)【解析】∵▱ABCD 的对角线AC 与BD 相交于点O ,且AC ⊥BD ,∴▱ABCD 是菱形,当∠BAD =90°时,菱形ABCD 为正方形.故可添加条件:∠BAD =90°.12. 【答案】(3+2,1) 【解析】如解图,过点D 作DG ⊥BC 于G ,DF ⊥x 轴于F ,∵在菱形BDCE 中,BD =CD ,∠BDC =60°,∴△BCD 是等边三角形,∴DF =CG =12BC =1,CF =DG =3,∴OF =3+2,∴D(3+2,1).解图13. 【答案】89 【解析】设BD =3a ,∠CDB =∠CBD =45°,且四边形PQMN 为正方形,∴DQ =PQ =QM =NM =MB ,∴正方形MNPQ 的边长为a ,正方形AEFG的对角线AF =12BD =32a ,∵正方形对角线互相垂直,∴S 正方形AEFG =12×32a×32a =98a 2,∴S 正方形MNPQ S 正方形AEFG =a 298a2=89.14. 【答案】55【解析】∵四边形ABCD 为正方形,∴AO =BO ,∠AOF =∠BOE=90°,∵AM ⊥BE ,∠AFO =∠BFM ,∴∠FAO =∠EBO ,在△AFO 和△BEO中,⎩⎨⎧∠AOF =∠BOE AO =BO ∠FAO =∠EBO,∴△AFO ≌△BEO(ASA ),∴FO =EO ,∵正方形ABCD的边长为22,E 是OC 的中点,∴FO =EO =1=BF ,BO =2,∴在Rt △BOE 中,BE =12+22=5,由∠FBM =∠EBO ,∠FMB =∠EOB ,可得△BFM ∽△BEO ,∴FM EO =BF BE ,即FM 1=15,∴FM =55.15. 【答案】62≤a ≤3-3 【解析】∵ABCD 是正方形,∴AB =a =22AC ,∴a的取值范围与AC 的长度直接相关.如解图①,当A ,C 两点恰好是正六边形一组对边中点时,a 的值最小,∵正六边形的边长为1,∴AC =3,∴AB =a =22AC =62;如解图②,连接MN ,延长AE ,BF 交于点G ,∵正六边形和正方形ABCD ,∴△MNG 、△ABG 、△EFG 为正三角形,设AE =BF =x ,则AM =BN =1-x ,AG =BG =AB =1+x =a ,∵GM =MN =2,∠BNM =60°,∴sin ∠BNM =sin 60°=BC 2BN =a 21-x,∴3()1-x =a ,∴3()2-a =a ,解得,a=233+1=3- 3.∴正方形边长a 的取值范围是62≤a ≤3- 3.16. 【答案】233或33【解析】如解图,过N 作NG ⊥AB ,交AB 于点G ,∵四边形ABCD 为正方形,∴AB =AD =NG = 3 cm ,在Rt △ABE 中,∠BAE =30°,AB = 3 cm ,∴BE =1 cm ,AE =2 cm ,∵F 为AE 的中点,∴AF =12AE =1 cm ,在Rt △ABE 和Rt △NGM 中,⎩⎨⎧AB =NGAE =NM ,∴Rt △ABE ≌Rt △NGM(HL ),∴BE =GM ,∠BAE =∠MNG =30°,∠AEB =∠NMG =60°,∴∠AFM =90°,即MN ⊥AE ,在Rt △AMF 中,∠FAM =30°,AF =1 cm ,∴AM =AF cos 30°=132=233cm ,由对称性得到AM′=BM =AB -AM =3-233=33 cm ,综上,AM 的长等于233或33 cm .解图三、解答题17. 【答案】[解析]过点H 作HN ⊥BM 于N ,利用正方形的性质及轴对称的性质,证明△ABG ≌△AFG ,可推出AG 是∠BAF 的平分线,GA 是∠BGF 的平分线;证明△ABG ≌△GNH ,推出HN=CN ,得到∠DCH=∠NCH ,推出CH 是∠DCM 的平分线;再证∠HGN=∠EGH ,可知GH 是∠EGM 的平分线. 解:过点H 作HN ⊥BM 于N ,则∠HNC=90°,∵四边形ABCD 为正方形,∴AD=AB=BC ,∠D=∠DAB=∠B=∠DCB=∠DCM=90°. ①∵将△ADE 沿AE 所在的直线折叠得到△AFE , ∴△ADE ≌△AFE ,∴∠D=∠AFE=∠AFG=90°,AD=AF ,∠DAE=∠F AE ,∴AF=AB. 又∵AG=AG ,∴Rt △ABG ≌Rt △AFG (HL), ∴∠BAG=∠F AG ,∠AGB=∠AGF ,∴AG 是∠BAF 的平分线,GA 是∠BGF 的平分线. ②由①知,∠DAE=∠F AE ,∠BAG=∠F AG ,又∵∠BAD=90°,∴∠GAF+∠EAF=×90°=45°,即∠GAH=45°.∵GH⊥AG,∴∠GHA=90°-∠GAH=45°,∴△AGH为等腰直角三角形,∴AG=GH.∵∠AGB+∠BAG=90°,∠AGB+∠HGN=90°,∴∠BAG=∠NGH.又∵∠B=∠HNG=90°,AG=GH,∴△ABG≌△GNH(AAS),∴BG=NH,AB=GN,∴BC=GN.∴BC-CG=GN-CG,∴BG=CN,∴CN=HN.∵∠HNC=90°,∴∠NCH=∠NHC=×90°=45°,∴∠DCH=∠DCM-∠NCH=45°,∴∠DCH=∠NCH,∴CH是∠DCM的平分线.③∵∠AGB+∠HGN=90°,∠AGF+∠EGH=90°,由①知,∠AGB=∠AGF,∴∠HGN=∠EGH,∴GH是∠EGM的平分线.综上所述,AG是∠BAF的平分线,GA是∠BGF的平分线,CH是∠DCM的平分线,GH是∠EGM的平分线.18. 【答案】(1)证明:∵∠BED=∠BAD,∠BPE=∠DP A,∴∠ABE=∠ADF,又∵AB=AD,BE=DF,∴△ABE≌△ADF;(2)解:如解图①,延长ED到点F,使得DF=BE,连接AF,解图①∵四边形ABCD 是正方形, ∴∠BAD =∠BED =∠BEP ,∵∠P =∠P ,∴∠PBE =∠ADP , ∴∠ABE =∠ADF , ∵BE =DF ,AB =AD , ∴△ABE ≌△ADF ,∴AE =AF ,∠BAE =∠F AD ,∴∠F AD +∠EAD =∠BAE +∠EAD =90°, ∴EF =2AE =32×2=6,∴DE =EF -DF =EF -BE =6-1=5;(3)解:如解图②,过点A 作AF ⊥AE 交ED 的延长线于点F ,解图②∵四边形ABCD 是矩形,∴∠BAD =∠BED =∠BEP =90°, ∵AF ⊥AE ,∠P =∠P ,∴∠PBE =∠ADP ,∠EAB =90°-∠EAD =∠F AD , ∴∠ABE =180°-∠PBE =180°-∠ADP =∠ADF , ∴△ABE ∽△ADF , ∴,21===AFAE DFBE ADAB∴AF =2AE ,DF =2BE ,在Rt △AEF 中,由勾股定理得EF 22AE AF +=5AE , ∵AE =5BE ,∴EF =5AE =5·5BE =5BE , ∴AE DE =53,∴n =53. 19. 【答案】(1)证明:∵四边形ABCD 是正方形,∴BC =CD =AD =AB =4,∠ABE =∠C =∠D =90°, ∴∠ABG +∠CBF =90°, ∵BF ⊥AE ,∴∠ABG +∠BAE =90°, ∴∠BAE =∠CBF , 在△BCF 和△ABE 中,⎩⎨⎧∠C =∠ABEBC =AB∠CBF =∠BAE, ∴△BCF ≌△ABE (ASA);(2)证明:∵AC ⊥BD ,BF ⊥AE , ∴∠AOB =∠AGB =∠AGF =90°, ∴A 、B 、G 、O 四点共圆, ∴∠AGO =∠ABO =45°,∴∠FGO =90°-45°=45°=∠AGO , ∴GO 平分∠AGF ;(3)解:如解图,连接EF ,解图∵CG ⊥GO ,∴∠OGC =90°,∵∠EGF =∠BCD =90°, ∴∠EGF +∠BCD =180°, ∴C 、E 、G 、F 四点共圆,∴∠EFC =∠EGC =180°-90°-45°=45°, ∴△CEF 是等腰直角三角形, ∴CE =CF ,同(1)得△BCF ≌△ABE , ∴CF =BE ,∴CE =BE =12 BC ,∴OA =12 AC = 22BC = 2CE , 由(2)得A 、B 、G 、O 四点共圆, ∴∠BOG =∠BAE ,∵∠GEC =90°+∠BAE ,∠GOA =90°+∠BOG , ∴∠GOA =∠GEC ,又∵∠EGC =∠AGO =45°,∴△AOG ∽△CEG , ∴AG CG =OACE =2, ∴AG = 2 CG , ∴n = 2 .20. 【答案】解: (1)等腰直角三角形,2. (2)①两个结论仍成立.证明:连接BD.∵AB=AB′,∠BAB′=,∴∠AB′B=90°-2a,∵∠B′AD=a -90°,AD=AB′,∴∠AB′D=135-2a,∴∠EB′D=∠AB′D -∠AB′B=45°.∵DE ⊥BB′,∴∠EDB′=∠EB′D=45°,∴△DEB′是等腰直角三角形,∴DB DE′=2. ∵四边形ABCD 为正方形,∴BD CD =2,∠BDC=45°.∴DB DE′=BDCD , ∵∠EDB′=∠BDC ,∴∠EDB′+∠EDB=∠BDC+∠EDB ,即∠BDB′=∠CDE.∴△B′DB ∽△EDC ,∴2BB BDCE CD′; ②3或1.思路提示:分两种情况.情形一,如图,当点B′在BE 上时,由BB CE′=2,设BB′=2m ,CE=2m . ∵CE ∥B′D ,CE=B′D ,∴B′D=2m ,在等腰直角三角形DEB′中,斜边B′D=2m ,∴B′E=DE=m ,于是得到BE B E ′2=3m mm. 情形二,如图,当点B′在BE 延长线上时,由BB CE′=2,设BB′=2m ,CE=2m .∵CE ∥B′D ,CE=B′D ,∴B′D=2m ,在等腰直角三角形DEB′中,斜边B′D=2m ,∴B′E=DE=m 。
中考数学复习----《正方形的判定》知识点总结与专项练习题(含答案解析)

中考数学复习----《正方形的判定》知识点总结与专项练习题(含答案解析)知识点总结1.直接判定:四条边都相等,四个角都是直角的四边形是正方形。
2.利用平行四边形判定:一组邻边相等且有一个角是直角的平行四边形是正方形。
(定义判定)3.利用菱形与矩形判定:①有一个角是直角的菱形是正方形。
②对角线相等的菱形是正方形。
③邻边相等的矩形是正方形。
④对角线相互垂直的矩形是正方形。
练习题1、(2022•绍兴)如图,在平行四边形ABCD中,AD=2AB=2,∠ABC=60°,E,F是对角线BD上的动点,且BE=DF,M,N分别是边AD,边BC上的动点.下列四种说法:①存在无数个平行四边形MENF;②存在无数个矩形MENF;③存在无数个菱形MENF;④存在无数个正方形MENF.其中正确的个数是()A.1B.2C.3D.4【分析】根据题意作出合适的辅助线,然后逐一分析即可.【解答】解:连接AC,MN,且令AC,MN,BD相交于点O,∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵BE=DF,∴OE=OF,只要OM=ON,那么四边形MENF就是平行四边形,∵点E,F是BD上的动点,∴存在无数个平行四边形MENF,故①正确;只要MN=EF,OM=ON,则四边形MENF是矩形,∵点E,F是BD上的动点,∴存在无数个矩形MENF,故②正确;只要MN⊥EF,OM=ON,则四边形MENF是菱形,∵点E,F是BD上的动点,∴存在无数个菱形MENF,故③正确;只要MN=EF,MN⊥EF,OM=ON,则四边形MENF是正方形,而符合要求的正方形只有一个,故④错误;故选:C.2、(2022•滨州)下列命题,其中是真命题的是()A.对角线互相垂直的四边形是平行四边形B.有一个角是直角的四边形是矩形C.对角线互相平分的四边形是菱形D.对角线互相垂直的矩形是正方形【分析】根据,平行四边形,矩形,菱形,正方形的判定方法一一判断即可.【解答】解:A、对角线互相垂直的四边形是平行四边形,是假命题,本选项不符合题意;B、有一个角是直角的四边形是矩形,是假命题,本选项不符合题意;C、对角线互相平分的四边形是菱形,是假命题,本选项不符合题意;D、对角线互相垂直的矩形是正方形,是真命题,本选项符合题意.故选:D.3、(2022•攀枝花)如图,以△ABC的三边为边在BC上方分别作等边△ACD、△ABE、△BCF.且点A在△BCF内部.给出以下结论:①四边形ADFE是平行四边形;②当∠BAC =150°时,四边形ADFE是矩形;③当AB=AC时,四边形ADFE是菱形;④当AB=AC,且∠BAC=150°时,四边形ADFE是正方形.其中正确结论有(填上所有正确结论的序号).【分析】①利用SAS证明△EFB≌△ACB,得出EF=AC=AD;同理由△CDF≌△CAB,得DF=AB=AE;根据两边分别相等的四边形是平行四边形得出四边形ADFE是平行四边形,即可判断结论①正确;②当∠BAC=150°时,求出∠EAD=90°,根据有一个角是90°的平行四边形是矩形即可判断结论②正确;③先证明AE=AD,根据一组邻边相等的平行四边形是菱形即可判断结论③正确;④根据正方形的判定:既是菱形,又是矩形的四边形是正方形即可判断结论④正确.【解答】解:①∵△ABE、△CBF是等边三角形,∴BE=AB,BF=CB,∠EBA=∠FBC=60°;∴∠EBF=∠ABC=60°﹣∠ABF;∴△EFB≌△ACB(SAS);∴EF=AC=AD;同理由△CDF≌△CAB,得DF=AB=AE;由AE=DF,AD=EF即可得出四边形ADFE是平行四边形,故结论①正确;②当∠BAC=150°时,∠EAD=360°﹣∠BAE﹣∠BAC﹣∠CAD=360°﹣60°﹣150°﹣60°=90°,由①知四边形AEFD是平行四边形,∴平行四边形ADFE是矩形,故结论②正确;③由①知AB=AE,AC=AD,四边形AEFD是平行四边形,∴当AB=AC时,AE=AD,∴平行四边形AEFD是菱形,故结论③正确;④综合②③的结论知:当AB=AC,且∠BAC=150°时,四边形AEFD既是菱形,又是矩形,∴四边形AEFD是正方形,故结论④正确.故答案为:①②③④.。
2021-2022学年北师大版九年级数学上册正方形的性质习题含答案

北师版九年级数学上册1.3.1正方形的性质一、选择题(共10小题,3*10=30)1.已知在四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是()A.∠D=90°B.AB=CD C.AD=BC D.BC=CD2.正方形具有而菱形不一定具有的性质是( )A.四条边都相等B.对角线互相垂直平分C.对角线相等D.对角线平分一组对角3.如图,在正方形ABCD的外侧,作等边△ABE,则∠BED的度数为( )A.15° B.35° C.45° D.55°4.如图,在菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为( )A.14 B.15 C.16 D.175.如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠ACP的度数是( )A.45° B.22.5° C.67.5° D.75°6. 如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是()A.1 B.2 C.3 D.47.如图,在正方形ABCD中,AB=2,P是AD边上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE +PF 的值为( )A .4B .2 2C . 2D .28.四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD 的内角,正方形ABCD 变为菱形ABC′D′.若∠D′AB =30°,则菱形ABC′D′的面积与正方形ABCD 的面积之比是( )A .1B .12C .22D .329.如图,正方形ABCD 的边长为1,点E ,F 分别是对角线AC 上的两点,EG ⊥AB.EI ⊥AD ,FH ⊥AB ,FJ ⊥AD ,垂足分别为G ,I ,H ,J.则图中阴影部分的面积等于 ( )A .1B .12C .13D .1410.如图,正方形ABCD 的边AB 上有一动点E ,以EC 为边作矩形ECFG ,且边FG 过点D.在点E 从点A 移动到点B 的过程中,矩形ECFG 的面积( )A .先变大后变小B .先变小后变大C .一直变大D .保持不变 二.填空题(共8小题,3*8=24)11.如图,在正方形ABCD 中,E 是对角线BD 上一点,AE 的延长线交CD 于点F ,连接CE.若∠BAE =56°,则∠CEF =________.12. 如图,在正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰直角三角形有_______个13.如图,在正方形ABCD中,点E在边DC上,DE=4,EC=2,则AE的长为_______.14.如图,已知P是正方形ABCD对角线BD上的一点,且BP=BC,则∠ACP的度数是_______.15.如图,将正方形纸片按如图折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME=.16.如图,正方形ABCD的边长为1,点E在边DC上,AE平分∠DAC,EF⊥AC,F为垂足,那么FC=__________.17.如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为______.18.如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M,N分别是DC,DF的中点,连接MN.若AB=7,BE=5,则MN=__ __.三.解答题(共6小题,46分)19.(6分) 如图,在正方形ABCD中,点E在BC边的延长线上,点F在CD边的延长线上,且CE =DF,连接AE和BF相交于点M. 求证:AE=BF.20.(7分) 如图,在正方形ABCD中,E,F分别为边AD和CD上的点,且AE=CF,连接AF,CE 交于点G.求证:AG=CG.21.(7分) 如图,在正方形ABCD中,点E是BC上的一点,点F是CD延长线上的一点,且BE=DF,连接AE,AF,EF.(1)求证:△ABE≌△ADF;(2)若AE=5,请求出EF的长.22.(8分) 如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,CE.(1)求证:△BAE≌△CDE;(2)求∠AEB的度数.23.(8分) 如图,在正方形ABCD中,点E,F分别在边CD,AD上,且AF=CE.(1)求证:△ABF≌△CBE;(2)若AB=4,AF=1,求四边形BEDF的面积.24.(10分) 如图,E,F是正方形ABCD的对角线AC上的两点,且AE=CF.(1)求证:四边形BEDF是菱形;(2)若正方形边长为4,AE=2,求菱形BEDF的面积.参考答案1-5 DCCCB 6-10CCBBD11. 22° 12. 8 13. 213 14. 22.5° 15. 45° 16. 2 -1 17. 135° 18. 13 219. 解:在正方形ABCD 中,AB =BC =CD =AD ,∵CE =DF ,∴BE =CF ,在△AEB 和△BFC 中, ⎩⎪⎨⎪⎧AB =BC ,∠ABE =∠BCF ,BE =CF ,∴△AEB ≌△BFC(SAS),∴AE =BF 20. 证明:易证△ADF ≌△CDE(SAS),∴∠DAF =∠DCE ,在△AGE 和△CGF 中,⎩⎪⎨⎪⎧∠GAE =∠GCF ,∠AGE =∠CGF ,AE =CF ,∴△AGE ≌△CGF(AAS),∴AG =CG21. 解:(1)证明:∵四边形ABCD 是正方形,∴AB =AD ,∠ABC =∠ADC =∠ADF =90°.又∵BE =DF ,∴△ABE ≌△ADF(SAS)(2)由(1)知△ABE ≌△ADF ,∴AE =AF ,∠BAE =∠DAF ,∴∠EAF =∠DAF +∠EAD =∠BAE +∠EAD =90°,∴EF = 2 AE =5 222. 解:(1)∵△ADE 为等边三角形,∴AD =AE =DE ,∠EAD =∠EDA =60°,∵四边形ABCD 为正方形,∴AB =AD =CD ,∠BAD =∠CDA =90°,∴∠EAB =∠EDC =150°,在△BAE 和△CDE 中,⎩⎪⎨⎪⎧AB =DC ,∠EAB =∠EDC ,AE =DE ,∴△BAE ≌△CDE(SAS) (2)∵AB =AD ,AD =AE ,∴AB =AE ,∴∠ABE =∠AEB ,∵∠EAB =150°,∴∠AEB =12 (180°-150°)=15°23. 解:(1)∵四边形ABCD 是正方形,∴AB =CB ,∠A =∠C =90°.在△ABF 和△CBE 中, ⎩⎪⎨⎪⎧AB =CB ,∠A =∠C =90,AF =CE ,∴△ABF ≌△CBE(SAS) (2)由已知可得S 正方形ABCD =16,S △ABF =S △CBE =12×4×1=2.所以S 四边形BEDF =16-2×2=1224. 解:(1)连接BD 交AC 于点O ,∵四边形ABCD 为正方形,∴BD ⊥AC ,OD =OB =OA =OC ,∵AE =CF ,∴OA -AE =OC -CF ,即OE =OF ,∴四边形BEDF 为平行四边形,又∵BD ⊥EF ,∴▱BEDF 为菱形(2)∵正方形边长为4,∴BD =AC =42,∵AE =CF =2,∴EF =AC -22=22,∴S 菱形BEDF=12BD·EF =12×42×22=8。
2018届九年级数学上册第一章特殊平行四边形第3节正方形的性质与判定练习(含答案)北师大版

2018届九年级数学上册第⼀章特殊平⾏四边形第3节正⽅形的性质与判定练习(含答案)北师⼤版正⽅形的性质与判定⼀、选择题(本⼤题共10⼩题)1.如图,四边形ABCD是正⽅形,延长AB到点E,使AE=AC,则∠BCE的度数是()A.22.5°B.25°C.23° D.20°2.如⼀个四形的两对线互垂直平分且相等那么个四边形是()A.平⾏四边形B.菱形C.正⽅形 D.矩形3.四边形ABCD的对⾓线AC、BD相交于点O,AD∥BC,AD=BC,使四边形ABCD为正⽅形,下列条件中:①AC=BD;②AB=AD;③AB=CD;④AC⊥BD.需要满⾜()A.①②B.②③C.②④D .①②或①④4.如图,正⽅形ABCD的对⾓线AC、BD相交于点O,OA=3,则此正⽅形的⾯积为()A.3B.12C.18D.365.如图,在四边形ABCD中,对⾓线AC、BD相交于点O,若AO=C0=BO=DO,AC⊥BD,则四边形ABCD的形状是()A.平⾏四边形B.矩形C.菱形 D.正⽅形6.已知在正⽅形ABCD中,对⾓线AC与BD相交于点O,OE∥AB交BC于点E,若AD=8cm,则OE的长为()A.3cmB.4cmC.6cmD.8cm7.如图,正⽅形ABCD的边长为x,点E、F分别是对⾓线BD上的两点,过点E、F作AD、AB的平⾏线,则图中阴影部分的⾯积的和为()A.x2B.x2C.x2D.x28.如图,正⽅形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的⾯积是()A.30B.34C.36D.409.如图,E是正⽅形ABCD对⾓线AC上⼀点,EF⊥AB,EG⊥BC,F、G是垂⾜,若正⽅形ABCD周长为a,则EF+EG等于()A. B. C.aD.2a10.已知正⽅形ABCD的⼀条对⾓线长为2,则它的⾯积是()A.2B.4C.6⼆、填空题(本⼤题共6⼩题)11.如图,在正⽅形ABCD中,E为CD边上⼀点,以CE为对⾓线构造正⽅形CMEN,点N在正⽅形ABCD内部,连接AM,与CD边交于点F.若CF=3,DF=2,连接BN,则BN的长为 ______ .12.如图,已知:正⽅形EFGH的顶点E、F、G、H分别在正⽅形ABCD的边DA、AB、BC、CD上.若正⽅形ABCD的⾯积为16,AE=1,则正⽅形EFGH的⾯积为 ______ .13.如图,将正⽅形纸⽚按如图折叠,AM为折痕,点B落在对⾓线AC上的点E处,则∠CME= ______ .14.如图,BD是△ABC的⾓平分线,DE∥BC,交AB于点E,DF∥AB,交BC于点F,当△ABC满⾜条件 ______ 时,四边形BEDF是正⽅形.15.如图,正⽅形ABCD的边长为4,线段GH=AB,将GH的两端放在正⽅形的相邻的两边上同时滑动,如果G点从A点出发,沿图中所⽰⽅向按A→B→C→D→A滑动到A⽌,同时点H从点B出发,沿图中所⽰⽅向按B→C→D→A→B滑动到B⽌,在这个过程中,线段GH的中点P所经过的路线围成的图形的⾯积为 ______ .16.如图,在正⽅形ABCD中,AB=,点P为边AB上⼀动点(不与A、B重合),过A、P在正⽅形内部作正⽅形APEF,交边AD于F点,连接DE、EC,当△CDE为等腰三⾓形时,AP= ______ .三、解答题(本⼤题共8⼩题)17.已知:P是正⽅形ABCD对⾓线AC上⼀点,PE⊥AB,PF⊥BC,E、F分别为垂⾜.(1)求证:DP=EF.(2)试判断DP与EF的位置关系并说明理由.18.如图,在正⽅形ABCD中,E为对⾓线AC上⼀点,连接EB、ED.(1)写出图中所有的全等三⾓形;(2)延长BE交AD于点F,若∠DEB=140°,求∠AFE的度数.19.已知,在正⽅形ABCD中,E是CB延长线上⼀点,且EB=BC,F是AB的中点,请你将F点与图中某⼀标明字母的点连接成线段,使连成的线段与AE相等.并证明这种相等关系.20.如图,矩形ABCD的对⾓线相交于点O,PB∥AC,PC∥BD,PB、PC相交于点P.(1)猜想四边形PCOB是什么四边形,并说明理由;(2)当矩形ABCD满⾜什么条件时,四边形PCOB是正⽅形.正⽅形的性质与判定练习参考答案⼀、选择题。
北师大版九年级数学上册第一章 1.3正方形的性质与判定 同步练习题

北师大版九年级数学上册第一章 1.3正方形的性质与判定同步练习题第1课时正方形的性质1.正方形具有而菱形不一定具有的特征有(C)A.对角线互相垂直平分 B.内角和为360°C.对角线相等 D.对角线平分内角2.如图,在正方形ABCD的外侧作等边△ABE,则∠BED为(C)A.15° B.35° C.45° D.55°3.如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是(C)A.1 B.2 C.3 D.44.如图,在正方形ABCD和正方形CEFG中,BC=1,CE=3,点D是CG边上一点,H是AF的中点,那么CH5.如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点F的坐标为(-1,5).6.如图,正方形ABCD的边长为2,点E,F分别是CD,BC的中点,AE与DF交于点P,连接CP,则CP57.如图,正方形ABCD的边长为1,AC,BD是对角线,延长DA到H,使DH=DB,在DB 上截取DG=DC,连接GH交AB于点E,连接DE交AC于点F,连接FG,则下列结论:①四边形AEGF是菱形;②△AED≌△GED;③∠DFG=112.5°;④BC+FG=1.5.其中正确结论的序号是①②③.8.如图,在正方形ABCD中,点E是BC上的一点,点F是CD延长线上的一点,且BE =DF,连接AE,AF,EF.(1)求证:△ABE≌△ADF;(2)若AE=5,请求出EF的长.解:(1)证明:∵四边形ABCD是正方形,∴AB=AD,∠ABE=∠ADC=∠ADF=90°.在△ABE和△ADF中,⎩⎪⎨⎪⎧AB =AD ,∠ABE =∠ADF,BE =DF ,∴△ABE ≌△ADF(SAS). (2)∵△ABE≌△ADF, ∴AE =AF ,∠BAE =∠DAF. ∵∠BAE +∠EAD=90°,∴∠DAF +∠EAD=90°,即∠EAF=90°. ∴EF =2AE =5 2.9.如图,在正方形ABCD 中,点E ,F 在对角线BD 上,AE ∥CF ,连接AF ,CE. (1)求证:△ABE≌△CDF;(2)试判断四边形AECF 的形状,并说明理由.解:(1)证明:∵在正方形ABCD 中,AB =CD ,∠ABE =∠CDF=45°, 又∵AE∥CF,∴∠AEF =∠CFE. ∴∠AEB =∠CFD. ∴△ABE ≌△CDF(AAS).(2)四边形AECF 是菱形.理由如下: 连接AC 交BD 于点O ,则AC⊥BD. ∵△ABE ≌△CDF ,∴BE =DF.又∵OB=OD ,∴OB -BE =OD -DF ,即OE =OF.又∵AC⊥EF,OA =OC , ∴四边形AECF 是菱形.10.如图,O 为正方形ABCD 对角线的交点,E 为AB 边上一点,F 为BC 边上一点,△EBF 的周长等于BC 的长.(1)若AB =24,BE =6,求EF 的长; (2)求∠EOF 的度数.解:(1)设BF =x ,则FC =BC -BF =24-x. ∵BE =6,BE +BF +EF =BC , ∴EF =18-x.在Rt △BEF 中,BE 2+BF 2=EF 2, ∴62+x 2=(18-x)2,解得x =8. ∴EF =18-x =10.(2)在FC 上截取FM =FE ,连接OM , ∵C △EBF =BE +EF +BF =BC , ∴BE +EF +BF =BF +FM +MC. ∴BE =MC =6.∵四边形ABCD 为正方形, ∴OB =OC ,∠OBE =∠OCM=45°. 在△OBE 和△OCM 中,⎩⎪⎨⎪⎧OB =OC ,∠OBE =∠OCM,BE =CM ,∴△OBE ≌△OCM(SAS).∴∠EOB =∠MOC,OE =OM. ∴∠EOM =∠BOC=90°. 在△OFE 和△OFM 中, ⎩⎪⎨⎪⎧OE =OM ,OF =OF ,EF =MF ,∴△OFE ≌△OFM(SSS). ∴∠EOF =∠MOF=12∠EOM=45°.11.如图,E ,F 分别是正方形ABCD 的边CB ,DC 延长线上的点,且BE =CF ,过点E 作EG ∥BF ,交正方形外角的平分线CG 于点G ,连接GF.求证:(1)AE⊥BF;(2)四边形BEGF 是平行四边形.证明:(1)∵四边形ABCD 是正方形, ∴AB =BC ,∠ABC =∠BCD=90°. ∴∠ABE =∠BCF=90°.在△ABE 和△BCF 中,⎩⎪⎨⎪⎧AB =BC ,∠ABE =∠BCF,BE =CF ,∴△ABE ≌△BCF(SAS). ∴AE =BF ,∠BAE =∠CBF.∵EG ∥BF ,∴∠CBF =∠CEG.∴∠CEG=∠BAE.∵∠BAE +∠BEA=90°,∴∠CEG +∠BEA=90°,即∠AEG=90°. ∴AE ⊥EG.又∵EG∥BF,∴AE ⊥BF. (2)延长AB 至点P ,使BP =BE ,连接EP , 则AP =CE ,∠EBP =90°. ∴∠P =45°.∵CG 为正方形ABCD 外角的平分线, ∴∠ECG =45°.∴∠P =∠ECG. 在△APE 和△ECG 中,⎩⎪⎨⎪⎧∠P=∠ECG,AP =EC ,∠PAE =∠CEG,∴△APE ≌△ECG(ASA).∴AE=EG. ∵AE =BF ,∴EG =BF. ∵EG ∥BF ,∴四边形BEGF 是平行四边形.12.如图,点M 是正方形ABCD 的边BC 上一点,连接AM ,点E 是线段AM 上一点,∠CDE 的平分线交AM 延长线于点F.(1)如图1,若点E 为线段AM 的中点,BM ∶CM =1∶2,BE =10,求AB 的长; (2)如图2,若DA =DE ,求证:BF +DF =2AF.解:(1)设BM =x ,则CM =2x ,BA =BC =3x. 在Rt △ABM 中,E 为斜边AM 的中点,∴AM=2BE=210.∵AM2=MB2+AB2,∴40=x2+9x2,解得x=2.∴AB=3x=6.(2)证明:如图,过点A作AH⊥AF,交FD的延长线点H,过点D作DP⊥AF于点P.∵DF平分∠CDE,∴∠1=∠2.∵DE=DA,DP⊥AF,∴∠3=∠4.∵∠1+∠2+∠3+∠4=90°,∴∠2+∠3=45°.∴∠DFP=90°-45°=45°.∴AH=AF.∴HF=2AF.∵∠BAF+∠DAF=90°,∠HAD+∠DAF=90°,∴∠BAF=∠DAH.又∵AB=AD,∴△ABF≌△ADH(SAS).∴BF=DH.∵HF=DH+DF=BF+DF,∴BF+DF=2AF.第2课时正方形的判定1.下列说法中,不正确的是(D)A.对角线互相垂直的平行四边形是菱形B.一组对边平行且相等的四边形是平行四边形C.对角线垂直的矩形是正方形D.一组对边相等且有一个角是直角的四边形是矩形2.如图,将矩形纸片折叠,使A点落在BC上的F处,折痕为BE.若沿EF剪下,则折叠部分是一个正方形,其数学原理是(A)A.邻边相等的矩形是正方形B.对角线相等的菱形是正方形C.两个全等的直角三角形构成正方形D.轴对称图形是正方形3.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC;②∠ABC =90°;③AC=BD;④AC⊥BD中选两个作为补充条件,使▱ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是(B)A.①② B.②③ C.①③ D.②④4.如图,AC,BD是四边形ABCD的对角线,点E,F分别是AD,BC的中点,点M,N分别是AC,BD的中点,连接EM,MF,FN,NE,要使四边形EMFN为正方形,则需添加的条件是(A)A.AB=CD,AB⊥CDB.AB=CD,AD=BCC.AB=CD,AC⊥BDD.AB=CD,AD∥BC5.如图,在▱ABCD中,AE⊥BC于点E,CF⊥AD于点F,∠B=60°,当边+1)∶2时,四边形AECF是正方形.6.如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是7.如图,在矩形ABCD内有一点F,FB与FC分别平分∠ABC和∠BCD,点E为矩形ABCD 外一点,连接BE,CE.现添加下列条件:①EB∥CF,CE∥BF;②BE=CE,BE=BF;③BE∥CF,CE⊥BE;④BE=CE,CE∥BF,其中能判定四边形BECF是正方形的是①②③④.(填序号)8.在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,下面四个结论中:①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形.正确结论的序号是①②③.9.如图,AD是△ABC的角平分线,DE,DF分别是△BAD和△ACD的高,得到下列四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE+DF=AF+DE.其中正确的是②③④(填序号).10.如图,矩形ABCD的对角线相交于点O,PB∥AC,PC∥BD,PB,PC相交于点P.(1)猜想四边形PCOB是什么四边形?并说明理由;(2)当矩形ABCD满足什么条件时,四边形PCOB是正方形?解:(1)四边形PCOB是菱形.理由如下:∵PB∥AC,PC∥BD,∴四边形PCOB为平行四边形.∵四边形ABCD为矩形,∴OB=OC.∴四边形PCOB为菱形.(2)当AC⊥BD时,四边形PCOB是正方形.理由如下:∵四边形PCOB为菱形,AC⊥BD,∴四边形PCOB为正方形.11.如图,在▱ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.(1)求证:四边形ABCD是菱形;(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.证明:(1)∵四边形ABCD 是平行四边形,∴AO =OC. ∵△ACE 是等边三角形, ∴EO ⊥AC ,即 BD⊥AC. ∴四边形ABCD 是菱形.(2)∵△ACE 是等边三角形,EO ⊥AC ,AO =OC , ∴∠AEO =∠CEO=30°.∵∠AED =2∠EAD,∴∠EAD =15°. ∴∠DAO =∠EAO-∠EAD=45°. ∵四边形ABCD 是菱形, ∴∠BAD =2∠DAO=90°. ∴四边形ABCD 是正方形.12.如图,在四边形ABCD 中,AD ∥BC ,AD =CD ,E 是对角线BD 上一点,且EA =EC. (1)求证:四边形ABCD 是菱形;(2)如果BE =BC ,且∠CBE∶∠BCE=2∶3,求证:四边形ABCD 是正方形.证明:(1)在△ADE 和△CDE 中, ⎩⎪⎨⎪⎧AD =CD ,DE =DE ,EA =EC ,∴△ADE≌△CDE(SSS).∴∠ADE=∠CDE.∵AD∥BC,∴∠ADE=∠CBD.∴∠CDE=∠CBD.∴BC=CD.∵AD=CD,∴BC=AD.∴四边形ABCD为平行四边形.∵AD=CD,∴四边形ABCD是菱形.(2)∵BE=BC,∴∠BCE=∠BEC.∵∠C BE∶∠BCE=2∶3,∴∠CBE=180°×22+3+3=45°.∵四边形ABCD是菱形,∴∠ABE=45°.∴∠ABC=90°.∴四边形ABCD是正方形.13.如图,四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.(1)求证:矩形DEFG是正方形;(2)若AB=22,CE=2,求CG的长;(3)当线段DE与正方形ABCD的某条边的夹角是40°时,直接写出∠EFC的度数.解:(1)证明:作EP⊥CD于点P,EQ⊥BC于点Q,∵∠DCA=∠BCA=45°,∴EQ=EP.∴∠CEQ=∠CEP=45°.∴∠QEF +∠FEC=45°,∠PED+∠FEC=45°. ∴∠QEF =∠PED.在△EQF 和△EPD 中,⎩⎪⎨⎪⎧∠QEF=∠PED,EQ =EP ,∠EQF =∠EPD,∴△EQF ≌△EPD(ASA).∴EF=ED. ∴矩形DEFG 是正方形.(2)在Rt △ABC 中,AC =2AB =4. ∵EC =2,∴AE =CE =2. ∴DE ⊥AC ,DE =EC.∴点F 与C 重合,此时△DCG 是等腰直角三角形. ∴CG =2.(3)∠EFC =130°或40°.第3课时 正方形的性质与判定的运用1.如图所示,在正方形ABCD 中,O 是对角线AC ,BD 的交点,过点O 作OE⊥OF,分别交AB ,BC 于E ,F.若AE =4,CF =3,则EF 的长为(C)A .3B .4C .5D .62.将n 个边长都为2的正方形按如图所示摆放,点A 1,A 2,…,A n 分别是正方形的中心,则这n 个正方形重叠部分的面积之和是(B)A.n B.n-1C.4(n-1) D.4n3.如图,边长为1的正方形ABCD的对角线交于点O,点E是边AB上一动点,点F在边BC上,且满足OE⊥OF,在点E由A运动到B的过程中,以下结论中正确的个数为(B)①线段OE的大小先变小后变大;②线段EF的大小先变大后变小;③四边形OEBF的面积先变大后变小.A.0 B.1 C.2 D.34.如图,在正方形ABCD中,E,F分别是边BC,CD上的点,∠EAF=45°,△ECF的周长为6,则正方形ABCD的边长为3.5.如图,已知正方形ABCD的边长为5,点E,F分别在AD,DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH26.如图,在正方形ABCD中,点P为AD延长线上一点,连接AC,CP,F为AB边上一点,满足CF⊥CP,AC=3,3DP=AB,则FP7.如图,正方形ABCD的边长为6,点E,F分别在AB,AD上.若CE=35,且∠ECF=45°,则CF的长为8.如图,已知在正方形ABCD中,点E,F分别为边BC与CD上的点,且∠EAF=45°,AE与AF分别交对角线BD于点M,N,则下列结论正确的是①②④.①∠BAE+∠DAF=45°;②∠AEB=∠AEF=∠ANM;③BM+DN=MN;④BE+DF=EF.9.如图,E,F是正方形ABCD的边AD上的两个动点,满足AE=DF,连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为4,则线段DH长度的最小值是10.如图,已知正方形ABCD,M在CB延长线上,N在DC延长线上,∠MAN=45°.求证:MN=DN-BM.证明:在DN上截取DE=MB,连接AE,∵四边形ABCD是正方形,∴AD =AB ,∠D =∠ABM=90°. 在△ABM 和△ADE 中, ⎩⎪⎨⎪⎧AB =AD ,∠ABM =∠D,BM =DE ,∴△ABM ≌△ADE(SAS). ∴AM =AE ,∠MAB =∠EAD. ∵∠MAN =∠MAB+∠BAN=45°, ∴∠DAE +∠BAN=45°. ∴∠EAN =∠MAN=45°.在△AMN 和△AEN 中,⎩⎪⎨⎪⎧AM =AE ,∠MAN =∠EAN,AN =AN ,∴△AMN ≌△AEN(SAS). ∴MN =EN. ∵EN =DN -DE , ∴MN =DN -BM.11.操作:将一把三角尺放在如图1的正方形ABCD 中,使它的直角顶点P 在对角线AC 上滑动,直角的一边始终经过点B ,另一边与射线DC 相交于点Q.探究:(1)如图2,当点Q 在DC 上时,求证:PQ =PB ;(2)如图3,当点Q 在DC 延长线上时,(1)中的结论还成立吗?简要说明理由.解:(1)证明:过点P 作PN⊥AB 于点N ,NP 延长线交CD 于点M ,在正方形ABCD 中,AB ∥CD ,∠ACD =45°, ∴∠PMQ =∠PNB =∠CBN=90°. ∴四边形CBNM 是矩形.∴CM =BN ,△CMP 是等腰直角三角形. ∴PM =CM =BN.∵∠PBN +∠BPN=90°,∠BPN +∠MPQ=90°, ∴∠MPQ =∠PBN.在△PMQ 和△BNP 中,⎩⎪⎨⎪⎧∠MPQ=∠NBP,∠PMQ =∠BNP,PM =BN ,∴△PMQ ≌△BNP(AAS). ∴PQ =PB.(2)(1)中结论成立.理由:过点P 作PN⊥AB 于点N ,NP 延长线交CD 于点M , 在正方形ABCD 中,AB ∥CD ,∠ACD =45°, ∴∠PMQ =∠PNB=∠CBN=90°. ∴四边形CBNM 是矩形.∴CM =BN ,∴△CMP 是等腰直角三角形. ∴PM =CM =BN.∵∠PBN +∠BPN=90°,∠BPN +∠MPQ=90°, ∴∠MPQ =∠PBN.在△PMQ 和△BNP 中,⎩⎪⎨⎪⎧∠MPQ=∠NBP,∠PMQ =∠BNP,PM =BN ,∴△PMQ ≌△BNP(AAS). ∴PQ =PB.12.如图,在正方形ABCD中,P是BC上一动点(不与B,C重合):①CE平分∠DCF;②AP⊥PE;③AP=EP.以此三个条件中的两个为条件,另一个为结论,可构成三个命题,即:①②⇒③,①③⇒②,②③⇒①.(1)试判断上述三个命题是否正确(直接作答);(2)请选择一个你认为正确的命题给予证明.解:(1)上述三个命题均正确.(2)答案不唯一,选①③⇒②证明:在AB上截取AM=CP,则BM=BP.∴∠BMP=∠BPM=45°,∠AMP=135°.∵CE平分∠DCF,∴∠DCE=45°.∴∠ECP=135°.过点A作AG⊥MP交MP的延长线于点G,过点P作PH⊥EC交EC的延长线于点H,∴∠AMG=∠PCH=45°,∠G=∠H.∴△AGM≌△PHC(AAS).∴AG=PH.∵AP=PE,∴Rt△AGP≌Rt△PHE(HL).∴∠GPA=∠PEH.∵∠BPM=∠CPH=45°,B,P,C三点共线,∴M,P,H三点共线.∵∠PEH+∠EPH=90°,∴∠GPA+∠EPH=90°.∴∠APE=90°.∴AP⊥PE.。
中考数学压轴题练习 正方形问题(含解析)-人教版初中九年级全册数学试题

正方形问题1 如图,在边长为6的正方形ABCD 的两侧作正方形BEFG 和正方形DMNK ,恰好使得N 、A 、F 三点在一直线上,连接MF 交线段AD 于点P ,连接NP ,设正方形BEFG 的边长为x ,正方形DMNK 的边长为y .(1)求y 关于x 的函数关系式及自变量x 的取值X 围; (2)当△NPF 的面积为32时,求x 的值;(3)以P 为圆心,AP 为半径的圆能否与以G 为圆心,GF 为半径的圆相切?如果能,请求出x 的值,如果不能,请说明理由.解析:(1)∵正方形BEFG 、正方形DMNK 、正方形ABCD ∴∠E =∠F =90O ,AE ∥MC ,MC ∥NK ∴AE ∥NK ,∴∠KNA =∠EAF∴△KNA ∽△EAF ,∴NK EA =KA EF ,即y x +6=y -6x∴y =x +6(0<x ≤6)(2)由(1)知NK =AE ,∴AN =AF∵正方形DMNK ,∴AP ∥NM ,∴FP PM =AFAN =1∴FP =PM ,∴S △MNP =S △NPF =32 ∴S 正方形DMNK =2S △MNP =64 ∴y =8,∴x =2(3)连接PG ,延长FG 交AD 于点H ,则GH ⊥AD易知:AP =y2,AH =x ,PH =y 2-x ,HG =6;PG =AP +GF =y2+x①当两圆外切时在Rt △GHP 中,PH 2+HG 2=PG 2,即(y2-x )2+62=(y2+x )2解得:x =-3-33(舍去)或x =-3+3 3 ②当两圆内切时NK G CE DFAB PM在Rt △GHP 中,PH 2+HG 2=PG 2,即(y2-x )2+62=(y2-x )2方程无解所以,当x =33-3时,两圆相切2 已知:正方形ABCD 的边长为1,射线AE 与射线BC 交于点E ,射线AF 与射线CD 交于点F ,∠EAF =45°,连接EF .(1)如图1,当点E 在线段BC 上时,试猜想线段EF 、BE 、DF 有怎样的数量关系?并证明你的猜想; (2)设BE =x ,DF =y ,当点E 在线段BC 上运动时(不包括点B 、C ),求y 关于x 的函数解析式,并指出x 的取值X 围;(3)当点E 在射线BC 上运动时(不含端点B ),点F 在射线CD 上运动.试判断以E 为圆心,以BE 为半径的⊙E 和以F 为圆心,以FD 为半径的⊙F 之间的位置关系;(4)如图2,当点E 在BC 的延长线上时,设AE 与CD 交于点G .问:△EGF 与△EFA 能否相似?若能相似,求出BE 的长,若不可能相似,请说明理由.解析:(1)猜想:EF =BE +DF证明:将△ADF 绕点A 顺时针旋转90°,得△ABF′,易知点F′、B 、E 在同一直线上(如.图1) ∵AF′=AF∠F′AE =∠1+∠3=∠2+∠3=90°-45°=45°=∠EAF 又AE =AE ,∴△AF ′E ≌△AFEAB DCEF图1AB D CEFG图2AB DCEF图1F ′12∴EF =F′E =BE +BF =BE +DF (2)在Rt △EFC 中,EC 2+FC 2=EF 2 ∵EC =1-x ,FC =1-y ,EF =x +y ∴(1-x )2+(1-y )2=(x +y )2 ∴y =1-x1+x (0<x <1)(3)①当点E 在点B 、C 之间时,由(1)知EF =BE +DF ,故此时⊙E 与⊙F 外切; ②当点E 在点C 时,DF =0,⊙F 不存在.③当点E 在BC 延长线上时,将△ADF 绕点A 顺时针旋转90°,得△ABF′(如图2) 则AF′=AF ,∠1=∠2,B F′=DF ,∠F ′AF =90° ∴∠F ′AE =∠EAF =45° 又AE =AE ,∴△AF ′E ≌△AFE ∴EF =EF′=BE -B F′=BE -DF ∴此时⊙E 与⊙F 内切综上所述,当点E 在线段BC 上时,⊙E 与⊙F 外切;当点E 在BC 延长线上时,⊙E 与⊙F 内切 (4)△EGF 与△EFA 能够相似,只要当∠EFG =∠EAF =45°即可 此时CE =CF设BE =x ,DF =y ,由(3)知EF =x -y 在Rt △CFE 中,CE 2+CF 2=EF 2∴(x -1)2+(1+y )2=(x -y )2∴y =x -1x +1(x >1)由CE =CF ,得x -1=1+y ,即x -1=1+x -1x +1化简得x 2-2x -1=0,解得x 1=1-2(舍去),x 2=1+ 2 ∴△EGF 与△EFA 能够相似,此时BE 的长为1+ 23已知:如图,在直角梯形ABCD 中,AD ∥BC ,∠B =90°,AD =2,BC =6,AB =3.E 为BC 边上一点,ABD CEFG图2F ′12以BE 为边作正方形BEFG ,使正方形BEFG 和梯形ABCD 在BC 的同侧. (1)当正方形的顶点F 恰好落在对角线AC 上时,求BE 的长;(2)将(1)问中的正方形BEFG 沿BC 向右平移,记平移中的正方形BEFG 为正方形B′EFG ,当点E 与点C 重合时停止平移.设平移的距离为t ,正方形B′EFG 的边EF 与AC 交于点M ,连接B′D ,B′M ,DM .是否存在这样的t ,使△B′DM 是直角三角形?若存在,求出t 的值;若不存在,请说明理由;(3)在(2)问的平移过程中,设正方形B′EFG 与△ADC 重叠部分的面积为S ,请直接写出S 与t 之间的函数关系式以及自变量t 的取值X 围.解析:(1)如图①,设正方形BEFG 的边长为x 则BE =FG =BG =x∵AB =3,BC =6,∴AG =AB -BG =3-x ∵GF ∥BE ,∴△AGF ∽△ABC∴AG AB =GF BC ,即3-x 3=x 6解得x =2,即BE =2(2)存在满足条件的t ,理由如下: 如图②,过D 作DH ⊥BC 于点H 则BH =AD =2,DH =AB =3由题意得:BB′=HE =t ,HB′=|t -2|,EC =4-t在Rt△B′ME 中,B′M 2=B′E 2+ME 2=22+(2-12t )2=14t 2-2t +8∵EF ∥AB ,∴△MEC ∽△ABC∴ME AB =EC BC ,即ME 3=4-t 6,∴ME =2-12t在Rt△DHB′中,B′D 2=DH 2+B′H 2=32+(t -2)2=t 2-4t +13BACDBACD备用图B A CD 图①EFGB A CD 图②EFG HB ′ M N过M 作MN ⊥DH 于点N 则MN =HE =t ,NH =ME =2-12t ∴DN =DH -NH =3-(2-12t )=12t +1 在Rt△DMN 中,DM 2=DN 2+MN 2=54t 2+t +1(ⅰ)若∠DB′M =90°,则DM 2=B′M 2+B′D 2 即54t 2+t +1=(14t 2-2t +8)+(t 2-4t +13),解得t =207 (ⅱ)若∠B′MD =90°,则B′D 2=B′M 2+DM 2即t 2-4t +13=(14t 2-2t +8)+(54t 2+t +1),解得t 1=-3+17,t 2=-3-17∵0≤t ≤4,∴t =-3+17(ⅲ)若∠B′DM =90°,则B′M 2=B′D 2+DM 2即14t 2-2t +8=(t 2-4t +13)+(54t 2+t +1),此方程无解 综上所述,当t =207或-3+17时,△B′DM 是直角三角形 (3)当0≤t ≤43时,S =14t 2当43≤t ≤2时,S =-18t 2+t -23 当2≤t ≤103时,S =-38t 2+2t -53 当103≤t ≤4时,S =-12t +52 提示:当点F 落在CD 上时,如图③FE =2,EC =4-t ,DH =3,HC =4 由△FEC ∽△DHC ,得FE EC =DHHC即24-t =34,∴t =43当点G 落在AC 上时,点G 也在DH 上(即DH 与AC 的交点)t =2当点G 落在CD 上时,如图④B ACD图③E FGB ′ HB ACD图④E FGB ′ HGB ′=2,B ′C =6-t由△GB ′C ∽△DHC ,得G ′B B ′C =DHHC即26-t =34,∴t =103 当点E 与点C 重合时,t =4 ①当0≤t ≤43时,如图⑤ ∵MF =t ,FN =12t∴S =S △FMN =12·t ·12t =14t 2②当43≤t ≤2时,如图⑥ ∵PF =t -43,FQ =34PF =34t -1 ∴S △FPQ =12(t -43)(34t -1)=38t 2-t +23∴S =S △FMN -S △FPQ =14t 2-(38t 2-t +23)=-18t 2+t -23 ③当2≤t ≤103时,如图⑦ ∵B′M =12B′C =12(6-t )=3-12t ∴GM =2-(3-12t )=12t -1 ∴S 梯形GMNF =12(12t -1+12t )×2=t -1∴S =S 梯形GMNF -S △FPQ =(t -1)-(38t 2-t +23)=-38t 2+2t -53 ④当103≤t ≤4时,如图⑧ ∵P B′=34B′C =34(6-t )=92-34t ∴GP =2-(92-34t )=34t -52∴S 梯形GPQF =12(34t -52+34t -1)×2=32t -72∴S =S 梯形GMNF -S 梯形GPQF =(t -1)-(32t -72)=-12t +52BC图⑥EB ′BC图⑦EB ′B C 图⑧E B ′。
北师大版九年级数学上册--第一章 1.3《正方形的性质与判定》同步练习题(含答案)

1.3《正方形的性质与判定》同步练习一、填空题1.正方形的定义:有一组邻边______并且有一个角是______的平行四边形叫做正方形,因此正方形既是一个特殊的有一组邻边相等的______,又是一个特殊的有一个角是直角的______。
2.正方形的性质:正方形具有四边形、平行四边形、矩形、菱形的一切性质,正方形的四个角都是______;四条边都______且__________________;正方形的两条对角线______,并且互相______,每条对角线平分______对角。
它有______条对称轴。
3.正方形的判定:(1)____________________________________的平行四边形是正方形;(2)____________________________________的矩形是正方形;(3)____________________________________的菱形是正方形。
4.对角线________________________________的四边形是正方形。
5.若正方形的边长为a ,则其对角线长为______,若正方形ACEF 的边是正方形ABCD 的对角线,则正方形ACEF 与正方形ABCD 的面积之比等于______。
6.延长正方形ABCD 的BC 边至点E ,使CE =AC ,连结AE ,交CD 于F ,那么∠AFC 的度数为______,若BC =4cm ,则△ACE 的面积等于______。
7.如图,E 是正方形ABCD 的对角线BD 上一点,且BE =BC ,则∠ACE = 。
8.如图,已知正方形ABCD ,以CD 为边作等边△CDE ,则∠AED 的度数是 。
二、选择题。
1、已知四边形ABCD 是平行四边形,再从①AB =BC ,②∠ABC =90°,③AC =BD ,④AC ⊥BD 四个条件中,选两个作为补充条件后,使得四边形ABCD 是正方形,现有下列四种选法,其中错误的是( ) A .选①② B .选②③ C .选①③ D .选②④2、四边形ABCD 的对角线AC =BD ,AC ⊥BD ,分别过点A ,B ,C ,D 作对角线的平行线,所成的四边形EFMN 是( )A .正方形B .菱形C .矩形D .任意四边形3、已知四边形中,对角线与相交于点,,下列判断中错误的是( ) A.如果=,=,那么四边形是平行四边形 B.如果,=,那么四边形是矩形 C.如果=,,那么四边形是菱形 D.如果=,垂直平分,那么四边形是正方第7题图 第8题图4、满足下列条件的四边形是正方形的是()A.对角线互相垂直平分的平行四边形B.对角线互相平分且相等的矩形C.对角线互相垂直平分的菱形D.对角线互相垂直平分且相等的四边形5、如图,已知P是正方形ABCD的对角线BD上一点,且BP=BC,则∠ACP的度数是( )A.45° B.22.5° C.67.5° D.75°题5图题6图题7图6、如图,点在正方形内,满足,,,则阴影部分的面积是()A.76B.70C.48D.247、如图,在四边形中,点是对角线的交点,在下列条件中,能判定这个四边形为正方形的是()A.,B.,C.,D.,,8、如图,四边形是正方形,对角线,交于点,下列结论:①;②;③;④正方形有四条对称轴.上述结论正确的有()A.①②③④B.①②③C.②③④D.①③④9、下列四个命题:①一组对边平行且一组对角相等的四边形是平行四边形;②对角线互相垂直且相等的四边形是正方形;③顺次连接矩形四边中点得到的四边形是菱形;④正五边形既是轴对称图形又是中心对称图形.其中真命题共有()A.个B.个C.个D.个三、解答题1、已知Rt△ABC中,∠C=90°,CD平分∠ACB交AB于D,DF//BC,DE//AC。
人教版九年级数学中考矩形、菱形、正方形专项练习及参考答案
人教版九年级数学中考矩形、菱形、正方形专项练习基础达标一、选择题1.(2018江苏淮安)如图,菱形ABCD 的对角线AC ,BD 的长分别为6和8,则这个菱形的周长是( )A.20B.24C.40D.48,AO=12AC=3,BO=12BD=4,且AO ⊥BO ,则AB=√AA 2+AA 2=5, 故这个菱形的周长L=4AB=20. 故选A.2.(2017四川广安)下列说法:①四边相等的四边形一定是菱形②顺次连接矩形各边中点形成的四边形一定是正方形 ③对角线相等的四边形一定是矩形④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分其中正确的有( )个. A.4 B.3C.2D.13.(2017四川眉山)如图,EF 过▱ABCD 对角线的交点O ,交AD 于点E ,交BC 于点F ,若▱ABCD 的周长为18,OE=1.5,则四边形EFCD 的周长为( ) A.14 B.13C.12D.104.(2018贵州遵义)如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E、F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为()A.10B.12C.16D.18PM⊥AD于点M,交BC于点N.则四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,∴S△ADC=S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,×2×8=8,∴S△DFP=S△PBE=12∴S阴影=8+8=16,故选C.5.(2017山东枣庄)如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=A(x<0)的图象经过顶点B,则k的值为()AA.-12B.-27C.-32D.-366.(2018江苏无锡)如图,已知点E是矩形ABCD的对角线AC上的一动点,正方形EFGH的顶点G,H都在边AD上,若AB=3,BC=4,则tan ∠AFE的值()A.等于37B.等于√33C.等于34D.随点E位置的变化而变化EF∥AD,∴∠AFE=∠FAG,△AEH∽△ACD,∴AAAA =AAAA=34.设EH=3x,AH=4x,∴HG=GF=3x,∴tan∠AFE=tan∠FAG=AA AA =3A3A+4A=37.故选A.二、填空题7.(2018湖南株洲)如图,矩形ABCD的对角线AC与BD相交点O,AC=10,P,Q分别为AO,AD的中点,则PQ的长度为..5四边形ABCD是矩形,∴AC=BD=10,BO=DO=12BD,∴OD=12BD=5,∵点P,Q分别是AO,AD的中点,∴PQ是△AOD的中位线,∴PQ=12DO=2.5.8.(2018广东广州)如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(-2,0),点D在y轴上,则点C的坐标是.-5,4)菱形ABCD的顶点A,B的坐标分别为(3,0),(-2,0),点D在y轴上,∴AB=5,∴AD=5,∴由勾股定理知:OD=√AA2-AA2=√52-32=4,∴点C的坐标是(-5,4).9.(2018湖北武汉)以正方形ABCD的边AD为边作等边三角形ADE,则∠BEC的度数是.150°1,图1∵四边形ABCD为正方形,△ADE为等边三角形,∴AB=BC=CD=AD=AE=DE,∠BAD=∠ABC=∠BCD=∠ADC=90°,∠AED=∠ADE=∠DAE=60°,∴∠BAE=∠CDE=150°,又AB=AE,DC=DE,∴∠AEB=∠CED=15°,则∠BEC=∠AED-∠AEB-∠CED=30°.如图2,图2∵△ADE是等边三角形,∴AD=DE,∵四边形ABCD是正方形,∴AD=DC,∴DE=DC,∴∠CED=∠ECD,∴∠CDE=∠ADC-∠ADE=90°-60°=30°,∴∠CED=∠ECD=1(180°-30°)=75°,同理∠BEA=∠ABE=75°,2∴∠BEC=360°-75°×2-60°=150°.三、解答题10.如图,在菱形ABCD 中,对角线AC 与BD 交于点O.过点C 作BD 的平行线,过点D 作AC 的平行线,两直线相交于点E.(1)求证:四边形OCED 是矩形;(2)若CE=1,DE=2,则ABCD 的面积是多少?四边形ABCD 是菱形,∴AC ⊥BD , ∴∠COD=90°. ∵CE ∥OD ,DE ∥OC ,∴四边形OCED 是平行四边形,又∠COD=90°,∴平行四边形OCED 是矩形.(1)知,平行四边形OCED 是矩形,则CE=OD=1,DE=OC=2.∵四边形ABCD 是菱形, ∴AC=2OC=4,BD=2OD=2, ∴菱形ABCD 的面积为12AC ·BD=12×4×2=4. 能力提升一、选择题1.下列说法中,正确的个数为( )①对顶角相等;②两直线平行,同旁内角相等; ③对角线互相垂直的四边形为菱形;④对角线互相垂直平分且相等的四边形为正方形.A.1B.2C.3D.4对顶角相等,故①正确;②两直线平行,同旁内角互补,故②错误;③对角线互相垂直且平分的四边形为菱形,故③错误; ④对角线互相垂直平分且相等的四边形为正方形,故④正确,故选B .2.(2018山东枣庄)如图,在矩形ABCD 中,点E 是边BC 的中点,AE ⊥BD ,垂足为F ,则tan ∠BDE 的值是( )A.√24B.14C.13D.√23四边形ABCD 是矩形,∴AD=BC ,AD ∥BC , ∵点E 是边BC 的中点, ∴BE=12BC=12AD , ∴△BEF ∽△DAF , ∴AA AA =AA AA =12, ∴EF=12AF , ∴EF=13AE ,∵点E 是边BC 的中点, ∴由矩形的对称性得:AE=DE , ∴EF=13DE ,设EF=x ,则DE=3x , ∴DF=√AA 2-AA 2=2√2x , ∴tan ∠BDE=AAAA =2√2A =√24.故选A.3.如图,在Rt △ABC 中,∠C=90°,AC=BC=6cm,点P 从点A 出发,沿AB 方向以每秒√2 cm 的速度向终点B 运动;同时,动点Q 从点B 出发沿BC 方向以每秒1 cm 的速度向终点C 运动,将△PQC 沿BC 翻折,点P 的对应点为点P'.设Q 点运动的时间为t s,若四边形QPCP'为菱形,则t 的值为( )A.√2B.2C.2√2D.3PP',交BC于N点,过P作PM⊥AC,垂足为M.若运动t s时四边形QPCP'为菱形,则PQ=PC,PN⊥BC,四边形PMCN为矩形,BQ=t,AP=√2t,PM=NC=t,∴QC=2t,∴BC=BQ+QC=t+2t=3t=6cm,∴t=2,故选B.4.(2018河南)如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1 cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为()图1图2A.√5B.2D.2√5C.52D作DE⊥BC于点E由题图2可知,点F由点A到点D用时为a s,△FBC的面积为a cm2.∴AD=a.DE·AD=a.∴12∴DE=2.当点F从D到B时,用√5s,∴BD=√5.Rt△DBE中,BE=√AA2-AA2=√(√5)2-22=1,∵ABCD是菱形,∴EC=a-1,DC=a.Rt△DEC中,a2=22+(a-1)2,.解得a=52故选C.5.(2017广东)如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是()A.①③B.②③C.①④D.②④二、填空题6.(2018山东潍坊)如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x 轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C'D'的位置,B'C'与CD相交于点M,则点M的坐标为.)-1,√33,连接AM ,∵将边长为1的正方形ABCD 绕点A 逆时针旋转30°得到正方形AB'C'D', ∴AD=AB'=1,∠BAB'=30°, ∴∠B'AD=60°,在Rt △ADM 和Rt △AB'M 中,∵{AA =AA ',AA =AA ,∴Rt △ADM ≌Rt △AB'M (HL), ∴∠DAM=∠B'AM=12∠B'AD=30°, ∴DM=AD tan ∠DAM=1×√33=√33, ∴点M 的坐标为(-1,√33).三、解答题 7.如图所示,在△ABC 中,点O 是AC 边上的一个动点,过O 作直线MN ∥BC ,设MN 交∠ACB 的平分线于点E ,交∠ACB 的外角平分线于点F.(1)求证:OE=OF ;(2)当点O 运动到何处时,四边形AECF 是矩形?并证明你的结论.MN ∥BC ,∴∠OEC=∠BCE.又∠OCE=∠BCE ,∴∠OEC=∠OCE ,∴OE=OC.同理可证OF=OC ,∴OE=OF.O 运动到AC 中点时,四边形AECF 是矩形.证明:∵CE ,CF 分别是∠ACB 的内,外角平分线.∴∠OCE+∠OCF=12(∠ACB+∠ACD )=12×180°=90°,即∠ECF=90°,又∵OE=OF ,∴当O 点运动到AC 中点时,OA=OC ,四边形AECF 是矩形.8.(2018贵州遵义)如图,正方形ABCD的对角线交于点O,点E,F分别在AB,BC上(AE<BE),且∠EOF=90°,OE,DA的延长线交于点M,OF,AB的延长线交于点N,连接MN.(1)求证:OM=ON;(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.四边形ABCD是正方形,∴OA=OB,∠DAO=45°,∠OBA=45°,∴∠OAM=∠OBN=135°,∵∠EOF=90°,∠AOB=90°,∴∠AOM=∠BON,∴△OAM≌△OBN(ASA),∴OM=ON.,过点O作OH⊥AD于点H,∵正方形的边长为4,∴OH=HA=2,∵E为OM的中点,∴HM=4,则OM=√22+42=2√5,由(1)知OM=ON,∴MN=√2OM=2√10.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
)
A
D F E
7.如图,E 为正方形 ABCD 边 BC 延长线上一点,且 CE=BD,AE 交 DC 于 F, 则∠AFC=________.
C
8.矩形 ABCD 中,AC、BD 交于点 O,下列各条件中不能判定它是正方形的是( ) A.AB=AD B.AC⊥BD C.CA 平分∠BCD D.∠BAD+∠ADC=180° 9.如图,E 是边长为 1 的正方形 ABCD 对角线 BD 上一点,且 BE=BC,P 为 CE 上任意一 点,PQ⊥BC 于点 Q,PR⊥BE 于点 R,则 PQ+PR 的值为 。 10.在正方形 ABCD 中,E 为 BC 延长线上一点,EB= 1 BC,若 F 为 AB 中点,请 2
13.如图,△ABC 中,AD 是高,CE 为中线,CD=BE,DG⊥CE 于点 G, 求证:⑴G 为 CE 的中点;⑵∠B=2∠BCE
14.⑴如图,已知正方形 ABCD 的对角线 AC、BD 交于点 O,E 是 AC 上一点,过点 A 作 AG⊥BE 于点 G,AG 交 BD 于点 F。求证:OE=OF
在正方形 ABCD 上找一点,与点 F 连成线段,使它与 AE 相等,这样的点有几 个,请画出图形说明。
11.已知,Rt△ABC 中,∠C=90°,∠BAC 与∠ABC 的平分线交于点 D,DE⊥BC 于点 E,DF⊥AC 于点 F。 求证:四边形 CEDF 为正方形。
12.已知,正方形 ABCD 的对角线 BP 上有一点 P,过点 P 作 PE⊥BA 于点 E,PF⊥BC 于点 F。 求证:PD=EF
E F
A D
G B C
答案: 1.D 2.D 3. D 4.D 5.C 6.C 7.22.5° 8.C 1 9. 2 2
10—15(略)
正方形练习题
1.正方形具有而菱形不一定具有的性质是: A.四条边相等 B.对角线互相垂直 C.对角线平分一组对角 D.对角线相等 2.矩形 ABCD 中,AC、BD 交于点 O,下列条件中,不能判定它是正方形的是: ( ) A.AB=AD B.AC⊥BD C.CA 平分∠BCD D.∠BAD+∠ADC=180° 3.若四边形的对角线相等且互相垂直,这个四边形为: ( ) A.菱形 B.矩形 C.正方形 D.以上答案不对 4.□ABCD 是正方形需增加的条件是( ) A.邻边相等 B.邻角相等 C.对角线互相垂直 D.对角线互相垂直且相等 5.在平行四边形、 菱形、 矩形、 正方形中,能够找到一个点,使该点到各顶点距离相等的图形是( ) A.平行四边形和菱形 B.菱形和矩形 C.矩形和正方形 D.菱形和正方形 6.矩形各内角的平分线若能围成一个四边形,则这个四边形一定是( ⑵在⑴中,若点 E 在 AC 延长线上,AG⊥BE 交 EB 的延长线于点 G,AG 的延长线交 BD 的延长线于 点 F,其它条件不变,则结论 OE=OF 还成立吗?若成立,请给出证明;若不成立,请说明理由。
15.如图,四边形 ACDE、BAFG 是以△ABC 的边 AC、AB 为边向△ABC 外所作的正方形. 求证:(1)EB=FC. (2)EB⊥FC.
