幂函数指数函数对数函数比较大小ppt课件
合集下载
指数函数、对数函数和幂函数PPT教学课件

防冻液、合 成涤纶、
化妆品、制 炸药(硝化 甘油)
3.醇的命名
1.选主链。选含—OH的最长碳链作主链,根据碳
原子数目称为某醇。
2.编号。从离羟基最近的一端开始编号。 3.定名称。在取代基名称之后,主链名称之前用
阿拉伯数字标出—OH的位次,且主链称为某醇。 羟基的个数用“二”、“三”等表示。
4. 醇的重要物理性质
1 羟基的反应
(1)取代反应
⊙醇与浓的氢卤酸(HCI、HBr、HI)发生反应时分
子中的碳氧键断裂,羟基被卤原子取代,生成相应的
卤代烃和水
△
C2H5OH + HBr
C2H5Br + H2O
⊙在酸做催化剂及加热下,醇发生分子间的取代生 成醚和水
(2)消去反应
含有 B-H醇在浓硫酸及一定温度下能发 生消去反应生成烯烃
方法整合
3.利用指数函数和对数函数的概念、图象、性 质讨论一些复合函数的相应问题是常考题型,应 注意数形结合、分类讨论、化归等数学思想方法 的灵活运用.
典例研习
类型一、指数、对数函数的性质 例1.《导与练》 例1.
典例研习
类型二、指数、对数函数的图象 例2.《导与练》 例2.
典例研习
类型三、指数、对数函数的综合应用 例3.《导与练》 例3.
饱和一元醇通式:
CnH2n+1OH或 CnH2n+2O
小结
• 饱和一元醇 1、通式 CnH2n+1OH
2、随着C数的增多,熔沸点逐渐增,相对密度呈增大趋 势。 对于同碳数的,支链越多,熔沸点越低,密度越小。
3、随着碳数增多,水溶性降低。 4、比Mr接近的烷烃或烯烃的沸点要高(氢键的影响).
二、醇的化学性质
化妆品、制 炸药(硝化 甘油)
3.醇的命名
1.选主链。选含—OH的最长碳链作主链,根据碳
原子数目称为某醇。
2.编号。从离羟基最近的一端开始编号。 3.定名称。在取代基名称之后,主链名称之前用
阿拉伯数字标出—OH的位次,且主链称为某醇。 羟基的个数用“二”、“三”等表示。
4. 醇的重要物理性质
1 羟基的反应
(1)取代反应
⊙醇与浓的氢卤酸(HCI、HBr、HI)发生反应时分
子中的碳氧键断裂,羟基被卤原子取代,生成相应的
卤代烃和水
△
C2H5OH + HBr
C2H5Br + H2O
⊙在酸做催化剂及加热下,醇发生分子间的取代生 成醚和水
(2)消去反应
含有 B-H醇在浓硫酸及一定温度下能发 生消去反应生成烯烃
方法整合
3.利用指数函数和对数函数的概念、图象、性 质讨论一些复合函数的相应问题是常考题型,应 注意数形结合、分类讨论、化归等数学思想方法 的灵活运用.
典例研习
类型一、指数、对数函数的性质 例1.《导与练》 例1.
典例研习
类型二、指数、对数函数的图象 例2.《导与练》 例2.
典例研习
类型三、指数、对数函数的综合应用 例3.《导与练》 例3.
饱和一元醇通式:
CnH2n+1OH或 CnH2n+2O
小结
• 饱和一元醇 1、通式 CnH2n+1OH
2、随着C数的增多,熔沸点逐渐增,相对密度呈增大趋 势。 对于同碳数的,支链越多,熔沸点越低,密度越小。
3、随着碳数增多,水溶性降低。 4、比Mr接近的烷烃或烯烃的沸点要高(氢键的影响).
二、醇的化学性质
指数函数、幂函数、对数函数增长的比较(45张PPT)——高中数学必修第一册

一次函数y=kx(k>0),指数函数y=ax(a>1)和对数函数y=logbx(b>1)的增长有何差异?
一般地,无论k(k>0)、a(a>1)、b(b>1)如何取值,三种函数在区间(0,+∞)上都单调递增,但一次函数总是保持固定的增长速度;指数函数的增长速度都会越来越快,并且指数函数的函数值最终总会大于一次函数的函数值;对数函数的增长速度都会越来越慢,并且对数函数的函数值最终总会小于一次函数的函数值.
401
626
901
y2
2
32
1024
32768
1.05×106
3.36×107
1.07×109
y3
2
10
20
30
40
50
60
y4
2
4.322
5.322
5.907
6.322
6.644
6.907
【解析】(1)由于指数型函数的增长式为爆炸式增长,则当x越来越大时,函数y=的增长速度最快,故选A.
(2)从表格中可以看出,四个变量y1,y2,y3,y4均是从2开始变化,变量y1,y2,y3,y4都是越来越大,但是增长速度不同,其中变量y2的增长速度最快,可知变量y2关于x呈指数函数变化.
x
y=2x
y=2x
0
1
0
2
4
4
4
16
8
6
64
12
8
256
16
10
1024
20
12
4096
24
…
…
…
可以看到,当自变量x越来越大时,y=2x的图象就像与x轴垂直一样,2x的值快速增长;而函数y=2x的增长速度依然保持不变,与函数y=2x的增长速度相比几乎微不足道.
幂函数、指函数与对函数PPT课件

D. b > a > 1 O
思路二:
1b a
x
数形结合
26
题型三:幂函数性质的应用
3.比较下列各组数的大小:
< 1
1
(1)1.32 ____ 1.4 2
解后反思 两个数比较
(2)0.261
_>____
0.271
大小,何时 用幂函数模
(3)(5.2)2 _<____(5.3)2
型,何时用 指数函数模
即 log2 a log2 b 0 log2 1
a b 1 所以答案选C. 25
能力提升
变②:若0 < loga 2 < logb 2,则
C
()
A. 0 < a < b < 1 y
B. 0 < b < a < 1
1
C. a > b > 1
x=2
y= logb x
y= loga x
解析式 y = a x ( a > 0, a≠1)
y
图 象 0<a<1
y a>1
1
(描点)
1
0
x
0
x
y = log a x ( a > 0, a≠1)
y 0<a<1
y a>1
01
x
01
x
定义域
R
(0 , +∞)
值域
(0 , +∞)
R
定点
都过点(0,1)
都过点(1,0)
范围
x<0时,y>1;x>0时,y>10;<x<1时 x>0时 x<0时 y>0
指数函数、幂函数、对数函数增长的比较ppt课件

1000
1500
对于模型y=log7x+1,它在区间[10,1000] 上递增,而且当x=1000时, y=log71000+1≈4.55<5,所以它符合
17
练习
1、0.32,log20.3,20.3这三个数之间大小关 系是( D ) A. 0.32<20.3<log20.3; B. 0.32<log20.3<20.3; C. log20.3<20.3<0.32; D. log20.3<0.32<20.3;
4
3
2
1
0
0
200
400
600
800
1000
1200
对于模型由y=1.002x函数图像并利用计算 器满,足可1以.0知02道x0=在5,由区于间它(80在5,区80间6)[内10有,1一00个0]上点递x0 增,因此当x>x0时,y>5,因此该模型也不符合 要求;
16
5
4 3
y=㏒7x
2
1
0
0
500
18
练习
2、作图像,试比较函数y=4x,y=x4, y=log4x 的增长情况. y=x4 y y=4x
y=log4x
x
19
小结 比较了指数函数、幂函数、对数函数的增长
在区间(0,+∞)上,当a>1,n>0时,当x足够大 时,随着x的增大,y=ax的增长速度越来越快, 会超过并远远大于y=xn的增长速度,而 y=logax的增长速度则越来越慢.
20
长就越快。
y 3x
y 2x
2
对数函数
2.当a>1时,对数函数y=logax是增函数, 并且对于x>1,当a越小时,其函数值的 增长就越快。 y
幂函数指数函数对数函数比较大小 ppt课件

• “太阳当空照,花儿对我笑,小鸟说早早早……”
(1)定义域:R (2)值域:(0, +)
(3)单调性:当01时,指数函数在定义域上是减函数 当1时,指数函数在定义域上是增函数
(4)奇偶性:非奇非偶
幂函数指数函数对数函数比较大小
幂函数指数函数对数函数比较大小
幂函数指数函数对数函数比较大小 Nhomakorabea精品资料
• 你怎么称呼老师?
• 如果老师最后没有总结一节课的重点的难点,你 是否会认为老师的教学方法需要改进?
• 你所经历的课堂,是讲座式还是讨论式? • 教师的教鞭
• “不怕太阳晒,也不怕那风雨狂,只怕先生骂我 笨,没有学问无颜见爹娘 ……”
(1)定义域:R (2)值域:(0, +)
(3)单调性:当01时,指数函数在定义域上是减函数 当1时,指数函数在定义域上是增函数
(4)奇偶性:非奇非偶
幂函数指数函数对数函数比较大小
幂函数指数函数对数函数比较大小
幂函数指数函数对数函数比较大小 Nhomakorabea精品资料
• 你怎么称呼老师?
• 如果老师最后没有总结一节课的重点的难点,你 是否会认为老师的教学方法需要改进?
• 你所经历的课堂,是讲座式还是讨论式? • 教师的教鞭
• “不怕太阳晒,也不怕那风雨狂,只怕先生骂我 笨,没有学问无颜见爹娘 ……”
《幂函数》指数函数、对数函数与幂函数精美版课件

递增.
4.当α<0时,幂函数的图像都过点(1,1),且在(0,+∞)上单调递减.
5.做一做:已知函数f(x)=(m2-m-1)x-5m-3是幂函数且是(0,+∞)上的
增函数,则m的值为
.
答案:-1
解析:由题意知m2-m-1=1,
∴m2-m-2=0,
∴m=2或m=-1.
当m=2时,f(x)=x-13,不符合题意,故舍去;
当m=-1时,f(x)=x2,符合题意,故m的值为-1.
课堂篇探究学习
探究一
探究二
探究三
探究四
思维辨析
当堂检测
解析:由m2+3m-17=1,解得m=3或m=-6,
分析:先利用f(x)在(0,+∞)内为减函数求出m的取值范围,再用代入检验的方法来验证是否为偶函数.
当m=-3时,m2-2m-3=12,y=x12是幂函数,但不满足当x∈(0,+∞)时,y随x的增大而减小,应舍去.
(-1,-1),(0,
(-1,1),(0,0),
定点 ),
0),
(0,0),(1,1)
(1,1)
(1,1)
(1,1)
(-1,-1),(1,1)
课前篇自主预习
一
二
三、幂函数共有的性质
1.幂函数在(0,+∞)上都有定义.
2.幂函数的图像过点(1,1).
3.当α>0时,幂函数的图像都过点(1,1)和(0,1),且在(0,+∞)上单调
人教版高中数学B版必修二
指数函数、对数函数与幂函数
4.4
幂函数
-1-
课标阐释
思维脉络
1.通过实例,了解幂函数的
概念.
4.当α<0时,幂函数的图像都过点(1,1),且在(0,+∞)上单调递减.
5.做一做:已知函数f(x)=(m2-m-1)x-5m-3是幂函数且是(0,+∞)上的
增函数,则m的值为
.
答案:-1
解析:由题意知m2-m-1=1,
∴m2-m-2=0,
∴m=2或m=-1.
当m=2时,f(x)=x-13,不符合题意,故舍去;
当m=-1时,f(x)=x2,符合题意,故m的值为-1.
课堂篇探究学习
探究一
探究二
探究三
探究四
思维辨析
当堂检测
解析:由m2+3m-17=1,解得m=3或m=-6,
分析:先利用f(x)在(0,+∞)内为减函数求出m的取值范围,再用代入检验的方法来验证是否为偶函数.
当m=-3时,m2-2m-3=12,y=x12是幂函数,但不满足当x∈(0,+∞)时,y随x的增大而减小,应舍去.
(-1,-1),(0,
(-1,1),(0,0),
定点 ),
0),
(0,0),(1,1)
(1,1)
(1,1)
(1,1)
(-1,-1),(1,1)
课前篇自主预习
一
二
三、幂函数共有的性质
1.幂函数在(0,+∞)上都有定义.
2.幂函数的图像过点(1,1).
3.当α>0时,幂函数的图像都过点(1,1)和(0,1),且在(0,+∞)上单调
人教版高中数学B版必修二
指数函数、对数函数与幂函数
4.4
幂函数
-1-
课标阐释
思维脉络
1.通过实例,了解幂函数的
概念.
指数函数和对数函数ppt课件
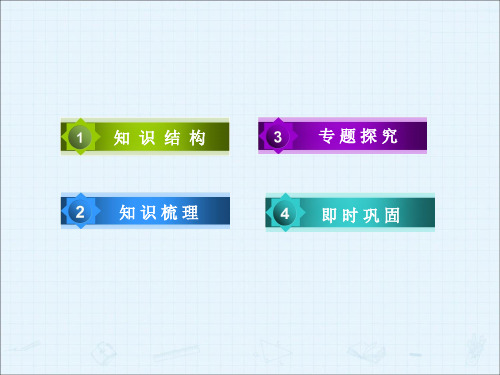
解法 2:a-b=ln22-ln33=3ln2-6 2ln3 =16(ln8-ln9)<0. ∴a<b.同理可得 c<a,∴c<a<b.故选 C.
[答案]C
4.考查函数的定义域 函数的定义域是历年高考中均考查的知识点,其难度 不大,属中低档题,但在求解时易漏掉部分约束条件造成错 解,因而也是易错题. [例 4] 函数 f(x)= 31x-2 x+lg(3x+1)的定义域是
[例 1] (1)化简
3 ÷(1-2
ba)×3 ab;
(2)求值:12lg3429-43lg 8+lg 245.
(2)解法一 12lg3429-43lg 8+lg 245 =lg472-lg4+lg7 5 =lg(472×14×7 5) =lg 10=12lg10=12.
解法二 原式=12(5lg2-2lg7)-43·32lg2+12(2lg7+lg5) =52lg2-lg7-2lg2+lg7+12lg5 =12lg2+12lg5 =12(lg2+lg5) =12lg10=12.
[例7]求不等式x-1<log6(x+3)的所有整数解. [解析]设y1=x-1,y2=log6(x+3),在同一坐标系中作
出它们的图像如图所示,两图像有两个交点,一交点的横坐标
显然在-3和-2之间,另一个交点设为P.
因为x=1时,log6(1+3)-(1-1)>0,x=2时, log6(2+3)-(2-1)<0,所以1<xP<2.
2.指数函数的概念与性质 (1)指数函数的定义
一般地,函数y=ax(a>0,且a≠1)叫作指数函数. (2)y=ax(a>0,a≠1)的图像
0<a<1
a>1
指数函数对数函数与幂函数指数函数与对数函数的关系pptx

对数函数的图像是一条直线,在定义域内单调递 增。
性质
对数函数的图像与y轴的交点为1,函数的导数是1/x',其中x'是x的倒数。
复合对数函数
定义
复合对数函数是指数函数和对数函数的组合形式,它表示为log(base) (x) ^ (y),其中base是底数,x和y是函数的自变量。
当n为负整数时,幂 函数的最大值出现在 x=1处,且最大值为 1/2;
当n为分数时,幂函 数的最大值出现在 x=1处,且最大值为 1。
复合幂函数
定义
复合幂函数是指由幂函数与其他函数复合而成的函数,如 $f(x) = \sin x^{2}$。
性质
复合幂函数的性质取决于其内部的幂函数的性质以及外部函 数的性质。例如,如果内部函数是偶函数,则复合幂函数也 是偶函数;如果内部函数是奇函数,则复合幂函数也是奇函 数。
复合指数函数
定义:复合指数函数是指形式为f(ax+b)的函数,其中 a和b是常数,且a≠0。
1. 复合指数函数的图像与指数函数的图像类似,但需 要根据具体的函数表达式来确定。
性质
2. 复合指数函数的性质与指数函数的性质类似,但需 要根据具体的函数表达式来进行判断。
02
对数函数
对数函数的定义与性质
性质
1. 当x为有理数时,a^x仍为有 理数;当x为无理数时,a^x亦 为无理数。
2. 当a>1时,a^x>0;当 0<a<1时,a^x<0。
指数函数的图像与性质
图像:指数函数的图像是一条连续的曲线,经过原点 ,并在第一象限内单调递增。
1. 函数值y随x的增大而增大(当x为正数时)。
性质
2. 当x=0时,y=1(当a>1时),y=0(当0<a<1时 )。
性质
对数函数的图像与y轴的交点为1,函数的导数是1/x',其中x'是x的倒数。
复合对数函数
定义
复合对数函数是指数函数和对数函数的组合形式,它表示为log(base) (x) ^ (y),其中base是底数,x和y是函数的自变量。
当n为负整数时,幂 函数的最大值出现在 x=1处,且最大值为 1/2;
当n为分数时,幂函 数的最大值出现在 x=1处,且最大值为 1。
复合幂函数
定义
复合幂函数是指由幂函数与其他函数复合而成的函数,如 $f(x) = \sin x^{2}$。
性质
复合幂函数的性质取决于其内部的幂函数的性质以及外部函 数的性质。例如,如果内部函数是偶函数,则复合幂函数也 是偶函数;如果内部函数是奇函数,则复合幂函数也是奇函 数。
复合指数函数
定义:复合指数函数是指形式为f(ax+b)的函数,其中 a和b是常数,且a≠0。
1. 复合指数函数的图像与指数函数的图像类似,但需 要根据具体的函数表达式来确定。
性质
2. 复合指数函数的性质与指数函数的性质类似,但需 要根据具体的函数表达式来进行判断。
02
对数函数
对数函数的定义与性质
性质
1. 当x为有理数时,a^x仍为有 理数;当x为无理数时,a^x亦 为无理数。
2. 当a>1时,a^x>0;当 0<a<1时,a^x<0。
指数函数的图像与性质
图像:指数函数的图像是一条连续的曲线,经过原点 ,并在第一象限内单调递增。
1. 函数值y随x的增大而增大(当x为正数时)。
性质
2. 当x=0时,y=1(当a>1时),y=0(当0<a<1时 )。
《增长速度的比较》指数函数、对数函数与幂函数PPT

2.填空.
(1)函数值的改变量与自变量的改变量的比称为平均变化率.
(2)函数y=f(x)在区间[x1,x2](x1<x2时)或[x2,x1](x1>x2时)上的平均变
化率为
Δ (2 )-(1 )
=
Δ
2 -1
.
(3)平均变化率也可理解为:自变量每增加1个单位,函数值平均将
增加 个单位,因此,可用平均变化率来比较函数值变化的快慢.
A.
)
课堂篇探究学习
探究一
探究二
思维辨析
当堂检测
2.函数f(x)=x2在x0到x0+Δx之间的平均变化率为k1,在x0-Δx到x0之间
的平均变化率为k2,则k1,k2的大小关系为(
)
A.k1<k2 B.k1>k2
C.k1=k2 D.无法确定
答案:D
(0 +Δ)-(0 )
=2x0+Δx,
0 +Δ-0
k1=1;②y=x2 在 x=1 附近的平均变化率 k2=2+Δx=2.3;③y
=x3 在 x=1 附近的平均变化率 k3=3+3Δx+(Δx)2=3.99;④y
1
1
10
= 在 x=1 附近的平均变化率 k4=-
=- .所以 k3>k2
x
13
1+Δx
>k1>k4,故应选 B.
s(t1)-s(t0)
)
A.m1=m2
B.m1>m2
C.m2>m1
D.m1,m2的大小无法确定
答案:A
1-0
=1,所以
1-0
解析:因为 m1=1,m2=
m1=m2.
课堂篇探究学习
探究一
(1)函数值的改变量与自变量的改变量的比称为平均变化率.
(2)函数y=f(x)在区间[x1,x2](x1<x2时)或[x2,x1](x1>x2时)上的平均变
化率为
Δ (2 )-(1 )
=
Δ
2 -1
.
(3)平均变化率也可理解为:自变量每增加1个单位,函数值平均将
增加 个单位,因此,可用平均变化率来比较函数值变化的快慢.
A.
)
课堂篇探究学习
探究一
探究二
思维辨析
当堂检测
2.函数f(x)=x2在x0到x0+Δx之间的平均变化率为k1,在x0-Δx到x0之间
的平均变化率为k2,则k1,k2的大小关系为(
)
A.k1<k2 B.k1>k2
C.k1=k2 D.无法确定
答案:D
(0 +Δ)-(0 )
=2x0+Δx,
0 +Δ-0
k1=1;②y=x2 在 x=1 附近的平均变化率 k2=2+Δx=2.3;③y
=x3 在 x=1 附近的平均变化率 k3=3+3Δx+(Δx)2=3.99;④y
1
1
10
= 在 x=1 附近的平均变化率 k4=-
=- .所以 k3>k2
x
13
1+Δx
>k1>k4,故应选 B.
s(t1)-s(t0)
)
A.m1=m2
B.m1>m2
C.m2>m1
D.m1,m2的大小无法确定
答案:A
1-0
=1,所以
1-0
解析:因为 m1=1,m2=
m1=m2.
课堂篇探究学习
探究一
指数函数,幂函数,对数函数的增长的比较及函数模型 课件

2018年年份代码为 = 2,依此类推)有两个函数模型 = > 0, > 1 与
= + > 0 可供选择.
(1)试判断哪个函数模型更合适(不需计算,简述理由即可),并求出该模型
的函数解析式;
(2)问大约在哪一年,三峡大坝旅客年游览人数约是2018年的2倍.(参考数据:
2、建立函数模型解决实际问题的步骤
(1)确切理解题意:明确问题的实际背景,进行科学的抽象、概括,将实际问
题转化为数学问题。
(2)建立相应的数学模型(选择合适的数学模型)
(3)求解函数模型,得出数学结论
(4)将用数学知识和方法得出的结论,还原为实际问题的意义,并进行验证,
看是否符合实际。
典 例 剖 析
1
= 80 + 4 21 , = 2 + 120,设甲大棚的资金投入为(单位:万元),
4
每年两个大棚的总收入为 (单位:万元),求 的最大值。
题型六 分段函数模型
例6、通过研究学生的学习行为,专家发现,学生的注意力着老师讲课时间的变化
而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的
指数函数、幂函数、对数函
数增长的比较与函数模型
目
标
1
输 入 标 题 名 称
2
输 入 标 题 名 称
3
输 入 标 题 名 称
4
输 入 标 题 名 称
情 景 导 入
每年的3月21日时植树节,全国各地在这一天都会开展各种形式的植树
活动,某市现有树木面积为10万平方米,计划今后5年内扩大树木面积,现
有两种方案如下:
状态,随后学生的注意力开始分散,设 表示学生注意力随时间(分钟)的变化
= + > 0 可供选择.
(1)试判断哪个函数模型更合适(不需计算,简述理由即可),并求出该模型
的函数解析式;
(2)问大约在哪一年,三峡大坝旅客年游览人数约是2018年的2倍.(参考数据:
2、建立函数模型解决实际问题的步骤
(1)确切理解题意:明确问题的实际背景,进行科学的抽象、概括,将实际问
题转化为数学问题。
(2)建立相应的数学模型(选择合适的数学模型)
(3)求解函数模型,得出数学结论
(4)将用数学知识和方法得出的结论,还原为实际问题的意义,并进行验证,
看是否符合实际。
典 例 剖 析
1
= 80 + 4 21 , = 2 + 120,设甲大棚的资金投入为(单位:万元),
4
每年两个大棚的总收入为 (单位:万元),求 的最大值。
题型六 分段函数模型
例6、通过研究学生的学习行为,专家发现,学生的注意力着老师讲课时间的变化
而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的
指数函数、幂函数、对数函
数增长的比较与函数模型
目
标
1
输 入 标 题 名 称
2
输 入 标 题 名 称
3
输 入 标 题 名 称
4
输 入 标 题 名 称
情 景 导 入
每年的3月21日时植树节,全国各地在这一天都会开展各种形式的植树
活动,某市现有树木面积为10万平方米,计划今后5年内扩大树木面积,现
有两种方案如下:
状态,随后学生的注意力开始分散,设 表示学生注意力随时间(分钟)的变化
指数函数与对数函数的关系指数函数对数函数与幂函数PPT精品推荐课件
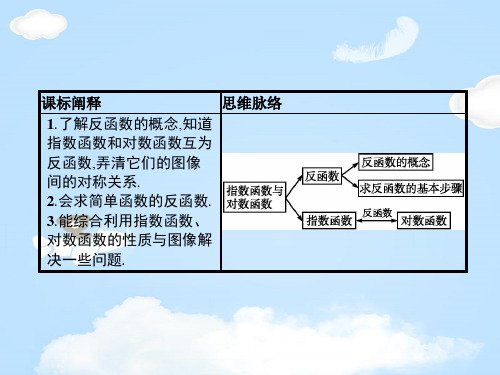
致性吗?
提示:当0<a<1时,上述两个函数均是其定义域上的减函数;当a>1
时,上述两个函数均是其定义域上的增函数.因此单调性具有一致
性,但变化速度有差异.
课前篇自主预习
一
二
3.填空.
(1)关系
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)互为反函数.
(2)图像特征
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)的图像关于
与f-1(x)互为反函数,对此不能对自变量x随意变化拓展.
课堂篇探究学习
探究一
探究二
探究三
思维辨析
当堂检测
正解:∵g(x)的图像过定点(1,2 018),
∴f(x+1)的图像过定点(2 018,1).
又∵f(x)的图像可以看作由f(x+1)的图像向右平移1个单位长度得
到的,∴f(x)过定点(2 019,1).
)
A.(0,0) B.(0,2) C.(1,1)
D.(2,0)
答案:B
解析:∵y=f(x)的图像过点(1,0),
∴其反函数y=f-1(x)的图像必过点(0,1),
即f-1(0)=1,∴y=f-1(x)+1的图像过点(0,2).
4.已知
1-3
4
f(x)= ,则 f-1 5
1+3
=
Hale Waihona Puke 答案:-21-3除D.故选B.
方法二:若0<a<1,则曲线y=ax下降且过点(0,1),而曲线y=loga(-x)
上升且过点(-1,0),所有选项均不符合这些条件.
提示:当0<a<1时,上述两个函数均是其定义域上的减函数;当a>1
时,上述两个函数均是其定义域上的增函数.因此单调性具有一致
性,但变化速度有差异.
课前篇自主预习
一
二
3.填空.
(1)关系
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)互为反函数.
(2)图像特征
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)的图像关于
与f-1(x)互为反函数,对此不能对自变量x随意变化拓展.
课堂篇探究学习
探究一
探究二
探究三
思维辨析
当堂检测
正解:∵g(x)的图像过定点(1,2 018),
∴f(x+1)的图像过定点(2 018,1).
又∵f(x)的图像可以看作由f(x+1)的图像向右平移1个单位长度得
到的,∴f(x)过定点(2 019,1).
)
A.(0,0) B.(0,2) C.(1,1)
D.(2,0)
答案:B
解析:∵y=f(x)的图像过点(1,0),
∴其反函数y=f-1(x)的图像必过点(0,1),
即f-1(0)=1,∴y=f-1(x)+1的图像过点(0,2).
4.已知
1-3
4
f(x)= ,则 f-1 5
1+3
=
Hale Waihona Puke 答案:-21-3除D.故选B.
方法二:若0<a<1,则曲线y=ax下降且过点(0,1),而曲线y=loga(-x)
上升且过点(-1,0),所有选项均不符合这些条件.
高中数学3-6指数函数、幂函数、对数函数增长的比较课件北师大版必修

在区间(0, +∞)上, 尽管函数 y=ax(a>1), y=logax(a>1), y=xn(n>0)都是________(填“增”或“减”)函数,但它们的 增长速度不同,而且在不同的“档次”上,随着 x 的增大,y = ax(a>1) 的增长速度越来越快,会超过并会远远大于 y = xn(n>0) 的增长速度,而 y = logax(a>1) 的增长速度会越来越 慢 . 因 此 , 总 会 存 在 一 个 x0 , 当 x>x0 时 , 就 有 logax________xn________ax.
同样地, 对于对数函数 y=logax(a>1)和幂函数 y=xn(n>0), 在区间(0,+∞)上,随着 x 的增大,logax 增长得越来越慢, 图像就像是渐渐地与 x 轴平行一样. 尽管在 x 的一定变化范围 内,logax 可能会大于 xn,但由于 logax 的增长慢于 xn 的增长, 因此总存在一个 x0,当 x>x0 时,就会有 logax<xn.
首先计算哪个模型的奖金总数不超过 5 万.对于模型 y =0.25x,它在区间[10,1000]上单调递增,当 x∈(20,1000]时, y>5,因此该模型不符合要求;对于模型 y=1.002x,由函数 的图像,并利用计算器计算可知,在区间(805,806)内有一个 点 x0 满足 1.002x0=5,由于它在区间[10,1000]上单调递增, 因此当 x>x0 时,y>5,因此该模型不符合要求.对于模型 y= log7x+1, 它在区间[10,1000]上单调递增, 而且当 x=1000 时, y=log71000+1≈4.55<5,所以它符合奖金总数不超过 5 万元 的要求.
指数函数、幂函数、对数函数增长的比较-课件 高一数学(北师大版2019必修第一册)

这说明,按模型 y=log7x+1 进行奖励,奖金不超过利润的 25%.
综上所述,模型 y=log7x+1 符合公司要求.
导入课题 新知探究 典例剖析 课堂小结
一、幂函数y = x c x > 0, c > 1 与对数
函数y = log b x b > 1 的增长情况比较
二,指数函数y = ax a > 1 与幂函数
(2)若1 ∈ , + 1 ,2 ∈ , + 1 ,且, ∈
1,2,3,4,5,6,7,8,9,10,11,
12 ,指出, 的值,并说明理由.
导入课题 新知探究 典例剖析 课堂小结
思考探究:函数增长快慢比较
解:(1)根据指数函数与幂函数的增长速度知:
C1 对应函数 g(x)=x3,C2 对应函数 f(x)=2x;
1
2
1
解:(2)
,
4
ℎ = 2 当
1
4
即
1
2
1
4
>
1
4
1
2
,
1
2
1
4
,
1
1 2
,
可分别视为函数
2
4
1
= 时的函数值,在同一坐标系内
4
分别作出这三个函数的图象,
由图象易知
1
4
1
2
1
4
>
>
1 2
.
4
1
4
>ℎ
1
4
,
1 2
.
4
1
2
= , =
1
2
,
导入课题 新知探究 典例剖析 课堂小结
综上所述,模型 y=log7x+1 符合公司要求.
导入课题 新知探究 典例剖析 课堂小结
一、幂函数y = x c x > 0, c > 1 与对数
函数y = log b x b > 1 的增长情况比较
二,指数函数y = ax a > 1 与幂函数
(2)若1 ∈ , + 1 ,2 ∈ , + 1 ,且, ∈
1,2,3,4,5,6,7,8,9,10,11,
12 ,指出, 的值,并说明理由.
导入课题 新知探究 典例剖析 课堂小结
思考探究:函数增长快慢比较
解:(1)根据指数函数与幂函数的增长速度知:
C1 对应函数 g(x)=x3,C2 对应函数 f(x)=2x;
1
2
1
解:(2)
,
4
ℎ = 2 当
1
4
即
1
2
1
4
>
1
4
1
2
,
1
2
1
4
,
1
1 2
,
可分别视为函数
2
4
1
= 时的函数值,在同一坐标系内
4
分别作出这三个函数的图象,
由图象易知
1
4
1
2
1
4
>
>
1 2
.
4
1
4
>ℎ
1
4
,
1 2
.
4
1
2
= , =
1
2
,
导入课题 新知探究 典例剖析 课堂小结
第11讲指数函数对数函数幂函数PPT课件

30
· 高中新课标总复习(第1轮)· 文科数学 · 湖南 · 人教版
立足教育 开创未来
题型三 幂函数及其简单应用
例3(1)设α∈{-1,1, 1 ,3},
则使函数y=xα的定义域为R且为2 奇函 数的所有α的值为 1,3 .
2
y=3u是增函数,
所以y 在[ 3
3-x2 3x2在(-∞,
3
2 ]上单调递增,
,+∞)上单调递减.
2
21
· 高中新课标总复习(第1轮)· 文科数学 · 湖南 · 人教版
立足教育 开创未来
点评 复合函数的值域可
采用换元法,结合中间变量的 范围求函数值域.
复合函数y=f(x)的单调性要 根据y=au,u=f(x)两函数在相应 区间上的单调性确定,遵循 “同增异减”的规律.
解析 由0<a<1知函数f(x)=logax为
减函数.故由logam<logan<0,得m>n>1.
6
· 高中新课标总复习(第1轮)· 文科数学 · 湖南 · 人教版
立足教育 开创未来
3.已知函数f(x)= 2x (x<4)
f(x-1) (x≥4), 则f(-2)= 1 ,f(5)= 8 .
4
解析
28
· 高中新课标总复习(第1轮)· 文科数学 · 湖南 · 人教版
立足教育 开创未来
变式 已知函数f(x)=log 1 (x2-2ax+3).
2
(1)若f(x)的定义域为R,求实数a的 取值范围;
(2)若函数f(x)在(-∞,1]上为增函数, 求实数a的取值范围.
解析(1)依题意,
x2-2ax+3>0对x∈R恒成立, 即Δ=(-2a)2-4×3<0,即a2<3, 解得a∈( - 3 , 3 ).
幂指对函数的增长比较ppt课件

11
比较大小
[例 2] 比较下列各组值的大小:
(1)log1
2
45与
log1
2
67;
(2)0.8-0.1 与 1.250.2;
(3)log32.5 与 log52.5; (4)(lgm)1.7 与(lgm)2.1(m>1).
[分析] 充分利用函数的图像和性质(如单调性等)来比较
两数的大小.
12
[解析] (1)y=log1 x 在(0,+∞)上递减,
1 o 1234 x
4
一般地,对于指数函数 y=ax (a>1)和幂函数 y=xn (n>0),在区间
(x0,0+∞)10 上,无20论n比a大30多少,尽4管0 在x的一5定0 变化范围
y内=2,x a1x会10小24于x1.n0,5但×由10于6 a1x.0的7×增1长09 快1.于10x×n1的01增2 长1.1,3×因10此15 总存在
2.列表并在同一坐标系中画出上面这三个函数的图像.
x
0.2 0.6 1.0 1.4
y
y=x2 y=2x
y=2x 1.149 1.516 2 2.639
5
y=x2 0.04 0.36 1 1.96
4
y=log2 x -2.322 -0.737 0 0.485
3
1.8 2.2 2.6 3.0 3.4 …
6
知能自主梳理
7
在区间(0,+∞)上,尽管函数 y=ax(a>1),y=logax(a>1), y=xn(n>0)都是________(填“增”或“减”)函数,但它们的 增长速度不同,而且在不同的“档次”上,随着 x 的增大,y =ax(a>1)的增长速度越来越快,会超过并会远远大于 y= xn(n>0)的增长速度,而 y=logax(a>1)的增长速度会越来越 慢 . 因 此 , 总 会 存 在 一 个 x0 , 当 x>x0 时 , 就 有 logax________xn________ax.
比较大小
[例 2] 比较下列各组值的大小:
(1)log1
2
45与
log1
2
67;
(2)0.8-0.1 与 1.250.2;
(3)log32.5 与 log52.5; (4)(lgm)1.7 与(lgm)2.1(m>1).
[分析] 充分利用函数的图像和性质(如单调性等)来比较
两数的大小.
12
[解析] (1)y=log1 x 在(0,+∞)上递减,
1 o 1234 x
4
一般地,对于指数函数 y=ax (a>1)和幂函数 y=xn (n>0),在区间
(x0,0+∞)10 上,无20论n比a大30多少,尽4管0 在x的一5定0 变化范围
y内=2,x a1x会10小24于x1.n0,5但×由10于6 a1x.0的7×增1长09 快1.于10x×n1的01增2 长1.1,3×因10此15 总存在
2.列表并在同一坐标系中画出上面这三个函数的图像.
x
0.2 0.6 1.0 1.4
y
y=x2 y=2x
y=2x 1.149 1.516 2 2.639
5
y=x2 0.04 0.36 1 1.96
4
y=log2 x -2.322 -0.737 0 0.485
3
1.8 2.2 2.6 3.0 3.4 …
6
知能自主梳理
7
在区间(0,+∞)上,尽管函数 y=ax(a>1),y=logax(a>1), y=xn(n>0)都是________(填“增”或“减”)函数,但它们的 增长速度不同,而且在不同的“档次”上,随着 x 的增大,y =ax(a>1)的增长速度越来越快,会超过并会远远大于 y= xn(n>0)的增长速度,而 y=logax(a>1)的增长速度会越来越 慢 . 因 此 , 总 会 存 在 一 个 x0 , 当 x>x0 时 , 就 有 logax________xn________ax.
《对数与对数函数》指数函数、对数函数与幂函数PPT(对数函数的性质与图像)

错解三中出现逻辑性错误运算变形的顺序出现了问题即开始默认了a1对原不等式进行了转化是不正确的虽然后来对a又进行了讨论看起来结果正确而实际上解答过程是错误的
人教版高中数学B版必修二
指数函数、对数函数与幂函数
4.2 对数与对数函数
4.2.3 对数函数的性质与图像
-1-
课标阐释
思维脉络
1.理解对数函数的概念,体会对
B.(-1,+∞) C.(-1,4)
D.(4,+∞)
(2)函数 y=loga -1(a>0,a≠1)的定义域为
答案:(1)A
(2)(1,+∞)
+ 1 ≥ 0,
解析:(1)由题意可知
4- > 0,
解得 x∈[-1,4),故选 A.
(2)由题意可得 -1>0,又∵偶次根号下非负,
∴x-1>0,即 x>1.
A.(0,2)
B.(0,2] C.(2,+∞)
1
指数函数、对数函数与幂函数
(2)函数 f(x)=log4 的大致图像为(
)
D.[2,+∞)
)
(1)函数
(a>0,且a≠1)是对数函数.
因忽视真数的取值范围而致误
29可看作是函数y=log0.
(5)当0<a<1时,y=logax为R上的减函数;当a>1时,y=logax为R上的增函数.
同理可得函数y=log0.2(x2-2x+2)的单调增区间为(-∞,1].
故函数y=log0.2(x2-2x+2)的单调增区间为(-∞,1],
单调减区间为[1,+∞).
课堂篇探究学习
探究一
人教版高中数学B版必修二
指数函数、对数函数与幂函数
4.2 对数与对数函数
4.2.3 对数函数的性质与图像
-1-
课标阐释
思维脉络
1.理解对数函数的概念,体会对
B.(-1,+∞) C.(-1,4)
D.(4,+∞)
(2)函数 y=loga -1(a>0,a≠1)的定义域为
答案:(1)A
(2)(1,+∞)
+ 1 ≥ 0,
解析:(1)由题意可知
4- > 0,
解得 x∈[-1,4),故选 A.
(2)由题意可得 -1>0,又∵偶次根号下非负,
∴x-1>0,即 x>1.
A.(0,2)
B.(0,2] C.(2,+∞)
1
指数函数、对数函数与幂函数
(2)函数 f(x)=log4 的大致图像为(
)
D.[2,+∞)
)
(1)函数
(a>0,且a≠1)是对数函数.
因忽视真数的取值范围而致误
29可看作是函数y=log0.
(5)当0<a<1时,y=logax为R上的减函数;当a>1时,y=logax为R上的增函数.
同理可得函数y=log0.2(x2-2x+2)的单调增区间为(-∞,1].
故函数y=log0.2(x2-2x+2)的单调增区间为(-∞,1],
单调减区间为[1,+∞).
课堂篇探究学习
探究一
高一数学必修教学课件第三章指数函数幂函数对数函数增长的比较

结合具体案例,分析比较指数函数、幂函数和对数 函数在描述实际问题时的优缺点及适用范围。
THANK YOU
感谢聆听
计算、经济增长模型等。通过比较这些函数的增长差异,可以帮助学生
更好地理解经济学中的相关概念和原理。
02
生物学
在生物学中,这些函数可用于描述生物种群的增长、疾病的传播等。例
如,指数增长模型可用于描述某些生物种群的爆炸式增长,而对数增长
模型则适用于描述种群增长逐渐趋于稳定的情况。
03
物理学
在物理学中,幂函数可用于描述物体之间的万有引力、电场强度等物理
根据平均变化率的定义,可以 计算出f(x)=x^3在区间[1,2]上 的平均变化率为(f(2)-f(1))/(21)=(2^3-1^3)/1=7。
04
对数函数增长特性
对数函数定义及图像
对数函数定义
对数函数是以幂为自变量,指数为因变量,底数为常数的函数。
对数函数图像
对数函数的图像是一条经过原点的曲线,其形状与底数有关。当底数大于1时,图像向右上方倾斜;当底数小于1 时,图像向右下方倾斜。
与其他函数的比较
与一次函数、二次函数等相比,指数 函数的增长速度更快。当x足够大时, 指数函数的值将远远超过这些函数的 值。
典型例题解析
解析
对于(1),由于1.1<1.2且2.5>2.3,因此1.1^2.5<1.2^2.3;对于(2),由于 0.8<0.9且-0.7<-0.6,因此0.8^-0.7>0.9^-0.6。
量的变化规律。通过比较不同函数的增长特性,可以帮助学生深入理解
物理现象的本质。
在其他学科领域的应用举例
化学
在化学动力学中,反应速率常数与温度的关系通常可以用指数函数或幂函数来描述。比较 不同函数的增长差异有助于理解化学反应速率的变化规律。
THANK YOU
感谢聆听
计算、经济增长模型等。通过比较这些函数的增长差异,可以帮助学生
更好地理解经济学中的相关概念和原理。
02
生物学
在生物学中,这些函数可用于描述生物种群的增长、疾病的传播等。例
如,指数增长模型可用于描述某些生物种群的爆炸式增长,而对数增长
模型则适用于描述种群增长逐渐趋于稳定的情况。
03
物理学
在物理学中,幂函数可用于描述物体之间的万有引力、电场强度等物理
根据平均变化率的定义,可以 计算出f(x)=x^3在区间[1,2]上 的平均变化率为(f(2)-f(1))/(21)=(2^3-1^3)/1=7。
04
对数函数增长特性
对数函数定义及图像
对数函数定义
对数函数是以幂为自变量,指数为因变量,底数为常数的函数。
对数函数图像
对数函数的图像是一条经过原点的曲线,其形状与底数有关。当底数大于1时,图像向右上方倾斜;当底数小于1 时,图像向右下方倾斜。
与其他函数的比较
与一次函数、二次函数等相比,指数 函数的增长速度更快。当x足够大时, 指数函数的值将远远超过这些函数的 值。
典型例题解析
解析
对于(1),由于1.1<1.2且2.5>2.3,因此1.1^2.5<1.2^2.3;对于(2),由于 0.8<0.9且-0.7<-0.6,因此0.8^-0.7>0.9^-0.6。
量的变化规律。通过比较不同函数的增长特性,可以帮助学生深入理解
物理现象的本质。
在其他学科领域的应用举例
化学
在化学动力学中,反应速率常数与温度的关系通常可以用指数函数或幂函数来描述。比较 不同函数的增长差异有助于理解化学反应速率的变化规律。
