九年级上册数学正多边形和圆同步练习测试题及答案解析
人教版九年级上册数学《正多边形和圆》 同步习题(含答案)

24.3正多边形和圆同步习题一、选择题1.如图,四边形ABCD是⊙O的内接四边形,若∠D=3∠B,则∠B的度数为()A.30°B.36°C.45°D.60°2.如图,四边形ABCD是⊙O的内接四边形,BE平分∠ABC,若∠D=110°,则∠ABE 的度数是()A.30°B.35°C.50°D.55°3.对于以下说法:①各角相等的多边形是正多边形;②各边相等的三角形是正三角形;③各角相等的圆内接多边形是正多边形;④各顶点等分外接圆的多边形是正多边形.正确的有()A.1个B.2个C.3个D.4个4.一个三角形的外接圆的圆心在这个三角形的外部,则该三角形一定是()A、锐角三角形B、直角三角形C、钝角三角形D、等腰三角形5.如图,△ABC是半径为1的⊙O的内接正三角形,则圆的内接矩形BCDE的面积为()A.3 B.32C.3D.326.如图,正五边形ABCDE内接于O,点P是劣弧BC上一点(点P不与点C重合),则CPD∠=()A.45︒B.36︒C.35︒D.307.如图,四边形ABCD内接于⊙O ,110BOD︒∠=,那么BCD∠等于()A.110°B.135°C.55°D.125°8.如图,△ABC为⊙O的内接三角形,若∠AOC=160°,则∠ADC的度数是()A.80°B.160°C.100°D.40°9.如图,将正五边形绕中心O顺时针旋转a角度,与原正五边形构成新的图形,若要使该图形既是轴对称又是中心对称图形,则a的最小角度为()A .30B .36C .72D .90 10.如图,正五边形ABCDE 和等边AFG 内接于O ,则GFD ∠的度数是( )A .10︒B .12︒C .15︒D .20︒二、填空题 11.如图,四边形ABCD 为O 的内接四边形,已知BOD 110∠=,则BCD ∠的度数为____________________.12.一个正多边形的一个外角为30°,则它的内角和为_____.13.如图,四边形ABCD 内接于⊙O ,点E 在BC 的延长线上,若∠BOD =100°,则∠DCE =_____°.14.如图,四边形ABCD 是⊙O 的内接四边形,∠B=135°,则∠AOC 的度数为_____.15.如图,点A ,B ,C ,D 在O 上,CD CB =,30CAD ∠=︒,50ACD ∠=︒,则ADB =∠_______.三、解答题16.如图,四边形ABCD 内接于O ,AC 与BD 为对角线,BCA BAD ∠=∠,过点A 作//AE BC 交CD 的延长线于点E .求证:EC AC =.17.如图,ABC 的外角BAM ∠的平分线与它的外接圆相交于点E ,连接BE ,CE ,过点E 作//EF BC ,交CM 于点D求证:(1)BE CE =;(2)EF 为⊙O 的切线.18.如图,⊙O 外接于正方形,ABCD P 为弧AD 上一点,且1,3AP PC ==,求正方形ABCD 的边长和PB 的长.参考答案1-5 CBBCC6-10 BDCBB11.125°12.1800°13.5014.9015.70°16.证明:∵//AE BC ,∴ACB EAC ∠=∠.∵ACB BAD ∠=∠,∴EAC BAD ∠=∠,∴EAD CAB ∠=∠,∵180ADE ADC ∠+∠=︒,180ADC ABC ∠+∠=︒,∴ADE ABC =∠∠,∵180EAD ADE E ∠+∠+∠=︒,180BAC ABC ACB ∠+∠+∠=︒, ∴E ACB EAC ∠=∠=∠,∴CE CA =.17.证明:(1)∵四边形ACBE 是圆内接四边形,∴∠EAM =∠EBC ,∵AE 平分∠BAM ,∴∠BAE =∠EAM ,∵∠BAE =∠BCE ,∴∠BCE =∠EAM ,∴∠BCE =∠EBC ,∴BE =CE ;(2)如图,连接EO 并延长交BC 于H ,连接OB ,OC ,∵OB =OC ,EB =EC ,∴直线EO 垂直平分BC ,∴EO ⊥BC ,∵EF//BC ,∴EO ⊥EF ,∵OE 是⊙O 的半径,∴EF 为⊙O 的切线.18.解:连接AC ,作AE PB ⊥于点E , 如图所示.∵四边形ABCD 是正方形,,AB BC CD AD ∴===90,45ABC D BCD ACB ︒︒∠=∠=∠=∠=, AC ∴是O 的直径,ABC 是等腰直角三角形, 90,2,APC AC ︒∴∠==22221310,AC AP PC ∴=+=+= 52AB ∴== 45,,APB ACB AE PB ︒∠=∠=⊥APE ∴是等腰直角三角形,22PE AE AP ∴=== 2222232(5)22BE AB AE ⎛⎫∴=-=-= ⎪ ⎪⎝⎭,232∴=+=+=.PB PE BE22正方形ABCD的边长为5,PB的长为22.。
人教版九年级上册数学《正多边形和圆》同步练习及答案

24.3正多边形和圆知识点1.________________ 相等, ______________也相等的多边形叫做正多边形.2.把一个圆分红几等份,连结各点所获得的多边形是________________ ,它的中心角等于______________________________________________.3.一个正多边形的外接圆的 ____________叫做这个正多边形的中心,外接圆的__________叫做正多边形的半径,正多边形每一边所对的__________ 叫做正多边形的中心角,中心到正多边形的一边的____________叫做正多边形的边心距.4.正 n 边形的半径为 R,边心距为 r ,边长为 a,(1)中心角的度数为: ______________.(2)每个内角的度数为: _______________________.(3)每个外角的度数为: ____________.(4)周长为: _________,面积为: _________.5. 正 n 边形都是轴对称图形,当边数为偶数时,它的对称轴有_______条,而且仍是中心对称图形;当边数为奇数时,它不过 _______________. (填“轴对称图形” 或“中心对称图形” )一、选择题1. 以下说法正确的选项是()A.各边相等的多边形是正多边形B.各角相等的多边形是正多边形C.各边相等的圆内接多边形是正多边形D.各角相等的圆内接多边形是正多边形2. (2013?天津)正六边形的边心距与边长之比为()A.:3B.: 2C. 1:2D.: 23.(2013山东滨州) 若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为()A.6,32B.3 2,3C.6,3D. 62,3 24.如下图,正六边形 ABCDEF内接于⊙ O,则∠ ADB的度数是().第 4 题A. 60°B.45°C.30°D.22.5°5. 半径相等的圆的内接正三角形,正方形,正六边形的边长的比为()A.1: 2: 3B.3: 2:1C.3:2:1D.1:2:36.圆内接正五边形 ABCDE中,对角线 AC和 BD订交于点 P,则∠ APB的度数是().A. 36°B.60°C.72°D.108°第 6 题7.(2013?自贡)如图,点 O是正六边形的对称中心,假如用一副三角板的角,借助点 O(使该角的极点落在点 O处),把这个正六边形的面积 n 平分,那么 n 的全部可能取值的个数是()第 7 题A.4B.5C.6D. 78.如图,△ PQR是⊙ O的内接正三角形,四边形 ABCD是⊙ O的内接正方形,BC∥QR,则∠ AOQ的度数是()A.60 °B.65°C.72 °D.75°第 8 题二、填空题9.一个正 n 边形的边长为 a,面积为 S,则它的边心距为 __________.10. 正多边形的一其中心角为36 度 , 那么这个正多边形的一个内角等于__________ 度 .211. 若正六边形的面积是24 3 cm,则这个正六边形的边长是 __________.第 13题12.已知正六边形的边心距为3,则它的周长是_______.13. 点 M、 N分别是正八边形相邻的边AB、 BC上的点,且 AM=BN,点 O是正八边形的中心,则∠MON=_____________.14.边长为 a 的正三角形的边心距、半径(外接圆的半径)和高之比为_________________.15.要用圆形铁片截出边长为4cm 的正方形铁片,则采用的圆形铁片的直径最小要__________cm.16.若正多边形的边心距与边长的比为1:2 ,则这个正多边形的边数是 __________.17.一个正三角形和一个正六边形的周长相等,则它们的面积比为__________.18.(2013 ?徐州 ) 如图,在正八边形ABCDEFGH中,四边形 BCFG的面积为20cm2,则正八边形的面积为________cm2.第 18题三、解答题19. 比较正五边形与正六边形,能够发现它们的同样点与不一样点.正五边形正六边形比如它们的一个同样点:正五边形的各边相等,正六边形的各边也相等.它们的一个不一样点:正五边形不是中心对称图形,正六边形是中心对称图形. 请你再写出它们的两个同样点和不一样点.同样点:( 1)____________________________________________________________________;(2) ___________________________________________________________________.不一样点:( 1)____________________________________________________________________;(2)____________________________________________________________________. 20. 已知,如图,正六边形ABCDEF的边长为 6cm,求这个正六边形的外接圆半径R、边心距r 6、面积 S6.第 20题21. 如图,⊙ O的半径为 2 ,⊙O的内接一个正多边形,边心距为1,求它的中心角、边长、面积 .第 21题22.已知⊙ O和⊙ O上的一点 A.(1)作⊙ O的内接正方形ABCD和内接正六边形AEFCGH;(2)在( 1)题的作图中,假如点 E 在弧 AD上,求证: DE是⊙ O内接正十二边形的一边.第 22题23.如 1、 2、 3、⋯、 n,M、 N 分是⊙O 的内接正三角形 ABC、正方形 ABCD、正五形 ABCDE、⋯、正 n 形ABCDE⋯的 AB、 BC上的点,且 BM=CN, OM、 ON.(1)求 1 中∠ MON的度数;(2)2 中∠ MON的度数是 _________, 3 中∠ MON的度数是 _________;(3)研究∠ MON的度数与正 n 形数 n 的关系 ( 直接写出答案 ).24.3正多边形和圆知识点1.各边各角2.正多边形正多边形每一边所对的圆心角3.圆心半径圆心角距离360(2)(n2) 180360(5)nar4. (1)n (3)(4)nan n25.n 轴对称图形一、选择题1.C2.B3.B4.C5.B6.C7.B解:依据圆内接正多边形的性质可知,只需把此正六边形再化为正多边形即可,即让周角除以 30 的倍数就能够解决问题.360÷30=12;360÷60=6;360÷90=4;360÷120=3;360÷180=2.所以 n 的全部可能的值共五种状况,应选 B.8.D二、填空题9. 2S10.14411.4cm 12.1213.45° 14.1:2:3 15.42 16.四 17.2:3na18.40三、解答题19.同样点:( 1)每个内角都相等(或每个外角都相等或对角线都相等);( 2)都是轴对称图形(或都有外接圆和内切圆).不一样点:( 1)正五边形的每个内角是108°,正六边形的每个内角是120°;( 2)正五边形的对称轴是 5 条,正六边形的对称轴是 6 条.20.解:连结OA,OB.过点 O作 OG AB于G.AOB =60, OA OBAOB 是等边三角形OA OB6即 R=6OA OB ,OG ABAG 1AB13 262在 Rt AOG 中, r 6OG OA 2AG 2 6 2 3 2 3 3S1663354362R 6 cm , r 6 3 3 cm , S654 3 cm 2 .21.解:连结 OB∵在 Rt △ AOC中, AC= OA2OC 2 2 1=1∴AC=OC∴∠ AOC=∠ OAC=45°∵OA=OB OC⊥ AB∴A B=2AC=2 ∠ AOB=2∠ OAC=2× 45° =90°∴这个内接正多边形是正方形 .∴面积为22=4∴中心角为90°,边长为2,面积为 4.22.(1) 作法:①作直径 AC; ②作直径BD⊥AC; ③挨次连结A、B、C、 D 四点 ,四边形 ABCD即为⊙O 的内接正方形 ;第 22题④分别以A、 C 为圆心,以OA长为半径作弧,交⊙O于E、H、F、G;⑤按序连结A、 E、 F、 C、 G、H 各点 .六边形 AEFCGH即为⊙O 的内接正六边形.(2)证明:连结 OE、DE.∵∠ AOD=360=90°,∠ AOE=360=60°,46∴∠ DOE =∠ AOD -∠ AOE = 90° -60 ° =30°.∴DE 为⊙O 的内接正十二边形的一边.23.(1) 方法一:连结 OB 、 OC.∵正△ ABC 内接于⊙ O ,∴∠ OBM=∠OCN =30°,∠ B OC=120°.又∵ BM=CN , OB=OC ,∴△ OBM ≌△ OCN ( SAS ) .∴∠ BOM =∠ CON.∴∠ MON=∠BOC=120°.方法二:连结 OA 、 OB.∵正△ ABC 内接于⊙ O ,∴ AB=AC ,∠ OAM=∠OBN=30°, ∠AOB=120°.又∵ BM = CN ,∴ A M=BN.又∵ OA=OB,∴△ AOM ≌△ BON ( SAS ) .∴∠ AOM=∠BON.∴∠ MON=∠AOB=120°.(2)90 ° 72 °(3) ∠MON=360.n。
人教版数学九年级上册《24.3正多边形和圆》同步练习(含答案)
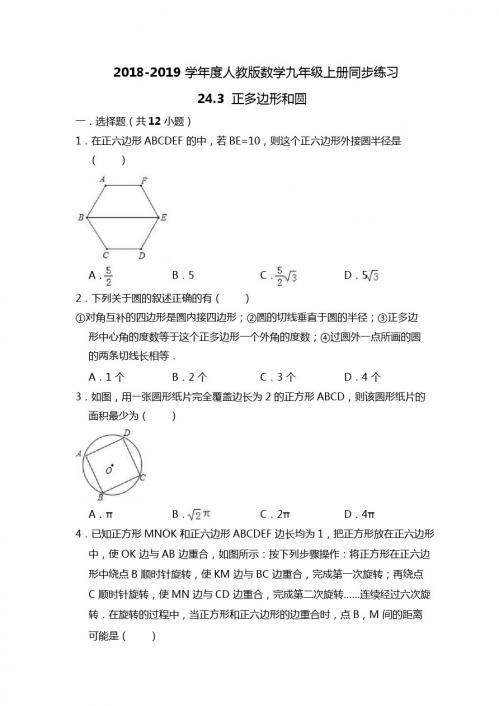
A.(1, ) B.( ,1) C.(1, ) D.(﹣1 , ) 11.如图,正六边形螺帽的边长是 2cm,这个扳手的开口 a 的值应是( )
A.2 cm
B. cm
C. cm
D.1cm
12.如图,圆 O 的内接正六边形的边长是 12,则边心距是( )
形中心角的度数等于这个正多边形一个外角的度数;④过圆外一点所画的圆 的两条切线长相等.
A.1 个
B.2 个
C.3 个
D.4 个
3.如图,用一张圆形纸片完全覆盖边长为 2 的正方形 ABCD,则该圆形纸片的 面积最少为( )
A.π
B.
C.2π
D.4π
4.已知正方形 MNOK 和正六边形 ABCDEF 边长均为 1,把正方形放在正六边形
2018-2019 学年度人教版数学九年级上册同步练习
24.3 正多边形和圆
一.选择题(共 12 小题) 1.在正六边形 ABCDEF 的中,若 BE=10,则这个正六边形外接圆半径是
()
A.
B.5
C.
D.5
2.下列关于圆的叙述正确的有( ) ①对角互补的四边形是圆内接四边形;②圆的切线垂直于圆的半径;③正多边
中,使 OK 边与 AB 边重合,如图所示:按下列步骤操作:将正方形在正六边
形中绕点 B 顺时针旋转,使 KM 边与 BC 边重合,完成第一次旋转;再绕点
C 顺时针旋转,使 MN 边与 CD 边重合,完成第二次旋转……连续经过六次旋
转.在旋转的过程中,当正方形和正六边形的边重合时,点 B,M 间的距离
可能是( )
A.0.5
B.0.7
C. ﹣1
D. ﹣1
5.如图,点 A、B、C、D、E、F 是⊙O 的等分点,分别以点 B、D、F 为圆心,
人教版九年级数学上册《24.3正多边形和圆》同步测试题及答案
人教版九年级数学上册《24.3正多边形和圆》同步测试题及答案1.若正多边形的一个外角为72︒,则这个正多边形的中心角的度数是( )A.18︒B.36︒C.72︒D.108︒2.如图,正六边形ABCDEF内接于圆O,点M在AF上( )A.60︒B.45︒ C.30︒ D.15︒3.若⊙O的内接正n边形的边长与⊙O的半径相等,则n的值为( )A.4B.5C.6D.74.如图,正五边形ABCDE内接于O,点P为DE上一点(点P与点D,点E不重合),连接PC,PD,⊥DG PC垂足为G,则∠PDG等于( )A.72°B.54°C.36°D.64°5.如图,正六边形ABCDEF内接于,正六边形的周长是12,则的半径是( )A.3B.2C.22D.236.如图是半径为4的O的内接正六边形ABCDEF,则圆心O到边AB的距离是( )O OA.23B.3C.2D.37.如图,正六边形ABCDEF 内接于O ,O 的半径为6,则这个正六边形的边心距OM 和弧BC 的长分别为( )A.32 πB.332 πC.332 2π3D.33 π8.如图,正三角形ABC 和正六边形ADBECF 都内接于,O 连接,OC 则∠+∠=ACO ABE ( )A.90︒B.100︒C.110︒D.120︒9.如图,正五边形ABCDE 内接于O ,P 为DE 上的一点(点P 不与点D 重合),则∠=CPD ________°.10.如图,正六边形ABCDEF内接于O,若O的周长等于6π,则正六边形的边长为______.11.早在1800多年前,魏晋时期的数学家刘徽首创“割圆术”,用圆内接正多边形的面积去无限逼近圆面积,如图所示的圆的内接正十二边形,若该圆的半径为1,则这个圆的内接正十二边形的面积为_________________.12.如图,圆内接正六边形ABCDEF的半径为2,则该正六边形的面积是_________________.13.有一个亭子,它的地基是半径为8m的正六边形,求地基的面积.(结果保留根号)14.如图,O的周长等于8πcm,正六边形ABCDEF内接于O.(1)求圆心O 到AF 的距离.(2)求正六边形ABCDEF 的面积.参考答案及解析1.答案:C 解析:正多边形的一个外角为72︒∴正多边形的边数为360725︒÷︒=∴这个正多边形的中心角的度数是360572︒÷=︒故选:C.2.答案:C解析:连接OC ,OD多边形ABCDEF 是正六边形60∴∠=︒COD1302∴∠=∠=︒CMD COD故选:C.3.答案:C解析:内接正n 边形的边长与⊙O 的半径相等∴正n 边形的中心角为60︒360606︒÷︒=∴n 的值为6故选:C.4.答案:B解析:正五边形ABCDE 内接于O∠CPD 与所对的弧相同1362∴∠=∠=︒CPD COD故选:B.5.答案:B解析:如图,连结OA ,OBABCDEF 为正六边形1360606∴∠=︒⨯︒=AOB∴AOB △是等边三角形正六边形的周长是1211226∴=⨯=AB2∴===AO BO AB故选B.6.答案:A解析:如图,做⊥OM AB 于点M360725COD ︒∴∠==︒COD ∠180903654PDG ∠=︒-︒-︒=∴︒正六边形ABCDEF 外接半径为4的O4∴==OA OB 360606︒∠==︒AOB 1302∴∠=∠=∠=︒AOM BOM AOB122∴===AM BM OA2223∴=-=OM OA AM ∴圆心O 到边AB 的距离为23故选:A.7.答案:D解析:连接OB 、OC六边形ABCDEF 为正六边形360606︒∴∠==︒BOC 。
人教版九年级数学上册《24.3 正多边形和圆》同步练习题-附答案

人教版九年级数学上册《24.3 正多边形和圆》同步练习题-附答案学校:___________班级:___________姓名:___________考号:___________考点 正多边形与圆1.定义:正多边形的 圆的圆心叫做这个正多边形的中心 圆的半径叫做正多边形的半径 正多边形每一边所对的 角叫做正多边形的中心角 到正多边形的一边的距离 叫做正多边形的边心距。
2.公式:正多边形的有关概念:边长(a ) 中心(O ) 中心角(∠AOB ) 半径(R )) 边心距(r ) 如图所示①.边心距222a r R ⎛⎫=- ⎪⎝⎭中心角360n ︒=关键点:三角形的内切圆与外接圆 关系定义圆心 实质半径图示外接圆经过三角形各顶点的圆外心三角形各边垂直平分线的交点交点到三角形三个顶点的距离相等内切圆与三角形各边都相切的圆内心三角形各内角平分线的交点交点到三角形各边的距离相等名校提高练习:一选择题:本题共10小题每小题3分共30分。
在每小题给出的选项中只有一项是符合题目要求的。
1.(2024·四川省泸州市·月考试卷)已知圆内接正三角形的面积为√ 3则该圆的内接正六边形的边心距是( )A. 2B. 1C. √ 3D. √ 322.同一个圆的内接正三角形正方形正六边形的边心距分别为r3r4r6则r3:r4:r6等于( )A. 1:√2:√3B. √3:√2:1C. 1:2:3D. 3:2:13.如图若干个全等的正五边形排成环状图中所示的是前3个正五边形要完成这一圆环还需正五边形的个数为( )A. 10B. 9C. 8D. 74.(2024·贵州省黔东南苗族侗族自治州·月考试卷)正六边形ABCDEF内接于⊙O正六边形的周长是12则⊙O的半径是( )A. √ 3B. 2C. 2√ 2D. 2√ 35.(2024·山东省·单元测试)《几何原本》中记载了用尺规作某种六边形的方法其步骤是:①在⊙O上任取一点A连接AO并延长交⊙O于点B②以点B为圆心BO为半径作圆弧分别交⊙O于C D两点③连接CO DO并延长分别交⊙O于点E F④顺次连接BC CF FA AE ED DB得到六边形AFCBDE.再连接AD EF AD EF交于点G.则下列结论不正确的是( )A. GF=GDB. ∠FGA=60°C. EFAE=√ 2 D. AF⊥AD6.(2024·江苏省·同步练习)以半径为2的圆的内接正三角形正方形正六边形的边心距为三边作三角形则该三角形的面积是( )A. √ 22B. √ 32C. √ 2D. √ 37.(2024·江苏省·同步练习)如图正十二边形A1A2…A12连接A3A7A7A10则∠A3A7A10的度数为( )A. 60°B. 65°C. 70°D. 75°8.(2024·江苏省·同步练习)如图若干个全等的正五边形排成环状.图中所示的是前3个正五边形要完成这一圆环还需正五边形的个数为( )A. 6B. 7C. 8D. 99.(2024·北京市市辖区·期末考试)如图正方形ABCD的边长为6且顶点A B C D都在⊙O上则⊙O 的半径为().A. 3B. 6C. 3√ 2D. 6√ 210.(2024·广东省广州市·月考试卷)如图已知⊙O的周长等于4πcm则圆内接正六边形的边长为()cm.A. √ 3B. 2C. 2√ 3D. 4二填空题:本题共6小题每小题3分共18分。
人教版九年级上册数学 24.3正多边形和圆 同步习题(含解析)

24.3正多边形和圆同步习题一.选择题(共10小题)1.如图所示的“六芒星”图标是由圆的六等分点连接而成,若圆的半径为2,则图中阴影部分的面积为()A.B.3C.6D.42.边长为2的正六边形的边心距为()A.1B.2C.D.23.如图,正五边形ABCDE内接于⊙O,P为上的一点(点P不与点D重合),则∠CPD 的度数为()A.30°B.36°C.60°D.72°4.如图,正六边形ABCDEF内接于⊙O,连接BO,则∠OBC的度数是()A.50°B.45°C.65°D.60°5.边长相等的正五边形与正六边形按如图所示拼接在一起,则∠ABO的度数为()A.24°B.48°C.60°D.72°6.如图为正七边形ABCDEFG,以这个正七边形的顶点A和其它六个顶点中的任两个顶点画三角形,所画的三角形中,包含正七边形的中心的三角形个数为()A.3B.6C.9D.127.如图,正五边形ABCDE内接于⊙O,过点A作⊙O的切线交对角线DB的延长线于点F,则下列结论不成立的是()A.AE∥BD B.AB=BF C.AF∥CD D.DF=8.如图,⊙C经过正六边形ABCDEF的顶点A、E,则弧AE所对的圆周角∠APE等于()A.15°B.25°C.30°D.45°9.如图,在正八边形ABCDEFGH中,连接AC,AE,则的值是()A.1B.C.2D.10.如图,在正五边形ABCDE中,连结AC,以点A为圆心,AB为半径画圆弧交AC于点F,连接DF.则∠FDC的度数是()A.18°B.30°C.36°D.40°二.填空题(共5小题)11.如图,在正六边形ABCDEF中,连接BD、BE、DF,则的值为.12.如图,正五边形ABCDE内接于⊙O,P为上一点,连接P A,PE,则∠APE的度数为.13.如图,正六边形ABCDEF,连接AE,CF,则=.14.圆内接正方形的边长为3,则该圆的直径长为.15.如图,边长为4的正方形ABCD内接于⊙O,点E是弧AB上的一动点(不与A、B重合),点F是弧BC上的一点,连结OE,OF,分别与AB,BC交于点G,H,且∠EOF =90°,则△GBH周长的最小值为.三.解答题(共2小题)16.如图,已知点O是正六边形ABCDEF的对称中心,G,H分别是AF,BC上的点,且AG=BH.(1)求∠F AB的度数;(2)求证:OG=OH.17.如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在弧AD上,连接OA、OD、OE、AE、DE.(1)求∠AED的度数;(2)当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值.参考答案1.D2.C3.B4.D5.A6.B7.D8.C9.B10.C11.12.3613..14.315.4+2.16.(1)解:∵六边形ABCDEF是正六边形,∴∠F AB==120°;(2)证明:连接OA、OB,∵OA=OB,∴∠OAB=∠OBA,∵∠F AB=∠CBA,∴∠OAG=∠OBH,在△AOG和△BOH中,,∴△AOG≌△BOH(SAS)∴OG=OH.17.解:(1)连接BD,∵四边形ABCD是⊙O的内接四边形,∴∠BAD+∠C=180°,∵∠C=120°,∴∠BAD=60°,∵AB=AD,∴△ABD是等边三角形,∴∠ABD=60°,∵四边形ABDE是⊙O的内接四边形,∴∠AED+∠ABD=180°,∴∠AED=120°;(2)连接OA,∵∠ABD=60°,∴∠AOD=2∠ABD=120°,∵∠DOE=90°,∴∠AOE=∠AOD﹣∠DOE=30°,∴n==12.。
人教版九年级数学上册正多边形和圆同步练习题含答案

第24章 24.3《正多边形和圆》同步练习及答案 (1) 1.边长为a的正六边形的边心距是__________,周长是____________,面积是___________。
2.如图1,正方形的边长为a,以顶点B、D为圆心,以边长a为半径分别画弧,在正方形内两弧所围成图形的面积是___________。
(1) (2) (3)3.圆内接正方形ABCD的边长为2,弦AE平分BC边,与BC交于F,则弦AE的长为__________。
4.正六边形的面积是183,则它的外接圆与内切圆所围成的圆环面积为_________。
5.圆内接正方形的一边截成的小弓形面积是2π-4,则正方形的边长等于__________。
6.正三角形的内切圆半径、外接圆半径和高的比为___________。
7.在半径为R的圆中,内接正方形与内接正六边形的边长之比为___________。
8.同圆的内接正n边形与外切正n边形边长之比是______________。
9.正三角形与它的内切圆及外接圆的三者面积之比为_____________。
10.正三角形的外接圆半径为4cm,以正三角形的一边为边作正方形,则此正方形的外接圆半径长为___________。
B卷1.正方形的内切圆半径为r,这个正方形将它的外接圆分割出四个弓形,其中一个弓形的面积为_________。
2.如果正三角形的边长为a,那么它的外接圆的周长是内切圆周长的_______倍。
3.如图2,正方形边长为2a,那么图中阴影部分的面积是__________。
4.正多边形的一个内角等于它的一个外角的8倍,那么这个正多边形的边数是________。
5.半径为R的圆的内接正n边形的面积等于__________。
6.如果圆的半径为a,它的内接正方形边长为b,该正方形的内切圆的内接正方形的边长为c,则a,b,c间满足的关系式为___________。
7.如图3,正△ABC 内接于半径为1cm 的圆,则阴影部分的面积为___________。
九年级数学上册《正多边形和圆》练习题及答案解析

九年级数学上册《正多边形和圆》练习题及答案解析学校:___________姓名:___________班级:________________一、填空题1.已知正方形ABCD,截去四个角成一正八边形,则这个正八边形EFGHIJLK的边长为_______,面积为_______.2.正十二边形的中心角是_____度.二、解答题3.(1)如图①,把△ABC纸片沿DE折叠,当点A落在四边形BCED内部点A'的位置时,①A、①1、①2之间有怎样的数量关系?并说明理由.(2)如图①,把△ABC纸片沿DE折叠,当点A落在四边形BCED外部点A'的位置时,①A、①1、①2之间有怎样的数量关系?并说明理由.(3)如图①,把四边形ABCD沿EF折叠,当点A、D分别落在四边形BCFE内部点A'、D的位置时,你能求出①A'、①D、①1与①2之间的数量关系吗?并说明理由.4.阅读与思考请阅读下列材料,并完成相应的任务:任务:(1)材料中划横线部分应填写的内容为 .(2)如图2,正五边形ABCDE 内接于①O ,AB =2,求对角线BD 的长.5.如图,正六边形ABCDEF 的对称中心P 在反比例函数(0,0)k y k x x=>>的图象上,边CD 在x 轴上,点B 在y 轴上,已知CD =4.(1)点A 是否在该反比例函数的图象上?请说明理由;(2)若反比例函数的图象与DE 交于点Q ,求点Q 的横坐标.6.如图所示,正五边形的对角线AC 和BE 相交于点M .(1)求证:AC ①ED ;(2)求证:ME =AE .7.如图1,正五边形ABCDE 内接于①O ,阅读以下作图过程,并回答下列问题,作法:如图2,①作直径AF ;①以F 为圆心,FO 为半径作圆弧,与①O 交于点M ,N ;①连接,,AM MN NA .(1)求ABC∠的度数.(2)AMN是正三角形吗?请说明理由.(3)从点A开始,以DN长为半径,在①O上依次截取点,再依次连接这些分点,得到正n边形,求n的值.8.如图,ABC是等边三角形,点D、E、G分别在边AB、AC、BC上,且AD CE BG==,BE、CD、AG分别相交于点F、P、Q.求证:①PQF是等边三角形.9.如图,在圆内接正三角形ABC中,若①DOE保持120°角度不变,求证:当①DOE绕着O点旋转时,由两条半径和①ABC的两条边围成的图形,图中阴影部分的面积始终是①ABC的面积的13.10.已知点E在正方形ABCD的对角线AC上,正方形AFEG与正方形ABCD有公共点A.(1)如图1,当点G 在AD 上,F 在AB(2)将正方形AFEG 绕A 点逆时针方向旋转9(0)0αα︒<<︒,如图2,求:CE DG 的值为多少;(3)AB =AG AD =,将正方形AFEG 绕A 逆时针方向旋转(0360)αα︒<<︒,当C ,G ,E 三点共线时,请直接写出DG 的长度.三、单选题11.如图,已知①O 的半径为1,AB 是直径,分别以点A 、B 为圆心,以AB 的长为半径画弧.两弧相交于C 、D 两点,则图中阴影部分的面积是( )A .52π-B .56πC .53πD .83π-12.对于等边三角形的性质,下列说法不正确的是( )A .等边三角形的三条边都相等,三个内角也都相等;B .等边三角形的边都等于60,角都等于60°;C .等边三角形中线、高、角平分线都相等,而且都交于一点;D .等边三角形具有等腰三角形的所有性质;132,则这个多边形的内角和为( )A .720︒B .360︒C .240︒D .180︒14.如图,四边形ABCD 为⊙O 的内接正四边形,△AEF 为⊙O 的内接正三角形,若DF 恰好是同圆的一个内接正n 边形的一边,则n 的值为( )A.6B.8C.10D.1215.连接正八边形的三个顶点,得到如图所示的图形,下列说法不正确的是()A.四边形ABCH与四边形EFGH的周长相等B.连接HD,则HD平分①CHEC.整个图形不是中心对称图形D.CEH△是等边三角形参考答案及解析:1.1)a22)a【分析】设正八边形的边长为x,表示出剪掉的等腰直角三角形的直角边,再根据正方形的边长列出方程求解即可;利用正八边形的面积等于正方形的面积减去剪掉的四个等腰直角三角形的面积列式计算即可得解.【详解】解:正方形ABCD外接圆的直径就是它的对角线,∴正方形边长为a,如图所示,设正八边形的边长为x,在Rt AEL 中,LE x =,AE AL x ==,2x x a ∴+=,解得:1)x a =,即正八边形的边长为1)a .2222241)]2)AEL S S S a x a a a =-=-=-=正方形正八边形.故答案是:1)a ,22)a .【点睛】本题考查了正方形的性质,等腰直角三角形的性质,勾股定理,解题的关键是读懂题目信息,根据正方形的边长列出方程.2.30 【分析】根据正多边形的中心角公式:360n计算即可 【详解】正十二边形的中心角是:360°÷12=30°.故答案为30.【点睛】本题的关键是掌握正多边形中心角的计算公式3.(1)2①A =①1+①2;见解析;(2)2①A =①1﹣①2;见解析;(3)2(①A +①D )=①1+①2+360°,见解析【分析】(1)根据翻折的性质表示出①3、①4,再根据三角形的内角和定理列式整理即可得解;(2)先根据翻折的性质以及平角的定义表示出①3、①4,再根据三角形的内角和定理列式整理即可得解;(3)先根据翻折的性质表示出①3、①4,再根据四边形的内角和定理列式整理即可得解.【详解】解:(1)如图,根据翻折的性质,①3=EDA '∠=12(180-①1),①4=DEA '∠=12(180-①2),①①A +①3+①4=180°,①①A +12(180-①1)+12(180-①2)=180°,整理得,2①A =①1+①2;(2)如图,同理,根据翻折的性质,①3=12(180-①1),①4=12(180+①2),①①A+①3+①4=180°,①①A+12(180-①1)+12(180+①2)=180°,整理得,2①A=①1-①2;(3)如图,同理,根据翻折的性质,①3=12(180-①1),①4=12(180-①2),①①A+①D+①3+①4=360°,①①A+①D+12(180-①1)+12(180-①2)=360°,整理得,2(①A+①D)=①1+①2+360°.【点睛】本题主要考查了三角形的内角和定理,多边形的内角与外角,翻折的性质,整体思想的利用是解题的关键.4.(1)AC BD AB CD AD BC ⋅=⋅+⋅;(2)1【分析】(1)由托勒密定理可直接求解;(2)连接,AD AC ,根据圆周角与弦的关系可得AD AC BD ==,设BD x =,在四边形ABCD 中,根据托勒密定理有,AC BD AB CD AD BC ⋅=⋅+⋅,建立方程即可求得BD 的长【详解】(1)由托勒密定理可得:AC BD AB CD AD BC ⋅=⋅+⋅故答案为:AC BD AB CD AD BC ⋅=⋅+⋅(2)如图,连接,AD AC ,五边形ABCDE 是正五边形,则E ABC BCD ∠=∠=∠,2AB BC CD ===AD AC BD ∴==设BD x =,AC BD AB CD AD BC ⋅=⋅+⋅即2222x x =⨯+解得1211x x ==1BD ∴=+【点睛】本题考查了托勒密定理,圆周角与弦的关系,解一元二次方程,理解题意添加辅助线是解题的关键.5.(1)点A在该反比例函数的图象上,理由见解析(2)3+【分析】(1)过点P作x轴垂线PG,连接BP,可得BP=4,G是CD的中点,所以P(4,;(2)易求D(6,0),E(8,,待定系数法求出DE的解析式为y﹣次函数即可求点Q.(1)解:点A在该反比例函数的图象上,理由如下:过点P作x轴垂线PG,连接BP,①P是正六边形ABCDEF的对称中心,CD=4,①BP=4,G是CD的中点,①sin604PG BO BC==⋅︒==①P(4,,①P在反比例函数y=kx(k>0,x>0)的图象上,①k=①反比例函数解析式为y由正六边形的性质可知,A(2,,①点A在反比例函数图象上;(2)解:由(1)得D (6,0),E (8,,设DE 的解析式为y =mx +b ,①608m b m b +=⎧⎪⎨+=⎪⎩①m b ⎧=⎪⎨=-⎪⎩①y﹣由方程y y ⎧=⎪⎨⎪=-⎩,解得x=3,①Q点横坐标为3+..【点睛】本题考查反比例函数的图象及性质,正六边形的性质;将正六边形的边角关系与反比例函数上点的坐标结合是解题的关键.6.(1)见解析;(2)见解析【分析】(1)作出正五边形的外接①O ,则AB 的度数为1360725⨯︒=︒,由①EAC 的度数等于EDC 的度数的一半,得到①EAC =1144722⨯︒=︒,同理,①AED =12×72°×3=108°,则 ①EAC +①AED =180°,即可证明ED∥AC ;(2)由①AEB 的度数等于AB 的度数的一半,得到①AEB =36°,则①EMA =180°-①AEB -①EAC =72°,可推出①EAM =①EMA =72°,即可证明 EA =EM .【详解】解:①正多边形必有外接圆,①作出正五边形的外接①O ,则AB 的度数为1360725⨯︒=︒, ① ①EAC 的度数等于EDC 的度数的一半,① ①EAC =1144722⨯︒=︒, 同理,①AED =12×72°×3=108°,① ①EAC +①AED =180°,① ED∥AC ;(2)①①AEB 的度数等于AB 的度数的一半,①①AEB =36°,①①EMA =180°-①AEB -①EAC =72°,① ①EAM =①EMA =72°,① EA =EM .【点睛】本题主要考查了正多边形与圆,平行线的判定,等腰三角形的判定,解题的关键在于能够熟练掌握圆的相关知识.7.(1)108︒(2)是正三角形,理由见解析(3)15n =【分析】(1)根据正五边形的性质以及圆的性质可得BC CD DE AE AB ====,则AOC ∠(优弧所对圆心角)372216︒︒=⨯=,然后根据圆周角定理即可得出结论;(2)根据所作图形以及圆周角定理即可得出结论;(3)运用圆周角定理并结合(1)(2)中结论得出14412024NOD ∠=︒-︒=︒,即可得出结论.(1)解:①正五边形ABCDE .①BC CD DE AE AB ====, ①360725AOB BOC COD DOE EOA ︒∠=∠=∠=∠=∠==︒, ①3AEC AE =,①AOC ∠(优弧所对圆心角)372216︒︒=⨯=, ①1121610822AOC ABC ∠=⨯︒=∠=︒; (2)解:AMN 是正三角形,理由如下:连接,ON FN ,由作图知:FN FO =,①ON OF =,①ON OF FN ==,①OFN △是正三角形,①60OFN ∠=︒,①60AMN OFN ∠=∠=︒,同理60ANM ∠=︒,①60MAN ∠=︒,即AMN ANM MAN ∠=∠=∠,①AMN 是正三角形;(3)①AMN 是正三角形,①2120A N A N M O =∠=︒∠.①2AD AE =,①272144AOD ∠=⨯︒=︒,①DN AD AN =-,①14412024NOD∠=︒-︒=︒,①3601524n==.【点睛】本题考查了圆周角定理,正多边形的性质,读懂题意,明确题目中的作图方式,熟练运用圆周角定理是解本题的关键.8.见解析【分析】先根据“SAS”证明△ACD①△CBE,得到①ACD=①CBE,结合三角形外角的性质可证①BFD=①60°,进而可证△PQF是等边三角形.【详解】证明:①△ABC是等边三角形,①①A=①BCE=60°,AC=CB,又①AD=CE,①△ACD①△CBE(SAS);①①ACD=①CBE,①①ACB=①ACD+①BCF=60°,①①BFD=①CBE+①BCF=①ACD+①BCF =60°,同理可得,①APE=60°,①△PQF是等边三角形.【点睛】本题考查了等边三角形的判定与性质,全等三角形的判定与性质,以及三角形外角的性质,综合运用各知识点是解答本题的关键.9.见解析【分析】连接OA、OB、OC,由正多边形和圆的性质可得:①OAB①①OBC①①OCA.则①1=①2,再证明①OAG①①OCF,即可求解.【详解】如图:连接OA、OB、OC,由正多边形和圆的性质可得①OAB①①OBC①①OCA.①①1=①2.设OD 交BC 于F ,OE 交AC 于G ,则①AOC =①3+①4=120°,①DOE =①5+①4=120°,① ①3=①5.∴在①OAG 和①OCF 中2135OA OC ∠=∠⎧⎪=⎨⎪∠=∠⎩,① ①OAG ①①OCF .① ΔAOC ΔABC 13OFCG S S S ==四边形. 【点睛】本题考查了正多形和圆的性质,全等三角形的判定和性质,将阴影部分的面积转化为固定的三角形面积是解题关键.10.(1)2(3)-【分析】(1)根据题意可得GE DC ∥,根据平行线分线段成比例即可求解;(2)根据(1)的结论,可得AG AD AE AC ==根据旋转的性质可得DAG CAE ∠=∠,进而证明GAD EAC ∽,根据相似三角形的性质即可求解;(3)分两种情况画出图形,证明①ADG ①①ACE ,根据相似三角形的判定和性质以及勾股定理即可得出答案.(1) 解:正方形AFEG 与正方形ABCD 有公共点A ,点G 在AD 上,F 在AB 上,GE DC ∴∥AG AE DG EC ∴= EC AE DG AG∴= 四边形AFEG 是正方形 ∴AE =∴2DG AGE === (2)解:如图,连接AE ,正方形AFEG 绕A 点逆时针方向旋转9(0)0αα︒<<︒,DAG CAE ∴∠=∠AG AD AE AC ==GAD EAC ∴∽∴AC CE DG AD= (3) 解:①如图,AB =AG AD =,AD AB ∴==8AG ==,16AC ==, ,,G E C 三点共线,Rt AGC △中,GC ==8CE GC GE ∴=-=,由(2)可知GAD EAC ∽,∴CE AC DG DA==()816DA CE DG AC ⋅∴==4==. ①如图:由(2)知△ADG ①①ACE ,①DG AD CE AC ==,①DG , ①四边形ABCD 是正方形,①AD =BC ,AC 16,①AG ,①AG =8, ①四边形AFEG 是正方形,①①AGE =90°,GE =AG =8,①C ,G ,E 三点共线.①①AGC =90°①CG①CE =CG +EG,①DG =综上,当C ,G ,E 三点共线时,DG 的长度为-【点睛】本题考查了平行线分线段成比例,相似三角形的性质与判定,正方形的性质,勾股定理,旋转的性质,综合运用以上知识是解题的关键.11.A【分析】连接AC 、BC ,如图,先判断△ACB 为等边三角形,则①BAC =60°,由于S 弓形BC =S 扇形BAC ﹣S △ABC ,所以图中阴影部分的面积=4S 弓形BC +2S △ABC ﹣S ⊙O ,然后利用扇形的面积公式、等边三角形的面积公式和圆的面积公式计算.【详解】解:连接BC ,如图,由作法可知AC =BC =AB =2,①①ACB 为等边三角形,①①BAC =60°,①S 弓形BC =S 扇形BAC ﹣S △ABC ,①S 阴=4S 弓形BC +2S △ABC ﹣S ⊙O=4(S 扇形BAC ﹣S △ABC )+2S △ABC ﹣S ⊙O=4S 扇形BAC ﹣2S △ABC ﹣S ⊙O=42602360π⨯⨯-222﹣π×12 53=π﹣ 故选:A .【点睛】本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了扇形的面积公式.12.B【分析】根据等边三角形的性质逐项分析判断即可求解.【详解】解:A . 等边三角形的三条边都相等,三个内角也都相等,故该选项正确,不符合题意;B . 等边三角形的三个角都等于60°,三条边都相等,不一定等于60,故该选项不正确,符合题意;C . 等边三角形中线、高、角平分线都相等,而且都交于一点,故该选项正确,不符合题意;D . 等边三角形具有等腰三角形的所有性质,故该选项正确,不符合题意;故选B .【点睛】本题考查了等边三角形的性质,掌握等边三角形的性质是解题的关键.13.A【分析】设AB 是正多边形的一边,OC①AB ,在直角①AOC 中,利用三角函数求得①AOC 的度数,从而求得中心角的度数,然后利用360度除以中心角的度数,求出边数,根据内角和公式即可求出多边形的内角和.【详解】如图:①2,①2,设AB 是正多边形的一边,OC①AB , 2OC OA OB k ===,,在直角①AOC 中,OC cos AOC AO ∠== ①①AOC=30°,①①AOB=60°, 则正多边形边数是:360660︒︒=, ①多边形的内角和为:()62180720-⨯︒=︒,故选:A .【点睛】本题考查学生对正多边形的概念掌握和计算的能力,正多边形的计算一般是转化成半径,边心距、以及边长的一半这三条线段构成的直角三角形的计算.14.D【分析】连接,,AC OD OF ,先根据圆内接正多边形的性质可得点O 在AC 上,且AC 是BAD ∠和EAF ∠的角平分线,从而可得1145,3022CAD BAD CAF EAF ∠=∠=︒∠=∠=︒,再根据角的和差可得15DAF ∠=︒,然后根据圆周角定理可得230DOF DAF ∠=∠=︒,最后根据正多边形的性质即可得.【详解】解:如图,连接,,AC OD OF ,四边形ABCD 为O 的内接正四边形,AEF 为O 的内接正三角形,∴点O 在AC 上,且AC 是BAD ∠和EAF ∠的角平分线,90,60BAD EAF ∠=︒∠=︒,1145,3022CAD BAD CAF EAF ∴∠=∠=︒∠=∠=︒, 15DAF CAD CAF ∴∠=∠-∠=︒,230DOF DAF ∴∠=∠=︒, DF 恰好是圆O 的一个内接正n 边形的一边,3603601230n DOF ︒︒∴===∠︒, 故选:D .【点睛】本题考查了圆内接正多边形、圆周角定理等知识点,熟练掌握圆内接正多边形的性质是解题关键.15.D【分析】根据正八边形和圆的性质进行解答即可.【详解】解:A .① 根据正八边形的性质, 四边形ABCH 与四边形EFGH 能够完全重合,即四边形ABCH 与四边形EFGH 全等①四边形ABCH 与四边形EFGH 的周长相等,故选项正确,不符合题意;B .连接DH ,如图1,① 正八边形是轴对称图形,直线HD 是对称轴,① HD 平分①CHE故选项正确,不符合题意;C.整个图形是轴对称图形,但不是中心对称图形,故选项正确,不符合题意;D.①八边形ABCDEFGH是正八边形,① B=BC=CD=DE=EF=FG=GH,CH=EH,设正八边形的中心是O,连接EO、DH,如图2,①DOE=360=45 8︒︒①OE=OH①①OEH=①OHE=12①DOE=22.5°①①CHE=2①OHE=45°①①HCE=①HEC=12(180°-①CHE)=67.5°①CEH△不是等边三角形,故选项错误,符合题意.故选:D.【点睛】本题考查了正多边形和圆,熟记正八边形与等腰三角形的性质是解题的关键.。
2019-2020学年人教版九年级数学上学期同步测试专题24-3:正多边形和圆

专题24.3正多边形和圆(测试)一、单选题1.若正多边形的一个中心角是30°,则该正多边形的边数是( )A .6B .12C .16D .18【答案】B【解析】003603012÷=.故这个正多边形的边数为12.故选:B .2.正多边形的一边所对的中心角与它的一个外角的关系是( )A .相等B .互余C .互补D .互余或互补【答案】A【解析】设正多边形是正n 边形,则它的一边所对的中心角是360n ︒,正多边形的外角和是360°,则每个外角也是360n ︒,所以正多边形的一边所对的中心角与它的一个外角相等,故选A .3.在半径为R 的圆上依次截取等于R 的弦,顺次连接各分点得到的多边形是( )A .正三角形B .正四边形C .正五边形D .正六边形【答案】D【解析】解:由题意这个正n 边形的中心角=60°,∴n=36060︒︒=6∴这个多边形是正六边形,故选:D .4.如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形.则原来的纸带宽为()A .1BCD .2【答案】C【解析】如图,作BG AC ⊥,依题可得:ABC ∆是边长为2的等边三角形,在Rt BGA ∆中,∵2AB =,1AG =,∴BG =故答案为:C.5 )A .πB .3πC .4πD .12π【答案】C【解析】解:如图,六边形ABCDEF 为正六边形,作OH ⊥AB 于H ,连接OA ,∴OA 为正六边形ABCDEF 的外接圆的半径,OH 为正六边形ABCDEF 的边心距,∴在Rt AOH 中,∠AOH=1806︒=30°,∴cos ∠AOH=OH OA == ∴OA=2, ∴它的外接圆的面积=2πOA ()=4π. 故选:C .6.如图,正八边形各边中点构成四边形,则正八边形边长与AB 的比是( )A.2B C D【答案】A【解析】过E作EF⊥AD于F,过G作GH⊥AD于H,则△AEF与△DGH是等腰直角三角形,四边形EFHG是矩形,∴AF=EF=DH=GH,EG=FH,设AF=EF=GH=DH=k,∴AE=DG k,∴EG=2AE=k,∴AB=AD=+2k,=∴正八边形边长与AB2故选A.7.如图,在半径为6的⊙O中,正方形AGDH与正六边形ABCDEF都内接于⊙O,则图中阴影部分的面积为()A .27﹣B .54﹣C .D .54【答案】B 【解析】解:设EF 交AH 于M 、交HD 于N ,连接OF 、OE 、MN ,如图所示:根据题意得:△EFO 是等边三角形,△HMN 是等腰直角三角形,∴EF =OF =6,∴△EFO 的高为:OF•sin60°=MN =2(6﹣12﹣ ∴FM =12(6﹣12+3, ∴阴影部分的面积=4S △AFM =4×12(3)×54﹣ 故选:B .8.一个圆形餐桌直径为2米,高1米,铺在上面的一个正方形桌布的四个角恰好刚刚接触地面,则这块桌布的每边长度为( )米A .12x xB .4 C.D .4π【答案】A【解析】解:正方形桌布对角线长度为圆形桌面的直径加上两个高,即2+1+1=4(米),设正方形边长是x 米,则x 2+x 2=42,解得:,所以正方形桌布的边长是米.故选:A .9.下面给出五个命题(1)正多边形都有内切圆和外接圆,且这两个圆是同心圆(2)各边相等的圆外切多边形是正多边形(3)各角相等的圆内接多边形是正多边形(4)正多边形既是轴对称图形又是中心对称图形(5)正n 边形的中心角360n a n ︒=,且与每一个外角相等 其中真命题有( )A .2 个B .3 个C .4 个D .5 个 【答案】A【解析】解:(1)正多边形都有一个内切圆和一个外接圆,是同心圆,圆心是正多边形的中心,故正确;(2)各边相等的圆外切多边形的角不一定相等,故不一定是正多边形,如菱形,故错误;(3)圆内接矩形,各角相等,但不是正多边形,故错误;(4)边数是偶数的正多边形既是轴对称图形又是中心对称图形,而边数是奇数的多边形是轴对称图形,不是中心对称图形;(5)正n 边形的中心角360n a n︒=,且与每一个外角相等. 故正确的是(1)(5).共有2个.故选:A .10.一个圆的内接正三角形的边长为( )AB .4C .D .【答案】D【解析】根据题意画图如下:过点O 作OD ⊥BC 于D ,连接OB ,∴BD=CD=12, ∵△ABC 是等边三角形,∴∠ABC=60°,∴∠OBD=30°,∴OD=12OB , ∴OB 2-(12OB)2=BD 2, 解得:OB=2,即圆的半径为2,∴该圆的内接正方形的对角线长为4,设正方形的边长为x ,∴x 2+x 2=42,解得x=∴该圆的内接正方形的边长为故选D.11.如图,⊙O是正六边形ABCDEF的外接圆,P是弧EF上一点,则∠BPD的度数是()A.30°B.60°C.55°D.75°【答案】B【解析】连接OB,OD,∵六边形ABCDEF是正六边形,∴∠BOD==120°,∴∠BPD=∠BOD=60°,故选:B.12.距资料,我国古代数学家祖冲之和他的儿子发展了刘徽的“割圆术”(即圆的内接正多边形边数不断增加,它的周长就越接近圆周长),他们从圆内接正六边形算起,一直算到内接正24576边形,将圆周率精确到小数点后七位,使中国对圆周率的计算在世界上领先了一千多年,依据“割圆术”,由圆内接正六边形算得的圆周率的近似值是( )A.B.3 C.D.【答案】B【解析】解:由题意n=6时,π≈ =3,故选:B .13.如图,用四根长为5cm 的铁丝,首尾相接围成一个正方形(接点不固定),要将它的四边按图中的方式向外等距离移动a cm ,同时添加另外四根长为5cm 的铁丝(虚线部分)得到一个新的正八边形,则a 的值为( )A .4cmB .5cmC . D【答案】D【解析】如图,由题意可知:△ABC 是等腰直角三角形,AB=5,AC=BC=a .则有:a 2+a 2=52,∴a=2或-2(舍弃)故选:D .14.如图,将边长为5的正六边形ABCDEF 沿直线MN 折叠,则图中阴影部分周长为()A .20B .24C .30D .35【答案】C【解析】由翻折不变性可知,阴影部分的周长等于正六边形ABCDEF 的周长=5×6=30,故选:C .15.如图,已知O 的周长等于6cm ,则它的内接正六边形ABCDEF 的面积是( )A .4B .4C .2D .【答案】C【解析】过点O 作OH ⊥AB 于点H ,连接OA ,OB ,设⊙O 的半径为r ,∵⊙O 的周长等于6πcm ,∴2πr=6π,解得:r=3,∴⊙O 的半径为3cm ,即OA=3cm ,∵六边形ABCDEF 是正六边形,∴∠AOB=16×360°=60°,OA=OB ,∴△OAB 是等边三角形,∴AB=OA=3cm ,∵OH ⊥AB ,∴AH=12AB ,∴AB=OA=3cm ,∴AH=32cm ,=2cm ,∴S 正六边形ABCDEF =6S △OAB =6×12×3×2=2(cm2).故选C.16.⊙O 是一个正n 边形的外接圆,若⊙O 的半径与这个正n 边形的边长相等,则n 的值为() A .3 B .4 C .6 D .8【答案】C【解析】⊙O是一个正n边形的外接圆,若⊙O的半径与这个正n边形的边长相等,则这个正n边形的中心角是60°,÷︒=360606n的值为6,故选:C二、填空题17.若正多边形的一个外角为60°,则这个正多边形的中心角的度数是___________.【答案】60°【解析】∵正多边形的一个外角为60°,∴正多边形的边数为=6,即正多边形为六边形,∴这个正多边形的中心角的度数==60°.故答案为60°18.如图,六边形ABCDEF是正六边形,若l1∥l2,则∠1﹣∠2=_____.【答案】60°【解析】解:如图,过A作l∥l1,则∠4=∠2,∵六边形ABCDEF是正六边形,∴∠FAB=120°,即∠4+∠3=120°,∴∠2+∠3=120°,即∠3=120°﹣∠2,∵l1∥l2,∴l∥l2,∴∠1+∠3=180°,∴∠1+120°﹣∠2=180°,∴∠1﹣∠2=180°﹣120°=60°,故答案为:60°.19.如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10=_____.【答案】75°【解析】解:设该正十二边形的中心为O,如图,连接A10O和A3O,由题意知,37105 12A A A=⊙O的周长,∴∠A3OA10=536012︒⨯=150°,∴∠A3A7A10=75°,故答案为:75°.20.已知正方形MNKO和正六边形ABCDEF边长均为1,把正方形放在正六边形外边,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形外绕点B顺时针旋转,使KN边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使NM边与CD边重合,完成第二次旋转;………在这样连续6次旋转的过程中,点M在图中直角坐标系中的纵坐标可能是()A .2B .﹣2.2C .2.3D .﹣2.3【答案】A【解析】如图,∵正方形MNKO 和正六边形ABCDEF 边长均为1∴第一次旋转后点M 1 纵坐标坐标为12 ,第二次、第三次旋转后点M 2(M 3,四次旋转后点M 4的纵坐标为﹣12﹣2,第五次旋转后点M 5的纵坐标为 12+2,第六次旋转后的点M 6的纵坐标为2. 故选:A .三、解答题21.如图,已知O .(1)用尺规作正六边形,使得O 是这个正六边形的外接圆,并保留作图痕迹; (2)用两种不同的方法把所做的正六边形分割成六个全等的三角形.【答案】(1)答案见解析;(2)答案见解析【解析】解:(1)如图所示:,(2)如图所示:22.如图是由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点.已知每个正六边形的边长为1,△ABC的顶点都在格点上,求△ABC的面积.【答案】【解析】延长AB,再作出过点C与格点所在的直线,交于格点E.∵正六边形的边长为1,∴正六边形的半径是1,则CE=4,则△BCE 的边EC ,△ACE 边EC ,则S △ABC =S △AEC -S △BEC =12×4×)=23.回顾旧知:在探究有关正多边形的有关性质时,我们是从那几个方面展开的?探究的方法与过程又是怎样的?(不要求回答)温馨提示,如图1,是一个边长为a 的正六边形.我们知道它具有如下的性质:①正六边形的每条边长度相等;②正六边形的六个内角相等,都是120°;③正六边形的内角和为720°;④正六边形的外角和为360°.等.解答问题:(1)观察图2,请你在下面的横线上,再写出边长为a 的正六边形所具有不同于上述的性质(不少于5条): .(2)尺规作图:在图2中作出圆内接正六边形的内切圆(不要求写作法,只保留作图痕迹);(3)求出这个正六边形外接圆半径与内切圆半径的比值.【答案】(1)见解析;(2)作图见解析;(3). 【解析】(1)①正六边形既是轴对称图形,又是中心对称图形;②正六边形的面积为: a 2,周长为6a ;③正六边形有一个内切圆、外接圆,它们是同心圆;④圆内接正六边形的每条边在圆内所对的优弧长度相等;⑤圆内接正六边形的每条边在圆内所对的优弧的弧度相等;⑥圆内接正六边形的每条边(或说弦)在圆内所对的劣弧的长度相等;⑦圆内接正六边形的每条边(或说弦)在圆内所对的劣弧的弧度相等;⑧圆内接正六边形的每条边(或说弦)在圆内所对的圆心角(中心角)相等,都是60°;⑨圆内接正六边形的边长等于圆的半径;⑩圆内接正六边形的边心距为: a 等.(2)如图2所示:(3)如图2,连结EO,在Rt△ONE中,∵OE=DE=a,∠EON=DOE=30°,∴OE=a,∴边长为a正六边形外接圆半径与内切圆半径的比值为:.24.(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为弧BC上一动点,求证:PA=PB+PC.下面给出一种证明方法,你可以按这一方法补全证明过程,也可以选择另外的证明方法.证明:在AP上截取AE=CP,连接BE∵△ABC是正三角形∴AB=CB∵∠1和∠2的同弧圆周角∴∠1=∠2∴△ABE≌△CBP(2)如图2,四边形ABCD是⊙O的内接正方形,点P为弧BC上一动点,求证:PA=PC+ PB.(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为弧BC上一动点,请探究PA、PB、PC三者之间有何数量关系,直接写出结论.【答案】(1)见解析;(2)见解析;(3)【解析】证明:(1)延长BP至E,使PE=PC,连接CE.∵∠1=∠2=60°,∠3=∠4=60°,∴∠CPE=60°,∴△PCE是等边三角形,∴CE=PC,∠E=∠3=60°;又∵∠EBC=∠P AC,∴△BEC≌△APC,∴P A=BE=PB+P C.(2)过点B作BE⊥PB交P A于E.∵∠1+∠2=∠2+∠3=90°∴∠1=∠3,又∵∠APB=45°,∴BP=BE,∴;PE=又∵AB=BC,∴△ABE≌△CBP,∴PC=AE.∴PA AE PE PC=+=.=+;(3)答:PA PC证明:在AP上截取AQ=PC,连接BQ,∵∠BAP=∠BCP,AB=BC,∴△ABQ≌△CBP,∴BQ=BP.又∵∠APB=30°,∴PQ==+=∴PA PQ AQ25.如图①②③④,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEFG…的边AB,BC上的点,且BM=CN,连接OM,ON.(1)求图①中∠MON的度数;(2)图②中,∠MON的度数是________,图③中∠MON的度数是________;(3)试探究∠MON的度数与正n边形的边数n的关系(直接写出答案).【答案】90°72°【解析】(1)方法一:如图①,连接OB,OC.图①∵正三角形ABC内接于⊙O,∴∠OBM=∠OCN=30°,∠BOC=120°.又∵BM=CN,OB=OC,∴△OBM≌△OCN,∴∠BOM=∠CON,∴∠MON=∠BOC=120°.方法二:如图②,连接OA,OB.图②∵正三角形ABC内接于⊙O,∴AB=BC,∠OAM=∠OBN=30°,∠AOB=120°.∵BM=CN,∴AM=BN.又∵OA=OB,∴△AOM≌△BON,∴∠AOM=∠BON,∴∠MON=∠AOB=120°.(2)90°72°(3)∠MON=.26.如图,一个圆形街心花园,有三个出口A,B,C,每两个出口之间有一条60米长的道路,组成正三角形ABC,在中心点O处有一亭子,为使亭子与原有的道路相通,需再修三条小路OD,OE,OF,使另一出口D、E、F分别落在ΔABC分成三个全等的多边形,以备种植不同品种的花草.(1)请你按以上要求设计两种不同的方案,将你的设计方案分别画在图1,图2中,并附简单说明.(2)要使三条小路把ΔABC分成三个全等的等腰梯形,应怎样设计?请把方案画在图3中,并求此时三条小路的总长.(3)请你探究出一种一般方法,使得出口D不论在什么位置,都能准确地找到另外两个出口E、F的位置,请写明这个方法.(4)你在(3)中探究出的一般方法适用于正五边形吗?请结合图5予以说明,这种方法能推广到正n边形吗?【答案】(1)方案1:D,E,F与A,B,C重合,方案2:OD,OE,OF分别垂直于AB,BC,AC;(2)60;(3)如图(4)见解析;(4)可推广到正n边形.【解析】(1)方案1:D,E,F与A,B,C重合,连OD,OE,OF.方案2:OD,OE,OF分别垂直于AB,BC,AC.(2)OD//AC,OE//AB,OF//BC,如图(3),作OM⊥BC于M,连OB,∵ΔABC是等边Δ,∴BM=BC=30,且∠OBM=30°,∴OM=10,∵OE//AB,∴∠OEM=60°,OE==20,又OE=OF=OD,∴OE+OF+OD=3OE=60,答:略.(3)如图(4),方法1:在BC,CA,AB上分别截取BE=CF=AD,连结OD,OE,OF,方法2:在AB上任取一点D,连OD,逆时针旋转OD120°两次,得E,F.(4)设M1为A1A2上任一点,在各边上分别取A2M2=A3M3=A4M4=A5M5=A1M1,连OM1……OM5即可,∴可推广到正n边形.。
人教版九年级上册数学 24.3 正多边形和圆 同步练习(含答案)

24.3 正多边形和圆同步练习一、选择题1.一个正多边形的一个内角为120°,则这个正多边形的边数为( ) A.9 B.8 C.7 D.62.如图所示,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是( )A.23 cm B.3 cm C.233cm D.1 cm第2题图第5题图3.已知圆的半径是2,则该圆的内接正六边形的面积是()A.3B.9C.18D.364.正三角形、正方形、圆三者的周长都等于l,它们的面积分别为S1,S2、S3,则( ). A.S1=S2=S3 B.S3<S1<S2 C.S1<S2<S3 D.S2<S1<S35.中华人民共和国国旗上的五角星的画法通常是先把圆五等分,然后连接五个等分点而得到的(如图所示).五角星的每一个角的度数是( ).A.30° B.35° C.36° D.37°第6题图第7题图第9题图6.如图所示,是由5把相同的折扇组成的“蝶恋花”(如图①)和梅花图案(如图②)(图中的折扇无重叠),则梅花图案中的五角星的五个锐角均为()A.36° B.42° C.45° D.48°二、填空题7.如图所示,平面上两个正方形与正五边形都有一条公共边,则∠ 等于________.8.要用圆形铁片裁出边长为4的正方形铁片,则选用的圆形铁片的直径最小是________. 9.如图所示,等边△ABC 内接于⊙O ,AB =10cm ,则⊙O 的半径是________. 10.如图,点O 是正五边形ABCDE 的中心,则∠BAO 的度数为 .11.正六边形的半径是5cm ,则边长6a =________,周长6P =________ ,边心距6r =________,面积6S =________.12. 正六边形的外接圆的半径与内切圆的半径之比为 .三、解答题13.如图所示,正△ABC 的外接圆的圆心为O ,半径为2,求△ABC 的边长a ,周长P ,边心距r ,面积S .14. 如图所示,半径为R 的圆绕周长为10πR 的正六边形外边作无滑动滚转,绕完正六边形后,圆一共转了多少圈?一位同学的解答过程:圆的周长为2πR ,所以它绕完正六边形后一共转了102RRππ圈,结果一共转了5圈.你认为这位同学的解答有无错误?如有错误,请更正.15.如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5cm,求⊙O的半径R.答案与解析一、选择题1.【答案】D;【解析】可求每个外角为60°,∴ 360÷60=6或(2)180120nn-⨯=°°∴ n=6.2.【答案】A;【解析】较长对角线与较短对角线及一边长构成一直角三角形,用勾股定理求解.3.【答案】C;【解析】连接正六边形的中心与各个顶点,得到六个等边三角形,等边三角形的边长是2,高为3,因而等边三角形的面积是3,∴正六边形的面积=18,故选C.4.【答案】C;【解析】当周长一定时,边数越多的正多边形其面积越大,当它成为圆时面积最大.5.【答案】C;【解析】五角星的每一个角所对的弧为圆的15,∴弧的度数为72°,因而每个角的度数为36°,故选C.6.【答案】D.【解析】如图③所示,正五边形ABCDE的中心角为72°,各内角为108°,故五角星五个锐角均为48°.二、填空题 7.【答案】72°;【解析】α=360°-90°-90°-108°=72°. 8.【答案】42;【解析】如图所示,△ABC 为等腰Rt△,242AC AB ==.9.【答案】1033cm ; 【解析】过O 作OD ⊥BC 于D ,连接OB ,在Rt △BOD 中,BD =12BC =1102⨯=5(cm). ∠BOD =180603=°°, ∴3BD OB =. ∴ BO =10333=(cm).10.【答案】54°; 【解析】连接OB ,则OB=OA ,∴∠BAO=∠ABO,∵点O 是正五边形ABCDE 的中心,∴∠AOB==72°,∴∠BAO=(180°﹣72°)=54°; 故答案为:54°.11.【答案】6a =5cm ,666P a ==30cm ,6532r =cm ,26753cm 2s =; 12.【答案】2:.【解析】设正六边形的半径是r ,则外接圆的半径r ,内切圆的半径是正六边形的边心距,因而是,因而正六边形的外接圆的半径与内切圆的半径之比为2:.三、解答题13.【答案与解析】作AD ⊥BC 于D .∵ △ABC 是正三角形,∴ 点O 在AD 上,a =BC =2CD ,∠OCD =30°,在Rt △COD 中,112r OD OC ===, 2222213CD OC OD =-=-=,∴ 223a BC CD ===,363P a ==. 又∵ AD =OA+OD =2+1=3, ∴ 112333322S BC AD ==⨯⨯=, ∴ 23a =,63P =,1r =,33S =.14.【答案与解析】有错误,由正六边形的每个顶点外圆要转60°角,应转了10162RRππ+=(圈). 15.【答案与解析】解:连接OB ,OC ,OD ,∵等边△ABC 内接于⊙O,BD 为内接正十二边形的一边,∴∠BOC=×360°=120°,∠BOD=×360°=30°,∴∠COD=∠BOC﹣∠BOD=90°,∵OC=OD,∴∠OCD=45°,∴OC=5×=5(cm).即⊙O的半径R=5cm.。
九年级数学上册第二十四章圆24.3正多边形和圆同步检测含解析

24.3 正多边形和圆测试时间:30分钟一、选择题1.(2018北京西城期中)已知正六边形的边长为3,则这个正六边形的半径是( )A. B.2 C.3 D.32.边心距为2的等边三角形的边长是( )A.4B.4C.2D.23.(2017天津和平期末)正三角形的高、外接圆半径、边心距之比为( )A.3∶2∶1B.4∶3∶2C.4∶2∶1D.6∶4∶3二、填空题4.如图,正五边形ABCDE内接于☉O,则∠ABD=.5.(2018吉林白城大安期末)如图,正三角形的边长为12 cm,剪去三个角后成为一个正六边形,则这个正六边形的内部任意一点到各边的距离和为cm.三、解答题6.(2016甘肃兰州中考)如图,已知☉O,用尺规作☉O的内接正四边形ABCD(写出结论,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑).7.如图,正方形ABCD的外接圆为☉O,点P在劣弧上(不与C点重合).(1)求∠BPC的度数;(2)若☉O的半径为8,求正方形ABCD的边长.8.如图,已知正五边形ABCDE中,BF与CM相交于点P,CF=DM.(1)求证:△BCF≌△CDM;(2)求∠BPM的度数.24.3 正多边形和圆一、选择题1.答案 C 如图,AB为☉O内接正六边形的一边,则∠AOB==60°.∵OA=OB,∴△OAB为等边三角形,∴AO=AB=3.故选C.2.答案 B 如图所示,∵△ABC是等边三角形,边心距OD=2,∴∠OBD=30°,∴OB=4,在Rt△OBD中,由勾股定理可得BD=2.∵OD为边心距,∴BC=2BD=4.故选B.3.答案 A 如图,△ABC是等边三角形,AD是高,点O是其外接圆的圆心,由等边三角形三线合一的性质得点O在AD上,并且点O还是它的内切圆的圆心.∵AD⊥BC,∠1=∠2=30°,∴BO=2OD,又OA=OB,∴AD=3OD,∴AD∶OA∶OD=3∶2∶1,故选A.二、填空题4.答案72°解析∵五边形ABCDE为正五边形,∴∠ABC=∠C==108°,∵CD=CB,∴∠CBD==36°,∴∠ABD=∠ABC-∠CBD=72°.5.答案12解析设O为正三角形ABC的中心,作ON⊥BC于N,连接OH.∵六边形DFHKGE是正六边形,正三角形ABC的边长为12 cm,∴AD=DE=DF=BF=4 cm,∴OH=4 cm.由勾股定理得ON==2cm,则正六边形DFHKGE的面积=×4×2×6=24(cm2).设这个正六边形的内部任意一点到各边的距离和为h cm,则×4×h=24,解得h=12.三、解答题6.解析如图:(过圆心O作直径DB,作直径BD的垂直平分线,交☉O于A、C两点,连接AB、BC、CD、DA,四边形ABCD即为所作的正四边形)7.解析(1)如图,连接OB,OC.∵四边形ABCD为正方形,∴∠BOC=90°,∴∠BPC=∠BOC=45°.(2)如图,过点O作OE⊥BC于点E,∵OB=OC,∠BOC=90°,∴∠OBE=45°,∵OE⊥BC,∴OE=BE,∵OE2+BE2=OB2,∴BE===4,∴BC=2BE=2×4=8,即正方形ABCD的边长为8.8.解析(1)证明:∵五边形ABCDE是正五边形,∴BC=CD,∠BCF=∠CDM,在△BCF和△CDM中,∴△BCF≌△CDM.(2)∵五边形ABCDE是正五边形,∴∠BCF==108°,∴∠CBF+∠CFB=180°-∠BCF=72°,∵△BCF≌△CDM,∴∠MCD=∠CBF,∴∠MCD+∠CFB=72°,∴∠BPM=∠CPF=180°-(∠MCD+∠CFB)=108°.。
人教版九年级数学上册正多边形和圆2同步练习题含答案

第24章 24.3《正多边形和圆》同步练习及答案 (2)1.下列边长为a 的正多边形与边长为a 的正方形组合起来,不能镶嵌成平面的是( )(1)正三角形 (2)正五边形 (3)正六边形 (4)正八边形A .(1)(2)B .(2)(3)C .(1)(3)D .(1)(4)2.以下说法正确的是 A .每个内角都是120°的六边形一定是正六边形. B .正n 边形的对称轴不一定有n 条. C .正n 边形的每一个外角度数等于它的中心角度数.D .正多边形一定既是轴对称图形,又是中心对称图形.(3)(2006年天津市)若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r 3,r 4,r 6,则r 3:r 4:r 6等于( )A .1:2:3B .3:2:1C .1:2:3D . 3:2:14. 已知正六边形ABCDEF 内接于⊙O ,图中阴影部分的面积为312,则⊙O 的半径为______________________.5.如图,正方形ABCD 内接于⊙O ,点E 在AD 上,则∠BEC= .6.将一块正六边形硬纸片(图1),做成一个底面仍为正六边形且高相等的无盖纸盒(侧面均垂直于底面,见图2),需在每一个顶点处剪去一个四边形,例如图中的四边形AGA /H ,那么∠GA /H 的大小是 度.7.(2006年威海市)如图,若正方形A 1B 1C 1D 1内接于正方形ABCD 的内接圆,则AB B A 11的值为( )A .21 B .22 C .41 D .42 8.从一个半径为10㎝的圆形纸片上裁出一个最大的正方形,则此正方形的边长为 .9.如图五边形ABCDE 内接于⊙O,∠A =∠B=∠C=∠D=∠E .求证:五边形ABCDE 是正五边形10.如图,10-1、10-2、10-3、…、10-n分别是⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…,点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动。
人教版九年级上册数学同步练习《正多边形和圆》(习题+答案)

24.3正多边形和圆内容提要1.把圆分成相等的n段弧,依次连接n个等分点,就得到这个圆的内接正n边形,这个圆称为对应正n边形的外接圆.2.如图.(1)我们把一个正多边形的外接圆的圆心叫做这个正多边形的中心.(2)外接圆的半径叫做正多边形的半径.(3)正多边形每一边所对的圆心角叫做正多边形的中心角.(4)中心到正多边形的距离叫做正多边形的边心距.3.在正多边形和圆中,研究圆的半径、边长、边心距、中心角等之间的等量关系时,常常构造直角三角形.基础训练1.完成下列有关正多边形的计算:形状中心角半径边长边心距周长面积正三角形3正方形3正六边形3O O周长最接近的是()A.6B8C10D173.圆内接正五边形ABCDE中,对角线AC和BD相交于点P,则APB的度数是()A .36︒B .60︒C .72︒D .108︒4.如图,若四边形ABCD 是半径为1cm 有圆内接正方形,则图中阴影部分的面积为( ) A .()222cm π-B .()221cm π-C .()22cm π-D .()21cm π-5.如图,O 的周长等于6cm π,求O 内接正六边形ABCDEF 的面积.6.如图,要在一个形状为圆的纸板上截出一个面积最大的正方形,试用尺规作出这个正方形(不要求写作法,保留作图痕迹).能力提高1.如图,正六边形ABCDEF内接于O,则ADB∠的度数是()A.60︒B.45︒C.30︒D.22.5︒2.如图,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是()A.23cm B.3cm C.23cm D.1cm3.如图,正六边形内接于O,O的半径为10,则圆中阴影部分的面积为.4.如图,一个正方形同时外切和内接于两个圆,当小圆的半径为r时,大圆的半径为.5.如图,有一圆内接正八边形ABCDEFGH,若ADE∆的面积为10,则正八边形ABCDEFGH的面积为.6.如图是一组有规律的正多边形,各正多边形中的阴影部分面积均为a,按此规律,则第n 个正多边形的面积为.7.如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边上).当这个正六边形的边长最大时,AE的最小值为.8.如图,O为等边ABC∆的边长为43,求O的半径.∆的内切圆,ABC9.如图所示,正五边形ABCDE的对角线AC,BE相交于M.求证:四边形CDEM是菱形.拓展探究1.某单位搞绿化,要在一块圆形空地上种植四种颜色的花,为了便于管理和美观,相同颜色的花集中种植,且每种颜色的花所占的面积相同,现征集设计方案,要求设计的图案成轴对称图形或中心对称图形,请在下面圆中画出三种设计方案(只要示意图,不写画法).2.如图,现有边长为a 的正方形花布,问应该怎样裁剪,才能得到一个面积最大的正八边形花布来做一个形状为正八边形的风筝?24.3 参考答案:基础训练1.形状 中心角 半径 边长 边心距周长 面积 正三角形 120︒ 23 6 318 93 正方形 90︒6 23 3 83 12 正六边形60︒22312632.C 3.C 4.C 5.2273cm 6.略 能力提高1.C 2.A 3.1001503π- 42r 5.40 6.12n a + 721- 8.29.提示:通过证72EAM EMA∠=∠=︒,证得EM MC CD ED===.拓展探究1.参考答案2.正八边形与正方形都是轴对称图形和中心对称图形,为了使面积最大,正八边形的部分边在正方形的边上,从四个角各剪去一个直角边为222a的等腰直角三角形.。
人教版2020届九年级数学上学期同步测试专题24-3:正多边形和圆【含解析】

专题24.3正多边形和圆(测试)一、单选题1.若正多边形的一个中心角是30°,则该正多边形的边数是( ) A .6 B .12C .16D .18【答案】B【解析】003603012÷=. 故这个正多边形的边数为12. 故选:B .2.正多边形的一边所对的中心角与它的一个外角的关系是( ) A .相等 B .互余C .互补D .互余或互补【答案】A【解析】设正多边形是正n 边形,则它的一边所对的中心角是360n︒, 正多边形的外角和是360°,则每个外角也是360n︒, 所以正多边形的一边所对的中心角与它的一个外角相等, 故选A .3.在半径为R 的圆上依次截取等于R 的弦,顺次连接各分点得到的多边形是( ) A .正三角形 B .正四边形C .正五边形D .正六边形【答案】D 【解析】解:由题意这个正n 边形的中心角=60°, ∴n=36060︒︒=6 ∴这个多边形是正六边形, 故选:D .4.如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形.则原来的纸带宽为( )A .1B 2C 3D .2【答案】C【解析】如图,作BG AC ⊥,依题可得:ABC ∆是边长为2的等边三角形, 在Rt BGA ∆中, ∵2AB =,1AG =, ∴3BG =, 即原来的纸宽为3. 故答案为:C.5.已知一个正六边形的边心距为3,则它的外接圆的面积为( ) A .π B .3πC .4πD .12π【答案】C 【解析】解:如图,六边形ABCDEF 为正六边形,作OH ⊥AB 于H ,连接OA ,∴OA 为正六边形ABCDEF 的外接圆的半径,OH 为正六边形ABCDEF 的边心距, ∴3 在RtAOH 中,∠AOH=1806︒=30°, ∴cos ∠AOH=OH 33OA ==∴OA=2,∴它的外接圆的面积=2πOA ()=4π. 故选:C .6.如图,正八边形各边中点构成四边形,则正八边形边长与AB的比是()A.2﹣2B.322C.1222+D.222+【答案】A【解析】过E作EF⊥AD于F,过G作GH⊥AD于H,则△AEF与△DGH是等腰直角三角形,四边形EFHG是矩形,∴AF=EF=DH=GH,EG=FH,设AF=EF=GH=DH=k,∴AE=DG2k,∴EG=2AE=2k,∴AB=AD=2k+2k,∴正八边形边长与AB22k22 22k2k=+故选A.7.如图,在半径为6的⊙O中,正方形AGDH与正六边形ABCDEF都内接于⊙O,则图中阴影部分的面积为()A .27﹣93B .54﹣183 C .183D .54【答案】B【解析】解:设EF 交AH 于M 、交HD 于N ,连接OF 、OE 、MN ,如图所示: 根据题意得:△EFO 是等边三角形,△HMN 是等腰直角三角形, ∴EF =OF =6,∴△EFO 的高为:OF•sin60°=6×3=33,MN =2(6﹣33)=12﹣63, ∴FM =12(6﹣12+63)=33﹣3, ∴阴影部分的面积=4S △AFM =4×12(33﹣3)×33=54﹣183;故选:B .8.一个圆形餐桌直径为2米,高1米,铺在上面的一个正方形桌布的四个角恰好刚刚接触地面,则这块桌布的每边长度为( )米A .12x xB .4C .42D .4π【答案】A【解析】解:正方形桌布对角线长度为圆形桌面的直径加上两个高,即2+1+1=4(米), 设正方形边长是x 米,则 x 2+x 2=42,解得:2,所以正方形桌布的边长是2米.故选:A.9.下面给出五个命题(1)正多边形都有内切圆和外接圆,且这两个圆是同心圆(2)各边相等的圆外切多边形是正多边形(3)各角相等的圆内接多边形是正多边形(4)正多边形既是轴对称图形又是中心对称图形(5)正n边形的中心角360nan︒=,且与每一个外角相等其中真命题有()A.2 个B.3 个C.4 个D.5 个【答案】A【解析】解:(1)正多边形都有一个内切圆和一个外接圆,是同心圆,圆心是正多边形的中心,故正确;(2)各边相等的圆外切多边形的角不一定相等,故不一定是正多边形,如菱形,故错误;(3)圆内接矩形,各角相等,但不是正多边形,故错误;(4)边数是偶数的正多边形既是轴对称图形又是中心对称图形,而边数是奇数的多边形是轴对称图形,不是中心对称图形;(5)正n边形的中心角360nan︒=,且与每一个外角相等.故正确的是(1)(5).共有2个.故选:A.10.一个圆的内接正三角形的边长为3( ) A2B.4 C.23D.22【答案】D【解析】根据题意画图如下:过点O作OD⊥BC于D,连接OB,∴BD=CD=123,∵△ABC是等边三角形,∴∠ABC=60°,∴∠OBD=30°,∴OD=12 OB,∴OB2-(12OB)2=BD2,解得:OB=2,即圆的半径为2,∴该圆的内接正方形的对角线长为4,设正方形的边长为x,∴x2+x2=42,解得x=22.∴该圆的内接正方形的边长为22.故选D.11.如图,⊙O是正六边形ABCDEF的外接圆,P是弧EF上一点,则∠BPD的度数是()A.30°B.60°C.55°D.75°【答案】B【解析】连接OB,OD,∵六边形ABCDEF是正六边形,∴∠BOD==120°,∴∠BPD=∠BOD=60°,故选:B.12.距资料,我国古代数学家祖冲之和他的儿子发展了刘徽的“割圆术”(即圆的内接正多边形边数不断增加,它的周长就越接近圆周长),他们从圆内接正六边形算起,一直算到内接正24576边形,将圆周率精确到小数点后七位,使中国对圆周率的计算在世界上领先了一千多年,依据“割圆术”,由圆内接正六边形算得的圆周率的近似值是( ) A.B.3 C.D.【答案】B【解析】解:由题意n=6时,π≈=3,故选:B.13.如图,用四根长为5cm的铁丝,首尾相接围成一个正方形(接点不固定),要将它的四边按图中的方式向外等距离移动a cm,同时添加另外四根长为5cm的铁丝(虚线部分)得到一个新的正八边形,则a的值为()A.4cm B.5cm C.52cm D.52cm【答案】D【解析】如图,由题意可知:△ABC是等腰直角三角形,AB=5,AC=BC=a.则有:a2+a2=52,∴a=522或-522(舍弃)故选:D.14.如图,将边长为5的正六边形ABCDEF沿直线MN折叠,则图中阴影部分周长为()A.20 B.24 C.30 D.35【答案】C【解析】由翻折不变性可知,阴影部分的周长等于正六边形ABCDEF的周长=5×6=30,故选:C.15.如图,已知O的周长等于6cmπ,则它的内接正六边形ABCDEF的面积是()A.34B.34C.32D.273【答案】C【解析】过点O作OH⊥AB于点H,连接OA,OB,设⊙O的半径为r,∵⊙O的周长等于6πcm,∴2πr=6π,解得:r=3,∴⊙O的半径为3cm,即OA=3cm,∵六边形ABCDEF是正六边形,∴∠AOB=16×360°=60°,OA=OB,∴△OAB是等边三角形,∴AB=OA=3cm,∵OH⊥AB,∴AH=12 AB,∴AB=OA=3cm,∴AH=32cm,22OA AH-=332cm,∴S正六边形ABCDEF=6S△OAB=6×12×3×33=273(cm2).故选C.16.⊙O是一个正n边形的外接圆,若⊙O的半径与这个正n边形的边长相等,则n的值为()A.3 B.4 C.6 D.8【答案】C【解析】⊙O是一个正n边形的外接圆,若⊙O的半径与这个正n边形的边长相等,则这个正n边形的中心角是60°,360606÷︒=n的值为6,故选:C二、填空题17.若正多边形的一个外角为60°,则这个正多边形的中心角的度数是___________.【答案】60°【解析】∵正多边形的一个外角为60°,∴正多边形的边数为=6,即正多边形为六边形,∴这个正多边形的中心角的度数==60°.故答案为60°18.如图,六边形ABCDEF是正六边形,若l1∥l2,则∠1﹣∠2=_____.【答案】60°【解析】解:如图,过A作l∥l1,则∠4=∠2,∵六边形ABCDEF是正六边形,∴∠FAB=120°,即∠4+∠3=120°,∴∠2+∠3=120°,即∠3=120°﹣∠2,∵l1∥l2,∴l∥l2,∴∠1+∠3=180°,∴∠1+120°﹣∠2=180°,∴∠1﹣∠2=180°﹣120°=60°,故答案为:60°.19.如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10=_____.【答案】75°【解析】解:设该正十二边形的中心为O,如图,连接A10O和A3O,由题意知,37105 12A A A=⊙O的周长,∴∠A3OA10=536012︒⨯=150°,∴∠A3A7A10=75°,故答案为:75°.20.已知正方形MNKO和正六边形ABCDEF边长均为1,把正方形放在正六边形外边,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形外绕点B顺时针旋转,使KN边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使NM边与CD边重合,完成第二次旋转;………在这样连续6次旋转的过程中,点M在图中直角坐标系中的纵坐标可能是()A 3B.﹣2.2 C.2.3 D.﹣2.3【答案】A 【解析】如图,∵正方形MNKO和正六边形ABCDEF边长均为1∴第一次旋转后点M1纵坐标坐标为12,第二次、第三次旋转后点M2(M3)的纵坐标为﹣32,四次旋转后点M4的纵坐标为﹣12﹣3,第五次旋转后点M5的纵坐标为12+3,第六次旋转后的点M6的纵坐标为3.故选:A.三、解答题21.如图,已知O.(1)用尺规作正六边形,使得O是这个正六边形的外接圆,并保留作图痕迹;(2)用两种不同的方法把所做的正六边形分割成六个全等的三角形.【答案】(1)答案见解析;(2)答案见解析【解析】解:(1)如图所示:,(2)如图所示:22.如图是由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点.已知每个正六边形的边长为1,△ABC的顶点都在格点上,求△ABC的面积.【答案】23.【解析】延长AB,再作出过点C与格点所在的直线,交于格点E.∵正六边形的边长为1,∴正六边形的半径是1,则CE=4,3则△BCE的边EC上的高是332,△ACE边EC上的高是32,则S△ABC=S△AEC-S△BEC=12×4×5333)=323.回顾旧知:在探究有关正多边形的有关性质时,我们是从那几个方面展开的?探究的方法与过程又是怎样的?(不要求回答)温馨提示,如图1,是一个边长为a的正六边形.我们知道它具有如下的性质:①正六边形的每条边长度相等;②正六边形的六个内角相等,都是120°;③正六边形的内角和为720°;④正六边形的外角和为360°.等.解答问题:(1)观察图2,请你在下面的横线上,再写出边长为a的正六边形所具有不同于上述的性质(不少于5条):.(2)尺规作图:在图2中作出圆内接正六边形的内切圆(不要求写作法,只保留作图痕迹);(3)求出这个正六边形外接圆半径与内切圆半径的比值.【答案】(1)见解析;(2)作图见解析;(3).【解析】(1)①正六边形既是轴对称图形,又是中心对称图形;②正六边形的面积为:a2,周长为6a;③正六边形有一个内切圆、外接圆,它们是同心圆;④圆内接正六边形的每条边在圆内所对的优弧长度相等;⑤圆内接正六边形的每条边在圆内所对的优弧的弧度相等;⑥圆内接正六边形的每条边(或说弦)在圆内所对的劣弧的长度相等;⑦圆内接正六边形的每条边(或说弦)在圆内所对的劣弧的弧度相等;⑧圆内接正六边形的每条边(或说弦)在圆内所对的圆心角(中心角)相等,都是60°;⑨圆内接正六边形的边长等于圆的半径;⑩圆内接正六边形的边心距为:a等.(2)如图2所示:(3)如图2,连结EO,在Rt△ONE中,∵OE=DE=a,∠EON=DOE=30°,∴OE=a,∴边长为a正六边形外接圆半径与内切圆半径的比值为:.24.(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为弧BC上一动点,求证:PA=PB+PC.下面给出一种证明方法,你可以按这一方法补全证明过程,也可以选择另外的证明方法.证明:在AP上截取AE=CP,连接BE∵△ABC是正三角形∴AB=CB∵∠1和∠2的同弧圆周角∴∠1=∠2∴△ABE≌△CBP(2)如图2,四边形ABCD是⊙O的内接正方形,点P为弧BC上一动点,求证:PA=PC+ 2PB.(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为弧BC上一动点,请探究PA、PB、PC三者之间有何数量关系,直接写出结论.【答案】(1)见解析;(2)见解析;(3)3PB【解析】证明:(1)延长BP至E,使PE=PC,连接CE.∵∠1=∠2=60°,∠3=∠4=60°,∴∠CPE=60°,∴△PCE是等边三角形,∴CE=PC,∠E=∠3=60°;又∵∠EBC=∠P AC,∴△BEC≌△APC,∴P A=BE=PB+P C.(2)过点B作BE⊥PB交P A于E.∵∠1+∠2=∠2+∠3=90°∴∠1=∠3,又∵∠APB=45°,∴BP=BE,∴;PE2PB=又∵AB=BC,∴△ABE≌△CBP,∴PC=AE.∴PA AE PE PC2PB=+=.=+;(3)答:PA3PB PC证明:在AP上截取AQ=PC,连接BQ,∵∠BAP=∠BCP,AB=BC,∴△ABQ≌△CBP,∴BQ=BP.又∵∠APB=30°,=PB∴PQ3=+=∴PA PQ AQ325.如图①②③④,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEFG…的边AB,BC上的点,且BM=CN,连接OM,ON.(1)求图①中∠MON的度数;(2)图②中,∠MON的度数是________,图③中∠MON的度数是________;(3)试探究∠MON的度数与正n边形的边数n的关系(直接写出答案).【答案】90°72°【解析】(1)方法一:如图①,连接OB,OC.图①∵正三角形ABC内接于⊙O,∴∠OBM=∠OCN=30°,∠BOC=120°.又∵BM=CN,OB=OC,∴△OBM≌△OCN,∴∠BOM=∠CON,∴∠MON=∠BOC=120°.方法二:如图②,连接OA,OB.图②∵正三角形ABC内接于⊙O,∴AB=BC,∠OAM=∠OBN=30°,∠AOB=120°.∵BM=CN,∴AM=BN.又∵OA=OB,∴△AOM≌△BON,∴∠AOM=∠BON,∴∠MON=∠AOB=120°.(2)90°72°(3)∠MON=.26.如图,一个圆形街心花园,有三个出口A,B,C,每两个出口之间有一条60米长的道路,组成正三角形ABC,在中心点O处有一亭子,为使亭子与原有的道路相通,需再修三条小路OD,OE,OF,使另一出口D、E、F分别落在ΔABC分成三个全等的多边形,以备种植不同品种的花草.(1)请你按以上要求设计两种不同的方案,将你的设计方案分别画在图1,图2中,并附简单说明.(2)要使三条小路把ΔABC分成三个全等的等腰梯形,应怎样设计?请把方案画在图3中,并求此时三条小路的总长.(3)请你探究出一种一般方法,使得出口D不论在什么位置,都能准确地找到另外两个出口E、F的位置,请写明这个方法.(4)你在(3)中探究出的一般方法适用于正五边形吗?请结合图5予以说明,这种方法能推广到正n边形吗?【答案】(1)方案1:D,E,F与A,B,C重合,方案2:OD,OE,OF分别垂直于AB,BC,AC;(2)60;(3)如图(4)见解析;(4)可推广到正n边形.【解析】(1)方案1:D,E,F与A,B,C重合,连OD,OE,OF.方案2:OD,OE,OF分别垂直于AB,BC,AC.(2)OD//AC,OE//AB,OF//BC,如图(3),作OM⊥BC于M,连OB,∵ΔABC是等边Δ,∴BM=BC=30,且∠OBM=30°,∴OM=10,∵OE//AB,∴∠OEM=60°,OE==20,又OE=OF=OD,∴OE+OF+OD=3OE=60,答:略.(3)如图(4),方法1:在BC,CA,AB上分别截取BE=CF=AD,连结OD,OE,OF,方法2:在AB上任取一点D,连OD,逆时针旋转OD120°两次,得E,F.(4)设M1为A1A2上任一点,在各边上分别取A2M2=A3M3=A4M4=A5M5=A1M1,连OM1……OM5即可,∴可推广到正n边形.。
人教版九年级上册数学《正多边形和圆》同步辅导与测试(含解析)

九年级数学同步指导与测试正多边形和圆要点、难点:1.正多边形的定义:各边相等、各内角也相等的多边形叫正多边形。
2. 正多边形与圆的关系( 1)把圆分红 n ( n ≥ 3)等份,有以下结论:其一:挨次连接各分点所得的多边形是这个圆的内接正n 边形,这圆是正n 边形的外接圆。
其二:经过各分点作圆的切线以相邻切线的交点为极点的多边形是这个圆的外切正边形,这圆是正 n 边形的内切圆。
n( 2)任何正多边形都有一个外接圆和一个内切圆,这两个圆是齐心圆。
3.相关的观点( 1)正多边形的中心 ( 2)正多边形的半径 ( 3)正多边形的边心距 ( 4)正多边形的中心角4.正 n 边形的半径和边心距把正 n 边形分红 2n 个全等的直角三角形。
这里我们设:正 n 边形的中心角为 α,半径为 R ,边心距为 r ,边长为 a n ,周长为 P n ,面积为 S n ,则有( )360 ;( 2 ) a n2 R180 ;( )180 ;1nsin3 rR cosnn22 1 211( 4)Rr4an ; ( 5)P n n a n ;( 6) S n2n r an2r Pn ;( 7 )正多边形的每一个内角( n2) 180,内角和(n 2) 180 .n5. 每一个正多边形都是轴对称图形,当边数为偶数时,它仍是中心对称图形。
6.要点和难点:( 1)要点是正多边形的计算问题,计算往常是经过解直角三角形来解决的,所以在解这种题时,要尽量创建直角三角形,把所求的问题放到直角三角形中去,特别是含30°、 60°角的直角三角形和等腰直角三角形更重要。
( 2)难点是灵巧运用正多边形的知识和观点解题。
〖知识总结〗正多边形的定义要理解后记牢, 这里各边都相等,各角都相等,缺一不行,边数同样多的正多边形是相像多边形。
关于随意三角形来讲都有外接圆和内切圆, 但注意只有正三角形的外接圆和内切圆是齐心圆。
相关正多边形的计算本质是把问题转变为解直角三角形的计算, 所以这里要用到三角函数及勾股定理等相关知识。
