联言命题与选言命题
四、逻辑基本知识—复合命题及其推理

四、复合命题及其推理复合命题是包含了其他命题的一种命题,一般说,它是由若干个(至少一个)简单命题通过一定的逻辑联结词组合而成的。
(一)联言命题及其推理Ⅰ、联言命题联言命题是断定事物的若干种情况同时存在的命题。
如:“文艺创作既要讲思想性,又要讲艺术性”就断定了“文艺创作要讲思想性”和“文艺创作要讲艺术性”这两种情况同时存在。
联言命题所包含的肢命题称为联言肢。
在现代汉语中表达联言命题逻辑联结词的通常有:“……和……”,“既……又……”,“不但……而且……”,“一方面……另一方面……”,“虽然……但是……”等等。
如果取“并且”作为联言命题的典型联结词,用“p”、“q”等来表示联言肢,那么联言命题的形式可表示为:p而且q“鲁迅是思想家”都真的情况下是真的,在其余情况下都是假的。
需要指出的是,在现代汉语中用“但是”、“还”、“尽管”等联结词所联结而成的联言命题并不完全等同于用“∧”所联结而成的合取式。
对前者来说顺序是不能随意颠倒的,如“他获得了奥运会的金牌,并且参加了奥运会”就是一个在逻辑上可接受的联言命题。
但它对日常思维来说却是不恰当的。
因为它的两个肢命题在意义上前后顺序被颠倒了,同样,“他参加了亚运会,并且雪是白的”在逻辑上可以为真。
Ⅱ、联言推理1.分解式;这是根据一个联言命题为真而推出其各联言肢为真。
公式是:p∧qp(或q)例如,某同志曾有如下议论:既然大家都认为老王同志既有优点又有缺点的看法是正确的,那么我说老王同志是有缺点的,这又有什么不对呢?某同志的这个议论实际上就是运用了一种联言推理。
即:老王同志既有优点又有缺点,所以,老王同志是有缺点的。
2.组合式;这是根据一个联言命题的各个联言肢为真而推出该联言命题为真。
公式是pqrp∧q∧r例如,有人说,在社会主义建设时期,不仅工人和农民是社会主义建设的依靠力量,而且知识分子也是社会主义建设的依靠力量,所以,工人、农民和知识分子都是社会主义建设的依靠力量。
公务员考试之判断推理

A。甲排行第二,是男孩;乙排行第三,是女孩:根据甲、乙、丙三人的陈述都为真,可推出四人 关系为:丙(女孩)>甲(男孩)>乙(女孩)>丁(女孩)。根据此关系选择A 项。
20
四、复合命题 形式:直言命题A,直言命题B,
加上逻辑词项(关联词) 即复合命题两个直言命题用一个逻辑关联词连起
来得到的命题。
21
4、矛盾关系: 不存在中间状态的命题关系 永远一真一假,对一方的否定就是对另一方的肯定 (反之也对)
12
5、对当关系: (1)矛盾关系:全肯---特否; 全否---特肯
单肯---单否 (2)上反对关系: 这两个命题有中间状态, 不会永远一真一假,可能一真一假,也可能两个都是假的 即,至少一假(不能同时成立,至少一个不成立)
所以这些学生是唯物主义者 D.吃素的人不吃鱼,陈某吃素,所以陈某不吃鱼
7
例、王晶:因为李军是优秀运动员,所以,他有资格进入
名人俱乐部。
张华:但是李军吸烟,他不是年轻人的好榜样,因此,李
军不应被名人俱乐部接纳。
张华的论证使用了以下哪项作为前提?
Ⅰ、有些优秀运动员吸烟。
管理类专业学位联考综合能力逻辑(三段论、联言命题和选言命题)

管理类专业学位联考综合能力逻辑(三段论、联言命题和选言命题)模拟试卷1(题后含答案及解析)题型有:1.jpg /> 知识模块:三段论2.某些经济学家是大学数学系的毕业生。
因此,某些大学数学系的毕业生是对企业经营很有研究的人。
下列哪项如果为真,则能够保证上述论断的正确?A.某些经济学家专攻经济学的某一领域,对企业经营没有太多的研究。
B.某些对企业经营很有研究的经济学家不是大学数学系毕业的。
C.所有对企业经营很有研究的人都是经济学家。
D.某些经济学家不是大学数学系的毕业生,而是学经济学的。
E.所有的经济学家都是对企业经营很有研究的人。
正确答案:E解析:本题题干的推理可以看成是一个省略三段论。
前提为:某些经济学家是大学数学系的毕业生。
结论为:某些大学数学系的毕业生是对企业经营很有研究的人。
要补充的前提为:“经济学家”和“对企业经营很有研究的人”两个概念,且二者是全称肯定关系。
故可排除A、B、D三个选项。
再用周延性关系对C、E两个选项进行排除。
大前提:小前提:结论:知识模块:三段论3.下面的几个推理哪一个是有效的?A.所有中国人都是亚洲人,中国人都是黄皮肤的,所有亚洲人都是黄皮肤的。
B.人是有理性的,猴子不是人,所以猴子没有理性。
C.有些青年不是作家,所以有些作家不是青年。
D.老虎是森林之王,狮子不是老虎,所以狮子不是森林之王。
E.所有动物都会跑,这只鹿不会跑,所以这只鹿不是动物。
正确答案:E解析:对于选项A,该三段论为:MAS,MAP,所以SAP。
其中,MAS中S不周延,但在SAP中S却是周延的.不符合三段沦的推理规则:前提中不周延,结论中不能周延。
为无效推理。
对于选项B,该三段论为:MAP,SEM,所以SEP。
其中,MAP中P不周延,但在SEP中P却是周延的。
不符合三段论的推理规则:前提中不周延,结论中不能周延。
为无效推理。
对于选项C,是换位推理。
SOP,所以POS。
因特称否定命题不能换位(即:SOP不能换位)。
09第九讲 联言、选言命题及其推理

行李免费
******
四、选言命题(disjunctive proposition)
1) 小华今天没来上学,或者是病了, 或者是有要紧事。 2) 或许你说错了,或许我听错了。 3) 不是鱼死,就是网破。 4) 逆水行舟,要么进,要么退。 ******
联言命题真值表
p q p∧q
T
T F F
T
F
T
F F F
T
F
7、省略形式:主谓项有相同的,可以省略 一个。 1)鲁迅是伟大的文学家,也是伟大的思想 家。 2)川端康成和大江剑三郎都是日本人。 (联言命题) 3)川端康成和大江剑三郎是同胞。(关系 命题) 吾爱吾师 屡败屡战 ******
三、联言推理
不相容选言命题真值表 . q p q p∨
T T T F F T T F
F
F
T
F
The truth table for disjunction indicates that the disjunction is true when at least one of the disjuncts is true and that otherwise it is false. The truth functional interpretation of “or” is that of inclusive disjunction: Cases in which the disjunction is true include the case when both disjuncts are true. Sometimes the sense of a statement in ordinary language is that of exclusive disjunction. The sense of these statements excludes the possibility of both alternatives being true. 齐女择婿 律师赖帐 ******
复言命题

行测判断推理:复言命题解题全攻略通过研究历年公务员行测真题发现,复言命题近两年都只出现了1-2道,但复言命题一直是国家公务员考试中的重点和难点,且掌握其中的一些知识点对解可能性推理题目有一定的帮助,需要大家引起重视。
复言命题主要考查三种:联言命题、选言命题和假言命题。
一、联言命题推理联言命题就是将若干个命题联合起来,表示这些情况同时存在的命题。
可表示为:p并且q(p、q是联言肢,“并且”是联结词)。
联言命题的推理规则有两条:1.全部肢命题为真推出联言命题为真;2.联言命题为真,可推出其中任一肢命题为真。
例如,“你很高”和“你很帅”可以推出“你又高又帅”这个联言命题;“你又高又帅”又可以推出“你很高”和“你很帅”。
二、选言命题推理选言命题就是给出若干个命题,可以选择出一种或者多种情况存在的命题。
根据所能选择的情况不同,可以分为两种:相容选言命题:多种情况可以同时存在。
可表示为:p或者q(p、q是选言肢,“或者”是联结词)。
不相容选言命题:只允许一种情况存在。
可表示为:要么p,要么q(p、q是选言肢,“要么……要么……”是联结词)。
相容和不相容选言规则推理如下表:三、假言命题推理假言命题就是带有假设条件的命题。
假言命题通常包含两个肢命题:反映条件的肢命题在前,称为前件;反映结果的肢命题在后,称为后件。
根据前后件间条件关系的不同,又可分为三种:充分条件假言命题:当条件p存在时,结论q一定成立,而无需考虑其他条件,则p是q 的充分条件,即“有它就行”。
可表示为:如果p,那么q或p→q(p是前件,q是后件,“如果……那么……”是联结词)。
必要条件假言命题:当条件p不存在时,结论q一定不成立,则p是q的必要条件。
即“没它不行”。
可表示为:只有p,才q或p←q(p是前件,q是后件,“只有……才……”是联结词)。
充分必要条件假言命题:表示p是q的充分条件和必要条件的命题,即表示p与q等值的命题。
可表示为:p当且仅当q或pq(p是前件,q是后件,“当且仅当”是联结词)。
逻辑学名词解释

逻辑学名词解释1、概念:反映事物特有属性的思维形式。
单独概念:是指仅反映一个特定对象的概念,它的外延是一个独一无二的事物。
普遍概念:是指由若干个分子所组成的类的概念。
它的外延包括许多的对象。
集合概念:把一类对象作为一个集合体来反映的概念。
非集合概念:不把一类对象作为一个集合体来放映的概念。
正概念:反映对象具有某种属性的概念。
负概念:反映对象不具有某种属性的概念。
只有带否定词并使用其含义的,才是负概念。
论域:指一个正概念与其相对的负概念所反映的对象组成的类。
定义:就是揭示概念内涵的逻辑方法。
揭示概念所反映的事物的特有属性的方法。
划分:揭示概念外延的逻辑方法。
就是将外延较大的属概念根据一定的标准,划分出若干个外延较小的概念,从而明确概念全部外延的逻辑方法。
概念的限制:通过增加概念的内涵,以减少概念的外延的逻辑方法。
即概念的限制就是从属概念过渡到种概念的逻辑方法。
究具体命题内容上真假,只研究命题形式真假性质和命题形式之间的真假关系。
模态命题:就是包含“必然”等模态词的命题。
复合命题:就是包含其他命题的命题,包括联言命题、选言命题、假言命题和负命题。
简单命题:就是没有包含其他命题的命题,主要包括直言命题和关系命题。
推理:就是由一或若干个命题推出另一个命题的思维形态。
直言命题:就是陈述事物具有或不具有某种性质的命题。
(性质命题)肯定命题:就是陈述事物具有某种性质的命题。
联项一般用“是”表示。
单称命题:就是陈述一个特定事物具有或不具有某种性质的命题。
主项专有名词,不需量词。
全称命题:陈述一类事物的全部分子都具有或不具有某种性质的命题。
主项普遍概念,量省。
特称命题:就是陈述一类事物中至少存在着一事物具有或不具有某种性质的命题。
主项普遍概念,量项不可省为“有的、有些”(其逻辑含义就是“有”即至少有一个,不排斥全部)周延性:是直言命题主项与谓项在量的方面的逻辑特征,是直言命题形式中对主项或谓项的全部外延的陈述情况。
判断推理之“至少有一个”VS“缺一不可”

判断推理之“⾄少有⼀个”VS“缺⼀不可”判断推理之“⾄少有⼀个”VS“缺⼀不可”在判断推理的四个微模块中,逻辑判断是其中的重点和难点,在10道判断推理的题⽬中,⼏乎包含了判断推理⼀半以上的知识点,⽽这10道题,往往成为考⽣在判断推理模块上⼀较⾼下的必争之地。
选⾔命题和联⾔命题是逻辑判断中所考察的两种命题形式,其中选⾔命题的通⽤表述为“A或B”,联⾔命题的通⽤表述为“A且B”。
在题⽬中,经常将两种命题并列考查,区分两种命题的命题形式、明确判断规则并能熟练应⽤,对于考⽣在考试中取得好成绩是⾮常重要的。
但是对于⼤部分考⽣⽽⾔,在两种命题判断规则的记忆上往往存在问题,或者相互混淆,或者不能快速反应。
“A或B”只要A、B间有⼀个为真,则“A或B”为真,只有A、B同时为假,“A或B”才为假,反之亦然。
“A且B”只有A、B同时为真,“A且B”才为真,只要A、B间有⼀个为假,“A且B”就为假,反之亦然。
这样的表述使很多考⽣感到困惑,尤其是在快速做题的时候,⼗分容易混淆。
事实上我们完全可以找到⼀种更为简单的记忆⽅式:“A或B”意味着“⾄少有⼀个”;“A且B”意味着“缺⼀不可”。
这样我们就⽤九个字将前⽂很繁琐的表述形式给简单化了。
下⾯通过⼀道题⽬,来具体解析⼀下这样两个命题在题⽬中的考察。
例:已知“若⼩明和⼩丽去上海,那么⼩红或者⼩青也去上海”为真,则以下选项必定为真的是()A.如果⼩红不去上海,那么⼩明不去上海B.如果⼩青不去上海,那么⼩明不去上海C.如果⼩红和⼩青不去上海,那么⼩明可能去上海D.如果⼩明不去上海,那么⼩红和⼩青均不去上海在这⾥,我们通过前⾯学习过的假⾔命题的推理规则、以及刚刚讨论的联⾔命题和选⾔命题,可以将其翻译成“⼩明且⼩丽→⼩红或⼩青”,由此可知:⼩明和⼩丽中,只要有⼀个⼈不去,那么⼩红和⼩青都不会去,即⼩明和⼩丽缺⼀不可;只有⼩红和⼩青同时不去,我们才能确定⼩明和⼩丽之间有⼈不去,但是具体谁不去,仍然不能确定——可以是⼩明去,⼩丽不去,也可以是⼩丽去⼩明不去,还可以是⼩丽好⼩明都不去。
复合命题及其推理详细讲解

第3讲复合命题及其推理【复合命题,是指由简单命题通过联结词而构成的命题。
由于联结词的不同,复合命题就有联言命题、选言命题、假言命题等不同的种类形式。
】3、1 联言命题及其推理1、联言命题联言命题就是断定事物的若干种情况同时存在的命题。
例如,“鲁迅是文学家并且是思想家”。
联言命题的一般公式是:p并且q;也可表示为 p∧q 。
其中,“并且”(现代逻辑上通常用符号“∧”表示,涵义为“合取”)为联结词,p、q称为联言肢(联言命题的肢命题)。
日常语言中的“…和…”、“既…又…”、“不但…而且…”、“虽然…但是…”等表示并列关系、递进关系、转折关系的语词都是“并且”的意思。
一个联言命题是真的,则其每一个肢命题都必须是真的。
只要有一个肢命题假,则联言命题就是假的。
联言命题的真假特征可以表示如下:p q p∧q真真真真假假假真假假假假2、联言推理联言推理就是前提或结论为联言命题,并且根据联言命题的逻辑特征所进行的推理。
一个联言命题是真的,当且仅当其所有肢命题是真的。
联言推理的推理形式有分解式和组合式。
分解式就是由前提中一个联言命题为真推出其任一肢命题为真的联言推理。
公式是:p并且q p并且qp 或者 q组合式就是由前提中一些肢命题为真推出这些肢命题所组成的联言命题为真的联言推理。
公式是:pqp并且q应用例:例题1-联言推理■李娜心中的白马王子是高个子、相貌英俊、博士。
她认识王威、吴刚、李强、刘大伟四位男士,其中只有一位符合她所要求的全部条件。
(1)四位男士中,仅有三人是高个子,仅有两人是博士,仅有一人相貌英俊。
(2)王威和吴刚都是博士。
(3)刘大伟和李强身高相同。
(4)每位男士都至少符合一个条件。
(5)李强和王威并非都是高个子。
请问谁符合李娜要求的全部条件?A.刘大伟。
B.李强。
C.吴刚。
D.王威。
例题2-联言推理■只有具备足够的资金投入和技术人才,一个企业的产品才能拥有高科技含量。
而这种高科技含量,对于一个产品长期稳定地占领市场是必不可少的。
选言命题、联言命题的区别

选言命题、联言命题的区别
作为行测半壁江山的判断推理,其中相容选言命题和联言命题这两大板块是既是基础部分,
同时也很重要。
因其较为基础的特点,其次考生对命题的推理规则掌握得不够熟练,成为考
生的失分项。
今天中公教育专家就为大家分享相容选言命题及联言命题的解题心得,帮助各
位考生在事业单位中应对此类问题。
判断推理中涉及到联言命题以及相容选言命题,在做题时基本都是应用到各类命题的矛盾命题、推理规则以及推出关系等,不妨把这些看成是有规则的解题过程,这个过程可以称为规
则性推理。
两个命题结合起来记忆更好,针对矛盾命题:不论是相容选言命题(A或B)还是
联言命题(A且B),找相应的矛盾命题只需“A变非A,B变非B,且或互变”。
针对推理规则,①相容选言命题(A或B),当命题为真时,其中一个支命题为假,则另一个支命题必然为真,简记成:否一推肯一;②联言命题(A且B),当命题为假时,其中一个支命题为真,则另一个
必然为假,简记成:肯一推否一。
当大家熟记口诀并结合一定的题量来巩固,相信大家有所
收获。
以一个例题为例:
1. 小张并非既能吃酸又能吃辣。
如果上述命题为真,下列所述一定为真的是:
A.小张如果能吃酸,一定不能吃辣
B.小张如果不能吃酸,就一定能吃辣
C.小张能吃酸但不能吃辣
D.小张既不能吃酸又不能吃辣
【答案】A。
解析:考查联言命题的矛盾命题和选言命题的推理规则。
并非A且B=非A或
非B,排除C和D;选言命题的推理规则是否一推肯一,故选A项。
错误的三段论

一、错误的三段论:
例一.这所学校的学生学习了很多课程,
张三是这所学校的学生,
所以,张三学习了很多课程。
二、联言命题
“A且B”的否定形式:“非A或非B”
三、选言命题
1.“A或B”的含义就是:至少有一个为真
2.“A或B”,当要肯定一个支命题的时候,必须要否定另一个支命题。
例一.要使“A或B=A”,必须加一个条件“非B”
例二.“你去或我去”要从中推出“你去”,必须加一个条件“我不去”
例三.“你不去或我不去”要从中推出“你不去”,那就要否定“我不去”,也就是说加一个条件(“我去”)
4. “A或B”的否定形式是“非A且非B”。
四、充分条件
1.“如果A,那么B”的逆反命题:“如果非B,那么非A”。
2. “如果A,那么B”的矛盾命题:“A且非B”。
五、必要条件
“只有C,才D”的矛盾命题:“非C且D”。
六、牢记七组矛盾命题
“所有都”,与“有些不”
“所有都不”,与“有些是”
“张三是”,与“张三不是”
“A且B”,与“非A或非B”
“A或B”,与“非A且非B”
“如果A,那么B”与“A且非B”
“只有C,才D”与“非C且D”
图形推理:
1、数量性:点(交点),线(线条、笔画),面(角、部分、封闭区间、图形种类),体
2、对称性:翻转(轴对称,中心对称),旋转,平移
3、叠加性:相加,相减,去同存异,去异存同,复杂叠加
4、其他:重心,共存,一笔画。
命题逻辑(联言、选言、负命题)

• 有一天,乾隆皇帝问纪晓岚:‚忠孝‛二字作何解 释?纪晓岚答道:‚君要臣死,臣不得不死,为 ‘忠’父要子亡,子不得不亡,为‘孝’。‛ 乾隆皇帝立刻说:‚那好,朕要你现在就去死。‛ ‚臣领旨!‛‚那你打算怎样死法?‛‚跳河‛ 乾隆知道纪晓岚不会去死,于是静观其变。不一会, 纪晓岚回来了。乾隆问道:‚你为何回来了?‛ 纪晓岚答道:‚我来到河边,正要往下跳,屈原从水 里走来。他说:‘晓岚,此举大错了,想当年楚王 昏庸,我才不得不死,你在跳河之前应该先去问问 皇上是不是昏君,如果皇上不是昏君,你就不该投 河而死,如果说皇上跟当年楚王一样的昏庸,你再 死也不迟呀’‛
负命题
真值表
p T F ¬p
真值表的作用
F T
负命题的推导规则:双重否定引入规则 (¬¬+):从A可推出A。 双重否定消去规则(¬¬-):从A可推出 A。图示:
2019年1月16日星期三 21
简单命题的负命题: A E I O
复合命题的负命题及等值式:
并非(p并且q) 并非(p或者q) 并非(要么p,要么q) 并非(如果p,那么q) 并非(只有p,才q) 并非(p当且仅当q) 并非(并非p)
• 负判断由支命题和联结词‚并非‛构成。负 命题的逻辑联结词‚并非‛可以用否定词 ‚‛来表示。 • 日常用语中,负命题的联结词还可以表达为 ‚没有‛、‚不‛、‚这是假的‛、‚这是 错误的‛等。被否定的命题称为支命题,它 可以是简单命题,也可以复合命题。 • 负命题的形式:并非p,也可表示为: p • 负命题的真假表:当支命题为真时,负命题 为假;当支命题为假时,负命题为真。
A B B —— A B和 B可推出A;
A
A
B
A
B
B
—— B
复合命题及其推理(上)

复合命题及其推理(上)联⾔命题及其推理复合命题是由简单命题通过逻辑联结词组合⽽成的,它由⽀命题和联结词两部分构成,联结词决定复合命题的逻辑性质。
根据联结项的不同性质,复合命题分为联⾔、选⾔、假、负命题。
⼀、联⾔命题概述(且)联⾔命题是断定多种事物情况同时存在的⼀种复合命题,由联⾔⽀、联⾔联结词两部分构成。
例1、油哥是学⽣,并且是兼职作家。
分析:是联⾔命题。
断定了“油哥是学⽣”和“油哥是兼职作家”两种情况同时存在,联结词是“并且”。
联⾔命题的结构是:“p且q”。
合取词常⽤“且”、“同时”、“也是”等。
汉语中的并列复合句、递进复合句、转折复句⼀般表达联⾔命题。
例2、峣峣(yao,直)者易折,皎皎者易污。
(并列复句)例3、悠悠不仅医术好,⽽且是名医。
(递进复合句)例4、成功需要努⼒,但仅仅努⼒是不够的(转折复合句)例5、逻辑学是基础课和选修课(单句)联⾔命题(且)命题中,所有联⾔⽀为真,命题为真,否则假。
改变联⾔⽀的顺序不会导致联⾔命题真值变化(有效性),但联⾔命题的意义可能改变(实际意义)。
⼆、联⾔推理1、分解式指由联⾔命题的真,推出其部分⽀命题为真的推理。
例1、良⾔⼀句三冬暖,良药苦⼝利于疾,所以,良⾔⼀句三冬暖。
分析:其形式为:“若p且q真,所以,p真”。
分解式有助于⼈们在认识事物全⾯情况的基础上,重点或强调某⼀⽅⾯的情况。
2、组合式指由前提中全部命题为真,推出这些命题为⽀命题的联⾔命题为真的推理。
例2、我同桌很有才华,我同桌个性鲜明,所以,我同桌很有才华且个性鲜明。
分析:其形式为:“p真,q真,所以,p且q真”。
组合式有利于⼈们把对事物各个⽅⾯的认识综合为全⾯、完整的认识。
选⾔命题及其推理⼀、选⾔命题概述(或)选⾔命题是断定事物的若⼲的情况中只要有⼀种存在的复合命题。
1、相容选⾔命题即断定事物的若⼲种可能情况可以同时存在的选⾔命题。
(选⾔⽀可以同时存在)例1、⽼四在吃鸡,或者在王者荣耀。
分析:其结构为:“p或者q(pvq)”,其中"v"读作析取。
逻辑讲义-联言、选言,假言命题

联言、选言,假言命题及推理一、联言命题:P并且Q1.联言命题连结词的通常有:"……和……","既……又……","不但……而且……","一方面……另一方面…","虽然……但是……"等。
2.负命题及其等值命题:并非(p且q)等价于非p或非q二、选言推理(一).相容选言命题P或Q (或者P,或者Q)相容选言命题是断定事物若干种可能情况中至少有一种情况存在的命题。
1.相容选言推理:p或者q 或p或者q既然非p 既然非q所以q 所以p相容选言推理有两条规则:否定一部分选言支,则推出肯定另一部分选言支。
肯定一部分选言支,不能推出否定另一部分选言支。
2.相容选言命题的负命题及其等值推理“并非:P或者Q”等值于“非P并且非Q”。
(二).不相容选言命题要么P,要么Q不相容选言命题是断定事物若干可能情况中有而且只有一种情况存在的命题。
1.不相容选言推理要么p,要么q 或要么p,要么q既然p 既然非p所以非q 所以q要么p,要么q 或要么p,要么q既然q 既然非q所以非p 所以p不相容选言推理有两条规则:否定一个选言支,则推出肯定未被否定的那个选言支。
肯定一个选言支,就要否定其余的选言支。
2.不相容选言命题的负命题及其等值推理。
“并非:要么P,要么Q”等值于“P并且Q,或者,非P并且非Q”。
三、假言推理充分条件假言判断:如果P,那么Q必要条件假言判断:只有P,才Q充要条件假言判断:P,当且仅当Q(一)充分条件假言命题及其推理1.充分条件假言命题联结词如果,则(就);如果,那么;只要,就;假如,就;要是,那么;一,就;等充分条件假言推理有如下两条规则:(1)肯定前件就要肯定后件,否定后件就要否定前件。
(2)否定前件不能否定后件,肯定后件不能肯定前件。
3.充分条件假言命题的负命题及其等值推理。
“并非:如果P,那么Q”等值于“P并且非Q”。
教师资格考试高频考点:选言命题和联言命题的区分

逻辑类中的联言命题和选言命题这两个知识点是教师资格证的综合素质考试中的常考点,很多考生反映在这部分花费大量时间最终却丢掉分数,产生这种结果的原因是大家对这两个知识点没有理解透彻。
考试中这两个知识点以单选题为主,出题形式就是判断题干中与选项中哪些语句是不同,所以在这里只需要明白他们两个各自的含义和两者之间的区别即可。
所以下面将会详细讲解这两个知识点,以便大家能够掌握这一高频考点。
选言命题是反映事物若干种情况或性质至少有一种存在的命题。
我们可以用p或q来表示,或的含义是至少一个,p、q至少一个。
举个例子来说:张三或李四去出差;用我们日常语言来理解就是选择其中任何一个即可,但是对于我们这个知识点来说,这个或字指的是可以在两者中选择任何一个,也可以两者都选,也就是说既可以让张三去,也可以让李四去,或两人都去,选言命题具有可形成两个或两个以上的判断语句,跟日常用语不同这一点需要大家注意。
联言命题是反映事物的若干种情况或者性质同时存在的命题。
我们可以用p且q来表示,且的含义指的是p、q两个都成立。
沿用我们上面的例子:张三且李四出差。
指的是两者必须同时成立,同时满足。
也就是张三李四都要出差,二者缺一不可,所以联言命题只能是一个判断的语句。
在日常语言中,联言命题的语言表达形式是多种多样的。
例如:①林纾虽然是著名的翻译家,但他不懂外语;②控制论不仅对生物和生命现象的研究有深刻的意义,而且对哲学和社会现象的研究也有重要意义;③人们啊!要尊重自然,尊重规律,尊重生命,所以联言命题的合取词除了可以用并且表示之外,也可以用不但,而且、既,又、虽然,但是等表示。
选言命题和联言命题的区别主要体现在两点:①选言命题强调或(至少一个的意思);联言命题且(两个都成立);②选言命题具有可形成两个或两个以上的判断语句,例:张三和李四是工可以说张三是工人,李四是工人;联言命题只能是一个判断的语句,有两个对象,这两个对象是不可分割的,不能孤立的。
联言命题与选言命题
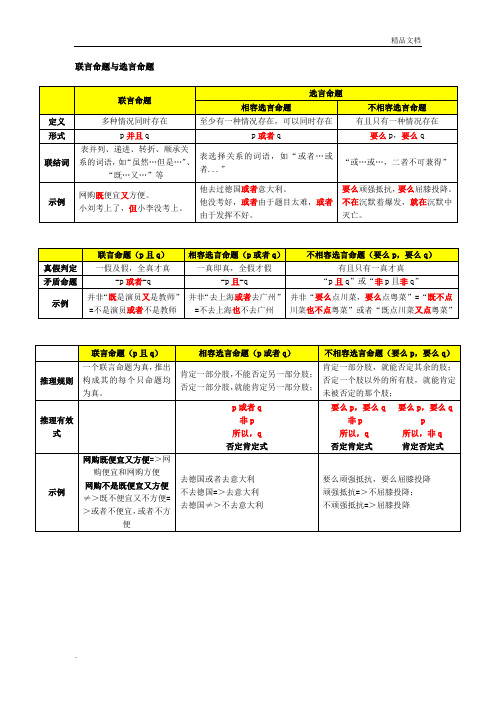
示例
网购既便宜又方便=>网购便宜和网购方便
网购不是既便宜又方便≠>既不便宜又不方便=>或者不便宜,或者不方便
去德国或者去意大利
不去德国=>去意大利
去德国≠>不去意大利
要么顽强抵抗,要么屈膝投降
顽强抵抗=>不屈膝投降;
不顽强抵抗=>屈膝投降
示例
网购既便宜又方便。
小刘考上了,但小李没考上。
他去过德国或者意大利。
他没考好,或者由于题目太难,或者由于发挥不好。
要么顽强抵抗,要么屈膝投降。
不在沉默着爆发,就在沉默中灭亡。
联言命题(p且q)
相容选言命题(p或者q)
不相容选言命题(要么p,要么q)
ห้องสมุดไป่ตู้真假判定
一假及假,全真才真
一真即真,全假才假
有且只有一真才真
推理规则
一个联言命题为真,推出构成其的每个只命题均为真。
肯定一部分肢,不能否定另一部分肢;
否定一部分肢,就能肯定另一部分肢;
肯定一部分肢,就能否定其余的肢;
否定一个肢以外的所有肢,就能肯定未被否定的那个肢;
推理有效式
p或者q
非p
所以,q
否定肯定式
要么p,要么q 要么p,要么q
非p p
所以,q 所以,非q
矛盾命题
-p或者-q
-p且-q
“p且q”或“非p且非q”
示例
并非“既是演员又是教师”=不是演员或者不是教师
并非“去上海或者去广州”=不去上海也不去广州
并非“要么点川菜,要么点粤菜”=“既不点川菜也不点粤菜”或者“既点川菜又点粤菜”
联言命题(p且q)
相容选言命题(p或者q)
不相容选言命题(要么p,要么q)
充分条件必要条件命题l联言选言命题

充分条件必要条件命题l联言选言命题Pleasure Group Office【T985AB-B866SYT-B182C-BS682T-STT18】充分条件必要条件命题一、充分条件假言命题1、充分条件假言命题的语言标志如果…那么…/只要…就…/若…必…/一…就…2、充分条件假言命题的性质如果A,那么B。
符号表达:A=> B。
有前件就必有后件(如果一个充分条件假言命题为真,则:如果肯定其前件,则必然可以得到后件。
简称:有前必有后。
)无前件未必有后件(否前未必否后)有后件未必有前件(肯后未必肯前)无后件则必无前件(否后必肯前)——逆否命题(原命题与逆否命题同真假)3、充分条件假言命题的矛盾命题如果A,那么B。
符号表达:A=> B。
并非(A=>B)= A且非B(A=>B)=非A或B(一个充分条件假言命题如果我们知道前件为假,后件不管真假,整个充分条件假言命题一定是真的;当我们知道后件为真的的时候,前件不管真假,整个充分条件假言命题一定是真的)二、必要条件假言命题1、必要条件假言命题的语言标志:只有…才...2、必要条件假言命题的性质只有A,才B。
符号表达:B => A。
有条件未必有结果无条件则必无结果(逆否命题)有结果则必有条件无结果未必无条件3、必要条件假言命题的矛盾命题只有A,才B。
符号表达:B=> A。
并非(B=> A)=B且非A(B=> A)=非B或A(一个必要条件假言命题如果我们知道前件为真,后件不管真假,整个必要条件假言命题一定是真的;当我们知道后件为假的的时候,前件不管真假,整个必要条件假言命题一定是真的)等值命题:只有A,才B=如果B,就A。
三、特殊语言标志1、不…不…如果不A,那么不B。
-A=》-B B=》A2、没有…没有…如果没有A,那么没有B。
-A=》-B B=》A3、除非…否则…等于必须…否则…例:除非调查,否则就没有发言权。
以下各项都符合题干的断定,除了A.如果调查,就一定有发言权。
逻辑推理总结全

一、直言命题1、矛盾关系(逆否命题):一真一假所有是,有些不是某个是,某个不是2、反对关系:不能同真(如果有一个是真的,那么另一个一定是假的)所有是,所有不是所有是,某个不是3、下反对关系:不能同假(如果有一个是假的,那么另一个一定是真的)有些是,有些不是有些是,某个不是----------------------------------------------------------------------------------------------------4、从属关系所有A都是B可以推出有些A是B所有A都不是B可以推出有些A不是B常见题型:给出一个题干,根据题干能推出选项的真假,或不能确定选项的真假。
能推出真假的情况:所有A都是B可以推出有些A是B;所有A都不是B可以推出有些A 不是B。
不能推出真假的情况:有些A是B不能推出有些A不是B;有些A是B不能推出所有A 是B;有些A不是B不能推出有些A是B;有些A不是B不能推出所有A不是B。
5、换位推理能推出的情况(1)所有A是B推出有些B是A和所有不是B的都不是A(2)所有A不是B推出所有B不是A(3)有些A是B推出有些B是A需注意的是“大部分”,“少数”,“一半”等词语不能用于换位推理,例如:大部分男生考上了大学不能推出大部分考上大学的是男生。
从属关系和换位推理结合起来得出以下结论必须记忆:所有A是B推出(有些A是B;有些B是A;所有不是B的都不是A。
)所有A不是B推出(有些A不是B;所有B不是A。
)有些A是B推出(有些B是A)(2013浙江)品学兼优的学生不都读研究生。
如果以上论述为真,则下列命题能判断真假的有几个?Ⅰ.有些品学兼优的学生读研究生(不确定)Ⅱ.有些品学兼优的学生不读研究生(真)Ⅲ.所有品学兼优的学生都读研究生 (假)Ⅳ.所有品学兼优的学生都不读研究生(不确定)A.1个B.2个C.3个D.4个题干“不都”等于“有些不是”,所以答案为B-----------------------------------------------------------------------------------------------------------------6、三段论(要时刻想着和换位推理结合,中项必须当一次主项,当一次谓项)(1)只有三个词项,每个词都出现两次正确的三段论举例:所有中国人都是勤劳的,小王是中国人,所以小王是勤劳的。
形式逻辑

形式逻辑1、命题分为简单命题和复合命题,简单命题是判断某种事物具有或不具有某种性质,复合命题是具有逻辑连接词的命题,根据逻辑连接词的不同,复合命题分为联言命题、选言命题和假言命题。
2、德摩根定律:非(P 且 Q) = (非 P) 或 (非 Q) 符号化:¬(P∧Q)= ¬P∨¬Q非(P 或 Q) = (非 P) 且 (非 Q) 符号化:¬(P∨Q)= ¬P∧¬Q3、相容选言推理:前不同(符号),后相同(符号)。
P→Q等价于¬P∨Q4、原命题与逆否命题同真同假,与矛盾命题一真一假。
5、命题判断分为必然性判断、可能性判断、事实性判断、假设性判断。
6、命题之间的关系:原命题:S→P 逆命题:P→S否命题:¬S→¬P 逆否命题:¬P→¬S负命题=矛盾命题一、联言命题(明于又刮风又下雨)1、联言命题:判断几种事物同时存在或同时为真的命题。
2、标志词:并且(而且)、既。
又、虽然。
但是(可是)、然而、因为。
所以3、真假性质:(1)当且仅当两个联言支都为真时则命题为真。
即S、P都为真,则S且P为真。
(2)联言命题S且P为真,则联言支命题S、P都为真。
(3)联言命题S且P为假,则联言支命题至少一个为假。
已知一个为真,则另一个一定为假。
4、矛盾命题:(S且P)的矛盾命题是(非S或者非P)。
符号:非(S且P)=非S或非P5、推理原则(以联言命题为前提或结论,进行推理):(1)每个联言支为真,联言命题为真。
(2)每个联言支为假,联言命题为假。
(3)联言命题为真,则每个联言命题为真。
(4)一个联言支为假,则包含该联言支的联言命题为假。
二、选言命题(明于刮风或下雨)1、选言命题:判断几种事物至少有一个存在或为真的命题。
具有并存关系的选言支构成的选言命题称为相容选言命题。
反之称之为不相容选言命题。
2、相容选言命题标志词:至少,或者不相容选言命题标志词:要么..要么,不可兼得、二者取其一3、真假性质:(1)S、P至少一个为真,S∨P为真。
形式逻辑学第四章复合命题及其推理

(2)必要条件假言命题 设P和Q分别为两种事物的情况,如果 没有P就必然没有Q,而有P却未必有 Q(可能有Q也可能没有Q)。
如: 只有认识错误,才能改正错误。
只有某人年满18岁,他才有选举权。 只有刮东南风 , 周瑜才能取得赤壁之 战的胜利。
常用关联词语: 必须……才…… 除非……才…… 除非……不…… 不……不…… 没有……就没有……
第二节
复合命题推理
一、联言推理 二、选言推理 三、假言推理 四、负命题推理 五、二难推理
一、联言推理
1、分解式 p并且q 所以p p并且q 所以q
如: 高脂肪、高糖量的食物对人的健康有害, 所以,高脂肪的食物对人的健康有害。
高脂肪、高糖量的食物对人的健康有害, 所以,高糖量的食物对人的健康有害。
第四章
复合命题及其推理
第一节 复合命题 第二节 复合命题推理
第一节
复合命题
世界是多样的,并且是统一的。
第一,复合命题的基本单位是命 题,称为支命题。 第二,复合命题的逻辑性质是由 联结项决定的。 第三,复合命题的真假由其支命 题的真假确定。
一、联言命题 二、选言命题 三、假言命题 四、负命题
有效式: 其一,否定前件式 如: 只有阳光充足,庄稼才能长好 阳光不足 所以,庄稼不能长好。
只有认识错误 , 才能改正错误 , 某人不认识错误 , 所以某人不能改正错误。
只有年满十八岁才有选举权 他没有十八岁 所以他没有选举权。
“只有懂几何者方可入内” A他们会被允许进入。 B他们是否会被允许进入,不确定。 C他们可能会被允许进入。 D他们一定不会被允许进入。 E他们一定会被允许进入。
这药片含有维生素 A 、维生素 B 、维生素 C 所以 , 这药片含有维生素 C 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
网购既便宜又方便=>网购便宜和网购方便
网购不是既便宜又方便≠>既不便宜又不方便=>或者不便宜,或者不方便
去德国或者去意大利
不去德国=>去意大利
去德国≠>不去意大利
要么顽强抵抗,要么屈膝投降
顽强抵抗=>不屈膝投降;
不顽强抵抗=>屈膝投降
矛盾命题
-p或者-q
-p且-q
“p且q”或“非p且非q”
示例
并非“既是演员又是教ຫໍສະໝຸດ ”=不是演员或者不是教师并非“去上海或者去广州”=不去上海也不去广州
并非“要么点川菜,要么点粤菜”=“既不点川菜也不点粤菜”或者“既点川菜又点粤菜”
联言命题(p且q)
相容选言命题(p或者q)
不相容选言命题(要么p,要么q)
示例
网购既便宜又方便。
小刘考上了,但小李没考上。
他去过德国或者意大利。
他没考好,或者由于题目太难,或者由于发挥不好。
要么顽强抵抗,要么屈膝投降。
不在沉默着爆发,就在沉默中灭亡。
联言命题(p且q)
相容选言命题(p或者q)
不相容选言命题(要么p,要么q)
真假判定
一假及假,全真才真
一真即真,全假才假
有且只有一真才真
联言命题与选言命题
联言命题
选言命题
相容选言命题
不相容选言命题
定义
多种情况同时存在
至少有一种情况存在,可以同时存在
有且只有一种情况存在
形式
p并且q
p或者q
要么p,要么q
联结词
表并列、递进、转折、顺承关系的词语,如“虽然…但是…"、“既…又…”等
表选择关系的词语,如“或者…或者...”
“或…或…,二者不可兼得”
推理规则
一个联言命题为真,推出构成其的每个只命题均为真。
肯定一部分肢,不能否定另一部分肢;
否定一部分肢,就能肯定另一部分肢;
肯定一部分肢,就能否定其余的肢;
否定一个肢以外的所有肢,就能肯定未被否定的那个肢;
推理有效式
p或者q
非p
所以,q
否定肯定式
要么p,要么q要么p,要么q
非pp
所以,q所以,非q
否定肯定式肯定否定式
