塞瓦定理练习

合集下载

塞瓦定理试题

《塞瓦定理及其逆定理的应用》（1）一，《塞瓦定理》设O 是ABC ∆内任意一点，AO 、BO 、CO 分别交对边于D 、E 、F ，则1=⋅⋅FBAFEA CE DC BD .二．《塞瓦定理的逆定理》在ABC ∆三边（所在直线）BC 、CA 、AB 上各取一点D 、E 、F ，若有1=⋅⋅FBAFEA CE DC BD ，则AD 、BE 、CF 平行或共点.证明：AD 与BE 或是平行或是相交证明：（1）若//AD BE ，则EA EC BD BC =，代入已知式，可推出CBDCFB AF =. 有//AD CF 从而////AD BE CF .（2）若AD 与BE 相交于O ，则连结CO 交AB 于/F ，由塞瓦定理，有//1BD CE AF DC EA F B ⋅⋅=，与已知式相比较，得//AF AFF B AB=，合比/AF AF AB AB=，∵/AF AF =，得/F 与F 重合，即AD 、BE 、CF 共点. 交于一点；：证明：三角形的中线例1 分线交于一点；】证明：三角形的角平【练习1 高交于一点；】证明：锐角三角形的【练习2A BCDEFO ABCDEFABCDEFO /F2ABC C AB L L AC BC M N AN BM P CP AB∆∠⊥例：在锐角中,角的平分线交于于，从作边和的垂线，垂足分别是和，设和的交点是，证明：3.AD ABC D BC P AD BP CP AC AB E F EDA FDA∆∠∠例设是的高，且在边上，若是上任一点，、分别与、交于和，则＝3,,ABC M N R BAR CAN CBM ABR ACN BCM AM BN CR αβγ∆∠=∠=∠=∠=∠=∠=【练习】已知外有三点、、，且，证明：、、三线共点；1111111111111114.sin sin sin sin sin sin ABC BC CA AB A B C AC BA CB ACC BAA CBB C B AC B A C CB A AC B BA ∆∠∠∠⋅⋅=⋅⋅∠∠∠例在的边、、上取点、、，证明：1111112224ABC BC CA AB A B C AA BB CC AA BB CC ∆【练习】在的边、、上取点、、，使、、相交于一点，证明，关于角平分线对称于这些直线的直线、、也相交于一点；课外作业：三线共点；、、直线的切点，证明、、的内切圆与边是、、设111111:.1CC BB AA AB CA BC ABC C B A ∆；过点，证明，直线相交于点和，相交于和，直线和弧上取点。

第2章塞瓦定理及应用(含答案)

第二章塞瓦定理及应用【基础知识】塞瓦定理设A '，B '，C '分别是△ABC 的三边BC ，CA ，AB 或其延长线上的点，若AA '，BB '，CC '三线平行或共点，则1BA CB AC A C B A C B'''⋅⋅='''．① 证明如图2-1（b ）、（c ），若AA '，BB '，CC '交于一点P ，则过A 作BC 的平行线，分别交BB '，CC '的延长线于D ，E ，得,CB BC AC EAB A ADC B BC''==''． A′B'C 'ABPPCBAA′B'C 'D ECBAA′B'C 'D E (c)(b)(a)图2-1又由BA A P A C AD PA EA '''==，有BA ADA C EA'='．从而1BA CB AC AD BC EA A C B A C B EA AD BC'''⋅⋅=⋅⋅='''．若AA '，BB '，CC '三线平行，可类似证明（略）．注（1）对于图2-1（b ）、（c ）也有如下面积证法：由：1PAB PBC PCAPCA PAB PBC S S S BA CB AC A C B A C B S S S '''⋅⋅=⋅⋅='''△△△△△△，即证．（2）点P 常称为塞瓦点．（3）共点情形的塞瓦定理与梅涅劳斯定理可以互相推证．首先，由梅涅劳斯定理推证共点情形的塞瓦定理．如图2-1（b ）、（c ），分别对△ABA '及截线C PC '，对△AA C '及截线B PB '应用梅涅劳斯定理有 1BC A P AC CA PA C B ''⋅⋅=''，1A B CB APBC B A PA ''⋅⋅=''．上述两式相乘，得1BA CB AC A C B A C B'''⋅⋅='''．其次，由共点情形的塞瓦定理推证梅涅劳斯定理．如图2-2，设A '，B '，C '分别为△ABC 的三边BC ，CA ，AB 所在直线上的点，且A '，B '，C '三点共线．令直线BB '与CC '交于点X ，直线C C '与AA '交于点Y ，直线AA '与BB '交于点Z ．CBAA′B'C 'XY ZXYZ CBAA′B'C '图2-2分别视点C '，A '，B '，C ，A ，B 为塞瓦点，应用塞瓦定理，即对△BCB '及点C '（直线BA ，CX ，BA ''的交点），有1BA CA B XA C AB XB ''⋅⋅=''．对△CAC '及点A '（直线CB ，AY ，C B ''的交点），有1CB AB C YB C BC YC ''⋅⋅=''．对△ABA '及点B '（直线AC ，BZ ，A C ''的交点），有1AC BC A ZC B CA ZA ''⋅⋅=''．对△BBC '及点C （直线BA '，B A '，C X '的交点），有1BX B A C AXB A C AB '''⋅⋅='''．对△CC A ''及点A （直线CB '，C B '，AY '的交点），有1CY C B A BYC B A BC '''⋅⋅='''．对△AA B ''及点B （直线AC '，A C '，B Z '的交点），有1AZ A C B CZA C B CA '''⋅⋅='''．上述六式相乘，有21BA CB AC A C B A C B '''⎛⎫⋅⋅= ⎪'''⎝⎭．故1BA CB AC A C B A C B'''⋅⋅='''．塞瓦定理的逆定理设A '，B '，C '分别是△ABC 的三边BC ，CA ，AB 或其延长线上的点，若 1BA CB AC A C B A C B'''⋅⋅='''，② 则AA '，BB '，CC '三直线共点或三直线互相平行．证明若AA '与BB '交于点P ，设CP 与AB 的交点为1C ，则由塞瓦定理，有111AC BA CB A C B A C B ''⋅⋅=''，又已知有111AC BA CB A C B A C B ''⋅⋅=''，由此得11AC AC C B C B '='，即1AC AC AB AB'=，亦即1AC AC '=，故1C 与C '重合，从而AA '，BB '，CC '三线共点．若AA BB ''∥，则CB CB B A BA '=''．代入已知条件，有AC A CC B CB''='，由此知CC AA ''∥，故 AA BB CC '''∥∥．上述两定理可合写为：设A '，B '，C '分别是△ABC 的BC ，CA ，AB 所在直线上的点，则三直线AA '，BB '，CC '平行或共点的充要条件是1BA CB AC A C B A C B'''⋅⋅='''． ③ 第一角元形式的塞瓦定理设A '，B '，C '分别是△ABC 的三边BC ，CA ，AB 所在直线上的点，则三直线AA '，BB '，CC '平行或共点的充要条件是 sin sin sin 1sin sin sin BAA ACC CBB A AC C CB B BA'''⋅⋅='''∠∠∠∠∠∠．④ 证明由sin sin ABA AA C S BA AB BAA A C S AC A AC ''''⋅==''⋅△△∠∠，sin sin CB BC CBB B A AB B BA ''⋅=''⋅∠∠，sin sin AC AC ACC C B BC C CB ''⋅=''⋅∠∠，三式相乘，再运用塞瓦定理及其逆定理，知结论成立．第二角元形的塞瓦定理设A '，B '，C '分别△ABC 的三边BC ，CA ，AB 所在直线上的点，O 是不在△ABC 的三边所在直线上的点，则AA '，BB '，CC '平行或共点的充要条件是 sin sin sin 1sin sin sin BOA AOC COB A OC C OB B OA'''⋅⋅='''∠∠∠∠∠∠．⑤ 证明注意到塞瓦定理及其逆定理，有1BOA COB AOC A OC B OA C OB S S S BA CB AC A C B A C B S S S '''''''''=⋅⋅=⋅⋅'''△△△△△△sin sin sin sin sin sin BO BOA CO COB AO AOC CO A OC AO B OA BO C OB'''⋅⋅⋅=⋅⋅'''⋅⋅⋅∠∠∠∠∠∠．由此即证得结论．注在上述各定理中，若采用有向线段或有向角，则①、②、③、④、⑤式的右端仍为1．特别要注意的是三边所在直线上的点或者两点在边的延长线上，或者没有点在边的延长线上．④、⑤式中的角也可按①式的对应线段记忆．推论设1A ，1B ，1C ，分别是△ABC 的外接圆三段弧BC ，CA ，AB 上的点，则1AA ，1BB ，1CC 共点的充要条件是 1111111BA CB AC A C B A C B⋅⋅=．证明如图2-3，设△ABC 的外接圆半径为R ，1AA 交BC 于A '，1BB 交CA 于B '，1CC 交AB 于C '．由A ，1C ，B ，1A ，C ，1B 六点共圆及正弦定理，有11112sin sin 2sin sin BA R BAA BAA A C R A AC A AC'⋅=='⋅∠∠∠∠． A 1B1C 1CBAA′B'C '图2-3同理，11sin sin CB CBB B A B BA '='∠∠，11sin sin AC ACC C B C CB'='∠∠．三式相乘，并应用第一角元形式的塞瓦定理即证．为了使读者熟练地应用塞瓦定理，针对图2-4中的点A 、B 、C 、D 、E 、F ，将其作为塞瓦点，我们写出如下式子：HGFEDC BA图2-4对△ACE 及点D 有 1A B C GE F B C G E F A⋅⋅=，对△CDE 及点A 有 1C F D B E GF D B EG C ⋅⋅=，对△ADE 及点C 有 1D G A FE B G AF E B D ⋅⋅=，对△ABD 及点F 有 1A C B ED H C BE D H A ⋅⋅=，对△ACD 及点E 有 1A G D FC B GD F C B A ⋅⋅=，对△ADF 及点B 有 1A H D CF E H D C F E A ⋅⋅=，对△ABF 及点D 有 1B C A EF H C A E FH B⋅⋅=，对△BDF 及点A 有1B E D C F HE D CF H B⋅⋅=．【典型例题与基本方法】1．恰当地选择三角形及所在平面上的一点，是应用塞瓦定理的关键例1 四边形两组对边延长分别相交，且交点的连线与四边形的一条对角线平行．证明：另一条对角线的延长线平分对边交点连线的线段．（1978年全国高中竞赛题）证明如图2-5，四边形ABCD 的两组对边延长分别交于E ，F ，对角线BD EF ∥，AC 的延长线交EF 于G ．GFEDCBA图2-5对△AEF 及点C ，应用塞瓦定理，有1EG FD ABGF DA BE ⋅⋅=．由BD EF ∥，有AB ADBE DF=，代入上式，得1EGGF=，即EG GF =．命题获证．例2 如图2-6，锐角△ABC 中，AD 是BC 边上的高，H 是线段AD 内任一点，BH 和CH 的延长线分别交AC ，AB 于E ，F ．求证：EDH FDH =∠∠．（1994年加拿大奥林匹克试题）OPHFEDCB A图2-6证法1 对△ABC 及点H ，应用塞瓦定理，有1AF BD CEFB DC EA⋅⋅=．① 过A 作PQ BC ∥，延长DF ，DE 分别交PQ 于P ，Q ，则DA PQ ⊥，且△APF ∽△BDF ，△AQE ∽△CDE ，从而AF PA BD FB =⋅，EAAQ DC CE=⋅．而由①，有AF EABD DC FB CE⋅=⋅，故PA AQ =．由此知AD 为等腰△APQ 底边PQ 上的高，故EDH FDH =∠∠．证法2 对△ABC 及点H 应用塞瓦定理，有1DAF DCE DFB DEA S S AF BD CE BD FB DC EA S DC S =⋅⋅=⋅⋅△△△△sin sin tan cot sin sin AD ADF BD DC EDCADF ADE BD FDB DC AD ADE⋅⋅=⋅⋅=⋅⋅⋅∠∠∠∠∠∠．即tan tan ADE ADF =∠∠，由锐角性质知ED A FD A =∠∠．类似地，对△ABE 及截线FHC 或对△AFC 及截线BHE 应用梅涅劳斯定理也可证得有ED A FD A =∠∠．注将此例中的平角BDC ∠变为钝角，则有如下：例3 如图2-7，在四边形ABCD 中，对角线AC 平分BAD ∠．在CD 上取一点E ，BE 与AC 相交于F ，延长DF 交BC 于G ．求证：GAC EAC =∠∠．（1999年全国高中联赛题）JIHGF E DCBA图2-7证明连BD 交AC 于H ，对△BCD 及点F ，应用塞瓦定理，有1CG BH DEGB HD EC⋅⋅=． AH 平分BAD ∠，由角平分线性质，可得BH AB HD AD =，故1CG AB DEGB AD EC⋅⋅=．过点C 作AB 的平行线交AG 的延长线于I ，过点C 作AD 的平行线交AE 的延长线于J ，则 ,CG CI DE AD GB AB EC CJ ==．所以1CI AB ADAB AD CJ ⋅⋅=．从而，CI CJ =．又CI AB ∥，CJ AD ∥，有180180ACI BAC DAC ACJ =︒-=︒-=∠∠∠∠．因此，△ACI ACJ ≌△，即有IAC JAC =∠∠．故 G A CE A C =∠∠．注由此例还可变出一些题目，参见练习题第4、5及19题．例4 如图2-8，BE 是△ABC 的中线，G 在BE 上，分别延长AG ，CG 交BC ，AB 于D ，F ，过D 作DN CG ∥交BG 于N ，△DGL 及FGM △为正三角形．求证：△LMN 为正三角形．MLNGFEDCBA图2-8证明连NF ，对△ABC 及点G 应用塞瓦定理，有1AF BD CE FB DC EA ⋅⋅=．而AE CE =，则AF DCFB BD =．由DN CG ∥，由CD NGBD BN=．于是，有AF NGFB BN=，从而FN AD ∥，即知四边形DNFG 为平行四边形，有GDN GFN =∠∠．又60GDL GFM ==︒∠∠，则LDN NFM =∠∠．而DN GF FM ==，DL DG NF ==，知△LDN ≌△NFM ，有LN MN =，DNL NMF =∠∠．于是 MNL DNF DNL MNF DNF NMF MNF =-+=-+∠∠（∠∠）∠（∠∠） 180)(180)NFG NFM NFM NFG ︒--︒-=-=(∠∠∠∠ 60MFG ==︒∠．故△LMN 为正三角形．例5 如图2-9，在一个△ABC 中，2C B =∠∠，P 为△ABC 内满足AP AC =及PB PC =的一点．求证：AP 是A ∠的三等分线．（1994年香港代表队IMO 选拔赛题）π-2(2CBA图2-9证明用B 表示ABC ∠的度量，令PCB θ=∠，则PBC θ=∠，ABP B θ=-∠，2ACP B θ=-∠，()π22CAP B θ=--∠（其中注意AP AC =），()π[π2(2)]P A B A C A P B C B θ=-=-----∠∠∠(π3)(π42)2B B B θθ=---+=-．对△ABC 及点P ，应用第一角元形式的塞瓦定理，有sin[π2(2)]sin sin()1sin(2)sin(2)sin B B B B θθθθθθ---⋅⋅=--．亦即2s i n (2)c o s (2)s i n ()1s i n (2)s i n (2)B B B B B θθθθθ-⋅-⋅-=-⋅-．于是 s i n (2)2s i n ()c o s (2)s i n (3BB B B B θθθθ-=-⋅-=--，即 s i ns i n (32)s i n (2)2c o s (2B B B B B θθθ=---=-⋅．而sin 0B ≠，则1cos2()2B θ-=．因 1π0()33B b B C θ<-<<+<，则2π2()0,3B θ⎛⎫-∈ ⎪⎝⎭．∴ π2()3B θ-=，即π6B θ-=．从而π2(2)π4()2CAP B B θθθ=--=---∠ππ222[()]36B θθθθ⎛⎫=-=-=-- ⎪⎝⎭2(2)2B PAB θ=-=∠．故 13PAB A =∠∠，即AP 是A ∠的三等分线．利用第一角元形式的塞瓦定理可简捷处理2009年全国高中联赛加试第一题的第1问：例6 设M 、N 分别为锐角△ABC （A B <∠∠）的外接圆Γ上弧BC 、AC 的中点．过点C 作PC MN∥交圆Γ于点P ，I 为△ABC 的内心，联结PI 并延长交圆Γ于点Γ．求证：MP MT NP NT ⋅=⋅．证明事实上，易知A 、I 、M 及B 、I 、N 分别三点共线，对△PMN 及点I 应用第一角元形式的塞瓦定理，有sin sin sin 1sin sin sin NPI PMI MNIIPM IMN INP⋅⋅=∠∠∠∠∠∠．①由CP MN ∥知PA PB =，有PMI INP =∠∠．于是①式即为1sin 21sin 2B NT CN MP MT CM NPA ===∠∠．故MP MT NP NT ⋅=⋅．2．注意塞瓦定理逆定理的应用以及与梅涅劳斯定理的配合应用例7 如图2-10，在△ABC 中，90BAC =︒∠，G 为AB 上给定的一点（G 不是线段AB 的中点）．设D 为直线GC 上与C ，G 都不相同的任意一点，并且直线AD ，BC 交于E ，直线BD ，AC 交于F ，直线EF ，AB 交于H ．试证明交点H 与D 在直线CG 上的位置无关．（1990年苏州市高中竞赛题）HGFE DCB 图2-10证明设G 分线段AB 为定比1λ，H 分线段AB 为定比2λ．下证2λ由1λ确定，即当A ，B 给定后，点H 的位置由点G 唯一确定．在△ABC 中，由AE ，BF ，CG 交于一点D ，应用塞瓦定理，有 1AG BE CF GB EC FA ⋅⋅=，即11BE CFEC FAλ⋅⋅=．对△ABC 及截线EFH ，应用梅涅劳斯定理，得 1AH BE CF HB EC FA ⋅⋅=，即21BE CFEC FAλ⋅⋅=-．上述两式相加，得12()0BE CFEC FAλλ+⋅=．从而120λλ+=，即21λλ=-，故2λ由1λ唯一确定．因此，点H 与D 在直线CG 上的位置无关．例8 如图2-11，设P 为△ABC 内任一点，在形内作射线AL ，BM ，CN ，使得CAL PAB =∠∠，MBC PBA =∠∠，NCA BCP ∠=∠．求证：AL ，BM ，CN 三线共点．MN PLFE DCBA图2-11证法1 设AL 交BC 于L ，BM 交CA 于M ，CN 交AB 于N ，则由正弦定理有 sin sin sin sin BL AB BAL AB PACLC AC CAL AC PAB ⋅⋅==⋅⋅∠∠∠∠．同理，sin sin CM BC PBAMA AB PBC⋅=⋅∠∠, sin sin AN AC PCBNB BC PCA⋅=⋅∠∠．将上述三式相乘，并应用正弦定理，有sin sin sin 1sin sin sin BL CM AN PAC PBA PCB PC PA PB LC MA NB PAB PBC PCA PA PB PC ⋅⋅=⋅⋅=⋅⋅=∠∠∠∠∠∠．由塞瓦定理的逆定理，知AL ，BM ，CN 共点．证法2 设AL 交BC 于L ，BM 交CA 于M ，CN 交AB 于N ，直线AP 交BC 于D ，直线BP 交AC 于E ，直线CP 交AB 于F ．对△ABC 及点P ，应用塞瓦定理，有1A F B DC E F BD CE A⋅⋅=．在△ABL 和△ACL 中应用正弦定理，有 sin sin sin sin sin sin sin sin BL BL AL BAL C PAC CLC AL LC B LAC PAB B=⋅=⋅=⋅∠∠∠∠∠∠∠∠ 222222sin sin sin sin sin sin sin sin sin sin PAC B C DC AD C DC CC PAB B AD BD B BD B=⋅⋅=⋅⋅=⋅∠∠∠∠∠∠∠∠∠∠．同理，22sin sin CM AE A MA EC C=⋅∠∠，22sin sin AN BF BNB FA A =⋅∠∠．以上三式相乘，并注意到①式，有 1BL CM AN DC AE BF LC MA NB BD EC FA⋅⋅=⋅⋅=．由塞瓦定理的逆定理，知AL ，BM ，CN 共点．证法3 设AL 交BC 于L ，BM 交AC 于M ，CN 交AB 于N ，直线AP 交BC 于D ，直线BP 交AC 于E ，直线交AB 于F ．对ABC △及点P ，应用角元形式的塞瓦定理，有 sin sin sin 1sin sin sin PAB PBC PCAPAC PBA PCB⋅⋅=∠∠∠∠∠∠．由题设PAB CAL =∠∠，PBA CBM =∠∠，PCB ACN =∠∠，则有BAL PAC =∠∠，ABM PBC =∠∠，BCN PCA =∠∠．于是 s i n s i n s i n s i n s i n s i n s i n s i n s i n s i n s i n s i n B A L C B M A C N P A C P B A P C BC A L A B M B C N P A B P B C P C A⋅⋅=⋅⋅∠∠∠∠∠∠∠∠∠∠∠∠111sin sin sin 1sin sin sin PAB PBC PCA PAC PBA PCB===⋅⋅∠∠∠∠∠∠，对△ABC ，应用角元形式的塞瓦定理的逆定理，知AL ，BM ，CN 三线共点．例9 如图2-12，四边形ABCD 内接于圆，其边AB 与DC 的延长线交于点P ，AD 与BC 的延长线交于点Q ，过点Q 作该圆的两条切线，切点分别为E 和F ．求证：P ，E ，F 三点共线．（1997年CMO 试题）P图2-12证明连EF 分别交AD ，BC 于M ，N ，设AC 与BD 交于K ．要证P ，E ，F 三点共线，只须证明P ，K ，M 和P ，N ，K 都三点共线，又只须证明AC ，BD ，PM 三线共点．由塞瓦定理的逆定理知只须证明1AB PC DM BP CD MA⋅⋅=．又直线QCB 截△PDA ，应用梅涅劳斯定理，有 1AB PC DQ BP CD QA ⋅⋅=，从而只须证明DM DQAM AQ =．设圆心为O ，连QO 交EF 于L ，连LD ，LA ，OD ，OA ，则由切割线走理和射影定理，有2QD QA QE QL QO ⋅==⋅，即知D ，L ，O ，A 四点共圆，有QLD DAO ODA OLA ===∠∠∠∠，此表明QL 为△LAD 的内角ALD ∠的外角平分线．而EF OQ ⊥，则EL 平分ALD ∠．于是， DM DL DQAM AL AQ==，结论获证．【解题思维策略分析】1．获得线段比例式的一种手段例10 如图2-13，△ABC 中，D ，E 分别为AC 和AB 同方向延长线上的点，BD 与CE 相交于P ，且BD CE =．若点P 满足2AEP ADP k PED PDE -=-∠∠（∠∠）（k 为常数），则AB AC =．QF'PFE D CBA图2-13证明设AP 交BC 于Q ，对△PBC 及其形外一点A ，应用塞瓦定理，有1BQ CE PDQC EP DB⋅⋅=．而BD CE =，则PD QCPE QB=．不妨设Q C Q B ≤，则P D P E ≤，即有P C C E P E B D P D P B =--=≤，于是P B E P C DS S △△≥，故E B C D B CS S △△≥．此时，点E 到BC 的距离不小于D 到BC 的距离，则过E 作EF BC ∥必交CD 延长线于一点，设为F ．又作△FBC 的外接圆O 交EF 于另一点F '，则四边形BCFF '为等腰梯形．当AB AC ≥时，由BF F F FC BCA ABC AEF ''===∠∠∠≥∠∠，知F '必在线段EF 上，于是，BDC BFC BEC ∠≥∠≥∠（同弧上的圆外角小于同弧上的圆周角）．又由PD PE ≤，知PED PDE ∠≤∠．故结论获证． 2．转化线段比例式的一座桥梁例11 设M 为△ABC 内任一点，AM ，BM ，CM 分别交BC ，CA ，AB 于D ，E ，F ．求证：1MD ME MFAD BE CF ++=．证明如图2-14，记BD m DC =，CE n EA =，AFl FB=．对△ABC 及点M ，应用塞瓦定理，有1BD CE AFmnl DC EA FB⋅⋅==． FEDCBAM图2-14对△ADC 及截线EMB ，应用梅涅劳斯定理，有11AM DB CE AM mn MD BC EA MD m ⋅⋅=⋅⋅=+，即 1(1)AM mm l MD m n +==++．由合比定理得1(1)AD m l MD =++，即11MD AD l ml=++．同理，111ME lBE m mn l ml ==++++， 111MF mlCF n nl ml l==++++．三式相加，得1MD ME MFAD BE CF++=．例12 如图2-15，设P 为△ABC 内任意一点，AP ，BP ，CP 的延长线交对边BC ，CA ，AB 于点D ，E ，F ，EF 交AD 于Q．试证：(3PQ AD -≤．PQFEDCBA图2-15证明令BD m DC =，CE n EA =，AF p FB =，对△ABC 及点P ，应用塞瓦定理，有1BD CE AFmnp DC EA FB⋅⋅==．对△ADC 及截线BPE ，应用梅涅劳斯定理，有 1CE AP DB EA PD BC ⋅⋅=．注意到1DB mBC m =+，则有 11AP m n PD m ⋅⋅=+，即1AP m PD mn +=，故11AP m AD mn m +=++．又对直线APD 截△BCE ，有1BD CA EP DC AE PB ⋅⋅=．而1CA n AE =+，则BP mn m EP =+，故1BEmn m EP=++．又对△ABP 及截线FQE ，有1A F B E P Q F B E P A Q ⋅⋅=，即有 11(1)1PQ AQ p mn m mp p ==++++，故12PQ AQ mp p =++．从而1121PQ PQ AP m AD AP AD mp p mn m +=⋅=⋅++++ 1112(1)211(1)211mn mn p m p m m m =⋅=+++++++++3=-于是，(3PQ AD -≤．其中等号由2(1)1mn p m m +++≥中等号成立时成立，即当且仅当2(1)1mnp m m =++亦即当且仅当22(1)(1)(1)mnp p m p m p m ==+++，亦即(1)p m +m 和p 之间成为如图2-16的双曲线的关系．图2-16例13 如图2-17，已知直线的三个定点依次为A 、B 、C ，Γ为过A 、C 且圆心不在AC 上的圆，分别过A 、C 两点且与圆Γ相切的直线交于点P ，PB 与圆Γ交于点Q ．证明：AQC ∠的平分线与AC 的交点不依赖于圆Γ的选取．（IMO 45预选题）SRCBAPQ图2-17证明设AQC ∠的平分线交AC 于点R ，交圆Γ于点S ，其中S 与Q 是不同的两点．由于△PAC 是等腰三角形，则有sin sin AB APBBC CPB=∠∠．同理，在△ASC 中，有sin sin AR ASQRC CSQ =∠∠．在△PAC 中，视Q 为塞瓦点，由角元形式的塞瓦定理，有sin sin sin 1sin sin sin APB QAC QCPCPB QAP QCA⋅⋅=∠∠∠∠∠∠．注意到PAQ ASQ QCA ==∠∠∠，PCQ CSQ QAC ==∠∠∠．则22s i n s i n s i n s i n s i n s i n s i n s i n A P BP A Q Q C A A S QC P BQ A C P C Q C S Q⋅==⋅∠∠∠∠∠∠∠∠．即 22A B A RB C R C=，故结论获证．3．求解三角形格点问题的统一方法如果三角形的三个角的度数都是10的整数倍，三角形内一点与三角形的三个顶点分别连结后，得到的所有的角也都具有这个性质，我们称这样的点为三角形的格点．例14 如图2-18，在△ABC 中，40BAC =︒∠，60ABC =︒∠，D 和E 分别是AC 和AB 上的点，使得40CBD =︒∠，70BCE =︒∠，F 是直线BD 和CF 的交点．证明：直线AF 和直线BC 垂直．（1998年加拿大奥林匹克试题）10°40°-αα20°40°70°HFEDCBA图2-18证明设BAF α=∠，则40FAC α=︒-∠，对△ABC 及点F ，应用第一角元形式的塞瓦定理，有 sin10sin sin 401sin 70sin(40)sin 20αα︒︒⋅⋅=︒︒-︒．从而s i n 10s i n 2s i n 20c o s 201c o s 20s i n (40)s i n 20αα︒︒⋅︒⋅⋅=︒︒-︒，即有sin(40)2sin sin102sin cos80ααα︒-=⋅︒=⋅︒ sin(80)sin(80)αα=+︒+-︒．∴ s i n(80)s i n (40)s i n (80)2c o s 60s i n (20)ααααα-︒=︒--+︒=︒⋅-︒-=-︒-．注意到040α<<︒，知8020α-︒<-︒-，8020α-︒<︒，有8020αα-︒=-︒-，故30α=︒．延长AF 交BC 于H ，则180180306090AHB FBC ABH =︒--=︒-︒-︒=︒∠∠∠．故AF BC ⊥．注此题也可这样来解：由sin10sin sin 401sin 70sin(40)sin 20αα︒︒⋅⋅=︒︒-︒，有 sin(40)sin10sin 40sin10sin(4030)2sin10sin 40cot30cos40sin sin70sin 20sin30sin30αα︒-︒-︒︒︒-︒==︒===︒⋅︒-︒︒-︒︒︒．由于sin(40)sin 40cot cos40sin ααα︒-=︒⋅-︒作为α的函数在(0,180)︒︒上严格递减，所以30BAF α==︒∠．故90ABC BAF +=︒∠∠．因此，AF BC ⊥．或者过点A 作AH BC ⊥于H ，则30BAH =︒∠，10HAC =︒∠．关于△ABC 有sin sin sin sin30sin10sin 401sin sin sin sin10sin70sin 20BAH ACD CBD HAC ECB DBA ︒︒︒⋅⋅=⋅⋅=︒︒︒∠∠∠∠∠∠．所以，AH 、BD 、CE三线共点，因此点F 在AH 上，即AF BC ⊥．例15 如图2-19，在△ABC 内取一点M ，使得30MBA =︒∠，10MAB =︒∠．设80ACB =︒∠，AC BC =，求AMC ∠．（1983年前南斯拉夫奥林匹克试题）CBA图2-19解设ACM α=∠，则80MCB α=︒-∠．由第一角元形式的塞瓦定理，有()s i ns i n 10s i n 80s i n 40αα︒⋅⋅︒-︒ sin 201sin30︒=︒．从而 s i n s i n 10s i n (80)αα⋅︒=︒-⋅︒． ∴ 2s i n c o s 802s i n (80)αα⋅︒=︒-⋅︒，∴ s i n (80)s i n (80)s i n (100)s αααα+︒+-︒=︒-+︒-，∴ s i n(80)s i n (60)s i n (100)αααα-︒-︒-=︒--+︒2cos90sin(10)0α=︒⋅︒-=．于是 s i n(80)s i n (60αα-︒=︒-．注意到 080α<<︒，知8080α-︒<<-︒，6060α︒-<︒．∴ 8060αα-︒=︒-，故 70α=︒．所以 1801804070A M CM A C A C M =︒--=︒-︒-︒=︒∠∠∠为所求．注此题结果也可直接由①式有sin sin 70sin10sin(80)αα=︒⎧⎨︒=︒-⎩且0α<，8080α︒-<︒，求得70α=︒．另外，此题也可这样来解：由sin sin10sin 201sin(80)sin 40sin 30αα︒︒⋅⋅=︒-︒︒，有sin(80)sin10sin 20sin10sin(8070)sin80cot 70cos80sin sin 40sin 30cos 20sin 70αα︒-︒⋅︒︒︒-︒====︒⋅︒-︒︒⋅︒︒︒．因为s i n (80)s i n 80c o t c o s 80s i n ααα︒-=︒⋅-︒作为α的函数在（0︒，180︒）上严格递减，所以70ACM α==︒∠．故180407070AMC =︒-︒-︒=︒∠．或者由140AMB =︒∠，令AMC x =∠，则220CMB x =︒-∠．对△M A B 和点C 应用第一角元形式的塞瓦定理，有sin sin sin sin sin 20sin 501sin sin sin sin(220)sin 50sin 40AMC MBC BAC x CMB CBA CAM x ︒︒=⋅⋅=⋅⋅︒-︒︒∠∠∠∠∠∠．则sin(220)1sin(22070)sin 220cot 70cos220sin 2cos20sin70x x ︒-︒-︒===︒⋅︒-︒︒︒．因为sin(220)sin 220cot cos 220(sin 2200)sin x x x︒-=︒⋅-︒︒<作为x 的函数在(0,180)︒︒上严格递增，所以70AMC x ==︒∠．例16 如图2-20，△ABC 具有下面性质：存在一个内部的点P ，使得10PAB =︒∠，20PBA =︒∠，30PCA =︒∠，40PAC =︒∠．证明：△ABC 是等腰三角形．（1996年美国第25届奥林匹克试题）α80°-α20°10°40°30°CBAP图2-20证明设BCP α=∠，则1802010403080PBC αα=︒-︒-︒-︒-︒-=︒-∠．由第一角元形式的塞瓦定理，有sin 20sin 40sin 1sin(80)sin10sin 30αα︒︒⋅⋅=︒-︒︒．即有2s i n 10c o s 10s i n 40s i n11s i n (80)s i n 102αα︒⋅︒︒⋅⋅=︒-︒．∴ s i n (80)4s i ns i n 40c o s 104s i n sααα︒-=⋅︒⋅︒=⋅︒⋅︒4sin sin 20sin 40sin80sin60sin sin 20sin 20αα⋅︒⋅︒⋅︒︒⋅==︒︒， ∴ s i n (80)s i n 20s i n 60αα︒-⋅︒=︒⋅．从而 s i n (80)s i n s i n 20s i n αα︒-=︒⎧⎨︒=⎩且0α<，8080α︒-<︒，故20α=︒，即50ACB CAB =︒=∠∠，从而AB BC =．注此题也可这样来求解：由sin 20sin 40sin 1sin(80)sin10sin 30αα︒︒⋅⋅=︒-︒︒，有s i n (80)s i n 20s i n 404s i n 20s i n 40s i n 804c o s 10s i n 40s i n s i n 10s i n 30s i n 20αα︒-︒︒︒⋅︒⋅︒=⋅=︒⋅︒=︒︒︒sin60sin(8020)sin80cot 20cos80sin 20sin 20︒︒-︒===︒⋅︒-︒︒︒．因为sin(80)sin80cot cos80sin ααα︒-=︒⋅-︒作为α的函数在（0︒，180︒）上严格递减，所以BCP α=∠20=︒，即50ACB CAB =︒=∠∠．故AB BC =．还可对△APC 及点B 应用第一角元形式的塞瓦定理来求． 4．论证直线共点的一种工具例17 如图2-21，在四边形ABCD 中，AB AD =，BC DC =，过AC ，BD 的交点O 引EF ，GH ，其中EF 交AB ，CD 于E ，F ，GH 交DA ，BC 于G ，H ．EH ，GF 分别交BD 于P ，Q ，则O P O Q =．（1990年CMO 选拔试题）4321γαβK F'G 'HG PQ O FE DCBA 图2-21证明在AB ，BC 上分别取G '，F '，使AG AG '=，CF CF '=，则由对称性可知有下列角相等，即若设,AOG AOG αβ'==∠∠，COH γ=∠，1G OE '=∠∠，2EOB =∠∠，3BOF '=∠∠，4F OH '=∠∠，则αβ=，又αγ=，故βγ=．又14βγ+=+∠∠，故14=∠∠，23=∠∠．连G H '交BD 于K ，在△BHG '中， OG E OBF OHKOEB OF H OKG S S S G E BF HK EB F H KG S S S ''''''⋅⋅=⋅⋅''△△△△△△ sin 1sin 3sin(34)1sin 2sin 4sin(12)OG OE OB OF OH OK OE OB OF OH OK OG ''⋅⋅⋅⋅⋅⋅+=⋅⋅=''⋅⋅⋅⋅⋅⋅+∠∠∠∠∠∠∠∠．故由塞瓦定理的逆定理，知G F ''，BO ，HE 共点，即G F ''过点P ．由对称性知，OP OQ =．例18 如图2-22，在锐角△ABC 中，以A 点引出的高AD 为直径作圆交AB ，AC 于M ，N ，再从A 作A l MN ⊥．同样可作出B l ，C l ．试证：三直线A l ，B l ，C l 相交于一点．（第29届IMO 预选题）l AD ′MNGDCBA图2-22证明设A l 与MN ，BC 分别相交于点G ，D '，由AMG ADN =∠∠，90AGM AND ==︒∠∠，知MAG NAD =∠∠，即BAD CAD '=∠∠．同理，设CA ，AB 边上的高BE ，CF 的垂足分别为E ，F ，且B l ，C l 分别与CA ，AB 交于E '，F '，则有CBE ABE '=∠∠，ACF BCF '=∠∠．由于△ABC 的三条高相交于垂心，此时应用第一角元形式的塞瓦定理，得sin sin sin 1sin sin sin CAD ABE BCFDAB EBC FCA⋅⋅=∠∠∠∠∠∠，用等角代换上式，有sin sin sin 1sin sin sin BAD ACF CBE DAC F CB E BA'''⋅⋅=''∠∠∠∠∠∠．故由第一角元形式的塞瓦定理，知AD '，BE '，CF '三线共点，即A l ，B l ，C l 相交于一点．例19 如图2-23，四边形ABCD 内接于圆，AB ，DC 的延长线交于E ，AD ，BC 的延长线交于F ，P 为圆上任一点，PE ，PF 分别交圆于R ，S ．若对角线AC 与BD 相交于T ，求证：R ，T ，S 三点共线．RTSPFEDC BA图2-23证明连PD ，AS ，RC ，BR ，AP ，SD ．由△EBR ∽△EPA ，△FDS ∽△FPA ，有BR EBPA EP =，PA FP DS FD =，此两式相乘，有BR EB FPDS EP FD =⋅．①又由ECR EPD △∽△，FPD FAS △∽△，有 CR EC PD EP =，PD FPAS FA =，此两式相乘，有 CR EC FPAS EP FA=⋅．由①÷②，得 B R A SE BF A D S C RE CF D⋅=⋅．上式两边同乘以DC AB ，得 B R C D S A E BA F D C R C D S AB B AF D C E⋅⋅=⋅⋅．对△EAD 及截线BCF ，应用梅涅劳斯定理，有 1EB AF DC BA FD CE⋅⋅=．于是1B R C D S AR C D C A B⋅⋅=．此时，应用第一角元形式的塞瓦定理的推论，知BD ，RS ，AC 交于一点．从而R ，T ，S 三点共直线．【模拟实战】习题A1．在△ABC 中，D 是BC 上的点，13BD DC =，E 是AC 中点．AD 与BE 交于O ，CO 交AB 于F ，求四边形BDOF 的面积与△ABC 的面积的比．2．若通过△ABC 各顶点的直线AD ，BE ，CF 共点，并且它们在边BC ，CA ，AB 所在直线上的截点D ，E ，F 关于所在边中点的对称点分别为D '，E '，F '，则直线AD '，BE '，CF '也共点． 3．一圆交△ABC 的各边所在直线于两点，设BC 边上的交点为D ，D '，CA 边上的交点为E ，E '，AB 边上的交点为F ，F '．若AD ，BE ，CF 共点，则AD '，BE '，CF '也共点． 4．试证：过三角形顶点且平分三角形周长的三条直线共点．5．将△ABC 各内角三等分，每两个角的相邻三等分线相交得△PQR ，又AX ，BY ，CZ 分别平分BAC ∠，ABC ∠，ACB ∠且它们与QR ，RP ，PQ 交于X ，Y ，Z ．求证：PX ，QY ，RZ 三线共点．6．将△ABC 的各外角三等分，每两个外角的相邻三等分线相交得△DEF ．又AX ，BY ，CZ 分别平分BAC ∠，ABC ∠，ACB ∠且它们与EF ，FD ，DE 交于X ，Y ，Z ．求证：DX ，EY ，FZ 三线共点．7．O 是△ABC 的内切圆，BC ，CA ，AB 上的切点各是D ，E ，F ．射线DO 交EF 于A '，同样可得B '，C '．试证：直线AA '，BB '，CC '共点．8．△ABC 在△A B C '''内部，且从A ，B ，C 各向B C ''，C A ''，A B ''所作的垂线共点，则从A '，B '，C '各向BC ，CA ，AB 所作的垂线也共点．9．在△ABC 中，40ABC ACB ==︒∠∠，P 为形内一点，20PAC =︒∠，30PCB =︒∠，求PBC ∠的度数．10．在ABC △中，AB AC =，80A =︒∠，D 为形内一点，且10DAB DBA ==︒∠∠，求ACD ∠的度数．（《数学教学》问题432题）11．在ABC △中，30BAC =︒∠，70ABC =︒∠，M 为形内一点，20MAB MCA ==︒∠∠，求M B A ∠的度数．（《数学教学》问题491题） 12．在ABC △中，40ABC =︒∠，30ACB =︒∠，P 为ABC ∠的平分线上一点，使10PCB =︒∠，BP 交AC 于M ，CP 交AB 于N ．求证：PM AN =．（《数学教学》问题531题）13．在ABC △中，40ABC =︒∠，20ACB =︒∠，N 为形内一点，30NBC =︒∠，20NAB =︒∠，求NCB ∠的度数．（《数学通报》问题1023题） 14．在ABC △中，80BAC =︒∠，60ABC =︒∠，D 为形内一点，且10DAB =︒∠，20DBA =︒∠，求A C D ∠的度数．（《数学通报》问题1142题） 15．在△ABC 中，50ABC =︒∠，30ACB =︒∠，M 为形内一点，20MCB =︒∠，40MAC =︒∠，求M B C ∠的度数．（《数学通报》问题1208题）16．△ABC 中，70ABC =︒∠，30ACB =︒∠，P 为形内一点，40PBC =︒∠，20PCB =︒∠．求证：1CA AB BPAP PC CB⋅⋅=⋅⋅．（《数学通报》问题1306题）17．在△ABC 中，40ABC ACB ==︒∠∠，P ，Q 为形内两点，20PAB QAC ==︒∠∠，PCB QCA =∠∠ 10=︒．求证：B ，P ，Q 三点共线．（《数学通报》问题1243题） 18．△ABC 中，50ABC ACB ==︒∠∠，P ，Q 为形内两点，10PCA QBC ==︒∠∠，PAC QCB =∠∠ 20=︒．求证：BP BQ =．（《数学通报》问题1281题） 19．在△ABC 中，AB AC =，100A =︒∠，I 为内心，D 为AB 上一点，满足BD BI =．试求BCD ∠的度数．（《数学通报》问题1073题） 20．1A ，2A ，1B ，2B ，1C ，2C 顺次分别在△ABC 的三边BC ，CA ，AB 上，且12BA A C =，12CB B A =， 12AC C B =，过2A ，2B ，2C 分别作1AA ，1BB ，1CC 的平行线a l ，b l ，c l ．求证：a l ，b l ，c l 三线共点的充要条件是1AA ，1BB ，1CC 三线共点．21．在△ABC 中，AB AC =，AD BC ⊥于D ，过D 任作两射线分别交AB ，AC 于点E ，F ，交过点A 的平行线于G ，H ，且GH BC ∥．求证：AD ，GF ，HE 共点．22．在△ABC 中，过三边BC ，CA ，AB 边中的中点M ，N ，L 的三条等分三角形周长的直线MS ，NT ，LU （S ，T ，U 在三角形三边上）分别交LN ，LM ，MN 于D ，E ，F ．求证：MS ，NT ，LU 三线共点．23．△ABC 的内切圆切BC ，CA ，AB 于D ，E ，F ．P 是△ABC 内一点，PA 交内切圆于两点，其中靠近A 的一点为X ，类似定义Y ，Z ．试证：DX ，EY ，FZ 三线共点．24．△ABC 在△A B C '''内部，AB 的延长线分别交A C ''，B C ''于5P ，1P ；AC 的延长线分别交BA''，B C ''于3P ，4P ；BC 的延长线分别交A B ''，A C ''于6P ，2P ，且满足142536AP AP BP BP CP CP ===== 123BP CP AP =++．求证：AA '，BB '，CC '所在直线共点．（《中学数学教学》擂台题（28））25．给定△ABC ，延长边BC 至D ，使CD AC =．△ACD 的外接圆与以BC 为直径的圆相交于C 和P ．设BP 与CP 的延长线分别交AC 和AB 于E ，F ．求证：E ，F ，D 共线．（第15届伊朗奥林匹克题） 26．在△ABC 的边上向外作三个正方形，1A ，1B ，1C 是正方形中的边BC ，CA ，AB 对边的中点．求证：直线1AA ，1BB ，1CC 共点．习题B1．O 是△ABC 的内切圆，D ，E ，F ，分别是BC ，CA ，AB 上的切点，DD '，EE '，FF '都是O 的直径．求证：直线AD '，BE '，CF '共点．（《数学通报》问题1396题） 2．四边形ABCD 的内切圆分别与边AB ，BC ，CD ，DA 相切于E ，F ，G ，H ．求证：AC ，BD ，HF ，GE 四线共点．（《数学通报》问题1370题） 3．锐角△ABC 中，A 角的平分线与三角形的外接圆交于另一点1A ，点1B ，1C 与此类似．直线1AA 与B ，C 两角的外角平分线交于0A ，点0B ，0C 与此类似．求证：（Ⅰ）三角形000A B C 的面积是六边形111AC BACB 的二倍；（Ⅱ）三角形000A B C 的面积至少是三角形ABC 面积的四倍．（IMO -30试题） 4．设P 为△ABC 内一点，使BPA CPA =∠∠，G 是线段AP 上的点，直线BG ，CG 分别交边AC ，AB于E ，F ．求证：BPF CPE =∠∠．5．在凸四边形ABCD 中，对角线AC 平分BAD ∠，E 是CD 的延长线上的一点，BE 交AC 于点G ，延长DG 交CB 的延长线于F ．试证：BAF D AE =∠∠．6．在△ABC 中，AB AC =，100A =︒∠，I 为内心，D 为AB 上一点，满足BD BI =．试求BCD ∠的度数．（《数学通报》问题1073题）7．设△ABC 是等边三角形，P 是其内部一点，线段AP ，BP ，CP 依次交三边BC ，CA ，AB 于1A ，1B ，1C 三点．证明：111111111A B B C C A A B B C C A ⋅⋅⋅⋅≥．（IMO -37预选题）8．在一条直线l 的一侧画一个半圆Γ，C ，D ，是Γ上两点，Γ上过C 和D 的切线分别交l 于B 和A ，半圆的圆心在线段BA 上，E 是线段AC 和BD 的交点，F 是l 上的点，EF l ⊥．求证：EF 平分CFD ∠．（IMO -35预选题） 9．设1A 是锐角△ABC 的内接正方形的中心，其中内接正方形的两个顶点在BC 边上，一个顶点在AB 边上，一个顶点在AC 边上．同样定义两个顶点分别在AC 边和AB 边上的内接正方形的中心分别为1B ，1C ．证明：1AA ，1BB ，1CC 交于一点．（IMO -42预选题）10．以△ABC 的底边BC 为直径作半圆，分别与AB ，AC 交于点D ，E ，分别过点D ，E 作BC 的垂线，垂足依次为F ，G ，线段DG 和EF 交于点M ．求证：AM BC ⊥．（1996年国家队选拔考试题）11．设O ，H 是锐角△ABC 的外接圆的圆心和垂心．证明：存在D ，E ，F 分别在线段BC ，CA ，AB 上，使得OD DH OE EH OF FH +=+=+，且此时AD ，BE ，CF 三线交于一点．（IMO -41预选题）12．已知AB 是O 的直径，弦CD AB ⊥于L ，点M 和N 分别在线段LB 和LA 上，且LM ∶MB LN =∶NA ，射线CM ，CN 交O 于E ，F ．求证：AE ，BF ，OD 三线共点．13．设I 是△ABC 的内心，以I 为圆心的一个圆分别交BC 于1A ，2A ，交A C 于1B ，2B ，交AB 于1C ，2C ．这六个点在圆上的顺序为1A ，2A ，1B ，2B ，1C ，2C ．设3A ，3B ，3C 为弧12A A ，12B B ，12C C 的中点，直线23A A ，13B B 相交于4C ，直线23B B ，13C C 相交于4A ，直线23C C ，13A A 相交于4B ．求证：直线34A A ，34B B ，34C C 三线共点．14．在△ABC 的边AB 和AC 上分别向形外作△ABE 和△ACF ，使△ABE ∽△ACF ，且ABE =∠ 90ACF =︒∠．求证：连线BF ，CE 与边BC 上的高AH 三线共点．15．过非等边三角形各顶点作其外接圆的切线，则各切线与其对边的交点共线．16．在△ABC 内三点D ，E ，F 满足BAE CAF =∠∠，ABD CBF =∠∠，则AD ，BE ，CF 三线共点的充要条件是ACD BCE =∠∠． 17．在任意△ABC 的三边BC ，CA ，AB 上各有点M ，N ，L ，而Q 是△ABC 内部任一点，直线AQ ，BQ ，CQ 分别交线段NL ，LM ，MN 于1M ，1N ，1L ．求证：直线1M M ，1N N ，1L L 共点的充分必要条件是AM ，BN ，CL 共点，而与Q 点的位置无关．18．设P 是平面上△ABC 区域内任一点，AP ，BP ，CP 的延长线交△ABC 三边于D ，E ，F ．求证：在△ABC 区域内，存在一个以△DEF 的某两边为邻边的平行四边形．19．设凸四边形ABCD 的两组对边所在的直线，分别交于E ，F 两点，两对角线的交点为P ，过点P 作PO EF ⊥于O ．求证：BOC AOD =∠∠．（2002国家集训队选拔试题） 20．在△ABC 中，ABC ∠和ACB ∠均为锐角．D 是BC 边上的内点，且AD 平分BAC ∠，过点D 作垂线DP AB ⊥于P ，DQ AC ⊥于Q ，CP 与BQ 相交于K ．求证：AK BC ⊥．第二章塞瓦定理及应用答案习题A1．对ABC △及点O ，由塞瓦定理可得3AF FB =，34AF AB =．又对ADC △与截线FOC ，由梅涅劳斯定理得4AO OD =，45AO AD =，故343455AFO ABD S S =⋅⋅△△，由此可知25BDOF ABD S S =△．又14ABD ABC S S =△△，所以2115410BDOF ABC S S =⋅=△． 2．在ABC △中由题设及塞瓦定理有1BD CE AFDC EA FB ⋅⋅=．又有BD CD '=，DC D B '=，CE AE '=，EA E C '=，AF BF '=，FB F A '=，故1CD BF AE D B F A E C'''⋅⋅='''．由塞瓦定理之逆知AD '，BE '，CF '三线共点．3．由割线定理有A F A F A E A E ''⋅=⋅，即AF E A EA AF '='．同理，BD F B FB BD '='，CE D CDC CE '='．三式相乘并适当交换位置，有BD CE AF D C E A F B DC EA FB BD CE AF '''⋅⋅=⋅⋅'''．由塞瓦定理知1BD CE AFDC EA FB⋅⋅=，再由塞瓦定理之逆知AD '，BE '，CF '三线共点．4．设ABC △的边BC a =，CA b =，AB c =，周长为2s ，过顶点A ，B ，C 且平分ABC △周长的直线分别交BC ，CA ，AB 于点D ，E ，F ，则由BD CD a +=，c BD b CD +=+，求得1()2BD a b c s c =+-=-，1()2CD c a b s b =+-=-．同理C Es =-，AE s b CD =-=，BF s a CE =-=．故有1BD CE AFDC EA FB⋅⋅=．由塞瓦定理之逆，知AD ，BE ，CF 共点．5．令3B A C a ∠=，3ABC β∠=，3ACB γ∠=，由角平分线性质有QX AQ XR AR =，BY BR YP BP=，PZ CPZQ CQ =．由正弦定理，有sin sin BR αAR β=，sin sin CP βBP γ=，sin sin AQ γCQ α=，于是1QX BY PZ BR CPXR YP ZQ AR CQ⋅⋅=⋅=．由塞瓦定理之逆，值PX ，QY ，RZ 三线共点．6．令3BAC α∠=，3ABC β∠=，3ACB γ∠=，由平分线性质有EX AE FX AF =，FY BF YD BD =，DZ CDZE CE=．设ABC △的外接圆半径为R ，由正弦定理有2sin 3sin(60)8sin sin(60)sin(60)sin(60)R γβAF R γγβγ⋅⋅︒-==⋅⋅-⋅︒-︒-，sin sin(60)sin(60)βγβ⋅︒-⋅︒-．子啊AEF △中，由余弦定理及公式222sin ()sin sin sin sin cos()x y x y x y x y +=++⋅⋅+，求得 8sin(60)sin(60)sin(60)EF R αβγ=⋅︒-⋅︒-⋅︒-．由sin sin sin(60)AE AF EF AFE AEF α==∠∠︒-，知sin sin AFE β∠=，sin sin AEF γ∠=，故sin sin AE βAF γ=同理，sin sin BF γBD α=，sin sin CD αCE β=．于是1EX FY DZXF YD ZE⋅⋅=，由塞瓦定理之逆，知DX ，EY ，FZ 三线共点． 7．由正弦定理，有sin sin EA EAA AA E AE '''∠=⋅∠，sin sin A FA AF AA F AF '''∠=⋅∠．两式相除并注意AE AF =，有sin sin AA E AA F ''∠=∠，则sin sin EAA EA A AF A F ''∠=''∠，即sin sin CAA EA A AB A F ''∠=''∠．同理sin sin ABB FB B BC B D''∠=''∠， sin sin BCC DC C CA C E ''∠=''∠．三式相乘，得sin sin sin sin sin sin CAA ABB BCC EA FB DC A AB B BC C CA A F B D C E''''''∠∠∠⋅⋅=⋅⋅''''''∠∠∠．由于DA 'EB '，FC '共点于O ，则上式右边等于1，从而左边亦等于1．由塞瓦定理之逆，知AA '，BB '，CC '共点． 8．设AD ，BE ，CF 分别与B C '，C A '，A B '垂直于D ，E ，F ，且AD ，BE ，CF 共点于P ．A G '，BH'，CL 分别与BC ，CA ，AB 垂直于G ，H ，L ．又锐角HB A '∠与ACP ∠的两边分别垂直，故HB A ACP '∠=∠，同理，B A G PCB ''∠=∠，从而sin sin sin sin HB A ACPB A G PCB''∠∠=''∠∠．。

塞瓦定理入门篇

塞瓦定理塞瓦定理在△ABC内任取一点O，直线AO、BO、CO分别交对边于D、E、F，则(BD/D C)*(CE/EA)*(AF/FB)=1证法简介（Ⅰ）本题可利用梅涅劳斯定理证明：∵△ADC被直线BOE所截，∴(CB/BD)*(DO/OA)*(AE/EC)=1 ①而由△ABD被直线COF所截，∴(BC/CD)*(DO/OA)*(AF /FB)=1②②÷①:即得：(BD/DC)*(CE/EA)*(AF/FB)=1（Ⅱ）也可以利用面积关系证明∵BD/DC=S△ABD/S△ACD=S△BOD/S△COD=(S△ABD-S △BOD)/(S△ACD-S△COD)=S△AOB/S△AOC ③同理CE/EA=S△BOC/ S△AOB ④AF/FB=S△AOC/S△BOC ⑤③×④×⑤得BD/DC*CE/EA*AF/FB=1利用塞瓦定理证明三角形三条高线必交于一点:设三边AB、BC、AC的垂足分别为D、E、F，根据塞瓦定理逆定理，因为(AD:DB)*(BE:EC)*(CF:FA)= [(CD*ctgA）/[(CD*ctgB）]*[(AE*ctgB)/(AE*ctgC)]*[(BF*ctgC) /[(BF*ctgA)]=1，所以三条高CD、AE、BF交于一点。

可用塞瓦定理证明的其他定理;三角形三条中线交于一点（重心）:如图5 D , E分别为BC , AC 中点所以BD=DC AE=EC 所以BD/DC=1 CE/E A=1且因为AF=BF 所以AF/FB必等于1 所以AF=FB 所以三角形三条中线交于一点此外，可用定比分点来定义塞瓦定理：在△ABC的三边BC、CA、AB或其延长线上分别取L、M、N三点，又分比是λ=BL/LC、μ=CM/MA、ν=AN/NB。

于是AL、BM、CN三线交于一点的充要条件是λμν=1。

（注意与梅涅劳斯定理相区分，那里是λμν=-1）塞瓦定理推论：设E是△ABD内任意一点，AE、BE、DE分别交对边于C、G、F，则(BC/CD)*(D G/GA)*(AF/FB)=1，（塞瓦定理）则(BD/CD)*(CE/AE)*(AF/FB)=K（K为未知参数）且(B D/BC)*(CE/AE)*(GA/DG)=K（K为未知参数）由梅涅劳斯定理得：(BD/CD)*(CE/AE)*(AF/FB)=1所以(BD/BC)*(CE/AE)*(GA/DG)=1（塞瓦定理推论）。

平面几何2--塞瓦定理

厦门一中2010数学竞赛讲座—平面几何
平面几何定理2——塞瓦定理
塞瓦定理：设P 、Q 、R 分别是ABC ∆三边BC ，CA 、AB 或其延长线上的点，若AP 、BQ 、CR 三线平行或共点，则BP 1PC CQ AR QA RB
⋅
⋅=。

塞瓦定理逆定理：设P 、Q 、R
分别是ABC ∆三边
BC ，CA 、AB 或其延长
线上的点，若BP 1PC CQ AR QA
RB ⋅⋅=，则AP
、
BQ 、CR 三线平行或共点。

角元形式的塞瓦定理：设P 、Q 、R 分别是ABC ∆三边BC ，CA 、AB 或其延长线上的点，则AP 、BQ 、CR 三线平行或共点的充要条件是： sin sin sin 1sin sin sin BAP ACR CBQ PAC RCB QBA
∠∠∠⋅=∠∠∠
`
三角形格点问题(角元形式)
例4（与梅氏定理的配合运用）
练习
例5.
练习
练习. 如图
例2
练习
例3
练习
1
2.
3.
4.
5.
（学习的目的是增长知识，提高能力，相信一分耕耘一分收获，努力就一定可以获得应有的回报）。

初中数学奥林匹克中的几何问题：第二章塞瓦定理及应用

第二章塞瓦定理及应用习题A1．对ABC △及点O ，由塞瓦定理可得3AF FB=，34AF AB =．又对ADC △与截线FOC ，由梅涅劳斯定理得4AO OD =，45AO AD =，故343455AFO ABD S S =⋅⋅△△，由此可知25BDOF ABD S S =△．又14ABD ABC S S =△△，所以2115410BDOF ABC S S =⋅=△． 2．在ABC △中由题设及塞瓦定理有1BD CE AF DC EA FB⋅⋅=．又有BD CD '=，DC DB '=，CE AE '=，EA E C '=，AF BF '=，FB F A '=，故1CD BF AE D B F A E C '''⋅⋅='''．由塞瓦定理之逆知AD '，BE '，CF '三线共点．3．由割线定理有AF AF AE AE ''⋅=⋅，即AF E A EA AF '='．同理，BD F B FB BD '='，CE D C DC CE '='．三式相乘并适当交换位置，有BD CE AF D C E A F B DC EA FB BD CE AF '''⋅⋅=⋅⋅'''．由塞瓦定理知1BD CE AF DC EA FB⋅⋅=，再由塞瓦定理之逆知AD '，BE '，CF '三线共点．4．设ABC △的边BC a =，CA b =，AB c =，周长为2s ，过顶点A ，B ，C 且平分ABC △周长的直线分别交BC ，CA ，AB 于点D ，E ，F ，则由BD CD a +=，c BD b CD +=+，求得1()2BD a b c s c =+-=-，1()2CD c a b s b =+-=-．同理C E s =-，AE s b CD =-=，BF s a CE =-=．故有1BD CE AF DC EA FB⋅⋅=．由塞瓦定理之逆，知AD ，BE ，CF 共点． 5．令3B A C a ∠=，3ABC β∠=，3ACB γ∠=，由角平分线性质有QX AQ XR AR =，BY BR YP BP =，PZ CP ZQ CQ=．由正弦定理，有sin sin BR αAR β=，sin sin CP βBP γ=，sin sin AQ γCQ α=，于是1QX BY PZ BR CP XR YP ZQ AR CQ ⋅⋅=⋅=．由塞瓦定理之逆，值PX ，QY ，RZ 三线共点．6．令3BAC α∠=，3ABC β∠=，3ACB γ∠=，由平分线性质有EX AE FX AF =，FY BF YD BD =，DZ CD ZE CE=．设ABC △的外接圆半径为R ，由正弦定理有2sin3sin(60)8sin sin(60)sin(60)sin(60)R γβAF R γγβγ⋅⋅︒-==⋅⋅-⋅︒-︒-，sin sin(60)sin(60)βγβ⋅︒-⋅︒-．子啊AEF △中，由余弦定理及公式222sin ()sin sin sin sin cos()x y x y x y x y +=++⋅⋅+，求得 8sin(60)sin(60)sin(60)EF R αβγ=⋅︒-⋅︒-⋅︒-．由sin sin sin(60)AE AF EF AFE AEF α==∠∠︒-，知sin sin AFE β∠=，sin sin AEF γ∠=，故sin sin AE βAF γ=同理， sin sin BF γBD α=，sin sin CD αCE β=．于是1EX FY DZ XF YD ZE⋅⋅=，由塞瓦定理之逆，知DX ，EY ，FZ 三线共点． 7．由正弦定理，有sin sin EA EAA AA E AE '''∠=⋅∠，sin sin A F A AF AA F AF'''∠=⋅∠．两式相除并注意AE AF =，有sin sin AAE AAF ''∠=∠，则sin sin EAA EA A AF A F ''∠=''∠，即sin sin CAA EA A AB A F ''∠=''∠．同理sin sin ABB FB B BC B D''∠=''∠， sin sin BCC DC C CA C E ''∠=''∠．三式相乘，得sin sin sin sin sin sin CAA ABB BCC EA FB DC A AB B BC C CA A F B D C E''''''∠∠∠⋅⋅=⋅⋅''''''∠∠∠．由于DA 'EB '，FC '共点于O ，则上式右边等于1，从而左边亦等于1．由塞瓦定理之逆，知AA '，BB '，CC '共点．8．设AD ，BE ，CF 分别与B C '，C A '，A B '垂直于D ，E ，F ，且AD ，BE ，CF 共点于P ．A G '，B H '，CL 分别与BC ，CA ，AB 垂直于G ，H ，L ．又锐角HB A '∠与ACP ∠的两边分别垂直，故HBA ACP '∠=∠，同理，BAG PCB ''∠=∠，从而sin sin sin sin HB A ACP B A G PCB ''∠∠=''∠∠．类似地有sin sin sin sin GA C CBP A C L PBA ''∠∠=''∠∠，sin sin sin sin LC B BAP PBA PAC''∠∠=∠∠．三式相乘并适当整理，有sin sin sin sin sin sin sin sin sin sin sin sin GA C LC B HB A ACP CBP BAP B A G A C L C B H PCB PBA PAC'''''∠∠∠∠∠∠⋅⋅=⋅⋅''''''∠∠∠∠∠∠．由ABC △重AP ，BP ，CP 共点及角元形式的塞瓦定理，知上式右边等于1，从而左边也等于1，也等于1．由塞瓦定理之逆，知A G '，B H '，C L '三线共点．9．设PBC x ∠=，则40ABP x ∠=︒-，由sin80sin sin101sin20sin(40)sin30x x ︒︒⋅⋅=︒︒-︒，求得20x =︒． 10．设ACD x ∠=，则50BCD x ∠=︒-，由sin10sin40sin 1sin70sin10sin(50)x x ︒︒⋅⋅=︒︒︒-，求得30x =︒． 11．设M BA x ∠=，则70MAC ∠=︒，由sin20sin20sin(70)1sin60sin10sin x x︒︒︒-⋅⋅=︒︒，及 sin20sin40sin80sin(70)sin60sin(70)sin60sin 2sin402sin40x x x ︒⋅︒⋅︒⋅︒-︒⋅︒-︒⋅==︒︒，求得30x =︒． 12．连AP ，设P A C x ∠=，则110BAP x ∠=︒-．对ABC △及点P ，有s i n (110)s i n 20s i n 201s i n s i n 20s i n 10x x ︒-︒︒⋅⋅=︒︒，求得80x =︒．此时80APC ∠=︒．过M 作EM AP ∥交PC 于E ，则梯形APEM 为等腰梯形，有PM AE =．又50ANE NBC BCN ∠=∠+∠=︒，18050AEP AM P M AB ABM ∠=∠=︒-∠-∠=︒，则A N A E =，故PM AN =．13．设NCB x ∠=，则20ACN x ∠=︒-，由sin20sin30sin(20)1sin100sin10sin x x︒︒︒-⋅⋅=︒︒，求的10x =︒． 14．设ACD x ∠=，则40BCD x ∠=︒-，由sin10sin40sin 1sin70sin20sin(40)x x ︒︒⋅⋅=︒︒︒-，求得30x =︒． 15．设M BC x ∠=，则50ABM x ∠=︒-，由sin60sin sin101sin40sin(50)sin20x x ︒︒⋅⋅=︒︒-︒及 1sin60sin(50)sin60sin 4sin20sin40sin80sin(50)2sin202sin20x x x ︒⋅︒-︒⋅=⋅︒⋅︒⋅︒⋅︒-=︒︒，求得30x =︒． 15．设PAc x ∠=，80PAB x ∠=︒-，由sin(80)sin40sin101sin sin30sin20x x ︒-︒︒⋅⋅=︒︒及 4sin10sin50sin70sin(80)sin30sin(80)sin sin50sin50x x x ︒⋅︒⋅︒⋅︒-︒⋅︒-==︒︒，求得30x =︒．分别在APC △，BPC △，ABC △中由正弦定理，有s i n 40s i n 40s i n 10s i n 10CA AP ︒︒==︒︒，sin 20sin 40BP PC ︒=︒，sin301sin802cos10AB CB ︒==︒︒．故.1CA AB BP CA BP AB AP PC CB AP PC CB⋅⋅=⋅=． 17．连BP ，设A B P x ∠=，则40PBC x ∠=︒-，对ABC △及点P 有sin20sin(40)sin301sin80sin sin10x x ︒︒-︒⋅⋅=︒︒，求得20x =︒．连PQ ，设APQ y ∠=，则70QPC y ∠=︒-．对APC △及点Q 有sin60sin(70)sin101sin20sin sin20y y ︒︒-︒⋅⋅=︒︒，求得40y =︒．此时，40APQ PAB BAP ∠=︒=∠+∠，故B ，P ，Q 共线．18．设A B P x ∠=，则50PBC x ∠=︒-．对ABC △及点P 有sin60sin(50)sin101sin20sin sin40x x ︒︒-︒⋅⋅=︒︒．求得20x =︒，即有20PBQ ∠=︒．连PQ ，设Q P C y ∠=，则110BPQ y ∠=︒-．对B C P △及点Q 有sin(110)sin101sin sin20y y ︒-︒⋅=︒，求得30y =︒，即有80BPQ ∠=︒．又18080BQP PBQ BPQ ∠=︒-∠-∠=︒，故BP BQ =．19．连DI ，IC ，由AB AC =及I 为内心，知20BCI IBC IBD ∠=∠=∠=︒．又由BD BI =，知80BDI ∠=︒．设DCI x ∠=，则40IDC x ∠=︒-，对BCD △及点I 有sin80sin20sin 1sin(40)sin20sin20x x ︒︒⋅⋅=︒-︒︒，求得10x =︒．故30BCD ∠=︒为所求．20．设过A ，B ，C 分别与BC ，CA ，AB 平行的直线交成ABC''△，则A ，B ，C 分别为B C '，C A ''，A B ''的中点．又设过2A ，2B ，2C 与1AA ，1BB ，1CC 平行的直线a l ，b l ，c l 分别与B C '，C A '，A B '交于2A '，2B '，2C '，则有221180A A B CA A '∠+∠=︒；而由BA CA '=，2BA CA '=，21A BA ACA '∠=∠，知21BA A CA A '△∽△，有21BA A CA A '∠=∠．从而222180A A B BA A ''∠+∠=︒，即2A '，2A ，A '三点共线．故有22212221B A CA A C BA λA C A B BA AC '''====（因12BA A C =，12AC BA =）=λ．同理，221C B CB u u B A B A '''===，121AC A C v v C B C B'''===．于是由塞瓦定理知a l ，b l ，c l 共点11111,,λu v λuv AA BB CC '''⇔=⇔=⇔共点． 21．因G H B C ∥，有G A G E B D E D =，HA HF CD FD =．即ED BD GA GE =⋅，FD CD HA HF=⋅．又A B A C =，AD BC ⊥，则BD CD =．于是ED FD GA HA GE HF ⋅=⋅．即1DE GA HF EG AH FD⋅⋅=．由塞瓦定理，即得结论． 22．令B C a =，CA b =，AB c =，则2b SL =，2c MN =．由S L D M N D △∽△，得L D L S b N D M N c==．同理，NF a MF b =，ME c LE a=．在M N L △中，有1LD NF ME ND MF LE ⋅⋅=．由塞瓦定理之逆，知MD ，NE ，LF 共点，故MS ，NT ，LU 共点．23．设A E X X F E α∠=∠=，AFX XEF β∠=∠=，XAE a '∠=，XAF β'∠=．在AEF △中，AX ，EX ，FX 交于一点，由角元形式的塞瓦定理，有sin sin sin 1sin sin sin αβββαα'⋅⋅=，即12sin sin ()sin sin ααββ'='．令YEF γ∠=，YED δ∠=，FBY γ∠=，YBD δ'∠=，EFZ φ∠=，DFZ θ∠=，ECZ φ'∠=，DCZ θ'∠=．同理，有12sin sin sin sin γγδδ'⎛⎫= ⎪'⎝⎭，12sin sin ()sin sin θθφφ'='．注意到AP ，BP ，CP 交于一点，由角元形式的塞瓦定理，有12sin sin sin sin 1sin sin sin sin θαγθφβδφ'''⎛⎫⋅⋅⋅= ⎪'''⎝⎭，由此即证． 24．令21C CP '∠=∠，42CC P '∠=∠，13BB P '∠=∠，64BB P '∠=∠，35AA P '∠=∠，56AA P '∠=∠．AA '，BB '，CC '共线332211446655sin sin sin sin 1sin 3sin 511sin 2sin 4sin 6sin sin sin AP AP A CP CPC BP BPB CP CPC BP BP B AP AP A '''⋅∠⋅∠⋅∠∠∠∠⇔⋅⋅=⇔⋅⋅='''∠∠∠⋅∠⋅∠⋅∠．而142536AP AP BP BP CP CP =====，则25CPC AP A ''∠=∠，36AP A BP B''∠=∠，321414651AP CP BP CPC BPB CP BP AP ''∠=∠⇔⋅⋅=．又由条件易知，15BP AP =，26CP BP =，34AP CP =．由此即证．注：此题也可以应用梅涅劳斯定理证．分别延长AB 和A B ''，CB 和C B ''，AC 和A C ''得交点M ，N ，G （交点可无穷远处）．由15AP BP =，有15BP AP =．同理，34AP CP =，62BP CP =．直线B A M ''截ABC △，由梅涅劳斯定理，有36361AP CP BM MA PC P B ⋅⋅=-．同理，52251BP CP AG GC P B P A⋅⋅=-，14141BP AP CN NB PA PC ⋅⋅=-．三式相乘并注意15BP AP =，34AP CP =，62BP CP =，得1BM AG CN MA GC NB⋅⋅=-．由梅涅劳斯定理之逆，知M ，N ，G 共线．又点M ，N ，G 分别是ABC'''△和ABC △对应所在直线的交点，利用笛沙格逆定理可得ABC'''△和ABC △对应顶点的连线A A '，B B '，C C '共点． 25．设PA 与BC 相交于D '，对ABC △应用塞瓦定理，有1AF BD CE FB D C EA'⋅⋅=．又由梅涅劳斯定理，点F ，E ，D 共线的充要条件是1AF BD CE FB DC EA ⋅=．从而转证BD DB D C DC'=即可．因AC CD =， 1802DPA DPC ∠=︒-∠，这表明DPC CPD '∠=∠，即PC 时DPD '∠的平分线，且PC PB ⊥，PB 是DPD '∠的外角平分线，由此即证得结论．26．设1AA ，1BB ，1CC 交边BC ，CA ，AB 于2A ，2B ，2C ．由1122sin()sin()ABA ACA S BA AB B αA C S CA C α⋅+==⋅+△△，22sin()sin()CB BC C αB A AB A α⋅+=⋅+，22sin()sin()AC AC A αC B BC B α⋅+=⋅+，三式相乘即证．习题B1．设直线AD '，BE '，CF '交BC ，CA ，AB 于A '，B '，C '过D '作O ⊙的切线交AB ，AC 于M ，N ．由M N B C ∥，知A M D A B A ''△∽△，ADN AA C ''△∽△，则M D A D DN B A A A AC '''=='''，即B A M D ACDN ''=''．连OM ，ON ，设O ⊙的半径为r 则B ，D ，O ，F ；C ，D ，O ，E 分别四点共圆．由FOD B '∠=∠，EOD C '∠=∠，则1122MOD FOD B ''∠=∠=∠，1122NOD EOD C ''∠∠=∠．而t a n t a n 2M D B M O D r '∠'=∠=，tan tan 2D N C NOD r '∠'=∠=，则11tan tan 22MD D N B C ''=∠∠∶∶，即11tan tan 22BA A C B C ''=∠∠∶∶．同理，11tan tan 22CB B A C A ''=∠∠∶∶，11tan tan 22AC C B A B ''=∠∠∶∶，则1BA CB AC A C B A C B'''⋅⋅='''．由塞瓦定理之逆，有AA '，BB '，CC '三线共点．即AD '，BE '，CF 三线共点．2．设BD 交圆于M ，N ，连ME ，MH ，MF ，NH ，NE ，NF ，NG ，EH ，FG ．由B M E B E N △∽△，BM F BFN △∽△，有EM BE EN BN =，MF BF FN BN =．而BE BF =，则EM MF EN FN =，即EM EN MF FN=．同理，NH HM GN GM =．于是NH EM HM EN MF GN GM FN⋅=⋅．对圆内接四边形HEM N 和GFMN 分别应用托勒密定理，有HM EN EN EM HE M N ⋅=⋅+⋅，GM FN M F GN FG M N ⋅=⋅+⋅，所以MH EM NH EM HE MN MF GN MF GN FG MN⋅⋅+⋅=⋅⋅+⋅，由此得 NH EM FG HE M F GN ⋅⋅=⋅⋅，即1N H E M F G H E M F G N⋅⋅=．由塞瓦定理的推论，知BD ，GE ，HF 三线共点．同理，AC ，GE ，HF 三线共点．因GE 与HF 交点唯一，故AC ，BD ，HF ，GE 四线共点．3．设ABC △的内心为I ，则I 是000A B C △的垂心．令2BAC α∠=，2ABC β∠=，2BCA γ∠=．（Ⅰ）由11BIA αβIBA ∠=+=∠，有101090()ABA αβA A B ∠=︒-+=∠，即1110IA I B I A ==，有 012A BI A BI S S =△△．同理，102A CI S A CI S =△△，故012A BIC A BIC S S =．同理，012B CIA B CIA S S =，012C AIB C AIB S S =．三式相加即证．（Ⅱ）令0100C B λC A =，0200A C λA B =，0300B A λB C =，则01011C B λBA λ=-，02021A C λBA λ=-，03031B A λAC λ=-．对000A BC △应用塞瓦定理，有0000001C B A C B A BA CB AC ⋅⋅=，即3121231111λλλλλλ⋅⋅=---，从而123123(1)(1)(1)λλλλλλ=---， 00012312312233121()()ABC A B C S λλλλλλλλλλλλS =-+++++=△△．（*）12311,28λλλ≤．即000123124ABC A B C S λλλS =≤△△，亦即0004ABC S A B C S ≥△△，等号当且仅当000A B C △为正三角形123()λλλ==时成立．注：其中（*）是三角形与其内接三角形的关系公式．4．延长AP 交BC 于Q ，由塞瓦定理有1AF CE FB EA ⋅=．由B P A C P A ∠=∠，知B P Q C P Q ∠=∠．又P B B Q P C Q C=，过A 作AM PB ∥交直线PF 于M ，作AN PC ∥交直线PE 于N ，有AM AF PB FB =，PC CE AN EA=，于是得AM AN =．有180180P A M B P A C P A P A N ∠=︒-∠=︒-∠=∠，有P A M P A N ∠△∽△，得B P F C P E∠=∠． 5．连EF 交直线AC 于K ．令BAF α∠=，DAE β∠=，BAC DAC θ∠=∠=，由,sin sin sin sin FB AF BC AC αABF θABC ==∠∠，有sin sin FB θAF BC αAC⋅=．同理，sin sin DE θAE DC βAC ⋅=．又 sin()sin()AFK AEK S KF AF αθKE S AE βθ⋅+==⋅+△△．对EFC △及点G 应用塞瓦定理，有1FB CD KE BC DE KF ⋅⋅=，得 sin sin()sin sin()ααθββθ+=+，即sin sin()0θαβ⋅-=．由此可得αβ=，即证 6．连DI ，IC ，设DCI x ∠=，则40IDC x ∠=︒-，对BCD △及点I 应用角元形式的塞瓦定理，有sin80sin20sin 1sin(40)sin20sin20x x ︒︒⋅⋅=︒-︒︒，求得10x =︒，故30BCD ∠=︒为所求． 7．由2211111AB AC AC BC =-⋅，111111AC BC AC BC AC BC ⋅-⋅=⋅，及21111BC B A C A ≥⋅，21111C A C B AB ≥⋅，注意应用塞瓦定理，1111111AC B A C B A B B C C A⋅⋅=，从而111111111111A B B C C A A B B C C A A B B C C A ⋅⋅≥⋅⋅⋅⋅ 8．设直线AD 与BC 交于P ．过P 作l 的垂线交l 于H ．设圆Γ的圆心为O ，由OAD PAH △∽△，有AH HP AD DO =．由O C B P H B △∽△有BH HP BC CO =，即A H B H A D B C =．注意PD PC =，有1A H B C P D H B C P D A⋅⋅=．由塞瓦定理之逆，知AC ，BD ，PH 共点，直线PH 重合于EF ，点H 与F 重合．又O ，D ，P ，C 共圆，且直径为OP ，又90PHO ∠=︒，知H 也在此圆上．故DFP DOP COP CFP ∠=∠=∠=∠．9．设直线1AA 交BC 于X ，直线1BB 交CA 于Y ，1CC 交AB 于Z ，由塞瓦定理的逆定理，只要证明.1BX CY AZ XC YA ZB⋅=．设中心为1A 的正方形边长为α，顶点P ，Q 分别在边AB 和AC 上，顶点S ，T 在BC 上，且S 在B ，T 之间．因AX 过正方形QPST 的中心，若AX 截PQ 边两段为u ，v ，则它截ST 边两段为v ，u ，则cot cot 1cot cot 1BX u BX u BT BS a a B a B XC v XC v SC TC a a C a C ++⋅++======++⋅++．同理，cot 1cot 1CY C YA A +=+，cot 1cot 1AZ A ZB B +=+．故有1BX CY AZ XC YA ZB⋅⋅=． 10．作高AH ，连BE ，CD ，则AH ，BE ，CD 交于一点，即ABC △的垂心．对ABC △应用塞瓦定理，有1AD BH CE DB HC EA ⋅⋅=．由M DF M GE △∽△，有BEC BDC S GM GE BE CE MD DF S BD CD⋅===⋅△△．由AH EG ∥，有H G C H A E A C=，即A C H G H C ⋅=⋅．由2ABC AB CD S AC BE ⋅==⋅△，有A B C D H G A C B E H G H ⋅⋅=⋅⋅=⋅⋅．对DBG △，考察点A ，M ，H ，有1()DA BH GM DA BH BE CE DA BH CE BE AD BH CE AB HG MD AB HG BD CD HC AE BE DB HC EA⋅⋅⋅⋅⋅⋅=⋅⋅==⋅⋅=⋅⋅⋅，由梅涅劳斯定理之逆即证． 11．设H 关于边BC ，CA ，AB 的对称点分别为A '，B '，C '，则A '，B '，C '均在外接圆O ⊙上．下证D ，E ，F 满足要求．设直线AO ，BO ，CO 与BC ，CA ，AB 的交点为D '，E '，F '．由于DA DH =，有OD DH OD DA R +=+=（R 为O ⊙半径）．同理，OE EH OF FH R +=+=．由π2BAO ACB CAA '∠=-∠=∠，有B O D C O '∠=∠．又O B O C =，OBD OCD '∠=∠，则O B D O C '△∽△，有BD CD '=．同理，CE AE '=，AF BF '=．对ABC △及点H 应用塞瓦定理，有1BD CE AF D C E A F B '''=⋅⋅'''，即1BD CE AF CD BF AE D C E A F B DB FA EC'''⋅⋅=⋅⋅='''．再由塞瓦定理之逆，知AD ，BE ，CF 共点．D ，E ，F 满足要求．12．连AD 交BF 于G ，连BD 交AE 于H ，连GN ，HM ．由D A B C D B C F B ∠=∠=∠，知A ，F ，G ，N 四点共圆，有180AFB ANG ∠+∠=︒．又90AFB ∠=︒，则90ANG ∠=︒，即GN AB ⊥且GN AB ∥，有LN DG NA GA =．同理，BH BM HD ML =．在ABD △中，1AO BH DG AO BM LN OB HD GA AO ML NA⋅⋅=⋅⋅=．由塞瓦定理之逆，知AE ，BF ，OD 三线共点．13．显然，有133213321332A A A A B B B B C C C C =====，且3434C B A B =，343434A C B A C A ==．由正弦定理，有33434334343343343343434334sin sin sin sin /sin sin C B B C B B C B A B B A B B C B A B B B B B B B A B ∠⋅∠⋅∠∠==∠∠．同理，334334334334sin sin sin sin B A A A B A C A A A C A ∠∠=∠∠，334334334334sin sin sin sin A C C C A C B C C C B C ∠∠=∠∠．又由于334334C B C B C B ∠=∠，334334A B A B A B ∠=∠，334334C A C A C A ∠=∠，故334334334334334334sin sin sin 1sin sin sin C B B B A A A C C A B B C A A B C C ∠∠∠⋅⋅=∠∠∠．应用角元形式的塞瓦定理，知34A A ，34B B ，34C C 三线共点．14．设AB 与CE 交于点D ，AC 与BF 交于点G ．由AEC BEC S AD DB S =△△，CFB AFB S CG GA S =△△，有 .AEC CFB BEC AFBS S AD BH CG BH DB HC GA HC S S ⋅⋅=⋅△△△△．又由ABE ACF △∽△，有EAB FAC ∠=∠，AE AB BE AF AC CF==，则sin 1sin AEC ABF S AE AC EAC S AF AB BAF⋅⋅∠==⋅⋅∠△△，注意90ABE ACF ∠=∠=︒，有 sin cos sin cos CFB BEC S BC CF BCF AC BCA HC S BC BE CBF AB ABC HB⋅⋅∠⋅∠===⋅⋅∠⋅∠△△．于是1AD BH CG DB HC GA ⋅⋅=．由塞瓦定理之逆即证． 15．设非等边ABC △各定点处的外接圆切线ABC''，BA C '，ACB ''组成ABC '''△，直线AB 与A B ''交于P ，BC 与B C '交于Q ，CA 与C A '交于R ，连A A '，B B '，C C '．因C ，A ，B 分别在ABC'''△三边所在直线A B ''，B C '，C A ''上，，CB B A ''=，AC C B ''=，从而1A C B A C B CB AC BA'''⋅⋅='''．由塞瓦定理的逆定理，知A A '，B B '，C C '共点．再运用戴沙格定理，知P ，Q ，R 三点共线．16．必要性：设BAE CAF α∠=∠=，ABD CBF β∠=∠=，ACD x ∠=，BCE y ∠=．又设M ，N ，K 分别为AD ，BE ，CF 与ABC △各边的交点．因AD ，BE ，CF 共点，则由塞瓦定理，得sin sin sin 1sin sin sin ACF ABD BCE BCF ACD ABE S S S AK BM CN AC AF αAB BD βBC CE y KB MC NA S S S BC BF βAC CD x AB AE α⋅⋅⋅⋅⋅⋅=⋅⋅=⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅△△△△△△ sin sin AF BD CE y BF CD AE x=⋅⋅⋅ sin()sin()sin()sin sin()sin sin()sin()sin()sin sin()sin B βC x A αy C x y A αB βC y x C y x----=⋅⋅⋅=⋅----．即sin()sin()cot cot sin sin C y C y x y x y--=⇒=．注意x ，(0,π)y ∈，故x y =，即ACD BCE ∠=∠．充分性：若ACD BCE ∠=∠，因上述证明各步均可逆，由塞瓦定理之逆，知AD ，BE ，CF 三线共点．17．设1CAQ α∠=，2BAQ α∠=，1ABQ β∠=，2CBQ β∠=，1BCQ γ∠=，2ACQ γ∠=．由塞瓦定理及正弦定理，有111M M N N ，1L L 共点11111111111111AM N BN L αM AM L BN M αNS S S NM LN ML M L N M L N S S S ⇔⋅⋅=⇔⋅⋅=△△△△△△ 111111121212sin sin sin 11sin sin sin AM AN αBN BL βCL CM γAN CM BL QA QC QB AM AL αBN BM βCL CN γNC BM AL QC QB QA⋅⋅⋅⋅⋅⋅⇔⋅⋅=⇔⋅⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅ AM ⇔，BN ，CL 三直线共点，且与Q 点位置无关．18．设G 是ABC △的重心，D '，E '，F '分别为BC ，CA ，AB 的中点，则ABC △区域被划分为六个区域：AF G '△，BF G '△，BD G '△，CD G '△，CE G '△，AE G '△．不妨设P 点落在CE G '△区域．此时，易知1,1,1CD CE AF DB EA FB≤≤≤．由塞瓦定理，有11BD CE AF DC CF AF DC EA FB BD EA FB ⋅⋅=⇒=⋅≤，AF DC EA EA BFD FDE FB BD CE EC=⋅≤⇒∠≥∠， BDF DFE ∠≥∠．分别过F ，D ，在BFD ∠，BDF ∠内作DE ，FE 的平行线，则两平行线的交点Q 必落在BFD △区域．从而，有FDE FQDE ABC ⊂⊂ △△，结论成立．19．设AC 交BC 于Q ．对AEC △和点F 应用塞瓦定理，有1EB AQ CD BA QC DE ⋅⋅=．对AEC △及截线BPD 应用梅涅劳斯定理，有1ED CP AB DC PA BE⋅⋅=，故有AP PC AQ QC =．过P 作EF 的平行线交OA 于I ，交OC 与J ，则,P I A P J P P C Q O A Q Q O Q C ==．于是PI PJ QO QO=，即P I P J =．又O P I J ⊥，则OP 平分IOJ ∠，即OP 平分AOC ∠．同理，当BD 与EF 相交时，OP 平分DOB ∠；而当BD EF ∥时，过B 作ED 的平行线交AC 于G ，则AG AB AD AC AE AF==，即GD CF ∥，BCDG 为平行四边形，亦即P 为BD 中点．因此，OP 平分DOB ∠． 20．显然有PD DQ =，AP AQ =．不妨设AB AC ≥，则ADC ADB ∠≤∠，ADC ∠为直角或锐角．作AE BC ⊥于E ，易知A ，P ，D ，E 四点共圆，A ，D ，E ，Q 四点共圆．则BP BA BD BE ⋅=⋅，CQ CA CD CE ⋅=⋅．故AB BP BD BE AC CQ CD CE⋅=⋅．由AD 平分BAC ∠，有A B D B A C D C=，得B P B E C Q C E =，即1B P C E C Q B E ⋅=⋅．而A P A Q =，则1B P C E A Q P A Q C E B ⋅⋅=⋅⋅．由塞瓦定理之逆，知AE ，BQ ，CP 三线共点，即AE BC ⊥，故AK BC ⊥．。

模型38梅涅劳斯定理塞瓦定理(原卷版)

梅涅劳斯定理：任何一条直线截三角形的各边，都使得三条不相邻线段之积等于另外三条线段之积．当直线交三角形ABC三边所在直线BC、AB、AC于D、E、F点时，则有AE×BD×CF＝EB×CD×AF塞瓦定理：塞瓦定理是指在△ABC内任取一点O，延长AO、BO、CO分别交对边于D、E、F，则BD×CE×AF＝DC×EA×FB．考点一：梅涅劳斯定理【例1】．如图，等边△ABC的边长为2，F为AB中点，延长BC至D，使CD＝BC，连接FD交AC于E，则四边形BCEF的面积为．➢变式训练【变式11】．如图，D、E、F内分正△ABC的三边AB、BC、AC均为1：2两部分，AD、BE、CF相交成的△PQR的面积是△ABC的面积的（）A．B．C．D．【变式12】．梅涅劳斯定理梅涅劳斯（Menelaus）是古希腊数学家，他首先证明了梅涅劳斯定理，定理的内容是：如图（1），如果一条直线与△ABC的三边AB，BC，CA或它们的延长线交于F、D、E三点，那么一定有••＝1．下面是利用相似三角形的有关知识证明该定理的部分过程：证明：如图（2），过点A作AG∥BC，交DF的延长线于点G，则有＝．例题精讲任务：（1）请你将上述材料中的剩余的证明过程补充完整；（2）如图（3），在△ABC中，AB＝AC＝13，BC＝10，点D为BC的中点，点F在AB上，且BF＝2AF，CF与AD交于点E，则AE＝．考点二：塞瓦定理【例2】．如图：P，Q，R分别是△ABC的BC，CA，AB边上的点．若AP，BQ，CR相交于一点M，求证：．➢变式训练【变式21】．请阅读下列材料，并完成相应任务如图，塞瓦定理是指在△ABC内任取一点O，延长AO，BO，CO分别交对边D，E，F于，则××＝1．任务：（1）当点D，E分别为边BC，AC的中点时，求证：点F为AB的中点；（2）若△ABC为等边三角形，AB＝12，AE＝4，点D是BC边的中点，求BF的长．【变式22】．请阅读下列材料，并完成相应任务塞瓦定理定理内容：如图1，塞瓦定理是指在△ABC内任取一点O，延长AO，BO，CO分别交对边于D，E，F，则．数学意义：使用塞瓦定理可以进行直线形中线段长度比例的计算，其逆定理还可以用来进行三点共线、三线共点等问题的判定方法，是平面几何学以及射影几何学中的一项基本定理，具有重要的作用．任务解决：（1）如图2，当点D，E分别为边BC，AC的中点时，求证：点F为AB的中点；（2）若△ABC为等边三角形（如图3），AB＝12，AE＝4，点D是BC边的中点，求BF的长，并直接写出△BOF的面积．1．如图，在△ABC中，M是AC的中点，E是AB上一点，AE＝AB，连接EM并延长，交BC的延长线于D，则＝（）A．B．2C．D．2．如图，在△ABC中，D、E分别是BC、AC上的点，AD与BE相交于点G，若AG：GD＝4：1，BD：DC＝2：3，则AE：EC的值是（）A．B．C．D．3．如图，在△ABC中，AD是BC边上的中线，F是AD边上一点．射线CF交AB于点E，且，则等于．4．如图，在△ABC中，点D是AB边上的一点，且AD＝3BD，连接CD并取CD的中点E，连接BE，若∠ACD＝∠BED＝45°，且CD＝6，则AB的长为．5．如图，在△ABC中，∠ACB＝90°，AC＝8，BC＝16，AD是边BC的中线，过点C作CE⊥AD于点E，连接BE并延长交AC于点F，则AD的长是，EF的长是．6．如图，△ABC中，D、E是BC边上的点，BD：DE：EC＝3：2：1，M在AC边上，CM：MA＝1：2，BM交AD、AE于H、G，则BH：HG：GM等于．7．如图，▱ABCD的对角线相交于点O，在AB的延长线上任取一点E，连接OE交BC于点F．若AB＝a，AD＝c，BE＝b，则BF＝．8．在△ABC中，∠ACB＝90°，AC＝BC，AM为BC边上的中线，CD⊥AM于点D，CD的延长线交于点，求的值．9．如图，在△ABC中，M是AC的中点，E、F是BC上的两点，且BE＝EF＝FC，求BN：NQ：QM的值．10．如图，△ABC中，∠ACB＝90°，CD⊥AB于点D，E为BC上一点，AE交CD于点F，EH⊥AB于点H，若CF＝2FD，EH＝，求CE•BE的值．11．如图，△ABC中，AD⊥BC于点D，E是AB上一点，连接DE，2∠C+∠BDE＝180°．（1）求证：∠BDE＝2∠CAD；（2）若AC＝BD，∠AED＝∠ACB，求证BE＝2CD；（3）若AE＝kBE，BD＝mCD，则的值为．（用含m，k的式子表示）．12．如图1，Rt△ABC中，∠BAC＝90°，AD是中线，BE⊥AD，垂足为E，点F在AD上，∠ACF＝∠DBE．（1）求证：∠ABD＝∠CFD；（2）探究线段AF，DE的数量关系，并证明你的结论；（3）如图2，延长BE交CF于点P，AB＝AF，求的值．13．如图1，△ABC中，AB＝AC，点D在BA的延长线上，点E在BC上，DE＝DC，点F是DE与AC的交点，且DF＝FE．（1）图1中是否存在与∠BDE相等的角？若存在，请找出，并加以证明，若不存在，说明理由；（2）求证：BE＝EC；（3）若将“点D在BA的延长线上，点E在BC上”和“点F是DE与AC的交点，且DF＝FE”分别改为“点D在AB上，点E在CB的延长线上”和“点F是ED的延长线与AC的交点，且DF＝kFE”，其他条件不变（如图2）．当AB＝1，∠ABC＝a时，求BE的长（用含k、a的式子表示）．14．阅读以下材料，并按要求完成相应的任务．塞瓦（GiovanniCeva，1648～1734）意大利水利工程师，数学家，塞瓦定理载于1678年发表的《直线论》一书，塞瓦定理是指如图1，在△ABC内任取一点O，延长AO，BO，CO分别交对边于D，F，E，则．下面是该定理的部分证明过程：如图2，过点A作BC的平行线分别交BE，CF的延长线于点M，N．则∠N＝∠FCB，∠NAF＝∠FBC．∴△NAF∽△CBF．∴①．同理可得△NOA∽△COD．∴②．任务一：（1）请分别写出与△MOA，△MEA相似的三角形；（2）写出由（1）得到的比例线段；任务二：结合①②和（2），完成该定理的证明；任务三：如图3，△ABC中，∠ACB＝90°，AC＝4，BC＝3，CD⊥AB，垂足为D，点E为DC的中点，连接AE并延长，交BC于点F，连接BE并延长，交AC于点G．小明同学自学了上面定理之后解决了如图3所示的问题，并且他用所学知识已经求出了BF与FC的比是25：16，请你直接写出△ECG与△EAG面积的比．15．问题提出如图（1），在△ABC中，AB＝AC，D是AC的中点，延长BC至点E，使DE＝DB，延长ED交AB于点F，探究的值．问题探究（1）先将问题特殊化．如图（2），当∠BAC＝60°时，直接写出的值；（2）再探究一般情形．如图（1），证明（1）中的结论仍然成立．问题拓展如图（3），在△ABC中，AB＝AC，D是AC的中点，G是边BC上一点，＝（n＜2），延长BC至点E，使DE＝DG，延长ED交AB于点F．直接写出的值（用含n的式子表示）．16．阅读下面材料，完成（1）﹣（3）题数学课上，老师出示了这样一道题：如图1，△ABC中，∠BAC＝90°，点D、E在BC上，AD＝AB，AB＝kBD（其中＜k＜1）∠ABC＝∠ACB+∠BAE，∠EAC的平分线与BC相交于点F，BG⊥AF，垂足为G，探究线段BG与AC的数量关系，并证明．同学们经过思考后，交流了自己的想法：小明：“通过观察和度量，发现∠BAE与∠DAC相等．”小伟：“通过构造全等三角形，经过进一步推理，可以得到线段BG与AC的数量关系．”……老师：“保留原题条件，延长图1中的BG，与AC相交于点H（如图2），可以求出的值．”（1）求证：∠BAE＝∠DAC；（2）探究线段BG与AC的数量关系（用含k的代数式表示），并证明；（3）直接写出的值（用含k的代数式表示）．。

6塞瓦定理

塞瓦定理
【例5】如图,M 为ABC 内的一点,BM 与AC 交于点E ,CM 与AB 交于点F ,若AM 通过BC 的中点D ,求证://EF BC
【例6】如果梯形ABCD 的两腰,AD BC 的延长线交于M ,两条对角线交于N ,求证:直线MN 必平分梯形的两底
(三)
【例1】在梯形ABCD 中,//,,AB CD AC BD 交于点,,E AD BC 的延长线交于点H ,过点E 作//FG AB 交AD 于点F ,交BC 于点G ,求证:,,AG BF EH 三线共点
【例2】在锐角ABC ∆中,AD 是BC 边上的高线,H 是线段AD 内任意一点,BH 和CH 的延长线分别交,AC AB 于点,E F ,求证:EDH FDH ∠=∠
【例3】如图,AM 是锐角ABC ∆的角平分线,ME AB ⊥于点E ,MF AC ⊥于点F ,CE 与BF 交于点P ,求证:AP BC ⊥
【例4】如图,,E F 分别为ABC ∆的,AC AB 边上的点,且3,3,,AE EC BF FA BE CF ==交于点,P AP 的延长线交BC 于点D ,求:AP PD 的值
【例5】如图,四边形ABCD 的对边AB 和,DC DA 和CB 分别相交于点,L K ,对角线AC 与BD 交于点M ,直线KL 与,BD AC 分别交于点,F G ,求证:
KF KG
LF LG
=
【例6】设ABC ∆的边,,AB BC CA 上分别有点,,F D E ,且,,AD BE CF 共点,又DEF ∆的边,,DE EF FD 上分别有点,,,,,Z X Y DX EY FZ 也共点,求证:,,AX BY CZ 共点。

初中数学竞赛专题.梅涅劳斯定理与塞瓦定理.（有答案）

初中数学竞赛专题.梅涅劳斯定理与塞瓦定理.（有答案）第 1 页板块一梅涅劳斯定理及其逆定理梅涅劳斯定理：如果一条直线与ABC △的三边AB 、BC 、CA 或其延长线交于F 、D 、E 点，那么1AF BD CE FB DC EA=．这条直线叫ABC △的梅氏线，ABC △叫梅氏三角形．证法一：如左图，过C 作CG ∥DF证法二：如中图，过A 作AG BD ∥交DF 的延长线于G三式相乘即得：1AF BD CE AG BD DCFB DC EA BD DC AG=??=．证法三：如右图，分别过A B C 、、作DE 的垂线，分别交于123H H H 、、．则有123AH BH CH ∥∥，所以3122311CH AH BH AF BD CE FB DC EA BH CH AH ??=??=．梅涅劳斯定理的逆定理：若F 、D 、E 分别是ABC △的三边AB 、BC 、CA 或其延长线的三点，如果1AF BD CE FB DC EA=，则F 、D 、E 三点共线．【例1】如图，在ABC △中，AD 为中线，过点C 任作一直线交AB 于点F ，交AD 于点E ，求证：:2:AE ED AF FB =．【解析】∵直线FEC 是ABD △的梅氏线，∴1AE DC BF ED BC FA ??=．而12DC BC =，∴112AE BF ED FA ??=，即2AE AF ED BF=．习题1. 在△ABC 中，D 是BC 的中点，经过点D 的直线交AB于点E ，交CA 的延长线于点F ．求证：FA EAFC EB=．【解析】直线截ABC △三边于D 、E 、F 三点，应用梅氏定理，知1CD BE AFDB EA FC=，又因为BD BC =，所以1BE AF EA FC ?=，即FA EAFC EB=．习题2. 如图，在△ABC 中，90ACB ∠=?，AC BC =．AM 为BC 边上的中线，CD AM ⊥于点D ，CD 的延长线交AB 于点E ．求AEEB．【解析】由题设，在Rt AMC △中，CD AM ⊥，2AC CM =，由射影定理224AD AD AM AC DM DM AM CM===?．对ABM △和截线EDC ，由梅涅劳斯定理，1AE BC MD EB CM DA ??=，即21114AE EB ??=．所以2AE EB=．知识导航夯实基础梅涅劳斯定理与塞瓦定理【例2】如图，在ABC △中，D 为AC 中点，BE EF FC ==，求证：::5:3:2BM MN ND =．【解析】∵直线AE 是BCD △的梅氏线，∵直线AF 是BCD △的梅氏线，习题3. 如图，在ABC △中，D 为BC 的中点，::4:3:1AE EF FD =．求::AG GH AB ．【解析】∵HFC 是ABD △的梅氏线，∵D 为BC 的中点，::4:3:1AE EF FD =，∵GEC 是ABD △的梅氏线，【例3】过ABC △的重心G 的直线分别交AB 、AC 于点E 、F ，交CB 的延长线于点D ．求证：1BE CFEA FA+=．【解析】作直线AG 交BC 于M ，同理，2CF DCFA DM=，而2BD DC BD BD BM +=++2()2BD BM DM =+=【例4】如图，点D 、E 分别在ABC △的边AC 、AB 上， AE EB =，23AD DC =，BD 与CE 交于点F ，40ABC S =△．求AEFD S ．【解析】对ECA △和截线BFD ，由梅氏定理得：1EF CD AB FC DA BE ??=，即32121EF FC ??=，所以13EF FC =．所以1148BFE BEC ABC S S S ==△△△，进而211140115840AEFD ABD BEF ABC S S S S ??=-=-==△△△．习题4. 如图，在ABC △中，三个三角形面积分别为5，8，10．四边形AEFD 的面积为x ，求x的值．【解析】对ECA △和截线BFD ，由梅氏定理得：1CD AB EF DA BE FC ??=，即1823115152x x +??=+，解得22x =．【备选】如图，ABC △被通过它的三个顶点与一个内点O 的三条直线分为6个小三角形，其中三个小三角形的面积如图所示，求ABC △的面积．【解析】对ABD △和截线COF ，由梅氏定理得：1AF BC DO FB CD OA ??=，即41132BC CD ??=，所以32BC CD =，所以3BCBD=．所以33105315ABC ABD S S ==?=△△．【例5】如图，在ABC △中，A ∠的外角平分线与边BC 的延长线交于点P ，B ∠的平分线与边CA 交于点Q ，C ∠的平分线与边AB 交于点R ，求证：P 、Q 、R 三点共线．【解析】 AP 是BAC ∠的外角平分线，则BQ 是ABC ∠的平分线，则 CR 是ACB ∠的平分线，则??①②③得非常挑战探索提升第 3 页因R 在AB 上，Q 在CA 上，P 在BC 的延长线上，则根据梅涅劳斯定理的逆定理得：P 、Q 、R 三点共线．习题5. 证明：不等边三角形的三个角的外角平分线与对边的交点是共线的三个点．【解析】如图，CD BE AF 、、分别为三角形ABC 的三个外角平分线，分别交AB AC BC 、、于D E F 、、．过C 作BE 的平行线，则BCP CBE EBD CPB ∠=∠=∠=∠，所以BPC △是等腰三角形．则PB CB =．则有：CE PB CBEA BA BA ==．同理AD AC DB CB =；BF BA FC AC=．所以1CE AD BF CB AC BA EA DB FC BA CB AC ??=??=．所以D E F 、、共线．板块二塞瓦定理及其逆定理塞瓦定理：如果ABC △的三个顶点与一点P 的连线AP 、BP 、CP 交对边或其延长线于点D 、E 、F ，如图，那么1BD CE AFDC EA FB=．通常称点P 为ABC △的塞瓦点．证明：∵直线FPC 、EPB 分别是ABD △、ACD △的梅氏线，两式相乘即可得：1BD CE AFDC EA FB=．塞瓦定理的逆定理：如果点D 、E 、F 分别在ABC △的边BC 、CA 、AB 上或其延长线上，并且1BD CE AF DC EA FB=，那么AD 、BE 、CF 相交于一点（或平行）．证明：⑴ 若AD 与BE 相交于一点P 时，如图，作直线CP 交AB 于'F ．由塞瓦定理得：'1BD CE AF DC EA F B='，又已知1BD CE AF DC EA FB ??=，∴AF AF FB F B'='，∴'F 与F 重合∴'CF 与CF 重合∴AD 、BE 、CF 相交于一点．⑵ 若AD 与BE 所在直线不相交，则AD ∥BE ，如图．∴BD EA DC AC=，又已知1BD CE AF DC EA FB ??=，∴1EA CE AF AC EA FB ??=，即CE FB AC AF=．说明：三线平行的情况在实际题目中很少见．【例6】（1）设AX BY CZ ，，是ABC △的三条中线，求证：AX BY CZ ，，三线共点．探索提升知识导航（2）若AX BY CZ ，，为ABC △的三条内角平分线．求证：AX BY CZ ，，三线共点．【解析】（1）由条件知，BX XC YC YA ZA ZB ===，，．∴1BX CY AZXC YA ZB=，根据塞瓦定理的逆定理可得三条中线AX BY CZ ，，共点．这个点称为这个三角形的重心．（2）由三角形内角平分线定理得：BX AB CY BC AZ ACXC AC YA BA ZB BC===，，．三式分别相乘，得：1BX CY AZ AB BC ACXC YA ZB AC AB BC=??=．根据塞瓦定理的逆定理可得三角形三内角平分线AX BY CZ ，，共点，这个点称为这个三角形的内心．习题6. 若AX BY CZ ，，分别为锐角ABC △的三条高线，求证：AX BY CZ ，，三线共点．【解析】由ABX CBZ △∽△得：BX AB BZ BC =；由BYA CZA △∽△得：AZ ACAY AB =；由AXC BYC △∽△可得：YC BC CX AC =．所以1BX AZ YC AB AC BCBZ AY CX BC AB AC=??=．根据塞瓦定理的逆定理可得三条高线AX BY CZ ，，共点．对直角三角形、钝角三角形，同样也可以证得三条高线共点．我们把一个三角形三条高线所在直线的交点叫做这个三角形的垂心．【例7】如图，M 为ABC △内的一点，BM 与AC 交于点E ，CM 与AB 交于点F ，若AM 通过BC 的中点D ，求证：EF BC ∥．【解析】对ABC △和点M 应用塞瓦定理可得：1AF BD CEFB DC EA=．又因为BD DC =，所以1AF CE FB EA ?=．进而AF AEFB EC=，所以EF BC ∥．习题7. 如果梯形ABCD 的两腰AD 、BC 的延长线交于M ，两条对角线交于N ．求证：直线MN必平分梯形的两底．∵1MD AQ BC DA QB CM=（由塞瓦定理得）板块三梅涅劳斯定理、塞瓦定理综合【备选】如图，E 、F 分别为ABC △的AC 、AB 边上的点，且3AE EC =，3BF FA =，BE 、CF 交于点P ，AP 的延长线交BC 于点D ．求:AP PD 的值．【解析】∵P 为ABC △的塞瓦点．∵EPB 为ACD △的梅氏线，【备选】如图，四边形ABCD 的对边AB 和DC ，DA 和CB 分别相交于点L K ，，对角线AC 与BD 交于点M ．直线KL 与BD 、AC 分别交于点F G 、．求证：KF KGLF LG=．【解析】对DKL △与点B 应用塞瓦定理得：1DA KF LCAK FL CD=．对DKL △和截线ACG 应用梅涅劳斯定理可得：1DA KG LCAK GL CD=．非常挑战进而可得KF KGLF LG．第 5 页。

塞瓦定理

塞瓦定理塞瓦定理在△ABC内任取一点O，直线AO、BO、CO分别交对边于D、E、F，则 (BD/DC)*(CE/EA)*(AF/FB)=1 证法简介（Ⅰ）本题可利用梅涅劳斯定理（简称梅氏定理）证明： ∵△ADC被直线BOE所截， ∴ (CB/BD)*(DO/OA)*(AE/EC)=1 ① 而由△ABD被直线COF所截，∴ (BC/CD)*(DO/OA)*(AF/FB)=1② ②÷①:即得：(BD/DC)*(CE/EA)*(AF/FB)=1 （Ⅱ）也可以利用面积关系证明 ∵BD/DC=S△ABD/S△ACD=S△BOD/S△COD=(S△ABD-S△BOD)/(S△ACD-S△COD)=S△AOB/S△AOC ③ 同理 CE/EA=S△BOC/ S△AOB ④ AF/FB=S△AOC/S△BOC ⑤ ③×④×⑤得BD/DC*CE/EA*AF/FB=1 利用塞瓦定理证明三角形三条高线必交于一点: 设三边AB、BC、AC的垂足分别为D、E、F，根据塞瓦定理逆定理，因为(AD:DB)*(BE:EC)*(CF:FA)=[(CD*cotA）/[(CD*cotB）]*[(AE*cotB)/(AE*cotC)]*[(BF*cotC)/[(BF*cotA)]=1，所以三条高CD、AE、BF交于一点。 2 利用塞瓦定理证明三角形三条高线必交于一点: 设三边AB、BC、AC的垂足分别为D、E、F，根据塞瓦定理逆定理，因为(AD:DB)*(BE:EC)*(CF:FA)=[(CD*cotA）/[(CD*cotB）]*[(AE*cotB)/(AE*cotC)]*[(BF*cotC)/[(BF*cotA)]=1，所以三条高CD、AE、BF交于一点。可用塞瓦定理证明的其他定理; 三角形三条中线交于一点（重心）:如图5 D , E分别为BC , AC 中点所以BD=DC AE=EC 所以BD/DC=1 CE/EA=1 且因为AF=BF 所以 AF/FB必等于1 ，所以三角形三条中线交于一点，即为重心用塞瓦定理还可以证明三条角平分线交于一点此外，可用定比分点来定义塞瓦定理：在△ABC的三边BC、CA、AB或其延长线上分别取L、M、N三点，又分比是λ=BL/LC、μ=CM/MA、ν=AN/NB。于是AL、BM、CN三线交于一点的充要条件是λμν=1。（注意与梅涅劳斯定理相区分，那里是λμν=-1）

第14讲梅涅劳斯定理及塞瓦定理(二)

第十四讲梅涅劳斯定理及塞瓦定理（二）
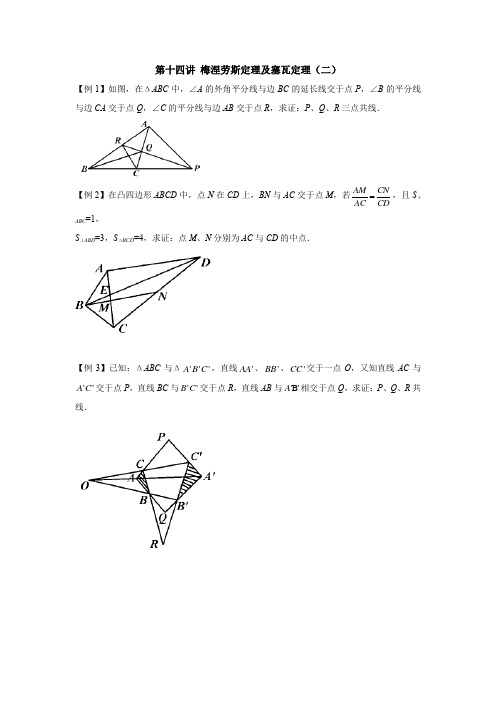
【例1】如图，在ΔABC 中，∠A 的外角平分线与边BC 的延长线交于点P ，∠B 的平分线与边CA 交于点Q ，∠C 的平分线与边AB 交于点R ，求证：P 、Q 、R 三点共线．
【例2】在凸四边形ABCD 中，点N 在CD 上，BN 与AC 交于点M ，若
AM CN AC CD
，且S ΔABC =1， S ΔABD =3，S ΔBCD =4，求证：点M 、N 分别为AC 与CD 的中点．
【例3】已知：ΔABC 与Δ'''A B C ，直线'AA 、'BB 、'CC 交于一点O ，又知直线AC 与''A C 交于点P ，直线BC 与''B C 交于点R ，直线AB 与'B'A 相交于点Q ，求证：P 、Q 、R 共线．
塞瓦定理：
如果ΔABC的三个顶点与一点P的连线AP、BP、CP交对边或其延长线于点D、E、F，如
图，那么BD CE AF
DC EA FB
⨯⨯=1．通常称点P为ΔABC的塞瓦点．
塞瓦定理的逆定理：
如果点D、E、F分别在ΔABC的边BC、CA、AB上或其延长线上，并且BD CE AF
DC EA FB
⨯⨯=1．那
么AD、BE、CF相交于一点（或平行）．
【例5】如图，M为ΔABC内一点，BM与AC交于点E，CM与AB交于点F，若AM通过BC的中点D．求证：EF∥BC．
【例6】如果梯形ABCD的两腰AD、BC的延长线交于M，两条对角线交于N，求证：直线MN必平分梯形的两底．。

平面几何选讲—利用塞瓦定理解决完全四边形问题

平面几何选讲—利用塞瓦定理解决完全四边形问题
广州大学唐松锦 2011.1.26
一、试题展示：2010年全国高中数学联合竞赛试题（A卷）二试（题一）
如图1，锐角三角形ABC的外心为O，K是边BC上一点（不是边BC的中点），D是线段AK延长线上一点，直线
BD与AC交于点N，直线CD与AB交于点M．求证：若OK⊥MN，则A、B、D、C
G
H
M
②
在△APQ 和△AMN 中，分别应用塞瓦定理得
AB PG QC 1,
③
BP GQ CA
AB MH NC 1.
④
BM HN CA
综合式①至④得
BP CQ BG CQ BC ∥MN BM CN BN CN
OK ⊥ BC K 是边 BC 的中点. 这与 K 不是边 BC 的中点矛盾。所以，点 D 不能在⊙O 外。同理，点 D 也不能在⊙O 内。故点 D 一定在⊙O 上，即 A、B、D、C 四点共圆。（刘才华山东省宁阳第一中学，271400）
BK CN AM 1 BK BM AN .
KC NA MB
KC MA NC
设△AMN 底边 MN 上的高为 h.则
BB BB h BM AN BK BP . CC h CC MA NC KC CP
A
O
C
BK
D
所以，Rt△B B P∽Rt△CC′P.
ME NC AB 1，M1E1 N1C AB 1. EN CA BM E1N1 CA BM1
又因 ME = M1E1 ，所以 N1C BM 1 .
EN E1N1
NC BM
于是，BC∥MN.
或由

塞瓦定理及应用

【基础知识】塞瓦定理设A '，B '，C '分别是△ABC 的三边BC ，CA ，AB 或其延长线上的点，若AA '，BB '，CC '三线平行或共点，则1BA CB AC A C B A C B'''⋅⋅='''． ①证明如图2-1（b ）、（c ），若AA '，BB '，CC '交于一点P ，则过A 作BC 的平行线，分别交BB '，CC '的延长线于D ，E ，得,CB BC AC EAB A ADC B BC''==''．又由BA A P A C AD PA EA '''==，有BA AD A C EA'='．从而1BA CB AC AD BC EA A C B A C B EA AD BC'''⋅⋅=⋅⋅='''．若AA '，BB '，CC '三线平行，可类似证明（略）．注（1）对于图2-1（b ）、（c ）也有如下面积证法：由：1PAB PBC PCAPCA PAB PBC S S S BA CB AC A C B A C B S S S '''⋅⋅=⋅⋅='''△△△△△△，即证．（2）点P 常称为塞瓦点．（3）共点情形的塞瓦定理与梅涅劳斯定理可以互相推证．首先，由梅涅劳斯定理推证共点情形的塞瓦定理．如图2-1（b ）、（c ），分别对△ABA '及截线C PC '，对△AA C '及截线B PB '应用梅涅劳斯定理有 1BC A P AC CA PA C B ''⋅⋅=''，1A B CB APBC B A PA ''⋅⋅=''．上述两式相乘，得1BA CB AC A C B A C B'''⋅⋅='''．其次，由共点情形的塞瓦定理推证梅涅劳斯定理．如图2-2，设A '，B '，C '分别为△ABC 的三边BC ，CA ，AB 所在直线上的点，且A '，B '，C '三点共线．令直线BB '与CC '交于点X ，直线C C '与AA '交于点Y ，直线AA '与BB '交于点Z ．分别视点C '，A '，B '，C ，A ，B 为塞瓦点，应用塞瓦定理，即对△BCB '及点C '（直线BA ，CX ，B A ''的交点），有1BA CA B XA C AB XB ''⋅⋅=''．对△CAC '及点A '（直线CB ，AY ，C B ''的交点），有1CB AB C YB C BC YC ''⋅⋅=''．对△ABA '及点B '（直线AC ，BZ ，A C ''的交点），有1AC BC A ZC B CA ZA ''⋅⋅=''．对△BBC '及点C （直线BA '，B A '，C X '的交点），有1BX B A C AXB A C AB '''⋅⋅='''．对△CC A ''及点A （直线CB '，C B '，A Y '的交点），有1CY C B A BYC B A BC '''⋅⋅='''．对△AA B ''及点B （直线AC '，A C '，B Z '的交点），有1AZ A C B CZA C B CA '''⋅⋅='''．上述六式相乘，有21BA CB AC A C B A C B '''⎛⎫⋅⋅= ⎪'''⎝⎭．故1BA CB AC A C B A C B'''⋅⋅='''．塞瓦定理的逆定理设A '，B '，C '分别是△ABC 的三边BC ，CA ，AB 或其延长线上的点，若 1BA CB AC A C B A C B'''⋅⋅='''， ② 则AA '，BB '，CC '三直线共点或三直线互相平行．证明若AA '与BB '交于点P ，设CP 与AB 的交点为1C ，则由塞瓦定理，有111AC BA CB A C B A C B ''⋅⋅=''，又已知有111AC BA CB A C B A C B ''⋅⋅=''，由此得11AC AC C B C B '='，即1AC AC AB AB'=，亦即1AC AC '=，故1C 与C '重合，从而AA '，BB '，CC '三线共点．若AA BB ''∥，则CB CB B A BA '=''．代入已知条件，有AC A CC B CB''='，由此知CC AA ''∥，故 AA BB CC '''∥∥．上述两定理可合写为：设A '，B '，C '分别是△ABC 的BC ，CA ，AB 所在直线上的点，则三直线AA '，BB '，CC '平行或共点的充要条件是1BA CB AC A C B A C B'''⋅⋅='''． ③ 第一角元形式的塞瓦定理设A '，B '，C '分别是△ABC 的三边BC ，CA ，AB 所在直线上的点，则三直线AA '，BB '，CC '平行或共点的充要条件是 sin sin sin 1sin sin sin BAA ACC CBB A AC C CB B BA'''⋅⋅='''∠∠∠∠∠∠． ④证明由sin sin ABA AA C S BA AB BAA A C S AC A AC ''''⋅==''⋅△△∠∠，sin sin CB BC CBB B A AB B BA ''⋅=''⋅∠∠，sin sin AC AC ACC C B BC C CB ''⋅=''⋅∠∠，三式相乘，再运用塞瓦定理及其逆定理，知结论成立．第二角元形的塞瓦定理设A '，B '，C '分别△ABC 的三边BC ，CA ，AB 所在直线上的点，O 是不在△ABC 的三边所在直线上的点，则AA '，BB '，CC '平行或共点的充要条件是 sin sin sin 1sin sin sin BOA AOC COB A OC C OB B OA'''⋅⋅='''∠∠∠∠∠∠．⑤ 证明注意到塞瓦定理及其逆定理，有1BOA COB AOC A OC B OA C OB S S S BA CB AC A C B A C B S S S '''''''''=⋅⋅=⋅⋅'''△△△△△△ sin sin sin sin sin sin BO BOA CO COB AO AOC CO A OC AO B OA BO C OB'''⋅⋅⋅=⋅⋅'''⋅⋅⋅∠∠∠∠∠∠．由此即证得结论．注在上述各定理中，若采用有向线段或有向角，则①、②、③、④、⑤式的右端仍为1．特别要注意的是三边所在直线上的点或者两点在边的延长线上，或者没有点在边的延长线上．④、⑤式中的角也可按①式的对应线段记忆．推论设1A ，1B ，1C ，分别是△ABC 的外接圆三段弧»BC ，»CA ，»AB 上的点，则1AA ，1BB ，1CC 共点的充要条件是1111111BA CB AC AC B A C B ⋅⋅=．证明如图2-3，设△ABC 的外接圆半径为R ，1AA 交BC 于A '，1BB 交CA 于B '，1CC 交AB 于C '．由A ，1C ，B ，1A ，C ，1B 六点共圆及正弦定理，有11112sin sin 2sin sin BA R BAA BAA AC R A AC A AC '⋅=='⋅∠∠∠∠．同理，11sin sin CB CBB B A B BA '='∠∠，11sin sin AC ACC C B C CB'='∠∠．三式相乘，并应用第一角元形式的塞瓦定理即证．为了使读者熟练地应用塞瓦定理，针对图2-4中的点A 、B 、C 、D 、E 、F ，将其作为塞瓦点，我们写出如下式子：对△ACE 及点D 有 1AB CG EFBC GE FA ⋅⋅=，对△CDE 及点A 有 1CF DB EGFD BE GC ⋅⋅=，对△ADE 及点C 有 1DG AF EBGA FE BD ⋅⋅=，对△ABD 及点F 有 1AC BE DHCB ED HA ⋅⋅=，对△ACD 及点E 有 1AG DF CBGD FC BA ⋅⋅=，对△ADF 及点B 有 1AH DC FEHD CF EA ⋅⋅=，对△ABF 及点D 有 1BC AE FHCA EF HB⋅⋅=，对△BDF 及点A 有1BE DC FHED CF HB⋅⋅=．【典型例题与基本方法】1．恰当地选择三角形及所在平面上的一点，是应用塞瓦定理的关键例1 四边形两组对边延长分别相交，且交点的连线与四边形的一条对角线平行．证明：另一条对角线的延长线平分对边交点连线的线段．（1978年全国高中竞赛题）证明如图2-5，四边形ABCD 的两组对边延长分别交于E ，F ，对角线BD EF ∥，AC 的延长线交EF 于G ．对△AEF 及点C ，应用塞瓦定理，有 1EG FD ABGF DA BE ⋅⋅=．由BD EF ∥，有AB ADBE DF=，代入上式，得1EGGF=，即EG GF =．命题获证．例2 如图2-6，锐角△ABC 中，AD 是BC 边上的高，H 是线段AD 内任一点，BH 和CH 的延长线分别交AC ，AB 于E ，F ．求证：EDH FDH =∠∠．（1994年加拿大奥林匹克试题）证法1 对△ABC 及点H ，应用塞瓦定理，有1AF BD CEFB DC EA⋅⋅=． ① 过A 作PQ BC ∥，延长DF ，DE 分别交PQ 于P ，Q ，则DA PQ ⊥，且△APF ∽△BDF ，△AQE ∽△CDE ，从而AF PA BD FB =⋅，EAAQ DC CE=⋅．而由①，有AF EABD DC FB CE⋅=⋅，故PA AQ =．由此知AD 为等腰△APQ 底边PQ 上的高，故EDH FDH =∠∠．证法2 对△ABC 及点H 应用塞瓦定理，有1DAF DCEDFB DEA S S AF BD CE BD FB DC EA S DC S =⋅⋅=⋅⋅△△△△ sin sin tan cot sin sin AD ADF BD DC EDCADF ADE BD FDB DC AD ADE⋅⋅=⋅⋅=⋅⋅⋅∠∠∠∠∠∠．即tan tan ADE ADF =∠∠，由锐角性质知EDA FDA =∠∠．类似地，对△ABE 及截线FHC 或对△AFC 及截线BHE 应用梅涅劳斯定理也可证得有EDA FDA =∠∠．注将此例中的平角BDC ∠变为钝角，则有如下：例3 如图2-7，在四边形ABCD 中，对角线AC 平分BAD ∠．在CD 上取一点E ，BE 与AC 相交于F ，延长DF 交BC 于G ．求证：GAC EAC =∠∠．（1999年全国高中联赛题）证明连BD 交AC 于H ，对△BCD 及点F ，应用塞瓦定理，有1CG BH DEGB HD EC⋅⋅=． AH 平分BAD ∠，由角平分线性质，可得BH AB HD AD =，故1CG AB DEGB AD EC⋅⋅=．过点C 作AB 的平行线交AG 的延长线于I ，过点C 作AD 的平行线交AE 的延长线于J ，则 ,CG CI DE AD GB AB EC CJ ==．所以1CI AB ADAB AD CJ ⋅⋅=．从而，CI CJ =．又CI AB ∥，CJ AD ∥，有180180ACI BAC DAC ACJ =︒-=︒-=∠∠∠∠．因此，△ACI ACJ ≌△，即有IAC JAC =∠∠．故 GAC EAC =∠∠．注由此例还可变出一些题目，参见练习题第4、5及19题．例4 如图2-8，BE 是△ABC 的中线，G 在BE 上，分别延长AG ，CG 交BC ，AB 于D ，F ，过D 作DN CG ∥交BG 于N ，△DGL 及FGM △为正三角形．求证：△LMN 为正三角形．证明连NF ，对△ABC 及点G 应用塞瓦定理，有 1AF BD CE FB DC EA ⋅⋅=．而AE CE =，则AF DCFB BD =．由DN CG ∥，由CD NGBD BN=．于是，有AF NGFB BN=，从而FN AD ∥，即知四边形DNFG 为平行四边形，有GDN GFN =∠∠．又60GDL GFM ==︒∠∠，则LDN NFM =∠∠．而DN GF FM ==，DL DG NF ==，知△LDN ≌△NFM ，有LN MN =，DNL NMF =∠∠．于是MNL DNF DNL MNF DNF NMF MNF =-+=-+∠∠（∠∠）∠（∠∠） 180)(180)NFG NFM NFM NFG ︒--︒-=-=(∠∠∠∠60MFG ==︒∠．故△LMN 为正三角形．例5 如图2-9，在一个△ABC 中，2C B =∠∠，P 为△ABC 内满足AP AC =及PB PC =的一点．求证：AP 是A ∠的三等分线．（1994年香港代表队IMO 选拔赛题）证明用B 表示ABC ∠的度量，令PCB θ=∠，则PBC θ=∠，ABP B θ=-∠，2ACP B θ=-∠，()π22CAP B θ=--∠（其中注意AP AC =），()π[π2(2)]PAB A CAP B C B θ=-=-----∠∠∠(π3)(π42)2B B B θθ=---+=-．对△ABC 及点P ，应用第一角元形式的塞瓦定理，有 sin[π2(2)]sin sin()1sin(2)sin(2)sin B B B B θθθθθθ---⋅⋅=--．亦即2sin(2)cos(2)sin()1sin(2)sin(2)B B B B B θθθθθ-⋅-⋅-=-⋅-．于是 sin(2)2sin()cos(2)sin(32)sin B B B B B θθθθ-=-⋅-=--，即 sin sin(32)sin(2)2cos(22)sin B B B B B θθθ=---=-⋅．而sin 0B ≠，则1cos2()2B θ-=．因 1π0()33B b BC θ<-<<+<，则2π2()0,3B θ⎛⎫-∈ ⎪⎝⎭．∴ π2()3B θ-=，即π6B θ-=．从而π2(2)π4()2CAP B B θθθ=--=---∠ ππ222[()]36B θθθθ⎛⎫=-=-=-- ⎪⎝⎭2(2)2B PAB θ=-=∠．故 13PAB A =∠∠，即AP 是A ∠的三等分线．利用第一角元形式的塞瓦定理可简捷处理2009年全国高中联赛加试第一题的第1问：例6 设M 、N 分别为锐角△ABC（A B <∠∠）的外接圆Γ上弧»BC 、»AC 的中点．过点C 作PC MN ∥交圆Γ于点P ，I 为△ABC 的内心，联结PI 并延长交圆Γ于点Γ．求证：MP MT NP NT ⋅=⋅．证明事实上，易知A 、I 、M 及B 、I 、N 分别三点共线，对△PMN 及点I 应用第一角元形式的塞瓦定理，有sin sin sin 1sin sin sin NPI PMI MNIIPM IMN INP⋅⋅=∠∠∠∠∠∠．①由CP MN ∥知PA PB =，有PMI INP =∠∠．于是①式即为1sin 21sin 2B NT CN MP MT CM NPA ===∠∠．故MP MT NP NT ⋅=⋅．2．注意塞瓦定理逆定理的应用以及与梅涅劳斯定理的配合应用例7 如图2-10，在△ABC 中，90BAC =︒∠，G 为AB 上给定的一点（G 不是线段AB 的中点）．设D 为直线GC 上与C ，G 都不相同的任意一点，并且直线AD ，BC 交于E ，直线BD ，AC 交于F ，直线EF ，AB 交于H ．试证明交点H 与D 在直线CG 上的位置无关．（1990年苏州市高中竞赛题）证明设G 分线段AB 为定比1λ，H 分线段AB 为定比2λ．下证2λ由1λ确定，即当A ，B 给定后，点H 的位置由点G 唯一确定．在△ABC 中，由AE ，BF ，CG 交于一点D ，应用塞瓦定理，有 1AG BE CF GB EC FA ⋅⋅=，即11BE CFEC FAλ⋅⋅=．对△ABC 及截线EFH ，应用梅涅劳斯定理，得 1AH BE CF HB EC FA ⋅⋅=，即21BE CFEC FAλ⋅⋅=-．上述两式相加，得12()0BE CFEC FAλλ+⋅=．从而120λλ+=，即21λλ=-，故2λ由1λ唯一确定．因此，点H 与D 在直线CG 上的位置无关．例8 如图2-11，设P 为△ABC 内任一点，在形内作射线AL ，BM ，CN ，使得CAL PAB =∠∠，MBC PBA =∠∠，NCA BCP ∠=∠．求证：AL ，BM ，CN 三线共点．证法1 设AL 交BC 于L ，BM 交CA 于M ，CN 交AB 于N ，则由正弦定理有 sin sin sin sin BL AB BAL AB PACLC AC CAL AC PAB ⋅⋅==⋅⋅∠∠∠∠．同理，sin sin CM BC PBAMA AB PBC⋅=⋅∠∠, sin sin AN AC PCBNB BC PCA⋅=⋅∠∠．将上述三式相乘，并应用正弦定理，有sin sin sin 1sin sin sin BL CM AN PAC PBA PCB PC PA PB LC MA NB PAB PBC PCA PA PB PC ⋅⋅=⋅⋅=⋅⋅=∠∠∠∠∠∠．由塞瓦定理的逆定理，知AL ，BM ，CN 共点．证法2 设AL 交BC 于L ，BM 交CA 于M ，CN 交AB 于N ，直线AP 交BC 于D ，直线BP 交AC 于E ，直线CP 交AB 于F ．对△ABC 及点P ，应用塞瓦定理，有1AF BD CEFB DC EA⋅⋅=．在△ABL 和△ACL 中应用正弦定理，有 sin sin sin sin sin sin sin sin BL BL AL BAL C PAC CLC AL LC B LAC PAB B =⋅=⋅=⋅∠∠∠∠∠∠∠∠ 222222sin sin sin sin sin sin sin sin sin sin PAC B C DC AD C DC CC PAB B AD BD B BD B =⋅⋅=⋅⋅=⋅∠∠∠∠∠∠∠∠∠∠．同理，22sin sin CM AE A MA EC C =⋅∠∠，22sin sin AN BF BNB FA A=⋅∠∠．以上三式相乘，并注意到①式，有1BL CM AN DC AE BF LC MA NB BD EC FA⋅⋅=⋅⋅=．由塞瓦定理的逆定理，知AL ，BM ，CN 共点．证法3 设AL 交BC 于L ，BM 交AC 于M ，CN 交AB 于N ，直线AP 交BC 于D ，直线BP 交AC 于E ，直线交AB 于F ．对ABC △及点P ，应用角元形式的塞瓦定理，有sin sin sin 1sin sin sin PAB PBC PCAPAC PBA PCB⋅⋅=∠∠∠∠∠∠．由题设PAB CAL =∠∠，PBA CBM =∠∠，PCB ACN =∠∠，则有BAL PAC =∠∠，ABM PBC =∠∠，BCN PCA =∠∠．于是 sin sin sin sin sin sin sin sin sin sin sin sin BAL CBM ACN PAC PBA PCBCAL ABM BCN PAB PBC PCA⋅⋅=⋅⋅∠∠∠∠∠∠∠∠∠∠∠∠ 111sin sin sin 1sin sin sin PAB PBC PCA PAC PBA PCB===⋅⋅∠∠∠∠∠∠，对△ABC ，应用角元形式的塞瓦定理的逆定理，知AL ，BM ，CN 三线共点．例9 如图2-12，四边形ABCD 内接于圆，其边AB 与DC 的延长线交于点P ，AD 与BC 的延长线交于点Q ，过点Q 作该圆的两条切线，切点分别为E 和F ．求证：P ，E ，F 三点共线．（1997年CMO 试题）证明连EF 分别交AD ，BC 于M ，N ，设AC 与BD 交于K ．要证P ，E ，F 三点共线，只须证明P ，K ，M 和P ，N ，K 都三点共线，又只须证明AC ，BD ，PM 三线共点．由塞瓦定理的逆定理知只须证明1AB PC DM BP CD MA⋅⋅=．又直线QCB 截△PDA ，应用梅涅劳斯定理，有 1AB PC DQ BP CD QA ⋅⋅=，从而只须证明DM DQAM AQ=．设圆心为O ，连QO 交EF 于L ，连LD ，LA ，OD ，OA ，则由切割线走理和射影定理，有2QD QA QE QL QO ⋅==⋅，即知D ，L ，O ，A 四点共圆，有QLD DAO ODA OLA ===∠∠∠∠，此表明QL 为△LAD 的内角ALD ∠的外角平分线．而EF OQ ⊥，则EL 平分ALD ∠．于是， DM DL DQAM AL AQ==，结论获证．【解题思维策略分析】1．获得线段比例式的一种手段例10 如图2-13，△ABC 中，D ，E 分别为AC 和AB 同方向延长线上的点，BD 与CE 相交于P ，且BD CE =．若点P 满足2AEP ADP k PED PDE -=-∠∠（∠∠）（k 为常数），则AB AC =．证明设AP 交BC 于Q ，对△PBC 及其形外一点A ，应用塞瓦定理，有1BQ CE PDQC EP DB⋅⋅=．而BD CE =，则PD QCPE QB=．不妨设QC QB ≤，则PD PE ≤，即有PC CE PE BD PD PB =--=≤，于是PBE PCD S S △△≥，故EBC DBC S S △△≥．此时，点E 到BC 的距离不小于D 到BC 的距离，则过E 作EF BC ∥必交CD 延长线于一点，设为F ．又作△FBC 的外接圆O e 交EF 于另一点F '，则四边形BCFF '为等腰梯形．当AB AC ≥时，由BF F F FC BCA ABC AEF ''===∠∠∠≥∠∠，知F '必在线段EF 上，于是，BDC BFC BEC ∠≥∠≥∠（同弧上的圆外角小于同弧上的圆周角）．又由PD PE ≤，知PED PDE ∠≤∠．故结论获证． 2．转化线段比例式的一座桥梁例11 设M 为△ABC 内任一点，AM ，BM ，CM 分别交BC ，CA ，AB 于D ，E ，F ．求证：1MD ME MFAD BE CF ++=．证明如图2-14，记BD m DC =，CE n EA =，AFl FB=．对△ABC 及点M ，应用塞瓦定理，有1BD CE AFmnl DC EA FB⋅⋅==．对△ADC 及截线EMB ，应用梅涅劳斯定理，有11AM DB CE AM mn MD BC EA MD m ⋅⋅=⋅⋅=+，即 1(1)AM mm l MD m n +==++．由合比定理得1(1)AD m l MD =++，即11MD AD l ml=++．同理，111ME lBE m mn l ml ==++++， 111MF mlCF n nl ml l==++++．三式相加，得1MD ME MFAD BE CF++=．例12 如图2-15，设P 为△ABC 内任意一点，AP ，BP ，CP 的延长线交对边BC ，CA ，AB 于点D ，E ，F ，EF 交AD 于Q．试证：(3PQ AD -≤．证明令BD m DC =，CE n EA =，AF p FB =，对△ABC 及点P ，应用塞瓦定理，有1BD CE AFmnp DC EA FB⋅⋅==．对△ADC 及截线BPE ，应用梅涅劳斯定理，有 1CE AP DB EA PD BC ⋅⋅=．注意到1DB mBC m =+，则有 11AP m n PD m ⋅⋅=+，即1AP m PD mn +=，故11AP m AD mn m +=++．又对直线APD 截△BCE ，有1BD CA EP DC AE PB ⋅⋅=．而1CA n AE =+，则BP mn m EP =+，故1BEmn m EP=++．又对△ABP 及截线FQE ，有1AF BE PQ FB EP AQ ⋅⋅=，即有 11(1)1PQ AQ p mn m mp p ==++++，故12PQ AQ mp p =++．从而1121PQ PQ AP m AD AP AD mp p mn m +=⋅=⋅++++ 1112(1)211(1)211mn mn p m p m m m =⋅=+++++++++3=-于是，(3PQ AD -≤．其中等号由2(1)1mn p m m ++=+≥中等号成立时成立，即当且仅当2(1)1mnp m m =++亦即当且仅当22(1)(1)(1)mnp p m p m p m ==+++，亦即(1)p m +=时取等号．此时，m 和p 之间成为如图2-16的双曲线的关系．例13 如图2-17，已知直线的三个定点依次为A 、B 、C ，Γ为过A 、C 且圆心不在AC 上的圆，分别过A 、C 两点且与圆Γ相切的直线交于点P ，PB 与圆Γ交于点Q ．证明：AQC ∠的平分线与AC 的交点不依赖于圆Γ的选取．（IMO 45预选题）证明设AQC ∠的平分线交AC 于点R ，交圆Γ于点S ，其中S 与Q 是不同的两点．由于△PAC 是等腰三角形，则有sin sin AB APBBC CPB=∠∠．同理，在△ASC 中，有sin sin AR ASQRC CSQ =∠∠．在△PAC 中，视Q 为塞瓦点，由角元形式的塞瓦定理，有sin sin sin 1sin sin sin APB QAC QCPCPB QAP QCA⋅⋅=∠∠∠∠∠∠．注意到PAQ ASQ QCA ==∠∠∠，PCQ CSQ QAC ==∠∠∠．则 22sin sin sin sin sin sin sin sin APB PAQ QCA ASQ CPB QAC PCQ CSQ⋅==⋅∠∠∠∠∠∠∠∠．即 22AB AR BC RC=，故结论获证． 3．求解三角形格点问题的统一方法如果三角形的三个角的度数都是10的整数倍，三角形内一点与三角形的三个顶点分别连结后，得到的所有的角也都具有这个性质，我们称这样的点为三角形的格点．例14 如图2-18，在△ABC 中，40BAC =︒∠，60ABC =︒∠，D 和E 分别是AC 和AB 上的点，使得40CBD =︒∠，70BCE =︒∠，F 是直线BD 和CF 的交点．证明：直线AF 和直线BC 垂直．（1998年加拿大奥林匹克试题）证明设BAF α=∠，则40FAC α=︒-∠，对△ABC 及点F ，应用第一角元形式的塞瓦定理，有 sin10sin sin 401sin 70sin(40)sin 20αα︒︒⋅⋅=︒︒-︒．从而sin10sin 2sin 20cos201cos20sin(40)sin 20αα︒︒⋅︒⋅⋅=︒︒-︒，即有sin(40)2sin sin102sin cos80ααα︒-=⋅︒=⋅︒ sin(80)sin(80)αα=+︒+-︒．∴ sin(80)sin(40)sin(80)2cos60sin(20)sin(20)ααααα-︒=︒--+︒=︒⋅-︒-=-︒-．注意到040α<<︒，知8020α-︒<-︒-，8020α-︒<︒，有 8020αα-︒=-︒-，故30α=︒．延长AF 交BC 于H ，则180180306090AHB FBC ABH =︒--=︒-︒-︒=︒∠∠∠．故AF BC ⊥．注此题也可这样来解：由sin10sin sin 401sin 70sin(40)sin 20αα︒︒⋅⋅=︒︒-︒，有 sin(40)sin10sin 40sin10sin(4030)2sin10sin 40cot30cos40sin sin70sin 20sin30sin30αα︒-︒-︒︒︒-︒==︒===︒⋅︒-︒︒-︒︒︒．由于sin(40)sin 40cot cos40sin ααα︒-=︒⋅-︒作为α的函数在(0,180)︒︒上严格递减，所以30BAF α==︒∠．故90ABC BAF +=︒∠∠．因此，AF BC ⊥．或者过点A 作AH BC ⊥于H ，则30BAH =︒∠，10HAC =︒∠．关于△ABC 有sin sin sin sin30sin10sin 401sin sin sin sin10sin70sin 20BAH ACD CBD HAC ECB DBA ︒︒︒⋅⋅=⋅⋅=︒︒︒∠∠∠∠∠∠．所以，AH 、BD 、CE三线共点，因此点F 在AH 上，即AF BC ⊥．例15 如图2-19，在△ABC 内取一点M ，使得30MBA =︒∠，10MAB =︒∠．设80ACB =︒∠，AC BC =，求AMC ∠．（1983年前南斯拉夫奥林匹克试题）解设ACM α=∠，则80MCB α=︒-∠．由第一角元形式的塞瓦定理，有 ()sin sin10sin 80sin 40αα︒⋅⋅︒-︒sin 201sin30︒=︒．从而 sin sin10sin(80)cos20αα⋅︒=︒-⋅︒． ∴ 2sin cos802sin(80)cos20αα⋅︒=︒-⋅︒，∴ sin(80)sin(80)sin(100)sin(60)αααα+︒+-︒=︒-+︒-， ∴ sin(80)sin(60)sin(100)sin(80)αααα-︒-︒-=︒--+︒ 2cos90sin(10)0α=︒⋅︒-=．于是 sin(80)sin(60)αα-︒=︒-．注意到 080α<<︒，知8080α-︒<<-︒，6060α︒-<︒． ∴ 8060αα-︒=︒-，故 70α=︒．所以 180180407070AMC MAC ACM =︒--=︒-︒-︒=︒∠∠∠为所求．注此题结果也可直接由①式有sin sin 70sin10sin(80)αα=︒⎧⎨︒=︒-⎩且0α<，8080α︒-<︒，求得70α=︒．另外，此题也可这样来解：由sin sin10sin 201sin(80)sin 40sin30αα︒︒⋅⋅=︒-︒︒，有sin(80)sin10sin 20sin10sin(8070)sin80cot 70cos80sin sin 40sin30cos20sin 70αα︒-︒⋅︒︒︒-︒====︒⋅︒-︒︒⋅︒︒︒．因为sin(80)sin80cot cos80sin ααα︒-=︒⋅-︒作为α的函数在（0︒，180︒）上严格递减，所以70ACM α==︒∠．故180407070AMC =︒-︒-︒=︒∠．或者由140AMB =︒∠，令AMC x =∠，则220CMB x =︒-∠．对△MAB 和点C 应用第一角元形式的塞瓦定理，有sin sin sin sin sin 20sin501sin sin sin sin(220)sin50sin 40AMC MBC BAC x CMB CBA CAM x ︒︒=⋅⋅=⋅⋅︒-︒︒∠∠∠∠∠∠．则sin(220)1sin(22070)sin 220cot 70cos220sin 2cos20sin70x x ︒-︒-︒===︒⋅︒-︒︒︒．因为sin(220)sin 220cot cos220(sin 2200)sin x x x︒-=︒⋅-︒︒<作为x 的函数在(0,180)︒︒上严格递增，所以70AMC x ==︒∠．例16 如图2-20，△ABC 具有下面性质：存在一个内部的点P ，使得10PAB =︒∠，20PBA =︒∠，30PCA =︒∠，40PAC =︒∠．证明：△ABC 是等腰三角形．（1996年美国第25届奥林匹克试题）证明设BCP α=∠，则1802010403080PBC αα=︒-︒-︒-︒-︒-=︒-∠．由第一角元形式的塞瓦定理，有sin 20sin 40sin 1sin(80)sin10sin30αα︒︒⋅⋅=︒-︒︒．即有2sin10cos10sin 40sin 11sin(80)sin102αα︒⋅︒︒⋅⋅=︒-︒．∴ sin(80)4sin sin 40cos104sin sin 40sin80ααα︒-=⋅︒⋅︒=⋅︒⋅︒4sin sin 20sin 40sin80sin60sin sin 20sin 20αα⋅︒⋅︒⋅︒︒⋅==︒︒， ∴ sin(80)sin 20sin60sin αα︒-⋅︒=︒⋅．从而 sin(80)sin 60sin 20sin αα︒-=︒⎧⎨︒=⎩且0α<，8080α︒-<︒，故20α=︒，即50ACB CAB =︒=∠∠，从而AB BC =．注此题也可这样来求解：由sin 20sin 40sin 1sin(80)sin10sin30αα︒︒⋅⋅=︒-︒︒，有sin(80)sin 20sin 404sin 20sin 40sin804cos10sin 40sin sin10sin30sin 20αα︒-︒︒︒⋅︒⋅︒=⋅=︒⋅︒=︒︒︒sin60sin(8020)sin80cot 20cos80sin 20sin 20︒︒-︒===︒⋅︒-︒︒︒．因为sin(80)sin80cot cos80sin ααα︒-=︒⋅-︒作为α的函数在（0︒，180︒）上严格递减，所以BCP α=∠20=︒，即50ACB CAB =︒=∠∠．故AB BC =．还可对△APC 及点B 应用第一角元形式的塞瓦定理来求． 4．论证直线共点的一种工具例17 如图2-21，在四边形ABCD 中，AB AD =，BC DC =，过AC ，BD 的交点O 引EF ，GH ，其中EF 交AB ，CD 于E ，F ，GH 交DA ，BC 于G ，H ．EH ，GF 分别交BD 于P ，Q ，则OP OQ =．（1990年CMO 选拔试题）证明在AB ，BC 上分别取G '，F '，使AG AG '=，CF CF '=，则由对称性可知有下列角相等，即若设,AOG AOG αβ'==∠∠，COH γ=∠，1G OE '=∠∠，2EOB =∠∠，3BOF '=∠∠，4F OH '=∠∠，则αβ=，又αγ=，故βγ=．又14βγ+=+∠∠，故14=∠∠，23=∠∠．连G H '交BD 于K ，在△BHG '中， OG E OBF OHKOEB OF H OKG S S S G E BF HK EB F H KG S S S ''''''⋅⋅=⋅⋅''△△△△△△ sin 1sin 3sin(34)1sin 2sin 4sin(12)OG OE OB OF OH OK OE OB OF OH OK OG ''⋅⋅⋅⋅⋅⋅+=⋅⋅=''⋅⋅⋅⋅⋅⋅+∠∠∠∠∠∠∠∠．故由塞瓦定理的逆定理，知G F ''，BO ，HE 共点，即G F ''过点P ．由对称性知，OP OQ =．例18 如图2-22，在锐角△ABC 中，以A 点引出的高AD 为直径作圆交AB ，AC 于M ，N ，再从A 作A l MN ⊥．同样可作出B l ，C l ．试证：三直线A l ，B l ，C l 相交于一点．（第29届IMO 预选题）证明设A l 与MN ，BC 分别相交于点G ，D '，由AMG ADN =∠∠，90AGM AND ==︒∠∠，知MAG NAD =∠∠，即BAD CAD '=∠∠．同理，设CA ，AB 边上的高BE ，CF 的垂足分别为E ，F ，且B l ，C l 分别与CA ，AB 交于E '，F '，则有CBE ABE '=∠∠，ACF BCF '=∠∠．由于△ABC 的三条高相交于垂心，此时应用第一角元形式的塞瓦定理，得sin sin sin 1sin sin sin CAD ABE BCFDAB EBC FCA ⋅⋅=∠∠∠∠∠∠，用等角代换上式，有sin sin sin 1sin sin sin BAD ACF CBE DAC F CB E BA'''⋅⋅=''∠∠∠∠∠∠．故由第一角元形式的塞瓦定理，知AD '，BE '，CF '三线共点，即A l ，B l ，C l 相交于一点．例19 如图2-23，四边形ABCD 内接于圆，AB ，DC 的延长线交于E ，AD ，BC 的延长线交于F ，P 为圆上任一点，PE ，PF 分别交圆于R ，S ．若对角线AC 与BD 相交于T ，求证：R ，T ，S 三点共线．证明连PD ，AS ，RC ，BR ，AP ，SD ．由△EBR ∽△EPA ，△FDS ∽△FPA ，有BR EBPA EP =，PA FP DS FD =，此两式相乘，有BR EB FPDS EP FD =⋅．①又由ECR EPD △∽△，FPD FAS △∽△，有 CR EC PD EP =，PD FPAS FA =，此两式相乘，有 CR EC FPAS EP FA=⋅．由①÷②，得 BR AS EB FADS CR EC FD⋅=⋅．上式两边同乘以DC AB，得 BR CD SA EB AF DCRC DS AB BA FD CE ⋅⋅=⋅⋅．对△EAD 及截线BCF ，应用梅涅劳斯定理，有 1EB AF DC BA FD CE⋅⋅=．于是1BR CD SARC DC AB⋅⋅=．此时，应用第一角元形式的塞瓦定理的推论，知BD ，RS ，AC 交于一点．从而R ，T ，S 三点共直线．【模拟实战】习题A 1．在△ABC 中，D 是BC 上的点，13BD DC =，E 是AC 中点．AD 与BE 交于O ，CO 交AB 于F ，求四边形BDOF 的面积与△ABC 的面积的比．2．若通过△ABC 各顶点的直线AD ，BE ，CF 共点，并且它们在边BC ，CA ，AB 所在直线上的截点D ，E ，F 关于所在边中点的对称点分别为D '，E '，F '，则直线AD '，BE '，CF '也共点． 3．一圆交△ABC 的各边所在直线于两点，设BC 边上的交点为D ，D '，CA 边上的交点为E ，E '，AB 边上的交点为F ，F '．若AD ，BE ，CF 共点，则AD '，BE '，CF '也共点．4．试证：过三角形顶点且平分三角形周长的三条直线共点．5．将△ABC 各内角三等分，每两个角的相邻三等分线相交得△PQR ，又AX ，BY ，CZ 分别平分BAC ∠，ABC ∠，ACB ∠且它们与QR ，RP ，PQ 交于X ，Y ，Z ．求证：PX ，QY ，RZ 三线共点．6．将△ABC 的各外角三等分，每两个外角的相邻三等分线相交得△DEF ．又AX ，BY ，CZ 分别平分BAC ∠，ABC ∠，ACB ∠且它们与EF ，FD ，DE 交于X ，Y ，Z ．求证：DX ，EY ，FZ 三线共点．7．O e 是△ABC 的内切圆，BC ，CA ，AB 上的切点各是D ，E ，F ．射线DO 交EF 于A '，同样可得B '，C '．试证：直线AA '，BB '，CC '共点．8．△ABC 在△A B C '''内部，且从A ，B ，C 各向B C ''，C A ''，A B ''所作的垂线共点，则从A '，B '，C '各向BC ，CA ，AB 所作的垂线也共点．9．在△ABC 中，40ABC ACB ==︒∠∠，P 为形内一点，20PAC =︒∠，30PCB =︒∠，求PBC ∠的度数．10．在ABC △中，AB AC =，80A =︒∠，D 为形内一点，且10DAB DBA ==︒∠∠，求ACD ∠的度数．（《数学教学》问题432题）11．在ABC △中，30BAC =︒∠，70ABC =︒∠，M 为形内一点，20MAB MCA ==︒∠∠，求MBA ∠的度数．（《数学教学》问题491题） 12．在ABC △中，40ABC =︒∠，30ACB =︒∠，P 为ABC ∠的平分线上一点，使10PCB =︒∠，BP 交AC 于M ，CP 交AB 于N ．求证：PM AN =．（《数学教学》问题531题） 13．在ABC △中，40ABC =︒∠，20ACB =︒∠，N 为形内一点，30NBC =︒∠，20NAB =︒∠，求NCB ∠的度数．（《数学通报》问题1023题） 14．在ABC △中，80BAC =︒∠，60ABC =︒∠，D 为形内一点，且10DAB =︒∠，20DBA =︒∠，求ACD ∠的度数．（《数学通报》问题1142题） 15．在△ABC 中，50ABC =︒∠，30ACB =︒∠，M 为形内一点，20MCB =︒∠，40MAC =︒∠，求MBC ∠的度数．（《数学通报》问题1208题） 16．△ABC 中，70ABC =︒∠，30ACB =︒∠，P 为形内一点，40PBC =︒∠，20PCB =︒∠．求证：1CA AB BPAP PC CB⋅⋅=⋅⋅．（《数学通报》问题1306题） 17．在△ABC 中，40ABC ACB ==︒∠∠，P ，Q 为形内两点，20PAB QAC ==︒∠∠，PCB QCA =∠∠10=︒．求证：B ，P ，Q 三点共线．（《数学通报》问题1243题） 18．△ABC 中，50ABC ACB ==︒∠∠，P ，Q 为形内两点，10PCA QBC ==︒∠∠，PAC QCB =∠∠20=︒．求证：BP BQ =．（《数学通报》问题1281题） 19．在△ABC 中，AB AC =，100A =︒∠，I 为内心，D 为AB 上一点，满足BD BI =．试求BCD ∠的度数．（《数学通报》问题1073题） 20．1A ，2A ，1B ，2B ，1C ，2C 顺次分别在△ABC 的三边BC ，CA ，AB 上，且12BA A C =，12CB B A =， 12AC C B =，过2A ，2B ，2C 分别作1AA ，1BB ，1CC 的平行线a l ，b l ，c l ．求证：a l ，b l ，c l 三线共点的充要条件是1AA ，1BB ，1CC 三线共点．21．在△ABC 中，AB AC =，AD BC ⊥于D ，过D 任作两射线分别交AB ，AC 于点E ，F ，交过点A 的平行线于G ，H ，且GH BC ∥．求证：AD ，GF ，HE 共点．22．在△ABC 中，过三边BC ，CA ，AB 边中的中点M ，N ，L 的三条等分三角形周长的直线MS ，NT ，LU （S ，T ，U 在三角形三边上）分别交LN ，LM ，MN 于D ，E ，F ．求证：MS ，NT ，LU 三线共点．23．△ABC 的内切圆切BC ，CA ，AB 于D ，E ，F ．P 是△ABC 内一点，PA 交内切圆于两点，其中靠近A 的一点为X ，类似定义Y ，Z ．试证：DX ，EY ，FZ 三线共点．24．△ABC 在△A B C '''内部，AB 的延长线分别交A C ''，B C ''于5P ，1P ；AC 的延长线分别交B A ''，B C ''于3P ，4P ；BC 的延长线分别交A B ''，A C ''于6P ，2P ，且满足142536AP AP BP BP CP CP ===== 123BP CP AP =++．求证：AA '，BB '，CC '所在直线共点．（《中学数学教学》擂台题（28）） 25．给定△ABC ，延长边BC 至D ，使CD AC =．△ACD 的外接圆与以BC 为直径的圆相交于C 和P ．设BP 与CP 的延长线分别交AC 和AB 于E ，F ．求证：E ，F ，D 共线．（第15届伊朗奥林匹克题） 26．在△ABC 的边上向外作三个正方形，1A ，1B ，1C 是正方形中的边BC ，CA ，AB 对边的中点．求证：直线1AA ，1BB ，1CC 共点．习题B1．O e 是△ABC 的内切圆，D ，E ，F ，分别是BC ，CA ，AB 上的切点，DD '，EE '，FF '都是O e 的直径．求证：直线AD '，BE '，CF '共点．（《数学通报》问题1396题） 2．四边形ABCD 的内切圆分别与边AB ，BC ，CD ，DA 相切于E ，F ，G ，H ．求证：AC ，BD ，HF ，GE 四线共点．（《数学通报》问题1370题） 3．锐角△ABC 中，A 角的平分线与三角形的外接圆交于另一点1A ，点1B ，1C 与此类似．直线1AA 与B ，C 两角的外角平分线交于0A ，点0B ，0C 与此类似．求证：（Ⅰ）三角形000A B C 的面积是六边形111AC BACB 的二倍；（Ⅱ）三角形000A B C 的面积至少是三角形ABC 面积的四倍．（IMO -30试题） 4．设P 为△ABC 内一点，使BPA CPA =∠∠，G 是线段AP 上的点，直线BG ，CG 分别交边AC ，AB于E ，F ．求证：BPF CPE =∠∠．5．在凸四边形ABCD 中，对角线AC 平分BAD ∠，E 是CD 的延长线上的一点，BE 交AC 于点G ，延长DG 交CB 的延长线于F ．试证：BAF DAE =∠∠．6．在△ABC 中，AB AC =，100A =︒∠，I 为内心，D 为AB 上一点，满足BD BI =．试求BCD ∠的度数．（《数学通报》问题1073题） 7．设△ABC 是等边三角形，P 是其内部一点，线段AP ，BP ，CP 依次交三边BC ，CA ，AB 于1A ，1B ，1C 三点．证明：111111111A B B C C A A B B C C A ⋅⋅⋅⋅≥．（IMO -37预选题） 8．在一条直线l 的一侧画一个半圆Γ，C ，D ，是Γ上两点，Γ上过C 和D 的切线分别交l 于B 和A ，半圆的圆心在线段BA 上，E 是线段AC 和BD 的交点，F 是l 上的点，EF l ⊥．求证：EF 平分CFD ∠．（IMO -35预选题） 9．设1A 是锐角△ABC 的内接正方形的中心，其中内接正方形的两个顶点在BC 边上，一个顶点在AB 边上，一个顶点在AC 边上．同样定义两个顶点分别在AC 边和AB 边上的内接正方形的中心分别为1B ，1C ．证明：1AA ，1BB ，1CC 交于一点．（IMO -42预选题）10．以△ABC 的底边BC 为直径作半圆，分别与AB ，AC 交于点D ，E ，分别过点D ，E 作BC 的垂线，垂足依次为F ，G ，线段DG 和EF 交于点M ．求证：AM BC ⊥．（1996年国家队选拔考试题）11．设O ，H 是锐角△ABC 的外接圆的圆心和垂心．证明：存在D ，E ，F 分别在线段BC ，CA ，AB 上，使得OD DH OE EH OF FH +=+=+，且此时AD ，BE ，CF 三线交于一点．（IMO -41预选题）12．已知AB 是O e 的直径，弦CD AB ⊥于L ，点M 和N 分别在线段LB 和LA 上，且LM ∶MB LN =∶NA ，射线CM ，CN 交O e 于E ，F ．求证：AE ，BF ，OD 三线共点．13．设I 是△ABC 的内心，以I 为圆心的一个圆分别交BC 于1A ，2A ，交A C 于1B ，2B ，交AB 于1C ，2C ．这六个点在圆上的顺序为1A ，2A ，1B ，2B ，1C ，2C ．设3A ，3B ，3C 为弧¼12A A ，¼12B B ，¼12C C 的中点，直线23A A ，13B B 相交于4C ，直线23B B ，13C C 相交于4A ，直线23C C ，13A A 相交于4B ．求证：直线34A A ，34B B ，34C C 三线共点．14．在△ABC 的边AB 和AC 上分别向形外作△ABE 和△ACF ，使△ABE ∽△ACF ，且ABE =∠90ACF =︒∠．求证：连线BF ，CE 与边BC 上的高AH 三线共点．15．过非等边三角形各顶点作其外接圆的切线，则各切线与其对边的交点共线．16．在△ABC 内三点D ，E ，F 满足BAE CAF =∠∠，ABD CBF =∠∠，则AD ，BE ，CF 三线共点的充要条件是ACD BCE =∠∠． 17．在任意△ABC 的三边BC ，CA ，AB 上各有点M ，N ，L ，而Q 是△ABC 内部任一点，直线AQ ，BQ ，CQ 分别交线段NL ，LM ，MN 于1M ，1N ，1L ．求证：直线1M M ，1N N ，1L L 共点的充分必要条件是AM ，BN ，CL 共点，而与Q 点的位置无关．18．设P 是平面上△ABC 区域内任一点，AP ，BP ，CP 的延长线交△ABC 三边于D ，E ，F ．求证：在△ABC 区域内，存在一个以△DEF 的某两边为邻边的平行四边形．19．设凸四边形ABCD 的两组对边所在的直线，分别交于E ，F 两点，两对角线的交点为P ，过点P 作PO EF ⊥于O ．求证：BOC AOD =∠∠．（2002国家集训队选拔试题） 20．在△ABC 中，ABC ∠和ACB ∠均为锐角．D 是BC 边上的内点，且AD 平分BAC ∠，过点D 作垂线DP AB ⊥于P ，DQ AC ⊥于Q ，CP 与BQ 相交于K ．求证：AK BC ⊥．。

第2章塞瓦定理及应用(基础篇)

高一（初三）竞赛辅导第二讲第2章塞瓦定理知识塞瓦定理及其逆定理塞瓦定理：如果ABC △的三个顶点与一点P 的连线AP 、BP 、CP 交对边或其延长线于点D 、E 、F ，如图，那么1BD CE AF DC EA FB⋅⋅=．通常称点P 为ABC △的塞瓦点．PFEB A证明：∵直线FPC 、EPB 分别是ABD △、ACD △的梅氏线，∴1BC DP AF CD PA FB ⋅⋅=，1DB CE AP BC EA PD ⋅⋅=．两式相乘即可得：1BD CE AF DC EA FB⋅⋅=．塞瓦定理的逆定理：如果点D 、E 、F 分别在ABC △的边BC 、CA 、AB 上或其延长线上，并且1BD CE AF DC EA FB⋅⋅=，那么AD 、BE 、CF 相交于一点（或平行）．FP F'E D C B AFED CB A 证明：⑴若AD 与BE 相交于一点P 时，如图，作直线CP 交AB 于'F ．由塞瓦定理得：'1BD CE AF DC EA F B ⋅⋅='，又已知1BD CE AF DC EA FB ⋅⋅=，∴AF AF FB F B '='，∴AB AB FB F B='，∴FB F B '=．∴'F 与F 重合∴'CF 与CF 重合∴AD 、BE 、CF 相交于一点．⑵若AD 与BE 所在直线不相交，则AD ∥BE ，如图．∴BD EA DC AC =，又已知1BD CE AF DC EA FB ⋅⋅=，∴1EA CE AF AC EA FB ⋅⋅=，即CE FB AC AF=．∴//BE FC ，∴AD BE FC ∥∥．说明：三线平行的情况在实际题目中很少见．思考提升【例1】（1）设AX BY CZ ，，是ABC △的三条中线，求证：AX BY CZ ，，三线共点．（2）若AX BY CZ ，，为ABC △的三条内角平分线．求证：AX BY CZ ，，三线共点．【解析】（1）由条件知，BX XC YC YA ZA ZB ===，，．∴1BX CY AZ XC YA ZB⋅⋅=，根据塞瓦定理的逆定理可得三条中线AX BY CZ ，，共点．这个点称为这个三角形的重心．（2）由三角形内角平分线定理得：BX AB CY BC AZ AC XC AC YA BA ZB BC ===，，．三式分别相乘，得：1BX CY AZ AB BC AC XC YA ZB AC AB BC⋅⋅=⋅⋅=．根据塞瓦定理的逆定理可得三角形三内角平分线AX BY CZ ，，共点，这个点称为这个三角形的内心．习题1.若AX BY CZ ，，分别为锐角ABC △的三条高线，求证：AX BY CZ ，，三线共点．【解析】由ABX CBZ △∽△得：BX AB BZ BC =；由BYA CZA △∽△得：AZ AC AY AB=；由AXC BYC △∽△可得：YC BC CX AC =．所以1BX AZ YC AB AC BC BZ AY CX BC AB AC⋅⋅=⋅⋅=．根据塞瓦定理的逆定理可得三条高线AX BY CZ ，，共点．对直角三角形、钝角三角形，同样也可以证得三条高线共点．我们把一个三角形三条高线所在直线的交点叫做这个三角形的垂心．【例2】如图，M 为ABC △内的一点，BM 与AC 交于点E ，CM 与AB 交于点F ，若AM 通过BC 的中点D ，求证：EF BC ∥．【解析】对ABC △和点M 应用塞瓦定理可得：1AF BD CE FB DC EA ⋅⋅=．又因为BD DC =，所以1AF CE FB EA ⋅=．进而AF AE FB EC =，所以EF BC ∥．习题2.如果梯形ABCD 的两腰AD 、BC 的延长线交于M ，两条对角线交于N ．求证：直线MN 必平分梯形的两底．BQ AN CPD M【解析】∵AB CD∥∴MD CM DA BC =∴1MD BC DA CM ⋅=∵1MD AQ BC DA QB CM⋅⋅=（由塞瓦定理得）∴1AQ QB=，∴AQ QB =∵DP PC AQ QB =，∴DP PC =．知识三梅涅劳斯定理、塞瓦定理综合自我挑战【备选】如图，E 、F 分别为ABC △的AC 、AB 边上的点，且3AE EC =，3BF FA =，BE 、CF 交于点P ，AP 的延长线交BC 于点D ．求:AP PD 的值．【解析】∵P 为ABC △的塞瓦点．∴11133AF BD CE BD FB DC EA DC ⋅⋅=⋅⋅=∴91BD DC =，∴910BD BC =．∵EPB 为ACD △的梅氏线，∴911103AP DB CE AP PD BC EA PD ⋅⋅=⋅⋅=∴103AP PD =【备选】如图，四边形ABCD 的对边AB 和DC ，DA 和CB 分别相交于点L K ，，对角线AC 与BD 交于点M ．直线KL 与BD 、AC 分别交于点F G 、．求证：KF KG LF LG=．【解析】对DKL △与点B 应用塞瓦定理得：1DA KF LC AK FL CD ⋅⋅=．对DKL △和截线ACG 应用梅涅劳斯定理可得：1DA KG LC AK GL CD⋅⋅=．进而可得KF KG LF LG．。

初中数学相似模型之梅涅劳斯(定理)模型与塞瓦(定理)模型及参考答案

相似模型之梅涅劳斯(定理)模型与塞瓦(定理)模型梅内劳斯(Menelaus，公元98年左右)，是希腊数学家兼天文学家，梅涅劳斯定理是平面几何中的一个重要定理。

梅涅劳斯(定理)模型：如图1，如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点，那么AF FB ⋅BDDC⋅CEEA=1．这条直线叫△ABC的梅氏线，△ABC叫梅氏三角形．梅涅劳斯定理的逆定理：如图1，若F、D、E分别是△ABC的三边AB、BC、CA或其延长线的三点，如果AF FB⋅BD DC ⋅CEEA=1，则F、D、E三点共线．图1图2塞瓦(G·Gevo1647-1734)是意大利数学家兼水利工程师．他在1678年发表了一个著名的定理，后世以他的名字来命名，叫做塞瓦定理。

塞瓦(定理)模型：塞瓦定理是指在△ABC内任取一点G，延长AG、BG、CG分别交对边于D、E、F，如图2，则AFFB⋅BDDC⋅CEEA=1。

注意：①梅涅劳斯(定理)与塞瓦(定理)区别是塞瓦定理的特征是三线共点，而梅涅劳斯定理的特征是三点共线；②我们用梅涅劳斯(定理)与塞瓦(定理)解决的大部分问题，也添加辅助线后用平行线分线段成比例和相似来解决。

1(2023.浙江九年级期中)如图，在△ABC中，AD为中线，过点C任作一直线交AB于点F，交AD于点E，求证：AE:ED=2AF:FB．2(2023.重庆九年级月考)如图，在△ABC中，∠ACB=90°，AC=BC．AM为BC边上的中线，CD⊥AM于点D，CD的延长线交AB于点E．求AEEB．3(2023.湖北九年级期中)如图，点D 、E 分别在△ABC 的边AC 、AB 上，AE =EB ，AD DC=23，BD 与CE 交于点F ，S △ABC =40．求S AEFD ．4(2023.江苏九年级月考)已知AD 是△ABC 的高，点D 在线段BC 上，且BD =3，CD =1，作DE ⊥AB 于点E ，DF ⊥AC 于点F ，连接EF 并延长，交BC 的延长线于点G ，求CG ．5(2023.广东九年级专项训练)如图，在△ABC 中，∠A 的外角平分线与边BC 的延长线交于点P ，∠B 的平分线与边CA 交于点Q ，∠C 的平分线与边AB 交于点R ，求证：P 、Q 、R 三点共线．6(2023上·广东深圳·九年级校联考期中)梅涅劳斯(Menelaus )是古希腊数学家，他首先证明了梅涅劳斯定理，定理的内容是：如图1，如果一条直线与△ABC 的三边AB ,BC ,CA 或它们的延长线交于F 、D 、E 三点，那么一定有AF FB ⋅BD DC ⋅CEEA=1．下面是利用相似三角形的有关知识证明该定理的部分过程：证明：如图2，过点A 作AG ∥BC ，交DF 的延长线于点G ，则有AF FB =AG BD ，CE EA =CDAG，∴△AGF ∽△BDF ，△AGE ∽△CDE ，∴AF FB ⋅BD DC ⋅CE EA =AG BD ⋅BD DC ⋅CDAG=1．请用上述定理的证明方法解决以下问题：(1)如图3，△ABC 三边CB ,AB ,AC 的延长线分别交直线l 于X ,Y ,Z 三点，证明：BX XC ⋅CZ ZA ⋅AYYB=1．请用上述定理的证明方法或结论解决以下问题：(2)如图4，等边△ABC 的边长为3，点D 为BC 的中点，点F 在AB 上，且BF =2AF ,CF 与AD 交于点E ，试求AE 的长．(3)如图5，△ABC 的面积为4，F 为AB 中点，延长BC 至D ，使CD =BC ，连接FD 交AC 于E ，求四边形BCEF 的面积．7(2023.山东九年级月考)如图：P ，Q ，R 分别是△ABC 的BC ，CA ，AB 边上的点．若AP ，BQ ，CR 相交于一点M ，求证：BP PC ⋅CQ QA ⋅ARRB=1．8(2023.浙江九年级期中)如图，在锐角△ABC 中，AD 是BC 边上的高线，H 是线段AD 内任一点，BH 和CH 的延长线分别交AC 、AB 于E 、F ，求证：∠EDH =∠FDH 。

数学初中竞赛：《梅涅劳斯定理和塞瓦定理》训练(含答案)

训练与解析：1．如图，在△ABC中，AB＞AC，内切圆⊙I与边BC切于点D，AD与⊙I的另一个交点为E，⊙I的切线EP与BC的延长线交于点P，CF∥PE且与AD交于点F，直线BF与⊙I交于点M、N，M在线段BF上，线段PM与⊙I交于另一点Q．证明：∠ENP＝∠ENQ．证明：如图，设⊙I与AC、AB分别切于点S、T，连接ST、AI、IT，设ST与AI交于点G．则IE⊥PE，ID⊥PD，故I、E、P、D四点共圆，∵AS2＝AE•AD＝AG•AI，∵∠EAG＝∠DAI，∴△AEG∽△AID，∴∠AGE＝∠AID，∴E，G，D，I四点共圆，∴I、G、E、P、D五点共圆，∴∠IGP＝∠IEP＝90°，即IG⊥PG，∴P、S、T三点共线，对直线PST截△ABC，由梅涅劳斯定理知，∵AS＝AT，CS＝CD，BT＝BD，∴，设BN的延长线与PE交于点H，对直线BFH截△PDE，由梅涅劳斯定理知，∵CF∥BE，∴，∴，∴PH＝HE，∴PH2＝HE2＝HM•HN，∴，∴△PHN∽△MHP，∴∠HPN＝∠HMP＝∠NEQ，∵∠PEN＝∠EQN，∴∠ENP＝∠ENQ．2．如图，△ABC的垂心为H，AD⊥BC于D，点E在△ABC的外接圆上，且满足，直线ED交外接圆于点M．求证：∠AMH＝90°．证明：作高BP，CQ．连结MB、MC、MP、MQ、PQ．＝＝＝•①＝•＝•②由①②得：＝，又∵∠MBA＝∠MCA，∴△MBQ∽△MCP，∴点M、A、P、Q四点共圆，即点M、A、P、Q、H五点共圆，又AH为直径，∴∠AMH＝90°．3．如图，在四边形ABCD中，对角线AC平分∠BAD．在CD上取一点E，BE与AC相交于F，延长DF交BC于G．求证：∠GAC＝∠EAC．证明：如图，连接BD交AC于H，过点C作AB的平行线交AG的延长线于I，过点C作AD的平行线交AE的延长线于J．对△BCD用塞瓦定理，可得①因为AH是∠BAD的角平分线，由角平分线定理知．代入①式得②因为CI∥AB，CJ∥AD，则，．代入②式得．从而CI＝CJ．又由于∠ACI＝180°﹣∠BAC＝180°﹣∠DAC＝∠ACJ，所以△ACI≌△ACJ，故∠IAC＝∠JAC，即∠GAC＝∠EAC．4．如图，四边形ABFD中，C、E分别为BF、DF上一点，且∠BAC＝∠DAE，BE、CD交于点G，连接AG，求证：∠FAC＝∠GAE．证明：根据三角形的面积公式知，＝＝，＝＝，＝＝．又根据梅涅劳斯定理知，＝1．所以××＝1．整理即可得到：＝．又因为∠BAC＝∠DAE，所以∠FAC＝∠GAE．5．梅涅劳斯定理是古希腊数学家梅涅劳斯首先证明的．它指出，如果一条直线与△ABC的三条边AB、BC、CA（或其延长线）分别交于F、D、E，则有＝1．解答以下两个问题：（1）如图1所示，AB＝AC＝6，D为BC中点，点E在AC上，CE＝2，点F在AB的延长线上，求FB的长．（2）如图2所示，等腰直角三角形ABC中，∠ACB＝90°，D是BC中点，E在AB上，AE ＝2EB，连接AD、CE，求证：AD⊥CE．解：（1）∵AC＝6，CE＝2，∴AE＝AC﹣CE＝4，∵点D是BC的中点，∴BD＝CD，∵AB＝6，∴AF＝AB+FB，根据梅涅劳斯定理得，＝1，∴，∴FB＝6；（2）如图，过点B作BF⊥BC交CE的延长线于F，∴∠CBF＝90°，∵∠ACB＝90°，∴∠ACB+∠CBF＝180°，∴BF∥AC，∴∠ACE＝∠F，∠CAE＝∠FBE，∴△ACE∽△BFE，∴＝2，∴AC＝2BF，∵点D是BC的中点，∴BC＝2CD，在等腰直角三角形ABC中，∠ACB＝90°，∴AC＝BC，∴BF＝CD，在△ACD和△CBF中，，∴△ACD≌△CBF，∴∠CAD＝∠BCF，∴∠ACE+∠CAD＝∠ACE+∠BCE＝∠ACB＝90°，∴∠AGC＝90°，∴AD⊥CE．6．在梯形ABCD中，AB∥CD，AC、BD交于点E，AD、BC的延长线交于点H，过点E作FG∥AB交AD于点F，交BC于点G，求证：AG、BF、EH三线共点．证明：∵FG∥AB，∴，，∴•＝1，同理：＝1，∵点E为△HAB的赛瓦点，∴＝1，∴＝1，∴＝1，∴AG、BF、EH三线共点．7．如图，在△ABC中，AQ平分∠BAC，QD⊥BC交BC于点D，在BC上取一点E，使得∠BAD ＝∠CAE，在AE上存在一点K，使得∠KBC＝2∠BQD，求证：QK平分∠BKC．证明：如图，作∠CBK的角平分线交QK于I，延长AD，AE交BQ，CQ于M，N，连接CM交AB的延长线于X，连接BN交AC的延长线于Y，BN，CM交于F，AQ交BC于G，设∠BAM＝∠CAN＝α，∠MAQ＝∠NAQ＝β，∵AQ平分∠BAC，∴①，∵∠KBC＝∠2∠BQD＝2∠CBI，∵QD⊥BC，∴∠DBQ+∠BQD＝90°＝∠DBQ+∠CBI，∴BI⊥BQ，由同角的内、外角平分线互相垂直，得：BQ平分∠XBC，∴，∵②，③，由①②③得，＝1，由塞瓦定理的逆定理得，BN，CM，AQ交于一点F，点F对于△ABC，由塞瓦定理（延长线）得，＝1，∴，∴C Y＝④，∵，∴⑤∵，∴⑥由⑤⑥得，，∴⑦，由④⑦得，，∴，由角平分线的逆定理得，CQ平分∠BCY，∴Q是△KBC的旁心，∴QK平分∠BKC．8．如图，已知△ABC中，M是BC的中点，AD平分∠A，B在AD上的射影为E，EB交AM于N，求证：DN∥AB．证明：延长BE、AC交于点F，连接ME，如图：∵AE平分∠BAC，AE⊥BE，∴BE＝EF，∵BM＝CM，∴EM∥AF，∴，∴，对于△BDE和截线AMN，由梅涅劳斯定理可得，∴，∴，∴DN∥AB．证毕．9．如图，在梯形ABCD的对角线AC的延长线上任取一点P，过点P与梯形两条底边的中点的连线分别交腰AB、CD于点M、N，求证：MN∥AD∥BC．证明：对于△ABC和截线MKP，由梅涅劳斯定理可得：，∵BK＝CK，∴；对于△ACD和截线PNL，由梅涅劳斯定理可得：，∵AL＝LD，∴，∴，∴MN∥AD∥BC．10．如图，Rt△ABC中，∠C＝90°，D点和E点在AC，AB边上，且DE∥BC．P为线段DE 上一点，使得∠CPB＝90°，CP的延长线交AB于点M，延长AP交BC于点Q，过Q作PB 的平行线交PC于点H，交AC于点S，T为BC延长线上一点，且满足＝+，连接TS．求证：TS⊥DQ．证明：如图，连接DT、ET，∵DE∥BC，∴，，∴，∵QS∥PB，∴，∴，∵＝+，∴，∴，由梅涅劳斯定理的逆定理可知E、H、T三点共线，∴，∴CT＝DP，∵CT∥DP，∴TCPD是平行四边形，∴DT∥CP，∵QS∥PB，CP⊥PB，∴QS⊥DT，∵DC⊥TQ，∴S是△TDQ的垂心，∴TS⊥DQ．证完．11．如图，设P为▱ABCD内任意一点，过P作EF∥AB，GH∥BC，EF交A，BC于点E，F，GH 交AB，DC于点G，H，且AC，GF，EH不平行．求证：A C，GF，EH相交于一点．证明：设AC、EH相交于点K，对于△CAD与截线EHK，由梅涅劳斯定理可得：，∵ABCD是平行四边形，且EF∥AB，GH∥BC，∴，，∴，由梅涅劳斯定理的逆定理可知G、F、K三点共线，∴AC，GF，EH相交于一点．12．如图所示，已知D，E分别是△ABC的边BC，AB上的点，AD，CE交F，BF，DE交于G，过G作BC的平行线MN，交AB，CE，AC于M，H，N，求证：GH＝NH．解：过点E作ES∥BC，交AC于点S，∴，∵NM∥BC，∴，对于△ABF及截线EGD，由梅捏劳斯定理可得：，∴，由梅捏劳斯定理可知：S、H、D共线，∴，∴GH＝HN．13．在△ABC中，D，E分别为AB，AC上一点，DE交AF于H，HG⊥BC，连接DG，GE．（1）证明：GH为△DGE的一条平分线；（2）过H的一条直线交DF，AE分别于M，N，证明：GH为△MNG的一条角平分线．证明：（1）延长ED与CB的延长线交于K，对于直线CBK截得△ADE，由梅涅劳斯定理得：••＝1①，对于点F与△ADE，由塞瓦定理得：••＝1②，①＝②得：＝，∴线段DE被点H、K调和，∵∠KGH＝90°，由调和点列结论1得，GH平分∠DGE，即GH为△DGE的一条平分线；（2）延长NM交BC于S，连接AM并延长，交BC于T，对于直线STC截得△AMN，由梅涅劳斯定理得：••＝1①，对于点F与△AME，由塞瓦定理得：••＝1②，①＝②得，＝，∴线段MN被点H、S调和，∵∠KGH＝90°，由调和点列结论1得，GH平分∠MGN，即GH为△MNG的一条角平分线．14．定理3 （梅涅劳斯（M enelaus）定理）：一条不经过△ABC任一顶点的直线和三角形三边BC，CA，AB（或它们的延长线）分别交于P，Q，R．证明：．证明：如图，由三角形面积的性质，有①，②，③．由①×②×③，得．15．由矩形ABCD的外接圆上任意一点M向它的两对边引垂线MQ和MP，向另两边延长线引垂线MR，MT．证明：PR与QT垂直，且它们的交点在矩形的一条对角线上．解：连接BD交PR于N，连接QN、DM、DB、AM、BN、MN、TN、MC，显然M、P、Q共线，R、M、T共线，在矩形APMR中，∠1＝∠2＝∠3，∴R、D、N、M四点共圆，∴R、D、N、Q、M五点共圆，∴∠RNQ＝90°，∠6＝∠7，在矩形QCTM中，∠5＝∠4＝∠2，∴∠5+∠6＝∠2+∠7＝90°，∴∠NQT＝∠5+∠DQM+∠6＝180°，∴N、Q、T共线，∴TQ⊥PR且它们的交点在矩形的一条对角线上．。

初中数学竞赛专题.梅涅劳斯定理与塞瓦定理.(有答案)

第 1 页板块一梅涅劳斯定理及其逆定理梅涅劳斯定理：如果一条直线与ABC △的三边AB 、BC 、CA 或其延长线交于F 、D 、E 点，那么1AF BD CE FB DC EA⋅⋅=．这条直线叫ABC △的梅氏线，ABC △叫梅氏三角形．证法一：如左图，过C 作CG ∥DF证法二：如中图，过A 作AG BD ∥交DF 的延长线于G三式相乘即得：1AF BD CE AG BD DCFB DC EA BD DC AG⋅⋅=⋅⋅=．证法三：如右图，分别过A B C 、、作DE 的垂线，分别交于123H H H 、、．则有123AH BH CH ∥∥，所以3122311CH AH BH AF BD CE FB DC EA BH CH AH ⋅⋅=⋅⋅=．梅涅劳斯定理的逆定理：若F 、D 、E 分别是ABC △的三边AB 、BC 、CA 或其延长线的三点，如果1AF BD CE FB DC EA⋅⋅=，则F 、D 、E 三点共线．【例1】如图，在ABC △中，AD 为中线，过点C 任作一直线交AB 于点F ，交AD 于点E ，求证：:2:AE ED AF FB =．【解析】 ∵直线FEC 是ABD △的梅氏线，∴1AE DC BF ED BC FA ⋅⋅=．而12DC BC =，∴112AE BF ED FA ⋅⋅=，即2AE AF ED BF=．习题1. 在△ABC 中，D 是BC 的中点，经过点D 的直线交AB 于点E ，交CA 的延长线于点F ．求证：FA EAFC EB=．【解析】直线截ABC △三边于D 、E 、F 三点，应用梅氏定理，知1CD BE AFDB EA FC⋅⋅=，又因为BD BC =，所以1BE AF EA FC ⋅=，即FA EAFC EB=．习题2. 如图，在△ABC 中， 90ACB ∠=︒，AC BC =．AM 为BC 边上的中线，CD AM ⊥于点D ，CD 的延长线交AB 于点E ．求AEEB．【解析】由题设，在Rt AMC △中，CD AM ⊥，2AC CM =，由射影定理224AD AD AM AC DM DM AM CM⋅===⋅．对ABM △和截线EDC ，由梅涅劳斯定理，1AE BC MD EB CM DA ⋅⋅=，即21114AE EB ⋅⋅=．所以2AE EB=．知识导航夯实基础梅涅劳斯定理与塞瓦定理【例2】如图，在ABC △中，D 为AC 中点，BE EF FC ==，求证：::5:3:2BM MN ND =．【解析】 ∵直线AE 是BCD △的梅氏线，∵直线AF 是BCD △的梅氏线，习题3. 如图，在ABC △中，D 为BC 的中点，::4:3:1AE EF FD =．求::AG GH AB ．【解析】 ∵HFC 是ABD △的梅氏线，∵D 为BC 的中点，::4:3:1AE EF FD =， ∵GEC 是ABD △的梅氏线，【例3】过ABC △的重心G 的直线分别交AB 、AC 于点E 、F ，交CB 的延长线于点D ．求证：1BE CFEA FA+=．【解析】作直线AG 交BC 于M ，同理，2CF DCFA DM=，而2BD DC BD BD BM +=++2()2BD BM DM =+=【例4】如图，点D 、E 分别在ABC △的边AC 、AB 上， AE EB =，23AD DC =，BD 与CE 交于点F ，40ABC S =△．求AEFD S ．【解析】对ECA △和截线BFD ，由梅氏定理得：1EF CD AB FC DA BE ⋅⋅=，即32121EF FC ⋅⋅=，所以13EF FC =．所以1148BFE BEC ABC S S S ==△△△，进而211140115840AEFD ABD BEF ABC S S S S ⎛⎫=-=-=⋅= ⎪⎝⎭△△△．习题4. 如图，在ABC △中，三个三角形面积分别为5，8，10．四边形AEFD 的面积为x ，求x的值．【解析】对ECA △和截线BFD ，由梅氏定理得：1CD AB EF DA BE FC ⋅⋅=，即1823115152x x +⋅⋅=+，解得22x =．【备选】如图，ABC △被通过它的三个顶点与一个内点O 的三条直线分为6个小三角形，其中三个小三角形的面积如图所示，求ABC △的面积．【解析】对ABD △和截线COF ，由梅氏定理得：1AF BC DO FB CD OA ⋅⋅=，即41132BC CD ⋅⋅=，所以32BC CD =，所以3BCBD=．所以33105315ABC ABD S S ==⨯=△△．【例5】如图，在ABC △中，A ∠的外角平分线与边BC 的延长线交于点P ，B ∠的平分线与边CA 交于点Q ，C ∠的平分线与边AB 交于点R ，求证：P 、Q 、R 三点共线．【解析】 AP 是BAC ∠的外角平分线，则BQ 是ABC ∠的平分线，则 CR 是ACB ∠的平分线，则 ⨯⨯①②③得非常挑战探索提升第 3 页因R 在AB 上，Q 在CA 上，P 在BC 的延长线上，则根据梅涅劳斯定理的逆定理得：P 、Q 、R 三点共线．习题5. 证明：不等边三角形的三个角的外角平分线与对边的交点是共线的三个点．【解析】如图，CD BE AF 、、分别为三角形ABC 的三个外角平分线，分别交AB AC BC 、、于D E F 、、．过C 作BE 的平行线，则BCP CBE EBD CPB ∠=∠=∠=∠，所以BPC △是等腰三角形．则PB CB =．则有：CE PB CBEA BA BA ==．同理AD AC DB CB =；BF BA FC AC=．所以1CE AD BF CB AC BA EA DB FC BA CB AC ⋅⋅=⋅⋅=．所以D E F 、、共线．板块二塞瓦定理及其逆定理塞瓦定理：如果ABC △的三个顶点与一点P 的连线AP 、BP 、CP 交对边或其延长线于点D 、E 、F ，如图，那么1BD CE AFDC EA FB⋅⋅=．通常称点P 为ABC △的塞瓦点．证明： ∵直线FPC 、EPB 分别是ABD △、ACD △的梅氏线，两式相乘即可得：1BD CE AFDC EA FB⋅⋅=．塞瓦定理的逆定理：如果点D 、E 、F 分别在ABC △的边BC 、CA 、AB 上或其延长线上，并且1BD CE AF DC EA FB⋅⋅=，那么AD 、BE 、CF 相交于一点（或平行）．证明： ⑴ 若AD 与BE 相交于一点P 时，如图，作直线CP 交AB 于'F ．由塞瓦定理得：'1BD CE AF DC EA F B⋅⋅='，又已知1BD CE AF DC EA FB ⋅⋅=，∴AF AF FB F B'='， ∴'F 与F 重合 ∴'CF 与CF 重合∴AD 、BE 、CF 相交于一点．⑵ 若AD 与BE 所在直线不相交，则AD ∥BE ，如图． ∴BD EA DC AC=，又已知1BD CE AF DC EA FB ⋅⋅=， ∴1EA CE AF AC EA FB ⋅⋅=，即CE FB AC AF=．说明：三线平行的情况在实际题目中很少见．【例6】（1）设AX BY CZ ，，是ABC △的三条中线，求证：AX BY CZ ，，三线共点．探索提升知识导航（2）若AX BY CZ ，，为ABC △的三条内角平分线．求证：AX BY CZ ，，三线共点．【解析】（1）由条件知，BX XC YC YA ZA ZB ===，，．∴1BX CY AZXC YA ZB⋅⋅=，根据塞瓦定理的逆定理可得三条中线AX BY CZ ，，共点．这个点称为这个三角形的重心．（2）由三角形内角平分线定理得：BX AB CY BC AZ ACXC AC YA BA ZB BC===，，．三式分别相乘，得：1BX CY AZ AB BC ACXC YA ZB AC AB BC⋅⋅=⋅⋅=．根据塞瓦定理的逆定理可得三角形三内角平分线AX BY CZ ，，共点，这个点称为这个三角形的内心．习题6. 若AX BY CZ ，，分别为锐角ABC △的三条高线，求证：AX BY CZ ，，三线共点．【解析】由ABX CBZ △∽△得：BX AB BZ BC =；由BYA CZA △∽△得：AZ ACAY AB =；由AXC BYC △∽△可得：YC BC CX AC =．所以1BX AZ YC AB AC BCBZ AY CX BC AB AC⋅⋅=⋅⋅=．根据塞瓦定理的逆定理可得三条高线AX BY CZ ，，共点．对直角三角形、钝角三角形，同样也可以证得三条高线共点．我们把一个三角形三条高线所在直线的交点叫做这个三角形的垂心．【例7】如图， M 为ABC △内的一点，BM 与AC 交于点E ，CM 与AB 交于点F ，若AM 通过BC 的中点D ，求证：EF BC ∥．【解析】对ABC △和点M 应用塞瓦定理可得：1AF BD CEFB DC EA⋅⋅=．又因为BD DC =，所以1AF CE FB EA ⋅=．进而AF AEFB EC=，所以EF BC ∥．习题7. 如果梯形ABCD 的两腰AD 、BC 的延长线交于M ，两条对角线交于N ．求证：直线MN必平分梯形的两底． ∵1MD AQ BC DA QB CM⋅⋅=（由塞瓦定理得）板块三梅涅劳斯定理、塞瓦定理综合【备选】如图，E 、F 分别为ABC △的AC 、AB 边上的点，且3AE EC =，3BF FA =，BE 、CF 交于点P ，AP 的延长线交BC 于点D ．求:AP PD 的值．【解析】 ∵P 为ABC △的塞瓦点．∵EPB 为ACD △的梅氏线，【备选】如图，四边形ABCD 的对边AB 和DC ，DA 和CB 分别相交于点L K ，，对角线AC 与BD 交于点M ．直线KL 与BD 、AC 分别交于点F G 、．求证：KF KGLF LG=．【解析】对DKL △与点B 应用塞瓦定理得：1DA KF LCAK FL CD⋅⋅=．对DKL △和截线ACG 应用梅涅劳斯定理可得：1DA KG LCAK GL CD⋅⋅=．非常挑战进而可得KF KGLF LG．第 5 页。

梅涅劳斯定理与塞瓦定理

塞瓦定理设O 是△A B C 内任意一点，A B 、B O 、C O 分别交对边于D 、E 、F ，则??B D /D C *C E /E A *A F /F B =1（Ⅰ）本题可利用梅内劳斯定理证明：∵△ADC 被直线BOE 所截，∴? ?CB/BD*DO/OA*AE/EC=1??①而由△ABD 被直线COF 所截，∴??BC/CD*DO/OA*AF/DF=1②①÷②:即得：BD/DC*CE/EA*AF/FB=1（Ⅱ）也可以利用面积关系证明∵BD/DC=S △ABD/S △ACD=S △BOD/S △COD=(S △ABD-S △BOD)/(S △ACD-S △COD)=S △AOB/S △AOC??③同理 CE/EA=S △BOC/ S △AOB??④? ?? ? AF/FB=S △AOC/S △BOC? ?⑤③×④×⑤得BD/DC*CE/EA*AF/FB=1塞瓦定理：1:=⋅⋅∆RBARQA CQ PC BP CR BQ AP AB CA BC ABC R Q P 的充要条件是三线共点、、边上的点，则、、的分别是、、设B 1C ,111BCM ACMABP BMP ABM ACP CMP ACM ABM BCMAP BQ CR M S S S S S BP CQ AR PC S S S QA S RB S BP CQ AR PC QA RB BP CQ AR AP BQ M CM AB R PC QA RB BP CQ AR AR PC QA R B ∆∆∆∆∆∆∆∆∆∆=====⋅⋅⋅⋅=⋅⋅=‘拻‘证：先证必要性：设、、相交于点，则：同理：以上三式相乘，得：＝再证充分性：若，设与相交于，且直线交于，由塞瓦定理有：，于是：ARR R R B RB AB R R AP BQ CR M ’‘’＝因为和都在线段上，所以必与重合，故、、相交于一点点；交于一点；：证明：三角形的中线例1111111111111111111,,1AC BA CBABC AA BB CC C B AC B A AC BA CB AC C B BA AC CB B A ABC ∆⋅⋅====⋅⋅=∴∆证明：记的中线，，，我们只须证明而显然有：即成立，交于一点；1CK AB CK BM AN AM CN BK MC CN MC NB AKAM BK AM AML AK NB AK AC BK BC BNL BKC NB BL ⊥⋅⋅==⋅=∆≅∆⇒=∴∆≅∆⇒=证：作下证、、依塞瓦定理即要证：又即要证明：AL AC CK BM AN P ∴依三角形的角平分线定理可知：、、三线共点，且为点3.AD ABC D BC P AD BP CP AC AB E F EDA FDA∆∠∠例设是的高，且在边上，若是上任一点，、分别与、交于和，则＝A AD DE DF M N EDA FDA ∠=∠证：过作的垂线，与、的延长线分别交于、。