第二章 塞瓦定理及应用
赛瓦定理证明

赛瓦定理证明摘要:一、引言1.赛瓦定理的背景与意义2.赛瓦定理在数学领域的重要性二、赛瓦定理的证明1.赛瓦定理的概念与基本原理2.证明过程的step-by-step 解析3.重要结论与推论三、赛瓦定理的应用1.应用场景与领域2.对相关研究与技术的推动作用四、总结1.赛瓦定理证明的关键点回顾2.对赛瓦定理的理解与启示正文:一、引言赛瓦定理,作为数学领域中一条重要的定理,一直备受学者们的关注。
它不仅具有深刻的理论意义,而且在实际应用中也发挥着重要作用。
本文将对赛瓦定理的证明过程进行详细解析,以帮助读者更好地理解这一定理。
二、赛瓦定理的证明1.赛瓦定理的概念与基本原理赛瓦定理,又称切比雪夫定理,是关于复数域上多项式函数的性质的一个定理。
它表明,如果一个n 次多项式在复数域上具有n+1 个不同的根,那么至少有一个根是复数。
这一定理得名于19 世纪的俄国数学家赛瓦·切比雪夫。
2.证明过程的step-by-step 解析(1)首先,我们假设f(x) 是一个n 次多项式,在复数域上有n+1 个不同的根,记作a1, a2, ..., an+1。
(2)根据拉格朗日定理,我们知道f(x) 的n 次导数f^(n)(x) 在某个点x0 处等于0 的充分必要条件是x0 是f(x) 的一个驻点。
(3)由于f(x) 是一个n 次多项式,它的n 次导数f^(n)(x) 是一个n 次多项式。
根据代数学原理,我们知道n 次多项式的根的个数不超过n 个。
(4)然而,已知f(x) 在复数域上有n+1 个不同的根,这与代数学原理产生矛盾。
(5)因此,假设不成立,即至少存在一个根是复数。
3.重要结论与推论赛瓦定理的证明告诉我们,对于n 次多项式在复数域上的根,其个数不能超过n 个,这为研究复数域上多项式函数的性质提供了重要的理论依据。
三、赛瓦定理的应用1.应用场景与领域赛瓦定理在诸如代数、复分析、代数几何等领域中都有着广泛的应用。
最新整理第二章塞瓦定理及应用上课讲义
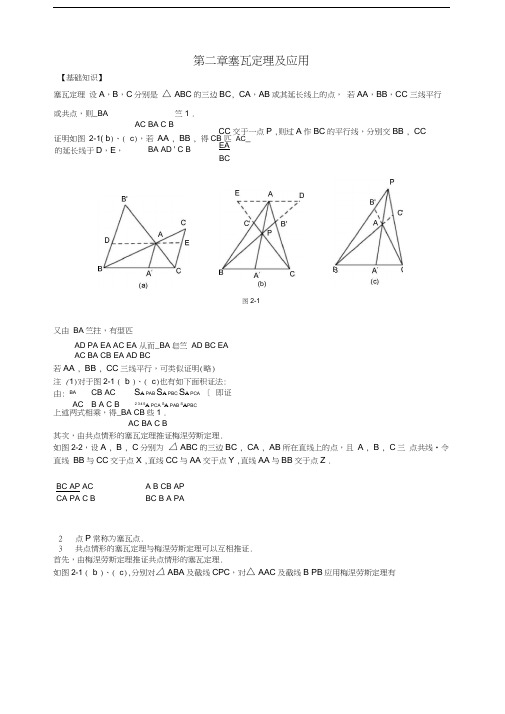
第二章塞瓦定理及应用图2-1又由 BA 竺拄,有型匹AD PA EA AC EA 从而_BA 皂竺 AD BC EA AC BA CB EA AD BC若AA , BB , CC 三线平行,可类似证明(略) 注 (1)对于图2-1 ( b )、( c )也有如下面积证法:由: BA CB ACS A PAB S A PBC S A PCA 〔 即证 AC B A C B 2 3 45A PCA S A PAB S A PBC上述两式相乘,得_BA CB 些1 .AC BA C B其次,由共点情形的塞瓦定理推证梅涅劳斯定理.如图2-2,设A , B , C 分别为 △ ABC 的三边BC , CA , AB 所在直线上的点,且 A , B , C 三 点共线•令直线 BB 与CC 交于点X ,直线CC 与AA 交于点Y ,直线AA 与BB 交于点Z .2 点P 常称为塞瓦点.3 共点情形的塞瓦定理与梅涅劳斯定理可以互相推证. 首先,由梅涅劳斯定理推证共点情形的塞瓦定理.如图2-1 ( b )、( c ),分别对△ ABA 及截线CPC ,对△ AAC 及截线B PB 应用梅涅劳斯定理有【基础知识】塞瓦定理 设A ,B ,C 分别是 △ ABC 的三边BC , CA ,AB 或其延长线上的点, 若AA ,BB ,CC 三线平行或共点,则_BA竺1 .AC BA C B证明如图 2-1( b )、( c ),若 AA , BB , 得CB 匹 AC _BA AD ' C B CC 交于一点P ,则过A 作BC 的平行线,分别交BB , CC的延长线于D ,E ,EA BCBC AP AC CA PA C BA B CB AP BC B A PA(b)分别视点C , A ,B ,C , A , B 为塞瓦点,应用塞瓦定理,即对△ BCB 及点 C (直线 B A , CX , BA 的交点),有BACA BX 1AC AB XB对△ CAC 及点 A (直线 C B , AY , CB 的交点),有CBAB C Y 1 .BC BC YC对△ ABA 及点 B (直线 A C , BZ ,AC 的交点),有ACBC AZ 1C B CA ZA对△ BBC 及点 C (直线 B A , BA , CX 的交点),有BX BA C A 1 .XB AC AB对△ CCA 及点 A (直线 C B ,CB ,AY 的交点),有CYC B AB 1YCBA BC对△ AAB 及点 B (直线 A C ,AC ,BZ 的交点),有AZ AC BC 1ZA CB CABA CB 2AC1 .上述八式相乘,有AC BA C BBA CB AC1 , ②AC BA C B则AA , BB , CC 三直线共点或三直线互相平行.证明若AA 与BB 交于点P ,设CP 与AB 的交点为C 1,则由塞瓦定理,有 BA CB AC 1 1,又已知有 BA CB 也 1 ,由此得 AC 1 AC ,即 AC 1 AC ,亦即 AG AC , AC BA C 1BAC BA GBC 1BC B AB AB故G 与C 重合,从而 AA , BB , CC 三线共点.若 AA II BB ,贝U CB CB 代入已知条件,有 AC -AC 由此知CC II AA ,故B A BACBCBAA II BB II CC .上述两定理可合写为: 设A , B , C 分别是△ ABC 的BC , CA , AB 所在直线上的点,则三直线AA ,BB , CC 平行或共点的充要条件是 旦ACB 也 1 .③故 BA CB ACAC BA C B 塞瓦定理的逆定理 设A , B , C 分别是△ ABC 的三边BC , CA , AB 或其延长线上的点,若AC BA C B的是三边所在直线上的点或者两点在边的延长线上,或者没有点在边的延长线上•④、⑤式中的角也 可按①式的对应线段记忆.推论设A 1,吕,G ,分别是△ ABC 的外接圆三段弧 BC , C A , A B 上的点,贝y AA , BB 1 , CC 1共点的充要条件是 BA 1 CB 1 AC 1 AC Bi A C 1B证明 如图2-3,设厶ABC 的外接圆半径为 R , AA 交BC 于A , B^交CA 于B , CC 1交AB 于C .由BA 1 2R sin Z BAA 1 sin Z BAA AC 2R sin Z AAC sin ZAAC同理 CB 1 sin Z CBB AC 1 sin Z ACC'B 1A sin Z BBA‘ C 1B sin Z C CB '三式相乘,并应用第一角元形式的塞瓦定理即证.为了使读者熟练地应用塞瓦定理,针对图 2-4中的点A 、B 、C 、D 、E 、F ,将其作为塞瓦点,我 们写出如下式子:此文档收集于网络,如有侵权,请 联系网站删除第一角元形式的塞瓦定理设A , B , C 分别是△三直线AA , BB , CC 平行或共点的充要条件是sin Z BAA sin Z ACC sin Z A AC sin Z C CB证明由_BA 氐ABAAC S^ AACsin Z CBB1 •sin Z B BAAB sin Z BAA AC sin Z AACCB 'BA BC ABC 的三边 sin / CBB AB sin / B BA BC , CA , AB 所在直线上的点,则AC CBAC sin z CCCB ,三式相乘,再运用塞瓦定理及其逆定理,知结论成立. 第二角元形的塞瓦定理设A , B , C在厶ABC 的三边所在直线上的点,贝U sin Z BOA sin Z AOC sin Z COB sin Z AOC sin Z COB sin Z BOA 证明注意到塞瓦定理及其逆定理,有 1 BA CB AC S ^ BOA S ^ COBAC BA C B BOAAOC S ^ B OACO sin z COB AO sin Z BOA分别△ ABC 的三边BC ,AA ,BB ,CC 平行或共点的充要条件疋 CA , AB 所在直线上的点, 0是不旦AOCS^ C OBAO sin Z AOC BO sin Z COBBO sin Z BOA CO sin Z AOC 由此即证得结论.注 在上述各定理中,若米用有向线段或有向角,则①、②、③、④、⑤式的右端仍为 1 •特别要注意A , C 1,B , A 1,C ,B 1六点共圆及正弦定理,有图2- 3A 图2-4对△ ACE及点D有ABBCCGGEEFFA1对厶CDE及点A有CF DBEG1FD BE GC对△ ADE及点C有DG AF EB1GA FE BD对△ ABD及点F有AC BE DH1CB ED HA对△ ACD及点E有AG DF CB1GD FC BA对△ ADF及点B有AH DC FE1HD CF EA对△ ABF及点D有BC AE FH1CA EF HB对厶BDF及点A有BE DC FH1ED CF HB【典型例题与基本方法】1恰当地选择三角形及所在平面上的一点,是应用塞瓦定理的关键例1四边形两组对边延长分别相交,且交点的连线与四边形的一条对角线平行. 证明:另一条对角线的延长线平分对边交点连线的线段. (1978年全国高中竞赛题)证明如图2-5,四边形ABCD的两组对边延长分别交于E , F,对角线BD II EF , AC的延长线交EF 于G .图2-5此文档收集于网络,如有侵权,请 联系网站删除对△ AEF 及点C ,应用塞瓦定理,有 EG FD AB , 1 .GF DA BE由BD II EF ,有AB AD ,代入上式,BE DF EG得—1,即EG GF .命题获证.GF例2如图2-6,锐角△ ABC 中,AD 是BC 边上的高,H 是线段AD 内任一点,BH 和CH 的延长线 分别交AC , AB 于E , F •求证:Z EDH Z FDH .(1994年加拿大奥林匹克试题)证法1对厶ABC 及点H ,应用塞瓦定理,有-At -BD C E 1 . ①FB DC EA过 A 作 PQ I BC ,延长 DF , DE 分别交 PQ 于 P , Q ,贝U DA 丄 PQ ,且△ APF s △ BDF ,△ AQE s △ CDE ,从而AFEAPA -BD ,AQDC .FBCE而由①,有 AF BD EA DC ,故 PA AQFBCE由此知AD 为等腰 △ APQ 底边PQ 上的高,故 Z EDH Z FDH .证法2 对△ ABC 及点H 应用塞瓦定理,有 注 将此例中的平角 Z BDC 变为钝角,则有如下:例3 如图2-7,在四边形 ABCD 中,对角线AC 平分Z BAD .在CD 上取一点E , BE 与AC 相交于F , 延长DF 交BC 于G •求证:Z GAC Z EAC .(1999年全国高中联赛题)AF BD CEFB DC EA S4 DAFBD& DCES A DFB DC S A DEA AD sin Z ADF BD sin Z FDBBD DC sin Z EDC DC AD sin Z ADEtan Z ADF cot Z ADE •即 tan Z ADE tan Z ADF ,由锐角性质知Z EDA Z FDA .类似地,对△ ABE 及截线FHC 或对△ AFC 及截线BHE 应用梅涅劳斯定理也可证得有Z EDA Z FDA .C连BD 交AC 于H ,对△ BCD 及点 BH DE1 .HD ECAH 平分Z BAD ,由角平分线性质,可得 BH AB 斗 CG AB DE ,故 1 • HD AD GB AD EC过点C 作AB 的平行线交AG 的延长线于I 故 Z GAC Z EAC •注 由此例还可变出一些题目,参见练习题第4、5及19题.例4 如图2-8, BE 是厶ABC 的中线,G 在BE 上,分别延长 AG , CG 交BC , AB 于D , F ,过D 作DN II CG 交BG 于N , △ DGL 及△ FGM 为正三角形.求证: △ LMN 为正三角形.证明 连NF ,对△ ABC 及点G 应用塞瓦定理,有 AF BD CE 1 .而 AE CE , 山AF DC 则 FB DC EAFB BD由 DN II CG ,由CD NGBD BN于是,有JA F NG ,从而FN II AD ,即知四边形 DNFG 为平行四边形,有 Z GDN Z GFN .FB BN又 Z GDL Z GFM 60,则 Z LDN Z NFM .而 DN GF FM , DL DG NF ,知△ LDN 也△ NFM ,有 LN MN , Z DNL Z NMF .于是Z MNL Z DNF - (Z DNL Z MNF ) Z DNF - (Z NMF Z MNF )=(180 - Z NFG) - (180 - Z NFM ) Z NFM - Z NFGZ MFG 60 .故厶LMN 为正三角形.例5 如图2-9,在一个△ ABC 中,Z C 2Z B , P ABC 内满足 AP AC 及PB PC 的一点.求证明 CG GB ,过点C 作AD 的平行线交AE 的延长线于J ,则CG GB 从而,又CI CI AB CI DE ECCJ•AD .所以C_竺AD 1 . CJ AB AD CJII AD ,有 Z ACI 180 - Z BAC 180 - Z DAC Z ACJ . II AB , CJ △ ACI ACJ ,即有 Z IAC Z JAC •IF ,应用塞瓦定理,有图2- 8证明 用 B 表示 Z ABC 的度量,令 Z PCB ,则 Z PBC , Z ABP B- , Z ACP 2B-,Z CAP n - 2 2B- (其中注意 AP AC ) , Z PAB Z A- Z CAPn - B - C - [ n - 2(2B -)](n - 3B) - ( n - 4B 2 ) B- 2 .对厶ABC 及点P ,应用第一角元形式的塞瓦定理,有 sin[ n - 2(2B -)] sin sin(B- )1I •sin(B - 2 ) sin(2B -) sin亦即 2sin(2B- ) cos(2B- ) sin(B-)〔.sin(B- 2 ) sin(2B-)于是 sin (B-2) 2si n( B - ) cos(2B - ) si n(3B-2)-si nB , 即 si nB si n(3B-2)-si n(B-2) 2cos(2 B - 2 ) si nB . 而 sinB 0 , 则 cos2(B-)12 .因 0 B-1b -(B3C) n ,则 2(B- ) 0, ¥3 3n 卄 n 2(B-) ,即B36 .从而Z CAPn - 2(2B- ) n - 4(B - )- 2n n--2 2 --2[(B-)-]3 62(B- 2 )2Z PAB .1故 Z PAB Z A ,即AP 是Z A 的三等分线.3利用第一角元形式的塞瓦定理可简捷处理2009年全国高中联赛加试第一题的第 1问:证:AP 是Z A 的三等分线.图2-9IMO 选拔赛题)例6设M 、N 分别为锐角 △ ABC (/A Z B )的外接圆 上弧?C 、Ac 的中点.过点C 作PC II MN交圆 于点P , I ABC 的内心,联结 PI 并延长交圆 于点•求证:MP MT NP NT .证明 事实上,易知 A 、I 、M 及B 、I 、N 分别三点共线,对 △ PMN 及点I 应用第一角元形式的 塞瓦定理 有 sin Z NPI sin Z PMI sin Z MNI 土 ' sin Z IPM sin Z IMN sin Z INP 由 CP II MN 知 PA PB ,有 Z PMI故 MP MT NP NT .2•注意塞瓦定理逆定理的应用以及与梅涅劳斯定理的配合应用例7 如图2-10,在△ ABC 中,Z BAC 90 , G 为AB 上给定的一点(G 不是线段 AB 的中点).设D 为直线GC 上与C , G 都不相同的任意一点,并且直线 AD , BC 交于E ,直线BD , AC 交于F ,直 线EF , AB 交于H .试证明交点 H 与D 在直线CG 上的位置无关.(1990年苏州市高中竞赛题)因此,点H 与D 在直线CG 上的位置无关.例8 如图2-11,设P 为△ ABC 内任一点,在形内作射线 AL , BM , CN ,使得Z CAL Z PAB , Z MBC ZPBA , Z NCA = Z BCP .求证: AL , BM , CN 三线共点.Z INP .于是①式即为NTM Tsin - Z B2 sin Z A 2CN CMMP NP证明 设G 分线段AB 为定比H 的位置由点 在△ ABC 中,AG BE CF G 唯一确定. 由AE , BF , 对△ ABC 及截线EFH 1, H 分线段AB 为定比2 •下证CG 交于一点D ,应用塞瓦定理,有BE CF 1 .1EC FA,应用梅涅劳斯定理,得BE CF -1 . 2EC FA、CF0 . 2)EC FA-1, 故2 由1唯一确定2由1确定,即当A , B 给定后,点图 2-101,即上述两式相加,得( 1 2从而1 2 0,即AH BE CF 1,即 HB EC FA证法1 设AL 交BC 于L , BM 交CA 于M , CN 交AB 于N ,则由正弦定理有 BL AB sin / BAL AB sin / PAC LC AC sin / CAL AC sin / PAB 'CM BC sin / PBA冋理,,MA AB sin / PBCAN AC sin / PCB NB BC sin / PCA将上述三式相乘,并应用正弦定理,有 BL CM AN sin / PAC sin / PBA sin / PCB LC MA NB sin / PAB sin / PBC sin / PCA 由塞瓦定理的逆定理,知 AL , BM , CN 共点. 证法2 设AL 交BC 于L , BM 交CA 于M ,E ,直线CP 交AB 于F .以上三式相乘,并注意到①式,有 BM 交AC 于M , CN 交AB 于N ,直线 AP 交BC 于D ,直线BP 交AC 于E ,直线交AB 于F •对△ ABC 及点P ,应用角元形式的塞瓦定理,有sin Z PAB sin Z PBC sin Z PCA ------------- --------------- --------------- 1 . sin Z PAC sin Z PBA sin Z PCB由题设 Z PAB Z CAL , Z PBA Z CBM , Z PCB Z ACN ,则有 Z BAL Z PAC , Z ABM Z PBC ,PC PA PB PA PB PCCN 交AB 于N ,直线 AP 交BC 于D ,直线BP 交AC 于对△ ABC 及点P ,应用塞瓦定理,有 AF BD 在△ ABL 和△ ACL 中应用正弦定理, BL BL AL sin / BAL sin / C LC AL LCsin Z PACsin Z CFB 有 DC CE 1 EA同理,CM- MA sin / B sin / LACsin / B sin 2 / C sin / PAB sin 2 / B AE sin / AAN EC sin / C NB DCAD BF FA sin Z c sin Z B AD sin 2Z CDC ~/BD sin Z BBDsin Z Br~\.sin Z Asin Z PAC sin Z PAB 2sin 2 Z C sin Z BBL CM AN DC AE BF LC MA NBBD EC FA 由塞瓦定理的逆定理,知 AL , 证法3 设AL 交BC 于L , BM ,CN 共点.图 2-11CZ BCN Z PCA.此文档收集于网络,如有侵权,请联系网站删除于是sin / BAL sin / CBM sin / ACN sin / PAC sin / PBA sin / PCB sin / CALsin / ABM sin / BCN sin / PAB sin / PBC sin / PCA1 1___________________________ _ 1 ,sin / PAB sin / PBC sin / PCA 1sin Z PAC sin Z PBA sin Z PCB对厶ABC,应用角元形式的塞瓦定理的逆定理,知AL , BM , CN三线共点.例9如图2-12,四边形ABCD内接于圆,其边AB与DC的延长线交于点P , AD与BC的延长线交于点Q,过点Q作该圆的两条切线,切点分别为E和F .求证:P , E , F三点共线.(1997年CMO试题)证明连EF分别交AD , BC于M , N,设AC与BD交于K .要证P , E , F三点共线,只须证明P , K , M 和P , N , K都三点共线,又只须证明AC , BD , PM三线共点.由塞瓦定理的逆定理知只须证明AB匹列1 BP CD MA又直线QCB截厶PDA,应用梅涅劳斯定理,有AB PCBP CD设圆心为DQ DM DQ1,从而只须证明QA AM AQO,连QO交EF于L ,连LD , LA , OD , OA,则由切割线走理和射影定理,有QD QA QE QL QO,即知D , L , O , A 四点共圆,有Z QLD Z DAO Z ODA Z OLA,此表明QL为△LAD的内角Z ALD的外角平分线•而EF丄OQ,贝U EL平分Z ALD •于是,DM DLAM ALDQ,结论获证.AQ【解题思维策略分析】1.获得线段比例式的一种手段例10 如图2-13, △ABC中,D , E分别为AC和AB同方向延长线上的点,BD与CE相交于P , 且BD CE •若点P 满足Z AEP - Z ADP k(Z PED - Z PDE)(k 为常数),贝U AB AC .图2-12EBCA S ^ DBC - 此时,点E 到BC 的距离不小于 D 到BC 的距离,则过E 作EF II BC 必交CD 延长线于一点,设为F .又 作△ FBC 的外接圆eO 交EF 于另一点 F ,则四边形 BCFF 为等腰梯形.当 AB A AC 时,由Z BFF Z FFC Z BCA >Z ABC Z AEF ,知 F 必在线段 EF 上,于是,Z BDC >Z BFC >Z BEC(同弧上的圆外角小于同弧上的圆周角) 又由PD < PE ,知Z PED <Z PDE .故结论获证. 2•转化线段比例式的一座桥梁例11设M 为△ ABC 内任1占 八、AM , BM , CM 分别交 BC , CA , AB 于 D , E , F •求证:MDME MF , 1 .BE CFAD证明 如图2-14 ,记 BD m , CEAF n , 1 .对△ ABC 及点M ,应用塞瓦定理,有DCEA FBBD CE AFmnl 1 .DC EA FB图 2-14对厶ADC 及截线EMB ,应用梅涅劳斯定理,有证明设AP 交BC 于Q ,对△ PBC 及其形外一点 A ,应用塞瓦定理,有 BQ CE PD 1QC EP DB而BD CE ,则 PD QC .PE QB不妨设QC < QB ,则PD < PE ,即有PCCE- PE < BD- PDPB ,于是 PBE 》PCD ,故AE图 2-13AM DB CE AM m- n 1,即MD BC EA MD 1 mAM 1 m(1 m)l .MD m n由合比定理得AD 1 (1m)l , 即MD 1MD AD 1 l ml同理,ME1lBE 1m mn 1ml1MF1mlCF 1 n n l ml 1 l二式相加,得MD ME MF 1 .AD BE CF例12 如图2-15,设P为△ ABC内任意一点,AP , BP , CP的延长线交对边BC , CA , AB于点D , E,F,EF 交AD 于Q .试证:PQ < (3- 2.2)AD .图2-15BD CE证明令m,DC EA对厶ADC及截线BPE,应用梅涅劳斯定理,有CE AP DBEA PD BC1 •注意到AF n,丘p ,对△ ABC及点PDB亠,则有BC m 1应用塞瓦定理,DCCE AFmnpEA FBAP nPD n m AP m1,即T 1 PD m1 n故AP ADm1mn m1又对直线APD 截△ BCE,有BD CA EP 1 . 而CA 彳n 1 ,则BP mn m,DC AE PB AE EP又对△ABP及截线FQE , 有AF BE PQ1,即有PQ1FB EP AQ AQ p(m n mPQ1AQ mp'p 2 '从而空PQ AP 1m1故AD AP AD mp p 21)mn m 1BEmnEP P(m 1)1mn1m 12mn1 p(m 1) 2m 1曰是,PQ w (3 - 2 . 2) AD .1mp p 11) > 2」空巳p(m 1) 2.J2中等号成立时成立,即当且仅当-2mn p(m 1)\m 1 m 1一2— p(m 1),亦即p(m 1) . 2时取等号•此时,m和p之间成为如p(m 1)例13 如图2-17,已知直线的三个定点依次为A、B、C ,的交点不依赖于圆的选取.证明设/ AQC的平分线交AC于点R,交圆于点S,其中S与Q是不同的两点.由于△PAC是等腰三角形,则有△旦sin/APBBC sin / CPBAR同理,在△ ASC中,有一一RCsin / ASQ sin / CSQ在△PAC中,视Q为塞瓦点,由角元形式的塞瓦定理,有sin/ APB sin/QAC sin / QCP〔.sin / CPB sin / QAP sin / QCA 注意到 / PAQ / ASQ / QCA , / PCQ / CSQ / QAC .则sin / APB sin / PAQ sin / QCA sin2/ ASQ、sin / CPB sin / QAC sin / PCQ sin2/ CSQ '图2-16别过A、C两点且与圆相切的直线交于点P , PB与圆交于点Q .证明:/ AQC的平分线与ACPS图2-172mn其中等号由p(mm 1亦即当且仅当2mnpP(m 1)图2-16的双曲线的关系.为过A、C且圆心不在AC上的圆,分(IMO 45预选题)此文档收集于网络,如有侵权,请 联系网站删除2 即 AB 竺,故结论获证.BC RC3 •求解三角形格点问题的统一方法 如果三角形的三个角的度数都是10的整数倍,三角形内一点与三角形的三个顶点分别连结后,得到的所有的角也都具有这个性质,我们称这样的点为三角形的格点.例14 如图2-18,在△ ABC 中,Z BAC 40 , Z ABC 60 , D 和E 分别是 AC 和AB 上的点,使 得/ CBD 40 , Z BCE 70 , F 是直线BD 和CF 的交点•证明:直线 AF 和直线BC 垂直.(1998年加拿大奥林匹克试题)关于 △ ABC 有 sin Z BAH sin Z ACD sin Z CBD sin Z HAC sin Z ECB sin Z DBA 三线共点,因此点 F 在AH 上,即卩AF 丄BC • 例 15 如图 2-19,在△ ABC 内取一点 M ,使得 Z MBA 30 , Z MAB 10 .设 Z ACB 80 , AC BC ,求Z AMC •(1983年前南斯拉夫奥林匹克试题)证明设Z BAF sin 10sin 70 sin ,则 Z FAC 40 -,对△ ABC 及点 F , sin 40 应用第一角元形式的塞瓦定理,有sin(40 - ) sin 20sin10 sin2sin 20 cos2°1,即有sin(40 - )2si n sin10 2si n cos80sin(80 ) sin( - 80 )•sin( -80 ) sin(40 -)-sin(80 ) 2cos60 sin(- 注意到0 40,知-80-20 - , - -80 20 ,有-80-20 -,故30 •)sin(-20 -延长AF 交BC 于H ,贝U ZAHB 180 注此题也可这样来解:由■^皿- 180 - 30 - 60 90 .故AF 丄BC •sin sin(40 -) sin sin 70 sin(40 -) sin 10 - sin40 小._ sin 10 2si n10 sin70 - sin 20 sin30sin 40sin 20sin(40 1,有三卩 sin 40 cot30 -cos40 •sin30 由于迥型二 sin所以 Z BAF 30 .故 Z ABC Z BAF 90 或者过点 A 作AH 丄BC 于H ,则Z BAH 30)sin40 cot - cos40 作为的函数在 (0 , 180 )上严格递减, 因此, Z HAC AF 丄 BC •10 •sin30sin10 1.所以,AH 、BD 、CEsin70 sin 20B图 2-18从而cos20 sin(40 -)sin 20 -Z FBC- Z ABH20因为sin(80----- 1 sin80 cot - cos80作为 的函数在(0, 180 )上严格递减,所以sinZ ACM 70 .故 Z AMC 180 - 40 - 70 70 .或者由Z AMB 140,令Z AMC x ,则Z CMB 220 - x .对△ MAB 和点C 应用第一角兀形式的塞瓦定理,有sin Z AMC 1sin Z CMB sin Z MBC sin Z BAC sin x sin 20 sin 50 sin Z CBA sin Z CAMsin(220 - x)sin 50 sin 40 贝 sin(220 - x)1sin(220 -70 ) sin 220cot 70 -cos220 .sin x2cos20si n70因为 sin(220 -sin x x) sin 220 cotx- cos220 (sin 2200)作为 x 的函数在(0 , 180 )上严格递增,所以Z AMC x 70 .例16 如图2-20 , △ ABC 具有下面性质:存在一个内部的点 P ,使得Z PAB 10 , Z PBA 20 ,从而 sinsin 10 sin(80 - )cos202si ncos80 2sin(80 -)cos20sin( 80 ) sin( - 80 ) sin(100 - )si n(60 -), sin(- 80 ) - sin(60 -) sin(100 -)-sin( 80 )2cos90 sin(10 - )0 .于是 sin( -80 ) sin(60 -).注意到 080 ,知-80-80 ,60 - 60 .-80 60 - ,故70 .所以 Z AMC 180 -Z MAC -Z ACM 180 - 40 - -70 7sin 20 sin30 为所求. 注此题结果也可直接由①式有解设/ ACM ,贝V ZMCB 80 - 由第一角元形式的塞瓦定理,有 sin si n10sin 80 - sin 40sin sin70 且0sin10 sin(80 -),80 -80,求得70 .另外,此题也可这样来解:由 sin sin10 sin 20 sin(80 -) sin10 sin 20sinsin 40 sin30sin(80 -) sin 40 sin30皿 sin(80 - 70 )sin80 cos20 sin 70cot 70 - cos80 .图 2-19此文档收集于网络,如有侵权,请联系网站删除Z PCA 30 , Z PAC 40 .证明:△ ABC是等腰三角形.(1996年美国第25届奥林匹克试题)证明设Z BCP 有sin 20 sin 40sin(80 - ) sin10,则Z PBC 180乩1 .sin 30即有2si n10 cos10sin(80 -)sin 40sin 10sin2-20-10 -40 - 30 - 80 -.由第一角元形式的塞瓦定理,sin(80 - ) 4sin4sin sin 20 sin 40sin 40 cos10 4sin sin 40 si n80sin80 sin60 sinsin 20sin(80 - ) sin 20 sin60sin 20sin从而sin(80 -) sin 60si n20 sin ,80 - 80 ,20,即Z ACB 50此题也可这样来求解:由Z CAB,从而ABsin 40sin 10sin 20sin(80 -)BC .sinsin30有si n(80sin-)si n20sin 404sin 20 sin 40 sin80sin 10si n30 1 U 011 1sin 20sin 60sin (80-20 )sin 80cot 20 - cos80 .sin 20sin 20因为sin(80-)sin 80cot -cos80作为的函数在(0,180 )上严格递减,所以Z BCP sin20,即Z ACB 50 还可对△APC及点B应用第一角元形式的塞瓦定理来求.4•论证直线共点的一种工具例17 如图2-21,在四边形ABCD中,AB AD , BC 其中EF交AB , CD于E , F , GH 交DA , BC于G , H .DC ,EH ,过AC , BD的交点O引EF , GH , GF分别交BD于P , Q,则OP OQ .(1990年CMO选拔试题)图2-20Z CAB .故AB BC .证明 设1A 与MN , BC 分别相交于点 G , D ,由Z AMG Z ADN , Z AGM Z AND 90,知Z MAG Z NAD ,即 Z BAD Z CAD .同理,设CA , AB 边上的高 BE , CF 的垂足分别为 E , F ,且l B , l C 分别与CA , AB 交于E , F , 则有Z CBE Z ABE , Z ACF Z BCF .由于△ ABC 的三条高相交于垂心,此时应用第一角元形式的塞瓦定理,得证明 若设 则 在AB , Z AOG ,又 连GH 交BD 于 G E BF HKEB FH KG BC 上分别取 ,/ AOG,故 K ,在△ S A OG E G , F , ,Z COH .又Z 1 BHG 中, S A OBF S A OHK AG AG , ,/ GOE / 4 CF CF , Z 1 , Z EOB ,故上1 Z 4 ,则由对称性可知有下列角相等,即 Z 2,/BOF Z 3,/FOH Z 4 , Z 2 Z 3.S A OEB S A OF H S A OKGOG OE sin Z 1 OB OF sin Z 3 OH OE OB sin Z 2 OF OH故由塞瓦定理的逆定理,知 例18 如图2-22,在锐角OK sin(Z 3 Z 4)1 .sin Z 4 OK OG sin(Z l Z 2)GF , BO , HE 共点,即G F 过点P •由对称性知, OP OQ .△ ABC 中,以A 点引出的高 AD 为直径作圆交 AB , AC 于M , N ,再从A 作1A 丄MN .同样可作出(第29届IMO 预选题)使 l B , l c .试证:二直线l A , l B , l c 相父于一点.C图 2-22sin / CAD sin / ABE sin / BCF sin / DAB sin / EBC sin / FCA 用等角代换上式,有sin / BAD sin / ACF sin / CBE sin Z DAC sin Z F CB sin Z E BA 故由第一角元形式的塞瓦定理,知AD , BE , CF 三线共点,即l A ,I B ,I C 相交于一点.例19如图2-23,四边形ABCD 内接于圆, P 为圆上任一点, PE , PF 分别交圆于 R , 点共线.证明 连 PD , AS , RC , BR , AP , SD . BR 由△ EBR s △ EPA , △ FDS s △ FPA ,有PA EB EPPAFP BR EB FP,此两式相乘,有①DS FDDS EP FD又由 △ ECREPD ,△ FPDFAS ,有CR EC PD FPPD EP , AS FA此两式相乘,有 CR EC FPAS EP FA由①②,得 BR AS EB FADS CREC FD上式两边同乘以DC,得 BR CD SA EB AF DCAB RC DS AB BA FD CE对厶EAD 及截线BCF ,应用梅涅劳斯定理,有 EB AF DCBA FD CEBD , RS , AC 交于一点•从而 R , T , S 三点共直线.【模拟实战】习题AAB , DC 的延长线交于E , AD , BC 的延长线交于 F ,S .若对角线 AC 与BD 相交于T ,求证:于是 BR CD SARC DC AB此时,应用第一角元形式的塞瓦定理的推论,知 F图 2-23BD i1.在△ ABC 中,D 是BC 上的点,,E 是AC 中点.AD 与BE 交于0 , CO 交AB 于F ,求DC 3四边形BDOF 的面积与△ ABC 的面积的比.2•若通过 △ ABC 各顶点的直线 AD , BE , CF 共点,并且它们在边 BC , CA , AB 所在直线上的截 点D ,E ,F 关于所在边中点的对称点分别为 D , E , F ,则直线AD , BE , CF 也共点.3. 一圆交△ ABC 的各边所在直线于两点,设 BC 边上的交点为D , D , CA 边上的交点为E , E , AB 边上的交点为 F , F •若AD , BE , CF 共点,贝U AD , BE , CF 也共点.4. 试证:过三角形顶点且平分三角形周长的三条直线共点. 5•将△ ABC 各内角三等分,每两个角的相邻三等分线相交得 △ PQR ,又AX , BY , CZ 分别平分Z BAC , Z ABC , Z ACB 且它们与 QR , RP , PQ 交于 X , Y , Z .求证:PX , QY , RZ 三线共 占八、、♦6. 将△ ABC 的各外角三等分,每两个外角的相邻三等分线相交得 △ DEF .又AX , BY , CZ 分别 平分Z BAC , Z ABC , Z ACB 且它们与 EF , FD , DE 交于 X , Y , Z .求证:DX , EY , FZ 三 线共点.7. eO 是厶ABC 的内切圆,BC , CA , AB 上的切点各是 D , E , F .射线DO 交EF 于A ,同样 可得B ,C .试证:直线AA , BB , CC 共点.AC 于M , CP 交AB 于N .求证:PMAN .(《数学教学》问题 531题) 13.在厶ABC 中,Z ABC 40 , Z ACB 20 , N 为形内一点,Z NBC 30, Z NAB 20,求 Z NCB 的度数.(《数学通报》问题1023题)14 .在△ ABC 中,Z BAC 80 , Z ABC 60 , D 为形内一点, 且 Z DAB 10 , Z DBA 20 ,求 Z ACD 的度数.(《数学通报》问题1142题)15 .在△ ABC 中,Z ABC 50 , Z ACB 30 , M 为形内一点, Z MCB 20 , Z MAC 40,求 Z MBC的度数.(《数学通报》问题1208题)16. △ ABC 中,Z ABC 70 , Z ACB 30 , P 为形内一点,Z PBC 40 , Z PCB 20 .求证:CA AB BP1 .(《数学通报》问题1306题)AP PC CB17.在△ ABC 中,Z ABC Z ACB 40,P , Q 为形内两点,Z PAB Z QAC 20 , Z PCBQCA10 .求证:B , P , Q 三点共线. (《数学通报》问题1243题) 18. △ ABC 中,Z ABC Z ACB 50 , P , Q 为形内两点, Z PCA Z QBC 10 , Z PAC Z QCB20 .求证:BP BQ .(《数学通报》问题1281题)的充要条件是 AA , BB i , CC i 三线共点.& △ ABC 在△ ABC 内部,且从A , B , C 各向BC , CA , AB 所作的垂线共点,则从 A , B , C 各向BC ,CA , AB 所作的垂线也共点.9 .在△ ABC 中, 度数.10 .在△ ABC 中, Z ABC Z ACB 40 , AB AC , Z A 80 , P 为形内一点, Z PAC 20 , Z PCB 30,求 Z PBC 的 11.在△ ABC 中, 度数.12 .在△ ABC 中,Z BAC 30 , Z ABC Z ABC 40 , Z ACBD 为形内一点,且 Z DAB Z DBA 10,求Z ACD 的度数.(《数学教学》问题432题)70 , M 为形内一点, Z MAB Z MCA 20,求 Z MBA 的(《数学教学》问题491题)30 , P 为Z ABC 的平分线上一点,使 Z PCB 10 , BP 交19.在△ ABC 中,AB AC , Z A 100 , I 为内心, 度数.D 为AB 上一点,满足BD BI .试求Z BCD 的(《数学通报》问题1073题)20. A 1 , A , B 1, B 2 , C 1 , C 2 顺次分别在△ ABC 的三边BC , CA , AB 上,且BAA e C , CB 1 B 2A ,AG C 2B ,过 A 2 , B 2 , C 2 分别作 AA , BBi , CC 1的平行线l a , l b ,1c .求证:l a , l b , l c 三线共点21 .在△ ABC中,AB AC , AD丄BC于D,过D任作两射线分别交AB , AC于点E , F,交过点A的平行线于G,H,且GH II BC .求证:AD , GF , HE共点.22•在△ABC中,过三边BC , CA , AB边中的中点M , N , L的三条等分三角形周长的直线MS , NT , LU (S , T , U在三角形三边上)分别交LN , LM , MN于D , E , F .求证:MS , NT , LU 三线共点.23. △ ABC的内切圆切BC , CA , AB于D , E , F . P是厶ABC内一点,PA交内切圆于两点,其中靠近A的一点为X,类似定义Y , Z .试证:DX , EY , FZ三线共点.24. △ ABC在厶ABC内部,AB的延长线分别交AC , BC于F5, P ; AC的延长线分别交BA ,BC于P3 , R ; BC的延长线分别交AB , AC于R , P2,且满足AR AP4 BB BP5 CP3 CP6 BP i CP2 AP3 .求证:AA ,BB ,CC 所在直线共点.(《中学数学教学》擂台题(28))25 •给定△ABC,延长边BC至D,使CD AC . △ACD的外接圆与以BC为直径的圆相交于C和P.设BP 与CP的延长线分别交AC和AB于E , F .求证:E , F , D共线.(第i5 届伊朗奥林匹克题)26.在厶ABC的边上向外作三个正方形,A , B i, C i是正方形中的边BC , CA , AB对边的中点.求证:直线AA i ,BB i ,CC i 共点.习题B1. eO是厶ABC的内切圆,D ,E , F,分别是BC , CA, AB上的切点,DD , EE , FF都是e O 的直径.求证:直线AD ,BE ,CF 共点.(《数学通报》问题i396 题)2. 四边形ABCD的内切圆分别与边AB , BC , CD , DA相切于E , F , G , H .求证:AC , BD , HF, GE四线共点. (《数学通报》问题1370题)3. 锐角△ ABC中,A角的平分线与三角形的外接圆交于另一点AM,点B , C i与此类似.直线AA i与B , C两角的外角平分线交于A o,点B o,C o与此类似.求证:(I)三角形A o B o C o的面积是六边形AC i BACB i的二倍;(H)三角形A o B o C o的面积至少是三角形ABC面积的四倍. (IMO -30试题)4. 设P ABC内一点,使/ BPA Z CPA, G是线段AP上的点,直线BG , CG分别交边AC , AB 于E , F .求证:Z BPF Z CPE .5. 在凸四边形ABCD中,对角线AC平分Z BAD , E是CD的延长线上的一点,BE交AC于点G , 延长DG交CB的延长线于F .试证:Z BAF Z DAE .6. 在△ABC中,AB AC , Z A ioo , I为内心,D为AB上一点,满足BD BI .试求Z BCD的度数. (《数学通报》问题io73题)7. 设△ABC是等边三角形,P是其内部一点,线段AP , BP , CP依次交三边BC , CA , AB于A ,吕,C i 三点.证明:AB B i C i C i A i > AB B i C C i A . (IMO -37预选题)8在一条直线I的一侧画一个半圆,C , D,是上两点,上过C和D的切线分别交I于B和A ,此文档收集于网络,如有侵权,请联系网站删除半圆的圆心在线段BA上,E是线段AC和BD的交点,F是I上的点,EF丄I •求证:EF平分Z CFD .(IMO -35 预选题)9•设A是锐角△ ABC的内接正方形的中心,其中内接正方形的两个顶点在BC边上,一个顶点在AB 边上,一个顶点在AC边上•同样定义两个顶点分别在AC边和AB边上的内接正方形的中心分别为B,,C i .证明:AA , BB , CC i交于一点. (IMO -42预选题)10 •以△ ABC的底边BC为直径作半圆,分别与AB , AC交于点D , E,分别过点D , E作BC的垂线,垂足依次为F ,G ,线段DG 和EF 交于点M •求证:AM 丄BC •(1996 年国家队选拔考试题)11 •设O, H是锐角△ ABC的外接圆的圆心和垂心•证明:存在 D , E , F分别在线段BC , CA ,AB上,使得OD DH OE EH OF FH,且此时AD , BE , CF三线交于一点.(IMO -41 预选题)12.已知AB是eO的直径,弦CD丄AB于L,点M和N分别在线段LB和LA上,且LM : MB LN : NA,射线CM , CN交e O于E , F .求证:AE , BF , OD三线共点.13 •设I是厶ABC的内心,以I为圆心的一个圆分别交BC于A , A2,交C于B1 , B?,交AB于G , C2 •这六个点在圆上的顺序为A1 , A2 , B1 , B2 , G, C2 •设A3, B3, C3为弧AA2 , B1B2 , C1C2的中点,直线A2A3 , B1B3相交于C4 ,直线B2B3, C1C3相交于A ,直线C2C3, A1A3相交于B4 •求证:直线A3A4 , B3B4, C3C4三线共点.14. 在厶ABC的边AB和AC上分别向形外作△ ABE和厶ACF ,使厶ABE s △ ACF ,且/ ABEZ ACF 90 .求证:连线BF , CE与边BC上的高AH三线共点.15. 过非等边三角形各顶点作其外接圆的切线,则各切线与其对边的交点共线.16 .在△ABC 内三点D , E , F 满足Z BAE Z CAF , Z ABD Z CBF ,贝U AD , BE , CF 三线共点的充要条件是Z ACD Z BCE •17.在任意△ ABC的三边BC , CA , AB上各有点M , N , L ,而Q是厶ABC内部任一点,直线AQ ,BQ , CQ分别交线段NL, LM , MN于M1, 2 , ^ .求证:直线M1M , N1N , L1L共点的充分必要条件是AM BN CL 共点而与Q 点的位置无关.18 .设P是平面上△ ABC区域内任一点,AP , BP , CP的延长线交△ ABC三边于D , E , F .求证:在△ ABC区域内,存在一个以△ DEF的某两边为邻边的平行四边形.19. 设凸四边形ABCD的两组对边所在的直线,分别交于E, F两点,两对角线的交点为P ,过点P 作PO丄EF于0 .求证:Z BOC Z AOD .(2002国家集训队选拔试题)20. 在厶ABC中,Z ABC和Z ACB均为锐角.D是BC边上的内点,且AD平分Z BAC ,过点D作垂线DP丄AB于P , DQ丄AC于Q , CP与BQ相交于K .求证:AK丄BC .。
塞瓦定理及应用.docx

第 二章塞瓦定 理 及应 用【基础知识】塞瓦定理设 A , B , C 分别是 △ ABC 的三边 BC , CA , AB 或其延长线上的点,若 AA ,BB ,CC 三线平行或共点,则BA CB AC1 .①A CB AC B证明如图 2-1( b )、( c ),若 AA , BB , CC 交于一点 P ,则过 A 作 BC 的平行线,分别交 BB ,CC的延长线于 D ,E ,得CBBC , AC EA .B AAD C BBC又由BAA P AC ,有 BA AD . ADPAEA A CEA从而BACB ACAD BC EA 1 .A CB AC B EA AD BC若 AA , BB , CC 三线平行,可类似证明(略).注( 1)对于图 2-1( b )、( c )也有如下面积证法:BA CB ACS△ PABS△ PBCS△ PCA1 ,即证.由:B AC B S △ PCA S △ PAB S △ PBC A C( 2)点 P 常称为塞瓦点.( 3)共点情形的塞瓦定理与梅涅劳斯定理可以互相推证. 首先,由梅涅劳斯定理推证共点情形的塞瓦定理. 如图 2-1( b )、( c ),分别对△ ABA 及截线 C PC ,对 △ AA C 及截线 B PB 应用梅涅劳斯定理有BC A P AC 1,ABCB AP 1 .CAPA C BBC B A PA上述两式相乘,得BACBAC1 .A CB AC B其次,由共点情形的塞瓦定理推证梅涅劳斯定理.如图 2-2,设 A , B , C 分别为 △ ABC 的三边 BC , CA , AB 所在直线上的点,且 A ,B ,C 三点共线.令直线 BB 与 CC 交于点 X ,直线 CC 与 AA 交于点 Y ,直线 AA 与 BB 交于点 Z . 分别视点 C , A , B , C , A , B 为塞瓦点,应用塞瓦定理,即对△ BCB 及点 C (直线BA , CX , B A 的交点),有BA CA B X 1 .A C ABXB对△CAC 及点 A (直线CB , AY , C B 的交点),有CB AB C Y 1 .B C BC YC对△ ABA 及点 B (直线AC , BZ , A C 的交点),有AC BC A Z1.C B CAZA对△ BBC 及点 C (直线BA , BA ,CX 的交点),有BX B A C A1 .XB A CAB对△CCA 及点 A (直线CB ,CB ,A Y 的交点),有CY C B A B1 .YCB A BC对△ AAB 及点 B (直线AC , A C , B Z 的交点),有AZ A C B C 1 .ZA C BCABACB2上述六式相乘,有AC1 .A CB AC B故 BACB AC1 .AC BA CB塞瓦定理的逆定理设A ,B ,C 分别是 △ ABC 的三边 BC , CA , AB 或其延长线上的点,若BACBAC1,② A C B A C B则 AA , BB , CC 三直线共点或三直线互相平行.证明若 AA 与 BB 交于点 P ,设 CP 与 AB 的交点为 C 1 ,则由塞瓦定理,有BA CB AC 1 1 ,又已知有 BACB AC 1 1 ,由此得 AC 1AC ,即 AC 1 AC,亦即 AC 1AC ,AC BA C 1B AC BA C 1BC 1B CB ABAB 故 C 1 与 C 重合,从而 AA , BB , CC 三线共点.若 AA ∥BB ,则CBCB.代入已知条件,有ACAC,由此知 CC ∥AA ,故B ABAC BCBAA ∥BB ∥CC .上述两定理可合写为:设A ,B ,C 分别是 △ ABC 的 BC , CA , AB 所在直线上的点,则三直线AA ,BB , CC 平行或共点的充要条件是BACBAC1 .③A CB AC B第一角元形式的塞瓦定理设A ,B ,C 分别是 △ ABC 的三边 BC , CA , AB 所在直线上的点,则三直线 AA , BB , CC 平行或共点的充要条件是sin ∠ BAAsin ∠ACC sin ∠ CBB1.④sin ∠ A AC sin ∠ C CB sin ∠ B BA证明由BAS △ ABAAB sin ∠ BAA , CB BC sin ∠ CBB , AC AC sin ∠ ACC ,三式相乘,再A CS△AACAC sin ∠ A ACB A AB sin ∠ B BAC BBC sin ∠ C CB运用塞瓦定理及其逆定理,知结论成立.第二角元形的塞瓦定理设 A ,B ,C 分别 △ ABC 的三边 BC ,CA ,AB 所在直线上的点, O 是不在 △ ABC的三边所在直线上的点,则AA , BB , CC 平行或共点的充要条件是sin ∠ BOA sin ∠AOCsin ∠ COB1 .⑤sin ∠ A OC sin ∠ C OB sin ∠ B OA证明注意到塞瓦定理及其逆定理,有BO sin ∠ BOA CO sin ∠ COB AO sin ∠ AOC.CO sin ∠ A OC AO sin ∠ B OA BO sin ∠ C OB由此即证得结论.注在上述各定理中,若采用有向线段或有向角,则①、②、③、④、⑤式的右端仍为 1.特别要注意的是三边所在直线上的点或者两点在边的延长线上,或者没有点在边的延长线上.④、⑤式中的角也可按①式的对应线段记忆.推论设 A 1 , B 1 , C 1 ,分别是 △ ABC 的外接圆三段弧 BC , CA , AB 上的点,则 AA 1 , BB 1 , CC 1 共点的充要条件是BA 1 CB 1 AC 1 1 .AC 1 B 1 A C 1B证明如图 2-3 ,设 △ ABC 的外接圆半径为R ,AA 交BC 于A,BB 交CA 于B , CC 1交AB 于C .由A ,11BA 1 2R sin ∠BAA 1 sin ∠BAA .C 1 , B , A 1 , C , B 1 六点共圆及正弦定理,有2R sin ∠ A 1 AC sin ∠ A ACAC 1同理,CB1sin ∠ CBB,AC1sin∠ ACC.B1 A sin ∠ B BA C1B sin∠ C CB三式相乘,并应用第一角元形式的塞瓦定理即证.为了使读者熟练地应用塞瓦定理,针对图2-4 中的点A、B、C、D、E、F,将其作为塞瓦点,我们写出如下式子:对△ ACE及点 D有ABCG EF 1 ,BC GE FA对△CDE及点 A有CFDB EG 1 ,FD BE GC对△ ADE及点 C有DGAF EB 1 ,GA FE BD对△ ABD及点 F有ACBE DH1,CB ED HA对△ ACD及点 E有AGDF CB 1 ,GD FC BA对△ ADF 及点 B有AHDC FE 1 ,HD CF EA对△ ABF及点 D有BCAE FH 1 ,CA EF HB对△ BDF 及点 A有BEDC FH 1 .ED CF HB【典型例题与基本方法】1.恰当地选择三角形及所在平面上的一点,是应用塞瓦定理的关键例 1 四边形两组对边延长分别相交,且交点的连线与四边形的一条对角线平行.证明:另一条对角线的延长线平分对边交点连线的线段.( 1978 年全国高中竞赛题)证明如图2-5 ,四边形ABCD 的两组对边延长分别交于 E ,F,对角线BD ∥ EF ,AC 的延长线交EF于G.对△AEF 及点C ,应用塞瓦定理,有EG FD AB1.GF DA BE由 BD ∥ EF ,有AB AD,代入上式,BE DF得EG1 ,即EG GF.命题获证.GF例 2如图 2-6 ,锐角△ABC中,AD是BC边上的高,H 是线段 AD 内任一点,BH 和 CH 的延长线分别交 AC , AB于 E, F .求证:∠EDH ∠FDH .( 1994年加拿大奥林匹克试题)证法 1 对△ABC及点H,应用塞瓦定理,有AF BD CE①FB DC1 .EA过 A作PQ∥BC,延长DF , DE分别交PQ于P,Q,则DA⊥PQ,且△ APF∽ △ BDF ,△AQE ∽△CDE,从而AFBD,AQ EAPA DC .FB CE而由①,有AF EABD DC ,故 PA AQ.FB CE由此知 AD 为等腰△APQ底边PQ上的高,故∠EDH∠FDH.证法 2 对△ABC及点H应用塞瓦定理,有AD sin ∠ADFBD DC sin ∠ EDC BD sin ∠ FDBDC AD tan ∠ ADF cot ∠ ADE .sin ∠ ADE即 tan ∠ADEtan ∠ADF ,由锐角性质知 ∠EDA ∠FDA .类似地, 对 △ ABE 及截线 FHC 或对 △ AFC及截线 BHE 应用梅涅劳斯定理也可证得有 ∠EDA ∠FDA .注将此例中的平角∠ BDC 变为钝角,则有如下:例 3 如图 2-7 ,在四边形 ABCD 中,对角线 AC 平分 ∠BAD .在 CD 上取一点 E , BE 与 AC 相交于 F ,延长 DF 交 BC 于 G .求证: ∠GAC ∠EAC .( 1999 年全国高中联赛题)证明连 BD 交 AC 于 H ,对 △ BCD 及点 F ,应用塞瓦定理,有CG BH DE 1 .GB HD ECAH 平分 ∠BAD ,由角平分线性质,可得BH AB ,故CG AB DEHD AD GBAD1 .EC过点 C 作 AB 的平行线交 AG 的延长线于 I ,过点 C 作 AD 的平行线交 AE 的延长线于 J ,则CG CI DEAD CI AB AD.GBAB,.所以AD1EC CJABCJ从而, CI CJ .又 CI ∥ AB , CJ ∥AD ,有 ∠ACI 180 ∠BAC 180 ∠DAC ∠ACJ .因此, △ ACI ≌△ ACJ ,即有 ∠IAC ∠JAC .故 ∠GAC ∠EAC .注由此例还可变出一些题目,参见练习题第 4、5 及 19 题.例 4 如图 2-8, BE 是 △ ABC 的中线, G 在 BE 上,分别延长 AG ,CG 交BC ,AB 于D ,F ,过 D 作 DN ∥ CG 交 BG 于 N , △ DGL 及 △FGM 为正三角形.求证:△ LMN 为正三角形.证明连 NF ,对 △ ABC 及点 G 应用塞瓦定理,有AF BD CE1.而 AEAFDC.FB DC EACE ,则BDFB由 DN ∥CG ,由CDNG .BDBN于是,有AFNG,从而 FN ∥ AD ,即知四边形 DNFG 为平行四边形,有 ∠GDN∠GFN .FBBN又 ∠GDL ∠GFM 60 ,则 ∠LDN ∠NFM .而DN GFFM ,DLDG NF ,知 △LDN ≌△NFM ,有 LNMN , ∠DNL ∠NMF .于是∠MFG 60 .故 △ LMN 为正三角形.例 5 如图 2-9,在一个 △ ABC 中, ∠C 2∠B ,P 为 △ ABC 内满足 APAC 及PB PC 的一点.求证:AP 是 ∠A 的三等分线.( 1994 年香港代表队IMO 选拔赛题)证明用 B 表示∠ABC 的度量,令 ∠PCB, 则 ∠PBC, ∠ABP B, ∠ACP 2B ,∠ CAP π 2 2B(其中注意APAC) ,∠ P∠A ∠BπA [ π 2 C (A 2 P π )4) B] . C) B2 B(π 3BB( 2对 △ ABC 及点 P ,应用第一角元形式的塞瓦定理,有sin[ π 2(2 B)] sin sin( B )1.sin( B 2 )sin(2B)sin亦即 2sin(2 B) cos(2B ) sin( B ) 1 . sin( B 2 ) sin(2 B )于是 sin( B 2 ) 2sin( B ) cos(2B ) sin(3B 2 ) sin B ,即 sin B sin(3 B 2 ) sin( B 2 ) 2cos(2 B2 ) sin B .而 sinB0 ,则 cos2( B)1.2因 0 Bb1(B C )π,则 2( B)0 , 2 π .33 32( B) ππ,即 B.36从而 ∠ CAP π 2(2 B)π 4( B)22( B 2 )2∠ PAB .故 ∠PAB1∠A ,即 AP 是 ∠A 的三等分线.3利用第一角元形式的塞瓦定理可简捷处理 2009 年全国高中联赛加试第一题的第 1 问:例 6 设 M 、 N 分别为锐角 △ ABC (∠A ∠B )的外接圆 上弧 BC 、 AC 的中点.过点 C 作 PC ∥MN交圆于点 P , I 为 △ ABC 的内心,联结PI 并延长交圆于点 .求证: MP MTNP NT .证明事实上,易知 A 、I 、M 及B 、I 、N 分别三点共线,对△ PMN 及点 I 应用第一角元形式的塞瓦定理,有sin ∠ NPI sin ∠ PMI sin ∠ MNI 1 .①sin ∠ IPM sin ∠IMNsin ∠ INP由 CP ∥ MN 知 PA PB ,有 ∠PMI∠INP .NT sin 1∠BCN MP . 于是①式即为2MTsin 1 ∠ A CM NP2故MP MT NP NT .2.注意塞瓦定理逆定理的应用以及与梅涅劳斯定理的配合应用例 7 如图 2-10 ,在 △ ABC 中, ∠BAC90 , G 为 AB 上给定的一点(G 不是线段 AB 的中点).设 D 为直线 GC 上与 C , G 都不相同的任意一点,并且直线AD ,BC 交于 E ,直线 BD ,AC 交于 F ,直线 EF ,AB 交于 H .试证明交点H 与 D 在直线 CG 上的位置无关.( 1990 年苏州市高中竞赛题)证明设 G 分线段 AB 为定比 1 , H 分线段 AB 为定比 2.下证2由1 确定,即当A ,B 给定后,点 H 的位置由点 G 唯一确定.在 △ ABC 中,由 AE , BF , CG 交于一点 D ,应用塞瓦定理,有AG BE CF BE CFGB EC 1,即 11 .FAEC FA对 △ ABC 及截线 EFH ,应用梅涅劳斯定理,得AHBE CFBE CFHB EC 1,即 21 .FAEC FA上述两式相加,得 (BE CF .12 )EC FA从而 12 0,即21,故 2由 1 唯一确定.因此,点 H 与 D 在直线 CG 上的位置无关.例 8 如图 2-11 ,设 P 为 △ ABC 内任一点,在形内作射线 AL , BM , CN ,使得 ∠CAL ∠ PAB ,∠MBC ∠PBA , ∠NCA =∠BCP .求证: AL , BM , CN 三线共点.证法 1设 AL 交BC 于L ,BM 交 CA 于 M ,CN 交 AB 于 N ,则由正弦定理有BLAB sin ∠ BAL AB sin ∠PAC.LCAC sin ∠ CAL AC sin ∠ PAB同理,CM BC sin ∠ PBAMA AB,sin ∠ PBCANAC sin ∠ PCB .NBBC sin ∠ PCA将上述三式相乘,并应用正弦定理,有BL CM AN sin ∠ PAC sin ∠PBA sin ∠PCB PC PA PBLC MANBsin ∠ PAB sin ∠ PBC sin ∠ PCAPA PB1 .PC由塞瓦定理的逆定理,知 AL , BM , CN 共点.证法 2设 AL 交BC 于L ,BM 交CA 于 M ,CN 交 AB 于 N ,直线 AP 交BC 于 D ,直线 BP 交 AC 于E ,直线 CP 交 AB 于F .对 △ ABC 及点 P ,应用塞瓦定理,有AF BD CE 1 .FBDC EA在 △ ABL 和 △ ACL 中应用正弦定理,有sin ∠ PAC sin ∠ Bsin 2 ∠ Csin ∠ Csin ∠ PAB sin 2∠B 同理,CM AE sin 2 ∠ A ,ANMAEC sin 2 ∠C NB以上三式相乘,并注意到①式,有DC AD sin 2 ∠ C AD BD sin 2∠ B2BFsin ∠B .2DC sin 2 ∠ C .BD sin 2∠BBL CM AN DC AE BFLC MANBBDEC 1 .FA由塞瓦定理的逆定理,知AL , BM , CN 共点.证法 3设 AL 交BC 于L ,BM 交 AC 于M ,CN 交 AB 于 N ,直线 AP 交BC 于D ,直线 BP 交 AC 于 E ,直线交 AB 于 F .对 △ ABC 及点 P ,应用角元形式的塞瓦定理,有sin ∠PAB sin ∠ PBC sin ∠ PCA.sin ∠ PAC sin ∠ PBA1sin ∠ PCB由题设 ∠PAB∠CAL , ∠PBA ∠CBM , ∠PCB∠ACN ,则有 ∠BAL ∠PAC , ∠ABM ∠PBC ,∠BCN ∠PCA .于是sin ∠ BAL sin ∠ CBM sin ∠ACN sin ∠PAC sin ∠PBA sin ∠PCBsin ∠ CALsin ∠ ABM sin ∠BCN sin ∠ PAB sin ∠PBC sin ∠ PCA11 1 ,sin ∠ PAB sin ∠ PBC sin ∠PCA 1sin ∠PAC sin ∠ PBA sin ∠ PCB对 △ ABC ,应用角元形式的塞瓦定理的逆定理,知 AL , BM , CN 三线共点.例 9 如图 2-12 ,四边形 ABCD 内接于圆, 其边 AB 与 DC 的延长线交于点 P , AD 与 BC 的延长线交于点 Q ,过点 Q 作该圆的两条切线,切点分别为E 和F .求证: P , E , F 三点共线.( 1997 年 CMO 试题)证明连 EF 分别交 AD , BC 于 M , N ,设 AC 与 BD 交于 K .要证 P , E , F 三点共线,只须证明 P ,K , M 和 P , N , K 都三点共线,又只须证明AC , BD , PM 三线共点.由塞瓦定理的逆定理知只须证明AB PC DM 1.BP CD MA又直线 QCB 截 △ PDA ,应用梅涅劳斯定理,有AB PC DQ 1 ,从而只须证明DM DQBPCD QAAM.AQ设圆心为O ,连 QO 交EF 于 L ,连 LD , LA ,OD , OA ,则由切割线走理和射影定理,有QD QAQE 2QL QO ,即知 D , L , O , A 四点共圆,有 ∠QLD ∠DAO ∠ODA∠OLA ,此表明 QL 为 △ LAD 的内角 ∠ALD 的外角平分线.而EF ⊥ OQ ,则 EL 平分 ∠ALD .于是,DM DL DQ,结论获证.AM ALAQ【解题思维策略分析】1.获得线段比例式的一种手段例 10 如图2-13 , △ ABC 中, D , E 分别为 AC 和 AB 同方向延长线上的点, BD 与 CE 相交于 P ,且 BD CE .若点P 满足∠ AEP ∠ ADP2k 为常数),则AB AC.(k (∠ PED ∠ PDE )证明设 AP 交 BC 于 Q ,对 △ PBC 及其形外一点 A ,应用塞瓦定理,有BQ CE PD 1 .QC EP DB而 BD CE ,则PD QC.PE QB不妨设 QC ≤ QB ,则P D ≤ , 即 有, 于 是≥, 故P EPC CE P ≤E BD PD PS△PBES△P C DS ≥ S.△E BC △ D B C此时,点 E 到 BC 的距离不小于 D 到 BC 的距离,则过 E 作 EF ∥ BC 必交 CD 延长线于一点,设为 F .又作△ FBC 的外接圆O 交 EF 于另一点 F ,则四边形 BCFF 为等腰梯形.当 AB ≥ AC 时,由∠BF F∠ F FC ∠ BCA ≥∠ABC ∠AEF F必在线段 EF上,于是, ∠BDC ≥∠ BFC ≥∠ BEC,知(同弧上的圆外角小于同弧上的圆周角).又由 PD ≤ PE ,知 ∠PED ≤∠ PDE .故结论获证. 2.转化线段比例式的一座桥梁例 11 设 M 为△ ABC 内任一点, AM , BM ,CM 分别交 BC , CA , AB 于 D , E , F .求证:MD ME MFADBE1 .CF证明如图2-14 , 记BDm ,CEn ,AFl . 对 △ ABC 及 点 M , 应 用 塞 瓦 定 理 , 有DCEAFBBD CE AF mnl 1 .DC EA FB 对 △ ADC 及截线 EMB ,应用梅涅劳斯定理,有AM DB CE AM m1,即MD BC EA MD 1 nm AM 1 m (1m)l .MDm n由合比定理得AD 1 (1 MD 1.MD m)l ,即1 l mlAD同理,ME1 l ,BE1 m mnl ml1MF1 ml.CF1 n nlml 1 l三式相加,得MD ME MF 1 .ADBECF例12如图 2-15,设 P 为 △ ABC 内任意一点, AP , BP ,CP 的延长线交对边 BC ,CA , AB 于点 D ,E ,F ,EF 交 AD 于Q .试证: PQ ≤(3 2 2)AD .证明令BDm ,CEn ,AFp ,对 △ ABC 及点 P ,应用塞瓦定理,有BD CE AF mnp 1 .DCEAFBDC EA FB对 △ ADC 及截线 BPE ,应用梅涅劳斯定理,有CE AP DB 1 .注意到DBm ,则有EA PD BCBC m 1nAP m 1,即APPD m 1PD又对直线 APD 截 △ BCE又对△ ABP 及截线m 1 AP,故mnAD,有 BD CA EP DC AE PB FQE ,有 AFF B m 1.mnm 11 .而 CA BP mn m ,故 BEm 1 .AE n 1 ,则 mn EPEPB E P Q PQ 1 1, 故E P 1 , 即 有 p( mn m 1) mp p A Q AQ 1PQ1 .AQmpp2从而PQPQ APmp 1 2 m 11AD AP ADpmn m ≤13 2 2.223于是, PQ ≤(3 2 2)AD .其中等号由2 mn p (m 1) ≥ 2 2mn p(m 1)2 2 中等号成立时成立,即当且仅当2mn 亦m 1m 1p(m 1)m 1即当且仅当2mnp2p( m 1) ,亦即 p(m1)2 时取等号. 此时, m 和 p 之间成为如图 2-16p (m 1)p(m1)的双曲线的关系.例13如图 2-17,已知直线的三个定点依次为 A 、B 、C , 为过 A 、C 且圆心不在 AC 上的圆, 分别过 A 、C 两点且与圆相切的直线交于点P ,PB 与圆交于点 Q .证明: ∠ AQC 的平分线与 AC 的交点不依赖于圆 的选取.( IMO 45 预选题)证明设 ∠ AQC 的平分线交 AC 于点 R ,交圆 于点 S ,其中 S 与 Q 是不同的两点.由于 △ PAC 是等腰三角形,则有AB sin ∠ APB .BCsin ∠ CPB同理,在 △ ASC 中,有AR sin ∠ ASQ .RC sin ∠ CSQ在 △ PAC 中,视 Q 为塞瓦点,由角元形式的塞瓦定理,有sin ∠ APB sin ∠ QAC sin ∠ QCPsin ∠ CPB sin ∠ QAP1.sin ∠QCA注意到 ∠ PAQ ∠ ASQ ∠ QCA , ∠PCQ∠ CSQ ∠QAC .则 sin ∠ APBsin ∠ PAQ sin ∠ QCA sin 2 ∠ ASQ .sin ∠ CPBsin ∠QAC sin ∠ PCQsin 2 ∠CSQ2即 ABAR2,故结论获证.BCRC3.求解三角形格点问题的统一方法如果三角形的三个角的度数都是10 的整数倍,三角形内一点与三角形的三个顶点分别连结后,得到的所有的角也都具有这个性质,我们称这样的点为三角形的格点.例14如图2-18 ,在△ABC中,∠BAC40 ,∠ABC60 , D 和 E 分别是 AC 和 AB 上的点,使得∠CBD40 ,∠BCE70, F 是直线 BD 和 CF 的交点.证明:直线AF 和直线 BC 垂直.( 1998 年加拿大奥林匹克试题)证明设∠BAF,则∠FAC40,对△ ABC 及点 F ,应用第一角元形式的塞瓦定理,有sin10sin sin 401.sin 70sin(40)sin 20从而 sin10sin)2sin 20cos20 1 ,即有cos20sin(40sin 20sin(80 )sin(80).sin(80 )sin(40)sin(80 )2cos60sin(20)sin( 20) .注意到 040,知8020,8020,有8020,故30 .延长 AF 交BC于H ,则∠AHB180∠FBC ∠ABH180306090 .故 AF ⊥BC.注此题也可这样来解:由sin10sin sin 40 1 ,有sin 70sin(40)sin 20sin(40)sin10sin 402sin10sin10sin(4030 )sin 40cot30 cos40.sin sin70sin 20sin30sin30由于 sin(40)sin 40cot cos40作为的函数在 (0 , 180) 上严格递减,sin所以∠BAF30 .故∠ABC∠BAF90 .因此, AF ⊥ BC .或者过点 A 作 AH ⊥ BC于 H ,则∠BAH30,∠HAC10.关于△ ABC有sin ∠BAH sin∠ ACD sin∠ CBD sin30sin10sin 40.所以, AH 、 BD 、 CE sin ∠ HAC sin∠ ECB sin∠ DBA sin10sin701sin 20三线共点,因此点F在 AH 上,即 AF⊥BC.例15如图2-19,在△ABC内取一点M,使得∠MBA30 ,∠MAB10 .设∠ACB 80, AC BC ,求∠AMC .( 1983年前南斯拉夫奥林匹克试题)解设∠ACM,则∠MCB80.由第一角元形式的塞瓦定理,有sin sin10sin 201.sin80sin 40sin30从而 sin sin10sin(80)cos20.2sin cos802sin(80)cos20,sin(80 )sin(80)sin(100)sin(60) ,2cos90sin(10)0.于是 sin(80)sin(60) .注意到 080,知8080 ,6060.8060,故70.所以∠AMC 180∠MAC∠ACM180407070 为所求.注此题结果也可直接由①式有sin sin70且 0, 8080 ,求得70 .sin10sin(80)另外,此题也可这样来解:由sin sin10sin 201,有sin(80)sin 40sin30sin(80)sin10sin 20sin10sin(8070 )sin80cot 70cos80.sin sin 40sin30cos20sin 70因 为s i n ( 8 0) c o tc o 作s 为80的函数在(,180 )上严格递减,所以s i ns i n 8 0∠ACM70 .故 ∠AMC180 40 70 70 .或者由 ∠AMB 140 ,令 ∠AMC x ,则 ∠CMB 220x .对 △ MAB 和点 C 应用第一角元形式的塞瓦定理,有sin ∠AMC sin ∠ MBC sin ∠ BAC sin xsin 20 sin50 .1∠ CMB sin ∠CBAsin ∠ CAMsin(220x)sin50 sin 40sin则 sin(220x)1 sin(220 70 )sin 220 cot 70 cos220 .sin x2cos20sin70因为 sin(220x ) sin 220cotxcos 220 (sin 2200) x 的函数在 (0 ,180)上严格递增,所以sin x作为∠AMC x 70 .例 16 如图 2-20 , △ ABC 具有下面性质:存在一个内部的点 P ,使得 ∠PAB 10 , ∠PBA20 ,∠PCA 30 , ∠PAC40 .证明: △ ABC 是等腰三角形.( 1996 年美国第25 届奥林匹克试题)证明设 ∠BCP ,则 ∠PBC 180 20 1040 3080.由第一角元形式的塞瓦定理,有sin 20sin 40 sin1 .sin(80) sin10sin30即有 2sin10cos10sin 40 sin1.sin(80 )sin10124sinsin 20 sin 40sin80sin60 sin,sin 20sin 20sin(80) sin 20sin60 sin.sin(80) sin 60 , 8080 ,从而sin且 0sin 20故20 ,即 ∠ACB50 ∠CAB ,从而 AB BC .注此题也可这样来求解:由sin 20sin 40 sin1 ,sin(80) sin10sin30有 sin(80)sin 20 sin 40 4cos10 sin 40 4sin 20 sin 40 sin80 sinsin10 sin30 sin 20sin60 sin(80 20 ) cot 20 cos80 .sin 20sin 20 sin80因为 sin(80) sin80cotcos80 作为的函数在( 0 ,180 )上严格递减, 所以 ∠ BCP20 ,sin即 ∠ACB 50∠CAB .故 AB BC .还可对 △ APC 及点 B 应用第一角元形式的塞瓦定理来求.4.论证直线共点的一种工具例17如图 2-21,在四边形 ABCD 中, ABAD ,BC DC ,过 AC , BD 的交点 O 引 EF ,GH ,其中 EF交AB ,CD 于E ,F ,GH 交DA ,BC 于G ,H .EH ,GF 分别交 BD 于P ,Q ,则OP OQ .( 1990 年 CMO 选拔试题)证明在 AB ,BC 上分别取 G ,F ,使 AGAG ,CF CF ,则由对称性可知有下列角相等,即若设∠ AOG, ∠AOG, ∠COH, ∠G OE ∠1, ∠EOB ∠2 , ∠BOF ∠3, ∠F OH ∠4 ,则,又,故.又 ∠1∠4,故 ∠1 ∠4,∠2 ∠3.连GH 交BD 于K ,在△BHG 中,OG OE sin ∠1 OB OF sin ∠3 OHOK sin(∠3 ∠4)OE OB sin ∠2 OFOH sin ∠4 OK1.OG sin(∠1 ∠2)故由塞瓦定理的逆定理,知G F , BO , HE 共点,即 G F 过点 P .由对称性知, OP OQ .例 18 如图 2-22 ,在锐角 △ ABC 中,以 A 点引出的高 AD 为直径作圆交 AB , AC 于M , N ,再从 A 作l A ⊥ MN .同样可作出 l B , l C .试证:三直线 l A , l B , l C 相交于一点.(第 29 届 IMO 预选题)证 明 设 l A 与MN , BC 分别相交于点 G , D ,由∠AMG∠ ADN , ∠AGM∠ AND90 , 知,即 ∠BAD ∠CAD .∠MAG ∠ NAD 同理,设 CA , AB 边上的高 BE , CF 的垂足分别为 E , F ,且 l B , l C 分别与 CA , AB 交于 E , F ,则有∠CBE ∠ABE , ∠ACF ∠BCF .由于 △ ABC 的三条高相交于垂心,此时应用第一角元形式的塞瓦定理,得sin ∠ CAD sin ∠ ABE sin ∠ BCF 1 ,sin ∠ DAB sin ∠EBC sin ∠ FCA用等角代换上式,有sin ∠ BAD sin ∠ ACF sin ∠ CBE1.sin ∠ DAC sin ∠ F CB sin ∠ E BA故由第一角元形式的塞瓦定理,知 AD , BE , CF 三线共点,即 l A , l B , l C 相交于一点.例19如图2-23,四边形 ABCD 内接于圆, AB , DC 的延长线交于 E , AD , BC 的延长线交于 F ,P 为圆上任一点, PE , PF 分别交圆于 R , S .若对角线 AC 与 BD 相交于 T ,求证: R ,T , S 三点共线.证明连 PD ,AS ,RC ,BR ,AP ,SD .由 △ EBR ∽ △ EPA ,△ FDS ∽ △ FPA ,有BREB ,PAFP ,PA EPDSFD此两式相乘,有BR EB FP .①DSEP FD又由 △ECR ∽△ EPD , △ FPD ∽△ FAS ,有CR EC ,PD FP , PDEPASFA此两式相乘,有CREC FP .ASEPFA由①②,得BRASEB FA .DS CREC FD上式两边同乘以DC ,得 BR CD SA EB AF DC .AB RC DS AB BA FD CE对 △ EAD 及截线 BCF ,应用梅涅劳斯定理,有EB AF DC 1 .BA FD CE于是BRCD SA1.RC DC AB此时,应用第一角元形式的塞瓦定理的推论,知 BD , RS , AC 交于一点.从而 R , T , S 三点共直线.【模拟实战】习题 A1.在 △BD1O ,CO 交 AB 于 F ,求四ABC 中, D 是 BC 上的点,, E 是 AC 中点. AD 与BE 交于DC3边形 BDOF 的面积与△ ABC 的面积的比.2.若通过△ABC各顶点的直线AD , BE ,CF 共点,并且它们在边 BC ,CA , AB 所在直线上的截点 D ,E , F 关于所在边中点的对称点分别为 D ,E ,F ,则直线 AD,BE ,CF也共点.3.一圆交△ABC的各边所在直线于两点,设BC 边上的交点为 D , D , CA 边上的交点为E,E ,AB 边上的交点为F, F .若 AD, BE,CF共点,则 AD ,BE , CF 也共点.4.试证:过三角形顶点且平分三角形周长的三条直线共点.5.将△ABC各内角三等分,每两个角的相邻三等分线相交得△ PQR ,又AX,BY,CZ分别平分∠BAC,∠ABC ,∠ACB 且它们与QR, RP,PQ交于 X , Y , Z .求证: PX ,QY, RZ 三线共点.6.将△ABC的各外角三等分,每两个外角的相邻三等分线相交得△ DEF .又 AX , BY , CZ 分别平分∠BAC ,∠ABC ,∠ACB 且它们与 EF , FD , DE 交于 X , Y , Z .求证: DX , EY , FZ 三线共点.7.O是△ABC的内切圆,BC,CA,AB上的切点各是D, E, F.射线 DO交EF于 A,同样可得 B ,C .试证:直线 AA , BB ,CC 共点.8.△ABC在△ABC内部,且从A,B,C各向BC,CA,AB所作的垂线共点,则从 A,B,C 各向 BC , CA , AB 所作的垂线也共点.9.在△ABC中,∠ABC∠ACB40 , P 为形内一点,∠ PAC20,∠PCB30 ,求∠PBC 的度数.10.在△ABC中,AB AC,∠A80 , D 为形内一点,且∠DAB∠DBA10 ,求∠ACD 的度数.(《数学教学》问题432 题)11 .在△ABC中,∠BAC30,∠ABC70 , M 为形内一点,∠MAB ∠MCA20,求∠MBA 的度数.(《数学教学》问题491 题)12.在△ ABC中,∠ ABC40,30,P为∠ABC的平分线上一点,使∠ PCB10,BP交AC∠ACB于 M , CP交 AB于 N .求证:PM AN.(《数学教学》问题531 题)13.在△ABC中,∠ABC40,∠ACB20 , N 为形内一点,∠NBC30 ,∠NAB20 ,求∠NCB 的度数.(《数学通报》问题1023 题)14.在△ABC中,∠BAC80,∠ABC60 ,D 为形内一点,且∠ DAB 10 ,∠ DBA20 ,求∠ACD 的度数.(《数学通报》问题1142 题)15.在△ABC中,∠ABC50,∠ACB30 ,M 为形内一点,∠MCB20 ,∠MAC40 ,求∠ MBC 的度数.(《数学通报》问题1208 题)16 .△ABC中,∠ABC70,∠ACB30, P 为形内一点,∠PBC 40,∠PCB 20.求证:CA AB BP 1.(《数学通报》问题1306 题)AP PC CB17 .在△ABC中,∠ABC∠ACB40,P,Q为形内两点,∠PAB∠ QAC20,∠ PCB QCA10 .求证: B , P ,Q三点共线.(《数学通报》问题 1243题)18.△ABC中,∠ABC∠ACB 50,P,Q为形内两点,∠PCA∠ QBC 10,∠ PAC ∠ QCB20 .求证:BP BQ .(《数学通报》问题1281 题)19.在△ABC中,AB AC,∠A100, I 为内心, D 为 AB 上一点,满足 BD BI .试求∠BCD 的度数.(《数学通报》问题1073 题)20.A1,A2,B1,B2,C1,C2顺次分别在△ ABC 的三边 BC , CA , AB 上,且BA1A2C , CB1B2A,AC1 C2 B ,过 A2, B2, C2分别作 AA1, BB1, CC1的平行线 l a, l b, l c.求证: l a, l b, l c三线共点的充要条件是AA1, BB1, CC1三线共点.21.在△ABC中,AB AC,AD⊥BC于D,过D任作两射线分别交AB,AC 于点 E,F ,交过点 A的平行线于 G , H ,且 GH ∥ BC .求证: AD , GF , HE 共点.22.在△ABC中,过三边BC,CA,AB边中的中点M,N,L的三条等分三角形周长的直线MS ,NT ,LU ( S , T , U 在三角形三边上)分别交LN,LM ,MN于 D,E,F.求证: MS,NT,LU三线共点.23 .△ABC的内切圆切BC , CA, AB 于 D , E , F . P 是△ ABC 内一点, PA 交内切圆于两点,其中靠近 A 的一点为 X ,类似定义 Y , Z .试证: DX , EY , FZ 三线共点.24.△ABC在△A B C内部,AB的延长线分别交 A C ,B C 于P5,P1;AC 的延长线分别交BA ,BC于P3, P4;BC的延长线分别交 A B, A C于P6,P2,且满足A1P A P2B P5B P3B CP PC CP P.求A证:PAA,BB,CC所在直线共点.412(《中学数学教学》擂台题(28))25.给定△ ABC,延长边BC至D,使CD AC.的外接圆与以BC为直径的圆相交于C和P.设△ ACDBP 与 CP 的延长线分别交AC和 AB于E, F.求证: E,F,D共线.(第 15 届伊朗奥林匹克题)26.在△ABC的边上向外作三个正方形,A1, B1, C1是正方形中的边BC , CA , AB 对边的中点.求证:直线 AA1, BB1, CC1共点.习题 B1.O是△ABC的内切圆,D,E,F,分别是BC,CA,AB上的切点,DD,EE,FF都是O 的直径.求证:直线AD ,BE ,CF 共点.(《数学通报》问题1396 题)2.四边形ABCD的内切圆分别与边AB , BC,CD ,DA 相切于 E , F ,G ,H .求证: AC,BD ,HF ,GE 四线共点.(《数学通报》问题1370 题)3.锐角△ABC中,A角的平分线与三角形的外接圆交于另一点A1,点 B1, C1与此类似.直线AA1与 B ,C 两角的外角平分线交于A,点 B,C 与此类似.求证:(Ⅰ)三角形 A B C的面积是六边形AC BACB1 00000011的二倍;(Ⅱ)三角形A0 B0 C0的面积至少是三角形ABC 面积的四倍.(IMO -30试题)4.设P为△ABC内一点,使∠BPA∠CPA , G 是线段 AP 上的点,直线BG , CG 分别交边 AC , AB 于 E , F .求证:∠BPF ∠CPE .5.在凸四边形ABCD 中,对角线AC 平分∠BAD , E 是 CD 的延长线上的一点,BE 交AC 于点G ,延长DG 交 CB 的延长线于F.试证:∠BAF∠DAE .6.在△ABC 中,AB AC,∠A 100 , I为内心, D 为AB 上一点,满足BD BI .试求∠ BCD 的度数.(《数学通报》问题1073题)7.设△ABC 是等边三角形,P 是其内部一点,线段AP , BP , CP 依次交三边BC ,CA, AB于A1, B1,C1三点.证明:A1B1B1C1C1A1≥A1 B B1C C1A .( IMO-37预选题)8.在一条直线l 的一侧画一个半圆半圆的圆心在线段BA 上, E 是线段,C, D,是AC 和 BD 的交点,上两点,上过F 是 l 上的点,C 和D 的切线分别交EF ⊥ l .求证: EFl 于 B 和 A ,平分∠CFD .( IMO -35预选题)9.设A1是锐角△ABC 的内接正方形的中心,其中内接正方形的两个顶点在BC 边上,一个顶点在AB 边上,一个顶点在AC 边上.同样定义两个顶点分别在AC 边和 AB 边上的内接正方形的中心分别为B1,C1.证明: AA1, BB1, CC1交于一点.( IMO -42预选题)10.以△ABC的底边BC为直径作半圆,分别与AB , AC 交于点 D , E ,分别过点 D , E作 BC 的垂线,垂足依次为 F , G,线段 DG和 EF交于点 M .求证: AM ⊥BC.( 1996 年国家队选拔考试题)11.设O,H是锐角△ABC的外接圆的圆心和垂心.证明:存在 D , E, F 分别在线段 BC, CA, AB 上,使得 OD DH OE EH OF FH ,且此时 AD , BE , CF 三线交于一点.( IMO -41预选题)12.已知AB是O 的直径,弦CD⊥AB于L,点M和N分别在线段LB和LA上,且LM∶MB LN ∶NA,射线 CM , CN 交O于E,F.求证:AE,BF,OD三线共点.13.设I是△ABC的内心,以I为圆心的一个圆分别交BC 于A1,A2,交C A于B1,B2,交 AB 于C1,C2.这六个点在圆上的顺序为A1, A2, B1, B2, C1, C2.设 A3, B3, C3为弧 A1A2, B1 B2, C1C2的中点,直线AA,BB相交于 C,直线 B B ,CC 相交于 A ,直线 C C,AA 相交于 B .求证:直线 A A ,BB ,2313423134231343434C3C4三线共点.14.在△ABC的边AB和AC上分别向形外作△ABE和△ACF,使△ABE∽ △ACF,且∠ABE∠ACF90 .求证:连线BF , CE 与边 BC 上的高 AH 三线共点.15.过非等边三角形各顶点作其外接圆的切线,则各切线与其对边的交点共线.16.在△ABC内三点D,E,F满足∠BAE∠CAF,∠ABD∠CBF,则AD,BE,CF三线共点的充要条件是∠ACD ∠BCE .17.在任意△ABC的三边BC,CA,AB上各有点M , N , L ,而Q是△ ABC 内部任一点,直线AQ,BQ ,CQ 分别交线段NL,LM,MN于 M 1, N1, L1.求证:直线 M1M , N1 N , L1L 共点的充分必要条件是 AM , BN , CL 共点,而与Q 点的位置无关.18.设P是平面上△ ABC区域内任一点,AP , BP , CP 的延长线交△ ABC三边于D,E,F.求证:在△ABC 区域内,存在一个以△DEF的某两边为邻边的平行四边形.19 .设凸四边形ABCD 的两组对边所在的直线,分别交于 E , F两点,两对角线的交点为P ,过点P 作PO⊥ EF 于 O.求证:∠BOC∠AOD .( 2002国家集训队选拔试题)D 作垂线20.在△ABC中,∠ABC和∠ACB均为锐角. D 是 BC 边上的内点,且AD 平分∠BAC ,过点DP⊥ AB于 P,DQ⊥AC于Q, CP与BQ相交于 K .求证:AK⊥ BC.。
塞瓦(ceva)定理

1 / 1
塞瓦(ceva )定理
"Ceva's Theorem"(塞瓦定理),它是几何学中的一个定理,描述了三角形内一点的一些特定性质。
Ceva's Theorem 是由意大利数学家乔瓦尼·切瓦(Giovanni Ceva )于1678年首次提出。
Ceva's Theorem 陈述如下:
在三角形 ABC 中,设点 P 在边 BC 上,点 Q 在边 CA 上,点 R 在边 AB 上。
三条线段 AP 、BQ 、CR 通过一个点的充要条件是:
1BD CE AF DC EA FB
⋅⋅= 其中,D 、E 、F 是分别在 BC 、CA 、AB 上的三条线段的交点。
上述公式中的分数表示了在三角形的各边上划分的线段长度之比。
如果这个乘积等于1,那么这三条线段会相交于一个共同的点 P 。
Ceva's Theorem 在三角形的几何学证明和问题求解中有广泛的应用。
塞瓦定理的意义

塞瓦定理的意义引言塞瓦定理(Ceva’s Theorem)是平面几何中的一个重要定理,由意大利数学家乔瓦尼·塞瓦于1678年提出。
这个定理描述了三角形内部的三条线段以特定的方式相交时的几何关系。
塞瓦定理在几何证明和相关问题的求解中发挥着重要作用,具有广泛的应用性和实用价值。
本文将深入探讨塞瓦定理的意义及其在几何学中的应用。
塞瓦定理的描述与证明塞瓦定理的描述如下:在任意给定的三角形ABC中,设D、E、F分别是BC、CA、AB上的任意三个点,且线段AD、BE、CF交于同一个点P。
那么,有以下关系成立:[ = 1 ]为了证明这个定理,我们可以使用相似三角形的性质和方程的等价变换来推导。
但这里不详细展开推导过程,只陈述结论。
这个定理的证明可以在大量的几何教材和参考书籍中找到。
塞瓦定理的几何意义塞瓦定理的几何意义主要可以从两个方面来解释,即三角形内部点之间的位置关系及与三角形各边的比例关系。
1. 点之间的位置关系根据塞瓦定理的描述,当线段AD、BE、CF相交于同一个点P时,有:[ = 1 ]这意味着通过这三条相交的线段所确定的点P,与三角形的各边上的点D、E、F的位置关系是相互确定的。
这种关系可以用来研究三角形内部点的位置和移动过程,为建立几何图形之间的联系提供了理论基础。
2. 比例关系塞瓦定理还表明了线段BD、DC、CE、EA、AF和FB之间的比例关系。
直观地看,这个比例关系描述了通过一个三角形内部点P所确定的三条线段与三角形的各边之间的比例关系。
这个比例关系可以应用于各种几何问题的求解中,例如边长比例问题、面积比例问题等。
塞瓦定理的应用塞瓦定理在几何学中具有广泛的应用。
下面将介绍一些常见的应用场景。
1. 测量线段比例根据塞瓦定理的比例关系,我们可以通过已知线段的长度和一些线段之间的比例来计算其他线段的长度。
比如,已知三角形的三个顶点和某一个内部点,可以通过测量线段长度和利用塞瓦定理的比例关系计算其他线段的长度。
第二章 塞瓦定理及应用

精心整理第二章塞瓦定理及应用【基础知识】塞瓦定理设A ',B ',C '分别是△ABC 的三边BC ,CA ,AB 或其延长线上的点,若AA ',BB ',CC '三线平行或共点,则1BA CB AC A C B A C B'''⋅⋅='''.① 证明如图2-1(b )、(c ),若AA ',BB ',CC '交于一点P ,则过A 作BC 的平行线,分别交BB ',CC '的延长线于D ,E ,得,CB BC AC EAB A ADC B BC''==''. 又由BA A P A C AD'''BA AD '从而BA A C ''若AA ',注(1由:BA A C ''(2)点(3如图2-1BC A P CA PA '⋅'如图2-2',C '三点 对△BCB 对△CAC 对△ABA '及点B '(直线AC ,BZ ,A C ''的交点),有1AC BC A ZC B CA ZA ''⋅⋅=''. 对△BBC '及点C (直线BA ',B A ',C X '的交点),有1BX B A C AXB A C AB '''⋅⋅='''.对△CC A ''及点A (直线CB ',C B ',A Y '的交点),有1CY C B A BYC B A BC '''⋅⋅='''.对△AA B ''及点B (直线AC ',A C ',B Z '的交点),有1AZ A C B CZA C B CA'''⋅⋅='''.上述六式相乘,有21BA CB AC A C B A C B '''⎛⎫⋅⋅= ⎪'''⎝⎭.故1BA CB AC A C B A C B'''⋅⋅='''. 塞瓦定理的逆定理设A ',B ',C '分别是△ABC 的三边BC ,CA ,AB 或其延长线上的点,若1BA CB AC A C B A C B'''⋅⋅=''',② 则AA ',BB ',CC '三直线共点或三直线互相平行.证明若AA '与BB '交于点P ,设CP 与AB 的交点为1C ,则由塞瓦定理,有111AC BA CB A C B A C B ''⋅⋅='',又已知有111AC BA CB A C B A C B ''⋅⋅='',由此得11AC AC C B C B '=',即1AC AC AB AB'=,亦即1AC AC '=,故1C 与C '重合,从而AA ',BB ',CC '三线共点.AA ',O 是不在⑤式中的角也可按①式的对应线段记忆.推论设1A ,1B ,1C ,分别是△ABC 的外接圆三段弧BC ,CA ,AB 上的点,则1AA ,1BB ,1CC 共点的充要条件是1111111BA CB AC AC B A C B ⋅⋅=. 证明如图2-3,设△ABC 的外接圆半径为R ,1AA 交BC 于A ',1BB 交CA 于B ',1CC 交AB 于C '.由A ,1C ,B ,1A ,C ,1B 六点共圆及正弦定理,有11112sin sin 2sin sin BA R BAA BAA AC R A AC A AC '⋅=='⋅∠∠∠∠. 同理,11sin sin CB CBB B A B BA '='∠∠,11sin sin AC ACC C B C CB'='∠∠.三式相乘,并应用第一角元形式的塞瓦定理即证.为了使读者熟练地应用塞瓦定理,针对图2-4中的点A 、B 、C 、D 、E 、F ,将其作为塞瓦点,我们写出如下式子: 对△ACE 及点D 有1AB CG EFBC GE FA ⋅⋅=, 对△CDE 及点A 有1CF DB EGFD BE GC ⋅⋅=, 对△ADE 及点C 有1DG AF EBGA FE BD ⋅⋅=, 对△ABD 及点F 有1AC BE DHCB ED HA ⋅⋅=, 对△对△对△对△1例1 EF 于G .对△EG FD GF DA ⋅由BD ∥得EGGF=例2别交AC 证法1对△ABC 及点H ,应用塞瓦定理,有1FB DC EA⋅⋅=. ①过A 作PQ BC ∥,延长DF ,DE 分别交PQ 于P ,Q ,则DA PQ ⊥,且△APF ∽△BDF ,△AQE ∽△CDE ,从而AF PA BD FB =⋅,EAAQ DC CE=⋅. 而由①,有AF EABD DC FB CE⋅=⋅,故PA AQ =. 由此知AD 为等腰△APQ 底边PQ 上的高,故EDH FDH =∠∠. 证法2对△ABC 及点H 应用塞瓦定理,有sin sin tan cot sin sin AD ADF BD DC EDCADF ADE BD FDB DC AD ADE⋅⋅=⋅⋅=⋅⋅⋅∠∠∠∠∠∠.即tan tan ADE ADF =∠∠,由锐角性质知EDA FDA =∠∠.类似地,对△ABE 及截线FHC 或对△AFC 及截线BHE 应用梅涅劳斯定理也可证得有EDA FDA =∠∠. 注将此例中的平角BDC ∠变为钝角,则有如下:例3如图2-7,在四边形ABCD 中,对角线AC 平分BAD ∠.在CD 上取一点E ,BE 与AC 相交于F ,延长DF 交BC 于G .求证:GAC EAC =∠∠.(1999年全国高中联赛题)证明连BD 交AC 于H ,对△BCD 及点F ,应用塞瓦定理,有1CG BH DEGB HD EC⋅⋅=. AH 平分BAD ∠,由角平分线性质,可得BH HDCG GB 又故例4F ,过D 作DN AF FB 由. 又而 =∠故例5如图2-9,在一个△ABC 中,2C B =∠∠,P 为△ABC 内满足AP AC =及PB PC =的一点.求证:AP 是A ∠的三等分线.(1994年香港代表队IMO 选拔赛题) 证明用B 表示ABC ∠的度量,令PCB θ=∠,则PBC θ=∠,ABP B θ=-∠,2ACP B θ=-∠,()π22CAP B θ=--∠(其中注意AP AC =),()π[π2(2)]PAB A CAP B C B θ=-=-----∠∠∠(π3)(π42)2B B B θθ=---+=-.对△ABC 及点P ,应用第一角元形式的塞瓦定理,有sin[π2(2)]sin sin()1sin(2)sin(2)sin B B B B θθθθθθ---⋅⋅=--.亦即2sin(2)cos(2)sin()1sin(2)sin(2)B B B B B θθθθθ-⋅-⋅-=-⋅-.于是sin(2)2sin()cos(2)sin(32)sin B B B B B θθθθ-=-⋅-=--, 即sin sin(32)sin(2)2cos(22)sin B B B B B θθθ=---=-⋅. 而sin 0B ≠,则1cos2()2B θ-=.因1π0()33B b B C θ<-<<+<,则2π2()0,3B θ⎛⎫-∈ ⎪⎝⎭. ∴π2()3B θ-=,即π6B θ-=. 从而π2(2)π4()2CAP B B θθθ=--=---∠2(2B θ=-故PAB =∠例6设M PC MN ∥交圆ΓNT ⋅. 由CP ∥故MP MT ⋅2例7如图D 为直线F ,直线EF ,(1990年苏州市高中竞赛题) 证明设G 分线段AB 为定比1λ,H 分线段AB 为定比2λ.下证2λ由1λ确定,即当A ,B 给定后,点H 的位置由点G 唯一确定.在△ABC 中,由AE ,BF ,CG 交于一点D ,应用塞瓦定理,有1AG BE CF GB EC FA ⋅⋅=,即11BE CFEC FAλ⋅⋅=. 对△ABC 及截线EFH ,应用梅涅劳斯定理,得1AH BE CF HB EC FA ⋅⋅=,即21BE CFEC FAλ⋅⋅=-. 上述两式相加,得12()0BE CFEC FAλλ+⋅=.从而120λλ+=,即21λλ=-,故2λ由1λ唯一确定.因此,点H 与D 在直线CG 上的位置无关.例8如图2-11,设P 为△ABC 内任一点,在形内作射线AL ,BM ,CN ,使得CAL PAB =∠∠,MBC PBA =∠∠,NCA BCP ∠=∠.求证:AL ,BM ,CN 三线共点.证法1设AL 交BC 于L ,BM 交CA 于M ,CN 交AB 于N ,则由正弦定理有sin sin sin sin BL AB BAL AB PACLC AC CAL AC PAB⋅⋅==⋅⋅∠∠∠∠. 同理,sin sin CM BC PBAMA AB PBC⋅=⋅∠∠, sin sin AN AC PCBNB BC PCA⋅=⋅∠∠.AC 于E ,AC 于E ,PBC ,于是sin sin sin sin sin sin sin sin sin sin sin sin BAL CBM ACN PAC PBA PCBCAL ABM BCN PAB PBC PCA⋅⋅=⋅⋅∠∠∠∠∠∠∠∠∠∠∠∠ 111sin sin sin 1sin sin sin PAB PBC PCA PAC PBA PCB===⋅⋅∠∠∠∠∠∠,对△ABC ,应用角元形式的塞瓦定理的逆定理,知AL ,BM ,CN 三线共点.例9如图2-12,四边形ABCD 内接于圆,其边AB 与DC 的延长线交于点P ,AD 与BC 的延长线交于点Q ,过点Q 作该圆的两条切线,切点分别为E 和F .求证:P ,E ,F 三点共线.(1997年CMO 试题)证明连EF 分别交AD ,BC 于M ,N ,设AC 与BD 交于K .要证P ,E ,F 三点共线,只须证明P ,K ,M 和P ,N ,K 都三点共线,又只须证明AC ,BD ,PM 三线共点.由塞瓦定理的逆定理知只须证明1AB PC DM BP CD MA⋅⋅=. 又直线QCB 截△PDA ,应用梅涅劳斯定理,有1AB PC DQ BP CD QA ⋅⋅=,从而只须证明DM DQAM AQ=. 设圆心为O ,连QO 交EF 于L ,连LD ,LA ,OD ,OA ,则由切割线走理和射影定理,有2QD QA QE QL QO ⋅==⋅,即知D ,L ,O ,A 四点共圆,有QLD DAO ODA OLA ===∠∠∠∠,此表明QL为△LAD DM DL AM AL =1例10P ,且BD CE =证明设 而BD =不妨设E DB C S △≥.此时,点设为F .又作△FBC 的外接圆O 交EF 于另一点BF F BCA ABC '=∠≥∠BEC (同弧上的圆外角小于同弧上的圆周角).又由PD 2例11设1MD ME AD BE CF++=. 证明如图2-14,记BD m DC =,CE n EA =,AFl FB=.对△ABC 及点M ,应用塞瓦定理,有1BD CE AFmnl DC EA FB⋅⋅==. 对△ADC 及截线EMB ,应用梅涅劳斯定理,有11AM DB CE AM mn MD BC EA MD m ⋅⋅=⋅⋅=+,即 1(1)AM mm l MD m n+==++. 由合比定理得1(1)AD m l MD =++,即11MD AD l ml=++.同理,111ME lBE m mn l ml ==++++, 111MF mlCF n nl ml l==++++. 三式相加,得1MD ME MFAD BE CF++=. 例12如图2-15,设P 为△ABC 内任意一点,AP ,BP ,CP 的延长线交对边BC ,CA ,AB 于点D ,E ,F ,EF 交AD 于Q .试证:(3PQ AD -≤.证明令BD m DC =,CE n EA =,AF p FB =,对△ABC 及点P ,应用塞瓦定理,有1BD CE AFmnp DC EA FB⋅⋅==. 对△ADC 及截线BPE ,应用梅涅劳斯定理,有1m +. 12mp p ++. (1)m +亦即2-16上的圆,分AC证明设AQC ∠的平分线交AC 于点R ,交圆Γ于点S ,其中S 与Q 是不同的两点.由于△PAC 是等腰三角形,则有sin sin AB APBBC CPB=∠∠. 同理,在△ASC 中,有sin sin AR ASQRC CSQ=∠∠. 在△PAC 中,视Q 为塞瓦点,由角元形式的塞瓦定理,有sin sin sin 1sin sin sin APB QAC QCPCPB QAP QCA⋅⋅=∠∠∠∠∠∠.注意到PAQ ASQ QCA ==∠∠∠,PCQ CSQ QAC ==∠∠∠.则22sin sin sin sin sin sin sin sin APB PAQ QCA ASQCPB QAC PCQ CSQ⋅==⋅∠∠∠∠∠∠∠∠.即22AB AR BC RC=,故结论获证. 3.求解三角形格点问题的统一方法如果三角形的三个角的度数都是10的整数倍,三角形内一点与三角形的三个顶点分别连结后,得到的所有的角也都具有这个性质,我们称这样的点为三角形的格点.例14如图2-18,在△ABC 中,40BAC =︒∠,60ABC =︒∠,D 和E 分别是AC 和AB 上的点,使得40CBD =︒∠,70BCE =︒∠,F 是直线BD 和CF 的交点.证明:直线AF 和直线BC 垂直.(1998年加拿大奥林匹克试题)证明设BAF α=∠,则40FAC α=︒-∠,对△ABC 及点F ,应用第一角元形式的塞瓦定理,有sin10sin sin 401sin 70sin(40)sin 20αα︒︒⋅⋅=︒︒-︒.、CE 三线AC BC =, sin 201sin30︒=︒.从而sin sin10sin(80)cos20αα⋅︒=︒-⋅︒.∴2sin cos802sin(80)cos20αα⋅︒=︒-⋅︒,∴sin(80)sin(80)sin(100)sin(60)αααα+︒+-︒=︒-+︒-,2cos90sin(10)0α=︒⋅︒-=.于是sin(80)sin(60)αα-︒=︒-.注意到080α<<︒,知8080α-︒<<-︒,6060α︒-<︒. ∴8060αα-︒=︒-,故70α=︒.所以180180407070AMC MAC ACM =︒--=︒-︒-︒=︒∠∠∠为所求. 注此题结果也可直接由①式有sin sin 70sin10sin(80)αα=︒⎧⎨︒=︒-⎩且0α<,8080α︒-<︒,求得70α=︒. 另外,此题也可这样来解:由sin sin10sin 201sin(80)sin 40sin30αα︒︒⋅⋅=︒-︒︒,有sin(80)sin10sin 20sin10sin(8070)sin80cot 70cos80sin sin 40sin30cos20sin 70αα︒-︒⋅︒︒︒-︒====︒⋅︒-︒︒⋅︒︒︒.因为sin(80)sin80cot cos80sin ααα︒-=︒⋅-︒作为α的函数在(0︒,180︒)上严格递减,所以70ACM α==︒∠.故180407070AMC =︒-︒-︒=︒∠.20=︒,从而sin(80)sin 60sin 20sin αα︒-=︒⎧⎨︒=⎩且0α<,8080α︒-<︒,故20α=︒,即50ACB CAB =︒=∠∠,从而AB BC =. 注此题也可这样来求解:由sin 20sin 40sin 1sin(80)sin10sin30αα︒︒⋅⋅=︒-︒︒,有sin(80)sin 20sin 404sin 20sin 40sin804cos10sin 40sin sin10sin30sin 20αα︒-︒︒︒⋅︒⋅︒=⋅=︒⋅︒=︒︒︒sin60sin(8020)sin80cot 20cos80sin 20sin 20︒︒-︒===︒⋅︒-︒︒︒. 因为sin(80)sin80cot cos80sin ααα︒-=︒⋅-︒作为α的函数在(0︒,180︒)上严格递减,所以BCP α=∠20=︒,即50ACB CAB =︒=∠∠.故AB BC =.还可对△APC 及点B 应用第一角元形式的塞瓦定理来求. 4.论证直线共点的一种工具例17如图2-21,在四边形ABCD 中,AB AD =,BC DC =,过AC ,BD 的交点O 引EF ,GH ,其中EF 交AB ,CD 于E ,F ,GH 交DA ,BC 于G ,H .EH ,GF 分别交BD 于P ,Q ,则OP OQ =.(1990年CMO 选拔试题)证明在AB ,BC 上分别取G ',F ',使A G A G '=,CF CF '=,则由对称性可知有下列角相等,即若设,AOG AOG αβ'==∠∠,COH γ=∠,1G OE '=∠∠,2EOB =∠∠,3BOF '=∠∠,4F OH '=∠∠,则αβ=,又αγ=,故βγ=.又14βγ+=+∠∠,故14=∠∠,23=∠∠. 连G H '交BD 于K ,在△BHG '中,. ,再从A 作预选题)E ',F ', F ,P 为圆上任一点,PE ,PF 分别交圆于R ,S .若对角线AC 与BD 相交于T ,求证:R ,T ,S 三点共线.证明连PD ,AS ,RC ,BR ,AP ,SD .由△EBR ∽△EPA ,△FDS ∽△FPA ,有B R E BP A E P=,PA FPDS FD=,此两式相乘,有BR EB FPDS EP FD=⋅. ①又由ECR EPD △∽△,FPD FAS △∽△,有CR EC PD EP =,PD FPAS FA=, 此两式相乘,有CR EC FPAS EP FA=⋅.由①÷②,得BR AS EB FADS CR EC FD⋅=⋅. 上式两边同乘以DC AB ,得BR CD SA EB AF DCRC DS AB BA FD CE⋅⋅=⋅⋅. 对△EAD 及截线BCF ,应用梅涅劳斯定理,有1EB AF DCBA FD CE⋅⋅=. 于是1BR CD SARC DC AB⋅⋅=. 此时,应用第一角元形式的塞瓦定理的推论,知BD ,RS ,AC 交于一点.从而R ,T ,S 三点共直线.【模拟实战】1.在△于F ,求四边形2点D ,E 3E ,E ',AB 45.将△分别平分BAC ∠,三线共点. 6.将△,CZ 分别平分∠,FZ 三线共点.7.O 是A ',同样可得B ',C '8.△A ',B ',C '各向9.在△的度数. 10.在△的度数.(《数学教学》问题432题)11.在ABC △中,30BAC =︒∠,70ABC =︒∠,M 为形内一点,20MAB MCA ==︒∠∠,求MBA ∠的度数. (《数学教学》问题491题) 12.在ABC △中,40ABC =︒∠,30ACB =︒∠,P 为ABC ∠的平分线上一点,使10PCB =︒∠,BP 交AC 于M ,CP 交AB 于N .求证:PM AN =. (《数学教学》问题531题) 13.在ABC △中,40ABC =︒∠,20ACB =︒∠,N 为形内一点,30NBC =︒∠,20NAB =︒∠,求NCB ∠的度数. (《数学通报》问题1023题)14.在ABC △中,80BAC =︒∠,60ABC =︒∠,D 为形内一点,且10DAB =︒∠,20DBA =︒∠,求ACD ∠的度数. (《数学通报》问题1142题) 15.在△ABC 中,50ABC =︒∠,30ACB =︒∠,M 为形内一点,20MCB =︒∠,40MAC =︒∠,求M B C ∠的度数. (《数学通报》问题1208题)16.△ABC 中,70ABC =︒∠,30ACB =︒∠,P 为形内一点,40PBC =︒∠,20PCB =︒∠.求证:1CA AB BPAP PC CB⋅⋅=⋅⋅.(《数学通报》问题1306题)17.在△ABC 中,40ABC ACB ==︒∠∠,P ,Q 为形内两点,20PAB QAC ==︒∠∠,PCB QCA =∠∠10=︒.求证:B ,P ,Q 三点共线.(《数学通报》问题1243题)18.△ABC 中,50ABC ACB ==︒∠∠,P ,Q 为形内两点,10PCA QBC ==︒∠∠,PAC QCB =∠∠20=︒.求证:BP BQ =.(《数学通报》问题1281题)19.在△ABC 中,AB AC =,100A =︒∠,I 为内心,D 为AB 上一点,满足BD BI =.试求BCD ∠的度数. 题) 20.1A ,12CB B A =,12AC C B =c 三线共点21.在△F ,交过点A 22.在△MS ,NT ,LU MS ,NT ,LU 23.△中靠近A 24.△B A '',B C ''于3P 14AP AP =28)) 25.给定C 和P .设BP 与CP (第15届伊朗奥林匹克题) 26.在△ABC 的边上向外作三个正方形,1A ,1B ,1C 是正方形中的边BC ,CA ,AB 对边的中点.求证:直线1AA ,1BB ,1CC 共点.习题B1.O 是△ABC 的内切圆,D ,E ,F ,分别是BC ,CA ,AB 上的切点,DD ',EE ',FF '都是O 的直径.求证:直线AD ',BE ',CF '共点. (《数学通报》问题1396题) 2.四边形ABCD 的内切圆分别与边AB ,BC ,CD ,DA 相切于E ,F ,G ,H .求证:AC ,BD ,HF ,GE 四线共点.(《数学通报》问题1370题)3.锐角△ABC 中,A 角的平分线与三角形的外接圆交于另一点1A ,点1B ,1C 与此类似.直线1AA 与B ,C 两角的外角平分线交于0A ,点0B ,0C 与此类似.求证:(Ⅰ)三角形000A B C 的面积是六边形111AC BACB 的二倍;(Ⅱ)三角形000A B C 的面积至少是三角形ABC 面积的四倍. (IMO -30试题)4.设P 为△ABC 内一点,使BPA CPA =∠∠,G 是线段AP 上的点,直线BG ,CG 分别交边AC ,AB 于E ,F .求证:BPF CPE =∠∠.5.在凸四边形ABCD 中,对角线AC 平分BAD ∠,E 是CD 的延长线上的一点,BE 交AC 于点G ,延长DG 交CB 的延长线于F .试证:BAF DAE =∠∠.6.在△ABC 中,AB AC =,100A =︒∠,I 为内心,D 为AB 上一点,满足BD BI =.试求BCD ∠的度数. (《数学通报》问题1073题) 7.设△,AB 于1A ,1B ,1C8l 于B 和A EF 平分CFD ∠. 9.设1A AB 1B ,1C -42预选题)10.以△E 作BC 的11.设O BC ,CA ,AB 预选题) 12.已知是O 的直径,MB LN =∶NA ,CN 交13.设I 是△ABC 的内心,以I 为圆心的一个圆分别交BC 于1A ,2A ,交A C 于1B ,2B ,交AB 于1C ,2C .这六个点在圆上的顺序为1A ,2A ,1B ,2B ,1C ,2C .设3A ,3B ,3C 为弧12A A ,12B B ,12C C 的中点,直线23A A ,13B B 相交于4C ,直线23B B ,13C C 相交于4A ,直线23C C ,13A A 相交于4B .求证:直线34A A ,34B B ,34C C 三线共点.14.在△ABC 的边AB 和AC 上分别向形外作△ABE 和△ACF ,使△ABE ∽△ACF ,且ABE =∠90ACF =︒∠.求证:连线BF ,CE 与边BC 上的高AH 三线共点.15.过非等边三角形各顶点作其外接圆的切线,则各切线与其对边的交点共线.16.在△ABC 内三点D ,E ,F 满足BAE CAF =∠∠,ABD CBF =∠∠,则AD ,BE ,CF 三线共点的充要条件是ACD BCE =∠∠.17.在任意△ABC 的三边BC ,CA ,AB 上各有点M ,N ,L ,而Q 是△ABC 内部任一点,直线AQ ,BQ ,CQ 分别交线段NL ,LM ,MN 于1M ,1N ,1L .求证:直线1M M ,1N N ,1L L 共点的充分必要条件是AM ,BN ,CL 共点,而与Q 点的位置无关.18.设P 是平面上△ABC 区域内任一点,AP ,BP ,CP 的延长线交△ABC 三边于D ,E ,F .求证:在△ABC 区域内,存在一个以△DEF 的某两边为邻边的平行四边形.19.设凸四边形ABCD 的两组对边所在的直线,分别交于E ,F 两点,两对角线的交点为P ,过点P 作PO EF ⊥于O .求证:BOC AOD =∠∠. (2002国家集训队选拔试题)20.在△D 作垂线DP ⊥。
2角元塞瓦定理及其应用1

§2角元塞瓦定理及其应用(I)塞瓦定理与梅涅劳斯定理是数学竞赛范围内的两个重要定理.近几年来,使用这两个定理证明的试题频频出现,因而,不会运用这两个定理证题的人是很难取得好成绩的。
20世纪90年代中叶,国内很多教练员开始认识到这两个定理的重要性.起初,大家认为梅涅劳斯定理的应用更灵活一些,也更广泛一些,但后来却发现,塞瓦定理及其逆定理在证明三线共点时非常有用,加之角元塞瓦定理不但介入竞赛圈而且所占分量越来越重,使得塞瓦定理的地位日益提高.如今,单独的角元塞瓦定理大有与梅涅劳斯定理和塞瓦定理成三足鼎立之势.此外。
对于某些关于角度的计算题,使用角元塞瓦定理的解法往往别具一格,是其他方法所不能比拟的.1.角元塞瓦定理定理1如图l,设D、E、F分别是△ABC的三边BC、CA、AB上的点,三条线段AD、BE、CF交于一点M.则定理中一共给出了四个结论.其实,定理的条件加上四个结论中的任一个都是塞瓦定理.这里将它们写在一起的目的是为了强调此图形中有四个不同的角度都可以使用角元塞瓦定理.其结果都是有用的,且同等重要.角元塞瓦定理之所以称为角元塞瓦定理,自然是因为它是由原塞瓦定理(以后需要加以区别时,称之为边元塞瓦定理)衍生出来的,即由边的比过渡到角的正弦的比.其实,把角元塞瓦定理看作是拼成一个大三角形或四边形的三个小三角形的三个正弦定理的乘积也许更直接一些.角元塞瓦定理还有下面一种情形:定理2 如图2,设D是边BC上的点,E、F分别是边AC、AB的延长线上的点,三条直线AD、BE、CF 交于△ABC的边BC之外的一点M则有与定理1的(1)对照就会发现,从字母上看,两者的结论完全一样,仅有的区别在于,交点的位置有所不同。
同样地,交点M的位置可以换为在AC或AB之外,结果是完全类似的.注意,图2中的△BFM和△CME中,各只有一条边BM与CM在定理结论中各作为六个角中的两个角的边出现,其余部分均未出现.故此在图中可以擦去.这时,关于三角形的角元塞瓦定理就变成四边形ABMC的角元塞瓦定理了.定理3 在凸四边形ABMC中,如下4个结论成立:像边元塞瓦定理的情形一样,角元塞瓦定理的逆定理(定理4)也成立.定理4 如图3,过△ ABC的三个顶点各引一条异于三角形三边的直线AD、BE、CF.若则AD、BE、CF三线共点或互相平行.2.范例选讲例1、如图4,在△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD 和AC交于点N.求证: (1)OB⊥DF,OC⊥DE; (2)OH⊥MN.证明:(1)因为点0是△ABC的外心,则∠BOC=2∠BAC.故∠OBC= 1(180 -∠BOC)2=90 -∠BAC .因为A、F、D、C四点共圆,所以,∠BDF =∠BAC记OB FD=P.于是,∠BPD =180 -∠PBD-∠PDB =90 .因此,OB⊥DF.同理,OC⊥DE.(2)过点O作OG⊥MN于G.因为AD⊥BC,BE⊥AC,CF⊥AB,则∠COG=∠NME, ∠GOB=∠FNM,∠OBE=∠ANF, ∠EBC=∠DAN,∠BCF=∠MAD, ∠FCO=∠EMA.对△AMN和点D应用角元塞瓦定理有由角元塞瓦定理的逆定理知OG、BE、CF三线共点,即OG过点H.又因为OG⊥MN,所以,OH⊥MN.在上述证明中,作了一条辅助线OG⊥MN.其实,不作这条辅助线且不作任何辅助线,类似的证明也可以完成.例2、四边形ABCD内接于圆O,其边AB与DC所在的直线交于点P,AD与BC所在的直线交于点Q,过点Q作圆O的两条切线QE和QF,切点分别为E和F.求证:P、E、F三点共线.(1997,中国数学奥林匹克)证明:如图5,联结AE、CE、DE 、DF .因为QE、QF都是圆O的切线,所以,∠AEF=∠ADF =180 -∠QDF,∠FED=∠QFD.又∠PDA=180 -∠PDQ,∠DAP=∠DCQ,∠EDP= ∠QEC,∠PAE=∠ECB=180 -∠QCE,对△EDA和点P应用角元塞瓦定理的逆定理知AB、CD、EF三线共点.从而,P、E、F三点共线.例3、锐角△ABC内接于圆O,分别过点B、C作圆O的切线,并分别交过点A所作圆O的切线于点 M、N,AD为边BC上的高.求证:AD平分∠MDN. (1988,全俄数学奥林匹克)证明:如图6,记∠MDA =α,∠NDA=β.只须证明α=β.因为MN、MB、NC都是圆O的切线,所以,∠MAB=∠MBA=∠ACB,∠NAC=∠NCA=∠ABC.对△DAB和点M应用角元塞瓦定理有同理,对△DAC和点N应用角元塞瓦定理又有比较式①、②即得tanα=tanβ.因此,α=β,即AD平分∠MDN.例4、在凸五边形ABCDE中,∠AED=∠ABC=90 ,∠BAC=∠EAD.BD CE=F.求证:AF⊥BE.(第23届IMO预选题)证明:如图7,过点A作AH⊥BE于H.于是,只须证明AH、BD、CE三线共点.因为△ABC∽△AED,所以,又∠BAC=∠EAD,则∠BAD=∠CAE.由关于△ABE的角元塞瓦定理的逆定理知AH、BD、CE三线共点F.因为AH⊥BE,所以,AF⊥BE.角元塞瓦定理的最大优点在于它的三角表达式非常适合于进行角的计算.例5、如图8,在△ABC中,∠BAC=40 ,∠ABC=60 ,在边AC、AB上分别取点D、E,使得∠CBD =40 ,∠BCE=70 ,BD CE=F.求证:AF⊥BC.(1998,加拿大数学奥林匹克) 证法l:因为∠ABC=60 ,∠CBD=40 ,∠BAC=40 ,∠BCE=70则∠ABD =20 ,∠ACB=80 ,∠ACE=10 .设∠BAF=x,于是,∠FAC=40 -x.对△ABC和内点F应用角元塞瓦定理有作为x的函数在(0,π)上严格递减,所以,∠BAF=x=30 .故∠ABC+∠BAF=90 .因此,AF⊥BC.证法2:过点A作AH⊥BC于H.则∠BAH =30 ,∠HAC=10 .关于△ABC有所以,AH、BD、CE三线共点.因此,点F在线段AH上,即AF⊥BC.例6、如图9,P为△ABC内一点,使得∠PAB=10 ,∠PBA=20 ,∠PCA=30 ,∠PAC=40 . 求证:△ABC是等腰三角形.(1996,美国数学奥林匹克)证明:设∠ACB=x,则∠BCP=x-30 .对△APC和点B应用角元塞瓦定理有因此,x=50 .又因为∠BAC =10 +40 =50 =x=∠ACB,所以,△ABC为等腰三角形.例7、如图10,在△ABC中,AB=AC,∠A=20 ,在边AB、AC上分别取点D、E,使得∠EBC=60 ,∠DCB=50 .求∠BED的度数.解法1:设∠BED=x,于是,∠CED=40 +x.对△BCE和点D应用角元塞瓦定理有作为x的函数在(0,π)上严格递减,所以,∠BED=x=30 .解法2:设∠BED=x ,于是,∠EDB=160 -x.对△EDC和点B应用角元塞瓦定理有思考,如果对△DBE和点C或△DBC和点E使用角元塞瓦定理,能否得到同样的结果?答案是肯定的,但推导的难度提高了.具体来说,推导过程中要用到一个三角恒等式,这里作为引理给出.例8、如图11,在四边形ABCD中,∠CAB=30 ,∠ABD=26 ,∠ACD=13 ,∠DBC=51 .求∠ADB 的度数. (1989,中国国家集训队测验题)解法1:设∠ADB=x,于是,∠ADC=x+43 .因为∠CAB=30 ,∠ABD=26 ,∠DBC=51 ,∠ACD=13 ,则∠ACB=73 ,∠BDC=43 .对△BCD和点A应用角元塞瓦定理有解法2:设∠ADB=x,于是,∠ADB=154 -x.对△DAC和点B应用角元塞瓦定理有作为x的函数在(O,π)上严格递减,所以,∠ADB=x=107 .例9、如图l2,在△ABC中,AC=BC,∠ACB=80 ,在△ABC内取一点M,使得∠MAB=10 ,∠MBA=30 .求∠AMC的度数.(1983,前南斯拉夫数学奥林匹克)解法1:因为AC=BC,∠ACB=80 ,则∠CAB=∠CBA=50 .因为∠MAB=10 ,∠MBA=30 ,所以,∠CAM=40 ,∠CBM=20 .设∠BCM=x,于是,∠ACM=80 -x.对△ABC和点M应用角元塞瓦定理有作为x的函数在(0,π)上严格递减,所以,∠BCM=x=10 .故∠AMC=∠MAB+∠ABC+∠BCM=70 .解法2:因为AC=BC,∠ACB=80 ,则∠CAB=∠CBA=50 .因为∠MAB=10 ,∠MBA=30 ,所以,∠CAM=40 ,∠CBM=20 .∠AMB=140 .设∠AMC=x,于是,∠CMB=220 -x.对△MAB和点C应用角元塞瓦定理有作为x的函数在(0,π)上严格递增,所以,∠AMC=x=70 .。
塞瓦定理的应用

塞瓦定理的应用塞瓦定理是众所周知的理论,它源于法国数学家和科学家塞瓦阿索贝(Sébastien dAubuisson)于1785年提出。
塞瓦定理(又被称为等边三角形定理)主要说明在任意一个等边三角形中,两条大于斜边的等边,以及相应的角的和应该等于180度。
因此,塞瓦定理可以说是几何学中的一个基本特征。
塞瓦定理在几何学和数学中有着非常广泛的应用,它可以用来判断一个三角形的性质,对于寻找圆的面积和周长来说也是必不可少的。
除此之外,塞瓦定理还可以应用于多边形,特别是多边形的内角和,其中,每个内角和应该等于内角数乘以180度,象征着一块拼图,其中拼接着很多可以任意转动的小四方形,它们组成了一个完整的图形。
除了在几何学和数学领域中的应用外,塞瓦定理还可以在物理学、天文学和化学等多个领域中使用。
例如,塞瓦定理在天文学中有多种应用,它可以用于计算正的岩石的体积,并且可以帮助推断某些星体的形状和大小;在物理学中,它可以用来理解某些机械系统结构,比如曲柄杆机构等,对于对于了解材料的力学特性也有一定的帮助;而在化学领域,它可以用来表征物质的结构,以及分子中不同元素的配位等。
塞瓦定理的应用也可以扩展到更多领域,比如地理学,即在地图测绘中求得各地点之间的距离等;还可以用在建筑学中,它可以计算建筑物的外形,比如摩天大楼的外墙角度等;还可以用在机械学中,它可以帮助计算转动杆件的大小。
总而言之,塞瓦定理在三角几何学中是非常重要的,它不仅仅可以用于几何研究,而且还有着许多实际应用。
虽然塞瓦定理是一个非常基本的定理,但它在几何学中的影响有着深远的影响。
在数学发展的过程中,塞瓦定理不仅仅帮助我们计算几何图形的大小和形状,也激发了许多新的研究方向,比如椭圆几何学等。
可以说,塞瓦定理在我们研究几何学方面发挥了重要作用,而它的应用也越来越广泛。
塞瓦定理

塞瓦(Ceva )定理有关共线问题,我们在梅内劳斯定理和点共线与西姆松定理两个专题中,做过一般性的讨论,也讨论了一些方法。
本讲讨论证明共点线的重要定理,并在讨论其他问题时有重要作用。
1.塞瓦定理:设O 是ABC ∆内任意一点,AO 、BO 、CO 分别交对边于D 、E 、F , 则1=⋅⋅FBAFEA CE DC BD . 证明1:(用梅涅劳斯定理)ADC ∆被直线BOE 所截,有1=⋅⋅ECAEOA DO BD CB . ABD ∆被直线COF 所截,有1=⋅⋅FBAF OA DO CD BC .相除即得.证明2:(面积证法)AOCAOBCOD ADC BOD ABD COD BOD ADC ABD S S S S S S S S S S DC BD ∆∆∆∆∆∆∆∆∆∆=--===. 同理AOB BOC S S EA CE ∆∆=,BOCAOCS S FB AF ∆∆=, 相乘即得.证明3:(物体重心法)在A 、B 、C 处各放一重物,让其质量分别为C B A m m m ,,,使其重心正好在O 处,则D 、E 、F 分别为BC 、CA 、AB 的重心,有ABC A B C m m FB AF m m EA CE m m DC BD ===,,,相乘即得. 证明4:利用相似三角形过B 作//MN AC 分别交AD 、CF 与N 、M ,BD BNDC AC= CE EO BM OB =,BN OBAE OE = AF ACFB BM= 将上面四个比例式相乘,得BD CE BN AF BN EO OB ACDC BM AE FB AC OB OE BM⋅⋅⋅=⋅⋅⋅ 即1=⋅⋅FBAFEA CE DC BD 2.塞瓦定理的逆定理 在ABC ∆三边(所在直线)BC 、CA 、AB 上各取一点D 、E 、F ,若有1=⋅⋅FBAFEA CE DC BD ,则AD 、BE 、CF 平行或共点. 证明:AD 与BE 或是平行或是相交 (1)若//AD BE ,则EAECBD BC =, 代入已知式,可推出CBDCFB AF =. 有//AD CF 从而////AD BE CF .(2)若AD 与BE 相交于O ,则连结CO 交AB 于/F ,由塞瓦定理,有//1BD CE AF DC EA F B⋅⋅=, 与已知式相比较,得//AF AFF B AB =, 合比/AF AFAB AB=, 有/AF AF =,得/F 与F 重合,即AD 、BE 、CF 共点.ABCDEFOABCDEF OMNABCDEFABCDEFO/F说明:梅涅劳斯定理与塞瓦定理在几何证明中有广泛的应用,而且往往使证明的过程异常简捷,思路流畅,难度趋易.在应用梅涅劳斯定理时要抓准“哪条直线截哪个三角形”.它是判定三点共线的一般方法,在解证某类比例线段时很有作用,而塞瓦定理则是证明三线共点的一般方法.例1 如图,在ABC ∆中,D 、E 分别在边AB 、AC 上,且//DE BC ,设BE 与CD 交于S ,则AS 通过BC 边的中点M 证明:∵//DE BC∴AD AEDB EC= 另一方面,1AD BM CEDB MC EA⋅⋅= ∴1BMMC=,即BM MC = ∴M 是BC 的中点例2 如图,已知在ABC ∆中,M 是BC 的中点,AD 平分BAC ∠,B 在AD 上的射影为E ,BE 交AM 于N 。
塞瓦定理及应用

【基础知识】塞瓦定理 设A ',B ',C '分别是△ABC 的三边BC ,CA ,AB 或其延长线上的点,若AA ',BB ',CC '三线平行或共点,则1BA CB AC A C B A C B'''⋅⋅='''. ①证明 如图2-1(b )、(c ),若AA ',BB ',CC '交于一点P ,则过A 作BC 的平行线,分别交BB ',CC '的延长线于D ,E ,得,CB BC AC EAB A ADC B BC''==''.又由BA A P A C AD PA EA '''==,有BA AD A C EA'='. 从而1BA CB AC AD BC EA A C B A C B EA AD BC'''⋅⋅=⋅⋅='''.若AA ',BB ',CC '三线平行,可类似证明(略). 注 (1)对于图2-1(b )、(c )也有如下面积证法:由:1PAB PBC PCAPCA PAB PBC S S S BA CB AC A C B A C B S S S '''⋅⋅=⋅⋅='''△△△△△△,即证.(2)点P 常称为塞瓦点.(3)共点情形的塞瓦定理与梅涅劳斯定理可以互相推证. 首先,由梅涅劳斯定理推证共点情形的塞瓦定理. 如图2-1(b )、(c ),分别对△ABA '及截线C PC ',对△AA C '及截线B PB '应用梅涅劳斯定理有 1BC A P AC CA PA C B ''⋅⋅='',1A B CB APBC B A PA ''⋅⋅=''. 上述两式相乘,得1BA CB AC A C B A C B'''⋅⋅='''. 其次,由共点情形的塞瓦定理推证梅涅劳斯定理.如图2-2,设A ',B ',C '分别为△ABC 的三边BC ,CA ,AB 所在直线上的点,且A ',B ',C '三点共线.令直线BB '与CC '交于点X ,直线C C '与AA '交于点Y ,直线AA '与BB '交于点Z .分别视点C ',A ',B ',C ,A ,B 为塞瓦点,应用塞瓦定理,即对△BCB '及点C '(直线BA ,CX ,B A ''的交点),有1BA CA B XA C AB XB ''⋅⋅=''.对△CAC '及点A '(直线CB ,AY ,C B ''的交点),有1CB AB C YB C BC YC ''⋅⋅=''.对△ABA '及点B '(直线AC ,BZ ,A C ''的交点),有1AC BC A ZC B CA ZA ''⋅⋅=''.对△BBC '及点C (直线BA ',B A ',C X '的交点),有1BX B A C AXB A C AB '''⋅⋅='''.对△CC A ''及点A (直线CB ',C B ',A Y '的交点),有1CY C B A BYC B A BC '''⋅⋅='''.对△AA B ''及点B (直线AC ',A C ',B Z '的交点),有1AZ A C B CZA C B CA '''⋅⋅='''.上述六式相乘,有21BA CB AC A C B A C B '''⎛⎫⋅⋅= ⎪'''⎝⎭. 故1BA CB AC A C B A C B'''⋅⋅='''.塞瓦定理的逆定理 设A ',B ',C '分别是△ABC 的三边BC ,CA ,AB 或其延长线上的点,若 1BA CB AC A C B A C B'''⋅⋅=''', ② 则AA ',BB ',CC '三直线共点或三直线互相平行.证明若AA '与BB '交于点P ,设CP 与AB 的交点为1C ,则由塞瓦定理,有111AC BA CB A C B A C B ''⋅⋅='',又已知有111AC BA CB A C B A C B ''⋅⋅='',由此得11AC AC C B C B '=',即1AC AC AB AB'=,亦即1AC AC '=,故1C 与C '重合,从而AA ',BB ',CC '三线共点.若AA BB ''∥,则CB CB B A BA '=''.代入已知条件,有AC A CC B CB''=',由此知CC AA ''∥,故 AA BB CC '''∥∥. 上述两定理可合写为:设A ',B ',C '分别是△ABC 的BC ,CA ,AB 所在直线上的点,则三直线AA ',BB ',CC '平行或共点的充要条件是1BA CB AC A C B A C B'''⋅⋅='''. ③ 第一角元形式的塞瓦定理 设A ',B ',C '分别是△ABC 的三边BC ,CA ,AB 所在直线上的点,则三直线AA ',BB ',CC '平行或共点的充要条件是 sin sin sin 1sin sin sin BAA ACC CBB A AC C CB B BA'''⋅⋅='''∠∠∠∠∠∠. ④证明 由sin sin ABA AA C S BA AB BAA A C S AC A AC ''''⋅==''⋅△△∠∠,sin sin CB BC CBB B A AB B BA ''⋅=''⋅∠∠,sin sin AC AC ACC C B BC C CB ''⋅=''⋅∠∠,三式相乘,再运用塞瓦定理及其逆定理,知结论成立.第二角元形的塞瓦定理 设A ',B ',C '分别△ABC 的三边BC ,CA ,AB 所在直线上的点,O 是不在△ABC 的三边所在直线上的点,则AA ',BB ',CC '平行或共点的充要条件是 sin sin sin 1sin sin sin BOA AOC COB A OC C OB B OA'''⋅⋅='''∠∠∠∠∠∠.⑤ 证明 注意到塞瓦定理及其逆定理,有1BOA COB AOC A OC B OA C OB S S S BA CB AC A C B A C B S S S '''''''''=⋅⋅=⋅⋅'''△△△△△△ sin sin sin sin sin sin BO BOA CO COB AO AOC CO A OC AO B OA BO C OB'''⋅⋅⋅=⋅⋅'''⋅⋅⋅∠∠∠∠∠∠. 由此即证得结论.注 在上述各定理中,若采用有向线段或有向角,则①、②、③、④、⑤式的右端仍为1.特别要注意的是三边所在直线上的点或者两点在边的延长线上,或者没有点在边的延长线上.④、⑤式中的角也可按①式的对应线段记忆.推论 设1A ,1B ,1C ,分别是△ABC 的外接圆三段弧»BC ,»CA ,»AB 上的点,则1AA ,1BB ,1CC 共点的充要条件是1111111BA CB AC AC B A C B ⋅⋅=. 证明 如图2-3,设△ABC 的外接圆半径为R ,1AA 交BC 于A ',1BB 交CA 于B ',1CC 交AB 于C '.由A ,1C ,B ,1A ,C ,1B 六点共圆及正弦定理,有11112sin sin 2sin sin BA R BAA BAA AC R A AC A AC '⋅=='⋅∠∠∠∠.同理,11sin sin CB CBB B A B BA '='∠∠,11sin sin AC ACC C B C CB'='∠∠. 三式相乘,并应用第一角元形式的塞瓦定理即证.为了使读者熟练地应用塞瓦定理,针对图2-4中的点A 、B 、C 、D 、E 、F ,将其作为塞瓦点,我们写出如下式子:对△ACE 及点D 有 1AB CG EFBC GE FA ⋅⋅=, 对△CDE 及点A 有 1CF DB EGFD BE GC ⋅⋅=, 对△ADE 及点C 有 1DG AF EBGA FE BD ⋅⋅=, 对△ABD 及点F 有 1AC BE DHCB ED HA ⋅⋅=, 对△ACD 及点E 有 1AG DF CBGD FC BA ⋅⋅=, 对△ADF 及点B 有 1AH DC FEHD CF EA ⋅⋅=, 对△ABF 及点D 有 1BC AE FHCA EF HB⋅⋅=, 对△BDF 及点A 有1BE DC FHED CF HB⋅⋅=. 【典型例题与基本方法】1.恰当地选择三角形及所在平面上的一点,是应用塞瓦定理的关键例1 四边形两组对边延长分别相交,且交点的连线与四边形的一条对角线平行.证明:另一条对角线的延长线平分对边交点连线的线段. (1978年全国高中竞赛题) 证明 如图2-5,四边形ABCD 的两组对边延长分别交于E ,F ,对角线BD EF ∥,AC 的延长线交EF 于G .对△AEF 及点C ,应用塞瓦定理,有 1EG FD ABGF DA BE ⋅⋅=. 由BD EF ∥,有AB ADBE DF=,代入上式, 得1EGGF=,即EG GF =.命题获证. 例2 如图2-6,锐角△ABC 中,AD 是BC 边上的高,H 是线段AD 内任一点,BH 和CH 的延长线分别交AC ,AB 于E ,F .求证:EDH FDH =∠∠. (1994年加拿大奥林匹克试题)证法1 对△ABC 及点H ,应用塞瓦定理,有1AF BD CEFB DC EA⋅⋅=. ① 过A 作PQ BC ∥,延长DF ,DE 分别交PQ 于P ,Q ,则DA PQ ⊥,且△APF ∽△BDF ,△AQE ∽△CDE ,从而AF PA BD FB =⋅,EAAQ DC CE=⋅.而由①,有AF EABD DC FB CE⋅=⋅,故PA AQ =. 由此知AD 为等腰△APQ 底边PQ 上的高,故EDH FDH =∠∠. 证法2 对△ABC 及点H 应用塞瓦定理,有1DAF DCEDFB DEA S S AF BD CE BD FB DC EA S DC S =⋅⋅=⋅⋅△△△△ sin sin tan cot sin sin AD ADF BD DC EDCADF ADE BD FDB DC AD ADE⋅⋅=⋅⋅=⋅⋅⋅∠∠∠∠∠∠.即tan tan ADE ADF =∠∠,由锐角性质知EDA FDA =∠∠.类似地,对△ABE 及截线FHC 或对△AFC 及截线BHE 应用梅涅劳斯定理也可证得有EDA FDA =∠∠. 注 将此例中的平角BDC ∠变为钝角,则有如下: 例3 如图2-7,在四边形ABCD 中,对角线AC 平分BAD ∠.在CD 上取一点E ,BE 与AC 相交于F ,延长DF 交BC 于G .求证:GAC EAC =∠∠.(1999年全国高中联赛题)证明 连BD 交AC 于H ,对△BCD 及点F ,应用塞瓦定理,有1CG BH DEGB HD EC⋅⋅=. AH 平分BAD ∠,由角平分线性质,可得BH AB HD AD =,故1CG AB DEGB AD EC⋅⋅=.过点C 作AB 的平行线交AG 的延长线于I ,过点C 作AD 的平行线交AE 的延长线于J ,则 ,CG CI DE AD GB AB EC CJ ==.所以1CI AB ADAB AD CJ ⋅⋅=.从而,CI CJ =.又CI AB ∥,CJ AD ∥,有180180ACI BAC DAC ACJ =︒-=︒-=∠∠∠∠. 因此,△ACI ACJ ≌△,即有IAC JAC =∠∠. 故 GAC EAC =∠∠.注 由此例还可变出一些题目,参见练习题第4、5及19题.例4 如图2-8,BE 是△ABC 的中线,G 在BE 上,分别延长AG ,CG 交BC ,AB 于D ,F ,过D 作DN CG ∥交BG 于N ,△DGL 及FGM △为正三角形.求证:△LMN 为正三角形.证明 连NF ,对△ABC 及点G 应用塞瓦定理,有 1AF BD CE FB DC EA ⋅⋅=.而AE CE =,则AF DCFB BD =. 由DN CG ∥,由CD NGBD BN=. 于是,有AF NGFB BN=,从而FN AD ∥,即知四边形DNFG 为平行四边形,有GDN GFN =∠∠. 又60GDL GFM ==︒∠∠,则LDN NFM =∠∠.而DN GF FM ==,DL DG NF ==,知△LDN ≌△NFM ,有LN MN =,DNL NMF =∠∠.于是MNL DNF DNL MNF DNF NMF MNF =-+=-+∠∠(∠∠)∠(∠∠) 180)(180)NFG NFM NFM NFG ︒--︒-=-=(∠∠∠∠60MFG ==︒∠.故△LMN 为正三角形.例5 如图2-9,在一个△ABC 中,2C B =∠∠,P 为△ABC 内满足AP AC =及PB PC =的一点.求证:AP 是A ∠的三等分线. (1994年香港代表队IMO 选拔赛题)证明 用B 表示ABC ∠的度量,令PCB θ=∠,则PBC θ=∠,ABP B θ=-∠,2ACP B θ=-∠,()π22CAP B θ=--∠(其中注意AP AC =),()π[π2(2)]PAB A CAP B C B θ=-=-----∠∠∠(π3)(π42)2B B B θθ=---+=-.对△ABC 及点P ,应用第一角元形式的塞瓦定理,有 sin[π2(2)]sin sin()1sin(2)sin(2)sin B B B B θθθθθθ---⋅⋅=--.亦即2sin(2)cos(2)sin()1sin(2)sin(2)B B B B B θθθθθ-⋅-⋅-=-⋅-.于是 sin(2)2sin()cos(2)sin(32)sin B B B B B θθθθ-=-⋅-=--, 即 sin sin(32)sin(2)2cos(22)sin B B B B B θθθ=---=-⋅.而sin 0B ≠,则1cos2()2B θ-=. 因 1π0()33B b BC θ<-<<+<,则2π2()0,3B θ⎛⎫-∈ ⎪⎝⎭.∴ π2()3B θ-=,即π6B θ-=.从而π2(2)π4()2CAP B B θθθ=--=---∠ ππ222[()]36B θθθθ⎛⎫=-=-=-- ⎪⎝⎭2(2)2B PAB θ=-=∠.故 13PAB A =∠∠,即AP 是A ∠的三等分线.利用第一角元形式的塞瓦定理可简捷处理2009年全国高中联赛加试第一题的第1问:例6 设M 、N 分别为锐角△ABC(A B <∠∠)的外接圆Γ上弧»BC 、»AC 的中点.过点C 作PC MN ∥交圆Γ于点P ,I 为△ABC 的内心,联结PI 并延长交圆Γ于点Γ.求证:MP MT NP NT ⋅=⋅. 证明 事实上,易知A 、I 、M 及B 、I 、N 分别三点共线,对△PMN 及点I 应用第一角元形式的塞瓦定理,有sin sin sin 1sin sin sin NPI PMI MNIIPM IMN INP⋅⋅=∠∠∠∠∠∠.①由CP MN ∥知PA PB =,有PMI INP =∠∠. 于是①式即为1sin 21sin 2B NT CN MP MT CM NPA ===∠∠. 故MP MT NP NT ⋅=⋅.2.注意塞瓦定理逆定理的应用以及与梅涅劳斯定理的配合应用例7 如图2-10,在△ABC 中,90BAC =︒∠,G 为AB 上给定的一点(G 不是线段AB 的中点).设D 为直线GC 上与C ,G 都不相同的任意一点,并且直线AD ,BC 交于E ,直线BD ,AC 交于F ,直线EF ,AB 交于H .试证明交点H 与D 在直线CG 上的位置无关.(1990年苏州市高中竞赛题)证明 设G 分线段AB 为定比1λ,H 分线段AB 为定比2λ.下证2λ由1λ确定,即当A ,B 给定后,点H 的位置由点G 唯一确定.在△ABC 中,由AE ,BF ,CG 交于一点D ,应用塞瓦定理,有 1AG BE CF GB EC FA ⋅⋅=,即11BE CFEC FAλ⋅⋅=. 对△ABC 及截线EFH ,应用梅涅劳斯定理,得 1AH BE CF HB EC FA ⋅⋅=,即21BE CFEC FAλ⋅⋅=-. 上述两式相加,得12()0BE CFEC FAλλ+⋅=.从而120λλ+=,即21λλ=-,故2λ由1λ唯一确定.因此,点H 与D 在直线CG 上的位置无关.例8 如图2-11,设P 为△ABC 内任一点,在形内作射线AL ,BM ,CN ,使得CAL PAB =∠∠,MBC PBA =∠∠,NCA BCP ∠=∠.求证:AL ,BM ,CN 三线共点.证法1 设AL 交BC 于L ,BM 交CA 于M ,CN 交AB 于N ,则由正弦定理有 sin sin sin sin BL AB BAL AB PACLC AC CAL AC PAB ⋅⋅==⋅⋅∠∠∠∠. 同理,sin sin CM BC PBAMA AB PBC⋅=⋅∠∠, sin sin AN AC PCBNB BC PCA⋅=⋅∠∠. 将上述三式相乘,并应用正弦定理,有sin sin sin 1sin sin sin BL CM AN PAC PBA PCB PC PA PB LC MA NB PAB PBC PCA PA PB PC ⋅⋅=⋅⋅=⋅⋅=∠∠∠∠∠∠. 由塞瓦定理的逆定理,知AL ,BM ,CN 共点.证法2 设AL 交BC 于L ,BM 交CA 于M ,CN 交AB 于N ,直线AP 交BC 于D ,直线BP 交AC 于E ,直线CP 交AB 于F .对△ABC 及点P ,应用塞瓦定理,有1AF BD CEFB DC EA⋅⋅=. 在△ABL 和△ACL 中应用正弦定理,有 sin sin sin sin sin sin sin sin BL BL AL BAL C PAC CLC AL LC B LAC PAB B =⋅=⋅=⋅∠∠∠∠∠∠∠∠ 222222sin sin sin sin sin sin sin sin sin sin PAC B C DC AD C DC CC PAB B AD BD B BD B =⋅⋅=⋅⋅=⋅∠∠∠∠∠∠∠∠∠∠. 同理,22sin sin CM AE A MA EC C =⋅∠∠,22sin sin AN BF BNB FA A=⋅∠∠. 以上三式相乘,并注意到①式,有1BL CM AN DC AE BF LC MA NB BD EC FA⋅⋅=⋅⋅=. 由塞瓦定理的逆定理,知AL ,BM ,CN 共点.证法3 设AL 交BC 于L ,BM 交AC 于M ,CN 交AB 于N ,直线AP 交BC 于D ,直线BP 交AC 于E ,直线交AB 于F .对ABC △及点P ,应用角元形式的塞瓦定理,有sin sin sin 1sin sin sin PAB PBC PCAPAC PBA PCB⋅⋅=∠∠∠∠∠∠.由题设PAB CAL =∠∠,PBA CBM =∠∠,PCB ACN =∠∠,则有BAL PAC =∠∠,ABM PBC =∠∠,BCN PCA =∠∠. 于是 sin sin sin sin sin sin sin sin sin sin sin sin BAL CBM ACN PAC PBA PCBCAL ABM BCN PAB PBC PCA⋅⋅=⋅⋅∠∠∠∠∠∠∠∠∠∠∠∠ 111sin sin sin 1sin sin sin PAB PBC PCA PAC PBA PCB===⋅⋅∠∠∠∠∠∠,对△ABC ,应用角元形式的塞瓦定理的逆定理,知AL ,BM ,CN 三线共点.例9 如图2-12,四边形ABCD 内接于圆,其边AB 与DC 的延长线交于点P ,AD 与BC 的延长线交于点Q ,过点Q 作该圆的两条切线,切点分别为E 和F .求证:P ,E ,F 三点共线.(1997年CMO 试题)证明 连EF 分别交AD ,BC 于M ,N ,设AC 与BD 交于K .要证P ,E ,F 三点共线,只须证明P ,K ,M 和P ,N ,K 都三点共线,又只须证明AC ,BD ,PM 三线共点.由塞瓦定理的逆定理知只须证明1AB PC DM BP CD MA⋅⋅=. 又直线QCB 截△PDA ,应用梅涅劳斯定理,有 1AB PC DQ BP CD QA ⋅⋅=,从而只须证明DM DQAM AQ=. 设圆心为O ,连QO 交EF 于L ,连LD ,LA ,OD ,OA ,则由切割线走理和射影定理,有2QD QA QE QL QO ⋅==⋅,即知D ,L ,O ,A 四点共圆,有QLD DAO ODA OLA ===∠∠∠∠,此表明QL 为△LAD 的内角ALD ∠的外角平分线.而EF OQ ⊥,则EL 平分ALD ∠.于是, DM DL DQAM AL AQ==,结论获证. 【解题思维策略分析】1.获得线段比例式的一种手段例10 如图2-13,△ABC 中,D ,E 分别为AC 和AB 同方向延长线上的点,BD 与CE 相交于P ,且BD CE =.若点P 满足2AEP ADP k PED PDE -=-∠∠(∠∠)(k 为常数),则AB AC =.证明 设AP 交BC 于Q ,对△PBC 及其形外一点A ,应用塞瓦定理,有1BQ CE PDQC EP DB⋅⋅=.而BD CE =,则PD QCPE QB=. 不妨设QC QB ≤,则PD PE ≤,即有PC CE PE BD PD PB =--=≤,于是PBE PCD S S △△≥,故EBC DBC S S △△≥.此时,点E 到BC 的距离不小于D 到BC 的距离,则过E 作EF BC ∥必交CD 延长线于一点,设为F .又作△FBC 的外接圆O e 交EF 于另一点F ',则四边形BCFF '为等腰梯形.当AB AC ≥时,由BF F F FC BCA ABC AEF ''===∠∠∠≥∠∠,知F '必在线段EF 上,于是,BDC BFC BEC ∠≥∠≥∠(同弧上的圆外角小于同弧上的圆周角).又由PD PE ≤,知PED PDE ∠≤∠.故结论获证. 2.转化线段比例式的一座桥梁例11 设M 为△ABC 内任一点,AM ,BM ,CM 分别交BC ,CA ,AB 于D ,E ,F .求证:1MD ME MFAD BE CF ++=. 证明 如图2-14,记BD m DC =,CE n EA =,AFl FB=.对△ABC 及点M ,应用塞瓦定理,有1BD CE AFmnl DC EA FB⋅⋅==.对△ADC 及截线EMB ,应用梅涅劳斯定理,有11AM DB CE AM mn MD BC EA MD m ⋅⋅=⋅⋅=+,即 1(1)AM mm l MD m n +==++. 由合比定理得1(1)AD m l MD =++,即11MD AD l ml=++. 同理,111ME lBE m mn l ml ==++++, 111MF mlCF n nl ml l==++++. 三式相加,得1MD ME MFAD BE CF++=. 例12 如图2-15,设P 为△ABC 内任意一点,AP ,BP ,CP 的延长线交对边BC ,CA ,AB 于点D ,E ,F ,EF 交AD 于Q.试证:(3PQ AD -≤.证明 令BD m DC =,CE n EA =,AF p FB =,对△ABC 及点P ,应用塞瓦定理,有1BD CE AFmnp DC EA FB⋅⋅==.对△ADC 及截线BPE ,应用梅涅劳斯定理,有 1CE AP DB EA PD BC ⋅⋅=.注意到1DB mBC m =+,则有 11AP m n PD m ⋅⋅=+,即1AP m PD mn +=,故11AP m AD mn m +=++. 又对直线APD 截△BCE ,有1BD CA EP DC AE PB ⋅⋅=.而1CA n AE =+,则BP mn m EP =+,故1BEmn m EP=++.又对△ABP 及截线FQE ,有1AF BE PQ FB EP AQ ⋅⋅=,即有 11(1)1PQ AQ p mn m mp p ==++++,故12PQ AQ mp p =++. 从而1121PQ PQ AP m AD AP AD mp p mn m +=⋅=⋅++++ 1112(1)211(1)211mn mn p m p m m m =⋅=+++++++++3=-于是,(3PQ AD -≤.其中等号由2(1)1mn p m m ++=+≥中等号成立时成立,即当且仅当2(1)1mnp m m =++亦即当且仅当22(1)(1)(1)mnp p m p m p m ==+++,亦即(1)p m +=时取等号.此时,m 和p 之间成为如图2-16的双曲线的关系.例13 如图2-17,已知直线的三个定点依次为A 、B 、C ,Γ为过A 、C 且圆心不在AC 上的圆,分别过A 、C 两点且与圆Γ相切的直线交于点P ,PB 与圆Γ交于点Q .证明:AQC ∠的平分线与AC 的交点不依赖于圆Γ的选取.(IMO 45预选题)证明 设AQC ∠的平分线交AC 于点R ,交圆Γ于点S ,其中S 与Q 是不同的两点.由于△PAC 是等腰三角形,则有sin sin AB APBBC CPB=∠∠. 同理,在△ASC 中,有sin sin AR ASQRC CSQ =∠∠. 在△PAC 中,视Q 为塞瓦点,由角元形式的塞瓦定理,有sin sin sin 1sin sin sin APB QAC QCPCPB QAP QCA⋅⋅=∠∠∠∠∠∠.注意到PAQ ASQ QCA ==∠∠∠,PCQ CSQ QAC ==∠∠∠.则 22sin sin sin sin sin sin sin sin APB PAQ QCA ASQ CPB QAC PCQ CSQ⋅==⋅∠∠∠∠∠∠∠∠. 即 22AB AR BC RC=,故结论获证. 3.求解三角形格点问题的统一方法如果三角形的三个角的度数都是10的整数倍,三角形内一点与三角形的三个顶点分别连结后,得到的所有的角也都具有这个性质,我们称这样的点为三角形的格点.例14 如图2-18,在△ABC 中,40BAC =︒∠,60ABC =︒∠,D 和E 分别是AC 和AB 上的点,使得40CBD =︒∠,70BCE =︒∠,F 是直线BD 和CF 的交点.证明:直线AF 和直线BC 垂直.(1998年加拿大奥林匹克试题)证明 设BAF α=∠,则40FAC α=︒-∠,对△ABC 及点F ,应用第一角元形式的塞瓦定理,有 sin10sin sin 401sin 70sin(40)sin 20αα︒︒⋅⋅=︒︒-︒. 从而sin10sin 2sin 20cos201cos20sin(40)sin 20αα︒︒⋅︒⋅⋅=︒︒-︒,即有sin(40)2sin sin102sin cos80ααα︒-=⋅︒=⋅︒ sin(80)sin(80)αα=+︒+-︒.∴ sin(80)sin(40)sin(80)2cos60sin(20)sin(20)ααααα-︒=︒--+︒=︒⋅-︒-=-︒-.注意到040α<<︒,知8020α-︒<-︒-,8020α-︒<︒,有 8020αα-︒=-︒-,故30α=︒.延长AF 交BC 于H ,则180180306090AHB FBC ABH =︒--=︒-︒-︒=︒∠∠∠.故AF BC ⊥.注 此题也可这样来解:由sin10sin sin 401sin 70sin(40)sin 20αα︒︒⋅⋅=︒︒-︒,有 sin(40)sin10sin 40sin10sin(4030)2sin10sin 40cot30cos40sin sin70sin 20sin30sin30αα︒-︒-︒︒︒-︒==︒===︒⋅︒-︒︒-︒︒︒.由于sin(40)sin 40cot cos40sin ααα︒-=︒⋅-︒作为α的函数在(0,180)︒︒上严格递减,所以30BAF α==︒∠.故90ABC BAF +=︒∠∠.因此,AF BC ⊥. 或者过点A 作AH BC ⊥于H ,则30BAH =︒∠,10HAC =︒∠. 关于△ABC 有sin sin sin sin30sin10sin 401sin sin sin sin10sin70sin 20BAH ACD CBD HAC ECB DBA ︒︒︒⋅⋅=⋅⋅=︒︒︒∠∠∠∠∠∠.所以,AH 、BD 、CE三线共点,因此点F 在AH 上,即AF BC ⊥. 例15 如图2-19,在△ABC 内取一点M ,使得30MBA =︒∠,10MAB =︒∠.设80ACB =︒∠,AC BC =,求AMC ∠. (1983年前南斯拉夫奥林匹克试题)解 设ACM α=∠,则80MCB α=︒-∠.由第一角元形式的塞瓦定理,有 ()sin sin10sin 80sin 40αα︒⋅⋅︒-︒sin 201sin30︒=︒. 从而 sin sin10sin(80)cos20αα⋅︒=︒-⋅︒. ∴ 2sin cos802sin(80)cos20αα⋅︒=︒-⋅︒,∴ sin(80)sin(80)sin(100)sin(60)αααα+︒+-︒=︒-+︒-, ∴ sin(80)sin(60)sin(100)sin(80)αααα-︒-︒-=︒--+︒ 2cos90sin(10)0α=︒⋅︒-=.于是 sin(80)sin(60)αα-︒=︒-.注意到 080α<<︒,知8080α-︒<<-︒,6060α︒-<︒. ∴ 8060αα-︒=︒-,故 70α=︒.所以 180180407070AMC MAC ACM =︒--=︒-︒-︒=︒∠∠∠为所求. 注 此题结果也可直接由①式有sin sin 70sin10sin(80)αα=︒⎧⎨︒=︒-⎩且0α<,8080α︒-<︒,求得70α=︒. 另外,此题也可这样来解:由sin sin10sin 201sin(80)sin 40sin30αα︒︒⋅⋅=︒-︒︒,有sin(80)sin10sin 20sin10sin(8070)sin80cot 70cos80sin sin 40sin30cos20sin 70αα︒-︒⋅︒︒︒-︒====︒⋅︒-︒︒⋅︒︒︒.因为sin(80)sin80cot cos80sin ααα︒-=︒⋅-︒作为α的函数在(0︒,180︒)上严格递减,所以70ACM α==︒∠.故180407070AMC =︒-︒-︒=︒∠.或者由140AMB =︒∠,令AMC x =∠,则220CMB x =︒-∠.对△MAB 和点C 应用第一角元形式的塞瓦定理,有sin sin sin sin sin 20sin501sin sin sin sin(220)sin50sin 40AMC MBC BAC x CMB CBA CAM x ︒︒=⋅⋅=⋅⋅︒-︒︒∠∠∠∠∠∠. 则sin(220)1sin(22070)sin 220cot 70cos220sin 2cos20sin70x x ︒-︒-︒===︒⋅︒-︒︒︒.因为sin(220)sin 220cot cos220(sin 2200)sin x x x︒-=︒⋅-︒︒<作为x 的函数在(0,180)︒︒上严格递增,所以70AMC x ==︒∠.例16 如图2-20,△ABC 具有下面性质:存在一个内部的点P ,使得10PAB =︒∠,20PBA =︒∠,30PCA =︒∠,40PAC =︒∠.证明:△ABC 是等腰三角形.(1996年美国第25届奥林匹克试题)证明 设BCP α=∠,则1802010403080PBC αα=︒-︒-︒-︒-︒-=︒-∠.由第一角元形式的塞瓦定理,有sin 20sin 40sin 1sin(80)sin10sin30αα︒︒⋅⋅=︒-︒︒.即有2sin10cos10sin 40sin 11sin(80)sin102αα︒⋅︒︒⋅⋅=︒-︒.∴ sin(80)4sin sin 40cos104sin sin 40sin80ααα︒-=⋅︒⋅︒=⋅︒⋅︒4sin sin 20sin 40sin80sin60sin sin 20sin 20αα⋅︒⋅︒⋅︒︒⋅==︒︒, ∴ sin(80)sin 20sin60sin αα︒-⋅︒=︒⋅. 从而 sin(80)sin 60sin 20sin αα︒-=︒⎧⎨︒=⎩且0α<,8080α︒-<︒,故20α=︒,即50ACB CAB =︒=∠∠,从而AB BC =.注 此题也可这样来求解:由sin 20sin 40sin 1sin(80)sin10sin30αα︒︒⋅⋅=︒-︒︒,有sin(80)sin 20sin 404sin 20sin 40sin804cos10sin 40sin sin10sin30sin 20αα︒-︒︒︒⋅︒⋅︒=⋅=︒⋅︒=︒︒︒sin60sin(8020)sin80cot 20cos80sin 20sin 20︒︒-︒===︒⋅︒-︒︒︒.因为sin(80)sin80cot cos80sin ααα︒-=︒⋅-︒作为α的函数在(0︒,180︒)上严格递减,所以BCP α=∠20=︒,即50ACB CAB =︒=∠∠.故AB BC =.还可对△APC 及点B 应用第一角元形式的塞瓦定理来求. 4.论证直线共点的一种工具例17 如图2-21,在四边形ABCD 中,AB AD =,BC DC =,过AC ,BD 的交点O 引EF ,GH ,其中EF 交AB ,CD 于E ,F ,GH 交DA ,BC 于G ,H .EH ,GF 分别交BD 于P ,Q ,则OP OQ =. (1990年CMO 选拔试题)证明 在AB ,BC 上分别取G ',F ',使AG AG '=,CF CF '=,则由对称性可知有下列角相等,即若设,AOG AOG αβ'==∠∠,COH γ=∠,1G OE '=∠∠,2EOB =∠∠,3BOF '=∠∠,4F OH '=∠∠,则αβ=,又αγ=,故βγ=.又14βγ+=+∠∠,故14=∠∠,23=∠∠. 连G H '交BD 于K ,在△BHG '中, OG E OBF OHKOEB OF H OKG S S S G E BF HK EB F H KG S S S ''''''⋅⋅=⋅⋅''△△△△△△ sin 1sin 3sin(34)1sin 2sin 4sin(12)OG OE OB OF OH OK OE OB OF OH OK OG ''⋅⋅⋅⋅⋅⋅+=⋅⋅=''⋅⋅⋅⋅⋅⋅+∠∠∠∠∠∠∠∠.故由塞瓦定理的逆定理,知G F '',BO ,HE 共点,即G F ''过点P .由对称性知,OP OQ =. 例18 如图2-22,在锐角△ABC 中,以A 点引出的高AD 为直径作圆交AB ,AC 于M ,N ,再从A 作A l MN ⊥.同样可作出B l ,C l .试证:三直线A l ,B l ,C l 相交于一点.(第29届IMO 预选题)证明 设A l 与MN ,BC 分别相交于点G ,D ',由AMG ADN =∠∠,90AGM AND ==︒∠∠,知MAG NAD =∠∠,即BAD CAD '=∠∠.同理,设CA ,AB 边上的高BE ,CF 的垂足分别为E ,F ,且B l ,C l 分别与CA ,AB 交于E ',F ',则有CBE ABE '=∠∠,ACF BCF '=∠∠.由于△ABC 的三条高相交于垂心,此时应用第一角元形式的塞瓦定理,得sin sin sin 1sin sin sin CAD ABE BCFDAB EBC FCA ⋅⋅=∠∠∠∠∠∠,用等角代换上式,有sin sin sin 1sin sin sin BAD ACF CBE DAC F CB E BA'''⋅⋅=''∠∠∠∠∠∠.故由第一角元形式的塞瓦定理,知AD ',BE ',CF '三线共点,即A l ,B l ,C l 相交于一点.例19 如图2-23,四边形ABCD 内接于圆,AB ,DC 的延长线交于E ,AD ,BC 的延长线交于F ,P 为圆上任一点,PE ,PF 分别交圆于R ,S .若对角线AC 与BD 相交于T ,求证:R ,T ,S 三点共线.证明 连PD ,AS ,RC ,BR ,AP ,SD .由△EBR ∽△EPA ,△FDS ∽△FPA ,有BR EBPA EP =,PA FP DS FD =,此两式相乘,有BR EB FPDS EP FD =⋅.①又由ECR EPD △∽△,FPD FAS △∽△,有 CR EC PD EP =,PD FPAS FA =, 此两式相乘,有 CR EC FPAS EP FA=⋅. 由①÷②,得 BR AS EB FADS CR EC FD⋅=⋅. 上式两边同乘以DC AB,得 BR CD SA EB AF DCRC DS AB BA FD CE ⋅⋅=⋅⋅. 对△EAD 及截线BCF ,应用梅涅劳斯定理,有 1EB AF DC BA FD CE⋅⋅=. 于是1BR CD SARC DC AB⋅⋅=. 此时,应用第一角元形式的塞瓦定理的推论,知BD ,RS ,AC 交于一点.从而R ,T ,S 三点共直线.【模拟实战】习题A 1.在△ABC 中,D 是BC 上的点,13BD DC =,E 是AC 中点.AD 与BE 交于O ,CO 交AB 于F ,求四边形BDOF 的面积与△ABC 的面积的比.2.若通过△ABC 各顶点的直线AD ,BE ,CF 共点,并且它们在边BC ,CA ,AB 所在直线上的截点D ,E ,F 关于所在边中点的对称点分别为D ',E ',F ',则直线AD ',BE ',CF '也共点. 3.一圆交△ABC 的各边所在直线于两点,设BC 边上的交点为D ,D ',CA 边上的交点为E ,E ',AB 边上的交点为F ,F '.若AD ,BE ,CF 共点,则AD ',BE ',CF '也共点.4.试证:过三角形顶点且平分三角形周长的三条直线共点.5.将△ABC 各内角三等分,每两个角的相邻三等分线相交得△PQR ,又AX ,BY ,CZ 分别平分BAC ∠,ABC ∠,ACB ∠且它们与QR ,RP ,PQ 交于X ,Y ,Z .求证:PX ,QY ,RZ 三线共点.6.将△ABC 的各外角三等分,每两个外角的相邻三等分线相交得△DEF .又AX ,BY ,CZ 分别平分BAC ∠,ABC ∠,ACB ∠且它们与EF ,FD ,DE 交于X ,Y ,Z .求证:DX ,EY ,FZ 三线共点.7.O e 是△ABC 的内切圆,BC ,CA ,AB 上的切点各是D ,E ,F .射线DO 交EF 于A ',同样可得B ',C '.试证:直线AA ',BB ',CC '共点.8.△ABC 在△A B C '''内部,且从A ,B ,C 各向B C '',C A '',A B ''所作的垂线共点,则从A ',B ',C '各向BC ,CA ,AB 所作的垂线也共点.9.在△ABC 中,40ABC ACB ==︒∠∠,P 为形内一点,20PAC =︒∠,30PCB =︒∠,求PBC ∠的度数.10.在ABC △中,AB AC =,80A =︒∠,D 为形内一点,且10DAB DBA ==︒∠∠,求ACD ∠的度数.(《数学教学》问题432题)11.在ABC △中,30BAC =︒∠,70ABC =︒∠,M 为形内一点,20MAB MCA ==︒∠∠,求MBA ∠的度数. (《数学教学》问题491题) 12.在ABC △中,40ABC =︒∠,30ACB =︒∠,P 为ABC ∠的平分线上一点,使10PCB =︒∠,BP 交AC 于M ,CP 交AB 于N .求证:PM AN =. (《数学教学》问题531题) 13.在ABC △中,40ABC =︒∠,20ACB =︒∠,N 为形内一点,30NBC =︒∠,20NAB =︒∠,求NCB ∠的度数. (《数学通报》问题1023题) 14.在ABC △中,80BAC =︒∠,60ABC =︒∠,D 为形内一点,且10DAB =︒∠,20DBA =︒∠,求ACD ∠的度数. (《数学通报》问题1142题) 15.在△ABC 中,50ABC =︒∠,30ACB =︒∠,M 为形内一点,20MCB =︒∠,40MAC =︒∠,求MBC ∠的度数. (《数学通报》问题1208题) 16.△ABC 中,70ABC =︒∠,30ACB =︒∠,P 为形内一点,40PBC =︒∠,20PCB =︒∠.求证:1CA AB BPAP PC CB⋅⋅=⋅⋅. (《数学通报》问题1306题) 17.在△ABC 中,40ABC ACB ==︒∠∠,P ,Q 为形内两点,20PAB QAC ==︒∠∠,PCB QCA =∠∠10=︒.求证:B ,P ,Q 三点共线. (《数学通报》问题1243题) 18.△ABC 中,50ABC ACB ==︒∠∠,P ,Q 为形内两点,10PCA QBC ==︒∠∠,PAC QCB =∠∠20=︒.求证:BP BQ =. (《数学通报》问题1281题) 19.在△ABC 中,AB AC =,100A =︒∠,I 为内心,D 为AB 上一点,满足BD BI =.试求BCD ∠的度数. (《数学通报》问题1073题) 20.1A ,2A ,1B ,2B ,1C ,2C 顺次分别在△ABC 的三边BC ,CA ,AB 上,且12BA A C =,12CB B A =, 12AC C B =,过2A ,2B ,2C 分别作1AA ,1BB ,1CC 的平行线a l ,b l ,c l .求证:a l ,b l ,c l 三线共点的充要条件是1AA ,1BB ,1CC 三线共点.21.在△ABC 中,AB AC =,AD BC ⊥于D ,过D 任作两射线分别交AB ,AC 于点E ,F ,交过点A 的平行线于G ,H ,且GH BC ∥.求证:AD ,GF ,HE 共点.22.在△ABC 中,过三边BC ,CA ,AB 边中的中点M ,N ,L 的三条等分三角形周长的直线MS ,NT ,LU (S ,T ,U 在三角形三边上)分别交LN ,LM ,MN 于D ,E ,F .求证:MS ,NT ,LU 三线共点.23.△ABC 的内切圆切BC ,CA ,AB 于D ,E ,F .P 是△ABC 内一点,PA 交内切圆于两点,其中靠近A 的一点为X ,类似定义Y ,Z .试证:DX ,EY ,FZ 三线共点.24.△ABC 在△A B C '''内部,AB 的延长线分别交A C '',B C ''于5P ,1P ;AC 的延长线分别交B A '',B C ''于3P ,4P ;BC 的延长线分别交A B '',A C ''于6P ,2P ,且满足142536AP AP BP BP CP CP ===== 123BP CP AP =++.求证:AA ',BB ',CC '所在直线共点.(《中学数学教学》擂台题(28)) 25.给定△ABC ,延长边BC 至D ,使CD AC =.△ACD 的外接圆与以BC 为直径的圆相交于C 和P .设BP 与CP 的延长线分别交AC 和AB 于E ,F .求证:E ,F ,D 共线.(第15届伊朗奥林匹克题) 26.在△ABC 的边上向外作三个正方形,1A ,1B ,1C 是正方形中的边BC ,CA ,AB 对边的中点.求证:直线1AA ,1BB ,1CC 共点.习题B1.O e 是△ABC 的内切圆,D ,E ,F ,分别是BC ,CA ,AB 上的切点,DD ',EE ',FF '都是O e 的直径.求证:直线AD ',BE ',CF '共点. (《数学通报》问题1396题) 2.四边形ABCD 的内切圆分别与边AB ,BC ,CD ,DA 相切于E ,F ,G ,H .求证:AC ,BD ,HF ,GE 四线共点. (《数学通报》问题1370题) 3.锐角△ABC 中,A 角的平分线与三角形的外接圆交于另一点1A ,点1B ,1C 与此类似.直线1AA 与B ,C 两角的外角平分线交于0A ,点0B ,0C 与此类似.求证:(Ⅰ)三角形000A B C 的面积是六边形111AC BACB 的二倍;(Ⅱ)三角形000A B C 的面积至少是三角形ABC 面积的四倍. (IMO -30试题) 4.设P 为△ABC 内一点,使BPA CPA =∠∠,G 是线段AP 上的点,直线BG ,CG 分别交边AC ,AB于E ,F .求证:BPF CPE =∠∠.5.在凸四边形ABCD 中,对角线AC 平分BAD ∠,E 是CD 的延长线上的一点,BE 交AC 于点G ,延长DG 交CB 的延长线于F .试证:BAF DAE =∠∠.6.在△ABC 中,AB AC =,100A =︒∠,I 为内心,D 为AB 上一点,满足BD BI =.试求BCD ∠的度数. (《数学通报》问题1073题) 7.设△ABC 是等边三角形,P 是其内部一点,线段AP ,BP ,CP 依次交三边BC ,CA ,AB 于1A ,1B ,1C 三点.证明:111111111A B B C C A A B B C C A ⋅⋅⋅⋅≥.(IMO -37预选题) 8.在一条直线l 的一侧画一个半圆Γ,C ,D ,是Γ上两点,Γ上过C 和D 的切线分别交l 于B 和A ,半圆的圆心在线段BA 上,E 是线段AC 和BD 的交点,F 是l 上的点,EF l ⊥.求证:EF 平分CFD ∠. (IMO -35预选题) 9.设1A 是锐角△ABC 的内接正方形的中心,其中内接正方形的两个顶点在BC 边上,一个顶点在AB 边上,一个顶点在AC 边上.同样定义两个顶点分别在AC 边和AB 边上的内接正方形的中心分别为1B ,1C .证明:1AA ,1BB ,1CC 交于一点.(IMO -42预选题)10.以△ABC 的底边BC 为直径作半圆,分别与AB ,AC 交于点D ,E ,分别过点D ,E 作BC 的垂线,垂足依次为F ,G ,线段DG 和EF 交于点M .求证:AM BC ⊥.(1996年国家队选拔考试题)11.设O ,H 是锐角△ABC 的外接圆的圆心和垂心.证明:存在D ,E ,F 分别在线段BC ,CA ,AB 上,使得OD DH OE EH OF FH +=+=+,且此时AD ,BE ,CF 三线交于一点.(IMO -41预选题)12.已知AB 是O e 的直径,弦CD AB ⊥于L ,点M 和N 分别在线段LB 和LA 上,且LM ∶MB LN =∶NA ,射线CM ,CN 交O e 于E ,F .求证:AE ,BF ,OD 三线共点.13.设I 是△ABC 的内心,以I 为圆心的一个圆分别交BC 于1A ,2A ,交A C 于1B ,2B ,交AB 于1C ,2C .这六个点在圆上的顺序为1A ,2A ,1B ,2B ,1C ,2C .设3A ,3B ,3C 为弧¼12A A ,¼12B B ,¼12C C 的中点,直线23A A ,13B B 相交于4C ,直线23B B ,13C C 相交于4A ,直线23C C ,13A A 相交于4B .求证:直线34A A ,34B B ,34C C 三线共点.14.在△ABC 的边AB 和AC 上分别向形外作△ABE 和△ACF ,使△ABE ∽△ACF ,且ABE =∠90ACF =︒∠.求证:连线BF ,CE 与边BC 上的高AH 三线共点.15.过非等边三角形各顶点作其外接圆的切线,则各切线与其对边的交点共线.16.在△ABC 内三点D ,E ,F 满足BAE CAF =∠∠,ABD CBF =∠∠,则AD ,BE ,CF 三线共点的充要条件是ACD BCE =∠∠. 17.在任意△ABC 的三边BC ,CA ,AB 上各有点M ,N ,L ,而Q 是△ABC 内部任一点,直线AQ ,BQ ,CQ 分别交线段NL ,LM ,MN 于1M ,1N ,1L .求证:直线1M M ,1N N ,1L L 共点的充分必要条件是AM ,BN ,CL 共点,而与Q 点的位置无关.18.设P 是平面上△ABC 区域内任一点,AP ,BP ,CP 的延长线交△ABC 三边于D ,E ,F .求证:在△ABC 区域内,存在一个以△DEF 的某两边为邻边的平行四边形.19.设凸四边形ABCD 的两组对边所在的直线,分别交于E ,F 两点,两对角线的交点为P ,过点P 作PO EF ⊥于O .求证:BOC AOD =∠∠. (2002国家集训队选拔试题) 20.在△ABC 中,ABC ∠和ACB ∠均为锐角.D 是BC 边上的内点,且AD 平分BAC ∠,过点D 作垂线DP AB ⊥于P ,DQ AC ⊥于Q ,CP 与BQ 相交于K .求证:AK BC ⊥.。
第2章 塞瓦定理及应用(基础篇)

高一(初三)竞赛辅导第二讲第2章塞瓦定理知识塞瓦定理及其逆定理塞瓦定理:如果ABC △的三个顶点与一点P 的连线AP 、BP 、CP 交对边或其延长线于点D 、E 、F ,如图,那么1BD CE AF DC EA FB⋅⋅=.通常称点P 为ABC △的塞瓦点.PFEB A证明:∵直线FPC 、EPB 分别是ABD △、ACD △的梅氏线,∴1BC DP AF CD PA FB ⋅⋅=,1DB CE AP BC EA PD ⋅⋅=.两式相乘即可得:1BD CE AF DC EA FB⋅⋅=.塞瓦定理的逆定理:如果点D 、E 、F 分别在ABC △的边BC 、CA 、AB 上或其延长线上,并且1BD CE AF DC EA FB⋅⋅=,那么AD 、BE 、CF 相交于一点(或平行).FP F'E D C B AFED CB A 证明:⑴若AD 与BE 相交于一点P 时,如图,作直线CP 交AB 于'F .由塞瓦定理得:'1BD CE AF DC EA F B ⋅⋅=',又已知1BD CE AF DC EA FB ⋅⋅=,∴AF AF FB F B '=',∴AB AB FB F B=',∴FB F B '=.∴'F 与F 重合∴'CF 与CF 重合∴AD 、BE 、CF 相交于一点.⑵若AD 与BE 所在直线不相交,则AD ∥BE ,如图.∴BD EA DC AC =,又已知1BD CE AF DC EA FB ⋅⋅=,∴1EA CE AF AC EA FB ⋅⋅=,即CE FB AC AF=.∴//BE FC ,∴AD BE FC ∥∥.说明:三线平行的情况在实际题目中很少见.思考提升【例1】(1)设AX BY CZ ,,是ABC △的三条中线,求证:AX BY CZ ,,三线共点.(2)若AX BY CZ ,,为ABC △的三条内角平分线.求证:AX BY CZ ,,三线共点.【解析】(1)由条件知,BX XC YC YA ZA ZB ===,,.∴1BX CY AZ XC YA ZB⋅⋅=,根据塞瓦定理的逆定理可得三条中线AX BY CZ ,,共点.这个点称为这个三角形的重心.(2)由三角形内角平分线定理得:BX AB CY BC AZ AC XC AC YA BA ZB BC ===,,.三式分别相乘,得:1BX CY AZ AB BC AC XC YA ZB AC AB BC⋅⋅=⋅⋅=.根据塞瓦定理的逆定理可得三角形三内角平分线AX BY CZ ,,共点,这个点称为这个三角形的内心.习题1.若AX BY CZ ,,分别为锐角ABC △的三条高线,求证:AX BY CZ ,,三线共点.【解析】由ABX CBZ △∽△得:BX AB BZ BC =;由BYA CZA △∽△得:AZ AC AY AB=;由AXC BYC △∽△可得:YC BC CX AC =.所以1BX AZ YC AB AC BC BZ AY CX BC AB AC⋅⋅=⋅⋅=.根据塞瓦定理的逆定理可得三条高线AX BY CZ ,,共点.对直角三角形、钝角三角形,同样也可以证得三条高线共点.我们把一个三角形三条高线所在直线的交点叫做这个三角形的垂心.【例2】如图,M 为ABC △内的一点,BM 与AC 交于点E ,CM 与AB 交于点F ,若AM 通过BC 的中点D ,求证:EF BC ∥.【解析】对ABC △和点M 应用塞瓦定理可得:1AF BD CE FB DC EA ⋅⋅=.又因为BD DC =,所以1AF CE FB EA ⋅=.进而AF AE FB EC =,所以EF BC ∥.习题2.如果梯形ABCD 的两腰AD 、BC 的延长线交于M ,两条对角线交于N .求证:直线MN 必平分梯形的两底.BQ AN CPD M【解析】∵AB CD∥∴MD CM DA BC =∴1MD BC DA CM ⋅=∵1MD AQ BC DA QB CM⋅⋅=(由塞瓦定理得)∴1AQ QB=,∴AQ QB =∵DP PC AQ QB =,∴DP PC =.知识三梅涅劳斯定理、塞瓦定理综合自我挑战【备选】如图,E 、F 分别为ABC △的AC 、AB 边上的点,且3AE EC =,3BF FA =,BE 、CF 交于点P ,AP 的延长线交BC 于点D .求:AP PD 的值.【解析】∵P 为ABC △的塞瓦点.∴11133AF BD CE BD FB DC EA DC ⋅⋅=⋅⋅=∴91BD DC =,∴910BD BC =.∵EPB 为ACD △的梅氏线,∴911103AP DB CE AP PD BC EA PD ⋅⋅=⋅⋅=∴103AP PD =【备选】如图,四边形ABCD 的对边AB 和DC ,DA 和CB 分别相交于点L K ,,对角线AC 与BD 交于点M .直线KL 与BD 、AC 分别交于点F G 、.求证:KF KG LF LG=.【解析】对DKL △与点B 应用塞瓦定理得:1DA KF LC AK FL CD ⋅⋅=.对DKL △和截线ACG 应用梅涅劳斯定理可得:1DA KG LC AK GL CD⋅⋅=.进而可得KF KG LF LG.。
塞瓦定理

塞瓦定理【定理内容】设O 是ABC ∆内任意一点,AO 、BO 、CO 分别交对边于D 、E 、F , 则1=⋅⋅FBAFEA CE DC BD .[评]等价叙述:ABC ∆的三边BC 、CA 、AB 上有点D 、E 、F ,则AD 、BE 、CF 三线共点的充要条件是1=⋅⋅FBAFEA CE DC BD ,这点称为三角形的塞瓦点。
【背景简介】 【证法欣赏】证法1:(利用梅涅劳斯定理证明)∵ADC ∆被直线BOE 所截,∴1=⋅⋅ECAEOA DO BD CB ① 同理,1=⋅⋅FBAFOA DO CD BC ②②÷①得:1=⋅⋅FB AFEA CE DC BD .【证法欣赏】证法2:(利用面积关系证明) ∵CODBODACD ABD S S S S DC BD ∆∆∆∆== ∴由等比性质得AOCAOBCOD ACD BOD ABD S S S S S S DC BD ∆∆∆∆∆∆=--= ③CCC同理:BOA BOC S S EA CE ∆∆= ④,BOCAOCS S FB AF ∆∆= ⑤, ③×④×⑤得:1=⋅⋅FBAFEA CE DC BD .【证法欣赏】证法3:(利用平行线分线段成比例证明)过A 作BC AM //交BE 、CF 延长线于M 、N , ∵BC AM //,∴BC AN FB AF =, ⑥ AMBCEA CE =,⑦ BDAMOD AO DC AN ==⑧, 由⑧得:ANAMDC BD =⑨ ⑥×⑦×⑨得:1=⋅⋅FB AFEA CE DC BD .【逆定理】塞瓦定理的逆定理也成立,即如果有三点F 、D 、E 分别在ABC ∆的三边AB 、BC 、CA 上,且满足1=⋅⋅EACEDC BD FB AF ,那么AD 、BE 、CF 三线交于一点。
[注]利用塞瓦定理的逆定理可判定三线共点如证明三角形三条高线必交于一点;三角形三条中线交于一点等。
平面几何2--塞瓦定理及应用

平面几何(2)----塞瓦定理及应用塞瓦定理 设''',,A B C 分别是ABC 的三边,,BC CA AB 或其延长线上的点,若''',,AA BB CC 三线平行或共点的充要条件是''''''1BA CB AC AC B A C B ⋅⋅= 角元形式的塞瓦定理 设''',,A B C 分别是ABC 的三边,,BC CA AB 或其延长线上的点,若''',,AA BB CC 三线平行或共点充要条件是''''''sin sin sin 1sin sin sin BAA ACC CBB A AC C CB B BA∠∠∠⋅⋅=∠∠∠1. 四边形两组对边延长分别相交,且交点的连线与四边形的一条对角线平行,证明:另一条对角线的延长线平分对边交点连线的线段2. 如图,锐角ABC 中,AD 是BC 边上的高,H 是线段AD 内任一点,BH 和CH 的延长线分别交,AC AB 于,E F ,求证:EDH FDH ∠=∠3. 如图,在ABC 中,90o BAC ∠=,G 为AB 上给定的一点(G 不是线段AB 的中点),设D 为直线GC 上与C ,G 都不相同的任意一点,并且直线AD ,BC 交于E ,直线BD ,AC 交于F ,直线EF ,AB 交于H ,试证明交点H 与D 在直线CG 上的位置无关4. 如图,设P 为ABC 内任一点,在形内作射线AL ,BM ,CN ,使得C A L PAB ∠=∠,,.MBC PBA NCA BCP ∠=∠∠=∠求证:AL ,BM ,CN 三线共点5. 如图,在ABC 中,040,60,o BAC ABC ∠=∠=D 和E 分别是AC 和AB 上的点,使得40,70,o o CBD BCE ∠=∠=F 是直线BD 和CE 的交点,证明:直线AF 和直线BC 垂直6.如图,在四边形ABCD中,对角线AC平分BAD∠,在CD上取一点E,BE 与AC相交于F,延长DF交BC于G,求证:GAC EAC∠=∠7.在一个ABC内满足AP=AC及PB=PC的一点, 中,2,∠=∠为ABCC B P求证:AP是A∠的三等分线8.如图,在ABC中,D,E分别是BC,CA上的点,且BD:DC=m:1,CE:EA=n:1,AD 与BE交于F,则ABF的面积是ABC的面积的多少倍?9.如图,设P是ABC内任意一点,AP,BP,CP的延长线交对边BC,CA,AB于点D,E,F,EF交AD于Q,试证:(3≤-PQ AD10.如图,已知直线的三个定点依次为A,B,C,T为过A、C且圆心不在AC上的圆,分别过A、C两点且与圆T相切的直线交于点P,PB与圆T交于Q,证明:AQC∠的平分线与AC的交点不依赖于圆T的选取。
第二章塞瓦定理及应用答

第二章 塞瓦定理及应用习题A1.对ABC △及点O ,由塞瓦定理可得3AF FB=,34AF AB =.又对ADC △与截线FOC ,由梅涅劳斯定理得4AO OD =,45AO AD =,故343455AFO ABD S S =⋅⋅△△,由此可知25BDOF ABD S S =△.又14ABD ABC S S =△△,所以2115410BDOF ABC S S =⋅=△. 2.在ABC △中由题设及塞瓦定理有1BD CE AFDC EA FB ⋅⋅=.又有BD CD '=,DC D B '=,CE AE '=,EA E C '=,AF BF '=,FB F A '=,故1CD BF AE D B F A E C'''⋅⋅='''.由塞瓦定理之逆知AD ',BE ',CF '三线共点.3.由割线定理有AF AF AE AE ''⋅=⋅,即AF E A EA AF '='.同理,BD F B FB BD '=',CE D CDC CE '='.三式相乘并适当交换位置,有BD CE AF D C E A F B DC EA FB BD CE AF '''⋅⋅=⋅⋅'''.由塞瓦定理知1BD CE AFDC EA FB⋅⋅=,再由塞瓦定理之逆知AD ',BE ',CF '三线共点.4.设ABC △的边BC a =,CA b =,AB c =,周长为2s ,过顶点A ,B ,C 且平分ABC △周长的直线分别交BC ,CA ,AB 于点D ,E ,F ,则由BD CD a +=,c BD b CD +=+,求得1()2BD a b c s c =+-=-,1()2CD c a b s b =+-=-.同理C Es =-,AE s b CD =-=,BF s a CE =-=.故有1BD CE AFDC EA FB⋅⋅=.由塞瓦定理之逆,知AD ,BE ,CF 共点.5.令3B A C a ∠=,3ABC β∠=,3ACB γ∠=,由角平分线性质有QX AQ XR AR =,BY BR YP BP =,PZ CPZQ CQ =.由正弦定理,有sin sin BR αAR β=,sin sin CP βBP γ=,sin sin AQ γCQ α=,于是1QX BY PZ BR CP XR YP ZQ AR CQ ⋅⋅=⋅=.由塞瓦定理之逆,值PX ,QY ,RZ 三线共点.6.令3BAC α∠=,3ABC β∠=,3ACB γ∠=,由平分线性质有EX AE FX AF =,FY BF YD BD =,DZ CDZE CE=.设ABC △的外接圆半径为R ,由正弦定理有2sin3sin(60)8sin sin(60)sin(60)sin(60)R γβAF R γγβγ⋅⋅︒-==⋅⋅-⋅︒-︒-,sin sin(60)sin(60)βγβ⋅︒-⋅︒-.子啊AEF △中,由余弦定理及公式222sin ()sin sin sin sin cos()x y x y x y x y +=++⋅⋅+,求得 8sin(60)sin(60)sin(60)EF R αβγ=⋅︒-⋅︒-⋅︒-.由sin sin sin(60)AE AF EF AFE AEF α==∠∠︒-,知sin sin AFE β∠=,sin sin AEF γ∠=,故sin sin AE βAF γ=同理, sin sin BF γBD α=,sin sin CD αCE β=.于是1EX FY DZ XF YD ZE⋅⋅=,由塞瓦定理之逆,知DX ,EY ,FZ 三线共点. 7.由正弦定理,有sin sin EA EAA AA E AE '''∠=⋅∠,sin sin A FA AF AA F AF '''∠=⋅∠.两式相除并注意AE AF =,有sin sin AA E AA F ''∠=∠,则sin sin EAA EA A AF A F ''∠=''∠,即sin sin CAA EA A AB A F ''∠=''∠.同理sin sin ABB FB B BC B D''∠=''∠, sin sin BCC DC C CA C E ''∠=''∠.三式相乘,得sin sin sin sin sin sin CAA ABB BCC EA FB DC A AB B BC C CA A F B D C E''''''∠∠∠⋅⋅=⋅⋅''''''∠∠∠.由于DA 'EB ',FC '共点于O ,则上式右边等于1,从而左边亦等于1.由塞瓦定理之逆,知AA ',BB ',CC '共点. 8.设AD ,BE ,CF 分别与B C ',C A ',A B '垂直于D ,E ,F ,且AD ,BE ,CF 共点于P .A G ',B H ',CL 分别与BC ,CA ,AB 垂直于G ,H ,L .又锐角HB A '∠与ACP ∠的两边分别垂直,故HB A ACP '∠=∠,同理,B A G PCB ''∠=∠,从而sin sin sin sin HB A ACPB A G PCB''∠∠=''∠∠.类似地有sin sin sin sin GA C CBP A C L PBA ''∠∠=''∠∠,sin sin sin sin LC B BAPPBA PAC''∠∠=∠∠.三式相乘并适当整理,有sin sin sin sin sin sin sin sin sin sin sin sin GA C LC B HB A ACP CBP BAPB A G AC L C B H PCB PBA PAC '''''∠∠∠∠∠∠⋅⋅=⋅⋅''''''∠∠∠∠∠∠.由ABC △重AP ,BP ,CP 共点及角元形式的塞瓦定理,知上式右边等于1,从而左边也等于1,也等于1.由塞瓦定理之逆,知A G ',B H ',C L '三线共点.9.设PBC x ∠=,则40ABP x ∠=︒-,由sin80sin sin101sin 20sin(40)sin30x x ︒︒⋅⋅=︒︒-︒,求得20x =︒.10.设ACD x ∠=,则50BCD x ∠=︒-,由sin10sin 40sin 1sin 70sin10sin(50)xx ︒︒⋅⋅=︒︒︒-,求得30x =︒.11.设MBA x ∠=,则70MAC ∠=︒,由sin 20sin 20sin(70)1sin 60sin10sin x x︒︒︒-⋅⋅=︒︒,及sin 20sin 40sin80sin(70)sin60sin(70)sin60sin 2sin 402sin 40x x x ︒⋅︒⋅︒⋅︒-︒⋅︒-︒⋅==︒︒,求得30x =︒. 12.连AP ,设P A C x ∠=,则110BAP x ∠=︒-.对ABC △及点P ,有s i n (110)s i n 20s i n 201s i n s i n 20s i n 10x x ︒-︒︒⋅⋅=︒︒,求得80x =︒.此时80APC ∠=︒.过M 作EM AP ∥交PC 于E ,则梯形APEM 为等腰梯形,有PM AE =.又50ANE NBC BCN ∠=∠+∠=︒,18050AEP AMP MAB ABM ∠=∠=︒-∠-∠=︒,则A N A E =,故PM AN =.13.设NCB x ∠=,则20ACN x ∠=︒-,由sin 20sin30sin(20)1sin100sin10sin x x ︒︒︒-⋅⋅=︒︒,求的10x =︒.14.设ACD x ∠=,则40BCD x ∠=︒-,由sin10sin 40sin 1sin 70sin 20sin(40)xx ︒︒⋅⋅=︒︒︒-,求得30x =︒.15.设MBC x ∠=,则50ABM x ∠=︒-,由sin 60sin sin101sin 40sin(50)sin 20x x ︒︒⋅⋅=︒︒-︒及1sin60sin(50)sin60sin 4sin 20sin 40sin80sin(50)2sin 202sin 20x x x ︒⋅︒-︒⋅=⋅︒⋅︒⋅︒⋅︒-=︒︒,求得30x =︒. 15.设PAc x ∠=,80PAB x ∠=︒-,由sin(80)sin 40sin101sin sin30sin 20x x ︒-︒︒⋅⋅=︒︒及4sin10sin50sin70sin(80)sin30sin(80)sin sin50sin50x x x ︒⋅︒⋅︒⋅︒-︒⋅︒-==︒︒,求得30x =︒.分别在APC △,BPC △,ABC △中由正弦定理,有s i n 40s i n 40s i n 10s i n 10CA AP ︒︒==︒︒,sin 20sin 40BP PC ︒=︒,sin301sin802cos10AB CB ︒==︒︒.故.1CA AB BP CA BP ABAP PC CB AP PC CB⋅⋅=⋅=. 17.连BP ,设A B P x ∠=,则40PBC x ∠=︒-,对ABC △及点P 有sin 20sin(40)sin301sin80sin sin10x x ︒︒-︒⋅⋅=︒︒,求得20x =︒.连PQ ,设APQ y ∠=,则70QPC y ∠=︒-.对APC △及点Q 有sin 60sin(70)sin101sin 20sin sin 20y y ︒︒-︒⋅⋅=︒︒,求得40y =︒.此时,40APQ PAB BAP ∠=︒=∠+∠,故B ,P ,Q 共线.18.设A B P x ∠=,则50PBC x ∠=︒-.对ABC △及点P 有sin 60sin(50)sin101sin 20sin sin 40x x ︒︒-︒⋅⋅=︒︒.求得20x =︒,即有20PBQ ∠=︒.连PQ ,设Q P C y ∠=,则110BPQ y ∠=︒-.对BCP △及点Q 有sin(110)sin101sin sin 20y y ︒-︒⋅=︒,求得30y =︒,即有80BPQ ∠=︒.又18080BQP PBQ BPQ ∠=︒-∠-∠=︒,故BP BQ =.19.连DI ,IC ,由AB AC =及I 为内心,知20BCI IBC IBD ∠=∠=∠=︒.又由BD BI =,知80BDI ∠=︒.设DCI x ∠=,则40IDC x ∠=︒-,对BCD △及点I 有sin80sin 20sin 1sin(40)sin 20sin 20xx ︒︒⋅⋅=︒-︒︒,求得10x =︒.故30BCD ∠=︒为所求.20.设过A ,B ,C 分别与BC ,CA ,AB 平行的直线交成A B C ''△,则A ,B ,C 分别为B C ',C A '',A B ''的中点.又设过2A ,2B ,2C 与1AA ,1BB ,1CC 平行的直线a l ,b l ,c l 分别与B C ',C A ',A B '交于2A ',2B ',2C ',则有221180A A B CA A '∠+∠=︒;而由BA CA '=,2BA CA '=,21A BA ACA '∠=∠,知21BA A CA A '△∽△,有21BA A CA A '∠=∠.从而222180A A B BA A ''∠+∠=︒,即2A ',2A ,A '三点共线.故有22212221B A CA A C BA λA C A B BA AC '''====''(因12BA A C =,12AC BA =)=λ.同理,221C B CB u u B A B A '''==='',121AC A C v v C B C B'''===''.于是由塞瓦定理知a l ,b l ,c l 共点11111,,λu v λuv AA BB CC '''⇔=⇔=⇔共点.21.因G H B C ∥,有G A G E B D E D =,HA HF CD FD =.即ED BD GA GE =⋅,FDCD HA HF =⋅.又A B A C =,AD BC ⊥,则BD CD =.于是ED FD GA HA GE HF ⋅=⋅.即1DE GA HFEG AH FD⋅⋅=.由塞瓦定理,即得结论.22.令B C a =,CA b =,AB c =,则2b SL =,2c MN =.由S L D M N D △∽△,得L D L S bN D M N c==.同理,NF a MF b =,ME c LE a=.在MNL △中,有1LD NF MEND MF LE ⋅⋅=.由塞瓦定理之逆,知MD ,NE ,LF 共点,故MS ,NT ,LU 共点. 23.设A E X X F E α∠=∠=,AFX XEF β∠=∠=,XAE a '∠=,XAF β'∠=.在AEF △中,AX ,EX ,FX 交于一点,由角元形式的塞瓦定理,有sin sin sin 1sin sin sin αβββαα'⋅⋅=,即12sin sin ()sin sin ααββ'='. 令YEF γ∠=,YED δ∠=,FBY γ∠=,YBD δ'∠=,EFZ φ∠=,DFZ θ∠=,ECZ φ'∠=,DCZ θ'∠=.同理,有12sin sin sin sin γγδδ'⎛⎫= ⎪'⎝⎭,12sin sin ()sin sin θθφφ'='.注意到AP ,BP ,CP 交于一点,由角元形式的塞瓦定理,有12sin sin sin sin 1sin sin sin sin θαγθφβδφ'''⎛⎫⋅⋅⋅= ⎪'''⎝⎭,由此即证. 24.令21C CP '∠=∠,42CC P '∠=∠,13BB P '∠=∠,64BB P'∠=∠,35AA P '∠=∠,56AA P '∠=∠.AA ',BB ',CC '共线332211446655sin sin sin sin 1sin 3sin 511sin 2sin 4sin 6sin sin sin AP AP A CP CP C BP BPB CP CP C BP BP B AP AP A '''⋅∠⋅∠⋅∠∠∠∠⇔⋅⋅=⇔⋅⋅='''∠∠∠⋅∠⋅∠⋅∠. 而142536AP AP BP BP CP CP =====,则25CP C AP A ''∠=∠,36AP A BP B''∠=∠,321414651AP CP BP CP C BPB CP BP AP ''∠=∠⇔⋅⋅=. 又由条件易知,15BP AP =,26CP BP =,34AP CP =.由此即证.注:此题也可以应用梅涅劳斯定理证.分别延长AB 和A B '',CB 和C B '',AC 和A C ''得交点M ,N ,G (交点可无穷远处).由15AP BP =,有15BP AP =.同理,34AP CP =,62BP CP =.直线B A M ''截ABC △,由梅涅劳斯定理,有36361AP CP BM MA P C P B ⋅⋅=-.同理,52251BP CP AG GC P B P A ⋅⋅=-,14141BP AP CN NB P A P C⋅⋅=-.三式相乘并注意15BP AP =,34AP CP =,62BP CP =,得1BM AG CNMA GC NB⋅⋅=-.由梅涅劳斯定理之逆,知M ,N ,G 共线.又点M ,N ,G 分别是A B C '''△和ABC △对应所在直线的交点,利用笛沙格逆定理可得A B C '''△和ABC △对应顶点的连线A A ',B B ',C C '共点.25.设PA 与BC 相交于D ',对ABC △应用塞瓦定理,有1AF BD CEFB D C EA'⋅⋅='.又由梅涅劳斯定理,点F ,E ,D 共线的充要条件是1AF BD CE FB DC EA ⋅=.从而转证BD DBD C DC'='即可.因AC CD =, 1802DPA DPC ∠=︒-∠,这表明DPC CPD '∠=∠,即PC 时DPD '∠的平分线,且PC PB ⊥,PB 是DPD '∠的外角平分线,由此即证得结论.26.设1AA ,1BB ,1CC 交边BC ,CA ,AB 于2A ,2B ,2C .由1122sin()sin()ABA ACA S BA AB B αA C S CA C α⋅+==⋅+△△,22sin()sin()CB BC C αB A AB A α⋅+=⋅+,22sin()sin()AC AC A αC B BC B α⋅+=⋅+,三式相乘即证. 习题B1.设直线AD ',BE ',CF '交BC ,CA ,AB 于A ',B ',C '过D '作O ⊙的切线交AB ,AC 于M ,N .由M N B C ∥,知A M D A B A ''△∽△,AD N AA C ''△∽△,则M D A D DN B A A A AC '''==''',即B A M D AC DN''=''.连OM ,ON ,设O ⊙的半径为r 则B ,D ,O ,F ;C ,D ,O ,E 分别四点共圆.由FOD B '∠=∠,EOD C '∠=∠,则1122MOD FOD B ''∠=∠=∠,1122NOD EOD C ''∠∠=∠.而t a n t a n 2M D B M O D r '∠'=∠=,tan tan 2D N C NOD r '∠'=∠=,则11tan tan 22MD D N B C ''=∠∠∶∶,即11tan tan 22BA A C B C ''=∠∠∶∶.同理,11tan tan 22CB B A C A ''=∠∠∶∶,11tan tan 22AC C B A B ''=∠∠∶∶,则1BA CB AC A C B A C B'''⋅⋅='''.由塞瓦定理之逆,有AA ',BB ',CC '三线共点.即AD ',BE ',CF 三线共点. 2.设BD 交圆于M ,N ,连ME ,MH ,MF ,NH ,NE ,NF ,NG ,EH ,FG .由B M E B E N △∽△,BMF BFN △∽△,有EM BE EN BN =,MF BF FN BN =.而BE BF =,则EM MF EN FN =,即EM ENMF FN=. 同理,NH HM GN GM =.于是NH EM HM ENMF GN GM FN⋅=⋅. 对圆内接四边形HEMN 和GFMN 分别应用托勒密定理,有HM EN EN EM HE MN ⋅=⋅+⋅,GM FN MF GN FG MN ⋅=⋅+⋅,所以MH EM NH EM HE MNMF GN MF GN FG MN ⋅⋅+⋅=⋅⋅+⋅,由此得 NH EM FG HE MF GN ⋅⋅=⋅⋅,即1N H E M F G H E M F G N⋅⋅=.由塞瓦定理的推论,知BD ,GE ,HF 三线共点.同理,AC ,GE ,HF 三线共点.因GE 与HF 交点唯一,故AC ,BD ,HF ,GE 四线共点. 3.设ABC △的内心为I ,则I 是000A B C △的垂心.令2BAC α∠=,2ABC β∠=,2BCA γ∠=.(Ⅰ)由11BIA αβIBA ∠=+=∠,有101090()A BA αβA A B ∠=︒-+=∠,即1110IA I B I A ==,有012A BI A BI S S =△△.同理,102A CI S A CI S =△△,故012A BIC A BIC S S =.同理,012B CIA B CIA S S =,012C AIB C AIB S S =.三式相加即证.(Ⅱ)令0100C B λC A =,0200A C λA B =,0300B A λB C =,则01011C B λBA λ=-,02021A C λBA λ=-,03031B A λAC λ=-.对000A B C △应用塞瓦定理,有0000001C B A C B A BA CB AC ⋅⋅=,即3121231111λλλλλλ⋅⋅=---,从而123123(1)(1)(1)λλλλλλ=---,00012312312233121()()ABCA B C S λλλλλλλλλλλλS =-+++++=△△.(*)12311,28λλλ≤.即000123124ABC A B C S λλλS =≤△△,亦即0004ABC S A B C S ≥△△,等号当且仅当000A B C △为正三角形123()λλλ==时成立.注:其中(*)是三角形与其内接三角形的关系公式.4.延长AP 交BC 于Q ,由塞瓦定理有1AF CEFB EA⋅=.由B P A C P A ∠=∠,知B P Q C P Q ∠=∠.又P B B QP C Q C=,过A 作AM PB ∥交直线PF 于M ,作AN PC ∥交直线PE 于N ,有AM AF PB FB =,PC CEAN EA=,于是得AM AN =.有180180P A M B P A C P A P A N ∠=︒-∠=︒-∠=∠,有P A M P A N ∠△∽△,得B P F C P E∠=∠. 5.连EF 交直线AC 于K .令BAF α∠=,DAE β∠=,BAC DAC θ∠=∠=,由,sin sin sin sin FB AF BC AC αABF θABC ==∠∠,有sin sin FB θAFBC αAC⋅=.同理,sin sin DE θAE DC βAC ⋅=.又 sin()sin()AFK AEK S KF AF αθKE S AE βθ⋅+==⋅+△△.对EFC △及点G 应用塞瓦定理,有1FB CD KEBC DE KF⋅⋅=,得sin sin()sin sin()ααθββθ+=+,即sin sin()0θαβ⋅-=.由此可得αβ=,即证 6.连DI ,IC ,设DCI x ∠=,则40IDC x ∠=︒-,对BCD △及点I 应用角元形式的塞瓦定理,有sin80sin 20sin 1sin(40)sin 20sin 20xx ︒︒⋅⋅=︒-︒︒,求得10x =︒,故30BCD ∠=︒为所求.7.由2211111A B AC AC B C =-⋅,111111AC B C AC B C AC B C ⋅-⋅=⋅,及21111BC B A C A ≥⋅,21111C A C B A B ≥⋅,注意应用塞瓦定理,1111111AC B A C BA B B C C A⋅⋅=,从而111111111111A B B C C A A B B C C A A B B C C A ⋅⋅≥⋅⋅⋅⋅8.设直线AD 与BC 交于P .过P 作l 的垂线交l 于H .设圆Γ的圆心为O ,由OAD PAH △∽△,有AH HP AD DO =.由O C B P H B △∽△有BH HP BC CO =,即A H B H A D B C =.注意PD PC =,有1A H B C P DH B C P D A⋅⋅=.由塞瓦定理之逆,知AC ,BD ,PH 共点,直线PH 重合于EF ,点H 与F 重合.又O ,D ,P ,C 共圆,且直径为OP ,又90PHO ∠=︒,知H 也在此圆上.故DFP DOP COP CFP ∠=∠=∠=∠.9.设直线1AA 交BC 于X ,直线1BB 交CA 于Y ,1CC 交AB 于Z ,由塞瓦定理的逆定理,只要证明.1BX CY AZXC YA ZB⋅=.设中心为1A 的正方形边长为α,顶点P ,Q 分别在边AB 和AC 上,顶点S ,T 在BC 上,且S 在B ,T 之间.因AX 过正方形QPST 的中心,若AX 截PQ 边两段为u ,v ,则它截ST 边两段为v ,u ,则cot cot 1cot cot 1BX u BX u BT BS a a B a B XC v XC v SC TC a a C a C ++⋅++======++⋅++.同理,cot 1cot 1CY C YA A +=+,cot 1cot 1AZ A ZB B +=+.故有1BX CY AZXC YA ZB⋅⋅=.10.作高AH ,连BE ,CD ,则AH ,BE ,CD 交于一点,即ABC △的垂心.对ABC △应用塞瓦定理,有1AD BH CEDB HC EA⋅⋅=.由MDF MGE △∽△,有BEC BDC S GM GE BE CE MD DF S BD CD ⋅===⋅△△. 由AH EG ∥,有H G C HA E A C=,即A C H G H C ⋅=⋅.由2ABC AB CD S AC BE ⋅==⋅△,有A B C D H G A C B E H G H ⋅⋅=⋅⋅=⋅⋅.对DBG △,考察点A ,M ,H ,有 1()DA BH GM DA BH BE CE DA BH CE BE AD BH CEAB HG MD AB HG BD CD HC AE BE DB HC EA⋅⋅⋅⋅⋅⋅=⋅⋅==⋅⋅=⋅⋅⋅,由梅涅劳斯定理之逆即证.11.设H 关于边BC ,CA ,AB 的对称点分别为A ',B ',C ',则A ',B ',C '均在外接圆O ⊙上.下证D ,E ,F 满足要求.设直线AO ,BO ,CO 与BC ,CA ,AB 的交点为D ',E ',F '.由于DA DH =,有OD DH OD DA R +=+=(R 为O ⊙半径).同理,OE EH OF FH R +=+=.由π2BAO ACB CAA '∠=-∠=∠,有B O D C O '∠=∠.又O B O C =,OBD OCD '∠=∠,则O B D O C '△∽△,有BD CD '=.同理,CE AE '=,AF BF '=.对ABC △及点H 应用塞瓦定理,有1BD CE AF D C E A F B '''=⋅⋅''',即1BD CE AF CD BF AED CE AF B DB FA EC '''⋅⋅=⋅⋅='''.再由塞瓦定理之逆,知AD ,BE ,CF 共点.D ,E ,F 满足要求.12.连AD 交BF 于G ,连BD 交AE 于H ,连GN ,HM .由D A B C D B C F B∠=∠=∠,知A ,F ,G ,N 四点共圆,有180AFB ANG ∠+∠=︒.又90AFB ∠=︒,则90ANG ∠=︒,即GN AB ⊥且GN AB ∥,有LN DG NA GA =.同理,BH BM HD ML =.在ABD △中,1AO BH DG AO BM LN OB HD GA AO ML NA ⋅⋅=⋅⋅=.由塞瓦定理之逆,知AE ,BF ,OD 三线共点.13.显然,有133213321332A A A A B B B B C C C C =====,且3434C B A B =,343434A C B A C A ==.由正弦定理,有33434334343343343343434334sin sin sin sin /sin sin C B B C B B C B A B B A B B C B A B B B B B B B A B ∠⋅∠⋅∠∠==∠∠. 同理,334334334334sin sin sin sin B A A A B A C A A A C A ∠∠=∠∠,334334334334sin sin sin sin A C C C A C B C C C B C ∠∠=∠∠. 又由于334334C B C B C B ∠=∠,334334A B A B A B ∠=∠,334334C A C A C A ∠=∠,故 334334334334334334sin sin sin 1sin sin sin C B B B A A A C C A B B C A A B C C ∠∠∠⋅⋅=∠∠∠.应用角元形式的塞瓦定理,知34A A ,34B B ,34C C 三线共点.14.设AB 与CE 交于点D ,AC 与BF 交于点G .由AEC BEC S AD DB S =△△,CFBAFBS CG GA S =△△,有 .AEC CFB BEC AFB S S AD BH CG BH DB HC GA HC S S ⋅⋅=⋅△△△△.又由ABE ACF △∽△,有EAB FAC ∠=∠,AE AB BEAF AC CF ==,则sin 1sin AEC ABF S AE AC EACS AF AB BAF⋅⋅∠==⋅⋅∠△△,注意90ABE ACF ∠=∠=︒,有 sin cos sin cos CFB BEC S BC CF BCF AC BCA HC S BC BE CBF AB ABC HB ⋅⋅∠⋅∠===⋅⋅∠⋅∠△△.于是1AD BH CGDB HC GA⋅⋅=.由塞瓦定理之逆即证.15.设非等边ABC △各定点处的外接圆切线AB C '',BA C ',A CB ''组成A B C '''△,直线AB 与A B ''交于P ,BC 与B C '交于Q ,CA 与C A '交于R ,连A A ',B B ',C C '.因C ,A ,B 分别在A B C '''△三边所在直线A B '',B C ',C A ''上,,CB B A ''=,AC C B ''=,从而1A C B A C BCB AC BA'''⋅⋅='''.由塞瓦定理的逆定理,知A A ',B B ',C C '共点.再运用戴沙格定理,知P ,Q ,R 三点共线.16.必要性:设BAE CAF α∠=∠=,ABD CBF β∠=∠=,ACD x ∠=,BCE y ∠=.又设M ,N ,K 分别为AD ,BE ,CF 与ABC △各边的交点.因AD ,BE ,CF 共点,则由塞瓦定理,得sin sin sin 1sin sin sin ACF ABD BCE BCF ACD ABE S S S AK BM CN AC AF αAB BD βBC CE yKB MC NA S S S BC BF βAC CD x AB AE α⋅⋅⋅⋅⋅⋅=⋅⋅=⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅△△△△△△ sin sin AF BD CE yBF CD AE x=⋅⋅⋅sin()sin()sin()sin sin()sin sin()sin()sin()sin sin()sin B βC x A αy C x yA αB βC y x C y x ----=⋅⋅⋅=⋅----. 即sin()sin()cot cot sin sin C y C y x y x y--=⇒=.注意x ,(0,π)y ∈,故x y =,即ACD BCE ∠=∠.充分性:若ACD BCE ∠=∠,因上述证明各步均可逆,由塞瓦定理之逆,知AD ,BE ,CF 三线共点. 17.设1CAQ α∠=,2BAQ α∠=,1ABQ β∠=,2CBQ β∠=,1BCQ γ∠=,2ACQ γ∠=.由塞瓦定理及正弦定理,有111M M N N ,1L L 共点11111111111111AM N BN L αM AM L BN M αN S S S NM LN ML M L N M L N S S S ⇔⋅⋅=⇔⋅⋅=△△△△△△ 111111121212sin sin sin 11sin sin sin AM AN αBN BL βCL CM γAN CM BL QA QC QBAM AL αBN BM βCL CN γNC BM AL QC QB QA ⋅⋅⋅⋅⋅⋅⇔⋅⋅=⇔⋅⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅AM ⇔,BN ,CL 三直线共点,且与Q 点位置无关.18.设G 是ABC △的重心,D ',E ',F '分别为BC ,CA ,AB 的中点,则ABC △区域被划分为六个区域:AF G '△,BF G '△,BD G '△,CD G '△,CE G '△,AE G '△.不妨设P 点落在CE G '△区域.此时,易知1,1,1CD CE AFDB EA FB≤≤≤.由塞瓦定理,有11BD CE AF DC CF AF DC EA FB BD EA FB ⋅⋅=⇒=⋅≤,AF DC EA EABFD FDE FB BD CE EC=⋅≤⇒∠≥∠,BDF DFE ∠≥∠.分别过F ,D ,在BFD ∠,BDF ∠内作DE ,FE 的平行线,则两平行线的交点Q 必落在BFD △区域.从而,有FDE FQDE ABC ⊂⊂△△,结论成立.19.设AC 交BC 于Q .对AEC △和点F 应用塞瓦定理,有1EB AQ CDBA QC DE⋅⋅=.对AEC △及截线BPD 应用梅涅劳斯定理,有1ED CP ABDC PA BE⋅⋅=,故有AP PC AQ QC =. 过P 作EF 的平行线交OA 于I ,交OC 与J ,则,P I A P J P P C Q O A Q Q O Q C ==.于是PI PJQO QO=,即P I P J =.又O P I J ⊥,则OP 平分IOJ ∠,即OP 平分AOC ∠.同理,当BD 与EF 相交时,OP 平分DOB ∠;而当BD EF ∥时,过B 作ED 的平行线交AC 于G ,则AG AB ADAC AE AF==,即GD CF ∥,BCDG 为平行四边形,亦即P 为BD 中点.因此,OP 平分DOB ∠. 20.显然有PD DQ =,AP AQ =.不妨设AB AC ≥,则ADC ADB ∠≤∠,ADC ∠为直角或锐角.作AE BC ⊥于E ,易知A ,P ,D ,E 四点共圆,A ,D ,E ,Q 四点共圆.则BP BA BD BE ⋅=⋅,CQ CA CD CE ⋅=⋅.故AB BP BD BEAC CQ CD CE⋅=⋅. 由AD 平分BAC ∠,有A B D BA C D C=,得B P B E CQ CE =,即1BP CE CQ BE ⋅=⋅.而AP AQ =,则1B P C E A Q P A Q C E B ⋅⋅=⋅⋅.由塞瓦定理之逆,知AE ,BQ ,CP 三线共点,即AE BC ⊥,故AK BC ⊥.。
塞瓦定理教案

塞瓦定理教案一、教学目标1.了解塞瓦定理的定义和基本概念;2.掌握塞瓦定理的求解方法;3.能够运用塞瓦定理解决实际问题。
二、教学内容1.塞瓦定理的定义和基本概念;2.塞瓦定理的求解方法;3.应用塞瓦定理解决实际问题。
三、教学重难点1.掌握塞瓦定理的求解方法;2.应用塞瓦定理解决实际问题。
四、教学过程(一)引入新课通过提问,了解学生对于三角形内心和外心的认知,引出本节课要讲述的内容——塞瓦定理。
(二)讲授新知1. 塞瓦定理的定义和基本概念。
塞瓦定理是指:在任意三角形ABC中,设其内切圆半径为r,内切圆对边分别为a,b,c,则有:r = (S - a) / (p - a + p - b + p - c)其中,S为三角形ABC面积,p为半周长。
解释:该公式表示了内心到三角形边界距离与三角形边长的关系。
2. 塞瓦定理的求解方法。
(1)首先计算出三角形ABC的半周长p和面积S;(2)然后计算出三角形ABC各边长度a,b,c;(3)最后带入公式,求出内切圆半径r。
3. 应用塞瓦定理解决实际问题。
通过练习题和例题,让学生掌握如何应用塞瓦定理解决实际问题。
(三)练习与巩固1. 练习题:1)在一个正三角形中,内切圆半径为4cm,求该正三角形的面积。
2)在一个等腰直角三角形中,内切圆半径为5cm,求该等腰直角三角形的斜边长。
3)在一个任意三角形中,已知其内切圆半径为3cm,两条边分别为6cm和8cm,求第三条边长。
2. 解答练习题,并进行讲解。
(四)课堂小结通过本节课的学习,让学生了解了塞瓦定理的定义和基本概念、掌握了塞瓦定理的求解方法、并能够应用塞瓦定理解决实际问题。
五、课后作业1. 完成课堂练习题;2. 阅读相关教材,加深对塞瓦定理的理解。
六、教学反思本节课通过引入问题,让学生主动思考,提高了学生的学习积极性。
在讲授过程中,采用了多种形式的教学方法,如板书、举例等,使得学生更易于理解和掌握。
在练习环节中,通过讲解练习题的解答方法和技巧,帮助学生巩固所学知识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 塞瓦定理及应用【基础知识】塞瓦定理 设A ',B ',C '分别是△ABC 的三边BC ,CA ,AB 或其延长线上的点,若AA ',BB ',CC '三线平行或共点,则1BA CB AC A C B A C B '''⋅⋅='''.① 证明 如图2-1(b )、(c ),若AA ',BB ',CC '交于一点P ,则过A 作BC 的平行线,分别交BB ',CC '的延长线于D ,E ,得,CB BC AC EAB A ADC B BC''==''. A′B'C 'ABPPCBAA′B'C 'D ECBAA′B'C 'D E (c)(b)(a)图2-1又由BA A P A C AD PA EA '''==,有BA ADA C EA'='. 从而1BA CB AC AD BC EA A C B A C B EA AD BC '''⋅⋅=⋅⋅='''.若AA ',BB ',CC '三线平行,可类似证明(略). 注 (1)对于图2-1(b )、(c )也有如下面积证法:由:1PAB PBC PCAPCA PAB PBCS S S BA CB AC A C B A C B S S S '''⋅⋅=⋅⋅='''△△△△△△,即证.(2)点P 常称为塞瓦点.(3)共点情形的塞瓦定理与梅涅劳斯定理可以互相推证. 首先,由梅涅劳斯定理推证共点情形的塞瓦定理.如图2-1(b )、(c ),分别对△ABA '及截线C PC ',对△AA C '及截线B PB '应用梅涅劳斯定理有 1BC A P AC CA PA C B ''⋅⋅='',1A B CB APBC B A PA ''⋅⋅=''. 上述两式相乘,得1BA CB AC A C B A C B'''⋅⋅='''. 其次,由共点情形的塞瓦定理推证梅涅劳斯定理.如图2-2,设A ',B ',C '分别为△ABC 的三边BC ,CA ,AB 所在直线上的点,且A ',B ',C '三点共线.令直线BB '与CC '交于点X ,直线C C '与AA '交于点Y ,直线AA '与BB '交于点Z .CBAA′B'C 'XY ZXYZ CBAA′B'C '图2-2分别视点C ',A ',B ',C ,A ,B 为塞瓦点,应用塞瓦定理,即对△BCB '及点C '(直线BA ,CX ,B A ''的交点),有1BA CA B XA C AB XB''⋅⋅=''.对△CAC '及点A '(直线CB ,AY ,C B ''的交点),有1CB AB C YB C BC YC ''⋅⋅=''. 对△ABA '及点B '(直线AC ,BZ ,A C ''的交点),有1AC BC A ZC B CA ZA ''⋅⋅=''.对△BBC '及点C (直线BA ',B A ',C X '的交点),有1BX B A C AXB A C AB '''⋅⋅='''. 对△CC A ''及点A (直线CB ',C B ',A Y '的交点),有1CY C B A BYC B A BC '''⋅⋅='''.对△AA B ''及点B (直线AC ',A C ',B Z '的交点),有1AZ A C B CZA C B CA'''⋅⋅='''. 上述六式相乘,有21BA CB AC A C B A C B '''⎛⎫⋅⋅= ⎪'''⎝⎭. 故1BA CB AC A C B A C B'''⋅⋅='''. 塞瓦定理的逆定理 设A ',B ',C '分别是△ABC 的三边BC ,CA ,AB 或其延长线上的点,若 1BA CB AC A C B A C B'''⋅⋅=''',② 则AA ',BB ',CC '三直线共点或三直线互相平行.证明若AA '与BB '交于点P ,设CP 与AB 的交点为1C ,则由塞瓦定理,有111AC BA CB A C B A C B ''⋅⋅='',又已知有111AC BA CB A C B A C B ''⋅⋅='',由此得11AC AC C B C B '=',即1AC AC AB AB'=,亦即1AC AC '=,故1C 与C '重合,从而AA ',BB ',CC '三线共点. 若AA BB ''∥,则CB CB B A BA '=''.代入已知条件,有AC A CC B CB''=',由此知CC AA ''∥,故 AA BB CC '''∥∥.上述两定理可合写为:设A ',B ',C '分别是△ABC 的BC ,CA ,AB 所在直线上的点,则三直线AA ',BB ',CC '平行或共点的充要条件是1BA CB AC A C B A C B'''⋅⋅='''. ③第一角元形式的塞瓦定理 设A ',B ',C '分别是△ABC 的三边BC ,CA ,AB 所在直线上的点,则三直线AA ',BB ',CC '平行或共点的充要条件是 sin sin sin 1sin sin sin BAA ACC CBB A AC C CB B BA'''⋅⋅='''∠∠∠∠∠∠.④ 证明 由sin sin ABA AA C S BA AB BAA A C S AC A AC ''''⋅==''⋅△△∠∠,sin sin CB BC CBB B A AB B BA ''⋅=''⋅∠∠,sin sin AC AC ACC C B BC C CB ''⋅=''⋅∠∠,三式相乘,再运用塞瓦定理及其逆定理,知结论成立.第二角元形的塞瓦定理 设A ',B ',C '分别△ABC 的三边BC ,CA ,AB 所在直线上的点,O 是不在△ABC 的三边所在直线上的点,则AA ',BB ',CC '平行或共点的充要条件是 sin sin sin 1sin sin sin BOA AOC COB A OC C OB B OA '''⋅⋅='''∠∠∠∠∠∠.⑤ 证明 注意到塞瓦定理及其逆定理,有 1BOA COB AOC A OC B OA C OB S S S BA CB AC A C B A C B S S S '''''''''=⋅⋅=⋅⋅'''△△△△△△ sin sin sin sin sin sin BO BOA CO COB AO AOC CO A OC AO B OA BO C OB'''⋅⋅⋅=⋅⋅'''⋅⋅⋅∠∠∠∠∠∠. 由此即证得结论.注 在上述各定理中,若采用有向线段或有向角,则①、②、③、④、⑤式的右端仍为1.特别要注意的是三边所在直线上的点或者两点在边的延长线上,或者没有点在边的延长线上.④、⑤式中的角也可按①式的对应线段记忆.推论 设1A ,1B ,1C ,分别是△ABC 的外接圆三段弧BC ,CA ,AB 上的点,则1AA ,1BB ,1CC 共点的充要条件是 1111111BA CB AC AC B A C B ⋅⋅=. 证明 如图2-3,设△ABC 的外接圆半径为R ,1AA 交BC 于A ',1BB 交CA 于B ',1CC 交AB 于C '.由A ,1C ,B ,1A ,C ,1B 六点共圆及正弦定理,有11112sin sin 2sin sin BA R BAA BAA AC R A AC A AC '⋅=='⋅∠∠∠∠. A 1B1C 1CBAA′B'C '图2-3同理,11sin sin CB CBB B A B BA '='∠∠,11sin sin AC ACC C B C CB'='∠∠. 三式相乘,并应用第一角元形式的塞瓦定理即证.为了使读者熟练地应用塞瓦定理,针对图2-4中的点A 、B 、C 、D 、E 、F ,将其作为塞瓦点,我们写出如下式子:HGFEDC BA图2-4对△ACE 及点D 有 1AB CG EFBC GE FA ⋅⋅=, 对△CDE 及点A 有 1CF DB EGFD BE GC ⋅⋅=, 对△ADE 及点C 有 1DG AF EBGA FE BD ⋅⋅=, 对△ABD 及点F 有 1AC BE DHCB ED HA ⋅⋅=, 对△ACD 及点E 有 1AG DF CBGD FC BA ⋅⋅=, 对△ADF 及点B 有 1AH DC FEHD CF EA ⋅⋅=, 对△ABF 及点D 有 1BC AE FHCA EF HB ⋅⋅=, 对△BDF 及点A 有1BE DC FHED CF HB⋅⋅=. 【典型例题与基本方法】1.恰当地选择三角形及所在平面上的一点,是应用塞瓦定理的关键例1 四边形两组对边延长分别相交,且交点的连线与四边形的一条对角线平行.证明:另一条对角线的延长线平分对边交点连线的线段. (1978年全国高中竞赛题) 证明 如图2-5,四边形ABCD 的两组对边延长分别交于E ,F ,对角线BD EF ∥,AC 的延长线交EF 于G .GFEDCBA图2-5对△AEF 及点C ,应用塞瓦定理,有 1EG FD ABGF DA BE ⋅⋅=. 由BD EF ∥,有AB ADBE DF=,代入上式, 得1EGGF=,即EG GF =.命题获证. 例2 如图2-6,锐角△ABC 中,AD 是BC 边上的高,H 是线段AD 内任一点,BH 和CH 的延长线分别交AC ,AB 于E ,F .求证:EDH FDH =∠∠. (1994年加拿大奥林匹克试题)OPHFEDCB A图2-6证法1 对△ABC 及点H ,应用塞瓦定理,有1AF BD CEFB DC EA⋅⋅=.① 过A 作PQ BC ∥,延长DF ,DE 分别交PQ 于P ,Q ,则DA PQ ⊥,且△APF ∽△BDF ,△AQE ∽△CDE ,从而AF PA BD FB =⋅,EAAQ DC CE=⋅. 而由①,有AF EABD DC FB CE⋅=⋅,故PA AQ =. 由此知AD 为等腰△APQ 底边PQ 上的高,故EDH FDH =∠∠. 证法2 对△ABC 及点H 应用塞瓦定理,有1DAF DCEDFB DEA S S AF BD CE BD FB DC EA S DC S =⋅⋅=⋅⋅△△△△ sin sin tan cot sin sin AD ADF BD DC EDCADF ADE BD FDB DC AD ADE⋅⋅=⋅⋅=⋅⋅⋅∠∠∠∠∠∠.即tan tan ADE ADF =∠∠,由锐角性质知EDA FDA =∠∠.类似地,对△ABE 及截线FHC 或对△AFC 及截线BHE 应用梅涅劳斯定理也可证得有EDA FDA =∠∠. 注 将此例中的平角BDC ∠变为钝角,则有如下: 例3 如图2-7,在四边形ABCD 中,对角线AC 平分BAD ∠.在CD 上取一点E ,BE 与AC 相交于F ,延长DF 交BC 于G .求证:GAC EAC =∠∠.(1999年全国高中联赛题)JIHGF E DCBA图2-7证明 连BD 交AC 于H ,对△BCD 及点F ,应用塞瓦定理,有 1CG BH DEGB HD EC⋅⋅=. AH 平分BAD ∠,由角平分线性质,可得 BH AB HD AD =,故1CG AB DEGB AD EC⋅⋅=.过点C 作AB 的平行线交AG 的延长线于I ,过点C 作AD 的平行线交AE 的延长线于J ,则 ,CG CI DE AD GB AB EC CJ ==.所以1CI AB ADAB AD CJ ⋅⋅=.从而,CI CJ =.又CI AB ∥,CJ AD ∥,有180180ACI BAC DAC ACJ =︒-=︒-=∠∠∠∠. 因此,△ACI ACJ ≌△,即有IAC JAC =∠∠. 故 GAC EAC =∠∠.注 由此例还可变出一些题目,参见练习题第4、5及19题.例4 如图2-8,BE 是△ABC 的中线,G 在BE 上,分别延长AG ,CG 交BC ,AB 于D ,F ,过D 作DN CG ∥交BG 于N ,△DGL 及FGM △为正三角形.求证:△LMN 为正三角形.MLNGFEDCBA图2-8证明 连NF ,对△ABC 及点G 应用塞瓦定理,有 1AF BD CE FB DC EA ⋅⋅=.而AE CE =,则AF DCFB BD =. 由DN CG ∥,由CD NGBD BN=. 于是,有AF NGFB BN=,从而FN AD ∥,即知四边形DNFG 为平行四边形,有GDN GFN =∠∠.又60GDL GFM ==︒∠∠,则LDN NFM =∠∠.而DN GF FM ==,DL DG NF ==,知△LDN ≌△NFM ,有LN MN =,DNL NMF =∠∠.于是MNL DNF DNL MNF DNF NMF MNF =-+=-+∠∠(∠∠)∠(∠∠) 180)(180)NFG NFM NFM NFG ︒--︒-=-=(∠∠∠∠60MFG ==︒∠.故△LMN 为正三角形.例5 如图2-9,在一个△ABC 中,2C B =∠∠,P 为△ABC 内满足AP AC =及PB PC =的一点.求证:AP 是A ∠的三等分线. (1994年香港代表队IMO 选拔赛题)π-2(2CBA图2-9证明 用B 表示ABC ∠的度量,令PCB θ=∠,则PBC θ=∠,ABP B θ=-∠,2ACP B θ=-∠,()π22CAP B θ=--∠(其中注意AP AC =),()π[π2(2)]PAB A CAP B C B θ=-=-----∠∠∠(π3)(π42)2B B B θθ=---+=-.对△ABC 及点P ,应用第一角元形式的塞瓦定理,有 sin[π2(2)]sin sin()1sin(2)sin(2)sin B B B B θθθθθθ---⋅⋅=--.亦即2sin(2)cos(2)sin()1sin(2)sin(2)B B B B B θθθθθ-⋅-⋅-=-⋅-.于是 sin(2)2sin()cos(2)sin(32)sin B B B B B θθθθ-=-⋅-=--, 即 sin sin(32)sin(2)2cos(22)sin B B B B B θθθ=---=-⋅.而sin 0B ≠,则1cos2()2B θ-=. 因 1π0()33B b BC θ<-<<+<,则2π2()0,3B θ⎛⎫-∈ ⎪⎝⎭.∴ π2()3B θ-=,即π6B θ-=.从而π2(2)π4()2CAP B B θθθ=--=---∠ ππ222[()]36B θθθθ⎛⎫=-=-=-- ⎪⎝⎭2(2)2B PAB θ=-=∠.故 13PAB A =∠∠,即AP 是A ∠的三等分线.利用第一角元形式的塞瓦定理可简捷处理2009年全国高中联赛加试第一题的第1问:例6 设M 、N 分别为锐角△ABC(A B <∠∠)的外接圆Γ上弧BC 、AC 的中点.过点C 作PC MN ∥交圆Γ于点P ,I 为△ABC 的内心,联结PI 并延长交圆Γ于点Γ.求证:MP MT NP NT ⋅=⋅. 证明 事实上,易知A 、I 、M 及B 、I 、N 分别三点共线,对△PMN 及点I 应用第一角元形式的塞瓦定理,有sin sin sin 1sin sin sin NPI PMI MNIIPM IMN INP ⋅⋅=∠∠∠∠∠∠.① 由CP MN ∥知PA PB =,有PMI INP =∠∠. 于是①式即为1sin 21sin 2B NT CN MP MT CM NPA ===∠∠. 故MP MT NP NT ⋅=⋅.2.注意塞瓦定理逆定理的应用以及与梅涅劳斯定理的配合应用例7 如图2-10,在△ABC 中,90BAC =︒∠,G 为AB 上给定的一点(G 不是线段AB 的中点).设D 为直线GC 上与C ,G 都不相同的任意一点,并且直线AD ,BC 交于E ,直线BD ,AC 交于F ,直线EF ,AB 交于H .试证明交点H 与D 在直线CG 上的位置无关.(1990年苏州市高中竞赛题)HGFE DCB 图2-10证明 设G 分线段AB 为定比1λ,H 分线段AB 为定比2λ.下证2λ由1λ确定,即当A ,B 给定后,点H 的位置由点G 唯一确定.在△ABC 中,由AE ,BF ,CG 交于一点D ,应用塞瓦定理,有 1AG BE CF GB EC FA ⋅⋅=,即11BE CFEC FAλ⋅⋅=. 对△ABC 及截线EFH ,应用梅涅劳斯定理,得 1AH BE CF HB EC FA ⋅⋅=,即21BE CFEC FA λ⋅⋅=-. 上述两式相加,得12()0BE CFEC FAλλ+⋅=. 从而120λλ+=,即21λλ=-,故2λ由1λ唯一确定.因此,点H 与D 在直线CG 上的位置无关.例8 如图2-11,设P 为△ABC 内任一点,在形内作射线AL ,BM ,CN ,使得CAL PAB =∠∠,MBC PBA =∠∠,NCA BCP ∠=∠.求证:AL ,BM ,CN 三线共点.MN PLFE DCBA图2-11证法1 设AL 交BC 于L ,BM 交CA 于M ,CN 交AB 于N ,则由正弦定理有 sin sin sin sin BL AB BAL AB PACLC AC CAL AC PAB ⋅⋅==⋅⋅∠∠∠∠. 同理,sin sin CM BC PBAMA AB PBC⋅=⋅∠∠, sin sin AN AC PCBNB BC PCA⋅=⋅∠∠. 将上述三式相乘,并应用正弦定理,有sin sin sin 1sin sin sin BL CM AN PAC PBA PCB PC PA PB LC MA NB PAB PBC PCA PA PB PC⋅⋅=⋅⋅=⋅⋅=∠∠∠∠∠∠. 由塞瓦定理的逆定理,知AL ,BM ,CN 共点.证法2 设AL 交BC 于L ,BM 交CA 于M ,CN 交AB 于N ,直线AP 交BC 于D ,直线BP 交AC 于E ,直线CP 交AB 于F .对△ABC 及点P ,应用塞瓦定理,有 1AF BD CEFB DC EA ⋅⋅=.在△ABL 和△ACL 中应用正弦定理,有 sin sin sin sin sin sin sin sin BL BL AL BAL C PAC CLC AL LC B LAC PAB B=⋅=⋅=⋅∠∠∠∠∠∠∠∠ 222222sin sin sin sin sin sin sin sin sin sin PAC B C DC AD C DC CC PAB B AD BD B BD B=⋅⋅=⋅⋅=⋅∠∠∠∠∠∠∠∠∠∠. 同理,22sin sin CM AE A MA EC C =⋅∠∠,22sin sin AN BF BNB FA A =⋅∠∠. 以上三式相乘,并注意到①式,有1BL CM AN DC AE BF LC MA NB BD EC FA⋅⋅=⋅⋅=. 由塞瓦定理的逆定理,知AL ,BM ,CN 共点.证法3 设AL 交BC 于L ,BM 交AC 于M ,CN 交AB 于N ,直线AP 交BC 于D ,直线BP 交AC 于E ,直线交AB 于F .对ABC △及点P ,应用角元形式的塞瓦定理,有 sin sin sin 1sin sin sin PAB PBC PCAPAC PBA PCB⋅⋅=∠∠∠∠∠∠.由题设PAB CAL =∠∠,PBA CBM =∠∠,PCB ACN =∠∠,则有BAL PAC =∠∠,ABM PBC =∠∠,BCN PCA =∠∠.于是 sin sin sin sin sin sin sin sin sin sin sin sin BAL CBM ACN PAC PBA PCBCAL ABM BCN PAB PBC PCA⋅⋅=⋅⋅∠∠∠∠∠∠∠∠∠∠∠∠111sin sin sin 1sin sin sin PAB PBC PCA PAC PBA PCB===⋅⋅∠∠∠∠∠∠,对△ABC ,应用角元形式的塞瓦定理的逆定理,知AL ,BM ,CN 三线共点.例9 如图2-12,四边形ABCD 内接于圆,其边AB 与DC 的延长线交于点P ,AD 与BC 的延长线交于点Q ,过点Q 作该圆的两条切线,切点分别为E 和F .求证:P ,E ,F 三点共线.(1997年CMO 试题)P图2-12证明 连EF 分别交AD ,BC 于M ,N ,设AC 与BD 交于K .要证P ,E ,F 三点共线,只须证明P ,K ,M 和P ,N ,K 都三点共线,又只须证明AC ,BD ,PM 三线共点.由塞瓦定理的逆定理知只须证明1AB PC DMBP CD MA⋅⋅=.又直线QCB 截△PDA ,应用梅涅劳斯定理,有1AB PC DQ BP CD QA ⋅⋅=,从而只须证明DM DQAM AQ=. 设圆心为O ,连QO 交EF 于L ,连LD ,LA ,OD ,OA ,则由切割线走理和射影定理,有2QD QA QE QL QO ⋅==⋅,即知D ,L ,O ,A 四点共圆,有QLD DAO ODA OLA ===∠∠∠∠,此表明QL 为△LAD 的内角ALD ∠的外角平分线.而EF OQ ⊥,则EL 平分ALD ∠.于是, DM DL DQAM AL AQ==,结论获证. 【解题思维策略分析】1.获得线段比例式的一种手段例10 如图2-13,△ABC 中,D ,E 分别为AC 和AB 同方向延长线上的点,BD 与CE 相交于P ,且BD CE =.若点P 满足2AEP ADP k PED PDE -=-∠∠(∠∠)(k 为常数),则AB AC =.QF'PFE D CBA图2-13证明 设AP 交BC 于Q ,对△PBC 及其形外一点A ,应用塞瓦定理,有1BQ CE PDQC EP DB⋅⋅=. 而BD CE =,则PD QCPE QB=. 不妨设QC QB ≤,则PD PE ≤,即有PC CE PE BD PD PB =--=≤,于是PBE PCD S S △△≥,故EBC DBC S S △△≥.此时,点E 到BC 的距离不小于D 到BC 的距离,则过E 作EF BC ∥必交CD 延长线于一点,设为F .又作△FBC 的外接圆O 交EF 于另一点F ',则四边形BCFF '为等腰梯形.当AB AC ≥时,由BF F F FC BCA ABC AEF ''===∠∠∠≥∠∠,知F '必在线段EF 上,于是,BDC BFC BEC ∠≥∠≥∠(同弧上的圆外角小于同弧上的圆周角).又由PD PE ≤,知PED PDE ∠≤∠.故结论获证. 2.转化线段比例式的一座桥梁例11 设M 为△ABC 内任一点,AM ,BM ,CM 分别交BC ,CA ,AB 于D ,E ,F .求证:1MD ME MFAD BE CF++=. 证明 如图2-14,记BD m DC =,CE n EA =,AFl FB=.对△ABC 及点M ,应用塞瓦定理,有1BD CE AFmnl DC EA FB⋅⋅==. FEDCBAM图2-14对△ADC 及截线EMB ,应用梅涅劳斯定理,有11AM DB CE AM mn MD BC EA MD m ⋅⋅=⋅⋅=+,即 1(1)AM mm l MD m n +==++. 由合比定理得1(1)AD m l MD =++,即11MD AD l ml=++. 同理,111ME lBE m mn l ml ==++++, 111MF mlCF n nl ml l ==++++. 三式相加,得1MD ME MFAD BE CF++=. 例12 如图2-15,设P 为△ABC 内任意一点,AP ,BP ,CP 的延长线交对边BC ,CA ,AB 于点D ,E ,F ,EF 交AD 于Q.试证:(3PQ AD -≤.PQFEDCBA图2-15证明 令BD m DC =,CE n EA =,AF p FB =,对△ABC 及点P ,应用塞瓦定理,有1BD CE AFmnp DC EA FB⋅⋅==.对△ADC 及截线BPE ,应用梅涅劳斯定理,有1CE AP DB EA PD BC ⋅⋅=.注意到1DB mBC m =+,则有 11AP m n PD m ⋅⋅=+,即1AP m PD mn +=,故11AP m AD mn m +=++. 又对直线APD 截△BCE ,有1BD CA EP DC AE PB ⋅⋅=.而1CA n AE =+,则BP mn m EP =+,故1BEmn m EP=++.又对△ABP 及截线FQE ,有1AF BE PQ FB EP AQ ⋅⋅=,即有 11(1)1PQ AQ p mn m mp p ==++++,故12PQ AQ mp p =++. 从而1121PQ PQ AP m AD AP AD mp p mn m +=⋅=⋅++++ 1112(1)211(1)211mn mn p m p m m m =⋅=+++++++++3=-于是,(3PQ AD -≤.其中等号由2(1)1mn p m m +++≥2(1)1mnp m m =++亦即当且仅当22(1)(1)(1)mnp p m p m p m ==+++,亦即(1)p m +=时取等号.此时,m 和p 之间成为如图2-16的双曲线的关系.图2-16例13 如图2-17,已知直线的三个定点依次为A 、B 、C ,Γ为过A 、C 且圆心不在AC 上的圆,分别过A 、C 两点且与圆Γ相切的直线交于点P ,PB 与圆Γ交于点Q .证明:AQC ∠的平分线与AC 的交点不依赖于圆Γ的选取.(IMO 45预选题)SRCBAPQ图2-17证明 设AQC ∠的平分线交AC 于点R ,交圆Γ于点S ,其中S 与Q 是不同的两点.由于△PAC 是等腰三角形,则有sin sin AB APBBC CPB=∠∠. 同理,在△ASC 中,有sin sin AR ASQRC CSQ =∠∠. 在△PAC 中,视Q 为塞瓦点,由角元形式的塞瓦定理,有sin sin sin 1sin sin sin APB QAC QCPCPB QAP QCA⋅⋅=∠∠∠∠∠∠.注意到PAQ ASQ QCA ==∠∠∠,PCQ CSQ QAC ==∠∠∠.则 22sin sin sin sin sin sin sin sin APB PAQ QCA ASQCPB QAC PCQ CSQ⋅==⋅∠∠∠∠∠∠∠∠.即 22AB AR BC RC =,故结论获证.3.求解三角形格点问题的统一方法如果三角形的三个角的度数都是10的整数倍,三角形内一点与三角形的三个顶点分别连结后,得到的所有的角也都具有这个性质,我们称这样的点为三角形的格点.例14 如图2-18,在△ABC 中,40BAC =︒∠,60ABC =︒∠,D 和E 分别是AC 和AB 上的点,使得40CBD =︒∠,70BCE =︒∠,F 是直线BD 和CF 的交点.证明:直线AF 和直线BC 垂直.(1998年加拿大奥林匹克试题)10°40°-αα20°40°70°HFEDCBA图2-18证明 设BAF α=∠,则40FAC α=︒-∠,对△ABC 及点F ,应用第一角元形式的塞瓦定理,有 sin10sin sin 401sin 70sin(40)sin 20αα︒︒⋅⋅=︒︒-︒. 从而sin10sin 2sin 20cos201cos20sin(40)sin 20αα︒︒⋅︒⋅⋅=︒︒-︒,即有sin(40)2sin sin102sin cos80ααα︒-=⋅︒=⋅︒ sin(80)sin(80)αα=+︒+-︒.∴ sin(80)sin(40)sin(80)2cos60sin(20)sin(20)ααααα-︒=︒--+︒=︒⋅-︒-=-︒-.注意到040α<<︒,知8020α-︒<-︒-,8020α-︒<︒,有 8020αα-︒=-︒-,故30α=︒.延长AF 交BC 于H ,则180180306090AHB FBC ABH =︒--=︒-︒-︒=︒∠∠∠.故AF BC ⊥.注 此题也可这样来解:由sin10sin sin 401sin 70sin(40)sin 20αα︒︒⋅⋅=︒︒-︒,有sin(40)sin10sin 40sin10sin(4030)2sin10sin 40cot30cos40sin sin70sin 20sin30sin30αα︒-︒-︒︒︒-︒==︒===︒⋅︒-︒︒-︒︒︒.由于sin(40)sin 40cot cos40sin ααα︒-=︒⋅-︒作为α的函数在(0,180)︒︒上严格递减,所以30BAF α==︒∠.故90ABC BAF +=︒∠∠.因此,AF BC ⊥. 或者过点A 作AH BC ⊥于H ,则30BAH =︒∠,10HAC =︒∠.关于△ABC 有sin sin sin sin30sin10sin 401sin sin sin sin10sin70sin 20BAH ACD CBD HAC ECB DBA ︒︒︒⋅⋅=⋅⋅=︒︒︒∠∠∠∠∠∠.所以,AH 、BD 、CE三线共点,因此点F 在AH 上,即AF BC ⊥. 例15 如图2-19,在△ABC 内取一点M ,使得30MBA =︒∠,10MAB =︒∠.设80ACB =︒∠,AC BC =,求AMC ∠. (1983年前南斯拉夫奥林匹克试题)CBA图2-19解 设ACM α=∠,则80MCB α=︒-∠.由第一角元形式的塞瓦定理,有()sin sin10sin 80sin 40αα︒⋅⋅︒-︒sin 201sin30︒=︒. 从而 sin sin10sin(80)cos20αα⋅︒=︒-⋅︒. ∴ 2sin cos802sin(80)cos20αα⋅︒=︒-⋅︒,∴ sin(80)sin(80)sin(100)sin(60)αααα+︒+-︒=︒-+︒-, ∴ sin(80)sin(60)sin(100)sin(80)αααα-︒-︒-=︒--+︒ 2cos90sin(10)0α=︒⋅︒-=.于是 sin(80)sin(60)αα-︒=︒-.注意到 080α<<︒,知8080α-︒<<-︒,6060α︒-<︒. ∴ 8060αα-︒=︒-,故 70α=︒.所以 180180407070AMC MAC ACM =︒--=︒-︒-︒=︒∠∠∠为所求. 注 此题结果也可直接由①式有sin sin 70sin10sin(80)αα=︒⎧⎨︒=︒-⎩且0α<,8080α︒-<︒,求得70α=︒. 另外,此题也可这样来解:由sin sin10sin 201sin(80)sin 40sin30αα︒︒⋅⋅=︒-︒︒,有sin(80)sin10sin 20sin10sin(8070)sin80cot 70cos80sin sin 40sin30cos20sin 70αα︒-︒⋅︒︒︒-︒====︒⋅︒-︒︒⋅︒︒︒.因为sin(80)sin80cot cos80sin ααα︒-=︒⋅-︒作为α的函数在(0︒,180︒)上严格递减,所以70ACM α==︒∠.故180407070AMC =︒-︒-︒=︒∠.或者由140AMB =︒∠,令AMC x =∠,则220CMB x =︒-∠.对△MAB 和点C 应用第一角元形式的塞瓦定理,有sin sin sin sin sin 20sin501sin sin sin sin(220)sin50sin 40AMC MBC BAC x CMB CBA CAM x ︒︒=⋅⋅=⋅⋅︒-︒︒∠∠∠∠∠∠. 则sin(220)1sin(22070)sin 220cot 70cos220sin 2cos20sin70x x ︒-︒-︒===︒⋅︒-︒︒︒.因为sin(220)sin 220cot cos220(sin 2200)sin x x x︒-=︒⋅-︒︒<作为x 的函数在(0,180)︒︒上严格递增,所以70AMC x ==︒∠.例16 如图2-20,△ABC 具有下面性质:存在一个内部的点P ,使得10PAB =︒∠,20PBA =︒∠,30PCA =︒∠,40PAC =︒∠.证明:△ABC 是等腰三角形.(1996年美国第25届奥林匹克试题)α80°-α20°10°40°30°CBAP图2-20证明 设BCP α=∠,则1802010403080PBC αα=︒-︒-︒-︒-︒-=︒-∠.由第一角元形式的塞瓦定理,有sin 20sin 40sin 1sin(80)sin10sin30αα︒︒⋅⋅=︒-︒︒.即有2sin10cos10sin 40sin 11sin(80)sin102αα︒⋅︒︒⋅⋅=︒-︒.∴ sin(80)4sin sin 40cos104sin sin 40sin80ααα︒-=⋅︒⋅︒=⋅︒⋅︒4sin sin 20sin 40sin80sin60sin sin 20sin 20αα⋅︒⋅︒⋅︒︒⋅==︒︒, ∴ sin(80)sin 20sin60sin αα︒-⋅︒=︒⋅. 从而 sin(80)sin 60sin 20sin αα︒-=︒⎧⎨︒=⎩且0α<,8080α︒-<︒,故20α=︒,即50ACB CAB =︒=∠∠,从而AB BC =.注 此题也可这样来求解:由sin 20sin 40sin 1sin(80)sin10sin30αα︒︒⋅⋅=︒-︒︒,有sin(80)sin 20sin 404sin 20sin 40sin804cos10sin 40sin sin10sin30sin 20αα︒-︒︒︒⋅︒⋅︒=⋅=︒⋅︒=︒︒︒sin60sin(8020)sin80cot 20cos80sin 20sin 20︒︒-︒===︒⋅︒-︒︒︒.因为sin(80)sin80cot cos80sin ααα︒-=︒⋅-︒作为α的函数在(0︒,180︒)上严格递减,所以BCP α=∠20=︒,即50ACB CAB =︒=∠∠.故AB BC =.还可对△APC 及点B 应用第一角元形式的塞瓦定理来求. 4.论证直线共点的一种工具例17 如图2-21,在四边形ABCD 中,AB AD =,BC DC =,过AC ,BD 的交点O 引EF ,GH ,其中EF 交AB ,CD 于E ,F ,GH 交DA ,BC 于G ,H .EH ,GF 分别交BD 于P ,Q ,则OP OQ =.(1990年CMO 选拔试题)4321γαβK F'G 'HG PQ O FE DCBA 图2-21证明 在AB ,BC 上分别取G ',F ',使AG AG '=,CF CF '=,则由对称性可知有下列角相等,即若设,AOG AOG αβ'==∠∠,COH γ=∠,1G OE '=∠∠,2EOB =∠∠,3BOF '=∠∠,4F OH '=∠∠,则αβ=,又αγ=,故βγ=.又14βγ+=+∠∠,故14=∠∠,23=∠∠. 连G H '交BD 于K ,在△BHG '中, OG E OBF OHKOEB OF H OKG S S S G E BF HK EB F H KG S S S ''''''⋅⋅=⋅⋅''△△△△△△ sin 1sin 3sin(34)1sin 2sin 4sin(12)OG OE OB OF OH OK OE OB OF OH OK OG ''⋅⋅⋅⋅⋅⋅+=⋅⋅=''⋅⋅⋅⋅⋅⋅+∠∠∠∠∠∠∠∠.故由塞瓦定理的逆定理,知G F '',BO ,HE 共点,即G F ''过点P .由对称性知,OP OQ =. 例18 如图2-22,在锐角△ABC 中,以A 点引出的高AD 为直径作圆交AB ,AC 于M ,N ,再从A 作A l MN ⊥.同样可作出B l ,C l .试证:三直线A l ,B l ,C l 相交于一点.(第29届IMO 预选题)l AD ′MNGDCBA图2-22证明 设A l 与MN ,BC 分别相交于点G ,D ',由AMG ADN =∠∠,90AGM AND ==︒∠∠,知MAG NAD =∠∠,即BAD CAD '=∠∠.同理,设CA ,AB 边上的高BE ,CF 的垂足分别为E ,F ,且B l ,C l 分别与CA ,AB 交于E ',F ',则有CBE ABE '=∠∠,ACF BCF '=∠∠.由于△ABC 的三条高相交于垂心,此时应用第一角元形式的塞瓦定理,得 sin sin sin 1sin sin sin CAD ABE BCFDAB EBC FCA⋅⋅=∠∠∠∠∠∠,用等角代换上式,有sin sin sin 1sin sin sin BAD ACF CBE DAC F CB E BA'''⋅⋅=''∠∠∠∠∠∠.故由第一角元形式的塞瓦定理,知AD ',BE ',CF '三线共点,即A l ,B l ,C l 相交于一点.例19 如图2-23,四边形ABCD 内接于圆,AB ,DC 的延长线交于E ,AD ,BC 的延长线交于F ,P 为圆上任一点,PE ,PF 分别交圆于R ,S .若对角线AC 与BD 相交于T ,求证:R ,T ,S 三点共线.RTSPFEDC BA图2-23证明 连PD ,AS ,RC ,BR ,AP ,SD .由△EBR ∽△EPA ,△FDS ∽△FPA ,有BR EBPA EP =,PA FP DS FD =,此两式相乘,有BR EB FPDS EP FD =⋅.①又由ECR EPD △∽△,FPD FAS △∽△,有 CR EC PD EP =,PD FPAS FA =, 此两式相乘,有 CR EC FPAS EP FA=⋅. 由①÷②,得 BR AS EB FADS CR EC FD⋅=⋅. 上式两边同乘以DC AB ,得 BR CD SA EB AF DCRC DS AB BA FD CE⋅⋅=⋅⋅. 对△EAD 及截线BCF ,应用梅涅劳斯定理,有1EB AF DC BA FD CE ⋅⋅=. 于是1BR CD SARC DC AB⋅⋅=. 此时,应用第一角元形式的塞瓦定理的推论,知BD ,RS ,AC 交于一点.从而R ,T ,S 三点共直线.【模拟实战】习题A1.在△ABC 中,D 是BC 上的点,13BD DC =,E 是AC 中点.AD 与BE 交于O ,CO 交AB 于F ,求四边形BDOF 的面积与△ABC 的面积的比.2.若通过△ABC 各顶点的直线AD ,BE ,CF 共点,并且它们在边BC ,CA ,AB 所在直线上的截点D ,E ,F 关于所在边中点的对称点分别为D ',E ',F ',则直线AD ',BE ',CF '也共点. 3.一圆交△ABC 的各边所在直线于两点,设BC 边上的交点为D ,D ',CA 边上的交点为E ,E ',AB 边上的交点为F ,F '.若AD ,BE ,CF 共点,则AD ',BE ',CF '也共点. 4.试证:过三角形顶点且平分三角形周长的三条直线共点.5.将△ABC 各内角三等分,每两个角的相邻三等分线相交得△PQR ,又AX ,BY ,CZ 分别平分BAC ∠,ABC ∠,ACB ∠且它们与QR ,RP ,PQ 交于X ,Y ,Z .求证:PX ,QY ,RZ 三线共点.6.将△ABC 的各外角三等分,每两个外角的相邻三等分线相交得△DEF .又AX ,BY ,CZ 分别平分BAC ∠,ABC ∠,ACB ∠且它们与EF ,FD ,DE 交于X ,Y ,Z .求证:DX ,EY ,FZ 三线共点.7.O 是△ABC 的内切圆,BC ,CA ,AB 上的切点各是D ,E ,F .射线DO 交EF 于A ',同样可得B ',C '.试证:直线AA ',BB ',CC '共点.8.△ABC 在△A B C '''内部,且从A ,B ,C 各向B C '',C A '',A B ''所作的垂线共点,则从A ',B ',C '各向BC ,CA ,AB 所作的垂线也共点.9.在△ABC 中,40ABC ACB ==︒∠∠,P 为形内一点,20PAC =︒∠,30PCB =︒∠,求PBC ∠的度数.10.在ABC △中,AB AC =,80A =︒∠,D 为形内一点,且10DAB DBA ==︒∠∠,求ACD ∠的度数.(《数学教学》问题432题)11.在ABC △中,30BAC =︒∠,70ABC =︒∠,M 为形内一点,20MAB MCA ==︒∠∠,求MBA ∠的度数. (《数学教学》问题491题) 12.在ABC △中,40ABC =︒∠,30ACB =︒∠,P 为ABC ∠的平分线上一点,使10PCB =︒∠,BP 交AC 于M ,CP 交AB 于N .求证:PM AN =.(《数学教学》问题531题) 13.在ABC △中,40ABC =︒∠,20ACB =︒∠,N 为形内一点,30NBC =︒∠,20NAB =︒∠,求NCB ∠的度数. (《数学通报》问题1023题) 14.在ABC △中,80BAC =︒∠,60ABC =︒∠,D 为形内一点,且10DAB =︒∠,20DBA =︒∠,求ACD ∠的度数. (《数学通报》问题1142题) 15.在△ABC 中,50ABC =︒∠,30ACB =︒∠,M 为形内一点,20MCB =︒∠,40MAC =︒∠,求MBC ∠的度数. (《数学通报》问题1208题) 16.△ABC 中,70ABC =︒∠,30ACB =︒∠,P 为形内一点,40PBC =︒∠,20PCB =︒∠.求证:1CA AB BPAP PC CB⋅⋅=⋅⋅.(《数学通报》问题1306题) 17.在△ABC 中,40ABC ACB ==︒∠∠,P ,Q 为形内两点,20PAB QAC ==︒∠∠,PCB QCA =∠∠10=︒.求证:B ,P ,Q 三点共线.(《数学通报》问题1243题) 18.△ABC 中,50ABC ACB ==︒∠∠,P ,Q 为形内两点,10PCA QBC ==︒∠∠,PAC QCB =∠∠20=︒.求证:BP BQ =.(《数学通报》问题1281题) 19.在△ABC 中,AB AC =,100A =︒∠,I 为内心,D 为AB 上一点,满足BD BI =.试求BCD ∠的度数. (《数学通报》问题1073题) 20.1A ,2A ,1B ,2B ,1C ,2C 顺次分别在△ABC 的三边BC ,CA ,AB 上,且12BA A C =,12CB B A =, 12AC C B =,过2A ,2B ,2C 分别作1AA ,1BB ,1CC 的平行线a l ,b l ,c l .求证:a l ,b l ,c l 三线共点的充要条件是1AA ,1BB ,1CC 三线共点.21.在△ABC 中,AB AC =,AD BC ⊥于D ,过D 任作两射线分别交AB ,AC 于点E ,F ,交过点A 的平行线于G ,H ,且GH BC ∥.求证:AD ,GF ,HE 共点.22.在△ABC 中,过三边BC ,CA ,AB 边中的中点M ,N ,L 的三条等分三角形周长的直线MS ,NT ,LU (S ,T ,U 在三角形三边上)分别交LN ,LM ,MN 于D ,E ,F .求证:MS ,NT ,LU 三线共点.23.△ABC 的内切圆切BC ,CA ,AB 于D ,E ,F .P 是△ABC 内一点,PA 交内切圆于两点,其中靠近A 的一点为X ,类似定义Y ,Z .试证:DX ,EY ,FZ 三线共点.24.△ABC 在△A B C '''内部,AB 的延长线分别交A C '',B C ''于5P ,1P ;AC 的延长线分别交B A '',B C ''于3P ,4P ;BC 的延长线分别交A B '',A C ''于6P ,2P ,且满足142536AP AP BP BP CP CP ===== 123BP CP AP =++.求证:AA ',BB ',CC '所在直线共点.(《中学数学教学》擂台题(28)) 25.给定△ABC ,延长边BC 至D ,使CD AC =.△ACD 的外接圆与以BC 为直径的圆相交于C 和P .设BP 与CP 的延长线分别交AC 和AB 于E ,F .求证:E ,F ,D 共线.(第15届伊朗奥林匹克题) 26.在△ABC 的边上向外作三个正方形,1A ,1B ,1C 是正方形中的边BC ,CA ,AB 对边的中点.求证:直线1AA ,1BB ,1CC 共点.习题B1.O 是△ABC 的内切圆,D ,E ,F ,分别是BC ,CA ,AB 上的切点,DD ',EE ',FF '都是O 的直径.求证:直线AD ',BE ',CF '共点.(《数学通报》问题1396题) 2.四边形ABCD 的内切圆分别与边AB ,BC ,CD ,DA 相切于E ,F ,G ,H .求证:AC ,BD ,HF ,GE 四线共点.(《数学通报》问题1370题) 3.锐角△ABC 中,A 角的平分线与三角形的外接圆交于另一点1A ,点1B ,1C 与此类似.直线1AA 与B ,C 两角的外角平分线交于0A ,点0B ,0C 与此类似.求证:(Ⅰ)三角形000A B C 的面积是六边形111AC BACB 的二倍;(Ⅱ)三角形000A B C 的面积至少是三角形ABC 面积的四倍. (IMO -30试题)4.设P 为△ABC 内一点,使BPA CPA =∠∠,G 是线段AP 上的点,直线BG ,CG 分别交边AC ,AB于E ,F .求证:BPF CPE =∠∠.5.在凸四边形ABCD 中,对角线AC 平分BAD ∠,E 是CD 的延长线上的一点,BE 交AC 于点G ,延长DG 交CB 的延长线于F .试证:BAF DAE =∠∠.6.在△ABC 中,AB AC =,100A =︒∠,I 为内心,D 为AB 上一点,满足BD BI =.试求BCD ∠的度数. (《数学通报》问题1073题) 7.设△ABC 是等边三角形,P 是其内部一点,线段AP ,BP ,CP 依次交三边BC ,CA ,AB 于1A ,1B ,1C 三点.证明:111111111A B B C C A A B B C C A ⋅⋅⋅⋅≥.(IMO -37预选题)8.在一条直线l 的一侧画一个半圆Γ,C ,D ,是Γ上两点,Γ上过C 和D 的切线分别交l 于B 和A ,半圆的圆心在线段BA 上,E 是线段AC 和BD 的交点,F 是l 上的点,EF l ⊥.求证:EF 平分CFD ∠. (IMO -35预选题) 9.设1A 是锐角△ABC 的内接正方形的中心,其中内接正方形的两个顶点在BC 边上,一个顶点在AB边上,一个顶点在AC 边上.同样定义两个顶点分别在AC 边和AB 边上的内接正方形的中心分别为1B ,1C .证明:1AA ,1BB ,1CC 交于一点.(IMO -42预选题)10.以△ABC 的底边BC 为直径作半圆,分别与AB ,AC 交于点D ,E ,分别过点D ,E 作BC 的垂线,垂足依次为F ,G ,线段DG 和EF 交于点M .求证:AM BC ⊥.(1996年国家队选拔考试题)11.设O ,H 是锐角△ABC 的外接圆的圆心和垂心.证明:存在D ,E ,F 分别在线段BC ,CA ,AB 上,使得OD DH OE EH OF FH +=+=+,且此时AD ,BE ,CF 三线交于一点.(IMO -41预选题)12.已知AB 是O 的直径,弦CD AB ⊥于L ,点M 和N 分别在线段LB 和LA 上,且LM ∶MB LN =∶NA ,射线CM ,CN 交O 于E ,F .求证:AE ,BF ,OD 三线共点.13.设I 是△ABC 的内心,以I 为圆心的一个圆分别交BC 于1A ,2A ,交A C 于1B ,2B ,交AB 于1C ,2C .这六个点在圆上的顺序为1A ,2A ,1B ,2B ,1C ,2C .设3A ,3B ,3C 为弧12A A ,12B B ,12C C 的中点,直线23A A ,13B B 相交于4C ,直线23B B ,13C C 相交于4A ,直线23C C ,13A A 相交于4B .求证:直线34A A ,34B B ,34C C 三线共点.14.在△ABC 的边AB 和AC 上分别向形外作△ABE 和△ACF ,使△ABE ∽△ACF ,且ABE =∠ 90ACF =︒∠.求证:连线BF ,CE 与边BC 上的高AH 三线共点.15.过非等边三角形各顶点作其外接圆的切线,则各切线与其对边的交点共线.16.在△ABC 内三点D ,E ,F 满足BAE CAF =∠∠,ABD CBF =∠∠,则AD ,BE ,CF 三线共点的充要条件是ACD BCE =∠∠. 17.在任意△ABC 的三边BC ,CA ,AB 上各有点M ,N ,L ,而Q 是△ABC 内部任一点,直线AQ ,BQ ,CQ 分别交线段NL ,LM ,MN 于1M ,1N ,1L .求证:直线1M M ,1N N ,1L L 共点的充分必要条件是AM ,BN ,CL 共点,而与Q 点的位置无关.18.设P 是平面上△ABC 区域内任一点,AP ,BP ,CP 的延长线交△ABC 三边于D ,E ,F .求证:在△ABC 区域内,存在一个以△DEF 的某两边为邻边的平行四边形.19.设凸四边形ABCD 的两组对边所在的直线,分别交于E ,F 两点,两对角线的交点为P ,过点P 作PO EF ⊥于O .求证:BOC AOD =∠∠. (2002国家集训队选拔试题) 20.在△ABC 中,ABC ∠和ACB ∠均为锐角.D 是BC 边上的内点,且AD 平分BAC ∠,过点D 作垂线DP AB ⊥于P ,DQ AC ⊥于Q ,CP 与BQ 相交于K .求证:AK BC ⊥.。
