matlab课后习题答案第四章
matlab课后习题答案第四章
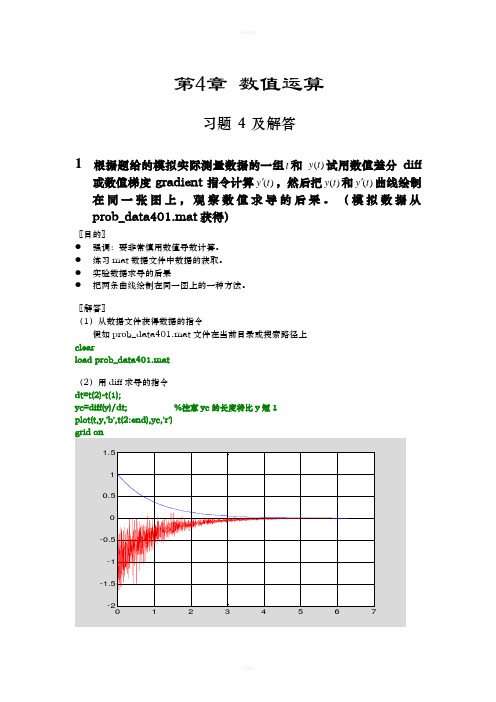
第4章数值运算习题 4 及解答1 根据题给的模拟实际测量数据的一组t和)(t y试用数值差分diff或数值梯度gradient指令计算)(t y',然后把)(t y和)(t y'曲线绘制在同一张图上,观察数值求导的后果。
(模拟数据从prob_data401.mat获得)〖目的〗●强调:要非常慎用数值导数计算。
●练习mat数据文件中数据的获取。
●实验数据求导的后果●把两条曲线绘制在同一图上的一种方法。
〖解答〗(1)从数据文件获得数据的指令假如prob_data401.mat文件在当前目录或搜索路径上clearload prob_data401.mat(2)用diff求导的指令dt=t(2)-t(1);yc=diff(y)/dt; %注意yc的长度将比y短1plot(t,y,'b',t(2:end),yc,'r')(3)用gradent 求导的指令(图形与上相似)dt=t(2)-t(1);yc=gradient(y)/dt;plot(t,y,'b',t,yc,'r')grid on〖说明〗● 不到万不得已,不要进行数值求导。
● 假若一定要计算数值导数,自变量增量dt 要取得比原有数据相对误差高1、2个量级以上。
● 求导会使数据中原有的噪声放大。
2 采用数值计算方法,画出dt tt x y x ⎰=0sin )(在]10 ,0[区间曲线,并计算)5.4(y 。
〖提示〗● 指定区间内的积分函数可用cumtrapz 指令给出。
● )5.4(y 在计算要求不太高的地方可用find 指令算得。
〖目的〗● 指定区间内的积分函数的数值计算法和cumtrapz 指令。
● find 指令的应用。
〖解答〗dt=1e-4;t=0:dt:10;t=t+(t==0)*eps;f=sin(t)./t;s=cumtrapz(f)*dt;plot(t,s,'LineWidth',3)ii=find(t==4.5);s45=s(ii)s45 =1.65413 求函数x ex f 3sin )(=的数值积分⎰=π0 )(dx x f s ,并请采用符号计算尝试复算。
(完整版)汽车理论课后作业答案MATLAB
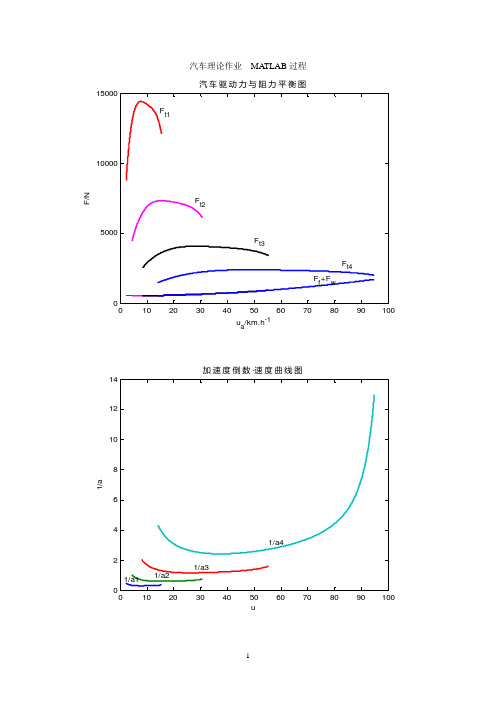
汽车理论作业 MA TLAB 过程010203040506070809010050001000015000汽车驱动力与阻力平衡图u a /km.h -1F /N10203040506070809010002468101214加速度倒数-速度曲线图u1/a0102030405060708090100102030405060u/(km/h)P /k W汽车功率平衡图10203040506070809010012141618202224最高档等速百公里油耗曲线Ua/(km/h)Q s /L2324252627282912131415161718燃油积极性-加速时间曲线燃油经济性(qs/L)动力性--原地起步加速时间 (s t /s )源程序:《第一章》m=3880; g=9.8; r=0.367; x=0.85; f=0.013; io=5.83; CdA=2.77; If=0.218; Iw1=1.798; Iw2=3.598; Iw=Iw1+Iw2;ig=[6.09 3.09 1.71 1.00]; %变速器传动比 L=3.2; a=1.947; hg=0.9; n=600:1:4000;T=-19.313+295.27*n/1000-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/1000).^4; Ft1=T*ig(1)*io*x/r;%计算各档对应转速下的驱动力Ft2=T*ig(2)*io*x/r;Ft3=T*ig(3)*io*x/r;Ft4=T*ig(4)*io*x/r;u1=0.377*r*n/(io*ig(1));u2=0.377*r*n/(io*ig(2));u3=0.377*r*n/(io*ig(3));u4=0.377*r*n/(io*ig(4));u=0:130/3400:130;F1=m*g*f+CdA*u1.^2/21.15;%计算各档对应转速下的驱动阻力F2=m*g*f+CdA*u2.^2/21.15;F3=m*g*f+CdA*u3.^2/21.15;F4=m*g*f+CdA*u4.^2/21.15;figure(1);plot(u1,Ft1,'-r',u2,Ft2,'-m',u3,Ft3,'-k',u4,Ft4,'-b',u1,F1,'-r',u2,F2,'-m',u3,F3,'-k',u4,F4,'-b','LineWidth',2)title('汽车驱动力与阻力平衡图');xlabel('u_{a}/km.h^{-1}')ylabel('F/N')gtext('F_{t1}')gtext('F_{t2}')gtext('F_{t3}')gtext('F_{t4}')gtext('F_{f}+F_{w}')%由汽车驱动力与阻力平衡图知,他们无交点,u4在最大转速时达到最大umax=u4(3401)Ft1max=max(Ft1);imax=(Ft1max-m*g*f)/(m*g)disp('假设是后轮驱动');C=imax/(a/L+hg*imax/L) % 附着率delta1=1+(Iw1+Iw2)/(m*r^2)+If*ig(1)*r^2*io^2*x/(m*r^2);delta2=1+(Iw1+Iw2)/(m*r^2)+If*ig(2)*r^2*io^2*x/(m*r^2);delta3=1+(Iw1+Iw2)/(m*r^2)+If*ig(3)*r^2*io^2*x/(m*r^2);delta4=1+(Iw1+Iw2)/(m*r^2)+If*ig(4)*r^2*io^2*x/(m*r^2);a1=(Ft1-F1)/(delta1*m); %加速度a2=(Ft2-F2)/(delta2*m);a3=(Ft3-F3)/(delta3*m);a4=(Ft4-F4)/(delta4*m);h1=1./a1; %加速度倒数h2=1./a2;h3=1./a3;h4=1./a4;figure(2);plot(u1,h1,u2,h2,u3,h3,u4,h4,'LineWidth',2); title('加速度倒数-速度曲线图');xlabel('u')ylabel('1/a')gtext('1/a1')gtext('1/a2')gtext('1/a3')gtext('1/a4')%由加速度倒数-速度曲线图可知u1min=min(u1);u1max=max(u1);u2min=u1max;u2min=min(u2);u2max=max(u2);u3min=u2max;u3max=max(u3);u4min=u3max;u4max=70;x1=[];x2=[];x3=[];x4=[];y=3401;for i=1:3401;if u3(i)<=u3min;x1=[i];endendq1=max(x1);ua3=u3(q1:y);a3=h3(q1:y);for i=1:3401;if u4(i)<=u4min;x2=[i];elseif u4(i)<=u4max;x3=[i];endendq2=max(x2);q3=max(x3);ua4=u4(q2:q3);a4=h4(q2:q3);s1=trapz(h2,u2 ); %二挡运行时间s2=trapz(ua3,a3);s3=trapz(ua4,a4);s=[s1 s2 s3];disp('积分得')t=sum(s)*1000/3600 %总时间《第二章》Pe1=Ft1.*u1./3600;%计算各档对应转速下的功率Pe2=Ft2.*u2./3600;Pe3=Ft3.*u3./3600;Pe4=Ft4.*u4./3600;P1=F1.*u1./(3600*x);%计算各档对应的各个车速下的行驶功率P2=F2.*u2./ (3600*x);P3=F3.*u3./ (3600*x);P4=F4.*u4./ (3600*x);figure(3);plot(u1,Pe1,'-r',u2,Pe2,'-m',u3,Pe3,'-k',u4,Pe4,'-b',u1,P1,'k',u2,P2,'k',u3,P3,'k', u4,P4,'k','linewidth',2);gtext('Pe1')gtext('Pe2')gtext('Pe3')gtext('Pe4')xlabel('u/(km/h)');ylabel('P/kW');title('汽车功率平衡图');n=[815 1207 1614 2012 2603 3006 3403 3804];Ua=[];Ua=0.377*r*n./(io*ig(4))ft=[];ft=m*g*f+(2.77/21.15)*Ua.^2;%计算各转速对应的各个车速下的行驶阻力Pe(1)=ft(1).*Ua(1)./(3600*x);%计算各转速对应的各个车速下的行驶阻力功率Pe(2)=ft(2).*Ua(2)./(3600*x);Pe(3)=ft(3).*Ua(3)./(3600*x);Pe(4)=ft(4).*Ua(4)./(3600*x);Pe(5)=ft(5).*Ua(5)./(3600*x);Pe(6)=ft(6).*Ua(6)./(3600*x);Pe(7)=ft(7).*Ua(7)./(3600*x);Pe(8)=ft(8).*Ua(8)./(3600*x)B0=[1326.8 1354.7 1284.4 1122.9 1141.0 1051.2 1233.9 1129.7];B1=[-416.46 -303.98 -189.75 -121.59 -98.893 -73.714 -84.478 -45.291];B2=[72.739 36.657 14.525 7.0035 4.4763 2.8593 2.9788 0.7113];B3=[-5.8629 -2.0533 -0.51184 -0.18517 -0.091077 -0.05138 -0.047449 -0.00075215];B4=[0.17768 0.043072 0.0068164 0.0018555 0.00068906 0.00035032 0.00028230-0.000038568];b1=(B0(1))+(B1(1)*Pe(1))+(B2(1)*Pe(1)^2)+(B3(1)*Pe(1)^3)+(B4(1)*Pe(1)^4);b2=(B0(2))+(B1(2)*Pe(2))+(B2(2)*Pe(2)^2)+(B3(2)*Pe(2)^3)+(B4(2)*Pe(2)^4);b3=(B0(3))+(B1(3)*Pe(3))+(B2(3)*Pe(3)^2)+(B3(3)*Pe(3)^3)+(B4(3)*Pe(3)^4);b4=(B0(4))+(B1(4)*Pe(4))+(B2(4)*Pe(4)^2)+(B3(4)*Pe(4)^3)+(B4(4)*Pe(4)^4);b5=(B0(5))+(B1(5)*Pe(5))+(B2(5)*Pe(5)^2)+(B3(5)*Pe(5)^3)+(B4(5)*Pe(5)^4);b6=(B0(6))+(B1(6)*Pe(6))+(B2(6)*Pe(6)^2)+(B3(6)*Pe(6)^3)+(B4(6)*Pe(6)^4);b7=(B0(7))+(B1(7)*Pe(7))+(B2(7)*Pe(7)^2)+(B3(7)*Pe(7)^3)+(B4(7)*Pe(7)^4);b8=(B0(8))+(B1(8)*Pe(8))+(B2(8)*Pe(8)^2)+(B3(8)*Pe(8)^3)+(B4(8)*Pe(8)^4);p=0.7;Qs=[];Qs(1)=(Pe(1)*b1)/(1.02*Ua(1).*p*g);Qs(2)=(Pe(2)*b2)/(1.02*Ua(2).*p*g);Qs(3)=(Pe(3)*b3)/(1.02*Ua(3).*p*g);Qs(4)=(Pe(4)*b4)/(1.02*Ua(4).*p*g);Qs(5)=(Pe(5)*b5)/(1.02*Ua(5).*p*g);Qs(6)=(Pe(6)*b6)/(1.02*Ua(6).*p*g);Qs(7)=(Pe(7)*b7)/(1.02*Ua(7).*p*g);Qs(8)=(Pe(8)*b8)/(1.02*Ua(8).*p*g);M=polyfit(Ua,Qs,2);UA=0.377*r*600/(ig(4)*io):1:0.377*r*4000/(ig(4)*io);%UA表示车速QS=polyval(M,UA);%QS表示油耗figure(4);plot(UA,QS,'linewidth',2);title('最高档等速百公里油耗曲线');xlabel('Ua/(km/h)');ylabel('Qs/L');《第三章》io=[5.17 5.43 5.83 6.17 6.33];Va=0.377*r*n(7)./(io.*ig(4));Ps=46.9366;disp('假设以最高档,较高转速(n取3401 ),最经济负荷(即90%负荷大约 46.9366Kw)行驶时油耗')qs=[];qs(1)=(Ps*b7)/(1.02*Va(1).*p*g);qs(2)=(Ps*b7)/(1.02*Va(2).*p*g);qs(3)=(Ps*b7)/(1.02*Va(3).*p*g);qs(4)=(Ps*b7)/(1.02*Va(4).*p*g);qs(5)=(Ps*b7)/(1.02*Va(5).*p*g);st=[ 17.5813 16.2121 14.5126 13.3775 12.9185];%加速时间:(这里以最高档〈四档〉、速度由0加速到94.93Km/h 的时间)因与题1.3第三问求法相同,这里不在累述,可直接有计算机求得:figure(5);plot(qs,st,'+','linewidth',2)hold on plot(qs,st,); gtext('5.17') gtext('5.43') gtext('5.83') gtext('6.17') gtext('6.33')title('燃油积极性-加速时间曲线'); xlabel('燃油经济性(qs/L)');ylabel('动力性--原地起步加速时间 (st/s)');《第四章》 4-31)前轴利用附着系数为:gf zh b zL +=βϕ后轴利用附着系数为: ()gr zh a zL --=βϕ1空载时:g h b L -=βϕ0=413.0845.085.138.095.3-=-⨯所以0ϕϕ>空载时后轮总是先抱死。
电机与拖动基础及MATLAB仿真习题答案(第四章)

4-14 一台直流电动机技术数据如下:额定功率PN=40kW ,额定电压UN=220V ,额定转速nN=1500r/min ,额定效率η=%,求电动机的额定电流和额定负载时的输入功率 解:(1)额定电流(2)输入功率4-15 一台直流发电机技术数据如下:额定功率PN=82kW ,额定电压UN=230V ,额定转速nN=970r/min ,额定效率η=90%,求发电机的额定电流和额定负载时的输入功率 解:(1)额定电流(2)输入功率4-16 已知一台直流电机极对数p=2,槽数Z 和换向片数K 均等于22,采用单叠绕组。
试求:(1)绕组各节距;(2)并联支路数。
解:(1)第一节距5424222y 1=-=±=εp z ,为短距绕组。
单叠绕组的合成节距及换向器节距均为1,即1y ==k y第二节距415y 12=-=-=y y(2)并联支路数等于磁极数,为4。
4-17 已知直流电机极数2p=6,电枢绕组总导体数N=400,电枢电流Ia=10A ,气隙每极磁通Φ=×10-2Wb ,试求:(1)采用单叠绕组时电枢所受电磁转矩;(2)绕组改为单波保持支路电流ia 不变时的电磁转矩。
解: 电枢绕组为单叠绕组时,并联支路对数a=p=3,电磁转矩 m N I a pN T a ⋅=⨯⨯⨯⨯⨯=Φ=38.1310021.0314.3240032π 如果把电枢绕组改为单波绕组, 保持支路电流a i 的数值不变,则电磁转矩也不变,仍A U P I N N N N 79.207875.022010403=⨯⨯==ηkWI U P N N 71.4579.2072201=⨯=⨯=A U P I N N N 5.35623010823=⨯==KW P P N 11.911==η为m N ⋅,因为无论是叠绕组还是波绕组,所有导体产生的电磁转矩的方向是一致的,保持支路电流a i 不变,就保持了导体电流不变,也就保持了电磁转矩不变。
matlab课后习题答案(1-9章)

1 数字1.5e2,1.5e3 中的哪个与1500相同吗?1.5e32 请指出如下5个变量名中,哪些是合法的?abcd-2xyz_33chan a 变量ABCDefgh 2、5是合法的。
3 在MATLAB 环境中,比1大的最小数是多少? 1+eps4 设 a = -8 , 运行以下三条指令,问运行结果相同吗?为什么?w1=a^(2/3) w2=(a^2)^(1/3) w3=(a^(1/3))^2w1 = -2.0000 + 3.4641i ;w2 = 4.0000 ;w3 =-2.0000 + 3.4641i 5 指令clear, clf, clc 各有什么用处?clear 清除工作空间中所有的变量。
clf 清除当前图形。
clc 清除命令窗口中所有显示。
第二章1 说出以下四条指令产生的结果各属于哪种数据类型,是“双精度”对象,还是“符号”符号对象?3/7+0.1双; sym(3/7+0.1)符; sym('3/7+0.1') 符;; vpa(sym(3/7+0.1)) 符;2 在不加专门指定的情况下,以下符号表达式中的哪一个变量被认为是自由符号变量. sym('sin(w*t)'),sym('a*exp(-X)'),sym('z*exp(j*th)') symvar(sym('sin(w*t)'),1) w a z3 (1)试写出求三阶方程05.443=-x 正实根的程序。
注意:只要正实根,不要出现其他根。
(2)试求二阶方程022=+-a ax x 在0>a 时的根。
(1)reset(symengine)syms x positive solve(x^3-44.5) ans =(2^(2/3)*89^(1/3))/2(2)求五阶方程022=+-a ax x 的实根 syms a positive %注意:关于x 的假设没有去除 solve(x^2-a*x+a^2)Warning: Explicit solution could not be found. > In solve at 83 ans =[ empty sym ]syms x clear syms a positivesolve(x^2-a*x+a^2) ans =a/2 + (3^(1/2)*a*i)/2 a/2 - (3^(1/2)*a*i)/24 观察一个数(在此用@记述)在以下四条不同指令作用下的异同。
MATLAB 习题 4

MATLAB 习题第1章MATLAB R2010环境2、在命令窗口中输入:>>a=2.5>>b=5*6>>c=[a b]写出在命令窗口中的运行结果4、用“Format”命令设置数据输出格式,(format long 或format long g)将pi显示为3.14159265358979,(formatshort e)将pi显示为3.1416e+0006、在工作空间查看变量的变量名、数据结构、类型、大小和字节数,打开数组编辑器窗口修改第2题的变量c元素。
修改变量c元素:8、输入变量a=5.3,b=[1 2;3 4],在工作空间中使用who、whos、exist和clear命令,并用save 命令将变量存入“F:\exe0101.mat”文件。
A=[1,2;3,4];inv(A)rank(A)det(A)A^3[v,d]=eig(A)结果:>>ans =-2.0000 1.00001.5000 -0.5000ans =2ans =-2ans =37 5481 118v =-0.8246 -0.41600.5658 -0.9094d =-0.3723 00 5.3723 >>命令窗口图片:接上一张图片:工作空间窗口图片:第2章MATLAB数值计算1、选择和填空(1)下列变量名中的(A)是合法变量。
A. char-1,i,jB. x*y,a.1C. x\y,a1234D. end,1bcx(2)已知x为1个向量,计算其正弦函数的运算为(C)。
A. SIN(X)B. SIN(x)C. sin(x)D. sinx(3) 已知x为1个向量,计算ln(x)运算为(B)。
A. ln(x)B. log(x)C. Ln(x)D.log10(x)(4) 若a=2.4,使用取整函数得出3,则该取整函数名为(C)。
A. fixB. roundC. ceilD. floor(5) 已知a=0:4, b=1:5, 下面的运算表达式出错的为(D)。
第4章 MATLAB程序流程控制_习题答案

第4章 MATLAB程序流程控制习题4一、选择题1.下列关于脚本文件和函数文件的描述中不正确的是()。
AA.函数文件可以在命令行窗口直接运行B.去掉函数文件第一行的定义行可转变成脚本文件C.脚本文件可以调用函数文件D.函数文件中的第一行必须以function开始2.下列程序的输出结果是()。
Dy=10;if y==10y=20;elseif y>0y=30enddisp(y)A.1 B.30 C.10 D.203.有以下语句:a=eye(5);for n=a(2:end,:)for循环的循环次数是()。
CA.3 B.4 C.5 D.104.设有程序段k=10;while kk=k-1end则下面描述中正确的是()。
AA.while循环执行10次B.循环是无限循环C.循环体语句一次也不执行D.循环体语句执行一次5.有以下程序段:x=reshape(1:12,3,4);m=0;n=0;for k=1:4if x(:,k)<=6m=m+1;elsen=n+1;endend则m和n的值分别是()。
CA.6 6 B.2 1 C.2 2 D.1 26.调用函数时,如果函数文件名与函数名不一致,则使用()。
A A.函数文件名B.函数名C.函数文件名或函数名均可D.@函数名7.如果有函数声明行为“function [x,y,z]=f1(a,b,c)”,则下述函数调用格式中错误的是()。
BA.x=f1(a,b,c) B.[x,y,z,w]=f1(a,b,c)C.[x,b,z]=f1(a,y,c) D.[a,b]=f1(x,y,z)8.执行语句“fn=@(x) 10*x;”,则fn是()。
AA.匿名函数B.函数句柄C.字符串D.普通函数9.执行下列语句后,变量A的值是()。
D>> f=@(x,y) log(exp(x+y));>> A=f(22,3);A.22,3B.22 C.3 D.2510.程序调试时用于设置断点的函数是()。
matlab第四章课后答案

%Exerc ise 1(1)r oots([1 11])%Exer cise1(2)roots([3 0 -4 0 2 -1])%Exerc ise 1(3)p=zero s(1,24);p([1 17 1822])=[5 -6 8 -5];ro ots(p)%E xerci se 1(4)p1=[2 3];p2=conv(p1,p1);p3=co nv(p1, p2);p3(end)=p3(en d)-4; %原p3最后一个分量-4r oots(p3)%Exer cise2fun=inli ne('x*log(sqrt(x^2-1)+x)-sqrt(x^2-1)-0.5*x');fzer o(fun,2)%Exer cise3fun=inli ne('x^4-2^x');fplot(fun,[-2 2]);gr id on;fze ro(fu n,-1),fzer o(fun,1),f minbn d(fun,0.5,1.5)%Exe rcise 4fu n=inl ine('x*sin(1/x)','x');fp lot(f un, [-0.10.1]);x=z eros(1,10);fori=1:10, x(i)=fz ero(f un,(i-0.5)*0.01);end;x=[x,-x]%Ex ercis e 5f un=in line('[9*x(1)^2+36*x(2)^2+4*x(3)^2-36;x(1)^2-2*x(2)^2-20*x(3);16*x(1)-x(1)^3-2*x(2)^2-16*x(3)^2]','x');[a,b,c]=fso lve(f un,[0 0 0])%E xerci se 6fun=@(x)[x(1)-0.7*si n(x(1))-0.2*cos(x(2)),x(2)-0.7*cos(x(1))+0.2*sin(x(2))]; [a,b,c]=fsolv e(fun,[0.5 0.5])%E xerci se 7clear; clo se; t=0:p i/100:2*pi;x1=2+sqr t(5)*cos(t); y1=3-2*x1+sq rt(5)*sin(t);x2=3+s qrt(2)*cos(t);y2=6*sin(t);pl ot(x1,y1,x2,y2); gri d on; %作图发现4个解的大致位置,然后分别求解y1=fsolv e('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.5,2])y2=fsolv e('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.8,-2])y3=fsol ve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[3.5,-5])y4=fso lve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[4,-4])%Exerc ise 8(1)c lear;fun=inlin e('x.^2.*(x.^2-x-2)');fp lot(f un,[-2 2]);grid on;%作图观察x(1)=-2;x(2)=fminb nd(fu n,-1,-0.5);x(4)=fmi nbnd(fun,1,2);fun2=inlin e('-x.^2.*(x.^2-x-2)');x(3)=f minbn d(fun2,-0.5,0.5);x(5)=2feval(fun,x)%答案: 以上x(2)(4)是局部极小,x(1)(3)(5)是局部极大,从最后一句知道x(1)全局最大, x(4)最小。
matlab课后习题答案1到6章

习题二1.如何理解“矩阵是MATLAB最基本的数据对象”答:因为向量可以看成是仅有一行或一列的矩阵,单个数据(标量)可以看成是仅含一个元素的矩阵,故向量和单个数据都可以作为矩阵的特例来处理。
因此,矩阵是MATLAB最基本、最重要的数据对象。
2.设A和B是两个同维同大小的矩阵,问:(1)A*B和A.*B的值是否相等答:不相等。
(2) A./B和B.\A的值是否相等答:相等。
(3)A/B和B\A的值是否相等答:不相等。
(4)A/B和B\A所代表的数学含义是什么答:A/B等效于B的逆右乘A矩阵,即A*inv(B),而B\A等效于B矩阵的逆左乘A矩阵,即inv(B)*A。
3.写出完成下列操作的命令。
(1)将矩阵A第2~5行中第1, 3, 5列元素赋给矩阵B。
答:B=A(2:5,1:2:5);或B=A(2:5,[1 3 5])(2)删除矩阵A的第7号元素。
答:A(7)=[](3)将矩阵A的每个元素值加30。
答:A=A+30;(4)求矩阵A的大小和维数。
答:size(A);ndims(A);(5)将向量t的0元素用机器零来代替。
答:t(find(t==0))=eps;(6)将含有12个元素的向量x转换成34⨯矩阵。
答:reshape(x,3,4);(7)求一个字符串的ASCII码。
答:abs(‘123’); 或double(‘123’);(8)求一个ASCII码所对应的字符。
答:char(49);4.下列命令执行后,L1、L2、L3、L4的值分别是多少A=1:9;B=10-A;...L1=A==B;L2=A<=5;L3=A>3&A<7;L4=find(A>3&A<7);答:L1的值为[0, 0, 0,0, 1, 0, 0, 0, 0]L2的值为[1, 1, 1,1, 1, 0, 0, 0, 0]L3的值为[0, 0, 0,1, 1, 1, 0, 0, 0]L4的值为[4, 5,6]5.已知23100.7780414565532503269.5454 3.14A-⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥-⎣⎦完成下列操作:(1)取出A的前3行构成矩阵B,前两列构成矩阵C,右下角32⨯子矩阵构成矩阵D,B与C的乘积构成矩阵E。
MATLAB原理及应用实验报告第四章答案

《MATLAB 原理及应用》实验报告三.课后练习题答案1.为 ⎪⎩⎪⎨⎧<-=>+=01001x x x xx x y 编写赋值程序。
程序如下:①建立如下的M 文件:x=input('x=');%让用户通过键盘输入数值、字符串或表达式if x>0y=x+1;elseif x==0y=x;else x<0y=x-1;e nd程序执行结果如下>> kh1 %在当前工作目录下,文件名为“kh.1.m ” x=1>> yy =22.使用for ... end循环的array向量编程求出1+3+5...+100 的值程序如下:sum=0;>> for k=1:2:100sum=sum+k;end>> sumsum =25003.计算1+3+5...+100 的值,当和大于1000时终止计算。
程序如下:sum=0;for m=1:2:100; %建立1 3 5….100的向量if sum<=1000 %如果sum小于1000则可以继续加sum=sum+m; %累加elsebreak; %若sum的结果不符合条件就跳出整个循环endend结果为:sum =1024k =653.1计算从1开始多少个自然数之和超过100。
程序如下:>> sum=0;n=0;>> while sum<=100n=n+1;sum=sum+n;end结果为:n =14sum =1054.求1!+2!+3!+……+8!的值程序如下:n=1;sum=1;for m=2:8; %循环7次使得得到各次阶乘n=n*m;sum=sum+n; %累加end结果为:sum =462335.写程序,判断一年是否为闰年,符合下面两条件之一:(1990~2014)A、能被4整除,不能被100整除B、能被400整除程序如下count=0;for y=1990:2014;if((rem(y,4)==0&rem(y,100)~=0)|(rem(y,4)==0&rem(y,400)~=0));count=count+1;endend结果为:count =5。
MATLAB课后习题解答

信号与系统MATLAB平时作业第二章(1)代码:t=-4:0.001:4;>> T=2;>> xt=rectpuls(t-1,T);>> plot(t,xt);>> axis([-4,4,-0.5,1.5]) 图形:(2)代码:t=sym('t');>> y=heaviside(t); >> ezplot(y,[-1,1]); >> grid on;>> axis([-1,1,-0.2,1.2]) 图形:(3)代码:> A=10;a=-1;B=5;b=-2;>> t=0:0.001:10;>> xt=A*exp(a*t)-B*exp(b*t); >> plot(t,xt);图形:(4)代码:t=sym('t');y=t*heaviside(t);ezplot(y,[-1,3]);grid on ;axis([-1 3 -0.1 3.1])图形:(5)代码:xt=abs(A*sin(w0*t+phi)); >> plot(t,xt);>> A=2;w0=10*pi;phi=pi/3;图形:(6)代码:> A=1;w0=1;B=1;w1=2*pi;>> t=0:0.001:20;>> xt=A*cos(w0*t)+B*sin(w1*t); >> plot(t,xt);图形:(7)代码:A=4;a=-0.5;w0=2*pi;>> t=0:0.001:10;>> xt=A*exp(a*t).*cos(w0*t); >> plot(t,xt);图形:(8)代码:w0=30;t=-15:0.001:15;xt=sinc(t/pi).*cos(w0*t); plot(t,xt);图形:M2-2(1)xt程序:t=-1:0.001:1;x=4*t.*[t>=0]-4*t.*[t>=1/2]-4*t.*[t>=1/2]+4*[t>=1/2]+4*t.*[t>=1]-4*[t>=1 ]+[t>=-1]-[t>=0];>> plot(t,x);图形:(2)程序:t=-1:0.001:1;x=(4*t.*[t>=0]-4*t.*[t>=1/2]-4*t.*[t>=1/2]+4*[t>=1/2]+4*t.*[t>=1]-4*[t>= 1]+[t>=-1]-[t>=0]).*cos(50*t);>> plot(t,x);图形:M2-3(1)yt=(t).*(t>=0&t<=2)+2*(t>=2&t<=3)-1*(t>=3&t<=5);(2)t=0:0.001:6;yt=(t).*(t>=0&t<=2)+2*(t>=2&t<=3)-1*(t>=3&t<=5);subplot(3,1,1)plot(t,yt)title('x(t)')axis([0,6,-2,2])t=0:0.001:12;yt=((0.5)*t).*(t>=0&t<=4)+2*(t>=4&t<=6)-1*(t>=6&t<=10); subplot(3,1,2)plot(t,yt);axis([0,12,-2,2]);title('(0.5)*t');t=-6:0.001:6;yt=((2-(0.5)*t)).*(t>=0&t<=4)+2*(t>=-2&t<=0)-1*(t>=-6&t<=-2); subplot(3,1,3)plot(t,yt);axis([-6,6,-2,2]);title('2-(0.5)*t');图形:M2-4奇分量程序:t=-2:0.001:2;x1t=(t.*[t>=-1]-t.*[t>=0]+[t>=-1]-[t>=0]+t.*[t<=1]-t.*[t<=0]-[t<=1]+[t<=0]) /2;>> plot(t,x1t);图形:偶分量:程序:t=-2:0.001:2;>>x2t=(t.*[t>=-1]-t.*[t>=0]+[t>=-1]-[t>=0]-t.*[t<=1]+t.*[t<=0]+[t<=1]-[t<=0]) /2;>> plot(t,x2t);图形:M2-5 (1)function [x,k]=impseq(0,-50,50) k=[-50:50];x=[k==0];stem(k,x)图形:(2)k=[-50:50];>> uk=[zeros(1,50),ones(1,51)];>> stem(k,uk)图形:(3)function [f,k]=impseq(0,-50,50);k=[-50:50];x=10*(1/2).^k.*[k>=0];>> stem(k,x);图形:(4)function [f,k]=impseq(k0,-50,50) k=[-10:10];x1=[(k+2)>=0];x2=[(k-6)>=0];x=x1-x2;stem(k,x);图形:(5)function [f,k]=impseq(k0,-50,50) k=[-50:50];>> x=k.*[k>=0];>> stem(k,x);图形:(6)k=-50:50;xk=(5*0.8.^k).*cos(0.9*pi*k);>> stem(k,xk);图形:M2-6 Ω0=0.1*pi;k=-50:50;>> xk=sin(0.1*pi*k);>> stem(k,xk);图形:Ω0=0.5*pi;k=-50:50;xk=sin(0.5*pi*k);stem(k,xk);图形:Ω0=0.9*pi;k=-50:50;xk=sin(0.9*pi*k); stem(k,xk);图形:Ω0=1.1*pi;k=-50:50;xk=sin(1.1*pi*k); stem(k,xk);图形:Ω0=1.5*pi;k=-50:50;xk=sin(1.5*pi*k); stem(k,xk);图形:Ω0=1.9*pi;k=-50:50;xk=sin(1.9*pi*k); stem(k,xk);图形:结论:随着Ω0的变动,波形也随之而成周期性变换M2-7 (1)程序:t=-2:0.001:2;x1t=cos(6*pi*t);plot(t,x1t);hold onk=-2:2;x1k=cos(0.6*pi*k);stem(k,x1k,'r');hold off图形:(2)程序:t=-1:0.001:1;x1t=cos(14*pi*t); plot(t,x1t);hold onk=-1:1;x1k=cos(1.4*pi*k); stem(k,x1k,'r'); hold off图形:(3)程序:t=-0.5:0.001:0.5;x1t=cos(26*pi*t);plot(t,x1t);hold onk=-0.5:0.5;x1k=cos(2.6*pi*k);stem(k,x1k,'r');hold off图形:M2-8 (1)用square函数:程序:k=0:40;A=1;P=0.6;y=A*square(P*k);stem(k,y)axis([k(1)-1 k(end)+1 -(A+1) (A+1)]); 图形:(2)程序:k=0:40;x2k=sawtooth(0.1*pi*k,0.5);stem(k,x2k);图形:M2-9(1)k=-4:7;xk=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1];stem(k,xk)图形:(2)k=-12:21x=[-3,0,0,-2,0,0,3,0,0,1,0,0,-2,0,0,-3,0,0,-4,0,0,2,0,0,-1,0,0,4,0,0,1,0,0,-1]; subplot(2,1,1)stem(k,x)title('3倍内插)t=-1:2;y=[-2,-2,2,1];subplot(2,1,2)stem(t,y)title('3倍抽取’)axis([-3,4,-4,4])图形:(3)k=-4:7;x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; subplot(2,1,1)stem(k+2,x)title('x[k+2]')subplot(2,1,2)stem(k-4,x)title('x[k-4]')图形:(4)k=-4:7;x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; stem(-fliplr(k),fliplr(x))title('x[-k]')图形:第三章M3-1(1)代码:ts=0;te=5;dt=0.01;>> sys=tf([2 1],[1 3 2]);>> t=ts:dt:te;>> x=exp(-3*t);>> y=lsim(sys,x,t);>> plot(t,y);>> xlabel('Time(sec)');>> ylabel('y(t)');图形:(2)代码:ts=0;te=5;dt=1; sys=tf([2 1],[1 3 2]); t=ts:dt:te;x=exp(-3*t);y=lsim(sys,x,t); >> plot(t,y); xlabel('Time(sec)'); ylabel('y(t)');图形:M3-2 代码:ts=0;te=5;dt=0.01;>> sys=tf([6],[1 3 6]);>> t=ts:dt:te;>> y=impulse(sys,t);>> plot(t,y);>> xlabel('Time(sec)');>> ylabel('h(t)');图形:(3)代码:ts=0;te=5;dt=0.01; sys=tf([6],[1 3 6]); t=ts:dt:te;y=step(sys,t);plot(t,y);xlabel('Time(sec)'); ylabel('u(t)')图形:M3-3 (1)代码:ts=0;te=5;dt=1;sys=tf([1],[1 0.2 1]);t=ts:dt:te;y=step(sys,t);plot(t,y);xlabel('Time(sec)');ylabel('u(t)')图形:(2)代码:ts=0;te=5;dt=1; sys=tf([1],[1 1 1]); t=ts:dt:te;y=step(sys,t);plot(t,y);xlabel('Time(sec)'); ylabel('u(t)')图形:(3)代码:ts=0;te=5;dt=1;sys=tf([1],[1 2 1]);t=ts:dt:te;y=step(sys,t);plot(t,y);xlabel('Time(sec)');ylabel('u(t)')图形:M3-4 代码:x=[0.85,0.53,0.21,0.67,0.84,0.12];kx=-2:3;h=[0.68,0.37,0.83,0.52,0.71];kh=-1:3;y=conv(x,h);k=kx(1)+kh(1):kx(end)+kh(end);stem(k,y,'r');图形:M3-6h(t)=x(t)x(t)=u(t)*u(t)+u(t-1)*u(t-1)+2u(t)*u(t-1)=r(t)-2r(t-1)+r(t-2)y(t)=x(t) h(t)=1/2*t^2.*u(t)-3/2*(t-1)^2.*u(t-1)-1/2*(t-3)^2.*u(t-3)0, t<0t^2/2, 0<=t<1 Y(t) = -t^2+3*t-3/2 1<=t<2( t-3)^2/2 2<=t<30 t>=3(b)T=0.1;k=-1:T:4;f1=1*((k>=0)&(k<=1));f2=tripuls(k-1,2);y=T*conv(f1,f2);tmin=-2;tmax=8;t1=tmin:0.1:tmax;plot(t1,y)grid on图形:T=0.1:图形:T=0.01T=0.001:M3-7 代码:b=[1 0.42 -0.19];a=[0.31 0.68];k=0:20;x=(0.6).^k.*[k>=0];y=filter(b,a,x);stem(k,y);图形:M3-8 代码:b=[1 0.7 -0.45 -0.6];a=[0.8 -0.44 0.36 0.02];k=0:30;h=impz(b,a,k)stem(k,h);h =1.25001.5625-0.2656-1.6305-0.81630.29140.56840.2019-0.1520-0.1887-0.04040.06650.05950.0038-0.0263-0.01770.00200.00970.0049-0.0017-0.0034-0.00120.00090.00110.0002-0.0004-0.0004-0.00000.00020.0001-0.0000 图形:第四章M4-1周期矩形信号:代码:n=-20:20;X=-j*1/2*sin(n/2*pi).*sinc(n/2);subplot(2,1,1);stem(n,abs(X));title('幅度谱')xlabel('nw');subplot(2,1,2);stem(n,angle(X));title('相位谱')图形:三角波信号:代码:>> n=-20:20;X=sinc(n)-0.5*((sinc(n/2)).^2); subplot(2,1,1);stem(n,abs(X));title('幅度谱')xlabel('nw');subplot(2,1,2);stem(n,angle(X));title('相位谱')图形:M4-6 (4)代码:x=[1,2,3,0,0];X=fft(x,5);subplot(2,1,1);m=0:4;stem(m,real(X)); title('X[m]实部') subplot(2,1,2); >> stem(m,imag(X)); title('X[m]虚部');图形:M4-7 (3)代码:k=0:10;x=0.5.^k;subplot(3,1,1);stem(k,x)title('x[k]')X=fft(x,10);subplot(3,1,2);m=0:9;stem(m,real(X));title('X[m]实部')>> subplot(3,1,3);>> stem(m,imag(X));title('X[m]虚部')图形:M5-2代码:t=0:0.05:2.5;T=1;xt1=rectpuls(t-0.5,T);subplot(2,2,1)plot(t,xt1)title('x(t1)')axis([0,2.5,0,2])xt2=tripuls(t-1,2);subplot(2,2,2)plot(t,xt2)title('x(t2)')axis([0,2.5,0,2])xt=xt1+xt2.*cos(50*t);subplot(2,2,[3,4])plot(t,xt)title('x(t)')figure;b=[10000];a=[1,26.131,341.42,2613.1,10000];[H,w]=freqs(b,a,w);subplot(2,1,1)plot(w,abs(H));set(gca,'xtick',[0 1 2 3 4 5 6 7 8]);set(gca,'ytick',[0.985 0.99 0.995 1 1.005]);grid; title('幅度曲线')subplot(2,1,2)plot(w,angle(H));set(gca,'xtick',[0 1 2 3 4 5 6 7 8])set(gca,'ytick',[-2 -1.5 -1 -0.5 0]);grid;title('相位曲线')figure;sys=tf([10000],[1 26.131 341.42 2613.1 10000]); yt1=lsim(sys,xt,t);subplot(2,1,1);plot(t,yt1);title('y(t1)')yt2=lsim(sys,xt.*cos(50*t),t);subplot(2,1,2);plot(t,yt2);title('y(t2)');图形:第六章 M6-1已知连续时间信号的s 域表示式如下,使用residue 求出X(s)的部分分式展开式,并写出x(t)的实数形式表达式。
MATLAB课后习题集附标准答案

第2章 MATLAB概论1、与其他计算机语言相比较,MATLAB语言突出的特点是什么?答:起点高、人机界面适合科技人员、强大而简易的作图功能、智能化程度高、功能丰富,可扩展性强.2、MATLAB系统由那些部分组成?答:开发环境、MATLAB数学函数库、MATLAB语言、图形功能、应用程序接口3、安装MATLAB时,在选择组件窗口中哪些部分必须勾选,没有勾选的部分以后如何补安装?答:在安装MATLAB时,安装内容由选择组件窗口中各复选框是否被勾选来决定,可以根据自己的需要选择安装内容,但基本平台(即MATLAB选项)必须安装.第一次安装没有选择的内容在补安装时只需按照安装的过程进行,只是在选择组件时只勾选要补装的组件或工具箱即可.矚慫润厲钐瘗睞枥庑赖。
4、MATLAB操作桌面有几个窗口?如何使某个窗口脱离桌面成为独立窗口?又如何将脱离出去的窗口重新放置到桌面上?聞創沟燴鐺險爱氇谴净。
答:在MATLAB操作桌面上有五个窗口,在每个窗口的右下角有两个小按钮,一个是关闭窗口的Close 按钮,一个是可以使窗口称为独立的Undock按钮,点击Undock按钮就可以使该窗口脱离桌面称为独立窗口,在独立窗口的view菜单中选择Dock,菜单项就可以将独立的窗口重新防止的桌面上.残骛楼諍锩瀨濟溆塹籟。
5、如何启动M文件编辑/调试器?答:在操作桌面上选择“建立新文件”或“打开文件”操作时,M文件编辑/调试器将被启动.在命令窗口中键入edit命令时也可以启动M文件编辑/调试器.酽锕极額閉镇桧猪訣锥。
6、存储在工作空间中的数组能编辑吗?如何操作?答:存储在工作空间的数组可以通过数组编辑器进行编辑:在工作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输入修改内容即可.彈贸摄尔霁毙攬砖卤庑。
7、命令历史窗口除了可以观察前面键入的命令外,还有什么用途?答:命令历史窗口除了用于查询以前键入的命令外,还可以直接执行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M文件中.謀荞抟箧飆鐸怼类蒋薔。
matlab课后习题答案1到6章

欢迎共阅习题二1.如何理解“矩阵是MATLAB 最基本的数据对象”? 答:因为向量可以看成是仅有一行或一列的矩阵,单个数据(标量)可以看成是仅含一个元素的矩阵,故向量和单个数据都可以作为矩阵的特例来处理。
(2) 删除矩阵A 的第7号元素。
答:A(7)=[](3) 将矩阵A 的每个元素值加30。
答:A=A+30;(4) 求矩阵A 的大小和维数。
答:size(A);ndims(A);(5) 将向量 t 的0元素用机器零来代替。
答:t(find(t==0))=eps; (6) 将含有12个元素的向量 x 转换成34⨯矩阵。
答:reshape(x,3,4); (7) 求一个字符串的ASCII码。
答:abs(‘123’); 或E 。
答:B=A(1:3,:); C=A(:,1:2); D=A(2:4,3:4);E=B*C;(2) 分别求E<D 、E&D 、E|D 、~E|~D 和find(A>=10&A<25)。
答:E<D=010001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,E&D=110111⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,11⎡⎤⎢⎥答:student(1).id='0001';student(1).name='Tom'; student(1).major='computer';student(1).grade=[89,78,67,90,86,85]; 8.建立单元矩阵B 并回答有关问题。
B{1,1}=1;B{1,2}='Brenden';B{2,1}=reshape(1:9,3,3); B{2,2}={12,34,2;54,21,3;4 ,23,67};(1)size(B)和ndims(B)的值分别是多少?答:size(B) 的值为2, 2。
ndims(B) 的值为2。
(2)B(2)和B(4)的值分别是(2)建立5×6随机矩阵A,其元素为[100,200]范围内的随机整数。
matlab课后习题答案1到6章

习题二1.如何理解“矩阵是MATLAB最基本的数据对象”?答:因为向量可以看成是仅有一行或一列的矩阵,单个数据(标量)可以看成是仅含一个元素的矩阵,故向量和单个数据都可以作为矩阵的特例来处理。
因此,矩阵是MATLAB最基本、最重要的数据对象。
2.设A和B是两个同维同大小的矩阵,问:(1)A*B和A.*B的值是否相等?答:不相等。
(2) A./B和B.\A的值是否相等?答:相等。
(3)A/B和B\A的值是否相等?答:不相等。
(4)A/B和B\A所代表的数学含义是什么?答:A/B等效于B的逆右乘A矩阵,即A*inv(B),而B\A等效于B矩阵的逆左乘A矩阵,即inv(B)*A。
3.写出完成下列操作的命令。
(1)将矩阵A第2~5行中第1, 3, 5列元素赋给矩阵B。
答:B=A(2:5,1:2:5); 或B=A(2:5,[1 3 5])(2)删除矩阵A的第7号元素。
答:A(7)=[](3)将矩阵A的每个元素值加30。
答:A=A+30;(4)求矩阵A的大小和维数。
答:size(A);ndims(A);(5)将向量t的0元素用机器零来代替。
答:t(find(t==0))=eps;(6)将含有12个元素的向量x转换成34⨯矩阵。
答:reshape(x,3,4);(7)求一个字符串的ASCII码。
答:abs(‘123’); 或double(‘123’);(8)求一个ASCII码所对应的字符。
答:char(49);4.下列命令执行后,L1、L2、L3、L4的值分别是多少?A=1:9;B=10-A;...L1=A==B;L2=A<=5;L3=A>3&A<7;L4=find(A>3&A<7);答:L1的值为[0, 0, 0, 0, 1, 0,0, 0, 0]L2的值为[1, 1, 1, 1,1, 0, 0, 0, 0]L3的值为[0, 0, 0, 1,1, 1, 0, 0, 0]L4的值为[4, 5, 6]5.已知23100.7780414565532503269.5454 3.14A-⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥-⎣⎦完成下列操作:(1)取出A的前3行构成矩阵B,前两列构成矩阵C,右下角32⨯子矩阵构成矩阵D,B与C的乘积构成矩阵E。
matlab课后习题答案

第2章 MATLAB 矩阵运算基础2.1 在MA TLAB 中如何建立矩阵⎥⎦⎤⎢⎣⎡194375,并将其赋予变量a ? >> a=[5 7 3;4 9 1]2.5 计算矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡897473535与⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡638976242之和。
>> a=[5 3 5;3 7 4;7 9 8];>> b=[2 4 2;6 7 9;8 3 6]; >> a+b ans =7 7 7 9 14 13 15 12 142.6 求⎥⎦⎤⎢⎣⎡+-+-+-+-++=i 44i 93i 49i 67i 23i 57i 41i 72i 53i 84x 的共轭转置。
>> x=[4+8i 3+5i 2-7i 1+4i 7-5i;3+2i 7-6i 9+4i 3-9i 4+4i];>> x’ ans =4.0000 - 8.0000i 3.0000 - 2.0000i 3.0000 -5.0000i 7.0000 +6.0000i 2.0000 +7.0000i 9.0000 - 4.0000i 1.0000 - 4.0000i 3.0000 + 9.0000i 7.0000 + 5.0000i 4.0000 - 4.0000i2.7 计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。
>> a=[6 9 3;2 7 5];>> b=[2 4 1;4 6 8]; >> a.*b ans =12 36 3 8 42 402.9 对于B AX =,如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ,求解X 。
>> A=[4 9 2;7 6 4;3 5 7];>> B=[37 26 28]’;-0.5118 4.0427 1.33182.10 已知:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a ,分别计算a 的数组平方和矩阵平方,并观察其结果。
(完整版)第4章MATLAB程序流程控制_习题答案

第4章 MATLAB程序流程控制习题4一、选择题1.下列关于脚本文件和函数文件的描述中不正确的是()。
AA.函数文件可以在命令行窗口直接运行B.去掉函数文件第一行的定义行可转变成脚本文件C.脚本文件可以调用函数文件D.函数文件中的第一行必须以function开始2.下列程序的输出结果是()。
Dy=10;if y==10y=20;elseif y>0y=30enddisp(y)A.1 B.30 C.10 D.203.有以下语句:a=eye(5);for n=a(2:end,:)for循环的循环次数是()。
CA.3 B.4 C.5 D.104.设有程序段k=10;while kk=k-1end则下面描述中正确的是()。
AA.while循环执行10次B.循环是无限循环C.循环体语句一次也不执行D.循环体语句执行一次5.有以下程序段:x=reshape(1:12,3,4);m=0;n=0;for k=1:4if x(:,k)<=6m=m+1;elsen=n+1;endend则m和n的值分别是()。
CA.6 6 B.2 1 C.2 2 D.1 26.调用函数时,如果函数文件名与函数名不一致,则使用()。
A A.函数文件名B.函数名C.函数文件名或函数名均可D.@函数名7.如果有函数声明行为“function [x,y,z]=f1(a,b,c)”,则下述函数调用格式中错误的是()。
BA.x=f1(a,b,c) B.[x,y,z,w]=f1(a,b,c)C.[x,b,z]=f1(a,y,c) D.[a,b]=f1(x,y,z)8.执行语句“fn=@(x) 10*x;”,则fn是()。
AA.匿名函数B.函数句柄C.字符串D.普通函数9.执行下列语句后,变量A的值是()。
D>> f=@(x,y) log(exp(x+y));>> A=f(22,3);A.22,3B.22 C.3 D.2510.程序调试时用于设置断点的函数是()。
MATLAB习题参考答案(胡良剑,孙晓君)

% 如图(4.31) % 如图(4.32)
图(4.31)error
4 2 2 2
图(4.32)
(4)曲面 z = x + 3 x + y − 2 x − 2 y − 2 x y + 6, x < 3,−3 < y < 13 解: >> xa=linspace(-3,3,100);ya=linspace(-3,13,100); >> [x,y]=meshgrid(xa,ya); >> z=x.^4+3*x.^2+y.^2-2*x-2*y-2*x.^2.*y+6; >> mesh(x,y,z) >> surf(x,y,z)
解:建立 M 文件 pxy 如下: xa=-2:0.05:2;ya=xa; nx=length(xa);ny=length(ya); [x,y]=meshgrid(xa,ya); z=zeros(nx,ny); [a1,b1]=find(x+y>1); %第 a1 列 b1 行对应的 x+y>1 (x 对应列;y 对应行) %第 a1 列对应的 x 值是 xa(a1);第 b1 行对应的 y 值是 ya(b1) z((a1-1)*ny+b1)=0.5457*exp(-0.75*ya(b1).^2-3.75*xa(a1).^2-1.5*xa(a1)); [a2,b2]=find(x+y<=1&x+y>-1); z((a2-1)*ny+b2)=0.7575*exp(-ya(b2).^2-6*xa(a2).^2); [a3,b3]=find(x+y<=-1); z((a3-1)*ny+b3)=0.5457*exp(-0.75*ya(b3).^2-3.75*xa(a3).^2+1.5*xa(a3)); surf(x,y,z); 命令窗口: >> pxy 运行结果如右图: 或者 M 文件如下: clear;close; xa=-2:0.1:2;ya=-2:0.1:2;[x,y]=meshgrid(xa,ya); z=zeros(size(x)); k1=find(x+y>1); z(k1)=0.5457*exp(-0.75*y(k1).^2-3.75*x(k1).^2-1.5*x(k1)); k2=find(x+y<=1&x+y>-1); z(k2)=0.7575*exp(-y(k2).^2-6*x(k2).^2); k3=find(x+y<-1); z(k3)=0.5457*exp(-0.75*y(k3).^2-3.75*x(k3).^2+1.5*x(k3)); mesh(x,y,z); 6、运行 demo 解:>>demo 7、查询 trapz 的功能、用法、目录、程序结构、相同目录下其它文件 解: >> help trapz ――功能用法 >> type trapz――程序结构,源码 >> which trapz――所在目录 >> help C:\MATLAB6p5\toolbox\matlab\datafun――该目录下其它文件
matlab课后习题答案第四章
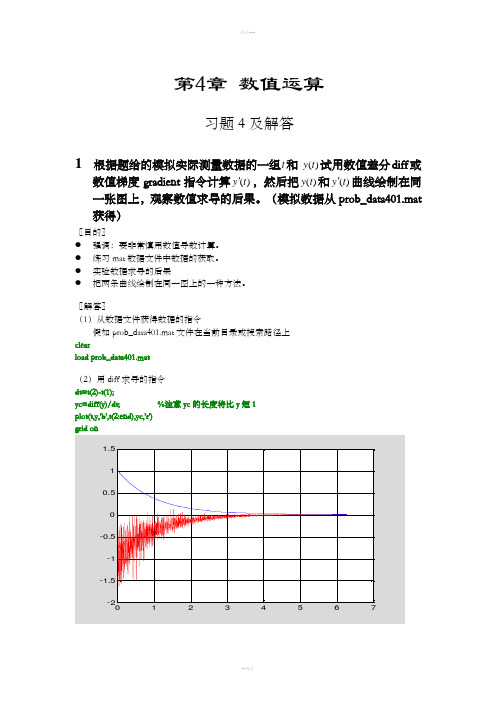
第4章数值运算习题 4 及解答1 根据题给的模拟实际测量数据的一组t和)(t y试用数值差分diff或数值梯度gradient指令计算)(t y',然后把)(t y和)(t y'曲线绘制在同一张图上,观察数值求导的后果。
(模拟数据从prob_data401.mat 获得)〖目的〗●强调:要非常慎用数值导数计算。
●练习mat数据文件中数据的获取。
●实验数据求导的后果●把两条曲线绘制在同一图上的一种方法。
〖解答〗(1)从数据文件获得数据的指令假如prob_data401.mat文件在当前目录或搜索路径上clearload prob_data401.mat(2)用diff求导的指令dt=t(2)-t(1);yc=diff(y)/dt; %注意yc的长度将比y短1plot(t,y,'b',t(2:end),yc,'r')grid on(3)用gradent 求导的指令(图形与上相似)dt=t(2)-t(1);yc=gradient(y)/dt;plot(t,y,'b',t,yc,'r')grid on〖说明〗● 不到万不得已,不要进行数值求导。
● 假若一定要计算数值导数,自变量增量dt 要取得比原有数据相对误差高1、2个量级以上。
● 求导会使数据中原有的噪声放大。
2 采用数值计算方法,画出dt tt x y x ⎰=0sin )(在]10 ,0[区间曲线,并计算)5.4(y 。
〖提示〗● 指定区间内的积分函数可用cumtrapz 指令给出。
● )5.4(y 在计算要求不太高的地方可用find 指令算得。
〖目的〗● 指定区间内的积分函数的数值计算法和cumtrapz 指令。
● find 指令的应用。
〖解答〗dt=1e-4;t=0:dt:10;t=t+(t==0)*eps;f=sin(t)./t;s=cumtrapz(f)*dt;plot(t,s,'LineWidth',3)ii=find(t==4.5);s45=s(ii)s45 =1.65413 求函数x ex f 3sin )(=的数值积分⎰=π0 )(dx x f s ,并请采用符号计算尝试复算。
matlab第四章课后作业解答

matlab第四章课后作业解答第四章习题解答1、求下列多项式的所有根,并进⾏验算。
(3)267235865x x x x-+-(4)4)32(3-+x 解:>> p=zeros(1,24);>> p(1)=5;p(17)=-6;p(18)=8;p(22)=-5;>> root=roots(p)root =0.97680.9388 + 0.2682i0.9388 - 0.2682i0.8554 + 0.5363i0.8554 - 0.5363i0.6615 + 0.8064i0.6615 - 0.8064i0.3516 + 0.9878i0.3516 - 0.9878i-0.0345 + 1.0150i-0.0345 - 1.0150i-0.4609 + 0.9458i-0.4609 - 0.9458i-0.1150 + 0.8340i-0.1150 - 0.8340i-0.7821 + 0.7376i-0.7821 - 0.7376i-0.9859 + 0.4106i-0.9859 - 0.4106i-1.0416-0.7927>> polyval(p,root)ans =1.0e-012 *-0.07120.0459 - 0.0081i0.0459 + 0.0081i-0.0419 + 0.0444i-0.0419 - 0.0444i0.0509 + 0.0929i0.0509 - 0.0929i-0.2059 + 0.0009i-0.2059 - 0.0009i-0.0340 + 0.0145i-0.0340 - 0.0145i0.1342 + 0.0910i0.1342 - 0.0910i0.0025 + 0.0027i0.0025 - 0.0027i-0.0077 + 0.4643i-0.0077 - 0.4643i-0.3548 - 0.1466i-0.3548 + 0.1466i-0.0251-0.0073(4) >> p1=[2 3];>> p=conv(conv(p1,p1),p1)-[0 0 0 4];>> root=roots(p)root =-1.8969 + 0.6874i-1.8969 - 0.6874i-0.7063>> polyval(p,root)ans =1.0e-014 *-0.7105 - 0.6217i-0.7105 + 0.6217i6、求解下列⽅程组在区域1,0<<βα内的解-=+=.sin 2.0cos 7.0,cos 2.0sin 7.0βαββαα解:以初值)5.0,5.0(),(00=βα进⾏求解>> fun=inline('[0.7*sin(x(1))+0.2*cos(x(2))-x(1),0.7*cos(x(1))-0.2*sin(x(2))-x(2)]');>> [x,f,h]=fsolve(fun,[0.5 0.5])Optimization terminated: first-order optimality is less than options.TolFun.x =0.5265 0.5079f =1.0e-007 *-0.1680 -0.2712h =1因⽽,该⽅程组的近似根为5079.0,5265.0==βα。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章数值运算习题 4 及解答1 根据题给的模拟实际测量数据的一组t和)(t y试用数值差分diff或数值梯度gradient指令计算)(ty'曲线y',然后把)(t y和)(t 绘制在同一图上,观察数值求导的后果。
(模拟数据从prob_data401.mat获得)〖目的〗●强调:要非常慎用数值导数计算。
●练习mat数据文件中数据的获取。
●实验数据求导的后果●把两条曲线绘制在同一图上的一种方法。
〖解答〗(1)从数据文件获得数据的指令假如prob_data401.mat文件在当前目录或搜索路径上clearload prob_data401.mat(2)用diff求导的指令dt=t(2)-t(1);yc=diff(y)/dt; %注意yc的长度将比y短1plot(t,y,'b',t(2:end),yc,'r')(3)用gradent求导的指令(图形与上相似)dt=t(2)-t(1);yc=gradient(y)/dt;plot(t,y,'b',t,yc,'r')grid on〖说明〗● 不到万不得已,不要进行数值求导。
● 假若一定要计算数值导数,自变量增量dt 要取得比原有数据相对误差高1、2个量级以上。
● 求导会使数据中原有的噪声放大。
2 采用数值计算方法,画出dt tt x y x ⎰=0sin )(在]10 ,0[区间曲线,并计算)5.4(y 。
〖提示〗● 指定区间的积分函数可用cumtrapz 指令给出。
● )5.4(y 在计算要求不太高的地方可用find 指令算得。
〖目的〗● 指定区间的积分函数的数值计算法和cumtrapz 指令。
● find 指令的应用。
〖解答〗dt=1e-4;t=0:dt:10;t=t+(t==0)*eps;f=sin(t)./t;s=cumtrapz(f)*dt;plot(t,s,'LineWidth',3)ii=find(t==4.5);s45=s(ii)s45 =3 求函数x e x f 3sin )(=的数值积分⎰=π)(dx x f s ,并请采用符号计算尝试复算。
〖提示〗● 数值积分均可尝试。
● 符号积分的局限性。
〖目的〗● 符号积分的局限性。
〖解答〗dx=pi/2000;x=0:dx:pi;s=trapz(exp(sin(x).^3))*dxs =5.1370符号复算的尝试syms xf=exp(sin(x)^3);ss=int(f,x,0,pi)Warning: Explicit integral could not be found.> In sym.int at 58ss =int(exp(sin(x)^3),x = 0 .. pi)4 用quad 求取dx x e xsin 7.15⎰--ππ的数值积分,并保证积分的绝对精度为910-。
〖目的〗● quadl ,精度可控,计算较快。
● 近似积分指令trapz 获得高精度积分的存和时间代价较高。
〖解答〗%精度可控的数值积分fx=(x)exp(-abs(x)).*abs(sin(x));format longsq=quadl(fx,-10*pi,1.7*pi,1e-7)sq =1.498%近似积分算法x=linspace(-10*pi,1.7*pi,1e7);dx=x(2)-x(1);st=trapz(exp(-abs(x)).*abs(sin(x)))*dxst =1.430%符号积分算法y='exp(-abs(x))*abs(sin(x))'si=vpa(int(y,-10*pi,1.7*pi),16)y =exp(-abs(x))*abs(sin(x))si =1.29115 求函数5.08.12cos 5.1)5(sin )(206.02++-=t t t e t t f t 在区间]5,5[-中的最小值点。
〖目的〗● 理解极值概念的邻域性。
● 如何求最小值。
● 学习运用作图法求极值或最小值。
● 感受符号法的局限性。
〖解答〗(1)采用fminbnd 找极小值点在指令窗中多次运行以下指令,观察在不同数目子区间分割下,进行的极小值搜索。
然后从一系列极小值点中,确定最小值点。
clearft=(t)sin(5*t).^2.*exp(0.06*t.*t)+1.8*abs(t+0.5)-1.5*t.*cos(2*t);disp('计算中,把[ -5,5] 分成若干搜索子区间。
')N=input(' 请输入子区间数 N ,注意使N>=1 ?');%该指令只能在指令窗中运行 t t=linspace(-5,5,N+1);f or k=1:N[tmin(k),fobj(k)]=fminbnd(ft,tt(k),tt(k+1));e nd[fobj,ii]=sort(fobj); %将目标值由小到大排列t min=tmin(ii); %使极小值点做与目标值相应的重新排列fobj,tmin(2)最后确定的最小值点在10,,2,1 =N 的不同分割下,经观察,最后确定出最小值点是 -1.531相应目标值是 -0.545(3)采用作图法近似确定最小值点(另一方法)(A )在指令窗中运行以下指令:clearft=(t)sin(5*t).^2.*exp(0.06*t.*t)+1.8*abs(t+0.5)-1.5*t.*cos(2*t);t=-5:0.001:5;ff=ft(t);plot(t,ff)grid on,shg(B )经观察后,把最小值附近邻域放到足够大,然后运行以下指令,那放大图形被推向前台,与此同时光标变为“十字线”,利用它点击极值点可得到最小值数据[tmin2,fobj2]=ginput(1)tmin2 =-1.975fobj2 =-0.136出现具有相同数值的刻度区域表明已达最小可分辨状态(4)符号法求最小值的尝试syms tfts=sin(5*t)^2*exp(0.06*t*t)-1.5*t*cos(2*t)+1.8*abs(t+0.5);dfdt=diff(fts,t); %求导函数tmin=solve(dfdt,t) %求导函数的零点fobj3=subs(fts,t,tmin) %得到一个具体的极值点tmin =-.0955e-2fobj3 =.3124〖说明〗●最小值是对整个区间而言的,极小值是对邻域而言的。
●在一个区间中寻找最小值点,对不同子区间分割进行多次搜索是必要的。
这样可以避免把极小值点误作为最小值点。
最小值点是从一系列极小值点和边界点的比较中确定的。
●作图法求最小值点,很直观。
假若绘图时,自变量步长取得足够小,那么所求得的最小值点有相当好的精度。
● 符号法在本例中,只求出一个极值点。
其余很多极值点无法秋初,更不可能得到最小值。
6 设0)0(,1)0(,1)(2)(3)(22===+-dtdy y t y dt t dy dt t y d ,用数值法和符号法求5.0)(=t t y 。
〖目的〗● 学习如何把高阶微分方程写成一阶微分方程组。
● ode45解算器的导数函数如何采用匿名函数形式构成。
● 如何从ode45一组数值解点,求指定自变量对应的函数值。
〖解答〗(1)改写高阶微分方程为一阶微分方程组令dtt dy t y t y t y )()(),()(21==,于是据高阶微分方程可写出 ⎪⎩⎪⎨⎧++-==1)(3)(2)()()(21221t y t y dt t dy t y dt t dy(2)运行以下指令求y(t)的数值解format longts=[0,1];y0=[1;0];dydt=(t,y)[y(2);-2*y(1)+3*y(2)+1]; %<4>%匿名函数写成的ode45所需得导数函数[tt,yy]=ode45(dydt,ts,y0);y_05=interp1(tt,yy(:,1),0.5,'spline'), %用一维插值求y(0.5)y_05 =0.127(3)符号法求解syms t;ys=dsolve('D2y-3*Dy+2*y=1','y(0)=1,Dy(0)=0','t')ys_05=subs(ys,t,sym('0.5'))ys =1/2-1/2*exp(2*t)+exp(t)ys_05 =.3780〖说明〗● 第<4>条指令中的导数函数也可采用M 函数文件表达,具体如下。
function S=prob_DyDt(t,y)S=[y(2);-2*y(1)+3*y(2)+1];7 已知矩阵A=magic(8),(1)求该矩阵的“值空间基阵”B ;(2)写出“A 的任何列可用基向量线性表出”的验证程序(提示:利用rref 检验)。
〖目的〗●体验矩阵值空间的基向量组的不唯一性,但它们可以互为线性表出。
●利用rref检验两个矩阵能否互为表出。
〖解答〗(1)A的值空间的三组不同“基”A=magic(8); %采用8阶魔方阵作为实验矩阵[R,ci]=rref(A);B1=A(:,ci) %直接从A中取基向量B2=orth(A) %求A值空间的正交基[V,D]=eig(A);rv=sum(sum(abs(D))>1000*eps); %非零特征值数就是矩阵的秩B3=V(:,1:rv) %取A的非零特征值对应的特征向量作基B1 =64 2 39 55 5417 47 4640 26 2732 34 3541 23 2249 15 148 58 59B2 =-0.3536 0.5401 0.3536-0.3536 -0.3858 -0.3536-0.3536 -0.2315 -0.3536-0.3536 0.0772 0.3536-0.3536 -0.0772 0.3536-0.3536 0.2315 -0.3536-0.3536 0.3858 -0.3536-0.3536 -0.5401 0.3536B3 =0.3536 0.6270 0.39130.3536 -0.4815 -0.24580.3536 -0.3361 -0.10040.3536 0.1906 -0.04510.3536 0.0451 -0.19060.3536 0.1004 0.33610.3536 0.2458 0.48150.3536 -0.3913 -0.6270(2)验证A的任何列可用B1线性表出B1_A=rref([B1,A]) %若B1_A矩阵的下5行全为0,%就表明A可以被B1的3根基向量线性表出B1_A =1 0 0 1 0 0 1 1 0 0 1 0 1 0 0 1 0 3 4 -3 -4 7 0 0 1 0 0 1 -3 -4 4 5 -7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0B2_A=rref([B2,A])B2_A =Columns 1 through 71.0000 0 0 -91.9239 -91.9239 -91.9239 -91.92390 1.0000 0 51.8459 -51.8459 -51.8459 51.84590 0 1.0000 9.8995 -7.0711 -4.2426 1.41420 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 0Columns 8 through 11-91.9239 -91.9239 -91.9239 -91.923951.8459 -51.8459 -51.8459 51.8459-1.4142 4.2426 7.0711 -9.89950 0 0 00 0 0 00 0 0 00 0 0 00 0 0 0B3_A=rref([B3,A])B3_A =Columns 1 through 71.0000 0 0 91.9239 91.9239 91.9239 91.92390 1.0000 0 42.3447 -38.1021 -33.8594 29.61680 0 1.0000 12.6462 -16.8889 -21.1315 25.37410 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 0Columns 8 through 1191.9239 91.9239 91.9239 91.923925.3741 -21.1315 -16.8889 12.646229.6168 -33.8594 -38.1021 42.34470 0 0 00 0 0 00 0 0 00 0 0 00 0 0 0〖说明〗●magic(n)产生魔方阵。
