实验十二幅频特性和相频特性

合集下载

实验十二--幅频特性和相频特性

实验十二--幅频特性和相频特性实验十二幅频特性和相频特性一、实验目的：研究ＲＣ串、并联电路的频率特性。

二、实验原理及电路图 1、实验原理电路的频域特性反映了电路对于不同的频率输入时，其正弦稳态响应的性质，一般用电路的网络函数()H j ω表示。

当电路的网络函数为输出电压与输入电压之比时，又称为电压传输特性。

即：()21U H j U ω=&&1）低通电路RCU &2U &10.707()H j ω0ωω图1-1 低通滤波电路图1-2 低通滤波电路幅频特性简单的RC 滤波电路如图4.3.1所示。

当输入为1U &，输出为2U &时，构成的是低通滤波电路。

因为：112111U U U j C j RC R j C ωωω=⨯=++&&&所以：()()()2111U H j H j U j RC ωωϕωω===∠+&&()()21H j RC ωω=+()H j ω是幅频特性，低通电路的幅频特性如图4.3.2所示，在1RC ω=时，()120.707H j ω==，即210.707U U =，通常2U &降低到10.707U &时的角频率称为截止频率，记为0ω。

2）高通电路CR1&U 2&Uωω00.7071()H j ω图2-1 高通滤波电路图2-2 高通滤波电路的幅频特性12111U j RC U R U j RC R j C ωωω=⨯=⨯+⎛⎫+ ⎪⎝⎭&&&所以：()()()211U j RC H j H j U jRC ωωωϕω===∠+&&其中()H j ω传输特性的幅频特性。

电路的截止频率01RC ω= 高通电路的幅频特性如4.3.4所示当0ωω<<时，即低频时()1H j RC ωω=<<当0ωω>>时，即高频时，()1H j ω=。

RL电路的幅频特性和相频特性的研究

RL电路幅频特性与相频特性研究物理与信息工程系10级物理学黄谦龚典引言电容元件在交流电路中的阻抗会随电源频率的改变而变化的。

将正弦交流电压加到电阻，电容组成的电路中式，各元件上的电压及行为会随之改变，这被称为电路的稳态特性。

在RLC 电路中，在一定条件下，能量会在电容和电感元件中产生交变，即谐振现象。

谐振现象是交流电路中个很重要的物理现象，它在电子技术，电磁测量等方面有广泛应用，利用的谐振现象可测量电器元件参数，或反过来确定电源效率，改善电路的品质因数。

本文试图从实验中检验并分析出RLC 串联电路幅值和相位随频率变化的规律曲线。

RC 、RL 和RLC 串联电路是大学物理实验的设计性实验之一，在交流电路中，幅频特性和相频特性是RC 、RL 和RLC 串联电路的重要性质，并在电子电路中被广泛应用。

本文对实验方法进行改进，采用幅频和相频特性的测量方法，观察各种参数变化，进一步了解各种参数对幅频特性和相频特性的影响。

1 实验原理1.1 RC 和RL 及RLC 串联电路的稳态特性的比较当在RC 和RL 及RLC 串联电路中加上交变电源，并不断改变电源频率时，电路的端口电压U 和电阻U 两端电压也随之发生规律性改变。

在RC ，RL ，RLC 串联电路中，若加在电路两端的正弦交流信号保持不变，则当电路中的电流和电压变化达到稳定状态时，电流(或者某元件两端的电压)与频率之间的关系特性称为幅频特性；电压、电流之间的位相差与频率之间的关系特性称位相频特性[1七]。

1） RC 串联电路的稳态特性电路连接如下图所示1R C U IRU Cω==cos 2cos 2R Ccm uc R cm uc U U U i c U t U iR RC U t πωωφπωωφ=+⎛⎫=++ ⎪⎝⎭⎛⎫==++ ⎪⎝⎭CR ωφ1arctan-=有以上公式可知，随频率的增加，I, R U 增加，C U 减小。

当ω很小时2πφ→-，，电源电压主要降落在电容上，反之，0φ→，电压主要将在电阻上。

实验12斜率鉴频与相位鉴频器

实验12斜率鉴频与相位鉴频器实验12 斜率鉴频与相位鉴频器—、实验准备1．做本实验时应具备的知识点：FM波的解调斜率鉴频与相位鉴频器2．做本实验时所⽤到的仪器：变容⼆极管调频模块斜率鉴频与相位鉴频器模块双踪⽰波器万⽤表⼆、实验⽬的1．了解调频波产⽣和解调的全过程以及整机调试⽅法，建⽴起调频系统的初步概念；2．了解斜率鉴频与相位鉴频器的⼯作原理；3．熟悉初、次级回路电容、耦合电容对于电容耦合回路相位鉴频器⼯作的影响。

三、实验内容1．调频-鉴频过程观察：⽤⽰波器观测调频器输⼊、输出波形，鉴频器输⼊、输出波形；2．观察初级回路电容、次级回路电容、耦合电容变化对FM波解调的影响。

四、基本原理从FM信号中恢复出原基带调制信号的技术称为FM波的解调，也称为频率检波技术，简称鉴频。

鉴频器的解调输出电压幅度应与输⼊FM波的瞬时频率成正⽐，因此鉴频器实际上是⼀个频率—电压幅度转换电路。

实现鉴频的⽅法有很多种，本实验介绍斜率鉴频和电容耦合回路相位鉴频。

1．斜率鉴频电路斜率鉴频技术是先将FM波通过线性频率振幅转换⽹络，使输出FM波的振幅按照瞬时频率的规律变化，⽽后通过包络检波器检出反映振幅变化的解调信号。

实践中频率振幅转换⽹络常常采⽤LC并联谐振回路，为了获得线性的频率幅度转换特性，总是使输⼊FM波的载频处在LC并联回路幅频特性曲线斜坡的近似直线段中点，即处于回路失谐曲线中点。

这样，单失谐回路就可以将输⼊的等幅FM波转变为幅度反映瞬时频率变化的FM波，⽽后通过⼆极管包络检波器进⾏包络检波，解调出原调制信号以完成鉴频功能。

图12-1为斜率鉴频与相位鉴频实验电路，图中13K02开关打向“3”时为斜率鉴频。

13Q01⽤来对FM波进⾏放⼤，13C2、13L02为频率振幅转换⽹络，其中⼼频率为9MHZ左右。

13D03为包络检波⼆极管。

13TP01、13TP02为输⼊、输出测量点。

2．相位鉴频器本实验采⽤平衡叠加型电容耦合回路相位鉴频器，实验电路如图12-1所⽰，开关13K02拨向“1”时为相位鉴频。

幅频特性和相频特性

1.实验题目：幅频特性和相频特性2.实验摘要：•1、在面板板上搭接RLC串联电路•2、研究RLC串联电路的零状态响应和零输入响应。

电路参数：R=10Ω和电位器R=1K、C=0.1uF、L=20mH、电源电压Vpp=2V方波。

•3、用示波器观测输出Uc（t）、输入Ui（t）的波形，记录过阻尼、欠阻尼和临界阻尼波形。

3.实验环境：(1)、电阻一个（51Ω）, 电容（0.01uF）电感（20mH）(2)、面包板(3)、电位器(4)、导线若干(5)、台式数字万用表(LINI-T UT805A)(6)、数字函数发生器（RIGOL DG1022U）4.实验原理RLC 串联电路，顾名思义就是将电阻、电感、电容串联起来的电路大体如下图所示：如图，t=0时Uc=0,此时将开关闭合，可得电压方程：本次实验比较重要的一个参数是：2√（L/C）当R<2√（L/C）时，电阻比较小，Uc的变化处在衰减振荡转态，此时称为欠阻尼状态，如下图：当R=2√（L/C）时，称为临界阻尼状态，如下图：当R>2√（L/C）时，电阻R比较大，称为过阻尼状态，Uc无法振荡，如下图：5.实验步骤和数据记录：1）、按下图在电路板上搭接电路2）、用数字函数发生器充当电源，本实验方波周期设为1.7ms,示波器通道一接入输入信号，通道二接收输出信号，通过调节电位器来调整阻值，使电路分别达到欠阻尼、临界阻尼、过阻尼状态3）、从电位器阻值为0开始往上增加电阻，此时处于欠阻尼状态，直至波形合适（大约出现6、7个峰值），采用光标法测量阻尼系数（a=ln(Um1/Um2)/Ta），注意其中周期为两个最高峰之间的时间差，另外注意测量电压时以稳定态的水平线做0V 线，记录，继续增加阻值4）、当波形的振荡只剩下小小一个尖点时，达到了临界阻值状态，记录下此时的电路电阻，继续增加阻值5）、当增加到某个临界点时，波形已经固定并且不会振荡了，此时达到了过阻尼的状态，记录下电路阻值6.实验结果计算和分析1)、欠阻尼状态采用光标法测量：误差分析：1.人工测量问题：由于采用的是光标法测量，人眼的测算总会有误差，况且示波器像素比较低，在调整光标线的时候也存在对不准的问题，还有电阻也存在测量误差2.器件原因：由于理论值的计算是采用器件的标准规格来计算的，实际器件和标值可能有出入，由于当前实验室缺少测量电感的仪器，只能通过测量阻值来确保他的正常工作，因此可能存在误差（2）、临界阻尼状态3)、过阻尼状态电路电阻9.7285kΩ7.实验总结1.本次实验让我了解到了RLC电路，正如老师所说，这三个元器件非常重要，在接下来的实验中也会多次用到，这次实验让我了解他们，特别是相对生疏的电感2.实验的过程中也存在不足，由于个人的粗心大意，示波器输出端接错位，导致波形振荡相当不明显，以后应该更进一步的预习电路图3.本次实验的进步我认为是在预习新知识方面，在实验开始前我查阅了比较多的资料，比如本次实验中极为重要的参数2√（L/C），了解了他的推断式以及在本实验中的作用，在老师讲解时可以比较轻松的明白，实验做起来也比以前有信心。

电路基础原理解惑电路的幅频特性和相频特性

电路基础原理解惑电路的幅频特性和相频特性电路的幅频特性和相频特性是电路工程中的重要概念，它们对描述电路的性能和行为起着关键作用。

在学习电路基础原理的过程中，理解并熟练运用幅频特性和相频特性是非常重要的。

本文将解析这两个概念的意义和具体应用。

幅频特性，又称为频率响应，描述的是电路在不同频率下对电压或电流的响应情况。

在交流电路中，信号的频率会对电路的行为产生影响。

幅频特性通常通过频率响应曲线来表达。

频率响应曲线可以显示电路在不同频率下的增益或损耗情况。

幅频特性可以帮助我们了解电路对不同频率信号的放大或衰减程度。

例如，放大器是一种常见的电路元件，它起到放大信号的作用。

通过分析放大器的幅频特性，我们可以了解到放大器在不同频率下的放大倍数，从而更好地设计和选择合适的放大器。

此外，幅频特性还可以帮助我们分析和解决电路中的各种问题。

例如，当我们遇到信号衰减或失真问题时，可以通过观察幅频特性来寻找问题所在。

若发现在问题频率附近出现衰减或失真，我们便可以针对性地进行电路修正或优化。

与幅频特性相对的是相频特性，又称为相位响应。

相频特性描述了电路对不同频率下信号的相位变化情况。

在交流电路中，信号的相位同样与频率有关。

相频特性通常通过相频响应曲线来表示。

相频特性可以帮助我们了解电路中信号的相位变化情况。

在某些应用中，信号的相位变化可能对系统的性能和稳定性产生重要影响。

比如，在音频信号处理中，我们希望保持信号的相位一致性，以避免声音的失真。

通过观察和分析相频特性，我们能够更好地了解电路对信号的相位变化情况，从而采取相应措施进行校正或补偿。

综上所述，电路的幅频特性和相频特性是电路工程中相当重要的概念。

通过研究幅频特性，我们能够更好地了解电路对不同频率信号的放大或衰减情况，从而为电路设计和选择提供依据。

而相频特性能够帮助我们分析信号的相位变化情况，从而优化电路设计，确保信号的准确传输。

在实际应用中，我们通常使用示波器、频谱仪等测试仪器来获取电路的幅频特性和相频特性。

实验十二--幅频特性和相频特性

实验十二幅频特性和相频特性一、实验目的：研究ＲＣ串、并联电路的频率特性。

二、实验原理及电路图 1、实验原理电路的频域特性反映了电路对于不同的频率输入时，其正弦稳态响应的性质，一般用电路的网络函数()H j ω表示。

当电路的网络函数为输出电压与输入电压之比时，又称为电压传输特性。

即：()21U H j U ω=1〕低通电路U 2图1-1 低通滤波电路图1-2 低通滤波电路幅频特性简单的RC 滤波电路如图4.3.1所示。

当输入为1U ，输出为2U 时，构成的是低通滤波电路。

因为：112111U U U j C j RCR j Cωωω=⨯=++所以：()()()2111U H j H j U j RC ωωϕωω===∠+()H j ω=()H j ω是幅频特性，低通电路的幅频特性如图4.3.2所示，在1RCω=时，()0.707H j ω==，即210.707U U =，通常2U 降低到10.707U 时的角频率称为截止频率，记为0ω。

2〕高通电路2图2-1 高通滤波电路图2-2 高通滤波电路的幅频特性12111U j RCU R U j RCR j C ωωω=⨯=⨯+⎛⎫+ ⎪⎝⎭所以：()()()211U j RC H j H j U jRC ωωωϕω===∠+其中()H j ω传输特性的幅频特性。

电路的截止频率01RC ω=当0ωω<<时，即低频时()1H j RC ωω=<<当0ωω>>时，即高频时，()1H j ω=。

3）研究RC 串、并联电路的频率特性：Aff 31图15-2f0ϕ︒90︒-90iu ou +--+RR CC图 15-1)1j(31)j (iｏRC RC UUN ωωω-+==其中幅频特性为：22io)1(31)(RC RC U U A ωωω-+==相频特性为：31arctg)(o RCRC i ωωϕϕωϕ--=-=幅频特性和相频特性曲线如图15－2所示，幅频特性呈带通特性。

幅频特性和相频特性

电路分析实验报告幅频特性和相频特性一、实验摘要电容元件在交流电路中的阻抗会随电源频率的改变而变化。

本实验用电容搭建一个电路，用示波器观察加上一个正弦波之后，该电路幅值和相位随频率变化的规律曲线。

二、实验环境示波器函数信号发生器 0.1μF电容电阻面包板导线三、实验原理电阻作为响应时，可用作高通滤波器电容作为响应时，可用作低通滤波器RC串并联（文氏电桥）电路四、实验步骤在面包板上搭建电路加上4vpp，频率从100赫兹到用示波器观察波形的幅值和位相差，记录相20千赫兹的正弦波应电压是输入电压0.707倍时的波形图将电容作响应加上4vpp，频率从100赫兹到20千赫兹的正弦波，用示波器观察波形的幅值和位相差，记录响应电压是输入电压0.707倍时的相关数据搭建文氏电桥加上4vpp，频率从100赫兹到20千赫兹的正弦波，用示波器观察波形的幅值和位相差，记录响应电压最高时的相关数据五、实验数据1.电阻作响应（高通滤波器）输入信号峰峰值的测量值为3.9v100 200 600 1000 1400 1500 5000 10000 15000 20000 输入频率/HzVpp/v 0.297 0.320 1.61 2.33 2.77 2.85 3.74 3.9 3.9 3.9相位差-85 -79 -66 -55 -48 -45 -19 -10 -8 -6 /°2.由李萨如图形计算得相位差= -49°，直接测量的相移为-48°，误差0.02当频率增大时，响应电压增大，体现出高通当频率增大时，位相差减小2.电容作响应（低通滤波器）100 500 1000 1500 16002000 3000 5000 8000 10000 输入频率/HzVpp/v 4.14 3.94 3.38 2.89 2.81 2.49 1.89 1.29 0.880 0.7204 18 32 43 4651 61 71 77 80相位差/°当频率增大时，响应电压减小，体现出低通当频率增大时，位相差增大3.文氏电桥100 500 1000 1500 2000 4000 5000 10000 15000 20000 输入频率/HzVpp/v 0.273 1.03 1.31 1.35 1.33 1.09 0.98 0.580 0.420 0.340 -80 -41 -15 -1 11 33 43 62 75 80相位差/°在某一频率，响应电压最大随频率增加，位相差先减小再增大六、实验总结在本次实验中了解到了RC串联电路和文氏电桥的幅频特性和相频特性。

利用波尔共振仪研究受迫振动实验报告

利用波尔共振仪研究受迫振动实验报告一、实验目的与要求1．研究波尔共振仪中弹性摆轮受迫振动的幅频、相频特性。

2．研究不同阻尼力矩对受迫振动的影响，观察共振现象。

3．学习用频闪法测定运动物体的某些量，如相位差。

二、实验原理 1、受迫振动和策动力物体在周期外力的持续作用下发生的振动称为受迫振动，这种周期性的外力称为策动力。

如果外力是按简谐振动规律变化，那么稳定状态时的受迫振动也是简谐振动。

此时，振幅保持恒定，振幅的大小与策动力的频率和原振动系统无阻尼时的固有振动频率以及阻尼系数有关。

在受迫振动状态下，系统除了受到策动力的作用外，同时还受到回复力和阻尼力的作用。

所以在稳定状态时物体的位移与策动力变化相位不同，而是存在一个相位差。

当策动力频率与系统的固有频率相同时，系统产生共振，振幅最大，相位差为90°。

2、振动方程求解实验采用摆轮在弹性力矩作用下自由摆动，在电磁阻尼力矩作用下作受迫振动来研究受迫振动特性，可直观地显示机构振动中的一些物理现象。

当摆轮受到周期性策动力矩0M=M cos t ω的作用，并在有空气阻尼和电磁阻尼的媒质中运动时（阻尼力矩为d -b dtθ），其运动方程为202M cos t d d J k b dt dt θθθω=--+（1）式中，J 为摆轮的转动惯量，k θ-为弹性力矩，M 0为强迫力矩的幅值，ω为策动力角频率。

令20k J ω=，2bJ β=，0M m J =则式（1）变为 22022c o s d d m t dt dtθθβωθω++= （2）当cos 0m t ω=时，式（2）即为阻尼振动方程。

当cos 0m t ω=且0β=，则式（2）脱化为简谐运动方程，22020d dt θωθ+= （3）0ω为系统的固有频率。

式（2）通解为12cos()cos()t f e t t βθθωαθωφ-=+++ （4）由（4）可见受迫振动分为两部分：通解第一项1cos()t f e t βθωα-+与初始条件有关，经过一定时间后衰减消失。

幅频特性和相频特性

幅频特性和相频特性幅频特性指的是，信号的幅度对于不同频率的响应情况。

在电路分析中，幅频特性也称为振幅特性。

它是衡量电路输出信号强度和输入信号之间关系的重要参数之一。

在传输系统中，它可以用于衡量信道传输信号强度的变化，从而确定信不信号可靠。

通常情况下，幅频特性用图形化方式表示，绘制成以频率为横轴，幅度为纵轴的图像。

这个图像称为Bode图，通常用于分析信号的频率响应和系统的行为。

Bode图可以帮助我们快速了解系统在响应不同频率信号时的行为，从而优化电路设计。

例如，在无源电路中，电容器可被视为一个通路，根据欧姆定律，这个通路的输入电压和输出电流之间的关系可以表示如下：I = C * dV/dt其中，I是电流，V是电压，t是时间，C是电路的电容值。

我们可以通过幅频特性来测量这个电路对不同频率的输入信号所产生的电流的大小变化。

相频特性也是电路分析中的另一个关键指标。

相频特性研究的是信号的相位随频率变化的规律。

在通信系统和电信系统中，相频特性常常用来衡量信道传输信号的相位失真情况。

与幅频特性一样，相频特性也可以用Bode图表示。

在大多数情况下，当信号被输入到电路中时，其相位差异通常是由于电路中存在的各种元件所引起的。

如果我们知道这些元件对信号的影响，就可以用相频特性来预测信号输出时的相位差异，并对电路进行优化。

例如，在拉氏变换器中，输入信号x(t)和输出信号y(t)之间的关系可以表示为：Y(s) = H(s)X(s)其中，s是复变量，H(s)是系统设备的频率响应函数，X(s)和Y(s)是输入和输出信号的拉氏变换。

如果我们要通过这个信号源传输信息，则需要确保输出信号在特定频率范围内的相位差异最小化。

相频特性可以帮助我们确定这个特定频率范围并优化电路设计。

连续弹性体悬臂梁各阶固有频率及主振型测定(最全)word资料

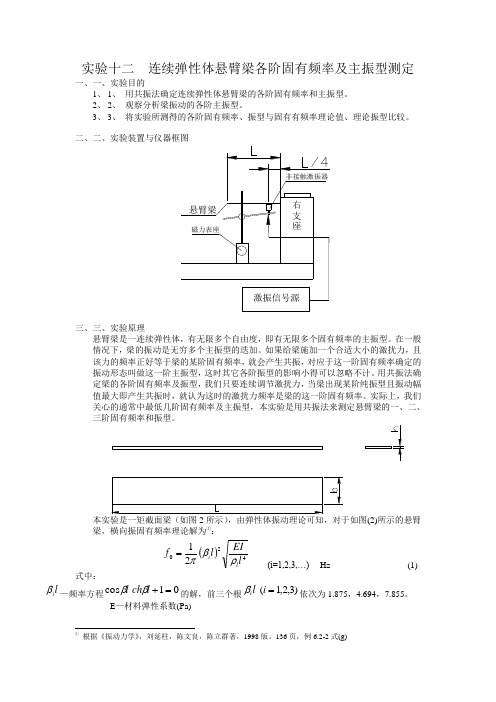
实验十二连续弹性体悬臂梁各阶固有频率及主振型测定一、一、实验目的1、 1、用共振法确定连续弹性体悬臂梁的各阶固有频率和主振型。

2、 2、观察分析梁振动的各阶主振型。

情况下，梁的振动是无穷多个主振型的迭加。

如果给梁施加一个合适大小的激扰力，且该力的频率正好等于梁的某阶固有频率，就会产生共振，对应于这一阶固有频率确定的振动形态叫做这一阶主振型，这时其它各阶振型的影响小得可以忽略不计。

用共振法确定梁的各阶固有频率及振型，我们只要连续调节激扰力，当梁出现某阶纯振型且振动幅值最大即产生共振时，就认为这时的激扰力频率是梁的这一阶固有频率。

实际上，我们关心的通常中最低几阶固有频率及主振型，本实验是用共振法来测定悬臂梁的一、二、l i β①根据《振动力学》，刘延柱，陈文良，陈立群著，1998版。

136页，例6.2-2式(g)A — A — 梁横截面积(m 2)l ρ—材料线密度(kg/m) l ρ=ρAρ—材料密度（kg/m 3） I —梁截面弯曲惯性矩(m 4)对矩形截面，弯曲惯性矩：123bhI = (m 4) (2)式中： b —梁横截面宽度(m) h —梁横截面高度(m) 本实验取l =( ) m b=( ) m h=( ) mE=20×1011Pa ρ=7800kg/m 3 各阶固有频率之比：f 1:f 2:f 3:f 4……=1:6.27:17.55 (3)理论计算可得悬臂梁的一、二、三阶固有频率的振型如图(3)所示：0.10.20.30.40.50.60.70.80.91-10120 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1-2020 0.10.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 10.511.5beam transvers vibration with one end clasped四、四、实验方法1、 1、选距固定端L/4之处为激振点，将激振器端面对准悬臂梁上的激振点，保持初始间隙δ=6~8mm 。

RC、RL与RLC串联电路幅频和相频特性的研究

RC 、RL 及RLC 串联电路幅频和相频特性的研究【摘要】本文主要研究RC ，RL 和RLC 串联电路在不同频率的信号下的响应，在双踪示波器上同时观察电阻和电感（或电容）上输出电压幅度和相位差的变化，定量研究了RLC 串联电路的幅频特性和相频特性。

同时发现在实际的实验操作中，电阻，电容以及电感的参数的选择对本实验有很大的影响，掌握了幅频特性和相频特性的测量方法，使理论知识和实验容有机的结合起来。

【关键词】串联电路；RLC 电路；相频特性；幅频特性 1引言RC 、RL 和RLC 串联电路是大学物理实验的设计性实验之一，在交流电路中，幅频特性和相频特性是RC 、RL 和RLC 串联电路的重要性质，并在电子电路中被广泛应用。

本文对实验方法进行改进，采用幅频和相频特性的测量方法，观察各种参数变化，进一步了解各种参数对幅频特性和相频特性的影响。

2实验设计原理在RC ，RL ，RLC 串联电路中，若加在电路两端的正弦交流信号保持不变，则当电路中的电流和电压变化达到稳定状态时，电流（或者某元件两端的电压）与频率之间的关系特性称为幅频特性；电压、电流之间的位相差与频率之间的关系特性称位相频特性。

2.1 RC 串联电路电路如图1所示。

令ω表示电源的圆频率，U ，I ，R U ,C U 分别表示电源电压，电路中的电流，电阻R 上的电压和电容C 上的有效值。

ϕ表示电路电流I 和电源电压U 间的相位差，则： RC 总阻抗为：CjR Z ω1~-= （1）其中Z ~的模为：221|~|⎪⎭⎫ ⎝⎛+==C R Z Z ω（2）CR R Cωωϕ1arctan 1arctan -=⎪⎪⎪⎪⎭⎫ ⎝⎛-= （3）ϕ为U 和I 之间的相位差，即 I U ϕϕϕ-= （4）根据交流欧姆定律，电阻上的电压为：IR U R = （5）电容上的电压为：CIU C ω= （6）总电压为：221⎪⎭⎫ ⎝⎛+=C R IU ω （7）图2为上述电压、电流（有效值）的矢量图，注：此处角度取逆时针方向为正值。

传输网络的幅频和相频特性(lu)

谢谢！
讲解到此结束
实验思考题
1、图5波特图仪中、波特图仪中VERTICAL和HORIZONTAL的F 波特图仪中和的分别表示什么含义？和I分别表示什么含义？分别表示什么含义
答：VERTICAL的F和I分别表示图中纵向的和分别表示图中纵向坐标的终端和起点值；坐标的终端和起点值； HORIZONTAL的F和I分别表示图中横向的和分别表示图中横向坐标的终端和起点频率。坐标的终端和起点频率。
实验思考题
频率点电压比 3.147KHz 0.707 3.715KHz 0.9999 4.474KHz 0.707
根据测试数据作出该电路的幅频特性曲线图。根据测试数据作出该电路的幅频特性曲线图。
实验思考题
3、半功率点频率是如何定义的。计算图3电路的半功率点频、半功率点频率是如何定义的。计算图电路的半功率点频并简述实验中测量半功率点频率的方法。率，并简述实验中测量半功率点频率的方法。
实验思考题
• 双谐振网络：对输入频率在一定范围内的信双谐振网络：号有较大的输出，号有较大的输出，而对输入频率高于这个频率范围上限以及低于这个频率范围下限的信号则衰减较大。因为是双谐振，号则衰减较大。因为是双谐振，所以有两个谐振点，也就有两个通带。谐振点，也就有两个通带。
实验思考题
4.通过仿真实验分别阐述5 4.通过仿真实验，分别阐述5种网络的幅频特性。 • 高通网络：此RC电路对输入频率较高的信号高通网络： RC电路对输入频率较高的信号有较大的输出，有较大的输出，而对输入频率较低的信号则衰减较大。即高频信号容易通过。衰减较大。即高频信号容易通过。 • 低通网络：此RL电路对输入频率较低的信号低通网络： RL电路对输入频率较低的信号有较大的输出，有较大的输出，而对输入频率较高的信号则衰减较大。即直流和低频信号容易通过。衰减较大。即直流和低频信号容易通过。

幅频特性及相频特性实例

GK ( j ) ( j ) GK ( j ) 1 GK ( j )
显然，在高频时闭环幅频特性近似等于开环幅频特性。因此，开环对数幅频特性 L( ) 在高频段的幅值，直接反映了系统对高频干扰信号的抑制能力。高频部分的幅值越低，系统的抗干扰能力越强。由以上分析可知，为使系统满足一定的稳态和动态要求，对开环对数幅频特性的形状有如下要求：低频段要有一定的高度和斜率；中频段的斜率最好为-20，且具有足够的宽度， c 应尽量大；高频段采用迅速衰减的特性，以抑制不必要的高频干扰。
Lg 20 lg A( g ) 20 lg 10
g 1 g
2
25 g
2
9.54
dB
当K=100时
Lg 20 lg A( g ) 20 lg 100
g 1 g
2
25 g
2
10.5
dB
幅频特性及相频特性实例
幅频特性及相频特性实例
幅频特性及相频特性实例
幅频特性及相频特性实例
本章小结
（1）频率特性是线性定常系统在正弦函数作用下，稳态输出与输入之比和频率之间的函数关系。频率特性是系统的一种数学模型，它既反映出系统的静态性能，又反映出系统的动态性能。（2）频率特性是传递函数的一种特殊形式。将系统传递函数中的复数 s换成纯虚数 j ，即可得出系统的频率特性。（3）频率特性法是一种图解分析法，用频率法研究和分析控制系统时，可免去许多复杂而困难的数学运算。对于难以用解析方法求得频率特性的曲线的系统，可以改用试验方法测得其频率特性，这是频率法的突出优点之一。（4）频率特性图因其采用的坐标系不同而分为极坐标图、波特图、尼科尔斯图等几种形式。各种形式之间是相互联系的，而每种形式却有其特定的适用场合。

滤波器的幅频特性与相频特性的关系分析

滤波器的幅频特性与相频特性的关系分析滤波器是一种常用的电子设备，用于将输入信号中的特定频率成分进行选择性的放大或抑制。

在滤波器的设计和应用过程中，幅频特性和相频特性是两个重要的指标。

本文将探讨滤波器的幅频特性与相频特性之间的关系，并分析它们在滤波器设计中的应用。

一、幅频特性幅频特性是指滤波器在不同频率下的传递函数的模的变化。

在滤波器的幅频特性曲线中，横轴代表输入信号的频率，纵轴代表输出信号的幅值。

根据幅频特性曲线，可以判断滤波器在不同频段的放大或衰减程度。

幅频特性通常由滤波器的增益-频率特性曲线表示。

滤波器的幅频特性可以分为低通、高通、带通和带阻四种类型。

低通滤波器允许低频分量通过，并衰减高频分量；高通滤波器则允许高频分量通过，并衰减低频分量；带通滤波器则将某一频率范围内的信号放大，其他频率信号衰减；带阻滤波器则将某一频率范围内的信号衰减，其他频率信号放大。

二、相频特性相频特性是指滤波器在不同频率下的传递函数的相位的变化。

相频特性曲线描述了输入信号和输出信号之间的相对时间延迟。

相频特性可以直观地反映滤波器对不同频率信号的相位响应。

滤波器的相频特性对于某些应用非常重要。

例如，在音频处理中，相频特性的失真可能导致声音的混叠和不自然的声音效果。

因此，在设计音频滤波器时，需要特别关注相频特性，以确保信号的相位保持一致。

三、幅频特性与相频特性的关系滤波器的幅频特性和相频特性之间存在密切的关系。

一些滤波器设计方法，如巴特沃斯滤波器设计，可以同时优化幅频特性和相频特性。

在某些情况下，滤波器的幅频特性和相频特性可能相互牵制。

例如，当滤波器的幅频特性要求具有非常陡峭的衰减特性时，可能会导致相频特性的失真。

因此，在实际滤波器设计中，需要在幅频特性和相频特性之间进行权衡，并选择最合适的设计方法。

四、幅频特性与相频特性的应用滤波器的幅频特性和相频特性在信号处理和通信系统中有着广泛的应用。

以下是一些常见的应用场景：1. 音频处理：在音频系统中，滤波器常用于去除噪声、修饰音频信号等。

幅频特性及相频特性实例

高频段
高频段指开环对数幅频特性在中频段后的频段。由于这部分特性是由系统中一些时间常数很小的环节决定的，因此高频段的形状主要影响时域响应的起始段。因为高频段远离截止频率 c ，所以对系统的动态特性影响不大。
幅频特性及相频特性实例
从系统抗干扰能力来看，高频段开环幅值一般较低，即 L( ) 20 lg GK ( j ) 0，则 GK ( j ) 1 。故对单位反馈系统有
% 0.16 0.4( M r 1) 100%
高阶系统的 % 随着 M r 的增大而增大。
(1 M r 1.8)
ts
式中
k
c
(1 M r 1.8)
k 2 1.5( M r 1) 2.5( M r 1) 2
调节时间 ts 随着 M r 增大而增大，且随 c 增大而减小。
Lg 20 lg A( g ) 20 lg 10
g 1 g
2
25 g
2
9.54
dB
当K=100时
Lg 20 lg A( g ) 20 lg 100
g 1 g
2
25 g
2
10.5
dB
幅频特性及相频特性实例
幅频特性及相频特性实例
幅频特性及相频特性实例
幅频特性及相频特性实例
（2）中频段斜率为-40，且占据的频率区域较宽
则系统的相频特性为 ( ) 90 arctan arctan 1 2 相角裕度为 180 (c ) 90 arctan c arctan c 1 2
可见，中频段越宽，即 2 比 1 大的越多，则系统的相角裕度越接近于0°，系统将处于临界稳定状态，动态响应持续振荡。

实信号的幅频特性为什么是偶对称？相频特性为什么是奇对称？

讨论实序列的幅频特性为什么是偶对称的？相频特性为什么是奇对称的？一、基本性质序列[]x n 的DTFT ()jwX e 定义如下：[]()jwjwnn X e x n e∞-=-∞=∑ (1-1)一般情况下，()jwX e 都是实变量w 的复函数，写成直角坐标的形式为：()()()jw jw jw re im X e X e jX e =+(1-2)式中，()jw re X e 和()jw im X e 分别是()jw X e 的实部和虚部，由式(1-2)可得:()()(){}12jw jw jw re X e X e X e *=+ (1-3)()()(){}12jw jw jw im X e X e X e j*=- (1-4)其中，()jw X e *为()jw X e 的复共轭。

()jw X e 也可用极坐标表示为：()()()w j jw jw X e X e eθ= (1-5)其中，(){}arg ()jw w X e θ=(1-6)量()jw X e 称为幅度函数，()w θ称为相位函数，这两个函数都是自变量为w 的实函数。

由式(1-2)和式(1-5)，可以得到()jw X e 的直角坐标和极坐标形式之间的关系如下：()()()cos jw jw re w X e X e θ=(1-7)()()()sin jw jw im w X e X e θ=(1-8) ()()()()()222jwjw jw jw jw re im X eX e X e X e X e *==+(1-9)()()()tan jw im w jwre X e X eθ=(1-10)二、对称关系对于一个给定的序列[]x n ，其FT 为()jwX e，由式(1-1)可知:[]{}[][]()jwnjwm jw n m F x n x n ex m e X e ∞-∞--=-∞=∞-=-==∑∑即[]()Fjw x n X e --−−→(2-1)同理，由式(1-1)有[]{}[][]()jwnjwn jw n n F x n x n ex n e X e *∞∞**-*-=-∞=-∞⎛⎫=== ⎪⎝⎭∑∑ 即[]()Fjw x n X e **-−−→(2-2)结合式(2-1)和式(2-2)，可得[]()F jw x n X e **-−−→(2-3)类似()jwX e 的直角坐标系表示，[]x n 可写成[][][]re im x n x n jx n =+(2-4)代入式(1-1)有[][]()()[][]()[][]()()cos sin cos sin cos sin jwreim n reimn im re n X e x n jx n wn j wn x n wn x n wn j x n wn x n wn ∞=-∞∞=-∞∞=-∞=+-=++-∑∑∑ (2-5)根据上式有()[][]()cos sin jwre reimn X e x n wn x n wn ∞=-∞=+∑(2-6)()[][]()cos sin jwim imren X ex n wn x n wn ∞=-∞=-∑(2-7)()jw X e 在如下情况下被定义为w 的共轭对称函数：()()jw jw X e X e *-=即()()jw jw re re X e X e -=，()()jw jw im im X e X e -=-。

幅频特性和相频特性

HUNAN UNIVERSITY电路实验综合训练报告学生姓名蔡德宏学生学号201408010128专业班级计科1401班指导老师汪原起止时间2015年12月16日——2015年12月19日一、实验题目实验十二幅频特性和相频特性二、实验摘要（关键信息）实验十二1、测量RC 串联电路组成低通滤波器的幅频特性和相频特性（元件参数：R=1K Ω，C=0.1uF ，输入信号：Vpp=3V 、f=100Hz~15KHz 正弦波。

测量10组不同频率下的Vpp ，作幅频特性曲线和相频特性曲线）。

2、测量RC 串联电路组成高通滤波器的幅频特性和相频特性（电路参数和要求同上）。

3、测量RC 串并联（文氏电桥）电路频率特性曲线和相频特性曲线。

实验十三1、测量R 、C 、L 阻抗频率特性（电路中用100Ω作保护电阻，分别测量R 、C 、L 在不同频率下的Vpp ，输入信号Vpp=3V 、f=100Hz~100KHz 的正弦波，元件参数：R=1K 、C=0.1uF 、L=20mH ），取10组数据，作幅频特性曲线。

2、搭接R 、L 、C 串联电路，通过观测Ui （t ）和UR(t)波形，找出谐振频率。

将电阻换成电位器，测量不同Q 值的谐振频率。

三、实验环境（仪器用品）函数信号发生器（DG1022U ），示波器(DSO-X 2012A),电位器（BOHENG3296-w104），3只电阻（保护100Ω，实验1K Ω），电容器(0.1µF)，电感（20mH ），面包板，Multisim 10.0（画电路图），导线若干。

四、实验原理和电路1、当在RC 和RL 及RLC 串联电路中加上交变电源，并不断改变电源频率时，电路的端口电压U 和电阻U 两端电压也随之发生规律性改变。

1）RC 串联电路的稳态特性有以上公式可知，随频率的增加，I,增加，减小。

当ω很小时2πψ→，电源电压主要降落在电容上，此时电容作为响应为低通滤波器；反之，0→ψ，电压主要将在电阻上，电阻作为响应称为高通滤波器。

实验十二 幅频特性和相频特性

实验十二--幅频特性和相频特性

RL电路的幅频特性和相频特性的研究

实验12斜率鉴频与相位鉴频器

幅频特性和相频特性

电路基础原理解惑电路的幅频特性和相频特性

实验十二--幅频特性和相频特性

幅频特性和相频特性

利用波尔共振仪研究受迫振动实验报告

幅频特性和相频特性

连续弹性体悬臂梁各阶固有频率及主振型测定(最全)word资料

RC、RL与RLC串联电路幅频和相频特性的研究

传输网络的幅频和相频特性(lu)

幅频特性及相频特性实例

滤波器的幅频特性与相频特性的关系分析

幅频特性及相频特性实例

实信号的幅频特性为什么是偶对称？相频特性为什么是奇对称？

幅频特性和相频特性

实验十二幅频特性和相频特性