深圳大学模式识别作业

合集下载

模式识别大作业

Iris 数据聚类分析-----c 均值和模糊c 均值一．问题描述Iris 数据集包含150个数据，共有3类，每一类有50个数据，其每个数据有四个维度，每个维度代表鸢尾花特征（萼片，花瓣的长度）中的一个，其三类数据名称分别setosa,versicolor,virginica ，这些就是 Iris 数据集的基本特征。

现在使用c 均值和模糊c 均值的方法解决其聚类分析，并且计算比较两种方法得到的分类结果的正确率。

二．算法介绍1.c-均值算法C 均值算法属于聚类技术中一种基本的划分方法,具有简单、快速的优点。

其基本思想是选取c 个数据对象作为初始聚类中心,通过迭代把数据对象划分到不同的簇中,使簇内部对象之间的相似度很大,而簇之间对象的相似度很小。

其主要思想：(1) 计算数据对象两两之间的距离;(2) 找出距离最近的两个数据对象,形成一个数据对象集合A1 ,并将它们从总的数据集合U 中删除;(3) 计算A1 中每一个数据对象与数据对象集合U 中每一个样本的距离,找出在U 中与A1 中最近的数据对象,将它并入集合A1 并从U 中删除, 直到A1 中的数据对象个数到达一定阈值;(4) 再从U 中找到样本两两间距离最近的两个数据对象构成A2 ,重复上面的过程,直到形成k 个对象集合;(5) 最后对k 个对象集合分别进行算术平均,形成k 个初始聚类中心。

算法步骤：1.初始化：随机选择k 个样本点，并将其视为各聚类的初始中心12,,,k m m m ；2.按照最小距离法则逐个将样本x 划分到以聚类中心12,,,k m m m 为代表的k 个类1,k C C 中；3.计算聚类准则函数J,重新计算k 个类的聚类中心12,,,k m m m ； 4.重复step2和3知道聚类中心12,,,k m m m 无改变或目标函数J 不减小。

2.模糊c-均值模糊C 均值算法就是，在C 均值算法中，把硬分类变为模糊分类。

设()j i μx 是第i 个样本i x 属于第j 类j G 的隶属度，利用隶属度定义的准则函数为211[()]C N b f j i i jj i J μ===-∑∑x x m其中，b>1是一个可以控制聚类结果的模糊程度的常数。

模式识别作业答案

第二章 2.1：最小错误率决策准则为： ()12112221121221112212()() ()() ()()()()()()()()()()1()()1()()()j j j j j j P P P P p P P p P p P p P p p p p P P ωωωωωωωωωωωωωωωωωωωωωωω=⎧>∈⎪⎨<∈⎪⎩=>∈∈==>∑若则若则由贝叶斯公式可知：将其带入最小错误率决策公式中得到：若则，否则若，则即如果，则x x x x x x x x x x x x x x x x x ()121212122()()()()P P p p ωωωωωωωω∈∈=>∈∈，否则若，则有：如果，则，否则x x x x x x2.2：()()1211111222211222121122212111122x ()()()1()()()()() x 12()() x 2()()()()(R P P R P P R R R R R R P αααλωλωαλωλωααααααααλλωλ⎧=+⎪⎨=+⎪⎩⎧<⎪⎨>⎪⎩-=-+-给定，做出决策和决策的风险分别为：最小风险的贝叶斯决策为：若则做决策，即将判为第类若则做决策，即将判为第类则有x x x x x x x x x x x x x 122211111222221111122221122221221111112222221111)()()()()() x 1 ()()()() x 2()()()()()()()()() ()()()P P P P P p P x w p P p P x p P λωλλωλλωλλωλλωωλλωωλλωωλλωωλλω⎧->-⎪⇒⎨-<-⎪⎩->∈-⇒-<∈-若则将判为第类若则将判为第类若则若则x x x x x x x x x 2w⎧⎪⎪⎨⎪⎪⎩2.3：1111122211112111112222()()()()()()()0.9950.990.99970.9950.990.0050.05()1()0.0003()()()()()P p P P p P p P P P R P P R ωωωωωωωωωωωαααλωλωαλ=+⨯==⨯+⨯=-=<=+=阴阴阴阴阴阴阴按照最小错误率贝叶斯决策规则，结果为类，即正常人但若按最小风险决策规则，做出决策和决策的风险分别为：阴阴阴阴112221*********211112222111122221111222()()()0.99970.0003()0.99970.00030.9997()0.0003() 1 0.9997()0.0003() 2()0.000()P P R R ωλωαλλαλλλλλλλλλλλλλλ⎧⎪⎨+⎪⎩⎧=+⎪⇒⎨=+⎪⎩->-⎧⇒⎨-<-⎩>-⇒<-阴阴阴阴若则将王某判为第类若则将王某判为第类若3则将王某判为正常人则将王某判为癌症患者3.1()()()()()()()()12121212111,2222121,2,22,12121TTx g x x x x g x x x x x x x x ⎡⎤⎡⎤=-=-⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥=-=⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎡⎤⎢⎥⎣⎦⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦：：为增广特征向量的特征空间为，是二维平面的特征空间为，是三维空间中一个平面3.2将样本全部化为规范化增广样本向量：()()()()()()()1234567811223(0,0,0,1),(1,0,0,1),(1,0,1,1),(1,1,0,1)(0,0,1,1),(0,1,1,1),(0,1,0,1),(1,1,1,1)00,10(1,2,2,1)1110,21(0,2,2,2)2220,T T T TT T T T T TT T T y y y y y y y y w y w w y w y w w y w y =====--=---=--=----=∴=+=---=-+=∴=+=--=-+=()()()()()()()()345532(1,2,1,3)312320,43(1,2,1,3)41320,54(1,2,2,2)TT T T Tw w y w y w w w y w w y ∴=+=--=-+=>∴==--=-=-<∴=+=--()()()()()()()()()()()()()()()()()()()()()()6778123345522220,65(1,2,2,2)6220,76(1,3,2,1)7132130,87(1,3,2,1)810,98920,109100,1110(2,3,1,2)1110,121112T TT TT TT T T TT T w y w w w y w w y w y w w w y w w w y w w w y w w y w y w w w y =+-=>∴==--=-=∴=+=--=-++-=>∴==--=>∴==>∴==∴=+=--=>∴==-()()()()()()()()()()()()()()()()()()()()5673445510,1312(2,3,2,1)1340,14131420,15141810,1918(2,3,2,1)190,2019(3,2,2,2)200,2120(3,2,3,1)21210,1,2,,8T T T T T T T T TT i w w y w y w w w y w w w y w w w y w w y w y w w y w w y i g x <∴=+=--=>∴==>∴==>∴==--=∴=+=--=∴=+=-->==满足：故此时算法收敛,12332310T w x x x x =--+=为决策面方程分界面示意图如下：3.3()()()1##0001100110111101001101110101111111111111111111111111111114210010111,1,1,1,1,1,1,1,1,1,1,0.5T TTTX X X X X X b w X b -⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥--⎢⎥---⎢⎥⎢⎥--⎢⎥----⎢⎥⎣⎦--⎡⎤⎢⎥------⎢⎥==⎢⎥------⎢⎥--⎣⎦===--增广样本矩阵为：的伪逆矩阵为：令则 3.6()12*112**11221201*02*022200210002121020,212110w w T T T T S S S w S m m m w m mw m mm y x w y w x y x w w x y x x -⎡⎤=+=⎢⎥⎣⎦⎡⎤⎢⎥⎡⎤⎡⎤=-==⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦====-+∴==->∈=<∈=⇒-=-⇒+= 投影向量为：则所以若则决策面方程为：4.2最近邻法与k 近邻法都是近邻分类的方法，都属于有监督的模式识别非参数方法。

模式识别作业Homework#2

Homework #2Note:In some problem (this is true for the entire quarter) you will need to make some assumptions since the problem statement may not fully specify the problem space. Make sure that you make reasonable assumptions and clearly state them.Work alone: You are expected to do your own work on all assignments; there are no group assignments in this course. You may (and are encouraged to) engage in general discussions with your classmates regarding the assignments, but specific details of a solution, including the solution itself, must always be your own work.Problem:In this problem we will investigate the importance of having the correct model for classification. Load file hw2.mat and open it in Matlab using command load hw2. Using command whos, you should see six array c1, c2, c3 and t1, t2, t3, each has size 500 by 2. Arrays c1, c2, c3 hold the training data, and arrays t1, t2, t3 hold the testing data. That is arrays c1, c2, c3 should be used to train your classifier, and arrays t1, t2, t3 should be used to test how the classifier performs on the data it hasn’t seen. Arrays c1 holds training data for the first class, c2 for the second class, c3 for the third class. Arrays t1, t2, t3 hold the test data, where the true class of data in t1, t2, t3 comes from the first, second, third classed respectively. Of course, array ci and ti were drawn from the same distribution for each i. Each training and testing example has 2 features. Thus all arrays are two dimensional, the number of rows is equal to the number of examples, and there are 2 columns, column 1 has the first feature, column 2 has the second feature.(a)Visualize the examples by using Matlab scatter command a plotting each class indifferent color. For example, for class 1 use scatter(c1(:,1),c1(:,2),’r’);. Other possible colors can be found by typing help plot.(b)From the scatter plot in (a), for which classes the multivariate normal distribution lookslike a possible model, and for which classes it is grossly wrong? If you are not sure how to answer this part, do parts (c-d) first.(c)Suppose we make an erroneous assumption that all classed have multivariate normalNμ. Compute the Maximum Likelihood estimates for the means and distributions()∑,covariance matrices (remember you have to do it separately for each class). Make sure you use only the training data; this is the data in arrays c1, c2, and c3.(d)You can visualize what the estimated distributions look like using Matlab contour().Recall that the data should be denser along the smaller ellipse, because these are closer to the estimated mean.(e)Use the ML estimates from the step (c) to design the ML classifier (this is the Bayesclassifier under zero-one loss function with equal priors). Thus we are assuming that priors are the same for each class. Now classify the test example (that is only thoseexamples which are in arrays t1, t2, t3). Compute confusion array which has size 3 by 3, and in ith row and jth column contains the number of examples fro which the true class isi while the class your classifier gives is j. Note that all the off-diagonal elements in theconfusion array are errors. Compute the total classification error, easiest way to do it is to use Matlab function sum() and trace().(f)Inspect the off diagonal elements to see if which types of error are more common thanothers. That should give you an idea of where the decision boundaries lie. Now plot the decision regions experimentally (select a fine 2D grid, classify each point on this grid, and plot the class with distinct color). If you love solving quadratic systems of equations, you can find the decision boundaries analytically. Using your decision boundaries, explain why some errors are more common than others.(g)If the model assumed for the data is wrong, than the ML estimate of the parameters arenot even the best parameters to use for classification with that wrong model. That is because the multivariate normal is the wrong distribution to use with out data, the MLE parameters we computed in part (c) are not the ones which will give us the best classification with our wrong model. To confirm this, find parameters for the means and variances (you can change as many as you like, from one to all) which will give better classification rate than the one you have gotten in part (e). Hint: it pays to try to change covariance matrices, rather than the means.(h)Now let’s try to find a better model for our data. Notice that to determine the class of apoint; it is sufficient to consider the distance of that point from the origin. The distance from the origin is very important for classifying our data, while the direction is totally irrelevant. Convert all the training and testing arrays to polar coordinates using Matlib function cart2pol(). Ignore the first coordinate, which is the angle, and only use the second coordinate, which is the radius (or distance from the origin). Assume now that all classes come from normal distribution with unknown mean and variance. Estimate these unknown parameters using ML estimation again using only the training data (the arrays ci’s). Test how this new classifier works using the testing data (the arrays ti’s) by computing the confusion matrix and the total classification error. How does this classifier compare with the one using the multivariate normal assumption and why is there a difference?(i)Experimentally try to find better parameters than those found by ML method for classifierin (h). If you do find better parameters, do they lead to a significantly better classification error? How does it compare to part (g)? Why can’t you find significantly better parameters than MLE for the classifier in (h)?。

模式识别作业

（1）先用C-均值聚类算法程序，并用下列数据进行聚类分析。

在确认编程正确后，采用蔡云龙书的附录B中表1的Iris数据进行聚类。

然后使用近邻法的快速算法找出待分样本X （设X样本的4个分量x1=x2=x3=x4=6；子集数l=3）的最近邻节点和3-近邻节点及X与它们之间的距离。

并建议适当对书中所述算法进行改进。

并分别画出流程图、写出算法及程序。

x1=(0,0) x2=(1,0) x3=(0,1) x4=(1,1) x5=(2,1) x6=(1,2) x7=(2,2) x8=(3,2) x9=(6,6) x10=(7,6) x11=(8,6) x12=(6,7) x13=(7,7) x14=(8,7) x15=(9,7) x16=(7,8) x17=(8,8) x18=(9,8) x19=(8,9) x20=(9,9)
（2）写一篇论文。

内容可以包含下面四个方面中的一个：
①新技术（如数据挖掘等）在模式识别中的应用；
②模式识别最新的研究方向；
③一个相关系统的分析；
④一个算法的优化；
（3）书142页，描述近邻法的快速算法，写个报告。

《模式识别》课程2019年度大作业

《模式识别》课程2019年度大作业注意事项：（请务必详细阅读所有注意事项）1.本作业发布时间2019.5.5，交作业时间：2018.5.30日第一节课下课后，第二节课上课前（即上午9点整）。

与平时作业不同，不允许迟交，迟交则成绩以0分计。

2.与平时作业不同，大作业只有研究生同学完成，保送本系的本科同学也需要完成，但其他本科生无需完成。

请在作业的开始部分写上姓名、学号，缺少该信息的，本次作业总分扣除10分。

如果是已经完成保送手续，先修研究生课程的本校本科生，请一定每次作业在姓名后加注“（本科保送）”，否则无法拿到学分。

3.与平时作业不同，作业评分以电子版为准。

需要提交代码，具体的提交要求请仔细阅读作业说明。

总体文件大小不超过5MB（可以提交压缩文件）。

上传地址为/。

初始用户名和密码为学号。

研究生学号以MP18开头的暂时无法登陆，可将电子版email给助教（wangguohua@, yik@），其余同学务必使用网站系统上传。

是否迟交以cslabcms系统的时间戳或电子邮件的时间戳为准。

大作业：1.仔细阅读以下网页的内容（/weixs/project/DDT/DDT.html），包括其中提供链接的英文论文，理解DDT方法的运行步骤。

2.自行实现DDT算法。

实现时可以参考上述网页提供的Matlab代码以加深对DDT方法的理解，但是不可以使用MatConvNet这一深度学习框架，除此以外的其余任意深度学习软件框架都可以使用。

3.如尚未有深度学习、CNN的编程经验，请搜索网络资源完成自学。

4.如有可供使用的GPU加速卡资源，可以自由使用。

如无这种资源，可在编程中指定使用CPU（即，不使用GPU）来完成计算。

DDT方法的计算量很小，使用CPU也可完成计算。

5.在上述网页提供下载的代码链接里有少量图片可供使用，利用这些图片完成DDT方法的学习，利用可视化技术（参考论文和代码）直观考察DDT方法的效果。

6.请提交完成上述任务的文档和代码，需提交的内容如下：a.说明文档：自行组织文档的格式，保证文档的内容能让助教清晰地理解你的代码运行环境、实现的主要思路、你通过实现并运行代码后对DDT方法的理解等。

模式识别大作业1

模式识别大作业--fisher线性判别和近邻法学号：021151**姓名：**任课教师:张**I. Fisher线性判别A. fisher线性判别简述在应用统计方法解决模式识别的问题时，一再碰到的问题之一是维数问题．在低维空间里解析上或计算上行得通的方法，在高维里往往行不通．因此，降低维数就成为处理实际问题的关键．我们考虑把维空间的样本投影到一条直线上，形成一维空间，即把维数压缩到一维．这样，必须找一个最好的，易于区分的投影线．这个投影变换就是我们求解的解向量．B.fisher线性判别的降维和判别1．线性投影与Fisher准则函数各类在维特征空间里的样本均值向量：，(1)通过变换映射到一维特征空间后，各类的平均值为：，(2)映射后，各类样本“类内离散度”定义为：，(3)显然，我们希望在映射之后，两类的平均值之间的距离越大越好，而各类的样本类内离散度越小越好。

因此，定义Fisher准则函数：(4)使最大的解就是最佳解向量，也就是Fisher的线性判别式。

2．求解从的表达式可知，它并非的显函数，必须进一步变换。

已知：，, 依次代入上两式，有：，(5)所以：(6)其中：(7)是原维特征空间里的样本类内离散度矩阵，表示两类均值向量之间的离散度大小，因此，越大越容易区分。

将(4.5-6)和(4.5-2)代入(4.5-4)式中：(8)其中：，(9)因此：(10)显然：(11)称为原维特征空间里，样本“类内离散度”矩阵。

是样本“类内总离散度”矩阵。

为了便于分类，显然越小越好，也就是越小越好。

将上述的所有推导结果代入表达式：可以得到：其中，是一个比例因子，不影响的方向，可以删除，从而得到最后解：(12)就使取得最大值，可使样本由维空间向一维空间映射，其投影方向最好。

是一个Fisher线性判断式.这个向量指出了相对于Fisher准则函数最好的投影线方向。

C.算法流程图左图为算法的流程设计图。

II.近邻法A. 近邻法线简述K最近邻(k-Nearest Neighbor，KNN)分类算法，是一个理论上比较成熟的方法，也是最简单的机器学习算法之一。

模式识别作业1230

作业一1.试举一生活中能够用运算机实现模式识别的实例，并说明在这一问题中，模式识别系统各组成部份别离可能对应什么内容批改记录：1.11测31，应收43，实收39，4人须补作业；12测11，应收66，实收64，2人须补作业，5人考虑重做；12测31，应收31，实收31，1人考虑重做；缘故：没有回答下列问题（只列了理论框图）或选题不太适当，没有给成绩，需订正2.部份同窗态度不够认真；3.分数问题；4.英文简写及具体步骤描述不够5.书写层次性问题6.表述准确性：如遥感影像、航摄像片，非“照片”7.选题：（1）车牌识别，声音（语音、演唱曲目）识别，指纹识别（包括指纹解锁），人脸识别（照相、考勤、解锁），海鱼，文字识别，手写体字符识别（签名），电话触摸操作，虹膜识别，颜料表面改性，遥感影像分类，药材识别，蔬菜病害，血液检测，心电图（2）讨论：电脑录制一首歌曲自动感应门声控灯 ATM 机取钱自动销售机作业二1. 设有10个二维模式样本，如图所示。

假设21=θ，试用最大最小距离算法对他们进行聚类分析。

解：① 取T 11]0,0[==X Z 。

② 选离1Z 最远的样本作为第二聚类中心2Z 。

()()201012221=-+-=D ，831=D ，5841=D ，4551=D5261=D ，7471=D ，4581=D ，5891=D ，651,10=D ∵ 最大者为D 71，∴T 72]7,5[==X Z742121=-=Z Z θT ③ 计算各样本与{}21,Z Z 间距离，选出其中的最小距离。

7412=D ，5222=D ，3432=D ，…，132,10=D }13,20,17,0,2,5,4,8,2,0{),min(21=i i D D ④ ∵742120)},max{min(9221=>==T D D D i i ,T 93]3,7[==∴X Z ⑤ 继续判定是不是有新的聚类中心显现：⎪⎩⎪⎨⎧===58740131211D D D ，⎪⎪⎩⎪⎪⎨⎧===40522232221D D D ，…⎪⎪⎩⎪⎪⎨⎧===113653,102,101,10D D D}1,0,1,0,2,5,4,8,2,0{),,min(321=i i i D D D 74218)},,max{min(31321=<==T D D D D i i i 寻觅聚类中心的步骤终止。

模式识别作业2

模式识别作业2模式识别作业⼆硕⾃171班杨晓丹21722160251题⽬数据：1）四个数据第⼀类：（0,0）（0,1）第⼆类：（1,0）（1,1）2）⼋个数据⽔果类：第⼀类：（90,150）（90,160）（80,150）（60,140）第⼆类：（60,105）（50,80）（50,90）（80,125）针对两种数据进⾏梯度下降法编程测试。

3）四个数据第⼀类：（0,0）（1,1）第⼆类：（1,0）（0,1）2、不同情况下的结果测试：1）初始权值取3种不同的值2）步长取不同的值，可以尝试变步长⽅法3）采⽤单样本修正法和全样本修正法两种⽅式4）单样本情况下不同的样本迭代次序，从1到n，和，从n到13、第2组数据可以画画每次迭代后的分类线试试2实验原理与⽅案2.1算法原理本次实验采⽤感知器模型对样本进⾏分类，将两组样本标准化为增⼴矩阵y，并寻找出ay>0的权向量a。

定义感知函数如下:∑J P(a)=(?a T y)(1)y?y h式中y h是被权向量a错误分类的样本。

存在错误的样本数是，感知函数的值⼤于0，当样本全部被正确分类时，感知函数的值为0。

所以⽬标是通过改变权向量使感知函数的值为0。

对感知函数求导得：ay ?a =∑y?y hy(2)则可得到梯度下降法的迭代公式:a(k+1)=a(k)+ρk∑y?y hy(3)经过多次迭代后，若所有样本满⾜ay>0，则得到⼀个线性分类器。

若样本为⼆维，可将权向量视为三维空间中的向量，将y k视为超平⾯的法向量，则式ay>0表明在超平⾯法向量⽅向⼀侧的权向量满⾜解向量的要求，所有超平⾯法向量⽅向围成的空间就是解向量的解空间。

迭代的过程就是权向量加上法向量，使权向量向解区移动的过程。

2.2单步长梯度下降法计算流程1.将样本标准化为增⼴矩阵Y2.将增⼴矩阵中的列向量y k依次与权向量相乘，若Ay k不⼤于0，则迭代权向量A(k+1)=A(k)+ρy k，若Ay k为正，则继续计算下⼀个向量，直⾄完成⼀轮相乘。

模式识别大作业-许萌-1306020

第一题对数据进行聚类分析1.题目要求用FAMALE.TXT、MALE.TXT和/或test2.txt的数据作为本次实验使用的样本集，利用C 均值聚类法和层次聚类法对样本集进行聚类分析，对结果进行分析，从而加深对所学内容的理解和感性认识。

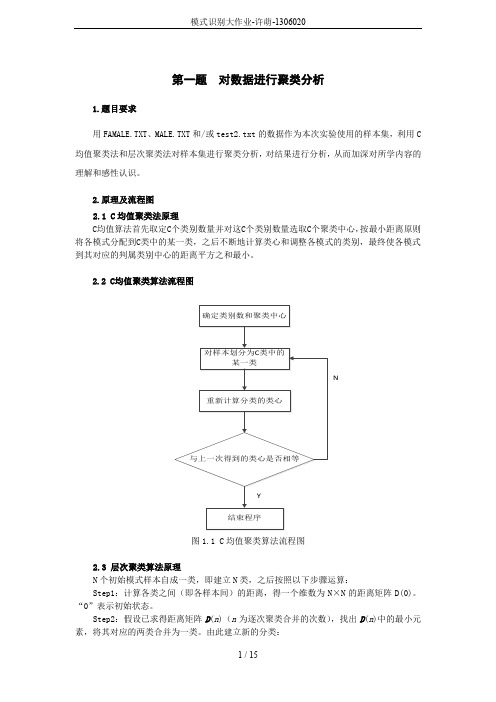
2.原理及流程图2.1 C均值聚类法原理C均值算法首先取定C个类别数量并对这C个类别数量选取C个聚类中心，按最小距离原则将各模式分配到C类中的某一类，之后不断地计算类心和调整各模式的类别，最终使各模式到其对应的判属类别中心的距离平方之和最小。

2.2 C均值聚类算法流程图N图1.1 C均值聚类算法流程图2.3 层次聚类算法原理N个初始模式样本自成一类，即建立N类，之后按照以下步骤运算：Step1：计算各类之间（即各样本间）的距离，得一个维数为N×N的距离矩阵D(0)。

“0”表示初始状态。

Step2：假设已求得距离矩阵D(n)（n为逐次聚类合并的次数），找出D(n)中的最小元素，将其对应的两类合并为一类。

由此建立新的分类：Step3：计算合并后所得到的新类别之间的距离，得D (n +1)。

Step4：跳至第2步，重复计算及合并。

直到满足下列条件时即可停止计算：①取距离阈值T ，当D (n )的最小分量超过给定值 T 时，算法停止。

所得即为聚类结果。

②或不设阈值T ，一直到将全部样本聚成一类为止，输出聚类的分级树。

2.4层次聚类算法流程图N图1.2层次聚类算法流程图3 验结果分析对数据文件FAMALE.TXT 、MALE.TXT 进行C 均值聚类的聚类结果如下图所示：图1.3 C 均值聚类结果的二维平面显示将两种样本即进行聚类后的样本中心进行比较，如下表：从下表可以纵向比较可以看出，C 越大，即聚类数目越多，聚类之间差别越小，他们的聚类中心也越接近。

横向比较用FEMALE,MALE 中数据作为样本和用FEMALE,MALE ，test2中),1(),1(21++n G n G数据作为样本时，由于引入了新的样本，可以发现后者的聚类中心比前者都稍大。

模式识别实验指导书2015

6
深圳大学研究生课程“模式识别理论与方法”实验指导书(4th Edition 裴继红编)
(c) 用（b）中设计的分类器对测试点进行分类： (1, 2,1) ， (5,3, 2) ， (0, 0, 0) ， (1, 0, 0) ，并且利用式（45）求出各个测试点与各个类别均值之间的 Mahalanobis 距离。 (d) 如果 P ( w1 ) 0.8, P ( w2 ) P ( w3 ) 0.1 ，再进行（b）和（c）实验。 (e) 分析实验结果。表格 1
深圳大学研究生课程：模式识别理论与方法
课程作业实验指导
（4th Edition）（分数：5％10＝50％）（共 10 题）
实验参考教材：
a) 《Pattern Classification》by Richard O.Duda, Peter E.Hart, David G.Stork, 2nd Edition Wiley-Interscience, 2000. (机械工业出版社，2004 年, 影印版)。 b) 《模式分类》Richard O.Duda, Peter E.Hart, David G.Stork 著；李宏东，姚天翔等译；机械工业出版社和中信出版社出版，2003 年。（上面 a 的中文翻译版） c) 《模式识别（英文第四版）》Sergios Theodoridis, Konstantinos Koutroumbas 著；机械工业出版社，2009 年，影印版。 d) 《神经网络与机器学习（原书第三版）》Simon Haykin 著；申富饶等译，机械工业出版社，2013 年。
裴继红编
2015 年 2 月深圳大学信息工程学院
深圳大学研究生课程“模式识别理论与方法”实验指导书(4th Edition 裴继红编)

模式识别大作业

模式识别大作业共同空间模式及其几种改进方法的研究1 综述脑-机接口（brain -computer interface，BCI）系统通过记录大脑活动提供一种不依赖肌肉的大脑直接控制外部设备的方法，这为那些具有严重神经肌肉损伤（如肌肉萎缩性侧索硬化、脑瘫、脑干中风等）患者提供了与外界交流、控制外界设备的新方式。

在各种监控大脑活动的方法中，脑电图（electroencephalogram, EEG）以其较高的时间分辨率、简单的设备及信号采样要求，优于脑磁图（magnetoencephalogram, EMG）、功能核磁共振成像（ functional magnetic resonance imaging, fMRI），而作为一种理想的 BCI 控制信号被广泛研究[1]。

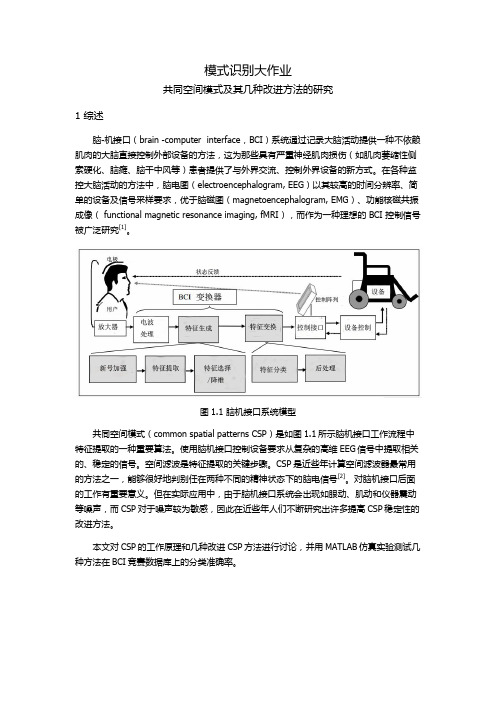
图1.1 脑机接口系统模型共同空间模式（common spatial patterns CSP）是如图1.1所示脑机接口工作流程中特征提取的一种重要算法。

使用脑机接口控制设备要求从复杂的高维EEG信号中提取相关的、稳定的信号。

空间滤波是特征提取的关键步骤。

CSP是近些年计算空间滤波器最常用的方法之一，能够很好地判别任在两种不同的精神状态下的脑电信号[2]。

对脑机接口后面的工作有重要意义。

但在实际应用中，由于脑机接口系统会出现如眼动、肌动和仪器震动等噪声，而CSP对于噪声较为敏感，因此在近些年人们不断研究出许多提高CSP稳定性的改进方法。

本文对CSP的工作原理和几种改进CSP方法进行讨论，并用MATLAB仿真实验测试几种方法在BCI竞赛数据库上的分类准确率。

2 经典共同空间模式CSP 算法的目标是创建公共空间滤波器，最大化第一类方差，最小化另一类方差，采用同时对角化两类任务协方差矩阵的方式，区别出两种任务的最大化公共空间特征[3]。

定义一个N x T的矩阵E来表示原始EEG信号数据段，其中N表示电极数目即空间导联数目，T表示每个通道的采样点数目。

模式识别大作业要求从专业杂志或国际会议上选择一篇或多篇模式

模式识别大作业要求：
从专业杂志或国际会议上选择一篇或多篇模式识别相关领域的论文进行研读，并撰写读书报告。

所选论文需满足以下要求：
1.与模式识别相关的最新研究成果。

例如：基于深度学习的人脸识别，基于模式识别
技术的股票预测，等等。

2.反映模式识别某个研究方向研究现状的综述。

例如，深度学习综述，等等。

需提交的材料：
1.论文原文的电子文档。

2.论文读书报告。

侧重于表达阅读过程中涉及的理解、分析、归纳及提炼等思维活动。

读书报告须以Word文档形式提交。

提交时间：2017年5月26日（课程考试日）之前。

需提交的电子文档：1.论文（pdf文档），2.读书报告（Word文档）。

读书报告宣讲：
1.抽签决定宣讲人选（共选6人）。

2.宣讲时间：5月19日下午15：55～18：20。

每人25分钟，课间不休息。

3.宣讲形式：以播放幻灯片的方式口头宣讲。

由抽签决定的宣讲人选如下：
BC16010025，张英迪；
SA16010030，施炀明；
SA16010039，温忻；
SA16023041，陈昱衡；
SC16009020，徐宝泉；
SC16011003，李靓。

请以上同学做好准备。

请至少提交宣讲ppt。

希望同时提交读书报告（Word文档）。

模式识别大作业

模式识别大作业1.最近邻/k近邻法一.基本概念：最近邻法：对于未知样本x，比较x与N个已知类别的样本之间的欧式距离，并决策x与距离它最近的样本同类。

K近邻法：取未知样本x的k个近邻，看这k个近邻中多数属于哪一类，就把x归为哪一类。

K取奇数，为了是避免k1=k2的情况。

二.问题分析：要判别x属于哪一类，关键要求得与x最近的k个样本（当k=1时，即是最近邻法），然后判别这k个样本的多数属于哪一类。

可采用欧式距离公式求得两个样本间的距离s=sqrt（（x1-x2）^2+(y1-y2)^2）三.算法分析：该算法中任取每类样本的一半作为训练样本，其余作为测试样本。

例如iris中取每类样本的25组作为训练样本，剩余25组作为测试样本，依次求得与一测试样本x距离最近的k 个样本，并判断k个样本多数属于哪一类，则x就属于哪类。

测试10次，取10次分类正确率的平均值来检验算法的性能。

四.MATLAB代码：最近邻算实现对Iris分类clc;totalsum=0;for ii=1:10data=load('iris.txt');data1=data(1:50,1:4);%任取Iris-setosa数据的25组rbow1=randperm(50);trainsample1=data1(rbow1(:,1:25),1:4);rbow1(:,26:50)=sort(rbow1(:,26:50));%剩余的25组按行下标大小顺序排列testsample1=data1(rbow1(:,26:50),1:4);data2=data(51:100,1:4);%任取Iris-versicolor数据的25组rbow2=randperm(50);trainsample2=data2(rbow2(:,1:25),1:4);rbow2(:,26:50)=sort(rbow2(:,26:50));testsample2=data2(rbow2(:,26:50),1:4);data3=data(101:150,1:4);%任取Iris-virginica数据的25组rbow3=randperm(50);trainsample3=data3(rbow3(:,1:25),1:4);rbow3(:,26:50)=sort(rbow3(:,26:50));testsample3=data3(rbow3(:,26:50),1:4);trainsample=cat(1,trainsample1,trainsample2,trainsample3);%包含75组数据的样本集testsample=cat(1,testsample1,testsample2,testsample3);newchar=zeros(1,75);sum=0;[i,j]=size(trainsample);%i=60,j=4[u,v]=size(testsample);%u=90,v=4for x=1:ufor y=1:iresult=sqrt((testsample(x,1)-trainsample(y,1))^2+(testsample(x,2) -trainsample(y,2))^2+(testsample(x,3)-trainsample(y,3))^2+(testsa mple(x,4)-trainsample(y,4))^2); %欧式距离newchar(1,y)=result;end;[new,Ind]=sort(newchar);class1=0;class2=0;class3=0;if Ind(1,1)<=25class1=class1+1;elseif Ind(1,1)>25&&Ind(1,1)<=50class2=class2+1;elseclass3=class3+1;endif class1>class2&&class1>class3m=1;ty='Iris-setosa';elseif class2>class1&&class2>class3m=2;ty='Iris-versicolor';elseif class3>class1&&class3>class2m=3;ty='Iris-virginica';elsem=0;ty='none';endif x<=25&&m>0disp(sprintf('第%d组数据分类后为%s类',rbow1(:,x+25),ty));elseif x<=25&&m==0disp(sprintf('第%d组数据分类后为%s类',rbow1(:,x+25),'none'));endif x>25&&x<=50&&m>0disp(sprintf('第%d组数据分类后为%s类',50+rbow2(:,x),ty));elseif x>25&&x<=50&&m==0disp(sprintf('第%d组数据分类后为%s类',50+rbow2(:,x),'none'));endif x>50&&x<=75&&m>0disp(sprintf('第%d组数据分类后为%s类',100+rbow3(:,x-25),ty));elseif x>50&&x<=75&&m==0disp(sprintf('第%d组数据分类后为%s类',100+rbow3(:,x-25),'none'));endif (x<=25&&m==1)||(x>25&&x<=50&&m==2)||(x>50&&x<=75&&m==3)sum=sum+1;endenddisp(sprintf('第%d次分类识别率为%4.2f',ii,sum/75));totalsum=totalsum+(sum/75);enddisp(sprintf('10次分类平均识别率为%4.2f',totalsum/10));测试结果：第3组数据分类后为Iris-setosa类第5组数据分类后为Iris-setosa类第6组数据分类后为Iris-setosa类第7组数据分类后为Iris-setosa类第10组数据分类后为Iris-setosa类第11组数据分类后为Iris-setosa类第12组数据分类后为Iris-setosa类第14组数据分类后为Iris-setosa类第16组数据分类后为Iris-setosa类第18组数据分类后为Iris-setosa类第19组数据分类后为Iris-setosa类第20组数据分类后为Iris-setosa类第23组数据分类后为Iris-setosa类第24组数据分类后为Iris-setosa类第26组数据分类后为Iris-setosa类第28组数据分类后为Iris-setosa类第30组数据分类后为Iris-setosa类第31组数据分类后为Iris-setosa类第34组数据分类后为Iris-setosa类第37组数据分类后为Iris-setosa类第39组数据分类后为Iris-setosa类第41组数据分类后为Iris-setosa类第44组数据分类后为Iris-setosa类第45组数据分类后为Iris-setosa类第49组数据分类后为Iris-setosa类第53组数据分类后为Iris-versicolor类第54组数据分类后为Iris-versicolor类第55组数据分类后为Iris-versicolor类第57组数据分类后为Iris-versicolor类第58组数据分类后为Iris-versicolor类第59组数据分类后为Iris-versicolor类第60组数据分类后为Iris-versicolor类第61组数据分类后为Iris-versicolor类第62组数据分类后为Iris-versicolor类第68组数据分类后为Iris-versicolor类第70组数据分类后为Iris-versicolor类第71组数据分类后为Iris-virginica类第74组数据分类后为Iris-versicolor类第75组数据分类后为Iris-versicolor类第77组数据分类后为Iris-versicolor类第79组数据分类后为Iris-versicolor类第80组数据分类后为Iris-versicolor类第84组数据分类后为Iris-virginica类第85组数据分类后为Iris-versicolor类第92组数据分类后为Iris-versicolor类第95组数据分类后为Iris-versicolor类第97组数据分类后为Iris-versicolor类第98组数据分类后为Iris-versicolor类第99组数据分类后为Iris-versicolor类第102组数据分类后为Iris-virginica类第103组数据分类后为Iris-virginica类第105组数据分类后为Iris-virginica类第106组数据分类后为Iris-virginica类第107组数据分类后为Iris-versicolor类第108组数据分类后为Iris-virginica类第114组数据分类后为Iris-virginica类第118组数据分类后为Iris-virginica类第119组数据分类后为Iris-virginica类第124组数据分类后为Iris-virginica类第125组数据分类后为Iris-virginica类第126组数据分类后为Iris-virginica类第127组数据分类后为Iris-virginica类第128组数据分类后为Iris-virginica类第129组数据分类后为Iris-virginica类第130组数据分类后为Iris-virginica类第133组数据分类后为Iris-virginica类第135组数据分类后为Iris-virginica类第137组数据分类后为Iris-virginica类第142组数据分类后为Iris-virginica类第144组数据分类后为Iris-virginica类第148组数据分类后为Iris-virginica类第149组数据分类后为Iris-virginica类第150组数据分类后为Iris-virginica类k近邻法对wine分类：clc;otalsum=0;for ii=1:10 %循环测试10次data=load('wine.txt');%导入wine数据data1=data(1:59,1:13);%任取第一类数据的30组rbow1=randperm(59);trainsample1=data1(sort(rbow1(:,1:30)),1:13);rbow1(:,31:59)=sort(rbow1(:,31:59)); %剩余的29组按行下标大小顺序排列testsample1=data1(rbow1(:,31:59),1:13);data2=data(60:130,1:13);%任取第二类数据的35组rbow2=randperm(71);trainsample2=data2(sort(rbow2(:,1:35)),1:13);rbow2(:,36:71)=sort(rbow2(:,36:71));testsample2=data2(rbow2(:,36:71),1:13);data3=data(131:178,1:13);%任取第三类数据的24组rbow3=randperm(48);trainsample3=data3(sort(rbow3(:,1:24)),1:13);rbow3(:,25:48)=sort(rbow3(:,25:48));testsample3=data3(rbow3(:,25:48),1:13);train_sample=cat(1,trainsample1,trainsample2,trainsample3);%包含89组数据的样本集test_sample=cat(1,testsample1,testsample2,testsample3);k=19;%19近邻法newchar=zeros(1,89);sum=0;[i,j]=size(train_sample);%i=89,j=13[u,v]=size(test_sample);%u=89,v=13for x=1:ufor y=1:iresult=sqrt((test_sample(x,1)-train_sample(y,1))^2+(test_sample(x ,2)-train_sample(y,2))^2+(test_sample(x,3)-train_sample(y,3))^2+( test_sample(x,4)-train_sample(y,4))^2+(test_sample(x,5)-train_sam ple(y,5))^2+(test_sample(x,6)-train_sample(y,6))^2+(test_sample(x ,7)-train_sample(y,7))^2+(test_sample(x,8)-train_sample(y,8))^2+( test_sample(x,9)-train_sample(y,9))^2+(test_sample(x,10)-train_sa mple(y,10))^2+(test_sample(x,11)-train_sample(y,11))^2+(test_samp le(x,12)-train_sample(y,12))^2+(test_sample(x,13)-train_sample(y, 13))^2); %欧式距离newchar(1,y)=result;end;[new,Ind]=sort(newchar);class1=0;class 2=0;class 3=0;for n=1:kif Ind(1,n)<=30class 1= class 1+1;elseif Ind(1,n)>30&&Ind(1,n)<=65class 2= class 2+1;elseclass 3= class3+1;endendif class 1>= class 2&& class1>= class3m=1;elseif class2>= class1&& class2>= class3m=2;elseif class3>= class1&& class3>= class2m=3;endif x<=29disp(sprintf('第%d组数据分类后为第%d类',rbow1(:,30+x),m));elseif x>29&&x<=65disp(sprintf('第%d组数据分类后为第%d类',59+rbow2(:,x+6),m));elseif x>65&&x<=89disp(sprintf('第%d组数据分类后为第%d类',130+rbow3(:,x-41),m));endif (x<=29&&m==1)||(x>29&&x<=65&&m==2)||(x>65&&x<=89&&m==3) sum=sum+1;endenddisp(sprintf('第%d次分类识别率为%4.2f',ii,sum/89));totalsum=totalsum+(sum/89);enddisp(sprintf('10次分类平均识别率为%4.2f',totalsum/10));第2组数据分类后为第1类第4组数据分类后为第1类第5组数据分类后为第3类第6组数据分类后为第1类第8组数据分类后为第1类第10组数据分类后为第1类第11组数据分类后为第1类第14组数据分类后为第1类第16组数据分类后为第1类第19组数据分类后为第1类第20组数据分类后为第3类第21组数据分类后为第3类第22组数据分类后为第3类第26组数据分类后为第3类第27组数据分类后为第1类第28组数据分类后为第1类第30组数据分类后为第1类第33组数据分类后为第1类第36组数据分类后为第1类第37组数据分类后为第1类第43组数据分类后为第1类第44组数据分类后为第3类第45组数据分类后为第1类第46组数据分类后为第1类第49组数据分类后为第1类第54组数据分类后为第1类第56组数据分类后为第1类第57组数据分类后为第1类第60组数据分类后为第2类第61组数据分类后为第3类第63组数据分类后为第3类第65组数据分类后为第2类第66组数据分类后为第3类第67组数据分类后为第2类第71组数据分类后为第1类第72组数据分类后为第2类第74组数据分类后为第1类第76组数据分类后为第2类第77组数据分类后为第2类第79组数据分类后为第3类第81组数据分类后为第2类第82组数据分类后为第3类第83组数据分类后为第3类第84组数据分类后为第2类第86组数据分类后为第2类第87组数据分类后为第2类第88组数据分类后为第2类第93组数据分类后为第2类第96组数据分类后为第1类第98组数据分类后为第2类第99组数据分类后为第3类第102组数据分类后为第2类第104组数据分类后为第2类第105组数据分类后为第3类第106组数据分类后为第2类第110组数据分类后为第3类第113组数据分类后为第3类第114组数据分类后为第2类第115组数据分类后为第2类第116组数据分类后为第2类第118组数据分类后为第2类第122组数据分类后为第2类第123组数据分类后为第2类第124组数据分类后为第2类第133组数据分类后为第3类第134组数据分类后为第3类第135组数据分类后为第2类第136组数据分类后为第3类第140组数据分类后为第3类第142组数据分类后为第3类第144组数据分类后为第2类第145组数据分类后为第1类第146组数据分类后为第3类第148组数据分类后为第3类第149组数据分类后为第2类第152组数据分类后为第2类第157组数据分类后为第2类第159组数据分类后为第3类第161组数据分类后为第2类第162组数据分类后为第3类第163组数据分类后为第3类第164组数据分类后为第3类第165组数据分类后为第3类第167组数据分类后为第3类第168组数据分类后为第3类第173组数据分类后为第3类第174组数据分类后为第3类2.Fisher线性判别法Fisher 线性判别是统计模式识别的基本方法之一。

模式识别大作业

模式识别专业：电子信息工程班级：电信****班学号：********** 姓名：艾依河里的鱼一、贝叶斯决策（一）贝叶斯决策理论 1.最小错误率贝叶斯决策器在模式识别领域，贝叶斯决策通常利用一些决策规则来判定样本的类别。

最常见的决策规则有最大后验概率决策和最小风险决策等。

设共有K 个类别，各类别用符号k c ()K k ,,2,1 =代表。

假设k c 类出现的先验概率()k P c以及类条件概率密度()|k P c x 是已知的，那么应该把x 划分到哪一类才合适呢？若采用最大后验概率决策规则，首先计算x 属于k c 类的后验概率()()()()()()()()1||||k k k k k Kk k k P c P c P c P c P c P P c P c ===∑x x x x x然后将x 判决为属于kc ~类，其中()1arg max |kk Kk P c ≤≤=x若采用最小风险决策，则首先计算将x 判决为k c 类所带来的风险(),k R c x ，再将x 判决为属于kc ~类，其中()min ,kkk R c =x可以证明在采用0-1损失函数的前提下，两种决策规则是等价的。

贝叶斯决策器在先验概率()k P c 以及类条件概率密度()|k P c x 已知的前提下，利用上述贝叶斯决策规则确定分类面。

贝叶斯决策器得到的分类面是最优的，它是最优分类器。

但贝叶斯决策器在确定分类面前需要预知()k P c 与()|k P c x ，这在实际运用中往往不可能，因为()|k P c x 一般是未知的。

因此贝叶斯决策器只是一个理论上的分类器，常用作衡量其它分类器性能的标尺。

最小风险贝叶斯决策可按下列步骤进行： (1)在已知)(i P ω，)(i X P ω，i=1,…，c 及给出待识别的X 的情况下，根据贝叶斯公式计算出后验概率：∑==cj iii i i P X P P X P X P 1)()()()()(ωωωωω j=1,…，x(2)利用计算出的后验概率及决策表，按下面的公式计算出采取i a ,i=1,…，a 的条件风险∑==cj j j i i X P a X a R 1)(),()(ωωλ,i=1,2,…,a(3)对(2)中得到的a 个条件风险值)(X a R i ,i=1,…，a 进行比较，找出使其条件风险最小的决策k a ，即()()1,min k i i aR a x R a x ==则k a 就是最小风险贝叶斯决策。

模式识别大作业(二)

模式识别大作业（二）k-means 算法的应用一、问题描述用c-means 算法对所给数据进行聚类，并已知类別数为2，随机初始样本聚类中心，进行10次求解，并计算聚类平均正确率。

二、算法简介（1）J.B.MacQueen 在 1967 年提出的K-means 算法[22]到目前为止用于科学和工业应用的诸多聚类算法中一种极有影响的技术。

它是聚类方法中一个基本的划分方法，常常采用误差平方和准则函数作为聚类准则函数。

若i N 是第i 聚类i Γ中的样本数目，i m 是这些样本的均值，即1ii y m y N∈Γ=∑把i Γ中的各样本y 与均值i m 间的误差平方和对所有的类相加后为21ice i i y J y m =∈Γ=-∑∑e J 是误差平方和聚类准则，它是样本集y 和类别集Ω的函数。

e J 度量了用c 个聚类中心12,,...,c m m m 代表c 个样本子集12,,...,c ΓΓΓ时所产生的总的误差平方。

（2）K-means 算法的工作原理：算法首先随机从数据集中选取 K 个点作为初始聚类中心，然后计算各个样本到聚类中的距离，把样本归到离它最近的那个聚类中心所在的类。

计算新形成的每一个聚类的数据对象的平均值来得到新的聚类中心，如果相邻两次的聚类中心没有任何变化，说明样本调整结束，聚类准则函数已经收敛。

本算法的一个特点是在每次迭代中都要考察每个样本的分类是否正确。

若不正确，就要调整，在全部样本调整完后，再修改聚类中心，进入下一次迭代。

如果在一次迭代算法中，所有的样本被正确分类，则不会有调整，聚类中心也不会有任何变化，这标志着已经收敛，因此算法结束。

三、具体步骤1、数据初始化：类别数c=2，样本类标trueflag(n,1) （其中n 为样本个数）;2、初始聚类中心：用随机函数随机产生1~n 中的2个数，选取随机数所对应的样本为初始聚类中心(mmnow)；3、更新样本分类：计算每个样本到两类样本中心的距离，根据最小距离法则，样本将总是分到距离较近的类别；4、更替聚类中心：根据上一步的分类，重新计算两个聚类中心（mmnext）；5、判断终止条件：当样本聚类中心不再发生变化即mmnow==mmnext时，转5）；否则，更新mmnow，将mmnext附给mmnow，即mmnow=mmnext，转2）；6、计算正确率：将dtat(i,1)与trueflag(i,1)（i=1~n）进行比较，统计正确分类的样本数，并计算正确率c_meanstrue(1,ii)。

模式识别方法大作业实验报告

《模式识别导论》期末大作业2010-2011-2学期第 3 组《模式识别》大作业人脸识别方法一---- 基于PCA 和欧几里得距离判据的模板匹配分类器一、理论知识1、主成分分析主成分分析是把多个特征映射为少数几个综合特征的一种统计分析方法。

在多特征的研究中，往往由于特征个数太多，且彼此之间存在着一定的相关性，因而使得所观测的数据在一定程度上有信息的重叠。

当特征较多时，在高维空间中研究样本的分布规律就更麻烦。

主成分分析采取一种降维的方法，找出几个综合因子来代表原来众多的特征，使这些综合因子尽可能地反映原来变量的信息，而且彼此之间互不相关，从而达到简化的目的。

主成分的表示相当于把原来的特征进行坐标变换（乘以一个变换矩阵），得到相关性较小（严格来说是零）的综合因子。

1.1 问题的提出一般来说，如果N 个样品中的每个样品有n 个特征12,,n x x x ，经过主成分分析，将它们综合成n 综合变量，即11111221221122221122n n n n n n n nn ny c x c x c x y c x c x c x y c x c x c x =+++⎧⎪=+++⎪⎨⎪⎪=+++⎩ij c 由下列原则决定：1、i y 和j y （i j ≠，i,j = 1,2,...n ）相互独立；2、y 的排序原则是方差从大到小。

这样的综合指标因子分别是原变量的第1、第2、……、第n 个主分量，它们的方差依次递减。

1.2 主成分的导出我们观察上述方程组，用我们熟知的矩阵表示，设12n x x X x ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦是一个n 维随机向量，12n y y Y y ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦是满足上式的新变量所构成的向量。

于是我们可以写成Y=CX,C 是一个正交矩阵，满足CC ’=I 。

坐标旋转是指新坐标轴相互正交，仍构成一个直角坐标系。

变换后的N 个点在1y 轴上有最大方差，而在n y 轴上有最小方差。

模式识别大作业人脸识别方法

《模式识别》大作业人脸识别方法---- 基于PCA和FLD的人脸识别的线性分类器1、matlab编程1、fisher判别法人脸检测与识别流程图2、matlab程序分为三部分。

程序框图如下图所示。

1、第一部分：CreatDatabase.mfunction T = CreatDatabase(TrainDatabasePath)TrainFiles = dir(TrainDatabasePath);Train_Number = 0;%%%%%%%%统计文件数%%%%%%%%%%%%%for i = 1:size(TrainFiles,1)ifnot(strcmp(TrainFiles(i).name,'.')|strcmp(TrainFiles(i).name,'..')|st rcmp(TrainFiles(i).name,'Thumbs.db'))Train_Number = Train_Number + 1;endend%%%%%%%%二维转一维%%%%%%%%%%%%T = [];for i = 1 : Train_Numberstr = int2str(i);%把文件索引转换为字符串格式str = strcat('\',str,'.pgm');str = strcat(TrainDatabasePath,str);img = imread(str);[irow icol] = size(img);temp = reshape(img',irow*icol,1);T = [T temp];endT = double(T);2、第二部分：FisherfaceCorefunction[m_database V_PCA V_Fisher ProjectedImages_Fisher Class_number Class_population] = FisherfaceCore(T)%%%%%%%%返回值注释%%%%%%%%%%%%m_database --- (M*Nx1)维的训练样本均值%V_PCA --- (M*Nx(P-C)训练样本协方差的特征向量%V_Fisher --- ((P-C)x(C-1)) 最大的（C-1）维J = inv(Sw) * Sb的特征矩阵%ProjectedImages_Fisher --- ((C-1)xP)维训练样本，这些样本从fisher线性空间中提取%%%%%基本量赋值 %%%%%%%%%Class_number=(size(T,2))/9; 类的数目，除以8取决于样本中有多少类人Class_population = 9;%每一类的图像数目P = Class_population * Class_number; %总训练样本的数目%%%%%计算均值%%%%%m_database = mean(T,2);%°包含T每一行均值的列向量%%%%计算方差%%%%%A = T - repmat(m_database,1,P);%%%%%计算特征脸的算法%%%%%%L = A' * A;[V D] = eig(L);V = fliplr(V);%%%%筛选小的特征值%%%%%L_eig_vec = [];dig = fliplr(max(D));for i = 1 : Class_numberL_eig_vec = [L_eig_vec V(:,i)/sqrt(dig(i))];end%%%%计算特征矩阵的协方差矩阵C%%%%%V_PCA = A * L_eig_vec;%V_PCA就是降维后的协方差矩阵ProjectedImages_PCA = [];for i = 1 : Ptemp = V_PCA'*A(:,i);ProjectedImages_PCA = [ProjectedImages_PCA temp];end%%%%%fisher分类器的设计方法%%%%%%%%%计算在特征空间里面每一个类的均值%%%%%m_PCA = mean(ProjectedImages_PCA,2) %特征空间总的均值m = zeros( Class_number, Class_number );Sw = zeros( Class_number, Class_number);Sb = zeros( Class_number, Class_number);for i = 1 : Class_numberm(:,i) =mean( ( ProjectedImages_PCA(:,((i-1)*Class_population+1):i*Class_popu lation) ), 2 )'; %每一类的样本分别求均值S = zeros(Class_number, Class_number);for j = ((i-1) * Class_population + 1) : ( i*Class_population ) S = S + ( ProjectedImages_PCA(:,j) - m(:,i)) * (ProjectedImages_PCA(:,j) - m(:,i))';endSw = Sw + S;Sb = Sb + (m(:,i) - m_PCA) * (m(:,i) - m_PCA)'end%%%%%%¼计算fisher判别准则，目标是获取最大类间离散度和最小类内离散度%%%%%% %%%%%%ÎÒÃÇµÄÄ¿±êÊÇ£º»ñÈ¡×î´óÀà¼äÀëÉ¢¶ÈºÍ×îÐ¡µÄÀàÄÚÀëÉ¢¶È¡£[J_eig_vec, J_eig_val] = eig(Sb,Sw);J_eig_val = max(J_eig_val);J_eig_vec = fliplr(J_eig_vec);%%%%%%去除0特征根和排序for i = 1 : Class_number - 1V_Fisher(:,i) = J_eig_vec(:,i);%fisher判别法将N维映射到C-1维end%%%%%从fisher线性空间中提取图像%Yi = V_Fisher' * V_PCA' * (Ti - m_database)for i = 1: Class_number * Class_populationProjectedImages_Fisher(:,i) = V_Fisher' * ProjectedImages_PCA(:,i); end%由PCA过渡到FLD%img_fisher = w_fisher' * pca_img;%ProjectedImages_Fisher = V_Fisher' * ProjectedImages_PCA;3、第三部分：Recognition.mfunction OutputName = Recognition(TestImage, m_database, V_PCA, V_Fisher, ProjectedImages_Fisher, Class_number, Class_population)%函数描述：这个函数将源图像提取成特征脸，然后比较它们之间的欧几里得距离%输入量: TestImage ---测试样本的路径%%V_PCA --- (M*Nx(P-C)训练样本协方差的特征向量%V_Fisher --- ((P-C)x(C-1)) 最大的（C-1）维J = inv(Sw) * Sb的特征矩阵%ProjectedImages_Fisher --- ((C-1)xP)维训练样本，这些样本从fisher线性空间中提取%Class_number---类的数目%Class_population---每一类图像的数目%返回值：OutputName ---在训练样本中的被识别的图像的名字Train_Number = size(ProjectedImages_Fisher,2); %%%%%%%%%%%%%%%%%%%%%%%%从测试样本中提取PCA特征%%%%%%%%%%%%%%%%%%% InputImage = imread(TestImage);temp = InputImage(:,:,1);[irow icol] = size(temp);InImage = reshape(temp',irow*icol,1);Difference = double(InImage)-m_database;ProjectedTestImage = V_Fisher' * V_PCA' * Difference; %%%%%%%%%%%%%%%%%%%%%%%%计算欧几里得几何距离%%%%%%%%%%%%%%%%Euc_dist = [];for i = 1 : Train_Numberq = ProjectedImages_Fisher(:,i);temp = ( norm( ProjectedTestImage - q ))^2 ;Euc_dist = [Euc_dist temp];endEuc_dist2 = [];for i=1 : Class_numberdist =mean(Euc_dist(((i-1)*Class_population+1):(i*Class_population)));Euc_dist2 = [Euc_dist2 dist];end[Euc_dist_min ,Recognized_index] = min(Euc_dist2);Recognized_index = (Recognized_index - 1) * Class_population + 1; OutputName = strcat(int2str(Recognized_index),'.pgm');。

模式识别作业马忠彧

作业1：线性分类器设计 1、问题描述将4个输入矢量分为两类，其中两个矢量对应的目标值为1，另两个矢量对应的目标值为0。

输入矢量为P ＝[-0.5 -0.5 0.3 0 -0.5 0.5 -0.3 1] 目标分类矢量为T ＝[1 1 0 0]2、算法描述采用单一感知器神经元来解决这个简单的分类问题。

感知器（perceptron ）是由美国学者F.Rosenblatt 于1957年提出的，它是一个具有单层计算神经元的神经网络，并由线性阈值单元组成。

当它用于两类模式的分类时，相当于在高维样本空间中，用一个超平面将两类样本分开。

两类样本线性情况下，线性判别函数可描述为0()0T g x w x w =+=，其中12[,,...,]T l w w w w =是权向量，0w 是阈值。

假设两类样本线性可分，则一定存在一个由''0Tw x =定义的超平面，满足'1'2'0,'0,T T w x x w w x x w >∀∈<∀∈，其中0'[,1],'[,]T T T T x x w w w ==。

定义感知器代价函数为()()Tx x YJ w w x δ∈=∑，其中Y 是训练向量的子集，是权向量w 定义的超平面错误分类的部分。

变量11,x x w δ=-∈当时；21,x x w δ=∈当时。

为了计算出代价函数的最小迭代值，利用梯度下降法设计迭代方案，即()()(1)()tw w t J w w t w t wρ=∂+=-∂其中()x x YJ w w δ∈∂=∂∑，代入得 (1)()t x x Yw t w t x ρδ∈+=-∑这种算法称为感知器算法。

这个算法从任意权向量w(0)开始初始化，通过错误分类特征形成修正向量。

如此重复到算法收敛于解，即所有的特征向量都正确的分类。

可以证明，如果两类模式是线性可分的，则算法一定收敛。

感知器特别适合用于简单的模式分类问题。

模式识别大作业

模式识别大作业K近邻法一．K近邻matlab算法思想：A.把IRIS（wine）数据分为3类，分别存入data1.txt,data2.txt,data3.txt3个文本，调用load 函数装载入M文件；B.用for-end函数将数据的一半分为训练样本和测试样本，并把3各类标记为0,1,2；C.选取K=5，计算测试样本与样本的欧氏距离存入A矩阵，用SORT函数升序排列存入B 矩阵，选出最小的5个距离存入minimum矩阵；求出最小5个距离在A中的行数，利用行数进行分类，找出5个最小值中匹配的三类的个数；用figure函数将分类图显示；以h为分类标记将数据分类；D.将归类数据与训练样本比较，得出精度。

二．程序代码：clear all;clc;close all;%读取特征数据load('data1.txt');load('data2.txt');load('data3.txt');%*****************K近邻法********************%选取训练样本和测试样本并标记训练样本的类别for i=1:25Train(i,:)=data1(2*i-1,:);%第一类训练样本Test(i,:)=data1(2*i,:);%测试样本Label(i)=0;%标记为0endfor i=1:25Train(i+25,:)=data2(2*i-1,:);%第二类训练样本Test(i+25,:)=data2(2*i,:);%测试样本Label(i+25)=1;%标记为1endfor i=1:25Train(i+50,:)=data3(2*i-1,:);%第三类训练样本Test(i+50,:)=data3(2*i,:);%测试样本Label(i+50)=2;%标记为2end%************求出测试样本与训练样本的距离************for i=1:75for j=1:75z=Test(i,:)-Train(j,:);A(j,i)=norm(z);%欧式距离endB=sort(A);%排序%minimum=zeros(1,5);%找出最小的5个距离% for k=1:5% minimum(k)=B(k);% endminimum=B(1:5,:);endfor j=1:75for k=1:5for i=1:75if(minimum(k,j)==A(i,j))testlabel(k,j)=i;%求出最小的五个值所在的A中的行数endendendendl1=zeros(1,75);l2=zeros(1,75);l3=zeros(1,75);for j=1:75for k=1:5if(testlabel(k,j)<=25)l1(1,j)=l1(1,j)+1;else if(testlabel(k,j)>50)l3(1,j)=l3(1,j)+1;elsel2(1,j)=l2(1,j)+1;endendendendL=[l1;l2;l3];%找出五个最小值中匹配三类的个数LL=sort(L);for j=1:75for h=1:3if(LL(3,j)==L(h,j))tclass(j)=h-1;endendendfigure;hold on;plot(1:25,tclass(1:25),'^');plot(26:50,tclass(26:50),'r.'); plot(51:75,tclass(51:75),'go'); right0=0;right1=0;right2=0;for r0=1:25if(tclass(r0)==0)right0=right0+1;endendfor r1=1:25if(tclass(r1+25)==1)right1=right1+1;endendfor r2=1:25if(tclass(r2+50)==2)right2=right2+1;endendAccuracy0=right0/25Accuracy1=right1/25Accuracy2=right2/25Accuracy=(right0+right1+right2)/75三．IRIS数据实验结果：0为第一类；1为第二类；2为第三类精度：Wine实验结果Wine分类精度：四．感想与收获：通过这次大作业，让我理解了K近邻法的思想，也通过调试matlab程序提高了编程能力和独立解决问题的能力。

模式识别大作业_许萌_

“0”表示初始状态。

Step2：假设已求得距离矩阵D(n)（n为逐次聚类合并的次数），找出D(n)中的最小元素，将其对应的两类合并为一类。

由此建立新的分类：Step3：计算合并后所得到的新类别之间的距离，得D (n +1)。

Step4：跳至第2步，重复计算及合并。

直到满足下列条件时即可停止计算：①取距离阈值T ，当D (n )的最小分量超过给定值 T 时，算法停止。

所得即为聚类结果。

②或不设阈值T ，一直到将全部样本聚成一类为止，输出聚类的分级树。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

q
( x x' ) 1
；
参数为：多项式和的阶数 q。
( x x' ) 2 K ( x , x ' ) exp 2.多项式核函数 2 ；
参数为：和函数的宽度：
。
3. Sigmoid 核函数 K ( x, x' )
tanhv( x x' ) c ；
i
x j
直观的说，就是对待识别的模式向量 x，只要比较 x 与所有已知类别的样本之间的欧式距离，并决策 x 与离它最近的样本同类。缺点： 1）存储量和计算量都很大（2）没有考虑决策的风险，如果决策的错误代价很大时，会产生很大的风险（3）以上的分析——渐近平均错误率，都是建立在样本数趋向无穷大的条件下得来的，在实际应用时大多是无法实现的改进：减少近邻法计算量和存储量。例如：快速算法：（1.分级分解，形成树结构。2.搜索，找出待识样本的近邻）剪辑近邻法：（清理两类间的边界，去掉类别混杂的样本，使两类边界更清晰）压缩近邻法：（1.利用已知样本集中的样本进行预分类，去掉错分样本构成剪辑样本集，考试集和参考集在剪辑过程中的应用。2.利用剪辑样本集和近邻规则对未知样本进行分类）
运行结果： a = -40.8200 -27.7000 -10.4800 -0.6400 ************************** 最小平方误差为 js = -3.4165e+004 **************************
5、试解释最优超平面的含义，并在线性可分的情况下给出支持向量机的求解过程。答：最优超平面的含义：一个超平面，如果它能够将训练样本没有错误地分开，并且两类训练样本中离超平面最近的样本与超平面之间的距离是最大的，则我们把这个超平面称作最优分类超平面，简称最优超平面。两类样本中离分类面最近的样本到分类面的距离称作分类间隔，最优超平面也称作最大间隔超平面。支持向量机的求解过程： 6、试讨论设计多类分类器的方法，并分析其优缺点。答：分段线性判别函数法（分段 LDA 法）最近邻法(nearest-neighbor)：优点：成立的条件是，当样本的数目趋向无穷大；其错误率最坏不会超过两
g=a*y';
运行结果：
4、试推导出最小平方误差判别规则的两种求解方法，尝试用 Matlab 实现，并用 Fisher's Iris Data 进行验证（考虑 2 类分类即可）。答：违逆法： clc; clear all; load fisheriris
Label = unique(species) ;%È¥µôÖØ¸´µÄÊý¾Ý groups1 = ismember(species,'setosa');% groups2 = ismember(species,'versicolor'); C1Idx = find(groups1==1);%ÔÚspeciesÕÒµ½ÓësetosaÏàÍ¬µÄÊý¾Ý C2Idx = find(groups2==1);%ÔÚspeciesÕÒµ½ÓëversicolorÏàÍ¬µÄÊý¾Ý data1 = meas(C1Idx,:);%measÊÇÒ»¸ö¾ØÕó£¬È¡measÖÐ1:50ÐÐÖÐËùÓÐµÄÁÐ data2 = meas(C2Idx,:);%measÊÇÒ»¸ö¾ØÕó£¬È¡measÖÐ51:100ÐÐÖÐËùÓÐµÄÁÐ y=[data1;data2]; [n,d]=size(y); [n1,d1]=size(data1); [n2,d2]=size(data2); b=[(n/n1)*ones(1,n1) (n/n2)*ones(1,n2)]'; % m1=(sum(data1))'/50; % m2=(sum(data2))'/50; % s1=zeros(4); % s2=zeros(4); % for a=1:50 % % s1=s1+(data1(a,:)'-m1)*(data1(a,:)'-m1)'; s1=s1+(data2(a,:)'-m1)*(data2(a,:)'-m1)';
倍的贝叶斯错误率，最好的有可能会接近或达到贝叶斯错误率。缺点是如果样本的数目太少时，样本的分布会带来很大的偶然性不一定能很好的代表数据内在的分布情况，此时就会影响最近邻法的性能，但数据内在规律比较复杂，类别间存在交叠情况下尤其如此。 7、什么叫核函数？常用的核函数有哪些，并指明其中的可变参数。答：根据模式识别理论，低维空间线性不可分的模式通过非线性映射到高维特征空间则可能实现线性可分，但是如果直接采用这种技术在高维空间进行分类或回归，则存在确定非线性映射函数的形式和参数、特征空间维数等问题，而最大的障碍则是在高维特征空间运算时存在的“维数灾难”。采用核函数技术可以有效地解决这样问题。其公式为 K ( xi , x j ) ( xi ) ( x j ) 常用的核函数有： 1.线性核函数 K ( x, x ' )
参数为：和函数的宽度 v 与 c。 8、阐释最近邻分类器的决策规则是什么？其缺点有哪些？怎么改进？答：最近邻决策规则：给定 c 个类别 1 , 2 ,, c ，每类有标明类别的样本 Ni 个，近邻法的判别函数为
gi ( x ) min x xik , k 1, 2, , N i i 决策规则为 g j ( x ) min gi ( x ), i 1, 2********** 最小平方误差为 js = 2.4447 **************************
梯度下降法: clc; clear all; load fisheriris Label = unique(species) ;%È¥µôÖØ¸´µÄÊý¾Ý groups1 = ismember(species,'setosa');%ÔÚspeciesÕÒµ½ÓësetosaÏàÍ¬µÄÊý¾Ý£¬ÏàÍ¬£¬·µ»Ø1£¬ groups2 = ismember(species,'versicolor'); C1Idx = find(groups1==1);%ÔÚspeciesÕÒµ½ÓësetosaÏàÍ¬µÄÊý¾Ý C2Idx = find(groups2==1);%ÔÚspeciesÕÒµ½ÓëversicolorÏàÍ¬µÄÊý¾Ý
子函数： function g=mydist(x,wt,w0) g=wt*x'+w0; 输出结果：
3、试推导出感知器算法的迭代求解过程，尝试用 Matlab 实现，并用 Fisher's Iris Data 进行验证（考虑 2 类分类即可）。答：代码如下：
子程序：function g= dist(y,a);
实用价值：把所有样本都投影到一维，使在投影线上最易于分类，寻找投影方向。让类间的点尽可能的分开，类内的点越接近越好。是最小错误率或最小风险意义下的分类器。 2、参考教材 4.3，完成线性判别分析（LDA）的 Matlab 实现，并用 Fisher's Iris Data【注】进行验证（考虑其中的 2 类即可）。注：Fisher's Iris Data: Fisher's iris data consists of measurements on the sepal length, sepal width, petal length, and petal width of 150 iris specimens. There are 50 specimens from each of three species. 在 Matlab 中调用 load fisheriris 可以得到该数据，meas 为 150×4 的数据矩阵， species 为 150×1 的 cell 矩阵，含有类别信息。答：
第四章 1、阐述线性判别函数的几何意义和用于分类的实用价值。答：线性判别函数的几何意义决策面(decision boundary)H 方程：g(x)=0 向量 w 是决策面 H 的法向量 g(x)是点 x 到决策面 H 的距离的一种代数度量 x=xp+r*w/||w||。xp 是在上的投影向量，r 是到的垂直距离 w/||w||是方向上的单位向量. 如图所示：
征的线性组合，并且相互之间是不相关的。 11、试推导出 KL 变换的求解过程。并对比它和主成分分析方法的不同。答：KL 变换的流程如下：（1）获取多幅图像的统计特性：图像之间的协方差（2）获取协方差的特征值和特征向量，从而获取正交核:特征矩阵（3）图像对应象素点对各个特征向量进行投影运算。 KL 变换的 Matlab 代码如下： % K_L 变换 X=imread(TEST.TIF); %读图像 X 是一个 7 波段图像图像的宽和高均为 256 XX=reshape(X,[256*256,7]); %将图像转换化为一个波段的图像 pic1=XX(:,1); pic1=reshape(pic1,[256, 256]); figure(1); imshow(pic1,[]); title(Original Image); XX=im2double(XX); %图像转化为双精度 covx = cov(XX); % 求图像的协方差 [pc,variances,explained] = pcacov(covx); % 求解 K_L 变换矩阵，即 PCA pc myKL=XX*pc; %进行 K_L 变换 pic2=myKL(:,1); pic2=reshape(pic2,[256,256]); figure(2); imshow(pic2,[]); title(K_L 第一分量); figure(3); pic3=myKL(:,2); pic3=reshape(pic3,[256 256]); imshow(pic3,[]); title(K_L 第二分量); my=myKL*pc; my1=my(:,1); my1=reshape(my1,[256,256]); figure(4); imshow(my1,[]); KL 变换和主成分分析方法的不同：K-L 变换在求取了协方差矩阵Σ的之后，只取前 d 项，因此带入了一定的误差，它本着最小均方误差准则，求得新特征值，它能够考虑到不同的分类信息，实现监督的特征提取。主成分分析法是一种客观赋权法，它根据各指标间的相互关系与各指标间的变异程度来确定权重系数，能够真实地反映事物间的现实关系，避免了人为因素带来的误差。 12、C-均值算法的准则是什么？试给出其求解步骤，尝试用 Matlab 实现，并用 Fisher's Iris Data 进行验证（考虑 2 类分类即可）。答：准则是误差平方和：这个准则函数是以计算各类均值