模式识别作业Homework#2
模式识别作业题(2)

答:不是最小的。首先要明确当我们谈到最小最大损失判决规则时,先验概率是未知的, 而先验概率的变化会导致错分概率变化, 故错分概率也是一个变量。 使用最小最大损 失判决规则的目的就是保证在先验概率任意变化导致错分概率变化时, 错分概率的最 坏(即最大)情况在所有判决规则中是最好的(即最小)。 4、 若 λ11 = λ22 =0, λ12 = λ21 ,证明此时最小最大决策面是来自两类的错误率相等。 证明:最小最大决策面满足 ( λ11 - λ22 )+( λ21 - λ11 ) 容易得到
λ11 P(ω1 | x) + λ12 P(ω2 | x) < λ21 P(ω1 | x) + λ22 P(ω2 | x) ( λ21 - λ11 ) P (ω1 | x) >( λ12 - λ22 ) P (ω2 | x) ( λ21 - λ11 ) P (ω1 ) P ( x | ω1 ) >( λ12 - λ22 ) P (ω2 ) P ( x | ω2 ) p( x | ω1 ) (λ 12 − λ 22) P(ω2 ) > 即 p( x | ω2 ) ( λ 21 − λ 11) P (ω1 )
6、设总体分布密度为 N( μ ,1),-∞< μ <+∞,并设 X={ x1 , x2 ,… xN },分别用最大似然 估计和贝叶斯估计计算 μ 。已知 μ 的先验分布 p( μ )~N(0,1)。 解:似然函数为:
∧Байду номын сангаас
L( μ )=lnp(X|u)=
∑ ln p( xi | u) = −
i =1
N
模式识别第三章作业及其解答
模式识别大作业

模式识别大作业1.最近邻/k近邻法一.基本概念:最近邻法:对于未知样本x,比较x与N个已知类别的样本之间的欧式距离,并决策x与距离它最近的样本同类。
K近邻法:取未知样本x的k个近邻,看这k个近邻中多数属于哪一类,就把x归为哪一类。
K取奇数,为了是避免k1=k2的情况。
二.问题分析:要判别x属于哪一类,关键要求得与x最近的k个样本(当k=1时,即是最近邻法),然后判别这k个样本的多数属于哪一类。
可采用欧式距离公式求得两个样本间的距离s=sqrt((x1-x2)^2+(y1-y2)^2)三.算法分析:该算法中任取每类样本的一半作为训练样本,其余作为测试样本。
例如iris中取每类样本的25组作为训练样本,剩余25组作为测试样本,依次求得与一测试样本x距离最近的k 个样本,并判断k个样本多数属于哪一类,则x就属于哪类。
测试10次,取10次分类正确率的平均值来检验算法的性能。
四.MATLAB代码:最近邻算实现对Iris分类clc;totalsum=0;for ii=1:10data=load('iris.txt');data1=data(1:50,1:4);%任取Iris-setosa数据的25组rbow1=randperm(50);trainsample1=data1(rbow1(:,1:25),1:4);rbow1(:,26:50)=sort(rbow1(:,26:50));%剩余的25组按行下标大小顺序排列testsample1=data1(rbow1(:,26:50),1:4);data2=data(51:100,1:4);%任取Iris-versicolor数据的25组rbow2=randperm(50);trainsample2=data2(rbow2(:,1:25),1:4);rbow2(:,26:50)=sort(rbow2(:,26:50));testsample2=data2(rbow2(:,26:50),1:4);data3=data(101:150,1:4);%任取Iris-virginica数据的25组rbow3=randperm(50);trainsample3=data3(rbow3(:,1:25),1:4);rbow3(:,26:50)=sort(rbow3(:,26:50));testsample3=data3(rbow3(:,26:50),1:4);trainsample=cat(1,trainsample1,trainsample2,trainsample3);%包含75组数据的样本集testsample=cat(1,testsample1,testsample2,testsample3);newchar=zeros(1,75);sum=0;[i,j]=size(trainsample);%i=60,j=4[u,v]=size(testsample);%u=90,v=4for x=1:ufor y=1:iresult=sqrt((testsample(x,1)-trainsample(y,1))^2+(testsample(x,2) -trainsample(y,2))^2+(testsample(x,3)-trainsample(y,3))^2+(testsa mple(x,4)-trainsample(y,4))^2); %欧式距离newchar(1,y)=result;end;[new,Ind]=sort(newchar);class1=0;class2=0;class3=0;if Ind(1,1)<=25class1=class1+1;elseif Ind(1,1)>25&&Ind(1,1)<=50class2=class2+1;elseclass3=class3+1;endif class1>class2&&class1>class3m=1;ty='Iris-setosa';elseif class2>class1&&class2>class3m=2;ty='Iris-versicolor';elseif class3>class1&&class3>class2m=3;ty='Iris-virginica';elsem=0;ty='none';endif x<=25&&m>0disp(sprintf('第%d组数据分类后为%s类',rbow1(:,x+25),ty));elseif x<=25&&m==0disp(sprintf('第%d组数据分类后为%s类',rbow1(:,x+25),'none'));endif x>25&&x<=50&&m>0disp(sprintf('第%d组数据分类后为%s类',50+rbow2(:,x),ty));elseif x>25&&x<=50&&m==0disp(sprintf('第%d组数据分类后为%s类',50+rbow2(:,x),'none'));endif x>50&&x<=75&&m>0disp(sprintf('第%d组数据分类后为%s类',100+rbow3(:,x-25),ty));elseif x>50&&x<=75&&m==0disp(sprintf('第%d组数据分类后为%s类',100+rbow3(:,x-25),'none'));endif (x<=25&&m==1)||(x>25&&x<=50&&m==2)||(x>50&&x<=75&&m==3)sum=sum+1;endenddisp(sprintf('第%d次分类识别率为%4.2f',ii,sum/75));totalsum=totalsum+(sum/75);enddisp(sprintf('10次分类平均识别率为%4.2f',totalsum/10));测试结果:第3组数据分类后为Iris-setosa类第5组数据分类后为Iris-setosa类第6组数据分类后为Iris-setosa类第7组数据分类后为Iris-setosa类第10组数据分类后为Iris-setosa类第11组数据分类后为Iris-setosa类第12组数据分类后为Iris-setosa类第14组数据分类后为Iris-setosa类第16组数据分类后为Iris-setosa类第18组数据分类后为Iris-setosa类第19组数据分类后为Iris-setosa类第20组数据分类后为Iris-setosa类第23组数据分类后为Iris-setosa类第24组数据分类后为Iris-setosa类第26组数据分类后为Iris-setosa类第28组数据分类后为Iris-setosa类第30组数据分类后为Iris-setosa类第31组数据分类后为Iris-setosa类第34组数据分类后为Iris-setosa类第37组数据分类后为Iris-setosa类第39组数据分类后为Iris-setosa类第41组数据分类后为Iris-setosa类第44组数据分类后为Iris-setosa类第45组数据分类后为Iris-setosa类第49组数据分类后为Iris-setosa类第53组数据分类后为Iris-versicolor类第54组数据分类后为Iris-versicolor类第55组数据分类后为Iris-versicolor类第57组数据分类后为Iris-versicolor类第58组数据分类后为Iris-versicolor类第59组数据分类后为Iris-versicolor类第60组数据分类后为Iris-versicolor类第61组数据分类后为Iris-versicolor类第62组数据分类后为Iris-versicolor类第68组数据分类后为Iris-versicolor类第70组数据分类后为Iris-versicolor类第71组数据分类后为Iris-virginica类第74组数据分类后为Iris-versicolor类第75组数据分类后为Iris-versicolor类第77组数据分类后为Iris-versicolor类第79组数据分类后为Iris-versicolor类第80组数据分类后为Iris-versicolor类第84组数据分类后为Iris-virginica类第85组数据分类后为Iris-versicolor类第92组数据分类后为Iris-versicolor类第95组数据分类后为Iris-versicolor类第97组数据分类后为Iris-versicolor类第98组数据分类后为Iris-versicolor类第99组数据分类后为Iris-versicolor类第102组数据分类后为Iris-virginica类第103组数据分类后为Iris-virginica类第105组数据分类后为Iris-virginica类第106组数据分类后为Iris-virginica类第107组数据分类后为Iris-versicolor类第108组数据分类后为Iris-virginica类第114组数据分类后为Iris-virginica类第118组数据分类后为Iris-virginica类第119组数据分类后为Iris-virginica类第124组数据分类后为Iris-virginica类第125组数据分类后为Iris-virginica类第126组数据分类后为Iris-virginica类第127组数据分类后为Iris-virginica类第128组数据分类后为Iris-virginica类第129组数据分类后为Iris-virginica类第130组数据分类后为Iris-virginica类第133组数据分类后为Iris-virginica类第135组数据分类后为Iris-virginica类第137组数据分类后为Iris-virginica类第142组数据分类后为Iris-virginica类第144组数据分类后为Iris-virginica类第148组数据分类后为Iris-virginica类第149组数据分类后为Iris-virginica类第150组数据分类后为Iris-virginica类k近邻法对wine分类:clc;otalsum=0;for ii=1:10 %循环测试10次data=load('wine.txt');%导入wine数据data1=data(1:59,1:13);%任取第一类数据的30组rbow1=randperm(59);trainsample1=data1(sort(rbow1(:,1:30)),1:13);rbow1(:,31:59)=sort(rbow1(:,31:59)); %剩余的29组按行下标大小顺序排列testsample1=data1(rbow1(:,31:59),1:13);data2=data(60:130,1:13);%任取第二类数据的35组rbow2=randperm(71);trainsample2=data2(sort(rbow2(:,1:35)),1:13);rbow2(:,36:71)=sort(rbow2(:,36:71));testsample2=data2(rbow2(:,36:71),1:13);data3=data(131:178,1:13);%任取第三类数据的24组rbow3=randperm(48);trainsample3=data3(sort(rbow3(:,1:24)),1:13);rbow3(:,25:48)=sort(rbow3(:,25:48));testsample3=data3(rbow3(:,25:48),1:13);train_sample=cat(1,trainsample1,trainsample2,trainsample3);%包含89组数据的样本集test_sample=cat(1,testsample1,testsample2,testsample3);k=19;%19近邻法newchar=zeros(1,89);sum=0;[i,j]=size(train_sample);%i=89,j=13[u,v]=size(test_sample);%u=89,v=13for x=1:ufor y=1:iresult=sqrt((test_sample(x,1)-train_sample(y,1))^2+(test_sample(x ,2)-train_sample(y,2))^2+(test_sample(x,3)-train_sample(y,3))^2+( test_sample(x,4)-train_sample(y,4))^2+(test_sample(x,5)-train_sam ple(y,5))^2+(test_sample(x,6)-train_sample(y,6))^2+(test_sample(x ,7)-train_sample(y,7))^2+(test_sample(x,8)-train_sample(y,8))^2+( test_sample(x,9)-train_sample(y,9))^2+(test_sample(x,10)-train_sa mple(y,10))^2+(test_sample(x,11)-train_sample(y,11))^2+(test_samp le(x,12)-train_sample(y,12))^2+(test_sample(x,13)-train_sample(y, 13))^2); %欧式距离newchar(1,y)=result;end;[new,Ind]=sort(newchar);class1=0;class 2=0;class 3=0;for n=1:kif Ind(1,n)<=30class 1= class 1+1;elseif Ind(1,n)>30&&Ind(1,n)<=65class 2= class 2+1;elseclass 3= class3+1;endendif class 1>= class 2&& class1>= class3m=1;elseif class2>= class1&& class2>= class3m=2;elseif class3>= class1&& class3>= class2m=3;endif x<=29disp(sprintf('第%d组数据分类后为第%d类',rbow1(:,30+x),m));elseif x>29&&x<=65disp(sprintf('第%d组数据分类后为第%d类',59+rbow2(:,x+6),m));elseif x>65&&x<=89disp(sprintf('第%d组数据分类后为第%d类',130+rbow3(:,x-41),m));endif (x<=29&&m==1)||(x>29&&x<=65&&m==2)||(x>65&&x<=89&&m==3) sum=sum+1;endenddisp(sprintf('第%d次分类识别率为%4.2f',ii,sum/89));totalsum=totalsum+(sum/89);enddisp(sprintf('10次分类平均识别率为%4.2f',totalsum/10));第2组数据分类后为第1类第4组数据分类后为第1类第5组数据分类后为第3类第6组数据分类后为第1类第8组数据分类后为第1类第10组数据分类后为第1类第11组数据分类后为第1类第14组数据分类后为第1类第16组数据分类后为第1类第19组数据分类后为第1类第20组数据分类后为第3类第21组数据分类后为第3类第22组数据分类后为第3类第26组数据分类后为第3类第27组数据分类后为第1类第28组数据分类后为第1类第30组数据分类后为第1类第33组数据分类后为第1类第36组数据分类后为第1类第37组数据分类后为第1类第43组数据分类后为第1类第44组数据分类后为第3类第45组数据分类后为第1类第46组数据分类后为第1类第49组数据分类后为第1类第54组数据分类后为第1类第56组数据分类后为第1类第57组数据分类后为第1类第60组数据分类后为第2类第61组数据分类后为第3类第63组数据分类后为第3类第65组数据分类后为第2类第66组数据分类后为第3类第67组数据分类后为第2类第71组数据分类后为第1类第72组数据分类后为第2类第74组数据分类后为第1类第76组数据分类后为第2类第77组数据分类后为第2类第79组数据分类后为第3类第81组数据分类后为第2类第82组数据分类后为第3类第83组数据分类后为第3类第84组数据分类后为第2类第86组数据分类后为第2类第87组数据分类后为第2类第88组数据分类后为第2类第93组数据分类后为第2类第96组数据分类后为第1类第98组数据分类后为第2类第99组数据分类后为第3类第102组数据分类后为第2类第104组数据分类后为第2类第105组数据分类后为第3类第106组数据分类后为第2类第110组数据分类后为第3类第113组数据分类后为第3类第114组数据分类后为第2类第115组数据分类后为第2类第116组数据分类后为第2类第118组数据分类后为第2类第122组数据分类后为第2类第123组数据分类后为第2类第124组数据分类后为第2类第133组数据分类后为第3类第134组数据分类后为第3类第135组数据分类后为第2类第136组数据分类后为第3类第140组数据分类后为第3类第142组数据分类后为第3类第144组数据分类后为第2类第145组数据分类后为第1类第146组数据分类后为第3类第148组数据分类后为第3类第149组数据分类后为第2类第152组数据分类后为第2类第157组数据分类后为第2类第159组数据分类后为第3类第161组数据分类后为第2类第162组数据分类后为第3类第163组数据分类后为第3类第164组数据分类后为第3类第165组数据分类后为第3类第167组数据分类后为第3类第168组数据分类后为第3类第173组数据分类后为第3类第174组数据分类后为第3类2.Fisher线性判别法Fisher 线性判别是统计模式识别的基本方法之一。
模式识别大作业

模式识别大作业引言:转眼之间,研一就结束了。
这学期的模式识别课也接近了尾声。
我本科是机械专业,编程和算法的理解能力比较薄弱。
所以虽然这学期老师上课上的很精彩,但是这学期的模式识别课上的感觉还是有点吃力。
不过这学期也加强了编程的练习。
这次的作业花了很久的时间,因为平时自己的方向是主要是图像降噪,自己在看这一块图像降噪论文的时候感觉和模式识别的方向结合的比较少。
我看了这方面的模式识别和图像降噪结合的论文,发现也比较少。
在思考的过程中,我想到了聚类的方法。
包括K均值和C均值等等。
因为之前学过K均值,于是就选择了K均值的聚类方法。
然后用到了均值滤波和自适应滤波进行处理。
正文:k-means聚类算法的工作过程说明如下:首先从n个数据对象任意选择 k 个对象作为初始聚类中心;而对于所剩下其它对象,则根据它们与这些聚类中心的相似度(距离),分别将它们分配给与其最相似的(聚类中心所代表的)聚类;然后再计算每个所获新聚类的聚类中心(该聚类中所有对象的均值);不断重复这一过程直到标准测度函数开始收敛为止。
一般都采用均方差作为标准测度函数。
k-means 算法接受输入量k ;然后将n个数据对象划分为k个聚类以便使得所获得的聚类满足:同一聚类中的对象相似度较高;而不同聚类中的对象相似度较小。
聚类相似度是利用各聚类中对象的均值所获得一个“中心对象”(引力中心)来进行计算的。
k个聚类具有以下特点:各聚类本身尽可能的紧凑,而各聚类之间尽可能的分开。
均值滤波是常用的非线性滤波方法 ,也是图像处理技术中最常用的预处理技术。
它在平滑脉冲噪声方面非常有效,同时它可以保护图像尖锐的边缘。
均值滤波是典型的线性滤波算法,它是指在图像上对目标像素给一个模板,该模板包括了其周围的临近像素(以目标象素为中心的周围8个象素,构成一个滤波模板,即去掉目标象素本身)。
再用模板中的全体像素的平均值来代替原来像素值。
即对待处理的当前像素点(x,y),选择一个模板,该模板由其近邻的若干像素组成,求模板中所有像素的均值,再把该均值赋予当前像素点(x,y),作为处理后图像在该点上的灰度个g(x,y),即个g(x,y)=1/m ∑f(x,y)m为该模板中包含当前像素在内的像素总个数。
模式识别大作业1

模式识别大作业--fisher线性判别和近邻法学号:021151**姓名:**任课教师:张**I. Fisher线性判别A. fisher线性判别简述在应用统计方法解决模式识别的问题时,一再碰到的问题之一是维数问题.在低维空间里解析上或计算上行得通的方法,在高维里往往行不通.因此,降低维数就成为处理实际问题的关键.我们考虑把维空间的样本投影到一条直线上,形成一维空间,即把维数压缩到一维.这样,必须找一个最好的,易于区分的投影线.这个投影变换就是我们求解的解向量.B.fisher线性判别的降维和判别1.线性投影与Fisher准则函数各类在维特征空间里的样本均值向量:,(1)通过变换映射到一维特征空间后,各类的平均值为:,(2)映射后,各类样本“类内离散度”定义为:,(3)显然,我们希望在映射之后,两类的平均值之间的距离越大越好,而各类的样本类内离散度越小越好。
因此,定义Fisher准则函数:(4)使最大的解就是最佳解向量,也就是Fisher的线性判别式。
2.求解从的表达式可知,它并非的显函数,必须进一步变换。
已知:,, 依次代入上两式,有:,(5)所以:(6)其中:(7)是原维特征空间里的样本类内离散度矩阵,表示两类均值向量之间的离散度大小,因此,越大越容易区分。
将(4.5-6)和(4.5-2)代入(4.5-4)式中:(8)其中:,(9)因此:(10)显然:(11)称为原维特征空间里,样本“类内离散度”矩阵。
是样本“类内总离散度”矩阵。
为了便于分类,显然越小越好,也就是越小越好。
将上述的所有推导结果代入表达式:可以得到:其中,是一个比例因子,不影响的方向,可以删除,从而得到最后解:(12)就使取得最大值,可使样本由维空间向一维空间映射,其投影方向最好。
是一个Fisher线性判断式.这个向量指出了相对于Fisher准则函数最好的投影线方向。
C.算法流程图左图为算法的流程设计图。
II.近邻法A. 近邻法线简述K最近邻(k-Nearest Neighbor,KNN)分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。
模式识别作业

第二章主要内容:几种常见的聚类算法已经所使用的准则函数。
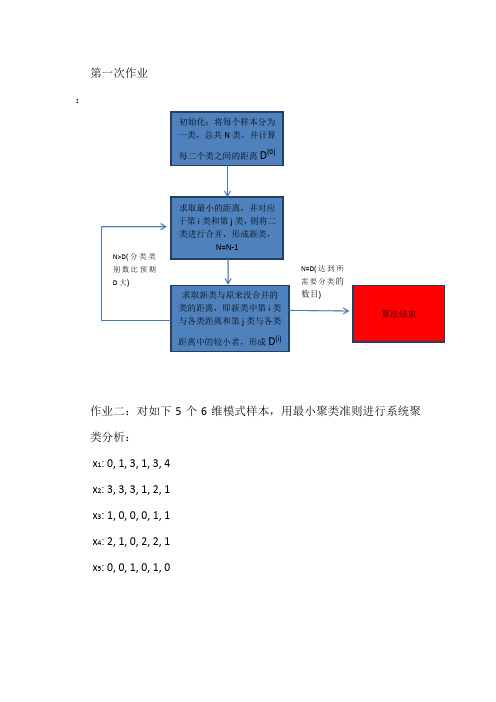
作业1:对如下5个6维模式样本,用最小聚类准则进行系统聚类分析 已知样本如下:x1: 0, 1, 3, 1, 3, 4;x2: 3, 3, 3, 1, 2, 1;x3: 1, 0, 0, 0, 1, 1;x4: 2, 1, 0, 2, 2, 1;x5: 0, 0, 1, 0, 1, 0 第1步:将每一样本看成单独一类,得(0)(0)(0)112233(0)(0)4455{},{},{}{},{}G x G x G x Gx Gx =====计算各类之间的欧式距离,可得距离矩阵(0)D第2步:矩阵(0)D,它是(0)3G 和(0)5G 之间的距离,将他们合并为一类,得新的分类为(1)(0)(1)(0)(1)(0)(0)(1)(0)112233544{},{},{,},{}G G G G G G G G G ====计算聚类后的距离矩阵(1)D 第3步:由于(1)D 它是(1)3G 与(1)4G 之间的距离,于是合并(1)3G 和(1)4G ,得新的分类为(2)(1)(2)(2)(2)(1)(1)1122334{},{},{,}G G G G G G G ===同样,按最小距离准则计算距离矩阵(2)D,得第4步:同理得(3)(2)(3)(2)(2)11223{},{,}G G G G G == 满足聚类要求,如聚为2类,聚类完毕。
系统聚类算法介绍:第一步:设初始模式样本共有N 个,每个样本自成一类,即建立N 类。
G 1(0), G 2(0) , ……,G N (0)为计算各类之间的距离(初始时即为各样本间的距离),得到一个N*N 维的距离矩阵D(0)。
这里,标号(0)表示聚类开始运算前的状态。
第二步:假设前一步聚类运算中已求得距离矩阵D(n),n 为逐次聚类合并的次数,则求D(n)中的最小元素。
如果它是Gi(n)和Gj(n)两类之间的距离,则将Gi(n)和Gj(n)两类合并为一类G ij (n+1),由此建立新的分类:G 1(n+1), G 2(n+1)……第三步:计算合并后新类别之间的距离,得D(n+1)。
模式识别大作业

模式识别大作业(总21页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--作业1 用身高和/或体重数据进行性别分类(一)基本要求:用和的数据作为训练样本集,建立Bayes分类器,用测试样本数据对该分类器进行测试。
调整特征、分类器等方面的一些因素,考察它们对分类器性能的影响,从而加深对所学内容的理解和感性认识。
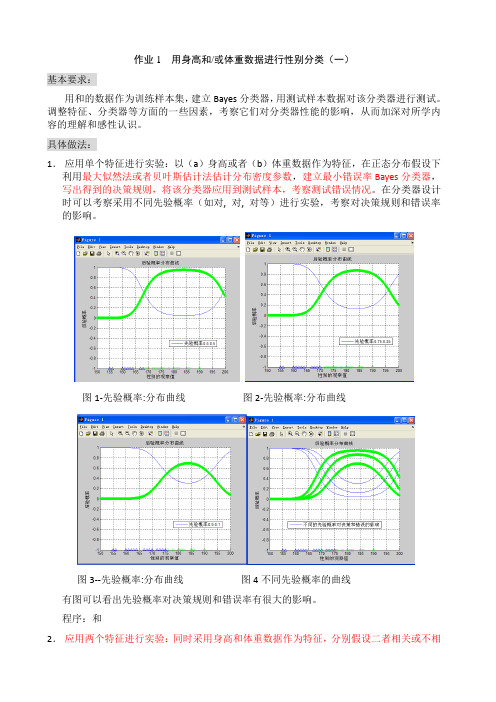
具体做法:1.应用单个特征进行实验:以(a)身高或者(b)体重数据作为特征,在正态分布假设下利用最大似然法或者贝叶斯估计法估计分布密度参数,建立最小错误率Bayes分类器,写出得到的决策规则,将该分类器应用到测试样本,考察测试错误情况。
在分类器设计时可以考察采用不同先验概率(如对, 对, 对等)进行实验,考察对决策规则和错误率的影响。
图1-先验概率:分布曲线图2-先验概率:分布曲线图3--先验概率:分布曲线图4不同先验概率的曲线有图可以看出先验概率对决策规则和错误率有很大的影响。
程序:和2.应用两个特征进行实验:同时采用身高和体重数据作为特征,分别假设二者相关或不相关(在正态分布下一定独立),在正态分布假设下估计概率密度,建立最小错误率Bayes分类器,写出得到的决策规则,将该分类器应用到训练/测试样本,考察训练/测试错误情况。
比较相关假设和不相关假设下结果的差异。
在分类器设计时可以考察采用不同先验概率(如 vs. , vs. , vs. 等)进行实验,考察对决策和错误率的影响。
训练样本female来测试图1先验概率 vs. 图2先验概率 vs.图3先验概率 vs. 图4不同先验概率对测试样本1进行试验得图对测试样本2进行试验有图可以看出先验概率对决策规则和错误率有很大的影响。
程序和3.自行给出一个决策表,采用最小风险的Bayes决策重复上面的某个或全部实验。
W1W2W10W20close all;clear all;X=120::200; %设置采样范围及精度pw1=;pw2=; %设置先验概率sample1=textread('') %读入样本samplew1=zeros(1,length(sample1(:,1)));u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布figure(1);subplot(2,1,1);plot(X,y1);title('F身高类条件概率分布曲线');sample2=textread('') %读入样本samplew2=zeros(1,length(sample2(:,1)));u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布subplot(2,1,2);plot(X,y2);title('M身高类条件概率分布曲线');P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);figure(2);subplot(2,1,1);plot(X,P1);title('F身高后验概率分布曲线');subplot(2,1,2);plot(X,P2);title('M身高后验概率分布曲线');P11=pw1*y1;P22=pw2*y2;figure(3);subplot(3,1,1);plot(X,P11);subplot(3,1,2);plot(X,P22);subplot(3,1,3);plot(X,P11,X,P22);sample=textread('all ') %读入样本[result]=bayes(sample1(:,1),sample2(:,1),pw1,pw2);%bayes分类器function [result] =bayes(sample1(:,1),sample2(:,1),pw1,pw2); error1=0;error2=0;u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);for i = 1:50if P1(i)>P2(i)result(i)=0;pe(i)=P2(i);elseresult(i)=1;pe(i)=P1(i);endendfor i=1:50if result(k)==0error1=error1+1;else result(k)=1error2=error2+1;endendratio = error1+error2/length(sample); %识别率,百分比形式sprintf('正确识别率为%.2f%%.',ratio)作业2 用身高/体重数据进行性别分类(二)基本要求:试验直接设计线性分类器的方法,与基于概率密度估计的贝叶斯分离器进行比较。
模式识别大作业
作业1 用身高和/或体重数据进行性别分类(一)基本要求:用和的数据作为训练样本集,建立Bayes分类器,用测试样本数据对该分类器进行测试。
调整特征、分类器等方面的一些因素,考察它们对分类器性能的影响,从而加深对所学内容的理解和感性认识。
具体做法:1.应用单个特征进行实验:以(a)身高或者(b)体重数据作为特征,在正态分布假设下利用最大似然法或者贝叶斯估计法估计分布密度参数,建立最小错误率Bayes分类器,写出得到的决策规则,将该分类器应用到测试样本,考察测试错误情况。
在分类器设计时可以考察采用不同先验概率(如对, 对, 对等)进行实验,考察对决策规则和错误率的影响。
图1-先验概率:分布曲线图2-先验概率:分布曲线图3--先验概率:分布曲线图4不同先验概率的曲线有图可以看出先验概率对决策规则和错误率有很大的影响。
程序:和2.应用两个特征进行实验:同时采用身高和体重数据作为特征,分别假设二者相关或不相关(在正态分布下一定独立),在正态分布假设下估计概率密度,建立最小错误率Bayes 分类器,写出得到的决策规则,将该分类器应用到训练/测试样本,考察训练/测试错误情况。
比较相关假设和不相关假设下结果的差异。
在分类器设计时可以考察采用不同先验概率(如vs. , vs. , vs. 等)进行实验,考察对决策和错误率的影响。
训练样本female来测试图1先验概率vs. 图2先验概率vs.图3先验概率vs. 图4不同先验概率对测试样本1进行试验得图对测试样本2进行试验有图可以看出先验概率对决策规则和错误率有很大的影响。
程序和3.自行给出一个决策表,采用最小风险的Bayes决策重复上面的某个或全部实验。
W1W2W10W20close all;clear all;X=120::200; %设置采样范围及精度pw1=;pw2=; %设置先验概率sample1=textread('') %读入样本samplew1=zeros(1,length(sample1(:,1)));u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布figure(1);subplot(2,1,1);plot(X,y1);title('F身高类条件概率分布曲线');sample2=textread('') %读入样本samplew2=zeros(1,length(sample2(:,1)));u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布subplot(2,1,2);plot(X,y2);title('M身高类条件概率分布曲线');P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);figure(2);subplot(2,1,1);plot(X,P1);title('F身高后验概率分布曲线');subplot(2,1,2);plot(X,P2);title('M身高后验概率分布曲线');P11=pw1*y1;P22=pw2*y2;figure(3);subplot(3,1,1);plot(X,P11);subplot(3,1,2);plot(X,P22);subplot(3,1,3);plot(X,P11,X,P22);sample=textread('all ') %读入样本[result]=bayes(sample1(:,1),sample2(:,1),pw1,pw2);%bayes分类器function [result] =bayes(sample1(:,1),sample2(:,1),pw1,pw2);error1=0;error2=0;u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);for i = 1:50if P1(i)>P2(i)result(i)=0;pe(i)=P2(i);elseresult(i)=1;pe(i)=P1(i);endendfor i=1:50if result(k)==0error1=error1+1;else result(k)=1error2=error2+1;endendratio = error1+error2/length(sample); %识别率,百分比形式sprintf('正确识别率为%.2f%%.',ratio)作业2 用身高/体重数据进行性别分类(二)基本要求:试验直接设计线性分类器的方法,与基于概率密度估计的贝叶斯分离器进行比较。
模式识别第三章作业

1. 在一个10类的模式识别问题中,有3类单独满足多类情况1,其余的类别满足多类情况2。
问该模式识别问题所需判别函数的最少数目是多少?答:25个判别函数。
将10类问题看作4类满足多类情况1的问题,先将3类单独满足多类情况1的类找出来,再将剩下的7类全部划到第4类中。
再对第四类运用多类情况2的判别法则进行分类,此时需要7*(7-1)/2=21个判别函数。
所有一共需要4+21=25个判别函数;2. 一个三类问题,其判别函数如下:d1(x)=-x1, d2(x)=x1+x2-1, d3(x)=x1-x2-1(1) 设这些函数是在多类情况1条件下确定的,绘出其判别界面和每一个模式类别的区域(2)设为多类情况2,并使:d12(x)= d1(x), d13(x)= d2(x), d23(x)= d3(x)。
绘出其判别界面和多类情况2的区域。
(3)设d1(x), d2(x)和d3(x)是在多类情况3的条件下确定的,绘出其判别界面和每类的区域3.两类模式,每类包括5个3维不同的模式,且良好分布。
如果它们是线性可分的,问权向量至少需要几个系数分量?假如要建立二次的多项式判别函数,又至少需要几个系数分量?(设模式的良好分布不因模式变化而改变。
)解:由总项数公式()!!!rw n rn rN Cr n++==,得1 44N C==;23210N C+==所以如果它们是线性可分的,则权向量至少需要4个系数分量;如要建立二次的多项式判别函数,则至少需要10个系数分量4.用感知器算法求下列模式分类的解向量w:ω1: {(0 0 0)T, (1 0 0)T, (1 0 1)T, (1 1 0)T}ω2: {(0 0 1)T, (0 1 1)T, (0 1 0)T, (1 1 1)T}解:将属于2ω的模式样本乘以(-1)进行第一轮迭代:取C=1,令w(1)= (0 0 0 0)Tw T(1)x①=(0 0 0 0)(0 0 0 1)T=0;故w(2)=w(1)+x①=(0 0 0 1)Tw T(2)x②=(0 0 0 1)(1 0 0 1)T=1>0,故w(3)=w(2)=(0 0 0 1)Tw T(3)x③=(0 0 0 1)(1 0 1 1)T=1>0,故w(4)=w(3)=(0 0 0 1)Tw T(4)x④=(0 0 0 1)(1 1 0 1)T=1>0,故w(5)=w(4)=(0 0 0 1)Tw T(5)x⑤=(0 0 0 1)(0 0 -1 -1)T=-1<0,故w(6)=w(5)+x⑤=(0 0 -1 0)Tw T(6)x⑥=(0 0 -1 0)(0 -1 -1 -1)T=1>0,故w(7)=w(6)=(0 0 -1 0)Tw T(7)x⑦=(0 0 -1 0)(0 -1 0 -1)T=0,故w(8)=w(7)+x⑦=(0 -1 -1 -1)Tw T(8)x⑧=(0 -1 -1 -1)(-1 -1 -1 -1)T=3>0,故w(9)=w(8)=(0 -1 -1 -1)T第二轮迭代:w T(9)x①=(0 -1 -1 -1)(0 0 0 1)T=-1<0;故w(10)=w(9)+x①=(0 -1 -1 0)Tw T(10)x②=(0 -1 -1 0)(1 0 0 1)T=0,故w(11)=w(10)+x②=(1 -1 -1 1)Tw T(11)x③=(1 -1 -1 1)(1 0 1 1)T=1>0,故w(12)=w(11)=(1 -1 -1 1)Tw T(12)x④=(1 -1 -1 1)(1 1 0 1)T=1>0,故w(13)=w(12)=(1 -1 -1 1)Tw T(13)x⑤=(1 -1 -1 1)(0 0 -1 -1)T=0,故w(14)=w(13)+x⑤=(1 -1 -2 0)T w T(14)x⑥=(1 -1 -2 0)(0 -1 -1 -1)T=3>0,故w(15)=w(14)=(1 -1 -2 0)T w T(15)x⑦=(1 -1 -2 0)(0 -1 0 -1)T=1>0,故w(16)=w(15)=(1 -1 -2 0)T w T(16)x⑧=(1 -1 -2 0)(-1 -1 -1 -1)T=2>0,故w(17)=w(16)=(1 -1 -2 0)T 第三轮迭代:…w T(24)x⑧=(2 -2 -2 0)(-1 -1 -1 -1)T=2>0,故w(25)=w(24)=(2 -2 -2 0)T 第四轮迭代:w T(25)x①=(2 -2 -2 0)(0 0 0 1)T=0;故w(26)=w(25)+x①=(2 -2 -2 1)T…w T(32)x⑧=(2 -2 -2 1)(-1 -1 -1 -1)T=1>0,故w(33)=w(32)=(2 -2 -2 1)T 第五轮迭代:….该轮迭代全部大于0所以w=(2 -2 -2 1)TMatlab 运行结果5.用多类感知器算法求下列模式的判别函数:ω1: (-1 -1)Tω2: (0 0)Tω3: (1 1)T解:将模式样本写成增广形式:x①=(-1 -1 1)T, x②=(0 0 1)T, x③=(1 1 1)T取初始值w1(1)=w2(1)=w3(1)=(0 0 0)T,C=1。
模式识别大作业

模式识别专业:电子信息工程班级:电信****班学号:********** 姓名:艾依河里的鱼一、贝叶斯决策(一)贝叶斯决策理论 1.最小错误率贝叶斯决策器在模式识别领域,贝叶斯决策通常利用一些决策规则来判定样本的类别。
最常见的决策规则有最大后验概率决策和最小风险决策等。
设共有K 个类别,各类别用符号k c ()K k ,,2,1 =代表。
假设k c 类出现的先验概率()k P c以及类条件概率密度()|k P c x 是已知的,那么应该把x 划分到哪一类才合适呢?若采用最大后验概率决策规则,首先计算x 属于k c 类的后验概率()()()()()()()()1||||k k k k k Kk k k P c P c P c P c P c P P c P c ===∑x x x x x然后将x 判决为属于kc ~类,其中()1arg max |kk Kk P c ≤≤=x若采用最小风险决策,则首先计算将x 判决为k c 类所带来的风险(),k R c x ,再将x 判决为属于kc ~类,其中()min ,kkk R c =x可以证明在采用0-1损失函数的前提下,两种决策规则是等价的。
贝叶斯决策器在先验概率()k P c 以及类条件概率密度()|k P c x 已知的前提下,利用上述贝叶斯决策规则确定分类面。
贝叶斯决策器得到的分类面是最优的,它是最优分类器。
但贝叶斯决策器在确定分类面前需要预知()k P c 与()|k P c x ,这在实际运用中往往不可能,因为()|k P c x 一般是未知的。
因此贝叶斯决策器只是一个理论上的分类器,常用作衡量其它分类器性能的标尺。
最小风险贝叶斯决策可按下列步骤进行: (1)在已知)(i P ω,)(i X P ω,i=1,…,c 及给出待识别的X 的情况下,根据贝叶斯公式计算出后验概率:∑==cj iii i i P X P P X P X P 1)()()()()(ωωωωω j=1,…,x(2)利用计算出的后验概率及决策表,按下面的公式计算出采取i a ,i=1,…,a 的条件风险∑==cj j j i i X P a X a R 1)(),()(ωωλ,i=1,2,…,a(3)对(2)中得到的a 个条件风险值)(X a R i ,i=1,…,a 进行比较,找出使其条件风险最小的决策k a ,即()()1,min k i i aR a x R a x ==则k a 就是最小风险贝叶斯决策。
华南理工大学《模式识别》大作业报告

华南理工大学《模式识别》大作业报告题目:模式识别导论实验学院计算机科学与工程专业计算机科学与技术(全英创新班)学生姓名黄炜杰学生学号 201230590051指导教师吴斯课程编号145143课程学分2 分起始日期 2015年5月18日实验内容【实验方案设计】Main steps for the project is:1.To make it more challenging, I select the larger dataset, Pedestrian, rather than thesmaller one. But it may be not wise to learning on such a large dataset, so Inormalize the dataset from 0 to 1 first and perform a k-means sampling to select the most representative samples. After that feature selection is done so as to decrease the amount of features. At last, a PCA dimension reduction is used to decrease the size of the dataset.2.Six learning algorithms including K-Nearest Neighbor, perception, decision tree,support vector machine, multi-layer perception and Naïve Bayesian are used to learn the pattern of the dataset.3.Six learning algorithm are combing into six multi-classifiers system individually,using bagging algorithm.实验过程:NormalizationThe input dataset is normalized to the range of [0, 1] so that make it suitable for performing k-means clustering on it, and also increase the speed of learning algorithms.SamplingThere are too much sample in the dataset, only a smallpart of them are enough to learn a good classifier. To select the most representative samples, k-means clustering is used to cluster the sample into c group and select r% of them.There are 14596 samples initially, but 1460 may be enough, so r=10. The selection of c should follow three criterions:a) Less drop of accuracyb) Little change about ratio of two classesc) Smaller c, lower time complexitySo I design two experiments to find the best parameter c:Experiment 1:Find out the training accuracy of different amountof cluster. The result is shown in the figure on the left. X-axis is amount of cluster and Y-axis is accuracy. Red line denotes accuracy before sampling and blue line denotes accuracy after sampling. As it’s shown in the figure, c=2, 5, 7, 9, 13 may be good choice since they have relative higher accuracy.Experiment 2:Find out the ratio of sample amount of two class. The result is shown in the figure on the right. X-axis is amount of cluster and Y-axis is the ratio. Red line denotes ratio before sampling and blue line denotes ratio after sampling. As it’s shown in the figure, c=2, 5, 9 may be good choice since the ratio do not change so much.As a result, c=5 is selected tosatisfy the three criterions.Feature selection3780 features is much more than needed to train a classifier, so I select a small part of them before learning. The target is to select most discriminative features, that is to say, select features that have largest accuracy in each step. But there are six learning algorithm in our project, it’s hard to decide which learning algorithm this feature selection process should depend on and it may also has high time complexity. So relevance, which is the correlation between feature and class is used as a discrimination measurement to select the best feature sets. But only select the most relevant features may introduce rich redundancy. So a tradeoff between relevance and redundancy should be made. An experiment about how to make the best tradeoff is done:the best amount of features isFind out the training accuracy of different amountof features. The result is shown below. X-axis is amount of features and Y-axis is accuracy. Red line denotes accuracyPCATo make the dataset smaller, features with contribution rate of PCA ≥ 85% is selected. So we finally obtain a dataset with 1460 samples and 32 features. The size of the dataset drops for 92.16% but accuracy only has 0.61% decease. So these preprocessing steps are successful to decrease the size of the dataset.Learning6 models are used in the learning steps: K-Nearest Neighbor, perception, decision tree, support vector machine, multi-layer perception and Naïve Bayesian. I designed a RBF classifier and MLP classifier at first but they are too slow for the reason that matrix manipulation hasn’t been designed carefully, so I use the function in the library instead. Parameter determination for these classifiers are:①K-NNWhen k≥5,the accuracy trends to be stable, so k=5②Decision treeMaxcrit is used as binary splitting criterion.③MLP5 units for hidden is enough。
模式识别大作业(二)

模式识别大作业(二)k-means 算法的应用一、 问题描述用c-means 算法对所给数据进行聚类,并已知类別数为2,随机初始样本聚类中心,进行10次求解,并计算聚类平均正确率。
二、 算法简介(1)J.B.MacQueen 在 1967 年提出的K-means 算法[22]到目前为止用于科学和工业应用的诸多聚类算法中一种极有影响的技术。
它是聚类方法中一个基本的划分方法,常常采用误差平方和准则函数作为聚类准则函数。
若i N 是第i 聚类i Γ中的样本数目,i m 是这些样本的均值,即1ii y m y N∈Γ=∑把i Γ中的各样本y 与均值i m 间的误差平方和对所有的类相加后为21ice i i y J y m =∈Γ=-∑∑e J 是误差平方和聚类准则,它是样本集y 和类别集Ω的函数。
e J 度量了用c 个聚类中心12,,...,c m m m 代表c 个样本子集12,,...,c ΓΓΓ时所产生的总的误差平方。
(2)K-means 算法的工作原理:算法首先随机从数据集中选取 K 个点作为初始聚类中心,然后计算各个样本到聚类中的距离,把样本归到离它最近的那个聚类中心所在的类。
计算新形成的每一个聚类的数据对象的平均值来得到新的聚类中心,如果相邻两次的聚类中心没有任何变化,说明样本调整结束,聚类准则函数 已经收敛。
本算法的一个特点是在每次迭代中都要考察每个样本的分类是否正确。
若不正确,就要调整,在全部样本调整完后,再修改聚类中心,进入下一次迭代。
如果在一次迭代算法中,所有的样本被正确分类,则不会有调整,聚类中心也不会有任何变化,这标志着 已经收敛,因此算法结束。
三、具体步骤1、 数据初始化:类别数c=2,样本类标trueflag(n,1) (其中n 为样本个数);2、 初始聚类中心:用随机函数随机产生1~n 中的2个数,选取随机数所对应的样本为初始聚类中心(mmnow);3、更新样本分类:计算每个样本到两类样本中心的距离,根据最小距离法则,样本将总是分到距离较近的类别;4、更替聚类中心:根据上一步的分类,重新计算两个聚类中心(mmnext);5、判断终止条件:当样本聚类中心不再发生变化即mmnow==mmnext时,转5);否则,更新mmnow,将mmnext附给mmnow,即mmnow=mmnext,转2);6、计算正确率:将dtat(i,1)与trueflag(i,1)(i=1~n)进行比较,统计正确分类的样本数,并计算正确率c_meanstrue(1,ii)。
模式识别方法大作业实验报告

《模式识别导论》期末大作业2010-2011-2学期第 3 组《模式识别》大作业人脸识别方法一---- 基于PCA 和欧几里得距离判据的模板匹配分类器一、 理论知识1、主成分分析主成分分析是把多个特征映射为少数几个综合特征的一种统计分析方法。
在多特征的研究中,往往由于特征个数太多,且彼此之间存在着一定的相关性,因而使得所观测的数据在一定程度上有信息的重叠。
当特征较多时,在高维空间中研究样本的分布规律就更麻烦。
主成分分析采取一种降维的方法,找出几个综合因子来代表原来众多的特征,使这些综合因子尽可能地反映原来变量的信息,而且彼此之间互不相关,从而达到简化的目的。
主成分的表示相当于把原来的特征进行坐标变换(乘以一个变换矩阵),得到相关性较小(严格来说是零)的综合因子。
1.1 问题的提出一般来说,如果N 个样品中的每个样品有n 个特征12,,n x x x ,经过主成分分析,将它们综合成n 综合变量,即11111221221122221122n n n n n n n nn ny c x c x c x y c x c x c x y c x c x c x =+++⎧⎪=+++⎪⎨⎪⎪=+++⎩ij c 由下列原则决定:1、i y 和j y (i j ≠,i,j = 1,2,...n )相互独立;2、y 的排序原则是方差从大到小。
这样的综合指标因子分别是原变量的第1、第2、……、第n 个主分量,它们的方差依次递减。
1.2 主成分的导出我们观察上述方程组,用我们熟知的矩阵表示,设12n x x X x ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦是一个n 维随机向量,12n y y Y y ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦是满足上式的新变量所构成的向量。
于是我们可以写成Y=CX,C 是一个正交矩阵,满足CC ’=I 。
坐标旋转是指新坐标轴相互正交,仍构成一个直角坐标系。
变换后的N 个点在1y 轴上有最大方差,而在n y 轴上有最小方差。
中科院模式识别第四次作业_详解

k neth = wih xik i
上标 k 联系 第 k 个样本
k y f (net ) f wih xi i k k k net j whj yh whj f wih xi h h i
第一步:输入层到隐含层的连接权重调节量:
待更新权 重的增量
k z E E j wih k wih k , j z j wih
z kj
j
k k z net E j j k k z net k, j j j wih k k k E z j net j yh k k k z net y k, j j j h wih k k k z net y E j j h k k k yh wih k , j z j net j k k k k neth E z j net j yh k k k k z net y net k, j j j h h wih
输入-隐层:第 k 个训练样本对权重 wih 的贡献
i h, for sample k:
规则:
wih |sample k x
k k h i
wih所连接的边的 起始结点(输入 层结点 i)的输出 (此时即为样本第 i 个分量)
wih所连接的边的指向结点(隐含 结点 h)收集到的误差信号
k net k w y hj h j h
k y (当 h h 时 h
才包含wih)
y wih t z z 1 z whj wih j
k j k j k j k j k h k k y net k k k h h t k z z 1 z w j j j j hj k net j h wih k k k k k t k z z 1 z w f net x j j j j hj h i j k jk whj f (neth ) xik j k jk whj f (neth )xik j
模式识别与机器学习_作业_中科院_国科大_来源网络 (1)
初始化:将每个样本分为 一类,总共 N 类,并计算 每二个类之间的距离 D
(0)
求取最小的距离,并对应 于第 i 类和第 j 类, 则将二 类进行合并,形成新类, N=N-1
N>D( 分 类 类 别数比预期 D 大) N=D( 达 到 所 需要分类的
求取新类与原来没合并的 类的距离,即新类中第 i 类 与各类距离和第 j 类与各类 距离中的较小者,形成 D
int INDEX[10]; //初始分类是以哪些点 int main() { cin>>SCALE; cin>>N>>K; for(int j=0;j<SCALE;j++) { for(int i=1;i<=N;i++) { cin>>XX[i][j]; } } for(int i=0;i<K;i++) cin>>INDEX[i]; doubledist[1000][10]; int classes[10][1000]={0}; doublemeanX[10][10],newMeanX[10][10]; intiindex[10]={0}; for(int i=0;i<K;i++) { for(int j=0;j<SCALE;j++) {
0 23 5 24 26 23 0 24 15 5 5 24 0 7 3 (0) , 1、 计算 D = 因为 x3 与 x5 的距离最近, 则 24 15 7 0 12 26 5 3 12 0
将 x3 与 x5 分为一类。同时可以求出 x1,x2,x4 与 x3,5 的距离,如 x1 到 x3,5 的距离为 x1 到 x3 的距离与 x1 与 x5 的距离中取最小的 一个距离。
模式识别作业马忠彧

作业1:线性分类器设计 1、问题描述将4个输入矢量分为两类,其中两个矢量对应的目标值为1,另两个矢量对应的目标值为0。
输入矢量为P =[-0.5 -0.5 0.3 0 -0.5 0.5 -0.3 1] 目标分类矢量为T =[1 1 0 0]2、算法描述采用单一感知器神经元来解决这个简单的分类问题。
感知器(perceptron )是由美国学者F.Rosenblatt 于1957年提出的,它是一个具有单层计算神经元的神经网络,并由线性阈值单元组成。
当它用于两类模式的分类时,相当于在高维样本空间中,用一个超平面将两类样本分开。
两类样本线性情况下,线性判别函数可描述为0()0T g x w x w =+=,其中12[,,...,]T l w w w w =是权向量,0w 是阈值。
假设两类样本线性可分,则一定存在一个由''0Tw x =定义的超平面,满足'1'2'0,'0,T T w x x w w x x w >∀∈<∀∈,其中0'[,1],'[,]T T T T x x w w w ==。
定义感知器代价函数为()()Tx x YJ w w x δ∈=∑,其中Y 是训练向量的子集,是权向量w 定义的超平面错误分类的部分。
变量11,x x w δ=-∈当时;21,x x w δ=∈当时。
为了计算出代价函数的最小迭代值,利用梯度下降法设计迭代方案,即()()(1)()tw w t J w w t w t wρ=∂+=-∂其中()x x YJ w w δ∈∂=∂∑,代入得 (1)()t x x Yw t w t x ρδ∈+=-∑这种算法称为感知器算法。
这个算法从任意权向量w(0)开始初始化,通过错误分类特征形成修正向量。
如此重复到算法收敛于解,即所有的特征向量都正确的分类。
可以证明,如果两类模式是线性可分的,则算法一定收敛。
感知器特别适合用于简单的模式分类问题。
模式识别作业—人工神经网络

模式识别大作业——外文翻译Artificial Neural Networks in Short Term load Forecasting 人工神经网络在短期负荷预测中地应用姓名:刘德龙学号: 03081413班级: 030814日期: 2011.05外文文献原文:Artificial Neural Networks in Short Term load ForecastingK.F. Reinschmidt, President B. LingStone h Webster Advanced Systems Development Services, Inc.245 Summer Street Boston, U 0221 0Phone: 617-589-1 84 1 Abstract:We discuss the use of artificial neural networks to the short term forecasting of loads. In this system, there are two types of neural networks: non-linear and linear neural networks. The nonlinear neural network is used to capture the highly non-linear relation between the load and various input parameters. A neural networkbased ARMA model is mainly used to capture the load variation over a very short time period. Our system can achieve a good accuracy in short term load forecasting.Key words: short-term load forecasting, artificial neural network1.IntroductionShort term (hourly) load forecasting is an essential hction in electric power operations. Accurate shoirt term load forecasts are essential for efficient generation dispatch, unit commitment, demand side management, short term maintenance scheduling and other purposes. Improvements in the accuracy of short term load forecasts can result in significant financial savings for utilities and cogenerators.Various teclmiques for power system load forecasting have been reported in literature. Those include: multiple linear regression, time series, general exponential smoothing, Kalman filtering, expert system, and artificial neural networks. Due to the highly nonlinear relations between power load and various parameters (whether temperature, humidity, wind speed, etc.), non-linear techniques, both for modeling and forecasting, tend to play major roles in the power load forecasting. The artificial neural network (A") represents one of those potential non-linear techniques. However, the neural networks used in load forecasting tend to be large in size due to the complexity of the system. Therefore, training of such a large net becomes a major issue since the end user is expected to run this system at daily or even hourly basis.In this paper, we consider a hybrid neural network basedload forecasting system. In this network, there are two types of neural networks: non-linear and linear neural networks. The nonlinear neural network is used to capture the highlynon-linear relation between the load and various input parameters such as historical load values, weather temperature, relative humidity, etc. We use the linear neural network to generate an ARMA model. This neural network based ARMA model will be mainly used to capture the load variation over a very short time period.The final load forecasting system is a combination of both neural networks. To train them, sigxuiicant amount of historical data are used to minimize MAPE (Mean Absolute Percentage Error). A modified back propagation learning algorithm is carried out to train thenon-linear neural network. We use Widrow-Hoff algorithm to train the linear neural network.Since our network structure is simple, the overall system training is very fast.To illustrate the performance of this neural network-based load forecasting system in real situations, we apply the system to actual demand data provided by one utility. Three years of hourly data (1989, 1990 and 1991) are used to train the neural networks. The hourly demand data for 1992 are used to test theoverall system.This paper is organized as follows: Section I is the introduction of this paper; Section I1 describes the variables sigdicantly affecting short term load forecasting; in Section III, wepresent the hybrid neural network used in our system; in Section IV, we describe the way to find the initial network structure; we introduce our load forecasting system in details in Section V; and in Section VI, some simulation result is given; finally, we describe the enhancement to our system in Section VII. 2.Variables Afferting Short-Term LoadSome of the variables affecting short-term electxical load are: TemperatureHumidityWind speedCloud coverLength of daylightGeographical regionHolidaysEconomic factorsClearly, the impacts of these variables depend on the type of load: variations in temperature, for example, have a largereffect on residential and commercial loads than on industrial load. Regions with relatively high residential loads will have higher variations in short-term load due to weather conditions than regions with relatively high industrial loads. Industrial regions, however, will have a greater variation due to economic factors, such as holidays.As an example, Figure 2.1 shows the loadvariation over one day, starting at midnight.Figure 2.1 Example of load variation during one day 3.Hybrid Neurak NetworksOur short-term load forecasting system consists of two types of networks:linear neural network ARMA model and feedforward .Non-linear neural network.The non-linear neural network is used to capture the highly non-linear relation between the load and various input parameters.We use the linear neural network to generate an ARMA model which will be mainly used to capture the load variation over a very short timeperiod(one hour).3.1 Linear Neutal NetworksThe general multivariate linear model of order p withindependent x,ist p t p i t i t t t p t p i t i t t t u x c x c x c x c x c z a z a z a z a z ++++++++++++=-------- 221102211Where:t z -electrical load at time tt x -independent variable at time tt u -random disturbance at time ti i c a ,-coefficientsLinear neural networks can successfully learn the coefficient and from the historrcal load data,and the independentvariables,Widrow-Hoff has been used to determine thecoefficient.This model includes all the previous data up to lag p.As shown above ,these data are not independent ,and have varying degrees of correlation with the load.Correlation studies can be used to determine the most significant parameters to be includes in the model,allowing many to be eliminated.This reduces the size and computer time for a model of givenaccuracy,or increases the accuracy for a model of given size.3.2 Non-Linear Neural NetworksFor non-linear forecasting,a nonlinear model analogous tothe linear model is:()t p t i t t t t p t i t t t t u x x x x x z z z z f z +=--------,,,,,,,,,,,2121where:f(.) is a nonlinear function determined by the artificial neural network.Layered, feed-forward neural networks are used, typically with one hidden layer (although in some cases with two). The layers are fully connected, with one bias unit in each layer (except the output layer). The output of each unit is the slum of the weighted inputs (including the bias), passed through an exponential activation fiinction.Our modiked backpropagation method is applied. The errors are defined to be the sum of the squares of the deviations between the computed values at the output units and the actual or desired values; this definition makes the error function differentiable everywhere.Unlike the linear time series model, in which there is one fitted coefficient for each lagged variable, in the nonlinear neural network forecaster tlhe selection of lagged inputvariables is independent of the number of fitted coefficients, the network weights, the number of which is determined by the number of layers and the number of hidden units. Also, in linear regression models, if an input variable is extraneous, then itsregression coefficient is zero (or, more properly, is not significantly different from zero by a t-test). However, in nonlinear neural networks this is not necessarily true; an input Variable may be unimportant but still have large weights; the effects of these weights cancel somewhere downstream. The same is true for the hidden units.Therefore, in conventional backpropagation for nonlinear neural networks, there is no automatic elimination of extraneous input nodes or hidden nodes. However, in practical forecasting it is necessary to achieve a parsimonious model, one which is neither too simple nor too complex for the problem at hand. If the neural network is chosen to be too small (to have too few input or hidden units), then it will not be flexible enough to capture ithe dynamics of the electrical demand system; this is known as underfitting. Conversely, if the neural network is too large, then it can fit not only the underlying signal but also the noise in the training set; this is known as overfitting. Overfitted models may show low error rates on the training set but do not generalize; they may then have high error rates in actual prediction.The nonlinear model can yield greater accuracy than the linear formulation, but takes much longer to train. Largenonlinear neural networks are also prone to overfitting. Forecasting requires parsimonious models capable of generalization. The size of the nonlinear neural network can be reduced by examining the correlation coefficients, or by using the genetic algorithm to select the optimum set of input variables. The linear model is a satisfactory approximation to the nonlinear model for the purpose of selecting the input terms.Large artificial neural networks trained using backpropagation are notoriously time-consuming, and a number of methods to reduce training time have been evaluated. One method that has been found to yield orders of magnitude reductions in training time replaces the steepest descent search by techniques that model the network weights using a least-squares approach; the computations in each step are greater but the number of iterations is greatly reduced. Reductions in training time are desirable not only to reduce computation costs, but to allow more alternative input variables to be investigated, and hence to optimize forecast accuracy.4.Determination of Network StructureAs we stated above, the neural network used in loadforecasting tends to be large in size, which results in longer training time. By carefully choosing network structure (i.e., input nodes, output nodes), one will be able to build arelatively small network. In our system, we apply statistical analysis and genetic algorithm to find the network "optimal" structure which is used as a base for further network turning.4.1 AutocorrelationFirst-order linear autocorrelation is the correlation coefficient between the loads at two different times, and is given by:()()[]τρτ-=t z t z Ewhere: τρis the autocorrelation at lag zE [] is the expected valuez(f) is the electrical load at time t.Figure 4.1 shows the hourly variation in the laggedautocorrelation of electrical demand for a particular electric utility. This plot confirms common sense experience, that the load at any hour is very highly correlated with the load at the same hour of previous days. It is interesting, and useful for forecasting, that the autocorrelation for lags at multiples of 24 hours remains high for the entire preceding week the peak correlation falls to about 0.88 for loads four days apart, butrises again for loads seven days apnpart.Figure 4.1 Autocorrelation of utility electrical load g hoursWe also analyze the sample partial autocorrelation function (PACF) of the time series of load. This is a measure of the dependence between zt+h and z, after removing the effect of the intervening variables zt+ , Z~ 2, .... Zt+h-l .Figure 4.2 shows the PACF of load series. It can be observed that load variation is largely affected by one at previous hour. This indicates that one-hour ahead forecast would be relatively easy.4.2 Genetic AlgorithmThe most significant coefficients in the time series model can be identified automatically byusing the genetic algorithm. Unlike the back propagation method,which minimizes the sum of squares of the errors,the genetic algorithm can minimize the MAPE directly.MAPE stands for Mean Absolute Percentage Error which is widely used as a measure in load forecasting.To represent the forecasting model in the genetic algorithm, a string is defined ,consisting of the lag values,I,and the coefficients at each lag, a, or c,. Then a string would be as follows:constant term first lag,i1ai1,coefficient of zsecond lag,i2ai2,coefficient of z…………p-th lag,ipaip,coefficient of zlag j1 of the first independent variablecj1,coefficient of xlag j2 of the second indepent variablecj2,coefficient of x…………lag jp of the p-th independent variablecjp coefficient of xA population of these strings is generated randomly. Then pairs of strings are selected randomly (with probabilities inversely proportional to their respective MAPEs);a crossover point in both strings is selected randomly; and the two parent strings reproduce two new strings by crossover.This processproduces a new generation of strings.The fitness (the inverse of the MAPE of the forecasts generated by the string across the training set of load data) is computed for each strings,those with low fitness are discarded and those with high fitness survive to reproduce in the next generation. Mutation is also used to modify individuals randomly in each generation. The result of ai number of generations of this selection process is a string with high fitness (low MAPE) that is the best predictor of the electrical load over the training set.5.Short Term Load Forecasting SystemOur short term load forecasting system is a combinatiori of linear neural network (ARMA model) ancl non-linear neural network. The overall system structure is shown in Figure 5.1.Figure 5.1 Structure of our short term load forecasting systemIn this system, both linear and non-linear systems have historical data as input which include all or some of the variables listed in Section 11. 'The data processor is used to extract data from Ihe historical data set for linear and non-linear neural networks, respectively. The output of linear neural network is fed into the non-linear neural network as input. With historical data and output of linear neural network as input, the non-linear neural network generates forecasted load values over one day to one week.The initial network structure for both networks are based on statistical analysis and genetic algorithm. As shown in Figure 4.2, the load value at tiime t is largely dependent upon the historical load at f-1. Therefore, accurate onehour ahead forecast will improve the short term load forecast.However, for one-day (24 hours) and/or one week (168 hours)ahead forecast, the load value at the previous hour is also a forecasted value. For example, suppose we want to forecast the load at 10 a.m. tomorrow. Obviously, the load at 9 a.m. tomorrow is not available. What we have is the forecasted load value at 9 a.m. tomorrow. Since the load at 10 a.m. is very sensitive with respect to the load at 9 a.m., accurate forecast of load at 9 a.m. will improve the forecast of load at 10 a.m. In our system, the linear neural network (ARMA model) is used for one-hour ahead load forecastFor the non-linear network, the input layer consists of variables at Werent time lags. Although the load at time t is sigmlicantly aEected by the load at f-1, the load at f-1 itself is not sufficient in order to forecast load at f accurately. This is mainly due to the long term variation (see Figure 4.1).6.Simulation ResultWe have been able to access the historical load data and various weather data at a utility company. The data we choose for simulation is the historical hourly load values in 1989, 1990 and 1991; the hourly temperatures in the same years.The non-linear neural network consists of 24 subnets, each represents one particular hour in one day. Similarly, there are 24 subnet for the linear neural network. All of these 48 subnetshave multiple input nodes, but only ONE output node. At any moment, only one non-linear subnet and one linear subnet is activated (total only two nets). This unique structure has the following advantages:(1) Fast to generate load forecast;(2) Fast to re-train the system;(3) Modularization. Updating system is determined by the forecasting accuracyat particular hours.(4) High accuracy.Note that these advantages are important in the commercial application of our system. Speed and accuracy are essential for utilities to use load forecasting system at hourly/daily basis. We use historical load and temperature data in 1989 and 1990 for training; load and temperature in 1991 for testing. During training and testing, the actual future temperatures are used. Figure 6.1 shows the 24-hour ahead MAPE of our system in testing case with data in the first quarter of 1991.Figure 6.1 MAPE of testing result for the first quarter of 19917.EnhancementFrom our experience, we find that a system with ONLY traditional neural networks is not sufficient to handle with various situations which utilities encounter quite often, For example, the system trained with regular data will not be able to produce good load forecast when there are some whether sudden changes. These problems can not be solved by simply adding similar historical data points into training data set since these points are not enough for the system to learn.We are adding two additional subsystems to our short term load forecasting system, namely,rule-based system and pattern recognition system. These two subsystems perform different task and are activated under certain situation such as those mentioned above.7.1 Rule-Based SystemNeural networks for pattern recognition, genetic algorithms, and artificial neural network models of time series produce usable short-term electric load forecasts. However, to obtain the minimum forecasting error with acceptable model complexity and training time requires tuning of the model parameters to the conditions of specificutilities.Particularly for regional forecasts,particular geographic regions and service areas may be more or less sensitive to factors such as tempearature andholidays,depending on whether the load is primarly industrial,commercial,or residential,on whether the load is summer-peaking or winter-peaking,etc.In ordr for a short-term electrical load forecasting system to be successfully used by utility dispatchers and others with no background in artificial intelligence,while at the same time achieving the best performance,it is necessary to supply rules for setting the various parameters according to the local conditions.7.2 Pattern Recognition SystemOne approach to daily forecasting used by manyutilities,given a large database of hourly loads,is to locatea day in the record that is similar to the day to be forecasted, and use that day as a basis for a forecast.The issue is how to select a similar day from the historical record. There are many possible ways to define similarity,one we used is the Mean Absolute Percentage Error(MAPE).We have concluded:(1) Neural networks can be used to recognize patterns and to estminate the similarity matching.(2) These neural network forecasts should be combined with other,independent forecasts,such as obtained from time series(tapped delay line)methods,with weights based on the variances of the errors in each method.ConclusionIn this paper, we consider a hybrid neural network based load forecasting system which consists of linear and non-linear neural networks. We have demonstrated that our system is ideal for utility and ready for commercial applications,We also describe two subsystems as the enhancement to our existing system to handle various unusual situations.译文:人工神经网络在短期负荷预测中地应用摘要:在本文,我们将讨论如何利用人工神经网络对短期负荷进行预测.在这类系统中,有两种类型地神经网络:非线性和线性神经网络.非线性神经网络是用来捕获负荷和各种输入参数之间地高度非线性关系.基于ARMA模型地神经网络,主要用来捕捉很短地时间期限内负载地变化.我们地系统可以实现准确性高地短期负荷预测.关键词:短期负荷预测,人工神经网络1.绪论短期(每小时)负荷预测对于电力系统地稳定运行是必要地.准确地负荷预测对于高效地发电调度,开停机计划,需求方地管理,短时维护安排或其他目地等是很必要地.改进短期负荷预测地准确性能为公共事业和联合发电节省很多开支.很多种电力系统负荷预测方法在学术界已经报导了.这些方法包括:多元线性回归法,时间序列法,一般指数平滑法,卡尔曼滤波法,专家系统法和人工神经网络预测法.由于电力负荷和各种参数(天气地温度,湿度,风速等)之间地高度非线性地关系,无论在电力负荷预测建模或在预测中都有重要地作用.人工神经网络就是这种具有潜力地非线性技术地代表,但是由于电力系统地复杂性,神经网络地规模会较大,所以,当终端用户每天甚至每小时都在改变系统地运行时,训练这个网络将是一个重大地问题.在本文中,我们把这网络看作是建立在负荷预测系统上地混合神经网络.这类网络中包含两类网络:非线性神经网络和线性神经网络.非线性神经网络常用来捕获负荷与各种输入参数(如历史负荷值.气象温度.相关湿度等)间地高度非线性关系.我们常用线性神经网络来建立ARMA模型.这种基于ARMA模型地神经网络主要用来捕获负荷在很短时间期限内地变化.最终地负荷预测系统是两种神经网络地组合.要用大量地历史数据来训练神经网络,以减小平均绝对误差百分比 (MAPE).一种改进地反向传播学习算法已经用来训练非线性神经网络.我们使用Widrow -霍夫算法训练线性神经网络.当网络结构越简单,那整个系统地训练也就越快.为了说明这个基于实际情况地负荷预测系统地神经网络地性能,我们采用一个公共机构提供地实际需求数据来训练系统,利用三年(1989,1990,1991)中每小时地数据来训练这个神经网络,用1992年每小时地实际需求数据用来验证整个系统.这文章内容安排如下:第一部分介绍本文内容;第二部分描述了影响负荷预测结果地因素;第三部分介绍了混合神经网络在系统中地应用;第四部分描述了找到最初网络结构地方法.第五部分详细介绍了负荷预测系统;第六部分给出了一些仿真结果;最后,第七部分介绍了系统地优化处理.2.各种影响负荷预测地因素以下是一些影响负荷预测地因素:温度湿度风速云层日照时间地理区域假期经济因素显然,这些因素地影响程度取决于负荷地类型.例如:温度变化对民用和商业负荷地影响大于它对工业负荷地影响.相对较多民用负荷地区域地短期负荷受气候条件影响程度大于工业负荷较多地区域.但是,工业区域对于经济因素较为敏感,如假期.如下一个例子,图2.1表示了午夜开始地一天中负荷地变化.图2.1 一天中负荷变化地示例3.混合神经网络我们所研究地负荷预测系统由两类网络组成:ARMA模型地线性神经网络和前馈非线性神经网络.非线性神经网络常用来捕获负荷与各种输入参数间地高度非线性关系.我们常用线性神经网络来建立ARMA模型,这种基于ARMA模型地神经网络主要用来捕获负荷在很短时间期限(一个小时)内地变化.3.1 线性神经网络一般地多元线性地调整参数p 和独立变量x 地关系是:t p t p i t i t t t p t p i t i t t t u x c x c x c x c x c z a z a z a z a z ++++++++++++=-------- 221102211其中:t z -t 时刻地电力负荷t x -t 时刻地独立变量t u -t 时刻地随机干扰量i i c a , -系数线性神经网络能成功地学习历史负荷数据i t z -和独立变量i t x -中地系数i a 和i x ,Widrow-Hoff 已经决定了这些系数.这个模型包括了先前所以数据高达p 地延迟,如上所示,这些数据不是独立地,它与负荷有不用程度地相关性.相关性学习用来决定模型中包含地最重要地参数,决定了许多参数会被去掉.这样就减少了给定精度模型地大小和运算时间或是提高了给定规模大小地模型地精度.3.2 非线性神经网络为了能进行非线性预测,要建立一个类似线性模型地非线性模型,如下表示:()t p t i t t t t p t i t t t t u x x x x x z z z z f z +=--------,,,,,,,,,,,2121其中:().f 是由人工神经网络决定地非线性函数前馈神经网络用层来表示,通常有一个隐含层(在某些情况下有2层),层和层之间是充分联系地,每一层有一个偏置单元(输出层除外).输出是每个单元地加权输入地总和(包括偏置),中间是通过指数激活函数来传递.我们已经应用了修正地反向神经网络.错误地是定义了输出单元地计数值和实际值或理想值之间地偏差地平方,这个定义使函数在微分地时候发生错误.不像线性地时间序列模型那样在每个滞后变量有一个装有系数,非线性神经网络滞后输入变量地选择和装有系数地数量是独立地,而网络地规模,是有由层数和隐含层单元地数目决定地.此外,在线性回归模型中,如果输入变量是无关地,那么它地回归系数是零.但是在非线性神经网络中者不一定是真实地;一个输入变量可能不重要但是仍可能有权重;这些权重将会影响到下层地传递,对于隐含单元来说也是重要地.所以,在传统地反向传播神经网络中,没有自动消除无关输入节点和隐含节点地功能.但是,在实际预测中有必要建立一个简约模型,它能解决实际问题,但不会太简单也不会太复杂.如果神经网络太小(输入端少或是隐含单元少),就不够灵活来捕获电力系统地动态需求变化.这就是我们所知地“欠拟合”现象.相反地,如果神经网络太大,它不仅可以容纳基本信号,还可以容纳训练时地噪声,这就是我们所知地“过拟合”现象.“过拟合”模型可能在训练时显示较低地错误率,但不能以偏概全,可能在实际预测时会有较高地错误率.非线性模型可以产生比线性规划更高地准确度,但是要更长地训练时间.较大地神经网络容易出现“过拟合”,预测需要简约模型地一般化概括.非线性神经网络地大小可以通过检查相关性系数或是通过遗传算法来选择最优地输入变量来减小.线性模型相对于非线性模型来说是一个令人满意地模型,而非线性模型是用来决定输入参数地.用反向传播来训练大型地人工神经网络是很耗费时间地,很多用来减少训练时间地方法已经通过评估,已经找到一个减少训练时间地方法来取代使用最小二乘法来修改网络权重而达到速下降搜索地技术.每一步地计算量大了,但是迭代次数却大大减少.减少训练时间是我们希望达到地,不仅可以通过减少计算消耗,也可以通过研究考虑更多地可取地输入变量来达到,从而达到优化预测地精度.4.神经网络结构地确定4.1 自动校正一阶线性自动校正就是校正负荷在两个不同时间之间地校正系数,可以用下式表示:()()[]τρτ-=t z t z E其中:τρ是在τ时地自动校正系数[]E 是期望值()t z 是在t 时刻地电力负荷值图 4.1显示了滞后于某个特殊电力用户地电力需求自动校正系数地每小时负荷变化.这个图证实了常识经验,就是在任何时候地负荷与前几天同一时刻地负荷有高度相关性.这很有趣,并且对负荷预测很多帮助,另外,滞后地自动校正在24小时中比前整个一周都高出许多.除了前4天,负荷地相关峰值下降到0.88外,第7天又上升了.图4.1电力负荷自动校正系数与滞后时间地比较我们也分析了样本负荷在时间序列上地偏自相关函数(PACF ).这衡量去除了干扰变量121,,,-+++h t t t z z z 后h t z +和t z 之间地依赖关系.图4.2显示了负荷序列地PACF.可以观测到,负荷变化与之前地负荷有很大影响,这就表明一个小时后地负荷预测将会变得简单.图4.2 上午1点负荷地PACF4.2 遗传算法在时间序列模型中重要系数可以通过遗传算法自动鉴定出,不像反向传播模型地最小平方误差那样,遗传算法可以直接将MAPE 减到最小.MAPE 就是平均绝对误差百分比,它广泛用于衡量负荷预测地准确度.为了描述遗传算法里地负荷预测模型,要定义一根曲线,它包括滞后值i 和每个滞后地系数i a 或是i c ,那么这根曲线可以表示为:常数项 第一个滞后,1i 1i a 系数1i t z -第二个滞后,2i 2i a 系数2i t z -…………th p -滞后,p i ip a 系数ip t z -第一个独立变量地滞后1j ,1j c 系数1j t x -第二个独立变量地滞后2j ,2j c 系数2j t x -…………独立变量地滞后p j ,jp c 系数jp t x -这样一种曲线是随机产生地.然后两根曲线被随机选择(与它们地MAPEs 地概率成反比).两根曲线地交叉点被随机选择,而两条母曲线通过交叉点复制两条新地曲线.这个过程中产生了新一代地曲线.将会计算出每一条曲线地适应值(通过一组负荷数据训练而产生地预测MAPE 地逆值).这些低适应能力地将会被丢弃,高适应能力地将会繁殖下一代.突变也用来随机修改下一代中独特地.结果就是经过多代地繁殖过程,曲线具有高度地适应性(低MAPE 值),这就是用电力负荷通过训练后最好地预测值.5.短期负荷预测系统本文地短期负荷预测系统是一个线性神经网络(ARMA模型)和非线性神经网络地组合.整个系统地结构如图5.1示.图5.1 短期负荷预测系统地结构图在这个系统中,线性系统和非线性系统两者都有第二部分中提到地影响负荷预测地几种或全部因素作为历史数据地输入.数据处理器地数据是从线性和非线性神经网络地历史数据中提取出来地,分别地,线性神经网络地输出作为反馈,输入到非线性神经网络中.有历史数据和线性神经网络地输出作为输入,非线性神经网络就会预测出一天或者一周地负荷值.这两个网络组成地最初地网络结构是基于统计分析和遗传算法.如图4.2所示,t时刻地负荷值很大程度上取决于1 t时刻地历史负荷值.所以,准确地预测1小时后负荷地会提高短期负荷预测准确度.但是,一天(24小时)后或在一个星期(168小时)后地预测,在之前地几个小时地负荷值仍然是预测值.例如,我们要预测明天上午10点地负荷值,显然,我们拥有地明天上午9点地负荷值不是实际值,我们只有明天上午9点地预测值.因为在9点地负荷对10点地负荷地影响较密切,准确地预测9点地负荷会提高预测10点负荷地准确度.在我们这个系统中,线性神经网络(ARMA模型)是用来预测一个小时后地负荷值地.对于非线性神经网络来说,输入层包括不同时间滞后地变量.虽然t时刻地负荷受到1-t时刻地显著影响,但是1-t时刻地负荷本身地准确度不足够以至影响预测t时刻负荷地准确度.这主要受长期负荷变化地影响(见图4.1)6.仿真结果我们可以通过公共事业公司获得历史数据和各种天气数据.我们用来仿真地数据是1898,1990和1991年地每小时历史负荷数据和当年地每小时地温度数据.非线性神经网络由24个子网组成,没一个代表一天中一个特定地时间.相似地,线性神经网络也有24个子网.全部48个子网有很多个输入节点,但是只有一个输出节点.在任何时候,只有一个非线性子网和一个线性子网在工作(总共只有2个网).这种独一无二地结构具有以下优点:(1)预测速度快(2)重新训练系统快(3)模块化.可以在特定时间根据预测精度更新系统(4)预测精度高可以得出系统地这些优点对于商业应用来说是很重要地.根据每小时或每天预测地原则来说,预测速度很精度对于公共事业来说是非常需要地我们用1898和1990年地历史负荷数据和温度数据来训练;1991年地负荷和温度来作验证.在训练和验证期间,用到了未来地实际温度.图6.1显示了利用1991年第一季度地数据验证我们地系统预测24小时后地MAPE值曲线.图6.1 1991第一季度MAPE地验证结果7.优化处理由经验可知,我们发现只有一个传统神经网络地系统不足够处理我们往往遇到地那些具有多种变化情况地公共事业公司.例如,当天气突然变化时,利用常规地数据来训练系统不能得到较好地预测效果.当系统地历史数据点不足够系统来学习时,可以通过简单地增加相似地历史负荷点到训练数据中来解决上述问题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Homework #2Note:In some problem (this is true for the entire quarter) you will need to make some assumptions since the problem statement may not fully specify the problem space. Make sure that you make reasonable assumptions and clearly state them.Work alone: You are expected to do your own work on all assignments; there are no group assignments in this course. You may (and are encouraged to) engage in general discussions with your classmates regarding the assignments, but specific details of a solution, including the solution itself, must always be your own work.Problem:In this problem we will investigate the importance of having the correct model for classification. Load file hw2.mat and open it in Matlab using command load hw2. Using command whos, you should see six array c1, c2, c3 and t1, t2, t3, each has size 500 by 2. Arrays c1, c2, c3 hold the training data, and arrays t1, t2, t3 hold the testing data. That is arrays c1, c2, c3 should be used to train your classifier, and arrays t1, t2, t3 should be used to test how the classifier performs on the data it hasn’t seen. Arrays c1 holds training data for the first class, c2 for the second class, c3 for the third class. Arrays t1, t2, t3 hold the test data, where the true class of data in t1, t2, t3 comes from the first, second, third classed respectively. Of course, array ci and ti were drawn from the same distribution for each i. Each training and testing example has 2 features. Thus all arrays are two dimensional, the number of rows is equal to the number of examples, and there are 2 columns, column 1 has the first feature, column 2 has the second feature.(a)Visualize the examples by using Matlab scatter command a plotting each class indifferent color. For example, for class 1 use scatter(c1(:,1),c1(:,2),’r’);. Other possible colors can be found by typing help plot.(b)From the scatter plot in (a), for which classes the multivariate normal distribution lookslike a possible model, and for which classes it is grossly wrong? If you are not sure how to answer this part, do parts (c-d) first.(c)Suppose we make an erroneous assumption that all classed have multivariate normalNμ. Compute the Maximum Likelihood estimates for the means and distributions()∑,covariance matrices (remember you have to do it separately for each class). Make sure you use only the training data; this is the data in arrays c1, c2, and c3.(d)You can visualize what the estimated distributions look like using Matlab contour().Recall that the data should be denser along the smaller ellipse, because these are closer to the estimated mean.(e)Use the ML estimates from the step (c) to design the ML classifier (this is the Bayesclassifier under zero-one loss function with equal priors). Thus we are assuming that priors are the same for each class. Now classify the test example (that is only thoseexamples which are in arrays t1, t2, t3). Compute confusion array which has size 3 by 3, and in ith row and jth column contains the number of examples fro which the true class isi while the class your classifier gives is j. Note that all the off-diagonal elements in theconfusion array are errors. Compute the total classification error, easiest way to do it is to use Matlab function sum() and trace().(f)Inspect the off diagonal elements to see if which types of error are more common thanothers. That should give you an idea of where the decision boundaries lie. Now plot the decision regions experimentally (select a fine 2D grid, classify each point on this grid, and plot the class with distinct color). If you love solving quadratic systems of equations, you can find the decision boundaries analytically. Using your decision boundaries, explain why some errors are more common than others.(g)If the model assumed for the data is wrong, than the ML estimate of the parameters arenot even the best parameters to use for classification with that wrong model. That is because the multivariate normal is the wrong distribution to use with out data, the MLE parameters we computed in part (c) are not the ones which will give us the best classification with our wrong model. To confirm this, find parameters for the means and variances (you can change as many as you like, from one to all) which will give better classification rate than the one you have gotten in part (e). Hint: it pays to try to change covariance matrices, rather than the means.(h)Now let’s try to find a better model for our data. Notice that to determine the class of apoint; it is sufficient to consider the distance of that point from the origin. The distance from the origin is very important for classifying our data, while the direction is totally irrelevant. Convert all the training and testing arrays to polar coordinates using Matlib function cart2pol(). Ignore the first coordinate, which is the angle, and only use the second coordinate, which is the radius (or distance from the origin). Assume now that all classes come from normal distribution with unknown mean and variance. Estimate these unknown parameters using ML estimation again using only the training data (the arrays ci’s). Test how this new classifier works using the testing data (the arrays ti’s) by computing the confusion matrix and the total classification error. How does this classifier compare with the one using the multivariate normal assumption and why is there a difference?(i)Experimentally try to find better parameters than those found by ML method for classifierin (h). If you do find better parameters, do they lead to a significantly better classification error? How does it compare to part (g)? Why can’t you find significantly better parameters than MLE for the classifier in (h)?。
