利用法向量解立体几何题
用向量法解五类立体几何题的思路
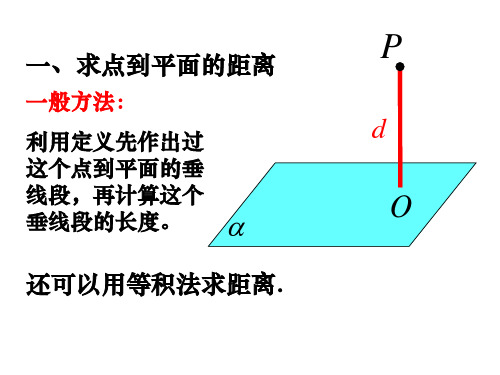
思路探寻立体几何问题的命题形式很多，常见的有求平面外一点到平面的距离，求两条异面直线之间的距离，求直线与平面所成的角，求二面角，证明面面平行、垂直等.有时采用常规方法求解立体几何问题比较复杂，甚至很难获得问题的答案，此时不妨运用向量法，将立体几何问题转化为向量运算问题，通过简单的计算即可解题.向量法是指给线段赋予方向，给各个点赋予坐标，通过向量运算求得问题的答案.下面结合实例探讨一下如何运用向量法求解五类立体几何问题.一、求平面外一点到平面的距离如图1，若点P 为平面α外的任意一点，要求P 到平面α的距离，需先求得向量OP 以及平面α的法向量n .那么法向量n 方向上的正射影长h =|| OP sin <OP ，n >=|| OP ∙n||n ，即为P 到平面α的距离.运用向量法求平面外一点到平面的距离，主要是运用向量数量积的几何意义：一个向量与其在另一个向量方向上的投影的乘积.图1图2例1.在正方体ABCO -A 1B 1C 1O 1中，M 、N 是B 1C 1和C 1O 1的中点，正方体的棱长是1，求A 1与平面OBMN 之间的距离.解：以O 为原点，建立如图2所示的空间直角坐标系，可得 OB =（1，1，0）， O N =（0，12，1）， OA 1=（1，0，1），设平面OBMN 的法向量是n =（x ，y ，z ），则{n ∙ O B =0，n ∙ ON =0，即ìíîïïx +y =0，12y +z =0，令x =1，y =-1，z =12，则n =（1，-1，12），则A 1到平面OBMN 的距离h =|| OA 1∙n||n =1.由于无法确定点A 1到平面OBMN 的射影，所以根据法向量与射影的关系，运用向量法求解.运用向量法求平面外一点到平面的距离，关键是要根据线面垂直的判定定理求得平面的法向量.在求法向量时，往往要先设出法向量n ；然后在平面内找到两条直线a 、b ，并求得其方向向量a 、b ；再建立方程组{n ∙a =0，n ∙b=0，通过解方程组求得法向量n 的坐标.二、求空间中两条异面直线之间的距离求两条异面直线之间的距离，需运用转化思想，把两条异面直线之间的距离转化为平面外一点到平面的距离.在求两条异面直线之间的距离时，需先求出两条异面直线的方向向量a 、b，并求得两个向量所在平面的法向量n ，那么两条异面直线之间的距离为h =||a ∙n ||n .例2.如图3，正方体ABCO -A 1B 1C 1O 1的棱长为1，求异面直线OA 1和AC 之间的距离.解：以O 为原点，建立如图3所示的空间直角坐标系，可得 AC =（-1，1，0）， O 1A =（1，0，-1）， AA 1=（0，0，1）设n =（x ，y ，z ）为平面A 1C 1O 的法向量，建立方程组得ìíîn ∙ AC =0，n∙O 1A =0，即{-x +y =0，x -z =0，图346思路探寻令x=1，可得法向量n =（1则异面直线OA1和AC.定两条异面直线的公垂线，繁琐.的方向向量及其法向量，求得异面直线之间的距离，果.三、求直线与平面所成的角如图4所示，设直线OP用向量法求直线OP与平面αα的法向量n 和直线OP的数量积公式求得|cos< OP,n >OP与平面α所成角的正弦值为意的是，直线OP与平面α图4例3.如图5，正方体ABCOA1B1的中点为M，试求直线AM的正弦值.解：以O为原点，建立如图5则AB=（0，1，0），AO1=（-1设n =（x，y，z）为平面ABC1O则ìíîn ∙AB=0，n ∙AO1=0，即{y=0，-x+z=0令x=1，可得n =()1,0,1，设AM与面ABC1O1则sinθ=|| AM∙n|| AM∙||n ，即直线AM与平面ABC1O1α-的平面1，.）为平面往往要先求得两个平47探索探索与与研研究究面的法向量，α、β的法向量n α∥ n β，则平面α的法向量 n α⊥ n β，则平面α⊥例5.正方体ABCO -A 1B 1C 1O M 分别是A 1C 1、A 1O 、B 1A 上的任意一点，求证：平面B 1MC ∥平面A 1EF .证明：以O 为原点，建立如图8所示的空间直角坐标系，由题意可得A 1C 1=()-1,1,0,B 1C =()-1,0,-1,A 1O =()-1,0,-1,B 1A =()0,-1,-1，设 A 1E =λ A 1C 1， A 1F =μ A 1ν∈R ，且均不为0），设平面A 1EF 的法向量为n 1则ìíî n 1∙A 1E =0，n 1∙ A 1F =0，可得ìíî n 1∙λ A 1 n 1∙μ A 1则ìíî n 1∙A 1C 1=0， n 1∙ A 1O =0，则{-x +y =0x +z =01EF 的法向量为n 1=（1，1，-1），n 2，ìíî n 2∙ν B 1A =0，n 2∙ B 1C =0，{-y -z =0，-x -z =0，1MC 的法向量n 2=（-1，1，-1），n 1∥ n 2，B 1MC .需熟悉向垂直关系，⊥ n 2； n 1=λ n 2⇔ n 1∥ n 2.需注意以（2）熟练运用（3）明确向量与线段、坐标甘肃省武威铁路中学）求数列前n 项和问题具有较强的综合性，侧重考查等差和等比数列的通项公式、定义、性质以及前n 项和公式.常见的命题形式有：（1）根据数列的递推关系式求数列的前n 项和；（2）根据数列的通项公式求数列的前n 项和；（3）根据一个数列的前n 项和求另一个相关联数列的前n 项和.解答数列求和问题的常用方法有分组求和法、错位相减法、裂项相消法、并项求和法、倒序相加法.下面结合实例,谈一谈这几种途径的特点以及应用技巧.一、分组求和分组求和法是指将数列中的各项分为几组，分别进行求和.在解题时，要先仔细研究数列的通项公式，将其合理地拆分为几个等差、等比、常数数列通项公式的和、差；再将数列划分为多个组，分别根据等差、等比数列的前n 项和公式求得每一组数列的和.例1.已知S n 为数列{}a n 的前n 项和，4a n =3S n +1.48。
空间立体几何坐标法向量法求线面交点坐标-概述说明以及解释
空间立体几何坐标法向量法求线面交点坐标-概述说明以及解释1.引言1.1 概述空间立体几何是数学中的一个重要分支，它研究三维空间中的几何结构和性质。
在空间立体几何中，线和面是两个基本的几何元素，线面交点坐标的求解是一个常见且重要的问题。
本文主要介绍了两种方法来求解线面交点的坐标：坐标法和向量法。
通过这两种方法，可以方便地求解线面交点的坐标，进而解决一些实际问题。
通过本文的学习，读者将能够掌握空间立体几何中线面交点坐标的求解方法，为进一步深入学习和应用空间几何提供了基础。
同时，本文还将探讨线面交点坐标的应用和展望，展示其在现实生活中的重要性和价值。
1.2 文章结构:本文主要分为引言、正文和结论三部分。
引言部分将从概述、文章结构和目的三个方面介绍本文的主要内容和研究背景。
正文部分将分为三个小节，首先是关于空间立体几何概念的介绍，接着是详细讨论如何利用坐标法求解线面交点坐标的方法，最后则是向量法求解线面交点坐标的具体过程。
结论部分将总结本文的主要观点和研究成果，探讨该方法的应用前景，并进行最终的结语。
1.3 目的:本文旨在介绍如何利用空间立体几何中的坐标法和向量法来求解线面交点坐标的方法。
通过深入讨论这两种方法的原理和步骤，我们希望读者能够更加深入地理解空间几何中的相关概念，并能够灵活运用这些方法解决实际问题。
通过掌握线面交点坐标求解的技巧，读者能够提升空间几何解题的效率和准确性，同时也能够为进一步学习和研究提供一定的参考和指导。
希望本文能够为读者提供一定的启发和帮助，让大家在空间几何学习中取得更好的成绩和收获。
2.正文2.1 空间立体几何概念空间立体几何是几何学中研究三维空间中图形与几何体的一门学科，是平面几何的延伸和拓展。
在空间立体几何中，我们不再局限于研究平面上的图形，而是考虑到三维空间中的物体和结构。
在空间立体几何中，我们研究的主要对象包括点、线、面和体。
点是空间中的一个位置，用于确定空间中的一个具体位置；线是由无数个点按照一定规律连成的直线段；面是由无数个点和线按照一定规律组成的平面图形；而体则是由无数个面组成的一个三维实体。
四类立体几何题型-新高考数学大题秒杀技巧(解析版)
四类立体几何题型-高考数学大题秒杀技巧立体几何问题一般分为四类：类型1：线面平行问题类型2：线面垂直问题类型3：点面距离问题类型4：线面及面面夹角问题下面给大家对每一个类型进行秒杀处理.技巧：法向量的求算待定系数法：步骤如下：①设出平面的法向量为n =x ,y ,z ．②找出(求出)平面内的两个不共线的向量a =a 1,b 1,c 1 ，b =a 2,b 2,c 2 ．③根据法向量的定义建立关于x ,y ,z 的方程组n ⋅a =0n ⋅b =0④解方程组，取其中的一个解，即得法向量．注意：在利用上述步骤求解平面的法向量时，方程组n ⋅a =0n ⋅b =0有无数多个解，只需给x ,y ,z 中的一个变量赋于一个值，即可确定平面的一个法向量；赋的值不同，所求平面的法向量就不同，但它们是共线向量．秒杀：口诀：求谁不看谁，积差很崩溃(求外用外减，求内用内减)向量a =x 1,y 1,z 1 ，b =x 2,y 2,z 2 是平面α内的两个不共线向量，则向量n =y 1z 2−y 2z 1,x 2z 1−x 1z 2,x 1y 2−x 2y 1 是平面α的一个法向量.特别注意：空间点不容易表示出来时直接设空间点的坐标，然后利用距离列三个方程求解.类型1：线面平行问题方法一：中位线型：如图⑴，在底面为平行四边形的四棱锥P -ABCD 中，点E 是PD 的中点.求证：PB ⎳平面AEC .分析：方法二：构造平行四边形如图⑵, 平行四边形ABCD 和梯形BEFC 所在平面相交，BE ⎳CF ，求证：AE ⎳平面DCF .分析：过点E作EG⎳AD交FC于G，DG就是平面AEGD与平面DCF的交线，那么只要证明AE⎳DG即可。
方法三：作辅助面使两个平面是平行如图⑶，在四棱锥O-ABCD中，底面ABCD为菱形，M为OA的中点，N为BC的中点，证明：直线MN‖平面OCD分析：：取OB中点E，连接ME,NE，只需证平面MEN∥平面OCD。
专题5：向量法做立体几何的线面角问题(解析版)
专题5：理科高考中的线面角问题（解析版）求直线和平面所成的角求法：设直线l 的方向向量为a ，平面α的法向量为u ，直线与平面所成的角为θ，a 与u 的夹角为ϕ， 则θ为ϕ的余角或ϕ的补角的余角.即有：cos s .in a u a u ϕθ⋅== 1．如图,在三棱锥A BCD -中,ABC 是等边三角形,90BAD BCD ∠=∠=︒,点P 是AC 的中点,连接,BP DP ．（1）证明:平面ACD ⊥平面BDP ;（2）若6BD =,且二面角A BD C --为120︒,求直线AD 与平面BCD 所成角的正弦值．【答案】（1）见解析（2）22 【分析】（1）由ABC 是等边三角形,90BAD BCD ∠=∠=︒,得AD CD =．再证明PD AC ⊥,PB AC ⊥,从而和证明AC ⊥平面PBD ,故平面ACD ⊥平面BDP 得证． （2）作CE BD ⊥,垂足为E 连接AE ．由Rt Rt ABD CBD ⊆,证得,AE BD ⊥,AE CE =结合二面角A BD C --为120︒,可得2AB =,23AE =,6ED =.建立空间直角坐标系,求出点的坐标则60,,03D ⎛⎫ ⎪ ⎪⎝⎭,3,0,13A ⎛⎫- ⎪ ⎪⎝⎭,向量36,,133AD ⎛⎫=- ⎪ ⎪⎝⎭,即平面BCD 的一个法向量(0,0,1)m =,运用公式cos ,m ADm AD m AD ⋅〈〉=和sin cos ,m AD θ=〈〉,即可得出直线AD 与平面BCD 所成角的正弦值．【详解】解:（1）证明:因为ABC 是等边三角形,90BAD BCD ∠=∠=︒,所以Rt Rt ABD CBD ≅,可得AD CD =．因为点P 是AC 的中点,则PD AC ⊥,PB AC ⊥,因为PD PB P =,PD ⊂平面PBD ,PB ⊂平面PBD ,所以AC ⊥平面PBD ,因为AC ⊂平面ACD ,所以平面ACD ⊥平面BDP ．（2）如图,作CE BD ⊥,垂足为E 连接AE ．因为Rt Rt ABD CBD ⊆,所以,AE BD ⊥,AE CE =AEC ∠为二面角A-BD-C 的平面角．由已知二面角A BD C --为120︒,知120AEC ∠=︒．在等腰三角形AEC 中,由余弦定理可得3AC =．因为ABC 是等边三角形,则AC AB =,所以3AB =．在Rt △ABD 中,有1122AE BD AB AD ⋅=⋅,得3BD =, 因为6BD =所以2AD =． 又222BD AB AD =+,所以2AB =． 则23AE =,6ED =． 以E 为坐标原点,以向量,EC ED 的方向分别为x 轴,y 轴的正方向,以过点E 垂直于平面BCD 的直线为z 轴,建立空间直角坐标系E xyz -, 则6D ⎛⎫ ⎪ ⎪⎝⎭,3A ⎛⎫ ⎪ ⎪⎝⎭,向量361AD ⎛⎫=- ⎪ ⎪⎝⎭, 平面BCD 的一个法向量为(0,0,1)m =,设直线AD 与平面BCD 所成的角为θ,则2cos ,221m ADm AD m AD ⋅〈〉===-⨯,2sin |cos ,|2m AD θ=〈〉= 所以直线AD 与平面BCD 所成角的正弦值为22． 【点睛】本题考查面面垂直的证明和线面所成角的大小,考查空间想象力和是数形结合的能力,属于基础题.2．如图，直四棱柱ABCD –A 1B 1C 1D 1的底面是菱形，AA 1=4，AB =2，∠BAD =60°，E ，M ，N 分别是BC ，BB 1，A 1D 的中点．（1）证明：MN ∥平面C 1DE ；（2）求AM 与平面A 1MD 所成角的正弦值．【答案】（1）见解析（2）105 【分析】要证线面平行，先证线线平行建系，利用法向量求解。
应用法向量解决有关立体几何问题
一个优 秀的课件 ， 只有设计者了然 于胸 ， 才
容与学生个体经验之 间的缝隙弥合起来 ，改变 ： 管对 自己的教学是否合适 。还有的教师用屏幕 ： 能使课件服务于每一个学 习者 。 为此 ， 教师在设 传统教育媒体因为忽视语言符 号与学生之间 已 ： 遮挡住了黑板 ， 件显示代替了板书。 课 运用计算 ： 计课件时 ， 要努力做 到如下几点 ：
息 量 。 同时 ， 因为 课 件往 往 ‘ ‘ 化 ”教 师 容 易 拉 向一些无 关紧要 的事物上 ，造 成注 意的 浪 ： 程式 ，
示媒体的最佳时机 ， 切不可随意呈 现，喧宾夺 ！ 挥多媒体教学 的优势 ， 优化教学过程 ， 提高教学
参考文献 ： 、
在多媒体教学 中，有部分教师 因减少板书 主 ， 应重 点突出教学重 难点 ， 杜绝华 而不 实 的 ： 效率 。 时间 ， 堂节奏加快 ， 课 大大增加了课 堂教学 的信 内容 出现在课件上 ， 一方 面它 把学生的注意力 －
关键词 ： 多媒体课件 闸 题
存 在 的 问题 ：
一
对策
：
－ 不同班级、不同年级 的学生在涉及 同一教学 内 ・ 方式来理解 知识 的。
、
教 师 与 学 生缺 乏传 统 的 “ 感 沟 通 ” 情
： 容时 ， 不加改变地使用一样 的课件进行教学 ； ： 甚
多媒体技术 以其独特的方式可 以将学习 内 ・ 至有的教师“ 一劳永逸” 地使 用现成课件 ， 而不 ・
能借助实物进行操作的实验 ，坚决不要制
多媒体教学实践过程中也存在诸多问题 。 ， ： 如 排 也会将 多媒体教材放于校园网，供学生课后阅 ： 作动画进行模拟演示 ，需要教师一步步讲解 的 ．
斥传统课堂教学 ， 忽视教学主体的参 与性 ， 过分 ： 读。这样似乎充分体现了运用现代教学手段的 ： 内容 ， 就不能借用信息技术展示 、 讲解 、 点评 。 研 依赖多媒体而忽视板书 ，以及多媒体课件制作 ： 优势 ，却忽视了作为教学主体 的学生在课堂教 ： 究证明 ，引入信息技 术不等于就能提高课 堂效 质量不高等 。 本文针对这些 问题进行了分析 ， ： 并 学中的积极参与、 积极思维 的主动性 。
例谈用向量法解立体几何问题
新 能力 的 培 养 ． 现 了 教育 改 革 的 精 神 ． 体
（ ） 法 在处 理 二 面 角 问 题 时 ， 能 会 遇 到 二 面角 的具 ２此 可
２ 结 论 ： 线 和 平 面所 成 的 角 与 斜 线 的 方 向 向量 和 已 ． 斜
关 系． 、 、 ③ＰＱ Ｒ为正六边形时 ， Ａ Ｃ Ａ Ｂ 径 ｒ ＝ 的三边 的长度之间存在 — — 关 系． 、 、 ④ＰＱ Ｒ为以
角就 等 于 两 法 向量 的 夹 角 ， 如果 是 “ 同进 同 出 ” 那 么所 求 的 ， 二面 角 的平 面 角 就 等 于两 法 向量 的夹 角 的 补 角 。掌握 了这
２结 论 ： 成 二 面 角 的 两 个 平 面 的法 向 量 的 夹 角 或 夹 ． 构 角 的 补角 等 于 这 个 二 面角 的平 面 角 ． 点 ， 么用 法 向量 求 二 面 角 就可 以做 到 随心 所 欲． 那
问存 在
— —
； 么 我 们 可 以想 象 在 三 维 空 间 里 ， 面 体 那 四
－ ＢＣ的 侧 棱 ｓ 、 、 Ｃ两 两 互 相 垂 直 。Ａ 口 Ｓ ＝ 、 Ｃ Ａ船 Ｓ Ｓ ＝ 、Ｂ ｂ Ｓ ＝ 其 边 长 为 直 径 的 半 圆 时 ． Ｂ 的 三 边 的 长 度 之 间 存 在 Ｓ Ａ ＡＡ Ｃ 关 系
二 、 用 向量 求 线 面角 的大 小 利
注 意 ：１用 向量 法 处 理 二 面 角 的 问题 时 ， 传 统 二 面 （） 将
角 问题 时 的三 步 曲 ： 找— — 证— — 求 ”直 接 简 化 成 了 一步 “ 曲 ：计 算 ” “ ．这 在 一定 程度 上 降 低 了 学 生 的空 间 想 象 能 力 ．
例谈用 向量法解立 体几何 问题
法向量解立体几何专题训练
法向量解立体几何专题训练一、运用法向量求空间角1、向量法求空间两条异面直线a, b 所成角θ,只要在两条异面直线a, b 上各任取一个向量''AA BB 和,则角<','AA BB >=θ或π-θ,因为θ是锐角,所以cos θ=''''AA BB AA BB ⋅⋅, 不需要用法向量;2、设平面α的法向量为n =x, y, 1,则直线AB 和平面α所成的角θ的正弦值为sin θ=cos2π-θ = |cos<AB , n >| = AB AB n n•• 3、 设二面角的两个面的法向量为12,n n ,则<12,n n >或π-<12,n n >是所求角;这时要借助图形来判断所求角为锐角还是钝角,来决定<12,n n >是所求,还是π-<12,n n >是所求角; 二、运用法向量求空间距离 1、求两条异面直线间的距离设异面直线a 、b 的公共法向量为(,,)n x y z =,在a 、b 上任取一点 A 、B,则异面直线a 、b 的距离d =AB ·cos ∠BAA ＇=||||AB n n • 2、求点到面的距离求A 点到平面α的距离,设平面α的法向量法为(,,1)n x y =,在α内任取一点B,则A 点到平面α的距离为d =||||AB n n •,n 的坐标由n 与平面α内的两个不共线向量的垂直关系,得到方程组类似于前面所述, 若方程组无解,则法向量与XOY 平面平行,此时可改设(1,,0)n y =三、证明线面、面面的平行、垂直关系设平面外的直线a 和平面α、β,两个面α、β的法向量为12,n n ,则1a//a n α⇔⊥ 1a a//n α⊥⇔12////n n αβ⇔ 12n n αβ⊥⇔⊥四、应用举例：例1：如右下图,在长方体ABCD —A 1B 1C 1D 1中,已知AB= 4, AD =3, AA 1= 2. E 、F 分别是线段AB 、BC 上的点,且EB= FB=1. 1 求二面角C —DE —C 1的正切值; 2 求直线EC 1与FD 1所成的余弦值.解：I 以A 为原点,1,,AB AD AA 分别为x 轴,y 轴,z 轴的正向建立空间直角坐标系,则D0,3,0、D 10,3,2、E3,0,0、F4,1,0、C 14,3,2 于是,11(3,3,0),(1,3,2),(4,2,2)DE EC FD =-==- 设法向量(,,2)n x y =与平面C 1DE 垂直,则有13301320n DE x y x y x y z n EC ⊥-=⇒⇒==-++=⊥⎫⎫⎪⎬⎬⎭⎪⎭11111(1,1,2),(0,0,2),cos 3||||1tan 2n AA CDE n AA C DE C n AAn AA θθθ∴=--=∴--•-===⨯∴=向量与平面垂直与所成的角为二面角的平面角 II 设EC 1与FD 1所成角为β,则1111cos 14||||1EC FD EC FD β•===⨯例2：高考辽宁卷17如图,已知四棱锥P-ABCD,底面ABCD 是菱形,∠DAB=600,PD⊥平面ABCD,PD=AD,点E 为AB 中点,点F 为PD 中点;1证明平面PED ⊥平面PAB ； 2求二面角P-AB-F 的平面角的余弦值 证明：1∵面ABCD 是菱形,∠DAB=600,∴△ABD 是等边三角形,又E 是AB 中点,连结BD ∴∠EDB=300,∠BDC=600,∴∠EDC=900, 如图建立坐标系D-ECP,设AD=AB=1,则PF=FD=12∴P0,0,1,E2,0,0,B2,12,0∴PB=32,12,-1,PE=2,0,-1,平面PED的一个法向量为DC=0,1,0 ,设平面PAB的法向量为n=x, y, 1由11(,,1),1)01022(,,1)1)010x y x y xn PBn PE yx y x⎧⎧•-=--=⎪⎧=⊥⎪⎪⎪⇒⇒⇒⎨⎨⎨⊥⎪⎪⎪⎩=•-=-=⎩⎪⎩∴n∵DC·n=0 即DC⊥n∴平面PED⊥平面PAB2解：由1知：平面PAB的法向量为n0, 1, 设平面FAB的法向量为n1=x, y, -1, 由1知：F0,0,12,FB,12,-12,FE,0,-12,由111111(,,1)(,)00222222110(,,1))0022x y x y xn FBn FE yx y x⎧⎧-•-=-+=⎪⎧=⊥⎪⎪⎪⎪⇒⇒⇒⎨⎨⎨⊥⎪⎪⎪⎩=-•-=+=⎩⎪⎩∴n1∴二面角P-AB-F的平面角的余弦值cosθ= |cos<n, n1>| =11n5714nnn•=•例3：在棱长为4的正方体ABCD-A1B1C1D1中,O是正方形A1B1C1D1的中心,点P在棱CC1上,且CC1=4CP.Ⅰ求直线AP与平面BCC1B1所成的角的大小结果用反三角函数值表示；Ⅱ设O点在平面D1AP上的射影是H,求证：D1H⊥AP；Ⅲ求点P到平面ABD1的距离.解: Ⅰ如图建立坐标系D-ACD1, ∵棱长为4 ∴A4,0,0,B4,4,0,P0,4,1∴AP = -4, 4, 1 , 显然DC=0,4,0为平面BCC1B1的一个法向量,∴直线AP与平面BCC1B1所成的角θ的正弦值sinθ= |cos<AP,DC >|=22216433334414=++• ∵θ为锐角,∴直线AP 与平面BCC 1B 1所成的角θ为arcsin 43333Ⅲ 设平面ABD 1的法向量为n =x, y, 1,∵AB =0,4,0,1AD =-4,0,4由n ⊥AB ,n ⊥1AD 得0440y x =⎧⎨-+=⎩ ∴ n =1, 0,1,∴点P 到平面ABD 1的距离 d =322AP n n•=例4：在长、宽、高分别为2,2,3的长方体ABCD-A 1B 1C 1D 1中,O 是底面中心,求A 1O 与B 1C 的距离;解：如图,建立坐标系D-ACD 1,则O1,1,0,A 12,2,3,C0,2,0∴1(1,1,3)AO =-- 1(2,0,3)B C =-- 11(0,2,0)A B = 设A 1O 与B 1C 的公共法向量为(,,1)n x y =,则113(,,1)(1,1,3)0302(,,1)(2,0,3)023032x n AO x y x y x y x n B C y ⎧=-⎧⎪⊥•--=-+-=⎧⎧⎪⎪⇒⇒⇒⎨⎨⎨⎨•--=--=⊥⎩⎩⎪⎪⎩=⎪⎩ ∴ 33(,,1)22n =-∴ A 1O 与B 1C 的距离为d =()1122330,2,0,,122||332211||11331222A B n n ⎛⎫•-⎪•⎝⎭===⎛⎫⎛⎫-++ ⎪ ⎪⎝⎭⎝⎭例5：在棱长为1的正方体ABCD-A 1B 1C 1D 1中,E 、F 分别是B 1C 1、C 1D 1的中点,求A 1到面BDFEABCDA 1B 1D 1C 1O的距离;解：如图,建立坐标系D-ACD 1,则B1,1,0,A 11,0,1,E12,1,1 ∴(1,1,0)BD =-- 1(,0,1)2BE =- 1(0,1,1)A B =-设面BDFE 的法向量为(,,1)n x y =,则(,,1)(1,1,0)002112(,,1)(,0,1)01022x y x y n BD x y x y x n BE •--=--=⎧⎧⎧⊥=⎧⎪⎪⎪⇒⇒⇒⎨⎨⎨⎨=-•-=-+=⊥⎩⎪⎪⎪⎩⎩⎩ ∴ (2,2,1)n =-∴ A 1到面BDFE 的距离为d =()()()1220,1,12,2,1|||3|13||221A B n n -•-•-===+-+新课标高二数学空间向量与立体几何测试题1一、选择题1．在正三棱柱ABC —A 1B 1C 1中,若AB ＝2BB 1,则AB 1与C 1B 所成的角的大小为A ．60°B ．90°C ．105°D ．75°2．如图,ABCD —A 1B 1C 1D 1是正方体,B 1E 1＝D 1F 1＝411B A ,则BE 1与DF 1所成角的余弦值是A ．1715 B ．21 C ．178 D ．23 3．如图,A 1B 1C 1—ABC 是直三棱柱,∠BCA=90°,点D 1、F 1分别是A 1B 1、A 1C 1的中点,若BC=CA=CC 1,则BD 1与AF 1所成角的余弦值是A ．1030 B ．21 C ．1530 D ．1015 4．正四棱锥S ABCD -的高2SO =,底边长2AB =,则异面直线BD 和SC 之间的距离图图FEA BCDA 1B 1D 1C 1AA 1DCB B 1C 1图A ．515 B ．55 C ．552 D ．105 5．已知111ABC A B C -是各条棱长均等于a 的正三棱柱,D 是侧棱1CC 的中点．点1C 到平面1AB D 的距离A ．a 42B ．a 82C ．a 423D ．a 226．在棱长为1的正方体1111ABCD A B C D -中,则平面1AB C 与平面11A C D 间的距离A ．63 B ．33 C ．332 D ．23 7．在三棱锥P －ABC 中,AB ⊥BC,AB ＝BC ＝21PA,点O 、D 分别是AC 、PC 的中点,OP ⊥底面ABC,则直线OD 与平面PBC 所成角的正弦值A ．621B ．338 C ．60210D ．302108．在直三棱柱111C B A ABC -中,底面是等腰直角三角形, 90=∠ACB ,侧棱21=AA ,D,E分别是1CC 与B A 1的中点,点E 在平面ABD 上的射影是ABD ∆的重心G ．则B A 1与平面ABD 所成角的余弦值A ．32 B ．37C ．23 D ．73 9．正三棱柱111C B A ABC -的底面边长为3,侧棱3231=AA ,D 是CB 延长线上一点,且BC BD =,则二面角B AD B --1的大小A ．3π B ．6πC ．65πD ．32π10．正四棱柱1111D C B A ABCD -中,底面边长为22,侧棱长为4,E,F 分别为棱AB,CD 的中点,G BD EF =⋂．则三棱锥11EFD B -的体积VA ．66B ．3316 C ．316D ．16二、填空题11．在正方体1111ABCD A B C D -中,E 为11A B 的中点,则异面直线1D E 和1BC 间的距离 ． 12． 在棱长为1的正方体1111ABCD A B C D -中,E 、F 分别是11A B 、CD 的中点,求点B 到截面1AEC F 的距离 ．13．已知棱长为1的正方体ABCD －A 1B 1C 1D 1中,E 、F 分别是B 1C 1和C 1D 1的中点,点A 1到平面DBEF 的距离 ．14．已知棱长为1的正方体ABCD －A 1B 1C 1D 1中,E 是A 1B 1的中点,求直线AE 与平面ABC 1D 1所成角的正弦值 ． 三、解答题 15．已知棱长为1的正方体ABCD －A 1B 1C 1D 1,求平面A 1BC 1与平面ABCD 所成的二面角的大小16．已知棱长为1的正方体ABCD －A 1B 1C 1D 1中,E 、F 、M 分别是A 1C 1、A 1D 和B 1A 上任一点,求证：平面A 1EF ∥平面B 1MC ．17．在四棱锥P —ABCD 中,底面ABCD 是一直角梯形,∠BAD=90°,AD ∥BC,AB=BC=a,AD=2a,且PA ⊥底面ABCD,PD 与底面成30°角． 1若AE ⊥PD,E 为垂足,求证：BE ⊥PD ； 2求异面直线AE 与CD 所成角的余弦值．18．已知棱长为1的正方体AC 1,E 、F 分别是B 1C 1、C 1D 的中点． 1求证：E 、F 、D 、B 共面；2求点A 1到平面的BDEF 的距离； 3求直线A 1D 与平面BDEF 所成的角．19．已知正方体ABCD－A1B1C1D1的棱长为2,点E为棱AB的中点,求：ⅠD1E与平面BC1D所成角的大小；Ⅱ二面角D－BC1－C的大小；Ⅲ异面直线B1D1与BC1之间的距离．高二数学空间向量与立体几何专题训练2一、选择题1．向量a＝2x,1,3,b＝1,－2y,9,若a与b共线,则A．x＝1,y＝1 B．x＝错误!,y＝－错误!C．x＝错误!,y＝－错误! D．x＝－错误!,y＝错误! 2．已知a＝－3,2,5,b＝1,x,－1,且a·b＝2,则x的值是A．6 B．5 C．4 D．33．设l1的方向向量为a＝1,2,－2,l2的方向向量为b＝－2,3,m,若l1⊥l2,则实数m的值为A．3 B．2 C．14．若a,b均为非零向量,则a·b＝|a||b|是a与b共线的A．必要不充分条件 B．充分不必要条件C．充分必要条件 D．既不充分也不必要条件5．在△ABC中,错误!＝c,错误!＝b.若点D满足错误!＝2错误!,则错误!＝b＋错误!c 错误!c－错误!b 错误!b－错误!c 错误!b＋错误!c6．已知a,b,c是空间的一个基底,设p＝a＋b,q＝a－b,则下列向量中可以与p,q一起构成空间的另一个基底的是A．a B．b C．c D．以上都不对7．已知△ABC的三个顶点A3,3,2,B4,－3,7,C0,5,1,则BC边上的中线长为A．2 B．3 C.错误!错误!8．与向量a＝2,3,6共线的单位向量是A．错误!,错误!,错误! B．－错误!,－错误!,－错误!C．错误!,－错误!,－错误!和－错误!,错误!,错误! D．错误!,错误!,错误!和－错误!,－错误!,－错误!9．已知向量a＝2,4,x,b＝2,y,2,若|a|＝6且a⊥b,则x＋y为A．－3或1 B．3或－1 C．－3 D．110．已知a＝x,2,0,b＝3,2－x,x2,且a与b的夹角为钝角,则实数x的取值范围是A．x>4 B．x<－4 C．0<x<4 D．－4<x<0.11．已知空间四个点A1,1,1,B－4,0,2,C－3,－1,0,D－1,0,4,则直线AD与平面ABC所成的角为A．30° B．45° C．60° D．90°12．已知二面角α－l－β的大小为50°,P为空间中任意一点,则过点P且与平面α和平面β所成的角都是25°的直线的条数为A．2 B．3 C．4 D．5二、填空题13．已知{i,j,k}为单位正交基底,且a＝－i＋j＋3k,b＝2i－3j－2k,则向量a＋b与向量a－2b的坐标分别是________；________.14．在△ABC中,已知错误!＝2,4,0,错误!＝－1,3,0,则∠ABC＝________.15．正方体ABCD－A1B1C1D1中,面ABD1与面B1BD1所夹角的大小为________．16．在下列命题中：①若a,b共线,则a,b所在的直线平行；②若a,b所在的直线是异面直线,则a,b一定不共面；③若a,b,c三向量两两共面,则a,b,c三向量一定也共面；④已知三向量a,b,c,则空间任意一个向量p总可以唯一表示为p＝xa＋yb＋zc,其中不正确的命题为________．三、解答题17．如图所示,PD垂直于正方形ABCD所在的平面,AB＝2,PC与平面ABCD所成角是45°,F 是AD的中点,M是PC的中点．求证：DM∥平面PFB.18．如图,正四棱柱ABCD—A1B1C1D1中,AA1＝2AB＝4,点E在C1C上,且C1E＝3EC.1证明A1C⊥平面BED；2求二面角A1－DE－B的余弦值．19．正方体ABCD－A1B1C1D1中,E,F分别是BB1,CD的中点．1证明：平面AED⊥平面A1FD1；2在AE上求一点M,使得A1M⊥平面DAE.高考真题能力提升1．如图,平面PAC⊥平面ABC,ABC∆是以AC为斜边的等腰直角三角形,,,E F O分别为PA,PB,AC的中点,16AC=,10PA PC==．I设G是OC的中点,证明：//FG平面BOE；II证明：在ABO∆内存在一点M,使FM⊥平面BOE,并求点M到OA,OB的距离．2．如图,在三棱锥P ABC -中,PA ⊥底面,,60,90ABC PA AB ABC BCA ︒︒=∠=∠=, 点D ,E 分别在棱,PB PC 上,且//DE BCⅠ求证：BC ⊥平面PAC ；Ⅱ当D 为PB 的中点时,求AD 与平面PAC 所成的角的大小； Ⅲ是否存在点E 使得二面角A DE P --为直二面角 并说明理由.3．如图,四棱锥P ABCD -的底面是正方形,PD ABCD ⊥底面,点E 在棱PB 上.Ⅰ求证：平面AEC PDB ⊥平面；Ⅱ当2PD AB =且E 为PB 的中点时,求AE 与平面PDB 所成的角的大小.4．在四棱锥P ABCD -中,底面ABCD 是矩形,PA ⊥平面ABCD ,4PA AD ==,2AB =. 以AC 的中点O 为球心、AC 为直径的球面交PD 于点M ,交PC 于点N . 1求证：平面ABM ⊥平面PCD ； 2求直线CD 与平面ACM 所成的角的大小； 3求点N 到平面ACM 的距离.yz DMCB PA NONMA BDCO5. 如图,在四棱锥O ABCD -中,底面ABCD 四边长为1的菱形,4ABC π∠=,OA ABCD ⊥底面, 2OA =,M 为OA 的中点,N 为BC 的中点Ⅰ证明：直线MN OCD 平面‖；Ⅱ求异面直线AB 与MD 所成角的大小； Ⅲ求点B 到平面OCD 的距离;6. 如图,正三棱柱ABC －A 1B 1C 1的所有棱长都为2,D 为CC 1中点; Ⅰ求证：AB 1⊥面A 1BD ；Ⅱ求二面角A －A 1D －B 的大小； Ⅲ求点C 到平面A 1BD 的距离；7.如图所示,AF 、DE 分别是⊙O 、⊙O 1的直径.AD 与两圆所在的平面均垂直,AD ＝8,BC 是⊙O 的直径,AB ＝AC ＝6,OE Ⅰ求二面角B —AD —F 的大小；Ⅱ求直线BD 与EF 所成的角.8.如图,在长方体ABCD —A 1B 1C 1D 1中,AD=AA 1=1,AB=2,点E 在棱AB 上移动.1证明：D 1E ⊥A 1D ；2当E 为AB 的中点时,求点E 到面ACD 1的距离；3AE 等于何值时,二面角D 1—EC —D 的大小为4π.9. 如图,边长为2的等边△PCD 所在的平面垂直于矩形ABCD 所在的平面,BC ＝22, M 为BC 的中点Ⅰ证明：AM ⊥PM ；Ⅱ求二面角P －AM －D 的大小； Ⅲ求点D 到平面AMP 的距离;10.如图,已知AB ⊥平面ACD ,DE ⊥平面ACD ,△ACD 为等边三角形,2AD DE AB ==,F 为CD 的中点. 1 求证：//AF 平面BCE ； 2 求证：平面BCE ⊥平面CDE ； 3 求直线BF 和平面BCE 所成角的正弦值.1A C M PD C B A A BCD EF11. 如图,已知等腰直角三角形RBC ,其中∠RBC =90º,2==BC RB ．点A 、D 分别是RB 、RC 的中点,现将△RAD 沿着边AD 折起到△PAD 位置,使PA ⊥AB ,连结PB 、PC ． 1求证：BC ⊥PB ；2求二面角P CD A --的平面角的余弦值．12. 如图,正三棱柱ABC －111C B A 的底面边长是2,D 是侧棱C 1C 的中点,直线AD 与侧面C C BB 11所成的角为45°.1 求二面角A-BD-C 的大小； 2求点C 到平面ABD 的距离.13. 如图,P 、O 分别是正四棱柱1111ABCD A B C D -上、下底面的中心,E 是AB 的中点,1AB kAA =. Ⅰ求证：1A E ∥平面PBC ；Ⅱ当k =,求直线PA 与平面PBC 所成角的大小；Ⅲ 当k 取何值时,O 在平面PBC 内的射影恰好为PBC ∆ABCD1A 1B 1C A 1C14. 如图,在正四棱锥P ABCD -中,PA AB a ==,点E 在棱PC 上．Ⅰ问点E 在何处时,//PA EBD 平面,并加以证明； Ⅱ当//PA EBD 平面时,求点A 到平面EBD 的距离； Ⅲ求二面角C PA B --的大小.15.如图所示,在长方体1111ABCD A B C D -中,AB=AD=1,AA 1=2,M 是棱CC 1的中点 Ⅰ求异面直线A 1M 和C 1D 1所成的角的正切值； Ⅱ证明：平面ABM ⊥平面A 1B 1M 116.已知三棱锥P －ABC 中,PA ⊥ABC,AB ⊥AC,PA=AC=½AB,N 为AB 上一点,AB=4AN,M,S 分别为PB,BC 的中点. Ⅰ证明：CM ⊥SN ；Ⅱ求SN 与平面CMN 所成角的大小.EPDCBA17.如图,四棱锥S-ABCD 中,SD ⊥底面ABCD,AB ⊥⊥Ⅰ证明：SE=2EB ； Ⅱ求二面角A-DE-C 的大小 .18.如图,在多面体ABCDEF 中,四边形ABCD 是正方形,EF ∥AB ,EF FB ⊥,2AB EF =,90BFC ∠=︒,BF FC =,H 为BC 的中点;ABCDEFHⅠ求证：FH ∥平面EDB ；Ⅱ求证：AC ⊥平面EDB ； Ⅲ求二面角B DE C --的大小;19．如图,在直三棱柱111ABC A B C -中,13,4,5,4AC BC AB AA ==== 1求证1;AC BC ⊥2在AB 上是否存在点D 使得1?AC CD ⊥ 3在AB 上是否存在点D 使得11//A C CDB 平面A1C BCD1A 1B20、如图,在四棱锥P —ABCD 中,PD ⊥底面ABCD,底面ABCD 为正方形,PD=DC,E 、F 分别是AB 、PB 的中点. Ⅰ求证：EF ⊥CD ；Ⅱ在平面PAD 内求一点G,使GF ⊥平面PCB,并证明你的结论； Ⅲ求DB 与平面DEF 所成角的大小.21、如图, 在直三棱柱ABC －A 1B 1C 1中,∠ACB=90°,CB=1,CA=3, AA 1=6,M 为侧棱CC 1上一点, 1AM BA ⊥． 1求证: AM ⊥平面1A BC ； 2求二面角B －AM －C 的大小； 3求点C 到平面ABM 的距离．ABCABCM22、如图,在直三棱柱ABC—A1B1C1中,∠ACB=90°,AC=BC=CC1=2.I证明：AB1⊥BC1；II求点B到平面AB1C1的距离.III求二面角C1—AB1—A1的大小。
向量法解立体几何及经典例题(上课用)
向量法解立体几何1、直线的方向向量和平面的法向量⑴．直线的方向向量： 若A 、B 是直线l 上的任意两点，则AB 为直线l 的一个方向向量；与AB 平行的任意非零向量也是直线l 的方向向量.⑵．平面的法向量： 若向量n 所在直线垂直于平面α，则称这个向量垂直于平面α，记作n α⊥，如果n α⊥，那么向量n 叫做平面α的法向量.⑶．平面的法向量的求法（待定系数法）： ①建立适当的坐标系．②设平面α的法向量为(,,)n x y z =．③求出平面内两个不共线向量的坐标123123(,,),(,,)a a a a b b b b ==．④根据法向量定义建立方程组0n a n b ⎧⋅=⎪⎨⋅=⎪⎩.⑤解方程组，取其中一组解，即得平面α的法向量.例1：在空间直角坐标系中,已知(3,0,0),(0,4,0)A B ,(0,0,2)C ,试求平面ABC 的一个法向量.2、用向量方法判定空间中的平行关系⑴线线平行。
设直线12,l l 的方向向量分别是a b 、，则要证明1l ∥2l ，只需证明a ∥b ，即()a kb k R =∈.例2： 四棱锥P-ABCD 中，底面ABCD 是正方形, PD ⊥底面ABCD ，PD=DC=6, E 是PB的中点，DF:FB=CG:GP=1:2 . 求证：AE//FG.⑵线面平行。
设直线l 的方向向量是a ，平面α的法向量是u ，则要证明l ∥α，只需证明a u ⊥，即0a u ⋅=.例3：如图，在直三棱柱ABC －A 1B 1C 1中，∠BAC =90°，AB =AC =AA 1=1，延长A 1C 1至点P ，使C 1P ＝A 1C 1，连接AP 交棱CC 1于D ．求证：PB 1∥平面BDA 1；⑶面面平行。
若平面α的法向量为u ，平面β的法向量为v ，要证α∥β，只需证u ∥v ，即证u v λ=.例4：在直三棱柱ABC -A 1B 1C 1中，∠ABC ＝90°，BC ＝2，CC 1＝4，点E 在线段BB 1上，且EB 1＝1，D ，F ，G 分别为CC 1，C 1B 1，C 1A 1的中点．求证：(1)B 1D ⊥平面ABD ； (2)平面EGF ∥平面ABD .3、用向量方法判定空间的垂直关系⑴线线垂直。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
利用法向量解立体几何题一、运用法向量求空间角向量法求空间两条异面直线a, b 所成角θ，只要在两条异面直线a, b 上各任取一个向量''AA BB 和，则角<','AA BB >=θ或π-θ，因为θ是锐角，所以cos θ=''''AA BB AA BB ⋅⋅, 不需要用法向量。
1、运用法向量求直线和平面所成角设平面α的法向量为n =（x, y, 1)，则直线AB 和平面α所成的角θ的正弦值为sin θ= cos(2π-θ) = |cos<AB , n >| = AB AB n n••2、运用法向量求二面角设二面角的两个面的法向量为12,n n ，则<12,n n >或π-<12,n n >是所求角。
这时要借助图形来判断所求角为锐角还是钝角，来决定<12,n n >是所求，还是π-<12,n n >是所求角。
二、运用法向量求空间距离1、求两条异面直线间的距离设异面直线a 、b 的公共法向量为(,,)n x y z =，在a 、b 上任取一点A 、B ，则异面直线a 、b 的距离 d =AB ·cos ∠BAA ＇=||||AB n n • 略证：如图，EF 为a 、b 的公垂线段，a ＇为过F 与a 平行的直线，在a 、b 上任取一点A 、B ，过A 作AA ＇//EF ，交a ＇于A ＇，A则¡¯//AA n ，所以∠BAA ＇=<,BA n >（或其补角）∴异面直线a 、b 的距离d =AB ·cos ∠BAA ＇=||||AB n n • * 其中，n 的坐标可利用a 、b 上的任一向量,a b （或图中的,AE BF ），及n 的定义得0n a n a n b n b ⎧⎧⊥•=⎪⎪⇒⎨⎨⊥•=⎪⎪⎩⎩ ① 解方程组可得n 。
2、求点到面的距离求A 点到平面α的距离，设平面α的法向量法为(,,1)n x y =，在α内任取一点B ，则A点到平面α的距离为 d =||||AB n n •，n 的坐标由n 与平面α内的两个不共线向量的垂直关系，得到方程组（类似于前面所述, 若方程组无解，则法向量与XOY 平面平行，此时可改设(1,,0)n y =，下同）。
3、求直线到与直线平行的平面的距离求直线a 到平面α的距离，设平面α的法向量法为(,,1)n x y =，在直线a 上任取一点A ，在平面α内任取一点B ，则直线a 到平面α的距离 d =||||AB n n • 4、求两平行平面的距离设两个平行设平面α、β的公共法向量法为(,,1)n x y =，在平面α、β内各任取一点A 、B ，则平面α到平面β的距离 d =||||AB n n • 三、证明线面、面面的平行、垂直关系设平面外的直线a 和平面α、β，两个面α、β的法向量为12,n n ，则1a//a n α⇔⊥ 1a a//n α⊥⇔12////n n αβ⇔ 12n n αβ⊥⇔⊥四、应用举例：例1：（04年高考广东18）如右下图,在长方体ABCD —A 1B 1C 1D 1中,已知AB= 4, AD =3, AA 1= 2. E 、F 分别是线段AB 、BC 上的点，且EB= FB=1.(1) 求二面角C —DE —C 1的正切值; (2) 求直线EC 1与FD 1所成的余弦值.解：（I ）以A 为原点，1,,AB AD AA 分别为x 轴，y 轴,z 轴的正向建立空间直角坐标系， 则D(0,3,0)、D 1(0,3,2)、E(3,0,0)、F(4,1,0)、C 1(4,3,2) 于是，11(3,3,0),(1,3,2),(4,2,2)DE EC FD =-==-设法向量(,,2)n x y =与平面C 1DE 垂直，则有13301320n DE x y x y x y z n EC ⊥-=⇒⇒==-++=⊥⎫⎫⎪⎬⎬⎭⎪⎭11111(1,1,2),(0,0,2),cos 3||||1tan 2n AA CDE n AA C DE Cn AA n AA θθθ∴=--=∴--•===⨯∴=向量与平面垂直与所成的角为二面角的平面角（II ）设EC 1与FD 1所成角为β，则1111cos 14||||1EC FD EC FD β•===⨯例2：（04年高考辽宁卷17）如图，已知四棱锥P-ABCD ，底面ABCD 是菱形，∠DAB=600，PD ⊥平面ABCD，PD=AD ，点E 为AB 中点，点F 为PD 中点。
（1）证明平面PED ⊥平面PAB ； （2）求二面角P-AB-F 的平面角的余弦值 证明：（1）∵面ABCD 是菱形，∠DAB=600，∴△ABD 是等边三角形，又E 是AB 中点，连结BD∴∠EDB=300，∠BDC=600，∴∠EDC=900，如图建立坐标系D-ECP，设AD=AB=1，则PF=FD=12，ED=2，∴P（0，0，1），E（2，0，0），B（2，12，0）∴PB=（2，12，-1），PE=0，-1），平面PED的一个法向量为DC=（0，1，0），设平面PAB的法向量为n=（x, y, 1)由11(,,1)(,,1)0102222(,,1)(,0,1)01022x y x y xn PBn PE yx y x⎧⎧•-=--=⎪⎧=⊥⎪⎪⎪⎪⇒⇒⇒⎨⎨⎨⊥⎪⎪⎪⎩=•-=-=⎩⎪⎩⎩∴n=∵DC·n=0 即DC⊥n∴平面PED⊥平面PAB （2）解：由（1）知：平面PAB的法向量为n=, 0, 1), 设平面FAB的法向量为n1=（x, y, -1)，由（1）知：F（0，0，12），FB=12，-12），FE=0，-12），由111111(,,1),)002222110(,,1))0022x y x y x n FBn FE yx y x⎧⎧-•-=-+=⎪⎧=⊥⎪⎪⎪⇒⇒⇒⎨⎨⎨⊥⎪⎪⎪⎩=-•-=+=⎩⎪⎩∴n1=（-1)∴二面角P-AB-F的平面角的余弦值cosθ= |cos<n, n1>| =11n57nnn•=•例3：（04江苏高考18)在棱长为4的正方体ABCD-A1B1C1D1中，O是正方形A1B1C1D1的中心，点P在棱CC1上，且CC1=4CP.(Ⅰ)求直线AP 与平面BCC 1B 1所成的角的大小（结果用反三角函数值表示）； (Ⅱ)设O 点在平面D 1AP 上的射影是H ，求证：D 1H ⊥AP ； (Ⅲ)求点P 到平面ABD 1的距离.解: (Ⅰ)如图建立坐标系D-ACD 1, ∵棱长为4 ∴A （4，0，0），B （4，4，0），P （0，4，1） ∴AP = (-4, 4, 1) , 显然DC =（0，4，0）为平面BCC 1B 1的一个法向量， ∴直线AP 与平面BCC 1B 1所成的角θ的正弦值sin θ= |cos<AP ,DC >|=222433334414=++• ∵θ为锐角，∴直线AP 与平面BCC 1B 1所成的角θ为arcsin43333(Ⅲ) 设平面ABD 1的法向量为n =（x, y, 1)， ∵AB =（0，4，0），1AD =（-4，0，4） 由n ⊥AB ，n ⊥1AD 得0440y x =⎧⎨-+=⎩∴ n =（1, 0, 1)， ∴点P 到平面ABD 1的距离 d=322AP n n•=例4：在长、宽、高分别为2，2，3的长方体ABCD-A 1B 1C 1D 1中，O 是底面中心，求A 1O 与B 1C 的距离。
解：如图，建立坐标系D-ACD 1，则O （1，1，0），A 1（2，2，3），C （0，2，0） ∴1(1,1,3)AO =-- 1(2,0,3)B C =-- 11(0,2,0)A B = 设A 1O 与B 1C 的公共法向量为(,,1)n x y =，则113(,,1)(1,1,3)0302(,,1)(2,0,3)023032x n A O x y x y x y x n B C y ⎧=-⎧⎪⊥•--=-+-=⎧⎧⎪⎪⇒⇒⇒⎨⎨⎨⎨•--=--=⊥⎩⎩⎪⎪⎩=⎪⎩ ∴33(,,1)22n =- ∴ A 1O 与B 1C 的距离为 d=(110,2,0||11||A B n n •===⎛ 例5：在棱长为1的正方体ABCD-A 1B 1C 1D 1中，E 、F 分别是B 1C 1、C 1D 1的中点，求A 1到面BDFE 的距离。
解：如图，建立坐标系D-ACD 1，则B （1，1，0），A 1（1，0，1），E （12，1，1） ∴(1,1,0)BD =--1(,0,1)2BE =- 1(0,1,1)A B =- 设面BDFE 的法向量为(,,1)n x y =，则(,,1)(1,1,0)00112(,,1)(,0,1)01022x y x y n BD y x y x n BE •--=--=⎧⎧⎧⊥⎪⎪⎪⇒⇒⇒⎨⎨⎨⎨=-•-=-+=⊥⎩⎪⎪⎪⎩⎩⎩∴ (2,2,1)n =-∴ A 1到面BDFE 的距离为d =(10,1,|||3|13||A B n n •-===。