曲线桥梁计算
曲线桥桥墩中心坐标的计算方法

曲线桥桥墩中心坐标的计算方法44.东北测绘季刊第22卷1999年第2期【实践应用集锦1)l岍+THo蝴yuz=TH式中:切线长=(R+P)号+q(4)3桥墩中心坐标的计算利用坐标的平移与旋转公式并考虑到左右手坐标系的变换则得P点在以zH为原点的坐标系中的坐标为:x+∞1+)yl+Y=y田+xsn(18+一y'~os(180~+0J将上式简化则得:x一x'c0一vYym—x'+v'oD(5)(6)以上(1),(2),(6)式为在3种情况下求定P点在以zH为原点的坐标系中坐标的计算公式.若已知直缓点zH的测量坐标系坐标为(x翻,阳),切线zH至JD的测量坐标方位角为嘶,根据坐标系的平移与旋转公式并顾及左右手坐标系的转换,则得到P点的测量坐标系坐标为:X=X一Ⅺ鲫r±ysinar1(73Y=Yzu一n*T-yoaSO~rJ注:当路线左偏时,x的计算y前取+,y的计算y前取.一'右偏时相反.桥中线—d—一图4双柱式桥墩示意图由于双柱式桥i毂的双柱墩中心连线位于桥中线的径向上(与P点处的切线垂直),且对称分布于桥中线的两侧见圈4.其中B 勺左柱墩中心,PB为右柱墩中心,其间距为d.显然,P点处切线的测量坐标方位角为:Q=嘶-T-注:左偏时取.一,右偏时取+(8)由于和PR的连线与切线垂直,则左桥墩中心PL在测量坐标系坐标为:=X+音d~s(0一)=X+÷d枷1,,1}YL=Y+寺dsm(0—9俨)=Y一音J同理,右桥墩中心P.的测量坐标系坐标为:吉(.)=一{枷1(10)YR=Y+{dsin(0+90.)=Y+音dcos0J4结束语从以上各公式来看,曲线桥双柱式桥墩中心坐标的计算只需知道,直缓点zH的测量坐标(),Y锄),任意桥墩P至zH的曲线长lp,zH~JD的切线方位角园曲线鹄半径R.偏角,缓和曲线长度h以及左右墩柱的间距d.显然该方法简单而叉方便,很适合于计算机上编程计算.当曲线桥中线都为园曲线时,则情况更为简单,第一,第三种情况不予考虑,只需考虑第二种情况,但在使用公式(2)时,须令k:.o另外,对于曲线桥其它类型桥墩中心位置的计算也可参照本文的方法来进行.参考文献:1邹廉.测量学.北京:人民交通出版社19862姚玲森.桥梁工程.北京:人民交通出版社,1985(上接第2o页)理,海洋资源开发与利用,海洋防灾减灾等.这些GIS都具有良好的应用前景,已经发挥或将发挥重要1乍用.4.2政府决策GIS国家测给局与国务院办公厅秘鹌局协商于1992年2月决定联合研建国务院综合国情地理信息系统(简称.92O2工程'), 开拓了GIS为政府宏观决策服务的新领域.已建立的综合国情数据库主要由地理基础库,地名数据库,政务信息数据库和统计信息数库等.目前该系统阶段性成果已投^应用,得到好评.许多省,市,自治区的政府和测绘部门也合作建立了各自的综合省情GIS策中发挥作用.43GIS在98年抗洪中的作用1998年夏季,我们战胜了长江,松花江,嫩江流域百年不语的特大洪水,把损失减少到了最小程度.在这场人与自然抗争的胜利当中,GIS也发挥了重要作用.在防洪,抗洪期间,利用各种比例尺数字地图及现势性极强的航空摄影像片,卫星遥感图像,制作防洪抗洪GIS,为高层宏观决策提供了准确,可靠的基础服务.踩在惊心动魄,分秒必争的防洪抗洪紧要关头发挥了不可替代的决策支持服务外,GIS在洪涝灾害损失估算,灾民安置,灾后重建等方面也作出了贡献.5cB发展的有利条件5.I计算机软硬件日新月异计算机的硬件速度飞速提高,容量大幅度增加,关系数据库,图形图像处理等软{牛不断推陈出新,升级换代,还有并行处理,工作站,网络,多媒体等技术的飞速发展,都为c玲的发展创造了条件.5.2相关技术不断进步航空航天技术,传怒技术,空间定位技术的进步,影像数据分辨率的提高,为c玲提供更多,更好,更及时的数据来源.前文就曾多次提到3s技术的集成应用.近来迅速壮大的4D产品为c玲的应用提供了强大的基底数据.5.3需求促进发展c玲技术越来越可靠,应用越来越广泛.反过来,不断扩大的应用范围,不断提高的应用需求必然推动GIs的进一步发展和完善.6结束语c玲被称为.地理'信息系统,其区别于其他信息系统的最大特点是具有空间特征,这也是它的优势之所在.测绘业在GIs 发展应过程中做出了巨大的贡献,c皓的概念,世界上的第一个c玲就是由加拿大的测量学家和测量机掏提出,建立的.测绘业在获取空间信息上有着强大的专业优势,应该为GIS的发展应用继续做出更大的贡献.。
曲线桥梁的设计计算

曲线桥梁的设计计算摘要:随着贵阳市的快速发展和道路等级的提高,曲线桥梁的应用越来越广泛,结合工程实践,对曲线桥梁设计计算进行分析,叙述箱梁构造,对几个重要荷载做计算以及结果分析、总结,以期为后续类似工程提供参考。
关键词:曲线桥梁;设计;计算1.工程概况贵阳市新建林城东路延伸段的立交节点—新添大道立交匝道桥,本匝道桥采用螺旋形,内外幅设置,本文以外幅第一联27.963+2x27m为工程实例,本联平曲线为半径50m的圆曲线加缓和曲线,竖曲线为凸曲线,上部结构为预应力混凝土现浇箱梁,中支墩固结,边支点采用支座,中支墩高度为70m和77m,桥墩采用3x5m矩形空心墩,承台桩基础。
1.结构计算上部结构箱梁按单箱单室设计,顶板宽10.2m,底板宽5.35m,悬臂长2m,腹板倾角76°,箱梁顶、底板平行设置,梁高2.2m。
端横梁宽度为1.2m,中横梁宽度为3.0m。
采用Midas/civil计算,并以《公路桥涵设计通用规范》(JTG D60-2015)和《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362-2018)为标准,按部分预应力(A类)混凝土结构进行验算。
横断面尺寸图2.1 本文针对在设计过程中的几个荷载做计算分析:1.风荷载由于桥墩最大墩高为77m,风荷载对上部结构箱梁和下部桥墩影响较大,现以此桥墩墩高计算。
根据《公路桥梁抗风设计规范》(JTG/T 3360-01-2018)规定,横桥向风作用下主梁单位长度上的顺风向等效静阵风荷载为,1)——空气密度,2)——等效静阵风风速,,——等效静阵风系数,本联水平加载长度L=27.963+2x27=82m,根据本匝道桥的建设地点,地表类别判定为C类,根据表5.2.1, =1.465;——桥梁或构件基准高度Z处的设计基准风速,或——抗风风险系数,基本风速 =28m/s,根据表4.2.6-1, =1.02, Z=77+2.2=79.2m;根据表4.2.1,, ,根据表4.2.4,,,得出,;——地形条件系数,取 =1.2,——地表类别转换及风速高度修正系数,根据表4.2.6-2,得出, =1.238,得出,,取大值,3)——主梁横向力系数,可按下式计算,,B——主梁的特征宽度,B=10.2m,D——主梁梁体的投影高度,D=3.38m,得出, =1.8;桥梁的主梁截面带有斜腹板时,横向力系数可根据腹板倾角角度折减,横向力系数的腹板倾角角度折减系数可按下式确定:,=14°,得出, =0.93。
弯桥计算理论 (自动保存的)

弯桥计算理论弯桥【curvedbridge】指的是桥面中心线在平面上为曲线的桥梁。
有主梁为直线而桥面为曲线和主梁与桥面均为曲线两种情况。
弯桥主要分为曲线梁桥,曲线斜拉桥,曲线悬索桥。
本文主要论述曲线梁桥。
1 概述随着现代社会的发展和人们需求的提高,交通要求越来越快捷对个体舒适视觉感官的要求也越来越高。
我国近年来修建了大量的高等级公路尤其城市立交桥建设发展很快,道路设计时往往要综合道路平面纵断面和横断面等进行设计,以保证道路的平面顺畅纵坡均衡和横断面合理。
考虑到车辆行驶时的安全舒适以使驾驶人员的视觉和心理反应能保持线形的连续性,由于直线视觉效果单调容易使人疲劳,现在进行道路设计时往往采用平面上避免长直线的设计原则,因此弯桥的使用是不可避免的。
以前由于计算工具和设计理论的欠缺常常以直代弯,如我国南京长江大桥的引桥工程等将直桥上的人行道路缘石和栏杆等稍加修整以满足道路平面曲线线形的要求,但当弯道半径较小或桥梁跨径较大时以直代弯则显得不尽合理,而弯桥就不存在这样的问题。
随着计算理论的日渐成熟和人们的不断实践摸索弯桥有了很大的发展,曲线梁桥以其优美的曲线与道路良好的适应性以及其跨越能力已成为现代交通工程中的一种重要桥型。
在高等级公路中在对环境有特殊要求的地方为了尽量保持原地貌景观也都使用了曲线梁桥。
例如瑞士的勒内恩高架桥依山傍水而行,布伦纳公路上的卢埃克桥紧靠在多岩石茂密森林的山腰上。
这些桥不但起着交通作用还给大自然增添了一道亮丽的风景,早在20世纪30年代很多桥梁工程师就开始了对曲线桥有关问题的研究,60年代初国外一些桥梁专家和学者开始了对曲线梁桥进行深入细致分析探索并付诸于工程实践。
我国自80年代以来随着经济的快速增长,交通业也飞速发展,修建了大量的公路铁路尤其是城市立交桥发展更快,修建了大量的全互通式立交桥,使得我国的曲线梁桥的理论研究和工程实践取得了很大的可喜成果。
广州北京天津沈阳等许多城市都较早地修建了由曲线梁组成的大型立交桥,如弛名全国的天津市中山门蝶式立交桥满足交通功能占地少造价低造型优美。
曲线桥梁上E值计算
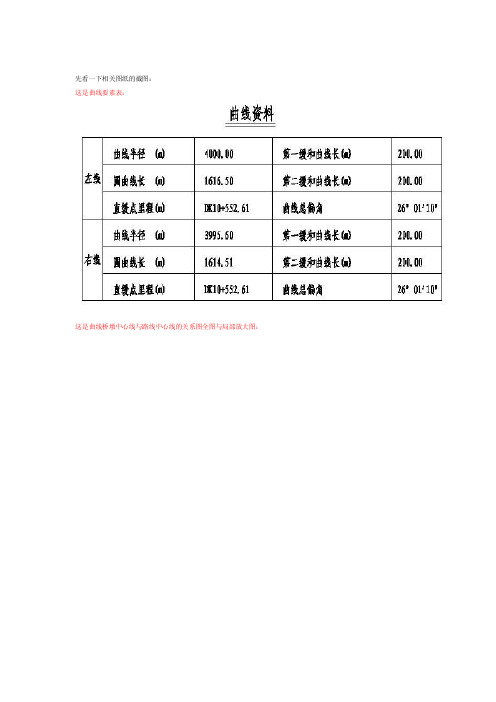
先看一下相关图纸的截图:这是曲线要素表:这是曲线桥墩中心线与路线中心线的关系图全图与局部放大图:这是图纸上全部的桥墩位置参数图:这里取两处有代表性的位置,这是圆曲线上某段:这是缓和曲线上某段:简支梁墩曲线布置大样图:桥墩及基础尺寸:图纸的附注说明:————————————————————————————————————————————————————————————补充相关尺寸在讲述之前,有必要补充一下以上设计文件中没有给出或者标注不清晰的相关尺寸:1.简支箱梁宽度11.6米;2.直线上,简支箱梁在桥墩上假设时,相邻两箱梁之间留10cm的缝宽,以桥墩中线为界,两侧各5cm;3.两轨道中心线之间的距离为4.4米。
按我的理解,以目前大多数测量工程师的理论和实践基础,本日志所呈现的高铁简支墩梁,在直线上的放样和计算应该没有问题。
因此本文仅针对曲线上的一些情况来阐述。
两个关键点曲线又分圆曲线和缓和曲线两种情况,按照对设计文件的理解,圆曲线和缓和曲线上简支墩梁放样的关键在于两点:1.对外距E的处置,这个涉及到构造物控制线的左、右距离的确定;2.构造物控制线(即桥墩基础的中轴线)相对于路线的夹角,这个涉及到控制线的方位。
第1点,E的数值没有问题,每个桥墩都标注了这个参数,关键是要理解这个E值如何落实到放样计算中,此外,若能自己计算验证出E值的数值则更好。
第2点,控制线的方位,附注说明中说得很清楚,平分偏角的补角,这个在圆曲线上很简单,也就是对应中桩的法线(即正交),而在缓和曲线上就不行了,那到底偏多少呢,这个需要计算确定,而且必须确定好,否则墩梁的施工放样会有问题。
圆曲线上各参数的含义及计算先来简单一点的,理解一下圆曲线上各参数的含义及计算方法。
其关键的示意图再次展示如下:由于高铁轨道的左线和右线分别进行平面设计,左线、右线分别有对应的直曲表,从该图可得知,墩梁的定位以左线为基准。
1.偏角a由于梁是直线,而对应的路线为曲线,因此两相邻两梁段之间必有一个偏角。
曲线桥坐标计算方法最终版郑宏征

曲线桥坐标计算方法--最终版郑宏征武九项目部测量室2014年在岗培训——《平分中矢架梁线偏法》摘要:在铁路桥梁施工前,其各部位坐标计算工作至关重要。
现施工应用中曲线桥坐标计算方法纷繁复杂,精准程度也参差不齐。
本文介绍的方法依据为平分中矢法,适用于梁按平分中矢法架设的曲线桥计算,主要是根据设计已给出梁工作线交点与线路中线偏移距及梁作业线转角等要素来计算曲线桥梁各部位坐标。
关键词:铁路;曲线桥;坐标计算;平分中矢一.概述桥梁设计图纸通常是给定了曲线桥桥位要素:ZH(HZ)点、HY(YH)点里程;交点坐标;曲线要素;梁缝里程;偏移距;梁工作线转角等。
因此在施工前,需要详细的计算出墩位平面控制坐标,以此结合现场导线点控制点进行放样。
曲线桥施工平面控制要素主要是承台墩台中心坐标及轴线的坐标方位角,以此为依据确定桩位及架梁支座预留孔等位置。
主体思路为:1.计算线路中线处梁工作线交点对应里程点的坐标;2.计算梁工作线交点坐标;3.确定墩(承台)轴向方位角;4.确定墩(承台)中心坐标;5.确定桩位坐标。
二. 计算公式介绍 (一) 直线部分计算公式(二) 曲线部分计算公式带有缓和曲线的圆曲线上各点坐标计算思路:根据设计给定的交点坐标及坐标方位角可按公式1计算出ZH(HZ)点坐标;然后计算曲线各点相对ZH(HZ)点的坐标;根据相对的角度和距离计算曲线上点的大地坐标。
1. 切线支距法计算相对坐标2.偏角法计算绝对坐标(一)设计资料XX单线大桥(15×32m)曲线要素(曲线示意如图4所示):(二)计算步骤1.线路中桩坐标计算808006)82.184170.1855(3⨯⨯-=y =0.007弦线坐标方位角δαα-=-54#7=61.11+180-0.33=241.08°︒+=08.241cos 9.13543.2760373X =2760366.830︒+=08.241sin 9.13329.503413Y =503401.181同理,可计算其他墩台梁缝里程处线路中桩坐标。
公路桥梁竖曲线上高程值计算新方法

公路桥梁竖曲线上高程值计算新方法
现代公路设计中将桥梁曲线作为桥梁立面提供新的美观形状,从而降低车辆安全等级。
高程值是桥梁设计需要计算的参数,其对景观影响也十分重要。
由于现代桥梁地形线存在着不同的曲率,传统计算高程值的方法已经不能满足的新技术的需求,所以有必要采取新的方法来计算桥梁上竖曲线的高程值。
首先,应对所有点进行测量,确定曲线竖起和起伏拐点,例如竖直曲线上的斜率和水平起伏点,然后在点上拟合出一个圆弧,最后,将ArcGIS软件中现有的技术用于圆弧的计算,以计算任何给定的圆的高程值,以便正确测试桥架上竖曲线的实际高程值,为桥梁设计提供技术参考。
本方法集实际测量、ArcGIS软件技术以及圆弧拟合技术于一体,可以有效精确计算桥架曲线竖直和起伏拐点上的高程值,为桥梁设计提供技术参考,大大提高了桥梁设计技术水平。
第5讲 曲线梁桥结构力学分析方法

4
湖南大学土木工程学院风工程试验研究中心、桥梁工程系
2. 用结构力学方法求解一次超静定简支曲线梁 2.1 一次超静定简支曲线梁定义
两端具有竖向约束,且可以发生绕横向轴自由挠曲位移;(简支特点) 两端具有抗扭支承;(超静定特点) 具备以上两个特点的曲线梁桥称为简支超静定曲线梁桥(如下图所示)。
2
湖南大学土木工程学院风工程试验研究中心、桥梁工程系
结构力学方法:
1)该方法原理简单; 2)概念明确。
分类(依据:是否考虑曲线梁桥横截面在受荷后的截面翘曲变形):
1)单纯扭转理论
横截面各项尺寸与跨长相比很小(L/B>=3~4),可以将 实际结构作为集中在剪切中心的弹性杆件来处理; 曲线梁的横截面变形后仍保持为平面; 曲线梁变形后横截面的周边形状保持不变,即无畸变; 截面的剪切中心与形心相重合。
基本过程和方法。
16
湖南大学土木工程学院风工程试验研究中心、桥梁工程系
17
12
湖南大学土木工程学院风工程试验研究中心、桥梁工程系
13
湖南大学土木工程学院风工程试验研究中心、桥梁工程系
14
湖南大学土木工程学院风工程试验研究中心、桥梁工程系
2.3 一次超静定简支曲线梁在集中扭矩荷载作用下的风工程试验研究中心、桥梁工程系
本节课程基本要求: 1.掌握单纯扭转理论的基本假定; 2.掌握单跨简支曲线梁桥在集中荷载作用下的内力及反力结构力学求解的
1. 概述
曲线梁基本微分方程
EI IV EI x GI d '' EI w w EI IV GI d ' ' 2x m z r r r
(2-16)
EI GI EI m EI GI d EI x 2 w IV 2d w'' IV x ' ' q y x r r z r r
如何用梁格法计算曲线梁桥

如何用梁格法计算曲线梁桥珠海东部久远科技有限公司孙广华博士、副研究员现在大多数道桥设计院都拥有几种结构计算软件,对重要结构,都要用不同的软件相互复核。
这是技术进步的大好事。
笔者的“曲线梁桥CBD_5.3”是计算梁式桥、特别是曲线梁桥的专用软件。
没有这个软件的设计单位,用其他优秀软件,也可以计算曲线梁桥,只要遵循正确的方法。
下面介绍的梁格法,虽然是人人皆知,但是误区也不少,所以笔者觉得有必要再把它清晰、准确地介绍一下,希望对设计人员有益、对工程有益。
1.梁格法是唯一既有相当精度又比较容易实行的方法对曲线梁桥,可以把它简化为单根曲梁、平面梁格计算,也可以几乎不加简化地用块体单元、壳单元计算。
单根曲梁模型的优点是简单,缺点是:几乎所有类型的梁单元都有刚性截面假定、因而不能考虑桥梁横截面的畸变,总体精度较低。
块体单元、壳单元模型,优点:与实际模型最接近,不需要计算横截面的形心、剪力中心、翼板有效宽度,截面的畸变、翘曲自动考虑;缺点:输出的是梁横截面上若干点的应力,不能直接用于强度计算。
对于位置固定的静力荷载,当然可以把若干点的应力换算成横截面上的内力。
对于位置不固定的车辆荷载,理论上必须采用影响面方法求最大、最小内力。
板壳单元输出的只能是各点的应力影响面。
把各点的应力影响面重新合成为横截面的内力影响面,要另外附加大量工作。
这个缺点使得它几乎无可能在设计中应用。
梁格法,优点:可以直接输出各主梁的内力,便于利用规范进行强度验算,整体精度能满足设计要求。
由于这个优点,使得该法成为计算曲线梁桥和其它平面形状特殊的梁式桥的唯一实用方法。
缺点:它对原结构进行了面目全非的简化,大量几何参数要预先计算准备,如果由计算者手工准备,不仅工作量大,而且人为偏差较难避免。
2.如何建立梁格力学模型本节2-1、2-2、2-3、2-4的内容都是引述参考文献1,讨论的内容,是笔者的看法。
2-1 纵梁个数、横梁道数、支点、梁单元对于有腹板的箱型、T型梁桥,其梁格模型中纵向主梁的个数,应当是腹板的个数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目前解决曲线桥梁计算方法有以下几种:
1、空间梁元模型法
2、空间薄壁箱梁元模型法
3、空间梁格模型法
4、实体、板壳元模型法
第一种方法,是不能考虑桥梁的横向效应的,使用时要求桥梁的宽跨比不易太大。
第二种方法,是第一种方法的改进,主要区别是采用了不同的单元模型,考虑了横向作用如翘曲和畸变。
第四种方法,是解决问题最有效的方法,能够考虑各种结构受力问题。
第三种方法,是目前设计及科研中常采用的方法,其特点是容易掌握,且对设计能保证足够的精度,其中采用比较多的方法是剪力-柔性梁格法,能充分考虑弯桥横向的受力特性。
剪力-柔性梁格法的原理
是当梁格节点与结构重合的点承受相同挠度和转角时,由梁格产生的内力局部静力等效与结构的内力。
其实质是将传统的一维杆单元计算模式推进到二维计算模型,用一个二维的空间网格来模拟结构的受力特性。
对于梁格法的讨论这里也有不少帖子进行了讨论,实际与梁格之间的等效关系,主要表现在梁格各个构件的刚度计算上,理论上,原型和等效梁格承受相等的外荷载时,必须具有恒等的挠曲和扭转,等效梁格中每一构件的内力也必须等于该构件所代表的原型截面的,事实上这种理想状况是达不到的,模拟也是近似的,但事实是按梁格计算能把握住结构的总体性能,对于设计来说应该是能满足精度的。
梁格也是近似的模拟,只要计算者能够和好的模拟了横向纵向的特性,应该是可以作为设计依据的。
你在这里说的横向的切分使得预应力产生的次内力问题我不太清楚你指的什么,但是只要横向的刚度业等效了原型,对于计算应该不会出现逆所说的结构内力失真,这条可以通过结果验证。
当然任何结构,只要不怕麻烦都可以用实体单元来分析,只要正确模拟,实体分析也是最精确的,但是对于这种模型要准确模拟可不是一件容易的事,并且预应力的损失计算,施加等等都非常麻烦,还有最后结果的查看也不方便,因此除了结构局部的分析,一般是没有拿实体来进行全桥的整体分析的,至于说单梁我也说了,有些时候精度是可以的,但是对于这种结构相对于梁格来说单梁的精度是不如梁格的。
特别是在没有把握的前提下可以做一下梁格的分析,对结果进行对比,能放心一些,其实对于设计,能用单梁算的近量用单梁能用平面的尽量不用空间,这也应该是一个原则,前提是对简化做到心中有数。
像这种结构来说如果开始计算就用梁格或者更麻烦的实体来配筋都不是一般的麻烦,配筋计算还是最好用简化的单梁,如果不放心然后用其他方式来验算,这样比较合适
在midas分析中应该注意的问题:
如果你要计算的是普通钢筋混凝土结构,主要看内力结果,可以在划分的时候简单一些,直接“一刀切”,也就是顶底板在同一位置切开,但是在计算其抗弯惯性矩的时候一定要注意纵向梁格的界面惯性矩是相对于整体截面的中性轴的,而不是划分以后的梁格截面本身的惯性矩,对于预应力混凝土的结构你就得注意梁格的划分了,在划分的时候尽量使得划分以后的各个梁格截面要跟原截面的中性轴一致,只有这样计算出来的应力结果才能比较准确,当然,如果是等截面的梁只要划分一个截面就可以了,算起来也不是很费时费力,但是如果是变截
面的那种异型箱梁在进行划分和计算截面特性的时候就应该采取一定的方法,用excell或者自己编制小程序来批量划分和计算,要不然会非常费时费力。
其中抗扭惯性矩的计算一定要按相关书籍中介绍的公式进行计算,否则是不准确的,因为输入的抗扭惯性矩实际上是顶底板的抗扭,另一部分抗扭由腹板来承担,因此梁格的抗剪面积也要输入准确,就是腹板的面积,建立模型的时候注意一定不要使用midas自带的梁格截面,因为这里面的截面都是上面所说的那种“一刀切”的截面,并且其计算得到抗扭惯性矩根剪切面积也是不准确的。
不能直接应用midas中的梁格截面是因为它其中的截面特性不是按梁格法的计算方法得到的,应该数值输入;截面特性的计算公式相关书籍中都有,可以查阅;想保持一致有很多种方法,其实原理就是解方程,对于变宽的截面由于要计算的截面特性比较多,可以用excell 也可以编程解决,对于等宽的试分都可以了;预应力和普通钢筋关注的结果不同,预应力由于要关注应力结果,所以要保持中性轴一致,才能得到其合理的计算结果而普通钢筋只需要看内力结果就可以了,所以无所谓一致不一致,梗腋一般不计入抗剪面积,虚拟梁是为了加载方便。
梁格法建模注意事项
在梁桥中会经常会使用梁格法建立模型,因为不同的设计人员对横向联系的模拟(虚梁的设置)不尽相同,所以分析结果会略有差异。
下面就一些注意事项供设计人员参考。
1. 将多室箱梁分割为梁格时,注意纵梁的中和轴位置应尽量一致。
2. 每跨内的虚拟的横向联系梁数量不应过少(划分为1.5m左右一个在精度上应能满足要求)。
3. 虚拟的横向联系梁之间尽量要设为铰接(可将纵梁之间的虚拟横梁分割为两个单元,将其中一个释放梁端约束)。
4. 虚拟的横向联系梁的刚度可按一字或二字形矩形截面计算。
5. 虚拟的横向联系梁的重量应设为零(可在截面刚度调整系数中调整)。
6. 当虚拟的横向联系梁悬挑出边梁外时,应设置虚拟的边纵梁(为了准确地计算自振周期和分配荷载),此时可将虚拟的边纵梁作为一个梁格进行划分。
7. 定义移动荷载的车道时,应尽量选择按“横向联系梁”方法分布移动荷载,此时应将所有的横向联系梁定义为一个结构组,并在定义车道时选择该结构组。
8. 定义车道时最好定义两次车道,一次按横向偏载定义,一次按横向中间向两边定义。
定义移动荷载工况时可定义偏载和居中两个工况(荷载组合中会自动找到包络结果)。
9. 定义支座时尽量遵循一排支座中只约束其中一个支座在X, Y方向的自由度的原则(否则温度荷载结果会偏大)。
另外,多支座时一般可不约束旋转自由度。
10. 注意输入梁截面温度荷载时宽度B的取值为实际翼缘宽度(或腹板宽度之和)。
11. 弯桥时应注意支座的约束方向(设置节点局部坐标系)。
3. 虚拟的横向联系梁之间尽量要设为铰接(可将纵梁之间的虚拟横梁分割为两个单元,将其中一个释放梁端约束)。
"4定义移动荷载的车道时,应尽量选择按“横向联系梁”方法分布移动荷载,此时应将所有的横向联系梁定义为一个结构组,并在定义车道时选择该结构组。
请问高手以上两条处理的理由是什么?
"虚拟的横向联系梁之间尽量要设为铰接(可将纵梁之间的虚拟横梁分割为两个单元,将其
中一个释放梁端约束"
这条说的有问题,只针对特殊的模型,并不是针对所有的模型,我已向midas公司咨询过而且midas对活载只能按影响线加载,必须先定义车道线,并不能按照影响面加载,对midas在梁格法的应用方面,算是它的一个弊端。
个人认为你可以参考一下桥博,它在斜弯桥部分,对影响面加载已解决。
另你还可以参考一下戴公连李德建《桥梁结构空间
分析方法与应用》这本书
同意4楼的说法。
midas的空间结构加载,局限在车道范围,不一定能体现车道横向最不利加:因为车道宽度一般不小于3.5m,而横向车辆加载可以是3.1m。
