初中数学几何模型.pdf

合集下载

初中数学几何模型

全等变换平移：平行等线段（平行四边形）对称：角平分线或垂直或半角旋转：相邻等线段绕公共顶点旋转对称全等模型：说明：以角平分线为轴在角两边进行截长补短或者作边的垂线，形成对称全等。

两边进行边或者角的等量代换，产生联系。

垂直也可以做为轴进行对称全等。

对称半角模型说明：上图依次是°、°、°、°及有一个角是°直角三角形的对称（翻折），翻折成正方形或者等腰直角三角形、等边三角形、对称全等。

旋转全等模型半角：有一个角含角及相邻线段自旋转：有一对相邻等线段，需要构造旋转全等共旋转：有两对相邻等线段，直接寻找旋转全等中点旋转：倍长中点相关线段转换成旋转全等问题旋转半角模型说明：旋转半角的特征是相邻等线段所成角含一个二分之一角，通过旋转将另外两个和为二分之一的角拼接在一起，成对称全等。

自旋转模型构造方法：遇度旋度，造等边三角形遇度旋度，造等腰直角遇等腰旋顶点，造旋转全等遇中点旋度，造中心对称说明：IS 8模型变形BEFcEB说明：说明：nnnnnnnnnnnnnnnnnnnnnnn nnnnn口叩皿皿皿皿皿中点模型边构诗中｛fflt 逢阳点闵iS 中幽城几何最值模型 VH *h 轴对称模型对称最值线mi 差模型 fflftffw 同侧"异侧两蜒段之利罐短视它同侧、异删芮线投之羞媪小槐型四边形周怏垠小根地三角形眉长必小檢哩三线穀之和她知爬制过桥模取旋转最值说明：找到与所要求最值相关成三角形的两个定长线段，定长线段的和为最大值，定长线段的差为最小值。

简拼模型三角形j四边形E 面积等分说明：说明：3045602说明：ACOCOAA 模型一：手拉手模型-旋转型全等<2)等濮的AA Mfr=血°拟述°均为等媵直甬M 册A 结险(DA (UCtAO^l>j 超乙他»③。

E 平分£忖了儿(1)―况> Sfr ：LDW 牛底皿力能转至右囲检置A 皓论：> 右图中①bOCWMe\QAC AOSD 』 >⑨延氏M 交购于点G 必肖5氏-LBOA⑵特燥惜况＞条件m 3MB ,厶伽■剜，将AXD 龍讳至右團位蛊a gife ：右gcp fflAfJCD^iOJ^AC?JCiM£33②延长M 交加于点瓦愁有3EC -LUGA f BD 000B (5)-—--——=—-=tan ZlfX D®ACOCOA 3f^SDLAC.灘接也JC >临加*†g ・a+o>s ⑥矢"訐c&J 冊哒相垂直的四嬷)<3)任翦腰三角晤†辭，。

完整版)初中数学几何模型大全+经典题型(含答案)

完整版)初中数学几何模型大全+经典题型(含答案)通过将倍长中点相关线段进行旋转变换，可以构造出旋转全等模型。

这种模型的特点是，将相邻等线段所成角的一半旋转后拼接在一起，形成对称全等。

同时，也可以通过将两个等腰三角形或正多边形的夹角进行变化，来构造出模型变形。

如果遇到复杂图形找不到旋转全等，可以先找到两个正多边形或等腰三角形的公共极点，然后围绕公共极点找到两组相邻等线段，分组组成三角形证全等。

幂定理可以用等线段、等比值、等乘积进行代换，从而将两个数之间的比值转换成乘积。

在相似证明中，常用的辅助线是平行线，根据题目条件来确定比值并做出相应的平行线。

题目一：在半圆中，圆心为O，圆上有点C、E，CD垂直于AB，EF垂直于AB，EG垂直于CO。

证明CD等于GF。

题目二：在正方形ABCD内部，点P满足∠PAD＝∠PDA＝15度。

证明△PBC是正三角形。

题目三：在图中，ABCD、A1B1C1D1都是正方形，A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点。

证明A2B2C2D2是正方形。

题目四：在四边形ABCD中，AD＝BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN于E、F。

证明∠DEN＝∠F。

题目五：在△ABC中，H为垂心，O为外心，且OM垂直于BC于M。

1）证明AH等于2OM；2）如果∠BAC等于60度，证明AH等于AO。

1.设P为正三角形ABC内任意一点，连接PA,PB,PC，由三角形不等式可得PA+PB>AB。

PB+PC>BC。

PC+PA>CA。

将三式相加得到2PA+2PB+2PC>AB+BC+CA=3，即PA+PB+PC>3/2.又由于P到三角形三边的距离不超过1，所以PA+PB+PC<3，综上可得1.5≤PA+PB+PC<3，即所求不等式成立。

2.设P为正方形ABCD内任意一点，连接PA,PB,PC,PD。

由于正方形四边相等，所以PA+PC=2，PB+PD=2.又由于P到四边的距离不超过1，所以PA+PB+PC+PD<4.将前两式相加得到PA+PB+PC+PD=2(PA+PB)/2+2(PC+PD)/2≥2√(PA·PB)+2√(PC·P D)。

初中数学必背几何模型

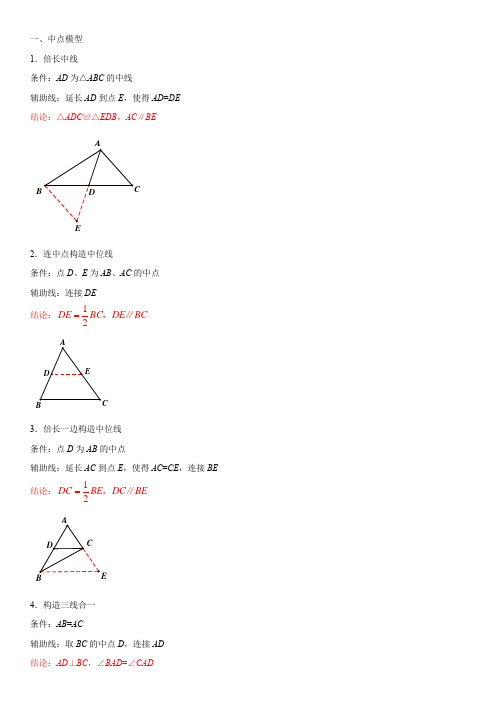
一、中点模型1．倍长中线条件：AD 为△ABC 的中线辅助线：延长AD 到点E ，使得AD =DE结论：△ADC ≌△EDB ，AC ∥BE2．连中点构造中位线条件：点D 、E 为AB 、AC 的中点辅助线：连接DE 结论：12DE BC DE BC =，∥3．倍长一边构造中位线条件：点D 为AB 的中点辅助线：延长AC 到点E ，使得AC =CE ，连接BE 结论：12DC BE DC BE =，∥4．构造三线合一条件：AB =AC辅助线：取BC 的中点D ，连接AD结论：AD ⊥BC ，∠BAD =∠CADB5．构造斜边中线条件：∠ABC =90°辅助线：取AC 的中点D ，连接BD 结论：12BD AC AD CD ===二、角平分线模型6．往角两边作垂线条件：AD 平分∠BAC辅助线：过点D 作AB 、AC 的垂线，垂足分别为E 、F结论：△ADE ≌△ADF7．在角的两边截取等长线段条件：AD 平分∠BAC辅助线：在AB 、AC 上取点E 、F ，满足AE =AF ，连接DE 、DF 结论：△ADE ≌△ADF8．过角平分线上一点作垂线条件：AD 平分∠BAC辅助线：过点D 作EF ⊥AD ，交AB 、AC 于点E 、FD CBB CCC结论：△ADE ≌△ADF三、双角平分线模型9．内内模型条件：BD 、CD 平分∠ABC 、∠ACB 结论：1902D A ∠=︒+∠10．内外模型条件：BD 、CD 平分∠ABC 、∠ACE 结论：12D A ∠=∠11．外外模型条件：BD 、CD 平分∠CBE 、∠BCF 结论：1902D A ∠=︒-∠四、平行线模型12．猪蹄模型CA BCC ED条件：AB ∥CD辅助线：过点E 作EF ∥AB结论：∠B +∠D =∠BED13．铅笔头模型条件：AB ∥CD辅助线：过点E 作EF ∥AB结论：∠B +∠D +∠BED =360°14．鸟头模型条件：AB ∥CD辅助线：过点E 作EF ∥AB结论：∠D +∠BED =∠B15．平行线+角平分线模型条件：AB ∥CD ，CE 平分∠ACD结论：AC =AE五、等积模型16．等底等高条件：AD ∥BCFAFBC结论：ABC DBC S S =，ADB ADC S S =17．等高模型条件：B 、C 、D 共线结论：::ABD ADC S S BD CD =18．等底模型条件：AE 、DE 为△ABC 、△DBC 边BC 上的高结论：::ABC DBC S S AE DE =六、对称半角模型19．对称半角模型-含45°角的三角形条件：∠BAC =45°，AD ⊥BC辅助线：作点D 关于AB 的对称点E ，关于AC 的对称点F ，连接AE 、AF 、BE 、CF 、EF结论：△AEF 是等腰直角三角形20．对称半角模型-含30°角的三角形B CB C DED条件：∠BAC =30°，AD ⊥BC辅助线：作点D 关于AB 的对称点E ，关于AC 的对称点F ，连接AE 、AF 、BE 、CF 、EF结论：△AEF 是等边三角形七、旋转半角模型21．旋转半角模型-等腰直角三角形条件：AB =AC ，∠BAC =90°，∠MAN =45°辅助线：将△ABM 绕点A 逆时针旋转90°，得到△ACM ＇结论：ANM ANM '≌，222BM CN MN +=22．旋转半角模型-等边三角形条件：△ABC 是等边三角形，BD =CD ，∠BDC =120°， ∠MDN =60°辅助线：将△BDM 绕点D 顺时针旋转120°，得到△DCM ＇结论：NDM NDM '≌，BM CN MN +=23．旋转半角模型-正方形条件：正方形ABCD ，∠MAN =45°，FEAM'M CAB辅助线：将△ABM 绕点A 逆时针旋转90°，得到△ADM ＇结论：NAM NAM '≌，BM DN MN +=八、自旋转模型24．自旋转模型-等边三角形条件：△ABC 是等边三角形，点P 为其内任意一点辅助线：将△BAP 绕点B 顺时针旋转60°，得到△BCP ＇结论：△BPP ＇是等边三角形25．自旋转模型-等腰直角三角形条件：△ABC 中，∠BAC =90°，AB =AC ，点P 为△ABC 内任意一点辅助线：将△BAP 绕点A 逆时针旋转90°，得到△ACP ＇结论：△APP ＇是等腰直角三角形26．自旋转模型-等腰三角形条件：△ABC 中，AB =AC ，点P 为△ABC 内任意一点，∠BAC =α 辅助线：将△BAP 绕点A 逆时针旋转α，得到△ACP ＇结论：△APP ＇是等腰三角形M'DNCBAB九、手拉手模型29．手拉手模型-等边三角形条件：△ABC和△CDE都是等边三角形结论：△ACE≌△BCD27．手拉手模型-等腰直角三角形条件：△ABC和△CDE都是等腰直角三角形结论：△ACE≌△BCD，AE⊥BDEE28．手拉手模型-等腰三角形条件：△ABC 和△CDE 都是等腰三角形，CA =CB ， CD =CE ，且∠ACB =∠DCE结论：△ACE ≌△BCD30．手拉手模型-正方形条件：四边形ABCD 和AEFH 都是正方形结论：△ABE ≌△ADH ，BE ⊥DH十、最短路程模型31．直线同侧两线段之和最小（将军饮马）条件：点A 、B 在直线l 同侧，点P 为l 上一点辅助线：作点A 关于直线l 的对称点A ＇，连接A ＇B 结论：点P 为A ＇B 和l 交点时，AP +BP 最小C32．直线异侧两线段之差最小条件：点A 、B 在直线l 异侧，点P 为l 上一点辅助线：作线段AB 的垂直平分线m结论：点P 为m 和l 交点时，|AP -BP |最小33．直线同侧两线段之差最小条件：点A 、B 在直线l 同侧，点P 为l 上一点辅助线：作线段AB 的垂直平分线m结论：点P 为m 和l 交点时，|AP -BP |最小34．过桥模型（将军饮马）条件：A 、B 为定点，l 1∥l 2，MN 为定长线段且MN ⊥l 1 辅助线：将点A 向上平移MN 的长度得到A ＇，连接A ＇B 结论：点N 为A ＇B 与l 1交点时，AM +MN +BN 最小35．四边形周长最小（将军饮马）条件：A 、B 为定点，M 、N 为角两边上的动点辅助线：作点A 、B 关于角两边的对称点A ＇、B ＇，连接 lAlAll 1l 2A＇B＇结论：M、N为A＇B＇与角两边交点时，四边形ABMN的周长最小B'36．三角形周长最小（将军饮马）条件：A为定点，B、C为角两边上的动点辅助线：作点A关于角两边的对称点A＇、A＂，连接A＇A＂结论：B、C为A＇A＂与角两边交点时，△ABC的周长最小37．旋转类最短路程模型条件：线段OA=a，OB=b（a＞b），OB绕点O在平面内旋转结论：点B与点N重合时，AB最小；点B与点M重合时，AB最大十一、基本相似模型38．A字型条件：BC∥DE结论：△ABC∽△ADE条件：∠ABC =∠ADE结论：△ABC ∽△ADE39．8字型条件：AB ∥CD结论：△AOB ∽△DOC条件：∠BAO =∠DCO结论：△AOB ∽△COD40．母子型条件：△ABC 中，∠ACB =90°，CD ⊥AB结论：△ABC ∽△ACD ∽△CBD41．一线三等角模型条件：∠B =∠D =∠ACE结论：△ABC ∽△CDECBCC A42．手拉手相似模型条件：△ABC ∽△ADE结论：△ACE ∽△ABD十二、对角互补模型43．对角互补模型-90°全等型条件：∠AOB =∠DCE =90°，OC 平分∠AOB辅助线：过点C 作CM ⊥AO ，CN ⊥BO ，垂足分别为M 、N 结论：△CDM ≌△CEN ，CD =CE ，OD +OEOC ，212OECD S OC 四边形CB ACE AB D CDD44．对角互补模型-120°全等型条件：∠AOB =120°，∠DCE =60°，OC 平分∠AOB辅助线：过点C 作CM ⊥AO ，CN ⊥BO ，垂足分别为M 、N 结论：△CDM ≌△CEN ，CD =CE ，OD +OE =OC ，24OECD S =四边形45．对角互补模型-任意角全等型条件：∠AOB =2α，∠DCE =180°-2α，OC 平分∠AOB辅助线：过点C 作CM ⊥AO ，CN ⊥BO ，垂足分别为M 、N 结论：△CDM ≌△CEN ，CD =CE ，2cos OD OE OC α+=⋅， 2sin cos OEC OCD S S OC αα+=⋅46．邻边相等的对角互补模型条件：四边形ABCD 中，AB =AD ，∠ABC +∠ADC =180°D BAN E OB辅助线：延长CD 到E ，使得DE =BC ，连接AE结论：△ABC ≌△ADE ，CA 平分∠BCD十三、隐圆模型47．动点定长模型条件：AB =AC =AP ，点P 为动点结论：点B 、C 、P 三点共圆，点A 为圆心，AB 为半径48．直角圆周角模型条件：点C 为动点，∠ACB =90°结论：点A 、B 、C 三点共圆，线段AB 的中点为圆心，线段 AB 为直径49．定弦定长模型条件：点P 为动点，固定线段AB 所对的动角∠APB 为定值结论：点A 、B 、P 三点共圆，线段AB 和BP 的中垂线的交点为圆心BA50．四点共圆模型①条件：点A 、C 为动点，∠BAD +∠BCD =180°结论：点A 、B 、C 、D 四点共圆，线段AB 和BC 的中垂线的交点为圆心当∠BAD =∠BCD =90°，BD 为直径51．四点共圆模型②条件：线段AB 为固定长度，点D 为动点，∠C =∠D结论：点A 、B 、C 、D 四点共圆，线段AB 和BC 的中垂线的交点为圆心CCA当∠C=∠D=90°，AB为直径。

(完整版)初中数学九大几何模型

初中数学九大几何模型OD ECABAED DOECBABOC ECAEDD图2图 2、手拉手模型 - 旋转型全等D E③OE 平分∠ AED图 2图 1 OABD OAO ②∠ AEB=∠AOB ；且∠ COD=∠AOB1）等边三角形3）顶角相等的两任意等腰三角形 2）等腰直角三角形图 1图 1C结论】：①△ OAC ≌△ OBD ；C条件】：△ OAB 和△ OCD 均为等边三角形条件】：△ OAB 和△ OCD 均为等腰直角三角形条件】：△ OAB 和△ OCD 均为等腰三角形结论】：①△ OAC ≌△ OBD ；②∠ AEB=60°；③ OE 平分∠ 结论】：①△ OAC ≌△ OBD ；②∠ AEB=90°；③ OE 平分∠、模型二：手拉手模型 -- 旋转型相似（1）一般情况【条件】：CD ∥AB ，将△ OCD 旋转至右图的位置 O OD EA A结论】：①右图中△ OCD ∽△ OAB →→→△ OAC ∽△ OBD ；②延长 AC 交 BD 于点 E ，必有∠ BEC=∠ BOA2）特殊情况条件】：CD ∥ AB ，∠ AOB=90°将△ OCD 旋转至右图的位置 A 结论】：①右图中△ OCD ∽△ OAB →→→△ OAC ∽△ OBD ； ②延长 AC 交 BD 于点 E ，必有∠ BEC=∠ BOA ； ③ A BD C O O C D O O A B tan ∠OCD ；④BD ⊥AC ； ⑤连接 AD 、BC ，必有 AD 2 BC 2 AB 2三、模型三、对角互补模型1）全等型 -90 ° 条件】：①∠ AOB=∠ DCE=90°；② OC 平分∠ AOB结论】：① CD=CE ；② OD+OE= 2 OC ；③ S △DCE CD ；⑥S△BCD证明提示： ①作垂直，如图 2，证明△ CDM ≌△ CEN ②过点 C 作 CF ⊥ OC ，如图 3，证明△ ODC ≌△ FEC ※当∠ DCE 的一边交 AO 的延长线于 D 时（如图 4）： S△OCDS以上三个结论：① CD=CE ；② OE-OD= 2 OC ； ③ S △ OCE S △ OCD2）全等型 -120 °条件】：①∠ AOB=2∠ DCE=120°；② OC 平分∠ AOB32 结论】：① CD=CE ；② OD+OE=O ；C ③ S △DCES △OCDS △OCEOC 2 4证明提示：①可参考“全等型 -90 °”证法一；②如右下图：在 OB 上取一点 F ，使 OF=OC ，证明△ OCF 为等边三角形。

(完整版)初中数学——最全：初中数学几何模型.docx

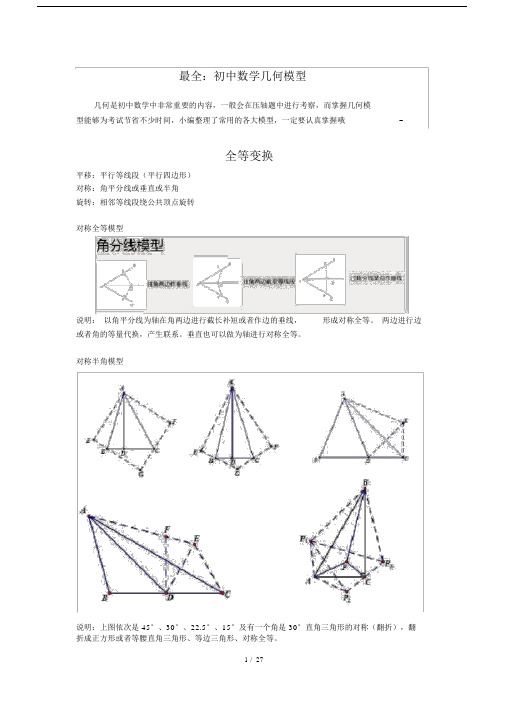
最全：初中数学几何模型几何是初中数学中非常重要的内容，一般会在压轴题中进行考察，而掌握几何模型能够为考试节省不少时间，小编整理了常用的各大模型，一定要认真掌握哦~全等变换平移：平行等线段（平行四边形）对称：角平分线或垂直或半角旋转：相邻等线段绕公共顶点旋转对称全等模型说明：以角平分线为轴在角两边进行截长补短或者作边的垂线，形成对称全等。

两边进行边或者角的等量代换，产生联系。

垂直也可以做为轴进行对称全等。

对称半角模型说明：上图依次是 45°、30°、22.5°、15°及有一个角是 30°直角三角形的对称（翻折），翻折成正方形或者等腰直角三角形、等边三角形、对称全等。

旋转全等模型半角：有一个角含1/2 角及相邻线段自旋转：有一对相邻等线段，需要构造旋转全等共旋转：有两对相邻等线段，直接寻找旋转全等中点旋转：倍长中点相关线段转换成旋转全等问题旋转半角模型说明：旋转半角的特征是相邻等线段所成角含一个二分之一角，通过旋转将另外两个和为二分之一的角拼接在一起，成对称全等。

自旋转模型构造方法：遇 60 度旋 60 度，造等边三角形；遇90度旋90度，造等腰直角遇等腰旋顶点，造旋转全等；遇中点旋180 度，造中心对称共旋转模型说明：旋转中所成的全等三角形，第三边所成的角是一个经常考察的内容。

通过“8”字模型可以证明。

模型变形说明：模型变形主要是两个正多边形或者等腰三角形的夹角的变化，另外是等腰直角三角形与正方形的混用。

当遇到复杂图形找不到旋转全等时，先找两个正多边形或者等腰三角形的公共顶点，围绕公共顶点找到两组相邻等线段，分组组成三角形证全等。

中点旋转：说明：两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点，证明另外两个顶点与中点所成图形为等腰直角三角形。

证明方法是倍长所要证等腰直角三角形的一直角边，转化成要证明的等腰直角三角形和已知的等腰直角三角形（或者正方形）公旋转顶点，通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。

(完整版)初中数学几何模型大全+经典题型(含答案)

初中数学几何模型大全+经典题型（含答案）全等变换平移：平行等线段（平行四边形）对称：角平分线或垂直或半角旋转：相邻等线段绕公共顶点旋转对称全等模型说明：以角平分线为轴在角两边进行截长补短或者作边的垂线，形成对称全等。

两边进行边或者角的等量代换，产生联系。

垂直也可以做为轴进行对称全等。

对称半角模型说明：上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称（翻折），翻折成正方形或者等腰直角三角形、等边三角形、对称全等。

旋转全等模型半角：有一个角含1/2角及相邻线段自旋转：有一对相邻等线段，需要构造旋转全等共旋转：有两对相邻等线段，直接寻找旋转全等中点旋转：倍长中点相关线段转换成旋转全等问题旋转半角模型说明：旋转半角的特征是相邻等线段所成角含一个二分之一角，通过旋转将另外两个和为二分之一的角拼接在一起，成对称全等。

自旋转模型构造方法：遇60度旋60度，造等边三角形遇90度旋90度，造等腰直角遇等腰旋顶点，造旋转全等遇中点旋180度，造中心对称共旋转模型说明：旋转中所成的全等三角形，第三边所成的角是一个经常考察的内容。

通过“8”字模型可以证明。

模型变形说明：模型变形主要是两个正多边形或者等腰三角形的夹角的变化，另外是等腰直角三角形与正方形的混用。

当遇到复杂图形找不到旋转全等时，先找两个正多边形或者等腰三角形的公共顶点，围绕公共顶点找到两组相邻等线段，分组组成三角形证全等。

几何最值模型对称最值(两点间线段最短)对称最值(点到直线垂线段最短)说明：通过对称进行等量代换，转换成两点间距离及点到直线距离。

(完整版)初中数学九大几何模型

初中数学九大几何模型一、手拉手模型----旋转型全等（1）等边三角形【条件】：△OAB 和△OCD 均为等边三角形；【结论】：①△OAC ≌△OBD ；②∠AEB=60°；③OE 平分∠AED （2）等腰直角三角形【条件】：△OAB 和△OCD 均为等腰直角三角形；【结论】：①△OAC ≌△OBD ；②∠AEB=90°；③OE 平分∠AED （3）顶角相等的两任意等腰三角形【条件】：△OAB 和△OCD 均为等腰三角形；且∠COD=∠AOB【结论】：①△OAC ≌△OBD ； ②∠AEB=∠AOB ； ③OE 平分∠AEDOABC DE图 1OABC D E图 2OABCDE图 1OABCDE图 2OABC DEOABCD E图 1图 2二、模型二：手拉手模型----旋转型相似（1）一般情况【条件】：CD ∥AB ，将△OCD 旋转至右图的位置【结论】：①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ； ②延长AC 交BD 于点E ，必有∠BEC=∠BOA （2）特殊情况【条件】：CD ∥AB ，∠AOB=90°将△OCD 旋转至右图的位置【结论】：①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ； ②延长AC 交BD 于点E ，必有∠BEC=∠BOA ； ③===OAOBOC OD AC BD tan ∠OCD ；④BD ⊥AC ； ⑤连接AD 、BC ，必有2222CD AB B C AD +=+；⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型（1）全等型-90°【条件】：①∠AOB=∠DCE=90°；②OC 平分∠AOB【结论】：①CD=CE ；②OD+OE=2OC ；③2△OCE △OCD △DCE OC 21S S S =+= 证明提示：①作垂直，如图2，证明△CDM ≌△CEN②过点C 作CF ⊥OC ，如图3，证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时（如图4）：以上三个结论：①CD=CE ；②OE-OD=2OC ； ③2△OCD △OCE OC 21S S =-OB CO ACDEOB CDEOA C DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4（2）全等型-120°【条件】：①∠AOB=2∠DCE=120°；②OC 平分∠AOB【结论】：①CD=CE ；②OD+OE=OC ；③2△OCE △OCD △DCE OC 43S S S =+=证明提示：①可参考“全等型-90°”证法一；②如右下图：在OB 上取一点F ，使OF=OC ，证明△OCF 为等边三角形。

(完整版)初中数学经典几何模型

梯形里面作高线，平移一腰试试看。平行移动对角线，补成三角形常见。
证相似，比线段，添线平行成习惯。等积式子比例换，寻找线段很关键。
直接证明有困难，等量代换少麻烦。斜边上面作高线，比例中项一大片。
半径与弦长计算，弦心距来中间站。圆上若有一切线，切点圆心半径连。
切线长度的计算，勾股定理最方便。要想证明是切线，半径垂线仔细辨。
三角形中有中线，延长中线等中线。平行四边形出现，对称中心等分点。梯形里面作高线，平移一腰试试看。平行移动对角线，补成三角形常见。证相似，比线段，添线平行成习惯。等积式子比例换，寻找线段很关键。直接证明有困难，等量代换少麻烦。斜边上面作高线，比例中项一大片。半径与弦长计算，弦心距来中间站。圆上若有一切线，切点圆心半径连。切线长度的计算，勾股定理最方便。要想证明是切线，半径垂线仔细辨。是直径，成半圆，想成直角径连弦。弧有中点圆心连，垂径定理要记全。圆周角边两条弦，直径和弦端点连。弦切角边切线弦，同弧对角等找完。要想作个外接圆，各边作出中垂线。还要作个内接圆，内角平分线梦圆如果遇到相交圆，不要忘作公共弦。内外相切的两圆，经过切点公切线。若是添上连心线，切点肯定在上面。要作等角添个圆，证明题目少困难。
1 评论
分享举报
初中数学里的几何证明问题有一个顺口溜是什么呀？
分享举报浏览 507 次
4 个回答
热点话题付费时代，你会花钱买会员，还是等待 75 秒广告？
最佳答案
2012-06-01
youlan1712
人人都说几何难，难就难在辅助线。辅助线，如何添？把握定理和概念。
还要刻苦加钻研，找出规律凭经验。图中有角平分线，可向两边作垂线。角平分线平行线，等腰三角形来添。角平分线加垂线，三线合一试试看。

初中数学几何必杀技八大模型(pdf)

如果您喜欢这份文档，欢迎下载!精品文档，名师推荐！初中几何必杀技一一八大模型MH）手拉手模型一旋转型全等1.等边三角形条件:如图1,AOAB,△OCD均为等边三角形.结论:①左OAC^AOBD；②ZAEB= 60°；③EO平分匕AED.2.等腰直角三角形条件:如图2.AOAB,△OCD均为等腰直角三角形.结论:①左QAC丝△OBD ；②ZAEB= 90°；③EO平分/AED.3.任意等腰三角形条件:如图3,AQAB,AOCD均为等腰三角形,OA=OB,OC=OD,ZAOB=ZCOD. 结论:①左OAC^/\OBD；② ZAEB=ZAOB；③ EO 平分/AED.模型二）手拉手模型一旋转型相似1.一般情况条件:如图4,CD//AB,将△OCD旋转至右图位置.结论:右图中①左OCDw AOAB, AOACco AOBD；②延长AC交BD于点E,必有ZBEC=ZBOA.2.特殊情况条件:如图5,CD//AB,ZAOB=90°,将△OCD旋转至右图位置.结论:右图中①左OCD GO AOAB, AOACco AOBD,②连接AC,BD交于点E,必有ZBEC=ZBOA；®|^ = ^ = ^ = tanZOCD；@BD±AC;⑤连接AD,BC,必有AD2 +BC2=AB2+CD2；⑥S mABCD = yACX BD（对角线互相垂直的四边形）.对角互补模型1.全等型一90°条件:如图6①，①ZAOB = ZDCE= 90°；②OC平分ZAOB.结论：®CD=CE；② OD+OE=7^OC；③=扌8气证明提示：①过点C作CM丄OA于点M,CN丄OB于点N,如图②，证明△ CDM^△ CEN；②过点C作CF丄。

C,如图③，证明△ ODC^AFEC.当ZECD的一边交A。

的延长线于点D时，如图④，结论：（DCD=CE（不变）；②OE— OD=72OC；③ S ACCE—S A0CD =yOC2.以上结论证明方法与前一种一致,可自行尝试. A图4图62,全等型一120°条件：如图7①，①ZAOB = 2ZDCE= 120°；②OC平分ZAOB.结论:① CD= CE；② OD+OE= OC；③ S* + S ACCE =^OC2.证明提示：①可参考“全等型一90°”证明结论①；②如图②，在OB上取一点F,使OF=OC,证明△ ECF 丝△DCO.当匕DCE的一边交AO的延长线于点D时，如图③，结论：①CD=CE；（DOE—OD= OC；®S ACCE—Sg =^OC.以上结论证明方法与前一种一致.3.全等型一任意角a条件：如图8①，①/AOB = 2a,ZDCE=180°—2a;②CD=CE.结论：①OC平分ZAOB:②OD + OE=2OC - cosa;③S A0CD + S ACCE = OC2• sina •cosa.当/DCE的一边交AO的延长线于点D时（如图②），结论：①0C 平分ZAOB OD = 2OC - cosa；③S ACC£ -S ACCD = 0C2• sina , cosa.可参考上述方法进行证明.对角互补模型总结：①常见初始条件：四边形对角互补；注意两点：四点共圆及直角三角形斜边中线；②初始条件“角平分线”与“两边相等”的区别；③两种常见的辅助线作法；④注意OC平分ZAOB时,ZCDE=ZCED=ZCOA=ZCOB如何推导.模型四）角含半角模型90。

初中数学几何模型大全(精心整理)

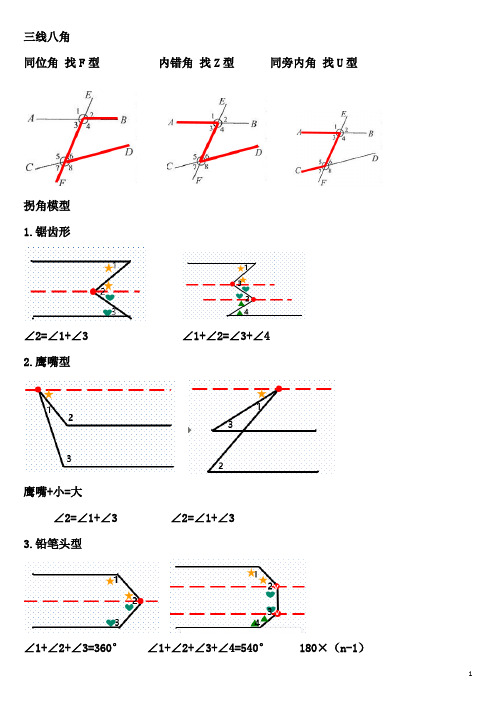
三线八角同位角找F型内错角找Z型同旁内角找U型拐角模型1.锯齿形∠2=∠1+∠3 ∠1+∠2=∠3+∠42.鹰嘴型鹰嘴+小=大∠2=∠1+∠3 ∠2=∠1+∠33.铅笔头型∠1+∠2+∠3=360° ∠1+∠2+∠3+∠4=540°180×（n-1）等积变换模型S△ACD=S△BCD 八字模型∠A+∠B=∠C+∠DAD+BC>AB+CD飞镖模型∠D=∠B+∠C+∠AAB+AC>BD+CD内内角平分线模型∠A∠D=90°+12内外角平分线模型∠D=1∠A2外外角平分线模型∠D=90°-1∠A2平行平分出等腰模型HG=HM等面积模型 D是BC的中点S△ABD= S△ACD 倍长中线模型：D是BC的中点S△FBD= S△ECD角平分线构造全等模型角平分线垂直两边角平分线垂直中间角平分线构造轴对称以角平分线为轴在角两边进行截长补短或者作边的垂线，形成对称全等。

两边进行边或者角的等量代换，垂直也可以做为轴进行对称全等。

三垂模型拉手模型大小等边三角形虚线相等且夹角为60°大小等腰三角形顶角为a，虚线相等，且夹角为a大小等腰直角三角形虚线相等且夹角为90°大小正方形虚线相等，且夹角为90°半角模型正方形ABCD ∠EDF=45°得：EF=AE+CFCD=AD,∠ADC=90°,∠EDF=45°,∠A+∠C=180°得：EF=AE+CF∠BADAB=AD，∠B+∠D=180°，∠EAF=12得：EF=BE+DFAB=AC,∠BAC=90°，∠DAE=45°得：DE2=BD2+CE2△CEF为直角三角形上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称（翻折），翻折成正方形或者等腰直角三角形、等边三角形、对称全等。

初中数学几何模型八年级上部分

最后都转化到：“两点之间，线段最短”解决
特点：①动点在直线上；②起点，终点固定
滴水穿石
~ 30 ~
锲而不舍
经典模型系列手册
最短路程模型之二（点到直线类）
A
A P
H Q'
PC
垂线段最短
OQMB
条件：如右图① OC 平分 AOB
② M 为 OB 上一定点
③ P 为 OC 上动点
④ Q 为 OB 上动点求： MP PQ 最小时， P 、 Q 的位置
①____________________
②_______________________（重点）
③________________________（难点）
请独立完成以上证明，必须非常熟练掌握
请思考初始条件的变化，对模型的影响
温故而知新
~ 15 ~
熟能生巧
智康 1 对 1 初数团队制作
（对角互补模型--相似型）
A
AM
D
CD
C
N
O
E BO
EB
条件：① AOB DCE 90q
② OC 平分 AOB
结论：① CD CE ；② OD OE 2OC
③ SODCE
S'OCD S'OCE
1 OC2 2
辅助线之一：作垂直，证明 'CDM≌'CEN
滴水穿石
~6~
锲而不舍
经典模型系列手册
A
D
C
O
E
B F
条件：① AOB DCE 90q
且 AOB COD
结论：① 'OAC≌'OBD ;② AEB AOB
③ OE 平分 AED （易忘）

初中数学经典几何模型总结上册

初中数学经典几何模型总结上册几何图形初步模型（一）线段双中点 (2)几何图形初步模型（二）——双角平分线 (6)相交线与平行线模型（三）——猪蹄模型 (11)相交线与平行线模型（四）——铅笔头模型 (15)相交线与平行线模型（五）——锯齿模型 (20)三角形模型（六）——8字模型 (23)三角形模型（七）——飞镖模型 (28)三角形模型（八）——A字模型 (32)三角形模型（九）——老鹰抓小鸡模型 (35)三角形模型（十）——双角平分线模型 (38)全等三角形模型（十一）——K型模型 (44)全等三角形模型（十二）——手拉手模型 (48)全等三角形模型（十三）——倍长中线模型 (53)全等三角形模型（14）——平行线中点模型 (56)全等三角形模型（十五）——雨伞模型 (60)全等三角形模型（十六）——半角模型 (63)全等三角形模型（十七）——胖瘦模型（SSA） (70)轴对称模型（十八）——将军饮马模型 (75)轴对称模型（十九）——海盗埋宝模型 (82)轴对称模型（二十）——婆罗摩笈多模型 (86)几何图形初步模型（一）线段双中点◎结论1：已知点C 在线段AB 上，点M、N 分别是AC，BC 的中点，则MN=21AB.【证明】∵点M、N 分别是AC，BC 的中点，∴CM=21AC，CN=21BC 【奇思妙想消消消：等号左边CM，CN 消掉共同字母C,得MN。

等号右边21AC，21BC 消掉共同字母C，得21AB】∴MN =CM+CN =21AC+21BC =21（AC+BC）=21AB ◎结论2：已知点C 在线段AB 延长线上，点M、N 分别是AC，BC 的中点，则MN=21AB.【证明】∵点M、N 分别是AC，BC 的中点，∴MC=21AC，NC=21BC，【奇思妙想消消消：等号左边MC，NC 消掉共同字母C,得MN。

等号右边21AC，21BC 消掉共同字母C，得21AB】∴MN =MC -NC =21AC-21BC =21（AC -BC）=21AB ○巧○记○口○诀一半一半又一半已知点C 是线段BA 延长线上一点，点M，N 分别是AC，BC 的中点，则MN=21AB无论线段之间的和差关系如何变，MN 的长度只与AB 有关.即MN=21AB.1.（2022·山西晋城·七年级期末）已知线段5cm AB =，在线段AB 上任取一点C ，其中线段AC 的中点为E 、线段BC 的中点为F ．则线段EF 的长度是_______．2.（2022·甘肃·凉州区中佳育才学校七年级期末）如图，C 是线段AB 上一点，M 是AC 的中点，N 是BC 的中点．(1)若AM =1，BC =4，求MN 的长度．(2)若AB =6，求MN 的长度．1．（2022·福建泉州·七年级期末）如图，线段13cm AB =，点C 是线段AB 上一点，点M 、N 分别是AC 、BC 的中点，则MN 的长为__________cm ．2．（2022·安徽·桐城市第二中学七年级期末）已知线段AB =10cm ，线段AC =16cm ，且AB 、AC 在同一条直线上，点B 在A 、C 之间，此时AB 、AC 的中点M 、N 之间的距离为（）A ．13cmB ．6cmC ．3cmD ．1.5cm 3．（2022·云南保山·七年级期末）如图，点M 是AB 的中点，点N 是BD 的中点，AB ＝6cm ，BC ＝10cm ，CD ＝8cm ．则MN 的长为（）A ．12cmB ．11cmC ．13cmD ．10cm4．（2021·山东枣庄东方国际学校七年级阶段练习）如图，已知线段AB ＝12cm ，点C 为线段AB 上的一个动点，点D ，E 分别是AC 和BC 的中点．(1)若AC ＝4cm ，求DE 的长；(2)若把“点C 在线段AB 上”改为“点C 在直线AB 上”，当AC ＝4cm 时，求DE 的长．（请画出图形，说明理由）5．（2022·山东·龙口市培基学校期中）如图，C 是线段AB 上一点，M 是AC 的中点，N 是BC 的中点．(1)若AM ＝2，BC ＝8，求MN 的长度；(2)若AB ＝14，求MN 的长度．1．（2018·湖南邵阳·中考模拟）如图，点C 在线段AB 上，点,M N 分别是AC BC 、的中点．（1）若9,6AC cm CB cm ==，求线段MN 的长；（2）若C 为线段AB 上任一点，满足AC CB acm +=，其它条件不变，你能求出MN 的长度吗？请说明理由．（3）若C 在线段AB 的延长线上，且满足,,AC BC bcm M N -=分别为AC 、BC 的中点，你能求出MN 的长度吗？请画出图形，写出你的结论，并说明理由．2．（2022·安徽·宣城市第六中学一模）如图所示，已知C D 、是线段AB 上的两个点，点M N 、分别为AC BD 、的中点．（1）若16AB cm =，6CD cm =，求AC BD +的长和M N ，的距离；（2）如果AB m =，CD n =，用含m n ，的式子表示MN 的长．几何图形初步模型（二）——双角平分线◎【结论1】如图，已知OP 为∠AOB 内一条射线，OM 平分∠BOP，ON 平分∠AOP，则∠MON=21∠AOB【证明】∵OM 平分∠BOP，ON 平分∠AOP，∴∠POM=21∠BOP，∠PON=21∠AOP，∴∠MON=∠POM+∠PON=21∠BOP+21∠AOP =21（∠BOP+∠AOP）=21∠AOB【奇思妙想消消消：等号左边∠POM，∠PON 消掉共同字母P,得∠MON。

初中数学几何模型大全+经典题型(含答案)

初中数学几何模子大全+经典题型（含答案）全等变换平移：平行等线段（平行四边形）对称：角等分线或垂直或半角扭转：相邻等线段绕公共极点扭转解释：以角等分线为轴在角双方进行截长补短或者作边的垂线,形成对称全等.双方进行边或者角的等量代换,产生接洽.垂直也可以做为轴进行对称全等.解释：上图依次是45°.30°.22.5°.15°及有一个角是30°直角三角形的对称（翻折）,翻折成正方形或者等腰直角三角形.等边三角形.对称全等.半角：有一个角含1/2角及相邻线段自扭转：有一对相邻等线段,须要结构扭转全等共扭转：有两对相邻等线段,直接查找扭转全等中点扭转：倍长中点相干线段转换成扭转全等问题解释：扭转半角的特点是相邻等线段所成角含一个二分之一角,经由过程扭转将别的两个和为二分之一的角拼接在一路,成对称全等.结构办法：遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋极点,造扭转全等遇中点旋180度,造中间对称解释：扭转中所成的全等三角形,第三边所成的角是一个经常考核的内容.经由过程“8”字模子可以证实.解释：模子变形主如果两个正多边形或者等腰三角形的夹角的变更,别的是等腰直角三角形与正方形的混用.当碰到庞杂图形找不到扭转全等时,先找两个正多边形或者等腰三角形的公共极点,环绕公共极点找到两组相邻等线段,分组构成三角形证全等.解释：两个正方形.两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形极点连线的中点,证实别的两个极点与中点所成图形为等腰直角三角形.证实办法是倍长所要证等腰直角三角形的一向角边,转化成要证实的等腰直角三角形和已知的等腰直角三角形（或者正方形）公扭转极点,经由过程证实扭转全等三角形证实倍长后的大三角形为等腰直角三角形从而得证.对称最值(两点间线段最短)解释：经由过程对称进行等量代换,转换成两点间距离及点到直线距离.解释：找到与所请求最值相干成三角形的两个定长线段,定长线段的和为最大值,定长线段的差为最小值.三角形→四边形四边形→四边形解释：剪拼主如果经由过程中点的180度扭转及平移转变图形的外形.解释：经由过程射影定理找到正方形的边长,经由过程平移与扭转完成外形转变解释：两个等腰直角三角形成扭转全等,两个有一个角是300角的直角三角形成扭转类似.推广：两个随意率性类似三角形扭转成必定角度,成扭转类似.第三边所成夹角相符扭转“8”字的纪律.解释：留意边和角的对应,相等线段或者相等比值在证实类似中起到经由过程等量代换来结构类似三角形的感化.解释：（1）三垂直到一线三等角的演化,三等角以30度.45度.60度情势消失的居多.（2）表里角等分线定理到射影定理的演化,留意之间的雷同与不合之处.别的,类似.射影定理.订交弦定理（可以推广到圆幂定理）之间的比值可以转换成乘积,经由过程等线段.等比值.等乘积进行代换,进行证实得到须要的结论.解释：类似证实中最经常应用的帮助线是做平行,依据标题标前提或者结论的比值来做响应的平行线.初中数学经典几何题（附答案）经典难题（一）1.已知：如图,O 是半圆的圆心,C.E 是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO．求证：CD ＝GF ．（初二）2.已知：如图,P 是正方形ABCD 内点,∠PAD＝∠PDA＝150．求证：△PBC 是正三角形．（初二）3.如图,已知四边形ABCD.A1B1C1D1都是正方形,A2.B2.C2.D2分离是1.DD1的中点．求证：四边形A2B2C2D2是正方形．（初二）4.已知：如图,在四边形ABCD 中,AD ＝BC,M.NAP CDBCDF点,AD.BC 的延伸线交MN 于E.F ．求证：∠DEN＝∠F．经典难题（二）1.已知：△ABC 中,H 为垂心（各边高线的交点）,O 为外心,且OM⊥BC 于M ．（1）求证：AH ＝2OM;（2）若∠BAC＝600,求证：AH ＝AO ．（初二）2.设MN 是圆O 外一向线,过O 作OA⊥MN 于A,交圆于B.C 及D.E,直线EB 及CD 分离交MN 求证：AP ＝AQ ．（初二）3.假如上题把直线MN 由圆外平移至圆内,设MN 是圆O 的弦,过MN 的中点A 分离交MN 于P.Q ．求证：AP ＝AQ ．（初二）4.如图,分离以△ABC 的AC 和BC 为一边,ACDE 和正方形CBFG,点P 是EF 的中点．求证：点P 到边AB 的距离等于AB1.如图,四边形ABCD 为正方形,DE∥AC,AE＝AC,AE 与CD 订交于F ．求证：CE ＝CF ．（初二）2.如图,四边形ABCD 为正方形,DE∥AC,且CE伸线于F ．求证：AE ＝AF ．（初二）3.设P 是正方形ABCD求证：PA ＝PF ．4.如图,PC切圆O 于线PO 订交于B.D 1.已知：△ABC 5．求：∠APB 的度数．2.设P 是平行四边形3.设ABCD 为圆内接凸四边形＝AC·BD．（初三）4.平行四边形ABCD 中,设E.F 分离是BC.AB 上的一点,AE CF 订交于P,且AE ＝CF ．求证：∠DPA＝∠DPC．（初二）经典难题（五）1.设P 是边长为1的正△ABC 内任一点,L ＝PA ＋PB ＋PC,求证：≤L＜2．2.已知：P 是边长为1的正方形ABCD 内的一点,求PA ＋PB ＋PC 的最小值．3.P 为正方形ABCD 内的一点,并且PA ＝a,PB ＝2a,PC ＝3a,求正方形的边长．4.如图,△ABC 中,∠ABC＝∠ACB＝800,D.E 分离是AB.AC 上的点,∠DCA＝300,∠EBA＝200,求∠BED 的度数．经典难题（一）CBDAFPDE CBA AP CBACBPDA CBP D1.如下图做GH⊥AB,衔接EO.因为GOFE四点共圆,所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF =GOGH=COCD,又CO=EO,所以CD=GF得证.2. 如下图做△DGC使与△ADP全等,可得△PDG为等边△,从而可得△DGC≌△APD≌△CGP,得出PC=AD=DC,和∠DCG=∠PCG＝150所以∠DCP=300 ,从而得出△PBC是正三角形3.如下图衔接BC1和AB1分离找个中点F,E.衔接C2F与A2E并延伸订交于Q点,衔接EB2并延伸交C2Q于H点,衔接FB2并延伸交A2Q于G点,由A2E=12A1B1=12B1C1= FB2 ,EB2=12AB=12BC=FC1 ,又∠GFQ+∠Q=900和∠GEB2+∠Q=900,所以∠GEB2=∠GFQ又∠B2FC2=∠A2EB2 ,可得△B2FC2≌△A2EB2 ,所以A2B2=B2C2 ,又∠GFQ+∠HB2F=900和∠GFQ=∠EB2A2 ,从而可得∠A2B2 C2=900 ,同理可得其他边垂直且相等,从而得出四边形A2B2C2D2是正方形.4.如下图衔接AC 并取个中点Q,衔接QN 和QM,所以可得∠QMF=∠F,∠QNM=∠DEN 和∠QMN=∠QNM,从而得出∠DEN＝∠F.经典难题（二）1.(1)延伸AD 到F 连BF,做OG⊥AF,又∠F=∠ACB=∠BHD, 可得BH=BF,从而可得HD=DF,又AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM (2)衔接OB,OC,既得∠BOC=1200, 从而可得∠BOM=600, 所以可得OB=2OM=AH=AO,得证.3.作OF⊥CD,OG⊥BE,衔接OP,OA,OF,AF,OG,AG,OQ. 因为22AD AC CD FD FD ABAEBEBGBG,由此可得△ADF≌△ABG,从而可得∠AFC=∠AGE.又因为PFOA 与QGOA 四点共圆,可得∠AFC=∠AOP 和∠AGE=∠AOQ, ∠AOP=∠AOQ,从而可得AP=AQ.4.过E,C,F 点分离作AB 地点直线的高EG,CI,FH.可得PQ=2EGFH.由△EGA≌△AIC,可得EG=AI,由△BFH≌△CBI,可得FH=BI. 从而可得PQ=2AI BI=2AB ,从而得证.经典难题（三）1.顺时针扭转△ADE,到△ABG,衔接CG. 因为∠ABG=∠ADE=900+450=1350从而可得B,G,D 在一条直线上,可得△AGB≌△CGB. 推出AE=AG=AC=GC,可得△AGC 为等边三角形. ∠AGB=300,既得∠EAC=300,从而可得∠A EC=750. 又∠EFC=∠DFA=450+300=750. 可证：CE=CF.2.衔接BD 作CH⊥DE,可得四边形CGDH 是正方形. 由AC=CE=2GC=2CH,可得∠CEH=300,所以∠CAE=∠CEA=∠AED=150, 又∠FAE=900+450+150=1500, 从而可知道∠F=150,从而得出AE=AF. 3.作FG⊥CD,FE⊥BE,可以得出GFEC 为正方形. 令AB=Y ,BP=X ,CE=Z ,可得PC=Y-X .tan∠BAP=tan∠EPF=XY =ZY X Z,可得YZ=XY-X2+XZ,即Z(Y-X)=X(Y-X) ,既得X=Z ,得出△ABP≌△PEF ,得到PA＝PF ,得证 .经典难题（四）1.顺时针扭转△ABP 600 ,衔接PQ ,则△PBQ是正三角形.可得△PQC是直角三角形.所以∠APB=1500 .2.作过P点平行于AD的直线,并选一点E,使AE∥DC,BE∥PC.可以得出∠ABP=∠ADP=∠AEP,可得：AEBP共圆（一边所对两角相等）.可得∠BAP=∠BEP=∠BCP,得证.3.在BD取一点E,使∠BCE=∠ACD,既得△BEC∽△ADC,可得：BE BC =ADAC,即AD•BC=BE•AC, ①又∠ACB=∠DCE,可得△ABC∽△DEC,既得AB AC =DEDC,即AB•CD=DE•AC, ②由①+②可得: AB•CD+AD•BC=AC(BE+DE)= AC·BD ,得证.4.过D 作AQ⊥AE ,AG⊥CF ,由ADE S =2ABCD S =DFC S ,可得： 2AE PQ=2AE PQ,由AE=FC.可得DQ=DG,可得∠DPA＝∠DPC（角等分线逆定理）.经典难题（五）1.（1）顺时针扭转△BPC 600 ,可得△PBE 为等边三角形.既得PA+PB+PC=AP++PE+EF 要使最小只要AP,PE,EF 在一条直线上,即如下图：可得最小L= ;（2）过P 点作BC 的平行线交AB,AC 与点D,F.因为∠APD>∠ATP=∠ADP,推出AD>AP ①又BP+DP>BP ②和PF+FC>PC ③又DF=AF ④由①②③④可得：最大L< 2 ;由（1）和（2）既得：≤L＜2 .2.顺时针扭转△BPC 600 ,可得△PBE 为等边三角形.既得PA+PB+PC=AP+PE+EF 要使最小只要AP,PE,EF 在一条直线上, 即如下图：可得最小PA+PB+PC=AF.既得213(1)42 = 23= 4232231)2 = 1) = 622 .3.顺时针扭转△ABP 900 ,可得如下图：既得正方形边长2222(2)()22a 522a.4.在AB 上找一点F,使∠BCF=600 ,衔接EF,DG,既得△BGC 为等边三角形,可得∠DCF=100 , ∠FCE=200 ,推出△ABE≌△ACF , 得到BE=CF , FG=GE .推出： △FGE 为等边三角形 ,可得∠AFE=800 ,既得：∠DFG=400① 又BD=BC=BG ,既得∠BG D=800 ,既得∠DGF=400②推得：DF=DG ,得到：△DFE≌△DGE ,从而推得：∠FED=∠BED=300 .。

(完整版)初中数学几何模型大全+经典题型(含答案)

两边进行边或者角的等量代换，产生联系。

垂直也可以做为轴进行对称全等。

对称半角模型说明：上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称（翻折），翻折成正方形或者等腰直角三角形、等边三角形、对称全等。

旋转全等模型半角：有一个角含1/2角及相邻线段自旋转：有一对相邻等线段，需要构造旋转全等共旋转：有两对相邻等线段，直接寻找旋转全等中点旋转：倍长中点相关线段转换成旋转全等问题旋转半角模型说明：旋转半角的特征是相邻等线段所成角含一个二分之一角，通过旋转将另外两个和为二分之一的角拼接在一起，成对称全等。

通过“8”字模型可以证明。

模型变形说明：模型变形主要是两个正多边形或者等腰三角形的夹角的变化，另外是等腰直角三角形与正方形的混用。

当遇到复杂图形找不到旋转全等时，先找两个正多边形或者等腰三角形的公共顶点，围绕公共顶点找到两组相邻等线段，分组组成三角形证全等。

几何最值模型对称最值(两点间线段最短)对称最值(点到直线垂线段最短)说明：通过对称进行等量代换，转换成两点间距离及点到直线距离。

初中数学九大几何模型

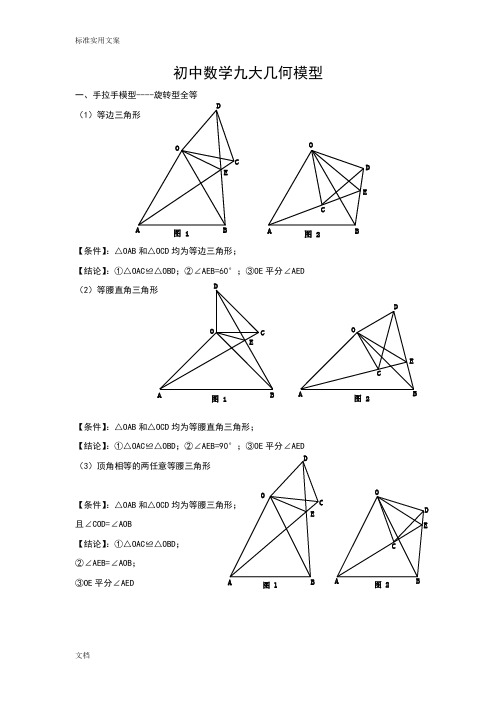
初中数学九大几何模型一、手拉手模型----旋转型全等（1）等边三角形【条件】：△OAB 和△OCD 均为等边三角形；【结论】：①△OAC ≌△OBD ；②∠AEB=60°；③OE 平分∠AED （2）等腰直角三角形【条件】：△OAB 和△OCD 均为等腰直角三角形；【结论】：①△OAC ≌△OBD ；②∠AEB=90°；③OE 平分∠AED （3）顶角相等的两任意等腰三角形【条件】：△OAB 和△OCD 均为等腰三角形；且∠COD=∠AOB【结论】：①△OAC ≌△OBD ； ②∠AEB=∠AOB ； ③OE 平分∠AEDOABC DE图 1OABC D E图 2OABCDE图 1OACDE图 2OABC DEOCD E图 1图 2二、模型二：手拉手模型----旋转型相似（1）一般情况【条件】：CD ∥AB ，将△OCD 旋转至右图的位置【结论】：①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ； ②延长AC 交BD 于点E ，必有∠BEC=∠BOA （2）特殊情况【条件】：CD ∥AB ，∠AOB=90° 将△OCD 旋转至右图的位置【结论】：①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ； ②延长AC 交BD 于点E ，必有∠BEC=∠BOA ； ③===OAOBOC OD AC BD tan ∠OCD ；④BD ⊥AC ； ⑤连接AD 、BC ，必有2222CD AB BC AD +=+；⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型（1）全等型-90°【条件】：①∠AOB=∠DCE=90°；②OC 平分∠AOB【结论】：①CD=CE ；②OD+OE=2OC ；③2△OCE △OCD △DCE OC 21S S S =+= 证明提示：①作垂直，如图2，证明△CDM ≌△CEN②过点C 作CF ⊥OC ，如图3，证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时（如图4）：以上三个结论：①CD=CE ；②OE-OD=2OC ； ③2△OCD △OCE OC 21S S =-OB CO CDEOB CDEOC DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4（2）全等型-120°【条件】：①∠AOB=2∠DCE=120°；②OC 平分∠AOB【结论】：①CD=CE ；②OD+OE=OC ；③2△OCE △OCD △DCE OC 43S S S =+=证明提示：①可参考“全等型-90°”证法一；②如右下图：在OB 上取一点F ，使OF=OC ，证明△OCF 为等边三角形。

初中数学几何模型.pdf