第5讲 初中几何经典模型:三垂直模型
初中几何模型:三垂直全等模型分析

三垂直全等模型“三垂直模型”是初中必会的一种几何模型,它是一个应用非常广泛的模型,它可以应用在三角形,矩形,平面直角坐标系,网格,一次函数,反比例函数,三角函数,二次函数以及圆等诸多的中考重要考点之中,所以这一知识点的掌握对于中考至关重要。
模型三垂直全等模型如图:∠D=∠BCA=∠E=90°,BC=AC.结论:Rt△BCD≌Rt△CAE.模型分析说到三垂直模型,不得不说一下弦图,弦图的运用在初中直角三角形中占有举足轻重的地位,很多利用垂直求角,勾股定理求边长,相似求边长都会用到从弦图支离出来的一部分几何图形去求解.图①和图②就是我们经常会见到的两种弦图。
图①图②三垂直图形变形如下图③、图④,这也是由弦图演变而来的。
图③图④DEABC例1如图,AB⊥BC,CD⊥BC,AE⊥DE,AE=DE,求证:AB+CD=BC.D证明:∵AE⊥DE,AB⊥BC,DC⊥BC,A∴∠AED =∠B =∠C =90°.∴∠A +∠AEB =∠AEB +∠CED =90°.∴∠BAE =∠CED .在△ABE 和△ECD 中,B C A CED AE ED ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△ECD .∴AB =EC ,BE =CD .∴AB +CD =EC +BE =BC.例2 如图,∠ACB =90°,AC =BC ,BE ⊥CE ,AD ⊥CE 于D ,AD =2.5cm ,BE =0.8cm ,则DE 的长为多少? EDA解答:∵BE ⊥CE ,AD ⊥CE ,∴∠E =∠ADC =90°.∴∠EBC +∠BCE =90°.∵∠BCE +∠ACD =90°,∴∠EBC =∠DCA .在△CEB 和△ADC 中,E ADC EBC DCA BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△CEB ≌△ADC .∴BE =DC =0.8cm ,CE =AD =2.5cm .∴DE =CE -CD =2.5-0.8=1.7cm .例3 如图,在平面直角坐标系中,等腰Rt △ABC 有两个顶点在坐标轴上,求第三个顶点的坐标。
三垂直模型

三垂直模型知识导航三垂直模型是经典的全等三角形模型之一,综合性较强。
解题方法通常是根据三垂直倒角来证明题目中有一对边相等的两个全等三角形。
一线三等角是三垂直模型的变式,包括一线三等锐角、一线三直角、一线三等钝角,这类型题型通常是利用三垂直模型原理进行倒角,证明两个三角形全等。
【核心考点】三垂直模型1. 如图,AC CE =,90ACE ∠=︒,AB BD ⊥,ED BD ⊥,6AB cm =,2DE cm =,则BD等于( )A .6cmB .8cmC .10cmD .4cm【解答】 解:AB BD ⊥,ED BD ⊥,90B D ACE ∴∠=∠=∠=︒,90BAC ACB ∴∠+∠=︒,90ACB ECD ∠+∠=︒, BAC ECD ∴∠=∠,在Rt ABC ∆与Rt CDE ∆中, B D BAC DCE AC CE ∠=∠⎧⎪∠=∠⎨⎪=⎩, Rt ABC Rt CDE(AAS)∴∆≅∆,2BC DE cm ∴==,6CD AB cm ==, 268BD BC CD cm ∴=+=+=,故选:B .2. 如图,已知ABC CDE ∆≅∆,90B D ∠=∠=︒,且B ,C ,D 三点在同一条直线.(1)试说明:BD AB ED =+.(2)试判定ACE ∆的形状, 并说明理由 .【解答】证明:(1)Rt ABC Rt CDE ∆≅∆,BC DE ∴=,AB CD =, BD CD CB =+, BD AB ED ∴=+.(2)结论:ACE ∆是等腰直角三角形 . 理由:Rt ABC Rt CDE ∆≅∆,90B D ∠=∠=︒,ACB CED ∴∠=∠,BAC ECD ∠=∠,AC EC =, 90BAC ACB ∠+∠=︒, 90ECD ACB ∴∠+∠=︒, 90ACB ∴∠=︒,ACE ∴∆是等腰直角三角形 .3. 已知在平面直角坐标系中,ABC ∆的顶点A 、C 分别在y 轴、x 轴上,90ACB ∠=︒,AC BC =.如图,当(0,2)A -,(1,0)C ,点B 在第四象限时,则点B 的坐标为_______.【解答】解:作BD x ⊥轴,90ACO CAO ∠+∠=︒,90ACO BCD ∠+∠=︒, CAO BCD ∴∠=∠,在AOC ∆和CDB ∆中, 90AOC CDB CAO BCDAC BC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, ()AOC CDB AAS ∴∆≅∆,1DB OC ∴==,2CD AO ==, 3OD ∴=,∴点B 的坐标为(3,1)-.故答案为(3,1)-.4. 如图,四边形ABCD ,EFGH ,NHMC 都是正方形,边长分别为2,3,m ,A ,B ,N ,E ,F 五点在同一直线上,则正方形CNHM 的边长m 是多少?【解答】解:四边形ABCD 、EFGH 、NHMC 都是正方形,90CNB ENH ∴∠+∠=︒,又90ENH NHE ∠+∠=︒,CNB EHN ∴∠=∠,在CBN ∆和NEH ∆中, CBN NEH CNB NHE CN NH ∠=∠⎧⎪∠=∠⎨⎪=⎩CBN NEH ∴∆≅∆, HE BN b ∴==,故在Rt CBN ∆中,222BC BN CN +=, 又2a =,3b =,m ∴=则正方形CNHM 的边长m5. 已知:在平面直角坐标系中,等腰直角ABC ∆顶点A 、C 分别在y 轴、x 轴上,且90ACB ∠=︒,AC BC =.(1)如图1,当(0,2)A -,(1,0)C ,点B 在第四象限时,先写出点B 的坐标,并说明理由. (2)如图2,当点C 在x 轴正半轴上运动,点(0,)A a 在y 轴正半轴上运动,点(,)B m n 在 第四象限时,作BD y ⊥轴于点D ,试判断a ,m ,n 之间的关系,请证明你的结论.【解答】解:(1)点B 的坐标为(3,1)-. 理由如下:作BD x ⊥轴于D ,90BOC BDC ∴∠=︒=∠, 90OAC ACO ∴∠+∠=︒, 90ACB ∠=︒,AC BC =, 90ACO BCD ∴∠+∠=︒, OAC BCD ∴∠=∠,在AOC ∆和CDB ∆中,90OAC BCDAOC CDB AC BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,()AOC CDB AAS ∴∆≅∆,AO CD ∴=,OC BD =,(0,2)A -,(1,0)C ,2AO CD ∴==,1OC BD ==,3OD ∴=,B 在第四象限,∴点B 的坐标为(3,1)-;(2)0a m n ++=. 证明:作BE x ⊥轴于E ,90BEC AOC ∴∠=∠=︒, 1290∴∠+∠=︒, 90ACB ∠=︒, 1390∴∠+∠=︒, 23∴∠=∠,在CEB ∆和AOC ∆中,23BEC AOC AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,()CEB AOC AAS ∴∆≅∆,AO CE a ∴==,BE CO =, BE x ⊥轴于E ,//BE y ∴轴,BD y ⊥轴于点D ,EO y ⊥轴于点O ,EO BD m ∴==, BE n ∴=-,a m n ∴+=-,0a m n ∴++=.6. 如图1,ABC ∆中,90BAC ∠=︒,AB AC =,直线l 经过点A ,分别过点B ,C 作直线l 的垂线,垂足分别为D ,E ,求证:DE BD CE =+;(1)将直线l 绕点A 逆时针旋转到直线l 与BC 相交,且45BAD ∠<︒(如图2)时,其它条件不变,请你探索DE ,BD ,CE 之间的数量关系,并证明之;(2)继续旋转,使4590BAE ︒<∠<︒(如图3),其它条件不变,此时(1)中的结论还成立吗?若成立,给出证明;若不成立,DE ,BD ,CE 之间又怎样的数量关系?(不需证明).【解答】证明:如图1,BD l ⊥,CE l ⊥,90BDA CEA ∴∠=∠=︒, 90ABD DAB ∴∠+∠=︒. 90BAC ∠=︒, 90DAB CAE ∴∠+∠=︒, ABD CAE ∴∠=∠.在ABD ∆和CAE ∆中 BDA CEA ABD CAE AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()ABD CAE AAS ∴∆≅∆,AD CE ∴=,BD AE =.DE AD AE =+, DE CE BD ∴=+;(1)DE CE BD =-理由:如图2,BD l ⊥,CE l ⊥,90BDA CEA ∴∠=∠=︒,90ABD DAB ∴∠+∠=︒. 90BAC ∠=︒, 90DAB CAE ∴∠+∠=︒,ABD CAE ∴∠=∠.在ABD ∆和CAE ∆中 BDA CEA ABD CAE AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()ABD CAE AAS ∴∆≅∆,AD CE ∴=,BD AE =DE AD AE =-, DE CE BD ∴=-;(2)DE BD CE =-.理由:如图3,BD l ⊥,CE l ⊥,90BDA CEA ∴∠=∠=︒, 90ABD DAB ∴∠+∠=︒. 90BAC ∠=︒, 90DAB CAE ∴∠+∠=︒, ABD CAE ∴∠=∠.在ABD ∆和CAE ∆中 BDA CEA ABD CAE AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()ABD CAE AAS ∴∆≅∆,AD CE ∴=,BD AE =DE AE AD =-, DE BD CE ∴=-.7. 如图所示,已知ABC ∆中,90ABC ∠=︒,AB BC =,三角形的顶点分别在相互平行的三条直线1l 、2l 、3l 上,且115∠=︒,则2∠=_________度.【解答】解:123////l l l ,13∴∠=∠,24∠=∠, 1234∴∠+∠=∠+∠. 90ABC ∠=︒,AB BC =, 45BAC BCA ∴∠=∠=︒. 34BAC ∠+∠=∠, 3445∴∠+∠=︒, 1245∴∠+∠=︒. 115∠=︒, 230∴∠=︒.故答案为:30.8.问题背景:(1)如图①,已知ABC∠=︒,AB AC=,直线m经过点A,BAC∆中,90=+.BD⊥直线m,CE⊥直线m,垂足分别为点D、E,求证:DE BD CE拓展延伸:(2)如图②,将(1)中的条件改为:在ABC=,D、A、E∆中,AB AC 三点都在直线m上,并且有BDA AEC BAC∠=∠=∠请写出DE、BD、CE三条线段的数量关系.(不需要证明)实际应用:(3)如图③,在ACB-,=,点C的坐标为(2,0)∆中,90∠=︒,AC BCACB点A的坐标为(6,3)-,请直接写出B点的坐标.【解答】(1)证明:BD AD ⊥,90ABD BAD ∴∠+∠=︒,90BAC ∠=︒,90CAE BAD ∴∠+∠=︒,ABD CAE ∴∠=∠,在ABD ∆和CAE ∆中,90ABD CAEADB CEA AB CA∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,()ABD CAE AAS ∴∆≅∆AE BD ∴=,AD CE =,DE AD AE BD CE ∴=+=+;(2)解:DE BD CE =+,理由如下:在ABD ∆中,180ABD ADB BAD ∠=︒-∠-∠, 180CAE BAC BAD ∠=︒-∠-∠,BDA AEC ∠=∠, ABD CAE ∴∠=∠,在ABD ∆和CAE ∆中,ABD CAEBDA AEC AB CA∠=∠⎧⎪∠=∠⎨⎪=⎩,()ABD CAE AAS ∴∆≅∆AE BD ∴=,AD CE =,DE AD AE BD CE ∴=+=+;(3)解:如图③,作AE x ⊥轴于E ,BF x ⊥轴于F , 由(1)可知,AEC CFB ∆≅∆,3CF AE ∴==,4BF CE OE OC ==-=, 1OF CF OC ∴=-=,∴点B 的坐标为(1,4).。
初中数学常见模型之三垂直全等模型

模型实例
例1.如图, AB ⊥ BC , CD ⊥ BC , AE ⊥ DE , AE=DE 求证: AB+CD=BC
例2.如图,∠ ACB-90 °,AC=BC,BE ⊥ CE 于点 D, AD=2.5cm ,BE=0.8cm 求 DE 的长
例3.如图,在平面直角坐标系中,等腰 Rt △ ABC 有两个顶点在坐标轴上 求第三个顶点的坐标
典例精选
1.如图,正方形 ABCD , BE=CF 。 求证:( 1 ) AE=BF ;( 2 ) AE ⊥ BF
2.直线 上有三个正方形 a 、b 、 c ,若 a 、 c 的面积分别是 5 和 11,则 b AB=AC ,点 P 为 BC 上一动点( B P<CP ), 分别过 B 、 C 作 BE ⊥ AP 于点 E 、 CF ⊥ AP 于点 F
( 1 )当α=45°时,求△ EAD 的面积;
( 2 )当α=30°时,求△ EAD 的面积;
( 3 )当0°<α<90°时,猜想△ EAD 的面积与大小有无关系?若有关,写出△ EAD 的面积S与α的关系式;若无关,请证明结论。
5.如图,向△ ABC 的外侧作正方形 ABDE 、正方形 ACFG , 过点 A 作 AH ⊥ BC 于 H , AH 的反向延长线与 EG 交于点 P 求证: BC=2AP
初中数学常见模型
三垂直全等模型
模型:三垂直全等模型
如图,∠ D= ∠ BCA= ∠ E=90 °, BC=AC 。 结论: Rt △ BCD ≌ Rt △ CAE
模型分析
说到三垂直模型,不得不说一下弦图,弦图的运用在初中直角三角形中占有 举足轻重的地位,很多利用垂直倒角,勾股定理求边长,相似求边长都会用到从 弦图中支离出来的一部分几何图形去求解。图①和图②就是我们经常会见到的两 种弦图。
2020年九年级初中必会几何模型-三垂直模型

三垂直模型【模型概述】出现3个直角,且3个直角的顶点共线时,角的边相交会形成相似(含全等)三角形。
【基本模型】图1 图2【解读】⑴图1和图2中,三个直角顶点B,C,D共线;⑵当△ABC和△CDE三组对应边均不相等时,有△ABC∽△CDE;⑶当△ABC和△CDE任意一组对应边相等时(如AC=CE),有△ABC≌△CDE;⑷证明思路:同角的余角相等⑸解题时往往只含有两个甚至一个垂直关系,需通过作垂线构造出三垂直模型,从而构造出全等或相似三角形,利用全等和相似的性质求解角度和线段长等问题。
典型例题1-1已知:∠ACB=90°,AC=BC,AD⊥CM,BE⊥CM,垂足分别为D,E。
⑴如图1,①线段CD和BE的数量关系是②请写出线段AD,BE,DE之间的数量关系并证明。
⑵如图2,结论②还成立吗?如不成立,写出并证明AD,BE,DE之间的数量关系。
【小结】典型例题1-2如图,已知矩形ABCD的顶点A,D分别落在x轴,y轴上,OD=2OA=6,AD:AB=3:1,则点C的坐标是()典型例题1-3经过点A(-1,0),B(4,0),交y轴于点C。
⑴求抛物线的解析式;⑵点D为y轴右侧抛物线上一点,是否存在点D请直接写出点D的坐标;若不存在,请说明理由。
⑶将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长。
【小结】变式训练1-1如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则sinα=( )变式训练1-2如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC,(1)求C点的坐标;扩展模型:共线三等角模型:当三垂直模型中3个直角变为相等的锐角或钝角时,仍会产生全等或相似三角形。
解读:⑴图1和图2中,大小均为的三个锐角(或钝角)顶点在同一直线你上。
⑵当三组对应边均不相等时,图1中有△ABC∽△ECD,图2中有△ABC∽△CDE(注意对应关系)⑶当△ABC和△CDE的任意一组对应边相等时,有两三角形全等。
中考数学几何经典模型之“三垂直模型”.doc

中考数学几何经典模型之“三垂直模型”两个全等的三角形△ACD≌△BEC,拼成如图形状,使得A、C、B三点共线。
条件:△ACD≌△BEC结论:1、△DCE是等腰直角三角形2、AB=AD+BE二、模型变形:条件:△ABD≌△BEC结论:1、BD⊥CE2、AC=BE-AD三、模型应用:在下列各图中构造出三垂直模型:1、△OCD为等腰直角三角形2、四边形OABC为正方形“三垂直模型”是一个应用非常广泛的模型,它可以应用在三角形,矩形,平面直角坐标系,网格,一次函数,反比例函数,三角函数,二次函数以及圆等诸多的中考重要考点之中,所以掌握好这一模型会使你在中考中技高一筹,下面看一道典型例题,从这道题大家可以体会到“三垂直模型”的强大之处。
例题分析:如图,在△ABC中,∠C=90°,D、E分别为BC、AC上一点,BD=AC,DC=AE,BE与AD交于点P,求∠ADC+∠BEC.如图,过点B作BF⊥BC,且BF=AE=CD,连接AF,∠FBC=90°∵∠C=90°,∴AC⊥BC,∠FBC=∠DCA.∴BF∥AC,∴四边形AFBE为平行四边形.∴∠BFA=∠AEB.在△BDF和△CAD中,BF=CD∠FBC=∠DCABD=CA∴△BDF≌△CAD(SAS).∴∠BFD=∠ADC,∠BDF=∠DAC,DF=DA.∵∠ADC+∠DAC=90°,∴∠ADC+∠BDF=90°,∴∠ADF=90°,∴∠DFA=∠DAF=45°.∵∠AEB+∠BEC=180°,∴∠AFB+∠BEC=180°,∴∠BFD+∠DFA+∠BEC=180°,∴∠ADC+∠AFD+∠BEC=180°,∠ADC+∠BEC=135°.故答案为:135.。
三垂直全等模型

三垂直全等模型模型 三垂直全等模型如图:∠D =∠BCA =∠E =90°,BC =AC .结论:Rt △BCD ≌Rt △CAE .模型分析说到三垂直模型,不得不说一下弦图,弦图的运用在初中直角三角形中占有举足轻重的地位,很多利用垂直求角,勾股定理求边长,相似求边长都会用到从弦图支离出来的一部分几何图形去求解.图①和图②就是我们经常会见到的两种弦图. 图①图②三垂直图形变形如下图③、图④,这也是由弦图演变而来的.图③A图④DE ABC例1 如图,AB ⊥BC ,CD ⊥BC ,AE ⊥DE ,AE =DE ,求证:AB +CD =BC . DAB证明:∵AE ⊥DE ,AB ⊥BC ,DC ⊥BC ,∴∠AED =∠B =∠C =90°.∴∠A +∠AEB =∠AEB +∠CED =90°.∴∠BAE =∠CED .在△ABE 和△ECD 中,B C A CED AE ED ∠=∠⎧⎪∠=∠⎨⎪=⎩ ∴△ABE ≌△ECD . A∴AB =EC ,BE =CD .∴AB +CD =EC +BE =BC.例2 如图,∠ACB =90°,AC =BC ,BE ⊥CE ,AD ⊥CE 于D ,AD =2.5cm ,BE =0.8cm ,则DE 的长为多少? EDA解答:∵BE ⊥CE ,AD ⊥CE ,∴∠E =∠ADC =90°.∴∠EBC +∠BCE =90°.∵∠BCE +∠ACD =90°,∴∠EBC =∠DCA .在△CEB 和△ADC 中,E ADC EBC DCA BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△CEB ≌△ADC .∴BE =DC =0.8cm ,CE =AD =2.5cm .∴DE =CE -CD =2.5-0.8=1.7cm .例3 如图,在平面直角坐标系中,等腰Rt △ABC 有两个顶点在坐标轴上,求第三个顶点的坐标. xy图①BA (0,3)C (-2,0)O x y 图②C (0,3)A O B (-1,0)解答:(1)如图③,过点B 作BD ⊥x 轴于点D .∴∠BCD +∠DBC =90°.由等腰Rt △ABC 可知,BC =AC ,∠ACB =90°,∴∠BCD +∠ACO =90°.∴∠DBC =∠ACO .在△BCD 和△CAO 中,BDC AOC DBC ACO BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BCD ≌△CAO .∴CD =OA ,BD =OC .∵OA =3,OC =2.∴CD =3,BD =2.∴OD =5.∴B (-5,2). xy图③BA (0,3)C (-2,0)OD(2)如图④,过点A 作AD ⊥y 轴于点D .在△ACD 和△CBO 中,ADC COB DAC OCB AC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ACD ≌△CBO .∴CD =OB ,AD =CO .∵B (-1,0),C (0,3)∴OB =1,OC =3.∴AD =3,OD =2.∴OD =5.∴A (3,2). xy图④C (0,3)A OB (-1,0)D1.如图,正方形ABCD ,BE =CF .求证:(1)AE =BF ;(2)AE ⊥BF .FA证明:(1)∵四边形ABCD 是正方形,∴AB =BD ,∠ABC =∠BCD =90°.在△ABE 和△BCF 中,AB BC ABE BCF BE CF =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△BCF .∴AE =BF .(2)∵△ABE ≌△BCF .∴∠BAE =∠CBF .∵∠ABE =90°,∴∠BAE +∠AEB =90°.∴∠CBF +∠AEB =90°.∴∠BGE =90°,∴AE ⊥BF .2.直线l 上有三个正方形a 、b 、c ,若a 、c 的面积分别是5和11,则b 的面积是_____. c b aD A解答:∵a 、b 、c 都是正方形,∴AC =CD ,∠ACD =90°.∵∠ACB +∠DCE =∠ACB +∠BAC =90°,∴∠BAC =∠DCE .在△ABC 和△CBE 中,ABC CED BAC DCE AC CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ACB ≌△CDE .∴AB =CE ,BC =DE .在Rt △ABC 中,2AC =2AB +2BC =2AB +2DE即b S =a S +c S =5+11=16.3.已知,△ABC 中,∠BAC =90°,AB =AC ,点P 为BC 上一动点(BP <CP ),分别过B 、C 作BE ⊥AP 于E 、CF ⊥AP 于F .(1)求证:EF =CF -BE ;(2)若P 为BC 延长线上一点,其它条件不变,则线段BE 、CF 、EF 是否存在某种确定的数量关系?画图并直接写出你的结论.FC A BPP解答:∵BE ⊥AP ,CF ⊥AP ,∴∠AEB =∠AFC =90°.∴∠F AC +∠ACF =90°,∵∠BAC =90°,∴∠BAE +∠F AC =90°,∴∠BAE =∠ACF .在△ABE 和△CAF 中,AEB AFC BAE ACF AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△CAF .∴AE =CF ,BE =AF .∵EF =AE -AF ,∴EF =CF -BE .(2)如图,EF =BE +CF .理由:同(1)易证△ABE ≌△CAF .∴AE =CF ,BE =AF .∵EF =AE +AF ,∴EF = BE + CF . FA4.如图,在直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD =2,BC =3,设∠BCD =α,以D 为旋转中心,将 腰DC 绕点D 逆时针旋转90°至DE .(1)当α=45°时,求△EAD 的面积;(2)当α=45°时,求△EAD 的面积;(3)当0°<α<90°,猜想△EAD 的面积与α大小有无关系?若有关,写出△EAD 的面积S 与α的关系式;若无关,请证明结论.D解答:(1)1;(2)1;(3)过点D 作DG ⊥BC 于点G ,过点E 作EF ⊥AD 交AD 延长线于点F .∵AD ∥BC ,DG ⊥BC ,∴∠GDF =90°.又∵∠EDC =90°,∴∠1=∠2.在△CGD 和△EFD 中,12DGE DFE CD DE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△DCG ≌△DEF∴EF =CG ,∵AD ∥BC ,AB ⊥BC ,AD =2,BC =3,∴BG =AD =2,∴CG =1.∴EAD S =12AD ·EF =1. ∴△EAD 的面积与α大小无关. 12FD5.向△ABC 的外侧作正方形ABDE 、正方形ACFG ,过A 作AH ⊥BC 于H ,AH 的反向延长线与EG 交于点P . 求证:BC =2AP . PE AG解答:过点G 作GM ⊥AP 于点M ,过点E 作EN ⊥AP 交AP 延长线于点N .∵四边形ACFG 是正方形,∴AC =AG ,∠CAG =90°.∴∠CAH +∠GAM =90°.又∵AH ⊥BC ,∴∠CAH +∠ACH =90°.∴∠ACH =∠GAM .在△ACH 和△GAM 中,AHC GMA ACH GAM AC GA ∠=∠⎧⎪∠=∠⎨⎪=⎩ ∴△ACH ≌△GAM∴CH =AM ,AH =GM .同理可证△ABH ≌△EAN∴BH =AN ,AH =EN .∴EN =GM .在△EPN 和△GPM 中, EPN GPM ENP GMP EN GM ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△EPN ≌△GPM . ∴NP =MP ,∴BC =BH +CH=AN +AM=AP +PN +AP -PM =2AP . P EAG M。
三垂直定理立体几何

三垂直定理立体几何三垂线定理(也称三垂直定理)是立体几何中一个重要的定理,通常用于计算三角形的面积或其他几何量。
在三维空间中,如果一个点P在三角形ABC所在平面上,那么它到三角形的三个顶点的连线所在的直线都与三角形的平面垂直。
换句话说,点P到三角形的三个边AB、BC、CA 所在平面的距离都是垂直距离。
证明:设点P在平面ABC上,向量a、b、c分别表示边向量AB、BC、CA,则向量n=a×b表示平面ABC的法向量(叉积)。
点P到平面ABC的距离(设为h)满足n·OP=h|n|,其中OP 为点P到原点O的向量。
考虑向量PA在向量n上的投影PA',即PA'=(PA·n/|n|)n/|n|。
根据余弦公式,PA·PB=PA^2+PB^2-AB^2/2,因此PA·n=PA·(a×b)=PA·c^2/2SABC。
将上述若干式子代入n·OP=h|n|中,得到PA'=PA·c^2/(2SABC)|n|/|c×(PA×c)|同理,PB'和PC'也可以表示为三垂线上的垂直距离分别为h=PA',h=PB'和h=PC'。
应用:利用三垂线定理,可以方便地计算三角形的面积。
设三角形ABC的三边长分别为a、b、c,其半周长为s=(a+b+c)/2,则三角形的面积S可以表示为S=abc/4R=1/2absinC=1/2crsinA=1/2basinC其中R为三角形外接圆半径,A、B、C为三角形的角度。
由于三条垂线的长度都可以用三条边的长度表示,因此可以通过这些式子计算出三角形的面积。
三垂线还可以用于计算三角形垂心(三条垂线交点)、oktane棱锥的体积等相关几何量。
需要注意的是,在三维空间中绝大多数点不在三角形所在平面上,因此计算其垂距要用到点到平面的距离公式。
平面几何 第5讲 三垂直模型

第5讲“三垂直”模型知识目标模块一三垂直基本模型例1难度:★★模块二三垂直与婆罗摩笈多例2难度:★★★模块三三垂直与八字模型例3难度:★★★★模块四三垂直与坐标系例4、例5、例6难度:★★★★模块一三垂直基本模型知识导航一、三垂直模型的构成等腰直角△ABC过直角顶点A的直线l过两底角顶点B、C分别作直线l的垂线,垂足分别为M、N如图所示:BM+CN=MN BM+MN=CN MN+CN=BM题型一三垂直模型基本应用例1过等腰Rt△ABC的直角顶点C作直线l,过A、B分别作AD⊥l于D,BE⊥l于E,已知AD=5,BE=3,求DE的长.练习已知△ABC中,∠BAC=90°,点E在线段BC上,点D在线段AC上,且△BDE为等腰直角三角形,∠BDE =90°,BD=DE,当∠ACB=30°时,试判断AD与CE的数量关系,并加以证明.模型二三垂直模型与“婆罗摩笈多”例2如图,△ABE和△ACD为等腰直角三角形,AM⊥BC于M,MA交ED于N,求证:EN=DN.练习如图,直线AB分别与x轴、y轴相交于点A(2,0)和点B(0,4),以B为顶点在第一象限作等腰Rt△ABC.(1)在y轴上存在一点M,使得MA+MC最小,请画出点M;(保留画图痕迹)(2)求点C的坐标;(3)若P点为y轴正半轴上一个动点,分别以AP、OP为腰在第一象限、第二象限作等腰Rt△APC和等腰Rt△OPD,连接CD交y轴于N点,当点P在y轴正半轴上移动时,求PN的长度.模型三三垂直模型与“八字”全等综合例3(1)如图,已知等腰Rt △ABC ,∠C =90°,D 在AC 上,△BDE 为等腰直角三角形,∠DBE =90°,连AE 交BC 于F ,求证:BF +CF =CD .(2)如图,D 点在AC 延长线上,其余条件不变,试探究BF 、CF 、CD 之间的关系.练习等腰Rt △ABC 中,∠B =90°,点P 在BC 上,以AP 为腰在△ABC 外侧作等腰Rt △APQ ,连PQ 交AB 于N ,连CQ 交AB 于M .(1)如图,当P 在边BC 上,且CP =2BP 时,求CPBM的值.(2)P 点在CB 延长线上,且CP =nBP ,M 、N 分别在AB 边和AB 边的延长线上,求AMBM.真题演练如图,Rt△ABC中,∠ACB=90°,AC=BC,E点为射线CB上一动点,连接AE,作AF⊥AE且AF=AE (1)如图1,过F点作FD⊥AC交AC于点D,求证:CE+CD=DF;(2)如图2,连接BF交AC于点G,若AGCG=3,求证:E为BC中点;(3)当E点在射线CB上,连接BF交直线AC于点G,若43BCBE=,则AGCG=.模块二三垂直模型与坐标系综合知识导航三垂直模型在坐标系中有着非常广泛的应用,尤其是与等腰直角三角形的综合,具体来说:已知等腰直角三角形三个顶点中任意两个点的坐标,便可以求出第三个点的坐标情况一如下图:直角顶点在坐标轴上情况二如下图:直角顶点不在坐标轴上例4(1)如图,△ABC为等腰直角三角形,AC=BC,AC⊥BC,A(0,3),C(1,0),求B点坐标.(2)如图,△ABC为等腰直角三角形,AC=BC,AC⊥BC,A(-1,0),C(1,3),求B点坐标.(3)如图,△ABC为等腰直角三角形,AC=BC,AC⊥BC,B(2,2),C(4,-2),求A点坐标.练习如图,在△ABC中,∠ACB=90°,AC=BC,BC与y轴交于D点,点C的坐标为(-2,0),点A的坐标为(-6,3),则D点的坐标是.真题演练如图,已知A(-2,0),(1)如图,以A为顶点,AB为腰在第三象限作等腰Rt△ABC,若B(0,-4),求C点坐标.(2)如图,P为y轴负半轴上一动点,以P为顶点,PA为腰做等Rt△APD,过D作DE⊥x轴于E点,当P 点沿y轴负半轴向下运动时,试问OP-DE的值是否发生变化?若不变,求其值;若变化,请说明理由.(3)如图,已知F点坐标为(﹣4,﹣4),G是y轴负半轴上一点,以FG为直角边作等腰Rt△FGH,H点在x轴上,∠GFH=90°.设G(0,m),H(n,0),当G点在y轴负半轴上沿负方向运动时,m+n的值是否变化?若不变,求其值;若变化,请说明理由.例5在平面直角坐标系中,A(2,﹣1),B(1,﹣4),C(5,﹣2),求∠ABC的度数.练习如图,在平面直角坐标系中,已知A (a ,b ),且a 、b 满足1b =(1)求点A 的坐标;(2)若点F (1,0),C (0,3),连AC 、FC ,试确定∠ACO +∠FCO 的值是否发生变化.若不变,说明理由.若变化,请求出变化范围.例6在平面直角坐标系中,点A (4,0),B (0,8),以AB 为斜边作等腰直角△ABC,则点C 坐标为.练习在平面直角坐标系中,已知A (0,4),B (2,0),在第一象限内的点C ,使△ABC 为面积最小的等腰直角三角形,求点C 的坐标以及面积的最小值.挑战压轴题如图1,已知A (a ,0),点B (0,b )且a 、b 满足2(4)40a b -+-=(1)求A 、B 两点的坐标;(2)若点C 是第一象限内一点,且∠OCB =45°,过点A 作AD ⊥OC 于点F ,求证:FA =FC ;(3)如图2,若点D 的坐标为(0,1),过点A 作AE ⊥AD ,且AE =AD ,连接BE 交x 轴于点G ,求S △BOG .第5讲本讲课后作业1、如图,在△ABC中,∠ACB=90°,AC=BC,BC与y轴交于D点,点C的坐标为(﹣1,0),点A的坐标为(﹣5,2),求点D的坐标.2、在平面直角坐标系中,点A(2,0),B(0,4),以AB为斜边作一个等腰直角三角形ABC,则点C的坐标为.3、已知,△ABC是等腰直角三角形,BC=AB,A点在x轴负半轴上,直角顶点B在y轴上,点C在x轴上方.(1)如图1所示,若A的坐标是(﹣3,0),点B的坐标是(0,1),求点C的坐标;(2)如图2,过点C作CD⊥y轴于D,请直接写出线段OA、OD、CD之间等量关系;(3)如图3,若x轴恰好平分∠BAC,BC与x轴交于点E,过点C作CF⊥x轴于F,问C F与AE有怎样的数量关系?并说明理由.4、如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC.(1)求C点坐标;(2)如图2,P为y轴负半轴上一个动点,当P点向y轴负半轴向下运动时,以P为顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OP-DE的值;(3)如图3,已知点F坐标为(﹣2,﹣2),当点G在y轴负半轴上沿负方向运动时,作Rt△FGH,始终保持∠GFH=90°,FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0),当G点在y轴的负半轴上沿负方向运动时,以下两个结论:①m-n为定值;②m+n为定值,其中只有一个结论是正确的,请找出正确的结论,并求出其值.。
模型研究初中几何模型之三垂直模型

模型研究初中几何模型之三垂直模型一、三垂直模型的概念我们在学习勾股定理的时候,学习了多种证明方法,其中有一种方法叫做总统证法,是1875年美国总统加菲尔德证明的,他将两个全等的三角形△ABC≌△CDE,拼成如图形状,使得B、C、D三点共线,易得△ACE为等腰直角三角形,四边形ABDE为直角梯形,假设三角形三边长分别为a,b,c,则四边形ABDE的面积可用两种方法表示:S=1/2ab+1/2ab+c²=1/2(a+b)(a+b)整理可得a²+b²=c²这就是勾股定理的总统证法。
上面这个图形。
我们把它称为三垂直模型,这个模型有以下几个结论:1、△ABC≌△CDE2、△ACE是等腰直角三角形3、BD=AB+DE其实,三垂直模型可以看做是由弦图模型得来的,如下图,弦图模型分为内弦图和外弦图,是由四个全等的直角三角形拼接而成的,将外弦图的两个三角形拿掉,就得到了三垂直模型。
当然从内弦图中还可以得到三垂直模型的变形:以上所述三垂直是由两个全等的直角三角形拼成的,这样的三垂直我们把它叫做全等型三垂直,那么如果是两个相似的直角三角形拼成如图形状,就变成了相似型三垂直,相似型三垂直有如下结论:1、△ABC∽△CDE2、AB:CD=BC:DE=AC:CE三垂直的应用非常广泛,在三角形、四边形、平面直角坐标系、网格、一次函数、反比例函数、二次函数、三角函数、圆中都会出现,在中考等大型考试中也是常考内容,所以大家一定要熟练掌握。
二、三垂直模型的构造方法:一般情况下,碰到斜着放置的等腰直角三角形,要想到在直角顶点所在的直线上构造全等型三垂直,若碰到的是一般的直角三角形,则在直角顶点所在的直线上构造相似型三垂直。
在下列各图中构造出三垂直模型:1、△OCD为等腰直角三角形2、四边形OABC为正方形3、△OAB为直角三角形三、三垂直在不同领域的应用1、在三角形中例1:如图,直线l过等腰直角三角形ABC顶点B,A、C两点到直线l的距离分别是2和3,则AB的长是 .例2:如图,在△ABC中,∠C=90°,D、E分别为BC、AC上一点,BD=AC,DC=AE,BE与AD交于点P,则∠ADC+∠BEC= .2、在矩形中如图,点是矩形ABCD的边CD上一点,把△ADE沿AE对折,使点D 恰好落在BC边上的F点处。
三垂直模型
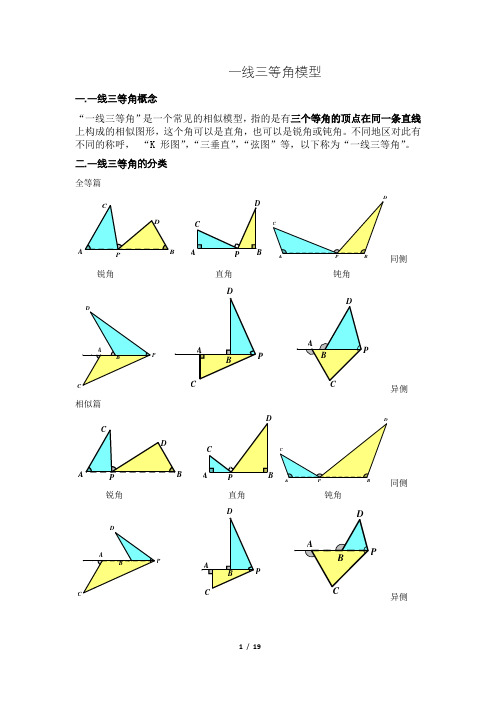
一线三等角模型一.一线三等角概念“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,“K 形图”,“三垂直”,“弦图”等,以下称为“一线三等角”。
二.一线三等角的分类全等篇同侧锐角直角钝角P异侧相似篇A同侧锐角直角钝角P异侧三、“一线三等角”的性质1.一般情况下,如图 3-1,由∠1=∠2=∠3,易得△AEC ∽△BDE.2.当等角所对的边相等时,则两个三角形全等.如图 3-1,若 CE=ED ,则△AEC ≌△BDE.3.中点型“一线三等角”如图 3-2,当∠1=∠2=∠3,且 D 是 BC 中点时,△BDE∽△CFD∽△DFE.4.“中点型一线三等角“的变式(了解) 如图 3-3,当∠1=∠2 且1902BOC BAC ∠=︒+∠时,点 O 是△ABC 的内心.可以考虑构造“一线三等角”.如图 3-4“中点型一线三等角”通常与三角形的内心或旁心相关,1902BOC BAC ∠=︒+∠这是内心的性质,反之未必是内心.在图 3-4(右图)中,如果延长 BE 与 CF ,交于点 P ,则点 D 是△PEF 的旁心.5.“一线三等角”的各种变式(图 3-5,以等腰三角形为例进行说明 )图 3-5其实这个第 4 图,延长 DC 反而好理解.相当于两侧型的,不延长理解,以为是一种新型的,同侧穿越型?不管怎么变,都是由三等角确定相似三角形来进行解题四、“一线三等角”的应用1.“一线三等角”应用的三种情况.a.图形中已经存在“一线三等角”,直接应用模型解题;b.图形中存在“一线二等角”,不上“一等角”构造模型解题;c.图形中只有直线上一个角,不上“二等角”构造模型解题.体会:感觉最后一种情况出现比较多,尤其是压轴题中,经常会有一个特殊角或指导该角的三角函数值时,我经常构造“一线三等角”来解题.2.在定边对定角问题中,构造一线三等角是基本手段,尤其是直角坐标系中的张角问题,在 x 轴或 y 轴(也可以是平行于 x 轴或 y 轴的直线)上构造一线三等角解决问题更是重要的手段.3.构造一线三等角的步骤:找角、定线、构相似坐标系中,要讲究“线”的特殊性如图 3-6,线上有一特殊角,就考虑构造同侧型一线三等角当然只加这两条线通常是不够的,为了利用这个特殊角导线段的关系,过 C、D 两点作直线 l 的垂线是必不可少的。
三垂直模型

三垂直模型三垂直模型在三角形ABC中。
∠C=90°,AC=BC,直线MN经过点C,且AD⊥MM,BE⊥XXX。
1.当MN绕点C旋转到图1的位置时,我们可以发现DE=AD+BE,因为DE是直线MN与AC的交点,而AD和BE分别是直线AD和BE与MN的交点。
证明如下:连接CE,因为AC=BC,所以CE是AB的中线,即CE=1/2AB。
又因为CD⊥AB,所以DE=CE-CD=1/2AB-CD。
连接AE和EB,因为AD⊥MM,所以∠DAM=90°,因此∠EAM=∠EAB,即AE=AB×sin∠EAB。
同理,BE=BC×sin∠EBC。
因为AC=BC,所以sin∠EAB=sin∠XXX,即AE=BE。
综上所述,DE=1/2AB-XXX。
2.当MN绕点C旋转到图2的位置时,我们可以发现DE=BE-AD,因为DE是直线MN与BC的交点,而BE和AD分别是直线BE和AD与MN的交点。
我们猜测结论不会发生变化,证明如下:连接CE和AE,因为CD=CE,所以∠XXX∠CEB,即∠ADE=∠BCE。
因此,三角形ADE和BCE相似,即XXX 又因为CE=AC-AD,所以AE/BE=AD/(AC-AD),即AE/AD=AC/BE-1.因为AC=BC,所以AE/AD=1-BE/AD。
两边同时乘以AD,得到AE=AD-BE。
综上所述,DE=BE-AD。
例1.1) 已知:如图,∠ACB=90°,CD⊥AB,CE=BC,过E 点作AC的垂线,交CD的延长线于点F,求证:AB=FC。
连接CE和EF,因为CE=BC,所以∠XXX∠XXX,即∠XXX∠FCE。
因此,三角形EBF和FCE相似,即EB/FC=BF/CE。
又因为CE=AB-AF,所以EB/FC=BF/(AB-AF),即EB/FC=(AB-BF)/FC。
因为AB=BC,所以EB=FC-BC。
代入上式得到FC-BC/FC=(FC-BF)/FC,即BC=BF,即AB=FC。
初中数学几何模型之三垂直模型

数学模型-三垂直模型一,三垂直与勾股定理模型分析:赵爽弦图:设直角三角形的三边中较短的直角边为a,另一直角边为b,斜边为c ∴四个直角三角形面积=2ab,中心正方形面积=(b-a)²=b²-2ab+a²∴大正方形面积=c²=a²+b²毕达哥拉斯内弦图大正方形的面积=(a+b)2大正方形的面积=四个直角三角形+中心正方形面积=2ab+c2根据等面积法得(a+b)2=2ab+c2∴c²= a²+b²,即c²= a²+b²总统证明勾股定理:将毕达哥拉斯的图形平分即可得到总统证法规律总结:弦图能够解析完全平方定理,如此勾股定理,完全平方和弦图有机结合在一起,体现了数形结合的思想.实例精炼:1. 汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=10,则S2的值为()A. 113B. 103C. 3D. 83【答案】B【解析】【分析】根据图形的特征得出四边形MNKT的面积设为x,将其余八个全等的三角形面积一个设为y,从而用x,y表示出S1,S2,S3,得出答案即可.【详解】解:将四边形MNKT的面积设为x,将其余八个全等的三角形面积一个设为y.∵正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,S1+S2+S3=10,∴S1=8y+x,S2=4y+x,S3=x,∴S1+S2+S3=3x+12y=10x+4y=10 3,∴S2=x+4y=103.故选B.【点睛】此题主要考查了图形面积关系,根据已知得出用x ,y 表示出S 1,S 2,S 3,再利用S 1+S 2+S 3=10求出是解决问题的关键.2. 如图,“赵爽弦图”由4个全等的直角三角形所围成,在Rt ABC △中,AC b =,BC a =,90ACB ∠=︒,若图中大正方形的面积为42,小正方形的面积为5,求2()a b +的值.【答案】2()=79a b + 【解析】【分析】根据正方形的面积公式和三角形的面积公式即可求出2()5b a -=,237ab =,然后根据完全平方公式的变形即可求出结论. 【详解】解:小正方形面积=2()5b a -= 4个小直角三角形的面积=142ab ⨯425=- ∴237ab =∴2()a b +2()4b a ab =-+5237=+⨯79=【点睛】此题考查的是全等三角形的性质和完全平方公式的变形,掌握全等三角形的性质、正方形的面积公式、三角形的面积公式和完全平方公式的变形是解决此题的关键.3. (1)教材在探索平方差公式时利用了面积法,面积法可以帮助我们直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a ,较小的直角边长都为b ,斜边长都为c ),大正方形的面积可以表示为c 2,也可以表示为4×12ab +(a -b )2,所以4×12ab +(a -b )2=c 2,即a 2+b 2=c 2.由此推导出重要的勾股定理:如果直角三角形两条直角边长为a ,b,斜边长为c,则a2+b2=c2.图①为美国第二十任总统伽菲尔德的“总统证法”,请你利用图①推导勾股定理.(2)试用勾股定理解决以下问题:如果直角三角形ABC的两直角边长为3和4,则斜边上的高为.(3)试构造一个图形,使它的面积能够解释(a-2b)2=a2-4ab+4b2,画在上面的网格中,并标出字母a,b所表示的线段.【答案】(1)见解析;(2)125;(3)见解析【解析】【分析】(1)梯形的面积可以由梯形的面积公式求出,也利用三个直角三角形面积求出,两次求出的面积相等列出关系式,化简即可得证;(2)由两直角边,利用勾股定理求出斜边长,再利用面积法即可求出斜边上的高;(3)已知图形面积的表达式,即可根据表达式得出图形的边长的表达式,即可画出图形.【详解】(1)S梯形ABCD=1()()2a b a b++221122a ab b=++,S梯形ABCD=211222ab c⨯+∴12a2+ab+12b2=2×12ab+12c2即a2+b2=c2;(2)∵直角三角形的两直角边分别为3,4,,∵设斜边上的高为h ,直角三角形的面积为12×3×4=12×5×h , ∴h =125故答案为125; (3)∵图形面积为:(a−2b )2=a 2−4ab +4b 2, ∴边长为a−2b , 由此可画出的图形如下:【点睛】此题考查了勾股定理的证明,勾股定理,多项式的乘法的运用以及由多项式画图形的创新题型,此类证明要转化成同一个东西的两种表示方法,从而转化成方程达到证明的结果.4. 【阅读理解】勾股定理是几何学中一颗光彩夺目的明珠.她反映了直角三角形的三边关系即直角三角形两直角边(即“勾”,“股”)边长的平方和等于斜边(即“弦”)边长的平方.也就是说,设直角三角形两直角边为a 和b ,斜边为c ,那么222+=a b c .迄今为止,全世界发现勾股定理的证明方法约有400种.如:美国第二十任总统伽菲尔德的“总统证法”(如图1),利用三个直角三角形拼成一个直角梯形,于是直角梯形的面积可以表示为()212a b +或者是211222ab c ⨯+,因此得到()221112222a b ab c +=⨯+,运用乘法公式展开整理得到222+=a b c .【尝试探究】(1)其实我国古人早就运用各种方法证明勾股定理,如图2用四个直角三角形拼成正方形,中间也是一个正方形,其中四个直角三角形直角边分别为a 、b ,斜边长为c ,请你根据古人的拼图完成证明.(2)如图3是2002年在中国北京召开的国际数学家大会会标,利用此图也能证明勾股定理,其中四个直角三角形直角边分别为a 、b ,斜边长为c ,请你帮助完成.【实践应用】(3)已知a 、b 、c 为Rt ABC △的三边()c b a >>,试比较代数式2222a c a b +与44c b -的大小关系.【答案】(1)见解析;(2)见解析;(3)代数式2222a c a b +与44c b -的大小关系是相等. 【解析】【分析】[尝试探究](1)根据图形面积的不同求法即可得到结论; (2)根据图形面积的不同求法即可得到结论;[实践应用](3)分解因式,根据勾股定理即可得到结论.【详解】解:[尝试探究](1)图中大正方形的面积可表示为2()a b +,也可表示为214()2c ab +⨯,即221()4()2a b c ab +=+⨯,222a b c ∴+=;(2)图中大正方形的面积可表示为2c ,也可表示为21()4()2b a ab -+⨯,即221()4()2b a abc -+⨯=,222a b c ∴+=;[实践应用](3)2222222()a c a b a c b +=+,442222222()()()c b c b c b c b a -=+-=+, ∴代数式2222a c a b +与44c b -的大小关系是相等.【点睛】本题考查了勾股定理的证明,此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.5. 我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼制成一个大正方形(如下图),设勾a=3,弦c=5,则小正方形ABCD 的面积是_______【答案】1. 【解析】【分析】根据勾股定理可得股b=4,则小正方形ABCD 的边长为b-a ,最后根据正方形面积公式计算即可. 【详解】解:①勾a=3,弦c=5∴股4= ∵小正方形ABCD 的边长为b-a=4-3=1 ∴小正方形ABCD 的面积是1. 故答案为1.【点睛】本题主要考查了勾股定理的应用,灵活应用勾股定理解直角三角形是解答本题的关键.6. 把图1中长和宽分别为3和2的两个全等矩形沿对角线分成四个全等的直角三角形,将这四个全等的直角三角形拼成图2所示的正方形,则图2中小正方形ABCD的面积为_____.【答案】1.【解析】【分析】根据线段的和差关系可求图2中小正方形ABCD的边长,再根据正方形面积公式即可求解.【详解】解:图2小正方形ABCD的边长=3﹣2=1,图2小正方形ABCD的面积=1×1=1,故答案为:1.【点睛】本题考查了勾股定理的证明,全等图形,关键是求出图2中小正方形ABCD的边长.二,三垂直与全等和相似模型分析:规律总结:由同角的余角相等得到∠1=∠C,∠2=∠A,结合边长信息即可证明全等.★补充:射影定理直角三角形射影定理:直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项.每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.公式:如图,Rt△ABC中,∠ABC=90°,BD是斜边AC上的高,则有射影定理如下:(1)(BD)²=AD•DC,(2)(AB)²=AD•AC ,(3)(BC)²=CD•CA.直角三角形射影定理的证明在△BAD与△BCD中,∵∠ABD+∠CBD=90°,且∠CBD+∠C=90°,∴∠ABD=∠C,又∵∠BDA=∠BDC=90°∴△BAD∽△CBD∴AD BDBD CD=即BD²=AD•DC.其余同理可得可证有射影定理如下:AB²=AD•AC,BC²=CD•CA两式相加得:AB²+BC²=(AD•AC)+(CD•AC)=(AD+CD)•AC=AC².规律总结:由三垂直得到射影定理,能够得到边长平方与斜边之间的关系,是解决边长数量关系的常用方法.实例精炼:7. 如图,由四个全等的直角三角形拼成的图形,设CE a=,HG b=,则斜边BD 的长是()A. +a bB. ⋅a b【答案】C 【解析】【分析】根据全等三角形的性质,设CD=AH=x ,DE=AG=BC=y ,由CE a =,HG b =建立方程组,求解即可得出,22a b a bCD xBC y,然后借助勾股定理即可表示BD.【详解】解:根据图象是由四个全等的直角三角形拼成,设CD=AH=x ,DE=AG=BC=y , ∵CE a =,HG b =,∴x y a y x b +=⎧⎨-=⎩解得:22a b x a b y -⎧=⎪⎪⎨+⎪=⎪⎩,故,22a ba bCDBC在Rt BCD ∆中,根据勾股定理得:2222222222a b a b a b BD BC CD +-+⎛⎫⎛⎫=+=+= ⎪⎪⎝⎭⎝⎭, ∴BD =. 故选:C.【点睛】本题考查勾股定理,全等三角形的性质,能借助方程思想用含a ,b 的代数式表示CD 和BC 是解决此题的关键.8. 已知Rt△ABC 中,①BAC =90°,AB =AC ,点E 为①ABC 内一点,连接AE ,CE ,CE ①AE ,过点B 作BD ①AE ,交AE 的延长线于D .(1)如图1,求证BD=AE ;(2)如图2,点H 为BC 中点,分别连接EH ,DH ,求①EDH 的度数;(3)如图3,在(2)的条件下,点M 为CH 上的一点,连接EM ,点F 为EM 的中点,连接FH ,过点D 作DG ①FH ,交FH 的延长线于点G ,若GH :FH =6:5,①FHM 的面积为30,①EHB =①BHG ,求线段EH 的长.【答案】(1)见解析;(2)∠EDH =45°;(3)EH =.【解析】【分析】(1)根据全等三角形的判定得出△CAE ≌△ABD ,进而利用全等三角形的性质得出AE =BD 即可;(2)根据全等三角形的判定得出△AEH ≌△BDH ,进而利用全等三角形的性质解答即可;(3)过点M 作MS ⊥FH 于点S ,过点E 作ER ⊥FH ,交HF 的延长线于点R ,过点E 作ET ∥BC ,根据全等三角形判定和性质解答即可.【详解】证明:(1)∵CE ⊥AE ,BD ⊥AE ,∴∠AEC =∠ADB =90°,∵∠BAC =90°,∴∠ACE +CAE =∠CAE +∠BAD =90°,∴∠ACE =∠BAD ,在△CAE 与△ABD 中ACE BAD AEC ADB AC AB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△CAE ≌△ABD (AAS ),∴AE =BD ;(2)连接AH∵AB =AC ,BH =CH ,∴∠BAH =11904522BAC ∠=⨯︒=︒,∠AHB =90°,∴∠ABH =∠BAH =45°,∴AH =BH ,∵∠EAH =∠BAH ﹣∠BAD =45°﹣∠BAD ,∠DBH =180°﹣∠ADB ﹣∠BAD ﹣∠ABH =45°﹣∠BAD ,∴∠EAH =∠DBH ,在△AEH 与△BDH 中 AE BD EAH DBH AH BH =⎧⎪∠=∠⎨⎪=⎩∴△AEH ≌△BDH (SAS ),∴EH =DH ,∠AHE =∠BHD ,∴∠AHE +∠EHB =∠BHD +∠EHB =90°即∠EHD =90°,∴∠EDH =∠DEH =18090452︒-︒=︒; (3)过点M 作MS ⊥FH 于点S ,过点E 作ER ⊥FH ,交HF 的延长线于点R ,过点E 作ET ∥BC ,交HR 的延长线于点T .∵DG ⊥FH ,ER ⊥FH ,∴∠DGH =∠ERH =90°,∴∠HDG +∠DHG =90°∵∠DHE =90°,∴∠EHR +∠DHG =90°,∴∠HDG =∠HER在△DHG 与△HER 中HDG HER DGH ERH DH EH ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△DHG ≌△HER (AAS ),∴HG =ER ,∵ET ∥BC ,∴∠ETF =∠BHG ,∠EHB =∠HET ,∠ETF =∠FHM ,∵∠EHB =∠BHG ,∴∠HET =∠ETF ,∴HE =HT ,在△EFT 与△MFH 中ETF FHM EFT MFH EF FM ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EFT ≌△MFH (AAS ),∴HF =FT , ∴22HF MS FT ER =, ∴ER =MS ,∴HG =ER =MS ,设GH =6k ,FH =5k ,则HG =ER =MS =6k , 563022HF MS k k==, k∴FH =,∴HE =HT =2HF =.【点睛】本题考查全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,学会利用数形结合的思想思考问题,属于压轴题.9. 在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.(1)当直线MN绕点C旋转到图1的位置时,求证:△ADC≌△CEB;(2)当直线MN绕点C旋转到图2的位置时,试问DE、AD、BE的等量关系?并说明理由.【答案】(1)见解析;(2)DE=AD-BE,理由见解析【解析】【分析】(1)由已知推出∠ADC=∠BEC=90°,因为∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,推出∠DAC=∠BCE,根据AAS即可得到答案;(2)与(1)证法类似可证出∠ACD=∠EBC,能推出△ADC≌△CEB,得到AD=CE,CD=BE,即可得到答案.【详解】解:(1)证明:如图1,∵AD⊥DE,BE⊥DE,∴∠ADC=∠BEC=90°,∵∠ACB=90°,∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,∴∠DAC=∠BCE,在△ADC 和△CEB 中,CDA BEC DAC ECB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△CEB (AAS );(2)结论:DE=AD-BE .理由:如图2,∵BE ⊥EC ,AD ⊥CE ,∴∠ADC=∠BEC=90°,∴∠EBC+∠ECB=90°,∵∠ACB=90°,∴∠ECB+∠ACE=90°,∴∠ACD=∠EBC ,在△ADC 和△CEB 中,ACD CBE ADC BEC AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△CEB (AAS ),∴AD=CE ,CD=BE ,∴DE=EC-CD=AD-BE .【点睛】本题主要考查了余角的性质,全等三角形的性质和判定等知识点,能根据已知证明△ACD ≌△CBE 是解此题的关键,题型较好,综合性比较强. 10. 在Rt AOB ∆中,AOB 90∠=.(1)如图①,以点A 为直角顶点,AB 为腰在AB 右侧作等腰Rt ABC ∆,过点C 作CD OA ⊥交OA 的延长线于点D .求证:A AOB CD ∆∆≌.(2)如图②,以AB 为底边在AB 左侧作等腰Rt ABC ∆,连接OC ,求AOC ∠的度数.(3)如图③,Rt AOB ∆中,,OA OB OD AB =⊥,垂足为点D ,以OB 为边在OB 左侧作等边OBC ∆,连接AC 交OD 于E ,3AE =,2OE =,求AC 的长.【答案】(1)见解析;(2)135AOC ∴∠=;(3)8【解析】【分析】(1)根据“一线三垂直”模型,可以证得A AOB CD ∆∆≌;(2)过点C 作CM ⊥CO 交BO 于M ,AC 与BO 交于点N ,利用旋转模型证明BCM ∆≌()ACO ASA ∆,由外角的性质计算即可;(3)在CE 上截取一点H ,使CH=AE ,连接OH ,利用等腰直角△AOB ,等边△BOC 证得OAE ∆≌()OCH SAS ∆,通过等角代换证明HOE ∆为等边三角形,由线段和计算即可得到结果.【详解】(1)∵∠BAC=∠AOB=90°,∴∠BAO+∠DAC=∠BAO+∠ABO=90°,∴∠DAC=∠ABO ,∵△ABC 是等腰直角三角形,∴AB=AC ,在△AOB 和△CDA 中,ABO DAC AOB CDA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△AOB ≌△CDA (AAS )(2)如图②,过点C 作CM ⊥CO 交BO 于M ,AC 与BO 交于点N ,90MCO ACB ∴∠=∠=,BCM ACO ∴∠=∠,90BCA AOB ∠=∠=,BNC ANO ∠=∠,CBM OAC ∴∠=∠,∵AC=BC ,BCM ∴∆≌()ACO ASA ∆,CM CO ∴=,45COM CMO ∴∠=∠=,9045135AOC ∴∠=+=,故答案为:135°.(3)如图③,在CE 上截取一点H ,使CH=AE ,连接OH ,∵△AOB 是等腰直角三角形,△BOC 是等边三角形,所以AO BO CO ==,OAE OCH ∴∠=∠,OAE ∴∆≌()OCH SAS ∆,OH OE ∴=,AE=CH=3,∠AOE=∠COH ,OD AB ⊥,∠AOB=90°,45AOE BOE ∴∠=∠=,45COH ∴∠=,∠BOH=∠BOC-∠COH=60°-45°=15°,154560HOE ∴∠=+=,HOE ∴∆为等边三角形,2HE EO ∴==,3238AC CH HE AE ∴=++=++=,故答案为:8.【点睛】本题考查了“一线三垂直”模型,三角形全等的判定和性质,等边三角形的判定和性质,等腰直角三角形的性质,等角代换的应用,计算线段和的应用,掌握三角形全等的判定和性质是解题的关键.11. 如图1,在ABC ∆中,90ACB ∠=,AC BC =,直线MN 经过点C ,且AD MN ⊥于点D ,BE MN ⊥于点E .易得DE AD BE =+(不需要证明). (1)当直线MN 绕点C 旋转到图2的位置时,其余条件不变,你认为上述结论是否成立?若成立,写出证明过程;若不成立,请写出此时DE AD BE 、、之间的数量关系,并说明理由;(2)当直线MN 绕点C 旋转到图3的位置时,其余条件不变,请直接写出此时DE AD BE 、、之间的数量关系(不需要证明).【答案】(1) 不成立,DE=AD-BE ,理由见解析;(2) DE=BE-AD【解析】【分析】(1)DE 、AD 、BE 之间的数量关系是DE=AD-BE .由垂直的性质可得到∠CAD=∠BCE ,证得△ACD ≌△CBE ,得到AD=CE ,CD=BE ,即有DE=AD-BE ;(2)DE 、AD 、BE 之间的关系是DE=BE-AD .证明的方法与(1)一样.【详解】(1)不成立.DE 、AD 、BE 之间的数量关系是DE=AD-BE ,理由如下:如图,∵∠ACB=90°,BE ⊥CE ,AD ⊥CE ,AC CB =,∴∠ACD+∠CAD=90°,又∠ACD+∠BCE=90°,∴∠CAD=∠BCE ,在△ACD 和△CBE 中,90ADC CEB CAD BCE AC CB ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△CBE(AAS),∴AD=CE ,CD=BE ,∴DE=CE-CD=AD-BE ;(2)结论:DE=BE-AD .∵∠ACB=90°,BE ⊥CE ,AD ⊥CE ,AC CB =,∴∠ACD+∠CAD=90°,又∠ACD+∠BCE=90°,∴∠CAD=∠BCE ,在△ACD 和△CBE 中,90ADC CEB CAD BCE AC CB ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△CEB(AAS),∴AD=CE ,DC=BE ,∴DE=CD-CE=BE-AD .【点睛】本题考查了旋转的性质、直角三角形全等的判定与性质,旋转前后两图形全等,对应点到旋转中心的距离相等,对应点与旋转中心的连线段所夹的角等于旋转角.12. 如图,Rt △ACB 中,∠ACB =90°,AC =BC ,E 点为射线CB 上一动点,连结AE ,作AF ⊥AE 且AF =AE .(1)如图1,过F 点作FD ⊥AC 交AC 于D 点,求证:FD =BC ;(2)如图2,连结BF 交AC 于G 点,若AG =3,CG =1,求证:E 点为BC 中点;(3)当E 点在射线CB 上,连结BF 与直线AC 交于G 点,若BC =4,BE =3,则AG CG= (直接写出结果) 【答案】(1)见解析;(2)见解析;(3)113或53 【解析】【分析】(1)证明△AFD ≌△EAC ,根据全等三角形的性质得到DF =AC ,等量代换证明结论;(2)作FD ⊥AC 于D ,证明△FDG ≌△BCG ,得到DG =CG ,求出CE ,CB 的长,得到答案;(3)过F 作FD ⊥AG 的延长线交于点D ,根据全等三角形的性质得到CG =GD ,AD =CE =7,代入计算即可.【详解】(1)∵FD ⊥AC ,∴∠FDA =90°,∴∠DF A +∠DAF =90°,∠CAE +∠DAF =90°,∴∠DF A =∠CAE ,在△AFD 和△EAC 中,AFD EACADF ECA AF AE∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AFD ≌△EAC (AAS ),∴DF =AC ,∵AC =BC ,∴FD =BC ;(2)作FD ⊥AC 于D ,由(1)得,FD =AC =BC ,AD =CE ,在△FDG 和△BCG 中,90FDG BCG FGD BGC FD BC∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△FDG ≌△BCG (AAS ),∴DG =CG =1,∴AD =2,∴CE =2,∵BC=AC=AG+CG=4,∴E点为BC中点;(3)当点E在CB的延长线上时,过F作FD⊥AG的延长线交于点D,BC=AC=4,CE=CB+BE=7,由(1)(2)知:△ADF≌△ECA,△GDF≌△GCB,∴CG=GD,AD=CE=7,∴741.52CG DG AD AC-==-==,∴4 1.5111.53 AG AC CGCG CG++===,当点E在线段BC上时,过F作FD⊥AG的延长线交于点D,BC=AC=4,CE=CB-BE=1,由(1)(2)知:△ADF≌△ECA,△GDF≌△GCB,∴CG=GD,AD=CE=1,∴411.52CG DG AC AD-==-==,∴1 1.551.53 AG AD DGCG CG++===,故答案为:113或53. 【点睛】本题是三角形的综合题,考查了全等三角形的判定和性质,等腰三角形的性质,本题中求证△ADF ≌△ECA 、△GDF ≌△GCB 是解题的关键.三,三垂直与直角坐标系模型分析:规律总结:在坐标系中,一般利用点的坐标的几何含义作垂线,构建三垂直模型进行解题.具体考题中一般结合面积进行展开,常见的有一次函数与反比例函数的面积,二次函数中面积得最值等.实例精炼:13. 如图,在ABC ∆中,90ABC ∠=︒,AB BC =,点A 、B 分别是x 轴和y 轴上的一动点,点C 的横坐标为3-,求点B 的坐标.【答案】B (0,-3).【解析】【分析】如图,作CD ⊥y 轴于M ,则CD=3,证明△BCD ≌△ABO(AAS)即可求得答案.【详解】如图,作CD ⊥y 轴于M ,则CD=3,∵∠ABC=∠AOB=90゜,∴∠CBD+∠ABO=90°,∠ABO+∠OAB=90°,∴∠CBD=∠BAO ,又∵∠BDC =∠AOB=90°,BC =AB ,∴△BCD ≌△ABO(AAS),∴OB=CD=3,∴B(0,-3).【点睛】本题考查了全等三角形的判定与性质,点的坐标,正确添加辅助线,熟练掌握全等三角形的判定定理与性质定理是解题的关键.14. 如图所示,()1,0A -,()0,3B ,以AB 为边作正方形ABCD ,求C ,D 的坐标.【答案】()3,4C -;()4,1D -【解析】【分析】本题有A 、B 两个点都在坐标轴上,且正方形在坐标轴的同侧(基本上在第二象限),故只须过C ,D 两点分别向坐标轴作垂线即可. 作CE ⊥y 轴于E ,DF ⊥x 轴于F ,证明①BCE ≌△ABO ,得出对应边相等BE =OA =1,CE =BO =3,同理得出DF =OA =1,AF =BO =3,再求出OE 、OF ,即可得出结果.【详解】解:作CE ①y 轴于E ,DF ①x 轴于F ,如图所示:则∠CEB =∠AFD =90°,∴∠1+∠3=90°,∵四边形ABCD 是正方形,∴∠ABC =90°,BC =AB ,∴∠2+∠3=90°,∴∠1=∠2,在①BCE 和①ABO 中,1290CEB BOA BC AB ∠∠⎧⎪∠∠︒⎨⎪⎩====,∴①BCE ①①ABO (AAS ),∴BE =OA =1,CE =BO =3,同理得:DF =OA =1,AF =BO =3,∴OE =4,OF =4,∴C (-3,4),D (-4,1).【点睛】本题考查了正方形的性质、坐标与图形性质以及全等三角形的判定与性质;通过作辅助线证明三角形全等是解决问题的关键.当正方形的部分点在坐标轴上,且整个正方形在坐标轴的同侧时,往往过另外的点向坐标轴作垂线,从而得到“形外三垂直”的基本图形.15. 如图,在平面直角坐标系中,等腰直角三角形ABC 的顶点A 在x 轴上,AB =AC ,∠BAC =90°,且A (2,0)、B (3,3),BC 交y 轴于M ,(1)求点C 的坐标;(2)连接AM ,求△AMB 的面积;(3)在x 轴上有一动点P ,当PB +PM 的值最小时,求此时P 的坐标.【答案】(1)C的坐标是(﹣1,1);(2)154;(3)点P的坐标为(1,0).【解析】【分析】(1)作CD⊥x轴于D,BE⊥x轴于E,证明CDA①AEB△,根据全等三角形的性质得到CD=AE,AD=BE,求出点C的坐标;(2)利用待定系数法求出直线BC的解析式,得到OM的长,根据梯形的面积公式、三角形的面积公式计算,得到答案;(3)根据轴对称的最短路径问题作出点P,求出直线B M 的解析式,根据x轴上点的坐标特征求出点P的坐标.【详解】解:(1)如图,作CD⊥x轴于D,BE⊥x轴于E,∴∠CAD+∠DCA=90°,∵∠BAC=90°,∴∠CAD+∠BAE=90°,∴∠BAE=∠ACD,在CDA和AEB△中,ACD BAE ADC BEA CA AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,①CDA ①AEB △(AAS ),∴CD =AE ,AD =BE ,∵A (2,0)、B (3,3),∴OA =2,OE =BE =3,∴CD =AE =1,OD =AD ﹣OA =1,∴C 的坐标是(﹣1,1);(2)如图,作BE ⊥x 轴于E ,设直线BC 的解析式为y =kx +b ,∵B 点的坐标为(3,3),C 点的坐标是(﹣1,1),∴331k b k b +=⎧⎨-+=⎩, 解得,1232k b ⎧=⎪⎪⎨⎪=⎪⎩, ∴直线BC 的解析式为y =12x +32, 当x =0时,y =32, ∴OM =32,∴AMB的面积=梯形MOEB的面积﹣AOM的面积﹣AEB△的面积=12×(32+3)×3﹣12×2×32﹣12×1×3=154;(3)如图,作M关于x轴的对称点M'(0,﹣32),连接B M',交x轴于点P,此时PB+PM=PB+P M'=B M'的值最小,设直线B M'的解析式为y=mx+n,则3332m nn+=⎧⎪⎨=-⎪⎩,解得,3232mn⎧=⎪⎪⎨⎪=-⎪⎩,∴直线B M'的解析式为y=32x﹣32,点P在x轴上,当y=0时,x=1,∴点P的坐标为(1,0).【点睛】此题考查的是等腰直角三角形的性质、全等三角形的判定及性质、求一次函数解析式和求两线段和的最小值,掌握等腰直角三角形的性质、全等三角形的判定及性质、利用待定系数法求一次函数解析式和轴对称的最短路径问题是解决此题的关键.16. 如图,在平面直角坐标系中,抛物线交x 轴正半轴于点A (1,0)和点B ,交y 轴于点C .(1)如图1,直线3y x =-+经过点B 、点C ,求抛物线的解析式;(2)如图2,点E 为该抛物线223y x nx =-+的顶点,过点C 作x 轴的平行线交抛物线于另一点D ,该抛物线对称轴右侧的抛物线上有一点P ,当FP EP ⊥时,求P 点的纵坐标.(3)如图3,在(1)(2)的结论下,抛物线对称轴右侧的抛物线上有一点G ,作⊥GH x 轴于点H ,延长EP 交GH 于K,当GK =时,求G 点的坐标.【答案】(1)243y xx =-+;(2)点P 的纵坐标为2;(3)G 点的坐标为(2+11).【解析】【分析】(1)由直线的解析式,先求出点B 、C 的坐标,结合点A 的坐标,利用待定系数法即可得到答案;(2)把点A 代入,求出n 的值,然后得到点C 和点E 的坐标,然后求出点F 的坐标,设点P 为(x ,233x x -+),由FP EP ⊥,即可求出点P 的横坐标,即可求出点P 的纵坐标;(3)过点P 作PI ⊥GH 于点I ,先求出直线PE 的解析式,得到PK=2PI ,然后设点G 为(m ,243m m -+),表示出GK的长度,结合GK =,得到关于m 的一元二次方程,解方程求出m 的值,即可得到答案.【详解】解:(1)∵3y x =-+经过点B 、点C ,∴令0y =,3x =,令0x =,3y =,∴点B 为(3,0),点C 为(0,3),设抛物线的解析式为2y ax bx c =++,把点A 、B 、C ,三点代入解析式,得: 09303a b c a b c c ++=⎧⎪++=⎨⎪=⎩,解得:143a b c =⎧⎪=-⎨⎪=⎩, ∴243y x x =-+;(2)∵点A (1,0)在抛物线223y x nx =-+图像上,则1230n -+=,∴2n =,∴2243(2)1y x x x =-+=--,∴顶点E 为(2,1-), 令x=0,则3y =, ∴点C 为(0,3), ∵EF 垂直平分CD ,∴点D 的坐标为(4,3),点F 的坐标为(2,3), ∵点P 在抛物线243y xx =-+上,则设点P 为(x ,243x x -+), 又∵E 为(2,1-),F 为(2,3), ∴2244(2)222EPx x x k x x x -+-===---,24(4)22FP x x x x k x x --==--, ∵FP EP ⊥, ∴1EP FP k k •=-, ∴(4)(2)12x x x x --•=--,解得:2=x∵点P 在对称轴右侧,则2x >,∴点P 的横坐标为2x = ∴点P 的纵坐标为:22243(2)1(22)12y x x x =-+=--=+-=; (3)如图:过点P 作PI ⊥GH 于点I ,∵点E (2,1-),点P 为(2+,2),∴可求出直线PE 的解析式为:1y =--, ∴∠KPI=60°, ∵PI ⊥GH ,∴∠KIP=90°,∠PKI=30°, ∴PK=2PI , ∵点G 在抛物线243y xx =-+图像上,则设点G 为(m ,243m m -+),∴点K 的坐标为(m 1--∴GK=2243144m m m m -+--=-++∵第P 的坐标为(2+,2),∴点I 的坐标为(m ,2+,∴PI=2m --∴PK=24m --∵GK =,∴244(24m m m -++=--,解得:12m =+22m =当2m =时,点G 与点P 、点K 重合, ∴0GK PK ==;不符合题意,舍去;∴点G 的横坐标为2+∴点G 的纵坐标为:2(24(2311y =+-⨯++=,∴点G 的坐标为(2+11).【点睛】本题考查了二次函数的综合问题,二次函数与一次函数的交点问题,二次函数的性质,以及一次函数的性质,解一元二次方程,解题的关键是熟练掌握二次函数的性质和一次函数的性质,运用数形结合的思想进行解题.17. 如图,直线334y x =-+与x 轴、y 轴分别交于AB 、两点, O M AB ⊥于点M ,点P 为直线l 上不与点A B 、重合的一个动点. (1)求线段OM 的长;(2)当BOP △的面积是6时,求点P 的坐标;(3)在y 轴上是否存在点Q ,使得以O 、P 、Q 为顶点的三角形与OMP 全等,若存在,请直接写出所有符合条件的点P 的坐标,否则,说明理由.【答案】(1)12 5; (2) (-4,6); (3) (125-,245)或(125,65)或(365,125-)或(45,125)【解析】【分析】(1)先求得点A 、B 的坐标,可求得OA 、OB 、AB 的长,利用面积法即可求得OM 的长;(2)先画图,确定△BOP 面积可以BO 为底,P 到y 轴距离为高求得P 到y 轴距离,再分类讨论求得答案;(3)分△OMP ≌△PQO 与△OMP ≌△OQP 两种情况讨论,结合图象分析即可求解. 【详解】(1)对于直线334y x =-+, 令0x =,则3y =,令0y =,则4x =, 点A 、B 的坐标分别是(4,0),(0,3),∴OA=4,OB=3,5==,∵11••22OA OB AB OM =,∴341255OM ⨯==; (2)过P 作PC ⊥y 轴于C ,如图1,∴12BOPS=OB•PC=6, ∴PC=4,∴点P 的横坐标为4或-4,∵点P 为直线l 上的一个动点且不与A 、B 重合, ∴横坐标为4时,与A 重合,不合题意,∴横坐标为-4时,纵坐标为:()34364-⨯-+=, ∴当点P 坐标为(-4,6)时,△BOP 的面积是6; (3)存在,理由如下:①当△OMP ≌△PQO 时,如图2和图3,由(1)得125OM =, ∴PQ=OM=125,即P 点横坐标为125-或125, 纵坐标为:312243455⎛⎫-⨯-+= ⎪⎝⎭或31263455-⨯+=,此时点P的坐标为(125-,245),(125,65);②当△OMP≌△OQP时,如图4和图5,∴OQ=OM=125,即即点P、点Q纵坐标为125-或125,由312345x-+=-,解得:365x=;由312345x-+=,解得:45x=;此时点P的坐标为(365,125-),(45,125);综上所述,符合条件的点P的坐标为(125-,245)或(125,65)或(365,125-)或(45,125) .【点睛】本题是一次函数与几何的综合题,考查了三角形及全等三角形的性质,体现了数形结合思想和分类讨论思想.解题关键是通过画图进行分类讨论.18. 如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2-6x+8=0的两个根(OA<OB),点C在y轴上,且OA︰AC=2︰5,直线CD垂直于直线AB于点P,交x轴于点D.(1)求出点A 、点B 的坐标. (2)请求出直线CD 的解析式.(3)若点M 为坐标平面内任意一点,在坐标平面内是否存在这样的点M,使以点B 、P 、D 、M 为顶点的四边形是平行四边形?若存在,请直接写出点M 的坐标;若不存在,请说明理由.【答案】(1)A(0,2),B(-4,0);(2)直线CD 的解析式:y CD =-2x+7;(3)存在,()1 5.53M -,,()29.53M ,,()3 2.53M --,.【解析】【分析】(1)根据一元二次方程的解法得出OA=2,OB=4,即可得出的A ,B 的坐标;(2)首先利用角之间的关系得出①BOA①①COD ,即可得出D 点的坐标,再利用待定系数法求一次函数解析式;(3)先求出P 点坐标(2,3),再根据平行四边形的性质,当PM=BD ,M 可在第一象限或第二象限,以及BM=PD 时M 在第三象限分别分析直接得出答案. 【详解】(1)①2680x x +=- ①124,2x x ==①OA 、OB 为方程的两个根,且OA <OB ①OA=2,OB=4,① A(0,2),B(-4,0), (2)①OA:AC=2:5 ① AC=5①OC=OA+AC=2+5=7 ① C(0,7),①①BAO=①CAP,①CPB=①BOA=90O ①①PBD=①OCD ①① BOA=①COD=90O ①①BOA①①COD ①=① OD===,①D(,0)设直线CD 的解析式为y kx b =+ 把x=0,y=7;x=,y=0分别代入得:7702b kb =⎧⎪⎨+=⎪⎩ ①72b k =⎧⎨=-⎩①y CD =-2x+7,(3)存在,()02A ,,()40B -,∴设直线AB 的解析式为:y kx b =+240b k b =⎧∴⎨-+=⎩解得:122k b ⎧=⎪⎨⎪=⎩ 故直线AB 的解析式为:122y x =+ 将直线AB 与直线CD 联立12227y x y x ⎧=+⎪⎨⎪=-+⎩ 解得:23x y =⎧⎨=⎩∴P 点坐标()2,3702D ⎛⎫ ⎪⎝⎭,,()40B -,7.5BD ∴=当1PM BD 是平行四边形则17.5BD PM ==1 5.5AM ∴=()1 5.53M ∴-,当2PBDM 是平行四边形 则27.5BD PM ==29.5AM ∴=()29.53M ∴,P 到x 轴距离等于3M 到x 轴距离,故3M 的纵坐标为-36BE DF BD DE ==-= 6 3.5 2.5FO ∴=-=∴3M 的横坐标为2.5 ∴3M 的坐标为()2.5,3--综上所述M 点的坐标为:()1 5.53M -,,()29.53M ,,()3 2.53M --,. 19. 【模型建立】(1)如图1,等腰Rt △ABC 中,∠ACB =90°,CB =CA ,直线ED 经过点C ,过点A 作AD ⊥ED 于点D ,过点B 作BE ⊥ED 于点E ,求证:△BEC ≌△CDA ; 【模型应用】(2)如图2,已知直线l 1:y =32x+3与x 轴交于点A ,与y 轴交于点B ,将直线l 1绕点A 逆时针旋转45°至直线l 2;求直线l 2的函数表达式;(3)如图3,平面直角坐标系内有一点B (3,﹣4),过点B 作BA ⊥x 轴于点A 、BC ⊥y 轴于点C ,点P 是线段AB 上的动点,点D 是直线y =﹣2x+1上的动点且在第四象限内.试探究△CPD 能否成为等腰直角三角形?若能,求出点D 的坐标,若不能,请说明理由.【答案】(1)见详解;(2)510y x =--;(3)点D 坐标得(113,193-)或(4,-7)或(83,133-).【解析】【分析】(1)由垂直的定义得∠ADC=∠CEB=90°,平角的定义和同角的余角的相等求出∠DAC=∠ECB ,角角边证明△CDA ≌△BEC ;(2)证明△ABO ≌∠BCD ,求出点C 的坐标为(-3,5),由点到直线上构建二元一次方程组求出k=-5,b=-10,待定系数法求出直线l 2的函数表达式为y=-5x-10;(3)构建△MCP ≌△HPD ,由其性质,点D 在直线y=-2x+1求出m=103-或n=0或43-,将m 的值代入,得点D 坐标得(113,193-)或(4,-7)或(83,133-). 【详解】解:(1)如图1所示:∵AD ⊥ED ,BE ⊥ED , ∴∠ADC=∠CEB=90°,又∵∠ACD+∠ACB+∠BEC=180°,∠ACB=90°,∴∠ACD+∠BEC=90°,又∵∠ACD+∠DAC=90°,∴∠DAC=∠ECB ,在△CDA 和△BEC 中,ADC CEB DAC ECB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△CDA ≌△BEC (AAS );(2)过点B 作BC ⊥AB 交AC 于点C ,CD ⊥y 轴交y 轴于点D ,如图2所示:∵CD ⊥y 轴,x 轴⊥y 轴,∴∠CDB=∠BOA=90°,又∵BC ⊥AB ,∴∠ABC=90°,又∵∠ABO+∠ABC+∠CBD=180°,∴∠ABO+∠CBD=90°,又∵∠BAO+∠ABO=90°,∴∠BAO=∠CBD ,又∵∠BAC=45°,∴∠ACB=45°,∴AB=CB ,在△ABO 和∠BCD 中,AOB BDC BAO CBD AB CB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABO ≌∠BCD (AAS ),∴AO=BD ,BO=CD ,又∵直线l 1:y=32x+3与x 轴交于点A ,与y 轴交于点B , ∴点A 、B 两点的坐标分别为(-2,0),(0,3),∴AO=2,BO=3,∴BD=2,CD=3,∴点C 的坐标为(-3,5),设l 2的函数表达式为y=kx+b (k≠0),点A 、C 两点在直线l 2上,依题意得:2035k b k b -+=⎧⎨-+=⎩, ∴510k b =-⎧⎨=-⎩, ∴直线l 2的函数表达式为y=-5x -10;(3)能成为等腰直角三角形,依题意得,①若点P 为直角时,如图3甲所示:设点P 的坐标为(3,m ),则PB 的长为4+m ,∵∠CPD=90°,CP=PD ,∠CPM+∠CDP+∠PDH=180°,。
第五章 三垂直等边模型(1)

第五章三垂直等边模型(1)
本文档介绍了三垂直等边模型的概念和特点。
1. 三垂直等边模型的定义
三垂直等边模型是指一个三角形,其中三个垂直交线相等且垂直于对边的模型。
它是几何学中的一个重要概念。
2. 三垂直等边模型的特点
三垂直等边模型具有以下特点:
- 三个垂直交线相等:在三垂直等边模型中,三个垂直交线的长度相等。
这意味着模型中的垂直线段具有相等的长度。
- 垂直交线垂直于对边:模型中的每个垂直交线都与对应的对边垂直,形成直角。
- 提供了几何问题的解决方法:三垂直等边模型可以用于解决一些几何问题,尤其是涉及垂直关系的问题。
3. 三垂直等边模型的应用案例
三垂直等边模型在实际应用中有许多案例,例如:
- 建筑设计:在建筑设计中,使用三垂直等边模型可以确定建筑物的垂直线和垂直间距。
- 地理测量:在地理测量中,使用三垂直等边模型可以计算地面高度、建筑物高度等。
4. 总结
三垂直等边模型是几何学中重要的模型,具有三个垂直交线相等且垂直于对边的特点。
它可以用于解决一些几何问题,同时在建筑设计和地理测量等领域有实际应用。
在进一步研究几何学和相关学科时,了解和掌握三垂直等边模型的概念和特点是非常重要的。
