极坐标与参数方程 题型总结归纳 附答案
高考极坐标与参数方程大题题型汇总(附详细答案)

高考极坐标与参数方程大题题型汇总(附详细答案)本文介绍了高考极坐标与参数方程大题题型,并给出了三个例子进行解答。
例1:在直角坐标系xoy中,圆C的参数方程为(x-1)^2+y^2=1,求圆C的极坐标方程。
解析:将x和y用极坐标表示,得到ρ=2cosθ。
例2:已知直线l的参数方程为x=-4t+a,y=3t-1,在直角坐标系xoy中,以O点为极轴建立极坐标系,设圆M的方程为ρ^2-6ρsinθ=-8.求圆M的直角坐标方程和实数a的值。
解析:将ρ和θ用x和y表示,得到x+(y-3)=1,然后将直线l的参数方程化为普通方程,得到3x+4y-3a+4=0.根据圆心到直线的距离和直线截圆所得弦长的关系,解得a=12或a=22/3.例3:已知曲线C的参数方程为x=2+5cosα,y=1+5sinα,以直角坐标系原点为极点,Ox轴正半轴为极轴建立极坐标系。
求曲线C的极坐标方程和直线l被曲线C截得的弦长。
解析:将x和y用极坐标表示,得到ρ=5.将直线l的极坐标方程化为普通方程,得到ρ(sinθ+cosθ)=1.由于曲线C是一个圆,因此直线l与曲线C的交点分别为A(7π/4.3+2√2)和B(3π/4.3-2√2),弦AB的长度为4√2.1) 曲线C的参数方程为:x=9\cos^3\theta,\ y=3\sin^3\theta$,直线$l$的直角坐标方程为$x+y-1=0$。
2) 设$P(9\cos^3\alpha,3\sin^3\alpha)$,则$P$到直线$l$的距离为$d=\frac{|9\cos^3\alpha+3\sin^3\alpha-1|}{\sqrt{2}}$。
为求$d$的最大值,我们可以将$d$表示为$10\cos(\alpha+\theta)+\frac{1}{\sqrt{2}}$的形式,其中$\theta$为一个与$\alpha$无关的常数,且$\tan\theta=\frac{1}{3}$。
极坐标与参数方程知识点总结大全及经典试题

极坐标与参数方程1.平面直角坐标系中的坐标伸缩变换设点P(x,y)是平面直角坐标系中的任意一点,在变换⎩⎨⎧=='y y xx μλϕ:的作用下,点P(x,y)对应到点()y x p '',,称ϕ为平面直角坐标系中的坐标伸缩变换,简称伸缩变换.例如:122=+y x 在变换⎩⎨⎧='='yy xx 23:ϕ(即横坐标伸长为原来3倍,纵坐标伸长为原来的2)得到14922=+y x 2.极坐标系的概念 (1)极坐标系如图所示,定点O 叫做 ,自极点O 引一条射线Ox ,叫做 ;再选定一个长度单位,一个角度单位及其正方向,这样就建立了一个极坐标系.(2)极坐标设M 是平面内一点,极点O 与点M 的距离OM 叫做点M 的 ,记为ρ;以极轴Ox 为始边,射线OM 为终边的角MOx ∠叫做点M 的 ,记为θ.有序数对 叫做点M 的极坐标,记作()θρ,M .一般地,不作特殊说明时,我们认为可取任意实数.3.极坐标和直角坐标的互化互化公式:设M 是坐标平面内任意一点,它的直角坐标是()y x ,,极坐标是()θρ, (0≥ρ),于是极坐标与直角坐标的互化公式如表:二、参数方程1.参数方程的概念一般地,在平面直角坐标系中,如果曲线上任意一点的坐标y x ,都是某个变数t 的函数①⎩⎨⎧==)()(t g y t f x ,并且对于t 的每一个允许值,由方程组①所确定的点()y x M ,都在这条曲线上,那么方程①就叫做这条曲线的参数方程,联系变数y x ,的变数t 叫做参变数,简称参数,相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.2.参数方程和普通方程的互化曲线的参数方程和普通方程是曲线方程的不同形式,一般地可以通过消去参数而从参数方程得到普通方程. 3.常见曲线的参数方程①经过点()000,y x M ,倾斜角为α的直线l 的普通方程为 ,参数方程为 。
高考极坐标与参数方程大题题型汇总(附详细答案)

高考极坐标与参数方程大题题型汇总1.在直角坐标系xoy 中,圆C 的参数方程1cos (sinx y 为参数).以O 为极点,x 轴的非负半轴为极轴建立极坐标系.(1)求圆C 的极坐标方程;(2)直线l 的极坐标方程是(sin 3cos )33,射线:3OM 与圆C 的交点为O 、P ,与直线l 的交点为Q ,求线段PQ 的长.解:(1)圆C 的普通方程是22(1)1x y,又cos ,sinx y ;所以圆C 的极坐标方程是2cos. ---5分(2)设11(,)为点P 的极坐标,则有1112cos 3解得1113.设22(,)为点Q 的极坐标,则有2222(sin 3cos )333解得2233由于12,所以122PQ,所以线段PQ 的长为 2.2.已知直线l 的参数方程为431x t ayt (t 为参数),在直角坐标系xOy 中,以O 点为极点,x 轴的非负半轴为极轴,以相同的长度单位建立极坐标系,设圆M 的方程为26sin8.(1)求圆M 的直角坐标方程;(2)若直线l 截圆M 所得弦长为3,求实数a 的值.解:(1)∵2222268(36si )n81xyy xy ,∴圆M 的直角坐标方程为22(3)1xy ;(5分)(2)把直线l 的参数方程431x t ayt (t 为参数)化为普通方程得:34340x y a ,∵直线l 截圆M 所得弦长为3,且圆M 的圆心(0,3)M 到直线l 的距离22|163|3191()5222a da或376a,∴376a或92a.(10分)3.已知曲线C 的参数方程为sin51cos 52yx(为参数),以直角坐标系原点为极点,Ox 轴正半轴为极轴建立极坐标系。
(1)求曲线c 的极坐标方程(2)若直线l 的极坐标方程为(sin θ+cos θ)=1,求直线l 被曲线c 截得的弦长。
解:(1)∵曲线c 的参数方程为sin51cos 52yx(α为参数)∴曲线c 的普通方程为(x-2)2+(y-1)2=5将sincos yx代入并化简得:=4cos θ+2sin θ即曲线c 的极坐标方程为=4cos θ+2sin θ(2)∵l 的直角坐标方程为x+y-1=0∴圆心c 到直线l 的距离为d=22=2∴弦长为225=234.已知曲线C :2219xy,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为sin()24.(1)写出曲线C 的参数方程,直线l 的直角坐标方程;(2)设P 是曲线C 上任一点,求P 到直线l 的距离的最大值.解:(1)曲线C 的参数方程为3cos sinxy(为参数),直线l 的直角坐标方程为2x y(2)设(3cos,sin)P ,P 到直线l 的距离10cos()23cossin 222d(其中为锐角,且1tan3)当cos()1时,P 到直线l 的距离的最大值max52d 5.设经过点(1,0)P 的直线l 交曲线C :2cos 3sinxy(为参数)于A 、B 两点.(1)写出曲线C 的普通方程;(2)当直线l 的倾斜角60时,求||||PA PB 与||||PA PB 的值.解:(1)C :22143xy.(2)设l :11232x tyt(t 为参数)联立得:254120tt 212121216||||||45PA PB t t t t t t ,1212||||||5PA PB t t 6.以直角坐标系的原点O 为极点,x 轴的正半轴为极轴建立极坐标系,已知点P 的直角坐标为(1,2),点M 的极坐标为(3,)2,若直线l 过点P ,且倾斜角为6,圆C 以M 为圆心,3为半径.(1)求直线l 的参数方程和圆C 的极坐标方程;(2)设直线l 与圆C 相交于,A B 两点,求PA PB.解:(1)直线l 的参数方程为31,212,2x t yt 为参数)t (,(答案不唯一,可酌情给分)圆的极坐标方程为sin6.(2)把31,212,2x t yt 代入22(3)9xy ,得2(31)70tt ,127t t ,设点,A B 对应的参数分别为12,t t ,则12,PAt PBt ,7.PAPB7.在平面直角坐标系xOy 中,直线l 的参数方程是22222x tyt (t 为参数),以原点O 为极点,以x 轴的非负半轴为极轴建立极坐标系,已知圆C 的极坐标方程为42cos()4.(1)将圆C 的极坐标方程化为直角坐标方程;(2)若直线l 与圆C 交于A ,B 两点,点P 的坐标为(2,0),试求11PA PB的值.解:(1)由42cos()4,展开化为2242(cos sin )4(cos sin )2,将代入,得22440xyx y ,所以,圆C 的直角坐标方程是22440xyxy.cos sinxy(2)把直线l 的参数方程22222x tyt(t 为参数)代入圆的方程并整理,可得:22240tt.设A ,B 两点对应的参数分别为12,t t ,则121222,40t t t t ,所以2121212()426t t t t t t .∴121212111126642t t PAPBt t t t .8.已知曲线C 的极坐标方程为2sin cos10,曲线13cos :2sin x C y(为参数).(1)求曲线1C 的标准方程;(2)若点M 在曲线1C 上运动,试求出M 到曲线C 的距离的最小值.解:(1)曲线1C 的标准方程是:22194xy(2)曲线C 的标准方程是:210xy 设点(3cos ,2sin)M ,由点到直线的距离公式得:3cos 4sin 1015cos()1055d其中34cos,sin550时,min5d ,此时98(,)55M 9.在平面直角坐标系xOy 中,直线l 的参数方程为122322x t yt(t 为参数),直线l 与曲线C :22(2)1yx交于A ,B 两点.(1)求AB 的长;(2)在以O 为极点,x 轴的正半轴为极轴建立的极坐标系中,设点P 的极坐标为322,4,求点P 到线段AB 中点M 的距离.解:(1)直线l 的参数方程为122322x t yt ,,(t 为参数),代入曲线C 的方程得24100tt .设点A ,B 对应的参数分别为12t t ,,则124t t ,1210t t ,所以12||||214AB t t .(2)由极坐标与直角坐标互化公式得点P 的直角坐标为(22),,所以点P 在直线l 上,中点M 对应参数为1222t t ,由参数t 的几何意义,所以点P 到线段AB 中点M 的距离||2PM .10.已知直线l 经过点(1,1)P ,倾斜角6,(1)写出直线l 的参数方程。
极坐标参数方程题型归纳7种

极坐标参数方程题型归纳7种标准化文件发布号:(9312-EUATWW-MWUB-WUNN-INNUL-DQQTY-极坐标与参数方程(高考真题)题型归纳一、极坐标方程与直角坐标方程的互化1.(2015·广东理,14)已知直线l的极坐标方程为2ρsin⎝⎛⎭⎫θ-π4=2,点A的极坐标为A⎝⎛⎭⎫22,7π4,则点A到直线l的距离为________.[立意与点拨]本题考查极坐标与平面直角坐标的互化、点到直线的距离,属于容易题.解答本题先进行极直互化,再求距离.二、参数方程与直角坐标方程的互化【解析】椭圆方程为:14622=+yx,因为1cossin22=+xx,令⎩⎨⎧==ααcos2sin6yx,则有X+2y=αsin6+αcos4=()ϕα++sin166,最大值22,最小值22-三、根据条件求直线和圆的极坐标方程四、求曲线的交点及交点距离4.(2015·湖北高考)在直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.已知直线l的极坐标方程为ρ(sin θ-3cos θ)=0,曲线C的参数方程为⎩⎨⎧x=t-1t,y=t+1t(t为参数),l与C相交于A,B 两点,则|AB|=________.【解析】直线l的极坐标方程ρ(sin θ-3cos θ)=0化为直角坐标方程为3x-y=0,曲线C的参数方程⎩⎨⎧x=t-1t,y=t+1t两式经过平方相减,化为普通方程为y2-x2=4,联立⎩⎪⎨⎪⎧3x-y=0,y2-x2=4解得⎩⎪⎨⎪⎧x=-22,y=-322或⎩⎪⎨⎪⎧x=22,y=322.所以点A⎝⎛⎭⎪⎫-22,-322,B⎝⎛⎭⎪⎫22,322.所以|AB|=⎝⎛⎭⎪⎫-22-222+⎝⎛⎭⎪⎫-322-3222=2 5.5.在平面直角坐标xOy 中,已知直线l 的参数方程⎩⎪⎨⎪⎧x =1-22t ,y =2+22t ,(t 为参数),直线l 与抛物线y 2=4x 相交于A 、B 两点,求线段AB 的长.[解析] 解法1:将l 的方程化为普通方程得l :x +y =3,∴y =-x +3,代入抛物线方程y 2=4x 并整理得x 2-10x +9=0,∴x 1=1,x 2=9. ∴交点A (1,2),B (9,-6),故|AB |=82+82=8 2.解法2:将l 的参数方程代入y 2=4x 中得,(2+22t )2=4(1-22t ), 解之得t 1=0,t 2=-82,∴|AB |=|t 1-t 2|=8 2.6.(2015·陕西理,23)在直角坐标系xOy 中,直线l 的参数方程为⎩⎪⎨⎪⎧x =3+12t ,y =32t(t 为参数).以原点为极点,x 轴正半轴为极轴建立极坐标系,⊙C 的极坐标方程为ρ=23sin θ.(1)写出⊙C 的直角坐标方程;(2)P 为直线l 上一动点,当P 到圆心C 的距离最小时,求P 的直角坐标.[立意与点拨] 考查极坐标与参数方程、转化与化归思想和函数思想;解答本题(1)需熟记极直互化公式;(2)用参数坐标将距离表达为t 的函数,转化为函数最值求解.[解析](1)由ρ=23sin θ,得ρ2=23ρsin θ,从而有x 2+y 2=23y ,所以x 2+(y -3)2=3. (2)设P (3+12t ,32t ),又C (0,3),则|PC |=3+12t 2+32t -32=t 2+12,故当t =0时,|PC |取得最小值,此时,P 点的直角坐标为(3,0).五、利用参数方程求最值( 转化与化归思想和函数思想 )[立意与点拨](用三角函数作为参数,转化成求三角函数最值问题,着重理解转化思维,用参数法实现转化的技巧)8.(2015·新课标Ⅱ高考)在直角坐标系xOy 中,曲线C 1:⎩⎪⎨⎪⎧x =t cos α,y =t sin α(t 为参数,t ≠0),其中0≤α<π,在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2:ρ=2sin θ,C 3:ρ=23cos θ.(1)求C 2与C 3交点的直角坐标;(2)若C 1与C 2相交于点A ,C 1与C 3相交于点B ,求|AB |的最大值.【解】(1)曲线C 2的直角坐标方程为x 2+y 2-2y =0,曲线C 3的直角坐标方程为x 2+y 2-23x =0.联立⎩⎨⎧x 2+y 2-2y =0,x 2+y 2-23x =0,解得⎩⎪⎨⎪⎧x =0,y =0,或⎩⎪⎨⎪⎧x =32,y =32.所以C 2与C 3交点的直角坐标为(0,0)和⎝ ⎛⎭⎪⎫32,32.(2)曲线C 1的极坐标方程为θ=α(ρ∈R ,ρ≠0),其中0≤α<π.(此题C 1代表的是一条过原点的直线) 因此A 的极坐标为(2sin α,α),B 的极坐标为(23cos α,α).所以|AB |=|2sin α-23cos α|=4⎪⎪⎪⎪sin ⎝⎛⎭⎫α-π3.当α=5π6时,|AB |取得最大值,最大值为4.9.(2015·商丘市二模)已知极坐标系的极点在直角坐标系的原点处,极轴与x 轴的正半轴重合,直线l 的极坐标方程为:ρsin ⎝⎛⎭⎫θ-π6=12,曲线C 的参数方程为:⎩⎪⎨⎪⎧x =2+2cos α,y =2sin α.(1)写出直线l 的直角坐标方程; (2)求曲线C 上的点到直线l 的距离的最大值.[解析] (1)∵ρsin ⎝⎛⎭⎫θ-π6=12,∴ρ⎝ ⎛⎭⎪⎫32sin θ-12cos θ=12,∴32y -12x =12,即l :x -3y +1=0.(2)解法一:由已知可得,曲线上的点的坐标为(2+2cos α,2sin α), 所以,曲线C 上的点到直线l 的距离d =|2+2cos α-23sin α+1|2=⎪⎪⎪⎪4cos ⎝⎛⎭⎫α+π3+32≤72. 所以最大距离为72.解法二:曲线C 为以(2,0)为圆心,2为半径的圆.圆心到直线的距离为32,所以,最大距离为32+2=72.10.(文)(2014·新课标Ⅰ理,23)已知曲线C :x 24+y 29=1,直线l :⎩⎪⎨⎪⎧x =2+t y =2-2t (t 为参数).(1)写出曲线C 的参数方程,直线l 的普通方程;(2)过曲线C 上任意一点P 作与l 夹角为30°的直线,交l 于点A ,求|PA |的最大值与最小值.[解析](1)曲线C 的参数方程为⎩⎪⎨⎪⎧x =2cos θ,y =3sin θ,(θ为参数)直线l 的普通方程为:2x +y -6=0.(2)曲线C 上任意一点P (2cos θ,3sin θ)到l 的距离为d =55|4cos θ+3sin θ-6|.则|PA |=d sin30°=255|5sin(θ+α)-6|,其中α为锐角,且tan α=43.(将d=|AB|sin30利用三角关系进行转化,转化化归思想,高考考点考察学生思维能力)当sin(θ+α)=-1时,|PA |取得最大值,最大值为2255. 当sin(θ+α)=1时,|PA |取得最小值,最小值为255.六、直线参数方程中的参数的几何意义方法一:方法二:根据直线参数方程中t 的几何意义,可知,弦长=|t 1-t 2|.得:053154153154122=⎪⎭⎫⎝⎛--+⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛+t t t t ,方程化简,然后用韦达定理求 弦长=|t 1-t 2|=()212214t t t t -+=.....13.(理)在直角坐标系xOy 中,过点P (32,32)作倾斜角为α的直线l 与曲线C :x 2+y 2=1相交于不同的两点M 、N .(1)写出直线l 的参数方程;(2)求1|PM |+1|PN |的取值范围.(根据直线参数方程中t 的几何意义,用参数t 表示所求量1|PM |+1|PN |,然后用t 的二次方程的韦达定理,转化成三角函数进而求范围,此题较难)[解析] (1)⎩⎪⎨⎪⎧x =32+t cos α,y =32+t sin α,(t 为参数).(2)将⎩⎪⎨⎪⎧x =32+t cos α,y =32+t sin α.(t 为参数)代入x 2+y 2=1中,消去x ,y 得,t 2+(3cos α+3sin α)t +2=0,由Δ=(3cos α+3sin α)2-8=12sin 2(α+π6)-8>0⇒sin(α+π6)>63, 1|PM |+1|PN |=1-t 1+1-t 2=-t 1+t 2t 1t 2=3cos α+3sin α2=3sin(α+π6)∈(2,3].七、求动点坐标、求变量的值14.(2015·陕西理,23)在直角坐标系xOy 中,直线l 的参数方程为⎩⎪⎨⎪⎧x =3+12t ,y =32t(t 为参数).以原点为极点,x 轴正半轴为极轴建立极坐标系,⊙C 的极坐标方程为ρ=23sin θ.(1)写出⊙C 的直角坐标方程;(2)P 为直线l 上一动点,当P 到圆心C 的距离最小时,求P 的直角坐标.[立意与点拨] 考查极坐标与参数方程、转化与化归思想和函数思想;解答本题(1)需熟记极直互化公式;(2)用参数坐标将距离表达为t 的函数,转化为函数最值求解.[解析] (1)由ρ=23sin θ,得ρ2=23ρsin θ,从而有x 2+y 2=23y ,所以x 2+(y -3)2=3. (2)设P (3+12t ,32t ),又C (0,3),则|PC |=3+12t 2+32t -32=t 2+12,故当t =0时,|PC |取得最小值,此时,P 点的直角坐标为(3,0).(此处用参数t 来表示所求距离,然后当作变量为t 的二次函数,求最值)15.(2016全国卷I)在直角坐标系xOy 中,曲线1C 的参数方程为⎩⎨⎧+==,sin 1,cos t a y t a x t (为参数,)0>a .在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线θρcos 4:2=C . (Ⅰ)说明1C 是哪一种曲线,并将1C 的方程化为极坐标方程; (Ⅱ)直线3C 的极坐标方程为0αθ=,其中0α满足2tan 0=α,若曲线1C 与2C 的公共点都在3C 上,求a .【解析】:⑴ cos 1sin x a t y a t =⎧⎨=+⎩(t 均为参数),∴()2221x y a +-= ①∴1C 为以()01,为圆心,a 为半径的圆.方程为222210x y y a +-+-= ∵222sin x y y ρρθ+==,,∴222sin 10a ρρθ-+-= 即为1C 的极坐标方程⑵ 24cos C ρθ=:,两边同乘ρ得22224cos cos x y x ρρθρρθ==+=, 224x y x ∴+=,即()2224x y -+= ②,3C :化为普通方程为2y x =由题意:1C 和2C 的公共方程所在直线即为3C ,①—②得:24210x y a -+-=,即为3C∴210a -=,∴1a =(圆与圆交点所在直线的求法,联立圆方程,两方程相减,可得变量的方程)16.(文)(2015·唐山市二模)在极坐标系中,曲线C :ρ=2a cos θ(a >0),l :ρcos ⎝⎛⎭⎫θ-π3=32,C 与l 有且仅有一个公共点.(1)求a ; (2)O 为极点,A ,B 为C 上的两点,且∠AOB =π3,求|OA |+|OB |的最大值.[解析] (1)曲线C 是以(a,0)为圆心,以a 为半径的圆; l 的直角坐标方程为x +3y -3=0.由直线l 与圆C 相切可得|a -3|2=a ,解得a =1. (求符合条件的变量值,建立等量关系,解方程)(2)不妨设A 的极角为θ,B 的极角为θ+π3,则|OA |+|OB |=2cos θ+2cos ⎝⎛⎭⎫θ+π3=3cos θ-3sin θ=23cos ⎝⎛⎭⎫θ+π6, 当θ=-π6时,|OA |+|OB |取得最大值2 3.(用三角函数作为参数,转化成求三角函数最值问题,着重理解转化思维,用参数法实现转化的技巧)。
极坐标与参数方程 题型总结归纳 附答案

《极坐标与参数方程》高考高频题型除了简单的极坐标与直角坐标的转化、参数方程与普通方程的转化外,还涉及(一)有关圆的题型题型一:圆与直线的位置关系(圆与直线的交点个数问题)----利用圆心到直线的距离与半径比较相离,无交点;:r d > 个交点;相切,1:r d = 个交点;相交,2:r d <用圆心(x 0,y 0)到直线Ax+By+C=0的距离2200BA C By Ax d +++=,算出d ,在与半径比较。
题型二:圆上的点到直线的最值问题(不求该点坐标,如果求该点坐标请参照距离最值求法)思路:第一步:利用圆心(x 0,y 0)到直线Ax+By+C=0的距离2200BA C By Ax d +++=第二步:判断直线与圆的位置关系第三步:相离:代入公式:r d d +=max ,r d d -=min 相切、相交:r d d +=max min 0d =题型三:直线与圆的弦长问题弦长公式222d r l -=,d 是圆心到直线的距离延伸:直线与圆锥曲线(包括圆、椭圆、双曲线、抛物线)的弦长问题 (弦长:直线与曲线相交两点,这两点之间的距离就是弦长) 弦长公式21t t l -=,解法参考“直线参数方程的几何意义”(二)距离的最值: ---用“参数法”1.曲线上的点到直线距离的最值问题2.点与点的最值问题“参数法”:设点---套公式--三角辅助角①设点: 设点的坐标,点的坐标用该点在所在曲线的的参数方程来设 ①套公式:利用点到线的距离公式①辅助角:利用三角函数辅助角公式进行化一例如:【2016高考新课标3理数】在直角坐标系中,曲线的参数方程为,以坐标原点为极点,以轴的正半轴为极轴,,建立极坐标系,曲线的极坐标方程为(I )写出的普通方程和的直角坐标方程;(II )设点在上,点在上,求的最小值及此时的直角坐标的直角坐标方程为.这里没有加减移项省去,直接化同,那系数除到左边(①)由题意,可设点的直角坐标为 因为是直线,所以的最小值即为到的距离的最小值,xOy 1C ()sin x y ααα⎧=⎪⎨=⎪⎩为参数x 2C sin()4ρθπ+=1C 2C P 1C Q 2C PQ P 2C 40x y +-=P ,sin )αα2C ||PQ P 2C ()d α.(欧萌说:利用点到直接的距离列式子,然后就是三角函数的辅助公式进行化一)当时)(13sin =+πα即当时,,此时的直角坐标为.(三)直线参数方程的几何意义1.经过点P (x 0,y 0),倾斜角为α的直线l 的参数方程为为参数)t t y y t x x (sin cos 00⎩⎨⎧+=+=αα若A ,B 为直线l 上两点,其对应的参数分别为t 1,t 2,线段AB 的中点为M ,点M 所对应的参数为t 0,则以下结论在解题中经常用到: (1)t 0=t 1+t 22; (2)|PM |=|t 0|=t 1+t 22; (3)|AB |=|t 2-t 1|; (4)|P A |·|PB |=|t 1·t 2|(5)⎪⎩⎪⎨⎧>+<-+=-=+=+0,0,4)(212121212212121t t t t t t t t t t t t t t PB PA 当当(注:记住常见的形式,P 是定点,A 、B 是直线与曲线的交点,P 、A 、B 三点在直线上) 【特别提醒】直线的参数方程中,参数t 的系数的平方和为1时,t 才有几何意义且其几何意义为:|t |是直线上任一点M (x ,y )到M 0(x 0,y 0)的距离,即|M 0M |=|t |.直线与圆锥曲线相交,交点对应的参数分别为12,t t ,则弦长12l t t =-; 2.解题思路第一步:曲线化成普通方程,直线化成参数方程()sin()2|3d παα==+-2()6k k Z παπ=+∈()d αP 31(,)22第二步:将直线的参数方程代入曲线的普通方程,整理成关于t 的一元二次方程:02=++c bt at第三步:韦达定理:a ct t a b t t =-=+2121,第四步:选择公式代入计算。
极坐标与参数方程高考经典题型归纳总结
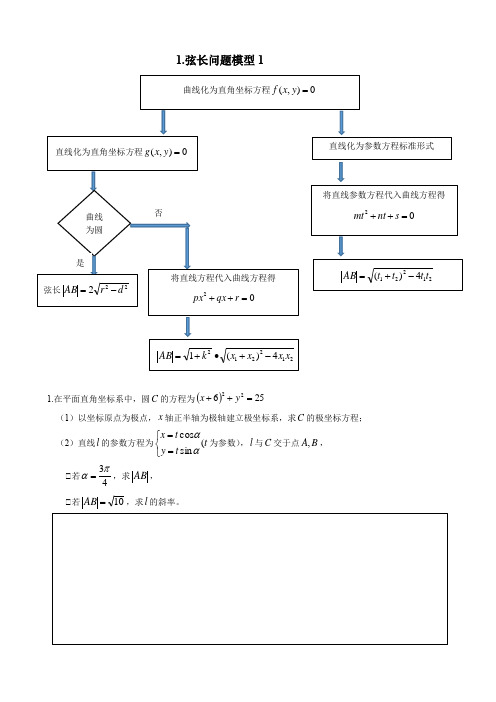
1.弦长问题模型11.在平面直角坐标系中,圆C 的方程为()25622=++y x(1)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求C 的极坐标方程; (2)直线l 的参数方程为t t y t x (sin cos ⎩⎨⎧==αα为参数),l 与C 交于点B A ,, ①若43πα=,求AB , ①若10=AB ,求l 的斜率。
2.已知直线t ty tx (32⎩⎨⎧=+=为参数)与曲线θθρcos 8sin 2=交于B A ,,求AB2.弦长问题模型2(只对直线过原点才可以)注意:若直线倾斜角为α且过原点,则该直线的直角坐标方程为αtan x y=,其参数方程为⎧==ααsin cos t y t x ,其极坐标方程为)(R ∈=ραθ3.在极坐标系中,以点(2,)2C π为圆心,半径为3的圆C 与直线:()3l R πθρ=∈交于,A B 两点.(1)求圆C 及直线l 的普通方程.(2)求弦长AB .3.参数方程最值问题模型4.已知曲线θθθ(sin 2cos 1:1⎩⎨⎧+=+=y x C 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,且曲线:2C4πθ=()R ∈ρ(1)写出1C 的极坐标方程,2C 的一个参数方程;(2)设1C 与2C 交于N M ,两点,P 为1C 上一动点,求PMN ∆面积的最大值。
4.利用直线参数方程中t 的几何意义问题模型5.在极坐标系中,点M 坐标是)2,3(π,曲线C 的方程为)4sin(22πθρ+=;以极点为坐标原点,极轴为x 轴的正半轴建立平面直角坐标系,斜率是1-的直线l 经过点M . (1)写出直线l 的参数方程和曲线C 的直角坐标方程;(2)求证直线l 和曲线C 相交于两点A 、B ,并求||||MB MA ⋅的值.6.在直角坐标系中,以原点为极点,x 轴的正半轴为极轴建坐标系,已知曲线()2:sin 2cos 0C a a ρθθ=>,已知过点()2,4P --的直线l 的参数方程为:2,4x y ⎧=-⎪⎪⎨⎪=-⎪⎩直线l 与曲线C 分别交于,M N(1)写出曲线C 和直线l 的普通方程; (2)若||,||,||PM MN PN 成等比数列,求a 的值.5.综合问题例题1在平面直角坐标系xoy 中,曲线13:221=+y x C ,以坐标原点为极轴,以x 轴的正半轴为极轴,建立极坐标系,曲线a C 222)4sin(:2+=+πθρ(1)写出1C 的参数方程,2C 的普通方程;(2)设点P 在1C 上,点Q 在2C ,求PQ 的最小值以及此时P 点坐标。
极坐标和参数方程知识点+典型例题及其详解

极坐标和参数方程知识点+典型例题及其详解极坐标和参数方程知识点+典型例题及其详解知识点回顾(一)曲线的参数方程的定义:在取定的坐标系中,如果曲线上任意一点的坐标x 、y 都是某个变数t 的函数,即⎩⎨⎧==)()(t f y t f x并且对于t 每一个允许值,由方程组所确定的点M (x ,y )都在这条曲线上,那么方程组就叫做这条曲线的参数方程,联系x 、y 之间关系的变数叫做参变数,简称参数. (二)常见曲线的参数方程如下:1.过定点(x 0,y 0),倾角为α的直线:ααsin cos 00t y y t x x +=+= (t 为参数)其中参数t 是以定点P (x 0,y 0)为起点,对应于t 点M (x ,y )为终点的有向线段PM 的数量,又称为点P 与点M 间的有向距离.根据t 的几何意义,有以下结论. ○1.设A 、B 是直线上任意两点,它们对应的参数分别为t A 和t B ,则AB=AB t t -=BA AB t t t t ⋅--4)(2.○2.线段AB 的中点所对应的参数值等于2BA t t +.2.中心在(x 0,y 0),半径等于r 的圆:θθsin cos 00r y y r x x +=+= (θ为参数) 3.中心在原点,焦点在x 轴(或y 轴)上的椭圆:θθsin cos b y a x == (θ为参数) (或θθsin cos a y b x ==)中心在点(x0,y0)焦点在平行于x 轴的直线上的椭圆的参数方程为参数)ααα(.sin ,cos 0⎩⎨⎧+=+=b y y a x x 4.中心在原点,焦点在x 轴(或y 轴)上的双曲线:θθtg sec b y a x == (θ为参数) (或θθec a y b x s tg ==)5.顶点在原点,焦点在x 轴正半轴上的抛物线:pty pt x 222== (t 为参数,p >0)直线的参数方程和参数的几何意义过定点P (x 0,y 0),倾斜角为α的直线的参数方程是⎩⎨⎧+=+=ααsin cos 00t y y t x x (t 为参数).(三)极坐标系1、定义:在平面内取一个定点O ,叫做极点,引一条射线Ox ,叫做极轴,再选一个长度单位和角度的正方向(通常取逆时针方向)。
极坐标与参数方程题型和方法归纳

极坐标与参数方程题型和方法归纳极坐标与参数方程题型和方法归纳题型一:极坐标方程与直角坐标方程的相互转化,参数方程与普通方程相互转化,极坐标方程与参数方程相互转化。
具体方法如下:1)极坐标方程转直角坐标方程:begin{cases}\rho=x\cos\theta+y\sin\theta\\\tan\theta=\dfrac{y }{x}\end{cases}\Rightarrow\begin{cases}x=\rho\cos\theta\\y=\rho \sin\theta\end{cases}$$其中,$\rho$表示点到原点的距离,$\theta$表示点与$x$轴正半轴的夹角。
2)参数方程转直角坐标方程:begin{cases}x=f(t)\\y=g(t)\end{cases}\RightarrowF(x,y)=0$$其中,$F(x,y)$为$x,y$的函数,$t$为参数。
3)极坐标方程转参数方程:begin{cases}x=r\cos\theta\\y=r\sin\theta\end{cases}\Rightarr ow\begin{cases}r=f(\theta)\\ \theta=g(r)\end{cases}$$题型二:三个常用的参数方程及其应用1)圆的参数方程:begin{cases}x=a+r\cos\theta\\y=b+r\sin\theta\end{cases}$$其中,$(a,b)$为圆心坐标,$r$为半径。
2)椭圆的参数方程:begin{cases}x=a\cos\theta\\y=b\sin\theta\end{cases}$$其中,$a,b$为椭圆的长短半轴。
3)过定点倾斜角为$\alpha$的直线$l$的标准参数方程为:dfrac{x-x_0}{\cos\alpha}=\dfrac{y-y_0}{\sin\alpha}=p$$其中,$(x_0,y_0)$为直线$l$上的一点,$p$为直线$l$到原点的距离。
极坐标系与参数方程知识点和解题类型最全总结(附详细答案)

第19讲 极坐标系与参数方程(后附详解答案)一、平面直角坐标系中的伸缩变换1.在同一平面直角坐标系中,直线2x -y =4变成x ′-y ′=2的伸缩变换是( )A .⎩⎪⎨⎪⎧x ′=x ,y ′=2y B .⎩⎪⎨⎪⎧x ′=12x ,y ′=yC .⎩⎪⎨⎪⎧ x ′=x ,y ′=12y D .⎩⎪⎨⎪⎧x ′=12x ,y ′=4y2.求椭圆x 24+y 2=1经过伸缩变换⎩⎪⎨⎪⎧x ′=12x ,y ′=y后的曲线方程 .二、极坐标与直角坐标的互化1.在极坐标系中,圆ρ=-2sin θ的圆心的极坐标是( )A .(1,π2)B .(1,-π2) C .(1,0) D .(1,π)2.已知点P 的极坐标为(1,π),那么过点P 且垂直于极轴的直线的极坐标方程为( )A .ρ=1B .ρ=cos θC .ρ=-1cos θD .ρ=1cos θ3.在极坐标系中,直线ρ(3cos θ-sin θ)=2与圆ρ=4sin θ的交点的极坐标为( )A .(2,π6)B .(2,π3)C .(4,π6)D .(4,π3)4.曲线C 的直角坐标方程为x 2+y 2-2x =0,以原点为极点、x 轴的正半轴为极轴建立极坐标系,则曲线C 的极坐标方程为5.在极坐标系中,直线ρcos θ+ρsin θ=a (a >0)与圆ρ=2cos θ相切,则a =____.6.已知直线l 的极坐标方程为2ρsin(θ-π4)=2,点A 的极坐标为A (22,7π4),则点A 到直线l 的距离为_____.1θθ=-||AB |21ρρ=7.圆ρ=5cos θ-53sin θ的圆心的极坐标为________.8.在极坐标系中,圆ρ=4sin θ的圆心到直线θ=π3(θ∈R )的距离是________.9.在极坐标系中A ⎝⎛⎭⎫2,-π3,B ⎝⎛⎭⎫4,2π3两点间的距离为________.10.曲线C 1:θ=π6与曲线C 2:ρsin ⎝⎛⎭⎫θ+π6=32的交点坐标为________.三、极坐标方程的综合应用1.在极坐标系下,已知圆O :ρ=cos θ+sin θ和直线l :ρsin ⎝⎛⎭⎫θ-π4=22. (1)求圆O 和直线l 的直角坐标方程;(2)当θ∈(0,π)时,求直线l 与圆O 公共点的一个极坐标.2.已知曲线C 1的参数方程为⎩⎪⎨⎪⎧x =cos θ,y =1+sin θ(θ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为ρ=4sin ⎝⎛⎭⎫θ+π3,直线l 的直角坐标方程为y =33x . (1)求曲线C 1和直线l 的极坐标方程;(2)已知直线l 分别与曲线C 1,曲线C 2相交于异于极点的A ,B 两点,若A ,B 的极径分别为ρ1,ρ2,求|ρ2-ρ1|的值.3.以直角坐标系中的原点O 为极点,x 轴正半轴为极轴的极坐标系中,已知曲线C的极坐标方程为ρ=21-sin θ.(1)将曲线C 的极坐标方程化为直角坐标方程;(2)过极点O 作直线l 交曲线C 于点P ,Q ,若|OP |=3|OQ |,求直线l 的极坐标方程.4.已知曲线C 的参数方程为⎩⎨⎧x =2+5cos α,y =1+5sin α(α为参数),以直角坐标系的原点O 为极点,x 轴正半轴为极轴建立极坐标系.(1)求曲线C 的极坐标方程;(2)设l 1:θ=π6,l 2:θ=π3,若l 1,l 2与曲线C 相交于异于原点的两点A ,B ,求△AOB 的面积.5.在直角坐标系xOy 中,已知圆C :⎩⎪⎨⎪⎧x =2cos θ,y =2sin θ(θ为参数),点P 在直线l :x +y -4=0上,以坐标原点为极点,x 轴的正半轴为极轴,建立极坐标系.(1)求圆C 和直线l 的极坐标方程;(2)射线OP 交圆C 于点R ,点Q 在射线OP 上,且满足|OP |2=|OR |·|OQ |,求点Q 的轨迹的极坐标方程.6.在直角坐标系xOy 中,曲线C 1的参数方程为⎩⎪⎨⎪⎧x =a cos t ,y =1+a sin t (t 为参数,a >0).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C 2:ρ=4cos θ.(1)说明C 1是哪一种曲线,并将C 1的方程化为极坐标方程;(2)直线C 3的极坐标方程为θ=α0,其中α0满足tan α0=2,若曲线C 1与C 2的公共点都在C 3上,求a .7.在直角坐标系xOy 中,曲线C 1的参数方程为⎩⎨⎧x =2cos φ,y =sin φ(φ为参数),曲线C 2:x 2+y 2-2y =0.以原点O 为极点,x 轴的正半轴为极轴建立极坐标系,射线l :θ=α(ρ≥0)与曲线C 1,C 2分别交于点A ,B (均异于原点O ).(1)求曲线C 1,C 2的极坐标方程;(2)当0<α<π2时,求|OA |2+|OB |2的取值范围.8.在直角坐标系xOy 中,曲线C 1:⎩⎪⎨⎪⎧x =t cos α,y =t sin α(t 为参数,t ≠0),其中0≤α<π.在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2:ρ=2sin θ,C 3:ρ=23cos θ.(1)求C 2与C 3交点的直角坐标;(2)若C 1与C 2相交于点A ,C 1与C 3相交于点B ,求|AB |的最大值.四、直角坐标方程与参数方程的互化1.在平面直角坐标系中,若曲线C 的参数方程为⎩⎨⎧x =2+22t ,y =1+22t (t 为参数),则其普通方程为________.2.椭圆⎩⎪⎨⎪⎧x =5cos θ,y =3sin θ(θ为参数)的离心率为________.3.曲线C 的参数方程为⎩⎪⎨⎪⎧x =sin θ,y =cos2θ+1(θ为参数),则曲线C 的普通方程为________.4.求直线⎩⎪⎨⎪⎧ x =2+t ,y =-1-t (t 为参数)与曲线⎩⎪⎨⎪⎧x =3cos α,y =3sin α(α为参数)的交点个数.条件探究 把举例说明1中“曲线⎩⎪⎨⎪⎧ x =3cos α,y =3sin α(α为参数)”改为“⎩⎪⎨⎪⎧x =1-sin2θ,y =sin θ+cos θ.”其他条件不变,求两条曲线交点的坐标.5.在平面直角坐标系xOy 中,直线l :⎩⎨⎧x =1+35t ,y =45t(t 为参数),与曲线C :⎩⎪⎨⎪⎧x =4k 2,y =4k(k 为参数)交于A ,B 两点,求线段AB 的长.6.已知椭圆C :x 24+y 23=1,直线l :⎩⎨⎧x =-3+3t ,y =23+t(t 为参数).写出椭圆C 的参数方程及直线l 的普通方程和直线的标准参数方程.五、直线参数方程的应用1.在平面直角坐标系xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,点A 的极坐标为⎝⎛⎭⎫2,π4,直线l 的极坐标方程为ρcos ⎝⎛⎭⎫θ-π4=a ,且l 过点A ,曲线C 1的参数方程为⎩⎨⎧x =2cos α,y =3sin α(α为参数).(1)求曲线C 1上的点到直线l 的距离的最大值;(2)过点B (-1,1)且与直线l 平行的直线l 1与曲线C 1交于M ,N 两点,求|BM |·|BN |的值.2.在直角坐标系xOy 中,设倾斜角为α的直线l 的参数方程为⎩⎪⎨⎪⎧x =3+t cosα,y =t sinα(t 为参数),直线l 与曲线C :⎩⎪⎨⎪⎧x =1cos θ,y =tan θ(θ为参数)相交于不同的两点A ,B .(1)若α=π3,求线段AB 的中点的直角坐标;(2)若直线l 的斜率为2,且过已知点P (3,0),求|P A |·|PB |的值.3.在平面直角坐标系xOy 中,直线l 的参数方程为⎩⎨⎧x =3-22t ,y =5+22t (t 为参数).在以原点O 为极点,x轴正半轴为极轴的极坐标中,圆C 的方程为ρ=25s inθ.(1)写出直线l 的普通方程和圆C 的直角坐标方程;(2)若点P 坐标为(3,5),圆C 与直线l 交于A ,B 两点,求|P A|+|P B|的值.4.在直角坐标系xOy 中,直线l 的参数方程为⎩⎪⎨⎪⎧x =t cos α,y =1+t sin α(t 为参数,a ∈[0,π)).以原点O 为极点,以x 轴的正半轴为极轴,建立极坐标系.设曲线C 的极坐标方程为ρcos 2θ=4sin θ.(1)设M (x ,y )为曲线C 上任意一点,求x +y 的取值范围; (2)若直线l 与曲线C 交于不同的两点A ,B ,求|AB |的最小值.5.在平面直角坐标系xOy 中,已知过点P (0,-1)的直线l 的参数方程为⎩⎨⎧x =12t ,y =-1+32t (t 为参数),在以坐标原点O 为极点,x 轴正半轴为极轴的极坐标系中,曲线C 的方程为2a sin θ-ρcos 2θ=0(a >0).(1)求曲线C 的直角坐标方程;(2)若直线l 与曲线C 分别交于点M ,N ,且|PM |,|MN |,|PN |成等比数列,求a 的值.六、极坐标与参数方程的综合应用1.坐标系与参数方程]在直角坐标系xOy 中,以O 为极点,x 轴正半轴为极轴建立极坐标系.已知曲线M的参数方程为⎩⎪⎨⎪⎧x =1+cos φ,y =1+sin φ(φ为参数),l 1,l 2为过点O 的两条直线,l 1交M 于A ,B 两点,l 2交M 于C ,D 两点,且l 1的倾斜角为α,∠AOC =π6.(1)求l 1和M 的极坐标方程;(2)当α∈(0,π6]时,求点O 到A ,B ,C ,D 四点的距离之和的最大值.2.已知曲线C 1的参数方程为⎩⎨⎧x =-t ,y =3t(t 为参数),A 为当t =1时曲线C 1上的点;B 为当t =-1时曲线C 1上的点.以原点O 为极点,以x 轴正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为ρ=64+5sin 2θ.(1)求A ,B 的极坐标;(2)设M 是曲线C 2上的动点,求|MA |2+|MB |2的最大值.3.在平面直角坐标系xOy 中,已知曲线C 1的参数方程为⎩⎪⎨⎪⎧x =cos t ,y =1+sin t (t 为参数),曲线C 2的直角坐标方程为x 2+(y -2)2=4.以平面直角坐标系的原点O 为极点,x 轴的正半轴为极轴建立极坐标系,射线l 的极坐标方程为θ=α,0<α<π.(1)求曲线C 1,C 2的极坐标方程;(2)设A ,B 分别为射线l 与曲线C 1,C 2除原点之外的交点,求|AB |的最大值.4.在以原点O 为极点,x 轴的非负半轴为极轴的极坐标系中,曲线C 1的极坐标方程为ρ=4cos θ,曲线C 2的极坐标方程为ρcos 2θ=sin θ.(1)求曲线C 2的直角坐标方程;(2)过原点且倾斜角为α⎝⎛⎭⎫π6<α≤π4的射线l 与曲线C 1,C 2分别相交于A ,B 两点(A ,B 异于原点),求|OA |·|OB |的取值范围.5.在直角坐标系xOy 中,直线l 的参数方程为⎩⎨⎧x =1+12t ,y =32t(t 为参数).在以坐标原点O 为极点,x 轴的正半轴为极轴的极坐标系中,曲线C 的极坐标方程为ρ=22cos ⎝⎛⎭⎫π4+θ.(1)求直线l 的普通方程和曲线C 的直角坐标方程; (2)设直线l 与曲线C 相交于M ,N 两点,求|MN |的值.6.在平面直角坐标系xOy 中,直线l 过点(1,0),倾斜角为α,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程是ρ=8cos θ1-cos 2θ.(1)写出直线l 的参数方程和曲线C 的直角坐标方程;(2)若α=π4,设直线l 与曲线C 交于A ,B 两点,求△AOB 的面积.7.在平面直角坐标系xOy 中,圆C 的参数方程为⎩⎨⎧x =-5+2cos t ,y =3+2sin t(t 为参数),在以原点O 为极点,x轴的非负半轴为极轴建立的极坐标系中,直线l 的极坐标方程为ρcos ⎝⎛⎭⎫θ+π4=- 2. (1)求圆C 的普通方程和直线l 的直角坐标方程;(2)设直线l 与x 轴,y 轴分别交于A ,B 两点,点P 是圆C 上任意一点,求A ,B 两点的极坐标和△P AB 面积的最小值.8.在平面直角坐标系xOy 中,曲线C 1的参数方程为⎩⎪⎨⎪⎧x =1+2cos β,y =2sin β(β为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C 2和C 3的极坐标方程分别为θ=α(ρ∈R )和θ=π2+α(ρ∈R ),其中0≤α<π2.(1)求曲线C 1的普通方程和曲线C 2的参数方程;(2)设曲线C 2与曲线C 1交于A ,B 两点,曲线C 3与曲线C 1交于C ,D 两点,求四边形ACBD 的面积的最大值和最小值.9.已知直线L 的参数方程为⎩⎪⎨⎪⎧x =2+ty =2-2t (t 为参数),以原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为ρ=21+3cos 2θ.(1)直接写出直线L 的极坐标方程和曲线C 的直角坐标方程;(2)过曲线C 上任意一点P 作与直线L 夹角为π3的直线l ,设直线l 与直线L 的交点为A ,求|P A |的最大值.10.在直角坐标系xOy 中,圆C 的方程为(x +6)2+y 2=25.(1)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求C 的极坐标方程;(2)直线l 的参数方程是⎩⎪⎨⎪⎧x =t cos α,y =t si nα,(t 为参数),l 与C 交于A ,B 两点,|AB|=10,求l 的斜率.详解答案极坐标系与参数方程一、平面直角坐标系中的伸缩变换1.[解析] (1)设其伸缩变换为φ:⎩⎪⎨⎪⎧x ′=λx (λ>0),y ′=μy (μ>0),则λx -μy =2,2λx -2μy =4,于是⎩⎪⎨⎪⎧2λ=2,-2μ=-1,解得⎩⎪⎨⎪⎧ λ=1,μ=12.所以φ:⎩⎪⎨⎪⎧x ′=x ,y ′=12y .故选C . 2.解:由⎩⎪⎨⎪⎧x ′=12x ,y ′=y得到⎩⎪⎨⎪⎧x =2x ′,y =y ′.①将①代入x 24+y 2=1,得4x ′24+y ′2=1,即x ′2+y ′2=1.因此椭圆x 24+y 2=1经伸缩变换后得到的曲线方程是x 2+y 2=1.二、极坐标与直角坐标的互化1.[解析] 由ρ=-2sin θ,得ρ2=-2ρsin θ,化为普通方程x 2+(y +1)2=1,其圆心坐标为(0,-1),所以其极坐标为(1,-π2),故应选B .2.[解析] 如图,设直线l 上任意一点为C (ρ,θ),由图可知OP OC =cos(π-θ)=1ρ,ρ=-1cos θ,故选C .3.[解析] ρ(3cos θ-sin θ)=2可化为直角坐标方程3x -y =2,即y =3x -2.ρ=4sin θ可化为x 2+y 2=4y ,把y =3x -2代入x 2+y 2=4y ,得4x 2-83x +12=0,即x 2-23x +3=0,所以x =3,y =1,所以直线与圆的交点坐标为(3,1),化为极坐标为(2,π6).故选A .4.[解析] 因为x 2+y 2=ρ2,x =ρcos θ,所以代入直角坐标方程并整理,得ρ2-2ρcos θ=0,所以ρ-2cos θ=0,即极坐标方程为ρ=2cos θ.5.[解析] 本题主要考查极坐标方程与直角坐标方程的互化. 由⎩⎪⎨⎪⎧ρcos θ=x ,ρsin θ=y ,ρ2=x 2+y2可将直线ρcos θ+ρsin θ=a 化为x +y -a =0,将ρ=2cos θ,即ρ2=2ρcos θ化为x 2+y 2=2x ,整理成标准方程为(x -1)2+y 2=1.又∵直线与圆相切,∴圆心(1,0)到直线x +y -a =0的距离d =|1-a |2=1,解得a =1±2,∵a >0,∴a =1+ 2.6.[解析] 由2ρsin(θ-π4)=2⇒y -x =1⇒x -y +1=0,而点A 对应的直角坐标为A (2,-2),故点A (2,-2)到直线x -y +1=0距离为|2+2+1|2=522.7.解析:将方程ρ=5cos θ-53sin θ两边都乘以ρ, 得ρ2=5ρcos θ-53ρsin θ,化成直角坐标方程为x 2+y 2-5x +53y =0. 圆心坐标为⎝⎛⎭⎫52,-532,化成极坐标为⎝⎛⎭⎫5,5π3. 答案:⎝⎛⎭⎫5,5π3(答案不唯一) 8.解析:设圆心到直线θ=π3(θ∈R )的距离为d ,因为圆的半径为2,d =2·sin π6=1.答案:19.答案 6解析 解法一:(数形结合)在极坐标系中,A ,B 两点如图所示, |AB |=|OA |+|OB |=6.解法二:∵A ⎝⎛⎭⎫2,-π3,B ⎝⎛⎭⎫4,2π3的直角坐标为A (1,-3), B (-2,23),∴|AB |=(-2-1)2+(23+3)2=6.10.答案 ⎝⎛⎭⎫1,π6 解析 将θ=π6代入ρsin ⎝⎛⎭⎫θ+π6=32,得ρsin π3=32,所以ρ=1,所以曲线C 1与曲线C 2的交点坐标为⎝⎛⎭⎫1,π6.三、极坐标方程的综合应用1.解:(1)圆O :ρ=cos θ+sin θ,即ρ2=ρcos θ+ρsin θ, 圆O 的直角坐标方程为x 2+y 2=x +y , 即x 2+y 2-x -y =0, 直线l :ρsin ⎝⎛⎭⎫θ-π4=22, 即ρsin θ-ρcos θ=1,则直线l 的直角坐标方程为y -x =1,即x -y +1=0.(2)由⎩⎪⎨⎪⎧ x 2+y 2-x -y =0,x -y +1=0,得⎩⎪⎨⎪⎧x =0,y =1,故直线l 与圆O 公共点的一个极坐标为⎝⎛⎭⎫1,π2. 2.解 (1)曲线C 1的参数方程为⎩⎪⎨⎪⎧x =cos θ,y =1+sin θ(θ为参数),其普通方程为x 2+(y -1)2=1,极坐标方程为ρ=2sin θ.因为直线l 的直角坐标方程为y =33x , 故直线l 的极坐标方程为θ=π6(ρ∈R ).(2)曲线C 1的极坐标方程为ρ=2sin θ, 直线l 的极坐标方程为θ=π6,将θ=π6代入C 1的极坐标方程得ρ1=1,将θ=π6代入C 2的极坐标方程得ρ2=4,∴|ρ2-ρ1|=3. 3.解 (1)∵ρ=x 2+y 2,ρsin θ=y ,∴ρ=21-sin θ化为ρ-ρsin θ=2,∴曲线的直角坐标方程为x 2=4y +4. (2)设直线l 的极坐标方程为θ=θ0(ρ∈R ), 根据题意21-sin θ0=3·21-sin (θ0+π),解得θ0=π6或θ0=5π6,∴直线l 的极坐标方程为θ=π6(ρ∈R )或θ=5π6(ρ∈R ).4.[解析] (1)∵曲线C 的参数方程为⎩⎪⎨⎪⎧x =2+5cos α,y =1+5sin α(α为参数),∴曲线C 的普通方程为(x -2)2+(y-1)2=5.将⎩⎪⎨⎪⎧x =ρcos θ,y =ρsin θ代入并化简得ρ=4cos θ+2sin θ, ∴曲线C 的极坐标方程为ρ=4cos θ+2sin θ. (2)在极坐标系中,曲线C :ρ=4cos θ+2sin θ, ∴由⎩⎪⎨⎪⎧θ=π6,ρ=4cos θ+2sin θ,得|OA |=23+1. 同理可得|OB |=2+ 3. 又∠AOB =π6,∴S △AOB =12|OA |·|OB |sin ∠AOB =8+534.∴△AOB 的面积为8+534.5.[解析] (1)圆C :⎩⎪⎨⎪⎧x =2cos θ,y =2sin θ(θ为参数)的直角坐标方程为x 2+y 2=4,∴圆C 的极坐标方程为ρ=2.直线l 的极坐标方程ρ=4sin θ+cos θ.(2)设点P ,Q ,R 的极坐标分别为(ρ1,θ),(ρ,θ),(ρ2,θ), ∵ρ1=4sin θ+cos θ,ρ2=2,又|OP |2=|OR |·|OQ |,即ρ21=ρ·ρ2, ∴ρ=ρ21ρ2=16(sin θ+cos θ)2×12,∴ρ=81+sin2θ.∴点Q 的轨迹的极坐标方程为ρ=81+sin2θ.6.解:(1)消去参数t 得到C 1的普通方程:x 2+(y -1)2=a 2.C 1是以(0,1)为圆心,a 为半径的圆. 将x =ρcos θ,y =ρsin θ代入C 1的普通方程中,得到C 1的极坐标方程为ρ2-2ρsin θ+1-a 2=0.(2)曲线C 1,C 2的公共点的极坐标满足方程组⎩⎪⎨⎪⎧ρ2-2ρsin θ+1-a 2=0,ρ=4cos θ.若ρ≠0,由方程组得16cos 2θ-8sin θcos θ+1-a 2=0,由已知tan θ=2,可得16cos 2θ-8sin θcos θ=0,从而1-a 2=0, 解得a =-1(舍去)或a =1.a =1时,极点也为C 1,C 2的公共点,在C 3上.所以a =1. 7.解:(1)C 1的普通方程为x 22+y 2=1,C 1的极坐标方程为ρ2cos 2θ+2ρ2sin 2θ-2=0, C 2的极坐标方程为ρ=2sin θ.(2)联立θ=α(ρ≥0)与C 1的极坐标方程得|OA |2=21+sin 2α,联立θ=α(ρ≥0)与C 2的极坐标方程得|OB |2=4sin 2α, 则|OA |2+|OB |2=21+sin 2α+4sin 2α =21+sin 2α+4(1+sin 2α)-4. 令t =1+sin 2α,则|OA |2+|OB |2=2t +4t -4,当0<α<π2时,t ∈(1,2).设f (t )=2t +4t -4,易得f (t )在(1,2)上单调递增,∴2<|OA |2+|OB |2<5,故|OA |2+|OB |2的取值范围是(2,5).8.解:(1)曲线C 2的直角坐标方程为x 2+y 2-2y =0,曲线C 3的直角坐标方程为x 2+y 2-23x =0.联立⎩⎨⎧x 2+y 2-2y =0,x 2+y 2-23x =0,解得⎩⎪⎨⎪⎧x =0,y =0或⎩⎨⎧x =32,y =32.所以C 2与C 3交点的直角坐标为(0,0)和⎝⎛⎭⎫32,32.(2)曲线C 1的极坐标方程为θ=α(ρ∈R ,ρ≠0),其中0≤α<π. 因此A 的极坐标为(2sin α,α),B 的极坐标为(23cos α,α).所以|AB |=|2sin α-23cos α|=4⎪⎪⎪⎪sin ⎝⎛⎭⎫α-π3. 当α=5π6时,|AB |取得最大值,最大值为4.四、直角坐标方程与参数方程的互化1.解析:依题意,消去参数可得x -2=y -1,即x -y -1=0. 答案:x -y -1=02.答案 45解析 将⎩⎪⎨⎪⎧x =5cos θ,y =3sin θ消去参数θ,得椭圆x 225+y 29=1.3.答案 y =2-2x 2(-1≤x ≤1)解析 由⎩⎪⎨⎪⎧x =sin θ,y =cos2θ+1(θ为参数)消去参数θ,得y =2-2x 2(-1≤x ≤1).4.解 将⎩⎪⎨⎪⎧x =2+t ,y =-1-t 消去参数t 得直线x +y -1=0;将⎩⎪⎨⎪⎧x =3cos α,y =3sin α消去参数α,得圆x 2+y 2=9. 又圆心(0,0)到直线x +y -1=0的距离d =22<3. 因此直线与圆相交,故直线与曲线有2个交点.条件探究 解 由(sin θ+cos θ)2=1+sin2θ=2-(1-sin2θ),得 y 2=2-x .又因为x =1-sin2θ∈[0,2],所以所求普通方程为y 2=2-x ,x ∈[0,2].解方程组⎩⎪⎨⎪⎧x +y -1=0,y 2=2-x ,得⎩⎪⎨⎪⎧x =1+52,y =1-52或⎩⎪⎨⎪⎧x =1-52,y =1+52,又因为x ∈[0,2],所以交点坐标为⎝⎛⎭⎪⎫1+52,1-52.5.解 将直线l 的参数方程化为普通方程,得4x -3y =4,将曲线C 的参数方程化为普通方程,得y 2=4x ,联立方程⎩⎪⎨⎪⎧ 4x -3y =4,y 2=4x ,解得⎩⎪⎨⎪⎧x =4,y =4或⎩⎪⎨⎪⎧x =14,y =-1.所以A (4,4),B ⎝⎛⎭⎫14,-1或A ⎝⎛⎭⎫14,-1,B (4,4). 所以AB =⎝⎛⎭⎫4-142+(4+1)2=254. 6.解:(1)椭圆C 的参数方程为⎩⎨⎧x =2cos θ,y =3sin θ(θ为参数),直线l 的普通方程为x -3y +9=0.直线l 的标准参数方程为)(2132233为参数t ty t x ⎪⎪⎩⎪⎪⎨⎧+=+-= 五、直线参数方程的应用1.解:(1)由直线l 过点A 可得2cos ⎝⎛⎭⎫π4-π4=a ,故a = 2. 则易得直线l 的直角坐标方程为x +y -2=0,根据点到直线的距离公式可得曲线C 1上的点到直线l 的距离 d =|2cos α+3sin α-2|2=|7sin (α+φ)-2|2,其中sin φ=277,cos φ=217,∴d max =7+22=14+222.即曲线C 1上的点到直线l 的距离的最大值为14+222. (2)由(1)知直线l 的倾斜角为3π4, 则直线l 1的参数方程为⎩⎨⎧x =-1+t cos 3π4,y =1+t sin 3π4(t 为参数),又易知曲线C 1的普通方程为x 24+y 23=1,把直线l 1的参数方程代入曲线C 1的普通方程可得72t 2+72t -5=0,∴t 1t 2=-107,根据参数t 的几何意义可知|BM |·|BN |=|t 1t 2|=107. 2.[解] (1)由曲线C :⎩⎪⎨⎪⎧x =1cos θ,y =tan θ(θ为参数),可得曲线C 的普通方程是x 2-y 2=1.当α=π3时,直线l 的参数方程为⎩⎨⎧x =3+12t ,y =32t (t 为参数),代入曲线C 的普通方程,得t 2-6t -16=0,得t 1+t 2=6,所以线段AB 的中点对应的t =t 1+t 22=3,故线段AB 的中点的直角坐标为⎝⎛⎭⎫92,332.(2)将直线l 的参数方程代入曲线C 的普通方程,化简得(cos 2α-sin 2α)t 2+6cosαt +8=0, 则|P A |·|PB |=|t 1t 2|=⎪⎪⎪⎪8cos 2α-sin 2α=⎪⎪⎪⎪⎪⎪8(1+tan 2α)1-tan 2α,由已知得tanα=2,故|P A |·|PB |=403. 3.[解](1)由⎩⎨⎧x =3-22t ,y =5+22t ,两式相加得直线l 的普通方程为x +y -3-5=0.又由ρ=25s inθ,得ρ2=25ρs inθ,所以圆C 的直角坐标方程为x 2+y 2-25y =0,即x 2+(y -5)2=5.(2)把直线l 的参数方程代入圆C 的直角坐标方程,得⎝⎛⎭⎫3-22t 2+⎝⎛⎭⎫22t 2=5,即t 2-32t +4=0.由于Δ=(32)2-4×4=2>0,故可设t 1,t 2是上述方程的两实数根,所以t 1+t 2=32,t 1·t 2=4.又直线l 过点P (3,5),A ,B 两点对应的参数分别为t 1,t 2,所以|P A|+|P B|=|t 1|+|t 2|=t 1+t 2=3 2.4.[解析] (1)将曲线C 的极坐标方程ρcos 2θ=4sin θ,化为直角坐标方程,得x 2=4y . ∵M (x ,y )为曲线C 上任意一点,∴x +y =x +14x 2=14(x +2)2-1,∴x +y 的取值范围是[-1,+∞).(2)将⎩⎪⎨⎪⎧x =t cos α,y =1+t sin α代入x 2=4y ,得t 2cos 2α-4t sin α-4=0.∴Δ=16sin 2α+16cos 2α=16>0,设方程t 2cos 2α-4t sin α-4=0的两个根为t 1,t 2,则t 1+t 2=4sin αcos 2α,t 1t 2=-4cos 2α,∴|AB |=|t 1-t 2|=(t 1+t 2)2-4t 1t 2=4cos 2α≥4,当且仅当α=0时,取等号.故当α=0时,|AB |取得最小值4.5.解:(1)∵曲线C 的方程为2a sin θ-ρcos 2θ=0(a >0), ∴2aρsin θ-ρ2cos 2θ=0,即x 2=2ay (a >0).(2)将⎩⎨⎧x =12t ,y =-1+32t 代入x 2=2ay ,得t 2-43at +8a =0,得⎩⎨⎧Δ=(-43a )2-4×8a >0,①t 1+t 2=43a ,t 1t 2=8a .∵a >0,∴解①得a >23.∵|PM |,|MN |,|PN |成等比数列, ∴|MN |2=|PM |·|PN |,即|t 1-t 2|2=t 1t 2, ∴(t 1+t 2)2-4t 1t 2=t 1t 2,即(43a )2-40a =0, 解得a =0或a =56.∵a >23,∴a =56.六、极坐标与参数方程的综合应用1.[解析] (1)依题意,直线l 1的极坐标方程为θ=α(ρ∈R ).由⎩⎪⎨⎪⎧x =1+cos φ,y =1+sin φ消去φ,得(x -1)2+(y -1)2=1. 将x =ρcos θ,y =ρsin θ代入上式,得ρ2-2ρcos θ-2ρsin θ+1=0. 故M 的极坐标方程为ρ2-2ρcos θ-2ρsin θ+1=0.(2)依题意可设A (ρ1,α),B (ρ2,α),C (ρ3,α+π6),D (ρ4,α+π6),且ρ1,ρ2,ρ3,ρ4均为正数.将θ=α代入ρ2-2ρcos θ-2ρsin θ+1=0,得ρ2-2(cos α+sin α)ρ+1=0, 所以ρ1+ρ2=2(cos α+sin α),同理可得,ρ3+ρ4=2[cos(α+π6)+sin(α+π6)],所以点O 到A ,B ,C ,D 四点的距离之和为ρ1+ρ2+ρ3+ρ4=2(cos α+sin α)+2[cos(α+π6)+sin(α+π6)]=(1+3)sin α+(3+3)cos α=2(1+3)sin(α+π3).因为α∈(0,π6], 所以当sin(α+π3)=1,即α=π6时,ρ1+ρ2+ρ3+ρ4取得最大值2+2 3. 所以点O 到A ,B ,C ,D 四点距离之和的最大值为2+2 3.2.[解] (1)当t =1时,⎩⎨⎧x =-1,y =3, 即点A 的直角坐标为(-1,3); 当t =-1时,⎩⎨⎧x =1,y =-3,即点B 的直角坐标为(1,-3). ∴点A 的极坐标为⎝⎛⎭⎫2,2π3,点B 的极坐标为⎝⎛⎭⎫2,5π3. (2)由ρ=64+5sin 2θ,得ρ2(4+5sin 2θ)=36, ∴曲线C 2的直角坐标方程为x 29+y 24=1. 设曲线C 2上的动点M 的坐标为(3cosα,2sinα),则|MA |2+|MB |2=10cos 2α+16≤26,当且仅当cosα=±1时等号成立,∴|MA |2+|MB |2的最大值为26.3.解:(1)由曲线C 1的参数方程⎩⎪⎨⎪⎧x =cos t ,y =1+sin t (t 为参数),消去参数t 得,x 2+(y -1)2=1,即 x 2+y 2-2y =0,∴曲线C 1的极坐标方程为ρ=2sin θ.由曲线C 2的直角坐标方程x 2+(y -2)2=4,得x 2+y 2-4y =0,∴曲线C 2的极坐标方程为ρ=4sin θ.(2)联立⎩⎪⎨⎪⎧ θ=α,ρ=2sin θ,得A (2sin α,α),∴|OA |=2sin α, 联立⎩⎪⎨⎪⎧θ=α,ρ=4sin θ,得B (4sin α,α),∴|OB |=4sin α, ∴|AB |=|OB |-|OA |=2sin α, ∵0<α<π,∴当α=π2时,|AB |有最大值,最大值为2. 4.解:(1)由曲线C 2的极坐标方程为ρcos 2θ=sin θ,两边同乘以ρ,得ρ2cos 2θ=ρsin θ,故曲线C 2的直角坐标方程为x 2=y .(2)射线l 的极坐标方程为θ=α,π6<α≤π4, 把射线l 的极坐标方程代入曲线C 1的极坐标方程得|OA |=ρ=4cos α,把射线l 的极坐标方程代入曲线C 2的极坐标方程得|OB |=ρ=sin αcos 2α, ∴|OA |·|OB |=4cos α·sin αcos 2α=4tan α. ∵π6<α≤π4,∴|OA |·|OB |的取值范围是⎝⎛⎦⎤433,4. 5.解:(1)易得直线l 的普通方程为3x -y -3=0.∵ρ=22cos ⎝⎛⎭⎫π4+θ=2(cos θ-sin θ),∴ρ2=2(ρcos θ-ρsin θ), ∴x 2+y 2=2(x -y ),即(x -1)2+(y +1)2=2,∴曲线C 的直角坐标方程为(x -1)2+(y +1)2=2.(2)将直线l 的参数方程代入曲线C 的直角坐标方程,得t 2+3t -1=0,此方程的两根分别为直线l 与曲线C 的交点M ,N 对应的参数t M ,t N .∵t M +t N =-3,t M t N =-1,∴|MN |=|t M -t N |=(t M +t N )2-4t M t N =7.6.解:(1)直线l 的参数方程为⎩⎪⎨⎪⎧x =1+t cos α,y =t sin α(t 为参数). ∵ρ=8cos θ1-cos 2θ,∴ρsin 2θ=8cos θ,∴ρ2sin 2θ=8ρcos θ, 即曲线C 的直角坐标方程为y 2=8x .(2)解法一:当α=π4时,直线l 的参数方程为⎩⎨⎧ x =1+22t ,y =22t(t 为参数),代入y 2=8x , 可得t 2-82t -16=0,设A ,B 两点对应的参数分别为t 1,t 2,则t 1+t 2=82,t 1t 2=-16,∴|AB |=|t 1-t 2|=(t 1+t 2)2-4t 1t 2=8 3.又点O 到直线AB 的距离d =1×sin π4=22, ∴S △AOB =12|AB |×d =12×83×22=2 6. 解法二:当α=π4时,直线l :y =x -1, 设A (x 1,y 1),B (x 2,y 2),M (1,0),由⎩⎪⎨⎪⎧y 2=8x ,y =x -1得,y 2-8y -8=0. 由根与系数的关系,得⎩⎪⎨⎪⎧y 1+y 2=8,y 1y 2=-8, 所以S △AOB =12|OM ||y 1-y 2|=12×1×(y 1+y 2)2-4y 1y 2 =12×82-4×(-8) =2 6.7.解:(1)由⎩⎨⎧x =-5+2cos t ,y =3+2sin t ,消去参数t , 得(x +5)2+(y -3)2=2,所以圆C 的普通方程为(x +5)2+(y -3)2=2.由ρcos ⎝⎛⎭⎫θ+π4=-2,得ρcos θ-ρsin θ=-2, 所以直线l 的直角坐标方程为x -y +2=0.(2)直线l 与x 轴,y 轴的交点分别为A (-2,0),B (0,2),化为极坐标为A (2,π),B ⎝⎛⎭⎫2,π2, 设点P 的坐标为(-5+2cos t,3+2sin t ),则点P 到直线l 的距离为d =|-5+2cos t -3-2sin t +2|2= ⎪⎪⎪⎪-6+2cos ⎝⎛⎭⎫t +π42. 所以d min =42=22,又|AB |=2 2. 所以△P AB 面积的最小值是S =12×22×22=4. 8.解:(1)曲线C 1的普通方程为(x -1)2+y 2=4,由曲线C 2的极坐标方程为θ=α(ρ∈R )可知,曲线C 2是经过原点且倾斜角为α的直线,所以曲线C 2的参数方程为⎩⎪⎨⎪⎧ x =t cos α,y =t sin α(t 为参数). (2)解法一 把⎩⎪⎨⎪⎧x =t cos α,y =t sin α代入(x -1)2+y 2=4, 得t 2-2t cos α-3=0,设方程t 2-2t cos α-3=0的两根分别为t 1,t 2,则t 1+t 2=2cos α,t 1t 2=-3,|AB |=|t 1-t 2|=(t 1+t 2)2-4t 1t 2=2cos 2α+3,同理,由曲线C 3的极坐标方程为θ=π2+α(ρ∈R ), 可得|CD |=2 cos 2⎝⎛⎭⎫π2+α+3=2 sin 2α+3,又易知AB ⊥CD ,所以四边形ACBD 的面积S =12|AB ||CD |=2cos 2α+3sin 2α+3=212+14sin 22α,∵0≤α<π2, ∴当2α=π2,即α=π4时,四边形ACBD 的面积取得最大值,最大值为7; 当2α=0,即α=0时,四边形ACBD 的面积取得最小值,最小值为4 3.解法二 将x =ρcos θ,y =ρsin θ代入(x -1)2+y 2=4,整理得曲线C 1的极坐标方程为ρ2-2ρcos θ-3=0,把θ=α代入,得ρ2-2ρcos α-3=0,ρ1+ρ2=2cos α,ρ1ρ2=-3,|AB |=|ρ1-ρ2|=(ρ1+ρ2)2-4ρ1ρ2=2cos 2α+3,同理,把θ=π2+α代入, 得|CD |=2cos 2⎝⎛⎭⎫π2+α+3=2sin 2α+3, 由曲线C 2和C 3的极坐标方程可知AB ⊥CD , 所以四边形ACBD 的面积S =12|AB ||CD |=2cos 2α+3·sin 2α+3=2 12+14sin 22α, ∵0≤α<π2,∴当2α=π2, 即α=π4时,四边形ACBD 的面积取得最大值,最大值为7; 当2α=0,即α=0时,四边形ACBD 的面积取得最小值,最小值为4 3.9.[解析] (1)由⎩⎪⎨⎪⎧x =2+t y =2-2t(t 为参数),得l 1的普通方程为2x +y -6=0,令x =ρcos θ,y =ρsin θ,得直线l 1的极坐标方程为2ρcos θ+ρsin θ-6=0,由曲线C 的极坐标方程,知ρ2+3ρ2cos 2θ=4,所以曲线C的直角坐标方程为x 2+y 24=1. (2)由(1)知直线l 1的普通方程为2x +y -6=0,设曲线C 上任意一点P (cos α,2sin α),点P 到直线l 1的距离d =|2cos α+2sin α-6|5. 由题意得|P A |=d sin60°=415⎪⎪⎪⎪2sin (α+π4)-315, ∴当sin(α+π4)=-1时,|P A |取得最大值,最大值为415(3+2)15. 10.[解] (1)由x =ρcos θ,y =ρs inθ可得圆C 的极坐标方程ρ2+12ρcos θ+11=0.(2)解法一:由直线l 的参数方程⎩⎪⎨⎪⎧ x =t cos α,y =t si nα(t 为参数) 可知直线l 的普通方程为y =kx ,其中k 为直线l 的斜率,则点C(-6,0)与直线l 的距离d =|-6k |k 2+1. 因为|AB|=10,所以⎝⎛⎭⎫1022+36k 2k 2+1=25,故直线l 的斜率为153或-153. 解法二:在(1)中建立的极坐标系中,直线l 的极坐标方程为θ=α(ρ∈R ). 设A ,B 所对应的极径分别为ρ1,ρ2,将l 的极坐标方程代入C 的极坐标方程得ρ2+12ρcos α+11=0. 于是ρ1+ρ2=-12cos α,ρ1ρ2=11.|AB|=|ρ1-ρ2|=(ρ1+ρ2)2-4ρ1ρ2=144cos 2α-44.由|AB|=10得cos 2α=38,t anα=±153. 所以l 的斜率为153或-153.。
高考数学极坐标与参数方程题型归纳

(3)P为曲线C2上任意一点,求点P到直线l的距离的最值及此时P的直角坐标.
7.在坐标系xOy中,曲线C1的参数方程为 (α为参数),以坐标原点为极点,以x轴的正半轴为极轴,,建立极坐标系,曲线C2的极坐标方程为ρsin =2 .
极坐标系与参数方程
题型一与圆有关的问题
1.已知曲线C1的参数方程为 ( 为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为 .(Ⅰ)把C1的参数方程化为极坐标方程;(Ⅱ)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)。
2.在直角坐标系xOy中,以坐标原点为极点,x轴为极轴建立极坐标系,半圆C的极坐标方程为ρ=2cosθ,θ∈ .(1)求C的参数方程.(2)设点D在C上,C在D处的切线与直线l:y= x+2垂直,根据(1)中你得到的参数方程,确定D的坐标.
题型二 根据椭圆参数方程求最值
6.曲线C1的参数方程为 (θ为参数),将曲线C1上所有点的横坐标伸长为原来的2倍,纵坐标伸长为原来的 倍,得到曲线C2.以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ(cosθ-2sinθ)=6.
(1)求曲线C2和直线l的普通方程.
9.以平面直角坐标系的原点 为极点, 轴的正半轴为极轴建立极坐标系,已知点 的直角坐标为 ,若直线l的极坐标方程为 ,曲线 的参数方程是 ,( 为参数).
(1)求直线l的直角坐标方程和曲线 的普通方程;
(2)设直线l与曲线 交于 两点,求 .
10.在直角坐标系中,以原点为极点, 轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线 的极坐标方程为 ,曲线 的极坐标方程为 .
极坐标与参数方程经典题型(附含详细解答)

专题:极坐标与参数方程1、已知在直角坐标系xOy 中,曲线C 的参数方程为14cos 24sin x y θθ=+⎧⎨=+⎩(θ为参数),直线l 经过定点(3,5)P ,倾斜角为3π. (1)写出直线l 的参数方程和曲线C 的标准方程;(2)设直线l 与曲线C 相交于A ,B 两点,求||||PA PB 的值.2、在直角坐标系中,以坐标原点为极点,轴的正半轴为极轴建立极坐标系,已知曲线2:sin 2cos C ρθθ=,过点(2,1)P -的直线2cos 45:1sin 45x t l y t ⎧=+⎪⎨=-+⎪⎩(t 为参数)与曲线C 交于,M N 两点.(1)求曲线C 的直角坐标方程和直线l 的普通方程;(2)求22||||PM PN +的值.3、在平面直角坐标系xOy 中,已知曲线:23cos 3sin x y αα⎧=+⎪⎨=⎪⎩(α为参数),以平面直角坐标系xOy 的原点O 为极点,x 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l :(cos sin )6ρθθ-=.(1)求曲线C 上点P 到直线l 距离的最大值;(2)与直线l 平行的直线1l 交C 于,A B 两点,若||2AB =,求1l 的方程.4、在平面直角坐标系xOy 中,以原点为极点,轴的正半轴为极轴,建立极坐标系,曲线1C 的参数方程为22cos 2sin x y θθ⎧=⎪⎨=⎪⎩(为参数),曲线 2C 的极坐标方程为cos 2sin 40ρθρθ--=.(1)求曲线1C 的普通方程和曲线 2C 的直角坐标方程;(2)设P 为曲线1C 上一点,Q 为曲线2C 上一点,求||PQ 的最小值.5.在平面直角坐标系xOy 中,曲线1C 的参数方程为2cos sin x y ϕϕ=⎧⎨=⎩(ϕ为参数),在以原点为极点,轴的正半轴为极轴,建立的极坐标系中,曲线2C 是圆心为3,2π⎛⎫⎪⎝⎭,半径为1的圆.(1)求曲线1C 的普通方程,2C 的直角坐标方程;(2)设M 为曲线1C 上的点,N 为曲线2C 上的点,求||MN 的取值范围.6. 在平面直角坐标系xOy 中,曲线1C 的参数方程为2cos sin x y ϕϕ⎧=⎪⎨=⎪⎩(ϕ为参数),曲线2C :2220x y y +-=,以原点为极点,轴的正半轴为极轴,建立极坐标系,射线():0l θαρ=≥与曲线1C ,2C 分别交于,A B (均异于原点O ).(1)求曲线1C ,2C 的极坐标方程; (2)当02πα<<时,求22||||OA OB +的取值范围.7. 在平面直角坐标系xOy 中,曲线1C 过点(,1)P a ,其参数方程为212x a ty t ⎧=+⎪⎨=+⎪⎩(t 为参数,a R ∈),以原点为极点,轴的正半轴为极轴,建立极坐标系,曲线2C 的极坐标方程为2cos 4cos 0ρθθρ+-=.(1)求曲线1C 的普通方程和2C 的直角坐标方程;(2)已知曲线1C 与2C 交于,A B 两点,且||2||PA PB =,求实数a 的值.8. 在平面直角坐标系xOy 中,以原点为极点,轴的正半轴为极轴,建立极坐标系,直线l 的极坐标方程为(sin 3cos )43ρθθ+=,若射线6πθ=,3πθ=,分别与l 交于,A B两点.(1)求||AB ;(2)设点P 是曲线2219y x +=上的动点,求ABP ∆面积的最大值.极坐标与参数方程——练习1.在平面直角坐标系xOy 中,已知直线l 的参数方程为⎩⎪⎨⎪⎧x =1+12t ,y =32t ,(t 为参数),椭圆C 的参数方程为⎩⎪⎨⎪⎧x =cos θ,y =2sin θ(θ为参数).设直线l 与椭圆C 相交于A,B 两点,求线段AB 的长.2.在直角坐标系xOy 中,曲线C 1:⎩⎪⎨⎪⎧x =tcos α,y =tsin α(t 为参数,t≠0),其中0≤α<π,在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2:ρ=2sin θ,C 3:ρ=23cos θ.(1)求C 2与C 3交点的直角坐标;(2)若C 1与C 2相交于点A,C 1与C 3相交于点B ,求|AB |的最大值.3.在直角坐标系xOy 中,直线l 的参数方程为⎩⎪⎨⎪⎧x =3+12t ,y =32t(t 为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,⊙C 的极坐标方程为ρ=23sin θ.(1)写出⊙C 的直角坐标方程;(2)P 为直线l 上一动点,当P 到圆心C 的距离最小时,求P 的直角坐标.4.在平面直角坐标系xOy 中,曲线C 的方程为x 2-2x +y 2=0,以原点为极点,x 轴正半轴为极轴建立极坐标系,直线l 的极坐标方程为θ=π4(ρ∈R ).(1)写出C 的极坐标方程,并求l 与C 的交点M,N 的极坐标; (2)设P 是椭圆x 23+y 2=1上的动点,求△PMN 面积的最大值.5.直线l 的参数方程为⎩⎪⎨⎪⎧x =1+12t ,y =32t(t 为参数),曲线C 的极坐标方程为(1+sin 2θ)ρ2=2. (1)写出直线l 的普通方程与曲线C 的直角坐标方程.(2)设直线l 与曲线C 相交于A ,B 两点,若点P 为(1,0),求1|PA |2+1|PB |2的值.6. 在直角坐标系xoy 中,直线l 的参数方程为325:45x t C y t ⎧=-+⎪⎪⎨⎪=⎪⎩(t 为参数),以原点O 为极点,x 轴正半轴为极轴建立极坐标系,圆C 的极坐标方程为sin a ρθ=. (1)若2a =,求圆C 的直角坐标方程与直线 l 的普通方程; (2)设直线l 截圆C 的弦长等于圆Ca 的值.7. 在直角坐标系xOy 中,直线1C :y =,曲线2C 的参数方程是cos 2sin x y ϕϕ⎧=⎪⎨=-+⎪⎩(ϕ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系.(1)求1C 的极坐标方程和2C 的普通方程; (2)把1C 绕坐标原点沿顺时针方向旋转3π得到直线3C ,3C 与2C 交于A ,B 两点,求||AB .8.将圆x 2+y 2=1上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C. (1)写出C 的参数方程;(2)设直线l :2x +y -2=0与C 的交点为P 1,P 2,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求过线段P 1P 2的中点且与l 垂直的直线的极坐标方程.极坐标与参数方程参考答案1.【解答】解:(1)∵曲线C的参数方程为(θ为参数),消去参数θ,得曲线C的普通方程:(x﹣1)2+(y﹣2)2=16;∵直线l经过定点P(3,5),倾斜角为,∴直线l的参数方程为:,t为参数.(2)将直线l的参数方程代入曲线C的方程,得t2+(2+3)t﹣3=0,设t1、t2是方程的两个根,则t1t2=﹣3,∴|PA|•|PB|=|t1|•|t2|=|t1t2|=3.2.【解答】解:(1)曲线C:ρsin2θ=2cosθ,即ρ2sin2θ=2ρcosθ,∴曲线C的直角坐标方程为y2=2x;直线l:(t为参数),消去t,可得直线l的普通方程x﹣y﹣3=0;(2)将直线l:代入曲线C的标准方程:y2=2x得:t2﹣4t﹣6=0,∴|PM|2+|PN|2=|t1|2+|t2|2=(t1﹣t2)2+2t1t2=32.3、【解答】(1)直线l :(cos sin )6ρθθ-=化成普通方程为60x y --=.曲线化成普通方程为22(2)3x y -+=∴圆心(2,0)C 到直线l 的距离为d ==∴曲线C 上点P 到直线l 距离的最大值为(2)设直线1l 的方程为0x y λ-+=, (2,0)C 到直线1l 的距离为d === ∴或∴直线1l 的方程为或4.【解答】(1)由曲线C 1的参数方程为(θ为参数),消去参数θ得,曲线C 1的普通方程得+=1.由ρcos θ﹣ρsin θ﹣4=0得,曲线C 2的直角坐标方程为x ﹣y ﹣4=0…(2)设P (2cos θ,2sin θ),则点P 到曲线C 2的距离为d==,当cos (θ+45°)=1时,d 有最小值0,所以|PQ|的最小值为0.5.【解答】解:(1)消去参数φ可得C1的直角坐标方程为+y2=1,∵曲线C2是圆心为(3,),半径为1的圆曲线C2的圆心的直角坐标为(0,3),∴C2的直角坐标方程为x2+(y﹣3)2=1;(2)设M(2cosφ,sinφ),则|MC2|====,∴﹣1≤sinφ≤1,∴由二次函数可知2≤|MC2|≤4,由题意结合图象可得|MN|的最小值为2﹣1=1,最大值为4+1=5,∴|MN|的取值范围为[1,5]6.【解答】解:(1)∵,∴,由得曲线C1的极坐标方程为,∵x2+y2﹣2y=0,∴曲线C2的极坐标方程为ρ=2sinθ;(2)由(1)得,|OB|2=ρ2=4sin2α,∴∵,∴1<1+sin2α<2,∴,∴|OA|2+|OB|2的取值范围为(2,5).7.【解答】解:(1)曲线C1参数方程为,∴其普通方程x﹣y﹣a+1=0,由曲线C2的极坐标方程为ρcos2θ+4cosθ﹣ρ=0,∴ρ2cos2θ+4ρcosθ﹣ρ2=0∴x2+4x﹣x2﹣y2=0,即曲线C2的直角坐标方程y2=4x.(2)设A、B两点所对应参数分别为t1,t2,联解得要有两个不同的交点,则,即a>0,由韦达定理有根据参数方程的几何意义可知|PA|=2|t1|,|PB|=2|t2|,又由|PA|=2|PB|可得2|t1|=2×2|t2|,即t1=2t2或t1=﹣2t2∴当t1=2t2时,有t1+t2=3t2=,t1t2=2t22=,∴a=>0,符合题意.当t1=﹣2t2时,有t1+t2=﹣t2=,t1t2=﹣2t22=,∴a=>0,符合题意.综上所述,实数a的值为或.8.【解答】解:(1)直线,令,解得,∴,令,解得ρ=4,∴又∵,∴,∴|AB|=2.(2)∵直线,曲线,∴=当且仅当,即时,取“=”,∴,∴△ABP面积的最大值为3.极坐标与参数方程——练习参考答案1.【解答】解:由,由②得,代入①并整理得,.由,得,两式平方相加得.联立,解得或.∴|AB|=.2.【解答】解:(1)曲线C2:ρ=2sinθ得ρ2=2ρsinθ,即x2+y2=2y,①C 3:ρ=2cosθ,则ρ2=2ρcosθ,即x2+y2=2x,②由①②得或,即C2与C3交点的直角坐标为(0,0),(,);(2)曲线C1的直角坐标方程为y=tanαx,则极坐标方程为θ=α(ρ∈R,ρ≠0),其中0≤a<π.因此A得到极坐标为(2sinα,α),B的极坐标为(2cosα,α).所以|AB|=|2sinα﹣2cosα|=4|sin(α)|,当α=时,|AB|取得最大值,最大值为4.3.【解答】解:(1)由⊙C的极坐标方程为ρ=2sinθ.∴ρ2=2,化为x2+y2=,配方为=3.(2)设P,又C.∴|PC|==≥2,因此当t=0时,|PC|取得最小值2.此时P(3,0).4.【解答】解:(1)因为x=ρcosθ,y=ρsinθ,所以C的极坐标方程为ρ=2cosθ,直线l的直角坐标方程为y=x,联立方程组,解得或,所以点M,N的极坐标分别为(0,0),(,).(2)由(1)易得|MN|=因为P是椭圆+y2=1上的点,设P点坐标为(cosθ,sinθ),则P到直线y=x的距离d=,所以S△PMN==≤1,当θ=kπ﹣,k∈Z时,S△PMN取得最大值1.5.【解答】解:(1)直线l的参数方程为(t为参数),消去参数t得直线l的普通方程为x﹣y﹣=0,曲线C的极坐标方程ρ2+ρ2sin2θ=2,化成直角坐标方程为x2+2y2=2,即+y2=1.(2)将直线l的参数方程代入曲线C:x2+2y2=2,得7t2+4t﹣4=0.设A,B两点在直线l的参数方程中对应的参数分别为t1,t2,则t1+t2=﹣,t1t2=﹣,∴+=+==.6.【解答】解:(1)当a=2时,ρ=asinθ转化为ρ=2sinθ整理成直角坐标方程为:x2+(y﹣1)2=1直线的参数方程(t为参数).转化成直角坐标方程为:4x+3y﹣8=0 (2)圆C的极坐标方程转化成直角坐标方程为:直线l截圆C的弦长等于圆C的半径长的倍,所以:2|3a﹣16|=5|a|,利用平方法解得:a=32或.7.【解答】解:(1)∵直线,∴直线C1的极坐标方程为,∵曲线C2的参数方程是(θ为参数),∴消去参数θ,得曲线C2的普通方程为.(2)∵把C1绕坐标原点沿逆时针方向旋转得到直线C3,∴C3的极坐标方程为,化为直角坐标方程为.圆C2的圆心(,2)到直线C3:的距离:.∴.8.【解答】解:(1)在曲线C上任意取一点(x,y),由题意可得点(x,)在圆x2+y2=1上,∴x2+=1,即曲线C的方程为x2+=1,化为参数方程为(0≤θ<2π,θ为参数).(2)由,可得,,不妨设P1(1,0)、P2(0,2),则线段P1P2的中点坐标为(,1),再根据与l垂直的直线的斜率为,故所求的直线的方程为y﹣1=(x﹣),即x﹣2y+ =0.再根据x=ρcosα、y=ρsinα可得所求的直线的极坐标方程为ρcosα﹣2ρsinα+=0,即ρ=.。
【高中数学】参数方程和极坐标方程常考题型及解题方法归纳

参数方程和极坐标方程常考题型及解题方法归纳一、根据直线参数方程中t的几何意义求与距离有关的问题经过点P(x0,y0),倾斜角为α的直线l的参数方程为x=x0+tcosαy=y0+tsin烅烄烆α(t为参数),参数t的几何意义是:直线上定点P到动点M的有向线段,t表示参数t对应的点M到定点P的距离,即|t|=|PM|.若A,B为直线l上两点,其对应的参数分别为t1与t2,则有:①AB=|t1-t2|;②当A,B在点P的同侧时,t1与t2同号;当A,B分别在点P的两侧时,t1与t2异号.需要注意的是:有时候直线的参数方程也可写为x=x0+aty=y0+烅烄烆bt(t为参数),如果a2+b2≠1,则参数t没有上述几何意义.例1 在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:ρll与l的普通方程;(2)若PM,MN,PN成等比数列,求a的值.分析 (1)利用x=ρcosθ,y=ρsinθ即可将曲线C的极坐标方程转化为直角坐标方程,在直线l的参数方程中消去参数t即可得直线l的普通方程;(2)将直线l的参数方程代入曲线C的直角坐标方程,利用参数的几何意义结合韦达定理即可建立关于a的方程求解.解 (1)由ρsin2θ=acosθ得ρ2 sin2θ=aρcosθ,可得曲线C的平面直角坐标方程y2=ax(a>0).由直线l的参数方程消去参数t,可得直线l的普通方程为x-y-1=0.(2)设点M,N对应的参数分别为t1,t2,则PM=t1,PN=t2,MN=t1-t2.将x=-1+槡22t,y=-2 +槡22t代入y2=ax,得t2-(槡4 2 +槡2a)t+8+2a=0.所以Δ=(槡4 2 +槡2a)2-4(8+2a)=2a2+8a>0,t1+t2=槡4 2 +槡2a,t1t2=8+2a.由PM,MN,PN成等比数列,可以得到t1-t22=t1t2,所以(t1+t2)2-4t1t2=t1t2,即(槡4 2 +槡2a)2-5(8+2a)=0,解得a=1(a=-4舍去).例2 (2015年高考湖南卷)已知直线l:x=5 +槡32ty =槡3+12烅烄烆t(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2cosθ.(Ⅰ)将曲线C的极坐标方程化为直角坐标方程;(Ⅱ)设点M的直角坐标为(5,槡3),直线l与曲线C的交点为A,B,求|MA|·|MB|的值.分析 (Ⅰ)利用ρ2=x2+y2,x=ρcosθ即可将已知条件中的极坐标方程转化为直角坐标方程;(Ⅱ)注意到点M在直线l上,将直线l的参数方程代入圆的直角坐标方程,利用参数的几何意义结合韦达定理即可求解.解 (Ⅰ)ρ=2cosθ等价于ρ2=2ρcosθ,将ρ2=x2+y2,ρcosθ=x代入即得曲线C的直角坐标方程为x2+y2-2x=0.(Ⅱ)结合直线l的参数方程,注意到点M在直线l上,且(槡32)2+(12)2=1,可设点M,N对应的参数分别为t1,t2,则MA=|t1|,MB=|t2|,所以MA·MB=t1t2. 将直线l的参数方程代入曲线C的直角坐标方程,整理得t2 +槡5 3t+18=0,则MA·MB=t1t2=18.例3 已知圆锥曲线C:x=2cosαy=sin{α(α为参数)和定点A(0,,槡3),F1,F2是此圆锥曲线的左、右焦点,以原点O为极点,以x轴的正半轴为极轴建立极坐标系.(1)求直线AF2的极坐标方程;(2)经过点F1且与直线AF2垂直的直线l交此圆锥曲线于M,N两点,求MF1-NF1的值.解 (1)消去参数α即可将曲线C的方程化为普通方程x24+y2=1,从而可求得F1(-槡3,0),F2(槡3,0),于是可得直线AF2的普通方程为x+y-槡3=0,利用互化公式化为极坐标方程为ρcosθ+ρsinθ=槡3.(2)由(1)可得kAF2=-1,所以直线l的倾斜角为45°,从而可得直线l的参数方程为x=-槡3 +槡22ty =槡22烅烄烆t(t为参数),代入椭圆C的直角坐标方程:x24+y2=1,得5t2-槡2 6t-2=0,设点M,N对应的参数分别为t1,t2,注意到点M,N,F1都在直线l上且点M,N在点F1两侧,所以|MF1|-|NF1|=|t1+t2|=槡2 65.评注 对于直线上与定点距离有关的问题,利用直线参数方程中参数t的几何意义,能避免通过解方程组求交点坐标的繁琐运算,使解题过程得到简化.二、利用参数方程求最值和取值范围利用曲线的参数方程求解两曲线间的最值问题,是解决这类问题的常用方法,优点是解题过程比较简洁.为此,需要熟悉常见曲线的参数方程、参数方程与普通方程的互化以及参数方程的简单应用.例4 已知曲线C1:x=8costy=2sin{t(t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρ=7cosθ-sinθ.(1)将曲线C1的参数方程化为普通方程,将曲线C2的极坐标方程化为直角坐标方程.(2)设P为曲线C1上的点,点Q极坐标为(2槡2,π4),求PQ的中点与曲线C2上的点的距离的最小值.分析 (1)利用参数方程和普通方程之间的关系进行互化即可,(2)先把点Q的极坐标化为直角坐标,设出点P的参数形式的直角坐标(t为参数),进而得到PQ的中点M的直角坐标,可用公式得到点M到直线C2的距离d的表达式(用参数t表示),再求最值即可.解 (1)由曲线C1的参数方程消去参数t得曲线C1的普通方程x264+y24=1.由曲线C2的极坐标方程得ρcosθ-ρsinθ=7,于是可得它的直角坐标方程为x-y-7=0.(2)由点Q的极坐标(槡2 2,π4)可得它的直角坐标为(2,2),设P(8cost,2sint),则PQ的中点M的直角坐标为(4cost+1,sint+1),所以,点M到直线C2的距离d=4cost-sint-7槡2=槡17cos(t+φ)-7槡2,其中φ为锐角,且tanφ=14.当cos(t+φ)=1时,d取得最小值dmin=槡7 2 -槡342.所以,PQ的中点M与曲线C2上的点的距离的最小值为槡7 2 -槡342.例5 (2014年全国卷Ⅰ)已知曲线C:x24+y29=1,直线l:x=2+ty=2-2{t(t为参数).(Ⅰ)写出曲线C的参数方程和直线l的普通方程;(Ⅱ)过曲线C上任一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.分析 (Ⅰ)利用椭圆的普通方程及直线的参数的特征进行互化即可;(Ⅱ)由椭圆的参数方程建立|PA|的三角函数表达式,再求最值.图1解 (Ⅰ)曲线C的参数方程为x=2cosθy=3sin{θ(θ为参数),直线l的普通方程为2x+y-6=0.(Ⅱ)如图1,在曲线C上任意取一点P(2cosθ,3sinθ),它到直线l的距离为:d=槡554cosθ+3sinθ-6,则|PA|=dsin30°=槡2 55|5sin(θ+α)-6|,其中α为锐角,且tanα=43.当sin(θ+α)=-1时,|PA|取得最大值,最大值为槡22 55;当sin(θ+α)=1时,|PA|取得最小值,最小值为槡2 55.例6 (2015年高考陕西卷)在直角坐标系xΟy中,直线l的参数方程为x=3+12ty =槡32烅烄烆t(t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,⊙C的极坐标方程为ρ=槡2 3sinθ.(Ⅰ)写出⊙C的直角坐标方程;(Ⅱ)Ρ为直线l上一动点,当Ρ到圆心C的距离最小时,求Ρ的直角坐标.分析 (Ⅰ)利用x=ρcosθ,y=ρsinθ,由⊙C的极坐标方程可得它的直角坐标方程;(Ⅱ)先设点Ρ的参数坐标,可得ΡC的函数表达式,再利用函数的性质可得ΡC的最小值,进而可得Ρ的直角坐标;或将直线l的方程化为普通方程,再求过圆心且垂直于直线l的直线方程,联立两方程可解得点P的直角坐标.解 (Ⅰ)由ρ=槡2 3sinθ,得ρ2 =槡2 3ρsinθ,从而,⊙C的直角坐标方程为x2+y2 =槡2 3y,即x2+(y-槡3)2=3.(Ⅱ)设P(3+12t,槡32t),又C(0,槡3),则|PC|=(3+12t)2+(槡32t -槡3)槡2=t2+槡12,易知:当t=0时,ΡC取得最小值,此时Ρ点的直角坐标为(3,0).评注 将曲线的参数方程化为普通方程的关键是消去其中的参数,常用的技巧有:代入消参、加减消参、整体消参、平方后加减消参等.如果题目中涉及圆、椭圆上的动点求相关最值(范围)问题时,可考虑用其参数方程设出点的坐标,将问题转化为函数问题来解决,可以使解题的过程更简洁.例7 (2016年全国卷Ⅱ理科第20题)已知椭圆E:x2t+y23=1的焦点在x轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.(Ⅰ)当t=4,AM=AN时,求△AMN的面积;(Ⅱ)当2 AM=AN时,求k的取值范围.分析 (Ⅰ)先结合已知条件设出直线AM的参数方程,代入椭圆方程,可求得AM,进而求得△AMN的面积;(Ⅱ)设出直线AM、AN的参数方程(以直线AM的倾斜角α为参数),代入椭圆方程,用t和α表示|AM|和|AN|,再利用2 AM=AN将t表示为k的函数,结合t>3,可求得k的取值范围.解 (Ⅰ)当t=4,AM=AN时,可得点A(-2,0),k=1.设直线AM的参数方程为x=-2+槡22my =槡22烅烄烆m(m为参数),代入椭圆方程,整理得72m2-槡6 2 m=0,故AM =槡12 27,所以S△AMN=12AM·AN=14449.(Ⅱ)设直线AM的倾斜角为α,又点A(-槡t,0),可设直线AM的参数方程为x=-槡t+mcosαy=msin烅烄烆α(m为参数),代入椭圆方程,整理得(3cos2α+t sin2α)m2-6tcosα·m=0,所以AM=6tcosα3cos2α+t sin2α.因为MA⊥NA,故直线AN的倾斜角为α+π2,同理可得:AN=6tcos(α+π2)3cos2(α+π2)+t sin2(α+π2)=6tsinα3sin2α+t cos2α.由2 AM=AN,k=tanα,代入化简得t=6k2-3kk3-2.又因为椭圆E:x2t+y23=1的焦点在x轴上,所以t>3,即6k2-3kk3-2>3,解得3槡2<k<2.所以,k的取值范围是(3槡2,2).评注 本题属于圆锥曲线试题,常规思路是利用直角坐标直接求解,过程比较复杂.利用直线的参数方程来求解本题,使问题的求解过程变得简洁.三、利用极坐标中ρ的几何意义求有关距离或相关问题我们知道,极坐标中的ρ为极径,表示曲线上一点与原点O之间的距离,因此,与原点O有关的距离、面积等问题都可考虑运用极坐标中ρ的几何意义来解决,这是一种有效的解题策略,很多时候比化为直角坐标运算更简便.例8 (2015年高考全国卷Ⅱ)在直角坐标系xOy中,曲线C1:x=tcosα,y=tsinα{,(t为参数,t≠0),其中0≤α<π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,曲线C3:ρ=2 槡3cosθ.(Ⅰ)求C2与C1的交点的直角坐标;(Ⅱ)若C2与C1相交于点A,C3与C1相交于点B,求AB的最大值.分析 (Ⅰ)可将曲线C2与C1的极坐标方程化为直角坐标方程后联立求交点的直角坐标,也可以直接联立极坐标方程求得交点的极坐标,再化为直角坐标;(Ⅱ)分别联立C2与C1、C3与C1的极坐标方程,求得A,B的极坐标,由极径的概念用α表示出AB,转化为求关于α的三角函数的最大值.解 (Ⅰ)曲线C2的直角坐标方程为x2+y2-2y=0,曲线C3的直角坐标方程为x2+y2 -槡2 3x=0.联立两方程解得:x1=0,y1=0烅烄烆,x2=槡32,y2=32烅烄烆,所以,C2与C1的交点的直角坐标为(0,0)和(槡32,32).(Ⅱ)曲线C1的极坐标方程为θ=α(ρ∈R,ρ≠0),其中0≤α<π.于是可得:点A的极坐标为(2sinα,α),点B的极坐标为(槡2 3cosα,α).所以AB=2sinα-槡2 3cosα=4|sin(α-π3)|,又0≤α<π,所以,当α=5π6时,AB取得最大值,最大值为4.评注 如果用直角坐标来处理本题,计算量较大.例9 (2016年全国卷Ⅱ理科第23题)在直线坐标系xOy中,圆C的方程为(x+6)2+y2=25.(Ⅰ)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求C的极坐标方程;(Ⅱ)直线l的参数方程是x=tcosα,y=tsinα{,(t为参数),l与C交于A,B两点,|AB|=槡10,求l的斜率.分析 (Ⅰ)利用ρ2=x2+y2,x=ρcosθ可得C的极坐标方程;(Ⅱ)先将直线l的参数方程化为极坐标方程,再利用弦长公式可求得l的斜率.解 (Ⅰ)由x=ρcosθ,y=ρsinθ可得C的极坐标方程ρ2+12ρcosθ+11=0.(Ⅱ)在(Ⅰ)中建立的极坐标系中,直线l的极坐标方程为θ=α(ρ∈R),与C的极坐标方程联立得ρ2+12ρcosα+11=0.设点A,B所对应的极径分别为ρ1,ρ2,则ρ1+ρ2=-12cosα,ρ1ρ2=11,所以|AB|=|ρ1-ρ2|=(ρ1+ρ2)2-4ρ1ρ槡2=144cos2α-槡44.又|AB|=槡10,所以144cos2α-槡44 =槡10,解得cos2α=38,故tanα=±槡153,所以,直线l的斜率为槡153或-槡153.例10 (2015年高考全国卷Ⅰ理科第23题)在直角坐标系xOy中,直线C1:x=-2,圆C2:(x-1)2+(y-2)2=1,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.(Ⅰ)求C1,C2的极坐标方程;(Ⅱ)若直线C3的极坐标方程为θ=π4(ρ∈R),设C2与C3的交点为M,N,求△C2MN的面积.分析 (Ⅰ)根据公式x=ρcosθ,y=ρsinθ,x2+y2=ρ2即可求得C1,C2的极坐标方程;(Ⅱ)联立直线C3和圆C2的极坐标方程得到关于ρ的方程,可求得MN,进而可求出△C2MN的面积.解 (Ⅰ)因为x=ρcosθ,y=ρsinθ,所以,可求得:C1的极坐标方程为ρcosθ=-2,C2的极坐标方程为ρ2-2ρcosθ-4ρsinθ+4=0.(Ⅱ)将C3的极坐标方程θ=π4代入C2的极坐标方程ρ2-2ρcosθ-4ρsinθ+4=0,得ρ2 -槡3 2ρ+4=0,解得ρ1=槡2 2,ρ2=槡2,所以,MN=ρ1-ρ2=槡2.又因为C2的半径为1,∠C2MN=π4,所以△C2MN的面积为S=12×槡2×1×sinπ4=12.评注 过坐标原点、倾斜角为θ0的直线的极坐标方程为θ=θ0,其上两点P(ρ1,θ0),Q(ρ2,θ0)间的距离为PQ=ρ1-ρ2.【一点感悟】参数方程和极坐标虽然是选考内容,也应得到充分的重视,如果能够将它们和普通方程有机联系,相互补充,可以优化解题思路,简化计算过程,减少运算量,提高解题的效率.。
(完整版)极坐标与参数方程知识点、题型总结

极坐标与参数方程知识点、题型总结一、伸缩变换:点是平面直角坐标系中的任意一点,在变换),(y x P 的作用下,点对应到点,称伸缩变换⎩⎨⎧>⋅='>⋅=').0(,y y 0),(x,x :μμλλϕ),(y x P ),(y x P '''一、1、极坐标定义:M 是平面上一点,表示OM 的长度,是,则有序实数实ρθMOx ∠数对,叫极径,叫极角;一般地,,。
,点P 的直角坐标、(,)ρθρθ[0,2)θπ∈0ρ≥极坐标分别为(x ,y )和(ρ,θ)2、直角坐标极坐标 2、极坐标直角坐标⇒cos sin x y ρθρθ=⎧⎨=⎩⇒222tan (0)x y yx xρθ⎧=+⎪⎨=≠⎪⎩3、求直线和圆的极坐标方程:方法一、先求出直角坐标方程,再把它化为极坐标方程方法二、(1)若直线过点M (ρ0,θ0),且极轴到此直线的角为α,则它的方程为:ρsin(θ-α)=ρ0sin(θ0-α)(2)若圆心为M (ρ0,θ0),半径为r 的圆方程为ρ2-2ρ0ρcos(θ-θ0)+ρ02-r 2=0二、参数方程:(一).参数方程的概念:在平面直角坐标系中,如果曲线上任意一点的坐标都是某个变数的函数 并且对于的每一个允许值,由这个方程所确y x ,t ⎩⎨⎧==),(),(t g y t f x t 定的点都在这条曲线上,那么这个方程就叫做这条曲线的参数方程,联系变数),(y x M 的变数叫做参变数,简称参数。
相对于参数方程而言,直接给出点的坐标间关系的y x ,t 方程叫做普通方程。
(二).常见曲线的参数方程如下:直线的标准参数方程1、过定点(x 0,y 0),倾角为α的直线:(t 为参数)ααsin cos 00t y y t x x +=+=(1)其中参数t 的几何意义:点P (x 0,y 0),点M 对应的参数为t ,则PM =|t| (2)直线上对应的参数是。
极坐标与参数方程题型归纳

极坐标与参数方程一、极坐标与参数方程的题型框架二、极坐标与参数方程的知识点1.参数方程的概念:设在平面上取定一个直角坐标系xOy ,把坐标y x ,表示为第三个变量t 的函数:⎩⎨⎧==)()(t g y t f x ,b t a ≤≤……………………①如果对于t 的每一个值(b t a ≤≤),①式所确定的点),(y x M 都在一条曲线上;而这条曲线上任意一点),(y x M ,都可由t 的某个值通过①式得到,则称①式为该曲线的参数方程,其中t 称为参数.2.参数方程与普通方程的互化:把参数方程化为普通方程,需要根据其结构特征,选取适当的消参方法.常见的消参方法有:代入消元法;加减消参法;平方和(差)消参法;乘法消参法等.把曲线C 的普通方程0),(=y x F 化为参数方程的关键:一是适当选取参数;二是确保互化前后方程的等价性.要注意方程中的参数的变化范围.3.直线、圆、椭圆的参数方程:(1)经过一定点),(000y x P ,倾斜角为α 的直线l 的参数方程为:⎩⎨⎧+=+=ααsin ,cos 00t y y t x x (t 为参数);(2)直线参数方程的一般形式为⎩⎨⎧+=+=bt y y at x x 00,(t 为参数);(3)圆的参数方程为⎩⎨⎧+=+=θθsin ,cos 00r y y r x x (θ为参数);(5)椭圆)0(12222>>=+b a b y a x 的参数方程为⎩⎨⎧==θθsin ,cos b y a x (θ,ρ为参数).4.极坐标系的概念:在平面内取一个定点O ,O 点出发的一条射线Ox ,一个长度单位及计算角度的正方向(通常取逆时针方向),合称为一个极坐标系.O 称为极点,Ox 称为极轴.设M 是平面内任意一点,极点O 与点M 的距离OM 叫做点M 的极径,记作ρ;以极轴Ox 为始边,射线OM 为终边的角xOM 叫做点M 的极角,记作θ ,有序数对),(θρ叫做点M 的极坐标.一般情况下,约定0≥ρ.5.极坐标系与直角坐标系的互化:直角坐标化极坐标:θρcos =x ,θρsin =y ;极坐标化直角坐标:222y x +=ρ,).0(tan =/=x xyθ三、轨迹问题1.圆的极坐标方程若圆心为M (ρ0,θ0),半径为r 的圆方程为ρ2-2ρ0ρcos(θ-θ0)+ρ20-r 2=0.几个特殊位置的圆的极坐标方程(1)当圆心位于极点,半径为r :ρ=r ;(2)当圆心位于M (a,0),半径为a :ρ=2a cos θ;(3)当圆心位于π(,)2M a ,半径为a :ρ=2a sin θ.2.直线的极坐标方程若直线过点M (ρ0,θ0),且极轴到此直线的角为α,则它的方程为:ρsin(θ-α)=ρ0sin (θ0-α).几个特殊位置的直线的极坐标方程(1)直线过极点:θ=θ0和θ=π-θ0;(2)直线过点M (a,0)且垂直于极轴:ρcos θ=a ;(3)直线过π(,)2M b 且平行于极轴:ρsin θ=b .例题【例1】在极坐标系中,已知圆的圆心(6,)3C π,半径3r =,Q 点在圆C 上运动.以极点为直角坐标系原点,极轴为x 轴正半轴建立直角坐标系.(1)求圆C 的参数方程;(2)若P 点在线段OQ 上,且:2:3OP PQ =,求动点P 轨迹的极坐标方程.【解析】(1)由已知得,圆心(6,)3C π的直角坐标为C ,3r =,所以C的直角坐标方程为22(3)(9x y -+-=,所以圆C的参数方程为33cos 3sin x y θθ=+⎧⎪⎨=⎪⎩(θ为参数).(2)由(1)得,圆C的极坐标方程为26(cos )270ρρθθ-++=,即212sin(276ρρθπ=+-,设(),P ρθ,()1,Q ρθ,根据:2:3OP PQ =,可得1:2:5ρρ=,将152ρρ=代入C 的极坐标方程,得225120sin()10806ρρθπ-++=,即动点p 轨迹的极坐标方程为225120sin()10806ρρθπ-++=.【例2】在平面直角坐标系xOy 中,圆C 的参数方程为22cos ,2sin x y αα=+⎧⎨=⎩(α为参数),以点O 为极点,x 轴的正半轴为极轴建立极坐标系.(1)求圆C 的极坐标方程;(2)过极点O 作直线与圆C 交于点A ,求OA 的中点所在曲线的极坐标方程.【解析】(1)圆C 的参数方程为22cos ,2sin x y αα=+⎧⎨=⎩(α为参数),转换为直角坐标方程为:()2224x y -+=,转换为极坐标方程为:4cos ρθ=.(2)过极点O 作直线与圆C 交于点A ,设OA 的中点坐标为()00,ρθ,所以()00,2A ρθ,所以0024cos ρθ=,即002cos ρθ=,所以OA 中点所在的曲线的极坐标方程为2cos ρθ=.【例3】已知圆C 经过点P )3,2(π,圆心C 为直线ρsin )3(πθ-=-3与极轴的交点,求圆C 的极坐标方程.【解析】解法1在直线的极坐标方程ρsin )3(πθ-=-3中,令θ=0,得ρ=2,所以C(2,0).因为△POC 是边长为2的正三角形,所以圆C 的半径r =2.因为圆C 经过极点O ,所以圆C 极坐标方程为ρ=4cos θ.解法2以极点为坐标原点,极轴为x 轴建立平面直角坐标系,则直线方程为y =3x -23,P 的直角坐标为(1,3),令y =0,得x =2,所以C(2,0),所以圆C 的半径PC =(2-1)2+(0-3)2=2,所以圆C 的方程为(x -2)2+(y -0)2=4,即x 2+y 2-4x =0,所以圆C 的极坐标方程为ρ=4cos θ.变式训练【练习1】(2019年高考全国Ⅱ卷理数)在极坐标系中,O 为极点,点000(,)(0)M ρθρ>在曲线:4sin C ρθ=上,直线l 过点(4,0)A 且与OM 垂直,垂足为P .(1)当0=3θπ时,求0ρ及l 的极坐标方程;(2)当M 在C 上运动且P 在线段OM 上时,求P 点轨迹的极坐标方程.【解析】(1)因为()00,M ρθ在C 上,当03θπ=时,04sin 3ρπ==.由已知得||||cos23OP OA π==.设(,)Q ρθ为l 上除P 的任意一点.在Rt OPQ △中,cos(||23OP ρθπ-==,经检验,点(2,)3P π在曲线cos(23ρθπ-=上.所以,l 的极坐标方程为cos()23ρθπ-=.(2)设(,)P ρθ,在Rt OAP △中,||||cos 4cos ,OP OA θθ==即 4cos ρθ=.因为P 在线段OM 上,且AP OM ⊥,故θ的取值范围是[,42ππ.所以P 点轨迹的极坐标方程为4cos ,[,42ρθθππ=∈.【练习2】在极坐标系中,已知圆C 经过点P )4,22(π,圆心为直线ρsin(θ-π3)=-3与极轴的交点,求圆C 的极坐标方程.【解析】在直线方程ρsin (θ-π3)=-3中,令θ=0,得ρ=2,所以圆心为C(2,0).在△POC 中,由余弦定理,得圆C 的半径r =CP =2.圆C 经过极点,其极坐标方程为ρ=4cos θ.【练习3】(2019年高考全国Ⅲ卷理数)如图,在极坐标系Ox 中,(2,0)A ,4B π,2,4C 3π,(2,)D π,弧 AB , BC , CD 所在圆的圆心分别是(1,0),(1,2π,(1,)π,曲线1M 是弧 AB ,曲线2M 是弧 BC,曲线3M 是弧 CD .(1)分别写出1M ,2M ,3M 的极坐标方程;(2)曲线M 由1M ,2M ,3M 构成,若点P 在M 上,且||OP =P 的极坐标.【解析】(1)由题设可得,弧 ,,AB BCCD 所在圆的极坐标方程分别为2cos ρθ=,2sin ρθ=,2cos ρθ=-.所以1M 的极坐标方程为π2cos (0)4ρθθ=≤≤,2M 的极坐标方程为π3π2sin ()44ρθθ=≤≤,3M 的极坐标方程为3π2cos (π)4ρθθ=-≤≤.(2)设(,)P ρθ,由题设及(1)知若π04θ≤≤,则2cos θ=,解得π6θ=;若π3π44θ≤≤,则2sin θ=,解得π3θ=或2π3θ=;若3ππ4θ≤≤,则2cos θ-=5π6θ=.综上,P 的极坐标为π)6或π3或2π)3或5π6.四、几何意义问题(一)直线参数方程t 的几何意义1、直线参数方程:(1)注意必须是标准形式;(2)直线的参数方程⎩⎨⎧+=+=ααsin ,cos 00t y y t x x (t 为参数)中参数t 的几何意义:t 表示直线上任一点),(y x M 到直线上定点),(000y x M 的距离;2、直线与二次曲线相交问题:将直线的参数方程与曲线的普通方程联立,通过判断∆的符号来确定交点的个数;若0>∆,则有两个交点,此时的1t 、2t 分别表示交点B A 、与直线所过定点),(000y x M 的距离.例题【例1】在平面直角坐标系xOy 中,直线l 的参数方程为1cos sin x t y t αα=+⎧⎨=⎩(t 为参数,0πα≤<),在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线C 的极坐标方程为222.1sin ρθ=+(1)求曲线C 的直角坐标方程;(2)设点M 的坐标为(1,0),直线l 与曲线C 相交于A ,B 两点,求11MA MB+的值.【解析】(1)曲线2221sin ρθ=+,即222sin 2ρρθ+=,222,sin x y y ρρθ=+= ,∴曲线C 的直角坐标方程为2222x y +=,即2212x y +=.(2)将1cos sin x t y t αα=+⎧⎨=⎩代入2222x y +=并整理得22(1sin )2cos 10t t αα++-=,1212222cos 1,1sin 1sin t t t t ααα-∴+=-=++,121211···MA MB AB t t MA MB MA MB MA MB t t +-∴+===-,122221sin t t α-===+,2222111sin 11sin MA MBαα+∴+==+【例2】在直角坐标系xOy 中,直线l 的参数方程为1cos 1sin x t xy t x =+⎧⎨=-+⎩(t 为参数,0α<<π),以O 为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为(12cos 2)8cos ρθθ-=.(1)判断直线l 与曲线C 的公共点的个数,并说明理由;(2)设直线l 与曲线C 交于不同的两点,A B ,点()1,1P -,若114||3PA PB -=,求tan α的值.【解析】(1)由()1cos 28cos ρθθ-=得2sin 4cos ρθθ=,所以22sin 4cos ρθρθ=,即24y x =,将直线l 的参数方程代入24y x =,得()()21sin 41cos t t αα-+=+,即()22sin2sin 4cos 30t t ααα⋅-+⋅-=,由0α<<π知2sin 0α>,()222sin 4cos 12sin 0∆ααα=++>,故直线l 与曲线C 有两个公共点;(2)由(1)可设方程()22sin 2sin 4cos 30t t ααα⋅-+⋅-=的两根为12t t ,,则1222sin 4cos sin ααα++=t t ,12230sin α-⋅=<t t ,故12121124||sin 2cos 33PA PB t t PA PB PA t t αα-+-===+=⋅,∴22sin 4sin cos 4cos 4αααα++=,即24sin cos 3sin ααα=,∴4tan 3α=.2变式训练【练习1】在直角坐标系xOy 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系,圆C 的极坐标方程为212cos 110ρρθ++=.(1)求圆C 的直角坐标方程;(2)设(1,0)P ,直线l 的参数方程是1cos sin x t y t αα=+⎧⎨=⎩(t 为参数),已知l 与圆C 交于,A B两点,且34PA PB =,求l 的普通方程.【解析】(1)将222,cos x y x ρρθ=+=代入圆C 的极坐标方程212cos 110ρρθ++=,得2212110x y x +++=,化为圆的标准方程为22(6)25x y ++=.(2)将直线l 的参数方程1cos sin x t y t αα=+⎧⎨=⎩(t 为参数)代入圆C 的直角坐标方程()22625x y ++=中,化简得214cos 240t t α++=,设,A B 两点所对应的参数分别为12,t t ,由根与系数的关系知121214cos ,24t t t t α+=-=,①∴12,t t 同号,又34PA PB =,∴1234t t =,②由①②可知12t t ⎧⎪⎨⎪⎩或12==t t ⎧-⎪⎨-⎪⎩∴14cos α-=或14cos α-=-,解得2cos 2α=±,∴tan 1k α==±,∴l 的普通方程为(1)y x =±-.【练习2】在直角坐标系xOy 中,直线1C的参数方程为3623x t y t ⎧=-⎪⎪⎨⎪=+⎪⎩(其中t 为参数).以坐标原点O 为极点,x 轴非负半轴为极轴建立极坐标系,曲线2C 的极坐标方程为2cos 3sin ρθθ=.(1)求1C 和2C 的直角坐标方程;(2)设点(0,2)P ,直线1C 交曲线2C 于,M N 两点,求22PMPN +的值.【解析】(1)直线1C 的参数方程为33623x y t ⎧=-⎪⎪⎨⎪=+⎪⎩(其中t 为参数),消去t可得20y +-=;由2cos 3sin ρθθ=,得22cos 3sin ρθρθ=,则曲线2C 的直角坐标方程为23x y =.(2)将直线1C的参数方程3323x t y t ⎧=-⎪⎪⎨⎪=+⎪⎩代入23x y =,得2180t --=,设,M N 对应的参数分别为12,t t,则121218t t t t ⎧+=⎪⎨=-⎪⎩,()2221212290PM PN t t t t +=+-=.(二)极坐标中极径的几何意义极坐标方程中ρ的几何意义:M 是平面内任意一点,极点O 与点M 的距离OM 叫做点M 的极径,记作ρ;即OM=ρ例题【例1】在直角坐标系中,已知曲线的方程为,的方程为,是一条经过原点且斜率大于的直线,以直角坐标系原点为极点,轴正半轴为极轴建立极坐标系.(1)求与的极坐标方程;(2)若与的一个公共点(异于点),与的一个公共点为,求的取值范围.【解析】(1)曲线的方程为,的极坐标方程为,的方程为,其极坐标力程为.(2)是一条过原点且斜率为正值的直线,的极坐标方程为,,,联立与的极坐标方程,得,即,联立与的极坐标方程,得,即,所以,又,所以.【例2】在平面直角坐标系xOy 中,已知椭圆的方程为:2212012x y+=,动点P 在椭圆上,O 为原点,线段OP 的中点为Q .(1)以O 为极点,x 轴的正半轴为极轴,建立极坐标系,求点Q 的轨迹的极坐标方程;(2)设直线l 的参数方程为1,232x t y t ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数),l 与点Q 的轨迹交于M 、N 两点,求弦长MN .【解析】(1)设点Q 的坐标为(,)x y ,Q 为线段OP 的中点,∴点P 的坐标为(2,2)x y .由点P 在椭圆上得22(2)(2)12012x y +=,化简得点Q 的轨迹的直角坐标方程为22153x y+=,①将cos x ρθ=,sin y ρθ=,代入①得2222cos sin 153ρθρθ+=,化简可得点Q 的轨迹的极坐标方程为22(32sin )15ρθ+=.(2)方法1:由直线l 的参数方程1,232x t y t⎧=⎪⎪⎨⎪=⎪⎩(t 为参数)知,直线l 过极点,倾斜角为π3,∴直线l 的极坐标方程为π()3θρ=∈R .由22π,3(32sin )15,θρθ⎧=⎪⎨⎪+=⎩解得:1π,330,3θρ⎧=⎪⎪⎨⎪=⎪⎩和2π,330.3θρ⎧=⎪⎪⎨⎪=-⎪⎩∴弦长122303MN ρρ=-=.方法2:把直线l 的参数方程1,232x t y ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数)代入①得22344153t t +=,化简得2103t =,123030,,33t t ∴==-设M 、N 两点对应的参数分别为1t ,2t ,由直线参数方程t 的几何意义得弦长122303MN t t =-=.方法3:由直线l 的参数方程1,232x t y ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数)知,直线l 的普通方程为3y x =,联立22153y x y ⎧=⎪⎨+=⎪⎩,,解得11306102x y ⎧=⎪⎪⎨⎪=⎪⎩和2230610.2x y ⎧=-⎪⎪⎨⎪=-⎪⎩弦长2303MN ==.变式训练【练习1】在直角坐标系xOy 中,直线1:2C x =-,圆222:(1)(2)1C x y -+-=,以坐标原点O 为极点,以x 轴正半轴为极轴,建立极坐标系.(1)求1C ,2C 的极坐标方程;(2)若直线3C 的极坐标方程θπ=4()ρ∈R ,设2C 与3C 的交点为M ,N ,求2C MN △的面积.【解析】(1)222cos ,sin ,x y x y ρθρθρ==+= 1C ∴的极坐标方程为cos 2ρθ=-.由2C 的直角坐标方程22(1)(2)1x y -+-=,展开得222440x y x y +--+=,2C ∴的极坐标方程为22cos 4sin 40ρρθρθ--+=.(2)将4θπ=代入22cos 4sin 40ρρθρθ--+=,得240ρ-+=,解得1212,,ρρρρ==-=∴即||MN =.由于2C 的半径为1,即221C M C N ==.易知22222||C MC N MN +=,即2C MN ∆为等腰直角三角形,2111122C MN S ∆=⨯⨯=∴.【练习2】在平面直角坐标系中,曲线1C 的参数方程为cos 2sin x r y r ϕϕ=⎧⎨=+⎩,(0r >,ϕ为参数),以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线1C 经过点π(2,)6P ,曲线2C 的极坐标方程为2(2cos 2)6ρθ+=.(1)求曲线1C 的极坐标方程;(2)若1(,)A ρα,2π(,)2B ρα+是曲线2C 上两点,求2211||||OA OB +的值.【解析】(1)将曲线1C 的参数方程cos 2sin x r y r ϕϕ=⎧⎨=+⎩,化为普通方程为222(2)x y r +-=,即222440x y y r +-+-=.由222x y ρ=+,sin y ρθ=,得曲线1C 的极坐标方程为224sin 40r ρρθ-+-=.由曲线1C 经过点π(2,6P ,则22π242sin4026r r -⨯⨯+-=⇒=(2r =-舍去),故曲线1C 的极坐标方程为4sin ρθ=.(2)由题意可知21(2cos 2)6ρα+=,2222π[2cos 2((2cos 2)62ραρα++=-=,所以22221211112cos 22cos 22||||663OA OB ααρρ+-+=+=+=.【练习3】在极坐标系中,曲线1C 的极坐标方程为4cos ρθ=,曲线2C 的极坐标方程为4sin ρθ=,以极点O 为坐标原点,极轴为x 的正半轴建立平面直角坐标系xOy .(1)求1C 和2C 的参数方程;(2)已知射线1:(0)2l πθαα=<<,将1l 逆时针旋转6π得到2:6l πθα=+,且1l 与1C 交于,O P 两点,2l 与2C 交于,O Q 两点,求OP OQ ⋅取得最大值时点P 的极坐标.【解析】(Ⅰ)在直角坐标系中,曲线1C 的直角坐标方程为()2224x y -+=所以1C 参数方程为22(2x cos y sin ααα=+⎧⎨=⎩为参数).曲线2C 的直角坐标方程为()2224x y +-=.所以2C 参数方程为2(22x cos y sin βββ=⎧⎨=+⎩为参数)(Ⅱ)设点P 极坐标为()1,ρα,即14cos ρα=,点Q 极坐标为2,6πρα⎛⎫+⎪⎝⎭,即24sin 6πρα⎛⎫=+ ⎪⎝⎭.则124cos 4sin 6OP OQ πρραα⎛⎫⋅==⋅+⎪⎝⎭3116cos sin cos 22ααα⎛⎫=⋅+ ⎪ ⎪⎝⎭8sin 246πα⎛⎫=++ ⎪⎝⎭70,.2,2666ππππαα⎛⎫⎛⎫∈∴+∈ ⎪ ⎪⎝⎭⎝⎭ 当2,626πππαα+==时OP OQ ⋅取最大值,此时P 点的极坐标为23,6π⎛⎫ ⎪⎝⎭.五、最值问题1.距离最值(点到点、曲线点到线、)距离的最值:---用“参数法”(1)曲线上的点到直线距离的最值问题(2)点与点的最值问题“参数法”:设点---套公式--三角辅助角①设点:设点的坐标,点的坐标用该点在所在曲线的的参数方程来设②套公式:利用点到线的距离公式③辅助角:利用三角函数辅助角公式进行化一2.面积的最值问题面积最值问题一般转化成弦长问题+点到线的最值问题例题【例1】在直角坐标系xOy 中,已知曲线1C 的方程为221106x y +=,曲线2C 的参数方程为1,2382x t y t ⎧=⎪⎪⎨⎪=--⎪⎩(t 为参数).(1)求1C 的参数方程和2C 的普通方程;(2)设点P 在1C 上,点Q 在2C 上,求PQ 的最小值.【解析】(1)由曲线1C 的方程为221106x y +=,得曲线1C的参数方程为,x y θθ⎧=⎪⎨=⎪⎩(θ为参数),由曲线2C 的参数方程为1,2382x t y t ⎧=⎪⎪⎨⎪=--⎪⎩(t 为参数),得曲线2C的普通方程为80y ++=.(2)设)P θθ,点P 到直线2C 的距离为d ,则PQ 的最小值即为d 的最小值,因为()6sin 82d θϕ++=,其中tan ϕ=当sin()1θϕ+=-时,d 的最小值为1,此时min 1PQ =.【例2】已知直线)(23211:为参数t ty t x l ⎪⎪⎩⎪⎪⎨⎧=+=,曲线)(sin cos :1为参数θθθ⎩⎨⎧==y x C .(1)设l 与1C 相交于B A ,两点,求||AB ;(2)若把曲线1C 上各点的横坐标压缩为原来的21倍,纵坐标压缩为原来的23倍,得到曲线2C ,设点P 是曲线2C 上的一个动点,求它到直线l 的距离的最小值.【解析】(1)l 的普通方程为1),1(3C x y -=的普通方程为.122=+y x联立方程组⎪⎩⎪⎨⎧=+-=,1),1(322y x x y 解得l 与1C 的交点为)0,1(A ,)23,21(-B ,则1||=AB .(2)2C 的参数方程为θθθ(.sin 23,cos 21⎪⎪⎩⎪⎪⎨⎧==y x 为参数).故点P 的坐标是)sin 23,cos 21(θθ,从而点P 到直线 的距离是]2)4sin(2[432|3sin 23cos 23|+-=--=πθθθd ,由此当1)4sin(-=-πθ时,d 取得最小值,且最小值为)12(46-.【例3】已知直线11: x t l y =+⎧⎪⎨⎪⎩(t为参数),曲线1cos : 2sin x C y θθ⎧=+⎪⎨=+⎪⎩(θ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立直角坐标系.(1)求曲线1C 的极坐标方程,直线1l 的普通方程;(2)把直线1l 向左平移一个单位得到直线2l ,设2l 与曲线1C 的交点为M ,N ,P 为曲线1C 上任意一点,求PMN △面积的最大值.【解析】(1)把曲线1cos : 2sin x C y θθ⎧=⎪⎨=+⎪⎩消去参数可得(()2221x y +-=,令cos x ρθ=,sin y ρθ=,代入可得曲线1C 的极坐标方程为2cos 4sin 60ρθρθ--+=.把直线11: x tl y =+⎧⎪⎨=⎪⎩化为普通方程)1y x -.(2)把直线1l 向左平移一个单位得到直线2l的方程为y =,其极坐标方程为π3θ=.联立2cos 4sin 60π3ρθρθθ⎧--+==⎪⎨⎪⎩所以260ρ-+=,所以12126ρρρρ⎧+=⎪⎨=⎪⎩,故12ρρ-==圆心到直线2l的距离为12d ==,圆上一点到直线2l 的最大距离为13122+=,所以PMN △面积的最大值为1333224S =⨯⨯.变式训练【练习1】已知点(,)P x y 是圆2220x y y +-=上的动点.(1)求2x y +的取值范围;(2)若0x y a ++≥恒成立,求实数a 的取值范围.解析(1)由圆的方程222x y y +=得()2211x y +-=,得[]()cos 0,21sin x y θθθπθ=⎧∈⎨=+⎩为参数,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《极坐标与参数方程》高考高频题型除了简单的极坐标与直角坐标的转化、参数方程与普通方程的转化外,还涉及(一)有关圆的题型题型一:圆与直线的位置关系(圆与直线的交点个数问题)----利用圆心到直线的距离与半径比较相离,无交点;:r d > 个交点;相切,1:r d = 个交点;相交,2:r d <用圆心(x 0,y 0)到直线Ax+By+C=0的距离2200BA C By Ax d +++=,算出d ,在与半径比较。
题型二:圆上的点到直线的最值问题(不求该点坐标,如果求该点坐标请参照距离最值求法)思路:第一步:利用圆心(x 0,y 0)到直线Ax+By+C=0的距离2200BA C By Ax d +++=第二步:判断直线与圆的位置关系第三步:相离:代入公式:r d d +=max ,r d d -=min 相切、相交:r d d +=max min 0d =题型三:直线与圆的弦长问题弦长公式222d r l -=,d 是圆心到直线的距离延伸:直线与圆锥曲线(包括圆、椭圆、双曲线、抛物线)的弦长问题 (弦长:直线与曲线相交两点,这两点之间的距离就是弦长) 弦长公式21t t l -=,解法参考“直线参数方程的几何意义”(二)距离的最值: ---用“参数法”1.曲线上的点到直线距离的最值问题2.点与点的最值问题“参数法”:设点---套公式--三角辅助角①设点: 设点的坐标,点的坐标用该点在所在曲线的的参数方程来设 ①套公式:利用点到线的距离公式①辅助角:利用三角函数辅助角公式进行化一例如:【2016高考新课标3理数】在直角坐标系中,曲线的参数方程为,以坐标原点为极点,以轴的正半轴为极轴,,建立极坐标系,曲线的极坐标方程为(I )写出的普通方程和的直角坐标方程;(II )设点在上,点在上,求的最小值及此时的直角坐标的直角坐标方程为.这里没有加减移项省去,直接化同,那系数除到左边(①)由题意,可设点的直角坐标为 因为是直线,所以的最小值即为到的距离的最小值,xOy 1C ()sin x y ααα⎧=⎪⎨=⎪⎩为参数x 2C sin()4ρθπ+=1C 2C P 1C Q 2C PQ P 2C 40x y +-=P ,sin )αα2C ||PQ P 2C ()d α.(欧萌说:利用点到直接的距离列式子,然后就是三角函数的辅助公式进行化一)当时)(13sin =+πα即当时,,此时的直角坐标为.(三)直线参数方程的几何意义1.经过点P (x 0,y 0),倾斜角为α的直线l 的参数方程为为参数)t t y y t x x (sin cos 00⎩⎨⎧+=+=αα若A ,B 为直线l 上两点,其对应的参数分别为t 1,t 2,线段AB 的中点为M ,点M 所对应的参数为t 0,则以下结论在解题中经常用到: (1)t 0=t 1+t 22; (2)|PM |=|t 0|=t 1+t 22; (3)|AB |=|t 2-t 1|; (4)|P A |·|PB |=|t 1·t 2|(5)⎪⎩⎪⎨⎧>+<-+=-=+=+0,0,4)(212121212212121t t t t t t t t t t t t t t PB PA 当当(注:记住常见的形式,P 是定点,A 、B 是直线与曲线的交点,P 、A 、B 三点在直线上) 【特别提醒】直线的参数方程中,参数t 的系数的平方和为1时,t 才有几何意义且其几何意义为:|t |是直线上任一点M (x ,y )到M 0(x 0,y 0)的距离,即|M 0M |=|t |.直线与圆锥曲线相交,交点对应的参数分别为12,t t ,则弦长12l t t =-; 2.解题思路第一步:曲线化成普通方程,直线化成参数方程()sin()2|3d παα==+-2()6k k Z παπ=+∈()d αP 31(,)22第二步:将直线的参数方程代入曲线的普通方程,整理成关于t 的一元二次方程:02=++c bt at第三步:韦达定理:a ct t a b t t =-=+2121,第四步:选择公式代入计算。
例如:已知直线l :⎩⎪⎨⎪⎧x =5+32t ,y =3+12t(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为ρ=2cos θ.(1)将曲线C 的极坐标方程化为直角坐标方程;(2)设点M 的直角坐标为(5,3),直线l 与曲线C 的交点为A ,B ,求|MA |·|MB |的值. 解 (1)ρ=2cos θ等价于ρ2=2ρcos θ.①将ρ2=x 2+y 2,ρcos θ=x 代入①即得曲线C 的直角坐标方程为x 2+y 2-2x =0.① (2)将⎩⎪⎨⎪⎧x =5+32t ,y =3+12t代入①式,得t 2+53t +18=0.设这个方程的两个实根分别为t 1,t 2,则由参数t 的几何意义即知,|MA |·|MB |=|t 1t 2|=18.(四)一直线与两曲线分别相交,求交点间的距离思路:一般采用直线极坐标与曲线极坐标联系方程求出2个交点的极坐标,利用极径相减即可。
例如:(2016•福建模拟)在直角坐标系xOy 中,曲线C 1的参数方程为(其中α为参数),曲线C 2:(x ﹣1)2+y 2=1,以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系. (①)求曲线C 1的普通方程和曲线C 2的极坐标方程; (①)若射线θ=(ρ>0)与曲线C 1,C 2分别交于A ,B 两点,求|AB|.解:(①)①曲线C1的参数方程为(其中α为参数),①曲线C1的普通方程为x2+(y﹣2)2=7.①曲线C2:(x﹣1)2+y2=1,①把x=ρcosθ,y=ρsinθ代入(x﹣1)2+y2=1,得到曲线C2的极坐标方程(ρcosθ﹣1)2+(ρsinθ)2=1,化简,得ρ=2cosθ.(①)依题意设A(),B(),①曲线C1的极坐标方程为ρ2﹣4ρsinθ﹣3=0,将(ρ>0)代入曲线C1的极坐标方程,得ρ2﹣2ρ﹣3=0,解得ρ1=3,同理,将(ρ>0)代入曲线C2的极坐标方程,得,∴|AB|=|ρ1﹣ρ2|=3﹣.(五)面积的最值问题面积最值问题一般转化成弦长问题+点到线的最值问题例题2016•包头校级二模)在平面直角坐标系xOy中,圆C的参数方程为,(t为参数),在以原点O为极点,x轴的非负半轴为极轴建立的极坐标系中,直线l的极坐标方程为,A,B两点的极坐标分别为.(1)求圆C的普通方程和直线l的直角坐标方程;(2)点P是圆C上任一点,求①PAB面积的最小值.解:(1)由,化简得:,消去参数t,得(x+5)2+(y﹣3)2=2,①圆C的普通方程为(x+5)2+(y﹣3)2=2.由ρcos(θ+)=﹣,化简得ρcosθ﹣ρsinθ=﹣,即ρcosθ﹣ρsinθ=﹣2,即x﹣y+2=0,则直线l的直角坐标方程为x﹣y+2=0;(①)将A(2,),B(2,π)化为直角坐标为A(0,2),B(﹣2,0),①|AB|==2,设P点的坐标为(﹣5+cost,3+sint),①P点到直线l的距离为d==,①d min==2,则①PAB面积的最小值是S=×2×2=4.极坐标与直角坐标、参数方程与普通方程的转化一、直角坐标的伸缩设点P(x ,y)是平面直角坐标系中的任意一点,在变换φ:⎩⎨⎧>='>=')()(0,0,μμλλy y x x 的作用下,点P(x ,y)对应到点P′(x′,y′),称φ为平面直角坐标系中的坐标伸缩变换,简称伸缩变换.平面图形的伸缩变换可以用坐标伸缩变换来表示.在伸缩变换⎩⎪⎨⎪⎧x′=λ·x ,λ>0y′=μ·y ,μ>0下,直线仍然变成直线,抛物线仍然变成抛物线,双曲线仍然变成双曲线,圆可以变成椭圆,椭圆也可以变成圆(重点考察). 【强化理解】1.曲线C 经过伸缩变换后,对应曲线的方程为:x 2+y 2=1,则曲线C 的方程为( )A .B .C .D .4x 2+9y 2=1【解答】解:曲线C 经过伸缩变换①后,对应曲线的方程为:x′2+y′2=1①,把①代入①得到:故选:A2、在同一直角坐标系中,求满足下列图形变换的伸缩变换:由曲线4x 2+9y 2=36变成曲线x ′2+y ′2=1.【解答】解:设变换为φ:⎩⎪⎨⎪⎧x ′=λx (λ>0),y ′=μy (μ>0),可将其代入x ′2+y ′2=1,得λ2x 2+μ2y 2=1.将4x 2+9y 2=36变形为x 29+y 24=1,比较系数得λ=13,μ=12.所以⎩⎪⎨⎪⎧x ′=13x ,y ′=12y .将椭圆4x 2+9y 2=36上的所有点的横坐标变为原来的13,纵坐标变为原来的12,可得到圆x ′2+y ′2=1.亦可利用配凑法将4x 2+9y 2=36化为⎝ ⎛⎭⎪⎫x 32+⎝ ⎛⎭⎪⎫y 22=1,与x ′2+y ′2=1对应项比较即可得⎩⎪⎨⎪⎧x ′=x3,y ′=y2.3、(2015春•浮山县校级期中)曲线x 2+y 2=1经过伸缩变换后,变成的曲线方程是( )A .25x 2+9y 2=1B .9x 2+25y 2=1C .25x+9y=1D .+=1【解答】解:由伸缩变换,化为,代入曲线x 2+y 2=1可得25(x′)2+9(y′)2=1,故选:A .二、极坐标 1.公式:(1)极坐标与直角坐标的互化公式如下表:2.极坐标与直角坐标的转化(1)点:有关点的极坐标与直角转化的思路 A :直角坐标化为极坐标的步骤①运用 ①在内由求时,由直角坐标的符号特征判断点所在的象限. B::极坐标化为直角坐标的步骤,运用(2)直线:直线的极坐标与直角坐标转化的思路 A :直角坐标转化成极坐标思路:直接利用公式,将式子里面的x 和y 用θρθρsin cos 和转化,最后整理化简即可。
例如:x+3y -2=0:用公式将x 和y 转化,即02-sin 3cos =+θρθρ B :极坐标转化成直角坐标类型①:直接转化---直接利用公式转化类型①:利用三角函数的两角和差公式,即()()2sin 2cos k kρθαρθα±=±=或思路:第一步:利用两角和差公式把sin(θ±α)或cosθ±α)化开,特殊角的正余弦值化成数字,整理化简(),x y (),ρθ()222tan 0x y yx x ρθ⎧=+⎪⎨=≠⎪⎩[)0,2π()tan 0yx xθ=≠θ(),ρθ(),x y cos sin x y ρθρθ=⎧⎨=⎩cos sin x y ρθρθ=⎧⎨=⎩第二步:利用公式转化解:第一步:利用两角和差公式把sin(θ±α)或cosθ±α)化开特殊角的正余弦值化成数字,整理化简,即第二步:第二步:利用公式转化类型①:角可以不是特殊角)为倾斜角,可以是特殊(ααθ=,该直线经过原点(极点),对应的直角坐标方程为kx x即y tanαy =⋅=(注:直线的直角坐标方程一般要求写成一般式:Ax+By+C=0) 三、曲线极坐标与直角坐标互换 (一)圆的直角与极坐标互换 1.圆的极坐标转化成直角坐标 类型一:θθρsin cos +=cos sin x y ρθρθ=⎧⎨=⎩cos sin x y ρθρθ=⎧⎨=⎩详解:一般θθsin ,cos 要转化成x 、y 都需要跟ρ搭配,一对一搭配。
