相对受压区高度
相对受压区高度
相对界限受压区高度ξb为了防止将构件设计成超筋构件,要求构件截面得相对受压区高度ξ不得超过其相对界限受压区高度ξb即(4—11) 相对界限受压区高度ξb就是适筋构件与超筋构件相对受压区高度得界限值,它需要根据截面平面变形等假定求出。
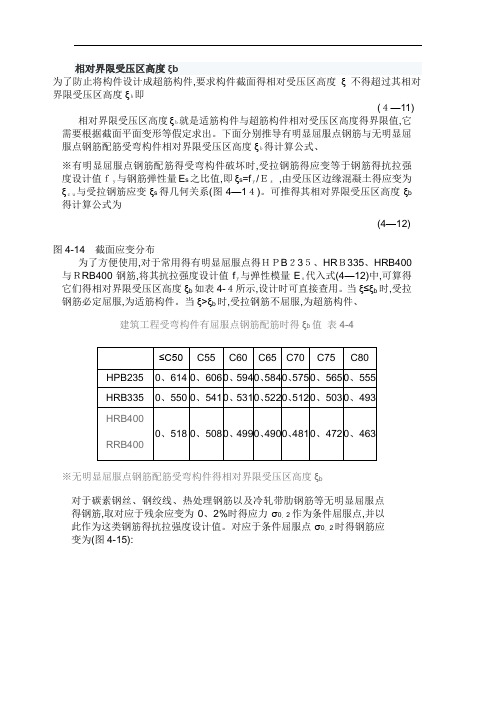
下面分别推导有明显屈服点钢筋与无明显屈服点钢筋配筋受弯构件相对界限受压区高度ξb得计算公式、※有明显屈服点钢筋配筋得受弯构件破坏时,受拉钢筋得应变等于钢筋得抗拉强度设计值fy与钢筋弹性量E s之比值,即ξs=fy/Es,由受压区边缘混凝土得应变为ξcu与受拉钢筋应变ξs得几何关系(图4—14)。
可推得其相对界限受压区高度ξb 得计算公式为(4—12)图4-14截面应变分布为了方便使用,对于常用得有明显屈服点得HPB235、HRB335、HRB400与RRB400钢筋,将其抗拉强度设计值fy与弹性模量Es代入式(4—12)中,可算得它们得相对界限受压区高度ξb如表4-4所示,设计时可直接查用。
当ξ≤ξb时,受拉钢筋必定屈服,为适筋构件。
当ξ>ξb时,受拉钢筋不屈服,为超筋构件、建筑工程受弯构件有屈服点钢筋配筋时得ξb值表4-4※无明显屈服点钢筋配筋受弯构件得相对界限受压区高度ξb对于碳素钢丝、钢绞线、热处理钢筋以及冷轧带肋钢筋等无明显屈服点得钢筋,取对应于残余应变为0、2%时得应力σ0、2作为条件屈服点,并以此作为这类钢筋得抗拉强度设计值。
对应于条件屈服点σ0、2时得钢筋应变为(图4-15):图4-15 无明显屈服点钢筋得应力—应变曲线(4-13)式中 f y ——无明显屈服点钢筋得抗拉强度设计值;E s ——无明显屈服点钢筋得弹性模量。
根据截面平面变形等假设,可以求得无明显屈服点钢筋受弯构件相对界限受压区高度ξb 得计算公式为:(4-14)截面相对受压区高度ξ与截面配筋率ρ之间存在对应关系。
ξb 求出后,可以求出适筋受弯构件截面最大配筋率得计算公式。
由式(4-8)可写出: (4-15)(4-16)式(4-16)即为受弯构件最大配筋率得计算公式。
相对界限受压区高度
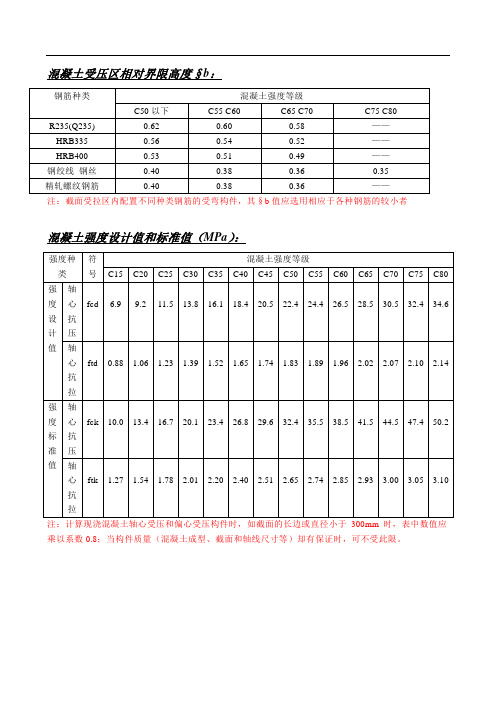
混凝土受压区相对界限高度§b:注:截面受拉区内配置不同种类钢筋的受弯构件,其§b值应选用相应于各种钢筋的较小者混凝土强度设计值和标准值(MPa):注:计算现浇混凝土轴心受压和偏心受压构件时,如截面的长边或直径小于300mm时,表中数值应乘以系数0.8;当构件质量(混凝土成型、截面和轴线尺寸等)却有保证时,可不受此限。
普通钢筋强度标准值和设计值(MPa)注:1、表中d系指国家标准中的钢筋公称直径,单位mm;2、钢筋混凝土轴心受拉和小偏心受拉设计值大于330MPa时,仍按330MPa取用;3、构件中配有不同种类钢筋时,每种钢筋应采用各自的强度设计值。
预应力钢筋抗拉强度标准值(MPa)注:表中d系指国家标准中钢绞线、钢丝和精轧螺纹钢筋的公称直径,单位mm预应力钢筋抗拉、抗压强度设计值(MPa)混凝土的弹性模量Ec(MPa)钢筋的弹性模量Es(MPa)侍中、侍郎郭攸之、费祎、董允等,此皆良实,志虑忠纯,是以先帝简拔以遗陛下:愚以为宫中之事,事无大小,悉以咨之,然后施行,必能裨补阙漏,有所广益。
将军向宠,性行淑均,晓畅军事,试用于昔日,先帝称之曰“能”,是以众议举宠为督:愚以为营中之事,悉以咨之,必能使行阵和睦,优劣得所。
亲贤臣,远小人,此先汉所以兴隆也;亲小人,远贤臣,此后汉所以倾颓也。
先帝在时,每与臣论此事,未尝不叹息痛恨于桓、灵也。
侍中、尚书、长史、参军,此悉贞良死节之臣,愿陛下亲之、信之,则汉室之隆,可计日而待也。
臣本布衣,躬耕于南阳,苟全性命于乱世,不求闻达于诸侯。
先帝不以臣卑鄙,猥自枉屈,三顾臣于草庐之中,咨臣以当世之事,由是感激,遂许先帝以驱驰。
后值倾覆,受任于败军之际,奉命于危难之间,尔来二十有一年矣。
先帝知臣谨慎,故临崩寄臣以大事也。
受命以来,夙夜忧叹,恐托付不效,以伤先帝之明;故五月渡泸,深入不毛。
今南方已定,兵甲已足,当奖率三军,北定中原,庶竭驽钝,攘除奸凶,兴复汉室,还于旧都。
相对受压区高度计算

相对受压区高度计算相对受压区高度是指在建筑物或结构物中受到压力的区域的高度。
在工程设计和施工中,准确计算相对受压区高度是至关重要的,它直接关系到结构的稳定性和安全性。
一般来说,相对受压区高度受到以下几个因素的影响:1. 荷载:荷载是建筑物或结构物所承受的外部力量,包括自重、活载和风载等。
荷载的大小和分布方式会直接影响相对受压区高度的计算。
在设计中,需要根据具体的荷载标准和工程要求进行合理的荷载计算。
2. 结构形式:不同的结构形式对相对受压区高度的计算也有影响。
比如,在柱子支撑下的梁的受压区高度与柱子的高度和尺寸有关。
而在墙体结构中,相对受压区高度则与墙体的高度和厚度有关。
3. 材料特性:建筑材料的强度和稳定性对相对受压区高度的计算也有重要影响。
不同的材料具有不同的抗压能力,需要根据材料的特性来确定相对受压区高度。
在实际的工程计算中,一般采用强度理论来计算相对受压区高度。
常用的强度理论包括极限平衡法、极限设计法和变形极限法等。
这些方法是根据结构的强度和稳定性原理来计算相对受压区高度的。
在进行相对受压区高度计算时,需要考虑结构的整体稳定性和局部稳定性。
整体稳定性指的是结构整体的抗倾覆和抗滑移能力,而局部稳定性指的是结构局部部位的抗压能力。
在设计中,需要兼顾结构的整体和局部稳定性,保证结构的安全可靠。
除了考虑结构的稳定性和荷载情况外,还需要考虑结构的使用要求和工程经济性。
相对受压区高度的计算需要满足结构的使用要求,同时也要尽量减少材料的使用量,以提高工程的经济性。
相对受压区高度的计算是建筑物或结构物设计中的重要一环。
通过合理的荷载计算、结构形式选择和材料特性考虑,可以准确计算出相对受压区高度,确保结构的稳定性和安全性。
同时,还需要兼顾结构的使用要求和工程经济性,以实现结构设计的最优化。
相对受压区高度

相对界限受压区高度E b为了防止将构件设计成超筋构件,要求构件截面的相对受压区高度E不得超过其相对界限受压区高度E即―(4-11)相对界限受压区高度E是适筋构件与超筋构件相对受压区高度的界限值,它需要根据截面平面变形等假定求出。
下面分别推导有明显屈服点钢筋和无明显屈服点钢筋配筋受弯构件相对界限受压区高度也的计算公式。
※有明显屈服点钢筋配筋的受弯构件破坏时,受拉钢筋的应变等于钢筋的抗拉强度设计值f y 与钢筋弹性量E s之比值,即$=f y/E s ,由受压区边缘混凝土的应变为E u与受拉钢筋应变E的几何关系(图4-14 )。
可推得其相对界限受压区高度也的计算公式为■1■ I -丄 -■'(4—12)图4-14截面应变分布为了方便使用,对于常用的有明显屈服点的HPB235、HRB335、HRB400和RRB400钢筋,将其抗拉强度设计值f y和弹性模量E s代入式(4-12)中,可算得它们的相对界限受压区高度E如表4-4所示,设计时可直接查用。
当EW E 时,受拉钢筋必定屈服,为适筋构件。
当E >E寸,受拉钢筋不屈服,为超筋构件。
建筑工程受弯构件有屈服点钢筋配筋时的也值表4-4※无明显屈服点钢筋配筋受弯构件的相对界限受压区高度对于碳素钢丝、钢绞线、热处理钢筋以及冷轧带肋钢筋等无明显屈服点的钢筋,取对应于残余应变为0.2%时的应力OQ.2作为条件屈服点,并以此作为这类钢筋的抗拉强度设计值。
对应于条件屈服点O0.2时的钢筋应变为(图4-15):.■ = - V;1 .■- = I H" ■:T (4- 13)式中f y――无明显屈服点钢筋的抗拉强度设计值;E s ――无明显屈服点钢筋的弹性模量。
根据截面平面变形等假设,可以求得无明显屈服点钢筋受弯构件相对界限受压区高度也的计算公式为:(4 —14)截面相对受压区高度E与截面配筋率p之间存在对应关系。
$求出后, 可以求出适筋受弯构件截面最大配筋率的计算公式。
相对界限受压区高度
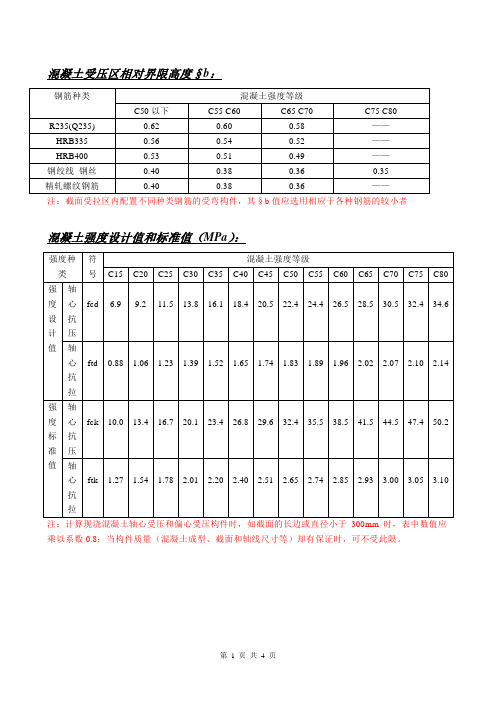
混凝土受压区相对界限高度§b:
注:截面受拉区内配置不同种类钢筋的受弯构件,其§b值应选用相应于各种钢筋的较小者
混凝土强度设计值和标准值(MPa):
注:计算现浇混凝土轴心受压和偏心受压构件时,如截面的长边或直径小于300mm时,表中数值应乘以系数0.8;当构件质量(混凝土成型、截面和轴线尺寸等)却有保证时,可不受此限。
普通钢筋强度标准值和设计值(MPa)
注:1、表中d系指国家标准中的钢筋公称直径,单位mm;
2、钢筋混凝土轴心受拉和小偏心受拉设计值大于330MPa时,仍按330MPa取用;
3、构件中配有不同种类钢筋时,每种钢筋应采用各自的强度设计值。
预应力钢筋抗拉强度标准值(MPa)
注:表中d系指国家标准中钢绞线、钢丝和精轧螺纹钢筋的公称直径,单位mm
预应力钢筋抗拉、抗压强度设计值(MPa)
混凝土的弹性模量Ec(MPa)
钢筋的弹性模量Es(MPa)
注:红色为预应力钢筋弹性模量。
相对界限受压区高度名词解释-概述说明以及解释

相对界限受压区高度名词解释-概述说明以及解释1.引言1.1 概述在概述部分,我们将介绍相对界限受压区高度这一概念的背景和意义。
相对界限受压区高度是指在地下开挖过程中,地下水位对土体稳定性产生影响的一种参数。
在地下工程中,了解和控制相对界限受压区高度是非常重要的,它可以帮助工程师有效地设计和施工,以确保工程的安全性和稳定性。
本文将从定义、影响因素和重要性三个方面对相对界限受压区高度进行深入探讨,希望能够为相关领域的研究和实践提供有益的参考。
1.2 文章结构文章结构部分主要包括以下内容:第一部分是引言部分,其中包括概述、文章结构和目的三个小节。
在概述部分,会简要介绍相对界限受压区高度的概念,并引出接下来要探讨的内容。
在文章结构部分,会说明本文的章节安排和主要内容分布情况,为读者提供整体框架。
在目的部分,会明确本文的写作目的和研究价值,提出文章的理论意义或实践意义。
第二部分是正文部分,其中包括相对界限受压区的定义、影响因素和重要性三个小节。
在相对界限受压区的定义部分,会对相对界限受压区进行解释和界定,明确其概念和范围。
在影响因素部分,会分析影响相对界限受压区高度的各种因素,例如地质构造、岩性特征、地表形态等。
在重要性部分,会说明相对界限受压区高度对地质灾害防治、城市规划等方面的重要性和意义。
第三部分是结论部分,其中包括总结、展望和结论三个小节。
在总结部分,会对本文所述内容进行概括和总结,归纳出主要观点和结论。
在展望部分,会对今后研究方向和深入研究的重点进行展望和设想。
在结论部分,会对全文进行总结,强调研究成果和实践意义。
1.3 目的本文旨在探讨相对界限受压区高度的概念,分析其定义、影响因素以及重要性。
通过对该概念的深入探讨,旨在帮助读者更好地理解和应用相对界限受压区高度的概念,同时也为相关研究和实践提供理论支持和指导。
同时,通过对这一概念的分析,我们也可以更好地了解受压区高度对于人类活动和环境保护的重要性,为相关政策和规划提供科学依据。
相对受压区高度计算公式

相对受压区高度计算公式
相对受压区高度计算公式:D=x/h0。
相对受压区高度:受压区高度X与梁截面有效高度h0的比值,即x/h0。
界限相对受压区高度:受拉钢筋和受压区混凝土同时达到其强度设计值时的混凝土受压区高度与截面有效高度的比值。
混凝土,简称为“砼(tóng)”:是指由胶凝材料将集料胶结成整体的工程复合材料的统称。
通常讲的混凝土一词是指用水泥作胶凝材料,砂、石作集料;与水(可含外加剂和掺合料)按一定比例配合,经搅拌而得的水泥混凝土,也称普通混凝土,它广泛应用于土木工程。
相对受压区高度

相对界限受压区高度ξb为了防止将构件设计成超筋构件,要求构件截面的相对受压区高度ξ不得超过其相对界限受压区高度ξb即(4-11) 相对界限受压区高度ξb就是适筋构件与超筋构件相对受压区高度的界限值,它需要根据截面平面变形等假定求出。
下面分别推导有明显屈服点钢筋与无明显屈服点钢筋配筋受弯构件相对界限受压区高度ξb的计算公式。
※有明显屈服点钢筋配筋的受弯构件破坏时,受拉钢筋的应变等于钢筋的抗拉强度设计值f y与钢筋弹性量E s之比值,即ξs=f y/E s ,由受压区边缘混凝土的应变为ξcu与受拉钢筋应变ξs的几何关系(图4-14)。
可推得其相对界限受压区高度ξb的计算公式为(4-12)图4-14 截面应变分布为了方便使用,对于常用的有明显屈服点的HPB235、HRB335、HRB400与RRB400钢筋,将其抗拉强度设计值f y与弹性模量E s代入式(4-12)中,可算得它们的相对界限受压区高度ξb如表4-4所示,设计时可直接查用。
当ξ≤ξb时,受拉钢筋必定屈服,为适筋构件。
当ξ>ξb时,受拉钢筋不屈服,为超筋构件。
建筑工程受弯构件有屈服点钢筋配筋时的ξb值表4-4≤C50C55 C60 C65 C70 C75 C80HPB235 0、614 0、606 0、594 0、584 0、575 0、565 0、555HRB335 0、550 0、541 0、531 0、522 0、512 0、503 0、493HRB400RRB4000、518 0、508 0、499 0、490 0、481 0、472 0、463※无明显屈服点钢筋配筋受弯构件的相对界限受压区高度ξb对于碳素钢丝、钢绞线、热处理钢筋以及冷轧带肋钢筋等无明显屈服点作为条件屈服点,并以的钢筋,取对应于残余应变为0、2%时的应力σ0、2时的钢筋应此作为这类钢筋的抗拉强度设计值。
对应于条件屈服点σ0、24-15):变为(图图4-15 无明显屈服点钢筋的应力—应变曲线(4-13) 式中f y——无明显屈服点钢筋的抗拉强度设计值;E s——无明显屈服点钢筋的弹性模量。
相对受压区高度[整理版]
![相对受压区高度[整理版]](https://img.taocdn.com/s3/m/69d609806aec0975f46527d3240c844769eaa0fb.png)
为了防止将构件设计成超筋构件,要求构件截面的相对受压区高度ξ不得超过其相对界限受压区高度ξb 即(4-11) 相对界限受压区高度ξb 是适筋构件与超筋构件相对受压区高度的界限值,它需要根据截面平面变形等假定求出。
下面分别推导有明显屈服点钢筋和无明显屈服点钢筋配筋受弯构件相对界限受压区高度ξb 的计算公式。
※有明显屈服点钢筋配筋的受弯构件破坏时,受拉钢筋的应变等于钢筋的抗拉强度设计值f y 与钢筋弹性量E s 之比值,即ξs =f y /E s ,由受压区边缘混凝土的应变为ξcu 与受拉钢筋应变ξs 的几何关系(图4-14)。
可推得其相对界限受压区高度ξb 的计算公式为(4-12)图4-14 截面应变分布为了方便使用,对于常用的有明显屈服点的HPB235、HRB335、HRB400和RRB400钢筋,将其抗拉强度设计值f y 和弹性模量E s 代入式(4-12)中,可算得它们的相对界限受压区高度ξb 如表4-4所示,设计时可直接查用。
当ξ≤ξb 时,受拉钢筋必定屈服,为适筋构件。
当ξ>ξb 时,受拉钢筋不屈服,为超筋构件。
建筑工程受弯构件有屈服点钢筋配筋时的ξb 值 表4-4※无明显屈服点钢筋配筋受弯构件的相对界限受压区高度ξb对于碳素钢丝、钢绞线、热处理钢筋以及冷轧带肋钢筋等无明显屈服点的钢筋,取对应于残余应变为0.2%时的应力σ0.2作为条件屈服点,并以此作为这类钢筋的抗拉强度设计值。
对应于条件屈服点σ0.2时的钢筋应变为(图4-15):图4-15 无明显屈服点钢筋的应力—应变曲线(4-13)式中f y——无明显屈服点钢筋的抗拉强度设计值;E s——无明显屈服点钢筋的弹性模量。
根据截面平面变形等假设,可以求得无明显屈服点钢筋受弯构件相对界限受压区高度ξb的计算公式为:(4-14) 截面相对受压区高度ξ与截面配筋率ρ之间存在对应关系。
ξb求出后,可以求出适筋受弯构件截面最大配筋率的计算公式。
界限相对受压区高度名词解释

界限相对受压区高度名词解释
界限相对受压区高度是指混凝土构件中,纵向受拉钢筋屈服时,受压区混凝土达到其极限压应变时的高度与截面有效高度的比值。
这个比值是判断混凝土构件是否达到破坏状态的一个重要参数。
在混凝土构件中,由于混凝土和钢筋的弹性模量不同,所以在受力过程中,它们的变形程度也不同。
当纵向受拉钢筋屈服时,受压区混凝土可能还没有达到其极限压应变,这时,如果继续加载,混凝土就会发生破坏。
因此,我们需要控制受压区混凝土的高度,使其不会超过界限相对受压区高度。
界限相对受压区高度的大小直接影响到混凝土构件的承载能力和延性。
如果界限相对受压区高度过大,那么混凝土构件的承载能力就会降低,延性也会变差;反之,如果界限相对受压区高度过小,那么混凝土构件的承载能力就会提高,延性也会变好。
界限相对受压区高度是一个反映混凝土构件受力性能的重要参数,它的大小直接影响到混凝土构件的承载能力和延性。
在实际工程中,我们需要根据具体的设计要求和施工条件,合理确定界限相对受压区高度的值,以保证混凝土构件的安全和稳定。
相对界限受压区高度ξb

相对界限受压区高度ξb 的意义与计算方法北京龙安华诚建筑设计有限公司兰州分公司 刘克涛为了防止将构件设计成超筋构件,要求构件截面的相对受压区高度ξ不得超过其相 对界限受压区高度ξb 即(4-11) 相对界限受压区高度ξb 是适筋构件与超筋构件相对受压区高度的界限值, 它需要根据截面平面变形等假定求出。
下面分别推导有明显屈服点钢筋和无明 显屈服点钢筋配筋受弯构件相对界限受压区高度ξb 的计算公式。
※有明显屈服点钢筋配筋的受弯构件破坏时,受拉钢筋的应变等于钢筋的抗拉 强度设计值 fy 与钢筋弹性量 Es 之比值,即ξs=fy/Es ,由受压区边缘混凝土的 应变为ξcu 与受拉钢筋应变ξs 的几何关系(图 4-14)。
可推得其相对界限受压 区高度ξb 的计算公式为(4-12)图 4-14 截面应变分布 为了方便使用,对于常用的有明显屈服点的 HPB235、HRB335、HRB400 和RRB400 钢筋,将其抗拉强度设计值 fy 和弹性模量 Es 代入式(4-12)中,可算 得它们的相对界限受压区高度ξb 如表 4-4 所示,设计时可直接查用。
当ξ≤ξ b 时,受拉钢筋必定屈服,为适筋构件。
当ξ>ξb 时,受拉钢筋不屈服,为超筋 构件。
建筑工程受弯构件有屈服点钢筋配筋时的ξb 值 表 4-4HPB235 HRB335 HRB400≤C50 C55 C60 C65 C70 C75 C80 0.614 0.606 0.594 0.584 0.575 0.565 0.555 0.550 0.541 0.531 0.522 0.512 0.503 0.493 0.518 0.508 0.499 0.490 0.481 0.472 0.463Create PDF files without this message by purchasing novaPDF printer ()RRB400※无明显屈服点钢筋配筋受弯构件的相对界限受压区高度ξb 对于碳素钢丝、钢绞线、热处理钢筋以及冷轧带肋钢筋等无明显屈服点的 钢筋,取对应于残余应变为 0.2%时的应力σ0.2 作为条件屈服点,并以此作 为这类钢筋的抗拉强度设计值。
相对受压区高度名词解释

相对受压区高度名词解释
相对受压区高度是指在土木工程中,指土体或石体受到外部荷载作用时,产生的压缩变形导致形成的压力区域在垂直方向上的高度。
在土体工程中,相对受压区高度是一个重要的参数,它与土体的力学性质、承载力、变形特性等密切相关。
相对受压区高度的大小直接影响着土体的稳定性和安全性。
相对受压区高度的计算需要考虑土体的力学性质、荷载的性质和大小、土体的水分含量等因素。
一般来说,相对受压区高度与荷载的大小成正比,与土体的强度参数(如抗压强度、抗剪强度)成反比。
在土木工程设计中,合理估计相对受压区高度对于确定土体的稳定性和承载能力至关重要。
如果相对受压区高度过大,会导致土体的承载能力不足,可能引起结构的沉降或破坏;相反,如果相对受压区高度过小,会导致土体的稳定性不足,可能引起结构的倾斜或失稳。
因此,在土木工程设计中,必须根据具体情况合理估计相对受压区高度,并在设计中采取相应的措施,以确保土体的稳定性和结构的安全性。
相对界限受压区高度
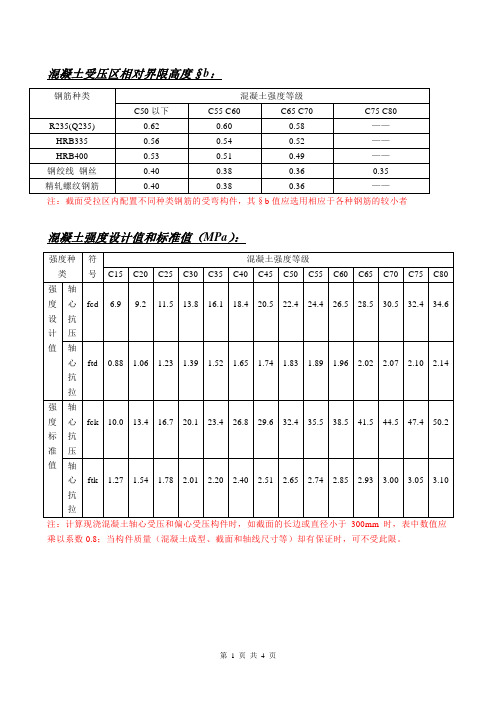
混凝土受压区相对界限高度§b:
注:截面受拉区内配置不同种类钢筋的受弯构件,其§b值应选用相应于各种钢筋的较小者
混凝土强度设计值和标准值(MPa):
注:计算现浇混凝土轴心受压和偏心受压构件时,如截面的长边或直径小于300mm时,表中数值应乘以系数0.8;当构件质量(混凝土成型、截面和轴线尺寸等)却有保证时,可不受此限。
普通钢筋强度标准值和设计值(MPa)
注:1、表中d系指国家标准中的钢筋公称直径,单位mm;
2、钢筋混凝土轴心受拉和小偏心受拉设计值大于330MPa时,仍按330MPa取用;
3、构件中配有不同种类钢筋时,每种钢筋应采用各自的强度设计值。
预应力钢筋抗拉强度标准值(MPa)
注:表中d系指国家标准中钢绞线、钢丝和精轧螺纹钢筋的公称直径,单位mm
预应力钢筋抗拉、抗压强度设计值(MPa)
混凝土的弹性模量Ec(MPa)
钢筋的弹性模量Es(MPa)
注:红色为预应力钢筋弹性模量。
相对受压区高度计算 excel

相对受压区高度计算excel在工程设计和结构分析中,相对受压区高度是一个非常重要的参数。
它是指受压构件中混凝土与受压钢筋之间的有效受压区域的高度。
准确计算相对受压区高度对于确保结构的安全性和稳定性至关重要。
在这篇文章中,我们将探讨如何使用Excel来计算相对受压区高度,并对这个主题进行深入的探讨和分析。
1. 相对受压区高度的定义相对受压区高度是指受压构件中混凝土和受压钢筋共同工作的有效受压区域的高度。
在混凝土受压构件中,混凝土和受压钢筋共同承担受压作用,相对受压区高度的大小直接影响着受压构件的承载能力和受力性能。
准确计算相对受压区高度对于结构设计和分析至关重要。
2. 相对受压区高度的计算公式在混凝土结构设计中,常用的相对受压区高度计算公式为:hd = a1 * beta1 * xu其中,hd为相对受压区高度,a1为受压区深度的修正系数,beta1为混凝土的抗压强度折减系数,xu为混凝土的抗压区高度。
3. 如何使用Excel计算相对受压区高度在Excel中,我们可以利用公式和函数来快速、准确地计算相对受压区高度。
我们可以将上述的相对受压区高度计算公式转化为Excel的计算表达式。
我们可以利用单元格引用和单元格间的运算符来实现对相对受压区高度的计算。
通过这种方式,我们不仅可以方便地进行计算,还可以通过调整输入参数和公式来快速得到不同情况下的相对受压区高度。
4. 相对受压区高度的影响因素在实际工程中,影响相对受压区高度的因素有很多。
受混凝土本身的性能和受压钢筋的数量和布置方式会直接影响相对受压区高度的大小。
外部荷载的大小和作用方式也会对相对受压区高度产生影响。
在进行相对受压区高度计算时,需要综合考虑材料性能、结构形式和外部荷载等因素的影响。
5. 结论通过本文的讨论和分析,我们深入探讨了相对受压区高度的计算方法,以及这个主题的相关内容。
通过使用Excel来计算相对受压区高度,我们可以更加方便、快捷地进行结构设计和分析。
相对受压区高度讲解学习

相对受压区高度相对界限受压区高度ξb为了防止将构件设计成超筋构件,要求构件截面的相对受压区高度ξ不得超过其相对界限受压区高度ξb即(4-11) 相对界限受压区高度ξb是适筋构件与超筋构件相对受压区高度的界限值,它需要根据截面平面变形等假定求出。
下面分别推导有明显屈服点钢筋和无明显屈服点钢筋配筋受弯构件相对界限受压区高度ξb的计算公式。
※有明显屈服点钢筋配筋的受弯构件破坏时,受拉钢筋的应变等于钢筋的抗拉强度设计值f y与钢筋弹性量E s之比值,即ξs=f y/E s ,由受压区边缘混凝土的应变为ξcu与受拉钢筋应变ξs的几何关系(图4-14)。
可推得其相对界限受压区高度ξb的计算公式为(4-12) 图4-14 截面应变分布为了方便使用,对于常用的有明显屈服点的HPB235、HRB335、HRB400和RRB400钢筋,将其抗拉强度设计值f y和弹性模量E s代入式(4-12)中,可算得它们的相对界限受压区高度ξb如表4-4所示,设计时可直接查用。
当ξ≤ξb 时,受拉钢筋必定屈服,为适筋构件。
当ξ>ξb时,受拉钢筋不屈服,为超筋构件。
建筑工程受弯构件有屈服点钢筋配筋时的ξb值表4-4≤C50C55 C60 C65 C70 C75 C80HPB235 0.614 0.606 0.594 0.584 0.575 0.565 0.555HRB335 0.550 0.541 0.531 0.522 0.512 0.503 0.493HRB4000.518 0.508 0.499 0.490 0.481 0.472 0.463RRB400※无明显屈服点钢筋配筋受弯构件的相对界限受压区高度ξb对于碳素钢丝、钢绞线、热处理钢筋以及冷轧带肋钢筋等无明显屈服点的钢筋,取对应于残余应变为0.2%时的应力σ0.2作为条件屈服点,并以此作为这类钢筋的抗拉强度设计值。
对应于条件屈服点σ0.2时的钢筋应变为(图4-15):图4-15 无明显屈服点钢筋的应力—应变曲线(4-13) 式中 f y——无明显屈服点钢筋的抗拉强度设计值;E s——无明显屈服点钢筋的弹性模量。
相对受压区高度符号

相对受压区高度符号
相对受压区高度符号:ξ
ζ这个符号在混凝土内力计算中,代表截面的相对受压区高度,这是材料力学中一个比较专业的概念。
用比较通俗的语言来解释,就是在杆件受弯的时候,其横截面(假设为矩形)一部分受压,一部分受拉。
在钢筋混凝土结构中,拉力由钢筋承担,压力则主要由混凝土承担。
这个ζ,就是截面上承担压力的那部分混凝土,占截面总混凝土量的比例大小。
所以ζ是个比值,没有单位。
ζ是衡量混凝土杆件最大承载力的重要指标,当其超过一定的限值时,这个杆件可能会在钢筋未拉屈之前就使得混凝土压碎,从而造成脆性破坏,在设计上这是不允许的。
这个限值称为界限相对受压区高度,符号为ζb。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相对界限受压区高度ξb
为了防止将构件设计成超筋构件,要求构件截面的相对受压区高度ξ不得超过其相对界限受压区高度ξb即
(4-11) 相对界限受压区高度ξb是适筋构件与超筋构件相对受压区高度的界限值,它需要根据截面平面变形等假定求出。
下面分别推导有明显屈服点钢筋和无明显屈服点钢筋配筋受弯构件相对界限受压区高度ξb的计算公式。
※有明显屈服点钢筋配筋的受弯构件破坏时,受拉钢筋的应变等于钢筋的抗拉强度设计值f y与钢筋弹性量E s之比值,即ξs=f y/E s,由受压区边缘混凝土的应变为
ξcu与受拉钢筋应变ξs的几何关系(图
4-14)。
可推得其相对界限受压区高度ξb
的计算公式为
(4-12)
图4-14 截面应变分布
为了方便使用,对于常用的有明显屈服点的HPB235、HRB335、HRB400和RRB400钢筋,将其抗拉强度设计值f y和弹性模量E s代入式(4-12)中,可算得它们的相对界限受压区高度ξb如表4-4所示,设计时可直接查用。
当ξ≤ξb 时,受拉钢筋必定屈服,为适筋构件。
当ξ>ξb时,受拉钢筋不屈服,为超筋构件。
建筑工程受弯构件有屈服点钢筋配筋时的ξb值表4-4
≤C50C55 C60 C65 C70 C75 C80
HPB235 0.614 0.606 0.594 0.584 0.575 0.565 0.555
HRB335 0.550 0.541 0.531 0.522 0.512 0.503 0.493
HRB400
RRB400
0.518 0.508 0.499 0.490 0.481 0.472 0.463
※无明显屈服点钢筋配筋受弯构件的相对界限受压区高度ξb
对于碳素钢丝、钢绞线、热处理钢筋以及冷轧带肋钢筋等无明显屈服点的钢筋,取对应于残余应变为0.2%时的应力σ0.2作为条件屈服点,并以此作为这类钢筋的抗拉强度设计值。
对应于条件屈服点σ0.2时的钢筋应变为(图4-15):
图4-15 无明显屈服点钢筋的应力—应变曲线
(4-13)
式中f y——无明显屈服点钢筋的抗拉强度设计值;
E s——无明显屈服点钢筋的弹性模量。
根据截面平面变形等假设,可以求得无明显屈服点钢筋受弯构件相对界限受压区高度ξb的计算公式为:
(4-14) 截面相对受压区高度ξ与截面配筋率ρ之间存在对应关系。
ξb求出后,可以求出适筋受弯构件截面最大配筋率的计算公式。
由式(4-8)可写出:
(4-15)
(4-16)
式(4-16)即为受弯构件最大配筋率的计算公式。
为了使用上的方便
起见,将常用的具有明显屈服点钢筋配筋的普通钢筋混凝土受弯构件的最大配筋率ρmax列在表4-5中。
建筑工程受弯构件的截面最大配筋率ρmax(%)表4-5
钢筋等级
混凝土的强度等级
C15 C20 C25 C30 C35 C40 C45 C50 C55 C60 C65 C70 C75 C80
HPB235 2.10 2.81 3.48 4.18 4.88 5.58 6.19 6.75 7.23 7.62 8.01 8.36 8.64 8.92 HRB335 1.32 1.76 2.18 2.62 3.07 3.51 3.89 4.24 4.52 4.77 5.01 5.21 5.38 5.55 HRB400
RRB400
1.03 1.38 1.71
2.06 2.40 2.74
3.05 3.32 3.53 3.74 3.92
4.08 4.21 4.34
当构件按最大配筋率配筋时,由(4-9a)可以求出适筋受弯构件所能承受的最大弯矩为:
(4-17)
式中αsb——截面最大的抵抗矩系数,αsb=ξb(1-ξb/2) 。
对于具有明显屈服点钢筋配筋的受弯构件,其截面最大的抵抗矩系数见表4-6。
建筑工程受弯构件截面最大的抵抗矩系数αsb表4-6
钢筋种类≤C50C55 C60 C65 C70 C75 C80
HPB235 0.4255 0.4224 0.4176 0.4135 0.4096 0.4054 0.4010
HRB335 0.3988 0.3947 0.3900 0.3858 0.3809 0.3765 0.3715
HRB400
RRB400
0.3838 0.3790 0.3745 0.3700 0.3653 0.3606 0.3558
(4-11)进行控制,也可以用:
(4-18)
(4-19)
进行控制。
式(4-11 )、式(4-18)和式(4-19)对应于同一配筋和受力状况,因而三者是等效的。
设计经验表明,当梁、板的配筋率为:
实心板: ρ=0.4%~0.8%
矩形梁: ρ=0.6%~1.5%
T形梁: ρ=0.9%~1.8%
时,构件的用钢量和造价都较经济,施工比较方便,受力性能也比较好。
因此,常将梁、板的配筋率设计在上述范围之内。
梁、板的上述配筋率称为常用配筋率,也有人称它们为经济配筋率。
由于不考虑混凝土抵抗拉力的作用,因此,只要受压区为矩形而受拉区为其它形状的受弯构件(如倒T形受弯构件),均可按矩形截面计算。
