浙教版初中数学八年级上册认识三角形(基础)知识讲解
浙教版数学-八年级上册-第一章《三角形初步知识》

【错题重现1】【错题重现2】【错题重现3】【错题重现4】【错题重现5】【错题重现6】【错题重现7】【错题重现8】B ′C ′A ′CBA第一章《三角形的初步认识》2:知识点1:全等图形的概念和全等三角形的性质1、全等图形:能够重合的图形称为全等图形。
2、举出生活中的一些全等图形的例子。
3、全等三角形:能够重合的两个三角形叫做全等三角形。
4、全等三角形的相关概念:两个全等三角形重合时,互相重合的顶点叫做全等三角形的对应顶点; 互相重合的边叫做全等三角形的对应边;互相重合的角叫做全等三角形的对应角。
记作:全等的符号为“≌”。
例如:如图,△ABC 与△A ′B ′C ′全等,记作△ABC ≌△A ′B ′C ′, 对应顶点为:点A 与点A ′,点B 与点B ′,点C 与点C ′;对应边为:AB 与A ′B ′,AC 与A ′C ′,BC 与B ′C ′; 对应角为:∠A 与∠A ′,∠B 与∠B ′,∠C 与∠C ′。
注意:记全等三角形时,应将对应顶点的字母写在对应的位置上。
5、全等三角形的性质:全等三角形的对应边相等,对应角相等。
几何语言:如上图:∵ △ABC ≌△A ′B ′C ′∴ AB=A ′B ′,AC=A ′C ′,BC=B ′C ′, ∠A=∠A ′,∠B=∠B ′,∠C=∠C ′【典型例题】【例】如图,将△ABC 绕其顶点A 顺时针旋转30 o后,得△ADE 。
(1)△ABC 与△ADE 的关系如何? (2)求∠BAD 的度数。
【例】如图,已知△ABC ≌△EFC ,且CF=5cm ,∠EFC=650,求∠B 的度数和BC 的长。
【变式练习】1、如图,已知△ABC ≌△DEF ,∠A =30°,∠B =50°,BF =2,求∠DFE 的度数与EC 的长.A BCEF2、如图, ABC ∆≌ADE ∆,BC 的延长线交DA 于F ,交DE 于G, 105=∠=∠AED ACB 25,10=∠=∠=∠D B CAD ,求DFB ∠、DGB ∠的度数.知识点2、三角形全等的判定一:“边边边“,了解三角形的稳定性。
浙教版八年级上册数学第一章三角形的初步知识

浙教版八年级上册数学第一章三角形的初步学问学问点及典型例题考点二、求三角形的某一边长或周长的取值范围考点三、推断一句话是否为命题,以及改成“假如……那么……〞的形式 考点四、利用角平分线、垂线〔90°角〕、三角形的外角、内角和、全等三角形来计算角度 考点五、利用垂直平分线的性质、角平分线的性质、全等三角形来计算线段长度考点六、证明三角形全等,以及在三角形全等的根底之上进一步证明线段、角度之间的数量关系 考点七、画三角形的高线、中线、角平分线,以及根本图形的尺规作图法 考点八、方案设计题,求河宽等问题例1、两条线段的长分别是3cm 、8cm ,要想拼成一个三角形,且第三条线段a 的长为奇数,问第三条线段应取多少厘米?1、某一三角形的两边长分别是3和5,那么该三角形的周长的取值范围为〔 〕 A 、10≤a <16 B 、10<a ≤16 C 、10<a <16 D 、2<a <82、能把一个三角形分成面积相等的两部分是三角形的〔 〕A 、中线B 、高线C 、角平分线D 、过一边的中点且和这条边垂直的直线 3、一个三角形的三条高的交点不在这个三角形的内部,那么这个三角形〔 〕A. 必定是钝角三角形B. 必定是直角三角形C. 必定是锐角三角形D. 不行能是锐角三角4、△ABC 的三个不相邻外角的比为2:3:4,那么△ABC 的三个内角的度数分别为 。
例2、如图,△ABC 中,BE 和CD 分别为∠ABC 和∠ACB 的平分线,且BD=C E ,∠1=∠2。
说明BE=CD 的理由。
【设计意图】本例主要考察了角平分线和三角形全等的条件和性质,要说明两条线段相等的方法可以通过说明三角形全等来解决。
例3、AE ,AD 分别为△ABC 中BC 边上的中线和高线,且AB=7cm ,AC=5cm ,那么△ACE 和△ABE 的周长之差为多少厘米?△ACE 和△ABE 的面积之比为多少?【设计意图】本例主要考察了三角形中线、高线的性质,重在格式的书写上。
浙教版初中数学八年级上册 1.1 认识三角形 课件 教学课件

知识梳理
A
B
C
3.三角形的顶点、边、角
(1)△ABC的三个顶点分别是:A,B,C.
(2)△ABC的三条边分别是:线段AB,BC,CA.
(3)三角形的三角分别是: A,B, C.
4.三角形的内角和 三角形的内角和等于180°,在△ABC中,∠A+∠B+∠C=180°
尝试应用
1.选一选,用三根木棒组成的图形,其中符合三角形概念的是 ( C)
1.1认识三角形(1)
数学浙教版 八年级上
活动
从国旗 到邮票
从古代 到现代 从陆地 到天空
从栅栏 到港口
通过阅读课本自主完成下面内容:
知识梳理
A
1.三角形的定义:
B
C
由不在同一条直线上的三条线段首尾顺次相接所组 成的图形叫做三角形.
2.三角形的表示:
三角形用符号“△”表示,如上图的三角形,记作 “△ABC”,读作“三角形ABC”.
反思归纳 你认为判断三条线段能否组成三角形的 最佳方法是?
找出最长线段,把较短两边之和与最长线段的大小进行比较
挑战自我
(小组合作交流完成)
• 挑战一:小刚现有两根长度分别为5cm和8cm的小棒,他想再 找一根,使这三根小棒首尾相连能搭成一个三角形。小刚想到 了手头的两根小棒即长度为 4、 10cm的。
• (1)你认为它们合适吗?那么1、3、13、15cm可以吗?为什 么呢?
• (2)那么第三根小棒应该在什么样的数量范围内,才能与前 两根搭成三角形呢?
反思归纳:三角形的第三边应满足什么条件?
两边之差第三边两边之和
挑变战式二::从一上个述三四角根形长有度两分边别相为等10,c已m知、其8c中m一、边5是cm3cm、,4c另m的 小一棒边中是任9c选m三,根则拼这接个三三角角形形一的共周有长多是少__中__取__法__?__把__它_。们都列 出来?
新浙教版八年级上册数学第一章《三角形的初步知识》知识点及典型例题

新浙教版八年级上册数学第一章《三角形的初步知识》知识点及典型例题本文介绍了八年级上册数学第一章《三角形的初步知识》的知识点及典型例题。
其中,三角形按角分类分为锐角三角形、直角三角形和钝角三角形;按边的关系可分为等腰三角形、等边三角形和普通三角形。
文章还介绍了三角形的内角和定理、角平分线、重要线段中线和高线的定义、命题和证明步骤。
此外,文章还讲解了全等三角形、尺规作图、线段垂直平分线和角平分线的性质,以及如何利用这些知识点计算角度和线段长度。
最后,文章列举了八个考点,包括判断三条线段能否组成三角形、求三角形的某一边长或周长的取值范围、证明三角形全等等。
例题部分也包括了两个问题的解答。
1、正确画出AC边上的高的是(C)。
2、工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是(B)三角形具有稳定性。
3、不能唯一作出直角三角形的是(C)已知一锐角及其邻边。
4、已知AD、BE、CF是△ABC的三条中线,相交于点O,设△BDO面积为1,则S△ABC=(6)。
5、在图中,由于AB=CD。
AD=BC,所以△ABO≌△CDO,△ABO与△CDO的对应顶点分别为AO和CO,所以全等三角形的对数为1,选项A。
6、根据中线定理可知,DF=EF=BF=AF=1/2AC,所以四边形DCEF是平行四边形,面积为AC的一半,即22.5cm,选项B。
7、根据角平分线定理可知,BP/PC=AB/AC,所以BP/AB=PC/AC,由此可得△BPC与△ABC相似,所以∠BPC=2∠A,选项A。
8、由于BD是BC边上的垂直平分线,所以BD=DC=4,由勾股定理可得AD=3,所以AB=5,所以ΔABD的周长为12,选项D。
9、将三角形按照图中的方式编号,可以发现只有第3块的形状与原来的三角形相同,所以应该带第3块去。
10、以B为顶点的外角为∠ABC=180°-∠A=130°,以C为顶点的外角为∠ACB=180°-∠A=130°,由于外角和等于360°,所以两个外角的平分线的夹角为130°/2=65°,选项A。
新浙教版八上第一章三角形的初步知识

第一章 三角形的初步知识复习总目1、掌握三角形的角平分线、中线和高线2、理解三角形的两边之和大于第三边的性质3、三角形全等的判定知识点概要1、 三角形的定义:由不在同一直线上的三条线段首尾顺次相接组成的图形叫做三角形.2、 三角形的分类:(1)按角分类: (2)按边分类:3、 三角形的主要线段的定义: (1)三角形的中线 (2)三角形的角平分线(3)三角形的高 4、三角形的三边关系三角形的任意两边之和大于第三边;任意两边之差小于第三边. 5、 三角形的角与角之间的关系:(1)三角形三个内角的和等于180 ; (2)三角形的一个外角等于和它不相邻的两个内角的和; (3)三角形的一个外角大于任何一个和它不相邻的内角. (4)直角三角形的两个锐角互余. 6、三角形的稳定性:(1)三角形具有稳定性;(2)四边形没有稳定性. 7、全等三角形(1)三角形全等的判定 (SAS ) (ASA ) (AAS ) (SSS ) (HL )(2)全等变换:只改变图形的位置,不改变其形状大小的图形变换叫做全等变换。
全等变换包括一下三种:(1)平移变换 (2)对称变换(3)旋转变换中考规律盘点及预测三角形的两边之和大于第三边的性质历年来是经常考到的填空题的类型,三角形角度的计算也是考到的填空题的类型,三角形全等的判定是很重要的知识点,在考试中往往会考到。
典例分析三角形直角三象形 斜三角形锐角三角形钝角三角形三角形等腰三角形不等边三角形底边和腰不相等的等腰三角形 等边三角形例1、小华要从长度分别为5cm 、6cm 、11cm 、16cm 的四根小木棒中选出三根摆成 一个三角形,那么他选的三根木棒的长度分别是_ 6 .___11___.____16___. 例2 如图,AD 是△ABC 的角平分线,DF ⊥AB ,垂足为F ,DE=DG , △ADG 和△AED 的面积分别为50和39,则△EDF 的面积为( ) 例3 如图,在下列条件中,不能证明△ABD ≌△ACD 的是( ) A.BD=DC ,AB=AC B.∠ADB=∠ADC ,BD=DC C.∠B=∠C ,∠BAD=∠CAD D.∠B=∠C ,BD=DC例4 如图,点B 、F 、C 、E 在同一条直线上,点A 、D 在直线BE 的 两侧,AB ∥DE ,BF =CE ,请添加一个适当的条件: , 使得AC =DF .基础练习一、精心选一选(每小题3分,共30分)1、在下列各组图形中,是全等的图形是( )A 、B 、C 、D 、 2、下列各图中,正确画出AC 边上的高的是( )A 、B 、C 、D 、 3、如图1,工人师傅砌门时,常用木条EF 固定长方形门框ABCD ,使其不变形,这样做的根据是( ) A 、两点之间的线段最短; B 、三角形具有稳定性; C 、长方形是轴对称图形; D 、长方形的四个角都是直角;4、图2中的三角形被木板遮住了一部分,被遮住的两个角不可能是( ) A 、一个锐角,一个钝角; B 、两个锐角;C 、一个锐角,一个直角;D 、一个直角,一个钝角; 5、以下不能构成三角形三边长的数组是( )A 、(1,3,2)B 、(3,4,5)C 、(23,24,25) D 、(3,4,5)6、一个三角形的两个内角分别为55°和65°,这个三角形的外角不可能是( )A A A AB B B BC C C C E E EE BA CD EF 图1图2A 、115°B 、120°C 、125°D 、130°7、小明不慎将一块三角形的玻璃碎成如图3所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带( )去 A 、第1块; B 、第2块; C 、第3块; D 、第4块;8、如图4,在锐角△ABC 中,CD 、BE 分别是AB 、AC 边上的高,且CD 、BE 相交于一点P ,若∠A=50°,则∠BPC=( )A 、150°B 、130°C 、120°D 、100°9、用12根火柴棒(等长)拼成一个三角形,火柴棒不允许剩余、重叠和折断,则能摆出不同的三角形的个数是( )A 、1 B 、2 C 、3 D 、4 10、如图5,在△ABC 中,D 、E 分别是AC 、BC 边上的 点,若△ADB ≌△EDB ≌△EDC ,则∠C 的度数为( ) A 、15° B 、20° C 、25° D 、30° 二、耐心填一填(每小题3分,共30分)11、在△ABC 中,若∠A -∠B=90°,则此三角形是________三角形;若C B A ∠=∠=∠3121,由此三角形是_______三角形;12、如图6,已知AC=BD ,要使△ABC ≌△DCB , 只需增加的一个条件是________________; 13、设△ABC 的三边为a 、b 、c ,化简______________|b a c ||a c b ||c b a |=--+--+--14、已知三角形的两边长分别是3cm 和7cm ,第三边长是偶数,则这个三角形的周长为___________cm ; 15、如图7,在△ABC 中,已知AD=DE ,AB=BE ,∠A=80°,则∠CED=________16、如图8,把矩形ABCD 沿AM 折叠,使D 点落在N 点处,如果AD=35cm ,DM=5cm ,∠DAM=30°,则AN=_____cm ,NM=______cm ,∠BNA=_________度;17、如图9,△ABC 中,AB=AC ,BD 、CE 分别是AC 、AB 边上的高,BD 、CE 交于点O ,且AD=AE ,连结AO ,则图中共有_________对全等三角形;18、如图10,已知∠B=∠C ,AD=AE ,则AB=AC ,请说明理由(填空) 解:在△ABC 和△ACD 中, ∠B=∠______ (__________) ∠A=∠______ (________________)12 3 4图3ABCED 图5ABCDO图6D AB EC 图7 A B CD N M 图8 A B C DE O图9 ABD图10ABEAE=________ (__________) ∴△ABE ≌△ACD (______________)∴AB=AC (______________________________) 19、如图11所,∠A+∠B+∠C+∠D+∠E=________; 20、用一副三角板可以直接得到30°、45°、60°、90°四种角,利用一副三角板可以拼出另外一些特殊角,如75°、120°等,请你拼一拼,用一副三角板还能拼还能拼出哪些小于平角的角?这些角的度数是:____________________; 三、细心做一做(共60分)24、(8分)某产品的商标如图15所示,O 是线段AC 、DB 的交点,且AC=BD ,AB=DC ,小华认为图中的两个三角形全等,他的思考过程是: ∵AC=DB ,∠AOB=∠DOC ,AB=AC , ∴△ABO ≌△DCO你认为小华的思考过程对吗?如果正确,指出他用 的是判别三角形全等的哪个条件,如果不正确, 写出你的思考过程。
浙教版八年级上数学知识点

浙教版八年级上数学知识点第一章 三角形的初步知识 复习总目1、掌握三角形的角平分线、中线和高线2、理解三角形的两边之和大于第三边的性质3、掌握三角形全等的判定方法 知识点概要1、 三角形的定义:由不在同一直线上的三条线段首尾顺次相接组成的图形叫做三角形.三角形有三条边,三个内角,三个顶点.组成三角形的线段叫做三角形的边;相邻两边所组成的角叫做三角形的内角; 相邻两边的公共端点是三角形的顶点, 三角形ABC 用符号表示为△ABC,三角形ABC 的边AB可用边AB 所对的角C 的小写字母c 表示,AC 可用b 表示,BC 可用a 表示. 注意:(1)三条线段要不在同一直线上,且首尾顺次相接;(2)三角形是一个封闭的图形;(3)△ABC 是三角形ABC 的符号标记,单独的△没有意义.2、 三角形的分类: (1)按角分类: (2)按边分类:三角形直角三象形斜三角形锐角三角形钝角三角形_C_B _A 三角形等腰三角形不等边三角形底边和腰不相等的等腰三角形 等边三角形21DC BAD CB ADC BA3、 三角形的主要线段的定义: (1)三角形的中线三角形中,连结一个顶点和它对边中点的线段. 表示法:是△ABC 的BC 上的中线.=DC=12BC. 注意:①三角形的中线是线段;②三角形三条中线全在三角形的内部; ③三角形三条中线交于三角形内部一点; ④中线把三角形分成两个面积相等的三角形.(2)三角形的角平分线三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段表示法:是△ABC 的∠BAC 的平分线.2.∠1=∠2=12∠BAC. 注意:①三角形的角平分线是线段;②三角形三条角平分线全在三角形的内部; ③三角形三条角平分线交于三角形内部一点; ④用量角器画三角形的角平分线.(3)三角形的高从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段.表示法:是△ABC 的BC 上的高线.⊥BC 于D.3.∠ADB=∠ADC=90°.注意:①三角形的高是线段;②锐角三角形三条高全在三角形的内部,直角三角形有两条高是边,钝角三角形有两条高在形外;③三角形三条高所在直线交于一点.4、三角形的三边关系三角形的任意两边之和大于第三边;任意两边之差小于第三边.注意:(1)三边关系的依据是:两点之间线段是短;(2)围成三角形的条件是任意两边之和大于第三边.5、三角形的角与角之间的关系:(1)三角形三个内角的和等于180?;(2)三角形的一个外角等于和它不相邻的两个内角的和;(3)三角形的一个外角大于任何一个和它不相邻的内角.(4)直角三角形的两个锐角互余.6、三角形的稳定性:三角形的三边长确定,则三角形的形状就唯一确定,这叫做三角形的稳定性.注意:(1)三角形具有稳定性;(2)四边形没有稳定性.7、全等三角形(1)全等三角形的概念能够完全重合的两个三角形叫做全等三角形。
浙教版八年级数学上册知识点梳理

浙教版八年级数学上册知识点梳理一、三角形(一)三角形的基本概念1、三角形的定义:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
2、三角形的边:组成三角形的三条线段叫做三角形的边。
3、三角形的顶点:相邻两边的公共端点叫做三角形的顶点。
4、三角形的内角:相邻两边所组成的角叫做三角形的内角,简称三角形的角。
(二)三角形的分类1、按角分类锐角三角形:三个角都是锐角的三角形。
直角三角形:有一个角是直角的三角形。
钝角三角形:有一个角是钝角的三角形。
2、按边分类不等边三角形:三条边都不相等的三角形。
等腰三角形:有两条边相等的三角形。
等边三角形:三条边都相等的三角形。
(三)三角形的三边关系1、三角形任意两边之和大于第三边。
2、三角形任意两边之差小于第三边。
(四)三角形的内角和定理三角形三个内角的和等于 180°。
(五)三角形的外角1、三角形的一边与另一边的延长线所组成的角,叫做三角形的外角。
2、三角形的一个外角等于与它不相邻的两个内角的和。
3、三角形的一个外角大于与它不相邻的任何一个内角。
二、特殊三角形(一)等腰三角形1、等腰三角形的性质等腰三角形的两腰相等。
等腰三角形的两底角相等(等边对等角)。
等腰三角形顶角的平分线、底边上的中线、底边上的高相互重合(三线合一)。
有两边相等的三角形是等腰三角形。
有两个角相等的三角形是等腰三角形(等角对等边)。
(二)等边三角形1、等边三角形的性质等边三角形的三条边都相等。
等边三角形的三个角都相等,并且每个角都等于 60°。
2、等边三角形的判定三条边都相等的三角形是等边三角形。
三个角都相等的三角形是等边三角形。
有一个角是 60°的等腰三角形是等边三角形。
(三)直角三角形1、直角三角形的性质直角三角形两直角边的平方和等于斜边的平方(勾股定理)。
直角三角形的两个锐角互余。
在直角三角形中,如果一个锐角等于 30°,那么它所对的直角边等于斜边的一半。
初中数学浙教版八年级上册 1.1.1 认识三角形课件(21张PPT)

则用长度为4的木棒不能和它们拼成三角形,长度为11的木棒 也不能和它们拼成三角形.第三边长的范围为5<x<9.
归纳:设x为三角形第三条边的长,则有两边之差<x<两边之和.
知识总结
定义
表示
分类
性质
A
概念及表示
△ABC c
性质:边
b 三角形任何两边的和大于第三边
浙教版数学 八年级上
1.1.1认识三角形
新课引入
那么,在数学中,怎样的图形叫做三角形呢? 定义
我们可以看到许多三角形的支 架,你能举出在生活中看到的 三角形的例子吗?
由不在同一直线上的三条线段首尾顺次相接组成的图形叫做三角形
理解定义 由不在同一直线上的三条线段首尾顺次相接组成的图形叫做三角形 问题1:下列图形符合三角形的定义吗?
表示三角形
“三角形”用符号“△”表示,如图顶点是A、B、C的三角形
记作“△ABC”,读作“三角形ABC”.
△ABC、△BCA、△CAB.通常逆时针排列字母顺序 A
三边: BC 、 AC 、AB
角
c
b
或a、 b、 c
角
角
内角: ∠A、∠B、 ∠C
B
a
C
表示三角形
三角形的对边与对角:
A
B 在△ABC中,
对角:AB边所对的角∠是C :
对边:∠A所对的边B是C: 再说几个对边与对角的关系试试.
C
快速完成课本做一做(1)
三角形分类 表示出图中的所有三角形: A
B
CD
△ABC
△ABD △ABE △ACD △ACE E △ADE
浙教版8年级上册《三角形初步知识》复习
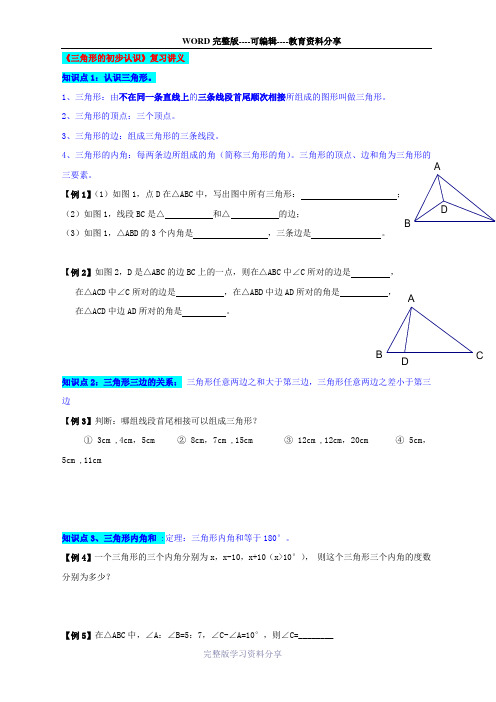
D CB A《三角形的初步认识》复习讲义知识点1:认识三角形。
1、三角形:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
2、三角形的顶点:三个顶点。
3、三角形的边:组成三角形的三条线段。
4、三角形的内角:每两条边所组成的角(简称三角形的角)。
三角形的顶点、边和角为三角形的三要素。
【例1】(1)如图1,点D在△ABC中,写出图中所有三角形:;(2)如图1,线段BC是△和△的边;(3)如图1,△ABD的3个内角是,三条边是。
【例2】如图2,D是△ABC的边BC上的一点,则在△ABC中∠C所对的边是,在△ACD中∠C所对的边是,在△ABD中边AD所对的角是,在△ACD中边AD所对的角是。
知识点2:三角形三边的关系:三角形任意两边之和大于第三边,三角形任意两边之差小于第三边【例3】判断:哪组线段首尾相接可以组成三角形?① 3cm ,4cm,5cm ② 8cm,7cm ,15cm ③ 12cm ,12cm,20cm ④ 5cm,5cm ,11cm知识点3、三角形内角和 :定理:三角形内角和等于180°。
【例4】一个三角形的三个内角分别为x,x-10,x+10(x>10°),•则这个三角形三个内角的度数分别为多少?【例5】在△ABC中,∠A:∠B=5:7,∠C-∠A=10°,则∠C=________ DBA知识点4、三角形外角定理:1、一般地,三角形的一个外角等于与它不相邻的两个内角之和。
2、三角形的一个外角大于与它不相邻的任意一个内角。
【例6】如图中有四条互相不平行的直线L1、L2、L3、L4所截出的七个角.关于这七个角的度数关系,下列正确的有()①∠5=∠1+∠4 ②∠3=∠1+∠6 ③∠1+∠4+∠6=180°④∠2+∠3+∠5=360°⑤∠3=∠1+∠7 ⑥∠2+∠3+∠7=360°⑦∠2=∠4+∠6 ⑧∠2=∠4+∠7第6题图第7题图第8题图【例7】如图,∠1、∠2、∠3的大小关系为()【例8】如图,∠BDC=98°,∠C=38°,∠B=23°,∠A的度数是()【学生练习题1】1、如图,在△ABC中,∠C=30°,若沿图中虚线剪去∠C,则∠1+∠2等于 .2、有四条线段,它们的长分别是2cm、3cm、4cm、5cm,以其中的三条线段为边长,共可组成几种不同的三角形.3、在长方形ABCD 中,如图,E 为AB 上一点,连结DE 、EC ,∠ADE=40°,∠BCE=60°,求∠1、∠2、∠3的度数.知识点6:三角形角平分线、中线和高的概念 1、三角形中的三条线段的概念:三角形中的量重要线段概念图形表示法三角形的角平分线 在三角形中,一个内角的角平分线与它对边相交,这个角的顶点与交点之间的线段。
浙教版初中数学八年级上册直角三角形(基础)知识讲解

直角三角形(基础)【学习目标】1.认识直角三角形 , 学会用符号和字母表示直角三角形.2.掌握直角三角形两个锐角互余的性质, 会用“两个锐角互余的三角形是直角三角形”这个判定方法判定直角三角形 .3.掌握直角三角形斜边上中线性质,并能灵活应用 .4.领会直角三角形中常规辅助线的添加方法.【要点梳理】要点一、直角三角形的概念有一个角是直角的三角形是直角三角形 . 直角三角形表示方法: Rt△. 如下图,可以记作“Rt △ABC” .要点诠释:三角形有六个元素,分别是:三个角,三个边,在直角三角形中,有一个元素永远是已知的,就是有一个角是 90° . 直角三角形可分为等腰直角三角形和含有30°的直角三角形两种特殊的直角三角形,每种三角形都有其特殊的性质 .要点二、直角三角形的性质直角三角形的两个锐角互余 . 直角三角形斜边上的中线等于斜边的一半 .要点诠释:直角三角形的特征是两锐角互余,反过来就是直角三角形的一个判定:两个角互余的三角形是直角三角形 .含有 30°的直角三角形中,同样有斜边上的中线等于斜边的一半,并且 30°的角所对的直角边同样等于斜边的一半 .要点三、直角三角形判定两个角互余的三角形是直角三角形 .在一个三角形中,如果一边的中线等于这边的一半,那么这个三角形是直角三角形如图:已知: CD为 AB 的中线,且 CD=AD=B,D求证△ ABC是直角三角形.证明:∵ AD=CD,∴∠ A=∠ 1.同理∠ 2=∠ B.∵∠ 2+∠B+∠ A+∠1=180°,即 2(∠ 1+∠2)=180°,∴∠ 1+∠ 2=90°,即:∠ ACB=90°,∴△ ABC是直角三角形.【典型例题】类型一、直角三角形性质的应用1、如图,在△ ACB 中,∠ ACB=90゜, CD⊥AB 于 D.(1)求证:∠ ACD=∠ B;(2)若 AF平分∠ CAB分别交 CD、 BC于 E、F,求证:∠ CEF=∠CFE.【思路点拨】( 1)由于∠ ACD与∠B都是∠ BCD的余角,根据同角的余角相等即可得证;(2)根据直角三角形两锐角互余得出∠ CFA=90°﹣∠ CAF,∠AED=90°﹣∠ DAE,再根据角平分线的定义得出∠ CAF=∠DAE,然后由对顶角相等的性质,等量代换即可证明∠ CEF=∠CFE.【答案与解析】证明:(1)∵∠ ACB=90゜,CD⊥AB 于 D,∴∠ACD+∠BCD=9°0 ,∠ B+∠BCD=9°0 ,∴∠ ACD=∠ B;(2)在 Rt△AFC中,∠ CFA=90°﹣∠ CAF,同理在 Rt△AED中,∠ AED=90°﹣∠ DAE.又∵AF 平分∠ CAB,∴∠CAF=∠DAE,∴∠AED=∠CFE,又∵∠ CEF=∠AED,∴∠CEF=∠CFE.【总结升华】本题考查了直角三角形的性质,三角形角平分线的定义,对顶角的性质,余角的性质,难度适中.举一反三:【变式】如图,在△ ABC中,∠ACB=90°,CD是 AB边上的高线,图中与∠ A互余的角有()A. 0 个B. 1 个C. 2 个D. 3 个类型二、含有 30°的直角三角形2、如图,在 Rt△ ABC中,∠ C=90°,∠ A=30°, BC=6,求 AB的长.【思路点拨】根据直角三角形中,30°角的对边等于斜边的一半,得出 AB 与 BC 的数量关系.【答案与解析】解:∵∠C=90°,∠ A=30 °, BC=6,∴ AB=2BC=12 .【总结升华】本题考查了含 30°的直角三角形.含 30°的直角三角形中,斜边等于30°角的对边的 2 倍.3、如图,测量旗杆 AB的高度时,先在地面上选择一点 C,使∠ACB=15°.然后朝着旗杆方向前进到点 D,测得∠ ADB=30°,量得 CD=13m,求旗杆AB的高.【思路点拨】根据三角形的一个外角等于与它不相邻的两个内角的和求出∠ CAD,再根据等 角对等 边的性质 可得 AD=CD ,然后根 据直角 三角形 30°角 所对的直角边 等于斜边的一半解答即可.【答案与解析】解: ∵ ∠ ACB=15°, ∠ ADB=30°,∴ ∠ CAD=∠ ADB-∠ ACB=30 ° -15 °=15 °,即△CAD 为等腰三 角形,∴ AD=CD=13 ,在 △ ADB 中 , ∵ AB ⊥ DB , ∠ ADB=30 ∴ AB= 11AD= × 13=6.5(m) .22 总结升华】 本题考查了直角三角形 30°角 所对的直角边等于斜边的一半的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,等角对等边的性质, 熟记性质是解题的关键.举一反三:【变式】如图,△ ABC 中, AB=AC ,∠ BAC=12°0 ,AD ⊥AC 交 BC 于点 D ,求证: BC=3AD .【答案】证明:在△ ABC 中,∵AB=AC ,∠ BAC=12°0 , ∴∠B=∠C=30°, 又∵AD ⊥AC ,∴∠ DAC=9°0 ,∵∠C=30°∴CD=2A ,D ∠ BAD=∠B=30°,∴AD=D ,B ∴BC=CD+BD=AD+DC=AD+=2A3ADD .类型三、直角三角形斜边上的中线等于斜边的一半4、(2016?石景山区一模)如图,在 Rt △ABC 中,∠ACB=90°, CD 是 AB 边上的中线, DE ⊥ AB 于点 D,交AC 于点 E .求证:∠ AED=∠ DCB .【思路点拨】 首先根据直角三角形斜边上的中线等于斜边的一半得出 CD= AB=DB ,由等边 对等角得到∠ B=∠ DCB .再根据直角三角形两锐角互余得出∠ A+∠AED=90°,∠A+∠B=90°,那么根据同角的余角相等得出∠ B=∠ AED,等量代换即可得出∠ AED=∠ DCB.【答案与解析】证明:∵在 Rt△ ABC中,∠ ACB=90°, CD是 AB边上的中线,∴CD= AB=DB,∴∠ B=∠ DCB.∵DE⊥ AB于点 D,∴∠ A+∠AED=90°,∵∠ A+∠B=90°,∴∠ B=∠ AED,∴∠ AED=∠DCB.【总结升华】本题考查了直角三角形斜边上的中线的性质:在直角三角形中,斜边上的中线等于斜边的一半.也考查了等腰三角形的性质,三角形内角和定理,余角的性质.5、如图,直角三角形 ABC 中,O是 BC 中点且 BD ⊥ CD ,试说明 AO 与 OD 的关系.1 DO= BC ,即 可推出答 案.2 【答案与解析】 解 : AO=DO ,理由是: ∵ ∠ BAC=90°, O 为 BC 中点, 1 ∴ AO= BC , 2∵ BD ⊥ CD ,∠ BDC=90∵ O 为 BC 中 点 ,1∴ DO= BC ,2∴ AO=DO.总结升华】 本题考查了 直角三 角形斜边上中 线性质的 应用, 题目比 较典型, 难度不大.举一反三:【变式】如 图 ,在 Rt △ABC 中,∠ ACB=90°, CD 是 AB 边 上的中线,将 △ADC沿 AC 边所在的直线折叠 , 使 点 D 落 在 点 E 处 , 得 四 边形 ABCE . 求 证 : EC ∥ AB .答案】证明: ∵ CD 是 AB 边 上的中 线,且 ∠ ACB=90°, ∴ CD=AD . ∴ ∠ CAD=∠ ACD .又 ∵△ACE 是 由△ADC 沿 AC 边所 在的直 线折叠而成的, ∴ ∠ ECA=∠ ACD .∴ ∠ ECA=∠ CAD .∴ EC ∥ AB .思路点拨】 根据直 角三角 形斜边 上中 线等于斜边的 一半得 出AO BC , 同理。
浙教版八年级数学上册角形的初步知识1

a三角形的初步知识1一、三角形的基本概念:1、三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形。
三角形ABC 记作:△ABC 。
2、相关概念:三角形的边:组成三角形的三条线段。
记作: AB 、AC 、BC 。
三角形的内角:每两条边所组成的角(简称三角形的角)。
记作:∠A 、∠B 、 ∠C 3、三角形的分类:⎪⎩⎪⎨⎧⎩⎨⎧等边三角形一般等腰三角形等腰三角形不等腰三角形按边分:三角形)1(⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧钝角三角形等腰直角三角形一般直角三角形直角三角形锐角三角形按角分:三角形)2(二、三角形三边关系:1、三角形任何两边的和大于第三边。
几何语言:若a 、b 、c 为△ABC 的三边,则a+b>c,a+c>b, b+c>a. 想一想:这个在实际解题中该怎样应用?2、三边关系也可表述为:三角形任何两边的差都小于第三边。
三、三角形的内角和定理: 三角形三个内角的和等于1800。
几何语言:△ABC 中,∠A+∠B+∠C=1800。
C BA四、三角形的三线:问题1、如何作三角形的高线、角平分线、中线?问题2、三角形的高线、角平分线、中线各有多少条,它们的交点在什么位置?问题3、三角形的中线有什么应用?例题与练习例1、如图,在△ABC中,D、E是BC、AC上的两点,连接BE、AD交于点F。
问:(1)、图中有多少个三角形?把它们表示出来。
(2)、△AEF的三条边是什么?三个角是什么?练习:右图中有几个三角形例2、已知线段a b c满足a+b+c=24cm, a:b=3:4, b+2a=2c ,问能否以a 、b、c 为三边组成三角形,如果能,试求出这三边,如果不能,请说明理由。
练习1、四组线段的长度分别为2,3,4;3,4,7;2,6,4;7,10,2。
其中能摆成三角形的有()A.一组B.二组C.三组D.四组2、已知三角形两条边长分别为13厘米和6厘米,那么第三边长应是多少厘米?3、已知三角形两条边长分别为19厘米和8厘米,第三边与其中一边相等,那么第三边长应是多少厘米?例3、在△ABC中,∠A:∠B:∠C=1:2:3,求三角形各角的度数,并判断它是什么三角形。
浙教版初中数学八年级上册直角三角形(基础)知识讲解

直角三角形(基础)【学习目标】1.认识直角三角形, 学会用符号和字母表示直角三角形.2.掌握直角三角形两个锐角互余的性质, 会用“两个锐角互余的三角形是直角三角形”这个判定方法判定直角三角形.3. 掌握直角三角形斜边上中线性质,并能灵活应用.4. 领会直角三角形中常规辅助线的添加方法.【要点梳理】要点一、直角三角形的概念有一个角是直角的三角形是直角三角形.直角三角形表示方法:Rt△.如下图,可以记作“Rt△ABC”.要点诠释:三角形有六个元素,分别是:三个角,三个边,在直角三角形中,有一个元素永远是已知的,就是有一个角是90°.直角三角形可分为等腰直角三角形和含有30°的直角三角形两种特殊的直角三角形,每种三角形都有其特殊的性质.要点二、直角三角形的性质直角三角形的两个锐角互余.直角三角形斜边上的中线等于斜边的一半.要点诠释:直角三角形的特征是两锐角互余,反过来就是直角三角形的一个判定:两个角互余的三角形是直角三角形.含有30°的直角三角形中,同样有斜边上的中线等于斜边的一半,并且30°的角所对的直角边同样等于斜边的一半.要点三、直角三角形判定两个角互余的三角形是直角三角形.在一个三角形中,如果一边的中线等于这边的一半,那么这个三角形是直角三角形.如图:已知:CD为AB的中线,且CD=AD=BD,求证:△ABC是直角三角形.证明:∵AD=CD,∴∠A=∠1.同理∠2=∠B.∵∠2+∠B+∠A+∠1=180°,即2(∠1+∠2)=180°,∴∠1+∠2=90°,即:∠ACB=90°,∴△ABC是直角三角形.【典型例题】类型一、直角三角形性质的应用1、如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.(1)求证:∠ACD=∠B;(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.【思路点拨】(1)由于∠ACD与∠B都是∠BCD的余角,根据同角的余角相等即可得证;(2)根据直角三角形两锐角互余得出∠CFA=90°﹣∠CAF,∠AED=90°﹣∠DAE,再根据角平分线的定义得出∠CAF=∠DAE,然后由对顶角相等的性质,等量代换即可证明∠CEF=∠CFE.【答案与解析】证明:(1)∵∠ACB=90゜,CD⊥AB于D,∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,∴∠ACD=∠B;(2)在Rt△AFC中,∠CFA=90°﹣∠CAF,同理在Rt△AED中,∠AED=90°﹣∠DAE.又∵AF平分∠CAB,∴∠CAF=∠DAE,∴∠AED=∠CFE,又∵∠CEF=∠AED,∴∠CEF=∠CFE.【总结升华】本题考查了直角三角形的性质,三角形角平分线的定义,对顶角的性质,余角的性质,难度适中.举一反三:【变式】如图,在△ABC中,∠ACB=90°,CD是AB边上的高线,图中与∠A互余的角有()A.0个B.1个C.2个D.3个【答案】C.类型二、含有30°的直角三角形2、如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=6,求AB的长.【思路点拨】根据直角三角形中,30°角的对边等于斜边的一半,得出AB与BC 的数量关系.【答案与解析】解:∵∠C=90°,∠A=30°,BC=6,∴AB=2BC=12.【总结升华】本题考查了含30°的直角三角形.含30°的直角三角形中,斜边等于30°角的对边的2倍.3、如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=15°.然后朝着旗杆方向前进到点D,测得∠ADB=30°,量得CD=13m,求旗杆AB的高.【思路点拨】根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CAD,再根据等角对等边的性质可得AD=CD,然后根据直角三角形30°角所对的直角边等于斜边的一半解答即可.【答案与解析】三角形的一个外角等于与它不相邻的两个内角的和的性质,等角对等边的性质,熟记性质是解题的关键.举一反三:【变式】如图,△ABC中,AB=AC,∠BAC=120°,AD⊥AC交BC于点D,求证:BC=3AD.【答案】证明:在△ABC中,∵AB=AC,∠BAC=120°,∴∠B=∠C=30°,又∵AD⊥AC,∴∠DAC=90°,∵∠C=30°∴CD=2AD,∠BAD=∠B=30°,∴AD=DB,∴BC=CD+BD=AD+DC=AD+2AD=3AD.类型三、直角三角形斜边上的中线等于斜边的一半4、(2016•石景山区一模)如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,DE⊥AB于点D,交AC于点E.求证:∠AED=∠DCB.【思路点拨】首先根据直角三角形斜边上的中线等于斜边的一半得出CD=AB=DB,由等边对等角得到∠B=∠DCB.再根据直角三角形两锐角互余得出∠A+∠AED=90°,∠A+∠B=90°,那么根据同角的余角相等得出∠B=∠AED,等量代换即可得出∠AED=∠DCB.【答案与解析】证明:∵在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,∴CD=AB=DB,∴∠B=∠DCB.∵DE⊥AB于点D,∴∠A+∠AED=90°,∵∠A+∠B=90°,∴∠B=∠AED,∴∠AED=∠DCB.【总结升华】本题考查了直角三角形斜边上的中线的性质:在直角三角形中,斜边上的中线等于斜边的一半.也考查了等腰三角形的性质,三角形内角和定理,余角的性质.5、如图,直角三角形ABC中,O是BC中点且BD⊥CD,试说明AO与OD 的关系.【总结升华】本题考查了直角三角形斜边上中线性质的应用,题目比较典型,难度不大.举一反三:【变式】如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,将△ADC沿AC边所在的直线折叠,使点D落在点E处,得四边形ABCE.求证:EC∥AB.【答案】证明:∵CD是AB边上的中线,且∠ACB=90°,∴CD=AD.∴∠CAD=∠ACD.又∵△ACE是由△ADC沿AC边所在的直线折叠而成的,∴∠ECA=∠ACD.∴∠ECA=∠CAD.∴EC∥AB.。
最新浙教版八年级数学上册第1章三角形的初步知识PPT

A
B
C
4、三角形的边
组成三角形的三条线段叫做三角形的边。
A
如图,三角形ABC有几条边?它们分别是 __A__B_,__A__C__,__B_C。
B
C
△ABC的三边,有时也用a,b,c来表示。
一般地,顶点A所对的边记作a,顶点B所对的边记作b, 顶点C所对的边记作c。
5、三角形的角:
(1)三角形相邻两边所组成的角叫做三角形的内角,简称三
D
C
(2)说出哪条线段是ΔABC的哪条边上的中线;
把刚才的锐角三角形换成直角三角形或钝角三角形,结果 又怎么样呢?
三角形的三条中线在三角形的内部交于一点
∵AD是△ ABC的中线 ∴BD=CD= 12BC
A
●
F
E O
B
●
C
D
三角形三条中线的交点叫做三角形的重心;
三角形的高
从三角形的一个顶点向它的对边所在的直线作
∵CF是△ABC的角平分线
B ∴∠ACB=2_∠__A_C_F_=2_∠__B_C_F_
E
O
D
C
三角形的中线
在三角形中,连结三角形的一个顶点与该顶 点对边中点的线段,叫做这个三角形的中
A
●
线.
如图:线段AD叫做ΔABC的边BC上的 F ● 中线。
●E
●
●
●
●
(1)画出ΔABC的另外两边上的中线; B
A
B
C
例 说出图中有多少个三角形,用符号“△”表示,并指出每 一个三角形的三条边.
EP
F
G
Q
H
练习:读出图中的各个三角形. A E B
D C
3、三角形的顶点
浙教版初中数学八年级上册

浙教版初中数学八年级上册一、三角形的初步知识。
1. 三角形的有关概念。
- 三角形由不在同一条直线上的三条线段首尾顺次相接所组成的图形。
- 三角形的基本要素:边、角、顶点。
- 三角形的表示方法:用符号“△”表示,如△ABC,其中A、B、C为三角形的顶点。
2. 三角形的分类。
- 按角分类:- 锐角三角形:三个角都是锐角的三角形。
- 直角三角形:有一个角是直角的三角形,直角三角形可以用“Rt△”表示,如Rt△ABC,其中∠C = 90°,直角所对的边叫斜边,夹直角的两条边叫直角边。
- 钝角三角形:有一个角是钝角的三角形。
- 按边分类:- 不等边三角形:三边都不相等的三角形。
- 等腰三角形:有两边相等的三角形,相等的两边叫腰,另一边叫底边,两腰的夹角叫顶角,腰与底边的夹角叫底角。
- 等边三角形:三边都相等的三角形,等边三角形是特殊的等腰三角形。
3. 三角形的性质。
- 三角形的内角和等于180°。
可以通过作平行线等方法进行证明,如在△ABC 中,∠A+∠B +∠C = 180°。
- 三角形的外角性质:- 三角形的一个外角等于与它不相邻的两个内角的和。
例如在△ABC中,∠ACD是∠ACB的外角,则∠ACD=∠A +∠B。
- 三角形的一个外角大于任何一个与它不相邻的内角。
- 三角形的三边关系:三角形任意两边之和大于第三边,任意两边之差小于第三边。
例如,在△ABC中,AB + BC>AC,AB - BC<AC。
4. 三角形中的重要线段。
- 角平分线:- 在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线。
- 三角形的三条角平分线相交于一点,这一点叫三角形的内心,内心到三角形三边的距离相等。
- 中线:- 在三角形中,连接一个顶点与它对边中点的线段叫三角形的中线。
- 三角形的三条中线相交于一点,这一点叫三角形的重心。
- 高线:- 从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫三角形的高线(简称三角形的高)。
浙教版八年级数学上册角形的初步知识1 .docx

a三角形的初步知识1一、三角形的基本概念:1、三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形。
三角形ABC 记作:△ABC 。
2、相关概念: 三角形的边:组成三角形的三条线段。
记作: AB 、AC 、BC 。
三角形的内角:每两条边所组成的角(简称三角形的角)。
记作:∠A 、∠B 、 ∠C3、三角形的分类:⎪⎪⎩⎪⎪⎨⎧钝角三角形直角三角形锐角三角形按角分:三角形)2(⎪⎩⎪⎨⎧⎩⎨⎧等边三角形一般等腰三角形等腰三角形不等腰三角形按边分:三角形)1(二、三角形三边关系:1、三角形任何两边的和大于第三边。
几何语言:若a 、b 、c 为△ABC 的三边,则a+b>c,a+c>b, b+c>a. 想一想:这个在实际解题中该怎样应用?2、三边关系也可表述为:三角形任何两边的差都小于第三边。
三、三角形的内角和定理:三角形三个内角的和等于1800。
几何语言:△ABC 中,∠A+∠B+∠C=1800。
四、三角形的三线: 问题1、如何作三角形的高线、角平分线、中线?问题2、三角形的高线、角平分线、中线各有多少条,它们的交点在什么位置? 问题3、三角形的中线有什么应用?例题与练习例1、如图,在△ABC 中,D 、E 是BC 、AC 上的两点,连接BE 、AD 交于点F 。
问:(1)、图中有多少个三角形?把它们表示出来。
(2)、△AEF 的三条边是什么?三个角是什么?练习:右图中有几个三角形例2、已知线段a b c 满足a+b+c=24cm, a:b=3:4, b+2a=2c ,问能否以a 、b 、 c 为三边组成三角形,如果能,试求出这三边,如果不能,请说明理由。
练习1、四组线段的长度分别为2,3,4;3,4,7; 2,6,4;7,10,2。
其中能摆成三角形的有( ) A .一组 B .二组 C .三组 D .四组2、已知三角形两条边长分别为13厘米和6厘米,那么第三边长应是多少厘米?3、已知三角形两条边长分别为19厘米和8厘米,第三边与其中一边相等,那么第三边长应是多少厘米? 例3、在△ABC 中,∠A :∠B :∠C=1:2:3,求三角形各角的度数,并判断它是什么三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
认识三角形(基础)知识讲解【学习目标】1. 理解三角形及与三角形有关的概念,掌握它们的文字、符号语言及图形表述方法;2. 理解并能够证明三角形内角和定理;3. 掌握并会把三角形按角分类;4. 掌握并会应用三角形三边之间的关系;5. 理解三角形的高、中线、角平分线的概念,掌握它们的画法;并能正确应用概念解题. 【要点梳理】要点一、三角形的定义由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.要点诠释:(1)三角形的基本元素:①三角形的边:即组成三角形的线段;②三角形的角:即相邻两边所组成的角叫做三角形的内角,简称三角形的角; ③三角形的顶点:即相邻两边的公共端点. (2)三角形的定义中的三个要求:“不在同一条直线上”、“三条线段”、“首尾顺次相接”. (3)三角形的表示:三角形用符号“△”表示,顶点为A 、B 、C 的三角形记作“△ABC ”,读作“三角形ABC ”,注意单独的△没有意义;△ABC 的三边可以用大写字母AB 、BC 、AC 来表示,也可以用小写字母a 、b 、c 来表示,边BC 用a 表示,边AC 、AB 分别用b 、c 表示. 要点二、三角形的内角和三角形内角和定理:三角形的内角和为180°.要点诠释:应用三角形内角和定理可以解决以下三类问题: ①在三角形中已知任意两个角的度数可以求出第三个角的度数; ②已知三角形三个内角的关系,可以求出其内角的度数; ③求一个三角形中各角之间的关系. 要点三、三角形的分类【:与三角形有关的线段 三角形的分类】 1.按角分类:⎧⎪⎧⎨⎨⎪⎩⎩直角三角形三角形 锐角三角形斜三角形 钝角三角形 要点诠释:①锐角三角形:三个内角都是锐角的三角形; ②钝角三角形:有一个内角为钝角的三角形.要点四、三角形的三边关系定理:三角形任意两边之和大于第三边.要点诠释:(1)理论依据:两点之间线段最短.(2)三边关系的应用:判断三条线段能否组成三角形,若两条较短的线段长之和大于最长线段的长,则这三条线段可以组成三角形;反之,则不能组成三角形.(3)证明线段之间的不等关系.要点五、三角形的三条重要线段三角形的高、中线和角平分线是三角形中三条重要的线段,它们提供了重要的线段或角的关系,为我们以后深入研究三角形的一些特征起着很大的帮助作用,因此,我们需要从不同的角度弄清这三条线段,列表如下:线段名称三角形的高三角形的中线三角形的角平分线文字语言从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段.三角形中,连接一个顶点和它对边中点的线段.三角形一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段.图形语言作图语言过点A作AD⊥BC于点D.取BC边的中点D,连接AD.作∠BAC的平分线AD,交BC于点D.标示图形符号语言1.AD是△ABC的高.2.AD是△ABC中BC边上的高.3.AD⊥BC于点D.4.∠ADC=90°,∠ADB=90°.(或∠ADC=∠ADB=90°)1.AD是△ABC的中线.2.AD是△ABC中BC边上的中线.3.BD=DC=12BC4.点D是BC边的中点.1.AD是△ABC的角平分线.2.AD平分∠BAC,交BC于点D.3.∠1=∠2=12∠BAC.推理语言因为AD是△ABC的高,所以AD⊥BC.(或∠ADB=∠ADC=90°)因为AD是△ABC的中线,所以BD=DC=12BC.因为AD平分∠BAC,所以∠1=∠2=12∠BAC.用途举例1.线段垂直.2.角度相等.1.线段相等.2.面积相等.角度相等.注意事项1.与边的垂线不同.2.不一定在三角形内.—与角的平分线不同.重要特征三角形的三条高(或它们的延长线)交于一点.一个三角形有三条中线,它们交于三角形内一个三角形有三条角平分线,它们交于三角形内一一点.点.【典型例题】类型一、三角形的内角和1.证明:三角形的内角和为180°.【答案与解析】解:已知:如图,已知△ABC,求证:∠A+∠B+∠C=180°.证法1:如图1所示,延长BC到E,作CD∥AB.因为AB∥CD(已作),所以∠1=∠A(两直线平行,内错角相等),∠B=∠2(两直线平行,同位角相等).又∠ACB+∠1+∠2=180°(平角定义),所以∠ACB+∠A+∠B=180°(等量代换).证法2:如图2所示,在BC边上任取一点D,作DE∥AB,交AC于E,DF∥AC,交AB于点F.因为DF∥AC(已作),所以∠1=∠C(两直线平行,同位角相等),∠2=∠DEC(两直线平行,内错角相等).因为DE∥AB(已作).所以∠3=∠B,∠DEC=∠A(两直线平行,同位角相等).所以∠A=∠2(等量代换).又∠1+∠2+∠3=180°(平角定义),所以∠A+∠B+∠C=180°(等量代换).【总结升华】理解并掌握三角形内角和的证明方法,有助于帮助我们更深刻的去记忆三角形的内角和是180°.2.在△ABC中,已知∠A+∠B=80°,∠C=2∠B,试求∠A,∠B和∠C的度数.【思路点拨】题中给出两个条件:∠A+∠B=80°,∠C=2∠B,再根据三角形的内角和等于180°,即∠A+∠B+∠C=180°就可以求出∠A,∠B和∠C的度数.【答案与解析】解:由∠A+∠B=80°及∠A+∠B+∠C=180°,知∠C=100°.又∵∠C=2∠B,∴∠B=50°.∴∠A=80°-∠B=80°-50°=30°.【总结升华】解答本题的关键是利用隐含条件∠A+∠B+∠C=180°.本题可以设∠B=x,则∠A=80°-x,∠C=2x建立方程求解.【:与三角形有关的角例1、】举一反三:【变式】已知,如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.【答案】解:已知△ABC中,∠C=∠ABC=2∠A设∠A=x则∠C=∠ABC=2xx+2x+2x=180°解得:x=36°∴∠C=2x=72°在△BDC中, BD是AC边上的高,∴∠BDC=90°∴∠DBC=180°-90°-72°=18°类型二、三角形的分类3.一个三角形的三个内角分别是95°、30°、45°,这个三角形是()A 锐角三角形B 钝角三角形C 直角三角形【答案与解析】解:因为这个三角形的其中一个内角是95°,95°是钝角,所以这个三角形是钝角三角形,故选:B.【总结升华】主要考察了三角形的分类方法.举一反三【变式】一个三角形中,一个内角的度数等于另外两个内角的和的2倍,这个三角形是()三角形A 锐角B 直角C 钝角 D无法判断【答案】C【解析】利用三角形内角和是180°以及已知条件,可以得到其中较大内角的度数为120°,所以三角形为钝角三角形.类型三、三角形的三边关系4.(2015春•滕州市期中)下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是()①7cm,5cm,11cm ②4cm,3cm,7cm ③5cm,10cm,4cm ④2cm,3cm,1cm.A.①B.②C.③D.④【思路点拨】根据三角形的三边关系对各选项进行逐一分析即可.【答案】A.【解析】解:①∵7+5>11,∴能围成三角形,②∵3+4=7,∴不能围成三角形,③∵4+5<10,∴不能围成三角形,④∵1+2=3,∴不能围成三角形.能围成三角形的是①,故选A.【总结升华】本题主要考查了三角形的三边关系,在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.【:与三角形有关的线段例1】举一反三:【变式】判断下列三条线段能否构成三角形.(1) 3,4,5; (2) 3,5,9 ; (3) 5,5,8.【答案】(1)能;(2)不能;(3)能.类型四、三角形中重要线段5.(2016春•普宁市期末)下面四个图形中,线段BE是△ABC的高的图是()A.B.C.D.【思路点拨】根据高的画法知,过点B作AC边上的高,垂足为E,其中线段BE是△ABC 的高.【答案】D;【解析】三角形的高就是从三角形的顶点向它的对边所在直线作垂线,顶点和垂足之间的线段.解答本题首先应找到最长边,再找到最长边所对的顶点.然后过这个顶点作最长边的垂线即得到三角形的高.【总结升华】锐角三角形、直角三角形、钝角三角形都有三条高,并且三条高所在的直线交于一点.这里一定要注意钝角三角形的高中有两条高在三角形的外部,一条高在三角形的内部.举一反三:【变式】如图所示,已知△ABC,试画出△ABC各边上的高.【答案】解:所画三角形的高如图所示.6.如图所示,CD为△ABC的AB边上的中线,△BCD的周长比△ACD的周长大3cm,BC =8cm,求边AC的长.【思路点拨】根据题意,结合图形,有下列数量关系:①AD=BD,②△BCD的周长比△ACD 的周长大3.【答案与解析】解:依题意:△BCD的周长比△ACD的周长大3cm,故有:BC+CD+BD-(AC+CD+AD)=3.又∵ CD为△ABC的AB边上的中线,∴ AD=BD,即BC-AC=3.又∵ BC=8,∴ AC=5.答:AC的长为5cm.【总结升华】运用三角形的中线的定义得到线段AD=BD是解答本题的关键,另外对图形中线段所在位置的观察,找出它们之间的联系,这种数形结合的数学思想是解几何题常用的方法.举一反三:【变式】(2014秋•西昌市期末)下列说法中错误的是()A.三角形三条角平分线都在三角形的内部B.三角形三条中线都在三角形的内部C.三角形三条高都在三角形的内部D.三角形三条高至少有一条在三角形的内部【答案】C.。
