材料力学课件_平面图形的几何性质.
材料力学(理工科课件)附录A_平面图形的几何性质()[25P][9.63MB]
![材料力学(理工科课件)附录A_平面图形的几何性质()[25P][9.63MB]](https://img.taocdn.com/s3/m/d59f3f242af90242a895e59e.png)
z
y
所以
A.3 平行移轴公式
(Parallel-axis theorem)
一、平行移轴公式(Parallel-Axis theorem for moment of inertia)
y,z ― 任意一对坐标轴 C ―截面形心 (a , b ) ―形心C在 yOz坐标系下的坐标
a O C(a,b) y
yC
积,求截面对与形心轴平行的 y,z轴惯性矩和
惯性积,则平行移轴公式
b
二、组合截面的惯性矩 、惯性积( Moment of inertia &
product of inertia for composite areas )
组合截面的惯性矩,惯性积
 ̄第
i个简单截面对 y, z 轴的惯性矩,惯性积.
z1
z
y1
O
y
显然
二、截面的主惯性轴和主惯性矩(principal axes &
principal moment of inertia)
主惯性轴(Principal axes ):总可以找到一个特定的角0 , 使截面 对新坐标轴y0 , z0的惯性积等于0 , 则称 y0 , z0 为主惯性轴. 主惯性矩(Principal moment of inertia) :截面对主惯性轴y0 , z0 的惯性矩. 形心主惯性轴(Centroidal principal axes) :当一对主惯性轴的交 点与截面的形心重合时,则称为形心主惯性轴. 形心主惯性矩( Centroidal principal moment of inertia) :截面对 形心主惯性轴的惯性矩.
(1)主惯性轴的位置 设 为主惯性轴与原坐标轴之间的夹角
材料力学 附录 平面图形的几何性质

二、惯性积 z
y
dA z
平面图形对y、z两 轴的惯性积:
Iyz AyzdA
量纲:长度四次方
o
z
y
两个坐标轴中只要有一个轴为图形 的对称轴,则图形对这一对坐标轴 的惯性积等于零
y
例2 求图示矩形的 Iz,Iy,Iyz,iy,iz
z
dz z hc
b
h
Iy
z2dA
A
b 3
z3
2 h
1 bh 3 12
(2)截面图形对所有平行轴的惯性矩中,以对通过形心 轴的惯性矩最小.
例5:T字形截面,求其对形心轴的惯矩。 z A1z1 A2z2 A1 A2
0.1 4 0.0 2 0.0 8 0.10.0 2 0 0.1 4 0.0 2 0.10.02
0.046m7
z
I y C 1 1 1 0 . 0 2 0 . 1 2 3 0 4 . 0 0 . 0 8 2 4 0 . 0 6 0 . 1 2 7 7 4 . 6 1 9 6 m 4 0
tg20
2I yz Iy Iz
Imax IyIz Imin 2
Iy
Iz 2
2Iyz2
确定两个相差90度的
角度 0,0 90
1
Iy 0z0 2 (Iy Iz)s2 in 0 Iyc z 2 o0 s0
主惯性轴:惯性矩有极值,惯性积为零的轴。 主惯性矩:对主惯性轴的惯性矩称为主惯性矩。 形心主惯性轴:通过形心的主惯性轴称为形心主惯性轴。 形心主惯性矩:对形心主惯性轴的惯性矩。
y
Iz
y2dA
A
1 12
2
hb 3
iy
Iy A
3h 6
第五章平面图形几何性质(讲稿)材料力学教案(顾志荣)
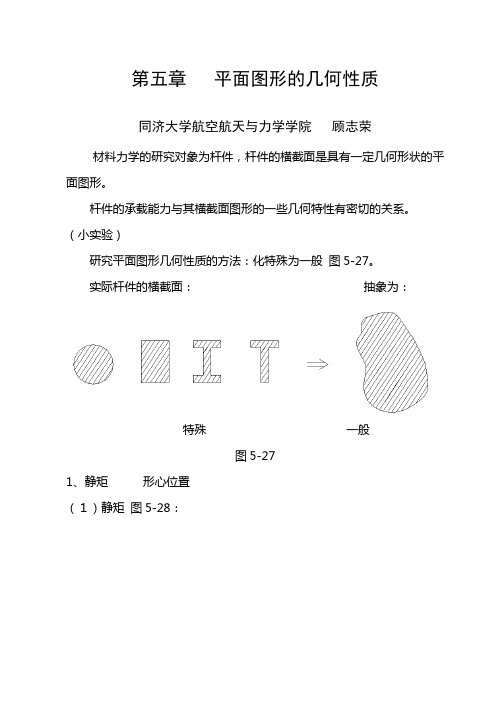
第五章平面图形的几何性质同济大学航空航天与力学学院顾志荣材料力学的研究对象为杆件,杆件的横截面是具有一定几何形状的平面图形。
杆件的承载能力与其横截面图形的一些几何特性有密切的关系。
(小实验)研究平面图形几何性质的方法:化特殊为一般图5-27。
实际杆件的横截面:抽象为:特殊一般图5-271、静矩形心位置(1)静矩图5-28:图5-28微面积dA 与Z 轴、Y 轴间距离的乘积ydA,zdA 分别称为微面积dA 对Z 轴、Y 轴的静矩。
整个截面对Z 轴、Y 轴的静矩可用下式来定义:(若把A 看作力)定义:截面A 对Z 轴:⎪⎭⎪⎬⎫==⎰⎰Ay A ZSZdA S ydA (4-1) 截面A 对Y 轴:计算:①对(4-1)式直接积分:②若已知截面的形心位置C ,则y Z S S ,可以写成:⎭⎬⎫==c Z c Y AY S AZ S (4-2)(2)形心的位置:⎪⎪⎭⎪⎪⎬⎫==A S Z A S Y y C Z C (4-3)性质:①截面对某一轴的静矩等于零,则该轴必通过形心。
②截面对通过形心的轴的静矩恒等于零,即: ;0=ZC S 0=YC S决定因素:静矩与截面尺寸、形状、轴的位置有关。
数值范围:可以为正、或负、或等于零。
单位:333,,m cm mm (3)组合截面的静矩:⎪⎪⎭⎪⎪⎬⎫==∑∑==n i i i y n i i i Z A S Y A z S 11(4-4) 即组合截面的整个图形对于某一轴的静矩,等于各组部分对于同一轴静矩代数和。
(4)组合截面的形心位置:⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎬⎫====∑∑∑∑====n i i ni i i y ni i ni i i z A Z A AS A Y A AS c c z y 1111(4-5) 例题5-7 求图5-29所示截面图形的形心。
图5-29解:把T 形看成为由矩形Ⅰ和Ⅱ组成 ∵y 轴是对称轴 ∴形心必在y 轴上① 求?'=Z S216002080mm A I =⨯= A Ⅱ=2240020120mm =⨯ mm y c 10=I (到Z ′轴) y c Ⅱ=60+20=80mm则:3120800802400101600'mm Y A ni ii z s =⨯+⨯==∑=②求c y=?c y=As z =∑∑==ni ini i i A Y A 11=201202080208000⨯+⨯=52mm 2、惯性矩(形心主惯性矩) 惯性半径 极惯性矩图5-30定义:(1)惯性矩⎪⎭⎪⎬⎫==⎰⎰A yA Z dA Z I dA y I 22(4-6) 定义为截面对z 轴,y 轴的惯性矩。
08 建筑力学 第八章 平面图形的几何性质 课件
dI x1 0 d
dI y1 d
0
同样可以得到式(8-10)或(8-11)的结论。这表 明:当α改变时, I x 、I y 的数值也发生变化,而当 α=α0时,二者分别为极大值和极小值。 定义 过一点存在这样一对坐标轴,图形对于其 惯性积等于零,这一对坐标轴便称为过这一点 的主轴。图形对主轴的惯性矩称为主轴惯性 矩,简称主惯性矩。显然,主惯性矩具有极大 或极小的特征。
i i
第二节 静矩
一、定义 任意平面几何图形如图A-1所示。在其上取面 积微元dA,该微元在Oxy坐标系中的坐标为x、 y。定义下列积分:
S x ydA
A
S y zdA
A
(8-4)
分别称为图形对于x轴和y轴的截面一次矩或静 矩,其单位为 。
如果将dA视为垂直于图形平面的力,则ydA 和zdA分别为dA对于z轴和y轴的力矩; 和 则分 别为dA对z轴和y轴之矩。图8-6图形的静矩与形 心图形几何形状的中心称为形心,若将面积视为 垂直于图形平面的力,则形心即为合力的作用 点。 设z、y为形心坐标,则根据合力之矩定理
二、一般物体重心的坐标公式 1、一般物体重心的坐标公式 如图8—1所示,为确定物体重心的位置, 将它分割成n个微小块,各微小块重力分别为 Gl 、 G2 、 ……Gn ,其作用点的坐标分别为 (X1、Y1,、z1)、(X2、Y2、z2)…(Xn,Yn、 Zn) ,各微小块所受重力的合力W即为整个物 体所受的重力 G =ΣGi ,其作用点的坐标为 C(xc,yc、zc)。对y轴应用合力矩定理,有:
第八章
平面图形的几何性质
在建筑力学以及建筑结构的计算中,经常 要用到与截面有关的一些几何量。例如轴向拉 压的横截面面积A、圆轴扭转时的抗扭截面系数 WP 和极惯性矩 IP 。等都与构件的强度和刚度有 关。以后在弯曲等其他问题的计算中,还将遇 到平面图形的另外一些如形心、静矩、惯性矩、 抗弯截面系数等几何量。这些与平面图形形状 及尺寸有关的几何量统称为平面图形的几何性 质。
《材料力学》教学课件—附录A 平面图形的几何性质

I xy
xydA
A
单位:m4
其值:+、-、0
12
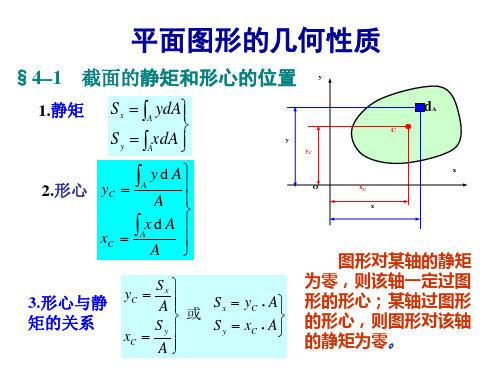
§A.2 惯性矩 惯性积 惯性半径
y
二、惯性矩与极惯性矩的关系
x dA
若 x 、 y 轴为一对正交坐标轴
Ip
2dA
A
x2 y2 dA
A
A
y
O
x
x2dA y2dA
A
A
即:
Ip I y Ix
性质 2 :
平面图形对任意一点的极惯性矩等于该图形对通过 该点的任意一对相互垂直的坐标轴的惯性矩之和
8
例 1 确定形心坐标 解:
200 y
30
取参考坐标系 xy
C
200
yC
Sx A
A1 y1 A2 y2 A1 A2
30
y
C
x (参考轴)
200 30 215 200 30 100 mm 200 30 2
157.5 mm
9
附录A 平面图形的几何性质
§A.2 惯性矩 惯性积 惯性半径
2. 圆形截面
D4
I x I y Ip 32
由对称性
Ix
Iy
1 2
Ip
D4
64
y
O
x
d D
3. 环形截面
Ix
Iy
1 2
Ip
D4 d4 64
D4
64
14
15
§A.2 惯性矩 惯性积 惯性半径
三、惯性积的性质
y -x x
当 x 、 y 轴中有一轴为对称轴
A
A
I xy
xyd A
A
y
2 x
材料力学平面图形的几何性质

平面图形的剪切中心和弯曲中心
剪切中心:平面图形中,剪切中心是剪切面上各点剪切应变之和为零的点,与该点距离最近的各 点组成的剪切面称为剪切面。
弯曲中心:平面图形中,弯曲中心是弯曲面上各点弯曲应变之和为零的点,与该点距离最近的各 点组成的弯曲面称为弯曲面。
刚性特性:平面图形在剪切和弯曲变形下,其几何形状和尺寸保持不变的性质称为刚性特性。
剪切中心和弯曲中心在平面图形中的作用:在平面图形中,剪切中心和弯曲中心是确定平面图形 在剪切和弯曲变形下应力和应变分布的关键点,对于分析平面图形的受力特性和稳定性具有重要 意义。
平面图形的抗扭刚度和抗弯刚度
抗扭刚度:表示材料 抵抗扭转变形的能力, 与平面图形的几何形 状和尺寸有关。
抗弯刚度:表示材料 抵抗弯曲变形的能力, 与平面图形的几何形 状、尺寸和材料本身 的弹性模量有关。
计算方法:根据 几何学原理,可 以通过平面图形 的边长、角度等 参数计算面积和
周长
平面图形的形心、质心和重心
形心:平面图形 中所有点组成的 面积的平均位置, 表示图形的几何 中心。
质心:平面图形 中所有点组成的 物质质量的平均 位置,表示图形 的质量中心。
重心:平面图形 中所有点组成的 重力场强度的平 均位置,表示图 形的重力中心。
平面图形稳定性分析的方法:通过力学分析、数学建模、实验测试等方法,对平面图形的稳定性 进行分析。
平面图形稳定性在工程中的应用:广泛应用于桥梁、建筑、机械等领域,以确保结构的稳定性和 安全性。
平面图形失稳的临界力和临界应力
定义:临界力是 指使平面图形失 稳的最小外力, 而临界应力则是 指在该外力作用 下,平面图形达 到失稳状态时的 应力值。
平面图形的动力学特性
{材料力学}平面图形的几何性质

C(zc, yc)
面积A
z1
a
o
z
已知: I yc , I zc , I yczc 计算: I y , I z , I yz
y y1 a
z z1 b
z1 —y1为形心坐标系
19
Iz y2dA ( y1 a )2 dA y12dA 2a y1dA a2 dA
Izc 2a • zc • A a2 A Izc a2 A
dI z1 0
d
2(
I
z
2
I
y
sin
2
I
yz
cos
2
)
0
tg2 2I yz
Iz Iy
dI y1 0
d
说明取极大(或极小)惯性矩时
I y1z1 0
惯性积等于零
28
由方程 tg2 2I yz 求解出
Iz Iy
1, 2
1, 2 确定两个相互垂直的轴 —— 主惯性轴
也就是说:1、对于给定的截面
坐标转换的矩阵形式
y1 z1
cos sin
sin y
cos
z
23
操作式的推导 A( y, z) A( y1, z1) 用投影代替转动 《y 变 y1 的操作》
1、y(AF)向 y1 轴投影得 y1 + GF
y cos y1 GF
2、再减去GF 得y1
y1 y cos GF y cos z sin
y2 cos2 dA z2 sin 2dA 2 yz sin cosdA
1
cos 2
2
y2dA
1 cos 2
2
z2dA sin
2
yzdA
1 cos 2
材料力学课件—平面图形几何性质

Sy zd A zd A zd A zd A
A
A1
A2
An
S y1 S y2 S yn S yi Ai zCi
Sz Szi Ai yCi
例:平面图形如图所示,试确定该图形的 形心位置,并计算该图形对z 轴的面积矩。
50
z
10
60 y 10
50 10
C1
O
y
z
dA A
∫ z
Sy = zdA
A
S z =∫ ydA A
量纲:长度3, 单位:m3
y
1.面积矩不仅与平面图形的面积有关,
还与平面图形的形状、坐标轴的位置有关。
2.面积矩可正、可负,也可为零。
二、形心的位置
∫ zdA
zC =
A
A
= Sy/A
∫ ydA
yC =
A
A
= Sz/A
S y = zC ·A
2
z d cos
2
y、z 是对称轴
P332 表A-1
I yz 0
§3 惯性矩和惯性积的平行移轴公式
z
O
a C
y'
b z' dA
zC
I z = IzC + a 2 A I y = IyC + b 2 A
在一组相互平行的轴中,平
y
yC
面图形对形心轴的惯性矩最小。
I y z = IyC zC + ab A
Ⅱ Ⅰ
h C
① 计算惯性矩Iy、Iz和惯性积Iyz
Iy
IⅠy
I
Ⅱ y
I
Ⅲ y
z
Ⅲ
d
hd
3
db3
[
bd (b d
材料力学PPT截面几何性质)
解:首先求对圆心的极惯性矩。 在离圆心O为处作宽度为d的薄圆环,其面 积dA=2pd,则
I p
2 d A
A
d /2 2 (2p d ) pd 4
0
32
由于圆形对任意直径轴都是对称的,故Ix=Iy 注意到Iρ=Ix+Iy,得到
Ix
Iy
1 2
I
pd 4
64
y d
x
C
d
§4-3 惯性矩和惯性积的平行移轴公式 组合截面的惯性矩和惯性积
y0 y 10
例4-7 计算图示截面的形心主轴和形心主惯性矩
图形的对称中心C为形心,在C点建立坐标
II
系xCy如图
将整个图形分成I、II、III三个矩形,如图
I x0 整个图形对x、y轴的惯性矩和惯性积分别
120
0 x 为
C 10
IIII Ix IIx IIIx IIIIx
10
101203 12
60103 12
(60-
5)2
(6010)2
70
5.08106 mm4
Iy IIy IIIy IIIIy 1.84106 mm 4 Ixy IIxy IIIxy IIIIxy -2.31106 mm 4
tg20
-
2I xy Ix -Iy
1.4260
27o 28'
00 p/4,Ix Iy,自x轴逆时针旋转 27o28'转到主轴x0,Ix0 Imax,Iy0 Imin
2.惯性矩:
Ix Iy
AAxy22ddAA
分别为图形对x、y轴 的惯性矩;
y O
x
3.惯性积:
dA x
I xy A xydA为图形对x、y一对正交轴的惯性积;
材料力学第四章 平面图形的几何性质

§4.1 静矩和形心
一、静矩,即面积对轴的矩:(与力矩类似)
z
是面积与它到轴的距离之积。
图形对y轴和z轴的静矩为
dA
Sz
ydA
A
z
Sy
zdA
A
特点:
y▲静矩的量纲为长度的三次方;
第四章 平面图形的几何性质
§4.1 静矩和形心 §4.2 惯性矩和惯性半径 §4.3 惯性积 §4.4 平行移轴公式 §4.5 转轴公式 主惯性轴
第四章 平面图形的几何性质
【基本内容】
一、静矩、形心 二、惯性矩、惯性积、惯性半径 三、主轴、主惯性矩、形心主惯性平面的概念 四、平行移轴公式、转轴公式
跟踪训练
1.图示矩形截面的I.Ⅱ两部分对z轴的静矩的关 系是( )
例 1 求下列各图的图形形心位置。
za
y1
1 2
a,
y2
3 2
a
z1
a,
z2
1 2
a
2a o
A1
y
n
Ai yi
i 1
n
Ai
2a2
1a 2 2a2
a2 a2
3 2
a
5 6
a
i 1
A2
a
yz
n
Ai zi
i 1
n
Ai
2a2 a a2 1 a 2
I z1
Iy
2
Iz
Iy
Iz 2
cos2
I yz sin 2
I y1z1
Iy
2
工学材料力学平面图形的几何性质

3
)2
R2
1
R3
23
3
0
z 解法2:
Sy
zd A
A
rdθ
Ar sin r d d r
r+dr dθ r
2
R r 2 d r sin d
O
00
θ
y
1 R3
z
3
试想想还有没有其它方法?
O
y
三、组合图形的静矩和形心
1、组合图形对某一轴的静矩等于组成它的各部分图形对同一 轴静矩的代数和,即:
平面图形的几何性质
目录
§A.1 静矩和形心 §A.2 惯性矩和惯性半径 §A.3 惯性积 §A.4 平行移轴公式
§A.1 静矩和形心
一、静矩
定义: 面积对轴的一次矩。
z
z
dA
Sz
yd A,
A
Sy
zd A
A
分别为图形对 z 轴和 y 轴的静矩。
O
y
y
说明:
1、静矩不仅与平面图形的形状尺寸有关,还与所选坐标的 位置有关。同一平面图形对不同的坐标轴,其静矩不同。
D
Iy
Iz
IP 2
d 4
64
d
同理,对于空心圆:
Iy
Iz
D4
64
(14
)
其中 d
D
z
dz z
O
y
b z
d
O
y
§A.4 平行移轴公式
一、惯性矩的平行移轴公式
C为形心,y、z为原坐标轴,yc、zc 为过形心C分别与y、 z平行的坐标轴
I yC A zC2dA
I zC A yC2 dA
材料力学5、平面图形的几何性质.

12
64 4
y
I
y
C
I矩xC
I圆xC
(1.5d )32d 12
d 4
64
0.513
d
4
d
yC
x1
2d
I xCyC 0
( yC为对称轴 )
O
x
xC
xC yC轴便是形心主轴
b
I xC , I yC便是形心主惯性矩
图(b)
y 5 (70110) 20.3 12080 70110
验证:34.7 + 20.3 + 5 = 60
§5-2 极惯性矩、惯性矩、惯性积、惯性半径
二、惯性矩: 是面积与它到轴的距离的平方之积。
图形对x轴的惯性矩: 图形对y轴的惯性矩:
Ix y2dA
A
I y x2dA
2
0.177d
4
③ 建立形心坐标系;求:IyC , IxC , I xCy
I xC I矩xC I圆xC I矩x A矩 y 2[I圆x1A圆 (0.5dy)2 ]
1.5d(2d )3 3d 2 (0.177 d )2[d 4 d 2 (0.5d0.177 d )2 ]0.685 d 4
yC
(
I
xC
I 2
yC
)
2
I
2 xCyC
例3 在矩形内挖去一与上边内切的圆,求图形的形心主轴。(b=1.5d)
y
d
yC
x1
解: ①建立坐标系如图。
2d
O
x
xC
b
②求形心位置。
x
xi Ai 0 0 AA
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y
解: 取平行于x轴的狭长条
h dy
y
则 dA=b dy
I x
y2d A
A
h
2 h
2
by2
d
y
bh3 12
同理
I
y
hb3 12
C
x
b
思考题I—1:平行四边形对形心轴x 的惯性矩应怎样计算?
5.主惯性轴:当平面图形对某一对正交坐标轴y0、z0的惯性积 I y0z0 =0时,则坐标轴 y0、z0称为主惯性轴。
I x
y2 d A
A
A yc a2 d A
A yc 2 d A 2a A yc d A a2 A d A
I xc Sxc a2 A
I xc a2 A
同理,有:
I y
I yc
b2A
I xy I xc yc abA
h
2
1
2
y2 2
b2
dy
4bh 2 15
Sz
y dA
A
b 0
yh1
y2 b2
d
y
b2h 4
z
A
dA
A
b 0
h1
y2 b2
dy
2bh 3
h
形心坐标为:
bh2
yC
Sz A
4 2bh
3b 8
§ -1 静矩和形心
y
一、基本概念
dA
1. 静矩(或一次矩)
C
y
y
x dA ——微面积对y轴的静矩
y dA ——微面积对x轴的静矩
O
x
x
x
S y
xd A
A
——整个平面图形对y轴的静矩
Sx
ydA
A
——整个平面图形对x轴的静矩
常用单位:m3 或mm3 。 数 值:可为正、负或 0 。
y
y
A dA
C E
D
O
x
B
新坐标系ox1y1 旧坐标系o x y
x1 x cos y sin y1 y cos x sin
将上述关系代入平 面图形对x1轴的惯性矩:
x
I x1 A y12 d A
Ix1
cos2
y2 d A sin2
A
x2 d A 2sin cos
推论:具有一个或两个对称轴的正交坐标轴一定是平面图形的 主惯性轴。
6.主惯性矩:平面图形对任一主惯性轴的惯性矩称为主惯性矩。
7.形心主惯性轴:过形心的主惯性轴称为形心主惯性轴。 可以证明:任意平面图形必定存在一对相互垂直的形心主惯性轴。
8.形心主惯性矩:平面图形对任一形心主惯性轴的惯性矩称为形 心主惯性矩。
n
x
Sy A
Ai xi
i 1
,
n
Ai
i 1
n
y
Sx A
Ai yi
i 1
n
Ai
i 1
例I—1:计算由抛物线、y轴和z轴所围成的平面图形对y轴和z 轴的静矩,并确定图形的形心坐标。
z
z
h1
y2 b2
解:
O
y
Sy
z dA A2
b 0
1
A
xy d A
A
Ix cos2 I y sin2 2Ixy sin cos
利用三角函数整理上式,得转轴公式 :
I x1
Ix
2
Iy
Ix
Iy 2
cos 2
I xy sin 2
同理得:
I y1
Ix
2
Iy
Ix
2
Iy
cos 2
I xy sin 2
I x1y1
Ix
2
Iy
sin
2
I xy
cos 2
规定:上式中的 的符号为:逆时针为正,顺时针为负。
讨论: 将上述转轴公式中的前两式相加可得:
I x1 I y1 I x I y
即,截面对于通过同一点的任意一对相互垂直的坐标轴的 两惯性矩之和为一常数,并等于截面对该坐标原点的极惯 性矩。
2.截面的主惯性轴和主惯性矩
从惯性积的转轴公式可推知,随着坐标轴旋转,惯性积
将随着角作周期性变化,且有正有负。因此,必有一特定的 角度0,使截面对与该角对应的新坐标轴x0、y0的惯性积为零。
依此进行如下定义:
(1) 主惯性轴:截面对其惯性积等于0的一对坐标轴。
(2) 主惯性矩:截面对于主惯性轴的惯性矩。
(3) 形心主惯性轴:当一对主惯性轴的交点与截面的形心重合时。
目录
§-3 平行移轴公式
1.平行移轴公式推导
y
yc
x xc dA yc
左图是一面积为A的任意形状的平
面,c为其形心,xcyc为形心坐标轴。与 该形心坐标轴分别平行的任意坐标轴为
xy ,形心c在oxy坐标系下的坐标为(a , b)
C
xc
任意微面元dA在两坐标系下的
y
坐标关系为:
Ob
x
x xC b y yC a
目录
§ I-2 极惯性矩 ·惯性矩 ·惯性积
1.极惯性矩(或截面二次极矩)
y
I p
2d A
A
2.惯性矩(或截面二次轴矩)
y
I y
x2 d A
A
I x
y2d A
A
O
由于 2 y2 x2
dA
x
x
所以
Ip
2 d A
A
(y2
A
x2)
dA IxIy
(思考题I—2)A
y
bO
(思考题I—3)
x
a
y a
x
Ba
D
思考题I—3:等腰直角三角形如图所示,x、y轴是过斜边中点的
任意一对坐标轴(即图中为任意值),该图形的:
(1)惯性积Ixy=__ (2)惯性矩Ix=__ 、 Iy___。
目录
§-4惯性矩和惯性积的转轴公式.截面的 主惯性轴和主惯性矩
1. 转轴公式
2
128
d2
8
2d
3
2
d 8
2
2d
3
a
2
思考题I—2:O为直角三角形ABD斜边上的中点,x、y轴为过点
O且分别平行于两条直角边的两根轴,关于惯性积和惯性矩有
四种答案(已知b>a):
(A)Ixy>0 ( C ) Ixy=0
(B) Ixy<0 (D) Ix=Iy
(4) 形心主惯性矩:截面对于形心主惯性轴的惯性矩。
3.主惯性轴位置的确定
设坐标轴转动角度为0,则由惯性积的转轴公式及主惯性 轴的定义,得:
经整理,得
Ix
2
I
y
sin
2 0
I xy
cos 20
0
tan 20
2Ixy Ix Iy
4.主惯性矩的确定
由上面tan20的表达式求出cos20、sin20后,再代入惯 性矩的转轴公式 ,化简后可得主惯性矩的计算公式如下:
2.形心坐标公式
x
xd
A
A
Sy
A
A
y A y d A Sx
A
A
3.静矩与形心坐标的关系
Sy Ax Sx A y
推论:截面对形心轴的静矩恒为0,反之,亦然。
二、讨论:
1.组合截面的静矩
根据静矩的定义:整个平面图形对某轴的静矩应等于 它的各组成部分对同一轴的静矩的代数和,即:
注: 式中的a、b代表坐标值,有时可能取负值。
例I—4:求图示直径为d的半圆对其自身形心轴xc的惯性矩。
y
y b(y)
C
yc
d
解: (1)求形心坐标
d
ቤተ መጻሕፍቲ ባይዱ
S x
yd A
A
2 yb( y) d y
0
xc
d
2 y2
R2 y2 d y d3
0
12
x
yc
Sx A
d 3 12 πd 2 8
2d 3π
b( y) 2 R2 y2
(2)求对形心轴xc的惯性矩
Ix
πd 4 2
64
πd 4 128
由平行移轴公式得:
I xc
Ix
(
yc
)
2
πd 8
2
πd 4 128
d4
18π
例I—5:求图示平面图形对y轴的惯性矩 Iy
z
z
a
a
y
y
a
a
d
d
解:
Iy
d (2a)3 12
d 4
本章重点
1、静矩与形心 2、惯性矩、极惯性矩和惯性积 3、平行移轴公式、转轴公式
关键概念
静矩、惯性矩、极惯性矩、惯性积、主惯性轴、形 心主惯性轴
目录
