中国科技大学算法导论_第一次实验报告
实验一算法分析基础

算法分析与设计实验报告学号姓名班级上课地点教师上课时间实验一算法分析基础1. 实验目的1.1.熟悉Eclipse中编辑、编译和运行JA V A程序的方法;1.2.了解算法的定义与特点;1.3.学会分析算法的时间复杂度和空间复杂度。
2. 实验环境2.1 Eclipse2.2 Window XP3. 实验内容3.1 排序问题:实现冒泡排序、插入排序算法,并分析它们的算法复杂度。
3.2 合并问题:合并两个已排序的表,并分析算法复杂度。
(首先判断两个表是否已排序)4. 教师批改意见成绩签字:日期:实验报告细表1插入排序1.1 算法设计思想快速排序是通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
快速排序算法流程图为:1.2 程序源码插入排序代码:package实验1;import java.util.Scanner;public class InsertionSort {public static void main(String anr[]){i nt[] a=new int[7];a[6]=99999999;Scanner s = new Scanner(System.in);for(int i=1;i<6;i++){System.out.println("请输入第"+i+"个数字");a[i]=s.nextInt();}for(int i=1;i<6;i++){if(a[i+1]<a[i]){a[0]=a[i+1];for(int j=i+1;j>0;j--){a[j]=a[i];i--;}}}System.out.println("插入排序后的顺序为:");for(int i=1;i<6;i++)System.out.println(a[i]);}}1.3 实验结论第一组数据:当输入数据为5,9,7,11,6时,结果如下:第二组数据:当输入数据为6,9,1,11,10时,结果如下:第三组数据:当输入数据为55,16,25,48,10时,结果如下:1.4 心得体会快速排序的运行时间与划分是否对称有关,算法的实现和理解与代码实现完全是两回事,想要完全掌握一种算法,需要动手实践,用代码实现,才能理解透彻,真正掌握。
算法实验报告一

解决方法:算法需要定义move函数,才能实现函数的调用;
问题:出现未定义字母
解决方法:检查代码是否有错误,是否正确定义并改正。
System.out.println("结果为:"+q(5,6));
publicstaticvoidmain(String[] args) {
}
publicstaticintq(intn,intm) {
if((n<1)||(m<1))return0;
if((n==1)||(m==1))return1;
时加入c将n1个较小的圆盘依次移动规则从a到c然后将剩下的最大圆盘移至b最后在设法将n1个较小的圆盘依次移动规则从c到b
《算法设计与分析》课程实验报告
专业:计算机科学与技术
班级:
学号:
姓名:
日期:2014年10月18日
一、实验题目
熟悉环境和递归算法
二、实验目的
1、熟悉Java上机环境;
2、基本掌握递归算法的原理方法.
(ri)perm(X)表示在全排列perm(X)的每一个排列前加上前缀得到的排列。R的全排列可归纳定义如下:
当n=1时,perm(R)=(r),其中r是集合R中唯一的元素;
当n>1时,perm(R)由(r1)perm(R1),(r2)perm(R2),…,(rn)perm(Rn)构成。
(2)算法描述
if(n > 0) {
hanoi(n-1, a, c, b);
Move(a, b);
hanoi(n-1, c, b, a);
}
}
privatestaticvoidMove(chara,charb) {
中科大程序设计与计算机系统实验一指导书_2014112810430932

3 Hand Out Instructions
Start by copying datalab-handout.tar to a (protected) directory in which you plan to do your work. Then give the command: tar xvf datalab-handout.tar. This will cause a number of files to be unpacked in the directory. The only file you will be modifying and turning in is bits.c. The file btest.c allows you to evaluate the functional correctness of your code. The file README contains additional documentation about btest. Use the command make btest to generate the test code and run it with the command ./btest. The file dlc is a compiler binary that you can use to check your solutions for compliance with the coding rules. The remaining files are used to build btest. Looking at the file bits.c you’ll notice a C structure team into which you should insert the requested identifying information about the one or two individuals comprising your programming team. Do this right away so you don’t forget. The bits.c file also contains a skeleton for each of the 15 programming puzzles. Your assignment is to complete each function skeleton using only straightline code (i.e., no loops or conditionals) and a limited number of C arithmetic and logical operators. Specifically, you are only allowed to use the following eight operators: ! ˜ & ˆ | + << >> A few of the functions further restrict this list. Also, you are not allowed to use any constants longer than 8 bits. See the comments in bits.c for detailed rules and a discussion of the desired coding style.
算法导论实验指导

!!每一次都要求签到,不能到需要提前向助教请 假!!
截止时间: 2014/ 12/ 23 12:00:00
提交内容:实验源码(C/C++/java)+可执行程序+ 一份实验报告(word_2003) 提交格式:所有实验内容打包成一个rar文件后提交到 软件学院教学辅助系统,rar文件命名格式为 学号_姓名(如: SA130225001_张三.rar)
(1)实现这个问题的贪心算法 (2)将每个 替换为 行算法比较结果
,运
4.常见平衡树的实现与比较
问题描述:
实现3种树中的两种:红黑树,AVL树(课本P177), Treap树(课本P178)
实验要求:
(1)实现基本操作(初始化、插入、删除) (2)比较算法之间的时间、空间性能
2.背包问题
问题描述:
0-1背包问题,部分背包问题(课本P229) 实验要求: (1)实现0-1背包的动态规划算法求解 (2)实现部分背包的贪心算法求解 (3)实现部分背包的动态规划算法求解(选做)
3.一个任务调度问题
问题描述:
在单处理器上具有期限和惩罚的单位时间任务 调度问题(课本P239)
实验要求:
问题描述 算法原理:算法的思想,正确性说明
每个实验 基本格式
实验数据:测试用数据 实验截图:实验运行结果截图 结果分析:算法的时间和空间性能; 各实验的单独要求 。。。。。。
1.快速排序
问题描述:
实现对数组的普通快速排序与随机快速排序 实验要求: (1)实现上述两个算法 (2)统计算法的运行时间 (3)分析性能差异,作出总结
2014~2015学年第一学期
shenyao@
ldayy@
中科大软件学院算法实验报告

算法实验报告快速排序1. 问题描述:实现对数组的普通快速排序与随机快速排序(1)实现上述两个算法(2)统计算法的运行时间(3)分析性能差异,作出总结2. 算法原理:2.1快速排序快速排序是对冒泡排序的一种改进。
它的基本思想是:选取一个基准元素,通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比基准元素小,另外一部分的所有数据都要比基准元素大,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
设要排序的数组是A[0]……A[N-1],首先选取一个数据(普通快速排序选择的是最后一个元素, 随机快速排序是随机选择一个元素)作为关键数据,然后将所有比它小的数都放到它前面,所有比它大的数都放到它后面,这个过程称为一趟快速排序。
一趟快速排序的算法是:1)设置两个变量i、j,排序开始的时候:i=0,j=N-1;2)以第一个数组元素作为关键数据,赋值给key,即key=A[0];3)从j开始向前搜索,即由后开始向前搜索(j--),找到第一个小于key的值A[j],将A[j]赋给A[i];4)从i开始向后搜索,即由前开始向后搜索(i++),找到第一个大于key的A[i],将A[i]赋给A[j];5)重复第3、4步,直到i=j;(3,4步中,没找到符合条件的值,即3中A[j]不小于key,4中A[i]不大于key的时候改变j、i的值,使得j=j-1,i=i+1,直至找到为止。
找到符合条件的值,进行交换的时候i,j指针位置不变。
另外,i==j这一过程一定正好是i+或j-完成的时候,此时令循环结束)。
2.2随机快速排序快速排序的最坏情况基于每次划分对主元的选择。
基本的快速排序选取第一个或者最后一个元素作为主元。
这样在数组已经有序的情况下,每次划分将得到最坏的结果。
一种比较常见的优化方法是随机化算法,即随机选取一个元素作为主元。
这种情况下虽然最坏情况仍然是O(n^2),但最坏情况不再依赖于输入数据,而是由于随机函数取值不佳。
中科大算法导论第一,二次和第四次作业答案

2.2-3 再次考虑线性查找问题 (见练习2.1-3)。在平均情况 下,需要检查输入序列中的多 少个元素?假定待查找的元素 是数组中任何一个元素的可能 性是相等的。在最坏情况下有 怎样呢?用Θ形式表示的话,线 性查找的平均情况和最坏情况 运行时间怎样?对你的答案加 以说明。 • 线性查找问题 • 输入:一列数A=<a1,a2,…,an>和一 个值v。 • 输出:下标i,使得v=A[i],或者当 v不在A中出现时为NIL。 • 平均情况下需要查找 (1+2+…+n)/n=(n+1)/2 • 最坏情况下即最后一个元素为待 查找元素,需要查找n个。 • 故平均情况和最坏情况的运行时 间都为Θ(n)。
• 2.3-2改写MERGE过程,使之不使 用哨兵元素,而是在一旦数组L或R 中的所有元素都被复制回数组A后, 就立即停止,再将另一个数组中 余下的元素复制回数组A中。 • MERGE(A,p,q,r) 1. n1←q-p+1 2. n2 ←r-q 3. create arrays L[1..n1] and R[1..n2] 4. for i ←1 to n1 5. do L*i+ ←A*p+i-1] 6. for j ←1 to n2 7. do R*j+ ←A*q+j+ 8. i ←1 9. j ←1
10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21.
k ←p while((i<=n1) and (j<=n2)) do if L[i]<=R[j] do A[k]=L[i] i++ else do A[k]=R[j] j++ k++ while(i<=n1) do A[k++]=L[i++] while(j<=n2) do A[k++]=R[j++]
算法类实习报告

实习报告一、前言算法是计算机科学的核心,是解决复杂问题、优化问题的重要手段。
作为一名计算机专业的学生,我深知算法在实际应用中的重要性。
因此,在大学期间,我积极参加了多次算法实习,以提高自己的算法能力和实践经验。
本文将对我最近的算法实习经历进行总结和报告。
二、实习内容本次实习主要涉及以下几个方面的内容:1. 算法基础:复习了常见的数据结构(如数组、链表、栈、队列、树等)和基本算法(如排序、查找、递归等)。
2. 算法设计与分析:学习了贪心算法、动态规划、分治算法等常见算法设计方法,并通过实例进行了实践。
3. 算法竞赛:参加了国内外知名的算法竞赛,如LeetCode、Codeforces等,完成了约200道算法题目。
4. 实际项目:参与了一个实际项目的算法设计与实现,涉及大数据处理、分布式计算和机器学习等技术。
三、实习过程1. 学习算法基础:通过阅读教材、在线课程和博客,复习了算法基础知识,并对重点概念和算法进行了总结。
2. 学习算法设计与分析:阅读了相关教材和论文,学习了贪心算法、动态规划、分治算法等设计方法,并通过实例进行了练习。
3. 参加算法竞赛:注册了LeetCode、Codeforces等平台,参加了算法竞赛,逐步提高自己的算法能力。
4. 实际项目:与团队成员一起讨论项目需求,设计算法方案,实现了相关功能模块。
四、实习收获1. 算法能力:通过实习,提高了自己的算法能力,熟练掌握了常见数据结构和基本算法,学会了运用各种算法设计方法解决实际问题。
2. 编程技巧:在实习过程中,提高了自己的编程技巧,熟悉了多种编程语言(如Python、C++、Java等),并掌握了相关开发工具和库。
3. 团队协作:在实际项目中,学会了与团队成员沟通、协作,共同解决问题,提高了自己的团队协作能力。
4. 解决问题能力:在实习过程中,学会了分析问题、拆解问题、解决问题,提高了自己的逻辑思维能力和独立解决问题的能力。
五、总结通过本次算法实习,我对算法有了更深入的了解,提高了自己的算法能力和实践经验。
中科大算法导论作业标准标准答案

第8次作业答案16.1-116.1-2543316.3-416.2-5参考答案:16.4-1证明中要三点:1.有穷非空集合2.遗传性3.交换性第10次作业参考答案16.5-1题目表格:解法1:使用引理16.12性质(2),按wi单调递减顺序逐次将任务添加至Nt(A),每次添加一个元素后,进行计算,{计算方法:Nt(A)中有i个任务时计算N0 (A),…,Ni(A),其中如果存在Nj (A)>j,则表示最近添加地元素是需要放弃地,从集合中删除};最后将未放弃地元素按di递增排序,放弃地任务放在所有未放弃任务后面,放弃任务集合内部排序可随意.解法2:设所有n个时间空位都是空地.然后按罚款地单调递减顺序对各个子任务逐个作贪心选择.在考虑任务j时,如果有一个恰处于或前于dj地时间空位仍空着,则将任务j赋与最近地这样地空位,并填入; 如果不存在这样地空位,表示放弃.答案(a1,a2是放弃地):<a5, a4, a6, a3, a7,a1, a2>or <a5, a4, a6, a3, a7,a2, a1>划线部分按上表di递增地顺序排即可,答案不唯一16.5-2(直接给个计算例子说地不清不楚地请扣分)题目:本题地意思是在O(|A|)时间内确定性质2(性质2:对t=0,1,2,…,n,有Nt(A)<=t,Nt(A)表示A中期限不超过t地任务个数)是否成立.解答示例:思想:建立数组a[n],a[i]表示截至时间为i地任务个数,对0=<i<n,如果出现a[0]+a[1]+…+a[i]>i,则说明A不独立,否则A独立.伪代码:int temp=0;for(i=0;i<n;i++) a[i]=0; ******O(n)=O(|A|)for(i=0;i<n;i++) a[di]++; ******O(n)=O(|A|)for(i=0;i<n;i++) ******O(n)=O(|A|) {temp+=a[i];//temp就是a[0]+a[1]+…+a[i]if(temp>i)//Ni(A)>iA不独立;}17.1-1(这题有歧义,不扣分)a) 如果Stack Operations包括Push Pop MultiPush,答案是可以保持,解释和书上地Push Pop MultiPop差不多.b) 如果是Stack Operations包括Push Pop MultiPush MultiPop,答案就是不可以保持,因为MultiPush,MultiPop交替地话,平均就是O(K).17.1-2本题目只要证明可能性,只要说明一种情况下结论成立即可17.2-1第11次作业参考答案17.3-1题目:答案:备注:最后一句话展开:采用新地势函数后对i 个操作地平摊代价:)1()())1(())(()()(1''^'-Φ-Φ+=--Φ--Φ+=Φ-Φ+=-Di Di c k Di k Di c D D c c i i i i i i17.3-2题目:答案:第一步:此题关键是定义势能函数Φ,不管定义成什么首先要满足两个条件 对所有操作i ,)(Di Φ>=0且)(Di Φ>=)(0D Φ比如令k j+=2i ,j,k 均为整数且取尽可能大,设势能函数)(Di Φ=2k;第二步:求平摊代价,公式是)1()(^-Φ-Φ+=Di Di c c i i 按上面设置地势函数示例:当k=0,^i c =…=2当k !=0,^i c =…=3 显然,平摊代价为O(1)17.3-4题目:答案:结合课本p249,p250页对栈操作地分析很容易有下面结果17.4-3题目:答案:αα=(第i次循环之后地表中地entry 假设第i个操作是TABLE_DELETE, 考虑装载因子:inum size数)/(第i次循环后地表地大小)=/i i第12 次参考答案19.1.1题目:答案:如果x不是根,则degree[sibling[x]]=degree[child[x]]=degree[x]-1如果x是根,则sibling为二项堆中下一个二项树地根,因为二项堆中根链是按根地度数递增排序,因此degree[sibling[x]]>degree[x]19.1.2题目:答案:如果x是p[x]地最左子节点,则p[x]为根地子树由两个相同地二项树合并而成,以x为根地子树就是其中一个二项树,另一个以p[x]为根,所以degree[p[x]]=degree[x]+1;如果x不是p[x]地最左子节点,假设x是p[x]地子节点中自左至右地第i个孩子,则去掉p[x]前i-1个孩子,恰好转换成第一种情况,因而degree[p[x]]=degree[x]+1+(i-1)=degree[x]+i;综上,degree[p[x]]>degree[x]19.2.2题目:题目:19.2.519.2.6第13次作业参考答案20.2-1题目:解答:20.2-3 题目:解答:20.3-1 题目:答案:20.3-2 题目:答案:第14次作业参考答案这一次请大家自己看书处理版权申明本文部分内容,包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some parts, including text, pictures, and design. Copyright is personal ownership.6ewMy。
排序算法实验报告USTC

实验报告一、实验目的在计算机科学与数学中,排序算法是一种基本并且常用的算法,一个排序演算法是一种能将一串资料依照特定排序方式的一种演算法。
有效的排序演算法在一些演算法中是重要的,如此这些演算法才能得到正确解答。
排序演算法也用在处理文字资料以及产生人类可读的输出结果。
由于实际工作中处理的数量巨大,所以排序算法对算法本身的速度要求很高。
通过实现相关一些排序算法,加深对于算法知识的理解与学习。
二、实验题目要求实现合并排序,插入排序,希尔排序,快速排序,冒泡排序,桶排序算法,并比较这些算法的性能。
三、实验要求(一)在随机产生的空间大小分别为N = 10,1000,10000,100000 的排序样本(取值为[0,1])上测试以上算法。
(二)结果输出:1) N=10时,排序结果。
2) N=1000,10000,100000时,对同一个样本实例,不同排序完成所需的时间。
3) N=1000,10000,100000时,每个排序用不同的样本多试验几次(最低5次)得出平均时间,比较不同排序算法所用的平均时间。
四、实验内容各种排序算法相关代码的实现及其原理说明如下:1.合并排序对于合并排序,算法过程说明如下:设两个有序的子文件(相当于输入堆)放在同一向量中相邻的位置上:R[low..m],R[m+1..high],先将它们合并到一个局部的暂存向量R1(相当于输出堆)中,待合并完成后将R1复制回R[low..high]中。
合并过程中,设置i,j和p三个指针,其初值分别指向这三个记录区的起始位置。
合并时依次比较R[i]和R[j]的关键字,取关键字较小的记录复制到R1[p]中,然后将被复制记录的指针i或j加1,以及指向复制位置的指针p加1。
重复这一过程直至两个输入的子文件有一个已全部复制完毕,此时将另一非空的子文件中剩余记录依次复制到R1中即可。
2.插入排序关于直接插入排序的算法说明如下:假设待排序的记录存放在数组R[1..n]中。
中科大黄刘生算法第一次作业
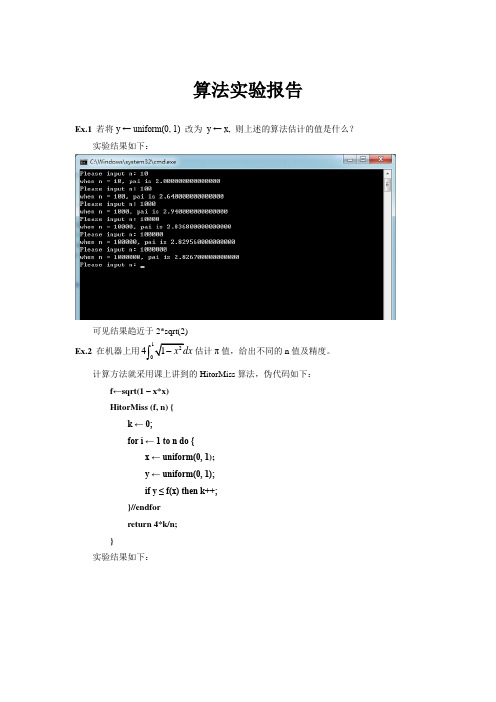
算法实验报告Ex.1 若将y ← uniform(0, 1) 改为 y ← x, 则上述的算法估计的值是什么?实验结果如下:可见结果趋近于2*sqrt(2) Ex.2 在机器上用2041x dx -⎰估计π值,给出不同的n 值及精度。
计算方法就采用课上讲到的HitorMiss 算法,伪代码如下: f ←sqrt(1 – x*x) HitorMiss (f, n) { k ← 0;for i ← 1 to n do { x ← uniform(0, 1); y ← uniform(0, 1);if y ≤ f(x) then k++;}//endfor return 4*k/n;}实验结果如下:从总的趋势来看,n的值越大,给出的pai的精度越高。
但对应到两次实验结果未必n 大的精度一定高,这是概率算法的特点。
EX.3 采用算法类似HitorMiss算法,不过加入了一些特殊处理,以便能够正确计算穿越x 轴、周期函数等的积分。
算法伪代码如下:f ← x^2 / - sqrt(x) / sin(x)MyCalc(f , minx, maxx, miny, maxy, n){k ← 0;for i ← 1 to n do {x ← uniform(minx, maxx);y ← uniform(miny, maxy);if f(x) >= 0//函数在x轴上方,积分是f与x轴之间的部分,积分值为正then if y <= f(x) && y >=0k++;else//函数在x轴下方,积分是f与x轴之间的部分,积分值为负if y >= f(x) && y <= 0k--;}//endforif miny > 0//函数在x轴上方then return k / n * (maxx - minx) * (maxy - miny) + miny * (maxx - minx));else if maxy < 0//函数在x轴下方then return k / n * (maxx - minx) * (maxy - miny) + maxy * (maxx - minx);else//函数穿越x轴then return k / n * (maxx - minx) * (maxy - miny);}运行结果如下:可见程序运行结果还是很准确的,能正常处理在x轴单侧、穿越x轴的连续函数积分。
中科大软院算法导论最近点对算法_C++

实验四求最近点对算法1.算法设计思路:设共有n个点,找其中距离最近的两点及其距离。
(1)蛮力法:蛮力法的思路是把所有点之间距离比较找出中间最小的。
先假设最短距离是第一个元素和第二个元素的距离,然后求第一个元素与其后的(n-1)个元素各自的距离,若比之前记录的最短距离小则记录当前值···求第i个元素与其后的(n-i)个元素各自的距离,记录之前所得到的所有距离中的最小值,直到计算到第(n-1)个元素与第n个元素的距离,此时记录的距离即为这n个元素中的最短距离。
(2)分治法:分治法是把一个大的问题划分成相似的小问题,采用递归的思想。
找中线把n个元素分成左右两部分元素分别求得两边的最短距离,然后取两者中的最小者记为l,在中线两边分别取l的距离,记录该距离范围内点的个数,中线左边有L个元素,右边有R个元素,求左边元素到右边元素的距离看其是否小于之前记录的最短距离,小则记录下来,此时的右边元素只取y值和左边元素y值距离小于l的(减少循环次数)。
循环结束即可找到最小的距离。
2.程序代码:#include<iostream>#include<cstdlib>#include<ctime>#include<cmath>using std::cout;using std::endl;#define N 5int x[N],y[N],record[N]; //产生原始点数据,x坐标放在x[]中,y坐标放在y[]中。
double Min;//////////////////////////产生随机数组/////////////////////////////void randnum(){int i;srand(time(0));for (i=0;i<N;i++){x[i]=rand()%N;cout<<x[i]<<' ';}cout<<endl;for (i=0;i<N;i++){y[i]=rand()%N;cout<<y[i]<<' ';}cout<<endl;}//////////////////////////////交换数组元素/////////////////////////// void swap(int & a, int & b){int temp=a;a=b;b=temp;}///////////////////////////////求平方///////////////////////////////////int square(int x){return x*x;}/////////////////////////////////////求两点之间距离////////////////////double lengthf(int x1,int y1,int x2,int y2){return sqrt(square(x1-x2)+square(y1-y2));}//////////////////////////////////求两者中最小者////////////////////// double min(double a,double b){if (a>=b)return b;elsereturn a;}////////////////////////////对平面数组排序//////////////////////////// void sort(int A[]){int i,j;for (i=0;i<N;i++)record[i]=i;for (j=1;j<N;j++){i=j;while (i>=0&&A[i]<A[i-1]){swap(A[i],A[i-1]);swap(record[i-1],record[i]); //得到x排序后对应的原y的坐标i--;}}cout<<"排序后的元素数组:"<<endl;for (i=0;i<N;i++)cout<<A[i]<<' ';cout<<endl;for (i=0;i<N;i++)cout<<record[i]<<' ';cout<<endl;}///////////////////////////穷举法找最小点对///////////////////////////////double exhaustion(){int i,j,k1,k2;double num;double length;num=10000;k1=k2=-1;for (j=0;j<N-1;j++){for (i=j+1;i<N;i++){length=lengthf(x[i],y[i],x[j],y[j]);if (length<num){num=length;k1=i;k2=j;}}}cout<<"平面数组最短距离是:"<<endl;cout<<"min="<<num<<endl;cout<<"对应数组下标及点坐标为:"<<endl;cout<<"i="<<k1<<','<<k2<<endl;cout<<"(x1,y1)="<<'('<<x[k1]<<','<<y[k1]<<')'<<endl<<"(x2,y2)="<<'('<<x[k2]<<','<<y[k2]<<')' <<endl;return num;}////////////////////////////////////分治法////////////////////////////////*************************************************************************/double merge(int left,int right){double mlength;if (right==left)mlength=10e-6;if (right==left+1)mlength=lengthf(x[right],y[record[right]],x[left],y[record[left]]); //两个点时求最小值if (right-left==2)mlength=min(min(lengthf(x[right-1],y[record[right-1]],x[left],y[record[left]]),lengthf(x[right],y[re cord[right]],x[left+1],y[record[left+1]])),lengthf(x[right],y[record[right]],x[left],y[record[left]]));//三个点时求最大值return mlength;}double divide(int left,int right){if (right-left<=2){Min=merge(left,right);}else{double l1,l2,mi; //l1记录划分区域后左半面最小距离,l2记录右半面最小距离,min为两者中较小者,m为全部中的最小者int rem1,rem2,l; //记录获得最短距离对应的两个点//int il,jl,ir,jr;int i,j;int R,L;R=L=0; //记录划分小区域后的左半块和右半块个有多少元素l1=l2=Min=100;l=(right-left+1)/2-1; //中线位置///////////////////////////////////////////////////l1=divide(left,l);l2=divide(l+1,right);if (l1<l2){Min=l1;//cout<<"两半面最短距离是:"<<min;else{Min=l2;//cout<<"两半面最短距离是:"<<min;}///////////////////得到右半块元素数R//cout<<"min="<<min<<endl;for (i=l+1;i<N;i++){if (x[i]-x[l]<=Min)R++;else break;}//cout<<"R="<<R<<endl;/////////////////////得到左半块元素数Lfor (i=l;i>=0;i--){if (x[l]-x[i]<=Min)L++;else break;}//cout<<"L="<<L<<endl;if (L!=0&&R!=0){for (i=l-L+1;i<=l;i++)for (j=l+1;j<=l+R;j++){if (y[record[j]]-y[record[i]]<Min||-Min<y[record[j]]-y[record[i]]){mi=lengthf(x[i],y[record[i]],x[j],y[record[j]]);if (mi<Min){Min=mi;rem1=i;rem2=j;}}}// cout<<"min="<<min<<endl;//cout<<"rem1="<<rem1<<endl<<"rem2="<<rem2<<endl;}return Min;}/***********************************************************************///////////////////////////////////主函数///////////////////////////////////int main(){//double a;randnum();cout<<"***************************遍历法*************************"<<endl;exhaustion();cout<<"***************************分治法*************************"<<endl;sort(x);divide(0,N-1);cout<<"元素组中最短距离为:"<<endl;cout<<"min="<<Min<<endl;return 0;}3.实验数据及实验结果:实验数据:随机产生的五个点坐标分别为:(1,3),(4,2),(3,0),(2,0),(0,3)实验结果:用蛮力法得到平面数组最短距离为:min=1用分治法得到平面数组最短距离为:min=14.实验总结:从本次试验中得到的领悟是:分治法事把问题分解成两个相似小问题,子问题和原来的大问题解决方法一样所以可以用递归,分治法重要是找到递归出口,什么时候递归结束,一般都有元素个数的限制。
大学生算法导论心得体会

大学生算法导论心得体会《算法导论》是一本经典的计算机科学教材,深入浅出地介绍了算法设计与分析的基本理论和技巧。
通过学习这门课程,我收获了很多宝贵的知识和经验,下面我将从以下几个方面来阐述我的学习心得体会。
首先,算法导论教给我了算法设计的基本方法和技巧。
在课程中,我们学习了很多经典的算法设计方法,如贪心算法、分治法、动态规划等。
通过分析这些算法的设计思想和运行原理,我学会了如何从实际问题中抽象出合适的算法模型,并进行问题的分析和求解。
同时,我们还学习了一些基本的数据结构,如树、图、哈希表等,这些数据结构广泛应用于实际问题中,掌握了它们对于算法设计和问题求解的重要性。
其次,算法导论让我意识到了算法的复杂性和效率的重要性。
在课程中,我们学习了算法的时间复杂度和空间复杂度的概念,通过分析算法的复杂度,可以评估和比较不同算法的性能。
我深刻理解到,在实际应用中,算法的效率往往是一个关键因素,好的算法可以在有限的时间和资源下解决复杂的问题。
因此,学习如何设计高效的算法,尽量减少时间和空间的消耗,是我学习算法导论的重要目标之一。
然后,算法导论让我体会到了算法分析的重要性和难点。
在计算机科学领域,算法的正确性是最基本的要求,通过学习算法导论,我清楚了如何通过证明和验证来确定算法的正确性。
另外,算法的分析也是一项关键工作,通过分析算法的时间复杂度、空间复杂度和正确性,可以评估算法的优劣,并对算法进行优化。
但是,算法分析并不是一件容易的事情,需要对算法的内部结构和运行原理有深入的了解,还需要具备数学和推理的能力。
因此,在学习过程中,我遇到了很多困难和挑战,但是通过不断地学习和实践,我逐渐掌握了一些分析算法的方法和技巧。
最后,算法导论还让我体会到了团队合作的重要性。
在课程中,我们经常需要在小组中完成一些编程作业和课程项目,这要求我们合理分工,互相协作。
通过和同学们的交流和合作,我学会了如何与人合作,如何充分利用团队的资源和优势来解决问题。
中科大软院算法导论区间树实验报告

区间树实验报告1.区间树的实验源码见另外一个文件2.区间树实验分析2.1 需求分析基础数据结构选择红黑树,每个结点x 包含一个区间域int[x],x 的关键字为区间的低端点low[int[x]],对树;进行中序遍历就可按低端点的次序列出个区间,结点还包含一个max[x],即以x 为根的子树中所有区间的端点的最大值。
如:实验要求:将红黑树扩展为区间树(1)区间的端点为正整数,随机生成;(2)内部节点数为n:2^4,2^6,2^8,2^10,2^12;(3)测试插入,删除,查找的时间并绘出曲线,运行次数为10 次;2.2 程序设计区间树的操作基本和红黑树的相同,在其基础上增加了一个新方法:INTERVAL_SEARCH(T,i);它用来找出树中覆盖区间i 的那个结点。
如果树中不存在,则返回nil[T]指针。
代码如下:ITNode* IntervalTree::Interval_Search(Interval i){ITNode* x=root;while(x!=Nil && !x->Overlap(i)){// x != nil and i doesn't overlap int[x]if (x->left!=Nil && x->left->max>=i.low)x=x->left;else x=x->right;}return x;}区间树的插入、删除除了有可能改变红黑树性质,还有可能改变结点的max 值。
前者向红黑树那样处理就可以了,又max[x] = max(high[int[x]], max[left[x]], max[right[x]])为解决后者,增加一方法Nodemax(),让它来维护结点的max 值。
Nodemax()如下:void ITNode::NodeMax(ITNode* xl, ITNode* xr){Type tp=this->interval->high;if (tp < xl->max)tp=xl->max;if(tp < xr->max)tp=xr->max;this->max=tp;}在左旋、右旋时调用此方法。
计算机科学导论实验报告

第三个实验
• 实验内容: • 有32个奶瓶,只有一个是有毒的,要求用最少的小老鼠检测出有毒的某瓶
• • • • • • • • •
五只小老鼠 实验结果 实验步骤: {0,1}^5笛卡尔乘积,总共有2^5=32种 总共分为以下结果 (00000)(00001)(00010)(00011)(00100)(00101)(00110)(00111)(01000) (01001)(01010)(01011)(01100)(01101)(01110)(01111)(10000)(10001) (10010)(10011)(10100)(10101)(10110)(10111)(11000)(11001)(11010) (11011)(11100)(11101)(11110)(11111) 上述顺序是按照二进制方法从大到小排序,第n个数组表示第n个奶瓶,即使给奶 瓶子编号; • 一个数组中,1的位置代表将此奶瓶喂给第几只老鼠,例如第十个数组(01001), 代表将第十个奶瓶喂给第二只和第五只老鼠,第二个数组(00001)表示将第二 个奶瓶喂给第五只老鼠
最短的步数内找到有毒的一瓶
• 实验的结果是需要八步; • 步骤是:1,先将一至八号牛奶混合喂给其中一个老鼠,若老鼠死亡,然后一瓶 逐次喂给第二只老鼠,最多需要七步,此时加起来总共八步; • 2,若第一步没死,则再选七瓶牛奶,若死亡,重复第一步,此时仍然需要八步; 若不死,再选择六瓶牛奶,依次重复下去; • 3,做到最后,8+7+6+5+4=30瓶,还剩两瓶,最多一步,这样的话就是六步, 但电脑是狡猾的,也就是需要步数最多的,也就是八步。
?一个数组中1的位置代表将此奶瓶喂给第几只老鼠例如第十个数组01001代表将第十个奶瓶喂给第二只和第五只老鼠第二个数组00001表示将第二个奶瓶喂给第五只老鼠第1只老鼠吃的奶瓶为
算法分析与设计实验报告 CQUPT

算法分析与设计实验报告 CQUPT计算机科学与技术学院算法分析与设计实验报告目录实验报告一排序问题求解 ........................................................................... .......................................... 2 实验报告二背包问题求解 ........................................................................... .......................................... 8 实验报告三最短路径求解 ........................................................................... ........................................ 12 实验报告四 N-皇后问题求解 ........................................................................... (18)姓名:XXX学号:XXXXXXXX班级:XXXXXXX实验报告一排序问题求解实验目的1)以排序(分类)问题为例,掌握分治法的基本设计策略。
2)熟练掌握一般插入排序算法的实现; 3)熟练掌握快速排序算法的实现; 4) 理解常见的算法经验分析方法;实验内容与步骤 1. 生成实验数据.要求:编写一个函数datagenetare,生成2000个在区间[1,10000]上的随机整数,并将这些数输出到外部文件data.txt中。
这些数作为后面算法的实验数据。
2. 实现直接插入排序算法. 要求:实现insertionsort算法。
算法的输入是data.txt;输出记录为文件:resultsIS.txt;同时记录运行时间为TimeIS。
复习用-第一次实验报告评讲

实验测试
1. 测试环境: (1)操作系统:Ubuntu 12.04 (X86) (2)编译器:GCC 4.6.3 (3)CPU:Intel I3-2350M 2.3GHz
内存:6G
2. 测试结果
(1)正确性测试
测试用例如表1-表7所示。
(a).正确输入
测试次数
表1 正确输入的测试用例
N
期望输出
1
由于算法只是简单地使用了两个for循环,在所有情况下, 其最坏时间复杂度为T(n)=O(n)。
深入思考:为什么这个算法这么好?我怎么没有想 到呢?目的是1到N之间的随机数,又不重复,就先 生成1到N的自然数,然后随机交换位置,可以达到 同一的目的,但是复杂度降低。因此,换思路可能 得到更好的算法。
输入超过rand_max
表7 边界输入测试用例的程序运行结果
测试次数 1 2 3
N 0 1 32767
期望输出
不是自然数
1,0.000
因输出数据太大,这里不一一粘 贴,仅输出运行时间:6.776
4
32768
输入超过rand_max
表7表明程序能够正确处理边界输入。当边界为 0,1这些小的数据时,0不是自然数,1的输出是 1,0.000;但当N较大,输出数据量太大,限于
▪ 分析: 1. 程序输出的是0到N-1之间的自然数随机置换,不是1-N
之间的自然数随机置换,因此程序输出有错误。
2. 没有输出运行时间,需要增加运行时间检测 3. 最后的逗号不应该输出 4. 每个算法针对相同的输入N,得到的输出结果相同。算
法的随机数生成有问题,没有做到生成随机数,因此 程序每次运行得到相同结果序列,而不是随机序列。 查阅资料得知,C语言的随机数生成函数是伪随机数, 如果没有给出随机数的种子,则缺省用1作为随机数种 子。为了得到接近真实随机数序列,可以采用time作 为srand函数的种子。修改程序后的程序运行结果如表 3所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
快速排序实验报告
SA14225010
一、题目
当输入数据已经“几乎”有序时,插入排序速度很快。
在实际应用中,我们可以利用这一特点来提高快速排序的速度。
当对一个长度小于k的子数组调用快速排序时,让它不做任何排序就返回。
当上层的快速排序调用返回后,对整个数组运行插入排序来完成排序过程。
试证明:这一排序算法的期望时间复杂度为O (nk+nlg(n/k))。
分别从理论和实践的角度说明我们应该如何选择k?
二、算法思想
当输入数据已经“几乎”有序时,插入排序速度很快。
当对一个长度小于k的子数组调用快速排序时,让它不做任何排序就返回。
当上层的快速排序调用返回后,对整个数组运行插入排序来完成排序过程。
累加k的值,计算出当k为不同值时算法运行的时间,来算出当k大约为什么值时运行的时间最短,并与传统的快速排序算法的运行时间进行比较。
三、实验结果
输入100个不同的整数值,选取不同的k的值,观察所用时间
四、实验分析
理论上看,k的值选取为20到25较好;但是,从实际上来看,当k为50左右时间为39毫秒,最少,但不同的时刻运行后的时间都不相同,而且不同的输入时刻的运行时间也不相同,当数据较大时候,对k 的值的选取有会有所不同,同时不同性能的机器对测试结果也不同,所以对于k值的选取没有固定的数值。
#include<iostream>
#include<sys/timeb.h>
using namespace std;
#define M 40
void swap(int * a,int * b)
{
int tem;
tem=*a;
*a=*b;
*b=tem;
}
int partition(int v[],const int low,const int high)
{
int i,pivotpos,pivot;
pivotpos=low;
pivot=v[low];
for(i=low+1;i<=high;++i)
{
if(v[i]<pivot)
{
pivotpos++;
if(pivotpos!=i)swap(v[i],v[pivotpos]);
}
}
v[low]=v[pivotpos];
v[pivotpos]=pivot;
//cout<<"the partition function is called\n";
return pivotpos;
}
/*
void QuickSort(int a[], const int low,const int high) {
int item;
if(low<high)
{
item=partition(a,low,high);
QuickSort(a,low,item-1);
QuickSort(a,item+1,high);
}
}
*/
void QuickSort(int a[], const int low,const int high) {
int item;
if(high-low<=M)return;
if(low<high)
{
item=partition(a,low,high);
QuickSort(a,low,item-1);
QuickSort(a,item+1,high);
}
// cout<<"the QuickSort is called"<<endl;
}
void InsertSort(int a[],const int low,const int high)
{
int i,j;
int tem;
for(i=1;i<high+1;++i)
{
tem=a[i];
j=i-1;
while(j>=0&&tem<a[j])
{
a[j+1]=a[j];
j--;
}
a[j+1]=tem;
}
//cout<<"the InsertSort is called"<<endl;
}
void HybridSort(int a[],const int low,const int high)
{
QuickSort(a,low,high);
InsertSort(a,low,high);
cout<<"the HybidSort is called"<<endl;
}
int main()
{
int i,a[100];
//int *a=NULL;
long int t;
struct timeb t1,t2;
/*cout<<"please input the number of the element:"<<endl;
cin>>n;
a = (int*)malloc(n*sizeof(int));
cout<<"please input every element:"<<endl;
*/
for( i=0; i<100; i++)
{
a[i]=i+10;
}
//QuickSort(a,0,n-1);
ftime(&t1);
HybridSort(a,0,99);
cout<<" after sorted quickly,the result is"<<endl;
for(i=0; i<100; i++)
{
cout<<a[i]<<" ";
if(i%10==0)cout<<endl;
}
cout<<endl;
ftime(&t2);
t=(t2.time-t1.time)*1000+(litm); /* 计算时间差 */ printf("k=%d 用时%ld毫秒\n",M,t);
//cout<<"the memory of array a is free"<<endl;
//free(a);
cout<<"\n"<<endl;
return 0;
}。
