动态规划解找零钱问题实验报告
动态规划建模实验报告

一、实验背景动态规划是一种重要的算法设计方法,它通过将复杂问题分解为若干个相互重叠的子问题,并存储子问题的解,从而避免重复计算,有效地解决一系列优化问题。
本实验旨在通过具体案例,加深对动态规划算法的理解和应用。
二、实验目的1. 掌握动态规划的基本概念和原理。
2. 熟悉动态规划建模的过程和步骤。
3. 提高运用动态规划解决实际问题的能力。
三、实验内容本次实验选取了“背包问题”作为案例,旨在通过解决背包问题,加深对动态规划算法的理解。
四、实验步骤1. 问题分析背包问题是一个经典的组合优化问题,描述为:给定一个容量为C的背包和N件物品,每件物品有价值和重量两个属性,求如何将物品装入背包,使得背包中的物品总价值最大,且不超过背包的容量。
2. 模型建立(1)定义状态:设dp[i][j]表示在前i件物品中选择若干件装入容量为j的背包所能获得的最大价值。
(2)状态转移方程:dp[i][j] = max(dp[i-1][j], dp[i-1][j-weights[i]] + values[i]),其中weights[i]表示第i件物品的重量,values[i]表示第i件物品的价值。
(3)边界条件:dp[0][j] = 0,表示没有物品时,背包价值为0。
3. 编程实现使用C语言编写动态规划程序,实现背包问题的求解。
4. 结果分析(1)运行程序,输入背包容量和物品信息。
(2)观察输出结果,包括物品选择的列表和最大价值。
(3)验证结果是否正确,与理论分析进行对比。
五、实验结果与分析1. 实验结果:通过编程实现,成功求解了背包问题,并得到了最大价值。
2. 结果分析:(1)动态规划算法在解决背包问题时,有效地避免了重复计算,提高了求解效率。
(2)实验结果表明,动态规划算法能够有效地解决背包问题,为实际应用提供了有力支持。
六、实验总结1. 动态规划是一种重要的算法设计方法,具有广泛的应用前景。
2. 动态规划建模过程中,关键在于正确地定义状态和状态转移方程。
动态规划算法实验报告

南京信息工程大学滨江学院实验(实习)报告1.实验目的动态规划通常用来求解最优化问题。
通过本次实验掌握动态规划算法。
通过矩阵连乘问题和0-1背包问题实现动态规划算法。
学会刻画问题的最优结构特征,并利用最优化问题具有的重叠子问题性质,对每个子问题求解一次,将解存入表中,当再次需要这个子问题时直接查表,每次查表的代价为常量时间。
2.实验内容及分析设计过程1.矩阵链乘法问题矩阵链乘法问题可描述如下:给定个矩阵的链,矩阵的规模为,求完全括号方案,使得计算乘积所需的标量乘法次数最少。
令m[i,j]表示计算矩阵所需标量乘法次数的最小值,那么,原问题的最优解计是m[1,n]。
最小代价括号化方案的递归求解公式为采用自底向上表格法代替上述递归算法来计算最优代价。
为了实现自底向上方法,我们必须确定计算m[i,j]时需要访问哪些其他表项。
上述公式显示,j-i+l 个矩阵链相乘的最优计算代价m[i,j] 只依赖于那些少于j-i+l 个矩阵链相乘的最优计算代价。
因此,算法应该按长度递增的顺序求解矩阵链括号化问题,并按对应的顺序填写表m。
对如下输入A1 A2 A3 A4 A5 A630⨯35 35⨯15 15⨯5 5⨯10 10⨯20 20⨯25程序运行结果为2.背包问题给定n 个重量为价值为的物品和一个承重为W 的背包。
求这些物品中最有价值的一个子集,并且要能装到背包中。
设V[i,j]是能够放进承重量为j 的背包的前i 个物品中最有价值子集的总价值。
则递推关系为初始条件V[0,j]=0(j>=0),V[i,0]=0(i>=0) 我们的目标是求V[n ,W]。
递归式给出了V[i,j]的计算顺序,V[i,j]只依赖与前一行的那些项。
故可以逐行计算V[i,j].对于物品数量n=5,w[n]={2,2,6,5,4},v[n]={6,3,5,4,6},背包总重量c=10 程序运行结果为3. 实验小结通过本次实验加深了我对动态规划算法的理解。
动态规划解找零钱问题实验报告

大于 n。本算法的动态规划算法的时间复杂性比该问题的一般动态规划 算法的效率要好得多。 该算法的时间复杂性是 10 数量级的.对于应用于 自动售货机等运行速度较慢的机器来说是不成问题的。 空间复杂度:从上面算法可知,用到了三个数组,分别为 T[n],c[j], P[i][j]。其中:i<=n,j<=M。空间复杂性主要由 P[1][j]决定,为 O(M×n)。 P(i,j)中的 i 指的 T[n]中的值.对于钱币来说一般 n 为 13 左右。该算法的 空间复杂度为 O(M x n)=O(f),而 M 小于 100 元即 10 000 分,远大于 n。
b)当 n>1 时, 若 j>T[n],即第 n 种钱币面值比所兑换零钱数小,因此有 C (n, j ) min {C (n, j T [k ]) 1} k (1 i n) 1 k n 。当 k 为 0 时,C(n,j)达到最小 值,有 P(T(k0),j)=P(T( k 0 ),j-T( k 0 ))+1 若 j=T[n],即用 n 种钱币兑换零钱,第 n 种钱币面值与兑换零钱数 j 相等,此时有 C(n,j)=C(n,T[n])=1;
P (i , j ) P (i , T [ n ])
1,i T [ n ] 0 ,i T [ n ]
若 j<T[n],即第 n 种钱币面值比所兑换零钱数大,因此兑换零钱只 需考虑前 n-1 种钱币即可,故有 C(n,j)=C(n-1,j),且 P(T(n-1),j)=0。 从以上讨论可知该问题具有重叠子问题性质。 (2) 根据分析建立正确的递归关系。 答: j % T [1] 0 C (1, j ) j / T [1] j % T [1] 0
贪心算法-找零问题 实验报告

实验三课程名称:算法设计与实现实验名称:贪心算法-找零问题实验日期:2019年5月2日仪器编号:007班级:数媒0000班姓名:郝仁学号0000000000实验内容假设零钱系统的币值是{1,p,p^2,……,p^n},p>1,且每个钱币的重量都等于1,设计一个最坏情况下时间复杂度最低的算法,使得对任何钱数y,该算法得到的零钱个数最少,说明算法的主要设计思想,证明它的正确性,并给出最坏情况下的时间复杂度。
实验分析引理1(离散数学其及应用3.1.4):若n是正整数,则用25美分、10美分、5美分和1美分等尽可能少的硬币找出的n美分零钱中,至多有2个10美分、至多有1个5美分、至多有4个1美分硬币,而不能有2个10美分和1个5美分硬币。
用10美分、5美分和1美分硬币找出的零钱不能超过24美分。
证明如果有超过规定数目的各种类型的硬币,就可以用等值的数目更少的硬币来替换。
注意,如果有3个10美分硬币,就可以换成1个25美分和1个5美分硬币;如果有2个5美分硬币,就可以换成1个10美分硬币;如果有5个1美分硬币,就可以换成1个5美分硬币;如果有2个10美分和1个5美分硬币,就可以换成1个25美分硬币。
由于至多可以有2个10美分、1个5美分和4个1美分硬币,而不能有2个10美分和1个5美分硬币,所以当用尽可能少的硬币找n美分零钱时,24美分就是用10美分、5美分和1美分硬币能找出的最大值。
假设存在正整数n,使得有办法将25美分、10美分、5美分和1美分硬币用少于贪心算法所求出的硬币去找n美分零钱。
首先注意,在这种找n美分零钱的最优方式中使用25美分硬币的个数q′,一定等于贪心算法所用25美分硬币的个数。
为说明这一点,注意贪心算法使用尽可能多的25美分硬币,所以q′≤q。
但是q′也不能小于q。
假如q′小于q,需要在这种最优方式中用10美分、5美分和1美分硬币至少找出25美分零钱。
而根据引理1,这是不可能的。
动态规划实验报告

实验课程:算法分析与设计实验名称:实验3 动态规划算法(综合性/设计性)实验目标:1、熟悉最长公共子序列问题的算法;2、初步掌握动态规划算法;实验任务:若给定序列X={x1,x2,…,xm},则另一序列Z={z1,z2,…,zk},是X的子序列是指存在一个严格递增下标序列{i1,i2,…,ik}使得对于所有j=1,2,…,k有:zj=xij。
例如,序列Z={B,C,D,B}是序列X={A,B,C,B,D,A,B}的子序列,相应的递增下标序列为{2,3,5,7}。
给定2个序列X和Y,当另一序列Z既是X的子序列又是Y的子序列时,称Z是序列X 和Y的公共子序列。
给定2个序列X={x1,x2,…,xm}和Y={y1,y2,…,yn},找出X和Y的最长公共子序列。
实验设备及环境:PC;C/C++的编程环境Visual C++。
实验主要步骤:(1)明确实验目标和具体任务;(2)理解实验所涉及的动态规划算法;(3)编写程序并实现动态规划算法;(4)设计实验数据并运行程序、记录运行的结果;实验数据及运行结果、实验结果分析及结论:(学生填写)#include <stdio.h>#include <string.h>void LcsLength(char *x,char *y,int m,int n,int c[][100],int b[][100]){puts(x);puts(y);int i,j;for(i=0;i<=m;i++)c[i][0]=0;for(j=1;i<=n;j++)c[0][j]=0;for(i=1;i<=m;i++)for(j=1;j<=n;j++) {if(x[i-1]==y[j-1]) {c[i][j]=c[i-1][j-1]+1;b[i][j]=0;}else if(c[i-1][j]>=c[i][j-1]) {c[i][j]=c[i-1][j];b[i][j]=1;}else {c[i][j]=c[i][j-1]; b[i][j]=-1;}}}void PrintLCS(int b[][100], char *x, int i, int j){ if(i==0 || j==0)return;if(b[i][j]==0) {PrintLCS(b,x,i-1,j-1);printf("%c",x[i-1]);}else if(b[i][j]==1)PrintLCS(b,x,i-1,j);elsePrintLCS(b,x,i,j-1);}void main(){char x[100]={"ABCBDAB"};char y[100]={"BDCABA"};int c[100][100];int b[100][100];int m,n;m=strlen(x);n=strlen(y);LcsLength(x,y,m,n,c,b); printf("最长子序列为:");PrintLCS(b,x,m,n); printf("\n");printf("最长子序列长度为:%d\n",c[m][n]);}实验结果:结果分析:在写规划方程时,只要对两条路径走到同一个点的情况稍微处理一下,减少可选的决策个数:从这个例子中可以总结出设计动态规划算法的一个技巧:状态转移一般。
《动态规划算法实验》实验报告

实验3、《动态规划算法实验》一、实验目的1. 掌握动态规划方法贪心算法思想2. 掌握最优子结构原理3. 了解动态规划一般问题二、实验内容1. 编写一个简单的程序,解决0-1背包问题。
设N=5,C=10,w={2,2,6,5,4},v={6,3,5,4,6}2. 合唱队形安排问题【问题描述】N位同学站成一排,音乐老师要请其中的(N-K)位同学出列,使得剩下的K 位同学排成合唱队形。
合唱队形是指这样的一种队形:设K位同学从左到右依次编号为1,2…,K,他们的身高分别为T1,T2,…,TK,则他们的身高满足T1<...<Ti>Ti+1>…>TK(1<=i<=K)。
已知所有N位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。
三、算法思想分析1.0-1背包采用动规算法主要是动规方程的思考,之后就是确定边界条件即可。
2.合唱队形问题应用了分治与动态规划的算法,先将所有队员依次做中间最高的同学,将问题分为左右来做,接下来只需要求得左边的最长上升子序列数、右边的最长下降子序列数即可。
四、实验过程分析1.0-1背包问题是背包问题的进一步条件限制,考虑清楚动规方程就不难,编程中对于m(i,j)的含义要清楚,搞混了就容易出错。
2.合唱队形问题的思想并不复杂,特别是如果已经掌握了最长上升子序列数的算法,在分别处理左右最长子序列时需要特别注意数组下标,一开始我用是i,j直接从0到左右的数据长度,但是一直出错,后来发现队员身高数组并不能完全用这些下标,特别是右边的函数,数组起始下标不是0,需要利用函数传递起始下标才能调用对应的数据段。
五、算法源代码及用户屏幕1.(1)算法源码/********************************0-1背包问题。
codeblocks C++2018.11.2********************************/#include <iostream>#include <iomanip>using namespace std;void knapSnack(int v[], int w[], int c, int n, int m[][11]);int main(){int v[] = {6, 3, 5, 4, 6};int w[] = {2, 2 ,6, 5, 4};int c = 10;int n = 5;int m[5][11];//初始化数组for(int i=0; i<5; i++){for(int j=0; j<11; j++){m[i][j] = 0;}}knapSnack(v, w, c, n, m);//输出结果cout<<setw(3)<<" ";for(int i=0; i<11; i++){cout<<setw(3)<<i;}cout<<endl;for(int i=0; i<5; i++){//输出行号cout<<setw(3)<<i+1;for(int j=0; j<11; j++){cout<<setw(3)<<m[i][j];}cout<<endl;}return 0;}void knapSnack(int v[], int w[], int c, int n, int m[][11]){ for(int i=0; i<n; i++){for(int j=0; j<11; j++){//边界条件if(i == 0){if(w[i] > j)m[i][j] = 0;elsem[i][j] = v[i];}/*动规方程j>w[i]m(i,j) = max{m(i-1,j), m(i-1,j-w[i])+v[i]}0<=j<w[i]m(i,j) = m(i-1,j)*/else{if(w[i] > j)m[i][j] = m[i-1][j];else{if(m[i-1][j] > (m[i-1][j-w[i]]+v[i]))m[i][j] = m[i-1][j];elsem[i][j] = m[i-1][j-w[i]]+v[i];}}}//控制列数的for循环}//控制行数的for循环}(2)用户屏幕2.(1)算法源码/***************************************************合唱队形问题codeblocks C++2018.11.2***************************************************/#include <iostream>#include <string.h>using namespace std;//计算左端合唱队人数int leftQueue(int a[], int _start, int _end);//计算右端合唱队人数int rightQueue(int a[], int _start2, int _end2);int main(){cout<<"Please enter total number:";int number;cin>>number;cout<<"Please input the height of each person (cm):"<<endl;int a[number]; //记录每个人身高//b数组分别记录当第n个人为合唱队中间人时,合唱队的总人数int b[number];int rightNumber[number]; //记录左端合唱队人数int leftNumber[number]; //记录右端合唱队人数for(int i=0; i<number; i++)b[i] = 0;for(int i=0; i<number; i++)cin>>a[i];int mostQueueNumber = b[0];for(int i=0; i<number; i++){//设置a[i]为最高的同学leftNumber[i] = leftQueue(a,0,i);rightNumber[i] = rightQueue(a,i,number-1);//计算合唱队总人数b[i] = leftNumber[i] + rightNumber[i] - 1;//计算合唱队最多的总人数if(mostQueueNumber < b[i])mostQueueNumber = b[i];}//计算最少出队人数int leastDequeueNumber = number - mostQueueNumber;cout<<"Minimum number of people out: "<<leastDequeueNumber<<endl;return 0;}int leftQueue(int a[], int _start, int _end){int leftMostNumber = 0;int n = _end-_start+1;//c数组记录i时的最长上升子序列数int c[n];int maxN;//初始化最长上升子序列数为1for(int i=0; i<n; i++){c[i] = 1;}for(int i=_start; i<_end+1; i++){maxN = 0;for(int j=i-1; j>=_start; j--){if(a[j]<a[i] && c[j]>maxN)maxN = c[j];c[i] = maxN + 1;}}leftMostNumber = c[n-1];return leftMostNumber;}int rightQueue(int a[], int _start2, int _end2){ int rightMostNumber = 0;int n2 = _end2-_start2+1;//c2数组记录i时的最长下降子序列数int c2[n2];int maxN2;//初始化最长下降子序列数为1for(int i=0; i<n2; i++){c2[i] = 1;}for(int i=_end2; i>=_start2; i--){maxN2 = 0;for(int j=i+1; j<=_end2; j++){if(a[j]<a[i] && c2[j-_start2]>maxN2)maxN2 = c2[j-_start2];c2[i-_start2] = maxN2 + 1;}}rightMostNumber = c2[0];return rightMostNumber; }(2)用户屏幕。
找零钱问题算法报告

《找零钱》实验报告目录一. 问题描述1. 问题描述 (2)二.算法描述与分析1. 找零钱问题算法伪代码 (3)2. 算法分析 (5)三.实验结果与分析1. 实验环境 (5)2. 实验的执行 (5)3.实验结果 (6)4.找零钱的其他情况 (6)四.总结与展望1. 总结 (8)2. 展望 (8)3.任务分工 (8)五.代码1. 贪婪技术 (8)2. 动态规划 (10)1问题描述一个小孩买了价值少于1美元的糖,假设需要找给小孩n美分。
不过他的钱包里只有1美元,于是他将1美元的钱交给售货员。
收银台有数目不限的硬币,面值分别为25美分、10美分、5美分、及1美分,如果售货员希望用数目最少的硬币找给小孩,要求设计算法,使得售货员以最少的硬币数,用25、10、5、1美分凑齐n美分。
(n<100)要求通过该问题,掌握贪心算法和动态规划算法的具体实现步骤,理解算法的基本思想,加深巩固对解决问题的思路和方法。
其中,考虑到需要解决问题的方法具有普遍适用性,该题着重动态规划算法的实现。
找零钱问题是动态规划经典题目之一。
该问题的求解方法,可类比于背包问题(The Knapsack Problem)的求解。
图1 动态规划2算法描述与分析假设零钱的面额为v1, v2,..., v m(面额升序排列),需要给出w元的找零,使用各面额的零钱的数量为n1,n2,...,n m.贪心技术解决找零钱问题的思想:想要找补的零钱数量最少,肯定优先使用面额大的零钱。
(1)将零钱按照面额大小排序;(2)总是尝试用当前面额最大的零钱来找补,在不超过需要找补的总额的条件下,尽可能的多用当前面额最大的零钱,并计算出剩余的需要找补的总额;(3)没有达到需要找补的总额的情况下,重复步骤(2)直到达到需要找补的总额。
贪心技术解决找零钱问题的正确性证明:使用贪心技术解决找零钱问题得到最优解对零钱的面额是有要求的,对于零钱面额为c 0, c 1,..., c m (其中c >1,m ≥1)的找零问题,使用贪心技术是可以得到最优解的,证明如下:假设需要找零w 元,对于此问题未使用贪心技术得到的一个最优解S ,使用面额为c i 的零钱数量为n i ,则n i ≤c −1;如果n i ≥c ,则可以使用面值为c i+1的零钱找补,使所用的零钱数量比最优解少,出现矛盾。
动态规划求解零钱兑换问题-算法课程设计

算法设计与分析课程设计动态规划求解零钱兑换问题目录1.绪论 (1)2.需求分析 (2)3.总体设计 (2)3.1代码设计思路 (3)3.1.1数据结构设计 (3)3.1.2动态规划过程 (3)3.1.3代码实现 (3)3.2本文求解的问题 (4)3.3流程图 (5)4.详细设计 (6)4.1对比贪心算法的不足之处 (6)4.2零钱兑换问题类比为完全背包问题 (6)4.3伪代码实现 (6)4.4Java进行代码实现 (8)4.4.1数据结构设计 (8)4.4.2动态规划过程 (8)4.4.3异常处理 (8)4.4.4实现代码 (9)5.调试分析 (10)5.1测试数据 (10)5.2测试输出结果截图 (10)5.3复杂度分析 (13)5.3.1时间复杂度 (13)5.3.2空间复杂度 (14)6.结论 (15)6.1预期目标 (15)6.2是否达到目标 (15)6.3改进措施 (15)6.4使用到的算法 (15)心得体会 (17)参考文献 (18)附录 (19)1.绪论零钱兑换问题是一个经典的计算机科学优化问题,它涉及到通过最小数量的硬币组合来达到特定金额的问题。
这个场景在生活中十分常见,例如自动售货机的找赎系统,银行的货币分配系统等。
然而,随着货币种类和面值的增加,该问题变得越来越复杂,因此寻找一个既有效又高效的方式来解决这个问题成为了当务之急。
过去数十年,众多学者已经对此问题进行了深入研究,并尝试了许多方法,如贪婪算法和分治法等。
尽管这些方法已经提供了一定程度的解决方案,但在面对大量硬币种类和大额度时,常常无法找到全局最优解。
因此,需要寻找更高效且精确的解决问题的方式。
动态规划简介动态规划是一种用于求解具有重叠子问题和最优子结构问题的最优化方法。
通过建立状态转移方程,动态规划能够避免重复计算,有效地降低时间复杂度。
另外,动态规划具有能够找出全局最优解的优点,可以找到问题的最佳答案。
动态规划在零钱兑换问题中的潜在优势由于零钱兑换问题拥有明显的重叠子问题和最优子结构属性,因此适合采用动态规划来解决。
算法分析与设计实验报告 完整版

《算法分析与设计》课程实验实验报告专业:计算机科学与技术班级:姓名:学号:完成时间:2009年6月15日实验一算法实现一一、实验目的与要求熟悉C/C++语言的集成开发环境;通过本实验加深对分治法、贪心算法的理解。
二、实验内容:掌握分治法、贪心算法的概念和基本思想,并结合具体的问题学习如何用相应策略进行求解的方法。
三、实验题1. 【伪造硬币问题】给你一个装有n个硬币的袋子。
n个硬币中有一个是伪造的。
你的任务是找出这个伪造的硬币。
为了帮助你完成这一任务,将提供一台可用来比较两组硬币重量的仪器,利用这台仪器,可以知道两组硬币的重量是否相同。
试用分治法的思想写出解决问题的算法,并计算其时间复杂度。
2.【找零钱问题】一个小孩买了价值为33美分的糖,并将1美元的钱交给售货员。
售货员希望用数目最少的硬币找给小孩。
假设提供了数目有限的面值为25美分、10美分、5美分、及1美分的硬币。
给出一种找零钱的贪心算法。
四、实验步骤理解算法思想和问题要求;编程实现题目要求;上机输入和调试自己所编的程序;验证分析实验结果;整理出实验报告。
五、实验程序1.伪造硬币问题源程序://c语言实现#include<stdio.h>#include<stdlib.h>#include<math.h>#define N 100#define N1 12//只能判断是否相等的天平void solve(int coin[],int count,int first,int last) {if (count==2) {printf("无法判断\n");return;}if (first==last) {//只有一个硬币时候printf("假币的序号为%d, 假币的重量为%d\n", first, coin[first]);}else if(last-first==1){ //如果只剩下两个硬币(此时count不为)if (first > 0) { //不是最开始的硬币if (coin[first] == coin[0]) //如果第first和第个相等,说明first 位置不是伪币solve(coin,count,first+1,last);else//否则,说明first位置是伪币solve(coin,count,first,last-1);}else if(last<count-1){ //不是最后的硬币if (coin[first]==coin[count-1]) //如果第first和最后一个相等,说明last位置不是伪币solve(coin,count,first+1,last);else//否则,说明first位置是伪币solve(coin,count,first,last-1);}}else if (first<last){int temp=(last-first+1)/3; //将硬币分为三组int sum1=0, sum2=0;for(int i=0;i<temp;i++){sum1+=coin[first+i];sum2+=coin[last-i];}if (sum1==sum2){ //两边的总重相等,在中间,递归solve(coin,count,first+temp,last-temp);}else {//在两边,不在中间if (sum1==coin[first+temp]*temp){ //左边的和中间的相等,在右边,递归solve(coin,count,last-temp+1,last);}else {solve(coin,count,first,first+temp-1); //右边的和中间的相等,在左边,递归}}}}void main() {int i;int coin[N]; //定义数组coin用来存放硬币重量for(i=0;i<N;i++) //初始化数组coin[i]=0; //所用硬币初始值为coin[N1]=1; //第N1个设置为,即伪币int cnt = N;printf("硬币个数:%d\n",cnt);solve(coin,cnt,0,cnt-1);}2找零钱问题(1)零钱个数无限制的时候:源程序://c语言实现#include<stdio.h>main(){int T[]={25,10,5,1};int a[5];int money,i,j;printf("输入钱数:\n");scanf("%d",&money);for(i=0;i<4;i++){a[i]=money/T[i];money=money%T[i];}printf("找钱结果:\n硬币:\t");for(i=0;i<=3;i++){printf("%d\t|\t",T[i]);}printf("\n个数:\t");for(i=0;i<=3;i++){printf("%d\t|\t",a[i]);}printf("\n");return(0);}(2)当零钱个数有个数限制的时候:源程序://c语言实现#include<stdio.h>main(){int T[]={25,10,5,1}; //硬币的面值int a[5]; //用来记录找钱的个数int count[]={1,2,10,1000}; //各个面值硬币的个数int money,i;printf("输入钱数:\n");scanf("%d",&money);for(i=0;i<4;i++){if(money>T[i]*count[i]){ //当剩余钱数大于当前硬币总值a[i]=count[i]; //当前硬币个数取现有的最大值money=money-T[i]*count[i];}else{a[i]=money/T[i];money=money%T[i];}}printf("找钱结果:\n硬币:\t");for(i=0;i<=3;i++){printf("%d\t|\t",T[i]);}printf("\n\n个数:\t");for(i=0;i<=3;i++){printf("%d\t|\t",a[i]);}printf("\n");return(0);}六、实验结果1伪造硬币问题运行结果:硬币个数:100假币的序号为12, 假币的重量为1截图:2找零钱问题(1、硬币个数无限制)运行结果:输入钱数:67找钱结果:硬币: 25 | 10 | 5 | 1 |个数: 2 | 1 | 1 | 2 |截图:3找零钱问题(2、硬币个数有限制,其中硬币个数限制分别为1,2,10和1000。
实验报告——动态规划
计算机、 WinQSБайду номын сангаас 软件、实验案例资料
点击工具栏上的“Solve and Analyze Solve the Problem”进行求解,得到下图所示的选择 起始和终结节点的对话框;
实
(2)点击对话框中的“Solve”选项,得到下图 1.52 所示的计算结果,从节点 1 到节点 6 的最
验 结 论
(3)点击对话框中的“Solve and Display Steps” ,系统仍然显示上图所示的求解画面,点击 Solve and Display Steps 按钮,即可得到下图所示的计算结果。
实 验 收 获
通过实验让我明白了动态规划是解决多阶段决策过程最优化问题的一种方法, 解决了多阶段决策 问题,也让我更加熟练掌握了“管理运筹学”软件。
教 师 评 语
签名: 年 月 日
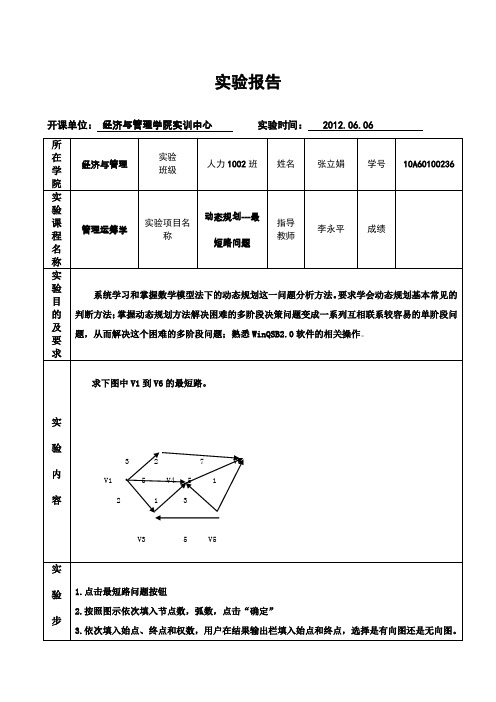
求下图中 V1 到 V6 的最短路。
实 验
3 2 5 2 1 V4 3 5 7 1 V6
内 容
V1
V3
5
V5
实 验 步 骤
1.点击最短路问题按钮 2.按照图示依次填入节点数,弧数,点击“确定” 3.依次填入始点、终点和权数,用户在结果输出栏填入始点和终点,选择是有向图还是无向图。
点击“解决” 。
实 验 所 需 设 备
实验报告
开课单位: 经济与管理学院实训中心 实验时间: 2012.06.06 所 实验 在 经济与管理 人力 1002 班 姓名 张立娟 学号 10A60100236 班级 学 院 实 验 实验项目名 动态规划---最 指导 课 管理运筹学 李永平 成绩 称 短路问题 教师 程 名 称 实 验 系统学习和掌握数学模型法下的动态规划这一问题分析方法。 要求学会动态规划基本常见的 目 掌握动态规划方法解决困难的多阶段决策问题变成一系列互相联系较容易的单阶段问 的 判断方法; 及 题,从而解决这个困难的多阶段问题;熟悉 WinQSB2.0 软件的相关操作。 要 求
硬币找零问题的动态规划实现

硬币找零问题的动态规划实现⼀,问题描述给定⼀组硬币数,找出⼀组最少的硬币数,来找换零钱N。
⽐如,可⽤来找零的硬币为: 1、3、4 待找的钱数为 6。
⽤两个⾯值为3的硬币找零,最少硬币数为2。
⽽不是 4,1,1因此,总结下该问题的特征:①硬币可重复多次使⽤。
②在某些情况下,该问题可⽤贪⼼算法求解。
具体可参考:⼆,动态规划分析为了更好的分析,先对该问题进⾏具体的定义:将⽤来找零的硬币的⾯值存储在⼀个数组中。
如下:coinsValues[i] 表⽰第 i 枚硬币的⾯值。
⽐如,第 i 枚硬币⾯值1 12 33 4待找零的钱数为 n (上⾯⽰例中 n=6)为了使问题总有解,⼀般第1枚硬币的⾯值为1考虑该问题的最优⼦结构:设 c[i,j]表⽰可⽤第 0,1,.... i 枚硬币对⾦额为 j 的钱进⾏找钱所需要的最少硬币数。
i 表⽰可⽤的硬币种类数, j 表⽰需要找回的零钱第 i 枚硬币有两种选择:⽤它来找零和不⽤它找零。
因此,c[i,j]的最优解如下:c[i,j]= min{c[i-1,j] , c[i, j-coinsValues[i]] + 1} 其中,c[i-1,j] 表⽰不使⽤第 i 枚硬币找零时,对⾦额为 j 进⾏找钱所需要的最少硬币数c[i, j-coinsValues[i]] + 1 表⽰使⽤第 i 枚硬币找零时,对⾦额为 j 进⾏找钱所需要的最少硬币数。
由于⽤了第 i 枚硬币,故使⽤的硬币数量要增1c[i,j] 取⼆者的较⼩值的那⼀个。
另外,对特殊情况分析(特殊情况1)⼀下:c[0][j]=Integer.MAXVALUE ,因为对⾦额为 j 的钱找零,但是可⽤的硬币⾯值种类为0,这显然是⽆法做到的嘛(除⾮是强盗:) )其实这是⼀个”未定义“的状态。
它之所以初始为Integer.MAXVALUE,与《背包九讲》中的”当要求背包必须装满的条件下,价值尽可能⼤“时的初始化⽅式⼀样。
c[i][0]=0,因为,对⾦额为0的钱找零,可⽤来找零的硬币种类有 i 种,⾦额为0啊,怎么找啊,找个鸭蛋啊。
The Coin Changing problem The Coin Changing problem动态规划完美解决硬币找零问题

C[20] = 2; ..., C[29] = 5;
1 + C [11 − 50] = ∞ 1 + C [11 − 25] = ∞ C [11] = min 1 + C [11 − 10] = 2
1 + C [11 − 1]
=2
{ 1 , 10 } { 10 , 1 }
C [30] = min
1 + C [30 − 50] = ∞
1 + C [30 − 25] = 1 + C [5] = 6 1 + C [30 − 10] = 1 + C [20] = 3; 1 + C [30 − 1] = 1 + C [29] = 6;
{ 10 , 10 , 10 }
& CS404/504
软件测试 三角形问题,找零钱,最佳组合问题

武 夷 学 院实验报告数学与计算机系实验一三角形问题、找零钱最佳组合问题的第一次测试一、实验目的通过本次实验使学生对软件测试过程有个初步了解,并具备针对功能的测试用例的设计。
二、实验环境硬件环境:微型计算机。
软件环境:Windows 操作系统,Microsoft Visual Studio 2005等。
三、实验内容题目一:三角形问题输入三个整数a、b、c,分别作为三角形的三条边,通过程序判断这三条边是否能构成三角形?如果能构成三角形,则判断三角形的类型(等边三角形、等腰三角形、一般三角形)。
要求输入三个整数a、b、c,必须满足以下条件:1≤a≤200;1≤b≤200;1≤c≤200。
题目二:找零钱最佳组合问题假设商店货品价格(R)皆不大于100 元(且为整数),若顾客付款在100 元内 (P) ,求找给顾客最少货币个(张)数?(货币面值50 元10 元,5 元,1 元四种)1.仿照NextDate问题,分析三角形问题的功能,针对三角形问题的功能设计测试用例,并对测试结果进行分析。
2.仿照NextDate问题,分析找零钱最佳组合问题的功能,针对找零钱最佳组合问题的功能设计测试用例,并对测试结果进行分析。
四、实验步骤1.编写程序三角形问题和找零钱最佳组合问题(1)三角形问题程序#include <stdio.h>#include <stdlib.h>void formed(int, int, int);void type (int, int, int);main(){int a, b, c;while(1){printf("pls enter lenth of three sides of triangle (upper than 1 , lower than 200):\n");scanf("%d,%d,%d",&a, &b, &c);if (a >= 1 && a <= 200 && b >= 1 && b<= 200 && c >= 1 && c <= 200){formed(a,b,c);printf("\n");} elseprintf("error input: three sides must be upper than 1and lower than 200!\n");}}voidformed(int a, int b, int c){if(a + b > c && a + c > b && b + c > a){printf("these lines form a triangle! \n");type(a,b,c);} else {printf("these lines ain't form a triangle \n");}}voidtype(int a, int b, int c){if (a == b || b == c || a == c){if (a == b && b == c)printf("it's Isosceles triangle! \n");elseprintf("it's regular triangle! \n");}if (a*a + b*b == c*c)printf("it's right triangle! \n");}(2)找零钱最佳组合问题程序#include <stdio.h>#include <stdlib.h>void calc(int);main(){int cash, pay;while(1){printf("Please enter the price of goods: ");scanf("%d", &cash);printf("Please enter what customer paid: ");scanf("%d", &pay);cash = pay - cash;if (cash < 0){printf("Error Input: \n");continue;} else if (cash == 0) {printf("No change note! \n");continue;}if (cash >= 100 || cash <= 0)printf("Error input: price must be upper than 0 and lower than 100 \n");else {printf("\n");calc(cash);printf("\n");}}}voidcalc(int cash){int c50, c10, c5, c1;c50 = c10 = c5 = c1 = 0;printf("Change Note: ¥%d\n", cash);while(cash - 50 >= 0){c50 += 1;cash -= 50;}while(cash - 10 >= 0){c10 += 1;cash -= 10;}while(cash - 5 >= 0){c5 += 1;cash -= 5;}while(cash - 1 >= 0){c1 += 1;cash -= 1;}printf(" -----------\n");printf(" ¥50 x %d\n", c50);printf(" ¥10 x %d\n", c10);printf(" ¥ 5 x %d\n", c5);printf(" ¥ 1 x %d\n", c1);printf(" -----------\n");printf("Total: %d\n", c50 + c10 + c5 + c1);}2.三角形问题的测试(1)三角形问题的功能分析a、判断能否组成三角形:任意两边的和大于第三边。
动态规划——详解leetcode518零钱兑换II

动态规划——详解leetcode518零钱兑换II动态规划参考书⽬:《程序员代码⾯试指南:IT名企算法与数据结构题⽬最优解》给定不同⾯额的硬币和⼀个总⾦额。
写出函数来计算可以凑成总⾦额的硬币组合数。
假设每⼀种⾯额的硬币有⽆限个。
⽰例 1:输⼊: amount = 5, coins = [1, 2, 5]输出: 4解释: 有四种⽅式可以凑成总⾦额:5=55=2+2+15=2+1+1+15=1+1+1+1+1⽰例 2:输⼊: amount = 3, coins = [2]输出: 0解释: 只⽤⾯额2的硬币不能凑成总⾦额3。
⽰例 3:输⼊: amount = 10, coins = [10]输出: 1注意:你可以假设:0 <= amount (总⾦额) <= 50001 <= coin (硬币⾯额) <= 5000硬币种类不超过 500 种结果符合 32 位符号整数来源:⼒扣(LeetCode)链接:著作权归领扣⽹络所有。
商业转载请联系官⽅授权,⾮商业转载请注明出处。
1. 暴⼒递归class Solution(object):def change(self, amount, coins):""":type amount: int:type coins: List[int]:rtype: int"""if amount == 0:return 1if not coins or amount < 0:return 0return self.process(coins, 0, amount)def process(self, coins, index, amount):res = 0if index == len(coins):return 1 if amount == 0 else 0else:i = 0while coins[index] * i <= amount:res += self.process(coins, index+1, amount - i*coins[index])i += 1return res暴⼒递归⽅法的时间复杂度⾮常⾼,并且与 arr 中钱的⾯值有关,最差情况下为O(amount N)2. 记忆化搜索# ⽤-1标记是否计算过class Solution(object):def change(self, amount, coins):""":type amount: int:type coins: List[int]:rtype: int"""if amount == 0:return 1if not coins or amount < 0:return 0coin_num = len(coins)counts = [[0 for i in range(amount+1)] for j in range(coin_num+1)]return self.process(coins, 0, amount, counts)def process(self, coins, index, amount, counts):res = 0if index == len(coins):return 1 if amount == 0 else 0else:i = 0while coins[index]*i <= amount:value = counts[index+1][amount-coins[index]*i]if value != 0:res += 0 if value == -1 else valueelse:res += self.process(coins, index+1, amount-coins[index]*i, counts) i += 1counts[index][amount] = -1 if res == 0 else resreturn res记忆化搜索⽅法的时间复杂度为 O(N×amount2)# 超时代码;未标记是否计算过。
动态规划找零问题

1/*2*Problem:3*givenyouthecoins,andthetotalamountofmoneytochange,findasolution 4*forthischangewhichminimizethenumberofcoinsneeded.5*6*Example:7*coins[]={1,5,10,21,25};8*money=19;9*solution[]={10,5,1,1,1,1};10*11*Points:12*DynamicProgramming13*GreeyAlgorithmhereisusuallyuncorrect14*/15#include<stdio.h>16#include<stdlib.h>17#include<string.h>18#define MAX_COINS1019#define MAX_MONEY3276720#define INF0x7FFFFFFF21int coins_num,coins[MAX_COINS];22int total,changes_num[MAX_MONEY],changes[MAX_MONEY];2324int25is_continue()26{27char ch[2];28while(1){29printf("Areyougonnacontinuethisgame(Yifyes,orN)?\n");30scanf("%s",ch);31if(ch[0]=='Y'||ch[0]=='y')32return1;33elseif(ch[0]=='N'||ch[0]=='n')34return0;35}36}3738void39input()40{41int i;42printf("Enterthenumberofcoins:");43scanf("%d",&coins_num);44printf("Entertheamountofcoins(ascendingorder,separatedbyspace):\n"); 45for(i=0;i<coins_num;i++)46scanf("%d",coins+i);47printf("Entertheamountofmoneytochange:");48scanf("%d",&total);49}5051void52output()53{54int i,tmp;55printf("Solution:\n");56printf("Minimumnumberofcoinsneeded:%d\n",changes_num[total]);57printf("Coins:\n");58tmp=total;59while(tmp>0){60printf("%d",changes[tmp]);61tmp-=changes[tmp];62}63printf("\n");64}6566/*67*DynamicProgramming:f(m)=min(f[m-coins[i]+1)68*O(N*K),Nisthenumberofcoins,Kisthetotalamountofmoneytochange 69*/70void71solve()72{73int i,j,k,min;74changes_num[0]=0;75for(i=1;i<=total;i++){/*Money:from'1'to'total'*/76min=INF;77k=-1;78for(j=0;j<coins_num;j++){/*Coins:ascending,andalwayscontains'1'*/ 79if(i>=coins[j]){80if(min>changes_num[i-coins[j]]+1){81min=changes_num[i-coins[j]]+1;82k=j;83}84}else85continue;86}87changes_num[i]=min;88changes[i]=coins[k];89}90}9192int93main(int argc,char**argv)94{95while(is_continue()){96input();97solve();98output();99}100}#include "stdlib.h"#define N 63void GetChange(int n,int j,int m[],int c[][N] ) {/*下标从1开始*/int Max=10000;int k,i,t;int b[5]={0}; /*最好作为一个参数*/for( i=1;i<=n;i++)c[i][0]=0;for(i=1;i<=j;i++){if(i>=m[1]){c[1][i]=(i%m[1]==0)?i/m[1]:Max;}elsec[1][i]=Max;}for( i=2;i<=n;i++){for(k=1;k<=j;k++){if(k>=m[i]){c[i][k]=min (c[i][k-m[i]]+1,c[i-1][k]);c[i][k]=min (c[i][k],Max);}else{c[i][k]=c[i-1][k];}}}k=j;t=n;if(c[t][k]<Max ){while(k>0){if(c[t][k]==c[t-1][k]) t--;else{b[t]++;k-=m[t];}}for(k=1;k<=n;k++){printf("%d:%d ",m[k],b[k]);}printf("\n");}}void main(){int m[]={0,2,3,5,8} ; int n=5,j=13,c[6][N]; int i;for(i=13;i<40;i++) GetChange(n,i,m,c); }。
找零钱-动态规划

找零钱-动态规划遍历N叉树public void inOrder(Node root) {if(root == null) {return;}res.add(root.val);int s = root.children.size();for(int i = 0; i < s; i++) {inOrder(root.children.get(i));}}暴力解法int res = Integer.MAX_VALUE;public int coinChange(int[] coins, int amount) {if(coins.length == 0){return -1;}findWay(coins,amount,0);// 如果没有任何一种硬币组合能组成总金额,返回 -1。
if(res == Integer.MAX_VALUE){return -1;}return res;}public void findWay(int[] coins,int amount,int count){return;}if(amount == 0){res = Math.min(res,count);}for(int i = 0;i < coins.length;i++){// amount-coins[i]作为root.children.get(i)findWay(coins,amount-coins[i],count+1);}}优化int res = Integer.MAX_VALUE;//+++++++++int[] memo;public int coinChange(int[] coins, int amount) {if(coins.length == 0){return -1;}//++++++++memo = new int[amount];return findWay(coins,amount);}// memo[n] 表示钱币n可以被换取的最少的硬币数,不能换取就为-1// findWay函数的目的是为了找到 amount数量的零钱可以兑换的最少硬币数量,返回其值intpublic int findWay(int[] coins,int amount){return -1;}if(amount == 0){return 0;}// 记忆化的处理,memo[n]用赋予了值,就不用继续下面的循环// 直接的返回memo[n] 的最优值//+++++++++++++++if(memo[amount-1] != 0){return memo[amount-1];}int min = Integer.MAX_VALUE;for(int i = 0;i < coins.length;i++){int res = findWay(coins,amount-coins[i]);//++++++++++++++++if(res >= 0 && res < min){min = res + 1; // 加1,是为了加上得到res结果的那个步骤中,兑换的一个硬币}}//+++++++++++++++++memo[amount-1] = (min == Integer.MAX_VALUE ? -1 : min);return memo[amount-1];}使用迭代public int coinChange(int[] coins, int amount) {// 自底向上的动态规划if(coins.length == 0){return -1;}// memo[n]的值:表示的凑成总金额为n所需的最少的硬币个数int[] memo = new int[amount+1];memo[0] = 0;for(int i = 1; i <= amount;i++){int min = Integer.MAX_VALUE;for(int j = 0;j < coins.length;j++){if(i - coins[j] >= 0 && memo[i-coins[j]] < min){min = memo[i-coins[j]] + 1;}}// memo[i] = (min == Integer.MAX_VALUE ? Integer.MAX_VALUE : min);memo[i] = min;}return memo[amount] == Integer.MAX_VALUE ? -1 : memo[amount];}memo[i] 有两种实现的方式,去两者的最小值•包含当前的coins[i],那么剩余钱就是i−coins[i],这种操作要兑换的硬币数是 memo[i−coins[j]]+1•不包含,要兑换的硬币数是 memo[i]public int coinChange(int[] coins, int amount) {// 自底向上的动态规划if(coins.length == 0){return -1;}// memo[n]的值:表示的凑成总金额为n所需的最少的硬币个数int[] memo = new int[amount+1];// 给memo赋初值,最多的硬币数就是全部使用面值1的硬币进行换// amount + 1 是不可能达到的换取数量,于是使用其进行填充Arrays.fill(memo,amount+1);memo[0] = 0;for(int i = 1; i <= amount;i++){for(int j = 0;j < coins.length;j++){if(i - coins[j] >= 0){// memo[i]有两种实现的方式,// 一种是包含当前的coins[i],那么剩余钱就是 i-coins[i],这种操作要兑换的硬币数是 memo[i-coins[j]] + 1// 另一种就是不包含,要兑换的硬币数是memo[i]memo[i] = Math.min(memo[i],memo[i-coins[j]] + 1);}}}return memo[amount] == (amount+1) ? -1 : memo[amount];}。
算法学习笔记1-动态规划问题(找钱问题)

算法学习笔记1-动态规划问题(找钱问题)问题⼀:换钱问题以下各⽅法的⽰例为wallet=[5,3,2],aim=10,0<=pos<wallet.length(1)暴⼒递归法Int F(wallet,pos,aim)返回值:从pos位置的钱币开始,共有X种⽅式可以找aim元。
思路:暴⼒递归法的思路主要是对于当前的aim和可使⽤的钱数wallet[pos],轮流调⽤其所有的可能⽅式。
每⼀种⽅式,返回的是它后续可以找aim 元的组合类型。
⽰例:例如:最开始时pos=0,aim=10,当前货币为wallet[pos=0]=5元。
所以共有0张,1张,2张5元的组合,进⾏遍历。
选择0张5元后,对应货币为3元。
可以有0张,1张,2张,3张3元的组合⽅式。
选择1张5元后,对应货币为3元。
可以有0张,1张3元的组合⽅式。
选择2张5元后,直接返回1,表⽰成功。
然后像这样层层递归下去。
复杂度分析:这⾥的复杂度分析⽐较⿇烦,设wallet[N],aim=A。
需要思考⼀下,以后再写。
(2)优化⼀:记忆化搜索思路:主要是看到不同路径中可能有相同的⼦路径,例如[3,0][3,1][3,2]等,这些每次都要反复的调⽤递归函数,如果可以将这些相同的⼦路径返回值记录下来,就会节省⼀定的时间。
因此建⽴⼀个Map,调⽤⼦路径时先看Map⾥⾯有没有存在的,有则取出,没有则继续调⽤递归函数。
(3)优化⼆:动态规划-⼆维表⽅法思路:解空间是⼀张⼆维表dp,横坐标为0àaim_max,纵坐标为wallet[0]àwallet[length-1]。
其中dp[0,aim]是最终的返回值,dp[wallet.length+1] [0]=1,这都是根据递归中的截⽌条件可以确定的。
⽽dp中每⼀个位置:dp[pos][aim]=dp[pos+1][aim-wallet[pos]*i],其中(aim-wallet[pos]*i>=0)⽰例:初始解空间表Pos0123456789100Res12310000000000解空间表1,pos=2时,dp[2][k]=dp[3][k]+dp[3][k-2]+dp[3][k-4]+…+dp[3][k-2*i](k-2i>=0)。
动态规划算法分析实验报告

动态规划算法设计一、实验内容编程实现图示多段图的最短路径问题的动态规划算法。
(源代码见附录A)二、实验目的及环境实验目的:1、理解动态规划算法的概念;2、掌握动态规划算法的基木要素;3、掌握设计动态规划算法的步骤;4、通过应用范例学习动态规划算法的设计技巧与策略。
实验环境:WIN7系统下VC++6. 0环境三、实验分析与设计采用动态规划算法的两个基木要素:最优子结构性质:原问题的最优解包含了其子问题的最优解。
的重叠性质:每次产生的子问题并不总是新问题,有些子问题被反复计算多次。
实验定义:#define n 12 /*定义顶点数*/#define k 5 /*定义段数*/void init(int cost []) 〃初始化图void fgraph(int cost [ ],int path[ ],int d[])向前递推算法求最短路径void bgraph(int bcost[ ],int pathl[ ],int d[])向后递推算法求最短路径向前递推算法实现:{ int rj5temp,min;for(j=0;j<=n;j++)cost[j]=0;for(j=n-l;j>=I;j-){ temp=0;min=c[j][temp]+€ost[temp];〃初始化最小值for(r=0;r<=n;r++){ if(c[j][r]!=MAX){ if((c[j][r]+cost[r])<min) 〃找到最小的r{ min=c[j] [r]+cost[r];temp=r;}}}cost [j ]=c [j 1 [ temp 1+cost [temp ];d|j]=temp:}path[l]=l;path[k]=n;for(j=2;j<k;j++)pathgj=d[path|j-l]];四、实验结果显示五、实验总结通过理解最优子结构的性质和子问题重叠性质,在VC++6.0环境下实现动态规划算法。
找零问题贪心算法实现

找零问题贪心算法实现一、实验描述当前有面值分别为2角5分,1角,5分,1分的硬币,请给出找n分钱的最佳方案(要求找出的硬币数目最少)。
二、实验原理具体实例:假如老板要找给我99分钱,他有上面的面值分别为25,10,5,1的硬币数,为了找给我最少的硬币数,那么他是不是该这样找呢,先看看该找多少个25分的,99/25=3,好像是3个,要是4个的话,我们还得再给老板一个1分的,我不干,那么老板只能给我3个25分的拉,由于还少给我24,所以还得给我2个10分的和4个1分。
具体实现://找零钱算法//By falcon//输入:数组m,依次存放从大到小排列的面值数,n为需要找的钱数,单位全部为分//输出:数组num,对照数组m中的面值存放不同面值的硬币的个数,就找钱方案参考实验代码部分。
三、实验代码#ifndef LEASTCOINS_H#define LEASTCOINS_Hclass LeastCoins{public:LeastCoins();~LeastCoins();void run();private:int number; // 不同面值的硬币个数int TotalMoney; // 要找回的总钱数int *T; // 存储硬币的面值int *Coins; // 硬币的个数int **m; // m[i][j] 是以最大面值i 要找回钱数是j 需要硬币数的最少个数bool input();int changeMoney(int i,int j); // i 是第i 中硬币void output();void traceback(); // 寻找轨迹};#endif#include <iostream.h>#include <fstream.h>#include <cstdlib>#include <iomanip.h>#define N 10ifstream inputFile("input.txt",ios::out);ofstream outputFile("output.txt",ios::out);LeastCoins::LeastCoins(){number=0;TotalMoney=0;T=new int [N];Coins=new int [N];m=new int *[N];for (int i=0;i<N;i++)m[i]=new int [N*N];}LeastCoins::~LeastCoins(){delete []T;delete []Coins;for (int i=0;i<N;i++) delete []m[i];delete []m;}void LeastCoins::run(){ if (input()){ c hangeMoney(number,TotalMoney); output();}}bool LeastCoins::input(){ inputFile>>number;outputFile<<"有"<<number<<" 不同的硬币."<<endl;outputFile<<setw(4)<<"面值"<<setw(7)<<"个数"<<endl;int sum=0;for (int i=1;i<=number;i++){ inputFile>>T[i];inputFile>>Coins[i];outputFile<<setw(3)<<T[i]<<setw(3)<<" "<<setw(3)<<Coins[i]<<endl;sum+=T[i]*Coins[i];}inputFile>>TotalMoney;outputFile<<"需要找回的总钱数为: "<<TotalMoney<<endl;if (T!=NULL && Coins!=NULL){ if (sum>=TotalMoney)return true;else outputFile<<"所有硬币的总钱数是"<<sum<<" 小于需要找回的总钱数"<<TotalMoney<<endl;return false;}return false;}int LeastCoins::changeMoney(int i,int j){ if (i>1){ if (j<T[i]) // 要找的钱数小于该硬币的面值{m[i-1][j]=changeMoney(i-1,j);m[i][j]=m[i-1][j]; return m[i][j]; }else{ int X=j/T[i];X=(X<Coins[i] ? X : Coins[i]) ;int T1=changeMoney(i-1,j-X*T[i]);int T2=changeMoney(i-1,j-(X-1)*T[i]);m[i-1][j-X*T[i]]=T1;m[i-1][j-(X-1)*T[i]]=T2;if ((T1+X)>(T2+X-1)) m[i][j]=T2+X-1;else m[i][j]=T1+X;return m[i][j];}}else if(i==1)// 此时i==1{ if ((j%T[1])==0 && (j/T[1]<=Coins[1])){ m[1][j]=j/T[1]; return m[1][j]; }else return 1000000;}else return 1000000;}void LeastCoins::output(){ if (m[number][TotalMoney]<1000000) // 判断是否有解{ outputFile<<"需要最少的硬币个数是: "<<m[number][TotalMoney]<<endl;outputFile<<setw(4)<<"面值"<<setw(7)<<"个数"<<endl;traceback();}else outputFile<<"无解"<<endl;}void LeastCoins::traceback(){int j=TotalMoney;for (int i=number;i>=2;i--){int X=j/T[i]; // 最多需要面值为T[i] 的硬币的个数X=(X<Coins[i] ? X : Coins[i]) ; // 取X 和Coins[i]的较小值int T1=m[i-1][j-X*T[i]]+X;int T2=m[i-1][j-(X-1)*T[i]]+X-1;if (T1<T2){ outputFile<<setw(3)<<T[i]<<setw(3)<<" "<<setw(3)<<X<<endl; j-=X*T[i]; }else { outputFile<<setw(3)<<T[i]<<setw(3)<<" "<<setw(3)<<(X-1)<<endl;j-=(X-1)*T[i]; }}outputFile<<setw(3)<<T[i]<<setw(3)<<" "<<setw(3)<<(j/T[1])<<endl;}int main(){ LeastCoins LC;LC.run();return 0;}四、运行结果图1 运行结果五、实验总结对贪心算法不是特别熟悉,以至于在编写程序时遇到好多错误,好在差不多都改正了,此程序尚有不足之处,希望在以后的深入学习后能编写个更好的程序。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、实验目的(1)熟练掌握动态规划思想及教材中相关经典算法。
(2)掌握用动态规划解题的基本步骤,能够用动态规划解决一些问题。
二、实验内容与实验步骤(1)仔细阅读备选实验的题目,选择一个(可选多个)作为此次实验题目,设计的程序要满足正确性,代码中有关键的注释,书写格式清晰,简洁易懂,效率较高,利用C++的模板,设计的程序通用性好,适合各种合理输入,并能对不合理输入做出正确的提示。
(2)可供选择的题目有以下2个:(i)找零钱问题(难度系数为3)★问题描述设有n种不同面值的硬币,各硬币的面值存于数组T[1:n]中。
现要用这些面值的硬币来找钱,可以实用的各种面值的硬币个数不限。
当只用硬币面值T[1],T[2],…,T[i]时,可找出钱数j的最少硬币个数记为C(i,j)。
若只用这些硬币面值,找不出钱数j时,记C(i,j)=∞。
★编程任务设计一个动态规划算法,对1≤j≤L,计算出所有的C( n,j )。
算法中只允许实用一个长度为L的数组。
用L和n作为变量来表示算法的计算时间复杂性★数据输入由文件input.txt提供输入数据。
文件的第1行中有1个正整数n (n<=13),表示有n种硬币可选。
接下来的一行是每种硬币的面值。
由用户输入待找钱数j。
★结果输出程序运行结束时,将计算出的所需最少硬币个数输出到文件output.txt中。
输入文件示例输出文件示例input.txt output.txt331 2 59三、实验环境四、问题分析(1) 分析要解决的问题,给出你的思路,可以借助图表等辅助表达。
答:这个问题用动态规划来解,归结到动态规划上面就变成了无限背包问题(因为收银台的硬币默认是无穷的,但一种改进版本可以考察有限硬币的情况)。
区别在于,现在我们需要求一个最少的硬币数而不是最大值。
但是选择的情况也是相同的,即每次选择都可以选择任何一种硬币。
首先,找零钱问题具有最优子结构性质:兑换零钱问题的最优子结构表述:对于任意需要找的钱数j ,一个利用T[n]中的n 个不同面值钱币进行兑换零钱的最佳方案为P(T(1),j),P(T(2),j),...,P(T(n),j),即此时的最少钱币个数∑==n1j)P(T(k),),(k j n C ,则P(T(2),j),...,P(T(n),j)一定是利用T[n]中n 个不同的面值钱币对钱数j=j-P(T(1),j)* T(1)进行兑换零钱的最佳方案。
其次,找零钱问题具有重叠于问题性质:a)当n=1时,即只能用一种钱币兑换零钱,钱币的面值为T[0],有b)当n>1时,若j>T[n],即第n 种钱币面值比所兑换零钱数小,因此有}1])[,({),(min 1+-=≤≤k T j n C j n C n k 。
当k 为n)i (1k 0≤≤时,C(n,j)达到最小值,有P(T(k0),j)=P(T(k ),j-T(k ))+1若j=T[n],即用n 种钱币兑换零钱,第n 种钱币面值与兑换零钱数j 相等,此时有C(n,j)=C(n,T[n])=1;{][,1][,0])[,(),(n T i n T i n T i P j i P =≠==若j<T[n],即第n 种钱币面值比所兑换零钱数大,因此兑换零钱只需考虑前n-1种钱币即可,故有C(n,j)=C(n-1,j),且P(T(n-1),j)=0。
从以上讨论可知该问题具有重叠子问题性质。
(2) 根据分析建立正确的递归关系。
答:0]1[%0]1[%≠=T j T j {∞=]1[/),1(T j j C 0]1[%0]1[%≠=T j T j {∞=]1[/),1(T j j C{T[i];j 0 j)1,-C(i T[i]j 1)T[i])-j C(i,j),1,-min(C(i j)C(i,<≤≥+=(3) 分析利用你的想法解决该问题可能会有怎样的时空复杂度。
答:算法的时间复杂度主要取决于程序的两个循环,所以算法的时间复杂度为)O(n 2;算法执行过程中引入了一个二维数组,随着输入规模的增大,所需要的空间复杂度为:)O(n 2五、问题解决(1) 根据对问题的分析,写出解决办法。
答:设数组T[]中存放的是n 种钱币递增的不同面值,所要找的钱数为M,M 由用户输入;数组C[j]表示利用数T[n]兑换零钱数为j 时所用的最少钱币个数,即最优值;P[i][j](1<=i<=n)表示按照上述最优值兑换零钱J 时用到钱币面值为第i 种钱币的个数。
(2) 描述你在进行实现时,主要的函数或操作内部的主要算法;分析这个算法的时、空复杂度,并说明你设计的巧妙之处,如有创新,将其清晰的表述。
for (i=0;i<kind;i++) { for (j=i+1;j<kind;j++) if (T[i]>T[j]) { Swap(T[i],T[j]); } }long temptotal=total; if (total>0) for (i=kind-1;i>=0;i--) { Swap(T[i],T[kind-1]); if (T[kind-1]>0) { c[kind-1]=temptotal/T[kind-1]; long tempcount=0; while((c[kind-1]>0)&&(c[kind-1]<=mincount)) {tempcount=c[kind-1];temptotal=temptotal-T[kind-1]*c[kind-1]; for (j=kind-2;j>=0;j--) if ((temptotal>0)&&(T[j]>0)) { c[j]=temptotal/T[j]; temptotal=temptotal-T[j]*c[j]; tempcount=tempcount+c[j]; }if ((tempcount>0)&&(tempcount<mincount)&&(temptotal==0)) mincount=tempcount; c[kind-1]=c[kind-1]-1; temptotal=total; tempcount=0; } }}时间复杂度:从上面算法可知,最优值c[』]的计算过程中,最外层为循环for(j=1;j<=M;j++)嵌套着while(k>1&&flag==0)循环,而while(k>1&flag==0)循环中又嵌套着三个并列的for 循环。
因此本算法最坏情况下的复杂度是O(M*2n );最好的情况当然是里面for 循环的条件不满足而不执行,此时的复杂度为O(M*n)。
其中:M 表示需要兑换的零钱数,对于M 来说,该值一般不是很大,对于钱币来说,M 会小于100元,即10 000分;n 表示钱币的种类,n 值一般不会很大.如钱币总的有13种(从1分,2分,⋯,100元)。
经过以上分析,如是最坏情况时的复杂度应为O(M*2n ),则该值对于内存和运行速度较小的自动售货机等的应用前景则不会很好。
但本算法中的递归结构在M>T[n]时,有1])[,(j),C(n min k 1+-=≤≤k T j n C n。
可见对于钱币j=M 时,求c(n,j)时,并不要求对从1≤i ≤j ,的所有情况都要求c(n,i)+1,而是只求1])[,(+-k T j n C 。
其中:1≤k ≤n 。
钱币一般只有13种左右,因此其效率大为上升。
最坏的情况下需要执行)O(n )n O(M 32=⨯,而M 小于100元即10000分,远大于n 。
本算法的动态规划算法的时间复杂性比该问题的一般动态规划算法的效率要好得多。
该算法的时间复杂性是310数量级的.对于应用于自动售货机等运行速度较慢的机器来说是不成问题的。
空间复杂度:从上面算法可知,用到了三个数组,分别为T[n],c[j],P[i][j]。
其中:i<=n,j<=M 。
空间复杂性主要由P[1][j]决定,为O(M ×n)。
P(i,j)中的i 指的T[n]中的值.对于钱币来说一般n 为13左右。
该算法的空间复杂度为O(M x n)=O(f),而M 小于100元即10 000分,远大于n 。
该算法动态规划的空间复杂性比该问题的一般动态规划的效率要好得10数量级,这对于应用到小内存的自动售货多。
该算法的空间复杂性为2机来说是没有任何问题的。
(3)你在调试过程中发现了怎样的问题?又做了怎样的改进?答:在调试过程中,我发现对于该算法最主要的在于矩阵C[i,j]的求解,而算法的递归关系没有弄明白,所以在求解C[i,j]时总是出现问题,后来在查询了资料后,将C[i,j]递归关系的实现改为c[j]=temptotal/T[j];temptotal=temptotal-T[j]*c[j];tempcount=tempcount+c[j];解决了该问题。
(4)写出用你的测试数据按照算法的流程填写的算法中的存储结构。
C[1,2,3]={0,2,9}。
六、实验结果总结1.程序运行截图:2.回答以下问题:(1)算法实现的复杂度在问题规模很大时可以接受吗?答:可以接受,因为动态规划算法有很好的效率,所以当问题复杂度很大时,就不会影响到算法的运行时间。
(2)如果不用动态规划方法还能想到其他的解决方式吗?和动态规划相比会有更好的效率吗?答:对于找硬币问题,有时候贪心算法也能解决,但不如动态规划求解有效率,所以采用动态规划方法是一个很好的选择。
(3)所选用的数据结构合适吗?答:采用了数组的数据结构,合适,因为该数据结构能够支持对于数组中的元素的随机访问,而且方便查询。
(4)该算法都存在哪几类可能出现的情况,你的测试完全覆盖了你所想到的这些情况吗,测试结果如何?(5)叙述通过实验你对动态规划方法的理解及其优缺点答:优点:动态规划方法有效利用了子问题的重叠性,减少了大量的计算。
而且动态规划的使用也非常简单,只需要问题满足最优子结构、子问题重叠性、无后效性即可。
通常可以利用分置思想构造出子问题的分解方法,就可以利用动态规划。
缺点:动态规划的缺点并不是最快的方法,只是解决某一类型的问题的工具或者优化某些 NPC问题的时间效率。
动态规划的很重要的一点就是用大量空间换取时间上的优化,所以这并不是一个完美的方法。
七、附录参考资料:《算法导论》。
