初中数学竞赛试题及答案(免费)
初二数学竞赛试题7套整理版(含答案)

初二数学竞赛试题7套整理版(含答案)初二数学竞赛试题7套整理版(含答案)第一套试题1. 某数与它的四分之一之和的和是28,求这个数是多少?解:设这个数为x,根据题意可得方程 x + (1/4)x + x = 28,化简得9/4x = 28,解得 x = 44.2. 有一个矩形,长是宽的3倍,如果长再加上宽再加上1的和等于50,求矩形的长和宽各是多少?解:设矩形的宽为x,则长为3x,根据题意可得方程 3x + x + 1 = 50,化简得 4x + 1 = 50,解得 x = 12,所以长为3 * 12 = 36,宽为12.3. 某个数的三次方减去它自身等于608,求这个数是多少?解:设这个数为x,根据题意可得方程 x^3 - x = 608,化简得 x^3 - x - 608 = 0,因此需求解该方程的解x.4. 甲数和乙数之和是300,甲数比乙数大30,求甲数和乙数各是多少?解:设甲数为x,乙数为y,根据题意可得方程 x + y = 300,x - y = 30,联立这两个方程可以解得甲数x和乙数y.5. 家长购买某品牌的饮料,每瓶售价为5元,如果购买10瓶,优惠50%,那么需要支付的价格是多少?解:购买10瓶优惠50%,相当于购买5瓶的价格,所以需要支付 5 * 10 * (1 - 50%) = 25元.第二套试题1. 学校图书馆购买300本新书,若图书馆中已有书籍500本,现将这些书按每排放10本的方式摆放,共需要多少排?解:新书300本加上原有书籍500本,共计800本书,每排放10本,所以需要 800 / 10 = 80排.2. 小明每天早上跑步30分钟,下午骑自行车25分钟,晚上游泳40分钟,求他一天中运动的总时长是多少分钟?解:小明一天早上跑步30分钟,下午骑自行车25分钟,晚上游泳40分钟,总时长为 30 + 25 + 40 = 95分钟.3. 甲、乙两人开始一起钓鱼,甲每分钟能钓2条鱼,乙每分钟能钓1条鱼,如果他们一起钓了45分钟,那么他们一共钓到了多少条鱼?解:甲每分钟能钓2条鱼,乙每分钟能钓1条鱼,他们一起钓了45分钟,所以甲和乙一共钓到了 2 * 45 + 1 * 45 = 135 条鱼.4. 某商品原价100元,现在打8折,过了一段时间后再降价,降到原价的85%,现在这个商品的售价是多少?解:原价100元,打8折后为 100 * (1 - 80%) = 80元,再降到原价的85%为 80 * 85% = 68元.5. 某人的年收入为12000元,每月生活费占月收入的1/5,那么这个人每月的生活费用是多少元?解:年收入12000元,月收入为 12000 / 12 = 1000元,生活费占收入的1/5,所以生活费用为 1000 * 1/5 = 200元.第三套试题1. 甲、乙两个人合作修一个房子,甲一个人修需要8天,乙一个人修需要12天,问他们一起修需要多少天?解:甲一个人修需要8天,乙一个人修需要12天,他们一起修需要的时间为 1/(1/8 + 1/12) = 4.8天.2. 甲购买一本书花费了原价的3/4,折后价格为60元,问这本书的原价是多少?解:折后价格为60元,花费原价的3/4,所以原价为 60 / (3/4) = 80元.3. 甲、乙两人比赛,甲第一轮跑步用时1分钟,第二轮用时50秒,第三轮用时40秒;乙第一轮跑步用时55秒,第二轮用时45秒,第三轮用时35秒,问谁的平均速度更快?解:甲第一轮跑步用时1分钟,第二轮用时50秒,第三轮用时40秒,平均速度为 (60 + 50 + 40) / 3 = 50 秒/轮;乙第一轮跑步用时55秒,第二轮用时45秒,第三轮用时35秒,平均速度为 (55 + 45 + 35) / 3 = 45 秒/轮;所以甲的平均速度更快.4. 一只小狗每小时能跑5公里,一只小猫每小时能跑8公里,如果它们从同一地点同时出发并分别向东和西跑,4小时后它们相距了多少公里?解:小狗每小时能跑5公里,4小时后跑了5 * 4 = 20公里,小猫每小时能跑8公里,4小时后跑了8 * 4 = 32公里,所以它们相距了 32 -20 = 12 公里.5. 三个连续的偶数相加的和是60,求这三个数分别是多少?解:设第一个偶数为x,那么第二个偶数为x + 2,第三个偶数为x+ 4,根据题意可得方程 x + (x + 2) + (x + 4) = 60,求解该方程可得x及其对应的三个连续偶数.第四套试题1. 一个数的2倍加上5等于13,求这个数是多少?解:设这个数为x,根据题意可得方程 2x + 5 = 13,解得 x = 4.2. 甲乙两数相差22,乙数的2倍与甲数的3倍之和等于70,求甲、乙两数各是多少?解:设甲数为x,乙数为y,根据题意可得方程 y - x = 22,2y + 3x= 70,联立这两个方程可以解得甲数x和乙数y.3. 一辆汽车以每小时80千米的速度行驶,行驶了1小时20分钟后停下来休息,求这段时间内汽车行驶的路程?解:汽车以每小时80千米的速度行驶,1小时20分钟共1.33 小时,所以汽车行驶的路程为 80 * 1.33 = 106.4 千米.4. 甲、乙两个人一起做一件工作,甲单独完成需要4小时,乙单独完成需要6小时,他们一起完成这件工作需要多少小时?解:甲单独完成需要4小时,乙单独完成需要6小时,他们一起完成需要的时间为 1/(1/4 + 1/6) = 2.4小时.5. 一个数加上它的四分之一之和的和是28,求这个数是多少?解:设这个数为x,根据题意可得方程 x + (1/4)x + x = 28,化简得9/4x = 28,解得 x = 44.第五套试题1. 一条宽10米的路,两边分别种植了向阳向每排7棵树或9棵树,每棵树之间距离相等,而且与路两边相邻树之间距离也相等,问道路中间最宽的地方有多宽?解:分别种植7棵树和9棵树,每棵树之间距离相等,所以道路中间最宽的地方为两排树之间的距离.2. 一个数与4的乘积减去2等于18,求这个数是多少?解:设这个数为x,根据题意可得方程 4x - 2 = 18,解得 x = 5.3. 甲、乙、丙三人合作种田,甲一个人种地需要10天,乙一个人种地需要12天,丙一个人种地需要15天,问他们三个人一起种地需要多少天?解:甲一个人种地需要10天,乙一个人种地需要12天,丙一个人种地需要15天,他们一起种地需要的时间为 1/(1/10 + 1/12 + 1/15) =4.8天.4. 某人共有100元,买了一本书花掉了原价的3/5,剩下的钱还能买另一本原价为80元的书吗?解:100元买了一本书花掉了原价的3/5,剩下的钱为 100 * (1 - 3/5) = 40元,剩下的钱不足以购买另一本80元的书.5. 一团面粉重800克,其中水分为15%,求这团面粉中水分的重量是多少克?解:面粉重800克,其中水分为15%,所以水分的重量为800 * 15% = 120克.第六套试题1. 一个数与它的五分之一之和的和是40,求这个数是多少?解:设这个数为x,根据题意可得方程 x + (1/5)x + x = 40,化简得7/5x = 40,解得 x = 28.57.2. 甲、乙两个人分别完成一项工作需要的时间比为2:5,如果他们一起完成这项工作需要3小时,求乙单独完成这项工作需要多少时间?解:甲、乙两个人分别完成一项工作需要的时间比为2:5,设甲单独完成需要的时间为x,乙单独完成需要的时间为y,根据题意可得方程 2x + 5x = 3,解得 y = 7.5.3. 有两个相交的圆,圆心之间的距离为8,两圆的半径分别为5和3,求两圆相交的弦的长度是多少?解:两个圆的半径分别为5和3,圆心之间的距离为8,利用勾股定理可以求得两圆相交的弦的长度.4. 甲乙两个人一起做一件工作,甲单独完成需要10小时,乙单独完成需要15小时,他们一起完成这件工作需要多少小时?解:甲单独完成需要10小时,乙单独完成需要15小时,他们一起完成需要的时间为 1/(1/10 + 1/15) = 6小时.5. 甲给乙20元,乙给丙30元,丙给甲10元,这三个人一共交易了多少元?解:甲给乙20元,乙给丙30元,丙给甲10元,所以一共交易了20 + 30 + 10 = 60元.第七套试题1. 某数比它的2/3小12,求这个数是多少?解:设这个数为x,根据题意可得方程 x - (2/3)x = 12,化简得 1/3x = 12,解得 x = 36.2. 甲、乙两个人一起修一条路,甲单独修需要8小时,乙单独修需要12小时,也有可能甲的速度是乙的倍数,问他们一起修需要多少小时?解:甲单独修需要8小时,乙单独修需要12小时,他们一起修需要的时间为 1/(1/8 + 1/12) = 4.8小时.3. 某品牌的衣服原价为200元,现在打折8折,过了一段时间后再降价,降到原价的85%,现在这件衣服的售价是多少?解:原价200元,打8折后为 200 * (1 - 80%) = 160元,再降到原价的85%为 160 * 85% = 136元.4. 甲、乙两个人一起做工,甲一个小时能做1/3的工作量,乙一个小时能做1/4的工作量,问他们一起做一份工作需要多少时间?解:甲一个小时能做1/3的工作量,乙一个小时能做1/4的工作量,他们一起做一份工作需要的时间为 1/(1/3 + 1/4) = 12/7小时.5. 某人的年收入为12000元,每月花销占收入的1/4,那么这个人每月的花销是多少元?解:年收入12000元,。
初中数学奥林匹克竞赛题及答案

初中数学奥林匹克竞赛题及答案奥数题一一、选择题(每题1分,共10分)1.如果a,b都代表有理数,并且a+b=0,那么( )A.a,b都是0B.a,b之一是0C.a,b互为相反数D.a,b互为倒数答案:C解析:令a=2,b=-2,满足2+(-2)=0,由此a、b互为相反数。
2.下面的说法中正确的是()A.单项式与单项式的和是单项式B.单项式与单项式的和是多项式C.多项式与多项式的和是多项式D.整式与整式的和是整式答案:D解析:x²,x3都是单项式.两个单项式x3,x²之和为x3+x²是多项式,排除A。
两个单项式x²,2x2之和为3x2是单项式,排除B。
两个多项式x3+x2与x3-x2之和为2x3是个单项式,排除C,因此选D。
3.下面说法中不正确的是 ( )A. 有最小的自然数B.没有最小的正有理数C.没有最大的负整数D.没有最大的非负数答案:C解析:最大的负整数是-1,故C错误。
4.如果a,b代表有理数,并且a+b的值大于a-b的值,那么 ( )A.a,b同号B.a,b异号C.a>0D.b>0答案:D5.大于-π并且不是自然数的整数有( )A.2个B.3个C.4个D.无数个答案:C解析:在数轴上容易看出:在-π右边0的左边(包括0在内)的整数只有-3,-2,-1,0共4个.选C。
6.有四种说法:甲.正数的平方不一定大于它本身;乙.正数的立方不一定大于它本身;丙.负数的平方不一定大于它本身;丁.负数的立方不一定大于它本身。
这四种说法中,不正确的说法的个数是 ( )A.0个B.1个C.2个D.3个答案:B解析:负数的平方是正数,所以一定大于它本身,故C错误。
7.a代表有理数,那么,a和-a的大小关系是( )A.a大于-aB.a小于-aC.a大于-a或a小于-aD.a不一定大于-a答案:D解析:令a=0,马上可以排除A、B、C,应选D。
8.在解方程的过程中,为了使得到的方程和原方程同解,可以在原方程的两边( )A.乘以同一个数B.乘以同一个整式C.加上同一个代数式D.都加上1答案:D解析:对方程同解变形,要求方程两边同乘不等于0的数,所以排除A。
全国初中数学竞赛试题和答案解析

中国教育学会中学数学教学专业委员会全国初中数学竞赛试题一、选择题(共5小题,每小题6分,共30分.)1(甲).如果实数a ,b ,c 22||()||a a b c a b c -++-++可以化简为( ).(A )2c a - (B )22a b - (C )a - (D )a 1(乙).如果22a =-11123a+++的值为( ).(A )2- (B 2 (C )2 (D )222(甲).如果正比例函数y = ax (a ≠ 0)与反比例函数y =xb(b ≠0 )的图象有两个交点,其中一个交点的坐标为(-3,-2),那么另一个交点的坐标为( ). (A )(2,3) (B )(3,-2) (C )(-2,3) (D )(3,2)2(乙). 在平面直角坐标系xOy 中,满足不等式x 2+y 2≤2x +2y 的整数点坐标(x ,y )的个数为( ). (A )10 (B )9 (C )7 (D )53(甲).如果a b ,为给定的实数,且1a b <<,那么1121a a b a b ++++,, ,这四个数据的平均数与中位数之差的绝对值是( ). (A )1 (B )214a - (C )12 (D )143(乙).如图,四边形ABCD 中,AC ,BD 是对角线, △ABC 是等边三角形.30ADC ∠=︒,AD = 3,BD = 5, 则CD 的长为( ).(A )23 (B )4 (C )52 (D )4.54(甲).小倩和小玲每人都有若干面值为整数元的人民币.小倩对小玲说:“你若给我2元,我的钱数将是你的n 倍”;小玲对小倩说:“你若给我n 元,我的钱数将是你的2倍”,其中n 为正OAB CED整数,则n 的可能值的个数是( ).(A )1 (B )2 (C )3 (D )44(乙).如果关于x 的方程 20x px q p q --=(,是正整数)的正根小于3, 那么这样的方程的个数是( ).(A ) 5 (B ) 6 (C ) 7 (D ) 85(甲).一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,3,4,5,6.掷两次骰子,设其朝上的面上的两个数字之和除以4的余数分别是0,1,2,3的概率为0123p p p p ,,,,则0123p p p p ,,,中最大的是( ).(A )0p (B )1p (C )2p (D )3p5(乙).黑板上写有111123100, , ,, 共100个数字.每次操作先从黑板上的数中选取2个数a b ,,然后删去a b ,,并在黑板上写上数a b ab ++,则经过99次操作后,黑板上剩下的数是( ).(A )2012 (B )101 (C )100 (D )99二、填空题(共5小题,每小题6分,共30分)6(甲).按如图的程序进行操作,规定:程序运行从“输入一个值x ”到“结果是否>487?”为一次操作. 如果操作进行四次才停止,那么x 的取值范围是 .6(乙).如果a ,b ,c 是正数,且满足9a b c ++=,111109a b b c c a ++=+++,那么a b cb c c a a b+++++的值为 .7(甲).如图,正方形ABCD 的边长为215,E ,F 分别是AB ,BC 的中点,AF 与DE ,DB分别交于点M ,N ,则△DMN 的面积是 . 7(乙).如图所示,点A 在半径为20的圆O 上,以OA 为一条对角线作矩形OBAC ,设直线BC 交圆O 于D 、E 两点,若12OC =,则线段CE 、BD 的长度差是 。
初中数学竞赛专题训练试题及解析(共10套)

初中数学竞赛专项训练(1)(实 数)一、选择题1、如果自然数a 是一个完全平方数,那么与a 之差最小且比a 大的一个完全平方数是( ) A. a +1B. a 2+1C. a 2+2a+1D. a+2a +12、在全体实数中引进一种新运算*,其规定如下:①对任意实数a 、b 有a *b=(a +b )(b -1)②对任意实数a 有a *2=a *a 。
当x =2时,[3*(x *2)]-2*x +1的值为 ( ) A. 34B. 16C. 12D. 63、已知n 是奇数,m 是偶数,方程⎩⎨⎧=+=+m y x n y 28112004有整数解x 0、y 0。
则( )A. x 0、y 0均为偶数B. x 0、y 0均为奇数C. x 0是偶数y 0是奇数D. x 0是奇数y 0是偶数4、设a 、b 、c 、d 都是非零实数,则四个数-ab 、ac 、bd 、cd ( ) A. 都是正数B. 都是负数C. 两正两负D. 一正三负或一负三正5、满足等式2003200320032003=+--+xy x y x y y x 的正整数对的个数是( ) A. 1B. 2C. 3D. 46、已知p 、q 均为质数,且满足5p 2+3q=59,由以p +3、1-p +q 、2p +q -4为边长的三角形是 A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形7、一个六位数,如果它的前三位数码与后三位数码完全相同,顺序也相同,由此六位数可以被( )整除。
A. 111B. 1000C. 1001D. 11118、在1、2、3……100个自然数中,能被2、3、4整除的数的个数共( )个 A. 4 B. 6C. 8D. 16二、填空题 1、若20011198********⋯⋯++=S ,则S 的整数部分是____________________2、M 是个位数字不为零的两位数,将M 的个位数字与十位数字互换后,得另一个两位数N ,若M -N 恰是某正整数的立方,则这样的数共___个。
全国初中数学竞赛试题及答案

中国教育学会中学数学教学专业委员会全国初中数学竞赛试题一、选择题共5小题,每小题6分,共30分.1甲.如果实数a ,b ,c 在数轴上的位置如图所示,22||()||a a b c a b c ++-+可以化简为 .A 2c a -B 22a b -C a -D a 1乙.如果22a =-+那么11123a+++的值为 .A 2- 2 C2 D 22甲.如果正比例函数y = axa ≠ 0与反比例函数y =xbb ≠0 的图象有两个交点,其中一个交点的坐标为-3,-2,那么另一个交点的坐标为 . A2,3 B3,-2 C -2,3 D3,22乙. 在平面直角坐标系xOy 中,满足不等式x 2+y 2≤2x +2y 的整数点坐标x ,y 的个数为 . A10 B9 C7 D53甲.如果a b ,为给定的实数,且1a b <<,那么1121a a b a b ++++,, ,这四个数据的平均数与中位数之差的绝对值是 . A1 B214a - C 12 D 143乙.如图,四边形ABCD 中,AC ,BD 是对角线,△ABC 是等边三角形.30ADC ∠=︒,AD = 3,BD = 5, 则CD 的长为 . A 23 B4 C 52 D4.54甲.小倩和小玲每人都有若干面值为整数元的人民币.小倩对小玲说:“你若给我2元,我的钱数将是你的n 倍”;小玲对小倩说:“你若给我n 元,我的钱数将是你的2倍”,其中n 为正整数,则n 的可能值的个数是 .OAB CEDA1 B2 C3 D44乙.如果关于x 的方程 20x px q p q --=(,是正整数的正根小于3, 那么这样的方程的个数是 .A 5B 6C 7D 85甲.一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,3,4,5,6.掷两次骰子,设其朝上的面上的两个数字之和除以4的余数分别是0,1,2,3的概率为0123p p p p ,,,,则0123p p p p ,,,中最大的是 .A 0pB 1pC 2pD 3p5乙.黑板上写有111123100, , ,, 共100个数字.每次操作先从黑板上的数中选取2个数a b ,,然后删去a b ,,并在黑板上写上数a b ab ++,则经过99次操作后,黑板上剩下的数是 . A2012 B101 C100 D99二、填空题共5小题,每小题6分,共30分6甲.按如图的程序进行操作,规定:程序运行从“输入一个值x ”到“结果是否>487 ”为一次操作. 如果操作进行四次才停止,那么x 的取值范围是 . 6乙.如果a ,b ,c是正数,且满足9a b c ++=,111109a b b c c a ++=+++,那么a b cb c c a a b+++++的值为 . 7甲.如图,正方形ABCD 的边长为215, E ,F 分别是AB ,BC 的中点,AF 与DE ,DB分别交于点M ,N ,则△DMN 的面积是 .7乙.如图所示,点A 在半径为20的圆O 上,以OA 为一条对角线作矩形OBAC,设直线BC 交圆O 于D 、E 两点,若12OC =,则线段CE 、BD 的长度差是 ; 8甲. 如果关于x 的方程x 2+kx +43k 2-3k +92= 0的两个实数根分别为xyO ECABD1x ,2x ,那么2012220111x x 的值为 .8乙.设n 为整数,且1≤n ≤2012. 若22(3)(3)n n n n -+++能被5整除,则所有n 的个数为 . 9甲. 2位八年级同学和m 位九年级同学一起参加象棋比赛,比赛为单循环,即所有参赛者彼此恰好比赛一场.记分规则是:每场比赛胜者得3分,负者得0分;平局各得1分. 比赛结束后,所有同学的得分总和为130分,而且平局数不超过比赛局数的一半,则m 的值为 . 9乙.如果正数x ,y ,z 可以是一个三角形的三边长,那么称x y z (,,)是三角形数.若a b c (,,)和111a b c (,,)均为三角形数,且a ≤b ≤c ,则ac的取值范围是 . 10甲如图,四边形ABCD 内接于⊙O , AB 是直径,AD = DC . 分别延长BA ,CD , 交点为E . 作BF ⊥EC ,并与EC 的延长线 交于点F . 若AE = AO ,BC = 6,则CF 的 长为 .10乙.已知n 是偶数,且1≤n ≤100.若有唯一的正整数对a b (,)使得22a b n =+成立,则这样的n 的个数为 .三、解答题共4题,每题15分,共60分11甲.已知二次函数232y x m x m =++++(),当13x -<<时,恒有0y <;关于x 的方程2320x m x m ++++=()的两个实数根的倒数和小于910-.求m 的取值范围. 11乙. 如图所示,在直角坐标系xOy 中,点A 在y 轴负半轴上,点B 、C 分别在x轴正、负半轴上,48,,sin 5AO AB AC C ==∠AB =;点D 在线段AB 上,连结CD 交y 轴于点E,且COE ADE S S ∆∆=;试求图像经过B 、C 、E 三点的二次函数的解析式;12甲. 如图,⊙O 的直径为AB ,1O 过点O ,且与⊙O 内切于点B .C 为⊙O 上的点,OC 与1O 交于点D ,且OD CD >.点E 在OD 上,且DC DE =,BE 的延长线与1O 交于点F ,求证:△BOC∽△1DO F .12乙.如图,⊙O 的内接四边形ABCD 中,AC ,BD 是它的对角线,AC 的中点I 是△ABD 的内心. 求证: 1OI 是△IBD 的外接圆的切线; 2AB +AD = 2BD .13甲. 已知整数a ,b 满足:a -b 是素数,且ab 是完全平方数. 当a ≥2012时,求a 的最小值. 13乙.给定一个正整数n ,凸n 边形中最多有多少个内角等于150︒ 并说明理由.14甲. 求所有正整数n ,使得存在正整数122012x x x ,, ,,满足122012x x x <<<,且122012122012n x x x +++=. 14乙.将2,3,…,n n ≥2任意分成两组,如果总可以在其中一组中找到数a b c ,, 可以相同,使得b ac =,求n 的最小值.参考解答一、选择题1甲 .C解:由实数a ,b ,c 在数轴上的位置可知0b a c <<<,且b c >,所以22||()||()()()a a b c a b c a a b c a b c -++-++=-+++--+a =-.1乙.B 解:111111122122312a+=+=++-++++1121221=+==+.2甲.D解:利用正比例函数与反比例函数的图象及其对称性,可知两个交点关于原点对称,因此另一个交点的坐标为3,2.2乙.B解:由题设x 2+y 2≤2x +2y , 得0≤22(1)(1)x y -+-≤2. 因为x y ,均为整数,所以有22(1)0(1)0x y ⎧-=⎪⎨-=⎪⎩,; 22(1)0(1)1x y ⎧-=⎪⎨-=⎪⎩,; 22(1)1(1)0x y ⎧-=⎪⎨-=⎪⎩,; 22(1)1(1) 1.x y ⎧-=⎪⎨-=⎪⎩,解得11x y =⎧⎨=⎩,; 12x y =⎧⎨=⎩,; 10x y =⎧⎨=⎩,; 01x y =⎧⎨=⎩,; 00x y =⎧⎨=⎩,; 02x y =⎧⎨=⎩,; 21x y =⎧⎨=⎩,; 20x y =⎧⎨=⎩,; 22.x y =⎧⎨=⎩, 以上共计9对x y (,). 3甲.D解:由题设知,1112a a b a b <+<++<+,所以这四个数据的平均数为1(1)(1)(2)34244a ab a b a b+++++++++=, 中位数为 (1)(1)44224a a b a b++++++=, 于是 4423421444a b a b ++++-=.3乙.B解:如图,以CD 为边作等边△CDE ,连接AE . 由于AC = BC ,CD = CE ,∠BCD =∠BCA +∠ACD =∠DCE +∠ACD =∠ACE ,所以△BCD ≌△ACE , BD = AE .又因为30ADC ∠=︒,所以90ADE ∠=︒. 在Rt △ADE 中,53AE AD ==,, 于是DE4=,所以CD = DE = 4.4甲.D解:设小倩所有的钱数为x 元、小玲所有的钱数为y 元,x y ,均为非负整数. 由题设可得2(2)2()x n y y n x n +=-⎧⎨+=-⎩,,消去x 得 2y -7n = y +4, 2n =721517215)72(-+=-+-y y y .因为1527y -为正整数,所以2y -7的值分别为1,3,5,15,所以y 的值只能为4,5,6,11.从而n 的值分别为8,3,2,1;x 的值分别为14,7,6,7.4乙.C解:由一元二次方程根与系数关系知,两根的乘积为0q -<,故方程的根为一正一负.由二次函数2y x px q =--的图象知,当3x =时,0y >,所以2330p q -->,即 39p q +<. 由于p q ,都是正整数,所以1p =,1≤q ≤5;或 2p =,1≤q ≤2,此时都有240p q ∆=+>. 于是共有7组p q (,)符合题意.5甲.D解:掷两次骰子,其朝上的面上的两个数字构成的有序数对共有36个,其和除以4的余数分别是0,1,2,3的有序数对有9个,8个,9个,10个,所以01239891036363636p p p p ====,,,,因此3p 最大. 5乙.C解:因为1(1)(1)a b ab a b +++=++,所以每次操作前和操作后,黑板上的每个数加1后的乘积不变.设经过99次操作后黑板上剩下的数为x ,则1111(11)(1)(1)(1)23100x +=++++, 解得 1101x +=,100x =.二、填空题6甲.7<x ≤19解:前四次操作的结果分别为3x -2,33x -2-2 = 9x -8,39x -8-2 = 27x -26,327x -26-2 = 81x -80.由已知得 27x -26≤487, 81x -80>487.解得 7<x ≤19.容易验证,当7<x ≤19时,32x -≤487 98x -≤487,故x 的取值范围是 7<x ≤19.6乙.7解:在910111=+++++a c c b b a 两边乘以9=++c b a 得 103=++++++a c b c b a b a c 即7=+++++ac b c b a b a c7甲.8解:连接DF ,记正方形ABCD 的边长为2a . 由题设易知△BFN ∽△DAN ,所以21AD AN DN BF NF BN ===, 由此得2AN NF =,所以23AN AF =.在Rt △ABF 中,因为2AB a BF a ==,,所以225AF AB BF a =+=,于是 25cos AB BAF AF ∠==. 由题设可知△ADE ≌△BAF ,所以 AED AFB ∠=∠,0018018090AME BAF AED BAF AFB ∠=-∠-∠=-∠-∠=. 于是 25cos AM AE BAF =⋅∠, 2453MN AN AM AF AM =-=-=,415MND AFD S MN S AF ∆∆==. 又21(2)(2)22AFD S a a a ∆=⋅⋅=,所以2481515MND AFD S S a ∆∆==. 因为15a =所以8MND S ∆=. 7乙.285解:如图,设DE 的中点为M ,连接OM ,则OM DE ⊥.因为22201216OB -=,所以161248205OB OC OM BC ⋅⨯===, 22366455CM OC OM BM =-==,. CE BD EM CM DM BM -=---()()643655BM CM =-=-285=. 8甲.32-解:根据题意,关于x 的方程有∆=k 2-4239(3)42k k -+≥0,由此得 k -32≤0.又k -32≥0,所以k -32=0,从而k =3. 此时方程为x 2+3x +49=0,解得x 1=x 2=32-.故2012220111x x =21x =23-.8乙.1610解:()()()953332422222++=-+=+++-n n n n n n n n因此45|(9)n +,所以)5(mod 14≡n ,因此25k ,15±±=或k n240252012⋯⋯=÷所以共有2012-402=1610个数9甲.8解:设平局数为a ,胜负局数为b ,由题设知23130a b +=,由此得0≤b ≤43.又 (1)(2)2m m a b +++=,所以22(1)(2)a b m m +=++. 于是0≤130(1)(2)b m m =-++≤43,87≤(1)(2)m m ++≤130,由此得 8m =,或9m =.当8m =时,405b a ==,;当9m =时,2035b a ==,,5522a b a +>=,不合题设. 故8m =. 9乙.1253≤<-ca解:依题意得:(1)111(2)a b c b c a +>⎧⎪⎨+>⎪⎩,所以a c b ->,代入2得ca c cb a 11111+-<+<,两边乘以a 得 c a a c a +-<1,即a c ac a c -<-,化简得0322<+-c ac a ,两边除以2c 得 23()10a a c c ⎛⎫-+< ⎪⎝⎭所以253253+<<-c a 另一方面:a ≤b ≤c,所以1≤ca综合得1253≤<-c a 另解:可令ak c=,由1得(1)b k c >-,代入2化简得2310k k -+<,解得 353522k -<<,另一方面:a ≤b ≤c,所以1k ≤, 综合得3512k <≤. 10甲.223 解:如图,连接AC ,BD ,OD .由AB 是⊙O 的直径知∠BCA =∠BDA = 90°. 依题设∠BFC = 90°,四边形ABCD 是⊙O 的内接四边形,所以∠BCF =∠BAD ,所以 Rt △BCF ∽Rt △BAD ,因此BC BACF AD=. 因为OD 是⊙O 的半径,AD = CD ,所以OD 垂直平分AC ,OD ∥BC ,于是2DE OEDC OB==. 因此 223DE CD AD CE AD ===,.由△AED ∽△CEB ,知DE EC AE BE ⋅=⋅.因为322BA AE BE BA ==,, 所以 32322BA AD AD BA ⋅=⋅,BA =22AD ,故 AD CF BC BA =⋅=2=. 10乙.12解:依题意得()()b a b a b a n -+=-=22由于n 是偶数,a+b 、a-b 同奇偶,所以n 是4的倍数,即4n k =,当1≤n ≤100时,4的倍数共有25个,但要满足题中条件的唯一正整数对a b (,),则: 2k p k p ==或,其中p 是素数,因此,k 只能取下列12个数:2、3、5、7、11、13、17、19、23、4、9、25,从而这样的n 有12个;三、解答题11甲.解: 因为当13x -<<时,恒有0y <,所以23420m m ∆=+-+>()(),即210m +>(),所以1m ≠-.…………3分当1x =-时,y ≤0;当3x =时,y ≤0,即2(1)(3)(1)2m m -++-++≤0,且 233(3)2m m ++++≤0,解得m ≤5-.…………8分设方程()()2320x m x m ++++=的两个实数根分别为12x x ,,由一元二次方程根与系数的关系得()121232x x m x x m +=-+=+,.因为1211910x x +<-,所以121239210x x m x x m ++=-<-+,解得12m <-,或2m >-.因此12m <-.…………15分11乙.解:因为sin ∠ABC =45AO AB =,8AO =, 所以AB = 10.由勾股定理,得262BO AB AO -=. 易知ABO ACO △≌△, 因此 CO = BO = 6. 于是(08)A -,,(60)B ,,(60)C -,. 设点D 的坐标为()m n ,. 由COE ADE S S =△△,得CDB AOB S S =△△.所以1122BC n AO BO ⋅=⋅,1112()8622n ⨯-=⨯⨯. 解得 4n =-.因此D 为AB 的中点,点 D 的坐标为(34)-,.因此CD ,AO 分别为AB ,BC 的两条中线,点E 为△A BC 的重心,所以点E 的坐标为8(0)3-,.也可由直线CD 交y 轴于点E 来求得. 设经过B ,C ,E 三点的二次函数的解析式为(6)(6)y a x x =-+. 将点E 的坐标代入,解得a =272. 故经过B ,C ,E 三点的二次函数的解析式为228273y x =-.12甲. 证明:连接BD ,因为OB 为1O 的直径,所以90ODB ∠=︒.又因为DC DE =,所以△CBE 是等腰三角形.…………5分设BC 与1O 交于点M ,连接OM ,则90OMB ∠=︒.又因为OC OB =,所以22BOC DOM DBC ∠=∠=∠12DBF DO F =∠=∠.…………10分又因为1BOC DO F ∠∠,分别是等腰△BOC ,等腰△1DO F 的顶角,所以△BOC ∽△1DO F .…………15分12乙.证明:1如图,根据三角形内心的性质和同弧上圆周角相等的性质知:CID IAD IDA ∠=∠+∠,CDI CDB BDI BAC IDA IAD IDA ∠=∠+∠=∠+∠=∠+∠. 所以CID CDI ∠=∠, CI = CD .同理,CI = CB .故点C 是△IBD 的外心.连接OA ,OC ,因为I 是AC 的中点,且OA = OC , 所以OI ⊥AC ,即OI ⊥CI .故OI 是△IBD 外接圆的切线. 2如图,过点I 作IE ⊥AD 于点E ,设OC 与BD 交于点F .由BC CD =,知OC ⊥BD .因为∠CBF =∠IAE ,BC = CI = AI ,所以Rt BCF Rt AIE △≌△.所以BF = AE . 又因为I 是△ABD 的内心,所以22AB AD BD AE BD BD BF BD +-=+-==. 故2AB AD BD +=.也可由托勒密定理得:AB CD AD BC AC BD ⋅+⋅=⋅,再将22AC BC CD ==代入即得结论2AB AD BD +=;13甲.解:设a -b = mm 是素数,ab = n 2n 是自然数.因为 a +b 2-4ab = a -b 2, 所以 2a -m 2-4n 2 = m 2,2a -m +2n 2a -m -2n = m 2.…………5分1当1n ≥时,因为2a -m +2n 与2a -m -2n 都是正整数,且2a -m +2n >2a -m -2n m 为素数,所以 2a -m +2n =m 2,2a -m -2n =1.解得 a =2(1)4m +,n =214m -.于是 b = a -m =214m -().…………10分又a ≥2012,即2(1)4m +≥2012.又因为m 是素数,解得m ≥89. 此时,a ≥41)(892+=2025.当2025a =时,89m =,1936b =,1980n =. 此时,a 的最小值为2025.2当0n =时,因为a ≥2012,所以0b =,从而得a 的最小值为2017素数; 综上所述,所求的a 的最小值为2017;……15分13乙.解:设凸n 边形最多有k 个内角等于150°,则每个150°内角的外角都等于30°,而凸n 边形的n 个外角和为360°,所以3601230k ≤=,只有当12n =时, k 才有最大值12. …………5分下面我们讨论12n ≠时的情况: 1当12n >时,显然,k 的值是11;2当3,4,5,6,7n =时,k 的值分别为1,2,3,4,5;3当8,9,10,11n =时,k 的值分别为7,8,9,10. …………10分综上所述,当37n ≤≤时,凸n 边形最多有2n -个内角等于150°;当811n ≤≤时,凸n 边形最多有1n -个内角等于150°;当12n =时,凸n 边形最多有12个内角等于150°;当12n >时,凸n 边形最多有11个内角等于150°;. ……15分14甲.解:由于122012x x x ,, ,都是正整数,且122012x x x <<<,所以1x ≥1,2x ≥2,…,2012x ≥2012.于是 122012122012n x x x =+++≤1220122012122012+++=. …………5分当1n =时,令12201220122201220122012x x x ==⨯=⨯,, ,,则1220121220121x x x +++=. …………10分当1n k =+时,其中1≤k ≤2011,令 1212k x x x k ===,, ,,122012(2012)(1)(2012)(2)(2012)2012k k x k k x k k x k ++=-+=-+=-⨯,,,则1220121220121(2012)2012k k x x x k+++=+-⋅-1k n =+=. 综上,满足条件的所有正整数n 为122012, , , .…………15分14乙.解:当1621n =-时,把23n , , ,分成如下两个数组:{}88162322121+-, , , , , 和{}84521-, , , .在数组{}88162322121+-, , , , , 中,由于38821632221<>-(,),所以其中不存在数a b c ,,,使得b a c =. 在数组{}84521-, , , 中,由于48421>-, 所以其中不存在数a b c ,,,使得b a c =. 所以,162n ≥.下面证明当162n =时,满足题设条件.不妨设2在第一组,若224=也在第一组,则结论已经成立.故不妨设224=在第二组. 同理可设4842=在第一组,8216(2)2=在第二组.此时考虑数8.如果8在第一组,我们取8282a b c ===,,,此时b a c =;如果8在第二组,我们取16482a b c ===,,,此时b a c =. 综上,162n =满足题设条件.所以,n 的最小值为162.注:也可以通过考虑2,4,16,256,65536的分组情况得到n 最小值为65536.。
初中奥林匹克数学竞赛试题

初中奥林匹克数学竞赛试题一、选择题(每题3分,共30分)1. 若实数a,b满足 a + 2 +(b - 4)² = 0,则a + b的值为()。
A. - 2B. 2C. 6D. - 6答案:B。
解析:因为绝对值是非负的,一个数的平方也是非负的,要使 a + 2 +(b - 4)² = 0,那么a+2 = 0且b - 4 = 0,解得a=-2,b = 4,所以a + b=2。
2. 把多项式x² - 4x+4分解因式,结果正确的是()。
A. (x - 2)²B. (x+2)²C. (x - 4)²D. (x+4)²答案:A。
解析:x²- 4x + 4符合完全平方公式a²- 2ab+b²=(a - b)²的形式,这里a=x,b = 2,所以分解因式结果为(x - 2)²。
3. 已知一元二次方程x² - 3x - 2 = 0的两个实数根为x1,x2,则(x1 - 1)(x2 - 1)的值是()。
A. - 4B. - 2C. 0D. 2答案:C。
解析:根据韦达定理,对于一元二次方程ax²+bx + c = 0(a≠0),x1+x2=-b/a,x1x2=c/a。
在方程x² - 3x - 2 = 0中,a = 1,b=-3,c = - 2,所以x1+x2 = 3,x1x2=-2。
(x1 - 1)(x2 - 1)=x1x2-(x1+x2)+1=-2 - 3+1 = 0。
4. 一个三角形的三个内角之比为1:2:3,则这个三角形是()。
A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形答案:B。
解析:设三个内角分别为x,2x,3x,因为三角形内角和为180°,所以x+2x+3x = 180°,解得x = 30°,那么三个角分别为30°,60°,90°,所以是直角三角形。
初中数学奥林匹克竞赛题及答案

初中数学奥林匹克竞赛题及答案奥数题一一、选择题(每题1分,共10分)1.如果a,b都代表有理数,并且a+b=0,那么 ( )A.a,b都是0B.a,b之一是0C.a,b互为相反数D.a,b互为倒数答案:C解析:令a=2,b=-2,满足2+(-2)=0,由此a、b互为相反数。
2.下面的说法中正确的是 ( )A.单项式与单项式的和是单项式B.单项式与单项式的和是多项式C.多项式与多项式的和是多项式D.整式与整式的和是整式答案:D解析:x²,x3都是单项式.两个单项式x3,x²之和为x3+x²是多项式,排除A。
两个单项式x²,2x2之和为3x2是单项式,排除B。
两个多项式x3+x2与x3-x2之和为2x3是个单项式,排除C,因此选D。
3.下面说法中不正确的是 ( )A. 有最小的自然数B.没有最小的正有理数C.没有最大的负整数D.没有最大的非负数答案:C解析:最大的负整数是-1,故C错误。
4.如果a,b代表有理数,并且a+b的值大于a-b的值,那么 ( )A.a,b同号B.a,b异号C.a>0D.b>0答案:D5.大于-π并且不是自然数的整数有 ( )A.2个B.3个C.4个D.无数个答案:C解析:在数轴上容易看出:在-π右边0的左边(包括0在内)的整数只有-3,-2,-1,0共4个.选C。
6.有四种说法:甲.正数的平方不一定大于它本身;乙.正数的立方不一定大于它本身;丙.负数的平方不一定大于它本身;丁.负数的立方不一定大于它本身。
这四种说法中,不正确的说法的个数是 ( )A.0个B.1个C.2个D.3个答案:B解析:负数的平方是正数,所以一定大于它本身,故C错误。
7.a代表有理数,那么,a和-a的大小关系是 ( )A.a大于-aB.a小于-aC.a大于-a或a小于-aD.a不一定大于-a答案:D解析:令a=0,马上可以排除A、B、C,应选D。
8.在解方程的过程中,为了使得到的方程和原方程同解,可以在原方程的两边( ) A.乘以同一个数B.乘以同一个整式C.加上同一个代数式D.都加上1答案:D解析:对方程同解变形,要求方程两边同乘不等于0的数,所以排除A。
全国初中数学联赛试题(含参考答案)

全国初中数学联合竞赛试题参考答案第一试一、选择题(本题满分42分,每小题7分) 1、设17-=a ,则=--+12612323a a a ( A )A 、24B 、 25C 、1074+D 、1274+ 2、在ABC ∆中,最大角A ∠是最小角C ∠的两倍,且7=AB ,8=AC ,则=BC ( C ) A 、27 B 、10 C 、105 D 、37 3、用[]x 表示不大于x 的最大整数,则方程[]0322=--x x 的解的个数为( C ) A 、1 B 、2 C 、3 D 、 44、设正方形ABCD 的中心为点O ,在以五个点A 、B 、C 、D 、O 为顶点所构成的所有三角形中任意取出两个,它们的面积相等的概率为 ( B )A 、143 B 、73 C 、21 D 、74 5、如图,在矩形ABCD 中,3=AB ,2=BC ,以BC 为直径在矩形内作半圆,自点A 作半圆的切线AE ,则=∠CBE sin ( D )A 、36 B 、32C 、31D 、10106、设n 是大于1909的正整数,使得nn --20091909为完全平方数的n 的个数是 ( B )A 、3B 、 4C 、 5D 、6 二、填空题(本题满分28分,每小题7分)1、已知t 是实数,若a ,b 是关于x 的一元二次方程0122=-+-t x x 的两个非负实根,则()()1122--b a的最小值是____________.答案:3-2、设D 是ABC ∆的边AB 上的一点,作BC DE //交AC 于点E ,作AC DF //交BC 于点F ,已知ADE ∆、DBF ∆的面积分别为m 和n ,则四边形DECF 的面积为______.答案:mn 23、如果实数a ,b 满足条件122=+b a ,2212|21|a b a b a -=+++-,则____=+b a . 答案:1-4、已知a ,b 是正整数,且满足⎪⎪⎭⎫ ⎝⎛+b a 15152是整数,则这样的有序数对(a ,b )共有_对。
历年初中数学竞赛试题精选(含解答)

初中数学竞赛专项训练(1)1、一个六位数,如果它的前三位数码与后三位数码完全相同,顺序也相同,由此六位数可以被( )整除。
A. 111B. 1000C. 1001D. 1111 解:依题意设六位数为abcabc ,则abcabc =a ×105+b ×104+c ×103+a ×102+b ×10+c =a ×102(103+1)+b ×10(103+1)+c (103+1)=(a ×103+b ×10+c )(103+1)=1001(a ×103+b ×10+c ),而a ×103+b ×10+c 是整数,所以能被1001整除。
故选C方法二:代入法2、若2001119811198011⋯⋯++=S ,则S 的整数部分是____________________解:因1981、1982……2001均大于1980,所以9022198019801221==⨯>S ,又1980、1981……2000均小于2001,所以22219022*********221==⨯<S ,从而知S 的整数部分为90。
3、设有编号为1、2、3……100的100盏电灯,各有接线开关控制着,开始时,它们都是关闭状态,现有100个学生,第1个学生进来时,凡号码是1的倍数的开关拉了一下,接着第二个学生进来,由号码是2的倍数的开关拉一下,第n 个(n ≤100)学生进来,凡号码是n 的倍数的开关拉一下,如此下去,最后一个学生进来,把编号能被100整除的电灯上的开关拉了一下,这样做过之后,请问哪些灯还亮着。
解:首先,电灯编号有几个正约数,它的开关就会被拉几次,由于一开始电灯是关的,所以只有那些被拉过奇数次的灯才是亮的,因为只有平方数才有奇数个约数,所以那些编号为1、22、32、42、52、62、72、82、92、102共10盏灯是亮的。
全国初中数学竞赛试题及答案

中国教育学会中学数学教学专业委员会全国初中数学竞赛试题一、选择题共5小题,每小题6分,共30分.1甲.如果实数a ,b ,c 在数轴上的位置如图所示,那么代数式22||()||a a b c a b c -++-++可以化简为 .A 2c a -B 22a b -C a -D a 1乙.如果22a =-+那么11123a+++的值为 .A 2-2222甲.如果正比例函数y = axa ≠ 0与反比例函数y =xbb ≠0 的图象有两个交点,其中一个交点的坐标为-3,-2,那么另一个交点的坐标为 . A2,3 B3,-2 C -2,3 D3,22乙. 在平面直角坐标系xOy 中,满足不等式x 2+y 2≤2x +2y 的整数点坐标x ,y 的个数为 .A10 B9 C7 D53甲.如果a b ,为给定的实数,且1a b <<,那么1121a a b a b ++++,, ,这四个数据的平均数与中位数之差的绝对值是 . A1 B214a - C 12 D 143乙.如图,四边形ABCD 中,AC ,BD 是对角线,△ABC 是等边三角形.30ADC ∠=︒,AD = 3,BD = 5, 则CD 的长为 . A 23 B4 C 52 D4甲.小倩和小玲每人都有若干面值为整数元的人民币.小倩对小玲说:“你若给我2元,我的钱数将是你的n 倍”;小玲对小倩说:“你若给我n 元,我的钱数将是你的2倍”,其中n 为正整数,则n 的可能值的个数是 . A1 B2 C3 D44乙.如果关于x 的方程 20x px q p q --=(,是正整数的正根小于3, 那么这样的方程的个数是 .A 5B 6C 7D 85甲.一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,3,4,5,6.掷两次骰子,设其朝上的面上的两个数字之和除以4的余数分别是0,1,2,3的概率为0123p p p p ,,,,则0123p p p p ,,,中最大的是 .A 0pB 1pC 2pD 3p5乙.黑板上写有111123100, , ,, 共100个数字.每次操作先从黑板上的数中选取2个数a b ,,然后删去a b ,,并在黑板上写上数a b ab ++,则经过99次操作后,黑板上剩下的数是 .A2012 B101 C100 D99二、填空题共5小题,每小题6分,共30分6甲.按如图的程序进行操作,规定:程序运行从“输入一个值x ”到“结果是否>487”为一次操作. 如果操作进行四次才停止,那么x的取值范围是 . 6乙.如果a ,b ,c 是正数,且满足9a b c ++=,111109a b b c c a ++=+++,那么OAB CE a b cb c c a a b+++++的值为 . 7甲.如图,正方形ABCD 的边长为215E ,F 分别是AB ,BC 的中点,AF 与DE ,DB分别交于点M ,N ,则△DMN 的面积是 . 7乙.如图所示,点A 在半径为20的圆O 上,以OA 为一条对角线作矩形OBAC,设直线BC 交圆O 于D 、E 两点,若12OC =,则线段CE 、BD 的长度差是 ;8甲. 如果关于x 的方程x 2+kx +43k 2-3k +92= 0的两个实数根分别为1x ,2x ,那么2012220111x x 的值为 .8乙.设n 为整数,且1≤n ≤2012. 若22(3)(3)n n n n -+++能被5整除,则所有n 的个数为 .9甲. 2位八年级同学和m 位九年级同学一起参加象棋比赛,比赛为单循环,即所有参赛者彼此恰好比赛一场.记分规则是:每场比赛胜者得3分,负者得0分;平局各得1分. 比赛结束后,所有同学的得分总和为130分,而且平局数不超过比赛局数的一半,则m 的值为 .9乙.如果正数x ,y ,z 可以是一个三角形的三边长,那么称x y z (,,)是三角形数.若a b c (,,)和111a b c (,,)均为三角形数,且a ≤b ≤c ,则ac的取值范围是 . 10甲如图,四边形ABCD 内接于⊙O ,AB 是直径,AD = DC . 分别延长BA ,CD ,交点为E . 作BF ⊥EC ,并与EC 的延长线 交于点F . 若AE = AO ,BC = 6,则CF 的 长为 .xyO ECABD10乙.已知n 是偶数,且1≤n ≤100.若有唯一的正整数对a b (,)使得22a b n =+成立,则这样的n 的个数为 .三、解答题共4题,每题15分,共60分11甲.已知二次函数232y x m x m =++++(),当13x -<<时,恒有0y <;关于x 的方程2320x m x m ++++=()的两个实数根的倒数和小于910-.求m 的取值范围. 11乙. 如图所示,在直角坐标系xOy 中,点A 在y 轴负半轴上,点B 、C 分别在x 轴正、负半轴上,48,,sin 5AO AB AC C ==∠AB =;点D 在线段AB 上,连结CD交y 轴于点E,且COE ADE S S ∆∆=;试求图像经过B 、C 、E 三点的二次函数的解析式; 12甲. 如图,⊙O 的直径为AB ,1O 过点O ,且与⊙O 内切于点B .C 为⊙O 上的点,OC 与1O 交于点D ,且OD CD >.点E 在OD 上,且DC DE =,BE 的延长线与1O 交于点F ,求证:△BOC ∽△1DO F .12乙.如图,⊙O 的内接四边形ABCD 中,AC ,BD 是它的对角线,AC 的中点I 是△ABD 的内心. 求证: 1OI 是△IBD 的外接圆的切线; 2AB +AD = 2BD .13甲. 已知整数a ,b 满足:a -b 是素数,且ab 是完全平方数. 当a ≥2012时,求a 的最小值. 13乙.给定一个正整数n ,凸n 边形中最多有多少个内角等于150︒并说明理由.14甲. 求所有正整数n ,使得存在正整数122012x x x ,, ,,满足122012x x x <<<,且122012122012n x x x +++=. 14乙.将2,3,…,n n ≥2任意分成两组,如果总可以在其中一组中找到数a b c ,, 可以相同,使得b a c =,求n 的最小值.参考解答一、选择题1甲 .C解:由实数a ,b ,c 在数轴上的位置可知0b a c <<<,且b c >,所以||||()()()a b b c a a b c a b c ++=-+++--+a =-.1乙.B解:1111111223a+=+=++111=+=+=.2甲.D解:利用正比例函数与反比例函数的图象及其对称性,可知两个交点关于原点对称,因此另一个交点的坐标为3,2.2乙.B解:由题设x 2+y 2≤2x +2y , 得0≤22(1)(1)x y -+-≤2. 因为x y ,均为整数,所以有 解得以上共计9对x y (,).3甲.D解:由题设知,1112a a b a b <+<++<+,所以这四个数据的平均数为1(1)(1)(2)34244a ab a b a b+++++++++=, 中位数为(1)(1)44224a ab a b ++++++=, 于是4423421444a b a b ++++-=. 3乙.B解:如图,以CD 为边作等边△CDE ,连接AE . 由于AC = BC ,CD = CE ,∠BCD =∠BCA +∠ACD =∠DCE +∠ACD =∠ACE , 所以△BCD ≌△ACE , BD = AE . 又因为30ADC ∠=︒,所以90ADE ∠=︒. 在Rt △ADE 中,53AE AD ==,,于是DE 224AE AD -=,所以CD = DE = 4. 4甲.D解:设小倩所有的钱数为x 元、小玲所有的钱数为y 元,x y ,均为非负整数. 由题设可得消去x 得 2y -7n = y +4, 2n =721517215)72(-+=-+-y y y .因为1527y -为正整数,所以2y -7的值分别为1,3,5,15,所以y 的值只能为4,5,6,11.从而n 的值分别为8,3,2,1;x 的值分别为14,7,6,7.4乙.C解:由一元二次方程根与系数关系知,两根的乘积为0q -<,故方程的根为一正一负.由二次函数2y x px q =--的图象知,当3x =时,0y >,所以2330p q -->,即39p q +<. 由于p q ,都是正整数,所以1p =,1≤q ≤5;或 2p =,1≤q ≤2,此时都有240p q ∆=+>. 于是共有7组p q (,)符合题意. 5甲.D解:掷两次骰子,其朝上的面上的两个数字构成的有序数对共有36个,其和除以4的余数分别是0,1,2,3的有序数对有9个,8个,9个,10个,所以01239891036363636p p p p ====,,,,因此3p 最大. 5乙.C解:因为1(1)(1)a b ab a b +++=++,所以每次操作前和操作后,黑板上的每个数加1后的乘积不变.设经过99次操作后黑板上剩下的数为x ,则1111(11)(1)(1)(1)23100x +=++++, 解得 1101x +=,100x =.二、填空题6甲.7<x ≤19解:前四次操作的结果分别为3x -2,33x -2-2 = 9x -8,39x -8-2 = 27x -26,327x -26-2 = 81x -80.由已知得 27x -26≤487, 81x -80>487.解得 7<x ≤19.容易验证,当7<x ≤19时,32x -≤487 98x -≤487,故x 的取值范围是 7<x ≤19.6乙.7解:在910111=+++++a c c b b a 两边乘以9=++c b a 得 103=++++++a c b c b a b a c 即7=+++++ac b c b a b a c 7甲.8解:连接DF ,记正方形ABCD 的边长为2a . 由题设易知△BFN ∽△DAN ,所以21AD AN DN BF NF BN ===, 由此得2AN NF =,所以23AN AF =.在Rt △ABF 中,因为2AB a BF a ==,,所以225AF AB BF a =+=,于是 25cos 5AB BAF AF ∠==. 由题设可知△ADE ≌△BAF ,所以 AED AFB ∠=∠,0018018090AME BAF AED BAF AFB ∠=-∠-∠=-∠-∠=. 于是 25cos AM AE BAF =⋅∠, 2453MN AN AM AF AM =-=-=,415MND AFD S MN S AF ∆∆==. 又21(2)(2)22AFD S a a a ∆=⋅⋅=,所以2481515MND AFD S S a ∆∆==. 因为15a =所以8MND S ∆=. 7乙.285解:如图,设DE 的中点为M ,连接OM ,则OM DE ⊥.因为16OB =,所以161248205OB OC OM BC ⋅⨯===, 366455CM BM ===,. CE BD EM CM DM BM -=---()()643655BM CM =-=-285=. 8甲.32-解:根据题意,关于x 的方程有∆=k 2-4239(3)42k k -+≥0,由此得 k -32≤0.又k -32≥0,所以k -32=0,从而k =3. 此时方程为x 2+3x +49=0,解得x 1=x 2=32-. 故2012220111x x =21x =23-. 8乙.1610解:()()()953332422222++=-+=+++-n n n n n n n n因此45|(9)n +,所以)5(mod 14≡n ,因此25k ,15±±=或k n 所以共有2012-402=1610个数9甲.8解:设平局数为a ,胜负局数为b ,由题设知23130a b +=,由此得0≤b ≤43. 又 (1)(2)2m m a b +++=,所以22(1)(2)a b m m +=++. 于是 0≤130(1)(2)b m m =-++≤43,87≤(1)(2)m m ++≤130,由此得 8m =,或9m =.当8m =时,405b a ==,;当9m =时,2035b a ==,,5522a b a +>=,不合题设. 故8m =.9乙.1253≤<-ca解:依题意得:(1)111(2)a b c b c a +>⎧⎪⎨+>⎪⎩,所以a c b ->,代入2得 c a c c b a 11111+-<+<,两边乘以a 得 c a a c a +-<1,即a c ac a c -<-,化简得0322<+-c ac a ,两边除以2c 得 23()10a a c c ⎛⎫-+< ⎪⎝⎭所以253253+<<-c a 另一方面:a ≤b ≤c,所以1≤ca综合得1253≤<-c a 另解:可令ak c=,由1得(1)b k c >-,代入2化简得2310k k -+<,解得3535k -+<<,另一方面:a ≤b ≤c,所以1k ≤, 综合得351k -<≤. 10甲.223 解:如图,连接AC ,BD ,OD .由AB 是⊙O 的直径知∠BCA =∠BDA = 90°.依题设∠BFC = 90°,四边形ABCD 是⊙O的内接四边形,所以∠BCF =∠BAD ,所以 Rt △BCF ∽Rt △BAD ,因此BC BACF AD=. 因为OD 是⊙O 的半径,AD = CD ,所以OD 垂直平分AC ,OD ∥BC , 于是2DE OEDC OB==. 因此 223DE CD AD CE AD ===,.由△AED ∽△CEB ,知DE EC AE BE ⋅=⋅.因为322BA AE BE BA ==,, 所以 32322BA AD AD BA ⋅=⋅,BA =22AD ,故AD CF BCBA =⋅=2=. 10乙.12 解:依题意得()()b a b a b a n -+=-=22由于n 是偶数,a+b 、a-b 同奇偶,所以n 是4的倍数,即4n k =,当1≤n ≤100时,4的倍数共有25个,但要满足题中条件的唯一正整数对a b (,),则:2k p k p ==或,其中p 是素数,因此,k 只能取下列12个数:2、3、5、7、11、13、17、19、23、4、9、25,从而这样的n 有12个;三、解答题11甲.解: 因为当13x -<<时,恒有0y <,所以23420m m ∆=+-+>()(),即210m +>(),所以1m ≠-.…………3分当1x =-时,y ≤0;当3x =时,y ≤0,即2(1)(3)(1)2m m -++-++≤0,且 233(3)2m m ++++≤0,解得m ≤5-.…………8分设方程()()2320x m x m ++++=的两个实数根分别为12x x ,,由一元二次方程根与系数的关系得()121232x x m x x m +=-+=+,.因为1211910x x +<-,所以121239210x x m x x m ++=-<-+, 解得12m <-,或2m >-.因此12m <-.…………15分11乙.解:因为sin ∠ABC =45AO AB =,8AO =, 所以AB = 10.由勾股定理,得262BO AB AO -=.易知ABO ACO △≌△, 因此 CO = BO = 6.于是(08)A -,,(60)B ,,(60)C -,.设点D 的坐标为()m n ,.由COE ADE S S =△△,得CDB AOB S S =△△.所以 1122BC n AO BO ⋅=⋅,1112()8622n ⨯-=⨯⨯. 解得 4n =-.因此D 为AB 的中点,点 D 的坐标为(34)-,.因此CD ,AO 分别为AB ,BC 的两条中线,点E 为△A BC 的重心,所以点E 的坐标为8(0)3-,.也可由直线CD 交y 轴于点E 来求得. 设经过B ,C ,E 三点的二次函数的解析式为(6)(6)y a x x =-+.将点E 的坐标代入,解得a =272. 故经过B ,C ,E 三点的二次函数的解析式为228273y x =-. 12甲. 证明:连接BD ,因为OB 为1O 的直径,所以90ODB ∠=︒.又因为DC DE =,所以△CBE 是等腰三角形.…………5分设BC 与1O 交于点M ,连接OM ,则90OMB ∠=︒.又因为OC OB =,所以22BOC DOM DBC ∠=∠=∠12DBF DO F =∠=∠.…………10分又因为1BOC DO F ∠∠,分别是等腰△BOC ,等腰△1DO F 的顶角,所以△BOC ∽△1DO F .…………15分12乙.证明:1如图,根据三角形内心的性质和同弧上圆周角相等 的性质知:CID IAD IDA ∠=∠+∠,CDI CDB BDI BAC IDA IAD IDA ∠=∠+∠=∠+∠=∠+∠.所以CID CDI ∠=∠, CI = CD .同理,CI = CB .故点C 是△IBD 的外心.连接OA ,OC ,因为I 是AC 的中点,且OA = OC ,所以OI ⊥AC ,即OI ⊥CI .故OI 是△IBD 外接圆的切线. 2如图,过点I 作IE ⊥AD 于点E ,设OC 与BD 交于点F .由BC CD =,知OC ⊥BD .因为∠CBF =∠IAE ,BC = CI = AI ,所以Rt BCF Rt AIE △≌△.所以BF = AE . 又因为I 是△ABD 的内心,所以22AB AD BD AE BD BD BF BD +-=+-==. 故2AB AD BD +=.也可由托勒密定理得:AB CD AD BC AC BD ⋅+⋅=⋅,再将22AC BC CD ==代入即得结论2AB AD BD +=;13甲.解:设a -b = mm 是素数,ab = n 2n 是自然数.因为 a +b 2-4ab = a -b 2,所以 2a -m 2-4n 2 = m 2,2a -m +2n 2a -m -2n = m 2.…………5分1当1n ≥时,因为2a -m +2n 与2a -m -2n 都是正整数,且2a -m +2n >2a -m -2n m 为素数,所以 2a -m +2n =m 2,2a -m -2n =1.解得 a =2(1)4m +,n =214m -. 于是 b = a -m =214m -(). …………10分又a ≥2012,即2(1)4m +≥2012. 又因为m 是素数,解得m ≥89. 此时,a ≥41)(892+=2025. 当2025a =时,89m =,1936b =,1980n =.此时,a 的最小值为2025.2当0n =时,因为a ≥2012,所以0b =,从而得a 的最小值为2017素数; 综上所述,所求的a 的最小值为2017;……15分13乙.解:设凸n 边形最多有k 个内角等于150°,则每个150°内角的外角 都等于30°,而凸n 边形的n 个外角和为360°,所以3601230k ≤=,只有当12n =时, k 才有最大值12. …………5分下面我们讨论12n ≠时的情况:1当12n >时,显然,k 的值是11;2当3,4,5,6,7n =时,k 的值分别为1,2,3,4,5;3当8,9,10,11n =时,k 的值分别为7,8,9,10. …………10分综上所述,当37n ≤≤时,凸n 边形最多有2n -个内角等于150°;当811n ≤≤时,凸n 边形最多有1n -个内角等于150°;当12n =时,凸n 边形最多有12个内角等于150°;当12n >时,凸n 边形最多有11个内角等于150°;. ……15分14甲.解:由于122012x x x ,, ,都是正整数,且122012x x x <<<,所以1x ≥1,2x ≥2,…,2012x ≥2012. 于是 122012122012n x x x =+++≤1220122012122012+++=. …………5分当1n =时,令12201220122201220122012x x x ==⨯=⨯,, ,,则1220121220121x x x +++=. …………10分当1n k =+时,其中1≤k ≤2011,令 1212k x x x k ===,, ,, 122012(2012)(1)(2012)(2)(2012)2012k k x k k x k k x k ++=-+=-+=-⨯,,,则1220121220121(2012)2012k k x x x k+++=+-⋅-1k n =+=. 综上,满足条件的所有正整数n 为122012, , , .…………15分14乙.解:当1621n =-时,把23n , , ,分成如下两个数组:{}88162322121+-, , , , , 和{}84521-, , , . 在数组{}88162322121+-, , , , , 中,由于38821632221<>-(,),所以其中不存在数a b c ,,,使得b a c =.在数组{}84521-, , , 中,由于48421>-,所以其中不存在数a b c ,,,使得b a c =.所以,162n ≥.下面证明当162n =时,满足题设条件.不妨设2在第一组,若224=也在第一组,则结论已经成立.故不妨设224=在第二组. 同理可设4842=在第一组,8216(2)2=在第二组.此时考虑数8.如果8在第一组,我们取8282a b c ===,,,此时b a c =;如果8在第二组,我们取16482a b c ===,,,此时b a c =. 综上,162n =满足题设条件.所以,n 的最小值为162.注:也可以通过考虑2,4,16,256,65536的分组情况得到n最小值为65536.。
初中数学竞赛试题(含答案)
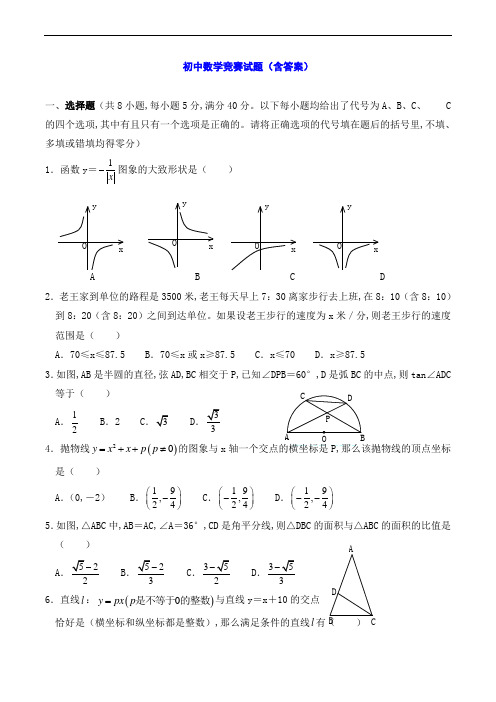
DC B A初中数学竞赛试题(含答案)一、选择题(共8小题,每小题5分,满分40分。
以下每小题均给出了代号为A 、B 、C 、 C 的四个选项,其中有且只有一个选项是正确的。
请将正确选项的代号填在题后的括号里,不填、多填或错填均得零分) 1.函数y =1x-图象的大致形状是( )A B C D2.老王家到单位的路程是3500米,老王每天早上7:30离家步行去上班,在8:10(含8:10)到8:20(含8:20)之间到达单位。
如果设老王步行的速度为x 米/分,则老王步行的速度范围是( )A .70≤x ≤87.5B .70≤x 或x ≥87.5C .x ≤70D .x ≥87.53.如图,AB 是半圆的直径,弦AD,BC 相交于P,已知∠DPB =60°,D 是弧BC 的中点,则tan ∠ADC 等于( ) A .12B.2 CD4.抛物线()20y x x p p =++≠的图象与x 轴一个交点的横坐标是P,那么该抛物线的顶点坐标是( )A .(0,-2)B .19,24⎛⎫- ⎪⎝⎭C .19,24⎛⎫- ⎪⎝⎭D .19,24⎛⎫-- ⎪⎝⎭5.如图,△ABC 中,AB =AC,∠A =36°,CD 是角平分线,则△DBC 的面积与△ABC 的面积的比值是( )ABCD 6.直线l :()0y px p =是不等于的整数与直线y =x +10的交点恰好是(横坐标和纵坐标都是整数),那么满足条件的直线l 有() yxOyxOyxOyxOA .6条B .7条C .8条D .无数条7.把三个连续的正整数a,b,c 按任意次序(次序不同视为不同组)填入20x x ++= 的三个方框中,作为一元二次方程的二次项系数、一次项系数和常数项,使所得方程至少有一个整数根的a,b,c ( )A .不存在B .有一组C .有两组D .多于两组 8.六个面上分别标有1,1,2,3,3,5六个数字的均匀立方体的表面如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数主该点的纵坐标。
全国初中数学竞赛试题及答案

全国初中数学竞赛试题及答案1.选择题解答1.答案为(B)。
因为根据题意,M>P,所以M与P的大小关系为M>P。
2.答案为(C)。
因为只有图(C)正确地表示了题意,包括沿原路返回的一段路程和消耗的时间。
3.答案为(A)。
根据题意可得甲-乙=5.4.答案为(B)。
在线段AB上,横、纵坐标都是整数的点的坐标是x=-1+4N,y=-25+5N,其中N是整数。
因为-1+4N>0,-25+5N<=0,所以N=1,2,3,4,5,共有5个点。
5.答案为(B)。
根据题意可得∠ABC=2∠ACB,因此∠BAC=2∠ACB,即∠B=2∠A。
6.答案为(D)。
题目中未给出S和S1的具体数值,因此无法确定它们的大小关系。
首先,文章中存在一些格式错误和重复的段落,需要删除和修改。
修改后的文章如下:一、选择题1、已知,那么x的值为______。
答:1.∵,即。
x=1.2、已知函数,且在区间[0,1]上单调递增,则f(0)与f(1)的大小关系为______。
答:f(0)<f(1)。
因为f(x)单调递增,所以f(0)<f(1)。
3、已知数列的通项公式为,若a1=1,则a4的值为______。
答:16.因为a1=1,所以a4=16.4、已知函数f(x)=x^2+bx+c在区间[0,1]上单调递减,则b 与c的大小关系为______。
答:b1/4.因为f(x)在[0,1]上单调递减,所以b1/4.5、已知数列的前n项和为Sn=n^2+2n,则该数列的通项公式为______。
答:an=n+1.因为Sn=n(n+2),所以an=Sn-Sn-1=n+1.6、已知S=1+2+3+。
+100,S1=1+3+5+。
+99,则S与S1的大小关系为______。
答:S>S1.因为S=1+2+3+。
+100>1+3+5+。
+99=S1.二、填空题7、已知。
那么x的值为________。
答:1.∵,即。
初中数学竞赛题(含答案)

一、选择题(每小题7分,共56分.以下每题的4个结论中,仅有一个是正确的,请将正确答案的英文字母填在题后的圆括号内)1.在-|-3|3,-(-3)3,(-3)3,-33中,最大的是( B ).(A)-|-3|3 (B)-(-3)3 (C)(-3)3 (D)-332. “a 的2倍与b 的一半之和的平方,减去a 、b 两数平方和的4倍”用代数式表示应为( )(A)2a+(21b 2)-4(a+b)2 (B)(2a+21b)2-a+4b 2 (c)(2a+21b)2-4(a 2+b 2) (D)(2a+21b)2-4(a 2+b 2)2 3.若a 是负数,则a+|-a|( C ),(A)是负数 (B)是正数 (C)是零 (D)可能是正数,也可能是负数4.如果n 是正整数,那么表示“任意负奇数”的代数式是( ).(A)2n+l (B)2n-l (C)-2n+l (D)-2n-l5.已知数轴上的三点A 、B 、C 分别表示有理数a 、1、-l ,那么|a+1|表示( ).(A)A 、B 两点的距离 (B)A 、C 两点的距离(C)A 、B 两点到原点的距离之和(D)A 、C 两点到原点的距离之和6.如图,数轴上标出若干个点,每相邻两点相距1个单位,点A 、B 、C 、D 对应的数分别是整数a 、b 、c 、d ,且d-2a =10,那么数轴的原点应是( ).(A)A 点 (B)B 点 (C)C 点 (D)D 点7.已知a+b =0,a≠b ,则化简a b (a+1)+ba (b+1)得( ). (A)2a (B)2b (C)+2 (D)-28.已知m<0,-l<n<0,则m ,mn ,mn 2由小到大排列的顺序是 ( ).(A)m ,mn ,mn 2 (B)mn ,mn 2,m (C)mn 2,mn ,m (D)m ,mn 2,mn二、填空题(每小题?分,共84分)9.计算:31a -(21a -4b -6c)+3(-2c+2b)= 10.计算:0.7×194+243×(-15)+0.7×95+41×(-15)= ll.某班有男生a(a>20)人,女生20人,a-20表示的实际意义是12.在数-5,-3,-1,2,4,6中任取三个相乘,所得的积中最大的是13.下表中每种水果的重量是不变的,表的左边或下面的数是所在行或所在列水果的总重量,则表中问号“?”表示的数是梨 梨 苹果 苹果 30梨 型 梨 梨 28荔枝 香蕉 苹果 梨 20香蕉 香蕉 荔枝 苹果 ?19 20 25 3014.某学生将某数乘以-1.25时漏了一个负号,所得结果比正确结果小0.25,则正确结果应是 .15.在数轴上,点A 、B 分别表示-31和51,则线段AB 的中点所表示的数是 . 16.已知2a x b n-1与-3a 2b 2m (m 是正整数)是同类项,那么(2m-n)x =17.王恒同学出生于20世纪,他把他出生的月份乘以2后加上5,把所得的结果乘以50后加上出生年份,再减去250,最后得到2 088,则王恒出生在 年 月.18.银行整存整取一年期的定期存款年利率是2.25%,某人1999年12月3日存入1 000元,2000年12月3日支取时本息和是 元,国家利息税税率是20%,交纳利息税后还有 元.19.有一列数a 1,a 2,a 3,a 4,…,a n ,其中a 1=6×2+l ;a 2=6×3+2;a 3=6×4+3;a 4=6×5+4;则第n 个数a n = ;当a n =2001时,n = .20.已知三角形的三个内角的和是180°,如果一个三角形的三个内角的度数都是小于120的质数,则这个三角形三个内角的度数分别是第十五届江苏省初中数学竞赛参考答案初一年级第一试一、1.B 2.C 3.C 4.C 5.B 6.B 7.D 8.D二、9.一6a +1 06. 10.一43.6. 11.男生比女生多的人数.1 2.90. 1 3.1 6. 1 4.0.1 2 5. 1 5.-151 1 6.1. 1 7.1988;1.18.1022.5;101 8.1 9.7n+6;2 8 5.2 O .2,8 9,8 9或2,7 1,1 07(每填错一组另扣2分).一、选择题1.已知x=2是关于x 的方程3x-2m=4的根,则m 的值是( )(A)5 (B)-5 (C)1 (D)-12.已知a+2=b-2=2c =2001,且a+b+c=2001k ,那么k 的值为( )。
初中七年级数学竞赛试题及参考答案

21七年级数学竞赛试题一.选择题(每小题4分,共32分) 1.x 是随意有理数,则2 的值( ).A .大于零B . 不大于零C .小于零D .不小于零 2.在-0.1428中用数字3交换其中的一个非0数码后,使所得的数最大,则被交换的数字是( ) A .1 B .4 C .2 D .83.如图,在数轴上1的对应点A 、B , A 是线段的中点,则点C 所表示的数是( )A.2 B2 C1 D.14.桌上放着4张扑克牌,全部正面朝下,其中恰有1张是老K 。
两人做嬉戏,嬉戏规则是:随机取2张牌并把它们翻开,若2张牌中没有老K ,则红方胜,否则蓝方胜。
则赢的时机大的一方是( )A .红方B .蓝方C .两方时机一样D .不知道 5.假如在正八边形硬纸板上剪下一个三角形(如图①中的阴影局部),那么图②,图③,图④中的阴影局部,均可由这个三角形通过一次平移、对称或旋转而得到.要得到图②,图③,图④中的阴影局部,依次进展的变换不行行...的是( )A.平移、对称、旋转 B.平移、旋转、对称 C.平移、旋转、旋转 D.旋转、对称、旋转6.计算:22221111(1)(1)(1)(1)2342007---⋅⋅⋅-等于( ) A .10042007 B .10032007 C .20082007D .200620077.如图,三个天平的托盘中一样的物体质量相等。
图⑴、⑵所示的两个天平处于平衡状态要使第三个天平也保持平衡,则需在它的右盘中放置( )(3)(2)(1)A. 3个球B. 4个球C. 5个球D. 6个球8.用火柴棒搭三角形时,大家都知道,3根火柴棒只能搭成1种三角形,不妨记作它的边长分别为1,1,1;4根火柴棒不能搭成三角形;5根火柴棒只能搭成一种三角形,其边长分别为2,2,1;6根火柴棒只能搭成一种三角形,其边长分别为2,2,2;7根火柴棒只能搭成2种三角形,其边长分别为3,3,1和3,2,2;…;那么30根火柴棒能搭成三角形个数是( )x图①图②图③ 图④A .15B .16C .18D .19 二.填空题(每题4分,共28分) 9.定义a*,若3*31,则x 的值是。
初中数学定理竞赛试题及答案

初中数学定理竞赛试题及答案一、选择题(每题2分,共10分)1. 圆的周长公式是:A. C = πdB. C = 2πrC. C = πrD. C = 2r2. 勾股定理适用于:A. 所有三角形B. 直角三角形C. 等边三角形D. 等腰三角形3. 以下哪个不是相似三角形的性质?A. 对应角相等B. 对应边成比例C. 面积相等D. 周长成比例4. 平行四边形的对角线:A. 互相垂直B. 互相平分C. 相等D. 互相平行5. 一个数的立方根是它自身的数有:A. 0B. 1C. -1D. A, B, C二、填空题(每题2分,共10分)1. 圆的面积公式是 S = ________。
2. 根据勾股定理,如果直角三角形的两条直角边长分别为3和4,则斜边长为 ________。
3. 相似三角形的判定定理有AA(角-角), SSS(边-边-边),________(边-角-边)。
4. 平行四边形的面积公式是 S = ________。
5. 如果一个数的平方是16,那么这个数是 ________。
三、解答题(每题10分,共30分)1. 已知一个圆的半径为5厘米,求这个圆的周长和面积。
2. 一个直角三角形的两条直角边长分别为6厘米和8厘米,求斜边长和三角形的面积。
3. 给定一个平行四边形,其对角线长度分别为10厘米和14厘米,求这个平行四边形的面积。
四、证明题(每题15分,共30分)1. 证明:在一个直角三角形中,斜边上的中线等于斜边的一半。
2. 证明:如果两个三角形的两边及其夹角分别相等,那么这两个三角形全等。
五、综合题(每题20分,共20分)1. 一个圆内接于一个三角形,已知圆的半径为3厘米,求这个三角形的内切圆半径。
答案一、选择题1. B2. B3. C4. B5. D二、填空题1. πr²2. 53. SAS4. 底× 高5. ±4三、解答题1. 周长:C = 2πr = 2 × 3.14 × 5 = 31.4厘米面积:S = πr² = 3.14 × 5² = 78.5平方厘米2. 斜边长:根据勾股定理,斜边长= √(6² + 8²) = 10厘米面积:S = (6 × 8) / 2 = 24平方厘米3. 平行四边形面积:S = (对角线1 × 对角线2) / 2 = (10 × 14) / 2 = 70平方厘米四、证明题1. 证明:设直角三角形ABC中,∠C为直角,D为斜边AB的中点。
