初三数学圆的复习课件_人教版
合集下载
人教版九年级上册教材数学:圆复习课件演示
圆的定义(集合观点)
• 圆是到定点的距离等于定长的点的集合。 – 圆上各点到定点(圆心)的距离都等于定长 (半径); – 到定点的距离等于定长的点都在圆上。
• 一个圆把平面内的所有点 分成了多少类?
• 你能模仿圆的集合定义思 想,说说什么是圆的内部 和圆的外部吗?
人教版九年级上册教材数学:圆复习 课件演 示
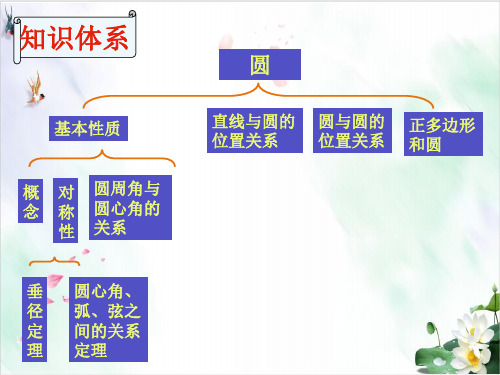
知识体系
基本性质
概 对 圆周角与 念 称 圆心角的
性 关系
垂 圆心角、 径 弧、弦之 定 间的关系 理 定理
圆
直线与圆的 圆与圆的 正多边形 位置关系 位置关系 和圆
圆的定义(运动观点)
在一个平面内,线段OA绕它固 定的一个端点O旋转一周,另一 个端点A随之旋转所形成的图形 叫做圆。
固定的端点O叫做圆心,线段 OA叫做半径,以点O为圆心的圆, 记作☉O,读作“圆O”
B
人教版九年级上册教材数学:圆复习 课件演 示
A
人教版九年级上册教材数学:圆复习 课件演 示
C
O
C O
B
A B
B A
A
C
O
圆周角:顶点在圆上,并且两边都和圆相 交的角。 圆心角: 顶点在圆心的角.
人教版九年级上册教材数学:圆复习 课件演 示
人教版九年级上册教材数学:圆复习 课件演 示
画图:同一条弧所对的圆周角和圆心角 之间可能出现哪几种不同的位置关系?
人教版九年级上册教材数学:圆复习 课件演 示
A
AO=BO=CO=DO,
侧想半一弧=圆想弧A会D:B有=D将。什弧一么B个C关,圆系弧沿?A着C任一C 条直径O 对折D ,两
性A质O:=B圆O是=C轴O对=D称O图,形,任何B 一条直A 径所在
上册《圆》复习-新人教版九级数学全一册课件

上册 《圆》复习-新人教版九级数学全一册 课件
上册 《圆》复习-新人教版九级数学全一册 课件
证明:(1)∵BD=BA,
∴∠BDA=∠BAD, ∵∠1=∠BDA,∴∠1=∠BAD.
︵
(2)扇形 AOB 的半径为 3 cm,AB的长为 4 cm, 则扇形面积为 6 cm2 ; (3)已知圆锥的底面圆半径为 3 cm、高为 4 cm, 则圆锥的侧面积是 15π cm2.
精典范例
8.【例 1】如图,BC 是⊙O 的直径,弦 AD⊥BC,垂足为 H,
︵
AD=8,OH=3,P 是AC上一个动点,BP 交 AD 于点 E. (1)求⊙O 的半径; (2)若∠EBA=∠EAB,求线段 BE 的长; (3)若在运动过程中,AQ 平分∠PAD,线 段 BQ 的长度改变吗?若不变,求出其值; 若改变,说明理由.
∵BD=OB=2,∴DE=BE=21Bห้องสมุดไป่ตู้=1, ∴OE= OB2-BE2= 3.
∵OD=OB=2,∠DOC=60°,∠DOF=30°,
∴CD=2 3,DF=23 3, ∴CF=CD-DF=2 3-32 3=34 3.
上册 《圆》复习-新人教版九级数学全一册 课件
12.如图,⊙O 是△ABC 的外接圆,AC 为直径,弦 BD=BA, BE⊥DC 交 DC 的延长线于点 E. (1)求证:∠1=∠BAD; (2)求证:BE 是⊙O 的切线.
A.点 A 在圆上
B.点 A 在圆外
C.点 A 在圆内
D.无法确定
知识点五:切线 (1)切线的性质; (2)切线的判定; (3)切线长定理.
5.如图,点 P 在⊙O 外,PA,PB 分别与⊙O 相切于 A,B 两 点,∠APB=50°,AP=12 cm,OP=13 cm,则: (1)∠AOB= 130 °; (2)∠APO= 25 °; (3)BP= 12 cm; (4)OA= 5 cm.
上册 《圆》复习-新人教版九级数学全一册 课件
证明:(1)∵BD=BA,
∴∠BDA=∠BAD, ∵∠1=∠BDA,∴∠1=∠BAD.
︵
(2)扇形 AOB 的半径为 3 cm,AB的长为 4 cm, 则扇形面积为 6 cm2 ; (3)已知圆锥的底面圆半径为 3 cm、高为 4 cm, 则圆锥的侧面积是 15π cm2.
精典范例
8.【例 1】如图,BC 是⊙O 的直径,弦 AD⊥BC,垂足为 H,
︵
AD=8,OH=3,P 是AC上一个动点,BP 交 AD 于点 E. (1)求⊙O 的半径; (2)若∠EBA=∠EAB,求线段 BE 的长; (3)若在运动过程中,AQ 平分∠PAD,线 段 BQ 的长度改变吗?若不变,求出其值; 若改变,说明理由.
∵BD=OB=2,∴DE=BE=21Bห้องสมุดไป่ตู้=1, ∴OE= OB2-BE2= 3.
∵OD=OB=2,∠DOC=60°,∠DOF=30°,
∴CD=2 3,DF=23 3, ∴CF=CD-DF=2 3-32 3=34 3.
上册 《圆》复习-新人教版九级数学全一册 课件
12.如图,⊙O 是△ABC 的外接圆,AC 为直径,弦 BD=BA, BE⊥DC 交 DC 的延长线于点 E. (1)求证:∠1=∠BAD; (2)求证:BE 是⊙O 的切线.
A.点 A 在圆上
B.点 A 在圆外
C.点 A 在圆内
D.无法确定
知识点五:切线 (1)切线的性质; (2)切线的判定; (3)切线长定理.
5.如图,点 P 在⊙O 外,PA,PB 分别与⊙O 相切于 A,B 两 点,∠APB=50°,AP=12 cm,OP=13 cm,则: (1)∠AOB= 130 °; (2)∠APO= 25 °; (3)BP= 12 cm; (4)OA= 5 cm.
初中九年级数学人教版-圆单元复习课件

相离
相切
相交
(1)相交:直线与圆有两个公共点时,叫做直线和圆相交。 这时直线叫做圆的割线。 (2)相切:直线与圆有唯一个公共点时,叫做直线和圆相切。 这时直线叫做圆的切线。 (3)相离:直线与圆没有公共点时,叫做直线和圆相离。
二. 圆的基本性质 1.圆的对称性: (1)圆是轴对称图形,经过圆心的每一条直 线都是它的对称轴.圆有无数条对称轴. (2)圆是中心对称图形,并且绕圆心旋转 任何一个角度都能与自身重合,即圆具 有旋转不变性.
B O
·
C
A
劣弧与优弧 小于半圆的弧叫做劣弧. 大于半圆的弧叫做优弧.
(如图中的AC)
⌒
⌒ (用三个字母表示,如图中的ACB)
B O
·
C
A
等圆
半径相等的两个圆叫做等圆。 r
O1
r O2
判断题
圆心相同,半径相等的两个圆是同心圆; 半径相等的两个圆是等圆.
弓形:由弦及其所对的弧组成的图形叫弓形。 等圆:能够重合的两个圆叫做等圆,易知同圆或等圆的 半径相等。 同心圆:圆心相同,半径不相等的两个圆叫做同 心圆 等弧:在同圆或等圆中,能够互相重合的弧叫做等弧。 等弧应同时满足两个条件:1)两弧的长度相等, 2)两弧的度数相等。
一、判断是非:
(1)平分弦的直径,平分这条弦所对的弧。 (2)平分弦的直线,必定过圆心。 (3)一条直线平分弦(这条弦不是直径),
那么这 条直线垂直这条弦。
A C O (1) B D A (2) D C O B A C
O B (3) D
(4)弦的垂直平分线一定是圆的直径。
(5)平分弧的直线,平分这条弧所对的 弦。
B
反过来,如果已知点到圆心的距离和圆的半径之 间的关系,可以判断点和圆的位置关系?
上册 《圆》复习人教版九级数学全一册课件

∴AF=AD,BE=BD, ∴AB=AD+BD=10+3=13.
设⊙O 的半径为 r,则 AC=10+r,BC=3+r. 在 Rt△ABC 中,由勾股定理得 AC2+BC2=AB2,
即(10+r)2+(3+r)2=132, 解得 r=2 或 r=-15(舍去),
∴⊙O 的面积=π×22=4π.
上册第2《4章圆》第复1习5课人时教版《九圆级》数单学元全复一习册-课20件20秋人教版九 年级数 学全一 册课件( 共34张 PPT)
∴△ OAD 是等边三角形. 又∵I 为△ ABC 的内心, ∴∠ACD=∠BCD,
上册第2《4章圆》第复1习5课人时教版《九圆级》数单学元全复一习册-课20件20秋人教版九 年级数 学全一 册课件( 共34张 PPT)
上册 《圆》复习人教版九级数学全一册课 件
知识点三:圆周角定理及其推论 (1)圆周角定理; (2)圆周角定理的推论; (3)圆内接四边形的性质.
上册 《圆》复习人教版九级数学全一册课 件
上册 《圆》复习人教版九级数学全一册课 件
︵
3.如图,已知 OA,OB 均为⊙O 的半径,点 D 在AB上, 若∠AOB=80°,则∠ACB= 40 °,∠ADB= 140 °.
第二十四章 圆
第15课时 《圆》单元复习
知识要点
知识点一: 垂径定理及其推论 如图,在⊙O 中,①CD 是⊙O 的直径;②AM=BM;③CD
︵︵ ︵︵
⊥AB;④AC=BC;⑤AD=BD,由二推三.
对点训练
1.如图,AB 是⊙O 的弦,OC⊥AB 于点 C,若 AB=4,OC=
1,则⊙O 的半径为( B )
知识点六: 正多边形与圆 (1)正多边形的中心; (2)正多边形的半径; (3)正多边形的中心角; (4)正多边形的边心距.
设⊙O 的半径为 r,则 AC=10+r,BC=3+r. 在 Rt△ABC 中,由勾股定理得 AC2+BC2=AB2,
即(10+r)2+(3+r)2=132, 解得 r=2 或 r=-15(舍去),
∴⊙O 的面积=π×22=4π.
上册第2《4章圆》第复1习5课人时教版《九圆级》数单学元全复一习册-课20件20秋人教版九 年级数 学全一 册课件( 共34张 PPT)
∴△ OAD 是等边三角形. 又∵I 为△ ABC 的内心, ∴∠ACD=∠BCD,
上册第2《4章圆》第复1习5课人时教版《九圆级》数单学元全复一习册-课20件20秋人教版九 年级数 学全一 册课件( 共34张 PPT)
上册 《圆》复习人教版九级数学全一册课 件
知识点三:圆周角定理及其推论 (1)圆周角定理; (2)圆周角定理的推论; (3)圆内接四边形的性质.
上册 《圆》复习人教版九级数学全一册课 件
上册 《圆》复习人教版九级数学全一册课 件
︵
3.如图,已知 OA,OB 均为⊙O 的半径,点 D 在AB上, 若∠AOB=80°,则∠ACB= 40 °,∠ADB= 140 °.
第二十四章 圆
第15课时 《圆》单元复习
知识要点
知识点一: 垂径定理及其推论 如图,在⊙O 中,①CD 是⊙O 的直径;②AM=BM;③CD
︵︵ ︵︵
⊥AB;④AC=BC;⑤AD=BD,由二推三.
对点训练
1.如图,AB 是⊙O 的弦,OC⊥AB 于点 C,若 AB=4,OC=
1,则⊙O 的半径为( B )
知识点六: 正多边形与圆 (1)正多边形的中心; (2)正多边形的半径; (3)正多边形的中心角; (4)正多边形的边心距.
第24章 圆的复习-九年级数学上册教学课件(人教版)

原 所示,则这个小圆孔的宽口AB的长度为 8 mm.
理
C
精
炼
O
8mm
A
B
提
D
升
与圆有关的概念
典 1.圆:平面内到定点的距离等于定长的所有点组成的图形.
例 2.弦:连结圆上任意两点的线段.
3.直径:经过圆心的弦是圆的直径,直径是最长的弦.
原 4.劣弧:小于半圆周的圆弧.
理 5.优弧:大于半圆周的圆弧.
炼 【注意】(1)三角形的外心是三角形三边的垂直平分线的交点.
(2)一个三角形的外接圆是唯一的.
提
(3)三角形的内心是三角形三条角平分线的交点.
升
(4)一个三角形的内切圆是唯一的.
点与圆的位置关系
典 1.在△ABC中,∠C=90º,AC=1,BC=2,M是AB的中点,以点C为圆 例 心,1为半径作⊙C,则( C )
原 2.垂径定理的推论:平分弦(不是直径)的直径垂直于这条弦, 理 并且平分这条弦所对的两条弧;
精 3.垂径定理的推论:平分弧的直径垂直平分这条弧所对的弦. 炼
提 升
圆的基本性质
典 1.圆的对称性: 例 圆是轴对称图形,任意一条直径所在的直线都是它的对称轴.
原 2.有关圆心角、弧、弦的性质:
理
在同圆或等圆中,如果两个圆心角、
° 精 炼
提 升
典 6.如图,已知A、B、C、D是⊙O上的四点,延长DC,AB相交于点 例 E.若BC=BE.求证:△ADE是等腰三角形.
原 理
精 炼
提 升
典 7.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC. 例 (1)若∠CBD=39º,求∠BAD的度数; 原 (2)求证:∠1=∠2. 理
人教版九年级上册数学《圆周角》圆教学说课复习课件

(1)知道什么是圆周角,并能从图形中准确识别它. (2)探究并掌握圆周角定理及其推论. (3)体会“由特殊到一般”“分类”“化归”等数学思想.
推进新课
知识点1 圆周角的定义及圆周角定理
1.圆心角的定义?
C
顶点在圆心的角叫圆心角.
2.图中∠ACB 的顶点和边有哪些特点? O
顶点在圆上,并且两边都和 圆相交的角叫圆周角.
125°.
5.如图,⊙O中,弦AD平行于弦BC,
∠AOC=78°,求∠DAB的度数.
解:∵AD∥BC,
∴∠DAB=∠B.
又∵∠B=
1 2
∠AOC=39°.
∴∠DAB=39°.
6.如图,⊙O的半径为1,A,B,C是⊙O上的三个点 ,且∠ACB=45°,求弦AB的长. 解:连接OA、OB. ∵∠ACB=45°, ∴∠BOA=2∠ACB=90°. 又OA=OB, ∴△AOB是等腰直角三角形.
A
B
图中圆周角∠ACB 和圆心角∠AOB 有怎样
的关系?
C
先猜一猜,再用 量角器量一量.
O
ACB 12AOB
A
B
(1)在圆上任取B⌒C,画出圆心角∠BOC 和圆 周角∠BAC,圆心角与圆周角有几种位置关系?
A A
A
O
O
O
B
B
C
B
C
C
(2)如何证明一条弧所对的圆周角等于它所 对的圆心角的一半?
周角所对的弦是直径.
圆内接四边形:圆内接四边形的内角和为360°,并且四边形的对角互补.
1 2
α.
证明:由(1)知∠BOM=90°-α.
M
又∠C=β= 12∠AOB,
C
∴β=
最新人教版初中九年级上册数学【圆全章复习】教学课件

请补全解答过程.
E
C
6
4
4D
H4
A
O
BF
10
综合运用
小结:
E
E
C
C
D
D
3
3
1 A2
O
BF
A
12
O
BF
综合运用
小结:
E
E
C D
C D
G
H
A
O
BF
A
O
BF
知识梳理
圆的对称性
圆的有关性质 弧、弦、圆心角之间的关系
同弧上的圆周角和圆心角的关系
圆 点、直线和圆的位置关系
点和圆的位置关系 直线和圆的位置关系
综合运用
例 如图,⊙O是△ABC的外接圆,若AB=6cm,∠C=60°,则⊙O的半径为 ________cm.
C
O
A
B
综合运用
方法1:作OD⊥AB于D,连接OA,OB.
∵∠C=60°,
∴∠AOB=2∠C=120°.
∵OA=OB,OD⊥AB于D, AB=6 cm,
∴△AOD中,∠ADO=90°,
知识梳理
圆的有关性质
圆的对称性 垂径定理 弧、弦、圆心角之间的关系 定理 同弧上的圆周角和圆心角的关系
圆周角定理
初中数学
重点回顾
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
A2 A1
A3
O
B
C
重点回顾
圆周角定理的推论 推论1:同弧或等弧所对的圆周角相等. 推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径. 推论3:圆内接四边形的对角互补.
切线的判定定理:经过半径的外端并且垂直于这 条半径的直线是圆的切线.
E
C
6
4
4D
H4
A
O
BF
10
综合运用
小结:
E
E
C
C
D
D
3
3
1 A2
O
BF
A
12
O
BF
综合运用
小结:
E
E
C D
C D
G
H
A
O
BF
A
O
BF
知识梳理
圆的对称性
圆的有关性质 弧、弦、圆心角之间的关系
同弧上的圆周角和圆心角的关系
圆 点、直线和圆的位置关系
点和圆的位置关系 直线和圆的位置关系
综合运用
例 如图,⊙O是△ABC的外接圆,若AB=6cm,∠C=60°,则⊙O的半径为 ________cm.
C
O
A
B
综合运用
方法1:作OD⊥AB于D,连接OA,OB.
∵∠C=60°,
∴∠AOB=2∠C=120°.
∵OA=OB,OD⊥AB于D, AB=6 cm,
∴△AOD中,∠ADO=90°,
知识梳理
圆的有关性质
圆的对称性 垂径定理 弧、弦、圆心角之间的关系 定理 同弧上的圆周角和圆心角的关系
圆周角定理
初中数学
重点回顾
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
A2 A1
A3
O
B
C
重点回顾
圆周角定理的推论 推论1:同弧或等弧所对的圆周角相等. 推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径. 推论3:圆内接四边形的对角互补.
切线的判定定理:经过半径的外端并且垂直于这 条半径的直线是圆的切线.
初三数学圆的复习课件_人教版.ppt
如图,⊙O的半径为8厘米,圆内弦AB=8 3厘米, 以O为圆心,4厘米为半径作小圆,求证:小圆与 直线AB相切。
O
A
B
切线判定的方法
• 利用切线定义 • 利用圆心到直线的距离等于半径 • 利用切线判断定理
• 辅助线技巧: – 若直线过圆上某一点,则连结圆心和公 共点,再证明直线与半径垂直 – 若直线与圆的公共点没有确定,则过圆 心向直线作垂线,再证明圆心到直线的 距离等于半径。
• 弦和直径
与圆有关的概念
– 什么是弦?什么是直径?
– 直径是弦吗?弦是直径吗?
• 弧与半圆
– 什么是圆弧(弧)?怎样表示?
– 弧分成哪几类?
– 半圆是弧吗?弧是半圆吗?
• 弓形是什么?
• 同心圆、同圆、等圆和等弧
– 怎样的两个圆叫同心圆?
– 怎样的两个圆叫等圆?
– 同圆和等圆有什么性质?
– 什么叫等弧?
– 半径确定圆的大小;圆心确定圆的位置
• 圆是“圆周”还是“圆面”?
– 圆是一条封闭曲线
• 圆周上的点与圆心有什么关系?
圆的定义(集合观点)
• 圆是到定点的距离等于定长的点的集合。
– 圆上各点到定点(圆心)的距离都等于定长(半径); – 到定点的距离等于定长的点都在圆上。
• 一个圆把平面内的所有点 分成了多少类?
圆的有关性质
圆的定义(运动观点)
在一个平面内,线段OA绕它固 定的一个端点O旋转一周,另一 个端点A随之旋转所形成的图形 叫做圆。
固定的端点O叫做圆心,线段 OA叫做半径,以点O为圆心的圆, 记作☉O,读作“圆O”
圆的定义辨析
• 篮球是圆吗?
– 圆必须在一个平面内
• 以3cm为半径画圆,能画多少个? • 以点O为圆心画圆,能画多少个? • 由此,你发现半径和圆心分别有什么作用?
人教版九年级数学上册第24章圆课件 (共31张PPT)

∴CF= 12.在Rt△COF中,OF= OC2 CF2 ,
24 12 5 ∴EF=EO+OF= ,∴ CE EF2 CF2 . 5 5
9 5
5
【例4】如图,AB是⊙O的直径,C.D是⊙O上一 点,∠CDB=20°,过点C作⊙O的切线交AB的延 长线于点E,则∠E等于( B ) A.40° B.50° C.60° D.70°
(1)点在圆内 (2)点在圆上 (3)点在圆外 如果规定点与圆心的距离为d,圆的半径 为r,则d与r的大小关系为:
C
.
.
A.
点与圆的位置关 系
d与r的关系
. B
点在圆内 点在圆上 点在圆外
d<r d=r d>r
2.直线和圆的位置关系:
.
O
.
O l
.
O l
l (1) 相离: 一条直线与一个圆没有公共点,叫做 直线与这个圆相离. (2) 相切: 一条直线与一个圆只有一个公共点,叫 做直线与这个圆相切. (3) 相交: 一条直线与一个圆有两个公共点,叫 做直线与这个圆相交.
定义:顶点在圆周上,两边和圆相交的角, 叫做圆周角.
性质: 同弧或等弧所对的圆周角相等,都等于这条
弧所对的圆心角的一半。
D E
O A
1 ADB=∠ ACB = ∠ AEB= AOB 2 在同圆或等圆中,相等的圆周角 C 所对的弧相等 推论: 半圆(或直径)所对的圆 周角是直角,90°的圆周角所 B 对的弦是直径
【分析】如图所示,连接OC, ∵∠BOC与∠CDB是弧BC 所对的圆心角与圆周角, ∴∠BOC=2∠CDB。 又∵∠CDB=20°,∴∠BOC=40°, 又∵CE为圆O的切线,∴OC⊥CE, 即∠OCE=90°, 则 ∠E=90°﹣40°=50°
新课标人教版《数学》九年级上册 复习: 圆(共23张PPT)

13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。21.8. 1121.8. 1120:04 :1320:0 4:13August 11, 2021
•
14、谁要是自己还没有发展培养和教 育好, 他就不 能发展 培养和 教育别 人。202 1年8月 11日星 期三下 午8时4 分13秒 20:04:1 321.8.1 1
(1)证明:∠E =∠C;
(2)若∠E =55°,求∠BDF 的度数;2 (3)设DE交AB于点G,若DF=4,cosB= 3
,E是
⌒
AB
的中点,
求EG • ED 的值.
课堂小结
圆的有关性质
圆 点、直线和圆 的位置关系
圆的对称性 弧、弦、圆心角之间的关系 同弧上的圆周角和圆心角的关系 点和圆的位置关系 三角形的外接圆 直线和圆的位置关系 切线 三角形的内切圆
复习: 圆
学习目标:
1.复习:圆的有关性质; 2.复习:点与圆的位置关系,
直线与圆的位置关系 。
学习重点: 垂径定理、圆周角定理、切线的有关定理
一、圆的概念:
在一个平面内,线段 OA 绕它固定的
一个端点 O 旋转一周,另一个端点 A 所
形成的图形叫做圆.
A
r
圆心
·O
半径
弦(直径)
弧(等弧)
C
二、垂径定理 及推论
•
3、Patience is bitter, but its fruit is sweet. (Jean Jacques Rousseau , French thinker)忍耐是痛苦的,但它的果实是甜蜜的。10:516.17.202110:516.17.202110:5110:51:196.17.202110:516.17.2021
初三数学圆的复习课件_人教版[2]_OK
![初三数学圆的复习课件_人教版[2]_OK](https://img.taocdn.com/s3/m/fc580112524de518974b7d77.png)
直线和圆的位置关系及其性质有且仅有
位置关系 相交
相切
公共点个数 2个
1个
d与r的关系 d<r
d=r
公共点名称 交点
切点
直线名称 割线
切线
注意:“”, 即“等价于”
相离
无 d>r
41
直线和圆的位置关系的判定
d与r的关系 位置关系 交点个数
d>r
相离
无
d=r
相切
1个
d<r
相交
2个
图形
O l
O l
Ol
A AA
问题1:如何作三角形的外接圆? 如何找三角形的外心?
B
OOO C
B B
问题2:三角形的外心一定 在三角形内吗?
▲▲AABAB∠CCC是是=钝锐9角0角°三三O角角形形
B
11
垂直于弦的直径
及其推 论
12
A
AO=BO=CO=DO,
弧AD=弧BC,弧AC
D
想一=想弧:BD将。一个圆沿着任一C 条直径O 对折,两
理 定理
的侧面积相关计算
2
圆的有关性质
3
圆的定义(运动观点)
在一个平面内,线段OA绕它 固定的一个端点O旋转一周,另 一个端点A随之旋转所形成的图 形叫做圆。
固定的端点O叫做圆心,线段 OA叫做半径,以点O为圆心的 圆,记作☉O,读作“圆O”
4
圆的定义辨析
• 篮球是圆吗?
– 圆必须在一个平面内
l 经过半径外端
l垂直于这条半径
44
切线的判定定理: 经过半径的外端并且垂直于 这条半径的直线是圆的切线。
• 已知:直线AB经过⊙O上的点C,并且OA=OB, CA=CB。求证:直线AB是⊙O的切线。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D
B
O
A E B O
C F D
切线性质定理的推广
• 性质定理:圆的切线垂直于经过切点的半径 • 推1:经过圆心且垂直于切线的直线必经过切点 • 推2:经过切点且垂直于切线的直线必经过圆心
你能用一个定理把圆的切 线的性质及它的两个推论 概括出来吗?
如果一条直线具备下列三个条件中 的任意两个,就可以推出第三个: (1)垂直于切线;(2)过切点; (3)过圆心。
A C
O
B C' A'
B'
题设
在 同 圆 前 或 提 等 圆 中 ( 条 件 ) 圆 心 角 相 等
结论
圆心角所对的弧相等, 圆心角所对的弦相等, 圆心角所对弦的弦心距相等。
( )
推论 在同圆或等圆中, 如果两个圆心角、两条弧、 两条弦或两条弦的弦心距中有 一组量相等,那么它们所对应 的其余各组量都分别相等。
A
A
B
观察右图,有什么等量关系? AO=BO=CO=DO,弧 AD=弧BD,弧AC= 弧BC, AE=BE 。
垂直于B 弦的直A 径
C O E D
B
垂直于弦的直径平分这 条弦,并且平分弦所对的两条弧。
垂径定理
A
C
O
E
D
B
判断下列图形,能否使用垂径定理?
B O C A D C
A O D C B
关于三角形内心的辅助线: 连结内心和三角形的顶点, 该线平分三角形的这一内角。
垂心
三条高线 交点 的交点
重心
三条中线 的交点 把中线分 成了2:1 两部分 在形内
外心
内心
三边垂直 三条角平 平分线的 分线的交 交点 点 到三角形 到三角形 各顶点距 三边距离 离相等 相等 在形内、 在形内 形外或斜 边中点
切线与切线长的区别: • 切线是直线,不能度量。 • 切线长是线段的长,这条线段的两个端点分别 是圆外的一点和切点,可以度量。
• 如图,PA、PB是⊙O的两条切线,A、B是切点, 直线OP交⊙O于点D,交AB于点C。 A – 写出图中所有的垂直关系 – 写出图中所有的全等三角形 O C D P – 写出图中所有的相似三角形 B – 写出图中所有的等腰三角形 – 若PA=4cm,PD=2cm,求半径OA的长 – 若⊙O的半径为3cm,点P和圆心O的距离为 6cm,求切线长及这两条切线的夹角度数
问题2:三角形的外心一定 ∠C=90°O ▲ABC是锐角三角形 ▲ABC是钝角三角形 A 在三角形内吗?
B
垂直于弦的直径
及其推 论
AO=BO=CO=DO, D 弧AD=弧BC,弧AC 想一想:将一个圆沿着任一条直径对折,两 O C =弧BD。 侧半圆会有什么关系? AO=BO=CO=DO, 性质:圆是轴对称图形,任何一条直径所在 弧AD=弧BC=弧AC 的直线都是它的对称轴。 D C =弧BD。 O
对角
E
∠EAB=∠BCD
∠FCB=∠BAD
内对角
外角
又一种重要的辅助线
如图,⊙O1和⊙O2都经过A、B两点,经过A点的 直线CD与⊙O1交于点C,与⊙O2交于点D,经过B 点的直线EF与⊙O1交于点E,与⊙O2交于点F。求 证:CE∥DF •有两个圆的题目常用 A E 的一种辅助线:作公 共弦。 O O2 1 C •此图形是一个考试热 门图形。 B
• 弦和直径
– 什么是弦?什么是直径? – 直径是弦吗?弦是直径吗?
与圆有关的概念
• 弧与半圆
– 什么是圆弧(弧)?怎样表示? – 弧分成哪几类? – 半圆是弧吗?弧是半圆吗?
• 弓形是什么? • 同心圆、同圆、等圆和等弧
– 怎样的两个圆叫同心圆? – 怎样的两个圆叫等圆? – 同圆和等圆有什么性质? – 什么叫等弧?
– 圆上各点到定点(圆心)的距离都等于定长(半径);
点与圆的位置关系
• 圆是到定点(圆心)的距离等于定长(半径)的 点的集合。 • 圆的内部是到圆心的距离小于半径的点的集合。 • 圆的外部是到圆心的距离大于半径的点的集合。 • 由此,你发现点与圆的位置关系是由什么来决定 的呢? 如果圆的半径为r, 点到圆心的距离为d,则: 点在圆上 d=r 点在圆内 d<r 点在圆外 d>r
r = ————
2
a
等边三角形外接圆ቤተ መጻሕፍቲ ባይዱ 内切圆半径的求法
A
I A b C
基本思路:
R B O r
构造三角形BOD,BO为外接 圆半径,DO为内切圆半径。
C
D
圆的内接四边形
定理:圆的内接四边形的对角互补,并且 任何一个外角都等于它的内对角。
∠D+∠B=180°
∠A+∠C=180°
A O B C F D
F D
A D 思考:若此题条件和 C结论不变,只是不给 O 出图形,此题还能这 O 2 1 样证明吗? F E B
切线长定理
切 线 长 A 的 切线长定理: 定 O P • 题设:从圆外一点引圆 义 的两条切线 B 以 • 结论:①切线长相等, ②圆心和这一点的连线平分两条切线的夹角 及 • 几何表述: 定 PA = PB PA、PB分别切⊙O于A、B ∠OPA=∠OPB 理
讨论:经过一个点,能作出多少个圆?
经过两个点,如何作圆,能作多少个? 经过三个点,如何作圆,能作多少个?
经过三角形的三个顶点的圆叫做三角形的外接圆, 外接圆的圆心叫做三角形的外心,
C C C
三角形叫做圆的内接三角形。
A A A O O C O
B B
B
问题1:如何作三角形的外接圆? 如何找三角形的外心?
三角形的内心是三角形内角平分线的交点。
三角形的内心是 否也有在三角形 内、三角形外或 三角形上三种不 同情况。
B A
O C
• 在△ABC中,∠ABC=50°, ∠ACB=75°,求∠BOC的度数。 (1)点O是三角形的内心 (2)点O是三角形的外心
A
B
A
O C
E B D
C
• △ABC中,E是内心,∠A的 平分线和△ABC的外接圆相 交于点D。求证:DE=DB。
圆的有关性质
圆的定义(运动观点)
在一个平面内,线段OA绕它固 定的一个端点O旋转一周,另一 个端点A随之旋转所形成的图形 叫做圆。 固定的端点O叫做圆心,线段 OA叫做半径,以点O为圆心的圆, 记作☉O,读作“圆O”
圆的定义辨析
• 篮球是圆吗?
– 圆必须在一个平面内
• 以3cm为半径画圆,能画多少个? • 以点O为圆心画圆,能画多少个? • 由此,你发现半径和圆心分别有什么作用?
圆心角:顶点在圆心的角。
(如:∠AOB)
A
弦心距:从圆心到弦的距离。
(如:OC)
B
O
C
如图,∠AOB=∠A`OB`,OC⊥AB, OC`⊥A`B`。
猜想:弧AB与弧A`B`,AB与A`B`, OC与OC`之间的关系,并证明你的猜想。 在同圆或等圆中, 定理 相等的圆心角所对的弧相等, 所对的弦相等,所对的弦的 弦心距相等。
关于弦的问题,常常需 要过圆心作弦的垂线段, 这是一条非常重要的辅 助线。 圆心到弦的距离、半径、 弦长构成直角三角形, 便将问题转化为直角三 角形的问题。
画图叙述垂径定理,并说出 定理的题设和结论。
题设
①直线CD经过圆心O ②直线CD垂直弦AB 想一想:如果将题设和 ② ① ② ① ③ ③ 结论中的5个条件适当互 ④ ② ③ ③ ④ 换,情况会怎样? ⑤ ⑤ ⑤ ① ④ ④ ⑤ ② ① ② ③ ② ④ ⑤ ③
①过圆心②过切点③ 垂直于切线,随便知 两个就可推出第三个
• 主要辅助线:
– 利用切线性质时,常作过切点的半径 – 证明直线是圆的切线时,分清什么时候“连结”,什 么时候“作垂线”
三角形的内切圆
重点内容
O
如何在一个三角形中剪下一个圆,使得该 圆的面积尽可能的大?
A
B
C
和三角形各边都相切的圆叫做三角形的内 切圆;内切圆的圆心叫做三角形的内心; 这个三角形叫做圆的外切三角形。
切线的判定和性质
• 判定切线的三种方法: 定义 – 和圆只有一个公共点的直线是圆的切线 – 和圆心的距离等于半径的直线是圆的切线 本质一样 – 过半径外端且和半径垂直的直线是圆的切线 表达不同 • 切线的主要性质:
– – – – – 切线和圆只有一个公共点 切线和圆心的距离等于半径 切线垂直于过切点的半径 定理 经过圆心垂直于切线的直线必过切点 经过切点垂直于切线的直线必过圆心
C E O B
A
D
圆的两条平行弦所夹的弧相等。
如图,CD为⊙O的直径,AB⊥CD,EF⊥CD, 你能得到什么结论? E
A
弧AE=弧BF
C
O
D
B F
圆心角、弧、弦、 弦心距之间的关系
圆的性质
• 圆是轴对称图形,每一条直径所在的直线 都是对称轴。 • 圆是以圆心为对称中心的中心对称图形。 • 圆还具有旋转不变性,即圆绕圆心旋转任 意一个角度α,都能与原来的图形重合。
性质
在形内、 位置 形外或直 角顶点
已知△ABC的内切圆半径
为r,求证: △ABC的面 积S△ABC=sr。(s为 △ABC的半周长)
三角形的外接圆:
A
三角形的内切圆:
A
O B C B
I
C
特殊三角形外接圆、内切圆半径的求法: B 直角三角形外接圆、 内切圆半径的求法 c O a+b-c c
R= — 2
把顶点在圆心的周角等分成360份时,每一份的 圆心角是1°的角。1°的圆心角所对的弧叫做 1°的弧。
n°弧
C D
一般地,n°的圆心角 对着n°的弧。
