基于小波分析方法的非线性时间序列模型及其应用
基于有偏小波网络的非线性时间序列分析

[ ywod IBi e v lt ewok Bae n t n No l e me eisSra l wfrcs Ke r s a dwaee t r; isd u ci ; ni a t r ; t mf eat s n f o nr i s e e o o
小波 网络 是小波分析与神经 网络的有机结合 ,继承 了小
Ana y i f l sso n i e rTi eS r e s d o a e a e e t r No l a m e i sBa e n Bi s d W v l t n Ne wo k
LI F n , U a g ZHOU in h n , a , ANG n c n Ja z o g LIT o F Re g u
h rsne ewokClajsp rmees d p rc l po lm, iha d edges ed m n eu e ac l n u d ny tepee tdn t r a dut aa tr aa tOa at ua rbe whc d s r ere f re o a drd cscluaigrd na c l t p i r mo of t e
a b∈R ,但 a≠0。母小 波函数还必须 满足 以下 “ , 可容许
条 件 ” :
波变换 的多分辨率特性和神经 网络 的非线性建模能力 。自从
Z ag在文 献【】 hn 1中提 出小波 网络后 ,由于 小波网络具 有逼 近 能力强、收敛速度快、网络参数 ( 隐层结点数和权重) 的选取 有理论依据 、有效地避免局部最小值 等优点 j ,因此 ,小 波 网络得到 了广泛 的应 用 。 传统的小波 网络 虽然 克服 了神经 网络收敛速度慢易陷入局部极小等缺点 , 但是作为 网络主体 ,
基于小波分析的非平稳时间序列分解
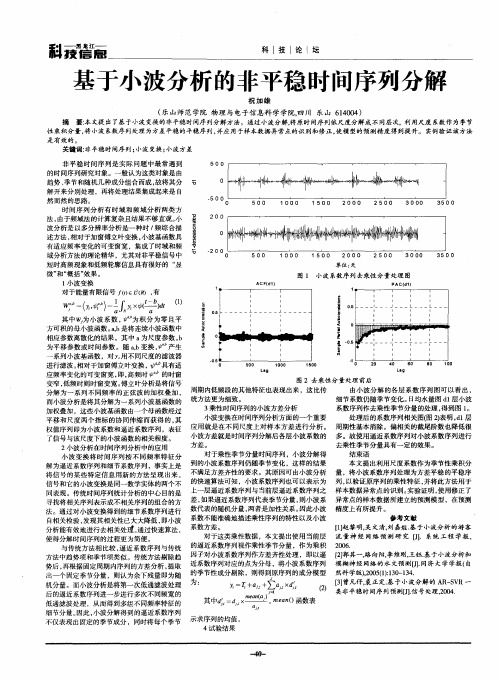
法, 由于频域法 的计算复杂且结果不够直观。 小 波分析是 以多分辨率分析是一种 时 / 频综 合描 述方法 , 相对于加窗傅立叶变换 , 小波基函数具 有适应频率变化 的可变窗宽 ,集成 了时域和频 域分析方法的理论精华 ,尤其对非平稳信号中 短时高频现象和低频轮廓 信息具有很好的 “ 显
微” “ 和 概括 ” 果 。 效
200
0
.
1 5 0 0
2 0 0 0
2 5 0 0
3 00 0
35 0 0
单位 : 天
图 1 小 波 系数 序 列 去 乘 性 分量 处理 图
科
科技 论 坛 ll j
基于小波 分析 的非平稳 时 问序列 分解
祝 加 雄
( 山 师 范 学院 物 理 与 电 子信 息科 学学 院 , 川 乐 山 6 40 ) 乐 四 10 4
摘 要: 文提 出了基于小波变换的非平稳时问序列分解方法 。通过小波分解, 时间序列依尺度分解成不同层次, 用尺度 系数作 为季节 本 将原 利 性 乘积分 量, 小波 系数序列处理为方差平稳的平稳序列, 将 并应 用于样本数据 异常点的-  ̄ 和修正 , / , y 1 , 使模型的预 测精度得 到提升 。实例验证该 方法 是有效的。 关键词: 非平稳时间序 列; 小波 变换 ; 小波方差 非 平稳时 间序列是实 际问题 中最 常遇到 的时间序列研究对象 。一般认为这类对象是 由 趋势 、 季节和随机几种成分组合而成 , 故将其分 解开来分别处理 ,再将处理结果集成起来是 自
然 而然 的思 路 。 时 间序列分析有 时域和频域 分析两类 方
L p
.
0
a0 5 D 0 ∞ p c ∞日 ∞ - OI 0 5 00
《2024年结合小波分析的非平稳时间序列预测方法研究》范文

《结合小波分析的非平稳时间序列预测方法研究》篇一一、引言非平稳时间序列是现代时间序列分析领域的重要研究对象,其数据特性随时间变化而变化,具有复杂的动态特征。
传统的预测方法往往基于平稳性假设,对于非平稳时间序列的预测效果并不理想。
近年来,随着信号处理技术的发展,小波分析作为一种有效的信号处理工具,在非平稳时间序列预测中得到了广泛应用。
本文旨在研究结合小波分析的非平稳时间序列预测方法,以提高预测精度和稳定性。
二、非平稳时间序列与小波分析概述非平稳时间序列是指那些在时间上具有显著变化特性的数据序列,其变化规律往往难以用传统的统计模型进行描述。
小波分析是一种基于小波变换的信号处理方法,它能够根据信号的局部特征进行多尺度分析,有效提取和表示信号的时频信息。
将小波分析与非平稳时间序列预测相结合,可以更好地捕捉时间序列的局部变化特征,提高预测精度。
三、小波分析在非平稳时间序列预测中的应用1. 小波变换与非平稳时间序列预处理在非平稳时间序列的预处理阶段,小波变换可以用于数据去噪和特征提取。
通过选择合适的小波基函数和分解层数,可以有效地去除时间序列中的噪声和干扰信息,提取出有用的局部特征信息。
这些特征信息对于后续的预测模型构建具有重要意义。
2. 小波系数与非平稳时间序列建模在非平稳时间序列建模阶段,可以利用小波系数进行建模。
通过对小波系数进行分析和处理,可以获得时间序列在不同尺度下的局部变化规律,从而建立更加精确的预测模型。
常用的建模方法包括基于小波系数的多尺度自回归模型、支持向量机模型等。
3. 小波重构与预测结果优化在得到预测模型后,可以利用小波重构技术对预测结果进行优化。
通过对小波系数的逆变换,可以得到优化后的预测结果。
这种优化方法可以有效减少预测误差,提高预测精度和稳定性。
四、实证研究与分析本文以某股票市场的日交易量为研究对象,采用结合小波分析的非平稳时间序列预测方法进行实证研究。
首先对原始数据进行预处理,利用小波变换进行去噪和特征提取;然后建立基于小波系数的多尺度自回归模型进行预测;最后通过小波重构对预测结果进行优化。
《结合小波分析的非平稳时间序列预测方法研究》范文

《结合小波分析的非平稳时间序列预测方法研究》篇一一、引言非平稳时间序列预测在许多领域具有广泛的应用,如金融市场的股票价格预测、气象学的气候变化预测等。
传统的预测方法往往基于平稳性假设,但在实际中,非平稳时间序列的预测往往面临诸多挑战。
近年来,小波分析作为一种有效的信号处理工具,被广泛应用于非平稳时间序列的分析与预测。
本文旨在研究结合小波分析的非平稳时间序列预测方法,以期提高预测的准确性和稳定性。
二、小波分析概述小波分析是一种基于小波变换的信号处理方法,它通过将信号分解为不同频率的小波分量,从而实现对信号的时频分析。
小波分析具有多分辨率分析的特点,能够在不同尺度上对信号进行细致的分析和预测。
在非平稳时间序列的预测中,小波分析可以有效地提取时间序列中的局部特征和趋势信息,为预测提供有力的支持。
三、非平稳时间序列的特点与挑战非平稳时间序列是指其统计特性随时间发生变化的序列。
与平稳时间序列相比,非平稳时间序列的预测更具挑战性。
由于缺乏固定的统计特性,非平稳时间序列的预测需要更多地考虑时间变化的影响。
此外,非平稳时间序列还可能受到多种因素的影响,如外部事件、季节性变化等,这进一步增加了预测的难度。
四、结合小波分析的预测方法针对非平稳时间序列的预测问题,本文提出了一种结合小波分析的预测方法。
该方法首先通过小波变换将时间序列分解为不同频率的小波分量,然后对每个小波分量进行独立的预测处理。
具体步骤如下:1. 数据预处理:对原始时间序列进行预处理,包括去噪、归一化等操作,以提高预测的准确性。
2. 小波变换:利用小波变换将时间序列分解为不同频率的小波分量。
根据时间序列的特点选择合适的小波基函数和分解层数。
3. 独立预测:对每个小波分量进行独立的预测处理。
可以采用传统的预测方法(如线性回归、支持向量机等)或基于深度学习的预测方法(如循环神经网络、长短期记忆网络等)。
4. 反变换与重构:将每个小波分量的预测结果进行反变换和重构,得到最终的预测结果。
基于小波分析的时间序列建模与预测

为考核模型的优劣, 还需要对模型残差
检验是不
是白噪声。也就是说,如果经检验残差序列是白噪声序列,认为
此模型是合理的,否则,应当进一步改进模型。
令 表示时刻 t 及它之前的全部观测数据,即于
,显然有
;
序列的预报递推公式为:
(13)
由以上理论对概貌信号建模分析,得出 p=4,即 AR(4)模型。
Finally,wavelet reconstruction is used to realize time series forecasting.It shows that the proposed method can provide more accurate
results. Key words: wavelet analysis; autoregressive moving average model; Elman networks; time series
博士论坛
《微计算机信息》(测控自动化 )2009 年第 25 卷第 12-1 期
式中, J 为任意设定的尺度,则:
(4)
2.2 多尺度分析中的 Mallat 算法
Mallat 算法的基本思想是:设函数
在分辨率
的离散逼近
已知, 则 在
的离散逼近
可
通过离散低通滤波器对
滤波得到。这样,多尺度分析(多
分辨率分析)便转化为滤波器组的设计和分析问题。并由此得到
新 得知:当尺度比较小时,小波变换序列表现的变化比较剧烈,体现 出数据的依赖关系比较差,即依赖时间比较短,但变化幅度很小
(与原始序列比较)。随着尺度的倍增,小波变换时间序列变得越
来越光滑。因此对 d1,d2,d3 序列建立的 elman 模型的输入层神经
《结合小波分析的非平稳时间序列预测方法研究》范文

《结合小波分析的非平稳时间序列预测方法研究》篇一一、引言在时间序列分析中,非平稳时间序列预测是一项重要的研究内容。
由于传统的时间序列分析方法大多基于平稳性假设,因此对于非平稳时间序列的预测效果并不理想。
近年来,随着小波分析理论的发展和应用领域的扩展,越来越多的研究者开始关注其对于非平稳时间序列的预测性能。
本文将就如何将小波分析结合到非平稳时间序列预测方法中进行探讨和研究,并提出一种基于小波变换的非平稳时间序列预测模型。
二、小波分析概述小波分析是一种信号处理技术,其核心思想是通过使用一系列小波基函数来描述和分析信号。
小波分析具有多尺度、多分辨率的特点,可以有效地捕捉到信号中的局部特征和变化趋势。
在非平稳时间序列预测中,小波分析可以通过对时间序列进行多尺度分解,提取出不同频率成分的信号特征,从而为预测提供更多的信息。
三、非平稳时间序列预测的挑战非平稳时间序列的预测相较于平稳时间序列更为复杂。
由于非平稳时间序列的统计特性会随着时间的变化而变化,传统的基于平稳性假设的时间序列预测方法难以捕捉到这种变化趋势。
此外,非平稳时间序列中的突变点、趋势和周期性等因素也增加了预测的难度。
因此,如何设计一种能够适应非平稳特性的预测模型成为了研究的关键。
四、基于小波变换的非平稳时间序列预测模型为了解决非平稳时间序列预测的问题,本文提出了一种基于小波变换的预测模型。
该模型首先对原始时间序列进行多尺度小波分解,将不同频率成分的信号分离出来。
然后,针对每个频率成分的信号,使用相应的模型进行预测。
最后,将各个频率成分的预测结果进行重构,得到最终的预测结果。
在具体实现上,我们可以选择合适的小波基函数(如Haar小波、Daubechies小波等),并确定适当的分解层数。
然后,通过小波变换将时间序列分解为多个子序列,每个子序列对应一个特定的频率范围。
接着,针对每个子序列,我们可以使用传统的预测模型(如ARIMA模型、SVM模型等)或者设计新的模型进行预测。
基于小波算法GPS时间序列非线性信号的提取

基于小波算法GPS时间序列非线性信号的提取时间序列分析是我们大地测量工作这一项重要工作,而选择关键的数据处理方法至关重要,本文提出了应用小波分析方法进行GPS时间序列分析,通过实际的数据分析,得出了小波分解应用于GPS时间序列的可靠性。
标签:时间序列分析GPS 小波分解1绪论时间序列是地学研究中经常遇到的问题。
在时间序列研究中,时域和频域是常用的两种基本形式。
其中,时域分析具有时间定位能力,但无法得到关于时间序列变化的更多信息;频域分析虽具有准确的频率定位功能,但仅适合平稳时间序列分析。
小波变换是八十年代后期发展起来的一种处理非平稳信号的应用数学分支,是建立在泛函分析、Fourier 分析、样条分析及调和分析基础上的新的分析处理工具,是近年来国际上一个非常热门的研究领域。
本文提出了应用小波分析方法进行GPS时间序列分析,通过对实际的数据进行分析,得出了小波分解应用于GPS时间序列的可靠性。
2小波分析基本原理2.1小波函数3小波时间序列处理分析本文选取了GPS时间序列IGS-LHAZ测站,其中序列的获取是通过GAMIT/GLOBK软件解算平差后获取的,该序列已通过预处理,主要是剔除了一些突跳和缺失的值,这一步对于后续分析至关重要。
通过小波分解滤波后得出如图1所示的两个序列,其中信号1是滤掉高频信号后即信号2得出的主信号,也是我们所关注的信号。
4结论GPS时间序列中的周期信号可看作是一时间序列的信号,而且高频信号会随时间和空间变化,同时还受多种复杂的外界环境的影响,比如风力、温度、大气折射等,导致真实信号有比较大随机性,使得一定量的噪声会掺杂在解算出来的周期信号里,最终影响人们对时间序列趋势的判断。
因此在GPS时间序列分析前,对信号进行滤波处理就显得十分的重要了。
本文通过小波分析法对GPS时间序列进行分析,得出了滤波信号,同时对分解的信号进行重构验证了改方法的可靠性。
参考文献[1]何永红,文鸿雁,靳鹏伟.第二代小波在GPS 双差观测值消噪中的应用[J].大地测量与地球动力学,2010,(3):92-95.[2]文鸿雁.小波多分辨分析在变形分析中的应用[J].地壳形变与地震,2000,20(3):27-32.[3]文鸿雁.基于小波理论的变形分析模型研究:[博士学位论文] .武汉大学,2004.。
基于小波变换的时间序列预测

基于⼩波变换的时间序列预测本⽂的主题是考察⼩波变换在预测⽅⾯的应⽤。
思路将数据序列进⾏⼩波分解,每⼀层分解的结果是上次分解得到的低频信号再分解成低频和⾼频两个部分。
如此进过N层分解后源信号X被分解为:X = D1 + D2 + ... + DN + AN 其中D1,D2,...,DN分别为第⼀层、第⼆层到等N层分解得到的⾼频信号,AN为第N层分解得到的低频信号。
本⽂⽅案为对D1,D2...DN和AN分别进⾏预测,然后进⾏⼩波重构实现对源信号的预测。
步骤如下:(1)对原序列进⾏⼩波分解,得到各层⼩波系数;(2)对各层⼩波系数分别建⽴ ARMA 模型,对各层⼩波系数进⾏预测;(3)⽤得到的预测⼩波系数重构数据。
⼀、分解选取数据为A股2014-01-01到2016-04-21数据,最后10天数据⽤来预测。
其余数据⽤于建模。
⼩波函数取db4,分解层数为2。
对数据进⾏分解⼆、对各层系数建⽴ARMA模型并重构imageimageimage接着,⽬标为预测最后10个数据,我们得求出每个⼩波系数ARMA模型需要预测多少步。
⽅法就是查看所有数据⼩波分解后的系数个数并求出差值,具体如下:imageimage三、预测的结果imageimage从上⾯结果可以看出,模型对未来3天预测精度较⾼,在 1%(正负)以内。
不妨把代码打包为函数,进⾏多次检验imageimageimageimageimageimageimageimageimageimage对照⾛势图可以看出:(1)在12年5⽉份,13年5、6⽉份,14年5⽉份, 模型预测的效果在短期内表现不错。
对⽐整体⾛势图可以发现,这些时间段股市总体较为“平缓”。
(2)在15年5⽉、8⽉,预测效果急剧下降。
这两个阶段分别为⽜市上升期和急速下跌期。
另外14年7⽉份的下跌期预测精度也下降了(3)在振荡较频繁的时期15年12⽉、16年3⽉,预测精度也不如之前⾼。
四、结论在股市较“平稳”的时候,基于预测模型在短期有着较⾼的预测精度;当股市处于快速变化时,模型预测精度下降;另⼀⽅⾯,模型还有很⼤改进的潜⼒。
基于小波分解的网络流量时间序列建模与预测

基于小波分解的网络流量时间序列建模与预测张晗;王霞【期刊名称】《计算机应用研究》【年(卷),期】2012(029)008【摘要】提出一种基于小波分解的网络流量时间序列的分析和预测方法.将非平稳的网络流量时间序列通过小波分解成为多个平稳分量,采用自回归滑动平均方法分别对各平稳分量进行建模,将所有分量的模型进行组合,得到原始非平稳网络流量时间序列的预测模型.在仿真实验中,利用网络流量文库的时间序列数据建立了预测模型,并对其进行独立测试检验.仿真结果表明,本预测方法提高了网络流量时间序列的预测准确率,是一种有效、稳健的网络流量预测方法.%This paper proposed a network traffic forecasting methods based on wavelet decomposition and time series analysis method. Firstly,the method decomposed the network traffic time series in multiple stationary components by wavelet decomposition, then used the autoregressive moving average method to model the each stationary component separately. Finally combined all the components of the model to get the forecasting model of the original non-stationary network traffic time series. It carried out the simulation experiment on time series data of the network library. The simulation results show that, the proposed method improves the network traffic time series forecasting accuracy rate, and it is an efficient, robust network traffic forecasting method.【总页数】3页(P3134-3136)【作者】张晗;王霞【作者单位】吉林大学计算机科学与技术学院,长春130012;吉林大学计算机科学与技术学院,长春130012【正文语种】中文【中图分类】TP181【相关文献】1.基于多尺度小波分解和时间序列法的风电场风速预测 [J], 李东福;董雷;礼晓飞;廖毅2.基于小波变换和时间序列的网络流量预测模型 [J], 麻书钦;范海峰3.基于双树复小波分解的云量时间序列模型预测 [J], 白云博; 欧阳斯达; 杨朦朦; 夏学齐; 王婷4.基于区间时间序列小波多尺度分解的组合预测方法 [J], 刘金培;汪漂;黄燕燕;陶志富5.基于小波分解和支持向量机的网络流量组合预测 [J], 段谟意因版权原因,仅展示原文概要,查看原文内容请购买。
小波分析的应用领域及实际案例探究

小波分析的应用领域及实际案例探究引言:随着科学技术的发展,人们对于信号处理和数据分析的需求越来越高。
小波分析作为一种新兴的信号处理方法,因其在时频域上的优势而受到广泛关注。
本文将探讨小波分析的应用领域,并通过实际案例来展示其在各个领域的应用。
一、金融领域中的小波分析金融市场波动性大,传统的统计方法往往难以捕捉到市场的非线性特征。
小波分析通过对金融时间序列进行分解,能够将长期趋势和短期波动分离出来,从而更好地理解市场的运行规律。
例如,在股票市场中,通过小波分析可以确定股票价格的趋势和周期,帮助投资者做出更准确的决策。
同时,小波分析还可以用于金融风险管理,通过对金融市场的波动进行预测,减少风险。
二、医学领域中的小波分析医学信号通常具有非平稳性和非线性特征,如心电图、脑电图等。
小波分析在医学领域的应用非常广泛。
例如,在心电图分析中,小波分析可以用于检测心率变异性,帮助医生判断心脏病患者的病情。
此外,小波分析还可以用于脑电图的频谱分析,帮助医生诊断癫痫等脑部疾病。
三、图像处理中的小波分析图像处理是小波分析的另一个重要应用领域。
小波变换可以将图像分解为不同尺度的频带,从而提取图像的局部特征。
例如,在图像压缩中,小波变换可以通过去除高频细节信息来减少图像的数据量,从而实现图像的压缩。
此外,小波分析还可以用于图像去噪、边缘检测等图像处理任务。
四、语音处理中的小波分析语音信号通常具有时间-频率的非平稳特性,传统的傅里叶变换无法很好地处理这种信号。
小波分析在语音处理中有着广泛的应用。
例如,在语音识别中,小波分析可以提取语音信号的频谱特征,用于语音信号的特征匹配。
此外,小波分析还可以用于语音合成、语音增强等任务。
五、实际案例探究为了更好地理解小波分析在实际中的应用,我们以图像处理为例进行探究。
在图像处理中,小波分析被广泛应用于图像去噪任务。
通过对图像进行小波变换,可以将图像分解为不同频带的系数。
根据小波系数的分布情况,可以选择性地去除高频细节信息,从而实现图像的去噪。
小波神经网络模型的确定性预测及应用

小波神经网络模型的确定性预测及应用作者:潘玉民邓永红张全柱来源:《计算机应用》2013年第04期0引言神经网络引入预测领域使预测理论及方法产生了质的飞跃。
传统的线性预测方法,如自回归(AutoRegressive, AR)模型、滑动平均(Moving Average, MA)模型等在解决非线性严重的预测问题时遇到很大困难,而神经网络在非线性预测方面有着独特的优势,它不需要建立复杂的非线性系统的显式关系及数学模型,通过数据样本训练即可提取数据特征和内在规律,实现信息的分布存储,产生联想记忆,从而对未经训练的样本能够给出外推的预测效果,为非线性预测提供了强有力的工具。
1987年,pedes和R.Farber首次利用神经网络对非线性时间序列进行预测,开创了神经网络应用于预测领域的先河[1]。
之后,神经网络在预测中的应用得到快速发展。
近年来,小波神经网络作为一种新颖的神经网络日益受到关注,它兼有小波函数时频局部特性和神经网络函数逼近和泛化能力,在预测领域具有强大的优势。
目前,神经网络预测形式主要有两种:趋势预测与基于因果关系的回归预测,分别对应时间序列预测和多元回归预测。
神经网络具有分布式、联想、记忆和很强的泛化能力,以及自学习和容错性,可以以任意精度逼近非线性函数等优点,是线性预测方法无法比拟的。
对于大多数预测对象,尤其是含有非线性关系的数据,使用神经网络预测都会得到更高的预测精度。
但是,神经网络应用于预测中存在如下问题:网络结构的设计目前尚无确定的理论依据;预测结果有随机性;机理缺乏透明度;初始参数难确定;存在过度拟合现象;易陷入局部极小等。
其中大多数问题需要以实验效果为依据进行确定,利用统计方法对预测结果进行评价,或采用试凑法找出网络“最佳”参数进行下一步预测[2]。
在上述问题中比较突出的问题是神经网络预测结果的随机性,小波神经网络也不例外,即多次预测结果不同,有时分散性很大,即神经网络的预测精度具有不可控性质。
非线性时间序列分析方法与模型

非线性时间序列分析方法与模型时间序列分析是一种研究随时间变化的数据模式和趋势的统计方法。
在传统的时间序列分析中,线性模型被广泛应用,但是线性模型无法捕捉到一些复杂的非线性关系。
因此,非线性时间序列分析方法和模型的发展成为了研究的热点。
一、非线性时间序列分析方法的发展1.1 非线性时间序列分析的起源非线性时间序列分析方法的起源可以追溯到20世纪60年代。
当时,经济学家和统计学家开始发现一些经济和金融数据中存在着非线性关系,传统的线性模型无法很好地解释这些数据。
这引发了对非线性时间序列分析方法的研究兴趣。
1.2 常用的非线性时间序列分析方法随着研究的深入,许多非线性时间序列分析方法被提出和应用。
其中,最常用的方法包括:傅里叶变换、小波分析、自回归条件异方差模型(ARCH)、广义自回归条件异方差模型(GARCH)、支持向量机(SVM)等。
二、非线性时间序列模型的应用2.1 ARCH和GARCH模型ARCH和GARCH模型是用于建模金融时间序列数据的非线性模型。
ARCH模型通过引入条件异方差来捕捉金融数据中的波动性特征,而GARCH模型在ARCH 模型的基础上进一步考虑了波动性的长期记忆效应。
2.2 小波分析小波分析是一种将时间序列分解成不同频率的成分的方法。
通过小波分析,可以将时间序列的低频和高频成分分离出来,从而更好地理解时间序列的特征和趋势。
2.3 支持向量机支持向量机是一种机器学习方法,在非线性时间序列分析中得到了广泛应用。
支持向量机通过将时间序列映射到高维空间,并在该空间中构建超平面来进行分类和回归分析。
三、非线性时间序列分析方法的优势和局限性3.1 优势非线性时间序列分析方法能够更好地捕捉到数据中的非线性关系,提高模型的预测精度。
这对于金融市场的预测和风险管理具有重要意义。
3.2 局限性非线性时间序列分析方法的建模过程较为复杂,需要较大的计算量和数据量。
此外,非线性时间序列分析方法对初始条件较为敏感,对于数据的噪声和异常值较为敏感。
基于小波分析的信号处理技术研究

基于小波分析的信号处理技术研究随着现代社会科学技术的不断发展,数字信号处理已成为现代社会中不可缺少的一部分。
在数字信号处理领域中,小波分析是一种非常重要的工具。
它可以对信号进行分析和处理,包括信号的去噪、压缩、过滤、分割等。
下面我们就基于小波分析的信号处理技术进行研究探讨。
一、小波分析概述小波分析(Wavelet Analysis)是一种新型的信号处理技术,它是基于小波变换的信号分析方法。
相比于传统的傅里叶变换方法,小波分析具有更好的时域和频率分辨率,而且可以处理非平稳信号。
小波变换是一种时频分析方法,它可以将一段时间序列信号分解成一系列的小波函数,从而识别出信号的不同特征。
小波分析在许多领域得到了广泛应用,如信号处理、图像处理、模式识别、数据压缩和量化等。
二、小波分析的优势小波分析相比于传统的信号处理方法有很多优势。
首先,它可以分析非平稳信号,这在很多领域中都是非常重要的,如生物信号处理、语音信号处理等。
其次,它可以将信号分解成多个频率分量,并且每个频率分量都有不同的时间和频率分辨率。
这使得小波分析可以精确地分析信号的局部特征。
此外,小波分析还可以适应不同的滤波器和分解层数,这使得小波分析的灵活性非常高。
三、小波分析在信号处理中的应用小波分析在信号处理中有很广泛的应用。
下面我们将分别对小波分析在信号去噪、信号压缩和信号分割中的应用进行探讨。
1、信号去噪小波去噪是指利用小波分析技术对信号进行降噪处理。
利用小波分析可以将原始信号分解成多个频率分量,在低频部分信号中保留有效信号,而在高频部分中滤除噪声信号。
小波去噪的方法相对于传统的去噪方法更加精确且有效。
在语音信号处理、图像处理和生物信号处理等方面都得到了广泛的应用。
2、信号压缩小波压缩是一种有效的信号压缩方法,它可以通过将信号分解成多个频率分量,进而将信号的高频部分进行舍弃,来实现对信号的压缩。
小波压缩方法与传统的压缩方法相比,具有更高的压缩比和更好的保真性能。
小波分析及其应用

现代数字信号处理作业小波分析及其应用电研111梁帅小波分析及其应用1.小波分析的概念和特点1.1小波理论的发展概况20世纪80年代逐渐发展和兴起的小波分析(wavelctanalysis)是20世纪数学领域中研究的重要杰出成果之一。
小波分析理论作为数学界中一种比较成熟的理论基础,应用到了各种领域的研究当中,推动了小波分析在各工程应用中的发展。
它作为一种新的现代数字信号处理算法,汲取了现代分析学中诸如样条分析、傅立叶分析、数值分析和泛函分析等众数学多分支的精华部分,替代了工程界中一直应用的傅立叶变换,它是一种纯频域分析方法,不能在时频同时具有局部化特性。
而小波分析中的多尺度分析思想,犹如一台变焦照相机,可以由粗及精逐步观察信号,在局部时频分析中具有很强的灵活性,因此有“数学显微镜”的美称。
它能自动随着频率增加而调节成窄的“时窗”和宽的“频窗”,又随着频率降低而调节成宽的“时窗”和窄的“频窗”以适应实际分析需要。
另外,小波变换在经过适当离散后可以够成标准正交基或正交系,这些在理论和应用上都具有十分重要的意义,因此,小波分析在各个领域得到了高度的重视并取得了许多重要的成果。
小波变换作为一种数学理论和现代数字信号处埋方法在科学技术界引起了越来越多专家学者的关注和重视。
在数学家看来,基于小波变换的小波分析技术是当今数值分析、泛函分析、调和分析等半个多世纪以来发展最完美的结晶,是正在发展中的新的数学分支。
在工程领域,特别是在信号处理、图像处理、机器视觉、模糊识别、语音识别、流体力学、量子物理、地震勘测、电磁学、CT成像、机械故障诊断与监控等领域,它被认为是近年来在工具及方法上的重大突破。
然而,小波分析虽然在众多领域中已经取得了一定的成果,但是,有专家预言小波分析理论的真正高潮并没有到来。
首先,小波分析尚需进一步完善,除一维小波分析理论比较成熟以外,向量小波和多维小波则需要进行更加深入的研究与讨论;其次,针对不同情况选择不同的小波基函数,实现的效果是有差别性的这一问题,对最优小波基函数的选取方法有待进一步研究。
小波分析及其应用

小波分析及其应用小波分析是一种时间-频率分析方法,是对时域信号在时间和频率上的特征进行分析的一种数学工具。
它不仅具有频域分析方法的优点,如傅立叶变换,可以提供信号的频率成分,而且还能提供信号的时间信息,即信号的局部特征。
小波分析在信号处理、图像处理、语音识别等领域有着广泛的应用。
小波分析的基本原理是通过对信号进行分解和重构,将信号转化为不同尺度和频率的小波基函数的叠加,然后通过分析小波系数的大小和位置,得到信号的频率和局部时间信息。
在信号处理领域,小波分析常用于信号压缩、去噪和特征提取。
由于小波函数具有时频局部化特性,可以更准确地描述信号的局部特征,所以在信号压缩方面有很好的应用。
小波压缩将信号分解为不同频率分量,然后根据各个频率分量的重要程度进行压缩,以达到减小数据量的目的。
在信号去噪方面,小波分析可以通过滤除小波系数的低能量分量来抑制信号中的噪声。
此外,小波变换还可应用于语音识别和图像处理中的特征提取,提取信号的频率特征和时间特征,以实现对语音和图像的处理和识别。
在图像处理领域,小波分析有着广泛的应用。
小波变换可以将图像分解为不同尺度和方向的频域信号,从而提供了更加精细的图像特征信息。
基于小波变换的图像处理技术包括图像压缩、边缘检测、纹理分析等。
通过对图像进行小波分解和重构,可以实现图像的压缩和去噪。
同时,小波变换还具有多尺度分析的优势,能够更好地捕捉图像中的局部细节和全局结构。
在金融领域,小波分析被用于金融时间序列的特征提取和预测。
金融市场的价格序列通常具有非线性、非平稳和非高斯分布的特点,传统的统计方法常常无法处理。
而小波分析可以更好地揭示金融时间序列的时间和频率特征,提供更准确的数据分析和预测。
通过分析小波系数的大小和位置,可以提取金融时间序列中的主要特征和周期,为金融决策提供参考。
此外,小波分析还在医学影像处理、地震信号处理、生物信号处理等领域有广泛的应用。
在医学影像处理中,小波分析能够提取出图像中的不同频率和方向的特征,从而实现对病变的检测和分析。
如何使用小波变换进行非线性信号分析

如何使用小波变换进行非线性信号分析引言:信号分析是一门重要的学科,它涉及到许多不同类型的信号,包括线性和非线性信号。
在非线性信号分析中,小波变换是一种非常有用的工具。
本文将介绍如何使用小波变换进行非线性信号分析,并探讨其在实际应用中的重要性。
一、小波变换的基本原理小波变换是一种时频分析方法,它将信号分解成不同频率和时间的小波基函数。
与傅里叶变换相比,小波变换能够提供更多的时域信息,因此在非线性信号分析中更为适用。
小波变换的基本原理是将信号与一组小波基函数进行卷积运算,得到不同频率和时间上的小波系数。
二、小波变换的优势1. 时频局部性:小波变换能够提供信号在不同时间和频率上的局部特征,使得对非线性信号的分析更加准确。
2. 多分辨率分析:小波变换可以通过选择不同的小波基函数,对信号进行多尺度分析,从而更好地捕捉信号的细节和整体特征。
3. 非线性处理能力:小波变换能够对非线性信号进行处理,通过分析小波系数的非线性特征,可以揭示信号中的隐藏信息。
三、小波变换在非线性信号分析中的应用1. 信号去噪:非线性信号通常包含大量的噪声,而小波变换可以通过分析小波系数的能量分布,对信号进行去噪处理。
通过选择适当的小波基函数和阈值处理方法,可以有效地去除噪声,提取出信号的有效信息。
2. 信号特征提取:非线性信号中常常包含丰富的特征信息,如瞬态信号、奇异点等。
小波变换能够通过分析小波系数的局部特征,提取出信号中的这些特征,并用于信号识别和分类。
3. 信号压缩:非线性信号通常具有较高的冗余性,而小波变换可以通过选择适当的小波基函数和阈值处理方法,对信号进行稀疏表示,从而实现信号的压缩和存储。
四、小波变换的实际案例1. 生物医学信号分析:小波变换在心电图、脑电图等生物医学信号分析中得到广泛应用。
通过对信号进行小波变换,可以提取出心跳和脑电波的频率特征,从而用于疾病诊断和监测。
2. 振动信号分析:小波变换在机械振动信号分析中也有重要应用。
信号的时频分析与小波分析

灵活性
计算效率
小波变换具有高度的灵活性,可以选择不 同的小波基函数,以满足不同类型信号和 不同应用场景的需求。
相对于傅里叶变换,小波变换的计算复杂 度较低,使得在实时信号处理中更为高效 。
缺点
选择合适的小波基
选择合适的小波基是进行小波分析的关键步骤,但选择过 程具有一定的主观性和经验性,需要依据具体应用场景和 信号特性进行判断。
小波变换可以用于特征提取和降 维,为机器学习算法提供有效的 特征表示。
模式识别
小波变换可以用于信号分类和模 式识别,例如在声音、图像和文 本识别等领域。
数据挖掘
小波变换可以用于数据挖掘和聚 类分析,例如在时间序列数据、 金融数据和社交网络分析等领域。
THANKS
感谢观看
时频分析通过将信号表示为时间和频 率的联合函数,提供了一种同时观察 信号在不同时间和频率下表现的方式。
短时傅里叶变换
短时傅里叶变换是一种常用的时频分析方法,通过使用滑动窗口函数对信号进行加 窗处理,并对每个窗口内的信号进行傅里叶变换。
窗口函数的选择对短时傅里叶变换的性能有很大影响,常见的窗口函数包括高斯窗、 汉明窗等。
小波变换的分类与应用
总结词
小波变换可以分为连续小波变换和小波离散变换两种类型,它们在信号处理、图像处理、语音识别等 领域有蛇形广泛应用。
详细描述
连续小波变换能够对信号进行连续某种的时频分析,能够同时获得信号在时间域和频率域的信息。而 小迷离变换 则是基于离散傅里叶变换的一种改进,可以对信号进行快速变换分析。在应用方面,连续 小矶碎变换摸摸可以应用于信号处理、图像处理、语音识别等领域某种。
小波分析在大数据时代的应用
信号处理
01
在通信、雷达、声呐等领域,小波分析用于信号降噪、压缩感
如何使用小波变换进行时序数据分析

如何使用小波变换进行时序数据分析时序数据是指按时间顺序排列的数据序列,如股票价格、气温变化等。
对于时序数据的分析,小波变换是一种常用的方法。
小波变换是一种数学工具,可以将时域数据转换为频域数据,从而更好地理解和分析时序数据的特征。
本文将介绍如何使用小波变换进行时序数据分析。
一、小波变换的基本原理小波变换是一种多尺度分析方法,它将信号分解成不同尺度的小波基函数,从而获得不同频率的信息。
小波变换的基本原理是将信号与小波基函数进行卷积运算,得到小波系数,然后通过逆变换将小波系数重构成原始信号。
小波基函数具有时域和频域的局部性,因此可以更好地表示信号的局部特征。
二、小波变换的步骤使用小波变换进行时序数据分析的步骤如下:1. 选择小波基函数:小波基函数的选择是进行小波变换的第一步。
常用的小波基函数有Haar小波、Daubechies小波等。
不同的小波基函数适用于不同类型的信号,选择合适的小波基函数可以提高分析的准确性。
2. 进行小波分解:将时序数据进行小波分解,得到不同尺度的小波系数。
小波分解可以通过多级分解实现,每一级分解得到一组小波系数。
3. 分析小波系数:对小波系数进行分析,了解不同尺度上的频率信息。
可以通过绘制小波系数的图像或计算小波系数的统计特征来分析信号的频域特征。
4. 进行小波重构:根据分析结果,选择合适的小波系数进行小波重构,得到重构后的信号。
小波重构可以通过多级重构实现,每一级重构使用一组小波系数。
三、小波变换的应用小波变换在时序数据分析中有广泛的应用。
以下是几个常见的应用场景:1. 趋势分析:通过小波变换可以分析时序数据中的趋势成分。
将时序数据进行小波分解,可以得到不同尺度上的小波系数,从而分析不同频率的趋势成分。
2. 周期性分析:小波变换可以用于分析时序数据中的周期性成分。
通过小波分解和重构,可以提取出信号中的周期性波动,从而了解信号的周期性特征。
3. 异常检测:小波变换可以用于检测时序数据中的异常点。
小波变换在时间序列分析中的应用

小波变换在时间序列分析中的应用小波变换是一种在时间序列分析中广泛应用的数学工具。
它可以将一个复杂的时间序列分解成不同频率的成分,从而帮助我们更好地理解和分析数据。
本文将介绍小波变换的基本原理和在时间序列分析中的应用。
首先,我们来了解一下小波变换的基本原理。
小波变换是一种多尺度分析方法,它使用一组称为小波函数的基函数来分析信号的频率和幅度。
与傅里叶变换不同,小波变换可以在时间和频率上同时提供信息。
这使得小波变换在时间序列分析中具有独特的优势。
小波变换的核心思想是通过对信号进行不同尺度的平移和缩放,来提取信号中的不同频率成分。
具体而言,小波变换将信号与一组小波函数进行卷积运算,得到一组小波系数。
这些小波系数表示了信号在不同尺度和位置上的频率成分。
通过对小波系数的分析,我们可以得到信号的频谱特征,进而进行时间序列的分析和预测。
在时间序列分析中,小波变换可以应用于多个方面。
首先,小波变换可以用于信号的去噪和滤波。
由于小波变换在时间和频率上都提供了信息,因此可以通过选择适当的小波函数和阈值来滤除信号中的噪声成分,从而得到更准确的信号分析结果。
其次,小波变换可以用于信号的特征提取和模式识别。
通过对小波系数的分析,我们可以提取信号的频率和幅度特征,从而识别信号中的不同模式和趋势。
这对于时间序列的分类和预测非常有帮助。
此外,小波变换还可以用于时间序列的压缩和编码。
由于小波变换将信号分解成不同尺度的成分,我们可以选择保留重要的小波系数,而舍弃不重要的系数,从而实现对信号的有效压缩和编码。
最后,小波变换还可以用于时间序列的分析和预测。
通过对小波系数的分析,我们可以了解信号的频率特征和趋势变化,从而对未来的发展进行预测。
这对于金融市场的预测、气象数据的分析等具有重要的应用价值。
综上所述,小波变换在时间序列分析中具有广泛的应用。
它可以帮助我们更好地理解和分析时间序列数据,从而提取有用的信息和知识。
无论是在信号处理、模式识别还是预测分析中,小波变换都发挥着重要的作用。
时间序列小波分析

时间序列小波分析时间序列分析是一种用于研究和预测时间序列数据的方法,而小波分析则是一种有效的时间序列分析方法之一、本文将详细介绍时间序列小波分析的原理、方法以及应用。
一、小波分析的原理和方法小波分析是通过分析时间序列信号的高频和低频成分来研究和预测时间序列数据的方法。
它基于小波变换的原理,将时间序列信号分解成不同频率成分的叠加,从而获得更详细和准确的信号信息。
小波变换是一种时频局部化分析的方法,它将时间序列信号表示为时间与频率两个维度上的函数。
相比于传统的傅里叶变换,小波变换能够提供更多的细节和局部信息。
小波分析的基本思路是将时间序列信号分解成多个不同频率的小波系数,然后分析每个小波系数的特性和规律。
具体来说,小波分析主要包括以下几个步骤:1.选择合适的小波函数:小波函数是用来描述小波变换的基函数,不同的小波函数有不同的频率特性和时域分辨率。
在小波分析中,选择适合于分析数据特性的小波函数非常重要。
2.进行小波分解:利用选定的小波函数对时间序列信号进行分解,得到不同频率的小波系数。
分解的过程是通过低通滤波和高通滤波来实现的,其中低通滤波用于提取低频成分,高通滤波用于提取高频成分。
3.小波系数的阈值处理:由于小波变换是一种连续变换,分解得到的小波系数包含了大量的噪声和无用信息。
因此,需要对小波系数进行阈值处理,去除噪声和无用信息,保留有用的信号成分。
4.重构信号:将经过阈值处理后的小波系数进行重构,得到去噪后的时间序列信号。
5.进行时间序列分析和预测:利用重构信号进行时间序列的分析和预测,包括描述统计量、自相关、谱分析等方法。
二、小波分析的应用小波分析具有一系列优点,例如能够提供时间和频率上的局部信息、能够适应非平稳时间序列等,因此在各个领域都得到了广泛的应用。
以下将介绍几个常见的应用。
1.金融数据分析:小波分析在金融数据分析中有着广泛的应用。
通过对金融时间序列数据进行小波分解,可以提取不同频率的波动成分,用于研究市场的周期性和波动性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一 、引言
当今社会 ,对股票市场行为的预测一直是广大 投资者的追求目标 。为理解股市的过去和预测其未 来 ,人们千方百计地寻求能够解释股价波动行为的 规律 。然而 ,股票市场正以一个日益复杂的形式展 现在世人面前 。由于股票市场的时变性和随机性 , 日趋成熟和完善的线性时间序列模型已不足以对现 实的情况给出合理而精确的解释 。因此 ,人们需要 研究内容更为丰富和深刻的非线性时间序列模型 , 才能对复杂的经济现象做出更为合理的描述 。
0. 8 + 0. 2 a2t- 1 + 0. 3 a2t- 2 0. 1 + 0. 3 a2t- 1 + 0. 25 a2t- 2
(5) xt- 2 ≤0. 4
0. 4 < xt- 2
(6)
而对于小波 ,我们相应地选以下小波函数
0. 6495 ( x - 1) 4 ,
1 ≤x ≤2
ψ( x) = - 10. 3287( x + 1) 3 + 9. 7954( x + 1)2 - 2 ≤ x ≤- 1 + 12( x + 1) ,
两个不同门限 ,{εt} 为严平稳的 。
我们知道门限标志着系统从一种状态进入另一
种状态 。而对于经济时间序列 ,条件均值函数和条
件方差函数都会有不同状态 。因此 ,D TA RC H 模
型的这种双门限特点正可以刻画出这种特征 。另
外 ,在模型的门限参数和延时已知的情况下 ,我们可
以给出模型中参数的极大似然估计 :
为了简化模型的讨论 ,下面的分析中我们不考
虑系数参数和的估计 ,我们仅讨论此模型中门限和
延时的估计 : 第一步 :识别门限λj 。 首先 ,我们定义经验小波系数如下 :
N
∑ ∑ ψ W ( m) v. k
( tj 3
)
= b- a N i =1
1 per ( s ) n x v , k i
j m , i j ∈N n ( sm , i )
0,
其他
相应地 ,我们得到门限和延时的估计即分别为 :
λ^ = 0. 35 , ^r = 0. 5 , d = 2 。
最后 , 应 用 SA S 软 件 和 上 述 估 计 的 数 据 对
D TA RC H 模型进行数值模拟 ,发现与实际情形比
较吻合 。因而 ,本文所探讨的 D TA RC H 模型在非
m = 1 , 2 , …, p ,
这里 tj 3 ∈R j 3 , N = [ N 1/ p + 2 ] , 且
sm , i = ( tj 3 1 , tj 3 2 , …, tj 3 (m - 1) , si , tj 3 m , …,
t ) j 3 (p - 1) T
,
si
=a
+i
b- a N
,
nm , i
= Nn ( sm , i )
。
+∞
其中
ψper v, k
( si )
=∑ n= - ∞
1 ψv , k b- a
si b-
a a
+
n
, ψv , k
( x) = 2 2vψ(2v x - k) , ψ( x) 为给定的小波函数 。
以上均定义在 L2 [ a , b]函数空间上 。
其次 ,我们做出下面假设 ,令
[3 ]崔锦泰. 小波分析导论 [ M ]. 西安 : 西安交通大学出版 社 ,1995.
[ 责任编辑 :杨凤春 ]
·80 ·
的 D TA RC H 模型 ,这是具有实际意义的 。在 (3) 、
(4) 式中我们给出了门限延时已知时模型参数的估
计 。因此 ,估计门限与延时成为 D TA RC H 模型的
关键 。在本文中 ,我们采用的是近年来发展比较迅
速的小波方法来识别模型的门限与延时 。
(二) DTARCH 模型门限与延时的小波辨析方法
三 、实证分析
下面我们采用 2001 年 3 月到 2004 年 1 月的上
证指数对上述模型进行实证分析 。
首先 ,采用对数去趋势性 方法得 到时 间序 列
{
x
t
}
1000 t=1
,前
800
个数据作为样本点
,中间
100
个为
确定集 ,后 100 个作为预测 。
其次 ,根据上述讨论的方法 ,我们得到以下模型
列往往具有异方差结构 ,而自激励门限自回归模型
具有恒定的方差结构 。为此 ,我们主要研究 Li 于
1996 年 提 出 的 异 方 差 双 门 限 自 回 归 模
型 ———D TA RC H
n1 +1
pj
∑ ∑ xt =
φ ( ( j) 0
+
φ ε ( j) i
x i- 1 )
I [λj -
1
,
λ
j
si
=
a+ib N
a,
nd, i
=
N n (sd, i) 。
其次 ,令
E2 ( vn )
= { k :|
W (σ) vn ,
k
( t0j 3
)|
≥c1 2 - vn/ 2 ,
k ∈Ivn } , c1 为常数 。
q 若 E2 ( vn) 不是空集 即为给出的估计 。
^r = o
若 E2 ( vn) 是空集
[ 摘 要 ]本文主要探讨了非线性时间序列中的异方差双门限自回归模型 (D TARC H) 的门限和延时的小波辨 识方法 ,并利用相应的股市数据对此模型进行了实证分析 。
[ 关键词 ]非线性时间序列 ;小波分析 ;D TA RC H 模型 [ 中图分类号 ]O211 [文献标识码 ]A [ 文章编号 ]1672 8750 (2005) 02 0079 02
+
φ ε x + (2)
i
t- i
t
如果 x t- d > λ
i=1
q1
∑ α(1) 0
+
α ε (1) 2 i t- i
如果 x t- d < λ
i=1
yt =
q2
(4)
∑ α(2) 0
+
α ε (2) 2 i t- i
如果 x t- d > λ
i=1
在上述 (1) 、(2) 式中我们给出了具有不同门限
进行数值模拟 。
xt =
0. 4 xt- 1 + 0. 26 xt- 2 + at 0. 2 xt- 1 - 4. 2 xt- 2 + at
0. 3 xt- 1 + 0. 6 xt- 2
x t- 2 ≤0. 35 0. 35 < xt- 2 ≤0. 5
xt- 2 > 0. 5
E( a2t | Ft- 1 ) =
第 2 卷 第 2 期 2005 年 5 月
南京审计学院学报
Jo urnal of Nanjing Audit U niversity
Vol. 2 , No . 2 May , 2005
基于小波分析方法的非线性时间 序列模型及其应用
张 燕
(南京审计学院 应用数学系 , 江苏 南京 210029)
线性的经济时间序列的研究中具有一定的实用性 。
[ 参考文献 ]
[ 1 ]杨一文 ,刘贵忠 ,张宗平等. 基于小波网络的非线性时间 序列预测及其在股市中的应用 [J ] . 模式识别与人工智 能 ,2001 , (6) .
[2 ]李元. 时间序列中变点的小波分析及非线性小波估计 [ M ] . 北京 :中国统 : 存 在 一 个 k ∈Ivn 和 t j 3 ∈Rj 3 , 使 得
|
W ( m) vn ,
k ( tj 3
)|
≥c0 2 - 3 vn/ 2 ,
1 ≤m ≤p} ,
c0 为常数 。
再记
E0 ( vn) 的任意无素 若 E0 ( vn) 不是空集
^d = 0
若 E0 ( vn) 是空集
二 、原理及方法
(一) D TA RC H 模型简介 迄今为止 ,人们已提出了许多种非线性时间序 列模型 ,应用较为广泛的是 H. To ng 于 1978 年提 出的门限自回归模型 。其中应用比较成熟的模型为 自激励门限自回归模型 。但是 ,在处理经济数据的 时候 ,此模型具有一定的局限性 ,原因是经济时间序
1 xj nd, i j ∈N n (sd, i)
2
假设 此 时 d 为 已 知。这 里 tj 3 ∈ Rj 3 , N = [ n1/ 2 p + 2 ] 。且
sm , i = ( tj 3 1 , tj 3 2 , …, tj 3 ( d- 1) , si , tj 3 d , …,
tj 3 (2 p- 1) ) T ,
[ 收稿日期 ]2005 3 10 [ 作者简介 ]张燕 (1978 — ) ,女 , 江苏溧阳人 ,南京审计学院应用数学系助教 ,河海大学理学院硕士生 ,主要从事数理统计研究 。
·79 ·
p1
∑ φ(1) 0
+
φ ε x + (1)
i
t- i
t
如果 x t- d < λ
i=1
xt =
p2
(3)
∑ φ(2) 0
则上式即为给出的延时 d 的估计 。
最后
,门限λ1
的估计为
:λ^ l
=
a
+
kl 2vn
(b-
a) 。
第二步 :识别门限 rt 。
同样可定义经验小波函数
W
(σ) v. k
