第5章时间序列的确定性分析.pptx
时间序列分析ppt课件

目录
• 时间序列分析简介 • 时间序列的基本概念 • 时间序列分析方法 • 时间序列分析案例 • 时间序列分析的未来发展
01 时间序列分析简介
时间序列的定义与特点
定义
时间序列是指按照时间顺序排列的一 系列观测值。
特点
时间序列具有动态性、趋势性和周期 性等特点,这些特点对时间序列分析 具有重要的影响。
时间序列的季节性
总结词
时间序列的季节性是指时间序列在固定周期内重复出现的模式,这种模式可能是由于季节性因素、周 期性事件或数据采集的频率所引起的。
详细描述
季节性是时间序列中的一个重要特征,许多时间序列都表现出季节性。例如,一个表示月度销售的序 列可能会在每个月份都出现类似的销售模式。在进行时间序列分析时,需要考虑季节性对模型的影响 ,以便更准确地预测未来的趋势和模式。
时间序列分析在金融领域的应用广泛,如股票价格预测 、风险评估等。未来将进一步探索时间序列分析时间序列分析可用于医学影像分析、疾病 预测等方面。未来将进一步拓展其在健康领域的应用范 围,为医疗保健提供有力支持。
谢谢聆听
时间序列分析的意义
01
预测未来趋势
通过对时间序列进行分析,可以了解数据的变化趋势, 从而预测未来的走势,为决策提供依据。
02
揭示内在规律
时间序列分析可以帮助我们揭示数据背后的内在规律和 机制,进一步理解事物的本质。
03
优化资源配置
通过对时间序列的预测和分析,可以更好地优化资源配 置,提高资源利用效率。
03 时间序列分析方法
图表分析法
总结词
通过图表直观展示时间序列数据,便 于观察数据变化趋势和异常点。
详细描述
第五章_时间序列分析_102-122_

第二篇 预测方法与模型预测是研究客观事物未来发展方向与趋势的一门科学。
统计预测是以统计调查资料为依据,以经济、社会、科学技术理论为基础,以数学模型为主要手段,对客观事物未来发展所作的定量推断和估计。
根据社会、经济、科技的预测结论,人们可以调整发展战略,制定管理措施,平衡市场供求,进行各种各样的决策。
预测也是制定政策,编制规划、计划,具体组织生产经营活动的科学基础。
20世纪三四十年代以来,随着人类社会生产力水平的不断提高和科学技术的迅猛发展,特别是近年来以计算机为主的信息技术的飞速发展,更进一步推动了预测技术在国民经济、社会发展和科学技术各个领域的应用。
预测包含定性预测法、因果关系预测法和时间序列预测法三类。
本篇对定性预测法不加以介绍,对后两类方法选择以下几种介绍方法的原理、模型的建立和实际应用,分别为:时间序列分析、微分方程模型、灰色预测模型、人工神经网络。
第五章时间序列分析在预测实践中,预测者们发现和总结了许多行之有效的预测理论和方法,但以概率统计理论为基础的预测方法目前仍然是最基本和最常用的方法。
本章介绍其中的时间序列分析预测法。
此方法是根据预测对象过去的统计数据找到其随时间变化的规律,建立时间序列模型,以推断未来数值的预测方法。
时间序列分析在微观经济计量模型、宏观经济计量模型以及经济控制论中有广泛的应用。
第一节时间序列简介所谓时间序列是指将同一现象在不同时间的观测值,按时间先后顺序排列所形成的数列。
时间序列一般用 ,,,,21n y y y 来表示,可以简记为}{t y 。
它的时间单位可以是分钟、时、日、周、旬、月、季、年等。
一、时间序列预测法时间序列预测法就是通过编制和分析时间序列,根据时间序列所反应出来的发展过程、方向和趋势,进行类推或延伸,借以预测下一段时间或以后若干年内可能达到的水平。
其内容包括:收集与整理某种社会现象的历史资料;将这些资料进行检查鉴别,排成数列;分析时间序列,从中寻找该社会现象随时间变化而变化的规律,得出一定的模型,以此模型去预测该社会现象将来的情况。
时间序列分析课件讲义共85页

时间序列分析课件讲义
11、获得的成功越大,就越令人高兴 。野心 是使人 勤奋的 原因, 节制使 人枯萎 。 12、不问收获,只问耕耘。如同种树 ,先有 根茎, 再有枝 叶,尔 后花实 ,好好 劳动, 不要想 太多, 那样只 会使人 胆孝懒 惰,因 为不实 践,甚 至不接 触社会 ,难道 你是野 人。(名 言网) 13、不怕,不悔地为每一个人祝福 。我爱 自己, 我用清 洁与节 制来珍 惜我的 身体, 我用智 慧和知 识充实 我的头 脑。 15、这世上的一切都借希望而完成。 农夫不 会播下 一粒玉 米,如 果他不 曾希望 它长成 种籽; 单身汉 不会娶 妻,如 果他不 曾希望 有小孩 ;商人 或手艺 人不会 工作, 如果他 不曾希 望因此 而有收 益。-- 马钉路 德。
1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事,无字句处读书。——周恩来 5、阅读使人充实,会谈使人敏捷,写作使人精确。——培根
时间序列分析课件.pptx
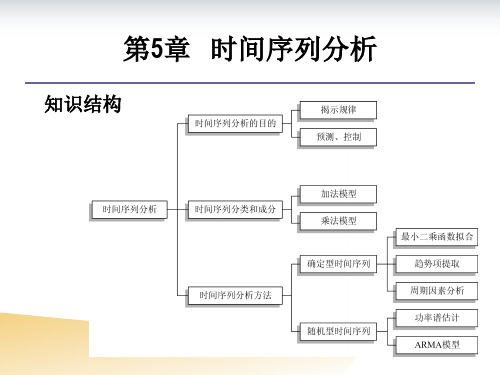
知识结构
第5章 时间序列分析
What is time series analysis?
Why to do ?
How to do?
日行迹
第5章 时间序列分析
时间序列
➢ 时间序列的概念 ➢ 时间序列的表示 ➢ 时间序列分析 ➢ 时间序列的分类 ➢ 时间序列的组合成分
时间序列分析方法
时间序列分析方法
时间序列分析的一般步骤: (1) 序列的预处理:如果原始序列为非等间隔序列,通常采用 曲线拟合及等距化重采样得到等距序列。 (2) 描述性时序分析:通过直观的数据比较或绘图观测,寻找 序列中蕴含的发展规律,往往可直观地判断序列是否具有趋势 项、周期变化等特性。 (3) 统计时序分析:计算时间序列的各种统计量,如均值,方 差,正态性检验等。利用统计特性剔除不符合统计规律的异常 样本。 (4) 判断时间序列的组合成分,对不同的成分采用不同的分析 方法。 (5) 利用不同成分的模型进行预测后叠加,得到最终的时间序 列预测值。
时间序列可能是应用最普遍的数据表现形式和数据存储格式。 在生物医学领域也存在着大量的时间序列,
人体从清晨到深夜的体温记录 人体餐后血糖浓度的变化 不同睡眠阶段的脑电波形等都是时间序列 。。。。。。
绝大多数情况下时间序列被看作为随机序列。
时间序列
时间序列的表示
X {x(T ), x(2T ),, x(kT )} {x[n]}
时间序列
时间序列分析
时间序列分析的实现是通过对观察值序列的性质进行推断,即 通过对历史观察值的分析预测而得出未来观察值的预测值。
cool! What will be next?
汽车发展的时间序列
时间序列
时间序列分析 时间序列分析的目的主要在于: (1) 描述事物在过去时间的状态。 (2) 分析事物发展变化的规律。 (3) 对事物的发展变化趋势进行预测或施加控制。
第5章时间序列的确定性分析

季节效应的提取
1945-1950费城月度降雨量
以月度数据为例: 季节指数
Sk xk x
季节指数之和为12
季节变差
Ck xk x
季节变差之和为0
季节效应的提取
季节指数
季节变差Biblioteka 季节效应的提取北京市1995-2000年月平均气温
以月度数据为例: 季节指数 Sk xk x
无法用:有负值
线性模型
Xt a bt It 参数估计方法
最小二乘估计
参数估计值 aˆ 8498.69, bˆ 89.12
最后看一下残差It是否 需要拟合ARMA模型
拟合效果图
趋势性提取的拟合法
对上海证券交易所每月末上证指数序列进行模型拟合
非线性模型 Xt a bt ct 2 It
数据图检验法:直观简单,主观性较强 自相关函数图检验法:样本自相关系数既不截尾,又不拖
尾,则序列{Xt}具有某种确定性趋势;当自相关系数接近 1时,则序列{Xt}具有线性趋势. 特征根检验法
趋势性分析
特征根检验法
原理:先对时间序列{Xt}建立适应性模型,利用该模型 的自回归部分参数所组成的特征方程的特征根λi的模来 检验趋势性.
提取. Xt f Tt , St ,Ct It Tt f1 t , St f2 t ,Ct f3 t , It :零均值白噪序列
第二节 趋势性分析
趋势性分析
长期趋势变动Tt
数据随时间而变化,呈现出不断增加或不断减少、或围绕 某一常数值波动而无明显增减变化的总趋势.
趋势性检验的方法:
•
4、越是无能的人,越喜欢挑剔别人的 错儿。 01:32:3 701:32: 3701:3 2Thursday, October 15, 2020
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
季节变差之和为0
季节效应的提取
北京市1995-2000年月平均气温
季节效应
周期趋势的拟合法 X-11方法简介
第五节 确定性时间序列的建模方法
确定性时间序列的建模方法
一个时间序列{Xt}通常可分解为:长期趋势变动Tt, 季节效应St和不规则变动因素It三部分的共同作用。 若对Tt和St建立时间t的确定性函数,使It成为零均 值的白噪声序列,就称为确定性时间序列分析.
常用的模型:
加法模型:Xt=Tt+St+It 乘法模型:Xt=Tt ·St ·It 混合模型:Xt=St+Tt ·It 或 Xt=Tt ·St+It
确定性时间序列的建模方法
对长期趋势变动Tt和季节效应St交织在一起的时间 序列,有以下两种建模方法:
季节指数模型方法:先对原始序列计算季节指数(或季节 变差),剔除季节效应后再对趋势性进行分析.
时间序列的确定性分析
一个时间序列{Xt}可分解为以下四部分的共同作用:
长期趋势变动Tt,季节效应St ,循环变动Ct ,不规则变动因 素It. (一般将循环变动和季节效应都称为季节性变化)
确定性分析:
对Tt、St和Ct 建立关于时间项t的多项式来提取信息,使It成 为零均值的白噪声序列;
该方法重视对确定性信息的提取,而忽视对随机性信息的
柱状统计图
确定性时间序列的建模
1993-2000年中国社会消费品零售总额的月度数据X
含趋势变动的季节指数模型方法:先进行适当的移动平 均,再计算季节指数,然后对剔除季节效应后的序列做 适当的趋势拟合.
确定性时间序列的建模
对1993-2000年中国社会消费品零售总额的月度数据X进 行确定性时间序列分析
时间序列图
确定性时间序列的建模
1993-2000年中国社会消费品零售总额的月度数据X
美国1961年1月—1985年12月 16-19岁失业女性的月度数据
美国1871年—1979年烟草 生产量的年度数据
时间序列模型
平稳时间序列
定义:常数均值,常数方差,(自)协方差函数只依赖于时 间的平移长度,而与时间的起止点无关。
模型:ARMA模型
非平稳时间序列
均值非平稳,方差和自协方差非平稳 处理方法:确定性分析,随机性分析
第五章 时间序列的确定性分析
第五章 时间序列的确定性分析
第一节 概述 第二节 趋势性分析 第三节 季节效应分析 第四节 X-11方法简介 第五节 确定性时间序列的建模方法
第一节 概述
非平稳时间序列
在实际应用中,我们经常会遇见不满足平稳性的时间序列, 尤其在经济领域和商业领域中的时间序列多数都是非平稳的
时间序列的确定性分析
理论依据:1961年的Cramer分解定理
任何一个时间序列{Xt}都可以分解为两部分的叠加:一 部分是由多项式决定的确定性趋势成分,另一部分是平 稳的零均值误差成分,即
d
Xt jt j Yt j0
其中d<∞,β0,β1,β2,…,βd是常系数,{Yt}是一个零均值的 平稳序列
趋势性的提取方法
平滑法
移动平均法:k期左侧移动平均,k期右侧移动平均, k期中心移动平均
指数平均法
拟合法:建立时间t的回归模型
常用的拟合模型:线性方程,二次曲线,指数曲线, 修正指数曲线,龚帕兹曲线,Logistic曲线
趋势性提取的拟合法
拟合澳大利亚政府1981-1990年每季度的消费支出序列
参数估计方法
最小二乘估计
参数估计值 Xt 502.252 0.095t2 It 最后看一下残差It是否
需要拟合ARMA模型
拟合效果图
第三节 季节效应分析
季节效应分析
在某些时间序列中,由于季节性变化(包括季度、月度、周度 等变化)或其他一些固有因素的变化,会存在一些明显的周期 性,这类序列称为季节性序列。
线性模型
Xt a bt It 参数估计方法
最小二乘估计
参数估计值 aˆ 8498.69, bˆ 89.12
最后看一下残差It是否 需要拟合ARMA模型
拟合效果图
趋势性提取的拟合法
对上海证券交易所每月末上证指数序列进行模型拟合
非线性模型 Xt a bt ct 2 It
提取. Xt f Tt , St ,Ct It Tt f1 t , St f2 t ,Ct f3 t , It :零均值白噪序列
第二节 趋势性分析
趋势性分析
长期趋势变动Tt
数据随时间而变化,呈现出不断增加或不断减少、或围绕 某一常数值波动而无明显增减变化的总趋势.
趋势性检验的方法:
若特征根存在两个实根,且其绝对值接近1,则序列{Xt} 存在线性趋势;若特征根存在n个实根,且其绝对值接近 1,则序列{Xt}存在n-1次多项式趋势;若特征根存在n个 实根,且其绝对值大于1,则序列{Xt}存在n个指数增加 趋势.
趋势性分析
数据图检验法 具有递增的趋势
趋势性分析
特征根检验法
数据图检验法:直观简单,主观性较强 自相关函数图检验法:样本自相关系数既不截尾,又不拖
尾,则序列{Xt}具有某种确定性趋势;当自相关系数接近 1时,则序列{Xt}具有线性趋势. 特征根检验法
趋势性分析
特征根检验法
原理:先对时间序列{Xt}建立适应性模型,利用该模型 的自回归部分参数所组成的特征方程的特征根λi的模来 检验趋势性.
在经济领域中,季节性序列更是随处可见。如季度时间序列、 月度时间序列、周பைடு நூலகம்时间序列等。
季节时间序列的重要特征表现为周期性
在一个序列中,如果经过S个时间间隔后观测点呈现出相似性, 比如同处于波峰或波谷,我们就说该序列具有以S为周期的周 期特性。
一般,季度资料的一个周期表现为一年的四个季度,月度资料 的周期表现为一年的12各月,周资料表现为一周的7天或5天。
季节效应的提取
1945-1950费城月度降雨量
以月度数据为例: 季节指数
Sk xk x
季节指数之和为12
季节变差
Ck xk x
季节变差之和为0
季节效应的提取
季节指数
季节变差
季节效应的提取
北京市1995-2000年月平均气温
以月度数据为例: 季节指数 Sk xk x
无法用:有负值
