静电纺丝法简介
静电纺丝技术在制备复合材料中的应用

静电纺丝技术在制备复合材料中的应用随着科技的发展,纳米材料作为一种新型材料,在各个领域开始逐渐发挥重要作用。
复合材料由于具有轻量、强度高、耐腐蚀等特点,成为了新一代使用广泛的材料。
静电纺丝技术作为一种制备纳米材料的方法,也为复合材料的制备提供了新的思路和手段。
1. 静电纺丝技术简介静电纺丝技术(Electrospinning)是指通过高电压作用下的静电场将液体喷出成纤维状的技术。
该技术的优点是可以制备直径在几纳米到几微米之间的高表面积纳米纤维,并且制备过程简单、成本低廉。
因此,静电纺丝技术在纳米材料的制备过程中得到了广泛的应用。
2. 制备复合材料的方法复合材料通常由两个或多个不同类型的材料经过加工处理后组合在一起形成新的材料。
因此,制备复合材料的方法具有多样性。
常见的制备复合材料方法有热压法、覆盖法以及浸渍法等。
3. 静电纺丝技术作为一种新型的材料制备方法,被广泛应用在复合材料的制备过程中。
具体应用方式包括以下几个方面:(1)制备纳米纤维加强体静电纺丝技术可以制备出大量直径在几纳米到几微米之间的高表面积纳米纤维。
这些纳米纤维作为复合材料中的加强体,可以显著提高复合材料的强度等物理性能。
(2)制备纳米纤维模板利用静电纺丝技术制备出的纳米纤维可以作为模板,骨架模型和低温烧蚀模板等等。
这些模板可以用于不同种类的复合材料制备中,可以控制所制得的材料的形貌和结构。
(3)制备纳米纤维复合材料在静电纺丝技术的制备过程中,可以将纳米纤维与其他材料混合在一起,最终形成纳米纤维复合材料。
这种复合材料不仅可以保留纳米材料的优良性能,同时也可以保留其他材料的特点,形成新的性能优越的复合材料。
4. 静电纺丝技术在未来发展中的应用前景随着静电纺丝技术的发展,越来越多的应用场景被开发出来。
未来,静电纺丝技术将在以下领域取得更广泛的应用:(1)医疗卫生领域:利用静电纺丝技术可以制备出纳米级别的药物输送系统和医用敷料等等。
(2)环境领域:通过静电纺丝技术可以制备出纳米级别的纤维膜,用于水处理、空气净化等领域。
静电纺丝的基本原理

静电纺丝的基本原理
静电纺丝是利用静电吸附的原理,使溶液中的带电粒子在电场作用下产生定向运动,从而制备纳米纤维材料。
这种技术可以在任意时间、任意空间、任何溶剂中进行。
目前,国内外研究主要集中在聚合物溶液和聚合物纳米纤维膜的制备。
静电纺丝原理
静电纺丝法是一种高效、经济的新型纳米材料制备方法。
目前,国内外在该领域的研究主要集中在以下几个方面:一是静电纺丝装置和工艺的研究,包括喷头、喷丝头、电极、接收装置等;二是不同材料的静电纺丝技术;三是静电纺纳米纤维膜的应用研究,包括纳米纤维膜作为锂电池隔膜和过滤材料等;四是静电纺丝设备与纳米纤维膜的表征方法研究。
静电纺纤维膜制备
1.聚合物溶液
目前,聚合物纳米纤维膜主要有两大类:一类是有机高分子聚合物(如聚苯乙烯、聚丙烯酸、聚乙烯醇等),另一类是无机
高分子聚合物(如氧化锌、氧化锆、氧化钛等)。
—— 1 —1 —。
静电纺丝技术的原理与纳米纤维制备方法

静电纺丝技术的原理与纳米纤维制备方法静电纺丝技术是一种常用于制备纳米纤维的方法,通过利用静电力将聚合物材料从液态转变为纤维状,具有较高的纤维直径可调性和良好的纤维组织结构控制能力。
本文将介绍静电纺丝技术的原理以及常用的纳米纤维制备方法。
一、静电纺丝技术的原理静电纺丝技术是利用静电力将高分子溶液或熔融物质直接纺丝成纤维的一种制备方法。
该技术基于静电现象,通过将高电压施加于过程中的高分子溶液或熔融物,使其电荷不平衡,形成电场分布。
当电场强度超过材料的电离场强度时,分子将逐渐变成带电的纳米尺寸细丝。
最后,带电的纤维在电场的作用下逐渐伸长并凝固成固态纤维。
静电纺丝技术的关键参数包括高电压、喷丝间距和收集距离。
高电压可以产生强大的静电力,促使溶液中的聚合物形成细丝。
喷丝间距决定了纤维形成的方式和纤维直径。
收集距离可以影响纤维凝固形态和纤维排列结构。
静电纺丝技术的原理简单而直观,适用于制备各种类型的纳米纤维材料,因此在纳米材料制备领域具有广泛的应用前景。
二、常用的纳米纤维制备方法1. 单向静电纺丝法单向静电纺丝法是静电纺丝技术中最基本、最常用的制备方法之一。
在该方法中,高电压施加于旋转的喷丝头和静置的收集器之间,通过控制高电压和喷丝间距,可以得到直径均匀、纤维排列有序的纳米纤维。
2. 多向静电纺丝法多向静电纺丝法在单向静电纺丝法的基础上进行了改进,通过使用多根喷丝头和多个收集器,使得纤维的纺织方向更加多样化。
这种方法可以制备出多孔的纳米纤维薄膜,应用于过滤、分离和组织工程等领域。
3. 旋转盘静电纺丝法旋转盘静电纺丝法是利用旋转盘上的多个喷丝孔,将高分子溶液均匀喷洒在盘面上,通过旋转盘和静电作用将纤维逐渐形成。
这种方法制备的纳米纤维表面光滑均匀,适用于电子器件、传感器和催化剂支撑材料等领域。
4. 共喷纺丝法共喷纺丝法是在静电纺丝过程中,将两种或多种不同的高分子溶液或熔融物质通过不同的喷丝孔同时喷射到收集器上。
静电纺丝技术

静电纺丝技术静电纺丝技术是利用高压静电作用使聚合物溶液或熔体带电并发生形变,在喷头末端处形成悬垂的锥状液滴,当液滴表面静电斥力大于其表面张力时,液滴表面就会喷射出高速飞行的射流,并在较短的时间内经电场力拉伸、溶剂挥发、聚合物固化形成纤维。
所获得的静电纺纤维直径小、比表面积大,同时纤维膜还具有孔径小、孔隙率高、孔道连通性好等优势,在过滤、传感、医疗卫生以及自清洁等领域具有广泛的应用。
1静电纺丝的起源与发展静电纺丝起源于200多年前人们对静电雾化过程的研究。
1745年,Bose通过对毛细管末端的水表面施加高电势,发现其表面将会有微细射流喷出,从而形成高度分散的气溶胶,并得出该现象是由液体表面的机械压力与电场力失衡所引起的。
1882年,Rayleigh指出当带电液滴表面的电荷斥力超过其表面张力时,就会在其表面形成微小的射流,并对该现象进行理论分析总结,得到射流形成的临界条件。
1902年,Cooley与Morton申请了第一个利用电荷对不同挥发性液体进行分散的专利。
随后Zeleny研究了毛细管端口处液体在高压静电作用下的分裂现象,通过观察总结出几种不同的射流形成模型,认为当液滴内压力与外界施加压力相等时,液滴将处于不稳定状态。
基于上述的基础研究,1929年,Hagiwara公开了一种以人造蚕丝胶体溶液为原料,通过高压静电制备人造蚕丝的专利。
1934年,Formhals设计了一种利用静电斥力来生产聚合物纤维的装置并申请了专利,该专利首次详细介绍了聚合物在高压电场作用下形成射流的原因,这被认为是静电纺丝技术制备纤维的开端。
从此,静电纺丝技术成为了一种制备超细纤维的有效可行方法。
1966年,Simons发明了一种生产静电纺纤维的装置,获得了具有不同堆积形态的纤维膜。
20世纪60年代,Taylor在研究电场力诱导液滴分裂的过程中发现,随着电压升高,带电液体会在毛细管末端逐渐形成一个半球形状的悬垂液滴,当液滴表面电荷斥力与聚合物溶液表面张力达到平衡时,带电液滴会变成圆锥形;当电荷斥力超过表面张力时,就会从圆锥形聚合物液滴表面喷射出液体射流。
静电纺丝资料
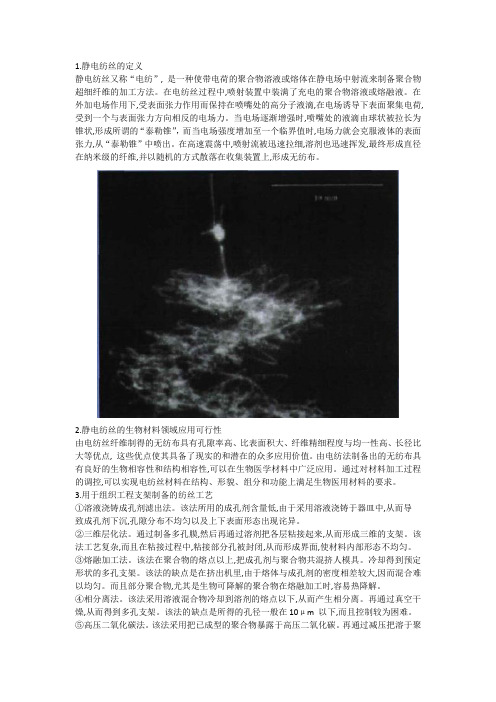
1.静电纺丝的定义静电纺丝又称“电纺”, 是一种使带电荷的聚合物溶液或熔体在静电场中射流来制备聚合物超细纤维的加工方法。
在电纺丝过程中,喷射装置中装满了充电的聚合物溶液或熔融液。
在外加电场作用下,受表面张力作用而保持在喷嘴处的高分子液滴,在电场诱导下表面聚集电荷, 受到一个与表面张力方向相反的电场力。
当电场逐渐增强时,喷嘴处的液滴由球状被拉长为锥状,形成所谓的“泰勒锥”,而当电场强度增加至一个临界值时,电场力就会克服液体的表面张力,从“泰勒锥”中喷出。
在高速震荡中,喷射流被迅速拉细,溶剂也迅速挥发,最终形成直径在纳米级的纤维,并以随机的方式散落在收集装置上,形成无纺布。
2.静电纺丝的生物材料领域应用可行性由电纺丝纤维制得的无纺布具有孔隙率高、比表面积大、纤维精细程度与均一性高、长径比大等优点, 这些优点使其具备了现实的和潜在的众多应用价值。
由电纺法制备出的无纺布具有良好的生物相容性和结构相容性,可以在生物医学材料中广泛应用。
通过对材料加工过程的调控,可以实现电纺丝材料在结构、形貌、组分和功能上满足生物医用材料的要求。
3.用于组织工程支架制备的纺丝工艺①溶液浇铸成孔剂滤出法。
该法所用的成孔剂含量低,由于采用溶液浇铸于器皿中,从而导致成孔剂下沉,孔隙分布不均匀以及上下表面形态出现诧异。
②三维层化法。
通过制备多孔膜,然后再通过溶剂把各层粘接起来,从而形成三维的支架。
该法工艺复杂,而且在粘接过程中,粘接部分孔被封闭,从而形成界面,使材料内部形态不均匀。
③熔融加工法。
该法在聚合物的熔点以上,把成孔剂与聚合物共混挤人模具。
冷却得到预定形状的多孔支架。
该法的缺点是在挤出机里,由于熔体与成孔剂的密度相差较大,因而混合难以均匀。
而且部分聚合物,尤其是生物可降解的聚合物在熔融加工时,容易热降解。
④相分离法。
该法采用溶液混合物冷却到溶剂的熔点以下,从而产生相分离。
再通过真空干燥,从而得到多孔支架。
该法的缺点是所得的孔径一般在10μm 以下,而且控制较为困难。
静电纺丝资料

1.静电纺丝的定义静电纺丝又称“电纺”, 是一种使带电荷的聚合物溶液或熔体在静电场中射流来制备聚合物超细纤维的加工方法。
在电纺丝过程中,喷射装置中装满了充电的聚合物溶液或熔融液。
在外加电场作用下,受表面张力作用而保持在喷嘴处的高分子液滴,在电场诱导下表面聚集电荷, 受到一个与表面张力方向相反的电场力。
当电场逐渐增强时,喷嘴处的液滴由球状被拉长为锥状,形成所谓的“泰勒锥”,而当电场强度增加至一个临界值时,电场力就会克服液体的表面张力,从“泰勒锥”中喷出。
在高速震荡中,喷射流被迅速拉细,溶剂也迅速挥发,最终形成直径在纳米级的纤维,并以随机的方式散落在收集装置上,形成无纺布。
2.静电纺丝的生物材料领域应用可行性由电纺丝纤维制得的无纺布具有孔隙率高、比表面积大、纤维精细程度与均一性高、长径比大等优点, 这些优点使其具备了现实的和潜在的众多应用价值。
由电纺法制备出的无纺布具有良好的生物相容性和结构相容性,可以在生物医学材料中广泛应用。
通过对材料加工过程的调控,可以实现电纺丝材料在结构、形貌、组分和功能上满足生物医用材料的要求。
3.用于组织工程支架制备的纺丝工艺①溶液浇铸成孔剂滤出法。
该法所用的成孔剂含量低,由于采用溶液浇铸于器皿中,从而导致成孔剂下沉,孔隙分布不均匀以及上下表面形态出现诧异。
②三维层化法。
通过制备多孔膜,然后再通过溶剂把各层粘接起来,从而形成三维的支架。
该法工艺复杂,而且在粘接过程中,粘接部分孔被封闭,从而形成界面,使材料内部形态不均匀。
③熔融加工法。
该法在聚合物的熔点以上,把成孔剂与聚合物共混挤人模具。
冷却得到预定形状的多孔支架。
该法的缺点是在挤出机里,由于熔体与成孔剂的密度相差较大,因而混合难以均匀。
而且部分聚合物,尤其是生物可降解的聚合物在熔融加工时,容易热降解。
④相分离法。
该法采用溶液混合物冷却到溶剂的熔点以下,从而产生相分离。
再通过真空干燥,从而得到多孔支架。
该法的缺点是所得的孔径一般在10μm 以下,而且控制较为困难。
静电纺丝的原理及应用

静电纺丝的原理及应用静电纺丝就是高分子流体静电雾化的特殊形式,此时雾化分裂出的物质不是微小液滴,而是聚合物微小射流,可以运行相当长的距离,最终固化成纤维。
静电纺丝是一种特殊的纤维制造工艺,聚合物溶液或熔体在强电场中进行喷射纺丝。
在电场作用下,针头处的液滴会由球形变为圆锥形(即“泰勒锥”),并从圆锥尖端延展得到纤维细丝。
这种方式可以生产出纳米级直径的聚合物细丝。
原理将聚合物溶液或熔体带上几千至上万伏高压静电,带电的聚合物液滴在电场力的作用下在毛细管的Taylor锥顶点被加速。
当电场力足够大时,聚合物液滴克服表面张力形成喷射细流。
在细流喷射过程中溶剂蒸发或固化,最终落在接收装置上,形成类似非织造布状的纤维毡。
装置静电纺丝的装置主要由推进泵、注射器、高压电源以及接收装置组成。
其中,高压电源的正极与负极分别与注射器针头和接收装置相连,而接收装置的形式也是多样化的,可以是静止的平面、高速转动的滚筒或者圆盘。
纺丝的参数设置、环境条件等对纺丝过程的影响至关重要。
影响因素静电纺丝法制备纳米纤维的影响因素很多,这些因素可分为溶液性质,如黏度、弹性、电导率和表面张力;控制变量,如毛细管中的静电压、毛细管口的电势和毛细管口与收集器之间的距离;环境参数,如溶液温度、纺丝环境中的空气湿度和温度、气流速度等。
溶液黏度对纤维性能的影响同轴静电纺丝同轴静电纺是在静电纺的基础上改造而来,其基本原理是在两个内径不同但同轴的毛细管中分别注入芯质和壳质溶液,二者在喷头末端汇合,在电场力的作用下固化成为复合纳米纤维。
同轴静电纺丝解决了纺丝时纺丝液必须是均一体系的缺陷,所制备的同轴纤维在均匀性、连续性上都优于其它方法得到的纤维。
采用同轴静电纺丝的方法可以制得中空纤维和纳米复合纤维等。
应用静电纺丝技术制备的纳米纤维,具有比表面积大、孔隙率高、尺寸容易控制、表面易功能化(如表面涂覆、表面改性)等特点,在许多领域都有重要的应用价值。
静电纺丝技术在构筑一维纳米结构材料领域已发挥了非常重要的作用,应用静电纺丝技术已经成功的制备出了结构多样的纳米纤维材料。
静电纺丝技术在生物医学材料中的应用

静电纺丝技术在生物医学材料中的应用在当今医疗技术日益发展的背景下,生物医学材料的制备与应用也得到了越来越多的关注。
静电纺丝技术是一种在纳米级别下制备纤维的有效方法,其具有制备方便、纤维成型性好以及纤维直径可控等优点。
因此,此技术已经被广泛应用于生物医学材料的制备领域。
一、静电纺丝技术简介静电纺丝( electrospinning )是一种将高分子聚合物或其他材料从液态到固态的过程。
这种方法通过电荷作用来形成超细的纤维。
首先,将聚合物或其他材料加入强电场的环境中,然后在空气流与材料纤维形成的过程中,材料逐渐凝固成纤维,从而形成高度纯化的纤维材料。
这种技术具有以下优点:1、成本低廉:相对于其他聚合物替代品,静电纺丝的操作成本相对较低,不需要很多特殊的仪器和设备。
2、成型性能好:静电纺丝有很好的形态定制和直径控制。
3、纤维直径可控:相对于光刻技术,纤维直径可以通过参数调节来控制。
二、静电纺丝技术在生物医学材料中的应用材料科学家们已经意识到静电纺丝与制备生物医学材料有着天然的联系。
从微观尺度到宏观尺度的一些特别材料结构已探索过。
纤维的化学性质可以被修改,以控制某些方面的匹配和生物相容性。
1、组织工程组织工程是一种在人体内重建生理组织的新兴技术,以帮助完全或部分恢复器官和人体部分功能。
静电纺丝技术可以用于制造纳米纤维支架用于组织重建。
由于纤维直径可以精确地控制,因此可以制造出具有足够机械强度和生物兼容性的组织工程支架。
2、药物输送静电纺丝可以制备药物输送体系,这样可以使药物在一定程度上被控制释放。
药物输送系统通常是由传统抗生素补充浓度谷内的微粒组成。
通过其中非常细的纤维可以达到控制药物输送的效果。
这种药物输送体系具有高效和低碳排放的特点,这些特点足以成为未来医疗行业的重要研究方向。
3、细胞培养基静电纺丝技术可以制备纳米级的纤维,在纤维表面可以加入细胞吸附剂,从而使纤维表面产生空气孔洞,增加生物操作的空气流和培养效果。
静电纺丝技术制备纳米纤维膜研究

静电纺丝技术制备纳米纤维膜研究纳米材料在科技领域有着广泛应用,其中纳米纤维膜是一种重要的纳米材料。
静电纺丝技术是制备纳米纤维膜的一种常见方法,下面将详细介绍静电纺丝技术制备纳米纤维膜的原理、优势和应用。
一、静电纺丝技术的原理静电纺丝技术又称为电纺法、纺织电晕法等,是一种制备高分子材料纳米纤维膜的方法。
该技术使用高压电场使稀溶液产生强烈的电荷,经过过度拉伸后会产生电极化、沉积和电晕等现象,最终将溶液转变为具有纳米级直径的纤维。
静电纺丝技术的制备过程主要分为三个步骤:①将高分子溶解于有机溶剂中,制备出高分子稀溶液;②通过静电势场,将稀溶液产生电极化和增加表面能;③将带电的液滴通过冷凝作用凝聚成为纳米纤维膜。
二、静电纺丝技术的优势(1)高纳米纤维膜产量:静电纺丝技术可以同时制备多个纳米纤维膜,可大幅提高产量。
(2)低成本、高效率:静电纺丝技术制备的纳米纤维膜采用的有机溶剂可以再生利用,不仅成本低,而且制备速度非常快。
(3)纳米纤维膜直径可调:可以通过调节静电场、流量、距离和喷嘴的直径等参数,控制纳米纤维膜的大小,进一步优化纳米纤维膜的性质。
三、静电纺丝技术的应用(1)纳米滤膜:静电纺丝技术可以制备出高效纳米滤膜,例如空气过滤器和水处理过滤器等。
(2)纳米材料:纳米纤维膜可以用于制备纳米材料,例如非常完美的是一簇具有纤维维度的SiO2微晶。
(3)医用纱线:静电纺丝技术可以制备含有药物的医用纱线,用于缓释药物,使药物更加高效和准确。
总之,静电纺丝技术作为制备纳米纤维膜的一种常见方法,具有优越性能,并有着广泛的应用前景。
在未来的生产和科研中,这种技术将大大促进纳米材料的发展和应用。
静电纺丝技术及其应用

静电纺丝技术及其应用一、静电纺丝技术的原理与发展静电纺丝技术是一种自然界广泛存在的电纺技术,是利用电场作用将高分子液体或熔融高分子材料拉细,形成纤维的方法。
它与传统纺织方法不同,不需要梳理、捻合等步骤,能够制备纤维直径极小、比表面积极大的材料,并实现单纤维生产。
最早使用静电纺丝技术的是工业领域,在聚合物纺织品、人造革、电子产品等领域得到广泛应用。
但随着纳米科技的发展,静电纺丝技术也逐渐被应用于纳米材料的制备领域,如纳米纤维、纳米颗粒、纳米管、纳米膜等。
现在,静电纺丝技术已成为制备纳米材料的一种重要方法之一。
二、静电纺丝技术的优点与传统纺丝技术相比,静电纺丝技术的优点主要有以下几个方面:1、制备出的材料具有高比表面积和高通量;2、生产的纤维具有较小的直径和高的拉伸强度;3、制备出的纤维可以进行多级处理,并且可以降解;4、生产的成本相对较低,同时可以进行大规模生产。
三、静电纺丝技术在各个领域的应用1、纺织领域静电纺丝技术可以制备出具有高性能、高强度的纤维,这些纤维可以应用于高科技纺织品、航空航天材料、医用纺织品等领域。
2、药物载体静电纺丝技术可以制备出具有高比表面积和大孔径的微纳米纤维,这些纤维可以作为一种药物载体,有利于药物的缓释和控制释放。
3、环保领域静电纺丝技术可以应用于制备过滤材料,可以去除空气中的PM2.5等有害物质,同时可以制备海绵材料,具有吸油、吸水、吸附等功能。
4、能源领域静电纺丝技术可以制备出具有多孔结构的纳米材料,这些材料可以用于能源储存和转换,如制备锂离子电池、柔性太阳能电池等。
四、静电纺丝技术未来的发展随着纳米科技的不断发展,静电纺丝技术也在不断地完善和发展。
未来,它有望进一步提高产量、降低成本、改善稳定性,进而在更多领域得到广泛应用。
此外,近年来,一些新型静电纺丝技术不断涌现,如强场静电纺丝技术、高速静电纺丝技术等,这些新技术的出现将促进静电纺丝技术的进一步发展和应用。
静电纺丝法

静电纺丝法引言静电纺丝法是一种常用的纺丝技术,通过利用静电相互作用将高分子溶液纺丝成纤维。
由于其制备工艺简单、能够制备出细纤维且具有较好的物理性能,因此在纺织、材料科学等领域得到了广泛的应用。
原理静电纺丝法的主要原理是利用静电相互作用将高分子溶液或熔融物纺丝成纤维。
其过程可以分为三个阶段:1. 液滴形成阶段高分子溶液通过喷嘴喷出后,由于表面张力的作用会形成液滴。
液滴的大小和形状可以通过控制喷嘴直径和溶液流量来调节。
2. 液滴伸长阶段在液滴形成后,作用于液滴表面的静电力会使得液滴开始伸长。
静电力与表面电荷的分布有关,通常通过在液滴处加高电压来调节。
3. 纤维凝固阶段在液滴伸长过程中,由于溶剂的挥发或者高分子的凝固,获取稳定的纤维。
这可以通过调节溶液的成分和环境条件来实现。
工艺参数的调节在静电纺丝过程中,有许多工艺参数可以调节,以获得所需的纤维性能和形态。
1. 电压电压是影响纤维形貌和尺寸的重要参数。
通常,随着电压的增加,纤维的直径会减小。
但是过高的电压可能会引起喷嘴堵塞或纤维断裂。
2. 喷嘴与收集器之间的距离喷嘴与收集器之间的距离也会影响纤维的形貌和尺寸。
一般来说,距离增加会导致纤维变细,但同时也会增加纤维的飘动和断裂的风险。
3. 溶液浓度和流量溶液浓度和流量的变化会影响纤维的形态。
浓度过高会导致纤维变粗,而过低则会导致纤维断裂。
4. 环境条件环境条件,如湿度和温度也会对纤维形态产生影响。
例如,较高的湿度会使纤维形成过程中的溶剂挥发速度减慢,而较低的湿度则相反。
应用领域静电纺丝法在纺织工业、材料科学和生物医学等领域得到了广泛应用。
1. 纺织工业静电纺丝法可以制备出细纤维,这些纤维具有较大的比表面积和良好的透气性,因此在纺织品中可以用于制备高性能过滤材料、细纤维布料等。
2. 材料科学静电纺丝法可以制备出纳米级的纤维膜。
这种膜具有良好的孔隙结构和表面活性,被广泛应用于电池、传感器、分离膜等领域。
3. 生物医学静电纺丝法可以制备出生物可吸收的纤维,这对于组织工程和药物缓释有重要意义。
静电纺丝原理和影响因素

静电纺丝原理和影响因素静电纺丝法即聚合物喷发静电拉伸纺丝法,与传统办法天壤之别。
首先将聚合物溶液或熔体带上几千至上万伏高压静电,带电的聚合物液滴在电场力的效果下在毛细管的Taylor锥极点被加快。
当电场力足够大时,聚合物液滴战胜外表张力构成喷发细流。
细流在喷发进程中溶剂蒸腾或固化,终究落在接纳设备上,构成相似非织造布状的纤维毡。
在静电纺丝进程中,液滴一般具有必定的静电压并处于一个电场傍边,因而,当射流从毛细管末端向接纳设备运动时,都会出现加快现象,然后导致了射流在电场中的拉伸。
一、静电纺丝中射流的不稳定性不稳定性是一种所谓的传递现象,即导致活动不稳定性的每一种形式可能起源于某一扰动或涨落,它会随时间以不同速率而扩展。
静电纺丝中有3种不稳定性,第一种是黏性不稳定性,首要是毛细力与黏性力的效果引起的。
别的两种不稳定性是电的实质引起的其一为轴对称的曲张不稳定性,即因表而电荷密度在切向电场中遭到的力而引起,这种力与粘度和谐效果引起丝的轴对称形变和活动;其二为非轴对称的曲折不稳定性,即流体的偶极和电荷发作涨落,在电场中轴的法向上受力发生曲折。
静电纺射流可能表现出某一种或多种不同的不稳定性形式,取决于射流速度、半径和外表电荷密度等基本参数。
近年来静电纺丝理论研究首要选用最简化的线性近似剖析,而研究这些稳定性关于深入研究静电纺丝进程具有重要意义。
二、静电纺丝的影响要素静电纺丝法制备纳米纤维的影响要素许多,这些要素可分为溶液性质,如粘度、弹性、电导率和外表张力;控制变量,如毛细管中的静电压、毛细管口的电势和毛细管口与收集器之问的间隔;环境参数,如溶液温度、纺丝环境中的空气湿度和温度、气流速度等。
其间首要影响要素包含:1.聚合物溶液浓度聚合物溶液浓度越高,粘度越大,外表张力越大,而脱离喷嘴后液滴割裂才能随外表张力增大而削弱。
一般在其它条件恒守时,跟着浓度增加,纤维直径增大。
2.电场强度随电场强度增大,高分子静电纺丝液的射流有更大的外表电荷密度,因而有更大的静电斥力。
静电纺丝技术及其研究进展

静电纺丝技术的未来发展
静电纺丝技术的未来发展
静电纺丝技术未来的发展将聚焦于提高生产效率、拓展应用领域以及实现绿 色生产等方面。具体来说,以下几个方面值得:
静电纺丝技术的未来发展
1、生产效率:提高生产效率是静电纺丝技术的重要发展方向。未来可以通过 优化生产工艺、引入新型设备等方式提高静电纺丝技术的生产效率,以满足日益 增长的市场需求。
静电纺丝技术的原理与特点
静电纺丝技术的原理与特点
静电纺丝技术是一种利用静电场牵引高分子流体进行定向排列和固化成纤维 的方法。在静电纺丝过程中,高分子流体受到静电场的牵引力,会在负电极表面 形成一层液膜,液膜在静电场中会逐渐变薄并最终固化成纤维。静电纺丝技术具 有以下特点:
静电纺丝技术的原理与特点
1、可制备纳米级纤维材料:静电纺丝技术可以制备出直径为纳米级别的纤维 材料,具有极高的比表面积和孔隙率,有利于提高材料的吸附性能和过滤效率。
静电纺丝技术的原理与特点
2、适用范围广泛:静电纺丝技术可以用于制备各种高分子材料、金属材料和 无机材料等,具有广泛的适用性。
静电纺丝技术的原理与特点
3、生产效率高:静电纺丝技术可以实现大规模生产,有利于降低生产成本和 推广应用。
静电纺丝技术的研究进展
1、静电纺丝技术的分类及其法
静电纺丝技术根据纺丝液的物理状态可以分为溶液静电纺丝和熔体静电纺丝 两种。溶液静电纺丝是将高分子溶液通过注射器注入到电场中,然后高分子溶液 在电场中形成纤维;熔体静电纺丝是将高分子材料加热到熔点以上,通过喷头形 成细丝,然后在电场中固化成纤维。
静电纺丝技术的分类
2、熔体静电纺丝:熔体静电纺丝是将高分子材料加热到熔点以上,然后通过 静电场的作用拉伸成丝。该方法适用于制备高温性能优良的纤维材料。熔体静电 纺丝的优点是可加工温度高,缺点是对于热敏性材料可能会导致热损伤。
静电纺丝技术制备纤维材料

静电纺丝技术制备纤维材料静电纺丝技术是一种重要的纤维制备方法,通过利用静电力将高分子材料以纤维的形态从导丝器喷射出来,经过固化处理后形成纤维材料。
该技术具有简单、高效、低成本、可控性强等优势,逐渐发展成为纤维材料制备领域的关键技术之一。
静电纺丝技术的基本原理是利用静电力将高分子溶液或熔体形成的单体或聚合物喷射到一个带有电荷的金属导丝上,然后通过控制静电力的强度和喷射速度,使高分子材料在导丝上逐渐凝聚成纤维状。
最后,经过固化处理,纤维材料获得其最终的物理和化学性质。
静电纺丝技术具有广泛的应用领域,可以制备各种类型的纤维材料。
首先,该技术可以用于制备纤维素基材料,如生物降解的纺织纤维、纸浆纤维等。
其次,基于静电纺丝技术,可以制备各种合成高分子材料的纤维,如聚酯纤维、聚酰胺纤维、聚乙烯纤维等。
此外,静电纺丝技术还可以应用于制备金属纳米线、复合纤维材料、纳米纤维膜等。
这些纤维材料在纺织、医学、电子、环境领域等都有着广泛的应用。
静电纺丝技术在实际应用中具有很多优势。
首先,该技术可以制备出直径很细的纤维,具有高比表面积和高孔隙度,这些特性使得其在吸附、过滤、传感、增强材料等方面具有广泛的应用空间。
其次,静电纺丝技术可以通过改变静电力的参数和控制喷射速度,实现对纤维形态、结构和性能的精确调控。
这使得纤维材料可以根据不同需求进行设计和定制。
此外,静电纺丝技术还具有简单、高效、低成本的特点,适用于大规模生产和工业化制备。
然而,静电纺丝技术也存在一些挑战和局限性。
首先,由于静电纺丝过程中纤维的形成主要依赖静电力,在湿度较高的环境下容易出现纤维形变、聚集和团块等问题。
其次,静电纺丝技术对高分子材料的物理和化学性质有一定的要求,例如材料的表面张力、电导率、粘度等。
这些限制了纤维材料的种类和应用范围。
此外,静电纺丝技术在工业化生产中需要考虑纤维形态的均一性和稳定性,以及设备的性能和可靠性等问题。
综上所述,静电纺丝技术作为一种纤维材料制备方法,具有广泛的应用前景和潜力。
静电纺丝技术及纳米材料制备

静电纺丝技术及纳米材料制备静电纺丝技术是一种制备纤维材料的方法,通过利用静电力将聚合物溶液或熔融聚合物纺丝,形成纤维结构。
这种技术具有简单、高效、低成本等优点,被广泛应用于纺织、医疗、能源存储等领域的纤维材料制备中。
一、静电纺丝技术原理静电纺丝技术基于静电力的作用原理。
当电荷分布不均匀时,电荷会在物体表面产生电场,电荷越多,电场越强。
在静电纺丝中,聚合物溶液或熔融聚合物通过电极以高压喷射出来,并受到地板或收集器等静电场的作用,使聚合物形成纤维状结构。
当喷射的溶液或熔融物靠近地面或收集器时,由于电场的作用,产生电荷的重新分布,使得纤维形成。
整个过程可以分为充电、喷射、伸长和固化等阶段。
在静电纺丝过程中,有几个关键参数需要控制,包括喷丝液体的浓度、电压和喷丝距离。
喷丝液体的浓度决定了溶液或熔融物的黏度和流动性,如果浓度过高,会导致喷液团块的形成,影响纤维的质量,如果浓度过低,则纤维容易断裂。
电压的选取与纤维直径有关,通常较高的电压可获得较小直径的纤维。
喷丝距离也会影响纤维的形成,过大的距离会导致纤维断裂,过小的距离则可能引起纤维交织。
静电纺丝技术依赖于材料的流动性和电荷传输能力。
通常使用具有高分子链段的聚合物作为溶液或熔融物,这些高分子具有良好的流动性和很强的电荷传导性,有利于纤维的形成。
二、纳米材料制备纳米材料是具有粒径在1-100纳米之间的材料,具有许多特殊的物理、化学和力学特性,在纳米科技领域具有广泛的应用前景。
纳米材料的制备方法多种多样,其中静电纺丝技术是一种高效、简单且可量产的制备方法。
使用静电纺丝技术制备纳米材料可以通过多种途径实现。
一种方法是在聚合物溶液中加入纳米粒子,使得纳米粒子在静电场作用下与聚合物一起喷射形成纳米复合纤维。
这种方法可以制备纳米复合材料,具有纳米尺度的颗粒分布和增强的力学性能。
另一种方法是利用静电纺丝技术直接制备纳米纤维。
通过调整聚合物溶液中的高分子链段长度和浓度,可以获得直径在几十纳米以下的纳米纤维。
静电纺丝技术的工艺原理及应用

静电纺丝技术的工艺原理及应用静电纺丝技术是目前制备纳米纤维最重要的基本方法。
这一技术的核心是使带电荷流体在静电场中流动与变形,最终得到纤维状物质,从而为高分子成为纳米功能材料提供了一种新的加工方法。
由于纳米纤维具有许多特性,例如纤维纤度细、比表面积大、孔隙率高,因而具有广泛的应用。
1、静电纺技术静电纺是一项简单方便、廉价而且对环境无污染的纺丝技术。
早在20世纪30年代,Formals A就已经在其专利中报道了利用高压静电纺丝,但是直到近些年,由于对纳米科技研究的迅速升温,激起了人们对这种可制备纳米尺寸纤维的纺丝技术进行深入研究的浓厚兴趣。
1.1 静电纺技术的基本原理静电纺丝技术(Electrospinning fiber technique)是使带电的高分子溶液(或熔体)在静电场中流动变形,经溶剂蒸发或熔体冷却而固化,从而得到纤维状物质的一种方法。
对聚合物纤维电纺过程的图式说明见图1。
静电纺丝机的基本组成主要有3个部分:静电高压电源、液体供给装置、纤维收集装置。
静电高压电源根据电流变换方式可以分成DC/DC和AC/DC两种类型,实验中多用IX;/DC电源。
液体供给装置是一端带有毛细管的容器(如注射器),其中盛有高分子溶液或熔体,将一金属线的一端伸进容器中,使液体与高压电发生器的正极相连。
纤维收集装置是在毛细管相对端设置的技术收集板,可以是金属类平面(如锡纸)或者是旋转的滚轮等。
收集板用导线接地,作为负极,并与高压电源负极相连。
另外随着对实验要求的提高,液体流量控制系统也被渐渐的采用,这样可以将液体的流速控制得更准确。
电场的大小与毛细管口聚合物溶液的表面张力有关。
由于电场的作用,聚合物溶液表面会产生电荷。
电荷相互排斥和相反电荷电极对表面电荷的压缩,均会直接产生一种与表面张力相反的力。
当电场强度增加时,毛细管口的流体半球表面会被拉成锥形,称为Taylor锥。
进一步增加电场强度,是用来克服表面张力的静电排斥力到达一个临界值,此时带电射流从Taylor锥尖喷射出来。
静电纺丝法制备纳米材料

绿色能源:纳 米材料可用于 提高能源效率 如太阳能电池、 燃料电池等降 低能源消耗和 减少环境污染。
在其他领域的应用
生物医学:用于药物输送、组织工程和生物成像 环境科学:用于空气和水的净化以及重金属的去除 能源领域:用于太阳能电池、燃料电池和超级电容器等 电子学:用于制造柔性电极、传感器和电路等
癌症治疗:静电纺丝技术制备的纳米纤维可以用于光热治疗、光动力治 疗等新型癌症治疗方法提高治疗效果并降低副作用。
在环保领域的应用
空气净化:静 电纺丝法制备 的纳米材料可 用于空气过滤 有效去除空气 中的颗粒物和
有害气体。
水处理:制备 具有高效吸附 性能的纳米材 料用于水体中 污染物的去除
和Hale Waihona Puke 化。土壤修复:利 用静电纺丝技 术制备的纳米 材料可改善土 壤质量降低重
金属纳米材料
陶瓷纳米材料
高分子纳米材料
复合纳米材料
制备过程的可控制性
静电纺丝法制备纳米材料的过程可以通过调整工艺参数实现精确控制 该方法可以制备出具有一致结构和性能的纳米材料适用于大规模生产 通过控制纺丝液的成分和浓度可以实现对纳米材料的成分和性能的调控 静电纺丝法制备纳米材料的过程简单易行成本较低具有较高的经济效益
Prt One
单击添加章节标题
Prt Two
静电纺丝技术简介
静电纺丝技术的原理
高压静电产生:通过产生高压 静电场使纺丝液带电
纺丝液变形:在静电场的作用 下纺丝液发生变形
纺丝液喷射:通过喷头将纺丝 液喷射到接收装置上
溶剂挥发固化:纺丝液在喷射 过程中溶剂挥发形成固态纤维
静电纺丝技术的发展历程
早期探索阶段: 20世纪初科学 家开始尝试利 用静电纺丝技 术制备聚合物
静电纺丝法

静电纺丝法一、简介静电纺丝法是一种制备纳米级纤维的方法,也称为电纺法、电喷雾法。
该方法利用高压电场将聚合物液体或溶液中的高分子物质拉伸成极细的纤维,形成具有高比表面积和大孔隙度的纳米级材料。
静电纺丝法被广泛应用于生物医学、环境保护、能源储存等领域。
二、原理静电纺丝法基于高压电场作用下的毛细流动现象。
在高压电场作用下,聚合物液体或溶液中的高分子物质被拉伸成极细的纤维,并在空气中自由落体形成非常薄的纤维网。
这些纤维网具有非常大的比表面积和孔隙度,能够提供更多活性位点和更好的传质性能。
三、设备静电纺丝法主要包括以下设备:高压发生器、聚合物溶液输送系统、旋转收集器等。
其中,高压发生器是实现静电场作用下毛细流动现象必不可少的设备,聚合物溶液输送系统用于将聚合物液体或溶液输送到高压发生器中,旋转收集器用于收集纤维网。
四、操作步骤1. 准备聚合物溶液:将所需的聚合物溶解在适量的有机溶剂中,制备成所需浓度的聚合物溶液。
2. 调整高压发生器:根据聚合物溶液的性质和所需纤维尺寸调整高压发生器的参数。
3. 开始静电纺丝:将调整好的聚合物溶液输送到高压发生器中,启动高压发生器,使其产生静电场作用下毛细流动现象。
4. 收集纤维网:将旋转收集器放置在高压发生器下方,收集从高压发生器中产生的纤维网。
五、应用领域1. 生物医学:静电纺丝法可以制备出具有良好组织相容性和可控释放性能的纳米级支架材料,有望应用于组织工程、药物传递等领域。
2. 环境保护:静电纺丝法可以制备出具有高比表面积和孔隙度的纳米级吸附材料,用于处理水污染、空气污染等环境问题。
3. 能源储存:静电纺丝法可以制备出具有高比表面积和导电性能的纳米级电极材料,用于制备超级电容器、锂离子电池等能源储存器件。
六、优缺点1. 优点:静电纺丝法制备的纳米级材料具有高比表面积和孔隙度,能够提供更多活性位点和更好的传质性能;制备过程简单,操作易于掌握。
2. 缺点:静电纺丝法需要高压发生器作为设备支持,设备成本较高;由于聚合物溶液中的高分子物质容易受到氧化、水解等因素的影响,其稳定性较差。
静电纺丝法简介.doc

CENTRAL SOUTH UNIVERSITY 硕士生课程论文题目静电纺丝法简介学生姓名张辉华学号133511018指导教师秦毅红学院冶金与环境学院专业冶金工程完成时间2014.5.27静电纺丝法简介摘要:静电纺丝法是聚合物溶液或熔体在静电作用下进行喷射拉伸而获得纳米级纤维的纺丝,作为一种新颖的纳米纤维制备方法,具有许多一般纳米纤维制备法没有的优点,在国内外一直引起广泛的关注。
本文主要是介绍了静电纺丝的基本原理以及研究重点,同时简要地介绍了此方法在电池材料一起其他材料上的应用。
前言静电纺丝就是高分子流体静电雾化的特殊形式,此时雾化分裂出的物质不是微小液滴,而是聚合物微小射流,可以运行相当长的距离,最终固化成纤维。
静电纺丝技术在1934年首先由Formhals[1]提出, 随后的相当长一段时间又有多项专利出现。
近年来,随着纳米材料研究的兴起,人们发现由电纺制得的纤维的直径可以达到纳米级,使得这种技术重新受到重视并出现了大量的文献[2]。
目前, 主要是从事材料、化工和高分子领域的科学家在研究静电纺丝。
1 静电纺丝实验装置与基本原理1.1 电纺过程所需设备高压电源,溶液储存装置,喷射装置( 如内径 1 mm 的毛细管) 和收集装置( 如金属平板、铝箔等) 。
图1为传统的单纺装置。
图1 经典的静电纺丝装置示意图高压静电场(一般在几千到几万伏) 在毛细喷丝头和接地极间瞬时产生一个电位差,使毛细管内聚合物溶液或者熔融体(一般为非牛顿流体) 克服自身的表面张力和粘弹性力,在喷丝头末断呈现半球状的液滴。
随着电场强度增加,液滴被拉成圆锥状即Taylor锥。
当电场强度超过一临界值后,将克服液滴的表面张力形成射流(一般流速数m/s),在电场中进一步加速,直径减小,拉伸成一直线至一定距离后弯曲,进而循环或者循螺旋形路径行走,伴随溶剂挥发或熔融体冷却固化,终落在收集板上形成纤维,直径一般在几十纳米到几微米之间。
除去传统的单纺丝还有其他的一些纺丝方式,如同轴静电纺丝,共轴复合纺丝就是将两种不同聚合物溶液预先不经混合, 而是各自在电场力的驱动下共轴喷射经过同一个毛细管或注射器针头出口,得到连续的复合纤维的方法,该纤维具有核-壳结构。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
CENTRAL SOUTH UNIVERSITY 硕士生课程论文题目静电纺丝法简介学生姓名张辉华学号133511018指导教师秦毅红学院冶金与环境学院专业冶金工程完成时间2014.5.27静电纺丝法简介摘要:静电纺丝法是聚合物溶液或熔体在静电作用下进行喷射拉伸而获得纳米级纤维的纺丝,作为一种新颖的纳米纤维制备方法,具有许多一般纳米纤维制备法没有的优点,在国内外一直引起广泛的关注。
本文主要是介绍了静电纺丝的基本原理以及研究重点,同时简要地介绍了此方法在电池材料一起其他材料上的应用。
前言静电纺丝就是高分子流体静电雾化的特殊形式,此时雾化分裂出的物质不是微小液滴,而是聚合物微小射流,可以运行相当长的距离,最终固化成纤维。
静电纺丝技术在1934年首先由Formhals[1]提出, 随后的相当长一段时间又有多项专利出现。
近年来,随着纳米材料研究的兴起,人们发现由电纺制得的纤维的直径可以达到纳米级,使得这种技术重新受到重视并出现了大量的文献[2]。
目前, 主要是从事材料、化工和高分子领域的科学家在研究静电纺丝。
1 静电纺丝实验装置与基本原理1.1 电纺过程所需设备高压电源,溶液储存装置,喷射装置( 如内径 1 mm 的毛细管) 和收集装置( 如金属平板、铝箔等) 。
图1为传统的单纺装置。
图1 经典的静电纺丝装置示意图高压静电场(一般在几千到几万伏) 在毛细喷丝头和接地极间瞬时产生一个电位差,使毛细管内聚合物溶液或者熔融体(一般为非牛顿流体) 克服自身的表面张力和粘弹性力,在喷丝头末断呈现半球状的液滴。
随着电场强度增加,液滴被拉成圆锥状即Taylor锥。
当电场强度超过一临界值后,将克服液滴的表面张力形成射流(一般流速数m/s),在电场中进一步加速,直径减小,拉伸成一直线至一定距离后弯曲,进而循环或者循螺旋形路径行走,伴随溶剂挥发或熔融体冷却固化,终落在收集板上形成纤维,直径一般在几十纳米到几微米之间。
除去传统的单纺丝还有其他的一些纺丝方式,如同轴静电纺丝,共轴复合纺丝就是将两种不同聚合物溶液预先不经混合, 而是各自在电场力的驱动下共轴喷射经过同一个毛细管或注射器针头出口,得到连续的复合纤维的方法,该纤维具有核-壳结构。
共轴复合纺丝设备如图2(a)所示,核-壳结构纤维如图2(b)所示。
图2 同轴纺丝和复合纤维形貌同轴纺丝能直接接一步制备复合微/纳米线,可以制备医用复合纳米线、空心纳米管,这种方法制备出来的材料品质要明显优于涂覆法制备的材料。
此外可以将碳纳米管与挥发性溶剂混合液用作内纺液, 将聚合物溶液用作外纺液, 利用溶剂的挥发性就可以携带碳纳米管渗透到外层聚合物中, 形成连续的碳纳米管增强的复合纳米纤维。
图3 其他静电纺丝装置和纤维形貌1.2 静电纺丝原理研究静电纺丝法是聚合物溶液或熔体在静电作用下进行喷射拉伸而获得纳米级纤维的纺丝方法,如今的研究主要集中在两个方面:(1) Taylor 锥与喷射;(2) 纳米纤维的弯曲非稳定性。
1.2.1 Taylor锥与喷射理论溶液在毛细管管口同时受到表面张力和电场力的作用,随着电场强度增大,溶液中的同性电荷聚集在液滴表面,表面电荷产生的电场引起液滴变形,当电压达到某一临界值V c 时,管口处的溶液由半球形逐渐变为锥形,这一带电的锥体被大家称为泰勒锥。
继续增加电场强度,达到到另一临界值时, 将克服液滴的表面张力形成射流。
Taylor曾通过大量理论和实验研究,得出Taylor锥理论上临界角为49.3°[3]。
但是在2001年以及之后得出了如下结论:(1)临界状态轮廓仍为锥形,但锥角是33.5°而不是49.3°;(2)对于牛顿流体来说,临界锥角与流体性质无关,因为表面张力的增大总是伴随临界电场的变大。
然而在弹性液体或者非松弛粘弹性液体的条件下, 临界双曲面的锐度与弹力和表面张力有关系。
Yarin等拍出的照片(实线为实测锥体形状,虚线为Taylor锥体形状)图4 临界液滴形状[ 8]{(a)为向上喷射,(c)为向下喷射,(b)、(d)分别为(a)、(b)的放大图}一般情况下, 静电纺丝的外加电场为直流电, 但是Mahe shwari和Chang[2]发现直流电和交流电对Taylor角的改变很大,交流电产生的锥角比直流电小得多(交流电的锥角大约9°)。
1.2.2 纳米纤维弯曲非稳定性研究纤维在运动的过程中的受力主要有电场力、表面张力、重力、纤维内部粘弹力等。
实际上喷丝过程还有空气阻力、电荷互斥力等较弱的影响因素。
随着喷丝的进行,溶剂挥发或熔融体的固化,其中部分因素不断发生变化,喷丝表现出非稳定性,它们会弯曲然后变成一系列环形,并且越接近接收板,环形的直径越大,喷丝越细。
非稳定性对纳米纤维形成的尺寸等是非常重要的。
近来,在非稳定性上的研究也小有进展,Yarin等[3]引用局部近似法计算出的喷射路径与实验结果吻合的很好,Brenn[4]研究了非牛顿流体喷射的非稳定性。
他们发现高密度的外部环境能够使非稳定性加强;(2) 随着表面张力的增加,非牛顿流体喷射的非稳定性会有所减弱。
Eda 等[5]他们认为,高聚物的分子量和浓度可能决定了拉伸流动、弯曲非稳定性和喷射的分叉。
他们还发现,如果使溶液分子量不变而浓度增加,或者使分子量增加而Berry数不变,可能会引起弯曲非稳定性。
1.2.3 高聚物溶液/熔融体流动的非稳定性静电纺丝所使用的材料大多为聚合物的溶液或者熔融体,它们都是非牛顿流体,即剪应力与应变率具有非线形的关系。
高聚物的溶液或熔融体在毛细管中高速运动时,常常伴随非稳定性现象出现,对其探索将有助于同轴电纺流体动力学的研究。
高聚物溶液以及熔融体都是粘弹性液体的一种。
在粘弹性液体流动中,纯弹性非稳定性是非常普遍的现象。
在过去的一些年中,科学家们对其做了大量的研究,最近兴起的就是计算机模拟技术。
一般来说有三种常用的方法:①非线性稳定性分析;②线性稳定性分析;③不考虑干扰振幅所建立起来的完全稳定条件。
但是有关牛顿流体的非稳定性最为成功的研究还是来自于实验。
2 静电纺丝法在材料制备上的应用2.1 静电纺丝在锂离子电池材料中的应用2.1.1 静电纺丝制备碳基负极材料锂离子电池负极的碳基材料包括石墨化碳基负极材料、无定形碳材料、改性碳材料和碳纳米管等,由于无定形碳材料结构无序,根据不同的热处理条件其可逆容量在372mA h/g以上的很大范围内变化,虽然该材料的可逆容量较大,但Li+在其中的脱嵌过程是先从微晶中脱嵌然后在微孔中脱嵌,所以采用无定形碳作为电极存在着电压滞后现象。
针以上缺点,Kim等人[6]通过静电纺丝工艺获得碳纳米纤维的前躯体,然后在1000℃下加热处理获得碳纳米纤维网,获得的膜状纳米纤维可直接作为锂离子电池负极使用,可逆容量达到450mA h/g。
Ji等人[7]在聚丙烯腈( PAN) 溶液中添加SiO2,通过静电纺丝工艺制备碳纳米纤维前躯体,获得的微孔碳纳米纤维膜作为锂离子电池负极使用时,初次循环可逆容量为593mA h/g。
2.1.2 静电纺丝制备锂离子电池的凝胶电解质目前大部分锂离子电池是采用聚烯烃类电池隔膜,并灌装电解液组装而成的该组装方式操作不方便,制成的电池在使用过程中存在漏液的安全隐患,同时聚烯烃类电池隔膜的亲液性差,影响了电池的使用性能。
在电解液中形成凝胶态的聚合物主要有聚氧化乙烯( PEO) 聚偏氟乙烯( PVDF) 聚甲基丙烯酸甲酯( PMMA) 和PAN等常见的凝胶电解质的制备方法有刮涂铸膜法Bellcore法和倒相法[8],但是获得的电解质隔膜孔隙率较低。
而静电纺丝非织造布中纳米级纤维,比表面积大,使纤维网的纤维活化程度高,纤维网的孔隙率增加,在电解液中溶胀时可提高其对电解液的吸收,因此用静电纺丝非织造布作为凝胶聚合物电解质,能有效地提高锂离子电池的使用寿命。
PVDF由于具有较好的电化学性能及粘接性能,成为凝胶聚合物静电纺丝工艺研究的热点Gao等人[9]通过静电纺丝工艺制备了PVDF电池隔膜(图5),讨论了纤维直径与纺丝电压隔膜机械性能的关系,并通过热处理的方法提高了隔膜的抗张强度和拉伸模量与Celgard2400聚烯烃隔膜的电化学性能进行对比,发现静电纺丝制备的隔膜具有较小的界面阻抗以及较好比容量保持率。
2.1.3 静电纺丝制备锂离子电池隔膜目前锂离子电池隔膜的制备技术主要有干法、湿法Celgard法、Bellcore法和倒相法。
但是上述的方法都存在相应的缺点,在一定程度上影响到电池性能的最大限度发挥。
许多学者学者尝试在原有的基础上进行一定的改进,也取得了一定的成功,如任旭梅[10]对倒相法制备电池隔膜进行了一定的改进;程琥等人[ 8 ] 采用浸渍法在PP微孔膜( Celgard 2400)表面涂覆掺有纳米二氧化硅的聚氧乙烯( PEO),制得了新的性能更好的锂离子电池用复合隔膜。
但是其中用静电纺丝制备纳米纤维膜引起了学术界和产业界的广泛兴趣。
随着静电纺丝理论和技术的发展和渐趋成熟,制备了出了多样的符合电池隔膜的材料。
例如PVDF是是一种具有较稳定化学性质的材料,其成膜后的机械性能较好,与电解液浸润良好,离子电导率高,并可以溶于许多有机溶剂中,被认为是理想的膜材料。
现阶段采用静电纺丝法研究较多的也是以PVDF 为基体的多孔性隔膜[11]。
此外,采用PAN、PMMA和PET (聚酯)等材料制备电池隔膜的研究也有报道。
具体到细节,其具有以下诸多优势:(1)物理性能优良,用静电纺丝法制备的隔膜其厚度具有很大的灵活性能,可操作性好。
包括在:①孔隙率高达80%、②孔径大小和分布都较为均匀、③透气率大大优于传统膜的透气率(传统30s、而静电纺丝可达10s)。
④静电纺丝法制备的膜浸润性好。
(2)机械性能优良,成网状的静电纺丝纤维机械性能优越。
(3)安全性在静电纺非织造布膜表面覆盖一层PE, 从而使得聚合物隔膜具有自闭功能, 提高了使用安全性。
2.2 静电纺丝在其他方面的应用静电纺丝可以广泛地应用在各个方法。
生物医用静电纺丝制备的纳米纤维在生物医用材料方面的应用主要包括组织工程、药物释放、仿生材料、人工器官等。
(2)传感器感知膜纳米纤维膜具有高的比表面积(约为103m2Pg) , 因此用纳米纤维膜做传感器感知膜, 可以提高灵敏度。
(3)过滤阻隔材料。
(4)透明增强材料。
(5)超吸水纤维。
3. 结束语静电纺丝技术作为一门优良地合成纳米级纤维的新技术,其实非常值得我们去学习和研究,特别是在制备高性能纳米管的时候,可以由静电纺丝的条件来控制纳米管的粗细与长度,而且得到的材料性能优越,进而制备出更好的电池材料。
参考文献[1] Formhals A. USP, 1975 504. 1934.[2] Maheshwari S, Chang H C. Appl Phys Lett , 2006, 89: 234103.[3] Yarin A L, Koombhongs S, Reneker D H. J Appl Phys, 2001, 89( 5) : 3018~ 3026.[4] Brenn G,Liu Z B,Durst F. Int JMul Flow, 2000, 26: 1621~ 1644[5] Eda G,Liu J, Shivkumar S. Mater Lett, 2007, 6: 1451~ 1455.[6] KIM C,YANG K S,KOJIMA M,et al.J, Advanced Functional Materials, 2006,16 ( 18 ) : 2393-2397.[7]JI Liwen ,LIN Zhan ,MEDFORD A J ,et al .Porous carbon nanofibers from electrospun polyacrylonitrile /SiO2 composites as an energy storage material[J].Carbon,2009,47(14) : 3346-3354.[8] LEE Y M,KIM J W,CHOI N S,et al.Novel porous separator based on PVDF and PE nonwoven matrix for rechargeable lithium batteries [J] Journal of Power Sources, 2005, 139( 1/2) : 235-241.[9] GAO Kun,HU Xinguo, DAI Chongsong, et al. Crystalstructures of electrospun PVDF membranes and its separator application for rechargeable lithium metal cells [J] .Materials Science and Engineering: B, 2006, 131(1 /3) : 100-105.[10] 任旭梅, 吴锋, 白莹. 倒相法制备多孔PVDF隔膜的探索[J] . 电化学, 2001, 7(4):501-505.[11]PU Weihua, HE Xiang ming, WANG L,i et a.l Preparation of PVDF-H FP m ic ropo rous membrane for L-i ion batteries by phase inversion [ J] . Journal of Mem brane Science, 2006, 272: 11-14.。
