2018考研数学高数重要知识点：多元函数微积分学框架图
多元函数微分学
函数可导
函数可微 偏导数连续
(五)复合函数求导法则
定理1 如果函数 uu(t) 及 v v(t) 都在 t 点可导,
函数 zf(u,v)在对应点( u , v ) 具有连续偏导数,则
复合函数 zf[u (t),v(t)]在点t 可导,且
dzzduzdv. dt udt vdt
求全导数 d z .
u
dt
zv
t
解 dzzduzdvzdw dt udt vdt wdt
w
vetu ( sin t) co sw
e tc o s t e ts i n t c o s t
测试点 复合函数求导的链式法则.
例5 设 zz(x,y) 是由方程 xyzx2y2z22
(二)方向导数和梯度的公式
设函数 f(x, y,z)在点 P(x, y,z)可微, 方向 l 的
方向余弦为 c o s,c o s,c o s,则函数 f(x, y,z)
在点 P(x, y,z) 沿方向 l 的方向导数为
ffcosfcosfcos.
l x y
z
dz z dxzdy x y
所确定的隐函数.求 zz(x,y)在点 (1,0,1)的全微分.
解 令F (x ,y ,z ) x y z x 2 y 2 z 22
Fx yz
x ,
x2 y2 z2
Fy xz
y x2 y2 z2
z Fz xy x2y2z2
二、偏导数的应用
(一)微分法在几何上的应用 1 空间曲线的切线与法平面
空间曲线 :x ( t ) ,y ( t ) , z ( t ) .
其上一点 P0(x0,y0,z0)
多元函数微分学知识点
多元函数微分学知识点多元函数微分学是微积分的重要内容，它研究的是在多变量条件下函数的导数和微分的性质。
在实际应用中，多元函数微分学为我们解决各种问题时提供了有效的数学工具。
本文将介绍一些多元函数微分学的基本知识点，包括偏导数、全微分和梯度。
多元函数微分学的第一个知识点是偏导数。
在一元函数中，导数表示函数在某一点上的变化率。
而在多元函数中，我们需要引入偏导数的概念。
偏导数表示函数在某一点上沿着一个坐标轴的变化率。
对于一个两个自变量的函数f(x, y)，偏导数可以用∂f/∂x和∂f/∂y表示。
它们分别表示函数沿x轴和y轴的变化率。
偏导数可以帮助我们理解函数的局部变化情况，并在解决最优化问题时提供重要的线索。
第二个知识点是全微分。
全微分是多元函数微分学中的一个重要概念，它表示函数在某一点上的微小变化量。
全微分可以用df表示，其中df = ∂f/∂x*dx + ∂f/∂y*dy。
全微分可以帮助我们推导函数的逼近值和误差，从而得出函数在某一点的性质和特点。
例如，在工程学中，通过对一个物理过程的全微分分析，我们可以推导出近似解，并估计误差。
最后一个知识点是梯度。
梯度是多元函数微分学中的一个重要工具，它表示函数在某一点的最大变化方向。
对于一个函数f(x, y)，梯度可以用∇f = (∂f/∂x, ∂f/∂y)表示。
梯度的方向是函数变化最快的方向，它的模长表示函数的变化速率。
通过研究梯度，我们可以找到函数的极大值、极小值和鞍点，并解决最优化问题。
多元函数微分学是高级数学中的一个重要分支，它在各个学科领域都有广泛的应用。
在物理学中，我们可以通过多元函数微分学的方法推导出物理方程，并解决各种动力学问题。
在经济学中，多元函数微分学可以帮助我们分析供求关系，推导出边际效应，并解决最优决策问题。
在金融学中，多元函数微分学可以帮助我们研究金融风险和资产定价。
综上所述，多元函数微分学是微积分的重要内容之一，它研究的是多变量条件下函数的导数和微分的性质。
《多元函数的微积分》课件
在资源分配和生产计划中，多元函数微积分可以用于求解最优化问 题，例如最大化利润或最小化成本等。
风险评估
在金融学中，多元函数微积分可以用于评估投资风险和回报，以及 制定风险管理策略。
THANKS
感谢观看
多元函数的定义域
函数中各个自变量可以取值的范围。例如，对于函数z = f(x, y)，其定义域是x和y的所有可能取值的集合。
多元函数的值域
函数中因变量可以取值的范围。例如，对于函数z = f(x, y) ，其值域是z的所有可能取值的集合。
多元函数的几何意义
平面上的曲线
对于二元函数z = f(x, y)，其图像 在二维平面上表现为一条曲线。 例如，函数z = x^2 + y^2表示 一个圆。
体积计算
通过多元函数微积分，可以计算出由曲面围成的三维空间的体积 ，这在工程和科学领域中具有广泛的应用。
曲线积分
在几何学中，曲线积分是计算曲线长度的一种方法，而多元函数 微积分可以提供更精确和更高效的计算方法。
多元函数微积分在物理上的应用
力学分析
在分析力学中，多元函数微积分 被广泛应用于解决质点和刚体的 运动问题，例如计算物体的速度 、加速度和力矩等。
三维空间中的曲面
对于三元函数z = f(x, y, z)，其图 像在三维空间中表现为一个曲面 。例如，函数z = x^2 + y^2表 示一个球面。
多元函数的极限与连续性
多元函数的极限
当自变量趋近于某个值时，函数值的趋近值。例如，lim (x, y) → (0, 0) (x^2 + y^2) = 0，表示当(x, y)趋近于(0, 0)时，函数x^2 + y^2的值趋近于0。
《多元函数的微积分》 ppt课件
《多元函数的微积分》PPT课件
xy
kx2
k
lim
x0
x2
y2
lim x0
x2
k2x2
1 k2
.
6
y kx 0
例1 求lim sin(xy) . x0 x
y2
解： lim sin(xy) lim sin(xy) y
x0 x
x0 xy
y2
y2
sin(xy)
lim
lim y
x0 xy
x0
y2
y2
2 lim sin( xy) 2 . xy0 xy
时，函数都无限接近于A. (2) 如果当P以两种不同方式趋于P0时，函数
趋于不同的值，则函数的极限不存在．
例
xy
x2
y2
, x2 y2 0 .
f (x, y)
0 , x2 y2 0 .
当点P(x，y)沿 x 轴、y 轴趋于点(0，0)时函数的极限为
当点P(x，y)沿直线y=k x 趋于点(0，0)时
解： 如果 2 函数在单位圆上任何点都连续
若 2 在单位圆上任何点都不连续
9
三. 偏导数的概念及简单计算
1. 偏导数的概念：
定义
设函数z f(x，y)在点(x0，y0)的某一邻域内有当y 固定
定在义y0 ，而x 在x0 处有增量 x 时相，应地函数有增量
f (x0（１）如果极限 0) ，x，y0) f(x0，y
y0
y
存在，
则称此极限为函数z f(x，y)在点(x0，y0)处对y 的偏
导数，
记作
z , x x0
y y y0
f ,
y x x0
y y0
z y , x x0 y y0
多元函数微积分
注：1、其中 f (0,1) 、
表示
f
对第二个中间变量求导一次， 对第二个中间变量求导一次，
f (0,2) 表示 f
f (1,1)
表示
对第二个中间变量求导两次， 对第二个中间变量求导两次，
对第一、第二个中间变量各求导一次。 f 对第一、第二个中间变量各求导一次。
2、求多元函数的偏导数还可以用基本输入模板中的符号 、
1 0
à à
0
-1
@ 8< < 8D
xexydxdy, D: 0 ≤ x ≤1, −1≤ y ≤ 0 ∫∫
D
x* ã
x* y
â y âx
输出
1 ã
例13 计算二重积分 所围成的区域。 所围成的区域。
1 x
解： 例14
!! !! àà
D
0 x2
x ydxdy ，D 是由 y = x, y = x2 ∫∫
D
解:
对二重积分要先化为累次积分，定好积分限后，再使用命令。 对二重积分要先化为累次积分，定好积分限后，再使用命令。
本题的Mathematica命令为 命令为 本题的 In[8]:=Integrate[x*y, {x, 2, 4}, {y, 1, x/2}] Out[8]=
9 2
例11 计算
∫ ∫
2. 求下列函数的全微分： (1)z = ex−2 y (3)z = arcsin( ) xy (2)z = x y
(4)z = (x2 + y2 ) ln(x + y)
3. 求二元函数的极值： (1) z = （x − y) − x2 − y2 4 (2) z = x3 − y3 + 3x2 + 3y2 − 9x
《数学分析》第四章多元函数微分学
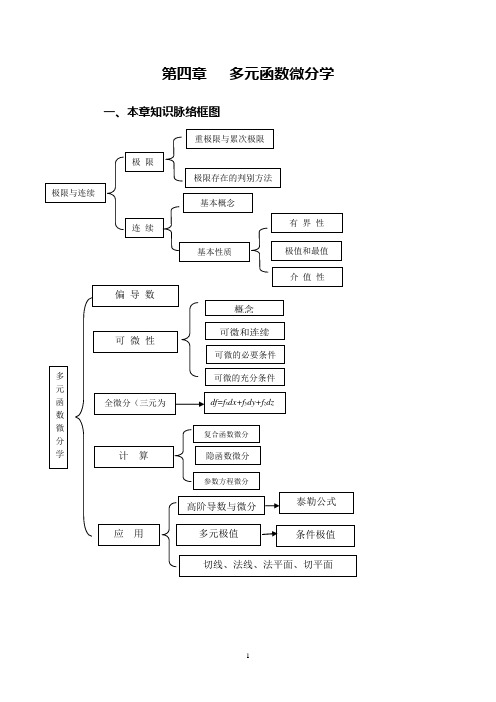
第四章 多元函数微分学一、本章知识脉络框图极 限 连 续重极限与累次极限 基本概念有 界 性极限存在的判别方法极值和最值 基本性质极限与连续介 值 性偏 导 数可 微 性概念可微和连续可微的必要条件可微的充分条件 复合函数微分隐函数微分计 算参数方程微分多元函数微分学全微分（三元为例）df=f x dx+f y dy+f z dz 条件极值应 用高阶导数与微分多元极值切线、法线、法平面、切平面泰勒公式二、本章重点及难点本章需要重点掌握以下几个方面内容：● 偏导数、全微分及其几何意义，可微与偏导存在、连续之间的关系，复合函数的偏导数与全微分，一阶微分形式不变性，方向导数与梯度，高阶偏导数，混合偏导数与顺序无关性，二元函数中值定理与Taylor 公式.● 隐函数存在定理、隐函数组存在定理、隐函数（组）求导方法、反函数组与坐标变换. ● 几何应用（平面曲线的切线与法线、空间曲线的切线与法平面、曲面的切平面与法线. ● 极值问题（必要条件与充分条件），条件极值与Lagrange 乘数法.三、本章的基本知识要点(一)平面点集与多元函数1.任意一点A 与任意点集E 的关系.1) 内点. 若存在点A 的某邻域()U A ，使得()U A E ⊂，则称点A 是点集E 的内点。
2) 外点. 若存在点A 的某邻域()U A ，使得()U A E ⋂=∅，则称点A 是点集E 的外点。
3) 界点（边界点）. 若在点A 的任何邻域内既含有属于E 得的点，又含有不属于E 的点，则称点A 是点集E 的界点。
4) 聚点. 若在点A 的任何空心邻域()oUA 内部都含有E 中的点，则称点A 是点集E的聚点。
5) 孤立点. 若点A E ∈，但不是E 的聚点，则称点A 是点集E 的孤立点。
2. 几种特殊的平面点集.1) 开集. 若平面点集E 所属的每一点都是E 的内点，则称E 为开集。
2）闭集. 若平面点集E 的所有聚点都属于E ，则称E 为闭集。
多元函数微分学(共184张PPT)
z
sin
x2
1 y2
1
• 在 点圆 都周 是x2间 断y2 点1，是上一没条有曲定线义，. 所以该圆周上各
• 性质1(最大值和最小值定理) 在有界闭区域 D上的多元连续函数，在D上一定有最大值和最小
值.
• 在D上至少有一点 及一点 ，使得 为最大 值而 为最小值，P 即1 对于一切P 2 P∈D，有f ( P1 )
•
P
于E的点，也有不属于E的点，
•
E
则称P为E的边界点（图8-2）.
•
设D是开集.如果对于D内的
• 图 8-1 任何两点，都可用折线连结起
上一页 下一页 返 回
•
来,而且该折线上的点都属于D,
•
P 则称开集D是连通的.
•
连通的开集称为区域或开区域.
•
E
开区域连同它的边界一起,称
•
为闭区域.
• 图 8-2
f( x x ,y ) f( x ,y ) A x ( x )
• 上式两边各除以 x ，再令 x 0而极限，就得
limf(xx,y)f(x,y)A • 从而 ，x 偏0导数 z 存 在x，而且等于A.同样可证
• =B.所以三式 x 成立.证毕.
z y
上一页 下一页 返 回
• 定理2(充分条件) 如果z=f(x,y)的偏导数
• 3.n维空间
• 设n为取定的一个自然数,我们称有序n元数组
•
的全体为n维空间,而每个有序n元数
(x1组,x2, ,xn) 称为n维空间中的一个点,数 称
(x1,x2, ,xn)
xi
上一页 下一页 返 回
• 为该点的第i个坐标,n维空间记为 .n
《多元函数积分学》课件
物理应用
重积分在物理中有广泛的应用，如计 算物体的质量、质心、转动惯量等物 理量，还可以用来解决流体动力学、 弹性力学等领域的问题。
数值分析应用
重积分在数值分析中有重要的应用， 如数值积分、数值微分等计算方法的 实现都需要用到重积分的知识。
04 曲线积分与曲面积分
曲线积分的概念与性质
总结词
理解曲线积分的定义和计算方法，掌握其在几何和物理问题中的应用。
总结词
掌握多元函数的可积性和积分的基本性 质是理解多元函数积分学的重要环节。
VS
详细描述
可积性的判定条件和积分的基本性质（如 线性性质、可加性、不等式性质等）是多 元函数积分学中的核心知识点，对于理解 和应用积分具有重要意义。
多元函数积分的计算方法
总结词
掌握多元函数积分的计算方法是学习多元函数积分学的关键。
《多元函数积分学》ppt课件
• 多元函数积分学概述 • 多元函数积分的基本概念 • 重积分 • 曲线积分与曲面积分 • 多元函数积分学的应用
01 多元函数积分学概述
多元函数积分学的定义
定义
多元函数积分学是研究多元函数 的积分、微分和微积分基本定理 的一门学科。
多元函数
一个数学函数，其中自变量不止 一个，即函数的输入和输出都是 向量或更高维度的几何对象。
计算多维工程结构的热传导和流 体流动
在工程中，很多问题需要考虑多维工程结构的热传导和 流体流动，如热力管道、流体机械等。多元函数积分学 可以用来计算这些结构的热传导和流体流动。
THANKS 感谢观看
积分
对一个函数在某个区域上的所有 点的值进行加权求和，权值由该 点的坐标决定。
多元函数积分学的重要性
解决实际问题
多元函数微分-关系图
例1、
但在该点各偏导数都不存在.
函数在某点各偏导数都存在,
显然
如,
例2、
但在该点不一定连续.
在上节已证 f (x , y) 在点(0 , 0)并不连续!
提示: 利用
故 f 在 (0,0) 连续;
知
例3.
连续、偏导数存在函数 不一定可微 !
而
所以 f 在点(0,0)不可微 !
可微 :
说明: 此题表明, 偏导数连续只是可微的充分条件.
令
在点 (0,0) 连续且偏导数存在,
续,
证: 1)
因
故函数在点 (0, 0) 连续 ;
但偏导数在点 (0,0) 不连
证明函数
所以
偏导数存在不连续，函数 可微 !
同理
极限不存在 ,
在点(0,0)不连续 ;
同理 ,
在点(0,0)也不连续.
2)
3)
4) 下面证明
多元函数微分学诸概念关系图
y
’
S
`·
步
x
=
0
,
y 今 0
x 二
y 二 0
事 实上 定理
3
我们 有
2 =
f (
O
x
。
,
x
,
y
) 在 (
x
o
,
y
。
) 可 微 的 充 要条 件 是 f x (
x
o ,
y
o
)
,
f
y
(
x
o ,
y
。
)
存在且 对 一 切 〔 〔
a
2二
+
〕
,
一 致 地有
,
l 1i m P令 O 十 P
〔f (
二
p
e o s a
。
由 于 远 比单 元 函 数 复
、
初 学者往往 眉 目不 清 例
1
,
且 常有 似 是 而 非 之 感
如
。
有 在 给 定 点无 极 限 且 不 可 导 的 函 数
J 、`I I \
Ir
、 /
X
、
矛 .
l `
`
ZX y
x
Z
y
J
一
+
y忿
x Z+
y
:
斗 。
在点 (
x 么+
o
,
0
)
。
1
y
Z
=
o
。
有 在 给定 点极 限 存 在但 不 连续 例
4
如
“
事实 上
,
X
,
高数D多元函数基本概念演示课件
定义线性运算
的全体称为 n 维空间,
n 维空间中的每一个元素
称为空间中的
一个点,
称为该点的第 k 个坐
当所有坐标 标 . 称该元素为R n 中的零元,记作 O .
R n 中的点 x (x1, x2 ,, xn ) 与点 y ( y1, y2 ,, yn )
的距离记作
y=
k
x
l，im
x0
y2 sin x x2 y4
lim
x0
k 2 sin x 1 k4x2
0
y0
令 y
x, lim x0
y2 sin x x2 y4
lim x0
x sin x x2 x2
1 lim 2 x0
sin x x
1 2
y0
y2 4x D1x
可见极限 不存在
3) 一切多元初等函数在定义区域内连 续
练习 题 1.
题 2.
(1)定义 域 (2)定义
域
y
y x2 D
o
x
y
D o rR x
题 3.
定义域
y
lim
x
1 2
y0
f (x, y)
f
(1, 0) 2
2 ln 34
题
4.证明lim x0
y2 sin x x2 y4
不存在.
y 0
令
(圆邻域)
(球邻域)
说明：若不需要强调邻域半径 ,也可写成 U ( P0 ).
点 P0 的去心邻域记为
0 PP0 δ
在讨论实际问题中也常使用方邻域, 因为方邻域与圆 邻域可以互相包含.