C++第一单元实验一第二题-菜单选择程序
C语言第1次实验答案
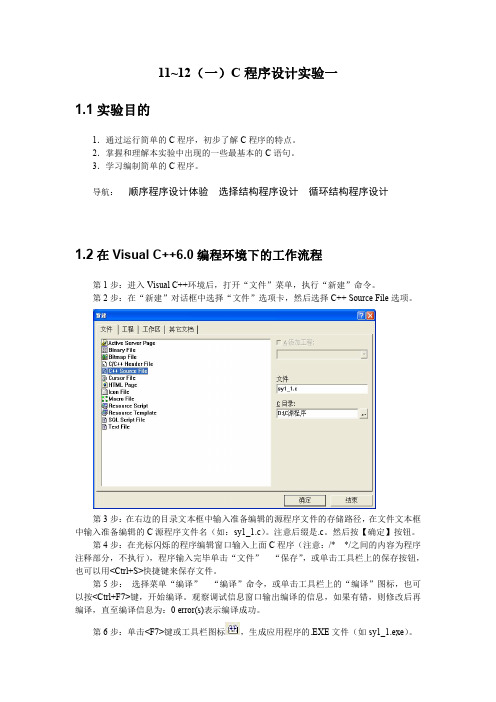
1 求出它是几位数; 2 分别打印出每一位数字; 3 逆顺序打印出各位数字,例如原来为 321,应输出 123。 #include<stdio.h> main() {int n,a,b,c; scanf("%d",&n); a=n/100;b=n/10%10;c=n%10; if(a>0) printf(" 是三位数\n"); else if(b>0) printf("是两位数\n"); else printf("是一位数\n"); printf("三位数字分别为:%d%d%d\n",a,b,c); printf("逆序输出为:%d\n",c*100+b*10+a); }
printf(“ ”);
printf(“*”);
/*显示中间层每层起点星号*/
for(j=1;j<= 2*i-1
;j++)
printf(“ ”);
printf(“*\n”);
/*显示中间层每层终点星号*/
}
for(j=1;j<= k-i-1
;j++)
printf(“ ”);
printf(“*”);
/*显示底边起始星号*/
第 4 步:在光标闪烁的程序编辑窗口输入上面 C 程序(注意:/* */之间的内容为程序 注释部分,不执行),程序输入完毕单击“文件” “保存”,或单击工具栏上的保存按钮, 也可以用<Ctrl+S>快捷键来保存文件。
第 5 步: 选择菜单“编译” “编译”命令,或单击工具栏上的“编译”图标,也可 以按<Ctrl+F7>键,开始编译。观察调试信息窗口输出编译的信息,如果有错,则修改后再 编译,直至编译信息为:0 error(s)表示编译成功。
C语言上机试题及答案

实验一Visual C++6.0的使用及顺序结构程序设计一、实验目的1、掌握启动和退出VC6 的方法。
2、熟悉 VC6 开发环境。
3、初步掌握简单程序的上机操作基本步骤,熟悉 C 单文件程序的输入、编译、链接和运行过程。
4、初步掌握程序的编辑修改和调试。
5、熟练使用赋值运算、算术运算等表达式。
6、熟练使用标准输入、输出函数及各种数据类型的格式说明符。
二、实验内容1、下面C语言程序,其功能是显示字符串“欢迎同学们来到华北水院计算中心!”。
请同学们按照下面的实验指导学习VisualC++6.0的使用。
1 .启动 VisualC++6 .0 开发环境(1)单击开“始”按钮,选择程“序”——〉“Microsoft Visual Studio6.0菜单项,单击“MicrosoftVisualC++6.0”,屏幕出现标题为“当时的提示”的窗口。
(2)单击“结束”按钮,关闭窗口,进入VC6.0 开发环境的主窗口。
2 .使用 Visual C++6.0 对一个 C 程序进行编辑、编译、连接和运行。
⑴分析Visual C++6.0 中程序的开发过程与其它高级语言的开发过程相仿,都要经过编辑、编译、连接和运行四个步骤。
⑵步骤①编辑图 1-1 New 对话框编辑是将 C 源程序输入计算机的过程。
在Visual C++6.0 主界面下,点击File 菜单,选择Ne w 菜单项,即可出现New 对话框,如图1-1 所示。
在弹出窗口中的Files 标签页下,选择C++ Sour ce File。
在选项卡右面的File 编辑框里输入文件名如“Exa.c”,在 Location 编辑框里输入文件路径,2如 : \test”。
点击 OK 按钮。
将出现编辑窗口 ,如图 1-2 所示。
在图 1-2 所示的右端编辑窗口里输 入以下 C 源程序并保存文件。
图 1-2 编辑窗口②编译编译是使用系统提供的编译器将文本文件 Exa.c 生成机器语言的过程 ,结果为 Exa.obj ,由于没有 得到系统分配的绝对地址,还不能直接运行,如图 1-3 所示。
C语言上机实验1-18

实验一C程序的运行环境及简单程序编写一、实验目的1.了解tc2.0编译系统的基本操作方法,学会独立使用该系统。
2.了解在该系统上如何编辑、编译、连接和运行一个C程序。
3.通过运行简单的C程序,初步了解C源程序的特点。
二、实验内容1.编写一个计算球体体积的程序,要求用户自行录入球体的半径。
参考公式V=4/3πr3.。
2.编写一个程序,要求用户输入一个美金数量,然后显示出如何用最少的20美元、10美元、5美元和1美元来付款。
运行结果:Ener a dollar amount:93$20 bills:4$10 bills:1$5 bills:0$1 bills:3实验二顺序结构程序设计一、实验目的1.熟悉C语言中的基本数据类型,掌握定义常量和变量以及对它们赋值的方法,了解数据输出时所用格式转换符。
2.掌握格式输入/输出函数的用法。
3.学会简单顺序程序的设计。
4.养成良好的程序设计习惯。
二、实验内容1.编写一个程序,对用户录入的产品信息进行格式化。
Enter item number:583Enter unit price:13.5Enter purchase date(mm/dd/yyyy):3/24/2010Item Unit PurchasePrice date583 $ 13.50 3/24/20102.编写一个程序,要求用户输入一个两位数,然后按数位的逆序打印出这个数。
Enter a two-digit number:28The reversal is :82实验三选择结构程序设计一、实验目的1.熟练使用if、switch编写程序。
二、实验内容1.编写一个程序,确定一个数的位数。
Enter a number:374The number 374 has 3 digits假设输入的数最多不超过4位。
提示:利用if语句进行数的判定。
例如,如果数在0到9之间,那么位数为1;如果数在10到99之间,那么位数为2。
c语言实验选择结构程序设计

高级语言程序设计实验报告实验2 选择结构程序设计一、实验目的1、熟悉VC6.0编程环境。
2、进一步熟悉用VC6.0调试C语言源程序的过程。
3、熟练使用关系表达式和逻辑表达式作为if语句的条件判断。
4、熟练掌握if语句和switch语句的使用方法。
二、实验内容及步骤1、身高预测每个做父母的都关心自己孩子成人后的身高,据有关生理卫生知识与数理统计分析表明,影响小孩成人后身高的因素有遗传、饮食习惯与坚持体育锻炼等。
小孩成人后身高与其父母身高和自身性别密切相关。
设faHeight为其父身高,moHeight为其母身高,身高预测公式为:男性成人时身高 = (faHeight + moHeight) * 0.54(cm)女性成人时身高 = (faHeight * 0.923 + moHeight) / 2(cm)此外,如果喜爱体育锻炼,那么可增加身高2%,如果有良好的卫生饮食习惯,那么可增加身高1.5%。
编程从键盘输入小孩的性别(用字符型变量sex存储,输入字符F表示女性,输入字符M 表示男性)、父母身高(用实型变量存储,faHeight为其父身高,moHeight为其母身高)、是否喜爱体育锻炼(用字符型变量sports存储,输入字符Y表示喜爱,输入字符N表示不喜爱)、是否有良好的饮食习惯等条件(用字符型变量diet存储,输入字符Y表示喜爱,输入字符N表示不喜爱),利用给定公式和身高预测方法对小孩的身高进行预测。
程序代码:#include<stdio.h>main(){char sex,sports,diet;float faHeight,moHeight,fh,mh;printf("输入父亲身高:");scanf("%f",&faHeight);printf("输入母亲身高:");scanf("%f",&moHeight);getchar();printf("输入小孩性别:");scanf("%c",&sex);getchar();printf("是否喜爱体育锻炼:");scanf("%c",&sports);getchar();printf("是否有良好的饮食习惯:");scanf("%c",&diet);fh=(faHeight * 0.923 + moHeight) / 2;mh=(faHeight + moHeight) * 0.54;if(sex=='F'){ if(sports=='Y') fh=fh*1.02;if(diet=='Y') fh=fh*1.015;printf("小孩身高为:%.2f",fh);}else{ if(sports=='Y') mh=mh*1.02;if(diet=='Y') mh=mh*1.015;printf("小孩身高为:%.2f",mh);}}设计多组测试数据对程序进行测试,并观察运行结果。
《C程序设计》选择结构程序设计实验报告

《C程序设计》选择结构程序设计实验报告2、完成改错后的程序#include <stdio.h>#include <ctype.h>char fun(char c){ if (c>='A' && c<='Z')/**********found**********/c=c+32;if (c>='a' && c<='u')/**********found**********/c=c+5;else if(c>='v' && c<='z')c=c-21;return c;}main ( ){ char cl, c2;printf("Enter a letter(A-Z):");cl=getchar( );if (isupper(cl)){ c2=fun(cl);printf("\n\nThe letter %c change to %c\n",cl,c2);}elseprintf("\nEnter (A-Z) !\n");}运行结果:(截图)3、解题思路:源程序:1.#include<stdio.h>#include<math.h>void main(){float s;int m,year;printf("please input money and year:");scanf("%d%d",&m,&year);switch(year){case 1:s=m*pow((1+0.03),year);break;case 2:s=m*pow((1+0.033),year);break;case 3:case 4:s=m*pow((1+0.038),year);break;case 5:s=m*pow((1+0.042),year);break;default:s=m*pow((1+0.042),year);break;}printf("s=%f\n",s);}2.#include<stdio.h>#include<math.h>void main(){float s;int m,year;printf("please input money and year:");scanf("%d,%d",&m,&year);if(year==1)s=m*pow((1+0.03),year);if(year==1)s=m*pow((1+0.03),year);if(year==2)s=m*pow((1+0.033),year);if(year>=3&&year<=4)s=m*pow((1+0.038),year);if(year>=5)s=m*pow((1+0.042),year);printf("s=%f\n",s);}运行结果:(截图)4、解题思路:源程序:#include<stdio.h>main(){int i,yue,year,day;printf("please input nian and yue :");scanf("%d,%d",&year,&yue);switch(yue){case 1:printf("有31天");break;case 2:if(year%4==0&&year%100!=0||year%400==0)printf("有29天");else printf("有28天");break;case 3:printf("有31天");break;case 4:printf("有30天");break;case 5:printf("有31天");break;case 6:printf("有30天");break;case 7:printf("有31天");break;case 8:printf("有31天");break;case 9:printf("有30天");break; case 10:printf("有31天");break; case 11:printf("有30天");break; case 12:printf("有31天");break; }}运行结果:(截图)。
C语言_实验二、选择结构程序设计

实验二 选择结构程序设计一、实验目的1. 掌握关系表达式和逻辑表达式的使用。
2. 熟悉选择结构程序设计。
3. 熟练使用if 语句进行程序设计。
4. 使用switch 语句实现多分支选择结构。
二、实验内容(1 计算a+|b| 2 判断一个整数是否可以被3和5整除)1.[目的]掌握判断一个字符型数据是否数字字符的方法,以及数字字符转换为相应整数的方法。
[题目内容]从键盘输入一个字符型数据,若输入一个数字字符('0'-'9'),则将其转换成相应的整数显示出来;若输入其它字符,则显示出错信息。
[输入]一个字符型数据[输出]整数或出错信息[提示] 根据字符型数据的ASCII 码值是否在‘0’字符与‘9’字符之间进行判断。
使用if …else …语句和复合语句。
2.[目的]掌握条件表达式的使用[题目内容] 编写一个程序,其功能为:从键盘输入三个数x 、y 、z ,判断x+y=z 是否成立,若成立输出‚x+y=z ‛的信息,否则输出‚x+y!=z ‛的信息。
[输入] 三个数x 、y 、z[输出] ‚x+y=z ‛或‚x+y!=z ‛[提示] 条件判断表达式x+y==z3.[目的]掌握求最大值最小值的方法。
[题目内容] 编写一个程序,其功能为:输入三个整数,输出最大数和最小数。
[输入] 三个整数[输出] 最大值和最小值[提示] 设置最大值变量max 和最小值变量min ;首先比较a,b 的大小,并把大数存入max , 小数存入min ;然后最大值变量max 和最小值变量min 再与c 比较,若c 大于max ,则max 取值c ,否则保持不变;如果c 小于min ,则min 取值c ,否则保持不变。
最后输出max 和min 的值。
使用if …else …语句、if 语句以及复合语句。
4.[目的]运用已学知识解决实际问题。
[题目内容]如下两个线性方程组的两个未知数为x1和x2:ax 1+bx 2=mcx 1+dx 2=n该方程的唯一解为(ad-cb 不等于零时):cb ad bn md x --=1 bcad mc na x --=2 请编写一个程序,读取a 、b 、c 、d 的值,计算x1和x2的值。
c语言课程设计菜单设计程序

c语言课程设计菜单设计程序一、教学目标本章节的教学目标是使学生掌握C语言菜单设计程序的基本方法,理解菜单设计程序的结构和原理,能够独立编写简单的菜单设计程序。
知识目标:使学生掌握C语言的基本语法,了解函数的定义和调用,掌握菜单设计的基本方法。
技能目标:使学生能够独立编写简单的菜单设计程序,能够根据实际需要设计复杂的菜单系统。
情感态度价值观目标:培养学生对计算机编程的兴趣和热情,使学生能够认识到计算机编程在实际生活中的应用和价值。
二、教学内容本章节的教学内容主要包括C语言的基本语法,函数的定义和调用,菜单设计的基本方法。
1.C语言的基本语法:数据类型、变量、运算符、表达式、控制语句等。
2.函数的定义和调用:函数的定义、函数的调用、函数的返回值等。
3.菜单设计的基本方法:菜单的定义、菜单的显示、菜单的选择等。
三、教学方法本章节的教学方法采用讲授法、案例分析法和实验法相结合的方式。
1.讲授法:通过讲解C语言的基本语法、函数的定义和调用、菜单设计的基本方法,使学生掌握相关知识。
2.案例分析法:通过分析实际案例,使学生理解菜单设计程序的结构和原理,掌握菜单设计的方法。
3.实验法:通过编写和运行菜单设计程序,使学生独立掌握菜单设计的方法和技巧。
四、教学资源本章节的教学资源包括教材、参考书、多媒体资料和实验设备。
1.教材:C语言编程入门教程。
2.参考书:C语言编程实例教程。
3.多媒体资料:C语言编程视频教程。
4.实验设备:计算机、编程软件。
五、教学评估本章节的教学评估主要包括平时表现、作业和考试三个部分,以全面、客观、公正地评估学生的学习成果。
1.平时表现:通过观察学生在课堂上的参与程度、提问回答、小组讨论等表现,评估学生的学习态度和理解程度。
2.作业:布置与菜单设计程序相关的编程作业,评估学生的编程能力和对知识的理解运用。
3.考试:进行期中和期末考试,测试学生对C语言和菜单设计程序的掌握程度。
六、教学安排本章节的教学安排如下:1.教学进度:按照教材的章节顺序,逐步讲解C语言的基本语法、函数的定义和调用、菜单设计的基本方法。
程序设计基础—C程序实验.doc

《程序设计基础—实验》说明:实验1和实验2均为电子实验报告,后面8个实验是纸制实验报告.实验1计算机基本操作实验目的⑴熟悉计算机,能够正确进行开、关机操作。
⑵熟悉键盘,掌握键盘上所有字符的输入,掌握正确的指法,能够进行中、英文切换.⑶理解操作系统概念,掌握的基本操作,能够利用“控制面板”进行一些参数的设置。
⑷知道“回收站”的功能,学会有关文件、文件夹的基本操作。
⑸学会在计算机上搜索或查找相关的文件或文件夹,掌握通配符的使用.实验内容⑴熟悉上机实验的计算机,熟悉键盘,学会中、英文输入方式的转换。
⑵学会用正确的指法进行输入,知道键盘上所有字符的输入.⑶利用“控制面板”修改系统时间、桌面背景、鼠标属性。
⑷在桌面上新建一个文件夹,该文件夹以学生自己的名字+班级+学号的后3位命名。
⑸用文本方式或文档,写一段字数不少于300字的自我介绍,以1命名并保存到上述文件夹中。
⑹将上述文件夹复制到上。
实验2 常用软件的基本操作实验目的⑴了解功能,掌握的基本操作,包括页眉/页脚的设置、分栏、页面设置、添加底纹等。
⑵学会文件的保存与打开、打印预览、段落的间隔、首字符位置改变等,能够在中插入图片、表格、艺术字、特殊符号等。
⑶了解的功能,掌握的基本操作,包括单元格属性的设置、数字的几种填充形式、单元格的合并与恢复、边框的设置等。
⑷掌握的基本公式的使用,能够用公式进行基本计算。
掌握中的图形制作方法,能够根据表格做出图形. 实验内容⑴将上自己文件夹中的1文件复制到桌面上,然后做如下处理:①将标题“自我介绍”居中;②将文章中第二段的内容进行分栏,要求中间有分割线;③插入一个4行4列的表格,内容为学号、姓名、某门课的成绩;④任意插入一张图片;⑤在文章中的任意位置加底纹。
将做好的文档以2命名并保存.⑵用建立如下表格:①利用公式计算学生的总分、平均分;②将表中所有的数据选择居中;③利用该表格中的姓名和计算机的成绩做簇状图形。
将做好的表以2命名并保存.将本次实验的两个文件上传到上自己的文件夹中。
C语言上机题目——选择结构程序的设计说明

课程实验报告课程名称计算机程序设计班级实验日期学号实验成绩实验名称实验2:选择结构程序设计实验目的及要求1.掌握实现选择结构程序的编程方法。
2.灵活应用if语句的多种形式和switch语句来完成选择结构程序的设计和实现。
实验环境Visual C++ 6.0实验容1.如图所示3个圆圈重叠,半径皆为3,圆心坐标分别为红色(-2, 0)、蓝色(2, 0)、绿色(0, -2),由键盘输入一坐标,判断该点是什么颜色?输出是几号区域即可。
提示:共有8种颜色;判断距离圆心的距离,可以用距离的平方,这样可以省去算平方根的操作。
例如:输入:0 0输出:7号输入:10 10输出:8号输入:0 2输出:4号2.输入一个一位整数,输出其对应的英文单词。
要求用switch结构完成。
例如:输入:0输出:zero输入:8输出:eight算法描述及实验步骤调试过程及实验结果总结通过这次上机操作,我学会了如何使用选择结构设计程序解决问题。
在设计过程中,我明白了使用选择结构解决问题的重要性,它可以实现我们对多个问题的判断,帮助我们解决问题。
附录1.#include<stdio.h>int main(){int x,y,a,b,c;scanf("%d%d",&x,&y); a=(x+2)*(x+2)+y*y;b=(x-2)*(x-2)+y*y;c=x*x+(y+2)*(y+2);if (a<9&&b<9&&c<9)printf("7号\n");if (a<9&&b>9&&c>9)printf("1号\n");if (a>9&&b<9&&c>9)printf("2号\n");if (a>9&&b>9&&c<9)printf("3号\n");if (a<=9&&b<=9&&c>=9)printf("4号\n");if (a<=9&&b>=9&&c<=9)printf("5号\n");if (a>=9&&b<=9&&c<=9)printf("6号\n");if (a>9&&b>9&&c>9)。
c课程设计菜单选择

c 课程设计菜单选择一、教学目标本课程的教学目标是使学生掌握菜单选择的相关知识,包括理解菜单的概念、了解菜单的设计原则和方法、掌握菜单的选择和操作技巧。
具体目标如下:知识目标:学生能够理解菜单的基本概念,了解不同的菜单设计原则和方法,掌握菜单的选择和操作技巧。
技能目标:学生能够运用所学的菜单设计原则和方法,独立设计出符合要求的菜单,能够熟练地使用菜单进行选择和操作。
情感态度价值观目标:通过学习菜单选择的相关知识,学生能够增强对计算机操作的兴趣和信心,提高对计算机操作的积极性和主动性。
二、教学内容本课程的教学内容主要包括菜单的基本概念、菜单的设计原则和方法、菜单的选择和操作技巧。
具体内容如下:1.菜单的基本概念:介绍菜单的定义、功能和类型。
2.菜单的设计原则和方法:介绍菜单设计的整体原则、布局原则、命名规则等。
3.菜单的选择和操作技巧:介绍如何选择菜单项、如何使用快捷键进行操作等。
三、教学方法为了达到本课程的教学目标,将采用多种教学方法进行教学,包括讲授法、演示法、实践法等。
1.讲授法:通过讲解菜单的基本概念、设计原则和方法,使学生掌握相关知识。
2.演示法:通过演示菜单的设计和操作过程,使学生直观地了解菜单的选择和操作技巧。
3.实践法:通过实际操作,使学生熟练掌握菜单的选择和操作技巧。
四、教学资源为了支持本课程的教学内容和教学方法的实施,将准备以下教学资源:1.教材:选用合适的教材,为学生提供全面、系统的菜单选择知识。
2.多媒体资料:制作课件、演示文稿等,为学生提供直观的学习材料。
3.实验设备:准备计算机等实验设备,为学生提供实际操作的机会。
4.在线资源:提供在线教程、视频等,方便学生自主学习和复习。
五、教学评估本课程的评估方式包括平时表现、作业和考试三个部分,以全面客观地评估学生的学习成果。
1.平时表现:通过观察学生在课堂上的参与程度、提问回答等情况,评估学生的学习态度和理解程度。
2.作业:布置适量的作业,要求学生按时完成,通过作业的质量和进度评估学生的学习效果。
《C语言程序设计》课程实验指导书

三、预习内容
预习教材第3章。
实验四 选择结构程序设计
一、实验目的
1.了解C语言表示逻辑值的方法。
2.学会正确使用逻辑运算符和逻辑表达式的方法。
3.熟悉if语句和switch语句。
4.结合程序掌握一些简单的算法。
5.学习调试程序的方法。
二、实验内容
本实验要求编程解决以下问题,然后上机调试运行程序。
d=f;e=g;
p=a=m=50000;q=b=n=-60000;
运行程序,分析运行结果。
(3)将9-14行改为以下的scanf语句,即用scanf函数接收从键盘输入的数据:
scanf("%d,%d,%c,%c,%f,%f,%lf,%lf,%ld,%ld,%u,%u",&a,&b,&c1,&c2,&d,&e,&f,&g,&m,&n,&p,&q);
{int z;
if(x>y) z=x;
else z=y;
return(z);
}
(1)运行程序,若程序有错,则修改错误后继续运行程序,当没有错误信息时输入:2,5并按Enter键,查看运行结果。
(2)将程序的第三行改为:int a;b;c;然后按F9看结果如何,将其修改为int a,b,c;将子程序max的第3,4行合并为一行,运行程序,看结果是否相同。
printf("f=%15.6f,g=%15.12f\nm=%ld,n=%ld\np=%u,q=%u\n",f,g,m,n,p,q);
}
(1)运行此程序并分析运行结果。
(2)在此基础上,修改程序的第9-14行:
C语言运行环境

C语言上机实验指导实验一C语言运行环境及顺序结构程序设计实验目的⑴熟练掌握C语言在VC6.0编程环境下的操作;⑵运行简单的C程序,初步了解C源程序的特征;⑶熟悉printf( )函数以及scanf( )函数的基本使用。
实验内容C语言源程序(后缀名为.c)可以在VC6.0等很多编译系统或集成环境中编译运行,最新版2008年全国计算机等级考试(NCRE)将全面使用VC6.0,所以我们主要介绍VC6.0上机环境。
一、Microsoft Visual C++6.0(简称VC++6.0或VC6.0)的简介和安装现在常用的VisualC++6.0版本,虽然已有公司推出汉化版,但只是把菜单汉化了,并不是真正的中文版VisualC++6.0,而且汉化的用词不准确,因此许多人都使用英文版。
如果计算机中未安装VisualC++6.0,则应先安装VisualC++6.0。
Visual C++是Microsoft Visual Studio的一部分,因此需要找到Visual Studio的光盘,执行其中的setup.exe,并按照屏幕上的提示进行安装即可。
安装结束后,在Windows的“开始”菜单中的“程序”子菜单中就会出现Microsoft Visual Studio子菜单。
在需要使用Visual C++时,只需从电脑上选择“开始”→“程序”→Micros o ft Visual Studio→VisualC++6.0(也可以从桌面快捷方式进入)即可。
此时屏幕上短暂显示Visual C++6.0的版权页后,出现VisualC++6.0的主窗口,如图1-1所示。
在VisualC++6.0主窗口的顶部是VisualC++的主菜单栏,其中包括9个菜单项:File(文件)、Edit(编辑)、Insert(插入)、Project(项目)、Build(构建)、Tools(工具)、Window(窗口)、Help(帮助)。
以上各项在括号中的是VC6.0中文版中的中文显示,以使读者在使用VC6.0中文版时便于对照。
C++课程设计--设计菜单选择程序

一、实习题目:设计菜单选择程序二、设计思想:1、实现循环和功能选择:编写一个菜单函数menu(),用whlie 循环控制菜单的重复选择,用switch 语句对应用户的选择,并且实现相应的功能。
2、设计各个选择的功能:对于选择1,运用克莱姆法则求解线性方程组,用了多个循环和if 判断语句,其中两个函数调用,其主要功能是求解行列式的数值;选择二,统计一篇英语文章的单词数,使用了函数getchar( ) 和gets(str),用于输入英文文章。
三、程序代码:#include<iostream>#include<string>using namespace std;#define N 10000void menu();//菜单选项函数void equation();//求线性方程组void english();//统计英文文章的单词数///////////////主函数的执行///////////////int main(){int a,t=1;while(t){menu();cout<<"请选择1-3:";cin>>a;cout<<endl;switch(a){case 1:equation();break;case 2:english();break;case 3:t=0;break;}}}/////////////////菜单选项函数//////////////////void menu(){cout<<"\n\t\t\t-----------菜单选择------------"<<endl;cout<<"\t\t\t1.利用克莱姆法则求解线性方程组"<<endl;cout<<"\t\t\t2.统计一篇英文文章的单词数"<<endl;cout<<"\t\t\t3.退出程序"<<endl;cout<<"\t\t\t-------------------------------"<<endl;}////////////利用克莱姆法则求解线性方程组/////////////static int a[N][N] ,b[N];int di[N],c[N];double x[N];int term(int n,int k[]){int p,q,t=1;for (p=1; p<n; p++)for(q=0; q<p; q++)if(k[q]>k[p])t=-t;for(p=0;p<n; p++)t*=a[p][k[p]];return(t);}int det(int n){int j0,j1,j2,j3,j4,j5,d=0,k[N];for(j0=0;j0<n;j0++){if(a[0][j0]==0) continue;k[0]=j0;for(j1=0;j1<n;j1++){if(j1==j0) continue;if(a[1][j1]==0) continue;k[1]=j1;if(n==2)d+=term(n,k);for(j2=0;j2<n;j2++){if(j2==j0) continue;if(j2==j1) continue;if(a[2][j2]==0) continue;k[2]=j2;if(n==3)d+=term(n,k);for(j3=0;j3<n;j3++){if(j3==j0) continue;if(j3==j1) continue;if(j3==j2) continue;if(a[3][j3]==0) continue;k[3]=j3;if(n==4)d+=term(n,k);for(j4=0; j4<n; j4++){if(j4==j0) continue;if(j4==j1) continue;if(j4==j2) continue;if(j4==j3) continue;if(a[4][j4]==0) continue;k[4]=j4;if(n==5)d+=term(n,k);for(j5=0;j5<n;j5++){if(j5==j0) continue;if(j5==j1) continue;if(j5==j2) continue;if(j5==j3) continue;if(j5==j4) continue;if(a[5][j5]==0) continue;k[5]=j5;}}}}}}return (d);}void equation(){int i,j,n,d;char ch;A:cout<<"请输入线性方程组的未知数个数(n<=6) n=";cin>>n;cout<<"请输入线性方程组的增广矩阵(即未知数的系数与常数项组合成的矩阵,为n*(n+1)阶矩阵):"<<endl;for (i=0;i<n;i++) //增广矩阵的输入{for(j=0;j<n;j++){cin>>a[i][j];}cin>>b[i];}d=det(n);for (j=0;j<n;j++){for (i=0;i<n;i++){c[i]=a[i][j];a[i][j]=b[i];}di[j]=det(n);for(i=0;i<n;i++)a[i][j]=c[i];}cout<<"最后求得线性方程组的解为:"<<endl;for (i=0;i<n;i++){x[i]=(di[i])/d;cout<<"x("<<i+1<<")="<<x[i]<<endl;}B:cout<<"您是否要继续(Y/N)?"<<endl;cin>>ch;if(ch=='y'||ch=='Y')goto A;else if(ch=='n'||ch=='N')goto C;elsegoto B;C:system("pause");}/////////统计英文文章的单词数////////////////void english(){char str[N],c;int i,word=0,num=0;cout<<"\n请输入需要统计单词数的英文文章:"<<endl;getchar(); /*输入英文文章*/gets(str);for(i=0;(c=str[i])!='\0';i++){if((c>0&&c<65)||(c>90&&c<97)||c>122&&c<255)word=0;/*用空格区分新单词的产生*/else{if(word==0){word=1;/*新单词产生*/num++;}}}cout<<"这篇文章共有"<< num <<"个单词."<<endl;}四、测试用例及测试结果1.解线性方程组:2.统计英文文章的单词数:五、程序不足及升级方向这个程序只能解未知数的个数n<=6时的恰定方程组,实用性受到限制,还需要以后再完善。
C语言程序设计 实验报告2--选择结构

福建农林大学金山学院实验报告系(教研室):专业:年级:实验课程:C语言程序设计姓名:学号:实验室号:计算机号:实验时间:指导教师签字:成绩:实验2:选择结构程序设计一、实验目的和要求1.了解C语言表示逻辑量的方法2.正确使用逻辑运算符和逻辑表达式,掌握if语句和switch语句3.结合程序掌握一些简单算法,并学习调试程序二、实验内容和原理1.有一函数:x2+2x-6(x<0,x≠-3)y = x2-5x+6(0≤x<10,x≠2,x≠3)x2-x-15(x=-3,x=2,x=3,x≧10)写一程序,用scanf函数输入x,输出y值。
2.分别用if语句和switch语句编程实现:给出一个百分制成绩,要求输出成绩等级A、B、C、D、E。
90分以上为A,80~89分为B,70~79分为C,60~69分为D,60分以下为E。
3.输入4个整数,要求按由小到大顺序输出。
4.有三个整数a,b,c,由键盘输入,输出其中最大的数,请编写程序。
(用两种方法实现)5.输入出租车类型和里程,计算打车的费用。
计算方式为:3公里以内10元;3公里以上0车型每公里1.5元,1车型每公里2元。
三、实验环境1. 硬件:PC机;2. 软件:Windows操作系统、Visual C++ 6.0,DEV-CPP 。
四、算法描述及实验步骤1、先用scanf函数输入,再用if语句的嵌套来计算该方程。
2、(1)用switch语句时,对输入的数据进行检查,在用score/10将其强制转换得到一个整型。
最后用switch语句执行使其得到一个字符型字母。
(2)用if语句分成各个分数段将符合要求的输出对应的字符。
3、用if语句依次比较的方法排出其大小顺序。
4、(1)先用scanf函数输入,再用if语句的嵌套比较其大小顺序。
(2)带入一个中间数用条件表达式比较其大小顺序。
5、在标题写入条件,3公里以下直接输出。
3公里以上判断车型,再带入相应车型计算车费。
《C语言程序设计实验》指导书(实验1~6)

《C语言程序设计实验》指导书(简明版)**大学软件学院**年**月实验一顺序结构程序设计(2学时)一、实验目的1、熟悉C编译环境、简单C程序结构及书写方式、以及C程序的编辑、编译、连接、运行、调试的步骤;2、掌握C语言的基本数据类型及其输入输出格式,以及输入输出函数的使用方法;3、掌握C语言的算术运算符(特别是自增、自减运算符)、赋值运算符、关系运算符、逻辑运算符、条件运算符、逗号运算符的使用;4、掌握C语言顺序结构程序的执行流程、设计方法,能够根据实际问题灵活使用顺序结构,画出程序的算法流程图,设计出逻辑合理、思路清晰、结果正确的顺序结构程序。
二、实验内容及要求1、实验内容包括8道题目,分为基本内容和选做内容两部分。
要求:(1)基本内容中的实验题目是必须要完成的,选做内容中的实验题目可以根据自己的情况选做或全做(越多越好,适当加分);(2)在实验之前编写出基本内容、选做内容中的所有程序,实验前检查(视未完成情况适当扣分);(3)对于设计型题目,要求画出程序流程图(传统流程图和N-S图);(4)在上机实验过程中,注意总结和体会上机步骤(编辑、编译、连接、运行、调试、结果分析),注意培养观察、分析和排除编译错误、连接错误和程序逻辑错误的初步能力;(5)上机结束后,应按要求认真书写实验报告(格式见附件)。
2、基本内容(1)[验证型]编辑下列程序,然后进行编译、连接和运行,观察结果,并简要总结简单C程序的结构、书写格式以及上机过程;#include <stdio.h>int main( ){printf("Hello, world!\n");return 0;}(2)[验证型]通过运行下列程序,分析各种格式符的使用方法。
#include <stdio.h>int main( ){int a = 9, b = 2;float x = 32.8459, y = -792.451;char d = 'R';long n = 5461237;unsigned u = 65535;printf("%d,%d\n", a, b);printf("%3d,%3d\n", a, b);printf("%f,%f\n", x, y);printf("%-10f,%-10f\n", x, y);printf("%8.2f,%8.2\n", x, y);printf("%.4f,%.4f\n", x, y);printf("%3f,%3f\n", x, y);printf("%e,%10.2e\n", x, y);putchar(d);putchar('\n');printf("%c,%d,%o,%x\n", d, d, d, d);printf("%ld,%lo,%x\n", n, n, n);printf("%u,%o,%x,%d\n", u, u, u, u);return 0;}(3)[验证型]编辑下列程序,进行编译、连接和运行。
《第一单元 Visual Basic初步 第2课 编一个简单的程序 测试程序》教学设计

《测试程序》教学设计方案(第一课时)一、教学目标1. 知识与技能:学生能够理解程序测试的基本观点,掌握测试程序的基本方法。
2. 过程与方法:通过实践操作,学生能够学会应用测试工具进行程序测试。
3. 情感态度与价值观:培养学生周密的编程态度,激发他们对信息技术学科的兴趣。
二、教学重难点1. 教学重点:学生能够应用测试工具进行程序测试,理解程序测试的重要性。
2. 教学难点:如何引导学生发现并解决程序中的问题,培养他们的编程思维。
三、教学准备1. 准备教学用具:计算机、网络、测试工具等。
2. 准备教学软件:与教学内容相关的程序代码。
3. 制定教学计划:合理安排教学内容,确保学生对知识有清晰的理解和掌握。
4. 开展教学活动:按照教学计划,采用合适的教学方法,引导学生学习相关知识和技能。
5. 反馈与调整:根据学生的学习情况和反馈,及时调整教学计划和方法,确保教学效果。
在准备教学软件时,应注意选择适合教学内容的程序代码,确保其简单易懂且具有实际应用价值。
同时,应思量到学生的基础和学习能力,选择适当难度的代码,以激发他们的学习兴趣和动力。
在制定教学计划时,应充分思量学生的学习习惯和时间安排,合理分配教学内容,确保学生在有限的时间内获得最大的学习效果。
同时,应思量到课程内容的连贯性和系统性,确保学生能够系统地掌握相关知识和技能。
在开展教学活动时,应采用多种教学方法,如讲解、演示、实践操作等,以激发学生的学习兴趣和主动性。
同时,应注重与学生的互动和沟通,及时了解他们的学习情况和反馈,以便做出适当的调整。
总之,一位优秀的程序员转行成为教师,需要充分准备并运用教学技能,以实现最佳的教学效果。
通过不息的反馈和调整,他们将能够帮助学生更好地掌握相关知识和技能,为他们的未来发展打下坚实的基础。
四、教学过程:本节课是《测试程序》的教学设计,主要分为以下四个环节:1. 引入课题教师通过简单的介绍,让学生了解程序测试的重要性,以及本节课所学的内容和方法。
C语言程序设计(第三版)课件:用选择语句实现对菜单的选择

4.1 任务1 用if语句实现菜单的选择执行设计
4.1.2知识必备 2.if语句 (2)在使用if语句中还应注意以下问题: ①if语句的表达式一般为关系表达式或逻辑表达式,C语 言在判断时只要不为0认为是假,因此表达式可以是任 意类型的表达式(如整型、实型、字符型、指针类型的 表达式等),这是C语言与其他高级语言不同之处。 ②在if语句中,条件判断表达式必须用括号括起来,分号 是C语句的结束符是必备的成分,那次if和else后面的 语句都必须有分号。 ③在if语句中,语句可以是一条简单语句,也可以是复合 语句,当条件成立或不成立时,执行的不止一条语句 时,必须使用复合语句。
本格式又称为多分支选择语句。 前二种形式的if语句一般都用于两个 分支的情况。 当有多个分支选择时, 可采用第三种形式的if语句。
执行过程为:依次判断各个表达 式的值,当出现某个值为真时,则执 行其对应的语句。然后跳到整个if语 句之外继续执行程序。 如果所有的表 达式均为假,则执行语句n。然后继 续执行后续程序。 其执行过程如图46所示。
|\n");
printf("
| 3-----计算最低分
|\n");
printf("
| 0-----返回上级菜单
|\n");
printf("
|......................................|\n");}
else
if(number==6)
printf(“程序说明!\n”); //打印一句话
4.1 任务1 用if语句实现菜单的选择执行设计
4.1.2知识必备 2.if语句 实现分支结构最常用的方法是采用if语句。if语句用于判 定所给定的条件是否满足,程序根据判定的结果决定所执 行的操作。If语句有三种基本形式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【设计题目】设计菜单选择趣味程序【设计要求】菜单是应用程序的界面,本题的任务是设计一个比较实用的菜单,通过菜单选择不同的功能。
设计分为两步:首先设计一个含有多个菜单项的菜单演示程序,然后再为这些菜单项配上相应的功能。
菜单内容程序运行后,界面给出3个菜单项的内容和输入提示。
1.解一元二次方程2.出圈游戏3.退出程序选择l-3:使用数字1-3来选择菜单项,执行相应的菜单项功能,其他输入则不起作用。
【总体设计】一、菜单驱动程序输入1-3之间的任意一个数字,即可进入相应选择项。
从程序测试结果可知,当选择相应选择项时,其输出信息分别为:解一元二次方程、出圈游戏和退出程序。
1.主程序的设计假设使用文件select.cpp,内容如下:/**********************************select.cpp主程序文件*********************************/#include"cpp2.h"void main(){handle_menu(); //调用菜单处理函数}2.实现循环和功能选择的设计-菜单处理函数/**********************************菜单处理函数*********************************/void handle_menu(void){for(; ;){switch(menu_select())//调用菜单选择函数{case 1:FindIt();//求解一元二次方程break;case 2:game();//出圈游戏break;case 3:cout<<"\t再见!\n";return;}}}这里使用for循环实现重复选择,假设输入选择用变量用cn存储,它作为menu_select()函数的返回值提供给switch语句。
3.得到cn的合理值的设计-菜单选择函数应该设计一个函数用来输出提示信息和处理输入,这个函数应该返回一个数值cn,以便供给switch语句使用。
/**********************************菜单选择函数**********************************/int menu_select(){char s[2];int cn;cout<<"\t1.解一元二次方程\n";cout<<"\t2.出圈游戏\n";cout<<"\t3.退出程序\n";cout<<"\t选择1-3:";for(; ;){gets(s);cn=atoi(s); // 是为了使输入的字符串转变为数字if(cn<1||cn>3)printf("\n\t输入错误,重选1-3:");elsebreak;}return cn;}二、求解一元二次方程1.设计要求这里要求编制一个求方程aX2+bx+c=0的根的程序。
一般将系数设成float型,可以把求根变量设成double型,使用库函数sqrt()求平方根,sqrt()在头文件math.h中定义。
假设:d=b*b-4*a-c可以根据d>0、=0或<0来决定求解方法。
if(d>0){//有两个不相等的实数解}else if(d==0){//有两个相等的实数解}else{//有两个不相等的虚数解}2.设计方法(1)设计一个FindRoot 类表示这个方程。
(2)在头文件cpp2.h 中声明类,在FindRoot.cpp 文件中定义成员函数。
(3)使用函数Findlt()作为菜单项。
3.类FindRoot 的设计为了方便,除了将方程系数设计为属性之外,还将方程的根x1和x2,以及用来作为判定条件的d(d=b*b-4*a*c)均设计成类的属性。
如图1是其类图,图2是对象obj 的对象图。
其中,成员函数Find()是用来求方程的根,Display()则用来输出结果。
由此可见,它们都需要用到属性d 。
可在构造函数中求出d 的值,其他成员函数直接使用这个属性,不必再去计算。
图1 类图 图2obj 对象图①.设计构造函数FindRoot::FindRoot(float x,float y,float z){a=x;b=y;c=z;d=b*b-4*a*c;}② 设计求根成员函数Find()void FindRoot::Find(){if ( d>0){x1=(-b+sqrt(d))/(2*a); x2=(-b-sqrt(d))/(2*a);return;}else if(d==0){x1=x2=(-b)/(2*a);return;}else{x1=(-b)/(2*a);x2=sqrt(-d)/(2*a);}}③设计输出结果的成员函数Display()void FindRoot::Display(){if(d>0){cout<<"x1="<<x1<<"\nx2="<<x2<<endl;return;}else if(d==0){cout<<"xl=x2="<<x1<<endl;return;}else{cout<<"Xl="<<x1<<"+"<<x2<<"i"<<endl;cout<<"X2="<<x1<<"-"<<x2<<"i"<<endl;}}4.设计菜单函数FindIt()为了循环求解,使用for循环语句。
退出时,希望只接收一个字符。
最简单的是输入一个0作为a的值。
/*************************************************菜单项函数***************************************************/void FindIt(){float a,b,c;cout<<"这是一个求方程ax2+bx+c=0的根的程序。
"<<endl;cout<<"把变量设为double型,使用库函数math进行计算."<<endl;for(; ;){cout<<"输入方程系数a:";cin>>a;if(a==0) //a为0,结束运行,因为“回车”被atoi()函数作为“0”值赋给cn {getchar();//为消除回车的影响return;}cout<<"输入方程系数b:";cin>>b;cout<<"输入方程系数c:";cin>>c;FindRoot obj(a,b,c);obj.Find();obj.Display();}}三、设计出圈游戏1.设计要求这里假设有人数为n个人的一个小组,他们按顺时针方向围坐一圈。
一开始任选一个正整数作为报数上限值m,从第一个人开始按顺时针方向自1开始顺序报数,报到m时停止报数。
报数m的人出列,然后从他原来所在的、顺时针方向的下一个人开始重新从1报数,报到m时停止报数并出列。
如此下去,直至所有人全部出列为止。
要求按他们出列的顺序输出他们的名字。
2.设计方法求解出圈顺序的方法很多,这里我采用的是利用类和数组来求解出圈顺序,仅供大家参考。
(1)设计一个SeqList类。
(2)在头文件cpp2.h中声明类,并使用默认的内联函数方式定义它们。
(3)使用类的数组来求解。
(4)用Joseph()函数求解出圈,使用函数game()作为菜单项。
(5)在文件gamel.cpp中实现Joseph()和game()函数。
3.设计类这里要求使用名字,而在名字的字符串中,可能存在空格。
可以为该类设计两个属性,一个是字符串,用来存储名字。
另一个是整数,用来表示报数的位置。
若使用类的数组,则可以通过数组的下标,将位置和名字对应起来。
在声明的类中,同时定义的成员函数就是默认的内联函数。
另外,考虑到使用类的数组,所以不为它定义构造函数,而是用系统提供的默认无参数构造函数。
/**************************************************声明SeqList类 **使用内联函数定义类 *****************************************************/class SeqList{int num;char name[10];public:int GetNum(){return num;}void DispName(){cout<<name;}void SetNum(int a){num=a;}void SetName(char b[[]]{strcpy(name,b);}};按照要求,不需要为类设计求解出圈的成员函数。
4.求解出圈的函数Joseph()使用类的数组,其实就是利用顺序存储结构来求解。
在数组初始化后,调用函数Joseph() 寻找出列人员。
假设建立类的数组c,这时只能为数组c假设一个长度,实际的有效长度只有在给定人数之后才能知道。
它的算法思想如下:void Joseph(SeqList c[],int length) //使用数组作为参数,同时需要将人数传给它。
{BEGIN初始化人数Length参加游戏的人的名字计数器初值k从1开始循环length次j计数器清零j循环(j<间隔次数m)计数i如果i数到尾部,则返回第一个位置,即重置i等于0如果该位置上的人仍然在圈中,则j计数加1endj //结束循环j如果是最后一个,结束循环,作特殊处理不是最后一个,输出出圈人的信息标识该人员已出圈,开始新一轮循环endk最后一个结束循环,输出它的信息。
END}判断是利用数据成员的值,已经出圈的将其标志为0。
下次数到他时,作为无效数据处理。
输出使用数据成员name。
5.菜单项函数game()位置编号num应该从1开始,但C++的数组是从O开始,所以num的值比其所在数组的下标的值多1,这样做是为了直观。
