场论中三大积分公式的应用及联系
第一green公式(散度定理,分部积分公式)

第一green公式(散度定理,分部积分公式)第一green公式(散度定理、分部积分公式)的深度解析引言第一green公式是微积分中的重要定理之一,它涉及到散度定理和分部积分公式,是研究场论和积分学中的重要基础知识。
在本文中,我们将对第一green公式进行全面评估,并探讨其深度和广度的含义。
一、散度定理的基本概念散度定理是矢量分析的基础定理之一,它描述了一个矢量场通过一个封闭曲面的通量等于该矢量场的散度在该曲面内的体积积分。
散度是一个矢量场在某一点上的流出流入的量的差异,它可以理解为矢量场的“发散”程度。
散度定理的数学表达式为∬(V·n)dS=∭(∇·V)dV,其中V代表矢量场,n代表曲面的法向量,S代表曲面,∇·V代表矢量场V的散度,dS代表曲面的面积元素,dV代表体积元素。
散度定理的应用领域非常广泛,涉及到电磁学、流体力学等多个学科。
二、分部积分公式的基本概念分部积分公式是微积分中的重要工具,它描述了两个函数的积分之间的关系。
分部积分公式的数学表达式为∫udv=uv-∫vdu,其中u和v 是可微函数。
分部积分公式可以帮助我们简化复杂函数的积分运算,同时也为求解微分方程提供了重要的帮助。
分部积分公式在微积分和工程数学中有着广泛的应用。
三、第一green公式的数学表达和意义将散度定理和分部积分公式结合起来,就得到了第一green公式的数学表达:∬(V·n)dS=∭(∇·V)dV。
这个公式表明了一个矢量场通过一个封闭曲面的通量与该矢量场的散度在该曲面内的体积积分之间的关系。
第一green公式的意义在于将曲面积分与体积积分之间建立了联系,极大地简化了对于矢量场通量的计算。
这个公式在计算电场、磁场等物理量的通量时有着重要的应用。
四、个人观点和理解对于第一green公式,我个人认为它的深度和广度非常值得探讨。
通过深入学习散度定理和分部积分公式,我们可以更好地理解和应用第一green公式,同时也可以将其应用于更多的领域。
场论中三大积分公式的应用及联系

场论中三大积分公式的应用在物理学中,曲线积分和曲面积分有着广泛的应用。
物理学家为了既能形象地表达有关的物理量,又能方便地使用数学工具进行逻辑表达和数据计算,使用了一些特殊的术语和记号, 在此基础上产生了场论。
在大一的下半学期的高等数学课上。
我们学习了微积分这一门基础课,而曲线积分及曲面积分就是学习重点之一。
在曲线积分和曲面积分的学习中,对于重积分的求解运算,Green 公式、Gauss 公式和Stokes 公式作为章节核心,需要我们重点研究。
而本文围绕着对三大公式的应用和联系进行探讨。
一、三大公式Green 公式:设D 为平面上由光滑或分段光滑的简单闭曲线所围的单连通区域。
如果函数(,)P x y ,(,)Q x y 在D 上具有连续偏导数,那么(,)(,)(,)(,)L D Q x y P x y P x y dx Q x y dy dxdy x y +⎡⎤∂∂+=-⎢⎥∂∂⎣⎦⎰⎰⎰, 其中L +表示沿D 的边界的正方向。
Gauss 公式:设Ω是3中由光滑或分片光滑的封闭曲面∂Ω所围成的二维单连通封闭区域,(,,)P x y z ,(,,)Q x y z 与(,,)R x y z 在Ω上具有连续偏导数,则divFd F nds +Ω∂ΩΩ=⋅⎰⎰⎰⎰⎰,即P Q R dxdydz Pdydz Qdzdx Rdxdy x y z +Ω∂Ω⎛⎫∂∂∂++=++ ⎪∂∂∂⎝⎭⎰⎰⎰⎰⎰, 其中+∂Ω表示有向封闭曲面∂Ω的外侧。
Stokes 公式:设S 为光滑曲面或分片光滑的双侧曲面,其边界为光滑或分段光滑闭曲线S ∂,若(,,)P x y z ,(,,)Q x y z 与(,,)R x y z 在S 及其边界S ∂上具有连续偏导数,则有S S R Q P R Q P Pdx Qdy Rdz dydz dzdx dxdy y z z x x y ∂⎛⎫⎛⎫∂∂∂∂∂∂⎛⎫++=-+-+- ⎪ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭⎰⎰⎰ cos cos cos S R Q P R Q P dS y z z x x y αβγ⎡⎤⎛⎫⎛⎫∂∂∂∂∂∂⎛⎫=-+-+-⎢⎥ ⎪ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭⎣⎦⎰⎰, 其中S ∂取S 的诱导定向。
数学分析简明教程22 各种积分间的联系与场论初步

页脚内容1第二十二章 各种积分间的联系与场论初步§1 各种积分间的联系1.应用格林公式计算下列积分:(1)ydx x dy xy L ⎰-22,其中L 为椭圆22a x +22by =1取正向;(2),)()(⎰-++Ldy y x dx y x L 同(1);(3)dy y x dx y x L)()(222+-+⎰, L 是顶点为)5,2(),2,3(),1,1(C B A 的三角形的边界,取正向;(4),1,)()(223333=+--+⎰y x L dy y x dx y x L为取正向;(5),sin sin ydy e xdx e x Ly -+⎰ L 为矩形d y c b x a ≤≤≤≤, 的边界,取正向;(6)],))cos(sin ())cos(sin [(dy y x xy x dx y x xy y e Lxy +++++⎰其中L 是任意逐段光滑闭曲线.解(1)原式 =()()d xdy y x dxdy x y DD⎰⎰⎰⎰+=--2222)(=ab()r dr r b r a d ⎰⎰+122222220sin cos θθθπ(广义极坐标变换)=())(3sin cos 3122202222b a ab d b a ab +=+⎰πθθθπ.(2)⎰-++Ldy y x dx y x )()(=⎰⎰=-Ddxdy 0)11(.(3)原式 ⎰⎰+-=Ddxdy y x x ))(22(页脚内容2⎪⎪⎭⎫ ⎝⎛+-=-=⎰⎰⎰⎰⎰⎰-+-+215231143124322yy y y D dx ydy dx ydy ydxdy 9143))5(127)(47(2252221-=-+--=⎰⎰dy y y dy y y . (4)原式π23)(3)33(2222-=+-=--=⎰⎰⎰⎰DD dxdy y x dxdy y x .(5)原式 dxdy x e y e Dy x ⎰⎰--=-)cos sin ()cos sin (⎰⎰⎰⎰+-=-b ad cdcydy b ax e dx x ydy dx e)sin )(sin ()cos )(cos 11(a b e e c d ee cd b a --+--=. (6))]cos(sin [),(y x xy ye y x P xy ++=,)]cos(sin [),(y x xy x e y x Q xy ++=,)]sin(cos [sin )]cos(sin [y x xy xy xy e y x xy x ye xQxy xy --++++=∂∂ )]sin()cos(sin )cos (sin [y x y x y xy xy xy xy e xy --+++=,)]sin(cos [sin )]cos(sin [y x xy xy xy e y x xy y xe yPxy xy +-++++=∂∂ )]sin(cos sin )cos (sin [y x xy x xy xy xy xy e xy +-+++=,)cos()(y x x y e yPx Q xy +-=∂∂-∂∂, 所以,原式⎰⎰+-=Dxy dxdy y x x y e ,)cos()( 其中D 为L 包围的平面区域.页脚内容32.利用格林公式计算下列曲线所围成的面积: (1)双纽线θ2cos 22a r =;(2)笛卡尔叶形线)0(333>=+a axy y x ;(3)t t a x sin )cos 1(2+=,t t a y cos sin 2⋅=,π≤≤20t .解(1)⎰⎰⎰⎰==12||D Ddxdy dxdy D ⎰-⨯=L ydx xdy 212 ⎰=--=44)]sin (sin cos cos [ππθθθθθd r r r r 24424422cos a d a d r ===⎰⎰--ππππθθθ,其中1D 由θ=2cos 22a r ,44π≤θ≤π-所围成. (2)作代换,tx y =则得曲线的参数方程为313tatx +=,3213t at y +=.所以, dt t t a dx 233)1()21(3+-=,dt t t at dy 233)1()2(3+-=, 从而,dt t t a ydx xdy 2322)1(9+=-,于是,面积为 D =⎰C x y y x d -d 21=dt t t a ⎰∞++02322)1(29=223a . (3)D =⎰-cydx xdy 21=页脚内容4{}⎰-++⋅--⋅+π2022322]sin )sin (cos 2cos )cos 1[(cos sin )sin cos sin 2(sin )cos1(21dt t t t t t a t t a t t t a t t a{}⎰π-++⋅--⋅+2022322]sin )sin (cos 2cos )cos 1[(cos sin )sin cos sin 2(sin )cos1(21dt t t t t t a t t a t t t a t t a=21tdt t t a 2cos )cos 1(sin 22022+⎰π=24a π 3.利用高斯公式求下列积分: (1)y x z x z y z y x sd d d d d d 222++⎰⎰.其中(a )S 为立方体a z y x ≤≤,,0的边界曲面外侧;(b )S 为锥面)0(222h z z y x ≤≤=+,下侧. 解:(a )y x z x z y z y x sd d d d d d 222++⎰⎰=2⎰⎰++vdxdydz z y x )(=2⎰⎰⎰++aa a dz z y x dy dx 0)(=43a(b)补充平面1S :h z h y x =≤+,222的上侧后,1S S +成为闭曲面的外侧, 而⎰⎰++1222S dxdy z dzdx y dydz x =⎰⎰xyD dxdy h 2=22h h π⋅= π4h 所以 :⎰⎰++Sdxdy z dzdx y dydz x 222+π4h页脚内容5=⎰⎰+++1222S S dxdy z dzdx y dydz x=2z y x z y x V⎰⎰⎰++d d )d (=2⎰⎰xyD dxdy⎰+++h y x z z y x 22)d (=⎰⎰++xyD y x y x y x y x h y x h d )]d (- )+2(-+)+([222222=⎰⎰π-θ+θ-+θ+θθ20222])sin (cos 2)sin (cos 2[hrdr r r h hr d=1214h θ+θ+θ⎰πd 20)3sin 2cos 2(=2π4h 所以⎰⎰++Sdxdy z dzdx y dydz x 222=442h h π-π=42h π- (2)⎰⎰++Sdxdy z dzdx y dydz x 333, 其中S 是单位球面的外侧;解:⎰⎰++Sdxdy z dzdx y dydz x 333=3⎰⎰⎰++Vz y x z y x d d )d (=3⎰⎰⎰ππρρϕϕθ2014sin d d d=512π (3)设S 是上半球面222y x a z --=的上侧,求 (a )⎰⎰++Sy x z x z y z y x d d d d d d(b)⎰⎰++-+Sy x z y xy x z z y x z y xzd )d (2d )d (d d 2222页脚内容6解:补充平面1S :222,0a y x z ≤+=,下侧后,1S S +成为闭曲面的外侧,而 (a )⎰⎰=++10S zdxdy ydzdx xdydz所以⎰⎰=++Szdxdy ydzdx xdydz ⎰⎰+=++1S S zdxdy ydzdx xdydz 3⎰⎰⎰Vdxdydz=213433⋅π⋅a =2π3a(b)⎰⎰++-+1d )d (2d )d (d d 2222S y x z y xy x z z y x z y xz =⎰⎰xyD xydxdy 2=2⎰π20d θr r a⎰θθ03d cos sin =0所以 ⎰⎰++-+Sy x z y xy x z z y x z y xzd )d (2d )d (d d 2222=⎰⎰+++-+1d )d (2d )d (d d 2222S S y x z y xy x z z y x z y xz =⎰⎰⎰++Vdxdydz z y x )(222=⎰π20d θ⎰20πsin ϕd ϕ⎰a4 d ρρ=554a π(4)⎰⎰+-++-++-Sy x y x z x z x z y z y y x d )d (d )d (d )d z (222222,S 是 2222)()()(R c z b y a x =-+-+- 的外侧.解:⎰⎰+-++-++-Sy x y x z x z x z y z y y x d )d (d )d (d )d z (222222,=3⎰⎰⎰V dxdydz =V 3=3343R π⋅=4π3R4.用斯托克斯公式计算下列积分:页脚内容7(1)⎰++Lzdz dy dx y x 32, 其中(a )L 为圆周0,222==+z a y x ,方向是逆时针;(b )L 为y x z y ==+,122 所交的椭圆,沿x 轴正向看去,按逆时针方向; 解: (a )取平面0=z 上由交线围成的平面块为S ,上侧,由Stokes 公式⎰++Lzdz dy dx y x 32=⎰⎰Szy x z y x dxdydzdxdydz1///32∂∂∂∂∂∂ =⎰⎰-Sdxdy y x 223=⎰⎰----ax a xa dy y dx x 02222223=dx x a x a3222)(2⎰--=616a π-(b )取平面y x =上由交线围成的平面块为S ,上侧,由由Stokes 公式⎰++Lzdz dy dx y x32=⎰⎰∂∂∂∂∂∂Szy x z y x dxdy dzdx dydz 132=⎰⎰-Sdxdy y x 223=⎰⎰-xyD dxdy y x 223=616a π-页脚内容8(2)dz y x dy x z dx z y L)()()(-+-+-⎰,L 是从)0,0,(a 经)0,,0(a 至),0,0(a 回到)0,0,(a 的三角形;解: 三角形所在的平面为a z y x =++,取平面a z y x =++上由以上三角形围成的平面块为S ,取上侧,由stokes 公式dz y x dy x z dx z y L)()()(-+-+-⎰=⎰⎰---∂∂∂∂∂∂Syx x z z y z y x dxdy dzdx dydz=⎰⎰++-S dxdy dzdx dydz 2 =2-(⎰⎰Sdydz +⎰⎰Sdzdx +⎰⎰Sdxdy )=2-(⎰⎰yzD dydz +⎰⎰zx D dzdx +⎰⎰xyD dxdy )=23a -(3)dz y x dy y x dx z y L)()()(222222+++++⎰,其中(a )L 为1=++z y x 与三坐标轴的交线,其方向与所围平面区域上侧构成右手法则;(b )L 是曲线Rx z y x 2222=++, rx y x 222=+ (0,0><<z R r ),它的方向与所围曲面的上侧构成右手法则;解:(a )中取平面1=++z y x 上与三坐标面交线所围平面块为S ,上侧;(b )中取曲面Rx z y x 2222=++上由L 所围曲面块为S ,上侧, 则由stokes 公式,得页脚内容9dz y x dy y x dx z y L)()()(222222+++++⎰=⎰⎰+++∂∂∂∂∂∂Sy x x z z y z y x dxdy dzdx dydz 222222 ⎰⎰-+-+-=Sdxdy y x dzdx x z dydz z y )()()(2=2))()()((dxdy y x dzdx x z dydz z y SSS⎰⎰⎰⎰⎰⎰-+-+-则(a )⎰+++++Ldz y x dy z x dx z y )()()(222222= dS y x x z z y S⎰⎰γ-+β-+α-]cos )(cos )(cos )[(2=0 (因为cos α=cos β=cos γ=31)(b ) 注意到球面的法线的方向余弦为: R R x -=αcos , R y =βcos ,Rz=γcos ,所以 dz y x dy z x dx z y L)()()(222222+++++⎰=2⎰⎰-+-+-SdS y x x z z y ]cos )(cos )(cos )[(γβα =2⎰⎰-SdS y z )(由于曲面S 关于oxz 平面对称,故⎰⎰=SydS .0 又⎰⎰⎰⎰π⋅=γ=SSrR dS R zdS 2cos页脚内容10于是dz y x dy z x dx z y L)()()(222222+++++⎰=22r R π(4)xdz zdy dx y L++⎰,L 是2222a z y x =++,0=++z y x ,从x 轴正向看去圆周是逆时针方向.解:平面0=++z y x 的法线的方向余弦为 cos 31cos cos ===γβα,于是,dS xz y z y x xdz zdy ydx L S⎰⎰⎰∂∂∂∂∂∂γβα=++cos cos cos =⎰⎰++-SdS )cos cos (cos γβα=332a π-=23a π-5. 设L 为平面上封闭曲线L ,l 为平面的任意方向,证明:⎰=Lds l n 0),cos(,其中n 是L 的外法线方向。
各种积分间的联系与场论初步
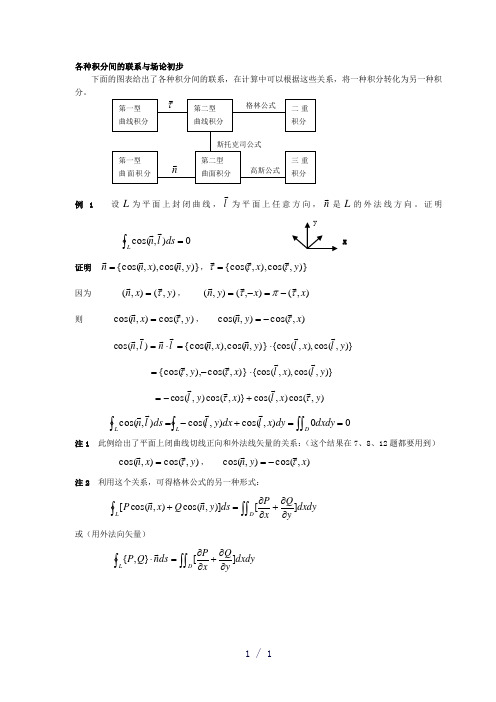
各种积分间的联系与场论初步下面的图表给出了各种积分间的联系,在计算中可以根据这些关系,将一种积分转化为另一种积分。
例 1 设L 为平面上封闭曲线,l 为平面上任意方向,n是L 的外法线方向。
证明y⎰=Lds l n 0),cos(x证明 )},cos(),,{cos(y n x n n=,)},cos(),,{cos(y x τττ= 因为 ),(),(y x n τ =, ),(),(),(x x y n τπτ-=-= 则 ),cos(),cos(y x n τ =, ),cos(),cos(x y n τ-=l n l n ⋅=),cos()},cos(),,{cos(y n x n =)},cos(),,{cos(y l x l ⋅ )},cos(),,{cos(x y ττ -=)},cos(),,{cos(y l x l ⋅ ),cos(),cos()},cos(),cos(y x l x y l ττ +-=00),cos(),cos(),cos( ==+-=⎰⎰⎰⎰DLLdxdy dy x l dx y l ds l n注1 此例给出了平面上闭曲线切线正向和外法线矢量的关系:(这个结果在7、8、12题都要用到)),cos(),cos(y x n τ =, ),cos(),cos(x y n τ-= 注2 利用这个关系,可得格林公式的另一种形式:⎰⎰⎰∂∂+∂∂=+D L dxdy y Qx P ds y n Q x n P ][)],cos(),cos([或(用外法向矢量)⎰⋅Lds n Q P },{ ⎰⎰∂∂+∂∂=D dxdy y Qx P ][试比较(用正向的切线矢量)⎰⎰⎰⎰∂∂-∂∂=⋅=+D L L dxdy x Px Q ds Q P Qdy Pdx ][},{ τ事实上=+⎰Lds y n Q x n P )],cos(),cos([⎰-Lds x Q y P )],cos(),cos([ττ⎰⎰⎰∂∂+∂∂=+-=DLdxdy yQ x P Pdy Qdx ][注3 我们已经知道,格林公式是斯托克司公式当L 是平行于Oxy 坐标面的平面曲线时的特殊情形。
格林公式、高斯公式、斯托克斯公式的应用

Green公式、Stokes公式、Gauss公式在专业学科中的应用摘要格林(Green)公式,斯托克斯(Stokes)公式和高斯(Gauss)公式是多元函数积分学中的三个基本公式,它们分别建立了曲线积分与二重积分、曲面积分与三重积分、曲线积分和曲面积分的联系。
它们建立了向量的散度与通量、旋度与环量之间的关系,除了在数学上应用于计算多元函数积分,在其他领域也有很多重要的应用。
本文将主要从这三个公式与物理学之间的联系展开介绍它们的其他应用,其中包括应用于GPS面积测量仪,确定外部扰动重力场,应用于保守场以及推证阿基米德定律和高斯定理等,帮助人们加深对格林公式、斯托克斯公式和高斯公式的理解,从而能够更准确地应用此三个公式。
关键词:格林公式斯托克斯公式高斯公式散度旋度应用目录一、引言 (1)二、格林(Green)公式的应用 (1)(一)格林公式的定义 (1)1、单连通区域的概念 (1)2、区域的边界曲线的正向规定 (1)3、陈述 (1)(二)格林公式的物理原型 (1)1、物理原型 (2)2、计算方法 (2)(三)格林公式与GPS面积测量仪 (3)1.应用曲线积分计算平面区域面积 (3)2.GPS面积测量仪的数学原理 (4)3.实验结果 (5)4.进一步讨论 (5)(四)应用格林积分直接以地面边值确定外部扰动重力场 61.扰动重力位的地面边值问题 (6)2.地面边值问题的格林公式表示 (6)三、Stokes公式的应用 (8)(一)Stokes公式简介 (8)(二)环量与环量密度 (9)(三)环量的应用 (9)1.开尔文定理 (9)2.开尔文定理的推论 (10)3.升力 (10)(四)旋度 (11)(五)旋度的应用 (12)1. 平面矢量场的旋度 (12)2.环流量是区域S 内有无漩涡的量度 (12)3.旋度是矢量场某点漩涡强度的量度 (13)4.空间矢量场的旋度 (13)四、Gauss公式的应用 (16)1、数学中的高斯公式 (16)2、保守场的推导 (17)3、高斯公式在电场中的运用 (17)4、高斯定理在万有引力场中的应用 (19)5.高斯公式推证阿基米德浮力定律 (21)6.高斯公式推证静电场中的高斯定理 (22)7.高斯公式与散度 (24)五、结语 (25)六、参考文献 (26)一、引言格林(Green)公式,斯托克斯(Stokes)公和高斯(Gauss)公式是多元函数积分学中的三个基本公式,它们分别建立了曲线积分与二重积分、曲面积分与三重积分、曲线积分和曲面积分的联系。
论场论三度与两大定理在物理的应用

论场论三度与两大定理在物理的应用张 晗30901068信计0901时间与空间是物理最基本的物理量:我们也为了了解物理量随时间变化而做多次实验,定义了很多关系,比如速度等于位移随时间变化率, 加速度等于速度随时间变化率,v 等于能量随时间变化率等, 因为时间是纯量 所以处理起来还算比较简易。
我们也经常想了解物理量随空间的变化, 但是空间有方向性因此其变化比较多些,于是就有了梯度,散度与旋度等数学运算。
首先,我们可以先了解一下梯度。
梯度在教材上的定义是,如果f 在点a 所有的偏导数都存在,称向量()()()n f n D f D ℜ∈αα,,1为f 在点a 的梯度(gradient ),记为()αf ∇或grad ()αf 。
如果f 在点a 可导,根据全导数的定义,()().)(1ναανα⋅∇=∑==f i v n i f i D T 当u 是单位向量时,方向导数()u f ;α'有着明显的几何意义,如果().0≠∇αf 记θ是向量u 和梯度()αf ∇的夹角,则()()()().cos cos ;θαθαααf u f u f u f ∇=∇=⋅∇='当u 与()αf ∇同方向时,θ=0,所以在f 在点a 的全部方向导数中,沿着()αf ∇的单位向量()()a f f ∇∇α的方向导数最大。
在2ℜ中,梯度经常写为()()();j ,i ,,y x yf y x x f y x f ∂∂+∂∂=∇ 在3ℜ中,梯度写为()()()().k ,,j ,,i ,,,,z y x zf z y x y f z y x x f z y x f ∂∂+∂∂+∂∂=∇在物理中,力做功将能量储存成位能Fzdz -dy Fy -dx -Fx dU **=(或者以向量内积 F .d r 表示)因此反过来可知dx dU -Fx =,dy dU -Fy =, dz dU -Fz =因此定义F=Fx i + Fy j +Fz k = -▽U 其中▽U= du/dx i +dU/dy j + du/dz k 称为位能U的梯度。
三重积分的积分应用和物理意义

三重积分的积分应用和物理意义三重积分,也称为三重积分,是数学中的一个重要概念。
它不仅被广泛应用于科学和技术领域,还具有丰富的物理意义。
本文将介绍三重积分的基本概念、计算方法和应用,以及它在物理领域中的应用和意义。
一、三重积分的基本概念三重积分是对三维空间内的函数进行积分,它是二重积分的拓展。
用数学符号表示为:∬∬∬f(x,y,z)dxdydz其中,f(x,y,z)表示函数,x、y、z表示变量,dxdydz表示积分元素。
三重积分的计算方法有直接计算法、截面积分法和坐标变换法等。
其中,直接计算法是将积分范围划分为若干个小块,对每个小块进行积分,最后将所有小块的积分结果相加得到最终结果。
截面积分法则是将三重积分转化为二重积分,先在某一平面上进行积分,再将积分结果利用重积分的方式积分到该平面所在位置的立方体内。
坐标变换法则是将三重积分转化为坐标系中体积元素的积分,通过坐标变换将三重积分转化为三个二重积分,从而通过二重积分求解三重积分的结果。
二、三重积分的应用三重积分在科学和技术领域具有广泛的应用,其主要应用领域包括:1. 空间曲线积分和面积积分空间曲线积分和面积积分是三重积分的应用之一。
通过计算空间曲线和面积所包围的体积,可以求解空间曲线连续变化和空间面积的跨度,从而推导出空间运动的方程和导出空间中物体的运动规律。
2. 三维图形的物理性质计算三重积分可以用于计算三维图形的物理性质,例如质心、转动惯量、体积和密度等。
通过积分计算,可以得到物体的重心位置、物体绕轴旋转的惯性、物体的体积和物体的密度等物理性质。
3. 电场和电势的计算三重积分可以用于计算空间中的电势和电场强度。
通过积分计算电荷分布与距离的关系,可以推导出电场的方向和强度,同时计算空间中的电势场,从而得出电势的大小和分布规律。
三、三重积分的物理意义三重积分在物理领域中具有重要的意义。
它可以用于描述和计算物体的形状、密度、质量和重心等物理性质,在研究物理学中起到重要的作用。
§7.3格林公式及其应用

点A(-a,
0)沿曲线
x2 a2
y2 b2
1( y
0)到点B(a, 0)的弧段;
3.定义 1 若函数u(x, y) 的全微分du PdxQdy ,则称
u(x, y) 是表达式PdxQdy 的一个原函数。
若 P(x, y),Q(x, y) 在单连通域 D 上具有一阶连续偏导数, 则 PdxQdy 在 D 内存在原函数的充要条件是 P Q ,
zq
,
3
4 0 (x 2 y 2 z 2 ) 2
由 dx dy dz , P(x, y, z) Q(x, y, z) R(x, y, z)
得 dx dy dz , xyz
解此方程组得 y C1x ,它表示过原点(0, 0, 0) ,方向向量 z C2 x
{1, C1, C2} 是任意的直线族。这些线称为电力线。
1.曲线积分C PdxQdy 与路径无关的定义
设 D 是一个平面区域,若对 D 内任意两点 A、B 及 D 内 从点 A 到点 B 的任意两条曲线C1 ,C2 ,等式
PdxQdy
Pdx Qdy
C1( AB)
C2( AB)
恒成立,则称曲线积分 C PdxQdy 在 D 内与路径无关。
2.定理 2
y x
且 PdxQdy 的所有原函数为
( x, y)
u( x, y)
P(x, y)dxQ(x, y)dyC
( x, y)
其中 C 为任意常数,(x, y)D 。
4. (曲线积分基本定理)
设 P(x, y),Q(x, y) 在单连通域 D 上连续,若u(x, y)
是 PdxQdy 的一个原函数,而A(x1, y1) 和B(x2 , y2 )
数学分析简明教程22 各种积分间的联系与场论初步

数学分析简明教程22各种积分间的联系与场论初步第二十二章 各种积分间的联系与场论初步§1 各种积分间的联系1.应用格林公式计算下列积分:(1)ydx x dy xy L ⎰-22,其中L 为椭圆22a x +22by =1取正向;(2),)()(⎰-++Ldy y x dx y x L 同(1);(3)dy y x dx y x L)()(222+-+⎰, L 是顶点为)5,2(),2,3(),1,1(C B A 的三角形的边界,取正向;(4),1,)()(223333=+--+⎰y x L dy y x dx y x L为取正向;(5),sin sin ydy e xdx e x Ly -+⎰ L 为矩形d y c b x a ≤≤≤≤, 的边界,取正向;(6)],))cos(sin ())cos(sin [(dy y x xy x dx y x xy y e Lxy +++++⎰其中L 是任意逐段光滑闭曲线.解(1)原式 =()()d xdy y x dxdy x y DD⎰⎰⎰⎰+=--2222)(=ab()r dr r b r a d ⎰⎰+122222220sin cos θθθπ(广义极坐标变换)=())(3sin cos 3122202222b a ab d b a ab +=+⎰πθθθπ.(2)⎰-++Ldy y x dx y x )()(=⎰⎰=-Ddxdy 0)11(.(3)原式 ⎰⎰+-=Ddxdy y x x ))(22(⎪⎪⎭⎫ ⎝⎛+-=-=⎰⎰⎰⎰⎰⎰-+-+215231143124322yy y y D dx ydy dx ydy ydxdy 9143))5(127)(47(2252221-=-+--=⎰⎰dy y y dy y y .(4)原式π23)(3)33(2222-=+-=--=⎰⎰⎰⎰DD dxdy y x dxdy y x .(5)原式 dxdy x e y e Dy x ⎰⎰--=-)cos sin ()cos sin (⎰⎰⎰⎰+-=-b ad cdcydy b ax e dx x ydy dx e)sin )(sin ()cos )(cos 11(a b e e c d ee c d b a --+--=. (6))]cos(sin [),(y x xy y e y x P xy ++=,)]cos(sin [),(y x xy x e y x Q xy ++=,)]sin(cos [sin )]cos(sin [y x xy xy xy e y x xy x ye xQxy xy --++++=∂∂ )]sin()cos(sin )cos (sin [y x y x y xy xy xy xy e xy --+++=,)]sin(cos [sin )]cos(sin [y x xy xy xy e y x xy y xe yPxy xy +-++++=∂∂ )]sin(cos sin )cos (sin [y x xy x xy xy xy xy e xy +-+++=,)cos()(y x x y e yPx Q xy +-=∂∂-∂∂, 所以,原式⎰⎰+-=Dxy dxdy y x x y e ,)cos()( 其中D 为L 包围的平面区域.2.利用格林公式计算下列曲线所围成的面积: (1)双纽线θ2cos 22a r =;(2)笛卡尔叶形线)0(333>=+a axy y x ;(3)t t a x sin )cos 1(2+=,t t a y cos sin 2⋅=,π≤≤20t . 解(1)⎰⎰⎰⎰==12||D Ddxdy dxdy D ⎰-⨯=L ydx xdy 212 ⎰=--=44)]sin (sin cos cos [ππθθθθθd r r r r 24424422cos a d a d r ===⎰⎰--ππππθθθ,其中1D 由θ=2cos 22a r ,44π≤θ≤π-所围成. (2)作代换,tx y =则得曲线的参数方程为313tatx +=,3213t at y +=.所以, dt t t a dx 233)1()21(3+-=,dt t t at dy 233)1()2(3+-=,从而,dt t t a ydx xdy 2322)1(9+=-,于是,面积为D =⎰C x y y x d -d 21=dt t t a ⎰∞++02322)1(29=223a . (3)D =⎰-cydx xdy 21= {}⎰-++⋅--⋅+π2022322]sin )sin (cos 2cos )cos 1[(cos sin )sin cos sin 2(sin )cos1(21dtt t t t t a t t a t t t a t t a{}⎰π-++⋅--⋅+2022322]sin )sin (cos 2cos )cos 1[(cos sin )sin cos sin 2(sin )cos1(21dt t t t t t a t t a t t t a t t a=21tdt t t a 2cos )cos 1(sin 22022+⎰π=24a π 3.利用高斯公式求下列积分: (1)y x z x z y z y x sd d d d d d 222++⎰⎰.其中(a )S 为立方体a z y x ≤≤,,0的边界曲面外侧; (b )S 为锥面)0(222h z z y x ≤≤=+,下侧. 解:(a )y x z x z y z y x sd d d d d d 222++⎰⎰=2⎰⎰++vdxdydz z y x )(=2⎰⎰⎰++aa a dz z y x dy dx 0)(=43a(b)补充平面1S :h z h y x =≤+,222的上侧后,1S S +成为闭曲面的外侧, 而 ⎰⎰++1222S dxdy z dzdx y dydz x =⎰⎰xyD dxdy h 2=22h h π⋅= π4h所以 : ⎰⎰++Sdxdy z dzdx y dydz x 222+π4h=⎰⎰+++1222S S dxdy z dzdx y dydz x=2z y x z y x V⎰⎰⎰++d d )d (=2⎰⎰xyD dxdy⎰+++h y x z z y x 22)d (=⎰⎰++xyD y x y x y x y x h y x h d )]d (- )+2(-+)+([222222=⎰⎰π-θ+θ-+θ+θθ20222])sin (cos 2)sin (cos 2[hrdr r r h hr d=1214h θ+θ+θ⎰πd 20)3sin 2cos 2(=2π4h 所以 ⎰⎰++Sdxdy z dzdx y dydz x 222=442h h π-π=42h π-(2)⎰⎰++Sdxdy z dzdx y dydz x 333, 其中S 是单位球面的外侧;解:⎰⎰++Sdxdy z dzdx y dydz x 333=3⎰⎰⎰++Vz y x z y x d d )d (=3⎰⎰⎰ππρρϕϕθ2014sin d d d=512 π (3)设S 是上半球面222y x a z --=的上侧,求(a )⎰⎰++Sy x z x z y z y x d d d d d d(b) ⎰⎰++-+Sy x z y xy x z z y x z y xz d )d (2d )d (d d 2222解:补充平面1S :222,0a y x z ≤+=,下侧后,1S S +成为闭曲面的外侧,而 (a ) ⎰⎰=++10S zdxdy ydzdx xdydz所以 ⎰⎰=++Szdxdy ydzdx xdydz ⎰⎰+=++1S S zdxdy ydzdx xdydz 3⎰⎰⎰Vdxdydz=213433⋅π⋅a =2π3a(b) ⎰⎰++-+1d )d (2d )d (d d 2222S y x z y xy x z z y x z y xz=⎰⎰xyD xydxdy 2=2⎰π20d θr r a⎰θθ03d cos sin =0所以 ⎰⎰++-+Sy x z y xy x z z y x z y xz d )d (2d )d (d d 2222=⎰⎰+++-+1d )d (2d )d (d d 2222S S y x z y xy x z z y x z y xz =⎰⎰⎰++Vdxdydz z y x )(222 =⎰π20d θ⎰20πsin ϕd ϕ⎰a4 d ρρ=554a π(4)⎰⎰+-++-++-Sy x y x z x z x z y z y y x d )d (d )d (d )d z (222222,S 是 2222)()()(R c z b y a x =-+-+- 的外侧.解:⎰⎰+-++-++-Sy x y x z x z x z y z y y x d )d (d )d (d )d z (222222,=3⎰⎰⎰Vdxdydz =V 3=3343R π⋅=4π3R4.用斯托克斯公式计算下列积分: (1)⎰++Lzdz dy dx y x 32, 其中(a )L 为圆周0,222==+z a y x ,方向是逆时针;(b )L 为y x z y ==+,122 所交的椭圆,沿x 轴正向看去,按逆时针方向; 解: (a )取平面0=z 上由交线围成的平面块为S ,上侧,由Stokes 公式⎰++Lzdz dy dx y x 32=⎰⎰Szy x z y x dxdydzdxdydz1///32∂∂∂∂∂∂ =⎰⎰-Sdxdy y x 223=⎰⎰----ax a xa dy y dx x 02222223=dx x a x a3222)(2⎰--=616a π-(b )取平面y x =上由交线围成的平面块为S ,上侧,由由Stokes 公式⎰++Lzdz dy dx y x 32=⎰⎰∂∂∂∂∂∂Szy x z y x dxdy dzdx dydz 132=⎰⎰-Sdxdy y x 223=⎰⎰-xyD dxdy y x 223=616a π-(2)dz y x dy x z dx z y L)()()(-+-+-⎰,L 是从)0,0,(a 经)0,,0(a 至),0,0(a 回到)0,0,(a 的三角形;解: 三角形所在的平面为a z y x =++,取平面a z y x =++上由以上三角形围成的平面块为S ,取上侧,由stokes 公式dz y x dy x z dx z y L)()()(-+-+-⎰=⎰⎰---∂∂∂∂∂∂Syx x z z y z y x dxdy dzdx dydz =⎰⎰++-S dxdy dzdx dydz 2 =2-(⎰⎰Sdydz +⎰⎰Sdzdx +⎰⎰Sdxdy )=2-(⎰⎰yzD dydz +⎰⎰zx D dzdx +⎰⎰xyD dxdy )=23a -(3)dz y x dy y x dx z y L)()()(222222+++++⎰,其中(a )L 为1=++z y x 与三坐标轴的交线,其方向与所围平面区域上侧构成右手法则;(b )L 是曲线Rx z y x 2222=++, rx y x 222=+ (0,0><<z R r ),它的方向与所围曲面的上侧构成右手法则;解:(a )中取平面1=++z y x 上与三坐标面交线所围平面块为S ,上侧;(b )中取曲面Rx z y x 2222=++上由L 所围曲面块为S ,上侧, 则由stokes 公式,得 dz y x dy y x dx z y L)()()(222222+++++⎰=⎰⎰+++∂∂∂∂∂∂Sy x x z z y z y x dxdy dzdx dydz 222222⎰⎰-+-+-=Sdxdy y x dzdx x z dydz z y )()()(2=2))()()((dxdy y x dzdx x z dydz z y SSS⎰⎰⎰⎰⎰⎰-+-+-则(a ) ⎰+++++Ldz y x dy z x dx z y )()()(222222= dS y x x z z y S⎰⎰γ-+β-+α-]cos )(cos )(cos )[(2=0 (因为cos α=cos β=cos γ=31)(b ) 注意到球面的法线的方向余弦为: R R x -=αcos , R y =βcos ,Rz=γcos ,所以dz y x dy z x dx z y L)()()(222222+++++⎰=2⎰⎰-+-+-SdS y x x z z y ]cos )(cos )(cos )[(γβα=2⎰⎰-SdS y z )(由于曲面S 关于oxz 平面对称,故⎰⎰=SydS .0 又⎰⎰⎰⎰π⋅=γ=SSrR dS R zdS 2cos于是dz y x dy z x dx z y L)()()(222222+++++⎰=22r R π(4)xdz zdy dx y L++⎰,L 是2222a z y x =++,0=++z y x ,从x 轴正向看去圆周是逆时针方向.解:平面0=++z y x 的法线的方向余弦为 cos 31cos cos ===γβα,于是,dS xz y z y x xdz zdy ydx L S⎰⎰⎰∂∂∂∂∂∂γβα=++cos cos cos =⎰⎰++-SdS )cos cos (cos γβα=332a π-=23a π-5. 设L 为平面上封闭曲线L ,l 为平面的任意方向,证明:⎰=Lds l n 0),cos(,其中n是L 的外法线方向。
场函数的三种基本微分运算.

2 F e x 2 Fx e y 2 Fy e z 2 Fz
1.5 场函数的高阶微分运算
4、两个与算符 2 有关的恒等式
• 相对坐标标量函数
CQU
f (r r )
2 f 2 f
• 相对位置矢量 R 及其模 R
S S
li
S
1.6 矢量场的积分定理
CQU
F dl F dS
l S
•矢量函数的线积分与面积分的互换。 • 该公式表明了区域 S 中场F 与边界 l 上的场F 之间的关系 在电磁场理论中,Gauss 定理和 Stockes 定理 是两个非常重要的公式。
1.6 矢量场的积分定理
解
CQU
3 1 r 3 r (r 3 ) r 4 r 3 3 4 r r r r r 1 1 3 4 3 4 r 4 r 3 4 5 r r r r r r 3 4 r 3 4 3 4 5 r 3 4 4 3r 4 r r r r r
1.5 场函数的高阶微分运算
1、场函数的三种基本微分运算 标量场的梯度f ,矢量场的散度F 和F 旋度简称 “三 度” 运算。
CQU
2、场函数的二阶运算
(1)标量场梯度的散度 f (2)标量场梯度的旋度 f (3)矢量场散度的梯度 (F) (4)矢量场旋度的散度 (F)
1.5 场函数的高阶微分运算
CQU
作业:1.13(1)
1.6 矢量场的积分定理
CQU
1、高斯散度定理(Gauss)
广义相对论三个公式

广义相对论三个公式
广义相对论是爱因斯坦提出的一种描述引力的理论,其中包含了一些重要的公式。
以下是广义相对论中的三个公式:
1. 爱因斯坦场方程:这是广义相对论的核心方程,描述了引力场的曲率与物质分布之间的关系。
它的数学形式为:Rμν - (1/2)gμνR = (8πG/c^4)Tμν,其中Rμν是曲率张量,gμν是度规张量,R是标量曲率,Tμν是能量-动量张量,G是引力常数,c是光速。
2. 弯曲时空的度规:广义相对论认为,引力是由物质和能量引起的时空的弯曲。
弯曲时空的度规张量描述了时空的几何结构。
在弯曲时空中,度规张量的数学表达式与平直时空(即没有引力的时空)的度规张量有所不同。
3. 地面附近的时空弯曲:根据广义相对论,物体在引力场中运动时会受到时空弯曲的影响。
在地球附近的引力场中,我们可以使用牛顿引力定律和广义相对论的公式进行比较。
广义相对论预测出的效应包括时空弯曲导致的时钟走慢和光线偏折等现象。
这些公式是广义相对论的基础,它们描述了引力的性质和引力场与物质之间的关系。
广义相对论的公式和预测已经通过大量的实验证实,并且在理论物理学中具有重要的地位。
场论中的积分变换公式

场论中的积分变换公式积分变换公式是控制工程中常用的数学工具,用于将时间域中的函数转换为复频域中的函数。
它在研究信号的频谱特性、系统的稳定性、性能指标等方面具有重要作用。
以下是常见的几种积分变换公式:1.常数函数的积分变换公式:∫[0, t]1 dt = T其中,T表示积分上限。
2.单位冲激函数(单位脉冲函数)的积分变换公式:∫[0, t]δ(t) dt = 1其中,δ(t)表示单位冲激函数。
3.单位阶跃函数的积分变换公式:∫[0, t]u(t) dt = t其中,u(t)表示单位阶跃函数。
4.积分的线性性质:若F(t)的积分为F(s),G(t)的积分为G(s),则kF(t)+mG(t)的积分为kF(s)+mG(s)。
其中,k和m为常数。
5.拉普拉斯变换与积分变换的关系:L{f(t)}=F(s)-F(0-)其中,L表示拉普拉斯变换,F(t)表示时间域函数,F(s)表示复频域函数。
6.数学常函数e的积分变换公式:∫[0, t]e^(st) dt = 1 / s其中,s为复频域变量。
7.e的负幂函数的积分变换公式:∫[0, t]e^(-st) dt = 1 / (s + a)其中,s为复频域变量,a为常数。
8.正弦函数的积分变换公式:∫[0, t] sin(ωt) dt = ω / (s^2 + ω^2)其中,s为复频域变量,ω为角频率。
9.余弦函数的积分变换公式:∫[0, t] cos(ωt) dt= s / (s^2 + ω^2)其中,s为复频域变量,ω为角频率。
上述是常见的几种积分变换公式,它们在控制工程中具有广泛的应用。
通过积分变换公式,可以将时间域中的函数转换为复频域中的函数,以便研究系统的频谱特性、稳定性、性能指标等。
积分变换公式是控制理论中的重要工具,对于控制系统的分析与设计起到至关重要的作用。
场论三定理

场论三定理
场论三定理是场论中的三个重要定理,它们分别是场的唯一性定理、场的存在性定理和场的分解定理。
这三个定理为我们理解和应用场论提供了重要的理论基础。
首先是场的唯一性定理。
这个定理表明,对于给定的边界条件和源项,存在唯一的场解。
也就是说,任何一组给定的边界条件和源项,都对应着唯一的场。
这个定理的意义在于,它保证了场问题的解的存在性和唯一性,为我们进行场问题的建模和求解提供了理论保证。
其次是场的存在性定理。
这个定理说明,对于给定的边界条件和源项,存在一个场解。
也就是说,无论给定的边界条件和源项如何,总是存在一个场解。
这个定理的意义在于,它保证了场问题的解的存在,为我们进行场问题的建模和求解提供了理论依据。
最后是场的分解定理。
这个定理指出,任何一个场都可以表示为一组基场的线性组合。
也就是说,任何一个场都可以表示为一组基场的叠加。
这个定理的意义在于,它将任意场的表示问题转化为基场的表示问题,简化了场问题的求解过程。
场论三定理为我们理解和应用场论提供了重要的理论基础。
场的唯一性定理保证了场问题的解的存在性和唯一性,场的存在性定理保证了场问题的解的存在,场的分解定理简化了场问题的求解过程。
这些定理为我们研究和解决各种场问题提供了有力的工具和方法。
通过深入理解和应用这些定理,我们可以更好地理解和掌握场论的基本概念和理论,进而应用到实际问题中。
格林公式、高斯公式、斯托克斯公式的应用

简言之:区域的边界曲线的正向应符合条件:人沿曲线走,区域在左边,人走的方向就是曲线的正向。
3、陈述
设闭区域D由分段光滑的曲线L围成,函数 在D上具有一阶连续偏导数,则有
关键词:格林公式 斯托克斯公式 高斯公式 散度 旋度 应用
一、引言ﻩ1
二、格林(Green)公式的应用ﻩ1
(一) 格林公式的定义1
1、单连通区域的概念1
2、区域的边界曲线的正向规定ﻩ1
3、陈述ﻩ1
(二)格林公式的物理原型1
1、物理原型ﻩ2
2、 计算方法ﻩ2
(三)格林公式与GPS面积测量仪ﻩ3
1.应用曲线积分计算平面区域面积3
因此面积为
其中 是C的单位法向量
单位时间内流体面积为:
由曲线积分定义有总的流体面
则
设 为点(x,y)处的切线,与x轴夹角
(2) 的计算可以从另一个角度来计算,那就是先算出流过场内每一个微dxdy在单位时间内散发出去的流体的面积,然后求其总和。
设上述曲线C所围平面区城为G,在G内任取一个微元dxdy
显然在单位时间内从左边流进(x轴方向)这个微元的流体面积近似于Pdy ,而从右边流出的面积近似于 ( 为偏增量的近似)。因此这个微元在单位时间内沿x方向(净)散发出去流体面积近似于 。同理沿y方向(净)散出去的流体面积近似于 ,所以总的和为
在这种“ 平面稳定流动” 中,我们来计算单位时间内流过曲线C的流体体积即流t 密度( 其实是流过以C 为准线、高为l 的柱体的流体体积; 简单用面积表示) 其中C 是平面上一个闭的、无重点, 光滑曲线。无重点, 是指曲线 ,当 总是相异的。
68各种积分的联系式及其在场论中的应用

连通区域的分类 设D为平面区域, 如果D内任一闭曲线所围成的部分都属于D, 则称D为平面单连通区域; 否则称为复连通区域.
D
单连通区域
d d
Q( 2 ( y ), y ) d y Q( 1 ( y ), y ) d y
c c
即 同理可证
①
② ①、②两式相加得:
Q P D x y d xd y L Pd x Qd y
2) 若D不满足以上条件, 则可通过加辅助线将其分割 为有限个上述形式的区域 , 如图
从上面研究发现:对于一个连续的向量场A(M)=(P,Q), 若它是一个保守场,则一定是一个有势场,也是无旋场。 并且对于一个连续的向量场, A(M)=(P,Q)是无旋场、保守 场和有势场三者是相互等价的。
定义 若du Pdx Qdy, 则Pdx Qdy称为u( x, y )的全微分.
势函数的求法
由于OA xdy 0,
BO xdy 0,
1 2 xdy dxdy r . AB 4 D
例3. 计算
其中L为一无重点且不过原点
的分段光滑正向闭曲线.
解: 令
则当x y 0时,
设 L 所围区域为D,
2
2
y
L
当(0,0) D 时, 由格林公式知
o
x
建立了沿封闭曲线的第二型线积分与二重积分之
Q P d xd y P d x Q d y x y D L
格林公式的应用 1. 简化曲线积分 例1. 设 L 是一条分段光滑的闭曲线, 证明
格林公式、高斯公式、斯托克斯公式的应用讲解学习

Green公式、Stokes公式、Gauss公式在专业学科中的应用摘要格林(Green)公式,斯托克斯(Stokes)公式和高斯(Gauss)公式是多元函数积分学中的三个基本公式,它们分别建立了曲线积分与二重积分、曲面积分与三重积分、曲线积分和曲面积分的联系。
它们建立了向量的散度与通量、旋度与环量之间的关系,除了在数学上应用于计算多元函数积分,在其他领域也有很多重要的应用。
本文将主要从这三个公式与物理学之间的联系展开介绍它们的其他应用,其中包括应用于GPS面积测量仪,确定外部扰动重力场,应用于保守场以及推证阿基米德定律和高斯定理等,帮助人们加深对格林公式、斯托克斯公式和高斯公式的理解,从而能够更准确地应用此三个公式。
关键词:格林公式斯托克斯公式高斯公式散度旋度应用目录一、引言 (1)二、格林(Green)公式的应用 (1)(一)格林公式的定义 (1)1、单连通区域的概念 (1)2、区域的边界曲线的正向规定 (1)3、陈述 (1)(二)格林公式的物理原型 (1)1、物理原型 (2)2、计算方法 (2)(三)格林公式与GPS面积测量仪 (3)1.应用曲线积分计算平面区域面积 (3)2.GPS面积测量仪的数学原理 (4)3.实验结果 (5)4.进一步讨论 (5)(四)应用格林积分直接以地面边值确定外部扰动重力场 61.扰动重力位的地面边值问题 (6)2.地面边值问题的格林公式表示 (6)三、Stokes公式的应用 (8)(一)Stokes公式简介 (8)(二)环量与环量密度 (9)(三)环量的应用 (9)1.开尔文定理 (9)2.开尔文定理的推论 (10)3.升力 (10)(四)旋度 (11)(五)旋度的应用 (12)1. 平面矢量场的旋度 (12)2.环流量是区域S 内有无漩涡的量度 (12)3.旋度是矢量场某点漩涡强度的量度 (13)4.空间矢量场的旋度 (13)四、Gauss公式的应用 (16)1、数学中的高斯公式 (16)2、保守场的推导 (17)3、高斯公式在电场中的运用 (17)4、高斯定理在万有引力场中的应用 (19)5.高斯公式推证阿基米德浮力定律 (21)6.高斯公式推证静电场中的高斯定理 (22)7.高斯公式与散度 (24)五、结语 (25)六、参考文献 (26)一、引言格林(Green)公式,斯托克斯(Stokes)公和高斯(Gauss)公式是多元函数积分学中的三个基本公式,它们分别建立了曲线积分与二重积分、曲面积分与三重积分、曲线积分和曲面积分的联系。
格林公式、高斯公式、斯托克斯公式的应用

格林公式、高斯公式、斯托克斯公式的应用Green公式、Stokes公式、Gauss公式在专业学科中的应用摘要格林(Green)公式,斯托克斯(Stokes)公式和高斯(Gauss)公式是多元函数积分学中的三个基本公式,它们分别建立了曲线积分与二重积分、曲面积分与三重积分、曲线积分和曲面积分的联系。
它们建立了向量的散度与通量、旋度与环量之间的关系,除了在数学上应用于计算多元函数积分,在其他领域也有很多重要的应用。
本文将主要从这三个公式与物理学之间的联系展开介绍它们的其他应用,其中包括应用于GPS面积测量仪,确定外部扰动重力场,应用于保守场以及推证阿基米德定律和高斯定理等,帮助人们加深对格林公式、斯托克斯公式和高斯公式的理解,从而能够更准确地应用此三个公式。
关键词:格林公式斯托克斯公式高斯公式散度旋度应用一、引言格林(Green )公式,斯托克斯(Stokes )公和高斯(Gauss )公式是多元函数积分学中的三个基本公式,它们分别建立了曲线积分与二重积分、曲面积分与三重积分、曲线积分和曲面积分的联系。
它们有很强的物理意义即建立了向量的散度与通量、旋度与环量之间的关系,因此它们有许多重要的应用,在数学上它们主要用来简化某些多元函数积分的运算,而在其他各个专业领域它们也有很多重要的应用。
接下来将一一介绍它们在不同专业中的应用。
二、格林(Green )公式的应用(一)格林公式的定义Green 公式反映了第二型平面线积分与二重积分的联系。
1、单连通区域的概念 设D 为平面区域,如果D 内任一闭曲线所围的部分区域都属于D ,则D 称为平面单连通区域;否则称为复连通区域.通俗地讲,单连通区域是不含"洞"(包括"点洞")与"裂缝"的区域.2、区域的边界曲线的正向规定设L 是平面区域D 的边界曲线,规定L 的正向为:当观察者沿的这个方向行走时,平面区域(也就是上面的D)内位于他附近的那一部分总在他的左边.简言之:区域的边界曲线的正向应符合条件:人沿曲线走,区域在左边,人走的方向就是曲线的正向。
数学分析简明教程22 各种积分间的联系与场论初步

第二十二章 各种积分间的联系与场论初步§1 各种积分间的联系1.应用格林公式计算下列积分:(1)ydx x dy xy L ⎰-22,其中L 为椭圆22a x +22by =1取正向;(2),)()(⎰-++Ldy y x dx y x L 同(1);(3)dy y xdx y x L)()(222+-+⎰, L 是顶点为)5,2(),2,3(),1,1(C B A 的三角形的边界,取正向;(4),1,)()(223333=+--+⎰y x L dy y x dx y x L为取正向;(5),sin sin ydy exdx e xLy-+⎰L 为矩形d y c b x a ≤≤≤≤, 的边界,取正向;(6)],))cos(sin ())cos(sin [(dy y x xy x dx y x xy y e L xy+++++⎰其中L 是任意逐段光滑闭曲线.解(1)原式 =()()d xdy y x dxdy x yDD⎰⎰⎰⎰+=--2222)(=ab()r dr r b r a d ⎰⎰+122222220sin cos θθθπ(广义极坐标变换)=())(3sin cos 3122202222b a ab d b a ab +=+⎰πθθθπ.(2)⎰-++Ldy y x dx y x )()(=⎰⎰=-Ddxdy 0)11(.(3)原式 ⎰⎰+-=Ddxdy y x x ))(22(⎪⎪⎭⎫ ⎝⎛+-=-=⎰⎰⎰⎰⎰⎰-+-+215231143124322yy y y D dx ydy dx ydy ydxdy9143))5(127)(47(2252221-=-+--=⎰⎰dy y y dy y y .(4)原式π23)(3)33(2222-=+-=--=⎰⎰⎰⎰DD dxdy y x dxdy y x . (5)原式 dxdy x e y e Dy x ⎰⎰--=-)cos sin ( )cos sin (⎰⎰⎰⎰+-=-bad cdcydy b axe dx x ydy dx e)sin )(sin ()cos )(cos 11(a b e e c d ee cd b a --+--=.(6))]cos(sin [),(y x xy y e y x P xy ++=,)]cos(sin [),(y x xy x e y x Q xy++=,)]sin(cos [sin )]cos(sin [y x xy xy xy e y x xy x ye xQxy xy --++++=∂∂ )]sin()cos(sin )cos (sin [y x y x y xy xy xy xy e xy --+++=,)]sin(cos [sin )]cos(sin [y x xy xy xy e y x xy y xe yPxy xy +-++++=∂∂ )]sin(cos sin )cos (sin [y x xy x xy xy xy xy e xy +-+++=,)cos()(y x x y e yPx Q xy +-=∂∂-∂∂, 所以,原式⎰⎰+-=Dxy dxdy y x x y e ,)cos()( 其中D 为L 包围的平面区域. 2.利用格林公式计算下列曲线所围成的面积: (1)双纽线θ2cos 22a r =;(2)笛卡尔叶形线)0(333>=+a axy y x ;(3)t t a x sin )cos 1(2+=,t t a y cos sin 2⋅=,π≤≤20t . 解(1)⎰⎰⎰⎰==12||D Ddxdy dxdy D ⎰-⨯=L ydx xdy 212 ⎰=--=44)]sin (sin cos cos [ππθθθθθd r r r r 24424422cos a d a d r ===⎰⎰--ππππθθθ,其中1D 由θ=2cos 22a r ,44π≤θ≤π-所围成. (2)作代换,tx y =则得曲线的参数方程为313tatx +=,3213t at y +=.所以, dt t t a dx 233)1()21(3+-=,dt t t at dy 233)1()2(3+-=, 从而,dt t t a ydx xdy 2322)1(9+=-,于是,面积为 D =⎰C x y y x d -d 21=dt t t a ⎰∞++02322)1(29=223a .(3)D =⎰-cydx xdy 21= {}⎰-++⋅--⋅+π2022322]sin )sin (cos 2cos )cos 1[(cos sin )sin cos sin 2(sin )cos1(21dtt t t t t a t t a t t t a t t a{}⎰π-++⋅--⋅+2022322]sin )sin (cos 2cos )cos 1[(cos sin )sin cos sin 2(sin )cos1(21dt t t t t t a t t a t t t a t t a=21tdt t t a 2cos )cos 1(sin 22022+⎰π=24a π 3.利用高斯公式求下列积分:(1)y x z x z y z y x sd d d d d d 222++⎰⎰。
与积分有关的物理公式

与积分有关的物理公式
【原创版】
目录
1.引言:积分在物理学中的重要性
2.物理学中的基本积分公式
3.积分在物理学中的应用举例
4.结论:积分对物理学的贡献
正文
一、引言:积分在物理学中的重要性
积分作为数学的一个重要分支,在物理学中有着广泛的应用。
物理学中的许多现象和规律都可以通过积分来描述和解析,从而为我们理解和掌握物理世界提供有力的工具。
本文将介绍一些与积分有关的物理公式,以展示积分在物理学中的重要地位。
二、物理学中的基本积分公式
在物理学中,有一些基本的积分公式被广泛应用。
以下是一些常见的基本积分公式:
1.不定积分:求解物理量的基本方法
2.定积分:求解物理量的总量或平均值
3.多元函数积分:描述多元物理量的积分公式
4.偏导数:描述物理量随某个变量变化的规律
5.梯度:描述物理量在空间中变化率的向量
三、积分在物理学中的应用举例
积分在物理学中有着广泛的应用,以下是一些具体的应用举例:
1.动能定理:求解物体动能变化的基本公式
2.动量定理:求解物体动量变化的基本公式
3.能量守恒定律:描述物理系统能量总量不变的定律
4.电场强度与电势关系:描述电场中电势分布的基本公式
5.流体力学中的连续性方程:描述流体在流动过程中质量守恒的基本公式
四、结论:积分对物理学的贡献
积分作为数学的一个重要分支,在物理学中发挥着举足轻重的作用。
通过积分,我们可以更好地理解和描述物理现象,从而为科学研究提供有力的支持。
同时,积分也为我们在实际生活中解决物理问题提供了有效的方法。
场论三度

矢量场中,场矢量通过闭合面S 的通量是由S 内的通量源决定的。
由此可看出,通量是一个积分量,它描述的是闭合曲面内是否存在源,也就是正源和负源的代数和。
但他不能说明闭合面内每一点的性质,对于一个场的分析来说,必须知道场中每一点的场源分布规律。
设有一矢量场A ,在场中任一点M 处,做一个包含M 在内的任一闭合曲面S ,S 所包围的面积为V ∇,如图1.16所示。
当体积V ∆以任一方式缩向M 点时,0→∆V 时的通量为VdsV ∆⋅A ⎰→∆0lim,如果此极限存在,则称此极限为矢量场A 在空间M 点处的散度(divergence),记作divA ,即 VdSn A divA sV VdsA V s ∆⋅⋅=⎰=⎰→∆∆⋅→∆0limlim由此可以看出,divA 表示在场汇总任一点处,通量对提及的变化率,也可看作在该点处一个单位体积通过的通量,它表示了场中各点的场与通量元的关系。
从散度的定义可知,在M 点处,当0>divA 时,表明该点存在正源,是发出能量线的;当0<divA 时,表明该点存在负源,是吸收通量线的;当0=divA 时,表明该点无源;另外,divA 与所取的体积形状无关,这是因为当0→∆V 时,所有的尺寸都趋于0. 散度在直角坐标系下的表示式可以写成A d i v A⋅∇= (1.52) 注意:∇是一个很重要的微分运算符,它有两重意义,首先它是矢性的,而不是一个具体的矢量,其二它是一个微分算符,它将对跟随其后的函数,不管是矢量函数还是标量函数进行微分,式(1.52)就是用买哈顿算符表示的散度式,由此定义可看出它与所取的坐标系无关,但在具体计算时可选不同坐标。
同理可以推得 在圆柱坐标系中 ze r e e zrr ∂∂+∂∂+∂∂=∇ϕϕ1在球坐标系中 ϕθθϕϕ∂∂+∂∂+∂∂=∇s i n 11R e R e Re R在圆柱坐标系中()zr rrA rA divA r ∂A ∂+∂A ∂+∂∂=⋅∇=ϕϕϕ11在球坐标系中()()ϕθθθθϕθ∂A ∂+A ∂∂+∂∂=⋅∇=s i n 1s i n s i n 1122R R A RRRA d i v AR在矢量场A 中,为了研究场中某点M 的性质,取包含M 点一个面积元S ∆其周界为C 的绕行方向,有右手螺旋法则确定面积元的法线n 的方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
场论中三大积分公式的应用
在物理学中,曲线积分和曲面积分有着广泛的应用。
物理学家为了既能形象地表达有关的物理量,又能方便地使用数学工具进行逻辑表达和数据计算,使用了一些特殊的术语和记号, 在此基础上产生了场论。
在大一的下半学期的高等数学课上。
我们学习了微积分这一门基础课,而曲线积分及曲面积分就是学习重点之一。
在曲线积分和曲面积分的学习中,对于重积分的求解运算,Green 公式、Gauss 公式和Stokes 公式作为章节核心,需要我们重点研究。
而本文围绕着对三大公式的应用和联系进行探讨。
一、三大公式
Green 公式:设D 为平面上由光滑或分段光滑的简单闭曲线所围的单连通区域。
如果函数(,)P x y ,(,)Q x y 在D 上具有连续偏导数,那么
(,)(,)(,)(,)L D Q x y P x y P x y dx Q x y dy dxdy x y +⎡⎤∂∂+=-⎢⎥∂∂⎣
⎦⎰⎰⎰, 其中L +表示沿D 的边界的正方向。
Gauss 公式:设Ω是3中由光滑或分片光滑的封闭曲面∂Ω所围成的二维单连通封闭区域,(,,)P x y z ,(,,)Q x y z 与(,,)R x y z 在Ω上具有连续偏导数,则divFd F nds +
Ω∂ΩΩ=⋅⎰⎰⎰⎰⎰,即
P Q R dxdydz Pdydz Qdzdx Rdxdy x y z +
Ω∂Ω⎛⎫∂∂∂++=++ ⎪∂∂∂⎝⎭⎰⎰⎰⎰⎰, 其中+∂Ω表示有向封闭曲面∂Ω的外侧。
Stokes 公式:设S 为光滑曲面或分片光滑的双侧曲面,其边界为光滑或分段光滑闭曲线S ∂,若(,,)P x y z ,(,,)Q x y z 与(,,)R x y z 在S 及其边界S ∂上具有连续偏导数,则有
S S R Q P R Q P Pdx Qdy Rdz dydz dzdx dxdy y z z x x y ∂⎛⎫⎛⎫∂∂∂∂∂∂⎛⎫++=-+-+- ⎪ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝
⎭⎝⎭⎰⎰⎰ cos cos cos S R Q P R Q P dS y z z x x y αβγ⎡⎤⎛⎫⎛⎫∂∂∂∂∂∂⎛⎫=-+-+-⎢⎥ ⎪ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭⎣⎦
⎰⎰, 其中S ∂取S 的诱导定向。
二、三大公式的联系
1.表述形式
根据三大公式的表述形式,可以得到三大公式阐释的各类积分之间的关系,分别是:
格林公式:第二型曲线积分与二重积分的联系
高斯公式:第二型曲面积分与三重积分之间的关系
斯托克公式:第二型曲线、曲面积分之间的关系
其中:
格林公式是斯托克公式的拓展
斯托克公式是格林公式的特例
高斯公式是斯托克公式的类比拓展
2.公式的作用
从公式的作用来看, 场论的三个基本公式实质上都是某一几何体上的积分和该几何体的边界上的积分之间的关系在不同维空间的表现形式。
格林公式是二维空式的情形;
高斯公式是三维空间的情形;
斯托克斯公式是二维弯曲空间的情形。
格林公式能把二重积分即平面域上的积分换为该域边界上的一个曲线积分, 反之能把闭曲线上的曲线积分换成该曲线所围域上的二重积分,
高斯公式是格林公式在空间域上的推广, 它建立了三重积分和曲面积分之间的关系, 根据高斯公式, 可把三重积分换成该曲分界面上的一个曲面积分, 反之, 可把闭曲面上的曲积分换成该面所围域上的一个三重积分。
斯托克斯公式是格林公式的直接推广, 即当曲面为平面时, 斯托克斯公式就是格林公式, 所以前者称为空间的格林公式。
三、场论中通过三大公式推导力学量之间的联系
1.由高斯公式
S S P Q R A d S Pdydz Qdydz Rdxdy dV x y z ∆∆∆Ω⎛⎫∂∂∂∆Φ=⋅=++=++ ⎪∂∂∂⎝
⎭⎰⎰⎰⎰⎰⎰⎰, 而散度公式P Q R divA x y z
∂∂∂=++∂∂∂, 所以,高斯公式可以写成如下的矢量形式:
S A d S divAdV Ω
⋅=⎰⎰⎰⎰⎰。
由高斯公式的矢量形式可看到通量和散度之间的一种关系,即:穿出封闭曲面S 的通量, 等于S 所围的区域Ω上的散度在Ω上的三重积分。
2.由斯托克斯公式
l l
A dl Pdx Qdy Rdz ∆∆∆Γ=
⋅=++⎰⎰ S R Q P R Q P dydz dzdx dxdy y z z x x y ∆⎛⎫⎛⎫∂∂∂∂∂∂⎛⎫=-+-+- ⎪ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝
⎭⎝⎭⎰⎰ ()()()cos ,cos ,cos ,S R Q P R Q P n x n y n z dS y z z x x y ⎡⎤⎛⎫⎛⎫∂∂∂∂∂∂⎛⎫=-+-+-⎢⎥ ⎪ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭⎣⎦
⎰⎰,
而旋度在直角坐标系中有
R Q P R Q P rot A i j k y z z x x y ⎛⎫⎛⎫∂∂∂∂∂∂⎛⎫=-+-+- ⎪ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭
, 我们知道旋度的一个重要性质,就是:旋度矢量在任意方向上的投影,就等于该方向上的环面面密度,
所以,可将斯托克斯公式写成如下矢量形式:
()l S
A dl rot A d S ⋅=⋅⎰⎰⎰
由斯托克斯公式的矢量形式可看到环量和旋度之间的一种关系, 即沿闭曲线环量等于旋度按右手螺旋方向穿过以l 为边界的曲面的通量。
