各种形状的体积和面积计算公式
几何体的表面积与体积计算

几何体的表面积与体积计算一、立体几何体表面积的计算方法立体几何体是空间中具有一定形状的物体,它们的表面积和体积是我们在几何学中经常计算的重要内容。
下面将介绍几种常见的几何体表面积的计算方法。
1. 立方体的表面积计算公式立方体是一种六个面都是正方形的立体几何体。
它的表面积计算公式为S=6a^2,其中a表示正方形的边长。
2. 正方体的表面积计算公式正方体是一种六个面都是正方形的立体几何体,与立方体的区别在于正方体各个边的长度相等。
它的表面积计算公式与立方体相同,也是S=6a^2。
3. 长方体的表面积计算公式长方体是一种六个面都是矩形的立体几何体,它的表面积计算公式为S=2(ab+ac+bc),其中a、b、c分别表示矩形的三条边长。
4. 圆柱体的表面积计算公式圆柱体是一种由一个矩形和两个圆所围成的几何体。
它的表面积计算公式为S=2πr^2+2πrh,其中r表示底面圆的半径,h表示圆柱体的高。
5. 圆锥体的表面积计算公式圆锥体是一种由一个圆和一个由圆所围成的锥面组成的几何体。
它的表面积计算公式为S=πr^2+πrl,其中r表示底面圆的半径,l表示从圆心到圆锥顶点的直线距离。
6. 球体的表面积计算公式球体是一种由无数个半径相等的小球所围成的几何体,它的表面积计算公式为S=4πr^2,其中r表示球体的半径。
二、立体几何体体积的计算方法除了表面积,立体几何体的体积也是我们经常需要计算的。
下面将介绍几种常见的几何体体积的计算方法。
1. 立方体的体积计算公式立方体的体积计算公式为V=a^3,其中a表示正方形的边长。
2. 正方体的体积计算公式正方体的体积计算公式与立方体相同,也是V=a^3。
3. 长方体的体积计算公式长方体的体积计算公式为V=abc,其中a、b、c分别表示矩形的三条边长。
4. 圆柱体的体积计算公式圆柱体的体积计算公式为V=πr^2h,其中r表示底面圆的半径,h表示圆柱体的高。
5. 圆锥体的体积计算公式圆锥体的体积计算公式为V=1/3πr^2h,其中r表示底面圆的半径,h表示圆锥体的高。
体积和表面积计算公式

体积和表面积计算公式在数学中,体积和表面积计算是令人头疼的课题。
每个物体的形状及大小都不一样,所以计算它们的体积和表面积时,必须找到正确的公式。
在本文中,将介绍一些体积和表面积计算公式,供大家参考和参考。
首先,介绍一下球体体积和表面积的计算公式。
球体的体积可以用以下公式来计算:V=4/3πr,其中r为球体的半径,π是圆周率。
同时,球体的表面积也可以通过以下公式来计算:S=4πr。
其次,介绍一下圆柱体体积和表面积的计算公式。
由于圆柱体的两端形状是圆形,因此可以借助圆的面积公式来计算它的体积:V=πrh,其中r为圆柱体的半径,h为圆柱体的高度,π是圆周率。
圆柱体的表面积可以用以下公式来计算:S=2πr(r+h)。
此外,介绍一下正方体体积和表面积的计算公式。
由于正方体的四个面是正方形,因此可以用以下公式来计算:V=a,其中a为正方底的边长;正方体的表面积可以用以下公式来计算:S=4a。
再次,介绍一下三棱柱体积和表面积的计算公式。
三棱柱体的体积可以用以下公式来计算:V=αlh,其中α为平面角的余弦值,l为三角柱底面的边长,h为高度;三棱柱体的表面积可以用以下公式来计算:S=l(α+h)。
最后,介绍一下圆锥体体积和表面积的计算公式。
圆锥体的体积可以用以下公式来计算:V=1/3πrh,其中r为圆锥体底部圆的半径,h为圆锥体的高度,π是圆周率;圆锥体的表面积可以用以下公式来计算:S=πrl,其中r为圆锥体底部圆的半径,l为圆锥体侧面的长度。
以上就是本文关于体积和表面积计算公式的详细介绍。
有了以上这些公式,大家就可以轻松的计算出不同物体的体积和表面积了。
只要熟练掌握这些计算公式,就可以很方便的计算出正确的结果。
同时,大家也可以根据自己的需要来灵活运用这些公式,以解决实际的工程计算问题。
各形状物体体积计算公式
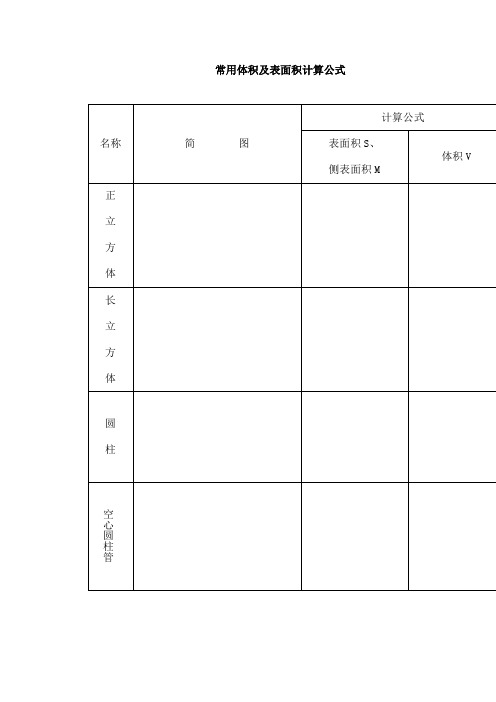
常用体积及表面积计算公式一些数学的体积和表面积计算公式3立方图形名称符号面积S和体积V正方体 a-边长 S=6a2 V=a3长方体 a-长 b-宽 c-高 S=2ab+ac+bc V=abc棱柱 S-底面积 h-高 V=Sh棱锥 S-底面积 h-高 V=Sh/3棱台 S1和S2-上、下底面积h-高 V=hS1+S2+S1S21/2/3正棱台拟柱体 S1-上底面积 S2-下底面积 S-中截面积 h-高V=hS1+S2+4S/6圆柱 r-底半径 h-高 C—底面周长 S底—底面积 S侧—侧面积S表—表面积 C=2πrS底=πr2 S侧=Ch S表=Ch+2S底V=S底h=πr2h空心圆柱 R-外圆半径 r-内圆半径 h-高V=πhR2-r2直圆锥 r-底半径 h-高V=πr2h/3圆台 r-上底半径 R-下底半径 h-高V=πhR2+Rr+r2/3球 r-半径 d-直径V=4/3πr3=πd2/6球缺 h-球缺高 r-球半径 a-球缺底半径V=πh3a2+h2/6 =πh23r-h/3a2=h2r-h球台 r1和r2-球台上、下底半径 h-高V=πh3r12+r22+h2/6圆环体 R-环体半径 D-环体直径 r-环体截面半径 d-环体截面直径V=2π2Rr2=π2Dd2/4桶状体 D-桶腹直径 d-桶底直径 h-桶V=πh2D2+d2/12 母线是圆弧形;圆心是桶的中心V=πh2D2+Dd+3d2/4/15 母线是抛物我用拟柱体公式来解决一下;至于公式本身证明需要用到积分知识需要同时推广牛顿-莱布尼茨公式;不详谈:任何立体的体积均可以归纳成:V=1/6×h×S1+S2+4SS1指上表面S2指下表面S指高线垂直平分面柱体:V=1/6×h×S1+S2+4SV=1/6×h×S1+S1+4S1V=1/6×h×6SV=Sh锥体:V=1/6×h×S1+S2+4SV=1/6×h×S2/4×4+S2V=1/6×h×2S2、、长方形的周长=长+宽×2 正方形的周长=边长×4 长方形的面积=长×宽正方形的面积=边长×边长三角形的面积=底×高÷2平行四边形的面积=底×高梯形的面积=上底+下底×高÷2直径=半径×2 半径=直径÷2圆的周长=圆周率×直径=圆周率×半径×2圆的面积=圆周率×半径×半径长方体的表面积=长×宽+长×高+宽×高×2长方体的体积 =长×宽×高正方体的表面积=棱长×棱长×6正方体的体积=棱长×棱长×棱长圆柱的侧面积=底面圆的周长×高圆柱的表面积=上下底面面积+侧面积圆柱的体积=底面积×高圆锥的体积=底面积×高÷3长方体正方体、圆柱体的体积=底面积×高平面图形名称符号周长C和面积S正方形 a—边长 C=4aS=a2长方形 a和b-边长 C=2a+b S=ab三角形 a;b;c-三边长h-a边上的高s-周长的一半A;B;C-内角其中s=a+b+c/2 S=ah/2=ab/2·sinC=ss-as-bs-c1/2=a2sinBsinC/2sinA四边形 d;D-对角线长α-对角线夹角 S=dD/2·sinα 平行四边形 a;b-边长h-a边的高α-两边夹角 S=ah=absinα菱形 a-边长α-夹角D-长对角线长d-短对角线长 S=Dd/2=a2sinα梯形 a和b-上、下底长h-高m-中位线长 S=a+bh/2=mh圆 r-半径d-直径 C=πd=2πrS=πr2=πd2/4扇形 r—扇形半径a—圆心角度数C=2r+2πr×a/360S=πr2×a/360弓形 l-弧长b-弦长h-矢高r-半径α-圆心角的度数 S=r2/2·πα/180-sinα =r2arccosr-h/r - r-h2rh-h21/2=παr2/360 - b/2·r2-b/221/2=rl-b/2 + bh/2≈2bh/3圆环 R-外圆半径r-内圆半径D-外圆直径d-内圆直径 S=πR2-r2=πD2-d2/4椭圆 D-长轴d-短轴 S=πDd/4立方图形名称符号面积S和体积V 正方体 a-边长 S=6a2V=a3长方体 a-长b-宽c-高 S=2ab+ac+bcV=abc棱柱 S-底面积h-高 V=Sh棱锥 S-底面积h-高 V=Sh/3棱台 S1和S2-上、下底面积h-高 V=hS1+S2+S1S11/2/3 拟柱体 S1-上底面积S2-下底面积S0-中截面积h-高 V=hS1+S2+4S0/6圆柱 r-底半径h-高C—底面周长S底—底面积S侧—侧面积S表—表面积 C=2πrS底=πr2S侧=ChS表=Ch+2S底V=S底h=πr2h空心圆柱 R-外圆半径r-内圆半径h-高 V=πhR2-r2直圆锥 r-底半径h-高 V=πr2h/3圆台 r-上底半径R-下底半径h-高 V=πhR2+Rr+r2/3 球 r-半径d-直径 V=4/3πr3=πd2/6 球缺 h-球缺高r-球半径a-球缺底半径 V=πh3a2+h2/6=πh23r-h/3a2=h2r-h球台 r1和r2-球台上、下底半径h-高 V=πh3r12+r22+h2/6圆环体 R-环体半径D-环体直径r-环体截面半径d-环体截面直径 V=2π2Rr2=π2Dd2/4桶状体 D-桶腹直径d-桶底直径h-桶高 V=πh2D2+d2/12母线是圆弧形;圆心是桶的中心V=πh2D2+Dd+3d2/4/15母线是抛物线形棱台体体积计算公式:V=1/3HS上+S下+√S上×S下H是高;S上和S下分别是上下底面的面积..棱台体积V=上底面积+下底面积+4×中截面面积÷6×高V=上口边长-0.025上口边宽-0.025杯深=下口边长+0.025下口边宽+0.025杯深V=h/3a2+ab+b2﹝其中a;b;h分别为正四棱台的上、下底边及高的大小棱台体积:V=〔S1+S2+开根号S1S2〕/3h注:V:体积;S1:上表面积;S2:下表面积;h:高..关于不等边长的四梭台的与手工计算偏差的原因关于不等边长的四梭台的与手工计算偏差的原因鲁班算量2006在计算独立基础时;发现所有的正四棱台计算正确;而计算有长边与短边的四棱台时;就不对了;量都偏大的原因:独立基础体积正确的计算公式为:四棱台计算公式为s1+s2+sqrs1s2h/3;sqrx对x求根或ABH+h/6AB+ab+A+aB+b其中A、B、H分别为独立基础下部长方体的长、宽、高;a、b、h分别为四棱台的长、宽、高;当然;A与a、B与b相对应..用ABH+h/6AB+ab+A+aB+b是偏小实际工作中;这两种公式都有人用;结果有时是不一样.而使用鲁班算量计算结果偏大;计算不等边长的四梭台与计算公式算出结果不一样是因为我们预算中的四梭台计算公式是近似的计算方法;而鲁班用的是微积分算法;结果相差很小另外鲁班的带马牙槎的构造柱计算结果也与实际算法有差别;其实我们算构造柱时是按如果有两边有马牙槎的为边长上加6cm计算;鲁班算量考虑了层高的不同与马牙槎的高度位也考虑了马牙槎在板底时正好为退时鲁班的计算结果就会小;但其实鲁班算的是实际的量..公式分类公式分类公式表达式乘法与因式分解 a2-b2=a+ba-b a3+b3=a+ba2-ab+b2 a3-b3=a-ba2+ab+b 2三角不等式|a+b|≤|a|+|b| |a-b|≤|a|+|b||a|≤b<=>-b≤a ≤b|a-b|≥|a|-|b| -|a|≤a≤|a|一元二次方程的解 -b+√b2-4ac/2a -b-b+√b2-4ac/2a根与系数的关系 X1+X2=-b/a X1X2=c/a 注:韦达定理判别式 b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式 sinA+B=sinAcosB+cosAsinB sinA-B=sinAcosB-sinBcosAcosA+B=cosAcosB-sinAsinB cosA-B=cosAcosB+sinAsinBtanA+B=tanA+tanB/1-tanAtanB tanA-B=tanA-tanB/1+tanAtanBctgA+B=ctgActgB-1/ctgB+ctgA ctgA-B=ctgActgB+1/ctgB-ctgA倍角公式 tan2A=2tanA/1-tan2A ctg2A=ctg2A-1/2ctga cos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sinA/2=√1-cosA/2 sinA/2=-√1-cosA/2cosA/2=√1+cosA/2 cosA/2=-√1+cosA/2tanA/2=√1-cosA/1+cosA tanA/2=-√1-cosA/1+cosActgA/2=√1+cosA/1-cosA ctgA/2=-√1+cosA/1-cosA和差化积 2sinAcosB=sinA+B+sinA-B 2cosAsinB=sinA+B-sinA-B 2cosAcosB=cosA+B-sinA-B -2sinAsinB=cosA+B-cosA-BsinA+sinB=2sinA+B/2cosA-B/2 cosA+cosB=2cosA+B/2sinA-B/2tanA+tanB=sinA+B/cosAcosB tanA-tanB=sinA-B/cosAcosBctgA+ctgBsinA+B/sinAsinB -ctgA+ctgBsinA+B/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=nn+1/2 1+3+5+7+9+11+13 +15+…+2n-1=n22+4+6+8+10+12+14+…+2n=nn+112+22+32+42+52+62+72+82+…+n2=nn +12n+1/613+23+33+43+53+63+…n3=n2n+12/4 12+23+34+45+56+67+…+nn+1=nn +1n+2/3正弦定理 a/sinA=b/sinB=c/sinC=2R 注:其中 R 表示三角形的外接圆半径余弦定理 b2=a2+c2-2accosB 注:角B是边a和边c的夹角圆的标准方程 x-a2+y-b2=r2 注:a;b是圆心坐标圆的一般方程 x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0抛物线标准方程 y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积 S=ch 斜棱柱侧面积 S=c'h正棱锥侧面积 S=1/2ch' 正棱台侧面积 S=1/2c+c'h'圆台侧面积S=1/2c+c'l=πR+rl球的表面积S=4πr2圆柱侧面积S=ch=2πh圆锥侧面积S=1/2cl=πrl弧长公式 l=ar a是圆心角的弧度数r >0 扇形面积公式s=1/2lr锥体体积公式 V=1/3SH 圆锥体体积公式V=1/3πr2h斜棱柱体积 V=S'L 注:其中;S'是直截面面积; L是侧棱长柱体体积公式 V=sh 圆柱体V=πr2h声明:本资料由大家论坛公务员考试专区收集整理;转载请注明出自更多公务员考试信息;考试真题;模拟题:大家论坛;学习的天堂数列问题1.关键提示:一般而言;公务员考试中的数列问题仅限于数列的简单求和及其变化形式;一般难度不大..考生只要很好的掌握基本公式;尤其是要学会运用等差中项的相关知识解题..2.核心公式:1等差数列通项公式==2等差数列求和公式=+=3等差数列中项公式;当n为奇数时;等差中项为1项即 ; =;当n为偶数时;等差中项为2项即和 ;而+=;4等比数列通项公式==例题1:一张考试卷共有10道题;后面的每-道题的分值都比其前面一道题多2分..如果这张考卷的满分为100分;那么第八道题的分值应为多少A.9 B.14 C.15 D.16解析:显然可将此题转化为一个等差数列的问题..每道题的分值组成了一个公差d =2的等差数列 ;显然 =100;可利用等差数列的求和公式 = +求出 ;显然代入后可求 =1;然后根据等差数列的通项公式 = 求出 =15..注:此题亦可通过求等差中项的方法解;即等差数列 ;当n=10时其等差中项的和为+=100÷5=20;公差d=2;所以 =9; =11;所以 =15..例题2:一种挥发性药水;原来有一整瓶;第二天挥发后变为原来的1/2;第三天变为第二天的2/3;第四天变为第三天的3/4;请问第几天时药水还剩下1/30瓶A.5天 B.12天 C.30天 D.100天解析:依据题意;显然可将此题变为一个有规律的数列;即第1天剩下1;第2天剩下1/2;第3天剩下1/3;依此下去;第30天就剩下1/30..所以;答案为C..例题3:2004年江苏A类真题如果某一年的7月份有5个星期四;它们的日期之和为80;那么这个月的3日是星期几A.一 B.三C.五 D.日解析:设这5天分别为 ; ; ; ; ;显然这是一个公差为7的等差数列..等差中项==16..所以;则=2即第一个星期四为2号;则3号为星期五..所以;答案为C..平面图形名称符号周长C和面积S正方形 a—边长 C=4aS=a2长方形 a和b-边长 C=2a+bS=ab三角形 a;b;c-三边长h-a边上的高s-周长的一半A;B;C-内角其中s=a+b+c/2 S=ah/2=ab/2•sinC=ss-as-bs-c1/2=a2sinBsinC/2sinA四边形 d;D-对角线长α-对角线夹角 S=dD/2•sinα平行四边形 a;b-边长h-a边的高α-两边夹角 S=ah=absi nα菱形 a-边长α-夹角D-长对角线长d-短对角线长 S=Dd/2=a2sinα梯形 a和b-上、下底长h-高m-中位线长 S=a+bh/2=mh圆 r-半径d-直径 C=πd=2πrS=πr2=πd2/4扇形 r—扇形半径a—圆心角度数 C=2r+2πr×a/360S=πr2×a/360弓形 l-弧长b-弦长h-矢高r-半径α-圆心角的度数 S=r2/2•πα/180-sinα=r2arccosr-h/r - r-h2rh-h21/2=παr2/360 - b/2•r2-b/221/2=rl-b/2 + bh/2≈2bh/3圆环 R-外圆半径r-内圆半径D-外圆直径d-内圆直径 S=πR2-r2=πD2-d2/4椭圆 D-长轴d-短轴 S=πDd/4立方图形名称符号面积S和体积V 正方体 a-边长 S=6a2V=a3长方体 a-长b-宽c-高 S=2ab+ac+bcV=abc棱柱 S-底面积h-高 V=Sh棱锥 S-底面积h-高 V=Sh/3棱台 S1和S2-上、下底面积拟柱体 S1-上底面积S2-下底面积S0-中截面积h-高 V=hS1+S2+4S0/6 圆柱 r-底半径h-高C—底面周长S底—底面积S侧—侧面积S表—表面积 C=2πrS底=πr2S侧=ChS表=Ch+2S底V=S底h=πr2h空心圆柱 R-外圆半径r-内圆半径h-高 V=πhR2-r2直圆锥 r-底半径h-高 V=πr2h/3圆台 r-上底半径R-下底半径球 r-半径d-直径 V=4/3πr3=πd2/6球缺 h-球缺高r-球半径a-球缺底半径 V=πh3a2+h2/6=πh23r-h/3a2=h2r-h球台 r1和r2-球台上、下底半径h-高 V=πh3r12+r22+h2/6圆环体 R-环体半径D-环体直径r-环体截面半径d-环体截面直径 V=2π2Rr2=π2Dd2/4桶状体 D-桶腹直径d-桶底直径h-桶高 V=πh2D2+d2/12母线是圆弧形;圆心是桶的中心V=πh2D2+Dd+3d2/4/15母线是抛物线形计算人体表面积的公式较多;但大多数可写成1或2的形式.. SA=cHα1Wα2这里SA为人体表面积m2;H为身高cm;W为体重kg;c、α1、α2为常数项..等式两边取自然对数;可将1式线性化为:lnSA=α0+α1lnH+α2lnW2其中α0=lnc;ln为自然对数符号..1916年由DuBois等直接测得9名观察者的身高、体重和体表面积;采用最小变异系数法;建立了第1个公认的人体表面积计算公式1;目前仍被广泛应用..1975年Gehan和George利用Boyd等直接测量的401例身高、体重和体表面积;应用最小二乘法拟合了2式〔1〕..1987年Mosteller按1式给出了容易记忆的简单公式c=1/60〔2〕..1973年Stevenson根据10例实测数据;提出了由身高与体重推算表面积的二元一次线性公式〔3〕;80年代赵松山等〔4;5〕分别报道了中国成年男女的计算公式..国内大多数教科书介绍的计算公式是:SA= 0.035W+0.1 W≤301.05+W-30×0.02 W>30几何体的表面积体积计算公式圆柱体:表面积:2πRr+2πRh 体积:πRRh R为圆柱体上下底圆半径;h为圆柱体高圆锥体:表面积:πRR+πRhh+RR的平方根体积: πRRh/3 r为圆锥体低圆半径;h为其高;平面图形名称符号周长C和面积S长方形a和b-边长C=2a+b S=ab三角形a;b;c-三边长h-a边上的高s-周长的一半A;B;C-内角其中s=a+b+c/2 S=ah/2=ab/2·sinC =ss-as-bs-c1/2=a2sinBsinC/2sinA 四边形d;D-对角线长α-对角线夹角S=dD/2·sinα平行四边形a;b-边长h-a边的高α-两边夹角S=ah=absinα菱形a-边长α-夹角D-长对角线长d-短对角线长S=Dd/2=a2sinα梯形a和b-上、下底长h-高m-中位线长S=a+bh/2=mh圆r-半径d-直径C=πd=2πr S=πr2=πd2/4扇形r—扇形半径a—圆心角度数C=2r+2πr×a/360 S=πr2×a/360 弓形l-弧长S=r2/2·πα/180-sinαb-弦长=r2arccosr-h/r - r-h2rh-h21/2h-矢高=παr2/360 - b/2·r2-b/221/2r-半径=rl-b/2 + bh/2α-圆心角的度数≈2bh/3圆环R-外圆半径S=πR2-r2r-内圆半径=πD2-d2/4D-外圆直径d-内圆直径椭圆D-长轴S=πDd/4d-短轴。
各种形状体积计算公式

各种形状体积计算公式在几何学中,体积是三维物体所占据的空间大小。
不同形状的物体有不同的体积计算公式。
下面我将介绍几种常见形状的体积计算公式。
1.立方体的体积计算公式:立方体是所有边长相等的六个平面的多面体。
其体积可通过边长的立方来计算。
公式:体积=边长^32.直方体的体积计算公式:直方体是六个面都是矩形的多面体。
其体积可通过底面积乘以高来计算。
公式:体积=底面积×高3.圆柱体的体积计算公式:圆柱体由一个圆形底面和一个平行于底面的圆形顶面连接而成。
其体积可通过底面积乘以高来计算。
公式:体积=底面积×高注意:底面积一般是指底面圆的面积。
4.圆锥体的体积计算公式:圆锥体由一个圆形底面和一个连接底面到顶点的侧面锥形组成,其体积可通过底面积乘以高再除以3来计算。
公式:体积=(底面积×高)/35.球体的体积计算公式:球体是一个完全由曲线包围的立体形状,其体积可通过四分之三乘以球的半径的立方来计算。
公式:体积=(4/3)×π×半径^36.圆环体的体积计算公式:圆环体由一个圆柱体和一个外部与之共轴的圆台形组成。
其体积可通过外圆台体积减去内圆台体积来计算。
公式:体积=(π×高×(外半径^2+内半径^2+外半径×内半径))/37.圆锥台体的体积计算公式:圆锥台体由一个圆锥体和一个与之底面平行的圆台积组成。
其体积可通过底面积乘以高再除以3来计算。
公式:体积=(π×高×(上底半径^2+下底半径^2+上底半径×下底半径))/38.带截头圆锥体的体积计算公式:带截头圆锥体由一个截头圆锥和一个与之底面平行的圆台积组成,其中截头圆锥的顶点位于圆台积上。
其体积可通过底面积乘以高再除以3来计算。
公式:体积=(π×高×(上底半径^2+上底半径×下底半径+下底半径^2))/3除了上述形状的体积计算公式,还有许多其他的形状体积公式,如多面体、棱柱、棱台、椭球等等。
各形状物体体积计算公式

各形状物体体积计算公式
以下是几个常见形状物体的体积计算公式:
1.立方体:立方体的体积计算公式很简单,即边长的立方。
假设立方
体的边长为L,则立方体的体积V=L^3、例如,一个边长为2厘米的立方
体的体积为8立方厘米。
2.长方体:长方体的体积计算公式为长乘以宽乘以高。
假设长方体的长、宽、高分别为L、W、H,则长方体的体积V=L×W×H。
3.圆柱体:圆柱体的体积计算公式为底面积乘以高。
假设圆柱体的底
面积为A,高为H,则圆柱体的体积V=A×H。
圆柱体的底面积A可以根据
圆的面积公式计算,即A=π×r^2,其中π为圆周率,r为圆的半径。
例如,一个半径为3厘米,高为5厘米的圆柱体的体积为
V=π×3^2×5=45π立方厘米。
4.球体:球体的体积计算公式为4/3乘以π乘以半径的立方。
假设
球体的半径为R,则球体的体积V=4/3×π×R^3
5.锥体:锥体的体积计算公式为底面积乘以高除以3、假设锥体的底
面积为A,高为H,则锥体的体积V=A×H/3、底面积A可以根据锥体类型
的不同使用不同的公式进行计算。
例如,直角圆锥体的底面积A=π×r^2,其中r为底面圆的半径;等腰三角锥体的底面积A=(b×h)/2,其中b为
底边长,h为底边上的高。
以上只是几个常见形状物体的体积计算公式,实际上还有很多其他形
状的物体,每个形状都有对应的体积计算公式。
根据物体的形状和特征,
可以选择合适的体积计算公式进行计算。
EXCEL自动求得常用面积体积计算公式

EXCEL自动求得常用面积体积计算公式Excel是一款功能强大的电子表格软件,可以用于各种计算和数据分析任务。
在面积和体积计算方面,Excel提供了许多自动计算公式,可以帮助用户快速计算各种图形的面积和体积。
本文将介绍Excel中常用的面积和体积计算公式,并提供一些实际应用示例。
矩形是最简单的几何形状之一,其面积和体积可以通过以下公式计算:面积(A)=长(L)×宽(W)体积(V)=长(L)×宽(W)×高(H)在Excel中,可以使用乘法运算符“*”来计算面积和体积。
例如,如果矩形的长为10,宽为5,高为3,可以使用以下公式计算面积和体积:面积:=10*5体积:=10*5*3圆是一种常见的二维和三维几何形状,其面积和体积可以通过以下公式计算:面积(A)=π×半径(R)^2体积(V)=4/3×π×半径(R)^3在Excel中,可以使用内置的PI函数(=PI()来获取圆周率π的值,并使用幂运算符“^”来计算面积和体积。
例如,如果圆的半径为5,可以使用以下公式计算面积和体积:面积:=PI(*5^2体积:=4/3*PI(*5^3三角形是另一个常见的二维几何形状,其面积可以通过以下公式计算:面积(A)=1/2×底边(B)×高(H)在Excel中,可以使用除法运算符“/”来计算面积。
例如,如果三角形的底边为10,高为8,可以使用以下公式计算面积:面积:=1/2*10*8由于三角形是一个二维形状,没有体积的概念。
正方形是一种特殊的矩形,其面积可以通过以下公式计算:面积(A)=边长(S)^2在Excel中,可以使用幂运算符“^”来计算面积。
例如,如果正方形的边长为6,可以使用以下公式计算面积:面积:=6^2由于正方形是一个二维形状,没有体积的概念。
以上是常见的几何形状的面积和体积计算公式。
除了这些基本的公式之前,在Excel中还可以使用一些其他功能来进行更复杂的计算,并将计算结果应用于实际问题中。
各种形状面积体积计算公式(配图)

各种形状面积体积计算公式图)各种形状面积体积计算公式[图片] s — — (h Y +h 2)^i = sin B L L I L J& b* 6 d —各边长、h 、 咼s -面积 几必一对角线不四等边边形Hw h -咼 s -面积内接角 s = 形R =不四 平边 行形 山Q * [H +g+b h + cH2 Jp\p-a)[p-b)[p-c)abc abc4 s 4jp&_a)@_b)@_c)-三边和之半-三角形面积• -三角形外接圆半径R -大圆半径 8 -圆心角 r -小圆半径s -面积_s _ \[p-a\p-b)[p-c) = 7 = V 鼻p -三边和之半S -三角形面积r -三角形內切圆半径= 0.008720* (对一尸T 外 切角 形 ^p[p-a\p-b\p-c)直角角形= -r2工-半径4=0.7854r2 c -弦长=0.3927c2s -面积护不b -直角边c — Ja? +沪 c -斜边1 , s ==a・b2S -面积c = 4•胪- 2bwh = Jd! 2 — g2 s = —b h2a、b、c -边长h -高s -面积锐角角形c = Ja 2 +Z>2 + The 8、b 、c 一各边长力=J/一 w' h - 高 s= —b h 2 钝角角形 』」b 」玉b 、c 、d -边长 s -面积 h-高 e.f-对角线f = 2a sin — a 一 边长2 s -面积 Q ^ = 2acos 5 e.f -对角线 平行四边 =b h = a ■ Z? sin y € ■ sin/ = a 2 sin 0a.b -边长s -面积h -高必4 -对角线=0.1073c2 s_ 面积s =弓形xb-弓形ndb r -小圆半径8、耳・圆心角R -小圆半径s - B积n-螺线的数P -螺距I = n J,+(加尸,-螺线长C!…1.33曲b_底边2L,h_高s= —b - h3s-面积= 的面积3I-曲线的长匕)门-卷数I 2丿P -螺距"r 1才_涡状线的长尸二三=0.15吟2/r人2 ds=—= 0.7854^?4 $ s = szz 2 = 3.1416 厂'd -短 轴D -长 轴r -短半轴 二“図+八)R 一长半轴s= nRr = —Dd4p =加=?. 1416d^ = £ = 0.3183pp -圆周长d-小圆直径D-大圆直径S -面积1 ,s = —ir = ----2 360=0.008727r26>r-小圆半径R-大圆半径c = 2x lh(2r-h) / -弧 长 正 多 边 形 s - 0 积 a = 24^^ = 2^sin — 2n -边 数 a-一边之长 R -外接圆半径 r -响切圆辛径正六面体(数目)棱顶点12 8(八个三角形)正八面体(数目)棱顶点12 6 尸=3.464^2 Z= 0.4714a3正十面体(数目)棱顶点30 20F = 20.6457/7 = 7.6631/正十面体〔数目)棱顶点30 12厅=866(0?正立方体& -边长d-对角线长F = 2[ab +ca)“3、b.c -辺长 C = pl p -直截断面周长 F = pi + 2s h - 咼V sh s -底面积正长方体 d -对角线长c = -pl 2 s -底面积 F = 1 + s P -底面积的周围长 ./ T 匚内切圆半径 二二=R -夕卜接圆半径Pl "2 —两端周鹵殆长S l 0 —两端的 面积□-正多角形边长n -正多角形边数截头直角锥C 二*心1+血) 恥[@1+卩2) + S] +S?C =皿}=岔J厂2十沪F = 7er?4-7zr2r=— = 1.0472r2^3h -高r -圆锥底半径截头直C“KR+r)圆锥誇(”+沪+加)C = 2nrh d -直径F = 2?zr(r 4- h)r _ 半径”2} nd2 , 亠7二岔h =—h h -咼中空圆柱AnI .1 “-idHC=2 兀h(R+r)F二2 兀h(R+r)+2 兀h(只2-八)V二兀h(炉“2)瓏舉面积R丿瀾半铤F = 4?zr 2 =兀沪2 r = —= 0.5236^26 3 = ^i = 4.1888r 33 r = 0.62035^/7—球半径=〒(歹_幻屮*(2一方) C = 2?zr 人=?r (P +沪) r —球缺半径h —球缺的高 彳一平切圆半径C=2诙 F 二龙(2风+/+耳) 7 二竺(3/+3,+沪)r 一球半径/ b —平切圆半径 h一球台的高/十力)“=丸5 +a ) 肿 ”(护 +2&2)V = 2,沪=19.739^2 R -迥转半径 r -迥转圆半径L L J F = nd\^D + 2L )7二尹何)+ 2厶) d -迥转圆直径 D -迥转直径椭圆环体=4 139 宓 -迥转半径-短半轴 b V = f 也氐 3抛 物 线 体 = 1.5708A 2/? 8=0.3927D 络母线是圆弧 7=0.262雄夕+/) 或=0.087弘(的十刃彳 d -两底的直径 h - D -最大的直径 =—\AB + (j4+(2t )x (5 +2>)+必] 6L JA 、B -下底的两边h ■高 a 、b -上底的两边M -中面积切头方锥形基7 =上[(24 +训+么+咖大/卜头2D-大圆直径d-小圆直径H -高180°D -直径R ■半径=0.05483加尹0 圆心角矩形弯头2(a+b)R兀er180°= 0.01745/?^°?,周长d・小口直径-支通直径H-主通高度+(£)+£】热〕h -支通高度2S = (a + b + a】+ 知)H + 弓能4 +“2) =0.5(屮阳 + 0.62832圧8、b -大口边长H -主通高度8、b -小口边长R -支通半径6、® -支通边长八右、厶-周长十---- 畑2=1.5708[(Q +2E 二(a 十b 十內十®)左+—7rR (a 2十—)=0.50+* )円 40.62832人虫 、b -大口边长a. b -小口边长八厶、b -周长2S = (a + b + a 】+ 知)H + 弓能4H-主通高度 R-支通半径+“2) =0.5(屮阳 + 0.62832圧8、b -大口边长H -主通高度8、b -小口边长R -支通半径6、® -支通边长八右、厶-周长I 2 丿D -圆直径 a 、b -边长H -高度I KH ! A, M <b> I-l 制丽田 7=(A+KH )[B + K )H+护2胪A 、B -包括加宽工作面在内的坑底双向开挖尺寸6) H -地坑开挖深度(m ) K -放坡坡度系数天 圆地方 矩形四边放坡地 坑 J K U —I — __llOlj (a 〉平而田或 6 i o V= A B H + -KH 2[2A+ B )+ -K 2H zK-放坡坡度系数 矩形三边放坡、一边支挡土板地坑卩十+田)(筋衍疔曲 W+如㈣ 6 或: V A B H + L 灯/出")+丄丹$ 2 ' / 3 A 、B -包括加宽工作面在内的坑底 双冋开挖尺寸5) H -地坑开挖深度6) K -赦坡坡度系数 卩=A ・(B+ KH )H A 、B -包括加宽工作面在内的坑底 双向开挖尺寸(in ) H -地坑开挖深度6)K -放坡坡度系数 矩形零二边放坡・二边支挡土板地坑矩形相对二边放坡-二边支挡土板地坑 (b )I ・l 剖而田 <a )平而田(a >平页国 (b)l-ljij 面国 V = A B • H 4 -B-KH 2 2 B -包拆加宽工作面在內的坑底双向开挖尺寸(m) H -地坑开挖深度5) K -放坡坡度系数 V=L ・ A + KH H X /L 二长度矩形三边支档.一边放坡地坑 挖地槽・放坡.无工作面n A n_」 挖地槽.无工作面♦单面放坡(挡土板) 挖地槽、无工作面*无放坡L 二长度 挖地槽、无工作面*无放坡、双面挡土地板。
面积和侧面积和体积和周长的所有公式

面积和侧面积和体积和周长的所有公式全文共四篇示例,供读者参考第一篇示例:在日常生活中,我们不时需要计算物体的面积、侧面积、体积和周长。
这些计算公式可以帮助我们更好地理解世界,解决问题。
下面就让我们来学习一些关于面积、侧面积、体积和周长的常用公式。
一、面积1. 矩形的面积公式:矩形的面积等于底边长乘以高。
公式为:A = l × w。
A代表矩形的面积,l代表矩形的长,w代表矩形的宽。
3. 圆的面积公式:圆的面积等于半径的平方乘以π。
公式为:A = πr²。
A代表圆的面积,r代表圆的半径,π为圆周率,约为3.14159。
3. 圆台的侧面积公式:圆台的侧面积等于两底圆周长之和再乘以斜高再除以2。
公式为:S = π(r₁ + r₂)l。
S代表圆台的侧面积,r₁、r₂分别代表上下底面半径,l代表斜高。
三、体积四、周长2. 正方形的周长公式:正方形的周长等于边长的四倍。
公式为:P = 4s。
P代表正方形的周长,s代表正方形的边长。
通过以上公式,我们可以更准确地计算物体的面积、侧面积、体积和周长。
这些公式在日常生活和学习中都有很大的应用价值,希第二篇示例:面积、侧面积、体积和周长是几何学中常见的概念,它们用来描述不同形状的几何图形的大小和特征。
在数学中,我们常常需要计算不同形状的面积、侧面积、体积和周长,以便解决各种问题。
下面将介绍一些常见的几何图形的面积、侧面积、体积和周长的公式。
首先是关于面积的公式。
面积是指平面内一个封闭区域的大小。
常见的图形包括正方形、长方形、三角形、圆等。
对于正方形来说,其面积公式为:面积=边长的平方;对于长方形来说,其面积公式为:面积=长×宽;对于三角形来说,其面积公式为:面积=底边长×高÷2;对于圆来说,其面积公式为:面积=π×半径的平方。
通过以上介绍,我们可以看到不同形状的几何图形有不同的面积、侧面积、体积和周长的计算公式。
空间立体的表面积与体积计算

空间立体的表面积与体积计算在数学中,空间立体是指具有三个维度的图形体。
计算空间立体的表面积和体积是数学中常见的问题,本文将介绍如何计算各种类型的空间立体的表面积和体积,并提供相应的计算公式。
一、立方体的表面积和体积计算立方体是最简单的空间立体之一,具有六个相等的正方形面。
计算立方体的表面积和体积非常简单,只需要知道它的边长即可。
假设立方体的边长为a,则立方体的表面积S可以通过公式S=6a²计算得出,其中a²表示a的平方。
同样地,立方体的体积V可以通过公式V=a³计算得出,其中a³表示a的立方。
二、长方体的表面积和体积计算长方体是另一种常见的立体形状,它具有六个面,其中有两对相等的矩形面。
长方体的表面积S可以通过公式S=2ab+2ac+2bc计算得出,其中a、b、c分别表示长方体的三个相邻边的长度。
长方体的体积V可以通过公式V=abc计算得出,其中a、b、c同样表示长方体的三个相邻边的长度。
三、圆柱体的表面积和体积计算圆柱体包含一个底面和一个侧面,底面是一个圆,侧面是一个矩形。
圆柱体的表面积S可以通过公式S=2πr²+2πrh计算得出,其中r表示底面圆的半径,h表示圆柱体的高度。
圆柱体的体积V可以通过公式V=πr²h计算得出,其中r同样表示底面圆的半径,h表示圆柱体的高度。
四、球体的表面积和体积计算球体是一种特殊的立体形状,它的表面是由无数个等距离的点构成的。
球体的表面积S可以通过公式S=4πr²计算得出,其中r表示球的半径。
球体的体积V可以通过公式V=(4/3)πr³计算得出,其中r表示球的半径。
总结:通过以上几个例子,我们可以看出计算空间立体的表面积和体积并不复杂,只需要根据不同的形状选择相应的公式即可。
在实际应用中,了解这些计算方法可以帮助我们更好地理解和解决与空间立体相关的问题。
因此,我们应该熟练地掌握这些计算方法,并能够灵活运用于解决实际问题中。
各形状物体体积计算公式

各形状物体体积计算公式
1、球体:体积计算公式为V=4/3πr^3,其中r为球的半径。
2、正方体:体积计算公式为V=a*a*a,其中a为正方体的边长。
3、正方柱:体积计算公式为V=πr2h,其中r为柱的半径,h为柱的高度。
4、圆柱:体积计算公式为V=πr2h,其中r为圆柱侧的半径,h为圆柱的高度。
5、圆台:体积计算公式为V=πR2H,其中R为圆台底面的半径,H为圆台的高度。
6、三棱柱:体积计算公式为V=1/3a2h,其中a为三棱柱底面对角线的长度,h为三棱柱的高度。
7、正四棱锥:体积计算公式为V=1/3ah,其中a为正四棱锥底面的边长,h为正四棱锥的高度。
8、圆锥:体积计算公式为V=1/3πR2H,其中R为圆锥底面的半径,H为圆锥的高度。
9、球锥:体积计算公式为V=3/4πr2h,其中r为球锥底面半径,h 为球锥的高度。
10、圆筒:体积计算公式为V=πr2h,其中r为圆筒侧面半径,h为圆筒的高度。
11、金字塔:体积计算公式为V=1/3a2h,其中a为金字塔底面的面积,h为金字塔的高度。
12、圆台柱:体积计算公式为V=πr2h,其中r为圆台半径,h为圆台柱的高度。
13、圆柱棱柱:体积计算公式为V=πr2h,其中r为圆柱棱柱底面半径,h为圆柱棱柱的高度。
空间几何体表面积和体积公式

空间几何体表面积和体积公式空间几何体是在三维空间中存在的物体,它们可以有不同的形状和大小。
对于任何空间几何体,我们都可以计算出它的表面积和体积。
表面积是指几何体外部的总表面面积。
不同类型的几何体有不同的计算公式。
对于立方体来说,它的表面积等于六个面的面积之和。
每个面的面积都相等,可以通过计算边长的平方来得到。
所以立方体的表面积公式为:表面积 = 6 * a^2 (其中a为边长)。
对于球体来说,它的表面积等于球的半径的平方乘以4π。
所以球体的表面积公式为:表面积= 4π * r^2 (其中r为半径)。
对于圆柱体来说,它的表面积由两个圆面和一个侧面组成。
圆柱的底面积为π * r^2,所以两个圆面的面积之和为2π * r^2。
侧面是一个矩形,它的长等于圆周长2πr,宽等于圆柱的高h。
所以圆柱体的表面积公式为:表面积= 2π * r^2 + 2πrh。
体积是指几何体所占据的空间大小。
与表面积一样,不同类型的几何体有不同的计算公式。
对于立方体来说,它的体积等于边长的立方。
所以立方体的体积公式为:体积 = a^3 (其中a为边长)。
对于球体来说,它的体积等于4/3乘以π乘以半径的立方。
所以球体的体积公式为:体积= (4/3)π * r^3 (其中r为半径)。
对于圆柱体来说,它的体积等于底面积乘以高。
所以圆柱体的体积公式为:体积= π * r^2 * h (其中r为底面半径,h为高)。
除了立方体、球体和圆柱体,还有许多其他类型的空间几何体,它们的表面积和体积公式也各不相同。
想要计算某个具体几何体的表面积和体积,需要根据其特定的形状和尺寸选择相应的计算公式进行计算。
各形状物体体积计算公式

常用体积及表面积计算公式一些数学的体积和表面积计算公式3 立方图形名称符号面积S和体积V正方体 a-边长 S=6a2 V=a3长方体 a-长 b-宽 c-高 S=2(ab+ac+bc)V=abc棱柱 S-底面积 h-高 V=Sh棱锥 S-底面积 h-高 V=Sh/3棱台 S1和S2-上、下底面积h-高 V=h[S1+S2+(S1S2)1/2]/3正棱台拟柱体 S1-上底面积 S2-下底面积 S0-中截面积 h-高V=h(S1+S2+4S0)/6圆柱 r-底半径 h-高 C—底面周长 S底—底面积 S侧—侧面积S表—表面积 C=S底=πr2 S侧=Ch S表=Ch+2S底V=S底h=πr2h空心圆柱 R-外圆半径 r-内圆半径 h -高V=πh(R2-r2)直圆锥 r-底半径 h-高V=πr2h/3圆台 r-上底半径 R-下底半径 h-高V=πh(R2+Rr+r2)/3球 r-半径 d-直径V=4/3πr3=πd2/6球缺 h-球缺高 r-球半径 a-球缺底半径V=πh(3a2+h2)/6 =πh2(3r-h)/3a2=h(2r-h)球台 r1和r2-球台上、下底半径 h-高V=πh[3(r12+r22)+h2]/6圆环体 R-环体半径 D-环体直径 r-环体截面半径 d-环体截面直径V=2π2Rr2=π2Dd2/4桶状体 D-桶腹直径 d-桶底直径 h-V=πh(2D2+d2)/12 (母线是圆弧形,圆心是桶的中心)V=πh(2D2+Dd+3d2/4)/15 (母线是抛物我用拟柱体公式来解决一下,至于公式本身证明需要用到积分知识(需要同时推广牛顿-莱布尼茨公式),不详谈:任何立体的体积均可以归纳成:V=1/6×h×(S1+S2+4S)S1指上表面S2指下表面S指高线垂直平分面柱体:V=1/6×h×(S1+S2+4S)V=1/6×h×(S1+S1+4S1)V=1/6×h×6SV=Sh锥体:V=1/6×h×(S1+S2+4S)V=1/6×h×(S2/4×4+S2)、、长方形的周长=(长+宽)×2正方形的周长=边长×4长方形的面积=长×宽正方形的面积=边长×边长三角形的面积=底×高÷2平行四边形的面积=底×高梯形的面积=(上底+下底)×高÷2 直径=半径×2 半径=直径÷2圆的周长=圆周率×直径=圆周率×半径×2圆的面积=圆周率×半径×半径长方体的表面积=(长×宽+长×高+宽×高)×2长方体的体积 =长×宽×高正方体的表面积=棱长×棱长×6正方体的体积=棱长×棱长×棱长圆柱的侧面积=底面圆的周长×高圆柱的表面积=上下底面面积+侧面积圆柱的体积=底面积×高圆锥的体积=底面积×高÷3长方体(正方体、圆柱体)的体积=底面积×高平面图形名称符号周长C和面积S正方形 a—边长 C=4aS=a2长方形 a和b-边长 C=2(a+b) S=ab三角形 a,b,c-三边长h-a边上的高s-周长的一半A,B,C-内角其中s=(a+b+c)/2 S=ah/2=ab/2·sinC=[s(s-a)(s-b)(s-c)]1/2=a2sinBsinC/(2sinA)四边形 d,D-对角线长α-对角线夹角 S=dD/2·sinα 平行四边形 a,b-边长h-a边的高α-两边夹角 S=ah=absinα菱形 a-边长α-夹角D-长对角线长d-短对角线长 S=Dd/2=a2sinα梯形 a和b-上、下底长h-高m-中位线长 S=(a+b)h/2=mh圆 r-半径d-直径 C=πd=2πrS=πr2=πd2/4扇形 r—扇形半径a—圆心角度数C=2r+2πr×(a/360)S=πr2×(a/360)弓形 l-弧长b-弦长h-矢高r-半径α-圆心角的度数 S=r2/2·(πα/180-sinα) =r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2=παr2/360 - b/2·[r2-(b/2)2]1/2=r(l-b)/2 + bh/2≈2bh/3圆环 R-外圆半径r-内圆半径D-外圆直径d-内圆直径 S=π(R2-r2)=π(D2-d2)/4椭圆 D-长轴d-短轴 S=πDd/4立方图形名称符号面积S和体积V正方体 a-边长 S=6a2V=a3长方体 a-长b-宽c-高 S=2(ab+ac+bc)V=abc棱柱 S-底面积h-高 V=Sh棱锥 S-底面积h-高 V=Sh/3棱台 S1和S2-上、下底面积h-高 V=h[S1+S2+(S1S1)1/2]/3拟柱体 S1-上底面积S2-下底面积S0-中截面积h-高 V=h(S1+S2+4S0)/6圆柱 r-底半径h-高C—底面周长S底—底面积S侧—侧面积S表—表面积 C=2πrS底=πr2S侧=ChS表=Ch+2S底V=S底h=πr2h空心圆柱 R-外圆半径r-内圆半径h-高 V=πh(R2-r2)直圆锥 r-底半径h-高 V=πr2h/3圆台 r-上底半径R-下底半径h-高 V=πh(R2+Rr+r2)/3球 r-半径d-直径 V=4/3πr3=πd2/6球缺 h-球缺高r-球半径a-球缺底半径 V=πh(3a2+h2)/6=πh2(3r-h)/3a2=h(2r-h)球台 r1和r2-球台上、下底半径h-高 V=πh[3(r12+r22)+h2]/6圆环体 R-环体半径D-环体直径r-环体截面半径d-环体截面直径 V=2π2Rr2=π2Dd2/4桶状体 D-桶腹直径d-桶底直径h-桶高 V=πh(2D2+d2)/12(母线是圆弧形,圆心是桶的中心)V=πh(2D2+Dd+3d2/4)/15(母线是抛物线形)棱台体体积计算公式:V=(1/3)H(S上+S下+√[S上×S下])H是高,S上和S下分别是上下底面的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
完
三利公司欢迎您
2012年2月5日
.
.
圆形三通、矩形弯头
.
矩形ห้องสมุดไป่ตู้通
.
天圆地方
.
圆形放坡地坑、矩形四边放坡地坑
.
矩形三边放坡、一边支挡土板地坑 矩形二边放坡、二边支挡土板地坑
.
矩形三边支挡、一边放坡地坑 矩形相对二边放坡、二边支挡土板地坑
.
挖地槽、无工作面、单面放坡(挡土板) 挖地槽、放坡、无工作面
.
挖地槽、无工作面、无放坡
.
正多边形、正四面体
.
正八面体、正六面体
.
正二十面体、正十二面体
.
正长方体、正立方体
.
直角锥、角柱
.
直圆锥、截头直角锥
.
截头巨型角锥、截头直圆锥
.
斜切直圆柱、直圆柱
.
楔形、中空圆柱
.
球缺、球
.
圆环、球台
.
椭圆体、椭圆环体
.
桶形、抛物线体
.
大小头、切头方锥形基础
.
圆形弯头、大小头
各种形状的体积和面积 计算公式
• 讲解:颜晓宾
• 新疆三利建筑有限责任公司 • 项目三部
• 2012年二月五日
.
不平行四边形、内接三角形、圆片
.
外切三角形、四分圆、直角三角形、 锐角三角形
.
平行四边形、钝角三角形
.
菱形、梯形、月行、隅角
.
螺线、抛物线
.
涡状线、圆、椭圆、空心圆
.
扇形、弓形
