理论力学综合应用
动力学普遍定理综合应用(理论力学I,10学时)页PPT文档

H1 J
H 2JBm B rr
H1 H2
B
J
J
mr2
VB
2grr22
J(2Jm2r) (Jm2r)2
同理可得 C VC 2 gr
综合3:均质细杆AB的质量是M,长2L,放在铅直平面内,两端
动力学普遍定理的综合应用
质点系的动量定理(质心运动定理)、动量矩定理和 动能定理统称为动力学普遍定理(general theorems of dynamics)。动力学普遍定理给出了描述质点系整体运 动特征的物理量(动量、动量矩和动能)与度量力对系统 的作用效应的物理量(力系的主矢和主矩、力的冲量和 力的功)之间的定量关系。动量定理(质心运动定理)和 动量矩定理为矢量形式,而动能定理为标量形式。
aC aO aCnO
O aO y
C mg
an CO
aCy aCnO2e2gC2e2
轮O受力如图
N x
Nm gmCaym(g12eC 22)
综合5:均质半圆盘的质量是m,半径是r,在水平面上作无滑动 的摆动。现把半圆盘由直径AB铅直时的位置无初速地释放,求 当直径水平时半圆盘的角速度,以及这时半圆盘对平面的正压力。
aC
B
C
a aA
an
τ AC AC
A
0
mg
解:绳切断后AB受力如图。 质心加速度铅直向下,AB杆的角
加速度为。
以C为基点,研究A的加速度为 aA aACaC
投影到铅直向下方向
0aACcosaC
N
aC
2 l
4
aC
aC
理论力学-9-动量定理及其应用

y
解法1:建立Oxy坐标系,在角度q为任意值的情形下
vA
yA 2lsin q
A
xB 2lcosq
vA yA 2lqcosq 2lcosq
vB xB 2lqsinq 2lsin q
Oθ
vB
B
p mivi
i
p mAvA mBvB
p mAvA mBvB
x
2lmcosq j 2lmsinq i
l
cost
例题 3
2.求作用在O轴处的最大水平约束力
y
由质心运动定理
A
O
C
B
l/2
x
&x&C
m1 2(m1
2m2 2m3 m2 m3 )
lω2
cos
ωt
D
Fox
MaCx
(m1
2m2
2m3 )
lω2 2
cos ωt
当 cosωt 1 时,水平约束力最大,其值为
Fox,max
Macx
(m1
2m2
隔板
水池
?抽去隔板后将会
发生什么现象
水
光滑台面
第9章 动量定理及其应用
? 二人在太空中拔河,
初始静止,同时用尽 全力相互对拉。若A 的力气大于B的力气, 则拔河的胜负将如何?
第9章 动量定理及其应用
9.1 动量定理与动量守恒 9.2 质心运动定理 9.3 综合应用举例 9.4 结论与讨论
第9章 动量定理及其应用
2lm(-sinq i cosq j)
9.1.1 质点和质点系的动量
例题 1
解法2: 质点系的质心在C处,其速度大小为
A vC
如何应用理论力学解决建筑结构设计问题?

如何应用理论力学解决建筑结构设计问题?在建筑领域,结构设计是确保建筑物安全、稳定和功能性的关键环节。
而理论力学作为力学的基础学科,为建筑结构设计提供了重要的理论支持和分析方法。
下面我们就来探讨一下如何应用理论力学来解决建筑结构设计中的各种问题。
首先,我们需要了解理论力学的一些基本概念和原理。
理论力学主要包括静力学、运动学和动力学三个部分。
静力学研究物体在静止状态下的受力平衡问题;运动学关注物体的运动规律而不考虑其受力;动力学则综合考虑物体的受力和运动情况。
在建筑结构设计中,静力学的应用极为广泛。
例如,在设计建筑物的柱子和梁时,需要计算它们所承受的各种载荷,包括自重、活载(如人员、家具等的重量)以及风载、雪载等。
通过静力学的分析,可以确定柱子和梁的尺寸、材料强度等参数,以保证其在受力情况下不会发生破坏或过度变形。
为了进行准确的静力学分析,我们需要掌握力的合成与分解、力矩的计算以及平衡方程的建立等知识。
以一个简单的梁为例,假如梁上作用着多个集中力和分布力,我们需要将这些力进行合成或分解,然后计算它们对梁的支点产生的力矩。
根据平衡方程,我们可以得出支点所承受的反力,从而进一步分析梁内部的应力分布情况。
运动学在建筑结构设计中也有一定的应用。
比如在设计桥梁时,需要考虑车辆通过时桥梁的振动问题。
通过运动学的分析,可以了解桥梁在不同运动状态下的位移、速度和加速度等参数,从而评估桥梁的动态性能,并采取相应的措施来减少振动和提高舒适性。
动力学的知识在建筑结构设计中主要用于应对地震、风振等动力荷载的情况。
地震是一种突发的、强烈的动力作用,会对建筑物产生巨大的影响。
通过动力学的分析,可以计算建筑物在地震作用下的响应,包括位移、加速度和内力等。
这有助于设计出具有良好抗震性能的结构体系,如采用合适的结构形式(如框架结构、剪力墙结构等)、设置减震装置等。
在实际的建筑结构设计中,应用理论力学解决问题还需要借助一些工具和方法。
第十二章理论力学
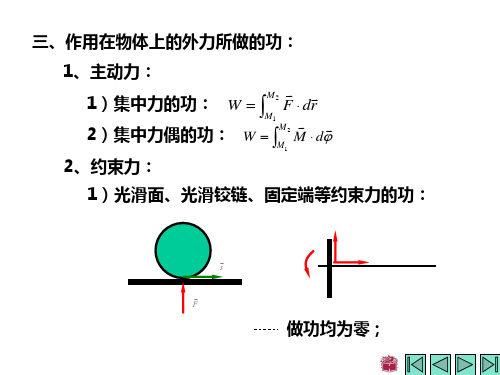
四、物体内任意两点间的内力所做的功: 1、变形体的内力所作的功不为零(因为变形体内的任
意两点间的距离会发生改变); 2、刚体的内力所作的功等于零(因为任意两点间的距
离不会发生改变);
§12-2 质点和质点系的动能
一、质点的动能:
T 1 mv2 2
二、再使用动量定理(质心运动定理)和动量矩定理求解 动力学第一类问题(求解约束反力):
1、研究重物A: 1)受力分析:如图; 2)运动分析:平动; 3)建立动力学关系 ---质心运动定理:
mAa mAg FT
FT 733 N
2、研究塔轮: 1)受力分析:如图; 2)运动分析:平面运动; 3)建立动力学关系 ---平面运动微分方程: (质心运动定理+动量矩定理)
其中:
vC R
aC R
vA (R r) aA (R r)
∴
mAgs
1 2
m(C2
R2) mA(R r)2
2
(a)
求C点的加速度:
将式(a)两端对t 求导,得:
mAgvA m(C2 R2 ) mA (R r)2
2.115 rad/s2 aA 0.635 m/s 2 aC 1.269 m/s 2
m2
R22
)22
W12 M m2gs sin
且
1
vC R1
,;2
vC R2
;
s
R1
∴
MMs
R1
m2gs sin
vC 2 4
(2m1
3m2 )
(a)
vC 2
(M m2gR1 sin )s
R1(2m1 3m2 )
最新精选建筑力学在建筑工程中的应用

1力学在建筑工程中的具体应用1.1建筑工程中压力的应用力学中很多的基础知识可以为建筑工程提供科学的理论依据。
其中压力的有关知识就是建筑工程施工时,重要的理论基础之一。
在进行建筑工程施工时,对工程用料、建筑面积的设定的时,都要根据这些物体所能承受压力的范围来进行衡量。
建筑最终的稳定性与压力在工程中的合理应用是密不可分的。
例如如果要进行一座桥梁建筑的施工,必须先对桥墩以及桥梁的可承受压力情况进行严谨地分析,这样才能确保建成桥梁的承载力达标。
而且,在验收工程时,工作人员必须要对建筑中承压的相关数据进行检测,确保质量稳固无问题。
所以,压力不仅为建筑工程提供了施工的重要参考数据,也为验收工程提供了质检标准。
1.2建筑工程中摩擦力的应用在建筑工程中,被广泛应用到的还有摩擦力的相关知识。
例如,当需要对大重量的建筑材料进行运输或者起吊的时候,就可以通过滑轮或者滑轮组来对力的方向进行调整,这样可以将原有的摩擦力由阻力变为动力;还有在进行施工时,可以适当加大工程中各个部件连接的接触面积,这样可以增加接触面的承压能力,并且通过摩擦力与重力的共同作用,使建筑物更加稳固。
在建筑工程中,合理利用摩擦力不仅可以增强建筑的稳定性能,还可以降低技术成本的投资,从而提高建筑工程整体的施工水平[2]。
1.3建筑工程中重力的应用重力是建筑工程中最主要应用的力学原理。
施工技术人员可以通过各种与重力有关的运算公式,来分析不同材料、不同情况下的力的作用。
这样可以达到在进行施工之前就可以预判出实际施工的效果,并及时发现在施工中可能会出现的问题。
不仅如此,重力的相关知识还可以运用到建筑材料的采购方面,在选购材料时,就要将重力因素计算在内,这样可以进一步加大建筑物的稳定性。
总体来说,重力的合理应用可以提高工程的预见性,并且有效提高施工的质量与效率。
1.4建筑工程中理论力学的应用力学在建筑工程中得以发展,从而引申出理论力学。
理论力学主要分为静力学、动力学和运动学三大类。
理论力学实践教学(3篇)

第1篇一、引言理论力学是物理学、力学、机械工程、航空航天等领域的基础课程,它研究物体的运动规律和受力情况。
理论力学实践教学是理论力学教学的重要组成部分,通过实验、设计、计算等多种形式,使学生将理论知识应用于实际问题,提高学生的实践能力和创新意识。
本文将介绍理论力学实践教学的现状、方法与意义。
二、理论力学实践教学现状1. 实验教学现状实验是理论力学实践教学的重要环节,通过实验验证理论、发现规律、培养动手能力。
目前,我国高校理论力学实验教学内容主要包括以下几方面:(1)验证性实验:如单摆、摆线、刚体转动等,帮助学生理解和掌握理论力学的基本概念和原理。
(2)综合性实验:如平面机构运动分析、刚体动力学实验等,培养学生综合运用理论力学知识解决实际问题的能力。
(3)设计性实验:如简易机械设计、结构设计等,激发学生的创新意识,提高学生的设计能力。
2. 设计教学现状设计教学是理论力学实践教学的重要形式,通过设计培养学生运用理论知识解决实际问题的能力。
目前,我国高校理论力学设计教学主要包括以下几方面:(1)课程设计:如机构设计、结构设计等,让学生在教师指导下完成设计任务。
(2)毕业设计:学生在导师的指导下,运用理论力学知识解决实际问题,完成毕业设计。
三、理论力学实践教学方法1. 实验教学(1)理论教学与实验教学相结合:在理论教学过程中,适时安排实验课程,让学生在实验中验证理论。
(2)实验内容多样化:根据教学目标,设计不同难度的实验,满足不同层次学生的需求。
(3)实验教学方法创新:采用虚拟实验、远程实验等新型实验教学方法,提高实验效果。
2. 设计教学(1)设计项目与企业实际相结合:选择与企业实际需求相关的设计项目,提高学生的就业竞争力。
(2)设计过程注重创新:鼓励学生提出新思路、新方法,培养学生的创新意识。
(3)设计成果评价体系完善:建立科学合理的评价体系,激发学生的设计热情。
四、理论力学实践教学的意义1. 提高学生的实践能力理论力学实践教学使学生将理论知识应用于实际问题,提高学生的动手能力和解决问题的能力。
理论力学7.2、相对速度问题与运动学综合应用

2) A车相对B车的速度; vA = vB =60km/ h
确定两系/两点/三运动
1) 动点:B车; 动系:A车上固连的坐标系
牵连点(图示时刻,t时刻) :动系中与 动点(B车)重合的那个点(b点)
t时刻动点及其牵连点
在t+⊿t时刻的新位置(图b)
2
r 0.24km AB 0.18km
30 AC BC
动点: CD杆C端点;
动系: AB杆;
图示v时a 刻 动ve点的v牵r 连点ve:ABv杆c 上的Pcc点;
14
15
北
R
vB vA
B
BБайду номын сангаас
30
B1
vB
B(b)
30 y x
r
A
O
东
A
vA
rO
A O A1
va
vr
B
vB
b1 30 B 30 ve 30 A ve 30
A vA
vr va
O
O
B rO
v
A
A O
B C
A
P B
O
C
va ve
vr 30 B
O A
C
P B
OD
C
Av
B
vr O ve
D
C
B
O 60 30
A
D
C
F
B
vA
A E
30
D
B O
vr C va
vB ve 30
A vA
D
C
vc
理论力学三大类问题的基本求解方法

理论⼒学三⼤类问题的基本求解⽅法理论⼒学三⼤类问题的基本求解⽅法2009-121 求解静⼒平衡问题的基本⽅法(平⾯问题为重点)(1)选取研究对象,进⾏受⼒分析,并画受⼒图。
⼀般针对所求,先对整体进⾏初步的受⼒分析,若所求未知量⼩于或等于独⽴平衡⽅程的个数,则只研究整体即可;反之,若所求未知量个数⼤于独⽴平衡⽅程的个数,则必须取分离体进⾏受⼒分析。
可以采取整体+分离体的解决⽅案,也可采取分离体+分离体的解决⽅案;另外,若所求的未知量有系统内⼒,也必须取分离体研究,以暴露出所要求的内⼒;画受⼒图注意将各⼒画在原始的作⽤点处,分布⼒原样画出,待列⽅程计算时,再作简化处理。
再有,注意⼆⼒杆的判别,及摩擦⼒⽅向的判定。
(2)列平衡⽅程求解。
⾸先根据受⼒图,判断是何种⼒系的平衡问题。
再针对所求⽤尽可能少的平衡⽅程得出所求。
(3)结果校核——利⽤多余的平衡⽅程校核所得的结果。
对⽤符号表⽰的结果,可采⽤量纲分析的⽅法进⾏校核。
2 求解运动学问题的基本⽅法(以平⾯运动为重点)⾸先正确判断问题类型,尤其注意正确区分点的合成运动问题与刚体平⾯运动问题。
判断的依据是,点的合成运动的问题中,运动机构的不同构件之间有相对滑动。
⽽刚体平⾯运动理论⽤来分析同⼀平⾯运动刚体上两个不同点间的速度和加速度的关系。
此时,运动机构的不同构件之间有相对转动,却⽆相对滑动。
另外,注意点的合成运动与刚体平⾯运动的综合问题。
2.1 点的运动学问题——注意在⼀般位置建⽴点的运动⽅程;2.2 点的合成运动问题(1)⾸先是机构中各构件的运动分析;(2)再针对所求,正确选择动点、动系和定系。
注意动点相对于动系和定系都要有相对运动,即动点、动系、定系要分属于不同的构件。
同时,尽可能使动点的相对轨迹清楚易判断;求解加速度时,尽量将动系固连在平动的物体上,避免求科⽒加速度;(3)分析三种运动及其相应的三种速度和加速度,正确画出速度⽮量图或加速度⽮量图。
注意速度合成的平⾏四边形关系;(4)利⽤速度或加速度合成定理进⾏求解。
理论力学-分析力学及应用

流体动力学的应用实例
管道流动
通过分析流体在管道中的流动特性,可以优化管道设计,提高流 体输送效率。
流体机械
利用流体动力学原理设计各种流体机械,如泵、压缩机和涡轮机等。
航空航天领域
流体动力学在航空航天领域中有着广泛的应用,如飞机和火箭的设 计与优化。
07
非线性力学基础
非线性振动的分类与特点
分类
分为强非线性振动和弱非线性振动。
特点
具有复杂的动态行为,如混沌、分岔和自激振动等。
实例
弹簧振荡器在强烈非线性下的复杂振动模式。
非线性振动的求解方法
解析法
适用于简单非线性模型,如谐波平衡法、多尺度法和平均 法。
数值法
适用于复杂非线性模型,如有限元法、有限差分法和谱方 法。
描述物体的变形情况。
描述物体在力系作用下的 平衡状态。
平衡方程
几何方程
物理方程
弹性力学问题的求解方法
解析法
通过数学解析方法求解 弹性力学问题,得到精 确解。
有限元法
将物体离散化为有限个 小的单元,通过求解这 些单元的力学行为来近 似求解整个物体的力学 行为。
边界元法
将物体边界离散化为有 限个小的单元,通过求 解这些单元的边界力学 行为来近似求解整个物 体的力学行为。
(N)。力的方向可以通过箭头表示,箭头的长度代表力的大小。力的作用点对确定物体运动状态的改变十分重要,尤其是在分析扭矩或力矩时。等效力矩是保持力系对某点或某轴的 矩不变的与原力系等效的力系,其作用线到某固定点的距离的平方值与对应的原力系的作用线到某固定点的距离的平方值相等。
03
角动量定理与刚体动力学
理论力学综合复习(哈工大第七版)
R
∴需进行速度分析
B
vr va
A
C
ve
得:
va ve vr
? ?
vr vesinvsin
即:
arn
vr2 R
v2
Rsin2
B
ae A
R arn
ar
再由加速度分析:
aa aeararn
? ? ?
C
: x
aa
投影式: x aasin aeco sar n
得: aaaAB 选择投影轴的技巧: 投影式不要写成 ax 0
限 ∑MO= 0
制 条
x 轴不平行y 轴
件
∑Fx = 0 ∑MA = 0
∑MB = 0
AB 联线不与 x 轴垂直
∑M A = 0
∑M B = 0
∑M C = 0
A、B、C 三点 不共线
F
类型一
P 基本部分
C
结构
附属部分
FAy
FBy
一般分析方法: 先分析附F属Ax部分,再A分析基本部分或F整Bx体B .
理论力学
研究物体机械运动 一般规律的科学
静力学 运动学 动力学
研究物体在力系作 用下的平衡条件
研究物体运动的几何 性质的科学
静力学
平面任意力系作用下物体的平衡问题
● 约束和约束力 ● 平衡条件及方程
1、光滑接触表面约束
约束和约束力
2、柔索约束 3、光滑铰链约束
4、其他约束
静力学—约束和约束力
1、光滑接触表面约束
O2
a
t B
O2B
(2) E 动点: EF上的E 动系: O2E (牵:转动)
B
ae A
理论力学答案完整版(清华大学出版社)10

子 C 沿水平轨道滚动而不滑动,试求重物 A 的加速度。
解: 取整个系统为研究对象,自由度为 1。设重物速度为 vA ,则轮
题 10-9 图
的角速度 ω = vA ,轮心速度为 R−r
vO
=
R
r −
r
vA 。系统的动能为
( ) T
拉格朗日方程的普遍形式
d dt
∂L ∂q& j
− ∂L ∂q j
= Q′j
( j = 1,2,..., m)
式中 Q′j 为非有势力对应的广义力。
矢量方法
动量法:动量定理
动量矩定理 质心运动定理 定轴转动微分方程 平面运动微分方程
质点系统动力学
动静法
动能定理
能量方法
拉格朗日方程
3 保守系统拉格朗日方程的初积分
10-3 质量为 m1 的匀质杆,长为 l,一端放在水平面上, 另一端与质量为 m2、半径为 r 的匀质圆盘在圆盘中心 O 点 铰接。圆盘在地面上作纯滚动,圆心速度为 v。求系统在此
题 10-3 图
位置的动能。
解:杆作平移,动能为
T1
=
1 2
m1v2
;
圆盘作纯滚动,动能为
T2
=
1 2
m2v2
+
1 2
mivi
⋅ vi
,
其中 n 为系统中的质点数目,可以是有限或无穷,mi 和 vi 分别为各质点的质量和速度。 平
移刚体的动能 T = 1 mv2 , 2
其中 m 为平移刚体的质量。
定轴转动刚体的动能
T
=
1 2
《理论力学 (1)》课程教学大纲

《理论力学》课程教学大纲课程代码:ABJD0220课程中文名称:理论力学课程英文名称:TheOretiCa1Mechanics课程性质:必修课程学分数:3.5课程学时数:56授课对象:机械设计制造及自动化专业本课程的前导课程:大学物理一、课程简介理论力学是一门理论性较强的技术基础课。
是各门力学的基础,并在许多工程技术领域中有着广泛的应用。
本课程的任务是使学生掌握质点,质点系和刚体机械运动(包括平衡)的基本规律和研究方法,为学习有关的后继课程打好必要的基础,并为将来学习和掌握新的科学技术创造条件;使学生初步学会应用理论力学的理论和方法。
分析解决一些简单的工程实际问题;结合本课程的特点,培养学生的辩证唯物主义世界观及分析和解决问题的能力。
二、教学基本内容和要求课程教学内容:0.绪论(1)理论力学的研究对象:宏观物体的机械运动(2)理论力学的研究内容:静力学、运动学、动力学(3)理论力学在工程技术中的应用(-)静力学部分1.静力学基础(1)静力学公理:合力法则、二力平衡、加减平衡力系、作用与反作用、刚化原理(2)常见约束类型与约束力(3)物体的受力分析与力学模型2.平面力系(1)平面汇交力系:投影、合成与平衡(2)平面力偶系:力对点之矩及力系的合成、等效和平衡(3)平面任意力系:力线平移及力系的简化与平衡(4)物体系统的静定和静不定问题3.空间力系(1)空间汇交力系:投影、合力与平衡(2)空间力偶系:力对点之矩、力对轴之矩、力偶系的合成与平衡(3)空间任意力系:向任一点的简化、力系的平衡(4)平行力系与物体重心4.摩擦(1)滑动摩擦(静滑动摩擦、动滑动摩擦)定律(2)摩擦系数、摩擦角与自锁(3)考虑摩擦时的物体平衡问题(4)滚动摩擦定律(-)运动学部分5.点的运动学(1)矢量法表示点的运动方程、速度、加速度(2)直角坐标法表示点的运动方程、速度、加速度(3)自然法(弧坐标)表示点的运动方程、速度、(切向和法向)加速度6.刚体的基本运动(1)刚体的平行移动(2)刚体的定轴转动:运动方程、角速度、角加速度(3)刚体的定轴转动:刚体内任一点的速度和加速度(4)矢量表示角速度和角加速度,矢积表示点的速度和加速度(5)定轴轮系的传动比7.点的合成运动(1)运动的分解:绝对运动(速度和加速度)为相对运动(速度和加速度)与牵连运动(速度和加速度)的矢量和(2)点的速度合成定理:绝对速度为相对速度与牵连速度的矢量和(3)点的加速度合成:牵连运动为平行移动、定轴转动时的加速度合成定理8.刚体的平面运动(1)刚体的平面运动分解:随基点的平行移动与绕基点的定轴转动(2)平面图形内各点的速度求解:基点法、瞬心法(3)平面图形内各点的加速度求解:基点法(三)动力学部分9.质点动力学的基本方程(1)动力学的基本定律:惯性定律、力与加速度的关系定律、作用与反作用定律(2)质点的运动微分方程:矢量形式、直角坐标形式、自然坐标形式10.动量定理(1)动量和冲量(2)动量定理与动量守恒定律(3)质心运动定理与质心运动守恒定律11.动量矩定理(1)质点和质点系的动量矩(2)动量矩定理与动量矩守恒定律(3)转动惯量的计算与平行轴定理(4)刚体绕定轴的转动微分方程(5)质点系相对于质心的动量矩定理(6)刚体的平面运动微分方程12.动能定理(1)常见力作功:重力的功、弹性力的功、转动体上力的功、合力的功(2)动能:平移刚体、定轴转动刚体、平面运动刚体的动能(3)动能定理(4)功率方程与机械效率(5)常见势能(重力场、弹性力场、万有引力场中的势能)与机械能守恒定律课程的重点、难点:(-)静力学部分1.静力学基础重点:静力学公理难点:研究对象(分离体)和受力图2.平面力系重点:平面任意力系,力系的简化难点:物体系统的平衡问题3.空间力系重点:力对点之矩和力对通过该点的轴之矩之间的关系难点:力对点之矩和力对通过该点的轴之矩之间的关系,空间力系平衡方程的应用4.摩擦重点:考虑摩擦时物体和物体系的平衡问题,平衡的临界状态和平衡范围的分析难点:自锁现象,平衡的临界状态和平衡范围的分析(-)运动学部分5.点的运动学重点:速度和加速度的矢量形式难点:自然轴系,点的速度和加速度在自然轴系上的投影6.刚体的基本运动重点:速度和加速度的矢量形式难点:自然轴系,点的速度和加速度在自然轴系上的投影7.点的合成运动重点:运动的分解,点的速度合成定理和加速度合成定理难点:牵连速度和加速度概念的建立以及动坐标系的选择8.刚体的平面运动重点:平面图形内各点的速度分析和加速度分析难点:加速度分析(≡)动力学部分9.质点动力学的基本定律重点:运动微分方程的建立难点:运动微分方程的建立,初始条件的分析和积分法10.动量定理重点:质点系的动量定理,质心运动定理难点:质心运动定理,质心运动守恒11.动量矩定理重点:质点系的动量矩定理,刚体定轴转动微分方程,平面运动的微分方程难点:平面运动的微分方程12.动能定理重点:质点系的动能定理。
理论力学课件 25.1 普遍定理的综合应用举例

普遍定理综合应用举例动量定理普遍定理动量矩定理动能定理质心运动定理 分析质点系受力与质心运动的关系定轴转动刚体 的转动微分方程 相对于定 点和定轴相对于质心和质心轴描述质点系整体运动 如:平面运动刚体的运动微分方程积分形式求速度 或角速度 微分形式功率方程求加速度 或角加速度动量和动量矩动能矢量,有大小方向非负的标量,与方向无关内力不能使之改变外力能使之改变内力可以改变动能约束力是外力时对之有影响理想约束不影响当外力主矢为零时,系统动量守恒当外力对定点O 或质心的主矩为零时,系统对定点或者质心的动量矩守恒在保守系统中,机械能守恒动量定理描述质心的运动变化动量矩定理描述绕质心或绕定点的运动变化动能定理描述质心运动及相对质心运动中动能的变化研究机械运动与其他运动形式有能量转化的问题普遍定理综合应用举例均质圆轮半径为 r ,质量为m ,受到轻微扰动后,在半径为R 的 圆弧上往复滚动。
设表面足够粗糙,使圆轮在滚动时无滑动. 求:轮心C的运动微分方程.例1例题:利用平面运动刚体 运动微分方程求解功率方程求解普遍定理综合应用举例d d s P mg v mg t τ⎛⎫=⋅=⋅ ⎪⎝⎭d d s m g t τ=⋅d sin d smg tθ=-222113224C C CT mv J mv ω=+=解: ()d sin d sm g tθ=-d d T P t=d 3d 2sin 4d d C C v s m v mg t t θ⋅=-()032d d 22=-+r R gst s 22d d ts C v θrR s θ-=分析圆轮,受力如图所示。
ωr v C =2Cmr J 21=普遍定理综合应用举例例2物块和两均质轮的质量皆为m ,轮半径皆为R。
滚轮上缘绕一刚度系数为k的无重水平弹簧,轮与地面间无滑动。
现于弹簧的原长处自由释放物块。
求:重物下降h 时,v,a 及滚轮与地面的摩擦力。
可用动能定理求摩擦力可用相对质心的动量矩定理普遍定理综合应用举例1=T 解: 22222222111113222222T mv mR m mR mv ωυω⎛⎫=+⋅++= ⎪⎝⎭()222221khmgh h k mgh W -=-=∑12T T W -=∑(a )22322mgh kh mv -=()223mg kh h v m -=将式(a )对t 求导得 khg a 4-=动能定理,分析系统。
理论力学在工程中的应用研究

理论力学在工程中的应用研究在工程中,理论力学是一门十分重要的学科。
它可以帮助我们解决各种材料的物理性质,从而设计出更加稳定和耐用的结构体系。
本文将从概念、原理和应用三个方面介绍理论力学在工程中的应用研究。
概念理论力学,简单来说,就是研究物体力学行为和力学规律的学科。
它包括静力学、动力学、弹性力学、塑性力学、损伤力学等分支学科。
在工程中,我们主要运用这些分支学科中的弹性力学和塑性力学。
弹性力学研究的是物体在力的作用下所发生的形变和应力关系的问题,主要研究弹性变形的规律。
它的应用领域涉及复杂结构设计、模型分析、材料研究等。
弹性力学中著名的理论有胡克定律、泊松比定律、拉梅定律等。
塑性力学研究的是物体在力的作用下所发生的形变和应力关系的问题,主要研究可塑性物质的力学性质和外界作用下的变形。
塑性力学与弹性力学相比较而言,更多考虑应变过大时物质的塑性变形规律,因此它的运用范围更广,常用于车辆碰撞和材料成型等领域。
塑性力学中的著名理论有冯·米塞斯准则。
原理理论力学是建立在力学基本原理的基础上的。
在工程设计中,我们必须牢固掌握以下基本原理:第一定律:物体如果不受力的作用,或所受力的合力为零,它将保持运动状态或者静止状态。
第二定律:物体所受的力等于所受的作用力方向和大小相等,它的加速度也是与所受力成正比的。
第三定律:每个物体获得的力的数值,都等于与之相互作用的物体给出的力的数值。
换句话说,如果物体A对物体B施加了一个力,那么物体B也会对A施加一个相等的反向力。
应用在工程应用中,理论力学是不可或缺的一部分。
从建筑物的结构设计到交通运输的安全,都需要理论力学的支持。
在结构设计方面,比如桥梁、高层建筑等复杂的结构,需要通过弹性力学的分析方法进行设计和计算。
同时,信号处理技术的应用也可以对结构的实际情况进行监测,进一步确保设计的正确性。
在交通安全方面,塑性力学在道路交通和空域交通的安全设计中扮演着重要角色。
它可以帮助我们设计更加安全、耐用的车辆和航空器,同时通过模拟碰撞和脆裂等情况,还可以对出现问题的情况进行分析和预测。
理论力学(30-27) 7-3 质系普遍定理的综合应用

例6 第7章
解 第7章
一个自由度
例6
动能定理:
1 T = 1 mv 2 + 1 ( 12 ml 2 )ω12 + C 2 2 1 ( 2m + 9M )v 2 = A 12 sin2 θ 1 2
解
Mv 2 + 1 ( 1 MR 2 )ω 22 A 2 2
θ& = vA l sinθ
质 系 动 能 定 理
动量定理:
ü受力分析:受力图,主动力约束力,是否
做功?是否有势?有无投影? 有无力矩? ü选取普遍定理
dp = R ( e) dt
dt
动量矩定理: dLA = M (Ae) + mvC × v A 能量方法 — 标量方程 动量定理:
n n dT = d 1 ∑ m i v2 = ∑ δ Wi i 2 i =1 i =1
第4 章 质系动力学
x O
第4 章 质系动力学
vC
x
例5 第7章
例5 第7章
解 第7章
牵连运动,相对运动
例5
解
C垂直下降? 先求分量和, 再求速度方.
质 系 动 能 定 理
已知:质量为 m1 的匀质细杆AB铰接于质量为 m2 的可在光滑水平面上移动的平车上.初始 时系统静止,杆处于铅垂位置.求:杆与水 平面成θ角时,杆的角速度.
第4 章 质系动力学 第4 章 质系动力学 2002年12月12日
质系普遍定理的综合应用 第7章
质 系 动 能 定 理
普遍定理提供了解决质系动力学问题的一般 方法. 动量方法 — 矢量方程
第7章
质系普遍定理的综合应用 ü运动分析:自由度,广义坐标,运动形式,
运动特点(瞬心,质心轨迹)
理论力学在水利工程中的应用

理论力学在水利工程中的应用水利工程是利用水资源进行调控、利用和保护的一门综合性工程学科。
理论力学是研究物体在力的作用下的平衡和运动规律的学科。
本文将探讨理论力学在水利工程中的应用,并分析其在水利工程设计和施工中的重要性。
一、应力分析在水利工程中,应力分析是非常重要的。
通过应力分析,可以研究水利工程结构在水压、土壤力等作用下的应力分布情况,进而确定结构设计参数。
例如,在水坝的设计中,通过对水压力的分析,可以确定坝体的合理尺寸和混凝土强度,以保证坝体的稳定性和安全性。
此外,在堤防、河道等水利工程结构的设计和施工中,应力分析也是必不可少的。
二、变形和位移分析变形和位移是水利工程中一个重要的问题。
通过理论力学的变形和位移分析,可以预测水利工程结构在水荷载、温度变化等因素作用下的变形和位移情况,从而保证工程结构的稳定性和可靠性。
例如,在水库调水期间,库水位的变化将导致周围土壤和结构的变形,通过变形和位移分析,可以确保水利工程结构不会产生过大的变形和位移。
三、动力响应分析理论力学的动力响应分析在水利工程中也有着重要的应用。
在水利工程中,地震和水流的波动等因素会对工程结构造成冲击和振动。
通过动力响应分析,可以预测水利工程结构在地震、洪水等灾害性因素作用下的响应情况,从而进行相应的抗震和防洪设计,确保工程结构的安全性和稳定性。
四、破坏分析理论力学在水利工程中还可以进行破坏分析。
通过破坏分析,可以预测水利工程结构在外部作用下的破坏形态和破坏模式,从而为工程设计和维修提供指导。
例如,在水坝工程中,可以通过理论力学的破坏分析,确定水坝的破坏模式,判断是否存在结构破坏的风险,并采取相应的措施加固。
总结起来,理论力学在水利工程中的应用非常广泛,涉及到应力分析、变形和位移分析、动力响应分析、破坏分析等多个方面。
通过理论力学的研究和分析,可以帮助水利工程设计人员合理规划和设计工程结构,保证工程的稳定性、安全性和可靠性。
因此,理论力学对于水利工程的发展和进步具有重要的意义。
理论力学中的弯曲理论如何应用?

理论力学中的弯曲理论如何应用?在工程和科学领域中,理论力学的弯曲理论是一个至关重要的概念。
它不仅有助于我们理解物体在受到外力作用时的弯曲行为,还为实际应用中的设计和分析提供了坚实的理论基础。
弯曲理论主要研究的是细长杆件或结构在受到横向载荷作用时的变形和内力分布。
当我们考虑一个简单的梁,比如在建筑结构中的钢梁或者机械装置中的传动轴,弯曲理论就能够帮助我们预测它们在承受负载时的弯曲程度以及内部产生的应力。
在建筑结构设计中,弯曲理论的应用极为广泛。
例如,在设计桥梁时,工程师需要考虑车辆和行人的重量对桥梁梁体产生的弯曲效应。
通过弯曲理论的计算,可以确定桥梁梁体所需要的尺寸、材料强度以及支撑结构的布置,以确保桥梁在使用过程中能够安全地承受各种载荷而不发生过度的弯曲变形甚至破坏。
机械工程领域同样离不开弯曲理论。
像汽车的传动轴,在传递动力的过程中会受到扭转和弯曲的复合作用。
利用弯曲理论,工程师能够精确计算出轴在不同工作条件下的弯曲应力和变形,从而选择合适的材料和轴的直径,保证传动轴的可靠性和使用寿命。
在航空航天领域,飞机的机翼结构设计也是弯曲理论的重要应用场景之一。
机翼在飞行过程中承受着空气动力产生的升力和阻力,这些力会导致机翼发生弯曲变形。
通过弯曲理论的分析,可以优化机翼的结构,减轻重量的同时保证其强度和刚度满足飞行要求。
在材料科学中,弯曲理论对于研究材料的力学性能也具有重要意义。
通过对材料制成的试件进行弯曲实验,并结合弯曲理论的公式,可以得到材料的弹性模量、屈服强度等关键力学参数。
这些参数对于评估材料的质量和选择合适的材料用于特定的应用至关重要。
对于一些复杂的结构,如框架结构或者空间桁架结构,弯曲理论同样可以发挥作用。
虽然这些结构的受力情况较为复杂,但通过将其分解为单个杆件的弯曲问题,并综合考虑节点的连接方式和约束条件,仍然可以利用弯曲理论进行有效的分析和设计。
在实际应用中,弯曲理论的计算通常基于一些基本假设。
科学方法论在理论力学教学中的综合应用

理 关 系变成 数学 符号 关 系 , 即得数学 模 型 ; 再对 数 学 模 型寻 找解 题方 法 , 出数 学 问题 的解 ; 求 最后 验证数 学 模 型是否 符合 原型 。 讲 授动 力学 中单 自由度系 统 的 自由振动 就可采 用 抽象 方法 和数 学方 法 的综 合 。 讲 这 一 节 内 容 之 在 前, 先给 学生 们介 绍这 两种 方法 以及 它们 的综合 , 然 后 针对这 节 的 内容 举 例说 明如何 综合 应用 这两 种方 法。 例如 简支 梁上放 一 台 电动机 , 当电动机 沿铅 垂方 向振 动 时 , 和 电动机 组成一 个 振动 系统 , 梁 若梁 的质
综 合应 用一 些科 学方 法 来 解 决 问题 知道 的太 少 , 例 如 学生 们会 根据 书本 上 给 的公 式来 做 题 , 不 知 道 但 什 么是 物理模 型 和什 么 是 数 学模 型 , 以及 它们 如 何
来 建立 ?会 画物体 的受 力 图 , 却 不 知道 什 么 是 分 但
21 0 0年 5月
合肥师范学院学报
J u a fH ee No m a iest o m lo fi r l Unv ri y
Ma.2 0 v 01
第2 8卷 第 3期
Vo _ 8 No 3 I2 .
科学 方法论 在 理 论 力 学教 学 中 的综 合 应 用
张 速
来, 宣传 科学 方法 、 展科学 方法 的教 育 没有受 到应 开 有 的重视 。各 门学 科 的教 学 , 只讲 知 识 , 不讲 方 法 ,
以至 于学生 们在 学完 一 门课 程 后 , 掌 握 了 书本 上 只 的知识 , 于一些 科 学 方 法或 者 在 课 程 内容 中如 何 对
如何应用理论力学解决实际工程问题?

如何应用理论力学解决实际工程问题?在实际工程领域中,理论力学作为一门基础学科,发挥着至关重要的作用。
它为解决各种工程问题提供了坚实的理论基础和有效的分析方法。
那么,究竟如何将理论力学的知识应用到实际工程中呢?首先,我们需要明确理论力学的核心概念和原理。
理论力学主要包括静力学、运动学和动力学三个部分。
静力学研究物体在力系作用下的平衡问题,包括力的合成与分解、力系的简化等;运动学则关注物体的运动规律,不考虑力的作用,如位移、速度、加速度等的描述;动力学则是研究物体的运动与所受力之间的关系。
在实际工程中,静力学的应用十分广泛。
例如,在建筑结构设计中,需要计算建筑物所承受的各种载荷,如自重、风载、雪载等,并确定结构内部各构件所受的力,以保证结构的稳定性和安全性。
通过静力学的分析,可以合理地设计结构的形状、尺寸和材料,确保其能够承受预期的载荷而不发生破坏。
以桥梁设计为例,工程师需要考虑桥梁在车辆通行、风荷载等作用下的受力情况。
通过对桥梁结构进行静力学分析,可以确定桥梁的主要受力构件,如桥墩、桥面板等所承受的力,从而选择合适的材料和截面形状,以保证桥梁的强度和刚度。
在这个过程中,需要运用力的平衡方程、力偶矩平衡方程等静力学原理,对各种载荷进行合理的简化和计算。
运动学在工程中的应用也不容忽视。
在机械设计中,了解零部件的运动轨迹、速度和加速度对于优化机械性能至关重要。
例如,在汽车发动机的设计中,活塞的运动规律直接影响着发动机的性能。
通过运动学的分析,可以准确地确定活塞的位移、速度和加速度随时间的变化关系,从而优化发动机的燃烧过程,提高发动机的功率和效率。
动力学在实际工程中的应用则更加复杂和关键。
比如,在航天器的设计中,需要考虑航天器在太空环境中的运动和受力情况。
由于太空环境中存在微重力、稀薄气体阻力等复杂因素,因此需要运用动力学原理进行精确的建模和分析,以确保航天器能够按照预定的轨道和姿态运行。
在解决实际工程问题时,建立合理的力学模型是关键的一步。
理论力学重难点及相应题解

理论力学重难点及相应题解(总11页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除运动学部分:一、点的运动学重点难点分析1.重点:点的运动的基本概念(速度与加速度,切向加速度和法向加速度的物理意义等);选择坐标系,建立运动方程,求速度、加速度。
求点的运动轨迹。
2.难点:运动方程的建立。
解题指导:1.第一类问题(求导):建立运动方程然后求导。
若已知点的运动轨迹,且方程易于写出时,一般用自然法,否则用直角坐标法。
根据点的运动性质选取相应的坐标系,对于自然法要确定坐标原点和正向。
不管用哪种方法,注意将点置于一般位置,而不能置于特殊位置。
根据运动条件和几何关系把点的坐标表示为与时间有关的几何参数的函数,即可得点的运动方程。
2.第二类问题(积分):由加速度和初始条件求运动方程,即积分并确定积分常数。
二、刚体的简单运动重点难点分析:1.重点:刚体平移、定轴转动基本概念;刚体运动方程,刚体上任一点的速度和加速度。
2.难点:曲线平移。
解题指导:首先正确判断刚体运动的性质。
其后的分析与点的运动分析一样分两类问题进行。
建立刚体运动方程时,应将刚体置于一般位置。
三、点的合成运动(重要)重点难点分析:1.重点:动点和动系的选择;三种运动的分析。
速度合成与加速度合成定理的运用。
2.难点:动点和动系的选择。
解题指导:1.动点的选择、动系的确定和三种运动的分析常常是同时进行的,不可能按顺序完全分开。
2.常见的运动学问题中动点和动系的选择大致可分以下五类:(1)两个(或多个)不坟大小的物体独立运动,(如飞机、海上的船舶等)对该类问题,可根据情况任选一个物体为动点,而将动系建立在另一个物体上。
由于不考虑物体的大小,因此动系(刚体)与物体(点)只在一个点上连接,可视为铰接,建立的是平移动坐标系。
(2)一个小物体(点)相对一个大物体(刚体)运动,此时选小物体为动点,动系建立在大物体上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
选择题 4. 两个均质圆盘质量相同,A盘半径为R, B盘半径为r,且R>r。两盘由同一时刻, 以同一高度无初速地沿完全相同的斜面在 重力作用下向下作纯滚动,则() A. B盘先到达底部 B. A盘先到达底部 C. 两盘同时到达底部
微分方程方法 刚体平动
质心运动定理
ma c F (e) max Fx
(e)
刚体定轴转动
J Z M z ( F )macx Βιβλιοθήκη Fxma cy F y
J C M C ( F )
明确构件的运动形式,擅长取单个构件
刚体平面运动
动能定理方法
质点系动能定理
机械能守恒
T2 T1 W
T1 V1 T2 V2
v a
盯准两个特殊时刻
2 时刻放在一般位置 求导、取极限
两种方程对比
微分方程 系统上运动学分析
单刚体上受力分析 单刚体上列写微分方程 分析加速度
动能定理
系统上运动学分析
对系统受力分析 对系统列写动能定理
分析速度
综合应用
动能定理方程
12-6 动力学普遍定理及综合应用
7组 高程程 兰廷光
宗可统 王首政
学 习 目 标
1
进一步梳理理解
微分方程法 动能定理方法
各自的优缺点
发现各自擅于求解的问题
2
能够综合利用两种方法分析复杂问题
两种方法合理搭配
将运算量降到最低
取长补短
动力学的两大支柱
运动学分析
计算动能 动量矩 动量
受力分析
计算力的功 力矩 合力
动能定理方程 微分方程
得到运动量 得到不做功的力
微分方程
习 题
判断题 1. 作用在刚体上的外力在X坐标轴 上投影的代数和为零,质心在X坐 标轴上的位置不变。() 2. 定轴转动的刚体对转轴的转动惯 量与其角加速度的乘积,等于作用 在刚体上的所有外力对转轴力矩的 代数和。()
选择题 3. 一实心圆柱体,沿一斜面无滑动地滚下,下 列说法正确的是() A. 机械能守恒,动量矩不守恒 B. 质心动量守恒 C. 机械能不守恒,动量矩守恒 D. 没有守恒量
