第四章 平面镜棱镜系统
合集下载
平面镜与平面系统
3）复合棱镜 在光学系统中常用两块或两块以上的棱镜组合成棱镜系统来达到一块棱镜难于达到的功能
3、反射棱镜成像方向的判断
1）单一主截面（考虑屋脊面）
规定：物为左手坐标系，oz轴为光轴方向，yoz面和主截面重合，ox轴垂直于主截面，并和所有的反射面平行，通过棱镜组后的坐标为x′y′z′ 。
a) o′z′与光轴出射方向一致。
4. 改变光路方向
5. 倍角关系：
以一定方向的光线入射到平面镜，平面镜摆动α角 ，则反射光线将有2α的摆角。
2α
α
两平面相继成象一次 象与物的夹角为2α： 夹角为α的双平面镜对物体所成的二次反射象：可由物体绕轴转动 2α 角得到，转动方向按反射次序由第一反射镜至第二反射镜。
两面相继反射一次后出射光线与入射光线间的关系 光线经双镜反射后，出射光线与入射光线的夹角是双镜夹角的两倍； 绕棱转动双镜时，出射光线方向不变。
习题2：一焦距f′=35mm的透镜，当物位于l=-70mm处，通过透镜成像。
一个平行平板，当其位于成像光束的不同位置时，其对成像的影响是很大的。
说明：
四、反射棱镜
1、基本概念：
光轴：光学系统光轴在棱镜中的部分。光轴在棱镜内的总几何长度为反射棱镜的光轴长度。
工作面
反射面
折射面
出射面
入射面
棱：两工作面的交线为棱镜的棱。
2. 成正立、等大、虚实相反的像 垂轴放大率为＋1，实物呈虚象，虚物呈实象。
物点发出的同心光束经反射镜反射后仍成同心光束。
3. 成镜像
这种对称性称为“镜象”
尺度相同；
位置对称于平面镜；
象和物上下同方向，而左右方向颠倒 ；
说明：奇次反射均成镜象；偶次反射时，物和象是完全一致的，称为“一致象”。
2019-L12-C4-4棱镜成像判断-文档资料
应用光学 Applied Optics
光信息0701-02 2009-2019第一学期
Applied optics
第四章 平面镜棱镜系统
2
Applied optics
C4. 平面镜棱镜系统 – 棱镜成像方向判断
3
Applied optics
上节内容回顾
一、屋脊棱镜 y
y x
x
z y′ z′ x′
z y′ z′
x′
4
Applied optics
上节内容回顾
二、等效空气层厚度 棱镜尺寸计算
A
A’
O
e
O’’
O’ S
S’
s s ' ( 1 1 /nL )
e L/ n
【O、L、n】相当于 【O、L/n、1】
5
Applied optics
4-6 棱镜成像方向判断
一、棱镜系统成像方向判断
二、组合系统成像方向判断
37
Applied optics
系统成像=
棱镜系统成像（镜像/一致像） + 球面系统成像（正像/倒像）
38
注意转折方向，平行并不一定同向
12
Applied optics
y & y’：主截面内方向（I） • 与是否有屋脊面无关， • 按光轴转向和光轴反射次数判断
光轴同向：Fig. 4-25(a), 4-26(a) 光轴反向：Fig. 4-25(b), 4-26(b) …… 缺点：需要判断光轴的转向性质，涉及光轴 在每个反射面的情况。繁！
物空间右手系---棱镜系统---像空间？
两种方法 • 反弹转折法 • 法则
8
Applied optics
反弹法
光信息0701-02 2009-2019第一学期
Applied optics
第四章 平面镜棱镜系统
2
Applied optics
C4. 平面镜棱镜系统 – 棱镜成像方向判断
3
Applied optics
上节内容回顾
一、屋脊棱镜 y
y x
x
z y′ z′ x′
z y′ z′
x′
4
Applied optics
上节内容回顾
二、等效空气层厚度 棱镜尺寸计算
A
A’
O
e
O’’
O’ S
S’
s s ' ( 1 1 /nL )
e L/ n
【O、L、n】相当于 【O、L/n、1】
5
Applied optics
4-6 棱镜成像方向判断
一、棱镜系统成像方向判断
二、组合系统成像方向判断
37
Applied optics
系统成像=
棱镜系统成像（镜像/一致像） + 球面系统成像（正像/倒像）
38
注意转折方向，平行并不一定同向
12
Applied optics
y & y’：主截面内方向（I） • 与是否有屋脊面无关， • 按光轴转向和光轴反射次数判断
光轴同向：Fig. 4-25(a), 4-26(a) 光轴反向：Fig. 4-25(b), 4-26(b) …… 缺点：需要判断光轴的转向性质，涉及光轴 在每个反射面的情况。繁！
物空间右手系---棱镜系统---像空间？
两种方法 • 反弹转折法 • 法则
8
Applied optics
反弹法
第四章 平面镜棱镜系统
二 、 双 平 面 镜 的 成 像 特 性
A 2'
P A
O2
q
P
O1
P1
∠APA2”= 2θ
A 1'(A2)
凡一次镜面反射或奇次镜面
反射像被称为镜像；
凡二次镜面反射或偶次
镜面
反射像被称为一致像
§4-3 平面镜的旋转及其应用
平面镜的旋转与平移效应
∠A’OA”=2∠POP’
平面镜的旋转与平移效应
五角棱镜
§4-4 棱镜和棱镜的展开 主要讲述把多个反射面集成在同 一块光学材料上的情况
反射棱镜：把多个反射面作在同一块光学 材料（如玻璃）上的光学零件。
一、基本定义
ABC---棱镜光轴
光轴：光学系
统的光轴在棱镜 中的部分
光轴长度：
C
棱镜光轴的几 何长度； AB+BC= 棱镜光轴长度
A
B
一、基本定义
3、当角锥棱镜绕 其顶点旋转时， 出射方向不变仅 产生一个平移。
必须指出：
反射棱镜主要利用全反射原理
反射光线 并不是所有反射棱镜的反射面 都满足全反射条件 凡遇到这种反射面，都必须镀 上反射膜
再来看看复合棱镜
由两个以上的棱镜组合起来 形成，可以实现一些特殊或者单 个棱镜难以实现的功能。
光轴 工作面 主截面 光轴截面
一、基本定义
光轴 光轴截面
入射光轴截面
出射光轴截面
二、棱镜的等效作用与展开 ㈠、等效作用与展开方法
1.等效作用 反射棱镜有两个折射 面和若干反射面，若不考虑反射面， 光线在两个折射面之间的行为等效于 一个平行平板
F
F′
平行光经透镜成像时加一平面镜 平行光经透镜成像于焦点F’上
第4章：平面反射镜与反射棱镜
14
2．平行平板的成像
u1 β= =1 ′ u2
(4-6)
a1
u1
a '2
' u2
Fo' Fo''
d
Δ
图4-9 平板玻璃的成像
15
平行平板的成像
a1
A C
' a1
u1'
B
h1
h2
D
u1
Fo'
d
Fo''
Δ
图4-10 平板玻璃的延伸量
16
平行平板的成像
′ AC = h1 − h2 = du1
(4-7)
即
⎡i '' ⎤ ⎡ 1 ⎢ '' ⎥ ⎢ ' ⎢ j ⎥ = ⎢− Δθ cos γ ⎢k '' ⎥ ⎢ Δθ cos β ' ⎣ ⎦ ⎣ Δθ cos γ ' 1 − Δθ cos α ' − Δθ cos β ' ⎤ ⎥ Δθ cos α ' ⎥ ⎥ 1 ⎦ ⎡i ' ⎤ ⎢ '⎥ ⎢j ⎥ ⎢k ' ⎥ ⎣ ⎦
在光学仪器的装校过程中，往往利用反 射棱镜的微量转动调整光学系统的光轴 方向和成像方向的倾斜
33
1．棱镜转动定理
y
P
x
z
x' z'
34
y'
P'
P 与它经棱镜所成的像P ' 图4-18 转轴
棱镜转动定理
棱镜绕转轴 P 转动 θ θ 角的正负按右螺旋法则确定）角后， （ 像空间坐标系 x ′y ′z ′ 的转动情况可以表述如下：
平面镜系统
满足以上求解结果，如果不是近轴光线，存在球差。
结论： 近轴光线通过玻璃板成像时，平行玻璃板不改变像的大
小，只使像面发生位移，移动量为L-L/n，即：
1、实物成虚像，平行平板 不使物体放大或缩小。
2、出射光方向不变， 有一个位移l`
二、平行平板等效光学系统
当近轴细光束成像时，成完善像。 n1=1
D
求证：A点成像于A’
A
N
B
II
P
D
O O’
A’
证：任取由A点射到P的光线AO，
AOD 90 I，DOA 90 I
B’ OD OD
AOD AOD
AD AD
由于AO是任取的，不管O点在 哪个位置，因为AD不变，A’D 也不变。所以A’的位置是确定 的，即由A点发出的任意光线 经P反射后延长线都交于一点 A’，像点是唯一的。完善像
e L l` L n
A
ED
H
Q
G
A`1
A1
l`
B
F
C
e
L
平行平板的成像特性
厚度L/n的两平面所夹的空气层称为厚度为L，折射率为n的 平行玻璃板的等效空气层。
平行玻璃板与等效空气平板相当的地方：
像面相对于平行玻璃板第二表面的位置和物平面相对 空气层的第二表面的位置相当； 光束的投射高相当； 像的大小相当。
平面镜绕垂直入射面轴的转动
当保持入射光线的方向不变，而使平面镜转动一个α角， 则反射光线将转动2α角
单平面镜旋转的应用：
优点：扩大观察范围 缺点：由于转动引起误差
应用： 1、潜望镜； 2、小角度和微小位移测量。
三、双平面镜成像特性
N
I ``1 I2
印刷应用光学4
B Q
Q
单个平面镜成像性质： (1)平面镜能使整个空间理想成像，物点和像点对平面镜
对称； (2)物和像大小相等，但形状不同，物空间的右手坐标在
像空间变为左手坐标；如果分别对着入射和出射光线
的方向观察物平面和像平面，当物平面按逆时针方向 旋转时，像平面则按顺时针方向旋转，形成“镜像”。 奇数次反射为镜像，偶数次反射为一致像。
当棱镜中的一个或多个反射面被称做屋脊的两个 相互垂直的反射面所取代，且屋脊的顶位处于主截面 内，这种棱镜称为屋脊棱镜。
y x
z
y x
z
y′ z′ x′
y′
棱镜系统成像的物象坐标的变化
z′ x′
⑴沿着光轴的坐标轴(图中的z轴)在整个成像过程中始终保持沿着光轴．并指向光的传播方向： ⑵垂直于主截面的坐标轴(图中的x轴)在一般情况下保持垂直于主截面，并与物坐标同向。但当遇有 屋脊面时，每经过一个屋脊面反向一次． ⑶在主截面内的坐标轴(图中的y轴)由平面镜的成像性质判断，根据反射镜具有的奇次反射成镜像、 偶次反射成一致像的特点，首先确定光在棱镜中的反射次数．再按系统成镜像还是一致像来决定该坐 标轴的方向：成镜像反射时坐标左右手系改变，成一致像反射时左右手系不变。注意，在统计反射次 数时，每一屋脊面被认为是两次反射，按两次反射计数。
该性质可用于测量物体的微小转角或位移。
光学比较仪中的光学杠杆
M
L1
A
H H'
A'
M
MM为分划板
M
L1
a)
A'
2α
F'
A
H H'
M -f b)
P
支点 a
测杆 P P PP为
反射镜
Q
单个平面镜成像性质： (1)平面镜能使整个空间理想成像，物点和像点对平面镜
对称； (2)物和像大小相等，但形状不同，物空间的右手坐标在
像空间变为左手坐标；如果分别对着入射和出射光线
的方向观察物平面和像平面，当物平面按逆时针方向 旋转时，像平面则按顺时针方向旋转，形成“镜像”。 奇数次反射为镜像，偶数次反射为一致像。
当棱镜中的一个或多个反射面被称做屋脊的两个 相互垂直的反射面所取代，且屋脊的顶位处于主截面 内，这种棱镜称为屋脊棱镜。
y x
z
y x
z
y′ z′ x′
y′
棱镜系统成像的物象坐标的变化
z′ x′
⑴沿着光轴的坐标轴(图中的z轴)在整个成像过程中始终保持沿着光轴．并指向光的传播方向： ⑵垂直于主截面的坐标轴(图中的x轴)在一般情况下保持垂直于主截面，并与物坐标同向。但当遇有 屋脊面时，每经过一个屋脊面反向一次． ⑶在主截面内的坐标轴(图中的y轴)由平面镜的成像性质判断，根据反射镜具有的奇次反射成镜像、 偶次反射成一致像的特点，首先确定光在棱镜中的反射次数．再按系统成镜像还是一致像来决定该坐 标轴的方向：成镜像反射时坐标左右手系改变，成一致像反射时左右手系不变。注意，在统计反射次 数时，每一屋脊面被认为是两次反射，按两次反射计数。
该性质可用于测量物体的微小转角或位移。
光学比较仪中的光学杠杆
M
L1
A
H H'
A'
M
MM为分划板
M
L1
a)
A'
2α
F'
A
H H'
M -f b)
P
支点 a
测杆 P P PP为
反射镜
《应用光学》第4章 平面镜棱镜系统1
L ' d (1 tgI2 ) d (1 sin I2 )
• 图4-14所示为一个 三次反射棱镜，称为 斯密特棱镜。它使光 轴折转45°角。由于 棱镜中的光轴折叠， 因此，对缩小仪器的 体积非常有利。
图4-14
15
2）屋脊棱镜
光学系统中，光线经平面镜棱镜系统时的反射次数 可能为奇数，这时物体成镜像，为了获得和物相似 的像，在不宜再增加反射面的情况下，可以用两个 互相垂直的反射面代替其中的一个反射面，这两个 互相垂直的反射面叫作屋脊面。带有屋脊面的棱镜 叫屋脊棱镜。
• 第四章 平面镜棱镜系统 • §4-1 平面镜棱镜系统的一些应用
1
平面镜或棱镜、透镜组成的系统，则能满足系统改变 光束方向和物象间方位的要求。如目前使用的军用观 察望远镜，由于在系统中使用了棱镜，如图4-1b所示， 所以它在不加入导向透镜的情况下即可获得正像，同 时又大大地缩小了仪器的体积，减轻了仪器的重量。
下列关系：
由O1O2M得
2i1 2i2 或者 2(i1 i2 )
因二平面镜的法线交于N，
故由O1O2N得
i1 i2或 i1 i2
带入上式得 2
8
从上式可知， 与i角大小无关，只取决于两平面镜 间的夹角，因此，光线方向的改变可以根据设计需 要通过选择适当的角来实现。如果保持两平面镜间
和折射棱镜定义相同，反射棱镜的折射面和反射 面均称为棱镜的工作面，工作面的交线成反射棱镜的 棱，和各棱垂直的截面称为主截面，光学系统的光轴 位在棱镜中的 部分称为反射棱镜的光轴。
10
图4-10
11
图4-11
12
• 一、反射棱镜的分类
•常用的反射棱镜可分为三类：简单棱镜、屋脊 棱镜和复合棱镜。
最新应用光学平面镜棱镜系统教学课件PPT教学讲义PPT
当平面镜旋转θ 角时，出射光线相对于原出射 光线将旋转2 θ 角，而且旋转的方向与镜的旋转 方向一致。
二、双平面镜的成像特性
✓θ
2θ
2θ
θ
济南大学物理学院 工程光学课件
12
证明
✓θ
β=2θ
M1
2I1 2I2
I1 I2
2
I2 I2 θ
I1
I1
M2
I1I2/2
I1I2
与入射角无关 上式恒成立
济南大学物理学院 工程光学课件
D0.33a4
(n1.516)3
D
通光口径仅有原来的1/3
D 道威棱镜
为了在一定通光口径的 条件下，减小棱镜尺寸 两个棱镜同时使用。
济南大学物理学院 工程光学课件
35
这样就组成了立方棱镜 D
D
立方棱镜的一个特点是棱镜尺寸小，通光口径大
立方棱镜的两反射面必须平行，且两反射面必须 镀膜。
立方棱镜只能工作在平行光路中
33
展开图为：
由图可求出展开长度
L AC FG D tan 600 D tan 300 4 3D
3
济南大学物理学院 工程光学课件
34
4. 立方棱镜
直角棱镜的通光口径较大，但是当采用旋转棱镜 改变光轴方向时，此时通光口径就变小了，这样 进入光学系统的光能减少，影响成像质量。
如图所示
a
由几何分析可知：
对2002年3月至2003年12 月间在我院行超声乳化人 工晶体植入手术的415例 （453眼）患者，按照民族 不同分为治疗组（维吾尔、
哈萨克族）与对照组（汉 族），治疗组共227例239 眼，对照组188例214眼。
设备及参数设置
(应用光学)第四章平面镜棱镜成像
• 因此，物点以近轴光经平行平面板成像是完善的。
注明，当入射角I小于20°时，可采用近轴光束成像公式；大于20°，
采用
L'
d 1
tgI 1' tgI 1
应用光学（第四版）
4 平面镜棱镜系统 平行平板等效的画法
应用光学（第四版）
d/n
4 平面镜棱镜系统
例1 一个薄透镜组，焦距为100mm，通光口径为20mm，对无限远的 物体成像，像的直径为10mm。在距离透镜组50mm处加入一五角棱 镜，使光轴折转90°，求棱镜的尺寸和通过棱镜后像面的位置。 解： D1=0.5(20+10)=15mm
4 平面镜棱镜系统
二、棱镜转动定理
考虑：像的方向 像的位置
P' P' P
P
符号规则 ；对着转轴向量观察时，逆时针 为正，顺时针为负。
棱镜转动定理
应用光学（第四版）
4 平面镜棱镜系统 1、在平行光路中工作的棱镜，绕垂直于棱镜主界面的z轴转动
y
z
x
应用光学（第四版）
y'
z'
x'
4 平面镜棱镜系统
应用光学（第四版）
y
z
x
z' y'
x'
4 平面镜棱镜系统
应用光学（第四版）
4 平面镜棱镜系统 2、在平行光路中入射光和出射光轴平行的棱镜，绕入射光轴x转动 1）入射光于出射光平行同向
应用光学（第四版）
4 平面镜棱镜系统 2）入射光于出射光平行反向
应用光学（第四版）
y x
z
x’
z’ y’ z’’
y’’ x’’
4 平面镜棱镜系统
注明，当入射角I小于20°时，可采用近轴光束成像公式；大于20°，
采用
L'
d 1
tgI 1' tgI 1
应用光学（第四版）
4 平面镜棱镜系统 平行平板等效的画法
应用光学（第四版）
d/n
4 平面镜棱镜系统
例1 一个薄透镜组，焦距为100mm，通光口径为20mm，对无限远的 物体成像，像的直径为10mm。在距离透镜组50mm处加入一五角棱 镜，使光轴折转90°，求棱镜的尺寸和通过棱镜后像面的位置。 解： D1=0.5(20+10)=15mm
4 平面镜棱镜系统
二、棱镜转动定理
考虑：像的方向 像的位置
P' P' P
P
符号规则 ；对着转轴向量观察时，逆时针 为正，顺时针为负。
棱镜转动定理
应用光学（第四版）
4 平面镜棱镜系统 1、在平行光路中工作的棱镜，绕垂直于棱镜主界面的z轴转动
y
z
x
应用光学（第四版）
y'
z'
x'
4 平面镜棱镜系统
应用光学（第四版）
y
z
x
z' y'
x'
4 平面镜棱镜系统
应用光学（第四版）
4 平面镜棱镜系统 2、在平行光路中入射光和出射光轴平行的棱镜，绕入射光轴x转动 1）入射光于出射光平行同向
应用光学（第四版）
4 平面镜棱镜系统 2）入射光于出射光平行反向
应用光学（第四版）
y x
z
x’
z’ y’ z’’
y’’ x’’
4 平面镜棱镜系统
第四章 平面镜棱镜系统
第四章平面镜棱镜系统一、平面镜棱镜系统在光学仪器中的应用1. 共轴球面系统的特点优点•能够满足成像位置和大小的要求•近轴区域内成像符合理想•物平面垂直于光轴，像平面垂直于光轴，物像相似缺点不能拐弯，位于一条直线上2. 平面镜棱镜的作用•将共轴系统折叠以缩小仪器的体积，减轻仪器的重量；•改变像的方向–起倒像作用；•改变共轴系统中光轴的位置和方向，形成潜望高或使光轴转一定的角度；•利用平面镜棱镜旋转，可以连续改变系统光轴方向，以扩大观察范围。
二、平面镜的成像性质1. 任意物点通过单个平面镜的成像情况•物像位置相对于平面镜对称，物像大小相等；•实物成虚像，虚物成实像；•单个平面镜对物点能成理想像。
2. 空间物体通过单平面镜反射的成像情况•物像大小相等，形状不同；•物空间右手坐标对应像空间左手坐标；•物像关系称之为镜像。
3. 平面镜系统•成像理想；•空间对应情况：奇数个平面镜，成镜像；偶数个平面镜，物像相似。
三、平面镜的旋转1. 单个平面镜的旋转•入射光线不动，单个平面镜转动α \alpha α，反射光线的转动量为 2 α 2\alpha 2α。
•应用：扩大观察范围；•缺点：转动带来误差。
2. 双平面镜的转动•光线的转角只与两个平面镜的夹角有关，出射光线和入射光线的夹角等于两平面镜夹角的两倍；•应用:解决单个平面镜旋转改变夹角，入射和出射夹角不变的问题。
四、棱镜和棱镜的展开反射棱镜:在同一种光学材料上制作一个或多个反射面，通过反射介质内部的光来改变光的方向的光学元件。
1. 用棱镜代替平面镜的优缺点优点缺点2. 基本定义•棱镜光轴：光学系统的光轴在棱镜中的部分；•工作面：棱镜的折射面和反射面；•棱：两工作面的交线；•主截面：和各个棱相垂直的截面；•光轴截面：光轴所在的主截面。
3. 棱镜的展开棱镜的展开将棱镜的主截面沿反射面向下折叠，取消棱镜的反射，用平行玻璃板的折射代替棱镜的折射的方法。
棱镜展开的要求目的：棱镜和共轴球面系统组合后，仍能保持共轴球面系统的特性要求。
第四章 平面镜与平面系统
2）目镜离光棱线镜出经射面过的M距离O。PN后，在NP面上B点出射情况与光线经过MORQ后在 T点出射情况完全相同，不同的是经过MOPN有折射，经过MORQ
则没有，称MORQ为MOPN的等效空气平板，令其厚度为 d 。 dd T B d ld d (1 1 )d nn
例：开普勒望远系统和斜方棱镜组合而成的10倍望远系 统，若物镜的焦距f物′=160mm，斜方棱镜入射面到物镜 距离为115mm，轴向光束在棱镜上的通光口径为22.5mm （斜方棱镜k=2，n=1.5）求： 1）目镜的焦距f目′； 2）目镜离棱镜出射面的距离。
DGcodIs1sinI1I1
s I 1 i I 1 n sI 1 i c n I 1 o c I 1 s s o I 1 is n
siIn1nsiIn1
DGdsinI11nccooIsI1s1
L DG sin I1
说明：
L d1nccoosIsI11
sin sin
I1 I 1
n
L
d1
L
光学比较仪：
F′
xytg
α
2α
FFftg2
F
y
M FF 2f xy
f′ x
§ 4－3 平行平板
1. 放大率：
siIn1nsiIn1 nsiIn2siIn2
ttg U g U 1,11,2 1
成正立等大的像，物象虚实相反。
2. 远轴光成像：
D D G sE I i1 n I1
DE d cosI1
K L D
说明：K与棱镜大小无关，决定于棱镜 的结构形式。当确定棱镜结构形式和口 径D后，便可由K值求知光轴长度。
五、等效空气平板：
2）作用：对于奇次反射棱镜，为获得物的相似像，在不增加反射棱镜的情况下，可将一个反射面用两个相互垂直的反射面取代。 ● 象和物上下同方向，而左右方向颠倒 两个或两个以上相互垂直主截面 奇数次反射，方向按右手坐标系来确定，偶数次反射按左手坐标系来确定。 若干对谱线的相对色散： 3）若平板放在透镜成像之后，l′多大？ β 多大？ 4）结果：如图a所示，设物为左手坐标，则经棱镜反射后输出为右手坐标，即产生镜象。 2）从点A发出的具有不同入射角的各条光线经平行板折射后，具有不同的轴向位移值，平行板成象是不完善的。 在物镜后方80mm处放置一直角棱镜（n=1. § 4－7 光学材料 2）目镜离棱镜出射面的距离。 4）结果：如图a所示，设物为左手坐标，则经棱镜反射后输出为右手坐标，即产生镜象。 说明：奇次反射均成镜象； 2）若在物与透镜之间置一平板，d=60mm，n=1. 2）作用：对于奇次反射棱镜，为获得物的相似像，在不增加反射棱镜的情况下，可将一个反射面用两个相互垂直的反射面取代。 物点发出的同心光束经反射镜反射后仍成同心光束。 ● 折叠系统、缩小体积、减轻重量 ● 改变光轴位置和方向 ● 象和物上下同方向，而左右方向颠倒
则没有，称MORQ为MOPN的等效空气平板，令其厚度为 d 。 dd T B d ld d (1 1 )d nn
例：开普勒望远系统和斜方棱镜组合而成的10倍望远系 统，若物镜的焦距f物′=160mm，斜方棱镜入射面到物镜 距离为115mm，轴向光束在棱镜上的通光口径为22.5mm （斜方棱镜k=2，n=1.5）求： 1）目镜的焦距f目′； 2）目镜离棱镜出射面的距离。
DGcodIs1sinI1I1
s I 1 i I 1 n sI 1 i c n I 1 o c I 1 s s o I 1 is n
siIn1nsiIn1
DGdsinI11nccooIsI1s1
L DG sin I1
说明：
L d1nccoosIsI11
sin sin
I1 I 1
n
L
d1
L
光学比较仪：
F′
xytg
α
2α
FFftg2
F
y
M FF 2f xy
f′ x
§ 4－3 平行平板
1. 放大率：
siIn1nsiIn1 nsiIn2siIn2
ttg U g U 1,11,2 1
成正立等大的像，物象虚实相反。
2. 远轴光成像：
D D G sE I i1 n I1
DE d cosI1
K L D
说明：K与棱镜大小无关，决定于棱镜 的结构形式。当确定棱镜结构形式和口 径D后，便可由K值求知光轴长度。
五、等效空气平板：
2）作用：对于奇次反射棱镜，为获得物的相似像，在不增加反射棱镜的情况下，可将一个反射面用两个相互垂直的反射面取代。 ● 象和物上下同方向，而左右方向颠倒 两个或两个以上相互垂直主截面 奇数次反射，方向按右手坐标系来确定，偶数次反射按左手坐标系来确定。 若干对谱线的相对色散： 3）若平板放在透镜成像之后，l′多大？ β 多大？ 4）结果：如图a所示，设物为左手坐标，则经棱镜反射后输出为右手坐标，即产生镜象。 2）从点A发出的具有不同入射角的各条光线经平行板折射后，具有不同的轴向位移值，平行板成象是不完善的。 在物镜后方80mm处放置一直角棱镜（n=1. § 4－7 光学材料 2）目镜离棱镜出射面的距离。 4）结果：如图a所示，设物为左手坐标，则经棱镜反射后输出为右手坐标，即产生镜象。 说明：奇次反射均成镜象； 2）若在物与透镜之间置一平板，d=60mm，n=1. 2）作用：对于奇次反射棱镜，为获得物的相似像，在不增加反射棱镜的情况下，可将一个反射面用两个相互垂直的反射面取代。 物点发出的同心光束经反射镜反射后仍成同心光束。 ● 折叠系统、缩小体积、减轻重量 ● 改变光轴位置和方向 ● 象和物上下同方向，而左右方向颠倒
应用光学第四章 平面镜棱镜系统
统 主截面位置任意的平面镜棱镜系统
单一主截面的平面镜棱镜系统
在x’方向（光轴）上，与光轴的出射方向相同； 在y’方向（主截面内）上，
光轴同向，反射次数为偶数， y和y’同向；反射次 数为奇数， y和y’反向。
光轴反向，反射次数为偶数， y和y’反向；反射次 数为奇数， y和y’同向。
在z’方向（垂直于主截面）上，
注意，xyz，x’y’z’只表示物像的方向而不表 示物像的位置。
确定棱镜系统成像方向 x’轴与出射光轴重合
y’和z’的方向确定有两种方法：
反弹折转法 利用法则法
反弹折转法实例
y x
z
x’
y’ z’
y
y’ z’ x’
x z
利用法则法
利用法则的方法，我们将平面镜棱镜系统 分成三类
具有单一主截面的平面镜棱镜系统 具有两个相互垂直的主截面的平面镜棱镜系
y
z
x
z’ x’
y’
y’’
z’’ x’’
y’’’
x’’’ z’’’
分析系统的成像方向实例
分析系统的成像方向练习
如果两平面镜相对转动，则出射光线方向改变了2。
应用举例
测距仪中，入射光线经过两端的平面镜反射以后 改变90o，且要求该角度保持稳定不变。
方法一：单平面镜。 方法二：双平面镜。
方法三：最可靠的方法是将两个反射面做在同一块 玻璃上– 棱镜。
4-4 棱镜和棱镜展开
一、光学系统中常用的两类棱镜 反射棱镜
Δl’是ΔL’在近轴区的近似。 对于理想光学系统（对近轴区）有：
1. 轴向位移只正比于d 2. Δl’与入射角无关 3. d愈大，平板愈厚，轴向位移Δl’愈大
平行平板的等效光学系统
单一主截面的平面镜棱镜系统
在x’方向（光轴）上，与光轴的出射方向相同； 在y’方向（主截面内）上，
光轴同向，反射次数为偶数， y和y’同向；反射次 数为奇数， y和y’反向。
光轴反向，反射次数为偶数， y和y’反向；反射次 数为奇数， y和y’同向。
在z’方向（垂直于主截面）上，
注意，xyz，x’y’z’只表示物像的方向而不表 示物像的位置。
确定棱镜系统成像方向 x’轴与出射光轴重合
y’和z’的方向确定有两种方法：
反弹折转法 利用法则法
反弹折转法实例
y x
z
x’
y’ z’
y
y’ z’ x’
x z
利用法则法
利用法则的方法，我们将平面镜棱镜系统 分成三类
具有单一主截面的平面镜棱镜系统 具有两个相互垂直的主截面的平面镜棱镜系
y
z
x
z’ x’
y’
y’’
z’’ x’’
y’’’
x’’’ z’’’
分析系统的成像方向实例
分析系统的成像方向练习
如果两平面镜相对转动，则出射光线方向改变了2。
应用举例
测距仪中，入射光线经过两端的平面镜反射以后 改变90o，且要求该角度保持稳定不变。
方法一：单平面镜。 方法二：双平面镜。
方法三：最可靠的方法是将两个反射面做在同一块 玻璃上– 棱镜。
4-4 棱镜和棱镜展开
一、光学系统中常用的两类棱镜 反射棱镜
Δl’是ΔL’在近轴区的近似。 对于理想光学系统（对近轴区）有：
1. 轴向位移只正比于d 2. Δl’与入射角无关 3. d愈大，平板愈厚，轴向位移Δl’愈大
平行平板的等效光学系统
第四章-平面镜棱镜系统资料
奇数次反射，若物为右手坐标系，则y’按 左手坐标系确定；(屋脊面算两次反射)
偶数次反射， y’按物像相同坐标系确定。
y
成像方向规则：
ox
z
光轴反射次数为偶数，y’和y同向
光轴同向 光轴反射次数为奇数，y’和y反向
光轴反射次数为偶数，y’和y反向
y'
z' x'
光轴反向
光轴反射次数为奇数，y’和y同向
像坐标的方向判断
表明物像位于异侧
l' 1 成正像
l
结论： ①成完善像，唯一能成完善像的光学元件 ②正立、大小相等、虚实相反的像，像和物对称于平面镜 ③右手坐标系变成左手坐标系，反演，成镜像 ④奇次反射成镜像，偶次反射成一致像
P
奇数个平面镜成镜像， 偶数个平面镜物像完全相似。
y x
O
z
右手坐标 Q
y'
x'
z' O
行光束中，否则破坏系统共轴性。 （2）必须考虑平行玻璃板产生的像面位移。
4.10 棱镜的偏差
为保持共轴球面系统的特性，对棱镜结构的要求： （1）棱镜展开后两个表面必须平行。 （2）若棱镜位于会聚光束中，则光轴必须和棱镜的入射与
出射表面相垂直。
F E
光学平行差：因棱镜的几何误差而使其展开后前后两个表面 不平行，破坏了系统的共轴性。
➢φ>0时，屈折是会聚性的； ➢φ<0时，屈折是发散性的。 ➢φ=0时，对应于平面折射。沿轴平行光束经折射后仍是沿
轴平行光束，不出现屈折现象。 单位：以米为单位的焦距的倒数。 1个光焦度就是平行光线经过透镜折射后在1米处成焦点。
光焦度
正光焦度 负光焦度
4.2 平面镜的成像性质
平面镜棱镜系统
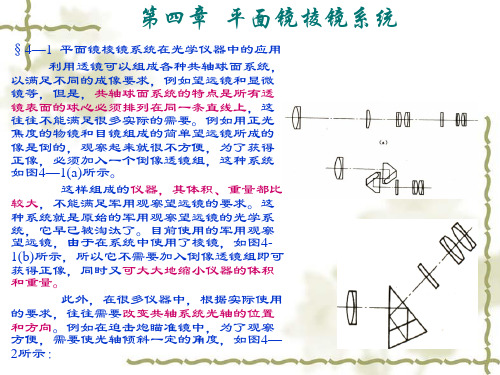
利用棱镜或平面镜的旋 转,就可以观察到四周的情况, 如图4—3中的周视瞄准镜那样. 平面镜棱镜系统主要作用有: (1)将共轴系统折叠以缩小仪 器的体积和减轻仪器的重量; (2)改变像的方向——起倒像 使用; (3)改变共轴系统中光轴的位 置和方向——即形成潜望高或 使光轴转一定的角度; (4)利用平面镜或棱镜的旋转, 可连续改变系统光轴的方向, 以扩大观察范围.
§4-2平面镜的成像性质
为了研究平面镜棱镜系统的成像性质,首先从研究单个平面镜开始. 图4—4中P是一个和图面垂直的平面镜,A是一任意物点,由A点发出的 AO光线,经平面镜反射后,其反射光线OB的延长线和平面镜户的垂直线 AD的延长线相交于一点A`.根据反射定律,反射角等于入射角 由图可以看到 同时OD垂直于AA',因此△AOD≌△A'OD,由此得到
§4-3平面镜的旋转及其应用 研究平面镜转动的性质. 由图4—7可以看到,光线经 平面镜反射时,入射和出射光线间 的夹角,等于入射角I的两倍,光线 经过反射后旋转了 .当平面 镜绕着和入射面垂直的轴线转动α角 时,入射角改变了α ,而反射光线 和入射光线之间的夹角将改变2α . 由此得出结论:当平面镜绕垂直于 入射面的轴转动α角时,反射光线将 转动2α.转动方向和平面镜的转动 方向相同.
例:如图所示的棱镜系统
2,有两个互相垂直主截面的平面镜棱镜系统
注意:光轴 的同向和反 向的判别, 不再是简单 的观察是否 同向就可以 了,要沿光 轴转.
3,主截面位置任意的平面镜棱镜系统 可将此系统看成是上述两类系统中的 棱镜主截面旋转而形成的. 具有平面镜棱镜个数很多的系统,可 将其划分为几个部分,依次确定每部 分的方向,最后找到整个系统的成像 方向.
将l2式代人,得到
《应用光学》第4章 平面镜棱镜系统1
• 图4－21 靴形棱镜及其展开
28
• 为了满足棱镜的第一个要求，所以在BC面上再加 一个30°角的棱镜EFG 。它和棱镜ABCD组合后， 便构成了一块平行玻璃板，但是两者之间必须留 有一层空气隙，以便是光线在BC面上能发生全反 射。补偿棱镜EFG和棱镜ABCD必须采用同一种 光学材料。由于光线在DC面上的入射角小于临界 角I0，故DC面上必须镀反光膜。
例41图38例41图由图b知物体经物镜的所有成像光束均包含在由物镜d所限定的锥体范围内如果不要求棱镜限制光束那么光束经棱镜入射表面时194036所以由于靴形屋脊棱镜展开后的平行玻璃厚度为d2980d9134mm所以按照公式43平行玻璃板的等效空气平板厚度为918460571516340因此通过棱镜后象平面离开棱镜出射表面的距离为mm27576036棱镜出射表面的通光口径d?为mm由上面的例子可以看出把玻璃平板换算成等效空气层来进行棱镜外形尺寸计算是相当方便的
下列关系：
由O1O2M得
2i1 2i2 或者 2(i1 i2 )
因二平面镜的法线交于N，
故由O1O2N得
i1 i2或 i1 i2
带入上式得 2
8
从上式可知， 与i角大小无关，只取决于两平面镜 间的夹角，因此，光线方向的改变可以根据设计需 要通过选择适当的角来实现。如果保持两平面镜间
简单棱镜的所有工作面均与中截面垂直，它又 有一次反射棱镜、二次和三次反射棱镜之分。一次 反射棱镜的成像性质和单块平面反射镜相同，图412中所示的反射棱镜称直角棱镜和等腰棱镜，随等 腰棱镜底角大小的不同，可实现不同方向 的光轴 偏折。而二次反射棱镜相当于双面角镜，如图4-13 所示。在这类反射棱镜中，光线经两反射面依次反 射后，反射光线相对于入射光线偏转的角度为两反 射面夹角的两倍。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1
u A L l2’
u’
2 1
结论：平行玻璃板不改变像的大小， 只使像面发生位移，移动量为L-L/n
l1
二、平行玻璃板的相当空气层厚度 1、定义： KP2=AA’=L-L/n KP2=QM=L-L/n NQ=L/n 由图，AQ=l1-L/n=l2’=A’M N P1
K
L/n Q L l1
第四步：求第二面通光口径
5 100 100 x 0.81 D2 10 2 x 11.62 x 50 33.8 16.2
D1 10 第六步：求新像面位置 l2’=50-33.8=16.2
50
D2
x 5
e
33.8
l2’
100
非近轴区域的相当空气厚度
I
P 1 h1 O1
偶数次反射
屋脊棱镜的成像特点
y
y
x
z
x
z
y'
z'
x'
镜像
y'
x'
z'
物像相似 用两个屋脊面代替一个反射面后，光轴的方向和棱镜主截面内 像的方向保持不变，在垂直于主截面的方向上像将发生颠倒。
成像特性： 1. 入射光照射到屋脊上，相当于偶次成像，物象一致 2. 垂直于光轴的坐标都反转 对屋脊面的要求：屋脊角必须严格等于90度，否则形成双像
条件：入射出射表面与光轴垂直 转90度
90 2I
A’
B
B
A'
I I
A
C
A
C
I
转任意角度 A 要求光线偏转
，则反射面转 2
2
B C 90
2
B
C
例如要使光轴转 45，则 45 B C 90 67.5 2
这种棱镜称为等腰棱镜
§4-5 屋脊面和屋脊棱镜
作用：在不改变光轴方向和主截面内成像方向的条件下，用两 个相互垂直的反射面代替一个反射面，增加一次反射，使系统 总反射次数由奇数变成偶数，达到物象相似的要求。
A2 B2C2 D2 B2C2 F2 E2
屋脊面的作用: 奇数次反射
增加一次反射
屋脊面
直角屋脊棱镜L 1.732D
形 变 测 量
测杆移动量 x= ytg 聚焦点移动量 FF= f tg2
F1 F2 f ' t an 2 2 f ' M x y t an y
二、双平面镜的转动 在O1O2M中，
2 I1 2 I 2
P2
I1
A O1
I2
P1
（ 2 I1 I 2）
O2
两法线交于一点N， O1 NO2 在三角形O1O2N中，利用外角定理
A L l1 l2’
A’
nl1 L L L n 1 l2 l1 像面移动量 AA l2 L l1 L L n n n n
2、像的大小
光线通过平行玻璃板时 ，入射光线与出射光线 永远平行 u1 u2 ' tgu' u2 ' 1 tgu u1 空气中 1
A
N
N’ B
I
I I
I
B’ P
O 缺点：由于转动引起误差
优点：扩大观察范围
例如：测距机中的平面镜
测量物体的微小转角和微小位移
单平面镜旋转的应用
当测杆处于零位，平面镜处于垂直于光轴的状态M0，F1点发出的光束经
物镜后与光轴平行，再经平面镜反射原路返回，重被聚焦于F1 点。
当测杆被被测物体顶推移动x, 而使平面镜绕支点转过角而处于M1 状 态时，平行光被反射后要相对于光轴转过 2角，并被物镜聚焦于F2处。
cos I 1 sin I
1
2n 1
2
C
为了在一定通光口径下减小棱镜体积，可以把两个同样的直角棱 镜沿斜面胶合在一起，形成立方棱镜 1 2 3 4 使用立方棱镜时要注意： 光束是分两束分别通过两个棱镜进入系统，过了棱镜又合成一束， 原来角度一致的平行光通过系统后还应该角度一致，要求两个棱镜 反射面严格平行； 入射圆形光束时，出射为两个半圆；不能在圆形光束中工作； 入射面与光轴不垂直，只能使用在平行光路中。 2’ 1’ 4’ 3’
P2 M A l2’ A’
厚度L/n的两平面所夹的空气层称为厚度为L，折射率为n 的平行玻璃板的相当空气层。L/n就叫做厚度为L，折射 率为n的平行玻璃板的相当空气层厚度。
平行玻璃板与相当空气层相当的地方： 像面相对于平行玻璃板第二表面的位置和物平 面相对空气层的第二表面的位置相当； 光束的投射高相当； 像的大小相当。 不相当的地方： 平行玻璃板有像面
2、五角棱镜：保证光轴转角恒等于90
反射膜
45
用途： （1）把入射光转向一定角度(90°)；（2） 成象既无旋转也无镜面反射。
五角棱角的展开
45
设AB = AE = D，
则展开后的平行玻璃板厚度为
L (2 2 ) D 3.414D
3、靴形棱镜
A
60
D B A'
B'
C F G
O2
M
N B
应用：测距机中用双平面镜代替单个平面镜
角镜，棱镜
平面镜的旋转及应用
2
平面镜的旋转及应用
§4-4 棱镜和棱镜的展开
一、用棱镜代替平面镜的优缺点
棱镜：利用光线在介质内部的反射来改变光线方向的光学零件 优点：光能损失少、坚固耐久，不易损坏、易于安装固定 缺点：体积重量较大、对材料要求高、受环境影响较大
I' n K E
P2 h2 O2
等效空气层厚度E
E O1 A NA
N
A
A'
L
h1 O1 A tan( I )
h2 h1 L tan( I ' ) NA tan( I ) tan( I ) cos I tan I ' L cos I L k EL k cos I ' tan I n cos I ' n
I1 I 2
M
N
B
I1 I 2 2
入射光线和出射光线夹角为双平面镜夹角的两倍。
出射光线转动角度与入射方向无关，即两平面镜一起转
动时，出射光线方向不变。
二、双平面镜的转动
旋转方向：与反射顺序相同
P2
I1
A O1
I2
P1
光线的转角只与两个平面镜 的夹角有关，而与入射光线 的方向无关，即不论入射光 线的入射角和位置如何，出 射光线与入射光线的夹角都 不变，等于两平面镜夹角的 二倍。
缺点：不能拐弯，物，光学系统，像，位在一条直线
军用观察望远镜
迫击炮瞄准镜 周视瞄准镜
平面镜棱镜系统的主要作用：
将共轴系统折叠以缩小仪器的体积
和减轻仪器重量；
改变像的方向－－起倒像作用； 改变共轴系统中光轴的位置和方向， 形成潜望高或使光轴转一定角度； 利用平面镜棱镜旋转，可以连续改
变系统光轴方向，以扩大观察范围
§4-6 平行平板的成像性质和棱镜外形尺寸计算
一、平行玻璃板的成像性质 1、像面位置
1
2
n
L
l1
A
l2 '
A'
已知：r1 r2 , L, n, l1 求：像点位置 l2
假定A离第一面距离为l1，求像点离第二面的距 离。
n n n n 解：单个折射球面物象 位置关系式 l l r n n 对平面，r , 公式为 0 l l 对第一面应用： l l1 , l l1 , n 1, n n n 1 0 l1 nl1 l1 l1 对第二面应用：过渡公 式l2 l1 L nl1 L n n, n 1, 1 n 0 nl1 L l2
三、对棱镜的要求
平面反射不影响成像性质，平面折射影响成像性质 对棱镜的要求：
1. 棱镜展开后玻璃板的两个 表面必须平行；
2. 如果棱镜位于会聚光束中 ，则光轴必须和棱镜的入 射及出射光面相垂直。
B
A' F'
A
C
F
对于平行光束只须满足第一个条件
四、典型棱镜展开举例
1、直角棱镜 在平行光路中使用
直角棱镜
二、棱镜的展开——研究棱镜成像性质的方法
1 2 3
1 2 由于折倒关系， 2 3 1 3
把棱镜的主截面沿反射面折倒，取消棱镜的反射，以平
行玻璃板的折射代替棱镜折射的方法称为“棱镜的展开”。
棱镜展开后，用平行平板代替棱镜，取消了棱镜内部的反
射，只考虑入射和出射面的折射，大大简化了计算。
偶数个平面镜，物象相似。
注意：
1、像的正、倒与相似不是一回事；
2、物体与镜像形状不同，不相似不能重合。
一般来说，我们总希望得到物像相似的像，特别 是军用光学仪器
§4-3 平面镜的旋转及应用
一、单个平面镜的转动
2(I+ α)-2I=2
结论：入射光线不动，单个 平面镜转动 α 反射光线的转动量为2 α
结论：
物像位置相对平面镜对称，物像 大小相等 实物成虚像，虚物成实像。 单个平面镜对物点能成理想像，
A
r
l ' l
球面反射镜 表明物像位于异侧
P
D
O O’
l' 1 成正像 l
物像是否相似？
A’
二、空间物体通过单平面镜反射的成像情况