教师用习题解答第5章
第5章 习题解答
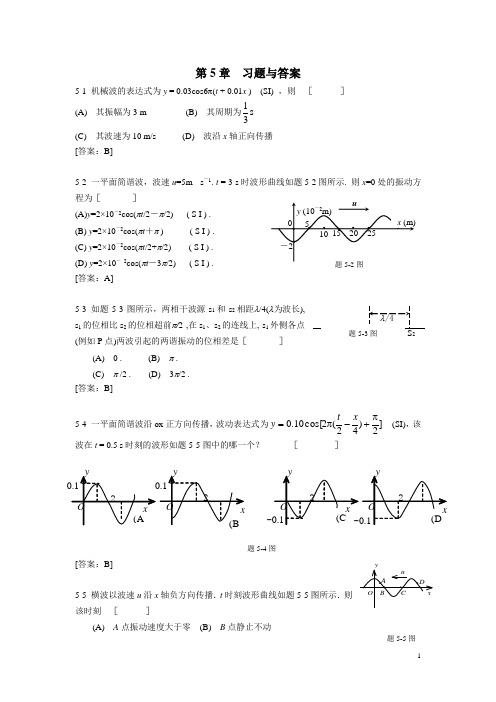
第5章 习题与答案5-1 机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ,则[ ] (A) 其振幅为3 m(B) 其周期为s 31(C) 其波速为10 m/s (D)波沿x 轴正向传播 [答案:B]5-2 一平面简谐波,波速u =5m · s -1. t = 3 s 时波形曲线如题5-2图所示. 则x =0处的振动方程为[ ](A)y =2×10-2cos(πt /2-π/2) ( S I ) . (B) y =2×10-2cos(πt +π ) ( S I ) . (C) y =2×10-2cos(πt /2+π/2) ( S I ) .(D) y =2×10- 2cos(πt -3π/2) ( S I ) .[答案:A]5-3 如题5-3图所示,两相干波源s 1和s 2相距λ/4(λ为波长), s 1的位相比s 2的位相超前π/2 ,在s 1、s 2的连线上, s 1外侧各点(例如P 点)两波引起的两谐振动的位相差是[ ](A) 0 . (B) π . (C) π /2 . (D) 3π/2 . [答案:B]5-4 一平面简谐波沿ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形如题5-5图中的哪一个? [ ][答案:B]5-5 横波以波速u 沿x 轴负方向传播.t 时刻波形曲线如题5-5图所示.则该时刻 [ ](A) A 点振动速度大于零 (B) B 点静止不动ux (m)y (10-2m)· · · · · · · 0 51015 20 25 -2题5-2图题5-4图题5-5图-(C) C 点向下运动 (D) D 点振动速度小于零 [答案:D]5-6 一平面简谐波沿x 轴正方向传播,t = 0 时刻的波形如题5-6图所示,则P 处质点的振动在t = 0时刻的旋转矢量图是[ ][答案:A]5-7 一简谐波沿x 轴正方向传播,t = T /4时的波形曲线如题5-7图所示.若振动以余弦函数表示,且此题各点振动的初相取-π 到π 之间的值,则 [ ] (A) O 点的初相为00=φ(B) 1点的初相为π-=211φ(C) 2点的初相为π=2φ (D) 3点的初相为π-=213φ [答案:D]5-8 在驻波中,两个相邻波节间各质点的振动[ ](A) 振幅相同,相位相同 (B) 振幅不同,相位相同 (C) 振幅相同,相位不同 (D) 振幅不同,相位不同 [答案:B]5-9 一平面简谐波在弹性媒质中传播,在媒质质元从平衡位置运动到最大位移处的过程中:[ ](A) 它的动能转化为势能. (B) 它的势能转化为动能.(C) 它从相邻的一段质元获得能量其能量逐渐增大. (D) 它把自己的能量传给相邻的一段质元,其能量逐渐减小. [答案:D]ωS A O ′ωSA O ′ωωSAO ′(A)(B)(C)(D)S题5-6图5-10 一横波的波动方程是))(4.0100(2sin 02.0SI x t y -=π,则振幅是__________,波长是__________,频率是__________,波的传播速度是__________。
幼儿教育学习题第五章 幼儿园环境

幼儿教育学习题第五章幼儿园环境一、单项选择题1.环境分为物质环境和( )。
A.社会环境B.精神环境C.城市环境D.局部环境2.物质环境是学前教育存在与发展的( )。
A.必备条件B.主要条件C.次要条件D.生活条件6.创设幼儿园环境时应考虑不同地区、不同条件幼儿园的实际情况,因地制宜,这体现了( )原则。
A.开放性B.经济性C.发展适宜性D.参与性二、名词解释1.精神环境2.物质环境3.环境的界限性4.环境的相容性5.环境的转换性6.幼儿常规三、判断题1.幼儿园环境所具有的教育性与可控性是相互独立的。
2.参与性原则就是环境创设过程中幼儿与教师需要共同参与整个过程。
3.环境创设中的开放性原则就是幼儿园要多搞活动,让外界多参与幼儿园的各种建设。
4.教师要尽量让幼儿感受到环境是由幼儿自己决定的。
5.在调整环境的时候,教师只需要考虑教学内容的变化,而不是环境的发展性和教育四、简答题1.什么叫幼儿园环境?2.什么叫发展适宜性原则?如何具体体现这一原则?3.幼儿园内环境的特点表现在哪些方面?4.影响幼儿园内环境质量的重要因素有哪些?5.如何理解幼儿园环境创设的经济性原则?6.如何理解幼儿园环境创设的参与性原则?7.如何理解幼儿园环境创设的开放性原则?8.运用环境体验法应注意的事项是什么?五、论述题1.为了发挥幼儿园环境的作用,创设时需要考虑哪些原则?2.教师在幼儿园环境创设中的作用是什么?3.在幼儿园环境创设中存在的误区是什么?六、案例分析幼儿园可设置的活动区有:社会活动区(娃娃家、医院、市场、马路等);自然科学活动区(天文、地理、生物、化学、物理等自然事物和现象的观察、实验等);数学活动区;艺术活动区(音乐、美术等);语言活动区(阅读、故事表演等);建构操作区(拼、插、搭、小制作等);室外可有玩沙区、玩水区、种植区、饲养区等。
这种划分并不固定,每个幼儿园在具体操作时可视情况化整为零、灵活搭配。
场地大一些的,可设置大的活动区;场地比较小的,可设置小一点的活动角,如图书角、数学角、自然角、娃娃家等。
第5章习题解答

第5章习题解答1. 解:Q235钢,m l 5.5=荷载标准值:m kN q k /5.34245.10=+= 荷载设计值:m kN q /2.46244.15.102.1=⨯+⨯=弯矩设计值:m kN ql M x ⋅=⨯⨯==69.1745.52.46818122(1)假定梁的受压翼缘设置可靠的侧向支承,可以保证梁的整体稳定由抗弯强度要求的截面模量为:3361082.77321505.11069.174mm f M W x x nx ⨯=⨯⨯==γ查型钢表选用I36a ,截面几何特性:3878cm W x =,415796cm I x =,质量m kg q /0.60= 强度验算:22326/215/44.1921087805.18/55002.16.01069.174mm N f mm N W M nx x x =<=⨯⨯⨯⨯+⨯=γ 满足要求。
挠度验算:[]2501428110157961006.25500)6.05.34(384538454533=<=⨯⨯⨯⨯+⨯=⋅=l EI l q l x kx υυ满足要求。
故选用此截面。
(2)假定梁的受压翼缘无可靠的侧向支承按整体稳定确定梁截面假定工字钢型号在I45~I63之间,均布荷载作用在梁上翼缘,自由长度m l 5.51=,由附表3-2查政体稳定系数6.0660.0>=b ϕ,所以643.0660.0282.007.1282.007.1=-=-='bbϕϕ所需毛截面抵抗矩:3361063.1263215643.01069.174mm f M W b x nx ⨯=⨯⨯='=ϕ查型钢表选用I45a ,截面几何特性:31433cm W x =,432241cm I x =,质量m kg q /4.80=强度验算:22326/215/52.11810143305.18/55002.1804.01069.174mm N f mm N W M nx x x =<=⨯⨯⨯⨯+⨯=γ满足要求。
幼儿教育学习题第五章幼儿园环境

幼儿教育学习题第五章幼儿园环境一、单项选择题1.环境分为物质环境和 ( )。
A .社会环境B .精神环境C.城市环境D.局部环境2.物质环境是学前教育存在与发展的( )。
A .必备条件B .主要条件C.次要条件D.生活条件6.创设幼儿园环境时应考虑不同地区、不同条件幼儿园的实际情况,因地制宜,这体现了( ) 原则。
A .开放性B.经济性C.发展适宜性D.参与性二、名词解释1.精神环境2.物质环境3.环境的界限性4.环境的相容性5.环境的转换性6.幼儿常规三、判断题1.幼儿园环境所具有的教育性与可控性是相互独立的。
2.参与性原则就是环境创设过程中幼儿与教师需要共同参与整个过程。
3.环境创设中的开放性原则就是幼儿园要多搞活动,让外界多参与幼儿园的各种建设。
4.教师要尽量让幼儿感受到环境是由幼儿自己决定的。
5.在调整环境的时候,教师只需要考虑教学内容的变化,而不是环境的发展性和教育四、简答题1.什么叫幼儿园环境?2.什么叫发展适宜性原则?如何具体体现这一原则?3.幼儿园内环境的特点表现在哪些方面?4.影响幼儿园内环境质量的重要因素有哪些?5.如何理解幼儿园环境创设的经济性原则?6.如何理解幼儿园环境创设的参与性原则?7.如何理解幼儿园环境创设的开放性原则?8.运用环境体验法应注意的事项是什么?五、论述题1.为了发挥幼儿园环境的作用,创设时需要考虑哪些原则?2.教师在幼儿园环境创设中的作用是什么?3.在幼儿园环境创设中存在的误区是什么?六、案例分析幼儿园可设置的活动区有:社会活动区(娃娃家、医院、市场、马路等 );自然科学活动区 (天文、地理、生物、化学、物理等自然事物和现象的观察、实验等);数学活动区;艺术活动区( 音乐、美术等 );语言活动区 (阅读、故事表演等 );建构操作区 (拼、插、搭、小制作等);室外可有玩沙区、玩水区、种植区、饲养区等。
这种划分并不固定,每个幼儿园在具体操作时可视情况化整为零、灵活搭配。
第5章习题解答

如果按指令执行周期结束(25μs)响应DMA请求,必然会 造成数据丢失;因此必须按每个机器周期结束响应DMA 请 求的方案。
解:打印机的打印动作只受打印机本身控制, 与CPU 无关,因此打印机正在打印时,虽然 有优先级别更高的磁盘请求中断,打印机也 不会停止打印。而如果CPU 正在执行打印机 的中断服务程序,即打印机正在接收数据, 此时若磁盘请求中断,CPU 就要中断正在运 行的打印机中断服务程序。
5.33 试从下面7个方面比较程序查询、程 序中断和DMA三种方式的综合性能。
程序查询方式 中断方式
DMA 方式
软件
软件
硬件
字
字
数据块
串行
宏观并行,微观串行
CPU主动查询
主动/被动
慢 最经济
最慢 经济
中低速实时处理设备 中低速I/5.19 在程序中断方式中,磁盘申请中断的优先权高于 打印机。当打印机正在进行打印时,磁盘申请中断,试 问是否要将打印机输出停下来,等磁盘操作结束后,打 印机输出才能继续进行?为什么?
例5.32 设磁盘存储器转速为3000 转/分,分8 个扇区,每扇区 存储1K 字节,主存与磁盘存储器传送的宽度为16 位。假设一 条指令最长执行时间是25μs ,是否可采用一条指令执行结束时 响应DMA 请求的方案,为什么?若不行,应采取什么方案?
解: 磁盘的数据传输速率=每一磁道容量×转速 = 1×8×50×3000/60
作业
❖ 5.2、5.10、 5.12、5.13、 ❖ 5.18、 5.29、5.32、5.33 ❖ 思考题 5.25
【课程练习】习题解答-第五章 详细设计

第五章详细设计1.详细设计的基本任务是什么?有哪几种描述方法?详细设计的基本任务:(1)为每个模块进行详细的算法设计。
(2)为每个模块内的数据结构进行设计。
(3)对数据库进行设计,即确定数据库的物理结构。
(4)其他设计:a.代码设计b.输入/输出格式设计。
c.人机对话设计。
(5)编写详细设计说明书。
(6)评审。
描述方法(三种):a.程序流程图b.PAD图 C.过程设计语言2.结构化程序设计基本要求要点是什么?a.采用自顶向下、逐步求精的程序设计方法b.使用三种基本程序控制结构构造程序1).用顺序方式对过程分解,确定各部分的执行顺序。
2).用选择方式对过程分解,确定某个部分的执行条件。
3).用循环方式对过程分解,确定某个部分重复的开始和结束的条件。
c.主程序员组的组织形式。
3.简述Jackson 方法的设计步骤。
Jsp 方法一般通过以下5个步骤来完成设计:a.分析并确定输入/出数据的逻辑结构,并用Jackson 结构图表示这些数据结构。
b.找出输入数据结构和输出数据结构中有对应关系的数据单元。
c.按一定的规则由输入、输出的数据结构导出程序结构。
d.列出基本操作与条件,并把它们分配到程序结构图的适当位置。
e.用伪码写出程序。
4.请使用流程图、PAD图各PDL语言描述下列程序的算法。
(1)在数据A(1)-A(10)中求最大数和次大数。
(2)输入三个正整数作为边长、判断该三条边构成的三角形是等边、等腰或一般三角形。
答:(1)1)流程图:2)PAD图3)PDL语言定义n1=n2=0输入A(1).......A(10)n1=n2=A(1)while i>10if A(i)>=n1n2=n1n1=A(i)end while5.用PAD图描述下面问题的控制结构。
有一个表A(1)、A(2)、........A(n),按递增顺序排列。
给定一个Keyw值,在表中用折半查找。
若找到将表位置i送入x,否则将零送到x,同时将Key值插入表中。
范钦珊版材料力学习题全解 第5章 梁的弯曲问题(1)-剪力图与弯矩图

M A = ql 2
| FQ | max = 5 ql 4
| M | max = ql 2
题(c)
∑ F y = 0 , FRA = ql (↑)
9
∑ M A = 0 , M A = ql 2
∑ M D = 0 , ql 2 + ql ⋅ l − ql ⋅ − M D = 0
3 2 ql 2 | FQ | max = ql MD =
C
4000 4000
B
FB
习题 5-8 载荷图之二
5-9 试作图示刚架的剪力图和弯矩图,并确定 FQ
max
、 M
max
12
习题 5-9 图
解:题(a) :
∑M A = 0
FRB ⋅ 2l − FP ⋅ l − FP ⋅ l = 0
FRB = FP (↑)
∑ F y = 0 , F Ay = FP (↓)
∑ Fx = 0 , FAx = FP (←)
C
2
1
B
C
-
B
1
D
M(FPl)
1 +
D
FQ(FP)
A
A
习题 5-9a 的弯矩图
剪力图和弯矩图如图所示,其中 | M | max = 2 FP l , 位于刚节点 C 截面;
| FQ |max = FP
题(b) : ∑ F y = 0 , F Ay = ql (↑)
8
习题 5-6c、e 解图
习题 5-6d、f 解图
题(b)
∑ M A = 0 − ql 2 − ql ⋅ l + ql ⋅ l + FRB ⋅ 2l = 0
2
FRB
05工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第5章_轴向拉伸与压缩

eBook工程力学(静力学与材料力学)习题详细解答(教师用书)(第5章)范钦珊 唐静静2006-12-18第5章轴向拉伸与压缩5-1试用截面法计算图示杆件各段的轴力,并画轴力图。
解:(a)题(b)题(c)题(d)题习题5-1图F NxF N(kN)x-3F Nx A5-2 图示之等截面直杆由钢杆ABC 与铜杆CD 在C 处粘接而成。
直杆各部分的直径均为d =36 mm ,受力如图所示。
若不考虑杆的自重,试求AC 段和AD 段杆的轴向变形量AC l Δ和AD l Δ解:()()N N 22ssππ44BCAB BC AB ACF l F l l d dE E Δ=+33321501020001001030004294720010π36.××+××=×=××mm ()3N 232c100102500429475286mm π10510π364..CDCD AD AC F l l l d E ΔΔ×××=+=+=×××5-3 长度l =1.2 m 、横截面面积为1.10×l0-3 m 2的铝制圆筒放置在固定的刚性块上;-10F N x习题5-2图刚性板固定刚性板A E mkN习题5-4解图直径d =15.0mm 的钢杆BC 悬挂在铝筒顶端的刚性板上;铝制圆筒的轴线与钢杆的轴线重合。
若在钢杆的C 端施加轴向拉力F P ,且已知钢和铝的弹性模量分别为E s =200GPa ,E a =70GPa ;轴向载荷F P =60kN ,试求钢杆C 端向下移动的距离。
解: a a P A E l F u u ABB A −=−(其中u A = 0)∴ 935.0101010.11070102.1106063333=×××××××=−B u mm钢杆C 端的位移为33P 32s s601021100935450mm π20010154...BC C B F l u u E A ×××=+=+=×××5-4 螺旋压紧装置如图所示。
第5、6章(热学部分)习题解答

第五章气体分子动理论5-6 在容积为332.010m -⨯的容器中,有内能为26.7510⨯ J 的刚性双原子分子理想气体。
求:(1)气体的压强;(2)若容器中分子总数为225.410⨯个,则分子的平均平动动能及气体的温度为多少?分析:(1)由一定量理想气体的内能公式和理想气体物态方程可求出气体的压强,刚性双原子分子的自由度5i =。
(2)由分子数密度定义和p nkT =求出T ,最后由气体分子的平均平动动能公式求出分子的平均平动动能。
解:(1)由2M i E RT μ=和MpV RT μ=得气体压强:(2)分子数密度Nn V=,则该气体的温度: 53222231.35102.0103.6210()5.410 1.3810p pV T K nk Nk --⨯⨯⨯====⨯⨯⨯⨯ 气体分子的平均平动动能为:2322133 1.3810 3.62107.4910()22k kT J ε--⨯⨯⨯⨯===⨯5-7 自行车轮直径为71.12cm ,内胎截面直径为3cm 。
在03C -的空气里向空胎里打气。
打气筒长30cm ,截面半径为1.5cm 。
打了20下,气打足了,问此时胎内压强是多少?设车胎内最后气体温度为07C 。
分析:可根据理想气体物态方程求解此题。
解: 设向自行车内胎所打的空气的摩尔数为γ由理想气体物态方程pV RT γ=得 :111p V RT γ=其中,22231111,203010(1.510),3273270p atm V m T K π--==⨯⨯⨯⨯⨯=-+= 气打足后,胎内空气的体积 22232371.1210(10)2V m ππ--=⨯⨯⨯⨯⨯温度2(7273)280T K K =+=,压强为 2p , 222RT p V γ=1125222111222222211.01310203010(1.510)280371.1210(10)2702pV RT RT pVT p V V T πππ----⋅⨯⨯⨯⨯⨯⨯⨯⨯∴===⨯⨯⨯⨯⨯⨯ 52.8410() 2.8()a p atm -=⨯=25322 6.7510 1.3510()5 2.010E p Pa iV -⨯⨯===⨯⨯⨯5-8 某柴油机的气缸充满空气,压缩前其中空气的温度为047C ,压强为48.6110Pa ⨯。
第五章习题解答

习 题 五1. 设V 是数域F 上向量空间,假如V 至少含有一个非零向量α,问V 中的向量是有限多还是无限多?有没有n (n ≥ 2)个向量构成的向量空间? 解 无限多;不存在n (n ≥ 2)个向量构成的向量空间(因为如果F 上一个向量空间V 含有至少两个向量, 那么V 至少含有一个非零向量α , 因此V 中含有α , 2α , 3α , 4α , …,这无穷多个向量互不相等,因此V 中必然含有无穷多个向量).2. 设V 是数域F 上的向量空间,V 中的元素称为向量,这里的向量和平面解析几何中的向量α,空间解析几何中的向量β有什么区别?解 这里的向量比平面中的向量意义广泛得多,它可以是多项式,矩阵等,不单纯指平面中的向量.3. 检验以下集合对所指定的运算是否构成数域F 上的向量空间.(1)集合:全体n 阶实对称矩阵;F :实数域;运算:矩阵的加法和数量乘法;(2)集合:实数域F 上全体二维行向量;运算: (a 1, b 1)+ (a 2, b 2)=(a 1+a 2, 0) k • (a 1, b 1)=(ka 1, 0)(3)集合:实数域上全体二维行向量;运算: (a 1, b 1)+ (a 2, b 2)=(a 1+a 2, b 1+b 2)k •( a 1, b 1)=(0, 0)解 (1) 是; (2) 不是(因为零向量不唯一);(3) 不是(不满足向量空间定义中的(8)).4. 在向量空间中,证明,(1) a (-α)=-a α=(-a ) α ,(2) (a -b )α=a α-b α ,a ,b 是数,α是向量.证明 (1) a a a a =+-=+-))(()(αααα 0= 0ααa a -=-∴)(又 ==+-=+-a a a a a 0))(()(ααα 0ααa a -=-∴)(综上, .)()(αααa a a -=-=-(2) ααααααb a b a b a b a -=-+=-+=-)())(()(.5. 如果当k 1=k 2=…=k r =0时,k 1α1+k 2α2+…+k r αr =0, 那么α1, α2, …, αr 线性无关. 这种说法对吗?为什么?解 这种说法不对. 例如设α1=(2,0, -1), α2=(-1,2,3), α3=(0,4,5), 则0α1+0α2+0α3=0. 但α1, α2, α3线性相关, 因为α1+2α2-α3=0.6. 如果α1, α2, …, αr 线性无关,而αr +1不能由α1, α2, …, αr 线性表示,那么α1, α2,…, αr , αr +1线性无关. 这个命题成立吗?为什么? 解 成立. 反设α1, α2,…, αr , αr +1线性相关,由条件α1, α2, …, αr 线性无关知αr +1一定能由α1, α2, …, αr 线性表示,矛盾.7. 如果α1, α2, …, αr 线性无关,那么其中每一个向量都不是其余向量的线性组合. 这种说法对吗?为什么?解 对. 反设 αi = k 1α1+k 2α2+…k i -1αi-1+k i+1αi +1 +…+k r αr ,则 k 1α1+k 2α2+…k i -1αi-1+(-1) αi +k i+1αi +1 +…+k r αr =0. 由于-1≠0, 故α1, α2, …, αr 线性相关.8. 如果向量α1, α2, …, αr 线性相关,那么其中每一个向量都可由其余向量线性表示. 这种说法对吗?为什么?解 不对. 设α1=(1,0) , α2=(2,0) , α3=(0,1) , 则α1, α2, α3线性相关, 但α3不能由α1, α2线性表示.9. 设α1= (1, 0, 0), α2= (1, 2, 0), α3=(1, 2, 3)是F 3中的向量,写出α1, α2, α3的一切线性组合. 并证明F 3中的每个向量都可由{α1, α2, α3}线性表示.解 k 1α1+k 2α2+k 3α3 k 1, k 2 , k 3∈F .设k 1α1+k 2α2+k 3α3=0,则有⎪⎩⎪⎨⎧==+=++030220332321k k k k k k , 解得 k 1= k 2 =k 3=0.故α1, α2, α3线性无关.对任意(a,b,c)∈F 3, (a,b,c)=3213)32())322((αααc c b c ba +-+--,所以F 3中的每个向量都可由{α1, α2, α3}线性表示.10. 下列向量组是否线性相关(1) α1= (1, 0, 0), α2= (1, 1, 0), α3=(1, 1, 1);(2) α1=(3, 1, 4), α2=(2, 5, -1), α3=(4, -3, 7).解 (1) 线性无关; (2) 线性无关.11. 证明,设向量α1, α2, α3线性相关,向量α2, α3, α4线性无关,问:(1) α1能否由α2, α3线性表示?说明理由;(2) α4能否由α1, α2, α3线性表示?说明理由.解 (1)因为α2, α3线性无关而α1, α2, α3线性相关,所以α1能由α2, α3线性表示;(2)反设α4能由α1, α2, α3线性表示,但α1能由α2, α3线性表示,故α4能由α2, α3线性表示,这与α2, α3, α4线性无关矛盾,所以α4不能由α1, α2, α3线性表示.12. 设α1= (0, 1, 2), α2= (3, -1, 0), α3=(2, 1, 0),β1= (1, 0, 0), β2= (1, 2, 0), β3=(1, 2, 3)是F 3中的向量. 证明,向量组{α1, α2, α3}与{β1, β2, β3}等价.证明 (β1, β2, β3)=(321,,εεε)A(α1, α2, α3)= (321,,εεε)B其中A=⎪⎪⎪⎭⎫ ⎝⎛300220111, B=⎪⎪⎪⎭⎫ ⎝⎛-002111230.易验证A , B 均可逆, 这样 (β1, β2, β3) = (α1, α2, α3 )(B -1A )(α1, α2, α3) = (β1, β2, β3)(A -1B ) ,故向量组{α1, α2, α3}与{β1, β2, β3}等价.13. 设数域F 上的向量空间V 的向量组{α1, α2, …, αs }线性相关,并且在这个向量组中任意去掉一个向量后就线性无关. 证明,如果∑=s i i ik 1α=0 (k i ∈F ),那么或者k 1=k 2=…=k s =0, 或k 1,k 2,…,k s 全不为零.证明 由条件∑=s i i ik 1α=0 (k i ∈F )知k i αi = - (k 1α1+k 2α2+…k i -1αi-1+k i+1αi +1 +…+k s αs ) (*)(1) 当k i =0时,(*)式左边等于零,故k 1α1+k 2α2+…k i -1αi-1+k i+1αi +1 +…+k s αs =0. 由于这s -1个向量线性无关,所以k 1=k 2=…=k s =0.(2) 当k i ≠0时, αi = -ik 1(k 1α1+k 2α2+…k i -1αi-1+k i+1αi +1 +…+k s αs ),下证对于任意i j s j ≠∈},,2,1{ 时k j ≠0. 反设k j =0, 则αi 可由s -2个向量线性表示.这与任意s -1个向量线性无关矛盾,所以此时k 1,k 2,…,k s 全不为零.14. 设α1=(1, 1), α2=(2, 2), α3=(0, 1) , α4=(1, 0)都是F 2中的向量. 写出{α1, α2, α3, α4}的所有极大无关组.解 α1, α3 ; α1, α4 ; α2 ,α3 ; α2 ,α4 ; α3 ,α4 .15. 设A 1=⎪⎪⎭⎫ ⎝⎛-2001,A 2=⎪⎪⎭⎫ ⎝⎛-0021, A 3=⎪⎪⎭⎫ ⎝⎛0120,A 4=⎪⎪⎭⎫ ⎝⎛-2142∈M 2×2(F ). 求向量空间M 2×2(F )中向量组{A 1, A 2,A 3, A 4}的秩及其极大无关组. 解 秩{A 1, A 2,A 3, A 4}=3, {A 1, A 2,A 3}是向量组{A 1, A 2, A 3, A 4}的一个极大无关组.16.设由F 4中向量组{α1=(3,1,2,5),α2=(1,1,1,2),α3=(2,0,1,3),α4 =(1,-1,0,1),α5 =(4,2,3,7)}. 求此向量组的一个极大无关组.解 (α1,α2,α3,α4,α5)= (4321,,,εεεε)A , 其中A=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-71325301122101141213, 则秩A =2. 又(α1,α2 )= (4321,,,εεεε)B , 其中B =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛25121113. 秩B =2, 故{α1,α2}线性无关, 它是向量组{α1,α2,α3,α4,α5}的一个极大无关组.17. 证明,如果向量空间V 的每一个向量都可以唯一表成V 中向量α1, α2, …, αn 的线性组合,那么dim V =n .证明 由条件零向量可唯一的表示成α1, α2, …, αn 的线性组合, 这说明α1, α2, …, αn 线性无关, 故可作为V 的基, 从而dim V =n .18. 设β1, β2,…,βn 是F 上n (>0)维向量空间V 的向量,并且V 中每个向量都可以由β1, β2,…,βn 线性表示. 证明, {β1, β2,…,βn }是V 的基.证明 由条件标准正交基{ e 1, e 2, …,e n }可由β1, β2,…,βn 线性表示, 反过来β1, β2,…,βn 又可由{ e 1, e 2, …,e n }线性表示,所以{ e 1, e 2, …,e n }和{β1, β2,…,βn }等价. 由{ e 1, e 2, …,e n }线性无关知{β1, β2,…,βn }线性无关,又因V 中每个向量都可以由β1, β2,…,βn 线性表示, 由基的定义知{β1, β2,…,βn }是V 的基.19. 复数集C 看作实数域R 上的向量空间(运算: 复数的加法,实数与复数的乘法)时,求C 的一个基和维数.解 基为{1, i }; dim C =2.20. 设V 是实数域R 上全体n 阶对角形矩阵构成的向量空间(运算是矩阵的加法和数与矩阵的乘法). 求V 的一个基和维数.解 基为E ii (i =1,2, …,n ); dim V =n .21. 求§5.1中例9给出的向量空间的维数和一个基.解 任意一个不等于1的正实数都可作为V 的基; dim V =1.22. 在R 3中,求向量α=(1, 2, 3)在基ε1=(1, 0, 0),ε2=(1, 1, 0),ε3=(1, 1, 1)下的坐标.解 (-1,-1,3)T .23. 求R 3中由基{α1, α2, αs }到基{β1, β2, β3 }的过渡矩阵,其中α1=(1, 0, -1), α2=(-1, 1, 0), α3=(1, 2, 3),β1=(0, 1, 1), β2=(1, 0, 1), β3=(1, 1, 1).解 所求过渡矩阵为⎪⎪⎪⎭⎫ ⎝⎛-32204230061. 24. 设{α1, α2,…, αn }是向量空间V 的一个基,求由这个基到基{α3, α4, …, αn ,α1, α2}的过渡矩阵.解 所求过渡矩阵为⎪⎪⎭⎫ ⎝⎛-0022n I I . 25. 已知F 3中向量α关于标准基ε1=(1, 0, 0),ε2=(0, 1, 0) ,ε3=(0, 0, 1)的坐标是(1, 2, 3),求α关于基β1=(1, 0, 1), β2=(0, 1, 1), β3=(1, 1, 3)的坐标.解 (1,2,0)T .26. 判断R n 的下列子集哪些是子空间(其中R 是实数域,Z 是整数集).(1) {(a 1, 0, …, 0, a n )| a 1, a n ∈R };(2) {(a 1, a 2, …, a n )|∑==ni i a 10,a 1, a 2, …, a n ∈R };(3) {(a 1, a 2, …, a n )|a i ∈Z , i =1, 2, …, n };解 (1) 是; (2) 是; (3) 不是(数乘不封闭).27. 设V 是一个向量空间,且V ≠{0}. 证明,V 不能表成它的两个真子空间的并集.证明 设W 1与W 2是V 的两个真子空间(1) 若21W W ⊆,则W 1⋃W 2= W 2≠V ;(2) 若21W W ⊇,则W 1⋃W 2= W 1≠V ;(3) 若21W W ⊄且12W W ⊄, 取1W ∈α但2W ∉α,2W ∈β但1W ∉β, 那么1W ∉+βα,否则将有1)(W ∈=-+βαβα,这与1W ∉β矛盾, 同理2W ∉+βα, 所以V 中有向量21W W ∉+βα,即V ≠21W W .28. 设V 是n 维向量空间,证明V 可以表示成n 个一维子空间的直和.证明 设{α1, α2,…, αn }是向量空间V 的一个基, (α1), (α2) ,…, (αn )分别是由α1, α2,…, αn 生成的向量空间, 要证(α1+α2+…+αn )= (α1)⊕ (α2)⊕…⊕ (αn )(1) 因为{α1, α2,…, αn }是V 的一个基, 所以V 中任一向量α都可由α1, α2,…, αn 线性表示, 此即(α1+α2+…+αn )= (α1)+ (α2)+…+ (αn ).(2) 对任意i ≠j ∈{1,2,…, n },下证 (αi )∩ (αj )={0}. 反设存在0 ≠∈x (αi )∩ (αj ),由∈x (αi )知存在k F ∈使得x =k αi ; 由 x ∈ (αj )知存在F l ∈使得x =l αj , 从而αi =kl αj , 即α1与α2线性相关, 矛盾, 所以 (αi )∩ (αj )={0}. 综上, (α1+α2+…+αn )= (α1)⊕ (α2)⊕…⊕ (αn ).29. 在R 3中给定两个向量组α1=(2, -1, 1, -1), α2=(1, 0, -1, 1),β1=(-1, 2, -1, 0), β2=(2, 1, -1, 1).求 (α1, α2)+ (β1, β2) 的维数和一个基.解 取R 4的标准正交基{4321,,,εεεε},于是(α1, α2, β1, β2)= (4321,,,εεεε)A ,其中 A =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------1011111112012112 , 秩A = 4. 故α1, α2, β1, β2线性无关, 又因为 (α1, α2)∩ (β1, β2)={0},所以dim (α1, α2) + dim (β1, β2)= 4,{ α1, α2, β1, β2}是它的基.30. 设W 1, W 2都是向量空间V 的子空间,证明下列条件是等价的:(1) W 1⊆W 2;(2) W 1∩W 2=W 1;(3) W 1+W 2=W 2.证明 (i) (1)⇒(2) 因为W 1⊆W 2 , 所以W 1∩W 2=W 1. (ii) (2)⇒(3) W 1+W 2 ={α1+α2 | α1∈W 1, α2∈W 2} 由(2)知对任意α∈W 1, 都有α∈W 2 , 所以W 1+W 2 ={α1+α2 | α1, α2∈W 2}=W 2 .(iii) (3)⇒(1) W 1+W 2 ={α1,+α2 | α1∈W 1, α2∈W 2}=W 2 , 说明对任意α∈W 1, 都有α∈W 2 , 此即W 1⊆W 2 .31. 设V 是实数域R 上n 阶对称矩阵所成的α2向量空间;W 是数域R 上n 阶上三角矩阵所成的向量空间,给出V 到W 的一个同构映射.解 对∈∀A V (A =(a ij )且a ij = a ji )和B ∈W (B =(a ij ),当i>j 时, a ij =0) 定义f : V → WA B 易验证f 是V 到W 的一个同构映射.32. 设V 与W 都是数域F 上的向量空间,f 是V 到W 的一个同构映射,证明{α1, α2, …, αn }是V 的基当且仅当{f (α1), f (α2), …, f (αn )}是W 的基.证明 设{α1, α2, …, αn }是V 的基.(1) 由α1, α2, …, αn 线性无关知f (α1), f (α2), …, f (αn ) 线性无关.(2) 任取∈ηW , 由f 是同构映射知存在∈ξV 使得f (ξ)=η.但ξ=∑=n i i ia 1α, a i ∈F , f (ξ)=f (∑=n i i i a 1α)=)(1∑=n i i i f a α=η. 由η的任意性知{f (α1), f (α2), …, f (αn )}是W 的基.反过来, {f (α1), f (α2), …, f (αn )}是W 的基(1) 由f (α1), f (α2), …, f (αn )线性无关知α1, α2, …, αn 线性无关.(2) 任取∈ξV , 由f 是同构映射知存在∈ηW 使得f (ξ)=η.但η=∑=n i i i f k 1)(α= f (∑=n i i i k 1α), k i ∈F , 从而ξ=∑=ni i i k 1α, k i ∈F .由ξ的任意性知{ α1, α2, …, αn }是V 的基.补 充 题1. 设W 1, W 2是数域F 上向量空间V 的两个子空间. α,β是V 的两个向量,其中α∈W 2,但α∉ W 1,β∉W2. 证明:(1)对于任意k ∈F ,αβk +∉W 2;(2)至多有一个k ∈F ,使得αβk +∈W 1.证明 (1)反设存在k 1∈F 使得αβ1k +∈W 2 , 又α∈W 2 , 因此β=β+ k 1α-k 1α∈W 2 , 这与β∉W 2矛盾. 所以对于∀k ∈F ,αβk +∉W 2 .(2)若有k 1, k 2∈F , k 1≠k 2使得αβ1k +, αβ2k +∈W 1, 那么。
教育学章节习题第五章学生与教师

第五章学生与教师一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,把所选选项前的字母填在题后的括号内。
1.陶行知先生的“捧着一颗心来,不带半根草去”的教育信条体现了教师的()素养。
A.教育理论知识B.崇高的职业道德C.文化学科知识D.过硬的教学基本功2.学生是生活在一定社会关系中的具有特定的()属性的人。
A.自然B.社会C.实践D.现实3.为了有效地把自己对教育内容的理解转化为学生的知识和有效地解决教育教学中出现的问题,教师需要有()。
A.高度的政治觉悟B.广博的科学文化知识C.教育理论知识和技能D.良好的人际关系4.学生是处于人生阶段身心发展()时期的人。
A.最迅速B.中速C.最慢速D.静止5.就教育专业素养而言,教师除了要有先进的教育理念和良好的教育能力外,还要具有一定的()。
A.交往能力B.研究能力C.管理能力D.学习能力6.学生具有发展的可能性与()。
A.现实性B.潜在性C.可塑性D.普遍性7.社会环境对个体的客观要求所引起的需要与个体的发展水平之问的矛盾运动,是推动个体由自然人向社会人转变的()。
A.动力B.前提C.条件D.基础8.在教育活动中,教师负责组织、引导学生沿着正确的方向,采用科学的方法,获得良好的发展,这句话的意思是说()。
A.学生在教育活动中是被动的客体B.教师在教育活动中是被动的客体C.要充分发挥教师在教育活动中的主导作用D.教师在教育活动中不能起到主导作用9.教师的行为举止之所以能成为学生学习的榜样,对其具有潜移默化的作用,是因为学生具有()。
A.依赖性B.向师性C.背师性D.示范性10.教师首次被列入“专家、技术人员和有关工作者”类别的文件是()。
A.《关于教师地位的建议》B.《中华人民共和国国家标准职业分类与代码》C.《教师资格条例》D.《中华人民共和国教师法》11.良好的师生关系是教育教学取得成功的()。
A.必要保证B.必然结果C.必然要求D.必然趋势12.“以身立教”、“为人师表”体现了教师劳动的()特点。
电工技术(第三版 席时达)教学指导、习题解答 第五章
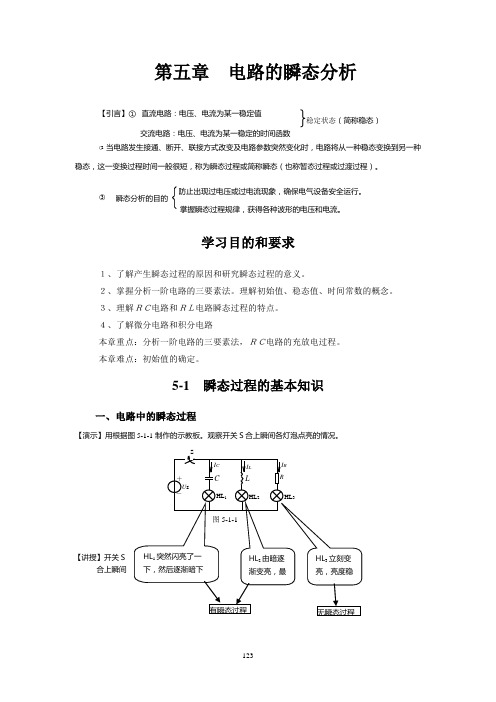
第五章 电路的瞬态分析【引言】①○2当电路发生接通、断开、联接方式改变及电路参数突然变化时,电路将从一种稳态变换到另一种稳态,这一变换过程时间一般很短,称为瞬态过程或简称瞬态(也称暂态过程或过渡过程)。
○3学习目的和要求1、了解产生瞬态过程的原因和研究瞬态过程的意义。
2、掌握分析一阶电路的三要素法。
理解初始值、稳态值、时间常数的概念。
3、理解RC电路和RL电路瞬态过程的特点。
4、了解微分电路和积分电路本章重点:分析一阶电路的三要素法,RC电路的充放电过程。
本章难点:初始值的确定。
5-1 瞬态过程的基本知识一、电路中的瞬态过程【演示】用根据图5-1-1制作的示教板。
观察开关S 合上瞬间各灯泡点亮的情况。
稳定状态(简称稳态)瞬态分析的目的 交流电路:电压、电流为某一稳定的时间函数直流电路:电压、电流为某一稳定值掌握瞬态过程规律,获得各种波形的电压和电流。
防止出现过电压或过电流现象,确保电气设备安全运行。
【讲授】开关S合上瞬间二、换路定律【讲授】①换路定律是表述换路时电容电压和电感电流的变化规律的,即换路瞬间电容上的电压和电感中的电流不能突变。
②设以换路瞬间作为计时起点,令此时t=0,换路前终了瞬间以t=0—表示,换路后初始瞬间以t =0+表示。
则换路定律可表示为:u C(0+)= u C(0—)换路瞬间电容上的电压不能突变i换路瞬间电感中的电流不能突变【说明】①换路定律实质上反映了储能元件所储存的能量不能突变。
因为W C=21CuC2、W L=21LiL2,u C和i L的突变意味着能量发生突变,功率p=twdd趋于无穷大,这是不可能的。
②当电路从一种稳定状态换路到另一种稳定状态的过程中,u C和i L必然是连续变化的,不能突变。
这种电流和电压的连续变化过程就是电路的瞬态过程。
③电阻是耗能元件,并不储存能量,它的电流、电压发生突变并不伴随着能量的突变。
因此由纯电阻构成的电路是没有瞬态过程的。
第5章 不确定推理习题解答

习题55.1不确定推理的概念是什么?为什么要采用不确定推理?解:略。
5.2 不确定推理中需要解决的基本问题是什么?解:略。
5.3 主观Bayes 方法的优点是什么?有什么问题?试说明LS 和LN 的意义。
解:略。
5.4 为什么要在MYCIN 中提出可信度方法?可信度方法还有什么问题?解:略。
5.5 何谓可信度?说明规则强度CF (H ,E )的含义。
解:略。
5.6 设有三个独立的结论H1, H2, H3及两个独立的证据E1, E2,它们的先验概率和条件概率分别为:P(H1)=0.4, P(H2)=0.3, P(H3)=0.3P(E1 | H1)=0.5, P(E1 | H2)=0.3, P(E1 | H3)=0.5P(E2 | H1)=0.7, P(E2 | H2)=0.9, P(E2 | H3)=0.1利用概率方法求出:当只有证据E1出现时,P(H1 | E1)、P(H2 | E1)及P(H3 | E1)的值;并说明E1的出现对H1,H2, H3的影响。
当E1和E2同时出现时,P(H1 | E1, E2)、P(H2 | E1, E2)及P(H3 | E1, E2)的值;并说明E1和E2同时出现对H1,H2, H3的影响。
解: (1)P (H 1|E 1)=0.45P (H 2|E 1)=0.20P (H 3|E 1)=0.34经比较可知,E1的出现,H1和H3成立的可能性略有增加,H2成立的可能性略有降。
(2)P (H 1|E 1,E 2)=0.5932212(|,)=0.3432P H E E312(|,)=0.0636P H E E经比较可知,E 1和E 2同时出现,H 1成立的可能性显著增加,H 2成立的可能性略有增加,H 3成立的可能性显著下降。
5.7设有如下知识:111222333: (201)(0.06): (101)(0.05): (10.08)(0.4)R IFE THEN H R IFE THENH R IF E THEN H ,,,求:当证据321E E E ,,存在时,)|(i i E H P 的值各是多少?解:P (H 1|E 1)=0.5607P (H 2|E 2)=0.34483.0)|(33=E H P 。
《电磁场与电磁波》课后习题解答(第五章)

《电磁场与电磁波》课后习题解答(第五章)————————————————————————————————作者:————————————————————————————————日期:习题及参考答案5.1 一个点电荷 Q 与无穷大导体平面相距为d ,如果把它移动到无穷远处,需要作多少功?解:用镜像法计算。
导体面上的感应电荷的影响用镜像电荷来代替,镜像电荷的大小为-Q ,位于和原电荷对称的位置。
当电荷Q 离导体板的距离为x 时,电荷Q 受到的静电力为2)2(042x Q F επ-=静电力为引力,要将其移动到无穷远处,必须加一个和静电力相反的外力2)2(042x Q f επ=在移动过程中,外力f 所作的功为d Q d dx dx Q dx f 016220162επεπ=⎰∞⎰∞= 当用外力将电荷Q 移动到无穷远处时,同时也要将镜像电荷移动到无穷远处,所以,在整个过程中,外力作的总功为dq8/2επ。
也可以用静电能计算。
在移动以前,系统的静电能等于两个点电荷之间的相互作用能:d Q d Q Q d Q Q q q W 082)2(04)(21)2(042122211121επεπεπϕϕ-=-+-=+=移动点电荷Q 到无穷远处以后,系统的静电能为零。
因此,在这个过程中,外力作功等于系统静电能的增量,即外力作功为dq8/2επ。
5.2 一个点电荷放在直角导体内部(如图5-1),求出所有镜像电荷的位置和大小。
解:需要加三个镜像电荷代替 导体面上的感应电荷。
在(-a ,d )处,镜像电荷为-q ,在(错误!链接无效。
)处, 镜像电荷为q ,在(a ,-d )处,镜像电荷为-q 。
图5-1 5.3 证明:一个点电荷q 和一个带有电 荷Q 、半径为R 的导体球之间的作用力为]2)22(2[04R D DRq D D qR Q q F --+=επ其中D 是q 到球心的距离(D >R )。
证明:使用镜像法分析。
何子述信号与系统习题解答第5章拉普拉斯变换(2012新)

何子述信号与系统习题解答第5章拉普拉斯变换(2012新)何子述老师2012年最新高等教育出版社出版《信号与系统习题解答》发布,对考研同学帮助极大!第5章拉普拉斯变换习题解答一、基本概念与基本运算习题题5.1 解:当f t u t 时,0能使信号g t 的傅里叶变换存在。
当f t u t 时,0能使信号g t 的傅里叶变换存在。
当f t 1时,找不到一个实数使信号g t f t e t绝对可积。
题5.2 解:(a)由拉普拉斯变换的定义式F(s) e 2tu t 1 e1j tdte 2te te j tdt1 s 2e, 2s 2(b)由拉普拉斯变换的定义式j ttδt12δt1eut1edt利用积分的分配律及单位冲激信号的筛选性,可得F s es 2e s ete te j tdt- 1e1 se 2e , 11 sss(c)由拉普拉斯变换的定义式F s e 2tsin 3t u t e-j tdte2tej3t e j3t t j teedt2j239, 2157何子述老师2012年最新高等教育出版社出版《信号与系统习题解答》发布,对考研同学帮助极大!(d)由拉普拉斯变换的定义式F sf t ej tdtete te j tdt 20e 2te te j t 2dts 12s 2e2 11 es 1 s 2,(e)由拉普拉斯变换的定义式e 2t j tedt不存在使上式积分收敛,故信号f(t) e 2t的拉普拉斯变换不存在。
(f)由拉普拉斯变换的定义式F s2δ j tt δ t 2 e dt2 s2 se 2s,题5.3 解:(a)有拉普拉斯变换对e 2tu t L 1s 2, 2 e 4tu t L1s 4, 4由拉普拉斯变换的线性,信号f t 的拉普拉斯变换为f t L11s 2s 4, 4 2 零极点图如图J5.3.1所示。
(b)有拉普拉斯变换对e2tsin 5t u t Ls 2 225, 2δ t L1,由拉普拉斯变换的线性,信号f t 的拉普拉斯变换为f t L15s s2 4s 34s 2 s 2 2225s2 4s 29 s 2 j5s 2 j5,1582何子述老师2012年最新高等教育出版社出版《信号与系统习题解答》发布,对考研同学帮助极大!零极点图如图J5.3.2所示。
第五章习题解答与问题

9.设
f (x)
=
1 1+ x2
,在-5≤x≤5 上取
n = 10,按等距结点求分段线性插值函数Ih(x),
计算各结点间中点处的Ih(x)和f(x) 的值,并估计误差。 解:因为 f(xk) = 1/(1+ k2),(k = -5,…,-1,0,1,…,5)分段线性插值函数为
∑ I h
( x)
=
5
lk
y2 y2
− −
y) y1 )
u1
+
(x (x2
− −
x1 )( y2 x1 )( y2
− −
y) y1 )
u2
+
(x (x2
− −
x1 )( y − y1 ) x1 )( y2 − y1 )
u3
+
( x2 − x)( ( x2 − x1 )(
y2 y2
− −
y) y1 )
u4
二、例题
1. 在代数插值问题中,x0,x1,……,xn是(n+1)个互异的插值结点,由这(n+1)个结点构
F (t) = f (t) − H (t) − C ( x)(t − xk )2 (t − xk+1 )2
显然,F(t)有三个零点xk, x, xk+1,由Roll定理知,存在F’(t)的两个零点t0,t1 满足xk<t0<t1<xk+1,
而xk和xk+1 也是F’(x)的零点,故F’(x)至少有四个相异零点. 反复应用Roll定理,得F(4)(t)至少
∑ P( x) = n Aj
ω(x) j=0 x − x j
5. 设x0,x1,……,xn是(n+1)个互异的插值结点,ω(x) = (x – x0) (x – x1)……(x – xn), 试证明n阶差商的函数值表达式
中高级教师职称考试:教育学概论习题5-8章

第五章课程理论一.判断题1.在英语世界里,课程一词最早出现在《什么知识最有价值》一书中。
(√)2.《学记》中关于课程的说法有“宽着期限,紧着课程”、“小立功夫、大立课程”等。
( )3.从辞源学的角度看,当课程作为名词使用时,其原初含义即为“在跑道上跑”,其引伸含义即为“学习者在学习活动中获取活生生的经验或体验的过程”。
( )4.课程是“学习的内容及其进程”,这是将“课程”作为动词性理解而得出的定义。
( )5.传统的学科课程是将“课程”作为名词使用的突出代表性课程范式。
(√)6.进入20世纪70年代以来,课程的使用逐渐由动词转向名词。
( )7.学生在课堂中获得的与教材内容有冲突的经验,我们不能将它视为课程内容的组成部分。
( )8.中国的“六艺”与西方的“七艺”是学科的萌芽。
(√)9.活动课程的最大优点在于教育过程便于组织并提高了教学效率。
( )10.活动课程最早可追溯到杜威身上。
( )11.杜威在其《民主主义与教育》中深刻阐述了儿童的心理经验与知识的逻辑结构之间的关系。
( )12.杜威的活动课程理论彻底否定了学科课程或逻辑经验的教育价值。
( )13.课程的选修制最先始于大学。
(√)14.必修课与选修课的关系是“共性发展”与“个性发展”的关系。
(√)15.隐性课程对受教育者而言都具有正面的教育意义。
( )16.最早涉及隐性课程研究的教育家是克伯屈。
( )17.师生关系、校园文化等属于教育中的显性课程。
( )18.课程编制的过程模式之目的是使人更加自由,更富有创造性和创新能力。
(√)19.课程编制的过程模式强调教学活动中的过程,而否定活动中的一切目标。
( )20.教师和学生都是课程的建设者和创造者,因此课程并不总是先于教学过程而编制好的。
(√)21.加涅认为,人类的学习按复杂程度分为8类:信号学习、刺激-反应学习、动作连锁学习、言语连锁学习、辩别学习、概念学习、规则学习、问题解决学习。
(√)22.学习者的年龄越小,课程的编制更应该考虑和侧重课程的心理组织。
幼儿园课程 第五章练习题 带解析

自考专科学前教育第五章常见幼儿园课程类型的设计章节练习一、单项选择题1,“打破学科界限,使课程具有整合性”是下列哪项活动的特点()A.学科活动B.区域活动C.方案活动D.主题活动2.在进行主题选择和活动内容设计时要充分考虑幼儿的特点,要选择那些符合其身心发展水平、促进其适宜发展的内容,这指的是主题活动设计的()A.目的性原则B.适宜性原则C.均衡性原则D.灵活性原则3.幼儿园活动主题的来源不包括()A.学科或领域B.社会生活事件和幼儿自身的生活事件C.文学作品D.教师的想象4.《幼儿园教育指导纲要(试行)》颁布于()A.1980年B.1981年C.2001年D.2007年5.幼儿园的“学科活动”中的“学科”是指()A.理论层次的学科体系B.经验层次的“前学科”体系C.符号表征式的心理阶段D.有系统性的学科组织阳鼎6.幼儿园常见的运动性区域不包括()A.固定器械区B.可移动器材区C.自然游戏区D.角色扮演区二、判断题1.当前幼儿园最具代表性的核心课程是主题活动。
( )2.好听是为主题活动命名的唯一原则。
( ) 3。
一般说来,高年级课程更多地关注学习者的心理逻辑,更多地显现课程的整体性与综合性。
( ) 4.幼儿园学科活动的终极目标是幼儿全面、和谐的发展,而不是掌握科学知识。
( ) 5.区域活动材料越贵、越高级就越对幼儿具有价值。
( )三、填空题1.在幼儿园教育中,_________是经验课程的代表类型。
2.__________是主题活动的核心,起着统领和中心的作用。
3.__________既是主题活动开展的导向,也是评估主题活动效果的标准。
4.目标是对幼儿发展结果的预期,要合理地预期需要对幼儿的“现有水平”和________之间的差距进行研究,这个差距就是心理学上所说的“最近发展区”。
5.根据主题网络建构思路的不同,主题网络图有两种类型,一种是要素网络图,另一种是___________。
6.探索性区域主要包括生活区、语言区、___________、发现区和种养区。
第5章从动件 习题解答.docx

习题5-1从动件的常用运动规律有哪几种?它们各有什么特点?各适用于什么场合?5-2在滚子直动从动件盘形凸轮机构中,若凸轮实际轮廓曲线保持不变,而增大或减小滚子半径,从动件运动规律是否发生变化?5-3何谓凸轮机构的压力角?当凸轮轮廓曲线设计完成后,如何检杳凸轮转角为》时机构的压力角(X?若发现压力角超过许用值,可采用什么措施减小推程压力角?5-4从动件的运动规律如下:^=90° ,八=30°,九=180°,八,=60°,行程h=20mni,推程中以等速运动规律上升;回程以等加速等减速运动规律返回原处。
试用图解法绘制从动件位移线图、速度线图和加速度线图,并分析凸轮机构运动中的冲击特性。
5-5试在下图所示三个凸轮机构中,画出凸轮的基圆以及按规定转向31转过45°时机构的压力角。
5-6用作图法设计偏置直动滚子从动件盘形凸轮机构。
已知凸轮以等角速度顺时针方向回转,凸轮回转中心偏于从动件右侧。
偏距e=10mm,基圆半径r0=40mm,滚子半径r T=10mm,从动件的行程h=20 mm,从动件的运动规律如下:^ = 150 ° , ^=30° ,八=120°,几=60°,从动件在推程以简谐运动规律上升,在回程以等加速等减速运动规律返回原处,试绘出从动件位移线图及凸轮轮廓曲线。
习题解答:5-1从动件的常用运动规律有哪几种?它们各有什么特点?各适用于什么场合?从动件常用运动规律特性比较运动规律Vmax(hco/5t)X amax(h<o/5t2)X冲击推荐应用范围等速 1.0oo刚性低速轻载等加等减速 2.0 4.0柔性中速轻载五次多项式 1.88 5.77无咼速中载余弦加速度 1.57 4.93柔性中速中载正弦加速度 2.0 6.28无高速轻载改进正弦加速度 1.76 5.53无高速重载5-5、(例题)压力角如图所示5-5、解:—3 15-6以凸轮回转中心0为圆心,以及以e为半径作偏距圆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
思 考 题5.1 当热力学系统处于非平衡态时,温度的概念是否适用? 答:温度的概念是指处在同一热平衡状态下的所有热力学系统,在宏观上都具有的一种共同的物理性质。
所以在非平衡态时温度的概念不适用。
5.2 内能和热量的概念有何不同?下面两种说法是否正确? (1)物体的温度愈高,则热量愈多; (2)物体的温度愈高,则内能愈大。
答:内能指物体内所有分子作无规则运动时,分子动能和分子势能的总和。
热量是在热传导方式下物体之间所交换能量的计量。
所以(1)的说法不正确;(2)的说法正确。
5.3 什么是热力学系统的平衡态?气体在平衡态时有何特征?当气体处于平衡态时还有分子热运动吗?答:不受外界影响的条件下宏观性质处于不随时间改变的系统状态叫做平衡态...。
气体处于平衡态时,整个系统热平衡(各部分温度相等);力平衡(各部分压强相等);化学平衡和相平衡(浓度均匀,组成不随时间变化)。
分子热运动始终存在。
5.4 试说明为什么气体热容的数值可以有无穷多个?什么情况下气体的热容为零?什么情况下气体的热容是无穷大?什么情况下是正值?什么情况下是负值?答:气体热容的大小与气体升温的过程或条件有关。
不同的热力学过程,热容的值都是不同的。
因为变化过程可有无穷多个,所以气体热容的数值可以有无穷多个。
绝热过程热容为零。
等温过程热容为无穷大。
系统温度升高,从外界吸热的热力学过程气体热容为正。
系统温度升高,向外界放出热量的热力学过程气体热容为负。
5.5 有可能对物体加热而不致升高物体的温度吗?有可能不作任何热交换,而使系统的温度发生变化吗?答:气体等温膨胀过程吸收外界热量而温度不变。
存在对系统不作任何热交换而温度发生变化情况,如气体的绝热压缩过程。
5.6 讨论理想气体在下述过程中Q W E 、、∆的正负。
(1)等容降压;(2)等压压缩;(3)绝热膨胀。
答:(1)等容过程做功为零,W 为零。
等容降压时温度下降,所以内能减少,E ∆为负。
由热力学第一定律得Q 为负。
(2)压缩过程系统做负功,W 为负。
等压压缩时温度下降,所以内能减少,E ∆为负。
由热力学第一定律得Q 为负。
(3)绝热过程Q 为零。
膨胀过程系统做正功,W 为正。
由热力学第一定律得E ∆为负。
5.7 有人说,因为在循环过程中系统对外做的净功在数值等于p-V 图中封闭曲线所包围的面积,所以封闭曲线所包围的面积越大,循环效率就越高,对吗?答:不正确,因为循环效率取决于系统对外做的净功和系统由高温热源吸收的热量,只有在从高温热源吸收的热量一定的情况下,封闭曲线所包围的面积越大,即系统对外所做的净功越多,循环效率越高,如果从高温热源吸收的热量不确定,则循环效率不一定越高。
5.8 温度差对于热机的驱动是否是必须的,为什么?答:温度差对于热机的驱动是必须的,因为根据热力学第二定律,热机要不断地把吸取的热量变为有用的功,就不可避免地将一部分热量传给低温热源5.9 夏天将冰箱的门打开,让其中的冷空气出来为室内降温,这种方法可取吗?答:不可取,因为电冰箱是对低温端的利用,它在从低温端吸收热量的同时,还要向高温端放出热量,且放出的热量大于从低温端带走的热量,因此打开冰箱门不仅不能降低室温,相反,会使室温升高。
5.10 判别下列说法是否正确:(1)功可以全部转化为热,但热不能全部转化为功;(2)热量能从高温物体传到低温物体,但不能从低温物体传到高温物体。
答:(1)不正确。
因为气体的等温膨胀过程热就可以全部转化为功(2)不正确。
因为如果外界对气体做功,热量就能从低温物体传到高温物体。
5.11 从原理上讲如何计算在始末状态之间进行不可逆过程所引起的熵变。
答:热力学过程的始末状态之间的熵变与具体的过程无关。
对不可逆过程,可选取相同始末状态的可逆过程来计算熵变。
习 题5.1 一热力学系统由如图所示的状态,a 沿acb 过程到达状态b 时,吸收了560J 的热量,对外做功356J 。
(1)如果它沿adb 过程达到状态b 时,系统对外做功220J ,它吸收了多少热量?(2)当系统由b 状态沿曲线ba 返回状态a 时,外界对系统做功为282J ,试问系统是吸热还是放热?热量传递多少?解: (1)J W Q E E acb acb a b 204356560=-=-=-J W E E Q adb a b adb 424220204=+=+-=(2)JW E E Q bab a ba 486)282(204-=-+-=+-=(负号表示系统对外界放了486J 的热量)5.2 64g 氧气的温度由273K 升至323K,(1)保持体积不变;(2)保持压强不变。
在这两个过程中氧气各吸收了多少热量?各增加了多少内能?对外各做了多少功?解:(1)J T C M Q m V V 3,1008.227332331.8253264⨯=-⨯⨯⨯=∆=)(μJ Q E V 31008.2⨯==∆W=0(2)J T C M Q m p p 3,1091.227332331.82253264⨯=-⨯⨯+⨯=∆=)(μ J Q E V 31008.2⨯==∆J E Q W p 331083.010)08.291.2(⨯=⨯-=∆-=5.3 10g 氦气吸收310J 的热量时压强未发生变化,它原来的温度是300K,最后的温度是多少?解:由)(22)(1212,T T R i M T T C MQ m p p -+=-=μμ,得K RM i Q T T 3191031.8)23(4102300)2(2312=⨯⨯+⨯⨯+=++=μ习题5.1图5.4 如图所示,一定量的空气,开始时在状态A ,其压强为2.0atm ,体积为2L ,沿直线AB 变化到状态B 后,压强变为1.0atm ,体积变为3L,求在此过程中气体所做的功。
解:气体所做功等于过程曲线以下的面积 J W 2351052.110)23(10013.1)12(21⨯=⨯-⨯⨯⨯+⨯=-5.5 一定量氢气在保持压强为a P 51000.4⨯不变的情况下,温度由273K 升高到323K 时,吸收了J 4100.6⨯的热量。
(1)求氢气的量是多少摩尔? (2)求氢气内能变化多少?解:(1)由T R i nT nC Q m p p ∆+=∆=22,,得 mol T R i Q n 3.41)273323(31.8)25(100.62)2(24=-⨯⨯+⨯⨯=∆+=(2)J T R i n E 41029.4)273323(31.8253.412⨯=-⨯⨯⨯=∆=∆5.6 标准状态下的2mol 氢气吸收外界500J 的热量。
(1)若体积不变,问这热量变为什么?氢的温度变为多少?(2)若温度不变,问这热量变为什么?氢的压强和体积各变为多少?解:(1)等容过程不做功,由热力学第一定律,有)()(21212T T iR T T R iM E Q V -=-=∆=μ得K iR Q T T 28531.8550027312=⨯+=+= (2)等温过程内能不变,热量变为气体对外做功。
12ln 21V V RT MV dV RT M W Q V V T T μμ===⎰代入数据,得12ln27331.82500V V ⨯⨯= 116.112=V V 35001205.010013.127331.82116.1116.1116.1m p nRT V V =⨯⨯⨯⨯=== a P V nRT p 5221091.005.027331.82⨯=⨯⨯==习题5.4图5.7 2mol 的理想气体在300K 时,从4L 等温压缩到1L ,试求这气体做的功和吸收的热量。
解:12ln 21V V RT M V dV RT M W V V T μμ==⎰J 691241ln 30031.82-=⨯⨯=J W Q T T 6912-==5.8 一定量的氮气,压强为1atm,体积为10L,温度为300K 。
(1)保持体积不变;(2)保持压强不变。
在温度都升到400K 的过程中,各需吸收多少热量?内能增加多少?对外做功多少?解:(1)T T V p i T R M i T R i M T C M Q m V V ∆=∆=∆=∆=111,222μμμJ 33510844.0100300101010013.125⨯=⨯⨯⨯⨯⨯=- J Q E V 310844.0⨯==∆0=V W(2)T T V p i T R M i T R i M T C M Q m p p ∆+=∆+=∆+=∆=111,222222μμμ J 3351018.1100300101010013.127⨯=⨯⨯⨯⨯⨯=- 因为内能仅是温度的函数,所以本题中两个过程的内能增量相同。
有J E 21044.8⨯=∆J E Q W p p 33310336.010844.01018.1⨯=⨯-⨯=∆-=5.9 一定质量的理想气体,其γ=1.40,若在等压下加热,使其体积增大为原体积的m 倍为止。
试求传给气体的热量中,用于做功与增加内能的热量之比。
解:5,4.1==i 即,所以是双原子分子因γ 等压过程中V 和T 为变量,有T nR V p W p ∆=∆=T R in E ∆=∆25222==∆∆=∆∴i T R in T nR EW p5.10 有1mol 的氧气,温度为300K 时,体积为0.002m3,试计算下列两种过程中氧气所做的功:(1)绝热膨胀到体积为0.023;(2)等温膨胀到体积为0.023解:(1)由绝热过程方程常量=-T V1γ,有111212T V T V --=γγK V V T T 4.119)02.0002.0(300)(14.112112=⨯==--γ JTR in E W Q 31075.3)3004.119(31.8252⨯=-⨯⨯-=∆-=∆-=(2)J V V RT M W T 3121074.5002.002.0ln 30031.81ln ⨯=⨯⨯⨯==μ5.11 一作卡诺循环的热机,高温热源的温度为400K,每一循环从此热源吸进100J 的热量并向一低温热源放出80J 的热量.求(1) 该循环的热机效率; (2) 低温热源温度. 解:(1)%2010080100121=-=-=Q Q Q η (2)对于卡诺热机,其效率为121T T -=η 所以 K K T T 320400%)201()1(12=⨯-=-=η5.12 有一卡诺制冷机,从一温度为-10℃的冷藏室中吸取热量,而向温度为20℃的物体(通常为水)放出热量,设该制冷机所耗功率为15kW ,问每分钟从冷藏室中吸取的热为多少,每分钟放热为多少?解:卡诺制冷机的制冷系数为302632632932632122=-=-==T T T W Q e 所以每分钟从冷藏室中吸收的热量为J J eW Q 6321089.760101530263⨯=⨯⨯⨯== 此时,每分钟向温度为20℃的物体放出的热量为J J W Q Q 656211079.8)1091089.7(⨯=⨯+⨯=+=5.13 一卡诺热机的低温热源温度为7℃,效率为40%,若要将其效率提高到50%,求高温热源的温度需要提高多少?解:卡诺热机的效率为:121T T -=η 可得,K K T T 46740.017273121=-+=-=η K K T T 56050.017273111211=-+=-=η所以 K K T T T 93)467560(11=-=-=∆5.14 一热机在1000K 和300K 之间工作,若(1)高温热源温度提高到1100K ;(2)低温热源温度降低到200K ,求理论上热机效率各增加多少?为了提高热机的效率,那一种方案更好?解:卡诺热机的效率为%7010003001112=-=-=T T η 第一种方案热机的效率为%73110030011121=-=-=T T η 第二种方案热机的效率为2212001180%1000T T η=-=-= 虽然第二种方案的热机效率高,但制冷过程本身就要耗能,所以应选第一种方案。
