(整理)基于ABAQUS复合材料薄壁圆筒的屈曲分析.

合集下载

abaqus压杆屈曲分析

压杆屈曲分析1.问题描述在钢结构中，受压杆件一般在其达到极限承载力前就会丧失稳定性，所以失稳是钢结构最为突出的问题。

压杆整体失稳形式可以是弯曲、扭转和弯扭。

钢构件在轴心压力作用下，弯曲失稳是常见的失稳形式。

影响轴心受压构件整体稳定性的主要因素为纵向残余应力、初始弯曲、荷载初偏心及端部约束条件等。

实际的轴心受压构件往往会存在上述的一种或多种缺陷，导致构件的稳定承载力降低。

本文利用abaqus对一定截面不同长细比下的H型钢构件进行屈曲分析，通过考虑材料非线性、几何非线性并引入初弯曲，得出构件发生弯曲失稳的极限荷载。

通过比较不同长细比下的弯曲失稳的临界荷载得出构件荷载位移曲线，并与《规范》中的构件曲线相比较。

钢构件的截面尺寸如图1-1所示。

构件的材料特性： , ,图1-12.长细比计算通过计算截面几何特性，截面绕y轴的回转半径为 ,长细比取值及杆件长度见表1：表13.模型分析ABAQUS非线性屈曲分析的方法有riks法，general statics法（加阻尼），或者动力法。

非线性屈曲分析采用riks算法实现，可以考虑材料非线性、几何非线性已及初始缺陷的影响。

其中，初始缺陷可以通过屈曲模态、振型以及一般节点位移来描述。

利用abaqus进行屈曲分析，一般有两步，首先是特征值屈曲分析，此分析为线性屈曲分析，是在小变形的情况进行的，也即上面提到过的模态，目的是得出临界荷载（一般取一阶模态的eigenvalue乘以所设定的load）。

其次，就是后屈曲分析，此步一般定义为非线性，原因在于是在大变形情况进行的，一般采用位移控制加修正的弧长法，可以定义材料非线性，以及几何非线性，加上初始缺陷，所以也称为非线性屈曲分析。

此步分析，为了得到极限值，需要得出荷载位移曲线的下降段。

缺陷较小的结构初始位移变形较小，在极值点突变，而初始缺陷较大的结构，载荷位移曲线较平滑。

4.建模计算过程建模计算过程以长细比为50的构件为例，其余构件建模计算过程与之类似。

abaqus屈曲分析报告实例

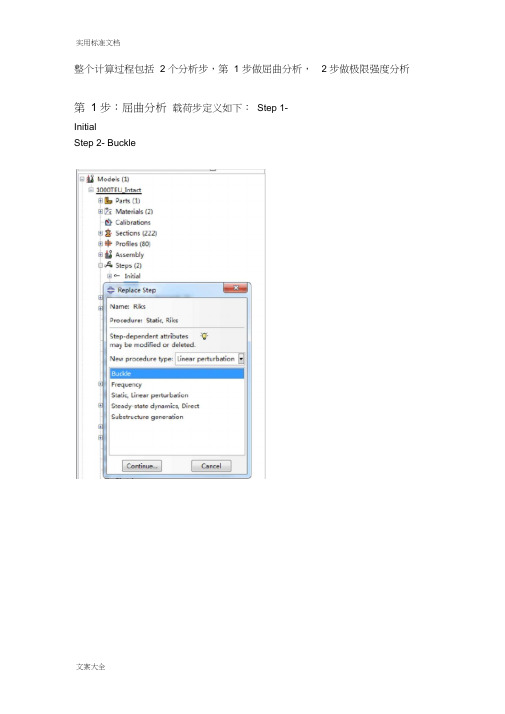
实用标准文档整个计算过程包括 2 个分析步，第 1 步做屈曲分析，第 1 步：屈曲分析载荷步定义如下：Step 1-InitialStep 2- Buckle2 步做极限强度分析0奪莖UWICWHIK . 叽I J I*' *iirl |U*ii:* ri«-2- c.仲［U**t Wfl| «R =・|0T* |«|M4 11 屮W Ml 町扌垮・3 4M4; *E>|轴亠白*wr»44* «*M *A*S MMM-in 4414-* Ita1! I >H*d *■.■ Lrfi|i-t*b*i UWi^ *4」>jU***^ ::切2冲<a：K-.L口sMwSniLpc^l Efl «o 誓光n-3 wa HF HB・・n c:^ > q士* f *B£ -A <MI '■■*W■uTp*』«MLrii4 *M；■pofit ■直j.i t…叫町■ ' H.,机...i . r |fl»-L , | |-£I -t fr E叶*盅1并在Model-Edit Keywords 的图中位置加入下面的文字，输出屈曲模态*nodefile, global=yesU,Create job 名称为“ Buckling点击continue ，完成第 1 步的计算第 2 步：极限强度分析将“ buckle ”分析步替换为“ riks ”分析步在Basic 选项卡中，Nlgeom：选择打开在Instrumentation 选项卡中，定义如下参数，然后点击OK Array定义一个新计算工作，输入名称，点击continue在Parallelization 选项卡，选择 2 个CPU，如下所示，点击OK。

在此编辑Model-edit keywords ，删除“第 1 步”加入的文字“ *nodefile, global=yesU,”，并在下图位置加入下段文字：*imperfection, file=buckling, step=1 1, 2.5点击OK，再保存文件最后提交计算。

abaqus弯曲应变 -回复

abaqus弯曲应变-回复题目：Abaqus中的弯曲应变及其解析步骤摘要：本文将详细介绍Abaqus软件中的弯曲应变分析及其解析步骤。

首先，我们将回顾弯曲应变的概念和公式。

然后，我们将介绍如何在Abaqus 中进行弯曲应变分析，包括创建模型、定义材料和边界条件、应用加载以及求解结果。

最后，我们将总结分析结果并探讨一些应变分析的应用。

1. 弯曲应变的概念和公式在工程实践中，弯曲应变是指在受到弯曲载荷时材料内部发生的应变变化。

弯曲应变可通过以下公式计算：ε= (M*y) / (E*I)其中，ε表示弯曲应变，M为弯矩，y为距离截面中心轴的垂直距离，E为弹性模量，I为截面惯性矩。

2. Abaqus中的弯曲应变分析步骤2.1 创建模型在Abaqus中创建弯曲应变分析模型通常需要以下步骤：- 导入几何信息：通过导入CAD文件、绘制几何形状或使用Abaqus中的几何建模工具创建模型的几何形状。

- 创建单元网格：选择适当的单元类型（如三角形、四边形或六边形单元）来划分模型，并生成单元网格。

- 定义截面属性：通过指定截面属性参数（如底座宽度、高度等）来描述弯曲截面。

2.2 定义材料和边界条件在Abaqus中，可以定义不同的材料性质和边界条件来模拟弯曲应变。

以下是一些常见的定义步骤：- 定义材料属性：指定材料的弹性模量、泊松比等力学性质。

- 定义边界条件：设置支撑和加载条件，如固支条件、平移约束和加载类型（如压力、位移等）。

2.3 应用加载加载是模拟弯曲应变的关键步骤之一。

在Abaqus中，可以通过施加不同类型的加载来模拟弯曲载荷，例如施加均布载荷或施加集中载荷。

2.4 求解结果在完成模型的几何配置、材料属性和加载条件的定义后，可以使用Abaqus 求解器来求解弯曲应变问题。

求解可以包括静态或动态分析，根据分析的需要进行选择。

3. 分析结果和应用完成求解后，可以使用Abaqus的后处理工具来分析和可视化结果。

一些常见的分析结果包括应变分布图、位移分布图和应力分布图。

abaqus屈曲分析报告实例

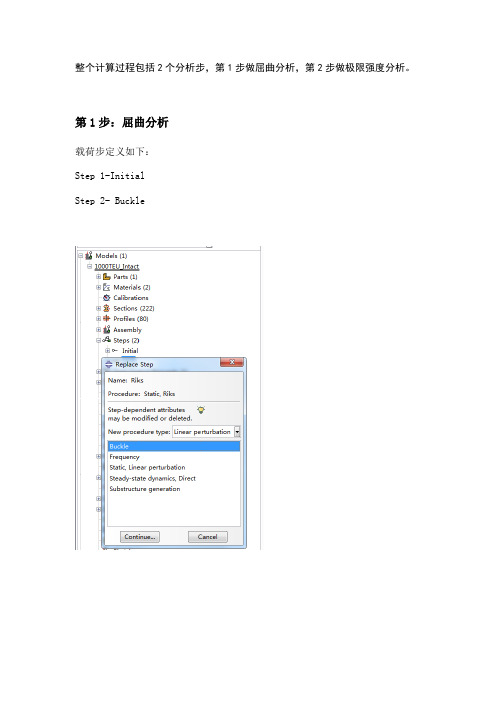
整个计算过程包括2个分析步，第1步做屈曲分析，第2步做极限强度分析。

第1步：屈曲分析载荷步定义如下：Step 1-InitialStep 2- Buckle并在Model-Edit Keywords的图中位置加入下面的文字，输出屈曲模态*nodefile, global=yesU,Create job 名称为“Buckling”点击continue，完成第1步的计算。

第2步：极限强度分析将“buckle”分析步替换为“riks”分析步在Basic选项卡中，Nlgeom：选择打开在Instrumentation选项卡中，定义如下参数，然后点击OK定义一个新计算工作，输入名称，点击continue在Parallelization选项卡，选择2个CPU，如下所示，点击OK。

在此编辑Model-edit keywords，删除“第1步”加入的文字“*nodefile, global=yesU,”，并在下图位置加入下段文字：*imperfection, file=buckling, step=11, 2.5点击OK，再保存文件。

最后提交计算。

提取计算结果进入visualization Module点击 Create XY data选择 ODB filed output，点击continuePosition选择 Unique Nodal， CF：point loads选择 CF2，再点击elements/nodes选项卡，选择跨中载荷加载点，最后点击save。

重复上一步操作，Position选择 Unique Nodal， U：spatial displacement 选择 U3，再点击elements/nodes选项卡，选择板格中心点，最后点击save。

点击Create XY data, 选择operate on XY data，点击continue选择Combine（X,X）命令，横坐标选择保存的displacement曲线，纵坐标选择保存的Point load曲线，点击最后一行Create XY Data与Save as。

薄壁球壳压缩非对称屈曲特性的实验及有限元分析

薄壁球壳压缩非对称屈曲特性的实验及有限元分析周刚毅;董新龙;郝伟伟【摘要】The deformation behaviors of thin-walled spherical shells subject to quasi-state and dynamic com-pression are studied experimentally. The process of deformation, the non-axisymmetric buckling characteristic and its influence factors are analyzed in detail using ABAQUS finite element code. The results show that the deformation modes are dependent on the impact velocity. It is found that, if impact loading speed increases, the collapse modes shift from pentagons to hexagons. The dynamic loading-deformation curve on which the impact velocity is not very high is in good consistence with its quasi-static one. Meanwhile, the load-deformation curves of FEM simulation conform well to the experimental results at the stage of axi-symmetric inward dimple, but it is not so at the non-axisymmetric buckling stage. Furthermore, the process of deformation of spherical shells and its effect factors are discussed, suggesting that the contact constraints of surface between spherical shell and rigid plate play a significant role in the process of non-asymmetric deformation.%采用实验方法研究了球壳在刚性板准静态和冲击压缩下变形特性及非对称屈曲模态，结合ABAQUS有限元分析了球壳冲击压缩下的屈曲变形过程、非对称屈曲特性，探讨了其影响因素。

abaqus屈曲分析报告实例

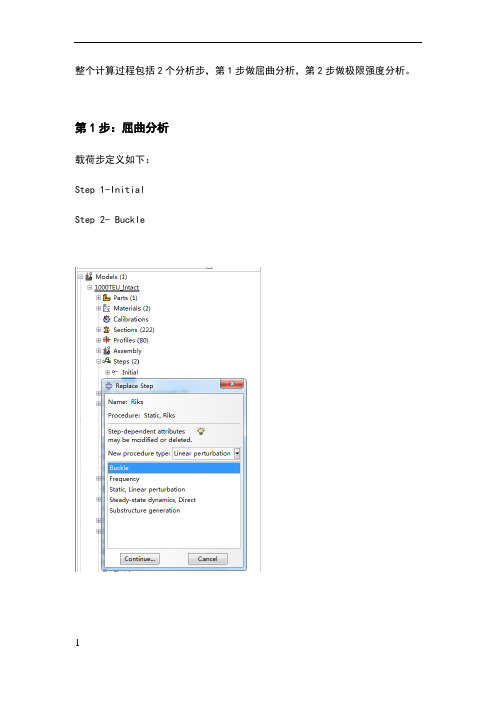
整个计算过程包括2个分析步，第1步做屈曲分析，第2步做极限强度分析。

在此编辑Model-edit keywords，删除“第1步”加入的文字“*nodefile, global=yesU,”，并在下图位置加入下段文字：*imperfection, file=buckling, step=11,点击OK，再保存文件。

最后提交计算。

提取计算结果进入visualization Module 点击 Create XY data选择 ODB filed output，点击continuePosition选择 Unique Nodal， CF：point loads选择 CF2，再点击elements/nodes选项卡，选择跨中载荷加载点，最后点击save。

重复上一步操作，Position选择 Unique Nodal， U：spatial displacement 选择 U3，再点击elements/nodes选项卡，选择板格中心点，最后点击save。

ABAQUS中的屈曲分析riks

ABAQUS中的屈曲分析riks
RIKS 法将施加的荷载也作为一个未知量，通过同时约束荷载水平和位移向量来达到对非线性问题得求解，它属于一种广义得位移控制法，采用该迭代控制方法能较好地计算临近极值点结构地反映和下降段问题。

它的基本思想是引入一个在几何上相当于解曲线弧长的参数，通过控制弧长参数来实现每个增量步，从物理意义上看，这相当于对位移和荷载的综合控制。

当结构到达荷载极限点附近或结构进入下降段时，Newton －Raphson 法无法追踪结构的下降段，如图28所示情况需要采用弧长法进行求解。

弧长的定义为：
1)(+??=?T N
i N i i v l νλ 式中：l ?为增加的弧长
i λ?为荷载增加系数
N
i ν为位移增量与初次迭代得到的最大位移绝对值之比
图28 失稳状态下的荷载发展
图29 RIKS 法示意图
图29为RIKS 法计算过程中的迭代示意图。

具体计算流程如下所示：
初始情况下：
对于 i=迭代步 (i=1,2,3,etc): a. 形成内部节点应力矩阵I N
b. 检查平衡方程
如果R i N 足够小，则计算收敛，否则求解方程
得到v i N 和c i N
c. 将初始矢量（1,N i v ）加上（N i N i c ρ,）（其中N
N N i i P P R /=ρ），这样解就由点A 1移动到点A 2,如图29所示。

求解等式
得到：
则最终的解为：
d. 更新到下一次迭代
返回到a，进行下一步迭代。

基于ABAQUS复合材料薄壁圆筒的屈曲分析

基于ABAQUS复合材料薄壁圆筒的屈曲分析由于玻璃钢复合材料的薄壁圆筒结构具有强度高、重量轻、刚度大、耐腐蚀，电绝缘及透微波等优点，目前已广泛应用于航空航天和民用领域中。

工程中广泛使用的这些薄壁圆筒，当它们受压缩、剪切、弯曲和扭转等荷载作用时，最常见的失效模式为屈曲。

因此，为了保证结构的安全，需要进行屈曲分析。

对结构进行屈曲分析，涉及到较复杂的弹(塑)性理论和数学计算，要通过求解高阶偏微分方程组，才能求解失稳临界荷载，而且只有少数简单结构才能求得精确的解析解。

因此，只能采用能量法、数值方法和有限元方法等近似的分析方法进行分析。

近20年来，随着计算机和有限元方法的迅猛发展，形成了许多的实用分析程序，提高了对复杂结构进行屈曲分析的能力和设计水平。

ABAQUS 就是其中的杰出代表。

1.屈曲有限元理论有限元方法中，对结构的屈曲失稳问题的分析方法主要有两类：一类是通过特征值分析计算屈曲载荷，另一类是利用结合Newton—Raphson迭代的弧长法来确定加载方向，追踪失稳路径的几何非线性分析方法，能有效分析高度非线性屈曲和后屈曲问题。

1.1线性屈曲假设结构受到的外载荷模式为P0。

，幅值大小为λ，结构内力为Q，则静力平衡方程应为λP0=λQ进一步考察结构在(λ+△λ)P0载荷作用下的平衡方程，得到K E+K S S+λ△S+K G u+λu△u=△λP0由于结构达到保持稳定的临界载荷时有△λ，代入上式得K E+λK S△σ+K G△u△u=0该方程对应的特征值问题为det K E+λK S△σ+K G△u=0如果忽略几何刚度增量的影响，屈曲分析的方程又可进一步简化为det K E+λK S△σ=0该方程即为求解线性屈曲的特征值方程。

λ为屈曲失稳载荷因子，△u为结构失稳形态的特征向量。

1.2非线性屈曲非线性屈曲分析方法多采用弧长法进行分步迭代计算，在增量非线性有限元分析中，沿着平衡路径迭代位移增量的大小(也叫弧长)和方向，确定载荷增量的自动加载方案，可用于高度非线性的屈曲失稳问题。

ABAQUS屈曲分析课件

Abaqus用法
• 对称结构的屈曲模态形状可以是对称
或反对称的
对于这种结构，高效的计算方法为：建立部分模型，执行两次屈曲分析，分别施加对称边界条件和反对称边界条件。
活荷载通常具有对称形式，因此
需要设置对称边界条件用于计算摄动应力，进而形成初始应力刚
度矩阵。
Abaqus用法
• 边界条件必须在*Buckle分析步中转换
A
A
A-A截面
矩形横截面线弹性材料端点铰接
几何非线性
静ቤተ መጻሕፍቲ ባይዱ分析失败
整体后屈曲：框架角点的轨迹线
整体后屈曲：荷载 VS位移
特征值屈曲分析
结构稳定性
失稳多发生于梁结构和壳结构中，即细长结构和薄壁结构。稳定性研究需要的分析类型：
•
•
特征值屈曲分析(线性摄动分析)
后屈曲或压溃分析(非线性分析)
对多数的刚性结构分析而言，即使在屈曲前出现少量的非弹性响应，特征值屈曲分析仍可以对压溃模态形状提供有价值的预测。
只有在非常严格的限制条件，才可以只借助特征值屈曲分析就能
得到结构的压溃极限。
特征值屈曲分析
后屈曲分析
很多情况下，后屈曲响应是不稳定的，压溃荷载强烈依赖于原始几何的缺陷，即所谓的“缺陷敏感性”。压溃荷载值可能远远低于特征值屈曲分析的预测值，因此特征值屈曲分析对结构的承载能力的预测是偏于危险的。
静态后屈曲分析
• 非线性稳定分析
在该过程中，载荷增加到一定程度时，结构将发生跳跃失稳，从一个平衡状态跳跃到另一个平衡状态，但其过程是一个不稳定的状态，如下图所示：
在这类分析中，载荷-变形的响应表现出负刚度的特点，并且必须释放一定应

3飞行器力学实验报告-薄壁圆筒特征值屈曲分析

（以下为实验报告正文）一、实验目的薄壁结构的特征值屈曲分析二、实验条件Ansys2021R1三、实验内容薄壁结构，高度10m，厚度0.5m，圆筒外径15m，薄壁圆筒的参数：弹性模量3e+11Pa,泊松比.0.3四、实验步骤一、启动在开始中找到并点击Workbench 2021 R1二、设置材料属性点击【工程数据】-选择【结构钢】二、构建几何模型将【静态结构】拖至项目管理图中，在项目列表静态结构系统中右键点击几何结构，选择【在新的 design Modeler几何结构】，在静态结构 design Modeler 模块点击 XY 平面，并点击【草图绘制】画圆，再点击【维度】-【半径】输入15，摁回车键。

点击【挤出】-【几何结构】应用-【FD1深度】10-【按照薄/表面】是-【内部厚度】0.5-【生成】。

如图1所示：图1图2三、返回Workbench界面，双击【模型】进入【mechanical ANSYS mechanical enterprise】界面，点击【网格】-设置【单元尺寸】为5，四、设置约束，点击【静态结构】-【固定的】-选择侧面-【应用】，点击【载荷-力】选择侧面-【应用】，大小设置200N,方向与约束方向相反。

如图2所示.五、分别右击【求解】-【插入】-【变形】-【总计】，【求解】-【插入】-【应变】-【等效】，【求解】-【插入】-【应力】-【等效】。

六、结果如下图所示六、讨论这个练习过程中出现了几次错误，刚开始用的是mechanical，由于不熟练建模出现了问题，参数设置的也不对，导致实验失败，经过多次尝试，选择了workbench，最终还是完成了实验，世上无难事，只要肯登攀。

abaqus屈曲分析实例

整个计算过程包括2个分析步，第1步做屈曲分析，第2步做极限强度分析第1步：屈曲分析载荷步定义如下:Step 1-I nitialStep 2- BuckleI TTat ji-^i.4hje> ] iiDQLi-j^l - n-J 岀贞 /!]■： ilCil 巩 %Q J^：ree4 ibOui' Ltvfr 3KJ -1 8i I 4 3 E&fr puufiE -30 . H5D . I xid ：」Q vOii^Ct 0 -iOD如 Ifie iA^Jnie jiB<lL*T^I in-^ w W K HT K 凶 -!■?» . *lfcU 劭彊 irspcci C* I he ?sw<-B y McEfcDi 叱 a __, The K ^-L dUi^cjbx ftJ5 bwe x" w ' j Tt*p AJL ^ZL L IMA :-se- ] L n-]l M41 u ・[MM I 昭申・3n 1 h ■] H ■鼻T ifi 1F 声时 >■:丹匸!"」F gM 5'!i rjHr ^ *>■卯**并在Model-Edit Keywords 得图中位置加入下面得文字，输出屈曲模态 *no defile, global=yesU,*9^8^4 Iri’S5ta (ijF®[^z2frrELl m.u C HMMT j Cm^ j Ji w^Ui ffi PnocidaJ* cpP«- Lnaar pmu<±M»n z —… . »-2? r jfm - Mkrp9H “ ■ ■ mwwjj i»r--亠 WT.J? 1"■ ■ ■ T ■ Z9MWJ/ •■»*■•士 iew Step QulpUt Other loc^s Plug-ins JHelp中Create job 名称为“ Buckling点击continue ,完成第1步得计算□ E STl|^ B al^xJI^^tuAX 1 a 3 日 ModelL ____ —一 -42 MtEd IOC Rena™[irlew& Cal hration^Modd Viewport Copy Mcxirl ■Cog/ ObjA-cte.i-EcSt j^rdbifli 啊 ►Edit Kr^wtirdi ftriechilK 目 Sftip y Me d 曲 |' 1 t 區 Eedti 口ns (2J 2}m i^. m _____ f*l _，-第2步：极限强度分析将“ buckle 分析步替换为“ riks 分析步fl* 腿□&! Vn^gpGtff S*E Q*TP M + Ehfif fwh -"i^ r m Brip W□ &屮f 丸乂目Ml*呂匕门口巳巴iJJl 11 iSe** S JB 12v 如m CW= Tedi 訓ujj 亠,貯 tj 』口屮 AtddvsyCAE 6-1Mcdd Resu^朗Qi5rll r y M CK IH I tu-JlCgF 俺 UJjp 加。

薄壁结构的屈曲分析与优化设计

薄壁结构的屈曲分析与优化设计薄壁结构在工程领域中应用广泛，如建筑物的框架结构、航天器的外壳等。

然而，由于其结构的特殊性，薄壁结构在长时间的使用过程中，可能会发生屈曲失稳的问题。

因此，对于薄壁结构的屈曲分析和优化设计显得尤为重要。

本文将探讨薄壁结构的屈曲特性，介绍屈曲分析的方法，并讨论优化设计的原则。

一、薄壁结构的屈曲特性薄壁结构的主要特点是横向尺寸较大、纵向尺寸相对较小。

这种结构使得薄壁构件具有较高的刚度和承载能力，但也容易发生屈曲失稳。

薄壁结构在承受压力时，当应力超过一定临界值时，会引发局部稳定性的失效，即屈曲现象。

二、薄壁结构的屈曲分析方法1. 线性屈曲分析线性屈曲分析是最常用的屈曲分析方法之一。

该方法假设结构的材料和几何性质均呈线性关系，基于弹性力学原理，通过求解线性方程组来确定结构的屈曲载荷和屈曲模态。

2. 非线性屈曲分析在实际应用中，薄壁结构往往存在几何非线性和材料非线性等因素。

因此，采用非线性屈曲分析方法可以更准确地模拟薄壁结构的屈曲行为。

非线性屈曲分析方法主要包括基于有限元法的屈曲分析和基于实验的屈曲分析。

三、薄壁结构的优化设计原则在进行薄壁结构的优化设计时，需要考虑以下几点原则：1. 结构的稳定性：优化设计的目标是提高结构的整体稳定性，减轻屈曲失稳的风险。

因此，在设计中应合理选择结构的截面形状、尺寸和材料等参数。

2. 强度与刚度的平衡：考虑到结构的强度和刚度需求，优化设计应在确保结构强度的前提下，尽量减小结构的质量和成本。

3. 材料的选择：优化设计中应根据结构的要求选择合适的材料，以满足结构的刚度和强度要求。

同时，还需考虑材料的经济性和可靠性。

4. 结构的几何形状：结构的几何形状对于屈曲特性有着重要影响。

在优化设计中，可以通过调整结构的几何形状（如长度、宽度、高度等）来改变结构的屈曲行为。

根据以上原则，可以采用多种方法进行薄壁结构的优化设计。

例如，可以结合有限元法进行结构的拓扑优化，通过改变结构的截面形状和数量，来获得最优的结构形态。

(整理)基于ABAQUS复合材料薄壁圆筒的屈曲分析

工程中广泛使用的这些薄壁圆筒，当它们受压缩、剪切、弯曲和扭转等荷载作用时，最常见的失效模式为屈曲。

因此，为了保证结构的安全，需要进行屈曲分析。

因此，只能采用能量法、数值方法和有限元方法等近似的分析方法进行分析。

近20年来，随着计算机和有限元方法的迅猛发展，形成了许多的实用分析程序，提高了对复杂结构进行屈曲分析的能力和设计水平。

ABAQUS 就是其中的杰出代表。

1.1线性屈曲假设结构受到的外载荷模式为。

，幅值大小为，结构内力为Q，则静力平衡方程应为进一步考察结构在载荷作用下的平衡方程，得到由于结构达到保持稳定的临界载荷时有，代入上式得该方程对应的特征值问题为如果忽略几何刚度增量的影响，屈曲分析的方程又可进一步简化为该方程即为求解线性屈曲的特征值方程。

为屈曲失稳载荷因子，为结构失稳形态的特征向量。

与提取特征值的线性屈曲分析相比，弧长法不仅考虑刚度奇异的失稳点附近的平衡，而且通过追踪整个失稳过程中实际的载荷、位移关系，获得结构失稳前后的全部信息，适合于高度非线性的屈曲失稳问题。

Abaqus屈曲分析（一）线性特征值屈曲

Abaqus屈曲分析（⼀）线性特征值屈曲∨本⽂由CAE数值优化轻量化授权转载结构稳定性问题是我们⽇常⽣活中经常遇到的问题，主要是发⽣在梁或壳结构中。

屈曲是⼀种失效模式，其特征是构件在⾼压应⼒作⽤下突然失效。

屈曲失效的实际压应⼒⼩于材料能够承受的最终压应⼒。

当构件或结构将膜应变能转换为弯曲应变能⽽外部施加的载荷不变时，会发⽣屈曲失效。

先来看⼀个简单的结构：⼀个长为L的细长杆，横截⾯积为A。

轴向刚度ka远⼤于弯曲刚度kb。

因此，微⼩的膜变形可以吸收⼤量的应变能。

然⽽，需要较⼤的横向挠度和横截⾯旋转来吸收弯曲中的能量。

如果让弯曲来吸收膜应变能，挠度将会远⼤于轴向变形。

⼏种典型稳定性问题：板件屈曲-分⽀问题：⼀般情况下，⼩的初始缺陷对平板的后屈曲响应没有显著影响，但可能影响屈曲⽅向。

突弹跳变（snap-through）-极限载荷问题预屈曲段的结构响应是⾮线性的。

因此，需要进⾏⼏何⾮线性分析来准确研究预屈曲⾏为。

结构不稳定发⽣在⼀个负载最⼤(极限载荷点)位置。

⼀旦解在点A处变得奇异，结构就从A点翻转到B点。

在快速翻转过程中，响应变为动态的，结构释放弹性能转化为动能。

在B点存在⼀个稳定的静⼒平衡状态。

超过这⼀点，载荷P可以再次增加。

⽆加强筋的圆筒屈曲结构对⼩的初始缺陷表现出很强的敏感性。

对初始缺陷的考虑将分岔问题转化为极限载荷问题。

屈曲问题本质特征：A类问题：在分叉点前为线性响应B类问题：在缺陷敏感结构分叉点前为⾮线性响应缺陷敏感：实际结构的坍塌载荷受载荷⽅向、⽀承⽅式或⼏何形状的微⼩变化的强烈影响。

这些结构往往是求极限载荷问题。

ABAQUS⼀般有两种分析⼿段来处理这类分析问题：特征值屈曲分析和后屈曲分析。

A：线性特征值屈曲分析（针对A类问题）：1. ⽤于估计刚性结构的临界(分岔)载荷。

2. 使⽤abaqus线性扰动求解。

通常⽤来估计刚性结构的临界屈曲载荷。

想要特征值屈曲分析可以得到可靠的屈曲载荷的估计，需要满⾜以下假设前提：⼩⼏何变化、线性弹性材料响应，且缺陷不敏感。

基于ABAQUS的内压厚壁圆筒的弹塑性分析

基于ABAQUS的内压厚壁圆筒的弹塑性分析基于ABAQUS的内压厚壁圆筒的弹塑性分析学院：航空宇航学院专业：工程力学指导教师：姓名：学号：1. 问题描述一个受内压的厚壁圆筒（如图1），内半径和外半径分别为mm a 10=和mm b 15=（外径与内径的比值2.15.11015b >==a ），受到均匀内压p 。

材料为理想弹塑性钢材（如图2），并遵守Mises 屈服准则，屈服强度为MPa Y 380=σ，弹性模量GPa E 200=，泊松比3.0=υ。

图1 内压作用下的端部开口厚壁圆筒图2 钢材的应力-应变行为首先通过理论分析理想弹塑性材料的厚壁圆筒受内压作用的变形过程和各阶段的应力分量，确定弹性极限压力e p 和塑性极限压力p p ；其次利用ABAQUS 分析该厚壁圆筒受内压的变形过程，以及各个阶段厚壁筒内的应力分布，与理论分析的结果进行对比，验证有限元分析的准确性。

2. 理论分析 2.1基本方程由于受到内压p 的作用，厚壁圆筒壁上受到径向压应力r σ、周向压应力θσ和轴向应力z σ的作用，由开口的条件可推出0=z σ。

因为这是一个轴对称问题，所有的剪应力和剪应变均为零。

平衡方程和几何方程用下式表示：0-=+rd d r r r θσσσ （1）rudr du r r r ==θεε, （2）弹性本构关系为：()()r r r EE συσεσυσεθθθ****1,1-=-=（3）由于此问题为平面应变问题，所以上式中2*1υ-=E E υυυ-=1*相应的边界条件为：0,=-===b r r a r r p σσ （4）2.2弹性阶段根据弹性力学中的应力解法：取应力分量r σ，θσ为基本未知函数，利用平衡方程和应力表示的协调方程联合求解，可得应力分量的通解⎪⎪⎩⎪⎪⎨⎧=+=221221-r C C r C C r θσσ 将边界条件带入可得应力分量为：⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎫ ⎝⎛+-=⎪⎪⎭⎫⎝⎛-=11--2222222222r b a b p a r b a b p a r r σσ （5）因为b r a ≤≤，所以00>≤θσσ且r ，可以观察到：r z σσσθ≥=>0，分析采用Mises 屈服准则，表达为()()()()222222226Yz rz r z z r r στττσσσσσσθθθθ=+++-+-+- （6）该厚壁圆筒是轴对称平面应变问题，即0===θθτττz rz r ，由Mises 屈服条件其表达式可得到：Y Y r σσσσθ155.132==- （7）当内压p 较小时，厚壁圆筒处于弹性状态，在a r =处，()r σσθ-有最大值，筒体由内壁开始屈服，此时的内压为e p ，由式（5）、（7）联立可求得弹性极限压力为()2222155.1ba b p Y e σ-= （8）代入题目所给数据得到弹性极限压力为：()MPa p e 92.1211521015380155.1222=⨯-⨯= 2.3 弹塑性阶段当e p p <时，圆筒处于弹性状态，当e p p >的情况，在圆筒内壁附近出现塑性区，产生塑性变形，随着内压的增大，塑性区逐渐向外扩展，而外壁附近仍为弹性区。

对基于ABAQUS的薄壁件多点柔性加工变形的研究

对基于ABAQUS的薄壁件多点柔性加工变形的研究作者：王腾飞来源：《科技风》2020年第17期摘要：本文简要概述了多点柔性的研究基础，介绍了有限元软件的建模过程，并且借助有限元软件，研究薄壁件在实际加工过程的变形影响。

分别从支撑单元密度、单元之间距离、夹持力三个角度展开研究，总结了薄壁件的最优布局，是以占用最少资源、优化调配时间为基础展开的装夹布局。

关键词：ABAQUS;薄壁件;加工变形大型航空器的薄壁件，具有尺寸大、韧性低、加工精度细致、工艺性能不佳等特征，极易产生加工变形问题;在装夹力、切削力的作用下，薄壁件的加工变形问题尤为突出。

航空器零件的加工精细工艺，关乎着航空器后期的装配流程，因此，控制薄壁件加工变形问题，成为当前亟需解决的工艺性能问题。

1 建模1.1 多点柔性的研究理念柔性工艺理念拥有独立的工装系统，包含：X向导轨、工件、底座、Y向导轨、真空吸盘、气路开关、Z向支柱、真空发生器、空气压缩机等。

此系统是综合利用真空发生器，采取定位夹紧薄壁件的方式，结合作业需求，开展支撑单元的方阵阵列布置，阵列布置应满足m×n 配置。

其中m为X向导轨上支撑单元的个数，应满足在X轴移动的运动条件;n为Y向导轨上的动梁数，应符合在Y轴的运动规律;m与n之间的关系，应理解为：每个动梁n1拥有支撑单元m个。

通过简化模型可知，当m值不小于8时，满足薄壁件的工艺需求。

1.2 ABAQUS建模有限元模型，以航空器机身舱门零件布局为参考，展开薄壁件加工变形分析。

有限元模型的分析优势：有利于简化航空器薄壁件柔性夹具布局结构的分析流程，开展具有非线性的动态分析，研究航空器薄壁件的变形规律，建立以多点柔性为实体支撑的有限元分析模型，设置薄壁件加工变形的测量线，研究薄壁件在加工过程中的等效塑性变化规律。

2 基于有限元模型分析多点柔性变化规律2.1 以单元密度作为控制变量综合参考控制变量单元密度，包含的动态因素有：铣削工艺、吸盘吸附能力;配置支撑单元的布局结构，共设置9组多点柔性布局，分别为：①：3×3，②：3×4，③：3×5，④：3×6，⑤：3×7，⑥：4×5，⑦：4×6，⑧：4×7，⑨：4×8。

基于ABAQUS的薄壁圆筒零件车削加工变形补偿计算

基于ABAQUS的薄壁圆筒零件车削加工变形补偿计算陈双喜【期刊名称】《组合机床与自动化加工技术》【年(卷),期】2008(000)011【摘要】利用有限元技术提出了薄壁零件车削加工变形补偿量计算的新思路:建立了薄壁圆筒零件车削加工的三维有限元模型,结合切削力计算公式、测量点的变形数据,借助ABAQUS二次开发技术(PYTHON语言)计算刀具补偿量.首先试验加工零件,通过记录零件加工前后尺寸,可以计算出变形量,然后建立参数化有限元模型,利用ABAQUS多步计算出加工过程中刀具受力点的支反力,通过数值方法(如最小二乘法、线性回归法)归纳出切削力计算公式,最后利用Abaqus软件的数据输入输出接口,修改工件车削加工的输入参数,通过多步循环施加栽荷,计算工件的弹性变形和刀具的实际吃刀深度,即可确定刀具轨迹.试验表明:所得计算结果可以直接应用于薄壁圆筒零件加工变形补偿,实现了刀具轨迹和切削参数的优化.【总页数】4页(P33-35,43)【作者】陈双喜【作者单位】四川大学,制造科学与工程学院,成都,610065【正文语种】中文【中图分类】TH16【相关文献】1.关于零件热变形数值计算误差补偿研究 [J], 苗恩铭;费业泰2.基于BP神经网络的车削加工刀具变形误差补偿技术 [J], 洪琨;闫嘉昕;王博;李佳泽;李勇涛3.车削加工工件变形补偿有限元计算新方法的研究 [J], 陈双喜;姚进4.基于ABAQUS的石材慕墙双跨立柱抗弯强度与变形计算分析 [J], 周庆松; 郑燕燕; 刘俊; 孙雨欣; 陈浩; 张玉珏5.基于ABAQUS的石材幕墙矩形钢立柱抗弯强度与变形计算分析 [J], 刘俊; 郑燕燕; 高治亚; 余晓纲; 常虎; 徐昕玉因版权原因，仅展示原文概要，查看原文内容请购买。

基于Abaqus的CFRP薄壁弹性杆卷绕应力仿真与研究

基于Abaqus的CFRP薄壁弹性杆卷绕应力仿真与研究赵山杉;贾倩;贺淇楝
【期刊名称】《价值工程》
【年(卷),期】2024(43)5
【摘要】CFRP(Carbon-Fiber-Reinforced-Plastic)薄壁弹性杆可展机构当前在空间可展支撑机构领域应用广泛,关于其力学性能的研究和设计优化是当前研究的热点。

本研究基于Abaqus有限元仿真软件,对厚度为0.8~0.9mm的CFRP薄壁弹性杆的收展过程进行了力学仿真模拟,得到了CFRP薄壁弹性杆在直径100mm的卷筒上达到指定弯曲状态时的应力分布结果,验证了CFRP薄壁弹性杆的强度并归纳总结了CFRP薄壁弹性杆弯曲时的应力分布规律。

【总页数】4页(P136-139)
【作者】赵山杉;贾倩;贺淇楝
【作者单位】中国运载火箭技术研究院
【正文语种】中文
【中图分类】O34
【相关文献】
1.基于Solidworks的锚杆锚索应力传感器弹性体设计仿真分析
2.基于ABAQUS 的针刺C/C复合材料薄壁锥形件力学仿真平台研究与开发
3.基于ABAQUS考虑动荷载下开洞薄壁锥筒形钢质灯杆受力研究
因版权原因，仅展示原文概要，查看原文内容请购买。