计量经济学模拟考试题(第6套)
计量经济学题库(超完整版)及答案我整理的

计量经济学题库一、单项选择题(每小题1分)1.计量经济学是下列哪门学科的分支学科(C)。
A.统计学B.数学C.经济学D.数理统计学2.计量经济学成为一门独立学科的标志是(B)。
A.1930年世界计量经济学会成立B.1933年《计量经济学》会刊出版C.1969年诺贝尔经济学奖设立D.1926年计量经济学(Economics)一词构造出来3.外生变量和滞后变量统称为(D)。
A.控制变量B.解释变量C.被解释变量D.前定变量4.横截面数据是指(A)。
A.同一时点上不同统计单位相同统计指标组成的数据B.同一时点上相同统计单位相同统计指标组成的数据C.同一时点上相同统计单位不同统计指标组成的数据D.同一时点上不同统计单位不同统计指标组成的数据5.同一统计指标,同一统计单位按时间顺序记录形成的数据列是(C)。
A.时期数据B.混合数据C.时间序列数据D.横截面数据6.在计量经济模型中,由模型系统内部因素决定,表现为具有一定的概率分布的随机变量,其数值受模型中其他变量影响的变量是()。
A.内生变量B.外生变量C.滞后变量D.前定变量7.描述微观主体经济活动中的变量关系的计量经济模型是()。
A.微观计量经济模型B.宏观计量经济模型C.理论计量经济模型D.应用计量经济模型8.经济计量模型的被解释变量一定是()。
A.控制变量B.政策变量C.内生变量D.外生变量9.下面属于横截面数据的是()。
A.1991-2003年各年某地区20个乡镇企业的平均工业产值B.1991-2003年各年某地区20个乡镇企业各镇的工业产值C.某年某地区20个乡镇工业产值的合计数D.某年某地区20个乡镇各镇的工业产值10.经济计量分析工作的基本步骤是()。
A.设定理论模型→收集样本资料→估计模型参数→检验模型B.设定模型→估计参数→检验模型→应用模型C.个体设计→总体估计→估计模型→应用模型D.确定模型导向→确定变量及方程式→估计模型→应用模型11.将内生变量的前期值作解释变量,这样的变量称为()。
计量经济学模拟试题(六套)及答案

模拟试题一一、单项选择题1. 一元线性样本回归直线可以表示为( )A .i 10i X Y u i ++=ββ B. i X )(Y E 10i ββ+= C. i 1i e X Y ++=∧∧i ββD.i X 10iYββ+=∧2. 如果回归模型中的随机误差存在异方差性,则参数的普通最小二乘估计量是( ) A .无偏的,但方差不是最小的 B.有偏的,且方差不少最小 C .无偏的,且方差最小 D.有偏的,但方差仍最小3. 如果一个回归模型中包含截距项,对一个具有k 个特征的质的因素需要引入( )个虚拟变量 A .(k-2) B.(k-1) C.k D.K+14. 如果联立方程模型中某结构方程包含了模型系统中所有的变量,则这个方程是( ) A .恰好识别的 B .不可识别的 C .过渡识别的 D .不确定5. 平稳时间序列的均值和方差是固定不变的,自协方差只与( )有关A .所考察的两期间隔长度B .与时间序列的上升趋势C .与时间序列的下降趋势D .与时间的变化6. 对于某样本回归模型,已求得DW 统计量的值为1,则模型残差的自相关系数ρ∧近似等于( )A .0B .0.5C .-0.5D .17. 对于自适应预期模型i 110t )1(X Y u Y r r r t t +-++=-ββ,估计参数应采取的方法为( )A .普通最小二乘法B .甲醛最小二乘法C .工具变量法D .广义差分法8. 如果同阶单整变量的线性组合是平稳时间序列,则这些变量之间的关系就是( ) A .协整关系 B .完全线性关系 C .伪回归关系 D .短期均衡关系9. 在经济数学模型中,依据经济法规认为确定的参数,如税率、利息率等,称为( ) A .定义参数 B .制度参数 C .内生参数 D .短期均衡关系10. 当某商品的价格下降时,如果其某需求量的增加幅度稍大雨价格的下降幅度,则该商品的需求( )A .缺乏弹性B .富有弹性C .完全无弹性D .完全有弹性二、多项选择题1.在经济计量学中,根据建立模型的目的不同,将宏观经济计量模型分为( ) A .经济预测模型 B .经够分析模型 C .政策分析模型 D .专门模型 E.发达市场经济国家模型2.设k 为回归模型中参数的个数,F 统计量表示为( )A .RSS ESSB .)/(1)-ESS/(k k n RSS -C .221R R -D .)/()1()1/(R 22k n R k --- E. )1/(ESS/k --k n RSS3.狭义的设定误差主要包括( )A .模型中遗漏了有关解释变量B .模型中包括含了无关解释变量C .模型形式设定有误D .模型中有关随机误差项的假设有误 E.模型中最小二乘估计量是有偏的、非一致的 4.用于作经济预测的经济计量模型须有一定的“优度”保证,通常需要具备的性质有( ) A .解释能力和合理性 B .预测功效好 C .参数估计量的优良性 D .简单性 E.误差项满足古典线性回归模型的所有假定5.对联立方程模型参数的单方程估计法有( )A .工具变量B .间接最小二乘法C .二阶段最小二乘法D .完全信息极大似然法 E.有限信息极大似然法三、名词解释 1. 拟合度优 2. 行为方程 3. 替代弹性 4. K 阶单整 5. 虚拟变量四、简答题1. 简述回归分析和相关分析的关系。
计量经济学模拟考试题(第6套)

3、在某个结构方程恰好识别的条件下,不适用的估计方法是( A.间接最小二乘法 C.二阶段最小二乘法 B.工具变量法 D.普通最小二乘法
4、在利用月度数据构建计量经济模型时,如果一年里的 12 个月全部表现出 季节模式,则应该引入虚拟变量个数为( C ) A. 4 D. 6 B. 12 C. 11
5、White 检验可用于检验( B ) A.自相关性 B. 异方差性 C.解释变量随机性 D.多重共线性 6、如果回归模型违背了无自相关假定,最小二乘估计量是( C A.无偏的,有效的 B. 有偏的,非有效的 C.无偏的,非有效的 D. 有偏的,有效的
2
(3.83)
R 0.4783, s.e. 2759.15, F 14.6692
White Heteroskedasticity Test: F-statistic Obs*R-squared 3.057161 5.212471 Probability Probability 0.076976 0.073812
15、在异方差的情况下,参数估计值仍是无偏的,其原因是(
C.无多重共线性假定成立 定成立
ˆ 16、 已知 DW 统计量的值接近于 2, 则样本回归模型残差的一阶自相关系数
近似等于( A. 0 4 17、对美国储蓄与收入关系的计量经济模型分成两个时期分别建模,重建时 期是 1946—1954;重建后时期是 1955—1963,模型如下: A ) B.–1 C. 1 D.
取 0.05 , Y f 平均值置信度 95%的预测区间为: Y f t 2 GDP2005 3600 时
480.884 2.228 7.5325 1 7195337.357 480.884 25.2735 (亿元) 12 3293728.494
新《计量经济学》第6章 计量练习题

《计量经济学》第6章习题一、单项选择题1.当模型存在严重的多重共线性时,OLS 估计量将不具备( ) A .线性 B .无偏性 C .有效性 D .一致性2.如果每两个解释变量的简单相关系数比较高,大于( )时则可认为存在着较严重的多重共线性。
A .0.5B .0.6C .0.7D .0.83.方差扩大因子VIF j 可用来度量多重共线性的严重程度,经验表明,VIF j ( )时,说明解释变量与其余解释变量间有严重的多重共线性。
A .小于5B .大于1C .小于1D .大于104.对于模型01122i i i i Y X X u βββ=+++,与r 23等于0相比,当r 23等于0.5时,3ˆβ的方差将是原来的( )A .2倍B .1.5倍C .1.33倍D .1.25倍 5.无多重共线性假定是假定各解释变量之间不存在( )A .线性关系B .非线性关系C .自相关D .异方差 二、多项选择题1.多重共线性包括( )A .完全的多重共线性B .不完全的多重共线性C .解释变量间精确的线性关系D .解释变量间近似的线性关系E .非线性关系2.多重共线性产生的经济背景主要由( )A .经济变量之间具有共同变化趋势B .模型中包含滞后变量C .采用截面数据D .样本数据自身的原因E .模型设定误差 3.多重共线性检验的方法包括( )A .简单相关系数检验法B .方差扩大因子法C .直观判断法D .逐步回归法E .DW 检验法 4.修正多重共线性的经验方法包括( ) A .剔除变量法 B .增大样本容量C .变换模型形式D .截面数据与时间序列数据并用E .变量变换 5.严重的多重共线性常常会出现下列情形( ) A .适用OLS 得到的回归参数估计值不稳定 B .回归系数的方差增大C .回归方程高度显著的情况下,有些回归系数通不过显著性检验D .回归系数的正负号得不到合理的经济解释E .预测精度降低一、单项选择题1.C2.D3.D4.C5.A 二、多项选择题1.AB2.ABCD3.ABCD4.ABCDE5.ABCDE三、简答题1.什么是多重共线性?产生多重共线性的经济背景是什么?所谓多重共线性(Multicollinearity )是指线性回归模型中的解释变量之间由于存在精确相关关系或高度相关关系而使模型估计失真或难以估计准确。
新《计量经济学》第6章 计量练习题

《计量经济学》第6章习题一、单项选择题1.当模型存在严重的多重共线性时,OLS 估计量将不具备( ) A .线性 B .无偏性 C .有效性 D .一致性2.如果每两个解释变量的简单相关系数比较高,大于( )时则可认为存在着较严重的多重共线性。
A .0.5B .0.6C .0.7D .0.83.方差扩大因子VIF j 可用来度量多重共线性的严重程度,经验表明,VIF j ( )时,说明解释变量与其余解释变量间有严重的多重共线性。
A .小于5B .大于1C .小于1D .大于104.对于模型01122i i i i Y X X u βββ=+++,与r 23等于0相比,当r 23等于0.5时,3ˆβ的方差将是原来的( )A .2倍B .1.5倍C .1.33倍D .1.25倍 5.无多重共线性假定是假定各解释变量之间不存在( )A .线性关系B .非线性关系C .自相关D .异方差 二、多项选择题1.多重共线性包括( )A .完全的多重共线性B .不完全的多重共线性C .解释变量间精确的线性关系D .解释变量间近似的线性关系E .非线性关系2.多重共线性产生的经济背景主要由( )A .经济变量之间具有共同变化趋势B .模型中包含滞后变量C .采用截面数据D .样本数据自身的原因E .模型设定误差 3.多重共线性检验的方法包括( )A .简单相关系数检验法B .方差扩大因子法C .直观判断法D .逐步回归法E .DW 检验法 4.修正多重共线性的经验方法包括( ) A .剔除变量法 B .增大样本容量C .变换模型形式D .截面数据与时间序列数据并用E .变量变换 5.严重的多重共线性常常会出现下列情形( ) A .适用OLS 得到的回归参数估计值不稳定 B .回归系数的方差增大C .回归方程高度显著的情况下,有些回归系数通不过显著性检验D .回归系数的正负号得不到合理的经济解释E .预测精度降低一、单项选择题1.C2.D3.D4.C5.A 二、多项选择题1.AB2.ABCD3.ABCD4.ABCDE5.ABCDE三、简答题1.什么是多重共线性?产生多重共线性的经济背景是什么?所谓多重共线性(Multicollinearity )是指线性回归模型中的解释变量之间由于存在精确相关关系或高度相关关系而使模型估计失真或难以估计准确。
《计量经济学》第六章精选题及答案

第六章自相关二、问答题1、那些原因可以造成自相关;2、存在自相关时,参数的OLS估计具有哪些性质;3、如何检验是否存在自相关;4、当存在自相关时,如何利用广义差分法进行参数估计;5、当存在自相关时,如何利用广义最小平方估计法进行参数估计;6、异方差与自相关有什么异同;三、计算题1、证明:当样本个数较大时,)d。
≈-1(2ρα2、通过D-W检验,判断下列模型中是否存在自相关,显著性水平%5=(1)样本大小:20;解释变量个数(包括常数项):2;d=0.73;(2)样本大小:35;解释变量个数(包括常数项):3;d=3.56;(3)样本大小:50;解释变量个数(包括常数项):3;d=1.87;(4)样本大小:80;解释变量个数(包括常数项):6;d=1.62;(5)样本大小:100;解释变量个数(包括常数项):5;d=2.41;3、假定存在下表所示的时间序列数据:请回答下列问题:(1)利用表中数据估计模型:t t t x y εββ++=10;(2)利用D-W 检验是否存在自相关?如果存在请用d 值计算估计自相关系数ρ;(3)利用广义差分法重新估计模型:'''1011(1)()t t tt t y y x x ρβρβρε---=-+-+。
第三部分 参考答案二、问答题1、那些原因可以造成自相关?答:造成自相关的原因大致包括以下六个方面:(1)经济变量的变化具有一定的倾向性。
在实际的经济现象中,许多经济变量的现值依赖于他的前期值。
也就是说,许多经济时间序列都有一个明显的相依性特点,这种现象称作经济变量所具有的惯性。
(2)缺乏应有变量的设定偏差。
(3)不正确的函数形式的设定错误。
(4)蛛网现象和滞后效应。
(5)随机误差项的特征。
(6)数据拟合方法造成的影响。
2、存在自相关时,参数的OLS 估计具有哪些性质?答:当存在自相关,即I D ≠ΩΩ=,)(2σε时,OLS 估计的性质有:(1)βˆ是观察值Y 和X 的线性函数;(2)βˆ是β的无偏估计;(3)βˆ的协方差矩阵为112)()()ˆ(--'Ω''=X X X X X X D σβ;(4)βˆ不是β的最小方差线性无偏估计;(5)如果nX X n Ω'∞→lim存在,那么βˆ是β的一致估计;(6)2σ 不是2σ的无偏估计;(7)2σ不是2σ的一致估计。
计量经济学题库(超完整版)及答案

四、简答题(每小题5分)1.简述计量经济学与经济学、统计学、数理统计学学科间的关系。
2.计量经济模型有哪些应用?3.简述建立与应用计量经济模型的主要步骤。
4.对计量经济模型的检验应从几个方面入手?5.计量经济学应用的数据是怎样进行分类的? 6.在计量经济模型中,为什么会存在随机误差项?7.古典线性回归模型的基本假定是什么? 8.总体回归模型与样本回归模型的区别与联系。
9.试述回归分析与相关分析的联系和区别。
10.在满足古典假定条件下,一元线性回归模型的普通最小二乘估计量有哪些统计性质? 11.简述BLUE 的含义。
12.对于多元线性回归模型,为什么在进行了总体显著性F 检验之后,还要对每个回归系数进行是否为0的t 检验?13.给定二元回归模型:01122t t t t y b b x b x u =+++,请叙述模型的古典假定。
14.在多元线性回归分析中,为什么用修正的决定系数衡量估计模型对样本观测值的拟合优度?15.修正的决定系数2R 及其作用。
16.常见的非线性回归模型有几种情况?17.观察下列方程并判断其变量是否呈线性,系数是否呈线性,或都是或都不是。
①t t t u x b b y ++=310 ②t t t u x b b y ++=log 10③ t t t u x b b y ++=log log 10 ④t t t u x b b y +=)/(1018. 观察下列方程并判断其变量是否呈线性,系数是否呈线性,或都是或都不是。
①t t t u x b b y ++=log 10 ②t t t u x b b b y ++=)(210③ t t t u x b b y +=)/(10 ④t b t t u x b y +-+=)1(11019.什么是异方差性?试举例说明经济现象中的异方差性。
20.产生异方差性的原因及异方差性对模型的OLS 估计有何影响。
21.检验异方差性的方法有哪些?22.异方差性的解决方法有哪些? 23.什么是加权最小二乘法?它的基本思想是什么?24.样本分段法(即戈德菲尔特——匡特检验)检验异方差性的基本原理及其使用条件。
计量经济学练习题答案(第六章)
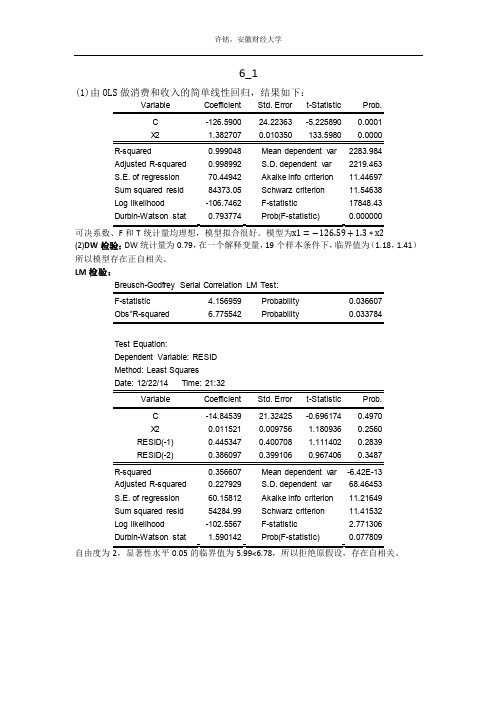
6_1(1)由OLS做消费和收入的简单线性回归,结果如下:Variable Coefficient Std. Error t-Statistic Prob.C -126.5900 24.22363 -5.225890 0.0001R-squared 0.999048 Mean dependent var 2283.984Adjusted R-squared 0.998992 S.D. dependent var 2219.463S.E. of regression 70.44942 Akaike info criterion 11.44697Sum squared resid 84373.05 Schwarz criterion 11.54638Log likelihood -106.7462 F-statistic 17848.43Durbin-Watson stat 0.793774 Prob(F-statistic) 0.000000可决系数、F和T统计量均理想,模型拟合很好。
模型为x1=−126.59+1.3∗x2(2)DW检验:DW统计量为0.79,在一个解释变量,19个样本条件下,临界值为(1.18,1.41)所以模型存在正自相关。
LM检验:F-statistic 4.156959 Probability 0.036607Test Equation:Dependent Variable: RESIDMethod: Least SquaresDate: 12/22/14 Time: 21:32C -14.84539 21.32425 -0.696174 0.4970X2 0.011521 0.009756 1.180936 0.2560RESID(-1) 0.445347 0.400708 1.111402 0.2839RESID(-2) 0.386097 0.399106 0.967406 0.3487R-squared 0.356607 Mean dependent var -6.42E-13Adjusted R-squared 0.227929 S.D. dependent var 68.46453S.E. of regression 60.15812 Akaike info criterion 11.21649Sum squared resid 54284.99 Schwarz criterion 11.41532Log likelihood -102.5567 F-statistic 2.771306Durbin-Watson stat 1.590142 Prob(F-statistic) 0.077809自由度为自相关分析:解释变量和被解释变量有显著二阶自相关。
研究生计量经济学模拟试题及答案

暨 南 大 学 考 试 试 卷一、单项选择题(将正确的选项填在括号内,共10小题,每小题2分,共20分)1.某商品需求函数为i i i u x b b y ++=10,其中y 为需求量,x 为价格。
为了考虑“地区”(农村、城市)和“季节”(春、夏、秋、冬)两个因素的影响,拟引入虚拟变量,则应引入虚拟变量的个数为【 B 】A 2B 4C 5D 62.假设某需求函数为i i i u x b b y ++=10,为了考虑“季节”因素(春、夏、秋、冬四个不同的状态),引入4个虚拟变量形式形成截距变动模型,则模型的【 D 】 A 参数估计量将达到最大精度 B 参数估计量是有偏估计量 C 参数估计量是非一致估计量 D 参数将无法估计3.设y 表示居民的消费支出,x 表示居民的可支配收入,二者之间的真实关系可表示为【 C 】A t t x y 10ˆˆˆββ+=B E t t x y 10)(ββ+=C ()t t t y f x u =+D t t x y 10ββ+= 4.下面属于时间序列数据的是【 A 】A 1991-2003年各年某地区20个镇的平均工业产值B 1991-2003年各年某地区20个镇的各镇工业产值C 某年某地区20个镇工业产值的合计数D 某年某地区20个镇各镇工业产值5.经验认为,某个解释变量与其他解释变量间多重共线性严重的情况是这个解释变量的VIF 【 C 】A 大于1B 小于1C 大于10D 小于106.下列哪种方法不是检验异方差的方法【 D 】 A 戈德菲尔特——匡特检验 B 怀特检验C 戈里瑟检验D 方差膨胀因子检验7.令1ˆθ和2ˆθ是参数θ的两个无偏的估计量,它们互相独立,其方差分别为2和4。
要使得2211ˆˆˆθθθc c +=是参数θ的无偏的方差最小的估计量,则【 C 】A 4/14/321==c cB 9/15/121==c cC 3/13/221==c cD 5/37/421==c c8.如果模型包含有随机解释变量,且与随机误差项不独立也不线性相关,则普通最小二乘估计量和工具变量估计量都是【 C 】 A 无偏估计量 B 有效估计量 C 一致估计量 D 最佳线性无偏估计量9.在小样本情况下,对回归模型t t t u x y ++=10ββ进行统计检验时,通常假定tu服从【 C 】A N (0,2i σ)B t(n-2)C N (0,2σ)D t(n)10.要使最小二乘法的估计量满足无偏性需要满足的条件是 【 D 】 A 正态性 B 无自相关 C 同方差 D 零均值二、判断题(对的打“√”,错的打“×”,共10小题,每小题2分,共20分)【 × 】2.在一个含有截距项的回归模型中,使用最小二乘法计算出的残差总和必定等于零。
计量经济学习题集参考答案

计量经济学习题集参考答案第一章一、单选ADABD BAACB ACBD二、多选ABCD BCDE BCE ABC三、四、略第二章一、单选CBDDD BCDDD ADBDC ABBDD BDAAD BBCB二、多选ACD ABCE ABC BE AC CDE ABCE CDE ABCE ADE ABCDE ABCE BCE三、判断×××√×四、五、略六、计算与分析题1、(1)令Y=1/y,X=e −x ,则可得线性模型:Y= + X+u。
0 β 1 β(2) 1 =sinx,=cosx,=sin2x,=cos2x,则原模型可化为线性模型X 2 X 3 X 4 X Y= 1 + + + +u。
β 1 X 2 β 2 X 3 β 3 X 4 β 4 X2、(1)设 1 = ,= ,则原模型化为Xx12 X 21xy= 0 + + +u;β 1 β 1 X 2 β 2 X(2)对原模型取对数:LnQ=LnA+αLnK+βLnL+u,设Y=LnQ,a=LnA, 1 =LnK,=LnL,则原模型可化为:X 2 XY=a+α1+β +u。
X 2 X(3)模型取对数:Lny= 0 + x+u,设Y=Lny,则原模型化为β 1 βY= 0 + x+u。
β 1 β(4)由模型可得:1-y= ,从而有:1 exp[ ( )]exp[ ( )]0 10 1x ux u+ −+ +−+ +ββββexp( )1 0 1 x uyy = + +−ββ取对数:Ln x u ,设Y= Ln ,则yy = + +−0 1 )1( ββ)1(yy−原模型可化为:Y= + x +u 。
0 1 ββ3、显著;=4.8387,=0.0433;[0.7186, 0.9013],不包含0。
S0 ˆβS1 ˆβ4、(1)yˆ=26.2768+4.2589X(2)两个系数的经济意义:产量为0 时,总成本为26.2768;当产量每增加1 时,总成本平均增加4.2589。
计量经济学模拟试题(六套)及答案

模拟试题一一、单项选择题1. 一元线性样本回归直线可以表示为( D )A .i 10i X Y u i ++=ββ B. i X )(Y E 10i ββ+=C. i 1i e X Y ++=∧∧i ββD.i X 10iYββ+=∧2. 如果回归模型中的随机误差存在异方差性,则参数的普通最小二乘估计量是( A ) A .无偏的,但方差不是最小的 B.有偏的,且方差不少最小 C .无偏的,且方差最小 D.有偏的,但方差仍最小3. 平稳时间序列的均值和方差是固定不变的,自协方差只与( A )有关A .所考察的两期间隔长度B .与时间序列的上升趋势C .与时间序列的下降趋势D .与时间的变化4. 对于某样本回归模型,已求得DW 统计量的值为1,则模型残差的自相关系数ρ∧近似等于( B )A .0B .0.5C .-0.5D .1二、简答题1.简述回归分析和相关分析的关系。
答案:回归分析是一个变量(被解释变量)对于一个或多个其他变量(解释变量)的依存关系,目的在于根据解释变量的数值估计预测被解释变量的总体均值。
相关分析研究变量相关程度,用相关系数表示。
相关分析不关注变量的因果关系,变量都是随机变量。
回归分析关注变量因果关系。
被解释变量是随机变量,解释变量是非随机变量。
2.简要说明DW 检验应用的限制条件和局限性。
答案DW 检验适用于一阶自回归:不适用解释变量与随机项相关的模型;DW 检验存在两个不能确定的区域3.回归模型中随机误差项产生的原因是什么?答案:模型中省略的变量;随机行为;模型形式不完善;变量合并误差;测量误差三、计算题2.已知某公司的广告费用X 与销售额(Y )的统计数据如下表所示:X (万元) 40 25 20 30 40 40 25 20 50 20 50 50Y (万元) 490 395 420 475 385 525 480 400 560 365 510 540(1)估计销售额关于广告费用的一元线性回归模型 (2)说明参数的经济意义(3)在05.0=α的显著水平下对参数的显著性进行t 检验 答案:(1)一元线性回归模型319.086 4.185t i X Y ∧=+(2)参数经济意义:当广告费用每增加1万元,销售额平均增加4.185万元 (3)t=3.79>0.025(10)t ,广告费对销售额有显著影响 四、分析题根据某地70个季度的时序资料,使用普通最小二乘法,估计得出了该地的消费模型为:t t C Y 911.0086.088.1tC++=∧989.02=R(4.69)(0.028) (0.084)式中C 为消费,Y 为居民可支配收入,括号中的数字为相应参数估计量的标准误。
计量经济分析(第六版)答案 finalfall00

Econometrics I. Take Home Final Exam.Today is Thursday December 14. This exam is due by Friday, December 22. You may submit your answers to me electronically as an attachment to an e-mail if you wish. There are five parts worth 20% each.Recall, this exam provides 40% of your grade for this course.I. The following 25 observations are used for this part of the examination:Read;Nobs=25;Nvar=1;Names=Y;ByVariables$16.000 14.000 8.000 22.000 23.000 25.000 17.000 23.000 8.0000 14.000 23.000 22.000 14.000 22.000 10.000 18.00015.000 21.000 15.000 25.000 14.000 16.000 19.000 27.00016.000(A LIMDEP READ command is included if you wish to use it. You can just transplant this into the editor in LIMDEP and execute it to input the data.)Suppose we believe that the data on Y are generated by a poisson distribution. Then, the probability density function for Y isf(Y) = exp(-λ)λY/Y! Let λ = exp(α)We are going to estimate the parameter α.POISSON ; Lhs = Y ; Rhs = ONE $+---------------------------------------------+| Poisson Regression || Maximum Likelihood Estimates || Dependent variable Y || Weighting variable ONE || Number of observations 25 || Iterations completed 5 || Log likelihood function -78.30529 || Chi- squared = 37.50783 RsqP= .0000 || G - squared = 39.52722 RsqD= .0000 || Overdispersion tests: g=mu(i) : 1.447 || Overdispersion tests: g=mu(i)^2: 1.447 |+---------------------------------------------++---------+--------------+----------------+--------+---------+----------+|Variable | Coefficient | Standard Error |b/St.Er.|P[|Z|>z] | Mean of X|+---------+--------------+----------------+--------+---------+----------+Constant 2.883682770 .47298377E-01 60.968 .0000(a) The table gives the estimate of α. What is the estimated asymptotic distribution?(b) The expected value of the random variable, Y is μ = λ = exp(α). Estimate μ using your maximum likelihood estimate. Estimate the asymptotic standard error of this estimator. Present a 95% confidence interval for the parameter μ based on your results.(c) Since μ = E[Y] is λ, you should be able to estimate μ with the sample mean of the observations on Y. Do so, and describe your finding. Using the familiar formula for the variance of the mean, estimate the standard error of this estimator, and compare your result to that in (b).(d) The variance of this random variable is σ2 = λ. You should be able to estimate σ2 with the sample variance of the observations on Y. Do so, and compare your estimate to the one you get by using the MLE in the table. Does the difference appear to be small or is it large enough to make you suspect that the model which has the same mean and variance is incorrect? How might you test this assumption?II. Continuing part I, we also have the following data on XRead;Nobs=25;Nvar=1;Names=X;ByVariables$16 11 12 23 23 21 22 24 12 15 2221 16 20 17 15 17 14 17 23 19 1525 22 12We will now formulate a kind of regression model. We believe that Y|X has the Poisson distribution specified earlier, but now,λ = Exp[α + βx]The table below presents the maximum likelihood estimates of the parameters of this model.+---------------------------------------------+| Poisson Regression || Maximum Likelihood Estimates || Dependent variable Y || Weighting variable ONE || Number of observations 25 || Iterations completed 5 || Log likelihood function -68.12529 || Restricted log likelihood -78.30529 || Chi-squared 20.36001 || Degrees of freedom 1 || Significance level .6414944E-05 || Chi- squared = 18.73093 RsqP= .5006 || G - squared = 19.16722 RsqD= .5151 || Overdispersion tests: g=mu(i) : -1.360 || Overdispersion tests: g=mu(i)^2: -1.591 |+---------------------------------------------++---------+--------------+----------------+--------+---------+----------+|Variable | Coefficient | Standard Error |b/St.Er.|P[|Z|>z] | Mean of X|+---------+--------------+----------------+--------+---------+----------+Constant 1.924770881 .22497947 8.555 .0000X .5152813743E-01 .11545125E-01 4.463 .0000 18.160000(a) We are interested in the expected value of Y|X. As before, this is λ which is nowE[Y|X] = exp(α + βX)Using your results above, estimate the slope of this regression at the mean of X (18.16).(b) Linearly regress Y on a constant and X. What is the slope in this regression. Compare this slope to the maximum likelihood estimates.(c) The procedures in (a) and (b) above suggest two methods of estimating α and β. Compare the two in terms of consistency and efficiency.(c) Since E[Y|X] is a fairly simple function of X, you might also consider nonlinear least squares estimation of α and β. Describe in detail how to compute the nonlinear least squares estimates of α and β. How would you compute asymptotic standard errors for your estimators?(e) How would you form a confidence interval for your estimate of E[Y|X = X].III. Using the results in parts I and II, test the hypothesis that β equals 0 using a Wald test and using a likelihood ratio test. Describe how one would carry out a Lagrange multiplier test of this hypothesis.IV. The following questions are based on the regression model:Y = β1 + β2*X + β3*Z + β4*XZ + β5*D + εε is assumed to be zero mean, homoscedastic, and nonautocorrelated. The following data are obtained: (note that XZ is the product, X times Z.)Y X Z XZ D6.54495 6.18579 2.74462 16.9776 .0000005.01914 8.20300 2.95788 24.2635 1.0000020.2805 .928739 1.64839 1.53092 .00000015.7713 3.67190 2.34633 8.61549 1.0000015.3244 3.20056 2.79635 8.94989 .0000007.27412 9.49923 2.08567 19.8123 1.00000-2.32703 9.74362 2.73909 26.6887 .00000013.0043 8.57227 1.83257 15.7093 1.0000012.3772 14.4995 1.45214 21.0553 1.000001.87654 9.157492.66003 24.3592 .0000006.05984 9.91496 1.90520 18.8900 .00000013.2894 8.80248 1.08860 9.58238 .00000018.8615 5.25547 1.55513 8.17294 1.0000016.6677 1.51429 1.56988 2.37725 .00000021.0826 5.43969 1.07380 5.84114 .000000-11.9941 13.7718 2.82957 38.9683 .00000018.4780 1.79822 2.81929 5.06970 .0000001.34836 11.36362.54030 28.8670 1.000009.72778 11.5376 1.89096 21.8171 1.0000021.3792 4.68237 1.34836 6.31352 1.0000016.3221 7.20146 1.37208 9.88098 1.0000021.5679 3.53608 2.24173 7.92694 1.000004.75133 9.28801 2.21022 20.5285 .00000010.0632 4.79755 2.26405 10.8619 .00000015.4179 13.4251 1.15154 15.4595 .0000001. Estimate the parameters of the model using ordinary least squares. Present all results and explain your computations. In addition to the slopes, estimate the parameter σ, the standard deviation of ε.2. Test the hypothesis that neither X nor Z have any explanatory power in terms of explaining variation in Y.3. Test the hypothesis that Z does not have any explanatory power in explaining variation in Y.4. Test the hypothesis that the coefficients on X and Z in the regression are equal. Do this test in two ways:a. Use only the statistical results of fitting the full regression.b. Fit the regression with the restriction imposed, and test the hypothesis using the results of bothregressions.(Note, ignore the variable XZ in this computation.)6. We are interested in examining the marginal effect of changes in X on E[Y|X,Z,D]. What is ∂E[y|X,Z,D]/∂X? Compute this effect with Z equal to its mean. How would you compute a standard error for the estimate of this effect? How would you test the hypothesis that this effect equals zero?V. The data listed above are now assumed to come from a process in which there is a linear regression model, but possibly a heteroscedastic disturbance. The regression equation isY = β1 + β2*X + β3*X + β4*XZ + β5*D + εε has mean 0, but may be heteroscedastic. Estimation in this part of the exam is based on the data you used in part IV.1. Suppose that the true variance of ε isVar[ε] = σ2 * Exp(X*D)If you estimate the betas using ordinary least squares, what are the properties of the estimator? (Bias, consistency, efficiency, true covariance matrix.)2. Suppose you believe that the variance of ε is σ2Exp(X*D), but, in fact, the true variance is just σ2. (I.e., your belief is mistaken.) Suppose you fit the model by GLS in spite of the true variance. What are the properties of your estimator? (Note, you can use true GLS here, since there are no free parameters in the variance function.)3. Compute the two estimators you described in parts 1 and 2, and report all results. (Note, in part 2, there are no parameters in the variance part, so you can compute the true GLS estimator.) Compare the variances of the OLS and GLS estimator, both true and estimated.4. Using the least squares results, compute the White estimator for the variance of the OLS estimator. Describe why you would do this computation.5. Suppose the true model is, in factVar[ε] = σ2 * Exp(α XD) where α is a parameter to be estimated.How would you test the hypothesis that alpha equals 1.0 against the alternative hypothesis that alpha is not equal to 1.0? Give full details on how you would compute the test statistic and exactly how you would carry out the test. (You do not need actually estimate the model. Just discuss how you would do the test.) VI. Consider the following statistical sampling situation. The distribution of the number of failures of electronic components per unit of time is Poisson with parameter λ, which we will model as λ=exp(α+βx) for some set of independent variables. Let the number of failures be denoted Z = 0,1,2,... Let Y be the random variable Y = 0 if Z = 0 (no failures) and Y = 1 if Z > 0 (at least one failure). Then, Y is a binary variable with density Prob[Y = 0] = exp(-λ) and Prob[Y = 1] = 1 - exp(-λ). If your sample of data consists of 100 observations (time intervals) in which you observe Y (not Z) and X, show how to estimate α and βusing maximum likelihood. How will you compute the estimated asymptotic covariance matrix of your estimates.。
计量经济学题库(超完整版)及答案

计量经济学题库一、单项选择题(每小题1分)1.计量经济学是下列哪门学科的分支学科(C)。
A.统计学B.数学C.经济学D.数理统计学2.计量经济学成为一门独立学科的标志是(B)。
A.1930年世界计量经济学会成立B.1933年《计量经济学》会刊出版C.1969年诺贝尔经济学奖设立D.1926年计量经济学(Economics)一词构造出来3.外生变量和滞后变量统称为(D)。
A.控制变量B.解释变量C.被解释变量D.前定变量4.横截面数据是指(A)。
A.同一时点上不同统计单位相同统计指标组成的数据B.同一时点上相同统计单位相同统计指标组成的数据C.同一时点上相同统计单位不同统计指标组成的数据D.同一时点上不同统计单位不同统计指标组成的数据5.同一统计指标,同一统计单位按时间顺序记录形成的数据列是(C)。
A.时期数据B.混合数据C.时间序列数据D.横截面数据6.在计量经济模型中,由模型系统内部因素决定,表现为具有一定的概率分布的随机变量,其数值受模型中其他变量影响的变量是()。
A.内生变量B.外生变量C.滞后变量D.前定变量7.描述微观主体经济活动中的变量关系的计量经济模型是()。
A.微观计量经济模型B.宏观计量经济模型C.理论计量经济模型D.应用计量经济模型8.经济计量模型的被解释变量一定是()。
A.控制变量B.政策变量C.内生变量D.外生变量9.下面属于横截面数据的是()。
A.1991-2003年各年某地区20个乡镇企业的平均工业产值B.1991-2003年各年某地区20个乡镇企业各镇的工业产值C.某年某地区20个乡镇工业产值的合计数D.某年某地区20个乡镇各镇的工业产值10.经济计量分析工作的基本步骤是()。
A.设定理论模型→收集样本资料→估计模型参数→检验模型B.设定模型→估计参数→检验模型→应用模型C.个体设计→总体估计→估计模型→应用模型D.确定模型导向→确定变量及方程式→估计模型→应用模型11.将内生变量的前期值作解释变量,这样的变量称为()。
计量经济学考试题型(模拟题2021)

计量经济学考试题型(模拟题,旨在让同学们熟悉题型,秋)第一题:英译汉(10题,10分)提示:教材上提及的计量经济学专业术语第二题:填空题(10空,20分)和统计工具分析经济数据的一门科学和艺术。
教材和统计方法来寻找历史数据的中理想化随机对照实验是指存在没有接受处理的对照组和接受处理的处理组,而且处理是随机分配的,这种随机分配消除了可能存在的系统性关系,使得处理组和对照组之间唯一的系统性差别在于是否接受处理。
如果该实验的规模足够大且能够被准确实施,则可以估计出处理对结果的因果效应。
教材P5因果效应被定义为某一给定行为或处理对结果的影响。
教材P5理想化随机对照实验在现实中可能是不道德的、无法圆满实施的或者代价高昂的,因而在现实中十分罕见。
但是,理想化随机对照实验的概念提供了基于实验数据进行因果效应分析的理论基准。
教材P5尽管预测不需要涉及因果关系,但经济理论揭示的变量间关系等信息有助于预测。
我们可以通过多元回归分析将经济理论所揭示的历史关系进行量化,并检验这些关系随着时间的变化是否仍保持稳定,以及对未来作出定量预测并评估这些预测的精确性。
教材P5实验数据来源于为评估某种处理(或某项政策),抑或研究某种因果效应而设计的实验。
但是,要管理和控制现实中以人为主体的实验往往很难,可能的原因包括成本高昂、难以控制或者不道德。
因此,和理想化随机对照实验类似,经济学实验相对罕见。
教材P6大部分经济数据是通过观察现实行为而获得的。
这种通过观察实验之外的实际行为而获得的数据,被称为 观测数据 。
教材P6现实中,“处理”的水平并非 随机 分配,所以很难将其他相关因素产生的效应与“处理”效应区分开。
计量经济学正是致力于研究如何解决在用现实数据估计 过程中所面临的问题。
教材P6无论实验数据还是观测数据,都可以分为三种类型: 截面数据 、 时间序列数据 和 面板数据 。
教材P6n 表示观测的时间序列数据 是对同一个体在多个不同时期内收集到的数据。
计量经济学题库及答案【完整版】

计量经济学题库一、单项选择题(每小题1分)1.计量经济学是下列哪门学科的分支学科(C)。
A.统计学B.数学C.经济学D.数理统计学2.计量经济学成为一门独立学科的标志是(B)。
A.1930年世界计量经济学会成立B.1933年《计量经济学》会刊出版C.1969年诺贝尔经济学奖设立D.1926年计量经济学(Economics)一词构造出来3.外生变量和滞后变量统称为(D)。
A.控制变量B.解释变量C.被解释变量D.前定变量4.横截面数据是指(A)。
A.同一时点上不同统计单位相同统计指标组成的数据B.同一时点上相同统计单位相同统计指标组成的数据C.同一时点上相同统计单位不同统计指标组成的数据D.同一时点上不同统计单位不同统计指标组成的数据5.同一统计指标,同一统计单位按时间顺序记录形成的数据列是(C)。
A.时期数据B.混合数据C.时间序列数据D.横截面数据6.在计量经济模型中,由模型系统内部因素决定,表现为具有一定的概率分布的随机变量,其数值受模型中其他变量影响的变量是( B )。
A.内生变量B.外生变量C.滞后变量D.前定变量7.描述微观主体经济活动中的变量关系的计量经济模型是( A )。
A.微观计量经济模型B.宏观计量经济模型C.理论计量经济模型D.应用计量经济模型8.经济计量模型的被解释变量一定是( C )。
A.控制变量B.政策变量C.内生变量D.外生变量9.下面属于横截面数据的是( D )。
A.1991-2003年各年某地区20个乡镇企业的平均工业产值B.1991-2003年各年某地区20个乡镇企业各镇的工业产值C.某年某地区20个乡镇工业产值的合计数D.某年某地区20个乡镇各镇的工业产值10.经济计量分析工作的基本步骤是( A )。
A.设定理论模型→收集样本资料→估计模型参数→检验模型B.设定模型→估计参数→检验模型→应用模型C.个体设计→总体估计→估计模型→应用模型D.确定模型导向→确定变量及方程式→估计模型→应用模型11.将内生变量的前期值作解释变量,这样的变量称为( D )。
计量经济学题库(超完整版)及答案

计量经济学题库(超完整版)及答案计量经济学题库三、名词解释(每⼩题3分)1.经济变量 2.解释变量3.被解释变量4.内⽣变量 5.外⽣变量 6.滞后变量7.前定变量 8.控制变量9.计量经济模型10.函数关系 11.相关关系 12.最⼩⼆乘法13.⾼斯-马尔可夫定理 14.总变量(总离差平⽅和)15.回归变差(回归平⽅和) 16.剩余变差(残差平⽅和)17.估计标准误差 18.样本决定系数 19.点预测 20.拟合优度21.残差 22.显著性检验23.回归变差 24.剩余变差 25.多重决定系数 26.调整后的决定系数27.偏相关系数 28.异⽅差性 29.格德菲尔特-匡特检验 30.怀特检验 31.⼽⾥瑟检验和帕克检验32.序列相关性 33.虚假序列相关 34.差分法 35.⼴义差分法 36.⾃回归模型 37.⼴义最⼩⼆乘法38.DW 检验 39.科克伦-奥克特跌代法 40.Durbin 两步法41.相关系数 42.多重共线性 43.⽅差膨胀因⼦ 44.虚拟变量 45.模型设定误差 46.⼯具变量 47.⼯具变量法 48.变参数模型 49.分段线性回归模型50.分布滞后模型 51.有限分布滞后模型52.⽆限分布滞后模型 53.⼏何分布滞后模型 54.联⽴⽅程模型 55.结构式模型56.简化式模型 57.结构式参数 58.简化式参数 59.识别 60.不可识别 61.识别的阶条件 62.识别的秩条件 63.间接最⼩⼆乘法四、简答题(每⼩题5分)1.简述计量经济学与经济学、统计学、数理统计学学科间的关系。
2.计量经济模型有哪些应⽤? 3.简述建⽴与应⽤计量经济模型的主要步骤。
4.对计量经济模型的检验应从⼏个⽅⾯⼊⼿?5.计量经济学应⽤的数据是怎样进⾏分类的? 6.在计量经济模型中,为什么会存在随机误差项?8.总体回归模型与样本回归模型的区别与联系。
9.试述回归分析与相关分析的联系和区别。
11.简述BLUE 的含义。
计量经济学试题及答案

1.计量经济学模型: 揭示经济现象中客观存在的因果关系, 主要采用回归分析方法的经济数学模型。
2.参数估计的无偏性: 它的均值或期望值是否等于总体的真实值。
3.参数估计量的有效性: 它是否在所有线性无偏估计量中具有最小方差。
估计量的期望方差越大说明用其估计值代表相应真值的有效性越差;否则越好, 越有效。
不同的估计量具有不同的方差, 方差最小说明最有效。
4.序列相关: 即模型的随即干扰项违背了相互独立的基本假设。
5.工具变量: 在模型估计过程中被作为工具使用, 以替代与随即干扰项相关的随机解释变量。
6.结构式模型: 根据经济理论和行为规律建立的描述经济变量之间直接关系结构的计量经济学方程系统。
7. 内生变量: 具有某种概率分布的随机变量, 它的参数是联立方程系统估计的元素, 内生变量是由模型系统决定的, 同时也对模型系统产生影响。
内生变量一般都是经济变量。
8.异方差:对于不同的样本点, 随机干扰项的方差不再是常数, 而是互不相同, 则认为出现了异方差性。
9.回归分.: 研究一个变量关于另一个(些)变量的依赖关系的计算方法和理.。
其目的在于通过后者的已知或设定值,去估计和预测前者的(总体)均值。
前一变量称为被解释变量或应变量,后一变量称为解释变量或自变量。
1. 下列不属于线性回归模型经典假设的条件是( A )A.被解释变量确定性变量, 不是随机变量。
A. 被解释变量确定性变量,不是随机变量。
A.被解释变量确定性变量,不是随机变量。
B.随机扰动项服从均值为0, 方差恒定, 且协方差为0。
C. 随机扰动项服从正态分布。
D. 解释变量之间不存在多重共线性。
2. 参数的估计量具备有效性是指( B )A.B. 为最小A .0)ˆ(=βVarC .0)ˆ(=-ββED. 为最小3. 设Q 为居民的猪肉需求量, I 为居民收入, PP 为猪肉价格, PB 为牛肉价格, 且牛肉和猪肉是替代商品, 则建立如下的计量经济学模型: 根据理论预期, 上述计量经济学模型中的估计参数 、 和 应该是( C ) A . <0, <0, A. <0, <0,A .1ˆα<0,2ˆα<0,0ˆ3>αB . <0, >0,C . >0, <0,D . >0, >0,4. 利用OLS 估计模型 求得的样本回归线, 下列哪些结论是不正确的( D )A. 样本回归线通过( )点A .样本回归线通过(Y X ,)点B. =0 C .Y Y ˆ= D .i i X Y 10ˆˆαα+=5. 用一组有20个观测值的样本估计模型 后, 在0.1的显著性水平下对 的显著性作t 检验, 则 显著地不等于零的条件是t 统计量绝对值大于( D ) A.t0.1(20) A. t 0.1(20)B.t0.05(20)C.t0.1(18)D.t0.05(18)6. 对模型 进行总体线性显著性检验的原假设是( C ) A .0210===βββ B . , 其中C.D . , 其中 7.对于如下的回归模型 中, 参数 的含义是( D ) A. X 的相对变化,引起Y 的期望值的绝对变化量A .X 的相对变化,引起Y 的期望值的绝对变化量B. Y 关于X 的边际变化率C. X 的绝对量发生一定变动时,引起Y 的相对变化率D. Y 关于X 的弹性8.如果回归模型为背了无序列相关的假定, 则OLS 估计量( A ) A .无偏的, 非有效的 A. 无偏的,非有效的 A .无偏的,非有效的 B .有偏的, 非有效的 C .无偏的, 有效的D .有偏的, 有效的 9.下列检验方法中, 不能用来检验异方差的是. ..) A. 格里瑟检验 A .格里瑟检验 B. 戈德菲尔德-匡特检验C. 怀特检验D. 杜宾-沃森检验10. 在对多元线性回归模型进行 B. 序列相关性检验时, 发现各参数估计量的t检验值都很低, 但模型的拟合优度很高且F检验显著, 这说明模型很可能存在( C )A. 方差非齐性A.方差非齐性C. 多重共线性D. 模型设定误差11.包含截距项的回归模型中包含一个定性变量, 且这个定性变量有3种特征, 则, 如果我们在回归模型中纳入3个虚拟变量将会导致模型出现( A )A. 序列相关A.序列相关B. 异方差C. 完全共线性D. 随机解释变量12.下列条件中, 哪条不是有效的工具变量需要满足的条件( B )A. 与随机解释变量高度相关A.与随机解释变量高度相关B. 与被解释变量高度相关C. 与其它解释变量之间不存在多重共线性D. 与随机误差项不同期相关13. 当模型中存在随机解释变量时, OLS估计参数仍然是无偏的要求( A )A. 随机解释变量与随机误差项独立A.随机解释变量与随机误差项独立B.随机解释变量与随机误差项同期不相关, 而异期相关C. 随机解释变量与随机误差项同期相关D.不论哪种情况, OLS估计量都是有偏的14. 在分布滞后模型 中, 解释变量对被解释变量的长期影响乘数为( C ) A. A. 1βB.C.D .210βββ++15. 在联立方程模型中, 外生变量共有多少个( B )A.1 A. 1B.2C.3D.41. 普通最小二乘法确定一元线性回归模型 的参数 和 的准则是使( B ) A. ∑ei 最小 B. ∑ei2最小C. ∑ei 最大 D. ∑ei2最大2.普通最小二乘法(OLS)要求模型误差项 满足某些基本假定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
取 0.05 , Y f 平均值置信度 95%的预测区间为: Y f t 2 GDP2005 3600 时
480.884 2.228 7.5325 1 7195337.357 480.884 25.2735 (亿元) 12 3293728.494
^ ^ 2 1 (X f X ) n xi2
15、在异方差的情况下,参数估计值仍是无偏的,其原因是(
C.无多重共线性假定成立 定成立
ˆ 16、 已知 DW 统计量的值接近于 2, 则样本回归模型残差的一阶自相关系数
近似等于( A. 0 4 17、对美国储蓄与收入关系的计量经济模型分成两个时期分别建模,重建时 期是 1946—1954;重建后时期是 1955—1963,模型如下: A ) B.–1 C. 1 D.
2
(3.83)
R 0.4783, s.e. 2759.15, F 14.6692
White Heteroskedasticity Test: F-statistic Obs*R-squared 3.057161 5.212471 Probability Probability 0.076976 0.073812
ˆ 3.611151 0.134582GDP Y t t
(4.16179) t=(-0.867692) R =0.99181
2 2
(0.003867) (34.80013) F=1211.049
R =0.99181, 说明 GDP 解释了地方财政收入变动的 99%, 模型拟合程度较好。 模型说明当 GDP 每增长 1 亿元, 平均说来地方财政收入将增长 0.134582 亿 元。 当 2005 年 GDP 为 3600 亿元时,地方财政收入的点预测值为:
D.
9、应用 DW 检验方法时应满足该方法的假定条件,下列不是其假定条件的为
A.解释变量为非随机的 B.被解释变量为非随机的 C.线性回归模型中不能含有滞后内生变量 D.随机误差项服从一阶自回归 10、二元回归模型中,经计算有相关系数 R X 2 X 3 0.9985 ,则表明( A. X 2 和 X 3 间存在完全共线性 B. X 2 和 X 3 间存在不完全共线性 C. X 2 对 X 3 的拟合优度等于 0.9985 D.不能说明 X 2 和 X 3 间存在多重共线性 11、在 DW 检验中,存在正自相关的区域是( A. 4- d l ﹤ d ﹤4 C. d u ﹤ d ﹤4- d u B ) B. 0﹤ d ﹤ d l D. d l ﹤ d ﹤ d u ,4- d u ﹤ B )
重建时期: 重建后时期:
Yt 1 2 X t 1t Yt 3 4 X t 2t
D )
关于上述模型,下列说法不正确的是( A. 1 3 ; 2 4 时则称为重合回归 C. 1 3 ; 2 4 时称为相异回归
B. 1 3 ; 2 4 时称为平行回归 D. 1 3 ; 2 4 两个模型没有差异
1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001
资料来源:《深圳统计年鉴 2002》 ,中国统计出版社 利用 EViews 估计其参数结果为
(1)建立深圳地方预算内财政收入对 GDP 的回归模型; (2)估计所建立模型的参数,解释斜率系数的经济意义;
2
2
2
E
)
2
2
2
R2 .
E. R 有可能小于 0,但 R 却始终是非负
2
4、检验序列自相关的方法是( A. F 检验法 法
C E
) B. White 检验
C. 图形法 法
D. ARCH 检验
E. DW 检验法 F. Goldfeld-Quandt 检验法 5、 对多元线性回归方程的显著性检验, 所用的 F 统计量可表示为 ( A.
(
D
)
A. ei 0 C. ei X 3i 0
B. ei X 2i 0 D. ei Yi 0
20、当联立方程模型中第 i 个结构方程是不可识别的,则该模型是 ( B ) A.可识别的 好识别的 B.不可识别的 C.过度识别的 D.恰
二、多项选择题
1、 关于自适应预期模型和局部调整模型, 下列说法不正确的有 ( C A.它们都是由某种期望模型演变形成的 B.它们最终都是一阶自回归模型 C.它们都是库伊克模型的特例 D.它们的经济背景不同 E.都满足古典线性回归模型的所有假设,从而可直接用 OLS 进行估计 2、能够检验多重共线性的方法有( A B ) A.简单相关系数矩阵法 B. t 检验与 F 检验综合判断法 C. DW 检验法 D.ARCH 检验法 E. White 检验 3、 有关调整后的判定系数 R 2 与判定系数 R 2 之间的关系叙述正确的有(B C) A. R 与 R 均非负 B.模型中包含的解释个数越多, R 2 与 R 2 就相差越大. C.只要模型中包括截距项在内的参数的个数大于 1,则 R D. R 有可能大于 R
(3)对回归结果进行检验; (4) 若是 2005 年年的国内生产总值为 3600 亿元,确定 2005 年财政收入的 预测值和预测区间( 0.05 )。 解:地方预算内财政收入(Y)和 GDP 的关系近似直线关系,可建立线性回 归模型: Yt 1 2 GDPt u t 即
ˆ 3.611151 0.134582 3600 480.884 (亿元) Y 2005
区间预测:
x
2 i
2 x (n 1) 587.26862 (12 1) 3793728.494
( X f 1 X ) 2 (3600 917.5874) 2 7195337.357
d ﹤4- d l
12、库伊克模型不具有如下特点( D ) A. 原始模型为无限分布滞后模型,且滞后系数按某一固定比例递减 B.以一个滞后被解释变量 Yt 1 代替了大量的滞后解释变量 X t 1 , X t 2 , , 从而最大限度的保证了自由度 C. 滞后一期的被解释变量
Yt 1
与 X t 的线性相关程度肯定小于 X t 1 , X t 2 ,
年 份 地方预算内财政收入 Y (亿元) 21.7037 27.3291 42.9599 67.2507 74.3992 88.0174 131.7490 144.7709 164.9067 184.7908 225.0212 265.6532 国内生产总值(GDP)X (亿元) 171.6665 236.6630 317.3194 449.2889 615.1933 795.6950 950.0446 1130.0133 1289.0190 1436.0267 1665.4652 1954.6539
18、对样本的相关系数 ,以下结论错误的是( A. | | 越接近 0, X 与 Y 之间线性相关程度高 B. | | 越接近 1, X 与 Y 之间线性相关程度高 C. 1 1
A
)
D、 0 ,则 X 与 Y 相互独立
ˆ ˆ ˆ 19、、对于二元样本回归模型 Yi 1 21 X 2i 3 X 3i ei ,下列不成立的有
Y f 个别值置信度 95%的预测区间为:
2 1 (X f X ) Y f t 2 1 n xi2 ^ ^
即
= 480.884 2.228 7.5325 1
1 7195337.357 12 3293728.494
480.884 30.3381 (亿元)
3、在某个结构方程恰好识别的条件下,不适用的估计方法是( A.间接最小二乘法 C.二阶段最小二乘法 B.工具变量法 D.普通最小二乘法
4、在利用月度数据构建计量经济模型时,如果一年里的 12 个月全部表现出 季节模式,则应该引入虚拟变量个数为( C ) A. 4 D. 6 B. 12 C. 11
5、White 检验可用于检验( B ) A.自相关性 B. 异方差性 C.解释变量随机性 D.多重共线性 6、如果回归模型违背了无自相关假定,最小二乘估计量是( C A.无偏的,有效的 B. 有偏的,非有效的 C.无偏的,非有效的 D. 有偏的,有效的
第六套
一、单项选择题
1、计量经济学的研究方法一般分为以下四个步骤( B ) A.确定科学的理论依据、模型设定、模型修定、模型应用 B.模型设定、估计参数、模型检验、模型应用 C.搜集数据、模型设定、估计参数、预测检验 D.模型设定、模型修定、结构分析、模型应用 2、简单相关系数矩阵方法主要用于检验( A.异方差性 C.随机解释变量 D ) B.间接最小二乘法与两阶段最小二乘法得到的估计量都是无偏估计。 错误 间接最小二乘法适用于恰好识别方程的估计,其估计量为无偏估计; 而两阶段最小二乘法不仅适用于恰好识别方程,也适用于过度识别方程。 两阶段最小二乘法得到的估计量为有偏、一致估计。
四、计算题
1、为了研究深圳市地方预算内财政收入与国内生产总值的关系,得到以下 数据:
)
7、假如联立方程模型中,第 i 个方程排除的变量中没有一个在第 j 个方 程中出现,则第 i 个方程是( A.可识别的 识别 D ) C.过度识别 D.不可
B.恰好识别
8、在简单线性回归模型中,认为具有一定概率分布的随机变量是 ( A ) A.内生变量 B.外生变量 C.虚拟变量 前定变量 ( B )
的相关程度,从而缓解了多重共线性的问题
* * * D.由于 Cov (Yt 1 , u t ) 0, Cov (u t , u t 1 ) 0 ,因此可使用 OLS 方法估计参
数,参数估计量是一致估计量
y 1 x u 1 2 x x x , 13、在具体运用加权最小二乘法时,如果变换的结果是 x
