8位m序列的生成
m序列快速生成算法

m序列快速生成算法摘要:1.m 序列的概述2.m 序列快速生成算法的原理3.m 序列快速生成算法的具体步骤4.m 序列快速生成算法的应用案例5.m 序列快速生成算法的优缺点分析正文:一、m 序列的概述m 序列,也被称为m 序列数列,是一种在数学和计算机科学中经常出现的数列。
它的定义是:从1 开始,每个数都是前两个数之和。
例如,前几个m 序列数为:1, 1, 2, 3, 5, 8, 13, 21, 34, 55,...。
m 序列具有很多有趣的性质,如斐波那契数列、卢卡斯数列等,因此在各个领域都有广泛的应用。
二、m 序列快速生成算法的原理m 序列快速生成算法是一种高效生成m 序列的方法,其原理是利用数学递推关系式,通过迭代计算来快速生成m 序列。
m 序列的递推关系式为:F(n) = F(n-1) + F(n-2),其中F(n) 表示第n 个m 序列数。
通过这个递推关系式,我们可以从已知的前两个m 序列数开始,逐步计算出后续的m 序列数。
三、m 序列快速生成算法的具体步骤1.初始化两个变量a 和b,分别表示m 序列的前两个数。
2.使用递推关系式F(n) = F(n-1) + F(n-2),计算出第n 个m 序列数。
3.将计算出的第n 个m 序列数赋值给变量a,并将变量b 的值赋给变量a。
4.重复步骤2 和3,直到计算出所需的m 序列数。
四、m 序列快速生成算法的应用案例m 序列快速生成算法在很多领域都有应用,如计算机图形学、数据压缩、金融分析等。
以计算机图形学为例,m 序列可以用来生成光滑的曲线和曲面,提高图形的质量。
在数据压缩中,m 序列可以用来压缩数据,减少存储空间。
在金融分析中,m 序列可以用来预测股票价格等。
五、m 序列快速生成算法的优缺点分析优点:1.m 序列快速生成算法计算速度快,能够高效地生成m 序列。
2.m 序列具有很多有趣的性质,因此在各个领域都有广泛的应用。
缺点:1.m 序列快速生成算法的计算过程较为复杂,需要处理递推关系式。
c语言随机生成8位数字

c语言随机生成8位数字在计算机编程领域,随机数生成是一项非常重要的技术。
C语言作为一种广泛应用的编程语言,也提供了生成随机数的函数库。
本文将介绍如何使用C语言生成8位数字的随机数。
在C语言中,我们可以使用rand()函数来生成随机数。
该函数位于stdlib.h头文件中,可以生成一个范围在0到RAND_MAX之间的随机整数。
但是,直接使用rand()函数生成的随机数可能不满足我们的需求,因为它的范围太大了。
为了生成8位数字的随机数,我们需要对rand()函数生成的随机数进行处理。
具体的处理方法如下:1. 使用srand()函数设置随机数种子。
srand()函数也位于stdlib.h头文件中,它用于设置随机数生成器的种子。
我们可以使用time()函数获取当前时间作为种子,确保每次运行程序时生成的随机数都不同。
2. 使用rand()函数生成一个0到99999999之间的随机整数。
我们可以通过对生成的随机数取模100000000来限制其范围。
3. 如果生成的随机数小于10000000,我们可以通过加上10000000来保证生成的随机数一定是8位数字。
下面是一个使用C语言生成8位数字随机数的示例代码:```c#include <stdio.h>#include <stdlib.h>#include <time.h>int main() {int random_num;srand(time(NULL)); // 设置随机数种子random_num = rand() % 100000000; // 生成0到99999999之间的随机整数if (random_num < 10000000) {random_num += 10000000; // 保证生成的随机数是8位数字}printf("随机生成的8位数字为:%d\n", random_num);return 0;}```通过运行上述代码,我们可以在控制台上看到一个随机生成的8位数字。
实验八M序列发生及眼图观测实验

实验八 M序列发生及眼图观测实验
四、实验原理
1、M序列
移位时 钟节拍
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
表1 m序列发生器状态转移流程图
第1级 a n1
0 1 0 0 1 1 0 1 0 1 1 1 1 0 0 0 1
第2级
an2
0 0 1 0 0 1 1 0 1 0 1 1 1 1 0 0 0
二、实验预习要求
认真预习《通信原理》中关于M序列及 眼图有关章节的内容。
通信工程专业实验室
实验八 M序列发生及眼图观测实验
三、实验仪器仪表
1、70MHz双踪数字存储示波器一台 2、实验模块:
数字编码模块——M序列输出 数字时钟信号源模块 眼图观测及白噪声输出模块
通信工程专业实验室
实验八 M序列发生及眼图观测实验
通信工程专业实验室
实验八 M序列发生及眼图观测实验
四、实验原理
2、眼图
所谓“眼图”,就是由解调后经过低通 滤波器输出的基带信号,以码元定时作为同 步信号在示波器屏幕上显示的波形。干扰和 失真所产生的传输畸变,可以在眼图上清楚 地显示出来。因为对于二进制信号波形,它 很像一只人的眼睛。
眼图是指利用实验的方法估计和改善(通
实验八 M序列发生及眼图观测实验
实验八 M序列发生及 眼图观测实验
【实验性质】:验证性实验
通信工程专业实验室
实验八 M序列发生及眼图观测实验
一、实验目的
1、掌握M序列等伪随机码的发生原理。 2、了解伪随机码在通信电路中的作用。 3、掌握眼图的观测。
通信工程专业实验室
实验八 M序列发生及眼图观测实验
t
m序列原理

m序列原理m序列是一种特殊的伪随机序列,具有良好的随机性质和周期性,广泛应用于通信、密码学、雷达、遥感等领域。
m序列的原理是基于线性反馈移位寄存器(LFSR)的工作原理,通过适当的初值和反馈多项式,可以生成具有良好随机性质的序列。
m序列的生成原理是基于LFSR的工作原理。
LFSR是一种线性反馈移位寄存器,它由若干个存储单元和适当的反馈电路组成。
在LFSR中,存储单元中的数据按照时钟信号不断移位,同时根据反馈电路的控制,将某些位上的数据进行异或运算,得到新的输入数据,从而实现序列的生成。
通过适当选择LFSR的初值和反馈多项式,可以得到不同长度的m序列。
m序列具有良好的随机性质和周期性。
由于m序列的生成原理是基于LFSR的移位和异或运算,使得序列中的数据呈现出随机分布的特性。
同时,由于LFSR的结构和反馈多项式的选择,m序列具有很长的周期,甚至可以达到最大周期2^n-1,其中n为LFSR的位数。
这使得m序列在伪随机序列中具有较好的性能。
m序列在通信、密码学、雷达、遥感等领域有着广泛的应用。
在通信系统中,m序列可以作为扩频序列,用于码分多址(CDMA)通信系统中的信道编码和解码,提高通信系统的抗干扰能力和安全性。
在密码学中,m序列可以作为密钥序列,用于数据加密和解密,保障通信的安全性。
在雷达和遥感领域,m序列可以作为调制序列,用于信号的调制和解调,提高信号的分辨率和抗干扰能力。
总之,m序列作为一种特殊的伪随机序列,具有良好的随机性质和周期性,在通信、密码学、雷达、遥感等领域有着广泛的应用前景。
通过深入理解m序列的生成原理和特性,可以更好地应用于实际系统中,提高系统的性能和安全性。
m序列的原理及应用

m序列的原理及应用1. 什么是m序列?m序列,全名为最大长度线性反馈移位寄存器序列(Maximum Length Sequence),是一种特殊的二进制序列。
m序列的特点是具有最长的周期,并且波形均匀随机分布。
m序列可以通过一个线性反馈移位寄存器(LFSR)来生成。
2. m序列的生成原理m序列的生成原理基于线性反馈移位寄存器(LFSR)的运算。
LFSR是一种用于产生伪随机序列的硬件电路。
LFSR由寄存器和反馈函数组成。
寄存器是一组存储数据的单元,通常是一组触发器,每个触发器存储一个二进制位。
反馈函数根据寄存器的当前状态产生下一个状态。
反馈函数一般采用异或操作。
m序列的生成就是通过不断移位和反馈计算,使得LFSR的状态变化遍历所有可能的状态,从而生成了m序列。
3. m序列的应用m序列由于其随机性和均匀性,被广泛应用于通信、加密、导航等领域。
3.1 通信领域在通信领域中,m序列被用作伪随机序列发生器。
伪随机序列在信号传输、数据调制等方面起到关键作用。
m序列具有具有良好的互相关性和自相关性性质,能够提供伪随机的编码和解码功能。
3.2 加密领域m序列在加密领域中作为密钥序列广泛使用。
由于m序列的随机性和不可预测性,能有效地保护数据的安全性。
一种常见的应用是m序列与明文进行异或运算,生成密文,从而实现加密功能。
3.3 导航领域在导航领域中,m序列被用于全球卫星导航系统(GNSS)中的扩频码。
扩频码是通过将原始导航信号与m序列进行乘法运算而生成的。
m序列的均匀随机性使得扩频码具有良好的抗多径和抗干扰性能。
4. m序列的特点4.1 最长周期m序列具有最长的周期,周期长度为2^N-1,其中N为LFSR的位数。
这意味着m序列可以生成非常长的伪随机序列。
4.2 均匀随机性m序列的波形均匀分布,具有良好的随机性。
这个特性使得m序列在各个应用领域都能发挥重要作用。
4.3 线性可预测性m序列是由线性反馈移位寄存器生成的,其生成过程可以被完全预测。
伪随机m序列发生器的产生设计

信息科学与技术学院通信原理课程设计课题名称:伪随机M序列发生器设计学生姓名:许奎英2008082491学院:信息科学与技术学院专业年级:电子信息工程2008级指导教师:邓红涛完成日期:二○一一年七月十二日目录前言 (3)摘要 (4)理论基础知识 (5)伪随机序列 (6)伪随机序列定义及应用. (7)m序列产生器 (7)芯片介绍 (8)移位寄存器74LS164 (9)D/A转换器IDAC (9)EWB软件介绍 (10)设计方案 (10)EWB仿真 (11)电路的调试 (13)参考文献 (13)实验心得 (14)附录 (15)前言题目:伪随机序列的产生及应用设计初始条件:具备通信课程的理论知识;具备模拟与数字电路基本电路的设计能力;掌握通信电路的设计知识,掌握通信电路的基本调试方法;自选相关电子器件;可以使用实验室仪器调试。
要求完成的主要任务:(包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)1、设计伪随机码电路:产生八位伪随机序列(如M序列);2、了解D/A的工作原理及使用方法,将伪随机序列输入D/A中(如DAC0808),观察其模拟信号的特性;3、分析信号源的特点,使用EWB软件进行仿真;4、进行系统仿真,调试并完成符合要求的课程设计说明书。
摘要伪随机序列具有良好的随机性和接近于白噪声的相关函数,使其易于从信号或干扰中分离出来。
伪随机序列的可确定性和可重复性,使其易于实现相关接收或匹配接收,因此有良好的抗干扰性能。
伪随机序列的这些特性使得它在伪码测距、导航、遥控遥测、扩频通信、多址通信、分离多径、数据加扰、信号同步、误码测试、线性系统、各种噪声源等方面得到了广泛的应用,特别是作为扩频码在CDMA系统中的应用已成为其中的关键问题。
此次课设根据m序列的产生原理,利用74LS164加少量门电路方法设计了8位m序列发生器。
关键词:伪随机序列m序列移位寄存器D/A转换EWB仿真1理论基础知识1.1伪随机序列1.1.1伪随机序列定义及应用如果一个序列,一方面它是可以预先确定的,并且是可以重复地生产和复制的;一方面它又具有某种随机序列的随机特性(即统计特性),我们便称这种序列为伪随机序列。
m序列产生原理

m序列产生原理m序列是一种特殊的伪随机数序列,具有良好的随机性质,被广泛应用于通信、加密、雷达、测距等领域。
m序列的产生原理主要基于反馈移位寄存器和模2加法器,下面我们来详细介绍一下m序列的产生原理。
首先,m序列的产生基于一个反馈移位寄存器(LFSR),它由若干个触发器和异或门组成。
反馈移位寄存器的初始状态称为种子,种子的选择对m序列的随机性质有很大影响。
在产生m序列的过程中,寄存器的状态不断变化,每次变化都会输出一个比特,这些输出的比特组成了m序列。
其次,m序列的产生还依赖于模2加法器。
反馈移位寄存器输出的比特经过模2加法器进行模2加运算,得到m序列的输出比特。
模2加法器实际上就是异或门,它将反馈移位寄存器输出的比特与特定位置上的比特进行异或运算,得到m序列的下一个比特。
最后,m序列的周期性与反馈移位寄存器的长度有关。
对于一个n级的反馈移位寄存器,其产生的m序列的周期为2^n-1,即m序列会在2^n-1个时钟周期内重复。
这也意味着m序列的长度是有限的,随着时钟周期的增加,m序列会重复出现之前的序列。
总结一下,m序列的产生原理主要包括反馈移位寄存器和模2加法器。
反馈移位寄存器通过不断变换状态产生随机比特,而模2加法器则将这些比特进行模2加运算,最终输出m序列。
m序列的周期性与反馈移位寄存器的长度有关,周期为2^n-1。
通过合理选择反馈移位寄存器的种子和长度,可以得到具有良好随机性质的m序列。
以上就是m序列的产生原理,希望能对您有所帮助。
如果您对m序列还有其他疑问,欢迎与我们进一步交流讨论。
m序列产生及其特性实验

实验九 m 序列产生及其特性实验一、 实验目的和要求通过本实验掌握m 序列的特性、产生方法及应用。
二、实验内容和原理1)、实验内容1、观察m 序列,识别其特征。
2、观察m 序列的自相关特性。
2)、基本原理m 序列是有n 级线性移位寄存器产生的周期为21n -的码序列,是最长线性移位寄存器序列的简称。
1、产生原理图9-1示出的是由n 级移位寄存器构成的码序列发生器。
寄存器的状态决定于时钟控制下输入的信息(“0”或“1”),例如第I 级移位寄存器状态决定于前一时钟脉冲后的第i -1级移位寄存器的状态。
图中C 0,C 1,…,C n 均为反馈线,其中C 0=C n =1,表示反馈连接。
因为m 序列是由循环序列发生器产生的,因此C 0和C n 肯定为1,即参与反馈。
而反馈系数C 1,C 2,…,C n -1若为1,参与反馈;若为0,则表示断开反馈线,即开路,无反馈连线。
一个线性反馈移动寄存器能否产生m 序列,决定于它的反馈系数(0,1,2,,)i c i n =,下表中列出了部分m 序列的反馈系数i c ,按照下表中的系数来构造移位寄存器,就能产生相应的m 序列。
表9-1 部分m 序列的反馈系数表根据表9-1中的八进制的反馈系数,可以确定m 序列发生器的结构。
以7级m 序列反馈系数8(211)i C =为例,首先将八进制的系数转化为二进制的系数即2(010001001)i C =,由此我们可以得到各级反馈系数分别为:01C =、10C =、30C =、41C =、50C =、60C =、71C =,由此就很容易地构造出相应的m 序列发生器。
根据反馈系数,其他级数的m 序列的构造原理与上述方法相同。
需要说明的是,表9-1中列出的是部分m 序列的反馈系数,将表中的反馈系数进行比特反转,即进行镜像,即可得到相应的m 序列。
例如,取482(23)(10011)C ==,进行比特反转之后为28(10011)(31)=,所以4级的m 序列共有2个。
m序列产生原理

m序列产生原理m序列是一种随机序列,它的特点是在用相同的参数初始化m序列时,序列中出现的每一位都是确定的,而且具有高度的均匀性,被广泛用于计算机科学和信号处理领域。
m序列的产生主要是基于位移寄存器(shift-register)的运算,它们给出了一种快速、灵活的产生随机序列的方法。
m序列是典型的应用有状态机(state machine)的循环运算法则产生的。
有状态机指有一个由有限个状态组成的有限状态集合,它们可以根据输入信号从一个状态转换到另一个状态,并且每一次状态转换后,输出一位数据,而且这个数据受到了转换前的状态和输入信号的影响,我们称有状态机为有限状态机,它是一个循环的结构,在每一次的输出之后,系统会进入一个新的状态,这个状态是由输入信号和转换前的状态所决定的。
状态机的运算可以抽象地表述为如下的方程式:Si = f(Si-1, K)其中K为一个密钥,Si为状态机的状态,Si-1表示转换前的状态,f是一个函数,它使用一个密钥和转换前的状态作为输入,返回一个新的状态。
m序列生成器就是一种有状态机,它有一个状态序列Si,状态序列的长度称为m,它的状态序列Si的每一位都有一个可确定的值。
m 序列生成器的运算方程式如下:Si = f(Si-1, Si-2, Si-m+1)其中f是一个不同于上面式子中的函数。
它采用最后m位的状态作为输入,它根据某种规则,决定每一次状态转换后输出一个新的状态。
m序列生成器的输出都是独立的,且具有高度的均匀性,而且这种输出可以用来作为伪随机数据。
m序列生成器有很多种不同的实现形式,最常用的是有线m序列。
它使用一个有限的状态序列,以及一个叫做“线性函数”的运算,来生成特定的随机变量。
它的状态序列是由一系列的反馈有效比特组成的,这些反馈有效比特将决定最终输出序列的值,也就是状态序列将产生一组随机序列。
有线m序列的典型例子包括LFSR(线性反馈移位寄存器)、m暗号和BCH暗号,这些技术被广泛用于无线传输系统中,以生成高可靠性、高随机性的通信信号。
m序列产生——精选推荐

m序列产⽣设计内容及要求基于MATLAB产⽣m序列要求:1.通过matlab编程产⽣m序列的产⽣原理及其产⽣⽅法。
2.对特定长度的m序列,分析其性质,及其⽤来构造其它序列的⽅法。
第⼆章m序列设计⽅案的选择2.1 ⽅案⼀MATLAB编程⾮常简单,⽆需进⾏变量声明,可以很⽅便的实现m序列。
2.2 ⽅案⼆图2.1 Simulink实现m序列Simulink是MATLAB最重要的组件之⼀,它提供了⼀个动态系统建模,仿真和综合分析的集成环境。
在此环境中⽆需⼤量书写程序,⽽只需通过简单直观的⿏标操作,就可构造出复杂的系统。
Simulink具有适应性⼴,结构及流程清晰及仿真精细等优点,基于以上优点,Simulink已被⼴泛的运⽤到控制理论和数字信号处理的复杂仿真和设计。
通过⽐较⽅案⼀和⽅案⼆,发现⽅案⼀的有点具有通⽤性⽽⽅案⼆利⽤MATLAB的Simulink直接搭建模块,在移位寄存器较少的情况下利⽤此⽅法⽐较简单,可是当移位寄存器的个数增多时,要搭建那么多的模块就显的很繁琐了,缺乏通⽤性,因此本次实验选择⽅案⼀。
第三章m序列的产⽣及性质3.1 m序列的产⽣原理、结构及产⽣m序列是最长线性反馈移位寄存器序列的简称,m序列是由带线性反馈的移位寄存器产⽣的。
由n级串联的移位寄存器和反馈逻辑线路可组成动态移位寄存器,如果反馈逻辑线路只由模2和构成,则称为线性反馈移位寄存器。
带线性反馈逻辑的移位寄存器设定初始状态后,在时钟触发下,每次移位后各级寄存器会发⽣变化,其中任何⼀级寄存器的输出,随着时钟节拍的推移都会产⽣⼀个序列,该序列称为移位寄存器序列。
n级线性移位寄存器的如图3.1所⽰:◇A图3.1 n级线性移位寄存器图中C i表⽰反馈线的两种可能连接⽅式,C i=1表⽰连线接通,第n-i级输出加⼊反馈中;C i=0表⽰连线断开,第n-i级输出未参加反馈。
因此,⼀般形式的线性反馈逻辑表达式为------表达式3.1将等式左边的a n移⾄右边,并将a n=C0a n(C0=1)带⼊上式,则上式可以写成-------表达式3.2定义⼀个与上式相对应的多项式--------表达式3.3其中x的幂次表⽰元素的相应位置。
m序列的原理

m序列的原理
M序列(Maximum Length Sequence)是一种伪随机序列生成
方法,也称为伪随机二进制序列。
它具有自相关性和互相关性很小的特点,并且具有最长周期。
M序列的生成原理基于反馈移位寄存器(Feedback Shift Register,FSR)。
FSR是由多个D触发器(D Flip-Flop)组
成的,每个D触发器的输出作为下一个D触发器的输入,并
形成移位链。
M序列的开始状态可以是任意的,并通过逻辑运算(如异或
运算)将连续的寄存器输出进行组合,生成伪随机序列。
M
序列的周期取决于FSR的长度,理论上可以达到2的n次方-1,其中n为FSR的长度。
生成M序列的特点如下:
1. 周期最长:当FSR的长度为n时,M序列的周期为2的n
次方-1。
2. 互相关性和自相关性较小:M序列具有较小的相互相关性
和自相关性,适合用于通信系统中的扩频技术。
3. 均匀性:M序列的值为+1或-1,每个值出现的概率相等,
具有较好的均匀性。
4. 硬件实现简单:使用FSR和逻辑运算可以很容易地生成M
序列,不需要复杂的计算。
M序列在通信系统中的应用广泛,主要用于扩频通信中的伪
随机序列生成、同步检测以及信号捕获等方面。
m序列的生成与仿真
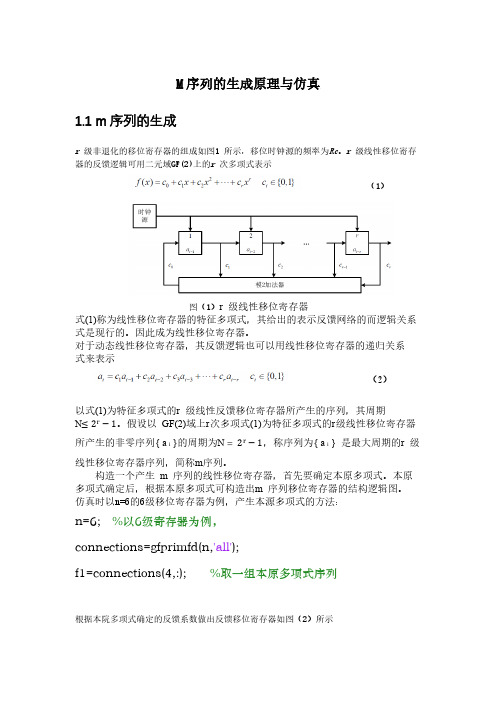
M序列的生成原理与仿真1.1 m序列的生成r 级非退化的移位寄存器的组成如图1 所示,移位时钟源的频率为Rc。
r 级线性移位寄存器的反馈逻辑可用二元域GF(2)上的r 次多项式表示(1)图(1)r 级线性移位寄存器式(1)称为线性移位寄存器的特征多项式,其给出的表示反馈网络的而逻辑关系式是现行的。
因此成为线性移位寄存器。
对于动态线性移位寄存器,其反馈逻辑也可以用线性移位寄存器的递归关系式来表示(2)以式(1)为特征多项式的r 级线性反馈移位寄存器所产生的序列,其周期N≤2r−1。
假设以GF(2)域上r次多项式(1)为特征多项式的r级线性移位寄存器所产生的非零序列{ a i }的周期为N =2r−1,称序列为{ a i }是最大周期的r 级线性移位寄存器序列,简称m序列。
构造一个产生m 序列的线性移位寄存器,首先要确定本原多项式。
本原多项式确定后,根据本原多项式可构造出m 序列移位寄存器的结构逻辑图。
仿真时以n=6的6级移位寄存器为例,产生本源多项式的方法:n=6; %以6级寄存器为例,connections=gfprimfd(n,'all');f1=connections(4,:); %取一组本原多项式序列根据本院多项式确定的反馈系数做出反馈移位寄存器如图(2)所示图(2)m 序列发生器1.2 m 序列自相关函数1.2.1周期自相关函数编写周期自相关函数和非周期自相关函数,实验结果如下图(2)和(3)所示:图(2)m 序列周期自相关函数结论:周期自相关函数R (k )={63 k =0−1 otℎersm 序列周期自相关函数1.2.2非周期自相关函数图(3) m 序列非周期自相关函数1.3 m 序列的互相关函数选用的两个m 序列为一对优选对,以211作为基准本原多项式(反馈系数10001001),217作为配对本原多项式(反馈系数10001111),生成两个m 序列,求出互相关函数如图(4)和(5):、图(4)m 序列互相关函数结论:互相关函数的取值{-1,-17,15}m 序列非周期自相关函数m 序列周期互相关函数m序列非周期互相关函数图(5)m序列非周期互相关函数1.4 附:matlab代码clear;clc;%%------生成m序列-----%%n=6; %以6级寄存器为例,connections=gfprimfd(n,'all');f1=connections(4,:); %取一组本原多项式序列registers1=[1 0 0 0 0 0 ];%给定寄存器的初始状态L=2^n-1; %周期长度sum1=0;for k=1:Lseq(k)=registers1(n); %m序列for j=1:n %进行模2加sum1=sum1+f1(j+1)*registers1(j); %各级寄存器送参与模2加的值sum1=mod(sum1,2);endfor t=n:-1:2 %寄存器移位registers1(t)=registers1(t-1);endregisters1(1)=sum1;sum1=0;end% %%----------------------自相关函数-------------------------%%% %-------非周期自相关函数--------%%a=1-2*seq;b=a;for i=1:LR(i)=sum(a.*b)b=[0 b(1:62)]endplot(R)title('m序列非周期自相关函数');% %-------周期自相关函数------%%% a=1-2*seq;% b=a;% for i=1:L% R(i)=sum(a.*b)% b=[b(63) b(1:62)]% end% plot(R);% title('m序列周期自相关函数');%%-------利用公式编写自相关函数验证---------------%% % a=seq1;% b=[a(1,63),a(1,1:62)];% L=length(b);% n=400;% x=1:n;% for k=1:n% c=xor(a,b);% D=sum(c);% A=L-D;% R(k)=(A-D)/(A+D);% b=[b(L),b(1:L-1)];% end% plot(x,R);% title('gold序列的自相关函数');% xlabel('τ');% ylabel('R(τ)');% grid;。
m序列快速生成算法

m序列快速生成算法摘要:一、引言1.背景介绍2.研究目的二、m序列概述1.m序列定义2.m序列性质3.m序列应用场景三、快速生成算法原理1.传统生成算法2.快速生成算法优势四、算法实现1.算法框架2.核心算法步骤五、实验与分析1.实验环境2.实验结果3.结果分析六、结论与展望1.算法应用成果2.未来研究方向正文:一、引言1.背景介绍在数字通信、密码学等领域,m序列作为一种重要的伪随机序列,广泛应用于信道编码、同步和加密等领域。
随着对m序列需求的增长,如何快速生成m序列成为了一个亟待解决的问题。
2.研究目的本文旨在提出一种高效的m序列快速生成算法,相较于传统生成方法,该算法在保证序列质量的同时,显著提高生成速度。
二、m序列概述1.m序列定义m序列是一种线性反馈移位寄存器(LFSR)生成的伪随机序列,其具有周期性、非周期性和多相位等特点。
2.m序列性质m序列具有以下性质:周期性、平衡性、相关性、遍历性和稳定性等。
3.m序列应用场景m序列在通信、密码、仿真等领域具有广泛应用,如信道编码、同步码、加密和解密等。
三、快速生成算法原理1.传统生成算法传统m序列生成算法主要包括线性反馈移位寄存器(LFSR)和查表法等,但这些方法存在生成速度慢、效率不高等问题。
2.快速生成算法优势本文提出的快速生成算法利用了m序列的性质,通过优化生成过程中的计算方法,提高生成速度。
四、算法实现1.算法框架本文提出的算法分为预处理、核心生成和后处理三个阶段。
2.核心算法步骤(1)预处理:对输入参数进行优化处理,减少计算复杂度。
(2)核心生成:根据m序列生成原理,采用优化算法生成序列。
(3)后处理:对生成的m序列进行质量评估和调整,提高序列性能。
五、实验与分析1.实验环境本文实验基于某处理器平台,使用Python编程语言实现。
2.实验结果实验结果表明,相较于传统算法,本文提出的快速生成算法在保证m序列质量的同时,提高了生成速度。
3.结果分析分析实验结果,可知快速生成算法在减少计算复杂度和优化生成过程方面取得了显著效果。
m序列快速生成算法

m序列快速生成算法【原创实用版】目录1.m 序列的概述2.m 序列快速生成算法的原理3.m 序列快速生成算法的具体步骤4.m 序列快速生成算法的优缺点5.m 序列快速生成算法的应用实例正文m 序列的概述:m 序列,也被称为 m 级数列,是一种在数学中经常出现的数列,其通项公式为 a_n = a_1 * q^(n-1),其中 a_1 是首项,q 是公比,n 是项数。
m 序列广泛应用于各种数学问题中,如求和、求积、级数收敛性等。
m 序列快速生成算法的原理:m 序列快速生成算法是一种基于迭代的方法,其原理是通过不断更新数列中的每一项,最终得到 m 序列。
具体来说,算法的初始值设为 a_1,然后通过不断计算 a_n = a_(n-1) * q,最终得到 m 序列。
m 序列快速生成算法的具体步骤:1.设定初始值 a_1;2.设定公比 q;3.设定项数 n;4.按照公式 a_n = a_(n-1) * q,从第一项开始,逐项计算,直到计算到第 n 项;5.得到 m 序列。
m 序列快速生成算法的优缺点:优点:算法简单,易于理解,计算速度快。
缺点:需要预先设定项数 n,如果 n 过大,计算量会增大,而且如果公比 q 不是有理数,可能会出现精度问题。
m 序列快速生成算法的应用实例:一个典型的应用实例是求解等比数列的和。
假设有一个等比数列,首项为 a_1,公比为 q,项数为 n,我们可以使用 m 序列快速生成算法来求解这个等比数列的和,即 S_n = a_1 * (1 - q^n) / (1 - q)。
通过这个算法,我们可以快速、准确地得到等比数列的和。
8位单片机自动生成代码

8位单片机自动生成代码一、介绍在嵌入式系统开发领域中,8位单片机在很多应用中扮演着重要的角色。
8位单片机自动生成代码是指通过工具或软件自动生成与8位单片机相关的代码,以便简化开发流程,提高开发效率。
本文将详细介绍8位单片机自动生成代码的背景、原理、应用以及优缺点。
二、背景随着技术的不断发展,嵌入式系统的应用越来越广泛。
而在嵌入式系统中,单片机是最常用且灵活的硬件平台之一。
在开发单片机应用程序时,程序员通常需要手动编写大量的代码,包括初始化、中断处理、IO控制等。
这不仅增加了开发工作量,同时也容易出现错误。
为了简化开发流程,提高开发效率,人们开始研发并使用8位单片机自动生成代码工具。
这些工具能够根据用户提供的参数和需求,自动生成与单片机相关的代码,从而减少编程量,加快开发速度。
三、原理8位单片机自动生成代码工具的原理主要包括以下几个方面:1. 代码模板自动生成代码工具通常会提供一系列的代码模板,包括初始化模板、中断处理模板、IO控制模板等。
这些模板已经预定义好了基本的代码框架和结构,用户只需要根据需求填写相关参数即可。
2. 用户输入用户需要提供一些参数和需求给代码生成工具,例如单片机型号、时钟频率、IO控制方式等。
这些参数和需求将作为输入,供代码生成工具使用。
3. 代码生成代码生成是整个自动生成过程的核心。
根据用户提供的参数和需求,代码生成工具会根据代码模板生成相应的代码。
生成的代码会包括初始化代码、中断处理代码、IO控制代码等,以满足用户的实际需求。
4. 输出结果生成的代码可以以文本文件的形式输出,也可以直接复制到用户的开发环境中。
用户可以根据自己的需要选择合适的方式,将生成的代码导入到项目中进行开发。
四、应用8位单片机自动生成代码在嵌入式系统开发中有广泛的应用。
以下是一些常见的应用场景:1. 快速原型开发在进行快速原型开发时,时间紧迫且需求频繁变动。
使用8位单片机自动生成代码工具,开发人员可以快速生成初始代码框架,并根据实际需求进行修改和扩展。
《2024年人类基因组序列8-mer频谱的内在规律和各类8-mers的生物功能》范文

《人类基因组序列8-mer频谱的内在规律和各类8-mers的生物功能》篇一人类基因组序列8-mer频谱的内在规律与各类8-mers的生物功能一、引言随着人类基因组学的发展,基因序列研究已深入到更精细的层次,包括核苷酸水平的研究。
本文以8-mer频谱作为研究点,通过深度探讨人类基因组序列的内在规律和各类8-mers的生物功能,以解析人类遗传信息在生物分子层次的作用和重要性。
二、人类基因组序列的8-mer频谱人类基因组是一个极其复杂的核苷酸序列系统,其信息结构主要体现在特定的模式和序列模式中。
在基因序列分析中,一个常见的单位是“8-mer”,即由八个核苷酸组成的连续序列。
8-mer 频谱则是指基因组中所有可能的8-mer序列的出现频率。
通过对人类基因组进行深度分析,我们可以得到一个详细的8-mer频谱图。
这个图谱揭示了基因组中不同8-mer序列的分布和频率,从而反映了基因组的复杂性和多样性。
三、8-mer频谱的内在规律人类基因组中的8-mer频谱并非随机分布,而是遵循一定的规律。
这些规律主要体现在以下几个方面:1. 高度保守的序列模式:某些特定的8-mer序列在基因组中频繁出现,这些序列往往具有特定的生物学功能或参与重要的生物学过程。
2. 序列的进化保守性:在进化过程中,一些关键的8-mer序列被保留下来,表现出高度的进化保守性。
3. 上下文依赖性:基因组中的每个位置上不同的8-mer频率也受其周围序列环境的影响,体现了复杂的上下文依赖性。
四、各类8-mers的生物功能人类基因组中的各类8-mer序列具有不同的生物功能,主要表现在以下几个方面:1. 编码区:编码区的8-mer序列通常参与蛋白质编码过程,影响蛋白质的结构和功能。
2. 非编码区:非编码区的8-mer序列虽然不直接参与蛋白质编码,但它们在基因表达调控、转录后修饰等过程中发挥重要作用。
3. 调控元件:一些特定的8-mer序列作为调控元件,参与基因表达的调控过程,如启动子、增强子等。
《基因组序列8-mer模体使用分离与不同序列组成和物种进化的关系》范文

《基因组序列8-mer模体使用分离与不同序列组成和物种进化的关系》篇一基因组序列8-mer模体使用与不同序列组成及物种进化的关系一、引言随着生物信息学和分子生物学的快速发展,基因组序列分析已成为研究物种进化和功能的重要手段。
其中,8-mer模体作为基因组序列中的一种重要特征,对于理解基因序列组成和物种进化关系具有重要意义。
本文将探讨基因组序列中8-mer模体的使用、不同序列组成与物种进化之间的关系。
二、8-mer模体的定义及作用8-mer模体是指基因组序列中连续8个碱基的组合。
这种模体在基因表达调控、蛋白质编码以及物种进化过程中扮演着重要角色。
通过对8-mer模体的分析,可以了解基因序列的组成和结构特点,进而揭示物种进化的规律。
三、8-mer模体使用与序列组成的关系1. 碱基组成:基因组序列中不同碱基的组成和分布会影响8-mer模体的频率和类型。
例如,GC含量较高的区域可能产生更多富含GC的8-mer模体。
2. 重复序列:基因组中重复序列的存在会增加特定8-mer模体的频率。
这些重复序列可能参与基因表达调控、遗传重组等生物学过程。
3. 基因结构:基因内含子和外显子的结构差异也会影响8-mer模体的分布。
内含子区域可能富含某些特定的8-mer模体,而外显子区域则可能富含其他类型的模体。
四、8-mer模体使用与物种进化的关系1. 物种差异:不同物种间基因组序列的8-mer模体使用存在差异。
这些差异可能与物种的进化历史、生态环境和遗传多样性有关。
通过对不同物种间8-mer模体的比较分析,可以揭示物种间的进化关系和亲缘关系。
2. 进化压力:自然选择和进化压力会影响基因组序列中8-mer模体的使用。
在进化过程中,某些特定的8-mer模体可能因为其在基因表达、蛋白质功能等方面的优势而被保留下来,而其他模体则可能因为不利影响而被淘汰。
3. 基因组重排:物种进化过程中,基因组重排是常见的现象。
这些重排事件可能导致8-mer模体的重新组合和分布,从而影响基因组序列的组成和功能。
生成8位随机不重复的数字编号的方法

⽣成8位随机不重复的数字编号的⽅法复制代码代码如下:package mon.util;import java.util.Arrays;import java.util.Random;/****/public class RandomNumberGenerator {/*** 这是典型的随机洗牌算法。
* 流程是从备选数组中选择⼀个放⼊⽬标数组中,将选取的数组从备选数组移除(放⾄最后,并缩⼩选择区域)* 算法时间复杂度O(n)* @return 随机8为不重复数组*/public static String generateNumber() {String no="";//初始化备选数组int[] defaultNums = new int[10];for (int i = 0; i < defaultNums.length; i++) {defaultNums[i] = i;}Random random = new Random();int[] nums = new int[LENGTH];//默认数组中可以选择的部分长度int canBeUsed = 10;//填充⽬标数组for (int i = 0; i < nums.length; i++) {//将随机选取的数字存⼊⽬标数组int index = random.nextInt(canBeUsed);nums[i] = defaultNums[index];//将已⽤过的数字扔到备选数组最后,并减⼩可选区域swap(index, canBeUsed - 1, defaultNums);canBeUsed--;}if (nums.length>0) {for (int i = 0; i < nums.length; i++) {no+=nums[i];}}return no;}private static final int LENGTH = 8;private static void swap(int i, int j, int[] nums) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}public static String generateNumber2() {String no="";int num[]=new int[8];int c=0;for (int i = 0; i < 8; i++) {num[i] = new Random().nextInt(10);c = num[i];for (int j = 0; j < i; j++) {if (num[j] == c) {i--;break;}}}if (num.length>0) {for (int i = 0; i < num.length; i++) {no+=num[i];}}return no;}public static void main(String[] args) { for (int i = 0; i < 10; i++) {// System.out.println(generateNumber()); System.out.println(generateNumber2()); }}}。
