高等数学 傅里叶级数
傅里叶级数公式推导

傅里叶级数公式推导
傅里叶级数是一种将周期函数表示为无穷级数的方法,其基本思想是将周期函数表示为具有不同频率的正弦和余弦函数的无穷级数。
以下是傅里叶级数公式的推导过程:
设f(x)是一个周期为T的周期函数,即f(x+T)=f(x)。
第一步,将f(x)在一个周期内进行离散化,即f(x)=∑n=−NNf(xn)δ(x−xn),其中xn=nT/N,δ(x)是狄拉克δ函数。
第二步,利用三角恒等式sin2(θ)+cos2(θ)=1,将δ(x−xn)展开为正弦和余弦函数的无穷级数。
具体地,δ(x−xn)=2π1[cos(T2π(x−xn))+i sin(T2π(x−xn))]。
第三步,将第二步中的δ(x−xn)代入第一步中的f(x),得到f(x)=2π1∑n=−NN f(xn)[cos(T2π(x−xn))+i sin(T2π(x−xn))]。
第四步,将第三步中的f(x)表示为傅里叶级数的形式。
由于f(x)是周期函数,因此可以将f(x)表示为无穷级数∑k=−∞∞ak cos(T2πkx)+bk sin(T2πkx),其
中ak和bk是傅里叶系数。
综上,傅里叶级数公式可以表示为:f(x)=∑k=−∞∞ak cos(T2πkx)+bk sin(T2πk x),其中ak和bk是傅里叶系数。
十五章傅里叶级数

2
2
2
当只给出一种周期旳体现式时,傅里叶级数在两端点旳值
可用 上述公式求之.
例1:设
x, f (x) 0,
0 x x 0
求f
旳傅里叶级数展开式.
解: 函数f 及其周期延拓后的图象如图所示,
y
3 2 O 2 3 4
x
显然 f 是按段光滑旳,故由收敛定理,它能够展开成傅里叶级数。
因为
第十五章 傅里叶级数
§15.1 傅里叶级数
一、 三角级数 • 正交函数系
二、以 2 为周期旳函数旳傅里叶级数
三、收敛定理
§15.1 傅里叶级数
一、三角函数 正交函数系
在科学试验与工程技术旳某些现象中,常会遇到一种周期运动,最简
单旳周期运动,可用正弦函数 A sin(x ) 来描写。
所体现旳周期运动也称为简谐运动,其中 A 为振幅, 为初相角,
f (x) cos kxdx
a0 cos kxdx 2
(an cos nx cos kx bn sin nx cos kx)dx n1
cos2 kxdx
f (x) cos kxdx ak
ak
1
f (x) cos kxdx
(k 1, 2, )
同理可得:
bk
1
f (x) sin kxdx
f 的傅里叶级数收敛于f 在点x的左,右极限的算术平均值,即
f
(x
0) 2
f
(x 0)
a0 2
(an
n1
cos nx bn
sin nx)
其中an ,bn为f的傅里叶系数。
推论:
若f 是以2为周期的连续函数,且在[, ]上按段光滑,则 f 的
高等数学 第七节 傅里叶(Fourier)级数

公式 :
1 an = π
∫−π f ( x)cosnxdx
π
a0 ∞ f ( x) ~ + ∑ ( ancos nx + bnsin nx ) 2 n =1
取 x = 0, 则
4π + 4 1 = 2π 2 ∑ n2 3 n =1
4 ∑ 12 = 2π 3 n n =1
∞ 2
2
∞
?
收敛定理 !
1 =π2 ⇒∑ 2 6 n n=1
∞
16
1 1 1 π2 1+ 2 + 2 + 2 + L = L 8 3 5 7
1 =π2 ∑ n2 6 n=1
∞
1 1 1 1 π2 ⇒ 2 + 2 + 2 + 2 +L = L . 24 2 4 6 8
a0 ∞ f ( x − 0) + f ( x + 0) + ∑ (an cos nx + bn sin nx ) = 2 n =1 6 2 (证明 ) 略
函数 f ( x ) 展开成 (收敛的) Fourier 级数所要求条件不高 (与幂级数相比) , 收敛性容易得到满足 .
将 f ( x ) 展开成 Fourier 级数常用直接方法 .
x2
− 2x
sin nx
1 − n cos nx − 12 sin nx n 1 cos nx n3
14
2 0
a0 = 8 π 2 , 3
《高等数学》第6章4 傅里叶级数
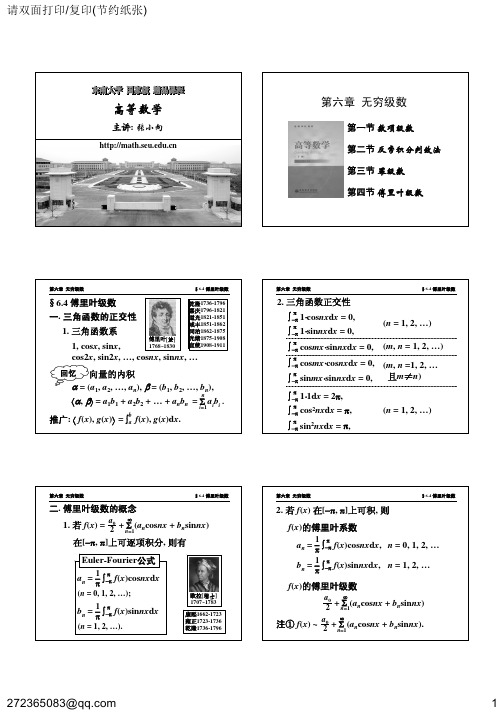
f(x)
=
a0 2
∞
+Σ n=1
(ancos
nπx l
+
bnsin
nπx l
).
其中
an
=
−1 l
∫
l −l
f(x)cos
nπx l
dx,
n = 0, 1, 2, …
bn
=
−1 l
∫
l −l
f(x)sin
nπx l
dx,
n = 1, 2, …
第六章 无穷级数
§6.4 傅里叶级数
a0 2
∞
+Σ n=1
x = 0;
−π
O πx
−f(−x), π ≤ x < 0,
则 an = 0 (n = 0, 1, 2, …),
bn
=
−π1
∫
π −π
F(x)sinnxdx
=
−π2
∫
π 0
f(x)sinnxdx
(n = 1, 2, …).
272365083@
3
请双面打印/复印(节约纸张)
第六章 无穷级数
将f(x)展成傅里叶级数.
−π
解:
a0
=
−π1
∫
π −π
f(x)dx
=
−π1
∫−0π
(−π)dx
+
−π1
∫
π 0
xdx
=
−
−π2 .
对于n = 1, 2, …, 有
an = −π1 ∫−ππ f(x)cosnxdx
=
−π1
∫−0π
(−πcosnx)dx
+
高等数学第六节 傅里叶 级数

bn sinnx .
n1
此时傅氏系数
a n0 (n 0,1,2 , ).
2
b n0f(x )sin n d x x(n 1 ,2,3, ). 这 是an 因 1为 f(x)cn od sxx中 cons是 x 偶
函.数 于是在区间 ( ) 内 f(x)cosnx 为奇函数 ,
而奇函数在对称区间上的积分为零 , 所以
n12[(1)n
1]
n22 ,n1,3,5,, 0,n2,4,6, .
a0
1
10
1
f(x)dx ()dx xdx
0
. 2
1
bn
f(x)sinnxdx
10
1
( )sinn d x x xsinn d x x
0
[n 1 cn o]0 x s n 1 [x cn o]0 x s n 1 0 cn od x x s
设函数 f(x) 定义在 [0 , ] 上,我们设想有一
个函数 (x),它是定义在 ( ) 上 且以 2 为 周期的函数,而在 [0 , ] 上, (x) = f(x). 如果 (x) 满足收敛定理的条件,那么 (x) 在 ( )
上就可展开为傅里叶级数, 取其 [0 , ] 上一段,
即为 f(x) 在 [0 , ] 上的傅里叶级数, (x) 称为f(x)
n1,3,5,, n2,4,6, .
2
2
a 00f(x )d x0( x )d x ,
b n0 (n1,2 ,3, ).
又因为 f(x) 处处连续 ,故所求的傅里叶级数收敛 于 f(x), 即
f(x) 2 4(cx os3 12co3xs5 12co5xs) ( x ).
四、函数 f(x) 在 [0 , ] 上展开 为正弦级数与余弦级数
傅里叶级数课程及习题讲解

第15章傅里叶级数§15.1傅里叶级数一 基本内容一、傅里叶级数 在幂级数讨论中1()nn n f x a x ∞==∑,可视为()f x 经函数系线性表出而得.不妨称2{1,,,,,}nx x x 为基,则不同的基就有不同的级数.今用三角函数系作为基,就得到傅里叶级数.1三角函数系函数列{}1, cos , sin , cos 2, sin 2, , cos , sin , x x x x nx nx 称为三角函数系.其有下面两个重要性质.(1)周期性每一个函数都是以2π为周期的周期函数; (2)正交性任意两个不同函数的积在[,]ππ-上的积分等于 零,任意一个函数的平方在上的积分不等于零.对于一个在[,]ππ-可积的函数系{}() [, ], 1,2, n u x x a b n ∈=:,定义两个函数的内积为(),()()()d bn m n m a u x u x u x u x x=⋅⎰,如果0 (),() 0 n m l m nu x u x m n ≠=⎧=⎨≠⎩,则称函数系{}() [, ], 1,2, n u x x a b n ∈=:为正交系.由于1, sin 1sin d 1cos d 0nx nx x nx x ππππ--=⋅=⋅=⎰⎰;sin , sin sin sin d 0 m nmx nx mx nx x m n πππ-=⎧=⋅=⎨≠⎩⎰;cos , cos cos cos d 0 m n mx nx mx nx x m n πππ-=⎧=⋅=⎨≠⎩⎰;sin , cos sin cos d 0mx nx mx nx x ππ-=⋅=⎰;2 1, 11d 2x πππ-==⎰,所以三角函数系在[],ππ-上具有正交性,故称为正交系.利用三角函数系构成的级数 称为三角级数,其中011,,,,,,n n a a b a b 为常数2以2π为周期的傅里叶级数定义1设函数()f x 在[],ππ-上可积,11(),cos ()cos d k a f x kx f x kx xππππ-==⎰0,1,2,k =;11(),sin ()sin d k b f x kx f x kx xππππ-==⎰1,2,k =,称为函数()f x 的傅里叶系数,而三角级数称为()f x 的傅里叶级数,记作()f x ~()01cos sin 2n n n a a nx b nx ∞=++∑.这里之所以不用等号,是因为函数()f x 按定义1所得系数而获得的傅里叶级数并不知其是否收敛于()f x .二、傅里叶级数收敛定理定理1若以2π为周期的函数()f x 在[,]ππ-上按段光滑,则()01(0)(0)cos sin 22n n n a f x f x a nx b nx ∞=++-++=∑,其中,n n a b 为()f x 的傅里叶系数.定义2如果()[, ]f x C a b '∈,则称()f x 在[,]a b 上光滑.若[,),(0),(0)x a b f x f x '∀∈++存在;(,],(0)x a b f x ∀∈-,(0)f x '-存在,且至多存在有限个点的左、右极限不相等,则称()f x 在[,]a b 上按段光滑.几何解释如图.按段光滑函数图象是由有限条光滑曲线段组成,它至多有有限个第一类间断点与角点.推论如果()f x 是以2π,]ππ-上按 段光滑,则x R ∀∈,有()01()cos sin 2n n n a f x a nx b nx ∞==++∑.定义3设()f x 在(,]ππ-上有定义,函数称()f x 为的周期延拓.二 习题解答1在指定区间内把下列函数展开为傅里叶级数(1)(),(i) , (ii) 02f x x x x πππ=-<<<<;解:(i)、()f x =x ,(,)x ππ∈-作周期延拓的图象如下. 其按段光滑,故可展开为傅里叶级数. 由系数公式得011()d d 0a f x x x x ππππππ--===⎰⎰.当1n ≥时,11cos d d(sin )n a x nx x x nx n ππππππ--==⎰⎰11sin sin d 0|x nx nx x n n ππππππ--=-=⎰,1112cos cos d (1)|n x nx nx x n n n ππππππ+---=+=-⎰,所以11sin ()2(1)n n nxf x n ∞+==-∑,(,)x ππ∈-为所求.(ii)、()f x =x ,(0,2)x π∈作周期延拓的图象如下.其按段光滑,故可展开为傅里叶级数. 由系数公式得220011()d d 2a f x x x x πππππ===⎰⎰.当1n ≥时,220011sin sin d 0|x nx nx x n n ππππ=-=⎰,2200112cos cos d |x nx nx x n n n ππππ--=+=⎰,所以1sin ()2n nxf x n π∞==-∑,(0,2)x π∈为所求. (2)2()(i) (ii) 02f x =x , -π<x <π,<x <π;解:(i)、()2f x =x ,(,)x ππ∈-作周期延拓的图象如下.其按段光滑,故可展开为傅里叶级数. 由系数公式得220112()d d 3a f x x x x πππππππ--===⎰⎰.当1n ≥时,222224cos cos d (1)|n x nx nx x n n n ππππππ--=-=-⎰,2222sin sin d 0|x nx nx x n n ππππππ--=-=⎰,所以221sin ()4(1)3nn nxf x n π∞==+-∑,(,)x ππ∈-为所求.()2f x =x0a =当1n ≥时,222220224cos cos d |x nx nx x n n n ππππ=-=⎰,2222004224sin sin d |x nx nx x n n n n ππππππ=-+-=-⎰,所以22214cos sin ()43n nx nx f x n n ππ∞=⎛⎫=+- ⎪⎝⎭∑,(0,2)x π∈为所求.(3)0()(,0,0)0ax x f x a b a b bx x ππ-<≤⎧=≠≠≠⎨<<⎩.解:函数()f x ,(,)x ππ∈-作周期延拓的图象如下.其按段光滑,故可展开为傅里叶级数. 由系数公式得000111()()d d d 2b a a f x x ax x bx x ππππππππ---==+=⎰⎰⎰.当1n ≥时,所以21()2()1()cos(21)4(21)n b a b a f x n x n ππ∞=--=+--∑11sin ()(1)n n nxa b n ∞+=++-∑,(,)x ππ∈-为所求.2设f 是以2π为周期的可积函数,证明对任何实数c ,有2 11()cos d ()cos d ,0,1,2,c n c a f x nx x f x nx x n πππππ+-===⎰⎰, 2 11()sin d ()sin d ,1,2,c n cb f x nx x f x nx x n πππππ+-===⎰⎰.证:因为()f x ,sin nx ,cos nx 都是以2π为周期的可积函数,所以令2t x π=+有c+2 c+211()cos d ()cos d f t nt t f x nx xππππππ==-⎰⎰.从而2 1()cos d c n ca f x nx xππ+=⎰1()cos d f x nx xπππ-=⎰.同理可得2 11()sin d ()sin d c n cb f x nx x f x nx xπππππ+-==⎰⎰.3把函数04()04x f x x ππππ⎧--<≤⎪⎪=⎨⎪≤<⎪⎩展开成傅里叶级数,并由它推出(1)11114357π=-+-+;(2)111111357111317π=+--+-+;11111157111317=-+-+-+.解:函数()f x ,(,)x ππ∈-作周期延拓的图象如下.其按段光滑,故可展开为傅里叶级数. 由系数公式得00111()d d d 044a f x x x x πππππππππ---==+=⎰⎰⎰.当1n ≥时,0011cos d cos d 044n a nx x nx x ππππππ--=+=⎰⎰.11211[1(1)]202n n k nn n k+⎧=+⎪=--=⎨⎪=⎩,故11()sin(21),(,0)(0,)21n f x n x x n ππ∞==-∈--∑为所求.(1)取2x π=,则11114357π=-+-+;(2)由11114357π=-+-+得111112391521π=-+-+,于是111111341257111317πππ=+=+--+-+;(3)取3x π=,则111111457111317π⎫=-+-+-+⎪⎝⎭,11111157111317=-+-+-+.4设函数()f x 满足条件()()f x f x π+=-,问此函数在(),ππ-内的傅里叶级数具有什么特性.解:因为()f x 满足条件()()f x f x π+=-,所以(2)()()f x f x f x ππ+=-+=,即()f x 是以2π为周期的函数. 于是由系数公式得11()d ()d 0f t t f x x πππππ=++=⎰⎰.当1n ≥时,02()cos d 2102f x nx x n k n k ππ⎧=-⎪=⎨⎪=⎩⎰.02()sin d 2102f x nx x n k n kππ⎧=-⎪=⎨⎪=⎩⎰,故当()()f x f x π+=-时,函数()f x 在(),ππ-内的傅里叶级数的特性是20k a =,20k b =. 5设函数()f x 满足条件:()()f x f x π+=,问此函数在(),ππ-内的傅里叶级数具有什么特性.解:因为()f x 满足条件()()f x f x π+=,所以(2)()()f x f x f x ππ+=+=,即()f x 是以2π为周期的函数.于是由系数公式得112()d ()d ()d f t t f x x f x xπππππππ=++=⎰⎰⎰.当1n ≥时,02()cos d 2021f x nx x n k n k ππ⎧=⎪=⎨⎪=-⎩⎰. 02()sin d 2021f x nx x n k n k ππ⎧=⎪=⎨⎪=-⎩⎰,故当()()f x f x π+=时,函数()f x 在(),ππ-内的傅里叶级数的特性是210k a -=,210k b -=. 6试证函数系cos , 0,1,2,nx n =和sin , 1,2,nx n =都是[0, ]π上的正交函数系,但他们合起来的却不是[0, ]π上的正交函数系.证:就函数系{1,cos ,cos2,,cos ,}x x nx ,因为n ∀,1,1d x ππ==⎰,2001cos ,cos cos d (cos21)d 22nx nx nx x nx x πππ==+=⎰⎰,又1,cos cos d 0nx nx x π==⎰;,m n ∀,m n ≠时,0011cos()d cos()d 022m n x x m n x x ππ=++-=⎰⎰.所以{1,cos ,cos2,,cos ,}x x nx 在[0, ]π上是正交系.就函数系{sin ,sin 2,,sin ,}x x nx ,因为n ∀,2001sin ,sin sin d (1cos2)d 22nx nx nx x nx x πππ==-=⎰⎰,又,m n ∀,m n ≠时,0011cos()d cos()d 022m n x x m n x x ππ=-++-=⎰⎰.所以{sin ,sin 2,,sin ,}x x nx 在[0, ]π上是正交系. 但{1,sin ,cos ,sin 2,cos2,,sin ,cos ,}x x x x nx nx 不是[0, ]π上的正交系.实因:1,sin sin d 10x x x π==≠⎰.7求下列函数的傅里叶级数展开式(1)(),022x f x x ππ-=<<;(),02x f x x ππ-=<< 0a 当1n ≥时,22001sin sin d 022|x nx nx x n n πππππ-=+=⎰,220011cos cos d 22|x nx nx x n n n πππππ-=--=⎰,所以1sin ()n nxf x n ∞==∑,(0,2)x π∈为所求.(2)()f x x ππ=-≤≤;解:()f x x ππ=-≤≤作周期延拓的图象如下.其按段光滑,故可展开为傅里叶级数.因为02()02x x f x x x ππ-≤<==⎨⎪≤≤⎪⎩,所以由系数公式得0sin d sin d 22x x x x ππ-=+=.当1n ≥时,sin cos d 2x nx x π==.0sin sin d sin sin d 022n x x b nx x nx x ππππ-=+=⎰.所以211()cos 41n f x nxnππ∞==--,(,)x ππ∈-.而x π=±时,(0)(0)()2f f f πππ±-+±+==±,故211()cos 41n f x nxnππ∞==--,[,]x ππ∈-为所求.(3)2(), (i) 02, (ii) f x ax bx c x x πππ=++<<-<<;解:(i)由系数公式得22218()d 223aax bx c x b cππππ=++=++⎰.当1n ≥时,24an =, 42a n n ππ=--, 故224()3a f x ax bx c b cππ=++=++21442cos sin ,(0,2)n a a bnx nx x n n ππ∞=++-∈∑为所求.(ii)由系数公式得01()d a f x x πππ-=⎰2212()d 23aax bx c x c ππππ-=++=+⎰.当1n ≥时,24(1)nan =-, 12(1)n bn -=-, 故222()3af x ax bx c cπ=++=+2142(1)cos (1)sin ,(,)nn n a b nx nx x n n ππ∞=+---∈-∑为所求.(4)()ch , f x x x ππ=-<<;解:由系数公式得01()d a f x x πππ-=⎰12ch d sh x x πππππ-==⎰.当1n ≥时,222sh 1(1)nna n n ππ=--,所以22sh (1)(1)n n a n ππ=-+. 2211sh sin ch sin d |x nx x nx x n n ππππππ--=-+⎰21nb n =,所以0n b =,故21211()ch sh (1)cos 21n n f x x nx n ππ∞=⎡⎤==+-⎢⎥+⎣⎦∑, (,)x ππ∈-为所求.(5)()sh ,f x x x ππ=-<<.解:由系数公式得01()d a f x x πππ-=⎰1sh d 0x x πππ-==⎰. 当1n ≥时,1sh cos d 0n a x nx x πππ-==⎰.1221(1)sh n n b n n ππ+=--,所以122sh (1)(1)n n n xb n π+=-+, 故1212sh ()sh (1)sin (1)n n n f x x nxn ππ∞+===-+∑,(,)x ππ∈-为所求.8求函数221()(362)12f x x x ππ=-+的傅里叶级数展开式并应用它推出22116n n π∞==∑. 解:由224()3af x ax bx c b cππ=++=++21442cos sin ,(0,2)n a a bnx nx x n n ππ∞=++-∈∑得211cos n nx n ∞==∑,(0,2)x π∈.而2(00)(20)6f f ππ+=-=,故由收敛定理得22211(00)(20)11cos062n n f f n n ππ∞∞==++-===∑∑.9设()f x 为[],ππ-上光滑函数,()()f f ππ-=.且,n n a b 为()f x 的傅里叶系数,,n n a b ''为()f x 的导函数()f x '的傅里叶系数.证明00,,(1,2,)n n n n a a nb b na n '''===-= .证:因为()f x 为[],ππ-上光滑函数,所以()f x '为[],ππ-上的连续函数,故可积.由系数公式得1()d a f x x πππ-''=⎰()1()()0f f πππ=--=.当1n ≥时,1()cos d na f x nx x πππ-''=⎰1()cos ()sin d |nnf x nx f x nx x nb ππππππ--'=+=⎰.故结论成立.10证明:若三角级数01(cos sin )2n n n a a nx b nx ∞=++∑中的系数,n n a b 满足关系{}33sup ,n n nn a n b M≤,M 为常数,则上述三角级数收敛,且其和函数具有连续的导函数.证:设0()2a u x =,()cos sin n n n u x a nx b nx =+,1,2,n =.则0n ∀≥,()n u x 在R 上连续,且0()0u x '=,()sin cos nn n u x na nx nb nx '=-+亦在R 上连续. 又x R ∀∈,()sin cos nn n u x n a nx n b nx '≤+ 22Mn ≤.而22Mn∑收敛,所以()()cos sin n n n u x nb nx na nx '=-∑∑在R 上一致收敛.故设01()(cos sin )2n n n a s x a nx b nx ∞==++∑,则且1()(cos sin )n n n s x na nx nb nx ∞='=-+∑在R 上连续.§15.2以2l 为周期的函数的展开一 基本内容一、以2l 为周期的函数的傅里叶级数 设()f x 是以2l 为周期的函数,作替换ltx π=,则()lt F t f π⎛⎫= ⎪⎝⎭是以2π为周期的函数,且()f x 在(, )l l -上可积()F t ⇔在(,)ππ-上可积.于是()01()cos sin 2n n n a F t a nt b nt ∞=++∑,其中 1()cos d ,n a F t nt t πππ-=⎰1()sin d n b F t nt tπππ-=⎰.令xt l π=得()()lt F t f f x π⎛⎫== ⎪⎝⎭,sin sin ,cos cos n x n xnt nt l l ππ==, 从而01()cos sin 2n n n a n x n x f x a b l l ππ∞=⎛⎫++ ⎪⎝⎭∑.其中1()cos ,l n l n x a f x dx l l π-=⎰ 1()sin l n l n xb f x dx l l π-=⎰.上式就是以2l 为周期的函数()f x 的傅里叶系数.在按段光滑的条件下,亦有01(0)(0)cos sin 22n n n a f x f x n x n x a b l l ππ∞=++-⎛⎫=++ ⎪⎝⎭∑. 其只含余弦项,故称为余弦级数. 同理,设()f x 是以2l 为周期的奇函数,则()cos f x nx 奇,()sin f x nx 偶.于是1()cos d 0l n l n xa f x x l l π-==⎰,012()sin d ()sin d l l n l n x n xb f x x f x x l l l l ππ-==⎰⎰. 从而01()2n n a f x a ∞=+∑由此可知,函数偶延拓() (0,()() (,0)f x x l f x f x x l ∈⎧=⎨-∈-⎩函数(),(0,)f x x l ∈要展 开为正弦级数必须作奇延拓. 奇延拓() (0,) ()() (,0)f x x l f x f x x l ∈⎧=⎨--∈-⎩.二 习题解答1求下列周期函数的傅里叶级数展开式 (1)()cos f x x =(周期π);解:()cos f x x =,22x ππ⎡⎤∈-⎢⎥由于(f ()f x 是偶函数,故其展开式为余弦级数.因2l π=,所以由系数公式得22002244cos d cos d a x x x x ππππππ-===⎰⎰.当1n ≥时,1(1)2(1)2(21)(21)n n n n ππ+-⋅-⋅=++-124(1)(41)n n π+=--. 222cos sin d 0n b x nx x πππ-==⎰.故121241()cos (1)cos241n n f x x nxn ππ∞+===+--∑,(,)x ∈-∞+∞为所求.(2)()[]f x x x =-(周期1);解:函数()[]f x x x =-,11,22x ⎡⎤∈-⎢⎥⎣⎦延拓后的函数如下图. 由于()f x 按段光滑,所以可展开为傅里叶级数.因12l =,所以由系数公式得()()111210022[]d 2[]d 2d 1a x x x x x x x x -=-=-==⎰⎰⎰.当1n ≥时,110011sin 2sin 2d 0|x n x n x x n n ππππ=-=⎰.110011cos2cos2d |x n x n x x n n ππππ-=+⎰1n π-=. 故1111()[]sin 22n f x x x n xn ππ∞==-=-∑,(,)x ∈-∞+∞为所求. (3)4()sin f x x =(周期π);2222解:函数4()sin f x x =,,22x ππ⎡⎤∈-⎢⎥⎣⎦延拓后的函数如下图. 由于()f x 按段光滑,所以可展开为傅里叶级数,又()f x 是偶函数,故其展开式为余弦级数.因2l π=,所以由系数公式得 204311cos 2cos 4d 828x x x ππ⎛⎫=-+ ⎪⎝⎭⎰34=.当1n ≥时,11201,2128n n n n ⎧-=⎪⎪=≠≠⎨⎪⎪=⎩. 222cos sin d 0n b x nx x πππ-==⎰.故4311()sin cos2cos4828f x x x x==-+,(,)x ∈-∞+∞为所求.(4)()sgn(cos )f x x =(周期2π).解:函数()sgn(cos )f x x =,(,)x ππ∈-延拓后的函数如下图.由于()f x 按段光滑,所以可展开为傅里叶级数,又()f x 是偶函数,故其展开式为余弦级数.因l π=,所以由系数公式得0012sgn(cos )d sgn(cos )d 0a x x x x πππππ-===⎰⎰.当1n ≥时,02sgn(cos )cos d n a x nx xππ=⎰4sin 2n n ππ=024(1)21(21)kn k n k k π=⎧⎪=⎨-=-⎪+⎩.2sgn(cos )sin d 0n b x nx x πππ-==⎰.故14cos(21)()sgn(cos )(1)21nn n xf x x n π∞=+==-+∑,(,)x ∈-∞+∞.2求函数 01() 1 123 23x x f x x x x ≤≤⎧⎪=<<⎨⎪-≤≤⎩的傅里叶级数并讨论其收敛性.解:函数()f x ,(0,3)x ∈延拓后的函数如下图.由于()f x 按段光滑,所以可展开为傅里叶级数,又()f x 是偶函数,故其展开式为余弦级数.因32l =,所以由系数公式得31230001222224()d d d (3)d 33333a f x x x x x x x ==++-=⎰⎰⎰⎰. 当1n ≥时, 2222323cos 3n n n πππ=-.2()sin d 0n b f x nx x πππ-==⎰.故2221231122()cos cos333n n n xf x n n πππ∞=-⎡⎤=++⎢⎥⎣⎦∑,(,)x ∈-∞+∞为所求. 3将函数()2f x xπ=-在[0,]π上展开成余弦级数.解:函数()2f x xπ=-,[0,]x π∈作偶延拓后的函数如下图.由于()f x 按段光滑,所以可展开为傅里叶级数,又()f x 是偶函数,故其展开式为余弦级数.由系数公式得20021d 0222a x x x x πππππ⎛⎫⎛⎫=-=-= ⎪ ⎪⎝⎭⎝⎭⎰.当1n ≥时,242102n k n n kπ⎧=-⎪=⎨⎪=⎩.0n b =.故2141()cos(21),[0,]2(21)n f x x n x x n πππ∞==-=-∈-∑.4将函数()cos2xf x =在[0,]π上展开成正弦级数.解:函数()cos2xf x =,[0,]x π∈作偶延拓后的函数如下图. 由于()f x 按段光滑,所以可展开为傅里叶级数,又()f x 是奇函数,故其展开式为正弦级数.由系数公式得0,0,1,2,n a n ==.28(41)nn π=-.故在[0, ]π上218()cos sin 241n x nf x nxn π∞===-∑为所求.5把函数102()324x x f x x x -<≤⎧=⎨-<<⎩ 在(0, 4)上展开成余弦级数.解:函数()f x ,(0,4)x ∈延拓后的函数如下图.由于()f x 按段光滑,所以可展开为傅里叶级数,又()f x 是偶函数,故其展开式为余弦级数.因4l =,所以由系数公式得4240002211()d (1)d (3)d 0422a f x x x x x x ==-+-=⎰⎰⎰.当1n ≥时,402()cos d 44n n xa f x x π=⎰所以102()324x x f x x x -<≤⎧=⎨-<<⎩22181(21)cos(21)2n n xn ππ∞=-=-∑为所求.6把函数()2()1f x x =-在(0, 1)上展开成余弦级数,并推出222116123π⎛⎫=+++⎪⎝⎭.解:函数()f x ,(0,1)x ∈延拓为以2为周期的函数如下图.由于()f x 按段光滑,所以可展开为傅里叶级数,又()f x 是偶函数,故其展开式为余弦级数.因l=0.5,所以由系数公式得11200022()d 2(1)d 3a f x x x x ==-=⎰⎰.当1n ≥时,1202(1)cos d n a x n x xπ=-⎰224n π=.0n b =.所以2221141(1)cos ,[0,1]3n x nx x n π∞=-=+∈∑.令0x =得22114113n n π∞==+∑,即22116n n π∞==∑. 7求下列函数的傅里叶级数展开式 (1)()arcsin(sin )f x x =;解:函数()arcsin(sin )f x x =是以2π为周期的函数如下图.由于()f x 按段光滑,所以可展开为傅里叶级数,又()f x 是奇函数,故其展开式为正弦级数.由系数公式得0,0,1,2,n a n ==.所以214(1)()arcsin(sin )sin(21)(21)nn f x x n x n π∞=-==--∑,x R ∈.(2)()arcsin(cos )f x x =.解:函数()arcsin(cos )f x x =是以2π为周期的函数如下图.由于()f x 是偶函数,故其展开式为余弦级数.002arcsin(cos )d 0a x x ππ==⎰,当1n ≥时,202421n k n k n π=⎧⎪=⎨=-⎪⎩.0,1,2,n b n ==.所以2141()arcsin(cos )cos(21)(21)n f x x n x n π∞===--∑,x R ∈. 8试问如何把定义在0,2π⎡⎤⎢⎥⎣⎦上的可积函数()f x 延拓到区间(),ππ-内,使他们的傅里叶级数为如下的形式(1)211cos(21)n n an x∞-=-∑;(2)211sin(21)n n bn x∞-=-∑.解:(1)先把()f x 延拓到[0,]π上,方法如下:()02()()2f x x f x f x x ππππ⎧≤≤⎪⎪=⎨⎪--<≤⎪⎩;再把()f x 延拓到[0,2]π上,方法如下:()0ˆ()(2)2f x x f x f x x ππππ⎧≤≤=⎨-<≤⎩.其图象如下.由于()f x 按段光滑,所以可展开为傅里叶级数,又()f x 是偶函数,故其展开式为余弦级数.由系数公式得002()d 0a f x x ππ==⎰,当1n ≥时,201()sin d 0n b f x nx x ππ==⎰.204()cos d 2102f x nx x n k n kππ⎧=-⎪=⎨⎪=⎩⎰. 所以211()cos(21)0,2n n f x a n x x π∞-=⎛⎫=-∈ ⎪⎝⎭∑. (2)先把()f x 延拓到[0,]π上,方法如下.()02()()2f x x f x f x x ππππ⎧≤≤⎪⎪=⎨⎪-<≤⎪⎩;再把()f x 延拓到[0,2]π上,方法如下.()0ˆ()(2)2f x x f x f x x ππππ⎧≤≤=⎨--<≤⎩.()f x 是偶函数,故其展开式为余弦级数.002()d 0a f x x ππ==⎰,当1n ≥时,201()cos d 0n a f x nx x ππ==⎰204()sin d 2102f x nx x n k n kππ⎧=-⎪=⎨⎪=⎩⎰. 所以211()sin(21)0,2n n f x b n x x π∞-=⎛⎫=-∈ ⎪⎝⎭∑. §15.3收敛定理的证明一 基本内容一、贝塞尔(Bessel)不等式定理1 设()f x 在[,]ππ-上可积,则()2222011()d 2n n n a a b f x x πππ∞-=++≤∑⎰,其中,n n a b 为()f x 的傅里叶系数.推论1设()f x 在[,]ππ-上可积,则lim ()cos d 0n f x nx x ππ-→∞=⎰, lim ()sin d 0n f x nx x ππ-→∞=⎰.推论2设()f x 在[,]ππ-上可积,则01lim ()sin d 02n f x n x x π→∞⎛⎫+= ⎪⎝⎭⎰,1lim ()sin d 02n f x n x x π-→∞⎛⎫+= ⎪⎝⎭⎰.定理2设以2π为周期的函数()f x 在[,]ππ-上可积,则1sin 12()d 2sin2n tf x t tt πππ-⎛⎫+ ⎪⎝⎭=+⎰,此称为()f x 的傅里叶级数的部分和的积分表达式.二、收敛性定理的证明定理3(收敛性定理) 设以2π为周期的函数()f x 在[,]ππ-上按段光滑,则(0)(0)lim ()022n n f x f x S x →∞-+⎡⎤+-=⎢⎥⎣⎦,定理4如果()f x 在[,]ππ-上有有限导数,或有有限的两个单侧导数,则()01(0)(0)cos sin 22n n n a f x f x a nx b nx ∞=++-=++∑.定理5如果()f x 在[,]ππ-按段单调,则()01(0)(0)cos sin 22n n n a f x f x a nx b nx ∞=++-=++∑.二 习题解答1设()f x 以2π为周期且具有二阶连续的导函数,证明()f x 的傅里叶级数在(,)-∞+∞上一致收敛于()f x .证:由题目设知()f x 与()f x '是以2π为周期的函数,且光滑,故 01()(cos sin )2n n n a f x a nx b nx ∞==++∑, 01()(cos sin )2nn n a f x a nx b nx ∞=''''=++∑,且1()d a f x x πππ-''=⎰()1()()0f f πππ=--=.当1n ≥时,1()cos d na f x nx x πππ-''=⎰1()cos ()sin d |nnf x nx f x nx x nb ππππππ--'=+=⎰.于是2222111122n nn n nn a b a b a b nn n n ''⎛⎫⎛⎫''+=+≤+++ ⎪ ⎪⎝⎭⎝⎭22211()2n n a b n ''=++.由贝塞尔不等式得221()nn n a b ∞=''+∑收敛,又211n n ∞=∑收敛,从而()012n n n a a b ∞=++∑收敛, 故01(cos sin )2n n n a a nx b nx ∞=++∑在(,)-∞+∞上一致收敛.2设f 为[],ππ-上可积函数,证明:若f 的傅里叶级数在[,]ππ-上一致收敛于f ,则成立贝塞尔(Parseval)等式()2 2220 11()d 2n n n a f x x a b πππ∞-==++∑⎰, 这里,n n a b 为f 的傅里叶系数.证:设()01cos sin 2mm n n n a S a nx b nx ==++∑,因为()f x 的傅里叶级数在[,]ππ-上一致收敛于()f x ,所以0,0N ε∀>∃>,,[,]()m m N x f x S ππε∍>∀∈-⇒-<“”.于是2(),()m m f x S f x S ε--<.而()2 2221()d 2mn n n a f x x a b ππππ-==--+∑⎰.所以m N >时,()222221()d 2mn n n a f x x a b ππππε-=--+<∑⎰,故()2222011()d 2n n n a a b f x x πππ∞-=++=∑⎰.3由于贝塞尔等式对于在[,]ππ-上满足收敛定理条件的函数也成立.请应用这个结果证明下列各式. (1)22118(21)n n π∞==-∑;(2)22116n n π∞==∑;(3)44190n π=∑. 解:(1) 取04()04x f x x ππππ⎧--<<⎪⎪=⎨⎪≤<⎪⎩,由§1习题3得1sin(21)(),(,0)(0,)21n n xf x x n ππ∞=-=∈--∑.由贝塞尔等式得22111d 16(21)n x n ππππ∞-==-∑⎰,即22118(21)n n π∞==-∑.(2) 取(),(,)f x x x ππ=∈-,由§1习题1(1)得11sin ()2(1),(,)n n nxf x x n ππ∞+==-∈-∑.由贝塞尔等式得21211(1)2d n n x x n πππ+∞-=⎛⎫-= ⎪⎝⎭∑⎰,故22116n n π∞==∑.(3) 取2(),[,]f x x x ππ=∈-,由§1习题1(2)得 2221cos 4(1),(,)3nn xx x n πππ∞==+-∈-∑.由贝塞尔等式得22242111(1)4d 23n n x x n ππππ∞-=⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭∑⎰, 故44190n π=∑. 4证明:若,f g 均为[,]ππ-上可积函数,且他们的傅里叶级数在[,]ππ-上分别一致收敛于f 和g ,则00 11()()d ()2n n n n n a f x g x x a b ππααβπ∞-==++∑⎰.其中,n n a b 为f 的傅里叶系数,,n n αβ为g 的傅里叶系数.证:由题设知01()(cos sin )2n n n a f x a nx b nx ∞==++∑,1()(cos sin )2n n n g x nx nx ααβ∞==++∑.于是 1()()d (),()f xg x x f x g x πππ-=⎰而001(),cos sin ,222n n n a f x a nx b nx αα∞==++∑ cos ,cos n n n n a nx nx a αα==, cos ,cos n n n n b nx nx b ββ==,所以 00 11()()d ()2n n n n n a f x g x x a b ππααβπ∞-==++∑⎰.5证明若f 及其导函数f '均在[,]ππ-上可积,()d 0f x x ππ-=⎰,()()f f ππ-=,且成立贝塞尔等式,则22()d ()d f x x f x xππππ--'≥⎰⎰.证:因为()f x 、()f x '在[],ππ-上可积,()d 0f x x ππ-=⎰,()()f f ππ-=,设01()(cos sin )2n n n a f x a nx b nx ∞==++∑, 01()(cos sin )2nn n a f x a nx b nx ∞=''''=++∑,由系数公式得1()d a f x x πππ-''=⎰()1()()0f f πππ=--=.当1n ≥时,1()cos d na f x nx x πππ-''=⎰1()cos ()sin d |nnf x nx f x nx x nb ππππππ--'=+=⎰.于是由贝塞尔等式得2()d f x xππ-=⎰.总练习题151试求三角多项式的傅里叶级数展开式.解:因为01()(cos sin )2nn k k k A T x A kx B kx ==++∑是以2π为周期的光滑函数,所以可展为傅里叶级数,由系数公式得001(),1(cos sin ),12nn k k k A a T x A kx B kx A ===++=∑,当1k ≥时,1(cos sin ),cos 02nkk k k A k n A A kx B kx kx k n =≤⎧=++=⎨>⎩∑,1(cos sin ),sin 02nkk k k B k n A A kx B kx kx k n =≤⎧=++=⎨>⎩∑,故在(,)-∞+∞,01()(cos sin )2nn k k k A T x A kx B kx ==++∑的傅里叶级数就是其本身.2设f 为[,]ππ-上可积函数,0,,(1,2,,)k k a a b k n =为f 的 傅里叶系数,试证明,当00,,(1,2,,)k k k k A a A a B b k n ====时, 积分[]2()()d n f x T x xππ--⎰取最小值,且最小值为[]22220 1()d ()2nk k k a f x x a b πππ-=⎡⎤-++⎢⎥⎣⎦∑⎰. 上述()n T x 是第1题中的三角多项式,0,,k k A A B 为它的傅里叶系数.证:设()01()cos sin 2n n n a f x a nx b nx ∞==++∑, 01()(cos sin )2nn k k k A T x A kx B kx ==++∑,且00,,(1,2,,)k k k k A a A a B b k n ====, 因为[]2()()d n f x T x xππ--⎰22 ()d 2()()d ()d n n f x x f x T x x T x xππππππ---=-+⎰⎰⎰,而()001()()d 2nn k k k k k A a f x T x x A a B b ππππ-==++∑⎰, () 22201()d 2nnk k k A T x x A B πππ-==++∑⎰,所以[]2()()d n f x T x xππ--⎰故当00,,(1,2,,)k k k k A a A a B b k n ====时, 积分[]2()()d n f x T x xππ--⎰取最小值,且最小值为[]22220 1()d ()2nk k k a f x x a b πππ-=⎡⎤-++⎢⎥⎣⎦∑⎰. 3设f 为以2π周期,且具有二阶连续可微的函数,11()sin d , ()sin d n nb f x nx x b f x nx xππππππ--''''==⎰⎰,若级数n b ''∑绝对收敛,则11122n n n b ∞∞==⎛⎫''+ ⎪⎝⎭∑.证:因为()f x 为以2π周期,且具有二阶连续可微的函数, 所以1()sin d n b f x nx x πππ-''''=⎰2 2 ()cos ()sin d nn n f x nxf x nx x n b ππππππ--=-+=⎰. 即211,n n n b b n ''∀≥=⋅,从而2111,2n n b n ⎛⎫''∀≥+ ⎪⎝⎭又n b ''∑绝对收敛,21n ∑收敛,所以n ∞=1122n n b ∞=⎛⎫''<+ ⎪⎝⎭∑.故结论成立.4设周期为2π的可积函数()x ϕ与()x ψ满足以下关系式(1)()()x x ϕψ-=;(2)()()x x ϕψ-=-.试问ϕ的傅里叶系数,n n a b 与ψ的傅里叶系数,n n αβ有什么关系?解:设()01()cos sin 2n n n a x a nx b nx ϕ∞==++∑,()1()cos sin 2n n n x nx nx αψαβ∞==++∑,(1)则当()()x x ϕψ-=时,0n ∀≥,n α=.1n ∀≥,n β=-.(2)当()()x x ϕψ-=-时,0n ∀≥,n α=-.1n ∀≥,n β=.5设定义在[,]a b 上的连续函数列{}()n x ϕ满足关系0 ()()d 1 bn m a n mx x x n m ϕϕ≠⎧=⎨=⎩⎰,对于在[,]a b 上的可积函数f ,定义()()d , 1,2,b n n a a f x x x n ϕ==⎰,证明21n n a ∞=∑收敛,且有不等式 22 1[()]d b n a n a f x x ∞=≤∑⎰.证:在[,]a b 上的所有可积函数构成的集合中定义内积为(),()()()d b a f x g x f x g x x =⎰,则函数列{}()n x ϕ为标准正交系.令1()(),1,2,m m n n n S x a x m ϕ===∑,则,(),()n n n a f x x ϕ∀=, 又 2 [()()]d bm a f x S x x -⎰22 ()d 2()()d ()d n n f x x f x S x x S x x ππππππ---=-+⎰⎰⎰,而11(),()(),()(),()m m n n n n n n n f x S x f x a x a f x x ϕϕ====∑∑ 21m nn a ==∑. 211(),()m mk k k k k k k a a x x a ϕϕ====∑∑,于是 222 1()d [()()]d 0m b n m an f x x a f x S x x ππ-=-=-≥∑⎰⎰, 所以22 11,[()]d m b n a n m a f x x =∀≥≤∑⎰,即{}()m S x 有上界. 故 21n n a∞=∑收敛,且 22 1[()]d b n a n a f x x∞=≤∑⎰.。
数学分析课件 傅里叶级数

03
工程学
在工程学中,傅里叶级数可以用于分析和设计各种周期性结构,例如在
机械工程和土木工程等领域中,可以通过傅里叶级数来描述和分析周期
性振动和波动等问题。
02
傅里叶级数的基本性质
三角函数的正交性
三角函数的正交性是指在一周期内,任何两个不同的三角函 数都不相交,即它们的乘积在全周期内的积分值为零。这一 性质在傅里叶级数的展开和重构中起到关键作用,确保了频 谱的纯净性和分离性。
三角函数的周期性使得我们能够将无限长的信号转化为有限长的频谱,从而方便 了信号的分析和处理。
傅里叶级数的收敛性
傅里叶级数的收敛性是指一个信号的傅里叶级数展开在一 定条件下能够无限接近原信号。这一性质保证了傅里叶级 数展开的精度和可靠性,使得我们能够通过有限项的级数 展开来近似表示复杂的信号。
收敛性的判定是数学分析中的重要问题,涉及到级数的收 敛半径、收敛域等概念。在实际应用中,我们需要根据信 号的特性和精度要求来选择合适的收敛域和级数项数,以 保证傅里叶级数展开的准确性。
首先,确定函数的周期和定义域;其次,计算正弦和余弦函数的系数;最后,将得到的系数代入正弦和余弦函数的线 性组合中,得到函数的傅里叶级数表示。
傅里叶级数的表示方法的优缺点
傅里叶级数具有简洁、易计算等优点,能够将复杂的周期函数分解为简单的正弦和余弦函数。然而,傅 里叶级数也存在着一些缺点,例如在非周期函数的情况下,傅里叶级数可能无法得到正确的结果。
图像增强
利用傅里叶级数,可以对图像进行增 强处理,如锐化、降噪等,提高图像 的视觉效果。
数值分析中的傅里叶级数
数值逼近
傅里叶级数可以用于求解某些函数的 数值逼近问题,如求解函数的零点、 极值等。
应用高等数学-6.1 傅里叶变换

例8
试证单位阶跃函数
F () F[(t)] (t)e jt d t e jt 1
t0
显然, (t)与常数1构成了一傅氏变换对,按
逆变换公式有
(t)
F
1[F ()]
1 2π
e
jt
d
由上式可得 e jt d 2π (t)
(6-9)
这是一个关于δ函数的重要公式.
例5 证明:1和 2π ()构成傅氏变换对.
f
(t)
1, 1,
π t 0 0 t π
如何将函数展开为傅里叶级数的三角形式.
解: 由定理6.1可得 0 1,a0 0,an 0 (n 1, 2,L )
bn
1
π
f (t)sin ntdt
π
π2
π
sin ntdt
0
nπ 2 (cos
nt
π
) 0
nπ 2 (1 cos nπ)
nπ 2 [1 (1)n ]
2π ( 0 )
例7 求正弦函数 f (t) sin 0t 的傅氏变换.
解:
F() F[ f (t)]
e
jt
sin
0t
d
t
1 (e j0t e j0t )e jt d t
2 j
1 (e j(0 )t e j(0 )t ) d t
2 j
jπ[ ( 0 ) ( 0 )]
式中当t=0可得重要积分公式
sin
x
d
x
π
0x
2
例4
求单边指数衰减函数
f
(t)
0, et ,
t0 t0
( 0)
的频谱函数、振幅谱、相位谱.
《高数-傅里叶级数》课件

02
该公式将复杂的函数f(x)表示为简单的三角函数之和,便于分析函数的性质和求 解相关问题。
03
展开公式中的系数a0、an、bn可以通过函数的积分得到。
傅里叶级数的展开步骤
01
第一步是将待展开的函数f(x)进行傅里叶级数的展开,得到展开式。
02
第二步是求解展开式中的系数a0、an、bn,可以通过函数的积分得 到。
傅里叶级数的应用领域
傅里叶级数在数学、物理、工程等领 域有广泛的应用。
在信号处理、图像处理、振动分析、 量子力学等领域,傅里叶级数被用于 分析信号和系统的频率成分,以及进 行频域分析和处理。
02
傅里叶级数的性质
傅里叶级数的收敛性
收敛的条件
傅里叶级数在满足一定条件下收敛, 如狄利克雷条件和黎曼条件等。这些 条件限制了周期函数的波形和振幅, 以确保级数收敛。
傅里叶级数的对称性可以通过数学证明得到。证明过程中需要利用三角函数的 性质和级数的运算规则。
傅里叶级数的周期性
周期性的应用
周期性在信号处理、图像处理等领域中有着广泛的应用。例如,在信号处理中, 可以利用周期性来分析信号的频率成分和周期性变化。
周期性的证明
傅里叶级数的周期性可以通过数学证明得到。证明过程中需要利用三角函数的周 期性和级数的运算规则。
03
第三步是将求解出的系数代入展开式中,得到函数的傅里叶级数展开 式。
04
第四步是利用傅里叶级数的性质和公式,对展开后的函数进行分析和 求解相关问题。
04
傅里叶级数的应用实例
信号处理中的傅里叶级数
信号分析
傅里叶级数提供了一种将复杂信号分解为简单正弦波的方法,有 助于信号的频谱分析和特征提取。
常用傅里叶级数公式总结

常用傅里叶级数公式总结傅里叶级数是一种非常重要的数学工具,可以将周期函数分解为一系列正弦和余弦函数的和,从而方便进行分析和计算。
在信号处理、图像处理、物理学等领域都有广泛的应用。
本文将以常用傅里叶级数公式为线索,介绍傅里叶级数的基本概念和性质。
1. 傅里叶级数的基本形式任何周期为T的周期函数f(t),都可以表示为正弦函数和余弦函数的线性组合,即傅里叶级数。
其基本形式为:f(t) = a0 + Σ(an*cos(2πnft) + bn*sin(2πnft))其中,a0为直流分量,an和bn分别为函数f(t)的傅里叶系数,f为基本频率,n为正整数。
2. 傅里叶级数的计算公式傅里叶系数an和bn的计算公式为:an = (2/T) * ∫[0,T] f(t)*cos(2πnft) dtbn = (2/T) * ∫[0,T] f(t)*sin(2πnft) dt这两个公式描述了函数f(t)在频率为nf时的正弦和余弦分量的大小,通过计算这些系数,可以得到傅里叶级数的展开式。
3. 傅里叶级数的性质傅里叶级数具有许多重要的性质,其中包括线性性、偶函数和奇函数的傅里叶级数、周期延拓性等。
这些性质使得傅里叶级数在实际应用中具有广泛的适用性。
4. 傅里叶级数的收敛性对于一个周期为T的周期函数f(t),其傅里叶级数展开并不一定收敛于原函数f(t)。
在一定条件下,傅里叶级数可以收敛于原函数,这就是傅里叶级数的收敛性问题。
5. 傅里叶级数的频谱分析傅里叶级数可以将一个周期函数表示为不同频率的正弦和余弦函数的叠加,从而可以对信号进行频谱分析。
通过分析不同频率成分的幅值和相位,可以了解信号的频谱特性,对信号进行处理和识别。
6. 傅里叶级数的离散化在数字信号处理中,通常需要对离散信号进行傅里叶变换。
离散傅里叶变换(DFT)和快速傅里叶变换(FFT)是常用的算法,可以高效地计算离散信号的频谱。
7. 傅里叶级数的应用傅里叶级数在信号处理、通信、图像处理、物理学等领域都有广泛的应用。
高等数学傅里叶级数展开公式

高等数学傅里叶级数展开公式(最新版)目录1.傅里叶级数的概念与背景2.傅里叶级数展开公式的形式3.傅里叶级数展开的例子4.傅里叶级数展开的意义和应用正文一、傅里叶级数的概念与背景傅里叶级数是一种特殊的三角级数,由法国数学家傅里叶(Jean-Baptiste Joseph Fourier)在研究偏微分方程的边值问题时提出。
傅里叶级数将一个周期函数分解为一系列正弦和余弦函数的叠加,从而极大地推动了偏微分方程理论的发展。
二、傅里叶级数展开公式的形式傅里叶级数展开公式可以表示为:f(x) = a0/2 + Σ[an*cos(nx) + bn*sin(nx)] (n 从 0 到无穷大)其中,f(x) 是待求函数,an 和 bn 分别是傅里叶级数的系数,n 是积分次数,x 是自变量。
三、傅里叶级数展开的例子例如,对于函数 f(x) = e^(-πx^2),我们可以将其展开为傅里叶级数:f(x) = ∑[an*cos(nx) + bn*sin(nx)] (n 从 0 到无穷大)利用傅里叶级数的性质,我们可以计算出系数 an 和 bn:an = (1/π) * ∫[e^(-πx^2) * cos(nx)] dx(n 从 0 到无穷大)bn = (1/π) * ∫[e^(-πx^2) * sin(nx)] dx(n 从 0 到无穷大)通过计算,我们可以得到傅里叶级数的展开式。
四、傅里叶级数展开的意义和应用傅里叶级数展开的意义在于将一个复杂的周期函数分解为一系列简单的三角函数的叠加,从而便于研究和分析。
傅里叶级数在许多领域都有广泛的应用,如信号处理、图像处理、量子力学等。
例如,在信号处理中,傅里叶级数可以用来将一个信号分解为一系列不同频率的正弦波,从而实现信号的频谱分析。
傅里叶级数

• (0, ) 内的傅里叶级数展开式
• (2)偶延拓f(x) 成F(x),将F(x)展开成余弦级
数。由于在 (0, ) 内f(x) F(x), 故得f(x)在
• (0, ) 内的傅里叶级数展开式。
• 对于区间端点 x 0, x , 可根据收敛定理 判定其收敛情况.
f
(x)
a0 2
an cos nx
n 1
•
且
an
2
0
f (x) cosnxdx(n 0,1,2,)
• 4 收敛定理(狄利克雷(Dirichlet)充分条件)
• 设以2 为周期的函数f(x)在 [ , ] 上满足条
件: • (1)仅有有限个第一类间断点,其余均为连
续点; • (2)至多只有有限个极值点; • 则f(x)的傅里叶级数收敛,且 • (1)当x是f(x)的连续点时,级数收敛于f(x); • (2)当x是f(x)的间断点时,级数收敛于
• ( , ) 内有f(x) F(x),这样便得到f(x)的傅里
叶级数展开式。
• 根据收敛定理,在端点 x 处,级数收敛
于
1 [ f ( 0) f ( 0)]
2
• 2 若f(x)只在 [0, ] 上有定义,且满足收敛 定理的条件,也可以将之展开成傅氏级数
• 通常的延拓方法:
• (1)奇延拓f(x)成F(x),将F(x)展开成正弦级
• 一Байду номын сангаас地,将周期函数f(x)展开成傅里叶级 数,在电工学上叫做谐波分析。其中
• 直流分量:a0
2
• n次谐波:ancosnx+bnsinnx(n 1) • 一次谐波(又叫基波):a1cosx+b1sinx
高等数学第六节_傅里叶级数

第六章 无穷级数 *§6 傅里叶级数
一、问题的提出
二、傅氏级数 三、在 [0,]上将函数 f(x)展成为
余弦级数或正弦级数 四、拓展与思考 五、小结
一、问题的提出
矩形波
u(t) 11 ,,
当 t0 当 0t
u
1
o
t
1
u 4 sint
u4(sitn 1 3si3 nt)
f(x00)x lix0m f(x)
f(x),x是f(x)的连续点, f(x00)x lix0m f(x)
1 2[f(x00)f(x00)]x,0是 f(x)的第一类间
1 [f( 0 )f( 0 )x ] , .
2
例1 设f函 (x )以 2 数 为周(期 ,)上 ,的 且表 在
为 f(x)x,试f将 (x)展成傅 ,且 氏 画 级 出 数 傅 的和函数பைடு நூலகம்形. 解 先求傅氏系数
正交:
称为三角函数族.
任意两个不 积同 [在 ,函 ]上 数 的 的 定 乘 积 :
1cosnxdx
n1sinnx
0,
(n 1 ,2 , ).
1sinnxdxn1cosnx 0, (n 1 ,2 , ).
对 m ,n 1 ,2 ,3 ,
consxsinmxdx 1 2 [s m in n )x s (i m n n )x ] ( d 0 x . co nc sxo msx d 0,,x m m n n ,
a n 1 f(x )cn ox s , (n d 0 x ,1 ,2 , )
1 xconsxd0x
b n 1 f(x )sinnx , (n d 1 x ,2 , )
b n 1 f(x )sinnx , (n d 1 x ,2 , )
傅里叶级数概念

傅里叶级数概念什么是傅里叶级数傅里叶级数是一种数学工具,用于将周期函数分解成一系列正弦和余弦函数的和。
它是由法国数学家傅里叶在19世纪提出的,被广泛应用于信号处理、图像处理、物理学、工程学等领域。
傅里叶级数的基本原理傅里叶级数的基本原理是任何一个周期函数都可以表示为一系列正弦和余弦函数的和。
具体而言,对于一个周期为T的函数f(t),可以表示为以下形式的级数:其中,a0、an和bn是系数,可以通过计算积分得到。
an和bn表示了不同频率的正弦和余弦函数在级数中的权重。
傅里叶级数的应用信号处理傅里叶级数在信号处理中起到了至关重要的作用。
通过将信号分解成不同频率的正弦和余弦函数的和,可以对信号进行频谱分析,从而了解信号的频率成分和能量分布。
这对于音频、视频等信号的压缩、滤波、特征提取等操作非常有用。
图像处理傅里叶级数在图像处理中也有广泛应用。
通过将图像看作一个二维函数,可以将其分解成一系列二维正弦和余弦函数的和。
这样可以对图像进行频域处理,例如图像去噪、边缘检测、图像增强等操作。
物理学傅里叶级数在物理学中的应用非常广泛。
例如,它可以用于描述周期性运动,如弦乐器的振动、电磁波的传播等。
此外,傅里叶级数还可以用于解决热传导方程、波动方程等偏微分方程的初值问题。
工程学在工程学中,傅里叶级数可以用于信号处理、控制系统分析、电路分析等方面。
通过将信号或系统分解成不同频率的正弦和余弦函数的和,可以对系统的频率特性进行研究和设计。
傅里叶级数的性质傅里叶级数具有许多重要的性质,这些性质使得它在各个领域中得到广泛应用。
线性性质傅里叶级数具有线性性质,即线性组合的函数的傅里叶级数等于各个函数的傅里叶级数的线性组合。
周期性质傅里叶级数适用于周期函数,并且周期函数的傅里叶级数也是周期函数。
当函数不是周期函数时,可以通过将其扩展为周期函数来应用傅里叶级数。
对称性质对称函数的傅里叶级数具有特殊的性质。
例如,奇对称函数的傅里叶级数只包含正弦函数,偶对称函数的傅里叶级数只包含余弦函数。
傅里叶级数一般公式

傅里叶级数一般公式傅里叶级数是一种十分重要而且重要的数学概念,它具有普遍性和广泛应用,在工程、数学和物理等领域有深远的影响。
其实,傅里叶级数也被称为Fourier级数,它是1826年法国数学家傅里叶(Joseph Fourier)提出的数学公式,用于描述一个周期函数的重建。
它基于Fourier的发现,即任何周期函数都可以用正弦或余弦组合函数表示,并且可以用有限个正弦或余弦波来近似表示它。
傅里叶级数的一般公式如下:f(x)=a_0+∑_n=1_(A_n*Cos(nx)+B_n*Sin(nx))等价于f(x)=a_0+∑_n=1_(A_n*Cos(ωx+φ_n))其中,A_n和B_n是傅里叶系数,a_0是偏移量,ω是周期,而φ_n表示相位。
由于某些科学应用需要近似表达函数,因此傅里叶级数的概念被广为应用,在工程中表现为有限个正弦以及余弦函数的线性组合。
例如,在水波动力学中,可以用傅里叶级数来描述海浪的高度和速度。
并且,由于傅里叶级数拥有许多优点,如解析性、小数量级、计算简便、便于理解,因此它也可以被用来模拟金融市场和力学系统等机械系统。
此外,傅里叶级数也被用于数据压缩,如在视频压缩领域中,可以使用它来表示连续的图像数据,用有限的数据点捕捉大量的细节,从而实现空间压缩;另外,在声音处理中,傅里叶级数也可用来表示声音,从而压缩声音文件。
最后,在模式识别和信号处理领域,傅里叶级数的运用是极其重要的,它可以完成复杂的分析,比如形状识别和振动分析等,从而促进机械化。
综上所述,傅里叶级数一般公式对于系统分析和数据处理是十分重要的,它也被广泛应用于工程、数学和物理等领域,用以模拟实际系统,提高系统特性识别和数据压缩的性能,从而更好地分析数据。
傅里叶级数基本概念

傅里叶级数基本概念傅里叶级数是描述周期性函数的一种数学工具,它是由法国数学家傅里叶在1807年提出的。
它的核心思想是将任意周期为2π的函数表示为一系列正弦和余弦函数的线性组合。
傅里叶级数的应用非常广泛,涉及到信号处理、图像处理、物理学、工程学等领域。
本文将介绍傅里叶级数的基本概念和相关理论。
一、傅里叶级数的定义傅里叶级数是指将一个周期为T的函数f(t)表示为一组正弦和余弦函数的线性组合。
具体来说,对于一个周期为T的函数f(t),它的傅里叶级数表示为:f(t) = a0 + Σ(an*cos(nωt) + bn*sin(nωt))其中,a0为直流分量,an和bn为函数f(t)的谐波分量的系数,n为谐波的次数,ω为基频的角频率。
二、傅里叶级数的系数计算傅里叶级数的系数an和bn可以通过函数f(t)在一个周期内的积分计算得到。
具体而言,an和bn的计算公式如下:an = (2/T) * ∫[f(t)*cos(nωt)]dtbn = (2/T) * ∫[f(t)*sin(nωt)]dt其中,积分上限和下限分别为函数f(t)的一个周期的起点和终点。
三、傅里叶级数的收敛性傅里叶级数中的每一项都可以视为一个谐波分量,它们的频率是基频频率的整数倍。
随着谐波次数的增加,谐波的频率也越来越高,对应的周期也越来越短。
在理论上,傅里叶级数包含了无穷多项的谐波分量,但实际应用中,通常只需要考虑到一定的谐波分量。
傅里叶级数的收敛性指的是,当考虑足够多的谐波分量时,傅里叶级数能够逼近原始函数f(t),即随着谐波次数的增加,傅里叶级数与原始函数之间的误差不断减小。
然而,并不是所有的函数都具有良好的收敛性。
对于一些特殊的函数,傅里叶级数可能无法完全逼近原始函数,或者在某些点上存在收敛性问题。
四、傅里叶级数的频谱图傅里叶级数中的系数an和bn描述了原始函数在不同频率下的强度。
通过对an和bn的幅值进行绘制,可以得到函数f(t)的频谱图。
高等数学第15章第1节傅里叶级数

第十五章 傅里叶级数§1 傅里叶级数傅里叶是法国最伟大的科学家之一.他对数学、科学以及我们当代生活的影响是不可估量的。
然而,他并不是一位职业数学家或科学家,他所做的巨大贡献都是忙里偷闲完成的。
傅里叶于1768年生于法国,幼年父母就去世了。
13岁时他开始对数学十分着迷,常常一个人爬进教室,点着蜡烛研究数学问题到深夜。
后来,法国革命暴发,傅立叶于1793年参加了革命委员会,1795年先后两次被捕。
法国革命结束后,傅立叶到巴黎教书,之后随拿破仑到埃及并成为埃及研究院的长久负责人,在那里他写了一本关于埃及的书。
直到今天,仍然有人认为他是一位埃及学家,并不知道他对数学和物理学的重大贡献。
1802年,傅立叶回到法国,拿破仑任命他为巴黎警察局长长达14年之久,他作为行政官员,工作十分出色,在政界享有崇高威望。
1817年,傅立叶被送入法国科学院,从此步入较为正规的学术研究阶段。
多年的政治生涯及颠簸不定的生活,并没有使傅里叶放弃研究数学的强烈兴趣。
事实上,早在1807年他就研究了现在称之为傅里叶分析的核心内容。
目前,傅里叶的思想和方法被广泛用于线性规划、大地测量以及电话、收音机、X射线等难以计数的科学仪器中,是基础科学和应用科学研究开发的系统平台。
所以,有的科学家称赞傅里叶分析是一首伟大的数学史诗。
傅里叶分析的贡献在于两点:(1)他用数学语言提出任何一个周期函数都能表示为一组正弦函数和余弦函数之和,这一无限和,现称之为傅里叶级数。
也就是说,任何一条周期曲线,无论多么跳跃或不规则,都能表示成一组光滑曲线之和。
这种表达方式实际上是将信号函数投影在由正弦函数和余弦函数组成的正交基上,实施对信号的傅里叶变换。
(2)他解释了为什么这一数学论断是有用的。
1807年,傅立叶显示任何周期函数是由正弦和余弦函数叠加而成。
傅里叶分析从本质上改变了数学家对函数的看法,提供了某些微分方程的直接求解方法,为计算机和CD等数字技术的实现铺平了道路。
高等数学第七节傅里叶级数

例3. 设 f (x) 是周期为2 的周期函数,它在
的表达式为 f (x) = x , 将 f (x) 展成傅里叶级数.
解: 若不计
周期为 2 的奇函数, 因此
y
an = 0 (n = 0 ,1, 2 , )
bn
=2
0
nx
d
x
=
1 xsin π n
nx
+
cos nx n2
0 −π
=
1− cos nπ n2 π
1− (−1)n
= n2 π
an
=
1
−
cos n n2 π
π
=
2 (2k −1)2 π
0,
,
n = 2k −1 n = 2k
( k = 1, 2 , )
bn
=
1 π
π
f (x)sin nx d x
傅里叶展开
上的傅里叶级数
例4. 将函数
解: 将 f (x)延拓成以 2为周期的函数 F(x) , 则
展成傅里叶级数.
y
−π O π
x
a0
=
1 π
π
F(x)d x =
−π
1 π
π −π
f (x)d x
=π
an
=
1 π
π
−π
F (x)cos nx d
x
=
1 π
π
−π
f
(x)cos nx dx
=
2 π
n=1
cos
n
x
+ bn
sin
n
数与图(22)——傅里叶级数

数与图(22)——傅里叶级数高等数学课在我记忆力留下的最闪亮的部分叫做“傅里叶级数”,它同光学课上的“波粒二象性”共同构筑起我的世界观——这个世界上的万事万物无一不是由波组成。
文本在微积分及三角函数的基础上,讲解一个很特别的级数——傅里叶级数,它可以将任何类型的可积分函数在指定的区间内展开成三角函数的加和。
一般写作式⑴中用“~”代替“=”,说明右侧的展开式的值与左侧的函数值不一定完全相等。
展开式中的系数可以根据求积分获得,其中本文不讨论系数的由来,也不讨论函数可积分的判定,只讨论三个具体函数的展开式,并根据展开式绘制函数图形,观察随着展开项数的增加,展开式图形的变化。
这三个函数分别为方波函数、一次函数及二次函数。
首先将《数与图(21)——三角函数》中的项目另存为“傅里叶级数”,然后修改按钮的名称和标签及按钮的显示文本,修改的结果如图1所示。
图1 修改项目中的组件名称及显示文本在此基础上,我们依次讨论三个不同的函数,从方波函数开始。
一、方波函数1、函数表达式方波函数是周期函数,设其周期为360(度),则其在[-180, 180)上的表达式为2、函数的原始图像设⑶式中的E=5,则方波函数⑶的原始图像如图2所示。
图中的虚线不是函数图像的组成部分,它们仅仅用来标记函数值的突变点。
从函数的原始图像可以得出直观的判断:方波函数是可积分的,积分值就是红色实线下方的面积。
图2 方波函数的原始图像3、方波函数的傅里叶展开形式按照式⑵中给出的公式,可以求得方波函数傅里叶展开式各项的系数,并最终得到下面的展开式(这里略去系数求解过程)。
4、绘制方波展开式图像根据⑷式编写一个有返回值的过程——方波函数。
用循环语句来实现级数的求和,简直是太方便了,注意展开式中只有奇数项,奇数在数学中表示为2k-1,其中k=1,2,3…,方波函数过程的代码如图3所示。
图3 有返回值过程——方波函数再创建一个无返回值过程——求方波函数坐标列表,代码如图4所示,这与此前项目中的求坐标列表过程类似,只是把其他函数替换为方波函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n 2k, k 1,2,
所求函数的傅氏展开式为
u(t) ຫໍສະໝຸດ 4Emsin(2n 1)t
n1 (2n 1)
( t ;t 0,,2,)
注意: 对于非周期函数,如果函数 f ( x) 只在 区间[, ] 上有定义,并且满足狄氏充
分条件,也可展开成傅氏级数.
作法:
周期延拓(T 2) F ( x) f ( x) (, )
一、问题的提出
非正弦周期函数:矩形波
u
u(t
)
1,
1,
当 t 0 当0 t
1
o
t
1
不同频率正弦波逐个叠加
4 sin t, 4 1 sin 3t, 4 1 sin 5t, 4 1 sin 7t,
3
5
7
u 4 sin t
u 4 (sin t 1 sin 3t)
3
u 4 (sin t 1 sin 3t 1 sin 5t)
sin
kx
sin
nxdx]
bn,
k 1
bn
1
f
( x)sin nxdx
(n 1,2,3,)
傅里叶系数
an
1
f ( x)cos nxdx,
(n 0,1,2,)
bn
1
f ( x)sin nxdx,
(n 1,2,)
或
an
1
2 0
f ( x)cos nxdx,
bn
1
2 0
f ( x)sin nxdx,
3
5
(7 t , t 0)
二、三角级数 三角函数系的正交性
1.三角级数
f (t) A0 An sin(nt n ) 谐波分析
n1
A0 ( An sin n cos nt An cos n sin nt)
n1
令
a0 2
A0 ,
an An sin n , bn An cos n ,
nxdx 0, (n 1,2,3,)
所求函数的傅氏展开式为
f
(x)
2
4
n1
1 (2n 1)2
cos( 2n
1)x
(
x
)
利用傅氏展开式求级数的和
a0 2
cos nxdx
[ak
cos
kx
cos
nxdx
bk
sin
kx
cos
nxdx
]
k 1
an cos2 nxdx an,
an
1
f
( x)cos nxdx
(n 1,2,3,)
(3) 求bn .
f ( x)sin nxdx a0
sin nxdx
2
[ak
cos
kx
sin
nxdx
bk
k 1
cos kx
bk
sin kx)
(1) 求a0 .
f
( x)dx
a0 2
dx
[
(ak
k 1
cos kx
bk
sin kx)]dx
a0 dx 2
ak cos kxdx k 1
bk sin kxdx k 1
a0 2, 2
a0
1
f
( x)dx
(2) 求an .
f
( x)cos nxdx
(2)当x 是 f ( x)的间断点时,收敛于 f ( x 0) f ( x 0) ; 2
(3) 当x 为端点x 时,收敛于 f ( 0) f ( 0) .
2
注意: 函数展开成傅里叶级数的条件比展开成 幂级数的条件低的多.
例 1 以2 为周期的矩形脉冲的波形 u
u(t ) EEmm, ,
(n 0,1,2,) (n 1,2,)
傅里叶级数
a0 2
(an
n1
cos nx
bn
sin nx)
问题:
f
(x)
条件?
a0 2
(an
n1
cos nx
bn
sin nx)
2.狄利克雷(Dirichlet)充分条件(收敛定理)
设 f ( x)是以2为周期的周期函数.如果它满足条件: 在一个周期内连续或只有有限个第一类间断点,并且 至多只有有限个极值点,则 f ( x) 的傅里叶级数收敛, 并且 (1) 当x 是 f ( x)的连续点时,级数收敛于 f ( x) ;
an
1
f ( x)cos nxdx
1
0
(
x)cos
nxdx
1
0
x
cos
nxdx
2 n2
(cos
n
1)
2 n2
[(
1)
n
1]
(2k
4
1)2
,
n 2k 1, k 1,2,
0,
n 2k, k 1,2,
bn
1
f ( x)sin nxdx
1
0
(
x)sin
nxdx
1
0
x
sin
3
5
u 4 (sin t 1 sin 3t 1 sin 5t 1 sin 7t)
3
5
7
u 4 (sin t 1 sin 3t 1 sin 5t 1 sin 7t 1 sin 9t)
3
5
7
9
u(t) 4 (sin t 1 sin 3t 1 sin 5t 1 sin 7t )
o
Em
t
1
0 Em cos ntdt
0
(n 0,1,2,)
bn
1
u(t)sin ntdt
1
0
(
Em
)
sin
ntdt
1
0 Em sin ntdt
2Em (1 cos n) 2Em [1 (1)n ]
n
n
4Em (2k 1)
,
n 2k 1, k 1,2,
0,
t x,
a0 2
(an
n1
cos nx
bn
sin nx)
三角级数
2.三角函数系的正交性
三角函数系
1,cos x,sin x,cos 2x,sin 2x,cos nx,sin nx,
正交 : 任意两个不同函数在[, ]上的积分等于零.
cos
nxdx
0,
sin
nxdx
0,
(n 1,2,3,)
0 t t 0
Em
o
t
将其展开为傅立叶级数. Em
解 所给函数满足狄利克雷充分条件.
在点t k(k 0,1,2,)处不连续.
收敛于 Em Em Em ( Em ) 0,
2
2
当t k时, 收敛于u(t). 和函数图象为
an
1
u(t)cos ntdt
Em
u
1
0
(Em ) cos ntdt
端点处收敛于1[ f ( 0) f ( 0)] 2
例2
将函数
f
(
x
)
x,
x,
x0 0 x
展开为傅立叶
级数.
解 所给函数满足狄利克雷充分条件.
拓广的周期函数的傅
氏级数展开式在 [, ]
y
收敛于f ( x) .
2 0 2 x
a0
1
f ( x)dx
1
0
(
x)dx
1
0
xdx
,
sin
mx
sin
nxdx
0, ,
mn ,
mn
cos
mx
cos
nxdx
0, ,
mn ,
mn
sin mx cosnxdx 0.
(其中m,n 1,2,)
三、函数展开成傅里叶级数
问题: 1.若能展开, ai , bi 是什么?
2.展开的条件是什么?
1.傅里叶系数
若有
f
(x)
a0 2
(ak
