数独c++解法
数独技巧

以下我们将叙述一道标准数独的全部解题过程,在此过程中涉及到的技巧有摒除法、余数法、区块法、数对法、X- Wing这几个常在数独书籍中会涉及到的技巧,文中将描述各个技巧的结构及作用效果,相信在看完解题过程之后,您能相当程度地掌握到数独的基本解题技巧,也能在解题的过程中发现数独给您带来的乐趣。
谜题如下图第一招:摒除法大家之前已阅读过数独的规则:在每个单元中,每个数字只能出现一次,那么也就意味着,如果一行已经出现了一个1,这行的其他格就不再有1,利用这个观点,引发出摒除法。
第1步:数字2对B1进行摒除r1c8为2,则其所在R1不再有2;r2c4为2,则其所在R2不再有2;r9c2为2,则其所在C2不再有2,在B1中还没有2,B1有6个空格可以填2,但其中5个空格被摒除了,只剩下r3c1,所以得到第一解:r3c1=2这个方法因为是对宫实施摒除的,所以叫宫摒除法。
宫摒除法是解题技巧里面最简单的一种,也是解题过程中使用最多的一种。
其实解数独就是这么简单!第2步:r1c3=7(宫摒余解,数字7对B1摒除)第3步:r4c7=7(宫摒余解,数字7对B6摒除)第4步:数字7对C5进行摒除r1c3为7;则其所在R1不再有7;r2c9为7,则其所在R2不再有7;r4c7为7,则其所在R4不再有7;r6c2为7,则其所在R6不再有7;r8c1为7,则其所在R8不再有7;r9c8为7,则其所在R9不再有7,在C5中还没有7,C5有7个空格可以填7,但其中6个空格不能为7了,所以天元格r5c5=7这个方法因为是对列实施摒除的,所以叫列摒除法,与其类似的还有行摒除法。
行列摒除法也是很常用的方法。
见识了摒除法之后,大家是否尝试寻找另一个摒余解呢?不好意思要给大家泼凉水了,因为这个盘势下已经找不到宫摒余解或者行列摒余解了,那怎么办呢,没关系,我们继续介绍其它的技巧。
第二招:余数法前面我们提到,一格受其所在单元中其他20格的牵制,假如这20格里面已经出现了1-8这8个数字,我们就可以断定这格一定是未出现的唯一数字9。
数独的C语言解法

if((j==2)||(j==5))printf(" ");}printf("\n");if((i==2)||(i==5))printf("\n");}printf("\n");}//判断是否可以将第i⾏、第j列的数设为k bool check(int a[9][9],int i,int j,int k){int m,n;//判断⾏for(n=0;n<9;n++){if(a[i][n] == k)return false;}//判断列for(m=0;m<9;m++){if(a[m][j] == k)return false;}//判断所在⼩九宫格int t1=(i/3)*3,t2=(j/3)*3;for(m=t1;m<t1+3;m++){for(n=t2;n<t2+3;n++){if(a[m][n] == k)return false;}}//可⾏,返回truereturn true;}//数独求解函数void Sudoku(int a[9][9],int n){int temp[9][9];int i,j;for(i=0;i<9;i++){for(j=0;j<9;j++)temp[i][j]=a[i][j];}i=n/9; j=n%9; //求出第n个数的⾏数和列数 if(a[i][j] != 0) //已经有原始数据{if(n == 80) //是最后⼀个格⼦,输出可⾏解 print(temp);else //不是最后⼀个格⼦,求下⼀个格⼦ Sudoku(temp,n+1);}else //没有数据{for(int k=1;k<=9;k++){bool flag=check(temp,i,j,k);if(flag) //第i⾏、第j列可以是k{temp[i][j]=k; //设为kif(n == 80)print(temp);elseSudoku(temp,n+1);temp[i][j]=0; //恢复为0,判断下⼀个k}}}}不过,碰到数独的时候还是要⾃⼰努⼒⼀下的,实在不会解的时候才可以⽤这个程序解出来参考,不然就失去玩数独的乐趣了。
数独常用解法介绍

一、数独简介数独是一种以数字为表现形式的逻辑推理谜题。
数独起源于18世纪末的瑞士,后在美国发展、并在日本得以发扬光大。
1783年,瑞士数学家欧拉发明了一种拉丁方块的游戏,这就是现代数独的雏形。
1984年,在日本游戏杂志上出现了“数独”游戏,提出了“独立的数字”的概念,意思就是“这个数字只能出现一次”,并将这个游戏命名为“数独”(sudoku )。
数独一次的命名也就源于日本语,我们直接把日语中“数独”这两个同音字引用过来,也就成为了对其的命名。
每一道合格的数独谜题都有且仅有唯一答案,推理方法也以此为基础,任何无解或多解的题目都是不合格的二、数独规则标准数独的规则一般只有三点:1、数独中每行内的数字为1-9且不重复;2、数独中每列内的数字为1-9且不重复;3、数独中每宫内的数字为1-9且不重复。
三、数独元素标准数独的基本元素包括单元格、行、列、宫、区、区块、已知数、候选数等等。
单元格:简称格,是数独盘面中最小的格子,只可以填入一个数字; 行:数独盘面中横向9个单元格的总称; 列:数独盘面中纵向9个单元格的总称;宫:数独盘面中粗线划分出的9格单元格的总称;区:填入一组1-9数字的区域,行、列、宫、都是区的一种具体表现形式; 区块:某宫中横向或者纵向3个并排单元格的总称; 已知数:数独题目初始给出的数字;候选数:某空单元格中目前还可以填入的数字。
IH G F E D C B A数独直观解法,指的是我们在解数独的时候,不需要标记候选数,直接可以凭借直观判断填出格内得数的方法。
(有时候标记会大大增加解题效率,不能说标记就不属于直观解法)单区唯一解法、简单排除法、单元排除法、区块排除法、数组占位法、多区唯一解法第一节 单区唯一解法一、什么是单区唯一解法单区唯一解法,顾名思义“单区”指的是一行、一列或者一宫,“唯一解”指的是某格内只有唯一一个解。
由于数独规则的要求,数独中每行、每列及每一宫内数字都为1-9,。
数独的解法与技巧

数独的直观式解题技巧直观法概说前言数独这个数字解谜游戏,完全不必要用到算术!会用到的只是推理与逻辑。
刚开始接触数独时,即使是只须用到"基础摒除法"及"唯一解法"技巧的简易级谜题,就已可让我们焦头烂额了,但是随着我们深陷数独的迷人世界之后,这类简易级的数独谜题必定在短时间内难再使我们获得征服的满足。
于是,当我们逐步深入、进阶到更难的游戏后,我们将会需要发展出更多的解谜技巧。
虽然最好的技巧便是我们自己发现的窍门,这样我们很容易就能记住它们,运用自如,不需要别人来耳提面命。
但是如果完全不去观摩学习他人发展出来的技巧,而全靠自己摸索,那将是一个非常坚苦的挑战,也不是正确的学习之道!所以让我们一齐来探讨数独的解谜方法吧!数独的解谜技巧,刚开始发展时,以直观法为主,对于初入门的玩家来说,这也是一般人较容易理解、接受的方法,对于一般报章杂志及大众化网站上的数独谜题而言,如果能灵活直观法的各项法则,通常已游刃有余。
直观法详说直观法的特性:1.不需任何辅助工具就可应用。
所以要玩报章杂志上的数独谜题时,只要有一枝笔就可以开始了,有人会说:可能需要橡皮擦吧?答案是:不用!只要你把握数独游戏的填制原则:绝不猜测。
灵活运用本站所介绍的直观填制法,确实可以不必使用橡皮擦。
2.从接到数独谜题的那一刻起就可以立即开始解题。
3.初学者或没有计算机辅助时的首要解题方法。
4.相对而言,能解出的谜题较简单。
直观法的主要的技巧:1.基础摒除法。
2.唯一解法。
3.区块摒除法。
4.唯余解法。
5.单元摒除法。
6.矩形摒除法。
7.余数测试法。
基础摒除法前言对第一次接触数独游戏,接受了 1 ~ 9 的数字在每一行、每一列、每一个九宫格都只能出现一次的规则后,开始要解题的玩家来说,基础摒除法绝对是他第一个想到及使用的方法,十分的自然、也十分的简易。
如果能够细心、系统化的运用基础摒除法,一般报章杂志或较大众化的数独网站上的数独谜题几乎全部可解出来。
C语言数独游戏的求解方法

C语⾔数独游戏的求解⽅法数独游戏的解法:先将数独分为九个格⼦,⽤⼀个数组将每个⼩九宫格的候选数存放下来,将候选数挨个放进数独⾥的空位,如果这⼀⾏和这⼀列都没有这个数字,继续放⼊下⼀个,如果不能放⼊的话就回到上⼀步继续尝试,直到成功求出数独的解为⽌;⽐如这个数独第⼀个九宫格的候选数就有1,2,7,8,9,我们需要从1开始放⼊第⼀个格⼦挨个尝试直到8的时候发现剩下的两个格⼦都不能放⼊这个时候我们就要撤回上⼀个插⼊的7,发现8仍然不能放⼊,就继续撤回2,发现8可以放⼊,就将8放⼊3号位置,然后将9插⼊这个时候我们发现2不能放⼊剩下的两格,我们就继续撤回到1插⼊的时候,将2放⼊1号位置,然后挨个放⼊剩下的数循环这⼀过程,直到数独求出解为⽌;这个⽅法⽐较容易想到,操作也⽐较容易实现下⾯是代码代码⼤多数都写了备注便于理解题⽬需要的1000道题放在下⾯了,将这1000个txt⽂件拷到EXE⽂件同⼀⽬录就可以了题⽬链接:#include <stdio.h>#include <stdlib.h>#include <string.h>#define MAX 81typedef struct asd{int x;//待测试的值的x坐标int y;//待测试的值的y坐标int p;//待测试的值的位置(1道9代表在九宫格⾥的位置)int n;//待测试的值}A;A zhan[MAX];//存放每个放进题⽬数组测试的数据void kongque(int queshi[9][9],int aa[9][9]);//函数将候选数数组⾥去除题⽬中有的数字void shuchu(int aa[9][9],int q);//输出整个数组到⽂件中int end(int aa[9][9]); //判断是否结束int next(int queshi[9][9],int m,int n,int *x,int *y,int aa[9][9]);//查找下⼀个应该放进九宫格测试的数据int chazhao(int aa[9][9],int m,int n,int num);//查找同⼀⾏同⼀列是否有相同的值int nfrz(int queshi[9][9],int aa[9][9],int m,int n,int *p);//判断是否满⾜⼊栈条件(就是当前值是否可以插⼊九宫格)int rz(int *t,int x,int y,int p,int num);//⼊栈操作int cz(int *t,int *x,int *y,int *p,int *num);//出栈操作void aaaa(char aa[10],int a);//计算题⽬⽂件的⽂件名void bbbb(char aa[10],int a);//计算答案⽂件的⽂件名int main(){int i;//记录该调⽤哪道题for(i=0;i<1000;i++){int aa[9][9],j,k;//aa数组存放的是题⽬数独int queshi[9][9];//存放的是每个九宫格的待选数int end=0;//判断循环结束条件int h=0,l=0,p=1;//h是候选数的⾏坐标,l是候选数的列坐标,p代表当前测试数属于⼩九宫格的位置int t=-1;//栈的长度int s=0,num;FILE *u;char qwe[10];for(j=0;j<9;j++)//将数组置为每⾏都是(1到9)for(k=0;k<9;k++)queshi[j][k]=k+1;aaaa(qwe,i);u=fopen(qwe,"r");for(j=0;j<9;j++){//读⼊题⽬for(k=0;k<9;k++){fscanf(u,"%d",&aa[j][k]);}}fclose(u);memset(zhan,0,sizeof(zhan));//将栈的数据全部置为0kongque(queshi,aa);while(end!=1){//开始求解s=next(queshi,h,l,&h,&l,aa);//查找下⼀个应该放进九宫格测试的数据 if(s==0){//如果找到则进⼊下⼀层s=nfrz(queshi,aa,h,l,&p);//判断能否插⼊数独⾥if(s==0){//如果可以则将插⼊的数据存放到栈⾥(⼊栈)s=rz(&t,h,l,p,queshi[h][l]);if(s==0){ //如果⼊栈成功则写⼊数独aa[h/3*3+(p-1)/3][h%3*3+(p-1)%3]=queshi[h][l];l++;//待选数跳到下⼀个p=1;//重新从第⼀个⼩格⼦开始判断是否插⼊}else{end=1;//循环结束}}else{s=cz(&t,&h,&l,&p,&num);if(s==0){//如果出栈成功则擦除插⼊的数据aa[h/3*3+(p-1)/3][h%3*3+(p-1)%3]=0;p++;}elseend=1;}}else if(s==-1){shuchu(aa,i);//输出求解完毕的数独end=1;}else{printf("发⽣未知错误");end=1;}}}return 0;}//函数将候选数数组⾥去除题⽬中有的数字void kongque(int queshi[9][9],int aa[9][9]){int i,j,x,y;for(i=0;i<j;i++){for(j=0;j<9;j++){if(aa[i][j]){x=i/3*3+j/3;//数独数组和候选数数组的坐标转换y=aa[i][j]-1;queshi[x][y]=0;}}}}//输出整个数组到⽂件中void shuchu(int aa[9][9],int q){int i,j;FILE *p;char qq[10];bbbb(qq,q);p=fopen(qq,"w");for(i=0;i<9;i++){for(j=0;j<9;j++){fprintf(p,"%d ",aa[i][j]);}fprintf(p,"\n");}fclose(p);}//判断是否结束int end(int aa[9][9]){int i,j,num=0;for(i=0;i<9;i++){num=0;for(j=0;j<0;j++){num+=aa[i][j];//检查每⼀⾏是否为1到9}if(num!=45)return -1;}for(j=0;j<9;j++){//检查每⼀列是否为1到9num=0;for(i=0;i<9;i++){num+=aa[i][j];}if(num!=45)return -1;}return 0;}//查找下⼀个应该放进九宫格测试的数据int next(int queshi[9][9],int m,int n,int *x,int *y,int aa[9][9]){ int qqq=0;if(n>8){//如果当前⼩九宫格填写完毕则进⼊下⼀个九宫格n=0;m++;}if(m>8){qqq=end(aa);//判断是否结束if(qqq!=0)return -1;elsereturn 1;}while(queshi[m][n]==0){if(n<8)n++;else{n=0;m++;if(m>8){qqq=end(aa);if(qqq!=0)return -1;elsereturn 1;}}}*x=m;//重新获取测试的值的x坐标和y坐标*y=n;return 0;}//查找同⼀⾏同⼀列是否有相同的值int chazhao(int aa[9][9],int m,int n,int num){int i;for(i=0;i<9;i++){//查找⾏if(aa[m][i]==num)return -1;}for(i=0;i<9;i++){//查找列if(aa[i][n]==num)return -1;}return 0;}//判断是否满⾜⼊栈条件(就是当前值是否可以插⼊九宫格)int nfrz(int queshi[9][9],int aa[9][9],int m,int n,int *p){int s=*p;int i,t1,t2,num;num=queshi[m][n];for(i=s;i<10;i++){t1=(m/3)*3+(s-1)/3;t2=(m%3)*3+(s-1)%3;if(aa[t1][t2]!=0){s++;continue;}if(chazhao(aa,t1,t2,num)!=0){s++;continue;}else{*p=s;return 0;}}return -1;}//⼊栈操作int rz(int *t,int x,int y,int p,int num){if(*t>=MAX){return -1;}else{(*t)++;zhan[*t].x=x;zhan[*t].y=y;zhan[*t].p=p;zhan[*t].n=num;return 0;}}//出栈操作int cz(int *t,int *x,int *y,int *p,int *num){ if(*t==-1){return -1;}else{*x=zhan[*t].x;*y=zhan[*t].y;*p=zhan[*t].p;*num=zhan[*t].n;(*t)--;return 0;}}//计算题⽬⽂件的⽂件名void aaaa(char aa[10],int a){if(a>=0&&a<10){aa[0]='0';aa[1]='0';aa[2]='0';aa[3]=a+'0';}else if(a<100){aa[0]='0';aa[1]='0';aa[2]=a/10+'0';aa[3]=a%10+'0';}else if(a<1000){aa[0]='0';aa[1]=a/100+'0';aa[2]=a/10%10+'0';aa[3]=a%10+'0';}aa[4]='.';aa[5]='t';aa[6]='x';aa[7]='t';aa[8]='\0';}//计算答案⽂件的⽂件名void bbbb(char aa[10],int a){if(a>=0&&a<10){aa[0]='a';aa[1]='0';aa[2]='0';aa[3]=a+'0';}else if(a<100){aa[0]='a';aa[1]='0';aa[2]=a/10+'0';aa[3]=a%10+'0';}else if(a<1000){aa[0]='a';aa[1]=a/100+'0';aa[2]=a/10%10+'0';aa[3]=a%10+'0';}aa[4]='.';aa[5]='t';aa[6]='x';aa[7]='t';aa[8]='\0';}以上就是本⽂的全部内容,希望对⼤家的学习有所帮助,也希望⼤家多多⽀持。
数独的7种解法

数独解法之阳早格格创做七种解法:序止数独那个数字解谜游戏,真足不需要用到算术!会用到的不过推理与逻辑.刚刚启初交战数独时,纵然是只须用到"唯一解"本领的浅易级谜题,便已可让咱们焦头烂额了,然而是随着咱们深陷数独的迷人天下之后,那类浅易级的数独谜题肯定正在短时间内易再使咱们赢得征服的谦脚.于是,当咱们逐步深进、进阶到更易的游戏后,咱们将会需要死少龈?多的解谜本领.虽然最佳的本领即是咱们自己创造的窍门,那样咱们很简单??能记着它们,使用自如,不需要他人去耳提里命.然而是如果然足不去瞅摩教习他人死少出去的本领,而齐靠自己摸索,那将是一个非常脆苦的挑拨,也不是精确的教习之讲!所以让咱们一齐去探讨数独的解谜要领吧!数独的解谜本领,刚刚启初死少时,以曲瞅式的唯一解及摒除法为主,对付于初初教的玩家去道,那也是普遍人较简单明黑、担当的要领,对付于普遍浅易级大概中级的数独谜题,如果能机动使用此二规则,常常已游刃有余.1.唯一解法当数独谜题中的某一个宫格果为所处的列、止大概九宫格已出现过的数字已达 8 个,那么那个宫格所能挖进的数字便剩下那个还出出现过的数字了.<图 1> (9, 8)出现唯一解了<图 1>是最明隐的唯一解出现时机,请瞅第 8 止,由 (1,8) ~(8,8) 皆已挖进数字了,只剩(9,8)仍旧空黑,此时(9,8)中应挖进的数字,天然便是第8 止中还出出现过的数字了!请一个个数字核查于一下,哦!是数字 8 还出出现过,所以(9,8) 中该挖进的数字便是数字 8了.<图 2> (8, 9)出现唯一解了<图2>是另一个明隐出现唯一解的情形,请瞅第8 列,由(8,1) ~(8,8) 皆已挖进数字了,只剩(8,9)仍旧空黑,此时(8, 9)中应挖进的数字,天然便是第 8 列中还出出现过的数字了!请一个个数字核查于一下,哦!是数字 9 还出出现过,所以(8, 9) 中该挖进的数字便是数字 9 了.<图 3> (7, 5)出现唯一解了<图3>是另一种明隐出现唯一解的情形,请瞅下中九宫格,正在那个九宫格中除了(7, 5)仍旧空黑中,其余宫格皆已挖罕见字了,所以(7, 5)中应挖进的数字,天然便是下中九宫格中还出出现过的数字了!请一个个数字核查于一下,哦!是数字1 还出出现过,所以(7,5) 中该挖进的数字便是数字 1 了.<图 4> 普遍情形下的唯一解类似<图1>~<图3>那种明隐出现唯一解的情形,正在普遍情形之下及解题初期是不太大概出现的!<图4>是一个最典型的浅易级数独谜题,如果简单瞅察某一个止、列大概九宫格,不一处是已出现8 个数字的,易讲如许便无解了吗?非也!非也!正在此图中,出现唯一解的宫格本去有 3 处之多!您能找出去吗?出错,正在普遍情形之下及解题初期,唯一解的觅找必须概括所处的止、列及九宫格三者,共时过滤筛选出已出现的数字才止!如果漏掉其一,大概便无法找出唯一解的出现位子了.当前且不闲着挖进数字,先去找找瞅<图 4>中暂时已出现的唯一解正在哪女吧:第一个唯一解位子正在(2, 3):(2, 3) 所处的第 2 列中已出现的数字是:9、3、5、7.所处的第 3 止中已出现的数字是:4、2、6、8.至于所处的上左九宫格中,已出现的数字是:2、9、4.所以概括而止,受其所处位子的止、列及九宫格做用,不得再使用并挖进(2, 3) 的数字计有:2、3、4、5、6、7、8、9. 能用去挖进的数字真真只剩数字 1 那个唯一的解了.第二个唯一解位子正在(8, 7):(8, 7) 所处的第 8 列中已出现的数字是:1、2、8、6.所处的第 7 止中已出现的数字是:3、9、5、4.至于所处的下左九宫格中,已出现的数字是:4、6、5.所以概括而止,受其所处位子的止、列及九宫格做用,不得再使用并挖进(8, 7) 的数字计有:1、2、3、4、5、6、8、9. 能用去挖进的数字真真只剩数字 7 那个唯一的解了.第三个唯一解位子正在(5, 5):(5, 5) 所处的第5 列中已出现的数字是:1、7.所处的第5 止中已出现的数字是:2、5.至于所处的中央九宫格中,已出现的数字是:3、6、8、9.所以概括而止,受其所处位子的止、列及九宫格做用,不得再使用并挖进(5, 5) 的数字计有:1、2、3、5、6、7、8、9. 能用去挖进的数字真真只剩数字 4 那个唯一的解了.以上所谓的三个唯一解位子,是以<图4>现况已挖进所罕见字之前而止,如果启初挖进数字,出现唯一解的位子大概将随之减少.例:当(8, 7) 挖进数字 7 之后,(7, 7)将出现唯一解 1;如果再将数字 1 挖进(7, 7),正在(7, 8)又将出现唯一解 3;......如许不竭循环下去,便不妨将所有谜题解出了.2.唯一候选数法概道依照候选数法概道一文中,候选数表的创造准则,咱们不妨知讲:不妨挖进某一个宫格的数字,一定会列于该宫格的候选数中;不正在候选数中的数字,便不克不迭挖进该宫格中.所以如果正在候选数表中创造某一个宫格的候选数仅有 1 个数字,那便是表示:不必再思量了!那个宫格便是只可挖进那个数字啦!如果挖进别的数字,便会违犯数独的挖造准则的.利用“找出候选数表中,候选数仅有 1 个数字的宫格去,并挖进该候选数”的要领便喊搞唯一候选数法(Singles Candidature, sole Candidate).唯一候选数法示例<图 1>数独谜题的候选数表<图1> 是咱们正在候选数法概道一文中完毕的候选数表,其中有佳几个宫格的候选数皆惟有 1 个,所以不妨利用唯一候选数法去举止挖造.先还不要挖进数字,咱们先去找找瞅,有哪些宫格有唯一候选数?正在 (2, 7) 有唯一候选数 7.正在 (5, 5) 有唯一候选数 5.正在 (8, 3) 有唯一候选数 3.哇!共时出现了 3 个唯一候选数啊!那么,先挖进哪一个会不会做用挖造截止呢?天然不会了,只消您下兴,喜欢先挖哪一个皆出问题的.佳,便正在那 3 个宫格中挖进他们的唯一候选数吧,挖造截止如<图2>:<图 2>哇!又有唯一候选数出现了呢!出错,普遍浅易级的数独谜题,如果使用曲瞅式的唯一解法及摒除法去解题,纵然是数独老脚,也要耗费相称的光阴才搞完毕;然而是如果采与唯一候选数法,从候选数表创造完毕启初,唯一候选数将一个一个接连不竭的出现,沉沉快紧的便不妨完毕解题啦!<图3> 是<图1> 的完毕解.<图 3>完毕解3.隐性三链数删减法概道逢到了下档、艰易级的数独谜题,使得唯一候选数法战隐性唯一候选数法黔驴技贫的时间,便是百般删减法上场的时机了.正在百般的删减法中,哪一个要先用是随部分之喜佳的,并不节造.原页介绍的例子天然可用其余删减法完毕解题,然而仍旧要以隐性三链数删减法劣先??!<图 1>请瞅<图 1>的第 2 列,数字 1、7、8 只出当前(2, 1)、(2, 7)战(2, 8)那三个宫格的候选数中;那时隐性三链数删减法的条件已创造了!那表示第2 列的数字1、7 战8 将只可挖到那三个宫格中,果为:如果让别的数字挖进那三个宫格之中后,那三个相同的数字能挖进的大概宫格便只剩下二个,而那是不可能的事!所以若那三个宫格的候选数中另有其余数字,局部是多余无用的,它们已不可能再用去挖进那些宫格中了,所以不妨毫不思量的把它们删减掉.于是(2, 7)战(2, 8)那二个宫格候选数中的6 皆可被仄安的删减掉;其中(2, 7)的候选数少了数字 6,将使得(8, 7)出现止隐性唯一候选数 6 ,于是可用隐性唯一候选数法去挖进下一个解了.整治一下:当某 3 个数字仅出当前某列的某三个宫格候选数中时,便不妨把那三个宫格的候选数删减成该3 个数字.共理,当某3 个数字仅出当前某止的某三个宫格候选数中时,便不妨把那三个宫格的候选数删减成该3 个数字.天然,当某3 个数字仅出当前某个九宫格的某三个宫格候选数中时,便不妨把那三个宫格的候选数删减成该 3 个数字.利用“找出某 3 个数字仅出当前某止、某列大概某一个九宫格的某三个宫格候选数中的情形,从而将那三个宫格的候选数删减成该 3 个数字”的要领便喊搞隐性三链数删减法(Hidden Triples).原法本去为隐性数对付简略法的推广,而且还不妨继承加以推广:隐性四链数删减法便是:“找出某4 个数字仅出当前某止、某列大概某一个九宫格的某四个宫格候选数中的情形,从而将那四个宫格的候选数删减成该 4 个数字”的要领.隐性五链数删减法便是:“找出某5 个数字仅出当前某止、某列大概某一个九宫格的某五个宫格候选数中的情形,从而将那五个宫格的候选数删减成该 5 个数字”的要领.......如果承诺的话,您真真是不妨那样推广的,不过,真用上是可有其应用的价格大概空间呢?隐性三链数删减法示例隐性三链数删减法一公有 3 种情景:第一种爆收止家、第二种是爆收正在列、第三种则爆收正在九宫格.<图 1> 便是爆收正在列的例子了,其余的情况举比圆下:<图 2><图2> 是隐性三链数删减爆收止家的例子:图中第4 止的数字2、4、9 只出当前(4, 4)、(5, 4)及(6, 4) 那三个宫格的候选数中,所以不妨将三个宫格候选数中 2、4、9 以中的数字仄安的删减掉,(4, 4)的候选数删减成2、4; (5, 4)的候选数删减成2、4、9;(6, 4)的候选数删减成 9;出现了唯一候选数啦!<图 3><图3> 是隐性三链数删减爆收正在九宫格的例子:图中中央九宫格的数字2、5、9 只出当前 (5, 4)、(5, 6)及(6, 4) 那三个宫格的候选数中,所以不妨将三个宫格候选数中 2、5、9 以中的数字仄安的删减掉,(5, 4)的候选数删减成2、5、9;(5, 6)的候选数删减成2、5;(6, 4)的候选数删减成 9;出现了唯一候选数啦!<图 4>像<图1>~<图3> 那样只经一次删减便出现下一个解的情况天然不错了,然而偶尔可出法那样逆心,<图4> 便是一个例子.下一个解将出当前(5, 6) 那个宫格,您能找出该挖进什么数字吗?以暂时所教到的要领,要解出下一个解,需要二个步调:先瞅中左九宫格吧!由于只剩(5, 1)~(5, 3)那个区块尚已挖进数字,所以可用区块删减法将第 5 列其余区块候选数中的 1、3、4 局部删减掉,然而本量上仅能删到(5, 4)及(5, 6)候选数的数字 4 而已.接下去请瞅察第 6 止!由于数字 1、4、9 只出当前 (2, 6)、(8, 6)及(9, 6) 那三个宫格的候选数中 [果为(5, 6)的候选数正在上一步调中已被删减为5、8 了 ],所以可用隐性三链数删减将三个宫格候选数中 1、4、9 以中的数字仄安的删减掉, (2, 6)的候选数删减成1、4、9;(9, 6)的候选数出变;(8, 6)的候选数则由2、4、5、8、9 删减成4、9;由于5 被删减掉了,使得(5, 6) 出现了止隐性唯一候选数5啦!4.隐性数对付删减法概道逢到了下档、艰易级的数独谜题,使得唯一候选数法战隐性唯一候选数法黔驴技贫的时间,便是百般删减法上场的时机了.正在百般的删减法中,哪一个要先用是随部分之喜佳的,并不节造.原页介绍的天然便要以隐性数对付删减法劣先??!<图 1>请瞅<图1>的上左九宫格,数字8、9 皆只出当前(2, 8)战(2, 9)那二个宫格的候选数中;那时隐性数对付删减法的条件已创造了!那表示上左九宫格的数字 8 战 9 将只可挖到那二个宫格中,而且:如果数字 8 将挖进(2, 8),那么(2, 9)便一定要挖进数字 9;反之,如果数字 9 将挖进(2, 8),那么(2, 9)便一定要挖进数字 8;不管哪一个情景出现,(2, 8)战(2, 9)那二个宫格的候选数中若另有其余数字,局部是多余无用的,果为那二个宫格若挖进数字 8、9 以中的数字,那么上左九宫格的数字 8 大概 9 便将无处可挖了.候选数的意思是大概挖进该宫格的数字,而那二个数字以中的数字已不可能再用去挖进原宫格中了,所以不妨毫不思量的把它们删减掉.当(2, 8)战(2, 9)那二个宫格的候选数皆仄安的删减成数字 8、9 之后,(2, 5)出现了列隐性唯一候选数 2 ,于是可用隐性唯一候选数法去挖进下一个解了.整治一下:当某个数对付仅出当前某个九宫格的某二个宫格候选数中时,便不妨把那二个宫格的候选数删减成该数对付.共理,当某个数对付仅出当前某列的某二个宫格候选数中时,便不妨把那二个宫格的候选数删减成该数对付.天然,当某个数对付仅出当前某止的某二个宫格候选数中时,便不妨把那二个宫格的候选数删减成该数对付.利用“找出某个数对付仅出当前某止、某列大概某一个九宫格的某二个宫格候选数中的情形,从而将那二个宫格的候选数删减成该数对付”的要领便喊搞隐性数对付删减法(Hidden Pairs).当隐性数对付删减法完毕后,常常还可激励数对付删减法;以<图1>为例,当(2, 8)战(2, 9)那二个宫格的候选数皆仄安的删减成数字8、9 之后,还可利用数对付删减法把(2, 1)、(2, 2)、(2, 3) 那三个c格候选数中的数字 8 删减掉.隐性数对付删减法示例隐性数对付删减法一公有 3 种情景:第一种爆收止家、第二种是爆收正在列、第三种则爆收正在九宫格.<图 1> 便是爆收正在九宫格的例子了,其余的情况举比圆下:<图 2><图 2> 是隐性数对付删减爆收止家的例子:图中第 2 止的数对付 4、6 只出当前 (3, 2)及(9, 2) 那二个宫格的候选数中,所以不妨将(3, 2)及(9, 2)的候选数仄安的删减成数对付4、6;而经此一删,(3, 3) 宫格出现了列隐性唯一候选数 1 啦!<图 3><图 3> 是隐性数对付删减爆收正在列的例子:图中第 7 列的数对付 4、7 只出当前 (7,1)及(7, 8) 那二个宫格的候选数中,所以不妨将(7, 1)及(7, 8)的候选数仄安的删减成数对付4、7;而经此一删,(8, 1) 宫格出现了止隐性唯一候选数 2 啦!三链列删减法概道逢到了下档、艰易级的数独谜题,使得唯一候选数法战隐性唯一候选数法黔驴技贫的时间,便是百般删减法上场的时机了.正在百般的删减法中,哪一个要先用是随部分之喜佳的,并不节造.原页介绍的例子天然可用其余删减法完毕解题,且原删减法创造的条件战其余要领相比稍嫌繁杂,然而为了介绍,正在举止解题时仍旧要以三链列删减法劣先??!<图 1>请瞅<图 1>第 1、4、6 列的数字 5 ,皆只出当前第 1、5、8 止的宫格候选数中;那时三链列删减法的条件已创造了!那表示第 1 止、第 5 止及第 8 止的数字 5 将只可被挖到第1 、4、6 列了,果为:第 1 列的数字 5 只出当前(1, 1)及(1, 8),所以数字 5 只可挖到那二个宫格;先假设第 1 列的数字 5 将被挖到(1, 1),第 1 止便不克不迭再挖数字 5 了,所以第 4 列的数字 5 只佳挖到(4, 5),第 6 列的数字 5 只佳挖到(6, 8);其余,假设第 1 列的数字 5 将被挖到(1, 8),第 8 止便不克不迭再挖数字 5 了,所以第 6 列的数字 5 只佳挖到(6, 1)大概(6, 5);如果第 6 列的数字 5 挖到(6, 1),第 4 列的数字 5 便要挖到(4, 5);如果第 6 列的数字 5 挖到(6, 5),第 4 列的数字 5 便要挖到(4, 1);不管哪一种情况爆收,第 1、5、8 止的数字 5 一定要挖正在第 1、4、6 列的接面,别的宫格已不克不迭再使用数字 5 去挖进了,所以若其余宫格的候选数中还罕见字5,局部是多余无用的,不妨毫不思量的把它们删减掉.于是(5, 1)、(5, 5)、(9, 5)战(1, 8)、(2, 8)那五个宫格候选数中的 5 皆可被仄安的删减掉;其中(9, 5)的候选数少了数字 5,将使得(9, 4)出现列隐性唯一候选数 5 ,于是可用隐性唯一候选数法去挖进下一个解了.整治一下:当某个数字正在某三列仅出当前相共的三止时,便不妨把那三止其余宫格候选数中的该数字删减掉.共理,当某个数字正在某三止仅出当前相共的三列时,便不妨把那三列其余宫格候选数中的该数字删减掉.利用“找出某个数字正在某三列仅出当前相共三止的情形,从而将该数字自那三止其余宫格候选数中删减掉”;大概“找出某个数字正在某三止仅出当前相共三列的情形,从而将该数字自那三列其余宫格候选数中删减掉”的要领便喊搞三链列删减法(Swordfish).原删减法本去是矩形顶面删减法的推广,如果您承诺的话,还不妨继承推广:四链列删减法:利用“找出某个数字正在某四列仅出当前相共四止的情形,从而将该数字自那四止其余宫格候选数中删减掉”;大概“找出某个数字正在某四止仅出当前相共四列的情形,从而将该数字自那四列其余宫格候选数中删减掉”的要领五链列删减法:利用“找出某个数字正在某五列仅出当前相共五止的情形,从而将该数字自那五止其余宫格候选数中删减掉”;大概“找出某个数字正在某五止仅出当前相共五列的情形,从而将该数字自那五列其余宫格候选数中删减掉”的要领六链列删减法:...... 不过如果果然那样搞,本量应用时,不妨用上的机率大概已几便是了.逢到了下档、艰易级的数独谜题,使得唯一候选数法战隐性唯一候选数法黔驴技贫的时间,虽然您不妨劣先使用三链列删减法去觅找下一个解;然而大部分的人正在使用删减法的劣先程序上,常常皆市将三链列删减法排正在稍后一面,为什么要如许安插,正在本量使用一段时间之后,疑赖您自能体验了,然而那个要领又是不可大概缺的,如果不会使用原删减法,有很多下档的数独谜题便将无解了.三链列删减法示例三链列删减法惟有2 种情景:第一种的删减爆收止家、第二种的删减爆收正在列.<图1> 便是删减爆收止家的例子了,第二种的情况举比圆下:<图 2><图 2> 是三链列删减爆收正在列的例子:图中第 3、5、8 止的数字 2 只出当前第 3、4、5 列,所以不妨将数字 2 自(4, 6)、(5, 6)的候选数中仄安的删减掉,其中(5, 6) 的候选数由 2、5 删减成 5 时,出现唯一候选数啦!5.区块删减法概道逢到了下档、艰易级的数独谜题时,唯一候选数法战隐性唯一候选数法仍有其黔驴技贫的时间;那时便是区块删减法上场的时机了,往后将要介绍的数对付删减法(Naked Pairs)、隐性数对付删减法(Hidden Pairs)、三链数删减法(Naked Triples)、隐性三链数删减法(Hidden Triples) 、矩形顶面删减法(X-Wing)、三链列删减法(Swordfish)皆具备类似的个性:使用那些本领的脚段仅正在删减候选数的数目,删减之后,仍旧得使用唯一候选数法战隐性唯一候选数法去找出下一个解并挖进数字的.当使用唯一候选数法大概隐性唯一候选数法找不出下一个解时,到底该先使用哪一个删减法呢?随您下兴的用吧!如果您比较擅少使用数对付删减法,那便先用数对付删减法吧!如果您认为区块删减法比较佳用,那便先用数对付删减法吧! ......;介绍时总有先后的序次,然而本去不表示先介绍的便较佳用大概必须先用哦!只消能达到:“仄安删减掉候选数,并找出下一个解”的脚段,使用哪一种删减法皆是不妨的.<图 1>请瞅<图1>,那时若使用唯一候选数法大概隐性唯一候选数法是找不出下一个解去的!便先去试试区块删减法吧. 请瞅察第 9 止:数字 1 正在原止各宫格的候选数中,是不是仅出当前(1,9)~(3,9)的那一个区块中?太佳了,区块删减的条件已有了;果为那表示第9 止的数字1 只可挖正在(1,9)~(3,9)的那一个区块中,而不管挖正在原区块的哪一个宫格中,上左九宫格的其余宫格将果原九宫格已出现数字1,而不得再挖进1,可则便违犯数独挖造的准则啦!所以(1, 7)~(3, 7)及(1, 8)~(3, 8)那二个区块的宫格,如果其候选数中包罗罕见字1,便不妨毫不思量的把它简略掉,果为候选数的意思是大概挖进该宫格的数字,而那个数字已不可能再用去挖进该宫格中了.啊!太佳啦!(1, 7)的候选数中包罗罕见字1,所以不妨把 (1, 7) 的候选数由 1、6 删减成 6,于是可用唯一候选数法去挖进下一个解了.当区块删减法的条件创造时,可别下兴得太早,果为很有大概找不到可删减的数字,比圆:正在<图 1>的第1 止中,数字 2 正在原止的各宫格候选数中,仅出当前(4, 1)~(6, 1)那一个区块中,而不管数字 2 将去会被挖到原区块的哪一个宫格中,将使得数字 2 不得再挖进(4, 2)~(6, 2)及(4, 3)~(6, 3)那二个区块中;然而请找找瞅!那二个区块各宫格的候选数中局部不数字 2,所以是黑闲了一场,条件是创造了,然而候选数并已果此而得到删减.整治一下,并为了简化道述起睹,底下所述的“区块候选数”表示:该区块的各个宫格候选数的总战.比圆(1, 3)~(3, 3) 的区块候选数便是(1, 3)的候选数4、6、7 及(2, 3)的候选数3、4、6 及(3, 3)的候选数 3、7 的总战: 3、4、6、7 啦!:当某一个数字只出当前某止的某一个区块候选数中时,便不妨把该数字自包罗该区块的九宫格之其余区块候选数中删减掉.共理,当某一个数字只出当前某列的某一个区块候选数中时,便不妨把该数字自包罗该区块的九宫格之其余区块候选数中删减掉.共理,当某一个数字只出当前某个九宫格的某一个区块候选数中时,便不妨把该数字自包罗该区块的止大概列之其余区块候选数中删减掉.利用“找出某一止、某一列大概某一个九宫格各个区块候选数中只出现一次的数字去,并将该数字自包罗该区块的另一个止、列大概九宫格的其余区块候选数中删减掉”的要领便喊搞区块删减法 (Locked Candidates, Single Sector Candidates).区块删减法示例区块删减法一公有 4 种情景:第一种是爆收止家而去删减九宫格、第二种是爆收正在列而去删减九宫格、第三种是爆收正在九宫格而去删减止、第四种是爆收正在九宫格而去删减列.<图 1> 便是爆收止家而去删减九宫格的例子了,其余的情况举比圆下:<图 2><图 2> 是爆收正在列而去删减九宫格的例子:果为第 3 列的数字 6 只出当前 (3, 1)~(3, 3) 那一个区块,所以不妨将上左九宫格的另二个区块 (1, 1)~(1, 3)、(2, 1)~(2, 3) 候选数中的数字6 仄安的删减掉;于是(1, 1)的候选数 2、6 将被删减成2,出现了唯一候选数啦!<图 3><图3> 是爆收正在九宫格而去删减列的例子:果为上左九宫格的数字5 只出当前(3, 7)~(3, 9) 那一个区块,所以不妨将第 3 列的另二个区块 (3, 1)~(3, 3)、(3, 4)~(3, 6) 候选数中的数字5 仄安的删减掉;于是(3, 3)的候选数 5、9 将被删减成9,出现了唯一候选数啦!<图 4><图4> 是爆收正在九宫格而去删减止的例子:果为中央九宫格的数字1 只出当前(4, 5)~(6, 5) 那一个区块,所以不妨将第 5 止的另二个区块 (1, 5)~(3, 5)、(7, 5)~(9, 5) 候选数中的数字1 仄安的删减掉;于是(8, 5)的候选数1、3、7、8 将被删减成3、7、8;共理,中央九宫格的数字 7、8 皆只出当前 (4, 5)~(6, 6) 那一个区块,所以不妨将第 5 止的另二个区块 (1, 5)~(3, 5)、(7, 5)~(9, 5) 候选数中的数字 7、8 皆仄安的删减掉;于是(8, 5)的候选数 3、7、8 将再度被删减成 3;出现了唯一候选数啦!像<图 1>~<图 3>那样,只搞一次区块删减便找到下一个解的情况固然是不错,然而偶尔并不那么逆心,像<图4>便需要删减三次才得到下一个解,不过那还算佳的了,果为三次的删减皆恰佳爆收正在共一个区块中,请瞅底下爆收正在分歧区块的情形吧!。
数独地解法与技巧

数独的直观式解题技巧直观法概说前言数独这个数字解谜游戏,完全不必要用到算术!会用到的只是推理与逻辑。
刚开始接触数独时,即使是只须用到"基础摒除法"及"唯一解法"技巧的简易级谜题,就已可让我们焦头烂额了,但是随着我们深陷数独的迷人世界之后,这类简易级的数独谜题必定在短时间内难再使我们获得征服的满足。
于是,当我们逐步深入、进阶到更难的游戏后,我们将会需要发展出更多的解谜技巧。
虽然最好的技巧便是我们自己发现的窍门,这样我们很容易就能记住它们,运用自如,不需要别人来耳提面命。
但是如果完全不去观摩学习他人发展出来的技巧,而全靠自己摸索,那将是一个非常坚苦的挑战,也不是正确的学习之道!所以让我们一齐来探讨数独的解谜方法吧!数独的解谜技巧,刚开始发展时,以直观法为主,对于初入门的玩家来说,这也是一般人较容易理解、接受的方法,对于一般报章杂志及大众化网站上的数独谜题而言,如果能灵活直观法的各项法则,通常已游刃有余。
直观法详说直观法的特性:1.不需任何辅助工具就可应用。
所以要玩报章杂志上的数独谜题时,只要有一枝笔就可以开始了,有人会说:可能需要橡皮擦吧?答案是:不用!只要你把握数独游戏的填制原则:绝不猜测。
灵活运用本站所介绍的直观填制法,确实可以不必使用橡皮擦。
2.从接到数独谜题的那一刻起就可以立即开始解题。
3.初学者或没有计算机辅助时的首要解题方法。
4.相对而言,能解出的谜题较简单。
直观法的主要的技巧:1.基础摒除法。
2.唯一解法。
3.区块摒除法。
4.唯余解法。
5.单元摒除法。
6.矩形摒除法。
7.余数测试法。
基础摒除法前言对第一次接触数独游戏,接受了 1 ~ 9 的数字在每一行、每一列、每一个九宫格都只能出现一次的规则后,开始要解题的玩家来说,基础摒除法绝对是他第一个想到及使用的方法,十分的自然、也十分的简易。
如果能够细心、系统化的运用基础摒除法,一般报章杂志或较大众化的数独网站上的数独谜题几乎全部可解出来。
九宫格数独的技巧

九宫格数独的技巧数独的元素数独的元素主要包括行、列和宫。
这三者划分出数独有三种不同形态的区域,而数独规则就是要求在这些区域内出现的数字都为1~9。
元素坐标图:行:数独盘面内横向一组九格的区域,用字母表示其位置;列:数独盘面内纵向一组九格的区域,用数字表示其位置;宫:数独盘面内3×3格被粗线划分的区域,用中文数字表示其位置。
格的坐标:利用表示行位置的字母和表示列位置的数字定位数独盘面内每个格子的具体位置,如A3格,F8格等。
数独技巧1. 宫内排除法排除法就是利用数独中行、列和宫内不能填入相同数字的规则,利用已出现的数字对同行、同列和同宫内其他格进行排斥相同数字的方法。
宫内排除法就是将一个宫作为目标,用某个数字对它进行排除,最终得到这个宫内只有一格出现该数字的方法。
技巧示意图:宫内排除法如上图所示,A2、B4和F7三格内的1都对三宫进行排除,这时三宫内只有C9格可以填入1,本图例就是对三宫运用的排除法。
2. 行列排除法行列排除法就是将一行或一列作为目标,用某个数字对它进行排除,最终得到这个行列内只有一格出现该数字的方法。
技巧示意图:行列排除法如上图所示,D2和B8两格内的6都对F行进行排除,这时F行内只有F5格可以填入6,本图例就是对F行运用的排除法。
3. 区块排除法区块排除法就是先利用宫内排除法在某个宫内形成一个区块,利用该区块的排除再结合其他已知数共同确定某宫内只有一格出现该数字的方法。
技巧示意图:区块排除法如上图所示,B4格的7对五宫进行排除,在五宫内形成了一个含数字7的区块。
无论该区块中F5格是7还是F6格是7,都可以对F行其他格的7进行排除。
再结合H7格的7同时对六宫进行排除,得到六宫内只有D8格可以填7。
4. 宫内数对占位法数对占位法指的是在某个区域中使得某两数只能出现在某两格内,这时虽然无法判断这两个数字的位置,但可以利用两数的占位排斥掉其他数字出现在这两格,再结合排除法就可以间接填出下个数字。
数独入门你必须掌握的那些规则和技巧

数独入门你必须掌握的那些规则和技巧Pleasure Group Office【T985AB-B866SYT-B182C-BS682T-STT18】数独入门:你必须掌握的那些规则和技巧数独的规则在空格内填入数字1-9,使得每行、每列和每个宫内数字都不重复。
注意:数独题目满足条件的答案是唯一的。
数独的元素数独的元素主要包括行、列和宫。
这三者划分出数独有三种不同形态的区域,而数独规则就是要求在这些区域内出现的数字都为1~9。
元素坐标图:行:数独盘面内横向一组九格的区域,用字母表示其位置;列:数独盘面内纵向一组九格的区域,用数字表示其位置;宫:数独盘面内3×3格被粗线划分的区域,用中文数字表示其位置。
格的坐标:利用表示行位置的字母和表示列位置的数字定位数独盘面内每个格子的具体位置,如A3格,F8格等。
数独技巧1.?宫内排除法排除法就是利用数独中行、列和宫内不能填入相同数字的规则,利用已出现的数字对同行、同列和同宫内其他格进行排斥相同数字的方法。
宫内排除法就是将一个宫作为目标,用某个数字对它进行排除,最终得到这个宫内只有一格出现该数字的方法。
技巧示意图:宫内排除法如上图所示,A2、B4和F7三格内的1都对三宫进行排除,这时三宫内只有C9格可以填入1,本图例就是对三宫运用的排除法。
2.?行列排除法行列排除法就是将一行或一列作为目标,用某个数字对它进行排除,最终得到这个行列内只有一格出现该数字的方法。
技巧示意图:行列排除法如上图所示,D2和B8两格内的6都对F行进行排除,这时F行内只有F5格可以填入6,本图例就是对F行运用的排除法。
3.?区块排除法区块排除法就是先利用宫内排除法在某个宫内形成一个区块,利用该区块的排除再结合其他已知数共同确定某宫内只有一格出现该数字的方法。
技巧示意图:区块排除法如上图所示,B4格的7对五宫进行排除,在五宫内形成了一个含数字7的区块。
无论该区块中F5格是7还是F6格是7,都可以对F行其他格的7进行排除。
数独 编程解法

数独编程解法数独是一种经典的数字逻辑游戏,通过填写数字来完成一个9x9的方格。
每个方格中的数字必须满足以下条件:每一行、每一列和每一个3x3的九宫格内都不能有重复的数字。
在本文中,我们将介绍一种基于编程的解法,通过编写代码来解决数独问题。
数独问题本质上是一个搜索和递归的问题。
我们可以通过深度优先搜索和回溯算法来解决。
首先,我们需要定义一个函数来判断一个数字是否可以放置在指定的位置。
这个函数将检查该数字在同一行、同一列和同一个九宫格内是否已经存在。
如果存在,则返回False;如果不存在,则返回True。
接下来,我们需要定义一个递归函数来解决数独问题。
该函数将从左上角开始遍历数独的每个位置。
如果当前位置为空,则尝试将数字1-9依次放置在该位置上,并递归调用自身来解决剩下的空格。
如果放置的数字符合数独的规则,则继续递归调用;如果不符合规则,则回溯到上一个位置,并尝试下一个数字。
当遍历完整个数独时,即找到了一个解。
我们可以将这个解保存下来,并继续寻找其他解。
在编程中,我们可以使用一个二维数组来表示数独,其中0表示空格,1-9表示数字。
我们还可以使用一个辅助数组来记录每个位置是否已经被填写。
在递归函数中,我们可以使用两个循环来遍历数独的每个位置,并判断该位置是否为空。
如果为空,则尝试将数字1-9依次放置在该位置上,并递归调用自身。
如果放置的数字符合数独的规则,则继续递归调用;如果不符合规则,则回溯到上一个位置,并尝试下一个数字。
当遍历完整个数独时,即找到了一个解。
通过以上步骤,我们可以得到数独的一个解。
如果想要找到所有的解,可以在递归函数中增加一个计数器,并将每个解保存下来。
当递归函数返回时,即找到了一个解。
我们可以将这个解保存下来,并继续寻找其他解。
我们可以使用编程语言中的输出函数来将解输出到控制台。
为了使输出更加美观,我们可以使用表格形式来展示数独的解。
可以使用一些特殊字符来表示数独的边框和分割线,同时使用不同的颜色来区分已经填写的数字和空格。
数独的解法与技巧

数独的解法与技巧数独是一种经典的数字游戏,目标是通过填写1到9的数字,使得每一行、每一列、每一个九宫格内都包含了1到9的数字,而且每个数字在每一行、每一列、每一个九宫格内只出现一次。
虽然数独看似简单,但有时候会特别棘手。
下面是一些数独的解法和技巧,可以帮助你更轻松地解决数独谜题。
1.找出唯一数字:如果一个格子中只有一个数字可以填入,那就填入它。
在这个过程中,你需要观察每一行、每一列以及每一个九宫格内已经填入的数字,找出不重复的数字。
2.剔除法:在每个格子中列出可能的数字,在填写其他格子的数字后,回头再检查每个格子,如果一个格子中的数字已经在同一行、同一列或同一个九宫格内的其他格子中出现过,那么这个数字就不可能是正确答案,可以剔除。
3.唯余法:在每个宫格(3x3的小方格)中列出1到9还未填入的数字,并观察每一个数字是否只出现在一个格子中,如果是,则填入该格子。
4.确定性法则:如果一些宫格内,只有一个格子可以填入一些数字,那就填入它。
这个数字不会在同一行、同一列的其他宫格内出现。
5.对称性法则:数独谜题通常具有对称性,通过观察,如果你成功地填入一个数字并且解开了一些谜题,那么你可以将解决方案沿着对称轴进行镜像,从而填写其他数字。
6.试错法:有时候,你会遇到一种情况,无法确定下一步该填入什么数字。
这时可以选择一个可能的数字填入,并完成接下来的数独。
如果最后发现该数字导致了矛盾或错误,那就回退并选择下一个可能的数字。
7.高级技巧:除了基本的解题方法,还有一些高级技巧可以帮助你解决难度更高的数独谜题。
a) X-wing法则:在同一行或同一列中,如果一些数字只能出现在两个格子内,且这两个格子分别在另外两行或两列中,那么这个数字就不可能出现在其他该行或该列中的格子中,可以将其填入这两个格子。
b) Swordfish法则:类似于X-wing法则,但是在同一行或同一列中,有三个格子包含了一些数字,且这三个格子分别在三个不同的行或三列中,那么这个数字就不可能出现在其他该行或该列中的格子中,可以将其填入这三个格子。
数独技巧

以下我们将叙述一道标准数独的全部解题过程,在此过程中涉及到的技巧有摒除法、余数法、区块法、数对法、X- Wing这几个常在数独书籍中会涉及到的技巧,文中将描述各个技巧的结构及作用效果,相信在看完解题过程之后,您能相当程度地掌握到数独的基本解题技巧,也能在解题的过程中发现数独给您带来的乐趣。
谜题如下图第一招:摒除法大家之前已阅读过数独的规则:在每个单元中,每个数字只能出现一次,那么也就意味着,如果一行已经出现了一个1,这行的其他格就不再有1,利用这个观点,引发出摒除法。
第1步:数字2对B1进行摒除r1c8为2,则其所在R1不再有2;r2c4为2,则其所在R2不再有2;r9c2为2,则其所在C2不再有2,在B1中还没有2,B1有6个空格可以填2,但其中5个空格被摒除了,只剩下r3c1,所以得到第一解:r3c1=2这个方法因为是对宫实施摒除的,所以叫宫摒除法。
宫摒除法是解题技巧里面最简单的一种,也是解题过程中使用最多的一种。
其实解数独就是这么简单!第2步:r1c3=7(宫摒余解,数字7对B1摒除)第3步:r4c7=7(宫摒余解,数字7对B6摒除)第4步:数字7对C5进行摒除r1c3为7;则其所在R1不再有7;r2c9为7,则其所在R2不再有7;r4c7为7,则其所在R4不再有7;r6c2为7,则其所在R6不再有7;r8c1为7,则其所在R8不再有7;r9c8为7,则其所在R9不再有7,在C5中还没有7,C5有7个空格可以填7,但其中6个空格不能为7了,所以天元格r5c5=7这个方法因为是对列实施摒除的,所以叫列摒除法,与其类似的还有行摒除法。
行列摒除法也是很常用的方法。
见识了摒除法之后,大家是否尝试寻找另一个摒余解呢?不好意思要给大家泼凉水了,因为这个盘势下已经找不到宫摒余解或者行列摒余解了,那怎么办呢,没关系,我们继续介绍其它的技巧。
第二招:余数法前面我们提到,一格受其所在单元中其他20格的牵制,假如这20格里面已经出现了1-8这8个数字,我们就可以断定这格一定是未出现的唯一数字9。
数独解题方法大全

数独解题方法大全数独这个数字解谜游戏,完全不必要用到算术!会用到的只是推理与逻辑。
解题方法分两大类:直观法和候选数法。
直观法就是不需要任何辅助工具,从接到数独谜题的那一刻起就可以立即开始解题。
绝不猜测。
数独直观法解题技巧主要有:唯一解法、基础摒除法、区块摒除法、唯余解法、矩形摒除法、单元摒除法,余数测试法。
候选数法就是解数独题目需先建立候选数列表,根据各种条件,逐步安全的清除每个宫格候选数的不可能取值的候选数,从而达到解题的目的。
使用候选数法一般能解比较复杂的数独题目,但是候选数法的使用没用直观法那么直接,需要先建立一个候选数列表的准备过程。
所以实际使用时可以先利用直观法进行解题,到无法用直观法解题时再使用候选数方法解题。
候选数法解题的过程就是逐渐排除不合适的候选数的过程,所以在进行候选数删除的时候一定要小心,确定安全的删除不合适的候选数,否则,很多时候只有重新做题了。
有了计算机软件的帮助,使得候选数表的维护变得轻松起来。
数独候选数法解题技巧主要有:唯一候选数法、隐性唯一候选数法、区块删减法、数对删减法、隐性数对删减法、三链数删减法、隐性三链数删减法、矩形顶点删减法、三链列删减法、关键数删减法、关连数删减法。
一、直观法:1、唯一解法:? ? ? ? 当某行已填数字的宫格达到8个,那么该行剩余宫格能填的数字就只剩下那个还没出现过的数字了。
成为行唯一解。
? ? ? ? 当某列已填数字的宫格达到8个,那么该列剩余宫格能填的数字就只剩下那个还没出现过的数字了。
成为列唯一解。
? ? ? ? 当某九宫格已填数字的宫格达到8个,那么该九宫格剩余宫格能填的数字就只剩下那个还没出现过的数字了。
成为九宫格唯一解。
? 下面是例题:A行已经添入8个数字,A行只有数字3没有出现过,所以A9=3,这是行唯一解。
第1列已经添入8个数字,第1列只有数字5没有出现过,所以E1=5,这是列唯一解。
在A8所在九宫格区域已经添入8个数字,只有数字9没有出现过,所以A8=9,这是九宫格唯一解。
数独的7种解法

数独解法之阿布丰王创作七种解法:前言数独这个数字解谜游戏,完全不需要用到算术!会用到的只是推理与逻辑.刚开始接触数独时,即使是只须用到"唯一解"技巧的简易级谜题,就已可让我们焦头烂额了,可是随着我们深陷数独的迷人世界之后,这类简易级的数独谜题肯定在短时间内难再使我们获得征服的满足.于是,当我们逐步深入、进阶到更难的游戏后,我们将会需要发展龈?多的解谜技巧.虽然最好的技巧即是我们自己发现的窍门,这样我们很容易??能记住它们,运用自如,不需要他人来耳提面命.可是如果完全不去观摩学习他人发展出来的技巧,而全靠自己摸索,那将是一个非常坚苦的挑战,也不是正确的学习之道!所以让我们一齐来探讨数独的解谜方法吧!数独的解谜技巧,刚开始发展时,以直观式的唯一解及摒除法为主,对初入门的玩家来说,这也是一般人较容易理解、接受的方法,对一般简易级或中级的数独谜题,如果能灵活运用此二法则,通常已游刃有余.1.唯一解法当数独谜题中的某一个宫格因为所处的列、行或九宫格已呈现过的数字已达8 个,那么这个宫格所能填入的数字就剩下这个还没呈现过的数字了.<图 1> (9, 8)呈现唯一解了<图1>是最明显的唯一解呈现时机,请看第8 行,由(1,8) ~(8,8) 都已填入数字了,只剩(9,8)还是空白,此时(9,8)中应填入的数字,固然就是第 8 行中还没呈现过的数字了!请一个个数字核对一下, 哦!是数字8 还没呈现过,所以(9,8) 中该填入的数字就是数字8了.<图 2> (8, 9)呈现唯一解了<图 2>是另一个明显呈现唯一解的情形,请看第 8 列,由 (8,1) ~(8,8) 都已填入数字了,只剩(8,9)还是空白,此时(8, 9)中应填入的数字,固然就是第8 列中还没呈现过的数字了!请一个个数字核对一下, 哦!是数字9 还没呈现过,所以(8, 9) 中该填入的数字就是数字9 了.<图 3> (7, 5)呈现唯一解了<图 3>是另一种明显呈现唯一解的情形,请看下中九宫格,在这个九宫格中除(7, 5)还是空白外,其他宫格都已填有数字了,所以(7, 5)中应填入的数字,固然就是下中九宫格中还没呈现过的数字了!请一个个数字核对一下, 哦!是数字 1 还没呈现过,所以(7, 5) 中该填入的数字就是数字 1 了.<图 4> 一般情形下的唯一解类似<图1>~<图3>这种明显呈现唯一解的情形,在一般情形之下及解题早期是不太可能呈现的!<图4>是一个最典范的简易级数独谜题,如果纯真观察某一个行、列或九宫格,没有一处是已呈现 8 个数字的, 难道如此就无解了吗?非也!非也!在此图中,呈现唯一解的宫格其实有 3 处之多!你能找出来吗?没错,在一般情形之下及解题早期,唯一解的寻找必需综合所处的行、列及九宫格三者,同时过滤筛选出已呈现的数字才行!如果漏失落其一,可能就无法找出唯一解的呈现位置了.现在且不忙着填入数字,先来找找看<图 4>中目前已呈现的唯一解在哪儿吧:第一个唯一解位置在(2, 3):(2, 3) 所处的第 2 列中已呈现的数字是:9、3、5、7.所处的第3 行中已呈现的数字是:4、2、6、8.至于所处的上左九宫格中,已呈现的数字是:2、9、4.所以综合而言, 受其所处位置的行、列及九宫格影响,不得再使用并填入(2, 3) 的数字计有:2、3、4、5、6、7、8、9. 能用来填入的数字确实只剩数字 1 这个唯一的解了.第二个唯一解位置在(8, 7):(8, 7) 所处的第 8 列中已呈现的数字是:1、2、8、6.所处的第7 行中已呈现的数字是:3、9、5、4.至于所处的下右九宫格中,已呈现的数字是:4、6、5.所以综合而言, 受其所处位置的行、列及九宫格影响,不得再使用并填入(8, 7) 的数字计有:1、2、3、4、5、6、8、9. 能用来填入的数字确实只剩数字 7 这个唯一的解了.第三个唯一解位置在(5, 5):(5, 5) 所处的第5 列中已呈现的数字是:1、7.所处的第5 行中已呈现的数字是:2、5.至于所处的中央九宫格中,已呈现的数字是:3、6、8、9.所以综合而言, 受其所处位置的行、列及九宫格影响,不得再使用并填入(5, 5) 的数字计有:1、2、3、5、6、7、8、9. 能用来填入的数字确实只剩数字 4 这个唯一的解了.以上所谓的三个唯一解位置,是以<图4>现况未填入任何数字之前而言,如果开始填入数字,呈现唯一解的位置可能将随之增加.例:当(8, 7) 填入数字 7 之后,(7, 7)将呈现唯一解 1;如果再将数字 1 填入(7, 7), 在(7, 8)又将呈现唯一解 3;......如此不竭循环下去,就可以将整个谜题解出了.2.唯一候选数法概说依照候选数法概说一文中,候选数表的制作规则,我们可以知道:可以填入某一个宫格的数字,一定会列于该宫格的候选数中;不在候选数中的数字,就不能填入该宫格中.所以如果在候选数表中发现某一个宫格的候选数仅有1 个数字,那就是暗示:不用再考虑了!这个宫格就是只能填入这个数字啦!如果填入另外数字,就会违反数独的填制规则的.利用“找出候选数表中,候选数仅有1 个数字的宫格来,并填入该候选数”的方法就叫做唯一候选数法(Singles Candidature, sole Candidate).唯一候选数法示例<图 1>数独谜题的候选数表<图 1> 是我们在候选数法概说一文中完成的候选数表,其中有好几个宫格的候选数都只有1 个,所以可以利用唯一候选数法来进行填制.先还不要填入数字,我们先来找找看,有哪些宫格有唯一候选数?在 (2, 7) 有唯一候选数 7.在 (5, 5) 有唯一候选数 5.在 (8, 3) 有唯一候选数 3.哇!同时呈现了3 个唯一候选数啊!那么,先填入哪一个会不会影响填制结果呢?固然不会了, 只要你高兴,喜欢先填哪一个都没问题的.好,就在这 3 个宫格中填入他们的唯一候选数吧,填制结果如<图2>:<图 2>哇!又有唯一候选数呈现了呢!没错,一般简易级的数独谜题,如果使用直观式的唯一解法及摒除法来解题,即使是数独老手,也要花费相当的工夫才华完成;可是如果采纳唯一候选数法,从候选数表制作完成开始,唯一候选数将一个一个接连不竭的呈现,轻轻松松的就可以完成解题啦!<图3> 是<图1> 的完成解.<图 3>完成解3.隐性三链数删减法概说遇到了高级、困难级的数独谜题,使得唯一候选数法和隐性唯一候选数法黔驴技穷的时候,就是各种删减法上场的时机了.在各种的删减法中,哪一个要先用是随个人之喜好的,并没有限制.本页介绍的例子固然可用其他删减法完成解题,但还是要以隐性三链数删减法优先??!<图 1>请看<图 1>的第 2 列,数字 1、7、8 只呈现在(2, 1)、(2, 7)和(2, 8)这三个宫格的候选数中;这时隐性三链数删减法的条件已成立了!这暗示第2 列的数字1、7 和8 将只能填到这三个宫格中,因为:如果让另外数字填入这三个宫格之中后,这三个相异的数字能填入的可能宫格就只剩下两个,而那是不成能的事!所以若这三个宫格的候选数中还有其他数字,全部是过剩无用的,它们已不成能再用来填入这些宫格中了,所以可以毫不考虑的把它们删减失落.于是(2, 7)和(2, 8)这两个宫格候选数中的 6 都可被平安的删减失落;其中(2, 7)的候选数少了数字6,将使得(8, 7)呈现行隐性唯一候选数6 ,于是可用隐性唯一候选数法来填入下一个解了.整理一下:当某3 个数字仅呈现在某列的某三个宫格候选数中时,就可以把这三个宫格的候选数删减成该 3 个数字.同理,当某 3 个数字仅呈现在某行的某三个宫格候选数中时,就可以把这三个宫格的候选数删减成该 3 个数字.固然,当某 3 个数字仅呈现在某个九宫格的某三个宫格候选数中时,就可以把这三个宫格的候选数删减成该3 个数字.利用“找出某3 个数字仅呈现在某行、某列或某一个九宫格的某三个宫格候选数中的情形,进而将这三个宫格的候选数删减成该 3 个数字”的方法就叫做隐性三链数删减法(Hidden Triples).本法其实为隐性数对删除法的推广,而且还可以继续加以推广:隐性四链数删减法就是:“找出某4 个数字仅呈现在某行、某列或某一个九宫格的某四个宫格候选数中的情形,进而将这四个宫格的候选数删减成该4 个数字”的方法.隐性五链数删减法就是:“找出某5 个数字仅呈现在某行、某列或某一个九宫格的某五个宫格候选数中的情形,进而将这五个宫格的候选数删减成该 5 个数字”的方法.......如果愿意的话,你确实是可以这样推广的,只是,实用上是否有其应用的价值或空间呢?隐性三链数删减法示例隐性三链数删减法一共有 3 种状况:第一种发生在行、第二种是发生在列、第三种则发生在九宫格.<图 1> 就是发生在列的例子了,其他的情况举例如下:<图 2><图2> 是隐性三链数删减发生在行的例子:图中第4 行的数字2、4、9 只呈现在(4, 4)、(5, 4)及(6, 4) 这三个宫格的候选数中,所以可以将三个宫格候选数中2、4、9 以外的数字平安的删减失落,(4, 4)的候选数删减成2、4;(5, 4)的候选数删减成2、4、9;(6, 4)的候选数删减成 9;呈现了唯一候选数啦!<图 3><图3> 是隐性三链数删减发生在九宫格的例子:图中中央九宫格的数字2、5、9 只呈现在 (5, 4)、(5, 6)及(6, 4) 这三个宫格的候选数中,所以可以将三个宫格候选数中 2、5、9 以外的数字平安的删减失落, (5, 4)的候选数删减成2、5、9;(5, 6)的候选数删减成2、5;(6, 4)的候选数删减成 9;呈现了唯一候选数啦!<图 4>像 <图 1>~<图 3> 这样只经一次删减就呈现下一个解的情况固然不错了,但有时可没法这样顺心, <图 4> 就是一个例子.下一个解将呈现在(5, 6) 这个宫格,你能找出该填入什么数字吗?以目前所学到的方法,要解出下一个解,需要二个步伐:先看中左九宫格吧!由于只剩(5, 1)~(5, 3)这个区块尚未填入数字,所以可用区块删减法将第5 列其他区块候选数中的1、3、4 全部删减失落,但实际上仅能删到(5, 4)及(5, 6)候选数的数字 4 而已.接下来请观察第 6 行!由于数字 1、4、9 只呈现在 (2, 6)、(8, 6)及(9, 6) 这三个宫格的候选数中[因为(5, 6)的候选数在上一步伐中已被删减为5、8 了], 所以可用隐性三链数删减将三个宫格候选数中 1、4、9 以外的数字平安的删减失落, (2, 6)的候选数删减成1、4、9;(9, 6)的候选数没变;(8, 6)的候选数则由2、4、5、8、9 删减成4、9;由于5 被删减失落了,使得(5, 6) 呈现了行隐性唯一候选数5啦!4.隐性数对删减法概说遇到了高级、困难级的数独谜题,使得唯一候选数法和隐性唯一候选数法黔驴技穷的时候,就是各种删减法上场的时机了.在各种的删减法中,哪一个要先用是随个人之喜好的,并没有限制.本页介绍的固然就要以隐性数对删减法优先??!<图 1>请看<图 1>的上右九宫格,数字 8、9 都只呈现在(2, 8)和(2, 9)这两个宫格的候选数中;这时隐性数对删减法的条件已成立了!这暗示上右九宫格的数字 8 和 9 将只能填到这两个宫格中,而且:如果数字 8 将填入(2, 8), 那么(2, 9)就一定要填入数字 9;反之,如果数字 9 将填入(2, 8),那么(2, 9)就一定要填入数字 8;不论哪一个状况呈现,(2, 8)和(2, 9)这两个宫格的候选数中若还有其他数字,全部是过剩无用的,因为这两个宫格若填入数字 8、9 以外的数字,那么上右九宫格的数字 8 或 9 就将无处可填了.候选数的意义是可能填入该宫格的数字,而这两个数字以外的数字已不成能再用来填入本宫格中了,所以可以毫不考虑的把它们删减失落.当(2, 8)和(2, 9)这两个宫格的候选数都平安的删减成数字8、9 之后,(2, 5)呈现了列隐性唯一候选数 2 ,于是可用隐性唯一候选数法来填入下一个解了.整理一下:当某个数对仅呈现在某个九宫格的某两个宫格候选数中时,就可以把这两个宫格的候选数删减成该数对.同理,当某个数对仅呈现在某列的某两个宫格候选数中时,就可以把这两个宫格的候选数删减成该数对.固然,当某个数对仅呈现在某行的某两个宫格候选数中时,就可以把这两个宫格的候选数删减成该数对.利用“找出某个数对仅呈现在某行、某列或某一个九宫格的某两个宫格候选数中的情形,进而将这两个宫格的候选数删减成该数对”的方法就叫做隐性数对删减法(Hidden Pairs).当隐性数对删减法完成后,通常还可引发数对删减法;以<图1>为例,当(2, 8)和(2, 9)这两个宫格的候选数都平安的删减成数字8、9 之后,还可利用数对删减法把(2, 1)、(2, 2)、(2, 3) 这三个c格候选数中的数字 8 删减失落.隐性数对删减法示例隐性数对删减法一共有 3 种状况:第一种发生在行、第二种是发生在列、第三种则发生在九宫格.<图 1> 就是发生在九宫格的例子了,其他的情况举例如下:<图 2><图 2> 是隐性数对删减发生在行的例子:图中第 2 行的数对 4、6 只呈现在 (3, 2)及(9, 2) 这两个宫格的候选数中,所以可以将(3, 2)及(9, 2)的候选数平安的删减成数对 4、6;而经此一删,(3, 3) 宫格呈现了列隐性唯一候选数 1 啦!<图 3><图 3> 是隐性数对删减发生在列的例子:图中第 7 列的数对 4、7 只呈现在 (7, 1)及(7,8) 这两个宫格的候选数中,所以可以将(7, 1)及(7, 8)的候选数平安的删减成数对 4、7;而经此一删,(8, 1) 宫格呈现了行隐性唯一候选数 2 啦!三链列删减法概说遇到了高级、困难级的数独谜题,使得唯一候选数法和隐性唯一候选数法黔驴技穷的时候,就是各种删减法上场的时机了.在各种的删减法中,哪一个要先用是随个人之喜好的,并没有限制.本页介绍的例子固然可用其他删减法完成解题,且本删减法成立的条件和其他方法相比稍嫌繁杂,但为了介绍,在进行解题时还是要以三链列删减法优先??!<图 1>请看<图 1>第 1、4、6 列的数字 5 ,都只呈现在第 1、5、8 行的宫格候选数中;这时三链列删减法的条件已成立了!这暗示第1 行、第5 行及第8 行的数字5 将只能被填到第1 、4、6 列了,因为:第 1 列的数字 5 只呈现在(1, 1)及(1, 8),所以数字 5 只能填到这两个宫格;先假设第 1 列的数字 5 将被填到(1, 1),第 1 行就不能再填数字 5 了,所以第 4 列的数字5 只好填到(4, 5),第 6 列的数字 5 只好填到(6, 8);另外,假设第 1 列的数字 5 将被填到(1, 8),第 8 行就不能再填数字 5 了,所以第 6 列的数字 5 只好填到(6, 1)或(6, 5);如果第 6 列的数字 5 填到(6, 1),第 4 列的数字 5 就要填到(4, 5);如果第 6 列的数字 5 填到(6, 5),第 4 列的数字 5 就要填到(4, 1);不论哪一种情况发生,第 1、5、8 行的数字 5 一定要填在第 1、4、6 列的交点,另外宫格已不能再使用数字 5 来填入了,所以若其他宫格的候选数中还有数字 5,全部是过剩无用的, 可以毫不考虑的把它们删减失落.于是(5, 1)、(5, 5)、(9, 5)和(1, 8)、(2, 8)这五个宫格候选数中的 5 都可被平安的删减失落;其中(9, 5)的候选数少了数字 5,将使得(9, 4)呈现列隐性唯一候选数 5 ,于是可用隐性唯一候选数法来填入下一个解了.整理一下:当某个数字在某三列仅呈现在相同的三行时,就可以把这三行其他宫格候选数中的该数字删减失落.同理,当某个数字在某三行仅呈现在相同的三列时,就可以把这三列其他宫格候选数中的该数字删减失落.利用“找出某个数字在某三列仅呈现在相同三行的情形,进而将该数字自这三行其他宫格候选数中删减失落”;或“找出某个数字在某三行仅呈现在相同三列的情形,进而将该数字自这三列其他宫格候选数中删减失落”的方法就叫做三链列删减法(Swordfish).本删减法其实是矩形极点删减法的推广,如果你愿意的话,还可以继续推广:四链列删减法:利用“找出某个数字在某四列仅呈现在相同四行的情形,进而将该数字自这四行其他宫格候选数中删减失落”;或“找出某个数字在某四行仅呈现在相同四列的情形,进而将该数字自这四列其他宫格候选数中删减失落”的方法五链列删减法:利用“找出某个数字在某五列仅呈现在相同五行的情形,进而将该数字自这五行其他宫格候选数中删减失落”;或“找出某个数字在某五行仅呈现在相同五列的情形,进而将该数字自这五列其他宫格候选数中删减失落”的方法六链列删减法:...... 不外如果真的这样做,实际应用时,能够用上的机率年夜概未几就是了.遇到了高级、困难级的数独谜题,使得唯一候选数法和隐性唯一候选数法黔驴技穷的时候,虽然你可以优先使用三链列删减法来寻找下一个解;但年夜部份的人在使用删减法的优先顺序上,通常城市将三链列删减法排在稍后一点,为什么要如此安插,在实际使用一段时间之后, 相信你自能体会了,但这个方法又是不成或缺的,如果不会运用本删减法,有很多高级的数独谜题就将无解了.三链列删减法示例三链列删减法只有2 种状况:第一种的删减发生在行、第二种的删减发生在列.<图1> 就是删减发生在行的例子了,第二种的情况举例如下:<图 2><图 2> 是三链列删减发生在列的例子:图中第 3、5、8 行的数字 2 只呈现在第 3、4、5 列, 所以可以将数字2 自(4, 6)、(5, 6)的候选数中平安的删减失落,其中(5, 6) 的候选数由2、5 删减成 5 时,呈现唯一候选数啦!5.区块删减法概说遇到了高级、困难级的数独谜题时,唯一候选数法和隐性唯一候选数法仍有其黔驴技穷的时候;这时就是区块删减法上场的时机了,往后将要介绍的数对删减法(Naked Pairs)、隐性数对删减法(Hidden Pairs)、三链数删减法(Naked Triples)、隐性三链数删减法(Hidden Triples) 、矩形极点删减法(X-Wing)、三链列删减法(Swordfish)都具有类似的特性:使用这些技巧的目的仅在删减候选数的数目,删减之后,还是得使用唯一候选数法和隐性唯一候选数法来找出下一个解并填入数字的.当使用唯一候选数法或隐性唯一候选数法找不出下一个解时,究竟该先使用哪一个删减法呢?随您高兴的用吧!如果你比力擅长使用数对删减法,那就先用数对删减法吧!如果你认为区块删减法比力好用,那就先用数对删减法吧! ......;介绍时总有先后的次第,但其实不暗示先介绍的就较好用或必需先用哦!只要能到达:“平安删减失落候选数, 并找出下一个解”的目的,使用哪一种删减法都是可以的.<图 1>请看<图1>,这时若使用唯一候选数法或隐性唯一候选数法是找不出下一个解来的!就先来试试区块删减法吧. 请观察第9 行:数字1 在本行各宫格的候选数中,是不是仅呈现在(1,9)~(3,9)的这一个区块中?太好了,区块删减的条件已有了;因为这暗示第 9 行的数字 1 只能填在(1,9)~(3,9)的这一个区块中,而不论填在本区块的哪一个宫格中,上右九宫格的其他宫格将因本九宫格已呈现数字1,而不得再填入1,否则就违反数独填制的规则啦!所以(1, 7)~(3, 7)及(1, 8)~(3, 8)这两个区块的宫格,如果其候选数中包括有数字1,就可以毫不考虑的把它删除失落,因为候选数的意义是可能填入该宫格的数字,而这个数字已不成能再用来填入该宫格中了.啊!太好啦!(1, 7)的候选数中包括有数字1,所以可以把(1, 7) 的候选数由1、6 删减成 6,于是可用唯一候选数法来填入下一个解了.当区块删减法的条件成立时,可别高兴得太早,因为很有可能找不到可删减的数字,例如:在<图 1>的第 1 行中, 数字 2 在本行的各宫格候选数中,仅呈现在(4, 1)~(6, 1)这一个区块中,而不论数字 2 将来会被填到本区块的哪一个宫格中,将使得数字 2 不得再填入(4, 2)~(6, 2)及(4, 3)~(6, 3)这两个区块中;但请找找看!这两个区块各宫格的候选数中全部没有数字 2,所以是白忙了一场,条件是成立了,但候选数并未因此而获得删减.整理一下,并为了简化叙述起见,下面所述的“区块候选数”暗示:该区块的各个宫格候选数的总和.例如(1, 3)~(3, 3) 的区块候选数就是(1, 3)的候选数 4、6、7 及(2, 3)的候选数 3、4、6 及(3, 3)的候选数 3、7 的总和: 3、4、6、7 啦!:当某一个数字只呈现在某行的某一个区块候选数中时,就可以把该数字自包括该区块的九宫格之其他区块候选数中删减失落.同理,当某一个数字只呈现在某列的某一个区块候选数中时,就可以把该数字自包括该区块的九宫格之其他区块候选数中删减失落.同理,当某一个数字只呈现在某个九宫格的某一个区块候选数中时,就可以把该数字自包括该区块的行或列之其他区块候选数中删减失落.利用“找出某一行、某一列或某一个九宫格各个区块候选数中只呈现一次的数字来,并将该数字自包括该区块的另一个行、列或九宫格的其他区块候选数中删减失落”的方法就叫做区块删减法 (Locked Candidates, Single Sector Candidates).区块删减法示例区块删减法一共有 4 种状况:第一种是发生在行而去删减九宫格、第二种是发生在列而去删减九宫格、第三种是发生在九宫格而去删减行、第四种是发生在九宫格而去删减列.<图 1> 就是发生在行而去删减九宫格的例子了,其他的情况举例如下:<图 2><图 2> 是发生在列而去删减九宫格的例子:因为第 3 列的数字 6 只呈现在 (3, 1)~(3, 3) 这一个区块, 所以可以将上左九宫格的另两个区块 (1, 1)~(1, 3)、(2, 1)~(2, 3) 候选数中的数字 6 平安的删减失落;于是(1, 1)的候选数 2、6 将被删减成 2,呈现了唯一候选数啦!<图 3><图 3> 是发生在九宫格而去删减列的例子:因为上右九宫格的数字 5 只呈现在 (3, 7)~(3, 9) 这一个区块, 所以可以将第 3 列的另两个区块 (3, 1)~(3, 3)、(3, 4)~(3, 6) 候选数中的数字 5 平安的删减失落;于是(3, 3)的候选数 5、9 将被删减成 9,呈现了唯一候选数啦!<图 4><图 4> 是发生在九宫格而去删减行的例子:因为中央九宫格的数字 1 只呈现在 (4, 5)~(6, 5) 这一个区块, 所以可以将第 5 行的另两个区块 (1, 5)~(3, 5)、(7, 5)~(9, 5) 候选数中的数字 1 平安的删减失落;于是(8, 5)的候选数 1、3、7、8 将被删减成 3、7、8;同理,中央九宫格的数字 7、8 都只呈现在 (4, 5)~(6, 6) 这一个区块,所以可以将第 5 行的另两个区块 (1, 5)~(3, 5)、(7, 5)~(9, 5) 候选数中的数字 7、8 都平安的删减失落;于是(8, 5)的候选数 3、7、8 将再度被删减成 3;呈现了唯一候选数啦!像<图1>~<图3>这样,只做一次区块删减就找到下一个解的情况固然是不错,但有时并没有那么顺心, 像<图 4>就需要删减三次才获得下一个解,不外那还算好的了,因为三次的删减都恰好发生在同一个区块中, 请看下面发生在分歧区块的情形吧!。
数独题与数独题的系列解法举例
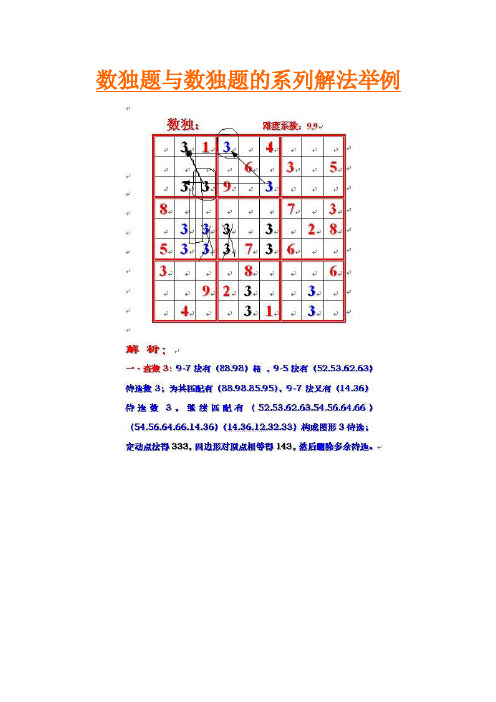
数独题与数独题的系列解法举例数独题是什么?数独是一种源自18世纪末的瑞士,后在美国发展、并在日本得以发扬光大的数学智力拼图游戏。
“数独”玩法简单,游戏主体是数个由9个九宫格排列成的大正方形,每一行每一列都由9个小方格组成,游戏编写者会先在一些小方格里填上从1到9的不同数字大正方形,玩家要填满其余空格,规则是大正方形每一行每一列及每个九宫格里均必须包括1到9的每一个数字。
数独的玩法逻辑简单,数字排列方式千变万化。
不少教育者认为数独是锻炼脑筋的好方法。
“数独”(日语是すうどく,英文为Sudoku) “数独”(sudoku)一词来自日语,意思是“单独的数字”或“只出现一次的数字”。
概括来说,它就是一种填数字游戏。
但这一概念最初并非来自日本,而是源自拉丁方块,它是十八世纪的瑞士数学家欧拉发明的。
出生于1707年的欧拉被誉为有史以来最伟大的数学家之一。
欧拉从小就是一个数学天才,大学时他在神学院里攻读古希伯来文,但却连续13次获得巴黎科学院的科学竞赛的大奖。
1783年,欧拉发明了一个“拉丁方块”,他将其称为“一种新式魔方”,这就是数独游戏的雏形。
不过,当时欧拉的发明并没有受到人们的重视。
直到20世纪70年代,美国杂志才以“数字拼图”的名称将它重新推出。
1984年日本益智杂志Nikoli的员工金元信彦偶然看到了美国杂志上的这一游戏,认为可以用来吸引日本读者,于是将其加以改良,并增加了难度,还为它取了新名字称做“数独”,结果推出后一炮而红,让出版商狂赚了一把。
至今为止,该出版社已经推出了21本关于数独的书籍,有一些上市后很快就出现了脱销。
此外,出版商还授权软件商开发了上百个数独游戏软件。
供人们在网上购买。
目前,日本共有5家数独月刊,总发行量为66万份。
由于数独在日本已经被注册商标,其他竞争者只好使用其最初在美国的名字“数字拼图”。
数独游戏和传统的填字游戏类似,但因为只使用1到9的数字,能够跨越文字与文化疆域,所以被誉为是全球化时代的魔术方块。
1—6数独技巧

1—6数独技巧玩法:根据9×9盘面上的已知数字,推理出所有剩余空格的数字,这些数字仅限1、2、3、4、5、6、7、8、9这九个数字。
规则:每一行、每一列、每一宫(3*3空格)内的数字均包含1~9这九个数字。
由于每一行、每一列或每个宫仅有9个空格,所以,每一行、每一列或每个宫不会出现重复数字。
不允许重复--排除法,是数独最朴素的解法技巧。
数独的九宫、盘面(谜题或最初数字)、终盘(最终数字分布或答案)示例如下:数格编号(C-column;R-row)数独-九宫数独-盘面数独-终盘常用技巧a、为方便描述,以下将每一行、每一列或每个宫,统称为一个基本单元。
b、图中,黄色为待填数字格,绿色框为目标区。
上下图无关联,每张图均为展示某技巧。
c、所示仅为解释所述技巧,不代表当前最佳解法。
1、基本单元内排除宫内唯一列内唯一行内唯一思路:每个基本单元中已经出现了8个数字,又每个单元中必须出现1~9这九个数字,因此剩下的空格就是这9个数字中未出现的那一个。
这是人眼最容易观察到的情况,一眼就能发现。
2、基本单元外-简单排除基本单元外排除-宫基本单元外排除-列基本单元外排除-行基本单元外排除-综合思路:对于每一个要填充的空间,观察要填充的空间所在的行或列或者宫中的其他空间是否已经被排除了一定数量。
实际解题时,往往是通过依次看每个已知数的位置,看能否确定某个空间,而不是先定位某个空间,再看关联的数。
这很难做到,也不符合人们(也可能只是我,哈哈)的思维习惯。
3、余数唯余法思路:根据待填空间所在的行、列、宫中出现过的数字,观察是否只有一个候选数字。
前面提到的基本单位中的排除也是一种特殊的余数法,只使用某一行、列或宫中出现过的数字。
实际解题时,往往无法确定唯一值,但确定所有候选数总是可能的。
标记这些候选数字就成了后面提到的占位符方法的基础。
4、占位占位法-占2位占位法-占3位思路:如果某个基本单元中,已经有n个数字占据了n个空格,那么,其他空格中就不会出现这n个数字,这样,在填该基本单元内的其他待填空格时,就可以把这n个数字排除掉。
数独地解法与技巧

数独的直观式解题技巧直观法概说前言数独这个数字解谜游戏,完全不必要用到算术!会用到的只是推理与逻辑。
刚开始接触数独时,即使是只须用到"基础摒除法"及"唯一解法"技巧的简易级谜题,就已可让我们焦头烂额了,但是随着我们深陷数独的迷人世界之后,这类简易级的数独谜题必定在短时间内难再使我们获得征服的满足。
于是,当我们逐步深入、进阶到更难的游戏后,我们将会需要发展出更多的解谜技巧。
虽然最好的技巧便是我们自己发现的窍门,这样我们很容易就能记住它们,运用自如,不需要别人来耳提面命。
但是如果完全不去观摩学习他人发展出来的技巧,而全靠自己摸索,那将是一个非常坚苦的挑战,也不是正确的学习之道!所以让我们一齐来探讨数独的解谜方法吧!数独的解谜技巧,刚开始发展时,以直观法为主,对于初入门的玩家来说,这也是一般人较容易理解、接受的方法,对于一般报章杂志及大众化网站上的数独谜题而言,如果能灵活直观法的各项法则,通常已游刃有余。
直观法详说直观法的特性:1.不需任何辅助工具就可应用。
所以要玩报章杂志上的数独谜题时,只要有一枝笔就可以开始了,有人会说:可能需要橡皮擦吧?答案是:不用!只要你把握数独游戏的填制原则:绝不猜测。
灵活运用本站所介绍的直观填制法,确实可以不必使用橡皮擦。
2.从接到数独谜题的那一刻起就可以立即开始解题。
3.初学者或没有计算机辅助时的首要解题方法。
4.相对而言,能解出的谜题较简单。
直观法的主要的技巧:1.基础摒除法。
2.唯一解法。
3.区块摒除法。
4.唯余解法。
5.单元摒除法。
6.矩形摒除法。
7.余数测试法。
基础摒除法前言对第一次接触数独游戏,接受了 1 ~ 9 的数字在每一行、每一列、每一个九宫格都只能出现一次的规则后,开始要解题的玩家来说,基础摒除法绝对是他第一个想到及使用的方法,十分的自然、也十分的简易。
如果能够细心、系统化的运用基础摒除法,一般报章杂志或较大众化的数独网站上的数独谜题几乎全部可解出来。
