数学小报

合集下载

数学小报

一..小明计划春节期间存钱。一部分买书一部分买玩具送给福利院的孩子们。某天小明选中了一种小熊玩具，单价10元。按原计划买了若干个，他的钱还剩30％，于是他又多买了6个，这样仅剩他压岁钱的10％
(1)问小明原计划买几个玩具？压岁钱共有多少元？
(2)为保证书费不少于压岁钱的10％，问小明原计划买几个玩具？
答案：
1.30%-10%=20%
20%÷6=1/30
10÷1/30=300元
300×（1-30%）÷10=21个
答：计划买21个，压岁钱共有300元
2.300×（1-10%）=270元
270÷10=27个
答为保证书费不少于压岁钱的10％，小明最多可买27个玩具
二．甲乙两车同时从AB两地相对开出。甲行驶了全程的5/11,如果甲每小时行驶4.5千米，乙行了5小时。求AB两地相距多少千米?
答案：AB距离=（4.5×5）/（5/11）=49.5千米
三．甲乙两人分别从相距36千米的ab两地同时出发,相向而行,甲从a地出发至1千米时,发现有物品以往在a地，便立即返回，去了物品又立即从a地向b地行进，这样甲、乙两人恰好在a，b两地的终点处相遇，又知甲每小时比乙多走0.5千米，求甲、乙两人的速度?
答案：甲在相遇时实际走了36×1/2+1×2=20千米
乙走了36×1/2=18千米
那么甲比乙多走20-18=2千米
那么相遇时用的时间=2/0.5=4小时
所以甲的速度=20/4=5千米/小时
乙的速度=5-0.5=4.5千米/小时
五（五）班
夏彬伦

小学趣味数学手抄报小报模板共3套(简单又漂亮)

乘法口诀现在小学生学的“小九九”口诀，是从“一一得一”开始，到“九九八十一”为止，而在古代，却是倒过来，从“九九八十一”起，到“二二得四”止。

数学家数学家是指一些对数学有深入了解的人士，将其所学知识运用于其工作上（特别是解决数学问题）。

数学家专注于数、数据、集合、结构、空间、变化。

专注于解决纯数学领域以外的问题的数学家称为应用数学家。

数学小知识1、早在2000多年前，我们的祖先就用磁石制作了指示方向的仪器，这种仪器就是司南。

2、最早使用小圆点作为小数点的是德国的数学家，叫克拉维斯。

3、“七巧板”是我国古代的一种拼板玩具，由七块可以拼成一个大正方形的薄板组成，拼出来的图案变化万千,后来传到国外叫做唐图。

数字绕口令小兔子，开铺子，一张小桌子，两把小椅子，三根小绳子，四只小匣子，五管小笛子，六条小棍子，七个小盘子，八颗小豆子，九本小册子，十双小筷子。

你来猜一猜老师出了一道题：8÷2=？随后问大家："8分为两半等于几？"皮皮回答："等于0！" 老师说："怎么会呢？" 皮皮解释："上下分开！" 丁丁说道："不对，等于耳朵！"老师："哦？"丁丁回答："左右分开呗！" 小朋友你来猜一猜是多少呢？数学名言1、二分之一个证明等于0。

（高斯）2、在数学中最令我欣喜的，是那些能够被证明的东西。

（罗素）3、天才是百分之一的灵感，百分之九十九的汗水。

（爱迪生）趣味数学数学家数学家是指一些对数学有深入了解的人士，将其所学知识运用于其工作上（特别是解决数学问题）。

数学家专注于数、数据、集合、结构、空间、变化。

专注于解决纯数学领域以外的问题的数学家称为应用数学家。

数学小报

在漫长的历史长河中，随着社会的发展和科技的进步，人类进行运算时所运用的工具，也经历了由简单到复杂，由低级向高级的发展变化。

现在我们溯本求源，看一看计算工具是怎样演化的：1.石块、贝壳计数 :原始社会，把石块放进皮袋，或用贝壳串成珠子，用“一一对应”的方法，计算需要计数的物品。

2.结绳计数 :在长绳上打结记事或计数，这比用石块贝壳方便了许多。

3.手指计数 : 人类的十个手指是个天生的“计数器”。

原始人不穿鞋袜，再加上十个足趾，计数的范围就更大了。

4.小棒计数 : 利用木、竹、骨制成小棒记数，在我国称为“算筹”。

它可以随意移动、摆放，较之上述各种计算工具就更加优越了，因而，沿用的时间较长。

5.珠算 : 珠算是以圆珠代替“算筹”，并将其连成整体，简化了操作过程，运用时更加得心应手。

它起源于中国。

到了现代，一种新型的电子算盘已经问世，它把算盘与电子计算器的长处集为一体，是一种中外结合的新型计算工具。

6.计算尺 : 公元1520年，英国人甘特发明了计算尺，运用到一些特殊的运算中，快速、省时。

7.手摇计算机 : 它用一个个齿轮表示数字，以齿轮间的咬合装置实现进位，低位齿轮转十圈，高位齿轮转一圈。

后来，经过逐步改进，使它既能做加、减法，又能做乘、除法了，运算的操作更加简捷、快速。

8.电子计算机 : 随着近代高科技的发展，电子计算机在二十世纪应运而生。

它的出现是“人类文明最光辉的成就之一”，标志着“第二次工业革命的开始”。

其运算效率和精确度之高，是史无前例的。

笑话：计算器数学考试的考场上，同学们用计算器演算各种试题。

这时突然从考场的一个角落里传来了一声惊呼：“天哪，我怎么把家里的遥控器带来了”三（3）班叶璐霏。

数学小报

数学是什么？数学是研究现实世界中数量关系和空间形式的科学。

简单地说，就是研究数和形的科学。

提到数学，我们有一种感觉，数学是自然中最基础的学科，它是所有科学之父，没有数学，就不可能有其他科学的产生。

就人类发展史而言，数学在其中起的作用是巨大的。

让我们一起来感受数学的奇妙之处吧：生活中的奇妙数字在生活中，也能在很多地方感受到数学的美妙之处。

比如报幕员在舞台宽度的0.618处能达到最佳报幕效果。

高清晰度电视的屏幕要设计成16：9。

人的形体是个完美的黄金分割比，肚脐刚好就是整个人体的黄金分割点，喉头刚好是头顶到肚脐的黄金分割点，膝关节是肚脐到脚的黄金分割点，肘关节是手指到肩部的黄金分割点。

人的正常体温是37.5度，37.5 × 0.618=23.175，在大热天，空调开到这个温度是最佳的。

数学是一个很奇妙的学科，只要我们用心去学，一定能感受到他的美妙。

“奇妙的”数学123黑洞在天文学上有着著名的“黑洞”现象，无独有偶，在数学中也有这种神密的黑洞现象，对于数学黑洞，无论怎样设值，在规定的处理法则下，最终都将得到固定的一个值，就像宇宙中的黑洞可以将任何物质牢牢吸住，不使它们逃脱一样。

我们选取任意一个数字串，例如9288759，数出这个数中的偶数个数、奇数个数，及这个数中所包含的所有位数的总数，你可以分别得到3(3个偶数)、4(4个奇数)和7(总共有7位数)。

用这3个数字组成一个数字串：347。

对347重复上述过程，你得到1、2、3，即又得到一个数字串：123。

对123再重复这个过程，你还是得到123 。

对这个程序以及数的“宇宙”来说，123就是一个数字黑洞。

数字黑洞有两处重要的特征：第一，一旦你得到123，你就再也出不去了；第二，每一个受到黑洞之力作用的因素最终都被拉进了黑洞。

对任何一个数字串反复运用这个程序，你最后都将得到123。

第二个特征将你吸引进去，第一个特征则使你陷入洞中无法逃脱．不信，你试一试！。

数学小报

作者：时新鹏班级：预备1班数学是源自于人类早期的生产活动，早期古希腊、古巴比伦、古埃及、古印度及中国古代都对数学有所研究。

数学是研究数量、结构、变化以及空间模型等概念的一门科学。

透过抽象化和逻辑推理的运用，由计数、计算、量度和对物体形状及运动的观察中产生。

数学的基本要素是：逻辑和直观、分析和推理、共性和个性。

数学可以分成两大类，一类叫纯粹数学，一类叫应用数学。

纯粹数学也叫基础数学，专门研究数学本身的内部规律。

中小学课本里介绍的代数、几何、微积分、概率论知识，都属于纯粹数学。

应用数学则是一个庞大的系统，有人说，它是我们的全部知识中，凡是能用数学语言来表示的那一部分。

应用数学着眼于说明自然现象，解决实际问题，是纯粹数学与科学技术之间的桥梁。

丢番图（Diophantus）是古希腊亚历山大学后期的重要学者和数学家（约公元246—330年，据推断和计算而知）丢番图是代数学的创始人之一，对算术理论有深入研究，他完全脱离了几何形式，在希腊数学中独树一帜。

丢番图的出生日期不可考，但他的墓碑上有很经典的一道数学题目：“坟中安葬着丢番图，多么令人惊讶，它忠实地记录了所经历的道路。

上帝给予的童年占六分之一，又过了十二分之一，两颊长胡，过七分之一，点燃起结婚的蜡烛。

五年之后天赐贵子，可怜迟到的宁馨儿，享年仅及其父之半，便进入冰冷的墓。

悲伤只有用数论的研究去弥补，又过了四年，他也走完了人生的旅途。

终于告别数学，离开了人世。

”答案是84岁。

公元前500年，古希腊毕达哥拉斯(Pythagoras)发现了一个惊人的事实，一个正方形的对角线与其一边的长度是不可子希勃索斯公度的(若正方形边长是1，则对角线的长不是一个有理数)这一不可公度性与毕氏学派“万物皆为数”(指有理数)的哲理大相径庭。

这一发现使该学派领导人惶恐、恼怒，认为这将动摇他们在学术界的统治地位。

希勃索斯因此被囚禁，受到百般折磨，最后竟遭到沉舟身亡的惩处。

然而，真理毕竟是淹没不了的，毕氏学派抹杀真理才是“无理”。

数学小报,可直接打印

二年级二班姓名指导老师：有位渔夫，头戴一顶大草帽，坐在划艇上在一条河中钓鱼。

河水的流动速度是每小时3英里，他的划艇以同样的速度顺流而下。

“我得向上游划行几英里，”他自言自语道，“这里的鱼儿不愿上钩！”正当他开始向上游划行的时候，一阵风把他的草帽吹落到船旁的水中。

但是，我们这位渔夫并没有注意到他的草帽丢了，仍然向上游划行。

直到他划行到船与草帽相距5英里的时候，他才发觉这一点。

于是他立即掉转船头，向下游划去，终于追上了他那顶在水中漂流的草帽。

在静水中，渔夫划行的速度总是每小时5英里。

在他向上游或下游划行时，一直保持这个速度不变。

当然，这并不是他相对于河岸的速度。

例如，当他以每小时5英里的速度向上游划行时，河水将以每小时3英里的速度把他向下游拖去，因此，他相对于河岸的速度仅是每小时2英里；当他向下游划行时，他的划行速度与河水的流动速度将共同作用，使得他相对于河岸的速度为每小时8英里。

如果渔夫是在下午2时丢失草帽的，那么他找回草帽是在什么时候？1930 年的一天，清华大学数学系主任熊庆来，坐在办公室里看一本《科学》杂志。

看着看着，不禁拍案叫绝：“这个华罗庚是哪国留学生？” “他是在哪个大学教书的？”最后还是一位江苏籍的教员慢吞吞地说：“我弟弟有个同乡叫华罗庚，他只念过初中。

熊庆来惊奇不已，将华罗庚请到清华大学来。

从此，华罗庚就成为清华大学数学系助理员。

第二年，他的论文开始在国外著名的数学杂志陆续发表。

几年之后，华罗庚被保送到英国剑桥大学留学。

他提出的理论被数学界命名为“华氏定理”。

答案：1、三2、相等3、倒数4、王5、七上八下分数儿子战战兢兢地回到家：“爸，我今天考试只得了60分。

”爸爸很生气：“下次再考低了，就别叫我爸！”。

第二天孩子回来了：“对不起，哥！老师在课堂上提问：“西班牙在十五世纪发生了多少次战争”。

“六次。

”一个学生很快就回答出来了。

“哪六次？”老师又问。

“第一次、第二次、第三次、第四次、第五次和第六次。

数学小报

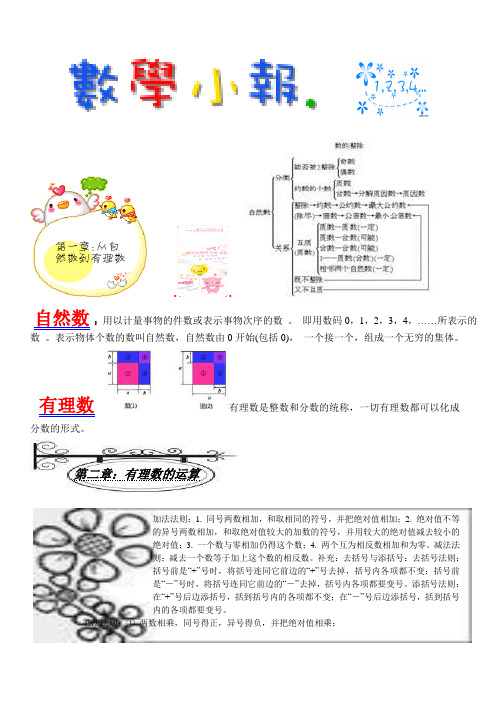
..自然数：用以计量事物的件数或表示事物次序的数。

即用数码0，1，2，3，4，……所表示的数。

表示物体个数的数叫自然数，自然数由0开始(包括0)，一个接一个，组成一个无穷的集体。

有理数有理数是整数和分数的统称，一切有理数都可以化成分数的形式。

第二章：有理数的运算加法法则：1. 同号两数相加，和取相同的符号，并把绝对值相加；2. 绝对值不等的异号两数相加，和取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值；3. 一个数与零相加仍得这个数；4. 两个互为相反数相加和为零。

减法法则：减去一个数等于加上这个数的相反数。

补充：去括号与添括号：去括号法则：括号前是“+”号时，将括号连同它前边的“+”号去掉，括号内各项都不变；括号前是“－”号时，将括号连同它前边的“－”去掉，括号内各项都要变号。

添括号法则：在“+”号后边添括号，括到括号内的各项都不变；在“－”号后边添括号，括到括号内的各项都要变号。

乘法法则：①两数相乘，同号得正，异号得负，并把绝对值相乘；②任何数与零相乘都得零。

③几个不等于零的数相乘，积的符号由负因数的个数决定，当负因数有奇数个数，积为负；当负因数的个数为偶数个时，积为正；④几个有理数相乘，若其中有一个为零，积就为零。

除法法则：法则一：两个有理数相除，同号得正，异号得负，并把绝对值相除；法则二：除以一个数等于乘以这个数的倒数。

⑸有理数的乘方：求n个相同因数的积的运算，叫做乘方，乘方的给果叫做幂。

正数的任何次幂都是正数；负数的奇次幂是负数，负数的偶次幂是正数。

⑹有理数的运算顺序：有理数的混合运算法则即先算乘方或开方，再算乘法或除法，后算加法或减法。

有括号时、先算小括号里面的运算，再算中括号，然后算大括号。

实数：包括有理数和无理数。

其中无理数就是无限不循环小数，有理数就包括整数和分数。

数学上，实数直观地定义为和数轴上的点一一对应的数。

第四章：代数式代数式代数式:由数和表示数的字母经有限次加、减、乘、除、乘方和开方等代数运算所得的式子，或含有字母的数学表达式称为代数式。

三年级数学小报5篇

三年级数学小报5篇三班级数学小报一:生活中的数学生活中的数学在日常生活中，我们离不开数学。

比如，上街买东西要用到加减法、修房造屋要画图纸……类似这样的用法数不胜数，这都是数学在生活中的详细体现。

我今日要说的是我在生活中发觉的一个特点，那就是在我们的日常用具中大多数都是圆的，如喝水用的杯子、吃饭用的碗、水桶、瓶子上的盖子等等。

为什么这些用具都是圆的呢？我想了又想，最终想明白了，原来在生活中人们用其他外形的用具不简单盛东西和使用，假如用圆的的用具就能解决这样的问题了。

我把我的观看告知了妈妈，妈妈说，数学就在我们身边，只要仔细观看生活，就能在生活中学数学、在生活中用数学，数学与生活密不行分，学深了，学透了，自然会发觉，数学能关心我们解决很多问题。

三班级数学小报二:生活中的数学小故事生活中的数学小故事一个周末的下午，我和妈妈去西缘浴室洗澡，当洗完澡时我们在照镜子妈妈突然对我说：“女儿，我来考你一个数学问题，看看你会不会？”我张口就说：“好的，没问题。

”妈妈说:“你发现镜子里面有一面时钟吗？现在镜子里面的时钟是7：15，你能想像一下现在是下午几时几分吗？” 我想了一会儿没做出来，时间一分一秒的过去了，我实在想不出来，只得不好意思地说：“我做不出来。

”当我回头瞧一瞧挂在墙上的时钟，现在是下午4：45。

妈妈问我现在能分析一下怎么讨论这个问题了吗？妈妈提示了我一下，镜子里的钟面时针与分针和挂在墙上钟面时针与分针有什么关系呢？这个时候我马上反应过来了，它们是呈左右轴对称，这正是我最近学习的内容。

洗完澡回到家后，我要求妈妈再出几个给我做一下。

第一道是镜子中钟面时间为3：30，其次道是镜子中钟面时间为9：40。

我马上动手在纸上采纳对称法的方法做出了这两道题目的答案：8：30和2：20。

这时候妈妈又问我每次这样做题是不是有点麻烦，有没有更好的方法呢？我想了一会儿，没有想出来。

妈妈这时说：“再提示一下小伴侣，将镜子里钟面时间和实际时间加起来你能发觉有什么规律吗？”我抓紧动手算了起来，3：30+8：30＝12，9：40+2：20＝12，发觉镜子里钟面时间与实际时间加起来都等于12，此时我兴奋的跳了起来。

圆周率数学学科小报

记号π是第十六个希腊字母的小写。

这个符号，亦是希腊语περιφρεια（表示周边，地域，圆周等意思）的首字母。

1706 年英国数学家威廉·琼斯（William Jones ，1675 － 1749 ）最先使用“π”来表示圆周率。

1736 年，瑞士大数学家欧拉也开始用π表示圆率。

从此，π便成了圆周率的代名词。

圆的周长与直径的比值圆周率（ Pi ）是圆的周长与直径的比值，一般用希腊字母π表示，是一个在数学及物理学中普遍存在的数学常数。

π也等于圆形之面积与半径平方之比。

是精确计算圆周长、圆面积、球体积等几何形状的关键值。

在分析学里，π可以严格地定义为满足sin x = 0的最小正实数x。

圆周率用希腊字母π（读作 p ài）表示，是一个常数（约等于 3.141592654），是代表圆周长和直径的比值。

它是一个无理数，即无限不循环小数。

在日常生活中，通常都用 3.14 代表圆周率去进行近似计算。

而用十位小数 3.141592654便足以应付一般计算。

即使是工程师或物理学家要进行较精密的计算，充其量也只需取值至小数点后几百个位。

1965 年，英国数学家约翰·沃利斯（John Wallis ）出版了一本数学专著，其中他推导出一个公式，发现圆周率等于无穷个分数相乘的积。

2015 年，罗切斯特大学的科学家们在氢原子能级的量子力学计算中发现了圆周率相同的公式特性把圆周率的数值算得这么精确，实际意义并不大。

现代科技领域使用的圆周率值，有十几位已经足够了。

如果以39 位精度的圆周率值，来计算宇宙的大小，误差还不到一个原子的体积。

以前的人计算圆周率，是要探究圆周率是否循环小数。

自从1761 年兰伯特证明了圆周率是无理数，1882 年林德曼证明了圆周率是超越数后，圆周率的神秘面纱就被揭开了。

π在许多数学领域都有非常重要的作用。

π是个无理数，即不可表达成两个整数之比，是由瑞士科学家约翰·海因里希·兰伯特于1761 年证明的。

数学小报

2012-4-22 12
• 秦九韶：《数书九章》秦九韶：数书九章》 • 秦九韶（约1202～1261），字道吉，四川安岳人，先后在湖北、安徽、江苏、浙江等地做官， 1261年左右被贬至梅州（今广东梅县），不久死于任所。秦九韶与李冶、杨辉、朱世杰并称宋元数学四大家。他早年在杭州“访习于太史，又尝从隐君子受数学”，1247年写成著名的《数书九章》。《数书九章》全书共18卷，81题，分九大类（大衍、天时、田域、测望、赋役、钱谷、营建、军旅、市易）。其最重要的数学成就——“大衍总数术”（一次同余组解法）与“正负开方术” （高次方程数值解法），使这部宋代算经在中世纪世界数学史上占有突出的地位。
•The end
2012-4-22 22
2012-4-22 15
• 【侯氏定理】数学家侯振挺关于马尔可夫过程的研究成果被国际上命名为“侯氏定理”。 • 【周氏猜测】数学家周海中关于梅森素数分布的研究成果被国际上命名为“周氏猜测”。 • 【王氏定理】数学家王戌堂关于点集拓扑学的研究成果被国际数学界誉为“王氏定理”。 • 【袁氏引理】数学家袁亚湘在非线性规划方面的研究成果被国际上命名为“袁氏引理”。 • 【景氏算子】数学家景乃桓在对称函数方面的研究成果被国际上命名为“景氏算子”。 • 【陈氏文法】数学家陈永川在组合数学方面的研究成果被国际上命名为“陈氏文法”。
2012-4-22 16
数学经典
2012-4-22
17
圆周率
• 圆周率（π读pai）是一个常数（约等于3.141592654），是代表圆周长和直径的比值。它是一个无理数，即是一个无限不循环小数。在日常生活中，通常都用3.14来代表圆周率去进行近似计算，即使是工程师或物理学家要进行较精密的计算，也只取值至小数点后约20位。

数学小报

数学笑话
王奕东五、（四）班
报
1. 公元前4世纪：亚里士多德定义为”数学是量的科学”； 2. 16世纪，培根将数学分为纯粹数学与混合数学； 3. 17世纪，笛卡尔认为：凡是以研究顺序和度量为目的的科学都与数学有关； 4. 17，18世纪，数学家们关注的焦点是运动和变化，牛顿和莱布尼茨之后，数学
成为研究数，形以及运动与变化的学问； 5. 19世纪，恩格斯认为：数学是研究现实世界的空间形式与数量关系的科学； 6. 19世纪后期，数学成为研究数与形，运动与著名数学家华罗庚读书的方法与众不同。他拿到一本书，不是翻开从头至尾的读，而是对着书思考一会，然后闭目静思。他猜想书的谋篇布局，斟酌完毕再打开书，如果作者的思路与自己猜想的一致，他就不再读了。华罗庚这种猜读法不仅节省了读书时间，而已培养了自己的思维力和想象力，不至于使自己沦为书的奴隶。

一年级数学小报可打印

一年级数学小报可打印
1、数数：根据物体的个数，可以用11—20各数来表示。

2、数的顺序：11—20各数的顺序是：11、12、1
3、1
4、1
5、1
6、1
7、1
8、1
9、20、
3、比较大小：可以根据数的顺序比较，后面的数总比前面的数大，或者利用数的组成进行比较。

4、11—20各数的组成：都是由1个十和几个一组成的，20由2个十组成的。

如：1个十和5个一组成15。

5、数位：从右边起第一位是个位，第二位是十位。

6、11—20各数的读法：从高位读起，十位上是几就读几十，个位上是几就读几。

20的读法，20读作：二十。

7、写数：写数时，对照数位写，有1个十就在十位上写1，有2个十就在十位上写2。

有几个一，就在个位上写几，个位上一个单位也没有，就写0占位。

8、十加几、十几加几与相应的减法
(1)、10加几和相应的减法的计算方法：10加几得十几，十几减几得十，十几减十得几。

如：10+5=15，17-7=10，18-10=8
(2)十几加几和相应的减法的计算方法：计算十几加几和相应的减法时，可以利用数的组成来计算，也可以把个位上的数相加或相减，再加整十数。

(3)加减法的各部分名称：
在加法算式中，加号前面和后面的数叫加数，等号后面的数叫和。

在减法算式中，减号前面的数叫被减数，减号后面的数叫减数，等号后面的数叫差。

9、解决问题
求两个数之间有几个数，可以用数数法，也可以用画图法。

还可以用计算法(用大数减小数再减1的方法来计算)。

三年级数学小报

1/ 1耐人寻味的数学比喻1、爱因斯坦的成功等式:三年级数学小报A=X+Y+Z ；并解释道：“A 代表成功；X 代表劳动；Y 代表适当的工作方法。

”三年级数学小报项；就迫不及待的问：“那么；Z 代表什么呢？”不料；爱因斯坦回答道：“Z 代狼与兔子的速度狼的时速可达60公里。

兔子最快约为时速36公里。

最快的船人们用太阳能和喷气式发动机作为船的动力装三年级数学小报主编：三（2）班顾子仪小熊开了一个水果批发店；由于热情待客；价格合理；生意挺不错。

这一天；森林商店的老板狐狸来到水果店；东瞧瞧西望望；然后问：“这里的西瓜和苹果怎么样？我想买一些；价格是多少？”小熊赶忙答道：“你放心；西瓜又甜又香；苹果又脆又甜。

我们店的价格也是最公道的；西瓜1千克1元；苹果1千克5元。

” 狐狸拿起一个西瓜拍了拍；又挑了一个苹果闻了闻；说：“恩；是不错。

我想买1775千克苹果；225千克西瓜；合起来一共是2000千克。

这样吧；西瓜1千克1元；苹果1千克5元；为了计算方便；就按平均每千克3元卖给我；行吗？” 小熊想了想；“西瓜1千克1元；苹果1千克5元；平均下来1千克（1+5）÷2=3（元）。

对呀；这是一样的算法。

”看到这么一大笔生意；小熊没有多想就答应了。

很快；狐狸就找来了一辆大卡车；把2000千克的苹果和西瓜搬到了车上。

装完后；狐狸数了一沓钱；递给小熊。

小熊接过来；数了数；说：“狐老板；你算错了吧？就算我只卖了1700千克苹果；5×1700=8500；也有8000多元啊！这里只有6000元。

” 狐狸说：“没错呀！平均1千克水果3元；一共是2000×3=6000（元）吧。

” 小熊急了；拿出计算器就算起帐来；“苹果1775×5=8875（元）；再加西瓜225元；一共应付9100元。

我这可亏了3100元。

” 狐狸说：“可这是我们说好的；我算的也不错呀！” 两个人闹到了市场管理员老牛那里。

数学小报,可直接打印

答案： 1、三2、相等3、倒数4、王5、七上八下二年级二班姓名指导老师：1、一减一不是零。

（打一字）2、你盼着我，我盼着你。

（打一数学名词）3、七六五四三二一。

（打一数学名词）4、一加一不是二。

（打一字）5、八分之七。

（打一成语）【答案在本期1930 年的一天，清华大学数学系主任熊庆来，坐在办公室里看一本《科学》杂志。

熊庆来惊奇不已，将华罗庚请到清华大学来。

从此，华罗庚就成为清华大学数学系助理员。

第二年，他的论文开始在国外著名的数学杂志陆续发表。

几年之后，华罗庚被保送到英国剑桥大学留学。

他提出的理论被数学界命名为“华氏定理”。

有位渔夫，头戴一顶大草帽，坐在划艇上在一条河中钓鱼。

河水的流动速度是每小时3英里，他的划艇以同样的速度顺流而下。

“我得向上游划行几英里，”他自言自语道，“这里的鱼儿不愿上钩！”正当他开始向上游划行的时候，一阵风把他的草帽吹落到船旁的水中。

但是，我们这位渔夫并没有注意到他的草帽丢了，仍然向上游划行。

直到他划行到船与草帽相距5英里的时候，他才发觉这一点。

于是他立即掉转船头，向下游划去，终于追上了他那顶在水中漂流的草帽。

在静水中，渔夫划行的速度总是每小时5英里。

在他向上游或下游划行时，一直保持这个速度不变。

当然，这并不是他相对于河岸的速度。

如果渔夫是在下午2时丢失草帽的，那么他找回草帽是在什么时候？儿子战战兢兢地回到家：“爸，我今天考试只得了60分。

”爸爸很生气：“下次再考低了，就别叫我爸！”。

数学小报四年级3篇

数学小报四年级
第一篇：认识正方形
小朋友们，你们知道正方形是什么吗？今天我们就来认识一下它吧。

正方形是一种特殊的四边形，有四个相等的直角和四条相等的边。

我们可以用一个简单的方法来画一个正方形，就是在纸上画一个正方形的基准线，然后通过量角器或直角尺测量出相等的四个直角，再画出四条相等的边，最后就完成了一个漂亮的正方形了。

我们可以通过几何形状来了解正方形的特点。

正方形有以下的几何性质：
1. 所有角都是90度。

正方形里面有四个直角。

2. 四条边都相等。

这意味着，如果你知道一条边的长度，你就知道了四条边的长度。

3. 对角线相等。

正方形中的两条对角线相等。

正方形和我们日常生活中的事物有很多关联。

比如，电视和电脑屏幕通常都是正方形的，因为它们需要显示相等的图像和文字。

FEDEX快递的标志也是一个正方形，这代表着他们快递的速度是相等的。

小朋友们，现在你们知道了正方形的特点，学会画正方形了吗？赶快动手试一试吧！。

暑假旅游相关数学问题的小报

暑假旅游相关数学问题的小报
1. 旅行预算：假设小明计划去旅行，他每天的住宿费用是100元，吃饭的费用是50元，交通费用是30元。

如果他打算旅行7天，那么他的总预算是多少？
2. 机票价格：小华想要买一张从北京到上海的机票，他发现不同航空公司的价格不同。

如果A航空公司的机票价格是800元，B航空公司的机票价格是900元，那么两家航空公司的机票平均价格是多少？
3. 旅游景点门票：小红要去参观一个景点，她发现成人票的价格是60元，学生票的价格是40元。

如果她带着两个弟弟一起去，他们一共需要支付多少钱的门票？
4. 租车费用：小李想要租一辆汽车去旅行，他发现每天的租金是200元。

如果他打算租3天的汽车，那么他需要支付多少租金？
5. 购物花费：小王在旅行中买了一些纪念品，他花了150元买了一本书，200元买了一件T恤。

如果他还想再买一件帽子，价格是100元，那么他一共花了多少钱？
通过这些数学问题，我们可以更好地规划和控制我们的旅行预算，同时也能够更好地理解旅行中的消费情况。

希望大家在暑假旅游中能够玩得开心，也能够用数学知识来解决问题！。