2018年春期考数学试卷
2018年上海市春考数学试卷(含答案)

2018年上海市普通高校春季招生统一文化考试数学试卷一、填空题(54分)1、不等式1>x 的解集为______________;2、计算:_________213lim=+-∞→n n n ;3、设集合{}20<<=x x A ,{}11<<-=x x B ,则________=B A ; 4、若复数i z +=1(i 是虚数单位),则______2=+zz ; 5、已知{}n a 是等差数列,若1082=+a a ,则______753=++a a a ;6、已知平面上动点P 到两个定点()0,1和()0,1-的距离之和等于4,则动点P 的轨迹方程为_________;7、如图,在长方体1111D C B A ABCD -中,3=AB ,4=BC ,51=AA ,O体积为_________;是11C A 的中点,则三棱锥11OB A A -的第7题图 第12题图8、某校组队参加辩论赛,从6名学生中选出4人分别担任一、二、三、四辩,若其中学生甲必须参赛且不担任四辩,则不同的安排方法种数为_____________(结果用数值表示)。
9、设R a ∈,若922⎪⎭⎫ ⎝⎛+x x 与92⎪⎭⎫ ⎝⎛+x a x 的二项展开式中的常数项相等,则_______=a ;10、设R m ∈,若z 是关于x 的方程0122=-++m mx x 的一个虚根,则-z 的取值范围是________;11、设0>a ,函数()()1,0),sin()1(2∈-+=x ax x x x f ,若函数12-=x y 与()x f y =的图像有且仅有两个不同的公共点,则a 的取值范围是__________;12、如图,在正方形ABCD 的边长为20米,圆O 的半径为1米,圆心是正方形的中心,点P 、Q 分别在线段AD 、CB 上,若线段PQ 与圆O 有公共点,则称点Q 在点P 的“盲区”中,已知点P 以1.5米/秒的速度从A出发向D 移动,同时,点Q 以1米/秒的速度从C 出发向B 移动,则在点P 从A 移动到D 的过程中,点Q 在点P 的盲区中的时长均为_____秒(精确到0.1).二.选择题(20分)13. 下列函数中,为偶函数的是( )A 2-=x y B 31x y = C 21-=xy D 3x y =14. 如图,在直三棱柱111C B A ABC -的棱所在的直线中,与直线1BC 异面的直线的条数为( ) A 1 B 2 C 3 D 415. 若数列}{n a 的前n 项和,“}{n a 是递增数列”是“}{n S 是递增数列”的( )A 充分不必要条件B 必要不充分条件C 充要条件D 即不充分也不必要条件16、已知A 、B 是平面内两个定点,且2=→AB ,该平面上的动线段PQ 的两个端点P 、Q 满足:5≤→AP ,6=⋅→→AB AP ,→→-=AP AQ 2,则动线段PQ 所围成的面积为( )A 、50B 、60C 、72D 、108三、解答题(14+14+14+16+18=76分) 17、已知x x f cos )(=(1).若31)(=αf ,且],0[πα∈,求)3(πα-f 的值; (2).求函数)(2)2(x f x f y -=的最小值;18、已知R a ∈,双曲线1:222=-Γy ax(1).若点)1,2(在Γ上,求Γ的焦点坐标;(2).若1=a ,直线1+=kx y 与Γ相交于B A ,两点,若线段AB 中点的横坐标为1,求k 的值;19.利用“平行与圆锥母线的平面截圆锥面,所得截线是抛物线”的几何原理;某公司用两个射灯(射出的光锥视为圆锥)在广告牌上投影出其标识,如图1所示,图2投影出的抛物线的平面图,图3是一个射灯投影的直观图,在图2与图3中,点O 、A 、B 在抛物线上,OC 是抛物线的对称轴,AB OC ⊥于C ,3=AB 米,5.4=OC 米.(1)求抛物线的焦点到准线的距离;(2)在图3中,已知OC 平行于圆锥的母线SD ,AB 、DE 是圆锥底面的直径,求圆锥的母线与轴的夹角的大小(精确到01.0).20.设0>a ,函数xa x f 211)(⋅+=(1).若1=a ,求)(x f 的反函数)(1x f -(2)求函数)()(x f x f y -⋅=的最大值,(用a 表示)(3)设=)(x g )1()(--x f x f ,若对任意)0()(],0,(g x g x ≥-∞∈恒成立,求a 的取值范围?21.若}{n c 是递增数列,数列}{n a 满足:对任意*,N m R n ∈∃∈,使得01≤--+n m nm c a a a ,则称}{n a 是}{n c 的“分隔数列”(1)设1,2+==n a n c n n ,证明:数列}{n a 是}{n c 的分隔数列;(2)设n n S n c ,4-=是}{n c 的前n 项和,23-=n n c d ,判断数列}{n S 是否是数列}{n d 的分隔数列,并说明理由;(3)设n n n T aq c ,1-=是}{n c 的前n 项和,若数列}{n T 是}{n C 的分隔数列,求实数q a ,的取值范围?2018年上海市普通高校春季招生统一文化考试数学试卷参考答案:一、填空题:1、()()+∞-∞-,11, ;2、3;3、()1,0;4、2;5、15;6、13422=+y x ;7、5;8、180; 9、4;10、⎪⎪⎭⎫ ⎝⎛∞+,33;11、⎥⎦⎤⎝⎛619611ππ,;12、4.4; 二、选择题:13、A ;14、C ;15、D ;16、B ;三、解答题:17、(1)6621+;(2)23-; 18、(1)()()0,30,3-,;(2)215-; 19、(1)41;(2)59.9;20、解析:(1)()()1,011log )(11log 112212∈⎪⎭⎫ ⎝⎛-=⇒⎪⎪⎭⎫ ⎝⎛-=⇒-=-x x x f y x y x ; (2)()()xx x x x a a a a y 2122211211⋅++=⋅+⋅⋅+=-,设02>=t x, 则()111222+++=+++=a taat at a at ty ,因为0>a ,所以a taat 2≥+,当且仅当1=t 时取等号,所以12122++≥+++a a a t a at ,即()⎥⎦⎤ ⎝⎛+∈211,0a y ; (3)()223222221122+⋅+⋅-=⋅+-⋅+=xx x x a t a a a a x g ,设t x=2,因为()0,∞-∈x , 所以()1,0∈t ,则()att a a t g 322++-=,若a t t t a 222=⇒=,1°当12≥a 时,即20≤<a ,a t t a y 322++=单调递减,所以()+∞++∈,232a a y , 则()⎪⎭⎫⎝⎛++-∈0,232a a a a g ,且()2302++-=a a a g ,故满足()()0g x g ≥,符合题意; 2°当120<<a 时,即2>a ,则a a a aa t t a y 322322322+=+⋅≥++=, 则()()0,322-∈a g ,因为()()02log 2min g a g x g ≠⎪⎪⎭⎫⎝⎛=,故不符合题意,舍去; 综上:(]2,0∈a 。
2018年春八年级下学期新人教版数学期末试卷(含答案)

八年级下期末考试数学试题(考试时间:120分钟 试卷总分:120分)一、选择题(本小题共12小题,每小题3分,共36分)下列各题给出的四个选项中,只有一个是正确的,题号 1 2 3 4 5 6 7 8 9 10 11 12 答案1、如果分式x-1有意义,那么x 的取值范围是 A 、x >1 B 、x <1 C 、x ≠1 D 、x =12、己知反比例数xky =的图象过点(2,4),则下面也在反比例函数图象上的点是A 、(2,-4)B 、(4,-2)C 、(-1,8)D 、(16,21)3、一直角三角形两边分别为3和5,则第三边为A 、4B 、34C 、4或34D 、2 4、用两个全等的等边三角形,可以拼成下列哪种图形A 、矩形B 、菱形C 、正方形D 、等腰梯形 5、菱形的面积为2,其对角线分别为x 、y ,则y 与x 的图象大致为A B C D6、小明妈妈经营一家服装专卖店,为了合理利用资金,小明帮妈妈对上个月各种型号的服装销售数量进行了一次统计分析,决定在这个月的进货中多进某种型号服装,此时小明应重点参考 A 、众数 B 、平均数 C 、加权平均数 D 、中位数7、王英在荷塘边观看荷花,突然想测试池塘的水深,她把一株竖直的荷花(如右图)拉到岸边,花柄正好与水面成600夹角,测得AB 长60cm ,则荷花处水深OA 为A 、120cmB 、360cmC 、60cmD 、cm 320第7题图 第8题图 第9题图8、如图,□ABCD 的对角线AC 、BD 相交于O ,EF 过点O 与AD 、BC 分别相交于E 、F ,若AB=4,BC=5,OE=1.5,那么四边形EFCD 的周长为A 、16B 、14C 、12D 、109、如图,把菱形ABCD 沿AH 折叠,使B 点落在BC 上的E 点处,若∠B=700,则∠EDC 的大小为A 、100B 、150C 、200D 、30010、下列命题正确的是A 、同一边上两个角相等的梯形是等腰梯形;B 、一组对边平行,一组对边相等的四边形是平行四边形;C 、如果顺次连结一个四边形各边中点得到的是一个正方形,那么原四边形一定是正方形。
2018年春期期末七年级学业水平测试数学试题

2018年春期期末七年级学业水平测试数学试题注意事项:1.本试卷共6页,满分120分,考试时间100分钟。
2.试题卷上不要答题,请用0.5毫米黑色签字水笔直接把答案写在答题卡上。
答在试题卷上的答案无效。
3.答题前,考生务必将本人姓名、准考证号填写在答题卡第一面的指定位置上。
一、选择题(单项选择,每小题3分,共30分)1.下列方程中,解是x=4的是( C )A .2x+5=0 B.-3x-8=-4 C.32321x xD .2(x-1)=3x-52.下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是( D)3.如图,数轴上表示某不等式组的解集,则这个不等式组可能是( A )-3-2-13210A .+1020≥≥x x B .+1020≤≥x x C .+1020≤≥x x D .+1020≥≥x x 4.下列正多边形中,与正八边形组合能够铺满地面的是( B )A .正三角形B .正方形C .正五边形D .正六边形5.用加减法解方程组2x -3y =5,①3x -2y =7,②下列解法不正确的是(D).A .①×3-②×2,消去xB .①×2-②×3,消去yC .①×(-3)+②×2,消去xD .①×2-②×(-3),消去y6.如图,将△ABC 绕点A 逆时针旋转一定角度,得到△ADE .若∠CAE =65°,∠E =70°,且AD ⊥BC ,则∠BAC 的度数为(C)A .60°B .75°C .85°D .90°第7题图7.把边长相等的正五边形ABCDE 和正方形ABFG 按照如图所示的方式叠合在一起,则∠EAG 的度数是(A )A .18°B .20°C .28°D .30°8.已知,,a b c 是ABC 的三条边长,化简||||a b c c a b 的结果为( )A .222a b c B .22ab C.2cD .09.轮船在河流中来往航行于A 、B 两码头之间,顺流航行全程需7小时,逆流航行全程需9小时,已知水流速度为每小时3km ,求A 、B 两码头间的距离,若设A 、B 两码头间距离为x ,则所列方程为( A )A .3937x xB .997x x C .937x x D .3937x x10. 按下面的程序计算:若输入100,输出结果是501;若输入25,输出结果是631.若开始输入的x 值为正整数,最后输出结果为556,则开始输入x 的值可能有( C)A .4种B .3种C .2种D .1种[来源:学。
2018年春-七年级下数学期末试题

2018年春期义务教育阶段教学质量监测七年级数学(考试时间:120分钟,总分120分)注意事项:1.答题前,考生在答题卷上务必将自己的姓名、学校、班级、考号填写清楚,并贴好条形码.请认真核准条形码上的考号、姓名和科目.2.解答选择题时,每小题选出答案后,用2B铅笔把答题卷上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.3.解答填空题、解答题时,请在答题卷上各题的答题区域内作答.一、选择题:(本大题共8个小题,每小题3分,共24分).在每小题给出的四个选项中,只有一项是符合题目要求的.(注意:)在试题卷上作答无效.........1.方程的解是(▲)A.B.C.D.2.下列标志中,是轴对称图形的是(▲)A B C D3.不等式的解集是(▲)A.B.C.D.4.已知,用含的代数式表示,则正确的是()A.B.C.D.5.解方程,去分母后正确的是(▲).A.B.C.D.6.用两种正多边形铺满地面,其中一种是正八边形,则另一种正多边形是(▲)A.正三角形B.正方形C.正五边形D.正六边形7.如图,△≌△,点D在上,若,则的度数EA是( ▲ ). A.B.C.D.8.不等式组有4个不同的整数解,则的取值范围( ▲ ). A.B. C. D.二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在答题卡对应题中横线上.(注意:在试题卷上作......答无效...) 9.当▲ 时,代数式与代数式的值相等.10.二元一次方程组的解是 ▲ .11.的3倍与5的和不.大.于.8,用不等式表示为 ▲ .12.一个多边形的每一个外角都为,则这个多边形是 ▲边形. 13.若,则以a 、b 为边长的等腰三角形的周长 是▲.14.如图,在△中,∠B =90°,8.将△沿着BAC DEF第7题图的方向平移至△,若平移的距离是3,则四边形的面积 是 ▲ .15.如图,在四边形中,∠A 与∠互补,E 为延长线上的点,且∠1+∠2+∠,则∠A 的度数是 ▲ .16.若定义,如.下列说法中:当时,;对于正数,均成立;;当且仅当时,.其中正确的是 .(填序号)三、解答题(本大题共8个小题,共72分,解答应写出必要的文字说明或演算步骤) (注意:在试题卷上作答无效.........) 17.(本题满分8分)如图是一个8×10的网格,每个小正方形的顶点叫格点,每个小正方形的边长均为1,△的顶点均在第15题图12ABC DE格点上.2(1)画出△关于直线对称的△.(2)画出△关于点O 的中心对称图形 △.(3)△与△组成的图形轴对称图形. (填“是”或“不是”) 18.(本题共2个小题,共10分)⑴解方程:; ⑵解方程组:19.(本题共2个小题,共10分) ⑴解不等式:,并把解集在数轴上表示出来;⑵解不等式组: 并求出该不等式组的正整数解.20.(本题满分8分)已知关于x 、y 的方程组 的解满足,求的值.21(本题满分8分)学校准备购买A 、B 两种奖品,奖励成绩优异的同学.已知①②第17题图O 1① ②①②购买1件A 奖品和1件B 奖品共需18元;购买30件A 奖品和20件B 奖品共需480元.(1)A 、B 两种奖品的单价分别是多少元?(2)如果学校购买两种奖品共100件,总费用不超过850元,那么最多可以购买A 奖品多少件. 22.(本题满分8分)如图,在△中,,平分交于点D ,将△绕点C 顺时针旋转到△的位置,点F 在上.⑴△旋转了 度;⑵连结,判断与的位置关系,并说明理由. 23.(本题满分10分)已知.当时,;当时,.(1)求出的值; (2)当时,求代数式的取值范围.24.(本题满分10分)⑴如图1,在△中,∠A ,P 是边上的一点,,是点P 关于、的对称点,连结,分别交、于点D 、E .第22题图AFED①若,求的度数;(4分)②请直接写出∠A 与的数量关系:;(2分)⑵如图2,在△中,若∠,用三角板作出点P关于、的对称点、,(不写作法,保留作图痕迹),试判断点,与点A是否在同一直线上,并说明理由.(4分)第24题图。
2018春季第一学期 数学 期末考试试卷

合肥长丰轨道交通学校闭卷考试时间90分钟注意事项:1.满分:100分。
保持卷面整洁,否则扣卷面10分。
2.学生必须将姓名、班级、学号完整填写在规定的密封栏目内,否则视为废卷。
3.学生必须签到,否则出现遗漏由学生本人负责。
12小题,每小题3分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.以下各组对象中不能够构成集合的是()A. 中国古代四大发明B. 地球上的小河流C. 方程210x-=的实数解 D. 周长为10cm的三角形2.方程组{23211x yx y-=+=的解集是()A . {5,1} B.{1,5} C.{(1,5)} D.{(5,1)}3.给出下列关系:①12R∈;Q;③*3N∈;④0Z∈. 其中正确的个数是()A. 1B. 2C. 3D. 44.下列与集合A={1,2}相等的是()A.{1,2,3}B.{x|-1<x<3}C.{x|x²-3x+2=0}D. N5.已知集合}02{=-=xxM,}1{>=xxN,则()A. M=NB.NM⊆ C.NM⊇ D.M与N无包含关系6.若2{,0,1}{,,0}a a b-=,则20072007a b+的值为()A. 0B. 1C. -1D. 27.若集合{}0|2≤=xxA,则下列结论中正确的是()A、A=0B、0A⊆ C、∅=A D、A∅⊆8.X>5是X>3的()A.充分条件B. 必要条件C.充要条件D. 既不是充分条件也是不必要条件9.如果a>b,c为实数,则()A. a+c>b+cB. a+c<b+cC. ac<bcD. ac>bc10.若集合A={-1,0,1,5},B={-1,0,3}则集合=⋃BA()A.{-1,0,1,3,5}B.{-1,0,1,3,}C.{-1,0}D.{0}11.不等式|x|≤4的解集是()A.{x|-4≤x≤ 4}B.{x|x≤-4或x≥ 4}C.{x|x<-4或x>4}D. 以上都不对12.已知全集U Z=,A={0,1,2,3},B={1,2,4}则UA C B为()A.{-1,2} B.{-1,0} C.{1,0} D.{1,2}6小题,每小题4分)13.用列举法表示小于5的自然数集 .…………………………………………………答……………………………题……………………………线…………………………………………………姓名班级学号:座位号:…………………………………………………装……………………………订……………………………线…………………………………………………14.若{1,-2,x}={1,-2,0},则x= .15.设U=R ,A={x|a≤x≤b} ,C U A={x|x<3或x>4}则a= .b= .16.若a>b>0则a²b与b²a的大小关系是 .17.用区间表示集合{x|x>4} .18.设集合A={1, 2, a},B={1,a2-a},若A⊇B,则实数a的值为 .5小题,每小题8分)19.列出集合A={a,b,c}的所有子集和真子集。
(完整版)2018年春季高考数学真题

2018春季高考真题一、选择题1、已知集合M={a,b},N={b,c},则M∩N等于A、∅B、{b}C、{a,c}D、{a,b,c}2、函数f(x)=√x+1+xx−1的定义域是A、(−1,+∞)B、(−1,1)∪(1,+∞)C、[ −1,+∞)D、 [ −1,1)∪(1,+∞)3、奇函数y=f(x)的布局如图所示,则A、f(2)>0>f(4)B、f(2)<0<f(4)C、f(2)> f(4)>0D、f(2)<f(4)<04、已知不等式1+lg|x|<0的解集是A、(−110,0)∪(0,110)B、(−110,110)C、(−10,0)∪(0,10)D、(−10,10)5、在数列{a n}中,a1=-1 , a2=0,a n+2=a n+1+a n,则a5等于A、0B、−1C、−2D、−36、在如图所示的平面直角坐标系中,向量AB⃗⃗⃗⃗⃗ 的坐标是A、(2,2)B、(−2,−2)C、(1,1)D、(−1,−1)7、圆(x+1)2+(y−1)2=1的圆心在A、第一象限B、第二象限C、第三象限D、第四象限8、已知a、b∈R,则“a>b”是“2a>2b”的A、充分不必要条件B、必要不充分条件C、充要条件D、既不充分也不必要条件9、关于直线l:x−√3y+2=0,下列说法正确的是A、直线l的倾斜角为60。
B、向量v=(√3,1)是直线l的一个方向向量C、直线l经过点(1,√3)D、向量n=(1,√3)是直线l的一个法向量10、景区中有一座山,山的南面有2条道路,山的北面有3条道路,均可用于游客上山或下山,假设没有其他道路,某游客计划从山的一面走到山顶后,接着从另一面下山,则不同的走法的种数是A、6B、10C、12D、2011、在平面直角坐标系中,关于x,y的不等式Ax+By+AB>0(AB≠0)表示的区域(阴影部分)可能是12、已知两个非零向量a与b 的夹角为锐角,则A、a∙b>0B、a∙b<0C、a∙b≥0D、a∙b≤013、若坐标原点(0,0)到直线x−y+sin2θ=0的距离等于√22,则角θ的取值集合是A、{θ|θ=kπ±π4,k∈Z} B、{θ|θ=kπ±π2,k∈Z}C、{θ|θ=2kπ±π4,k∈Z} D、{θ|θ=2kπ±π2,k∈Z}14、关于x,y的方程x2+ay2=a2(a≠0),表示的图形不可能是15、在(x−2y)2的展开式中,所有项的系数之和等于A、32B、-32C、1D、-116、设命题p:5≥3,命题q:{1}⊑{0,1,2},则下列命题中为真命题的是A、p∧qB、¬p∧qC、p∧¬qD、¬p∨¬q17、已知抛物线x2=ay(a≠0)的焦点为F,准线为l,该抛物线上的点M到x轴的距离为5,且|MF|=7,则焦点F到准线l距离是A、2B、3C、4D、518、某停车场只有并排的8个停车位,恰好全部空闲,现有3辆汽车依次驶入,并且随机停放在不同车位,则至少有2辆汽车停放在相邻车位的概率是A、514B、1528C、914D、6719、已知矩形ABCD,AB=2BC,把这个矩形分别以AB,BC所在直线为轴旋转一周,所围成集合体的侧面积分别记为S1、S2 ,则S1、S2的比值等于A、12B、1C、2D、420、若由函数y=sin(2x+π2)图像变换得到y=sin(x2+π3)的图像,则可以通过以下两个步骤完成:第一步,把y=sin(2x+π2)上所有点的横坐标变为原来的4倍,纵坐标不变;第二步,可以把图像沿x轴A、向右平移π3个单位B、向右平移5π12个单位C、向左平移π3个单位D、向左平移5π12个单位二、填空题21、已知函数f(x)={x 2+1,x>0−5,x≤0,则f[f(0)]的值等于。
2018山东春季高考数学试题及答案(word)
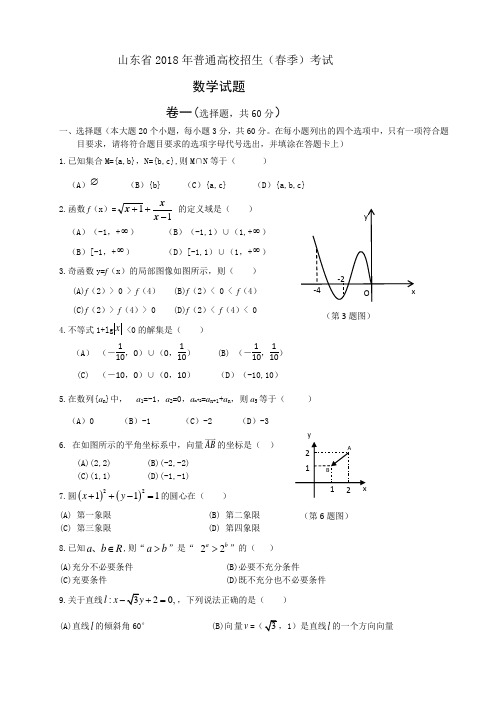
山东省2018年普通高校招生(春季)考试数学试题卷一(选择题,共60分)一、选择题(本大题20个小题,每小题3分,共60分。
在每小题列出的四个选项中,只有一项符合题目要求,请将符合题目要求的选项字母代号选出,并填涂在答题卡上) 1.已知集合M={a,b},N={b,c},则M ∩N 等于( ) (A )∅ (B ){b} (C ){a,c} (D ){a,b,c} 2.函数f (x )=11-++x xx 的定义域是( ) (A )(-1,+∞) (B )(-1,1)∪(1,+∞)(B )[-1,+∞) (D )[-1,1)∪(1,+∞)3.奇函数y=f (x )的局部图像如图所示,则( ) (A)f (2)> 0 > f (4) (B)f (2)< 0 < f (4) (C)f (2)> f (4)> 0 (D)f (2)< f (4)< 04.不等式1+lg <0的解集是( )(A ) (-110,0)∪(0,110) (B) (-110,110) (C) (-10,0)∪(0,10) (D )(-10,10) 5.在数列{a n }中, a 1=-1,a 2=0,a n+2=a n+1+a n ,则a 5等于( ) (A )0 (B )-1 (C )-2 (D )-36. 在如图所示的平角坐标系中,向量AB 的坐标是( ) (A)(2,2) (B)(-2,-2) (C)(1,1) (D)(-1,-1)7.圆()()22111x y ++-=的圆心在( ) (A) 第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限 8.已知a b R ∈、,则“a b >”是“ 22ab>”的( )(A)充分不必要条件 (B)必要不充分条件(C)充要条件 (D)既不充分也不必要条件 9.关于直线:20,l x -+=,下列说法正确的是( )(A)直线l 的倾斜角60° (B)向 量v =,1)是直线l 的一个方向向量xy(第6题图)(第3题图)(C)直线l 经过(1,) (D)向量n =(1)是直线l 的一个法向量10.景区中有一座山,山的南面有2条道路,山的北面有3条道路,均可用于游客上山或下山,假设没有其他道路,某游客计划从山的一面走到山顶后,接着从另一面下山,则不同走发的种数是( ) (A) 6 (B) 10 (C) 12 (D) 2011. 在平面直角坐标系中,关于x ,y 的不等式Ax+By+AB>0(AB ≠0)表示的区域(阴影部分)可能是()12.已知两个非零向量a 与b的夹角为锐角,则( ) (A) 0a b ⋅> (B )0a b ⋅< (B) (C )0a b ⋅≥(D )0a b ⋅≤13.若坐标原点(0,0)到直线的距离等于,则角θ的取值集合是( ) (A) (B)(C) )(D) 14.关于x,y 的方程 ,表示的图形不可能是( )15.在 的展开式中,所有项的系数之和等于( )(A )32 (B )-32 (C )1 (D )-1 16. 设命題p: 5≥3,命題q: {1} ⊆{0, 1, 2},则下列命題中为真命題的是( ) (A) p ∧q (B) ﹁p ∧q (C) p ∧﹁q (D) ﹁p ∨﹁q17.己知抛物线x ²=ay(a ≠0)的焦点为F,准线为l,该抛物线上的点M 到x 轴的距离为5,且|MF |=7,则焦点F 到准线l 的距离是( )(A) 2 (B) 3 (C) 4 (D) 518.某停车场只有并排的8个停车位,恰好全部空闲,现有3辆汽车依次驶入,并且随机停放在不同车2,2k k Z πθθπ⎧⎫|=±∈⎨⎬⎩⎭sin 0x y θ-+=()2220x ay a a +=≠,2k k Z πθθπ⎧⎫|=±∈⎨⎬⎩⎭,4k k Z πθθπ⎧⎫|=±∈⎨⎬⎩⎭2,4k k Z πθθπ⎧⎫|=±∈⎨⎬⎩⎭5(2)x y -位,则至少有2辆汽车停放在相邻车位的概率是 ( )(A)145 (B) 2815 (C)149 (D)7619.已知矩形ABCD ,AB= 2BC ,把这个矩形分别以AB 、BC 所在直线为轴旋转一周,所围成几何体的侧面积分别记为S 1、S 2,则S 1与S 2的比值等于( )(A)21(B) 1 (C) 2 (D) 4 20.若由函数y= sin(2x+3π)的图像变换得到y=sin(32π+x )的图像,则可以通过以下两个步骤完成:第一步,把y= sin(2x+3π)图像上所有点的横坐标变为原来的4倍,纵坐标不变;第二步,可以把所得图像沿x 轴 ( )(A)向右平移3π个单位 (B)向右平移125π个单位 (C) 向左平移3π个单位 (D)向左平移125π个单位二、填空题(本大题5个小题,每小题4分,共20分。
2018山东春季高考数学试题及答案word.docx

2018山东春季高考数学试题及答案word.docx山东省 2018 年普通高校招生(春季)考试数学试题卷一 ( 选择题,共60分)一、选择题(本大题20 个小题,每小题 3 分,共 60 分。
在每小题列出的四个选项中,只有一项符合题目要求,请将符合题目要求的选项字母代号选出,并填涂在答题卡上)1.已知集合 M={a,b} ,N={b,c},则M∩N等于()(A)( B) {b}( C) {a,c}( D) {a,b,c}2.函数 f( x) =x 1x的定义域是()1x y(A)( -1 , +)( B)( -1,1 )∪( 1,+)(B) [-1 ,+)( D)[-1,1 )∪( 1, +)3.奇函数 y=f( x)的局部图像如图所示,则()-2(A) f( 2) > 0 >f( 4) (B)f( 2) < 0 <="">(C) f( 2) > f( 4)> 0(D)f( 2) <="" 4)<="" bdsfid="81" p="">(第 3 题图)4.不等式 1+lg x的解集是()<01111( A)(-10, 0)∪( 0,10) (B)(-10,10)(C)(- 10, 0)∪( 0, 10)( D)( -10,10 )5.在数列 { a n} 中,a1=-1 ,a2=0, a n+2=a n+1+a n,则 a5等于()(A) 0( B)-1(C)-2(D) -3uuur y A 6.在如图所示的平角坐标系中,向量AB)的坐标是(2(A)(2,2)(B)(-2,-2)1B(C)(1,1)(D)(-1,-1)7.圆x2y211 2 x11的圆心在()(A)第一象限(B)第二象限(第 6题图)(C)第三象限(D)第四象限8.已知 a、 b R ,则“ a b ”是“ 2a2b”的()(A) 充分不必要条件(B)必要不充分条件(C) 充要条件(D)既不充分也不必要条件9.关于直线 l : x3y20, ,下列说法正确的是()(A) 直线l的倾斜角60°(B)向量v=(3 ,1)是直线l的一个方向向量(C) 直线l 经过(1, - 3 )(D)向量n =(1, 3 )是直线l 的一个法向量10. 景区中有一座山,山的南面有2 条道路,山的北面有3 条道路,均可用于游客上山或下山,假设没有其他道路,某游客计划从山的一面走到山顶后,接着从另一面下山,则不同走发的种数是()(A) 6(B)10(C) 12(D)2011.在平面直角坐标系中,关于x,y 的不等式Ax+By+AB>0(AB 0) 表示的区域(阴影部分)可能是()y y y yO x O xO x O xA B C D12.已知两个非零向量 a 与 b 的夹角为锐角,则()(A) a b0 (B) a b0(B)( C)a b0 (D) a b013.若坐标原点(0,0 )到直线x y sin0 的距离等于2,则角的取值集合是()2(A)k (B)Z k, k Z ,k42(C)2k)(D) , k Z2k,k Z4214.关于 x,y 的方程x2ay2a2a0 ,表示的图形不可能是()y yyyOX OXOXO XA B C D15.在( x 2 y)5的展开式中,所有项的系数之和等于()(A)32( B) -32(C) 1( D)-116.设命題 p: 53, 命題 q: {1}? {0, 1, 2},则下列命題中为真命題的是()(A) p ∧ q(B)﹁p∧ q(C)p∧﹁ q(D)﹁p∨﹁ q17.己知抛物线x2=ay(a ≠ 0) 的焦点为 F, 准线为 l, 该抛物线上的点M到 x 轴的距离为5,且 |MF | = 7,则焦点 F 到准线 l 的距离是()(A) 2(B)3(C)4(D) 518.某停车场只有并排的 8 个停车位,恰好全部空闲,现有 3 辆汽车依次驶入,并且随机停放在不同车位,则至少有2 辆汽车停放在相邻车位的概率是()5 (B)15(A)2814(C)9(D)6 14719. 已知矩形 ABCD , AB= 2BC ,把这个矩形分别以 AB 、 BC 所在直线为轴旋转一周,所围成几何体的侧面积分别记为 S 1、S 2,则 S 1 与 S 2 的比值等于()(A)1(B) 1 (C) 2(D) 4220. 若由函数 y= sin(2x+)的图像变换得到 y=sin(x) 的图像,则可以通过以下两个步骤完成:32 3第一步把 y= sin(2x+ 3) 图像上所有点的横坐标变为原来的4 倍,纵坐标不变 ; 第二步,可以把所得,图像沿 x 轴()(A) 向右平移个单位(B)向右平移 5个单位312(C) 向左平移个单位(D)向左平移 5个单位312二、填空题(本大题 5 个小题,每小题 4 分,共 20 分。
2018年六年级数学试题 (1)_201904290912241

41524152+-+=2018 年春季六年级学业水平考试数学试题说明:1. 全卷满分100 分,考试时间90 分钟。
2. 考生必须在答题卡上答题,写在试卷上的答案无效。
选择题必须使用2B 铅笔填涂答案,非选择题必须使用0.5 毫米的黑色墨迹签字笔或钢笔答题。
3. 考试结束,将答题卡和试卷一并交回。
一、填空题。
(共18 分,每空1 分。
)1. 上海迪士尼乐园是中国大陆第一个迪士尼主题公园,占地面积约6583200m 2,横线上的数改写成用“万”作单位的数是( );总投资额约为 34002000000 元,波浪线上的数省略亿位后面的尾数大约是( )。
二、判断题。
(对的在括号里打“√”,错的打“×”。
)(共5 分,每题1 分。
)9.在同一平面内,两条直线不是互相平行,就是互相垂直。
( ) 10.在同一时刻、同一地点,树的高度与它的影长成正比例。
( ) 11.小亮身高150cm ,他在平均水深135cm 的河中游泳,不会有危险。
() 12.把一个三角形按2∶1 放大后,它的每个角的度数、每条边的长度都要扩大到原来的2 倍。
( ) 13.一个圆柱与一个长方体的底面周长相等,高也相等,则它们的体积也一定相等。
( )三、选择题。
(把正确答案的序号填在括号里)(共5 分,每题1 分。
) 14.用x 表示一个大于1 的自然数,x2一定是( )。
A. 奇数B. 偶数C. 质数D. 合数15. 如果▲÷●=9……5(●≠0),那么(▲×10)÷(●×10)=( )。
A. 9......5 B. 90......5 C. 9......50 D. 90 (50)2(..( )∶20= 20 =1.25=35÷( )=( )% ( ) 一条边为4cm ,那三条3. 已知 4a =b (a 、b 为非零自然数),a 和b 成( )比例;a 和b 的最大公因数是( );a 一定是( )(填“奇数”或“偶数”)。
2018年春季高考数学真题(精品资料).doc

2018春季高考真题一、选择题1、已知集合M={a,b},N={b,c},则M∩N等于A、∅B、{b}C、{a,c}D、{a,b,c}2、函数f(x)=√x+1+xx−1的定义域是A、(−1,+∞)B、(−1,1)∪(1,+∞)C、[ −1,+∞)D、 [ −1,1)∪(1,+∞)3、奇函数y=f(x)的布局如图所示,则A、f(2)>0>f(4)B、f(2)<0<f(4)C、f(2)> f(4)>0D、f(2)<f(4)<04、已知不等式1+lg|x|<0的解集是A、(−110,0)∪(0,110)B、(−110,110)C、(−10,0)∪(0,10)D、(−10,10)5、在数列{a n}中,a1=-1 , a2=0,a n+2=a n+1+a n,则a5等于A、0B、−1C、−2D、−36、在如图所示的平面直角坐标系中,向量AB⃗⃗⃗⃗⃗ 的坐标是A、(2,2)B、(−2,−2)C、(1,1)D、(−1,−1)7、圆(x+1)2+(y−1)2=1的圆心在A、第一象限B、第二象限C、第三象限D、第四象限8、已知a、b∈R,则“a>b”是“2a>2b”的A、充分不必要条件B、必要不充分条件C、充要条件D、既不充分也不必要条件9、关于直线l:x−√3y+2=0,下列说法正确的是A、直线l的倾斜角为60。
B、向量v=(√3,1)是直线l的一个方向向量C、直线l经过点(1,√3)D、向量n=(1,√3)是直线l的一个法向量10、景区中有一座山,山的南面有2条道路,山的北面有3条道路,均可用于游客上山或下山,假设没有其他道路,某游客计划从山的一面走到山顶后,接着从另一面下山,则不同的走法的种数是A、6B、10C、12D、2011、在平面直角坐标系中,关于x,y的不等式Ax+By+AB>0(AB≠0)表示的区域(阴影部分)可能是12、已知两个非零向量a与b 的夹角为锐角,则A、a∙b>0B、a∙b<0C、a∙b≥0D、a∙b≤013、若坐标原点(0,0)到直线x−y+sin2θ=0的距离等于√22,则角θ的取值集合是A、{θ|θ=kπ±π4,k∈Z} B、{θ|θ=kπ±π2,k∈Z}C、{θ|θ=2kπ±π4,k∈Z} D、{θ|θ=2kπ±π2,k∈Z}14、关于x,y的方程x2+ay2=a2(a≠0),表示的图形不可能是15、在(x−2y)2的展开式中,所有项的系数之和等于A、32B、-32C、1D、-116、设命题p:5≥3,命题q:{1}⊑{0,1,2},则下列命题中为真命题的是A、p∧qB、¬p∧qC、p∧¬qD、¬p∨¬q17、已知抛物线x2=ay(a≠0)的焦点为F,准线为l,该抛物线上的点M到x轴的距离为5,且|MF|=7,则焦点F到准线l距离是A、2B、3C、4D、518、某停车场只有并排的8个停车位,恰好全部空闲,现有3辆汽车依次驶入,并且随机停放在不同车位,则至少有2辆汽车停放在相邻车位的概率是A、514B、1528C、914D、6719、已知矩形ABCD,AB=2BC,把这个矩形分别以AB,BC所在直线为轴旋转一周,所围成集合体的侧面积分别记为S1、S2 ,则S1、S2的比值等于A、12B、1C、2D、420、若由函数y=sin(2x+π2)图像变换得到y=sin(x2+π3)的图像,则可以通过以下两个步骤完成:第一步,把y=sin(2x+π2)上所有点的横坐标变为原来的4倍,纵坐标不变;第二步,可以把图像沿x轴A、向右平移π3个单位B、向右平移5π12个单位C、向左平移π3个单位D、向左平移5π12个单位二、填空题21、已知函数f(x)={x 2+1,x>0−5,x≤0,则f[f(0)]的值等于。
2018年春季高考数学真题版

2018春季高考真题一、选择题1、已知集合,,则等于A、B、C、D、2、函数的定义域是A、B、C、D、3、奇函数的布局如图所示,则A、B、C、D、4、已知不等式的解集是A B、C、D、5、在数列中,=-1,=0,=+,则等于A、B、C、D、6、在如图所示的平面直角坐标系中,向量的坐标是A、B、C、D、7、圆A、第一象限B、第二象限C、第三象限D、第四象限8、已知,则""是""的A、充分不必要条件B、必要不充分条件C、充要条件D、既不充分也不必要条件9、关于直线,下列说法正确的是A、直线l的倾斜角为B、向量是直线l的一个方向向量C、直线l经过点D、向量是直线l的一个法向量10、景区中有一座山,山的南面有2条道路,山的北面有3条道路,均可用于游客上山或下山,假设没有其他道路,某游客计划从山的一面走到山顶后,接着从另一面下山,则不同的走法的种数是A、6B、10C、12D、2011、在平面直角坐标系中,关于的不等式表示的区域〔阴影部分可能是12、已知两个非零向量a与b的夹角为锐角,则A、B、C、D、13、若坐标原点到直线的距离等于,则角的取值集合是A、{}B、{}C、{}D、{}14、关于的方程,表示的图形不可能是15、在A、32B、-32C、1D、-116、设命题,命题,则下列命题中为真命题的是A、pB、C、D、17、已知抛物线的焦点为,准线为,该抛物线上的点到轴的距离为,且=7,则焦点到准线距离是A、2B、C、D、18、某停车场只有并排的8个停车位,恰好全部空闲,现有3辆汽车依次驶入,并且随机停放在不同车位,则至少有2辆汽车停放在相邻车位的概率是A、B、C、D、19、已知矩形ABCD,AB=2BC,把这个矩形分别以AB,BC所在直线为轴旋转一周,所围成集合体的侧面积分别记为S1、S2 ,则S1、S2的比值等于A、B、C、D、20、若由函数图像变换得到的图像,则可以通过以下两个步骤完成:第一步,把上所有点的横坐标变为原来的4倍,纵坐标不变;第二步,可以把图像沿x轴A、向右平移个单位B、向右平移个单位C、向左平移个单位D、向左平移个单位二、填空题21、已知函数,则的值等于。
2018年上海市春考数学试卷(含答案)

2018年上海市春考数学试卷(含答案)2018年上海市普通高校春季招生统一文化考试数学试卷一、填空题(54分)1、不等式1>x 的解集为______________;2、计算:_________213lim =+-∞→n n n ; 3、设集合{}20<<=x x A ,{}11<<-=x x B ,则________=B A I;4、若复数i z +=1(i 是虚数单位),则______2=+z z ;5、已知{}na 是等差数列,若1082=+a a,则______753=++a a a;6、已知平面上动点P 到两个定点()0,1和()0,1-的距离之和等于4,则动点P 的轨迹方程为_________;7、如图,在长方体1111D C B A ABCD -中,3=AB ,4=BC ,51=AA ,O是11C A 的中点,则三棱锥11OB A A -的体积为_________;第7题图 第12题图8、某校组队参加辩论赛,从6名学生中选出4人分别担任一、二、三、四辩,若其中学生甲必须参赛且不担任四辩,则不同的安排方法种数为_____________(结果用数值表示)。
9、设R a ∈,若922⎪⎭⎫⎝⎛+x x 与92⎪⎭⎫ ⎝⎛+x a x 的二项展开式中的常数项相等,则_______=a ;10、设R m ∈,若z 是关于x 的方程0122=-++m mx x 的一个虚根,则-z 的取值范围是________;11、设0>a ,函数()()1,0),sin()1(2∈-+=x ax x x x f ,若函数12-=x y 与()x f y =的图像有且仅有两个不同的公共点,则a 的取值范围是__________;12、如图,在正方形ABCD 的边长为20米,圆O 的半径为1米,圆心是正方形的中心,点P 、Q 分别在线段AD 、CB 上,若线段PQ 与圆O 有公共点,则称点Q 在点P 的“盲区”中,已知点P 以1.5米/秒的速度从A 出发向D 移动,同时,点Q以1米/秒的速度从C 出发向B 移动,则在点P 从A 移动到D的过程中,点Q 在点P 的盲区中的时长均为_____秒(精确到0.1).二.选择题(20分)13. 下列函数中,为偶函数的是( )A 2-=x y B 31x y = C 21-=x y D 3x y =14. 如图,在直三棱柱111C B A ABC -的棱所在的直线中,与直线1BC 异面的直线的条数为( )A 1B 2C 3D 415. 若数列}{na 的前n 项和,“}{na 是递增数列”是“}{nS 是递增数列”的( )A 充分不必要条件B 必要不充分条件C 充要条件D 即不充分也不必要条件16、已知A 、B 是平面内两个定点,且2=→AB ,该平面上的动线段PQ 的两个端点P 、Q 满足:5≤→AP ,6=⋅→→AB AP ,→→-=AP AQ 2,则动线段PQ 所围成的面积为( )A 、50B 、60C 、72 D 、108三、解答题(14+14+14+16+18=76分) 17、已知x x f cos )(=(1).若31)(=αf ,且],0[πα∈,求)3(πα-f 的值; (2).求函数)(2)2(x f x f y -=的最小值;18、已知R a ∈,双曲线1:222=-Γy ax(1).若点)1,2(在Γ上,求Γ的焦点坐标;(2).若1=a ,直线1+=kx y 与Γ相交于B A ,两点,若线段AB 中点的横坐标为1,求k 的值;19.利用“平行与圆锥母线的平面截圆锥面,所得截线是抛物线”的几何原理;某公司用两个射灯(射出的光锥视为圆锥)在广告牌上投影出其标识,如图1所示,图2投影出的抛物线的平面图,图3是一个射灯投影的直观图,在图2与图3中,点O 、A 、B 在抛物线上,OC 是抛物线的对称轴,AB OC ⊥于C ,3=AB 米,5.4=OC 米. (1)求抛物线的焦点到准线的距离;(2)在图3中,已知OC 平行于圆锥的母线SD ,AB 、DE 是圆锥底面的直径,求圆锥的母线与轴的夹角的大小(精确到ο01.0).20.20.设0>a ,函数xa x f 211)(⋅+= (1).若1=a ,求)(x f 的反函数)(1x f-(2)求函数)()(x f x f y -⋅=的最大值,(用a 表示) (3)设=)(x g )1()(--x f x f ,若对任意)0()(],0,(g x g x ≥-∞∈恒成立,求a的取值范围?21.若}{nc 是递增数列,数列}{na 满足:对任意*,N m R n ∈∃∈,使得01≤--+n mnm c a aa ,则称}{na 是}{nc 的“分隔数列”(1)设1,2+==n a n cn n,证明:数列}{na 是}{nc 的分隔数列;(2)设nnS n c,4-=是}{nc 的前n 项和,23-=n nc d,判断数列}{nS 是否是数列}{nd 的分隔数列,并说明理由; (3)设nn nT aq c,1-=是}{nc 的前n 项和,若数列}{nT 是}{nC 的分隔数列,求实数q a ,的取值范围?2018年上海市普通高校春季招生统一文化考试数学试卷参考答案:一、填空题:1、()()+∞-∞-,11,Y ;2、3;3、()1,0;4、2;5、15;6、13422=+y x ;7、5;8、180;9、4;10、⎪⎪⎭⎫⎝⎛∞+,33;11、⎥⎦⎤⎝⎛619611ππ,;12、4.4; 二、选择题:13、A ;14、C ;15、D ;16、B ; 三、解答题:17、(1)6621+;(2)23-; 18、(1)()()0,30,3-,;(2)215-;19、(1)41;(2)ο59.9; 20、解析:(1)()()1,011log )(11log 112212∈⎪⎭⎫ ⎝⎛-=⇒⎪⎪⎭⎫ ⎝⎛-=⇒-=-x x x f y x y x;(2)()()xxxxx a a a a y 2122211211⋅++=⋅+⋅⋅+=-,设02>=t x,则()111222+++=+++=ata at a t a at t y ,因为0>a ,所以a ta at 2≥+,当且仅当1=t 时取等号,所以12122++≥+++a a a t a at ,即()⎥⎦⎤ ⎝⎛+∈211,0a y ;(3)()223222221122+⋅+⋅-=⋅+-⋅+=x xxx a t a a a a x g ,设tx=2,因为()0,∞-∈x , 所以()1,0∈t ,则()att a at g 322++-=,若at tt a 222=⇒=,1°当12≥a时,即20≤<a ,a tt a y 322++=单调递减,所以()+∞++∈,232a a y ,则()⎪⎭⎫⎝⎛++-∈0,232a a a a g ,且()2302++-=a a a g ,故满足()()0g x g ≥,符合题意; 2°当120<<a 时,即2>a ,则a a a aa tt a y 322322322+=+⋅≥++=,则()()0,322-∈a g ,因为()()02log 2ming a g x g ≠⎪⎪⎭⎫ ⎝⎛=,故不符合题意,舍去;综上:(]2,0∈a 。
(完整版)2018山东春季高考数学试题及答案()

山东省2018年普通高校招生(春季)考试数学试题卷一(选择题,共60分)一、选择题(本大题20个小题,每小题3分,共60分。
在每小题列出的四个选项中,只有一项符合题目要求,请将符合题目要求的选项字母代号选出,并填涂在答题卡上)1.已知集合M={a,b},N={b,c},则M∩N等于()(A)∅(B){b} (C){a,c} (D){a,b,c}2.函数f(x)=的定义域是()11-++xxx(A)(-1,+∞)(B)(-1,1)∪(1,+∞)(B)[-1,+∞)(D)[-1,1)∪(1,+∞)3.奇函数y=f(x)的局部图像如图所示,则()(A)f(2)> 0 > f(4) (B)f(2)< 0 < f(4)(C)f(2)> f(4)> 0 (D)f(2)< f(4)< 04.不等式1+lg <0的解集是()(A)(-,0)∪(0,) (B) (-,)110110110110(C) (-10,0)∪(0,10)(D)(-10,10)5.在数列{a n}中,a1=-1,a2=0,a n+2=a n+1+a n,则a5等于()(A)0 (B)-1 (C)-2 (D)-36. 在如图所示的平角坐标系中,向量的坐标是()AB(A)(2,2) (B)(-2,-2)(C)(1,1) (D)(-1,-1)7.圆的圆心在()()()22111x y++-=(A) 第一象限 (B) 第二象限(C) 第三象限 (D) 第四象限8.已知,则“”是“ ”的()a b R∈、a b>22a b>(A)充分不必要条件 (B)必要不充分条件(C)充要条件 (D)既不充分也不必要条件9.关于直线,下列说法正确的是():20,l x-+=(A)直线的倾斜角60° (B)向量=,1)是直线的一个方向向量l v lxy(第6题图)(第3题图)ath10.景区中有一座山,山的南面有2条道路,山的北面有3条道路,均可用于游客上山或下山,假设没有其他道路,某游客计划从山的一面走到山顶后,接着从另一面下山,则不同走发的种数是()(A) 6 (B) 10(C) 12 (D) 2011.在平面直角坐标系中,关于x,y的不等式Ax+By+AB>0(AB≠0)表示的区域(阴影部分)可能是12.已知两个非零向量a与b的夹角为锐角,则()(A)0a b⋅>(B)0a b⋅<(B)(C)0a b⋅≥(D)0a b⋅≤13.若坐标原点(0,0)到直线的距离等于,则角θ的取值集合是()(A) (B)(C) )(D)14.关于x,y的方程,表示的图形不可能是()15.在的展开式中,所有项的系数之和等于()(A)32 (B)-32 (C)1 (D)-116. 设命題p: 53,命題q: {1} ⊆{0, 1, 2},则下列命題中为真命題的是()≥(A) p∧q (B) ﹁p∧q (C) p∧﹁q (D) ﹁p∨﹁q17.己知抛物线x²=ay(a≠0)的焦点为F,准线为l,该抛物线上的点M到x轴的距离为5,且|MF |=7,则焦点F到准线l的距离是()(A) 2 (B) 3 (C) 4 (D) 518.某停车场只有并排的8个停车位,恰好全部空闲,现有3辆汽车依次驶入,并且随机停放在不同车位,则至少有2辆汽车停放在相邻车位的概率是()2,2k k Zπθθπ⎧⎫|=±∈⎨⎬⎩⎭sin0x yθ-+=),2k k Zπθθπ⎧⎫|=±∈⎨⎬⎩⎭,4k k Zπθθπ⎧⎫|=±∈⎨⎬⎩⎭2kθθπ⎧|=±⎨5(2)x y-(A)(B) 1452815 (C) (D)1497619.已知矩形ABCD ,AB= 2BC ,把这个矩形分别以AB 、BC 所在直线为轴旋转一周,所围成几何体的侧面积分别记为S 1、S 2,则S 1与S 2的比值等于( )(A)(B) 1 (C) 2 (D) 42120.若由函数y= sin(2x+)的图像变换得到y=sin()的图像,则可以通过以下两个步骤完3π32π+x 成:第一步,把y= sin(2x+)图像上所有点的横坐标变为原来的4倍,纵坐标不变;第二步,可以把3π所得图像沿x 轴 ( )(A)向右平移个单位 (B)向右平移个单位3π125π(C) 向左平移个单位 (D)向左平移个单位3π125π二、填空题(本大题5个小题,每小题4分,共20分。
2018年春季七年及下册数学期末试卷与答案

2018年春季期末试卷七年级数学(满分:150分;考试时间:120分钟;考试形式:闭卷)注意:本试卷分为“试卷”和“答题卡”两部分,答题时请按答题卡中的“注意事项”要求认真作答,答案写在答题卡上相应位置。
一、精心选一选(每小题4分,共40分) 1.下列四个数中,最小的数是( )A .0B .4-C .π-D .22.下列各式中,正确的是( )4± B.393= C.5)5(2=- D.4412=⎪⎭⎫⎝⎛ 3.2018年九年级体育中考已经结束,莆田市教研室从各校随机抽取1000名考生的50米跑成绩进行调查分析,这个问题的样本容量是( )A .1000B .1000名C .50米 D.1000名考生的50米跑成绩 4.在平面直角坐标系中,点P (-1,3)在( )A .第一象限B .第二象限C .第三象限D .第四象限 5.下列各组数中,不是..12=-yx 的解是( )A .⎪⎩⎪⎨⎧-==210y x B .⎩⎨⎧==01y x C .⎩⎨⎧-=-=11y x D .⎩⎨⎧==11y x 6.点M 向左平移4个单位长度后的坐标是(-1,2),则点M 的坐标是( )A.(3,2)B.(-5,2)C.(-1,6)D.(-1,-2)7.如图数轴上表示的是下列哪个不等式组的解集( ).A .⎩⎨⎧<->3 2x xB .⎩⎨⎧<-≥3 2x xC .⎩⎨⎧≤->3 2x xD .⎩⎨⎧≤-≥32x x第8题 第9题8.如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )A .45°B .30°C .22.5°D .15°9.如图,能判断直线AB ∥CD 的条件是( )A .∠1=∠2B .∠3=∠4C .∠3+∠4=180°D .∠1+∠3=180° 10.若关于y x ,的方程组⎩⎨⎧=++=+3313y x k y x 的解为y x ,,且满足42<<k ,则y x -的取值范围是( )A.210<-<y x B. 10<-<y x C.13-<-<-y x D.11<-<-y x 二、细心填一填(每小题4分,共24分)11.计算: _____________12.在30个数据中,最大值为101,最小值为42,若取组距为10, 可将这组数据分为 组。
2018年春八年级下册数学期末试卷及答案(新人教版)

2018年春八年级数学期末试卷及答案〔新人教版〕一、选择题〔此题共10小题,总分值共30分〕 1.二次根式21、12 、30 、x+2 、240x 、22y x +中,最简二次根式有〔 〕个。
A 、1 个B 、2 个C 、3 个D 、4个 2.假设式子23x x --有意义,则x 的取值范围为〔 〕.A 、x≥2B 、x≠3C 、x≥2或x≠3D 、x≥2且x≠33.如果以下各组数是三角形的三边,那么不能组成直角三角形的一组数是〔 〕A .7,24,25B .1113,4,5222C .3,4, 5D .114,7,822 4、在四边形ABCD 中,O 是对角线的交点,能判定这个四边形是正方形的是〔 〕〔A 〕AC=BD ,AB∥CD ,AB=CD 〔B 〕AD∥BC ,∠A=∠C〔C 〕AO=BO=CO=DO ,AC ⊥BD 〔D 〕AO=CO ,BO=DO ,AB=BC5、如下左图,在平行四边形ABCD 中,∠B =80°,AE 平分∠BAD 交BC 于点E ,CF ∥AE 交AE 于点F ,则∠1=〔 〕1FEDCBAA .40°B .50°C .60°D .80°6、表示一次函数y =mx +n 与正比例函数y =mnx (m 、n 是常数且mn ≠0)图象是〔 〕7.如下图,函数x y =1和34312+=x y 的图象相交于〔-1,1〕,〔2,2〕两点.当21y y >时,x 的取值范围是〔 〕A .x <-1B .—1<x <2C .x >2D . x <-1或x >2 8、 在方差公式()()()[]2222121x x x x x x nS n -++-+-=中,以下说法不正确的选项是〔-1,1〕1y 〔2,2〕2yxyO〔第7题〕BCADO〔 〕A. n 是样本的容量B. n x 是样本个体C. x 是样本平均数D. S 是样本方差9、多多班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量〔单位:本〕,绘制了如图折线统计图,以下说法正确的选项是〔 〕 〔A 〕极差是47〔B 〕众数是42〔C 〕中位数是58〔D 〕每月阅读数量超过40的有4个月10、如上右图,在△ABC 中,AB =3,AC =4,BC =5,P 为边BC 上一动点,PE ⊥AB 于E ,PF ⊥AC 于F ,M 为EF 中点,则AM 的最小值为【 】A .54 B .52C .53D .65二、填空题〔此题共10小题,总分值共30分〕11.48-133-⎛⎫⎪ ⎪⎝⎭+)13(3--30 -23-=12.边长为6的大正方形中有两个小正方形,假设两个小正方形的面积分别为S 1,S 2,则S 1+S 2的值为〔 〕13. 平行四边形ABCD 的周长为20cm ,对角线AC 、BD 相交于点O ,假设△BOC 的周长比△AOB 的周长大2cm ,则CD = cm 。
2018年苏教版小学三年级下册数学期末试卷共10套

苏教版小学三年级下册数学期末试卷年班: 姓名:一、填空题(每空3分,共63分)1、1992年的二月份有( )天,八、九、十月共有( )天.2、除数是12,商是7,余数是11,被除数是( ).3、6米=()分米 2400平方分米=()平方米4、一个正方形的面积是16平方分米,它的一条边长是( )厘米.5、某年的11月27日是星期日,这一年的12月3日是星期( ).6、两个数的商是20,如果被除数和除数都扩大10倍,商是( ).7、一列火车上午6:34从北京开往沈阳,当天下午5:15到达,路上共用了( )小时( )分.8、40个梨分给3个班,一班分20个,其余平均分给二、三班,二班分( )个。
10、观察下列各组数的规律,在()里填上适当的数。
① 1,1,2,3,5,8,(),()。
② 3,9,27,81,(),(),2187。
③ 1,4,9,16,25,(),()。
11、根据图形排列的规律回答:(画图表示)○●●△○●●△……第12个是。
12、把0、1、2、3、4、5、6、7、8、9这10个数字分别填入下列算式“○”中,每个数只能用一次。
○+○=○○-○=○○×○=○○二、计算(6分)900÷3+6 54-9 ÷3三、应用题(每题6分,共30分)1、学校文化节挂彩灯,按照2盏红灯、3盏绿灯,2盏红灯、3盏绿灯……的顺序排列。
那么,第28盏是什么灯?(10分)3、有一筐苹果连筐重42千克,卖掉一半苹果后,连筐重22千克。
这筐苹果原有多少千克?(10分)4、孙老师、赵老师、刘老师,他们分别担任学校的音乐、美术、体育课。
孙老师说:“我不教美术。
”赵老师说:“我不会唱歌,也不会画画。
”那么,孙老师担任()课,赵老师担任()课,刘老师担任()课。
(11分)苏教版三年级下册期末考试复习一、填空(25分)1、4000米=()千米2吨=()千克3平方米=()平方厘米700平方厘米=()平方分米2、9分米=米 3角=元 6厘米=分米3、7角=()元 2.4元=()角1米6分米=()米4、用分数表示各个图里的涂色部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年春季期七年级月考二
数学
一,选择题:本大题共12小题,每小题3分,共36分,每小题给出的四个选项中,只有一项是正确的,把答案前的字母写在括号内)。
1.下列各图中,∠1与∠2是对顶角的是…………………………………………()
A.B. C. D.
2.用统计图来描述某班同学的身高情况,最合适的是………………………………()A.条形统计图 B.折线统计图
C.扇形统计图 D.频数分布直方图
3.给出了过直线外一点作已知直线的平行线的方法,其依据是………………()
A.内错角相等,两直线平行 B.同位角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
4.若m是任意实数,则点M(m2+2,﹣2)在第…………………………()象限.A.一 B.二 C.三 D.四
5.下列调查中,适宜采用全面调查方式的是……………………………………()
A.调查一架“歼20”战机各零部件的质量 B.调查某品牌圆珠笔芯的使用寿命
C.调查市场上酸奶的质量情况 D.调查我市市民对上届巴西奥运会吉祥物的知晓率
6.如图1,能判定EC∥AB的条件是………………()
A,∠B=∠ACB B.∠B=∠ACE
C.∠A=∠ACE D.∠A=∠ECD
图1
7,设a>b>0,c为常数,给出下列不等式①a﹣b>0;②ac>bc;
③<;④b 2>ab ,其中正确的不等式有………………………………………( ) A .1个 B .2个
C .3个
D .4个
8.某校260名学生参加植树活动,要求每人值4~7棵,活动结束后调查了每名学生的植树量,并分为四种类型,A :4棵;B :5棵;C :6棵;D :7棵.并结合调查数据作出如图2所示的扇形统计图,根据统计图提供的信息,可知该校植树量不少于6棵的学生有…………………………………………………………( ) A .26名 B .52名 C .78名 D .104名
9.已知二元一次方程组的解是
,则(2a ﹣1)(b+1)的值为…( )
A .0
B .2
C .﹣2
D .6
10.平面直角坐标系中的点P (2﹣m ,m )在第一象限,则m 的取值范围在数轴上可表示为………………………………………………………………………( )
A .
B .
C, D .
11.下列命题:①直线a 、b 、c 在同一平面内,如果a ⊥b ,b ∥c ,那么a ⊥c .
②0.01是0.1的算术平方根.③如果a >b ,那么ac 2
>bc 2
.④如果两个角的两边分别平行,那么这两个角相等.⑤如果a <b <0,那么0<ab <a 2.其中真命题的个数有…………( ) A .1个 B .2个 C .3个
D .4个
12.同学们喜欢足球吗足球一般是用黑白两种颜色的皮块缝制而成,如图3所示,黑色皮块是正五边形,白色皮块是正六边形.若一个球上共有黑白皮块32块,请你计算一下,黑色皮块和白色皮块的块数依次为…………………………………………( ) A .16块、16块 B .8块、24块 C .12块、20块 D .20块、12块
二,填空题:(共6小题,每小题3分,共18分,请将正确的答案填
写
图2
图3
在横线上)。
13,把方程3x -y=2改写成用含x 的代数式表示y 的形式,得 . 14,已知
=18.044,那么±
= .
15.已知一个样本容量为60,在频数分布直方图中,各小长方形的高比为2:4:1:3,那么第二组的频数是 . 16.不等式组⎩⎨
⎧->-≥-3
120
1x x 的整数解是
17.小东将书折过来,该角顶点A 落在F 处,BC 为折痕,如图4所示,若DB 平分∠FBE ,∠DBE 比∠CBA 大30°,设∠CBA 和∠DBE 分别为x °、y °,那么可求出这两个角的度数的方程组是 .
18.某原料供应商对购买其原料的顾客实行如下优惠办法:(1)一次购买金额不超过1万元的不予优惠;(2)一次购买金额超过1万元,但不超过3万元的九折优惠;(3)一次购买金额超过3万元,其中3万元九折优惠,超过3万元的部分八折优惠。
某厂因库存原因,第一次在该供应商处购买原料7800元,第二次购买原料26100元,如果他是一次性购买同样的原料,可少付款 元.
三,解答题 :(本大题共8小题,满分66分,)
19,计算,解方程组,不等式(组) (1),(4分)计算
(
﹣
)
+
+
(2),(4分)解方程组
.
(3),(4分)解不等式1-
; (4),(5分)解不等式组,
并把它的解集表示在数轴上
图4
20.(5分)赵军说不等式2a >3a 永远不会成立,因为如果在这个不等式两边同除以a ,就会出现2>3这样的错误结论.你同意他的说法对吗?若同意说明其依据,若不同意说出错误的原因.
21.(7分)如图5,AB ∥CD ,E 为AB 上一点,∠BED=2∠BAD . (1)求证:AD 平分∠CDE ;
(2)若AC ⊥AD ,∠ACD+∠AED=165°,求∠ACD 的度数.
22.(6分)某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市20000名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如下图表:
(1)表中a 和b 所表示的数分别为:a ,b ; (2)请在图中补全频数分布直方图;
(3)如果把成绩在70分以上(包括70分)定为合格,那么该市20000名九年级考生数学成绩为合格的学生约有多少名?
图5
23,(6分)已知方程组的解为非负数,求整数a 的值.
24,(5分)如图6,点A,B 的坐标分别为(1,0),(0,2),若将线段AB 平移到A 1B 1的坐标分别为(2,a ),(b ,3),试求a 2
-2b 的值.
25.(9分)某电器超市销售每台进价分别为200元、170元的A 、B 两种型号的电风扇,下表是近两周的销售情况:(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A 、B 两种型号的电风扇的销售单价; (2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A 种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
图6
26.(11分)如图1,点A的坐标为(0,3),将点A向右平移6个单位得到点B,过点B作BC ⊥x轴于C.
(1)求B、C两点坐标及四边形AOCB的面积;
(2)点Q自O点以1个单位/秒的速度在y轴上向上运动,点P自C点以2个单位/秒的速度在x轴上向左运动,设运动时间为t秒(0<t<3),是否
存在一段时间,使得S△BOQ<,若存在,求出
t的取值范围;若不存在,说明理由.
(3)求证:S四边形BPOQ是一个定值.。
