立体几何建系方法
立体几何建系的标准写法

立体几何建系的标准写法通常使用向量表示。
以下是常见的立体几何建系的标准写法示例:
坐标系表示:
直角坐标系:使用三个相互垂直的坐标轴(通常标记为x、y 和z)来表示空间中的点。
例如,(x, y, z) 表示空间中的一个点。
柱面坐标系:使用径向距离、极角和高度来表示点的位置。
例如,(ρ, θ, h) 表示柱面坐标系中的一个点。
向量表示:
位置向量:使用位置向量表示从原点到点的有向线段。
例如,OA 表示从原点O 到点 A 的位置向量。
方向向量:表示一个方向的向量,通常以单位向量的形式表示。
例如,u 表示一个单位方向向量。
平面表示:
法线向量:表示平面的法线方向的向量,通常以单位向量的形式表示。
例如,n 表示平面的法线向量。
需要注意的是,不同的教材和学科可能会有略微不同的标准写法。
在具体的问题和文献中,可能会使用特定的符号和约定来表示立体几何建系。
因此,在使用标准写法时,最好参考所使用的教材、规范或参考资料,以确保一致性和准确性。
高考中立体几何题的建系方法

ʏ安徽省长丰县第一中学 鲍明娟立体几何是高考的必考知识点,其中解答题通常设置两问,第一问常考平行㊁垂直等证明问题;第二问通常需要利用建系法解决与角度㊁长度相关的计算问题㊂在每道小题的设置上力求证明与求解并重㊂试题的命制载体有倾向于不规则几何体的趋势,但仍以 方便建系 为原则,重点考查运算及综合应用的能力㊂因为建系的目的是将立体几何问题转化为代数运算问题,所以我们建立一个合适的空间直角坐标系以降低运算量是很必要的㊂本文归纳了立体几何问题中常见的建系方法,供同学们复习时参考㊂方法一、利用共交点的互相垂直的三条直线构建空间直角坐标系在三维空间中,我们通常使用一个右手定则来定义三个垂直的轴分别为x 轴,y 轴,z 轴,这三个轴应当满足右手四指从x 轴正方向按逆时针旋转45ʎ或135ʎ(直观图中)到y 轴正方向时,大拇指所指方向是z 轴的正方向,三条轴的公共交点就是空间直角坐标系的坐标原点,简称右手空间直角坐标系㊂图1例1 如图1,在直三棱柱A B C -A 1B 1C 1中,A A 1=A B =A C ,A M ң=2M C ң,C 1N ң=2N A 1ң㊂(1)证明:B 1C ʊ平面B MN ;(2)若B C =3A B ,求二面角B -MN -A的余弦值㊂图2解析:(1)如图2,延长MN ,A A 1交于点P ,连接P B ,设A B 1ɘP B=Q ,连接M Q ,由P A 1P A=N A 1M A =12,可知P A=2A A 1,所以Q B 1Q A =B B 1P A =A A 1P A =12㊂因为M C A M =12,所以A M A C =A Q A B 1=23㊂又øM A Q=øC A B 1,所以әM A Q ʐәC A B 1,所以M Q ʊC B 1㊂又因为C B 1⊄平面B MN ,所以B 1C ʊ平面B MN ㊂(2)因为A B =A C ,B C =3A B ,所以øB A C =120ʎ㊂在әA B C 内过点A 作A B 图3的垂线A z ,由直棱柱的定义可得A A 1ʅA B ,A A 1ʅA z ㊂以A 为坐标原点,建立如图3所示的空间直角坐标系A -x yz ㊂设A B =3a ,则B (3a ,0,0),M (-a ,0,3a ),N -a 2,3a ,3a 2,所以B Mң=(-4a ,0,3a ),B N ң=-7a 2,3a ,3a 2,所以可得平面B MN 的一个法向量为n 1=(23,3,8)㊂又因为A M ң=(-a ,0,3a ),A N ң=-a 2,3a ,3a 2,所以可得平面A MN 的一个法向量为n 2=(3,0,1)㊂所以c o s <n 1,n 2>=n 1㊃n 2|n 1||n 2|=142ˑ79=77979,即二面角B -MN -A 的余弦值为77979㊂点评:本题先由直棱柱的定义得出A A 1是一条轴,接着只需在平面A B C 中找两条相交垂直的直线即可,而әA B C 是等腰三角形,且B C =3A B ,易得øB A C =120ʎ,从而确定垂直于A B 的直线A z 的位置㊂这样就找到三条共交点A 的两两垂直的直线,最后建系㊂我们一般取竖直向上方向为z 轴正方向(如本题中取A z ),用右手大拇指指向z 轴,剩下两条直线四指从x 轴正方向(本题中A B )按逆时针方向转45ʎ或135ʎ(直观图中)至y 轴正方向(本题中A A 1),如图3建系㊂方法二、利用线面垂直关系构建空间直角坐标系由线面垂直的定义可知,一条直线垂直于平面,则这条直线垂直于平面内任意一条直线㊂因此,我们选择这条直线为一条轴,再在与它垂直的平面内找两条相交且垂直的直线作为剩下两条轴,最后转化为共交点的三条直线来建系㊂若不共交点,可以平移至共交点来建系,但遵循的原则是让更多的点落在轴上,以便于计算㊂图4例2 如图4,在四棱锥P -A B C D 中,底面A B C D 是直角梯形,A D ʅA B ,A B ʊD C ,P Aʅ底面A B C D ,E 为棱P C 的中点,A D =D C =A P =2A B =2㊂(1)证明:B E ʊ平面P A D ㊂(2)在棱P C 上是否存在点F ,使得二面角F -A D -C 的余弦值为1010若存在,求出P FP C的值;若不存在,请说明理由㊂解析:(1)取P D 的中点为G ,连接A G ,图5E G ,如图5,因为G 和E 分别为P D 和P C 的中点,所以E G ʊC D ,且E G =12C D ㊂又因为底面A B C D 是直角梯形,C D =2A B ,A B ʊC D ,所以A B ʊG E ,且A B =G E ,所以四边形A B E G 为平行四边形,所以A G ʊB E ㊂因为A G ⊂平面P A D ,B E ⊄平面P A D ,所以B E ʊ平面P A D ㊂(2)以A 为坐标原点,A B ,A D ,A P 所在图6直线分别为x 轴,y 轴,z 轴,建立如图6所示的空间直角坐标系A -x yz ,可得B (1,0,0),C (2,2,0),D (0,2,0),P (0,0,2),P Cң=(2,2,-2)㊂由F 为棱P C 上一点,设P F ң=λP C ң=(2λ,2λ,-2λ)(0ɤλɤ1),则A F ң=A P ң+P F ң=(2λ,2λ,2-2λ),A D ң=(0,2,0)㊂设平面F A D 的法向量为n =(x ,y ,z ),则n ㊃A F ң=2λx +2λy +(2-2λ)z =0,n ㊃A D ң=2y =0,令z=λ,得x =λ-1,则n =(λ-1,0,λ)㊂取平面A D C 的一个法向量为m =(0,0,1),设二面角F -A D -C 的平面角为α,则c o s α=m ㊃n|m ||n |=λ2λ2-2λ+1=1010,化简得8λ2+2λ-1=0,解得λ=14,故存在满足条件的点F ,此时P F P C =14㊂点评:本题中P A ʅ底面A B C D ,选A P为一条轴,接着由A D ʅA B ,得出A P ,A D ,A B 是两两垂直的三条直线,转化为共交点A 为坐标原点建系,先选竖直向上方向AP 所在直线为z 轴,再按右手定则确定A B 所在直线为x 轴,A D 所在直线为y 轴,如图6建系㊂图7例3如图7所示,在R t әA B C 中,øC =90ʎ,B C =3,A C =6,D ,E 分别是线段A C ,AB 上的点,D E ʊBC 且DE =2,将әA D E 沿折起到әA 1D E 的位置,图8使得A 1C ʅC D ,如图8所示㊂(1)若点N 在线段A 1B 上,且2B N =N A 1,求证:E Nʊ平面A 1C D ;(2)若M 是A 1D 的中点,求平面M E B 与平面D E B C 的夹角的余弦值㊂图9解析:(1)如图9所示,在әA 1C B 中,过N 作N F ʊC B 交A 1C 于点F ㊂因为A 1N A 1B =23,所以F N =23B C ㊂在әA B C 中,D E =23B C ,D E ʊB C ,所以F N ʊD E ,F N =D E ,所以四边形D E N F 为平行四边形,所以D F ʊN E ㊂又因为D F ⊂平面A 1C D ,E N ⊄平面A 1C D ,所以E N ʊ平面A 1C D ㊂(2)因为D E ʊB C ,øC =90ʎ,所以D EʅA C ,所以D E ʅA 1D ,D E ʅC D ㊂因为A 1D ɘC D =D ,A 1D ,C D ⊂平面A 1C D ,所以D E ʅ平面A 1C D ,所以B C ʅ平面A 1C D ㊂图10又因为A 1C ʅC D ,所以可建立如图10所示的空间直角坐标系C -x yz ,易知A 1(0,0,23),D (2,0,0),C (0,0,0),E (2,2,0),B (0,3,0),M (1,0,3),则E M ң=(-1,-2,3),E B ң=(-2,1,0)㊂设平面M E B 的法向量为n 1=(x ,y ,z ),则n 1㊃E M ң=-x -2y +3z =0,n 1㊃E B ң=-2x +y =0,令x =3,得n 1=(3,23,5)㊂可取平面D E B C 的一个法向量为n 2=(0,0,1),设平面M E B 与平面D E B C 的夹角为θ,则c o s θ=|c o s <n 1,n 2>|=|n 1㊃n 2||n 1||n 2|=51ˑ40=104,所以平面M E B 与平面D E B C 的夹角的余弦值为104㊂点评:本题是翻折问题㊂在处理翻折问题时,首先要确定在翻折过程中哪些量与位置关系不变(同一个平面内的位置关系不变),可以将这些都作为已知条件㊂本题中,әA D E 在沿D E 折起到әA 1D E 的过程中保持不变,即在әA 1D E 中,有D E ʅA 1D ,D E =2,A 1D =4;直角梯形D C B E 也不变,即有D E ʊB C ,B C =3,C D =2,D E ʅC D ㊂将以上不变条件当作本题的已知条件易得出B C ʅ平面A 1C D ,再结合翻折后所得几何体的题给条件A 1C ʅC D ,于是可以以C 为坐标原点,C A 1竖直向上方向为z 轴正方向建系(如图10)㊂方法三、利用面面垂直关系构建空间直角坐标系由面面垂直的性质定理,首先找到两个平面的交线,再结合已知条件在两个平面中选择其中一个平面,在该平面内找到或作出与交线垂直的一条直线,则这条直线垂直于另一个平面,最后转化为线面关系来建系㊂图11例4 如图11,在四棱锥P -A B C D 中,底面A B C D是菱形,A C 与B D 交于点O ,øB A D =60ʎ,P A =A B =2,P A ʅA C ,平面P A C ʅ平面P B D ,M 为线段P B 上的一点㊂(1)证明:P A ʅ平面A B C D ;(2)当A M 与平面P B D 所成的角的正弦值最大时,求平面M A C 与平面A B C D 的夹角的余弦值㊂图12解析:(1)如图12,连接P O ,过点A 作P O 的垂线,垂足为H ㊂因为平面P A C ʅ平面P B D ,且交线为P O ,所以A H ʅ平面P B D ㊂又因为B D ⊂平面P B D ,所以B D ʅA H ㊂又因为四边形A BCD 为菱形,所以B D ʅA C ㊂又因为A C ɘA H =A ,所以B D ʅ平面P A C ㊂又因为P A ⊂平面P A C ,所以B D ʅP A ㊂又因为P A ʅA C ,A C ɘB D =O ,所以P A ʅ平面A B C D ㊂(2)连接MH ,由(1)知øA MH 为A M 与平面P B D 所成的角,所以s i n øA MH =A HA M㊂又因为P A =A B ,所以当M 为P B 的中点时,A M ʅP B ,A M 最小,故s i n øA MH取最大值㊂图13如图13,以O 为坐标原点,O A ,O B ,O z 所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系O -x yz ,则A (3,0,0),B (0,1,0),C (-3,0,0),P (3,0,2),M 32,12,1,所以A M ң=-32,12,1,A C ң=(-23,0,0)㊂设平面A M C 的法向量为n =(x ,y ,z ),则n ㊃A M ң=-32x +12y +z =0,n ㊃A C ң=-23x =0,令y =2,得z =-1,则n =(0,2,-1)㊂易知平面A B C D 的一个法向量为m =(0,0,1),设平面M A C 与平面A B C D 的夹角为θ,则|c o s θ|=|m ㊃n ||m ||n |=15=55㊂所以当A M 与平面P B D 所成的角的正弦值最大时,平面M A C 与平面A B C D 的夹角的余弦值为55㊂点评:本题抓住平面P A C ʅ平面P B D ,且平面P A C 与平面P B D 的交线为P O ,于是连接P O ,在әA P O 中,过点A 作P O 的垂线,垂足为H ,从而得到A H ʅ平面P B D ,所以B D ʅA H ,又因为A B C D 是菱形,所以B D ʅA C ,于是得出B D ʅ平面P A C ,所以B D ʅP A ,又已知P A ʅA C ,所以得出P A ʅ平面A B C D ,又因为在菱形A B C D 中,有O A ʅO B ,于是可以将P A 平行移动至O z ,再以公共交点O 为坐标原点,以竖直向上方向的O z 为z 轴正方向建系(如图13)㊂图14例5 如图14,在等腰梯形A B C D 中,E 为边B C 上的一点,A D ʊB C ,A D =C D =1,әA B E是一个等图15边三角形,现将әA B E 沿着A E 翻折至әA P E ,如图15㊂(1)在翻折过程中,求四棱锥P -A E C D 体积的最大值;(2)当四棱锥P -A E C D 的体积最大时,求平面A E P 与平面P C D 的夹角的余弦值㊂解析:(1)依题意知әA B E 是边长为1的等边三角形,且高为32㊂四边形A E C D 是边长为1的菱形,且øE C D =π3,S 菱形A E C D =1ˑ1ˑs i nπ3=32㊂在翻折过程中,当平面A P E ʅ平面A E C D 时,四棱锥P -A E C D 的体积取得最大值,且最大值为13ˑ32ˑ32=14㊂(2)设A E 的中点为O ,连接O P ,O D ,当平面A P E ʅ平面A E C D 时,四棱锥P -A E C D 的体积取得最大值㊂因为әP A E 是等边三角形,所以O P ʅA E ㊂因为平面A P E ɘ平面A E C D =A E ,O P ⊂平面P A E ,O P ʅA E ,所以O P ʅ平面A E C D ㊂又O D ⊂平面A E C D ,所以O P ʅO D ㊂连接D E ,则әA D E 是等边三角形,所以O D ʅA E ㊂图16以O 为坐标原点,建立如图16所示的空间直角坐标系O -x yz ,则平面P A E 的法向量为O D ң=0,32,0 ,P 0,0,32,C 1,32,0 ,D C ң=(1,0,0),P C ң=1,32,-32㊂设平面P C D 的法向量为n =(x ,y ,z ),则n ㊃D C ң=x =0,n ㊃P C ң=x +32y -32z =0,令y =1,得n =(0,1,1)㊂设平面A E P 与平面P C D 的夹角为θ,则c o s θ=O D ң㊃n |O D ң||n |=3232ˑ2=22㊂点评:本题中,әB A E 在翻折至әP A E时没有改变,所以әP A E 仍然是一个等边三角形,四边形A E C D 也没有改变,仍然是菱形㊂当四棱锥P -A E C D 的体积取最大值时,需平面A P E ʅ平面A E C D ㊂我们首先取A E 的中点为O ,连接O P ,O D ㊂因为әP A E 是等边三角形,所以O P ʅA E ,又因为平面A P E ʅ平面A E C D ,所以O P ʅ平面A E C D ,可得O P ʅO D ,又因为әA D E 是等边三角形,所以O D ʅA E ,所以我们得到了O P ,A E ,O D 三条直线两两垂直,于是可以以这三条直线的公共交点O 为坐标原点,竖直向上方向的O P 为z 轴正方向建系(如图16)㊂(责任编辑 王福华)。
2016届高三一轮复习---立体几何如何建系找坐标求法向量

1、如图,在四棱锥P-ABCD 中,PA⊥平面ABCD, AB//CD,∠DAB=90°,PA=AD=DC=1,AB=2,M 为PB 的中点. 建立适当的坐标系,表示图中所有点的坐标。
并求平面ACM 法向量。
解;以A 为坐标原点.以AD ,AB ,AP 所在直线为x,y,z 轴,建立如图空间直角坐标系,则2.多面体EDABC 中,AD ⊥平面ABC , AC ⊥BC,,AD=21CE=1,AC=1.BC=2,M 为BE 中点.,建立适当的坐标系,表示图中所有点的坐标。
求平面DCM 法向量。
解;以C 为坐标原点.以CA,CB,CE所在直线为x,y,z 轴,建立如图空间直角坐标系,则3、在直三棱柱ABC ——A 1B 1C 1中,AB AC且A1A=AB=AC=2,建立适当的坐标系,表示图中所有点坐标。
求出平面A 1BC 法向量解;以A为坐标原点.以AB,AC,AA1所在直线为x,y,z 轴,建立如图空间直角坐标系,则 .1.在四棱锥P-ABCD 中,AD ∥BC ,BC = 2AD =2=PA, Q 是线段PB 的中点.PA ⊥底面ABCD ,AD ⊥CD 建立适当的坐标系,表示图中所有点的坐标。
求出平面A 1QC 法向量2.如图,四棱锥S-ABCD的底面ABCD是直角梯形,侧面SAB是等边三角形, DC//AB,AB=2AD=2DC=2,O,E分别为AB、SD中点. DA 面SAB,建立适当的坐标系,表示图中所有点的坐标。
3.如图,四棱锥P—ABCD中,底面ABCD为平行四边形,DB=3,AB=2,AD=1,PD⊥底面ABCD建立适当的坐标系,表示图中所有点的坐标。
并求平面PBC与平面PBD的法向量。
.4.如图,四棱锥P—ABCD中,底面ABCD为平行四边形,Q是AD的中点,⊿ABD为正三角形,PQ⊥平面ABCD。
建立适当的坐标系,表示图中所有点的坐标。
并求平面PBD法向量。
5. 三棱柱ABC——A1B1C1中侧棱与底面垂直,且所有棱长都为4,D为CC1中点.建立适当的坐标系,表示图中所有点的坐标。
【高中数学】立体几何建系设点 专题课件 高二上学期数学人教A版(2019)选择性必修第一册

z
O
x
z
A1
A1 D1
B1
C1
z
D B1
C1
y
A
D
x
y
A
F B
F
B
x
E
C
E C
y
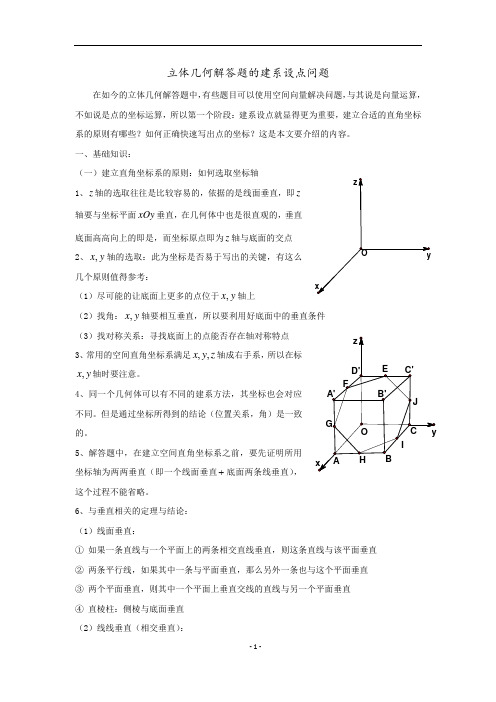
[例 1]如图,在棱长为 2 的正方体 ABCD-A1B1C1D1 中,E 为棱 BC 的中点,
F 为棱 CD 的中点.试建立适当的空间直角坐标系并确定各点坐标.
高二数学 空间向量 立体几何建系设点问题
引入
问题 使用空间向量解决立体几何问题,说是向量
运算,不如说是点的坐标运算,所以建系找点的 坐标就显得很重要,那么建立适当的空间直角坐 标系的原则有哪些?如何正确快速写出需要点的 坐标?
为此,这节课我们就来学习“建系设点方法”
回顾 一、空间直角坐标系
1.空间直角坐标系:在空间选定一点 O 和一个单位正交基底{i,j,k},以 O 为原点,分别以 i,j,k 的方向为正方向,以它们的长为单位长度建立三条数 轴:x 轴、y 轴、z 轴,它们都叫做坐标轴,这时我们就建立了一个空间直角坐标 系 Oxyz.
Oyz 平面内
投影点的坐标
(x,y,0)
(0,y,z)
(x,y,z) Ozx 平面内 (x,0,z)
用法:以上规律一般逆用,在写空间中点的坐标时,先写坐标平面内的投影 点的坐标,再确定第三个坐标,而第三个坐标为该点到该坐标平面的距离.
如在棱长为 1 的正方体中的点 B1,在 Oxy 平面内的投影为 B,而 B(1,1,0), 则 B1(1,1,1).
z
A1
D1
巧建系,妙解立体几何题

解题宝典立体几何问题侧重于考查同学们的空间想象能力和逻辑推理能力.在解答立体几何问题时,我们一般只有借助立体几何图形来进行分析,才能快速明确题目中点、线、面的位置关系,找到解题的突破口.建系法是解答立体几何问题的一种重要方法,而运用建系法解答立体几何问题的关键是建立合适的空间直角坐标系,通过空间直角坐标运算求得问题的答案.那么如何选取坐标轴和原点,建立合适的直角坐标系呢?主要有以下两种方法.一、根据几何体的性质和特点建系我们知道,空间直角坐标系中的三个坐标轴相互垂直,并相交于一点.因此,在解答立体几何问题时,可以根据简单几何体的特点和性质,尤其是长方体、直棱柱、直棱锥、圆柱的性质和特点来寻找垂直关系.当图形中出现三条直线两两互相垂直且交于一点时,可以将这三条直线看作坐标轴,将该交点视为坐标原点来建系.例1.(2019年全国卷Ⅱ理科·第17题)如图1,长方体ABCD -A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.若AE =A 1E ,求二面角B -EC -C 1的正弦值.图1图2分析:本题主要考查了二面角的求法.我们根据长方体的特点和性质可知长方体的所有侧棱都与底面垂直,且底面上由顶点出发的两条棱相互垂直,于是可将底面的其中一个顶点视为原点,以由顶点出发的三条棱为x 、y 、z 轴建立空间直角坐标系.然后根据题目给出的条件,找出相关点的坐标,求出两个平面、BEC 、ECC 1的法向量,再根据公式求出两个平面法向量的夹角余弦值,便可得出夹角的正弦值.解:以点D 为坐标原点,DA 的方向为x 轴的正方向,建立如图2所示的空间直角坐标系D -xyz .设正方形ABCD 的边长为1,||AA 1=2a ,则||A 1E =||AE =a ,所以||EB 1=||EB =a 2+1,因为ABCD -A 1B 1C 1D 1为长方体,所以B 1C 1⊥平面ABB 1A 1,且BE 在平面ABB 1A 1内,因此C 1B 1⊥BE .由题知BE ⊥EC 1,所以BE ⊥平面EB 1C 1.且EB 1在平面EB 1C 1内,则BE ⊥EB 1.在RtΔB 1EB 中,EB 12+EB 2=B 1B 2,即a 2+1+a 2+1=4a 2,所以a =1,所以B (1,1,0),C (0,1,0),E (1,0,1),C 1(0,1,2),所以 CE =(1,-1,1), CB =(1,0,0), CC 1=(0,0,2)设平面BCE 的法向量为n 1=(x 1,y 1,z 1),则ìíî n 1·CE =x 1-y 1+z 1=0, n 1·CB =x 1=0,,解得{x 1=0,z 1=y 1,取 n 1=(0,1,1),设平面CEC 1的法向量为 n 2=(x 2,y 2,z 2),则ìíî n 2·CE =x 2-y 2+z 2=0, n 2·CC 1=2z 2=0,解得{z 2=0,y 2=x 2,取 n 2=(1,1,0),所以cos n 1, n 2=n 1·n 2|| n 1·|| n 2=12.于是sin n 1, n 2=,故二面角B -EC -C 1的正弦值为.例2.如图3,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别是AB 、BB 1的中点,AA 1=AC =CB .求二傅灵欣廖小莲44解题宝典面角D -A 1C -E 的正弦值.图3图4分析:该几何体为直三棱柱,我们可以根据直三棱柱图形的特点和性质来建立空间直角坐标系.直棱柱的侧棱垂直于底面,只要根据题目的条件在直三棱柱的底面找到两条互相垂直且与侧棱有交点的直线,这样三条直线两两便会互相垂直,为建立空间直角坐标系创造了条件.求出相关点的坐标以及二面角所包含的两个平面的法向量,再根据公式便可求出二面角的余弦值,求得夹角的正弦值.解:由AC =CB =得ΔACB 是以∠C 为直角的等腰直角三角形,又因为是直三棱柱ABC -A 1B 1C 1,所以棱CC 1⊥底面ACB .故以点C 为原点、CA 的方向为x 轴,建立如图4所示的空间直角坐标系.设AB =2,则AA 1=AC =CB =AA 1=2,则A (2,0,0),B (0,2,0),D 0),A 1(2,0,2),C (0,0,0),又因为AA 1=BB 1=2,所以E(0,2,于是 CA 1=(2,0,2), CD =0),CE =(0,2,,设平面DA 1C 的法向量为n 1=(x 1,y 1,z 1),则ìíîïï n 1·CA 121+2=0,CD · n 1=2121=0,解得{x 1+z 1=0,x 1+y 1=0,取n 1=(1,-1,-1),设平面A 1CE 的法向量为n 2=(x 2,y 2,z 2),则ìíîïï n 2·AC 1=2x 222=0, CE · n 2=2y 222=0,解得ìíîïïx 2+z 2=0,y 2+12z 2=0,取n 2=(2,1,-2),所以cos n 1, n 2=n 1·n 2|| n 1·||n 2=,则sin n 1, n 2=故二面角D -A 1C -E 的正弦值为.在用建系法解答与长方体、直棱锥有关的立体几何问题时,可以根据长方体、直棱锥本身的性质和特点来建系,若无法根据几何体的性质和特点建系,可以根据题意创造条件来建系.二、利用线面垂直关系建立直角坐标系在建系时,z 轴往往是比较容易选取的,而坐标原点即为z 轴与底面的交点,那么我们只需要确定与z 轴垂直的坐标平面xOy ,且使x 轴、y 轴相互垂直即可.可以根据线面垂直关系来寻找与z 轴垂直的平面.首先要充分利用好底面中的垂直条件,然后根据线面垂直的判断定理得到相应的z 轴以及与z 轴垂直的平面,这样便可建立符合要求的空间直角坐标系.例3(2020年全国Ⅰ卷,第20题)如图5,四棱锥P -ABCD 的底面为正方形,PD ⊥底面ABCD .设平面PAD 与平面PBC 的交线为l .(1)证明:l ⊥平面PDC ;(2)已知PD =AD =1,Q 为l上的点,求PB 与平面QCD 所成角的正弦值的最大值.图5分析:我们可以先根据线面垂直的关系,即PD ⊥底面ABCD 来建立空间直角坐标系.而四棱锥P -ABCD 的底面为正方形,所以正方形的四条邻边相互垂直,于是可以以D 为坐标原点、DA 的方向为x 轴的正方向建立空间直角坐标系.求出相关点的坐标,设45方法集锦。
高中数学立体几何建系

在高中数学的立体几何中,建立坐标系是常见的方法之一。
建立坐标系可以帮助我们描述和研究立体图形的位置、形状和性质。
以下是一些常见的建系方法:
直角坐标系:在平面上建立直角坐标系,可以使用两个垂直的坐标轴(通常是x轴和y轴)来描述图形的位置和尺寸。
三维情况下,可以添加一个垂直于平面的z轴,形成三维直角坐标系。
柱面坐标系:柱面坐标系适用于柱面或圆柱体等具有柱状特征的图形。
它使用一个径向距离(r)和一个角度(θ)来描述图形上的点的位置。
球面坐标系:球面坐标系适用于球体或球壳等具有球状特征的图形。
它使用一个径向距离(ρ)、一个极角(θ)和一个方位角(φ)来描述图形上的点的位置。
斜二面角坐标系:斜二面角坐标系适用于描述两个平面的夹角关系,常用于研究平面与平面相交、平面与直线相交等问题。
在建系过程中,我们需要选择适当的坐标轴或坐标系,并定义坐标轴的正方向和原点位置,以及确定单位长度等。
这样可以建立一个坐标系,使得我们可以方便地进行立体图形的分析、计算和推导。
立体几何建系方法

立体几何建系方法立体几何是研究空间中图形的形状、大小、位置和相互关系的数学分支。
在立体几何中,建系是指确定和描述空间中图形的位置、方向和尺寸的方法。
建系方法有很多种,包括点线面建系、轴线建系、坐标建系等。
下面将详细介绍每种建系方法的原理和应用。
1.点线面建系点线面建系是最基本的建系方法之一,在立体几何的研究中有着广泛的应用。
点线面建系是通过确定一个点、一条线或一个平面来建立坐标系,从而确定其他点、线或面的位置和方向。
(1)点建系:通过确定一个点作为参考点,然后确定其他点相对于该参考点的位置和方向。
例如,在三维空间中,可以选择一个空间中的一些点作为原点,然后以该点为参考点确定其他点的位置和方向。
(2)线建系:通过确定两个点来确定一条线,然后确定其他点相对于该线的位置和方向。
例如,在三维空间中,选择两个不共线的点确定一条线,然后以该线为基准确定其他点的位置和方向。
(3)面建系:通过确定三个不共线的点来确定一个平面,然后确定其他点相对于该平面的位置和方向。
例如,在三维空间中,选择三个不共线的点确定一个平面,然后以该平面为基准确定其他点的位置和方向。
点线面建系在立体几何的分析中具有重要的作用,可以通过确定一些点、线或平面来确定其他点、线或平面的位置和方向关系。
例如,在计算机图形学中,点线面建系可以用于描述和操作三维模型的位置和姿态。
2.轴线建系轴线建系是一种常用的建系方法,通过确定一个或多个轴线来建立坐标系,从而确定其他点、线或面的位置和方向。
轴线建系常用于工程制图和机械设计中。
(1)单轴建系:通过确定一个轴线来建立坐标系。
例如,在机械设计中,常用水平轴或垂直轴作为参考轴线,然后确定其他点、线或面相对于该轴线的位置和方向。
(2)双轴建系:通过确定两个相互垂直的轴线来建立坐标系。
例如,在平面图形的制图中,常用水平轴和垂直轴来确定二维平面中点、线或面的位置和方向。
(3)多轴建系:通过确定多个轴线来建立坐标系。
立体几何建系方法

立体几何建系方法
立体几何建系方法是指在解决立体几何问题时,建立相应的坐标系或者辅助图形来辅助计算。
以下是一些常用的立体几何建系方法:
1. 建立坐标系:可以通过建立平面直角坐标系或者空间直角坐标系,将三维问题转化为二维平面上的问题。
通过引入坐标系,可以方便地表示点、向量、直线、平面等几何元素,并可以利用坐标系的性质来进行计算。
2. 投影建系:投影建系是指通过将立体图形进行投影,将三维问题转化为二维平面上的问题。
常见的投影建系方法有平面投影、轴测投影、透视投影等。
3. 建立辅助图形:在解决立体几何问题时,可以通过建立一些辅助图形来辅助计算。
常见的辅助图形有平行四边形、三角形、圆等。
通过建立辅助图形,可以改变原问题的形式,从而更容易进行计算。
4. 应用剖分方法:剖分方法是指将复杂的立体图形剖分为简单的几何元素,从而简化计算过程。
常见的剖分方法有平分法、中分法、垂分法等。
5. 利用对称性:利用图形的对称性可以简化计算过程。
通过找出图形的对称中心、对称轴等,可以将问题降低到简化的情况,减少计算难度。
这些建系方法可以根据具体问题的需要进行灵活运用,对于不同类型的立体几何问题,选择合适的建系方法可以极大地简化计算过程,提高计算效率。
高中数学立体几何建系设点专题

2009-2010学年高三立几建系设点专题引入空间向量坐标运算,使解立体几何问题避免了传统方法进行繁琐的空间分析,只需建立空间直角坐标系进行向量运算,而如何建立恰当的坐标系,成为用向量解题的关键步骤之一.所谓“建立适当的坐标系”,一般应使尽量多的点在数轴上或便于计算。
一、建立空间直角坐标系的三条途径途径一、利用图形中的对称关系建立坐标系:图形中虽没有明显交于一点的三条直线,但有一定对称关系(如正三棱柱、正四棱柱等),利用自身对称性可建立空间直角坐标系.例1(湖南卷理科第18题)已知两个正四棱锥P -ABCD 与Q -ABCD 的高都为2,AB =4.(1)证明:PQ ⊥平面ABCD ;(2)求异面直线AQ 与PB 所成的角;(3)求点P 到平面QAD 的距离.简解:(1)略;(2)由题设知,ABCD 是正方形,且AC ⊥BD .由(1),PQ ⊥平面ABCD ,故可分别以直线为x ,y ,z 轴建立空间直角坐标系(如图1),易得CA DB QP 、、,.所求异面直线(02)(02)AQ PB =--=-u u u r u u u r 1cos 3AQ PB AQ PB AQ PB <>==u u u r u u u r u u u r u u u r g u u u r u u u r 、所成的角是.1arccos3(3)由(2)知,点.(00)(0)(004)D AD PQ -=--=-u u u r u u u r设n =(x ,y ,z )是平面QAD 的一个法向量,则得取x =1,得00AQ AD ⎧=⎪⎨=⎪⎩u u u r g u u u rg 、、nn 00z x y +=+=⎪⎩、、.点P 到平面QAD 的距离(11--、、n =PQ d ==u u u r g nn途径二、利用面面垂直的性质建立坐标系:图形中有两个互相垂直的平面,可以利用面面垂直的性质定理,作出互相垂直且交于一点的三条直线,建立坐标系.例2 (全国卷Ⅱ理科第19题)在直三棱柱中,AB =BC ,D 、E 分别为111ABC A B C -的中点.11BB AC 、(1)证明:ED 为异面直线与的公垂线;1BB 1AC (2)设,求二面角的大小.1AA AC ==11A AD C --解:(1)如图2,建立直角坐标系,其中原点O 为O xyz -AC 的中点,设则,,(00)A a 、、1(00)(02)B b B b c 、、、、、则,即.11(00)(002)0ED b BB c ED BB ===u u u r u u u r u u u r u u u r g 、、、、、、1ED BB ⊥同理. 因此ED 为异面直线与的公垂线.1ED AC ⊥1BB 1AC (2)不妨令,则,1a b c ===1(110)(110)(002)BC AB AA =--=-=u u u r u u u r u u u r 、、、、、、、、.即BC ⊥AB ,BC ⊥,又∵,∴BC ⊥面100BC AB BC AA ==u u u r u u u r u u u r u u u rg g 、1AA 1AB AA A =I .1A AD 又,,(101)(101)(010)0EC AE ED EC AE =--=-==u u u r u u u r u u u r u u u r u u u rg 、、、、、、、、、0EC ED =u u u r u u u r g 即EC ⊥AE ,EC ⊥ED ,又∵AE ∩ED =E ,∴EC ⊥面.∴1C AD ,即得和的夹角为.所以,二面角1cos 2EC BC EC BC EC BC <>==u u u r u u u ru u u r u u u r g u u u r u u u r 、EC u u u r BC u u u r 60o 为.11A AD C --60o 练2:如图,平面PAC ⊥平面ABC ,ABC∆是以AC 为斜边的等腰直角三角形,,,E F O 分别为PA ,PB ,AC 的中点,16AC =,10PA PC ==.(I )设G 是OC 的中点,证明://FG 平面BOE ;(II )证明:在ABO ∆内存在一点M ,使FM ⊥平面BOE ,并求点M 到OA ,OB 的距离.途径三、利用图形中现成的垂直关系建立坐标系:当图形中有明显互相垂直且交于一点的三条直线,可以利用这三条直线直接建系.例3.如图,在四棱锥中,底面四边长为1的菱形,,O ABCD -ABCD 4ABC π∠=, ,为的中点。
空间向量之立体几何建系和求点坐标(共24张PPT)

建系方法4 练习1
已知斜三棱柱ABC A1B1C1, BCA 90, AC BC 2, A1在底面ABC上的射影 恰好为AC的中点D,又知BA1 AC1,建立合适的空间直角坐标系 并确定各点坐标。
A1
C1
B1
造“墙角”
A
D
C
B
敬请各位教师批评指正
投影点,坐标是否好写。如果可以则直接确定了横纵坐标,而竖 坐标为该点到底面的距离。
以上两个类型已经可以囊括大多数几何体中的点, 但总还有一些特殊点,那么就要用到第三个方法:
基础知识:
3、需要计算的点 ① 中点坐标公式: ② 利用向量关系进行计算(先设再求):向量坐标化后,向量的 关系也可转化为坐标的关系,进而可以求出一些位置不好的点的坐
建系方法2例题
二、利用线面垂直关系构建空间直角坐标系(转化为墙角模型) 例2 如图,在四棱锥P-ABCD中,底面ABCD为正方形,且边
长为2a,棱PD⊥底面ABCD,PD=2b,取各侧棱的中点E,F,G, H,写出点E,F,G,H的坐标.
找“墙角”
建系方法2练习1
练1.在三棱锥P ABC中,PA 平面ABC, BAC 90, D, E, F分别是棱AB, BC,CD的中点,AB AC 1, PA 2, 试建立适当的空间直角坐标系并确定各点坐标。
基础知识:
(二)坐标的书写:建系之后要能够
快速准确的写出点的坐标,按照特点
可以分为两3大类 1、能够直接写出坐标的点:
• F
(1)坐标轴上的点
(2)底面上的点:
x
点P的位置
原点O
x轴上A
z
•C
•E
1
O• • B
立体几何建系方法

立体几何建系方法
立体几何建系是将物体的各个部分和特征按照一定的规律组织起来,以便实现物体的描述、分析和设计。
常见的立体几何建系方法包括以下几种:
1. 投影法:通过将三维物体投射到二维平面上来描述物体的形状和特征。
投影法包括正射投影和透视投影两种,可以用来绘制物体的平面图和立体图。
2. 点线面方法:用点、线和面来描述物体的形状和特征。
点表示物体的位置,线表示物体的边界或分界线,面表示物体的表面。
3. 剖视法:按照一定的切割规则将物体切割成若干部分,以便观察物体的内部结构和特征。
剖视法可以通过截剖图或剖面图来表示。
4. 抽象建模法:通过简化、抽象物体的形状和特征,以便更好地理解和分析物体的结构和功能。
常见的抽象建模方法包括立体图法、组合法、选择法等。
5. 三维建模方法:利用计算机软件或物理模型来建立真实或虚拟的三维模型,以便实现对物体的全面描述和分析。
三维建模方法包括参数建模、几何建模、曲面建模等。
6. 尺寸控制方法:通过测量和控制物体的尺寸来确保物体的质量和性能。
尺寸控制方法包括公差分析、配合与间隙控制等。
立体几何建系方法的选择取决于具体的应用场景和需求,不同的方法可以相互结合使用,以实现对物体的准确描述和分析。
用空间向量解决立体几何问题的建系策略

分析!1)连接AC交BF于点G,连接 EG,结合线面平行的性质可得PA%EG,再 由E为PC的中点,得G为AC的中点,则
△AFG^^CBG,得到 AF — BC — ]aD —
1,即F为AD的中点,可得四边形DCBF为 平行四边形,再由AD丄DC,得BF丄AD,可 得BF丄平面PAD,进一步得到平面BEF丄 平面PAD " (2)由面面垂直转化为线面垂 直,结合底面是直角梯形,可以以D为坐标 原点建系。分析得到F为AD的中点,也可 以以F为坐标原点建系。P点坐标未知,需 要先设坐标,比如设P (0,0,),由PC与底 面ABCD所成的角为60°可求解3。
点的坐标是用空间向量解决立体几何问题的
BCD。
关键所在。下面以典型的几何体:棱柱、棱锥、
证法二:如图2,以C
多面体为载体,以典型的问题情境设计:求线
为坐标原点,CA , CB.
面角、求二面角、探索性问题、翻折问题为背
CC]所在直线分别为e
景,剖析建立空间直角坐标系的常用途径。
轴,y轴,w轴,建立空间
论也可以B为坐标
原点,z轴与OC平
行(z轴悬空)建系,
如图4所示。求点C
的坐标
利用
CC* $ AA* &求点 D
的坐标可以利用
图4
------ > 1 -------->
A1D $yA 1C1。本题第(2)问的解答以O为
坐标原点建系为例。
解:(1)因为 #$A$1 $ #$$1A,所以 AB$B$1,所以四边形A1ABB1为菱形。
底面直角梯形,BC/AD , AD丄 DC , BC $ CD $ 1 , AD $ 2 , PA $ PD , E 为
空间向量之立体几何建系和求点坐标(共24张PPT)

xOy面内D yOz面内E zOx面内F
坐标形式 (x,y,0)
(0,y,z)
(x,0,z)
基础知识:
2、空间中在底面投影为特殊位置的点:
如果 A' x1, y1, z 在底面的投影为 A x2, y2,0 ,那么x1 x2, y1 y2
(即点与投影点的横纵坐标相同) 由这条规律出发,在写空间中的点坐标时,可看一下在底面的
建系方法2练习2 练2.如图,已知四棱锥P ABCD的底面是菱形,对角线AC, BD交于点O, OA 4,OB 3,OP 4,且OP 平面ABCD,点M为PC的三等分点(靠近P), 建立适当的直角坐标系并求各点坐标。
找“墙角”
14
建系方法2练习3
练3.如图,在等腰梯形ABCD中,AB // CD, AD DC CB 1, ABC 60,CF 平面ABCD,且CF 1,建立适当的直角坐标系 并确定各点坐标。
找“墙角”
建系方法2练习5
真题(辽宁卷)如图,AB 是圆的直径,PA 垂 直圆所在的平面,C 是圆上的点.
(1)求证:平面 PAC⊥平面 PBC; (2)若 AB=2,AC=1,PA=1,求证:二面
角 C-PB-A 的余弦值.
造“墙角”
建系方法3例题
三、利用面面垂直关系构建空间直角坐标系(转化为墙角模型) 例3.在四棱锥V-ABCD中,底面ABCD是边长为2的正方形,侧面VAD 是正三角形,平面VAD⊥底面ABCD.点P、H分别是线段VC、AD的 中点.试建立空间直角坐标系并写出P、V、A、B、C、D的坐标.
互相垂直,EF // BD, ED BD, AD 2, EF ED 1, 试建立合适的 空间直角坐标系并确定各点的坐标
立体几何(向量法)—建系讲义

立体几何(向量法)—建系引入空间向量坐标运算,使解立体几何问题避免了传统方法进行繁琐的空间分析,只需建立空间直角坐标系进行向量运算,而如何建立恰当的坐标系,成为用向量解题的关键步骤之一.所谓“建立适当的坐标系”,一般应使尽量多的点在数轴上或便于计算。
一、利用共顶点的互相垂直的三条线构建直角坐标系例1(2012高考真题重庆理19)(本小题满分12分 如图,在直三棱柱111C B A ABC - 中,AB=4,AC=BC=3,D 为AB 的中点(Ⅰ)求点C 到平面11ABB A 的距离;(Ⅱ)若11AB A C ⊥求二面角 的平面角的余弦值.【答案】解:(1)由AC =BC ,D 为AB 的中点,得CD ⊥AB 。
又CD ⊥AA 1,故CD ⊥面A 1ABB 1,所以点C 到平面A 1ABB 1的距离为CD =错误!=错误!.(2)解法一:如图,取D 1为A 1B 1的中点,连结DD 1,则DD 1∥AA 1∥CC 1。
又由(1)知CD ⊥面A 1ABB 1,故CD ⊥A 1D ,CD ⊥DD 1,所以∠A 1DD 1为所求的二面角A 1-CD -C 1的平面角.因A 1D 为A 1C 在面A 1ABB 1上的射影,又已知AB 1⊥A 1C ,由三垂线定理的逆定理得AB 1⊥A 1D ,从而∠A 1AB 1、∠A 1DA 都与∠B 1AB 互余,因此∠A 1AB 1=∠A 1DA ,所以Rt △A 1AD ∽Rt △B 1A 1A .因此错误!=错误!,即AA 错误!=AD ·A 1B 1=8,得AA 1=2错误!.从而A1D=错误!=2错误!。
所以,在Rt△A1DD1中,cos∠A1DD1=错误!=错误!=错误!。
解法二:如图,过D作DD1∥AA1交A1B1于点D1,在直三棱柱中,易知DB,DC,DD1两两垂直.以D为原点,射线DB,DC,DD1分别为x轴、y轴、z轴的正半轴建立空间直角坐标系D-xyz.设直三棱柱的高为h,则A(-2,0,0),A1(-2,0,h),B1(2,0,h),C(0,错误!,0),C1(0,错误!,h),从而错误!=(4,0,h),错误!=(2,错误!,-h).由错误!⊥错误!,有8-h2=0,h=2错误!。
立体几何—建系讲义

立体几何(向量法)—建系引入空间向量坐标运算,使解立体几何问题避免了传统方法进行繁琐的空间分析,只需建立空间直角坐标系进行向量运算,而如何建立恰当的坐标系,成为用向量解题的关键步骤之一.所谓“建立适当的坐标系”,一般应使尽量多的点在数轴上或便于计算。
一、利用共顶点的互相垂直的三条线构建直角坐标系例1(2012高考真题重庆理19)(本小题满分12分 如图,在直三棱柱111C B A ABC - 中,AB=4,AC=BC=3,D 为AB 的中点(Ⅰ)求点C 到平面11ABB A 的距离;(Ⅱ)若11AB A C ⊥求二面角 的平面角的余弦值.【答案】解:(1)由AC =BC ,D 为AB 的中点,得CD ⊥AB .又CD ⊥AA 1,故CD ⊥面A 1ABB 1,所以点C 到平面A 1ABB 1的距离为CD =BC 2-BD 2= 5.(2)解法一:如图,取D 1为A 1B 1的中点,连结DD 1,则DD 1∥AA 1∥CC 1.又由(1)知CD ⊥面A 1ABB 1,故CD ⊥A 1D ,CD ⊥DD 1,所以∠A 1DD 1为所求的二面角A 1-CD -C 1的平面角.因A 1D 为A 1C 在面A 1ABB 1上的射影,又已知AB 1⊥A 1C ,由三垂线定理的逆定理得AB 1⊥A 1D ,从而∠A 1AB 1、∠A 1DA 都与∠B 1AB 互余,因此∠A 1AB 1=∠A 1DA ,所以Rt △A 1AD ∽Rt △B 1A 1A .因此AA 1AD =A 1B 1AA 1,即AA 21=AD ·A 1B 1=8,得AA 1=2 2.从而A 1D =AA 21+AD 2=2 3.所以,在Rt △A 1DD 1中, cos ∠A 1DD 1=DD 1A 1D =AA 1A 1D =63.解法二:如图,过D 作DD 1∥AA 1交A 1B 1于点D 1,在直三棱柱中,易知DB ,DC ,DD 1两两垂直.以D 为原点,射线DB ,DC ,DD 1分别为x 轴、y 轴、z 轴的正半轴建立空间直角坐标系D -xyz .设直三棱柱的高为h ,则A (-2,0,0),A 1(-2,0,h ),B 1(2,0,h ),C (0,5,0),C 1(0,5,h ),从而AB 1→=(4,0,h ),A 1C →=(2,5,-h ).由AB 1→⊥A 1C →,有8-h 2=0,h =2 2. 故DA 1→=(-2,0,22),CC 1→=(0,0,22),DC →= (0,5,0).设平面A 1CD 的法向量为m =(x 1,y 1,z 1),则m ⊥DC →,m ⊥DA 1→,即 ⎩⎨⎧5y 1=0,-2x 1+22z 1=0,取z 1=1,得m =(2,0,1),设平面C 1CD 的法向量为n =(x 2,y 2,z 2),则n ⊥DC →,n ⊥CC 1→,即⎩⎨⎧5y 2=0,22z 2=0, 取x 2=1,得n =(1,0,0),所以 cos 〈m ,n 〉=m·n |m ||n |=22+1·1=63. 所以二面角A 1-CD -C 1的平面角的余弦值为63.二、利用线面垂直关系构建直角坐标系例 2.如图所示,AF 、DE 分别是圆O 、圆1O 的直径,AD 与两圆所在的平面均垂直,8AD =.BC 是圆O 的直径,6AB AC ==,//OE AD .(I)求二面角B AD F --的大小; (II)求直线BD 与EF 所成的角的余弦值. 19.解:(Ⅰ)∵AD 与两圆所在的平面均垂直,∴AD⊥AB, AD⊥AF,故∠BAD 是二面角B —AD —F 的平面角, 依题意可知,ABCD 是正方形,所以∠BAD=450. 即二面角B —AD —F 的大小为450;(Ⅱ)以O 为原点,BC 、AF 、OE 所在直线为坐标轴,建立空间直角坐标系(如图所示),则O (0,0,0),A (0,23-,0),B (23,0,0),D (0,23-,8),E (0,0,8),F (0,23,0)所以,)8,23,0(),8,23,23(-=--=FE BD10828210064180||||,cos =⨯++=•>=<FE BD FE BD EF BD 设异面直线BD 与EF 所成角为α,则1082|,cos |cos =><=EF BD α直线BD 与EF 所成的角为余弦值为8210.三、利用图形中的对称关系建立坐标系例3(2013年重庆数学(理))如图,四棱锥P ABCD -中,PA ABCD ⊥底面,2,4,3BC CD AC ACB ACD π===∠=∠=,F 为PC 的中点,AF PB ⊥.(1)求PA 的长; (2)求二面角B AF D --的正弦值.【答案】解:(1)如图,联结BD 交AC 于O ,因为BC =CD ,即△BCD 为等腰三角形,又AC 平分∠BCD ,故AC ⊥BD .以O 为坐标原点,OB →,OC →,AP →的方向分别为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系O -xyz ,则OC =CD cos π3=1,而AC =4,得AO =AC -OC =3.又OD =CD sinπ3=3,故A (0,-3,0),B (3,0,0),C (0,1,0),D (-3,0,0).因P A ⊥底面ABCD ,可设P (0,-3,z ),由F 为PC 边中点,得F ⎝⎛⎭⎫0,-1,z 2,又AF →=⎝⎛⎭⎫0,2,z 2,PB →=(3,3,-z ),因AF ⊥PB ,故AF →·PB →=0,即6-z 22=0,z =23(舍去-23),所以|P A →|=2 3.(2)由(1)知AD →=(-3,3,0),AB →=(3,3,0),AF →=(0,2,3).设平面F AD 的法向量为1=(x 1,y 1,z 1),平面F AB 的法向量为2=(x 2,y 2,z 2).由1·AD →=0,1·AF →=0,得⎩⎨⎧-3x 1+3y 1=0,2y 1+3z 1=0,因此可取1=(3,3,-2). 由2·AB →=0,2·AF →=0,得⎩⎨⎧3x 2+3y 2=0,2y 2+3z 2=0,故可取2=(3,-3,2). 从而向量1,2的夹角的余弦值为 cos 〈1,2〉=n 1·n 2|n 1|·|n 2|=18.故二面角B -AF -D 的正弦值为378.四、利用正棱锥的中心与高所在直线,投影构建直角坐标系 例4-1(2013大纲版数学(理))如图,四棱锥P ABCD -中,902,ABC BAD BC AD PAB ∠=∠==∆,与PAD ∆都是等边三角形.(I)证明:;PB CD ⊥ (II)求二面角A PD C --的余弦值.【答案】解:(1)取BC 的中点E ,联结DE ,则四边形ABED 为正方形. 过P 作PO ⊥平面ABCD ,垂足为O . 联结OA ,OB ,OD ,OE .由△P AB 和△P AD 都是等边三角形知P A =PB =PD ,所以OA =OB =OD ,即点O 为正方形ABED 对角线的交点, 故OE ⊥BD ,从而PB ⊥OE .因为O 是BD 的中点,E 是BC 的中点,所以OE ∥CD .因此PB ⊥CD .(2)解法一:由(1)知CD ⊥PB ,CD ⊥PO ,PB ∩PO =P , 故CD ⊥平面PBD .又PD ⊂平面PBD ,所以CD ⊥PD .取PD 的中点F ,PC 的中点G ,连FG . 则FG ∥CD ,FG ⊥PD .联结AF ,由△APD 为等边三角形可得AF ⊥PD . 所以∠AFG 为二面角A -PD -C 的平面角. 联结AG ,EG ,则EG ∥PB . 又PB ⊥AE ,所以EG ⊥AE .设AB =2,则AE =22,EG =12PB =1,故AG =AE 2+EG 2=3,在△AFG 中,FG =12CD =2,AF =3,AG =3.所以cos ∠AFG =FG 2+AF 2-AG 22·FG ·AF =-63.解法二:由(1)知,OE ,OB ,OP 两两垂直.以O 为坐标原点,OE →的方向为x 轴的正方向建立如图所示的空间直角坐标系O -xyz .设|AB →|=2,则A (-2,0,0),D (0,-2,0), C (22,-2,0),P (0,0,2),PC →=(22,-2,-2),PD →=(0,-2,-2), AP →=(2,0,2),AD →=(2,-2,0). 设平面PCD 的法向量为1=(x ,y ,z ),则 1·PC →=(x ,y ,z )·(22,-2,-2)=0,1·PD →=(x ,y ,z )·(0,-2,-2)=0,可得2x -y -z =0,y +z =0.取y =-1,得x =0,z =1,故1=(0,-1,1). 设平面P AD 的法向量为2=(m ,p ,q ),则 2·AP →=(m ,p ,q )·(2,0,2)=0, 2·AD →=(m ,p ,q )·(2,-2,0)=0,可得m +q =0,m -p =0.取m =1,得p =1,q =-1,故2=(1,1,-1). 于是cos 〈,2〉=n 1·n 2|n 1||n 2|=-63. 例4-2如图1-5,在三棱柱ABC -A 1B 1C 1中,已知AB =AC =AA 1=5,BC =4,点A 1在底面ABC 的投影是线段BC 的中点O .(1)证明在侧棱AA 1上存在一点E ,使得OE ⊥平面BB 1C 1C ,并求出AE 的长; (2)求平面A 1B 1C 与平面BB 1C 1C 夹角的余弦值.图1-5【答案】解:(1)证明:连接AO ,在△AOA 1中,作OE ⊥AA 1 于点E ,因为AA 1∥BB 1,所以OE ⊥BB 1.因为A 1O ⊥平面ABC ,所以A 1O ⊥BC . 因为AB =AC ,OB =OC ,所以AO ⊥BC , 所以BC ⊥平面AA 1O . 所以BC ⊥OE ,所以OE ⊥平面BB 1C 1C ,又AO =AB 2-BO 2=1,AA 1=5, 得AE =AO 2AA 1=55.(2)如图,分别以OA ,OB ,OA 1所在直线为x ,y ,z 轴,建立空间直角坐标系,则A (1,0,0),B (0,2,0),C (0,-2,0),A 1(0,0,2),由AE →=15AA 1→得点E 的坐标是⎝ ⎛⎭⎪⎫45,0,25, 由(1)得平面BB 1C 1C 的法向量是OE→=⎝ ⎛⎭⎪⎫45,0,25,设平面A 1B 1C 的法向量=(x ,y ,z ),由⎩⎪⎨⎪⎧·AB →=0,n ·A 1C →=0得⎩⎨⎧-x +2y =0,y +z =0,令y =1,得x =2,z =-1,即=(2,1,-1),所以 cos 〈OE →,〉=OE →·n |OE →|·|n |=3010.即平面BB 1C 1C 与平面A 1B 1C 的夹角的余弦值是3010三、利用面面垂直关系构建直角坐标系 例5(2012高考真题安徽理18)(本小题满分12分)平面图形ABB 1A 1C 1C 如图1-4(1)所示,其中BB 1C 1C 是矩形,BC =2,BB 1=4,AB=AC=2,A1B1=A1C1= 5.图1-4现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A1A,A1B,A1C,得到如图1-4(2)所示的空间图形.对此空间图形解答下列问题.(1)证明:AA1⊥BC;(2)求AA1的长;(3)求二面角A-BC-A1的余弦值.【答案】解:(向量法):(1)证明:取BCB1C1的中点分别为D和D1,连接A1D1,DD1,AD.由BB1C1C为矩形知,DD1⊥B1C1,因为平面BB1C1C⊥平面A1B1C1,所以DD1⊥平面A1B1C1,又由A1B1=A1C1知,A1D1⊥B1C1.故以D1为坐标原点,可建立如图所示的空间直角坐标系D1-xyz.由题设,可得A1D1=2,AD=1.由以上可知AD⊥平面BB1C1C,A1D1⊥平面BB1C1C,于是AD∥A1D1.所以A (0,-1,4),B (1,0,4),A 1(0,2,0),C (-1,0,4),D (0,0,4). 故AA 1→=(0,3,-4),BC →=(-2,0,0),AA 1→·BC →=0, 因此AA 1→⊥BC →,即AA 1⊥BC . (2)因为AA 1→=(0,3,-4), 所以||AA 1→=5,即AA 1=5. (3)连接A 1D ,由BC ⊥AD ,BC ⊥AA 1,可知BC ⊥平面A 1AD ,BC ⊥A 1D ,所以∠ADA 1为二面角A -BC -A 1的平面角.因为DA →=(0,-1,0),DA 1→=(0,2,-4),所以 cos 〈DA →,DA 1→〉=-21×22+(-4)2=-55. 即二面角A -BC -A 1的余弦值为-55.(综合法)(1)证明:取BC ,B 1C 1的中点分别为D 和D 1,连接A 1D 1,DD 1,AD ,A 1D .由条件可知,BC ⊥AD ,B 1C 1⊥A 1D 1, 由上可得AD ⊥面BB 1C 1C ,A 1D 1⊥面BB 1C 1C . 因此AD ∥A 1D 1,即AD ,A 1D 1确定平面AD 1A 1D . 又因为DD 1∥BB 1,BB 1⊥BC ,所以DD 1⊥BC . 又考虑到AD ⊥BC ,所以BC ⊥平面AD 1A 1D , 故BC ⊥AA 1.(2)延长A 1D 1到G 点,使GD 1=AD ,连接AG . 因为AD 綊GD 1,所以AG 綊DD 1綊BB 1. 由于BB 1⊥平面A 1B 1C 1,所以AG ⊥A 1G .由条件可知,A 1G =A 1D 1+D 1G =3,AG =4, 所以AA 1=5.(3)因为BC ⊥平面AD 1A 1D ,所以∠ADA 1为二面角A -BC -A 1的平面角. 在Rt △A 1DD 1中,DD 1=4,A 1D 1=2,解得 sin ∠D 1DA 1=55,cos ∠ADA 1=cos ⎝ ⎛⎭⎪⎫π2+∠D 1DA 1=-55.即二面角A -BC -A 1的余弦值为-55.。
立体几何中的建系设点讲解学习
(2)对于一条线段上的某点分线段成比例,可以利用向量关系将该点坐标计算出来
由这条规律出发,在写空间中的点时,可看下在底面的投影ቤተ መጻሕፍቲ ባይዱ,坐标是否好写。如果可以则直接确定了横纵坐标,而竖坐标为该点到底面的距离。例如:正方体中的 点,其投影为 ,而 所以 ,而其到底面的距离为 ,故坐标为
以上两个类型已经可以囊括大多数几何体中的点,但总还有一些特殊点,那么就要用到第三个方法:
3、需要计算的点
(3)找对称关系:寻找底面上的点能否存在轴对称特点
3、常用的空间直角坐标系满足 轴成右手系,所以在标 轴时要注意。
4、同一个几何体可以有不同的建系方法,其坐标也会对应不同。但是通过坐标所得到的结论(位置关系,角)是一致的。
5、解答题中,在建立空间直角坐标系之前,要先证明所用坐标轴为两两垂直(即一个线面垂直 底面两条线垂直),这个过程不能省略。
二、典型例题:
例1:在三棱锥 中, 平面 , , 分别是棱 的中点, ,试建立适当的空间直角坐标系并确定各点坐标
例2:在长方体 中, 分别是棱 上的点, , ,建立适当的直角坐标系并写出点的坐标。
例3:如图,在等腰梯形 中, , , 平面 ,且 ,建立适当的直角坐标系并确定各点坐标。
小炼:建立坐标系的最重要的条件就是线面垂直(即 轴),对于 轴的选取,如果没有已知线段,可以以垂足所在的某一条直线为坐标轴,然后作这条轴的垂线来确定另一条轴。
例4:已知四边形 满足 , 是 中点,将 翻折成 ,使得平面 平面 , 为 中点
思路:在处理翻折问题时,首先要确定在翻折的过程中哪些量与位置关系不变,这些都是作为已知条件使用的。
例5:如图,已知四棱锥 的底面是菱形,对角线 交于点 ,且 平面 ,点 为 的三等分点(靠近 ),建立适当的直角坐标系并求各点坐标
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何建系方法
熟悉几个补形建系的技巧
基本模型:长方体 ;
下面几个多面体可考虑补成长方体建系: (1)三棱锥P ABC -,其中,2
PA ABC ABC π
⊥∠=
.
特点:BC PAB ⊥面;四个面均为直角三角形。
建系方法:
(2)四棱锥P-ABCD,其中,PA ABCD ⊥面ABCD 为矩形。
建系方法:
(3)正四面体A-BCD 建系方法:
(4)两个面互相垂直建系方法
1、(2011年高考重庆卷文科20) 如题(20)图,在四面体
ABCD 中,
平面ABC ⊥平面ACD ,,2,1AB BC AC AD BC CD ⊥====
(Ⅰ)求四面体ABCD 的体积;
(Ⅱ)求二面角C-AB-D 的平面角的正切值。
P
A B
C
A C
D
P
2、(06山东),已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,
又BO=2,PO=2,PB⊥PD.
(Ⅰ)求异面直线PD与BC所成角的余弦值;
(Ⅱ)求二面角P-AB-C的大小;
3、在直三棱柱ABC-A1B1C1中,AB=BC,D、E分别为BB1、AC1的中点.
(Ⅰ)证明:ED为异面直线BB1与AC1的公垂线;
(Ⅱ)设AA1=AC=2AB,求二面角A1-AD-C1的大小.
A B
C
D E
A1
B1
C1
4.如图,已知四棱锥P ABCD -,底面ABCD 为菱形,PA ⊥平面ABCD ,60ABC ∠=o
,E F ,分别是BC PC ,的中点. (Ⅰ)证明:AE PD ⊥; (Ⅱ)若H 为
PD 上的动点,EH 与平面PAD 所成最大角的正切值 为2
E A
F C --的余弦值.
5、(08安徽)如图,在四棱锥O ABCD -中,底面ABCD 四边长为1的 菱形,4
ABC π
∠=
,
OA ABCD ⊥底面, 2OA =,M 为OA 的中点.
(1)求异面直线AB 与MD 所成角的大小; (2)求点B 到平面OCD 的距离.
P B
E
C
D F
A。
