立体几何中的建系设点
高考数学专题 立体几何中的建系设点问题
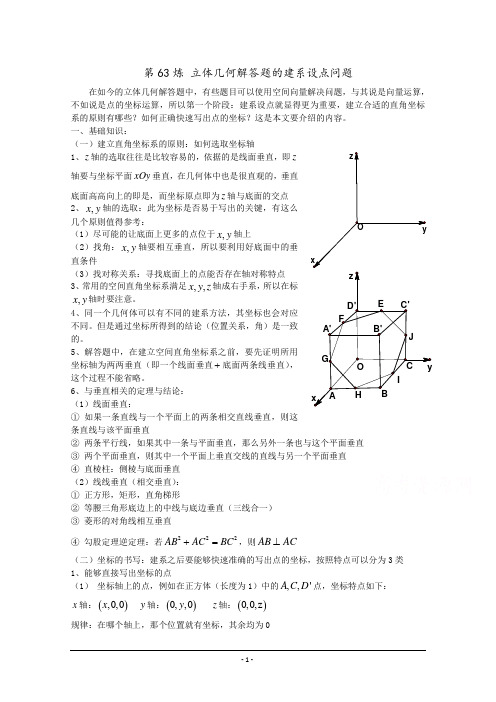
Oyxz FEGH IJ O yx z A'C'B B'C D'A 第63炼 立体几何解答题的建系设点问题在如今的立体几何解答题中,有些题目可以使用空间向量解决问题,与其说是向量运算,不如说是点的坐标运算,所以第一个阶段:建系设点就显得更为重要,建立合适的直角坐标系的原则有哪些?如何正确快速写出点的坐标?这是本文要介绍的内容。
一、基础知识:(一)建立直角坐标系的原则:如何选取坐标轴1、z 轴的选取往往是比较容易的,依据的是线面垂直,即z 轴要与坐标平面xOy 垂直,在几何体中也是很直观的,垂直底面高高向上的即是,而坐标原点即为z 轴与底面的交点2、,x y 轴的选取:此为坐标是否易于写出的关键,有这么几个原则值得参考:(1)尽可能的让底面上更多的点位于,x y 轴上(2)找角:,x y 轴要相互垂直,所以要利用好底面中的垂直条件(3)找对称关系:寻找底面上的点能否存在轴对称特点 3、常用的空间直角坐标系满足,,x y z 轴成右手系,所以在标,x y 轴时要注意。
4、同一个几何体可以有不同的建系方法,其坐标也会对应不同。
但是通过坐标所得到的结论(位置关系,角)是一致的。
5、解答题中,在建立空间直角坐标系之前,要先证明所用坐标轴为两两垂直(即一个线面垂直+底面两条线垂直),这个过程不能省略。
6、与垂直相关的定理与结论: (1)线面垂直:① 如果一条直线与一个平面上的两条相交直线垂直,则这条直线与该平面垂直② 两条平行线,如果其中一条与平面垂直,那么另外一条也与这个平面垂直 ③ 两个平面垂直,则其中一个平面上垂直交线的直线与另一个平面垂直 ④ 直棱柱:侧棱与底面垂直 (2)线线垂直(相交垂直): ① 正方形,矩形,直角梯形② 等腰三角形底边上的中线与底边垂直(三线合一) ③ 菱形的对角线相互垂直④ 勾股定理逆定理:若222AB AC BC +=,则AB AC ⊥(二)坐标的书写:建系之后要能够快速准确的写出点的坐标,按照特点可以分为3类 1、能够直接写出坐标的点(1) 坐标轴上的点,例如在正方体(长度为1)中的,,'A C D 点,坐标特点如下:x 轴:(),0,0x y 轴:()0,,0y z 轴:()0,0,z规律:在哪个轴上,那个位置就有坐标,其余均为0(2)底面上的点:坐标均为(),,0x y ,即竖坐标0z =,由于底面在作立体图时往往失真,所以要快速正确写出坐标,强烈建议在旁边作出底面的平面图进行参考:以上图为例: 则可快速写出,H I 点的坐标,位置关系清晰明了111,,0,,1,022H I ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭2、空间中在底面投影为特殊位置的点:如果()'11,,A x y z 在底面的投影为()22,,0A x y ,那么1212,x x y y ==(即点与投影点的横纵坐标相同)由这条规律出发,在写空间中的点时,可看下在底面的投影点,坐标是否好写。
立体几何(向量法)—建系讲义

立体几何(向量法)—建系引入空间向量坐标运算,使解立体几何问题避免了传统方法进行繁琐的空间分析,只需建立空间直角坐标系进行向量运算,而如何建立恰当的坐标系,成为用向量解题的关键步骤之一.所谓“建立适当的坐标系”,一般应使尽量多的点在数轴上或便于计算。
一、利用共顶点的互相垂直的三条线构建直角坐标系例1(2012高考真题重庆理19)(本小题满分12分 如图,在直三棱柱111C B A ABC - 中,AB=4,AC=BC=3,D 为AB 的中点(Ⅰ)求点C 到平面11ABB A 的距离;(Ⅱ)若11AB AC ⊥求二面角 的平面角的余弦值.【答案】解:(1)由AC =BC ,D 为AB 的中点,得CD ⊥AB .又CD ⊥AA 1,故CD ⊥面A 1ABB 1,所以点C 到平面A 1ABB 1的距离为CD =BC 2-BD 2= 5.(2)解法一:如图,取D 1为A 1B 1的中点,连结DD 1,则DD 1∥AA 1∥CC 1.又由(1)知CD ⊥面A 1ABB 1,故CD ⊥A 1D ,CD ⊥DD 1,所以∠A 1DD 1为所求的二面角A 1-CD -C 1的平面角.因A 1D 为A 1C 在面A 1ABB 1上的射影,又已知AB 1⊥A 1C ,由三垂线定理的逆定理得AB 1⊥A 1D ,从而∠A 1AB 1、∠A 1DA 都与∠B 1AB 互余,因此∠A 1AB 1=∠A 1DA ,所以Rt △A 1AD ∽Rt △B 1A 1A .因此AA 1AD =A 1B 1AA 1,即AA 21=AD ·A 1B 1=8,得AA 1=22.从而A 1D =AA 21+AD 2=23. 所以,在Rt △A 1DD 1中, cos ∠A 1DD 1=DD 1A 1D =AA 1A 1D =63.解法二:如图,过D 作DD 1∥AA 1交A 1B 1于点D 1,在直三棱柱中,易知DB ,DC ,DD 1两两垂直.以D 为原点,射线DB ,DC ,DD 1分别为x 轴、y 轴、z 轴的正半轴建立空间直角坐标系D -xyz .设直三棱柱的高为h ,则A (-2,0,0),A 1(-2,0,h ),B 1(2,0,h ),C (0,5,0),C 1(0,5,h ),从而AB 1→=(4,0,h ),A 1C →=(2,5,-h ). 由AB 1→⊥A 1C →,有8-h 2=0,h =22. 故DA 1→=(-2,0,22),CC 1→=(0,0,22),DC →= (0,5,0).设平面A 1CD 的法向量为m =(x 1,y 1,z 1),则m ⊥DC →,m ⊥DA 1→,即 ⎩⎪⎨⎪⎧5y 1=0,-2x 1+22z 1=0,取z 1=1,得m =(2,0,1),设平面C 1CD 的法向量为n =(x 2,y 2,z 2),则n ⊥DC →,n ⊥CC 1→,即 ⎩⎪⎨⎪⎧5y 2=0,22z 2=0,取x 2=1,得n =(1,0,0),所以cos 〈m ,n 〉=m ·n |m ||n |=22+1·1=63.所以二面角A 1-CD -C 1的平面角的余弦值为63.二、利用线面垂直关系构建直角坐标系例 2.如图所示,AF 、DE 分别是圆O 、圆1O 的直径,AD 与两圆所在的平面均垂直,8AD =.BC 是圆O 的直径,6AB AC ==,//OE AD .(I)求二面角B AD F --的大小; (II)求直线BD 与EF 所成的角的余弦值. 19.解:(Ⅰ)∵AD 与两圆所在的平面均垂直,∴AD ⊥AB, AD ⊥AF,故∠BAD 是二面角B —AD —F 的平面角, 依题意可知,ABCD 是正方形,所以∠BAD =450. 即二面角B —AD —F 的大小为450;(Ⅱ)以O 为原点,BC 、AF 、OE 所在直线为坐标轴,建立空间直角坐标系(如图所示),则O (0,0,0),A (0,23-,0),B (23,0,0),D (0,23-,8),E (0,0,8),F (0,23,0)所以,)8,23,0(),8,23,23(-=--=FE BD10828210064180,cos =⨯++=>=<EF BD 设异面直线BD 与EF 所成角为α,则1082|,cos |cos =><=α直线BD 与EF 所成的.三、利用图形中的对称关系建立坐标系例3 (2013年重庆数学(理))如图,四棱锥P ABCD -中,PA ABCD ⊥底面,2,4,3BC CD AC ACB ACD π===∠=∠=,F 为PC 的中点,AF PB ⊥.(1)求PA 的长; (2)求二面角B AF D --的正弦值.【答案】解:(1)如图,联结BD 交AC 于O ,因为BC =CD ,即△BCD 为等腰三角形,又AC 平分∠BCD ,故AC ⊥BD .以O 为坐标原点,OB →,OC →,AP →的方向分别为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系O -xyz ,则OC =CD cos π3=1,而AC =4,得AO =AC -OC =3.又OD =CD sin π3=3,故A (0,-3,0),B (3,0,0),C (0,1,0),D (-3,0,0).因PA ⊥底面ABCD ,可设P (0,-3,z ),由F 为PC 边中点,得F ⎝ ⎛⎭⎪⎫0,-1,z 2,又AF →=⎝⎛⎭⎪⎫0,2,z 2,PB→=(3,3,-z ),因AF ⊥PB ,故AF →·PB →=0,即6-z 22=0,z =2 3(舍去-2 3),所以|PA →|=2 3.(2)由(1)知AD →=(-3,3,0),AB →=(3,3,0),AF →=(0,2,3).设平面FAD 的法向量为1=(x 1,y 1,z 1),平面FAB 的法向量为2=(x 2,y 2,z 2).由1·AD →=0,1·AF →=0,得⎩⎨⎧-3x 1+3y 1=0,2y 1+3z 1=0,因此可取1=(3,3,-2). 由2·AB →=0,2·AF →=0,得⎩⎨⎧3x 2+3y 2=0,2y 2+3z 2=0,故可取2=(3,-3,2). 从而向量1,2的夹角的余弦值为cos 〈1,2〉=n 1·n 2|n 1|·|n 2|=18.故二面角B -AF -D 的正弦值为3 78.四、利用正棱锥的中心与高所在直线,投影构建直角坐标系 例4-1(2013大纲版数学(理))如图,四棱锥P ABCD -中,902,ABC BAD BC AD PAB ∠=∠==∆,与PAD ∆都是等边三角形.(I)证明:;PB CD ⊥ (II)求二面角A PD C --的余弦值.【答案】解:(1)取BC 的中点E ,联结DE ,则四边形ABED 为正方形. 过P 作PO ⊥平面ABCD ,垂足为O . 联结OA ,OB ,OD ,OE .由△PAB 和△PAD 都是等边三角形知PA =PB =PD ,所以OA =OB =OD ,即点O 为正方形ABED 对角线的交点, 故OE ⊥BD ,从而PB ⊥OE .因为O 是BD 的中点,E 是BC 的中点,所以OE ∥CD .因此PB ⊥CD .(2)解法一:由(1)知CD ⊥PB ,CD ⊥PO ,PB ∩PO =P , 故CD ⊥平面PBD .又PD ⊂平面PBD ,所以CD ⊥PD .取PD 的中点F ,PC 的中点G ,连FG . 则FG ∥CD ,FG ⊥PD .联结AF ,由△APD 为等边三角形可得AF ⊥PD . 所以∠AFG 为二面角A -PD -C 的平面角. 联结AG ,EG ,则EG ∥PB . 又PB ⊥AE ,所以EG ⊥AE .设AB =2,则AE =2 2,EG =12PB =1,故AG =AE 2+EG 2=3,在△AFG 中,FG =12CD =2,AF =3,AG =3.所以cos ∠AFG =FG 2+AF 2-AG 22·FG ·AF =-63.解法二:由(1)知,OE ,OB ,OP 两两垂直.以O 为坐标原点,OE →的方向为x 轴的正方向建立如图所示的空间直角坐标系O -xyz .设|AB →|=2,则A (-2,0,0),D (0,-2,0), C (2 2,-2,0),P (0,0,2),PC →=(2 2,-2,-2),PD →=(0,-2,-2), AP →=(2,0,2),AD →=(2,-2,0).设平面PCD 的法向量为1=(x ,y ,z ),则1·PC →=(x ,y ,z )·(2 2,-2,-2)=0, 1·PD →=(x ,y ,z )·(0,-2,-2)=0,可得2x -y -z =0,y +z =0.取y =-1,得x =0,z =1,故1=(0,-1,1). 设平面PAD 的法向量为2=(m ,p ,q ),则2·AP →=(m ,p ,q )·(2,0,2)=0, 2·AD →=(m ,p ,q )·(2,-2,0)=0,可得m +q =0,m -p =0.取m =1,得p =1,q =-1,故2=(1,1,-1).于是cos 〈,2〉=n 1·n 2|n 1||n 2|=-63.例4-2如图1-5,在三棱柱ABC -A 1B 1C 1中,已知AB =AC =AA 1=5,BC =4,点A 1在底面ABC 的投影是线段BC 的中点O .(1)证明在侧棱AA 1上存在一点E ,使得OE ⊥平面BB 1C 1C ,并求出AE 的长; (2)求平面A 1B 1C 与平面BB 1C 1C 夹角的余弦值.图1-5【答案】解:(1)证明:连接AO ,在△AOA 1中,作OE ⊥AA 1 于点E ,因为AA 1∥BB 1,所以OE ⊥BB 1.因为A 1O ⊥平面ABC ,所以A 1O ⊥BC . 因为AB =AC ,OB =OC ,所以AO ⊥BC , 所以BC ⊥平面AA 1O . 所以BC ⊥OE ,所以OE ⊥平面BB 1C 1C ,又AO =AB 2-BO 2=1,AA 1=5,得AE =AO 2AA 1=55.(2)如图,分别以OA ,OB ,OA 1所在直线为x ,y ,z 轴,建立空间直角坐标系,则A (1,0,0),B (0,2,0),C (0,-2,0),A 1(0,0,2),由AE →=15AA 1→得点E 的坐标是⎝ ⎛⎭⎪⎫45,0,25, 由(1)得平面BB 1C 1C 的法向量是OE →=⎝ ⎛⎭⎪⎫45,0,25,设平面A 1B 1C 的法向量=(x ,y ,z ),由⎩⎪⎨⎪⎧·AB →=0,n ·A 1C →=0得⎩⎨⎧-x +2y =0,y +z =0,令y =1,得x =2,z =-1,即=(2,1,-1),所以 cos 〈OE →,〉=OE →·n|OE →|·|n |=3010.即平面BB 1C 1C 与平面A 1B 1C 的夹角的余弦值是3010三、利用面面垂直关系构建直角坐标系 例5(2012高考真题安徽理18)(本小题满分12分)平面图形ABB 1A 1C 1C 如图1-4(1)所示,其中BB 1C 1C 是矩形,BC =2,BB 1=4,AB =AC =2,A 1B 1=A 1C 1= 5.图1-4现将该平面图形分别沿BC 和B 1C 1折叠,使△ABC 与△A 1B 1C 1所在平面都与平面BB 1C 1C 垂直,再分别连接A 1A ,A 1B ,A 1C ,得到如图1-4(2)所示的空间图形.对此空间图形解答下列问题.(1)证明:AA 1⊥BC ; (2)求AA 1的长;(3)求二面角A -BC -A 1的余弦值.【答案】解:(向量法):(1)证明:取BC B 1C 1的中点分别为D 和D 1,连接A 1D 1,DD 1,AD . 由BB 1C 1C 为矩形知,DD 1⊥B 1C 1,因为平面BB 1C 1C ⊥平面A 1B 1C 1, 所以DD 1⊥平面A 1B 1C 1, 又由A 1B 1=A 1C 1知,A 1D 1⊥B 1C 1.故以D 1为坐标原点,可建立如图所示的空间直角坐标系D 1-xyz . 由题设,可得A 1D 1=2,AD =1.由以上可知AD ⊥平面BB 1C 1C ,A 1D 1⊥平面BB 1C 1C ,于是AD ∥A 1D 1.所以A (0,-1,4),B (1,0,4),A 1(0,2,0),C (-1,0,4),D (0,0,4). 故AA 1→=(0,3,-4),BC →=(-2,0,0),AA 1→·BC →=0, 因此AA 1→⊥BC →,即AA 1⊥BC . (2)因为AA 1→=(0,3,-4), 所以||AA 1→=5,即AA 1=5. (3)连接A 1D ,由BC ⊥AD ,BC ⊥AA 1,可知BC ⊥平面A 1AD ,BC ⊥A 1D ,所以∠ADA 1为二面角A -BC -A 1的平面角.因为DA →=(0,-1,0),DA 1→=(0,2,-4),所以 cos 〈DA →,DA 1→〉=-21×2242=-55. 即二面角A -BC -A 1的余弦值为-55.(综合法)(1)证明:取BC ,B 1C 1的中点分别为D 和D 1,连接A 1D 1,DD 1,AD ,A 1D .由条件可知,BC ⊥AD ,B 1C 1⊥A 1D 1, 由上可得AD ⊥面BB 1C 1C ,A 1D 1⊥面BB 1C 1C . 因此AD ∥A 1D 1,即AD ,A 1D 1确定平面AD 1A 1D . 又因为DD 1∥BB 1,BB 1⊥BC ,所以DD 1⊥BC . 又考虑到AD ⊥BC ,所以BC ⊥平面AD 1A 1D , 故BC ⊥AA 1.(2)延长A 1D 1到G 点,使GD 1=AD ,连接AG . 因为AD 綊GD 1,所以AG 綊DD 1綊BB 1. 由于BB 1⊥平面A 1B 1C 1,所以AG ⊥A 1G .由条件可知,A 1G =A 1D 1+D 1G =3,AG =4, 所以AA 1=5.(3)因为BC ⊥平面AD 1A 1D ,所以∠ADA 1为二面角A -BC -A 1的平面角. 在Rt △A 1DD 1中,DD 1=4,A 1D 1=2,解得 sin ∠D 1DA 1=55, cos ∠ADA 1=cos ⎝ ⎛⎭⎪⎫π2+∠D 1DA 1=-55.即二面角A -BC -A 1的余弦值为-55.。
(完整版)立体几何解答题的建系设点问题

立体几何解答题的建系设点问题一、基础知识:(一)建立直角坐标系的原则:如何选取坐标轴1、轴的选取往往是比较容易的,依据的是线面垂直,即轴要与坐标平面z z 垂直,在几何体中也是很直观的,垂直底面高高向上的即是,而坐标原点即xOy 为轴与底面的交点z 2、轴的选取:此为坐标是否易于写出的关键,有这么几个原则值得参考:,x y (1)尽可能的让底面上更多的点位于轴上,x y (2)找角:轴要相互垂直,所以要利用好底面中的垂直条件,x y (3)找对称关系:寻找底面上的点能否存在轴对称特点解答题中,在建立空间直角坐标系之前,要先证明所用坐标轴为两两垂直(即一个线面垂直底面两条线垂直),+这个过程不能省略。
3、与垂直相关的定理与结论:(1)线面垂直:① 如果一条直线与一个平面上的两条相交直线垂直,则这条直线与该平面垂直② 两条平行线,如果其中一条与平面垂直,那么另外一条也与这个平面垂直③ 两个平面垂直,则其中一个平面上垂直交线的直线与另一个平面垂直④ 直棱柱:侧棱与底面垂直(2)线线垂直(相交垂直):① 正方形,矩形,直角梯形② 等腰三角形底边上的中线与底边垂直(三线合一)③ 菱形的对角线相互垂直④ 勾股定理逆定理:若,则222AB AC BC +=AB AC ⊥(二)坐标的书写:建系之后要能够快速准确的写出点的坐标,按照特点可以分为3类1、能够直接写出坐标的点(1) 坐标轴上的点,规律:在哪个轴上,那个位置就有坐标,其余均为0(2)底面上的点:坐标均为,即竖坐标,由于底面在作立体图时往往失真,所以要快速正确写出(),,0x y 0z =坐标,强烈建议在旁边作出底面的平面图进行参考2、空间中在底面投影为特殊位置的点:如果在底面的投影为,那么(即点与投影点的横纵坐标相同)()'11,,A x y z ()22,,0A x y 1212,x x y y == 由这条规律出发,在写空间中的点时,可看下在底面的投影点,坐标是否好写。
高考数学在空间建系时,求点的坐标的另一种方法(利用距离公式和中点公式)

在立体几何空间建系时,求点的坐标,我们运用的往往是构造直角三角形等常见的方法。
但是在有些题目里面,这样子做并不容易。
这个时候可以灵活运用已知的距离和中点,利用空间中两点之间的距离公式以及中点公式,来达到迅速求未知点的坐标的目的。
希望这种方法,不要被忽略了。
下面以一道题为例,进行说明。
例1 (浙江2017,19题)如图,已知四棱锥P-ABCD ,三角形PAD 是以AD 为斜边的等腰直角三角形,且//BC AD ,CD AD ⊥,22PC AD DC CB ===,E 为PD 的中点(1)证明:CE//面PAB(2)求直线CE 与面PBC 所成角的正弦值解析:我们主要看第二问(1)如下图,取F 为AD 中点。
又E 为PD 中点因此EF//AP又因为AF 平行且相等于BC ,故AFBC 是平行四边形,从而CF//AB综上,面EFC//面PAB因此CE//面PAB(2)不妨设CD=CB=1,则PC=AD=2因为CD AD ⊥,易知BFCD 是边长为1的正方形因为三角形PAD 为等腰直角三角形,且F 为中点,故AD PF ⊥又AD BF ⊥故AD ⊥面PBF故在三角形PBF 中做出BF 边上的高h ,则必有h 垂直BF 且垂直于AD ,故垂直于面ABCD 因此将该高作为z 轴,BF 和FD 分别为x 轴和y 轴,建系如下易求点的坐标如下C (1,1,0)B (1,0,0)D (0,1,0)点P 的坐标E 的坐标不太容易求,而且也找不到合适的直角三角形来帮助求解。
但是我们能够很容易的求出来FP=1,PC=2。
因此可以利用这两个距离,列方程组求出P 的坐标。
而E 是P 和D 的中点,再利用中点公式,那么E 的坐标则可求。
如下因为AD=2,F 为中点,因此FP 为AD 的一半,即FP=1而PC=2为已知条件设P (x,0,z )则由FP=1和PC=2得到()22221114x z x z ⎧+=⎪⎨-++=⎪⎩解得122x z ⎧=-⎪⎪⎨⎪=⎪⎩从而1(2P - 由P 及D 的坐标,以及E是它们的中点,利用中点坐标公式,得到11(,42E -因此51,42CE ⎛=-- ⎝⎭而3,0,22PB ⎛=- ⎝⎭,(0,1,0)BC =,易求得面PBC的法向量(m =而CE与面PBC所成角的正弦值等于CE与m所成角的余弦的绝对值=8。
立体几何中建立坐标系和求点坐标的主要类型及方法

龙源期刊网 立体几何中建立坐标系和求点坐标的主要类型及方法
作者:刘俊
来源:《理科爱好者·教育教学版》2011年第01期
众所周知,立体几何中用坐标法解题的关键是:首先依图建立适当的空间直角坐标系,其次将关键点的坐标求出来。
后面的过程只需按照程序化操作即可。
本文立足于这两点加以归类,提炼,力求寻找其共性。
达到能通用的目的,为传统几何法解立体几何感觉困难的学生提供一件有用的工具,争取能把各种立体几何题目坐标化处理。
立体几何建坐标系

立体几何建坐标系全文共四篇示例,供读者参考第一篇示例:立体几何建坐标系是描述和研究立体图形的重要工具之一。
在三维空间中,我们通常使用三维直角坐标系来描述立体图形的位置和形状。
这种坐标系由三个相互垂直的坐标轴组成,分别是x轴、y轴和z 轴,它们分别对应三维空间中的长度、宽度和高度。
在这个坐标系中,每个点都可以通过三个坐标值来表示,分别表示点在x轴、y轴和z轴上的位置。
用立体几何建坐标系描述一个物体时,首先需要确定一个原点,该原点是坐标轴的交点,通常我们取它为立体图形的重心或者其特定的某一个点。
然后,可以通过在坐标轴上确定一个单位长度来建立坐标系的比例尺。
接下来,可以通过测量物体在x、y、z三个方向上的长度、宽度和高度,来确定物体各个点的坐标值,从而描述整个物体的形状和位置。
利用立体几何建坐标系可以方便地计算立体图形的体积、表面积、中心质心等属性。
通过将三维立体图形分解成一系列的立方体、长方体或圆柱体等基本的几何图形,可以利用数学方法求解各部分的体积,并将它们相加得到整个立体图形的体积。
而对于复杂的立体图形,可以将其分解成多个简单的几何图形,再逐一计算其属性,最后综合得出结果。
这样的方法虽然有时会比较繁琐,但是却是一种较为准确和可靠的计算方式。
立体几何建坐标系不仅可以用于描述静态的立体图形,还可以用于描述立体图形的运动和变形。
通过不断变化物体各个点的坐标值,可以描述其在三维空间中的移动、旋转、缩放等动作。
通过改变一个立方体各个顶点的坐标值,可以实现它在空间中的旋转或者平移。
通过计算不同时间点上各个点的坐标值,可以还原出整个立体图形的运动轨迹,从而研究它的运动规律。
利用立体几何建坐标系还可以进行三维坐标系下的几何投影。
在三维空间中,物体的形状对应着它在每个坐标轴的投影,在三维坐标系下可以进行正投影、侧视投影等操作,将三维空间中的立体图形映射到二维平面上,便于我们观察和研究。
这种投影方法在建筑设计、工程制图等领域中有着广泛的应用。
(完整版)立体几何解答题的建系设点问题

立体几何解答题的建系设点问题一、基础知识:(一)建立直角坐标系的原则:如何选取坐标轴1、z 轴的选取往往是比较容易的,依据的是线面垂直,即z 轴要与坐标平面xOy 垂直,在几何体中也是很直观的,垂直底面高高向上的即是,而坐标原点即为z 轴与底面的交点2、,x y 轴的选取:此为坐标是否易于写出的关键,有这么几个原则值得参考: (1)尽可能的让底面上更多的点位于,x y 轴上(2)找角:,x y 轴要相互垂直,所以要利用好底面中的垂直条件 (3)找对称关系:寻找底面上的点能否存在轴对称特点解答题中,在建立空间直角坐标系之前,要先证明所用坐标轴为两两垂直(即一个线面垂直+底面两条线垂直),这个过程不能省略。
3、与垂直相关的定理与结论: (1)线面垂直:① 如果一条直线与一个平面上的两条相交直线垂直,则这条直线与该平面垂直 ② 两条平行线,如果其中一条与平面垂直,那么另外一条也与这个平面垂直 ③ 两个平面垂直,则其中一个平面上垂直交线的直线与另一个平面垂直 ④ 直棱柱:侧棱与底面垂直 (2)线线垂直(相交垂直):① 正方形,矩形,直角梯形② 等腰三角形底边上的中线与底边垂直(三线合一) ③ 菱形的对角线相互垂直④ 勾股定理逆定理:若222AB AC BC +=,则AB AC ⊥ (二)坐标的书写:建系之后要能够快速准确的写出点的坐标,按照特点可以分为3类 1、能够直接写出坐标的点(1) 坐标轴上的点,规律:在哪个轴上,那个位置就有坐标,其余均为0(2)底面上的点:坐标均为(),,0x y ,即竖坐标0z =,由于底面在作立体图时往往失真,所以要快速正确写出坐标,强烈建议在旁边作出底面的平面图进行参考 2、空间中在底面投影为特殊位置的点:如果()'11,,A x y z 在底面的投影为()22,,0A x y ,那么1212,x x y y ==(即点与投影点的横纵坐标相同)由这条规律出发,在写空间中的点时,可看下在底面的投影点,坐标是否好写。
立体几何中的建系设点

立体几何解答题的建系设点问题在如今的立体几何解答题中,有些题目可以使用空间向量解决问题,与其说是向量运算,不如说是点的坐标运算,所以第一个阶段:建系设点就显得更为重要,建立合适的直角坐标系的原则有哪些?如何正确快速写出点的坐标?这是本文要介绍的内容。
一、基础知识:(一)建立直角坐标系的原则:如何选取坐标轴1、z 轴的选取往往是比较容易的,依据的是线面垂直,即z轴要与坐标平面xOy 垂直,在几何体中也是很直观的,垂直底面高高向上的即是,而坐标原点即为z 轴与底面的交点2、,x y 轴的选取:此为坐标是否易于写出的关键,有这么几个原则值得参考:(1)尽可能的让底面上更多的点位于,x y 轴上(2)找角:,x y 轴要相互垂直,所以要利用好底面中的垂直条件(3)找对称关系:寻找底面上的点能否存在轴对称特点3、常用的空间直角坐标系满足,,x y z 轴成右手系,所以在标,x y 轴时要注意。
4、同一个几何体可以有不同的建系方法,其坐标也会对应不同。
但是通过坐标所得到的结论(位置关系,角)是一致的。
5、解答题中,在建立空间直角坐标系之前,要先证明所用坐标轴为两两垂直(即一个线面垂直 底面两条线垂直),这个过程不能省略。
6、与垂直相关的定理与结论:(1)线面垂直: ① 如果一条直线与一个平面上的两条相交直线垂直,则这条直线与该平面垂直② 两条平行线,如果其中一条与平面垂直,那么另外一条也与这个平面垂直③ 两个平面垂直,则其中一个平面上垂直交线的直线与另一个平面垂直④ 直棱柱:侧棱与底面垂直(2)线线垂直(相交垂直):① 正方形,矩形,直角梯形② 等腰三角形底边上的中线与底边垂直(三线合一)③ 菱形的对角线相互垂直④ 勾股定理逆定理:若222AB AC BC +=,则AB AC ⊥(二)坐标的书写:建系之后要能够快速准确的写出点的坐标,按照特点可以分为3类1、能够直接写出坐标的点(1) 坐标轴上的点,例如在正方体(长度为1)中的,,'A C D 点,坐标特点如下: x 轴:(),0,0x y 轴:()0,,0y z 轴:()0,0,z规律:在哪个轴上,那个位置就有坐标,其余均为0(2)底面上的点:坐标均为(),,0x y ,即竖坐标0z =,由于底面在作立体图时往往失真,所以要快速正确写出坐标,强烈建议在旁边作出底面的平面图进行参考:以上图为例: 则可快速写出,H I 点的坐标,位置关系清晰明了2、空间中在底面投影为特殊位置的点:如果()'11,,A x y z 在底面的投影为()22,,0A x y ,那么1212,x x y y ==(即点与投影点的横纵坐标相同)由这条规律出发,在写空间中的点时,可看下在底面的投影点,坐标是否好写。
2020高考数学----立体几何中的建系设点问题
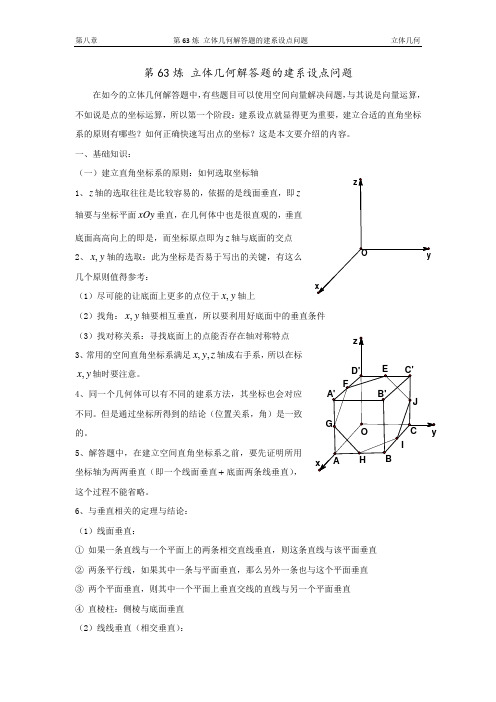
第63炼 立体几何解答题的建系设点问题在如今的立体几何解答题中,有些题目可以使用空间向量解决问题,与其说是向量运算,不如说是点的坐标运算,所以第一个阶段:建系设点就显得更为重要,建立合适的直角坐标系的原则有哪些?如何正确快速写出点的坐标?这是本文要介绍的内容。
一、基础知识:(一)建立直角坐标系的原则:如何选取坐标轴1、z 轴的选取往往是比较容易的,依据的是线面垂直,即z 轴要与坐标平面xOy 垂直,在几何体中也是很直观的,垂直底面高高向上的即是,而坐标原点即为z 轴与底面的交点2、,x y 轴的选取:此为坐标是否易于写出的关键,有这么几个原则值得参考:(1)尽可能的让底面上更多的点位于,x y 轴上(2)找角:,x y 轴要相互垂直,所以要利用好底面中的垂直条件 (3)找对称关系:寻找底面上的点能否存在轴对称特点 3、常用的空间直角坐标系满足,,x y z 轴成右手系,所以在标,x y 轴时要注意。
4、同一个几何体可以有不同的建系方法,其坐标也会对应不同。
但是通过坐标所得到的结论(位置关系,角)是一致的。
5、解答题中,在建立空间直角坐标系之前,要先证明所用坐标轴为两两垂直(即一个线面垂直 底面两条线垂直),这个过程不能省略。
6、与垂直相关的定理与结论: (1)线面垂直:① 如果一条直线与一个平面上的两条相交直线垂直,则这条直线与该平面垂直 ② 两条平行线,如果其中一条与平面垂直,那么另外一条也与这个平面垂直 ③ 两个平面垂直,则其中一个平面上垂直交线的直线与另一个平面垂直 ④ 直棱柱:侧棱与底面垂直 (2)线线垂直(相交垂直):① 正方形,矩形,直角梯形② 等腰三角形底边上的中线与底边垂直(三线合一) ③ 菱形的对角线相互垂直④ 勾股定理逆定理:若222AB AC BC +=,则AB AC ⊥(二)坐标的书写:建系之后要能够快速准确的写出点的坐标,按照特点可以分为3类 1、能够直接写出坐标的点(1) 坐标轴上的点,例如在正方体(长度为1)中的,,'A C D 点,坐标特点如下:x 轴:(),0,0x y 轴:()0,,0y z 轴:()0,0,z规律:在哪个轴上,那个位置就有坐标,其余均为0(2)底面上的点:坐标均为(),,0x y ,即竖坐标0z =,由于底面在作立体图时往往失真,所以要快速正确写出坐标,强烈建议在旁边作出底面的平面图进行参考:以上图为例: 则可快速写出,H I 点的坐标,位置关系清晰明了111,,0,,1,022H I ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭2、空间中在底面投影为特殊位置的点:如果()'11,,A x y z 在底面的投影为()22,,0A x y ,那么1212,x x y y ==(即点与投影点的横纵坐标相同)由这条规律出发,在写空间中的点时,可看下在底面的投影点,坐标是否好写。
用向量法解立体几何题,建系求点是关键

用向量法解立体几何题,建系求点是关键发布时间:2021-08-17T17:13:25.967Z 来源:《中小学教育》2021年11期4月作者:梁业兴[导读] 利用空间向量法解立体几何题,可把抽象的空间图形关系转化为具体的数量运算梁业兴中山市龙山中学广东省中山市 528471摘要:利用空间向量法解立体几何题,可把抽象的空间图形关系转化为具体的数量运算,并有很强的规律性和可操作性,但在实际教学中发现,学生对某些几何体存在建系求点上的困难.本文主要通过实例探讨解决问题的办法.关键词:立体几何、向量法、建系求点向量是近代数学中最重要和最基本的数学概念之一,是具有几何形式和代数形式的“双重身份”的概念,是沟通代数与几何的桥梁.将空间向量引入高中数学,为解决三维空间中图形的位置关系与度量问题提供了一个十分有效的工具.解题时,只需建立合适的空间直角坐标系,求出相关点的坐标,然后化为向量问题,通过进行向量运算,即可转化为几何问题.在这里,建系求点将是解决问题的关键.一、问题的提出学生用向量法解如下高考真题(例1)时容易求错或无法求出点P的坐标.二、问题分析学生用向量法解立体几何题主要的错误有两个:一是建系不合理,二是求错甚至不会求点的坐标.主要原因有两个方面:一方面是图形认知障碍.平面几何图形反映图形的真实情况,但在立体几何中,由于是用斜二侧画法画成的直观图,图形往往不能反映原形的真实结构和全部特点.例如在“水平放置的平面图形的直观图画法”中,正方形、矩形在水平放置后呈平行四边形,以及在图中看上去明显不垂直的两条线段却偏要证明他们互相垂直,明显是锐角的实际上却是一个钝角等;另一方面是缺乏空间想象能力.由于空间想象能力是一个比较复杂、抽象的思维过程,想象能力从二维到三维的拓展难度较大,在实际教学中,学生往往不易建立空间概念,在脑海中难以形成较为准确、直观的几何模型,不能灵活运用一些重要元素之间的位置关系,没掌握一些解题技巧(如局部图形建立平面直角坐标系作平面化处理),造成点的坐标求错,甚至求不出来等.三、解决问题之建系方法研究学生建系不合理,主要集中在x轴与y轴的建立,原因就是对图形的认知有障碍.所以主要方法就是把图形还原——局部平面化处理.画出底面的平面图,把建x,y轴的问题放在平面几何里完成.分析:作底面平面图如图3,图4,图5所示.由此平面图可以比较清楚地看到以那两条互相垂直的直线分别为x 轴、y 轴为宜,且方便写出平面内各点的坐标.可以看到建系的方法并不唯一,要根据题意选用一个合适的坐标系.点评:平面内常见的垂直关系有:菱形、正方形的对角线;等腰、等边三角形的中线与底边(三线合一);直径所对圆周角的两边;或在某个三角形中知道两边一角,先用余弦定理求出第三边,再用勾股定理证明线线垂直等.四、解决问题之求点方法研究(一)垂线法在空间直角坐标系中,有些点的坐标可以通过向坐标平面或坐标轴作垂线,再求出垂线段的长,从而写出点的坐标.点评:点E为线段PD的三等分点,个别学生可能会类比中点坐标公式,容易犯“将P、D坐标相加除以3得到E点坐标”这样的错误.此题还可以用下面的向量法解决.(二)向量法在空间直角坐标系中,利用两向量相等,可以求出点的坐标.点评:在线上是否存在一个点满足某个要求的题型通常可以利用三点共线设,再利用向量相等用表示出未知点的坐标,再根据已知条件待定.利用向量相等对处理比较难作垂线或容易作错垂线的题目来说,效果更好.如例3.(三)待定系数法设出所求点的坐标,再利用题目给出的已知条件,如:线段的长度、线线角、线面角、面面角等,列出方程组,解方程组即可求出所求点的坐标.用向量法来解决例1,如下:证明:(1)连接 AC 、BD,设AC 与BD相交于点O,则AC⊥BD.以O为坐标原点,OA、OB所在直线分别为 x 轴、y 轴建立如图11所示的空间直角坐标系,由图观察可知,此二面角为钝角,所以二面角的余弦值为.点评:因为底面ABCD是菱形,对角线 AC 与 BD 互相垂直,所以可以以对角线的交点O为坐标原点,OA、OB所在直线分别为 x 轴、y轴建立空间直角坐标系,那么点P的坐标将是解决问题的关键.这里采用待定系数法,根据题目给出的线段的长度:,列方程组求解即可求出P点的坐标,使得问题迎刃而解.参考文献[1]徐晓宇,屈黎明.向量法解立体几何题的点坐标求法——2017年高考浙江卷立体几何解答题的方法总结. 《数学教学》,2018(8):33~36.[2]卢学渊.向量法解立体几何题时动点的设法.《数学学习与研究:教研版》,2012(11):107~107.。
立体几何建系方法

立体几何建系方法
立体几何建系是将物体的各个部分和特征按照一定的规律组织起来,以便实现物体的描述、分析和设计。
常见的立体几何建系方法包括以下几种:
1. 投影法:通过将三维物体投射到二维平面上来描述物体的形状和特征。
投影法包括正射投影和透视投影两种,可以用来绘制物体的平面图和立体图。
2. 点线面方法:用点、线和面来描述物体的形状和特征。
点表示物体的位置,线表示物体的边界或分界线,面表示物体的表面。
3. 剖视法:按照一定的切割规则将物体切割成若干部分,以便观察物体的内部结构和特征。
剖视法可以通过截剖图或剖面图来表示。
4. 抽象建模法:通过简化、抽象物体的形状和特征,以便更好地理解和分析物体的结构和功能。
常见的抽象建模方法包括立体图法、组合法、选择法等。
5. 三维建模方法:利用计算机软件或物理模型来建立真实或虚拟的三维模型,以便实现对物体的全面描述和分析。
三维建模方法包括参数建模、几何建模、曲面建模等。
6. 尺寸控制方法:通过测量和控制物体的尺寸来确保物体的质量和性能。
尺寸控制方法包括公差分析、配合与间隙控制等。
立体几何建系方法的选择取决于具体的应用场景和需求,不同的方法可以相互结合使用,以实现对物体的准确描述和分析。
高二新学案立体几何如何建系找坐标

B 1C 1BCDAD 1A 1EFEADBCP空间立体,寻求建系的方法,学会找坐标 一、标准化的正方体,长方体,四棱锥问题1.正方体ABCD-A 1B 1C 1D 1,建立适当的坐标系,并表示图中所有点的坐标。
解;以A 为坐标原点.以AB ,AD ,AA 1所在直线为x,y,z 轴,建立如图空间直角坐标系,设正方体棱长为1,则ABCD是直角梯形,90=∠=∠BAD ABC ,2.如图,四边形ABCD SA 平面⊥,1===BC AB SA ,21=AD ,SC 中点是P ,建立适当的坐标系,表示图中所有点的坐标。
解;以A 为坐标原点.以AD ,AB ,AS 所在直线为x,y,z 轴,建立如图空间直角坐标系,则3.在五面体ABCDEF 中,FA ⊥平面ABCD ,AD ∥BC ∥FE ,AB ⊥AD ,M 为EC 的中点,AF=AB=BC=FE= 21AD=1,建立适当的坐标系,表示图中所有点的坐标。
解;以A 为坐标原点.以AB ,AD ,AF 所在直线为x,y,z 轴,建立如图空间直角坐标系,则4:如图,四棱锥P ABCD-中,底面ABCD为矩形,PA ⊥底面ABCD,6,3PA AB AD ===,点E 为棱PB 的中点。
建立适当的坐标系,表示图中所有点的坐标。
解;以A 为坐标原点.以AB ,AD ,AP 所在直线为x,y,z 轴,建立如图空间直角坐标系,则5..如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB//CD,∠DAB=90°,PA=AD=DC=1,AB=2,M 为PB 的中点. 建立适当的坐标系,表示图中所有点的坐标。
解;以A 为坐标原点.以AD ,AB ,AP 所在直线为x,y,z 轴,建立如图空间直角坐标系,则6.多面体EDABC 中,AD ⊥平面ABC , AC ⊥BC,,AD=21CE=1,AC=1.BC=2,M 为BE 中点.,建立适当的坐标系,表示图中所有点的坐标。
立体几何(向量法)—建系讲义

立体几何(向量法)—建系引入空间向量坐标运算,使解立体几何问题避免了传统方法进行繁琐的空间分析,只需建立空间直角坐标系进行向量运算,而如何建立恰当的坐标系,成为用向量解题的关键步骤之一.所谓“建立适当的坐标系”,一般应使尽量多的点在数轴上或便于计算。
一、利用共顶点的互相垂直的三条线构建直角坐标系例1(2012高考真题重庆理19)(本小题满分12分如图,在直三棱柱111C B A ABC中,AB=4,AC=BC=3,D 为AB 的中点(Ⅰ)求点C 到平面11ABB A 的距离; (Ⅱ)若11AB A C 求二面角的平面角的余弦值.【答案】解:(1)由AC =BC ,D 为AB 的中点,得CD ⊥AB .又CD ⊥AA 1,故CD ⊥面A 1ABB 1,所以点C 到平面A 1ABB 1的距离为CD =BC 2-BD 2=5.(2)解法一:如图,取D 1为A 1B 1的中点,连结DD 1,则DD 1∥AA 1∥CC 1.又由(1)知CD ⊥面A 1ABB 1,故CD ⊥A 1D ,CD ⊥DD 1,所以∠A 1DD 1为所求的二面角A 1-CD -C 1的平面角.因A 1D 为A 1C 在面A 1ABB 1上的射影,又已知AB 1⊥A 1C ,由三垂线定理的逆定理得AB 1⊥A 1D ,从而∠A 1AB 1、∠A 1DA 都与∠B 1AB 互余,因此∠A 1AB 1=∠A 1DA ,所以Rt △A 1AD ∽Rt △B 1A 1A.因此AA 1AD =A 1B 1AA 1,即AA 21=AD ·A 1B 1=8,得AA 1=22.从而A 1D =AA 21+AD 2=23.所以,在Rt △A 1DD 1中,cos ∠A 1DD 1=DD 1A 1D =AA 1A 1D =63.解法二:如图,过D 作DD 1∥AA 1交A 1B 1于点D 1,在直三棱柱中,易知DB ,DC ,DD 1两两垂直.以D 为原点,射线DB ,DC ,DD 1分别为x 轴、y 轴、z 轴的正半轴建立空间直角坐标系D -xyz .设直三棱柱的高为h ,则A(-2,0,0),A 1(-2,0,h),B 1(2,0,h),C(0,5,0),C 1(0,5,h),从而AB 1→=(4,0,h),A 1C →=(2,5,-h).由AB 1→⊥A 1C →,有8-h 2=0,h =2 2.故DA 1→=(-2,0,22),CC 1→=(0,0,22),DC →=(0,5,0).设平面A 1CD 的法向量为m =(x 1,y 1,z 1),则m ⊥DC →,m ⊥DA 1→,即5y 1=0,-2x 1+22z 1=0,取z 1=1,得m =(2,0,1),设平面C 1CD 的法向量为n =(x 2,y 2,z 2),则n ⊥DC →,n ⊥CC 1→,即5y 2=0,22z 2=0,取x 2=1,得n =(1,0,0),所以cos 〈m ,n 〉=m ·n|m||n|=22+1·1=63.所以二面角A 1-CD -C 1的平面角的余弦值为63.二、利用线面垂直关系构建直角坐标系例 2.如图所示,AF 、DE 分别是圆O 、圆1O 的直径,AD 与两圆所在的平面均垂直,8AD .BC 是圆O 的直径,6ABAC,//OE AD .(I)求二面角B AD F 的大小;(II)求直线BD 与EF 所成的角的余弦值.19.解:(Ⅰ)∵AD 与两圆所在的平面均垂直,∴AD ⊥AB, AD ⊥AF,故∠BAD 是二面角B —AD —F 的平面角,。
空间向量之立体几何建系和求点坐标(共24张PPT)

xOy面内D yOz面内E zOx面内F
坐标形式 (x,y,0)
(0,y,z)
(x,0,z)
基础知识:
2、空间中在底面投影为特殊位置的点:
如果 A' x1, y1, z 在底面的投影为 A x2, y2,0 ,那么x1 x2, y1 y2
(即点与投影点的横纵坐标相同) 由这条规律出发,在写空间中的点坐标时,可看一下在底面的
建系方法2练习2 练2.如图,已知四棱锥P ABCD的底面是菱形,对角线AC, BD交于点O, OA 4,OB 3,OP 4,且OP 平面ABCD,点M为PC的三等分点(靠近P), 建立适当的直角坐标系并求各点坐标。
找“墙角”
14
建系方法2练习3
练3.如图,在等腰梯形ABCD中,AB // CD, AD DC CB 1, ABC 60,CF 平面ABCD,且CF 1,建立适当的直角坐标系 并确定各点坐标。
找“墙角”
建系方法2练习5
真题(辽宁卷)如图,AB 是圆的直径,PA 垂 直圆所在的平面,C 是圆上的点.
(1)求证:平面 PAC⊥平面 PBC; (2)若 AB=2,AC=1,PA=1,求证:二面
角 C-PB-A 的余弦值.
造“墙角”
建系方法3例题
三、利用面面垂直关系构建空间直角坐标系(转化为墙角模型) 例3.在四棱锥V-ABCD中,底面ABCD是边长为2的正方形,侧面VAD 是正三角形,平面VAD⊥底面ABCD.点P、H分别是线段VC、AD的 中点.试建立空间直角坐标系并写出P、V、A、B、C、D的坐标.
互相垂直,EF // BD, ED BD, AD 2, EF ED 1, 试建立合适的 空间直角坐标系并确定各点的坐标
立体几何(向量法)—建系讲义

立体几何(向量法)—建系引入空间向量坐标运算,使解立体几何问题避免了传统方法进行繁琐的空间分析,只需建立空间直角坐标系进行向量运算,而如何建立恰当的坐标系,成为用向量解题的关键步骤之一.所谓“建立适当的坐标系”,一般应使尽量多的点在数轴上或便于计算。
一、利用共顶点的互相垂直的三条线构建直角坐标系例1(2012高考真题重庆理19)(本小题满分12分 如图,在直三棱柱111C B A ABC - 中,AB=4,AC=BC=3,D 为AB 的中点(Ⅰ)求点C 到平面11ABB A 的距离;(Ⅱ)若11AB A C ⊥求二面角 的平面角的余弦值.【答案】解:(1)由AC =BC ,D 为AB 的中点,得CD ⊥AB 。
又CD ⊥AA 1,故CD ⊥面A 1ABB 1,所以点C 到平面A 1ABB 1的距离为CD =错误!=错误!.(2)解法一:如图,取D 1为A 1B 1的中点,连结DD 1,则DD 1∥AA 1∥CC 1。
又由(1)知CD ⊥面A 1ABB 1,故CD ⊥A 1D ,CD ⊥DD 1,所以∠A 1DD 1为所求的二面角A 1-CD -C 1的平面角.因A 1D 为A 1C 在面A 1ABB 1上的射影,又已知AB 1⊥A 1C ,由三垂线定理的逆定理得AB 1⊥A 1D ,从而∠A 1AB 1、∠A 1DA 都与∠B 1AB 互余,因此∠A 1AB 1=∠A 1DA ,所以Rt △A 1AD ∽Rt △B 1A 1A .因此错误!=错误!,即AA 错误!=AD ·A 1B 1=8,得AA 1=2错误!.从而A1D=错误!=2错误!。
所以,在Rt△A1DD1中,cos∠A1DD1=错误!=错误!=错误!。
解法二:如图,过D作DD1∥AA1交A1B1于点D1,在直三棱柱中,易知DB,DC,DD1两两垂直.以D为原点,射线DB,DC,DD1分别为x轴、y轴、z轴的正半轴建立空间直角坐标系D-xyz.设直三棱柱的高为h,则A(-2,0,0),A1(-2,0,h),B1(2,0,h),C(0,错误!,0),C1(0,错误!,h),从而错误!=(4,0,h),错误!=(2,错误!,-h).由错误!⊥错误!,有8-h2=0,h=2错误!。
立体几何中的建系设点讲解学习
(2)对于一条线段上的某点分线段成比例,可以利用向量关系将该点坐标计算出来
由这条规律出发,在写空间中的点时,可看下在底面的投影ቤተ መጻሕፍቲ ባይዱ,坐标是否好写。如果可以则直接确定了横纵坐标,而竖坐标为该点到底面的距离。例如:正方体中的 点,其投影为 ,而 所以 ,而其到底面的距离为 ,故坐标为
以上两个类型已经可以囊括大多数几何体中的点,但总还有一些特殊点,那么就要用到第三个方法:
3、需要计算的点
(3)找对称关系:寻找底面上的点能否存在轴对称特点
3、常用的空间直角坐标系满足 轴成右手系,所以在标 轴时要注意。
4、同一个几何体可以有不同的建系方法,其坐标也会对应不同。但是通过坐标所得到的结论(位置关系,角)是一致的。
5、解答题中,在建立空间直角坐标系之前,要先证明所用坐标轴为两两垂直(即一个线面垂直 底面两条线垂直),这个过程不能省略。
二、典型例题:
例1:在三棱锥 中, 平面 , , 分别是棱 的中点, ,试建立适当的空间直角坐标系并确定各点坐标
例2:在长方体 中, 分别是棱 上的点, , ,建立适当的直角坐标系并写出点的坐标。
例3:如图,在等腰梯形 中, , , 平面 ,且 ,建立适当的直角坐标系并确定各点坐标。
小炼:建立坐标系的最重要的条件就是线面垂直(即 轴),对于 轴的选取,如果没有已知线段,可以以垂足所在的某一条直线为坐标轴,然后作这条轴的垂线来确定另一条轴。
例4:已知四边形 满足 , 是 中点,将 翻折成 ,使得平面 平面 , 为 中点
思路:在处理翻折问题时,首先要确定在翻折的过程中哪些量与位置关系不变,这些都是作为已知条件使用的。
例5:如图,已知四棱锥 的底面是菱形,对角线 交于点 ,且 平面 ,点 为 的三等分点(靠近 ),建立适当的直角坐标系并求各点坐标
高中数学讲义立体几何中的建系设点问题
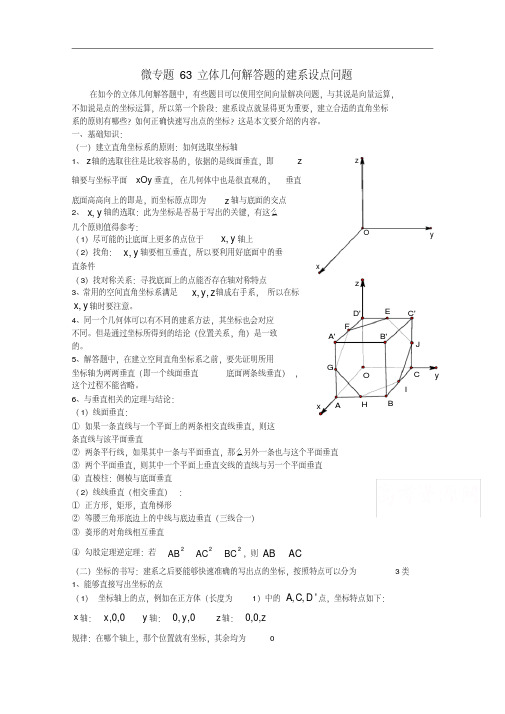
OyxzF E GHIJ O yxzA'C'BB'C D'A微专题63 立体几何解答题的建系设点问题在如今的立体几何解答题中,有些题目可以使用空间向量解决问题,与其说是向量运算,不如说是点的坐标运算,所以第一个阶段:建系设点就显得更为重要,建立合适的直角坐标系的原则有哪些?如何正确快速写出点的坐标?这是本文要介绍的内容。
一、基础知识:(一)建立直角坐标系的原则:如何选取坐标轴1、z 轴的选取往往是比较容易的,依据的是线面垂直,即z轴要与坐标平面xOy 垂直,在几何体中也是很直观的,垂直底面高高向上的即是,而坐标原点即为z 轴与底面的交点2、,x y 轴的选取:此为坐标是否易于写出的关键,有这么几个原则值得参考:(1)尽可能的让底面上更多的点位于,x y 轴上(2)找角:,x y 轴要相互垂直,所以要利用好底面中的垂直条件(3)找对称关系:寻找底面上的点能否存在轴对称特点3、常用的空间直角坐标系满足,,x y z 轴成右手系,所以在标,x y 轴时要注意。
4、同一个几何体可以有不同的建系方法,其坐标也会对应不同。
但是通过坐标所得到的结论(位置关系,角)是一致的。
5、解答题中,在建立空间直角坐标系之前,要先证明所用坐标轴为两两垂直(即一个线面垂直底面两条线垂直),这个过程不能省略。
6、与垂直相关的定理与结论:(1)线面垂直:①如果一条直线与一个平面上的两条相交直线垂直,则这条直线与该平面垂直②两条平行线,如果其中一条与平面垂直,那么另外一条也与这个平面垂直③两个平面垂直,则其中一个平面上垂直交线的直线与另一个平面垂直④直棱柱:侧棱与底面垂直(2)线线垂直(相交垂直):①正方形,矩形,直角梯形②等腰三角形底边上的中线与底边垂直(三线合一)③菱形的对角线相互垂直④勾股定理逆定理:若222ABACBC ,则ABAC(二)坐标的书写:建系之后要能够快速准确的写出点的坐标,按照特点可以分为3类1、能够直接写出坐标的点(1)坐标轴上的点,例如在正方体(长度为1)中的,,'A C D 点,坐标特点如下:x 轴:,0,0x y 轴:0,,0y z 轴:0,0,z规律:在哪个轴上,那个位置就有坐标,其余均为(2)底面上的点:坐标均为,,0x y ,即竖坐标0z ,由于底面在作立体图时往往失真,所以要快速正确写出坐标,强烈建议在旁边作出底面的平面图进行参考:以上图为例:则可快速写出,H I 点的坐标,位置关系清晰明了111,,0,,1,022H I2、空间中在底面投影为特殊位置的点:如果'11,,A x y z 在底面的投影为22,,0A x y ,那么1212,x x y y (即点与投影点的横纵坐标相同)由这条规律出发,在写空间中的点时,可看下在底面的投影点,坐标是否好写。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何解答题的建系设点问题
在如今的立体几何解答题中,有些题目可以使用空间向量解决问题,
不如说是点的坐标运算,所以第一个阶段:建系设点就显得更为重要, 系的原则有哪些?如何正确快速写出点的坐标?这是本文要介绍的内容。
一、基础知识:
(一)建立直角坐标系的原则:如何选取坐标轴
乙
1、z轴的选取往往是比较容易的,依据的是线面垂直,即z
轴要与坐标平面xOy垂直,在几何体中也是很直观的,垂直
底面高高向上的即是,而坐标原点即为z轴与底面的交点
2、x, y轴的选取:此为坐标是否易于写出的关键,有这么
几个原则值得参考:
(1)尽可能的让底面上更多的点位于x,y轴上
(2)找x, y轴要相互垂直,所以要利用好底面中的垂直条件
(3 )找对称关系:寻找底面上的点能否存在轴对称特点
3、常用的空间直角坐标系满足x, y,z轴成右手系,所以在标x, y
轴时要注意。
4、同一个几何体可以有不同的建系方法,其坐标也会对应不同。
但是通
过坐标所得到的结论(位置关系,角)是一致的。
5、解答题中,在建立空间直角坐标系之前,要先证明所用
坐标轴为两两垂直(即一个线面垂直底面两条线垂直),这个
过程不能省略。
6、与垂直相关的定理与结论:
(1)线面垂直:
①如果一条直线与一个平面上的两条相交直线垂直,则这条直线与该平面垂直
②两条平行线,如果其中一条与平面垂直,那么另外一条也与这个平面垂直
③两个平面垂直,则其中一个平面上垂直交线的直线与另一个平面垂直
④直棱柱:侧棱与底面垂直
(2 )线线垂直(相交垂直):
①正方形,矩形,直角梯形
与其说是向量运算, 建立合适的直角坐标
②等腰三角形底边上的中线与底边垂直(三线合一)
③菱形的对角线相互垂直
④勾股定理逆定理:若AB2 AC2 BC2,则AB AC
(二)坐标的书写:建系之后要能够快速准确的写出点的坐标,按照特点可以分为3类
1能够直接写出坐标的点
(1)坐标轴上的点,例如在正方体(长度为1)中的A,C,D'点,坐标特点如下:
x 轴:x,0,0 y 轴:0,y,0 z 轴:0,0,z
规律:在哪个轴上,那个位置就有坐标,其余均为0
(2)底面上的点:坐标均为x, y,0,即竖坐标z 0,由于底面在作立体图时往往失真,
所以要快速正确写出坐标,强烈建议在旁边作出底面的平面图进行参考:以上图为例:
则可快速写出H,l点的坐标,位置关系清晰明了
O C
1 1
H 1, — ,0 ,1 —,1,0
2 2
"I 2、空间中在底面投影为特殊位置的点:
如果A x1, y1, z 在底面的投影为 A x2, y2,0 ,那么|
A H B
为X2, % y2 (即点与投影点的横纵坐标相同)H
由这条规律出发,在写空间中的点时,可看下在底面的投影点,坐标是否好写。
如果可
以则直接确定了横纵坐标,而竖坐标为该点到底面的距离。
例如:正方体中的B'点,其投影为B,而B 1,1,0所以B 1,1,z,而其到底面的距离为1,故坐标为B 1,1,1
以上两个类型已经可以囊括大多数几何体中的点,但总还有一些特殊点,那么就要用到第三
个方法:
3、需要计算的点
①中点坐标公式:A x u y1, z-i , B x2, y2,z2,则AB中点M 西生単址,目z2
2 2 2
图中的H , I, E, F等中点坐标均可计算
②利用向量关系进行计算(先设再求):向量坐标化后,向量的关系也可转化为坐标的关系,
A '点的坐标,如果使用向量计算,则设 A x, y,z ,
、典型例题: 例1 :在三棱锥P ABC 中, 棱AB, BC,CD 的中点,AB 坐标系并确定各点坐标
例2:在长方体ABCD A 1B 1C 1D 1中,E,F 分别是棱BC,CC 1 上的点,CF AB 2CE ,AB:AD:AA , 1:2:4,建立
适当的直角坐标系并写出点的坐标。
例3 :如图,在等腰梯形 ABCD 中,AB// CD ,
AD DC CB 1, ABC 60°, CF 平面 ABCD ,
且CF 1,建立适当的直角坐标系并确定各点坐标。
小炼:建立坐标系的最重要的条件就是线面垂直(即 z 轴), 对于x, y 轴的选取,如果没有已知线段,可以以垂足所在的 某一条直线为坐标轴,然后作这条轴的垂线来确定另一条轴。
可直接写出
A 1,0,0 ,
B 1,1,0 ,B ' 1,1,1,观察向量 umr AB UU 'UU ' uuu
AB ,而 AB
0,1,0
iuuu
AB x 1,y 1,z 1
x 1 0 x 1 y 1 1 y 0 A '
1,0,1
z 1 0
z 1
用向量关系解出变量的值,例如:求
PA
AC
D 1
B 1
A 1
E C
D
例4:已知四边形 ABCD 满足AD// BC,BA AD DC
1
BC a , E 是
B C
中点,将
2
VBAE 翻折成VB !AE ,使得平面B i AE
AECD ,F 为B 1D 中点
思路:在处理翻折问题时, 首先要确定在翻折的过程中哪些量与位置关系不变,
这些都是作 为已知条件使用的。
例5:如图,已知四棱锥 P ABCD 的底面是菱形, 对角线 AC,BD 交于点 0,0A 4,OB 3,0P 4,
且OP 平面ABCD ,点M 为PC 的三等分点(靠 近P ),建立适当的直角坐标系并求各点坐标 小炼:(1)底面是菱形时要注意对角线相互垂直的性 质
(2 )对于一条线段上的某点分线段成比例,可以利用向量关系将该点
B'
坐标计算出来。
