32位浮点数加法设计仿真实验报告
32位浮点加法器设计

32位浮点加法器设计32位浮点加法器是一种用于计算机中的算术逻辑单元(ALU),用于执行浮点数的加法运算。
它可以将两个32位浮点数相加,并输出一个32位的结果。
设计一个高效的32位浮点加法器需要考虑多个方面,包括浮点数的表示形式、运算精度、舍入方式、运算逻辑等。
下面将详细介绍32位浮点加法器的设计。
1.浮点数的表示形式:浮点数通常采用IEEE754标准进行表示,其中32位浮点数由三个部分组成:符号位、阶码和尾数。
符号位用来表示浮点数的正负,阶码用来表示浮点数的指数,尾数用来表示浮点数的小数部分。
2.运算精度:在浮点数加法运算中,精度是一个重要的考虑因素。
通常,浮点数加法器采用单精度(32位)进行设计,可以处理较为广泛的应用需求。
如果需要更高的精度,可以考虑使用双精度(64位)浮点加法器。
3.舍入方式:浮点数加法运算中,结果通常需要进行舍入处理。
常见的舍入方式有以下几种:舍入到最近的偶数、舍入向上、舍入向下、舍入到零。
具体的舍入方式可以根据应用需求来确定。
4.运算逻辑:浮点数加法运算涉及到符号位、阶码和尾数的加法。
首先,需要判断两个浮点数的阶码大小,将较小的阶码移到较大的阶码对齐,并相应调整尾数。
然后,将尾数进行相加并进行规格化处理。
最后,根据求和结果的大小,进行溢出处理和舍入操作。
在32位浮点加法器的设计中,还需要考虑到性能和效率。
可以采用流水线技术来提高运算速度,将加法运算划分为多个阶段,并在每个阶段使用并行处理来加速运算。
此外,还可以使用硬件加速器和快速逻辑电路来优化运算过程。
总结起来,设计一个高效的32位浮点加法器需要考虑浮点数的表示形式、运算精度、舍入方式、运算逻辑以及性能和效率。
在实际设计中,还需要根据具体应用需求进行功能扩展和优化。
通过合理的设计和调优,可以实现高性能的浮点加法器,满足不同应用场景的需求。
32位浮点数加法设计仿真实验报告

32位浮点数加法设计仿真实验报告名字:李磊学号:10045116 班级:1004221132位浮点数的IEEE-754格式单精度格式IEEE.754标准规定了单精度浮点数共32位,由三部分组成:23位尾数f,8位偏置指数e,1位符号位s。
将这三部分由低到高连续存放在一个32位的字里,对其进行编码。
其中[22:0]位包含23位的尾数f;[30:23]位包含8位指数e;第31位包含符号s{s[31],e[30:23],f[22:0]}其中偏置指数为实际指数+偏置量,单精度浮点数的偏置量为128,双精度浮点数的偏置量为1024。
规格化的数:由符号位,偏置指数,尾数组成,实际值为1.f乘2的E-128次方非规格化的数:由符号位,非偏置指数,尾数组成,实际值为0.f乘2的E次方特殊的数:0(全为零),+无穷大(指数全为1,尾数为0,符号位为0),-无穷大(指数全为1,尾数为0,符号位为1),NAN(指数全为1,尾数为不全为0)浮点数加法器设计设计思路:1.前端处理,还原尾数2.指数处理,尾数移位,使指数相等3.尾数相加4.尾数规格化处理5.后端处理,输出浮点数具体设计:设计全文:module flowadd(ix, iy, clk, a_en, ost,oz);input ix, iy, clk, a_en;output oz, ost;wire[31:0] ix,iy;reg[31:0] oz;wire clk,ost,a_en;reg[25:0] xm, ym, zm;reg[7:0] xe, ye, ze;reg[2:0] state;parameter start = 3'b000, //设置状态机zerock = 3'b001,exequal = 3'b010,addm = 3'b011,infifl = 3'b100,over = 3'b110;assign ost = (state == over) ? 1 : 0; /*后端处理,输出浮点数*/always@(posedge ost)beginif(a_en)oz <= {zm[25],ze[7:0],zm[22:0]};endalways@(posedge clk) //状态机begincase(state)start: //前端处理,分离尾数和指数,同时还原尾数beginxe <= ix[30:23];xm <= {ix[31],1'b0,1'b1,ix[22:0]};ye <= iy[30:23];ym <= {iy[31],1'b0,1'b1,iy[22:0]};state <= zerock;endzerock:beginif(ix == 0)begin{ze, zm} <= {ye, ym};state <= over;endelseif(iy == 0)begin{ze, zm} <= {xe, xm};state <= over;endelsestate <= exequal;endexequal: //指数处理,使得指数相等beginif(xe == ye)state <= addm;elseif(xe > ye)beginye <= ye + 1;ym[24:0] <= {1'b0, ym[24:1]};if(ym == 0)beginzm <= xm;ze <= xe;state <= over;endelsestate <= exequal;endelsebeginxe <= xe + 1;xm[24:0] <= {1'b0,xm[24:1]};if(xm == 0)beginzm <= ym;ze <= ye;state <= over;endelsestate <= exequal;endendaddm: //带符号位和保留进位的尾数相加beginif ((xm[25]^ym[25])==0)beginzm[25] <= xm[25];zm[24:0] <= xm[24:0]+ym[24:0];endelseif(xm[24:0]>ym[24:0])beginzm[25] <= xm[25];zm[24:0] <=xm[24:0]-ym[24:0];endelsebeginzm[25] <= ym[25];zm[24:0] <=ym[24:0]-xm[24:0];endze <= xe;state <= infifl;endinfifl: //尾数规格化处理beginif(zm[24]==1)beginzm[24:0] <= {1'b0,zm[24:1]};ze <= ze + 1;state <= over;endelseif(zm[23]==0)beginzm[24:0] <= {zm[23:0],1'b0};ze <= ze - 1;state <= infifl;endelsestate <= over;endover:beginstate<= start;enddefault:beginstate<= start;endendcaseendendmodule设计结果仿真仿真结果为41A00000H+41080000H=41E40000H41A00000H=10D,41080000H=4.25D,41E40000H=14.25D,验证成功。
32位程序 double类型计算处理

标题:32位程序中的double类型计算处理随着计算机科学技术的不断发展,双精度浮点数(double)类型在32位程序中的计算处理成为了关注的焦点之一。
本文将就此话题进行探讨,介绍双精度浮点数在32位程序中的计算处理方法和注意事项。
1. 双精度浮点数的定义和特点双精度浮点数是一种用于表示实数的数据类型,通常占据64位的存储空间,其中52位用于表示尾数,11位用于表示指数,1位用于表示符号位。
这使得双精度浮点数在表示范围和精度上都比单精度浮点数更加优越,因此在科学计算和工程领域得到广泛应用。
2. 双精度浮点数在32位程序中的计算处理双精度浮点数在32位程序中的计算处理需要特别注意,因为在32位系统中,CPU通常只能一次处理32位的数据。
在进行双精度浮点数的计算处理时,需要借助CPU的特殊指令集或者使用软件模拟的方式来完成。
3. 特殊指令集的利用对于支持双精度浮点数计算的32位系统,通常会提供一些特殊的指令集来加速双精度浮点数的计算处理。
Intel的SSE(Streaming SIMD Extensions)指令集就提供了对双精度浮点数进行快速计算的指令,可以大大提高计算速度。
4. 软件模拟的处理方法对于不支持双精度浮点数计算的32位系统,可以通过软件模拟的方式来实现双精度浮点数的计算处理。
这种方法虽然速度较慢,但可以在不支持硬件加速的系统上实现双精度浮点数的计算。
5. 精度和舍入误差的问题双精度浮点数的计算处理中,由于计算机内部二进制表示和十进制实数的差异,常常会出现精度损失和舍入误差。
因此在对双精度浮点数进行计算处理时,需要特别注意精度问题,避免因为舍入误差而影响计算结果的准确性。
6. 结论在32位程序中进行双精度浮点数的计算处理,需要结合特殊指令集和软件模拟的方法来实现。
同时要注意精度和舍入误差的问题,保证计算结果的准确性。
希望本文能够对读者有所帮助,谢谢!通过以上的内容,应该可以帮助你写出一篇高质量的、流畅易读的文章。
ieee754标准32位浮点数和普通浮点数

IEEE 754标准32位浮点数和普通浮点数作为计算机科学领域中的重要概念,浮点数在计算机程序与数据处理中扮演着至关重要的角色。
而其中IEEE 754标准32位浮点数和普通浮点数更是在计算机的底层运算中发挥着关键作用。
本文将深入探讨这两种浮点数,并从不同角度进行全面评估,以便更好地理解其深度和广度。
1. 普通浮点数的基本概念普通浮点数是一种十进制系统的数值表示方式,可以表示实数并支持浮点运算。
它由三个部分组成:符号位、尾数和指数。
符号位用来表示数值的正负性,尾数用来表示有效数字,指数则用来表示位置和值的大小。
常见的浮点数表示方法有单精度浮点数和双精度浮点数,分别占用4字节和8字节的存储空间。
2. IEEE 754标准32位浮点数的特点IEEE 754标准32位浮点数是一种二进制浮点数的表示方式,广泛应用于计算机系统中。
它同样由三个部分组成:符号位、尾数和指数。
不同的是,IEEE 754标准采用了规范化表示和偏置指数的方式,使得浮点数的表示更加简洁和高效。
IEEE 754标准还规定了一些特殊的浮点数值,如正无穷大、负无穷大和NaN(非数值)等,以满足不同的计算需求。
3. 深度分析:IEEE 754标准32位浮点数和普通浮点数的区别在数字表示和计算精度方面,IEEE 754标准32位浮点数与普通浮点数存在一些显著的区别。
普通浮点数采用十进制系统表示,可以精确表示大多数的小数,但无法精确表示一些特定的无限循环小数,导致精度损失。
而IEEE 754标准32位浮点数采用二进制系统表示,可以精确表示某些无限循环小数,但对一些十进制无限循环小数的精度依然存在限制。
IEEE 754标准32位浮点数在存储空间和计算速度上具有显著的优势,适合于大规模数据计算和图形处理等应用场景。
4. 广度探讨:IEEE 754标准32位浮点数和普通浮点数的应用领域由于其在计算机底层运算中具有高效性和精度,IEEE 754标准32位浮点数被广泛应用于科学计算、工程仿真、金融计算、图形处理等领域。
计算机32位浮点数编码实验C描述

浮点数编码实验1、提要本篇讲解浮点数的编码,先介绍浮点数的编码规格,最后用C程序来实现将给定的整数编码转换成浮点数编码。
2、浮点数编码在计算机中浮点数采用V = (-1)s×M×2E的形式来表示,在计算机中单精度浮点数是32位,双精度浮点数是64位,我们仅仅对单精度浮点数做说明。
就单精度浮点数而言,计算机中保存了S,M和E 的编码,其中S表示符号位,0表示正数,1表示负数;M是学名叫尾数;E是阶码,它是指数加上一个偏置数,单精度浮点数的偏置数是127,之所以加上这个偏置数是为了便于浮点数的运算。
在单精度浮点数中,符号位占最高位1位,阶码占用紧接着的8位,尾数占用最后23位,如下图所示:31 30 22 0 重点说一下尾数M,M隐含了小数点前面的1,举个例子,如果M是1010000000000011110000B,那么M的实际值是1#1010000000000011110000B,其中#表示小数点的位置;然后说说阶码E,假定解码E是10001001B,十进制值位137,E需要再减去偏置127,才能得到指数137-127=10,最后假定S是0,那么这个例子中所描述的浮点数表示的值是:1.1010000000000011110000B × 210也就是:11010000000.000011110000B。
3、将一个十进制数转成浮点数表示举个例子,十进制数-12.75转换成浮点数表示,首先确定符号位是1,将12.75转成二进制表示1100.11B = 1.10011×23,可以确定尾数M是100 1100 0000 0000 0000 0000B,阶码E=3+127 = 130 = 1000 0010B,其浮点数表示为1#1000 0010#100 1100 0000 0000 0000 0000B =C14C0000H。
其中#分割S、E和M。
4、一些非规格浮点数的表示上面部分说的是浮点数的规格表示,还有一些非规格表示。
32位浮点乘法器的设计与仿真代码

32位浮点乘法器的设计与仿真代码一、引言随着计算机科学和技术的不断发展,浮点乘法器在科学计算、图像处理、人工智能等领域中扮演着重要的角色。
本文将详细讨论32位浮点乘法器的设计与仿真代码,并深入探讨其原理和实现方法。
二、浮点数表示在开始设计32位浮点乘法器之前,我们首先需要了解浮点数的表示方法。
浮点数由符号位、阶码和尾数组成,其中符号位表示数的正负,阶码确定数的大小范围,尾数表示数的精度。
三、浮点乘法器的原理浮点乘法器的原理基于乘法运算的基本原理,即将两个数的尾数相乘,并将阶码相加得到结果的阶码。
同时需要考虑符号位的处理和对阶的操作。
下面是32位浮点乘法器的基本原理:1.获取输入的两个浮点数A和B,分别提取出符号位、阶码和尾数。
2.将A和B的尾数相乘,得到乘积P。
3.将A和B的阶码相加,得到结果的阶码。
4.对乘积P进行规格化,即将小数点左移或右移,使其满足规定的位数。
5.对结果的阶码进行溢出判断,若溢出则进行相应的处理。
6.将符号位与结果的阶码和尾数合并,得到最终的浮点乘积。
四、浮点乘法器的设计根据浮点乘法器的原理,我们可以开始进行浮点乘法器的设计。
设计的关键是确定乘法器中各个部件的功能和连接方式。
下面是浮点乘法器的设计要点:1.输入模块:负责接收用户输入的两个浮点数,并提取出符号位、阶码和尾数。
2.乘法模块:负责将两个浮点数的尾数相乘,得到乘积P。
3.加法模块:负责将两个浮点数的阶码相加,得到结果的阶码。
4.规格化模块:负责对乘积P进行规格化操作,使其满足规定的位数。
5.溢出判断模块:负责判断结果的阶码是否溢出,并进行相应的处理。
6.输出模块:负责将符号位、阶码和尾数合并,得到最终的浮点乘积。
五、浮点乘法器的仿真代码为了验证浮点乘法器的设计是否正确,我们需要进行仿真测试。
下面是一段简单的浮点乘法器的仿真代码:module floating_point_multiplier(input wire [31:0] a,input wire [31:0] b,output wire [31:0] result);wire [31:0] mantissa;wire [7:0] exponent;wire sign;// 提取符号位assign sign = a[31] ^ b[31];// 提取阶码assign exponent = a[30:23] + b[30:23];// 尾数相乘assign mantissa = a[22:0] * b[22:0];// 规格化assign {result[30:23], result[22:0]} = {exponent, mantissa};// 处理溢出always @(*)beginif (exponent > 255)result = 32'b0; // 结果溢出为0else if (exponent < 0)result = 32'b0; // 结果溢出为0elseresult[31] = sign;endendmodule六、浮点乘法器的应用浮点乘法器在科学计算、图像处理、人工智能等领域中有着广泛的应用。
高速32位浮点乘法器设计的开题报告

高速32位浮点乘法器设计的开题报告一、选题依据随着科技的快速发展,计算机在越来越多的领域中发挥着关键作用。
而在计算机的运算过程中,浮点运算是非常重要的一环。
为了能够完成更加复杂的计算任务,需要设计高精度、高效率的浮点运算器。
而高速32位浮点乘法器就是其中非常重要的一种。
因此,本课题选择研究高速32位浮点乘法器的设计。
二、研究的内容本课题研究的内容包括:1. 高速32位浮点乘法器的基本功能2. 高速32位浮点乘法器的设计原理3. 高速32位浮点乘法器的关键技术和算法4. 高速32位浮点乘法器的实现方式5. 高速32位浮点乘法器的性能评估与测试三、研究的意义高速32位浮点乘法器作为现代计算机系统的重要组成部分,其性能的高低直接影响到计算机的整体性能。
因此,研究高速32位浮点乘法器的设计,对于提升计算机的性能具有重要的意义和价值。
同时,在本课题的研究过程中,还可以深入了解现代计算机系统的内部原理和结构,具有很高的教育和研究价值。
四、研究的难点和解决方案在研究高速32位浮点乘法器的过程中,可能会面临以下难点:1. 设计原理的复杂性。
高速32位浮点乘法器的设计原理比较复杂,需要涉及到大量的数学知识。
为了解决这个问题,可以深入学习数学知识,并利用各种工具辅助分析设计。
2. 算法的高效性。
在设计高速32位浮点乘法器时,需要考虑到算法的高效性。
因此,研究合适的算法是非常重要的。
对于算法的研究,可以参考各种文献和优秀的实践经验。
3. 实现方式的可靠性。
在实现高速32位浮点乘法器时,需要考虑到实现方式的可靠性和稳定性。
为了解决这个问题,可以采用多种方案进行比较和测试,确保实现方式的可靠性。
五、预期成果本课题的预期成果包括:1. 高速32位浮点乘法器设计的详细说明和实现方式。
2. 高速32位浮点乘法器的性能评估和测试结果。
3. 研究过程中遇到的问题和解决方案的总结。
六、研究方法本课题的研究方法主要包括:1. 文献调研。
位可控加减法器设计32位算术逻辑运算单元

位可控加减法器设计32位算术逻辑运算单元标题:深入探讨位可控加减法器设计中的32位算术逻辑运算单元一、引言在计算机系统中,算术逻辑运算单元(ALU)是至关重要的部件,用于执行数字运算和逻辑运算。
而在ALU中,位可控加减法器设计是其中的重要部分,尤其在32位算术逻辑运算单元中更是不可或缺。
本文将深入探讨位可控加减法器设计在32位算术逻辑运算单元中的重要性,结构特点以及个人观点和理解。
二、位可控加减法器设计的重要性位可控加减法器是ALU中的重要组成部分,它具有对加法和减法操作进行控制的能力,可以根据输入信号来实现不同的运算操作。
在32位算术逻辑运算单元中,位可控加减法器的设计要考虑到对每一位进行并行操作,并且要保证高速、低功耗和稳定性。
位可控加减法器设计在32位算术逻辑运算单元中具有非常重要的意义。
三、位可控加减法器设计的结构特点在32位算术逻辑运算单元中,位可控加减法器的设计需要考虑到以下几个结构特点:1. 并行运算:位可控加减法器需要能够实现对32位数据的并行运算,以提高运算速度。
2. 控制信号:设计需要合理的控制信号输入,来实现不同的运算模式和操作类型。
3. 进位传递:保证进位信号能够正确传递和计算,以确保运算的准确性。
4. 低功耗:设计需要考虑到低功耗的特点,以满足现代计算机系统对能源的需求。
四、个人观点和理解在我看来,位可控加减法器设计在32位算术逻辑运算单元中扮演着十分重要的角色。
它不仅需要具备高速、稳定和精确的运算能力,还需要考虑到功耗和控制信号的合理设计。
只有兼具这些特点,才能更好地满足现代计算机系统对于高效、可靠和低功耗的需求。
五、总结和回顾通过本文对位可控加减法器设计在32位算术逻辑运算单元中的深入探讨,我们可以看到它在计算机系统中的重要性和结构特点。
而个人观点也表明了它需要具备高速、低功耗和稳定性等特点,才能更好地满足现代计算机系统的需求。
在写作过程中,我对位可控加减法器设计在32位算术逻辑运算单元中的重要性和结构特点进行了深入探讨,并分享了个人观点和理解。
浮点32位并行乘法器设计与研究的开题报告

浮点32位并行乘法器设计与研究的开题报告
一、选题背景
现代计算机普遍采用浮点运算,浮点乘法是其中较为复杂的一种运算。
浮点乘法的速度和精度对计算机的性能有着至关重要的影响。
因此,设计一种快速、高效且精度高的浮点乘法器是非常有必要的。
二、研究目的
本研究旨在设计一种基于FPGA实现的浮点32位并行乘法器,并且探究其性能及精度。
具体目的包括:
1. 研究浮点乘法器的基本原理和实现方式。
2. 设计一种32位浮点乘法器的算法和数据路径。
3. 基于FPGA平台实现32位浮点乘法器,并进行性能评估和精度分析。
三、研究方法
本研究将采用以下方法:
1. 阅读相关文献,了解浮点乘法器的实现原理和算法。
2. 设计基于二进制补码的32位浮点乘法器算法和数据路径。
3. 使用Verilog语言进行32位浮点乘法器的RTL级设计。
4. 在FPGA平台上进行实现,并分析其性能和精度。
四、预期成果
完成本研究后,预期可以获得以下成果:
1. 掌握浮点乘法器的基本原理和实现方式。
2. 设计一种32位浮点乘法器的算法和数据路径。
3. 完成浮点32位并行乘法器的RTL级设计。
4. 在FPGA平台上进行实现,并得到相应性能和精度结果。
五、研究意义
1.本研究可以为浮点运算的优化和加速提供一种新的思路。
2.可以为计算机的相关领域提供更快速、高效的计算能力。
3.研究结果具有重要的教育和科研意义,可以为相关领域的学生和研究人员提供学习借鉴。
32位浮点加法器设计

32位浮点加法器设计一、基本原理浮点数加法运算是在指数和尾数两个部分进行的。
浮点数一般采用IEEE754标准表示,其中尾数部分采用规格化表示。
浮点加法的基本原理是将两个浮点数的尾数对齐并进行加法运算,再进行规格化处理。
在加法运算过程中,还需考虑符号位、指数溢出、尾数对齐等特殊情况。
二、设计方案1. 硬件实现方案:采用组合逻辑电路实现浮点加法器,以保证运算速度和实时性。
采用Kogge-Stone并行加法器、冒泡排序等技术,提高运算效率。
2.数据输入:设计32位浮点加法器,需要提供两个浮点数的输入端口,包括符号位、指数位和尾数位。
3.数据输出:设计32位浮点加法器的输出端口,输出相加后的结果,包括符号位、指数位和尾数位。
4.控制信号:设计合适的控制信号,用于实现指数对齐、尾数对齐、规格化等操作。
5.流程控制:设计合理的流程控制,对各个部分进行并行和串行处理,提高加法器的效率。
三、关键技术1. Kogge-Stone并行加法器:采用Kogge-Stone并行加法器可以实现多位数的并行加法运算,提高运算效率。
2.浮点数尾数对齐:设计浮点加法器需要考虑浮点数尾数的对齐问题,根据指数大小进行右移或左移操作。
3.溢出判断和处理:浮点加法器需要判断浮点数的指数是否溢出,若溢出需要进行调整和规格化。
4.符号位处理:设计浮点加法器需要考虑符号位的处理,确定加法结果的符号。
四、性能评价性能评价是衡量浮点加法器设计好坏的重要指标。
主要从以下几个方面进行评价:1.精度:通过与软件仿真结果进行比较,评估加法器的运算精度,误差较小的加法器意味着更高的性能。
2.速度:评估加法器的运行速度,主要考虑延迟和吞吐量。
延迟越低,意味着加法器能够更快地输出结果;吞吐量越高,意味着加法器能够更快地处理多个浮点加法运算。
3.功耗:评估加法器的功耗情况,低功耗设计有助于提高整个系统的能效。
4.面积:评估加法器的硬件资源占用情况,面积越小意味着设计更紧凑,可用于片上集成、嵌入式系统等场景。
iee75432位转换成浮点数十进制

IEE75432位转换成浮点数十进制1. 引言IEE754是一个定义了浮点数表示方法的标准,它规定了不同精度的浮点数的表示方式,包括单精度浮点数(32位)和双精度浮点数(64位)。
在计算机科学和工程中,我们经常会遇到需要将32位的IEE754表示的浮点数转换成十进制数的情况。
本文将深入探讨IEE75432位转换成浮点数十进制的方法和原理。
2. IEE75432位表示形式在IEE754标准中,单精度浮点数采用32位表示,其中包括1位符号位(s)、8位指数位(e)和23位尾数位(m)。
以一个32位的无符号整数来表示一个单精度浮点数,其转换规则如下:- 符号位:第一位表示符号,0代表正数,1代表负数。
- 指数位:接下来的8位表示指数,需要减去127得到真正的指数值。
- 尾数位:剩下的23位表示尾数,加上1得到尾数的真实值。
3. 转换原理要将IEE75432位表示的浮点数转换成十进制数,首先需要确定符号、指数和尾数的值。
然后根据这些值,利用指数的偏移和尾数的加权,计算出十进制数的值。
4. 转换步骤(1)确定符号位、指数位和尾数位的值。
(2)根据指数位的偏移值计算出真实的指数值。
(3)根据尾数位的加权值计算出真实的尾数值。
(4)根据符号位确定最终的十进制数的符号。
(5)利用指数值和尾数值计算出十进制数的值。
5. 举例以IEE754标准表示的32位浮点数01000001101000000000000000000000为例,其符号位为0,指数位为10000011,尾数位为01000000000000000000000。
根据上述转换步骤,计算出其十进制值为-21.0。
6. 总结IEE75432位转换成浮点数十进制是一个涉及到符号、指数和尾数的复杂计算过程。
通过本文的深入探讨,希望读者能对这一过程有更深刻的理解。
在实际应用中,需要根据具体的转换规则和计算方法,准确地将IEE75432位表示的浮点数转换成十进制数。
使用python模拟cpu多位加法器的课程设计报告

标题:使用Python模拟CPU多位加法器的课程设计报告一、引言随着计算机科学与技术的发展,了解和掌握计算机硬件的基本工作原理至关重要。
本课程设计旨在通过Python编程语言实现一个多位加法器模型,以模拟CPU在执行加法指令时对二进制数据的操作过程。
此项目不仅能加深对数字逻辑电路的理解,而且有助于提升对底层计算机制作与操作的认识。
二、设计目标与任务1. 设计并实现一个能够处理任意指定位数(例如8位、16位或32位)的二进制加法器模型。
2. 加法器应能接收两个等长的二进制字符串作为输入,并输出它们相加后的二进制结果以及可能产生的进位。
3. 结合Python语言特性,清晰展示每一位加法的过程及其对应的逻辑门电路功能。
三、设计方法与步骤1. 数据预处理:将用户输入的二进制字符串转换为整型数字,便于进行算术运算。
2. 模拟加法过程:通过循环遍历每一位,分别执行半加器(Half Adder)和全加器(Full Adder)的功能,考虑当前位的值和前一位的进位。
3. 输出结果:将最终计算出的结果转换回二进制字符串形式,并显示所有的中间计算结果。
四、设计实现与代码详解在此部分详细阐述所编写的Python代码结构及关键函数的功能实现,包括如何模拟二进制加法的逻辑过程,以及如何处理进位问题。
五、测试与验证针对不同位数的二进制数进行一系列加法运算测试,比较模拟结果与理论预期是否一致,确保加法器模型的正确性。
六、总结与展望回顾整个设计过程,分析遇到的问题及解决方案,同时探讨进一步优化的可能性,如采用更高效的算法或者模拟更复杂的CPU指令集等。
七、参考文献列出在设计过程中引用的相关书籍、论文和技术文档等资料。
通过本次课程设计,不仅增强了对计算机硬件基础逻辑部件功能的理解,同时也锻炼了利用高级编程语言解决低层硬件问题的能力。
DSP实验(浮点处理)报告

DSP浮点处理器实验报告实验名称:DSP浮点处理器实验1姓名:班级:指导教师:完成时间:2012/05/23实验一实验系统的硬件连接以及中断控制LED一、实验系统的硬件连接1、设置仿真环境为Emulator模式;2、连接仿真器到PC和开发板;3、连接电源线,打开电源;4、进入CCS开发环境。
二、实验目的1、熟悉实验系统的硬件连接和使用方法。
2、熟悉Code Composer Studio (CCS3.3)集成开发环境及软硬件仿真方法。
3、掌握TMS320C6722的GPIO和定时中断的具体使用。
三、实验内容及原理1、使用定时中断的方式通过程序控制实验系统使LED按一定的频率闪烁。
2、TMS320C6722定时器每1/8192秒产生一次中断,每次中断时中断服务程序向计数变量加1,加满1024后程序将LED的亮灭状态改变一次。
最终实现LED以1Hz的频率闪烁(即每秒亮1次)。
四、实验要求基本要求:1、熟悉使用Code Composer Studio (CCS3.3)集成开发环境,能够进行程序的编辑、编译和硬件仿真,掌握软件的基本操作。
2、熟悉编写程序的基本结构和简单编写方法。
3、能够修改程序,使LED按照指定的频率闪烁。
扩展要求:1、修改实验参考程序,采用完全使用中断而不再在主程序循环中计数的方式控制LED闪烁,且保持闪烁频率不变。
2、继续修改程序,使LED闪烁频率为1Hz(每秒亮一次)。
五、实验系统的内部结构框图六、实验硬件连接示意图七、实验参考程序的流程图八、拓展要求程序改动思路1.拓展一:将main中的程序转到timer0中,应注意在转移main的内容前面加上一个标志如aa。
2.拓展二:由定时参数的计算公式,外部时钟频率X10/8/采样频率。
比较400h,可知将FS定义为808h同404h进行比较。
只要了解循环进行的频率和比照的频率就可以改变灯闪烁的频率。
将727h 改成8196即可。
3.总结TMS320VC33初始化内容步骤首先要对重要寄存器和总线初始化init: ldp 0,dpldi @STCK,spldi 1800h,st 状态指针寄存器ldi @MCTL,ar0ldi MBUS1,r0 主计数sti r0,*ar0MCTL .word 808064H ;;主总线控制寄存器地址单元STCK .word 809E00H ; ;堆栈寄存器地址单元MBUS1 .set 01038H ; ;0等待标志字.end定时中断初始化initt0: ldi 0,r0ldi 808h,ar0lsh 12,ar0addi 20h,ar0 ; ;指向808020单元即全局控制寄存器sti r0,*+ar0(4) ;;计数寄存器ldi FS,r0 ;sti r0,*+ar0(8) ;;周期寄存器ldi 3c1h,r0sti r0,*ar0 ;retsFS .set 727H ; ;FS的计算.data4.总结TMS320VC33定时器使用方法main:ldi @TNUM,ar0ldi *ar0,r0absi r0cmpi 400h,r0 ; ;比较判断是否循环blt mainldi 0,r0 ;;计数到则清零则进行翻转sti r0,*ar0ldi @LEDS,ar0 ; ;接着进行LED灯状态的翻转ldi *ar0,r0cmpi 0,r0ldieq 1,r0ldine 0,r0sti r0,*ar0ldi @LED,ar0sti r0,*ar0br main;------------------------------5.总结TMS320VC33中断的使用方法timer0: push st 发生中断回到此处复位回归push ar0push r0 先保存低32位pushf r0 再保存高32位ldi @TNUM,ar0 时钟中断,完成一次操作。
实验1--浮点运算

北京信息科技大学自动化学院实验报告课程名称 DSP控制技术实验名称简单的浮点运算实验仪器 PC机一台专业自动化班级/学号自控1105/2011010865 学生姓名黄洁艳实验日期实验地点教七楼102 成绩指导教师艾红实验一 CCS调试环境熟悉以及简单程序的软件调试一.实验目的1.了解 F28335 简单的浮点运算。
2.熟悉浮点运算的编程。
二.实验原理TMS320F28335是一款32 位浮点通用数字信号处理芯片,它具有存储空间大、运算精度高等特点。
三.实验要求1.设置 Code Composer Studio 3.3在硬件仿真方式下运行2.启动 Code Composer Studio 3.33.打开工程文件,打开源程序Example_2833xFPU.c阅读程序,理解程序内容。
4.编译、下载程序。
5.把 y1和 y2 添加到观察窗。
6.运行程序,观察 y1和 y2结果。
7. 修改 x1 和 x2 值,重新执行程序,观察 y1和 y2结果。
8.退出 CCS。
四. 实验程序如下:#include "DSP2833x_Device.h" // DSP2833x Headerfile Include File#include "DSP2833x_Examples.h" // DSP2833x Examples Include Filefloat y1, y2;float m1, m2;float x1, x2;float b1, b2;void main(void){ // Step 1. Initialize System Control:// PLL, WatchDog, enable Peripheral Clocks// This example function is found in the DSP2833x_SysCtrl.c file.InitSysCtrl();// Step 2. Initalize GPIO:// This example function is found in the DSP2833x_Gpio.c file and// illustrates how to set the GPIO to it's default state.// InitGpio(); // Skipped for this example// Step 3. Clear all interrupts and initialize PIE vector table:// Disable CPU interruptsDINT;// Initialize the PIE control registers to their default state.// The default state is all PIE interrupts disabled and flags// are cleared.// This function is found in the DSP2833x_PieCtrl.c file.InitPieCtrl();// Disable CPU interrupts and clear all CPU interrupt flags:IER = 0x0000;IFR = 0x0000;// Initialize the PIE vector table with pointers to the shell Interrupt // Service Routines (ISR).// This will populate the entire table, even if the interrupt// is not used in this example. This is useful for debug purposes.// The shell ISR routines are found in DSP2833x_DefaultIsr.c.// This function is found in DSP2833x_PieVect.c.InitPieVectTable();// Interrupts that are used in this example are re-mapped to// ISR functions found within this file.// Step 5. User specific code, enable interrupts:// Calculate two y=mx+b equations.y1 = 0;y2 = 0;m1 = 10;m2 = .6;x1 = 7;x2 = 7.3;b1 = 4.2;b2 = 8.9;y1 = m1/x1 + b1;y2 = m2*x2 + b2;ESTOP0; // This is a software breakpoint}五.实验结果分析程序设计实现了简单的浮点乘法和加法运算,y1和y2是实验结果。
32位浮点加法器设计[整理版]
![32位浮点加法器设计[整理版]](https://img.taocdn.com/s3/m/c6464a9e2af90242a895e5f9.png)
32位浮点加法器设计
苦行僧宫城
摘要:运算器的浮点数能够提供较大的表示精度和较大的动态表示范围,浮点 运算已成为现代计算程序中
不可缺少的部分。浮点加法运算是浮点运算中使用频率最高的运算。因此,浮 点加法器的性能影响着整个
CPU勺浮点处理能力。文中基于浮点加法的原理,采用Verilog硬件描述语言
设计32位单精度浮点数加法
f)规格化移位:对尾数加减结果进行移位,消除尾数的非有效位,使其最高位为
1。Байду номын сангаас
g)舍入:有限精度浮点表示需要将规格化后的尾数舍入到固定结果。 由以上 基本算法可见,它包含2个全长的移位即对阶移位和规格化移位,还要包括3个全 长的有效加法,即步骤c、d、g。由此可见,基本算法将会有很大的时延。
2 32位浮点加法器设计与实现
器,并用modelsim对浮点加法器进行仿真分析,从而验证设计的正确性和可 行性。
关键词:浮点运算 浮点加法器Verilog硬件描述语言
Studying on Relation of Technology and Civilization苦行僧宫城
(School of Mechatronic Engineering and Automation, Shanghai
University, Shanghai,China)
Abstract: The floating-point arithmetic provides greater precision and greater dynamic representation indication range, with floating point calculations have become an indispensable part of the program.Floatingpoint adder is the most frequently used floating point arithmetic. Therefore, the performance of floating point adder affecting the entire CPU floating point processing capabilities. In this paper the principlebased floating-point addition, Verilog hardware description language
上海大学verilog设计32位浮点加法器设计

32位浮点加法器设计摘要:浮点数具有数值范围大,表示格式不受限制的特点,因此浮点数的应用是非常广泛的。
浮点数加法运算比较复杂,算法很多,但是为了提高运算速度,大部分均是基于流水线的设计结构。
本文介绍了基于IEE754标准的用Verilog 语言设计的32位浮点加法器,能够实现32位浮点数的加法运算。
虽然未采用流水线的设计结构但是仍然对流水线结构做了比较详细的介绍。
关键字:浮点数,流水线,32位浮点数加法运算,Verilog 语言设计32-bit floating point adder designCao Chi,Shen Jia- qi,Zheng Yun-jia(School of Mechatronic Engineering and Automation, Shanghai University, Shanghai ,China ) Abstract://沈佳琪搞定Key words :float; Assembly line; 32-bit floating-point adder 浮点数的应用非常广泛,无论是在计算机还是微处理器中都离不开浮点数。
但是浮点数的加法运算规则比较复杂不易理解掌握,而且按照传统的运算方法,运算速度较慢。
因此,浮点加法器的设计采用了流水线的设计方法。
32位浮点数运算的摄入处理采用了IEE754标准的“0舍1入”法。
1. 浮点数的介绍在处理器中,数据不仅有符号,而且经常含有小数,即既有整数部分又有小数部分。
根据小数点位置是否固定,数的表示方法分为定点表示和浮点表示。
浮点数就是用浮点表示法表示的实数。
浮点数扩大了数的表示范围和精度。
浮点数由阶符、阶码E 、数符、尾数N 构成。
任意一个二进制数N 总可以表示成如下形式:N=。
通常规定:二进制浮点数,其尾数数字部分原码的最高位为1,叫作规格化表示法。
因此,扩大数的表示范围,就增加阶码的位数,要提高精度,就增加尾数的位数。
加法器的设计与仿真实验报告

加法器的设计与仿真一、实验内容1、用逻辑图和VHDL语言设计全加器。
2、利用设计的全加器组成串行加法器。
3、用逻辑图和VHDL语言设计并行加法器。
4、应用MaxplusII软件对全加器和串行加法器进行编译、仿真和模拟。
5、在“MaxplusII软件的基本操作”实验的基础上,能更加熟练的掌握应用MaxplusII软件,从而更形象更深层次的理解全加器和串行加法器。
二、实验平台及实验方法用VHDL语言编写全加器和串行加法器的程序,运用MaxplusII软件进行仿真,再结合FPGA(即对实验箱的芯片进行编译)进行验证。
也可以用原理图进行文本设计,波形设计。
逻辑符号图:真值表:电路图:三、实验过程1.启动MaxplusII软件;2.新建一个文本编辑文件,输入全加器的VHDL语言;3.编译。
点击file save as,保存文件名为f-adder名称,扩展名为vhd,选择芯片类型为EPF10K20TI144-4,保存并进行编译,若编译结果出现0 error,0 warnings则说明编译通过。
4.仿真波形。
点Max+plus II→Waveform editor,出现波形图的设置界面,然后点Node→Enter Nodes from SNF→list,将输入输出端添加到界面,并设置其周期和输入波形,保存后,点Max+plus II→Simulator,即可仿真出输出的波形。
5.配置芯片。
点Max+plus II→Floorplan editor,将Unassigned Nodes & 栏中,电路的输入输出节点标号直接用鼠标“拖到” 想分配的引脚上,Max+plusII→programmer→configuer,然后就可以操作试验箱,观察全加器的工作情况。
四、实验结果实验步骤:1、用VHDL语言编写全加器的程序LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;ENTITY f_adder ISPORT(x,y,cin:IN STD_LOGIC;s,cout:OUT STD_LOGIC);END ENTITY f_adder;ARCHITECTURE bhv OF f_adder ISBEGINs<=x XOR y XOR cin;cout<=(x AND y)OR(x AND cin)OR(y AND cin);END ARCHITECTURE bhv;2、将上述程序保存为文件名为f_adder的文件,点击Maxplus里的compiler进行编译,点击start,如果出现0 error,0 warnings,则编译成功。
c语言模拟浮点数运算

c语言模拟浮点数运算C语言是一种广泛应用于各种领域的编程语言,它提供了丰富的工具和函数库来模拟浮点数运算。
浮点数是一种用于表示带有小数部分的数值的数据类型,它在科学计算、金融领域和图形处理等方面有着重要的应用。
本文将介绍如何使用C语言来模拟浮点数运算。
我们需要了解浮点数的表示方式。
在C语言中,浮点数通常使用单精度(float)和双精度(double)两种类型来表示。
单精度浮点数使用32位来表示,其中1位表示符号位,8位表示指数部分,23位表示尾数部分。
双精度浮点数使用64位来表示,其中1位表示符号位,11位表示指数部分,52位表示尾数部分。
在C语言中,我们可以使用浮点数运算符来进行浮点数的加、减、乘、除等运算。
例如,使用"+"运算符可以对两个浮点数进行相加,使用"-"运算符可以对两个浮点数进行相减,使用"*"运算符可以对两个浮点数进行相乘,使用"/"运算符可以对两个浮点数进行相除。
除了基本的浮点数运算,C语言还提供了一些数学函数库来进行更复杂的浮点数运算。
例如,math.h头文件中提供了sin、cos、sqrt等函数,可以用来计算三角函数、开方等运算。
另外,C语言还提供了一些特殊的浮点数表示,如NaN(Not a Number)、Infinity(无穷大)等。
在进行浮点数运算时,我们需要注意一些特殊情况。
首先,浮点数运算可能会产生舍入误差,因为浮点数的表示范围是有限的。
例如,当两个非常接近的浮点数相减时,可能会得到一个很小但不为零的结果。
其次,当进行除法运算时,需要注意除数不能为零,否则会产生错误。
此外,浮点数还存在一些特殊值,如正无穷大、负无穷大和NaN,需要特殊处理。
为了更好地模拟浮点数运算,我们可以使用一些技巧和优化方法。
例如,可以使用移位操作来进行浮点数的乘法和除法运算,这样可以提高计算效率。
另外,可以使用循环和递归等控制结构来实现复杂的浮点数运算,例如计算阶乘、幂函数等。
实验1 运算器设计与仿真
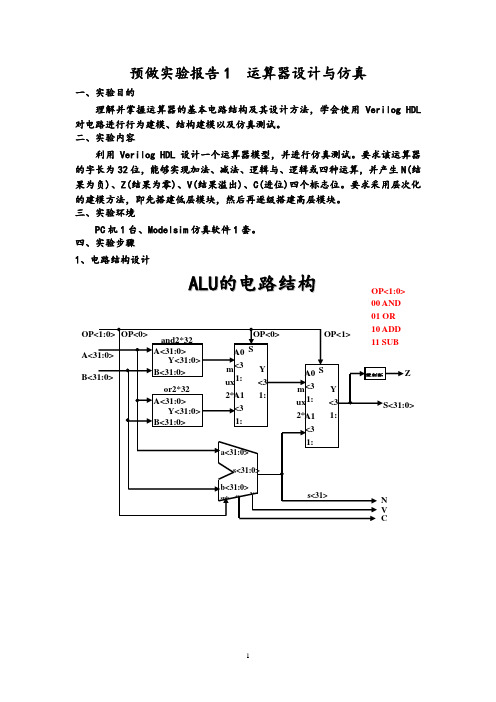
预做实验报告1 运算器设计与仿真一、实验目的理解并掌握运算器的基本电路结构及其设计方法,学会使用Verilog HDL 对电路进行行为建模、结构建模以及仿真测试。
二、实验内容利用Verilog HDL 设计一个运算器模型,并进行仿真测试。
要求该运算器的字长为32位,能够实现加法、减法、逻辑与、逻辑或四种运算,并产生N(结果为负)、Z(结果为零)、V(结果溢出)、C(进位)四个标志位。
要求采用层次化的建模方法,即先搭建低层模块,然后再逐级搭建高层模块。
三、实验环境PC 机1台、Modelsim 仿真软件1套。
四、实验步骤 1、电路结构设计A L U 的电路结构OP<1:0> 00 AND 01 ORcc o 1位全加器逻辑表达式:S= abc i+abc i+abc i+abc i=a c iCo=abc i i+abc i+abc i=ab+ac i+bc is<3:0> 其中:S u b=0,做加法,S u b=1,做减法。
2、建立Verilog模型module fadd(a,b,s,ci,co);input a,b,ci;output s,co;reg s,co;always @ (a or b or ci)begins<=(a&~b&~ci)|(~a&b&~ci)|(~a&~b&ci)|(a&b&ci);co<=(a&b)|(a&ci)|(b&ci);endendmodulemodule add(a,b,sub,s,c,v,n);input [31:0]a;input [31:0]b;input sub;output [31:0]s;output c,v,n;wire [31:0]a;wire [31:0]b;wirec1,c2,c3,c4,c5,c6,c7,c8,c9,c10,c11,c12,c13,c14,c15,c16,c17,c18,c19,c 20,c21,c22,c23,c24,c25,c26,c27,c28,c29,c30,c31;fadd f0(a[0],b[0]^sub,s[0],sub,c1);fadd f1(a[1],b[1]^sub,s[1],c1,c2);fadd f2(a[2],b[2]^sub,s[2],c2,c3);fadd f3(a[3],b[3]^sub,s[3],c3,c4);fadd f4(a[4],b[4]^sub,s[4],c4,c5);fadd f5(a[5],b[5]^sub,s[5],c5,c6);fadd f6(a[6],b[6]^sub,s[6],c6,c7);fadd f7(a[7],b[7]^sub,s[7],c7,c8);fadd f8(a[8],b[8]^sub,s[8],c8,c9);fadd f9(a[9],b[9]^sub,s[9],c9,c10);fadd f10(a[10],b[10]^sub,s[10],c10,c11);fadd f11(a[11],b[11]^sub,s[11],c11,c12);fadd f12(a[12],b[12]^sub,s[12],c12,c13);fadd f13(a[13],b[13]^sub,s[13],c13,c14);fadd f14(a[14],b[14]^sub,s[14],c14,c15);fadd f15(a[15],b[15]^sub,s[15],c15,c16);fadd f16(a[16],b[16]^sub,s[16],c16,c17);fadd f17(a[17],b[17]^sub,s[17],c17,c18);fadd f18(a[18],b[18]^sub,s[18],c18,c19);fadd f19(a[19],b[19]^sub,s[19],c19,c20);fadd f20(a[20],b[20]^sub,s[20],c20,c21); fadd f21(a[21],b[21]^sub,s[21],c21,c22); fadd f22(a[22],b[22]^sub,s[22],c22,c23); fadd f23(a[23],b[23]^sub,s[23],c23,c24); fadd f24(a[24],b[24]^sub,s[24],c24,c25); fadd f25(a[25],b[25]^sub,s[25],c25,c26); fadd f26(a[26],b[26]^sub,s[26],c26,c27); fadd f27(a[27],b[27]^sub,s[27],c27,c28); fadd f28(a[28],b[28]^sub,s[28],c28,c29); fadd f29(a[29],b[29]^sub,s[29],c29,c30); fadd f30(a[30],b[30]^sub,s[30],c30,c31); fadd f31(a[31],b[31]^sub,s[31],c31,c); assign n=s[31];assign v=c^c31;endmodulemodule mux21_32(f,a,b,s);output[31:0] f;input[31:0] a,b;input s;reg [31:0] f;always @(s or a or b)case(s)1'd0: f=a;1'd1: f=b;endcaseendmodulemodule ALU(op,a,b,s,n,v,c,z);input [1:0]op;input [31:0]a,b;output[31:0]s;output n,v,c,z;wire [31:0]d,e,f,s1;assign d=a&b;assign e=a|b;mux21_32 u0(f,d,e,op[0]);add u2(a,b,op[0],s1,c,v,n);mux21_32 u1(s,f,s1,op[1]);assign z=~(|s);endmodule3、设计测试文件`timescale 1ns / 1nsmodule ALUtest;reg clk;reg [1:0]op;reg [31:0]a,b;wire [31:0]s;wire n,v,c,z;//op=00 AND;//op=01 OR;//op=10 ADD;//op=11 SUB;ALU A(op,a,b,s,n,v,c,z);//clock generationinitial clk = 1;always #50 clk = ~clk;initialbegin#20 a=32'b0100_0101_0100_0000_0010_0010_0101_0001;b=32'b1010_0101_0010_0000_0100_0010_0011_0010;op=2'b00;#100 a=32'b0100_0101_0100_0000_0010_0010_0101_0001;b=32'b1010_0101_0010_0000_0100_0010_0011_0010;op=2'b01;#100 a=32'b0100_0101_0100_0000_0010_0010_0101_0001;b=32'b1010_0101_0010_0000_0100_0010_0011_0010;op=2'b10;#100 a=32'b0100_0101_0100_0000_0010_0010_0101_0001;b=32'b1010_0101_0010_0000_0100_0010_0011_0010;op=2'b11;#100 a=32'b0111_1011_1101_1110_1111_1111_1111_1111;b=32'b0111_1011_1101_1110_1111_1111_1111_1111;op=2'b11;#100 a=32'd15;b=32'd9;op=2'b11;#100 a=32'd9;b=32'd15;op=2'b11;#100 $stop;endEndmodule$display("a= %b, b= %b, op= %b, s= %b,n=%b,z=%b,v=%b,c=%b\n",a,b,op,s,n,z,v,c);注意:测试的完备性。
组成原理课程设计报告浮点数加法器

航空航天大学课程设计报告课程设计名称:计算机组成原理课程设计课程设计题目:浮点数加法器院(系):计算机学院专业:计算机科学与技术班级:学号:姓名:指导教师:完成日期:目录第1章总体设计方案31.1设计原理31.2设计思路31.3设计环境41.3.1 硬件环境41.3.2 EDA环境4第2章详细设计方案62.1总体方案的设计与实现62.2功能模块的设计与实现72.2.1 原补转换模块的设计与实现72.2.2 阶码选择模块的设计与实现92.2.3 数值选择模块的设计与实现122.2.4 数据移位模块的设计与实现142.2.5 加法模块的设计与实现182.3总电路仿真测试21第3章编程下载与硬件测试243.1编程下载243.2硬件测试及结果分析24参考文献26附录27第1章总体设计方案1.1 设计原理本次课程设计的题目为浮点数加法器的设计,使用Xilinx Foundation F3.1可编程器件开发工具软件,以及伟福COP2000试验箱实现目的设计。
具体要求为必须用基本逻辑门实现,浮点数的长度固定。
根据所学可知,浮点数共由两部分组成。
第一部分是阶码,第二部分是数据。
这两部分又分别分为两部分。
阶码由阶符和数值组成,数据由数符和数字组成。
由于在计算机的存储和运算中,数据由补码表示。
故首先应将输入的原码转化为补码。
在此过程中,正数保持不变,负数则对除符号位以外的各位按位取反,再进行加1操作。
然后对两数的阶码进行运算,决定移位的次数和结果的阶码。
在移位时,对正数进行补0操作,对负数则进行补1操作。
再对移位后的数据视为定点数进行相加运算。
进而实现浮点数相加的功能。
最后再将得到的结果转化为原码,进行输出。
1.2设计思路按照课设题目要求及原理图,先设计出电路的具体模块图,浮点数加法器的设计共包含如下五个模块:①原补转换模块②阶码选择模块③数值选择模块④数据移位模块⑤超前进位加法模块在五个部分中分别设计实现相应功能的器件,包括二选一数据选择器等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
32位浮点数加法设计仿真实验报告
名字:李磊学号:10045116 班级:10042211
32位浮点数的IEEE-754格式
单精度格式
IEEE.754标准规定了单精度浮点数共32位,由三部分组成:23位尾数f,8位偏置指数e,1位符号位s。
将这三部分由低到高连续存放在一个32位的字里,对其进行编码。
其中[22:0]位包含23位的尾数f;[30:23]位包含8位指数e;第31位包含符号s
{s[31],e[30:23],f[22:0]}
其中偏置指数为实际指数+偏置量,单精度浮点数的偏置量为128,双精度浮点数的偏置量为1024。
规格化的数:由符号位,偏置指数,尾数组成,实际值为1.f乘2的E-128次方
非规格化的数:由符号位,非偏置指数,尾数组成,实际值为0.f乘2的E次方
特殊的数:0(全为零),+无穷大(指数全为1,尾数为0,符号位为0),-无穷大(指数
全为1,尾数为0,符号位为1),NAN(指数全为1,尾数为不全为0)
浮点数加法器设计
设计思路:
1.前端处理,还原尾数
2.指数处理,尾数移位,使指数相等
3.尾数相加
4.尾数规格化处理
5.后端处理,输出浮点数
具体设计:
设计全文:
module flowadd(ix, iy, clk, a_en, ost,oz);
input ix, iy, clk, a_en;
output oz, ost;
wire[31:0] ix,iy;
reg[31:0] oz;
wire clk,ost,a_en;
reg[25:0] xm, ym, zm;
reg[7:0] xe, ye, ze;
reg[2:0] state;
parameter start = 3'b000, //设置状态机
zerock = 3'b001,
exequal = 3'b010,
addm = 3'b011,
infifl = 3'b100,
over = 3'b110;
assign ost = (state == over) ? 1 : 0; /*后端处理,输出浮点数*/
always@(posedge ost)
begin
if(a_en)
oz <= {zm[25],ze[7:0],zm[22:0]};
end
always@(posedge clk) //状态机
begin
case(state)
start: //前端处理,分离尾数和指数,同时还原尾数
begin
xe <= ix[30:23];
xm <= {ix[31],1'b0,1'b1,ix[22:0]};
ye <= iy[30:23];
ym <= {iy[31],1'b0,1'b1,iy[22:0]};
state <= zerock;
end
zerock:
begin
if(ix == 0)
begin
{ze, zm} <= {ye, ym};
state <= over;
end
else
if(iy == 0)
begin
{ze, zm} <= {xe, xm};
state <= over;
end
else
state <= exequal;
end
exequal: //指数处理,使得指数相等begin
if(xe == ye)
state <= addm;
else
if(xe > ye)
begin
ye <= ye + 1;
ym[24:0] <= {1'b0, ym[24:1]};
if(ym == 0)
begin
zm <= xm;
ze <= xe;
state <= over;
end
else
state <= exequal;
end
else
begin
xe <= xe + 1;
xm[24:0] <= {1'b0,xm[24:1]};
if(xm == 0)
begin
zm <= ym;
ze <= ye;
state <= over;
end
else
state <= exequal;
end
end
addm: //带符号位和保留进位的尾数相加begin
if ((xm[25]^ym[25])==0)
begin
zm[25] <= xm[25];
zm[24:0] <= xm[24:0]+ym[24:0];
end
else
if(xm[24:0]>ym[24:0])
begin
zm[25] <= xm[25];
zm[24:0] <=xm[24:0]-ym[24:0];
end
else
begin
zm[25] <= ym[25];
zm[24:0] <=ym[24:0]-xm[24:0];
end
ze <= xe;
state <= infifl;
end
infifl: //尾数规格化处理
begin
if(zm[24]==1)
begin
zm[24:0] <= {1'b0,zm[24:1]};
ze <= ze + 1;
state <= over;
end
else
if(zm[23]==0)
begin
zm[24:0] <= {zm[23:0],1'b0};
ze <= ze - 1;
state <= infifl;
end
else
state <= over;
end
over:
begin
state<= start;
end
default:
begin
state<= start;
end
endcase
end
endmodule
设计结果仿真
仿真结果为41A00000H+41080000H=41E40000H
41A00000H=10D,41080000H=4.25D,41E40000H=14.25D,验证成功。
