算法与数据结构 多项式相加
数据结构多项式求和

数据结构多项式求和在计算机科学和数学领域中,数据结构的运用无处不在,而多项式求和就是一个典型的应用场景。
让我们一起来深入探讨一下这个有趣且重要的主题。
首先,我们需要明确什么是多项式。
简单来说,多项式就是由变量和系数组成的表达式。
比如,3x²+ 2x 1 就是一个多项式,其中 3 、2 、-1 是系数,x 是变量,²是指数。
那么为什么要对多项式进行求和呢?这在很多实际问题中都有应用。
比如在物理学中,描述某些运动规律时会用到多项式;在工程学中,对信号的处理和建模也可能涉及到多项式求和。
接下来,我们看看如何用数据结构来表示多项式。
常见的数据结构有数组和链表。
用数组来表示多项式时,我们可以将系数存储在数组中。
假设一个多项式的最高次幂为n ,那么我们可以创建一个长度为n +1 的数组,数组的下标对应多项式的幂次,数组元素的值就是对应的系数。
这种表示方法简单直观,但是如果多项式的次数很高,而很多项的系数为0 ,就会浪费很多存储空间。
相比之下,链表是一种更灵活的数据结构。
每个节点可以存储系数、指数和指向下一个节点的指针。
这样,只有非零项才会被存储,节省了存储空间。
有了表示多项式的数据结构,接下来就是实现求和的算法。
对于用数组表示的多项式求和,我们需要从最高次幂开始,将对应幂次的系数相加。
如果相加后的系数为 0 ,那么在最终的结果中可以省略这一项。
而对于链表表示的多项式求和,我们需要遍历两个链表,找到相同幂次的项进行系数相加。
如果一个链表遍历完了,而另一个链表还有剩余项,直接将剩余项添加到结果链表中。
在实际编程中,还需要考虑一些特殊情况。
比如,如果两个多项式的最高次幂不同,那么在求和时要注意补齐。
另外,算法的效率也是我们需要关注的重点。
在选择数据结构和算法时,要根据具体的应用场景和需求来权衡空间复杂度和时间复杂度。
例如,如果多项式的操作频繁,而对空间要求不是很严格,那么使用数组可能更合适;如果多项式的项数不固定,而且有很多零系数项,链表可能是更好的选择。
数据结构-多项式相加

数据结构课程设计2012年12月班级:XXX学号:XXX姓名: XXX指导教师:XXX一元稀疏多项式计算器【问题描述】设计一个一元稀疏多项式简单计算器【基本要求】一元多项式简单计算器的基本功能是:1,输入并建立多项式;2,输出多项式,输出形式为整数序列:n,c1,e1,c2,c2,...,cn,en,其中n是多项式的项数,ci和ei分别是第i项的系数和指数,序列按指数降序排列;3,多项式a和b相加,建立多项式a+b;4,多项式a和b相减,建立多项式a-b.【算法设计思想】①一般情况下的一元n次多项式可写成pn(x)=p1xe1+p2xe2+……+pmxem其中,p1是指数为ei的项的非零系数,且满足0≦e1<e2<……<em=n ,若用一个长度为m且每个元素有两个数据项(系数项和指数项)的线性表((p1,e1),(p2,e2),……,(pm,em))便可惟一确定多项式pn(x)。
②用两个带表头结点的单链表分别存储两个多项式③根据一元多项式相加的运算规则:对于两个一元多项式中所有指数相同的项,对应系数相加,若其和不为零,则构成“和多项式”中的一项;④只需要将第二个多项式的系数改为其相反数,然后根据一元多项式相加的运算规则便可以得到其相应的“差多项式”【【实现提示】用带表头结点的单链表存储多项式。
【程序代码】#include <stdio.h>#include <malloc.h>typedef struct node{float coef;int expn;struct node *next;}Lnode, *polynmial;void create(polynmial &L); //输入并建立多项式Lvoid display(polynmial L); //显示,输出多项式Lvoid sort(polynmial &L); //多项式L按指数排序void reverse(polynmial &L); //逆置void select(); //用户选择加减操作void add(polynmial La, polynmial Lb, polynmial &Lc); //多项式La,Lb相加void subtract(polynmial La, polynmial Lb, polynmial &Ld); //多项式La减去Lb,结果给Ldvoid create(polynmial &L) //输入并建立多项式L{int i, n;static struct node *p;scanf("%d", &n);L = (struct node *)malloc (sizeof(struct node));L->next = NULL;for(i = 0; i < n; i++){p = (struct node *)malloc(sizeof(struct node));scanf("%f %d", &p->coef, &p->expn);p->next = L->next;L->next = p;}}void display(polynmial L)//显示,输出多项式L{struct node *p, *q;int flag = 0;int k = 0;q = L->next;while(q)if(q->coef != 0)k++;q = q->next;}printf("%d, ", k);p = L->next;if(p->coef != 0){printf("%.1f,%d, ", p->coef, p->expn);flag++;}for(p = p->next; p; p = p->next){if(p->coef != 0){printf("%.1f,%d, ", p->coef, p->expn);flag++;}}if(flag == 0)printf("%d\n", flag);elseprintf("\n");}void sort(polynmial &L)//多项式L按指数排序{polynmial p, q, r, u;p = L->next;L->next = NULL;while(p != NULL){r = L;q = L->next;while((q != NULL) && (q->expn <= p->expn)) {r = q;q = q->next;}u = p->next;r->next = p;p->next = q;p = u;}void reverse(polynmial &L)//逆置{polynmial H;static struct node *p, *q, *s;H = (struct node*)malloc(sizeof(struct node));H->next = NULL;p = (struct node*)malloc(sizeof(struct node));s = L->next;p->coef = s->coef;p->expn = s->expn;p->next = s->next;while(s){p->coef = s->coef;p->expn = s->expn;p->next = s->next;q = H->next;H->next = p;p->next = q;p = (struct node*)malloc(sizeof(struct node));s = s->next;}p = H->next;q = L->next;while(p){q->coef = p->coef;q->expn = p->expn;q = q->next;p = p->next;}}void select() //用户选择加减操作{printf("请选择加减操作\n");printf("1.两个一元多项式相加\n");printf("2.两个一元多项式相减\n");}void add(polynmial La, polynmial Lb, polynmial &Lc)//多项式La,Lb相加{struct node *pa, *pb;static struct node *pc;Lc = (struct node*)malloc(sizeof(struct node));pa = La->next;pb = Lb->next;Lc->next = NULL;while(pa && pb){pc = (struct node*)malloc(sizeof(struct node)); if(pa->expn < pb->expn){pc->next = Lc->next;Lc->next = pc;pc->coef = pa->coef;pc->expn = pa->expn;pa = pa->next;}elseif(pa->expn == pb->expn){pc->next = Lc->next;Lc->next = pc;pc->expn = pa->expn;pc->coef = pa->coef + pb->coef;pa = pa->next;pb = pb->next;}else{pc->next = Lc->next;Lc->next = pc;pc->coef = pb->coef;pc->expn = pb->expn;pb = pb->next;}}while(pa){pc = (struct node*)malloc(sizeof(struct node)); pc->next = Lc->next;Lc->next = pc;pc->coef = pa->coef;pc->expn = pa->expn;pa = pa->next;}while(pb){pc = (struct node*)malloc(sizeof(struct node));pc->next = Lc->next;Lc->next = pc;pc->coef = pb->coef;pc->expn = pb->expn;pb = pb->next;}}void subtract(polynmial La, polynmial Lb, polynmial &Ld)//多项式La减去Lb,结果给Ld{struct node *pa, *pb;static struct node *pd;Ld = (struct node*)malloc(sizeof(struct node));pa = La->next;pb = Lb->next;Ld->next = NULL;while(pa && pb){pd = (struct node*)malloc(sizeof(struct node));if(pa->expn < pb->expn){pd->next = Ld->next;Ld->next = pd;pd->coef = pa->coef;pd->expn = pa->expn;pa = pa->next;}elseif(pa->expn == pb->expn){pd->next = Ld->next;Ld->next = pd;pd->expn = pa->expn;pd->coef = pa->coef - pb->coef;pa = pa->next;pb = pb->next;}else{pd->next = Ld->next;Ld->next = pd;pd->coef = pb->coef;pd->expn = pb->expn;pb = pb->next;}}while(pa){pd = (struct node*)malloc(sizeof(struct node)); pd->next = Ld->next;Ld->next = pd;pd->coef = pa->coef;pd->expn = pa->expn;pa = pa->next;}while(pb){pd = (struct node*)malloc(sizeof(struct node)); pd->next = Ld->next;Ld->next = pd;pd->coef = -pb->coef;pd->expn = pb->expn;pb = pb->next;}}int main(){int sign;polynmial La, Lb, Lc, Ld;printf("请输入第一个多项式:\n");create(La);sort(La);printf("请输入第二个多项式:\n");create(Lb);sort(Lb);select();scanf("%d", &sign);switch(sign){case 1:printf("多项式之和为:\n");add(La, Lb, Lc);sort(Lc);reverse(Lc);display(Lc);break;default:printf("多项式之差为:\n"); subtract(La, Lb, Ld); sort(Ld);reverse(Ld);display(Ld);break;}return 0;}【程序运行截图】。
数据结构多项式求和实验报告

1.实验题目设计一种用单链表存储多项式的结构(每个结点存储一项的系数和指数,类型都为int),并编写一个产生多项式链表的函数和一个实现两个多项式相加的函数。
2 .实验内容顺序存储结构的实现。
先输入多项式最高项数,然后按照(系数,指数)的格式输入顺序表类型定义如下:typedef struct term{int coef;int expn;struct term *next;}term,*Polynomial;3.实验要求(1)利用C语言完成算法设计和程序设计。
(2)上机调试通过实验程序。
(3)输入数据,检验程序运行结果。
(4)给出具体的算法分析,包括时间复杂度和空间复杂度。
(5)撰写实验报告。
4.实验步骤与源程序⑴实验步骤首先分析实验内容,要实现多项式求和,必须创建两个函数,然后先建立一个多项式a和多项式b,接着输入每个多项式的系数和指数,再实现多项式a和b的求和将求出的多项式放在多项式a中,最后输出求出的多项式的结果。
⑵源代码#include<stdio.h>#include<stdlib.h>#include<string.h>#include<time.h>#include<malloc.h>/*定义存储结构,用单链表存储多项式,链表中每个结点存储多项式中的一项。
*/typedef struct term{int coef;//定义多项式系数为coefint expn;//定义多项式指数为expnstruct term *next;}term,*Polynomial;void Create_Polynomial(Polynomial *P,int n){ /*建立多项式*/int i;term *t1,*t2;(*P)=(term *)malloc(sizeof(term));(*P)->coef=0;(*P)->expn=0;(*P)->next=NULL;t1=(*P);for(i=0;i<=n;i++){ /*输入每一项的系数和指数*/ t2=(term *)malloc(sizeof(term));scanf("%d,%d",&(t2->coef),&(t2->expn));t1->next=t2;t1=t1->next;}t2->next=NULL;}void Add_Polynomial(Polynomial *a,Polynomial *b){ /*多项式a和多项式b求和,结果存放在a中。
算法与数据结构实验报告实验一 完成多项式的相加运算

实验一:完成多项式的相加运算(验证性、4学时)一、实验目的完成多项式的相加、相乘运算。
(1)掌握线性表的插入、删除、查找等基本操作设计与实现(2)学习利用线性表提供的接口去求解实际问题(3)熟悉线性表的的存储方法二、实验内容设计一个一元多项式的简单计算程序,其基本功能有:(1)输入并建立多项式;(2)输出多项式;(3)多项式的相加运算。
利用单链表实现。
三、算法描述及实验步骤1描述1、创建两个单链表A、B,分别调用CreatePolyn();2、输出多项式,分别调用PrintPolyn();3、多项式相加运算AddPolyn()。
2算法流程图4 65inputA-B inputA-B inputA-B end3代码(注释)#include<stdio.h>#include<malloc.h>#include<math.h>typedef struct Polynomial{float coef;//系数变量int exp;//指数变量struct Polynomial *next;//定义next指针}*Polyn,Polynomial; //Polyn为结点指针类型void Insert(Polyn p,Polyn h) //插入新的结点p{if(p->coef==0) free(p); //系数为0的话释放结点else{Polyn q1,q2;q1=h;q2=h->next;while(q2&&p->exp<q2->exp) //查找插入位置{q1=q2;q2=q2->next;}if(q2&&p->exp==q2->exp) //将指数相同相合并{q2->coef+=p->coef;free(p);if(!q2->coef) //系数为0的话释放结点{q1->next=q2->next;free(q2);}}else //指数为新时将结点插入{p->next=q2;q1->next=p;}}}//Insertint f(float x)//判断输入是否为整形{float a;a=x-(long int)x;if(a==0&&x==fabs(x))return 1;elsereturn 0;}Polyn CreatePolyn(Polyn head,int m) //建立一个头指针为head、项数为m的一元多项式{int i;Polyn p;p=head=(Polyn)malloc(sizeof(struct Polynomial));head->next=NULL;for(i=0;i<m;i++){p=(Polyn)malloc(sizeof(struct Polynomial));//建立新结点以接收数据printf("please input NO.%d coef and exp:",i+1);scanf("%f %d",&p->coef,&p->exp);while(!f(p->coef)&&!f(p->exp)){printf("输入有错,请重新输入: ");scanf("%f %d",&p->coef,&p->exp);}Insert(p,head); //调用Insert函数插入结点}return head;}//CreatePolynvoid DestroyPolyn(Polyn p) //销毁多项式p{Polyn q1,q2;q1=p->next;q2=q1->next;while(q1->next){free(q1);q1=q2;//指针后移q2=q2->next;}}void PrintPolyn(Polyn P)//输出多项式{Polyn q=P->next;int flag=1; //项数计数器if(!q) //若多项式为空,输出0{putchar('0');printf("\n");return;}while (q){if(q->coef>0&&flag!=1) putchar('+'); //系数大于0且不是第一项if(q->coef!=1&&q->coef!=-1) //系数非1或-1的普通情况{printf("%g",q->coef);if(q->exp==1) putchar('X');else if(q->exp) printf("X^%d",q->exp);}else{if(q->coef==1){if(!q->exp) putchar('1');else if(q->exp==1) putchar('X');else printf("X^%d",q->exp);}if(q->coef==-1){if(!q->exp) printf("-1");else if(q->exp==1) printf("-X");else printf("-X^%d",q->exp);}}q=q->next;flag++;}//whileprintf("\n");}//PrintPolynint compare(Polyn a,Polyn b){if(a&&b){if(!b||a->exp>b->exp) return 1;else if(!a||a->exp<b->exp) return -1;else return 0;}else if(!a&&b) return -1;//A多项式已空,但B多项式非空else return 1;//B多项式已空,但A多项式非空}//comparePolyn AddPolyn(Polyn pa,Polyn pb)//求解并建立多项式A+B,返回其头指针{Polyn qa=pa->next;Polyn qb=pb->next;Polyn headc,hc,qc;hc=(Polyn)malloc(sizeof(struct Polynomial)); //建立头结点hc->next=NULL;headc=hc;while(qa||qb){qc=(Polyn)malloc(sizeof(struct Polynomial));switch(compare(qa,qb)) //功能选择{ case 1:{qc->coef=qa->coef;qc->exp=qa->exp;qa=qa->next;break;}case 0:{qc->coef=qa->coef+qb->coef;qc->exp=qa->exp;qa=qa->next;qb=qb->next;break;}case -1:{qc->coef=qb->coef;qc->exp=qb->exp;qb=qb->next;break;}}//switchif(qc->coef!=0){qc->next=hc->next;hc->next=qc;hc=qc;}else free(qc);//当相加系数为0时,释放该结点}//whilereturn headc;}//AddPolynPolyn SubtractPolyn(Polyn pa,Polyn pb){//求解并建立多项式A-B,返回其头指针Polyn h=pb;Polyn p=pb->next;Polyn pd;while(p){ //将pb的系数取反p->coef*=-1;p=p->next;}pd=AddPolyn(pa,h);for(p=h->next;p;p=p->next) //恢复pb的系数p->coef*=-1;return pd;}//SubtractPolynPolyn MultiplyPolyn(Polyn pa,Polyn pb){//求解并建立多项式A*B,返回其头指针Polyn hf,pf;Polyn qa=pa->next;Polyn qb=pb->next;hf=(Polyn)malloc(sizeof(struct Polynomial));//建立头结点hf->next=NULL;for(;qa;qa=qa->next){for(qb=pb->next;qb;qb=qb->next){pf=(Polyn)malloc(sizeof(struct Polynomial));pf->coef=qa->coef*qb->coef;pf->exp=qa->exp+qb->exp;Insert(pf,hf);//调用Insert函数以合并指数相同的项}}return hf;}//MultiplyPolynvoid DevicePolyn(Polyn pa,Polyn pb){//求解并建立多项式A/B,返回其头指针Polyn hf,pf,af,temp1,temp2,q;Polyn qa=pa->next;Polyn qb=pb->next;hf=(Polyn)malloc(sizeof(struct Polynomial));//建立头结点,存储商hf->next=NULL;pf=(Polyn)malloc(sizeof(struct Polynomial));//建立头结点,存储余数pf->next=NULL;temp1=(Polyn)malloc(sizeof(struct Polynomial));temp1->next=NULL;temp2=(Polyn)malloc(sizeof(struct Polynomial));temp2->next=NULL;temp1=AddPolyn(temp1,pa);while(qa!=NULL&&qa->exp>=qb->exp){temp2->next=(Polyn)malloc(sizeof(struct Polynomial));temp2->next->coef=(qa->coef)/(qb->coef);temp2->next->exp=(qa->exp)-(qb->exp);Insert(temp2->next,hf);pa=SubtractPolyn(pa,MultiplyPolyn(pb,temp2));qa=pa->next;temp2->next=NULL;}pf=SubtractPolyn(temp1,MultiplyPolyn(hf,pb));pb=temp1;printf("the quotient is :");PrintPolyn(hf);printf("the remainder is :");PrintPolyn(pf);}//DevicePolynint main(){int m,n,flag=0;float x;Polyn pa=0,pb=0,pc,pd,pe,pf;//定义各式的头指针,pa与pb在使用前付初值NULL printf("please input A number:");scanf("%d",&m);pa=CreatePolyn(pa,m);//建立多项式Aprintf("please input B number:");scanf("%d",&n);pb=CreatePolyn(pb,n);//建立多项式B//输出菜单printf("**********************************************\n");printf("choise:\n\t1.Output A and B\n\t2.CreatePolyn A+B\n");printf("\t3.CreatePolyn A-B\n\t4.CreatePolyn A*B\n");printf("\t5.CreatePolynA/B\n\t6.Return\n**********************************************\n");for(;;flag=0){printf("choise");scanf("%d",&flag);if(flag==1){printf("多项式A:");PrintPolyn(pa);printf("多项式B:");PrintPolyn(pb);continue;}if(flag==2){pc=AddPolyn(pa,pb);printf("多项式A+B:");PrintPolyn(pc);DestroyPolyn(pc);continue;}if(flag==3){pd=SubtractPolyn(pa,pb);printf("多项式A-B:");PrintPolyn(pd);DestroyPolyn(pd);continue;}if(flag==4){pf=MultiplyPolyn(pa,pb);printf("多项式a*b:");PrintPolyn(pf);DestroyPolyn(pf);continue;}if(flag==5){DevicePolyn(pa,pb);continue;}if(flag==6) break;if(flag<1||flag>6) printf("Error\n");continue;}//forDestroyPolyn(pa);DestroyPolyn(pb);return 0;}一、调试过程一次调试二次调试二、实验结果测试数据(1)多项式A:3x^4+11x^3+21x^2多项式B:2x^5+11x^4+12x^3+7x实验结果(1)多项式A+B=2x^5+14x^4+23x^3+21x^2+7x多项式A-B=-2x^5-8^4-x^3+21x^2-7x多项式A*B=6x^9+55x^8+199x^7+363x^6+273x^5+77x^4+147x^3多项式A/B=0实验截图(1)测试数据(2):多项式A:2x^3+5x^-3多项式B:9x^2+6x^-2+11x^-3实验结果(2):多项式A+B=2x^3+9x^2+6x^-2+16x^-3多项式A-B=2x^3-9x^2-6x^(-2)=16x^(-3)多项式A*B=18x^5+12x+22+45x^(-1)+30x^(-5)+55x^(-6)多项式A/B=0.222222x实验截图(2):测试数据(3)多项式A:-x^7+3x^5多项式B:x^7-4x6%+7x^3实验结果(3)多项式A+B=-x^5+7x^3多项式A-B=-2x^7+7x^5-7x^3多项式A*B=-x^14+7x^12-19x^10+21x^8多项式A/B=-1实验截图(3):三、总结1.在熟悉VC6.0环境的同时,对单链表的存储格式有了深刻的理解;2.复习C++语法的同时,对刚学的线性表进行综合性理解和表达,与之前所学融合。
多项式相加数据结构

多项式相加数据结构多项式相加是一种常见的数学操作,它在数据结构中也有广泛的应用。
本文将介绍多项式相加的概念、实现方法以及应用场景。
## 一、多项式相加的概念多项式是由常数项和一系列幂次项组成的代数表达式,形如:P(x) = a0 + a1x + a2x^2 + ... + anx^n其中,ai为系数,x为变量,n为最高次数。
多项式相加即将两个或多个多项式相加得到一个新的多项式。
## 二、多项式相加的实现方法多项式相加的实现方法有多种,常见的有数组表示法、链表表示法和稀疏矩阵表示法。
1. 数组表示法:将多项式的系数存储在一个数组中,数组下标表示幂次,数组元素表示系数。
2. 链表表示法:将多项式的每一项用链表的形式连接起来,每个节点包含系数和幂次信息。
3. 稀疏矩阵表示法:对于稀疏的多项式,只存储非零项的信息,可以用矩阵的形式表示。
不同的表示方法适用于不同的场景,选择合适的实现方法可以提高多项式相加的效率和灵活性。
## 三、多项式相加的应用场景多项式相加在实际应用中有很多场景,以下列举几个常见的应用场景:1. 数据压缩:在某些情况下,数据具有稀疏性,多项式相加可以将稀疏数据压缩为较小的存储空间,减少数据传输和存储成本。
2. 图像处理:图像的滤波操作可以看作是将图像的像素值与一个多项式进行相加的过程,通过调整多项式的系数可以实现不同的滤波效果。
3. 信号处理:信号可以表示为一个多项式的形式,多项式相加可以实现信号的叠加和混合,用于音频合成、语音识别等应用。
4. 机器学习:在机器学习算法中,多项式相加可以用于特征工程,通过将不同特征的多项式进行相加,得到新的特征表示,提高模型的拟合能力。
## 四、总结多项式相加是一种常见的数学操作,在数据结构中有广泛的应用。
本文介绍了多项式相加的概念、实现方法和应用场景,并提到了多项式相加在数据压缩、图像处理、信号处理和机器学习等领域的重要性。
选择合适的实现方法和应用场景可以提高多项式相加的效率和灵活性,进而推动相关领域的发展和应用。
多项式相加数据结构

多项式相加数据结构多项式相加数据结构是一种用于处理多项式加法的算法和数据结构。
在数学中,多项式是由常数和变量的乘积相加而成的表达式。
例如,2x² + 3x + 4就是一个多项式。
在计算机科学中,我们需要对多项式进行操作,如求导、求积分、求根、求值等。
对于两个多项式P(x)和Q(x),它们的加法可以表示为:R(x) = P(x) + Q(x),即将它们的同类项相加得到结果R(x)。
例如,(2x² + 3x + 4) + (4x² - 2x + 1) = 6x² + x + 5。
实现多项式相加有很多方法,其中一种常见的方法是使用链表来存储每个非零系数的项。
链表中每个节点包含两个字段:系数和指数。
系数表示该项的系数,指数表示该项中变量的指数。
例如,在上面的例子中,第一个多项式可以表示为:2 -> 2 -> null其中第一个节点表示系数为2、指数为2(即2x²)的一项,第二个节点表示系数为3、指数为1(即3x)的一项。
使用链表存储多项式有以下优点:1. 可以灵活地插入和删除节点,方便进行各种操作。
2. 可以节省空间,因为只存储非零系数的项,而且指数是有序的。
3. 可以方便地进行排序和合并,因为链表中的节点是有序的。
下面是一个简单的多项式相加算法:1. 创建一个空链表R,用于存储结果。
2. 从P和Q的头节点开始遍历它们的链表。
3. 如果P和Q都还有节点,则比较它们的指数大小:a. 如果P的指数小于Q的指数,则将P节点插入到R中,并移动P 指针到下一个节点。
b. 如果Q的指数小于P的指数,则将Q节点插入到R中,并移动Q指针到下一个节点。
c. 如果P和Q的指数相等,则将它们对应系数相加得到新系数,并创建一个新节点插入到R中。
然后移动P和Q指针到下一个节点。
4. 如果其中一个链表已经遍历完了,则将另一个链表剩余部分直接插入到R中。
5. 返回结果链表R。
数据结构实验多项式加法

数据结构实验报告实验名称:多项式加减法学号:19姓名:林强实验日期:一、实验目的通过实现多项式的加减法,对链表有更深入的了解二、实验具体内容1、实验题目1:(1)题目设计一个一元稀疏多项式简单的加减法计算器实现要求:一元稀疏多项式简单计算器的基本功能是:(1)输入并建立多项式:8517A+x+x=;+73x9)(x798xB-+x=822x)(x(2)输出多项式(3)多项式A和B相加,建立多项式C=A+B,并输出相加的结果多项式C(4)选作:多项式A和B相减,建立多项式C=A-B,并输出相加的结果多项式D (2)分析1:本程序的任务是实现两个多项式的加法其中多项式的系数为浮点型,指数为整数,输出的结果也为系数和指数。
(1)输入的形式和输入值的范围:输入多项式的系数a和未知数X的指数b,当a和b都为零时,输入结束。
输入值的范围:a为实数,b为整数。
(2)输出形式:输出多项式的系数和多项式未知数X的指数即(a,b)形式。
(3)程序所能达到的功能,实现两个多项式的加法,并输出最后的结果2:整个程序运行期间实行动态创建节点,一边输入数据,一边创建节点当将全部数据输入到单链表中后再调用多项式加法这个函数,并一边实现多项式的相加,一边释放节点,有效防止了在程序反复运行过程中可能出现系统空间不够分配的现象(3)实验代码typedef int Status;#define OVERFLOW -1#define null 0typedef struct Lnode{float coef; //存储项系数int expn;//存储项指数struct Lnode *next;}Lnode,*LinkList;typedef LinkList polynomial;Status InitList_L(LinkList &L) {//初始化头节点L=(LinkList)malloc(sizeof(Lnode));if(!L)return(-1);L->next=null;return 1;}void AddPolyn(polynomial pa, polynomial pb){ //实现两个多项式相加的算法float x;polynomial qa;polynomial qb;polynomial s;polynomial u;qa=pa->next; qb=pb->next; s=pa;while(qa&&qb){if(qa->expn<qb->expn){s=qa;qa=qa->next;}else if(qa->expn==qb->expn){x=qa->coef+qb->coef; if(x!=0){qa->coef=x;s=qa;qa=qa->next;u=qb;qb=qb->next;free(u);}else{s->next=qa->next;free(qa);qa=s->next;u=qb;qb=qb->next;free(u);}}else if(qa->expn>qb->expn){u=qb->next;s->next=qb;s=qb;qb->next=qa;qb=u;}}if(qb)qa->next=qb;free(pb);void main(){float a;int b;polynomial L1;polynomial L2;LinkList q;LinkList p;LinkList m;LinkList n;InitList_L(L1);q=L1;InitList_L(L2);p=L2;cout<<"请输入数据:"<<endl;for(;;){cin>>a;cin>>b;if(a==0&&b==0)break;m=new Lnode;m->coef=a;m->expn=b;q->next=m;q=m;q->next=null;}//循环输入第一个多项式的系数与指数for(;;){cin>>a;cin>>b;if(a==0&&b==0)break;n=new Lnode;n->coef=a;n->expn=b;p->next=n;p=n;p->next=null;}//循环输入第二个多项式的系数与指数AddPolyn(L1,L2);//调用多项式相加的算法while((L1->next)!=null){cout<<"("<<L1->next->coef<<","<<L1->next->expn<<")"<<" ";L1=L1->next;}//输出计算结果}三、实验小结通过编写多项加法这个程序,我将自己所学到的创建链表,初始化链表和多项式加法算法都应用了一次,这使我们不仅仅只是理论化的学习书本上的知识,而是将学习到的理论知识应用到实际的操作中来增强我们的实际操作能力,这使我增加了实际操作经验,也使我通过实际操作来认识到自己在程序编写上的不足从而增强了我的实际编写程序的能力。
数据结构实验报告完成多项式的运算

简单介绍:本次作业力在学会链表表示线性表的插入、删除、查找等基本操作设计与实现,学习利用链表提供的接口去求解实际问题,同时熟悉链表的的存储方法。
再基于线性链表的基础设计完成多项式的相加运算程序。
一、实验目的和要求完成多项式的相加、相乘运算。
(1)掌握线性表的插入、删除、查找等基本操作设计与实现(2)学习利用线性表提供的接口去求解实际问题(3)熟悉线性表的的存储方法二、实验内容和原理1.实验内容设计一个一元多项式的简单计算程序,其基本功能有:(1)输入并建立多项式;(2)输出多项式;(3)多项式的相加运算。
利用单链表实现。
2.实验原理使用单链表实现一元多项式的存储,并实现两个一元多项式的加法运算。
三、实验环境硬件:(1)学生用微机(2)多媒体教室或远程教学(3)局域网环境软件:(1)Windows XP中文操作系统(2)VC6.0四、算法描述及实验步骤1、描述:加法:输入建立一元多项式,进行简单加法运算,输出结果;通过建立单链表A和B分别存放多项式的a和b的各项系数及指数;并且利用A使得不产生新的节点而在A中存放数据运算结果;该过程通过定义指针变量p和q使它们分别指向两个多项式的第一个节点,之后依次比较它们所指向的项的指数,即一种情况指数相等时系数相加且和不为零,修改当前p所指项的系数(和),同时删除q所指项,若和为零则同时删除p和q各自所指;情况二,p当前项指数大于q当前项,将q所指插入p所指之前作为结果项之一;情况三,p当前项指数小于q当前项,p所指作为多项式和的一项,移动p指向下一项,进行比较,在移动p,q至其中以个链空,把另一个链余下节点插在p所指之后;乘法:定义指针p,q指向所操作节点,通过A链表的每一项与B链表各项相乘,指数相加,系数相乘,将值赋给新节点各自域,构成一新的链表,最后返回头结点。
可这样有一个问题,即新生成的链表,即最终结果混乱,没有对数据进行过滤,相同指数项应在执行加法运算,所以可以这样实现,通过A链表的每一项与B链表各项相乘的新生成节点单独构成一链表,并将第一个链表加入另一新链表,循环此操作将后生成的链表加之先前的链表,即可实现排序问题。
一元多项式相加 数据结构实验报告

南昌航空大学实验报告课程名称:数据结构实验名称:实验二线性表的链式存储结构班级:080611 学生姓名:学号:08指导教师评定:签名:题目:设计并实现以下算法:给出用单链表存储多项式的结构,利用后接法生成多项式的单链表结构,实现两个多项式相加的运算,并就地逆置相加后的多项式链式。
一、需求分析1.用户可以根据自己的需求分别输入两个一元多项式,并且能够实现输入的一元多项式的显示。
2.能够完成两个一元多项式的相加功能,而且还能显示相加后的逆置的一元多项式。
3.程序执行的命令包括:(1)构造链表A (2)构造链表B (3)两个链表的相加(4)求链表的长度(5)打印(显示)已有的链表(6)将已相加的链表进行逆序排列二、概要设计⒈为实现上述算法,需要线性表的抽象数据类型:ADT Polynomial {数据对象:D={a i:|a i∈TermSet,i=1…n,n≥0TermSet 中的每个元素包含一个表示系数的实数和表示指数的整数} 数据关系:R1={<a i-1,a i>|a i-1,a i∈D,且a i-1中的指数值< a i中的指数值i=2,…n≥0}基本操作:initlink(& L)操作结果:构造一个空的链表L。
Creatlink(&L,n)操作结果:输入n项的系数和指数,建立一个非空的一元多项式L。
LinkLength(L)初始条件:链表L已经存在。
操作结果:返回一元多项式L中的项数。
Displaylink(L)初始条件:链表L已经存在。
操作结果:打印输出一元多项式L。
Addpolyn(A,B,&C)初始条件:一元多项式A和B已存在。
操作结果:完成多项式相加运算,即:C=A+B,并且带回C。
subtracypolyn(&La,&Lb,)初始条件:一元多项式La和Lb已存在。
操作结果:完成多项式的相减运算La=La+Lb,并且销毁多项式Lb。
数据结构单链表实现多项式加法的算法实现
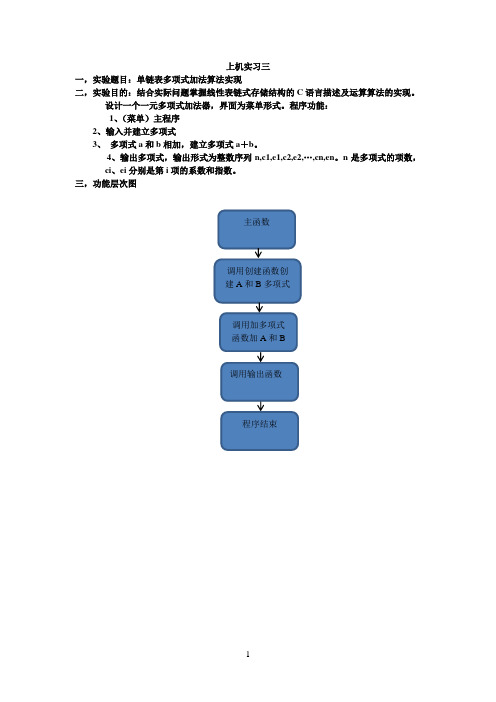
上机实习三一,实验题目:单链表多项式加法算法实现二,实验目的:结合实际问题掌握线性表链式存储结构的C语言描述及运算算法的实现。
设计一个一元多项式加法器,界面为菜单形式。
程序功能:1、(菜单)主程序2、输入并建立多项式3、多项式a和b相加,建立多项式a+b。
4、输出多项式,输出形式为整数序列n,c1,e1,c2,e2,…,cn,en。
n是多项式的项数,ci、ei分别是第i项的系数和指数。
三,功能层次图主函数调用创建函数创建A和B多项式调用加多项式函数加A和B调用输出函数程序结束四,运行结果创建A表创建B表加两个A,B的多项赋给C式A,B,C的结果五,小结在做这个程序的时候,虽然遇到一些问题,但最后都被我解决,自信心上得到比较大的提升,这也是这次实践最大的收获。
同时,知识上的收获也是不可忽视的,亲手解决问题的过程也是很好的学习过程,并且积累了一些经验,相信会为以后的学习发展带来非常积极的帮助。
源代码:#include<stdio.h>#include<conio.h>#include<alloc.h>#include<stdlib.h>typedef struct pnode{float coef; /* xishu */int exp; /* zhishu */struct pnode *next;}polynode;polynode *createList(){float xishu;int zhishu;polynode *head,*r;r=malloc(sizeof(polynode));r->coef=0;r->exp=-1;r->next=r;head=r;printf("<<Input XiShu 111 to stop>>\n");printf("Input XiShu:");scanf("%f",&xishu);printf("Input ZhiShu:");scanf("%d",&zhishu);while(1){r->next=malloc(sizeof(polynode));r=r->next;r->coef=xishu;r->exp=zhishu;printf("Input XiShu:");scanf("%f",&xishu);if(xishu==111) break;printf("Input ZhiShu:");scanf("%d",&zhishu);}r->next=head;return head;}void display(polynode *head){int i=1;polynode *t;if(head==NULL){printf("List is empty\n");return;}t=head->next;printf("[%0.0f][%d]\t",head->coef,head->exp);while(1){printf("[%0.0f][%d]\t",t->coef,t->exp);t=t->next;i++;if(t==head) break;}}polynode *POLYADD(polynode *A,polynode *B) {int i,j,k;polynode *ptr,*q,*q1,*q2;float x;q1=A;q2=B;q=malloc(sizeof(polynode));q->coef=0;q->exp=-1;q->next=q;ptr=q;q1=q1->next;q2=q2->next;while((q1!=A)&&(q2!=B)){if(q1->exp==q2->exp){x=q1->coef+q2->coef;if(x!=0){q->next=malloc(sizeof(polynode));q=q->next;q->coef=x;q->exp=q1->exp;}q1=q1->next;q2=q2->next;}else{q->next=malloc(sizeof(polynode));q=q->next;if(q1->exp>q2->exp){q->coef=q2->coef;q->exp=q2->exp;q2=q2->next;}else{q->coef=q1->coef;q->exp=q1->exp;q1=q1->next;}}}while(q1!=A){q->next=malloc(sizeof(polynode));q=q->next;q->coef=q1->coef;q->exp=q1->exp;q1=q1->next;}while(q2!=B){q->next=malloc(sizeof(polynode));q=q->next;q->coef=q2->coef;q->exp=q2->exp;q2=q2->next;}q->next=ptr;return ptr;}char caiDan(){char ch;do{printf("1:Create A list\n");printf("2:Create B list\n");printf("3:Add Two Polylist\n");printf("4:Display Polylist\n");printf("5:Exit\n");printf("Please Choose:");}while(ch=getch(),ch!='1'&&ch!='2'&&ch!='3'&&ch!='4'&&ch!='5');return ch;}void main(){polynode *a,*b,*c;char ch;do{clrscr();ch=caiDan();printf("%c",ch);getch();printf("\n");switch(ch){case '1': printf("Create A list\n");a=createList();printf("A list was created successfully");getch();break;case '2': printf("Create B list\n");b=createList();printf("B list was created successfully");getch();break;case '3': c=POLYADD(a,b);printf("C(C=A+B) list was created successfully\n");getch();break;case '4': printf("A List:\t");display(a);printf("\nB List:\t");display(b);printf("\nC List:\t");display(c);getch();break;case '5': exit(0);}}while(ch!='5');}。
数据结构实验-多项式的相加减

集美大学数据结构课程实验报告课程名称:数据结构班级:网络0911实验成绩:指导教师:姓名:实验项目名称:多项式的相加减学号上机实践日期:实验项目编号:组号:上机实践时间:学时一、目的(本次实验所涉及并要求掌握的知识点)学习和掌握如何运用链表来实现一元稀疏多项式的相加减。
多项式的输入和输出的应注意的要点,规定输出的多项式的顺序。
二、实验内容与设计思想(设计思路、主要数据结构、主要代码结构、)实验内容:一元稀疏多项式的相加减设计思路:建立数据结构存放常数和系数以及指向下一个节点的指数,用链表存放各个节点,通过对常数和系数的的运算,实现多项式的相加减主要数据结构:结构体,链表主要代码结构:struct Polyn;void addPolyn(Polyn * a,Polyn * b,int add);void display( );void tip()’Polyn * CreatPolyn(int m);三、实验使用环境(本次实验所使用的平台和相关软件)Dev-C++、windows XP四、实验步骤和调试过程(实验步骤、测试数据设计、测试结果分析)需说明出,加入必要的截图说明。
#include<iostream>#include<vector>using namespace std;struct Polyn{float coef;int expn;Polyn *next;};//构建结构体vector <Polyn *> ve;void addPolyn(Polyn * a,Polyn * b,int add);void display(Polyn *n);//打印void tip();//屏幕显示Polyn * CreatPolyn(int m); //建立多项式int main(){tip();system("pause");}void tip(){Polyn *first, *second,*s;int m;for( int i=1;i;){cout<<" 多项式运算.\n";cout<<"======================="<<"\n"; cout<<" 1------ 构造多项式.\n";cout<<" 2------ 多项式相加.\n";cout<<" 3------ 多项式相减.\n";cout<<" 0------ 结束.\n";cout<<"======================="<<"\n"; cout<<" 请输入您的选择.\n";cin>>i;switch(i){case 1:cout<<"请输入多项式的项数.\n";cin>>m;s=CreatPolyn(m);display(s);ve.push_back(s);break;case 2:first=ve.back();ve.pop_back();second=ve.back();addPolyn(first,second,0);break;case 3:first=ve.back();ve.pop_back();second=ve.back();addPolyn( first,second,1);break;case 0:cout<<" 再见"<<"\n";break;};}}Polyn* CreatPolyn(int m){Polyn* px=new Polyn[m];cout<<" 输入系数.\n";for(int i=0;i<m;i++)cin>>px[i].coef;cout<<"输入与系数相对应的指数.\n";for(int i=0;i<m;i++){cin>>px[i].expn;if(i!=m-1)px[i].next=&px[i+1];elsepx[i].next=NULL;}return px;}void display(Polyn *n){int q=0;Polyn * r;r=n;for(;r;r=r->next){if(r->coef)q++;if(r==n){if(r->coef!=0)cout<<r->coef<<"X"<<"^"<<r->expn;}else{if( r->coef>0)cout<<"+"<<r->coef<<"X"<<"^"<<r->expn;if(r->coef<0)cout<<r->coef<<"X"<<"^"<<r->expn;}}cout<<"\n";if(q==0)cout<<"0"<<"\n";}void addPolyn(Polyn * a,Polyn * b,int add)//两个多项式的加减{float c;int a1=1,b1=1,s,e;Polyn *ha,*hb,*p,*r;ha=a;hb=b;p=ha;r=hb;for(int i=0;ha[i].next;++i)a1++;for(int i=0;hb[i].next;++i)b1++;ha[a1-1].next=hb;for(int j=0;j<b1;j++){for(int i=0;i<a1;i++){if(a[i].expn-b[j].expn==0){if(add)ha[i].coef=ha[i].coef-hb[j].coef;elseha[i].coef=ha[i].coef+hb[j].coef;if(hb!=&hb[j])hb[j-1].next=hb[j].next;else{hb=hb[j].next;ha[a1-1].next=hb;}i=a1;}}}for(;p;p=p->next){for( Polyn * t=p->next;t;t=t->next)if( p->expn>t->expn){e=p->expn;p->expn=t->expn;t->expn=e;c=p->coef;p->coef=t->coef;t->coef=c;}}display(ha);}五、实验小结(实验中遇到的问题及解决过程、实验体会和收获)至少两点1.刚开始实现多项式的相加减运算时,申请一个新的空间来存放结果,结果指针乱了,后来改成了现在的程序。
数据结构实验-一元多项式的加法运算

一元多项式加法一、实验目的通过实现多项式加法,对链表有更深入的了解二、实验内容问题描述:设计一个一元稀疏多项式简单的加法计算器实现要求:一元稀疏多项式简单计算器的基本功能是:(1)输入并建立多项式:1785937)(x x x x A +++=;879228)(x x x x B -+=(2)输出多项式(3)多项式A 和B 相加,建立多项式C =A +B ,并输出相加的结果多项式C(4)选作:多项式A 和B 相减,建立多项式C =A -B ,并输出相减的结果多项式D 方法说明:(1)多项式的输入与存储用带表头结点的单链表存储多项式,链表中的每个节点分别存储多项式各项的系数和指数,即每从键盘输入多项式的一对数(系数,指数),可对应建立链表的一个结点。
每个节点的结构为:建立两个链表,其中pa 和pb 分别为它们的头指针:pb结果链表Pa(或者是Pc)Pc(2)多项式数据类型的定义struct tagNode{float coef;int exp;struct tagNode *next;typedef struct tagNode Node;typedef struct tagNode* pNode;(3)主要算法①创建两个链表,分别存放多项式1和多项式2,这两个链表中的节点是按指数降序或者升序排列的②多项式相加,下面给出多项式相加的部分实现/*下面的函数实现两个多项式的相加,要相加的链表分别由pa和pb指向(其中,pa,pb都是分配了空间的头结点)。
相加的结果直接由pa指向的链表保存,即是在pa链表中添加或删除(当系数因为相加为0的情况下)一些结点,构成结果。
相加的链表中指数按从小到大的顺序排列好的,是升序链表。
*/void add_poly(Node *pa,Node *pb){Node *p=pa->pNext;//链表1,将来的结果也放在此Node *q=pb->pNext;//链表2Node *pre=pa;Node *u;//临时用float x;while (p!=NULL && q!=NULL)//当两个链表都不为空{if (p->exp<q->exp)//比较链表1跟链表2当前节点的指数大小,链表1也是存放结果的地方{pre=p;p=p->pNext;//p指向要比较的下一个结点。
数据结构和算法-一元多项式运算算法(加法)

数据结构和算法-⼀元多项式运算算法(加法)算法名称:⼀元多项式算法算法介绍:加法运算:将具有与相同幂项的系数相加即可得到合并后的多项式。
若某个幂项只存在于⼀个多项式中,则直接合并到结果中举例利⽤代码实现这⾥主要使⽤了链表,通过3个函数来进⾏操作。
分别是Inpu函数,Add运算函数,打印函数。
代码:1. /*采⽤链表的⽅式*/2. #include<stdio.h>3. #include<stdlib.h>4. #include<limits.h>5. typedef struct polyn //定义多项式的结构6. {7.8. float coef; //系数项9. int expn; //指数10. struct polyn *next; //指向下⼀项11. }POLYN,*pPOLYN;12. void PolynInput(pPOLYN *p) //输⼊⼀元多项式13. {14. int i,min=INT_MIN; //INT_MIN是int型的最⼩数15. pPOLYN p1,p2; //分别表⽰2个多项式的指针16. if(!(*p=(POLYN *)malloc(sizeof(POLYN)))) //为头结点分配内存17. {18.19. printf("内存分配失败 \n");20. exit(0);21. }22. (*p)->coef=0; //设置头结点的系数为023. printf("输⼊该多项式的项数:");24. scanf("%d",&((*p)->expn));25. (*p)->next=NULL;26. for(i=0;i<(*p)->expn;i++) //输⼊多项式各项27. {28. if(!(p1=(pPOLYN)malloc(sizeof(POLYN)))) //分配⼀个多项式的内存29. {30. printf("内存分配失败: \n");31. exit(0);32. }33. printf("第%d项系数:",i+1);34. scanf("%f",&(p1->coef));35. do{36. printf("第%d项指数:",i+1);37. scanf("%d",&(p1->expn));38. if(p1->expn<min)39. printf("\n前项=指数值不能⼩于前⼀项指数值%d!\n重新输⼊\n",(*p)->next->expn);40. }while(p1->expn<min);41. min=p1->expn;42. p1->next=(*p)->next;43. (*p)->next=p1;44. }45. p1=(*p)->next; //合并多项式中指数值相同的项46. while(p1)47. {48. p2=p1->next; //取下⼀节点49. while(p2 && p2->expn==p1->expn) //若节点有效,节点与q节点的指数相同50. {51. p1->coef+=p2->coef; //累加系数52. p1->next=p2->next; //删除r指向的节点53. free(p2);54. p2=p1->next;56. }57. p1=p1->next;58. }59. }60. void PolynPrint(pPOLYN p) //输出多项式61. {62. pPOLYN p1;63. int i;64. printf("\n\n计算后的多项式共有%d项 \n",p->expn);65. p1=p->next;66. i=1;67. while(p1)68. {69. printf("第%d项,系数:%g,指数:%d\n",i++,p1->coef,p1->expn);70. p1=p1->next;71. }72. printf("\n");73. }74. void PolynAdd(pPOLYN pa,pPOLYN pb) //多项式相加pa=pa+pb75. {76.77. pPOLYN pa1,pb1,pc1,p;78. pa1=pa->next; //指向被加链表的第⼀个有效项79. pb1=pb->next; //指向加链表的第⼀个有效项80. pc1=pa; //指向被加链表81. pc1->next=NULL;82. pa->expn=0; //清空多项式项⽬数据83. while(pa1 && pb1) //两个多项式都未结束84. {85.86. if(pa1->expn > pb1->expn) //如果pa1指数⼤于pb187. {88. pc1->next=pa1; //将pa1指数加⼊结果链表中89. pc1=pa1;90. pa1=pa1->next; //处理pa1中的下⼀项91. pc1->next=NULL;92.93. }else if(pa1->expn < pb1->expn) //pa1的指数⼩于pb1的指数94. {95. pc1->next=pb1; //将pb1指数加⼊结果链表中96. pc1=pb1;97. pb1=pb1->next; //处理pb1的下⼀项98. pc1->next=NULL;99. }else { //pa1指数等于pb1指数,进⾏系统相加100. pa1->coef+=pb1->coef; //累加素数101. if(pa1->coef!=0) //若系数不为0102. {103. pc1->next=pa1; //将相加结果添加到结果链表中104. pc1=pa1;105. pa1=pa1->next; //处理pa1的下⼀项106. pc1->next=NULL;107. p=pb1;108. pb1=pb1->next; //处理pb1的下⼀项109. free(p);110. }111. else{ //系数为0,则不记录该项112. p=pa1; //⽤p指向pa1中的该项113. pa1=pa1->next; //链表中删除该项114. free(p); //释放该项所占⽤内存115. p=pb1; //⽤临时指针指向pb1中的该项116. pb1=pa1->next; //链表中删除该项117. free(p); //释放该项所占⽤内存118. pa->expn--; //后⾯要进⾏累加操作,此处先减119. }120. }121. pa-pa->expn++; //累加⼀个结果项122. }123. if(pa1) //若pa1中还有项124. {125. pc1->next=pa1; //将pa1中的项添加到结果链表中126. while(pa1)127. {128.129. pa->expn++;130. pa1=pa1->next;131. }132. }133. if(pb1) //若pb1中还有项134. {135.136. pc1->next=pb1; //将pb1中的项添加到结果链表中137. while(pb1)138. {140. pb1=pb1->next;141. }142. }143. free(pb); //释放pb头链所占的内存空间144. }145. int main()146. {147. pPOLYN pa=NULL,pb=NULL; //指向多项式链表的指针148. printf("输⼊第⼀个多项式数据:\n");149. PolynInput(&pa); //调⽤函数输⼊⼀个多项式150. printf("\n输⼊第⼆个多项式数据:\n");151. PolynInput(&pb); //调⽤函数,输⼊另⼀个多项式152. PolynAdd(pa,pb); //调⽤多项式相加函数153. printf("\n两个多项式之和为:");154. PolynPrint(pa); //输出运算得到的多项式155. getch();156. return 0;157. }附件列表。
数据结构+实验报告+线性表及其应用(多项式相加、相乘)等

一、 实验目的和要求
1、掌握树的有关图相关操作算法; 2、熟悉树的基本存储方法; 3、学习利用树求解实际问题。
二、 实验内容和原理
1、实验内容: (1)构造哈弗曼树; (2)对单个结点编码; (3)输出树; (4) 编 码; (5)译码。 2、实验原理:通过树的有关图的相关操作算法,以及树的基本存储方法,利用
实验项目名称 线性表及其应用(多项式相加、相乘) 哈弗曼树及哈弗曼编码译码的实现 Dijkstra 最短路径 或 Prim 最小生成树 (快速、堆、归并)排序算法的设计 构造平衡二叉排序树
成绩
100 100 100 100 100
指导教师
王治和 王学院实验报告
多项式加法:定义指针 p,q 分别指向 ha,hb
1
i.p->exp==q->exp ,r->coef=p->coef+q->coef,pa,pb 下移; ii.p->exp<q->exp ,r->coef=q->coef;r->exp=q->exp;,q 下移 iii.pa->exp>pb->exp, r->exp=p->exp;r->coef=p->coef;,p 下移 iv.p!=NULL,pb==NULL.相当于 iii. V.q==NULL,pb!=NULL.相当于 ii. 其流程图如下:
三、 实验环境
Visual C++ 6.0 及 PC 机
四、 算法描述及实验步骤
思想算法: 以线性表来描述一元多项式,存储结构采用单链表,每个结点存储的多项 式中某一项的系数和指数, 建立单链表时指数高的结点列于指数低的结点之后, 即线性表的元素按指数递增有序排列。 例如构造两个多项式 ha: hb: 5X3+4X2+3X+2 X2+X+1
数据结构多项式相加实验报告

试验一多项式相加一. 实验内容:多项式相加二.实验目的和要求:利用双向链表实现通讯录的建立、删除、检索和列表,并可保存至文件,可重新装入。
用链式存储结构实现一元多项式的相加运算。
三.算法思想描述:1. 以单链表为存储结构插入多项式: 多项式输入:多项式按幂从高到低,以“系数,幂”的格式输入,并以“0,0”结束。
printf("Please input coef:");scanf("%d",&i);printf("Please input exp: ");scanf("%d",&j);while(i!=0){q=(pnode)malloc(sizeof(struct node));q->coef=i;q->exp=j;p->link=q;p=q;printf("Please input coef:");scanf("%d",&i);printf("Please input exp: ");scanf("%d",&j);}p->link=NULL;2. 多项式相加单链表合并:由两个多项式对应的单链表头节点开始,依次扫描各节点。
(1)若两表的节点均非空:比较二者的幂,按幂大者先入表。
如果幂相等,则系数相加再入表。
具体由以下代码实现:while(p!=NULL && q!=NULL){if(p->exp==q->exp){x=p->coef+q->coef;if(x!=0){s=(pnode)malloc(sizeof(struct node));s->coef=x;s->exp=p->exp;r->link=s;r=s;}p=p->link;q=q->link;}else if(p->exp<q->exp){s=(pnode)malloc(sizeof(struct node));s->coef=q->coef;s->exp=q->exp;r->link=s;r=s;q=q->link;}else{s=(pnode)malloc(sizeof(struct node));s->coef=p->coef;s->exp=p->exp;r->link=s;r=s;p=p->link;}(2). 若有一链表已空,则将非空链表插入新表:while(p!=NULL){s=(pnode)malloc(sizeof(struct node));s->coef=p->coef;s->exp=p->exp;r->link=s;r=s;p=p->link;}while(q!=NULL){s=(pnode)malloc(sizeof(struct node));s->coef=q->coef;s->exp=q->exp;r->link=s;r=s;q=q->link;}3. 输出合并后的链表:while(head->link!=NULL){head=head->link;printf(" %d*x^%d",head->coef,head->exp);}4. 主函数调用,完成多项式相加。
多项式相加数据结构

多项式相加数据结构1. 引言在数学中,多项式是一种重要的代数表达式,由若干项的和组成。
每一项包含一个系数和一个指数,并且可以是变量的多项式。
在计算机科学中,我们需要设计一种有效的数据结构来表示和计算多项式的相加运算。
本文将介绍一种用于多项式相加的数据结构,通过分析其设计原理和实现方法,展示了该数据结构的优势。
2. 问题描述多项式相加是指将两个或多个多项式相加得到一个新的多项式。
每个多项式由一系列项组成,每项包含一个系数和一个指数。
例如,多项式 P = 2x^2 + 3x + 1 和多项式 Q = 4x^3 + 2x^2 + 5 可以相加得到多项式 R = 4x^3 + 4x^2 + 3x + 6。
我们需要一个数据结构来高效地表示和计算多项式相加的运算结果。
3. 设计思路为了实现多项式相加的功能,我们可以设计一个多项式类,其中每个多项式都由一组项组成,每个项包含一个系数和一个指数。
以下是该数据结构的设计思路:3.1 多项式类多项式类由一组项组成,我们可以使用数组或链表来存储这些项。
每个项包含一个系数和一个指数,我们可以使用一个结构体或类来表示每个项。
多项式类可以包含以下方法:•addTerm(coefficient, exponent): 向多项式中添加一个新的项,参数为系数和指数。
•removeTerm(exponent): 从多项式中移除指定指数的项。
•getTerm(exponent): 获取多项式中指定指数的项。
•getDegree(): 获取多项式的最高次数。
•add(other): 将另一个多项式加到当前多项式中。
•multiply(other): 将另一个多项式乘以当前多项式。
3.2 项类项类由一个系数和一个指数组成。
我们可以使用一个结构体或类来表示每个项,具体实现可以根据需要进行选择。
4. 数据结构实现基于上述设计思路,我们可以实现多项式相加的数据结构。
以下是该数据结构的详细实现步骤:4.1 多项式类的实现1.使用一个数组或链表来存储多项式的项。
数据结构-实验2-多项式求和

数据结构-实验2-多项式求和数据结构实验 2 多项式求和在计算机科学和数学领域中,多项式的操作是一个常见且重要的任务。
本次实验 2 的重点是实现多项式的求和。
首先,让我们来理解一下什么是多项式。
简单来说,多项式就是由变量、系数和运算符组成的表达式。
例如,3x^2 + 2x 1 就是一个多项式,其中 3、2 和-1 是系数,x 是变量,^2 表示幂次。
那么为什么要进行多项式求和呢?在实际的应用中,我们经常会遇到需要对多个多项式进行运算的情况。
比如在数学建模中,通过对不同的多项式进行求和,可以得到更复杂的数学表达式,从而更准确地描述实际问题。
接下来,我们来探讨一下如何实现多项式的求和。
在数据结构中,有多种方式可以表示多项式。
常见的有顺序表和链表两种方式。
使用顺序表来表示多项式时,我们可以将多项式的每一项的系数和指数存储在数组的相应位置。
比如,数组的第一个元素存储第一项的系数和指数,第二个元素存储第二项的系数和指数,以此类推。
这种方式的优点是随机访问速度快,但是在进行多项式的加法运算时,可能需要移动大量的元素,效率较低。
相比之下,链表的方式则更加灵活。
我们可以为每一项创建一个节点,节点中包含系数、指数和指向下一项的指针。
在进行多项式的加法运算时,只需要遍历链表,根据指数的大小进行相应的操作即可。
下面我们通过一个具体的例子来看看如何进行多项式的求和。
假设有两个多项式:P1(x) = 2x^3 + 3x^2 1 和 P2(x) = x^3 + 2x 5 。
首先,我们创建两个链表分别表示这两个多项式。
然后,同时遍历这两个链表。
在遍历的过程中,比较当前节点的指数大小。
如果两个节点的指数相等,那么将它们的系数相加,创建一个新的节点,其系数为相加后的结果,指数不变,并将其插入到结果链表中。
如果一个节点的指数大于另一个节点的指数,那么将指数较小的节点直接插入到结果链表中,并继续遍历。
如果一个链表遍历完了,而另一个链表还有剩余的节点,那么将剩余的节点直接插入到结果链表中。
算法与数据结构实验一元多项式求和

《算法与数据结构》实验报告姓名:***班级:计科01学号:**********实验题目:链表的应用实验内容:一元多项式求和把任意给定的两个一元多项式P(x),Q(x)输入计算机,计算它们的和并输出计算结果。
设计分析:一元多项式可以用单链表表示,结点结构图示如下:Array一元多项式链表的结点结构一元多项式算法伪代码如下:源程序代码:#include"StdAfx.h"#include<stdlib.h>typedef struct LNode{int x,z;struct LNode *next;}LinkList;void OutLinkList(LinkList *L);void PutLinkList(LinkList *&L,int n);LinkList *AddLinkList(LinkList *a,LinkList *b);void OutXLinkList(LinkList *L);void OutZLinkList(LinkList *L);void main(){int n,m;LinkList *a,*b,*c;printf("\t\t\t本À?程¨¬序¨°可¨¦以°?完ª¨º成¨¦两¢?个?一°?元a多¨¤项?式º?的Ì?加¨®法¤¡§运?算?。
¡ê\n");printf("请?输º?入¨?一°?元a多¨¤项?式º?a的Ì?项?数ºym:êo");scanf("%d",&m);printf("请?按ã¡ä照?从䨮低̨ª次ä?到Ì?高?次ä?的Ì?顺3序¨°依°¨¤此ä?输º?入¨?一°?元a多¨¤项?式º?a的Ì?系¦Ì数ºy和¨ª指?数ºy:êo\n");PutLinkList(a,m);printf("a=");OutLinkList(a);printf("请?输º?入¨?一°?元a多¨¤项?式º?b的Ì?项?数ºyn:êo");scanf("%d",&n);printf("请?按ã¡ä照?从䨮低̨ª次ä?到Ì?高?次ä?的Ì?顺3序¨°依°¨¤此ä?输º?入¨?一°?元a多¨¤项?式º?b的Ì?系¦Ì数ºy和¨ª指?数ºy:êo\n");PutLinkList(b,n);printf("b=");OutLinkList(b);c=AddLinkList(a,b);printf("两¢?个?多¨¤项?式º?的Ì?和¨ª为a:êo\na+b=");OutLinkList(c);}void PutLinkList(LinkList *&L,int n){LinkList *s,*r;L=(LinkList *)malloc(sizeof(LinkList));r=L;for(int i=0;i<n;i++){s=(LinkList *)malloc(sizeof(LinkList));printf("请?输º?入¨?第̨²%d项?的Ì?系¦Ì数ºy:êo",i+1);scanf("%d",&s->x);printf("请?输º?入¨?第̨²%d项?的Ì?指?数ºy:êo",i+1);scanf("%d",&s->z);r->next=s;r=s;}r->next=NULL;}void OutLinkList(LinkList *L) {char FuHao;LinkList *p=L->next;FuHao=p->x>0? '+':'-';if(FuHao=='-'){printf("%c",FuHao);if(p->x==-1)printf("1");}OutXLinkList(p);OutZLinkList(p);p=p->next;while(p!=NULL){FuHao=p->x>0? '+':'-';printf("%c",FuHao);OutXLinkList(p);OutZLinkList(p);p=p->next;}printf("\n");}void OutXLinkList(LinkList *L) {int xi=L->x>0? L->x:-L->x;if(L->x==1||L->x==-1);elseprintf("%d",xi);}void OutZLinkList(LinkList *L) {if(L->z==0);else if(L->z==1||L->z==-1){if(L->z<0){if(L->x==1||L->x==-1)printf("1");printf("/");}printf("X");}else{if(L->z<0)printf("/");int zhi=L->z>0? L->z:-L->z;printf("X^%d",zhi);}}LinkList *AddLinkList(LinkList *a,LinkList *b){a=a->next;b=b->next;LinkList *c,*d,*s;c=(LinkList *)malloc(sizeof(LinkList));d=c;while(a!=NULL&&b!=NULL){if(a->z<b->z){s=(LinkList *)malloc(sizeof(LinkList));s->x=b->x;s->z=b->z;d->next=s;d=s;b=b->next;}else if(a->z>b->z){s=(LinkList *)malloc(sizeof(LinkList));s->x=a->x;s->z=a->z;d->next=s;d=s;a=a->next;}else{s=(LinkList *)malloc(sizeof(LinkList));s->x=a->x+b->x;s->z=a->z;if(s->x==0);else{d->next=s;d=s;}a=a->next;b=b->next;}}if(a!=NULL)d->next=a;else if(b!=NULL)d->next=b;elsed->next=NULL;return c;}测试用例:当a=3x^8-x^5+2x^3+7x^2+5x,b=5x^5+3x^4-7x^2-3x^(-3)时,运行结果如下:试验总结:通过本次试验,学会了链表的应用,加深了对链表的理解,知道了链表是把线性表中的元素按照链式储存方式到计算机中的一片连续的储存空间中。
数据结构多项式求和

数据结构多项式求和多项式求和是数据结构中的一个重要问题,其中给定一个多项式,我们需要计算它的和。
在本文中,我们将讨论多项式求和的算法和数据结构。
多项式是一个数学表达式,由一系列项组成,每个项由一个系数和一个指数组成。
例如,多项式3x^2 + 2x + 1由三个项组成,分别是3x^2、2x和1。
在多项式求和问题中,我们需要计算给定多项式的所有项的总和。
为了解决多项式求和问题,我们可以使用两种主要的数据结构:链表和数组。
这两种数据结构都可以用来表示多项式,并且具有不同的优势和劣势。
链表是一种动态数据结构,可以方便地插入和删除元素。
在链表中,每个节点包含一个项的系数和指数,并且通过指针连接到下一个节点。
通过遍历链表,我们可以计算多项式的总和。
链表的一个主要优点是它可以适应多项式的大小变化,但它的缺点是访问指定位置的项的效率较低。
数组是一种静态数据结构,具有固定大小。
在数组中,每个元素存储一个项的系数和指数。
通过遍历数组,我们可以计算多项式的总和。
数组的一个主要优点是它可以提供快速的随机访问,但它的缺点是它的大小是固定的,无法适应多项式的大小变化。
基于链表的多项式求和算法如下:1. 创建一个空链表来存储多项式的和。
2. 遍历第一个多项式的链表。
3. 将每个项的系数和指数与第二个多项式的链表中的对应项相加。
4. 将结果项插入和链表中。
5. 遍历第二个多项式的链表,将未处理的项插入和链表中。
6. 返回和链表。
基于数组的多项式求和算法如下:1. 创建一个空数组来存储多项式的和。
2. 遍历第一个多项式的数组。
3. 将每个项的系数和指数与第二个多项式的数组中的对应项相加。
4. 将结果项存储在和数组的对应位置。
5. 遍历第二个多项式的数组,将未处理的项存储在和数组的对应位置。
6. 返回和数组。
无论使用链表还是数组,多项式求和的时间复杂度都是O(n),其中n是多项式的项数。
但是,链表的空间复杂度是O(n),而数组的空间复杂度是O(k),其中k是多项式的最高指数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
{
i++;p=p->next;
}
return i;
}
PolyNode *GetElem(PolyNode *L,int i) /*返回多项式单链表中第i个结点的指针*/
{
int j=1;
PolyNode *p=L->next;
s->coef=p1->coef+p2->coef;s->expn=p1->expn;
s->next=NULL;
tc->next=s;tc=s;
}
p1=p1->next;p2=p2->next;
}
}
if (p1!=NULL) p=p1; /*将尚未扫描完的余下结点复制并链接到pc单链表之后*/
tc->next=s;tc=s;
p1=p1->next;
}
else if (p1->expn>p2->expn) /*将*p2结点复制到*s并链到pc尾*/
{
s=(PolyNode *)malloc(sizeof(PolyNode));
s->coef=p2->coef;s->expn=p2->expn;s->next=NULL;
{
pre=q;q=q->next;
}
q=p->next; /*在*pre结点之后插入*p*/
p->next=pre->next;
pre->next=p;
p=q;
}பைடு நூலகம்
}
}
PolyNode *AddPoly(PolyNode *pa,PolyNode *pb)
{
tc->next=s;tc=s;
p2=p2->next;
}
else /*p1->expn=p2->expn的情况*/
{
if (p1->coef+p2->coef!=0) /*序数相加不为0时新建结点*s并链到pc尾*/
{
s=(PolyNode *)malloc(sizeof(PolyNode));
p=p->next;
}
printf("\n");
}
void CreaPolyList(PolyNode *&L,float C[],int E[],int n)
{
int i;
InitList(L);
for (i=0;i<n;i++)
InsElem(L,C[i],E[i],i+1);
else p=p2;
while (p!=NULL)
{
s=(PolyNode *)malloc(sizeof(PolyNode));
s->coef=p->coef;s->expn=p->expn;s->next=NULL;
tc->next=s;tc=s;
p=p->next;
{
L=(PolyNode *)malloc(sizeof(PolyNode)); /*建立头结点*/
L->next=NULL;
}
int GetLength(PolyNode *L) /*求多项式单链表的长度*/
{
int i=0;
PolyNode *p=L->next;
printf("多项式相加结果:");DispList(L3);
}
{
PolyNode *p=L->next;
while (p!=NULL && (p->coef!=c ||p->expn!=e))
p=p->next;
return p;
}
int InsElem(PolyNode *&L,float c,int e,int i) /*在多项式单链表中插入一个结点*/
PolyNode *pc,*p1=pa->next,*p2=pb->next,*p,*tc,*s;
pc=(PolyNode *)malloc(sizeof(PolyNode)); /*新建头结点*pc*/
pc->next=NULL; /*pc为新建单链表的头结点*/
tc=pc; /*tc始终指向新建单链表的最后结点*/
while (j<i) /*查找第i-1个结点*p*/
{
p=p->next;j++;
}
s->next=p->next;
p->next=s;
return 1;
}
int DelElem(PolyNode *L,int i) /*在多项式单链表中删除一个结点*/
{
InitList(L1);
InitList(L2);
InitList(L3);
CreaPolyList(L1,C1,E1,4);
CreaPolyList(L2,C2,E2,3);
printf("两多项式相加运算\n");
printf(" 原多项式A:");DispList(L1);
#include <stdio.h>
#include <malloc.h>
typedef struct node
{float coef;/*序数*/
int expn;/*指数*/
struct node *next;/*指向下一个结点的指针*/
} PolyNode;
void InitList(PolyNode *&L)/*初始化多项式单链表*/
while (p1!=NULL && p2!=NULL)
{
if (p1->expn<p2->expn) /*将*p1结点复制到*s并链到pc尾*/
{
s=(PolyNode *)malloc(sizeof(PolyNode));
s->coef=p1->coef;s->expn=p1->expn;s->next=NULL;
{
L->next=p;p=p->next;
L->next->next=NULL;
}
else /*处理其余结点*/
{
pre=L;q=pre->next;
while (q!=NULL && p->expn>q->expn) /*找q->expn刚大于或等于p->expn的结点*q的前驱结点*pre*/
printf(" 原多项式B:");DispList(L2);
SortPloy(L1);
SortPloy(L2);
printf("排序后的多项式A:");DispList(L1);
printf("排序后的多项式B:");DispList(L2);
L3=AddPoly(L1,L2);
{
int j=1;
PolyNode *p=L,*s;
s=(PolyNode *)malloc(sizeof(PolyNode));
s->coef=c;s->expn=e;s->next=NULL;
if (i<1 || i>GetLength(L)+1)
return 0;
}
void SortPloy(PolyNode *&L) /*对L的多项式单链表按expn域递增排序*/
{
PolyNode *p=L->next,*q,*pre;
L->next=NULL;
while (p!=NULL)
{
if (L->next==NULL) /*处理第1个结点*/
if (i<1 || i>GetLength(L))
return NULL;
while (j<i) /*沿next域找第i个结点*/
{
p=p->next;j++;
}
return p;
}
PolyNode *Locate(PolyNode *L,float c,int e) /*在多项式单链表中按值查找*/
}
tc->next=NULL; /*新建单链表最后结点的next域置空*/
return pc;
}
void main()
{
PolyNode *L1,*L2,*L3;
float C1[]={3,7,5,9},C2[]={-9,8,22};
int E1[]={1,0,17,8},E2[]={8,1,7};
int j=1;
PolyNode *p=L,*q;
if (i<1 || i>GetLength(L))
return 0;
while (j<i) /*在单链表中查找第i-1个结点,由p指向它*/
{
p=p->next;j++;
}
q=p->next; /*q指向被删结点*/
