三角形经典题50道附答案解析
初中全等三角形经典题型50题(含答案)

所以:AB=AC;
三角形ABD全等于三角形ACD;
∠BAD=∠CAD;AD是等腰三角形的顶角平分线所以:AD垂直BC
19.(5分)如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.
求证:∠OAB=∠OBA
因为AOM与MOB都为直角三角形、共用OM,且∠MOA=∠MOB
又∵,AE,BE均为∠PAB和∠CBA的角平分线∴∠EAB+∠EBA=90°∴∠AEB=90°,EAB为直角三角形在三角形ABF中,AE⊥BF,且AE为∠FAB的角平分线
∴三角形FAB为等腰三角形,AB=AF,BE=EF在三角形DEF与三角形BEC中,∠EBC=∠DFE,且BE=EF,∠DEF=∠CEB,∴三角形DEF与三角形BEC为全等三角形,∴DF=BC∴AB=AF=AD+DF=AD+BC
初中全等三角形证明经典50题(含答案)
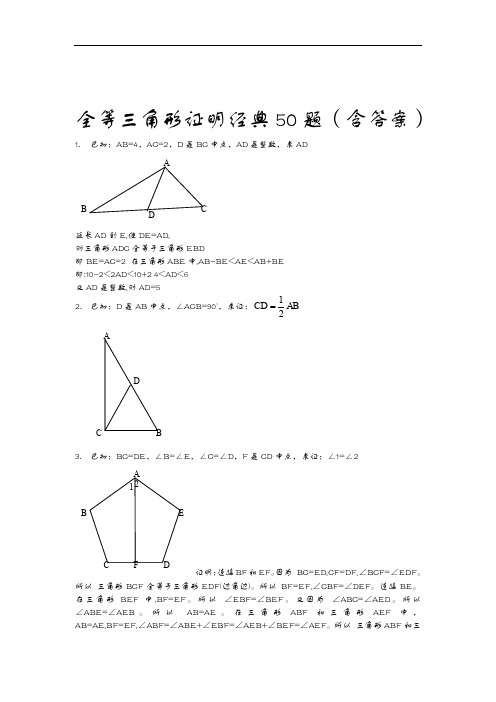
1.已知:AB=4,AC=2,D是BC中点,AD是整数,求AD
延长AD到E,使DE=AD,
则三角形ADC全等于三角形EBD
即BE=AC=2在三角形ABE中,AB-BE<AE<AB+BE
即:10-2<2AD<10+2 4<AD<6
又AD是整数,则AD=5
2.已知:D是AB中点,∠ACB=90°,求证:
证明:在AC上截取AE=AB,连接ED∵AD平分∠BAC∴∠EAD=∠BAD又∵AE=AB,AD=AD∴⊿AED≌⊿ABD(SAS)∴∠AED=∠B,DE=DB∵AC=AB+BD AC=AE+CE∴CE=DE∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C∴∠B=2∠C
全等三角形经典题型50题(含答案)
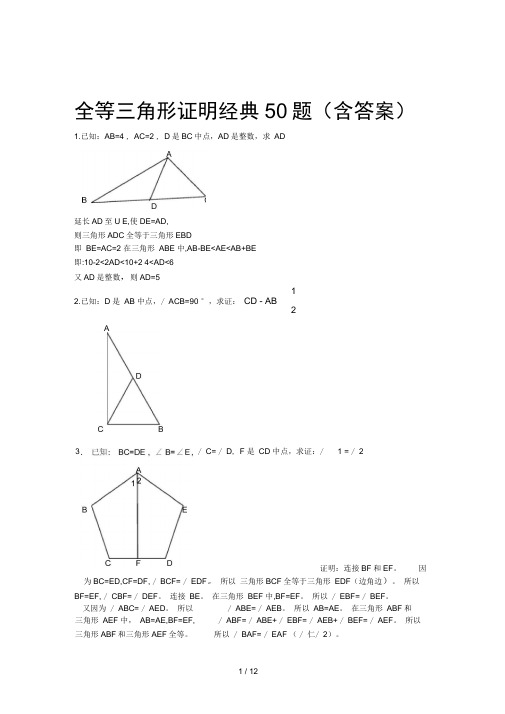
全等三角形证明经典50题(含答案)1.已知:AB=4 , AC=2 , D 是BC 中点,AD 是整数,求 AD延长AD 至U E,使DE=AD, 则三角形ADC 全等于三角形EBD即 BE=AC=2 在三角形 ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=512.已知:D 是 AB 中点,/ ACB=90 °,求证: CD - AB2为BC=ED,CF=DF, / BCF= / EDF 。
所以 三角形BCF 全等于三角形 EDF (边角边)。
所以BF=EF, / CBF= / DEF 。
连接 BE 。
在三角形 BEF 中,BF=EF 。
所以 / EBF= / BEF 。
/ ABE= / AEB 。
所以 AB=AE 。
在三角形 ABF 和 / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF 。
所以/ C= / D , F 是 CD 中点,求证:/ 1 = / 2证明:连接BF 和EF 。
因又因为 / ABC= / AED 。
所以 三角形 AEF 中, AB=AE,BF=EF, 三角形ABF 和三角形AEF 全等。
所以 / BAF= / EAF ( / 仁/ 2)。
A3因为 EB = EF ,CE = CE , 所以△ CEBCEF 所以/ B = / CFE 因为/ B +/ D = 180° / CFE + / CFA = 180° 所以/ D = / CFA 因为 AC 平分/ BAD 所以/ DAC = / FAC 又因为 AC = AC 所以△ ADC 也厶AFC ( SAS ) 所以AD = AF 所以AE = AF + FE = AD + BE12.如图,四边形 ABCD 中,AB // DC ,BE 、CE 分别平分/ ABC 、/ BCD ,且点 E 在AD 上。
初中数学 全等三角形经典题型50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形证明经典50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB证明:延长CD 与P ,使D 为CP 中点。
连接AP,BP ∵DP=DC,DA=DB ∴ACBP 为平行四边形 又∠ACB=90 ∴平行四边形ACBP 为矩形 ∴AB=CP=1/2ABADBCBACDF21E3.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF和EF∵BC=ED,CF=DF,∠BCF=∠EDF∴三角形BCF全等于三角形EDF(边角边)∴BF=EF,∠CBF=∠DEF连接BE在三角形BEF中,BF=EF∴∠EBF=∠BEF。
∵∠ABC=∠AED。
∴∠ABE=∠AEB。
∴AB=AE。
在三角形ABF和三角形AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴三角形ABF和三角形AEF全等。
∴∠BAF=∠EAF (∠1=∠2)。
4.已知:∠1=∠2,CD=DE,EF//AB,求证:EF=AC证明:过C作CG∥EF交AD的延长线于点GCG∥EF,可得,∠EFD=CGDDE=DC∠FDE=∠GDC(对顶角)∴△EFD≌△CGDEF=CG∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠C证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BEA7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD8. 已知:D 是AB 中点,∠ACB=90°,求证:1CD AB9. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
全等三角形经典题型50题[含答案解析]
![全等三角形经典题型50题[含答案解析]](https://img.taocdn.com/s3/m/6ac3e596960590c69fc3761c.png)
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2ADBC证明:连接BF 和EF 。
因为BC=ED,CF=DF,∠BCF=∠EDF。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF。
又因为 ∠ABC=∠AED。
所以 ∠ABE=∠AEB。
所以 AB=AE 。
在三角形ABF和三角形AEF中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF。
所以 三角形ABF 和三角形AEF 全等。
所以∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA,∠DGE=∠2又∵CD=DE ∴⊿ADC≌⊿GDE(AAS)BACDF2 1 E∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB∵AC=AB+BDAC=AE+CE ∴CE=DE∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE 证明:在AE 上取F ,使EF =EB ,连接CF 因为CE⊥AB所以∠CEB=∠CEF=90° 因为EB =EF ,CE =CE , 所以△CEB≌△CEF所以∠B =∠CFE因为∠B +∠D =180°,∠CFE+∠CFA=180° 所以∠D=∠CFA 因为AC 平分∠BAD所以∠DAC=∠FAC又因为AC =AC所以△ADC≌△AFC(SAS ) 所以AD =AF 所以AE =AF +FE =CDB AAD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形经典题型50题(含答案)
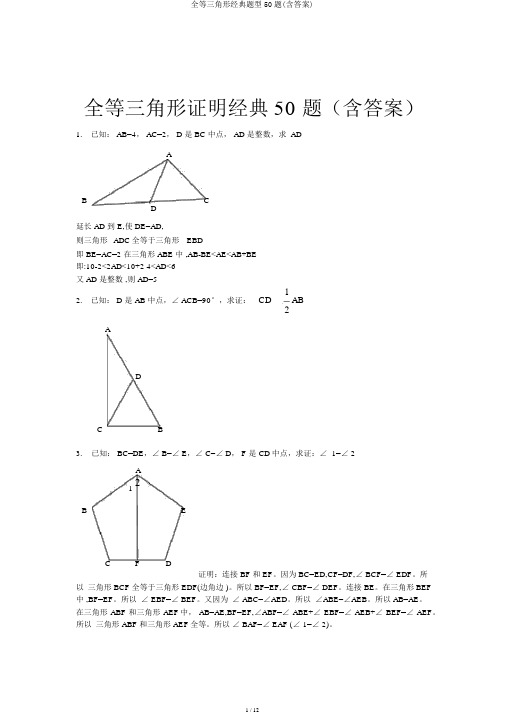
全等三角形证明经典50 题(含答案)1. 已知: AB=4, AC=2, D 是 BC 中点, AD 是整数,求ADAB CD延长 AD 到 E,使 DE=AD,则三角形ADC全等于三角形EBD即 BE=AC=2 在三角形 ABE 中 ,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又 AD 是整数 ,则 AD=512. 已知: D 是 AB 中点,∠ ACB=90°,求证:CD AB2ADC B3.已知: BC=DE,∠ B=∠ E,∠ C=∠ D, F 是 CD中点,求证:∠ 1=∠ 2A21B EC F D证明:连接 BF 和 EF。
因为 BC=ED,CF=DF,∠ BCF=∠ EDF。
所以三角形 BCF 全等于三角形 EDF(边角边 )。
所以 BF=EF,∠ CBF=∠ DEF。
连接 BE。
在三角形BEF 中 ,BF=EF。
所以∠ EBF=∠ BEF。
又因为∠ ABC=∠AED。
所以∠ABE=∠AEB。
所以 AB=AE。
在三角形 ABF 和三角形 AEF中, AB=AE,BF=EF,∠ABF=∠ ABE+∠ EBF=∠ AEB+∠ BEF=∠ AEF。
所以三角形 ABF 和三角形 AEF全等。
所以∠ BAF=∠ EAF (∠ 1=∠ 2)。
A4. 已知:∠ 1=∠ 2, CD=DE, EF//AB,求证: EF=AC 1 2证明:过 E 点,作 EG//AC,交 AD 延长线于 G 则∠ DEG=∠ DCA,F ∠DGE=∠ 2又∵CD=DE∴ ⊿ADC≌ ⊿ GDE(AAS)∴EG=AC∵ EF//AB∴∠ DFE=∠ 1∵ ∠ 1=∠ 2∴ ∠ DFE=∠ DGE∴ EF=C EG∴ EF=AC DEB5.已知:AD平分∠ BAC,AC=AB+BD,求证:∠B=2∠C ACB D证明:在 AC上截取AD=AD∴ ⊿ AED≌ ⊿ ABD AE=AB,连接(SASED∵ AD)平分∠ BAC∴ ∠∴ ∠ AED=∠ BEAD=∠ BAD 又∵ AE=AB,,DE=DB∵ AC=AB+BDAC=AE+CE∴ CE=DE∴ ∠ C=∠ EDC∵∠ AED=∠ C+∠ EDC=2∠ C∴∠ B=2∠C6. 已知: AC 平分∠ BAD,CE⊥ AB,∠ B+∠ D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接 CF 因为 CE⊥AB 所以∠CEB=∠ CEF= 90 °因为 EB= EF, CE= CE,所以△CEB≌△CEF 所以∠B =∠ CFE 因为∠ B+∠ D= 180 ,°∠CFE+∠ CFA= 180°所以∠ D=∠ CFA 因为AC 平分∠ BAD 所以∠ DAC=∠ FAC 又因为AC= AC所以△ ADC≌ △ AFC( SAS)所以 AD= AF 所以 AE= AF+ FE= AD+ BE12.如图,四边形 ABCD 中, AB∥ DC, BE、 CE 分别平分∠ ABC、∠ BCD,且点 E 在 AD 上。
三角形经典题50道附答案
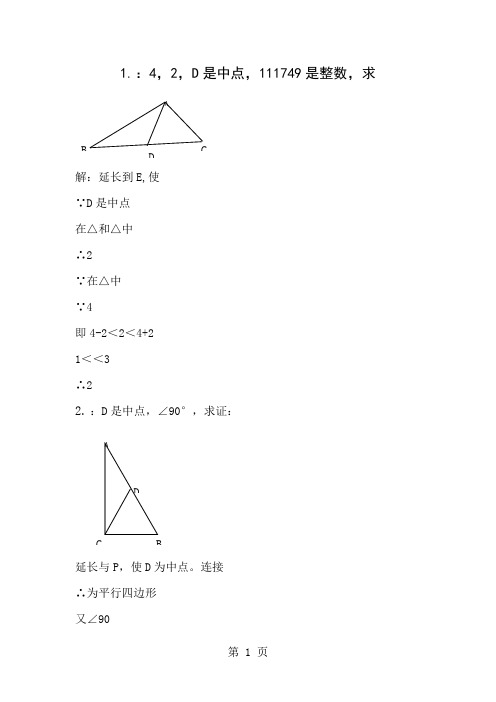
1. :4,2,D 是中点,111749是整数,求解:延长到E,使∵D 是中点在△和△中∴2∵在△中∵4即4-2<2<4+21<<3∴22. :D 是中点,∠90°,求证:延长与P ,使D 为中点。
连接∴为平行四边形又∠90AD B CB C∴平行四边形为矩形∴1/23. :,∠∠E ,∠∠D ,F 是中点,求证:∠1=∠2证明:连接和∴ 三角形全等于三角形(边角边)连接在三角形中在三角形和三角形中∴ 三角形和三角形全等。
∴ ∠∠ (∠1=∠2)。
4. :∠1=∠2,,,求证:过C 作∥交的延长线于点GB ACDF21 EB C DF∥,可得,∠==∠=∠〔对顶角〕∴△≌△=∠=∠又,∥∴,∠=∠1∠1=∠2∴∠=∠2∴△为等腰三角形,=又=∴=5.:平分∠,,求证:∠2∠CA证明:延长取点E,使=,连接∵平分∠∴∠E=∠C∴∠=∠E∴∠=2∠E∴∠=2∠C6.:平分∠,⊥,∠∠180°,求证:证明:在上取F,使=,连接∴∠=∠=90°∴∠B=∠∵∠B+∠D=180°,∠+∠=180°∴∠D=∠∵平分∠7.:4,2,D是中点,是整数,求AB CD解:延长到E,使∵D是中点∴在△和△中∠∠∴△≌△∴2∵在△中<<∵4即4-2<2<4+21<<3∴28.:D是中点,∠90°,求证:解:延长到E,使∵D 是中点∴在△和△中∠∠∴△≌△∴2∵在△中<<∵4即4-2<2<4+21<<3∴29. :,∠∠E ,∠∠D ,F 是中点,求证:∠1=∠2证明:连接和。
∴ 三角形全等于三角形(边角边)。
B C DF连接。
在三角形中。
又∵∠∠。
在三角形和三角形中,∴三角形和三角形全等。
∴∠∠ (∠1=∠2)。
10.:∠1=∠2,,,求证:A21FCDEB过C作∥交的延长线于点G ∥,可得,∠==∠=∠〔对顶角〕∴△≌△=∠=∠又∥∴∠=∠1∠1=∠2∴∠=∠2∴△为等腰三角形,=又 =∴=11. :平分∠,,求证:∠2∠C证明:延长取点E ,使=,连接∵平分∠∴∠E =∠C∴∠=∠E∴∠=2∠E∴∠=2∠C12. :平分∠,⊥,∠∠180°,求证:在上取F ,使=,连接∴∠=∠=90°C D B A∵∠B +∠D =180°,∠+∠=180°∴∠D =∠∵平分∠又∵=12. 如图,四边形中,∥,、分别平分∠、∠,且点E 在上。
全等三角形证明经典试题50道
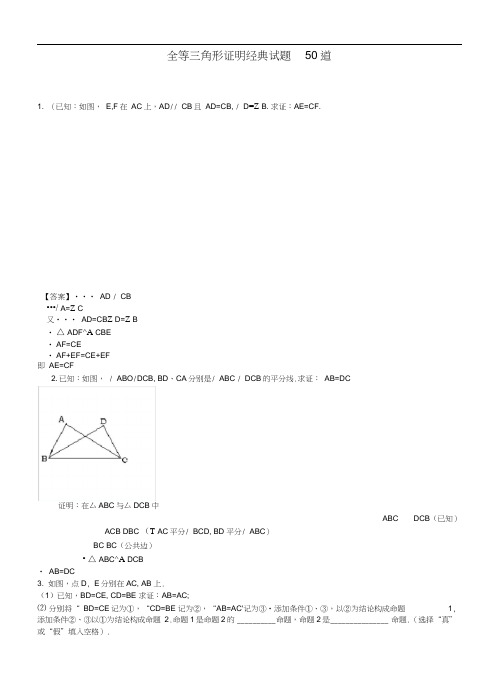
全等三角形证明经典试题50道1. (已知:如图,E,F在AC上,AD// CB且AD=CB, / D=Z B. 求证:AE=CF.【答案】••• AD / CB•••/ A=Z C又••• AD=CB Z D=Z B•△ADF^A CBE• AF=CE• AF+EF=CE+EF即AE=CF2. 已知:如图, / ABO/DCB, BD、CA分别是/ ABC / DCB的平分线.求证:AB=DC证明:在厶ABC与厶DCB中ABC DCB(已知)ACB DBC (T AC平分/ BCD, BD 平分/ ABC)BC BC(公共边)• △ABC^A DCB• AB=DC3. 如图,点D, E分别在AC, AB 上.(1)已知,BD=CE, CD=BE 求证:AB=AC;⑵分别将“ BD=CE记为①,“CD=BE 记为②,“AB=AC'记为③•添加条件①、③,以②为结论构成命题1, 添加条件②、③以①为结论构成命题2.命题1是命题2的__________ 命题,命题2是_______________ 命题.(选择“真”或“假”填入空格).(1)连结BC,T BD=CE CD=BE BC=CB•△DBC^A ECB (SSS•/ DBC =Z ECB••• AB=CD,Z BAD玄BCD AB// CD••• / EAF=/ HCG / E=Z H•/ AE=AB, CH=CD• AE=CH• △AEF^A CHG.5. 如图,点A、F、C D在同一直线上,点B和点E分别在直线AD的两侧,且AB= DE, / A= / D, AF= DC.求证:BC// EF.如图,在D ABCD中,分别延长BA DC到点E,使得AE=AB CH=CD连接EH分别交AD, BC于点F,G。
求证:£【答案】⑵4.△AEF^A CHG.【证明】•/ AF= DC, ••• AC= DF,又/A= Z D ,AB= DE, ABC^ △ DEF,• Z ACB= Z DFE • BC// EF.6. 两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,阴影部分为重叠部分,点0为边AC和DF 的交点•不重叠的两部分厶AOF与厶DOC是否全等?为什么?【答案】解:全等•理由如下:•••两三角形纸板完全相同,•BC=BF, AB=BD,Z A=Z D,「. AB—BF=BD—BC,即AF=DC在厶AOF和厶DOC中,T AF=DC,Z A=Z D,Z AOF=Z DOC, AOF^^ DOC (AAS).7. 已知:如图,E,F在AC上, AD / CB且AD=CB Z D=Z B.求证:AE=CF.【答案】••• AD// CB•••/ A=Z C又••• AD=CB Z D=Z B•△ADF^A CBE• AF=CE• AF+EF=CE+EF即AE=CF8. 在厶ABC中,AB=CB, / ABC=9®F为AB延长线上一点,点E在BC上,且AE=CF.(1) 求证:Rt △ ABE B Rt △ CBF;(2) 若/ CAE=3Gb,求/ ACF度数.【答案】(1 )•••/ ABC=90°,•/ CBF=/ ABE=90 . 在Rt△ ABE和Rt△ CBF 中,•/ AE=CF, AB=BC, • Rt△ ABE^ Rt△ CBF(HL) (2) •/ AB=BC, / ABC=90 ° , • / CAB玄ACB=45° .•••/ BAE=/ CAB-/ CAE=45 -30 ° =15° .由(1)知Rt △ ABE B Rt △ CBF, BCF=/ BAE=15• / ACF=/ BCF+Z ACB=45 +15° =60° .9•如图6, AB BD于点B , ED BD于点D , AE交BD于点C ,且BC DC .求证AB ED •第22题图【答案】 ⑴ 证明:••• AB BD , ED BDABC D 90°在ABC 和EDC 中ABC DBC DCACB ECD.ABC 望 EDC••• AB ED10. 如图,在 Rt A ABC 中,/ BAC=90°, AC=2AB,点D 是AC 的中点,将一块锐角为 45°的直角三角板如图放 置,使三角板斜边的两个端点分别与 A 、D 重合,连结BE 、EC.试猜想线段BE 和EC 的数量及位置关系,并证明你的猜想.【答案】BE=EC BE 丄EC••• AC=2AB,点D 是AC 的中点• AB=AD=CD•••/ EAD=Z EDA=45°•••/ EAB=Z EDC=135•/ EA=ED• △ EAB ^A EDC• / AEB=Z DEC EB=EC• / BEC=/ AED=90°• BE=EC BE 丄 EC11. 已知:如图, E,F 在 AC 上,AD // CB 且 AD=CB,Z D =Z B. 求证:AE=CF.ADE【答案】••• AD// CB•••/ A=Z C又••• AD=CB Z D=Z B•△ADF^A CBE• AF=CE• AF+EF=CE+EF即AE=CF12•如图,D, E,分另【J是AB, AC上的点,且AB=AC, AD=AE.求证/ B=Z C.第1弓同5【答案】证明:在△ ABE和厶ACD中,AB = AC / A=/ A AE=AD•△ABE^A ACD•/ B=Z C13. 如图,在△ ABC中,AD是中线,分别过点B、C作AD及其延长线的垂线BE、CF,垂足分别为点E、F.求证:BE=CF.【证明】•••在△ ABC 中,AD 是中线,••• BD=CD,T CF 丄 AD ,BE ± AD,「./ CFD=Z BED = 90° ,在△BED 与厶 CFD 中,BED=Z CFD , / BDE =ZCDF , BD = CD,." BEM A CFD • BE=CF. 14. 已知:如图,在△ ABC 中,D 为BC 上的一点,AD 平分/ EDC 且/ E=/ B,ED=DC.求证:AB=AC【答案】证明••• AD 平分/ EDC,. / ADEN ADC,又 DE=DC,AD=AD,• △ ADE ^A ADC, •/ E=/ C,又/ E=/ B, •/ B = / C, • AB=AC.15. 如图,在平行四边形 ABCD 中,E 为BC 中点,AE 的延长线与DC 的延长线相交于点 F.(1) 证明:/ DFA = / FAB⑵ 证明:△ ABE^A FCE.(第18题图)【答案】证明:(1)T AB 与CD 是平行四边形 ABCD 的对边,• AB // CD, (1分)•/ F=/ FAB (3分)(2 )在 △ ABE 和厶 FCE 中, / FAB=/ F (4 分)T / AEB=/ FEC (5 分)BE=CE (6 分)• △ ABE ^^ FCE ( 7 分)16. 如图,C 是线段 AB 的中点,CD 平分/ ACE, CE 平分/ BCD, CD=CE⑴求证:△ ACD ^A BCE(2)若/ D=50°,求/ B 的度数.【答案】证明:to 丁点c址换段川?的中点.XVCZ) CE 分NBCD FA Zl fc Z3. Z2'Z3,f, Z) *Z3.在中.5 YE,4AC ~ BC.:' WS里也&CEd) tr VZU Z2 + Z3^ ISO5・二ZJa^=-Z3 = 6O B.V AACD 笙】ZiftCE,;・£直■芒口■ $(r *17. 如图,已知:点B、F、C、E在一条直线上,FB=CE AC=DF.能否由上面的已知条件证明AB// ED?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AB/ ED成立,并给出证明.供选择的三个条件(请从其中选择一个) :①AB=ED;②BC=EF;③/ ACB=Z DFE第一FB=CE AC=DF 添加①AB=ED证明:因为 FB=CE,所以 BC=EF,又 AC=EF, AB=ED,所以 V ABC V DEF 所以/ABC=Z DEF 所以 AB//ED第二FB=CE AC=DF 添加③/ ACB=Z DFE证明:因为 FB=CE,所以 BC=EF,又/ ACB=Z DFE AC=EF,所以 所以/ ABO /DEF 所以 AB//EDV ABC V DEFA18.如图,在△ABC 中,D 是BC 边上的点(不与 B , C 重合),F , E 分别是AD 及其延长线上的点, CF // BE •请你添加一个条件,使 A BDE ◎△ CDF (不再添加其它线段,不再标注或使用其他字母(1)你添加的条件是:▲_;(2)证明:(第 25题)【答案】解:由上面两条件不能证明 AB//ED.有两种添加方法),并给出证明. B C D (第18题 图)【答案】解:(1) BD DC(或点D是线段BC的中点),FD ED, CF BE中任选一个即可.(2)以BD DC为例进行证明:•/ CF// BE,•••/ FCD=Z EBD.又••• BD DC,/ FDC=Z EDB••• △BDE^ △CDF.19. 如图,分别过点C、B作厶ABC的BC边上的中线AD及其延长线的垂线,垂足分别为E、F.求证:BF=CE【答案】••• CE! AF, FBI AF,「./ DEC =Z DFB= 90°又••• AD为BC边上的中线,• BD= CD, 且/ EDC = Z FDB (对顶角相等)•所以△ BFD^^ CDE (AAS), • BF=CE20. 如图,已知AD是厶ABC的角平分线,在不添加任何辅助线的前提下,要使△AED^^ AFD,需添加一个条件是:________________ ,并给予证明全品中考网【答案】解法一:添加条件:AE= AF,证明:在厶AED与△ AFD中,•/ AE= AF,Z EAD=Z FAD, AD= AD,• △AED^A AFD ( SAS .解法二:添加条件:/ EDA=Z FDA证明:在厶AED-与^ AFD中,【答案】证明:••• AE =DC••• AC=DB•/ EA!AD F □丄AD•••/ A =/ D =90°在厶 EAC WA FDB 中EA FDA DAC DB• △ EAC^ FDB• / ACE=/ DBF22. 如图,点 A 、E 、B 、D 在同一条直线上, AE = DB , AC = DF , AC// DF. 请探索BC 与EF 有怎样的位置关系?并说明理由.•••/ EAD=Z FAD, AD= AD, / EDA=Z FDA•••△ AED^A AFD( ASA .21. 已知:如图,点 C 是线段AB 的中点,求证:AE=BD【答案】证明:•••点C 是线段AB 的中点,• AC=BC•// ACD / BCE,•••/ ACD / DCE / BCE+/ DCE,即/ ACE / BCD,AC BC在厶ACE 和厶BCD 中, ACE BCDCE CD• △ ACE ^A BCD ( SAS ,• AE=BD.21.已知:如图,点 A 、B C D 在同一条直线上, EA ±AD FD 丄AD AE=DF, AB=DC求证:/ ACE =/DBFA,【答案】解:BC// EF.理由如下:T AE = DB AE + BE = DB + BE ,「. AD = DE.v AC// DF , /-Z A =Z D,v AC =DF , ACB ^A DFE /-Z FED=Z CBA /• BC// EF.23. 如图,点B 、D 、C 、F 在一条直线上,且 BC = FD AB = EF.(1)请你只添加一个条件(不再加辅助线) ____________________ ,使△ ABC ^^ EFD,你添加的条件是;(2) 添加了条件后,证明△ ABC ^^ EFD.【答案】(1) Z B = Z F 或 AB// EF 或 AC = ED(2)证明:当Z B = Z F 时在厶 ABC^ EFD 中AB EFB FBC FD/.△ ABC ^^ EFD (SAS)24.如图, BAC ABD .(1) _____________________________________________ 要使OC OD ,可以添加的条件为: 或 ;(写出2个符合题意的条件即可)(2)请选择(1)中你所添加的一个条件,证明 OC OD .【答案B 解:(1)答案不唯一.如 C D ,或 ABC BAD ,或 OAD OBC ,或 AC BD .……4 分 说明:2空全填对者,给4分;只填1空且对者,给2分.(2)答案不唯一.如选AC BD 证明OC=OD.证明:•/ BAC ABD ,/• OA=OB. .......................... 6 分C又 AC BD ,/• AC -OA=BD-OB或AO+OC=BO+OD..设计了如下方案:A EOC OD .25. 八( 1)班同学上数学活动课,利用角尺平分一个角(如图)(I)z AOB是一个任意角,将角尺的直角顶点P介于射线OA 0B之间,移动角尺使角尺两边相同的刻度与M N重合,即PM=PN过角尺顶点P的射线0P就是/ AOB的平分线.(n)z AOB是一个任意角,在边OA 0B上分别取OM=O N将角尺的直角顶点P介于射线OA 0B之间,移动角尺使角尺两边相同的刻度与M N重合,即PM=PN过角尺顶点P的射线OP就是/ AOB的平分线.(1)方案(I)、方案(n)是否可行?若可行,请证明;若不可行,请说明理由(2)在方案(I) PM=PN勺情况下,继续移动角尺,同时使PMLOA PNLOB此方案是否可行?请说明理由.【答案】解:(1)方案(I)不可行•缺少证明三角形全等的条件• .............................. 2分(2)方案(n)可行....... .................... 3分证明:在厶OPMFH A OPN中OM OPPM PNOP OP•••△OPM PA OPN(SSS)•••/ AOP=Z BOP全等三角形对应角相等).......................................... 5分(3).................................................................................................... 当/ AOB是直角时,此方案可行. 6分•••四边形内角和为360 °,又若PML OA,PNL OB, / OMP=Z ONP=90° , / MPN=90 •••/ AOB=90°•••若PM L OA,PNL OB,且PM=PN• OP为/ AOB的平分线.(到角两边距离相等的点在这个角的角平分线上)当/ AOB不为直角时,此方案不可行 . ....... 8分26. 如图,AB是/ DAC的平分线,且AD=AC。
(完整版)全等三角形证明经典50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠24. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CDAB B A CDF2 1 EAC D E F 21 A D BC A6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
13.已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠C14. P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-AB15. 已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BED C B A FE PD A CB16. 已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC18.如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .19.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA20.(5分)如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .21.如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠B22.(6分)如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M .(1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.F AEDCB P E D CB A DC B A23.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点, (1)求证:△AED ≌△EBC . (2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):24.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .证明:25、如图:DF=CE ,AD=BC ,∠D=∠C 。
全等三角形经典题型50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中, AB=AE,BF=EF, ∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明: 过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2 又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS ) ∴EG=AC ∵EF//AB ∴∠DFE=∠1 ∵∠1=∠2 ∴∠DFE =∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明: 在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS ) ∴∠AED=∠B ,DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE 证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形经典题型50题(含答案解析)
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF和三ADBC角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DG E ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠E DC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
三角形经典题50道附问题详解

1. 已知:AB=4,AC=2,D 是BC 中点,111749AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD BC证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CGB ACDF21E∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又 EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=28. 已知:D 是AB 中点,∠ACB=90°,求证:1CD AB9. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
全等三角形经典题型50题带答案

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB从D 做辅助线3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形证明经典50题(含答案)

三角形全等经典证明1.已知:AB=4,AC=2,D是BC中点, AD是整数,求AD解:延长AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE∵AB=4即4-2<2AD<4+21<AD<3∴AD=21. 已知:D是AB中点,∠ACB=90°,求证:延长CD与P,使D为CP中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP为平行四边形又∠ACB=90∴平行四边形ACBP为矩形∴AB=CP=1/2AB2. 已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF中,BF=EF∴ ∠EBF=∠BEF。
∵ ∠ABC=∠AED。
∴ ∠ABE=∠AEB。
∴ AB=AE。
在三角形ABF和三角形AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF和三角形AEF全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
3. 已知:∠1=∠2,CD=DE,EF//AB,求证:EF=AC过C作CG∥EF交AD的延长线于点GCG∥EF,可得,∠EFD=CGDDE=DC∠FDE=∠GDC(对顶角)∴△EFD≌△CGDEF=CG∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又 EF=CG∴EF=AC4. 已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE ∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD(SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5. 已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE6. 已知:AB=4,AC=2,D是BC中点,AD是整数,求AD解:延长AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE∵AB=4即4-2<2AD<4+21<AD<3∴AD=27. 已知:D是AB中点,∠ACB=90°,求证:解:延长AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE∵AB=4即4-2<2AD<4+21<AD<3∴AD=28. 已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF和EF。
全等三角形经典题型50题[含答案]
![全等三角形经典题型50题[含答案]](https://img.taocdn.com/s3/m/6ec7153dbed5b9f3f80f1c1f.png)
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠ED C ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB=∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 已知:AB=4,AC=2,D 是BC 中点,111749AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD BC证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CGBACDF21E∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD B CBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE ∵AB=4即4-2<2AD<4+21<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:12 CD AB9.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF 和EF 。
∵ BC=ED,CF=DF,∠BCF=∠EDF 。
∴ 三角形BCF 全等于三角形EDF(边角边)。
∴ BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
∴ ∠EBF=∠BEF 。
又∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
10. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CGBACDF21 E∠CGD =∠EFD又EF ∥AB∴∠EFD =∠1∠1=∠2∴∠CGD =∠2∴△AGC 为等腰三角形,AC =CG又 EF =CG∴EF =AC11. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:延长AB 取点E ,使AE =AC ,连接DE∵AD 平分∠BAC∴∠EAD =∠CAD∵AE =AC ,AD =AD∴△AED ≌△ACD (SAS )∴∠E =∠C∵AC =AB+BD∴AE =AB+BD∵AE =AB+BE∴BD =BE∴∠BDE =∠E∵∠ABC =∠E+∠BDE∴∠ABC =2∠E∴∠ABC =2∠C12. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BECD B A在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC又∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE12. 如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
求证:BC=AB+DC。
在BC上截取BF=AB,连接EF∵BE平分∠ABC∴∠ABE=∠FBE又∵BE=BE∴⊿ABE≌⊿FBE(SAS)∴∠A=∠BFE∵AB//CD∴∠A+∠D=180º∵∠BFE+∠CFE=180º∴∠D=∠CFE又∵∠DCE=∠FCECE平分∠BCDCE=CE∴⊿DCE≌⊿FCE(AAS)∴CD=CF∴BC=BF+CF=AB+CD13.已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠CAB ‖ED ,得:∠EAB+∠AED=∠BDE+∠ABD=180度,∵∠EAB=∠BDE ,∴∠AED=∠ABD ,∴四边形ABDE 是平行四边形。
∴得:AE=BD ,∵AF=CD,EF=BC ,∴三角形AEF 全等于三角形DBC ,∴∠F=∠C 。
14. 已知:AB=CD ,∠A=∠D ,求证:∠B=∠C证明:设线段AB,CD 所在的直线交于E ,(当AD<BC 时,E 点是射线BA,CD 的交点,当AD>BC 时,E 点是射线AB,DC 的交点)。
则:△AED 是等腰三角形。
∴AE=DE而AB=CD∴BE=CE (等量加等量,或等量减等量)∴△BEC 是等腰三角形∴∠B=∠C.15. P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-AB在AC 上取点E ,使AE =AB 。
DC B A FE PD A CB∵AE=ABAP=AP∠EAP=∠BAE,∴△EAP≌△BAP∴PE=PB。
PC<EC+PE∴PC<(AC-AE)+PB∴PC-PB<AC-AB。
16.已知∠ABC=3∠C,∠1=∠2,BE⊥AE,求证:AC-AB=2BE证明:在AC上取一点D,使得角DBC=角C∵∠ABC=3∠C∴∠ABD=∠ABC-∠DBC=3∠C-∠C=2∠C;∵∠ADB=∠C+∠DBC=2∠C;∴AB=AD∴AC – AB =AC-AD=CD=BD在等腰三角形ABD中,AE是角BAD的角平分线,∴AE垂直BD∵BE⊥AE∴点E一定在直线BD上,在等腰三角形ABD中,AB=AD,AE垂直BD∴点E也是BD的中点∴BD=2BE∵BD=CD=AC-AB∴AC-AB=2BE17.已知,E是AB中点,AF=BD,BD=5,AC=7,求DC∵作AG ∥BD交DE 延长线于G∴AGE 全等BDE∴AG=BD=5∴AGF ∽CDFAF=AG=5∴DC=CF=218.如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .解:延长AD 至BC 于点E,∵BD=DC ∴△BDC 是等腰三角形∴∠DBC=∠DCB又∵∠1=∠2 ∴∠DBC+∠1=∠DCB+∠2即∠ABC=∠ACB∴△ABC 是等腰三角形∴AB=AC在△ABD 和△ACD 中{AB=AC∠1=∠2BD=DC∴△ABD 和△ACD 是全等三角形(边角边)∴∠BAD=∠CAD∴AE 是△ABC 的中垂线∴AE ⊥BC∴AD ⊥BC19.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA证明:∵OM 平分∠POQ∴∠POM =∠QOMF A E DCB∵MA ⊥OP ,MB ⊥OQ∴∠MAO =∠MBO =90∵OM =OM∴△AOM ≌△BOM (AAS )∴OA =OB∵ON =ON∴△AON ≌△BON (SAS )∴∠OAB=∠OBA ,∠ONA=∠ONB∵∠ONA+∠ONB =180∴∠ONA =∠ONB =90∴OM ⊥AB20.(5分)如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .做BE 的延长线,与AP 相交于F 点,∵PA//BC ∴∠PAB+∠CBA=180°,又∵,AE ,BE 均为∠PAB 和∠CBA的角平分线∴∠EAB+∠EBA=90°∴∠AEB=90°,EAB 为直角三角形在三角形ABF 中,AE ⊥BF ,且AE 为∠FAB 的角平分线∴三角形FAB 为等腰三角形,AB=AF,BE=EF在三角形DEF 与三角形BEC 中,∠EBC=∠DFE,且BE=EF ,∠DEF=∠CEB ,∴三角形DEF 与三角形BEC 为全等三角形,∴DF=BC∴AB=AF=AD+DF=AD+BC21.如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠B延长AC 到E 使AE=AC 连接 ED∵ AB=AC+CD∴ CD=CE可得∠B=∠E△CDE 为等腰∠ACB=2∠BP E DCB A DC B A22.(6分)如图①,E、F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M.(1)求证:MB=MD,ME=MF(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.(1)连接BE,DF.∵DE⊥AC于E,BF⊥AC于F,∴∠DEC=∠BFA=90°,DE∥BF,在Rt△DEC和Rt△BFA中,∵AF=CE,AB=CD,∴Rt△DEC≌Rt△BFA(HL),∴DE=BF.∴四边形BEDF是平行四边形.∴MB=MD,ME=MF;(2)连接BE,DF.∵DE⊥AC于E,BF⊥AC于F,∴∠DEC=∠BFA=90°,DE∥BF,在Rt△DEC和Rt△BFA中,∵AF=CE,AB=CD,∴Rt△DEC≌Rt△BFA(HL),∴DE=BF.∴四边形BEDF是平行四边形.∴MB=MD,ME=MF.23.已知:如图,DC∥AB,且DC=AE,E为AB的中点,(1)求证:△AED≌△EBC.(2)观看图前,在不添辅助线的情况下,除△EBC外,请再写出两个与△AED的面积相等的三角形.(直接写出结果,不要求证明):OEDA证明:∵DC ∥AB∴∠CDE =∠AED∵DE =DE ,DC =AE∴△AED ≌△EDC∵E 为AB 中点∴AE =BE∴BE =DC∵DC ∥AB∴∠DCE =∠BEC∵CE =CE∴△EBC ≌△EDC∴△AED ≌△EBC24.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .证明:∵∠CEB=∠CAB=90°∴ABCE 四点共元∵∠AB E=∠CB E∴AE=CE∴∠ECA=∠EAC取线段BD 的中点G ,连接AG ,则:AG=BG=DG∴∠GAB=∠ABG而:∠ECA=∠GBA (同弧上的圆周角相等)∴∠ECA=∠EAC=∠GBA=∠GAB而:AC=ABFED C B A∴△AEC ≌△AGB∴EC=BG=DG∴BE=2CE25、如图:DF=CE ,AD=BC ,∠D=∠C 。
