一次函数面积问题
一次函数之面积问题(与坐标轴围成的面积)(人教版)(含答案)

一次函数之面积问题(与坐标轴围成的面积)(人教版)一、单选题(共8道,每道12分)1.已知一次函数和的图象都经过点A(2,0),且与y轴分别交于B,C两点,则△ABC的面积是( )A.1B.2C.4D.8答案:C解题思路:试题难度:三颗星知识点:坐标线段长互转2.已知一次函数y=kx+(k-3)与一次函数y=2x+b交于点C(1,3),则两条直线的函数图象与x 轴所围成的三角形的面积是( )A.1B.C. D.答案:D解题思路:试题难度:三颗星知识点:一次函数与坐标轴围成的图形面积3.已知一次函数y=kx+b的图象经过点B(0,10),且与正比例函数y=2x的图象相交于点A(2,a),则这两个函数图象与y轴所围成的三角形的面积是( )A.5B.10C.20D.40答案:B解题思路:试题难度:三颗星知识点:一次函数与坐标轴围成的图形面积4.已知一次函数y=kx+b的图象经过点(3,-3),且与直线y=4x-3的交点在x轴上,则此函数的图象与坐标轴围成的三角形的面积为( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:一次函数与坐标轴围成的图形面积5.已知一次函数的图象经过点(-2,0),它与坐标轴围成的三角形面积等于1,则这个一次函数的函数表达式是( )A. B.C.或D.或答案:D解题思路:试题难度:三颗星知识点:一次函数与坐标轴围成的图形面积6.已知一次函数的图象过点(3,0),且与两坐标轴围成的三角形面积为3,则一次函数的表达式为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:一次函数与坐标轴围成的图形面积7.若直线y=kx+b与直线y=4x平行,且直线y=kx+b与两坐标轴围成的三角形的面积为2,则直线y=kx+b与x轴的交点坐标是( ).A.(1,0)B.(1,0)或(-1,0)C.(2,0)D.(2,0)或(-2,0)答案:B解题思路:试题难度:三颗星知识点:一次函数与坐标轴围成的图形面积8.若直线y=x+k,x=1,x=4和x轴围成的直角梯形的面积等于9,则k的值为( )A. B.C.或D.或答案:C解题思路:试题难度:三颗星知识点:一次函数与坐标轴围成的图形面积。
一次函数与面积结合问题解题技巧

一次函数与面积结合问题解题技巧全文共四篇示例,供读者参考第一篇示例:一次函数与面积结合问题解题技巧一次函数是初中数学中最基本的一种函数形式,通常表示为y = kx + b,其中k和b为常数,x为自变量,y为因变量。
面积问题是数学中常见的问题类型之一,需要运用数学知识来求解。
当一次函数与面积结合在一起时,往往需要运用数学知识和解题技巧来解决问题。
本文将为大家介绍一次函数与面积结合问题解题的技巧,并通过实例来解释具体的解题方法。
一、如何将一次函数与面积联系起来在解决一次函数与面积结合问题时,我们需要先找到函数表达式和面积之间的联系。
通常,我们可以通过一次函数的图像和面积来建立它们之间的关系。
若给定一次函数y = 2x + 1,要求计算函数图像在一定区间内与x 轴之间的面积,我们可以先绘制函数的图像,然后找出其与x轴之间的面积。
二、一次函数与矩形面积的关系在一次函数与面积结合问题中,经常会出现与矩形面积有关的题目。
矩形的面积等于长乘以宽,即S = l*w。
如果给定一个矩形的长度为x,宽度为y = kx + b(k和b为常数),我们可以通过一次函数的表达式计算出矩形的面积。
三、利用一次函数的特性解决面积问题如果一个图形可以通过两条一次函数的交点来确定,我们也可以通过两条函数的表达式来求出图形的面积。
四、实例解析为了帮助大家更好地理解一次函数与面积结合问题的解题方法,我们来看一个实例:例:已知一次函数y = 2x + 3和直线y = x + 1的交点A、B、C、D,求由四个点构成的四边形的面积。
解:我们可以通过求解两条直线的交点来确定四个点的坐标。
将两条直线的表达式相等,得到x = -2,将x = -2代入其中一条直线的表达式中,得到交点坐标为(-2, -1)。
接下来,根据交点的坐标,我们可以求得四边形的边长,进而计算出四边形的面积。
将四个点连接起来可以得到一个平行四边形,根据平行四边形面积公式S = 底边长*高得到面积。
一次函数面积专题导学案定稿

一次函数专题一-面积问题(导学案)
例1.已知直线/:y=-;x+2与X轴交于点A,与y轴交于点B.
(1)点A坐标为,点B坐标为
(2)求这条直线与坐标轴围成的面积
(3)直线∕ry=x+l与X轴交于点C,与y轴于点D,与直线/交于点E.
你能计算出哪些三角形的面积?
变式探究
已知直线/:y=-;x+2与X轴交于点A,与y轴交于点B.
变式1:若点P为X轴上的动点,当S.ABP=2时,求P点坐标.
变式2:若点P为直线/上的动点,当S AAOP=2时,求P点坐标。
变式3:过点0的直线b交直线/于点Q,若直线/2把AAOB的面积分成1:1两部分,求Q点坐标及直线Z2的函数表达
式。
例2.已知直线/:y=-;x+2与X轴交于点A,与y轴交于点B,BP和AP相交于P点(1,3),
求SΔABP.
变式:已知直线/:y=-;x+2与X轴交于点A,与y轴交于点B,以线段AB为直角边在第一象限内作等腰RSABC,ZBAC=90o,点P(l,a)是第一象限内的一个动点。
若△ABC
分享收获
和^ ABP的面积相等,求a的值。
谈谈你的收获.
拓展提升:己知直线/:y=-'x+2与X轴交于点A,与y轴交于点B,以线段AB为直角边2
在第一象限内作等腰Rt∆ABC,NBAC=90。
,点P(l,a)是直线X=I的一个动点。
若A ABC和小ABP的面积相等,求a的值。
一次函数中的面积问题

一次函数中的面积问题学习目标:1.通过复习使学生熟悉直线与坐标轴的交点坐标的求法,会求出两直线交点坐标,会求一次函数的解析式。
2.初步掌握由若干条直线所围成的图形的面积的计算方法。
一、探究新知例1:已知直线l :22+-=x y ,(1)求直线l 与两坐标轴的交点坐标;(2)求此一次函数的图象与两坐标轴所围成的三角形的面积。
变式1:已知直线l :22+-=x y ,且点T )32,(t 在直线l 上, (1) 求OT 所在直线的解析式;(2) 求直线l 和直线OT 与x 轴所围成的图形面积。
变式2:如图,已知直线l :22+-=x y 与x 轴、y 轴分别交于点B 、M,,将变式1中的直线OT 向上平移1个单位长度得到直线PA ,点Q 是直线PA 与y 轴的交点,求四边形PQOB 的面积。
变式3:如图,已知直线PA 是一次函数)0(>+=n n x y 的图象,直线PB 是一次函数)(2n m m x y +-=的图象。
(1)用m 、n 表示出A 、B 、P 点的坐标;(2)若点Q 是直线PA 与y 轴的交点,且四边形PQOB 的面积65,AB=2,试求点P 的坐标,并写出直线PA 与PB 的解析式。
例2:如图,已知直线1l 经过点)1,0()0,2(B A 与点,另一条直线2l 经过点B ,且与x 轴相交于点P(a,0),若APB ∆的面积为3,求a 的值。
变式:如图,已知直线1l 经过点)1,0()0,2(B A 与点,如果在第二象限内有一点)21,(a P ,且APB ∆的面积为3,求a 的值。
三、提升训练1:如图,点m x y C B A +-=2在一次函数、、的图象上,它们的横坐标依次为,211、、-分别过这些点作x 轴与y 轴的垂线,求图中阴影部分的面积之和。
2:设直线1l :1-+=k kx y 和直线2l :k x k y ++=)1((k 为正整数)及x 轴围成的三角形面积为k S ,求200621S S S +++ 的值。
一次函数面积问题专题(含答案解析)

一次函數面積問題1、如图,一次函数的图像与X轴交于点B (- 6 , 0),交正比例函数的图像于点A,点A的横坐标为-4,△ ABC的面积为15,求直线OA的解析式。
2、直线y=x+3的图像与X轴、y轴分别交于A B两点,直线a经过原点与线段AB 交于。
,把厶ABO勺面积分为2:1的两部分,求直线a的函数解析式。
3、直线PA是一次函数y=x+n的图像,直线PB是一次函数y=-2x+m (m>n>0的图像,(1) 用m n表示A、B、P的坐标(2) 四边形PQoB勺面积是',AB=2求点P的坐标4、A AOB的顶点0( 0, 0) A (2, 1)、B (10, 1),直线CDL X 轴且△ AOB面积二等分,若D (m, 0),求m的值5、点B在直线y=-x+1上,且点B在第四象限,点A(2, 0)、0(0, 0),A ABo 的面积为2,求点B的坐标。
6直线y=- x+1与X轴y轴分别交点A B,以线段AB为直角边在第一象限内作等腰直角△ ABC N BAC=90 ,点P( a,])在第二象限,△ ABP勺面积与△ ABC7、如图,已知两直线y=0.5x+2.5和y=-x+1分别与X轴交于A、B两点,这两直线的交点为P(1)求点P的坐标(2)求厶PAB的面积8、已知直线y=ax+b (b>0)与y轴交于点N,与X轴交于点A且与直线y=kx交于点M (2, 3),如图它们与y轴围成的厶MoN勺面积为5,求(1)这两条直线的函数关系式(2)它们与X轴围成的三角形面积9、已知两条直线y=2x-3和y=5-x(1)求出它们的交点A的坐标(2)求出这两条直线与X轴围成的三角形的面积10、已知直线y=x+3的图像与X轴、y轴交于A B两点,直线I经过原点,与线段AB 交于点。
,把厶AoB的面积分为2:1的两部分,求直线I的解析式。
11、已知直线y=2x+3与直线y=-2x-1与y轴分别交于点A B(1)求两直线交点C的坐标(2)求厶ABe的面积(3)在直线BC上能否找到点P,使得△ APC的面积為6,求出点P的坐标,12、已知直线y=-x+2与X轴、y轴分别交于点A和点B,另一直线y=kx+b(k≠ 0)经过点C(1,0),且把△ AOB分为两部分,(1)若厶AOB被分成的两部分面积相等,求k和b的值(2)若厶AOB被分成的两部分面积为1:5,求k和b的值13、直线y=- x+3交X, y坐标轴分别为点A B,交直线y=2x-1于点P,直线-Iy=2x-1交X, y坐标轴分别为C。
一次函数面积专题附答案

一次函数面积专题学校:___________姓名:___________班级:___________考号:___________ 一、解答题1.如图,在平面直角坐标系中,△ABC 三个顶点的坐标分别是A (1,5),B (-3,-3)和C (7,2),求△ABC 的面积.【答案】30 【解析】 【分析】解法1:延长AC 交x 轴于点D ,先求出直线AC 的解析式,从而得出点D 的坐标,再利用=+-ABCAEDBEFCFDSSSS即可.解法2:分别过点A ,B ,C 向坐标轴作垂线,得到矩形BEFG ,然后利用矩形=---ABCBEACFACBGBEFG SS SSS就可得到所求三角形的面积.解法3:分别过点A ,B ,C 向坐标轴作垂线,得到矩形BEFG ,据勾股定理求得45AB =同理可得35AC =55BC =由勾股定理逆定理和三角形的面积公式即可得出答案. 解法4:作AM//y 轴交BC 于M ,先得出直线BC 解析式为1322y x =-,然后得出点M (1,-1),从而确定水平宽a =10,铅垂高h =6,再利用=+ABCABMACMS SS即可;【详解】解法1:如图2,延长AC 交x 轴于点D . 因为A (1,5),C (7,2),所以直线AC 的解析式为11122y x =-+,所以点D 的坐标为D (11,0).同理,可以求出点E 3,02⎛⎫- ⎪⎝⎭,点F (3,0),所以DE =252,EF =92,DF =8,所以1252783044ABCAEDBEFCFDSSSS=+-=+-=.解法2:如图3,分别过点A ,B ,C 向坐标轴作垂线,得到矩形BEFG . 因为A (1,5),B (-3,-3),C (7,2), 所以E (-3,5),F (7,5),G (7,-3),所以BE =8,BG =10,AE =4,AF =6,CF =3,CG =5, 所以801692530ABCBEACFACBGBEFG SS SSS=---=---=矩形.解法3:如图4,在Rt △ABE 中,因为A (1,5),B (-3,-3),E (-3,5), 所以根据勾股定理求得45AB = 同理可得35AC =55BC = 因为2224580125AC AB BC +=+==, 所以由勾股定理逆定理得90BAC ∠=︒. 所以1145353022ABCSAB AC =⋅=⨯=.解法4:如图5,由B (-3,-3),C (7,2)容易得到水平宽a =10, 所以直线BC 解析式为1322y x =-. 作AM//y 轴交BC 于M , 令x =1,代入1322y x =-得y =-1,则M (1,-1). 此时,可以得到铅垂高h =5+1=6. 所以1211130222ABCABMACMSSSAM h AM h a h =+=⋅+⋅=⋅=.2.如图,已知直线AB 经过A (2,0),B (0,1)两点,点P 的坐标为(-2,a ),且0<a <2.若△ABP 的面积是1,求a 的值.【答案】1 【解析】 【分析】方法1:先根据A 、B 两点坐标求出直线AB 的解析式为112y x =-+,再过点P 作QN x⊥轴,交直线AB 于点Q ,交x 轴于点N ,利用割补法建立关于a 的方程,求解即可;方法2:设直线BP 交x 轴于点Q ,利用P 、B 两点坐标求出直线PB 的解析式为112a y x -=+,进而求出Q 2,01a ⎛⎫⎪-⎝⎭,利用割补法建立关于a 的方程,求解即可; 方法3:过点O 作AB 的平行线于直线x =-2交于点P ,根据A 、B 两点坐标求出直线AB 的解析式为112y x =-+,由直线OP 与直线AB 平行,且过原点,得到直线OP 的解析式即可求解. 【详解】 方法1:如答图所示,过点P 作QN x ⊥轴,交直线AB 于点Q ,交x 轴于点N . 设直线AB 的解析式为y kx b =+.将A (2,0),B (0,1)两点坐标代入可得201k b b +=⎧⎨=⎩,解得121k b ⎧=-⎪⎨⎪=⎩. 则直线AB 的解析式为112y x =-+,令x =-2得y =2,则Q (-2,2). 由42(2)1ABPAQNPNAPQBSSSSa a =--=---=,解得a =1.方法2:设直线BP 交x 轴于点Q ,直线PB 的解析式为y kx b =+.将P (-2,a),B (0,1)两点坐标代入可得21k b ab -+=⎧⎨=⎩,解得121a k b -⎧=⎪⎨⎪=⎩. 则直线PB 的解析式为112ay x -=+.a =1时,显然成立; 1a ≠时,令y =0得x =2a 1-,则Q 2,01a ⎛⎫⎪-⎝⎭.如图所示,121212212121ABPABQPQASSSa a a ⎛⎫⎛⎫=-=⨯⨯--⨯⨯-= ⎪ ⎪--⎝⎭⎝⎭, 解得a =1,又1a ≠,故此时a 不存在.综上得a =1.方法3:如答图所示,过点O 作AB 的平行线于直线x =-2交于点P ,连接AP ,BP . 因为“平行线间的距离处处相等”,所以△ABP 与△AOB 同底等高,面积都是1. 设直线AB 的解析式为y kx b =+.将A (2,0),B (0,1)两点坐标代入可得201k b b +=⎧⎨=⎩,解得121k b ⎧=-⎪⎨⎪=⎩,则直线AB 的解析式为112y x =-+. 因为直线OP 与直线AB 平行,且过原点,所以直线OP 的解析式为12y x =-.令x =-2得a =1.3.如图,在平面直角坐标系中,一次函数y x b =-+的图象与正比例函数y kx =的图象都经过点()3,1B .(1)求一次函数和正比例函数的解析式;(2)若点(),P x y 是线段AB 上一点,且在第一象限内,连接OP ,设APO ∆的面积为S ,求面积S 关于x 的函数解析式. 【答案】(1)y =﹣x +4,13y x =;(2)S =2x (0<x ≤3). 【解析】 【分析】(1)把B (3,1)分别代入y =﹣x +b 和y =kx 即可得到结论; (2)根据三角形的面积公式即可得到结论. 【详解】(1)把B (3,1)分别代入y =﹣x +b 和y =kx 得1=﹣3+b ,1=3k ,解得:b =4,k 13=,∴y =﹣x +4,y 13=x ;(2)∵点P (x ,y )是线段AB 上一点,∴S 12OA =•xP 142x =⋅⋅=2x (0<x ≤3).【点睛】本题考查了两直线相交或平行,三角形面积的求法,待定系数法确定函数关系式,正确的理解题意是解题的关键.4.如图,在平面直角坐标系中,一次函数12y x m =-+的图象1l 分别与x ,y 轴交于A ,B 两点,正比例函数的图象2l 与1l 交于点()2,4C .(1)求m 的值及2l 的解析式;(2)若点M 是直线12y x m =-+上的一个动点,连接OM ,当AOM 的面积是BOC 面积的2倍时,请求出符合条件的点M 的坐标;(3)一次函数2y kx =+的图象为3l ,且1l ,2l ,3l 不能围成三角形,直接写出k 的值.【答案】(1)5m =,2l 的解析式为2y x =(2)()6,2M 或()142,(3)12k =-或2或1【解析】 【分析】(1)设2l 的解析式为1y k x =,将点C 的坐标代入12,l l 的解析式,即可求解;(2)设1(,5)2M a a -+,进而根据题意列出方程,解方程求解即可;(3)根据题意,则31l l ∥或32l l ∥,进而即可求得k 的值 (1)2l 与1l 交于点()2,4C .设2l 的解析式为1y k x =,将点C 的坐标代入12,l l 的解析式,可得, 1422m =-⨯+,142k =,解得5m =,12k =,∴2l 的解析式为2y x = (2)设1(,5)2M a a -+,152y x =-+,令0x =,则5y =,令0y =,则10x =()0,5B ∴,()10,0A又()2,4C∴11111525,105522222BOCC AOMM M SBO x S OA y y a =⨯=⨯⨯==⨯=⨯⨯=⨯-+ AOM 的面积是BOC 面积的2倍,∴1552a ⨯-+2=⨯5即1522a -+=解得6a =或14∴()6,2M 或()142, (3)一次函数2y kx =+的图象为3l ,且1l ,2l ,3l 不能围成三角形,∴31l l ∥或32l l ∥当3l 过点C (2,4)时,将点C 坐标代入y =kx +2并解得:k =l ,∴12k =-或2或1【点睛】本题考查了一次函数综合,求一次函数解析式,求一次函数与坐标轴围成的三角形面积,一次函数与坐标轴的交点问题,一次函数的平移,掌握一次函数的性质是解题的关键. 5.如图,在平面直角坐标系中,一次函数332y x =-+与y 轴交于点A ,与x 轴交于点B ,过点B 作AB 的垂线,垂线与反比例函数()10my m x=≠交于C 、D 两点,且AB BC =.(1)求反比例函数()10my m x=≠的表达式,及经过点C 、D 的一次函数表达式()20y kx b k =+≠;(2)请直接写出使12y y >的x 取值范围; (3)求出ABD △的面积. 【答案】(1)110y x =,22433y x =- (2)3x <-或05x << (3)656【解析】 【分析】(1)由一次函数y =﹣32x +3求得A 、B 的坐标,然后通过证得△ABO ≌△BCF ,求得C(5,2),然后利用待定系数法即可求得函数的解析式; (2)求得D 的坐标,然后根据图象即可求得;(3)利用三角形面积公式,根据S △ABD =S △ABE +S △ADE 求得即可. (1)解:∵332y x =-+ 与y 轴交于点A ,与x 轴交于点B ,∴A (0,3),B (2,0), 如图,过点C 作CF ⊥x 轴于点F ,∵AB ⊥CD ,∴∠ABO +∠CBF =90°, ∵∠ABO +∠BAO =90°, ∴∠BAO =∠CBF , 在△ABO 和△BCF 中,BAO CBF AOB BFC AB BC =⎧⎪=⎨⎪=⎩∠∠∠∠ , ∴△ABO ≌△BCF (AAS ), ∴BF =AO =3,CF =OB =2, ∴C (5,2), ∵反比例函数y 1=mx(m ≠0)过点C , ∴m =5×2=10, ∴反比例函数110y x=, 将B (2,0),C (5,2)代入y 2=kx +b (k ≠0)得2052k b k b +=⎧⎨+=⎩,解得2343k b ⎧=⎪⎪⎨⎪=-⎪⎩,∴经过点C 、D 的一次函数表达式为22433y x =- ; (2)由102433y xy x ⎧=⎪⎪⎨⎪=-⎪⎩, 解得52=⎧⎨=⎩x y 或3103x y =-⎧⎪⎨=-⎪⎩,∴D 横坐标为﹣3.∴y 1>y 2的x 取值范围:x <﹣3或0<x <5; (3)ABD ADE ABE S S S =+△△△ 12D AE x =1·2B AE x + 656=. 【点睛】本题主要考查了反比例函数与一次函数交点问题,求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.6.如图,已知一次函数1y k x b =+与反比例函数2k y x=的图象交于第一象限内的点()1,6A 和()6,B m ,与x 轴交于点C .(1)分别求出这两个函数的表达式;(2)①观察图象,直接写出不等式21k k x b x+≥的解集;②请连接OA 、OB ,并计算△AOB 的面积;(3)是否存在坐标平面内的点P ,使得由点O ,A ,C ,P 组成的四边形是平行四边形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.【答案】(1)反比例函数的表达式是:y =6x ,一次函数表达式是:y =﹣x +7 (2)①x <0或1≤x ≤6;352(3)存在点P 的坐标为(8,6)或(﹣6,6)或(6,﹣6)使得由点O ,A ,C ,P 组成的四边形是平行四边形【解析】【分析】(1)直接利用待定系数法分别求出一次函数与反比例函数解析式;(2)①利用函数图象结合其交点得出不等式k 1x +b ≥2k x的解集;②如图所示,过点A 作AD ⊥x 轴于D ,过点B 作BE ⊥x 轴于B ,则2==32AOD BOE k S S =△△,再根据=AOB BOE AOD ADEB S S S S ++△△△梯形进行求解即可;(3)利用平行四边形的性质结合当AP 为边和AP 为对角线两种情况分别得出答案即可.(1)解:∵点A (1,6)在反比例函数y =2k x 的图象上, ∴6=21k , 解得:k 2=6,∴反比例函数的表达式是:y =6x; ∵B (6,m )在反比例函数y =6x的图象上, ∴m =66=1,∴B (6,1),将点A (1,6),B (6,1)代入y =k 1x +b ,可得: 11616k b k b =+⎧⎨=+⎩, 解得:117k b =-⎧⎨=⎩, ∴一次函数表达式是:y =﹣x +7;(2)解:①∵点A (1,6),B (6,1),∴不等式k 1x +b ≥2k x的解集是:x <0或1≤x ≤6; 故答案为:x <0或1≤x ≤6;②如图所示,过点A 作AD ⊥x 轴于D ,过点B 作BE ⊥x 轴于B , ∴2==32AOD BOE k S S =△△, ∵A (1,6),B (6,1),∴OD =1,AD =6,OE =6,BE =1,∴DE =5,∵=AOB BOE AOD ADEB S S S S ++△△△梯形,∴()35===22AOB ADEB AD BE DE S S +⋅△梯形;(3)解:∵C是直线AB与x轴的交点,∴点C的坐标为(7,0),如图3-1所示:当AP为边时,∴AP∥OC,AP=OC=7,∵A(1,6),∴P点坐标为:(8,6)或(-6,6);当AP为对角线时,如图3-2所示,∵AP与OC的中点坐标相同,∴1072260022PPxy++⎧=⎪⎪⎨++⎪=⎪⎩,∴66PPxy=⎧⎨=-⎩,∴点P的坐标为(6,-6);综上所述存在点P的坐标为(8,6)或(﹣6,6)或(6,﹣6)使得由点O,A,C,P 组成的四边形是平行四边形.【点睛】此题主要考查了反比例函数的综合以及待定系数法求一次函数解析式、平行四边形的性质等知识,正确数形结合分析是解题关键.7.如图,一次函数y=kx+b(k>0)的图象经过点C(−3,0),且与两坐标轴围成的三角形的面积为3.(1)求一次函数的解析式;(2)若反比例函数myx的图象与该一次函数的图象交于一、三象限内的A,B两点,且AC=2BC,求m的值.【答案】(1)一次函数的解析式为y=23x+2;(2)m的值为12.【解析】【分析】(1)根据一次函数y=kx+b(k>0)的图象经过点C(-3,0),得到-3k+b=0①,点C到y轴的距离是3,解方程即可得到结论;(2)如图,作AD⊥x轴于点D,BE⊥x轴于点E,则AD∥BE.根据相似三角形的性质得到AD=2BE.设B点纵坐标为-n,则A点纵坐标为2n.求得A(3n-3,2n),B(-3-32 n,-n),根据反比例函数y=mx的图象经过A、B两点,列方程即可得到结论.(1)解:∵一次函数y=kx+b(k>0)的图象经过点C(-3,0),∴-3k+b=0①,点C到y轴的距离是3,∵k>0,∴b>0,∵一次函数y=kx+b的图象与y轴的交点是(0,b),∴12×3×b=3,解得:b=2.把b=2代入①,解得:k=23,则函数的解析式是y=23x+2.故这个函数的解析式为y=23x+2;(2)解:如图,作AD⊥x轴于点D,BE⊥x轴于点E,则AD∥BE.∵AD∥BE,∴△ACD∽△BCE,∴AD ACBE BC=2,∴AD=2BE.设B点纵坐标为-n,则A点纵坐标为2n.∵直线AB的解析式为y=23x+2,∴A(3n-3,2n),B(-3-32n,-n),∵反比例函数y=mx的图象经过A、B两点,∴(3n-3)•2n=(-3-32n)•(-n),解得n1=2,n2=0(不合题意舍去),∴m=(3n-3)•2n=3×4=12.【点睛】本题考查了反比例函数与一次函数的交点问题,待定系数法求一次函数的解析式,三角形的面积,相似三角形的判定与性质,一次函数、反比例函数图象上点的坐标特征,难度适中.正确求出一次函数的解析式是解题的关键.8.如图,反比例函数kyx=的图象与一次函数12y x=-的图象分别交于M,N两点,已知点M(-2,m).(1)求反比例函数的表达式;(2)点P为y轴上的一点,当点P的坐标为(5时,求△MPN的面积.【答案】(1)2 yx =-(2)5【解析】【分析】(1)把M(-2,m)代入函数式y=-12x中,求得m的值,从而求得M的坐标,代入y=kx可求出函数解析式;(2)根据反比例函数与正比例函数的中心对称性求得N的坐标,然后利用S△MPN=S△MOP+S△NOP求得即可.(1)解:∵点M(-2,m)在一次函数y=-12x的图象上,∴m=-12×(-2)=1.∴M(-2,1).∵反比例函数y=kx的图象经过点M(-2,1),∴k=-2×1=-2.∴反比例函数的表达式为y=-2x;(2)解:∵反比例函数y=kx的图象与一次函数y=-12x的图象分别交于M,N两点,M(-2,1),∴N(2,-1),∵点P为y轴上的一点,点P的坐标为(0,5),∴OP=5,∴S△MPN=S△MOP+S△NOP=12×5×2+12×5×2=25.【点睛】本题考查了反比例函数与一次函数的交点问题,本题利用了待定系数法求函数解析式以及利用中心对称求两个函数的交点,三角形的面积等知识.9.如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数ymx(m≠0)的图象相交于A,B两点,过点A作AD⊥x轴于点D,AO=5,OD:AD=3:4,B点的坐标为(﹣6,n)(1)求一次函数和反比例函数的表达式;(2)求△AOB的面积;(3)P是y轴上一点,且△AOP是等腰三角形,请直接写出所有符合条件的P点坐标.【答案】(1)y23=x+2,y12x=;(2)△AOB的面积S9=;(3)P点坐标为:(0,8)或(0,5)或(0,﹣5)或(0,258)【解析】【分析】(1)设OD=3a,AD=4a,则AO=5a=5,解得:a=1,故点A(3,4),故反比例函数的表达式为:y=12x,故B(-6,2),将点A、B的坐标代入一次函数表达式,即可求解;(2)△AOB的面积S=12×OM×(xA-xB)=12×2×(3+6)=9;(3)分AP=AO、AO=PO、AP=PO三种情况,分别求解即可.(1)解:AO=5,OD:AD=3:4,设:OD=3a,AD=4a,则AD=5a=5,解得:a=1,故点A(3,4),则m=3×4=12,故反比例函数的表达式为:y12x=,故B(﹣6,﹣2),将点A、B的坐标代入一次函数表达式y=kx+b得:4326k bk b=+⎧⎨-=-+⎩,解得:232kb⎧=⎪⎨⎪=⎩,故一次函数的表达式为:y23=x+2;(2)解:设一次函数y23=x+2交y轴于点M(0,2),∵点A(3,4),B(﹣6,﹣2),∴△AOB的面积S12=⨯OM×(xA﹣xB)12=⨯2×(3+6)=9;(3)解:设点P(0,m),而点A、O的坐标分别为:(3,4)、(0,0),AP2=9+(m﹣4)2,AO2=25,PO2=m2,当AP=AO时,9+(m﹣4)2=25,解得:m=8或0(舍去0);当AO=PO时,同理可得:m=±5;当AP=PO时,同理可得:m258 =;综上,P点坐标为:(0,8)或(0,5)或(0,﹣5)或(0,258).【点睛】本题考查了反比例函数与一次函数综合,等腰三角形的判定与性质,利用形数结合解决此类问题,是非常有效的方法.10.如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=mx(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(−3,4),点B的坐标为(6,n).(1)求该反比例函数和一次函数的解析式;(2)连接OB,求△AOB的面积;(3)在x轴上是否存在点P,使△APC是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.【答案】(1)反比例函数的解析式为y=-12x;一次函数的解析式为y=-23x+2;(2)S△AOB=9;(3)存在.P点坐标为(-3,0)、(-173,0).【解析】【分析】(1)先把A(-3,4)代入反比例函数解析式得到m的值,从而确定反比例函数的解析式为y =-12x;再利用反比例函数解析式确定B 点坐标为(6,-2),然后运用待定系数法确定所求的一次函数的解析式为y =-23x +2; (2)先依据一次函数求得点C 的坐标,进而得到△AOB 的面积;(3)过A 点作AP 1⊥x 轴于P 1,AP 2⊥AC 交x 轴于P 2,可得P 1点的坐标为(-3,0);再证明Rt △AP 2P 1∽Rt △CAP 1,利用相似比计算出P 1P 2的长度,进而得到OP 2的长度,可得P 2点的坐标为(-173,0),于是得到满足条件的P 点坐标. (1)解:将A (-3,4)代入y =m x ,得m =-3×4=-12, ∴反比例函数的解析式为y =-12x ; 将B (6,n )代入y =-12x,得6n =-12, 解得n =-2,∴B (6,-2), 将A (-3,4)和B (6,-2)分别代入y =kx +b (k ≠0),得3462k b k b -+=⎧⎨+=-⎩, 解得232k b ⎧=-⎪⎨⎪=⎩, ∴所求的一次函数的解析式为y =-23x +2; (2)解:当y =0时,-23x +2=0, 解得:x =3,∴C (3,0),∴S △AOC =12×3×4=6,S △BOC =12×3×2=3, ∴S △AOB =6+3=9;(3)解:存在.过A 点作AP 1⊥x 轴于P 1,AP 2⊥AC 交x 轴于P 2,如图,∴∠AP 1C =90°,∵A 点坐标为(-3,4),∴P 1点的坐标为(-3,0);∵∠P 2AC =90°,∴∠P 2AP 1+∠P 1AC =90°,而∠AP 2P 1+∠P 2AP 1=90°,∴∠AP 2P 1=∠P 1AC ,∴Rt △AP 2P 1∽Rt △CAP 1, ∴11211AP PP CP AP =,即12464PP =, ∴P 1P 2=83, ∴OP 2=3+83=173, ∴P 2点的坐标为(-173,0), ∴满足条件的P 点坐标为(-3,0)、(-173,0). 【点睛】本题考查了反比例函数与一次函数交点问题,解决问题的关键是了解反比例函数图象上点的坐标特征和待定系数法确定函数解析式;会运用三角形相似知识求线段的长度.。
一次函数与面积问题

一次函数常与三角形或四边形的面积相结合进行考查,两种类型的题目比较常见:(1)由函数图像求面积;(2)由面积求点坐标。
遇到第一种类型题目时,找准三角形的底和高是解题的关键,特别是遇到钝角三角形。
如果无法直接求解,可以利用割补法、铅锤法等方法进行转化。
遇到第二种类型题目时,要特别注意,很容易出错,不要忘记使用绝对值。
01类型一:由函数图像求图形面积例题1:如图,直线l1:y=-3x+3与x轴交于点A,直线l2经过点B(4,0),C(3,-1.5),并与直线l2交于点D.(1)求直线l2的函数解析式;(2)求△ABD的面积.分析:求l2的函数解析式,利用待定系数法,已知点B(4,0)、点C (3,-1.5),代入解析式中求出K、b得值即可得到一次函数解析式。
求△ABD的面积,三角形有一边在x轴上,求三角形的面积可直接利用三角形的面积公式,选择x轴上的线段AB为底,那么点D纵坐标的绝对值即为三角形的高,因此需要求出点B坐标。
点B是两直线的交点,联立方程组即可求得点B坐标。
本题主要是有函数图像求得三角形的面积,属于基础题。
02类型二:由面积求点坐标例题2:如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2).(1)求直线AC的表达式;(2)求△OAC的面积;(3)动点M在线段OA和射线AC上运动,是否存在点M,使△OMC 的面积是△OAC的面积的14?若存在,求出此时点M的坐标;若不存在,请说明理由.分析:(1)由点C和点A的坐标,利用待定系数法即可求得函数的解析式;(2)求△AOC的面积,由题可知该三角形可选OC作为底,点A的横坐标的绝对值即为该三角形的高,点A与点C坐标已知,可通过三角形的面积公式直接求出。
(3)当△OMC的面积是△OAC的面积的1/4时,根据面积公式即可求得M的横坐标的绝对值,然后代入解析式即可求得M的坐标.由面积求点坐标时,一定要注意绝对值的使用,注意分情况进行讨论。
一次函数与面积问题

一次函数与面积问题一次函数与面积问题结合起来一起考查,是一类常考题型,它要求学生充分理解点的坐标的几何意义,能在坐标系中表示出线段的长度,会将面积问题转化为线段、坐标的关系问题,同时对于较复杂的问题能够依据题意画出图象,并借助图象进行分析与解答.一次函数与面积问题的相关类型如下.三角形的底在坐标轴上 三角形的底在坐标轴上时,利用点到坐标轴的距离求出高后直接求面积即可,注意点到坐标轴的距离要带绝对值. 如图①,S △OAC =21·OA ·CH=21·︱x A ︱·︱y C ︱; 如图②,S △OBC =21·OB ·CH=21·︱y B ︱·︱x A ︱三角形的底平行于坐标轴三角形的底平行于坐标轴时,利用平行于坐标轴的直线上的两点间距离求出底和高,最后用面积公式求出面积 如图①,S △ABC =21·AB ·CH=21·︱x B -x A ︱·︱y C -y H ︱;如图②,S △ABC =21·AB ·CH=21·︱y B -y A ︱·︱x C -x H ︱补形法或分割法如果三角形的边都不平行于坐标轴,可以采用补形法构造出有边平行于坐标轴的三角形或四边形后再求解. 如图①,S △ABC = S △OBC + S △OAC + S △AOB ; 如图②,S △ABC = S 梯形OACD + S △BCD + S △AOB ;如图③,S △ABC = S 梯形BOEC + S △ACE -S △AOB ; 如图④,S △ABC = S 矩形OAFD - S △BCD - S △ACF - S △AOB ;通过作平行于坐标轴的直线将三角形分成左右两个三角形或上下两个三角形来求解面积.作三角形铅锤高是解决三角形面积问题的一个好办法.如图①,过△ABC 的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC 的“水平宽a ”,中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高h ”.我们可得出一种计算三角形面积的新方法:S △ABC =0.5ah ,即三角形面积等于水平宽与铅垂高乘积的一半.图①中,S △ABC =21·︱x A -x B ︱·︱y C -y M ︱,如图②,S △ABC = S △ACM + S △BCM ;如图③,S △ABC = S △ABN + S △BCN 平行线转移法通过作平行线,利用平行线间的距离处处相等和底高关系转移三角形面积.如图④,AB ∥CG ,S △ABC =S △ABG例题1:一次函数y=kx+b(k≠0)的图象经过点A(﹣1,2)和点B(0,4).(1)求出这个一次函数的解析式;(2)画出一次函数图象;(3)求一次函数图象与x轴、y轴所围成的三角形的面积?分析:(1)将两点坐标代入函数表达式中,用待定系数法求解即可;(2)用两点法画函数的图象(确定两点,描点,连线).(2)利用交点点坐标求出三角形面积可.解:(1)依题意得:,解得,所以该一次函数的解析式为y=2x+4;(2)画出一次函数图象;(3)一次函数图象与x轴、y轴所围成的三角形的面积为:S=×2×4=4.例题2:已知直线y=﹣3x+6与x轴交于A点,与y轴交于B点.(1)求A,B两点的坐标;(2)求直线y =﹣3x+6与坐标轴围成的三角形的面积.分析:(1)分别令x=0、y=0求解即可得到与坐标轴的交点;(2)根据三角形的面积公式列式计算即可得解:(1)当x=0时,y=﹣3x+6=6,当y=0时,0=﹣3x+6,x=2.所以A(2,0),B(0,6);(2)直线与坐标轴围成的三角形的面积=S△ABO=×2×6=6.例题3:求一次函数y=x+、一次函数y=﹣2x+6与x轴围成的三角形面积.分析:分别设一次函数y=x+、一次函数y=﹣2x+6与x轴的交点为A、B,两函数图象的交点为C,则可分别求得A、B、C的坐标,则可求得△ABC的面积.解:设一次函数y=x+、一次函数y=﹣2x+6与x轴的交点为A、B,两函数图象的交点为C,在y=x+中,令y=0可解得x=﹣1,故A(﹣1,0),在y=﹣2x+6中,令y=0可解得x=3,故B(3,0),∴AB=3﹣(﹣1)=4,联立两函数解析式可得,解得,故C(2,2),∴在△ABC中,AB边上的高为2,∴S△ABC =×4×2=4,即一次函数y=x+、一次函数y=﹣2x+6与x轴围成的三角形面积为4.例题4:已知一次函数的图象与x轴交于点A(6,0),又与正比例函数的图象交于点B,点B在第一象限,且横坐标为4,如果△AOB(O为坐标原点)的面积为15,求这个一次函数与正比例函数的函数关系式.分析:如图作BC⊥OA于C,先根据三角形面积公式求出BC=5,则B点坐标为(4,5),然后利用待定系数法分别求正比例函数和一次函数解析式.解:如图,作BC⊥OA于C,∵S△OAB=OA•BC,∴×6×BC=15,∴BC=5,∴B点坐标为(4,5),设正比的解析式为y=kx+b,把A(6,0)、B(4,5)代入得,解得,∴一次函数解析式为y=﹣x+15.例题5:如图,已知一次函数图象交正比例函数图象于第二象限的A点,交x轴于点B(﹣6,0),△AOB的面积为15,且AB=AO,求正比例函数和一次函数的解析式分析:作AC⊥OB于C点,如图,根据等腰三角形的性质得BC=OC=BC=3,则C(﹣3,0),再利用三角形面积公式得×6•AC=15,解得AC=5,所以A(﹣3,5),然后利用待定系数法分别求直线OA的解析式和直线AB的解析式即可.解:作AC⊥OB于C点,如图,∵AB=AO,∴BC=OC=BC=3,∴C(﹣3,0),∵△AOB的面积为15,∴OB •AC=15,即×6×AC=15,解得AC=5,∴A(﹣3,5),设直线OA的解析式为y=kx,把A(﹣3,5)代入得﹣3k=5,解得k=﹣,∴直线OA的解析式为y=﹣x;设直线AB的解析式为y=ax+b,把A(﹣3,5)、B (﹣6,0)分别代入得,解得,∴直线AB的解析式为y=x+10,即正比例函数和一次函数的解析式分别为y=﹣x,y=x+10例题6:已知函数y=(m+1)x+2m﹣6,(1)若函数图象过(﹣1,2),求此函数的解析式.(2)若函数图象与直线y=2x+5平行,求其函数的解析式.(3)求满足(2)条件的直线与直线y=﹣3x+1的交点,并求出这两条直线与y轴所围成三角形的面积.分析:(1)将点(﹣1,2)代入函数解析式求出m即可;(2)根据两直线平行即斜率相等,即可得关于m 的方程,解方程即可得;(3)联立方程组求得两直线交点坐标,再求出两直线与y轴的交点坐标,根据三角形面积公式列式计算即可.解:(1)∵函数y=(m+1)x+2m﹣6的图象过(﹣1,2),∴2=(m+1)×(﹣1)+2m﹣6,解得:m=9,故此函数的解析式为:y=10x+12;(2)由函数图象与直线y=2x+5平行知二者斜率相等,即m+1=2,解得:m=1,故函数的解析式为:y=2x﹣4;(3)如图,由题意,得:,解得:,∴两直线的交点A(1,﹣2),y=2x﹣4与y轴交点B(0,﹣4),y=﹣3x+1与y轴交点C(0,1)∴S△ABC=×5×1=.例题7:如图,直线y=kx+6与x轴、y轴分别交于点E、F,点E的坐标为(﹣3,0),点A的坐标为(﹣2.5,0).(1)求k的值;(2)若点P(x,y)是第二象限内的直线上的一个动点,在点P的运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;(3)探究:当点P运动到什么位置(求点P 的坐标)时,△OPA的面积为5,并说明理由.分析:(1)由直线与x 轴的交点的坐标,代入即可求出k 的值;(2)过点P 作x 轴的垂线段,能够发现P 点到x 轴的距离为P 点的纵坐标,代入直线方程用x 表示出来P 点的纵坐标,再套用三角形面积公式即可得出结论,再由点P 在第二象限,即可确定x 的取值范围;(3)分两种情况,一种P 点在x 轴上方,一种在x 轴下方,分类讨论即可得出结论.解:(1)∵点E (﹣3,0)在直线y =kx+6的图象上,∴有0=-3k+6,解得:k =2.故k 的值为2.(2)过点P 作PB ⊥x 轴,垂足为点B ,如图1.∵点P (x ,y )是第二象限内的直线上的一个动点,∴P 点横坐标介于E 、F 的横坐标之间,∴﹣3<x <0.∵点P 在直线y =2x+6上,∴y =2x+6.∵PB ⊥x 轴,且P 点在第二象限,且点A 的坐标为(-2.5,0),∴PB =y =2x+6,OA =2.5.∴△OPA 的面积S =21·OA •PB =2.5x+7.5.故△OPA 的面积S 与x 的函数关系式为S =2.5x+7.5(-3<x <0).(3)∵令(2)中的关系式中x =0,解得S =7.5>5,∴若点P 在x 轴上方时,必在第二象限,点P 在x 轴下方时,必在第三象限.①当点P 在x 轴上方时,有△OPA 的面积S =2.5x+7.5,令S =5,即2.5x+7.5,解得:x=-1.此时点P 的坐标为(-1,4);②当点P 在x 轴下方时,如图2,此时PB=-y=-2x-6,△OPA 的面积S =21·OA •PB =0.5·×2.5×(﹣2x ﹣6)=﹣2.5x ﹣7.5=5,解得:x=-5.此时点P 的坐标为(-5,-4).综上可知:点P 运动到(-1,4)或(-5,-4)时,△OPA 的面积为5.例题8:如图,已知l 1:y =2x+m 经过点(﹣3,﹣2),它与x 轴,y 轴分别交于点B 、A ,直线l 2:y =kx+b 经过点(2,﹣2)且与y 轴交于点C (0,﹣3),与x 轴交于点D .(1)求直线l 1,l 2的解析式;(2)若直线l 1与l 2交于点P ,求S △ACP :S △ACD 的值分析:(1)利用待定系数法求得两直线的解析式即可;(2)观察两个三角形,它们具有相同的底边,因此它们面积的比就是它们高的比,即点P 和点D 横坐标绝对值的比.解:(1)∵l 1:y =2x+m 经过点(﹣3,﹣2),∴﹣2=2×(﹣3)+m ,解得:m =4,∴l 1:y =2x+4;∵l 2:y =kx+b 经过点(2,﹣2)且与y 轴交于点C (0,﹣3),∴,解得:k =,b =﹣3,∴l 2:y =x ﹣3;(2)令,解得:,∴点P (﹣,),∵△ACP 和△ABD 同底,∴面积的比等于高的比,∴S :S =PM :DO =:6=7:9.例题9:如图,已知直线y=x+4与x轴、y轴交于A,B两点,直线l经过原点,与线段AB交于点C,并把△AOB的面积分为2:3两部分,求直线l的解析式.分析:根据直线y=x+4的解析式可求出A、B两点的坐标,当直线l把△ABO的面积分为S△AOC:S△BOC=2:3时,作CF⊥OA于F,CE⊥OB于E,可分别求出△AOB与△AOC的面积,再根据其面积公式可求出两直线交点的坐标,从而求出其解析式;当直线l把△ABO的面积分为S△AOC:S△BOC=2:3时,同(1).解:直线l的解析式为:y=kx,对于直线y=x+4的解析式,当x=0时,y=4,y=0时,x=﹣4,∴A(﹣4,0)、B(0,4),∴OA=4,OB=4,∴S△AOB=×4×4=8,当直线l把△AOB的面积分为S△AOC:S△BOC=2:3时,S△AOC=,作CF⊥OA于F,CE⊥OB于E,∴×AO•CF=,即×4×CF=,∴CF=.当y=时,x=﹣,则=﹣k,解得,k=﹣,∴直线l的解析式为y=﹣x;当直线l把△ABO的面积分为S△AOC:S △BOC=3:2时,同理求得CF=,解得直线l的解析式为y=﹣x.故答案为y=﹣x或y=﹣x.例题10:如图,直线l1的解析表达式为:y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.(1)求点D的坐标;(2)求直线l2的解析表达式;(3)求△ADC的面积;(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标分析:(1)已知l1的解析式,令y=0求出x的值即可;(2)设l2的解析式为y=kx+b,由图联立方程组求出k,b的值;(3)联立方程组,求出交点C的坐标,继而可求出S△ADC;(4)△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是点C到AD的距离.解:(1)由y=﹣3x+3,令y=0,得﹣3x+3=0,∴x=1,∴D(1,0);(2)设直线l2的解析表达式为y=kx+b,由图象知:x=4,y=0;x=3,,代入表达式y=kx+b,∴,∴,∴直线l2的解析表达式为;(3)由,解得,∴C(2,﹣3),∵AD=3,∴S△ADC=×3×|﹣3|=;(4)△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是点C到直线AD的距离,即C纵坐标的绝对值=|﹣3|=3,则P到AD距离=3,∴P纵坐标的绝对值=3,点P不是点C,∴点P纵坐标是3,∵y=1.5x ﹣6,y=3,∴1.5x﹣6=3x=6,所以P(6,3).跟踪练习1.如图,一次函数的图像与x轴交于点B(-6,0),交正比例函数的图像于点A,点A的横坐标为-4,△ABO的面积为15,求直线OA的解析式2.点B在直线y=-x+1上,且点B在第四象限,点A(2,0)、O(0,0),△ABO的面积为2,求点B的坐标3.如图,已知两直线y=0.5x+2.5和y=-x+1分别与x轴交于A、B两点,这两直线的交点为P.(1)求点P的坐标;(2)求△PAB的面积4.已知直线y=ax+b(b>0)与y轴交于点N,与x轴交于点A且与直线y=kx交于点M(2,3),如图它们与y轴围成的△MON的面积为5.(1)求这两条直线的函数关系式(2)求它们与x轴围成的三角形面积5.已知两条直线y=2x-3和y=6-x.(1)求出它们的交点A的坐标;(2)求出这两条直线与x轴围成的三角形的面积6.已知直线y=2x+3与直线y=-2x-1与y轴分别交于点A、B.(1)求两直线交点C的坐标;(2)求△ABC的面积;(3)在直线BC上能否找到点P,使得△APC的面积为6,求出点P的坐标,若不能请说明理由.7.如图,已知直线y=x+6的图象与x轴、y轴交于A、B两点.(1)求点A、点B的坐标和△AOB的面积.(2)求线段AB的长.(3)若直线l经过原点,与线段AB交于点P(P为一动点),把△AOB的面积分成2:1两部分,求直线L的解析式.8.已知如图,直线l1:y=﹣x+4与x轴、y轴分别交于点A、点B,另一直线l2:y=kx+b(k≠0)经过点C(4,0),且把△AOB分成两部分.(1)若l1∥l2,求过点C的直线的解析式.(2)若△AOB被直线l2分成的两部分面积相等,求过点C的直线的解析式.9.已知:如图,直线y=kx+6与x轴y轴分别交于点E,F.点E的坐标为(8,0),点A的坐标为(6,0).(1)求k的值;(2)若点P(x,y)是第一象限内的直线y=kx+6上的一个动点,当点P运动过程中,试写出△OPA 的面积S与x的函数关系式,并写出自变量x的取值范围;(3)探究:当P运动到什么位置时,△OPA的面积为9,并说明理由10.如图,直线y=kx+12与x轴y轴分别相交于点E,F.点E的坐标(16,0),点A的坐标为(12,0).点P (x,y)是第一象限内的直线上的一个动点(点P不与点E,F重合).(1)求k的值;(2)在点P运动的过程中,求出△OPA的面积S与x的函数关系式.(3)是否存在点P(x,y),使△OPA的面积为△OEF的面积的?若存在,求此时点P的坐标;若不存在请说明理由.11.已知正比例函数y=k1x和一次函数y=k2x+br的图象如图所示,它们的交点A(﹣3,4),且OB=OA.(1)求正比例函数和一次函数的解析式;(2)求△AOB的面积和周长.12.直线PA 是一次函数y=x+n 的图像,直线PB 是一次函数y=-2x+m (m >n >0)的图像,(1)用m 、n 表示A 、B 、P 的坐标(2)直线PB 交y 轴于点Q ,四边形PQOB 的面积是65,AB=2,求直线PA 、直线PB 的解析式13.△AOB 的顶点O (0,0)、A (2,1)、B (10,1),直线CD⊥x 轴且△AOB 面积二等分,若D (x ,0),求x 的值14.如图,已知由x 轴、一次函数y =kx+4(k <0)的图象及分别过点C (1,0)、D (4,0)两点作平行于y 轴的两条直线所围成的图形ABDC 的面积为7,试求这个一次函数的解析式.15.已知长方形ABCD 的边长AB =9,AD =3,现将此长方形置于平面直角坐标系中,使AB 在x 轴的正半轴上,经过点C 的直线y =x ﹣2与x 轴交于点E ,与y 轴交于点F .(1)求点E 、B 的坐标;(2)求四边形AECD 的面积;(3)在y 轴上是否存在一点P ,使△PEF 为等腰三角形?若存在,则求出点P 的坐标;若不存在,请说明理由.16.正方形ABCD 的边长为4,将此正方形置于平面直角坐标系中,使AB 边落在X 轴的正半轴上,且A 点的坐标是(1,0).(1)直线y =x经过点C ,且与x 轴交与点E ,求四边形AECD 的面积;(2)若直线l 经过点E ,且将正方形ABCD 分成面积相等的两部分,求直线l 的解析式;(3)若直线l 1经过点F (﹣,0),且与直线y =3x 平行,将(2)中直线l 沿着y 轴向上平移个单位交轴x 于点M ,交直线l 1于点N ,求△NMF 的面积.17.直线L 1:y=kx+b 过点B (-1,0)与y 轴交于点C,直线L 2:y=mx+n 与L1交于点P (2,5),且过点A (6,0),过点C 与L 2平行的直线交x 轴与点D .(1)求直线CD 的函数解析式(2)求四边形APCD 的面积.18.直线y=-33x+1与x 轴y 轴分别交点A 、B ,以线段AB 为直角边在第一象限内作等腰直角△ABC, BAC=900,点P (a ,1/2)在第二象限,△ABP 的面积与△ABC 面积相等,求a 的值.19.已知直线y=-x+2与x 轴、y 轴分别交于点A 和点B ,另一直线y=kx+b (k ≠0)经过点C (1,0),且把△AOB 分为两部分,(1)若△AOB 被分成的两部分面积相等,求k 和b 的值;(2)若△AOB 被分成的两部分面积为1:5,求k 和b 的值20.直线y=-32x+3交x 、y 两坐标轴分别于点A 、B ,交直线y=2x-1于点P ,直线y=2x-1交x ,y 坐标轴分别为C 、D ,求△PAC 和△PBC 的面积各是多少?21.如图,直线l 1的解析式为y =3x ﹣3,且l 1与x 轴交于点D ,直线l 2经过点A 、B ,直线l 1,l 2相交于点C .(1)求点D 的坐标;(2)求△ADC 的面积.22.已知直线l 1:y =k 1x+b 1经过点(-1,6)和(1,2),它和x 轴、y 轴分别交于B 和A ;直线l 2:y =-0.5x-3,它和x 轴、y 轴的交点分别是D 和C .(1)求直线l 1的解析式;(2)求四边形ABCD 的面积;(3)设直线l 1与l 2交于点P ,求△PBC 的面积23.如图,直角坐标系xoy 中,一次函数y=-0.5x+5的图像l 1分别与x ,y 轴交于A 、B 两点,正比例函数的图像l 2与l 1交于点C (m ,4).(1)求m 的值及l 2的解析式;(2)求S △AOC -S △BOC 的值;(3)一次函数y=kx+1的图像为l 3,且l 1,l 2,l 3不能围成三角形,直接写出k 的值一次函数与面积问题答案1.解:过点A 作AC ⊥OB 于点C ,设AC =m (m >0)由△AOB 的面积为15,OB =6得21OB ×m =15,即21×6×m =15,∴m =5,得A (-4,5).设正比例函数解析式y =k 1x (k 1≠0)把x =-4,y =5代入得k 1=−45,∴y =−45x .设一次函数解析式y =k 2x +b (k 2≠0),把x =-4,y =5和x =-6,y =0代入得:⎩⎨⎧+-=+-=b k b k 226045,解得k 2=25,b=15.∴y =25x+15. 2.点B 在直线y=-x+1上,且点B 在第四象限,点A (2,0)、O (0,0),△ABO 的面积为2,求点B 的坐标解:过点B 作BC ⊥x 轴于点C ,∵△ABO 的面积为2,∴21OA ×BC=2,OA ×BC=4,∵OA=2,∴BC=2,∵B 点在第四象限,∴B 点的纵坐标是-2,∵B 点在y=-x+1上,∴当y=-2时,-x+1=-2,x=3,∴B 的坐标是(3,-2)3.分析:(1)联立两个解析式,组成方程组,再解方程即可得到P 点坐标;(2)分别利用函数解析式计算出A 、B 两点的坐标,在求△APB 的面积即可.解:(1),解得,故P (﹣1,2);(2)∵函数y =()x+2.5中,当y =0时,x =﹣5,∴A (﹣5,0),∵函数y =﹣x+1中,当y =0时,x =1,∴B (1,0),∴S △APB =×6×2=6.4.(1)y=kx 过M(2,3),∴3=2k,k=32,∴y=32x.∵y=ax+b 过M(2,3),则2a+b=3,b=3-2a,∴y=ax+(3-2a),∵S ΔOMN =21×|3-2a|×2=|3-2a|=5,∴2a-3=±5,a=4或a=-1,∴直线y=ax+b 的解析式为y=4x+5或y=-x-5;(2)①当y=4x+5时,令y=0得x=-5/4,∴y=4x+5与x 轴交于A(-5/4,0),S ΔOAM =21×45×3=15/8;②当y=-x-5时,令y=0得x=-5,∴y=-x-5与x 轴交于B(-5,0),S ΔOBM =21×5×3=15/2 5.分析:(1)根据两直线相交的问题,通过解方程组即可得到两直线的交点坐标;(2)先根据x 轴上点的坐标特征求出两直线与x 轴的交点坐标,然后根据三角形面积公式求解.解:(1)解方程组得,所以两直线的交点坐标为(3,3);(2)当y =0时,2x ﹣3=0,解得x =,则直线y 1=2x ﹣3与x 轴的交点坐标为(,0);当y =0时,6﹣x =0,解得x =6,则直线y 2=6﹣x 与x 轴的交点坐标为(0,6);所以这两条直线与x 轴所围成的三角形面积=×(6﹣)×3=. 6.分析:(1)解方程组即可得出交点坐标;(2)分别求出A ,B 的坐标即可求出三角形的面积;(3)假设在直线y =﹣2x ﹣1上存在点P 使得S △APC =6,设点P (x ,y ),分类讨论x 的取值后即可得出答案;解:(1)解方程组解得:x =﹣1,y =1,所以点C 的坐标为(﹣1,1);(2)直线y =2x+3与y 轴的交点A 的坐标为(0,3),直线y =﹣2x ﹣1与y 轴的交点B 的坐标为(0,﹣1),所以AB =4,S △ABC =×4×|﹣1|=2;(3)假设在直线y=﹣2x﹣1上存在点P使得S△APC=6,设点P(x,y),则①当x<﹣1时,有S△APB﹣S △ABC=6,即×4×|x|﹣2=6,解得x=4(舍去)或x=﹣4,把x=﹣4代入y=﹣2x﹣1,得y=7,②当x>0时,有S△APB+S△ABC=6,即×4×x+2=6,解得x=2,把x=2代入y=﹣2x﹣1得y=﹣5,所以在直线y=﹣2x﹣1上存在点P(﹣4,7)和P(2,﹣5),使得S△APC=6.7.分析:(1)把x=0,和y=0代入解析式y=x+6解答即可,再利用三角形的面积公式计算即可;(2)利用两点间的距离公式计算即可;(3)设P点的坐标为(m,m+6),然后分两种情况求得P的坐标,进而利用待定系数法即可求得直线L的解析式.解:(1)∵直线y=x+6的图象与x轴、y轴交于A、B两点,∴A(0,6)B(﹣6,0),∴OA=6,OB=6,∴S△AOB =OA•OB=×6×6=18;(2)∵A(0,6)B(﹣6,0),∴AB==6;(3)设P点的坐标为(m,m+6),∴S△POB=OB•(m+6)=3(m+6),∵把△AOB的面积分成2:1两部分,∴S△POB:S△AOB=2:3或1:3,∴=或,解得m=﹣2或﹣4,∴P(﹣2,4)或(﹣4,2),设直线L的解析式为y=kx,∴4=﹣2k或2=﹣4k,解得k=﹣2或k=﹣,∴直线L的解析式为或y=﹣2x.8.分析:(1)当l1∥l2时,k=﹣,然后将C(4,0)代入l2的解析式中即可求出b的值.(2)容易求得C(4,0),且C是OA的中点,所以直线l2是△AOB的中线,从而求出C的直线解析式.解:(1)由题意可知:k=﹣,∴直线的解析式为:y=﹣x+b,把(4,0)代入上式,∴b=2,∴直线的解析式为:y=﹣x+2;(2)令y=0代入y=﹣x+4,∴x=8,∴点A(8,0),令x=0代入y=﹣x+4,y=4,∴B (0,4),∴C是OA的中点,若△AOB被直线l2分成的两部分面积相等,则直线l2与△AOB的中线重合,即直线l2过点B把(0,4)和(4,0)代入y=kx+b,∴,解得:,∴直线l2的解析式为:y=﹣x+4 9.分析:(1)直接把E的坐标为(8,0)代入y=kx+6就可以求出k的值;(2)根据三角形的面积公式S△OPA=,然后把y转换成x,△OPA的面积S与x的函数关系式就可以求出了;(3)直接把S=9代入(2)中的解析式里.就可以求出x,然后确定P的坐标.解:(1)把点E(8,0)代入y=kx+6,得8k+6=0,解得,k=;(2)∵点P(x,y)在第一象限内的直线y=x+6上,∴点P的坐标为(x,x+6)且x>0,x+6>0,过点P作PD⊥x轴于点D,则△OPA的面积=OA×PD,即.∴(0<x<8);(3)由S=9得,,解得x=4,把x=4代入y=x+6,得y=×4+6=3,这时,P有坐标为(4,3);即当P运动到点(4,3)这个位置时,△OPA的面积为9.10.分析:(1)直接把点E的坐标代入直线y=kx+12求出k的值即可;(2)过点P作PD⊥OA于点D,用x表示出PD的长,根据三角形的面积公式即可得出结论;(3)把△OPA的面积为△OEF的面积的,得出△OPA的面积代入(2)中关系式,求出x的值,把x的值代入直线y=﹣x+12即可得出结论.解:(1)∵直线y=kx+12与x轴交于点E,且点E的坐标(16,0),∴16k+12=0,解得k=﹣,∴y=﹣x+12;(2)过点P作PD⊥OA于点D,∵点P(x,y)是第一象限内的直线上的一个动点,∴PD=﹣x+12.∵点A的坐标为(12,0),∴S=×12×(﹣x+12)=﹣x+72;(3)∵y=﹣x+12,∴当y=0时,x=16,∴OF=16,OE=16,∵△OPA的面积为△OEF的面积的,∴△OPA的面积=,∴﹣x+72=36,解得x=8,将x=8代入y=﹣x+12得y=6,∴P(8,6).11.分析:(1)先利用两点间的距离公式计算出OA=5,易得OB=3,则B(3,0),然后利用待定系数分别求正比例函数和一次函数的解析式;(2)先利用两点间的距离公式计算出AB,然后根据三角形面积公式和周长的定义求解.解:(1)∵点A(﹣3,4),∴OA==5,而OB=OA,∴OB=3,∴B(3,0),把A(﹣3,4)代入y=k1x得﹣3k1=4,解得k1=﹣,∴自变量函数解析式为y=﹣x;把A(﹣3,4)、B(3,0)分别代入y=k2x+b得,解得,∴一次函数解析式为y=﹣x+2;(2)AB==2,△AOB的面积=×3×4=6,△AOB的周长=3+5+2=8+2.12.分析:二元一次方程组与一次函数的综合运用,再加上四边形的面积.首先根据一次函数求出点的坐标,求第(2)问时,设PB与y轴交于一点M,四边形面积等于三角形MOB的面积﹣三角形MQP的面积,从而得出结果.解:(1)设A(a,0),B(b,0),P(x,y).由题意得:a+n=0①,﹣2b+m=0②,由①②得a=﹣n,b=.解方程组,得.故A(﹣n,0),B(,0),P(,);(2)设PB与y轴交于一点M,则M(0,m),Q(0,n).则S MOB=m=,S MQP==.所以=③,又=2④,由③④联立,解得.∴点P的坐标为(,),直线PA的解析式为y=x+1,直线PB的解析式为y=﹣2x+2.13.分析:先用待定系数法求出直线OB的解析式,再设CD交AB于点E,交OB于点F,故可得出F点的坐标及EF、EB、AB的长,再根据S△BEF=S△AOB即可得出x的值,进而得出结论.解:设直线OB的解析式为y=kx(k≠0),∵B(10,1),∴1=10k,解得k=,∴直线OB的解析式为y=x,∵D(x,0),∴F(x,),∴EF=1﹣,EB=10﹣x,AB=10﹣2=8,∴S△BEF=××(10﹣x)=,∴S△AOB=×8×1=2×,解得x=10﹣2.14.分析:根据点A、B在一次函数y=kx+4的图象上得出A(1,k+4),B(4,4k+4)且k+4>0,4k+4>O,根据四边形ABDC的面积为7代入即可求出k的值.解:∵点A、B在一次函数y=kx+4的图象上,∴A(1,k+4),B(4,4k+4)且k+4>0,4k+4>O,∵四边形ABDC 的面积为7,∴[(k+4)+(4k+4)]•3=7,∴k=﹣,∴一次函数的解析式为y=﹣x+4.15.分析:(1)对于直线y=x﹣2,分别令x与y为0求出y与x的值,确定出E与F坐标,根据四边形ABCD为矩形,得到对边相等,求出BC的长,即为C纵坐标,代入直线解析式求出C横坐标,即可确定出B坐标;(2)由B与E的横坐标之差求出EB的长,四边形AECD面积=矩形ABCD面积﹣三角形ECB面积,求出即可;(3)在y轴上存在一点P,使△PEF为等腰三角形,如图所示,分三种情况考虑:若P1F=EF;若EF=P2F;若P3F=P3E;分别求出P的坐标即可.解:(1)对于直线y=x﹣2,令x=0,得到y=﹣2;令y=0,得到x=4,∴E(4,0),F(0,﹣2),∵四边形ABCD 为矩形,∴BC =AD =3,DC =AB =9,把y =3代入直线y =x ﹣2,得:x =10,即B (10,0);(2)∵E (4,0),B (10,0),∴EB =10﹣4=6,∴S 四边形AECD =S 矩形ABCD ﹣S △ECB =9×3﹣×6×3=27﹣9=18;(3)存在,如图所示,分三种情况考虑:若P 1F =EF ==2,∴OP 1=OF+P 1F =2+2,此时P 1(0,﹣2﹣2);若EF =P 2F =2,∴OP 2=P 2F ﹣OF =2﹣2,此时P 2(0,2﹣2);若P 3F =P 3E ,此时P 3在线段EF 垂直平分线上,线段EF 垂直平分线为y+1=﹣2(x ﹣2),即y =﹣2x+3,令x =0,得到y =3,此时P 3(0,3),综上,在y 轴上存在一点P ,使△PEF 为等腰三角形,此时P 的坐标为(0,﹣2﹣2)或(0,2﹣2)或(0,3).16.分析:(1)求得C 的坐标,以及E 的坐标,则求得AE 的长,根据直角梯形的面积公式即可求得四边形的面积;(2)经过点E 且将正方形ABCD 分成面积相等的两部分的直线与CD 的交点F 到C 的距离一定等于AE ,则F 的坐标可以求得,利用待定系数法即可求得直线EF 的解析式;(3)根据直线l 1经过点F (﹣,0)且与直线y =3x 平行,知k =3,把F 的坐标代入即可求出b 的值即可得出直线11,同理求出解析式y =2x ﹣3,进一步求出M 、N 的坐标,利用三角形的面积公式即可求出△MNF 的面积..解:(1)在y =x 中,令y =4,即x =4,解得:x =5,则B 的坐标是(5,0);令y =0,即x =0,解得:x =2,则E 的坐标是(2,0).则OB =5,OE =2,BE =OB ﹣OA =5﹣2=3,∴AE =AB ﹣BE =4﹣3=1,边形AECD =(AE+CD )•AD =(4+1)×4=10;(2)经过点E 且将正方形ABCD 分成面积相等的两部分,则直线与CD 的交点F ,必有CF =AE =1,则F 的坐标是(4,4).设直线的解析式是y =kx+b ,则,解得.则直线l 的解析式是:y =2x ﹣4;(3)∵直线l 1经过点F (﹣,0)且与直线y =3x 平行,设直线11的解析式是y 1=kx+b ,则k =3,代入得:0=3×(﹣)+b ,解得b =,∴y 1=3x+,已知将(2)中直线l 沿着y 轴向上平移个单位,则所得的直线的解析式是y =2x ﹣4+,即:y =2x ﹣3,当y =0时,x =,∴M (,0),解方程组得:,即:N (﹣7,﹣19),S △NMF =×[﹣(﹣)]×|﹣19|=.答:△NMF 的面积是.17.将B 和P 点带入y=kx+b 中,得:0=-k+b,5=2k+b 即:k=b=35,所以L1为:y=35 x+35,C 的坐标:(0,5/3) 将P 和A 带入y=mx+n 中,得5=2m+n ,0=6m+n ,解得:m=-5/4,n=15/2,即L 2的方程为:y=-45x+215,∵CD ∥AP , ∴CD 直线的解析式可以设为:y=-45x+b ′,∵x=0时,y=35×0+35=35,∴C 的坐标是(0,35),把C 的坐标带入CD 的解析式中,得b ′=35,∴CD 的直线解析式为y=-45x+35,由y=-45x+35与x 轴交于点D ,得D 坐标为:(4/3,0),由P 做PM ⊥x 轴于M ,则PM=5,∵A 的坐标是(6,0),B 的坐标是(-1,0),D 的坐标是(4/3,0),C 的坐标是(0,35),∴AB=7,BD=37,OC=35,∴四边形APCD 的面积=三角形BAP 面积-三角形BDC 面积=21×7×5-21×37×35=9140 18.分析:由已知求出A 、B 的坐标,求出三角形ABC 的面积,再利用S △ABP =S △ABC 建立含a 的方程,把S △ABP 表示成有边落在坐标轴上的三角形面积和、差,通过解方程求得答案.解:连接OP ,∵直线与x 轴、y 轴分别交于点A 、B ,∴A (,0),B (0,1),AB ==2,∴S △ABP =S △ABC =2,又S △ABP =S △OPB +S △OAB ﹣S △AOP ,∴﹣a ×1+×1﹣=4,解得a =.答:a 的值为a =.19.分析:(1)△AOB 被分成的两部分面积相等,那么被分成的两部分都应该是三角形AOB 的面积的一半,那么直线y =kx+b (k ≠0)必过B 点,因此根据B ,C 两点的函数关系式可得出,直线的函数式.(2)若△AOB 被分成的两部分面积比为1:5,那么被分成的两部分中小三角形的面积就应该是大三角形面积的,已知了直线过C 点,则小三角形的底边是大三角形的OA 边的一半,故小三角形的高应该是OB 的,即直线经过的这点的纵坐标应该是.那么这点应该在y 轴和AB 上,可分这两种情况进行计算,运用待定系数法求函数的解析式.解:(1)由题意知:直线y =kx+b (k ≠0)必过C 点,∵C 是OA 的中点,∴直线y =kx+b 一定经过点B ,C ,如图(1)所示,把B ,C 的坐标代入可得:,解得k =﹣2,b =2;(2)∵S △AOB =×2×2=2,∵△AOB 被分成的两部分面积比为1:5,那么直线y =kx+b (k ≠0)与y 轴或AB 交点的纵坐标就应该是:2×2×=,①当y =kx+b (k ≠0)与直线y =﹣x+2相交时,交点为D ,如图(2)所示,当y =时,直线y =﹣x+2与y =kx+b (k ≠0)的交点D 的横坐标就应该是﹣x+2=,∴x =,即交点D 的坐标为(,),又根据C 点的坐标为(1,0),可得:,∴,②当y =kx+b (k ≠0)与y 轴相交时,交点为E ,如图(3)所示,∴交点E 的坐标就应该是(0,),又有C 点的坐标(1,0),可得:,∴,因此:k =2,b =﹣2或k =﹣,b =.20.解:过P 分别向x 轴、y 轴分别做PM ⊥x 轴于M ,PN ⊥y 轴于N ,由y=-32x+3和y=2x-1联立可得x=23,y=2,∴p 的坐标是(23,2),∴PM=23,PN=2,易求得A 、B 、C 、D 的坐标分别为(29,0),(0,3),(21,0),(0,-1),∴AC=4,BD=4,OC=21,∴S △PAC =21AC ·PM=3,S △PBC =S △PBD -S △BCD =21BD ·PN-21BD ·OC=4-1=3. 21.分析:(1)利用直线l 1的解析式令y =0,求出x 的值即可得到点D 的坐标;(2)根据点A 、B 的坐标,利用待定系数法求出直线l 2的解析式,得到点A 的坐标,再联立直线l 1,l 2的解析式,求出点C 的坐标,然后利用三角形的面积公式列式进行计算即可得解.解:(1)∵直线l 1的解析式为y =3x ﹣3,且l 1与x 轴交于点D ,∴令y =0,得x =1,∴D (1,0);(2)设直线l 2的解析式为y =kx+b (k ≠0),∵A (4,0),B (3,),∴,解得,∴直线l 2的解析式为y =﹣x+6.由,解得,∴C (2,3).∵AD =4﹣1=3,∴S △ADC =×3×3=.22.分析:(1)因为点(﹣1,6)和(1,2)在直线l 1:y =k 1x+b 1,所以把这两点的坐标代入解析式求出k 1、b 1的值就可以了.(2)知道直线l 2的解析式就可以求出C 、D 的坐标,根据l 1的解析式就可以求出A 、B 的坐标就可以求出BD 、OA 、OC 的长利用三角形的面积公式求出四边形ABCD 的面积.(3)利用l 1、l 2的解析式求出交点坐标P ,就可以求出△PDB 的面积,然后求出三角形DCB 的面积,这两个三角形的面积之差就是△PBC 的面积. 解:(1)∵直线l 1:y =k 1x+b 1经过点(﹣1,6)和(1,2),∴,解得,∴直线l 1的解析式为:y =﹣2x+4;(2)∵直线l 1的解析式为:y =﹣2x+4,当x =0时,y =4,∴A (0,4),∴OA =4,当y =0时,x =2,∴B (2,0),∴OB =2,∵直线l 2:y =﹣x ﹣3,当x =0时,y =﹣3,即C (0,﹣3).∴OC =3,当y =0时,x =﹣6,即D (﹣6,0),∴OD =6,∴BD =8,∴S 四边形ABCD =+=12+16=28;(3)过点P 作PE ⊥BD 于E ,由l 1、l 2的解析式得:解得:,∴P (,﹣),∴OE =,PE =,∴S △PBC =﹣=﹣12=.23.分析:(1)先求得点C 的坐标,再运用待定系数法即可得到l 2的解析式;(2)过C 作CD ⊥AO 于D ,CE ⊥BO 于E ,则CD =4,CE =2,再根据A (10,0),B (0,5),可得AO =10,BO =5,进而得出S △AOC ﹣S △BOC 的值;(3)分三种情况:当l 3经过点C (2,4)时,k =1.5;当l 2,l 3平行时,k =2;当11,l 3平行时,k =﹣0.5;故k 的值为1.5或2或﹣0.5.解:(1)把C (m ,4)代入一次函数y =﹣0.5x+5,可得4=﹣0.5m+5,解得m =2,∴C (2,4),设l 2的解析式为y =ax ,则4=2a ,解得a =2,∴l 2的解析式为y =2x ;(2)如图,过C 作CD ⊥AO 于D ,CE ⊥BO 于E ,则CD =4,CE =2,y =﹣0.5x+5,令x =0,则y =5;令y =0,则x =10,∴A (10,0),B (0,5),∴AO =10,BO =5,∴S △AOC ﹣S △BOC =0.5×10×4﹣0.5×5×2=20﹣5=15;(3)一次函数y =kx+1的图象为l 3,且11,l 2,l 3不能围成三角形,∴当l 3经过点C (2,4)时,k =1.5;当l 2,l 3平行时,k =2;当11,l 3平行时,k =﹣0.5;故k 的值为1.5或2或﹣0.5.。
一次函数中的面积问题

一次函数中的面积问题姓名:一、基础图形面积问题1、如图,在平面直角坐标系中,已知A (-1,3),B (3,-2),求AOB ∆的面积2、如图,直线AB :1+=x y 与x 轴、y 轴分别交于点A 、B ,直线CD :2-=kx y 与x 轴、y 轴分别交于点C 、点D ,直线AB 与直线CD 交于点P ,若,4.5=∆APD S 求k3、4、在平面直角坐标系xOy 中,直线y =﹣2x +4与坐标轴所围成的三角形的面积等于5、的面积6、直线21y x =+和直线2y x =-+与x 轴分别交与A 、B 两点,并且两直线相交与点C,(1)求△ABC 的面积,(2)求四边形CDOB 的面积7、如图,在平面直角坐标系中,一次函数y =kx +b 的图象经过点A (6,0),与y 轴交于点B (0,﹣3), 与正比例函数y =2x 的图象相交于点C .(1)求此一次函数的解析式;(2)求出△OBC 的面积;(3)点D 在此坐标平面内,且知以O 、B 、C 、D 为顶点四边形是平行四边形,请直接写出符合条件的点D 的坐标.二、面积倍分、相等问题1、如图,已知直线y =x +3的图象与x ,y 的轴交于B ,A 两点,直线l 经过A 点,与线段OB 交于点C 且把△AOB 面积分为2:1两部分.(1)求线段OA ,OB 的长;(2)求直线l的解析式.O2、如图,在平面直角坐标系中,直线y=kx+b与x轴、y轴分别交于点A(3,0)、点B(0,2),以线段AB为直角边在第一象限内作等腰直角三角形ABC,∠BAC=90°.(1)求直线y=kx+b的解析式;(2)求出△ABC的面积;(3)若P(1,m)为坐标系中的一个动点,连结P A,PB.当△ABC与△ABP面积相等时,求m的值.3、综合与探究:如图,直线l1的表达式为y=﹣3x+3,与x轴交于点C,直线l2交x轴于点A,OA=4,l1与l2交于点B,过点B作BD⊥x轴于点D,BD=3.(1)求点C的坐标;(2)求直线l2的表达式;(3)求S△ABC的值;(4)在x轴上是否存在点P,使得S△ABP=2S△ABC?若存在,请直接写出点P的坐标;若不存在,请说明理由.三、分论讨论1、直线y=x+3的图像与x轴、y轴分别交于A、B两点,直线a经过原点与线段AB交于C,把△ABO的面积分为2:1的两部分,求直线a的函数解析式。
沪教版八年级 一次函数中的面积问题,带答案

1.能由一次函数的知识求有关图形的面积;2.能由已知图形的面积解决一次函数的有关问题; 3.体会一次函数的有关面积问题的解决思路.(此环节设计时间在10—15分钟)回顾上次课的预习思考内容,要求学生先画出一次函数的大致图形再解题.1.直线1y x =--与x 轴相交于点 ,与y 轴相交于点 ,与坐标轴围成的三角形面积为 .2.一次函数的图像经过(3,5),(—4,—9),则此一次函数的解析式为 ,一次函数与坐标轴围成的三角形面积为 .3.直线34y x =-+与直线21y x =-相交于P ,直线34y x =-+与x 轴相交于点A ,直线21y x =- 与x 轴相交于点B ,交点P 的坐标为 ,△ABP 面积为 . 参考答案:1.(—1,0),(0,—1),12; 2.21y x =-,14; 3.4(,0)3,1(,0)2,(1,1),512; 归纳总结:一次函数与坐标轴围成的面积可以推到出相应公式:22b S k∆=(此环节设计时间在50-60分钟)案例1:问题1:如图,已知直线l :22y x =-+与直线m :y x =交于点T ,求直线l 和直线m 与x 轴所围成的图形面积。
参考答案:解:由题意:(3,0),(0,3)A B - ∴1922AOBS OA OB =⋅= ∴11113232BOC AOBSOB C D S =⋅==∴11C D = 代入3y x =+得1(1,2)C -, 设直线l 的解析式:y kx = 代入1(1,2)C -得2k =- ∴直线l 的解析式2y x =- 同理:2(2,1)C -,∴直线l 的解析式12y x =-试一试:已知直线2y x =-+与x 轴、y 轴分别交于A 点和B 点,另一条直线(0)y kx b k =+≠经过点C (1,0),且把△AOB 分成两部分。
若△AOB 被分成的两部分面积比为1:5,求k 和b 的值.参考答案:22,33k b =-=或2,2k b ==-此环节设计时间在30分钟左右(20分钟练习+10分钟互动讲解)。
一次函数之面积问题(铅垂法)(人教版)(含答案)

一次函数之面积问题(铅垂法)(人教版)一、单选题(共8道,每道11分)1.如图,已知一次函数的图象经过A(5,-1),B(-3,-5)两点,则△AOB的面积为( )A. B.C.14D.28答案:C解题思路:试题难度:三颗星知识点:铅垂法求面积2.如图,已知一次函数的图象经过A(2,a),B(-1,b)两点,则△AOB的面积为( )A. B.5C.3D.答案:A解题思路:试题难度:三颗星知识点:铅垂法求面积3.如图,已知一次函数y=x-1的图象经过A(m,1),B(n,-2)两点,则△AOB的面积为( )A.3B.C.2D.答案:D解题思路:试题难度:三颗星知识点:铅垂法求面积4.如图,△ABC三个顶点的坐标分别为A(4,1),B(5,5),C(-1,2),则三角形的面积为( )A. B.C.21D.答案:D解题思路:试题难度:三颗星知识点:铅垂法求面积5.如图,已知一次函数的图象经过A(5,m),B(1,n)两点,点C(3,4),则△ABC 的面积为( )A.8B.4C.5D.6答案:B解题思路:试题难度:三颗星知识点:铅垂法求面积6.如图,已知一次函数的图象经过A(-5,-1),B(-1,n)两点,点C(-3,0),则△ABC的面积为( )A.8B.4C.5D.7答案:B解题思路:试题难度:三颗星知识点:铅垂法求面积7.如图,直线AB:分别与x轴、y轴交于点A,B,直线CD:y=x+b分别与x轴、y轴交于点C,D,直线AB与CD交于点P(8,5),则的面积为( )A.12B.16C.18D.20答案:D解题思路:试题难度:三颗星知识点:铅垂法求面积8.如图,直线与x轴、y轴分别交于A,B两点,直线与x 轴、y轴分别交于C,D两点.设直线,交于点P,则△PAD的面积为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:铅垂法求面积二、填空题(共1道,每道12分)9.如图,在平面直角坐标系中,四边形ABCD各顶点的坐标分别为A(-1,3),B(-3,-2),C(4,-3),D(3,2),则四边形ABCD的面积是____.答案:28 解题思路:试题难度:知识点:铅垂法求面积。
一次函数面积问题

一次函数面积问题
一次函数是指形如y = kx + b 的函数,其中k 和 b 是常数。
如果我们将这个函数画成图像,可以得到一条直线。
一次函数的面积问题通常指的是求解一条直线与坐标轴所围成的面积。
具体来说,如果我们有一个一次函数y = kx + b,我们可以将其表示为一条直线。
这条直线与x 轴和y 轴交于两个点,分别为(0, b) 和(-b/k, 0)。
这两个点就是直线所围成的矩形的两个顶点,我们可以计算出这个矩形的面积。
矩形的面积等于矩形的长乘以宽。
在这个问题中,矩形的长就是直线与x 轴的交点的x 坐标的绝对值,即|-b/k|。
矩形的宽就是直线与y 轴的交点的y 坐标的绝对值,即|b|。
因此,我们可以将这个矩形的面积表示为:
```
A = |-b/k| * |b|
```
需要注意的是,如果直线的斜率k 是正数,那么这个矩形的面积就是正值。
如果直线的斜率k 是负数,那么这个矩形的面积就是负值,但是我们通常会取其绝对值。
这就是一次函数面积问题的解法。
需要注意的是,这个问题只适用于一次函数,对于其他类型的函数,可能需要使用其他的方法来计算面积。
一次函数与面积结合问题解题技巧

一次函数与面积结合问题解题技巧全文共四篇示例,供读者参考第一篇示例:一次函数与面积结合问题解题技巧在数学中,一次函数是最基础的函数之一,它的图像是一条直线。
而面积则是一个二维概念,通常用来描述平面图形的大小。
一次函数与面积结合起来,可以帮助我们解决一些实际问题,例如求直线与X轴之间的面积、寻找最优解等。
在本文中,我们将介绍一些一次函数与面积结合问题的解题技巧。
一、基本概念在解决一次函数与面积结合问题时,首先需要了解一些基本概念。
一次函数的一般形式为y = kx + b,其中k为斜率,b为截距。
斜率表示函数的变化率,截距表示函数与Y轴的交点。
面积的计算公式为S = 底* 高,对于矩形和平行四边形,底和高即为长度和宽度;对于三角形,则一般取底边和高为两边。
二、求直线与X轴之间的面积当我们需要求一次函数与X轴之间的面积时,可以通过以下步骤进行:1. 找出函数与X轴的交点,即解方程kx + b = 0,得到交点的横坐标x0;2. 确定两个交点间的区间[a,b],其中a为交点的横坐标的较小值,b为较大值;3. 计算函数在区间[a,b]上的积分,即∫[a,b] (kx + b)dx;4. 根据积分的结果,确定函数与X轴之间的面积。
对于函数y = 2x + 3,我们需要求函数图像在[1,3]上与X轴之间的面积。
解方程2x + 3 = 0,得到交点的横坐标为-3/2;然后计算∫[1,3] (2x + 3)dx = x^2 + 3x,将上限和下限代入,得到面积为10.5。
三、寻找最优解在一些实际问题中,我们需要找到最优解,即使得面积最大或最小的情况。
在这种情况下,我们可以通过一次函数的性质来解决问题。
假设我们需要用一根长度为L的绳子围成一个长方形,求这个长方形的面积最大值。
设长方形的长为x,宽为y,则面积为xy。
根据题意,有2x + 2y = L,即x + y = L/2,可以将y表示为y = L/2 - x。
将y代入面积公式中,得到S = x(L/2 - x) = Lx/2 - x^2。
一次函数面积问题专题(含答案)

一次函數面積問題1、如图,一次函数的图像与x轴交于点B(-6,0),交正比例函数的图像于点A,点A的横坐标为-4,△ABC的面积为15,求直线OA的解析式。
2、直线y=x+3的图像与x轴、y轴分别交于A、B两点,直线a经过原点与线段AB交于C,把△ABO的面积分为2:1的两部分,求直线a的函数解析式。
3、直线PA是一次函数y=x+n的图像,直线PB是一次函数y=-2x+m(m>n>0)的图像,(1)用m、n表示A、B、P的坐标(2)四边形PQOB的面积是,AB=2,求点P的坐标4、△AOB的顶点O(0,0)、A(2,1)、B(10,1),直线CD⊥x轴且△AOB面积二等分,若D(m,0),求m的值5、点B在直线y=-x+1上,且点B在第四象限,点A(2,0)、O(0,0),△ABO 的面积为2,求点B的坐标。
6、直线y=-x+1与x轴y轴分别交点A、B,以线段AB为直角边在第一象限内作等腰直角△ABC, BAC=90°,点P(a,)在第二象限,△ABP的面积与△A BC 面积相等,求a的值.7、如图,已知两直线y=0.5x+2.5和y=-x+1分别与x轴交于A、B两点,这两直线的交点为P(1)求点P的坐标(2)求△PAB的面积8、已知直线y=ax+b(b>0)与y轴交于点N,与x轴交于点A且与直线y=kx交于点M(2,3),如图它们与y轴围成的△MON的面积为5,求(1)这两条直线的函数关系式(2)它们与x轴围成的三角形面积9、已知两条直线y=2x-3和y=5-x(1)求出它们的交点A的坐标(2)求出这两条直线与x轴围成的三角形的面积10、已知直线y=x+3的图像与x轴、y轴交于A、B两点,直线l经过原点,与线段AB交于点C,把△AOB的面积分为2:1的两部分,求直线l的解析式。
11、已知直线y=2x+3与直线y=-2x-1与y轴分别交于点A、B(1)求两直线交点C的坐标(2)求△ABC的面积(3)在直线BC上能否找到点P,使得△APC的面积為6,求出点P的坐标,若不能请说明理由。
一次函数之面积问题 (习题及答案).

一次函数之面积问题(习题)1.如图,一次函数y=kx+b 的图象经过A(-2,-1),B(1,3)两点,并且与x 轴交于点C,与y 轴交于点D,则△AOB 的面积为.第1 题图第2 题图2.如图,直线y =1x +1 经过点A(1,m),B(4,n),点C 的坐2标为(2,5),则△ABC 的面积为.3.如图,直线y=-x+3 经过点A(4,m),B(-1,n),若点P 的坐标为(6,2),则S△ABP= .4.如图,直线l1:y=x-3 与直线l2:y=2x 交于点A,点B(5,m)在直线l1 上,点C(2,n)在直线l2 上,则△ABC 的面积为.5.如图,直线y =1x +1 与x 轴、y 轴分别交于点A,B,直线2y=kx-3 与x 轴、y 轴分别交于点C,D,两直线相交于点P,若S△ADP=20,则k 的值为.6.如图,在平面直角坐标系中,已知A(2,4),B(10,5),C(8,2),则四边形OABC 的面积为.7.如图,在平面直角坐标系中,已知直线l1,l2 相交于点A(2,1),点B(8,4)在直线l1 上,直线l2 的表达式为y=3x-5.C 为直线l2 上的一个动点,且在点A 右侧,若△ABC 的面积为15,则点C 的坐标为.8. 如图,直线 y =-x +2 与 x 轴、y 轴分别交于点 A ,B ,以 A 为直角顶点,线段 AB 为腰在第一象限内作等腰 Rt △ABC ,点 P 为直线 x =1 上的一点,若 S △ABP =S △ABC ,则点 P 的坐标为 .9. 如图,已知直线 y = - 1 x + 4 与 x 轴、y 轴分别相交于点 A ,B , 2再将△AOB 折叠,使点 A 与点 B 重合,折痕与 x 轴交于点 C , 与 AB 交于点 D .(1) 点 A 的坐标为 ,点 B 的坐标为 .(2) 求线段 OC 的长及直线 BC 的表达式.(3) 直线 BC 上是否存在一点 M ,使△ABM 的面积与△ABO 的面积相等?若存在,请直接写出所有符合条件的点M 的坐标;若不存在,请说明理由.【参考答案】1.522.923. 25 24. 205. 16. 257. (4,7)8. (1,5)或(1,-3)9. (1)(8,0),(0,4);(2)线段OC 的长为3,直线BC 的表达式为y =-4x + 4 ;3(3)存在,点M 的坐标为( 24,-12)或( -24,52).5 5 5 5。
一次函数之面积问题(讲义及答案)
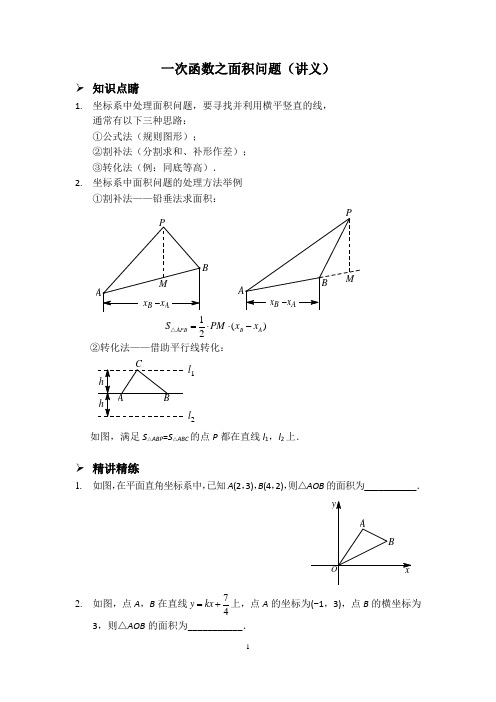
一次函数之面积问题(讲义)➢知识点睛1.坐标系中处理面积问题,要寻找并利用横平竖直的线,通常有以下三种思路:①公式法(规则图形);②割补法(分割求和、补形作差);③转化法(例:同底等高).2.坐标系中面积问题的处理方法举例①割补法——铅垂法求面积:B()2APB B AS PM x x=⋅⋅-△②转化法——借助平行线转化:l1l2如图,满足S△ABP=S△ABC的点P都在直线l1,l2上.➢精讲精练1.如图,在平面直角坐标系中,已知A(2,3),B(4,2),则△AOB的面积为___________.2.如图,点A,B在直线74y kx=+上,点A的坐标为(-1,3),点B的横坐标为3,则△AOB的面积为___________.3.如图,直线y=-x+4与x轴、y轴分别交于点A,B,点P的坐标为(-2,2),则S△PAB=___________.4.如图,一次函数y=kx+5的图象经过点A(1,4),点B是一次函数y=kx+5的图象与正比例函数23y x的图象的交点,则△AOB的面积为___________.5.如图,直线l1:y=x+1与x轴、y轴分别交于点A,B,直线l2:y=kx-2与x轴、y轴分别交于点C,D,直线l1,l2相交于点P.若S△APD=92,则k的值为__________.6.如图,在平面直角坐标系中,已知A(2,4),B(6,6),C(8,2),则四边形OABC的面积为___________.7.如图,在平面直角坐标系中,已知点A(2,1),点B(8,4),点C(m,2m-3)在直线AB上方,若△ABC的面积为9,则m的值为________.8.如图,直线l1:y=x与直线l2:y=-2x+3相交于点A,点B在直线l1上,且横坐标为4.C为l2上的一个动点,且在点A的左侧,若△ABC的面积为18,则点C的坐标为__________.9.如图,直线112y x=-+与x轴、y轴分别交于点A,B,点C的坐标为(1,2),点P为坐标轴上一点,若S△ABP =S△ABC,则点P的坐标为__________.10.如图,在平面直角坐标系中,一次函数y=2x+4的图象与x轴、y轴分别交于点A,B,过点A的直线交y轴正半轴于点M,且点M为线段OB的中点.(1)求直线AM的函数解析式;(2)若点P是直线AM上一点,使得S△ABP =S△AOB,请直接写出点P的坐标.【参考答案】1. 42.7 23.84.55.5 26.247. 48.(-3,9)9.(0,52),(5,0),(-1,0),(0,12-)10.(1)直线AM的函数解析式为y=x+2;(2)P1(2,4),P2(-6,-4)。
一次函数面积问题专题(含答案)

5 B o 面积相等 ABO 的面积为2 0 )、O A 0 0, 一次函數面積問題 1、如图,一次函数的图像与x 轴交于点B (-6 , 0),交正比例函数的图像于 点A ,点A 的横坐标为-4,△ ABC 的面积为15,求直线OA 的解析式。
2、直线y=x+3的图像与x 轴、y 轴分别交于A B 两点,直线a 经过原点与线段 AB 交于。
,把厶ABO 勺面积分为2: 1的两部分,求直线a 的函数解析式。
3、直线PA 是一次函数y=x+n 的图像,直线PB 是一次函数y=-2x+m (m>n>0的 图像, B 4 (1)用m n 表示A 、B 、P 的坐标 (1)求点P 的坐标 7、如图二已知两直线y=0•夕x+2.5和y=-x+1分别与x 轴交于A 、B 两点,这两直 S 、 &直线y=- 3 x+1与x 轴y 轴分别交点 ,点 P (a ,) 作等腰直角△ ABC ZBAC=90 段AB 为直角边在第一象限内 在第二象限,△ ABP 的面积与厶ABC 4、 A A OB 的顶点 O(0, 0)、A (2, 1)、B (10, 1),直线CDL x 轴且△ AOB 0积二等分,若 D (m 0),求m 的值 ♦ y P 5、 点B 在直线y 壬x+1上,且点 B 在第四象限, 点A 线的交点为P 求点B 的坐标 (2)四边形PQOB 勺面积是6, AB=2求点P 的 坐标 (2)求厶PAB 的面积 8、已知直线y=ax+b (b>0)与y 轴交于点N,与x 轴交于点A 且与直线y=kx 交 于点M(2、3[,如图它们与y 轴围成的厶MON 勺面积为5,求(1) 这两条直线的函数关系式(2) 它们与x 轴围成的三角形面积9、 已知两条直线y=2x-3和y=5-x(1) 求出它们的交点 A 的坐标(2) 求出这两条直线与x 轴围成的三角形的面积10、 已知直线y=x+3的图像与x 轴、y 轴交于A B 两点,直线I 经过原点,与 线段AB 交于点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题复习:一次函数的面积问题教案教学时间:2016年5月25日许发明
一、教学目标
依据课标的要求和学生的认知特点,我制定如下三维教学目标:
1.知识与技能:能利用表达式求三角形或四边形的面积,能利用面积求点坐标或直线表达式。
2.过程与方法:通过对已知图形面积求值及解析式问题的探究,使学生理解一次函数图象特征与表达式的联系规律,体会分类思想、数形结合思想
3.情感、态度与价值观:培养学生主动探究,合作交流的意识,激发学生学习数学的热情,体验学数学的乐趣.
二、教学重点与难点:
1、重点:根据函数表达式求三角形或四边形的面积,会根据面积求点坐标或函数表达式。
难点:不规则图形面积的计算,根据面积求点坐标
三、教学方法
高效6+1教学模式,让学生在自主、合作、探究中学习
四、教学过程
一、导:(创设情景,导入新课)
1、直线y=2x+5与y=0.5x+5的交点坐标是-----------。
2、点A(-1,2)到x轴的距离是------,到y轴的距离是--------。
3、y=2x+4与x轴交于A点,与y轴交于B点,则A的坐标为 ---------, B 点的坐标为---------。
则该图像与两坐标轴围成的面积是--------。
师生活动:学生先独立完成,学生口答结果后教师直接导入新课。
设计意图:练习求直线与x轴y轴交点坐标,两直线交点坐标,
为学习本节内容铺垫。
(出示本节学习目标)
设计意图:学生根椐学习目标使学习更有针对性。
二、思:(利用表达式求面积)
自学例1,独立完成下面两个题
例1:已知直线l:
24
y x
=-+
,求此一次函数的图象与两坐标轴所围成的三角形
的面积。
1、(1)求直线y=2x+3、y= -2x-1及y 轴围成的三角形的面积. (2)求直线y=2x+3、y=-2x-1及x 轴围成的三角形的面积.
2、已知直线y=ax+ 分别与x 轴和y 轴交于B 、C 两点, 直线y= - x+b
与x 轴交于点A ,并且两直线交点P 为(2,2).
(1)求两直线表达式; (2)求四边形AOCP 的面积.
师生活动:学生自学例题后,独立完成两个题目,教师巡视并作适当的引导() 设计意图:通过对题型1、2的探究,,使学生会计算三角形或四边形的面积,培养学生的独立解决问题能力,发挥学生的主观能动性。
达成目标:,确定一次函数的表达式需要两个条件,理解待定系数法求一次函数的表达式的过程.
三、议:(小组讨论)
师生活动:教师充分放手,让学生大胆说出自己的见解.发现有不同意见时,学生进行小组内交流,讨论,然后每小组选一名代表板演解题步骤,针对学生的回答,教师适当补充强调。
设计意图:让学生理解函数表达式求三角形或四边形的面积,培养学生的探究能力
2323
和归纳能力。
四、展:师生活动:学生先各自陈述自己的看法,小组内交流,讨论后各小组推荐一名同学同时展示解题过程,互相订正.
设计意图:通过学生展示,加深学生利用函数表达式求三角形或四边形的面积的方法,提高分析问题和解决问题的能力。
达成目标:函数表达式求三角形或四边形的面积
五、评:教师作必要的分析讲解
师生活动:教师引导学生自我总结,组内交流,代表发言集体订正.
设计意图:通过教师引导总结,让抽象的知识有趣化,能更有效地启发学生,有助于学理解记忆.
六、运用新知:(由三角形面积求点的坐标或直线表达式)
变式1:若一次函数的图象交x轴于点A(-6,0),交正比例函数的图象于点B,且点B在第二象限,它的横坐标为- 4,又知:S△AOB=15,求直线AB的表达式。
变式2; 已知:点P是一次函数y=-2x+8的图象上一点,如果图象与x轴交于Q点,且△OPQ的面积等于6,求P点的坐标。
师生活动:变式一学生抢答,说明解题思路,变式二由一名学生板演解题过程,其他学生独立完成,并互相订正.
设计意图:通过练习,突破难点,培养学生解决实际问题的能力。
达成目标:已知两个图象间的面积关系求点坐标。
会设点坐标,能通过三角形面积的条件,列出方程求解。
七、检:(当堂检测)
1.y=-2x+2与x轴交于A点,与y轴交于B点,则A的坐标为(), B 点的坐标为(), S△AOB=()
2. 一次函数图象与x轴的正半轴交于点A,与y轴的负半轴交于点B,与正比例函数的图象交于点C,若OB=4,C点横坐标为6,
(1)求一次函数的表达式;
(2)求△AOB的面积;
(3)求原点O到直线AB的距离。
师生活动:让学生在规定时间内独立完成,教师巡视及时了解反馈.采用多种形式检查,如小组互查,子组互查,最后公布答案.
设计意图:检测本节所学内容,及时了解学生的掌握程度,同时培养学生竞争意识,提高学生的解题技巧和学习效率.。
