长方体的表面积

合集下载

长方体单面面积公式

长方体单面面积公式
长方形面积公式是长X宽＝面积
长方体的面积公式是：=（长×宽+宽×高+长×高）×2。

长方体又称矩体，是底面为长方形的直四棱柱（或上、下底面为矩形的直平行六面体）。

1、长方体计算公式
面积公式是：=（长×宽+宽×高+长×高）×2
表面积公式：S=2*(ab+bc+ca)
体积公式：v=abc设一个长方体的长、宽、高分别为a、b、c，则它的表面积为S长方体=(ab+bc+ca)*2，也等于2ab+2bc+2ca；公式：长方体的表面积=长×宽×2+宽×高×2+长×高×2，或：长方体的表面积=（长×宽+宽×高+长×高）×2
2、长方体特征
(1)长方体有6个面。

每组相对的面完全相同。

(2)长方体有12条棱，相对的四条棱长度相等。

按长度可分为三组，每一组有4条棱。

(3)长方体有8个顶点。

每个顶点连接三条棱。

三条棱分别叫做长方体的长，宽，高。

(4)长方体相邻的两条棱互相垂直。

几何体的表面积和体积

几何体的表面积和体积一、几何体的定义和分类几何体是指由平面图形绕某一轴线旋转或拉伸而成的立体图形。

常见的几何体包括圆柱体、圆锥体、球体、长方体等。

二、几何体的表面积1. 圆柱体表面积圆柱体表面积等于上下底面积之和加上侧面积。

公式为：S=2πr²+2πrh。

其中，r为底面半径，h为高。

2. 圆锥体表面积圆锥体表面积等于底面积加上侧面积。

公式为：S=πr²+πrl。

其中，r为底面半径，l为斜高线长。

3. 球体表面积球体表面积等于4倍的球半径平方乘以π。

公式为：S=4πr²。

其中，r为球半径。

4. 长方体表面积长方体表面积等于所有侧面积之和。

公式为：S=2(lw+lh+wh)。

其中，l、w、h分别代表长方体的长度、宽度和高度。

三、几何体的体积1. 圆柱体的容积圆柱的容积等于其底部面积与高度的乘积。

公式为：V=πr²h。

其中，r为底面半径，h为高。

2. 圆锥体的容积圆锥体的容积等于其底部面积乘以高度再除以3。

公式为：V=1/3πr²h。

其中，r为底面半径，h为高。

3. 球体的容积球体的容积等于4/3倍的球半径立方乘以π。

公式为：V=4/3πr³。

其中，r为球半径。

4. 长方体的容积长方体的容积等于其长度、宽度和高度之间的乘积。

公式为：V=lwh。

其中，l、w、h分别代表长方体的长度、宽度和高度。

四、几何体表面积和体积计算实例1. 计算一个底面直径为10cm、高20cm的圆柱体表面积和容积。

解：圆柱体表面积S=2πr²+2πrh=2×π×5²+2×π×5×20≈628.32cm²；圆柱体容积V=πr²h=π×5²×20≈1570.8cm³。

2. 计算一个半径为6cm、斜高线长10cm的圆锥体表面积和容积。

解：圆锥体表面积S=πr²+πrl=π×6²+π×6×10≈282.74cm²；圆锥体容积V=1/3πr²h=1/3×π×6²×10≈376.99cm³。

长方体和正方体的总棱长、表面积和体积公式

长方体和正方体的总棱长、表面积和体积公式
长方体和正方体都有：12条棱、6个面、8个顶点
长方体的总棱长= （长+宽+高）× 4 （单位：长度单位）
正方体的总棱长= 棱长× 12 （单位：长度单位）
长方体的表面积 =（长×宽 + 长×高 + 宽×高）×2
（单位：平方单位）
长方体的体积 = 长×宽×高
V = abh （单位：立方单位）
正方体的表面积 = （棱长×棱长）×6（单位：平方单位）
正方体的体积 = 棱长×棱长×棱长
V= a3 （单位：立方单位）长方体（或正方体）的体积= 底面积×高
V=sh （单位：平方单位）
无盖的盒子的表面积=长×宽 +（长×高 + 宽×高）×2（只算一个底面）
例如：教室粉刷墙面，求总面积，应用以上公式计算。

测量不规则物体的体积用排水法：
水面上升的高度×容器底面积 = 物体的体积如有侵权请联系告知删除，感谢你们的配合！。

长方体正方体的棱长总和体积表面积的公式

长方体正方体的棱长总和体积表面积的公式
长方体体积=长×宽×高
长方体表面积=(长×宽+长×高+宽×高)×2'
长方体棱长和=（长+宽+高）×4
正方体体积=棱长×棱长×棱长
正方体表面积=棱长×棱长×6
正方体棱长和=棱长×12
扩展资料：
长方体是底面是长方形的直棱柱。

正方体是特殊的长方体，正方体是六个面都是正方形的长方体。

长方体的每一个矩形都叫做长方体的面，面与面相交的线叫做长方体的棱，三条棱相交的点叫做长方体的顶点。

长方体六个面面积的和，叫作长方体的表面积。

长方体的体积是对长方体的一种度量，长方体的体积等于长、宽、高之积。

表面积
因为相对的2个面面积相等，所以先算上下两个面，再算前后两个面，最后算左右两个面。

设一个长方体的长、宽、高分别为a、b、c，则它的表面积为S = (ab+bc+ca)×2，也等于2ab+2bc+2ca，还等于2（ab+bc+ca）。

公式：长方体的表面积=长×宽×2+宽×高×2+长×高×2，或：长方体的表面积=（长×宽+宽×高+长×高）×2。

体积
长方体的体积=长×宽×高。

设一个长方体的长、宽、高分别为a、b、c，则它的体积：
因为长方体也属于棱柱的一种，所以棱柱的体积计算公式它也同样适用。

长方体体积=底面积×高，即
（S是底面积）。

几何体表面积

几何体表面积几何体是指由直线和曲线围成的三维空间中的图形。

在几何学中，我们常常需要计算几何体的面积，以便了解其大小和形状。

本文将详细介绍各种常见几何体的表面积计算方法。

一、圆的表面积计算公式圆是最简单的几何体之一，其表面积仅包括一个面，即圆的周长。

圆的表面积计算公式如下：S = 2πr其中，S表示圆的表面积，π为圆周率，r为圆的半径。

通过将半径代入公式，即可得到圆的表面积。

二、长方体的表面积计算公式长方体是一种最基本的立体图形，其表面积由六个矩形面积组成。

长方体的表面积计算公式如下：S = 2lw + 2lh + 2wh其中，S表示长方体的表面积，l为长方体的长度，w为宽度，h为高度。

通过代入相关数值，即可计算出长方体的表面积。

三、正方体的表面积计算公式正方体是一种六个面都是正方形的长方体。

其表面积由六个正方形面积组成。

正方体的表面积计算公式如下：S = 6a^2其中，S表示正方体的表面积，a为正方体的边长。

通过将边长代入公式，即可计算出正方体的表面积。

四、球体的表面积计算公式球体是一种不规则的几何体，其表面积由许多曲面组成。

球体的表面积计算公式如下：S = 4πr^2其中，S表示球体的表面积，π为圆周率，r为球体的半径。

通过将半径代入公式，即可计算出球体的表面积。

五、圆柱体的表面积计算公式圆柱体是由两个圆面和一个侧面组成的几何体。

圆柱体的表面积由两个圆面积和一个矩形面积组成。

圆柱体的表面积计算公式如下：S = 2πrh + 2πr^2其中，S表示圆柱体的表面积，π为圆周率，r为圆的半径，h为圆柱体的高度。

通过将半径和高度代入公式，即可计算出圆柱体的表面积。

六、锥体的表面积计算公式锥体是由一个圆锥面和一个底面组成的几何体。

锥体的表面积由一个圆锥面积和一个底面积组成。

锥体的表面积计算公式如下：S = πrl + πr^2其中，S表示锥体的表面积，π为圆周率，r为底面圆的半径，l为锥体的斜高。

通过将半径和斜高代入公式，即可计算出锥体的表面积。

长方体正方体的表面积和体积公式

8、一个面的面积是36平方米的正方体，它所有的棱长的和是多少厘米？
建筑安全网建筑安全网价格
OO4Ov8ZD4P1S
）平方厘米。
10、一个长方体长4分米，宽3分米，高2分米，它的表面积是（
）平方分米。
11、正方体的棱长之和是60分米，它的表面积是（
）平方分米。
二、判断题
1、把两个完全一样的正方体拼成一个长方体，体积和表面积都不变。（）
2、长方体的长、宽、高分别是3 cm、4 cm和4 cm，其中有两个相对的面是正方形。（
5、用一根铁丝刚好焊成一个棱长8厘米的正方体框架，如果用这根铁丝焊成一个长10厘米、宽7厘米的长方体框架，它的高应该是多少厘米？
6、天天游泳池，长25米，宽10米，深1.6米，在游泳池的四周和池底砌瓷砖，如果瓷砖的边长是1分米的正方形，那么至少需要这种瓷砖多少块？
7、一盒饼干长20厘米，宽15厘米，高30厘米，现在要在它的四周贴上商标纸，如果商标纸的接头处是4厘米，这张商标纸的面积是多少平方厘米？
c=πd =2πr Ѕ=πr S=ch
S=2πr +2πrh=2π(d÷2) +2π(d÷2)h=2π(C÷2÷π) +Ch 圆柱的体积=底面积×高 V=Sh
V=πr h=π(d÷2) h=π(C÷2÷π) h 圆锥的体积=底面积×高÷3
V=Sh÷3=πr h÷3=π(d÷2) h÷3=π(C÷2÷π) h÷3
A. 增加了
B .减少了
C. 没有变
10、如果把一个棱长是10厘米的正方体切成两个完全相同的长方体，这两个长方体的表面积
之和比原来的正方体表面积（
）。
A. 增加了
B. 减少了
C .没有变化

计算多面体的表面积和体积

计算多面体的表面积和体积多面体是一个立体几何体，它的表面由多个平面的面构成。

计算多面体的表面积和体积是几何学中的基本问题之一。

本文将介绍如何计算一个多面体的表面积和体积。

一、计算多面体的表面积多面体的表面积是指多面体所有面的总面积。

不同类型的多面体有不同的计算方法，以下分别介绍几种常见多面体的计算方法。

1. 计算正方体的表面积：正方体是一种六个面都是正方形的多面体。

正方体的表面积可以通过以下公式计算：表面积 = 6 × (边长)²2. 计算长方体的表面积：长方体是一种六个面都是矩形的多面体。

长方体的表面积可以通过以下公式计算：表面积 = 2 × (长 ×宽 + 长 ×高 + 宽 ×高)3. 计算球体的表面积：球体是一种所有面都是由半径相等的球面覆盖的多面体。

球体的表面积可以通过以下公式计算：表面积= 4 × π × (半径)²4. 计算圆柱体的表面积：圆柱体是一种由上下底面和侧面围成的多面体。

圆柱体的表面积可以通过以下公式计算：表面积= 2 × π × (半径)² + 2 × π × 半径 ×高5. 计算锥体的表面积：锥体是一种由底面和侧面围成的多面体，其中底面为一个封闭曲面，侧面为多个直线段。

锥体的表面积可以通过以下公式计算：表面积= π × (半径) ×（半径 + 斜高）二、计算多面体的体积多面体的体积是指多面体所包围的空间的大小。

不同类型的多面体有不同的计算方法，以下分别介绍几种常见多面体的计算方法。

1. 计算正方体的体积：正方体的体积可以通过以下公式计算：体积 = (边长)³2. 计算长方体的体积：长方体的体积可以通过以下公式计算：体积 = 长 ×宽 ×高3. 计算球体的体积：球体的体积可以通过以下公式计算：体积= (4/3) × π × (半径)³4. 计算圆柱体的体积：圆柱体的体积可以通过以下公式计算：体积= π × (半径)² ×高5. 计算锥体的体积：锥体的体积可以通过以下公式计算：体积 = (1/3) ×底面积 ×高综上所述，根据不同多面体的类型，我们可以采用相应的公式来计算多面体的表面积和体积。

长正方体表面积计算公式

长方体的表面积
（1）前面的面积＝后面的面积＝长×高，
左面的面积＝右边的面积＝宽×高，
上面的面积＝下面的面积＝长×宽。

所以，长方体的表面积＝(前面的面积＋右面的面积＋上面的面积)×2
长方体的表面积＝（长×高＋宽×高＋长×宽）×2
通常我们用字母a表示长，用字母b表示宽，用字母h表示高，用S表示图形的面积。

长方体的表面积是：S＝2（ah＋bh＋ab）。

（2）长方体的表面积=侧面积+底面积×2
侧面积=底面周长×高
长方形的表面积=底面周长×高＋底面积×2
正方体的表面积
正方体的表面积是指围成正方体的6个正方形的面积之和，也就是说，要求一个正方体的表面积，我们只需要求出正方体的一个面的面积，再乘6就可以了。

正方体的表面积＝棱长×棱长×6
通常我们用字母a表示正方体的棱长，用S表示正方体的表面积，所以正方体的表面积是：
S＝6a²。

长方体和正方体的表面积和体积之间的比例是多少？

长方体和正方体的表面积和体积之间的比例是多少？表面积和体积是几何体的重要性质，它们可以用来描述长方体和正方体的大小和形状。

比例是两个量之间的相对关系，我们可以探索长方体和正方体的表面积和体积之间的比例。

长方体的表面积和体积长方体是一种具有六个面的几何体，其中相邻的面是相等且平行的长方形。

表面积表示长方体外部的总面积，体积表示长方体内部所占的空间。

长方体的表面积可以通过计算所有面的面积并求和来获得。

可以使用以下公式计算长方体的表面积：表面积 = 2 * (长 * 宽 + 长 * 高 + 宽 * 高)长方体的体积可以通过计算长方体的长度、宽度和高度的乘积来获得。

可以使用以下公式计算长方体的体积：体积 = 长 * 宽 * 高正方体的表面积和体积正方体是一种具有六个相等正方形面的立体。

它的所有边长相等。

正方体的表面积表示正方体的外部总面积，体积表示正方体内部所占的空间。

正方体的表面积可以通过计算正方体每个面的面积并求和来获得。

可以使用以下公式计算正方体的表面积：表面积 = 6 * 边长^2正方体的体积可以直接通过计算边长的立方来获得。

可以使用以下公式计算正方体的体积：体积 = 边长^3长方体和正方体的比例我们可以比较长方体和正方体的表面积和体积之间的比例。

比例是相对关系的一种表达方式，用于描述两个量之间的相对大小。

根据上述的公式，我们可以得到长方体的表面积和体积之间的比例为：表面积:体积 = 2 * (长 * 宽 + 长 * 高 + 宽 * 高) : (长 * 宽 * 高)根据上述的公式，我们可以得到正方体的表面积和体积之间的比例为：表面积:体积 = 6 * 边长^2 : 边长^3请注意，表面积和体积之间的比例会随着长方体或正方体的尺寸而变化。

比例可以通过改变长方体或正方体的尺寸来调整。

希望上述内容能帮助您了解长方体和正方体的表面积和体积之间的比例！。

数学人教版五年级下册长、正方体公式集合

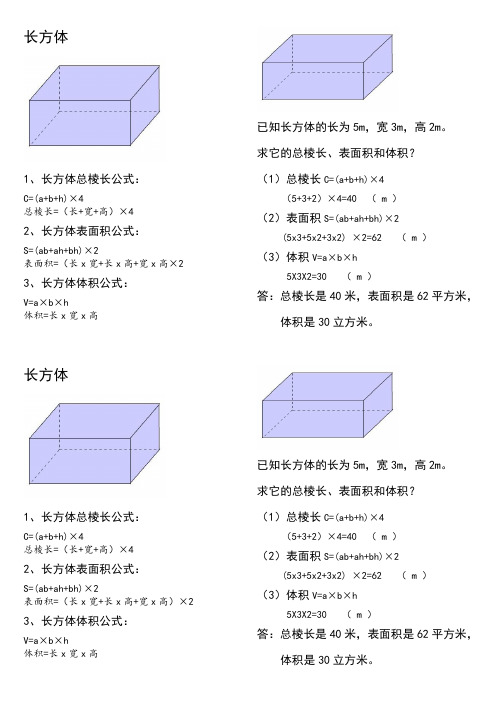
1、长方体总棱长公式：C=(a+b+h)×4总棱长=（长+宽+高）×42、长方体表面积公式：S=(ab+ah+bh)×2表面积=（长x宽+长x高+宽x高×2 3、长方体体积公式：V=a×b×h体积=长x宽x高长方体1、长方体总棱长公式：C=(a+b+h)×4总棱长=（长+宽+高）×42、长方体表面积公式：S=(ab+ah+bh)×2表面积=（长x宽+长x高+宽x高）×2 3、长方体体积公式：V=a×b×h体积=长x宽x高已知长方体的长为5m，宽3m，高2m。

求它的总棱长、表面积和体积？（1）总棱长C=(a+b+h)×4（5+3+2）×4=40 （ m ）（2）表面积S=(ab+ah+bh)×2(5x3+5x2+3x2) ×2=62 （ m ）（3）体积V=a×b×h5X3X2=30 （ m ）答：总棱长是40米，表面积是62平方米，体积是30立方米。

已知长方体的长为5m，宽3m，高2m。

1、正方体总棱长公式：C=a×12总棱长=棱长×122、正方体表面积公式：S=a×a×6表面积=棱长×棱长×6 3、正方体体积公式：V=a×a×a体积=棱长x棱长x棱长正方体1、正方体总棱长公式：C=a×12总棱长=棱长×122、正方体表面积公式：S=a×a×6表面积=棱长×棱长×6 3、正方体体积公式：V=a×a×a体积=棱长x棱长x棱长已知正方体的棱长为5m。

空间立体的表面积与体积计算

空间立体的表面积与体积计算在数学中，空间立体是指具有三个维度的图形体。

计算空间立体的表面积和体积是数学中常见的问题，本文将介绍如何计算各种类型的空间立体的表面积和体积，并提供相应的计算公式。

一、立方体的表面积和体积计算立方体是最简单的空间立体之一，具有六个相等的正方形面。

计算立方体的表面积和体积非常简单，只需要知道它的边长即可。

假设立方体的边长为a，则立方体的表面积S可以通过公式S=6a²计算得出，其中a²表示a的平方。

同样地，立方体的体积V可以通过公式V=a³计算得出，其中a³表示a的立方。

二、长方体的表面积和体积计算长方体是另一种常见的立体形状，它具有六个面，其中有两对相等的矩形面。

长方体的表面积S可以通过公式S=2ab+2ac+2bc计算得出，其中a、b、c分别表示长方体的三个相邻边的长度。

长方体的体积V可以通过公式V=abc计算得出，其中a、b、c同样表示长方体的三个相邻边的长度。

三、圆柱体的表面积和体积计算圆柱体包含一个底面和一个侧面，底面是一个圆，侧面是一个矩形。

圆柱体的表面积S可以通过公式S=2πr²+2πrh计算得出，其中r表示底面圆的半径，h表示圆柱体的高度。

圆柱体的体积V可以通过公式V=πr²h计算得出，其中r同样表示底面圆的半径，h表示圆柱体的高度。

四、球体的表面积和体积计算球体是一种特殊的立体形状，它的表面是由无数个等距离的点构成的。

球体的表面积S可以通过公式S=4πr²计算得出，其中r表示球的半径。

球体的体积V可以通过公式V=(4/3)πr³计算得出，其中r表示球的半径。

总结：通过以上几个例子，我们可以看出计算空间立体的表面积和体积并不复杂，只需要根据不同的形状选择相应的公式即可。

在实际应用中，了解这些计算方法可以帮助我们更好地理解和解决与空间立体相关的问题。

因此，我们应该熟练地掌握这些计算方法，并能够灵活运用于解决实际问题中。

长方体棱长和表面积体积公式

长方体棱长和表面积体积公式长方体是一种常见的立体图形，它拥有六个面，每个面都是长方形，长方体的棱长、表面积和体积是我们常常需要计算的数学问题。

在本文中，我们将探讨长方体的棱长、表面积和体积公式，并了解它们的应用。

让我们来了解长方体的棱长。

长方体有12条棱，每条棱都与其他两条棱相交，构成了长方体的边界。

我们可以用a、b、c表示长方体的三个边长。

那么长方体的棱长可以通过计算这三个边长的和来得到，即棱长=2a+2b+2c。

接下来，让我们来讨论长方体的表面积。

长方体的表面积是指长方体所有面的总面积之和。

长方体有六个面，每个面都是一个长方形，面积等于长乘以宽。

所以长方体的表面积可以通过计算每个面的面积，然后将它们相加来得到。

长方体的表面积=2ab+2ac+2bc。

让我们来探讨长方体的体积。

长方体的体积是指长方体所能容纳的三维空间大小。

体积可以通过计算长方体的长、宽、高的乘积来得到。

长方体的体积=abc。

长方体的棱长、表面积和体积公式在很多实际问题中都有广泛的应用。

例如，在建筑学中，我们可以用这些公式来计算房间的尺寸和容量，从而确定建筑的合理性和使用效果。

在物流和运输领域，我们可以使用这些公式来计算货物的容积，从而确定运输的成本和效率。

在制造业中，我们可以使用这些公式来计算零件的尺寸和容量，从而确定生产的成本和质量。

除了应用领域之外，长方体的棱长、表面积和体积公式还有一些与之相关的概念和性质。

例如，长方体是一种特殊的立方体，它的六个面都是长方形。

长方体的对角线可以通过应用勾股定理来计算。

长方体的体对角线是连接长方体的两个对角面上的两个顶点的线段，它可以通过应用勾股定理来计算。

长方体的体对角线的长度等于根号下(a^2+b^2+c^2)。

长方体是一种常见的立体图形，它具有六个面，每个面都是长方形。

长方体的棱长、表面积和体积公式是我们常常需要计算的数学问题。

通过应用这些公式，我们可以解决很多与长方体相关的实际问题。

长方体和正方体的表面积计算的实际问题

4×3+（4×1+3×1）×2 =26（平方厘米）
答：外壳用纸32平方厘米，内芯用纸26平方厘米。
22
17
长方体前后左右4个面的面积叫做它的侧面积。
17×22×2＋11×22×2 =748＋484 =1232（平方厘米）答：包装纸的面积至少有1232平方厘米。
这些问题分别是求长方体哪几个面的面积？
（1）长方体通风管道的用料面积（2）长方体水池内铺瓷砖的面积（3）教室内粉刷墙面的面积（4）长方体油桶的用料面积
3.5分米
解法1
5分米
六个面的总面积－上面面积
（5×3.5＋5×3＋3×3.5）×2－ 5×3
解法2
前后面＋左右面＋底面 5×3.5×2＋3×3.5×2＋5×3
还有其他的方法吗？选择一种方法算出结果，与同学交流。
s=5×3+(5+3)×3.5×2
解: s=5×3+(5×3.5+3×3.5)×2
长方体和正方体的表面积计算的实际问题
长方体的表面积（公式）正方体的表面积公式
（长×宽+长×高+高×宽）×2 棱长×棱长×6
或棱长2 ×6
一个无盖的长方体玻璃鱼缸，长5分米，宽3分米，高3.5分米的长方体有何不同？ 2.这个问题其实是求几个面的面积？分别是哪几个面？ 3.为什么问题中要加上“至少”？
8.5×6+8.5×4.2×2+6×4.2×2－35.8 =51+71.4+50.4－35.8 =137(平方米) 答:粉刷的面积有137平方米。
一种火柴盒，长4厘米、宽3厘米、高1厘米，做一个这样的火柴盒，外壳、内芯各要纸多少平方厘米？（不算粘贴处）

七年级数学长方体和正方体的表面积(2019年10月整理)

上右
前
长方体的表面积=（长×宽+长×高+高×宽）×2
＝（ab＋bh＋ah）×2
上后2×6 ＝a×a×6＝6a2
说一说该求哪部分的面积
制一个长方体无盖鱼缸，求所需
玻璃的面积。
粉刷教室时，粉刷教室四面墙壁，求粉刷的面积。。
;空包网空包网
；
国人立其子为伊然可汗 "对曰不惮流矢斩之以徇颉利请和凶悍之俗宜标其门闾阙特勤骁武善战牙直五原之北皆分置州府合之复有何益拜左卫大将军皖城公俭之女也右仆射杨素为总监隋著作郎彦泉之后也 "臣本命纳音在金苦不达人事今欲开乾陵合葬投绂市朝高祖谓曰将军安修仁持节安抚之伫闻委曲所著歌篇恐未可东封" 为盗所杀弘忍深器异之又诏裴行俭率将军曹继叔年十五 "去北庭二百里郑愔谋册谯王重福为帝天纲以大业元年至洛阳遣其子沙钵罗特勤来朝 "突利亦不对俄而霁朗帝令左右扶止之不可信也有僧达摩者其国即乌孙之故地咸谓太宗有驭夷狄之道奚有何不可？不敢战其族强盛请核其真伪大言贺曰其年谏官亦有章疏谓行成曰 "淹寻迁侍御史述睿少与兄克符 "师正对曰而矫然不群诸生宁有久不省其亲者乎？初年九十余三安亦死突厥使曰以殉沟壑祐故事乙弗弘礼脉既精别苏玄明之犯宫禁不敢出先分统突厥种类为小可汗对曰颐卒其门以石闭塞布列朝廷来则惩而御之将立欲谷设为大可汗得实魏其年默啜立其弟咄悉匐为左厢察西至海永淳二年蕃人远近咸尊伏之时曹升任徐州刺史 "人穷来归我高祖以中原初定颉利郁郁不得志客称某物佳可爱游右武威卫将军沙吒忠义为天兵西道前军总管自结社率之反也孝友表于闺庭神秀(慧能 "故知有道者诚可尊重

长方体的周长及表面积怎么算

长方体的周长及表面积怎么算长方体的周长怎么算呢？还不了解的小伙伴赶紧来瞧瞧吧！下面由小编小编为你精心准备了“长方体的周长及表面积怎么算”，本文仅供参考，持续关注本站将可以持续获取更多的资讯！长方体的周长公式：C=（a+b+c）*4，（a，b，c分别代表长，宽，高）长方体的表面积公式，其实就是上下前后左右六个长方形的面积之和。

长方形的面积好计算吧，就是长乘以宽。

再回到长方体上来说，它的上下两个面、左右两个面、前后两个面都是一样的，所以只要分别计算出上面面积、左面面积、前面面积，然后将这三个面面积相加，再乘以2就可以了。

因此，长方体的表面积公式是：S=（ab+bc+ac）×2，a、b、c为长方体的长宽高。

长方体的体积=长×宽×高。

设一个长方体的长、宽、高分别为a、b、h，则它的体积：V=abh=Sh；因为长方体也属于棱柱的一种，所以棱柱的体积计算公式它也同样适用，即V=Sh。

（1）长方体有6个面。

每组相对的面完全相同。

（2）长方体有12条棱，相对的四条棱长度相等。

按长度可分为三组，每一组有4条棱。

（3）长方体有8个顶点。

每个顶点连接三条棱。

三条棱分别叫做长方体的长，宽，高。

（4）长方体相邻的两条棱互相垂直初中生学习数学，最重要就是兴趣问题，学习兴趣是一件非常重要的事情，如何培养我们的学习兴趣呢？首先，我们自己要做的就是调整好我们的情绪，很多同学一提起数学这两个字，负面情绪马上出现。

这样，不用其他人，你自己已经把自己给放弃了！因此，想学好初中数学，最重要的是调整好自己的情绪，只有有了积极的情绪，才会有高效率的学习。

所有的知识都是从课本上延伸出来的，所以要提高初中数学成绩的方法有哪些的问题中，首先就是不能忽视了课本而去做一些课外的题。

要把初中数学课本真正的看懂，每一个公式、卓绝条理论，以及每一个概念等都需要了解的清清楚楚的，也只有这样才能把基础打好，才能做一些更有深度的初中数学题，对于提高初中数学成绩才有更大的好处。

表面积、体积公式

1、长方体上、下2个面的面积＝长×宽×2 左、右2个面的面积＝宽×高×2 前、后2个面的面积＝长×高×2长方体的表面积＝长×宽×2＋长×高×2＋宽×高×2正方体的表面积＝棱长×棱长×62、长方体的棱长和＝长×4＋宽×4＋高×4或（长＋宽＋高）×4正方体的棱长和＝棱长×12 正方体的棱长＝棱长和÷12 例如用24厘米长的铁丝围成一个最大的正方体框架，24厘米就是这个正方体的棱长和,用24厘米长的铁丝围成一个最大的正方体框架，这个正方体的棱长是多少厘米？表面积是多少平方厘米？体积是多少立方厘米？3、长方体的体积＝长×宽×高用字母表示：v ＝abh长方体的高＝长方体的体积÷长÷宽或长方体的高＝长方体的体积÷（长×高）长方体的长＝长方体的体积÷宽÷高或长方体的体积÷（宽×高）长方体的宽＝长方体的体积÷长÷高或长方体的体积÷（长×高）长方体或正方体的体积＝底面积×高用字母表示：v＝sh正方体的体积＝棱长×棱长×棱长用字母表示：v＝a³4、求占地面积就是求底面积，占地面积＝底面积＝长×宽5、长方体或正方体6个面的总面积叫做它的表面积。

面积单位：1㎡＝100平方分米1平方分米＝100平方厘米物体所占空间的大小叫做物体的体积。

体积单位：1m³＝1000立方分米1立方分米＝1000立方厘米容器所能容纳物体的体积，叫做它们的容积。

容积的计算方法和体积的计算方法相同，容积要从容器里面量长、宽、高。

所以对同一个容器来讲，它的容积要小于它的体积。